COPYRIGHT Lingo 12 Users Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 791 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- What is LINGO?
- Installing LINGO
- Variables box
- Constraints box
- Nonzeroes box
- Generator Memory Used box
- Elapsed Runtime box
- Solver Status box
- Model Class Field
- State Field
- Objective Field
- Infeasibility Field
- Iterations Field
- Extended Solver Status box
- Solver Type
- Solver Type Field
- Best Obj and Obj Bound Fields
- Steps Field
- Branch-and-Bound
- Modeling from the CommandLine
- Examining the Solution
- Using the Modeling Language
- Additional Modeling Language Features
- Maximum Problem Dimensions
- How to Contact LINDO Systems
- Why Use Sets?
- What Are Sets?
- The Sets Section of a Model
- The DATA Section
- Set Looping Functions
- Set Based Modeling Examples
- Summary
- Integer Variables
- Free Variables
- Bounded Variables
- SOS Variables
- Cardinality
- Semicontinuous Variables
- The DATA Section of a Model
- The INIT Section of a Model
- The CALC Section of a Model
- Summary
- Accessing Windows Commands
- Windows Commands In Brief
- Windows Commands In Depth
- 1. File Menu
- 2. Edit Menu
- Edit|Undo Ctrl+Z
- Edit|Redo Ctrl+Y
- Edit|Cut Ctrl+X
- Edit|Copy Ctrl+C
- Edit|Paste Ctrl+V
- Edit|Paste Special...
- Edit|Select All
- Edit|Find... Ctrl+F
- Edit|Find Next Ctrl+N
- Edit|Replace Ctrl+H
- Edit|Go To Line... Ctrl+T
- Edit|Match Parenthesis Ctrl+P
- Edit|Paste Function
- Edit|Select Font
- Edit|Insert New Object
- Edit|Links
- Edit|Object Properties Alt+Enter
- 3. LINGO Menu
- LINGO|Solve Ctrl+U
- LINGO|Solution Ctrl+W
- LINGO|Range Ctrl+R
- LINGO|Options Ctrl+I
- Interface Tab
- General Solver Tab
- Model Generator Tab
- Linear Solver Tab
- Nonlinear Solver Tab
- Integer PreSolver Tab
- Integer Solver Tab
- Global Solver Tab
- SP Solver Tab
- LINGO|Generate... Ctrl+G
- LINGO|Picture Ctrl+K
- LINGO|Debug
- LINGO|Model Statistics
- LINGO|Look... Ctrl+L
- 4. Window Menu
- 5. Help Menu
- The Commands In Brief
- The Commands In Depth
- 1. ILFTOL and 2. FLFTOL
- 3. INFTOL and 4. FNFTOL
- 5. RELINT
- 6. NOPTOL
- 7. ITRSLW
- 8. DERCMP
- 9. ITRLIM
- 10. TIMLIM
- 11. OBJCTS
- 12. MXMEMB
- 13. CUTAPP
- 14. ABSINT
- 15. HEURIS
- 16. HURDLE
- 17. IPTOLA
- 18. IPTOLR
- 19. TIM2RL
- 20. NODESL
- 21. LENPAG
- 22. LINLEN
- 23. TERSEO
- 24. STAWIN (Windows Only)
- 25. SPLASH (Windows Only)
- 26. OROUTE (Windows Only)
- 27. WNLINE (Windows Only) and 28. WNTRIM (Windows Only)
- 29. STABAR (Windows Only)
- 30. FILFMT (Windows Only)
- 31. TOOLBR (Windows Only)
- 32. CHKDUP
- 33. ECHOIN
- 34. ERRDLG (Windows Only)
- 35. USEPNM
- 36. NSTEEP
- 37. NCRASH
- 38. NSLPDR
- 39. SELCON
- 40. PRBLVL
- 41. SOLVEL
- 42. REDUCE
- 43. SCALEM
- 44. PRIMPR
- 45. DUALPR
- 46. DUALCO
- 47. RCMPSN
- 48. MREGEN
- 49. BRANDR
- 50. BRANPR
- 51. CUTOFF
- 52. STRONG
- 53. REOPTB
- 54. REOPTX
- 55. MAXCTP
- 56. RCTLIM
- Constraint Cut Types
- 67. SCLRLM (Windows Only)
- 68. SCLRDL (Windows Only)
- 69. PRNCLR (Windows Only)
- 70. MULTIS
- 71. USEQPR
- 72. GLOBAL
- 73-75. LNRISE, LNBIGM, LNDLTA
- 76. BASCTS
- 77. MAXCTR
- 78. HUMNTM
- 79. DECOMP
- 80. GLBOPT
- 81. GLBDLT
- 82. GLBVBD
- 83. GLBUBD
- 84. GLBBRN
- 85. GLBBXS
- 86. GLBREF
- 87. SUBOUT
- 88. NLPVER
- 89. DBGCLD and 90. DBGWRM
- 93. LOWMEM
- Standard Operators
- Mathematical Functions
- Financial Functions
- Probability Functions
- Variable Domain Functions
- Set Handling Functions
- Set Looping Functions
- Interface Functions
- Report Functions
- Miscellaneous Functions
- Cut and Paste Transfers
- Text File Interface Functions
- LINGO Command Scripts
- Specifying Files in the Commandline
- Redirecting Input and Output
- Managing LINGO Files
- Importing Data from Spreadsheets
- Exporting Solutions to Spreadsheets
- OLE Automation Links from Excel
- Embedding LINGO Models in Excel
- Embedding Excel Sheets in LINGO
- Summary
- ODBC Data Sources
- Importing Data from Databases with @ODBC
- Importing Data with ODBC in a PERT Model
- Exporting Data with @ODBC
- Exporting Data with ODBC in a PERT Model
- The LINGO Dynamic Link Library
- StaffScheduling Example Using the LINGO DLL
- Functions Exported by the LINGO DLL
- void LSclearPointersLng( pLSenvLINGO pL)
- int LScloseLogFileLng( pLSenvLINGO pL)
- pLSenvLINGO CALLTYPE LScreateEnvLng()
- pLSenvLINGO CALLTYPE LScreateEnvLicenseLng( char* pcLicenseKey, int* pnErr)
- int LSdeleteEnvLng( pLSenvLINGO pL)
- int LSexecuteScriptLng( pLSenvLINGO pL, char* pcScript)
- int LSgetCallbackInfoLng( pLSenvLINGO pL, int nObject, void* pResult)
- int LSgetCallbackVarPrimalLng( pLSenvLINGO pL, char* pcVarName, double* pdPrimals)
- int LSopenLogFileLng( pLSenvLINGO pL, char *pcLogFile)
- int LSsetCallbackErrorLng( pLSenvLINGO pL, lngCBFuncError_t pcbf, void* pUserData)
- int LSsetCallbackSolverLng( pLSenvLINGO pL, lngCBFuncError_t pcbf, void* pUserData)
- int CALLTYPE LSsetPointerLng( pLSenvLINGO pL, double* pdPointer, int* pnPointersNow)
- LINGO DLL Error Codes
- Name
- User Defined Functions
- Production Management Models
- Logistics Models
- Financial Models
- Queuing Models
- Marketing Models
- 2 Years
- Programming Features
- Programming Example: Binary Search
- Programming Example: Markowitz Efficient Frontier
- Programming Example: Cutting Stock
- Programming Example: Accessing Excel
- Summary
- Multistage Decision Making Under Uncertainty
- Recourse Models
- Scenario Tree
- Monte Carlo Sampling
- Setting up SP Models
- Language Features for SP Models
- Declaring Distributions
- Gas Buying Example
- Stock Option Example
- Investing Under Uncertainty Example
- Solvers Used Internally by LINGO
- Type of Constraints
- Local Optima vs. Global Optima
- Smooth vs. Nonsmooth Functions
- Guidelines for Nonlinear Modeling
- Supplying Bounds for Variables
- Supplying Initial Values for Variables
- Scale the Model to a Reasonable Range of Units
- Simplify Relationships
- Reduce Integer Restrictions
- Assembly Line Balancing Model: ASLBAL
- Bayes Rule; Conditional Probabilities Model: Bayes
- Blending of Ingredients I Model: BLEND
- Plant Location Model: CAPLOC
- Blending of Ingredients II Model: CHESS
- Chemical Equilibrium Model: CHMBL1
- Conjoint Analysis Model: CONJNT
- Data Envelopment Analysis Model: DEAMOD
- Generating Random Numbers Model: DEMRND
- Scenario-based Portfolio Model Model: DNRISK
- Staff Scheduling Model: STAFFDEM
- Dynamic Programming Model: DYNAMB
- Capacitated EOQ Model: EOQCAP
- Machine Repair Problem Model: EZMREPAR
- Newsboy Problem Model: EZNEWS
- Simple Queuing Example Model: EZQUEUE
- General Equilibrium of an Economy Model: GENEQ1
- Markowitz Portfolio Example Model: GENPRT
- Job Shop Scheduling Model: JOBSLT
- Knapsack Model Model: KNAPSACK
- Learning Curve Model: LEARNC
- Markov Chain Model Model: MARKOV
- Matching Model Model: MATCHD
- Computing Demand Backlog Model: METRIC
- The Mexican Steel Problem Model: MEXICO
- Multiprod. Capac. Lot Sizing Model: MPSCHD
- Machine Repair Model Model: MREPAR
- Material Requirements Planning Model: MRP
- Minimal Spanning Tree Model: MSPAN
- Multilevel Distribution Model: MULLDC
- Network Equilibrium Model: NETEQ1
- Minimize Traffic Congestion Model: NLTRAZ
- Newsboy with Fixed Order Charge Model: NUSBOY
- Optimal Airline Overbooking I Model: OBOOKO
- Optimal Airline Overbooking II Model: OBOOKT
- Black & Scholes Options Pricing Model: OPTION
- Binomial Options Pricing Model: OPTIONB
- Bond Portfolio Optimization Model: PBOND
- Simple ProductMix Model: PC
- Project Management Model: PERT
- Proj. Management with Crashing Model: PERTC
- ProductMix with Setup Costs Model: PRODMIX
- Scenario Portfolio Selection Model: PRTSCEN
- Quadratic Assignment Model: QASGN
- Economic Order Quantity Model: QDISCX
- Simple Queuing System Model: QMMC
- Minimal Cost Queuing Model: QUEUEL
- Steady State Queuing Model Model: QUEUEM
- Designing a Computer Cabinet Model: BOX
- Linear Regression Model: REGRES
- Acceptance Sampling I Model: SAMPLE
- Stratified Sampling Design Model: SAMPLE2
- Acceptance Sampling II Model: SAMSIZ
- Seasonal Sales Forecasting Model: SHADES
- Exponential Smoothing Model: SIMXPO
- Placing Songs on a Cassette Tape Model: SONGS
- Computing Sort Order Model: SORTIN
- Traveling Salesman Problem Model: TSP
- The Log Gamma Function Model: EZCOUNT
- Vehicle Routing Problem Model: VROUTE
- Home Mortgage Calculation Model: WHATIF
- Transportation Problem Model: WIDGETS


COPYRIGHT
The LINGO software and its related documentation are copyrighted. You may not copy the LINGO
software or related documentation except in the manner authorized in the related documentation or
with the written permission of LINDO Systems Inc.
TRADEMARKS
LINGO is a trademark, and LINDO is a registered trademark, of LINDO Systems Inc. Other product
and company names mentioned herein are the property of their respective owners.
DISCLAIMER
LINDO Systems, Inc. warrants that on the date of receipt of your payment, the disk enclosed in the
disk envelope contains an accurate reproduction of the LINGO software and that the copy of the
related documentation is accurately reproduced. Due to the inherent complexity of computer programs
and computer models, the LINGO software may not be completely free of errors. You are advised to
verify your answers before basing decisions on them. NEITHER LINDO SYSTEMS, INC. NOR
ANYONE ELSE ASSOCIATED IN THE CREATION, PRODUCTION, OR DISTRIBUTION OF
THE LINGO SOFTWARE MAKES ANY OTHER EXPRESSED WARRANTIES REGARDING
THE DISKS OR DOCUMENTATION AND MAKES NO WARRANTIES AT ALL, EITHER
EXPRESSED OR IMPLIED, REGARDING THE LINGO SOFTWARE, INCLUDING THE
IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE,
OR OTHERWISE. Further, LINDO Systems, Inc. reserves the right to revise this software and related
documentation and make changes to the content hereof without obligation to notify any person of such
revisions or changes.
Copyright © 2010 by LINDO Systems Inc. All rights reserved.
Published by
1415 North Dayton Street
Chicago, Illinois 60642
Technical Support: (312) 988-9421
E-mail: tech@lindo.com
WWW: http://www.lindo.com

iii
Contents
Contents................................................................................................................................................ iii
Preface ................................................................................................................................................. vii
New Features........................................................................................................................................ xi
1 Getting Started with LINGO............................................................................................................ 1
What is LINGO? ............................................................................................................................... 1
Installing LINGO............................................................................................................................... 1
Modeling from the Command-Line..................................................................................................21
Examining the Solution....................................................................................................................24
Using the Modeling Language.........................................................................................................25
Additional Modeling Language Features.........................................................................................35
Maximum Problem Dimensions.......................................................................................................38
How to Contact LINDO Systems.....................................................................................................39
2 Using Sets.......................................................................................................................................41
Why Use Sets?................................................................................................................................41
What Are Sets?...............................................................................................................................41
The Sets Section of a Model ...........................................................................................................42
The DATA Section...........................................................................................................................48
Set Looping Functions.....................................................................................................................49
Set Based Modeling Examples .......................................................................................................55
Summary.........................................................................................................................................73
3 Using Variable Domain Functions ................................................................................................75
Integer Variables.............................................................................................................................75
Free Variables.................................................................................................................................94
Bounded Variables..........................................................................................................................99
SOS Variables...............................................................................................................................100
Cardinality .....................................................................................................................................103
Semicontinuous Variables.............................................................................................................104
4 Data, Init and Calc Sections ........................................................................................................107
The DATA Section of a Model.......................................................................................................107
The INIT Section of a Model..........................................................................................................111
The CALC Section of a Model.......................................................................................................112
Summary.......................................................................................................................................115
5 Windows Commands ...................................................................................................................117
Accessing Windows Commands...................................................................................................117
Windows Commands In Brief........................................................................................................118
Windows Commands In Depth......................................................................................................121

iv CONTENTS
1. File Menu...................................................................................................................................121
2. Edit Menu..................................................................................................................................139
3. LINGO Menu.............................................................................................................................152
4. Window Menu............................................................................................................................240
5. Help Menu.................................................................................................................................244
6 Command-Line Commands.........................................................................................................251
The Commands In Brief ................................................................................................................251
The Commands In Depth ..............................................................................................................253
7 LINGO’s Operators and Functions..............................................................................................337
Standard Operators.......................................................................................................................337
Mathematical Functions ................................................................................................................341
Financial Functions .......................................................................................................................343
Probability Functions.....................................................................................................................343
Variable Domain Functions ...........................................................................................................346
Set Handling Functions .................................................................................................................346
Set Looping Functions...................................................................................................................349
Interface Functions........................................................................................................................350
Report Functions...........................................................................................................................351
Miscellaneous Functions...............................................................................................................362
8 Interfacing with External Files.....................................................................................................365
Cut and Paste Transfers ...............................................................................................................365
Text File Interface Functions.........................................................................................................367
LINGO Command Scripts..............................................................................................................375
Specifying Files in the Command-line...........................................................................................378
Redirecting Input and Output ........................................................................................................380
Managing LINGO Files..................................................................................................................380
9 Interfacing With Spreadsheets....................................................................................................383
Importing Data from Spreadsheets................................................................................................383
Exporting Solutions to Spreadsheets ............................................................................................388
OLE Automation Links from Excel.................................................................................................396
Embedding LINGO Models in Excel..............................................................................................400
Embedding Excel Sheets in LINGO ..............................................................................................406
Summary.......................................................................................................................................410
10 Interfacing with Databases..........................................................................................................411
ODBC Data Sources .....................................................................................................................412
Importing Data from Databases with @ODBC ..............................................................................419
Importing Data with ODBC in a PERT Model................................................................................421
Exporting Data with @ODBC ........................................................................................................423
Exporting Data with ODBC in a PERT Model................................................................................426
11 Interfacing with Other Applications............................................................................................431
The LINGO Dynamic Link Library..................................................................................................431

CONTENTS v
User Defined Functions.................................................................................................................473
12 Developing More Advanced Models...........................................................................................479
Production Management Models...................................................................................................480
Logistics Models............................................................................................................................494
Financial Models ...........................................................................................................................501
Queuing Models............................................................................................................................516
Marketing Models..........................................................................................................................523
13 Programming LINGO....................................................................................................................531
Programming Features..................................................................................................................531
Programming Example: Binary Search .........................................................................................549
Programming Example: Markowitz Efficient Frontier.....................................................................552
Programming Example: Cutting Stock...........................................................................................559
Programming Example: Accessing Excel......................................................................................565
Summary.......................................................................................................................................571
14 Stochastic Programming.............................................................................................................573
Multistage Decision Making Under Uncertainty.............................................................................573
Recourse Models ..........................................................................................................................575
Scenario Tree................................................................................................................................577
Monte Carlo Sampling...................................................................................................................579
Setting up SP Models....................................................................................................................580
Language Features for SP Models................................................................................................581
Declaring Distributions ..................................................................................................................583
Gas Buying Example.....................................................................................................................590
Stock Option Example...................................................................................................................600
Investing Under Uncertainty Example...........................................................................................608
15 On Mathematical Modeling..........................................................................................................617
Solvers Used Internally by LINGO.................................................................................................617
Type of Constraints .......................................................................................................................618
Local Optima vs. Global Optima....................................................................................................620
Smooth vs. Nonsmooth Functions ................................................................................................625
Guidelines for Nonlinear Modeling ................................................................................................626
Appendix A: Additional Examples of LINGO Modeling................................................................629
Appendix B: Error Messages .........................................................................................................717
Appendix C: Bibliography and Suggested Reading.....................................................................761
Index....................................................................................................................................................763

vii
Preface
LINGO is a comprehensive tool designed to make building and solving mathematical optimization
models easier and more efficient. LINGO provides a completely integrated package that includes a
powerful language for expressing optimization models, a full-featured environment for building and
editing problems, and a set of fast built-in solvers capable of efficiently solving most classes of
optimization models. LINGO's primary features include:
Algebraic Modeling Language
LINGO supports a powerful, set-based modeling language that allows users to express math
programming models efficiently and compactly. Multiple models may be solved iteratively using
LINGO's internal scripting capabilities.
Convenient Data Options
LINGO takes the time and hassle out of managing your data. It allows you to build models that
pull information directly from databases and spreadsheets. Similarly, LINGO can output solution
information right into a database or spreadsheet making it easier for you to generate reports in the
application of your choice. Complete separation of model and data enhance model maintenance
and scalability.
Model Interactively or Create Turnkey Applications
You can build and solve models within LINGO, or you can call LINGO directly from an
application you have written. For developing models interactively, LINGO provides a complete
modeling environment to build, solve, and analyze your models. For building turn-key solutions,
LINGO comes with callable DLL and OLE interfaces that can be called from user written
applications. LINGO can also be called directly from an Excel macro or database application.
LINGO currently includes programming examples for C/C++, FORTRAN, Java, C#.NET,
VB.NET, ASP.NET, Visual Basic, Delphi, and Excel.
Extensive Documentation and Help
LINGO provides all of the tools you will need to get up and running quickly. You get the LINGO
User Manual (in printed form and available via the online Help), which fully describes the
commands and features of the program. Also included with Super versions and larger is a copy of
Optimization Modeling with LINGO, a comprehensive modeling text discussing all major classes
of linear, integer and nonlinear optimization problems. LINGO also comes with dozens of real-
world based examples for you to modify and expand.
Powerful Solvers and Tools
LINGO is available with a comprehensive set of fast, built-in solvers for linear, nonlinear (convex
& nonconvex), quadratic, quadratically constrained, and integer optimization. You never have to
specify or load a separate solver, because LINGO reads your formulation and automatically
selects the appropriate one. A general description of the solvers and tools available in LINGO
follows:

viii PREFACE
General Nonlinear Solver
LINGO provides both general nonlinear and nonlinear/integer capabilities. The nonlinear license
option is required in order to use the nonlinear capabilities with LINDO API.
Global Solver
The global solver combines a series of range bounding (e.g., interval analysis and convex
analysis) and range reduction techniques (e.g., linear programming and constraint propagation)
within a branch-and-bound framework to find proven global solutions to nonconvex nonlinear
programs. Traditional nonlinear solvers can get stuck at suboptimal, local solutions. This is no
longer the case when using the global solver.
Multistart Solver
The multistart solver intelligently generates a sequence of candidate starting points in the solution
space of NLP and mixed integer NLPs. A traditional NLP solver is called with each starting point
to find a local optimum. For non-convex NLP models, the quality of the best solution found by the
multistart solver tends to be superior to that of a single solution from a traditional nonlinear solver.
A user adjustable parameter controls the maximum number of multistarts to be performed.
Barrier Solver
The barrier solver is an alternative way for solving linear, quadratic and second-order cone
problems. LINGO's state-of-the-art implementation of the barrier method offers great speed
advantages for large-scale, sparse models.
Simplex Solvers
LINGO offers two advanced implementations of the primal and dual simplex methods as the
primary means for solving linear programming problems. Its flexible design allows the users to
fine tune each method by altering several of the algorithmic parameters.
Mixed Integer Solver
The mixed integer solver’s capabilities of LINGO extend to linear, quadratic, and general
nonlinear integer models. It contains several advanced solution techniques such as cut generation,
tree reordering to reduce tree growth dynamically, and advanced heuristic and presolve strategies.
Stochastic Solver
The stochastic programming solver provides the opportunity of decision making under uncertainty
through multistage stochastic models with recourse. The user describes the uncertainity by
identifying the distribution functions, either built-in or user-defined, describing each random
variable. The stochastic solver will optimize the model to minimize the cost of the initial stage
plus the expected cost of future recourse actions over the planning horizon. Advanced sampling
modes are also available for approximating continuous distributions.
Model and Solution Analysis Tools
LINGO includes a comprehensive set of analysis tools for debugging infeasible linear, integer and
nonlinear programs, using advanced techniques to isolate the source of infeasibilities to the
smallest subset of the original constraints. It also has tools to perform sensitivity analysis to
determine the sensitivity of the optimal basis to changes in certain data components (e.g. objective
vector and right-hand-size values).

PREFACE ix
Quadratic Recognition Tools
The QP recognition tool is a useful algebraic pre-processor that automatically determines if an
arbitrary NLP is actually a convex, quadratic model. QP models may then be passed to the faster
quadratic solver, which is available as part of the barrier solver option. When the barrier solver
option is combined with the global option, LINGO will automatically recognize second-order
cone models, in addition to convex quadratic models.
Linearization Tools
Linearization is a comprehensive reformulation tool that automatically converts many non-smooth
functions and operators (e.g., max and absolute value) to a series of linear, mathematically
equivalent expressions. Many non-smooth models may be entirely linearized. This allows the
linear solver to quickly find a global solution to what would have otherwise been an intractable
nonlinear problem.

xi
New Features
for LINGO 12.0
LINDO Systems is proud to introduce LINGO 12.0. The new features in LINGO 12.0 include the
following:
All New Stochastic Programming (SP) Solver:
The SP solver supports decisionmaking under uncertainty through multistage stochastic models
with recourse. The user expresses the uncertainty via distribution functions, either built-in or
user-defined, and the stochastic solver will minimize the cost of the initial stage plus the expected
cost of recourse decisions over the planning horizon. Advanced sampling modes are also
available to approximate stochastic parameters from parametric distributions. Other features
include:
• Available for modeling linear, nonlinear and integer stochastic programs (SP).
• Supports most standard distributions, e.g., Normal and Poisson, as well as user defined.
• Full solutions for each of the possible scenarios are available at the scripting level (calc
sections) allowing for the creation of custom reports on variable values over the full
range of scenarios.
• Allows sampling scenarios through statistical sampling.
• Variance reduction with Latin-Hyper-Square sampling.
• Ability to generate statistically dependent samples based on Pearson, Spearman or
Kendall’s correlation measures.
• A pseudorandom number generator with long cycle length and excellent high dimension
uniformity.
• Ability to generate and display the underlying deterministic equivalent used to optimize
SP models.
Global Solver Improvements:
The global solver improvements now include:
• A new algorithm for convexifying models with quadratic terms, making the global solver
more efficient on non-convex quadratic models, as well as general nonlinear models with
quadratic terms.
• Automatic recognition of second-order cone quadratic problems, allowing for
dramatically faster solution times via the barrier solver.
• Reformulation capabilities that improve performance for a wide range of composite
functions.

xii PREFACE
Simplex Solver Improvements:
Large linear models solve an average of 20% faster with the enhanced dual and primal simplex
solvers.
MIP Solver Improvements:
LINGO's MIP solver improvements include:
• Enhancements in the feasibility-pump heuristic to help find improved feasible solutions
on many difficult problems.
• Enhancements in the rounding techniques exploit an even wider range of constraint
structures.
• Standard heuristics have been improved.
Loop Optimization:
Loop optimization reformulates expressions containing set looping functions in order to make
them more efficient, while maintaining mathematical equivalency. The end goal of loop
optimization is to minimize the number of passes through the inner loop of any nested loops in an
expression. Inefficiently formulated models can experience dramatic improvements in model
generation times.
Precision in Solution Reports:
In the past, LINGO's solution reports always displayed exactly 7 significant digits when reporting
numeric results. You may now control the degree of precision, with anywhere from 1 to 17
significant digits.
New Scripting Function Capabilities:
A number of calc section scripting functions were added or improved:
• @FORMAT may now be used to format output of strings in addition to numeric values.
• @GENDUAL generates the dual formulation of a linear program.
• @SMPS generates MPS format model files.
Variable Name Lengths Extended to 64 Characters:
Prior releases of LINGO had a limit of 32 characters on variable name lengths. This limit has
been increased to 64 characters.
We hope you enjoy this new release of LINGO. Many of the new features in this release are due to
suggestions from our users. If there are any features you'd like to see in the next release of LINGO,
please let us know. You can reach us at:
LINDO Systems Inc.
1415 N. Dayton St.
Chicago, Illinois 60642
(312) 988-7422
info@lindo.com
http://www.lindo.com
February 2010

1
1 Getting Started with
LINGO
What is LINGO?
LINGO is a simple tool for utilizing the power of linear and nonlinear optimization to formulate large
problems concisely, solve them, and analyze the solution. Optimization helps you find the answer that
yields the best result; attains the highest profit, output, or happiness; or achieves the lowest cost, waste,
or discomfort. Often these problems involve making the most efficient use of your resources—
including money, time, machinery, staff, inventory, and more. Optimization problems are often
classified as linear or nonlinear, depending on whether the relationships in the problem are linear with
respect to the variables.
If you are a new user, it is recommended you go through the first seven chapters to familiarize yourself
with LINGO. Then, you may want to see Chapter 15, On Mathematical Modeling, for more
information on the difference between linear and nonlinear models and how to develop large models. It
may also be helpful to view some sample models in Chapter 12, Developing More Advanced Models,
or Appendix A, Additional Examples of LINGO Modeling, to see if a particular template example is
similar to a problem you have. For users of previous versions of LINGO, the new features are
summarized in the Preface at the beginning of the manual.
Installing LINGO
This section discusses how to install LINGO on the Windows platform. To install LINGO on
platforms other than Windows, refer to the installation instructions included with your software.
Installing the LINGO software is straightforward. To setup LINGO for Windows, place your CD in the
appropriate drive and run the installation program SETUP contained in the LINGO folder. The LINGO
installation program will open and guide you through the steps required to install LINGO on your hard
drive.
Note: If there is a previous version of LINGO installed on your machine, then you may need to
uninstall it before you can install the new copy of LINGO. To uninstall the existing copy of
LINGO, click on the Windows Start button, select the Settings command, select Control
Panel, then double click on the Add or Remove Programs icon. You should then be able to
select LINGO and have the old version removed from your system.
2 CHAPTER 1
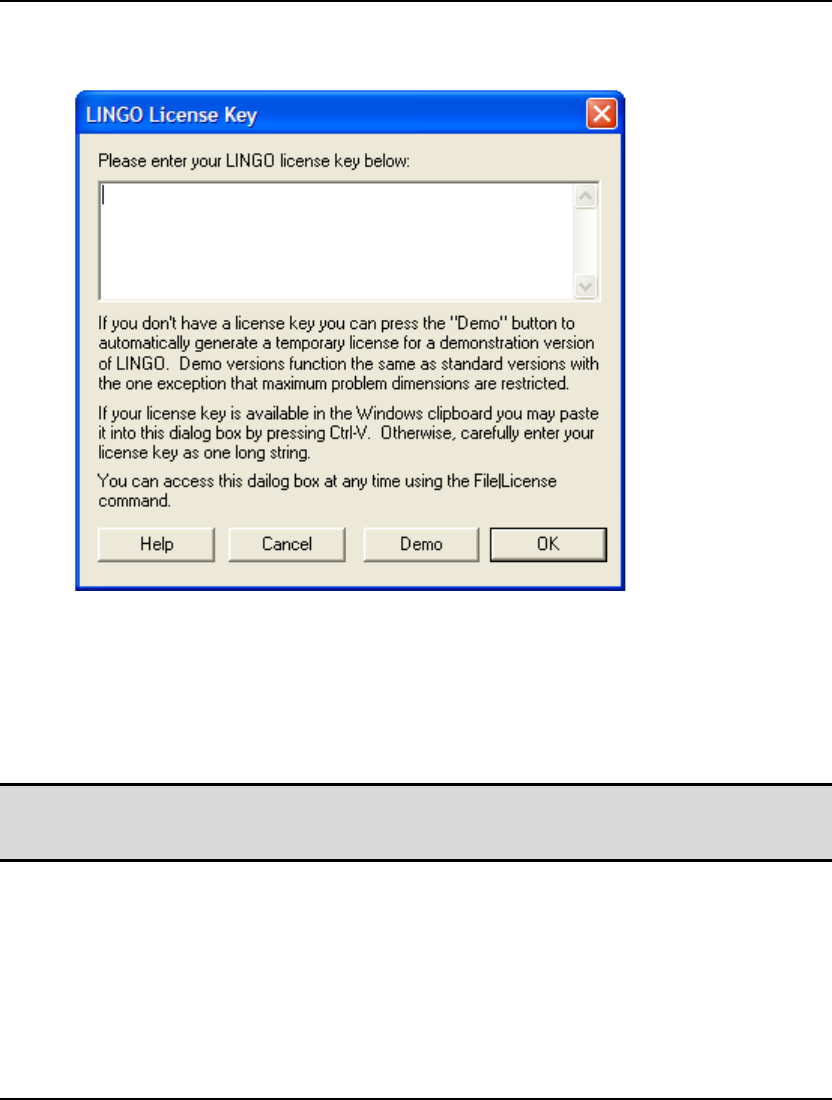
Most copies of LINGO come with their licenses preinstalled. However, some versions of LINGO
require you to input a license key. If your version of LINGO requires a license key, you will be
presented with the following dialog box when you start LINGO:
Your license key may have been included in an email sent to you when you ordered your software.
The license key is a string of letters, symbols and numbers, separated into groups of four by hyphens
(e.g., r82m-XCW2-dZu?-%72S-fD?S-Wp@). Carefully enter the license key into the edit field,
including hyphens. License keys are case sensitive, so you must be sure to preserve the case of the
individual letters when entering your key. Click the OK button and, assuming the key was entered
correctly, LINGO will then start. In the future, you will be able to run LINGO directly without
entering the key.
Note: If you received your license key by email, then you have the option of cutting-and-pasting it
into the license key dialog box. Cut the key from the email that contains it with the Ctrl+C
key, then select the key field in LINGO dialog box and paste the key with the Ctrl+V key.
If you don’t have a key, you can choose to run LINGO in demo mode by clicking the Demo button. In
demo mode, LINGO has all the functionality of a standard version of LINGO with the one exception
that the maximum problem size is restricted. Demo licenses expire after 30 days.
GETTING STARTED 3
Entering a Model in Windows
Starting LINGO
This section illustrates how to input and solve a small model in Windows. The text of the model’s
equations is platform independent and will be identical on all platforms. However, keep in mind that
the technique for entering a model is slightly different on non-Windows platforms. For instructions on
entering a model on platforms other than Windows, please refer to the Modeling from the
Command-Line section below.
When you start LINGO for Windows, your screen should resemble the following:
The outer window, labeled LINGO, is the main frame window. All other windows will be contained
within this window. The top of the frame window also contains all the command menus and the
command toolbar. See Chapter 5, Windows Commands, for details on the toolbar and menu
commands. The lower edge of the main frame window contains a status bar that provides various
pieces of information regarding LINGO's current state. Both the toolbar and the status bar can be
suppressed through the use of the LINGO|Options command.
The smaller child window labeled LINGO Model
−
LINGO1 is a new, blank model window. In the
next section, we will be entering a sample model directly into this window.

4 CHAPTER 1
Developing a LINGO Model in Windows
The Problem
For our sample model, we will create a small product-mix example. Let’s imagine that the
CompuQuick Corporation produces two models of computers—Standard and Turbo. CompuQuick can
sell every Standard unit it produces for a profit contribution of $100, and each Turbo unit for a
contribution of $150. At the CompuQuick factory, the Standard computer production line can produce,
at most, 100 computers per day. At the same time, the Turbo computer production line can turn out
120 computers per day. Furthermore, CompuQuick has a limited supply of daily labor. In particular,
there is a total of 160 hours of labor available each day. Standard computers require 1 hour of labor,
while Turbo computers are relatively more labor intense requiring 2 hours of labor. The problem for
CompuQuick is to determine the mix of Standard and Turbo computers to produce each day to
maximize total profit without exceeding line and labor capacity limits.
In general, an optimization model will consist of the following three items:
• Objective Function - The objective function is a formula that expresses exactly
what it is you want to optimize. In business oriented models, this will usually be
a profit function you wish to maximize, or a cost function you want to minimize.
Models may have, at most, one objective function. In the case of our
CompuQuick example, the objective function will compute the company’s profit
as a function of the output of Standards and Turbos.
• Variables - Variables are the quantities you have under your control. You must
decide what the best values of the variables are. For this reason, variables are
sometimes also called decision variables. The goal of optimization is to find the
values of a model’s variables that generate the best value for the objective
function, subject to any limiting conditions placed on the variables. We will
have two variables in our example−one corresponding to the number of
Standards to produce and the other corresponding to the number of Turbos to
produce.
• Constraints - Almost without exception, there will be some limit on the values
the variables in a model can assume—at least one resource will be limited (e.g.,
time, raw materials, your department’s budget, etc.). These limits are expressed
in terms of formulas that are a function of the model’s variables. These formulas
are referred to as constraints because they constrain the values the variables can
take. In our CompuQuick example, we will have one constraint for each
production line and one constraint on the total labor used.

GETTING STARTED 5
Entering the Model
We will now construct the objective function for our example. We will let the variables STANDARD
and TURBO denote the number of Standard and Turbo computers to produce, respectively.
CompuQuick’s objective is to maximize total profit. Total profit is calculated as the sum of the profit
contribution of the Standard computer ($100) multiplied by the total Standard computers produced
(STANDARD) and the profit contribution of the Turbo computer ($150) multiplied by the total Turbo
computers produced (TURBO). Finally, we tell LINGO we want to maximize an objective function by
preceding it with “MAX =”. Therefore, our objective function is written on the first line of our model
window as:
MAX = 100 * STANDARD + 150 * TURBO;
Note: Each mathematical expression in LINGO is terminated with a semicolon. These semicolons
are required. Your model will not solve without them. For more information on the syntax of
LINGO, see below.
Next, we must input our constraints on line capacity and labor supply. The number of Standard and
Turbo computers produced must be constrained to the production line limits of 100 and 120,
respectively. Do this by entering the following two constraints just below the objective function:
STANDARD <= 100;
TURBO <= 120;
In words, the first constraint says the number of Standard computers produced daily (STANDARD)
must be less-than-or-equal-to (<=) the production line capacity of 100. Likewise, the second constraint
says the number of Turbo computers produced daily (TURBO) must be less-than-or-equal-to (<=) its
line capacity of 120.
Note: Since most computers do not have less-than-or-equal-to keys (≤), LINGO has adopted the
convention of using the two character symbol <= to denote ≤. As an alternative, you may
simply enter < to signify less-than-or-equal-to. In a similar manner, >= or > are used to
signify greater-than-or-equal-to (≥).
The final constraint on the amount of labor used can be expressed as:
STANDARD + 2 * TURBO <= 160;
Specifically, the total number of labor hours used (STANDARD + 2 * TURBO) must be
less-than-or-equal-to (<=) the amount of labor hours available of 160.

6 CHAPTER 1
After entering the above and entering comments to improve the readability of the model, your model
window should look like this:
General LINGO Syntax
An expression may be broken up into as many lines as you want, but the expression must be
terminated with a semicolon. As an example, we could have used two lines rather than just one to
contain the objective function:
MAX = 100 * STANDARD
+ 150 * TURBO;
We have also entered some comments to improve the readability of our model. Comments begin with
an exclamation point (!) and end with a semicolon (;). All text between an exclamation point and
terminating semicolon is ignored by LINGO. Comments can occupy more than one line and can share
lines with other LINGO expressions. For example:
X = 1.5 * Y + Z / 2 * Y; !This is a comment;
X = 1.5 * !This is a comment in the middle
of a constraint; Y + Z / 2 * Y;
You may have noticed we used all uppercase letters for our variable names. This is not a requirement.
LINGO does not distinguish between uppercase and lowercase in variable names. Thus, the following
variable names would all be considered equivalent:
TURBO
Turbo
turbo
When constructing variable names in LINGO, all names must begin with an alphabetic character
(A-Z). Subsequent characters may be either alphabetic, numeric (0-9), or the underscore (_). Names
may be up to 64 characters in length.
A final feature you will notice is that LINGO’s editor is “syntax aware.” In other words, when it
encounters LINGO keywords it displays them in blue, comments are displayed in green, and all
remaining text is displayed in black. Matching parentheses are also highlighted in red when you
place the cursor immediately following a parenthesis. You should find this feature useful in tracking
down syntax errors in your models.
GETTING STARTED 7
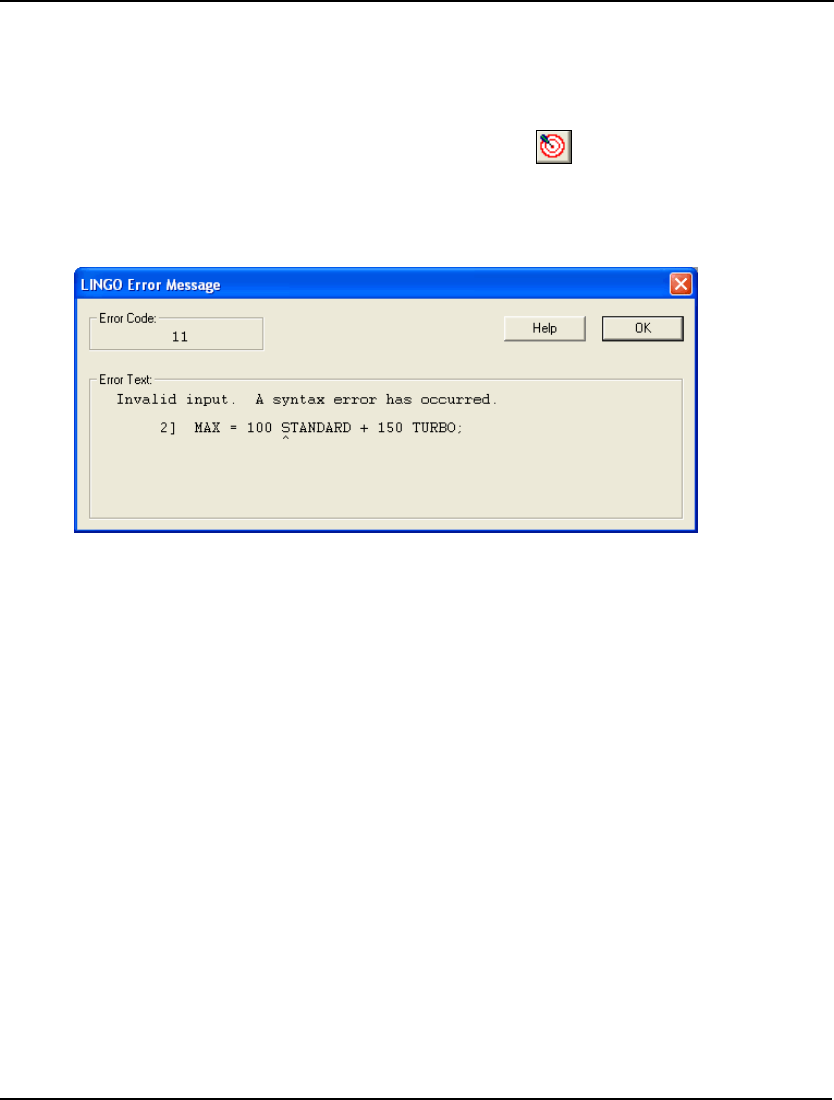
Solving the Model
Syntax Errors
Your model has now been entered and it is ready to be solved. To begin solving the model, select the
Solve command from the LINGO menu, or press the Solve button ( ) on the toolbar at the top of the
main frame window. LINGO will begin compiling the model. During this step, LINGO will determine
whether the model conforms to all syntax requirements. If the LINGO model doesn’t pass these tests,
you will be informed by an error message. In this model, for instance, if you forget to use the
multiplication sign, you will get an error like the following:
LINGO lets you know there is a syntax error in your model, lists the line of the model it is in, and
points to the place in the line where it occurred. For more information on error codes, see Appendix B,
Error Messages.
8 CHAPTER 1
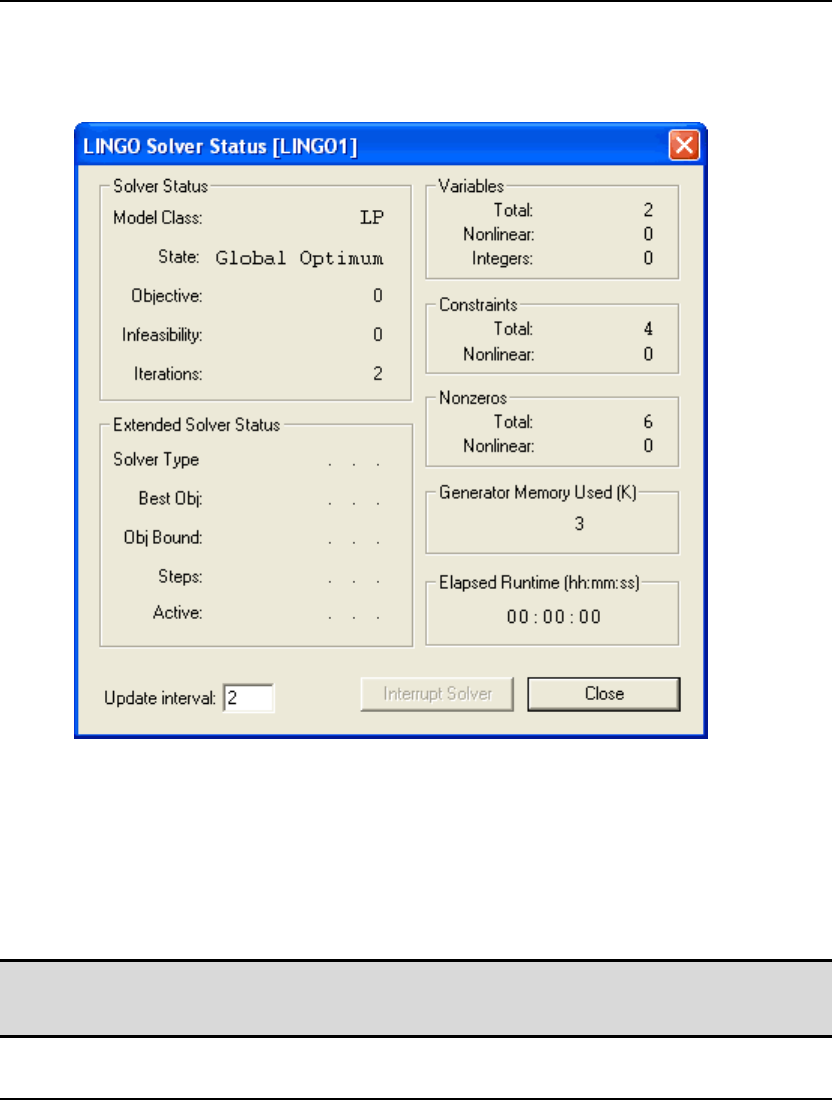
Solver Status Window
If there are no formulation errors during the compilation phase, LINGO will invoke the appropriate
internal solver to begin searching for the optimal solution to your model. When the solver starts, it
displays a solver status window on your screen resembling the following:
The solver status window is useful for monitoring the progress of the solver and the dimensions of
your model. The various fields are described in more detail below.
The solver status window also provides you with an Interrupt Solver button. Interrupting the solver
causes LINGO to halt the solver on the next iteration. In most cases, LINGO will be able to restore and
report the best solution found so far. The one exception is in the case of linear programming models
(i.e., linear models without integer variables). If a linear programming model is interrupted, the
solution returned will be meaningless and should be ignored. This should not be a problem because
linear programs generally solve quickly, thus minimizing the need to interrupt.
Note: You must be careful how you interpret solutions after interrupting the solver. These solutions
1) will definitely not be optimal, 2) may not be feasible to all the constraints, and 3) are
worthless if the model is a linear program.

GETTING STARTED 9
Next to the Interrupt Solver button is another button labeled Close. Hitting the Close button will close
the solver status window. This window can be reopened at any time by selecting the Window|Status
Window command.
At the bottom of the solver status window, you will find an Update Interval field. LINGO will update
the solver status window every n seconds, where n is the value contained in the Update Interval field.
You may set this interval to any value you desire. However, setting it to 0 will result in longer solution
times—LINGO will spend more time updating the solver status window than solving your model. On
larger models, LINGO may not always be able to update the solver status window on a regular
interval. So, don't be concerned if you sometimes must wait longer than the indicated interval.
Variables box
The Variables box shows the total number of variables in the model. The Variables box also displays
the number of the total variables that are nonlinear. A variable is considered to be nonlinear if it enters
into any nonlinear relationship in any constraint in the model. For instance, the constraint:
X + Y = 100;
would be considered linear because the graph of this function would be a straight line. On the other
hand, the nonlinear function:
X * Y = 100;
is quadratic and has a curved line as its graph. If we were to solve a model containing this particular
nonlinear constraint, the nonlinear variable count would be at least 2 to represent the fact that the two
variables X and Y appear nonlinearly in this constraint.
As another example, consider the constraint:
X * X + Y = 100;
In this case, X appears nonlinearly while Y appears as a linear variable. This constraint would not cause
Y to be counted as one of the nonlinear variables. See Chapter 15, On Mathematical Modeling, for
more information on the difference between linear and nonlinear equations.
The Variables box in the solver status window also gives you a count of the total number of integer
variables in the model. In general, the more nonlinear and integer variables your model has, the more
difficult it will be to solve to optimality in a reasonable amount of time. Pure linear models without
integer variables will tend to solve the fastest. For more details on the use of integer variables, refer to
Chapter 3, Using Variable Domain Functions.
The variable counts do not include any variables LINGO determines are fixed in value. For instance,
consider the following constraints:
X = 1;
X + Y = 3;
From the first constraint, LINGO determines X is fixed at the value of 1. Using this information in
constraint 2, LINGO determines Y is fixed at a value of 2. X and Y will then be substituted out of the
model and they will not contribute to the total variable count.
10 CHAPTER 1
Constraints box
The Constraints box shows the total constraints in the expanded model and the number of these
constraints that are nonlinear. A constraint is considered nonlinear if one or more variables appear
nonlinearly in the constraint.
LINGO searches your model for fixed constraints. A constraint is considered fixed if all the variables
in the constraint are fixed. Fixed constraints are substituted out of the model and do not add to the total
constraint count.
Nonzeroes box
The Nonzeros box shows the total nonzero coefficients in the model and the number of these that
appear on nonlinear variables. In a given constraint, only a small subset of the total variables typically
appears. The implied coefficient on all the non-appearing variables is zero, while the coefficients on
the variables that do appear will be nonzero. Thus, you can view the total nonzero coefficient count as
a tally of the total number of times variables appear in all the constraints. The nonlinear nonzero
coefficient count can be viewed as the number of times variables appear nonlinearly in all the
constraints.
Generator Memory Used box
The Generator Memory Used box lists the amount of memory LINGO's model generator is currently
using from its memory allotment. You may change the size of the generator's memory allotment using
the LINGO|Options command (see Chapter 5, Windows Commands).
Elapsed Runtime box
The Elapsed Runtime box shows the total time used so far to generate and solve the model. This is an
elapsed time figure and may be affected by the number of other applications running on your system.
Solver Status box
The Solver Status box shows the current status of the solver. A description of the fields appears in the
table below followed by a more in depth explanation:
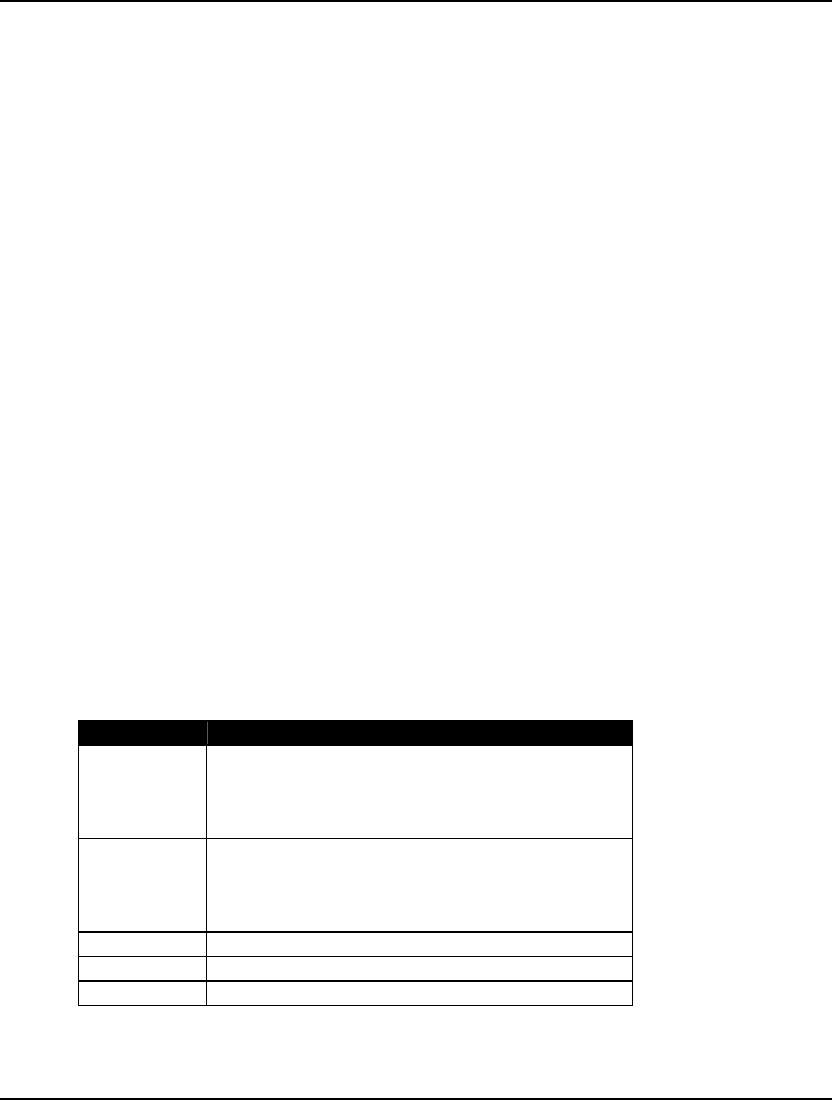
Field Description
Model Class Displays the model’s classification. Possible
classes are “LP”, “QP”, “MILP”, “MIQP”,
“PILP”, “PIQP”, “NLP”, “SOCP”, “MISOCP”,
“PISOCP”, “MINLP”, and “PINLP”.
State Gives the Status of the current solution. Possible
states are “Global Optimum”, “Local Optimum”,
“Feasible”, “Infeasible”, “Unbounded”,
“Interrupted”, and “Undetermined”.
Objective Current value of the objective function.
Infeasibility Amount constraints are violated by.
Iterations Number of solver iterations.

GETTING STARTED 11
Model Class Field
The Model Class field summarizes the properties of your model. The various classes you will
encounter are listed below, roughly ordered from easiest to hardest to solve:
Abbreviation Class Description
LP Linear
Program
All expressions are linear and the
model contains no integer
restrictions on the variables.
QP Quadratic
Program
All expressions are linear or
quadratic, the model is convex, and
there are no integer restrictions.
MILP Mixed
Integer
Linear
Program
All expressions are linear, and a
subset of the variables is restricted
to integer values.
MIQP Mixed
Integer
Quadratic
Program
All expressions are either linear or
quadratic, the model is convex, and
a subset of the variables has integer
restrictions.
PILP Pure
Integer
Linear
Program
All expressions are linear, and all
variables are restricted to integer
values.
PIQP Pure
Integer
Quadratic
Program
All expressions are linear or
quadratic, the model is convex, and
all variables are restricted to
integer values.
SOCP Second-
Order
Cone
Program
The model is a second-order cone
program and all variables are
continuous.
MISOCP Mixed
Integer
Second
Order
Cone
Program
The model is a second-order cone
program, and a subset of the
variables is restricted to integer
values.
PISOCP Pure
Integer
Second-
Order
Cone
Program
The model is a second-order cone
program, and all the variables are
restricted to integer values.
NLP Nonlinear
Program
At least one of the relationships in
the model is nonlinear with respect
to the variables.

12 CHAPTER 1
MINLP Integer
Nonlinear
Program
At least one of the expressions in
the model is nonlinear, and a
subset of the variables has integer
restrictions. In general, this class
of model will be very difficult to
solve for all but the smallest cases.
PINLP Pure
Integer
Nonlinear
Program
At least one of the expressions in
the model is nonlinear, and all
variables have integer restrictions.
In general, this class of model will
be very difficult to solve for all but
the smallest cases.
State Field
When LINGO begins solving your model, the initial state of the current solution will be
"Undetermined". This is because the solver has not yet had a chance to generate a solution to your
model.
Once the solver begins iterating, the state will progress to "Infeasible". In the infeasible state, LINGO
has generated tentative solutions, but none that satisfy all the constraints in the model.
Assuming a feasible solution exists, the solver will then progress to the "Feasible" state. In the feasible
state, LINGO has found a solution that satisfies all the constraints in your model, but the solver is not
yet satisfied it has found the best solution to your model.
Once the solver can no longer find better solutions to your model, it will terminate in either the
"Global Optimum" or "Local Optimum" state. If your model does not have any nonlinear constraints,
then any locally optimal solution will also be a global optimum. Thus, all optimized linear models will
terminate in the global optimum state. If, on the other hand, your model has one or more nonlinear
constraints, then any locally optimal solution may not be the best solution to your model. There may
be another "peak" that is better than the current one, but the solver's local search procedure is unable to
"see" the better peak. Thus, on nonlinear models, LINGO can terminate only in the local optimum
state. LINGO may, in fact, have a globally optimal solution, but, given the nature of nonlinear
problems, LINGO is unable to claim it as such. Given this fact, it is always preferred to formulate a
model using only linear constraints whenever possible. For more details on the concept of global vs.
local optimal points, refer to On Mathematical Modeling.
Note: LINGO’s optional global solver may be used to find globally optimal solutions to nonlinear
models. For more information on the global solver, refer to the Nonlinear Solver Tab help
topic.
If a model terminates in the "Unbounded" state, it means LINGO can improve the objective function
without bound. In real life, this would correspond to a situation where you can generate infinite profits.
Because such a situation is rare, if not impossible, you have probably omitted or mis-specified some
constraints in your model.

GETTING STARTED 13
Finally, the "Interrupted" state will occur when you prematurely interrupt LINGO's solver before it has
found the final solution to your model. The mechanics of interrupting the solver are discussed in more
detail above.
Objective Field
The Objective field gives the objective value for the current solution. If your model does not have an
objective function, then "N/A" will appear in this field.
Infeasibility Field
The Infeasibility field lists the amount that all the constraints in the model are violated by. Keep in
mind that this figure does not track the amount of any violations on variable bounds. Thus, it is
possible for the Infeasibility field to be zero while the current solution is infeasible due to violated
variable bounds. The LINGO solver may also internally scale a model such that the units of the
Infeasibility field no longer correspond to the unscaled version of the model. To determine whether
LINGO has found a feasible solution, you should refer to the State field discussed above.
Iterations Field
The Iterations field displays a count of the number of iterations completed thus far by LINGO's solver.
The fundamental operation performed by LINGO's solver is called iteration. Iteration involves finding
a variable, currently at a zero value, which would be attractive to introduce into the solution at a
nonzero value. This variable is then introduced into the solution at successively larger values until
either a constraint is about to be driven infeasible or another variable is driven to zero. At this point,
the iteration process begins anew. In general, as a model becomes larger, it will require more iterations
to solve and each iteration will require more time to complete.
Extended Solver Status box
The Extended Solver Status box shows status information pertaining to several of the specialized
solvers in LINGO. These solvers are:
♦ Branch-and-Bound Solver,
♦ Global Solver, and
♦ Multistart Solver.
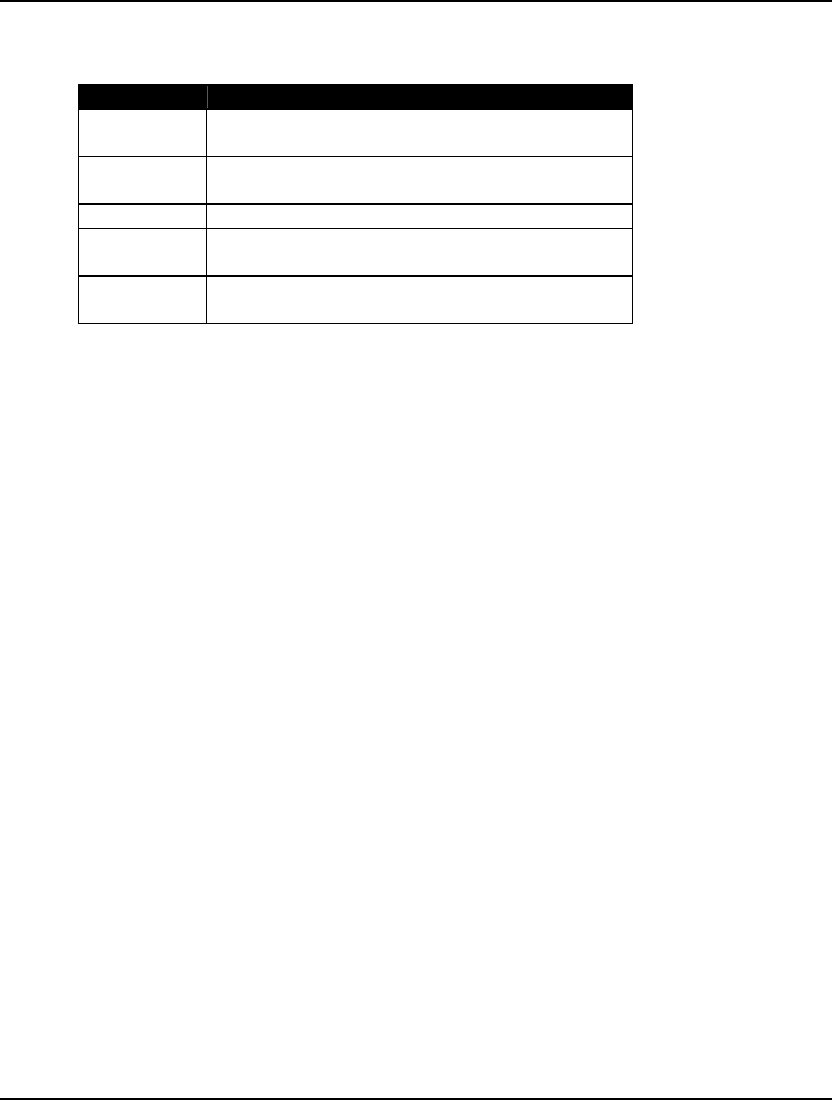
14 CHAPTER 1
The fields in this box will be updated only when one of these three specialized solvers is running.
The fields appearing in the Extended Solver Status box are:
Field Description
Solver Type The type of specialized solver in use. This will be
“B-and-B”, “Global”, or “Multistart”.
Best Obj The objective value of the best solution found so
far.
Obj Bound The theoretical bound on the objective.
Steps The number of steps taken by the Extended
Solver.
Active The number of active subproblems remaining to
be analyzed.
Solver Type Field
This field displays “B-and-B”, “Global”, or “Multistart” depending on the specialized solver in use.
LINGO employs a strategy called branch-and-bound to solve models with integer restrictions. Branch-
and-bound is a systematic method for implicitly enumerating all possible combinations of the integer
variables. Refer to Hillier and Lieberman (1995) for more information on the branch-and-bound
algorithm.
In addition to the branch-and-bound solver, there are two other specialized nonlinear solvers that may
be invoked: global solver and multistart solver. Many nonlinear models are non-convex and/or non-
smooth. For more information see the Chapter 15, On Mathematical Modeling. Nonlinear solvers that
rely on local search procedures (as does LINGO’s default nonlinear solver) will tend to do poorly on
these types of models. Typically, they will converge to a local, sub-optimal point that may be quite
distant from the true, globally optimal point. The multistart solver and the global solver are specialized
solvers that attempt to find the globally optimal solution to non-convex models. You can read more
about these solvers in the Nonlinear Solver Tab section.
Best Obj and Obj Bound Fields
The Best Obj field displays the best feasible objective value found so far. Obj Bound displays the
bound on the objective. This bound is a limit on how far the solver will be able to improve the
objective. At some point, these two values may become very close. Given that the best objective value
can never exceed the bound, the fact that these two values are close indicates that LINGO's current
best solution is either the optimal solution, or very close to it. At such a point, the user may choose to
interrupt the solver and go with the current best solution in the interest of saving on additional
computation time.

GETTING STARTED 15
Steps Field
The information displayed in the Steps field depends on the particular solver that is running. The table
below explains:
Solver Steps Field Interpretation
Branch-and-Bound Number of branches in the branch-
and-bound tree.
Global Number of subproblem boxes
generated.
Multistart Number of solver restarts.
Active Field
This field pertains to the branch –and –bound and global solvers. It lists the number of open
subproblems remaining to be evaluated. The solver must run until this valve goes to zero.
The Solution Report
When LINGO is done solving the CompuQuick model, there will be a new window created on your
screen titled Solution Report containing the details of the solution to your model. The solution report
should appear as follows:

16 CHAPTER 1
This solution tells us CompuQuick should build 100 Standards and 30 Turbos each day for a total daily
profit of $14,500. Refer to the Examining the Solution section below for additional details on the
various fields in this report.

GETTING STARTED 17
Printing Your Work in Windows
In Windows versions of LINGO, use the Print command in the File menu to print the active
(frontmost) window, or click on the Print button ( ). You may print any window, including model
and report windows. If you wish to print just a portion of a window, use the Cut and Paste commands
in the Edit menu to put the desired text in a new window before printing. You can also access the Cut
command by clicking on the Cut button ( ). Likewise, the Paste command can be accessed through
the Paste button ( ). To create a new window, use the File|New command, or click the New button
().
Saving Your Work in Windows
To save your model to a disk file, use the File|Save command or press the Save button ( ) in the
toolbar. Unless you specify otherwise, LINGO will automatically append a .LG4 extension to your file
name.
Opening a Sample Model
LINGO is shipped with a directory containing many sample models. These models are drawn from a
wide array of application areas. For a complete listing of these models, see Additional Examples of
LINGO Modeling. The sample model directory is titled Samples and is stored directly off the main
LINGO directory.
18 CHAPTER 1
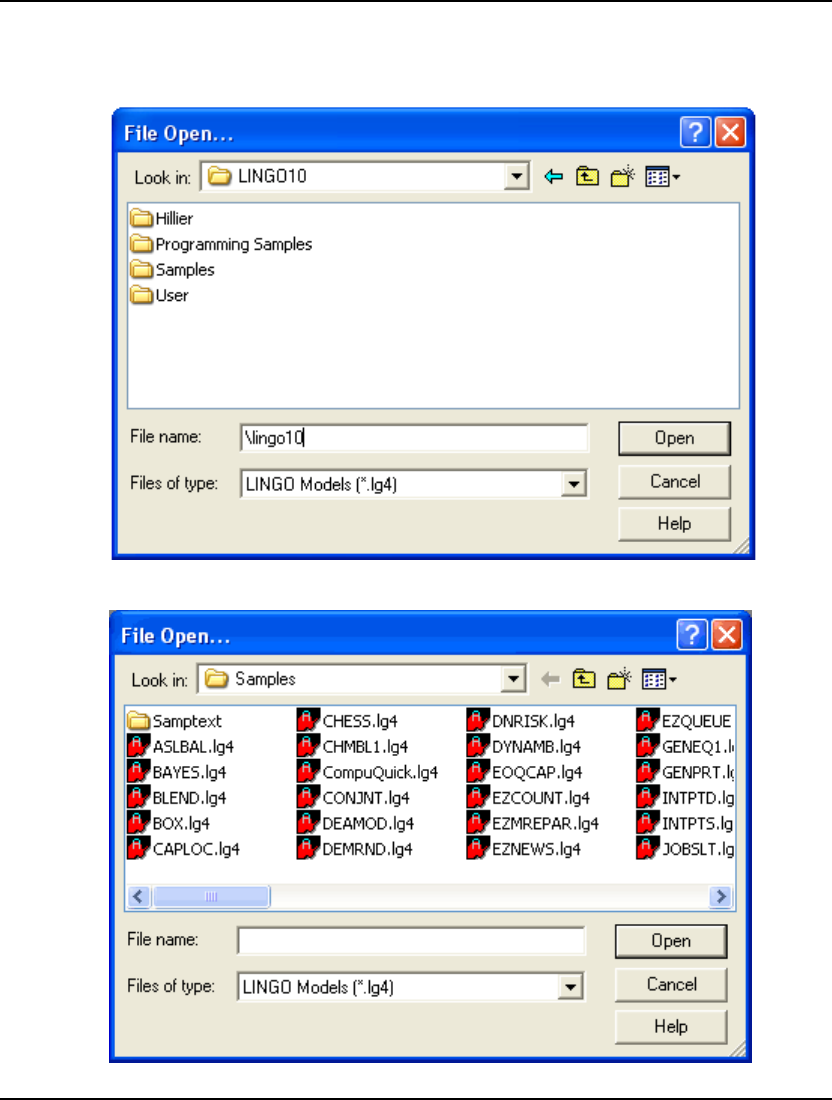
To open a sample model in LINGO, follow these steps:
1. Pull down the File menu and select the Open command. You should see the following dialog
box:
2. Double-click on the folder titled Samples, at which point you should see:
GETTING STARTED 19
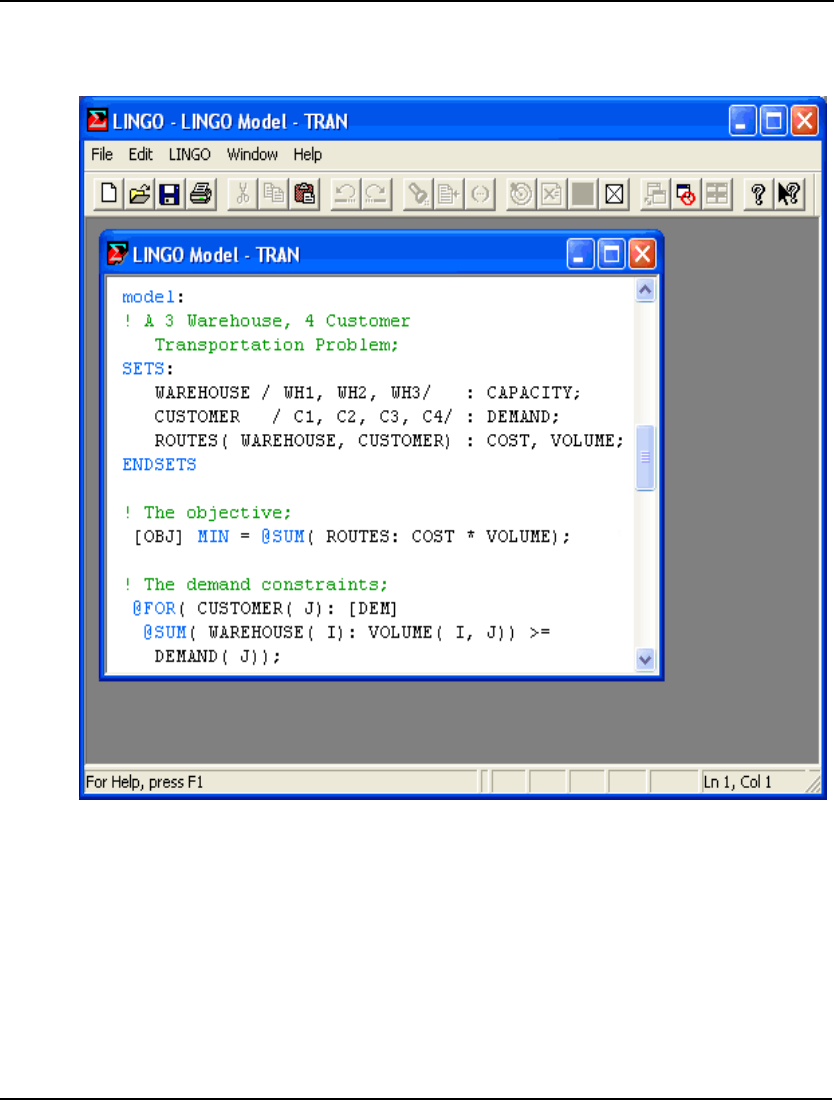
3. To read in a small transportation model, type Tran in the File Name field in the above dialog
box and press the Open button. You should now have the model in an open window in
LINGO as follows:
For details on developing a transportation model in LINGO see The Problem in Words in Getting
Started with LINGO.
20 CHAPTER 1
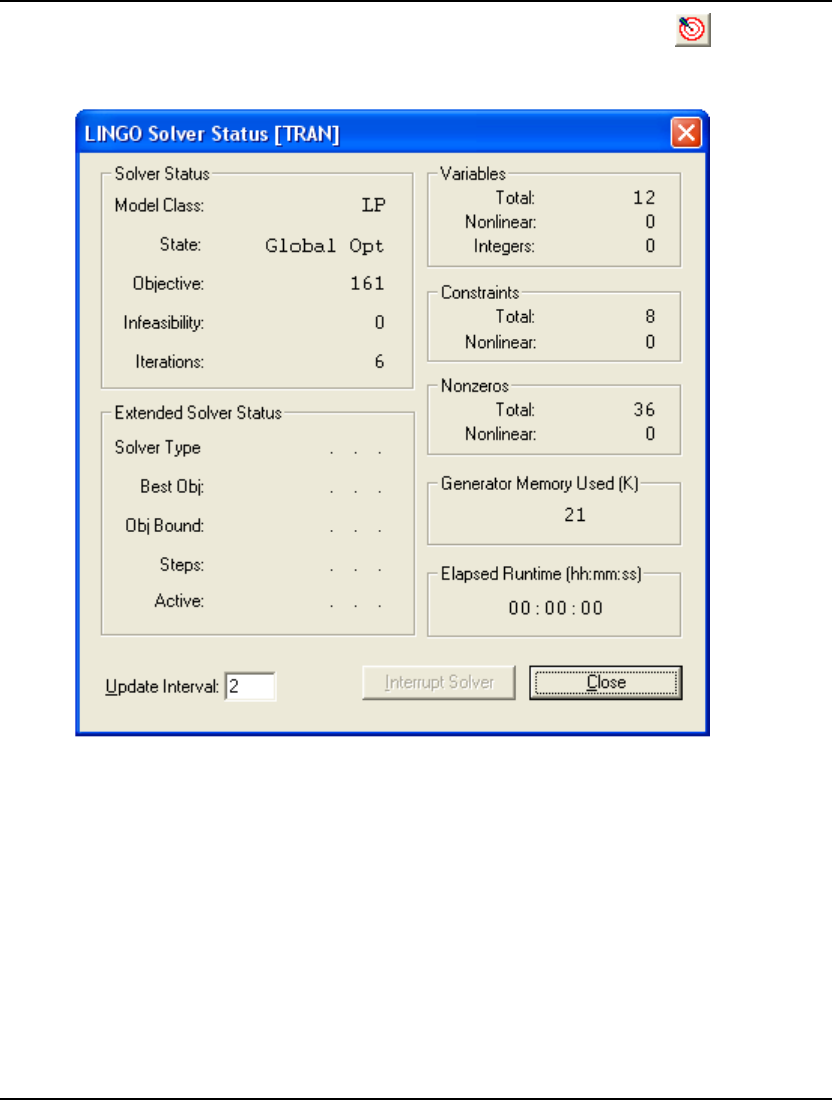
You may now solve the model using the LINGO|Solve command or by pressing the button on the
toolbar. The optimal objective value for this model is 161. When solved, you should see the following
solver status window:
Note the objective field has a value of 161 as expected. For an interpretation of the other fields in this
window, see Solver Status Window in Getting Started with LINGO.
GETTING STARTED 21
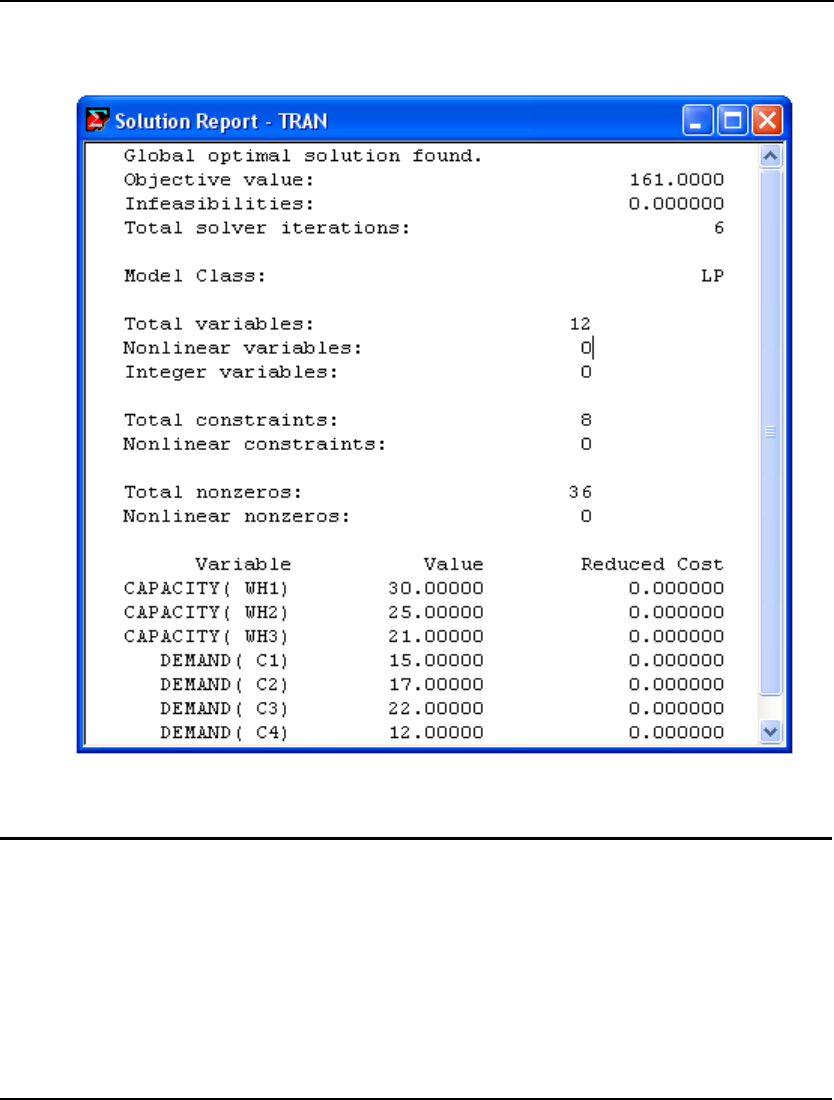
Behind the solver status window, you will find the solution report for the model. This report contains
summary information about the model as well as values for all the variables. This report’s header is
reproduced below:
For information on interpreting the fields in the solution report, see Sample Solution Report in Getting
Started with LINGO.
Modeling from the Command-Line
Starting LINGO
If you are running LINGO on a platform other than a Windows based PC, then you will interface with
LINGO through the means of a command-line prompt. All instructions are issued to LINGO in the
form of text command strings.

22 CHAPTER 1
When you start a command-line version of LINGO, you will see a colon command prompt as follows:
LINGO
Copyright (C) LINDO Systems Inc. Licensed material, all
rights reserved. Copying except as authorized in license
agreement is prohibited.
:
The colon character (:) at the bottom of the screen is LINGO’s prompt for input. When you see the
colon prompt, LINGO is expecting a command. When you see the question mark prompt, you have
already initiated a command and LINGO is asking you to supply additional information related to this
command such as a number or a name. If you wish to “back out” of a command you have already
started, you may enter a blank line in response to the question mark prompt and LINGO will return
you to the command level colon prompt. All available commands are listed in Chapter 6,
Command-line Commands.
Entering the Model
When you enter a model in the command-line interface, you must first specify to LINGO that you are
ready to begin entering the LINGO statements. This is done by entering the MODEL: command at the
colon prompt. LINGO will then give you a question mark prompt and you begin entering the model
line by line.
As an example, we will use the CompuQuick model discussed in the previous section. After entering
the CompuQuick model, your screen should resemble the following (Note that user input is in bold.):
LINGO
: MODEL:
? MAX = 100 * STANDARD + 150 * TURBO;
? STANDARD <= 100;
? TURBO <= 120;
? STANDARD + 2 * TURBO <= 160;
? END
:
The END command tells LINGO you are finished inputting the model. Once you enter the END
command and return to the colon prompt, the model is in memory and ready to be solved.
Solving the Model
To begin solving the model, type the GO command at the colon prompt and press the enter key.
LINGO will begin compiling the model. This means LINGO will determine whether the model
conforms to all syntax requirements. If the LINGO model doesn’t pass these tests, you will be
informed by an error message. For more information on error codes, see Appendix B, Error Messages.
If there are no formulation errors during the compilation phase, LINGO will invoke the appropriate
internal solver to begin searching for the optimal solution to your model. When LINGO is done
solving the CompuQuick model, it will send the following solution report to your screen:
: GO

GETTING STARTED 23
Global optimal solution found.
Objective value: 14500.00
Infeasibilities: 0.000000
Total solver iterations: 0
Model Class: LP
Total variables: 2
Nonlinear variables: 0
Integer variables: 0
Total constraints: 4
Nonlinear constraints: 0
Total nonzeros: 6
Nonlinear nonzeros: 0
Variable Value Reduced Cost
STANDARD 100.0000 0.000000
TURBO 30.00000 0.000000
Row Slack or Surplus Dual Price
1 14500.00 1.000000
2 0.000000 25.00000
3 90.00000 0.000000
4 0.000000 75.00000
This solution tells us that CompuQuick should build 100 Standards and 30 Turbos each day to give
them a total daily profit of $14,500. Refer to the Examining the Solution section below for additional
details on the various fields in this report.
Printing and Saving Your Work
For command-line (non-Windows) versions of LINGO, the DIVERT file command may be used to
send all LINGO reports to a file rather than to the screen. You may then route this file to a printer or
load it into a word processing program for printing.
For example, to create a text file for printing that contains a copy of your model and solution, issue the
commands:
DIVERT MYFILE !Opens an output file called MYFILE;
LOOK ALL !Sends formulation to the file;
GO !Sends solution to the file;
RVRT !Closes down output file;

24 CHAPTER 1
To save your model to disk, issue the SAVE command followed by the name of a file to store your
model under. For example, the command:
SAVE MYFILE.LNG
saves a copy of the current model to the file titled MYFILE.LNG. The model may be retrieved for use
later with the TAKE command.
Please refer to Chapter 6, Command-line Commands, for more detailed information on these and other
commands.
Examining the Solution
First, the solution report us that LINGO took 0 iterations to solve the model (the preprocessor was able
to deduce the optimal solution without having to iterate). Second, the maximum profit attainable is
$14,500. Third, the quantities of each computer to produce, STANDARD and TURBO, are 100 and 30,
respectively. What’s interesting to note is we make less of the relatively more “profitable” Turbo
computer due to its more intensive use of our limited supply of labor. The Reduced Costs, Slack or
Surplus, and Dual Price columns are explained in other sections.
Reduced Cost
In a LINGO solution report, you’ll find a reduced cost figure for each variable. There are two valid,
equivalent interpretations of a reduced cost.
First, you may interpret a variable’s reduced cost as the amount that the objective coefficient of the
variable would have to improve before it would become profitable to give the variable in question a
positive value in the optimal solution. For example, if a variable had a reduced cost of 10, the objective
coefficient of that variable would have to increase by 10 units in a maximization problem and/or
decrease by 10 units in a minimization problem for the variable to become an attractive alternative to
enter into the solution. A variable in the optimal solution, as in the case of STANDARD or TURBO,
automatically has a reduced cost of zero.
Second, the reduced cost of a variable may be interpreted as the amount of penalty you would have to
pay to introduce one unit of that variable into the solution. Again, if you have a variable with a reduced
cost of 10, you would have to pay a penalty of 10 units to introduce the variable into the solution. In
other words, the objective value would fall by 10 units in a maximization model or increase by 10
units in a minimization model.
Reduced costs are valid only over a range of values for the variable in questions. For more information
on determining the valid range of a reduced cost, see the LINGO|Range command in Chapter 5,
Windows Commands.
Slack or Surplus
The Slack or Surplus column in a LINGO solution report tells you how close you are to satisfying a
constraint as an equality. This quantity, on less-than-or-equal-to (≤) constraints, is generally referred to
as slack. On greater-than-or-equal-to (≥) constraints, this quantity is called a surplus.

GETTING STARTED 25
If a constraint is exactly satisfied as an equality, the slack or surplus value will be zero. If a constraint
is violated, as in an infeasible solution, the slack or surplus value will be negative. Knowing this can
help you find the violated constraints in an infeasible model—a model for which there doesn't exist a
set of variable values that simultaneously satisfies all constraints. Nonbinding constraints, will have
positive, nonzero values in this column.
In our CompuQuick example, note that row 3 (TURBO <= 120) has a slack of 90. Because the optimal
value of TURBO is 30, this row is 90 units from being satisfied as an equality.
Dual Price
The LINGO solution report also gives a dual price figure for each constraint. You can interpret the
dual price as the amount that the objective would improve as the right-hand side, or constant term, of
the constraint is increased by one unit. For example, in the CompuQuick solution, the dual price of 75
on row 4 means adding one more unit of labor would cause the objective to improve by 75, to a value
of 14,575.
Notice that “improve” is a relative term. In a maximization problem, improve means the objective
value would increase. However, in a minimization problem, the objective value would decrease if you
were to increase the right-hand side of a constraint with a positive dual price.
Dual prices are sometimes called shadow prices, because they tell you how much you should be
willing to pay for additional units of a resource. Based on our analysis, CompuQuick should be willing
to pay up to 75 dollars for each additional unit of labor.
As with reduced costs, dual prices are valid only over a range of values. Refer to the LINGO|Range
command in Chapter 5, Windows Commands, for more information on determining the valid range of a
dual price.
Using the Modeling Language
One of LINGO’s most powerful features is its mathematical modeling language. LINGO’s modeling
language lets you express your problem in a natural manner that is very similar to standard
mathematical notation. Rather than entering each term of each constraint explicitly, you can express a
whole series of similar constraints in a single compact statement. This leads to models that are much
easier to maintain and scale up.
Another convenient feature of LINGO’s modeling language is the data section. The data section
allows you to isolate your model’s data from the formulation. In fact, LINGO can even read data from
a separate spreadsheet, database, or text file. With data independent of the model, it’s much easier to
make changes, and there’s less chance of error when you do.
26 CHAPTER 1
The simple CompuQuick model discussed above uses scalar variables. Each variable is explicitly listed
by name (e.g., STANDARD and TURBO) and each constraint is explicitly stated
(e.g., TURBO <=120). In larger models, you’ll encounter the need to work with a group of several
very similar constraints and variables. Using the scalar modeling approach we have illustrated to this
point, you would need to undertake the repetitive task of typing in each term of each constraint.
Fortunately, LINGO’s ability to handle sets of objects allows you to perform such operations much
more efficiently.
The section below is an example of how to use sets to solve a shipping problem. After reviewing this
example, it should become clear that coupling the power of sets with LINGO’s modeling language
allows you to build large models in a fraction of the time required in a scalar oriented approach to
modeling (See Chapter 2, Using Sets, for a detailed description of sets).
Developing a Set Based Transportation Model
The Problem
For our example, suppose that the Wireless Widget (WW) Company has six warehouses supplying
eight vendors with their widgets. Each warehouse has a supply of widgets that cannot be exceeded, and
each vendor has a demand for widgets that must be satisfied. WW wants to determine how many
widgets to ship from each warehouse to each vendor so as to minimize the total shipping cost. This is a
classic optimization problem referred to as the transportation problem.
The following diagram illustrates the problem:
Wireless Widget’s Shipping Network
Since each warehouse can ship to each vendor, there are a total of 48 possible shipping paths, or arcs.
We will need a variable for each arc to represent the amount shipped on the arc.
GETTING STARTED 27
The following data is available:
Warehouse Widgets On Hand
1 60
2 55
3 51
4 43
5 41
6 52
Widget Capacity Data
Vendor Widget Demand
1 35
2 37
3 22
4 32
5 41
6 32
7 43
8 38
Vendor Widget Demand
V1 V2 V3 V4 V5 V6 V7 V8
Wh1 6 2 6 7 4 2 5 9
Wh2 4 9 5 3 8 5 8 2
Wh3 5 2 1 9 7 4 3 3
Wh4 7 6 7 3 9 2 7 1
Wh5 2 3 9 5 7 2 6 5
Wh6 5 5 2 2 8 1 4 3
Shipping Cost per Widget ($)
The Objective Function
Our first pass at formulating the model will be to construct the objective function. As mentioned, WW
wants to minimize total shipping costs. We will let the VOLUME_I_J variable denote the number of
widgets shipped from warehouse I to vendor J. Then, if we were to explicitly write out our objective
function using scalar variables, we would have:
MIN = 6 * VOLUME_1_1 + 2 * VOLUME_1_2 +
6 * VOLUME_1_3 + 7 * VOLUME_1_4 +
4 * VOLUME_1_5 +
.
.
.
8 * VOLUME_6_5 + VOLUME_6_6 + 4 * VOLUME_6_7 +
3 * VOLUME_6_8;
28 CHAPTER 1
For brevity, we included only 9 of the 48 terms in the objective. As one can see, entering such a
lengthy formula would be tedious and prone to errors. Extrapolate to the more realistic case where
vendors could number in the thousands, and it becomes apparent that scalar based modeling is
problematic at best.
If you are familiar with mathematical notation, you could express this long equation in a much more
compact manner as follows:
Minimize
Σ
ij COSTij
•
VOLUMEij
In a similar manner, LINGO’s modeling language allows you to express the objective function in a
form that is short, easy to type, and easy to understand. The equivalent LINGO statement is:
MIN = @SUM(LINKS(I,J): COST(I,J) * VOLUME(I,J));
In words, this says to minimize the sum of the shipping COST per widget times the VOLUME of
widgets shipped for all LINKS between the warehouses and vendors. The following table compares the
mathematical notation to the LINGO syntax for our objective function:
Math Notation LINGO Syntax
Minimize MIN =
Σ
ij @SUM(LINKS(I, J):
COSTij COST(I, J)
•
*
VOLUMEij VOLUME(I,J));
The Constraints
With the objective function in place, the next step is to formulate the constraints. There are two sets of
constraints in this model. The first set guarantees that each vendor receives the number of widgets
required. We will refer to this first set of constraints as being the demand constraints. The second set of
constraints, called the capacity constraints, ensures no warehouse ships out more widgets than it has on
hand.
Starting with the demand constraint for Vendor 1, we need to sum up the shipments from all the
warehouses to Vendor 1 and set them equal to Vendor 1’s demand of 35 widgets. Thus, if we were
using scalar-based notation, we would need to construct the following:
VOLUME_1_1 + VOLUME_2_1 + VOLUME_3_1 +
VOLUME_4_1 + VOLUME_5_1 + VOLUME_6_1 = 35;
You would then need to type seven additional demand constraints, in a similar form, to cover all eight
vendors. Again, as one can see, this would be a tedious and error prone process. However, as with our
objective function, we can use LINGO’s set based modeling language to simplify our task.
Using mathematical notation, all eight demand constraints can be expressed in the single statement:
Σ
i VOLUMEij = DEMANDj , for all j in VENDORS

GETTING STARTED 29
The corresponding LINGO modeling statement appears as follows:
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I): VOLUME(I, J)) =
DEMAND(J));
This LINGO statement replaces all eight demand constraints. In words, this says for all VENDORS, the
sum of the VOLUME shipped from each of the WAREHOUSES to that vendor must equal the
corresponding DEMAND of the vendor. Notice how closely this statement resembles the mathematical
notation above as the following table shows:
Math Notation LINGO Syntax
For all j in VENDORS @FOR(VENDORS(J):
Σ
i @SUM(WAREHOUSES(I):
VOLUMEij VOLUME(I, J))
= =
DEMANDj DEMAND(J));
Now, we will move on to constructing the capacity constraints. In standard mathematical notation, the
six capacity constraints would be expressed as:
Σ
j VOLUMEij <= CAPi , for all i in WAREHOUSES
The equivalent LINGO statement for all capacity constraints would be:
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J))<=
CAPACITY(I));
In words, this says, for each member of the set WAREHOUSES, the sum of the VOLUME shipped to
each of the VENDORS from that warehouse must be less-than-or-equal-to the CAPACITY of the
warehouse.
Putting together everything we’ve done so far yields the following complete LINGO model:
MODEL:
MIN = @SUM(LINKS(I, J):
COST(I, J) * VOLUME(I, J));
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I): VOLUME(I, J)) =
DEMAND(J));
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J)) <=
CAPACITY(I));
END
Model: WIDGETS
However, we still need to define sets of objects used in the model (vendors, warehouses and shipping
arcs) as well as the data. We will do this in two additional model sections called the sets section and
the data section.
30 CHAPTER 1
Defining the Sets
Whenever you are modeling some situation in real life, you will typically find there are one or more
sets of related objects. Examples would be such things as factories, customers, vehicles, and
employees. Usually, if a constraint applies to one member of a set, then it will apply equally to each
other member of the set. This simple concept is at the core of the LINGO modeling language. LINGO
allows you to define the sets of related objects in the sets section. The sets section begins with the
keyword SETS: on a line by itself and ends with ENDSETS on a line by itself. Once your set members
are defined, LINGO has a group of set looping functions (e.g., @FOR), which apply operations to all
members of a set using a single statement. See Chapter 2, Using Sets for more information.
In the case of our Wireless Widget model, we have constructed the following three sets:
♦ warehouses,
♦ vendors, and
♦ shipping arcs from each warehouse to customer.
The three sets are defined in the model's sets section as follows:
SETS:
WAREHOUSES: CAPACITY;
VENDORS: DEMAND;
LINKS( WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
The second line says that the set WAREHOUSES has an attribute called CAPACITY. The following
line declares the vendor set and that it has an attribute called DEMAND.
The final set, titled LINKS, represents the links in the shipping network. Each link has a COST and a
VOLUME attribute associated with it. The syntax used to define this set differs from the previous two.
By specifying:
LINKS( WAREHOUSES, VENDORS)
we are telling LINGO that the LINKS set is derived from the WAREHOUSES and VENDORS sets. In
this case, LINGO generates each ordered (warehouse, vendor) pair. Each of these 48 ordered pairs
becomes a member in the LINKS set. To help clarify this, we list selected members from the LINKS set
in the following table.
Member Index Shipping Arc
1 WH1
V1
2 WH1
V2
3 WH1
V3
… …
47 WH6
V7
48 WH6
V8
A nice feature of LINGO is that it will automatically generate the members of the LINKS set based on
the members of the WAREHOUSES and VENDORS sets, thereby saving us considerable work.

GETTING STARTED 31
Inputting the Data
LINGO allows the user to isolate data within the data section of the model. In our Wireless Widget
example, we have the following data section:
DATA:
!set members;
WAREHOUSES = WH1 WH2 WH3 WH4 WH5 WH6;
VENDORS = V1 V2 V3 V4 V5 V6 V7 V8;
!attribute values;
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
The data section begins with the keyword DATA: on a line by itself and ends with ENDDATA on a line
by itself.
Next, we input the list of warehouses and vendors. Had we preferred, we could have also used the
following shorthand notation to the same end:
!set members;
WAREHOUSES = WH1..WH6;
VENDORS = V1..V8;
LINGO interprets the double-dots to mean that it should internally generate the six warehouses and
eight vendors.
Both the CAPACITY attribute of the set WAREHOUSES and DEMAND attribute of the set VENDORS
are initialized in a straightforward manner. The COST attribute of the two-dimensional set LINKS is a
little bit trickier, however. When LINGO is initializing a multidimensional array in a data section, it
increments the outer index the fastest. Thus, in this particular example, COST( WH1, V1) is initialized
first, followed by COST( WH1, V2) through COST (WH1, V8). Then, the next one to be initialized with
be COST(WH2, V1), and so on.
In this particular example, we have isolated all the model’s data within a single data section. Given
that the data is the most likely feature to change from one run of a model to the next, isolating data, as
we have done here, makes modifications considerably easier. Contrast this to how difficult it would be
to track down and change the data in a large, scalar model where data is spread throughout all the
constraints of the model.
In order to facilitate data management further, LINGO has the ability to import data from external
sources. More specifically, a LINGO model can import data from external text files, establish real-time
OLE links to Excel, and/or create ODBC links to databases.

32 CHAPTER 1
Putting together the data section, the sets section, the objective, and the constraints, the completed
model is as follows:
MODEL:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES: CAPACITY;
VENDORS: DEMAND;
LINKS( WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
! Here is the data;
DATA:
!set members;
WAREHOUSES = WH1 WH2 WH3 WH4 WH5 WH6;
VENDORS = V1 V2 V3 V4 V5 V6 V7 V8;
!attribute values;
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
! The objective;
MIN = @SUM( LINKS( I, J):
COST( I, J) * VOLUME( I, J));
! The demand constraints;
@FOR( VENDORS( J):
@SUM( WAREHOUSES( I): VOLUME( I, J)) =
DEMAND( J));
! The capacity constraints;
@FOR( WAREHOUSES( I):
@SUM( VENDORS( J): VOLUME( I, J)) <=
CAPACITY( I));
END
Model: WIDGETS
Note that we have again added comments to improve the readability of the model. The model
is named WIDGETS, and can be found in the SAMPLES subdirectory off the main LINGO
directory.
Solving the Model
Now, let’s solve the model to determine the optimal shipping volume for each warehouse to vendor
link. In LINGO for Windows, choose Solve from the LINGO menu or press the Solve button ( ). On
other platforms, enter the GO command at the command-line prompt. LINGO will respond by solving
the model and returning a somewhat lengthy solution report containing the values for all the variables,
constraints, and data in the model. Most of this information is not of immediate interest. What we
would really like to know is the amount of widgets being shipped from the warehouses to the vendors.
GETTING STARTED 33
Note: Anytime you find the amount of LINGO’s output overwhelming, you can choose Options…
from the LINGO menu, select the Interface tab, and set the Output Level option to Terse.
LINGO will then display only the solutions status, objective value and number of iterations in
the solution window. In non-Windows versions of LINGO, enter the SET TERSEO 1
command before giving the GO command.
To obtain a report containing only the nonzero values for VOLUME, we select the Solution command
from the LINGO menu. We are then presented with the following dialog box:
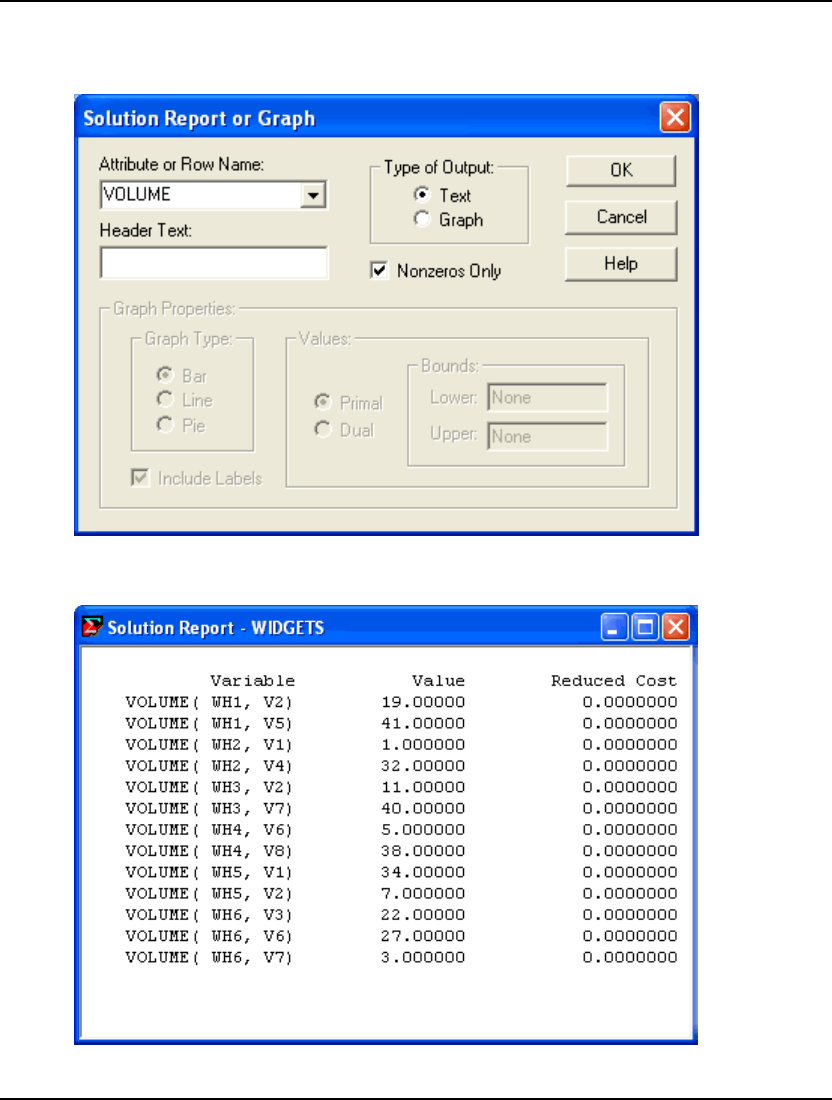
34 CHAPTER 1
Press down on the arrow button in the Attribute or Row Name field and select VOLUME from the list
of names in the drop-down box. To suppress the printing of variables with zero value, click on the
Nonzeros Only checkbox. Once you have done this, the dialog box should resemble:
Now, click the OK button and you will be presented with the following report that contains the
nonzero VOLUME variables:

GETTING STARTED 35
If you are running LINGO on a platform other than Windows, you can generate the same report by
issuing the NONZERO VOLUME command.
Summary
This section has begun to demonstrate the virtues of LINGO’s set based modeling language. By
moving to a set based approach to modeling, you will find that your models become easier to build,
easier to understand, and easier to maintain. Set based modeling takes a little more work to become
comfortable with, but the benefits should substantially outweigh the extra effort involved in the
learning process. We will delve further into the concepts of set based modeling in the following
chapter, Using Sets.
Additional Modeling Language Features
Constraint Names
LINGO gives you the ability to name the constraints in your model. This is a good practice for two
reasons. First, the constraint names are used in solution reports making them easier to interpret.
Secondly, many of LINGO’s error messages refer to a given constraint by name. If you don’t name
your constraints, tracking down the source of these errors may, at best, be difficult.
Note: LINGO does not require you to name your constraints. However, if you do not name your
constraints, LINGO defaults to using a name that corresponds to the internal index of the
constraint. This internal index may have little to do with the order in which you defined the
constraint, thus making the job of interpreting solution reports and error messages difficult.
Therefore, it is strongly recommended that you always use constraint names in your models.
Naming a constraint is quite simple. All you need do is insert a name in square brackets at the very
start of the constraint. The name must obey the standard requirements for a LINGO name. More
specifically, all names must begin with an alphabetic character (A-Z). Subsequent characters may be
either alphabetic, numeric (0-9), or the underscore (_). Names may be up to 64 characters in length.
Some examples of constraint names follow:
Example 1: [OBJECTIVE] MIN = X;
assigns the name OBJECTIVE to the model’s objective row,
Example 2: @FOR(LINKS(I, J): [DEMAND_ROW]
@SUM(SOURCES(I): SHIP(I, J)) >=
DEMAND(J));
assigns the name DEMAND_ROW to the demand constraints in a transportation model.

36 CHAPTER 1
To further illustrate the use of row names, we have updated the WIDGETS model from the previous
section to include constraint names (shown in bold):
MODEL:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES: CAPACITY;
VENDORS: DEMAND;
LINKS( WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
DATA:
!set members;
WAREHOUSES = WH1 WH2 WH3 WH4 WH5 WH6;
VENDORS = V1 V2 V3 V4 V5 V6 V7 V8;
!attribute values;
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
! The objective;
[OBJECTIVE] MIN = @SUM( LINKS( I, J):
COST( I, J) * VOLUME( I, J));
! The demand constraints;
@FOR( VENDORS( J): [DEMAND_ROW]
@SUM( WAREHOUSES( I): VOLUME( I, J)) =
DEMAND( J));
! The capacity constraints;
@FOR( WAREHOUSES( I): [CAPACITY_ROW]
@SUM( VENDORS( J): VOLUME( I, J)) <=
CAPACITY( I));
END
WIDGETS with Constraint Names
The row section of the solution report is now considerably easier to interpret:
Row Slack or Surplus Dual Price
OBJECTIVE 664.0000 1.000000
DEMAND_ROW(V1) 0.0000000 -4.000000
DEMAND_ROW(V2) 0.0000000 -5.000000
DEMAND_ROW(V3) 0.0000000 -4.000000
DEMAND_ROW(V4) 0.0000000 -3.000000
DEMAND_ROW(V5) 0.0000000 -7.000000
DEMAND_ROW(V6) 0.0000000 -3.000000
DEMAND_ROW(V7) 0.0000000 -6.000000
DEMAND_ROW(V8) 0.0000000 -2.000000
CAPACITY_ROW(WH1) 0.0000000 3.000000
CAPACITY_ROW(WH2) 22.00000 0.000000
CAPACITY_ROW(WH3) 0.0000000 3.000000
CAPACITY_ROW(WH4) 0.0000000 1.000000
CAPACITY_ROW(WH5) 0.0000000 2.000000
CAPACITY_ROW(WH6) 0.0000000 2.000000
Row Report for WIDGETS with Constraint Names

GETTING STARTED 37
Note that each row now has a name rather than a simple index number. Furthermore, if the constraint
is generated over a set using the @FOR function, LINGO qualifies the constraint name by appending
the corresponding set member name in parentheses.
Model Title
You can insert a title for a model anywhere you would normally enter a constraint. If a title is
included, it will be printed at the top of solution reports. The title is also used as a default argument in
the @ODBC function (see Chapter 10, Interfacing with Databases).
The model’s title must begin with the keyword TITLE and end with a semicolon. All text between
TITLE and the semicolon will be taken as the title of the model.
In the following, we have added a title to the beginning of the WIDGETS model:
MODEL:
TITLE Widgets;
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES: CAPACITY;
.
.
.
Excerpt from WIDGETS Model with a Title
Note that when we display the solution report, the title is now displayed along the top:
Model Title: Widgets
Variable Value Reduced Cost
CAPACITY( WH1) 60.00000 0.0000000
CAPACITY( WH2) 55.00000 0.0000000
CAPACITY( WH3) 51.00000 0.0000000
CAPACITY( WH4) 43.00000 0.0000000
.
.
.
Excerpt from Solution Report to WIDGETS Model with a Title
38 CHAPTER 1
Maximum Problem Dimensions
Some versions of LINGO limit one or more of the following model properties: total variables, integer
variables, nonlinear variables, global variables, and constraints. The total variable limit is on the total
number of optimizable variables in your model (i.e., variables LINGO was unable to determine as
being fixed at a particular value). The integer variable limit applies to the total number of optimizable
variables restricted to being integers with either the @BIN or @GIN functions. The nonlinear variable
limit applies to the number of optimizable variables that appear nonlinearly in the model’s constraints.
As an example, in the expression: X + Y, both X and Y appear linearly. However, in the expression:
X ^ 2 + Y, X appears nonlinearly while Y appears linearly. Thus, X would count against the nonlinear
variable limit. In some cases, nonlinear variables are allowed only if you have purchased the nonlinear
option for your LINGO software. The global variable limit applies to the total number of nonlinear
variables when using the global solver. The constraint limit refers to the number of formulas in the
model that contain one or more optimizable variables. Keep in mind that a single @FOR function may
generate many constraints.
The maximum sized problem your LINGO can handle depends on the version you have. The current
limits for the various versions are:
Version Total
Variables Integer
Variables Nonlinear
Variables Global
Variables
Constraints
Demo/Web 300 30 30 5 150
Solver Suite 500 50 50 5 250
Super 2,000 200 200 10 1,000
Hyper 8,000 800 800 20 4,000
Industrial 32,000 3,200 3,200 50 16,000
Extended Unlimited Unlimited Unlimited Unlimited Unlimited
You can also determine the limits of your version by selecting the About LINGO command from the
Help menu in Windows, or by typing HELP at the command-line prompt on other platforms. If you
determine you need a larger version of LINGO, upgrades are available from LINDO Systems. Please
feel free to contact us for pricing and availability.
Note 1: The limits of different LINGO versions are subject to change. Check our website,
http://www.lindo.com, for the most current sizes.
Note 2: In some versions of LINGO, the Nonlinear Variable limit will be 0 if you have not purchased
the nonlinear option for your copy of LINGO. Similarly, the global variable limit will be o if
the global solver option is not enabled.

GETTING STARTED 39
Note 3: LINGO has two other implicit limits not given by the table above—memory and time. Large
models may require more memory to solve than is available on your system, or they may
require more time to solve than one would normally be willing to wait. So, when building
large models, be aware that just because your model falls within LINGO’s limits there is no
guarantee it will be solvable in a reasonable amount of time on a particular machine.
How to Contact LINDO Systems
LINDO Systems can be reached at the following address and telephone numbers:
LINDO Systems, Inc.
1415 North Dayton Street
Chicago, IL 60642
Tel: 312-988-7422
Fax: 312-988-9065
e-mail: info@lindo.com
web: http://www.lindo.com
For sales and product information, please contact us at:
Tel: 1-800-441-2378 or 312-988-7422
e-mail: sales@lindo.com
For technical support, we prefer you send your model and questions by electronic mail to
tech@lindo.com. You may also speak to our technical support staff at 312-988-9421. Our technical
support staff can help you with questions regarding the installation and operation of LINGO. If you
have simple modeling questions, we can generally help get you pointed in the right direction. If you
have extensive modeling questions, we can recommend third party consultants well versed in the
specifics of LINGO and mathematical modeling in general, who can assist you in your modeling
efforts.

41
2 Using Sets
As we mentioned in the previous chapter, whenever you are modeling situations in real life there will
typically be one or more groups of related objects. Examples of such objects might include factories,
customers, vehicles, or employees. LINGO allows you to group these related objects together into sets.
Once the objects in your model are grouped into sets, you can make use of set based functions to
unleash the full power of the LINGO modeling language.
Having given you a brief introduction into the use of sets in Chapter 1, Getting Started with LINGO,
we will now go into greater depth as to how you construct sets and initialize set attributes with data.
This will then give us the ability to begin constructing some interesting and useful examples. Once
you’ve read this chapter, you should have a basic understanding of how to go about applying set based
modeling techniques to your own models.
Why Use Sets?
Sets are the foundation of LINGO’s modeling language—the fundamental building block of the
program’s most powerful capabilities. With an understanding of sets, you can write a series of similar
constraints in a single statement and express long, complex formulas concisely. This allows you to
express your largest models very quickly and easily. In larger models, you’ll encounter the need to
express a group of several very similar calculations or constraints. Fortunately, LINGO’s ability to
handle sets of information allows you to perform such operations efficiently.
For example, preparing a warehouse-shipping model for 100 warehouses would be tedious if you had
to write each constraint explicitly (e.g., “Warehouse 1 must ship no more than its present inventory,
Warehouse 2 must ship no more than its present inventory, Warehouse 3 must ship no more than its
present inventory…”, and so on). LINGO allows you to express formulas in the form easiest for you to
read and understand (e.g., “Each warehouse must ship no more than its present inventory”).
What Are Sets?
Sets are simply groups of related objects. A set might be a list of products, trucks, or employees. Each
member in the set may have one or more characteristics associated with it. We call these
characteristics attributes. Attribute values can be known in advance or unknowns that LINGO solves
for. For example, each product in a set of products might have a price attribute; each truck in a set of
trucks might have a hauling capacity attribute; and each employee in a set of employees might have a
salary attribute, as well as a birth date attribute.

42 CHAPTER 2
Types of Sets
LINGO recognizes two kinds of sets: primitive and derived.
A primitive set is a set composed only of objects that can’t be further reduced. In the Wireless Widgets
example (page 26), the WAREHOUSES set, which is composed of six warehouses, is a primitive set.
Likewise, the set composed of eight vendors is a primitive set.
A derived set is defined using one or more other sets. In other words, a derived set derives its members
from other preexisting sets. Again, using the Wireless Widgets example, the set composed of the links
between the six warehouses and eight vendors (LINKS) is a derived set. It derives its members from
the unique pairs of members of the WAREHOUSES and VENDORS sets. Although the LINKS set is
derived solely from primitive sets, it is also possible to build derived sets from other derived sets as
well. See the section below, Defining Derived Sets, for more information.
The Sets Section of a Model
Sets are defined in an optional section of a LINGO model called the sets section. Before you use sets
in a LINGO model, you have to define them in the sets section of the model. The sets section begins
with the keyword SETS: (including the colon), and ends with the keyword ENDSETS. A model may
have no sets section, a single sets section, or multiple sets sections. A sets section may appear
anywhere in a model. The only restriction is you must define a set and its attributes before they are
referenced in the model’s constraints.
Defining Primitive Sets
To define a primitive set in a sets section, you specify:
♦ the name of the set,
♦ optionally, its members (objects contained in the set), and
♦ optionally, any attributes the members of the set may have.
A primitive set definition has the following syntax:
setname [/ member_list /] [: attribute_list];
Note: The use of square brackets indicates an item is optional. In this particular case, a primitive
set’s attribute_list and member_list are both optional.
The setname is a name you choose to designate the set. It should be a descriptive name that is easy to
remember. The set name must conform to standard LINGO naming conventions. In other words, the
name must begin with an alphabetic character, which may be followed by up to 31 alphanumeric
characters or the underscore (_). LINGO does not distinguish between upper and lowercase characters
in names.
A member_list is a list of the members that constitute the set. If the set members are included in the set
definition, they may be listed either explicitly or implicitly. If set members are not included in the set
USING SETS 43
definition, then they may be defined subsequently in a data section of the model. For details on
defining set members in a data section, refer to Introduction to the Data Section.
When listing members explicitly, you enter a unique name for each member, optionally separated by
commas. As with set names, member names must also conform to standard naming conventions. In the
Wireless Widgets model, we could have used an explicit member list to define the set WAREHOUSES
in the sets section as follows:
WAREHOUSES / WH1 WH2 WH3 WH4 WH5 WH6/: CAPACITY;
When using implicit set member lists, you do not have to list a name for each set member. Use the
following syntax when using an implicit set member list:
setname / member1..memberN / [: attribute_list];
where member1 is the name of the first member in the set and memberN is the name of the last
member. LINGO automatically generates all the intermediate member names between member1 and
memberN. While this can be a very compact and convenient method for building a primitive set, there
is one catch in that only certain formats of names are accepted for the initial and terminal member
names. The following table details the available options:
Implicit Member List
Format Example Set Members
1..n 1..5 1, 2, 3, 4, 5
stringM..stringN TRUCKS3..TRUCKS204 TRUCKS3, TRUCKS4, …,
TRUCKS204
dayM..dayN MON..FRI MON, TUE, WED, THU,
FRI
monthM..monthN OCT..JAN OCT, NOV, DEC, JAN
monthYearM..monthYearN OCT2001..JAN2002 OCT2001, NOV2001,
DEC2001, JAN2002
When using the 1..n format, n may be any positive integer value, and the initial member must always
be a 1.
The stringM..stringN format allows you to use any string to start both the initial and terminal member
names as long as the string conforms to standard LINGO naming conventions. M and N must be
nonnegative and integer, such that M ≤ N.
The dayM..dayN format allows you to choose the initial and terminal member names for the names of
the days of the week. All names are abbreviated to three characters. Thus, the available options are:
Mon, Tue, Wed, Thu, Fri, Sat, and Sun.
The monthM..monthN format allows you to select from the months of the year, where all names are
abbreviated to three characters. The available options are: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep,
Oct, Nov, and Dec.
The monthYearM..monthYearN option allows you to specify a month and a four digit year.
As further illustration, in the Wireless Widgets example, we could have also defined the
WAREHOUSES set as:
WAREHOUSES / 1..6/: CAPACITY;

44 CHAPTER 2
As an alternative, when using this 1..n form of implicit definition, you may also place the length of the
set in a data section, and then reference this length in a subsequent sets section as we do here:
DATA:
NUMBER_OF_WH = 6;
ENDDATA
SETS:
WAREHOUSES / 1..NUMBER_OF_WH/: CAPACITY;
ENDSETS
Set members may have one or more attributes specified in the attribute_list of the set definition. An
attribute is simply some property each member of the set displays. For instance, in the WAREHOUSES
set above, there is a single attribute titled CAPACITY, which is used to represent the shipping capacity
of the WAREHOUSES. Attribute names must follow standard naming conventions and be separated by
commas.
For illustration, suppose our warehouses had additional attributes related to their location and the
number of loading docks. These additional attributes could be added to the attribute list of the set
declaration as follows:
WAREHOUSES / 1..6/: CAPACITY, LOCATION, DOCKS;
In addition to listing a primitive set's members in a model's sets section, primitive set members may
also be listed in a model's data section. Some users may prefer this alternative approach in that a set's
members are actually input data for the model. Therefore, listing set members in a model's data
section, along with all other data, is a more natural approach that makes a model more readable. All
the various techniques listed above for enumerating a primitive set's members are also valid in a data
section. Some examples of defining primitive set members in a data section follow:
SETS:
WAREHOUSES: CAPACITY;
ENDSETS
DATA:
WAREHOUSES = WH1 WH2 WH3 WH4 WH5 WH6;
ENDDATA
Example 1: Listing a Primitive Set in a Data Section
SETS:
WAREHOUSES: CAPACITY;
ENDSETS
DATA:
NUMBER_OF_WH = 6;
WAREHOUSES = 1..NUMBER_OF_WH;
ENDDATA
Example 2: Listing a Primitive Set in a Data Section
USING SETS 45
Defining Derived Sets
To define a derived set, you specify:
♦ the name of the set,
♦ its parent sets,
♦ optionally, its members, and
♦ optionally, any attributes the set members may have.
A derived set definition has the following syntax:
setname(parent_set_list) [ / member_list /] [: attribute_list];
The setname is a standard LINGO name you choose to name the set.
The parent_set_list is a list of previously defined sets, separated by commas. Without specifying a
member_list element, LINGO constructs all combinations of members from each parent set to create
the members of the new derived set. As an example, consider the following sets section:
SETS:
PRODUCT / A B/;
MACHINE / M N/;
WEEK / 1..2/;
ALLOWED(PRODUCT, MACHINE, WEEK);
ENDSETS
Sets PRODUCT, MACHINE, and WEEK are primitive sets, while ALLOWED is derived from parent
sets, PRODUCT, MACHINE, and WEEK. Taking all the combinations of members from the three
parent sets, we come up with the following members in the ALLOWED set:
Index Member
1 (A,M,1)
2 (A,M,2)
3 (A,N,1)
4 (A,N,2)
5 (B,M,1)
6 (B,M,2)
7 (B,N,1)
8 (B,N,2)
ALLOWED Set Membership
The member_list is optional, and is used when you want to limit the set to being some subset of the full
set of combinations derived from the parent sets. The member_list may alternatively be specified in a
model’s data section (for details on this see Introduction to the Data Section in Chapter 4, Data and
Init Sections).
If the member_list is omitted, the derived set will consist of all combinations of the members from the
parent sets. When a set does not have a member_list and, therefore, contains all possible combinations
of members, it is referred to as being a dense set. When a set includes a member_list that limits it to
being a subset of its dense form, we say the set is sparse.

46 CHAPTER 2
A derived set’s member_list may be constructed using either:
♦ an explicit member list, or
♦ a membership filter.
When using the explicit member list method to specify a derived set’s member_list, you must
explicitly list all the members you want to include in the set. Each listed member must be a member of
the dense set formed from all possible combinations of the parent sets. Returning to our small example
above, if we had used an explicit member list in the definition of the derived set, ALLOWED, as
follows:
ALLOWED(PRODUCT, MACHINE, WEEK)
/ A M 1, A N 2, B N 1/;
then ALLOWED would not have had the full complement of eight members. Instead, ALLOWED
would have consisted of the three member sparse set: (A,M,1), (A,N,2), and (B,N,1). Note that the
commas in the list of set members are optional and were added only for readability purposes.
If you have a large, sparse set, explicitly listing all members can become cumbersome. Fortunately, in
many sparse sets, the members all satisfy some condition that differentiates them from the
nonmembers. If you could just specify this condition, you could save yourself a lot of effort. This is
exactly how the membership filter method works. Using the membership filter method of defining a
derived set’s member_list involves specifying a logical condition that each potential set member must
satisfy for inclusion in the final set. You can look at the logical condition as a filter to keep out
potential members that don’t satisfy some criteria.
As an example of a membership filter, suppose you have already defined a set called TRUCKS, and
each truck has an attribute called CAPACITY. You would like to derive a subset from TRUCKS that
contains only those trucks capable of hauling big loads. You could use an explicit member list, and
explicitly enter each truck that can carry heavy loads. However, why do all that work when you could
use a membership filter as follows:
HEAVY_DUTY(TRUCKS)|CAPACITY(&1) #GT# 50000:
We have named the set HEAVY_DUTY and have derived it from the parent set, TRUCKS. The vertical
bar character (|) is used to mark the beginning of a membership filter. The membership filter allows
only those trucks that have a hauling capacity (CAPACITY(&1)) greater than (#GT#) 50,000 into the
HEAVY_DUTY set. The &1 symbol in the filter is known as a set index placeholder. When building a
derived set that uses a membership filter, LINGO generates all the combinations of parent set
members. Each combination is then “plugged” into the membership condition to see if it passes the
test. The first primitive parent set’s member is plugged into &1, the second into &2, and so on. In this
example, we have only one parent set (TRUCKS), so &2 would not have made sense. The symbol
#GT# is a logical operator and means “greater than”.
The logical operators recognized by LINGO are:
#EQ# equal
#NE# not equal
#GE# greater-than-or-equal-to
#GT# greater than
#LT# less than
#LE# less-than-or-equal-to

USING SETS 47
In addition to listing a derived set's members in a model's sets section, derived set members may also
be listed in a model's data section. Some users may prefer this alternative approach in that a set's
members are actually input data for the model. Therefore, listing set members in a model's data
section, along with all other data, is a more natural approach that makes a model more readable. All
the various techniques listed above for enumerating a primitive set's members are also valid in a data
section, with the exception of the membership filter method. An example of defining derived set
members in a data section follow:
SETS:
PRODUCT;
MACHINE;
WEEK;
ALLOWED( PRODUCT, MACHINE, WEEK);
ENDSETS
DATA:
PRODUCT = P1..P3;
MACHINE = M1..M3;
WEEK = W1..W4;
ALLOWED =
P1 M1 W1
P2 M1 W3
P3 M1 W2
P3 M3 W4
;
ENDDATA
Inputting a Derived Set in a Data Section
Summary
In summary, keep in mind that LINGO recognizes two types of sets—primitive and derived.
Primitive sets are the fundamental objects in a model and can't be broken down into smaller
components. Primitive sets can be defined using either an explicit or implicit list. When using an
explicit list, you enter each member individually in the set member list. With an implicit list, you enter
the initial and terminal set members and LINGO generates all the intermediate members.
Derived sets, on the other hand, are created from other component sets. These component sets are
referred to as the parents of the derived set, and may be either primitive or derived. A derived set can
be either sparse or dense. Dense sets contain all combinations of the parent set members (sometimes
this is also referred to as the Cartesian product or cross of the parent sets). Sparse sets contain only a
subset of the cross of the parent sets, and may be defined by two methods⎯⎯explicit listing or
membership filter. The explicit listing method involves listing the members of the sparse set. The
membership filter method allows you to specify the sparse set members compactly through the use of a
logical condition that all members must satisfy. The relationships amongst the various set types are
illustrated in the graph below.Derived sets, on the other hand, are created from other component sets.
These component sets are referred to as the parents of the derived set, and may be either primitive or
derived. A derived set can be either sparse or dense. Dense sets contain all combinations of the parent
set members (sometimes this is also referred to as the Cartesian product or cross of the parent sets).
Sparse sets contain only a subset of the cross of the parent sets and may be defined by two
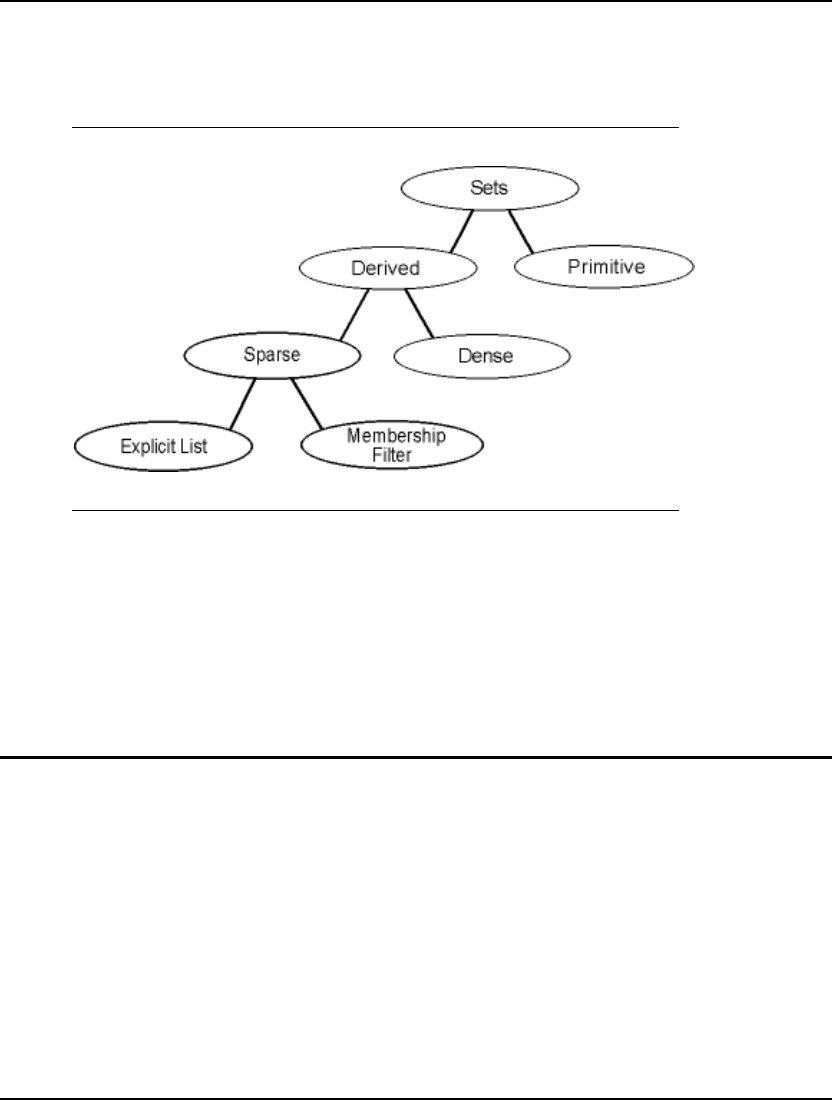
48 CHAPTER 2
methods⎯explicit listing or membership filter. The explicit listing method involves listing the
members of the sparse set. The membership filter method allows you to specify the sparse set members
compactly through the use of a logical condition all members must satisfy. The relationships amongst
the various set types are illustrated in the graph below:
LINGO Set Types
At this point, you are probably thinking that set definition is, at best, somewhat complicated. We will
be presenting you with plenty more examples in subsequent sections that should help to illustrate the
concepts introduced in this section, and demonstrate that set definition is nowhere near as difficult as it
may seem. For now, however, we will turn our attention to how data is input into a model. Then, we
will examine a group of functions that are designed to operate on set members. Once we have
accomplished this, we will be able to bring together all we have learned in order to begin building
some interesting and relevant examples of set based modeling.
The DATA Section
Typically, you will want to initialize the members of certain sets and assign values to certain set
attributes. For this purpose, LINGO uses a second optional section called the data section. The data
section allows you to isolate data from the equations of your model. This is a useful practice in that it
leads to easier model maintenance and facilitates scaling up a model to larger dimensions.
Similar to the sets section, the data section begins with the keyword DATA: (including the colon) and
ends with the keyword ENDDATA. In the data section, you can have statements to initialize the sets
and/or attributes you defined in a sets section. These expressions have the syntax:
object_list = value_list;
The object_list contains the names of a set and/or attributes you want to initialize, optionally separated
by commas. If there is more than one attribute name on in the object list, then all attributes must be

USING SETS 49
defined on the same set. Furthermore, if a set name appears in the object list, then it must be the parent
set of any attributes also in the object list. The value_list contains the values to assign to the objects in
the object list, optionally separated by commas. For example, consider the following model:
MODEL:
SETS:
SET1: X, Y;
ENDSETS
DATA:
SET1 = A B C;
X = 1 2 3;
Y = 4 5 6;
ENDDATA
END
We have two attributes, X and Y, defined on the set SET1. The three values of X are set to 1, 2, and 3,
while Y is set to 4, 5, and 6. We could have also used the following compound data statement to the
same end:
MODEL:
SETS:
SET1: X, Y;
ENDSETS
DATA:
SET1 X Y = A 1 4
B 2 5
C 3 6;
ENDDATA
END
An important fact to remember is that when LINGO reads a compound data statement's value list, it
assigns the first n values in the list to the first position of each of the n objects in the object list, the
second n values to the second position of each of the n objects, and so on. In other words, LINGO is
expecting the input data in column format rather than row format, which mirrors the flat file approach
used in relational databases.
This section has served to give you a brief introduction into the use of the data section. In Data and
Init Sections, you will learn more about the capabilities of the data section. You will learn data does
not have to actually reside in the data section as shown in examples here. In fact, your data section can
have OLE links to Excel, ODBC links to databases, and connections to text based data files.
Set Looping Functions
We have mentioned the power of set based modeling comes from the ability to apply an operation to
all members of a set using a single statement. The functions in LINGO that allow you to do this are
called set looping functions. If your models don’t make use of one or more set looping function, then
you are missing out on the power of set based modeling and, even worse, you’re probably working too
hard!

50 CHAPTER 2
Set looping functions allow you to iterate through all the members of a set to perform some operation.
There are currently four set looping functions in LINGO. The names of the functions and their uses
are:
Function Use
@FOR The most powerful of the set looping
functions, @FOR is used to generate
constraints over members of a set.
@SUM Probably the most frequently used set
looping function, @SUM computes the sum
of an expression over all members of a set.
@MIN Computes the minimum of an expression
over all members of a set.
@MAX Computes the maximum of an expression
over all members of a set.
@PROD Computes the product of an expression over
all members of a set.
The syntax for a set looping function is:
@function(setname [ (set_index_list) [|conditional_qualifier]] : expression_list);
where @function corresponds to one of the four set looping functions listed in the table above. setname
is the name of the set you want to loop over.
set_index_list is optional. It is used to create a list of indices. Each index corresponds to one of the
parent, primitive sets that form the set specified by setname. As LINGO loops through the members of
the set setname, it will set the values of the indices in the set_index_list to correspond to the current
member of the set setname.
The conditional_qualifier is optional, and may be used to limit the scope of the set looping function.
When LINGO is looping over each member of setname, it evaluates the conditional_qualifier. If the
conditional_qualifier evaluates to true, then the @function is performed for the set member.
Otherwise, it is skipped.
The expression_list is a list of expressions that are to be applied to each member of the set setname.
When using the @FOR function, the expression list may contain multiple expressions, separated by
semicolons. These expressions will be added as constraints to the model. When using the remaining set
looping functions (@SUM, @MAX, @MIN and @PROD), the expression list must contain one
expression only. If the set_index_list is omitted, all attributes referenced in the expression_list must be
defined on the set setname.
The following examples should help to illustrate the use of set looping functions.
@SUM Set Looping Function
In this example, we will construct several summation expressions using the @SUM function in order
to illustrate the features of set looping functions in general, and the @SUM function in particular.

USING SETS 51
Consider the model:
MODEL:
SETS:
VENDORS: DEMAND;
ENDSETS
DATA:
VENDORS, DEMAND = V1,5 V2,1 V3,3 V4,4 V5,6;
ENDDATA
END
Each vendor of the VENDORS set has a corresponding DEMAND. We could sum up the values of the
DEMAND attribute by adding the following expression after the ENDDATA statement:
TOTAL_DEMAND = @SUM(VENDORS(J): DEMAND(J));
LINGO evaluates the @SUM function by first initializing an internal accumulator to zero. LINGO then
begins looping over the members in the VENDORS set. The set index variable, J, is set to the first
member of VENDORS (i.e., V1) and DEMAND (V1) is then added to the accumulator. This process
continues until all DEMAND values have been added to the accumulator. The value of the sum is then
stored in the TOTAL_DEMAND variable.
Since all the attributes in our expression list (in this case, only DEMAND appears in the expression
list) are defined on the index set (VENDORS), we could have alternatively written our sum as:
TOTAL_DEMAND = @SUM(VENDORS: DEMAND);
In this case, we have dropped the superfluous index set list and the index on DEMAND. When an
expression uses this shorthand, we say the index list is implied. Implied index lists are not allowed
when attributes in the expression list have different parent sets.
Next, suppose we want to sum the first three elements of the attribute DEMAND. We can use a
conditional qualifier on the set index to accomplish this as follows:
DEMAND_3 = @SUM(VENDORS(J)|J #LE# 3: DEMAND(J));
The #LE# symbol is called a logical operator (see p. 339 for more details). This operator compares the
operand on the left (J) with the one on the right (3), and returns true if the left operand is
less-than-or-equal-to the one on the right. Otherwise, it returns false. Therefore, when LINGO
computes the sum this time, it plugs the set index variable, J, into the conditional qualifier J #LE# 3. If
the conditional qualifier evaluates to true, DEMAND(J) will be added to the sum. The end result is
LINGO sums up the first three terms in DEMAND, omitting the fourth and fifth terms, for a total sum
of 9.
Note: Before leaving this example, one subtle aspect to note in this last sum expression is the value
that the set index J is returning. Note, we are comparing the set index variable to the quantity
3 in the conditional qualifier J #LE# 3. In order for this to be meaningful, J must represent a
numeric value. Because a set index is used to loop over set members, one might imagine a set
index is merely a placeholder for the current set member. In a sense, this is true, but what set
indices really return is the index of the current set member in its parent primitive set. The
index returned is one-based. In other words, the value 1 is returned when indexing the first set
member, 2 when indexing the second, and so on. Given that set indices return a numeric
value, they may be used in arithmetic expressions along with other variables in your model.

52 CHAPTER 2
@MIN and @MAX Set Looping Functions
The @MIN and @MAX functions are used to find the minimum and maximum of an expression over
members of a set.
Again, consider the model:
MODEL:
SETS:
VENDORS: DEMAND;
ENDSETS
DATA:
VENDORS, DEMAND = V1,5 V2,1 V3,3 V4,4 V5,6;
ENDDATA
END
To find the minimum and maximum DEMAND, all one need do is add the two expressions:
MIN_DEMAND = @MIN( VENDORS( J): DEMAND( J));
MAX_DEMAND = @MAX( VENDORS( J): DEMAND( J));
The resulting model with the new statements in bold would then be as follows:
MODEL:
SETS:
VENDORS: DEMAND;
ENDSETS
DATA:
VENDORS, DEMAND = V1,5 V2,1 V3,3 V4,4 V5,6;
ENDDATA
MIN_DEMAND = @MIN( VENDORS( J): DEMAND( J));
MAX_DEMAND = @MAX( VENDORS( J): DEMAND( J));
END
As with the @SUM example, we can use an implied index list since the attributes are defined on the
index set. Using implied indexing, we can recast our expressions as:
MIN_DEMAND = @MIN( VENDORS: DEMAND);
MAX_DEMAND = @MAX( VENDORS: DEMAND);
In either case, when we solve this model, LINGO returns the expected minimum and maximum
DEMAND of:
Variable Value
MIN_DEMAND 1.000000
MAX_DEMAND 6.000000
For illustration purposes, suppose we had just wanted to compute the minimum and maximum values
of the first three elements of DEMAND. As with the @SUM example, all we need do is add the
conditional qualifier J #LE# 3. We then have:
MIN_DEMAND3 =
@MIN( VENDORS( J) | J #LE# 3: DEMAND( J));
MAX_DEMAND3 =
@MAX( VENDORS( J) | J #LE# 3: DEMAND( J));

USING SETS 53
with solution:
Variable Value
MIN_DEMAND3 1.000000
MAX_DEMAND3 5.000000
@FOR Set Looping Function
The @FOR function is used to generate constraints across members of a set. Whereas scalar based
modeling languages require you to explicitly enter each constraint, the @FOR function allows you to
enter a constraint just once, and LINGO does the work of generating an occurrence of the constraint
for each set member. Thus, the @FOR statement provides the set based modeler with a very powerful
tool.
To illustrate the use of @FOR, consider the following set definition:
SETS:
TRUCKS / MAC, PETERBILT, FORD, DODGE/: HAUL;
ENDSETS
Specifically, we have a primitive set of four trucks with a single HAUL attribute. If HAUL is used to
denote the amount a truck hauls, then we can use the @FOR function to limit the amount hauled by
each truck to 2,500 pounds with the following expression:
@FOR(TRUCKS(T): HAUL(T) <= 2500);
In this case, it might be instructive to view the constraints LINGO generates from our expression. You
can do this by using the LINGO|Generate|Display model command under Windows, or by using the
GENERATE command on other platforms. Running this command, we find LINGO generates the
following four constraints:
HAUL(MAC) <= 2500
HAUL(PETERBILT) <= 2500
HAUL(FORD) <= 2500
HAUL(DODGE) <= 2500
In other words, as we anticipated, LINGO generated one constraint for each truck in the set limiting it
to a load of 2,500 pounds.
Here is a model that uses an @FOR statement (listed in bold) to compute the reciprocal of any five
numbers placed into the VALUE attribute:
MODEL:
SETS:
NUMBERS /1..5/: VALUE, RECIPROCAL;
ENDSETS
DATA:
VALUE = 3 4 2 7 10;
ENDDATA
@FOR( NUMBERS( I):
RECIPROCAL( I) = 1 / VALUE( I)
);
END

54 CHAPTER 2
Solving this model gives the following values for the reciprocals:
Variable Value
RECIPROCAL(1) 0.3333333
RECIPROCAL(2) 0.2500000
RECIPROCAL(3) 0.5000000
RECIPROCAL(4) 0.1428571
RECIPROCAL(5) 0.1000000
Since the reciprocal of zero is not defined, we could put a conditional qualifier on our @FOR
statement that causes us to skip the reciprocal computation whenever a zero is encountered. The
following @FOR statement accomplishes this:
@FOR(NUMBERS(I)| VALUE(I) #NE# 0:
RECIPROCAL(I) = 1 / VALUE(I)
);
The conditional qualifier (listed in bold) tests to determine if the value is not equal (#NE#) to zero. If
so, the computation proceeds.
This was just a brief introduction to the use of the @FOR statement. There will be many additional
examples in the sections to follow.
@PROD Set Looping Function
The @PROD function is used to find the product of an expression across members of a set. As an
example, consider the model:
MODEL:
SETS:
COMPONENTS: P;
ENDSETS
DATA:
P = .95 .99 .98;
ENDDATA
P_FAIL = 1 - @PROD( COMPONENTS( I): P( I));
END
Here we have a system of three components arranged in a series. The probability that each component
functions successfully (.95, .99, and .98) is loaded into attribute P in the model’s data section. We
then compute the probability that the entire system will fail, P_FAIL, by taking the product of the
component probabilities and subtracting it from 1:
P_FAIL = 1 - @PROD( COMPONENTS( I): P( I));
As an aside, an interesting feature to note about this model is that we never initialized the
COMPONENTS set. When LINGO sees that an attribute of an undefined primitive set being
initialized to n values in a data section, it automatically initializes the parent primitive set to contain
the members: 1, 2, …, n. So, in this example, LINGO automatically assigned the member 1, 2 and 3 to
the COMPONENTS set.

USING SETS 55
Nested Set Looping Functions
The simple models shown in the last section use @FOR to loop over a single set. In larger models,
you’ll encounter the need to loop over a set within another set looping function. When one set looping
function is used within the scope of another, we call it nesting.
An example of a nested set looping function can be found in the Wireless Widgets shipping model
(p.26). If you remember, WW’s vendors had a demand for widgets that had to be met. The LINGO
statement that enforces this condition is:
! The demand constraints;
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I): VOLUME(I, J)) =
DEMAND(J));
Specifically, for each vendor, we sum up the shipments going from all the warehouses to that vendor
and set the quantity equal to the vendor’s demand. In this case, we have nested an @SUM function
within an @FOR function.
@SUM, @MAX, and @MIN can be nested within any set looping function. @FOR functions, on the
other hand, may only be nested within other @FOR functions.
Summary
This section demonstrated that set looping functions can be very powerful and can simplify the
modeler's task. If you aren't making use of sets and set looping functions, you will have a considerably
more difficult time building your models. Furthermore, the difficulty will grow dramatically as the
sizes of your models grow.
We now know how to create sets, how to initialize sets and attributes using the data section, and how
to work with sets using set looping functions. At this point, we now have the ability to start
constructing some meaningful example models.
Set Based Modeling Examples
Recall from the earlier discussion in this chapter, there are four types of sets that can be created in
LINGO. These set types are:
1. primitive,
2. dense derived,
3. sparse derived - explicit list, and
4. sparse derived - membership filter.
If you would like to review the four set types, refer to the sections What are Sets? and The Sets Section
of a Model at the beginning of this chapter. The remainder of this section will help develop your
talents for set based modeling by building and discussing four models, each introducing one of the set
types listed above.
56 CHAPTER 2
Primitive Set Example
The following staff scheduling model illustrates the use of a primitive set. In a staff scheduling model,
there is demand for staffing over a time horizon. The goal is to come up with a work schedule that
meets staffing demands at minimal cost.
The model used in this example may be found in the SAMPLES subdirectory off the main LINGO
directory under the name STAFFDEM.
The Staff Scheduling Problem
Suppose you run the popular Pluto Dogs hot dog stand that is open seven days a week. You hire
employees to work a five-day workweek with two consecutive days off. Each employee receives the
same weekly salary. Some days of the week are busier than others and, based on past experience, you
know how many workers are required on a given day of the week. In particular, your forecast calls for
these staffing requirements:
Day Mon Tue Wed Thu Fri Sat Sun
Staff Req'd 20 16 13 16 19 14 12
You need to determine how many employees to start on each day of the week in order to minimize the
total number of employees, while still meeting or exceeding staffing requirements each day of the
week.
The Formulation
The first question to consider when building a set based model is, "What are the relevant sets and their
attributes?". In this model, we have a single primitive set, the days of the week. If we call this set
DAYS, we can begin by writing our sets section as:
SETS:
DAYS;
ENDSETS
Next, we can add a data section to initialize the set members of the DAYS set:
SETS:
DAYS;
ENDSETS
DATA:
DAYS = MON TUE WED THU FRI SAT SUN;
ENDDATA
Alternatively, we could use LINGO’s implicit set definition capability and express this equivalently as:
SETS:
DAYS;
ENDSETS
DATA:
DAYS = MON..SUN;
ENDDATA

USING SETS 57
We will be concerned with two attributes of the DAYS set. The first is the number of staff required on
each day, and the second is the number of staff to start on each day. If we call these attributes
REQUIRED and START, then we may add them to the sets section to get:
SETS:
DAYS: REQUIRED, START;
ENDSETS
After defining the sets and attributes, it is useful to determine which of the attributes are data, and
which are decision variables. In this model, the REQUIRED attribute is given to us and is, therefore,
data. The START attribute is something we need to determine and constitutes the decision variables.
Once you've identified the data in the model, you may go ahead and initialize it. We can do this by
extending the data section as follows:
DATA:
DAYS = MON TUE WED THU FRI SAT SUN;
REQUIRED = 20 16 13 16 19 14 12;
ENDDATA
We are now at the point where we can begin entering the model's mathematical relations (i.e., the
objective and constraints). Let's begin by writing out the mathematical notation for the objective. Our
objective is to minimize the total number of employees we start during the week. Using standard
mathematical notation, this objective may be expressed as:
Minimize:
∑
i STARTi
The equivalent LINGO statement is very similar. Substitute "MIN=" for "Minimize:" and "@SUM(
DAYS( I):" for ∑i and we have:
MIN = @SUM( DAYS( I): START( I));
Now, all that is left is to come up with our constraints. There is only one set of constraints in this
model. Namely, we must have enough staff on duty each day to meet or exceed staffing requirements.
In words, what we want is:
Staff on duty today
≥
Staff required today, for each day of the week
The right-hand side of this expression, Staff required today, is easy to calculate. It is simply the
quantity REQUIRED( I). The left-hand side, Staff on duty today, is a bit trickier to compute. Given that
all employees are on a "five day on, two day off" schedule, the number of employees working today is:
Number working today = Number starting today +
Number starting 1 day ago + Number starting 2 days ago +
Number starting 3 days ago + Number starting 4 days ago.
In other words, to compute the number of employees working today, we sum up the number of people
starting today plus those starting over the previous four days. The number of employees starting five
and six days back don't count because they are on their days off. So, using mathematical notation, what
one might consider doing is adding the constraint:
∑
i = j-4, j STARTi
≥
REQUIRED j , for j
∈
DAYS
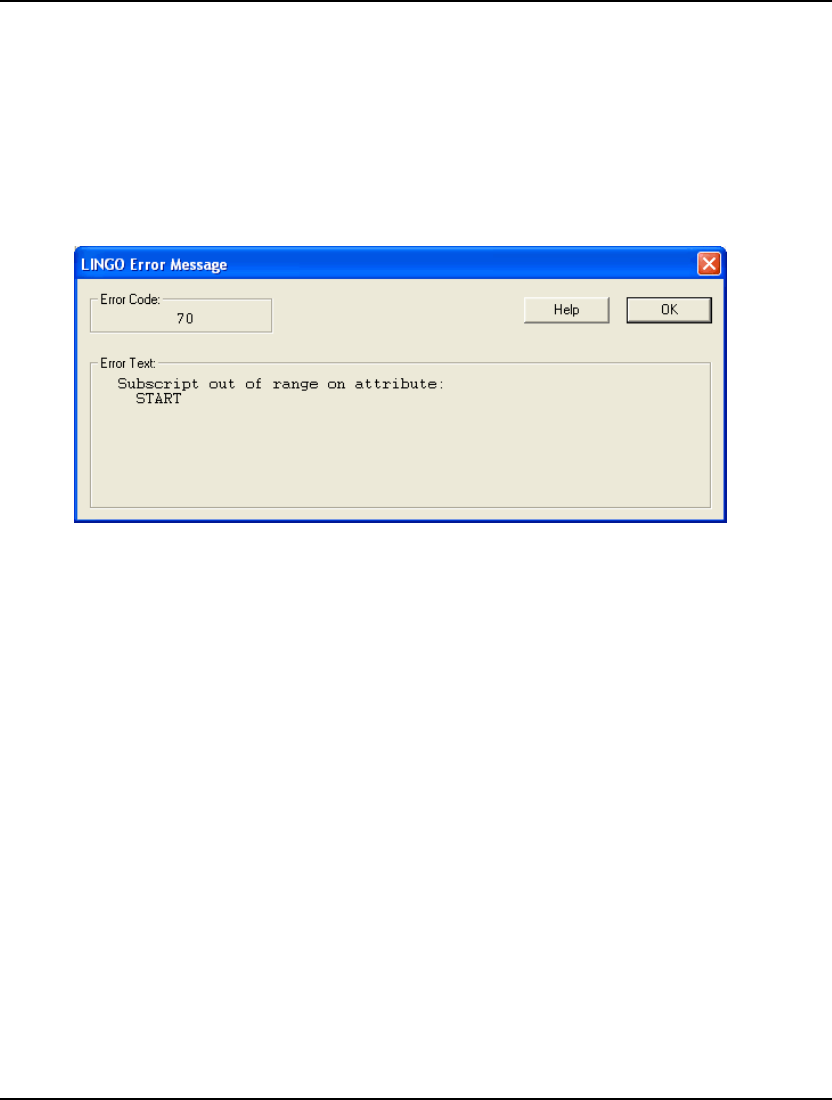
58 CHAPTER 2
Translating into LINGO notation, we can write this as:
@FOR( DAYS( J):
@SUM( DAYS( I) | I #LE# 5: START( J - I + 1))
>= REQUIRED( J)
);
In words, the LINGO statement says, for each day of the week, the sum of the employees starting over
the five day period beginning four days ago and ending today must be greater-than-or-equal-to the
required number of staff for the day. This sounds correct, but there is a slight problem. If we try to
solve our model with this constraint we get the error message:
To see why we get this error message, consider what happens on Thursday. Thursday has an index of 4
in our set DAYS. As written, the staffing constraint for Thursday will be:
START( 4 - 1 + 1) + START( 4 - 2 + 1) +
START( 4 - 3 + 1) + START( 4 - 4 + 1) +
START( 4 - 5 + 1) >= REQUIRED( 4);
Simplifying, we get:
START( 4) + START( 3) +
START( 2) + START( 1) +
START( 0) >= REQUIRED( 4);
The START( 0) term is the root of our problem. START is defined for days 1 through 7. START( 0) does
not exist. An index of 0 on START is considered "out of range.”
We would like to have any indices less-than-or-equal-to 0 wrap around to the end of the week.
Specifically, 0 would correspond to Sunday (7), -1 to Saturday (6), and so on. LINGO has a function
that does just this: @WRAP.
The @WRAP function takes two arguments⎯call them INDEX and LIMIT. Formally speaking,
@WRAP returns J such that J = INDEX - K * LIMIT, where K is an integer such that J is in the interval
[1, LIMIT]. Informally speaking, @WRAP will subtract or add LIMIT to INDEX until it falls in the
range 1 to LIMIT. Therefore, this is just what we need to "wrap around" an index in multiperiod
planning models.

USING SETS 59
Incorporating the @WRAP function, we get the corrected, final version of our staffing constraint:
@FOR( DAYS( J):
@SUM( DAYS( I) | I #LE# 5:
START( @WRAP( J - I + 1, 7)))
>= REQUIRED( J)
);
The Solution
Below is our staffing model in its entirety:
MODEL:
SETS:
DAYS: REQUIRED, START;
ENDSETS
DATA:
DAYS = MON TUE WED THU FRI SAT SUN;
REQUIRED = 20 16 13 16 19 14 12;
ENDDATA
MIN = @SUM( DAYS( I): START( I));
@FOR( DAYS( J):
@SUM( DAYS( I) | I #LE# 5:
START( @WRAP( J - I + 1, 7)))
>= REQUIRED( J)
);
END
Model: STAFFDEM

60 CHAPTER 2
Solving the model, we get the solution report:
Global optimal solution found.
Objective value: 22.00000
Infeasibilities: 0.000000
Total solver iterations: 5
Variable Value Reduced Cost
REQUIRED( MON) 20.00000 0.000000
REQUIRED( TUE) 16.00000 0.000000
REQUIRED( WED) 13.00000 0.000000
REQUIRED( THU) 16.00000 0.000000
REQUIRED( FRI) 19.00000 0.000000
REQUIRED( SAT) 14.00000 0.000000
REQUIRED( SUN) 12.00000 0.000000
START( MON) 8.000000 0.000000
START( TUE) 2.000000 0.000000
START( WED) 0.000000 0.000000
START( THU) 6.000000 0.000000
START( FRI) 3.000000 0.000000
START( SAT) 3.000000 0.000000
START( SUN) 0.000000 0.3333333
Row Slack or Surplus Dual Price
1 22.00000 -1.000000
2 0.000000 -0.3333333
3 0.000000 0.000000
4 0.000000 -0.3333333
5 0.000000 0.000000
6 0.000000 -0.3333333
7 0.000000 -0.3333333
8 0.000000 0.000000
Solution to STAFFDEM
The objective value of 22 means we need to hire 22 workers.
We start our workers according to the schedule:
Day Mon Tue Wed Thu Fri Sat Sun
Start 8 2 0 6 3 3 0
If we look at the surpluses on our staffing requirement rows (rows 2 - 7), we see that the slack values
are 0 on all of the days. This means there are no more workers than required and we just meet staffing
requirements on every day. Even though this is a small model, trying to come up with a solution this
efficient "by hand" would be a difficult task.
USING SETS 61
Dense Derived Set Example
The following model illustrates, among other things, the use of a dense derived set in a blending
model. In a blending model, one is blending raw materials into a finished product that must meet
minimal quality requirements on one or more dimensions. The goal is to come up with a blend of the
raw materials to satisfy the quality requirements at minimal cost.
This model may be found in the SAMPLES subdirectory off the main LINGO directory under the name
CHESS.
The Problem
The Chess Snackfoods Co. markets four brands of mixed nuts. The four brands of nuts are called the
Pawn, Knight, Bishop, and King. Each brand contains a specified ratio of peanuts and cashews. The
table below lists the number of ounces of the two nuts contained in each pound of each brand and the
price the company receives per pound of each brand:
Pawn Knight Bishop King
Peanuts (oz.) 15 10 6 2
Cashews (oz.) 1 6 10 14
Selling Price ($) 2 3 4 5
Chess has contracts with suppliers to receive 750 pounds of peanuts/day and 250 pounds of
cashews/day. Our problem is to determine the number of pounds of each brand to produce each day to
maximize total revenue without exceeding the available supply of nuts.
The Formulation
The primitive sets in this model are the nut types and the brands of mixed nuts. We can add them to the
sets section as follows:
SETS:
NUTS / PEANUTS, CASHEWS/: SUPPLY;
BRANDS / PAWN, KNIGHT, BISHOP, KING/:
PRICE, PRODUCE;
ENDSETS
The NUTS set has the single SUPPLY attribute, which we will use to store the daily supply of nuts in
pounds. The BRANDS set has PRICE and PRODUCE attributes, where PRICE stores the selling price
of the brands and PRODUCE represents the decision variables of how many pounds of each brand to
produce per day.
We need one more set, which is the dense derived set we have been promising. In order to input the
brand formulas, we will need a two dimensional table defined on the nut types and the brands. To do
this, we will generate a derived set from the cross of the NUTS and BRANDS sets. Adding this derived
set, we get the completed sets section:
SETS:
NUTS / PEANUTS, CASHEWS/: SUPPLY;
BRANDS / PAWN, KNIGHT, BISHOP, KING/:
PRICE, PRODUCE;
FORMULA(NUTS, BRANDS): OUNCES;
ENDSETS

62 CHAPTER 2
We have titled the derived set FORMULA. It has the single OUNCES attribute, which will be used to
store the ounces of nuts used per pound of each brand. Since we have not specified the members of this
derived set, LINGO assumes we want the complete, dense set that includes all pairs of nuts and brands.
Now that our sets are defined, we can move on to building the data section. We initialize SUPPLY,
PRICE, and OUNCES in the data section as follows:
DATA:
SUPPLY = 750 250;
PRICE = 2 3 4 5;
OUNCES = 15 10 6 2
1 6 10 14;
ENDDATA
With the sets and data established, we can begin to enter our objective function and constraints. The
objective function of maximizing total revenue is straightforward. We can express this as:
MAX = @SUM(BRANDS(I):
PRICE(I) * PRODUCE(I));
Our model has only one class of constraints. Namely, we can’t use more nuts than we are supplied
with on a daily basis. In words, we would like to ensure that:
For each nut i, the number of pounds of nut i used must be less-than-or-equal-to the
supply of nut i.
We can express this in LINGO as:
@FOR(NUTS(I):
@SUM(BRANDS(J):
OUNCES(I, J) * PRODUCE(J) / 16) <=
SUPPLY(I)
);
We divide the sum on the left-hand side by 16 to convert from ounces to pounds.

USING SETS 63
The Solution
Our completed blending model is:
SETS:
NUTS / PEANUTS, CASHEWS/: SUPPLY;
BRANDS / PAWN, KNIGHT, BISHOP, KING/:
PRICE, PRODUCE;
FORMULA(NUTS, BRANDS): OUNCES;
ENDSETS
DATA:
SUPPLY = 750 250;
PRICE = 2 3 4 5;
OUNCES= 15 10 6 2
1 6 10 14;
ENDDATA
MAX = @SUM(BRANDS(I):
PRICE(I) * PRODUCE(I));
@FOR(NUTS(I):
@SUM(BRANDS(J):
OUNCES(I, J) * PRODUCE(J) / 16) <=
SUPPLY(I)
);
Model: CHESS

64 CHAPTER 2
An abbreviated solution report to the model follows.
Global optimal solution found.
Objective value: 2692.308
Infeasibilities: 0.000000
Total solver iterations: 2
Variable Value Reduced Cost
SUPPLY( PEANUTS) 750.0000 0.000000
SUPPLY( CASHEWS) 250.0000 0.000000
PRICE( PAWN) 2.000000 0.000000
PRICE( KNIGHT) 3.000000 0.000000
PRICE( BISHOP) 4.000000 0.000000
PRICE( KING) 5.000000 0.000000
PRODUCE( PAWN) 769.2308 0.000000
PRODUCE( KNIGHT) 0.000000 0.1538462
PRODUCE( BISHOP) 0.000000 0.7692308E-01
PRODUCE( KING) 230.7692 0.000000
OUNCES( PEANUTS, PAWN) 15.00000 0.000000
OUNCES( PEANUTS, KNIGHT) 10.00000 0.000000
OUNCES( PEANUTS, BISHOP) 6.000000 0.000000
OUNCES( PEANUTS, KING) 2.000000 0.000000
OUNCES( CASHEWS, PAWN) 1.000000 0.000000
OUNCES( CASHEWS, KNIGHT) 6.000000 0.000000
OUNCES( CASHEWS, BISHOP) 10.00000 0.000000
OUNCES( CASHEWS, KING) 14.00000 0.000000
Row Slack or Surplus Dual Price
1 2692.308 1.000000
2 0.000000 1.769231
3 0.000000 5.461538
Solution to CHESS
This solution tells us that Chess should produce 769.2 pounds of the Pawn mix and 230.8 of the King
for total revenue of $2,692.30. Additional interesting information can also be found in the report. The
dual prices on the rows indicate Chess should be willing to pay up to $1.77 for an extra pound of
peanuts and $5.46 for an extra pound of cashews. If, for marketing reasons, Chess decides it must
produce at least some of the Knight and Bishop mixes, then the reduced cost figures tell us revenue
will erode by 15.4 cents with the first pound of Knight produced and 7.7 cents with the first pound of
Bishop produced.
Sparse Derived Set Example - Explicit List
In this example, we will introduce the use of a sparse derived set with an explicit listing. As you recall,
when we use this technique to define a sparse set, we must explicitly list all members belonging to the
set. This will usually be some small subset of the dense set resulting from the full Cartesian product of
the parent sets.
USING SETS 65
For our example, we will set up a PERT (Project Evaluation and Review Technique) model to
determine the critical path of tasks in a project involving the roll out of a new product. PERT is a
simple, but powerful, technique developed in the 1950s to assist managers in tracking the progress of
large projects. PERT is particularly useful in identifying the critical activities within a project, which,
if delayed, will delay the project as a whole. These time critical activities are referred to as the critical
path of a project. Having such insight into the dynamics of a project goes a long way in guaranteeing it
won’t get sidetracked and become delayed. In fact, PERT proved so successful, the Polaris project that
it was first used on was completed 18 months ahead of schedule. PERT continues to be used
successfully on a wide range of projects. For more information on PERT, and a related technique
called CPM (Critical Path Method), please refer to Schrage (2006) or Winston (1995).
The formulation for this model is included in the SAMPLES subdirectory off the main LINGO
directory under the name PERT.
The Problem
Wireless Widgets is about to launch a new product—the Solar Widget. In order to guarantee the
launch will occur on time, WW wants to perform a PERT analysis of the tasks leading up to the
launch. Doing so will allow them to identify the critical path of tasks that must be completed on time
in order to guarantee the Solar Widget’s timely introduction. The tasks that must be accomplished
before introduction and their anticipated times for completion are listed in the table below:
Task Weeks
Finalize Design 10
Forecast Demand 14
Survey Competition 3
Set Prices 3
Schedule Production Run 7
Cost Out 4
Train Salesmen 10
Certain tasks must be completed before others can commence. These precedence relations are shown
in the following graph:
Finalize
Design
Train
Salesman
Set
Prices
Survey
Competition
Cost Out
Schedule
Production Run
Forecast
Demand
Product Launch Precedence Relations
For instance, the two arrows originating from the Forecast Demand node indicate that the task must be
completed before the Schedule Production Run and the Set Prices tasks may be started.
Our goal is to construct a PERT model for the Solar Widget’s introduction in order to identify the tasks
on the critical path.

66 CHAPTER 2
The Formulation
We will need a primitive set to represent the tasks of the project. We can add such a set to the model
using the set definition:
TASKS / DESIGN, FORECAST, SURVEY, PRICE,
SCHEDULE, COSTOUT, TRAIN/: TIME, ES, LS, SLACK;
We have associated four attributes with the TASKS set. The definitions of the attributes are:
TIME Time to complete the task
ES Earliest possible start time for the task
LS Latest possible start time for the task
SLACK Difference between LS and ES for the task
The TIME attribute is given to us as data. We will compute the values of the remaining three attributes.
If a task has a 0 slack time, it means the task must start on time or the whole project will be delayed.
The collection of tasks with 0 slack time constitutes the critical path for the project.
In order to compute the start times for the tasks, we will need to examine the precedence relations.
Thus, we will need to input the precedence relations into the model. The precedence relations can be
viewed as a list of ordered pairs of tasks. For instance, the fact that the DESIGN task must be
completed before the FORECAST task could be represented as the ordered pair (DESIGN,
FORECAST). Creating a two-dimensional derived set on the TASKS set will allow us to input the list
of precedence relations. Specifically, we add the set definition:
PRED(TASKS, TASKS) /
DESIGN,FORECAST,
DESIGN,SURVEY,
FORECAST,PRICE,
FORECAST,SCHEDULE,
SURVEY,PRICE,
SCHEDULE,COSTOUT,
PRICE,TRAIN,
COSTOUT,TRAIN /;
Keep in mind that the first member of this set is the ordered pair (DESIGN, FORECAST)⎯not just the
single task DESIGN. Therefore, this set has a total of 8 members that all correspond to an arc in the
precedence relations diagram.
The set PRED is the sparse derived set with an explicit listing we want to highlight in this example.
The set is a subset derived from the cross of the TASKS set upon itself. The set is sparse because it
contains only 8 out of 49 possible members found in the complete cross of TASKS on TASKS. The set
is said to be an “explicit list” set, because we have explicitly listed the members we want included in
the set. Explicitly listing the members of a sparse set may not be convenient in cases where there are
thousands of members to select from, but it does make sense whenever set membership conditions are
not well defined and the sparse set size is small relative to the dense alternative.

USING SETS 67
Next, we can input the task times in the data section by including:
DATA:
TIME = 10, 14, 3, 3, 7, 4, 10;
ENDDATA
Now, with our sets and data established, we can turn our attention to building the formulas of the
model. We have three attributes to compute: earliest start (ES), latest start (LS), and slack time
(SLACK). The trick is computing ES and LS. Once we have these times, SLACK is merely the
difference of the two.
Let’s start by coming up with a formula to compute ES. A task cannot begin until all its predecessor
tasks are completed. Thus, if we find the latest finishing time of all predecessors to a task, then we
have also found its earliest start time. Therefore, in words, the earliest start time for task t is equal to
the maximum over all predecessors of task t of the sum of the earliest start time of the predecessor plus
its completion time. The corresponding LINGO notation is:
@FOR(TASKS(J)| J #GT# 1:
ES(J) = @MAX(PRED(I, J): ES(I) + TIME(I))
);
Note that we skip the computation for the first task by adding the conditional qualifier J #GT# 1. We
do this because the first task has no predecessors. We will give the first task an arbitrary start time as
shown below.
Computing LS is slightly trickier, but very similar to ES. In words, the latest time for task t to start is
the minimum over all successor tasks of the sum of the successor’s earliest start minus the time to
perform task t. If task t starts any later than this, it will prohibit at least one successor from starting at
its earliest start time. Converting into LINGO syntax gives:
@FOR(TASKS(I)| I #LT# LTASK:
LS(I) = @MIN(PRED(I, J): LS(J) - TIME(I))
);
Here, we omit the computation for the last task since it has no successor tasks.
Computing slack time is just the difference between LS and ES, and may be written as:
@FOR(TASKS(I): SLACK(I) = LS(I) - ES(I));
We can set the start time of the first task to some arbitrary value. For our purposes, we will set it to 0
with the statement:
ES(1) = 0;
We have now input formulas for computing the values of all the variables with the exception of the
latest start time for the last task. It turns out, if the last project were started any later than its earliest
start time, the entire project would be delayed. So, by definition, the latest start time for the last project
is equal to its earliest start time. We can express this in LINGO using the equation:
LS(7) = ES(7);

68 CHAPTER 2
This would work, but it’s probably not the best way to express the relation. Suppose you were to add
some tasks to your model. You’d have to change the 7 in this equation to the new number of tasks was.
The whole idea behind LINGO’s set based modeling language is the equations in the model should be
independent of the data. Expressing the equation in this form violates data independence. Here’s a
better way to do it:
LTASK = @SIZE(TASKS);
LS(LTASK) = ES(LTASK);
The @SIZE function returns the size of a set. In this case, it will return the value 7, as desired.
However, if we changed the number of tasks, @SIZE would also return the new, correct value. Thus,
we preserve the data independence of our model’s equations.
The Solution
The entire PERT formulation and portions of its solution appear below:
SETS:
TASKS / DESIGN, FORECAST, SURVEY, PRICE,
SCHEDULE, COSTOUT, TRAIN/: TIME, ES, LS, SLACK;
PRED(TASKS, TASKS) /
DESIGN,FORECAST,
DESIGN,SURVEY,
FORECAST,PRICE,
FORECAST,SCHEDULE,
SURVEY,PRICE,
SCHEDULE,COSTOUT,
PRICE,TRAIN,
COSTOUT,TRAIN /;
ENDSETS
DATA:
TIME = 10, 14, 3, 3, 7, 4, 10;
ENDDATA
@FOR(TASKS(J)| J #GT# 1:
ES(J) = @MAX(PRED(I, J): ES(I) + TIME(I))
);
@FOR(TASKS(I)| I #LT# LTASK:
LS(I) = @MIN(PRED(I, J): LS(J) - TIME(I));
);
@FOR(TASKS(I): SLACK(I) = LS(I) - ES(I));
ES(1) = 0;
LTASK = @SIZE(TASKS);
LS(LTASK) = ES(LTASK);
Model: PERT

USING SETS 69
Feasible solution found at step: 0
Variable Value
LTASK 7.000000
ES(DESIGN) 0.0000000
ES(FORECAST) 10.00000
ES(SURVEY) 10.00000
ES(PRICE) 24.00000
ES(SCHEDULE) 24.00000
ES(COSTOUT) 31.00000
ES(TRAIN) 35.00000
LS(DESIGN) 0.0000000
LS(FORECAST) 10.00000
LS(SURVEY) 29.00000
LS(PRICE) 32.00000
LS(SCHEDULE) 24.00000
LS(COSTOUT) 31.00000
LS(TRAIN) 35.00000
SLACK(DESIGN) 0.0000000
SLACK(FORECAST) 0.0000000
SLACK(SURVEY) 19.00000
SLACK(PRICE) 8.000000
SLACK(SCHEDULE) 0.0000000
SLACK(COSTOUT) 0.0000000
SLACK(TRAIN) 0.0000000
Solution to PERT
The interesting values are the slacks for the tasks. Both SURVEY and PRICE have slack in their start
times of 19 weeks and 8 weeks, respectively. Their start times may be delayed by as much as these
slack values without compromising the completion time of the entire project. The tasks DESIGN,
FORECAST, SCHEDULE, COSTOUT, and TRAIN, on the other hand, have 0 slack times. These tasks
constitute the critical path for the project and, if any of their start times are delayed, the entire project
will be delayed. Management will want to pay close attention to these critical path projects to be sure
they start on time and are completed within the allotted amount of time. Finally, the ES(TRAIN) value
of 35 tells us the estimated time to the start of the roll out of the new Solar Widget will be 45
weeks⎯35 weeks to get to the start of training, plus 10 weeks to complete training.
A Sparse Derived Set Using a Membership Filter
In this example, we introduce the use of a sparse derived set with a membership filter. Using a
membership filter is the third method for defining a derived set. When you define a set using this
method, you specify a logical condition each member of the set must satisfy. This condition is used to
filter out members that don’t satisfy the membership condition.
For our example, we will formulate a matching problem. In a matching problem, there are N objects
we want to match into pairs at minimum cost. The pair (I,J) is indistinguishable from the pair (J,I).
Therefore, we arbitrarily require I be less than J in the pair. Formally, we require I and J make a set of
ordered pairs. In other words, we do not wish to generate redundant ordered pairs of I and J, but only
those with I less than J. This requirement that I be less than J will form our membership filter.
The file containing this model may be found in the SAMPLES subdirectory off the main LINGO
directory under the name MATCHD.
70 CHAPTER 2
The Problem
Suppose you manage your company’s strategic planning department. You have a total of eight analysts
in the department. Furthermore, your department is about to move into a new suite of offices. There
are a total of four offices in the new suite and you need to match up your analysts into 4 pairs, so each
pair can be assigned to one of the new offices. Based on past observations, you know some of the
analysts work better together than they do with others. In the interest of departmental peace, you would
like to come up with a pairing of analysts that results in minimal potential conflicts. To this goal, you
have come up with a rating system for pairing your analysts. The scale runs from 1 to 10, with a 1
rating of a pair meaning the two get along fantastically. Whereas, a rating of 10 means all sharp objects
should be removed from the pair’s office in anticipation of mayhem. The ratings appear in the
following table:
Analysts 1 2 3 4 5 6 7 8
1 - 9 3 4 2 1 5 6
2 - - 1 7 3 5 2 1
3 - - - 4 4 2 9 2
4 - - - - 1 5 5 2
5 - - - - - 8 7 6
6 - - - - - - 2 3
7 - - - - - - - 4
Analysts’ Incompatibility Ratings
Since the pairing of analyst I with analyst J is indistinguishable from the pairing of J with I, we have
only included the above diagonal elements in the table. Our problem is to find the pairings of analysts
that minimizes the sum of the incompatibility ratings of the paired analysts.
The Formulation
The first set of interest in this problem is the set of eight analysts. This is a primitive set that can be
written simply as:
ANALYSTS / 1..8/;
The final set we want to construct is a set consisting of all the potential pairings. This will be a derived
set that we will build by taking the cross of the ANALYSTS set on itself. As a first pass, we could build
the dense derived set:
PAIRS(ANALYSTS, ANALYSTS);
This set, however, would include both PAIRS(I, J) and PAIRS(J, I). Since only one of these pairs is
required, the second is wasteful. Furthermore, this set will include “pairs” of the same analyst of the
form PAIRS(I, I). As much as each analyst might like an office of his or her own, such a solution is not
feasible. The solution is to put a membership filter on our derived set requiring each pair (I,J) in the
final set to obey the condition J be greater than I. We do this with the set definition:
PAIRS(ANALYSTS, ANALYSTS)|&2 #GT# &1;

USING SETS 71
The start of the membership filter is denoted with the vertical bar character (|). The &1 and &2
symbols in the filter are known as set index placeholders. Set index placeholders are valid only in
membership filters. When LINGO constructs the PAIRS set, it generates all combinations in the cross
of the ANALYSTS set on itself. Each combination is then “plugged” into the membership filter to see if
it passes the test. Specifically, for each pair (I,J) in the cross of the ANALYSTS set on itself, I is
substituted into the placeholder &1 and J into &2 and the filter is evaluated. If the filter evaluates to
true, (I,J) is added to the PAIRS set. Viewed in tabular form, this leaves us with just the above diagonal
elements of the (I,J) pairing table.
We will also be concerned with two attributes of the PAIRS set. First, we will need an attribute that
corresponds to the incompatibility rating of the pairings. Second, we will need an attribute to indicate
if analyst I is paired with analyst J. We will call these attributes RATING and MATCH. We append
them to the PAIRS set definition as follows:
PAIRS(ANALYSTS, ANALYSTS)|&2 #GT# &1:
RATING, MATCH;
We initialize the RATING attribute to the incompatibility ratings listed in the table above using the data
section:
DATA:
RATING =
9 3 4 2 1 5 6
1 7 3 5 2 1
4 4 2 9 2
1 5 5 2
8 7 6
2 3
4;
ENDDATA
We will use the convention of letting MATCH(I, J) be 1 if we pair analyst I with analyst J, otherwise 0.
Given this, the MATCH attribute contains the decision variables for the model.
Our objective is to minimize the sum of the incompatibility ratings of all the final pairings. This is just
the inner product on the RATING and MATCH attributes and is written as:
MIN = @SUM(PAIRS(I, J):
RATING(I, J) * MATCH(I, J));
There is just one class of constraints in the model. In words, it is:
For each analyst, ensure that the analyst is paired with exactly one other analyst.
Putting the constraint into LINGO syntax, we get:
@FOR(ANALYSTS(I):
@SUM(PAIRS(J, K)|J #EQ# I #OR# K #EQ# I:
MATCH(J, K)) = 1
);
The feature of interest in this constraint is the conditional qualifier (J #EQ# I #OR# K #EQ# I) on the
@SUM function. For each analyst I, we sum up all the MATCH variables that contain I and set them
equal to 1. In so doing, we guarantee analyst I will be paired up with exactly one other analyst. The
conditional qualifier guarantees we only sum up the MATCH variables that include I in its pairing.

72 CHAPTER 2
One other feature is required in this model. We are letting MATCH(I, J) be 1 if we are pairing I with J.
Otherwise, it will be 0. Unless specified otherwise, LINGO variables can assume any value from 0 to
infinity. Because we want MATCH to be restricted to being only 0 or 1, we need to apply the @BIN
variable domain function to the MATCH attribute. Variable domain functions are used to restrict the
values a variable can assume. Unlike constraints, variable domain functions do not add equations to a
model. The @BIN function restricts a variable to being binary (i.e., 0 or 1). When you have a model
that contains binary variables, it is said to be an integer programming (IP) model. IP models are much
more difficult to solve than models that contain only continuous variables. Carelessly formulated large
IPs (with several hundred integer variables or more) can literally take forever to solve! Thus, you
should limit the use of binary variables whenever possible. To apply @BIN to all the variables in the
MATCH attribute, add the @FOR expression:
@FOR(PAIRS(I, J): @BIN(MATCH(I, J)));
The Solution
The entire formulation for our matching example and parts of its solution appear below:
SETS:
ANALYSTS / 1..8/;
PAIRS(ANALYSTS, ANALYSTS)|&2 #GT# &1:
RATING, MATCH;
ENDSETS
DATA:
RATING =
9 3 4 2 1 5 6
1 7 3 5 2 1
4 4 2 9 2
1 5 5 2
8 7 6
2 3
4;
ENDDATA
MIN = @SUM(PAIRS(I, J):
RATING(I, J) * MATCH(I, J));
@FOR(ANALYSTS(I):
@SUM(PAIRS(J, K)|J #EQ# I #OR# K #EQ# I:
MATCH(J, K)) = 1
);
@FOR(PAIRS(I, J): @BIN(MATCH(I, J)));
Model: MATCHD

USING SETS 73
Global optimal solution found.
Objective value: 6.000000
Extended solver steps: 0
Total solver iterations: 0
Variable Value Reduced Cost
MATCH(1, 2) 0.0000000 9.000000
MATCH(1, 3) 0.0000000 3.000000
MATCH(1, 4) 0.0000000 4.000000
MATCH(1, 5) 0.0000000 2.000000
MATCH(1, 6) 1.000000 1.000000
MATCH(1, 7) 0.0000000 5.000000
MATCH(1, 8) 0.0000000 6.000000
MATCH(2, 3) 0.0000000 1.000000
MATCH(2, 4) 0.0000000 7.000000
MATCH(2, 5) 0.0000000 3.000000
MATCH(2, 6) 0.0000000 5.000000
MATCH(2, 7) 1.000000 2.000000
MATCH(2, 8) 0.0000000 1.000000
MATCH(3, 8) 1.000000 2.000000
MATCH(4, 5) 1.000000 1.000000
MATCH(4, 6) 0.0000000 5.000000
MATCH(4, 7) 0.0000000 5.000000
MATCH(4, 8) 0.0000000 2.000000
MATCH(5, 6) 0.0000000 8.000000
MATCH(5, 7) 0.0000000 7.000000
MATCH(5, 8) 0.0000000 6.000000
MATCH(6, 7) 0.0000000 2.000000
MATCH(6, 8) 0.0000000 3.000000
MATCH(7, 8) 0.0000000 4.000000
Solution to MATCHD
From the objective value, we know the total sum of the incompatibility ratings for the optimal pairings
is 6. Scanning the Value column for ones, we find the optimal pairings: (1,6), (2,7), (3,8), and (4,5).
Summary
In this chapter, we’ve discussed the concept of sets, how to declare sets, and demonstrated the power
and flexibility of set based modeling. You should now have a foundation of knowledge in the
definition and use of both primitive and derived sets. The next chapter will discuss the use of variable
domain functions, which were briefly introduced in this chapter when we used @BIN in the previous
matching model.

75
3 Using Variable Domain
Functions
Unless specified otherwise, variables in a LINGO model default to being non-negative and continuous.
More specifically, variables can assume any real value from zero to positive infinity. In many cases,
this default domain for a variable may be inappropriate. For instance, you may want a variable to
assume negative values, or you might want a variable restricted to purely integer values. LINGO
provides seven variable domain functions, which allow you to override the default domain of a
variable. The names of these functions and a brief description of their usage are:
@GIN restricts a variable to being an integer value,
@BIN makes a variable binary (i.e., 0 or 1),
@FREE allows a variable to assume any real value, positive or negative,
@BND limits a variable to fall within a finite range,
@SOS defines a set of binary variables and places restrictions on their collective
values,
@CARD defines a set of binary variables and places an upper limit on their sum, and
@SEMIC restricts variables to being either zero or grater than a specified constant.
In the remainder of this section, we'll investigate the mechanics of using these functions, and present a
number of examples illustrating their usage.
Integer Variables
LINGO gives the user the ability to define two types of integer variables⎯general and binary. A
general integer variable is required to be a whole number. A binary integer variable is further required
to be either zero or one. Any model containing one or more integer variables is referred to as an
integer programming (IP) model.
In many modeling projects, you will be faced with Yes/No types of decisions. Some examples would
include Produce/Don’t Produce, Open Plant/Close Plant, Supply Customer I from Plant J/Don’t
Supply Customer I from Plant J, and Incur a Fixed Cost/Don’t Incur a Fixed Cost. Binary variables are
the standard method used for modeling these Yes/No decisions.
General integer variables are useful where rounding of fractional solutions is problematic. For
instance, suppose you have a model that dictates producing 5,121,787.5 blue crayons in your crayon
factory. Whether you round the solution to 5,121,787 or 5,121,788 is inconsequential. On the other
hand, suppose your planning model for NASA determines the optimal number of space stations to
deploy is 1.5. Because building 0.5 space stations is impossible, you must very carefully consider how
to round the results. When whole numbers are required and rounding can make a significant
difference, general integer variables are appropriate.

76 CHAPTER 3
LINGO does not simply round or truncate values to come up with an integer answer. Rounding of a
solution will typically lead to either infeasible or suboptimal solutions. To illustrate this point, consider
the small model:
MAX = X;
X + Y = 25.5;
X <= Y;
By examining this model, one can deduce the optimal solution is X=Y=12.75. Now, suppose we want
an optimal solution with X being integer. Simply rounding X to 13 would make the model infeasible,
because there would be no value for Y that would satisfy both the constraints. Clearly, the optimal
solution is X=12 and Y=13.5. Unfortunately, “eyeballing” the optimal solution on larger models with
many integer variables is virtually impossible.
To solve these problems, LINGO performs a complex algorithm called branch-and-bound that
implicitly enumerates all combinations of the integer variables to determine the best feasible answer to
an IP model. Because of the extra computation time required by this algorithm, formulating your
problem to avoid the use of integer variables is advised whenever possible. Even so, although
computation times may grow dramatically when you add integer variables, it often makes sense to ask
LINGO for integer solutions when fractional values are of little or no use.
General Integer Variables
By default, LINGO assumes all variables in a model are continuous. In many applications, fractional
values may be undesirable. You won’t be able to hire two-thirds of a person, or sell half an
automobile. In these instances, you will want to make use of the general integer variable domain
function, @GIN.
The syntax of the @GIN function is:
@GIN(variable_name);
where variable_name is the name of the variable you wish to make general integer. The @GIN
function may be used in a model anywhere you would normally enter a constraint. The @GIN function
can be embedded in an @FOR statement to allow you to easily set all, or selected, variables of an
attribute to be general integers. Some examples of @GIN are:
Example 1: @GIN(X);
makes the scalar variable X general integer,
Example 2: @GIN(PRODUCE(5));
makes the variable PRODUCE(5) general integer,
Example 3: @FOR(DAYS(I): @GIN(START(I)));
makes all the variables of the START attribute general integer.

VARIABLE DOMAIN FUNCTIONS 77
General Integer Example - CompuQuick Product-Mix
To illustrate the use of @GIN in a full model, we will consider a variation on the CompuQuick
Corporation model in Chapter 1, Getting Started with LINGO. CompuQuick has successfully
rebalanced the Standard computer’s assembly line. In so doing, they are now able to build an
additional 3 Standard computers on the line each day, for a daily total of 103 computers. As a result,
the constraint on the Standard’s assembly line will now be:
STANDARD <= 103;
Incorporating this constraint into the original CompuQuick model, we have:
! Here is the total profit objective function;
MAX = 100 * STANDARD + 150 * TURBO;
! Constraints on the production line capacity;
STANDARD <= 103;
TURBO <= 120;
! Our labor supply is limited;
STANDARD + 2 * TURBO <= 160;
Solving this modified model, we get the solution:
Global optimal solution found.
Objective value: 14575.00
Infeasibilities: 0.000000
Total solver iterations: 0
Model Class: LP
Total variables: 2
Nonlinear variables: 0
Integer variables: 0
Total constraints: 4
Nonlinear constraints: 0
Total nonzeros: 6
Nonlinear nonzeros: 0
Variable Value Reduced Cost
STANDARD 103.0000 0.000000
TURBO 28.50000 0.000000
Row Slack or Surplus Dual Price
1 14575.00 1.000000
2 0.000000 25.00000
3 91.50000 0.000000
4 0.000000 75.00000

78 CHAPTER 3
Note the new optimal number of Turbo computers, 28.5, is no longer an integer quantity. CompuQuick
must produce whole numbers of computers each day. To guarantee this, we add @GIN statements to
make both the STANDARD and TURBO variables general integer. The revised model follows:
! Here is the total profit objective function;
MAX = 100 * STANDARD + 150 * TURBO;
! Constraints on the production line capacity;
STANDARD <= 103;
TURBO <= 120;
! Our labor supply is limited;
STANDARD + 2 * TURBO <= 160;
! Integer values only;
@GIN(STANDARD); @GIN(TURBO);
Solving the modified model results in the integer solution we were hoping for:
Global optimal solution found.
Objective value: 14550.00
Objective bound: 14550.00
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 0
Model Class: PILP
Total variables: 2
Nonlinear variables: 0
Integer variables: 2
Total constraints: 4
Nonlinear constraints: 0
Total nonzeros: 6
Nonlinear nonzeros: 0
Variable Value Reduced Cost
STANDARD 102.0000 -100.0000
TURBO 29.00000 -150.0000
Row Slack or Surplus Dual Price
1 14550.00 1.000000
2 1.000000 0.000000
3 91.00000 0.000000
4 0.000000 0.000000
Note that we now have a two new solution statistics: Extended solver steps and Objective bound.
For models with integer variables, such as this one, the extended solver steps statistic is a tally of the
number of times integer variables had to be forced to an integer value during the branch-and-bound
solution procedure. In general, this value is not of much practical use to the normal user, other than to
give you a notion of how hard LINGO is working at finding an integer solution. If the number of steps

VARIABLE DOMAIN FUNCTIONS 79
gets quite large, LINGO is having a hard time finding good integer solutions to your model. In this
case, given that the model is quite small, LINGO's preprocessor was able to find the optimal solution
without having to resort to the branch-and-bound solver.
The objective bound statistic gives us a bound on the best possible solution for the model. In other
words, there is no feasible solution to the model with an objective value better than the objective
bound statistic. Here we see that the bound and the objective value are both equal, which is further
evidence that we have a globally optimal solution. On larger models that take a while to run, you may
decide to interrupt LINGO before a global solution is found. In this case, the objective bound and the
objective value will probably not agree. In this case, the bound will let you know how far you are
from the true optimal solution. You may also find it useful to interrupt the solver once the bound and
objective value get close to one another, with the idea being that any further potential gains in the best
objective aren't worth the additional solve time.
Also of interest is the Model Class, which has changed from LP (Linear Program) to PILP (Pure
Integer Linear Program).
General Integer Example - Staff-Scheduling
Recalling the staff-scheduling example in Chapter 2, Using Sets, for the Pluto hot dog stand, you will
remember the solution told us how many employees to start on any given day of the week. You may
also remember the optimal solution had us starting whole numbers of employees on every day even
though we weren’t using integer variables. It turns out this was just a happy coincidence. Let’s return
to the staffing model to demonstrate this.

80 CHAPTER 3
In the original staffing model, we required the following number of people on duty for the seven days
of the week: 20, 16, 13, 16, 19, 14, and 12. Let’s change the second day requirement from 16 to 12 and
the third day’s requirement from 13 to 18. Incorporating this change into the model, we have:
MODEL:
SETS:
DAYS: REQUIRED, START;
ENDSETS
DATA:
DAYS = MON TUE WED THU FRI SAT SUN;
REQUIRED = 20 12 18 16 19 14 12;
ENDDATA
MIN = @SUM( DAYS( I): START( I));
@FOR( DAYS( J):
@SUM( DAYS( I) | I #LE# 5:
START( @WRAP( J - I + 1, 7)))
>= REQUIRED( J)
);
END
After making this modest change and re-solving, we no longer have a pure integer solution. In fact, all
the START variables are now fractional as the following, abbreviated solution report shows:
Global optimal solution found.
Objective value: 23.66667
Total solver iterations: 0
Variable Value Reduced Cost
START( MON) 9.666667 0.000000
START( TUE) 2.000000 0.000000
START( WED) 1.666667 0.000000
START( THU) 5.666667 0.000000
START( FRI) 0.000000 0.000000
START( SAT) 4.666667 0.000000
START( SUN) 0.000000 0.333333
In this particular model, we can always round the solution up and remain feasible. (In most models, we
won’t tend to be as lucky. Rounding the continuous solution in one direction or the other can lead to an
infeasible solution.) There may be some extra staff on some of the days, but, by rounding up, we will
never have a day without enough staff. Rounding the continuous solution up gives an objective of
10+2+2+6+5=25 employees.

VARIABLE DOMAIN FUNCTIONS 81
Now, let’s apply integer programming to the revised staffing model. First, we will need to use the
@GIN function to make the START variables general integers. We could do this by adding the
following to our model:
@GIN( START( MON));
@GIN( START( TUE));
@GIN( START( WED));
@GIN( START( THU));
@GIN( START( FRI));
@GIN( START( SAT));
@GIN( START( SUN));
However, an easier approach would be to embed the @GIN function in an @FOR function, so we can
apply @GIN to each member of START using the single statement:
@FOR( DAYS( I): @GIN( START( I)));
This new statement says, for each day of the week, make the variable corresponding to the number of
people to start on that day a general integer variable.
After inserting this @FOR statement at the end of our model and reoptimizing, we get the pure integer
solution:
Global optimal solution found.
Objective value: 24.00000
Extended solver steps: 0
Total solver iterations: 6
Variable Value Reduced Cost
START( MON) 10.00000 1.000000
START( TUE) 2.000000 1.000000
START( WED) 1.000000 1.000000
START( THU) 6.000000 1.000000
START( FRI) 0.000000 1.000000
START( SAT) 5.000000 1.000000
START( SUN) 0.000000 1.000000
Note that the objective of 24 beats the objective of 25 obtained by rounding. Thus, had we gone with
the rounded solution, we would have hired one more employee than required.

82 CHAPTER 3
Binary Integer Variables
A binary integer variable—also called a 0/1 variable—is a special case of an integer variable that is
required to be either zero or one. It’s often used as a switch to model Yes/No decisions.
The syntax of the @BIN function is:
@BIN( variable_name);
where variable_name is the name of the variable you wish to make binary. The @BIN function may be
used in a model anywhere you would normally enter a constraint. The @BIN function can be
embedded in an @FOR statement to allow you to easily set all, or selected, variables of an attribute to
be binary integers. Some examples of @BIN are:
Example 1: @BIN( X);
makes the scalar variable, X, a binary integer,
Example 2: @BIN( INCLUDE( 4));
makes the variable INCLUDE( 4) binary,
Example 3: @FOR( ITEMS: @BIN( INCLUDE));
makes all variables in the INCLUDE attribute binary.
Binary Integer Example - The Knapsack Problem
The knapsack model is a classic problem that uses binary variables. In this problem, you have a group
of items you want to pack into your knapsack. Unfortunately, the capacity of the knapsack is limited
such that it is impossible to include all items. Each item has a certain value, or utility, associated with
including it in the knapsack. The problem is to find the subset of items to include in the knapsack that
maximizes the total value of the load without exceeding the capacity of the knapsack.
Of course, the knapsack euphemism shouldn’t lead one to underestimate the importance of this class of
problem. The “knapsack” problem can be applied to many situations. Some examples are vehicle
loading, capital budgeting, and strategic planning.

VARIABLE DOMAIN FUNCTIONS 83
The Problem
As an example, suppose you are planning a picnic. You’ve constructed a list of items you would like to
carry with you on the picnic. Each item has a weight associated with it and your knapsack is limited to
carrying no more than 15 pounds. You have also come up with a 1 to 10 rating for each item, which
indicates how strongly you want to include the particular item in the knapsack for the picnic. This
information is listed below:
Item Weight Rating
Ant Repellent 1 2
Beer 3 9
Blanket 4 3
Bratwurst 3 8
Brownies 3 10
Frisbee 1 6
Salad 5 4
Watermelon 10 10
The Formulation
We have only one set in this model—the set of items we are considering carrying in the knapsack. This
is a primitive set, and we can define it in the sets section:
SETS:
ITEMS: INCLUDE, WEIGHT, RATING;
ENDSETS
We have associated the three attributes INCLUDE, WEIGHT, and RATING with the set. INCLUDE
will be the binary variables used to indicate if an item is to be included in the knapsack. WEIGHT is
used to store the weight of each item, and RATING is used to store each item's rating.
Next, we will need to construct a data section to input the set members of set ITEMS and their
associated weights and ratings. Here is a data section that accomplishes the task:
DATA:
ITEMS WEIGHT RATING =
ANT_REPEL 1 2
BEER 3 9
BLANKET 4 3
BRATWURST 3 8
BROWNIES 3 10
FRISBEE 1 6
SALAD 5 4
WATERMELON 10 10;
KNAPSACK_CAPACITY = 15;
ENDDATA
Note that we have also included the knapsack’s capacity in the data section. This is a good practice in
that it isolates data from the constraints of the model.

84 CHAPTER 3
Given that all the sets and data have been defined, we can turn to building our objective function. We
want to maximize the sum of the ratings of the items included in our knapsack. Note that INCLUDE(I)
will be 1 if item I is included. Otherwise, it will be 0. Therefore, if we take the inner product of
INCLUDE with the RATING attribute, we will get the overall rating of a combination of included
items. Putting this into LINGO syntax, we have:
MAX = @SUM( ITEMS: RATING * INCLUDE);
Note that we did not specify a set index variable in the @SUM function. Since all the attributes in the
function (RATING and INCLUDE) are defined on the index set (ITEMS), we can drop the set index
variable and use implicit indexing.
Our next step is to input our constraints. There is only one constraint in this model. Specifically, we
must not exceed the capacity of the knapsack. In a similar manner as the objective, we compute the
weight of a given combination of items by taking the inner product of the INCLUDE attribute with the
WEIGHT attribute. This sum must be less-than-or-equal-to the capacity of the knapsack. In LINGO
syntax, we express this as:
@SUM(ITEMS: WEIGHT * INCLUDE) <= KNAPSACK_CAPACITY;
Finally, we must make the INCLUDE variable binary. We could do this by adding:
@BIN( INCLUDE( @INDEX( ANT_REPEL)));
@BIN( INCLUDE( @INDEX( BEER)));
@BIN( INCLUDE( @INDEX( BLANKET)));
@BIN( INCLUDE( @INDEX( BRATWURST)));
@BIN( INCLUDE( @INDEX( BROWNIES)));
@BIN( INCLUDE( @INDEX( FRISBEE)));
@BIN( INCLUDE( @INDEX( SALAD)));
@BIN( INCLUDE( @INDEX( WATERMELON)));
(Note that the @INDEX function simply returns the index of a primitive set member in its set. )
However, a more efficient and data independent way of doing this would be to embed an @BIN
function in an @FOR function as follows:
@FOR( ITEMS: @BIN( INCLUDE));

VARIABLE DOMAIN FUNCTIONS 85
The Solution
The entire model for our knapsack example and excerpts from its solution are listed below. The model
formulation file may be found in your SAMPLES subdirectory off the main LINGO directory under the
name KNAPSACK:
MODEL:
SETS:
ITEMS: INCLUDE, WEIGHT, RATING;
ENDSETS
DATA:
ITEMS WEIGHT RATING =
ANT_REPEL 1 2
BEER 3 9
BLANKET 4 3
BRATWURST 3 8
BROWNIES 3 10
FRISBEE 1 6
SALAD 5 4
WATERMELON 10 10;
KNAPSACK_CAPACITY = 15;
ENDDATA
MAX = @SUM( ITEMS: RATING * INCLUDE);
@SUM( ITEMS: WEIGHT * INCLUDE) <=
KNAPSACK_CAPACITY;
@FOR( ITEMS: @BIN( INCLUDE));
END
Model: KNAPSACK

86 CHAPTER 3
Global optimal solution found.
Objective value: 38.00000
Objective bound: 38.00000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 0
Variable Value Reduced Cost
INCLUDE( ANT_REPEL) 1.000000 -2.000000
INCLUDE( BEER) 1.000000 -9.000000
INCLUDE( BLANKET) 1.000000 -3.000000
INCLUDE( BRATWURST) 1.000000 -8.000000
INCLUDE( BROWNIES) 1.000000 -10.00000
INCLUDE( FRISBEE) 1.000000 -6.000000
INCLUDE( SALAD) 0.000000 -4.000000
INCLUDE( WATERMELON) 0.000000 -10.00000
Solution to KNAPSACK
Your knapsack is fully packed at 15 pounds, and we take along everything, but the salad and
watermelon. Your lunch of beer, bratwurst and brownies may not be very healthy, but at least you will
be happy!
An Extension - Modeling a Logical Or Condition
Binary variables are very useful for modeling logical conditions. For instance, suppose your physician
reviews your picnic plans and, fearing for your health, insists you must take either the salad or the
watermelon along on your picnic. You could add this condition to your model by simply appending the
constraint:
INCLUDE( @INDEX( SALAD)) + INCLUDE( @INDEX( WATERMELON)) >= 1;
In order to satisfy this constraint, either the salad, the watermelon, or both must be included in the
knapsack. Unfortunately, constraints of this form are not good practice in that they are not data
independent. Suppose your list of picnic items changes. You may need to modify this new constraint to
reflect those changes. A well formulated model should require no changes to the constraints as a result
of changes to the data. The following model demonstrates a data independent way of incorporating
your physician’s request (additions to the original model are listed in bold):

VARIABLE DOMAIN FUNCTIONS 87
MODEL:
SETS:
ITEMS: INCLUDE, WEIGHT, RATING;
MUST_EAT_ONE( ITEMS);
ENDSETS
DATA:
ITEMS WEIGHT RATING =
ANT_REPEL 1 2
BEER 3 9
BLANKET 4 3
BRATWURST 3 8
BROWNIES 3 10
FRISBEE 1 6
SALAD 5 4
WATERMELON 10 10;
MUST_EAT_ONE = SALAD WATERMELON;
KNAPSACK_CAPACITY = 15;
ENDDATA
MAX = @SUM( ITEMS: RATING * INCLUDE);
@SUM( ITEMS: WEIGHT * INCLUDE) <=
KNAPSACK_CAPACITY;
@FOR( ITEMS: @BIN( INCLUDE));
@SUM( MUST_EAT_ONE( I): INCLUDE( I)) >= 1;
END
We have derived a set called MUST_EAT_ONE from the original picnic items, and used an explicit list
to include the items we must carry as members. Then, at the end of the model, we added a constraint
that forces at least one of the “must eat” items into the solution.
88 CHAPTER 3
For those interested, the solution to the modified model is:
Global optimal solution found.
Objective value: 37.00000
Objective bound: 37.00000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 0
Variable Value Reduced Cost
INCLUDE( ANT_REPEL) 0.000000 -2.000000
INCLUDE( BEER) 1.000000 -9.000000
INCLUDE( BLANKET) 0.000000 -3.000000
INCLUDE( BRATWURST) 1.000000 -8.000000
INCLUDE( BROWNIES) 1.000000 -10.00000
INCLUDE( FRISBEE) 1.000000 -6.000000
INCLUDE( SALAD) 1.000000 -4.000000
INCLUDE( WATERMELON) 0.000000 -10.00000
In short, we drop the ant repellent and blanket, and replace them with the salad.
Binary Integer Example – Product-Mix with Fixed Costs
In many situations, it is not unusual for a particular activity to incur a fixed cost. Examples where one
might incur a fixed cost include opening a plant, producing a product, paying a commission on an
order to buy stock, or retooling an assembly line.
In this next example, we will put together a product-mix model much like the CompuQuick example
from Chapter 1, Getting Started with LINGO. In this case, however, there is a fixed setup charge
associated with the production of an item. In other words, whenever we produce any amount of a
product, we incur a fixed charge independent of the output level of the product.
The Problem
You’re the manager of an airplane plant and you want to determine the best product-mix of your six
models to produce. The six models currently under production are the Rocket, Meteor, Streak, Comet,
Jet, and Biplane. Each plane has a known profit contribution. There is also a fixed cost associated with
the production of any plane in a period. The profit and fixed costs are given in the following table:
Plane Profit Setup
Rocket 30 35
Meteor 45 20
Streak 24 60
Comet 26 70
Jet 24 75
Biplane 30 30
VARIABLE DOMAIN FUNCTIONS 89
Each plane is produced using six raw materials—steel, copper, plastic, rubber, glass, and paint. The
units of these raw materials required by the planes as well as the total availability of the raw materials
are:
Rocket Meteor Streak Comet Jet Biplane Available
Steel 1 4 0 4 2 1 800
Copper 4 5 3 0 1 0 1160
Plastic 0 3 8 0 1 0 1780
Rubber 2 0 1 2 1 5 1050
Glass 2 4 2 2 2 4 1360
Paint 1 4 1 4 3 4 1240
The problem is to determine the final mix of products that maximizes net profit (gross profit - setup
costs) without exceeding the availability of any raw material. Your brand new Meteor model has the
highest profit per unit of anything you’ve ever manufactured and the lowest setup cost. Maybe you
should build nothing but Meteors? Then again, maybe not.
The Formulation
As you might guess, we will need two primitive sets in this model—one to represent the airplane
models and one to represent the raw materials. We can construct these sets as follows:
PLANES:
PROFIT, SETUP, QUANTITY, BUILD;
RESOURCES: AVAILABLE;
We added the following four attributes to the PLANES set:
♦ PROFIT stores profit contribution for the plane,
♦ SETUP stores setup cost to begin producing the plane,
♦ QUANTITY a variable for quantity of planes to produce, and
♦ BUILD a binary variable, 1 if we produce the plane, else 0.
The AVAILABLE attribute on the RESOURCES set will be used to store the availability of each
resource.
We will also need to derive a dense set by taking the cross of the RESOURCES set with the PLANES
set. We need this set in order to define a USAGE attribute to store the resource usage of each plane.
We will call this derived set RXP, which, after inclusion into the sets section, gives us:
SETS:
PLANES:
PROFIT, SETUP, QUANTITY, BUILD;
RESOURCES: AVAILABLE;
RXP( RESOURCES, PLANES): USAGE;
ENDSETS

90 CHAPTER 3
In our data section, we will initialize the set members: PLANES and RESOURCES, along with the data
attributes: PROFIT, SETUP, AVAILABLE, and USAGE. Here is the data section we will use:
DATA:
PLANES PROFIT SETUP =
ROCKET 30 35
METEOR 45 20
STREAK 24 60
COMET 26 70
JET 24 75
BIPLANE 30 30;
RESOURCES AVAILABLE =
STEEL,800 COPPER,1160 PLASTIC,1780
RUBBER,1050 GLASS,1360 PAINT,1240;
USAGE = 1 4 0 4 2 0
4 5 3 0 1 0
0 3 8 0 1 0
2 0 1 2 1 5
2 4 2 2 2 4
1 4 1 4 3 4;
ENDDATA
With the sets and data sections complete, we can now turn our attention to the objective function. For
our objective, we want to maximize total net profit. Specifically, this is computed as the sum of profit
times quantity produced of each plane, minus its setup cost multiplied by the BUILD binary variable.
In LINGO syntax, we express the objective as:
MAX = @SUM( PLANES:
PROFIT * QUANTITY - SETUP * BUILD);
Since all attributes are defined on the index set, we can drop the set index variable and use implicit
indexing.
For our first set of constraints, we want to be sure raw material supplies are not exceeded. In words,
what we want is:
For each resource i, the sum over each plane j of the quantity of plane j built
multiplied by the resource usage of resource i by plane j must be
less-than-or-equal-to the availability of resource i.

VARIABLE DOMAIN FUNCTIONS 91
Given the vagaries of the English language, it's highly likely one would find the equivalent LINGO
notation more concise and easier to understand:
@FOR( RESOURCES( I):
@SUM( PLANES( J):
USAGE( I, J) * QUANTITY( J)) <=
AVAILABLE( I)
);
Our next set of constraints is not quite as intuitive. We are using the binary variable BUILD to
represent if a plane is being built, so we can incorporate a fixed cost for the plane in the objective
function. What we need is some constraint mechanism to force BUILD( I) to be 1 when we produce a
nonzero quantity of plane I. The following constraint will do just that:
@FOR( PLANES:
QUANTITY <= 400 * BUILD;
@BIN( BUILD)
);
Given that BUILD is 0/1, as soon as QUANTITY goes nonzero the only feasible solution is for BUILD
to go to 1. Constraints of this form used to force a binary variable to an appropriate value are
sometimes referred to as forcing constraints.
The coefficient of 400 in our forcing constraints was chosen because we know from scanning our data
that no more than 400 of any plane can be built. Can you verify this? Coefficients used in this manner
are sometimes called BigM coefficients. For solver efficiency reasons, it's best to try to keep BigM
values as small as reasonably possible.
Because the BigM coefficient of 400 is dependent upon the model's data, it is actually bad modeling
practice to embed the coefficient in the model's constraints as we have done here. As we have
discussed, it is best to try to keep the constraints of your model independent of the data to facilitate
model maintenance. A more data independent formulation would actually involve calculations to come
up with a good BigM value. Can you think of how you might add such a feature to this model?
A reasonable question at this point would be: "We have the machinery to force BUILD to 1 when we
build a plane. What forces BUILD to zero when we don't build a plane?" The fact that BUILD appears
in the objective with a negative coefficient (we multiply it by SETUP and then subtract it from the
objective) guarantees this. If a plane was not being built and the corresponding BUILD variable was 1,
we could get a better solution by simply setting BUILD to 0. Since the goal is to maximize the
objective, BUILD will always be driven to 0 when a plane is not built.
One final feature of our forcing constraints to note is that we have piggybacked the @BIN function call
onto the @FOR statement for the forcing constraints. As you recall from the discussion of set looping
functions in Using Sets, an @FOR function may contain multiple expressions as long as they are
separated by a semicolon. We have capitalized on this feature by including the @BIN expression as
well.
As a final feature, we can make the QUANTITY variables general integers with the expression:
@FOR( PLANES: @GIN( QUANTITY));

92 CHAPTER 3
The Solution
The formulation in its entirety and a selected portion of the solution appear below. The formulation file
may be found in file PRODMIX.
MODEL:
SETS:
PLANES:
PROFIT, SETUP, QUANTITY, BUILD;
RESOURCES: AVAILABLE;
RXP( RESOURCES, PLANES): USAGE;
ENDSETS
DATA:
PLANES PROFIT SETUP =
ROCKET 30 35
METEOR 45 20
STREAK 24 60
COMET 26 70
JET 24 75
BIPLANE 30 30;
RESOURCES AVAILABLE =
STEEL,800 COPPER,1160 PLASTIC,1780
RUBBER,1050 GLASS,1360 PAINT,1240;
USAGE = 1 4 0 4 2 0
4 5 3 0 1 0
0 3 8 0 1 0
2 0 1 2 1 5
2 4 2 2 2 4
1 4 1 4 3 4;
ENDDATA
MAX = @SUM( PLANES:
PROFIT * QUANTITY - SETUP * BUILD);
@FOR( RESOURCES( I):
@SUM( PLANES( J):
USAGE( I, J) * QUANTITY( J)) <=
AVAILABLE( I);
);
@FOR( PLANES:
QUANTITY <= 400 * BUILD;
@BIN( BUILD);
);
@FOR( PLANES: @GIN( QUANTITY));
END
Model: PRODMIX

VARIABLE DOMAIN FUNCTIONS 93
Global optimal solution found.
Objective value: 14764.00
Objective bound: 14764.00
Infeasibilities: 0.000000
Extended solver steps: 7
Total solver iterations: 296
Variable Value Reduced Cost
QUANTITY( ROCKET) 96.00000 -30.00000
QUANTITY( METEOR) 0.000000 -45.00000
QUANTITY( STREAK) 195.0000 -24.00000
QUANTITY( COMET) 0.000000 -26.00000
QUANTITY( JET) 191.0000 -24.00000
QUANTITY( BIPLANE) 94.00000 -30.00000
BUILD( ROCKET) 1.000000 35.00000
BUILD( METEOR) 0.000000 20.00000
BUILD( STREAK) 1.000000 60.00000
BUILD( COMET) 0.000000 70.00000
BUILD( JET) 1.000000 75.00000
BUILD( BIPLANE) 1.000000 30.00000
Solution to PRODMIX
Surprisingly, we see from the solution that we build none of the "profitable" Meteors. Can you
determine why this is so? On the other hand, the Rocket, Streak, Jet and Biplane are produced, and, as
we anticipated, the BUILD variable for each of these planes has been correctly set to 1.
Dual Values and IP
In Chapter 1, Getting Started with LINGO, we introduced the concept of dual values. The dual values
of a solution are the reduced costs of the variables and dual prices on the constraints. We also
discussed the useful information that can be obtained from dual values. Unfortunately, in IP models
the interpretation of the dual values breaks down. Due to the discreet nature of IP models, the dual
values in the solution to an IP model are of no practical use to the average user. Given this, the dual
values should be ignored when your model contains integer variables created through the use of @BIN
or @GIN.
Summary
You should now be familiar with the use of the variable domain functions @BIN and @GIN, and how
they are used to introduce integer variables into a model. This section has shown how integer variables
bring a whole new dimension of power to the mathematical modeler. Given that we have only briefly
delved into the topic of modeling with integer variables, the user that would like to become more
familiar with the many practical applications of integer programming and their formulations can refer
to Schrage (2006), or Winston (1995).
94 CHAPTER 3
Free Variables
By default, a LINGO variable has a lower bound of zero and an upper bound of infinity. @FREE
removes the lower bound of zero and lets a variable take negative values, rendering it unconstrained in
sign, or free. The syntax is:
@FREE( variable_name);
where variable_name is the name of the variable you wish to make free.
The @FREE function may be used in a model anywhere you would normally enter a constraint. The
@FREE function can be embedded in an @FOR statement to allow you to easily make all, or selected,
variables of an attribute to be free. Some examples of @FREE are:
Example 1: @FREE( X);
makes the scalar variable, X, free,
Example 2: @FREE( QUANTITY( 4));
makes the variable QUANTITY( 4) free,
Example 3: @FOR( ITEMS: @FREE( QUANTITY));
makes all variables in the QUANTITY attribute free.
FREE Variable Example - Forecasting
You are the inventory controller for the successful new Shack4Shades retail chain. Your business
specializes exclusively in the retailing of sunglasses to the lover of the outdoors. You need to come up
with a model to forecast sales of sunglasses in the coming quarter in order to build up inventory levels.
You have created the following chart of your sales for the last eight quarters:

VARIABLE DOMAIN FUNCTIONS 95
Looking at this chart, you theorize that sales are growing according to a linear trend line, but with
rather sizable seasonal variations. Sales pick up in the summer months when people head to the
beaches and again in winter when they head for the ski slopes. Given this, you have come up with the
following theoretical function to forecast sales as a function of time:
Predicted_Sales(t) = Seasonal_Factor(t) * (Base + Trend * t)
where,
Predicted_Sales(t) represents predicted sales for quarter t,
Seasonal_Factor(t) is one of four multipliers (one for each quarter of the
year) to account for seasonal variations,
Base is the y-intercept of the hypothesized linear function, and
Trend is the slope of the linear function.
You would like to come up with a LINGO model to estimate the six parameters of your function (i.e.,
the four seasonal factors, the trend line base, and the trend line slope). To do this, you will let LINGO
choose values for the parameters that minimize the sum of the squared differences between predicted
and observed sales for the historical data.
The Formulation
We will need two primitive sets in our model. The first set will have eight members to represent the
quarters that we have historical data for. The second set will have four members corresponding to the
four quarters of the year. This second set is used for defining the four seasonal factors. Here is our sets
section that incorporates these two sets:
SETS:
PERIODS: OBSERVED, PREDICT, ERROR;
QUARTERS: SEASFAC;
ENDSETS
The three attributes on the PERIODS set—OBSERVED, PREDICT, and ERROR—correspond to the
observed sales values, predicted sales values, and the prediction error. The prediction error is simply
predicted sales minus observed sales. The SEASFAC attribute on the SEASONS set corresponds to the
seasonal sales factors and will be computed by LINGO.
We will also need to add a data section to initialize the set members and the OBSERVED attribute with
the historical sales data. We can do this with the following:
DATA:
PERIODS = P1..P8;
QUARTERS = Q1..Q4;
OBSERVED = 10 14 12 19 14 21 19 26;
ENDDATA
Next, we must add a formula to compute the error terms. As mentioned, the error term in a period is
the difference between the observed and predicted sales. We can express this in LINGO as:
@FOR( PERIODS: ERROR =
PREDICT - OBSERVED);
Our objective is to minimize the sum of the squared error terms, which may be written as:
MIN = @SUM( PERIODS: ERROR ^ 2);

96 CHAPTER 3
We choose to use squared error terms as a measure to minimize because we want to weight large errors
relatively more heavily. Another option might be to minimize the sum of the absolute values of the
errors, which would weight large and small errors proportionally the same.
In order to compute the error terms, we will also need to compute predicted sales. Using our
theoretical formula, we compute predicted sales as follows:
@FOR( PERIODS( P): PREDICT( P) =
SEASFAC( @WRAP( P, 4))
* ( BASE + P * TREND));
The @WRAP function is used here to allow us to apply the four seasonal factors over a time horizon
exceeding four periods. Had we simply used the index P, instead of @WRAP(P, 4), we would have
generated a subscript out of range error. For a more in depth explanation of the use of the @WRAP
function, please see the staff-scheduling example on page 56.
For esthetic reasons, we would like the seasonal factors to average out to a value of one. We can do
this by adding the constraint:
@SUM( QUARTERS: SEASFAC) = 4;
Finally, it is possible for the error terms to be negative as well as positive. Given that variables in
LINGO default to a lower bound of zero, we will need to use the @FREE function to allow the error
terms to go negative. By embedding the @FREE function in an @FOR loop, we can apply @FREE to
all the ERROR variables in the statement:
@FOR( PERIODS: @FREE( ERROR));

VARIABLE DOMAIN FUNCTIONS 97
The Solution
The entire formulation and excerpts from the solution appear below.
MODEL:
SETS:
PERIODS: OBSERVED, PREDICT, ERROR;
QUARTERS: SEASFAC;
ENDSETS
DATA:
PERIODS = P1..P8;
QUARTERS = Q1..Q4;
OBSERVED = 10 14 12 19 14 21 19 26;
ENDDATA
MIN = @SUM( PERIODS: ERROR ^ 2);
@FOR( PERIODS: ERROR =
PREDICT - OBSERVED);
@FOR( PERIODS( P): PREDICT( P) =
SEASFAC( @WRAP( P, 4))
* ( BASE + P * TREND));
@SUM( QUARTERS: SEASFAC) = 4;
@FOR( PERIODS: @FREE( ERROR);
@BND( -1000, ERROR, 1000));
END
Model: SHADES

98 CHAPTER 3
Local optimal solution found.
Objective value: 1.822561
Total solver iterations: 32
Variable Value
BASE 9.718878
TREND 1.553017
OBSERVED( P1) 10.00000
OBSERVED( P2) 14.00000
OBSERVED( P3) 12.00000
OBSERVED( P4) 19.00000
OBSERVED( P5) 14.00000
OBSERVED( P6) 21.00000
OBSERVED( P7) 19.00000
OBSERVED( P8) 26.00000
PREDICT( P1) 9.311820
PREDICT( P2) 14.10136
PREDICT( P3) 12.85213
PREDICT( P4) 18.80620
PREDICT( P5) 14.44367
PREDICT( P6) 20.93171
PREDICT( P7) 18.40496
PREDICT( P8) 26.13943
ERROR( P1) -0.6881796
ERROR( P2) 0.1013638
ERROR( P3) 0.8521268
ERROR( P4) -0.1938024
ERROR( P5) 0.4436688
ERROR( P6) -0.6828722E-01
ERROR( P7) -0.5950374
ERROR( P8) 0.1394325
SEASFAC( Q1) 0.8261096
SEASFAC( Q2) 1.099529
SEASFAC( Q3) 0.8938789
SEASFAC( Q4) 1.180482
Solution to SHADES
The solution is: TREND, 1.55; BASE, 9.72. The four seasonal factors are .826, 1.01, .894, and 1.18.
The spring quarter seasonal factor is .826. In other words, spring sales are 82.6% of the average. The
trend of 1.55 means, after the effects of season are taken into account, sales are increasing at an
average rate of 1,550 sunglasses per quarter. As one would expect, a good portion of the error terms
are negative, so it was crucial to use the @FREE function to remove the default lower bound of zero
on ERROR.
VARIABLE DOMAIN FUNCTIONS 99
Our computed function offers a very good fit to the historical data as the following graph illustrates:
Using this function, we can compute the forecast for sales for the upcoming quarter (quarter 1). Doing
so gives:
Predicted_Sales(9) = Seasonal_Factor(1) * (Base + Trend * 9)
=
0.826 * (9.72 + 1.55 * 9)
=
19.55
Given this, inventory levels should be brought to a level sufficient to support an anticipated sales level
of around 19,550 pairs of sunglasses.
Bounded Variables
Whereas @FREE sets the upper and lower bounds of the specified variable to plus and minus infinity
(effectively removing any bounds on the variable), the @BND function lets you set specific upper and
lower bounds on a variable. In other words, @BND limits a variable’s range within some specified
interval. The syntax for @BND is:
@BND(lower_bound, variable_name, upper_bound);
where variable_name is the variable to be bounded below by the quantity lower_bound and bounded
above by the quantity upper_bound. Both lower_bound and upper_bound must be either numeric
values or variables whose values have been set in a data section or calc section. @BND may be used
wherever you would normally enter a constraint in a model—including inside an @FOR looping
function.
In mathematical terms, LINGO interprets this @BND function as:
lower_bound ≤ variable_name ≤ upper_bound
100 CHAPTER 3
It is certainly possible to add constraints in lieu of the @BND function, but, from the standpoint of the
optimizer, @BND is an extremely efficient way of representing simple bounds on variables.
Specifying variable bounds using @BND rather than explicitly adding constraints can noticeably speed
up the solution times for larger models. Furthermore, @BND does not count against the limit on the
total number of constraints LINGO imposes on some versions. So, in general, it is a good idea to use
@BND in place of constraints whenever possible.
Some examples of @BND are:
Example 1: @BND( -1, X, 1);
constrains the variable X to lie in the interval [-1,1],
Example 2: @BND( 100, QUANTITY( 4), 200);
constrains the variable QUANTITY( 4) to fall within 100 to 200,
Example 3: @FOR( ITEMS: @BND( 10, Q, 20));
sets the bounds on all variables in the Q attribute to 10 and 20,
Example 4: @FOR( ITEMS: @BND( QL, Q, QU));
sets the bounds on all variables in the Q attribute to QL and QU (QL and
QU must have been previously set to some values in a data section).
SOS Variables
LINGO supports SOS (Special Ordered Sets) variables of Type 1, 2 and 3 via the @SOS1, @SOS2 and
@SOS3 functions, respectively. The properties of the three SOS types are:
SOS Type Property
SOS1 At most, only one variable belonging to an SOS1 set will be greater than 0.
SOS2 At most, only two variables in an SOS2 set can be different from 0. If two variables
are nonzero, then the variables will be adjacent to one another. SOS2 sets are
particularly useful for implementing piecewise-linear functions in models.
SOS3 Exactly one variable from a given SOS3 set will be equal to 1. All remaining
variables will be equal to 0.
Note: Any variables added to an SOS set will count against the integer variable limit imposed in
limited versions of LINGO. SOS sets are supported for linear models only.
The syntax for the @SOS declarations is as follows:
@SOS{1|2|3}( 'set_name', variable_reference);
The set_name argument is a unique label, or name, for the particular set of SOS variables. You add
additional variables to an SOS set by making subsequent calls to the @SOS function using the same set
name.
VARIABLE DOMAIN FUNCTIONS 101
Some examples of SOS sets are:
Example 1: @SOS3( 'SUM_TO_1', X); @SOS3( 'SUM_TO_1', Y); @SOS3(
'SUM_TO_1', Z);
In this example, an SOS Type 3 set forces either X, Y or Z to be equal to 1. The remaining
variables will be equal to 0.
Example 2: @FOR( CUST( J): @FOR( PLANTS( I): @SOS1( 'SNGSRC_' + CUST( J),
SHIP( I, J))));
Here, multiple SOS Type 1 sets force each customer to receive shipments from only one plant.
There is one SOS1 set created for each customer, each bearing the name
SNGSRC_customer_name.
An example of using Type 2 sets follows in the next section.
Piecewise Linear Example - Type SOS2 Set
As we mentioned above, SOS2 sets are particularly useful for implementing piecewise-linear
functions. Many cost curves exhibit the piecewise-linear property. For example, suppose we want to
model the following cost function, where cost is a piecewise-linear function of volume, X:
0
10
20
30
40
50
60
0 5 10 15 20 25
Piecewise-Linear Function Example
The breakpoints of the curve lie at the following points: (0,22), (5,10), (12,41) and (20,49).

102 CHAPTER 3
The following sample model, SOSPIECE.LG4, uses a Type 2 SOS set to model this piecewise-linear
function using what is referred to as the lambda method:
MODEL:
! Demonstrates the lambda method for
representing arbitrary, piecewise-linear
curves using an SOS2 set;
! See "Optimization Modeling with Lingo",
Section 11.2.7;
SETS:
! 4 breakpoints in this example;
B /1..4/: W, U, V;
ENDSETS
DATA:
! total cost at the breakpoints;
V = 22 10 41 49;
! the breakpoints;
U = 0 5 12 20;
ENDDATA
! set x to any value in interval--the cost
variable will automatically be set to the
correct total cost;
X = 8.5;
! calculate total cost;
COST = @SUM( B( i): V( i) * W( i));
! force the weights (w);
X = @SUM( B( I): U( I) * W( i));
!weights must sum to 1;
@SUM( B( I): W( I)) = 1;
! the weights are SOS2: at most two adjacent
weights can be nonzero;
@FOR( B( I): @SOS2( 'SOS2_SET', W( I)));
END
Model: SOSPIECE
We defined an attribute, W, whose members act as weights, placing us on an particular segment of the
curve. For example, if W(2)=W(3)=0.5, then we are exactly halfway between the second and third
breakpoints : (5,10) and (12,41), i.e., at point (8.5,25.5). In the case where we lie exactly on a
breakpoint, then only one of the W(i) will be nonzero and equal to 1.
For this strategy to work correctly, only two, at most, of the W(i) may be nonzero, and they must be
adjacent. As you recall, this is the definition of an SOS2 set, which we create at the end of the model
with the expression:
VARIABLE DOMAIN FUNCTIONS 103
! the weights are SOS2: at most two adjacent
weights can be nonzero;
@FOR( B( I): @SOS2( 'SOS2_SET', W( I)));
In particular, each weight W(i) is a member of the Type SOS2 set titled SOS2_SET.
For this particular example, we have chosen to pick an x-value and then let LINGO compute the
corresponding y-value, or cost. Running, the model, as predicted, we see that for an X value of 8.5,
total cost is 25.5:
Variable Value
X 8.500000
COST 25.50000
W( 1) 0.000000
W( 2) 0.5000000
W( 3) 0.5000000
W( 4) 0.000000
Solution to SOSPIECE
In addition to allowing the solver to work more efficiently, SOS sets also help to reduce the number of
variables and constraints in your model. In this particular example, had we not had the SOS2
capability, we would have needed to add an additional 0/1 attribute, Z, and the following expressions
to the model:
! Here's what we eliminated by using @sos2:
! Can be on only one line segment at a time;
w( 1) <= z( 1); w( @size( b)) <= z( @size( b));
@for( b( i) | i #gt# 1 #and# i #lt# @size( b):
w( i) <= z( i) + z( i + 1)
);
@sum( b( i): z( i)) = 1;
@for( b( i): @bin( z( i)));
Note: It may seem that piecewise linearity could be implemented in a more straightforward manner
through the use of nested @IF functions. Certainly, the @IF approach would be more natural
than the lambda method presented here. However, @IF functions would add discontinuous
nonlinearities to this model. This is something to try and avoid, in that such functions are
notoriously difficult to solve to global optimality. In the approach used above, we have
maintained linearity, which allows LINGO to use its faster, linear solvers, and converge to a
globally optimal solution.
Cardinality
Related to the SOS capability discussed above, LINGO also supports cardinality sets of variables via
the @CARD function. The cardinality feature allows you to specify a set of variables with a
cardinality of N, meaning that, at most, N of the variables in the set will be allowed to be nonzero.
As with SOS sets, cardinality sets help the integer solver branch more efficiently, and they reduce the
number of variables and constraints in your models. Also, as with SOS sets, each variable added to a
cardinality set will count against any integer variable limits imposed on your installation of LINGO.

104 CHAPTER 3
The syntax for the @CARD declarations is as follows:
@CARD( 'set_name', variable_reference|set_cardinality);
The set_name argument is a unique label, or name, for the particular cardinality set. You add
additional variables to an SOS set by making subsequent calls to the @CARD function using the same
set name with a different variable_reference. In addition to calling @CARD once for each variable in
a set, you will need to call @CARD once for each set passing an integer value as the second argument.
This integer argument is the set_cardinality, and may be either an actual integer number or a variable
set to an integer value in either a data or calc section.
Some examples of @CARD sets are:
Example 1: @CARD( 'PICK2', 2); @CARD( 'PICK2', X); @CARD( 'PICK2',
Y); @CARD( 'PICK2', Z);
In this example, at most, two out of the three variable X, Y, and Z will be nonzero.
Example 2: @FOR( PLANT( I): @CARD( 'OPENLIM', OPEN( I))); @CARD(
'OPENLIM', NCARD);
Here, we limit the maximum number of open plants to NCARD, where NCARD must be set
beforehand to an integer value in either a data or calc section.
Semicontinuous Variables
Many models require certain variables to either be 0 or lie within some nonnegative range, e.g., 10 to
20. Variables with this property are said to be semicontinuous. Modeling semicontinuity in LINGO in
the past meant having to add an additional 0/1 variable and two additional constraints. LINGO now
allows you to establish semicontinuous variables directly with the @SEMIC statement.
The syntax for the @SEMIC declarations is as follows:
@SEMIC( lower_bound, variable_reference, upper_bound);
This will restrict the variable, variable_reference, to be either 0 or to lie within the range
[lower_bound, upper_bound].
Note: Each semi-continuous variable will be counted against any integer variable limit for your
installation.

VARIABLE DOMAIN FUNCTIONS 105
Some examples of @SEMIC usage are:
Example 1: @SEMIC( 10, X, 20);
In this example, X will be restricted to being either 0, or to lie within the range [10,20].
Example 2: @FOR( PLANT( I): @SEMIC( MIN_HOURS, HOURS( I),
MAX_HOURS));
Here, we restrict the operating hours of each plant to be either 0, or to line in the range
[MIN_HOURS,MAX_HOURS]. Note that MIN_HOURS and MAX_HOURS must have
been set to explicit values beforehand in either a data or calc section.
Below, we have taken our familiar transportation model and modified it, via the use of @SEMIC, to
restrict shipments from each warehouse to each customer to be either 0, or between 3 and 10.
MODEL:
! A 3 Warehouse, 4 Customer Transportation Problem
that uses the semi-continuous (@SEMIC) to restrict
nonzero shipments to be between 3 and 10 units.;
SETS:
WAREHOUSE: CAPACITY;
CUSTOMER: DEMAND;
ROUTES( WAREHOUSE, CUSTOMER) : COST, VOLUME;
ENDSETS
DATA:
WAREHOUSE,CAPACITY = WH1,30 WH2,25 WH3,21;
CUSTOMER,DEMAND = C1,15 C2,17 C3,22 C4,12;
COST = 6 2 6 7
4 9 5 3
8 8 1 5;
ENDDATA
! The objective;
[R_OBJ] MIN = @SUM( ROUTES: COST * VOLUME);
! The demand constraints;
@FOR( CUSTOMER( J): [R_DEM]
@SUM( WAREHOUSE( I): VOLUME( I, J)) >=
DEMAND( J));
! The supply constraints;
@FOR( WAREHOUSE( I): [R_SUP]
@SUM( CUSTOMER( J): VOLUME( I, J)) <=
CAPACITY( I));
@FOR( ROUTES: @SEMIC( 3, VOLUME, 10));
END
Model: TRANSEMIC

106 CHAPTER 3
Solving this model yields the following optimal values for the semicontinuous attribute, VOLUME:
Global optimal solution found.
Objective value: 264.0000
Objective bound: 264.0000
Infeasibilities: 0.000000
Extended solver steps: 1
Total solver iterations: 32
Variable Value Reduced Cost
VOLUME( WH1, C1) 5.000000 0.000000
VOLUME( WH1, C2) 10.00000 -6.000000
VOLUME( WH1, C3) 6.000000 0.000000
VOLUME( WH1, C4) 0.000000 2.000000
VOLUME( WH2, C1) 10.00000 -1.000000
VOLUME( WH2, C2) 0.000000 2.000000
VOLUME( WH2, C3) 6.000000 0.000000
VOLUME( WH2, C4) 9.000000 -1.000000
VOLUME( WH3, C1) 0.000000 2.000000
VOLUME( WH3, C2) 7.000000 0.000000
VOLUME( WH3, C3) 10.00000 -5.000000
VOLUME( WH3, C4) 3.000000 0.000000

107
4 Data, Init and Calc
Sections
Typically, when dealing with a model’s data, you need to assign set members to sets and give values to
some set attributes before LINGO can solve your model. For this purpose, LINGO gives the user three
optional sections, the data section for inputting set members and data values, the init section for setting
the starting values for decision variables, and the calc section for performing computations on raw
input data.
The DATA Section of a Model
The DATA section allows you to isolate data from the rest of your model. This is a useful practice in
that it facilitates model maintenance and scaling of a model’s dimensions.
Basic Syntax
The data section begins with the keyword DATA: (including the colon) and ends with the keyword
ENDDATA. In the data section, you can have statements to initialize set members and/or the attributes
of the sets you instantiated in a previous sets section. These expressions have the syntax:
object_list = value_list;
The object_list contains the names of the attributes and/or a set whose members you want to initialize,
optionally separated by commas. There can be no more than one set name in object_list, while there
may be any number of attributes. If there is more than one attribute name in object_list, then the
attributes must be defined on the same set. If there is a set name in object_list, then all attributes in
object_list must be defined on this set.
The value_list contains the values you want to assign to the members of object_list, optionally
separated by commas. As an example, consider the following model:
SETS:
SET1 /A, B, C/: X, Y;
ENDSETS
DATA:
X = 1, 2, 3;
Y = 4, 5, 6;
ENDDATA

108 CHAPTER 4
We have two attributes, X and Y, defined on the SET1 set. The three values of X are set to 1, 2, and 3,
while Y is set to 4, 5, and 6. We could have also used the following compound data statement to the
same end:
SETS:
SET1 /A, B, C/: X, Y;
ENDSETS
DATA:
X, Y = 1, 4,
2, 5,
3, 6;
ENDDATA
Looking at this example, you might imagine X would be assigned the values 1, 4, and 2 because they
are first in the values list, rather than the true values of 1, 2, and 3. When LINGO reads a data
statement's value list, it assigns the first n values to the first position of each of the n attributes in the
attribute list, the second n values to the second position of each of the n attributes, and so on. In other
words, LINGO is expecting the input data in column form rather than row form.
As mentioned, we can also initialize the set members in the data section. Modifying our sample model
to use this approach by moving the set members from the sets section to the data section, we get:
SETS:
SET1: X, Y;
ENDSETS
DATA:
SET1, X, Y = A 1 4
B 2 5
C 3 6;
ENDDATA
This final method is, perhaps, the most elegant in that all model data—attribute values and set
members—are isolated within the data section.
Parameters
You are not limited to putting attributes and sets on the left-hand side of data statements. You may also
initialize scalar variables in the data section. When a scalar variable's value is fixed in a data section,
we refer to it as a parameter.
As an example, suppose your model uses an interest rate of 8.5% as a parameter. You could input the
interest rate as a parameter in the data section as follows:
DATA:
INTEREST_RATE = .085;
ENDDATA
As with set attributes, you can initialize multiple parameters in a single statement. Suppose you also
add the inflation rate to your model. You could initialize both the interest rate and inflation rate in the
same data statement as follows:
DATA:
INTEREST_RATE, INFLATION_RATE = .085, .03;
ENDDATA
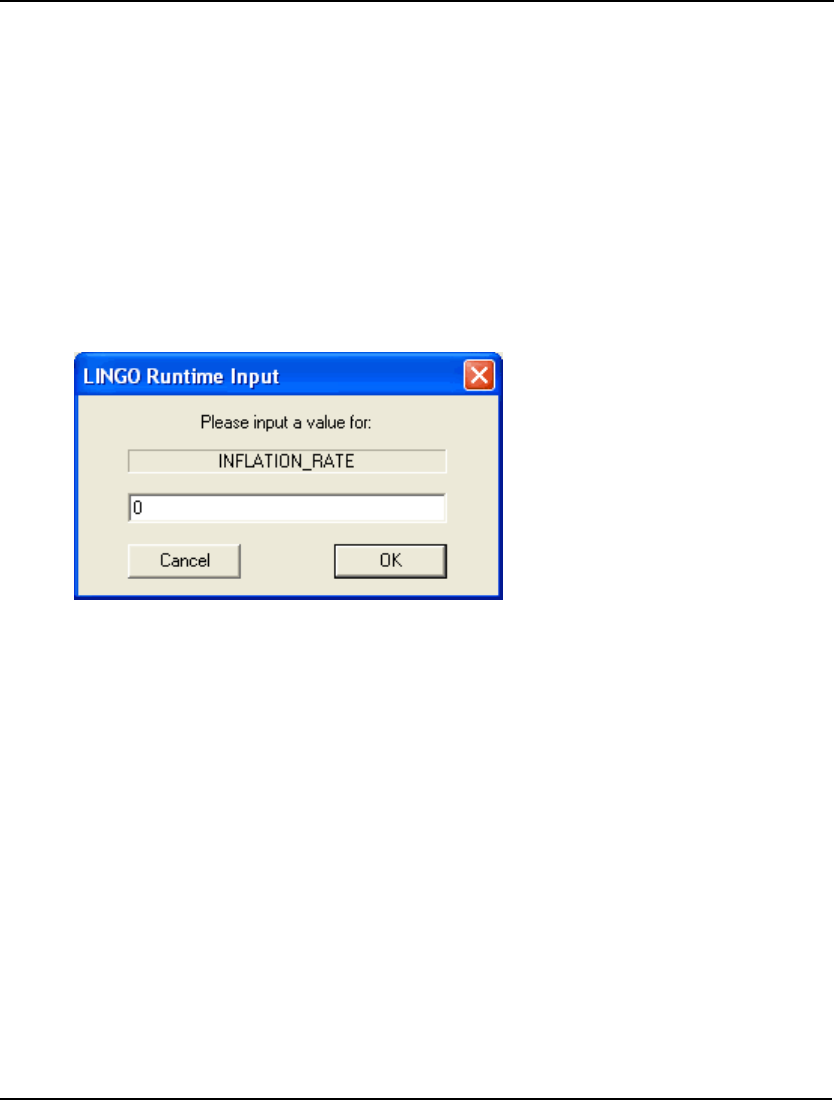
DATA, INIT AND CALC SECTIONS 109
What If Analysis
In some cases, you may not be sure what values to input for the data in your model. For example,
suppose your model uses the inflation rate as a parameter. You may be uncertain as to the exact rate of
inflation in the future, but you know it will most likely fall within a range of 2 to 6 percent. What you
would like to do is run your model for various values of the inflation rate within this range to see how
sensitive the model's results are to inflation. We refer to this as what if analysis, and LINGO has a
feature to facilitate this. To set up a parameter for what if analysis, input a question mark (?) as its
value in place of a number as in the following example:
DATA:
INFLATION_RATE = ?;
ENDDATA
LINGO will prompt you for a value for the INFLATION_RATE parameter each time you solve the
model. Under Windows, you will receive a dialog box resembling:
Simply input the desired value for the inflation rate and then press the OK button. LINGO will then set
INFLATION_RATE to the value you input and proceed with solving the model.
On platforms other than Windows, LINGO will write a prompt to your screen asking you to input a
value for INFLATION_RATE. Type in the value and then press the Enter key.
In addition to parameters, you can perform what if analysis on individual members of attributes by
initializing them to question marks in the data section, as well.
For an example of a model that uses what if analysis to compute the value of a home mortgage, see the
Home Mortgage Calculation model in Appendix A, Additional Examples of LINGO Modeling.
Initializing an Attribute to a Single Value
Suppose you want to initialize all the elements of an attribute to a single value. You can do this by
entering a single value on the right-hand side of the data statement. LINGO will initialize all the
elements of the attribute to this value. To perform what if analysis on the attribute, initialize it to a
single question mark and LINGO will prompt you for the values of all the members of the attribute
each time the model is solved.

110 CHAPTER 4
As an example, consider the following excerpt from a model:
SETS:
DAYS / MO, TU, WE, TH, FR, SA, SU/:
NEEDS;
ENDSETS
DATA:
NEEDS = 20;
ENDDATA
LINGO will initialize all the members of the NEEDS attribute to the value 20.
If there are multiple attributes on the left-hand side of the data statement, you will need one value on
the right-hand side for each attribute on the left. For instance, let's extend the previous example, so we
have an additional attribute called COST:
SETS:
DAYS / MO, TU, WE, TH, FR, SA, SU/:
NEEDS, COST;
ENDSETS
DATA:
NEEDS, COST = 20, 100;
ENDDATA
All seven members of NEEDS will be initialized to 20 and all seven members of COST to 100.
Omitting Values in a Data Section
You can omit values in a data statement to indicate that you don’t want to fix the values of particular
members. For instance, suppose you have a manufacturing company and you need to do some capacity
planning for the next 5 years. Furthermore, suppose it takes some time to boost capacity. As such, it
would be impossible to increase capacity over the next two years. In such a case, you might do
something like the following:
SETS:
YEARS /1..5/: CAPACITY;
ENDSETS
DATA:
CAPACITY = 34, 34, , , ;
ENDDATA
We have set CAPACITY for the first two years to 34, but have omitted values for the last three years.
LINGO will assume, therefore, that it is free to determine the values for CAPACITY in the last three
years.
Note: You must use commas when omitting values. If you do not use the commas, LINGO will
think you did not enter the correct number of values for the attribute, which will trigger an
error message.
DATA, INIT AND CALC SECTIONS 111
The INIT Section of a Model
The INIT section is another optional section offered by LINGO. In the init section, you enter
initialization statements that look much like the data statements found in the data section. The values
you input in the init section are used as starting points by LINGO’s solver. Unlike the variables that
are initialized in the data section, the solver is free to alter the values of variables initialized in the init
section.
Note: Starting points specified in an INIT section areof use only in nonlinearor integer models.
Starting points currently offer no help in purely linear models. If you are not sure whether
your model is linear or nonlinear, you can check the count of nonlinear constraints in the
solver status window. If there are any nonlinear constraints, then your model is nonlinear. For
more information on the nature of nonlinear models and how good starting points can be of
assistance, please see Chapter 15, On Mathematical Modeling.
Note: As an example, in a set defining a group of stocks, you may have a known price of each
stock, but the amount to buy or sell of each stock is unknown. You would typically initialize
the price attribute in the data section. If approximate values of the buy and sell attributes are
known, you can tell LINGO this information by entering it in the init section. LINGO then
uses the values specified as a starting point in its search for the optimal solution. If your
starting point is relatively close to an optimal solution, you may save on the solution time
required to run your model.
An init section begins with the keyword INIT: and ends with the keyword ENDINIT. The syntax rules
for init statements in the init section are identical to the rules for data section statements. You can have
multiple attributes on the left-hand side of a statement, you can initialize an entire attribute to a single
value, you can omit values in an attribute, and you can use the question mark to have LINGO prompt
you for an initialization value whenever you solve the model.
As an example of how a good starting point may help to reduce solution times, consider the small
model:
Y <= @LOG(X);
X^2 + Y^2 <=1;
The function @LOG(X) returns the natural logarithm of X. This model has only one feasible point of
(X,Y) = (1,0). If we solve this model without an init section, we get the solution:
Feasible solution found at step: 12
Variable Value
Y 0.5721349E-03
X 1.000419

112 CHAPTER 4
Note that it required 12 iterations to solve. Now, let’s add an init section to initialize X and Y to a point
close to the solution, so we have:
INIT:
X = .999;
Y = .002;
ENDINIT
Y <= @LOG(X);
X^2 + Y^2 <=1;
Solving this modified model, we get the solution:
Feasible solution found at step: 3
Variable Value
X 0.9999995
Y 0.0000000
Note that our solution required only 3 iterations compared to the 12 iterations required without the init
section.
The CALC Section of a Model
In many instances, your model’s raw input data will need additional massaging to get it into the proper
form. As an example, suppose your raw data consists of daily observations of a number of securities’
closing prices. Furthermore, let’s suppose that your model ultimately requires the covariance matrix
for the securities to be computed from the raw closing price data. You could certainly compute the
covariance matrix as part of the constraint section in your model. However, entering simple
computations as constraints will make your model artificially large. Another option, although
inconvenient, would be to compute the covariance matrix outside of LINGO and pass it to LINGO as
external data. Actually, what you would really like is a section in LINGO to perform data
manipulation in such a way that it doesn’t increase the size of the final optimization model passed
through to the solver engine. This is the function of the calc section.
A CALC section begins with the keyword CALC: and ends with the keyword ENDCALC. You may
input any expression in a calc section that you would in the constraint section of a model. However,
each expression must be in the form of an assignment statement. In an assignment statement, a single
variable appears on the left-hand side of an expression, followed by an equality sign, followed by an
arbitrary mathematical expression on the right-hand side. Furthermore, the right-hand side expression
may only contain references to variables that are set as part of the model’s input data (i.e., set in a
previous data section or calc expression.)

DATA, INIT AND CALC SECTIONS 113
As an example, here’s a model with a calc section that computes the average of three variables:
MODEL:
DATA:
X, Y, Z = 1, 2, 3;
ENDDATA
CALC:
AVG = ( X + Y + Z) / 3;
ENDCALC
END
Example of a valid calc section
Now, suppose we did not know the value of Y beforehand. The following model with Y dropped from
the data section would trigger an error in LINGO. The error occurs because the value of Y is an
unknown, which violates the requirement that all right-hand side variables in a calc expression must
have already had their values established in a previous data or calc section:
MODEL:
DATA:
X, Z = 1, 3;
ENDDATA
CALC:
AVG = ( X + Y + Z) / 3;
ENDCALC
END
Example of an invalid calc section
You may perform running calculations in a calc section, which means that you may break complex
calc expressions down into a series of smaller expressions. Here we break the computation from
above into two steps:
MODEL:
DATA:
X, Y, Z = 1, 2, 3;
ENDDATA
CALC:
AVG = X + Y + Z;
AVG = AVG / 3;
ENDCALC
END
Example of a running calc expression

114 CHAPTER 4
There is no limit to the number of times that a variable may appear on the left-hand side of a calc
expression. However, the final calc expression for the variable will determine its value in the final
solution report.
Calc expressions are computed sequentially in the order in which they appear in the model. So, if one
calc expression feeds its value into a subsequent expression, then it must appear before its dependent
expression. For example, the following calc section is valid:
CALC:
X = 1;
Y = X + 1;
ENDCALC
while this variation is not valid:
CALC:
Y = X + 1;
X = 1;
ENDCALC
In the second example, Y depends on X, but X is not defined until after Y.
Of course, Set looping functions may also be used in calc expressions. For example, consider the
following portfolio optimization model. In this model, we take the annual returns for three stocks and
in a calc section compute the following three pieces of information for the stocks: average return, the
covariance matrix, and the correlation matrix. This information is then used in a standard Markowitz
model to determine an optimal portfolio that meets a desired level of return while minimizing overall
risk.
MODEL:
SETS:
STOCKS: AVG_RET, WEIGHT;
DAYS;
SXD( DAYS, STOCKS): RETURN;
SXS( STOCKS, STOCKS): COVR, CORR;
ENDSETS
DATA:
DAYS = 1..12;
TARGET = .15;
STOCKS = ATT GMC USX;
RETURN = 0.300 0.225 0.149
0.103 0.290 0.260
0.216 0.216 0.419
-0.046 -0.272 -0.078
-0.071 0.144 0.169
0.056 0.107 -0.035
0.038 0.321 0.133
0.089 0.305 0.732
0.090 0.195 0.021
0.083 0.390 0.131
0.035 -0.072 0.006
DATA, INIT AND CALC SECTIONS 115
0.176 0.715 0.908;
ENDDATA
CALC:
!Average annual return for each stock;
@FOR( STOCKS( S):
AVG_RET( S) =
( @SUM( SXD( D, S): RETURN( D, S)) /
@SIZE( DAYS))
);
!Covariance matrix;
@FOR( SXS( S1, S2):
COVR( S1, S2) =
@SUM( DAYS( D):( RETURN( D, S1) - AVG_RET( S1)) *
( RETURN( D, S2) - AVG_RET( S2))) / @SIZE( DAYS)
);
!Although not required, compute the correlation matrix;
@FOR( SXS( S1, S2):
CORR( S1, S2) = COVR( S1, S2) /
( COVR( S1, S1) * COVR( S2, S2))^.5;
);
ENDCALC
!Minimize the risk of the portfolio
(i.e., its variance);
[R_OBJ] MIN = @SUM( SXS( S1, S2):
WEIGHT( S1) * WEIGHT( S2) * COVR( S1, S2));
!Must be fully invested;
[R_BUDGET] @SUM( STOCKS: WEIGHT) = 1;
!Must exceed target return;
[R_TARGET] @SUM( STOCKS: AVG_RET * WEIGHT) >= TARGET;
END
Model: MARKOW
Summary
You should now be comfortable with adding basic data, init and calc sections to your models. Keep in
mind that initialization performed in a data section fixes a variable's value. Initialization done in an init
section is used only as a temporary starting point, which may be of benefit in finding solutions to
nonlinear models. Initialization in a calc section holds until another calc expression redefining a
variable’s value is encountered. The benefit of placing computations in a calc section as opposed to
placing them in the general constraint section is that calc expressions are treated as side computations
and aren’t fed into the main solver, thereby improving execution times.
We have only touched on some of the basic features of data and init sections in this chapter. In
subsequent sections, you will see how to add hooks in your data and init sections to external files,
spreadsheets, and databases.
117
5 Windows Commands
In this chapter, we will discuss the pull down menu commands available in the Windows version of
LINGO. The following chapter, Command-line Commands, deals with the commands available
through LINGO’s command-line interface. If you’re not using a Windows version of LINGO, then you
will be primarily interested in the following chapter. If you are using a Windows version of LINGO,
then you will be primarily interested in this chapter. Windows users will also be interested in the
command-line interface if they plan to build command scripts to automate LINGO.
Accessing Windows Commands
Under Windows, commands may be accessed by either selecting them from a pull down menu,
pressing the command’s button in the toolbar, or, if applicable, entering the command’s keyboard
equivalent (also referred to as its accelerator key).
Menus
LINGO groups commands under the following five menus:
♦ File
♦ Edit
♦ LINGO
♦ Window
♦ Help
The File menu contains commands that primarily deal with handling input and output. The Edit menu
contains commands for editing the document in the current window. The LINGO menu contains
commands to solve a model and generate solution reports. The Window menu has commands that deal
with the mechanics of handling multiple windows. The Help menu provides access to LINGO’s help
facility.
The Toolbar
By default, the toolbar runs along the top of the screen and is illustrated in the following picture:
LINGO’s toolbar “floats”. Thus, you can reposition it by dragging it to any part of the screen. You can
also choose to suppress the toolbar by clearing the Toolbar button on the Interface tab of the
LINGO|Options dialog box.
Each button on the toolbar corresponds to a menu command. Not all menu commands have a toolbar
button, but, in general, the most frequently used commands have an equivalent button.

118 CHAPTER 5
LINGO displays “tool tips” for each button. When you position the mouse over a button, a short
description of what the button does appears in a pop up window and in the status bar at the bottom of
the screen.
Here is a list of the buttons and their equivalent commands:
File|New Edit|Match Parenthesis
File|Open LINGO|Solve
File|Save LINGO|Solution
File|Print LINGO|Options
Edit|Undo LINGO|Picture
Edit|Redo Window|Send To Back
Edit|Cut Window|Close All
Edit|Copy Window|Tile
Edit|Paste Help|Topics
Edit|Find Help|Pointer
Edit|Go To Line
Accelerator Keys
Along with accessing commands via the menus and toolbar, most commands may also be accessed by
a single, unique keystroke known as an accelerator. The equivalent accelerator key is listed alongside
each command in the menus.
Windows Commands In Brief
In this section, we give a brief listing of the commands available in the Windows version of LINGO.
The commands are categorized into the five main menus:
♦ File
♦ Edit
♦ LINGO
♦ Window
♦ Help
The next section in this chapter contains an in-depth description of the commands.

WINDOWS COMMANDS 119
1. File Menu Commands:
New Opens a new model window.
Open Opens an existing model previously saved to disk.
Save Saves the contents of the current window to disk.
Save As Saves the contents of the current window to a new name.
Close Closes the current window.
Print Prints the contents of the current window.
Print Setup Configures your printer.
Print Preview Displays the contents of the current window as it would
appear if printed.
Log Output Opens a log file for logging output to the command window.
Take Commands Runs a command script contained in a file.
Export File Exports a model in MPS or MPI file format.
License Prompts you for a new license password to upgrade your
system.
Database User Info Prompts you for a user id and password for database access
via the @ODBC() function.
Exit Exits LINGO.
2. Edit Menu Commands:
Undo Undoes the last change.
Redo Redoes the last undo command.
Cut Cuts the current selection from the document.
Copy Copies the current selection to the clipboard.
Paste Pastes the contents of the clipboard into the document.
Paste Special Pastes the contents of the clipboard into the document,
allowing choice as to how the object is pasted.
Select All Selects the entire contents of the current window.
Find Searches the document for the occurrence of a specified text
string.
Find Next Repeats the find operation for the last string specified.
Replace Replaces a specified text string with a new string.
Go To Line Moves the cursor to a specified line number.
Match Parenthesis Finds the parenthesis that closes a selected parenthesis.
Paste Function Pastes a template of a selected LINGO @function.
Select Font Specifies a font for a selected block of text.
Insert New Object Embeds an OLE (Object Linking and Embedding) object into
the document.
Links Controls the links to external objects in your document.
Object Properties Specifies the properties of a selected, embedded object.

120 CHAPTER 5
3. LINGO Menu Commands:
Solve Solves the model in the current window.
Solution Generates a solution report window for the current model.
Range Generates a range analysis report for the current window.
Options Sets system options.
Generate Generates the algebraic representation for the current
model.
Picture Displays a graphical picture of a model in matrix form.
Debug Tracks down formulation errors in infeasible and
unbounded linear programs.
Model Statistics Displays a brief report regarding the technical detail of a
model.
Look Generates a formulation report for the current window.
4. Window Menu Commands:
Command Window Opens a command window for command-line operation of
LINGO.
Status Window Opens the solver's status window.
Send to Back Sends the current window behind all other open windows.
Close All Closes all open windows.
Tile Arranges all open windows into a tile pattern.
Cascade Arranges all open windows into a cascading pattern.
Arrange Icons Aligns all iconized windows at the bottom of the main frame
window.
5. Help Menu Commands:
Help Topics Accesses LINGO's Help facility.
Register Registers your version of LINGO online.
AutoUpdate Checks to see if an updated copy of LINGO is available for
download on the LINDO Systems Web site.
About LINGO Displays the version and size of your copy of LINGO, along with
information on how to contact LINDO Systems.

WINDOWS COMMANDS 121
Windows Commands In Depth
In the remainder of this chapter, we will document all the commands specific to the Windows version
of LINGO. The commands are categorized into the five main menus described in the Windows
Commands In Brief section above.
1. File Menu
LINGO's File menu is pictured below. This menu contains
commands that generally pertain to the movement of files in and
out of LINGO.
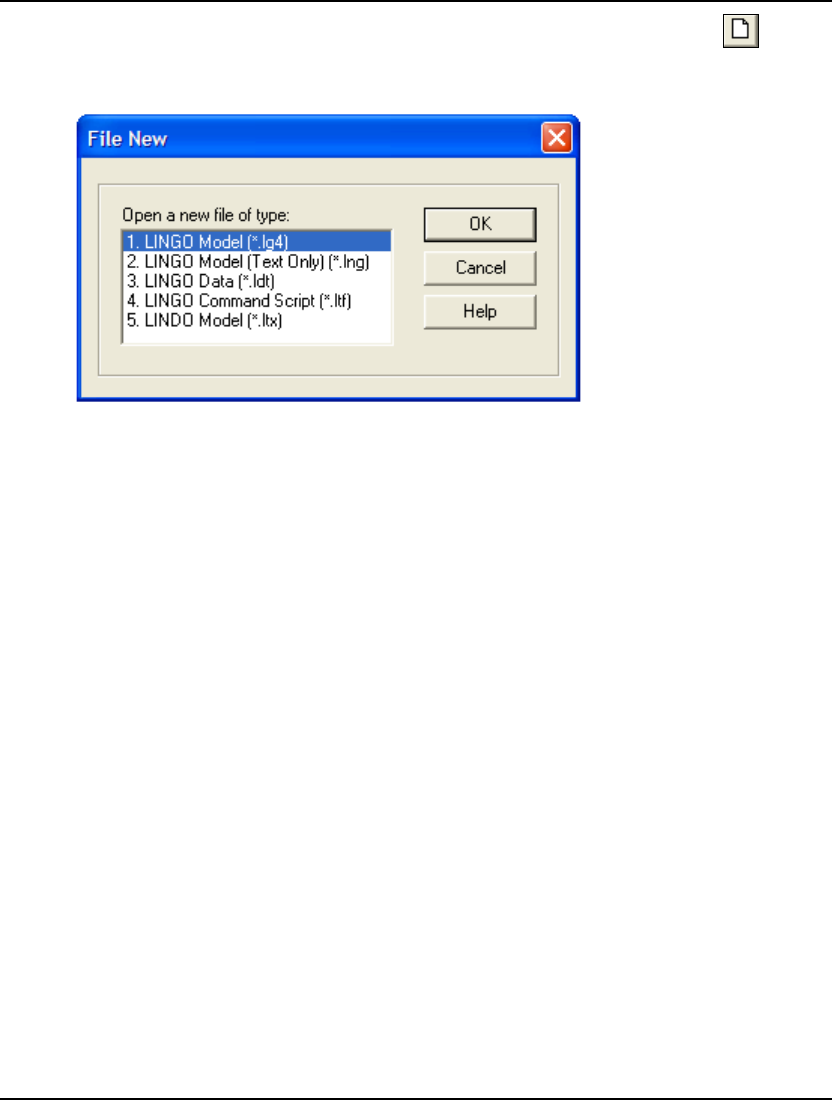
122 CHAPTER 5
File|New F2
The New command opens a new, blank window. When you select the New command, you will be
presented with the following dialog box:
You may then select the type of file you want to create. The file must be one of the four types:
1. LINGO Model (*.lg4)
The LG4 format was established with release 4.0 of LINGO. LG4 is the primary
file format used by LINGO to store models under Windows. This format
supports multiple fonts, custom formatting, and OLE (Object Linking and
Embedding). LG4 files are saved to disk using a proprietary binary format.
Therefore, these files can’t be read directly into other applications or transported
to platforms other than the PC. Use the LNG format (discussed next) to port a
file to other applications or platforms.
2. LINGO Model (Text Only) (*.lng)
The LNG format is a portable format for storing your models. It was the
standard file format used by LINGO in releases prior to 4.0 and remains in use
on all platforms other than Windows. LNG files are saved to disk as ASCII text
and may be read into any application or word processor that supports text files.
LNG files may also be ported to platforms besides the PC. LNG files do not
support multiple fonts, custom formatting, or OLE.
3. LINGO Data (*.ldt)
LDT files are data files typically imported into LINGO models using the @FILE
function. @FILE can only read text files. Given this, all LDT files are stored as
ASCII text. LDT files do not support multiple fonts, custom formatting, or OLE.
4. LINGO Command Script (*.ltf)
LTF files are LINGO command scripts. These are ASCII text files containing a
series of LINGO commands that can be executed with the File|Take Commands
command. For more information on commands that can be used in a LINGO
script, refer to the following chapter, Command-line Commands. LTF files do
not support multiple fonts, custom formatting, or OLE.
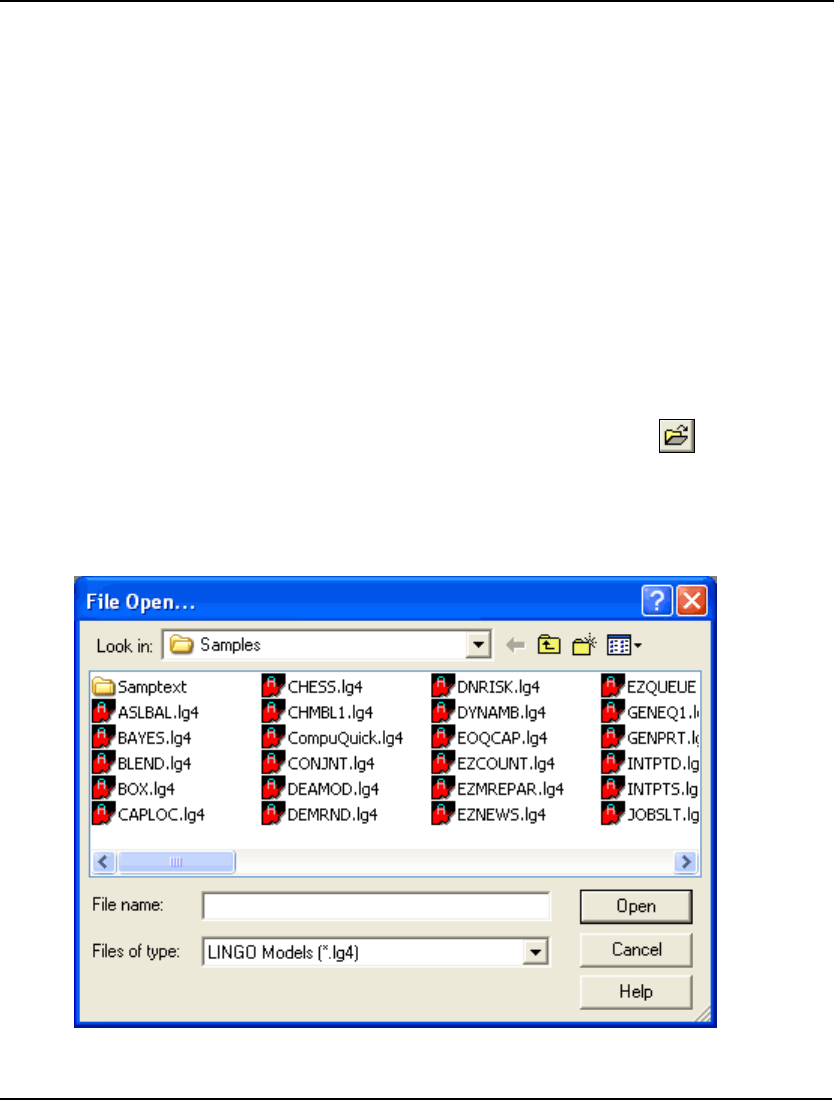
WINDOWS COMMANDS 123
5. LINDO Model (*.ltx)
LTX files are model files that use the LINDO syntax. Longtime LINDO users may
prefer LINDO syntax over LINGO syntax. LINDO syntax is convenient for quickly
entering small to medium sized linear programs. As long as a file has an extension
of .ltx, LINGO will assume that the model is written using LINDO syntax. Readers
interested in the details of LINDO syntax may contact LINDO Systems to obtain a
LINDO user’s manual.
When you simply press either the New toolbar button or the F2 key, LINGO assumes you want a
model file. Thus, LINGO does not display the file type dialog box and immediately opens a model file
of type LG4.
If you have used the LINGO|Options command to change the default model file format from LG4 to
LNG, LINGO will automatically open a model of type LNG when you press either the New button or
the F2 key.
You may begin entering text directly into a new model window or paste in text from other applications
using the Windows clipboard and the Edit|Paste command in LINGO.
File|Open... Ctrl+O
The Open command reads a saved file from disk and places it in a LINGO Window. The file can be a
LINGO model file (*.LG4), or any other file. If the file is not in LG4 format, it must be in ASCII text
format.
After issuing the Open command, you will be presented with a dialog box resembling the following:

124 CHAPTER 5
You can enter a file name in the File name edit box, or select a file name from the list of existing files
by double-clicking on a file. Press the Open button to open the file, the Cancel button to exit without
opening a file, or the Help button for assistance.
You may select a different file type from the Files of type list box causing LINGO to list only the files
of that type.
If the file to be opened has an extension of .MPS or .MPI, then LINGO will invoke its MPS or MPI
reader to parse the file. The MPS file format is an industry standard format developed by IBM, which
is useful for passing models from one solver or platform to another, while the MPI format was
developed by LINDO Systems as a portable format for representing arbitrary math programming
models. When importing either an MPS or MPI file, LINGO reads the file from disk, converts it to an
equivalent LINGO model, and places the model into a new model window. More details follow
immediately below. LINGO can also write MPS and MPI format files; this is discussed in the
File|Export File section below.
If you have just read in a LINGO model file (a LG4 or LNG file) and wish to solve it, use the
LINGO|Solve command.
Importing MPS and MPI Files
When LINGO reads an MPS file, it converts the formulation to an equivalent LINGO model. As an
example, consider the following, simple model:
ObjRow) Maximize 20X + 30Y
Subject To:
Row1) X < 50
Row2) Y < 60
Row3) X + 2Y < 120
The MPS file for this model is:
NAME SAMPLE
OBJSENSE
MAX
ROWS
N OBJROW
L ROW1
L ROW2
L ROW3
COLUMNS
X ROW3 1.0000000
X OBJROW 20.0000000
X ROW1 1.0000000
Y OBJROW 30.0000000
Y ROW2 1.0000000
Y ROW3 2.0000000
RHS
RHS ROW1 50.0000000
RHS ROW2 60.0000000
RHS ROW3 120.0000000
ENDATA

WINDOWS COMMANDS 125
And the MPI version of the model is:
BEGINMODEL SAMPL
! Number of Objective Functions: 1
! Number of Constraints : 3
! Number of Variables : 2
VARIABLES
! Name Lower Bound Initial Point
Upper Bound Type
X 0 1.23457
1e+030 C
Y 0 1.23457
1e+030 C
OBJECTIVES
OBJROW MAXIMIZE
EP_USRCOD -101
EP_PUSH_NUM 20
EP_PUSH_VAR X
EP_MULTIPLY
EP_PUSH_NUM 30
EP_PUSH_VAR Y
EP_MULTIPLY
EP_PLUS
CONSTRAINTS
ROW1 L
EP_USRCOD -101
EP_PUSH_VAR X
EP_PUSH_NUM 50
EP_MINUS
ROW2 L
EP_USRCOD -101
EP_PUSH_VAR Y
EP_PUSH_NUM 60
EP_MINUS
ROW3 L
EP_USRCOD -101
EP_PUSH_VAR X
EP_PUSH_NUM 2
EP_PUSH_VAR Y
EP_MULTIPLY
EP_PLUS
EP_PUSH_NUM 120
EP_MINUS
ENDMODEL
One thing to notice at this point is that MPS and MPI formats are not very compact methods for
storing a model⎯they are designed for portability, as opposed to efficiency.
Using the File|Open command to read this file into LINGO, we are presented with the following
window containing an equivalent LINGO model:
126 CHAPTER 5
Note how the model is automatically converted from MPS or MPI format to native LINGO format.
Should you wish to save the file again using MPS format rather than LINGO format, you may use the
File|Export File|MPS Format… command.
Note: The MPS and MPI file formats are intended primarily for exporting models to other
applications or platforms. The MPS format is purely scalar in nature—all set-based
information is lost upon converting a LINGO model to either MPS or MPI format. Thus,
when saving copies of a model on your own machine, you should always use the File|Save
command in order to save models in a native LINGO format (LG4 or LNG) in order to
preserve your model in its entirety.
When it comes to acceptable constraint and variable names, the MPS and MPI formats are less
restrictive than LINGO. To compensate for this fact, LINGO attempts to patch names when reading a
file, so that all the incoming names are compatible with its syntax. LINGO does this by substituting an
underscore for any character in a name that is not admissible. In most cases, this will work out OK.
However, there is a chance for name collisions where two or more names get mapped into one. For
instance, the variable names X.1 and X%1 would both get mapped into the single LINGO name X_1.
Of course, situations such as this entirely alter the structure of the model, rendering it incorrect.
However, you will be warned whenever LINGO has to patch a name with the following error message:
WINDOWS COMMANDS 127
This message displays the number of variable and row names that were patched to get them to conform
to LINGO syntax.
If name collisions are a problem, then LINGO has an option that will ensure that all names remain
unique. This option involves using RC format for names encountered during MPS I/O. RC format
involves renaming each row (constraint) in a model to be Rn, where n is the row’s index. Similarly,
each column (variable) is renamed to Cn. In addition, LINGO renames the objective row to be ROBJ.
To switch to RC format for MPS names, run the LINGO|Optionscommand, select the General Solver
tab, then click the checkbox titled Use R/C format names for MPS I/O, as illustrated here:
As an example, we will once again import the same MPS format model as above. However, this time
we will use RC naming conventions. Here is the model as it appears after importing it into LINGO:
Notice how the variable names now use RC format, guaranteeing that name collisions will not occur.
Another potential conflict is that MPS and MPI allow variable names to be duplicated as constraint
names and vice versa. LINGO does not allow for this. When you go to solve the model, you will
receive either error message 28 (Invalid use of a row name), or error message 37 (Name already in
use). Once again, you can switch to using RC name format to avoid this conflict.
As a final note, LINGO only supports free format MPS files, and does not support fixed format MPS
files. Therefore, variable and row names may not contain embedded blanks.
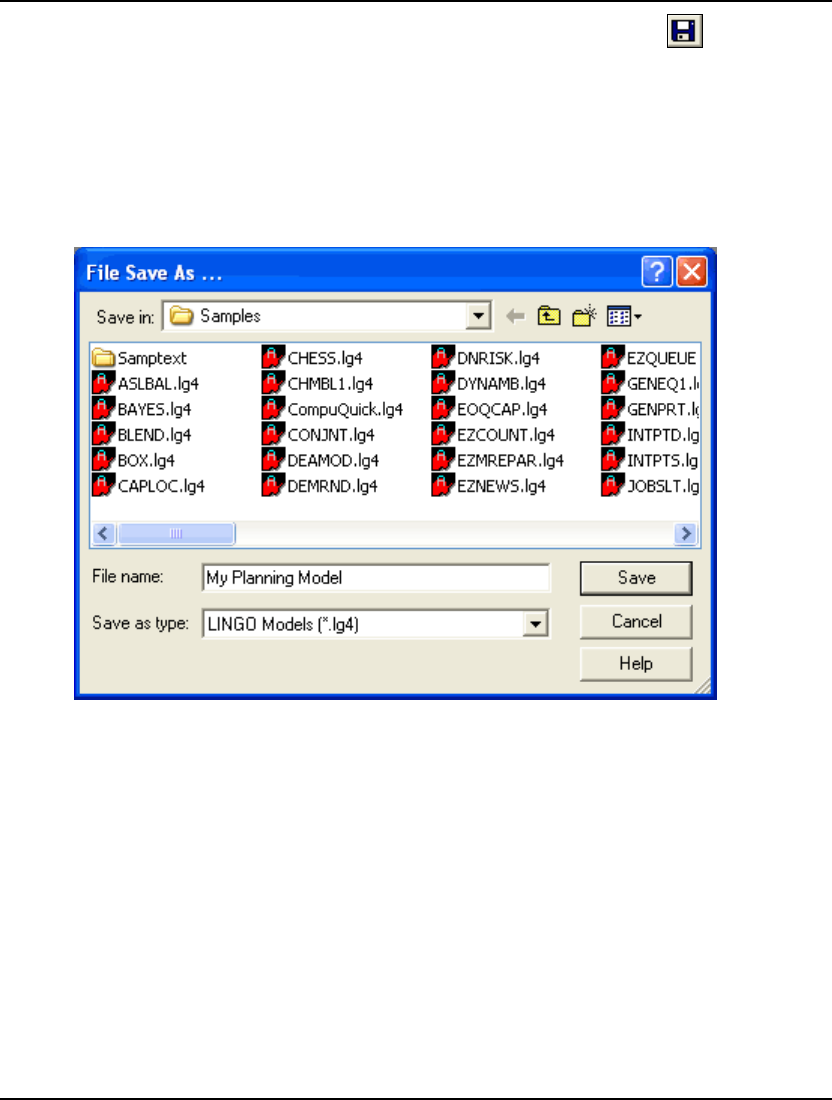
128 CHAPTER 5
File|Save Ctrl+S
The Save command saves the contents of the active window to disk using the existing file name for the
window. If the window has not been saved before, you will be prompted to provide a name for the file.
File|Save As... F5
The Save As command allows you to save the contents of the active window under a new file name.
When issuing the Save As command, you will be presented with a dialog box that resembles the
following:
You can enter a new file name in the File name edit box, or select a file name from the list of existing
files by double-clicking on it. If you do not specify a file extension, LINGO will append the extension
of the default model format to the name. If you want to prevent LINGO from appending an extension
to the name, place the file name in double quotes.
Press the Save button to save the model, the Cancel button to exit without saving, or the Help button
for assistance.
You may select a different file type from the Save as type list box. If your model has special fonts or
embedded objects, you must save it using the LG4 file format to preserve them. The LG4 format is a
special binary format readable only by LINGO. If you wish to create a text copy of your model, then
use the LNG file format. For further discussion of the available file formats under LINGO, refer to the
New command above.
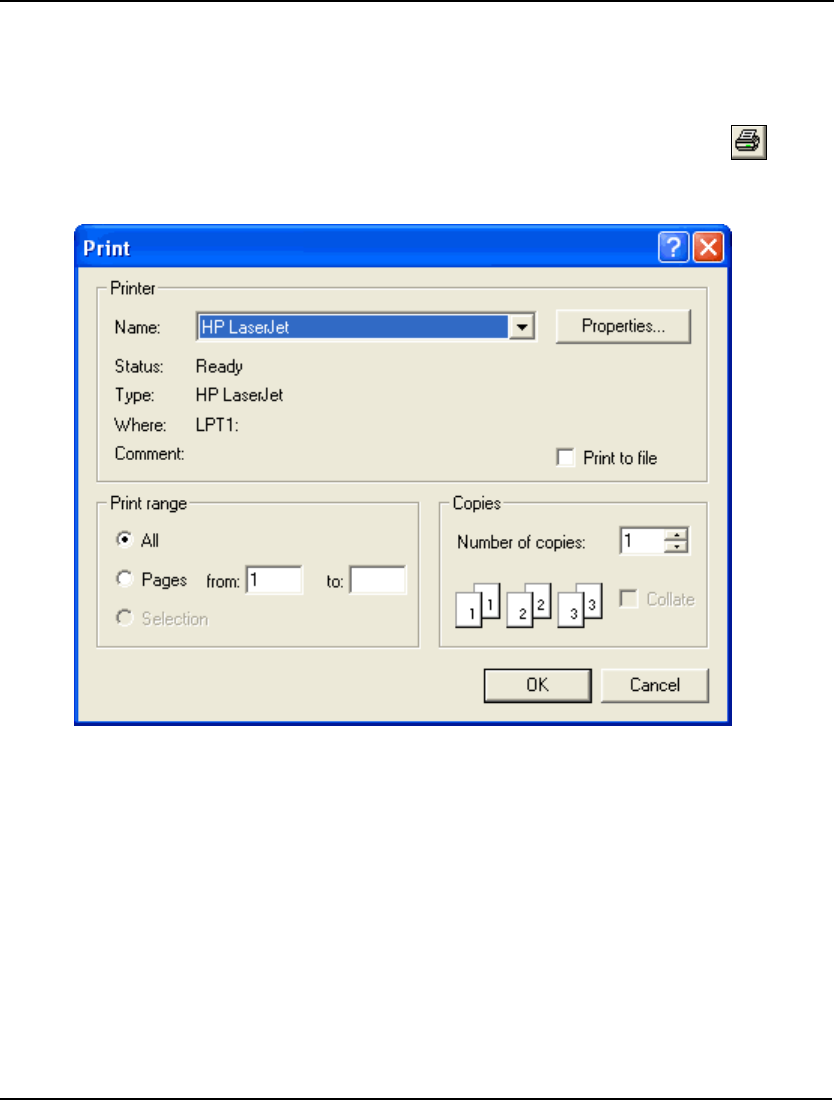
WINDOWS COMMANDS 129
File|Close F6
Use the Close command to close the active (front most) window. If the window has been modified
without being saved, you’ll be asked whether you want to save the changes.
File|Print... F7
Use the Print command to send the contents of the active window to your printer. First, LINGO will
display the Print dialog box:
Select the printer to route the output to from the Name list box. Modify the printer’s properties by
pressing the Properties button. Select a range of pages to print in the Print range group box. If you
need multiple copies, input the number desired in the Number of copies field and specify if you want
the copies collated (assuming your printer is capable of collating). Finally, press the OK button to
begin printing. Press the Cancel button to exit without printing.
130 CHAPTER 5
File|Print Setup... F8
Use the Print Setup command to configure your printer. You should see a dialog box that resembles
the following:
Select the target printer from the Name list box. Press the Properties button to set additional printer
properties. Select the type of paper and tray from the Paper group box. In the Orientation group box,
select whether you want portrait or landscape output. Press the Cancel button to exit without changing
the printer configuration. Press the OK button to save changes and exit the Print Setup command.
WINDOWS COMMANDS 131
File|Print Preview Shift+F8
Use the Print Preview command to display each page of the active window as it will appear when
printed. After issuing the Print Preview command, the contents of the active window will be placed in
a Preview window as follows:
The Print button sends the file to the printer. The Next Page button brings the next page into the
viewer. The Prev Page button brings the previous page into the viewer. The One Page button puts the
viewer into single page mode, while the Two Page button puts the viewer into double page mode. The
Zoom In button is used to have the viewer zoom in on a region of the document. The Zoom Out button
undoes the effect of a Zoom In. Press the Close button to close the print viewer and return to the
normal command mode of LINGO.
If you would like to change some of the printer specifications, such as landscape output, use the Print
Setup command (described above) before issuing the Print Preview command.
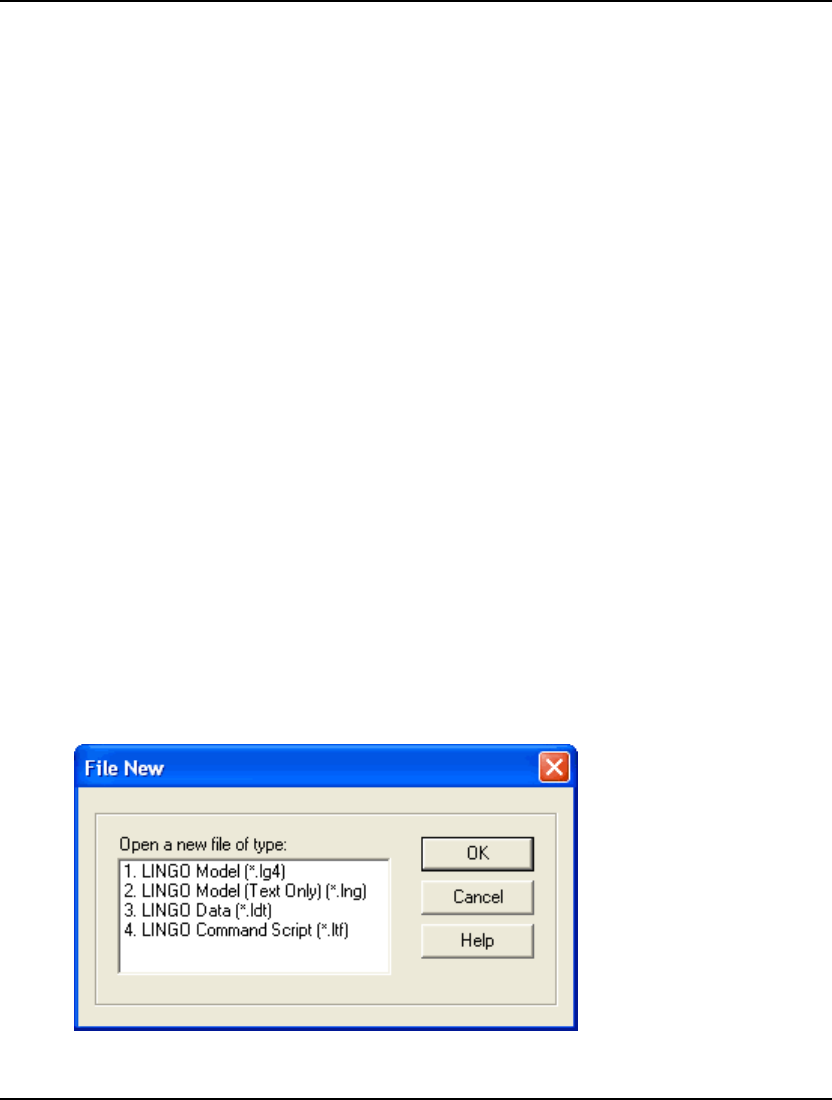
132 CHAPTER 5
File|Log Output... F9
Normally, when you are using LINGO for Windows, it is operating in a menu driven mode, where you
choose commands from the pull down menus and reports are displayed in individual windows. LINGO
can also operate in command mode, where text commands or command script files drive the
application and all output is routed to a window known as the command window. All input and output
passes through the command window when LINGO is in command mode. You can open a command
window at anytime by issuing the Window|Command Window command.
In general, you will only be interested in running LINGO in command mode if you are planning to
embed LINGO in a larger application. If you do use LINGO in command mode, you will find that the
command window can only hold a limited amount of output. Should you need to keep a disk-based
copy of all that transpires in the command window, you will need to use the Log Output command.
The Log Output command opens a standard Windows file dialog box from which you can name the
log file. You can echo the output to the command window as well as the file by checking the Echo to
screen checkbox. If you would like to append output to the end of an existing file, check the Append
output checkbox.
When you have selected a file for logging output, a check mark will appear in the File menu before the
Log Output command. To turn off Log Output, select the command again and the check mark will
disappear.
File|Take Commands... F11
The Take Commands command is used to submit a LINGO command script file for processing. For
more information on LINGO’s script language, refer to the following chapter, Command-line
Commands.
As an example, we will build a small script file that contains a small product-mix model and process it
using Take Commands.
To build a script file, issue the File|New command. LINGO will present you with the following dialog
box:
Select item 4, LINGO Command Script, and press the OK button. LINGO will open a blank script file.
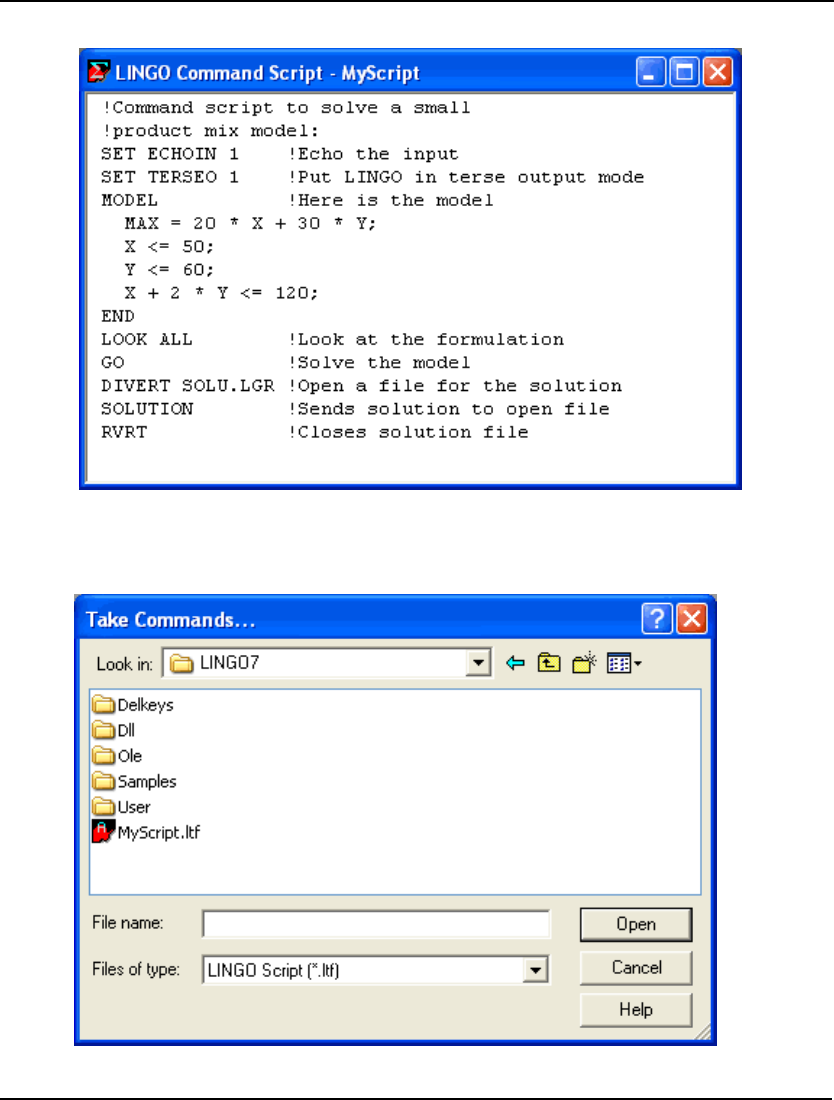
WINDOWS COMMANDS 133
Now, enter the following into the script file:
This is a command script that inputs a small product-mix model, solves it, and puts the solution in a
text file. Save the command script to a file titled MyScript.ltf using the File|Save As command.
To run the script, issue the File|Take Commands command. You should see the following:

134 CHAPTER 5
Double-click on the icon for MyScript.ltf to begin processing the command script. LINGO’s command
window will now appear, and you should be able to watch LINGO’s progress at processing the script
by watching commands and output as they are logged in the command window. When LINGO finishes
the command script, the command window will resemble the following:

WINDOWS COMMANDS 135
Also of interest is the solution file, SOLU.LGR, created as part of our command script. If you open this
file, you should find the following solution to the model:
Variable Value Reduced Cost
X 50.00000 0.000000
Y 35.00000 0.000000
Row Slack or Surplus Dual Price
1 2050.000 1.000000
2 0.000000 5.000000
3 25.00000 0.000000
4 0.0000000 15.00000
The output that was routed to the command window can be routed to a file using the Log Output
command described above.
File|Export File
The File|Export File command allows you to either export MPS or MPI format files. The MPS file
format is an industry standard format developed by IBM, and is useful for passing models from one
solver or platform to another. MPI file format was developed by LINDO Systems as a way to store all
math programs, from linear models to, in particular, nonlinear models
Exporting MPS Files
The File|Export File|MPS format command generates the underlying algebraic formulation for the
current model and then writes it to a selected disk file in MPS format. MPS format is a common format
for representing linear programming models. MPS files can be ported to any solver that reads MPS
files—this includes most commercial linear programming packages.
As an example of exporting an MPS file, consider the model:

136 CHAPTER 5
After issuing the File|Export File|MPS format command and opening the file containing the MPS
model, we will find:
NAME NO_TITLE
*****************************************************
* NOTICE: Generated by the MPS export utility for
* a maximization type problem.
*
* The objective coefficients have flipped signs.
* Interpret the objective value from the solution of
* this model accordingly.
*****************************************************
ROWS
N 1
L 2
L 3
L 4
COLUMNS
X 1 -20
X 2 1
X 4 1
Y 1 -30
Y 3 1
Y 4 2
RHS
RHS1 2 50
RHS1 3 60
RHS1 4 120
BOUNDS
ENDATA
Note 1: A model must be linear or quadratic to successfully export it in MPS format.
Note 2: When exporting an MPS file, LINGO truncates all variable names to 8 characters. For
instance, the two distinct LINGO names SHIP( WH1, C1) and SHIP( WH1, C2) would both
be truncated to the single 8 character name SHIPWH1C under MPS. Either choose names to
avoid collisions of truncated names, or enable the option for converting names to RC format
when doing MPS I/O. LINGO will display an error message if potential collisions exist.
Note 3: The MPS file format is intended primarily for exporting models to other applications or
platforms. The MPS format is purely scalar in nature—all set-based information is lost upon
converting a LINGO model to MPS format. Thus, when saving copies of a model on your
own machine, you should always use the File|Save command in order to preserve your model
in its entirety.
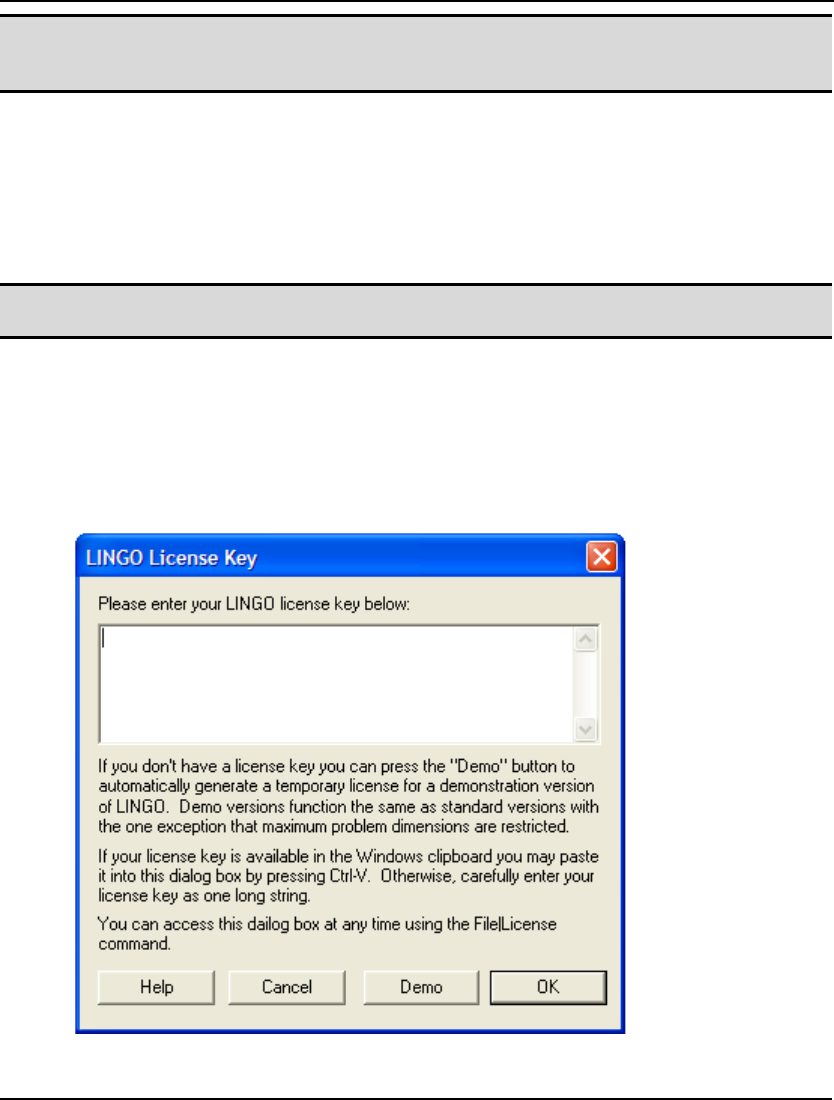
WINDOWS COMMANDS 137
Note 4: When exporting a stochastic program to MPS format, LINGO will write a total of three
SMPS format files, consisting of the core model, its stochastic declarations and its time
structure.
Exporting MPI Files
MPI file format was developed by LINDO Systems as a way to store all math programs, from linear
models to, in particular, nonlinear models. As with MPS files, the MPI format is scalar-based. Thus,
you will lose any sets in your model when saving it in this format. Most users will not have a need for
MPI formatted files. However, LINDO API users can load these files directly and may find this feature
useful.
Note 5: When exporting a stochastic program to MPI format, LINGO will write a total of four SMPI
format files, consisting of the core model, its stochastic declarations and its time structure.
File|License
Some versions of LINGO require the user to input a license key. Also, if you upgrade your copy of
LINGO, then you will need to enter a new password. The File|License command prompts you for a
new license key.
When you run the File|License command, you will be presented with the dialog box:
138 CHAPTER 5
Carefully enter the key into the edit field, including hyphens, making sure that each character is
correct. Click the OK button and, assuming the password was entered correctly, LINGO will display
the Help|About LINGO dialog box listing the features in the upgraded license. Verify that these
features correspond to the license you intended to install.
Note: If you were emailed your license key, then you have the option of cutting-and-pasting it into
the dialog box. Cut the cut the key from the email that contains it. Then, press Ctrl+V to paste
it into the LINGO File|License dialog box.
File|Database User Info
LINGO allows models to link directly with databases through use of the @ODBC() function. Many
times, the database you link your model to will require a user id and/or password. To avoid having to
enter your user id and password each time your model is run, you can input them once at the start of
your session using this command.
When you run the File|Database User Info command, you will be presented with the following dialog
box:
Enter any user id and/or password into the appropriate fields. For security reasons, LINGO does not
store this information from one session to the next. So, you will need to run this command at the start
of each session.
If security is not a concern, and you would like to store your database user information, then you can
create an AUTOLG.DAT file containing a DBUID command and a DBPWD command. Commands in
the AUTOLG.DAT file are executed automatically each time LINGO starts. Thus, DBUID and
DBPWD commands contained in an AUTOLG.DAT file will restore your database user information at
the start of each LINGO run. For more information on the use of AUTOLG.DAT files, refer to LINGO
Command Scripts section in Chapter 8, Interfacing with External Files.
File|Exit F10
Use the Exit command to quit LINGO. If any unsaved files are open, you will be prompted to save
them before LINGO shuts down.

WINDOWS COMMANDS 139
2. Edit Menu
LINGO’s Edit menu, pictured at left,
contains commands that generally
pertain to editing and modifying the text
within a window. Each command
contained in the Edit menu is discussed
below.
Edit|Undo Ctrl+Z
Use the Undo Command to undo the last modification made to the contents of a Window. Undo can
undo all operations except drag-and-drop. LINGO stores a limited amount of undo operations, so you
won’t be able to depend on LINGO to undo extensive changes.
Edit|Redo Ctrl+Y
This command will redo the last undo operation. LINGO stores a limited amount of redo operations, so
you won’t be able to depend on LINGO to redo extensive changes.

140 CHAPTER 5
Edit|Cut Ctrl+X
Use the Cut command to clear the selected block of text and place it on the clipboard for pasting. To
select a block of text for cutting, place the cursor immediately before the block and press down on the
left mouse button. Now, drag the mouse until the cursor appears immediately after the block of text.
The text block should now be displayed in reverse video. Now, issue the Cut command to remove the
selected text from the document, placing it in the Windows clipboard.
Edit|Copy Ctrl+C
Use the Copy command to copy the selected text to the clipboard for pasting. To select a block of text
for copying, place the cursor immediately before the block and press down on the left mouse button.
Now, drag the mouse until the cursor appears immediately after the block of text. The text block
should now be displayed in reverse video. Now, issue the Copy command to place a copy of the
selected text in the Windows clipboard.
The Copy command is a convenient way to transfer small amounts of data from LINGO to other
applications.
Edit|Paste Ctrl+V
Use the Paste command to replace the current selection in the active window with the contents of the
Windows clipboard. The Paste command is a convenient way to import small amounts of data from
other applications into your LINGO models.

WINDOWS COMMANDS 141
Edit|Paste Special...
Use the Paste Special command to insert the contents from the Windows clipboard into the active
window at the cursor insertion point. This command can do much more than insert just plain text as
done by the standard Paste command. Paste Special can be used to insert other objects and links to
other objects. This is particularly useful for adding links to supporting data for your model. By
inserting a link to your data sources, it is much easier to find and view them.
As an example, suppose we have the following transportation model:
! A 3 Warehouse, 4 Customer
Transportation Problem;
SETS:
WAREHOUSE / WH1, WH2, WH3/: CAPACITY;
CUSTOMER / C1, C2, C3, C4/: DEMAND;
ROUTES(WAREHOUSE, CUSTOMER): COST, VOLUME;
ENDSETS
! The objective;
MIN = @SUM(ROUTES: COST * VOLUME);
! The demand constraints;
@FOR(CUSTOMER(J):
@SUM(WAREHOUSE(I): VOLUME(I, J)) >=
DEMAND(J));
! The supply constraints;
@FOR(WAREHOUSE(I): [SUP]
@SUM(CUSTOMER(J): VOLUME(I, J)) <=
CAPACITY(I));
! Here are the parameters;
DATA:
CAPACITY = @OLE('D:\LNG\TRANLINKS.XLS');
DEMAND = @OLE('D:\LNG\TRANLINKS.XLS');
COST = @OLE('D:\LNG\TRANLINKS.XLS');
@OLE('D:\LNG\TRANLINKS.XLS') = VOLUME;
ENDDATA
As we can see from the data section, we are importing data from the Excel file TRANLINKS.XLS and
writing the solution back out to the same file.
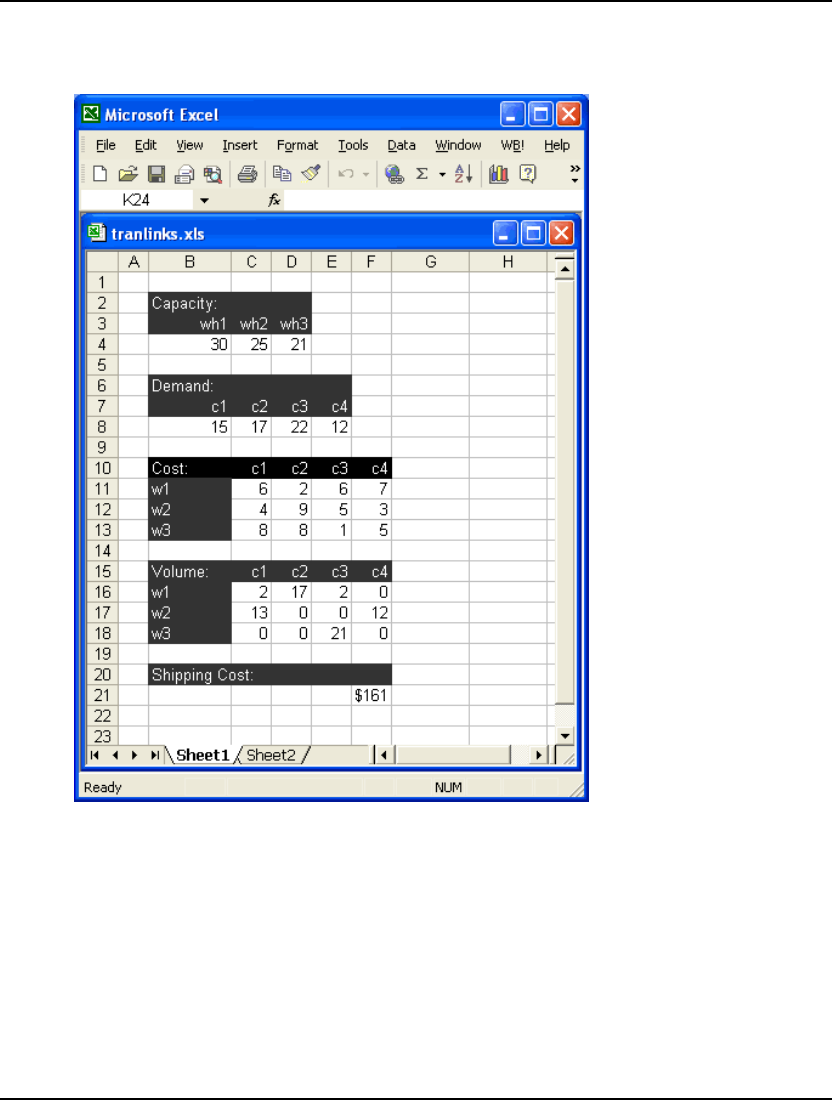
142 CHAPTER 5
A nice feature would be to insert a link to the spreadsheet into our model file. This way, we could view
the data and the solution without having to start Excel and load the spreadsheet. To do this, open Excel
and load the spreadsheet as we have done here:
For complete information on importing data from Excel, see Chapter 9, Interfacing with Spreadsheets.
WINDOWS COMMANDS 143
Now, select the range B2:F21 in the spreadsheet. Next, from Excel’s Edit menu, choose the Copy
command. Now, click on LINGO, place the cursor right before the data section, and give the
Edit|Paste Special command. Click on the Paste Link button in the dialog box, so you see the
following:
144 CHAPTER 5
Finally, click the OK button, and you should be able to see the spreadsheet contents in the LINGO
model:
This link will be saved as part of your LINGO file. Therefore, whenever you open the model, the
spreadsheet will be visible. Note that whenever you reopen the LINGO model, you may want to open
the link, so the contents are updated automatically. You can do this by selecting the spreadsheet in the
LINGO model, giving the Edit|Links command, and pressing the Open Links button in the dialog box.
As a final note, LINGO's compiler ignores all embedded links and objects. Thus, you are free to insert
links and objects wherever you choose in a model.
WINDOWS COMMANDS 145
Edit|Select All
Use the Select All command to select the entire contents of the active window. This is useful when you
want to copy the entire contents of the window elsewhere, or if you want to delete the contents of the
window.
Edit|Find... Ctrl+F
Use the Find command to search for a desired string of text in the active window. When you issue the
Find command, you should see the following dialog box:
Enter the text you wish to search for in the Find what box. Check the Match whole word only box to
have LINGO find only whole words of text (i.e., don’t search for occurrences of the text embedded in
other words). Check the Match case box to have LINGO search only for instances of the text with the
same capitalization. Click the Find Next button to find the next instance of the text.
Edit|Find Next Ctrl+N
Use the Find Next command to find the next instance of the text most recently searched for using the
Find command in the active window.
Edit|Replace Ctrl+H
Use the Replace command to replace one string of text with another in the active window. When you
issue the Replace command, you will see the following dialog box:
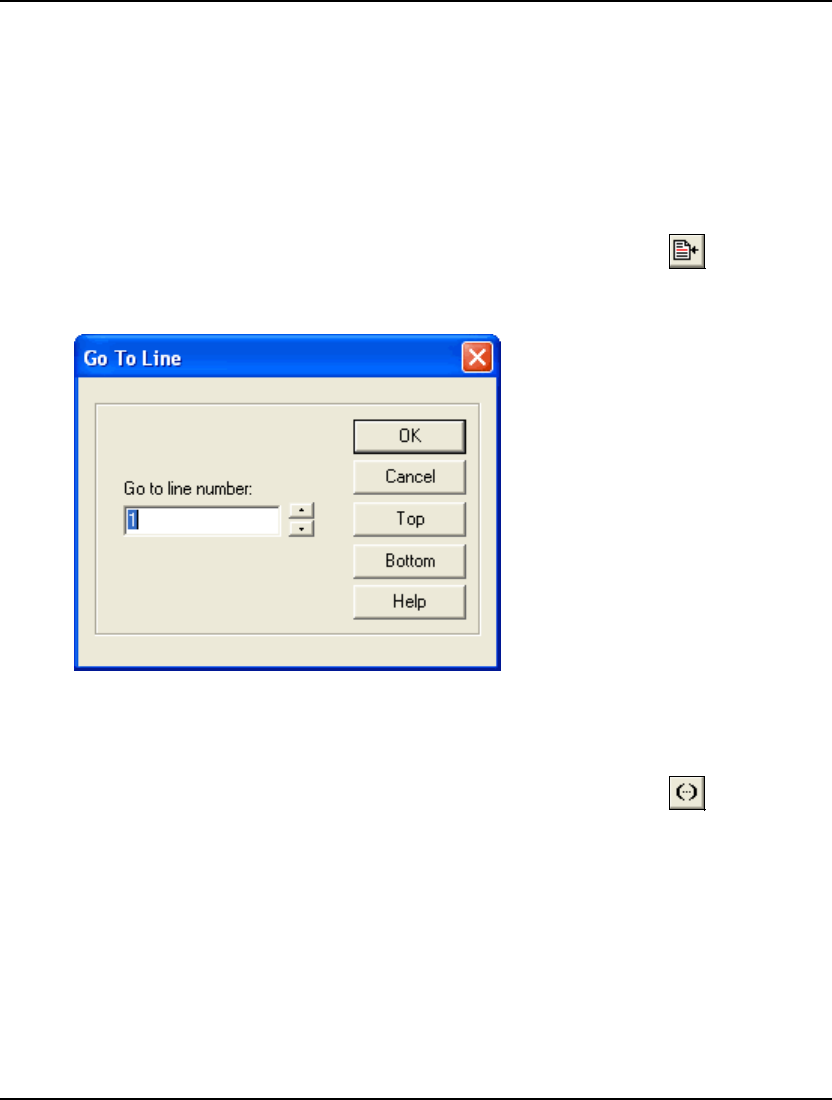
146 CHAPTER 5
Enter the name of the text you want to replace in the Find what box. Enter the text you want to replace
the old text with in the Replace with box. Clicking the Find Next button will cause LINGO to find the
next occurrence of the old text. Clicking the Replace button will cause the next occurrence of the old
text to be replaced by the new text. The Replace All button will replace all occurrences of the old text
with the new text throughout the entire document.
Check the Match whole word only box to have LINGO replace only whole words of the text (i.e., don’t
replace occurrences of the text embedded in other words). Check the Match case box to have LINGO
replace only instances of the text with the same capitalization.
Edit|Go To Line... Ctrl+T
Use the Go To Line command to jump to a selected line in the active window. When you issue the Go
To Line command, you will see the following dialog box:
Enter a line number in the Go to line number box. Then, press the OK button and LINGO will jump to
the desired line number. Press the Top button to go to the top of the document, or the Bottom button to
go to the bottom.
Edit|Match Parenthesis Ctrl+P
Select a parenthesis in a document. Then, use the Match Parenthesis command to find the closing
parenthesis for the selected parenthesis.
This command is useful when using nested statements such as:
@FOR(FXA(I, J):
JP(I, J) = MPF(I) * CAGF(I, J);
JP(I, J) = MPA(J) * CFGA(I, J));
where it may be difficult to find the close of a given parenthesis.
If no parenthesis is selected prior to issuing the Match Parenthesis command, LINGO will select the
parenthesis nearest to the current cursor position.
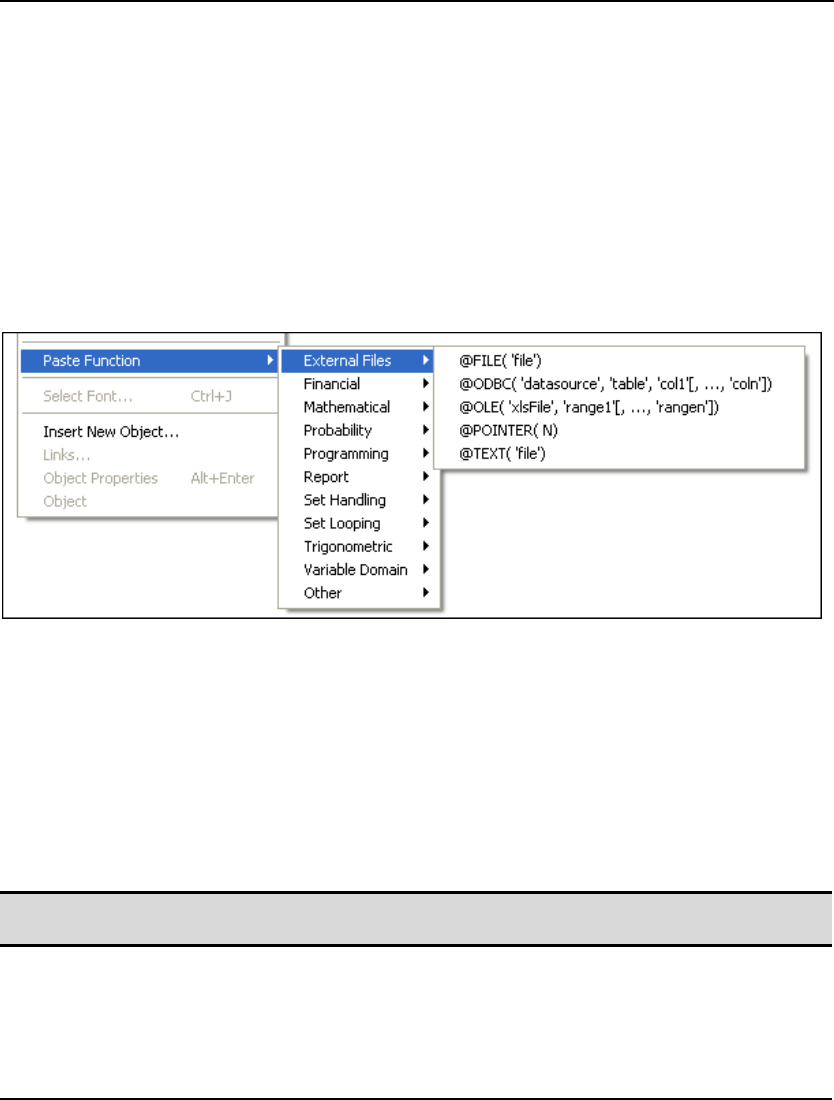
WINDOWS COMMANDS 147
In addition to this command, there is one other way to find matching parentheses. LINGO will
highlight matching parentheses in red when the Match Paren option is enabled under the
LINGO|Options command. By placing the cursor immediately after one of the parentheses of interest,
you will notice that the color of the parenthesis changes from black to red. LINGO will simultaneously
display the matching parenthesis in red. These parentheses will remain displayed in red until you move
the cursor to another position, at which point they will be returned to a black color.
Edit|Paste Function
Use the Paste Function command to paste any of LINGO’s built-in functions at the current insertion
point. Choose the category of the LINGO function you want to paste from the secondary menu, and
then select the function from the cascading menu.
In the following illustration, we have chosen the External Files category from the secondary menu:
On the right are all the functions that deal with external files. By selecting one of these functions,
LINGO will paste a template for the selected function into your document, with a suggestive
placeholder for each argument. You should then replace the argument placeholders with actual
arguments that are relevant to your model.
Edit|Select Font
Use the Select Font command to select a new font, size, style, color, or effect in which to display the
selected text. You may find it easier to read models and solution reports if you select a mono-spaced
font such as Courier. Custom fonts are preserved only when saving in the LG4 file format. (Refer to
the File|New command above for a description of LINGO’s various file types.)
Note: You cannot change the display color of text if syntax coloring is enabled. If you need to use
specific display colors in your document, you will need to disable syntax coloring.
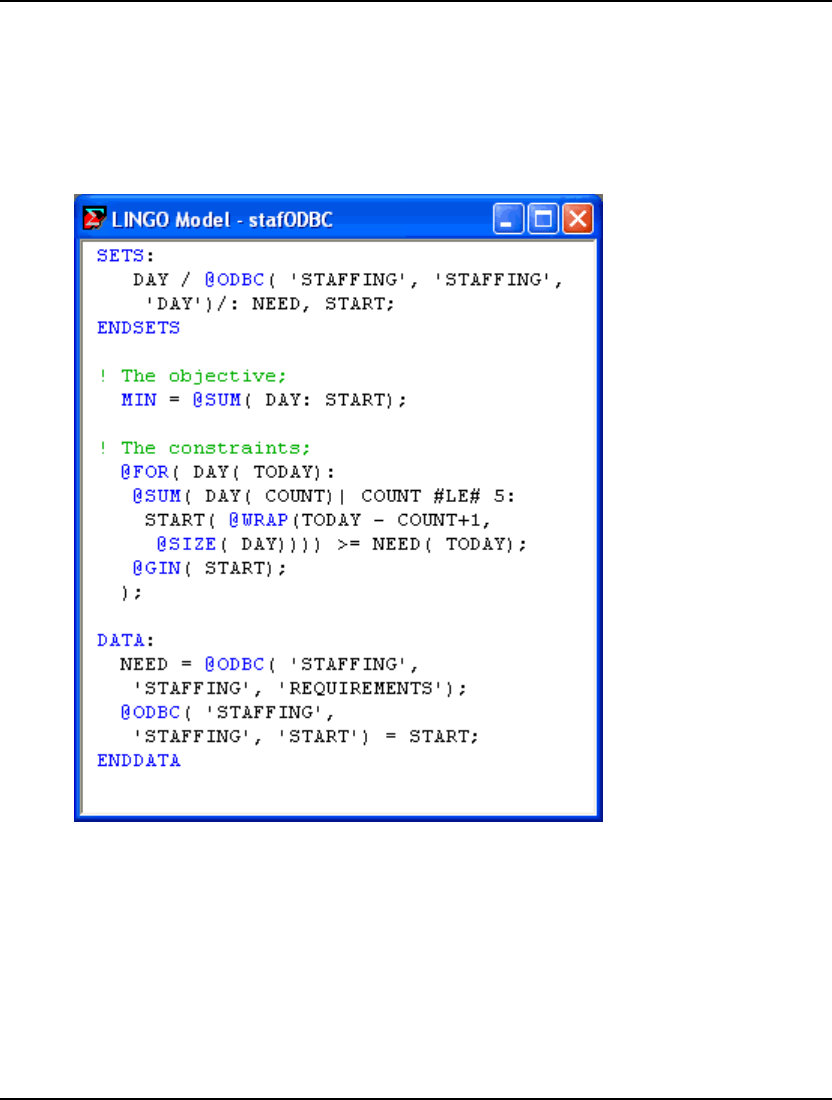
148 CHAPTER 5
Edit|Insert New Object
Use the Insert New Object command to insert an object or a link to an object into your model. As with
the Edit|Paste Special command, this command is helpful in that it allows you to insert links to your
model’s data sources. Unlike the Paste Special command, which links to portions of an external object,
the Insert New Object command can add a link to an entire object.
As an example, suppose you have the following staff-scheduling model:
From the model’s data section, we see that we are using the @ODBC function to retrieve the values for
the NEED attribute from the STAFFING ODBC data source. We are also using the @ODBC function
to send the optimal values for the START attribute back to the same data source. Because this data
source is an integral part of our model, it would be nice to place a link to it in our model, so we can
retrieve it easily each time we want to refer to it. We can do this with the Edit|Insert New Object
command as follows:
1. Position the cursor in the model where you would like the icon for the link
to appear (Note, the LINGO parser ignores links to external objects, so you
can insert the link anywhere you like).
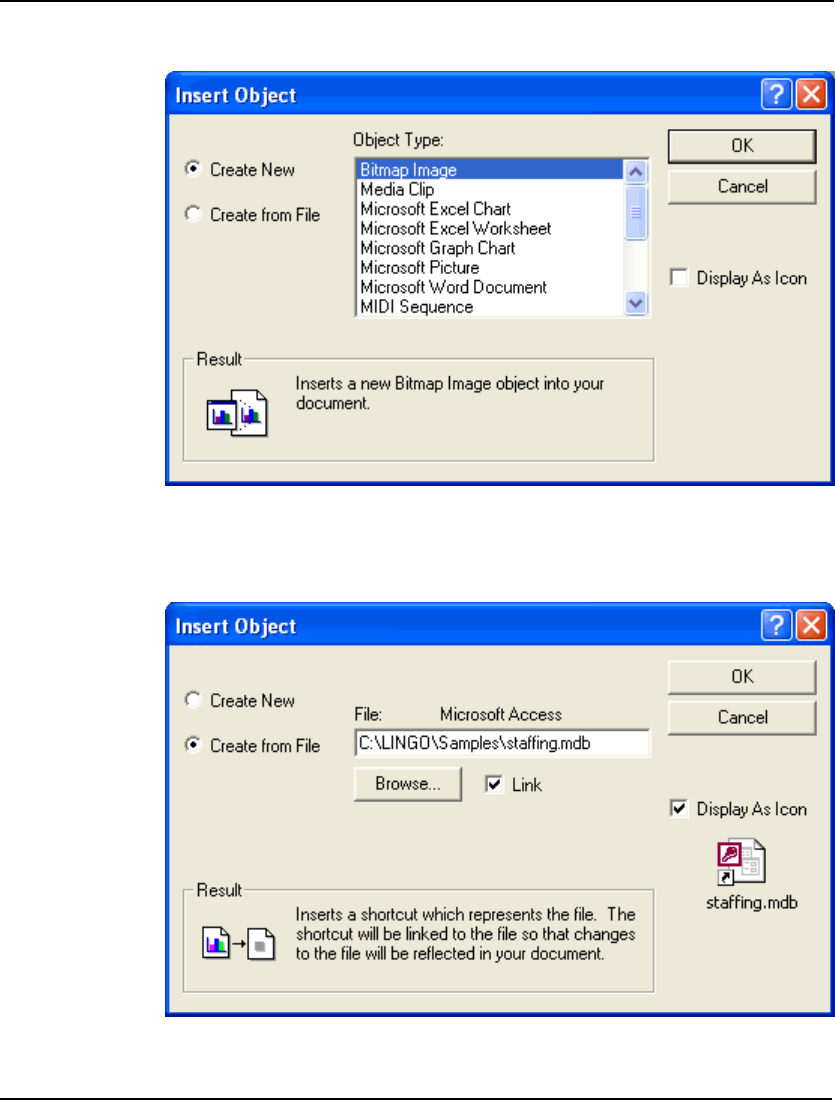
WINDOWS COMMANDS 149
2. Issue the Edit|Insert New Object command. You should see the following
dialog box:
3. Select the Create from File radio button.
4. Type in the name of the database file containing your data.
5. Click the Display As Icon button, so the box now resembles:
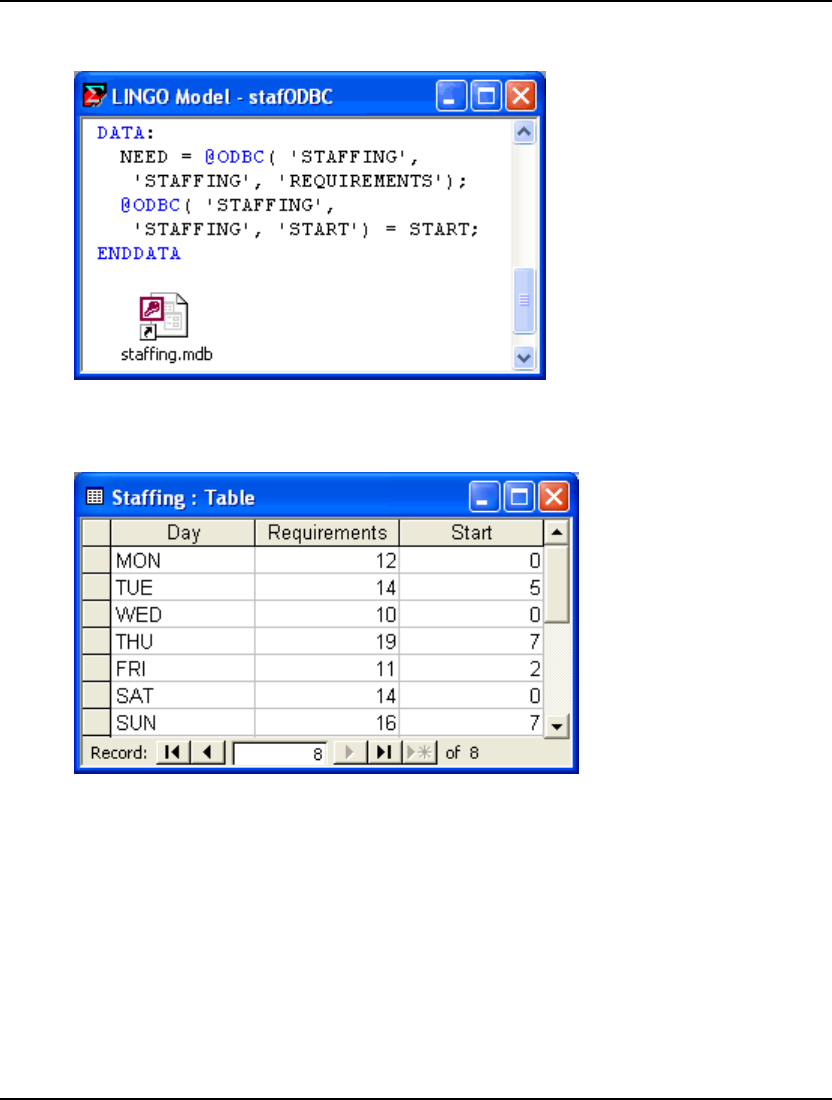
150 CHAPTER 5
6. Finally, click on the OK button, and an icon representing the linked
database will appear in your LINGO model as pictured below:
Now, whenever you want to edit or view the supporting database, all you need do is double-click on
the icon. In this case, Microsoft Access will start and load the staffing database, so you will see the
following on the screen:
As a final note, keep in mind linked objects are preserved only when a model is saved in LG4 format
(see the File|New command above for details on the LG4 file format).
For complete information on exchanging data and solution values with data sources, see Chapter 10,
Interfacing with Databases.
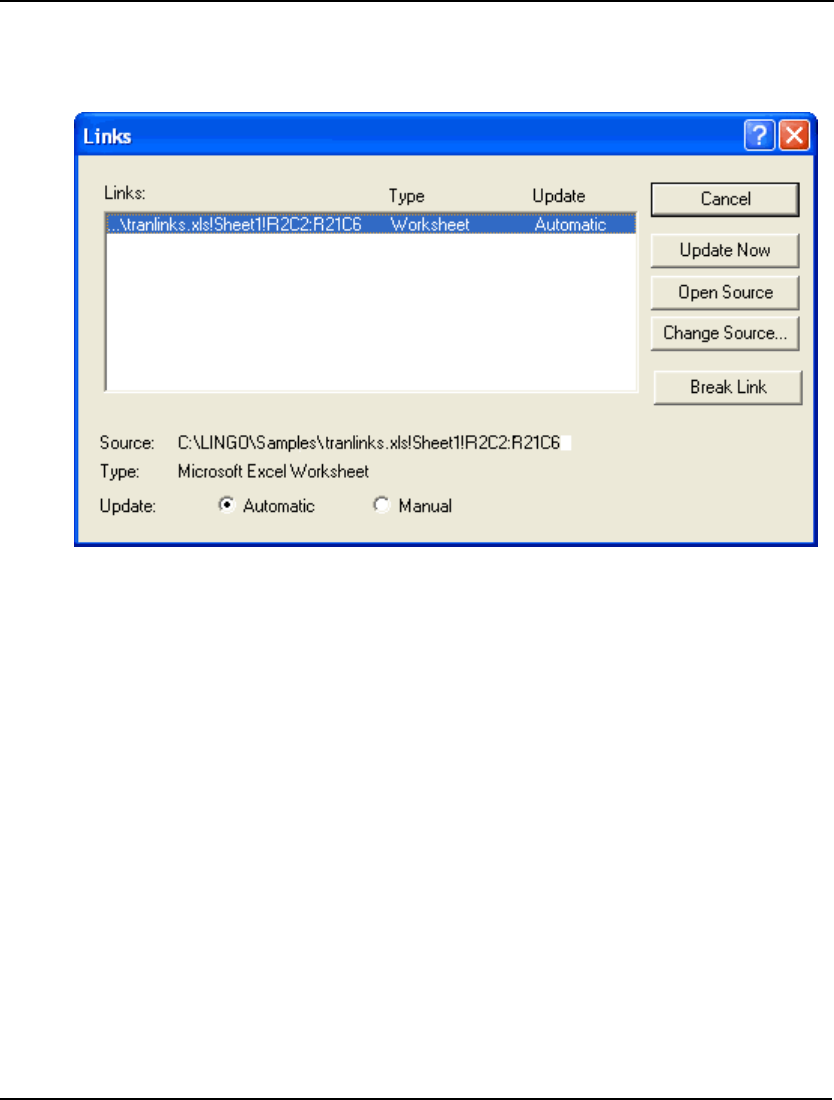
WINDOWS COMMANDS 151
Edit|Links
Use the Links command to modify the properties of the links to external objects in a LINGO
document. The dialog box appears as follows:
Select the Automatic radio button to have LINGO automatically update the object when the source file
is changed. The Manual radio button allows you to update the object only when you select the Update
Now button.
The Open Source button is used to open the connection to an automatic link. Once the link has been
opened, any changes to the source document will be reflected in the view of the object in your LINGO
model.
The Change Source button is used to attach the link to a different source file.
Finally, the Break Link button is used to break the connection to the external object.
Edit|Object Properties Alt+Enter
Select a linked or embedded object in your model by single-clicking it, and then you can use the
Object Properties command to modify the properties of the object. Properties you will be able to
modify include:
1. display of the object,
2. the object’s source,
3. type of update (automatic or manual),
4. opening a link to the object,
5. updating the object, and
6. breaking the link to the object.
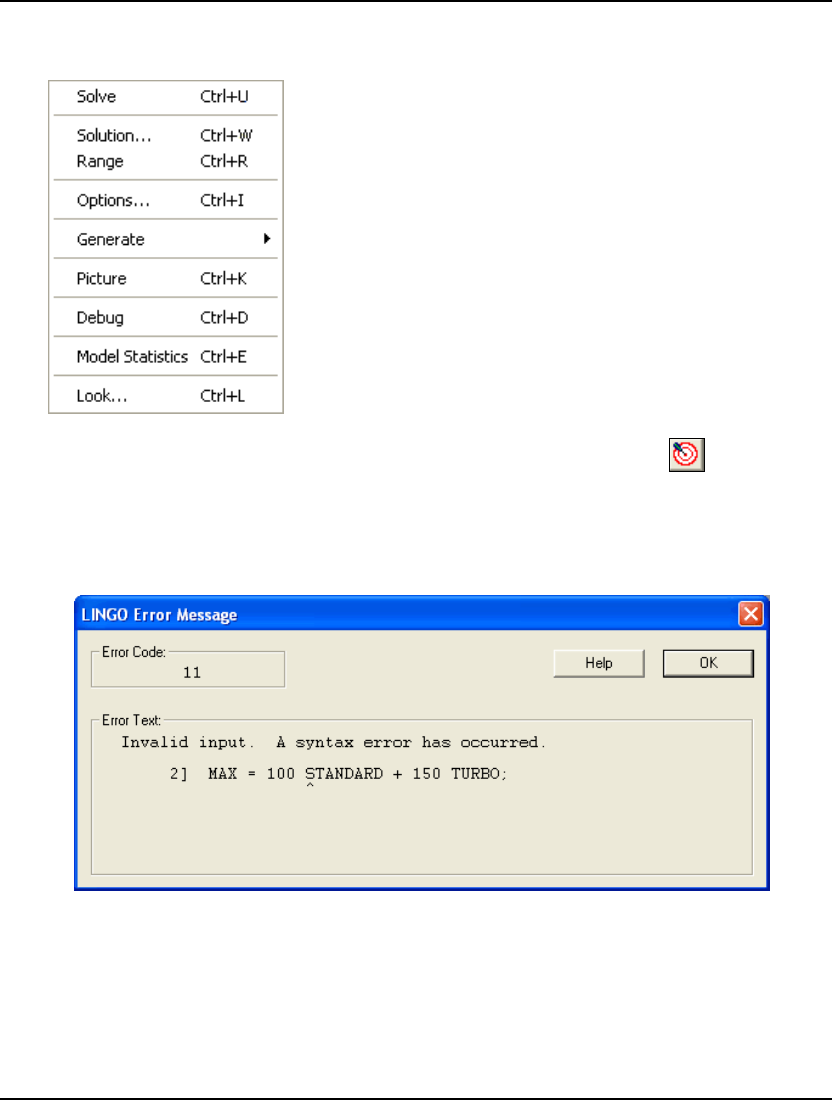
152 CHAPTER 5
3. LINGO Menu
The LINGO menu, pictured at left,
contains commands that generally
pertain to solving a model and
generating reports. This menu also
contains the Options command for
customizing LINGO’s configuration.
LINGO|Solve Ctrl+U
Use the Solve command to have LINGO solve the model in the active window. The Solve command is
available only for model windows—report, script, and data windows cannot be solved.
When you solve a model, LINGO first examines the model’s syntax to determine if it is valid. If
LINGO finds a mistake in the syntax, you will be presented with a dialog box similar to the following:
In the Error Text box, LINGO prints the line number where the syntax error occurred, the text of the
line, and points to where LINGO determines that the error occurred. In most cases, LINGO is good at
pointing to where the error occurred. Sometimes, however, the error may not be located exactly where
LINGO is pointing. Be sure to examine neighboring lines for possible flaws as well. In this particular
example, the syntax error occurred in line 2, where we forgot to insert the multiplication signs (*)
between the two coefficients and variable names.
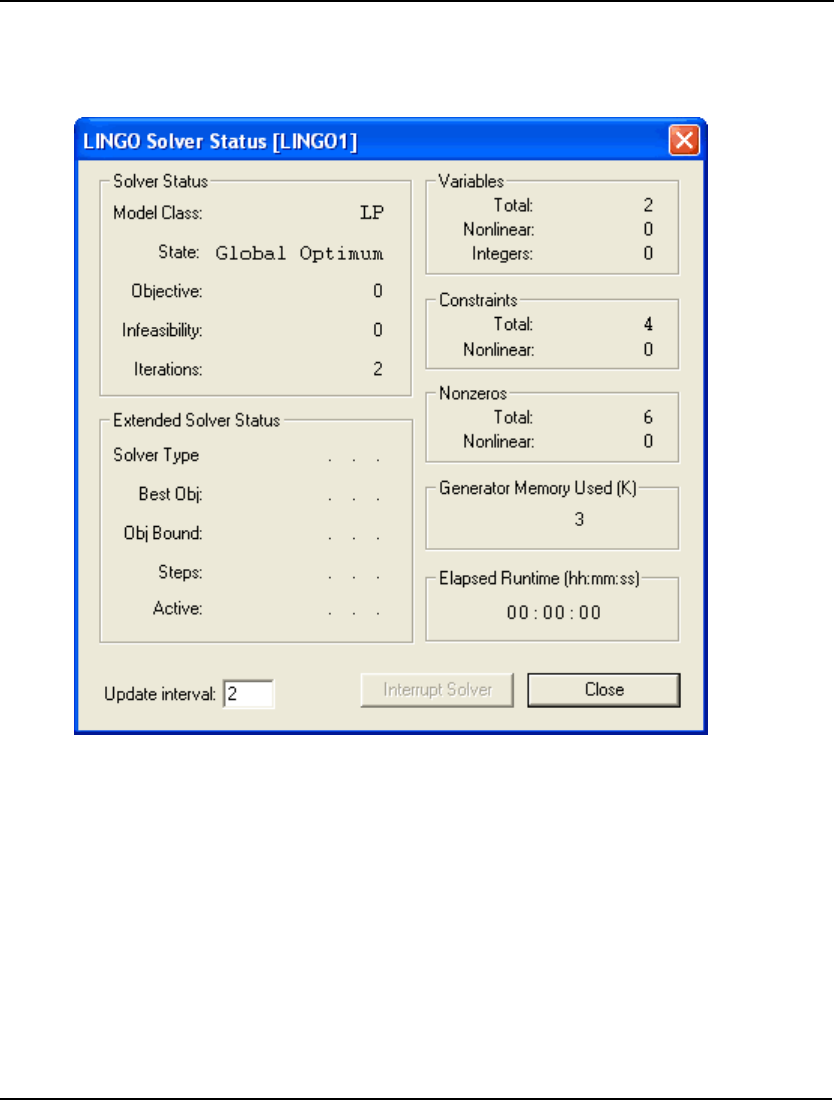
WINDOWS COMMANDS 153
When you issue the Solve command (assuming your model has no further syntax errors), LINGO will
post the solver status window. This window contains information about the composition of your model
and keeps you posted as to the progress of the solver. The solver status window resembles the
following:
For more information on the various fields in the solver status window, refer to Chapter 1, Getting
Started with LINGO.
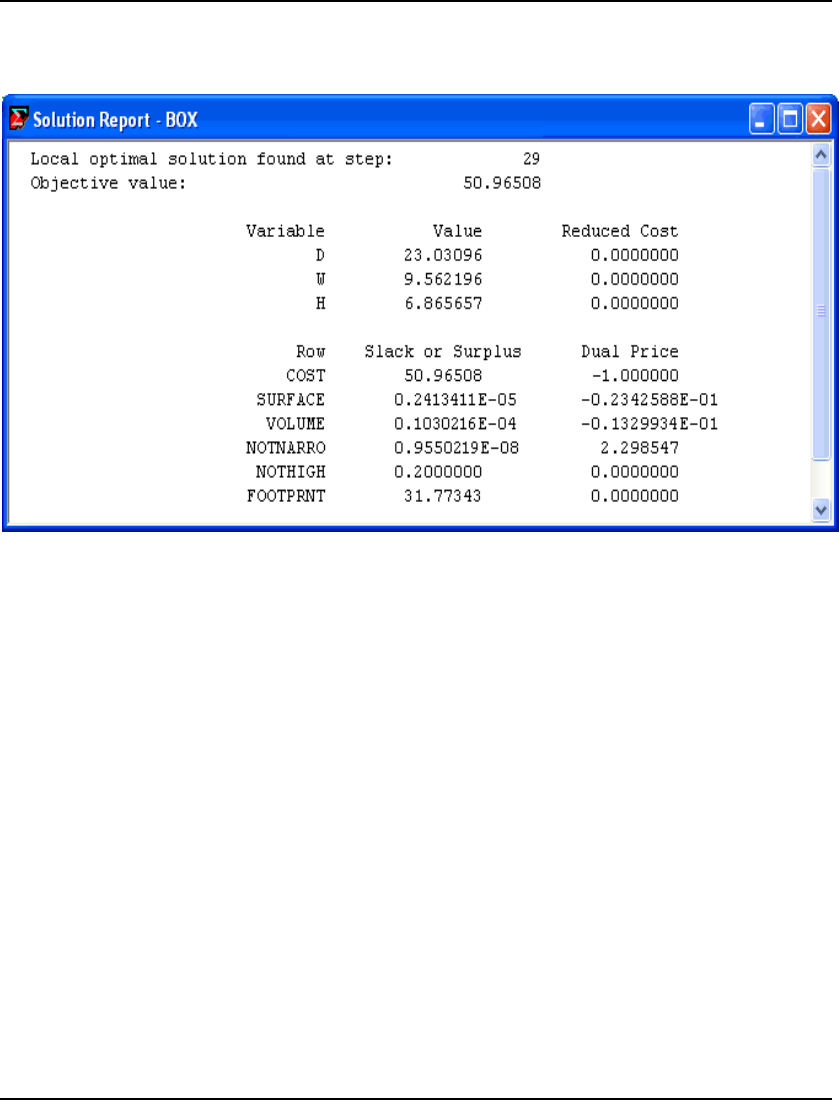
154 CHAPTER 5
Once the solver has completed processing your model, it will create a new window containing the
Solution Report for your model. You can scroll through this window to examine its contents, save it to
a text file, or queue it to your printer. The following is a sample solution report window:
WINDOWS COMMANDS 155
LINGO|Solution Ctrl+W
Use the Solution command to generate a solution report for the active window. The solution report
may be in text or graphical format.
After selecting the model window that you want to generate a solution for, issue the LINGO|Solution
command and you will be presented with this dialog box:
In the Attribute or Row Name list box, select an attribute or row name that you would like a report for.
If you do not select a name in this box, LINGO will generate a full solution report that includes all
attributes and rows.
In the Header Text box, enter whatever text (e.g., “Values for X”) you would like to appear at the head
of the report.
In the box labeled Type of Output, you can select either text or graphical output. If you select Text,
LINGO will create a new window containing the solution in text format. If you select Graph, a new
window containing the solution in one of several different graphical formats will be created. Current
supported graph formats are bar, line, and pie charts.
Check the Nonzeros Only box to see a report that contains only the variables with a nonzero value
and/or only the constraints that are binding.

156 CHAPTER 5
If you select to have the solution displayed as a graph, the Graph Properties box will be undimmed,
which allows you to select options influencing the display of the graph. In the Graph Type box, you
have the option of selecting a Bar, Line, or Pie chart. In the Values box, you can select to graph either
Primal or Dual values. The Bounds box gives you the option of placing bounds on the values
displayed in the graph. If a number is entered in the Lower bound field, LINGO will only display
points in the graph that are greater-than-or-equal-to the value. Conversely, if a value is placed in the
Upper bound field, LINGO will only graph points less-than-or-equal-to the bound. If the Include
Labels box is checked, LINGO will label each point on the graph with the name of the corresponding
variable.
When you click OK, LINGO creates a new solution window containing the solution report. You can
use Cut and Paste commands to move the contents of the report to other applications. If the report is in
text format, you can also save it to a file.
Note: LINGO maintains only one solution in memory. This is the solution to the last window you
issued the LINGO|Solve command for. If you try to issue the Solution command for a window
that LINGO does not currently have a solution for, you will receive an error message. Thus, if
you plan to work with two or more models that take a long time to solve, be sure to save
copies of your solutions. This will allow you to refer to them later without having to re-solve
your models.
LINGO|Range Ctrl+R
Use the Range command to generate a range report for the model in the active window. A range report
shows over what ranges you can: 1) change a coefficient in the objective without causing any of the
optimal values of the decision variables to change, or 2) change a row’s constant term (also referred to
as the right-hand side coefficient) without causing any of the optimal values of the dual prices or
reduced costs to change.
Note: The solver computes range values when you solve a model. Range computations must be
enabled in order for the solver to compute range values. Range computations are not enabled
by default. To enable range computations, select the General Solver Tab under
LINGO|Options and, in the Dual Computations list box, choose the Prices and Ranges option.
Range computations can take a fair amount of computation time, so, if speed is a concern,
you don’t want to enable range computations unnecessarily.
The example model below, when solved, yields the range report that follows:
[OBJECTIVE] MAX = 20 * A + 30 * C;
[ALIM] A <= 60;
[CLIM] C <= 50;
[JOINT] A + 2 * C <= 120;
WINDOWS COMMANDS 157
Here is the range report:
Ranges in which the basis is unchanged:
Objective Coefficient Ranges
Current Allowable Allowable
Variable Coefficient Increase Decrease
A 20.00000 INFINITY 5.000000
C 30.00000 10.00000 30.00000
Right-hand Side Ranges
Row Current Allowable Allowable
RHS Increase Decrease
ALIM 60.00000 60.00000 40.00000
CLIM 50.00000 INFINITY 20.00000
JOINT 120.0000 40.00000 60.00000
The first section of the report is titled Objective Coefficient Ranges. In the first column, titled Variable,
all the optimizable variables are listed by name. The next column, titled Current Coefficient, lists the
current coefficient of the variable in the objective row. The next column, Allowable Increase, tells us
the amount that we could increase the objective coefficient without changing the optimal values for the
variables. The final column, Allowable Decrease, lists the amount that the objective coefficient of the
variable could decrease before the optimal values of the variables would change. Information on the
allowable increases and decreases on objective coefficients can be useful when you need answers to
questions like, “How much more (less) profitable must this activity be before we should be willing to
do more (less) of it?”
Referring to the Objective Coefficient Ranges report for our example, we can say, as long as the
objective coefficient of A is greater-than-or-equal-to 15, the optimal values of the variables will not
change. The same may be said for the objective coefficient of variable C, as long as it falls within the
range of [0,40].
Note: Ranges are valid only if you are planning to alter a single objective or right-hand side
coefficient. The range information provided by LINGO cannot be applied in situations where
one is simultaneously varying two or more coefficients. Furthermore, ranges are only lower
bounds on the amount of change required in a coefficient to actually force a change in the
optimal solution. You can change a coefficient by any amount up to the amount that is
indicated in the range report without causing a change in the optimal solution. Whether the
optimal solution will actually change if you exceed the allowable limit is not certain.
The second section of the range report is Right-hand Side Ranges. The first column, Row, lists the
names of all the optimizable rows, or constraints, in the model. The second column, Current RHS,
gives the constant term, or right-hand side value, for the row. The next two columns, Allowable
Increase and Allowable Decrease, tell us how far we can either increase or decrease the right-hand
side coefficient of the row without causing a change in the optimal values of the dual prices or reduced
costs. If you recall, the dual prices on rows are, effectively, shadow prices that tell us at what price we
should be willing to buy (or sell) our resources for. The dual prices do not, however, tell us what
quantity we should be willing to buy (or sell) at the dual price. This information is obtained from the
allowable increases and decreases on the right-hand side coefficients for the row. So, for our example,
the dual prices and reduced costs will remain constant as long as the right-hand side of row ALIM falls
within the range [20,120], the right-hand side of CLIM is greater-than-or-equal-to 30, and the
right-hand side of JOINT is in [60,160].

158 CHAPTER 5
Note: We preceded all the constraints in our model with a name enclosed in square brackets. This is
an important practice if you wish to generate range reports. If you do not name your
constraints, LINGO assigns them a name that corresponds to the internal index of the
constraint. This internal index will not always correspond to the order of the constraint in the
text of the original model. So, to make the Right-hand Side Ranges section of range reports
meaningful, be sure to name all your constraints (See page 35 for details on assigning
constraint names).
If a variable is nonlinear in the objective, its value in the Current Coefficient column will be displayed
as NONLINEAR. Similarly, if a row is nonlinear, the value in the Current RHS column will be
displayed as NONLINEAR.
Coefficients that can be increased or decreased indefinitely will display a range of INFINITY.
Fixed variables are substituted out of a model and will not appear in a range report. Rows that contain
only fixed variables are also substituted out of models, and will also not appear in range reports. As an
example, suppose we changed the following inequality in our sample model from:
[ALIM] A <= 60;
to the equality:
[ALIM] A = 60;
LINGO can now solve directly for the value of A. The variable A is considered fixed, as is the row
ALIM (since it contains no optimizable variables). Given this, the variable A will no longer appear in
the Objective Coefficient Ranges section of the range report, and the row ALIM will not appear in the
Right-hand Side Ranges section. We can verify this by examining the updated range report:
Ranges in which the basis is unchanged:
Objective Coefficient Ranges
Current Allowable Allowable
Variable Coefficient Increase Decrease
C 30.00000 INFINITY 30.00000
Right-hand Side Ranges
Row Current Allowable Allowable
RHS Increase Decrease
CLIM 50.00000 INFINITY 20.00000
JOINT 60.00000 40.00000 60.00000
Note: LINGO maintains the range report for only one model in memory. This is the report for the
window that you last issued the LINGO|Solve command for. If you try to issue the Range
command for a window that LINGO does not currently have range information for, you will
receive an error message. If you plan to work with two or more models that take a long time
to solve, be sure to save copies of your range reports to disk, so you can refer to them later
without having to re-solve your models.
WINDOWS COMMANDS 159
Note: The barrier crossover option must be enabled if you plan to do range analysis. Range
computations cannot be performed if the final solution is not a basic solution.
LINGO|Options Ctrl+I
Use the LINGO|Options command to change a number of parameters that affect LINGO's user
interface, as well as the way LINGO solves your model. When issuing the Options command, you will
be presented with the following dialog box:
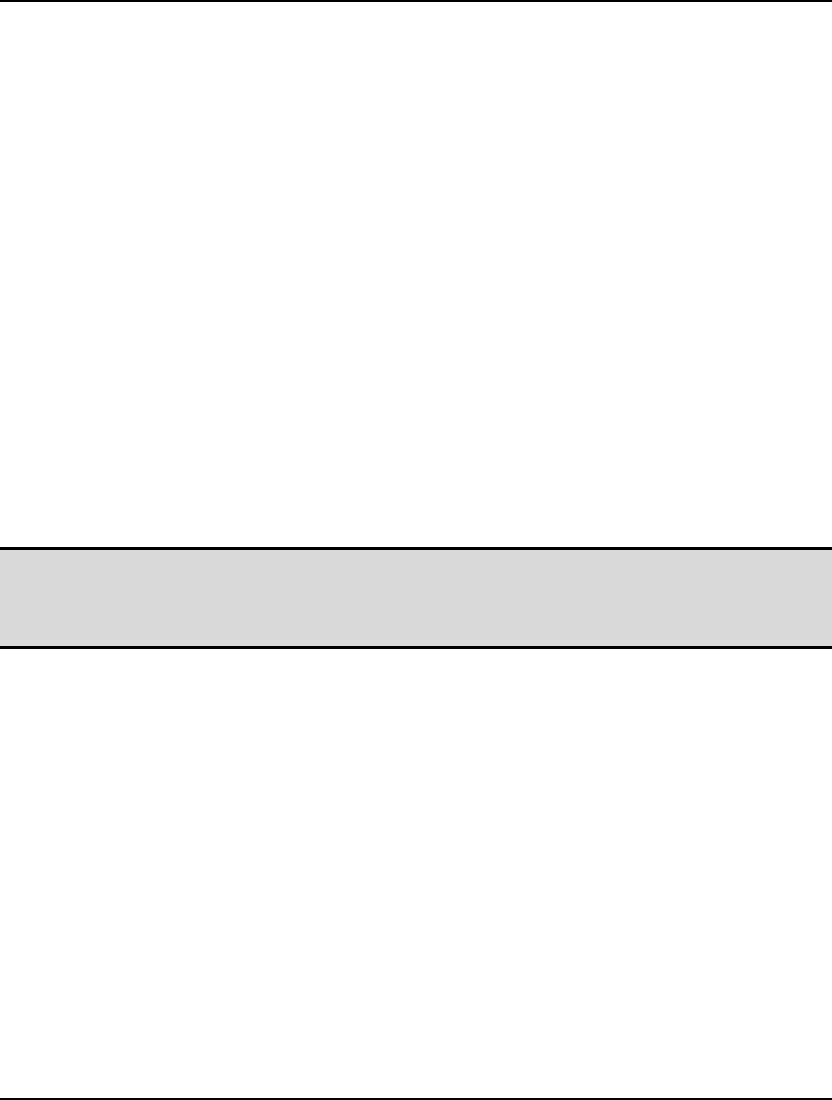
160 CHAPTER 5
Set these parameters to your personal preference and press the Apply button to set them for the extent
of the current LINGO session. The currently selected settings are also applied when you click the OK
button, with the one difference being that the OK button closes the dialog box. If you would like the
current parameter settings to be maintained for use in subsequent LINGO sessions, click the Save
button. The original default settings can be restored at any time by clicking the Default button.
There are nine tabs in the Options dialog box:
♦ Interface
♦ General Solver
♦ Linear Solver
♦ Nonlinear Solver
♦ Integer Pre-Solver
♦ Integer Solver
♦ Global Solver
♦ Model Generator
♦ SP Solver
The first time you run the Options command during a session, the Interface tab will be selected. The
Interface and General Solver tabs contain options of interest to most users. The remaining tabs (Linear
Solver, Nonlinear Solver, Integer Pre-Solver, Integer Solver, Global Solver and SP Solver) contain
advanced options that tend to be of interest primarily to the expert user. Follow the links above for
more details on the options available under each tab.
Note: LINGO uses the LINDO API as its solver engine. The LINDO API has a wealth of advanced
parameter settings to control its various solvers. Most of the more relevant parameters may
be set through the LINGO|Options command. However, some of the more advanced
parameters must be set using the APISET command.
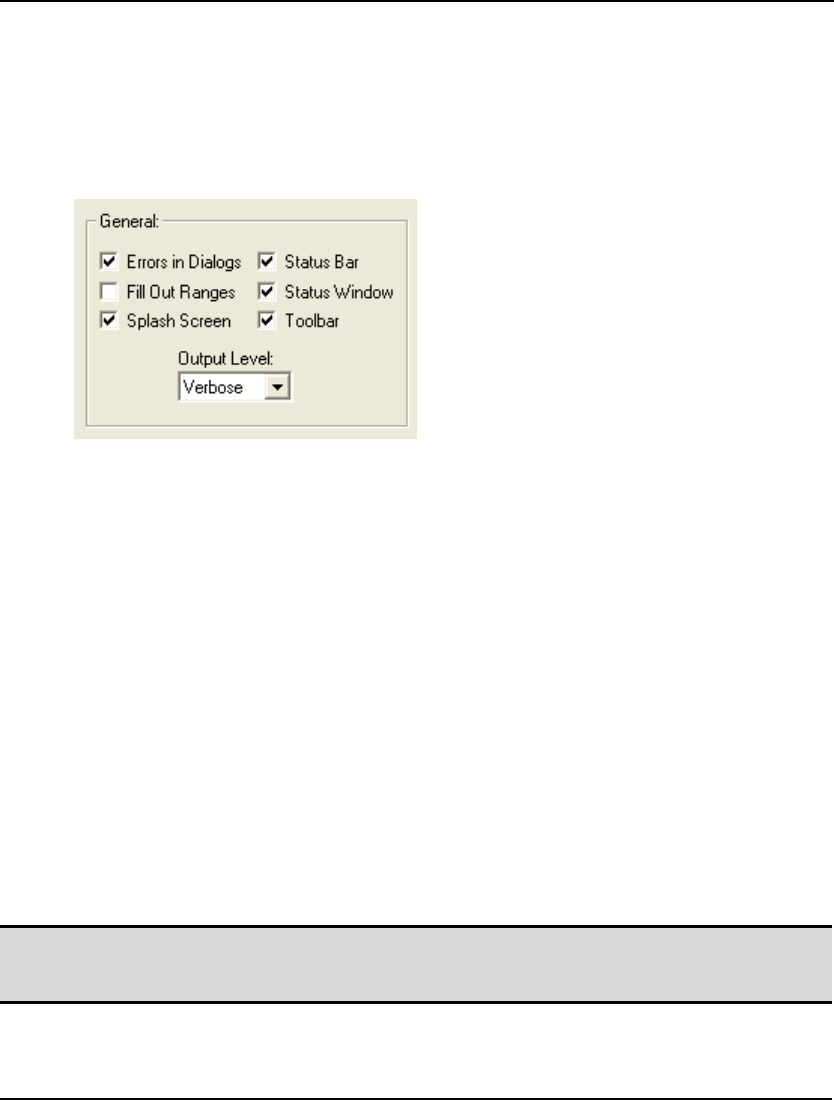
WINDOWS COMMANDS 161
Interface Tab
The Interface tab on the Options dialog box (shown above) can be used to control the appearance of
LINGO, LINGO’s output, and the default file format.
General Box
The General box on the Interface tab:
allows you to set the following general options:
♦ Errors In Dialogs,
♦ Status Bar,
♦ Fill Out Ranges and Tables,
♦ Status Window,
♦ Splash Screen,
♦ Toolbar, and
♦ Output Level.
Errors In Dialogs
If the Errors In Dialogs box is checked, LINGO will display error messages issued by the solver in a
modal dialog box. This dialog box must be cleared before LINGO proceeds with any other operation.
In some instances, you may have LINGO embedded in other applications, where it may not be
desirable, or possible, to have users clearing error dialogs. By unchecking this option, LINGO will
route the solver's error messages to the command window, where they will be displayed, and no user
intervention will be required to clear the messages.
The default is for solver errors to be displayed in dialog boxes.
Note: This option allows you to route only those error messages generated by LINGO's solver to the
report window. Error messages displayed by LINGO's interactive front-end will always be
posted in dialog boxes.

162 CHAPTER 5
Status Bar
If the Status Bar box is checked, LINGO displays a status bar along the bottom of the main frame
window. Among other things, the status bar displays the time of day, location of the cursor, menu tips,
and the current status of the program. To remove the status bar from the screen, clear the Status Bar
checkbox.
The default is for LINGO to display the status bar.
Fill Out Ranges and Tables
LINGO can export a model’s solution to Excel and databases. When exporting to Excel, LINGO
sends solutions to user defined ranges in a workbook. Solutions exported to a database are sent to
tables within the database. In either case, the target range or table may contain more space for values
than you are actually exporting. In other words, there may be cells at the end of ranges or records at
the end of tables that will not be receiving exported values from LINGO. The Fill Out Ranges and
Tables option determines how these extra cells and records are treated.
When the Fill Out Ranges and Tables option is enabled, LINGO overwrites the extra values.
Conversely, when the option is not enabled, LINGO leaves the extra values untouched.
Fill Out Ranges and Tables is disabled by default.
WINDOWS COMMANDS 163
Status Window
If the Status Window box is checked, LINGO displays a solver status window whenever you issue the
LINGO|Solve command. This window resembles the following:
The solver status window is useful for monitoring the progress of the solver and the dimensions of
your model. It is updated every n seconds, where n is the value in the Update interval field in the lower
right corner of the window. For a detailed description of the various fields in the solver status window,
see the section Solver Status Window in Chapter 1, Getting Started with LINGO.
The default is for the solver status window to be displayed.
Splash Screen
If the Splash Screen box is checked, LINGO will display its splash screen each time it starts up. The
splash screen lists the release number of LINGO and the software's copyright notice. If you disable this
option, LINGO will not display the splash screen.
The default is for the splash screen to be displayed.
164 CHAPTER 5
Output Level
You can use the Output Level setting to control the amount of output LINGO generates. There are
four settings available:
Verbose—Causes LINGO to display the maximum amount of output, including full solution
reports.
Terse—Less output than Verbose, with full solution reports suppressed. This is a good output
level if you tend to solve large models. LINGO also suppresses Export Summary Reports
generated when exporting data to spreadsheets or databases.
Errors Only—All output is suppressed, with the exception of error messages.
Nothing—LINGO suppresses all output. This level may be useful when taking advantage of
the programming capabilities in LINGO, in which case, you will add statements to your
model to generate all required output.
The default is for LINGO to be in verbose mode.
Toolbar
If the Toolbar box is checked, LINGO displays its command toolbar containing buttons, which act as
shortcuts to various commands contained in the LINGO menu. For definitions of the buttons on the
toolbar, please see the section The Toolbar at the beginning of this chapter. If the Toolbar checkbox is
unchecked, LINGO does not display its toolbar.
The default is for LINGO to display its toolbar.
Solution Display Box
The Solution Display box on the Interface tab:
allows you to set the following options:
♦ Show as 0, and,
♦ Precision.
Show as 0
On occasion, due to round-off error, some of the values returned by LINGO’s solver will be very small
(less than 1e9.) In reality, the true values of these variables are either zero or so small as to be of no
consequence. These tiny values can be distracting when interpreting a solution report. The Show as 0
parameter can be used to suppress small solution values. Any solution value less-than-or-equal-to
Show as 0 will be reported as being zero.
The default value for Show as 0 is 1e-9.

WINDOWS COMMANDS 165
Precision
LINGO defaults to displaying seven significant digits for values in standard solution reports. In some
cases, you may desire more or less than seven digits of precision, in which case, you will need to
adjust the Precision parameter.
For example, suppose we have a very simple model consisting of the single expression:
X = 1/3;
The default solution report for this model using seven digits of precision would contain:
Variable Value
X 0.3333333
Row Slack or Surplus
1 0.000000
Increasing the Precision parameter to 16 and resolving yields the following solution report with 16
significant digits:
Variable Value
X 0.3333333333333333
Row Slack or Surplus
1 0.000000000000000
The default value for Precision is seven significant digits.
File Format Box
The File Format box on the Interface tab:
is used to select the default file format that LINGO uses to save models to disk. There are three
different formats to choose from: LG4, LNG, or LTX.
The LG4 format is a binary format readable only by LINGO. This format enables you to have custom
formatting, fonts in your models, and to use LINGO as an OLE server and container. Files saved in the
LG4 format are readable only by Windows versions of LINGO.
The LNG format is a text-based format. Thus, models saved in the LNG format can be read into other
applications. LNG format models are transferable to other platforms running LINGO. Models saved in
LNG format cannot contain custom formatting or embedded objects.
LTX files are model files that use the LINDO syntax. Longtime LINDO users may prefer LINDO
syntax over LINGO syntax. LINDO syntax is convenient for quickly entering small to medium sized
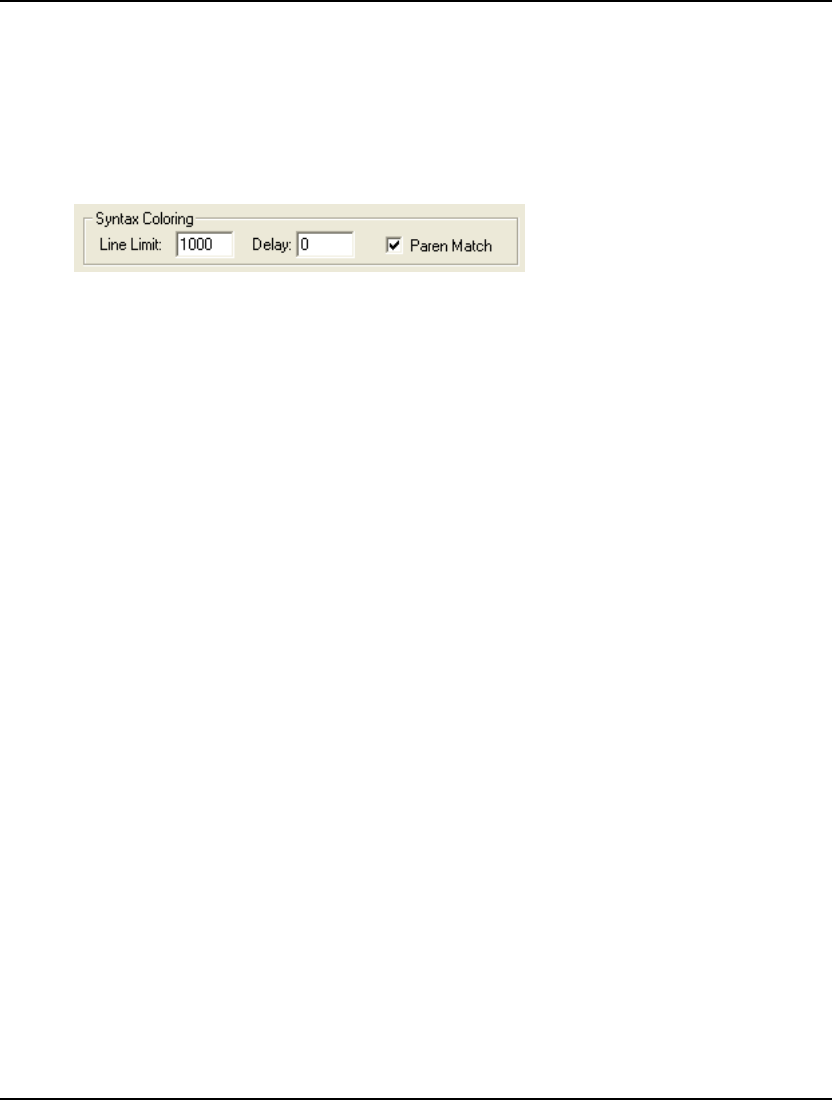
166 CHAPTER 5
linear programs. As long as a file has an extension of .ltx, LINGO will assume that the model is
written using LINDO syntax. Readers interested in the details of LINDO syntax may contact LINDO
Systems to obtain a LINDO user’s manual.
The default file format is LG4.
Syntax Coloring Box
The Syntax Coloring box on the Interface tab:
is used to control the syntax coloring capability in LINGO’s editor. LINGO’s editor is “syntax aware.”
In other words, when it encounters LINGO keywords, it displays them in blue. Comments are
displayed in green, and all remaining text is displayed in black. Matching parentheses are also
highlighted in red when you place the cursor immediately following a parenthesis.
The controls available in this box are: Line Limit, Delay, and Paren Match.
Line Limit
Syntax coloring can take a long time if you have very large files. The Line Limit field sets the
maximum acceptable file size for syntax coloring. Files with line counts exceeding this parameter will
not be syntax colored.
Setting this parameter to 0 will disable the syntax coloring feature. The default line limit is 1000 lines.
Delay
The Delay field sets the number of seconds LINGO waits after the last keystroke was typed before
re-coloring modified text. Users on slower machines may want to set this higher to avoid having
syntax coloring interfere with typing. Users on faster machines may want to decrease this value, so text
is re-colored quickly.
The default is 0 seconds.
Paren Match
If the Paren Match box is checked, LINGO will highlight matching parentheses in red when you place
the cursor immediately following a parenthesis. In other words, by placing the cursor immediately
after one of the parentheses of interest, you will notice that the color of the parenthesis changes from
black to red. LINGO will simultaneously display the matching parenthesis in red. These parentheses
will remain displayed in red until you move the cursor to another position, at which point they will be
returned to a black color.
The default is for parenthesis matching to be enabled.

WINDOWS COMMANDS 167
Command Window Box
The Command Window box on the Interface tab:
is used to customize the configuration of LINGO’s command window.
LINGO’s command window can be opened by using the Window|Command Window command. This
gives the user a command-line interface to LINGO. This interface is identical to ones used by LINGO
on platforms other than Windows. The command window is also useful for testing LINGO command
scripts. For more information on the commands available under LINGO’s command-line interface,
refer to Chapter 6, Command-line Commands.
Send Reports to Command Window
If the Send Reports to Command Windowbox is checked, LINGO will send any reports it generates to
the command window rather than to individual report windows. This is useful if you’d like to have
two or more LINGO generated reports contained in a single window.
The default is to not send reports to the command window.
Echo Input
When you run a LINGO command script with File|Take Commands, the commands LINGO processes
are normally not displayed. If the Echo Input box is checked, processed commands will be displayed in
the command window. This can be a useful feature when you are trying to develop and debug a
LINGO command script.
The default is to not echo input.
Line Count Limits
The Line Count Limits box on the Interface tab:
is used to control the total number of output lines that can be stored in the command window.

168 CHAPTER 5
When LINGO sends output to the command window, it places it at the bottom of the window. All
previous output is scrolled up to make way for the new output. The Maximum field sets the maximum
number of output lines allowed in the command window. When LINGO hits this limit, it starts
removing lines from the top of the command window until there are n lines left, where n is the value of
the Minimum field.
In general, output to the command window will become slower as the maximum and minimum line
counts are increased, or the difference between the maximum and minimum is decreased. If you have a
long session you need to save, you can use the File|Log Output command to log all command window
output to disk.
The default value for Line Count Limits is 800 lines maximum and 400 lines minimum.
Page Size Limits
The Page Size Limits box on the Interface tab:
is used to control the page length and width of the command window.
If you would like LINGO to pause after a certain number of lines have been written to the command
window, you can do so by setting the Length field in the Page Size Limits box. When LINGO hits this
limit, it will display the following button on your screen:
LINGO will wait until you press the More button to display any subsequent output in the command
window. The default is None, meaning no page length limit is imposed.
When LINGO generates reports, it limits output lines to a certain width. In some reports, lines will be
wrapped, so they fall within the line limit. In other reports, lines may be truncated. Because LINGO
concatenates variable names in performing set operations, a variable name such as
SHIPMENTS(WAREHOUSE1, CUSTOMER2) may result. This could be truncated in a solution report
if too narrow an output width is used. You can control this line width limit through the Width field of
the Page Size Limits box. You may set it anywhere between 64 and 200, with the default being 85.
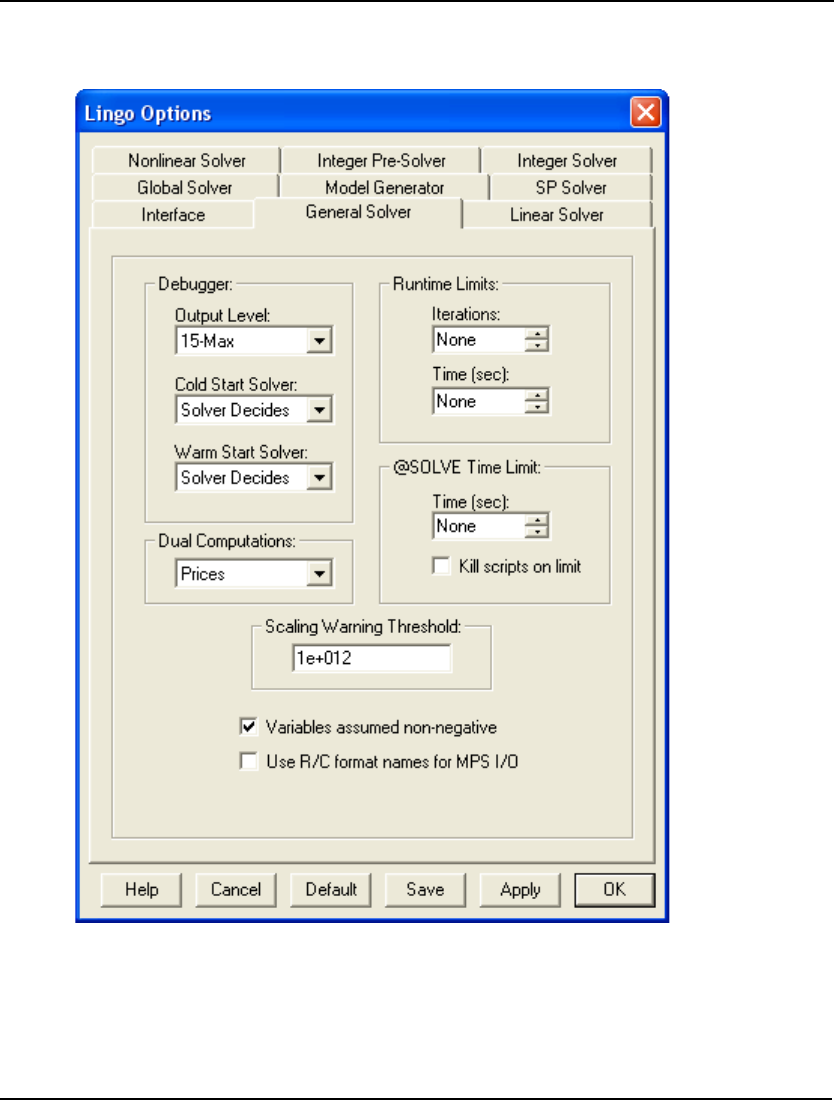
WINDOWS COMMANDS 169
General Solver Tab
The General Solver tab on the Options dialog box, shown here:
can be used to control several general parameters related to the functioning of LINGO’s solver.
170 CHAPTER 5
Debugger Box
The Debugger box on the General Solver tab:
gives you control over the output level and the solver used as part of the model debugging command,
LINGO|Debug. The debugger is very useful in tracking down problems in models that are either
infeasible or unbounded .
The Output Level option controls how much output the model debugger generates. Possible output
levels range from 1 (minimum output) to 15 (maximum output). In general, you will want to generate
as much output as possible. The only reason to restrict the amount of output would be to speed
debugging times on large models.
The default setting for the debugger output level is 15.
The Cold Start Solver and Warm Start Solver options control the solver used on linear models for cold
starts (starting without an existing basis in memory) and warm starts (restarting from an existing basis)
during the debugging process. In either case, the available options are
♦ Solver Decides — LINGO selects the solver it believes is the most appropriate,
♦ Primal — the primal simplex solver will be used,
♦ Dual — the dual simplex solver will be used, and
♦ Barrier — the barrier solver will be used (requires a barrier solver license).
With some models, you may find that choosing a particular solver improves overall performance of the
debugger.
LINGO defaults to Solver Decides for both the cold and warm debug solver.
WINDOWS COMMANDS 171
Runtime Limits Box
The Runtime Limits box on the General Solver tab:
is used to control the length of time the solver spends on your model.
The first field, Iterations, allows you to place an upper limit on the number of iterations the solver will
perform. An iteration is the fundamental operation performed by the solver. At the risk of
oversimplification, it is a process that involves forcing a variable, currently 0, to become nonzero until
some other variable is driven to zero, improving the objective as we go. In general, larger models will
take longer to perform an iteration and nonlinear models will take longer than linear models. The
default iteration limit is None, meaning no limit is imposed on the iteration count.
The second field in the Runtime Limits box, Time (sec), is a limit on the amount of elapsed time the
solver is allowed when optimizing a model. The default time limit is None, meaning no limit is
imposed on the length of time the solver can run.
If the solver hits either of these limits, it returns to normal command mode. If the model contains
integer variables, LINGO will restore the best solution found so far. You may need to be patient,
however, because the solver may have to perform a fair amount of work to reinstall the current best
solution after it hits a runtime limit.
Note: When the solver is interrupted, the only time it will return a valid solution is when the model
contains integer variables and an incumbent integer solution exists. In which case, the solver
backtracks to the incumbent solution before exiting. Interrupting a model without integer
variables will result in an undefined solution. Interrupting a model with integer variables but
no incumbent solution will also return an undefined solution.

172 CHAPTER 5
Dual Computations Box
The Dual Computations box on the General Solver tab:
is used to control the level of dual computations performed by the solver.
The choices for this option are:
♦ None,
♦ Prices,
♦ Prices and Ranges, and
♦ Prices Opt Only.
When the None option is selected, LINGO does not compute any dual and range information. This
option yields the fastest solution times, but is suitable only if you don’t require any dual information.
In fact, the LINGO|Range command will not execute when dual computations are turned off.
When the Prices option is selected, LINGO computes dual values, but not the ranges on the duals.
When Prices & Ranges is selected, LINGO computes both dual prices and ranges
When the Prices, Opt Only option is selected, LINGO computes dual values on the optimizable rows
only—fixed rows simply receive a dual value of 0. Ranges are also not computed under this option.
This can be a useful option if LINGO is spending a lot of time in the “Computing Duals…” phase of
the solution process. This phase is devoted to the computation of dual values on the fixed rows.
LINGO defaults to the Prices option (computing all the dual prices but not ranges.)
Note: If solution times are a concern, you should avoid unnecessarily enabling range computations.
@SOLVE Time Limit Box
The @SOLVE Time Limits box on the General Solver tab:
is used to set time limits on the runtime of @SOLVE commands, which is a command available in calc
sections for solving sub-models. The time limit, if specified, will be applied to each individual
@SOLVE command encountered in calc sections.
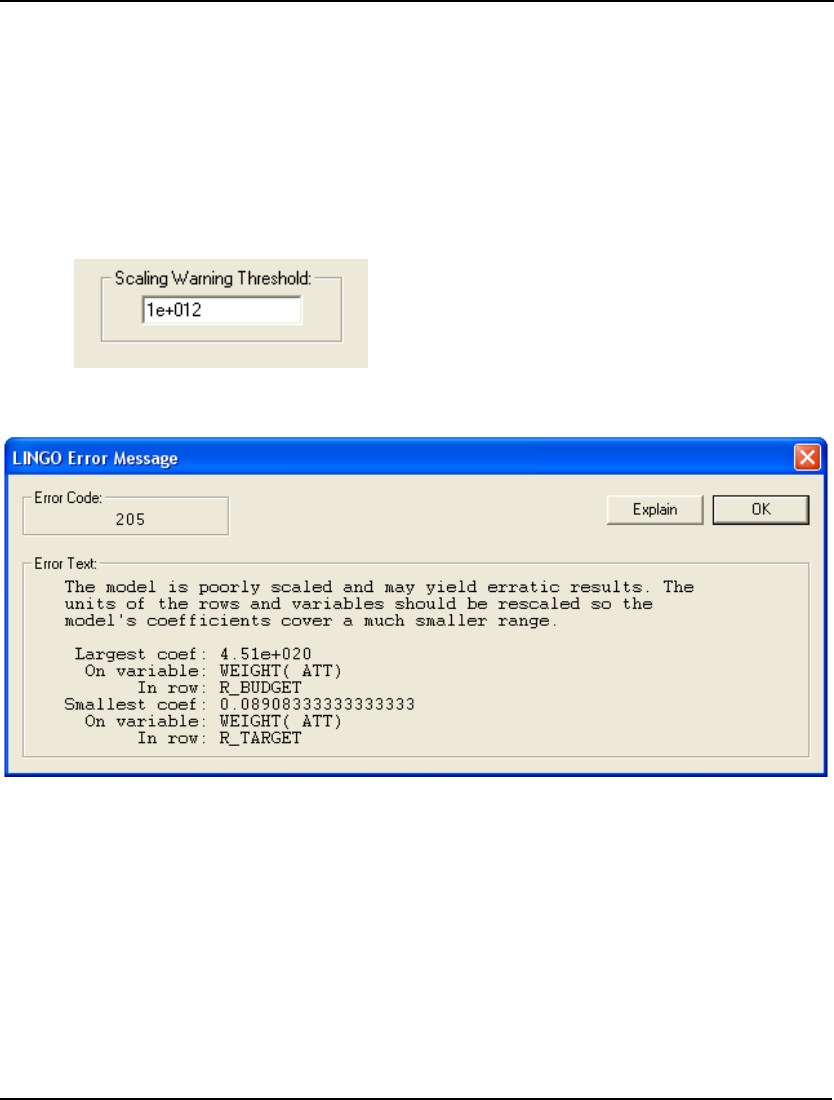
WINDOWS COMMANDS 173
When the None option is selected for the Time field, LINGO does not impose a time limit. Any
nonnegative value will be treated as a runtime limit, in seconds, for each @SOLVE command. If the
time limit is hit, the @SOLVE command will be interrupted, and the best solution found, up to that
point, will be returned.
LINGO defaults to the no time limit on @SOLVE commands and will not kill scripting when interrupts
occur
Scaling Warning Threshold
The Scaling Warning Threshold parameter on the General Solver tab:
controls when LINGO displays its scaling warning message:
When LINGO generates a model, it keeps track of the largest and smallest coefficient values in the
model. LINGO then computes the ratio of the largest to smallest coefficient, and if the absolute value
of this ratio exceeds the setting for Scaling Warning Threshold, LINGO will display the above error
message.
The scaling warning is to reminder that, due to finite precision, round-off error in arithmetic
calculations can result when the largest-to-smallest coefficient ratio becomes too large. Not all models
will necessarily experience round-off problems when the scaling warning is issued, however, it is
something you should be on the lookout for.
The recommended technique for eliminating the scaling warning is to rescale the model so as to reduce
the extreme coefficient ratio. Many times, just scaling units of measure (e.g., dollars to millions of

174 CHAPTER 5
dollars) is enough the bring a model's scaling into line. If this is not possible, or your model is
performing well in light of the poor scaling, you may choose to increase the Scaling Warning
Threshold in order to suppress the warning message.
The default value for the Scaling Warning Threshold is 1.e12.
Variables Assumed Non-Negative
When enabled, the Variables Assumed Non-Negative checkbox on the General Solver tab:
tells LINGO to place a default lower bound of 0 on all variables. In other words, unless otherwise
specified, variables will not be allowed to go negative. Should you want a variable to take on a
negative value, you may always override the default lower bound of 0 using the @BND() function. If
this option is disabled, then LINGO’s default assumption is that variables are unconstrained and may
take on any value, positive or negative. Unconstrained variables are also referred to as be being free
Use RC Format Names
The Use R/C Format names for MPS I/O checkbox on the General Solver tab:
tells LINGO to convert all variable and row names to RC notation when performing MPS file format
Input/Output.
RC format involves renaming each row (constraint) in a model to be Rn, where n is the row’s index.
Similarly, each column (variable) is renamed to Cn. In addition, LINGO renames the objective row to
be ROBJ. Refer to the Importing MPS Files section under the File|Open command earlier in this
chapter for a discussion of RC notation and why this option is useful.
By default, LINGO disables the use of RC format names.
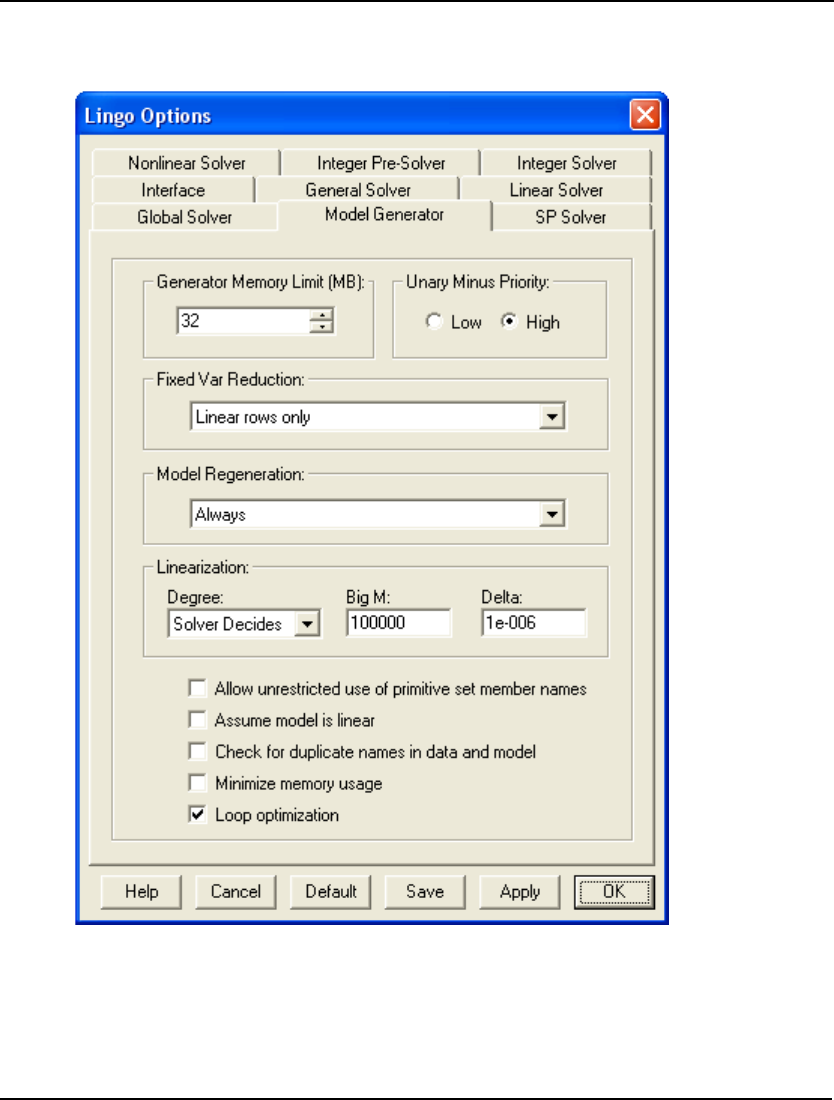
WINDOWS COMMANDS 175
Model Generator Tab
The Model Generator tab on the Options dialog box, shown here:
is used to control several parameters related to the generation of the model. The model generator takes
the expressions in your LINGO model and converts them to a format understood by the solver engines
that find the actual solutions to the model.
176 CHAPTER 5
Generator Memory Limit Box
The Generator Memory Limit box on the Model Generator tab:
is used to control the amount of memory set aside to use as workspace for generating a model.
Large models may run out of generator memory when you attempt to solve them. In this case, you will
receive the error message "The model generator ran out of memory.” To avoid this error, increase the
amount of memory in the Generator Memory Limit field. You will then need to click the Save button
and restart LINGO. Since LINGO sets aside this memory when it starts, changes in LINGO's generator
memory limit are not established until you restart the program.
To determine exactly how much generator memory LINGO was able to successfully allocate, run the
Help|About LINGO command. The About LINGO dialog box displays the amount of generator
memory allocated at startup.
The memory allocated to LINGO’s generator will not be available to the various solver engines
contained in LINGO. Thus, you should not allocate overly excessive amounts of memory to the
generator.
If you set LINGO's generator memory limit to None, LINGO will allocate all available memory when
it starts up. This is not a recommended practice. The default size for the workspace is 32Mb.
Note: By setting LINGO's generator memory limit abnormally high, both LINGO and Windows
will resort to swapping virtual memory to and from the hard drive, which can slow down your
machine dramatically and result in poor performance. In general, set the memory allocation to
a level high enough to comfortably handle your largest models, but not too much higher than
that. You can view the amount of memory used in the allotted workspace at any time by
opening the solver status window and examining the Generator Memory Used field.
Unary Minus Priority
The Unary Minus Priority box on the Model Generator tab:
is used to set the priority of the unary minus operator. The two available options are High and Low.

WINDOWS COMMANDS 177
There are two theories as to the priority that should be assigned to the unary minus (i.e., negation)
operator in mathematical expressions. On the one hand, there is the Excel practice that the unary
minus operator should have the highest priority, in which case, the expression -3^2 would evaluate to
+9. On the other hand, there is the mathematicians’ preference for assigning a lower priority to unary
minus than is assigned to exponentiation, in which case, -3^2 evaluates to -9. Note that regardless
which relative priority is used, one can force the desired result through the use of parenthesis.
LINGO defaults to the Excel approach of setting a higher priority (High) on negation than on
exponentiation.
Fixed Var Reduction
The Fixed Var Reduction box on the Model Generator tab:
is used to control the degree to which fixed variables are substituted out of the ultimate math program
passed to the solver engines.
For example, consider the model:
MAX= 20*X + 30*Y + 12*Z;
X = 2*Y;
X + Y + Z <= 110;
Y = 30;
If we run the LINGO|Generate command, we see that LINGO is able to reduce this model down to the
equivalent, but smaller model:
MAX= 12 * Z + 2100;
Z <= 20;
From the third constraint of the original model, it is obvious that Y is fixed at the value 30. Plugging
this value for Y into the first constraint, we can conclude that X has a value of 60. Substituting these
two fixed variables out of the original formulation yields the reduced formulation above.
In most cases, substituting out fixed variables yields a smaller, more manageable model. In some
cases, however, you may wish to avoid this substitution. An instance in which you might want to
avoid substitution would be when equations have more than one root. When multiple roots are
present, reduction may select a suboptimal root for a particular equation. On the other hand, the global
and multistart solvers are adept at handling equations containing multiple roots. Thus, when using
these solvers one may wish to forgo fixed variable reduction.
The available options are:
♦ None,
♦ Always,
♦ Always, but linear only with global and multi, and
♦ Linear rows only.
178 CHAPTER 5
Selecting None disables all fixed variable reduction. Selecting Always enables reduction. When
Always, but linear only with global and multi is selected, LINGO always enables reduction except
when either the global or multistart solvers are selected, in which case it will only perform reduction
on rows where the key variable appears linearly. The Linear rows only option always limits reduction
to rows in which the key variable is linear.
Note: You should be careful when turning off fixed variable reduction. If the model generator is
unable to substitute out fixed variables, you may end up turning a linear model into a more
difficult nonlinear model.
LINGO defaults to selecting Always, but linear only with global and multi for fixed variable reduction.
Model Regeneration Box
The Model Regeneration box on the Model Generator tab:
is used to control the frequency with which LINGO regenerates a model. Commands that will trigger
the model generator are LINGO|Solve, LINGO|Generate, LINGO|Model Statistics, LINGO|Picture,
LINGO|Debug, and File|Export File.
The choices available under this option are:
♦ Only when text changes - LINGO regenerates a model only when a change has been
made to the model’s text since the last generation took place.
♦ When text changes or with external references – LINGO regenerates whenever a change
is made to the model text or when the model contains references to external data sources
(e.g., text files, databases, or spreadsheets).
♦ Always - (default) LINGO always regenerates the model each time information regarding
the generated model is needed.
Linearization
The Linearization box on the Model Generator tab:
controls the linearization option in LINGO. Many nonlinear operations can be replaced by linear
operations that are mathematically equivalent. The ultimate goal is to replace all the nonlinear
operations in a model with equivalent linear ones, thereby allowing use of the faster and more robust
linear solvers. We refer to this process as linearization. For more information on linearization, please
refer to the section On Mathematical Modeling.

WINDOWS COMMANDS 179
Degree determines the extent to which LINGO will attempt to linearize models. The available options
are:
♦ Solver Decides,
♦ None,
♦ Math only,
♦ Math and Logic.
Under the None option, no linearization occurs. With the Math Only option, LINGO linearizes the
mathematical functions: @ABS(), @FLOOR(), @IF(), @MAX(), @MIN(), @SIGN(). @SMAX(), and
@SMIN() along with any products of binary and continuous variables. The Math and Logic option is
equivalent to the Math option plus LINGO will linearize all logical operators (#LT#, #LE#, #EQ#,
#GT#, #GE#, and #NE#). Under the Solver Decides option, LINGO will do maximum linearization if
the number of variables is less-than-or-equal-to 12, otherwise, LINGO will not perform any
linearization. LINGO defaults to the Solver Decides setting.
The Delta Coefficient is a tolerance indicating how closely you want the additional constraints added
as part of linearization to be satisfied. Most models won’t require any changes to this parameter.
However, some numerically challenging formulations may benefit from increasing Delta slightly.
LINGO defaults to a Delta of 1.e-6.
When LINGO linearizes a model, it will add forcing constraints to the mathematical program
generated to optimize your model. These forcing constraints are of the form:
f( x) = M • y
where M is the BigM Coefficient and y is a 0/1 variable. The idea is that if some activity in the
variables is occurring, then the forcing constraint will drive y to take on the value of 1. Given this, if
we set the BigM value to be too small, we may end up with an infeasible model. Therefore, the astute
reader might conclude that it would be smart to make BigM quite large, thereby minimizing the chance
of an infeasible model. Unfortunately, setting BigM to a large number can lead to numerical stability
problems in the solver resulting in infeasible or sub-optimal solutions. So, getting a good value for the
BigM Coefficient may take some experimentation.

180 CHAPTER 5
As an example of linearization, consider the following model:
MODEL:
SETS:
projects: baths, sqft, beds, cost, est;
ENDSETS
DATA:
projects, beds, baths, sqft, cost =
p1 5 4 6200 559608
p2 2 1 820 151826
p3 1 1 710 125943
p4 4 3 4300 420801
p5 4 2 3800 374751
p6 3 1 2200 251674
p7 3 2 3400 332426
;
ENDDATA
MIN = @MAX( projects: @abs( cost - est));
@FOR( projects:
est = a0 + a1 * beds + a2 * baths + a3 * sqft
);
END
Model: COSTING
This model estimates the cost of home construction jobs based on historical data on the number of
bedrooms, bathrooms, and square footage. The objective minimizes the maximum error over the
sample project set. Both the @MAX() and @ABS() functions in the objective are non-smooth nonlinear
functions, and, as a result, can present problems for LINGO’s default, local search NLP solver.
Running the model under the default settings with linearization disabled, we get the following result:
Local optimal solution found at step: 91
Objective value: 3997.347
Variable Value Reduced Cost
A0 37441.55 0.000000
A1 27234.51 0.000000
A2 23416.53 0.000000
A3 47.77956 0.000000
Enabling linearization and re-optimizing yields the substantially better solution:
Global optimal solution found at step: 186
Objective value: 1426.660
Variable Value Reduced Cost
A0 46814.64 0.000000
A1 22824.18 0.000000
A2 16717.33 0.000000
A3 53.74674 0.000000
Note that the maximum error has been reduced from 3,997 to 1,426!

WINDOWS COMMANDS 181
Linearization will substantially increase the size of your model. The sample model above, in un-
linearized form, has a mere 8 rows and 11 continuous variables. On the other hand, the linearized
version has 51 rows, 33 continuous variables, and 14 binary variables! Although linearization will
cause your model to grow in size, you will tend to get much better solution results if the model can be
converted entirely to an equivalent linear form.
Note: Linearization will be of most use when a nonlinear model can be 100% linearized. If LINGO
can only linearize a portion of your model, then you may actually end up with a more difficult
nonlinear model.
The linearization option is set to Solver Decides by default.
Allow Unrestricted Use of Primitive Set Member Names Check Box
The Allow unrestricted use of primitive set member names checkbox on the Model Generator tab:
allows for backward compatibility with models created in earlier releases of LINGO.
In many instances, you will need to get the index of a primitive set member within its set. Prior to
release 4 of LINGO, you could do this by using the primitive set member’s name directly in the
model’s equations. This can create problems when you are importing set members from an external
source. In this case, you will not necessarily know the names of the set members beforehand. When
one of the imported primitive set members happens to have the same name as a variable in your model,
unintended results can occur. More specifically, LINGO will not treat such a variable as optimizable.
In fact, it would treat it as if it were a constant equal to the value of the index of the primitive set
member!
In short, different primitive set names can potentially lead to different results. Therefore, starting with
release 4.0 of LINGO, models such as the following were no longer permitted:
MODEL:
SETS:
DAYS /MO TU WE TH FR SA SU/;
ENDSETS
INDEX_OF_FRIDAY = FR;
END
If you want the index of FR in the DAYS set, you should now use the @INDEX function:
INDEX_OF_FRIDAY = @INDEX(DAYS, FR);
By default, LINGO disables the use of primitive set member names.
Assume Model Is Linear
The Assume model is linear checkbox on the Model Generator tab:

182 CHAPTER 5
This option can be used for minimizing memory usage on models that are entirely linear. When this
option is in effect, the model generator can take steps to dramatically reduce overall memory
consumption without sacrificing performance. In fact, if all your models are linear, we recommend
that you enable this option permanently as the default for your installation. The one restriction is that
the model must prove to be entirely linear. If a single nonlinearity is detected, you will receive an
error message stating that the model is nonlinear and model generation will cease. At which point, you
should clear this option and attempt to solve the model again.
By default, the Assume model is linear option is disabled.
Check for Duplicate Names
The Check for duplicate names in data and model checkbox on the General Solver tab:
allows you to test your LINGO models from older releases for instances where primitive set members
appear in the model’s equations. The next time you run a model, LINGO will issue an error message if
duplicate names appear as set members and as variables in the model.
Earlier releases of LINGO allowed you to use primitive set names in the equations of a model.
Primitive set names in a model’s equations returned the index of the set member. Starting with release
4.0, LINGO required you to use the @INDEX function (see the Chapter 7, LINGO's Operators and
Functions) to get the index of a primitive set member.
By default, this option is disabled.
Minimize Memory Usage
The Minimize memory usage checkbox on the General Solver tab:
may be used to guide LINGO’s memory usage. Enabling Minimize memory usage causes LINGO to
opt for less memory usage when solving a model. The downside is that opting for less memory may
result in longer runtimes.
LINGO defaults to disabling Minimize memory usage.
Loop Optimization
The Loop optimization checkbox on the General Solver tab:
is used to either enable or disable LINGO's loop optimization step. Loop optimization reformulates
expressions containing set looping functions in order to make them more efficient, while maintaining
mathematical equivalency. The end goal of loop optimization is to minimize the number of passes
through the inner loop of any nested loops in an expression.

WINDOWS COMMANDS 183
As an example, consider the following transportation model fragment, that just contains constraints for
satisfying customer demand:
MODEL:
! A transportation problem fragment;
SETS:
WAREHOUSE /1..50/ : CAPACITY;
CUSTOMER /1..5000/ : DEMAND;
ROUTES( WAREHOUSE, CUSTOMER) : COST, VOLUME;
ENDSETS
! The demand constraints;
@FOR( CUSTOMER( J):
@SUM( ROUTES( I, J): VOLUME( I, J)) >= DEMAND( J)
);
END
Transportation Model Fragment with Inefficient Constraints
In the demand constraints expression there are two loops ⎯ an outer @FOR() over the CUSTOMER
set and an inner @SUM() over the ROUTES set. As written, the inner loop must be executed
5000*50*5000=1.25 billion times. Note that a valid reformulation of these demand constraints would
be:
! The demand constraints;
@FOR( CUSTOMER( J):
@SUM( WAREHOUSE( I): VOLUME( I, J)) >= DEMAND( J)
);
With the expression rewritten in this manner, the inner loop will now only be executed 50*5000 times,
reducing the total number of passes by a factor of 5000. LINGO's loop optimizer seeks out such
inefficient loops and, invisible to the user, rewrites them before the model gets passed to the generator.
Of course, the end result of such reformulations are faster generation times. In fact, the speedup from
reformulation can be quite dramatic in many cases. In this particular example, the reformulated
version ran over 400 times faster in the model generator.
Note that in some cases, particularly with models that primarily contain sparse sets, loop optimization
may actually increase runtimes. So, you should compare runtimes with, and without, the feature being
enabled.
By default, the Loop optimization feature is disabled.
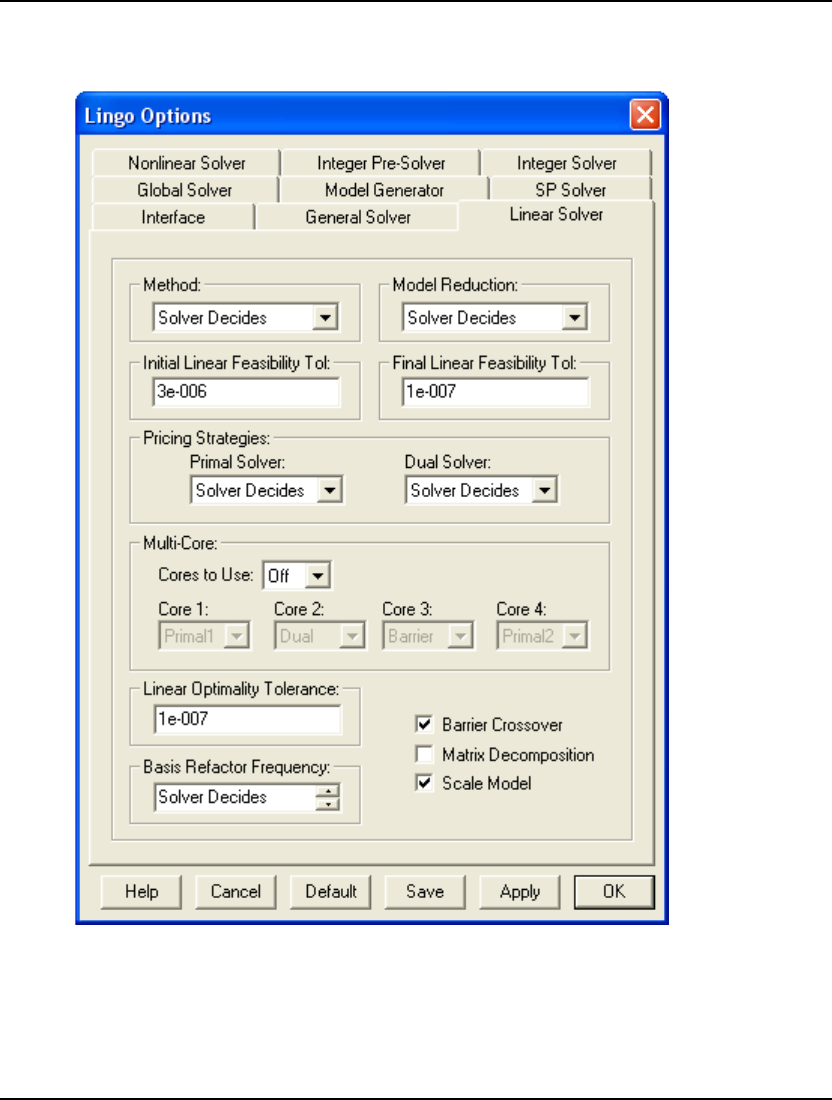
184 CHAPTER 5
Linear Solver Tab
The Linear Solver tab on the Options dialog box, pictured here:
can be used to control several options, discussed below, for tailoring the operation of LINGO’s linear
solver. The linear solver is used on linear models and on mixed integer linear models as part of the
branch-and-bound process.
WINDOWS COMMANDS 185
Method Box
The Method box on the Linear Solver tab:
is used to control the algorithm LINGO’s linear solver employs.
The current choices are:
♦ Solver Decides - LINGO selects the algorithm it determines is most appropriate.
♦ Primal Simplex - LINGO uses a primal simplex algorithm.
♦ Dual Simplex - LINGO uses a dual simplex algorithm.
♦ Barrier - LINGO uses a barrier algorithm (i.e., interior point).
The simplex algorithm moves around the exterior of the feasible region to the optimal solution, while
the interior point algorithm, Barrier, moves through the interior of the feasible region. In general, it is
difficult to say which algorithm will be fastest for a particular model. A rough guideline is Primal
Simplex tends to do better on sparse models with fewer rows than columns. Dual Simplex does well on
sparse models with fewer columns than rows. Barrier works best on densely structured models or very
large models.
The barrier solver is available only as an additional option to the LINGO package. Furthermore, if the
model has any integer variables, the barrier solver will be used for solving the LP at the initial root
node of the branch-and-bound tree, but may or may not be used on subsequent nodes. From a
performance point-of-view, the barrier solver’s impact will be reduced on integer models.
LINGO defaults to the Solver Decides option.
Model Reduction Box
The Model Reduction box on the Linear Solver tab:
is used to control the amount of model reduction performed by LINGO’s linear solver.
Your options are:
♦ Off - Disables reduction,
♦ On - Reduction is used on all models, and
♦ Solver Decides - LINGO decides whether or not to use reduction.
When this option is enabled, LINGO attempts to identify and remove extraneous variables and
constraints from the formulation before solving. In certain cases, this can greatly reduce the size of the
final model to be solved. Sometimes, however, reduction merely adds to solution times without
trimming back much on the size of the model.
LINGO defaults to the Solver Decides option.
186 CHAPTER 5
Feasibility Tolerance Boxes
The Initial Linear Feasibility Tol. and the Final Linear Feasibility Tol. boxes on the Linear Solver tab:
are used to control the feasibility tolerances for the linear solver. These tolerances are related to how
closely constraints must be satisfied in linear models. In general, if your models are well formulated,
you should not have to modify these tolerances. However, access to these tolerances is provided for the
expert user.
Due to the finite precision available for floating point operations on digital computers, LINGO can’t
always satisfy each constraint exactly. Given this, LINGO uses these two tolerances as limits on the
amount of violation allowed on a constraint while still considering it “satisfied”. These two tolerances
are referred to as the Initial Linear Feasibility Tolerance (ILFT) and the Final Linear Feasibility
Tolerance (FLFT). The default values for these tolerances are, respectively, .000003 and .0000001.
The ILFT is used when the solver begins iterating. In the early stages of the solution process, having
the solver less concerned with accuracy issues can boost performance. When LINGO thinks it has an
optimal solution, it switches to the more restrictive FLFT. At this stage in the solution process, you
want a relatively high degree of accuracy. Thus, the FLFT should be smaller than the ILFT.
One instance where these tolerances can be of use is when LINGO returns a solution that is almost
feasible. You can verify this by checking the values in the Slack or Surplus column in the model’s
solution report. If there are only a few rows with small negative values in this column, then you have a
solution that is close to being feasible. Loosening (i.e., increasing) the ILFT and FLFT may help you
get a feasible solution. This is particularly true in a model where scaling is poor (i.e., very large and
very small coefficients are used in the same model), and the units of measurement on some constraints
are such that minor violations are insignificant. For instance, suppose you have a budget constraint
measured in millions of dollars. In this case, a violation of a few pennies would be of no consequence.
Short of the preferred method of rescaling your model, loosening the feasibility tolerances may be the
most expedient way around a problem of this nature.
Pricing Strategies Box
The Pricing Strategies box on the Linear Solver tab:
is used to control the pricing strategy used by LINGO’s simplex solvers. Pricing determines the
relative attractiveness of the variables during the simplex algorithm.
WINDOWS COMMANDS 187
For the Primal Solver, you have the following choices:
♦ Solver Decides - LINGO selects the pricing method it believes is the most appropriate.
♦ Partial - LINGO prices out a small subset of variables at each iteration and intermittently
prices out all the variables to determine a new subset of interesting variables.
♦ Devex - Devex prices out all columns at each iteration using a steepest-edge
approximation (see below).
Partial pricing tends to yield faster iterations. Devex, while slower, results in fewer overall iteration
and can be helpful when models are degenerate. Thus, it is difficult to determine what method is
superior beforehand.
For the Dual Solver, you have these options:
♦ Solver Decides - LINGO selects the pricing method it believes is the most appropriate.
♦ Dantzig - The dual simplex solver will tend to select variables that offer the highest
absolute rate of improvement to the objective regardless of how far other variables may
have to move per unit of movement in the newly introduced variable.
♦ Steepest Edge - The dual solver spends a little more time selecting variables by looking at
the total improvement in the objective when adjusting a particular variable.
♦ Devex - Devex prices out all columns at each iteration using a steepest-edge
approximation.
♦ Approximate Devex - An simplified implementation of true Devex pricing.
Dantzig pricing generally yields faster iterations, however, the other variables in the model
may quickly hit a bound resulting in little gain to the objective. With the steepest-edge option,
each iteration will tend to lead to larger gains in the objective resulting in fewer overall
iterations, however, each iteration will tend to take more compute time due to increased time
spent in pricing. The Devex options approximate true steepest-edge pricing..
Multi-Core Box
The Multi-Core box on the Linear Solver tab:
may be used to perform parallel solves of linear programs on multiple cores. One of four different
linear solvers is chosen for each core. LINGO will take the solution from the solver that finishes first
and then interrupt the remaining solver threads.
The idea behind this approach is that different linear solvers will have relatively better or worse
performance on different classes of models. However, it may be difficult to predict beforehand the
solver that is most likely to outperform. So, by enabling multi-core solves, we guarantee that we will
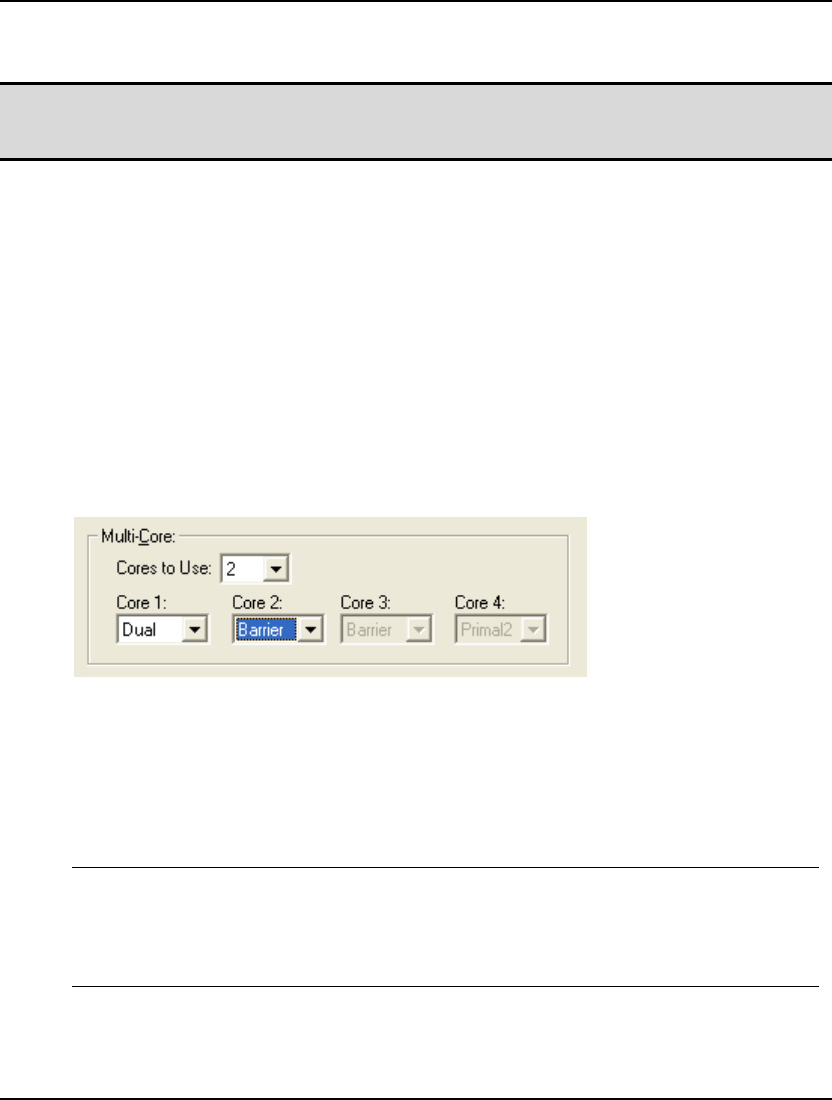
188 CHAPTER 5
always get top performance, even without knowledge beforehand of which solver is likely to run the
fastest.
Note: The multi-core feature requires that your machine have at least one core free for each solver
you wish to run. Using this feature with an inadequate number of cores will tend to decrease
overall performance.
For the Cores to Use parameter, you have the following choices: Off, 2, 3, or 4. When the default Off
option is selected, the multi-core feature is disabled, and LINGO will run only one solver on linear
programs, namely the one specified as part of the Solver Method option detailed above. When either
option 2, 3, or 4 is selected, LINGO will run linear solvers in the requested number of cores.
When selecting two or more cores, you will have the option to specify which of the linear solvers to
use in each of the running cores as part of the Core1 - Core4 list boxes. The available linear solvers
are:
♦ Primal1 - Primal simplex algorithm 1
♦ Dual - Dual simplex algorithm
♦ Barrier - Barrier/Interior point solver (available as a option)
♦ Primal2 - Primal simplex algorithm 2, installed as part of the Barrier option
As an example, the settings of the Multi-Core box below are requesting to run LP solvers in two cores,
with core 1 running the dual simplex solver and core 2 running the barrier solver:
While LINGO is solving linear programs it normally displays solver statistics in the Solver Status
Window. This will also be true with muti-core solves. However, LINGO reports the statistics from
only one of the solvers, specifically, the solver selected to run in Core 1. Once optimization is
complete, LINGO will populate the Solver Status Window with statistics from the solver that finished
first. Finally, as part of the solution report, LINGO will display a line indicating the solver that
finished first. In the solution report excerpt below, we see that the dual simplex solver was the first to
completion:
First returning solver: DUAL SIMPLEX
Global optimal solution found.
Objective value: 1272282.
Infeasibilities: 0.9313226E-09
Total solver iterations: 34862

WINDOWS COMMANDS 189
Linear Optimality Tolerance Box
The Linear Optimality Tolerance box on the Linear Solver tab:
allows you to control the setting for the linear optimality tolerance. This tolerance is used to determine
whether a reduced cost on a variable is significantly different from zero. You may wish to loosen this
tolerance (make it larger) on poorly scaled and/or large models to improve performance.
The default setting for the Linear Optimality Tolerance is 1.e-7.
Basis Refactor Frequency Box
The Basis Refactor Frequency box on the Linear Solver tab:
allows you to control the how frequently the linear solver refactors the basis matrix. The options are
either Solver Decides or some positive integer quantity. If an integer value, N, is selected, then the
linear solver will refactor every N iterations. Numerically tough and/or poorly scaled models may
benefit from more frequent refactoring. However, refactoring too frequently will cause the solver to
slow down.
The default setting for the Basis Refactor Frequency is Solver Decides, which will typically result in
refactoring about once every 100 iterations.
Barrier Crossover
The Barrier Crossover box on the Linear Solver tab:
is used to control whether or not the barrier solver performs a crossover operation. Unlike simplex
algorithms, the barrier solver does not automatically find basic (cornerpoint) solutions. Very roughly
speaking, basic solutions have the nice mathematical property that exactly m variables will have
nonzero values, where m is the number of constraints. The crossover procedure takes the barrier’s
non-basic solution, and, through the use of a simplex solver, converts the non-basic solution to a basic
one. If the basic solution property is not important for your models, then you may wish to disable
crossovers to improve performance when using the barrier solver.
Note: Barrier crossover must be enabled if you plan to do range analysis. Range computations
cannot be performed if the final solution is not a basic solution.
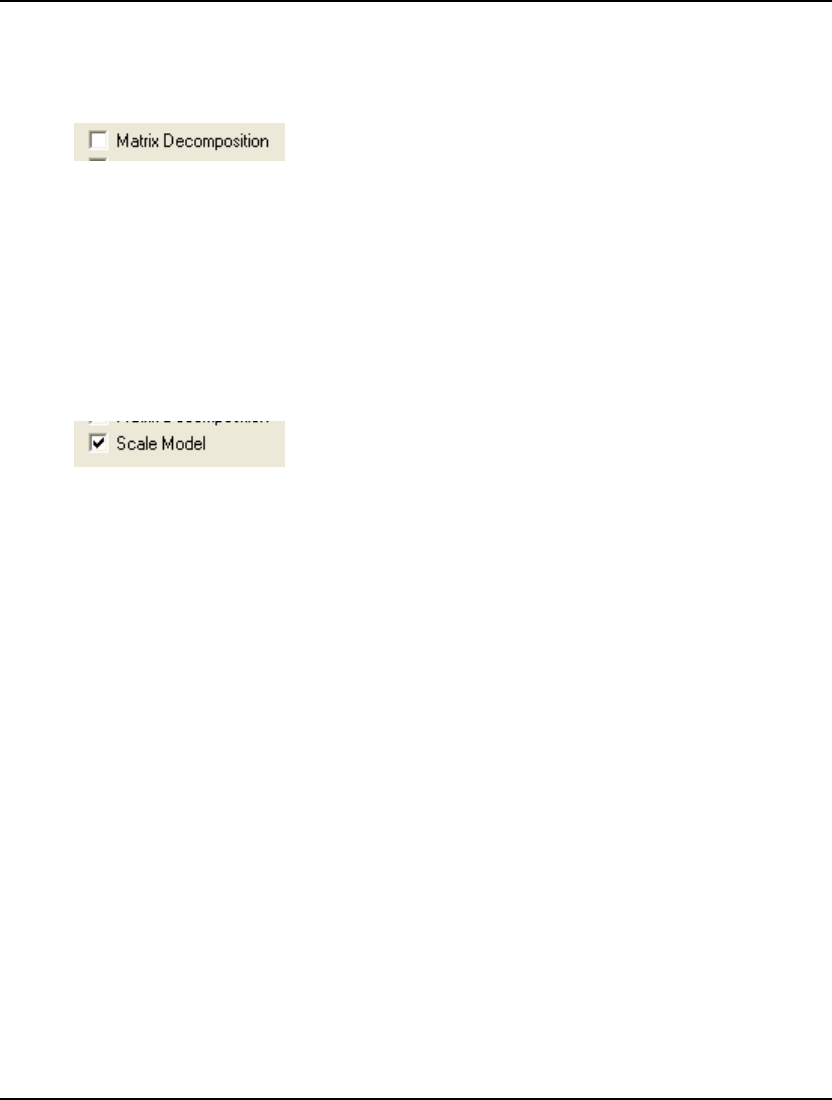
190 CHAPTER 5
The default is to perform crossovers.
Matrix Decomposition
The Matrix Decomposition box on the Linear Solver tab:
allows you to enable the matrix decomposition feature.
Many large-scale linear and mixed integer problems have constraint matrices that are totally
decomposable into a series of block structures. If total decomposition is possible, LINGO will solve
the independent problems sequentially and report a solution for the original model, resulting in
dramatic speed improvements.
LINGO defaults to not using matrix decomposition.
Scale Model Checkbox
The Scale Model box on the Linear Solver tab:
allows you to enable to matrix scaling option.
This option rescales the coefficients in the model’s matrix, so the ratio of the largest to smallest
coefficients is reduced. This reduces the chances of round-off error, which leads to greater numerical
stability and accuracy in the linear solver.
LINGO defaults to using scaling.
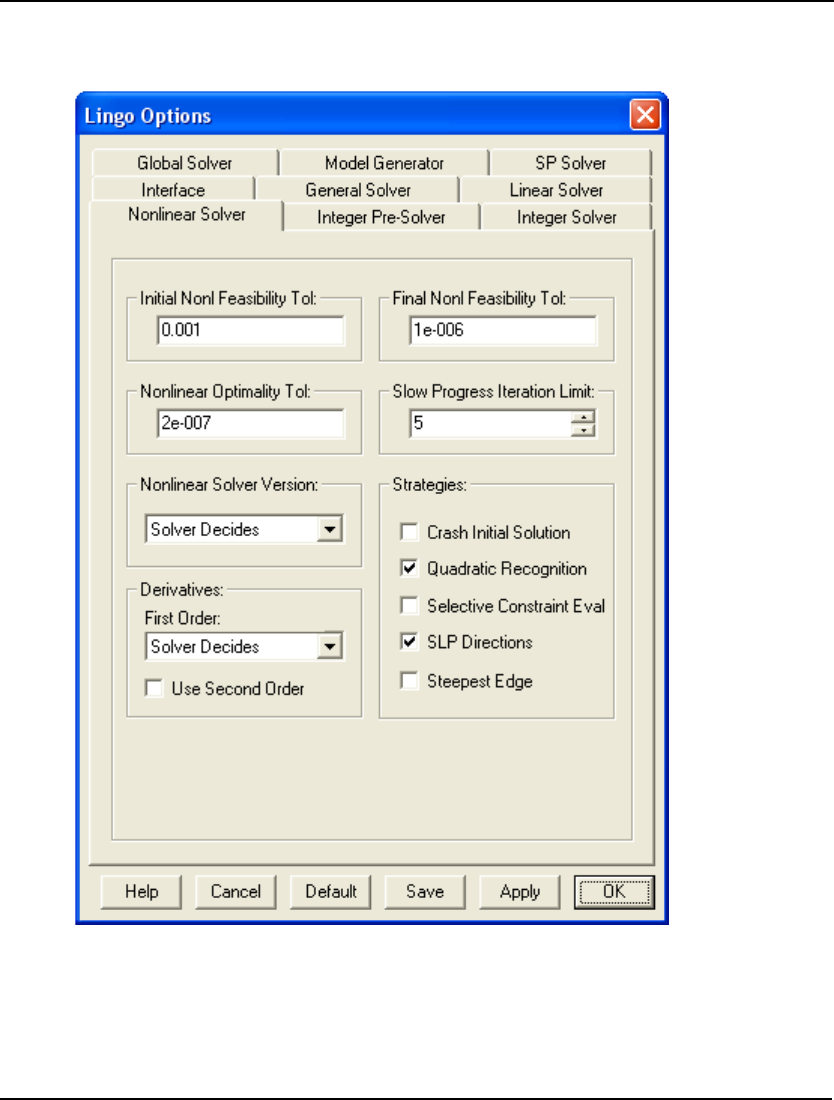
WINDOWS COMMANDS 191
Nonlinear Solver Tab
The Nonlinear Solver tab on the Options dialog box, pictured here:
controls several options that affect the operation of LINGO’s solver on nonlinear models.

192 CHAPTER 5
Initial Nonlinear Feasibility Tolerance
Final Nonlinear Feasibility Tolerance
The Initial Nonl Feasibility Tol and the Final Nonl Feasibility Tol boxes on the Nonlinear Solver tab:
are used to control the feasibility tolerances for the nonlinear solver in the same manner that the Initial
Linear and Final Linear Feasibility Tolerance are used by the linear solver. For information on how
and why these tolerances are useful, refer to the Feasibility Tolerances section in the Linear Solver
Tab section immediately above.
Default values for these tolerances are, respectively, .001 and .000001.
Nonlinear Optimality Tolerance
The Nonlinear Optimality Tol box on the Nonlinear Solver tab:
is used to control the adjustments to variables as described below.
While solving a model, the nonlinear solver is constantly computing a gradient. The gradient gives the
rate of improvement of the objective function for small changes in the variables. If the gradient’s rate
of improvement computation for a given variable is less-than-or-equal-to the Nonlinear Optimality
Tolerance, further adjustments to the variable’s value are not considered to be beneficial. Decreasing
this tolerance towards a limit of 0 will tend to make the solver run longer and may lead to better
solutions in poorly formulated or poorly scaled models.
The default value for the Nonlinear Optimality Tolerance is .0000001.
Slow Progress Iteration Limit
The Slow Progress Iteration Limit (SPIL) box on the Nonlinear Solver tab:
is used to terminate the solution process if little or no progress is being made in the objective value.
Specifically, if the objective function’s value has not improved significantly in n iterations, where n is
the value of SPIL, the nonlinear solver will terminate the solution process. Increasing this tolerance’s
value will tend to force the solver to run longer and may be useful in models with relatively “flat”
objective functions around the optimal solution.
The default value for SPIL is 5 iterations.
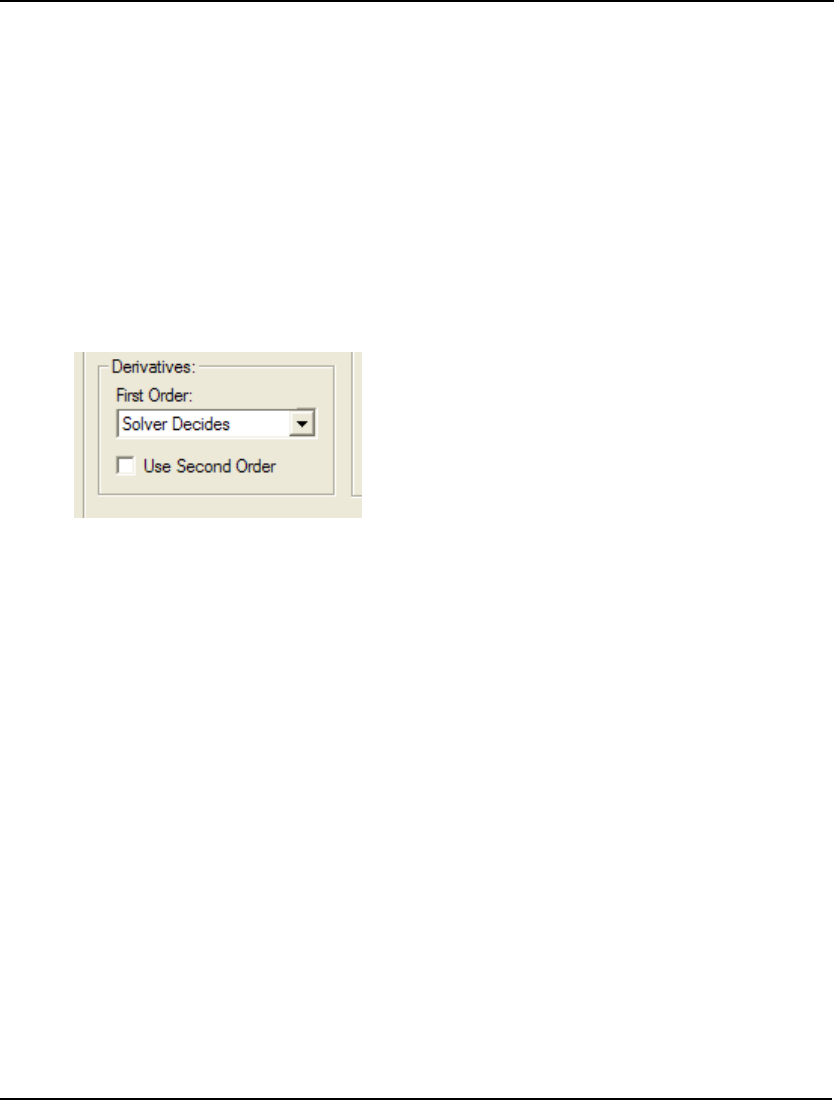
WINDOWS COMMANDS 193
Nonlinear Solver Version
The Nonlinear Solver Version box on the Nonlinear Solver tab:
♦ Solver Decides — LINGO selects the solver (ver 2.0 in this case),
♦ Ver 1.0, and
♦ Ver 2.0.
This option is available on the off chance that the older version of the nonlinear solver, Ver 1.0, should
perform better on a particular model.
LINGO defaults to Solver Decides for the nonlinear solver version.
Derivative Computation
The Derivatives box on the Nonlinear Solver tab:
The First Order option determines how the nonlinear solver computes first order derivatives. There
are two general methods available: numerical or analytical derivatives. Analytical derivatives are
computed directly by symbolically analyzing the arithmetic operations in a constraint. Numerical
derivatives are computed using finite differences. There are two types of numerical derivatives
available using either central differences or forward differences. There are also two types of analytical
derivatives available: backward analytical and forward analytical. Finally, a Solver Decides option is
also available. LINGO defaults to the Solver Decides setting for the First Order option, which
presently involves LINGO using backward analytical derivatives. However, one of the other choices
may be more appropriate for certain classes on nonlinear models. We suggest you try the various
derivative options to see which works best for your particular models.
The Use Second Order option determines if the nonlinear solver will use second order derivatives. If
used, second order derivatives will always be computed analytically. Computing second order
derivatives will take more time, but the additional information they provide may lead to faster runtimes
and/or more accurate solutions. LINGO defaults to not using second order derivatives.
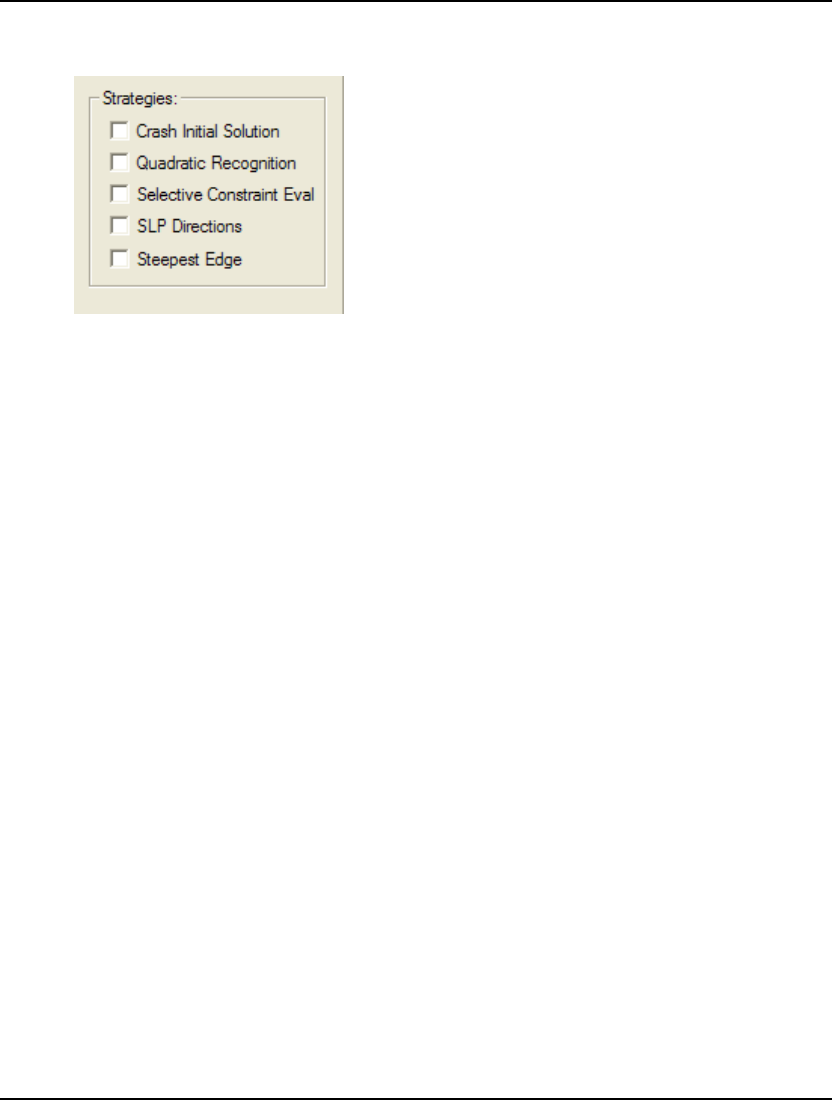
194 CHAPTER 5
Strategies Box
The Strategies box on the Nonlinear Solver tab:
allows you to set the following options:
♦ Crash Initial Solution,
♦ Global Solver,
♦ Quadratic Recognition,
♦ Selective Constraint Eval,
♦ SLP Directions, and
♦ Steepest Edge.
Crash Initial Solution
If the Crash Initial Solution box is checked, LINGO’s nonlinear solver will invoke a heuristic for
generating a “good” starting point when you solve a model. If this initial point is relatively good,
subsequent solver iterations should be reduced along with overall runtimes.
LINGO defaults to not crashing an initial solution.
Quadratic Recognition
If the Quadratic Recognition box is checked, LINGO will use algebraic preprocessing to determine if
an arbitrary nonlinear model is actually a quadratic programming (QP) model. If a model is found to
be a QP model, then it can be passed to the faster quadratic solver. Note that the QP solver is not
included with the standard, basic version of LINGO, but comes as part of the barrier option.
LINGO defaults to not using quadratic recognition
Selective Constraint Evaluation
If the Selective Constraint Eval box is checked, LINGO’s nonlinear solver will only evaluate
constraints on an as needed basis. Thus, not every constraint will be evaluated during each iteration.
This generally leads to faster solution times, but can also lead to problems in models that have
functions that are undefined in certain regions.
LINGO may not evaluate a constraint for many iterations only to find that it has moved into a region
where the constraint is no longer defined. In this case, there may not be a valid point for the solver to
retreat to, and the solution process terminates with an error. Turning off selective constraint evaluation
eliminates these errors.

WINDOWS COMMANDS 195
LINGO defaults to not using Selective Constraint Eval.
SLP Directions
If the SLP Directions box is checked, LINGO’s nonlinear solver will use successive linear
programming to compute new search directions. This technique uses a linear approximation in search
computations in order to speed iteration times. In general, however, the number of total iterations will
tend to rise when SLP Directions are used.
LINGO defaults to using SLP Directions.
Steepest Edge
If the Steepest Edge box is checked, LINGO’s nonlinear solver will use the steepest-edge strategy
when selecting variables to iterate on.
When LINGO is not in steepest-edge mode, the nonlinear solver will tend to select variables that offer
the highest absolute rate of improvement to the objective, regardless of how far other variables may
have to move per unit of movement in the newly introduced variable. The problem with this strategy is
that other variables may quickly hit a bound, resulting in little gain to the objective.
With the steepest-edge option, the nonlinear solver spends a little more time in selecting variables by
looking at the rate that the objective will improve relative to movements in the other nonzero
variables. Thus, on average, each iteration will lead to larger gains in the objective. In general, the
steepest-edge option will result in fewer iterations. However, each iteration will take longer.
LINGO defaults to not using the Steepest-Edge option.
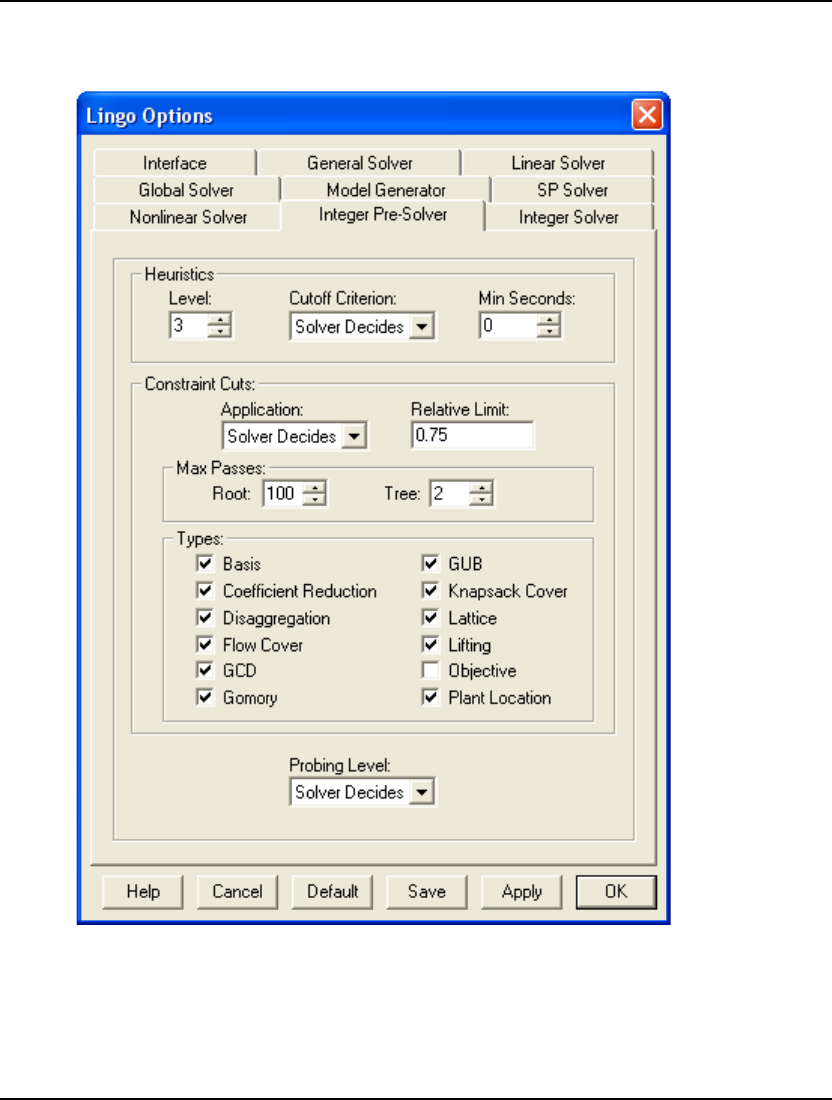
196 CHAPTER 5
Integer Pre-Solver Tab
The Integer Pre-Solver tab on the Options dialog box, pictured here:
can be used to control several options for tailoring the operation of LINGO’s integer programming
pre-solver. The integer pre-solver does a great deal of model reformulation, so that the final
formulation passed to the branch-and-bound solver may be solved as fast as possible. The reformulated
model is always mathematically equivalent to the original formulation, but it is structured in such a
way that it is best suited for solution by the branch-and-bound integer programming algorithm.
WINDOWS COMMANDS 197
The integer pre-solver operates only with linear integer models (i.e., models that make use of the
@BIN and @GIN functions to restrict one or more variables to integer values). Integer pre-solver
option settings have no effect on nonlinear integer models.
Probing Level
The Probing Level option on the Integer Pre-Solver tab can be used on mixed integer linear programs
to perform an operation known as probing. Probing involves taking a close look at the integer
variables in a model and deducing tighter variable bounds and right-hand side values. In many cases,
probing can tighten an integer model sufficiently to speed overall solution times. In other cases,
however, probing may not be able to do much tightening, and the overall solution time will increase
due to the extra time spent probing.
Pulling down the selection list for the Probing Level field:
you will see that you can choose one of eight different probing levels. A probing level of 1 means
probing is disabled, while levels 2 through 7 indicate successively higher degrees of probing. The
default setting for this option, Solver Decides, leaves the decision up to LINGO to select the probing
level.
Heuristics
The Heuristics box on the Integer Pre-Solver tab:
controls the level of integer programming heuristics used by the integer solver. These heuristics use the
continuous solution at each node in the branch-and-bound tree to attempt to quickly find a good integer
solution.
198 CHAPTER 5
The Cutoff Criterion is used to control the criterion for terminating heuristics. Choices here are Solver
Decides, Time, and Iterations. Under the Time setting, LINGO terminates heuristics after a certain
amount of elapsed time. The Iterations option terminates heuristics after a certain number of
iterations. In general, the Time setting results in the fastest performance. However, due to shifting
computational loads on a machine, solution paths may change under the Time setting from one solve to
the next, potentially resulting in non-reproducible solutions. If reproducibility of a runs is a concern,
then the Iterations option should be selected. Under the Solver Decides setting, LINGO chooses the
most appropriate strategy.
The Min Seconds field specifies the minimum amount of time to spend on heuristics at each node.
The default settings are 3 for Level, Solver Decides for Cutoff Criterion, and 0 for Min Seconds.
Constraint Cuts Box
The tolerances contained in the Constraint Cuts box on the Integer Pre-Solver tab:
can be used to control the solver’s cut generation phase on linear models.
LINGO’s integer programming pre-solver performs extensive evaluation of your model in order to add
constraint cuts. Constraint cuts are used to “cut” away sections of the feasible region of the continuous
model (i.e., the model with integer restrictions dropped) that are not contained in the feasible region to
the integer model.
On most integer models, this will accomplish two things. First, solutions to the continuous problem
will tend to be more naturally integer. Thus, the branch-and-bound solver will have to branch on fewer
variables. Secondly, the bounds derived from intermediate solutions will tend to be tighter, allowing
the solver to “fathom” (i.e., drop from consideration) branches higher in the branch-and-bound tree.
These improvements should dramatically speed solution times on most integer models.
Note: Cuts are not applied to nonlinear models. Thus, modifying any of the tolerances in the
Constraint Cuts box will have no bearing on nonlinear models.
WINDOWS COMMANDS 199
Application
In the Application drop-down box of the Constraint Cuts box:
you can control the nodes in the solution tree where the branch-and-bound solver adds cuts.
If you pull down the selection list, you will find three options:
♦ Root Only,
♦ All Nodes, and
♦ Solver Decides.
Under the Root Only option, the solver appends cuts only at the first node, or root node, in the solution
tree. With the All Nodes option, cuts are appended at each node of the tree. The Solver Decides option
causes the solver to dynamically decide when it is best to append cuts at a node.
The default is to let the solver decide when to append cuts. In general, this will offer superior
performance. There may be instances, however, where one of the other two options prevails.
Relative Limit
In the Relative Limit field of the Constraint Cuts box:
you can control the number of constraint cuts that are generated by the integer pre-solver. Most integer
programming models benefit from the addition of some constraint cuts. However, at some point
additional cuts take more time to generate than they save in solution time. For this reason, LINGO
imposes a relative limit on the number of constraint cuts.
The default limit is set to .75 times the number of true constraints in the original formulation. This
relative limit may be overridden by changing it in the Relative Limit field.
Max Passes
In the Max Passes box of the Constraint Cuts box:
you can control the number of iterative passes the integer pre-solver makes through a model to
determine appropriate constraint cuts to append to the formulation. In general, the benefits of each
successive pass decline. At some point, additional passes will only add to the total solution time. Thus,
LINGO imposes a limit on the maximum number of passes.

200 CHAPTER 5
The default limit is 100 passes at the root node of the branch-and-bound tree, and 2 passes at all
subsequent nodes. You can override these limits by changing the values in the Root and Tree fields.
Types
The Types box of the Constraint Cuts box:
is used to enable or disable the different strategies LINGO uses for generating constraint cuts. LINGO
uses twelve different strategies for generating constraint cuts. The default is for all cut generation
strategies to be enabled with the exception of Objective cuts.
It is beyond the scope of this manual to go into the details of the various strategies. Interested readers
may refer to any good text on integer programming techniques. In particular, see Nemhauser and
Wolsey (1988).
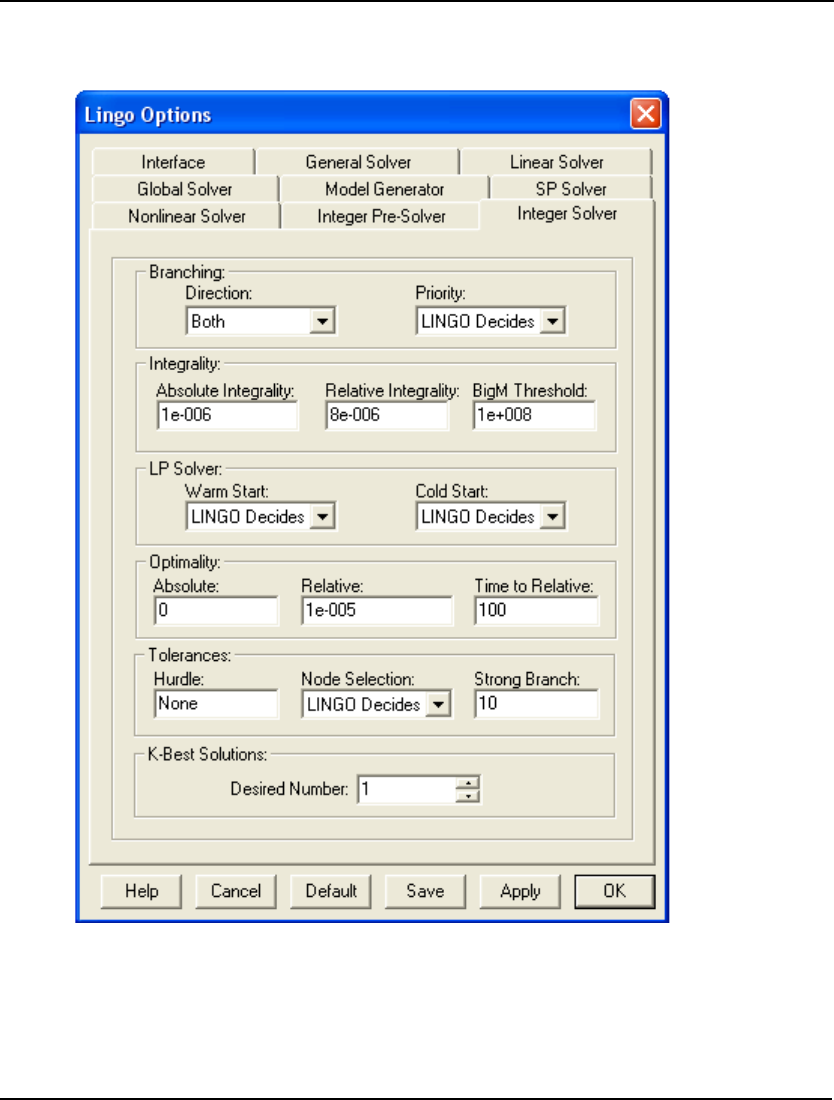
WINDOWS COMMANDS 201
Integer Solver Tab
The Integer Solver tab on the Options dialog box, pictured here:
can be used to control several tolerances for tailoring the operation of LINGO’s branch-and-bound
solver used on integer models (i.e., models making use of the @BIN and @GIN functions to restrict
one or more variables to integer values).
202 CHAPTER 5
Branching Box
The Branching box on the Integer Solver tab:
contains the following two options for controlling the branching strategy used by LINGO’s branch-
and-bound solver:
♦ Direction, and
♦ Priority.
Direction
LINGO uses a branch-and-bound solution procedure when solving integer programming models. One
of the fundamental operations involved in the branch-and-bound algorithm is branching on variables.
Branching involves forcing an integer variable that is currently fractional to either the next greatest or
the next lowest integer value. As an example, suppose there is a general integer variable that currently
has a value of 5.6. If LINGO were to branch on this variable, it would have to choose whether to set
the variable first to 6 or 5. The Direction field controls how LINGO makes this branching decision.
If you pull down the drop-down box for the Direction option, you’ll find the following:
The default, Both, involves LINGO making an intelligent guess as to whether it should branch up or
down first on each individual variable. If Up is selected, LINGO will always branch up first. If Down
is selected, LINGO will always branch down first. In most cases, the Both option will result in the best
performance.
Priority
When branching on variables, the branch-and-bound procedure can give priority to branching on the
binary variables first, or it can make an intelligent guess as to the next best variable to branch on,
regardless of whether it is binary or general. The Priority field controls how LINGO makes this
branching decision.
If you pull down the drop-down box for Priority, you’ll find the following:

WINDOWS COMMANDS 203
Select Binary to have LINGO give branching priority to the binary variables. Select LINGO Decides to
have LINGO select the next integer variable for branching based on an intelligent guess, regardless of
whether it is binary or general.
The default is LINGO Decides, which should generally give the best results.
Integrality Box
Due to the potential for round-off error on digital computers, it is not always possible for LINGO to
find exact integer values for the integer variables. The Integrality box on the Integer Solver tab:
contains the following three options for controlling the amount of deviation from integrality that will
be tolerated:
♦ Absolute Integrality,
♦ Relative Integrality, and
♦ BigM Threshhold.
Absolute Integrality
The Absolute Integrality tolerance is used by LINGO as a test for integrality in integer programming
models. Due to round-off errors, the “integer” variables in a solution may not have values that are
precisely integer. The absolute integrality tolerance specifies the absolute amount of violation from
integrality that is acceptable. Specifically, if X is an "integer" variable and I is the closest integer to X,
then X would be accepted as being integer valued if:
| X – I | <= Absolute Integrality Tolerance.
The default value for the absolute integrality tolerance is .000001. Although one might be tempted to
set this tolerance to 0, this may result in feasible models being reported as infeasible.
Relative Integrality
The Relative Integrality tolerance is used by LINGO as a test for integrality in integer programming
models. Due to round-off errors, the “integer” variables in a solution may not have values that are
precisely integer. The relative integrality tolerance specifies the relative amount of violation from
integrality that is acceptable. Specifically, if I is the closest integer value to X, X will be considered an
integer if:
| X – I | <= Relative Integrality Tolerance.
| X |
The default value for the relative integrality tolerance is .000008. Although one might be tempted to
set this tolerance to 0, this may result in feasible models being reported as infeasible.
BigM Threshold
Many integer programming models have constraints of the form:
204 CHAPTER 5
f(x) ≤ M * z
where f(x) is some function of the decision variables, M is a large constant term, and z is a binary
variable. These types of constraints are called forcing constraints and are used to force the binary
variable, z, to 1 when f(x) is nonzero. In many instances, the binary variable is multiplied by a fixed
cost term in the objective; a fixed cost that is incurred when a particular activity, represented by f(x),
occurs. The large constant term, M, Is frequently referred to as being a BigM coefficient.
Setting BigM too small can lead to infeasible or suboptimal models. Therefore, the BigM value will
typically have to be rather large in order to exceed the largest activity level of f(x). When BigM is
large, the solver may discover that by setting z slightly positive (within normal integrality tolerances),
it can increase f(x) to a significant level and thereby improve the objective. Although such solutions
are technically feasible to tolerances, they are invalid in that the activity is occurring without incurring
its associated fixed cost.
The BigM threshold is designed to avoid this problem by allowing LINGO to identify the binary
variables that are being set by forcing constraints. Any binary variable with a coefficient larger than
the BigM threshold will be subject to a much tighter integrality tolerance.
The default value for the BigM Threshold is 1.e8.
LP Solver Box
In a mixed linear integer programming model, LINGO’s branch-and-bound solver solves a linear
programming model at each node of the solution tree. LINGO has a choice of using the primal
simplex, dual simplex, or barrier solver (assuming the barrier option was purchased with your license)
for handling these linear programs. The LP Solver box on the Integer Solver tab:
contains the following two options for controlling this choice of linear program solver:
♦ Warm Start, and
♦ Cold Start
Warm Start
The Warm Start option controls the linear solver that is used by the branch-and-bound solver at each
node of the solution tree when a previous solution is present to use as a “warm start”. The cold start
option, discussed below, determines the solver to use when a previous solution does not exist.
If you pull down the drop-down box for Warm Start, you’ll find the following:
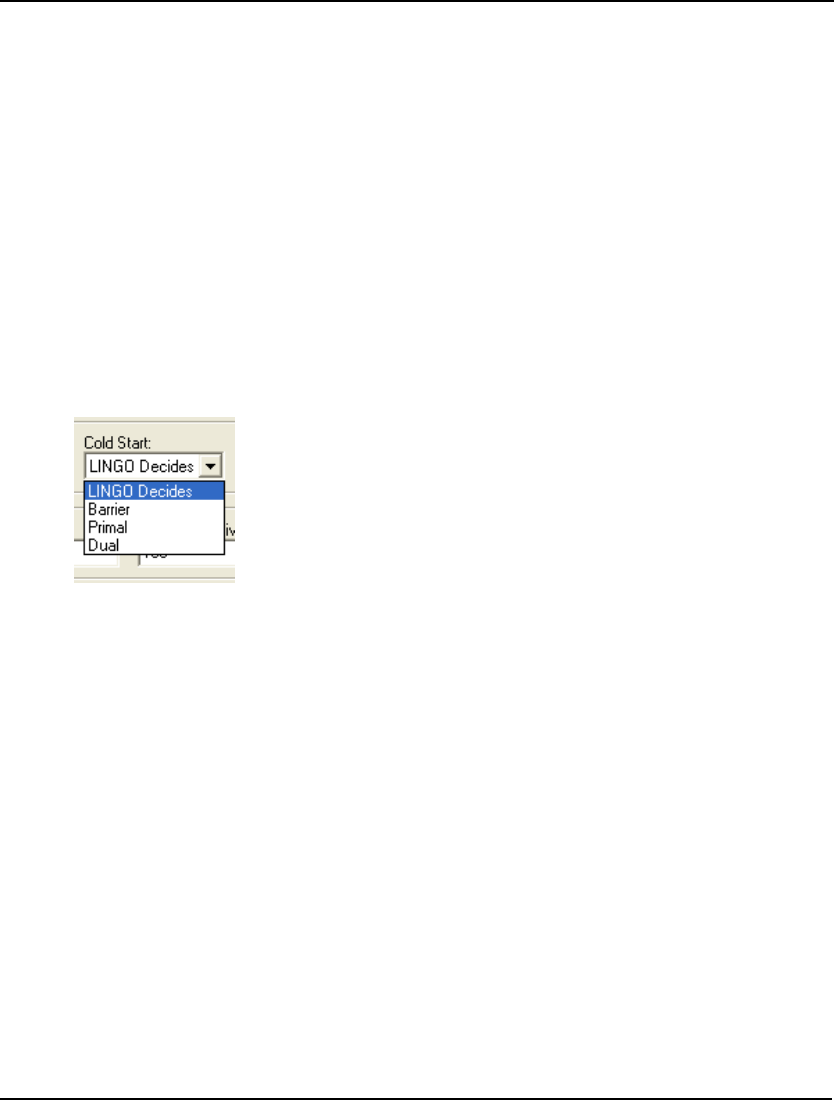
WINDOWS COMMANDS 205
The available options are:
♦ LINGO Decides – LINGO chooses the most appropriate solver.
♦ Barrier – LINGO uses the barrier method, assuming you have purchased a license for the
barrier solver. Otherwise, the dual solver will be used.
♦ Primal – LINGO uses the primal solver exclusively.
♦ Dual – LINGO uses the dual solver exclusively.
In general, LINGO Decides will yield the best results. The barrier solver can’t make use of a
pre-existing solution, so Barrier usually won’t give good results. In general, Dual will be faster than
Primal for reoptimization in branch-and-bound.
Cold Start
The Cold Start option controls the linear solver that is used by the branch-and-bound solver at each
node of the solution tree when a previous solution is not present to use as a “warm start”. The Warm
Start option, discussed above, determines the solver to use when a previous solution does exist.
If you pull down the drop-down box for Cold Start, you’ll find the following:
The available options are:
♦ LINGO Decides – LINGO chooses the most appropriate solver at each node.
♦ Barrier – LINGO uses the barrier method, assuming you have purchased a license for the
barrier solver. Otherwise, the dual solver will be used.
♦ Primal – LINGO uses the primal solver exclusively.
♦ Dual – LINGO uses the dual solver exclusively.
In general, LINGO Decides will yield the best results. However, experimentation with the other
options may be fruitful.

206 CHAPTER 5
Optimality Box
The Optimality Box on the Integer Solver tab:
is used to control three tolerances: Absolute, Relative, and Time to Relative. These tolerances control
how close you want the solver to come to the optimal solution. Ideally, we’d always want the solver to
find the best solution to a model. Unfortunately, integer programming problems are very complex, and
the extra computation required to seek out the absolute best solution can be prohibitive. On large
integer models, the alternative of getting a solution within a few percentage points of the true optimum
after several minutes of runtime, as opposed to the true optimum after several days, makes the use of
these tolerances quite attractive.
Absolute
The Absolute Optimality tolerance is a positive value r, indicating to the branch-and-bound solver that
it should only search for integer solutions with objective values at least r units better than the best
integer solution found so far. In many integer programming models, there are huge numbers of
branches with roughly equivalent potential. This tolerance helps keep the branch-and-bound solver
from being distracted by branches that can’t offer a solution significantly better than the incumbent
solution.
In general, you shouldn’t have to set this tolerance. Occasionally, particularly on poorly formulated
models, you might need to increase this tolerance slightly to improve performance. In most cases, you
should experiment with the relative optimality tolerance, discussed below, rather than the absolute
optimality tolerance in order to improve performance.
The default value for the absolute optimality tolerance is 8e-8.
Relative
The Relative Optimality tolerance is a value r, ranging from 0 to 1, indicating to the branch-and-bound
solver that it should only search for integer solutions with objective values at least 100*r% better than
the best integer solution found so far.
The end results of modifying the search procedure in this way are twofold. First, on the positive side,
solution times can be improved tremendously. Second, on the negative side, the final solution obtained
by LINGO may not be the true optimal solution. You will, however, be guaranteed the solution is
within 100*r% of the true optimum.
Typical values for the relative optimality tolerance would be in the range .01 to .05. In other words,
you would be happy to get a solution within 1% to 5% of the true optimal value. On large integer
models, the alternative of getting a solution within a few percentage points of the true optimum after
several minutes of runtime, as opposed to the true optimum after several days, makes the use of an
optimality tolerance quite attractive.

WINDOWS COMMANDS 207
Note: Generally speaking, the relative optimality tolerance is the tolerance that will most likely
improve runtimes on integer models. You should be sure to set this tolerance whenever
possible.
The default for the relative optimality tolerance is 5e-8.
Time to Relative
If an integer programming model is relatively easy to solve, then we would like to have the solver
press on to the true optimal solution without immediately resorting to a relative optimality tolerance,
discussed above. On the other hand, if, after running for a while, it becomes apparent that the optimal
solution won’t be immediately forthcoming, then you might want the solver to switch to using a
relative optimality tolerance.
The Time to Relative tolerance can be used in this manner. This tolerance is the number of seconds
before the branch-and-bound solver begins using the relative optimality tolerance. For the first n
seconds, where n is the value of the time to relative tolerance, the branch-and-bound solver will not
use the relative optimality tolerance and will attempt to find the true optimal solution to the model.
Thereafter, the solver will use the relative optimality tolerance in its search.
The default value for the time to relative tolerance is 100 seconds.
Tolerances Box
The Tolerances box on the Integer Solver tab:
contains three miscellaneous tolerances for controlling the branching strategy used by the
branch-and-bound solver on integer programming models. The three tolerances are Hurdle, Node
Selection, and Strong Branch.
Hurdle
If you know the objective value of a solution to a model, you can enter it as the Hurdle tolerance. This
value is used in the branch-and-bound solver to narrow the search for the optimum. More specifically,
LINGO will only search for integer solutions in which the objective is better than the hurdle value.
This comes into play when LINGO is searching for an initial integer solution. LINGO can ignore
branches in the search tree with objective values worse than the hurdle value, because a better solution
exists (i.e., the solution whose objective value equals the hurdle tolerance) on some alternate branch.
Depending on the problem, a good hurdle value can greatly reduce solution time. Once LINGO finds
an initial integer solution, however, the hurdle tolerance no longer has an effect. At this point, the
Relative Optimality tolerance comes into play.
Note: Be sure when entering a hurdle value that a solution exists that is at least as good or better
than your hurdle. If such a solution does not exist, LINGO will not be able to find a feasible
solution to the model.
The default hurdle value is None. In other words, the solver does not use a hurdle value.
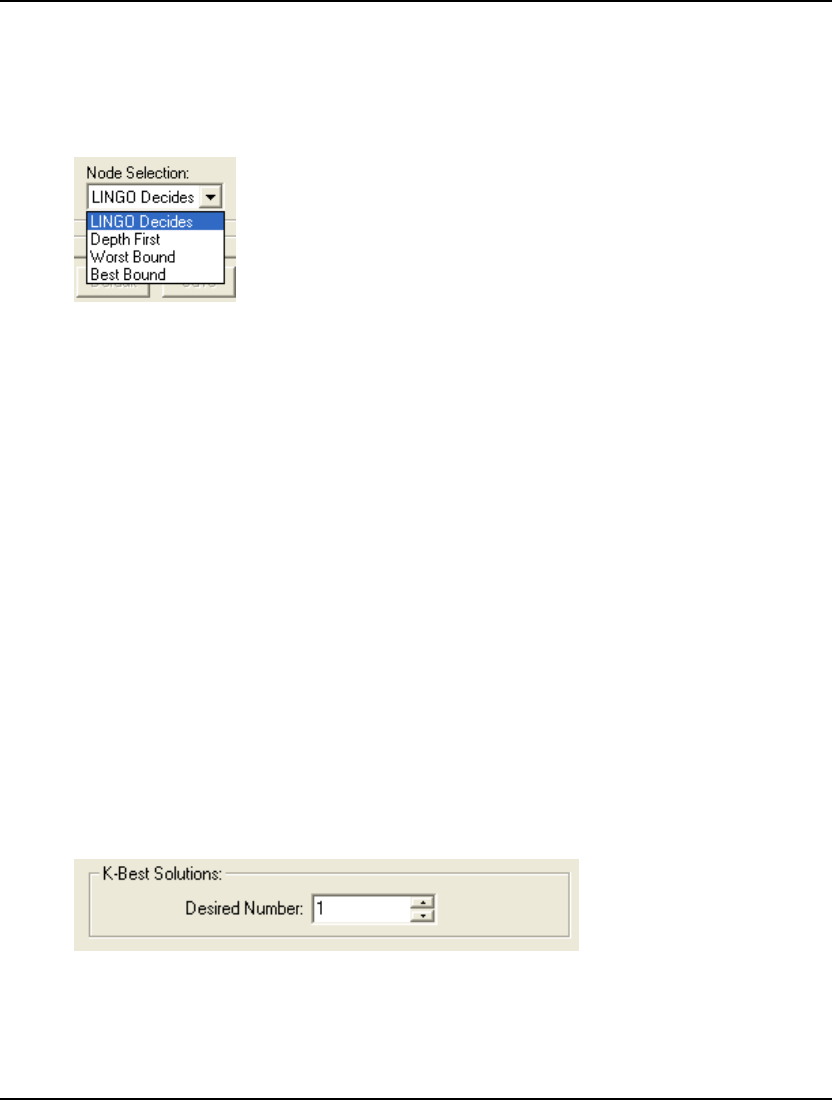
208 CHAPTER 5
Node Selection
The branch-and-bound solver has a great deal of freedom in deciding how to span the
branch-and-bound solution tree. The Node Selection option allows you to control the order in which
the solver selects branch nodes in the tree.
If you examine the pull down list for Node Selection, you will see the following:
The four choices function as follows:
♦ LINGO Decides – This is the default option. LINGO makes an educated guess as to the
best node to branch on next.
♦ Depth First – LINGO spans the branch-and-bound tree using a depth first strategy.
♦ Worst Bound – LINGO picks the node with the worst bound.
♦ Best Bound – LINGO picks the node with the best bound.
In general, LINGO Decides will offer the best results. Experimentation with the other three choices
may be beneficial with some classes of models.
Strong Branch
The Strong Branch field uses a more intensive branching strategy during the first n levels of the
branch-and-bound tree, where n is the value in Strong Branch. During these initial levels, LINGO
picks a subset of the fractional variables as branching candidates. LINGO then performs a tentative
branch on each variable in the subset, selecting as the final candidate the variable that offers the
greatest improvement in the bound on the objective. Although strong branching is useful in tightening
the bound quickly, it does take additional computation time. Therefore, you may want to try different
settings to determine what works best for your model.
The default strong branch setting is 10 levels.
K-Best Solutions Box
The K-Best Solutions box on the Integer Solver tab:
is used to set the number of solutions desired as part of the K-Best solutions feature of LINGO's mixed
integer solver. Whenever this value is greater than 1, say K, LINGO will will return up to K unique
solutions to the model. These solutions will have the property that they are the next best solutions
available in terms of their objective values. Less than K solutions may be returned if a sufficient
number of feasible solutions do not exist. An example of the K-Best feature follows.

WINDOWS COMMANDS 209
K-Best Solutions Example
In order to illustrate the K-Best feature, we will be using a variant of the knapsack model discussed
above in the Binary Integer Variables section. You may want to refer back to the earlier discussion if
you are not familiar with the knapsack model.
Here's our model:
MODEL:
SETS:
ITEMS: INCLUDE, WEIGHT, RATING;
MYFAVORITES( ITEMS);
ENDSETS
DATA:
KNAPSACK_CAPACITY = 15;
ITEMS WEIGHT RATING =
BRATS 3 1
BROWNIES 3 1
BEER 3 1
ANT_REPEL 7 1
BLANKET 4 6
FRISBEE 1 6
SALAD 5 10
WATERMELON 7 9;
MYFAVORITES = BRATS BROWNIES BEER;
ENDDATA
MAX = @SUM( ITEMS: RATING * INCLUDE);
@SUM( ITEMS: WEIGHT * INCLUDE) <=
KNAPSACK_CAPACITY;
@FOR( ITEMS: @BIN( INCLUDE));
NUMFAVE = @SUM( MYFAVORITES: INCLUDE);
END
Model: KBEST
In this example, we are packing a picnic basket for a picnic we will be taking with a friend. Our
friend's ratings of the candidate picnic items is given in the data section above. It turns out that our
friend is health conscious and does not care much for bratwurst, brownies nor beer. This is
unfortunate, because these happen to be our favorite items, which we indicate with a new subset of
ITEMS called MYFAVORITES.
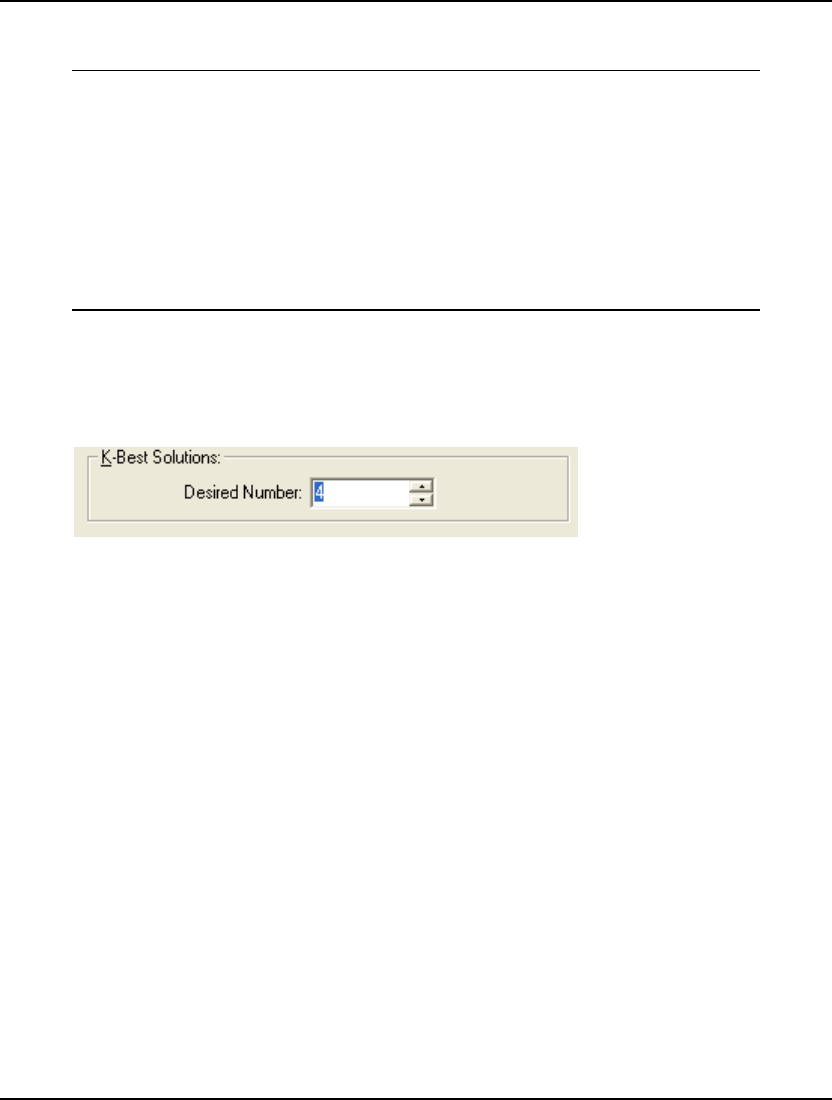
210 CHAPTER 5
If we solve the model as is, thus solely maximizing our friend's preferences, we get the following
solution:
Global optimal solution found.
Objective value: 25.00000
Variable Value
NUMFAVE 0.000000
INCLUDE( BRATS) 0.000000
INCLUDE( BROWNIES) 0.000000
INCLUDE( BEER) 0.000000
INCLUDE( ANT_REPEL) 0.000000
INCLUDE( BLANKET) 0.000000
INCLUDE( FRISBEE) 1.000000
INCLUDE( SALAD) 1.000000
INCLUDE( WATERMELON) 1.000000
As indicated by the NUMFAVE variable, none of our favorite items are included in the optimal basket.
Now, we like our friend a lot, and we want him to be happy. However, we are wondering if there isn't
another combination of items that our friend might like almost as much that includes at least one of our
favorite items. To investigate this question, we set the Desired Number parameter of the K-Best
Solutions box on the LINGO|Options Integer Solver tab to 4:
This means that we would like LINGO to generate the 4 best solutions to the model. We then click
OK and then run the LINGO|Solve command. At which point, the integer solver sees that the K-Best
feature is being requested, and it automatically generates the 4 best solutions to the model. At which
point, we are presented with the following dialog box:
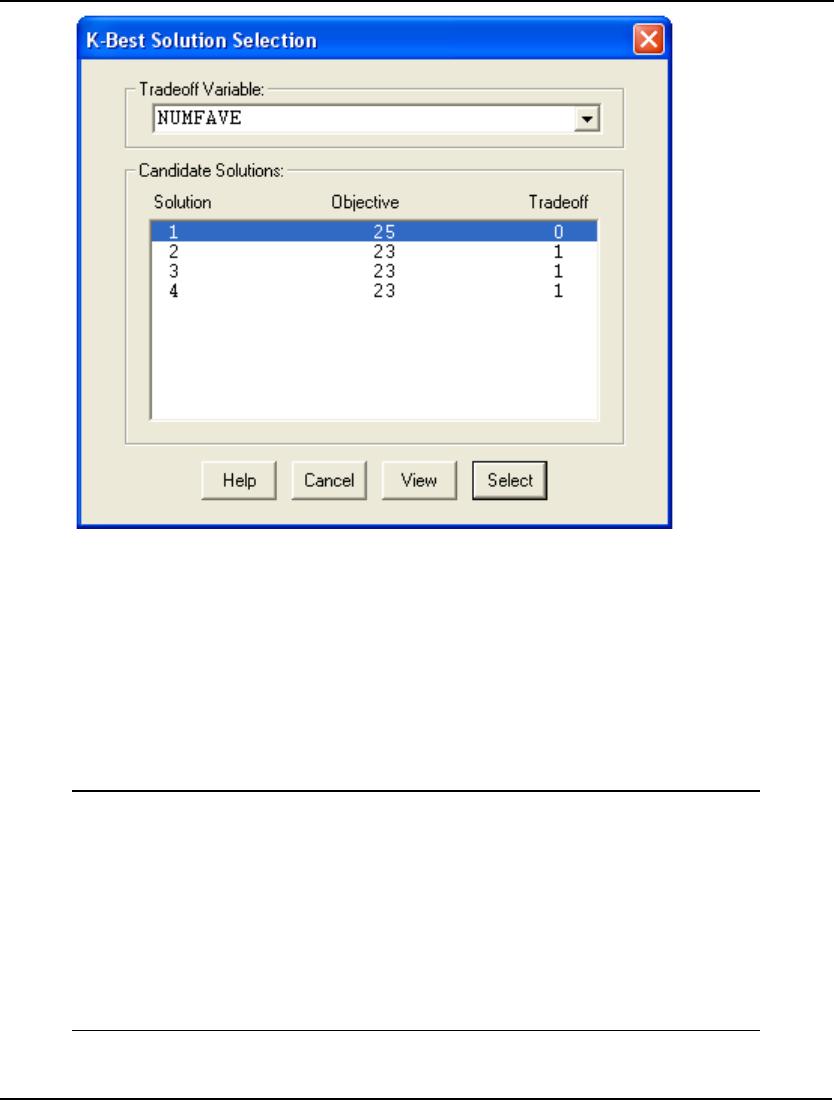
WINDOWS COMMANDS 211
In the Candidate Solutions window we see that the solver was able to find 4 feasible next-best
solutions to the model. The solutions are ranked in order by their objective values.
There is also a column labeled Tradeoff, which lists the value in each solution of a designated tradeoff
variable. Any scalar variable in a model can be selected as the tradeoff variable. In this example,
there is only one scalar variable, NUMFAVE, so it is automatically selected as the tradeoff variable.
The idea behind the tradeoff variable is that it allows you to weigh the tradeoffs in a model's objective
value with a secondary goal. In this case, our secondary goal is the number of our favorite items in the
picnic basket. In particular, we see that there are three solutions with slightly worse objective values
(23 vs. 25) that include one of our favorite items. For example, if we selected solution 2 and pressed
the View button, we'd see the following solution containing one of our favorite items, bratwurst:
Objective value: 23.00000
Variable Value
KNAPSACK_CAPACITY 15.00000
NUMFAVE 1.000000
INCLUDE( BRATS) 1.000000
INCLUDE( BROWNIES) 0.000000
INCLUDE( BEER) 0.000000
INCLUDE( ANT_REPEL) 0.000000
INCLUDE( BLANKET) 1.000000
INCLUDE( FRISBEE) 1.000000
INCLUDE( SALAD) 1.000000
INCLUDE( WATERMELON) 0.000000

212 CHAPTER 5
The following buttons are available along the bottom edge of the K-Best dialog box:
Help Displays online help regarding the K-Best feature.
Cancel Cancels out of K-Best mode, closing the dialog box.
View Displays any solutions selected in the Candidate Solutions box.
Select Allow you to select one of the candidate solutions as the final solution to the model.
These buttons allow you to examine selected solutions returned by the K-Best solver. Once you find a
solution you believe to be the best, you can select it as the final solution. Once a final solution is
selected, all subsequent solution reports will be based on that particular solution.
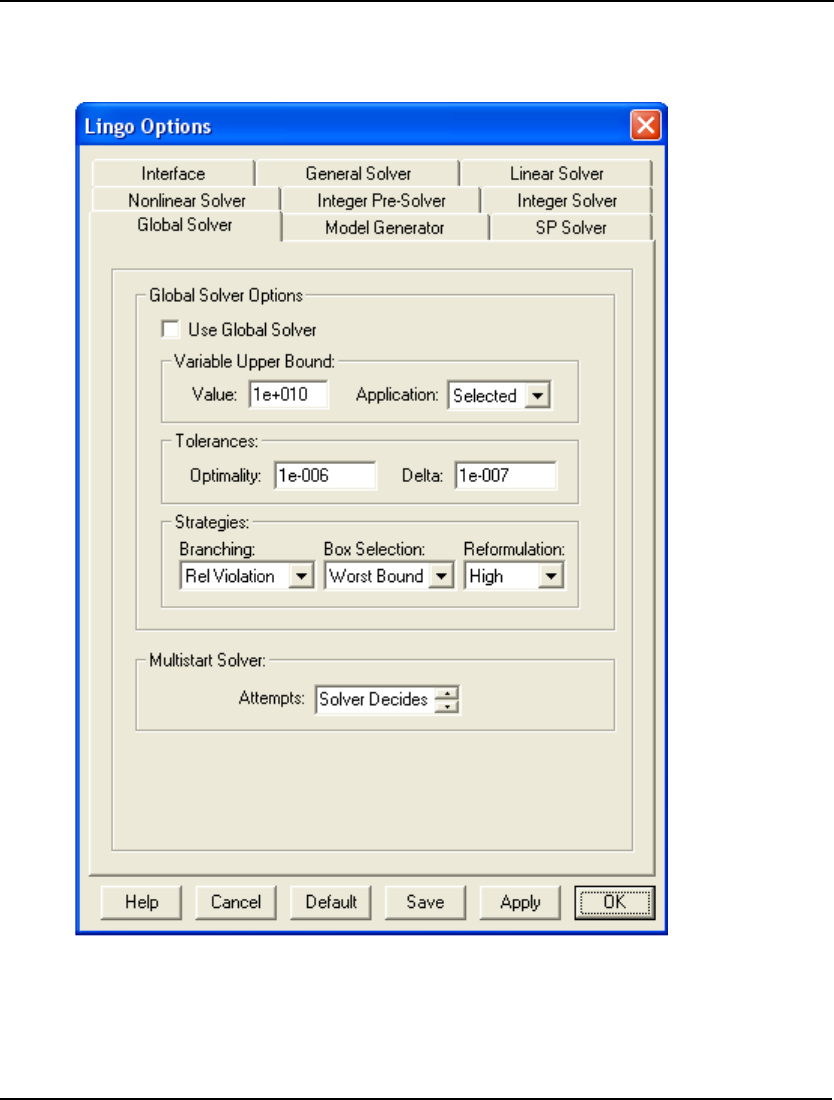
WINDOWS COMMANDS 213
Global Solver Tab
The Global Solver tab on the Options dialog box, pictured here:
can be used to control the operation of LINGO’s global solver capabilities. Please keep in mind that
the global solver toolkit is an add-on option to LINGO. You must specifically purchase the global
solver option as part of your LINGO license in order to make use of its capabilities.

214 CHAPTER 5
LINGO exploits the convex nature of linear models to find globally optimal solutions. However, we
aren’t as fortunate with nonlinear models. LINGO’s default NLP solver uses a local search procedure.
This can lead to LINGO stopping at locally optimal points when a model is non-convex and perhaps
missing a global point lying elsewhere. You may refer to Chapter 15, On Mathematical Modeling, for
more information on how and why this can happen. The global solver toolkit contains features
designed to sift through the local points in search of the globally optimal point.
The two primary features in LINGO’s global toolkit are a global solver and a multistart solver. The
global solver uses range bounding and reduction techniques within a branch-and-bound framework to
convert a non-convex model into a series of smaller, convex models. This divide-and-conquer strategy
ultimately results in convergence to the guaranteed globally optimal point. The multistart solver, on the
other hand, uses a heuristic approach of restarting the NLP solver several times from different initial
points. It is not uncommon for a different starting point to lead to a different local solution point. Thus,
if we restart from enough unique points, saving the best local solution as we go, we stand a much
better chance of finding the true global solution.
Use Global Solver
If the Use Global Solver box is checked, LINGO will invoke the global solver when you solve a
nonlinear model. Many nonlinear models are non-convex and/or non-smooth (for more information
see Chapter 15, On Mathematical Modeling.) Nonlinear solvers that rely on local search procedures (as
does LINGO’s default nonlinear solver) will tend to do poorly on these types of models. Typically,
they will converge to a local, sub-optimal point that may be quite distant from the true, global optimal
point. Global solvers overcome this weakness through methods of range bounding (e.g., interval
analysis and convex analysis) and range reduction techniques (e.g., linear programming and constraint
propagation) within a branch-and-bound framework to find global solutions to non-convex models.
The following example illustrates the usefulness of the global solver. Consider the simple, yet highly
nonlinear, model:
MODEL:
MIN = X * @COS( 3.1416 * X);
@BND( 0, X, 6);
END
The graph of the objective function is as follows:
WINDOWS COMMANDS 215
The objective function has three local minimal points over the feasible range. These points are
summarized in the following table:
Point X Objective
1 1.09 -1.05
2 3.03 -3.02
3 5.02 -5.01
Clearly, the third local point is also the globally best point, and we would like the NLP solver to
converge to this point. Below is the solution LINGO produces if the default nonlinear solver is
invoked:
Local optimal solution found at step: 11
Objective value: -1.046719
Variable Value Reduced Cost
X 1.090405 0.1181082E-07
Row Slack or Surplus Dual Price
1 -1.046719 -1.000000
216 CHAPTER 5
Unfortunately, as you can see, we converged to the least preferable of the local minimums. However,
after enabling the global solver by checking the Use Global Solver box, we do obtain the global
solution:
Global optimal solution found at step: 35
Objective value: -5.010083
Variable Value Reduced Cost
X 5.020143 -0.7076917E-08
Row Slack or Surplus Dual Price
1 -5.010083 -1.000000
Note: There is one drawback to using the global solver; it runs considerably slower than the default
nonlinear solver. Therefore, the preferred option is to always try and write smooth, convex
nonlinear models. By doing this, the faster, default local solver can be successfully invoked.
Keep in mind that the global solver supports most, but not all, of the functions available in the LINGO
language. The following is a list of the nonlinear functions not currently supported by the global
solver:
♦ @PBN()—Cumulative binomial probability
♦ @PCX()—Cumulative Chi-squared distrribution
♦ @PFD()—Cumulative F distribution
♦ @PHG()—Cumulative hypergeometric probability
♦ @PFS()—Poisson finite source
♦ @PPL()—Poisson linear loss
♦ @PTD()—Cumulative t distribution
♦ @USER()-User supplied function
Note: The global solver will not operate on models containing one or more unsupported nonlinear
operations that reference optimizable quantities; the default NLP solver will be called in this
case.
The global solver is disabled by default.
Variable Upper Bound Box
The Variable Upper Bound box:
sets the default variable bounds while the global solver is running. If this parameter is set to d, then
variables will not be permitted to assume values outside the range of [-d, d]. Setting this parameter as
tightly as possible in the Value Field restricts the global solver from straying into uninteresting regions
and will reduce run times. The default value for the Value Field is 1.e10.
WINDOWS COMMANDS 217
The Application list box has three options available: None, All and Selected. Selecting None removes
the variable bounds entirely, and is not recommended. The All setting applies the bound to all
variables. Finally, the Selected setting causes the global solver to apply the bound after an initial
solver pass to find the first local solution. The bound will only be applied to a variable if it does not
cutoff the initial local solution. LINGO defaults to the Selected setting.
Tolerances Box
The Tolerances box:
contains two tolerances used by the global solver: Optimality and Delta.
The Optimality tolerance specifies by how much a new solution must beat the objective value of the
incumbent solution in order to become the new incumbent. The default value for Optimality 1.e-6.
The Delta tolerance specifies how closely the additional constraints, added as part of the global
solver’s convexification process, must be satisfied. The default value for Delta is 1.e-7.
Strategies Box
The Strategies box:
allows you to control three strategies used by the global solver: Branching, Box Selection and
Reformulation.
The Branching strategy consists of six options to use when branching on a variable for the first time:
♦ Absolute Width,
♦ Local Width,
♦ Global Width,
♦ Global Distance,
♦ Absolute Violation, and
♦ Relative Violation.
The default setting for Branching is Relative Violation.
The Box Selection option specifies the strategy to use for choosing between all active nodes in the
global solver’s branch-and-bound tree. The choices are: Depth First and Worst Bound, with the
default being Worst Bound.
218 CHAPTER 5
The Reformulation option sets the degree of algebraic reformulation performed by the global solver.
Algebraic reformulation is critical for construction of tight, convex sub-regions to enclose the
nonlinear and nonconvex functions. The available settings are None, Low, Medium and High, with
High being the default.
Multistart Solver
LINGO exploits the convex nature of linear models to find globally optimal solutions. However, we
aren’t as fortunate with nonlinear models. With NLP models, LINGO’s default NLP solver uses a local
search procedure. This can lead to LINGO stopping at locally optimal points, perhaps missing a global
point lying elsewhere. You may refer to On Mathematical Modeling for more information on how and
why this can happen.
A strategy that has proven successful in overcoming this problem is to restart the NLP solver several
times from different initial points. It is not uncommon for a different starting point to lead to a
different local solution point. Thus, if we restart from enough unique points, saving the best local
solution as we go, then we stand a much better chance of finding the true global solution. We refer to
this solution strategy as multistart.
The Multistart Solver Attempts box on the Global Solver tab:
is used to set the number of times the multistart solver restarts the standard NLP solver in its attempt to
find successively better local solutions. Each new starting point is intelligently generated to maximize
the chances of finding a new local point.
The default option, Solver Decides, entails restarting 5 times on small NLPs and disabling multistart
on larger models. Setting multistart to 1 causes the NLP solver to be invoked only once, effectively
disabling multistart. Setting multistart to any value greater than 1 will cause the NLP solver to restart
that number of times on all NLPs. In general, we have found that setting the number of multistarts to
around 5 tends to be adequate for most models. Highly nonlinear models may require a larger setting.
Note: Keep in mind that multistart will dramatically increase runtimes, particularly if a large
number of restarts is selected. Thus, one should avoid using multistart unnecessarily on
convex models that will converge to a global point in a single pass without any additional
prodding.
The following example illustrates the usefulness of multistart. Consider the simple, yet highly
nonlinear, model:
MODEL:
MIN = X * @COS( 3.1416 * X);
@BND( 0, X, 6);
END
WINDOWS COMMANDS 219
The graph of the objective function is as follows:
The objective function has three local minimal points over the feasible range. These points are
summarized in the following table:
Point X Objective
1 1.09 -1.05
2 3.03 -3.02
3 5.02 -5.01
Clearly, the third local point is also the globally best point, and we would like the NLP solver to
converge to this point. Below is the solution you will get from LINGO if the multistart option is
disabled:
Local optimal solution found at step: 11
Objective value: -1.046719
Variable Value Reduced Cost
X 1.090405 0.1181082E-07
Row Slack or Surplus Dual Price
1 -1.046719 -1.000000

220 CHAPTER 5
Unfortunately, as you can see, we converged to the least preferable of the local minimums. However,
after setting the number of multistarts to five and re-solving, we do obtain the global solution:
Local optimal solution found at step: 39
Objective value: -5.010083
Variable Value Reduced Cost
X 5.020143 -0.7076917E-08
Row Slack or Surplus Dual Price
1 -5.010083 -1.000000
Note: Unlike the global solver, the multistart solver can only claim its solution to be locally optimal.
This is because there may always be a better solution out there that the multistart solver may,
or may not, be able to find with additional runs. The global solver, on the other hand, can
claim global optimality by having partitioned the original model into a series of smaller,
convex models.
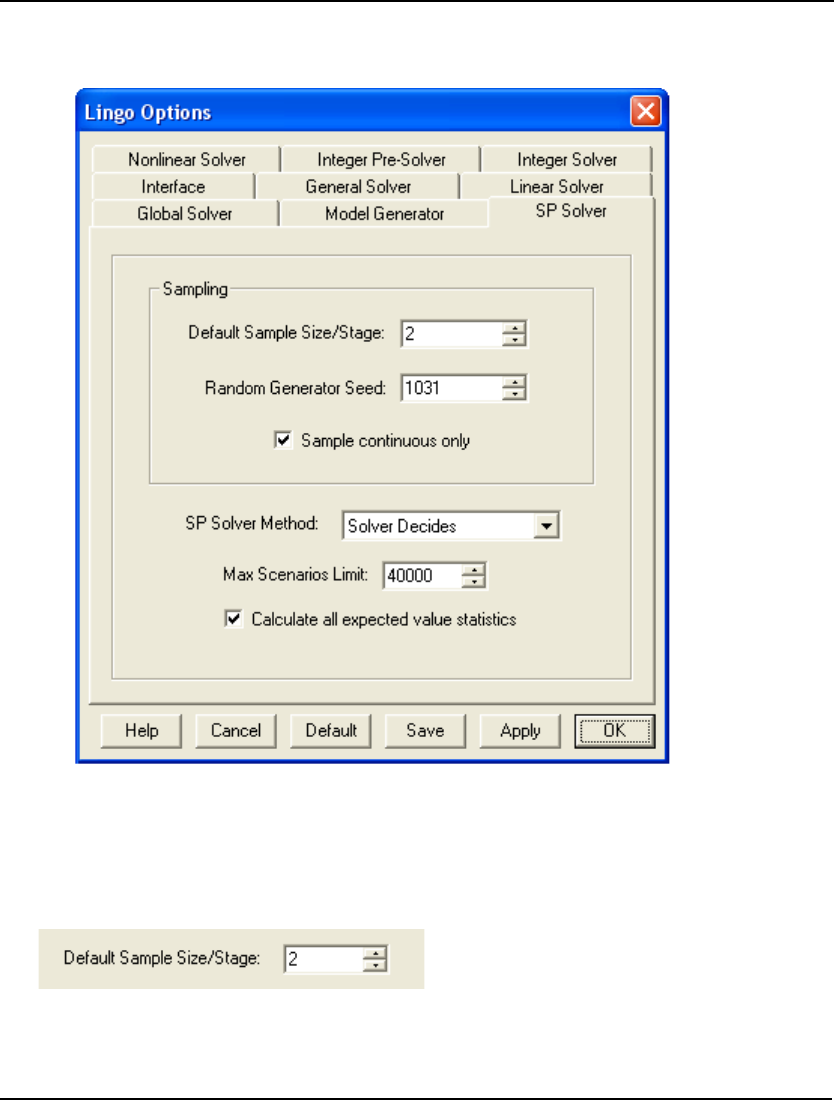
WINDOWS COMMANDS 221
SP Solver Tab
The SP Solver tab on the Options dialog box:
is used to control the operation of LINGO's SP (Stochastic Programming) solver. Please keep in mind
that the SP solver is an add-on option to LINGO. You must specifically purchase the SP solver option
as part of your LINGO license in order to make use of its capabilities.
Default Sample Size/Stage
The Default Sample Size/Stage parameter on the SP Solver tab:
is used to control the default sample size for random variables in stochastic programming (SP) whose
outcomes are determined via sampling.
222 CHAPTER 5
In many SP models, LINGO will generate a set of sample values for the some or all of the random
variables. This is particularly true when you have one or more continuous random variables, which
have an infinite number of possible outcomes. In such a case, sampling is the only viable alternative.
One way to specify the desired sample size for each stage is via the @SPSAMPSIZE function used
directly in the model's text. If, on the other hand, all or most stages should have the same sample size,
then you can use the Default Sample Size/Stage parameter to control the default sample size. Any
stage which has not had its sample size specified with @SPSAMPSIZE will default to a sample size
equal to the Default Sample Size/Stage parameter.
Note: In general, we prefer larger sample sizes to smaller ones in order to reduce sampling error.
However, SP models can become quite large if sample sizes aren't kept reasonably small.
This is particularly true for multiperiod models. For example, suppose we have a model with
just one random variable and ten periods/stages. If the default sample size is set to 3, then
there will be 3^10=59,049 possible scenarios. With this many scenarios, it would only take a
handful of decision variables to end up with an underlying deterministic equivalent model
approaching one million variables.
The Default Sample Size/Stage parameter defaults to a value of 2.
Random Generator Seed
The Random Generator Seed parameter on the SP Solver tab:
is used to establish the seed for the random number generator used in generating samples for random
variables in stochastic programming (SP) models.
In many SP models, LINGO will generate a set of sample values for the random variables. This is
particularly true when you have one or more continuous random variables, which leads to an infinite
number of possible outcomes. In such a case, sampling is the only viable alternative.
The Random Generator Seed parameter defaults to a value of 1013.
Sample Continuous Only
The Sample Continuous Only option on the SP Solver tab:
is used to control whether LINGO samples continuous distributions only for the random variables in
stochastic programs, or if it samples both continuous and discrete random variables. Obviously,
continuous random variables must be subject to sampling, given the infinite number of possible
outcomes. On the other hand, we have a choice when it comes to discretely distributed random
variables. If this option is enabled, then LINGO will generate one outcome for each density point in
the discrete distribution of the random variable. These outcomes will be weighted by their
corresponding probabilities.
WINDOWS COMMANDS 223
Note: If there are many density points in the distributions for the discrete random variables, the
deterministic equivalent generated to solve the SP may become exceedingly large, in which
case, disabling this option may be required. Once this option is disabled, discrete random
variables will be sampled in the same way as the continuous random variables.
The Sample Continuous Only option defaults to being on.
SP Solver Method
The SP Solver Method option:
on the SP Solver Tab is used to select the solution method for a stochastic programming (SP) model.
Presently, the available choices are:
♦ Solver Decides ⎯ LINGO decides the most appropriate method for solving the SP model.
♦ Deterministic Equivalent ⎯ LINGO generates and directly solves the deterministic
equivalent (DE) of the SP model.
♦ Nested Benders ⎯ The DE for realistic SP models can get to be quite large, in that the core
model is replicated once for every scenario. Fortunately, the DE displays strong block-
angular structure, which makes it adaptable to decomposition techniques, such as nested
Bender decomposition (NBD). Note that the model must be entirely linear to use NBD.
The default setting for the SP Solver Method option is Solver Decides.
Max Scenarios Limit
The Max Scenarios Limit parameter on the SP Solver tab:
is used to establish a limit on the maximum number of scenarios in a stochastic programming (SP)
model before forcing automatic sampling of the random variables.
The Max Scenarios Limit defaults to a value of 40,000.
Calculate All Expected Value Statistics
The Calculate All Expected Value Statistics option on the SP Solver tab:
controls whether LINGO displays information regarding the expected values for a number of statistics
when solving stochastic programming (SP) models. To illustrate, when solving the SPGAS.LG4 model
when this option is enabled, you will see the following expected values at the top of the solution
report:

224 CHAPTER 5
Expected value of:
Objective (EV): 1400.000
Wait-and-see model's objective (WS): 1326.667
Perfect information (EVPI = |EV - WS|): 73.33333
Policy based on mean outcome (EM): 1479.444
Modeling uncertainty (EVMU = |EM - EV|): 79.44444
The following is a brief description of these expected values:
Expected Value of Objective (EV)
⎯
is the expected value for the model's objective over all the
scenarios, and is the same as the reported objective value for the model.
Expected Value of Wait-and-See Model's Objective (WS)
⎯
reports the expected value of the
objective if we could wait and see the outcomes of all the random variables before making our
decisions. Such a policy would allow us to always make the best decision regardless of the
outcomes for the random variables, and, of course, is not possible in practice. For a minimization,
it's true that WS <= EV, with the converse holding for a maximization. Technically speaking, WS
is a relaxation of the true SP model, obtained by dropping the nonanticipativity constraints.
Expected Value of Perfect Information (EVPI)
⎯
is the absolute value of the difference between
EV and WS. This corresponds to the expected improvement to the objective were we to obtain
perfect information about the random outcomes. As such, this is a expected measure of how much
we should be willing to pay to obtain perfect information regarding the outcomes of the random
variables.
Expected Value of Policy Based On Mean Outcome (EM)
⎯
is an expected measure of the
objective if we were to follow a policy of assuming that the mean outcomes of the random
variables were always going to occur. EM is computed using a two-step process. First, the values
of all the random variables are fixed at their means, and the deterministic model is solved to yield
the optimal values for the stage 0 decision variables. Next, the stage 0 variables are fixed at their
optimal values from the previous step, while the random variables are freed up. At which point,
this SP is solved, with EM being equal to its objective value.
Expected Value of Modeling Uncertainty (EVMU)
⎯
is the absolute value of the difference
between EV and EM. As such, it's a measure of what we can expect to gain by incorporating
uncertainty into our modeling analysis, and not always assuming that we will be faced with mean
outcomes.
Note: Computing these expected value statistics can be very time consuming for large models. If
speed is an issue, you may wish to disable this feature.
The Calculate All Expected Value Statistics option is enabled by default.

WINDOWS COMMANDS 225
LINGO|Generate... Ctrl+G
Once you remove all the syntax errors from your LINGO model, there is still one very important step
required: model verification. LINGO’s set-based modeling capabilities are very powerful, and they
allow you to generate large, complex models quickly and easily. However, when you first develop a
model you will need to verify that the model being generated matches up to the model you actually
intended to generate. Many set-based models can be quite complex, and it is highly likely that logic
errors may creep into one or more expressions, thereby causing your generated model to be flawed.
The LINGO|Generate command is very useful for debugging such errors. It expands all of the model's
compact set-based expressions and then writes out the full scalarbased equivalent of the LINGO
model. The expanded model report explicitly lists all the generated constraints and variables in your
model. You will find that the Generate report can be an invaluable tool in tracking down errors.
When selecting the Generate command, you will be presented with a pop-up menu prompting you for
one of the following options:
♦ Display model,
♦ Don’t display model,
♦ Display nonlinear rows,
♦ Dual model,
♦ Explicit Deteq, and
♦ Scenario.

226 CHAPTER 5
Display Model
If you choose the Display model option of the LINGO|Generate command, LINGO will place a copy
of the generated model in a new window, which you may scroll through to examine, print, or save to
disk.
As an example of the output from the Generate command, consider the transportation model
developed in Chapter 1:
MODEL:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES: CAPACITY;
VENDORS: DEMAND;
LINKS( WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
DATA:
!set members;
WAREHOUSES = WH1 WH2 WH3 WH4 WH5 WH6;
VENDORS = V1 V2 V3 V4 V5 V6 V7 V8;
!attribute values;
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
! The objective;
[OBJECTIVE] MIN = @SUM( LINKS( I, J):
COST( I, J) * VOLUME( I, J));
! The demand constraints;
@FOR( VENDORS( J): [DEMAND_ROW]
@SUM( WAREHOUSES( I): VOLUME( I, J)) =
DEMAND( J));
! The capacity constraints;
@FOR( WAREHOUSES( I): [CAPACITY_ROW]
@SUM( VENDORS( J): VOLUME( I, J)) <=
CAPACITY( I));
END
Model: WIDGETS

WINDOWS COMMANDS 227
The objective will generate one expression, there should be one demand constraint generated for each
of the eight vendors and one supply constraint generated for each of the six warehouses, for a grand
total of 15 rows in the expanded model. Running the generate command to verify this reveals the
following report:
MODEL:
[OBJECTIVE] MIN= 6 * VOLUME_WH1_V1 + 2 * VOLUME_WH1_V2 + 6 *
VOLUME_WH1_V3 + 7 * VOLUME_WH1_V4 + 4 * VOLUME_WH1_V5 + 2 *
VOLUME_WH1_V6 + 5 * VOLUME_WH1_V7 + 9 * VOLUME_WH1_V8 + 4 *
VOLUME_WH2_V1 + 9 * VOLUME_WH2_V2 + 5 * VOLUME_WH2_V3 + 3 *
VOLUME_WH2_V4 + 8 * VOLUME_WH2_V5 + 5 * VOLUME_WH2_V6 + 8 *
VOLUME_WH2_V7 + 2 * VOLUME_WH2_V8 + 5 * VOLUME_WH3_V1 + 2 *
VOLUME_WH3_V2 + VOLUME_WH3_V3 + 9 * VOLUME_WH3_V4 + 7 *
VOLUME_WH3_V5 + 4 * VOLUME_WH3_V6 + 3 * VOLUME_WH3_V7 + 3 *
VOLUME_WH3_V8 + 7 * VOLUME_WH4_V1 + 6 * VOLUME_WH4_V2 + 7 *
VOLUME_WH4_V3 + 3 * VOLUME_WH4_V4 + 9 * VOLUME_WH4_V5 + 2 *
VOLUME_WH4_V6 + 7 * VOLUME_WH4_V7 + VOLUME_WH4_V8 + 2 *
VOLUME_WH5_V1 + 3 * VOLUME_WH5_V2 + 9 * VOLUME_WH5_V3 + 5 *
VOLUME_WH5_V4 + 7 * VOLUME_WH5_V5 + 2 * VOLUME_WH5_V6 + 6 *
VOLUME_WH5_V7 + 5 * VOLUME_WH5_V8 + 5 * VOLUME_WH6_V1 + 5 *
VOLUME_WH6_V2 + 2 * VOLUME_WH6_V3 + 2 * VOLUME_WH6_V4 + 8 *
VOLUME_WH6_V5 + VOLUME_WH6_V6 + 4 * VOLUME_WH6_V7 + 3 *
VOLUME_WH6_V8 ;
[DEMAND_ROW_V1] VOLUME_WH1_V1 + VOLUME_WH2_V1 +
VOLUME_WH3_V1 + VOLUME_WH4_V1 + VOLUME_WH5_V1 +
VOLUME_WH6_V1 = 35 ;
[DEMAND_ROW_V2] VOLUME_WH1_V2 + VOLUME_WH2_V2 +
VOLUME_WH3_V2 + VOLUME_WH4_V2 + VOLUME_WH5_V2 +
VOLUME_WH6_V2 = 37 ;
[DEMAND_ROW_V3] VOLUME_WH1_V3 + VOLUME_WH2_V3 +
VOLUME_WH3_V3 + VOLUME_WH4_V3 + VOLUME_WH5_V3 +
VOLUME_WH6_V3 = 22 ;
[DEMAND_ROW_V4] VOLUME_WH1_V4 + VOLUME_WH2_V4 +
VOLUME_WH3_V4 + VOLUME_WH4_V4 + VOLUME_WH5_V4 +
VOLUME_WH6_V4 = 32 ;
[DEMAND_ROW_V5] VOLUME_WH1_V5 + VOLUME_WH2_V5 +
VOLUME_WH3_V5 + VOLUME_WH4_V5 + VOLUME_WH5_V5 +
VOLUME_WH6_V5 = 41 ;
[DEMAND_ROW_V6] VOLUME_WH1_V6 + VOLUME_WH2_V6 +
VOLUME_WH3_V6 + VOLUME_WH4_V6 + VOLUME_WH5_V6 +
VOLUME_WH6_V6 = 32 ;
[DEMAND_ROW_V7] VOLUME_WH1_V7 + VOLUME_WH2_V7 +
VOLUME_WH3_V7 + VOLUME_WH4_V7 + VOLUME_WH5_V7 +
VOLUME_WH6_V7 = 43 ;
[DEMAND_ROW_V8] VOLUME_WH1_V8 + VOLUME_WH2_V8 +
VOLUME_WH3_V8 + VOLUME_WH4_V8 + VOLUME_WH5_V8 +
VOLUME_WH6_V8 = 38 ;
[CAPACITY_ROW_WH1] VOLUME_WH1_V1 + VOLUME_WH1_V2 +
VOLUME_WH1_V3 + VOLUME_WH1_V4 + VOLUME_WH1_V5 +
VOLUME_WH1_V6 + VOLUME_WH1_V7 + VOLUME_WH1_V8 <= 60 ;
[CAPACITY_ROW_WH2] VOLUME_WH2_V1 + VOLUME_WH2_V2 +
VOLUME_WH2_V3 + VOLUME_WH2_V4 + VOLUME_WH2_V5 +

228 CHAPTER 5
VOLUME_WH2_V6 + VOLUME_WH2_V7 + VOLUME_WH2_V8 <= 55 ;
[CAPACITY_ROW_WH3] VOLUME_WH3_V1 + VOLUME_WH3_V2 +
VOLUME_WH3_V3 + VOLUME_WH3_V4 + VOLUME_WH3_V5 +
VOLUME_WH3_V6 + VOLUME_WH3_V7 + VOLUME_WH3_V8 <= 51 ;
[CAPACITY_ROW_WH4] VOLUME_WH4_V1 + VOLUME_WH4_V2 +
VOLUME_WH4_V3 + VOLUME_WH4_V4 + VOLUME_WH4_V5 +
VOLUME_WH4_V6 + VOLUME_WH4_V7 + VOLUME_WH4_V8 <= 43 ;
[CAPACITY_ROW_WH5] VOLUME_WH5_V1 + VOLUME_WH5_V2 +
VOLUME_WH5_V3 + VOLUME_WH5_V4 + VOLUME_WH5_V5 +
VOLUME_WH5_V6 + VOLUME_WH5_V7 + VOLUME_WH5_V8 <= 41 ;
[CAPACITY_ROW_WH6] VOLUME_WH6_V1 + VOLUME_WH6_V2 +
VOLUME_WH6_V3 + VOLUME_WH6_V4 + VOLUME_WH6_V5 +
VOLUME_WH6_V6 + VOLUME_WH6_V7 + VOLUME_WH6_V8 <= 52 ;
END
Model: Generated Model Report for WIDGETS
As expected, there are 15 rows in the generated model: [OBJECTIVE], [DEMAND_ROW_V1]
through [DEMAND_ROW_V8], and [CAPACITY_ROW_WH1] through
[CAPACITY_ROW_WH6].
As a side note, it’s interesting to compare the generated model to the original, set-based model. The
generated model is the expanded version of the model, and has all sets and vector variables removed,
resulting in a fully scalar model. The scalar-based, generated model is mathematically equivalent to
the original vector-based model. However, we think most would agree that the set-based model is
much easier to comprehend, thereby illustrating one of the primary benefits of modern algebraic
languages over more traditional, scalar-based languages.
In addition to verifying that the correct number of rows is being generated, you should also examine
each of the rows to determine that the correct variables are appearing in each row along with their
correct coefficients.
Note: The reports generated by the LINGO|Generate command are valid LINGO models. You may
load Generate reports into a model window and solve them as you would any other LINGO
model.
One thing to keep in mind when examining generated model reports is that the LINGO model
generator performs fixed variable reduction. This means that any variables that are fixed in value are
substituted out of the generated model. For example, consider the simple model:
MODEL:
MAX = 200 * WS + 300 * NC;
WS = 60;
NC <= 40;
WS + 2 * NC <= 120;
END
If we generate this model we get the following, reduced model:

WINDOWS COMMANDS 229
MODEL:
MAX= 300 * NC + 12000 ;
NC <= 40 ;
2 * NC <= 60 ;
END
At first glance, it seems as if both the first constraint and the variable WS are missing from the
generated model. Note that by the first constraint in the original model (WS = 60), WS is fixed at a
value of 60. The LINGO model generator exploits this fact to reduce the size of the generated model
by substituting WS out of the formulation. The final solution report will still contain the values for all
the fixed variables, however, the fixed variables will not appear in the generated model report. If you
would like to suppress fixed variable reduction so that all variables appear in your generated model,
you may do so via the Fixed Var Reduction option.
Don't Display Model
If you choose the Don’t display model option, LINGO will generate the model without displaying it,
but will store the generated model for later use by the appropriate solver. This is a useful command for
verifying that your model contains no errors, while not actually having to pass it to the solver to be
optimized.
Display Nonlinear Rows
If you choose the Display Nonlinear Rows option of the Generate command, then LINGO will
generate the model and then display only those rows that contain nonlinearities. Please refer to the
Types of Constraints section for a discussion of linear vs. nonlinear expressions.
In general, one would prefer to always have purely linear models. Linear models solve faster and will
always converge to a global solution. Therefore, when developing a model, you will be interested in
carefully evaluating nonlinearities to see if they can either be eliminated or rewritten in a linear
fashion. The Display Nonlinear Rows is helpful in tracking down a model's nonlinearities.
Dual Model
The third option of the LINGO|Generate command, Dual Model, displays the dual formulation of the
current model. Every linear programming model has a corresponding, mirror-image formulation
called the dual. If the original model has M constraints and N variables, then its dual will have N
constraints and M variables.
Some interesting properties of the dual are that any feasible solution to the dual model provides a
bound on the objective to the original, primal model, while the optimal solution to the dual has the
same objective value as the optimal solution to the primal problem. It's also true that the dual of the
dual model is, once again, the original primal model. You may wish to refer to any good linear
programming text for a further discussion of duality theory.
If you run the LINGO|Generate|Dual Model command on the Widgets model shown above, you will
receive the following formulation:

230 CHAPTER 5
MODEL:
MAX = 35 * DEMAND_ROW_V1 + 37 * DEMAND_ROW_V2 + 22 *
DEMAND_ROW_V3 + 32 * DEMAND_ROW_V4 + 41 * DEMAND_ROW_V5
+ 32 * DEMAND_ROW_V6 + 43 * DEMAND_ROW_V7 + 38 *
DEMAND_ROW_V8 + 60 * CAPACITY_ROW_WH1 + 55 *
CAPACITY_ROW_WH2 + 51 * CAPACITY_ROW_WH3 + 43 *
CAPACITY_ROW_WH4 + 41 * CAPACITY_ROW_WH5 + 52 *
CAPACITY_ROW_WH6;
[ VOLUME_WH1_V1] DEMAND_ROW_V1 + CAPACITY_ROW_WH1 <= 6;
[ VOLUME_WH1_V2] DEMAND_ROW_V2 + CAPACITY_ROW_WH1 <= 2;
[ VOLUME_WH1_V3] DEMAND_ROW_V3 + CAPACITY_ROW_WH1 <= 6;
[ VOLUME_WH1_V4] DEMAND_ROW_V4 + CAPACITY_ROW_WH1 <= 7;
[ VOLUME_WH1_V5] DEMAND_ROW_V5 + CAPACITY_ROW_WH1 <= 4;
[ VOLUME_WH1_V6] DEMAND_ROW_V6 + CAPACITY_ROW_WH1 <= 2;
[ VOLUME_WH1_V7] DEMAND_ROW_V7 + CAPACITY_ROW_WH1 <= 5;
[ VOLUME_WH1_V8] DEMAND_ROW_V8 + CAPACITY_ROW_WH1 <= 9;
[ VOLUME_WH2_V1] DEMAND_ROW_V1 + CAPACITY_ROW_WH2 <= 4;
[ VOLUME_WH2_V2] DEMAND_ROW_V2 + CAPACITY_ROW_WH2 <= 9;
[ VOLUME_WH2_V3] DEMAND_ROW_V3 + CAPACITY_ROW_WH2 <= 5;
[ VOLUME_WH2_V4] DEMAND_ROW_V4 + CAPACITY_ROW_WH2 <= 3;
[ VOLUME_WH2_V5] DEMAND_ROW_V5 + CAPACITY_ROW_WH2 <= 8;
[ VOLUME_WH2_V6] DEMAND_ROW_V6 + CAPACITY_ROW_WH2 <= 5;
[ VOLUME_WH2_V7] DEMAND_ROW_V7 + CAPACITY_ROW_WH2 <= 8;
[ VOLUME_WH2_V8] DEMAND_ROW_V8 + CAPACITY_ROW_WH2 <= 2;
[ VOLUME_WH3_V1] DEMAND_ROW_V1 + CAPACITY_ROW_WH3 <= 5;
[ VOLUME_WH3_V2] DEMAND_ROW_V2 + CAPACITY_ROW_WH3 <= 2;
[ VOLUME_WH3_V3] DEMAND_ROW_V3 + CAPACITY_ROW_WH3 <= 1;
[ VOLUME_WH3_V4] DEMAND_ROW_V4 + CAPACITY_ROW_WH3 <= 9;
[ VOLUME_WH3_V5] DEMAND_ROW_V5 + CAPACITY_ROW_WH3 <= 7;
[ VOLUME_WH3_V6] DEMAND_ROW_V6 + CAPACITY_ROW_WH3 <= 4;
[ VOLUME_WH3_V7] DEMAND_ROW_V7 + CAPACITY_ROW_WH3 <= 3;
[ VOLUME_WH3_V8] DEMAND_ROW_V8 + CAPACITY_ROW_WH3 <= 3;
[ VOLUME_WH4_V1] DEMAND_ROW_V1 + CAPACITY_ROW_WH4 <= 7;
[ VOLUME_WH4_V2] DEMAND_ROW_V2 + CAPACITY_ROW_WH4 <= 6;
[ VOLUME_WH4_V3] DEMAND_ROW_V3 + CAPACITY_ROW_WH4 <= 7;
[ VOLUME_WH4_V4] DEMAND_ROW_V4 + CAPACITY_ROW_WH4 <= 3;
[ VOLUME_WH4_V5] DEMAND_ROW_V5 + CAPACITY_ROW_WH4 <= 9;
[ VOLUME_WH4_V6] DEMAND_ROW_V6 + CAPACITY_ROW_WH4 <= 2;
[ VOLUME_WH4_V7] DEMAND_ROW_V7 + CAPACITY_ROW_WH4 <= 7;
[ VOLUME_WH4_V8] DEMAND_ROW_V8 + CAPACITY_ROW_WH4 <= 1;
[ VOLUME_WH5_V1] DEMAND_ROW_V1 + CAPACITY_ROW_WH5 <= 2;
[ VOLUME_WH5_V2] DEMAND_ROW_V2 + CAPACITY_ROW_WH5 <= 3;
[ VOLUME_WH5_V3] DEMAND_ROW_V3 + CAPACITY_ROW_WH5 <= 9;
[ VOLUME_WH5_V4] DEMAND_ROW_V4 + CAPACITY_ROW_WH5 <= 5;
[ VOLUME_WH5_V5] DEMAND_ROW_V5 + CAPACITY_ROW_WH5 <= 7;
[ VOLUME_WH5_V6] DEMAND_ROW_V6 + CAPACITY_ROW_WH5 <= 2;
[ VOLUME_WH5_V7] DEMAND_ROW_V7 + CAPACITY_ROW_WH5 <= 6;
[ VOLUME_WH5_V8] DEMAND_ROW_V8 + CAPACITY_ROW_WH5 <= 5;
[ VOLUME_WH6_V1] DEMAND_ROW_V1 + CAPACITY_ROW_WH6 <= 5;
[ VOLUME_WH6_V2] DEMAND_ROW_V2 + CAPACITY_ROW_WH6 <= 5;
[ VOLUME_WH6_V3] DEMAND_ROW_V3 + CAPACITY_ROW_WH6 <= 2;
[ VOLUME_WH6_V4] DEMAND_ROW_V4 + CAPACITY_ROW_WH6 <= 2;
[ VOLUME_WH6_V5] DEMAND_ROW_V5 + CAPACITY_ROW_WH6 <= 8;

WINDOWS COMMANDS 231
[ VOLUME_WH6_V6] DEMAND_ROW_V6 + CAPACITY_ROW_WH6 <= 1;
[ VOLUME_WH6_V7] DEMAND_ROW_V7 + CAPACITY_ROW_WH6 <= 4;
[ VOLUME_WH6_V8] DEMAND_ROW_V8 + CAPACITY_ROW_WH6 <= 3;
@FREE( DEMAND_ROW_V1); @FREE( DEMAND_ROW_V2);
@FREE( DEMAND_ROW_V3); @FREE( DEMAND_ROW_V4);
@FREE( DEMAND_ROW_V5); @FREE( DEMAND_ROW_V6);
@FREE( DEMAND_ROW_V7); @FREE( DEMAND_ROW_V8);
@BND( -0.1E+31, CAPACITY_ROW_WH1, 0);
@BND( -0.1E+31, CAPACITY_ROW_WH2, 0);
@BND( -0.1E+31, CAPACITY_ROW_WH3, 0);
@BND( -0.1E+31, CAPACITY_ROW_WH4, 0);
@BND( -0.1E+31, CAPACITY_ROW_WH5, 0);
@BND( -0.1E+31, CAPACITY_ROW_WH6, 0);
END
Dual Formulation: WIDGETS
You will notice that in the dual formulation the variables from the primal model become the rows of
the dual. Similarly, the rows in the primal become the variables in the dual.
Note: The row names from the primal problem will become the variable names in the dual
formulation. For this reason, it is strongly recommended that you name all the rows in the
primal model. If a row is unnamed, then a default name will be generated for the
corresponding dual variable. The default name will consist of an underscore followed by the
row's internal index. These default names will not be very meaningful, and will make the
dual formulation difficult to interpret.
Explicit Deteq
The fourth option of the LINGO|Generate command, Explicit Deteq, displays the explicit deterministic
equivalent (DE) for the current model, assuming the current model is a stochastic program (SP).
Viewing the DE can be very helpful in determining if you have properly set up the SP components of
your model. You can refer to Chapter 15, Stochastic Programming, for more information on SP.
When LINGO solves an SP model, it is really solving the deterministic equivalent of the original SP.
The DE contains one instance of the original core model for each scenario, where the random variables
in each instance are replaced by their sampled values for the particular scenario. These core instances
are tied together by a probabilistically weighted objective of all the objectives form the individual
scenarios, plus a set of nonanticipativity constraints. The nonanticipativity constraints enforce the
condition that all scenarios with the same history must implement the same decisions, otherwise, the
DE would have the ability to anticipate future events.
As an example, if you were to load the SP gas buying sample model, SPGAS1.LG4, into LINGO and
run the LINGO|Generate|Explicit Deteq command, you will receive the following report, containing
the model's DE:

232 CHAPTER 5
MODEL:
TITLE _DETEQ;
[ _1] MIN = 0.3333333333333333 * PURCHASE_COST_SC1
+ 0.3333333333333333 * HOLD_COST_SC1 + 0.3333333333333333 *
PURCHASE_COST_SC2 + 0.3333333333333333 * HOLD_COST_SC2
+ 0.3333333333333333 * PURCHASE_COST_SC3 +
0.3333333333333333
* HOLD_COST_SC3;
[ _2_SC01] PURCHASE_COST_SC1 - 5 * PURCHASE_1_SC1 - 5 *
PURCHASE_2_SC1 = 0;
[ _3_SC01] HOLD_COST_SC1 - INVENTORY_1_SC1 -
INVENTORY_2_SC1 = 0;
[ _4_SC01] INVENTORY_1_SC1 - PURCHASE_1_SC1 = - 100;
[ _5_SC01] - INVENTORY_1_SC1 + INVENTORY_2_SC1 -
PURCHASE_2_SC1 = - 100;
[ _2_SC02] PURCHASE_COST_SC2 - 5 * PURCHASE_1_SC2 - 6 *
PURCHASE_2_SC2 = 0;
[ _3_SC02] HOLD_COST_SC2 - INVENTORY_1_SC2 -
INVENTORY_2_SC2 = 0;
[ _4_SC02] INVENTORY_1_SC2 - PURCHASE_1_SC2 = - 100;
[ _5_SC02] - INVENTORY_1_SC2 + INVENTORY_2_SC2 -
PURCHASE_2_SC2 = - 150;
[ _2_SC03] PURCHASE_COST_SC3 - 5 * PURCHASE_1_SC3 - 7.5 *
PURCHASE_2_SC3 = 0;
[ _3_SC03] HOLD_COST_SC3 - INVENTORY_1_SC3 -
INVENTORY_2_SC3 = 0;
[ _4_SC03] INVENTORY_1_SC3 - PURCHASE_1_SC3 = - 100;
[ _5_SC03] - INVENTORY_1_SC3 + INVENTORY_2_SC3 -
PURCHASE_2_SC3 = - 180;
[ _NAC01] INVENTORY_1_SC1 - INVENTORY_1_SC2 = 0;
[ _NAC02] PURCHASE_1_SC1 - PURCHASE_1_SC2 = 0;
[ _NAC03] INVENTORY_1_SC1 - INVENTORY_1_SC3 = 0;
[ _NAC04] PURCHASE_1_SC1 - PURCHASE_1_SC3 = 0;
END
Deterministic Equivalent: SPGAS1
The first row of the DE is the probabilistically weighted objective over the three scenarios (Normal,
Cold and Very Cold). Note that in the original core model, we had a variable called
PURCHASE_COST, which was used to compute the cost of the gas purchases. In the DE we now
have three PURCHASE_COST variables, or one for each of the three scenarios. LINGO appends the
strings _SC1, _SC2 or _SC3 to PUCHASE_COST so as to indicate the appropriate scenario. Each of
the constraints from the core model are also replicated across each of the scenarios with the
appropriate scenario tag appended to each row's name. Finally, at the bottom of the model, there are
four constraints beginning with the string: _NAC, which are the nonanticipativity constraints.
It's worthwhile pointing out that this report on the DE for SPGAS1 is a valid LINGO model. In fact,
you can copy this report into a new model window and solve it directly, in which case, you will get the
optimal solution to the original SP model.
WINDOWS COMMANDS 233
Scenario
As mentioned in the previous section, the ability to generate the deterministic equivalent (DE) of a
stochastic programming (SP) model can be very useful when initially formulating and debugging an
SP model. The only problem is that the DE can become quite unwieldy for all but the simplest SPs.
For example, if the core model has 500 variables and there are 1,000 scenarios, then the DE will have
500,000 variables. Tracking down problems in such a large model can be difficult. Fortunately, in
most cases when an SP is either infeasible or unbounded, LINGO will report the index of the first
scenario that is causing the problem. With such information, we can focus our attention on the model
for the isolated scenario that's causing the problem. This is where the Scenario command comes in ⎯
it allows us to generate the formulation for an individual scenario, as opposed to the entire DE, which
should substantially cut down on the burden of our debugging task.
As an example, we will work again with the SPGAS.LG4 gas buying model. After loading the model
and issuing the LINGO|Generate|Scenario command, we are prompted for the index of the scenario
we wish to view:
For our purposes, suppose we are interested in viewing scenario 2, in which case, we enter a 2 in the
edit box and then press the OK button. LINGO the displays the following report:
MODEL:
TITLE Scenario 2;
[ _1] MIN = PURCHASE_COST + HOLD_COST;
[ _2] PURCHASE_COST - 5 * PURCHASE_1 - 6 * PURCHASE_2 = 0;
[ _3] HOLD_COST - INVENTORY_1 - INVENTORY_2 = 0;
[ _4] INVENTORY_1 - PURCHASE_1 = - 100;
[ _5] - INVENTORY_1 + INVENTORY_2 - PURCHASE_2 = - 150;
END
You will note that this is the core model, with the period 2 random variable DEMAND replaced by its
sampled value of 150 in row 5. Nonanticipativity constraints are not generated as part of individual
scenario models.
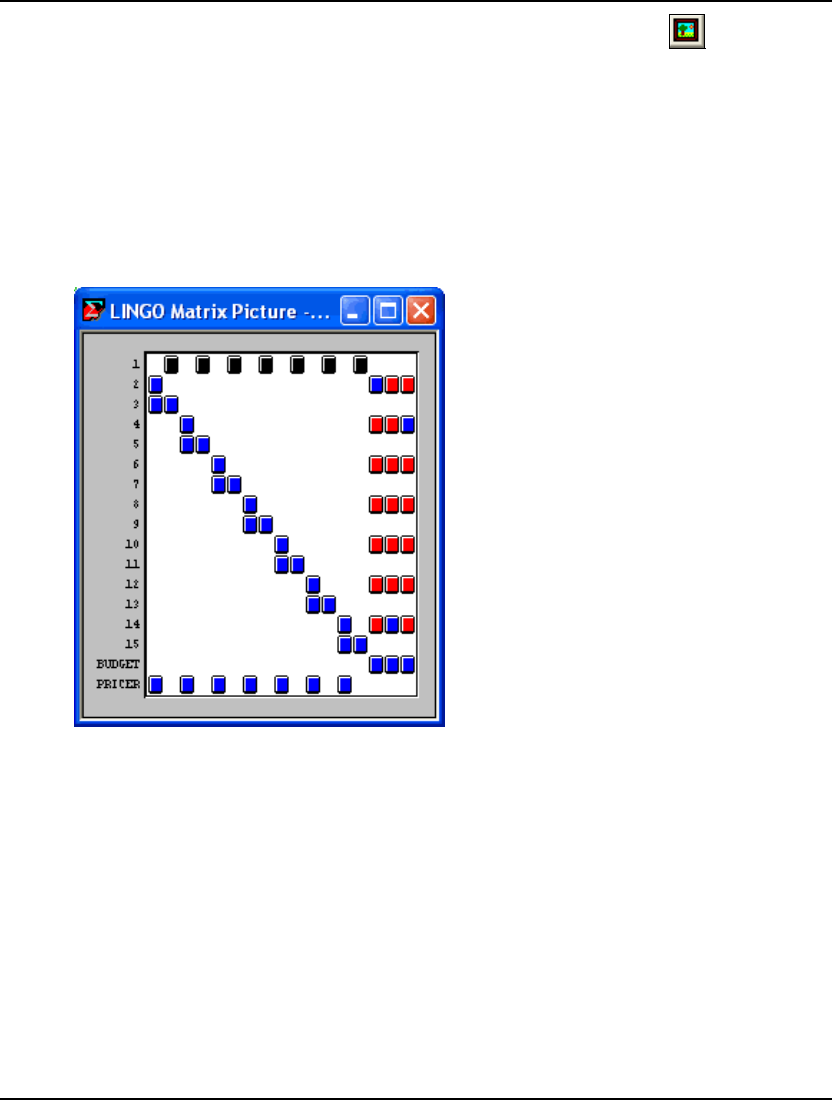
234 CHAPTER 5
LINGO|Picture Ctrl+K
The Picture command displays a model in matrix form. Viewing the model in matrix form can be
helpful in a couple of instances. First and perhaps most importantly, is the use of nonzero pictures in
debugging formulations. Most models have strong repetitive structure. Incorrectly entered sections of
the model will stand out in a model’s matrix picture. Secondly, a nonzero picture can be helpful when
you are attempting to identify special structure in your model. As an example, if your model displays
strong block angular structure, then algorithms that decompose the model into smaller fragments might
prove fruitful.
As an example, we loaded the DNRISK.LG4 model from LINGO’s sample model set. Issuing the
Picture command, we see the following:
Positive coefficients are represented with blue tiles, negatives with red, and variables that appear in a
row nonlinearly show up as black tiles.
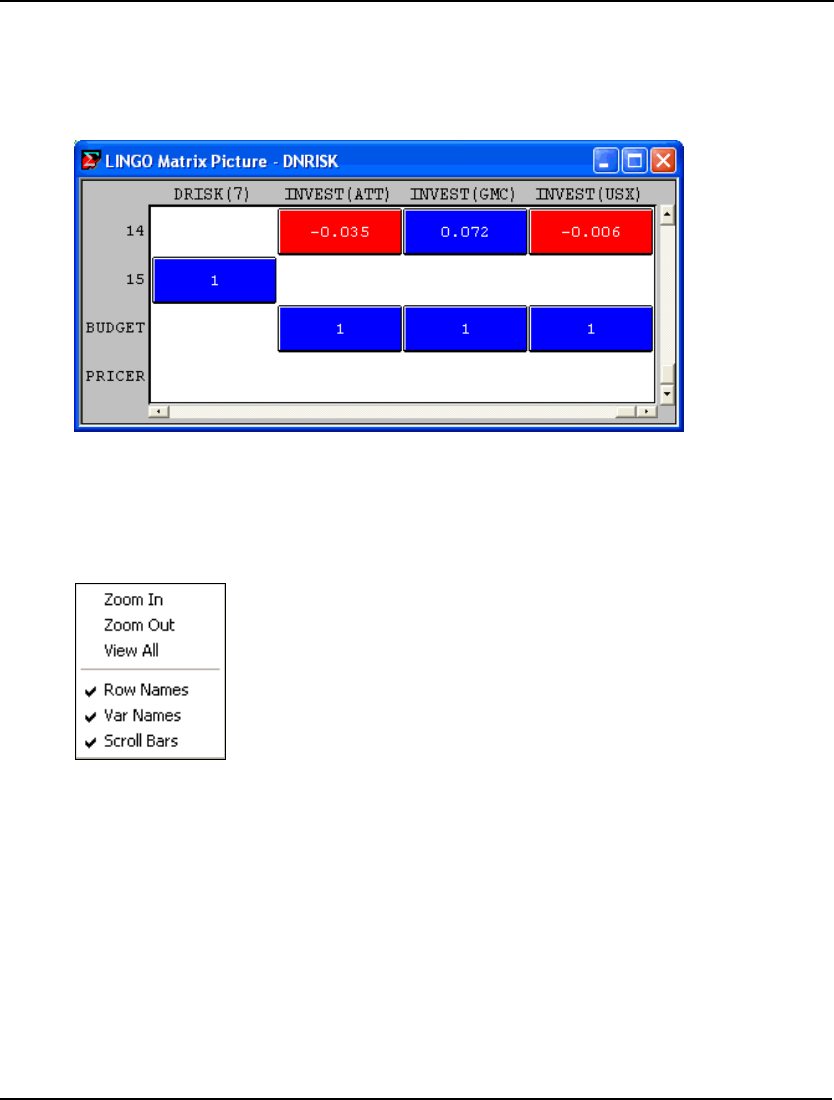
WINDOWS COMMANDS 235
You can zoom in on a selected range in the matrix for closer viewing. To do this, place the cursor on
the upper left corner of the range you wish to view, press and hold down the left mouse button. Next,
drag the mouse to the lower right-hand corner of the desired range. Now, release the left mouse button
and LINGO will zoom in on the selected range. As an example, here is a view of the matrix after
zooming in on a 4x4 range:
Note, we have zoomed in far enough to be able see the actual coefficient values, row names, and
variable names. Scroll bars have also appeared to allow scrolling through the matrix.
The matrix picture window supports several additional interactive features. To access these features,
place the cursor over the matrix picture and press and hold the right mouse button. This will bring up
the following menu:
A brief description of these features follows:
♦ Zoom In - Zooms the view in centered around the current cursor position
♦ Zoom Out - Zooms the view out centered around the current cursor position
♦ View All - Zooms all the way out to give a full view of the matrix
♦ Row Names - Toggles the display of row names on and off
♦ Var Names - Toggles the display of variable names on and off
♦ Scroll Bars - Toggles scroll bars on and off
At present, matrix pictures cannot be printed directly from LINGO. However, you can issue the
Edit|Copy command to place the matrix picture in the Windows clipboard. From the clipboard, the
picture can be pasted into any graphics program (e.g., Microsoft Paint) and printed from there.
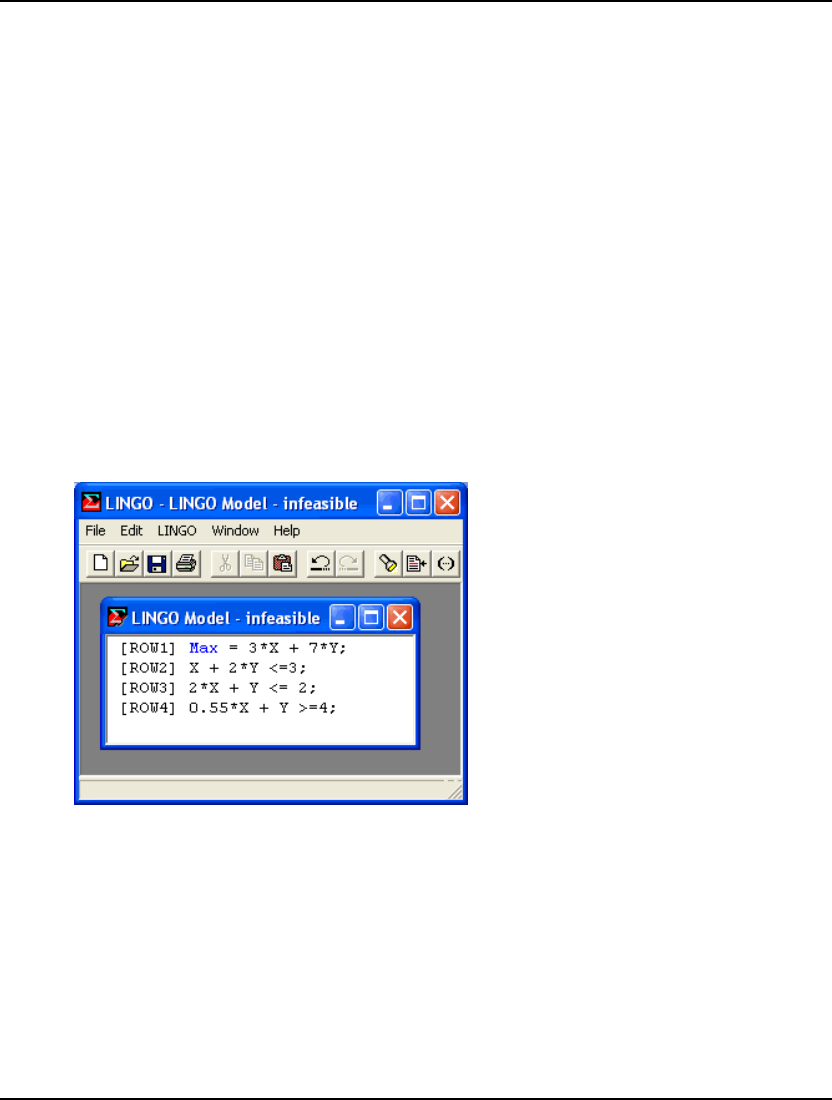
236 CHAPTER 5
LINGO|Debug
In the ideal world, all models would return an optimal solution. Unfortunately, this is not the case.
Sooner or later, you are bound to run across either an infeasible or unbounded model. This is
particularly true in the development phase of a project when the model will tend to suffer from
typographical errors.
Tracking down an error in a large model can prove to be a daunting task. The Debug command is
useful in narrowing the search for problems in both infeasible and unbounded linear programs. A small
portion of the original model is isolated as the source of the problem. This allows you to focus your
attention on a subsection of the model in search of formulation or data entry errors.
The Debug command identifies two types of sets: sufficient and necessary. Removing any sufficient
set object from the model is sufficient to fix the entire model. Not all models will have a sufficient set.
In which case, they will have a necessary set with the property that removing any object from this set
fixes the remaining objects within that set.
As an example, suppose you have an infeasible model. If the complete model would be feasible except
for a bug in a single row, that row will be listed as part of the sufficient set. If the model has a
necessary set, then, as long as all of them are present, the model will remain infeasible.
The following example illustrates. The coefficient .55 in row 4 should have been 5.5:
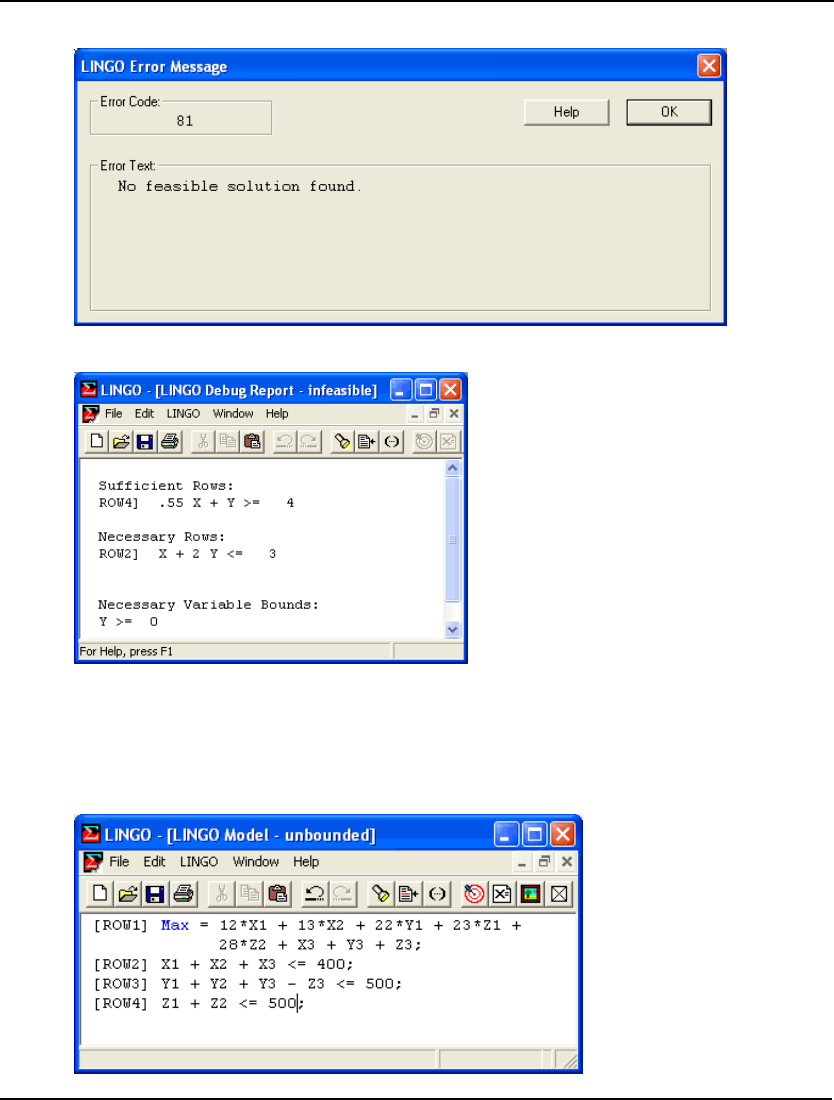
WINDOWS COMMANDS 237
When we attempt to solve this formulation, we get the following error:
Next, if we run the LINGO|Debug command, we are presented with the following report:
The Debug command has correctly identified that the erroneous ROW4, when eliminated, is sufficient
to make the entire model feasible.
Debug operates in a similar manner for unbounded models. In the following example, we introduced
an error by placing a minus sign instead of a plus sign in front of variable Z3 in ROW3. A look at
ROW3 reveals that Z3 can be increased indefinitely, leading to an unbounded objective.
238 CHAPTER 5
The resulting model is unbounded and, when issuing the LINGO|Solve command, we receive the
unbounded error message:
Issuing the Debug command, we receive the following breakdown:
The Debug command has successfully determined that bounding Z3 is sufficient to bound the entire
model.
Typically, the Debug command helps to substantially reduce the search effort. The first version of this
feature was implemented in response to a user who had an infeasible model. The user had spent a day
searching for a bug in a model with 400 constraints. The debug feature quickly found a necessary set
with 55 constraints, as well as one sufficient set constraint. The user immediately noticed that the
right-hand side of the sufficient set constraint was incorrect.
Note: Prior to release 10.0 of LINGO, the debugger was only capable of processing linear models.
Starting with release 10.0, all classes of models (LP, QP, IP and NLP) may now be debugged.
LINGO|Model Statistics
The Model Statistics command lists summary statistics for your model. The statistics vary slightly
depending on whether the model you’re working with is linear or nonlinear.
WINDOWS COMMANDS 239
In the following example, we open the linear transportation model, TRAN.LG4, issue the Model
Statistics command, and then discuss some of the details of the report. Here is the output generated by
Model Statistics for TRAN.LG4:
The statistics report consists of five lines.
In line one, the number of rows (constraints), variables (columns), and integer variables are shown.
The report also specifies when the model is linear by stating that all variables are linear.
Line two of the report gives a count of the number of nonzero coefficients appearing in the model. The
first count is the number of nonzero coefficients in the entire model. The Constraint nonz count is the
number of coefficients on the left-hand sides of all the constraints, excluding the nonzero objective and
right-hand side coefficients. Next, is a count of the number of constraint coefficients that are plus or
minus one. In general, a linear programming model is easier to solve when the number of percentage
of +/- 1 coefficient increases. Finally, LINGO reports a Density figure, which is defined as:
(total nonzeros) / [(number of rows) * (number of columns + 1)]. For large models, densities under .01
are common. High densities can mean that a problem will take longer to solve.
Line three lists the smallest and largest coefficients in the model in absolute value. For stability
reasons, the ratio of the largest coefficient to the smallest should, ideally, be close to 1. Also, in
absolute terms, it is best to keep coefficient values in the range of 0.0001 to 100,000. Values outside
this range can cause numerical difficulties for the solver.
Line four lists the number of constraints by type (<, =, and >), the sense of the objective, and an upper
bound on the number of Generalized Upper Bound (GUB) constraints. A GUB constraint is a
constraint that does not intersect with the remainder of the model. Given this, the GUB statistic is a
measure of model simplicity. If all the constraints were nonintersecting, the problem could be solved
by inspection by considering each constraint as a separate problem.
Line five lists the number of variables that appear in only one row. Such a variable is effectively a
slack. If you did not explicitly add slack variables to your model and the single column count is greater
than zero, then it suggests a misspelled variable name.
The following report was generated by the Model Statistics command for the nonlinear model,
DNRISK.LG4:
240 CHAPTER 5
The statistics report for nonlinear models drops information about the range of coefficient values, the
number of +/- 1 coefficient, and the GUB upper bound. A count of the number of nonlinear variables
and rows is added in line two. The nonlinear rows count includes the objective, while the nonlinear
constraint count does not.
LINGO|Look... Ctrl+L
Use the Look command to generate a report containing your model’s formulation. The Look
command’s dialog box, pictured below, lets you choose All or Selected rows for viewing from the
Rows to View:
When you choose Selected rows, the Beginning Row and Ending Row text boxes are available for entry
in the Selected Rows box. You must enter the indices of the range of rows you wish displayed. LINGO
will display the requested lines with line numbers in a new window.
4. Window Menu
The Window menu, pictured at left,
contains commands that generally
pertain to managing open windows.
WINDOWS COMMANDS 241
Window|Command Window Ctrl+1
In addition to the pull down menu commands, LINGO’s features can also be accessed through a
command language. For more details on the command language, refer to the following chapter,
Command-line Commands. A script file that contains LINGO commands may be run using the
File|Take Commands command. Alternatively, you can interactively enter script commands into
LINGO’s command window. The Window|Command Window command opens LINGO’s command
window. The following window should appear on your screen:
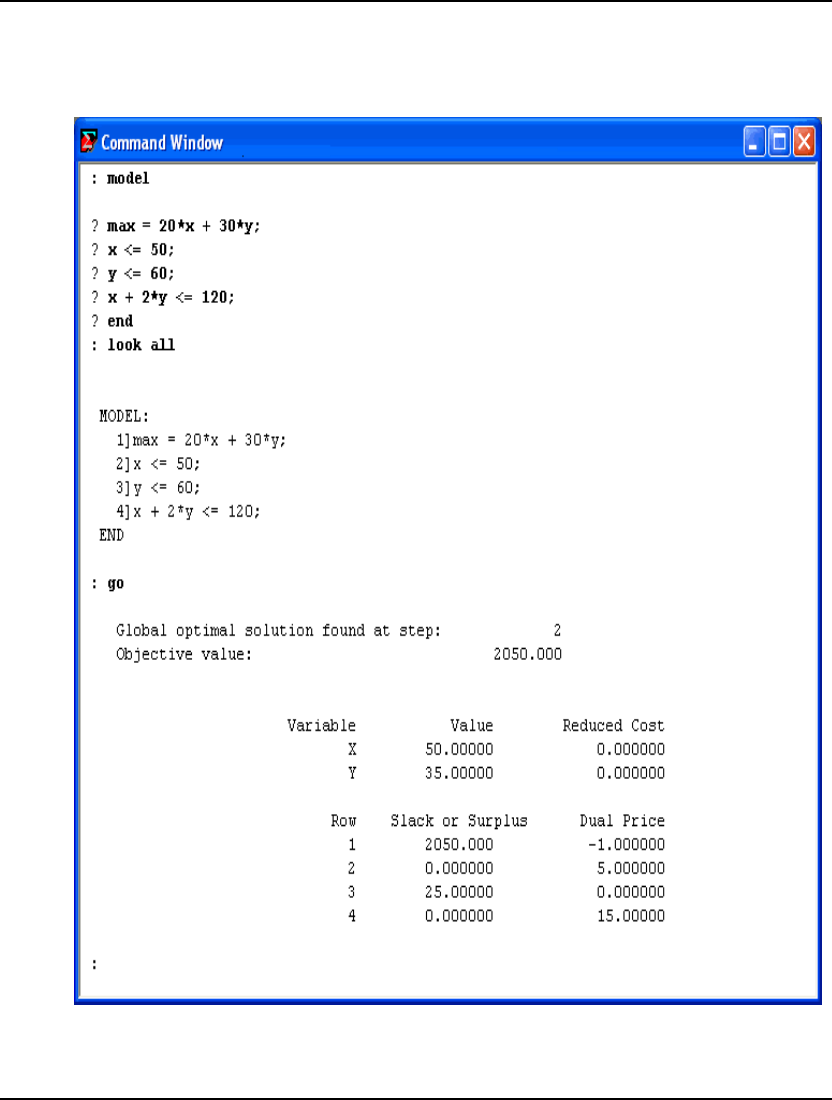
242 CHAPTER 5
You may enter any valid LINGO script commands to the colon prompt in the upper left corner of the
window. In the following example, we enter a small model with the MODEL command, display the
formulation with the LOOK ALL command, and then solve it using the GO command (user input is
shown in bold type):
In general, you will probably prefer to use the pull down menus and toolbar when using LINGO
interactively. The command window interface is primarily provided for users wishing to interactively
test command scripts.
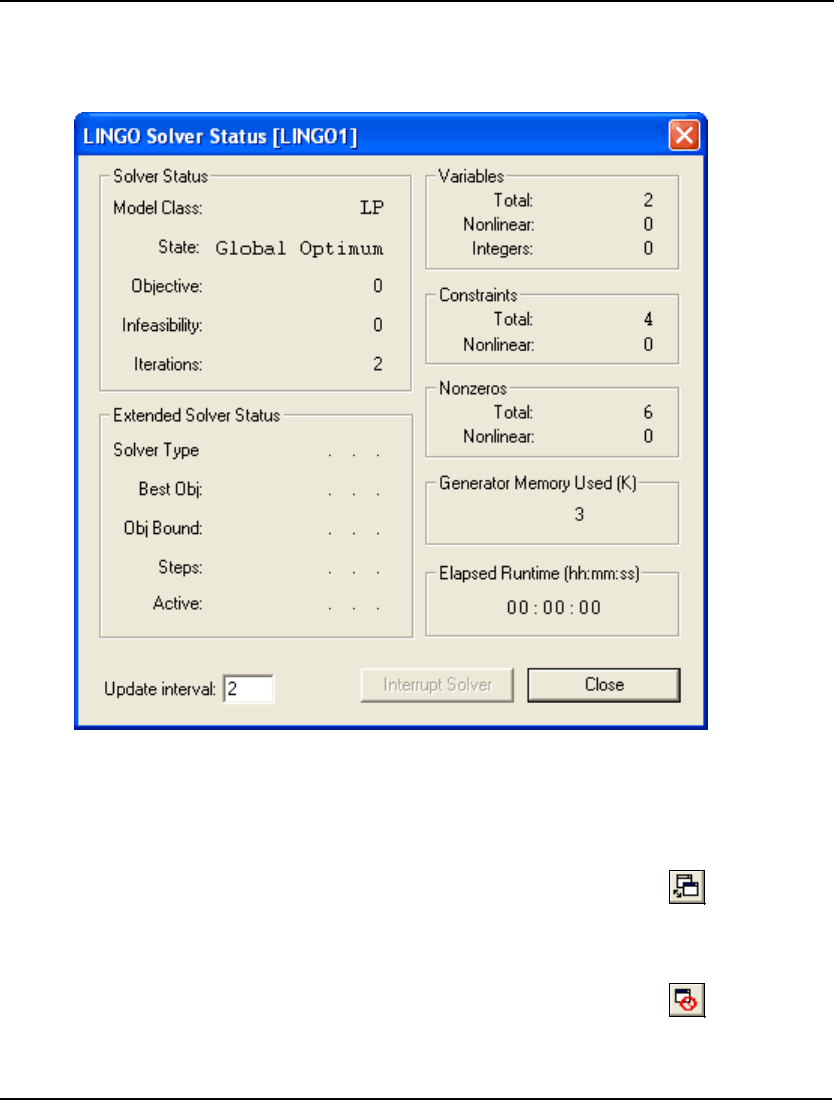
WINDOWS COMMANDS 243
Window|Status Window Ctrl+2
When you invoke LINGO’s Solve command, a status window is displayed on your screen that
resembles the following:
This window allows you to monitor the progress of the solver. You can close the status window at any
time. If you close the status window, it may be reopened with the Window|Status Window command.
If you would like to prevent LINGO from opening a status window, see the LINGO|Options command
above. For more information on the interpretation and use of the status window, see page 8.
Window|Send To Back Ctrl+B
The Window|Send To Back command sends the active window behind all others on the screen. This
command is useful when switching between a model and a solution window.
Window|Close All Ctrl+3
The Window|Close All command closes all open windows. If you made a change to a model window
without saving it, you will be prompted to save the model before it is closed.
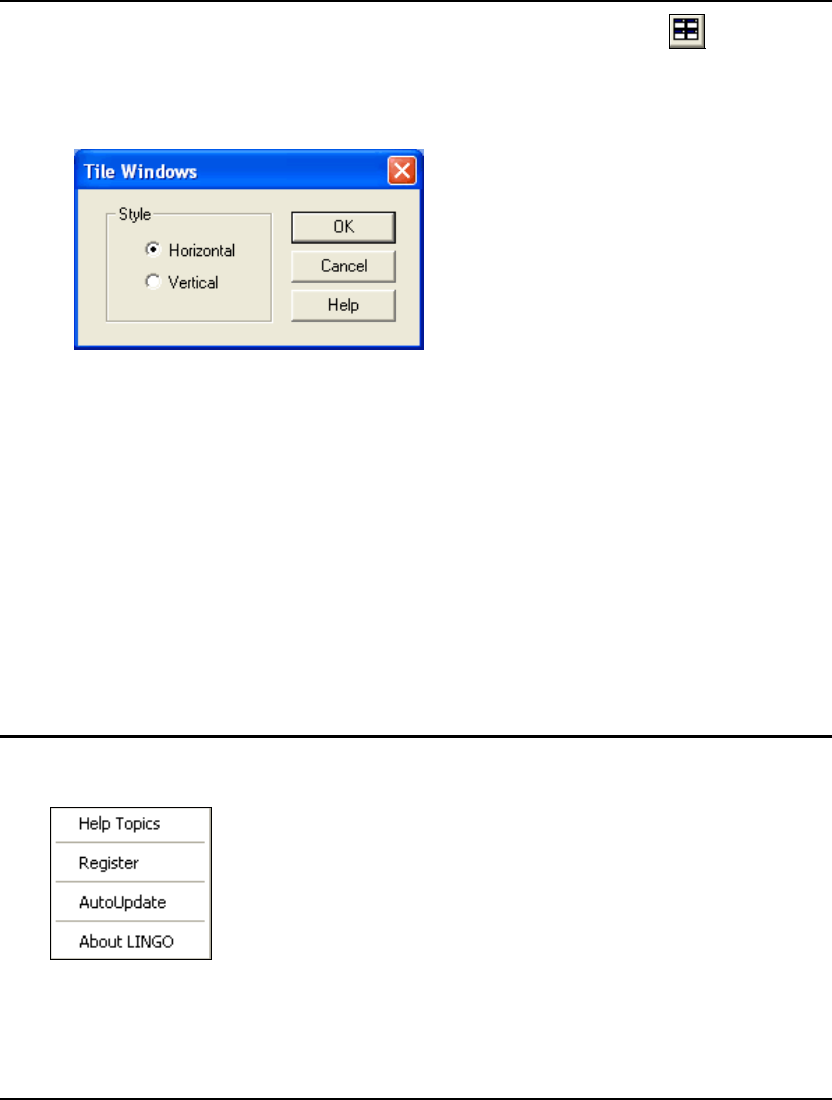
244 CHAPTER 5
Window|Tile Ctrl+4
The Window|Tile command arranges all the open windows in a tiled pattern. Each window is resized,
so all windows appear on the screen and are of roughly the same size.
When you issue the Window|Tile command, you will see the dialog box:
You have the choice of tiling the windows horizontally or vertically. If you tile Horizontally (or
Vertically), LINGO will maximize the horizontal (or vertical) dimension of each window.
If there are more than three open windows, LINGO will tile the windows, but the choice of horizontal
or vertical will no longer make a difference.
Window|Cascade Ctrl+5
The Window|Cascade command arranges all open windows in a cascade pattern starting in the upper
left corner of the mainframe window. The currently active window remains on top.
Window|Arrange Icons Ctrl+6
If you have minimized any open windows, so they appear as icons on the screen, you can issue the
Window|Arrange Icons command to line all the icons up in the lower left-hand corner of the frame
window.
5. Help Menu
The Help menu, pictured at left, contains
commands that generally pertain to
LINGO’s Help system, copyright notice,
and version specific information.
WINDOWS COMMANDS 245
Help|Help Topics
A portion of the dialog box displayed by the Help Topics command is displayed below:
Select the Contents tab to display a table of contents for the Help system. You can select any of the
topics that are of interest by double clicking on them.
Select the Index tab to display an index of topics for the Help system. Select an item for viewing by
double clicking on it.
Go to the Find tab to search the Help system for a particular item.
246 CHAPTER 5
Help|Register
Use the Help|Register command to register your version of LINGO online. You will need a
connection to the Internet open for this command to work. When you issue the Register command,
you will be presented with the following dialog box:
WINDOWS COMMANDS 247
Enter your personal information and select the Register button. Your information will be sent directly
to LINDO Systems via the Internet.
Once your registration is complete, the following dialog box will appear on your screen:
Select the OK button to be returned to the main LINGO environment.
LINDO Systems is constantly working to make our products faster and easier to use. Registering your
software with LINDO ensures that you will be kept up-to-date on the latest enhancements and other
product news. You can also register through the mail or by fax using the registration card included
with your software package.
Help|AutoUpdate
Turn the Help|AutoUpdate command on to have LINGO automatically check every time you start the
LINGO software whether there is a more recent version of LINGO available for download on the
LINDO Systems website. You will need a connection to the internet open for this command to work.
When you issue the AutoUpdate command or start a version of LINGO with AutoUpdate enabled,
LINGO will search the Internet to see if an updated version of the LINGO software is available for
download. If you currently have the most recent version, then you will be returned to the main LINGO
environment. If you have an outdated version of the software, you will be presented with the following
dialog box:
at which point, you may wish to go to the LINDO Systems Web site, www.lindo.com, to download the
latest build of the software.
If you want to disable the AutoUpdate feature, then select the Disable AutoUpdate button from the
AutoUpdate dialog box. The AutoUpdate feature is disabled by default.
248 CHAPTER 5
Help|About LINGO
When you issue the About LINGO command, you will be presented with a dialog box resembling the
following:
The first box lists size and release information of your copy of LINGO.

WINDOWS COMMANDS 249
The second box tells you where you can get in touch with LINDO Systems.
The third box, titled Limits for this Installation, lists various capacity limits of your version and the
current number of bytes allocated to LINGO's model generator. The maximum sized problem your
LINGO software can handle depends on the version you have. The current limits for the various
versions are:
Version Total
Variables Integer
Variables Nonlinear
Variables Global
Variables Constraints
Demo/Web 300 30 30 5 150
Solver Suite 500 50 50 5 250
Super 2,000 200 200 10 1,000
Hyper 8,000 800 800 20 4,000
Industrial 32,000 3,200 3,200 50 16,000
Extended Unlimited Unlimited Unlimited Unlimited Unlimited
For more information on the definitions of these limits see section Maximum Problem Dimensions. In
addition to the maximum problem limits, this box also lists the amount of memory allocated to
LINGO’s model generator. You can adjust the size of generator memory allocation on the General
Solver tab of the LINGO|Options dialog box.
The fourth box titled License Expiration lists the date at which your license expires. If your license
does not have an expiration date, this field will display Perpetual.
The box labeled License Usage lists whether your license is for commercial or educational use.
Educational licenses are restricted to use by faculty, staff, and students of educational institutions for
instructional or research purposes. Commercial licenses are not restricted to any particular use.
The box titled Licenses lists the number of users licensed to use your copy of LINGO.
The API Version box lists the version number of the LINDO API in use by your copy of LINGO. The
LINDO API is the library of solver tools used by LINGO to optimize your models.
The License Location box displays the location of the license file in effect for the current LINGO
session, while the Config Location box gives the location of LINGO's configuration file. The
configuration file is where LINGO stores non-default option settings, which are controlled by the
LINGO|Options command.
The final box, Additional License Information, contains information relevant to your particular license.
In most cases, your LINGO serial number can be found in this field. Scrolling through this field, you
will also find information as to the optional features included with your license (e.g., the barrier,
nonlinear, global and stochastic solvers.)
Help|Pointer
Press this button to switch the cursor into Help mode. Once the cursor is in Help mode, you can select
a menu command or a toolbar button and LINGO will display help information on the selected item.

251
6 Command-Line
Commands
This chapter discusses all of the command-line commands available to the LINGO user. On platforms
other than Windows based PC’s, the user interfaces with LINGO entirely through text commands
issued to LINGO’s command-line colon prompt.
If you are using a Windows version of LINGO, you will primarily be interested in the previous
chapter, Windows Commands, which details the commands available in the pull down menus of
LINGO’s Windows version. However, in Windows versions, LINGO command-line commands may
be entered using the command window (see the Window|Command Window section in Chapter 5,
Windows Commands) and may also be used to build command scripts. Command scripts may be run
automatically at startup or whenever the user desires. Command scripts are useful to both the Windows
user and users on other platforms. Thus, the Windows user may find this chapter of interest, too.
We will begin by briefly listing all the command-line commands according to their general function.
This will be followed up by an in-depth explanation of the commands.
The Commands In Brief
1. Information
CAT lists categories of available commands
COM lists available commands by category
HELP provides brief help on commands
MEM provides statistics about model generator memory usage
2. Input
FRMPS retrieves a model in free MPS format
MODEL begins input of a new model
RMPI retrieves a model in MPI format
RMPS retrieves a model in fixed MPS format
TAKE runs a command script from an external file

252 CHAPTER 6
3. Display
DUAL generates and displays the dual formulation for the model
GEN generates the algebraic formulation for the model
HIDE password protects the current model
LOOK displays the current model
PICTURE displays a picture of the model’s nonzero structure
SCENE generates the algebraic formulation for a specified scenario of a
larger stochastic program
SHOWNL generates the entire model, but only displays rows containing
nonlinearities
STATS gives summary statistics about the properties of a generated model
XDETEQ generates the algebraic formulation for a explicit deterministic
equivalent of a stochastic program
4. File Output
DIVERT opens a file for receiving output
RVRT closes a file previously opened with DIVERT
SAVE saves the current model to disk
SMPI exports a model in MPI format
SMPS sends a copy of the current model to a file in MPS format
5. Solution
DEBUG tracks down formulation errors in infeasible and unbounded
models
GO solves the current model
NONZ generates a nonzeros only solution report
RANGE generates a range analysis report
SOLU generates a solution report
6. Problem Editing
ALTER edits the contents of the model
DELETE deletes a selected row from the model
EXTEND adds rows to the end of the current model
7. Conversational Parameters
PAGE sets the page/screen length
PAUSE pauses for keyboard input
TERSE output level
VERBOSE switches to verbose output mode
WIDTH sets terminal display and input width

COMMAND-LINE COMMANDS 253
8. Tolerances
APISET allows access to advanced parameters in the LINDO API, which is
the solver library used by LINGO
DBPWD sets the password for database access via @ODBC
DBUID sets your user id for database access via @ODBC
FREEZE saves current tolerance settings to disk
SET overrides a number of LINGO defaults and tolerances
9. Miscellaneous
! inserts a comment
QUIT exits LINGO
TIME displays current elapsed time since start of session
The Commands In Depth
Each LINGO command-line command is discussed in detail in this section. Commands are grouped by
category based upon their general function.
Note: User input in the examples below is indicated through the use of bold typeface.
1. Information
The Information category contains commands related to on-line information.
CAT
The CAT command displays the nine categories of commands available in LINGO. You will be
prompted to input a number corresponding to one of the categories. If you input a number, LINGO
will display the commands available under the corresponding category. To exit out of the command,
input a blank line.
COM
The COM command lists all the command-line commands available in LINGO by category.
HELP
The HELP command combined with another LINGO command gives you information on the
command specified. The information is usually quite brief, but is often all that is needed.
The HELP command without an argument will give you general information about your version of
LINGO, along with the maximum number of constraints and variables that your version of LINGO can
handle.

254 CHAPTER 6
MEM
The MEM command displays statistics about the model generator's memory usage. The following is
some sample output from the MEM command:
: MEM
Total generator memory 5242880
Peak generator memory usage 12048
Current generator memory usage 1312
Total handles 96
Peak handle usage 9
Current handle usage 5
Total bytes moved 1552
Total blocks moved 6
Total heap compacts 0
Fragmentation ratio 0.002
:
The Total generator memory figure is the amount of memory LINGO has allocated for a working
memory heap for model generation. You can control the size of the heap using the SET command.
Peak generator memory usage refers to the maximum amount of memory the model generator used
during the current session. Current memory usage lists the amount of working memory currently in use
by the model generator.
Total handles is the maximum number of memory blocks LINGO can allocate. Peak handle usage lists
the maximum number of memory blocks LINGO allocated at any one time during this session. Current
handle usage represents the number of memory blocks currently in use by the model generator.
Total bytes moved lists the number of memory bytes the generator has had to move so far in order to
reallocate memory. Total blocks moved lists the number of memory blocks moved due to reallocation.
Total heap compacts lists the number of times the generator has had to compact the heap to make room
for growing memory needs. If the number of heap compacts is abnormally large, you should allocate
more working memory using the SET command.
The Fragmentation ratio is a statistic measuring how fragmented the memory heap is. A value of 1
would indicate high fragmentation, whereas a value of 0 indicates no fragmentation
2. Input
The Input category contains commands that initiate input into LINGO
FRMPS / RMPS
The FRMPS and RMPS commands are used to read MPS formatted models. The MPS file format is an
industry standard format developed by IBM and is useful for passing models from one solver or
platform to another.
FRMPS and RMPS don’t presently support quadratic MPS files, so the models read by these
commands must be either linear or mixed integer linear. FRMPS reads an MPS file in free format,
while RMPS reads fixed format MPS files.

COMMAND-LINE COMMANDS 255
When LINGO reads an MPS file, it converts the formulation to an equivalent LINGO model. As an
example, consider the following, simple model:
ObjRow) Maximize 20X + 30Y
Subject To:
Row1) X < 50
Row2) Y < 60
Row3) X + 2Y < 120
An equivalent MPS file for this model is:
NAME SAMPLE
OBJSENSE
MAX
ROWS
N OBJROW
L ROW1
L ROW2
L ROW3
COLUMNS
X ROW3 1.0000000
X OBJROW 20.0000000
X ROW1 1.0000000
Y OBJROW 30.0000000
Y ROW2 1.0000000
Y ROW3 2.0000000
RHS
RHS ROW1 50.0000000
RHS ROW2 60.0000000
RHS ROW3 120.0000000
ENDATA
As an aside, one thing to notice about the MPS representation is that it is not a very compact method
for storing a model.
In the following session, we read this MPS file into LINGO and then display the model with the
LOOK command. Note how the model is automatically converted from MPS format to LINGO format:
: rmps c:\sample.mps
: look all
1] TITLE SAMPLE;
2] [ OBJROW] MAX = 20 * X + 30 * Y;
3] [ ROW1] X <= 50;
4] [ ROW2] Y <= 60;
5] [ ROW3] X + 2 * Y <= 120;
:
Should you wish to save the file again using MPS format rather than LINGO format, you may use the
SMPS command (shown in the File Output section below).

256 CHAPTER 6
When it comes to acceptable constraint and variable names, MPS format is less restrictive than
LINGO. MPS allows for embedded blanks and other additional characters in names. To compensate
for this fact, LINGO attempts to patch names when reading an MPS file, so all the incoming names are
compatible with its syntax. LINGO does this by substituting an underscore for any character in a name
that is not admissible. In most cases, this will work out OK. However, there is a chance for name
collisions where two or more names get mapped into one. For instance, the variable names X.1 and
X%1 would both get mapped into the single LINGO name X_1. Of course, situations such as this
entirely alter the structure of the model rendering it incorrect.
You will be warned whenever LINGO has to patch a name with the following error message:
[Error Code: 179]
The MPS reader had to patch names to make them compatible:
var names patched: 1
row names patched: 0
Name collisions may have occurred.
This message displays the number of variable and row names that were patched to get them to conform
to LINGO syntax.
If name collisions are a problem, then LINGO has an option that will ensure all names remain unique.
This option involves using RC format for names encountered during MPS I/O. RC format involves
renaming each row (constraint) in a model to be Rn, where n is the row’s index. Similarly, each
column (variable) is renamed to Cn. In addition, LINGO renames the objective row to be ROBJ. To
switch to RC format for MPS names, you will need to use the SET command as follows:
: SET RCMPSN 1
This will cause LINGO to use RC naming conventions for all MPS reads and saves. To cancel the use
of RC names, type:
: SET RCMPSN 0
As an example, we will once again read the same MPS format model we read above, but this time we
will switch to RC naming conventions:
: set rcmpsn 1
Parameter Old Value New Value
RCMPSN 0 1
: rmps c:\sample.mps
: look all
1] TITLE SAMPLE;
2] [ ROBJ] MAX = 20 * C1 + 30 * C2;
3] [ R1] C1 <= 50;
4] [ R2] C2 <= 60;
5] [ R3] C1 + 2 * C2 <= 120;
Notice how the variable names now use RC format, guaranteeing that name collisions will not occur.

COMMAND-LINE COMMANDS 257
Another potential conflict is that MPS allows variable names to be duplicated as constraint names and
vice versa. LINGO does not allow for this. When you go to solve the model, you will either receive
error message 28 (Invalid use of a row name), or error message 37 (Name already in use). However,
once again, you can switch to using RC format for names to avoid this conflict.
MODEL
Use the MODEL command to begin inputting a new model into LINGO. LINGO prompts for each
new line of the model with a question mark. When you are through entering the model, enter END on a
single line by itself. LINGO will then return to normal command mode (indicated by the colon
prompt).
In the following example, we enter a small model with the MODEL command, display it with the
LOOK command, and then solve it with the GO command:
: MODEL
? !How many years does it take
? to double an investment growing
? 10% per year?;
? 1.1 ^ YEARS = 2;
? END
: LOOK ALL
1]!How many years does it take
2]to double an investment growing
3]10% per year?;
4]1.1 ^ YEARS = 2;
: GO
Feasible solution found at step: 0
Variable Value
YEARS 7.272541
Row Slack or Surplus
1 0.000000
:

258 CHAPTER 6
RMPI
The RMPI command is used to read MPI (Math Programmming Interface) formatted models. The
MPI file format was developed by LINDO Systems as a portable format for storing arbitrary math
programming models.
When LINGO reads an MPI file, it converts the formulation to an equivalent LINGO model. As an
example, consider the following, simple model:
ObjRow) Maximize 20X + 30Y
Subject To:
Row1) X < 50
Row2) Y < 60
Row3) X + 2Y < 120
The equivalent MPI file for this model is:

COMMAND-LINE COMMANDS 259
BEGINMODEL SAMPLE
! Number of Objective Functions: 1
! Number of Constraints : 3
! Number of Variables : 2
VARIABLES
! Name Lower Bound Initial Point
Upper Bound Type
X 0 1.23457
1e+030 C
Y 0 1.23457
1e+030 C
OBJECTIVES
OBJROW MAXIMIZE
EP_USRCOD -101
EP_PUSH_NUM 20
EP_PUSH_VAR X
EP_MULTIPLY
EP_PUSH_NUM 30
EP_PUSH_VAR Y
EP_MULTIPLY
EP_PLUS
CONSTRAINTS
ROW1 L
EP_USRCOD -101
EP_PUSH_VAR X
EP_PUSH_NUM 50
EP_MINUS
ROW2 L
EP_USRCOD -101
EP_PUSH_VAR Y
EP_PUSH_NUM 60
EP_MINUS
ROW3 L
EP_USRCOD -101
EP_PUSH_VAR X
EP_PUSH_NUM 2
EP_PUSH_VAR Y
EP_MULTIPLY
EP_PLUS
EP_PUSH_NUM 120
EP_MINUS
ENDMODEL

260 CHAPTER 6
As an aside, one thing to notice about the MPI representation is that it is not a very compact method
for storing a model⎯MPI is designed for portability, as opposed to efficiency.
In the following session, we read this MPI file into LINGO and then display the model with the LOOK
command. Note how the model is automatically converted from MPI format to native LINGO format:
: rmpi c:\sample.mpi
: look all
1] TITLE SAMPLE;
2] [OBJROW] MAX = 20 * X + 30 * Y;
3] [ROW1] X <= 50;
4] [ROW2] Y <= 60;
5] [ROW3] X + 2 * Y <= 120;
:
Should you wish to save the file again using MPS format rather than LINGO format, you may use the
SMPS command.
Note: The MPI file format is intended primarily for exporting models to other applications or
platforms. The MPI format is purely scalar in nature—all set-based information is lost upon
converting a LINGO model to MPI format. Thus, when saving copies of a model on your
own machine, you should always use the SAVE command in order to save models in native
LINGO format in order to preserve your model in its entirety.
When it comes to acceptable constraint and variable names, MPI format is less restrictive than
LINGO. MPI allows for embedded blanks and other additional characters in names. To compensate
for this fact, LINGO attempts to patch names when reading an MPI file so that all the incoming names
are compatible with its syntax. LINGO does this by substituting an underscore for any character in a
name that is not admissible. In most cases, this will work out OK. However, there is a chance for
name collisions where two or more names get mapped into one. For instance, the variable names X.1
and X%1 would both get mapped into the single LINGO name X_1. Of course, situations such as this
entirely alter the structure of the model rendering it incorrect.
You will be warned whenever LINGO has to patch a name with the following error message:
[Error Code: 179]
The MPS reader had to patch names to make them compatible:
var names patched: 1
row names patched: 0
Name collisions may have occurred.
This message displays the number of variable and row names that were patched to get them to conform
to LINGO syntax.
If name collisions are a problem, then LINGO has an option that will ensure that all names remain
unique. This option involves using RC format for names encountered during MPS I/O. RC format
involves renaming each row (constraint) in a model to be Rn, where n is the row’s index. Similarly,
each column (variable) is renamed to Cn. In addition, LINGO renames the objective row to be ROBJ.
To switch to RC format for MPS names, you will need to use the SET command as follows:
: SET RCMPSN 1

COMMAND-LINE COMMANDS 261
This will cause LINGO to use RC naming conventions for all MPI reads and saves. To cancel the use
of RC names, type:
: SET RCMPSN 0
As an example, we will once again read the same MPS format model we read above, but this time we
will switch to RC naming conventions.
: set rcmpsn 1
Parameter Old Value New Value
RCMPSN 0 1
: rmpi c:\sample.mpi
: look all
1] TITLE SAMPLE;
2] [ROBJ] MAX = 20 * C1 + 30 * C2;
3] [R1] C1 <= 50;
4] [R2] C2 <= 60;
5] [R3] C1 + 2 * C2 <= 120;
Notice how the variable names now use RC format, guaranteeing that name collisions will not occur.
Another potential conflict is that MPI allows variable names to be duplicated as constraint names, and
vice versa. LINGO does not allow for this. When you go to solve the model, you will either receive
error message 28 (Invalid use of a row name), or error message 37 (Name already in use). However,
once again, you can switch to using RC format for names to avoid this conflict.
TAKE
The TAKE command is used to 1) read models saved to disk using the SAVE command, and 2) execute
command scripts contained in external files. The syntax for the TAKE command is:
TAKE [filename]
If you omit a filename, LINGO will prompt you for one.
As an example, suppose you used the SAVE command to save a model to the file
C:\LINGOMOD\MYMODEL.LNG. You can read it back into LINGO by giving the command:
: TAKE C:\LINGOMOD\MYMODEL.LNG

262 CHAPTER 6
As a second example, we will use the TAKE command to execute a LINGO command script. A
command script is simply a text file that contains a series of LINGO commands. Suppose we have
built the following command script in an editor and have saved it in the text file
D:\LNG\MYSCRIPT.LTF:
MODEL:
!For a given probability P, this
model returns the value X such
that the probability that a unit
normal random variable is less
than or equal to X is P;
! Here is the probability;
P = .95;
! Solve for X;
P = @PSN(X);
END
!Terse output mode;
TERSE
!Solve the model;
GO
!Report X;
SOLU X
We can use the TAKE command to run the script as follows:
: TAKE D:\LNG\MYSCRIPT.LTF
Feasible solution found at step: 0
Variable Value
X 1.644854
:
3. Display
This category contains commands that display information.
DUAL
The DUAL command displays the dual formulation of the current model. Every linear programming
model has a corresponding, mirror-image formulation called the dual. If the original model has M
constraints and N variables, then its dual will have N constraints and M variables.
Some interesting properties of the dual are that any feasible solution to the dual model provides a
bound on the objective to the original, primal model, while the optimal solution to the dual has the
same objective value as the optimal solution to the primal problem. It's also true that the dual of the
dual model is, once again, the original primal model. You may wish to refer to any good linear
programming text for a further discussion of duality theory.

COMMAND-LINE COMMANDS 263
As an example, consider the following small transportation model:
MODEL:
! A 3 Warehouse, 4 Customer
Transportation Problem;
SETS:
WAREHOUSE / WH1, WH2, WH3/ : CAPACITY;
CUSTOMER / C1, C2, C3, C4/ : DEMAND;
ROUTES( WAREHOUSE, CUSTOMER) : COST, VOLUME;
ENDSETS
! The objective;
[OBJ] MIN = @SUM( ROUTES: COST * VOLUME);
! The demand constraints;
@FOR( CUSTOMER( J): [DEM]
@SUM( WAREHOUSE( I): VOLUME( I, J)) >=
DEMAND( J));
! The supply constraints;
@FOR( WAREHOUSE( I): [SUP]
@SUM( CUSTOMER( J): VOLUME( I, J)) <=
CAPACITY( I));
! Here are the parameters;
DATA:
CAPACITY = 30, 25, 21 ;
DEMAND = 15, 17, 22, 12;
COST = 6, 2, 6, 7,
4, 9, 5, 3,
8, 8, 1, 5;
ENDDATA
END
Model: TRAN.LNG
264 CHAPTER 6
If the sample session below, we load the sample model TRAN.LNG and use the DUAL command to
generate its dual formulation:
: take \lingo\samples\tran.lng
: dual
MODEL:
MAX = 15 * DEM_C1 + 17 * DEM_C2 + 22 * DEM_C3 + 12 * DEM_C4
+ 30 * SUP_WH1 + 25 * SUP_WH2 + 21 * SUP_WH3;
[ VOLUME_WH1_C1] DEM_C1 + SUP_WH1 <= 6;
[ VOLUME_WH1_C2] DEM_C2 + SUP_WH1 <= 2;
[ VOLUME_WH1_C3] DEM_C3 + SUP_WH1 <= 6;
[ VOLUME_WH1_C4] DEM_C4 + SUP_WH1 <= 7;
[ VOLUME_WH2_C1] DEM_C1 + SUP_WH2 <= 4;
[ VOLUME_WH2_C2] DEM_C2 + SUP_WH2 <= 9;
[ VOLUME_WH2_C3] DEM_C3 + SUP_WH2 <= 5;
[ VOLUME_WH2_C4] DEM_C4 + SUP_WH2 <= 3;
[ VOLUME_WH3_C1] DEM_C1 + SUP_WH3 <= 8;
[ VOLUME_WH3_C2] DEM_C2 + SUP_WH3 <= 8;
[ VOLUME_WH3_C3] DEM_C3 + SUP_WH3 <= 1;
[ VOLUME_WH3_C4] DEM_C4 + SUP_WH3 <= 5;
@BND( -0.1E+31, SUP_WH1, 0); @BND( -0.1E+31, SUP_WH2, 0);
@BND( -0.1E+31, SUP_WH3, 0);
END
:
You will notice that in the dual formulation the variables from the primal model become the rows of
the dual. Similarly, the rows in the primal become the variables in the dual.
Note: The row names from the primal problem will become the variable names in the dual
formulation. For this reason, it is strongly recommended that you name all the rows in the
primal model. If a row is unnamed, then a default name will be generated for the
corresponding dual variable. The default name will consist of an underscore followed by the
row's internal index. These default names will not be very meaningful, and will make the
dual formulation difficult to interpret.
GEN
Once you remove all the syntax errors from your LINGO model, there is still one very important step
required: model verification. LINGO’s set-based modeling capabilities are very powerful, and they
allow you to generate large, complex models quickly and easily. However, when you first develop a
model you will need to verify that the model being generated matches up to the model you actually
intended to generate. Many set-based models can be quite complex, and it is highly likely that logic
errors may creep into one or more expressions, thereby causing your generated model to be flawed.
The GEN (short for generate) command is very useful for debugging such errors. It expands all of the
model's compact set-based expressions and then writes out the full scalar-based equivalent of the
LINGO model. The expanded model report explicitly lists all the generated constraints and variables in
your model. You will find that the Generate report can be an invaluable tool in tracking down errors.

COMMAND-LINE COMMANDS 265
As an example of the output from the generate command, consider the transportation model developed
in Chapter 1:
MODEL:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES: CAPACITY;
VENDORS: DEMAND;
LINKS( WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
DATA:
!set members;
WAREHOUSES = WH1 WH2 WH3 WH4 WH5 WH6;
VENDORS = V1 V2 V3 V4 V5 V6 V7 V8;
!attribute values;
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
! The objective;
[OBJECTIVE] MIN = @SUM( LINKS( I, J):
COST( I, J) * VOLUME( I, J));
! The demand constraints;
@FOR( VENDORS( J): [DEMAND_ROW]
@SUM( WAREHOUSES( I): VOLUME( I, J)) =
DEMAND( J));
! The capacity constraints;
@FOR( WAREHOUSES( I): [CAPACITY_ROW]
@SUM( VENDORS( J): VOLUME( I, J)) <=
CAPACITY( I));
END
Model: WIDGETS

266 CHAPTER 6
The objective will generate one expression; there should be one demand constraint generated for each
of the eight vendors and one supply constraint generated for each of the six warehouses, for a grand
total of 15 rows in the expanded model. Running the generate command to verify this reveals the
following report:
MODEL:
[OBJECTIVE] MIN= 6 * VOLUME_WH1_V1 + 2 * VOLUME_WH1_V2 + 6 *
VOLUME_WH1_V3 + 7 * VOLUME_WH1_V4 + 4 * VOLUME_WH1_V5 + 2 *
VOLUME_WH1_V6 + 5 * VOLUME_WH1_V7 + 9 * VOLUME_WH1_V8 + 4 *
VOLUME_WH2_V1 + 9 * VOLUME_WH2_V2 + 5 * VOLUME_WH2_V3 + 3 *
VOLUME_WH2_V4 + 8 * VOLUME_WH2_V5 + 5 * VOLUME_WH2_V6 + 8 *
VOLUME_WH2_V7 + 2 * VOLUME_WH2_V8 + 5 * VOLUME_WH3_V1 + 2 *
VOLUME_WH3_V2 + VOLUME_WH3_V3 + 9 * VOLUME_WH3_V4 + 7 *
VOLUME_WH3_V5 + 4 * VOLUME_WH3_V6 + 3 * VOLUME_WH3_V7 + 3 *
VOLUME_WH3_V8 + 7 * VOLUME_WH4_V1 + 6 * VOLUME_WH4_V2 + 7 *
VOLUME_WH4_V3 + 3 * VOLUME_WH4_V4 + 9 * VOLUME_WH4_V5 + 2 *
VOLUME_WH4_V6 + 7 * VOLUME_WH4_V7 + VOLUME_WH4_V8 + 2 *
VOLUME_WH5_V1 + 3 * VOLUME_WH5_V2 + 9 * VOLUME_WH5_V3 + 5 *
VOLUME_WH5_V4 + 7 * VOLUME_WH5_V5 + 2 * VOLUME_WH5_V6 + 6 *
VOLUME_WH5_V7 + 5 * VOLUME_WH5_V8 + 5 * VOLUME_WH6_V1 + 5 *
VOLUME_WH6_V2 + 2 * VOLUME_WH6_V3 + 2 * VOLUME_WH6_V4 + 8 *
VOLUME_WH6_V5 + VOLUME_WH6_V6 + 4 * VOLUME_WH6_V7 + 3 *
VOLUME_WH6_V8 ;
[DEMAND_ROW_V1] VOLUME_WH1_V1 + VOLUME_WH2_V1 +
VOLUME_WH3_V1 + VOLUME_WH4_V1 + VOLUME_WH5_V1 +
VOLUME_WH6_V1 = 35 ;
[DEMAND_ROW_V2] VOLUME_WH1_V2 + VOLUME_WH2_V2 +
VOLUME_WH3_V2 + VOLUME_WH4_V2 + VOLUME_WH5_V2 +
VOLUME_WH6_V2 = 37 ;
[DEMAND_ROW_V3] VOLUME_WH1_V3 + VOLUME_WH2_V3 +
VOLUME_WH3_V3 + VOLUME_WH4_V3 + VOLUME_WH5_V3 +
VOLUME_WH6_V3 = 22 ;
[DEMAND_ROW_V4] VOLUME_WH1_V4 + VOLUME_WH2_V4 +
VOLUME_WH3_V4 + VOLUME_WH4_V4 + VOLUME_WH5_V4 +
VOLUME_WH6_V4 = 32 ;
[DEMAND_ROW_V5] VOLUME_WH1_V5 + VOLUME_WH2_V5 +
VOLUME_WH3_V5 + VOLUME_WH4_V5 + VOLUME_WH5_V5 +
VOLUME_WH6_V5 = 41 ;
[DEMAND_ROW_V6] VOLUME_WH1_V6 + VOLUME_WH2_V6 +
VOLUME_WH3_V6 + VOLUME_WH4_V6 + VOLUME_WH5_V6 +
VOLUME_WH6_V6 = 32 ;
[DEMAND_ROW_V7] VOLUME_WH1_V7 + VOLUME_WH2_V7 +
VOLUME_WH3_V7 + VOLUME_WH4_V7 + VOLUME_WH5_V7 +
VOLUME_WH6_V7 = 43 ;
[DEMAND_ROW_V8] VOLUME_WH1_V8 + VOLUME_WH2_V8 +
VOLUME_WH3_V8 + VOLUME_WH4_V8 + VOLUME_WH5_V8 +
VOLUME_WH6_V8 = 38 ;
[CAPACITY_ROW_WH1] VOLUME_WH1_V1 + VOLUME_WH1_V2 +
VOLUME_WH1_V3 + VOLUME_WH1_V4 + VOLUME_WH1_V5 +
VOLUME_WH1_V6 + VOLUME_WH1_V7 + VOLUME_WH1_V8 <= 60 ;
[CAPACITY_ROW_WH2] VOLUME_WH2_V1 + VOLUME_WH2_V2 +
VOLUME_WH2_V3 + VOLUME_WH2_V4 + VOLUME_WH2_V5 +
COMMAND-LINE COMMANDS 267
VOLUME_WH2_V6 + VOLUME_WH2_V7 + VOLUME_WH2_V8 <= 55 ;
[CAPACITY_ROW_WH3] VOLUME_WH3_V1 + VOLUME_WH3_V2 +
VOLUME_WH3_V3 + VOLUME_WH3_V4 + VOLUME_WH3_V5 +
VOLUME_WH3_V6 + VOLUME_WH3_V7 + VOLUME_WH3_V8 <= 51 ;
[CAPACITY_ROW_WH4] VOLUME_WH4_V1 + VOLUME_WH4_V2 +
VOLUME_WH4_V3 + VOLUME_WH4_V4 + VOLUME_WH4_V5 +
VOLUME_WH4_V6 + VOLUME_WH4_V7 + VOLUME_WH4_V8 <= 43 ;
[CAPACITY_ROW_WH5] VOLUME_WH5_V1 + VOLUME_WH5_V2 +
VOLUME_WH5_V3 + VOLUME_WH5_V4 + VOLUME_WH5_V5 +
VOLUME_WH5_V6 + VOLUME_WH5_V7 + VOLUME_WH5_V8 <= 41 ;
[CAPACITY_ROW_WH6] VOLUME_WH6_V1 + VOLUME_WH6_V2 +
VOLUME_WH6_V3 + VOLUME_WH6_V4 + VOLUME_WH6_V5 +
VOLUME_WH6_V6 + VOLUME_WH6_V7 + VOLUME_WH6_V8 <= 52 ;
END
Model: WIDGETS
As expected, there are 15 rows in the generated model: [OBJECTIVE], [DEMAND_ROW_V1]
through [DEMAND_ROW_V8], and [CAPACITY_ROW_WH1] through
[CAPACITY_ROW_WH6].
As a side note, it’s interesting to compare the generated model to the original, set-based model. We
think most would agree that the set-based model is much easier to comprehend, thereby illustrating one
of the primary benefits of modern algebraic languages over more traditional, scalar-based languages.
In addition to verifying that the correct number of rows is being generated, you should also examine
each of the rows to determine that the correct variables are appearing in each row along with their
correct coefficients.
Note: The reports generated by the GEN command are valid LINGO models. You may load
Generate reports into LINGO and solve them as you would any other model.
One thing to keep in mind when examining generated model reports is that the LINGO model
generator performs fixed variable reduction. This means that any variables that are fixed in value are
substituted out of the generated model. For example, consider the simple model:
MODEL:
MAX = 200 * WS + 300 * NC;
WS = 60;
NC <= 40;
WS + 2 * NC <= 120;
END
If we generate this model we get the following, reduced model:
MODEL:
MAX= 300 * NC + 12000 ;
NC <= 40 ;
2 * NC <= 60 ;
END
At first glance, it seems as if both the first constraint and the variable WS are missing from the
generated model. Note that by the first constraint in the original model (WS = 60), WS is fixed at a

268 CHAPTER 6
value of 60. The LINGO model generator exploits this fact to reduce the size of the generated model
by substituting WS out of the formulation. The final solution report will still contain the values for all
the fixed variables; however, the fixed variables will not appear in the generated model report. If you
would like to suppress fixed variable reduction so that all variables appear in your generated model,
you may do so via the Fixed Var Reduction option.
Note: To capture the results of the GEN command in a file, use the DIVERT command to open an
output file before issuing the GEN command.
HIDE
The HIDE command hides the text of a model from viewing by the user. This may be useful if you are
trying to protect proprietary ideas contained in your model.
When you enter the HIDE command, you’ll be prompted for a password. You may enter any password
with up to eight characters. LINGO will prompt you for this password once more for verification.
LINGO is sensitive to the case of the alphabetic characters in the password.
Once a model is hidden, commands allowing the user to view the model text (GEN, GENL, LOOK,
SMPS) are disabled. All other commands, however, will function as normal with the exception of
ALTER. If a model is hidden, ALTER will perform modifications, but they will not be echoed to the
screen.
When a hidden model is saved to disk, its text will be encrypted. This prevents the user from viewing
the model from outside of LINGO as well. You will want to distribute the encrypted version of the
model to those using your application. However, you should always keep an unhidden version of the
model at your site for safekeeping in the event you forget the password.
A hidden model may be returned to the normal unhidden state by once again issuing the HIDE
command with the correct password.

COMMAND-LINE COMMANDS 269
A sample session illustrating the use of the HIDE command follows:
: TAKE TRAN.LNG !Read in a model
: LOOK 4 6 !Display some rows
4] SUPPLY / WH1, WH2, WH3/ : CAP;
5] DEST / C1, C2, C3, C4/ : DEM;
6] LINKS(SUPPLY, DEST) : COST, VOL;
: HIDE !Now hide the model
Password?
TIGER
Please reenter password to verify:
TIGER
Model is now hidden.
: ! Model is hidden so LOOK will fail
: LOOK ALL
[Error Code: 111]
Command not available when model is hidden.
: ! We can still solve it though
: TERSE
: GO
Global optimal solution found at step: 6
Objective value: 161.0000
: !And get a solution report
: NONZ VOL
Variable Value Reduced Cost
VOL(WH1, C1) 2.000000 0.000000
VOL(WH1, C2) 17.00000 0.000000
VOL(WH1, C3) 1.000000 0.000000
VOL(WH2, C1) 13.00000 0.000000
VOL(WH2, C4) 12.00000 0.000000
VOL(WH3, C3) 21.00000 0.000000
: !Now, unhide the model
: HIDE
Password?
TIGER
Model is no longer hidden.
: !Once again, we can view the model
: LOOK 4 6
4] SUPPLY / WH1, WH2, WH3/ : CAP;
5] DEST / C1, C2, C3, C4/ : DEM;
6] LINKS(SUPPLY, DEST) : COST, VOL;
:

270 CHAPTER 6
LOOK
The LOOK command displays all or part of the current model. The syntax of the LOOK command is:
LOOK row_index|beg_row_index end_row_index|ALL
Thus, you can specify the index of a single row to view, a range of rows, or ALL to view the entire
model.
In this next example, we use several forms of the LOOK command to view the current model:
: LOOK ALL
1]!For a given probability P, this
2] model returns the value X such
3] that the probability that a unit
4] normal random variable is less
5] than or equal to X is P;
6]
7]! Here is the probability;
8] P = .95;
9]
10]! Solve for X;
11]P = @PSN(X);
12]
: LOOK 8
8] P = .95;
: LOOK 10 11
10]! Solve for X;
11]P = @PSN(X);
:

COMMAND-LINE COMMANDS 271
PICTURE
The PICTURE command displays the model in matrix form. For small to medium sized models, the
PICTURE command is a useful way to obtain a visual impression of the model and to hunt for
formulation errors.
The following letter codes are used to represent the linear coefficients in the PICTURE output:
Letter Code Coefficient Range
Z (.000000, .000001)
Y (.000001, .00001)
X (.00001, .0001)
W (.0001, .001)
V (.001, .01)
U (.01, .1)
T (.1, 1 )
A (1, 10)
B (10, 100)
C (100, 1000)
D (1000, 10000)
E (10000, 100000)
F (100000, 1000000)
G > 1000000
Single digit integers are shown explicitly rather than being displayed as a code. This is especially
handy, because many models have a large number of coefficients of positive or negative 1, which can
affect the solution procedure. If a variable appears nonlinearly in a row, then the PICTURE command
will represent its coefficient with a question mark.

272 CHAPTER 6
In this example, we read in a copy of the small transportation model supplied with LINGO and use the
PICTURE command to view the logical structure of the model:
: take \lingo\samples\tran.lng
: pic
V V V V V V V V V V V V
O O O O O O O O O O O O
L L L L L L L L L L L L
U U U U U U U U U U U U
M M M M M M M M M M M M
E E E E E E E E E E E E
( ( ( ( ( ( ( ( ( ( ( (
W W W W W W W W W W W W
H H H H H H H H H H H H
1 1 1 1 2 2 2 2 3 3 3 3
, , , , , , , , , , , ,
C C C C C C C C C C C C
1 2 3 4 1 2 3 4 1 2 3 4
) ) ) ) ) ) ) ) ) ) ) )
OBJ: 6 2 6 7 4 9 5 3 8 8 1 5 MIN
DEM(C1): 1 ' 1 ' 1 ' > B
DEM(C2): ' 1' ' '1 ' ' 1 ' > B
DEM(C3): ' 1 ' 1 ' 1 > B
DEM(C4): ' 1 ' 1 ' 1 > B
SUP(WH1): 1 1'1 1 ' ' ' ' ' < B
SUP(WH2): ' ' 1 1 1 1 ' < B
SUP(WH3): ' ' ' 1 1 1 1 < B
In this model, all the right-hand side values are in the range [12, 30]. Thus, they are all represented
using the letter B. Row names are displayed running down the left-hand side of the matrix, while
variable names are displayed along the top. The sense of the objective row and each of the constraints
are shown. Spaces stand in for zero coefficients, and single quote marks are inserted to give a grid-like
background.
Note: The PICTURE command is best used on small models. The amount of output generated for
large models can be cumbersome. For larger models, the LINGO|Picture command in
Windows versions of LINGO can compress the matrix picture of large models into a single
screen for easier viewing.
SCENE
The ability to generate the deterministic equivalent (DE) of a stochastic programming (SP) model via
the XDETEQ command can be very useful when initially formulating and debugging an SP model.
The only problem is that the DE can become quite unwieldy for all but the simplest SPs. For example,
if the core model has 500 variables and there are 1,000 scenarios, then the DE will have 500,000
variables. Tracking down problems in such a large model can be difficult. Fortunately, in most cases
when an SP is either infeasible or unbounded, LINGO will report the index of the first scenario that is
causing the problem. With such information, we can focus our attention on the model for the isolated
scenario that's causing the problem. This is where the Scenario command comes in ⎯ it allows us to
generate the formulation for an individual scenario, as opposed to the entire DE, which should
substantially cut down on the burden of our debugging task.

COMMAND-LINE COMMANDS 273
As an example, we will work again with the SPGAS gas buying model. In the following example, we
load the SP model and then use the SCENE command to generate the algebraic formulation of the
second scenario:
: take \lingo\samples\spgas.lng
: scene 2
MODEL:
TITLE Scenario 2;
[ _1] MIN = PURCHASE_COST + HOLD_COST;
[ _2] PURCHASE_COST - 5 * PURCHASE_1 - 6 * PURCHASE_2 =
0;
[ _3] HOLD_COST - INVENTORY_1 - INVENTORY_2 = 0;
[ _4] INVENTORY_1 - PURCHASE_1 = - 100;
[ _5] - INVENTORY_1 + INVENTORY_2 - PURCHASE_2 = -
150;
END
:
You will note that this is the core model, with the period 2 random variable DEMAND replaced by its
sampled value of 150 in row 5. Nonanticipativity constraints are not generated as part of individual
scenario models.
SHOWNL
The SHOWNL command will cause LINGO to generate the model and then display only those rows
that contain nonlinearities. Please refer to the Types of Constraints section for a discussion of linear
vs. nonlinear expressions.
In general, one would prefer to always have purely linear models. Linear models solve faster and will
always converge to a global solution. Therefore, when developing a model, you will be interested in
carefully evaluating nonlinearities to see if they can either be eliminated or rewritten in a linear
fashion. The Display Nonlinear Rows is helpful in tracking down a model's nonlinearities.
STATS
The STATS command lists summary statistics for your model. The statistics vary slightly depending on
whether the model you’re working with is linear or nonlinear. In this next example, we will read in a
linear transportation model, run the STATS command, and explain some of the details of the report.
: take \lingo\samples\tran.lng
: stats
Rows= 8 Vars= 12 No. integer vars= 0 (all are linear)
Nonzeros= 43 Constraint nonz= 24( 24 are +- 1) Density=0.413
Smallest and largest elements in abs value= 1.00000 30.0000
No. < : 3 No. =: 0 No. > : 4, Obj=MIN, GUBs <= 4
Single cols= 0
The STATS report for linear models consists of five lines.
In line one, we see the number of rows (constraints), variables (columns), and integer variables. The
STATS command lets us know the model is linear by stating that all the variables are linear.

274 CHAPTER 6
Line two of the report gives a count of the number of nonzero coefficients appearing in the model. The
first count is the number of nonzero coefficients in the entire model. The Constraint nonz count is the
number of coefficients on the left-hand sides of all the constraints, excluding the nonzero objective and
right-hand side coefficients. Next, STATS gives a count of the number of constraint coefficients that
are plus or minus one. In general, a linear programming model is easier to solve when the number of
unity coefficients increases. Finally, STATS reports a Density figure, defined as:
(total nonzeros) / [(number of rows) * (number of columns + 1)].
For large models, densities under .01 are common. High densities can mean that a problem will take
longer to solve.
Line three lists the smallest and largest coefficients in the model in absolute value. For stability
reasons, the ratio of the largest coefficient to the smallest should, ideally, be close to 1. Also, in
absolute terms, it is best to keep coefficient values in the range of 0.0001 to 100,000. Values outside
this range can cause numerical difficulties for the linear solver.
Line four lists the number of constraints by type (<, =, and >), the sense of the objective, and an upper
bound on the number of Generalized Upper Bound (GUB) constraints. A GUB constraint is a
constraint that does not intersect with the remainder of the model. Given this, the GUB statistic is a
measure of model simplicity. If all the constraints were nonintersecting, the problem could be solved
by inspection by considering each constraint as a separate problem.
Line five lists the number of variables that appear in only one row. Such a variable is effectively a
slack. If you did not explicitly add slack variables to your model and the single column count is greater
than zero, then it suggests a misspelled variable name.
In the next example, we read a nonlinear model, DNRISK.LG4, into LINGO and review it’s model
statistics.
: take c:\lingo\samples\dnrisk.lng
: stats
Rows= 17 Vars= 17 No. integer vars= 0
Nonlinear rows= 1 Nonlinear vars= 7 Nonlinear constraints= 0
Nonzeros= 68 Constraint nonz= 52 Density=0.222
No. < : 0 No. =: 8 No. > : 8, Obj=MIN Single cols= 0
The nonlinear STATS report drops information about the range of coefficient values, the number of
+/-1 coefficients, and the GUB upper bound. A count of the number of nonlinear rows and variables is
added in line two. The nonlinear rows count includes the objective, while the nonlinear constraint
count does not.
XDETEQ
The XDETEQ command displays the explicit deterministic equivalent (DE) for the current model,
assuming the current model is a stochastic program (SP). Viewing the DE can be very helpful in
determining if you have properly set up the SP components of your model. You can refer to Chapter
14, Stochastic Programming, for more information on SP.
When LINGO solves an SP model, it is really solving the deterministic equivalent of the original SP.
The DE contains one instance of the original core model for each scenario, where the random variables

COMMAND-LINE COMMANDS 275
in each instance are replaced by their sampled values for the particular scenario. These core instances
are tied together by a probabilistically weighted objective of all the objectives form the individual
scenarios, plus a set of nonanticipativity constraints. The nonanticipativity constraints enforce the
condition that all scenarios with the same history must implement the same decisions, otherwise, the
DE would have the ability to anticipate future events.
As an example below, we load the SP gas buying sample model, SPGAS, and run the XDETEQ
command:
: take \lingo\samples\spgas.lng
: xdeteq
MODEL:
TITLE _DETEQ;
[ _1] MIN = 0.3333333333333333 * PURCHASE_COST_SC1
+ 0.3333333333333333 * HOLD_COST_SC1 + 0.3333333333333333
*
PURCHASE_COST_SC2 + 0.3333333333333333 * HOLD_COST_SC2
+ 0.3333333333333333 * PURCHASE_COST_SC3 +
0.3333333333333333
* HOLD_COST_SC3;
[ _2_SC01] PURCHASE_COST_SC1 - 5 * PURCHASE_1_SC1 - 5 *
PURCHASE_2_SC1 = 0;
[ _3_SC01] HOLD_COST_SC1 - INVENTORY_1_SC1 -
INVENTORY_2_SC1 = 0;
[ _4_SC01] INVENTORY_1_SC1 - PURCHASE_1_SC1 = - 100;
[ _5_SC01] - INVENTORY_1_SC1 + INVENTORY_2_SC1 -
PURCHASE_2_SC1 = - 100;
[ _2_SC02] PURCHASE_COST_SC2 - 5 * PURCHASE_1_SC2 - 6 *
PURCHASE_2_SC2 = 0;
[ _3_SC02] HOLD_COST_SC2 - INVENTORY_1_SC2 -
INVENTORY_2_SC2 = 0;
[ _4_SC02] INVENTORY_1_SC2 - PURCHASE_1_SC2 = - 100;
[ _5_SC02] - INVENTORY_1_SC2 + INVENTORY_2_SC2 -
PURCHASE_2_SC2 = - 150;
[ _2_SC03] PURCHASE_COST_SC3 - 5 * PURCHASE_1_SC3 - 7.5
*
PURCHASE_2_SC3 = 0;
[ _3_SC03] HOLD_COST_SC3 - INVENTORY_1_SC3 -
INVENTORY_2_SC3 = 0;
[ _4_SC03] INVENTORY_1_SC3 - PURCHASE_1_SC3 = - 100;
[ _5_SC03] - INVENTORY_1_SC3 + INVENTORY_2_SC3 -
PURCHASE_2_SC3 = - 180;
[ _NAC01] INVENTORY_1_SC1 - INVENTORY_1_SC2 = 0;
[ _NAC02] PURCHASE_1_SC1 - PURCHASE_1_SC2 = 0;
[ _NAC03] INVENTORY_1_SC1 - INVENTORY_1_SC3 = 0;
[ _NAC04] PURCHASE_1_SC1 - PURCHASE_1_SC3 = 0;
END
:

276 CHAPTER 6
The first row of the DE is the probabilistically weighted objective over the three scenarios (Normal,
Cold and Very Cold). Note that in the original core model, we had a variable called
PURCHASE_COST, which was used to compute the cost of the gas purchases. In the DE we now
have three PURCHASE_COST variables, or one for each of the three scenarios. LINGO appends the
strings _SC1, _SC2 or _SC3 to PUCHASE_COST so as to indicate the appropriate scenario. Each of
the constraints from the core model are also replicated across each of the scenarios with the
appropriate scenario tag appended to each row's name. Finally, at the bottom of the model, there are
four constraints beginning with the string: _NAC, which are the nonanticipativity constraints.
It's worthwhile pointing out that this report on DE for SPGAS is a valid LINGO model, too. In fact,
you can copy this report from into a new model file and solve it directly, in which case, you will get
the optimal solution to the original SP model.
4. File Output
The File Output category contains commands that output model and session information to a file.
DIVERT
The DIVERT command opens a file and causes LINGO to route all subsequent reports (e.g.,
SOLUTION, RANGE, and LOOK commands) from the screen to the file. This command captures the
reports in text format in the file you specify. Since the files created by the DIVERT command are in
text format, they may be read into other programs, such as word processors and spreadsheets, or they
may be queued to your printer.
The syntax for the DIVERT command is:
DIVERT filename
where filename is the name of the file you wish to create.
The RVRT command reverses a DIVERT command by closing the DIVERT file and then rerouting
output back to the screen.

COMMAND-LINE COMMANDS 277
In the following example, we create a small model with the MODEL command, solve it with the GO
command, and then use the DIVERT command to create a file containing the formulation and solution:
: !Enter a small model
: MODEL
? MAX = 20*X + 30*Y;
? X <= 50;
? Y <= 60;
? X + 2*Y <= 120;
? END
: !Solve the model
: TERSE
: GO
Global optimal solution found at step: 1
Objective value: 2050.000
: !Create a DIVERT file with
: !the formulation & solution
: DIVERT MYFILE.TXT !Opens the file
: LOOK ALL !Sends model to file
: SOLU !Sends solution to file
: RVRT !Closes DIVERT file
:
Opening the DIVERT file created in this example, we find the following file with the formulation and
solution:
1]MAX = 20*X + 30*Y;
2]X <= 50;
3]Y <= 60;
4]X + 2*Y <= 120;
Variable Value Reduced Cost
X 50.00000 0.000000
Y 35.00000 0.000000
Row Slack or Surplus Dual Price
1 2050.000 1.000000
2 0.000000 5.000000
3 25.00000 0.000000
4 0.000000 15.00000
Note 1: Keep in mind that, when a DIVERT command is in effect, you will see little or no output on
your screen. This is because the majority of output is being routed to the DIVERT file rather
than to the screen.
Note 2: Also, be sure you choose a DIVERT filename different from your model filename. If not, you
will overwrite your model file and will be unable to retrieve it!
RVRT
The RVRT command closes an output file opened with the DIVERT command. For an example of its
use, see the DIVERT command immediately above.

278 CHAPTER 6
SAVE
The SAVE command saves the current model to a file. The syntax is:
SAVE filename
where filename is the name of the file to save your model in. LINGO saves the model in text format.
You can read the model back into LINGO with the TAKE command. We recommend you use an
extension of .LNG on your model files, so you can readily identify them.
You may want to use your own text editor to modify your model. If you do, be sure to save the LINGO
model in text (ASCII) format. Use the TAKE command to reopen the model in LINGO when you are
through editing it.
In the following example, we input a small model and save it in the file titled MYMODEL.LNG:
: !Enter a small model
: MODEL
? MAX = 20*X + 30*Y;
? X <= 50;
? Y <= 60;
? X + 2*Y <= 120;
? END
: !Save model to a file
: SAVE MYMODEL.LNG
:
If you open the model file, MYMODEL.LNG, in a text editor, you should see the following:
MODEL:
1]MAX = 20*X + 30*Y;
2]X <= 50;
3]Y <= 60;
4]X + 2*Y <= 120;
END
SMPI
The SMPI command saves your model in a special format called Mathematical Programming
Interface (MPI). MPI is a special format developed by LINDO Systems for representing all classes of
mathematical programs − linear, integer, and nonlinear. This format is not intended for permanent
storage of your models. LINDO API users may be interested in this format for exporting models to the
LINDO API.
Note 1: At present, LINGO does not read MPI format files. Thus, it is important that you do not use
this format for permanent storage. Use the SAVE command, discussed above, to permanently
save your files for later retrieval.
Note 2: When exporting a stochastic program to MPI format, LINGO will write a total of four SMPI
format files, consisting of the core model, its stochastic declarations and its time structure.

COMMAND-LINE COMMANDS 279
SMPS
The SMPS command generates the underlying algebraic formulation for the current model and then
writes it to a disk file in MPS format. MPS format is a common format for representing linear
programming models. MPS files can be ported to any solver that reads MPS files—this includes most
commercial linear programming packages.
The syntax for the SMPS command is:
SMPS filename
where filename is the name of the file you wish to save the MPS representation of the model under.
In the following example, we input a small model and then save it in an MPS file:
: !Enter a small model
: MODEL
? MAX = 20*X + 30*Y;
? X <= 50;
? Y <= 60;
? X + 2*Y <= 120;
? END
: !Save model to an MPS file
: SMPS MYMODEL.MPS
:
If you open the MPS file created in a text editor, you should find:
NAME LINGO GENERATED MPS FILE(MAX)
ROWS
N 1
L 2
L 3
L 4
COLUMNS
Y 1 30.0000000
Y 3 1.0000000
Y 4 2.0000000
X 1 20.0000000
X 2 1.0000000
X 4 1.0000000
RHS
RHS 2 50.0000000
RHS 3 60.0000000
RHS 4 120.0000000
ENDATA
Note 1: Your model must be entirely linear to be able to successfully export it using SMPS. If a model
is nonlinear, the MPS file will contain question marks in place of numbers for coefficients of
nonlinear variables.

280 CHAPTER 6
Note 2: SMPS truncates all variable names to 8 characters. For instance, the two distinct LINGO
names SHIP(WH1, C1) and SHIP(WH1, C2) would both be truncated to the single 8 character
name SHIPWH1C under SMPS . Either choose names to avoid collisions of truncated names
or enable the RCMPSN option for converting names to RC format when doing MPS I/O.
LINGO will print an error message if potential collisions exist.
Note 3: The MPS file format is intended primarily for exporting models to other applications or
platforms. The MPS format is purely scalar in nature—all set-based information is lost upon
converting a LINGO model to MPS format. Thus, when saving copies of a model on your
own machine, you should always use the SAVE command instead of the SMPS command.
Note 4: When exporting a stochastic program to MPS format, LINGO will write a total of three
SMPS format files, consisting of the core model, its stochastic declarations and its time
structure.
5. Solution
The Solution category contains commands for viewing a model’s solution.
DEBUG
In the ideal world, all models would return an optimal solution. Unfortunately, this is not the case.
Sooner or later, you are bound to run across either an infeasible or unbounded model. This is
particularly true in the development phase of a project when the model will tend to suffer from
typographical errors.
Tracking down an error in a large model can prove to be a daunting task. The DEBUG command is
useful in narrowing the search for problems in both infeasible and unbounded linear programs. A small
portion of the original model is isolated as the source of the problem. This allows you to focus your
attention on a subsection of the model in search of formulation or data entry errors.
The DEBUG command identifies two types of sets: sufficient and necessary. Removing any sufficient
set object from the model is sufficient to fix the entire model. Not all models will have a sufficient set.
In which case, they will have a necessary set with the property that removing any object from this set
fixes the remaining objects within that set.
As an example, suppose you have an infeasible model. If the complete model would be feasible except
for a bug in a single row, that row will be listed as part of the sufficient set. If the model has a
necessary set, then, as long as all of them are present, the model will remain infeasible.
The following example illustrates. The coefficient .55 in ROW4 should have been 5.5:
: look all
MODEL:
1][ROW1] Max = 3*X + 7*Y;
2][ROW2] X + 2*Y <= 3;
3][ROW3] 2*X + Y <= 2;
4][ROW4] 0.55*X + Y >=4;
END

COMMAND-LINE COMMANDS 281
When we attempt to solve this formulation, we get the following error:
: go
[Error Code: 81]
No feasible solution found.
Variable Value Reduced Cost
X 50.00000 0.000000
Y -23.50000 0.000000
Row Slack or Surplus Dual Price
ROW1 0.000000 -1.000000
ROW2 0.000000 8.500000
ROW3 -74.50000 0.000000
ROW4 0.000000 -10.00000
Next, if we run the DEBUG command, we are presented with the following report:
: debug
Sufficient Rows:
ROW4] .55 X + Y >= 4
Necessary Rows:
ROW2] X + 2 Y <= 3
Necessary Variable Bounds:
Y >= 0
The DEBUG command has correctly identified that the erroneous ROW4, when eliminated, is
sufficient to make the entire model feasible.
The debug feature operates in a similar manner for unbounded models. In the following example, we
introduced an error by placing a minus sign instead of a plus sign in front of variable Z3 in ROW3. A
look at ROW3 reveals that Z3 can be increased indefinitely, leading to an unbounded objective.
: look all
MODEL:
1][ROW1] Max = 12*X1 + 13*X2 + 22*Y1 + 23*Z1 +
2] 28*Z2 + X3 + Y3 + Z3;
3][ROW2] X1 + X2 + X3 <= 400;
4][ROW3] Y1 + Y2 + Y3 - Z3 <= 500;
5][ROW4] Z1 + Z2 <= 500;
END

282 CHAPTER 6
The resulting model is unbounded and, when issuing the LINGO|Solve command, we receive the
unbounded error message:
: go
[Error Code: 82]
Unbounded solution.
Issuing the DEBUG command, we receive the following breakdown:
: debug
Sufficient Variables:
Z3
Necessary Variables:
Y1
The DEBUG command has successfully determined that bounding Z3 is sufficient to bound the entire
model.
Typically, the DEBUG command helps to substantially reduce the search effort. The first version of
this feature was implemented in response to a user who had an infeasible model. The user had spent a
day searching for a bug in a model with 400 constraints. The debug feature quickly found a necessary
set with 55 constraints, as well as one sufficient set constraint. The user immediately noticed that the
right-hand side of the sufficient set constraint was incorrect.
GO
The GO command compiles and then solves the current model. When LINGO compiles the model, it
produces an internally executable version of the model and then runs it to produce the solution.
When LINGO finishes solving the model, it displays a full solution report on your screen. To suppress
the full solution report, issue the TERSE command before the GO command.
To capture the solution report generated by the GO command in a file, use the DIVERT command
before the GO command.
To set various parameters pertaining to the operation of LINGO’s solver, see the SET command later
in this chapter.
NONZ
The NONZ, or NONZEROS, command displays an abbreviated version of the solution for the current
model. NONZ is identical to the SOLUTION command with the exception that NONZ displays
information only about nonzero variables and binding rows (i.e., the slack or surplus is 0).
The syntax of the NONZ command is:
NONZ [‘header_text’] [var_or_row_name]
For a standard NONZ solution report, omit the two optional arguments and enter the NONZ command
by itself. LINGO will print primal and dual values for all nonzero variables and binding rows. LINGO
will label all the columns in the report.

COMMAND-LINE COMMANDS 283
The first optional field, header_text, will be displayed as a title header in the solution report. If the
header_text argument is included, LINGO prints primal values only, omitting all labels in the report.
The second optional field, var_or_row_name, is a variable or row name that, if included, will limit the
report to the given variable or row name.
As an example, in the following session, we load the Chess Snackfoods example from Chapter 2,
Using Sets, and then generate several solution reports using NONZ:
: TAKE CHESS.LNG
: TERSE
: GO
Global optimal solution found at step: 0
Objective value: 2692.308
: !Generate a standard NONZ report
: NONZ
Variable Value Reduced Cost
SUPPLY(PEANUTS) 750.0000 0.000000
SUPPLY(CASHEWS) 250.0000 0.000000
PRICE(PAWN) 2.000000 0.000000
PRICE(KNIGHT) 3.000000 0.000000
PRICE(BISHOP) 4.000000 0.000000
PRICE(KING) 5.000000 0.000000
PRODUCE(PAWN) 769.2308 0.000000
PRODUCE(KING) 230.7692 0.000000
FORMULA(PEANUTS, PAWN) 15.00000 0.000000
FORMULA(PEANUTS, KNIGHT) 10.00000 0.000000
FORMULA(PEANUTS, BISHOP) 6.000000 0.000000
FORMULA(PEANUTS, KING) 2.000000 0.000000
FORMULA(CASHEWS, PAWN) 1.000000 0.000000
FORMULA(CASHEWS, KNIGHT) 6.000000 0.000000
FORMULA(CASHEWS, BISHOP) 10.00000 0.000000
FORMULA(CASHEWS, KING) 14.00000 0.000000
Row Slack or Surplus Dual Price
1 2692.308 1.000000
2 0.000000 1.769231
3 0.000000 5.461538
: !Generate a NONZ report for PRODUCE
: NONZ PRODUCE
Variable Value Reduced Cost
PRODUCE(PAWN) 769.2308 0.000000
PRODUCE(KING) 230.7692 0.000000
: !Now add a header
: NONZ 'NONZERO PRODUCTION VALUES:' PRODUCE
NONZERO PRODUCTION VALUES:
769.2308
230.7692
If you would like to capture the solution report in a file, use the DIVERT command before the NONZ
command.
For more information on the interpretation of the various fields in the NONZ report, see Chapter 1,
Getting Started with LINGO.
284 CHAPTER 6
Note: If the solution report is scrolling off the screen, you can use the PAGE command to set the
page length to n lines, so LINGO will pause every time n lines are printed and wait until you
are ready to proceed with the next page.
RANGE
Use the RANGE command to generate a range report for the model in the active window. A range
report shows over what ranges you can: 1) change a coefficient in the objective without causing any of
the optimal values of the decision variables to change, or 2) change a row’s constant term (also
referred to as the right-hand side coefficient) without causing any of the optimal values of the dual
prices or reduced costs to change.
Note: The solver computes range values when you solve a model. Range computations must be
enabled in order for the solver to compute range values. Range computations are not enabled
by default, so you will need to switch them on with the command:
SET DUALCO 2
Range computations can take a fair amount of computation time. If speed is a concern, you
don’t want to enable range computations unnecessarily.
The example model below, when solved, yields the range report that follows:
[OBJECTIVE] MAX = 20 * A + 30 * C;
[ALIM] A <= 60;
[CLIM] C <= 50;
[JOINT] A + 2 * C <= 120;
Here is the range report:
Ranges in which the basis is unchanged:
Objective Coefficient Ranges
Current Allowable Allowable
Variable Coefficient Increase Decrease
A 20.00000 INFINITY 5.000000
C 30.00000 10.00000 30.00000
Right-hand side Ranges
Row Current Allowable Allowable
RHS Increase Decrease
ALIM 60.00000 60.00000 40.00000
CLIM 50.00000 INFINITY 20.00000
JOINT 120.0000 40.00000 60.00000
The first section of the report is titled Objective Coefficient Ranges. In the first column, Variable, all
the optimizable variables are listed by name. The next column, Current Coefficient, lists the current
coefficient of the variable in the objective row. The third column, Allowable Increase, tells us the
amount that we could increase the objective coefficient without changing the optimal values for the
variables. The final column, Allowable Decrease, lists the amount that the objective coefficient of the
variable could decrease before the optimal values of the variables would change. Information on the
allowable increases and decreases on objective coefficients can be useful when you need answers to
questions like, “How much more (less) profitable must this activity be before we should be willing to
do more (less) of it?”

COMMAND-LINE COMMANDS 285
Referring to the Objective Coefficient Ranges report for our example, we can say, as long as the
objective coefficient of A is greater-than-or-equal-to 15, the optimal values of the variables will not
change. The same may be said for the objective coefficient of variable C, as long as it falls within the
range of [0-40].
Note: Ranges are valid only if you are planning to alter a single objective or right-hand side
coefficient. The range information provided by LINGO cannot be applied in situations where
one is simultaneously varying two or more coefficients. Furthermore, ranges are only lower
bounds on the amount of change required in a coefficient to actually force a change in the
optimal solution. You can change a coefficient by any amount up to the amount that is
indicated in the range report without causing a change in the optimal solution. Whether the
optimal solution will actually change if you exceed the allowable limit is not certain.
The second section of the range report is titled Right-hand side Ranges. The first column, Row, lists
the names of all the optimizable rows, or constraints, in the model. The second column, Current RHS,
gives the constant term, or right-hand side value, for the row. The next two columns, Allowable
Increase and Allowable Decrease, tell us how far we can either increase or decrease the right-hand
side coefficient of the row without causing a change in the optimal values of the dual prices or reduced
costs. If you recall, the dual prices on rows are, effectively, shadow prices, which tell us at what price
we should be willing to buy (or sell) our resources for. The dual prices do not, however, tell us what
quantity we should be willing to buy (or sell) at the dual price. This information is obtained from the
allowable increases and decreases on the right-hand side coefficients for the row. So, for our example,
the dual prices and reduced costs will remain constant as long as the right-hand side of row ALIM falls
within the range [20-120], the right-hand side of CLIM is greater-than-or-equal-to 30, and the
right-hand side of JOINT is in [60-160].
Note: We preceded all the rows in our model with a name enclosed in square brackets. This is an
important practice if you wish to generate range reports. If you do not name your rows,
LINGO assigns them a name that corresponds to the internal index of the row. This internal
index will not always correspond to the order of the row in the text of the original model. To
make the Right-hand side Ranges section of range reports meaningful, be sure to name all
your rows. For details on assigning names to rows, see page 35.
If a variable is nonlinear in the objective, its value in the Current Coefficient column will be displayed
as NONLINEAR. Similarly, if a row is nonlinear, the value in the Current RHS column will be
displayed as NONLINEAR.
Coefficients that can be increased or decreased indefinitely will display a range of INFINITY.
Fixed variables are substituted out of a model and will not appear in a range report. Rows that contain
only fixed variables are also substituted out of models and will not appear in range reports. As an
example, suppose we changed the following inequality in our sample model from:
[ALIM] A <= 60;
to the equality:
[ALIM] A = 60;

286 CHAPTER 6
LINGO can now solve directly for the value of A. The variable A is considered fixed; as is the row
ALIM (since it contains no optimizable variables). Given this, the variable A will no longer appear in
the Objective Coefficient Ranges section of the range report, and the row ALIM will not appear in the
Right-hand Side Ranges section. We can verify this by examining the updated range report:
Ranges in which the basis is unchanged:
Objective Coefficient Ranges
Current Allowable Allowable
Variable Coefficient Increase Decrease
C 30.00000 INFINITY 30.00000
Right-hand Side Ranges
Row Current Allowable Allowable
RHS Increase Decrease
CLIM 50.00000 INFINITY 20.00000
JOINT 60.00000 40.00000 60.00000
As a final note, if the range report is scrolling off the screen, you can use the PAGE n command to set
the page length to n lines, so LINGO will pause every time n lines are printed and wait until you are
ready to proceed with the next page. In addition, if you would like to capture the solution report in a
file, use the DIVERT command before the SOLU command.
SOLU
The SOLU, or SOLUTION, command displays a solution report for the current model. The syntax of
the SOLU command is:
SOLU [‘header_text’] [ var_or_row_name]
For a standard solution report, omit the two optional arguments, and enter the SOLU command by
itself. LINGO will print primal and dual values for all the variables and rows in the model. LINGO
will label all the columns in the report.
The first optional field, header_text, will be displayed as a title header in the solution report. If the
header_text argument is included, LINGO prints primal values only, omitting all labels in the report.
The second optional field, var_or_row_name, is a variable or row name that, if included, will limit the
report to the given variable or row name.

COMMAND-LINE COMMANDS 287
As an example, in the following session, we load the Chess Snackfoods example from Chapter 2,
Using Sets, and then generate several solution reports using SOLU:
: TAKE CHESS.LNG
: TERSE
: GO
Global optimal solution found at step: 0
Objective value: 2692.308
: !Generate a standard SOLU report
: SOLU
Variable Value Reduced Cost
SUPPLY(PEANUTS) 750.0000 0.0000000
SUPPLY(CASHEWS) 250.0000 0.0000000
PRICE(PAWN) 2.000000 0.0000000
PRICE(KNIGHT) 3.000000 0.0000000
PRICE(BISHOP) 4.000000 0.0000000
PRICE(KING) 5.000000 0.0000000
PRODUCE(PAWN) 769.2308 0.0000000
PRODUCE(KNIGHT) 0.000000 0.1538461
PRODUCE(BISHOP) 0.000000 0.7692297E-01
PRODUCE(KING) 230.7692 0.0000000
FORMULA(PEANUTS, PAWN) 15.00000 0.0000000
FORMULA(PEANUTS, KNIGHT) 10.00000 0.0000000
FORMULA(PEANUTS, BISHOP) 6.000000 0.0000000
FORMULA(PEANUTS, KING) 2.000000 0.0000000
FORMULA(CASHEWS, PAWN) 1.000000 0.0000000
FORMULA(CASHEWS, KNIGHT) 6.000000 0.0000000
FORMULA(CASHEWS, BISHOP) 10.00000 0.0000000
FORMULA(CASHEWS, KING) 14.00000 0.0000000
Row Slack or Surplus Dual Price
1 2692.308 1.000000
2 0.000000 1.769231
3 0.000000 5.461538
: !Generate a SOLU report for PRODUCE
: SOLU PRODUCE
Variable Value Reduced Cost
PRODUCE(PAWN) 769.2308 0.0000000
PRODUCE(KNIGHT) 0.000000 0.1538461
PRODUCE(BISHOP) 0.000000 0.7692297E-01
PRODUCE(KING) 230.7692 0.0000000
: !Now add a header
: SOLU 'PRODUCTION QUANTITIES' PRODUCE
PRODUCTION QUANTITIES
769.2308
0.000000
0.000000
230.7692
If you would like to capture the solution report in a file, use the DIVERT command before the SOLU
command.
For more information on the interpretation of the various fields in the solution report, see page 22.
If the solution report is scrolling off the screen, you can use the PAGE command to set the page length
to n lines, so LINGO will pause every time n lines are printed and wait until you are ready to proceed
with the next page.

288 CHAPTER 6
6. Problem Editing
The Problem Editing category contains commands used in editing and modifying models.
ALTER
The ALTER command is used to edit the current model. The syntax of ALTER is:
ALTER [line_number|line_range|ALL] 'old_string'new_string'
where,
line_number is the index of a single line to edit,
line_range is a range of lines to edit,
ALL means edit all the lines in the model,
old_string is the old string to search for and replace, and
new_string is the string to replace all occurrences of old_string with in the
specified line range.

COMMAND-LINE COMMANDS 289
In the following sample session, we read in a small knapsack model and perform two ALTER
commands to modify the model:
: TAKE ALTER.LNG
: LOOK ALL
1]SETS:
2] THINGS /1..4/: VALUE, WEIGHT, X;
3]ENDSETS
4]DATA:
5] VALUE = 8 6 4 3;
6] WEIGHT = 66 44 35 24;
7]ENDDATA
8] MAX = @SUM(THINGS: VALUE * X);
9] @SUM(THINGS: WEIGHT * X) >= 100;
10] @FOR(THINGS: @BIN(X));
: !Change the direction of the constraint
: ALTER 9 '>='<='
9] @SUM(THINGS: WEIGHT * X) <= 100;
: !Change 'THINGS' to 'ITEMS' in ALL rows
: ALTER ALL 'THINGS'ITEMS'
2] ITEMS /1..4/: VALUE, WEIGHT, X;
8] MAX = @SUM(ITEMS: VALUE * X);
9] @SUM(ITEMS: WEIGHT * X) <= 100;
10] @FOR(ITEMS: @BIN(X));
: LOOK ALL
1]SETS:
2] ITEMS /1..4/: VALUE, WEIGHT, X;
3]ENDSETS
4]DATA:
5] VALUE = 8 6 4 3;
6] WEIGHT = 66 44 35 24;
7]ENDDATA
8] MAX = @SUM(ITEMS: VALUE * X);
9] @SUM(ITEMS: WEIGHT * X) <= 100;
10] @FOR(ITEMS: @BIN(X));
:
Note: In addition to the single quote character ('), LINGO also allows the use of the double quote
character (") for delimiting the text fields of the ALTER command.
DELETE
The DELETE command is used to delete one or more lines of text from the current model. The syntax
of DELETE is:
DELETE [line_number|line_range|ALL]
where,
line_number is the index of a single line to delete,
line_range is a range of lines to delete, and
ALL means delete the entire model.

290 CHAPTER 6
Some examples of the DELETE command follow:
Example 1: DELETE 3
deletes line 3 of the model,
Example 2: DEL 2 10
deletes lines 2 through 10 of the model, and
Example 3: DEL ALL
deletes the entire model.
EXTEND
The EXTEND command allows you to append lines to the current model. It puts LINGO in model
input mode just after the last line of the current model. When you use the EXTEND command, you’ll
see LINGO’s question mark prompt. Start entering your new lines of model text. When you’re done,
enter END at the prompt.
In the following sample session, we use the EXTEND command to append an additional constraint to a
small model:
: LOOK ALL
1]MAX 20*X + 30*Y;
2]X <= 50;
3]Y <= 60;
4]X + 2*Y <=120;
: ! Use EXTEND to add another line
: EXTEND
? X >= 30;
? END
: LOOK ALL
1]MAX 20*X + 30*Y;
2]X <= 50;
3]Y <= 60;
4]X + 2*Y <=120;
5]X >= 30;
:
7. Conversational Parameters
The Conversational Parameters category contains commands that control how information is
displayed.
PAGE
The PAGE command sets the length of the page or screen size in lines. The syntax for PAGE is:
PAGE n
where n is the desired number of lines per page of output. For instance, PAGE 25 will cause the
display to pause after 25 lines and await a carriage return before displaying the next 25 lines. The
PAGE command is convenient when you wish to page through long reports and not have them scroll
off the top of the screen.

COMMAND-LINE COMMANDS 291
When 0 is entered as the argument to PAGE, paging is turned off entirely. LINGO will no longer stop
output to wait for a carriage return. Entering PAGE 0 at the top of any command script is helpful in
that you generally want command scripts to run uninterrupted.
The PAGE command is equivalent to the SET LENPAG command and is maintained for backward
compatibility
PAUSE
The PAUSE command causes screen display to pause until a carriage return is typed. If you enter text
on the same line as the PAUSE command, the text will be displayed. The PAUSE command is useful in
command scripts for conveying information to the user.
TERSE
The TERSE command causes LINGO to suppress the automatic display of a solution report after a
model is solved with the GO command. When TERSE is enabled, you will need to use the NONZ or
SOLU commands to view the solution.
When LINGO is in terse output mode, export summary reports are also suppressed. Export summary
reports are normally generated each time you export solutions to spreadsheets or databases.
Once you enter the TERSE command, LINGO stays in terse output mode until you enter the VERBOSE
command (see below).
The TERSE command is equivalent to the SET TERSEO 1 command and is maintained for backward
compatibility.
VERBOSE
The VERBOSE command undoes the effects of the TERSE command, and places LINGO in verbose
output mode. Verbose output mode is the default mode. It results in the automatic display of solution
reports after solving a model. Verbose output mode also results in the automatic display of export
summary reports whenever export operations are performed to spreadsheets and databases.
The VERBOSE command is equivalent to the SET TERSEO 0 command and is maintained for
backward compatibility.
WIDTH
Use the WIDTH command to set the terminal width for input and output. The syntax of the WIDTH
command is:
WIDTH n
where n is the desired terminal width. You may set the width between 64 and 200. The default is 76.
When LINGO generates reports, it limits output lines to the terminal width length. In some reports,
lines will be wrapped, so they fall within the line limit. In other reports, lines may be truncated. Since
LINGO concatenates variable names in performing set operations, a variable name, such as
SHIPMENTS(WAREHOUSE1, CUSTOMER2), may result, which may be truncated in a solution report
if too narrow a terminal width is used.

292 CHAPTER 6
The WIDTH command is equivalent to the SET LINLEN command and is maintained for backward
compatibility.
8. Tolerances
The Tolerances category contains commands for setting system parameters in LINGO.
APISET
The APISET command gives you access to all the parameters in the LINDO API, which is the solver
library used by LINGO. LINGO allows access to most of the important solver parameters through the
SET command and, under Windows, via the LINGO|Options command. However, some of the more
advanced parameters may only be accessed through the APISET command. The syntax for this
command is:
APISET param_id {int|double} param_value
where param_id is the parameter’s index and param_value is the value you wish to set the parameter
to. You will also need to indicate if the parameter is an integer or double precision quantity.
Some examples of the APISET command follow:
Example 1: APISET 341 INT 10000
sets the MIP branch limit (LS_IPARAM_MIP_BRANCH_LIMIT=341) to 10000,
Example 2: HELP APISET
will cause LINGO to display all current APISET settings, and
Example 3: APISET DEFAULT
removes all custom LINDO API settings, returning to the defaults.
You will need to refer to the LINDO API documentation for a list of available parameters and their
indices. The LINDO API documentation is available at no charge as part of the LINDO API download
on the LINDO Systems Web site. The LINGO installation also comes with a macro definition file,
Lindo.h, which contains all the parameter indices for the LINDO API.
Parameter values set with the APISET command are not stored from one LINGO session to the next.
Give the HELP APISET command for a listing of parameters that are currently active. To remove all
APISET parameter settings type the command: APISET DEFAULT.
If there are some LINDO API parameters you wish to permanently set, you may place a series of
APISET commands in an AUTOLG.DAT script file that automatically gets run at the start of each
LINGO session.

COMMAND-LINE COMMANDS 293
DBPWD
The DBPWD command is used to input a password for accessing databases via the @ODBC()
function. Any password input with this command will not be permanently stored. Therefore, at the
start of each session, you will need to reenter your database password. The syntax for the command is:
DBPWD my_password
See the DBUID command below for entering any user id required by your database.
DBUID
The DBUID command is used to input a user id for accessing databases via the @ODBC() function.
Any user id input with this command will not be permanently stored. Therefore, at the start of each
session, you will need to reenter your database user id. The syntax for the command is:
DBUID my_user_id
See the DBPWD command above for entering any password required with your user id.
FREEZE
The FREEZE command saves your current configuration to LINGO’s configuration file, so it may be
automatically restored the next time LINGO starts. Any non-default features of the current
configuration are saved to the LINGO.CNF file in LINGO’s main directory. The LINGO.CNF
configuration file is a text file, and the curious user may examine it by simply opening it in a text
editor. All parameters controlled by the SET command, see below, are stored by the FREEZE
command.
Note: Be careful when saving a non-default configuration. The saved configuration will
automatically be restored next time you start LINGO. Settings of certain parameters will
affect the way models are solved, potentially leading to misleading results when used on a
different set of models. To restore the default configuration, use the following command
sequence:
: SET DEFAULT
: FREEZE
SET
The SET command allows you to override LINGO’s default tolerances and settings. All user
configurable options in LINGO are available through the SET command. The syntax for the SET
command is:
SET parameter_name|parameter_index [parameter_value]
where,
parameter_name is the name of the parameter to set,
parameter_index is the index of the parameter to set, and
parameter_value is the new value for the parameter that, if omitted, will cause
LINGO to display the current value for the specified
parameter.
294 CHAPTER 6
Use the FREEZE command, see above, to save any tolerances modified with the SET command to the
configuration file, so they will be automatically restored the next time LINGO starts. You may also
enter SET DEFAULT to return all parameters to their default values.
Some examples of the SET command follow:
Example 1: SET MXMEMB 128
FREEZE
sets the generator memory limit to 128MB and saves parameter settings to
the configuration file,
Example 2: SET 5 1.E-7
sets the relative integrality tolerance (RELINT) to 1.e-7,
Example 3: SET DEFAULT
restores all parameters to their default values, and
Example 4: HELP SET
causes LINGO to display all parameter settings.
The parameters accessible through the SET command are:
No. Name Default Description
1 ILFTOL 0.3e-5 Initial linear feasibility tolerance
2 FLFTOL 0.1e-6 Final linear feasibility tolerance
3 INFTOL 0.1e-2 Initial nonlinear feasibility tolerance
4 FNFTOL 0.1e-5 Final nonlinear feasibility tolerance
5 RELINT 0.8e-5 Relative integrality tolerance
6 NOPTOL 0.1e-6 NLP optimality tolerance
7 ITRSLW 5 Iteration limit for slow progress
8 DERCMP 0 Derivatives (0:LINGO chooses, 1:backward analytical, 2:forward
analytical, 3:central differences, 4:forward differences)
9 ITRLIM 0 Iteration limit (0:no limit)
10 TIMLIM 0 Solver time limit in seconds (0:no limit)
11 OBJCTS 0 Objective cuts (1:yes, 0:no)
12 MXMEMB 32 Memory limit in megabytes for LINGO’s model generator (N/A
on some machines)
13 CUTAPP 2 Cuts application (0:root, 1:all, 2:solver chooses)
14 ABSINT .000001 Absolute integrality tolerance
15 HEURIS 3 IP heuristics (0:none, 100:advanced)
16 HURDLE 0 Use an IP hurdle value (1:yes, 0:no)
17 IPTOLA 0 IP absolute optimality tolerance
18 IPTOLR .1e-4 IP relative optimality tolerance
19 TIM2RL 100 Seconds before switching to IP relative optimality tolerance
20 NODESL 0 0:LINGO decides, 1:depth first, 2:worst bound, 3:best bound
21 LENPAG 0 Terminal page length limit (0:none)
22 LINLEN 85 Terminal page width (0:none)
23 TERSEO 0 Output level (0:verbose, 1:terse, 2:errors only, 3:no output)
COMMAND-LINE COMMANDS 295
24 STAWIN 1 Post status window (1:yes, 0:no, Windows only)
25 SPLASH 1 Display splash screen (1:yes, 0:no, Windows only)
26 OROUTE 0 Route output to command window (1:yes, 0:no, Windows only)
27 WNLINE 800 Max command window lines (Windows only)
28 WNTRIM 400 Min command window lines (Windows only)
29 STABAR 1 Display status bar (1:yes, 0:no, Windows only)
30 FILFMT 1 File format (0:lng, 1:lg4, 2:ltx, Windows only)
31 TOOLBR 1 Display toolbar (1:yes, 0:no, Windows only)
32 CHKDUP 0 Check for duplicate model names in data (1:yes, 0:no)
33 ECHOIN 0 Echo command input to terminal (1:yes, 0:no)
34 ERRDLG 1 Route error messages to a dialog box (1:yes, 0:no, Windows
only)
35 USEPNM 0 Allow for unrestricted use of primitive set names (1:yes, 0:no)
36 NSTEEP 0 Use steepest edge variable selection in nonlinear solver (1:yes,
0:no)
37 NCRASH 0 Run crash procedure to get an initial starting point in nonlinear
models (1:yes, 0:no)
38 NSLPDR 0 Compute search directions in nonlinear solver using successive
linear programming (1:yes, 0:no)
39 SELCON 0 Use selective constraint evaluation in nonlinear solver (1:yes,
0:no)
40 PRBLVL 0 Specify probing level on MILPs (0:LINGO chooses, 1:none,
7:high)
41 SOLVEL 0 Specify linear solver (0:LINGO chooses, 1:primal, 2:dual,
3:barrier)
42 REDUCE 2 Perform model reduction (2:LINGO chooses, 1:yes, 0:no)
43 SCALEM 1 Scale the model (1:yes, 0:no)
44 PRIMPR 0 Select primal pricing method (0:LINGO chooses, 1:partial,
2:devex)
45 DUALPR 0 Select dual pricing method (0:LINGO chooses, 1:Dantzig,
2:steepest edge)
46 DUALCO 1 Specify dual computations (0:none, 1:prices only, 2:prices and
ranges, 3:prices only on optimizable rows)
47 RCMPSN 0 Use RC format names for MPS I/O (1:yes, 0:no)
48 MREGEN 2 Select model regeneration (0:only on modifications to model,
1:same as 0 plus whenever model has external references,
2:always)
49 BRANDR 0 Select branch direction (0:both, 1:up, 2:down)
50 BRANPR 0 Select branch priority (0:LINGO decides, 1:binary)
51 CUTOFF .1e-8 Cutoff solution values smaller than this
52 STRONG 10 Specify strong branch level
53 REOPTB 0 IP warm start LP (0:LINGO, 1:barrier, 2:primal, 3:dual)
54 REOPTX 0 IP cold start LP (0:LINGO, 1:barrier, 2:primal, 3:dual)
55 MAXCTP 100 Max top cuts passes
296 CHAPTER 6
56 RCTLIM .75 Relative cuts limit
57 GUBCTS 1 GUB cuts (1:yes, 0:no)
58 FLWCTS 1 Flow cuts (1:yes, 0:no)
59 LFTCTS 1 Lift cuts (1:yes, 0:no)
60 PLOCTS 1 Plant location cuts (1:yes, 0:no)
61 DISCTS 1 Disaggregation cuts (1:yes, 0:no)
62 KNPCTS 1 Knapsack cover cuts (1:yes, 0:no)
63 LATCTS 1 Lattice cuts (1:yes, 0:no)
64 GOMCTS 1 Gomory cuts (1:yes, 0:no)
65 COFCTS 1 Coefficient reduction cuts (1:yes, 0:no)
66 GCDCTS 1 Greatest common divisor cuts (1:yes, 0:no)
67 SCLRLM 1,000 Syntax coloring line limit (Windows only)
68 SCLRDL 0 Syntax coloring delay in seconds (Windows only)
69 PRNCLR 1 Matching parenthesis coloring (1:yes, 0:no, Windows only)
70 MULTIS 0 NLP multistart attempts (0:LINGO, n:number of attempts)
71 USEQPR 0 Use quadratic recognition (1:yes, 0:no)
72 GLOBAL 0 Use global solver on NLPs (1:yes, 0:no)
73 LNRISE 0 Linearization (0:LINGO, 1:none, 2:low, 3:high)
74 LNBIGM 100,000 Linearization BigM coefficient
75 LNDLTA .1e-5 Linearization Delta coefficient
76 BASCTS 1 Basis cuts (1:yes, 0:no)
77 MAXCTR 2 Max tree cuts passes
78 HUMNTM 0 Minimum heuristic time limit (seconds)
79 DECOMP 0 Matrix decomposition (1:yes, 0:no)
80 GLBOPT .1e-5 Global solver optimality tolerance
81 GLBDLT .1e-6 Global solver delta tolerance
82 GLBVBD .1e+11 Global solver variable bound limit
83 GLBUBD 2 Global solver bound use (0:no, 1:all, 2:some)
84 GLBBRN 5 Global solver branch selection (see below)
85 GLBBXS 1 Global solver box selection (0:depth first, 1:worst bound)
86 GLBREF 3 Global solver reformulation level (0:none, 3:high)
87 SUBOUT 2 Fixed variable reduction (0:none, 1:max, 2:not when using global
or multistart solvers, 3:linear variables only)
88 NLPVER 0 NLP solver version (0:LINGO, 1:1.0, 2:2.0)
89 DBGCLD 0 Debugging cold start solver (0:LINGO, 1:primal, 2:dual,
3:barrier)
90 DBGWRM 0 Debug warm start solver (0:LINGO, 1:primal, 2:dual, 3:barrier)
91 LCRASH 1 Use aggressive crashing for NLPs (0:no, 1:yes)
92 BCROSS 1 Perform a basis crossover on LPs when using barrier solver
(0:no, 1:yes)
93 LOWMEM 0 Opt for less memory usage (0:no, 1:yes)
94 FILOUT 0 Fill out workbook output ranges (0:no, 1:yes)
95 DBGLVL 15 Debugger output level (1:low, 15:high)
96 UNARYM 1 Unary minus priority (0:low, 1:high)

COMMAND-LINE COMMANDS 297
97 LINEAR 0 Assume model is linear to reduce memory consumption(0:no,
1:yes)
98 LOPTOL .1e-6 Linear optimality tolerance
99 SECORD 0 Use second order derivatives for NLPs (0:no, 1:yes)
100 NONNEF 1 Variables default to being non-negative (0:no, 1:yes)
101 BIGMVL 1.e8 BigM coefficient threshold value
102 KILLSC 0 Kill scripts on interrupts (0:no, 1:yes)
103 TATSLV 0 @SOLVE time limit in seconds
104 KBESTS 1 Number of K-Best MIP solutions to generate
105 LCORES 1 Number of concurrent LP solvers to run
106 LCORE1 1 LP Solver in Core 1 (1:prm1,2:dual,3:barrier,4:prim2)
107 LCORE2 2 LP Solver in Core 2
108 LCORE3 3 LP Solver in Core 3
109 LCORE4 4 LP Solver in Core 4
110 SCALEW 1.e12 Scaling warning threshold
111 REFRAQ 0 Basis refactor frequency (0:LINGO chooses, iteration count)
112 SPSMSZ 2 Default SP sample size per stage
113 SPSCON 1 Apply SP sampling to continuous random variables only (0:no,
1:yes)
114 SPSEED 1,031 SP sampling random number seed
115 SPMTHD 0 SP solution method (0:LINGO chooses, 1:deterministic
equivalent, 2:nested Benders, 3:augmented Lagrangian)
116 SPXVAL 1 Calculate all SP expected value statistics (0:no, 1:yes)
117 SPMAXS 40,000 Max scenarios allowed in an SP before auto sampling takes effect
118 PRECIS 7 Precision in digits for standard solution reports
119 LOOPOP 0 Perform loop optimization during model compiles (0:no, 1:yes)
120 HEUCUT 0 Heuristics cutoff criterion (0:LINGO chooses, 1:time,
2:iterations)
1. ILFTOL and 2. FLFTOL
Due to the finite precision available for floating point operations on digital computers, LINGO can’t
always satisfy each constraint exactly. Given this, LINGO uses these two tolerances as limits on the
amount of violation allowed on a constraint while still considering it “satisfied”. These two tolerances
are referred to as the initial linear feasibility tolerance (ILFTOL) and the final linear feasibility
tolerance (FLFTOL). The default values for these tolerances are, respectively, 0.000003 and
0.0000001.
ILFTOL is used when the solver first begins iterating. ILFTOL should be greater than FLFTOL. In the
early stages of the solution process, being less concerned with accuracy can boost the performance of
the solver. When LINGO thinks it has an optimal solution, it switches to the more restrictive FLFTOL.
At this stage in the solution process, one wants a relatively high degree of accuracy. Thus, FLFTOL
should be smaller than ILFTOL.
One instance where these tolerances can be of use is when LINGO returns a solution that is almost, but
not quite, feasible. You can verify this by checking the values in the Slack or Surplus column in the
model’s solution report. If there are only a few rows with small, negative values in this column, then

298 CHAPTER 6
you have a solution that is close to being feasible. Loosening (i.e., increasing the values of) ILFTOL
and FLFTOL may help you get a feasible solution. This is particularly true in a model where scaling is
poor (i.e., very large and very small coefficients are used in the same model), and the units of
measurement on some constraints are such that minor violations are insignificant. For instance,
suppose you have a budget constraint measured in millions of dollars. In this case, a violation of a few
pennies would be of no consequence. Short of the preferred method of rescaling your model, loosening
the feasibility tolerances may be the most expedient way around a problem of this nature.
3. INFTOL and 4. FNFTOL
The initial nonlinear feasibility tolerance (INFTOL) and the final nonlinear feasibility tolerance
(FNFTOL) are both used by the nonlinear solver in the same manner the initial linear and final linear
feasibility tolerances are used by the linear solver. For information on how and why these tolerances
are useful, refer to the section immediately above. Default values for these tolerances are, respectively,
0.001 and 0.000001.
5. RELINT
RELINT, the relative integrality tolerance, is used by LINGO as a test for integrality in integer
programming models. Due to round-off errors, the “integer” variables in a solution may not have
values that are precisely integral. The relative integrality tolerance specifies the relative amount of
violation from integrality that is acceptable. Specifically, if I is the closest integer value to X, X will be
considered an integer if:
|X - I| <= Relative Integrality Tolerance.
|X|
The default value for the relative integrality tolerance is .000008. Although one might be tempted to
set this tolerance to 0, doing so may result in feasible models being reported as infeasible.
6. NOPTOL
While solving a model, the nonlinear solver is constantly computing a gradient. The gradient gives the
rate of improvement of the objective function for small changes in the variables. If the gradient's rate
of improvement computation for a given variable is less-than-or-equal-to NOPTOL, the nonlinear
optimality tolerance, further adjustments to the variable's value are not considered to be beneficial.
The default value for the nonlinear optimality tolerance is .0000001. Decreasing this tolerance towards
a limit of 0 will tend to make the solver run longer and may lead to better solutions to poorly
formulated or poorly scaled models.
7. ITRSLW
LINGO’s nonlinear solver uses the ITRSLW, slow progress iteration limit, as a means of terminating
the solution process if little or no progress is being made in the objective value. Specifically, if the
objective function’s value has not improved significantly in n iterations, where n is the value of
ITRSLW, the nonlinear solver will terminate the solution process. Increasing this tolerance’s value will
tend to force the solver to run longer and may be useful in models that have relatively “flat” objective
functions around the optimal solution. The default value for ITRSLW is 5 iterations. Refer to the
description of ITRLIM below for a definition of iterations.

COMMAND-LINE COMMANDS 299
8. DERCMP
Use this parameter to set the style of derivative computation. Set DERCMP to 0 (Solver Decides) to
allow LINGO to select the method, 1 for backward analytical derivatives, 2 for forward analytical
derivatives, 3 for numerical derivatives using central differences, and 4 for numerical derivatives using
forward differences.
LINGO defaults to the Solver Decides setting, which presently involves using backward analytical
derivatives. However, we suggest you try the various derivative options to see which works best for
your particular models.
9. ITRLIM
Use this tolerance to place an upper limit on the number of iterations the solver will perform. An
iteration is the fundamental operation performed by the solver. At the risk of oversimplification, it is a
process that involves forcing a variable, currently at a zero value, to become nonzero until some other
variable is driven to zero, improving the objective as we go. In general, larger models will take longer
to perform an iteration, and nonlinear models will take longer than linear models. The default iteration
limit is 0, meaning no limit is imposed on the iteration count.
If the solver hits this limit, it returns to normal command mode. If the model contains integer variables,
LINGO will restore the best integer solution found so far. You may need to be patient, however,
because the solver may have to perform a fair amount of work to reinstall the current best solution
after it hits a runtime limit.
Note: Some caution is required when interrupting the solver. There must be an incumbent solution
available if you hope to interrupt the solver and have it return a valid solution. You can
always tell if an incumbent solution is available by examining the Best Obj field in the
Extended Solver Status box of the solver status window. If this field is blank, then an
incumbent solution does not exist, and the solution returned after an interrupt will be invalid.
If, on the other hand, this field contains a numeric value, then you should be able to interrupt
and return to a valid, if not globally optimal, solution.
10. TIMLIM
Use this tolerance to place a limit on the number of seconds the solver runs. If the solver hits this limit,
it will stop and return with the best solution found so far. The default limit is 0, meaning no time limit
is imposed on the solver.
If the solver hits this limit, it returns to normal command mode. If the model contains integer variables,
LINGO will restore the best integer solution found so far. You may need to be patient, however,
because the solver may have to perform a fair amount of work to reinstall the current best solution
after it hits a runtime limit.

300 CHAPTER 6
Note: Some caution is required when interrupting the solver. There must be an incumbent solution
available if you hope to interrupt the solver and have it return a valid solution. You can
always tell if an incumbent solution is available by examining the Best Obj field in the
Extended Solver Status box of the solver status window. If this field is blank, then an
incumbent solution does not exist, and the solution returned after an interrupt will be invalid.
If, on the other hand, this field contains a numeric value, then you should be able to interrupt
and return to a valid, if not globally optimal, solution.
11. OBJCTS
LINGO generates twelve different types of constraint cuts when solving mixed integer linear
programs. Using the options listed below, these various classes of cuts can be enabled by setting their
parameter value to 1, or disabled by setting their parameter value to 0.
The available cut classes are as follows:
Index Parameter Name Cut Type
11 OBJCTS Objective cuts
57 GUBCTS GUB
58 FLWCTS Flow
59 LFTCTS Lift
60 PLOCTS Plant location
61 DISCTS Disaggregation
62 KNPCTS Knapsack cover
63 LATCTS Lattice
64 GOMCTS Gomory
65 COFCTS Coefficient reduction
66 GCDCTS Greatest common divisor
76 BASCTS Basis cuts
By default, all cut classes are enabled with the exception of objective cuts (OBJCTS). Occasionally, on
some poorly formulated models, disabling one or more of the cut forms can help in finding feasible
solutions.
Cuts are not generated for nonlinear integer models. Thus, these options will not affect performance on
nonlinear models.
12. MXMEMB
Use this parameter to set an upper limit on the amount of memory, in megabytes, that LINGO allocates
as workspace for its model generator. When LINGO starts up, it sets aside a fixed amount of memory
to use as a generator workspace. The default workspace size is 32Mb. You can determine the size of
the current workspace and the amount of memory allotted in this workspace by issuing the MEM
command.
Large models may run out of generator memory when attempting to solve them. In this case, you will
receive the error message, “The model generator ran out of memory.” To avoid this error, increase the
value of MXMEMB and issue the FREEZE command to preserve the change. You must then restart
LINGO.
COMMAND-LINE COMMANDS 301
Note: Changes in LINGO’s generator memory limit are not established until you restart the
program.
The model generator is distinct from the actual solver engines. Memory allocated to the generator will
not be available to the solver engines. Thus, you shouldn’t allocate any more memory to the generator
than is required.
If you set MXMEMB to 0, LINGO will allocate all available memory when it starts up. This is not a
recommended practice.
Note: Setting LINGO’s generator memory limit abnormally high can result in poor performance of
LINGO and the operating system. By setting aside excessive amounts of memory for the
model generator, both LINGO and the operating system may have to resort to swapping of
virtual memory to and from the hard drive. Accessing the hard drive for memory swaps can
slow down your machine dramatically.
13. CUTAPP
Use this parameter to control the nodes in the solution tree where the branch-and-bound solver adds
constraint cuts in linear integer models. You have the following three options:
CUTAPP Setting Cuts Application at ...
0 Root only
1 All nodes
2 Solver decides
Under the Root Only option, the solver appends cuts only at the first node, or root node, in the solution
tree. With the All Nodes option, cuts are appended at each node of the tree. Under the Solver Decides
option, the solver dynamically decides when it is best to append cuts at a node.
The default is to let the solver decide when to append cuts. In general, this will offer superior
performance. There may be instances, however, where one of the other two options prevails.
14. ABSINT
Use this parameter to specify an absolute integrality tolerance. This tolerance is used by LINGO as a
test for integrality in integer programming models. Due to round-off errors, the "integer" variables in a
solution may not have values that are precisely integer. The absolute integrality tolerance specifies the
absolute amount of violation from integrality that is acceptable. Specifically, if X is an "integer"
variable and I is the closest integer to X, then X would be accepted as being integer valued if:
|X - I| <= Absolute Integrality Tolerance.
The default value for the absolute integrality tolerance is .000001. Although one might be tempted to
set this tolerance to 0, this may result in feasible models being reported as infeasible.
15. HEURIS
Use this parameter to control the level of integer programming heuristics used by the integer solver.
These heuristics use the continuous solution at each node in the branch-and-bound tree to attempt to
quickly find a good integer solution. If an integer solution better than the incumbent is found, then it is
used to fix or tighten global and local variable bounds. Heuristics are only applied to linear models.
Requesting heuristics on nonlinear models will result in no benefits.
302 CHAPTER 6
HEURIS may be set anywhere from 0 (none) to 100 (highest level), with 3 being the default.
16. HURDLE
If you know the objective value of a solution to a model, you can enter it as a hurdle tolerance. This
value is used in the branch-and-bound solver to narrow the search for the optimum. More specifically,
LINGO will only search for integer solutions where the objective is better than the hurdle value. This
comes into play when LINGO is searching for an initial integer solution. LINGO can ignore branches
in the search tree with objective values worse than the hurdle value, because a better solution exists
(i.e., the hurdle) on some alternate branch. Depending on the problem, a good hurdle value can greatly
reduce solution time. Once LINGO finds an initial integer solution, however, the Hurdle tolerance no
longer has an effect.
Note: Be sure when entering a hurdle value that a solution exists that is at least as good or better
than your hurdle. If such a solution does not exist, LINGO will not be able to find a feasible
solution to the model.
The default hurdle value is None. In other words, a hurdle value is not used by the solver. To clear an
existing hurdle value, type SET HURDLE NONE.
17. IPTOLA
Use this parameter to specify the absolute optimality tolerance. This tolerance is a positive value r,
indicating to the branch-and-bound solver that it should only search for integer solutions with objective
values at least r units better than the best integer solution found so far. In many integer programming
models, there are huge numbers of branches with roughly equivalent potential. This tolerance can help
to keep the branch-and-bound solver from being distracted by branches that can’t offer a solution
significantly better than the incumbent solution.
In general, you shouldn’t have to set this tolerance. Occasionally, particularly on poorly formulated
models, you might need to increase this tolerance slightly from zero to improve performance. In most
cases, you should experiment with the relative optimality tolerance rather than the absolute optimality
tolerance in order to improve performance.
The default value for the absolute optimality tolerance is 0.
18. IPTOLR
Use this parameter to specify the relative optimality tolerance. This tolerance is a value r, ranging
from 0 to 1, indicating to the branch-and-bound solver that it should only search for integer solutions
with objective values at least 100*r% better than the best integer solution found so far.
The end results of modifying the search procedure in this way are twofold. First, on the positive side,
solution times can be improved tremendously. Second, on the negative side, the final solution obtained
by LINGO may not be the true optimal solution. You will, however, be guaranteed the solution is
within 100*r% of the true optimum.
Typical values for the relative optimality tolerance would be in the range .01 to .05. In other words,
you would be happy to get a solution within 1% to 5% of the true optimal value. On larger integer
models, the alternative of getting a solution within a few percentage points of the true optimum after
several minutes of runtime, as opposed to the true optimum after several days, makes the use of an
optimality tolerance quite attractive.
COMMAND-LINE COMMANDS 303
Note: Generally speaking, the relative integrality tolerance is the tolerance that will most likely
improve runtimes on integer models. You should be sure to set this tolerance whenever
possible.
The default for the relative optimality tolerance is 1e-5.
19. TIM2RL
If an integer programming model is relatively easy to solve, then we would like to have the solver
press on to the true optimal solution without immediately resorting to a relative optimality tolerance
(discussed above). On the other hand, if, after running for a while, it becomes apparent that the optimal
solution won’t be immediately forthcoming, then you might want the solver to switch to using a
relative optimality tolerance. TIM2RL, the time to relative tolerance, can be used in this manner. This
tolerance is the number of seconds before the branch-and-bound solver begins using the relative
optimality tolerance. For the first n seconds, where n is the value of the time to relative tolerance, the
branch-and-bound solver will not use the relative optimality tolerance and will attempt to find the true
optimal solution to the model. Thereafter, the solver will use the relative optimality tolerance in its
search.
The default value for the time to relative tolerance is 100 seconds.
20. NODESL
The branch-and-bound solver has a great deal of freedom in deciding how to span the
branch-and-bound solution tree. NODESL, the node selection option, allows you to control the order in
which the solver selects branch nodes in the tree.
The four choices available for NODESL are as follows:
NODESL Setting Branch Selection
0 LINGO Decides –This is the default option. LINGO makes
an educated guess as to the best node to branch on.
1 Depth First – LINGO spans the branch-and-bound tree
using a depth first strategy.
2 Worst Bound – LINGO picks the node with the worst
bound.
3 Best Bound – LINGO picks the node with the best bound.
In general, LINGO Decides will offer the best results. Experimentation with the other options may be
beneficial with some classes of models.
21. LENPAG
The LENPAG parameter sets the length of the page or screen size in lines. For instance, setting
LENPAG to 25 will cause the display to pause after 25 lines and await a carriage return before
displaying the next 25 lines. This is convenient when you wish to page through long reports and not
have them scroll off the top of the screen.
When LENPAG is set to 0, paging is turned off entirely. LINGO will no longer stop output to wait for
a carriage return. Entering SET LENPAGE 0 at the top of any command script is helpful in that you
generally want command scripts to run uninterrupted.

304 CHAPTER 6
22. LINLEN
When LINGO generates reports, it limits output lines to a certain width. In some reports, lines will be
wrapped so that they fall within the line length limit. In other reports, lines may be truncated. Since
LINGO concatenates variable names in performing set operations, a variable name such as
SHIPMENTS( WAREHOUSE1, CUSTOMER2) may result, which may be truncated in a solution report
if too narrow an output width is used. You can control this line width limit through the LINLEN
parameter. You may set it anywhere between 64 and 200, with the default being 85.
23. TERSEO
You can use the TERSEO parameter to control the amount of output LINGO generates. There are four
settings available:
TERSEO Description
1 Verbose—Causes LINGO to display the maximum amount
of output, including full solution reports.
2 Terse—Less output than Verbose, with full solution reports
suppressed. This is a good output level if you tend to solve
large models. LINGO also suppresses Export Summary
Reports generated when exporting data to spreadsheets or
databases.
3 Errors Only—All output is suppressed, with the exception
of error messages
4 Nothing—LINGO suppresses all output. This level may be
useful when taking advantage of the programming
capabilities in LINGO, in which case, you will add
statements to your model to generate all required output.
The default setting for TERSEO is 1, or verbose mode.
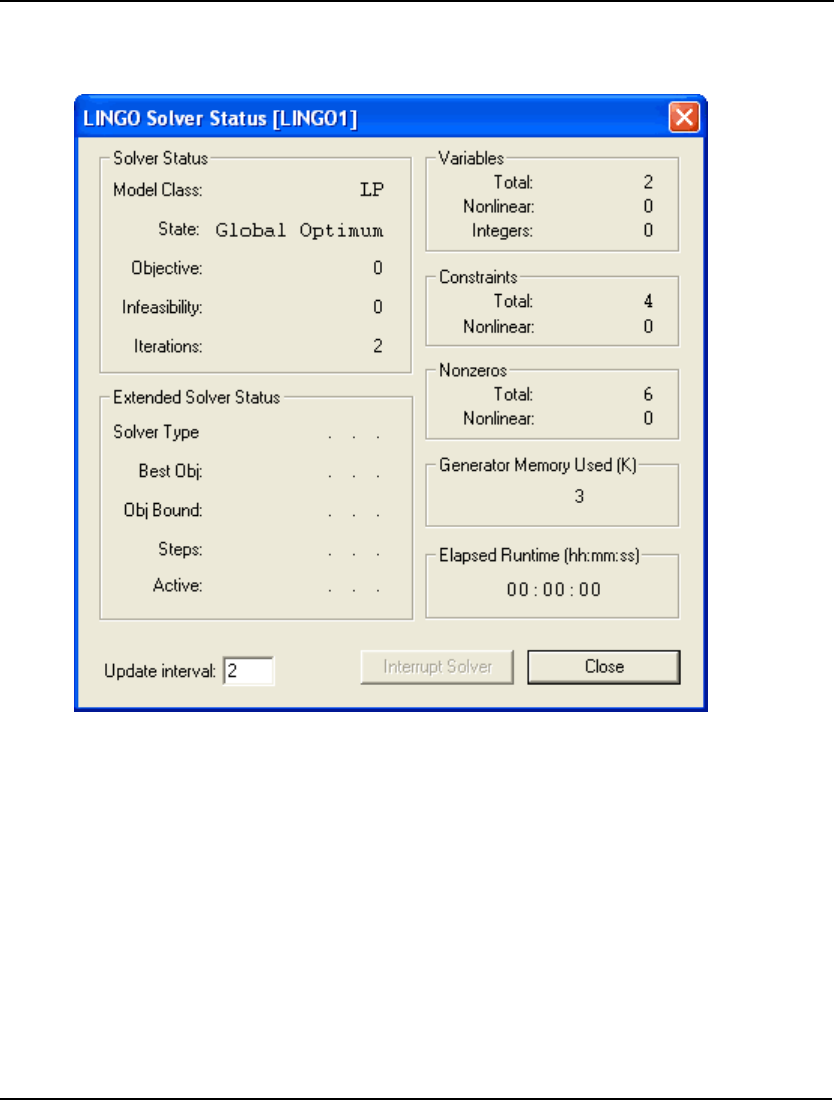
COMMAND-LINE COMMANDS 305
24. STAWIN (Windows Only)
If the STAWIN parameter is set to 1, LINGO displays a solver status window whenever you issue the
GO command. This window resembles the following:
The solver status window is useful for monitoring the progress of the solver and the dimensions of
your model. It is updated every n seconds, where n is the value in the Update interval field in the lower
right corner of the window. LINGO defaults to displaying the solver status window.
This option applies only to Windows versions of LINGO.
For a detailed description of the various fields in the solver status window, see Chapter 1, Getting
Started with LINGO.
25. SPLASH (Windows Only)
If the SPLASH parameter is set to 1, LINGO will display its splash screen each time it starts up. The
splash screen lists the release number of LINGO and the software’s copyright notice. Setting SPLASH
to 0 disables the splash screen. The default is for the splash screen to be displayed.
This option applies only to Windows versions of LINGO.

306 CHAPTER 6
26. OROUTE (Windows Only)
Set this parameter to 1 to send reports generated by LINGO to the command window, or 0 to send
them to individual report windows. Since you can log all output to the command window in a log file,
routing reports to the command window can be a useful way of logging all reports to disk. This may
also be a desirable option when you are using LINGO as part of an automated system where you need
LINGO to run without user input. The default is for LINGO to display reports in individual windows.
This option is available only on Windows versions of LINGO.
27. WNLINE (Windows Only) and 28. WNTRIM (Windows Only)
When LINGO sends output to the command window, it places new lines at the bottom of the window.
All previous output is scrolled up to make way for the new output. The total number of output lines
that can be stored in the command window is limited. When LINGO hits this limit, it begins deleting
lines from the top of the command window. You can control this feature by setting the WNLINE and
WNTRIM parameters.
The WNLINE parameter sets the maximum number of lines allowed in the command window. When
LINGO removes lines from the top of the command window, it stops once there are n lines left in the
command window, where n is the value of the WNTRIM parameter. In general, output to the command
window will become slower as you increase the maximum and minimum line counts.
The default values for WNLINE and WNTRIM are, respectively, 800 and 400. Minimum values are 200
and 100, while there are no upper limits.
These options are relevant only to Windows versions of LINGO.
29. STABAR (Windows Only)
If the STABAR parameter is set to 1, LINGO for Windows displays a status bar along the bottom of the
main frame window. Among other things, the status bar displays the time of day, location of the
cursor, menu tips, and the current status of the program.
To remove the status bar from the screen, set STABAR to 0.
The default is for LINGO to display the status bar.
This option applies only to Windows versions of LINGO.
30. FILFMT (Windows Only)
Use FILFMT to set the default file format LINGO uses when opening a new document. The options
are:
FILFMT File Type Description
0 LNG LINGO text
1 LG4 LINGO binary
2 LTX LINDO text
The LG4 format is the default file format for Windows versions of LINGO. This is a binary format
that is readable only by LINGO. This format enables you to have custom formatting and fonts in your
models, and allows you to use LINGO as an OLE server and container. Files written in LG4 format are
useful only on Windows hardware.

COMMAND-LINE COMMANDS 307
The LNG and LTX formats are text based. Given this, LNG and LTX files may be read into other
applications. However, these formats don’t support custom formatting and embedded objects. In
general, LNG files use LINGO syntax, while LTX files use LINDO syntax.
This option applies only to Windows versions of LINGO.
31. TOOLBR (Windows Only)
In Windows versions, LINGO can display a row of buttons that act as shortcuts to various commands
contained in the LINGO menu. This row of buttons is known as the toolbar. Set TOOLBR to 1 to
display the toolbar or 0 to remove it. The default is for LINGO to display the toolbar.
This option applies only to Windows versions of LINGO.
32. CHKDUP
Prior to release 4.0, LINGO allowed you to use primitive set names in the equations of a model.
Primitive set names in a model’s equations returned the index of the set member. Starting with release
4.0, LINGO required you to use the @INDEX function (see Chapter 7, LINGO's Operators and
Functions) to get the index of a primitive set member. If you would like to test your LINGO models
from releases prior to 4.0 for instances where primitive set members appear in the model’s equations,
set CHKDUP to 1. Whenever you run a model, LINGO will issue an error message if duplicate names
appear as set members and as variables in the model.
33. ECHOIN
When you run a LINGO command script with the TAKE command, the commands LINGO processes
are normally not displayed. If you would like the commands echoed to your screen, set the ECHOIN
parameter to 1. This can be a useful feature when you are trying to develop and debug a LINGO
command script.
34. ERRDLG (Windows Only)
Set the ERRDLG parameter to 1 and LINGO will display error messages issued by the solver in a
modal dialog box. This dialog box must be cleared before LINGO proceeds with any other operation.
In some instances, you may have LINGO embedded in other applications, where it may not be
desirable, or possible, to have users clearing the error dialog boxes. By setting ERRDLG to 0, LINGO
will route the solver’s error messages to the report window, where they will be displayed and no user
intervention will be required to clear the messages. Note that this option allows you to route only those
error messages generated by LINGO’s solver to the report window. Error messages displayed by
LINGO’s interactive front-end (error codes 1000 and above) will always be posted in dialog boxes.
The default is for solver errors to be displayed in dialog boxes.
This option applies only to Windows versions of LINGO.

308 CHAPTER 6
35. USEPNM
In many instances, you will need to get the index of a primitive set member within its set. Prior to
release 4 of LINGO, you could do this by using the primitive set member’s name directly in the
model’s equations. This can create problems when you are importing set members from an external
source. In this case, you will not necessarily know the names of the set members beforehand. When
one of the imported primitive set members happens to have the same name as a variable in your model,
unintended results can occur. More specifically, LINGO would not treat the variable as optimizable. In
fact, LINGO would treat it as if it were a constant equal to the value of the index of the primitive set
member! In short, different primitive set names could potentially lead to different results. Therefore,
starting with release 4.0 of LINGO, models such as the following are no longer permitted:
MODEL:
SETS:
DAYS /MO TU WE TH FR SA SU/;
ENDSETS
INDEX_OF_FRIDAY = FR;
END
If you want the index of FR in the DAYS set, you should use the @INDEX function (see Chapter 7,
LINGO's Operators and Functions):
INDEX_OF_FRIDAY = @INDEX(DAYS, FR);
If you are unable to update your models for some reason and you would like to allow for the direct use
of primitive set names, you can enable the USEPNM parameter by setting it to 1. The default is for
LINGO to disable USEPNM.
36. NSTEEP
Setting the NSTEEP parameter to 1 causes LINGO’s nonlinear solver to use steepest-edge variable
selection. When LINGO is not in steepest-edge mode, the nonlinear solver will tend to select variables
that offer the highest absolute rate of improvement to the objective, regardless of how far other
variables may have to move per unit of movement in the newly introduced variable. The problem with
this strategy is that other variables may quickly hit a bound, resulting in little gain to the objective.
With the steepest-edge option, the nonlinear solver spends a little more time in selecting variables by
looking at what rate the objective will improve relative to movements in the other nonzero variables.
Thus, on average, each iteration will lead to larger gains in the objective. In general, the steepest-edge
option will result in fewer iterations. However, each iteration will take longer. LINGO defaults to not
using the steepest-edge option.
37. NCRASH
If you set NCRASH to 1, LINGO’s nonlinear solver will invoke a heuristic for generating a “good”
starting point when you solve a model. If this initial point is relatively good, subsequent solver
iterations should be reduced along with overall runtimes. LINGO defaults to not crashing an initial
solution.
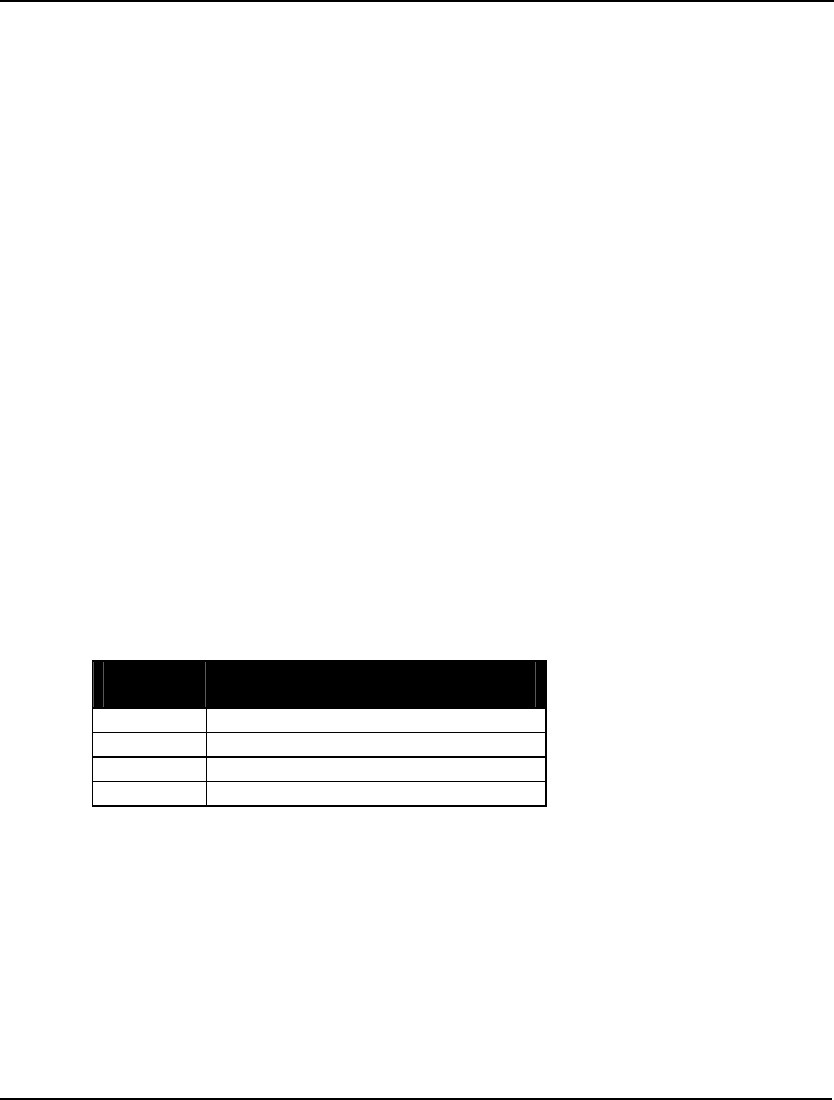
COMMAND-LINE COMMANDS 309
38. NSLPDR
If you set NSLPDR to 1, LINGO’s nonlinear solver will use successive linear programming (SLP) to
compute new search directions. This technique uses a linear approximation in search computations in
order to speed iteration times. In general, the number of total iterations will tend to rise when SLP
directions are used, but on some models overall runtimes may improve. LINGO defaults to not using
SLP directions.
39. SELCON
If you set SELCON to 1, LINGO’s nonlinear solver will only evaluate constraints on an as needed
basis. Thus, not every constraint will be evaluated at each iteration. This generally leads to faster
solution times, but can also lead to problems in models with undefined functions in certain regions.
LINGO may not evaluate a constraint for many iterations only to find that it has moved into a region
where the constraint is no longer defined. In this case, there may not be a valid point for the solver to
retreat to and the solution process terminates with an error. Turning off selective constraint evaluation
eliminates these errors. LINGO defaults to not using selective constraint evaluation.
40. PRBLVL
On a mixed-integer linear program, LINGO can perform an operation known as probing. Probing
involves taking a close look at the integer variables in a model and deducing tighter variable bounds
and right-hand side values. In many cases, probing can tighten an integer model sufficiently, thereby
speed overall solution times. In other cases, however, probing may not be able to do much tightening
and the overall solution time will increase due to the extra time spent probing. You can choose from
seven successive levels of probing ranging from 1 to 7. Level 1 disables probing completely, while
level 7 involves the highest degree of probing. Setting this option to 0 lets LINGO select the level of
probing. LINGO defaults to 0.
41. SOLVEL
This option allows you to choose the type of algorithm invoked by LINGO’s linear solver. At present,
LINGO offers the following four options:
SOLVEL
Value Linear Solver
Algorithm
0 LINGO chooses
1 Primal simplex
2 Dual simplex
3 Barrier (only available as an option)
In general, it is difficult to say what algorithm will be fastest for a particular model. A rough guideline
is that primal simplex tends to do better on sparse models with fewer rows than columns; the dual does
well on sparse models with fewer columns than rows; and the barrier works best on densely structured
models or very large models.
The barrier solver is available only as an additional option to the LINGO package.
LINGO defaults to 0, LINGO chooses.

310 CHAPTER 6
42. REDUCE
When this parameter is set to 1, LINGO’s linear solver tries to identify and remove extraneous
variables and constraints from the formulation before solving. In certain cases, this can greatly reduce
the size of the final model to be solved. Setting REDUCE to 1 enables reduction, while 0 disables it.
Setting REDUCE to 2 allows LINGO to choose whether or not to enable reduction. LINGO defaults to
this last option.
43. SCALEM
Setting SCALEM to 1 enables the scaling option in LINGO’s linear solver. This option rescales the
coefficients in the model’s matrix, causing the ratio of the largest to smallest coefficients to be
reduced. By doing this, LINGO reduces the chances of round-off error, which leads to greater
numerical stability and accuracy in the linear solver.
LINGO defaults to using scaling.
44. PRIMPR
Setting this parameter to 2 causes LINGO’s primal simplex linear solver to use devex pricing
techniques. If this parameter is set to 1, the primal simplex solver will use partial pricing. If this
parameter is set to 0, LINGO chooses the primal simplex pricing method.
LINGO defaults to choosing the primal pricing method.
45. DUALPR
If DUALPR is set to 2, LINGO’s dual simplex solver will use steepest edge pricing. If DUALPR is 1,
the dual solver will use Dantzig pricing methods. If DUALPR is 0, LINGO chooses the most
appropriate pricing method.
In Dantzig pricing mode, the dual simplex solver will tend to select variables that offer the highest
absolute rate of improvement to the objective, regardless of how far other variables may have to move
per unit of movement in the newly introduced variable. The problem with this strategy is that other
variables may quickly hit a bound, resulting in little gain to the objective. With the steepest-edge
option, the solver spends a little more time selecting variables by looking at the total improvement in
the objective by adjusting a particular variable. Thus, on average, each iteration will lead to larger
gains in the objective. In general, the steepest-edge option will result in fewer iterations. However,
each iteration will take longer.
LINGO defaults to choosing the pricing method for the dual solver.
46. DUALCO
The DUALCO parameter is used to set the level of dual computations performed by the solver. Setting
DUALCO to 0 will cause LINGO to not compute dual values and ranges. This is the fastest option, but
is suitable only if you don’t need this information. In fact, the RANGE command will not execute
when DUALCO is 0. When DUALCO is 1, LINGO will compute dual values, but not ranges. When
DUALCO is 2, LINGO computes both dual prices and ranges. Setting DUALCO to 3 causes LINGO to
compute the dual values on optimizable rows only (i.e., fixed rows are excluded) and forgo range
computations, LINGO defaults to a DUALCO value of 1.
Note: Range computations can take some time, so, if speed is a concern, you don’t want to enable
range computations unnecessarily.
COMMAND-LINE COMMANDS 311
Note: The barrier crossover option must be enabled if you plan to do range analysis. Range
computations cannot be performed if the final solution is not a basic solution.
47. RCMPSN
Setting RCMPSN to 1 causes LINGO to convert all variable and row names to RC notation when
performing MPS file format I/O. Refer to the RMPS command on page 254 for a discussion of why
this option is useful. By default, LINGO disables the use of RC format names.
48. MREGEN
The MREGEN parameter controls the frequency with which LINGO regenerates a model. With
MREGEN set to 0, LINGO regenerates a model only when a change has been made to the model’s text
since the last generation took place. When MREGEN is 1, LINGO regenerates whenever a change is
made to the model text or if it contains references to external data sources (e.g., text files, databases, or
spreadsheets). If MREGEN is 2, then LINGO always regenerates the model each time information
regarding the generated model is needed. Commands that will trigger a model generation are GO,
GEN, GENL, STATS, RMPS, FRMPS, SMPS, and PICTURE. LINGO defaults to a MREGEN value
of 2.
49. BRANDR
LINGO uses a branch-and-bound solution procedure when solving integer programming models. One
of the fundamental operations involved in the branch-and-bound algorithm is branching on variables.
Branching involves forcing an integer variable that is currently fractional to either the next greatest
integer value or to the next lowest integer value. As an example, suppose there is a general integer
variable that currently has a value of 5.6. If LINGO were to branch on this variable, it would have to
choose whether to set the variable first to 6 or 5. The BRANDR parameter controls how LINGO makes
this branching decision.
There are three possible settings for BRANDR:
BRANDR
Value Preferred Branching
Direction
0 Both up and down
1 Up
2 Down
The default option, Both up and down, involves LINGO making an intelligent guess as to whether it
should branch up or down first on each individual variable. If the Up option is selected, LINGO will
always branch up to the next highest integer first. If Down is selected, LINGO will always branch
down first. In most cases, the Both up and down option will result in the best performance.
Occasionally, models will benefit from use of one of the other two options.

312 CHAPTER 6
50. BRANPR
When branching on variables, the branch-and-bound procedure can give priority to branching on the
binary variables first, or it can make an intelligent guess as to the next best variable to branch on,
regardless of whether it is binary or general.
There are two possible settings for BRANPR:
BRANPR
Value Branching
Priority
0 LINGO decides
1 Binary variables first
Select the Binary variables first option to have LINGO give branching priority to the binary variables.
Select LINGO Decides to have LINGO select the next integer variable for branching based on an
intelligent guess regardless of whether it is binary or general. The default for this option is LINGO
Decides, which should generally give the best results. However, on occasion, the Binary option may
prevail.
51. CUTOFF
On occasion, due to round-off error, some of the values returned by LINGO’s solver will be very small
(less than 1e-10). In reality, the true values of these variables are either zero or so small as to be of no
consequence. These tiny values can be distracting when interpreting a solution report. The CUTOFF
parameter can be used to suppress small solution values. Any solution value less-than-or-equal-to
CUTOFF will be reported as being zero. The default value for CUTOFF is 1e-9.
52. STRONG
The strong branch option uses a more intensive branching strategy during the first n levels of the
branch-and-bound tree, where n is the value of the STRONG parameter. During these initial levels,
LINGO picks a subset of the fractional variables as branching candidates. LINGO then performs a
tentative branch on each variable in the subset, selecting as the final candidate the variable that offers
the greatest improvement in the bound on the objective. Although strong branching is useful in
tightening the bound quickly, it does take additional computation time. So, you may want to try
different settings to determine what works best for your model.
The default setting is 10 levels.
COMMAND-LINE COMMANDS 313
53. REOPTB
The warm start option controls the linear solver that is used by the branch-and-bound solver at each
node of the solution tree when a previous solution is present to use as a “warm start”. The cold start
option, discussed below, determines the solver to use when a previous solution does not exist.
There are four possible settings for REOPTB:
REOPTB
Value Warm Start
Solver
0 LINGO Decides – LINGO chooses the most
appropriate solver.
1 Barrier – LINGO uses the barrier method,
assuming you have purchased a license for the
barrier solver. Otherwise, the dual solver will be
used.
2 Primal – The primal solver will be used
exclusively.
3 Dual – The dual solver will be used exclusively.
In general, LINGO Decides will yield the best results. The barrier solver can’t make use of a
pre-existing solution, so Barrier usually won’t give good results. In general, Dual will be faster than
Primal for reoptimization in branch-and-bound.
54. REOPTX
The cold start option controls the linear solver that is used by the branch-and-bound solver at each
node of the solution tree when a previous solution is not present to use as a “warm start”. The warm
start option, discussed above, determines the solver to use when a previous solution does exist.
There are four possible settings for REOPTX :
REOPTX
Value Warm Start
Solver
0 LINGO Decides – LINGO chooses the most
appropriate solver.
1 Barrier – LINGO uses the barrier method,
assuming you have purchased a license for the
barrier solver. Otherwise, the dual solver will be
used.
2 Primal – The primal solver will be used
exclusively.
3 Dual – The dual solver will be used exclusively.
In general, LINGO Decides will yield the best results. However, experimentation with the other
options may be fruitful.

314 CHAPTER 6
55. MAXCTP
The integer pre-solver makes iterative passes through a model determining appropriate constraint cuts
to append to the formulation. In general, the marginal benefits of each additional pass declines. At
some point, additional passes will only add to total solution times. Thus, LINGO imposes a limit on
the maximum number of passes.
LINGO applies constraint cuts at both the top, or root, node of the branch-and-bound tree, and at all
subsequent nodes within the tree. The MAXCTP parameter limits the maximum number of cuts at the
top node, while the MAXCTR parameter sets the cut limit on all subsequent nodes in the tree. The
default limit is 100 passes.
56. RCTLIM
Most integer programming models benefit from the addition of some constraint cuts. However, at
some point, additional cuts take more time to generate than they save in solution time. For this reason,
LINGO imposes a relative limit on the number of constraint cuts that are generated. The default limit
is set to .75 times the number of true constraints in the original formulation. You may override this
relative limit by changing the setting of RCTLIM.
Constraint Cut Types
LINGO generates twelve different types of constraint cuts when solving mixed integer linear
programs. Using options listed below, these various classes of cuts can be enabled by setting their
parameter value to 1, or disabled by setting their parameter value to 0.
The available cut classes are as follows:
Index Parameter Name Cut Type
11 OBJCTS Objective cuts
57 GUBCTS GUB
58 FLWCTS Flow
59 LFTCTS Lift
60 PLOCTS Plant location
61 DISCTS Disaggregation
62 KNPCTS Knapsack cover
63 LATCTS Lattice
64 GOMCTS Gomory
65 COFCTS Coefficient reduction
66 GCDCTS Greatest common divisor
76 BASCTS Basis cuts
By default, all cut classes are enabled. Occasionally, on some poorly formulated models, disabling one
or more of the cut forms can help in finding feasible solutions.
Cuts are not generated for nonlinear integer models. Thus, these options will not affect performance on
nonlinear models.

COMMAND-LINE COMMANDS 315
67. SCLRLM (Windows Only)
The LINGO editor in Windows is “syntax aware.” In other words, when it encounters LINGO
keywords, it displays them in blue. Comments are displayed in green, and all remaining text is
displayed in black. Syntax coloring can take a long time if you have very large files. The SCLRLM
parameter sets the maximum acceptable file size for syntax coloring. Files with line counts exceeding
this parameter will not be syntax colored. Setting this parameter to 0 will disable the syntax coloring
feature. The default limit is 1000 lines.
This option applies only to Windows versions of LINGO.
68. SCLRDL (Windows Only)
The LINGO editor in Windows is “syntax aware”. In other words, when it encounters LINGO
keywords it displays them in blue. Comments are displayed in green, and all remaining text is
displayed in black. The SCLRDL parameter sets the number of seconds LINGO waits after the last
keystroke was typed before recoloring modified text. Users on slower machines may want to set this
higher to avoid having syntax coloring interfere with typing. Users on faster machines may want to
decrease this value, so text is recolored more quickly. The default is 0 seconds (i.e., LINGO recolors
modified text immediately).
This option applies only to Windows versions of LINGO.
69. PRNCLR (Windows Only)
The LINGO editor in Windows displays matching parentheses in red when you place the cursor
immediately following a parenthesis. The PRNCLR parameter allows you to disable this feature.
Setting PRNCLR to 0 will disable parenthesis matching, while setting it to 1 will enable it.
This option applies only to Windows versions of LINGO.
70. MULTIS
LINGO exploits the convex nature of linear models to find globally optimal solutions. However, we
aren’t as fortunate with nonlinear models. With nonlinear programming (NLP) models, LINGO’s
default NLP solver uses a local search procedure. This can lead to LINGO stopping at locally optimal
points, perhaps missing a global point lying elsewhere. Refer to Chapter 15, On Mathematical
Modeling, for more information on how and why this can happen.
A strategy that has proven successful in overcoming this problem is to restart the NLP solver several
times from different initial points. It is not uncommon for a different starting point to lead to a
different local solution point. The idea is that, if we restart from enough unique points, saving the best
local solution as we go, then we have a much better chance of finding the true global solution.
The MULTIS parameter allows you to set the number of times you would like the NLP solver to re-
solve your model, starting each time from an intelligently generated, new starting point. We refer to
this feature as multistart. The default value for MULTIS, 0, entails restarting 5 times on small NLPs
and disabling multistart on larger models. Setting MULTIS to 1 disables multistart on all NLPs. Setting
MULTIS to any value greater than 1 will cause the NLP solver to restart that number of times on all
NLPs. We have found that setting MULTIS around 5 tends to be adequate for most models. Highly
nonlinear models may require a larger setting.
316 CHAPTER 6
Keep in mind, however, that multistart will dramatically increase runtimes. Thus, one should avoid
using it unnecessarily on convex models that will converge to a global point in a single pass without
any additional prodding.
The following example illustrates the usefulness of multistart. Consider the simple, yet highly
nonlinear, model:
MODEL:
MIN = X * @COS( 3.1416 * X);
@BND( 0, X, 6);
END
The graph of the objective function is as follows:
The objective function has three local, minimal points over the feasible range. These points are
summarized in the following table:
Point X Objective
1 1.09 -1.05
2 3.03 -3.02
3 5.02 -5.01

COMMAND-LINE COMMANDS 317
Clearly, the third local point is also the globally best point, and we would like the NLP solver to
converge to this point. Below, we attempt this by loading the model, turning off the multistart option,
and then solving:
: take wavy.lng
: look all
MODEL:
1] MIN = X * @COS( 3.1416 * X);
2] @BND( 0, X, 6);
END
: set multis 1 !set solver attempts to 1 only (i.e., disable ms)
Parameter Old Value New Value
MULTIS 0 1
: go
Local optimal solution found at step: 11
Objective value: -1.046719
Variable Value Reduced Cost
X 1.090405 0.1181082E-07
Row Slack or Surplus Dual Price
1 -1.046719 -1.000000
Unfortunately, as you can see, we converged to the least preferable of the local minimums. Below, we
will do the same as in the previous run. However, this time, we will set the number of multistarts to
five:
: take wavy.lng
: look all
MODEL:
1] MIN = X * @COS( 3.1416 * X);
2] @BND( 0, X, 6);
END
: set multis 5
Parameter Old Value New Value
MULTIS 0 5
: go
Local optimal solution found at step: 39
Objective value: -5.010083
Variable Value Reduced Cost
X 5.020143 -0.7076917E-08
Row Slack or Surplus Dual Price
1 -5.010083 -1.000000
The extra four restarts allowed LINGO to find the global optimal point.

318 CHAPTER 6
71. USEQPR
The USEQPR parameter controls the Quadratic Recognition option. This option consists of an
algebraic preprocessor that automatically determines if an arbitrary nonlinear model is actually a
quadratic programming (QP) model. If a model is found to be a convex QP, then it can be passed to the
faster quadratic solver. Note that the QP solver is not included with the base version of LINGO, but
comes as part of the barrier option.
LINGO defaults to not using quadratic recognition. You may enable this option with the command:
SET USEQPR 1.
72. GLOBAL
Many nonlinear models are non-convex and/or non-smooth (for more information see Chapter 15, On
Mathematical Modeling). Nonlinear solvers that rely on local search procedures, as does LINGO’s
default nonlinear solver, will tend to do poorly on these types of models. Typically, they will converge
to a local, sub-optimal point that may be quite distant from the true, global optimal point. Global
solvers overcome this weakness through methods of range bounding (e.g., interval analysis and convex
analysis) and range reduction techniques (e.g., linear programming and constraint propagation) within
a branch-and-bound framework to find the global solutions to non-convex models. LINGO has a
global solver capability that is enabled through the GLOBAL parameter. Setting GLOBAL to 1 will
enable the global solver on nonlinear models, while setting it to 0 (the default) will not.
The following example illustrates the power of the global solver on a non-smooth model. Consider the
following model:
model:
sets:
projects: baths, sqft, beds, cost, est;
endsets
data:
projects, beds, baths, sqft, cost =
p1 5 4 6200 559608
p2 2 1 820 151826
p3 1 1 710 125943
p4 4 3 4300 420801
p5 4 2 3800 374751
p6 3 1 2200 251674
p7 3 2 3400 332426
;
enddata
min = @max( projects: @abs( cost - est));
@for( projects:
est = a0 + a1 * beds + a2 * baths + a3 * sqft
);
end
Model: COSTING

COMMAND-LINE COMMANDS 319
This model estimates the cost of home construction jobs based on historical data on the number of
bedrooms, bathrooms, and square footage. The objective minimizes the maximum error over the
sample project set. Both the @MAX() and @ABS() functions in the objective are non-smooth, and, as a
result, can present problems for LINGO’s default, local search NLP solver. Running the model under
the default settings with the global solver disabled, we get the following result:
Local optimal solution found at step: 91
Objective value: 3997.347
Variable Value Reduced Cost
A0 37441.55 0.000000
A1 27234.51 0.000000
A2 23416.53 0.000000
A3 47.77956 0.000000
Enabling the global solver with the SET GLOBAL 1 command and re-optimizing yields the substantially
better solution:
Global optimal solution found at step: 186
Objective value: 1426.660
Variable Value Reduced Cost
A0 46814.64 0.000000
A1 22824.18 0.000000
A2 16717.33 0.000000
A3 53.74674 0.000000
Note that the maximum error has been reduced from 3,997 to 1,426!
This example illustrates the power of the global solver. Unfortunately, there is a drawback. You will
find the global solver runs considerably slower than the default local solver, and may be swamped
when trying to solve larger models. Therefore, the preferred option is to always try to create smooth,
convex models, so that the faster, default local solver can successfully solve them.
Keep in mind that the global solver supports most, but not all, of the functions available in the LINGO
language. The following is a list of the nonlinear functions not currently supported by the global
solver:
♦ @PBN()—Cumulative binomial probability
♦ @PCX()—Cumulative Chi-squared distrribution
♦ @PFD()—Cumulative F distribution
♦ @PHG()—Cumulative hypergeometric probability
♦ @PFS()—Poisson finite source
♦ @PPL()—Poisson linear loss
♦ @PTD()—Cumulative t distribution
♦ @USER()-User supplied function
Note: The global solver will not operate on models containing one or more unsupported nonlinear
operations that reference optimizable quantities; the default NLP solver will be called in this
case.
The global solver is disabled by default.

320 CHAPTER 6
73-75. LNRISE, LNBIGM, LNDLTA
The LNRISE, LNBIGM, and LNDLTA parameters control the linearization option in LINGO. Many
nonlinear operations can be replaced by linear operations that are mathematically equivalent. The
ultimate goal is to replace all the nonlinear operations in a model with equivalent linear ones, thereby
allowing use of the faster and more robust linear solvers. We refer to this process as linearization.
The LNRISE parameter determines the extent to which LINGO will attempt to linearize models. The
available options are:
LNRISE Setting Linearization Level
0 Solver Decides
1 None
2 Math
3 Math and Logic
Under the None option, no linearization occurs. With the Math option, LINGO linearizes the
mathematical functions: @ABS(), @MAX(), @MIN(), @SMAX(), and @SMIN() along with any
products of binary and continuous variables. The Math and Logicoption is equivalent to the Math
option, plus LINGO will linearize all logical operators (#LT#, #LE#, #EQ#, #GT#, #GE#, and #NE#).
Under the Solver Decides option, LINGO will do maximum linearization if the number of variables
doesn’t exceed 12. Otherwise, LINGO will not perform any linearization. LINGO defaults to the
Solver Decides setting.
The LNDLTA parameter controls the Delta Coefficient, which is a tolerance indicating how closely you
want the additional constraints added as part of linearization to be satisfied. Most models won’t require
any changes to this parameter. However, some numerically challenging formulations may benefit from
increasing Delta slightly. LINGO defaults to a Delta of 1.e-6.
When LINGO linearizes a model, it adds forcing constraints to the mathematical program generated to
optimize your model. These forcing constraints are of the form:
f( x) ≤ M • y
where M is the BigM Coefficient and y is a 0/1 variable. The idea is that, if some activity in the
variables is occurring, then the forcing constraint will drive y to take on the value of 1. Given this, if
we set the BigM value to be too small, we may end up with an infeasible model. Therefore, the astute
reader might conclude that it would be smart to make BigM quite large, thereby minimizing the chance
of an infeasible model. Unfortunately, setting BigM to a large number can lead to numerical stability
problems in the solver resulting in infeasible or sub-optimal solutions. So, getting a good value for the
BigM Coefficient may take some experimentation. The default value for BigM is 100,000.

COMMAND-LINE COMMANDS 321
As an example of linearization, consider the following model:
model:
sets:
projects: baths, sqft, beds, cost, est;
endsets
data:
projects, beds, baths, sqft, cost =
p1 5 4 6200 559608
p2 2 1 820 151826
p3 1 1 710 125943
p4 4 3 4300 420801
p5 4 2 3800 374751
p6 3 1 2200 251674
p7 3 2 3400 332426
;
enddata
min = @max( projects: @abs( cost - est));
@for( projects:
est = a0 + a1 * beds + a2 * baths + a3 * sqft
);
end
Model: COSTING
This model estimates the cost of home construction jobs based on historical data on the number of
bedrooms, bathrooms, and square footage. The objective minimizes the maximum error over the
sample project set. Both the @MAX() and @ABS() functions in the objective are non-smooth nonlinear
functions, and, as a result, can present problems for LINGO’s default, local search NLP solver.
Running the model under the default settings with linearization disabled, we get the following result:
Local optimal solution found at step: 91
Objective value: 3997.347
Variable Value Reduced Cost
A0 37441.55 0.000000
A1 27234.51 0.000000
A2 23416.53 0.000000
A3 47.77956 0.000000
Enabling linearization and re-optimizing yields the substantially better solution:
Global optimal solution found at step: 186
Objective value: 1426.660
Variable Value Reduced Cost
A0 46814.64 0.000000
A1 22824.18 0.000000
A2 16717.33 0.000000
A3 53.74674 0.000000
Note that the maximum error has been reduced from 3,997 to 1,426!
Linearization will substantially increase the size of your model. The sample model above, in un-
linearized form, has a mere 8 rows and 11 continuous variables. On the other hand, the linearized

322 CHAPTER 6
version has 51 rows, 33 continuous variables, and 14 binary variables! Although linearization will
cause your model to grow in size, you will tend to get much better solution results if the model can be
converted entirely to an equivalent linear form.
Note: Linearization will be of most use when a nonlinear model can be 100% linearized. If LINGO
can only linearize a portion of your model, then you may actually end up with a more difficult
nonlinear model.
The linearization option is set to Solver Decides by default.
76. BASCTS
Please refer to the Constraint Cut Types section above for information on this parameter.
77. MAXCTR
This parameter controls the number of passes the branch-and-bound solver makes at each node of the
tree for cut generation. There is one exception in that MAXCTR does not control the number of passes
at the root node of the tree. You must use MAXCTP, see above, to control the number of passes at the
root node. The default value for MAXCTR is 2 passes.
78. HUMNTM
This parameter sets the minimum amount of time spent in heuristics at each node of the branch-and-
bound tree. The default value for HUMNTM is 0 seconds.
79. DECOMP
Many large scale linear and mixed integer problems have constraint matrices that are totally
decomposable into a series of block structures. If total decomposition is possible, LINGO can solve the
independent problems sequentially and report a solution for the original model, resulting in dramatic
speed improvements. Setting DECOMP to 1 enables the decomposition feature.
LINGO defaults to not using matrix decomposition.
80. GLBOPT
The GLBOPT tolerance specifies by how much a new solution must beat the objective value of the
incumbent solution in order to become the new incumbent in the global solver. The default value for
GLBOPT is 1. e-6.
81. GLBDLT
The GLBDLT tolerance specifies how closely the additional constraints, added as part of the global
solver’s convexification process, must be satisfied. The default value for GLBDLT is 1. e-7.
82. GLBVBD
The GLBVBD tolerance sets the default variable bounds while the global solver is running. If this
parameter is set to d, then variables will not be permitted to assume values outside the range of [-d, d].
Setting this parameter as tightly as possible in the Value Field restricts the global solver from straying
into uninteresting regions and will reduce run times. You may also need to set the GLBUBD tolerance
(see below) to control how the global solver uses the bound. The default value for GLBVBD is 1. e
+10.
83. GLBUBD
The GLBUBD tolerance controls how the global solver’s variable bound tolerance, GLBVBD (see
above), is applied. There are three choices available: 0:None, 1:All, and 2:Selected. Selecting None

COMMAND-LINE COMMANDS 323
removes the variable bound entirely and is not recommended. The All setting applies the bound to all
variables. Finally, the Selected setting causes the global solver to apply the bound after an initial solver
pass to find the first local solution. The bound will only be applied to a variable if it does not cut off
the initial local solution. LINGO defaults to the Selected setting.
84. GLBBRN
The GLBBRN tolerance specifies the branching direction for variables when the global solver initially
branches on them. Six options are available:
GLBBRN Setting Branching Direction
0 Absolute Width
1 Local Width
2 Global Width
3 Global Distance
4 Absolute Violation
5 Relative Violation
The default setting for branching is 5, or Relative Violation.
85. GLBBXS
The GLBBXS parameter specifies the strategy to use for choosing between all active nodes in the
global solver’s branch-and-bound tree. The choices are: 0:Depth First and 1:Worst Bound. The default
is 1, or Worst Bound.
86. GLBREF
The GLBREF option sets the degree of algebraic reformulation performed by the global solver.
Algebraic reformulation is critical for construction of tight, convex sub-regions to enclose the
nonlinear and nonconvex functions. The available settings are: 0:None, 1:Low, 2:Medium, and 3:High.
The default is 3, or High.
87. SUBOUT
The SUBOUT option is used to control the degree to which fixed variables are substituted out of the
ultimate math program passed to the solver engines.
For example, consider the model:
MAX= 20*X + 30*Y + 12*Z;
X = 2*Y;
X + Y + Z <= 110;
Y = 30;
If we run the GEN command, we see that LINGO is able to reduce this model down to the equivalent,
but smaller model:
MAX= 12 * Z + 2100;
Z <= 20;
324 CHAPTER 6
From the third constraint of the original model it is obvious that Y is fixed at the value 30. Plugging
this value for Y into the first constraint, we can conclude that X has a value of 60. Substituting these
two fixed variables out of the original formulation yields the reduced formulation above.
In most cases, substituting out fixed variables yields a smaller, more manageable model. In some
cases, however, you may wish to avoid this substitution. An instance in which you might want to
avoid substitution would be when equations have more than one root. When m multiple roots are
present, reduction may select a suboptimal root for a particular equation. On the other hand, the global
and multistart solvers are adept at handling equations containing multiple roots. Thus, when using
these solvers one may wish to forgo fixed variable reduction.
The available options are:
Selecting None disables all fixed variable reduction. Selecting Always enables reduction. When Not
with global and multistart is selected, LINGO disables reduction whenever either the global or
multistart solvers are selected, otherwise reduction is performed. With the Linear Only option, LINGO
will not substitute a variable out unless it is a linear variable.
Note: You should be careful when turning off fixed variable reduction. If the model generator is
unable to substitute out fixed variables, you may end up turning a linear model into a more
difficult nonlinear model.
LINGO defaults to the Linear Only setting for fixed variable reduction.
88. NLPVER
The NLPVER option determines the version of the nonlinear solver that is invoked:
NLPVER Setting Nonlinear Solver Version
0 Solver Decides — LINGO
selects the NLP solver version
(ver 2.0 in this case)
1 Ver 1.0
2 Ver 2.0
This option is available on the off chance that the older version of the nonlinear solver performs better
on a particular model.
SUBOUT Setting Reduction Degree
0 None
1 Always
2 Not with global and
multistart
3 Linear only

COMMAND-LINE COMMANDS 325
LINGO defaults to Solver Decides for the nonlinear solver version.
89. DBGCLD and 90. DBGWRM
These two parameters give you control over the linear solver that is used by the DEBUG command for
model debugging. The available choices are:
DBGCLD/DBGWRM Debug Linear Solver
0 Solver Decides — LINGO selects the solver
it believes is the most appropriate,
1 Primal — the primal simplex solver will be
used,
2 Dual — the dual simplex solver will be
used, and
3 Barrier — the barrier solver will be used
(requires a barrier solver license).
DBGCLD selects the solver for cold starts (starting without an existing basis in memory) and
DBGWRM selects the solver for warm starts (restarting from an existing basis).
LINGO defaults to Solver Decides for both the cold and warm debug solver.
91. LCRASH
The LCRASH parameter controls the use of aggressive crashing techniques on nonlinear programs.
Crashing is a heuristic process designed to find a good starting point for a model. The available
choices are: 0 for none, 1 for low and 2 for high. The default setting is 1, or low.
92. BCROSS
The BCROSS parameter controls whether or not the barrier solver performs a basis crossover on linear
programs. Barrier solvers do not normally return basic solutions. For example, if alternate optima
exist, the barrier method will return a solution that is, loosely speaking, the “average” of all alternate
optima. The basis crossover process converts a non-basic barrier solver solution to a basic (i.e., corner
point) solution. The available choices are: 0 for no crossover and 1 (the default) to perform a
crossover.
93. LOWMEM
The LOWMEM option may be used to guide LINGO’s memory usage. Enabling this option (SET
LOWMEM 1) causes LINGO to opt for less memory usage when solving a model. The downside is
that opting for less memory may result in longer runtimes.
LINGO defaults to disabling the LOWMEM option.
94. FILOUT
LINGO can export a model’s solution to Excel and databases. When exporting to Excel, LINGO
sends solutions to user defined ranges in a workbook. Solutions exported to a database are sent to
tables within the database. In either case, the target range or table may contain more space for values
than you are actually exporting. In other words, there may be cells at the end of ranges or records at

326 CHAPTER 6
the end of tables that will not be receiving exported values from LINGO. The Fill Out Ranges and
Tables option determines how these extra cells and records are treated.
When the Fill Out Ranges and Tables option is enabled (SET FILOUT 1), LINGO overwrites the
extra values. Conversely, when the option is not enabled (SET FILOUT 0), LINGO leaves the extra
values untouched.
Fill Out Ranges and Tables is disabled by default.
95. DBGLVL
The DBGLVL option gives you control over the output level of the model debugging command,
DEBUG. The debugger is very useful in tracking down problems in models that are either infeasible
or unbounded. Possible output levels range from 1 (minimum output) to 15 (maximum output). In
general, you will want to generate as much output as possible. The only reason to restrict the amount
of output would be to speed debugging times on large models.
The default setting for the debugger output level is 15.
96. UNARYM
The UNARYM option is used to set the priority of the unary minus operator. The two available
options are High (SET UNARYM 1) are Low (SET UNARYM 0).
There are two theories as to the priority that should be assigned to the unary minus (i.e., negation)
operator in mathematical expressions. On the one hand, there is the Excel practice that the unary
minus operator should have the highest priority, in which case, the expression 3^2 would evaluate to
+9. On the other hand, there is the mathematicians’ preference for assigning a lower priority to unary
minus than is assigned to exponentiation, in which case, 3^2 evaluates to 9. Note that regardless
which relative priority is used, one can force the desired result through the use of parenthesis.
LINGO defaults to the Excel approach of setting a higher priority (High) on negation than on
exponentiation.
97. LINEAR
The LINEAR option can be enabled (SET LINEAR 1) to minimize memory usage on models that are
entirely linear. When this option is in effect, the model generator can take steps to dramatically reduce
overall memory consumption without sacrificing performance. In fact, if all your models are linear,
we recommend that you enable this option permanently as the default for your installation. The one
restriction is that models must prove to be entirely linear. If a single nonlinearity is detected, you will
receive an error message stating that the model is nonlinear and model generation will cease. At which
point, you should clear this option and attempt to solve the model again.
By default, the LINEAR option is disabled.
98. LOPTOL
The LOPTOL parameter allows you to control the setting for the linear optimality tolerance. This
tolerance is used to determine whether a reduced cost on a variable is significantly different from zero.
You may wish to loosen this tolerance (make it larger) on poorly scaled and/or large models to
improve performance.
The default setting for the LOPTOL parameter is 1.e-7.

COMMAND-LINE COMMANDS 327
99. SECORD
The SECORD option determines if the nonlinear solver will use second order derivates. If used (SET
SECORD 1), second order derivatives will always be computed analytically, as opposed to using
numerical differences. Computing second order derivatives will take more time, but the additional
information they provide may lead to faster runtimes and/or more accurate solutions.
LINGO defaults to not using second order derivatives.
100. NONNEG
When enabled (SET NONNEG 1), the NONNEG option tells LINGO to place a default lower bound of
0 on all variables. In other words, unless otherwise specified, variables will not be allowed to go
negative. Should you want a variable to take on a negative value, you may always override the default
lower bound of 0 using the @BND() function. If this option is disabled, then LINGO’s default
assumption is that variables are unconstrained and may take on any value, positive or negative.
Unconstrained variables are also referred to as be being free.
By default, LINGO enables the non-negative option, thereby setting a default lower bound of 0 on all
variables.
101. BIGMVL
Many integer programming models have constraints of the form:
f(x) ≤ M * z
where f(x) is some function of the decision variables, M is a large constant term, and z is a binary
variable. These types of constraints are called forcing constraints and are used to force the binary
variable, z, to 1 when f(x) is nonzero. In many instances, the binary variable is multiplied by a fixed
cost term in the objective; a fixed cost that is incurred when a particular activity, represented by f(x),
occurs. The large constant tem, M, Is frequently referred to as being a BigM coefficient.
Setting BigM too small can lead to infeasible or suboptimal models. Therefore, the BigM value will
typically have to be rather large in order to exceed the largest activity level of f(x). When BigM is
large, the solver may discover that by setting z slightly positive (within normal integrality tolerances),
it can increase f(x) to a significant level and thereby improve the objective. Although such solutions
are technically feasible to tolerances, they are invalid in that the activity is occurring without incurring
its associated fixed cost.
The BIGMVL parameter, or BigM threshold, is designed to avoid this problem by allowing LINGO to
identify the binary variables that are being set by forcing constraints. Any binary variable with a
coefficient larger than the BigM threshold will be subject to a much tighter integrality tolerance.
The default value for the BigM Threshold is 1.e8.
102. KILLSC
LINGO allows the input of scripts in the calc section. These scripts are useful for running multiple
models, where the outputs of one model feed into subsequent models as input. Models are solved in
calc sections with the @SOLVE command. Time limits can be placed on @SOLVE's via the TATSLV
parameter (see below). If a time limit is hit while @SOLVE is running, LINGO will interrupt the solve
and either continue executing the script with the next command, or terminate all processing. When the
KILLSC option is set to 0 (default), processing continues with the next statement. Setting KILLSC to 1
328 CHAPTER 6
causes LINGO to terminate all processing whenever the @SOLVE time limit is hit, and LINGO will
subsequently return to command-prompt level.
103. TATSLV
LINGO allows the input of scripts in the calc section. These scripts are useful for running multiple
models, where the outputs of one model feed into subsequent models as input. Models are solved in
calc sections with the @SOLVE command. Time limits can be placed on @SOLVE's via the TATSLV
parameter. If a time limit is hit while @SOLVE is running, LINGO will interrupt the solver and either
continue executing the script with the next command, or terminate all processing based on the setting
for the KILLSC parameter (see above). LINGO defaults to placing no time limit on @SOLVE
commands.
104. KBESTS
The KBESTS parameter is used to set the number of solutions desired as part of the K-Best solutions
feature of LINGO's mixed integer solver. Whenever this value is greater than 1, say K, LINGO will
return up to K unique solutions to the model. These solutions will have the property that they are the
next best solutions available in terms of their objective values. Less than K solutions may be returned
if a sufficient number of feasible solutions do not exist. Please refer to section K-Best Solutions
Example for an example of the use of the K-Best feature. The default value for this parameter is 1,
meaning that LINGO will find only one solution to integer models, i.e, the K-Best feature is disabled
by default.
105. LCORES
The LCORES parameter may be used to perform parallel solves of linear programs on multiple-cored
machines. One of four different linear solvers is chosen for each core. Assignment of solvers to cores
is controlled by the LCORE1 - LCORE4 parameters (see below). LINGO will take the solution from
the solver that finishes first and then interrupt the remaining solver threads.
The idea behind this approach is that different linear solvers will have relatively better or worse
performance on different classes of models. However, it may be difficult to predict beforehand the
solver that is most likely to outperform. So, by enabling multi-core solves, you guarantee that you will
always get top performance, even without knowledge beforehand of which solver is likely to run the
fastest.
Note: The multi-core feature requires that your machine have at least one core free for each solver
you wish to run. Using this feature with an inadequate number of cores will tend to decrease
overall performance.
For the LCORES parameter, you have the following choices: 1, 2, 3, or 4. When the default 1 option is
selected, the multi-core feature is disabled, and LINGO will run only one solver on linear programs,
namely the one specified as part of the SOLVEL option detailed above. When either option 2, 3, or 4 is
selected, LINGO will run linear solvers in the requested number of cores. The choice of the actual
solvers used is controlled by the LCORE1 - LCORE4 parameters (see below).
106-109. LCORE1 - LCORE4
The LCORE1, LCORE2, LCORE3 and LCORE4 parameters are used in conjunction with the LCORES
parameter to perform parallel solves of linear programs on multiple-cored machines. One of four
different linear solvers is chosen for each core, with assignments controlled by the LCORE1 - LCORE4
parameters. LINGO will take the solution from the solver that finishes first and then interrupt the
remaining solver threads.

COMMAND-LINE COMMANDS 329
The LCORES parameter gives the number of parallel solves that are to be performed on linear
programs, while LCORE1 - LCORE4 control the selection of the actual LP solver to use in each core.
Parameters LCORE1 - LCORE4 are meaningful only when LCORES is greater than 1. In addition, if
LCORES=<n>, then only the parameters LCORE1 - LCORE<n> are meaningful. When the default 1
option is selected for LCORES, the multi-core feature is disabled, and LINGO will run only one solver
on linear programs, namely the one specified as part of the SOLVEL option detailed above. When
either option 2, 3, or 4 is selected for LCORES, LINGO will run linear solvers in the requested number
of cores. The choice of the actual solvers used is controlled by the LCORE1 - LCORE4 parameters.
The idea behind this approach is that different linear solvers will have relatively better or worse
performance on different classes of models. However, it may be difficult to predict beforehand the
solver that is most likely to outperform. So, by enabling multi-core solves, you guarantee that you will
always get top performance, even without knowledge beforehand of which solver is likely to run the
fastest.
Note: The multi-core feature requires that your machine have at least one core free for each solver
you wish to run. Using this feature with an inadequate number of cores will tend to decrease
overall performance.
For each of the LCORE1-4 parameters, you have the following choices:
LCORE(i) Setting LP Solver Used in Core i
1 Primal1 — Primal simplex algorithm 1
2 Dual — Dual simplex algorithm
3 Barrier — Barrier/Interior point solver (available as a
option)
4 Primal2 — Primal simplex algorithm 2, installed as
part of the Barrier option

330 CHAPTER 6
As an example, the following session runs an LP model in two cores (LCORES=2), with the barrier
solver in core 1 (LCORE1=3) and the dual simplex solver in core2 (LCORE2=2):
: set lcores 2 !run in 2 cores
Parameter Old Value New Value
LCORES 1 2
: set lcore1 3 !barrier in core 1
Parameter Old Value New Value
LCORE1 1 3
: set lcore2 2 !dual simplex in core 2
Parameter Old Value New Value
LCORE2 2 2
: take lp.lng !load the model
: set terseo 1 !minimal output
Parameter Old Value New Value
TERSEO 0 1
: go !solve the model
First returning solver: BARRIER
Global optimal solution found.
Objective value: 1272282.
Infeasibilities: 0.000000
Total solver iterations: 27
:
Once optimization is complete, LINGO will display a line indicating the solver that finished first. In
the solution report excerpt above, we see that the barrier solver was the first to completion.
110. SCALEW
After LINGO generates a model, it checks all the nonzero coefficients in the model and computes the
ratio of the largest to smallest coefficients. This ratio is an indicator of how well the model is scaled.
When the ratio gets to be too high, scaling is considered to be poor, and numerical difficulties may
result during the solution phase. If the scaling ratio exceeds the value of the SCALEW parameter,
LINGO will display error message 205. The default value for SCALEW is 1e12. Instead of simply
increasing the SCALEW setting to eliminate error 205, we strongly suggest that you attempt to rescale
the units of your model so as to reduce the largest-to-smallest coefficient ratio.
111. REFRAQ
The REFRAQ parameter allows you to control how frequently the linear solver refactors the basis
matrix. The options are either to set REFRAQ to 0, thereby letting LINGO determine the frequency,
or to set REFRAQ to some positive integer quantity. If an integer value, N, is selected, then the
linear solver will refactor every N iterations. Numerically tough and/or poorly scaled models may
COMMAND-LINE COMMANDS 331
benefit from more frequent refactoring. However, refactoring too frequently will cause the solver to
slow down.
The default setting for the REFRAQ is 0, which will typically result in refactoring about once every
100 iterations.
112. SPSMSZ
The SPSMSZ parameter is used to control the default sample size for random variables in stochastic
programming (SP) whose outcomes are determined via sampling.
In many SP models, LINGO will generate a set of sample values for the some or all of the random
variables. This is particularly true when you have one or more continuous random variables, which
have an infinite number of possible outcomes. In such a case, sampling is the only viable alternative.
One way to specify the desired sample size for each stage is via the @SPSAMPSIZE function used
directly in the model's text. If, on the other hand, all or most stages should have the same sample size,
then you can use the SPSMSZ parameter to control the default sample size. Any stage which has not
had its sample size specified with @SPSAMPSIZE will default to a sample size equal to the SPSMSZ
parameter.
Note: In general, we prefer larger sample sizes to smaller ones in order to reduce sampling error.
However, SP models can become quite large if sample sizes aren't kept reasonably small.
This is particularly true for multiperiod models. For example, suppose we have a model with
just one random variable and ten periods/stages. If the default sample size is set to 3, then
there will be 3^10=59,049 possible scenarios. With this many scenarios, it would only take a
handful of decision variables to end up with an underlying deterministic equivalent model
approaching one million variables.
The SPSMSZ parameter defaults to a value of 2.
113. SPSCON
The SPSCON parameter is used to control whether LINGO samples continuous distributions only for
the random variables in stochastic programs, or if it samples both continuous and discrete random
variables. Obviously, continuous random variables must be subject to sampling, given the infinite
number of possible outcomes. On the other hand, we have a choice when it comes to discretely
distributed random variables. If this option is enabled, then LINGO will generate one outcome for
each density point in the discrete distribution of the random variable. These outcomes will be
weighted by their corresponding probabilities.
Note: If there are many density points in the distributions for the discrete random variables, the
deterministic equivalent generated to solve the SP may become exceedingly large, in which
case, disabling this option may be required. Once this option is disabled, discrete random
variables will be sampled in the same way as the continuous random variables.
The SPSCON option defaults to being on.
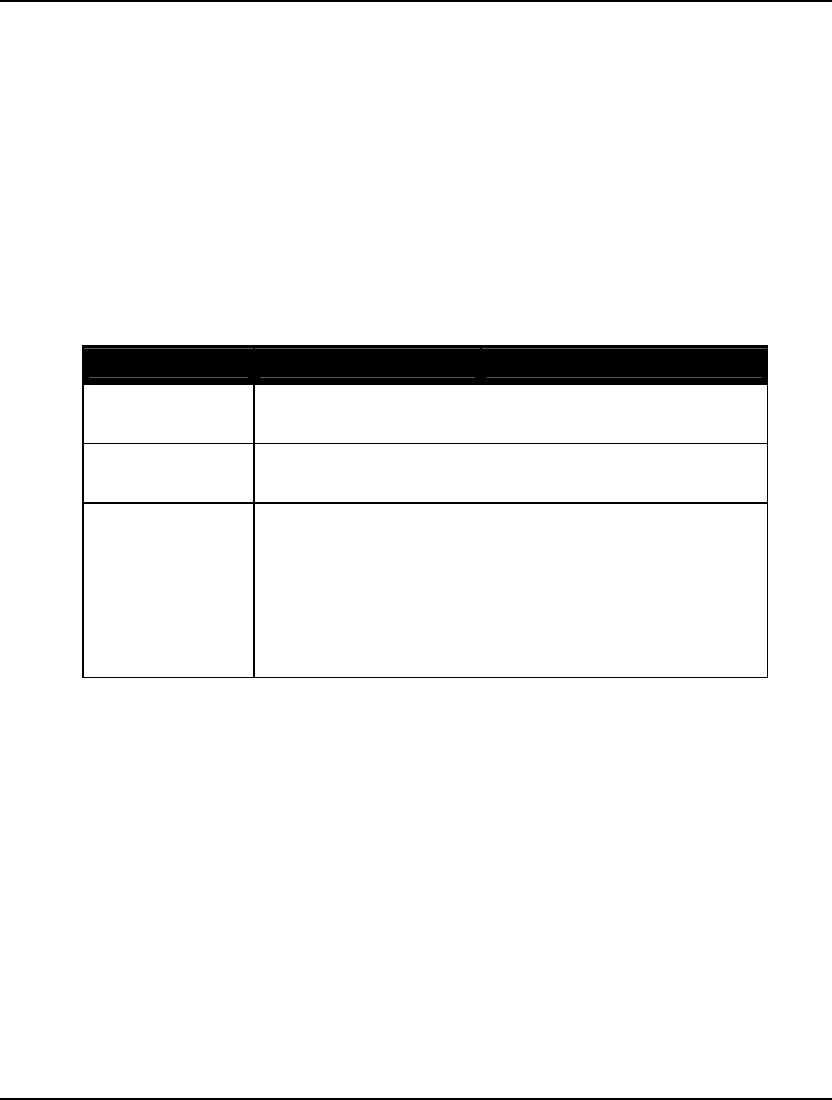
332 CHAPTER 6
114. SPSEED
The SPSEED parameter is used to establish the seed for the random number generator used in
generating samples for random variables in stochastic programming (SP) models.
In many SP models, LINGO will generate a set of sample values for the random variables. This is
particularly true when you have one or more continuous random variables, which leads to an infinite
number of possible outcomes. In such a case, sampling is the only viable alternative.
The SPSEED parameter defaults to a value of 1013.
115. SPMTHD
The SPMTHD, or SP Solver Method, option is used to select the solution method for a stochastic
programming (SP) model. Presently, the available choices are:
SPMTHD Setting SP Solver Method
0 Solver Decides — LINGO decides the most appropriate
method for solving the SP model
1 Deterministic Equivalent — LINGO generates and directly
solves the deterministic equivalent (DE) of the SP model
2 Nested Benders Decomposition — The DE for realistic SP
models can get to be quite large, in that the core model is
replicated once for every scenario. Fortunately, the DE
displays strong block-angular structure, which makes it
adaptable to decomposition techniques, such as nested Bender
decomposition (NBD). Note that the model must be entirely
linear to successfully use the NBD option.
The default setting for the SP Solver Method option is 0, or Solver Decides.
116. SPXVAL
The SPXVAL, or Calculate All Expected Value Statistics, option controls whether LINGO displays
information regarding the expected values for a number of statistics when solving stochastic
programming (SP) models. To illustrate, when solving the SPGAS.LG4 model when this option is
enabled, you will see the following expected values at the top of the solution report:
Expected value of:
Objective (EV): 1400.000
Wait-and-see model's objective (WS): 1326.667
Perfect information (EVPI = |EV - WS|): 73.33333
Policy based on mean outcome (EM): 1479.444
Modeling uncertainty (EVMU = |EM - EV|): 79.44444
The following is a brief description of these expected values:
COMMAND-LINE COMMANDS 333
Expected Value of Objective (EV)
⎯
is the expected value for the model's objective over all the
scenarios, and is the same as the reported objective value for the model.
Expected Value of Wait-and-See Model's Objective (WS)
⎯
reports the expected value of the
objective if we could wait and see the outcomes of all the random variables before making our
decisions. Such a policy would allow us to always make the best decision regardless of the
outcomes for the random variables, and, of course, is not possible in practice. For a minimization,
it's true that WS <= EV, with the converse holding for a maximization. Technically speaking, WS
is a relaxation of the true SP model, obtained by dropping the nonanticipativity constraints.
Expected Value of Perfect Information (EVPI)
⎯
is the absolute value of the difference between
EV and WS. This corresponds to the expected improvement to the objective were we to obtain
perfect information about the random outcomes. As such, this is a expected measure of how much
we should be willing to pay to obtain perfect information regarding the outcomes of the random
variables.
Expected Value of Policy Based On Mean Outcome (EM)
⎯
is an expected measure of the
objective if we were to follow a policy of assuming that the mean outcomes of the random
variables were always going to occur. EM is computed using a two-step process. First, the values
of all the random variables are fixed at their means, and the deterministic model is solved to yield
the optimal values for the stage 0 decision variables. Next, the stage 0 variables are fixed at their
optimal values from the previous step, while the random variables are freed up. At which point,
this SP is solved, with EM being equal to its objective value.
Expected Value of Modeling Uncertainty (EVMU)
⎯
is the absolute value of the difference
between EV and EM. As such, it's a measure of what we can expect to gain by incorporating
uncertainty into our modeling analysis, and not always assuming that we will be faced with mean
outcomes.
Note: Computing these expected value statistics can be very time consuming for large models. If
speed is an issue, you may wish to disable this feature.
The SPXVAL option is enabled by default.
117. SPMAXS
The SPMAXS, or Max Scenarios Limit, parameter is used to establish a limit on the maximum number
of scenarios in a stochastic programming (SP) model before forcing automatic sampling of the random
variables.
The SPMAXS parameter defaults to a value of 40,000 scenarios.
118. PRECIS
LINGO defaults to displaying seven significant digits for values in standard solution reports. In some
cases, you may desire more or less than seven digits of precision, in which case, you will need to
adjust the PRECIS parameter.
For example, suppose we have a very simple model consisting of the single expression:
X = 1/3;

334 CHAPTER 6
The default solution report for this model using seven digits of precision would contain:
Variable Value
X 0.3333333
Row Slack or Surplus
1 0.000000
Increasing the Precision parameter to 16 and resolving yields the following solution report with 16
significant digits:
Variable Value
X 0.3333333333333333
Row Slack or Surplus
1 0.000000000000000
The default value for the PRECIS parameter is seven significant digits.
119. LOOPOP
The LOOPOP, or Loop optimization, parameter is used to either enable or disable LINGO's loop
optimization step. Loop optimization reformulates expressions containing set looping functions in
order to make them more efficient, while maintaining mathematical equivalency. The end goal of loop
optimization is to minimize the number of passes through the inner loop of any nested loops in an
expression.
As an example, consider the following transportation model fragment, that just contains constraints for
satisfying customer demand:
MODEL:
! A transportation problem fragment;
SETS:
WAREHOUSE /1..50/ : CAPACITY;
CUSTOMER /1..5000/ : DEMAND;
ROUTES( WAREHOUSE, CUSTOMER) : COST, VOLUME;
ENDSETS
! The demand constraints;
@FOR( CUSTOMER( J):
@SUM( ROUTES( I, J): VOLUME( I, J)) >= DEMAND( J)
);
END
Transportation Model Fragment with Inefficient Constraints
In the demand constraints expression there are two loops ⎯ an outer @FOR() over the CUSTOMER
set and an inner @SUM() over the ROUTES set. As written, the inner loop must be executed
50*50*5000=1.25 million times. Note that a valid reformulation of these demand constraints would
be:

COMMAND-LINE COMMANDS 335
! The demand constraints;
@FOR( CUSTOMER( J):
@SUM( WAREHOUSE( I): VOLUME( I, J)) >= DEMAND( J)
);
With the expression rewritten in this manner, the inner loop will now only be executed 50*5000 times,
for a 98% reduction in total passes. LINGO's loop optimizer seeks out such inefficient loops and,
invisible to the user, rewrites them before the model gets passed to the generator. Of course, the end
result of such reformulations are faster generation times. In fact, the speedup from reformulation can
be quite dramatic in many cases. In this particular example, the reformulated version ran over 400
times faster in the model generator.
LINGO defaults to disabling the LOOPOP feature.
120. HEUCUT
The HEUCUT, or heuristics cutoff criterion, option controls the criterion for terminating integer
programming heuristics. The possible settings for HEUCUT are:
Under the Time setting, LINGO terminates heuristics after a certain amount of elapsed time. The
Iterations option terminates heuristics after a certain number of iterations. In general, the Time setting
results in the fastest performance. However, due to shifting computational loads on a machine,
solution paths may change under the Time setting from one solve to the next, potentially resulting in
non-reproducible solutions. If reproducibility of a runs is a concern, then the Iterations option should
be selected. Under the Solver Decides setting, LINGO chooses the most appropriate strategy.
The default setting for HEUCUT is 1, Solver Decides.
HEUCUT Value Cutoff Criterion
0 LINGO decides
1 Time
2 Iterations

336 CHAPTER 6
9. Miscellaneous
The Miscellaneous category contains various LINGO commands that don’t fall into one of the other
eight command categories.
!
Place an exclamation mark in a command and LINGO ignores the remainder of the line following the
exclamation mark.
QUIT
Issue the QUIT command to close the LINGO application. Be sure to save any changes made to your
model before quitting.
TIME
Displays the current elapsed time since the start of the current LINGO session as illustrated in the
following example:
: TIME
Cumulative HR:MIN:SEC = 2:22:39.54
:

337
7 LINGO’s Operators and
Functions
LINGO provides the mathematical modeler with a number of functions and operators. For our
purposes, we have broken them down into the following categories:
♦ Standard Operators - Arithmetic, logical, and relational operators such as +,
-, =, >=, and <=.
♦ Mathematical - Trigonometric and general mathematical functions.
♦ Financial - Common financial functions used to determine present values.
♦ Probability - Functions used to determine a wide range of probability and
statistical answers. Poisson and Erlang queuing functions are among those
provided.
♦ Variable Domain - Functions used to define the range of values (domain) a
variable can take on (e.g., lower and upper bounds or integer restrictions).
♦ Set Handling - Functions useful for manipulating sets.
♦ Set Looping - Looping functions used to perform an operation over a set
(e.g., to compute the sum, maximum, or minimum of a set of numbers).
♦ Import/Export - Functions used to create links to external data sources.
♦ Miscellaneous - Miscellaneous functions are listed under this heading.
In the remainder of this chapter, we will give an in-depth description of the operators and functions
available in LINGO.
Standard Operators
LINGO has three types of standard operators:
1. Arithmetic,
2. Logical, and
3. Relational.

338 CHAPTER 7
Arithmetic Operators
Arithmetic operators work with numeric operands. LINGO has five binary (two-operand) arithmetic
operators, shown here:
Operator Interpretation
^ Exponentiation
* Multiplication
/ Division
+ Addition
- Subtraction
Since these are binary operators, they require two arguments—one immediately to the left of the
operator and one immediately to the right.
The only unary (one-operand) arithmetic operator in LINGO is negation (-). In this case, the operator
applies to the operand immediately to the right of the negation sign.
These operators should be familiar to all readers. The priority of the operators is given in the
following:
Priority Level Operator(s)
Highest - (negation)
^
* /
Lowest + -
Operators with the highest priority are evaluated first, in order from left to right. As an example,
consider the expression:
4 + 6 / 2
The division operator (/) has higher priority than the addition operator (+). Thus, it is evaluated first,
leaving: 4 + 3. Evaluating the remaining addition gives a final result of 7.
The order of evaluation of the operators can be controlled with parentheses. LINGO evaluates the
equation in the innermost parentheses first and works out from there. If we recast the expression from
above as:
(4 + 6) / 2
we will now get a final result of 5, instead of 7. The 4 and 6 are added first because they appear in
parentheses. The resulting sum of 10 is divided by 2, giving the final result of 5.
Note: LINGO follows the Excel convention of assigning the highest priority to the negation
operator. Given this, LINGO evaluates -3^2 as positive 9. Some users may prefer to give the
unary minus operator a lower priority so that -3^2 evaluates to minus 9. You can do this by
setting the Unary Minus Priority option to Low via the Model Generator tab of the
LINGO|Options command. Once you set the unary minus operator’s priority is set to low its
priority will be lower than multiplication and division, but higher than addition and
subtraction.

OPERATORS AND FUNCTIONS 339
Logical Operators
Logical operators were used in Chapter 2, Using Sets, when we introduced set looping functions. In
LINGO, logical operators are primarily used in conditional expressions on set looping functions to
control which members of a set are to be included or excluded in the function. They also play a role in
building set membership conditions.
Logical operators return either TRUE or FALSE as a result. LINGO uses the value 1 to represent
TRUE, and the value 0 to represent FALSE. LINGO considers an argument to be FALSE if, and only
if, it is equal to 0. Thus, for example, arguments of 1, 7, -1, and .1234 would all be considered TRUE.
LINGO has nine logical operators, which are all binary with the single exception of the #NOT#
operator, which is unary. LINGO’s logical operators and their return values are listed below:
Logical Operator Return Value
#NOT# TRUE if the operand immediately to the right is FALSE, else
FALSE.
#EQ# TRUE if both operands are equal, else FALSE.
#NE# TRUE if both operands are not equal, else FALSE.
#GT# TRUE if the left operand is strictly greater than the right
operand, else FALSE.
#GE# TRUE if the left operand is greater-than-or-equal-to the right
operand, else FALSE.
#LT# TRUE if the left operand is strictly less than the right operand,
else FALSE.
#LE# TRUE if the left operand is less-than-or-equal-to the right
operand, else FALSE.
#AND# TRUE only if both arguments are TRUE, else FALSE.
#OR# FALSE only if both its arguments are FALSE, else TRUE.
The priority ranking of the logical operators is:
Priority Level Operator(s)
Highest #NOT#
#EQ# #NE# #GT# #GE# #LT# #LE#
Lowest #AND# #OR#
Relational Operators
In LINGO, relational operators are used in a model to specify whether the left-hand side of an
expression should be equal to, less-than-or-equal-to, or greater-than-or-equal-to the right-hand side.
Relational operators are used to form the constraints of a model. Relational operators are distinct from
the logical operators #EQ#, #LE#, and #GE#, in that they tell LINGO the optimal solution of the
model must satisfy the direction of the relational operator. Logical operators, on the other hand, merely
report whether or not a condition is satisfied.
Relational operators have the lowest priority of all the operators.

340 CHAPTER 7
The three relational operators are described below:
Relational Operator Interpretation
= The expression to the left must equal the one on the right.
<= The expression to the left must be less-than-or-equal-to the
expression on the right
>= The expression to the left must be greater-than-or-equal-to
the expression on the right
LINGO will also accept “<” for less-than-or-equal-to, and “>” for greater-than-or-equal-to.
Note: LINGO does not directly support strictly less than and strictly greater than relational
operators. In general, it would be unusual to find a good formulation that requires such a
feature. However, if you want A to be strictly less than B:
A < B,
then convert this expression to an equivalent less-than-or-equal-to expression as follows:
A + e ≤ B,
where e is a small constant term whose value is dependent upon how much A must be “less
than” B in order for you to consider them to be “not equal”.
Operator Priority Table
The following table combines all three types of operators⎯arithmetic, logical, and relational⎯into a
single table showing their relative priority rankings.
Priority Level Operator(s)
Highest #NOT# -(negation)
^
* /
+ -
#EQ# #NE# #GT# #GE# #LT# #LE#
#AND# #OR#
Lowest <= = >=
Note: LINGO follows the Excel convention of assigning the highest priority to the negation
operator. Given this, LINGO evaluates -3^2 as positive 9. Some users may prefer to give the
unary minus operator a lower priority so that -3^2 evaluates to minus 9. You can do this by
setting the Unary Minus Priority option to Low via the Model Generator tab of the
LINGO|Options command. Once you set the unary minus operator’s priority is set to low its
priority will be lower than multiplication and division, but higher than addition and
subtraction.

OPERATORS AND FUNCTIONS 341
Note: In the absence of parentheses, all operators of the same priority are processed from left to
right. Thus, 4^3^2 evaluates to 4096. Be forewarned that for the exponentiation operator,
"^", this differs from the convention that some mathematicians follow, namely, to have the
exponentiation operator evaluated from right to left, i.e., 4^3^2 would evaluate to 262144.
When in doubt, use parentheses to enforce your intentions, e.g., 4^(3^2) unambiguously
evaluates to 262144.
Mathematical Functions
LINGO offers a number of standard, mathematical functions. These functions return a single result
based on one or more scalar arguments. These functions are listed below:
@ABS(X)
Returns the absolute value of X.
@ACOS( X)
Returns the inverse cosine, or arccosine, of X, where X is an angle in radians.
@ACOSH( X)
Returns the inverse hyperbolic cosine of X, where X is an angle in radians.
@ASIN( X)
Returns the inverse sine, or arcsine, of X, where X is an angle in radians.
@ASINH( X)
Returns the inverse hyperbolic sine of X, where X is an angle in radians.
@ATAN( X)
Returns the inverse tangent, or arctangent, of X, where X is an angle in radians.
@ATAN2( Y, X)
Returns the inverse tangent of Y/X.
@ATANH( X)
Returns the inverse hyperbolic tangent of X, where X is an angle in radians.
@COS(X)
Returns the cosine of X, where X is an angle in radians.
@COSH( X)
Returns the hyperbolic cosine of X, where X is an angle in radians.
@EXP(X)
Returns e (i.e., 2.718281 ...) raised to the power X.
@FLOOR(X)
Returns the integer part of X. To be specific, if X ≥ 0, @FLOOR returns the
largest integer, I, such that I ≤ X. If X is negative, @FLOOR returns the most
negative integer, I, such that I ≥ X.

342 CHAPTER 7
@LGM(X)
Returns the natural (base e) logarithm of the gamma function of X (i.e., log of
(X - 1)!). It is extended to noninteger values of X by linear interpolation.
@LOG(X)
Returns the natural logarithm of X.
@LOG10(X)
Returns the base-10 logarithm of X.
@MOD( X,Y)
Returns the value of X modulo Y, or, in other words, the remainder of an integer divide of X
by Y.
@PI()
Returns the value of PI, i.e., 3.14159265....
@POW( X,Y)
Returns the value of X raised to the Y power.
@SIGN(X)
Returns -1 if X < 0, 0 if X = 0 and +1 if X > 0.
@SIN(X)
Returns the sine of X, where X is the angle in radians.
@SINH( X)
Returns the hyperbolic sine of X, where X is an angle in radians.
@SMAX (X1, X2, ..., XN)
Returns the maximum value of X1, X2, ..., and XN.
@SMIN(X1, X2, ..., XN)
Returns the minimum value of X1, X2, ..., and XN.
@SQR( X)
Returns the value of X squared.
@SQRT( X)
Returns the square root of X.
@TAN(X)
Returns the tangent of X, where X is the angle in radians.
@TANH( X)
Returns the hyperbolic tangent of X, where X is an angle in radians.

OPERATORS AND FUNCTIONS 343
Financial Functions
LINGO currently offers two financial functions. One computes the present value of an annuity. The
other returns the present value of a lump sum.
@FPA(I, N)
This returns the present value of an annuity. That is, a stream of $1 payments per period at an interest
rate of I for N periods starting one period from now. I is not a percentage, but a fraction representing
the interest rate (e.g., you would use .1 to represent 10%). To get the present value of an annuity
stream of $X payments, multiply the result by X.
@FPL(I, N)
This returns the present value of a lump sum of $1 N periods from now if the interest rate is I per
period. I is not a percentage, but a fraction representing the interest rate (e.g., you would use .1 to
represent 10%). To get the present value of a lump sum of $X, multiply the result by X.
Probability Functions
LINGO has a number of probability related functions. There are examples that make use of most of
these functions in Chapter 12, Developing More Advanced Models, and in Appendix A, Additional
Examples of LINGO Modeling.
@NORMINV( P, MU, SIGMA)
This is the inverse of the normal cumulative distribution. Given a probability, P, the mean of the of
the normal distribution, MU, and its standard deviation, SIGMA, this function returns the value Z such
that the probability of a normally distributed random variable being less-than-or-equal to Z is P.
@NORMSINV( P)
This is the inverse of the standard normal cumulative distribution. Given a probability, P, this function
returns the value Z such that the probability of a normally distributed random variable with a mean of 0
and a standard deviation of 1 being less-than-or-equal to Z is P.
@PBN(P, N, X)
This is the cumulative binomial probability. It returns the probability that a sample of N items, from a
universe with a fraction of P of those items defective, has X or less defective items. It is extended to
noninteger values of X and N by linear interpolation.
@PCX(N, X)
This is the cumulative distribution function for the Chi-squared distribution with N degrees of
freedom. It returns the probability that an observation from this distribution is less-than-or-equal-to X.
@PEB(A, X)
This is Erlang’s busy probability for a service system with X servers and an arriving load of A, with
infinite queue allowed. The result of @PEB can be interpreted as either the fraction of time all servers
are busy or the fraction of customers that must wait in the queue. It is extended to noninteger values of
X by linear interpolation. The arriving load, A, is the expected number of customers arriving per unit of
time multiplied by the expected time to process one customer.

344 CHAPTER 7
@PEL(A, X)
This is Erlang’s loss probability for a service system with X servers and an arriving load of A, no queue
allowed. The result of @PEL can be interpreted as either the fraction of time all servers are busy or the
fraction of customers lost due to all servers being busy when they arrive. It is extended to noninteger
values of X by linear interpolation. The arriving load, A, is the expected number of customers arriving
per unit of time multiplied by the expected time to process one customer.
@PFD(N, D, X)
This is the cumulative distribution function for the F distribution with N degrees of freedom in the
numerator and D degrees of freedom in the denominator. It returns the probability that an observation
from this distribution is less-than-or-equal-to X.
@PFS(A, X, C)
This returns the expected number of customers waiting for or under repair in a finite source Poisson
service system with X servers in parallel, C customers, and a limiting load A. It is extended to
noninteger values of X and C by linear interpolation. A, the limiting load, is the number of customers
multiplied by the mean service time divided by the mean repair time.
@PHG(POP, G, N, X)
This is the cumulative hypergeometric probability. It returns the probability that X or fewer items in
the sample are good, given a sample without replacement of N items from a population of size POP
where G items in the population are good. It is extended to noninteger values of POP, G, N, and X by
linear interpolation.
@PPL(A, X)
This is the linear loss function for the Poisson distribution. It returns the expected value of MAX(0,
Z-X), where Z is a Poisson random variable with mean value A.
@PPS(A, X)
This is the cumulative Poisson probability distribution. It returns the probability that a Poisson random
variable, with mean value A, is less-than-or-equal-to X. It is extended to noninteger values of X by
linear interpolation.
@PSL(X)
This is the unit normal linear loss function. It returns the expected value of MAX(0, Z-X), where Z is a
standard normal random variable. In inventory modeling, @PSL(X) is the expected amount that
demand exceeds a level X, if demand has a standard normal distribution.
@PSN(X)
This is the cumulative standard normal probability distribution. A standard normal random variable
has mean 0.0 and standard deviation 1.0 (the bell curve, centered on the origin). The value returned by
@PSN is the area under the curve to the left of the point on the ordinate indicated by X.
@PTD(N, X)
This is the cumulative distribution function for the t distribution with N degrees of freedom. It returns
the probability that an observation from this distribution is less-than-or-equal-to X.

OPERATORS AND FUNCTIONS 345
@QRAND(SEED)
The @QRAND function produces a sequence of “quasi-random” uniform numbers in the interval (0,
1). @QRAND is only permitted in a data section. It will fill an entire attribute with quasi-random
numbers. Generally, you will be filling two-dimensional tables with, say, m rows and n variables. m
represents the number of scenarios, or experiments, you want to run. n represents the number of
random variables you need for each scenario or experiment. Within a row, the numbers are
independently distributed. Among rows, the numbers are “super uniformly” distributed. That is, the
numbers are more uniformly distributed than you would expect by chance. These numbers are
generated by a form of “stratified sampling”.
For example, suppose m = 4 and n = 2. Even though the numbers are random, you will find that
there will be exactly one row in which both numbers are in the interval (0, .5), exactly one row in
which both numbers are in (.5, 1), and two rows in which one number is less than .5 and the other
is greater than .5. Using @QRAND allows you to get much more accurate results for a given
number of random numbers in a Monte Carlo model. If you want 8 ordinary random numbers,
then use @QRAND(1,8) rather than @QRAND(4,2). An example of @QRAND follows:
MODEL:
DATA:
M = 4;
N = 2;
SEED = 1234567;
ENDDATA
SETS:
ROWS /1..M/;
COLS /1..N/;
TABLE( ROWS, COLS): X;
ENDSETS
DATA:
X = @QRAND( SEED);
ENDDATA
END
Example of @QRAND function
If you don’t specify a seed value for @QRAND, then LINGO will use the system clock to construct a
seed value.
@RAND(SEED)
This returns a pseudo-random number between 0 and 1, depending deterministically on SEED.

346 CHAPTER 7
Variable Domain Functions
Unless specified otherwise, variables in a LINGO model default to being non-negative and continuous.
More specifically, variables can assume any real value from zero to positive infinity. In many cases,
this default domain for a variable may be inappropriate. For instance, you may want a variable to
assume negative values, or you might want a variable restricted to purely integer values. LINGO
provides seven variable domain functions, which allow you to override the default domain of a
variable. The names of these functions and a brief description of their usage are:
@GIN
This restricts a variable to being an integer value.
@BIN
This makes a variable binary (i.e., 0 or 1).
@FREE
This allows a variable to assume any real value, positive or negative.
@BND
This limits a variable to fall within a finite range.
@SOS
This defines a set of binary variables and places restrictions on their collective values.
@CARD
This defines a set of binary variables and places an upper limit on their sum.
@SEMIC
This restricts variables to being either zero or greater than a specified constant.
@PRIORITY
This is used to assign branching priorities to variables.
In the remainder of this section, we'll investigate the mechanics of using these functions, and present a
number of examples illustrating their usage.
Set Handling Functions
LINGO offers several functions that assist with handling sets. The @IN function determines if a set
element is contained in a set. The @INDEX function returns the index of a primitive set element within
its set. The @SIZE function returns the number of elements in a set. Finally, the @WRAP function is
useful for “wrapping” set indices from one end of a time horizon to another in multiperiod planning
models. These are described in more detail below.
@IN(set_name, primitive_1 [, primitive_2 ...])
This returns TRUE if the set member referenced by the primitive set member tuple (primitive_1,
primitive_2, ...) is contained in the set set_name. As the following example shows, the @IN operator is
useful for generating complements of subsets in set membership conditions:

OPERATORS AND FUNCTIONS 347
Example 1:
For example, to derive a set of open plants based on a subset of closed plants, your sets
section might resemble the following:
SETS:
PLANTS / SEATTLE, DENVER,
CHICAGO, ATLANTA/:;
CLOSED( PLANTS) /DENVER/:;
OPEN( PLANTS) |
#NOT# @IN( CLOSED, &1):;
ENDSETS
The OPEN set is derived from the PLANTS set. We use a membership condition containing
the @IN function to allow only those plants not contained in the CLOSED set to be in the
OPEN set.
Example 2:
In this example, we illustrate how to determine if the set element (B, Y) belongs to the derived
S3 set. In this case, (B, Y) is indeed a member of S3, so X will be set to 1. Note that, in order
to get the index of the primitive set elements B and Y, we made use of the @INDEX function,
which is discussed next.
SETS:
S1 / A B C/:;
S2 / X Y Z/:;
S3( S1, S2) / A,X A,Z B,Y C,X/:;
ENDSETS
X = @IN( S3, @INDEX( S1, B), @INDEX( S2, Y));
@INDEX( [set_name,] set_element)
This returns the index of a set element set_element in the optionally supplied set set_name. If the set
name is omitted, LINGO returns the index of the first primitive set element it finds with a name
matching set_element. If LINGO is unable to find set_element, then @INDEX will return 0.
As the following example illustrates, it is good practice to always specify a set name in the @INDEX
function:
Example 1:
A model’s set elements can come from external sources that the modeler may have little
control over. This can potentially lead to confusion when using the @INDEX function.
Consider the sets section:
SETS:
GIRLS /DEBBIE, SUE, ALICE/;
BOYS /BOB, JOE, SUE, FRED/;
ENDSETS

348 CHAPTER 7
Now, suppose you want to get the index of the boy named Sue within the set BOYS. The value
of this index should be 3. Simply using @INDEX(SUE) would return 2 instead of 3, because
LINGO finds SUE in the GIRLS set first. In this case, to get the desired result, you must
specify the set BOYS as an argument and enter @INDEX(BOYS, SUE).
Example 2:
@INDEX may also be used to return the index of a set member of a derived set. In this
case, assuming an n-dimensional derived set, set_member would consist of n primitive
set members separated by commas as illustrated for the 2-dimensional set rxc below:
SETS:
ROWS /R1..R27/;
COLS /C1..C3/;
RXC( ROWS, COLS): XRNG;
ENDSETS
! return the index of (r1,c3) in the rxc set;
NDX = @INDEX( RXC, R1, C3);
@WRAP(INDEX, LIMIT)
This allows you to “wrap” an index around the end of a set and continue indexing at the other end of
the set. That is, when the last (first) member of a set is reached in a set looping function, use of
@WRAP will allow you to wrap the set index to the first (last) member of the set. This is a particularly
useful function in cyclical, multiperiod planning models.
Formally speaking, @WRAP returns J such that J = INDEX - K * LIMIT, where K is an integer such
that J is in the interval [1-LIMIT]. Informally speaking, @WRAP will subtract or add LIMIT to INDEX
until it falls in the range 1 to LIMIT.
For an example on the use of the @WRAP function in a staff-scheduling model, refer to the Primitive
Set Example section in Chapter 2, Using Sets.
@SIZE(set_name)
This returns the number of elements in the set set_name. Using the @SIZE function is preferred to
explicitly listing the size of a set in a model. This serves to make your models more data independent
and, therefore, easier to maintain should the size of your sets change.
To view an example of the @SIZE function, refer to the PERT/CPM example in the Sparse Derived
Set Example - Explicit List section of Chapter 2, Using Sets.

OPERATORS AND FUNCTIONS 349
Set Looping Functions
Set looping functions operate over an entire set and, with the exception of the @FOR function,
produce a single result. The syntax for a set looping function is:
@function(setname [ (set_index_list) [ | conditional_qualifier]] : expression_list);
@function corresponds to one of the set looping functions listed below. setname is the name of the set
you want to loop over. The set_index_list is optional, and is used to create a list of indices, which
correspond to the parent primitive sets that form the set setname. As LINGO loops through the
members of the set setname, it will set the values of the indices in the set_index_list to correspond to
the current member of the set setname.
The conditional_qualifier is optional and may be used to limit the scope of the set looping function.
When LINGO is looping over each member of the set setname, it evaluates the conditional_qualifier.
If the conditional_qualifier evaluates to true, then @function is performed for the set member.
Otherwise, it is skipped.
The expression_list is a list of expressions to be applied to each member of the set setname. When
using the @FOR function, the expression_list may contain multiple expressions, separated by
semicolons. These expressions will be added as constraints to the model. When using the remaining
three set looping functions (@SUM, @MAX, and @MIN), the expression_list must contain one
expression only. If the set_index_list is omitted, all attributes referenced in the expression_list must be
defined on the set setname.
The available set looping functions are listed below:
@FOR (setname [ (set_index_list) [ | cond_qualifier]]: exp_list)
This generates the expressions contained in exp_list for all members of the set setname.
@MAX(setname [ (set_index_list) [ | cond_qualifier]]: expression)
This returns the maximum value of expression taken over the set setname.
@MIN(setname [ (set_index_list) [ | cond_qualifier]]: expression)
This returns the minimum value of expression taken over the set setname.
@PROD( setname [ ( set_index_list) [ | cond_qualifier]]: expression)
This returns the product of an expression over the setname set.
@SUM(setname [ (set_index_list) [ | cond_qualifier]]: expression)
This returns the sum of expression over the set setname.
Set looping functions are discussed in more detail in Chapter 2, Using Sets.

350 CHAPTER 7
Interface Functions
Interface functions allow you to link your model to external data sources such as text files, databases,
spreadsheets and external applications. With the exception of @FILE, interface functions are valid
only in sets and data sections, and may not be used in calc and model sections.The interface
functions currently available in LINGO are listed below.
@FILE( 'filename')
The @FILE function allows you to include data from external text files anywhere in your model,
where filename is the name of the file to include text form. This is particularly useful for
incorporating data stored in text files in your sets and data sections.
When this function is encountered in a model, LINGO will continue to take text from this file
until it encounters either the end-of-file or a LINGO end-of-record mark (~). For subsequent
@FILE references in the same model that use the same file name, LINGO resumes taking input
from the file at the point where it left off. Nesting of @FILE function calls (embedding an @FILE
in a file which is itself called by @FILE) is not allowed.
For more information on use of the @FILE function, refer to Interfacing with External Files.
@ODBC( ['data_source'[, 'table_name'[, 'col_1'[, 'col_2' ...]]]])
The @ODBC function is used to open ODBC links between LINGO and databases. You can use
@ODBC in the sets section to retrieve set members from a database, or in the data section to
import data and/or export solutions.
The data_source is the name of the ODBC data source you registered with the ODBC
Administrator. The table_name is the name of the table in the data_source you want to open a
link to. Finally, col_i is the column in the table table_name that you wish to link to.
The @ODBC function is discussed in detail in Interfacing with Databases.
@OLE( 'workbook_file'[, range_name_list])
The @OLE function is used to move data and solutions back and forth from Excel using OLE
based transfers. You can use @OLE in the sets section to retrieve set members from Excel, or in
the data section to import data and/or export solutions.
OLE transfers are direct memory transfers and do not make use of intermediate files. When using
@OLE for exports, LINGO loads Excel, tells Excel to load the desired spreadsheet, and sends
ranges of data containing solution values to the sheet. You must have Excel 5, or later, to use the
@OLE function. The @OLE function is valid only in data and sets sections. @OLE can export
two-dimensional ranges (rectangular ranges that lie on a single worksheet in Excel), but cannot
export three-dimensional ranges (ranges which traverse more than one worksheet in Excel) or
discontinuous ranges.
The workbook_file argument is the name of the workbook to link to. The range_name_list is the
list of named ranges in the sheet to link to.
For more information on use of the @OLE function, refer to Interfacing with Spreadsheets.
OPERATORS AND FUNCTIONS 351
@POINTER( N)
This function is strictly for use with the LINGO Dynamic Link Library (DLL) under Windows.
@POINTER allows you to transfer data directly through shared memory locations. For more
information on the use of the @POINTER function, refer to Interfacing with Other Applications.
@TEXT( [['filename'], ‘a’])
The @TEXT function is used in the data section of a model to export solutions to text files, where
filename is the name of the file you want to export the solution to. If filename is omitted, the
solution data will be sent to the standard output device (in most cases this corresponds to the
screen). If you specify a file name and you wish to append output to the file instead of
overwriting the file, include a second argument of ‘a’.
For additional documentation on the @TEXT function, see Interfacing with External Files.
Report Functions
Report functions are used to construct reports based on a model’s results, and are valid on both calc
and data sections. Combining report functions with interface functions in a data section allows you to
export the reports to text files, spreadsheets, databases, or your own calling application.
Note: The interested reader will find an exhaustive example of the use of report functions in the
sample model TRANSOL.LG4 in the Samples subfolder. This model makes extensive use of
many of the report functions to mimic the standard LINGO solution report.
@DUAL( variable_or_row_name)
The @DUAL function outputs the dual value of a variable or a row. For example, consider a
model with the following data section:
DATA:
@TEXT( 'C:\RESULTS\OUTPUT.TXT') =
@WRITEFOR( SET1( I): X( I), @DUAL( X( I)), @NEWLINE(1));
ENDDATA
When this model is solved, the values of attribute X and their reduced costs will be written to the file
C:\RESULTS\OUTPUT.TXT. Output may be routed to a file, spreadsheet, database or memory
location. The exact destination will depend on the export function used on the left-hand side of the
output statement.
If the argument to the @DUAL function is a row name, then the dual price on the generated row will
be output.
@FORMAT( value, format_descriptor)
@FORMAT may be used in @WRITE and @WRITEFOR statements to format a numeric or string
value for output as text, where value is the numeric or string value to be formatted, and
format_descriptor is a string detailing how the number is to be formatted. The format descriptor is
interpreted using C programming conventions. For instance, a format descriptor of ‘12.2f’ would
cause a numeric value to be printed in a field of 12 characters with 2 digits after the decimal point. For
a string values, such as a set member name, a format descriptor of '12s' would cause the string to be

352 CHAPTER 7
right justified in a field of 12 characters, while '-12s' would cause the string to be left justified in a field
of 12. You can refer to a C reference manual for more details on the available formatting options.
The following example uses the @FORMAT function to place a shipping quantity into a field of eight
characters with no trailing decimal value:
DATA:
@TEXT() = @WRITE( ' From To Quantity',
@NEWLINE(1));
@TEXT() = @WRITE( '--------------------------',
@NEWLINE(1));
@TEXT() = @WRITEFOR( ROUTES( I, J) | X( I, J) #GT# 0:
3*' ', WAREHOUSE( I), 4*' ',
CUSTOMER( J), 4*' ', @FORMAT( X( I, J), '8.0f'),
@NEWLINE( 1));
ENDDATA
The report will resemble the following:
From To Quantity
--------------------------
WH1 C1 2
WH1 C2 17
WH1 C3 1
WH2 C1 13
WH2 C4 12
WH3 C3 21
This next example, GRAPHPSN.LG4, graphs the standard normal function, @PSN, over the
interval [ –2.4, 2.4]. The @FORMAT function is used to print the X coordinates with one trailing
decimal point.

OPERATORS AND FUNCTIONS 353
! Graphs @PSN() over a specified
interval around 0;
DATA:
! height of graph;
H = 49;
! width of graph;
W = 56;
! interval around 0;
R = 2.4;
ENDDATA
SETS:
S1 /1..H/: X, FX;
ENDSETS
@FOR( S1( I):
! X can be negative;
@FREE( X);
! Compute x coordinate;
X( I) = -R + ( I - 1)* 2 * R / ( H - 1);
! Compute y coordinate = @psn( x);
FX( I) = @PSN( X( I));
);
DATA:
! Print the header;
@TEXT() = @WRITE(
'Graph of @PSN() on the interval [-',
R,',+',R,']:',@NEWLINE(1));
@TEXT() = @WRITE( '| 0 ',(W/2-5)*'-',
' 0.5 ',(W/2-5)*'-', '1.0 X(i)',@NEWLINE(1));
! Loop to print the graph over;
@TEXT() = @WRITEFOR( S1( I): '| ',
( W * FX( I) + 1/2) * '*',
@IF( X( I) #LT# 0, '', ' '), ( W -
( W * FX( I) + 1/2) + 3)*' ',
@FORMAT( X(I), '.1f'),@NEWLINE(1));
!Trailer;
@TEXT() = @WRITE( '| 0 ',(W/2-5)*'-',
' 0.5 ',(W/2-5)*'-', '1.0',@NEWLINE(1));
ENDDATA
Model: GRAPHPSN

354 CHAPTER 7
Here is how the graph will appear when the model is solved:
Graph of @PSN() on the interval [-2.4,+2.4]:
| 0 ----------------------- 0.5 -----------------------1.0 X(i)
| -2.4
| * -2.3
| * -2.2
| * -2.1
| * -2.0
| ** -1.9
| ** -1.8
| ** -1.7
| *** -1.6
| **** -1.5
| ***** -1.4
| ***** -1.3
| ****** -1.2
| ******** -1.1
| ********* -1.0
| ********** -0.9
| ************ -0.8
| ************** -0.7
| *************** -0.6
| ***************** -0.5
| ******************* -0.4
| ********************* -0.3
| ************************ -0.2
| ************************** -0.1
| **************************** 0.0
| ****************************** 0.1
| ******************************** 0.2
| *********************************** 0.3
| ************************************* 0.4
| *************************************** 0.5
| ***************************************** 0.6
| ****************************************** 0.7
| ******************************************** 0.8
| ********************************************** 0.9
| *********************************************** 1.0
| ************************************************ 1.1
| ************************************************** 1.2
| *************************************************** 1.3
| *************************************************** 1.4
| **************************************************** 1.5
| ***************************************************** 1.6
| ****************************************************** 1.7
| ****************************************************** 1.8
| ****************************************************** 1.9
| ******************************************************* 2.0
| ******************************************************* 2.1
| ******************************************************* 2.2
| ******************************************************* 2.3
| ******************************************************** 2.4
| 0 ----------------------- 0.5 -----------------------1.0

OPERATORS AND FUNCTIONS 355
@ITERS()
The @ITERS function returns the total number of iterations required to solve the model. @ITERS
is available only in the data and calc sections, and is not allowed in the constraints of a model.
For example, the following output statement writes the iteration count to the standard output
device:
DATA:
@TEXT() = @WRITE('Iterations= ', @ITERS());
ENDDATA
@NAME( var_or_row_reference)
Use @NAME to return the name of a variable or row as text. @NAME is available only in the
data and calc sections, and is not allowed in the constraints of a mode. The following example
prints a variable name and its value:
DATA:
@TEXT() = @WRITEFOR( ROUTES( I, J) |
X( I, J) #GT# 0: @NAME( X), ' ', X( I, J), @NEWLINE(1));
ENDDATA
The report will resemble the following:
X( WH1, C1) 2
X( WH1, C2) 17
X( WH1, C3) 1
X( WH2, C1) 13
X( WH2, C4) 12
X( WH3, C3) 21
@NEWLINE( n)
Use @NEWLINE to write n new lines to the output device. @NEWLINE is available only in the data
and calc sections, and is not allowed in the constraints of a model. See the example immediately
below in the @RANGED section.
@OBJBND()
@OBJBND returns the bound on the objective value.
@RANGED( variable_or_row_name)
@RANGED outputs the allowable decrease on a specified variable’s objective coefficient or on a
specified row’s right-hand side. @RANGED is available only in the data and calc sections, and is
not allowed in the constraints of a model. For example, consider a model with the following data
section:
DATA:
@TEXT( 'C:\RESULTS\OUTPUT.TXT') =
@WRITEFOR( SET( I): X( I), @RANGED( X( I), @NEWLINE(1));
ENDDATA

356 CHAPTER 7
When this model is solved, the values of attribute X and the allowable decreases on its objective
coefficients will be written to the file C:\RESULTS\OUTPUT.TXT. If @RANGED is passed a row
name it will output the allowable decrease on the right-hand side value for the row. Output may
be routed to a file, spreadsheet, database, or memory location. The exact destination will depend
on the export function used on the left-hand side of the output statement. Range computations
must be enabled in order for @RANGED to function properly. For more information on the
interpretation of allowable decreases, refer to the LINGO|Range command.
@RANGEU( variable_or_row_name)
@RANGEU outputs the allowable increase on a specified variable’s objective coefficient or on a
specified row’s right-hand side. For example, consider a model with the following data section:
DATA:
@TEXT( 'C:\RESULTS\OUTPUT.TXT') = @WRITEFOR( SET( I):
X, @RANGEU(X), @NEWLINE(1));
ENDDATA
When this model is solved, the values of X and the allowable increases on its objective
coefficients will be written to the file C:\RESULTS\OUTPUT.TXT. If @RANGEU is passed a row
name it will output the allowable increase on the right-hand side value for the row. Output may be
routed to a file, spreadsheet, database, or memory location. The exact destination will depend on
the export function used on the left-hand side of the output statement. Range computations must
be enabled in order for @RANGED to function properly. For more information on the
interpretation of allowable increases, refer to the LINGO|Range command.

OPERATORS AND FUNCTIONS 357
@STATUS()
This returns the final status of the solution process using the following codes:
@STATUS()
Code Interpretation
0 Global Optimum — The optimal solution
has been found.
1 Infeasible — No solution exists that
satisfies all constraints.
2 Unbounded — The objective can be
improved without bound.
3 Undetermined — The solution process
failed.
4 Feasible — A feasible solution was found
that may, or may not, be the optimal
solution.
5 Infeasible or Unbounded — The
preprocessor determined the model is
either infeasible or unbounded. If you
need to narrow the result down to either
infeasible or unbounded, then you will
need to turn off presolving and run the
model again.
6 Local Optimum — Although a better
solution may exist, a locally optimal
solution has been found.
7 Locally Infeasible — Although feasible
solutions may exist, LINGO was not able
to find one.
8 Cutoff — The objective cutoff level was
achieved.
9 Numeric Error — The solver stopped due
to an undefined arithmetic operation in
one of the constraints.
In general, if @STATUS does not return a code of 0, 4, 6 or 8, the solution is of little use and
should not be trusted. The @STATUS function is available only in the data and calc sections. The
@STATUS function is not allowed in the constraints of a model.

358 CHAPTER 7
For example, the following output statement uses @STATUS to print a message to let the user
know if the solution is globally optimal, or not:
DATA:
@TEXT() = @WRITE( @IF( @STATUS() #EQ# 0,
'Global solution found',
'WARNING: Solution *not* globally optimal!');
ENDDATA
For additional examples of the use of the @STATUS function, refer to Interfacing with Other
Applications.
@STRLEN( string)
Use @STRLEN to get the length of a specified string. This can be a useful feature when
formatting reports. As an example, @STRLEN( ‘123’) would return the value 3. @STRLEN is
available only in the data and calc sections, and is not allowed in the constraints of a model.
@TABLE( ‘attr|set’)
The @TABLE function is used to display either an attribute’s values or a set’s members in tabular
format. The @TABLE function is available only in the data section of a model. You can refer to
either QUEENS8.LG4 or PERT.LG4 for examples of @TABLE. These models can be found in
the SAMPLES folder off the main LINGO folder.
For instance, QUEENS8.LG4 is a model for positioning eight queens on a chessboard so that no
one queen can attack another. At the end of this model you will find the following data section:
DATA:
@TEXT() = ' The final chessboard:';
@TEXT() = @TABLE( X);
ENDDATA
Here we are using the @TABLE function to display the X attribute in the standard output window
via the @TEXT interface function (see below for more on @TEXT). The X attribute is an 8-by-8
table of 0’s and 1’s indicating if a queen is positioned in a given square of the chessboard, or not.
The output generated by @TABLE in this instance follows:
The final chessboard:
E1 E2 E3 E4 E5 E6 E7 E8
E1 0 1 0 0 0 0 0 0
E2 0 0 0 0 1 0 0 0
E3 0 0 0 0 0 0 1 0
E4 0 0 0 1 0 0 0 0
E5 1 0 0 0 0 0 0 0
E6 0 0 0 0 0 0 0 1
E7 0 0 0 0 0 1 0 0
E8 0 0 1 0 0 0 0 0
Note that all eight queens (indicated by the 1’s on the board) are safe from attack.

OPERATORS AND FUNCTIONS 359
In addition to displaying attributes, @TABLE can also display sets. When displaying a set,
@TABLE will print the letter X in the table cell if the corresponding set member exists, otherwise
it will leave the table cell blank.
The PERT.LG4 sample model is a project scheduling model. A project consists of many tasks,
and some tasks must be completed before others can begin. The list of all the tasks that must
precede certain other tasks is called the precedence relations. At the end of PERT4.LG4 there is
the following data section which uses @TABLE to display the precedence relations set, PRED:
DATA:
!Use @TABLE() to display the precedence relations set,
PRED;
@TEXT() = @TABLE( PRED);
ENDDATA
When we run the model, @TABLE displays the following table:
DESIGN FORECAST SURVEY PRICE SCHEDULE COSTOUT
TRAIN
DESIGN X X
FORECAST X X
SURVEY X
PRICE
X
SCHEDULE X
COSTOUT
X
TRAIN
Whenever one task must precede another, an ‘X’ appears in the particular cell of the table. So, for
instance, the DESIGN task must precede the FORECAST and SURVEY tasks.
If a line of a table exceeds the page width setting in Lingo, it simply gets wrapped around. So, if
you want to display wide tables without line wraps, you may need to increase the page width.
Note: Currently, @TABLE can only send tables to the standard solution window or to text files. In
other words, it is not possible to send tables to Excel, databases or to applications calling the
LINGO DLL.

360 CHAPTER 7
@TABLE can also display sets and attributes of more than two dimensions. In fact, @TABLE allows
you great control over how multidimensional objects get displayed. Specifically, four forms of
@TABLE are supported:
♦ @TABLE( attr/set) – This is the simplest form of @TABLE. If the object is of one
dimension, it will be displayed as a column. Otherwise, the first n-1 dimensions will
be displayed on the vertical axis, while the n-th dimension will be displayed on the
horizontal axis of the table. An example follows:
@TABLE( X)
♦ @TABLE( attr/set, num_horz_indices) – In this form, a second argument,
num_horz_indices, is supplied. This argument is an integer quantity equal to the
number of the object’s dimensions to display along the horizontal axis. In which
case, dimensions (n – num_horz_indices) to n will be displayed along the horizontal
axis of the table. The following example displays dimension 2 and 3 of a 3-
dimensional set along the horizontal axis:
@TABLE( MY_3_DIM_SET, 2)
♦ @TABLE( attr/set, prim_set1,...,prim_setn) – Here we specify the exact ordering of
the object’s n dimensions. In which case, the first n-1 dimensions specified will be
displayed along the vertical axis, while the last dimension specified will be displayed
along the horizontal axis. Here’s an example that displays a 4-dimensional attribute
with dimensions 3, 4 and 1 on the vertical, and dimension 2 on the horizontal:
@TABLE( MY_4_DIM_ATTRIBUTE, 3, 4, 1, 2)
♦ @TABLE( attr/set, prim_set1,...,prim_setn, num_horz_indices) – In this final form,
we again specify the ordering of all the indices, but a final integer argument is added
to specify the number of dimensions to be displayed on the horizontal axis. The
following example displays a 4-dimensional attribute with dimensions 3 and 4 on the
vertical, and dimensions 1 and 2 on the horizontal:
@TABLE( MY_4_DIM_ATTRIBUTE, 3, 4, 1, 2, 2)
@TIME()
The @TIME function returns the total runtime, in seconds, required so far to generate and solve the
model. @TIME is available only in the data and calc sections, and is not allowed in the constraints of a
model. For example, the following output statement writes the solution time to the standard output
device:
DATA:
@TEXT() = @WRITE('Solve time in seconds =', @TIME());
ENDDATA

OPERATORS AND FUNCTIONS 361
@WRITE(obj1[, …, objn])
Use @WRITE to output one or more objects. @WRITE is available only in the data and calc sections,
and is not allowed in the constraints of a model. In a data section, output from @WRITE may be
routed to a file, spreadsheet, or database. The exact destination will depend on the interface function
used on the left-hand side of the output statement. @WRITE is valid only in the data sections of a
model.
@WRITE may also be used to display computations that are a function of variable values. As an
example, the output statement below prints the ratio of the two variables X and Y:
DATA:
@TEXT() = @WRITE( 'The ratio of X to Y is: ', X / Y);
ENDDATA
@WRITEFOR( setname[ ( set_index_list) [ | cond_qualifier]]: obj1[, …, objn])
Use @WRITEFOR to output one or more objects across a set. @WRITEFOR is available only in the
data and calc sections, and is not allowed in the constraints of a model
@WRITEFOR operates like the other set looping functions in that you may, or may not, specify an
index list and a conditional qualifier. The ability to use a conditional qualifier allows great flexibility
in specifying exactly what you wish to display in your reports. @WRITEFOR may also be used to
display computations that are a function of variable values.
Using @WRITEFOR in conjunction with export functions in data sections allows you to route output
to a file, spreadsheet, or database. The exact destination will depend on the export function used on the
left-hand side of the output statement.
As an example, the output statement below prints the number of units to ship, the warehouse name,
and the customer name for each route with nonzero volume:
DATA:
@TEXT() = @WRITEFOR( ROUTES( I, J) | X( I, J) #GT# 0:
'Ship ', X( I, J), ' units from warehouse ', WAREHOUSE( I),
' to customer ', CUSTOMER( J), @NEWLINE( 1));
ENDDATA
The resulting report would appear as follows:
Ship 2 units from warehouse WH1 to customer C1
Ship 17 units from warehouse WH1 to customer C2
Ship 1 units from warehouse WH1 to customer C3
Ship 13 units from warehouse WH2 to customer C1
Ship 12 units from warehouse WH2 to customer C4
Ship 21 units from warehouse WH3 to customer C3
Text Replication Operator (*)
The text replication operator (*) may be used inside either the @WRITE or @WRITEFFOR functions
to repeat a string a specified number of times. The operator should be preceded by a numeric value
and then followed by a string (e.g., 3*’text’), which will cause the string to be printed n times, where n
is the numeric value.

362 CHAPTER 7
In the following example, the text replication operator is used twice to produce a simple graph of on-
duty staff during the seven days of the week:
DATA:
LEAD = 3;
@TEXT() = 'Staff on duty graph:';
@TEXT() = @WRITEFOR( DAY( D): LEAD*' ',
DAY( D), ' ', ON_DUTY( D), ' ', ON_DUTY( D)*'+',
@NEWLINE(1)
);
ENDDATA
The graph would appear as follows, with one plus sign displayed for each staff member on duty:
Staff on duty graph:
MON 20 ++++++++++++++++++++
TUE 16 ++++++++++++++++
WED 12 ++++++++++++
THU 16 ++++++++++++++++
FRI 19 +++++++++++++++++++
SAT 14 ++++++++++++++
SUN 13 +++++++++++++
Miscellaneous Functions
@IF(logical_condition, true_result, false_result)
The @IF function evaluates logical_condition and, if true, returns true_result. Otherwise, it returns
false_result. For example, consider the following simple model that uses @IF to compute fixed
production costs:
MIN = COST;
COST = XCOST +YCOST;
XCOST = @IF( X #GT# 0, 100, 0) + 2 * X;
YCOST = @IF( Y #GT# 0, 60, 0) + 3 * Y;
X + Y >= 30;
Model: IFCOST
We produce two products—X and Y. We want to minimize total cost, subject to producing at least 30
total units of X and Y. If we produce X, there is a fixed charge of 100 along with a variable cost of 2.
Similarly, for Y, these respective values are 60 and 3. We use the @IF function to determine if either
of the products are being produced in order to apply the relevant fixed cost. This is accomplished by
testing to see if their production levels are greater than 0. If so, we return the fixed cost value.
Otherwise, we return zero.
Experienced modelers know that, without the benefit of an @IF function, modeling fixed costs
requires invoking some “tricks” using binary integer variables. The resulting models are not as
intuitive as models constructed using @IF. However, the caveat is that the @IF function is not a linear

OPERATORS AND FUNCTIONS 363
function. At best, the graph of an @IF function will be piecewise linear. In our current example, the
@IF functions are piecewise linear with a discontinuous break at the origin.
It is always best to try and keep a model linear (see Chapter 15, On Mathematical Modeling). Barring
this, it is best for all functions in a nonlinear model to be continuous. The @IF function violates both
these conditions. Thus, models containing @IF functions may be tough to solve to global optimality.
Fortunately, LINGO has two options that can help overcome the difficult nature of models containing
@IF functions—linearization and global optimization.
To illustrate the difficulty in solving models with discontinuous functions such as @IF, we will solve
our example model with both linearization and global optimization disabled. When we do this, we get
the following solution:
Local optimal solution found at iteration: 42
Objective value: 160.0000
Variable Value
COST 160.0000
XCOST 160.0000
YCOST 0.000000
X 30.00000
Y 0.000000
This solution involves producing only X at a total cost of 160. Given that producing only Y and not X
will result in a lower total cost of 150, this is clearly a locally optimal point. In order to find the
globally optimal point, we must resort to either the linearization or global optimization features in
LINGO.
Briefly, linearization seeks to reformulate a nonlinear model into a mathematically equivalent linear
model. This is desirable for two reasons. First, linear models can always be solved to global optimality.
Secondly, linear models will tend to solve much faster than equivalent nonlinear models.
Unfortunately, linearization can not always transform a model into an equivalent linear state. In which
case, it may be of no benefit. Fortunately, our sample model can be entirely linearized. To enable the
linearization option, run the LINGO|Options command and set the Linearization Degree to High on the
General Solver tab.
Global optimization breaks a model down into a series of smaller, local models. Once this series of
local models has been solved, a globally optimal solution can be determined. To enable global
optimization, run the LINGO|Options command, select the Global Solver tab, then click on the Global
Solver checkbox. Note that the global solver is an add-on option to LINGO. The global solver feature
will not be enabled for some installations. Run the Help|About LINGO command to determine if your
installation has the global solver capability enabled.
Whether using the linearization option or the global solver, LINGO obtains the true, global solution:
Global optimal solution found at iteration: 6
Objective value: 150.0000
Variable Value
COST 150.0000
XCOST 0.000000
YCOST 150.0000
X 0.000000
Y 30.00000

364 CHAPTER 7
Note: Starting with release 9.0, the false branch of the @IF function may contain arithmetic errors
without causing the solver to trigger an error. This makes the @IF function useful in
avoiding problems when the solver strays into areas where certain functions become
undefined. For instance, if your model involves division by a variable, you might use @IF as
follows: @IF( X #GT# 1.E-10, 1/X, 1.E10).
@WARN(‘text’, logical_condition)
This displays the message ‘text’ if the logical_condition is met. This feature is useful for verifying the
validity of a model’s data. In the following example, if the user has entered a negative interest rate, the
message “INVALID INTEREST RATE” is displayed:
! A model of a home mortgage;
DATA:
! Prompt the user for the interest
rate, years, and value of mortgage.
We will compute the monthly payment;
YRATE = ?;
YEARS = ?;
LUMP = ?;
ENDDATA
! Number of monthly payment;
MONTHS = YEARS * 12;
! Monthly interest rate;
(1 + MRATE) ^ 12 = 1 + YRATE;
! Solve next line for monthly payment;
LUMP = PAYMENT * @FPA(MRATE, MONTHS);
! Warn them if interest rate is negative
@WARN('INVALID INTEREST RATE',
YRATE #LT# 0);
@USER(user_determined_arguments)
The user can supply this in an external DLL or object code file. For a detailed example on the use of
@USER, please see the User Defined Functions section in Chapter 11, Interfacing with Other
Applications.

365
8 Interfacing with External
Files
It can be cumbersome and impractical to try to maintain your data in a LINGO model file. In most
cases, your model’s data will reside externally in text files, spreadsheets, and databases. Also, a
solution generated by LINGO is of little use if you can’t export it to other applications. For these
reasons, LINGO has many methods to assist you in moving information in and out of the application.
The primary focus of this chapter is to illustrate how to move data in and out of LINGO through the
use of text based ASCII files. In Chapter 9, Interfacing with Spreadsheets, we will look at using
spreadsheets. In Chapter 10, Interfacing with Databases, we will illustrate the use of databases for
maintaining your model’s data.
Cut and Paste Transfers
Perhaps the simplest and most straightforward way to move data in and out of an application in
Windows is by using cut and paste commands. Windows maintains an information buffer called the
clipboard. Applications that support the cut command can move information into the clipboard.
Applications that support the paste command can move information from the clipboard into their
memory. Thus, cut and paste offers a simple, but effective, technique for moving small amounts of
data from one application to another.
Pasting in Data from Excel
You should be able to paste data into LINGO from any application that supports a cut command. For
illustration purposes, we will show how to paste data from an Excel worksheet into a LINGO model.
Recall our staff-scheduling model from Chapter 2, Using Sets, which is reproduced here with the data
for the REQUIRED attribute omitted from the data section:
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/:
REQUIRED, START;
ENDSETS
DATA:
REQUIRED = <data omitted>;
ENDDATA
MIN = @SUM(DAYS(I): START(I));
@FOR(DAYS(J):
@SUM(DAYS(I) | I #LE# 5:
START(@WRAP(J - I + 1, 7)))
>= REQUIRED(J)
);

366 CHAPTER 8
Suppose your staffing requirements data is maintained in an Excel worksheet resembling the
following:
To paste the staffing requirements data from Excel into the LINGO model above, follow these steps:
1. Select the range containing the data (C3:I3) by placing the cursor on the C3
cell, press and hold down the left mouse button, drag the mouse to cell I3,
then release the mouse button.
2. Select the Copy command from Excel’s Edit Menu.
3. Click once on the LINGO model window.
4. Place the LINGO cursor directly to the right of the data statement:
REQUIRED =.
5. Select the Paste command from LINGO’s Edit menu.
The data should now appear in the LINGO model as follows:
DATA:
REQUIRED = 20 16 13 16 19 14 12;
ENDDATA
You may need to adjust the font of the data to your liking. You can use the Edit|Select Font command
in LINGO to accomplish this. Your model now has the required data and is ready to be solved. Note
that LINGO also has features that allow you to import data directly from Excel. See Chapter 9,
Interfacing with Spreadsheets, for more information.
Pasting Data Out to Microsoft Word
Suppose you went ahead and solved the previous staffing model. LINGO will present you with a new
Window containing the solution to your model. Now, suppose you would like to get a copy of the
solution into MS Word for a report you are writing. You can do this by following these steps:
1. Select the solution report window in LINGO by clicking on it once.
2. Select all the text in the window by issuing the Edit|Select All command in
LINGO.
3. Place the solution into the clipboard by selecting the Edit|Copy command in
LINGO.
4. Activate MS Word by clicking once on the window containing the report
you are writing.
5. Paste the solution from the clipboard into the report by issuing the
Edit|Paste command in MS Word.

INTERFACING WITH EXTERNAL FILES 367
Text File Interface Functions
LINGO has several interface functions that perform input and output operations. There are interface
functions for dealing with text files, spreadsheets, and databases. There is even an interface function
that lets you pass data back and forth from other applications. In this chapter, we are focusing on
interfacing with text files, so we will investigate the @FILE function for importing the contents of
external text files and the @TEXT function for exporting solutions to text files.
Including External Files with @FILE
The @FILE interface function in LINGO allows you to include data from external text files anywhere
in your model. This is particularly useful for incorporating data stored in text files into your sets and
data sections.
The syntax for the @FILE function is:
@FILE(‘filename’)
where filename is the name of the file to include text from. When this function is encountered in a
model, LINGO will continue to take text from this file until it encounters either the end-of-file mark or
a LINGO end-of-record mark (~). For subsequent @FILE references in the same model that use the
same file name, LINGO resumes taking input from the file at the point where it left off. Nesting of
@FILE function calls (embedding an @FILE in a file that is itself called by @FILE) is not allowed.

368 CHAPTER 8
Using @FILE in a Transportation Model
As an example, we will use the Wireless Widgets transportation model developed in Chapter 1,
Getting Started with LINGO. It is reproduced in its original form below:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES /WH1 WH2 WH3 WH4 WH5 WH6/: CAPACITY;
VENDORS /V1 V2 V3 V4 V5 V6 V7 V8/ : DEMAND;
LINKS(WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
! The objective;
MIN = @SUM(LINKS(I, J):
COST(I, J) * VOLUME(I, J));
! The demand constraints;
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I): VOLUME(I, J)) =
DEMAND(J));
! The capacity constraints;
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J)) <=
CAPACITY(I));
! Here is the data;
DATA:
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
Model: WIDGETS
Note that data appears two places in the model. First, there are the lists of warehouses and vendors in
the sets section. Second, there is data on capacity, demand, and shipping costs in the data section.

INTERFACING WITH EXTERNAL FILES 369
In order to completely isolate the data from our model, we would like to move it to an external text
file, and modify the model so it will draw the data from the text file using the @FILE function. The
following modified version of the model has all the data removed. Changes are represented in bold
type:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES / @FILE('WIDGETS2.LDT')/: CAPACITY;
VENDORS / @FILE('WIDGETS2.LDT')/ : DEMAND;
LINKS(WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
! The objective;
MIN = @SUM(LINKS(I, J):
COST(I, J) * VOLUME(I, J));
! The demand constraints;
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I): VOLUME(I, J)) =
DEMAND(J));
! The capacity constraints;
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J)) <=
CAPACITY(I));
! Here is the data;
DATA:
CAPACITY = @FILE('WIDGETS2.LDT');
DEMAND = @FILE('WIDGETS2.LDT');
COST = @FILE('WIDGETS2.LDT');
ENDDATA
Model: WIDGETS2

370 CHAPTER 8
The model is now set to draw all data from the file WIDGETS2.LDT. The contents of this data file
appear below:
!List of warehouses;
WH1 WH2 WH3 WH4 WH5 WH6 ~
!List of vendors;
V1 V2 V3 V4 V5 V6 V7 V8 ~
!Warehouse capacities;
60 55 51 43 41 52 ~
!Vendor requirements;
35 37 22 32 41 32 43 38 ~
!Unit shipping costs;
6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3
File: WIDGETS2.LDT
Note: We use the convention of placing the extension of .LDT on all LINGO data files.
Sections of the data file between end-of-record marks (~) are called records. If an included file has no
end-of-record marks, LINGO reads the whole file as a single record. Notice that, with the exception of
the end-of-record marks, the model text and data appear just as they would if they were in the model
itself.
Also, notice how the end-of-record marks in the include file work along with the @FILE function calls
in the model. The first call to @FILE opens WIDGETS2.LDT and includes the first record. The second
call includes the second record, and so on.
The last record in the file does not need an end-of-record mark. When LINGO encounters an
end-of-file, it includes the last record and closes the file. If you end the last record in an include file
with an end-of-record mark, LINGO will not close the file until it is done solving the current model.
This could cause problems if multiple data files are opened in the model—files that remain open can
cause the limit on open files to be exceeded.
When using the @FILE function, think of the contents of the record (except for any end-of-record
mark) as replacing the text @FILE(‘filename’) in the model. This way, you can include a whole
statement, part of a statement, or a whole series of statements in a record. For example, the first two
records of the WIDGETS2.LDT file in the above example:
!List of warehouses;
WH1 WH2 WH3 WH4 WH5 WH6 ~
!List of vendors;
V1 V2 V3 V4 V5 V6 V7 V8 ~
are included in the model in the sets section as follows:
WAREHOUSES / @FILE('WIDGETS2.LDT')/: CAPACITY;
VENDORS / @FILE('WIDGETS2.LDT')/ : DEMAND;

INTERFACING WITH EXTERNAL FILES 371
The net effect of these @FILE calls is to turn the model statements into:
WAREHOUSES / WH1 WH2 WH3 WH4 WH5 WH6/: CAPACITY;
VENDORS / V1 V2 V3 V4 V5 V6 V7 V8/ : DEMAND;
Comments in the include file are ignored. The maximum number of include files a model can
simultaneously reference is 16.
Writing to Files Using @TEXT
The @TEXT interface function is used for exporting solutions to text files. The @TEXT function can
export both set members and attribute values. The syntax of the @TEXT function is:
@TEXT( ['filename', [‘a’]])
where filename is the name of the file you want to export the solution to. If filename is omitted, the
solution data will be sent to the standard output device (this is typically the screen). If the second
argument of ‘a’ is present, then LINGO will append output to the file, otherwise it will create a new
file for subsequent output, erasing any existing file. The @TEXT function may only appear on the left-
hand side of a data statement in the data section of a model.
We refer to data statements that use interface functions to generate output as output operations. Output
operations are only performed when the solver finishes running a model. The operations are run in the
sequence that they were encountered in the model.
Here are some examples of using @TEXT:
Example 1: @TEXT('RESULTS.TXT') = X;
Sends the value(s) for X to the file RESULTS.TXT. Any existing version of the file is
overwritten
Example 2: @TEXT() = DAYS, START;
In this example, we are exporting the DAYS set and the START attribute. We
routed the output to the screen by omitting the filename argument.
Example 3: @TEXT() = @WRITEFOR( DAYS( D) | START( D) #GT# 0:
DAYS( D), ' ', START( D));
In this example, we use the @WRITEFOR reporting function to loop over the
members of the DAYS set. Contrary to the previous example, we only print
information for those days where START( D) is greater than 0.
Now, let’s turn to a more detailed example of the use of @TEXT in our staff scheduling model.
372 CHAPTER 8
Example - Using @TEXT for Staff-Scheduling
Let’s once again make use of the staff scheduling model from Chapter 2, Using Sets. However, this
time we will modify it to use the @TEXT function and write the solution to a file. The model follows
with the critical change listed in bold type:
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/:
REQUIRED, START;
ENDSETS
DATA:
REQUIRED = 20 16 13 16 19 14 12;
@TEXT('OUT.TXT') = DAYS, START;
ENDDATA
MIN = @SUM(DAYS(I): START(I));
@FOR(DAYS(J):
@SUM(DAYS(I) | I #LE# 5:
START(@WRAP(J - I + 1, 7)))
>= REQUIRED(J)
);
We have added the one output operation:
@TEXT('OUT.TXT') = DAYS, START;
which writes the values of the DAYS set and the values of the START attribute to the file OUT.TXT.
Once you solve the model, LINGO will run this output operation, the file OUT.TXT will be generated,
and it will contain the members of the DAYS set and the optimal values for the START attribute:
MON 8.0000000
TUE 2.0000000
WED 0.0000000
THU 6.0000000
FRI 3.0000000
SAT 3.0000000
SUN 0.0000000
File: OUT.TXT
INTERFACING WITH EXTERNAL FILES 373
You may now import the data from OUT.TXT into other applications. For instance, if you want to
import the data into MS Access, you could use the File|Get External Data|Import command in Access
to read the data into a table. We defined a small table in Access called Start, and imported the data in
this manner yielding the following:
To import the data into an Excel sheet, you must first use the File|Open command on the OUT.TXT file
to get the data into a spreadsheet by itself, as we have done here:
Once the results are imported into a spreadsheet, you may cut and paste them to any other sheet you
desire.
Before we move on, suppose you are not interested in all the output generated by the standard LINGO
solution report. Suppose, in the case of this example, all you want to see is the objective value and the
values for the DAYS set and the START attribute. Here's how you can do it. First, add the additional
output operation, shown here in bold, to your data section, so it looks like:
DATA:
@TEXT('OUT.TXT') = DAYS, START;
@TEXT() = DAYS, START;
ENDDATA
The new output operation causes the values of DAYS and START to be sent to the screen (since we
omitted a file name). Next, you will need to suppress the normal LINGO solution report. In Windows
versions of LINGO, select the LINGO|Options command, click on the Interface tab in the Options
dialog box, check the Terse output checkbox, then press the OK button (on platforms other than

374 CHAPTER 8
Windows, enter the TERSE command). Now, solve your model and you will be presented with the
following, abbreviated report:
Global optimal solution found at step: 8
Objective value: 22.00000
MON 8.0000000
TUE 2.0000000
WED 0.0000000
THU 6.0000000
FRI 3.0000000
SAT 3.0000000
SUN 0.0000000
In the example above, we simply listed the names of set DAYS and attribute START on the right-hand
side of our output operation. This causes LINGO to display all values for DAYS and START. Suppose
we'd like more control over what values do and do not get displayed. In particular, suppose we are
only interested in viewing those days in which the value for START is nonzero. We can do this by
using the @WRITEFOR report function, which allows us to provide a condition to test before printing
output:
DATA:
@TEXT( ) = @WRITEFOR( DAYS( D) | START( D) #GT# 0:
DAYS( D), @FORMAT( START( D), '6.1f'));
ENDDATA
Note how we now only display the days where START > 0 in our new report:
Global optimal solution found at iteration: 15
Objective value: 22.00000
MON 8.0
TUE 2.0
THU 6.0
FRI 3.0
SAT 3.0
Another feature of this last example to note is the use of the @FORMAT function, which we used to
display the nonzero start values in a field of six columns with one trailing decimal point.
@WRITEFOR also allows us to form arithmetic expressions of the variable values. Here's an example
that we could add to our staff model to compute the number of staff on duty each day:
DATA:
@TEXT( ) = @WRITE( 'Day On-Duty');
@TEXT( ) = @WRITE( 14*'-');
@TEXT( ) = @WRITEFOR( DAYS( D): DAYS(D),
@FORMAT( @SUM( DAYS( D2) | D2 #LE# 5:
START( @WRAP( D - D2 + 1, 7))), '11.1f'));
ENDDATA
INTERFACING WITH EXTERNAL FILES 375
Here's the report generated by these output operations:
Day On-Duty
--------------
MON 20.0
TUE 16.0
WED 13.0
THU 16.0
FRI 19.0
SAT 14.0
SUN 12.0
This previous example also illustrates the use of the @WRITE function. The @WRITE function is
similar to the @WRITEFOR function with the exception that it does not accept a set to loop on, and,
therefore, is used to write single occurrences of text output. As with @WRITEFOR, @WRITE accepts
expressions of variables. Here's an example that calculates the maximum number of employees
starting on a particular day.
DATA:
@TEXT() = @WRITE( 'Max start = ', @MAX( DAYS: START));
ENDDATA
which yields the following output: Max start = 8.
LINGO Command Scripts
A LINGO command script is any text file containing a series of LINGO commands. In addition to
understanding the syntax of LINGO models, using command scripts requires some understanding of
LINGO’s command language (covered in Chapter 6, Command-line Commands). You can think of
these commands as a macro language that allows you to automate the running of frequently used
commands and/or models.
To run a command script in Windows versions of LINGO, use the File|Take Commands command. In
other versions of LINGO, use the TAKE command. In both cases, you will be prompted for the name
of a file that contains your command script. Once you have input the file name, LINGO will begin to
execute the commands in this file. Execution will continue until either a QUIT command is
encountered, causing LINGO to terminate, or an end-of-file is encountered, causing LINGO to return
to normal input mode.
376 CHAPTER 8
A Command Script Example
Once again, we will make use of the staff-scheduling model introduced on page 58 to illustrate the use
of a command script. Suppose, instead of one hot dog stand, our operations have expanded and we
now have three hot dog stands: Pluto Dogs, Mars Dogs, and Saturn Dogs. Our staffing requirements at
the three sites are:
Site Mon Tue Wed Thu Fri Sat Sun
Pluto 20 16 13 16 19 14 12
Mars 10 12 10 11 14 16 8
Saturn 8 12 16 16 18 22 19
Running staffing models for all three sites is cumbersome and prone to error. We would like to
automate the process by constructing a script file that runs all three staffing models automatically. To
do this, we construct the following script file:
! Have LINGO echo input to the screen;
SET ECHOIN 1
! Suppresses the standard solution report;
SET TERSEO 1
! Begins input of a new model;
MODEL:
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/:
REQUIRED, START;
ENDSETS
DATA:
REQUIRED = @FILE('PLUTO.LDT');
@TEXT('PLUTO.TXT') = START;
ENDDATA
MIN = @SUM(DAYS(I): START(I));
@FOR(DAYS(J):
@SUM(DAYS(I) | I #LE# 5:
START(@WRAP(J - I + 1, 7)))
>= REQUIRED(J)
);
@FOR(DAYS: @GIN(START));
END
! Solve Pluto Dogs model;
GO
! Alter model for Mars;
ALTER ALL 'PLUTO'MARS'
! Solve Mars model;
GO
! Alter model for Saturn;
ALTER ALL 'MARS'SATURN'
! Solve Saturn model;
GO
! Restore parameters;
SET TERSEO 0
SET ECHOIN 0
Command Script: DOGS.LTF

INTERFACING WITH EXTERNAL FILES 377
We use two SET commands to set two of LINGO’s parameters. First, we set ECHOIN to 1, which
causes LINGO to echo all command script input to the screen. This can be useful when you are trying
to debug a script file. Next, we set TERSEO to 1. This causes LINGO to go into terse output mode,
which suppresses the default solution report each time we solve a model.
Next, we include the MODEL: command to put LINGO into model input mode. It is important here to
remember the MODEL: statement is a command. When LINGO encounters this command in a script
file, it reads all subsequent text in the file as model text until it encounters the END command. This
model then becomes the current model in memory.
The key feature to note in our model is the data section:
DATA:
REQUIRED = @FILE('PLUTO.LDT');
@TEXT('PLUTO.TXT') = START;
ENDDATA
We use the @FILE function to include the staffing requirements from an external file and we use the
@TEXT function to send the values of the START attribute to a file.
After the END statement, we have a GO command to solve the model for the Pluto stand. We then
include an ALTER command to change all occurrences of PLUTO with MARS. This command will
change the data section to (changes in bold):
DATA:
REQUIRED = @FILE('MARS.LDT');
@TEXT('MARS.TXT') = START;
ENDDATA
Assuming we have the staffing requirements for the Mars stand in the file MARS.LDT, our model is
then ready to run again. However, this time it will solve for the START values for the Mars hot dog
stand. We include commands to do the same for the Saturn location as well. Finally, we have two SET
commands to restore the modified parameters.
You can run this command script by issuing the File|Take Commands command in Windows versions
of LINGO, or you can use the TAKE command in other versions. Once the command script has been
executed, you will find the three solution files: PLUTO.TXT, MARS.TXT, and SATURN.TXT. These
files will contain the optimal values for the START attribute for the three locations.
The AUTOLG.DAT Script File
LINGO has an option that allows you to automatically execute a command script each time LINGO
starts. To do this, simply name the command script AUTOLG.DAT and place it in LINGO’s working
directory. Each time LINGO starts, it will automatically execute the commands in this script file.

378 CHAPTER 8
Specifying Files in the Command-line
When a Windows version of LINGO starts up, it checks the command-line for the presence of the
following three commands:
Command Action at Runtime
-Tfilename LINGO executes a File|Take Commands command on the script file
filename. If an AUTOLG.DAT file is present in LINGO’s working
directory, it will be queued for execution before filename.
-Ofilename LINGO performs a File|Open command on filename, reading the
file into a standard window.
-Lfilename LINGO executes a File|Log Output command, causing all output
that would normally have been sent to the command window to be
routed to filename.
As an example, suppose we have the following command script:
! Input a small model
MODEL:
MAX = 20 * X + 30 * Y;
X <= 50;
Y <= 60;
X + 2 * Y <= 120;
END
! Terse output mode
SET TERSEO 1
! Solve the model
GO
! Open a file
DIVERT SOLU.TXT
! Send solution to the file
SOLUTION
! Close solution file
RVRT
! Quit LINGO
QUIT
Command Script: TEST.LTF
This script file inputs a small model, solves it, and then writes a solution report out to the file
SOLU.TXT. Let’s suppose the script file is titled TEST.LTF. We can instruct LINGO to automatically
execute this file by adding the following command to LINGO’s command-line: -tTEST.LTF. To do
this under Windows, you will first need to create a shortcut icon for LINGO. Click the right mouse
button on your desktop, and then select the New command followed by the Shortcut command. Press
INTERFACING WITH EXTERNAL FILES 379
the Browse button and then select the LINGO application file, which is found under the name
LINGO.EXE in your main LINGO directory. You should now have a LINGO shortcut icon on your
desktop that looks like:
To edit the command-line, you must right click on this icon and then select the Properties command.
You will then see the dialog box:
In the Target edit box, add the command -tTEST.LTF. If you want LINGO to run without opening up a
window, you can also select the Minimized option from the Run list box. Now, click the Apply
button followed by the OK button.

380 CHAPTER 8
You can now run LINGO and have it execute the script file by double clicking the shortcut icon on the
desktop. Once you have done this, the solution file, SOLU.TXT, should contain:
Variable Value Reduced Cost
X 50.00000 0.000000
Y 35.00000 0.000000
Row Slack or Surplus Dual Price
1 2050.000 1.000000
2 0.000000 5.000000
3 25.00000 0.000000
4 0.000000 15.00000
File: SOLU.TXT
Redirecting Input and Output
In most Unix environments, it is possible to redirect all screen output from LINGO to a text file. You
can also redirect all input from the keyboard to an input file. This is accomplished by specifying the
files in the command-line using the following syntax:
LINGO < input_file > output_file
Upon execution of this command, LINGO will take its input from input_file, and a text file will be
created called output_file, which contains everything that would have appeared on the screen had
LINGO been started normally. Path names may be included in the names of the input and output files.
Exploiting this capability allows you to use LINGO as a “black box” in larger turnkey applications. If
done properly, the user will not be aware LINGO is running in the background.
As an example, we could run the script file from the previous section, TEST.LTF, generating the same
solution file, SOLU.TXT, with the command:
LINGO < TEST.LTF > CAPTURE.TXT
The file CAPTURE.TXT is used to capture all screen output.
Managing LINGO Files
In order to help keep track of your files, you may want to adopt a file naming standard, at least as far
as the file name extensions are concerned. Here are some suggestions for file name extensions:
Extension Description
.LG4 model files (Windows only)
.LNG model files in text format
.LTF script files
.LDT included data files
.LRP report files

INTERFACING WITH EXTERNAL FILES 381
Note: If you use the default LINGO format (.LG4) for a model, the file will be saved in a special
binary format. Files in this format will only be readable by Windows versions of LINGO, and
will appear garbled if read into other applications. This binary format allows LINGO models
to function as both Object Linking and Embedding (OLE) containers and servers, allows for
embedding of objects (e.g., bitmaps), and permits custom formatting of model text. Thus, you
will generally want to use the .LG4 format. Cases where you must use a text format are:
1. a model that must be transferred to another platform or application,
2. a LINGO script file, or
3. a LINGO data file to be included with @FILE.
LINGO anticipates this by saving any file with an extension other than .LG4 as text.
You can force LINGO to always use the .LNG text format for models by checking the .LNG
box on the Interface tab of the LINGO|Options dialog box. Any special formatting of the text
(e.g., bold fonts) will be lost when a model is saved in this format. Also, models saved as text
may not function as OLE containers or servers.
On platforms other than Windows, LINGO always saves files in text format.

383
9 Interfacing With
Spreadsheets
As we have mentioned, it can be cumbersome and impractical to try to maintain your data in a LINGO
model file. This is particularly true if you have more than just a small handful of data—as is the case
with most practical models. Spreadsheets are adept at handling small to moderate amounts of data.
Spreadsheets are also very useful tools for manipulating and presenting the results generated by your
model. For these reasons, LINGO has a number of features that allow the user to import data from
spreadsheets and export solutions back out to spreadsheets. These features include real-time Object
Linking and Embedding (OLE) links to Excel, OLE automation links that can be used to drive LINGO
from Excel macros, and embedded OLE links that allow you to import the functionality of LINGO into
Excel. At present, all of these features are supported only under Windows versions of LINGO.
Importing Data from Spreadsheets
LINGO provides the @OLE function for importing data from spreadsheets. This function is only
available under Windows versions of LINGO. @OLE performs direct OLE transfers of data between
LINGO and Excel.
Using @OLE to Import Data from Excel
@OLE is an interface function for moving data back and forth from Excel using OLE based transfers.
OLE transfers are direct memory transfers and do not make use of intermediate files. When using
@OLE, LINGO loads Excel, tells Excel to load the desired spreadsheet, and requests ranges of data
from the sheet. You must have Excel 5, or later, to be able to use the @OLE function. The @OLE
function may be used in the data and init sections to import data.
@OLE can read both set members and set attributes—set members are expected in text format, while
set attributes are expected in numeric format. Primitive sets require one cell of data for each set
member (i.e., one set member per cell). You will need n cells of values to initialize each n-dimensional
derived set member, where the first n cells contain the first set member, the second n cells contain the
second set member, and so on.
@OLE can read one or two-dimensional ranges (ranges on a single worksheet in Excel), but cannot
read discontinuous ranges or three-dimensional ranges (ranges that traverse more than one worksheet
in Excel).
Ranges are read left-to-right, top-to-bottom.

384 CHAPTER 9
Importing in the Data and Init Sections with @OLE
The syntax for using @OLE to import data in both the data and init sections is:
object_list = @OLE([‘spreadsheet_file’] [, range_name_list]);
The object_list is a list of model objects, optionally separated by commas, which are to be initialized
from the spreadsheet. Object_list may contain any combination of set names, set attributes, and scalar
variables.
The spreadsheet_file is the name of the Excel spreadsheet file to retrieve the data from. If the name is
omitted, LINGO defaults to using whatever workbook is currently open in Excel.
The range_name_list is the list of named ranges in the sheet to retrieve the data from. The ranges must
contain exactly one element for each member in the object_list. There are three options available in
how you specify the ranges. First, you can omit the range arguments entirely. In which case, LINGO
defaults to using a list of range names identical to the list of object names in object_list. Second, you
can specify a single range name to retrieve all the data from. In which case, all the objects in
object_list must be defined on the same set, and LINGO reads the data as if it was a table. When
specifying a single range name for multiple objects, all the objects must be of the same data type.
Furthermore, you can’t mix set members (text) with set attributes (numeric). Finally, you can specify
one range name for each object in object_list. In which case, the objects do not have to be defined on
the same set and can be of differing data types. Examples of these three methods for using @OLE
follow:
Example 1: COST, CAPACITY = @OLE();
In this example we specify no arguments to the @OLE() function. In which case, LINGO
will supply the default arguments. Given that no workbook name was specified, LINGO
will use whatever workbook is currently open and active in Excel. In addition, no range
names were specified, so LINGO defaults to using the names of the model objects. Thus,
COST and CAPACITY are initialized to the values found, respectively, in the ranges COST
and CAPACITY in the currently open workbook in Excel.
Note: If you do not specify a workbook name in @OLE() function references, LINGO defaults to
using whatever workbook is currently open in Excel. Therfore, you will need to open Excel
and load the relevant workbook prior to solving your model.
Example 2: COST, CAPACITY = @OLE( 'SPECS.XLS', 'DATATABLE');
In this example, we are specifying a single range to initialize both COST and CAPACITY.
Assuming the range DATATABLE has two columns, LINGO initializes COST to the data in
column 1 and CAPACITY to the data in column 2. Note, in order for this method to work,
both COST and CAPACITY must be defined on the same set. Furthermore, they must both
be either sets or set attributes—mixed types aren’t allowed using this form.
Example 3: COST, CAPACITY = @OLE( 'SPECS.XLS', 'COST01', 'CAP01');
In this example, we are specifying individual ranges to initialize both COST and
CAPACITY. COST will be initialized with the data in the COST01 range and CAPACITY
will receive the values in the CAP01 range.

INTERFACING WITH SPREADSHEETS 385
As a final note, it is important to know that derived sets may be imported from either a single range or
from n ranges, where n is the dimension of the derived set. Here are two examples to illustrate:
Example 4: ARCS, COST = @OLE( 'TRAN.XLS', 'ARCS', 'COST');
You might find something similar to this example in a transportation model. ARCS is the
set of shipping arcs and COST is an attribute for storing the cost of shipping one unit down
each arc. Typically, ARCS would be a 2-dimensional derived set of from-to coordinate
pairs. In this example, we've chosen to bring the list of arcs in from a single workbook
range. Suppose there are 10 shipping arcs in our model, then the ARCS range would have
20 cells, with the first column of 10 cells being the ship-from points and the second column
of 10 cells being the ship-to points. Since we are using the single range method to input a
derived set, the two columns are adjacent and are both contained in the single range call
ARCS. This is in contrast to the following example…
Example 5: ARCS, COST = @OLE( 'TRAN.XLS', 'FROM', 'TO', 'COST');
…where we use two ranges to store the two-dimensional ARCS set. The first range,
FROM, would contain 10 ship-from points, while the second range, TO, would contain 10
ship-to points. These two ranges may lie in different areas of the workbook and need not
be adjacent.

386 CHAPTER 9
Importing in a Transportation Model with @OLE
We will now make use of the Wireless Widgets transportation model introduced in Chapter 1, Getting
Started with LINGO, to illustrate in more detail the use of the @OLE function. The model is
reproduced below with changes listed in bold type:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
! Import warehouses and vendors from Excel;
WAREHOUSES: CAPACITY;
VENDORS : DEMAND;
LINKS(WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
! The objective;
MIN = @SUM(LINKS(I, J):
COST(I, J) * VOLUME(I, J));
! The demand constraints;
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I):
VOLUME(I, J)) = DEMAND(J));
! The capacity constraints;
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J))
<= CAPACITY(I));
DATA:
! Import the data from Excel;
WAREHOUSES, VENDORS, CAPACITY, DEMAND, COST =
@OLE('\LINGO\SAMPLES\WIDGETS.XLS',
'WAREHOUSES', 'VENDORS', 'CAPACITY',
'DEMAND', 'COST');
ENDDATA
Model: WIDGETS3
Instead of explicitly listing the data in the text of the model, we are now importing it entirely from the
WIDGETS.XLS spreadsheet. Below is an illustration of the WIDGETS.XLS:
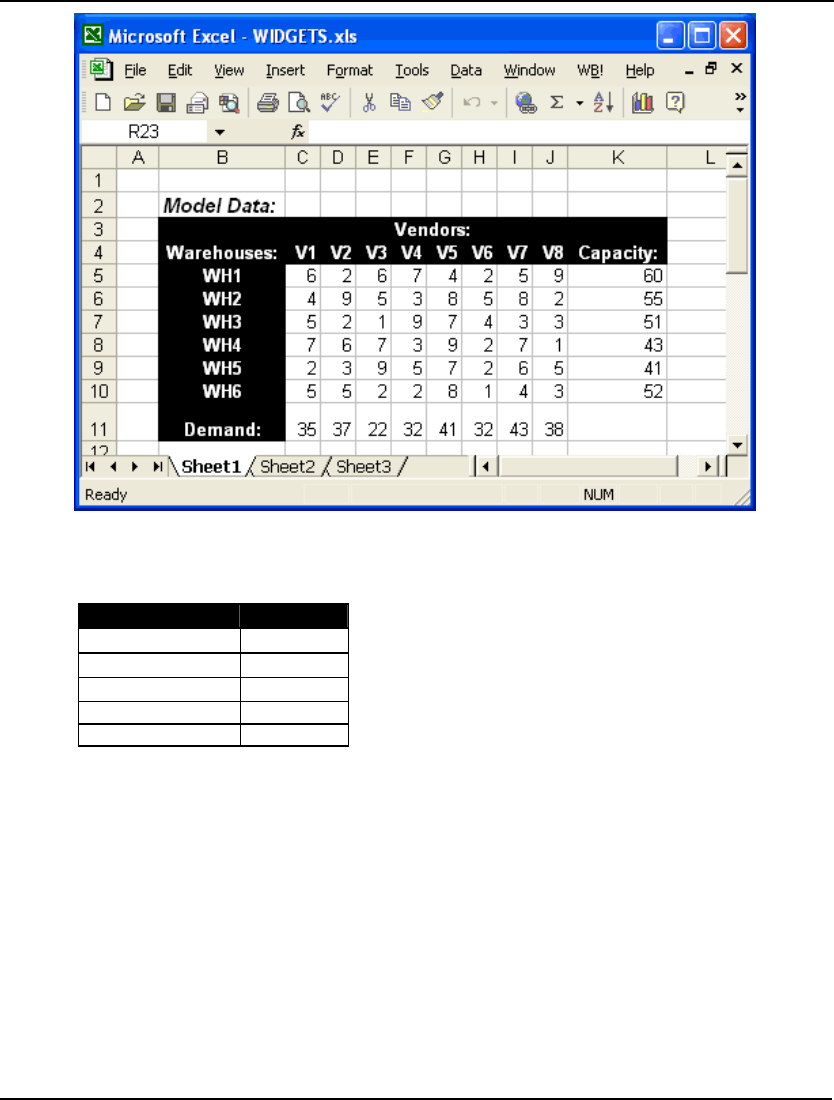
INTERFACING WITH SPREADSHEETS 387
In addition to inputting the data into this sheet, we also had to define range names for the cost,
capacity, demand, vendor name, and warehouse name regions. Specifically, we defined the following
range names:
Name Range
Capacity K5:K10
Cost C5:J10
Demand C11:J11
Vendors C4:J4
Warehouses B5:B10
To define a range name in Excel:
1) select the range by dragging over it with the mouse with the left button
down,
2) release the mouse button,
3) select the Insert|Name|Define command,
4) enter the desired name, and
5) click the OK button.
We use the following instance of the @OLE function in the data section of our model to import the
data from Excel:
WAREHOUSES, VENDORS, CAPACITY, DEMAND, COST =
@OLE('\LINGO\SAMPLES\WIDGETS.XLS',
'WAREHOUSES', 'VENDORS', 'CAPACITY',
'DEMAND', 'COST');

388 CHAPTER 9
Note that because the model objects are all either primitive sets or set attributes, and they have the
same names as their corresponding spreadsheet ranges, we could have dropped the range name
arguments and used the equivalent, but shorter, version:
WAREHOUSES, VENDORS, CAPACITY, DEMAND, COST =
@OLE('\LINGO\SAMPLES\WIDGETS.XLS');
As an aside, note that we used a single @OLE function call to read all the data for this model. This is
not a requirement, however. For clarity, you may choose to use multiple @OLE function
calls⎯perhaps one for each model object.
When we solve this model, LINGO will load Excel (assuming it isn't already running), load the
WIDGETS worksheet, and then pull the values for the CAPACITY, COST, and DEMAND attributes
from the worksheet, along with the members of the WAREHOUSES and VENDORS sets. Excerpts
from the solution appear below:
Global optimal solution found.
Objective value: 664.0000
Total solver iterations: 15
Variable Value Reduced Cost
VOLUME(WH1, V2) 19.00000 0.0000000
VOLUME(WH1, V5) 41.00000 0.0000000
VOLUME(WH2, V4) 32.00000 0.0000000
VOLUME(WH2, V8) 1.000000 0.0000000
VOLUME(WH3, V2) 12.00000 0.0000000
VOLUME(WH3, V3) 22.00000 0.0000000
VOLUME(WH3, V7) 17.00000 0.0000000
VOLUME(WH4, V6) 6.000000 0.0000000
VOLUME(WH4, V8) 37.00000 0.0000000
VOLUME(WH5, V1) 35.00000 0.0000000
VOLUME(WH5, V2) 6.000000 0.0000000
VOLUME(WH6, V6) 26.00000 0.0000000
VOLUME(WH6, V7) 26.00000 0.0000000
Exporting Solutions to Spreadsheets
LINGO allows you to place interface functions in a model’s data section to automatically perform
exports to Excel each time your model is solved. In this chapter, we will focus on how to place
interface functions in your model to export your model’s results to Excel.
In the previous section, we saw how the @OLE interface function can be used to import data from
Excel. As we will demonstrate here, this function may also be used to send solutions back out to Excel.
As with imports, @OLE uses OLE technology to create real time links with Excel.

INTERFACING WITH SPREADSHEETS 389
Using @OLE to Export Solutions to Excel
@OLE is an interface function for moving data back and forth from Excel using OLE based transfers.
OLE transfers are direct memory transfers and do not make use of intermediate files. When using
@OLE for exports, LINGO loads Excel, tells Excel to load the desired spreadsheet, and sends ranges
of data containing solution values to the sheet. @OLE can export one and two-dimensional ranges
(rectangular ranges that lie on a single spreadsheet in Excel), but cannot export discontinuous or
three-dimensional ranges (ranges that traverse more than one spreadsheet in Excel). In order to export
solutions with @OLE, you place calls to @OLE in the data section of your model. These @OLE
export instructions are executed each time your model is solved.
Syntax Form 1
The first form of syntax for using @OLE to export data is:
@OLE( ['spreadsheet_file’] [, range_name_list]) = object_list;
The object_list is a comma delimited list of sets, set attributes, and/or scalar variables to be exported.
The 'spreadsheet_file’is the name of the workbook file to export the values to. If the name is omitted,
LINGO defaults to using whatever workbook is currently open in Excel.
The range_name_list is the list of named ranges in the sheet to export solution values to. The ranges
must contain exactly one cell for each exported value for each object in the object_list. Primitive sets
and set attributes export one value per element. Derived sets, on the other hand, export one value for
each dimension of the set. Thus, a two-dimensional set exports two values per set member.
As an example, consider the following model and its solution:
SETS:
S1: X;
S2(S1, S1): Y;
ENDSETS
DATA:
S1,X = M1,1 M2,2 M3,3;
S2,Y = M1,M2,4 M3,M1,5;
ENDDATA
Variable Value
X(M1) 1.000000
X(M2) 2.000000
X(M3) 3.000000
Y(M1, M2) 4.000000
Y(M3, M1) 5.000000
X and Y, both set attributes, export one numeric value per element. More specifically, X exports 1,2,
and 3; while Y exports 4 and 5. S1, a primitive set, exports one text value per element, or the values:
M1, M2, and M3. S2, on the other hand, is a two-dimensional derived set. Thus, it exports two text
values per element. In this case, S2 has two members, so it exports the four values M1, M2, M3, and
M1.
390 CHAPTER 9
There are three options available for how you specify the range names. First, you can explicitly specify
one receiving range for each model object in object_list. Secondly, you can omit the range arguments
entirely. In that case, LINGO supplies the range names with default values that are the same as the
names of the model objects. Finally, you can specify a single range name to export all the solution
values to. In this final case, all the variables in object_list must be defined on the same set, and LINGO
exports the data in a tabular format. Examples of these three methods for using @OLE to export
solutions follow:
Example 1: @OLE('\XLS\DEVELOP.XLS', 'BUILD_IT', 'HOW_BIG') =
BUILD, SQ_FEET;
Here, an individual range for receiving each model object is specified. Thus, the values
of BUILD will be placed in the range BUILD_IT and SQ_FEET in the range HOW_BIG.
When specifying individual ranges, model objects are not required to be defined on the
same set.
Example 2: @OLE('\XLS\DEVELOP.XLS') = BUILD, SQ_FEET;
In this case, we omitted the range name argument. Thus, LINGO defaults to using the
model object names for the range names. So, LINGO exports BUILD and SQ_FEET to
ranges of the same name in the DEVELOP.XLS Excel sheet.
Example 3: @OLE('\XLS\DEVELOP.XLS', 'SOLUTION') = BUILD, SQ_FEET;
Here we have specified a single range, SOLUTION, to receive both model objects.
Assuming that the receiving range has two columns and our model objects are both
one-dimensional, the values of BUILD will be placed in column 1 and SQ_FEET in
column 2. In order for this method to work, BUILD and SQ_FEET must be defined on
the same set.
Note: The major difference to notice between using @OLE for exports, as opposed to imports, is the
side of the statement the @OLE function appears on. When the @OLE function appears on
the left of the equals sign, you are exporting. When it appears on the right, you are importing.
So, always remember:
@OLE( … ) = object_list; ↔ Export, and
object_list = @OLE( … ); ↔ Import.
Another way to remember this convention is that the left-hand side of the expression is
receiving the data, while the right-hand side is the source. For those familiar with computer
programming languages, this follows the convention used in assignment statements.
Syntax Form 2
As with @TEXT, you may also use the @WRITEFOR function in conjunction with @OLE to give you more
control over the values that are exported, which brings us to our second form of syntax for exporting to
Excel:
@OLE( ['spreadsheet_file’], range_name_list) = @WRITEFOR( setname
[ ( set_index_list) [ | conditional_qualifier]] : output_obj_1[,…,output_obj_n]);
One thing to note that differs from the previous syntax is that the range name list is now required when
exporting via the @WRITEFOR function. The range name list can be a single-cell range, a single
multiple-cell range, or a list of multiple-cell ranges.

INTERFACING WITH SPREADSHEETS 391
In the case of a single cell range, the i-th output object will be written to the (i-1)-th column to the right
of the named cell. Note that single-cell ranges act dynamically in that all values will be written to the
workbook even though, of course, they lie outside the single-cell range. When all output is written, the
original single-cell range will be at the upper left corner of the table of output values.
In the case of a single multiple-cell range, LINGO creates a table of all the output values, where output
object i forms the i-th column of the table. This table is then written to the output range. Items are
written from upper-left to lower-right. In general, your output range will have one column for each
output object. If not, the columns will get scrambled on output.
If a list of multiple cell ranges is specified, then you must specify one range name for each output
object. Each output object will be written to its output range in upper-left to lower-right direction.
@WRITEFOR functions like any other set looping function in that, as a minimum, you will need to
specify the set to loop over. Optionally, you may also specify an explicit set index list and a
conditional qualifier. If a conditional qualifier is used, it is tested for each member of the looping set
and output will not occur for any members that don't pass the test. It's this feature of being able to base
output on the results of a condition that distinguish this second style of syntax.
The list of output objects, of course, specifies what it is you want to output. As with the first form of
syntax, the output objects may be labels, set members and variable values. However, you have
additional latitude in that the output objects may now consist of complex expressions of the variable
values (e.g., you could compute the ratio of two variables). This is a useful feature when you need to
report statistics and quantities derived from the variable values. By placing these calculations in the
data section, as opposed to the model section, you avoid adding unnecessary complications to the
constraints of the model.
In general, you can do everything in the second form of syntax that you can do in the first, and more.
However, the first form has an advantage in that it can be very concise.
Some examples follow:
Example 1: @OLE( 'RESULTS.XLS', 'A1') =
@WRITEFOR( DAYS( D) | START( DAYS) #GT# 0:
DAYS( D), START( D));
Here, our target is the single cell A1. Starting at A1 we will write two columns. The first
column will contain the names of the DAYS set for which the attribute START is nonzero.
The second column will contain the START values. Assuming that there are five days that
have nonzero values, then range A1:A5 will contain the names of the days and B1:B5 will
contain the start values.
Example 2: @OLE( 'RESULTS.XLS', 'SKED') =
@WRITEFOR( DAYS( D) | START( DAYS) #GT# 0:
DAYS( D), START( D));
Here, our target is the multiple-cell range SKED. Assuming SKED is a two-column range,
column one will receive the DAYS set members and column 2 will receive the START
values.

392 CHAPTER 9
Example 3: @OLE( 'RESULTS.XLS', 'DAYS', 'START') =
@WRITEFOR( DAYS( D) | START( DAYS) #GT# 0:
DAYS( D), START( D));
In this example, we specify one named range for each output object. In which case, each
output object will be written to its corresponding range.
Note: When exporting to workbooks, receiving ranges that are larger than the number of exported
values can be filled out by either erasing the contents of the extra cells or leaving the extra
cells untouched. The default is to leave the extra cells untouched. If you would like to erase
the contents of the extra cells, you'll need to enable the Fill Out Ranges and Tables option.

INTERFACING WITH SPREADSHEETS 393
Exporting in a Transportation Model with @OLE
In a previous section of this chapter, @OLE Importing in a Transportation Model, we used the
Wireless Widgets transportation model to demonstrate the use of the @OLE function for importing
data from Excel. At the time, we did not use @OLE to export the solution back to the spreadsheet file.
We will now extend the model in order to have it also export the solution back to the spreadsheet. The
model is reproduced below with changes in the data section listed in bold type:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
! Import warehouses and vendors from Excel;
WAREHOUSES: CAPACITY;
VENDORS : DEMAND;
LINKS(WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
! The objective;
MIN = @SUM(LINKS(I, J):
COST(I, J) * VOLUME(I, J));
! The demand constraints;
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I):
VOLUME(I, J)) = DEMAND(J));
! The capacity constraints;
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J))
<= CAPACITY(I));
DATA:
! Import the data from Excel;
WAREHOUSES, VENDORS, CAPACITY, DEMAND, COST =
@OLE('\LINGO\SAMPLES\WIDGETS.XLS',
'WAREHOUSES', ' VENDORS', 'CAPACITY',
'DEMAND', 'COST');
! Export the solution back to Excel;
@OLE('\LINGO\SAMPLES\WIDGETS.XLS',
'VOLUME') = VOLUME;
ENDDATA
Model: WIDGETS5
We now use the @OLE function to send the decision variables contained in the VOLUME attribute
back to the Excel file WIDGETS.XLS with the statement:
@OLE('\LINGO\SAMPLES\WIDGETS.XLS', 'VOLUME') = VOLUME;
Note, since the attribute name is identical to the range name, we could have omitted the range name in
the @OLE function and simply used the following:
@OLE('\LINGO\SAMPLES\WIDGETS.XLS') = VOLUME;
394 CHAPTER 9
We will now need to add a range titled VOLUME for receiving the solution values in the WIDGETS
spreadsheet. Here is the range as it appears after adding it to the sheet:
We have also used the Insert|Name|Define command in Excel to assign the range name VOLUME to
the receiving range of C16:J21. To define a range name in Excel:
1. select the range by dragging over it with the mouse with the left button
down,
2. release the mouse button,
3. select the Insert|Name|Define command,
4. enter the desired name (VOLUME in this case), and
5. click the OK button.
INTERFACING WITH SPREADSHEETS 395
When we solve this model, LINGO will load Excel (assuming it isn't already running), load the
WIDGETS worksheet, and then pull the data for WAREHOUSES, VENDORS, CAPACITY, COST, and
DEMAND from the worksheet. Once the solver has found the optimal solution, LINGO will send the
values for the VOLUME attribute back to the worksheet storing them in the range of the same name
and the updated range will appear as follows:
Export Summary Reports
Whenever you use the @OLE function to export solutions to spreadsheets, you will receive a summary
of the results of the export process. This summary is called the export summary report. These reports
will be found at the top of the solution report window. There will be one export summary report for
each @OLE function in the model used for exporting solutions. Here is the export summary report
obtained when we exported the solution of the Wireless Widgets transportation model to Excel using
@OLE:
Export Summary Report
---------------------
Transfer Method: OLE BASED
Workbook: \LINGO\SAMPLES\WIDGETS.XLS
Ranges Specified: 1
VOLUME
Ranges Found: 1
Range Size Mismatches: 0
Values Transferred: 48
The Transfer Method field lists the type of transfer used. @OLE transfers will be listed as “OLE
BASED”.

396 CHAPTER 9
The Workbook field lists the name of the workbook the export was performed on.
The Ranges Specified field lists the total number of ranges specified in the export function followed by
a listing of the range names.
The Ranges Found figure lists the number of ranges actually found in the sheet from the total number
specified.
In general, the spreadsheet range should have one cell for each data value being exported. If a range
has too few or too many cells, it gets counted in the Range Size Mismatches field.
The Values Transferred field lists the total number of data values actually transferred into all the
specified ranges.
OLE Automation Links from Excel
LINGO allows you to place a LINGO command script in a range in an Excel spreadsheet and then pass
the script to LINGO by means of OLE Automation. This allows you to setup a client-server
relationship between Excel and LINGO.
To illustrate this feature, we will once again make use of the staff-scheduling model introduced in the
Primitive Set Example — Staff-Scheduling section in Chapter 2, Using Sets. This illustration assumes
the reader is moderately familiar with the use of Excel Visual Basic macros. If needed, you can refer to
the Excel documentation for more background.
INTERFACING WITH SPREADSHEETS 397
Consider the following Excel spreadsheet:
Spreadsheet: STAFOLE1.XLS
We have placed the staffing requirements in the range C16:I16 and assigned the name
REQUIREMENTS to this range. We have also assigned the name START to the range C18:I18. LINGO
will be sending the solution to the START range. We have also included two graphs in the sheet to help
visualize the solution. The graph on the left shows how many employees to start on each day of the
week, while the graph on the right compares the number on duty to the number required for each day.
398 CHAPTER 9
Note that our spreadsheet has a second tab at the bottom titled Model. Select this tab and you will find
the following:
Spreadsheet: STAFOLE1.XLS
This page contains the command script we will use to solve the staffing model. For more information
on command scripts, refer to page 375. In line 1, we turn on terminal echoing, so LINGO will echo the
command script to the command window as it is read. Lines 2 through 21 contain the text of the
model, which should be familiar by now. Note, in the data section, we are using two @OLE
functions—the first to import the data from the spreadsheet and the second to export the solution back
to the spreadsheet. The data is read from the range named REQUIRED, and the solution is written to
the START range on the first tab of the sheet. In line 22, we use the GO command to solve the model.
We have also assigned the range name MODEL to the range that contains this script (Model!A1:A23).

INTERFACING WITH SPREADSHEETS 399
Given that we have our LINGO command script contained in our spreadsheet, the next question is how
we pass it to LINGO to run it. This is where OLE Automation comes in. If you recall, the first tab of
our sheet (the tab labeled Data) had a Solve button. We added this button to the sheet and attached the
following Excel Visual Basic macro to it:
Sub LINGOSolve()
Dim iErr As Integer
iErr = LINGO.RunScriptRange("MODEL")
If (iErr > 0) Then
MsgBox ("Unable to solve model")
End If
End Sub
We use OLE Automation to call the LINGO exported method RunScriptRange, passing it the range
name MODEL. This, of course, is the name of the range that contains the command script. The
RunScriptRange routine calls Excel to obtain the contents of the range and begins processing the
commands contained therein. Processing continues until either a QUIT command is encountered or
there are no further commands remaining in the range.
RunScriptRange will return a value of 0 if it was successfully able to queue the script for processing. If
RunScriptRange was not successful, it will return one of the following error codes:
Error
Code
Description
1 Invalid argument
2 <Reserved>
3 Unable to open log file
4 Null script
5 Invalid array format
6 Invalid array dimension
7 Invalid array bounds
8 Unable to lock data
9 Unable to allocate memory
10 Unable to configure script reader
11 LINGO is busy
12 OLE exception
13 Unable to initialize Excel
14 Unable to read Excel range
15 Unable to find Excel range
We have also added the following Auto_Open macro to the sheet:
Dim LINGO As Object
Sub Auto_Open()
Set LINGO = CreateObject("LINGO.Document.4")
End Sub
An Auto_Open macro is automatically executed each time a sheet is opened. We declare LINGO as an
object and attach the LINGO object to the LINGO application with the CreateObject function.
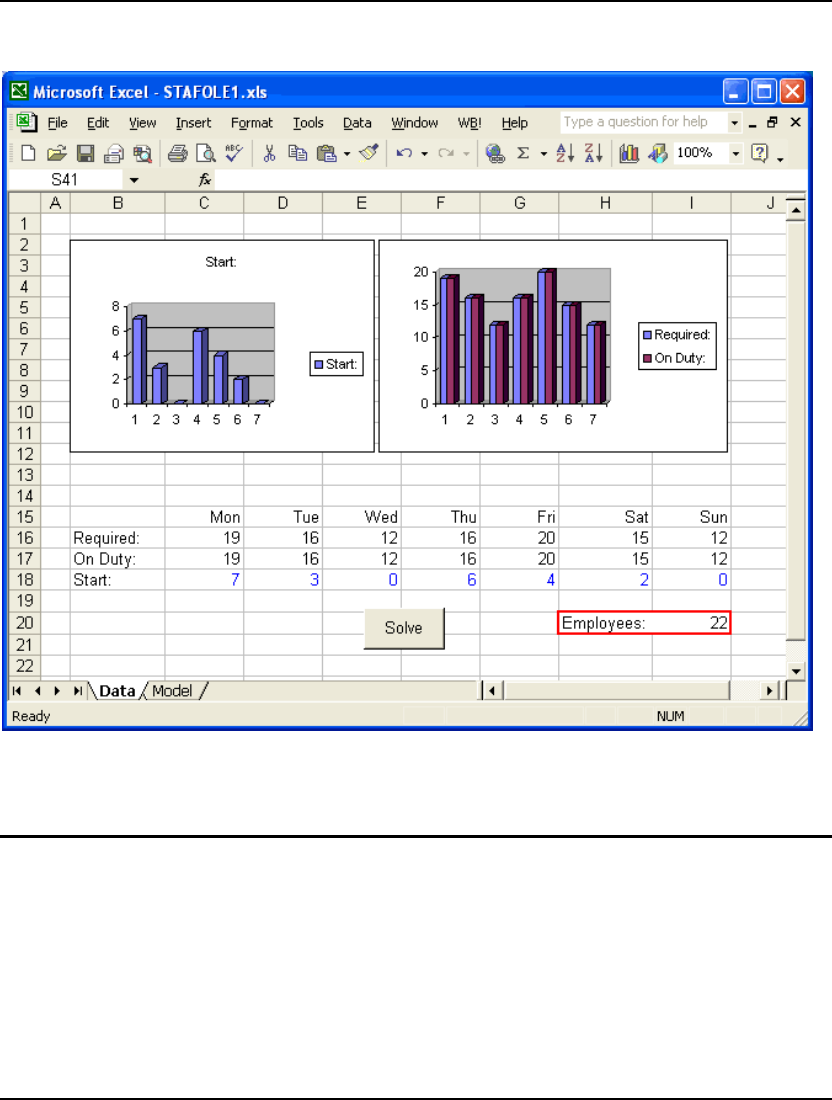
400 CHAPTER 9
Now, go back to the first tab on the workbook and press the Solve button. After a brief pause, you
should see the optimal solution installed, so the sheet resembles:
Spreadsheet: STAFOLE1.XLS
The optimal number of employees to start on each day of the week is now contained in the START
range (C18:I18), and the graphs have been updated to reflect this solution.
Embedding LINGO Models in Excel
LINGO is capable of functioning as an OLE server. This means you can embed a LINGO model in
any application that can function as an OLE container. Excel is one such application. Embedding a
LINGO model into Excel is convenient in that the LINGO model is always immediately available once
the spreadsheet is opened. You don’t have to worry about also starting LINGO and finding the correct
LINGO model that corresponds to the spreadsheet.
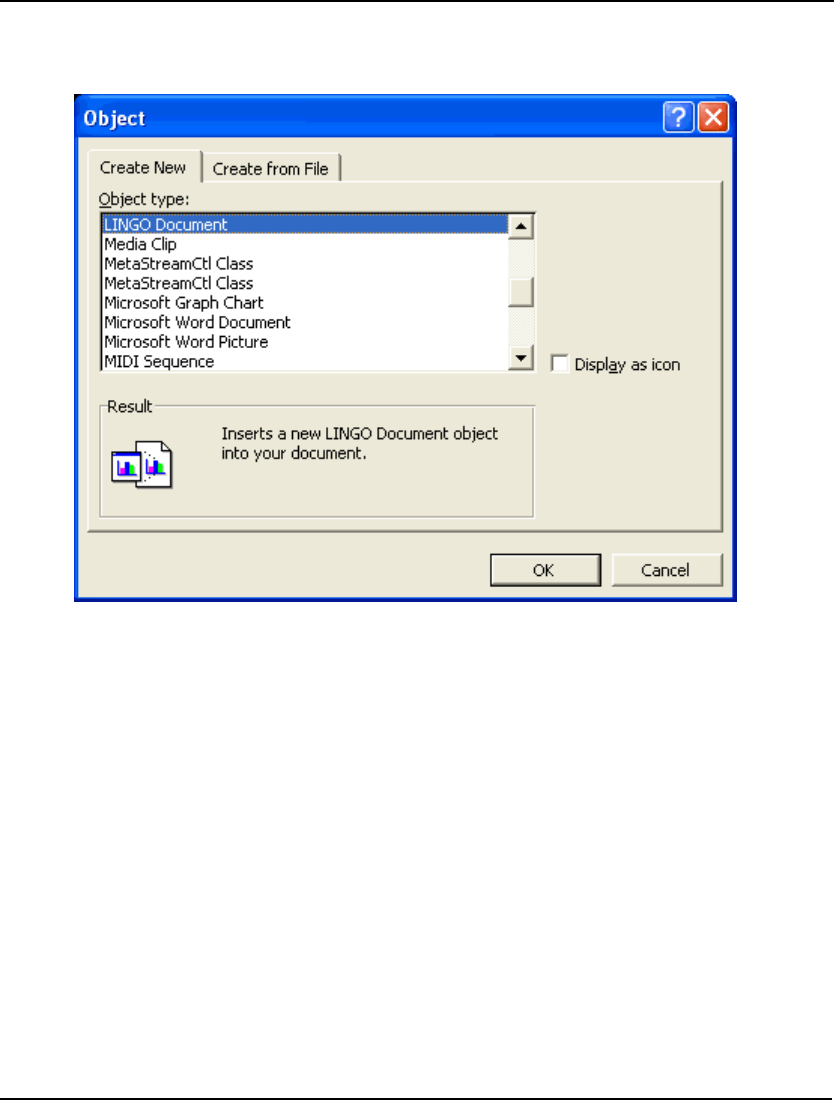
INTERFACING WITH SPREADSHEETS 401
To embed a LINGO document in an Excel file, select the Excel command Insert|Object. You will be
presented with a list of embeddable objects available on your system. Select the LINGO Document
object from this list as shown here:
Click the OK button and a blank LINGO model window will be embedded within the spreadsheet. You
can enter text directly into this window just as you would in LINGO, or you can paste it in from
another application. When you save the Excel sheet, the embedded LINGO model will automatically
be saved with it. Similarly, whenever you read the sheet back into Excel, the embedded LINGO model
will be restored, as well.
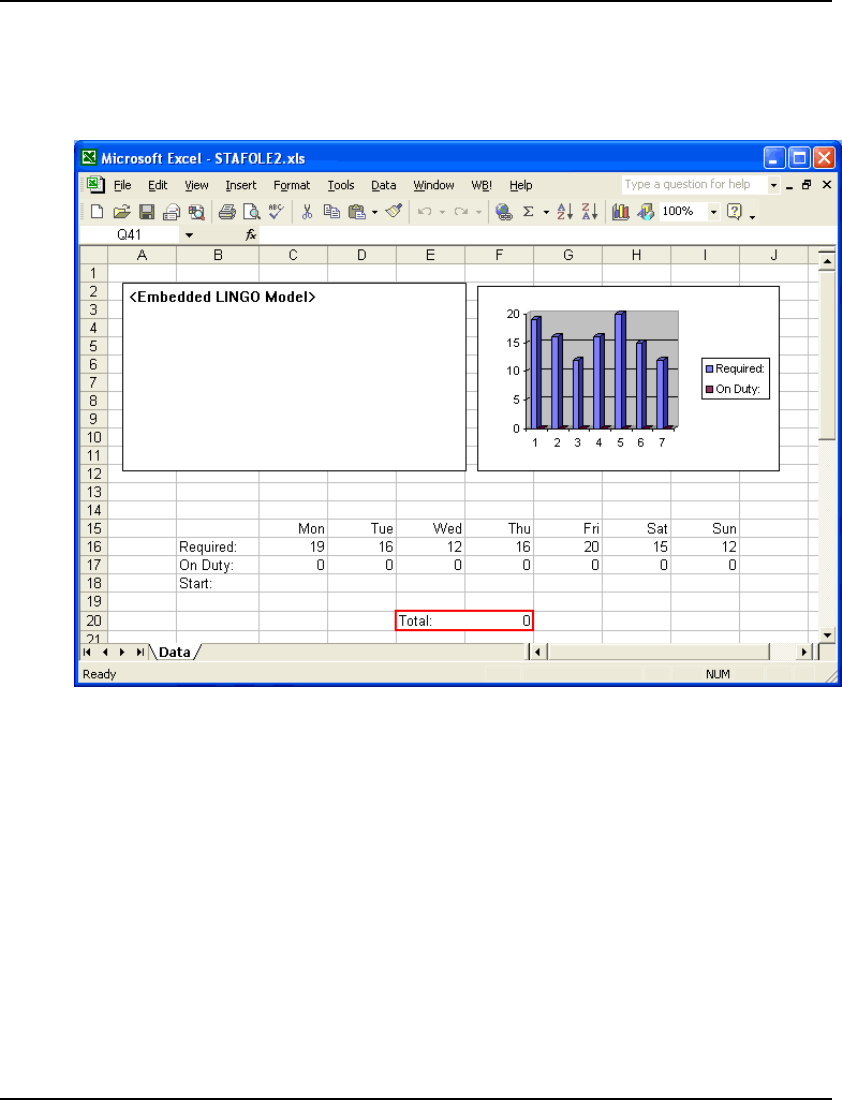
402 CHAPTER 9
To illustrate this feature, we will continue with the staffing model introduced in Chapter 2, Using Sets.
The spreadsheet will contain the data for the model, and it will also contain an embedded LINGO
model to perform the optimization and install the solution back into the spreadsheet. This example may
be found in the spreadsheet file SAMPLES\STAFOLE2.XLS. If you load this sheet into Excel, you
should see the following:
Spreadsheet: STAFOLE2.XLS
As in the previous example, the staffing requirements are in the range C16:I16. This range has been
titled REQUIRED. The range C18:I18 has been assigned the name START and will receive the solution
after the model is solved. In the upper right-hand corner of the sheet, we have defined a graph to help
visualize the solution.
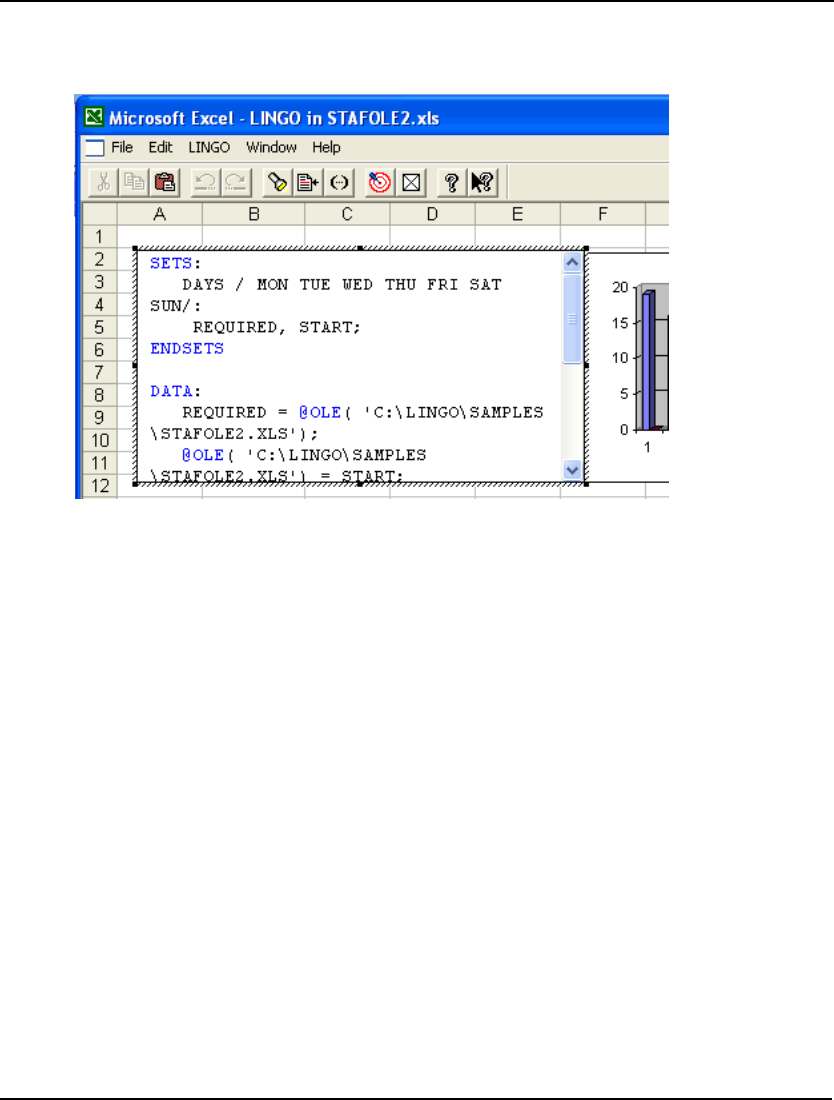
INTERFACING WITH SPREADSHEETS 403
In the upper left corner, there is a region labeled <Embedded LINGO Model>. This region contains a
LINGO model that will solve the staffing model and place the solution values into the spreadsheet. If
you double-click on this region, you will be able to see the model:
Spreadsheet: STAFOLE2.XLS
Note, when this LINGO model is active, the LINGO menus and toolbar replace the Excel menus and
toolbar. Thus, when working with an embedded LINGO model in Excel, you have all the functionality
of LINGO available to you. When you deselect the LINGO model, the Excel menus and toolbar will
automatically become available once again. This begins to illustrate the power of embedded OLE—it
allows the user to seamlessly combine the features of two or more applications together as if they were
a single, integrated application.

404 CHAPTER 9
You can drag the lower right-hand corner of the LINGO model region to expose the contents of the
entire model:
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/:
REQUIRED, START;
ENDSETS
DATA:
REQUIRED =
@OLE('C:\LINGO\SAMPLES\STAFOLE2.XLS');
@OLE('C:\LINGO\SAMPLES\STAFOLE2.XLS') = START;
ENDDATA
MIN = @SUM(DAYS: START);
@FOR(DAYS(J):
@SUM(DAYS(I) | I #LE# 5:
START(@WRAP(J - I + 1, 7)))
>= REQUIRED(J));
@FOR(DAYS: @GIN(START));
Once again, we are making use of our familiar staff-scheduling model. The main feature to note is that
we are using two instances of the @OLE function. The first instance gets the staffing requirements
from the spreadsheet. The second sends the solution back to the START range.
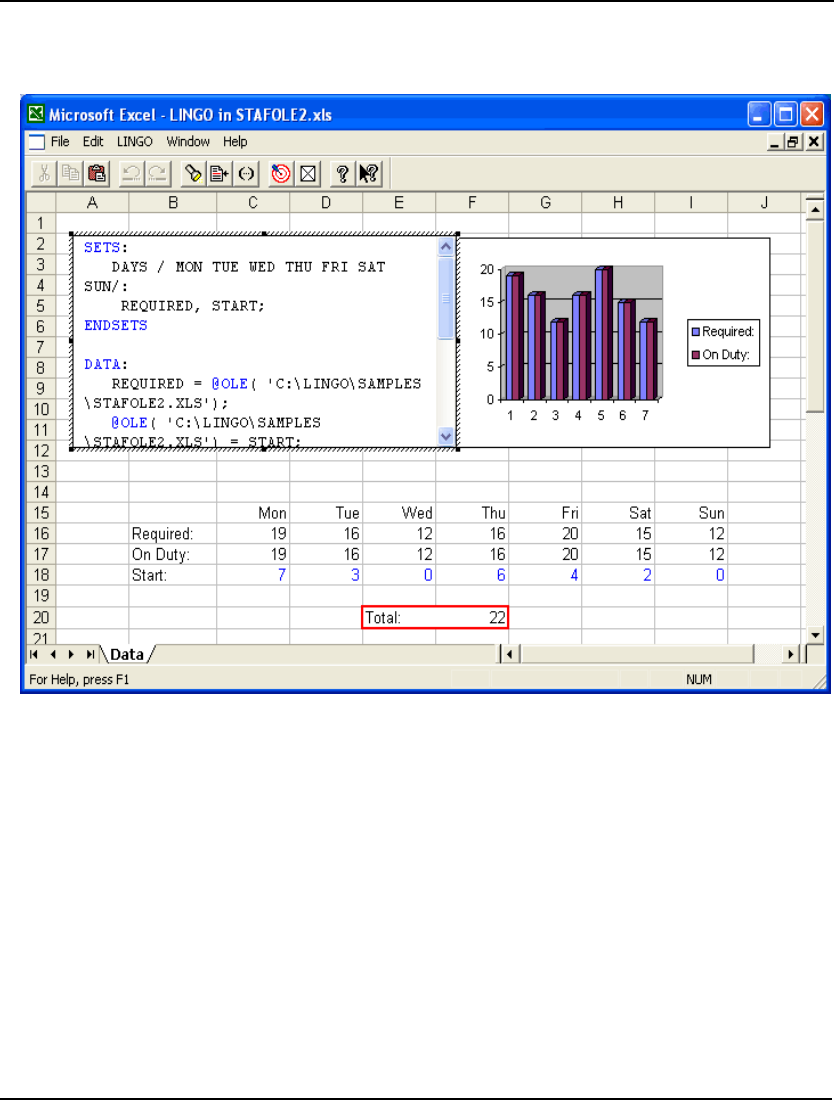
INTERFACING WITH SPREADSHEETS 405
To solve the model, double-click on the region containing the LINGO model. The LINGO command
menus will become visible along the top of the screen. Select the LINGO|Solve command. After
LINGO finishes optimizing the model, it will return the solution to the sheet and we will have:
Spreadsheet: STAFOLE2.XLS
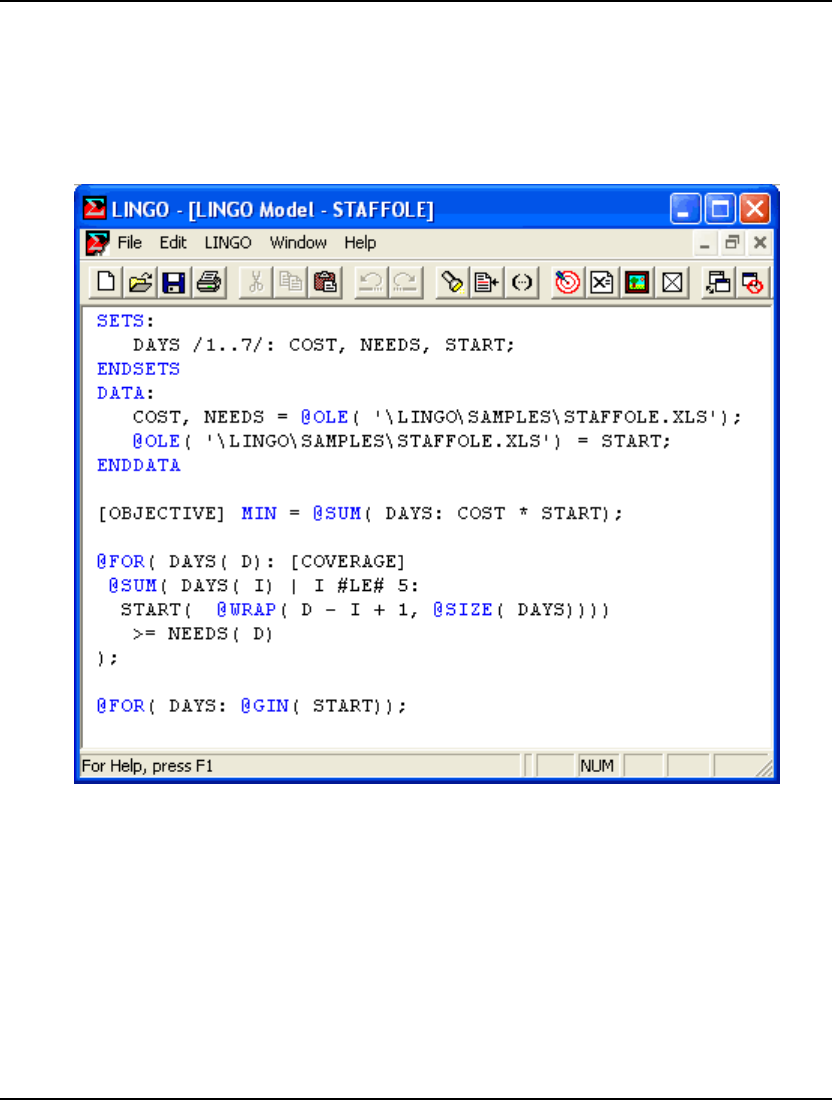
406 CHAPTER 9
Embedding Excel Sheets in LINGO
Just as you can embed a LINGO model into Excel, you can reverse the process and embed an Excel
sheet in a LINGO model. To illustrate this, load the STAFFOLE model from the SAMPLES
subdirectory into LINGO. Once again, this is our familiar staff-scheduling model and it appears as
follows:
Model: STAFFOLE
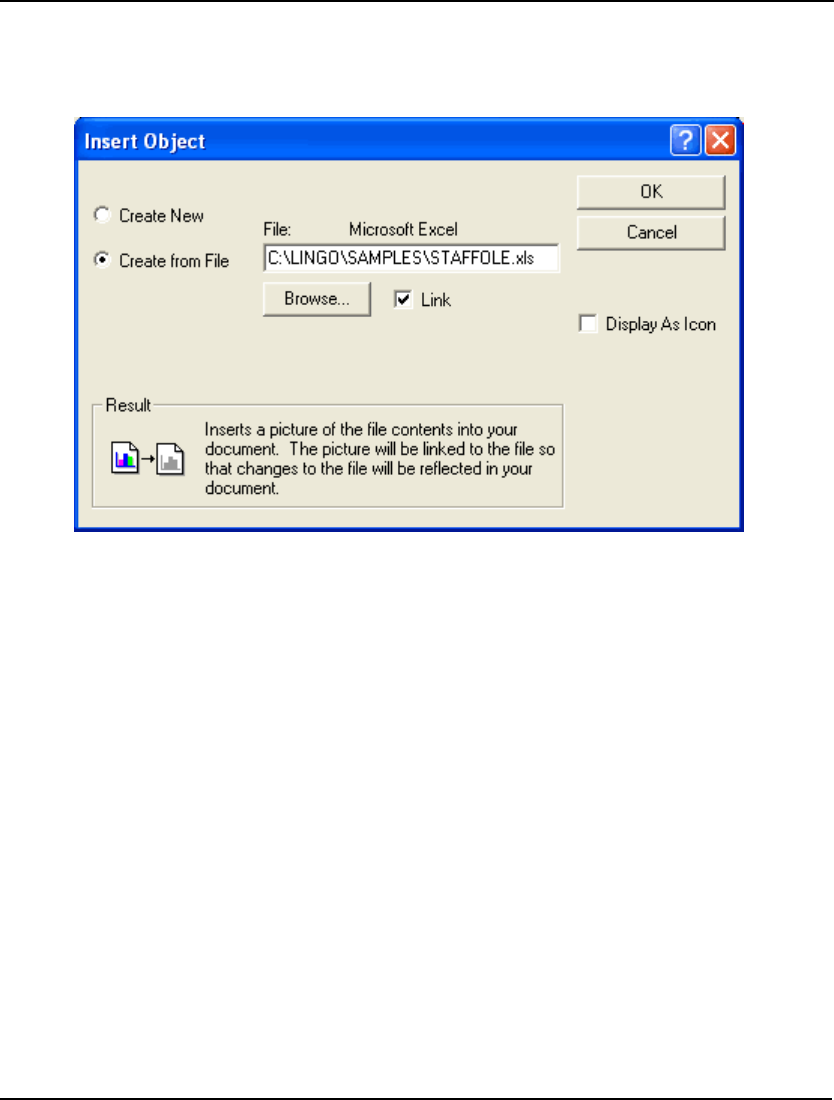
INTERFACING WITH SPREADSHEETS 407
This model reads data from and writes the solution to the Excel file STAFFOLE.XLS. To make our
lives easier, it would be nice to embed this spreadsheet in the LINGO model to avoid having to load it
into Excel each time we need to work with our model. To do this, select the Edit|Insert New Object
command in LINGO. You will be presented with the dialog box:
Click on the Create from File button, enter the spreadsheet file name in the File field, click on the Link
checkbox, and then press the OK button.
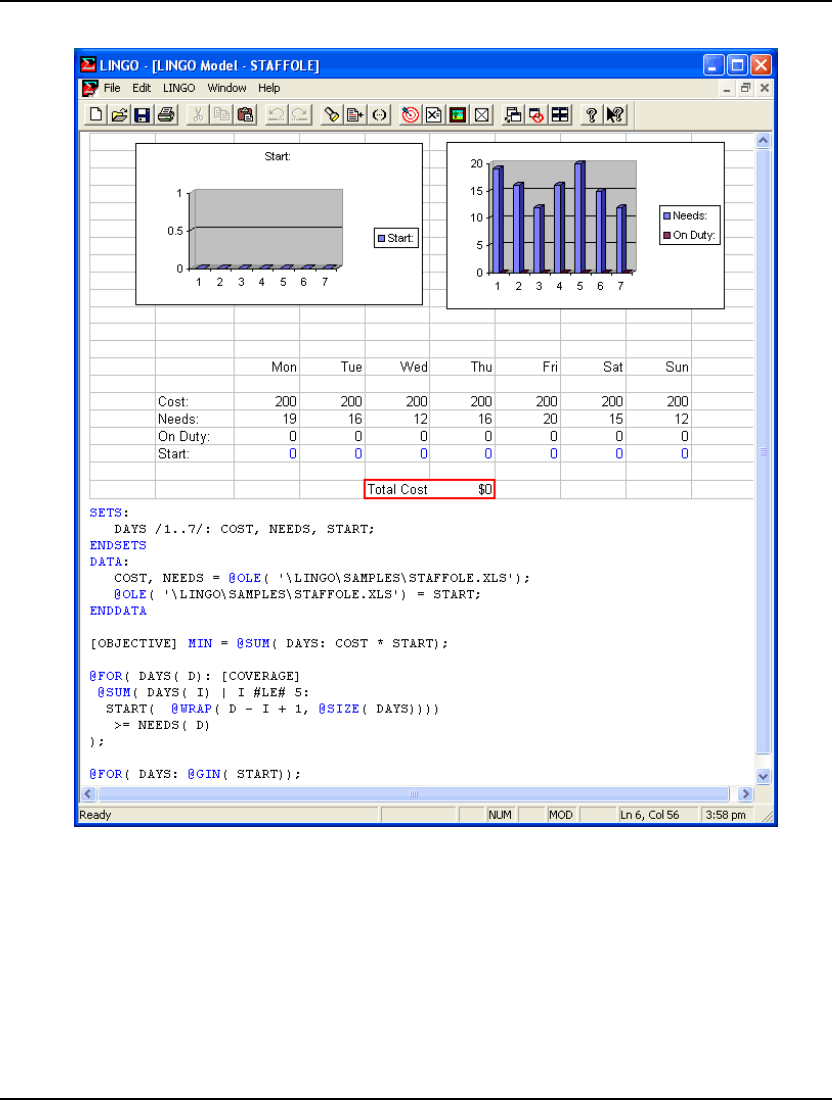
408 CHAPTER 9
Your LINGO model should now appear as:
The data spreadsheet is now embedded at the top of the LINGO document. You can easily edit the
spreadsheet by double-clicking on it. When you save the LINGO model, the link to the Excel file will
be saved as well.
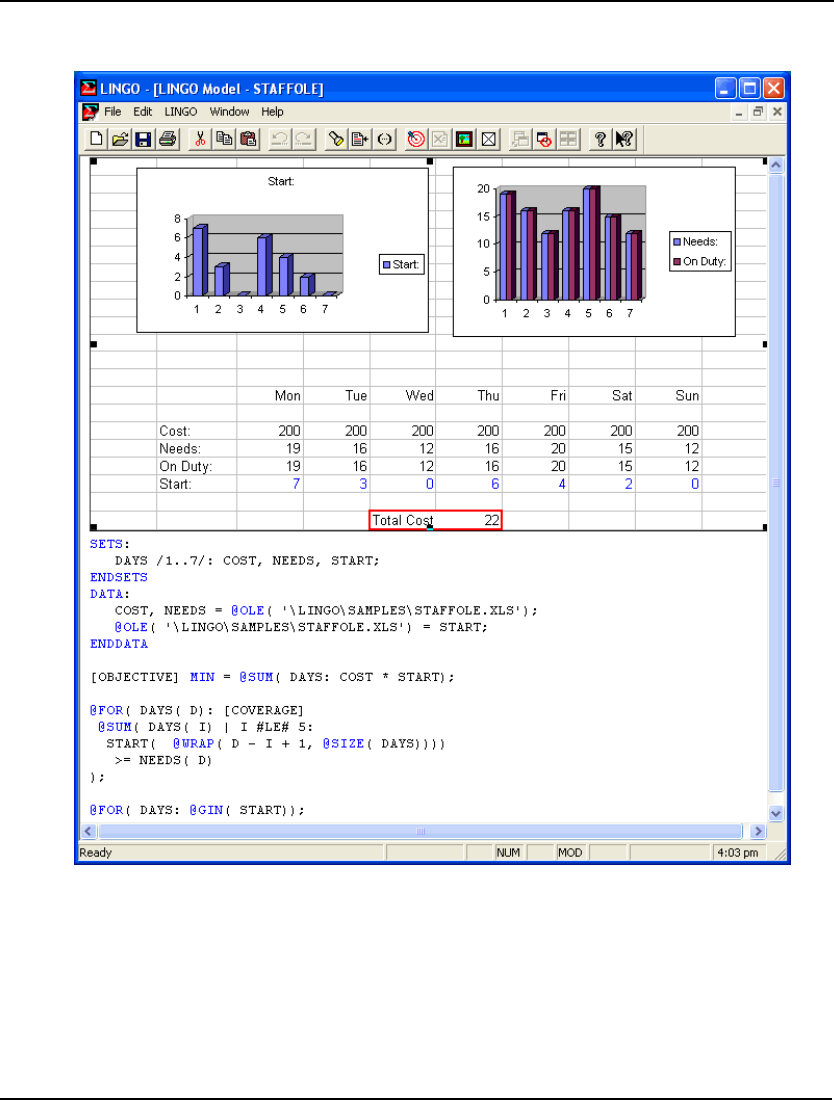
INTERFACING WITH SPREADSHEETS 409
At this point, go ahead and optimize the model by selecting the LINGO|Solve command. When LINGO
has finished solving the model, you should see the following:
The optimal solution now appears in the embedded spreadsheet and the graphs of the solution have
been updated.

410 CHAPTER 9
Summary
We have demonstrated a number of intriguing methods for combining the modeling features of
LINGO with the data management features of spreadsheets. The concise, structured nature of
LINGO’s modeling language makes reading and understanding even large models relatively easy.
Whereas, it can often be a challenge to discern the underlying mathematical relationships of large,
spreadsheet models with formulas spread throughout numerous cells on multiple tabbed sheets.
LINGO models are also easier to scale than spreadsheet models. As the dimensions of your problem
change, spreadsheet models can require the insertion or deletion of rows or columns and the editing of
cell formulas. Whereas, if your data is separate from the model, your LINGO formulation will
generally require little or no modification. Combining the power of model expression with LINGO and
the ease of data handling in spreadsheets gives the mathematical modeler the best of both worlds.

411
10 Interfacing with
Databases
Spreadsheets are good at managing small to moderate amounts of data. Once your models start dealing
with large amounts of data, database management systems (DBMSs) are, unquestionably, the tool of
choice. Also, in many business modeling situations, you will find most, if not all, of the data is
contained in one or more databases. For these reasons, LINGO supports links to any DBMS that has an
Open DataBase Connectivity (ODBC) driver (effectively all popular DBMSs). ODBC defines a
standardized interface to DBMSs. Given this standardized interface, LINGO can access any database
that supports ODBC.
LINGO has one interface function for accessing databases. This function’s name is @ODBC. The
@ODBC function is used to import data from and export data to any ODBC data source. @ODBC is
currently available only in Windows versions of LINGO.

412 CHAPTER 10
ODBC Data Sources
Windows versions of LINGO include a variation of the standard transportation model that retrieves all
data from a database, and writes a solution back to the same database. This file can be found in the file
SAMPLES\TRANDB.LG4. The contents of this model are displayed below:
MODEL:
! A 3 Plant, 4 Customer Transportation Problem;
! Data is retrieved from an either an Access database or
an Oracle database an ODBC link. You *MUST* use the
ODBC Administrator to register one of the supplied
databases under the name "Transportation" in order
to get this model to run. Refer to Chapter 10 for
more details.;
TITLE Transportation;
SETS:
PLANTS: CAPACITY;
CUSTOMERS: DEMAND;
ARCS(PLANTS, CUSTOMERS): COST, VOLUME;
ENDSETS
! The objective;
[OBJ] MIN = @SUM(ARCS: COST * VOLUME);
! The demand constraints;
@FOR(CUSTOMERS(C):
@SUM(PLANTS(P): VOLUME(P, C)) >= DEMAND(C));
! The supply constraints;
@FOR(PLANTS(P):
@SUM(CUSTOMERS(C): VOLUME(P, C)) <= CAPACITY(P));
DATA:
! Import the data via ODBC;
PLANTS, CAPACITY = @ODBC();
CUSTOMERS, DEMAND = @ODBC();
ARCS, COST = @ODBC();
! Export the solution via ODBC;
@ODBC() = VOLUME;
ENDDATA
END
Model: TRANDB
You will note that in the data section of this model, we use the @ODBC function to establish a link to
an ODBC data source to retrieve all the data and to export the final solution. The technical details of
the @ODBC function are discussed below. Right now, we will focus on how you set up an ODBC data
source that can be accessed by LINGO.
INTERFACING WITH DATABASES 413
An ODBC data source is a database that 1) resides in a DBMS for which you have an ODBC driver,
and 2) has been registered with the ODBC Administrator. Databases in an ODBC enabled DBMS do
not qualify as an ODBC data source until they have been registered with the ODBC Administrator.
The ODBC Administrator is a Windows Control Panel utility. Registering a database with the ODBC
Administrator is a straightforward process. In the following two sections, we will illustrate the
registration process for a Microsoft Access database and for an Oracle database.
Creating an ODBC Data Source from an Access Database
When you installed LINGO, a Microsoft Access database for the transportation model above was
included as part of the installation. This file is contained in the directory SAMPLES under the name
TRANDB.MDB. To register this database as an ODBC data source for our transportation model, you
must start the ODBC Administrator by doing the following:
1) double-click on the My Computer icon on your desktop,
2) find the Control Panel icon and double-click on it,
3) double-click on the Administrative Tools icon, and
4) search for the Data Sources (ODBC) icon and double-click on it.
You should now see the ODBC Administrator dialog box shown below:
414 CHAPTER 10
To install the TRANDB.MDB database as a data source, do the following:
1. Click the Add button in the ODBC Administrator dialog box to reveal the dialog box
below:
2. We are installing an Access data source, so select the Microsoft Access Driver option
and press the Finish button.
3. In the next dialog box:
INTERFACING WITH DATABASES 415
assign the data source the name Transportation in the Data Source Name field. In the
Description field, enter “Datasource for a LINGO transportation model”. Press the Select
button and enter the name of the database “LINGO\SAMPLES\TRANDB.MDB” (this
assumes LINGO has been installed in the LINGO directory—your installation may differ).
The dialog box should now resemble the one below:
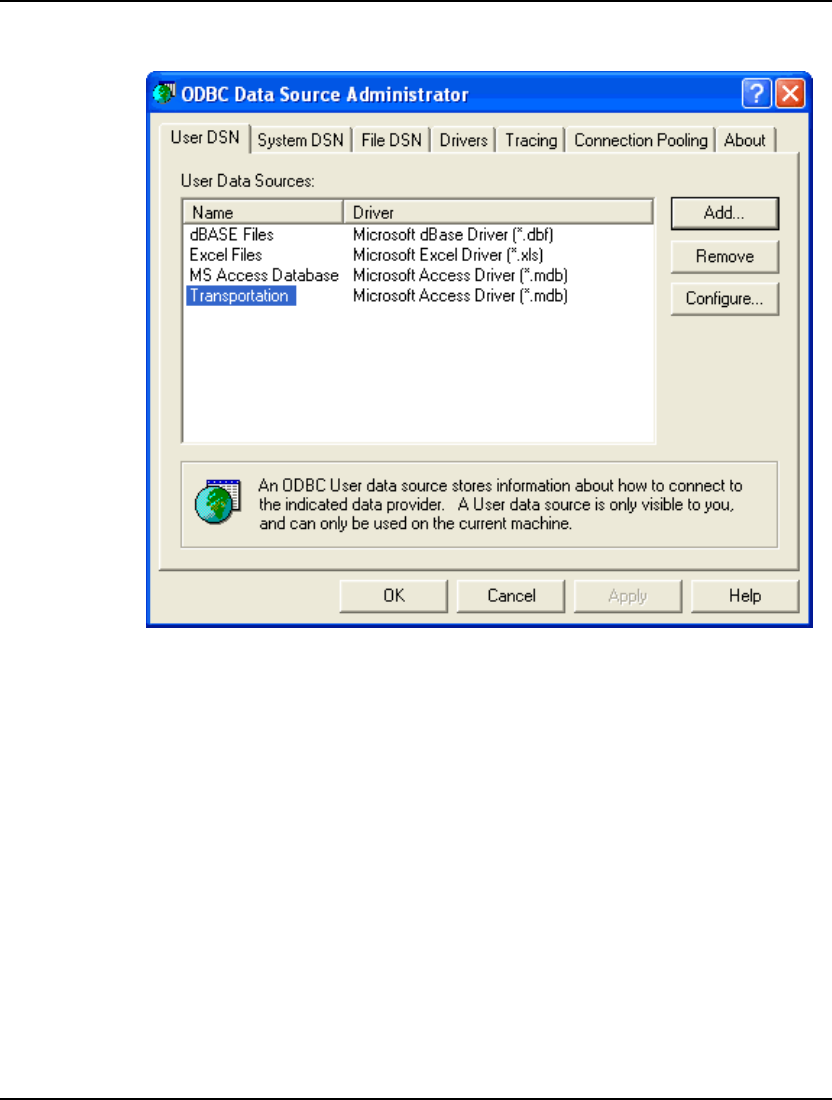
416 CHAPTER 10
4. Press the OK button and you should see the Transportation data source has been
added to the list of ODBC data sources:
5. Click the OK button to close the ODBC Administrator.

INTERFACING WITH DATABASES 417
You should now be able to start LINGO and solve the TRANDB.LG4 model. LINGO knows to go to
the Transportation data source for data because the model’s title (input with the TITLE statement) is
Transportation. If you solve this model, you should see the following results:
Global optimal solution found at step: 6
Objective value: 161.0000
Model Title: Transportation
Variable Value Reduced Cost
CAPACITY(PLANT1) 30.00000 0.0000000
CAPACITY(PLANT2) 25.00000 0.0000000
CAPACITY(PLANT3) 21.00000 0.0000000
DEMAND(CUST1) 15.00000 0.0000000
DEMAND(CUST2) 17.00000 0.0000000
DEMAND(CUST3) 22.00000 0.0000000
DEMAND(CUST4) 12.00000 0.0000000
COST(PLANT1, CUST1) 6.000000 0.0000000
COST(PLANT1, CUST2) 2.000000 0.0000000
COST(PLANT1, CUST3) 6.000000 0.0000000
COST(PLANT1, CUST4) 7.000000 0.0000000
COST(PLANT2, CUST1) 4.000000 0.0000000
COST(PLANT2, CUST2) 9.000000 0.0000000
COST(PLANT2, CUST3) 5.000000 0.0000000
COST(PLANT2, CUST4) 3.000000 0.0000000
COST(PLANT3, CUST1) 8.000000 0.0000000
COST(PLANT3, CUST2) 8.000000 0.0000000
COST(PLANT3, CUST3) 1.000000 0.0000000
COST(PLANT3, CUST4) 5.000000 0.0000000
VOLUME(PLANT1, CUST1) 2.000000 0.0000000
VOLUME(PLANT1, CUST2) 17.00000 0.0000000
VOLUME(PLANT1, CUST3) 1.000000 0.0000000
VOLUME(PLANT1, CUST4) 0.0000000 2.000000
VOLUME(PLANT2, CUST1) 13.00000 0.0000000
VOLUME(PLANT2, CUST2) 0.0000000 9.000000
VOLUME(PLANT2, CUST3) 0.0000000 1.000000
VOLUME(PLANT2, CUST4) 12.00000 0.0000000
VOLUME(PLANT3, CUST1) 0.0000000 7.000000
VOLUME(PLANT3, CUST2) 0.0000000 11.00000
VOLUME(PLANT3, CUST3) 21.00000 0.0000000
VOLUME(PLANT3, CUST4) 0.0000000 5.000000
Row Slack or Surplus Dual Price
OBJ 161.0000 1.000000
2 0.0000000 -6.000000
3 0.0000000 -2.000000
4 0.0000000 -6.000000
5 0.0000000 -5.000000
6 10.00000 0.0000000
7 0.0000000 2.000000
8 0.0000000 5.000000
TRANDB Solution

418 CHAPTER 10
As an interesting exercise, you may wish to redirect TRANDB.LG4 to use a second database that was
provided as part of your installation. The second database is called TRANDB2.MDB and is also located
in the SAMPLES directory. The main difference between the files is the dimension of data.
TRANDB.MDB involves only 3 plants and 4 customers, while TRANDB2.MDB contains 50 plants and
200 customers. If you return to the ODBC Administrator and register TRANDB2. MDB under the name
“Transportation2”, then you can redirect LINGO to use the new data source by changing the model
title from “Transportation” to “Transportation2” in the following line in the LINGO model:
TITLE Transportation2;
The new model will have 10,000 variables as opposed to the 12 variables generated with the smaller
data source. This ability to easily run different size data sets illustrates the usefulness of writing data
independent, set-based models.
Creating an ODBC Data Source from an Oracle Database
LINGO installs an SQL script that can be run by the SQL Plus utility in Oracle to build a small
database for the TRANDB.LG4 transportation model. The script file is named TRANDB.SQL and may
be found in the SAMPLES folder off the main LINGO directory. Here is the procedure you will need to
follow to set up this data source:
1. Start up the SQL Plus utility provided with Oracle by going to the Start menu in
Windows, select the Run command, type “SQLPLUSW”, and then click on the OK
button.
2. Enter your Oracle User ID and password. If you have a default installation of Oracle, the
User ID “sys” and the password “change_on_install” should be valid. A host name is
required only if Oracle is running remotely.
3. Run the TRANDB.SQL script by typing “@\LINGO\SAMPLES\TRANDB.SQL” to the
SQL Plus system prompt.
4. Exit SQL Plus by entering “EXIT” to the prompt.
5. Start up the ODBC Administrator as described in the previous section.
6. When selecting an ODBC driver, be sure to use the "Microsoft ODBC for Oracle" driver.
Do not use the "Oracle ODBC Driver", because it does not provide all the necessary
functionality.
7. Assign the data source the name “Transportation”.
8. Load TRANDB.LG4 into LINGO and solve it.
9. Enter your Oracle User ID and password as prompted.
If you would like to avoid entering your Oracle User ID and password each time LINGO accesses a
database, you may set them once at the start of your session with the File|Database User Info
command. For more information, see the File|Database User Info section above in Chapter 5,
Windows Commands.
INTERFACING WITH DATABASES 419
Creating an ODBC Data Source from an SQL Server Database
LINGO installs an SQL script that can be run by the SQL Analyzer utility in SQL Server to build a
small database for the TRANDB.LG4 transportation model. The script file is named
TRANDB_SQL.SQL and may be found in the SAMPLES folder off the main LINGO directory. Here is
the procedure you will need to follow to set up this data source:
1. Start up the SQL Analyzer utility provided with SQL Server by going to the Start menu in
Windows, selecting the Programs command, selecting the Microsoft SQL Server program
group, and then clicking on Query Analyzer.
2. Point the Query Analyzer to the machine running SQL Server.
3. Run the File|Open command and select the script file TRANDB_SQL.SQL from the LINGO
samples folder.
4. Run the script by issuing the Query|Execute command.
5. Exit the Query Analyzer.
6. Start up the ODBC Administrator as described in the section above: Creating an ODBC Data
Source from an Access Database.
7. Press the Add button to add a new ODBC data source: Select the SQL Server ODBC drive,
assign the data source the name "Transportation", and select the appropriate server machine.
8. You should now be able to load TRANDB.LG4 into LINGO and solve it.
Note: If you plan to use LINGO’s ODBC interface to write solutions to a table in SQL Server, then
the table must contain a field that is declared as a unique identifier. Failure to do so will
result in an error message claiming that the table is read-only.
Importing Data from Databases with @ODBC
To import a model’s data from an ODBC data source, we use the @ODBC function in the model’s
data section. @ODBC allows us to import both text formatted set members and numerical set attribute
values.
The syntax for using @ODBC to import data inside a data section is:
object_list = @ODBC([‘data_source’[, ‘table_name’
[,‘column_name_1’[, ‘column_name_2’ …]]]]);

420 CHAPTER 10
The object_list is a list, optionally separated by commas, containing model objects (i.e., attributes, sets,
or variables) that are to be initialized from the ODBC data source. Object_list may contain up to one
set and/or multiple set attributes. All set attributes in object_list must be defined on the same set. If
object_list contains a set, then all attributes in object_list must be defined on this set. The data_source
argument is the name of the ODBC data source that contains the data table. The table_name argument
is the name of the data table within the data source that contains the data. Finally, the column_name
arguments are the names of the data columns, or fields, in the data table table_name to retrieve the
initialization data from. Set attributes and primitive sets require one column name each to retrieve their
data from. Derived sets require one column name for each dimension of the set. Thus, a
two-dimensional derived set would require two columns of data to initialize its members.
If the data_source argument is omitted, the model's title is used in its place (see the discussion of the
TITLE statement in Chapter 1, Getting Started with LINGO). If table_name is omitted, the name of any
set in the object_list is used in its place. If there is no set in object_list, then the name of the set that the
attributes in object_list are defined on is used.
If the column_name arguments are omitted, LINGO will choose default names based on whether the
corresponding object in object_list is a set attribute, a primitive set, or a derived set. When the object
to be initialized is a set attribute or a primitive set, LINGO will use the name of the object as the
default column name. When the object is a derived set, LINGO will generate one default column name
for each dimension of the derived set, with each name being the same as the parent set that the given
dimension is derived from. As an example, a two-dimensional set named LINKS derived from the two
primitive sets SOURCE and DESTINATION would default to being initialized from the two columns
titled SOURCE and DESTINATION.
Keep in mind that LINGO expects to find set members in text format in the database, while set
attributes are expected to be in numeric format.
Some examples of using @ODBC to import data in a model's data section are:
Example 1: SHIPPING_COST =
@ODBC( 'TRANSPORTATION',
'LINKS','COST');
LINGO initializes the attribute SHIPPING_COST from the column COST contained in the
data table LINKS found in the ODBC data source TRANSPORTATION.
Example 2: VOLUME, WEIGHT =
@ODBC( 'TRUCKS', 'CAPACITY');
The database column names are omitted, so, assuming VOLUME and WEIGHT are set
attributes, LINGO defaults to using the attribute names (VOLUME and WEIGHT) as the
database column names. Therefore, LINGO initializes the attributes VOLUME and
WEIGHT from the columns also titled VOLUME and WEIGHT contained in the data table
named CAPACITY found in the ODBC data source TRUCKS.
Example 3: REQUIRED, DAYS = @ODBC();
In this example, we will assume a) we have titled the model PRODUCTION, b)
REQUIRED is a derived set derived from the two primitive sets JOB and WORKSTATION
( e.g., REQUIRED( JOB, WORKSTATION)), and c) DAYS is a set attribute defined on the
set REQUIRED. All arguments to the @ODBC function have been omitted, so LINGO
supplies PRODUCTION as the data source name; the set name REQUIRED as the data

INTERFACING WITH DATABASES 421
table name; and the three data column names JOB, WORKSTATION, and DAYS. Had we
wanted to be more specific, we could have explicitly included all the arguments to the
@ODBC function with the equivalent statement:
REQUIRED, DAYS = @ODBC( 'PRODUCTION', 'JOB',
'WORKSTATION', 'DAYS');
Importing Data with ODBC in a PERT Model
We will now modify the project scheduling model, PERT introduced in Chapter 2, Using Sets, to
demonstrate the use of @ODBC to import the set names of the project's tasks from a Microsoft Access
database. The modified model appears below, with changes listed in bold type:
SETS:
TASKS: TIME, ES, LS, SLACK;
PRED(TASKS, TASKS);
ENDSETS
DATA:
TASKS = @ODBC('PERTODBC', 'TASKS', 'TASKS');
PRED = @ODBC('PERTODBC', 'PRECEDENCE',
'BEFORE', 'AFTER');
TIME = @ODBC('PERTODBC');
ENDDATA
@FOR(TASKS(J)| J #GT# 1:
ES(J) = @MAX(PRED(I, J): ES(I) + TIME(I))
);
@FOR(TASKS(I)| I #LT# LTASK:
LS(I) = @MIN(PRED(I, J): LS(J) - TIME(I));
);
@FOR(TASKS(I): SLACK(I) = LS(I) - ES(I));
ES(1) = 0;
LTASK = @SIZE(TASKS);
LS(LTASK) = ES(LTASK);
Model: PERTODBC
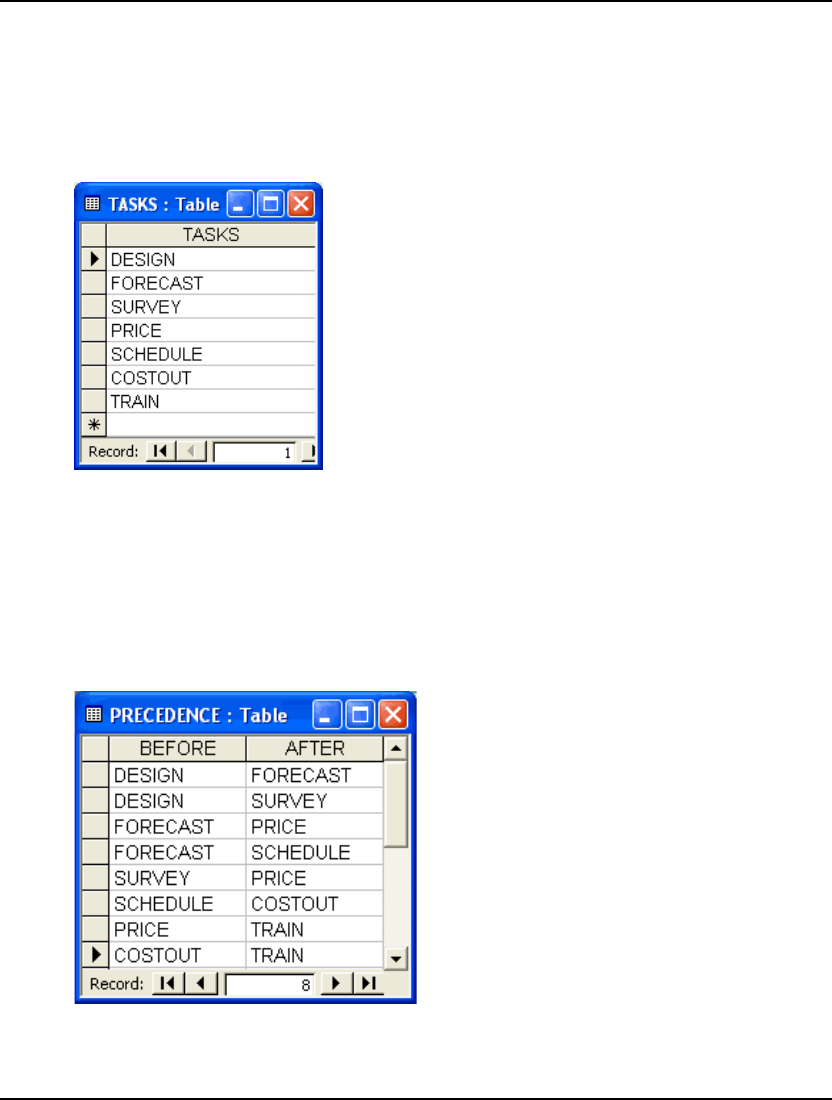
422 CHAPTER 10
With the statement:
TASKS = @ODBC('PERTODBC', 'TASKS', 'TASKS');
we now fetch the members of the TASKS set from our ODBC data source, as opposed to explicitly
listing them in the model. Specifically, we get the members of the TASKS set from the data column, or
field, TASKS contained in the table named TASKS from the ODBC data source PERTODBC. Here is
the data table as it appears in Access:
Access Database: PERTODBC.MDB
Next, we use the statement:
PRED = @ODBC('PERTODBC', 'PRECEDENCE',
'BEFORE', 'AFTER');
to fetch the members of the PRED set from an ODBC data source, as opposed to explicitly listing them
in the model. More specifically, we pull the members of the PRED set from the data columns
BEFORE and AFTER contained in the table named PRECEDENCE from the ODBC data source
PERTODBC. Here is the data table showing the precedence relations as it appears in Access:
Access Database: PERTODBC.MDB
Note that the PRECEDENCE set is a two-dimensional set. Thus, we must supply two database
columns containing the set members.
INTERFACING WITH DATABASES 423
In order to retrieve the values for the task times, we create the ODBC link:
TIME = @ODBC('PERTODBC');
Note that we only specified the ODBC data source name—the table and column names have been
omitted. In which case, LINGO supplies default values for the table and column. The object being
initialized, TIME, is a set attribute. Thus, LINGO supplies its parent set name, TASKS, as the default
table name. For the default column name, LINGO supplies the set attribute’s name, TIME. Had we
wanted to be specific, however, we could have explicitly entered all arguments to @ODBC with:
TIME = @ODBC('PERTODBC', 'TASKS', 'TIME');
Exporting Data with @ODBC
As is the case with most interface functions, @ODBC can export data as well as import it. Specifically,
you can use the @ODBC function in the data section of a model to export set members and attribute
values to ODBC data sources. In order to export solutions with @ODBC, you place calls to @ODBC
in the data section of your model. These @ODBC export instructions are executed each time your
model is solved.
The first form of syntax for using @ODBC to export data is:
@ODBC( ['data_source'[, 'table_name'[, 'column_name_1'[,…,
'column_name_n']]]]) = object_list;
Note: When importing, @ODBC appears on the right of the equality sign. When exporting, the
@ODBC function appears on the left of the equals sign.
The object_list is a list, optionally separated by commas, containing model objects (i.e., attributes, sets,
or variables) that are to be exported to the ODBC data source. Object_list may contain up to one set
and/or multiple set attributes. All set attributes in object_list must be defined on the same set. If
object_list contains a set, then all attributes in object_list must be defined on this set. The data_source
argument is the name of the ODBC data source containing the data table that will receive the exported
values. The table_name argument is the name of the data table within the data source that will receive
the data. Finally, the column_name arguments are the names of the receiving columns, or fields, in the
data table table_name. Set attributes and primitive sets require one receiving column name each.
Derived sets require one receiving column name for each dimension of the set. Thus, a two-
dimensional derived set would require two receiving columns in a data table.
If the data_source argument is omitted, the model's title is used in its place (see the discussion of the
TITLE statement in Chapter 1, Getting Started with LINGO). If table_name is omitted, the name of any
set in the object_list is used in its place. If there is no set in object_list, then the name of the set where
the attributes in object_list are defined is used.
If the column_name arguments are omitted, LINGO will choose default names based on whether the
corresponding object in object_list is either a set attribute, a primitive set, or a derived set. When the
object to be initialized is a set attribute or a primitive set, LINGO will use the name of the object as the
default column name. When the object is a derived set, LINGO will generate one default column name
for each dimension of the derived set, with each name being the same as the parent set that the given

424 CHAPTER 10
dimension is derived from. As an example, a two-dimensional set named LINKS derived from the
SOURCE and DESTINATION primitive sets would default to being exported to the two columns titled
SOURCE and DESTINATION.
Keep in mind that set members are exported as text, while set attributes are exported as double
precision floating point values.
Some examples of using @ODBC to export data values to an ODBC data source are:
Example 1: @ODBC( 'TRANSPORTATION',
'LINKS', 'VOLUME') = VOLUME;
LINGO sends the values of the VOLUME attribute to the column also titled VOLUME in
the data table LINKS in the ODBC data source TRANSPORTATION.
Example 2: @ODBC() = NUMBER_WORKING;
All arguments to the @ODBC function have been omitted and will default to the model's
title for the data source, the attributes parent set for the data table, and the attribute's name
for the column name. So, assuming we have used the TITLE statement to name this model
SCHEDULING, and the attribute NUMBER_WORKING is defined on the set
SCHEDULES, then LINGO exports the attribute NUMBER_WORKING to the column also
titled NUMBER_WORKING in the data table SCHEDULES in the ODBC data source
SCHEDULING.
The first form of syntax will generally be sufficient for most database export operations. However,
there may be times when you need to export only portions of the attributes, or you need to export
quantities computed from the attribute values. Our second form of syntax uses the @WRITEFOR
reporting function to handle these more general cases:
@ODBC( 'data_source', 'table_name', 'column_name_1'[,…,
'column_name_n']) = @WRITEFOR( setname
[ ( set_index_list) [ | conditional_qualifier]] : output_obj_1[,…, output_obj_n]);
@WRITEFOR functions like any other set looping function in that, as a minimum, you will need to
specify the set to loop over. Optionally, you may also specify an explicit set index list and a
conditional qualifier. If a conditional qualifier is used, it is tested for each member of the looping set
and output will not occur for any members that don't pass the test. It's this feature of being able to base
output on the results of a condition that distinguish this second style of syntax.
The list of output objects, of course, specifies what it is you want to output. As with the first form of
syntax, the output objects may be labels, set members and variable values. However, you have
additional latitude in that the output objects may now consist of complex expressions of the variable
values (e.g., you could compute the ratio of two variables). This is a useful feature when you need to
report statistics and quantities derived from the variable values. By placing these calculations in the
data section, as opposed to the model section, you avoid adding unnecessary complications to the
constraints of the model.
In general, you can do everything in the second form of syntax that you can do in the first, and more.
However, the first form has an advantage in that it can be very concise.
INTERFACING WITH DATABASES 425
Some examples of using @WRITEFOR for ODBC exports follow:
Example 1: @ODBC( 'TRANSPORTATION',
'SOLUTION', 'FROM', 'TO', 'VOLUME') =
@WRITEFOR( LINKS( I, J) | VOLUME( I, J) #GT# 0:
WAREHOUSE( I), CUSTOMER( J), VOLUME( I, J));
In this example, we exploit the ability to specify a conditional expression to weed zero
shipments out of the export. The nonzero values of the VOLUME attribute are sent to the
SOLUTION table in the TRANSPORTATION data source. The shipping warehouse set
name is placed in column FROM, the receiving customer set name goes to column TO, and
the shipping volume for the arc in placed in the VOLUME column.
Example 2: @ODBC( 'STAFFREP', 'STATS', 'RATIO') =
@WRITEFOR( DEPARTMENTS( D): ON_DUTY( D) / NEEDS( D));
Here, we make use of @WRITEFOR's ability to perform computations to compute a ratio
of two variables. Specifically, the ratio of on-duty staff to staffing needs by department is
placed into the column RATIO of table STATS in data source STAFFREP.
Note: When exporting to data tables, receiving columns that are longer than the number of exported
values can be filled out by either erasing the contents of the extra cells or leaving the extra
cells untouched. The default is to leave the extra cells untouched. If you would like to erase
the contents of the extra cells, you'll need to enable the Fill Out Ranges and Tables option. If
this option is enabled, extra text fields will be blanked out, while extra numeric fields will be
zeroed out.
426 CHAPTER 10
Exporting Data with ODBC in a PERT Model
Continuing from the PERT example used in the Importing Data with ODBC in a PERT Model section
above, we can add modifications to export the solution values of the earliest and latest start times (ES
and LS) back out to the PERTODBC data source. We will put these into a blank table titled
SOLUTION. We will also export the members of the TASKS set in order to label our table. The data
column, or field, that receives the TASKS members should be formatted as text, while the columns
receiving the ES and LS attributes should be declared as numeric. Here is a look at the blank table we
will be exporting to:
Access Database: PERTODBC.MDB
INTERFACING WITH DATABASES 427
After modifying the model to export the data back to the TASKS table, we have (with the relevant
changes in bold):
SETS:
TASKS: TIME, ES, LS, SLACK;
PRED(TASKS, TASKS);
ENDSETS
DATA:
TASKS = @ODBC('PERTODBC', 'TASKS', 'TASKS');
PRED = @ODBC('PERTODBC', 'PRECEDENCE', 'BEFORE', 'AFTER');
TIME = @ODBC('PERTODBC');
@ODBC('PERTODBC', 'SOLUTION', 'TASKS',
'EARLIEST START', 'LATEST START') =
TASKS, ES, LS;
ENDDATA
@FOR(TASKS(J)| J #GT# 1:
ES(J) = @MAX(PRED(I, J): ES(I) + TIME(I))
);
@FOR(TASKS(I)| I #LT# LTASK:
LS(I) = @MIN(PRED(I, J): LS(J) - TIME(I));
);
@FOR(TASKS(I): SLACK(I) = LS(I) - ES(I));
ES(1) = 0;
LTASK = @SIZE(TASKS);
LS(LTASK) = ES(LTASK);
Model: PERTODBC
With the data statement:
@ODBC('PERTODBC', 'SOLUTION', 'TASKS',
'EARLIEST START', 'LATEST START') =
TASKS, ES, LS;
we are sending the set TASKS to the text column TASKS, and the ES and LS attributes to the numeric
columns EARLIEST START and LATEST START. The data table is called SOLUTION, while the
ODBC data source name is PERTODBC.
428 CHAPTER 10
Once the model has been solved, the updated data table will resemble:
Access Database: PERTODBC.MDB
At the top of the solution report window, you will also notice an export summary report. There will be
one report for each @ODBC statement in the model used for exporting data. This report lists details as
to the operation of the @ODBC export. In the case of our PERT model, you should see the following
report:
Export Summary Report
---------------------
Transfer Method: ODBC BASED
ODBC Data Source: PERTODBC
Data Table Name: TASKS
Columns Specified: 3
TASKS
EARLIEST
LATEST
LINGO Column Length: 7
Database Column Length: 7
The Transfer Method will always list “ODBC BASED” when doing ODBC exports. Next, the data
source and table names are listed along with the number of columns specified and the column names.
The LINGO Column Length field lists the number of elements in each attribute. The Database Column
Length lists the length of the receiving columns in the database. In general, the LINGO Column
Length will agree with the Database Column Length. If not, LINGO must either truncate its output or
it will have insufficient data to fill out the columns in the database.
Export summary reports are not displayed when LINGO is in terse output mode. To place LINGO in
terse output mode, click on the Terse Output checkbox on the Interface tab of the LINGO|Options
dialog box.

INTERFACING WITH DATABASES 429
This version of the PERT model and its supporting database are contained in the SAMPLES directory.
Feel free to run the model to experiment with it if you like—you will find it under the name
PERTODBC. The supporting Access database file, PERTODBC.MDB, is also in the SAMPLES
subdirectory and you will need to register it with the ODBC Administrator as described above in
ODBC Data Sources.
Note that we exported start and finish times for all the tasks in the project. If we were dealing with a
large project there could be thousands of tasks to consider. With such an abundance of tasks, we might
be interested in reporting only those tasks that lie on the critical path. We'll modify our PERTODBC
example one last time to accomplish this using the @WRITEFOR reporting function.
For those unfamiliar with the concept of a critical path, it is the subset of tasks such that if any are
delayed the entire project will be delayed. Generally, and somewhat counterintuitive to what one
would expect, the set of tasks on the critical path will tend to be quite small compared to the total
number of tasks in a large project. A task is considered to be on the critical path when its earliest start
time is equal to its latest start time (i.e., there is no slack with respect to when the task must be started).
Below, we have modified PERTODBC to export only those tasks on the critical path.
MODEL:
SETS:
TASKS: TIME, ES, LS, SLACK;
PRED( TASKS, TASKS);
ENDSETS
DATA:
TASKS = @ODBC( 'PERTODBC', 'TASKS', 'TASKS');
PRED = @ODBC( 'PERTODBC', 'PRECEDENCE', 'BEFORE', 'AFTER');
TIME = @ODBC( 'PERTODBC');
@ODBC( 'PERTODBC', 'SOLUTION', 'TASKS',
'EARLIEST START', 'LATEST START') =
@WRITEFOR( TASKS( I) | ES( I) #EQ# LS( I):
TASKS( I), ES( I), LS( I));
ENDDATA
@FOR( TASKS( J)| J #GT# 1:
ES( J) = @MAX( PRED( I, J): ES( I) + TIME( I))
);
@FOR( TASKS( I)| I #LT# LTASK:
LS( I) = @MIN( PRED( I, J): LS( J) - TIME( I));
);
@FOR( TASKS( I): SLACK( I) = LS( I) - ES( I));
ES( 1) = 0;
LTASK = @SIZE( TASKS);
LS( LTASK) = ES( LTASK);
END
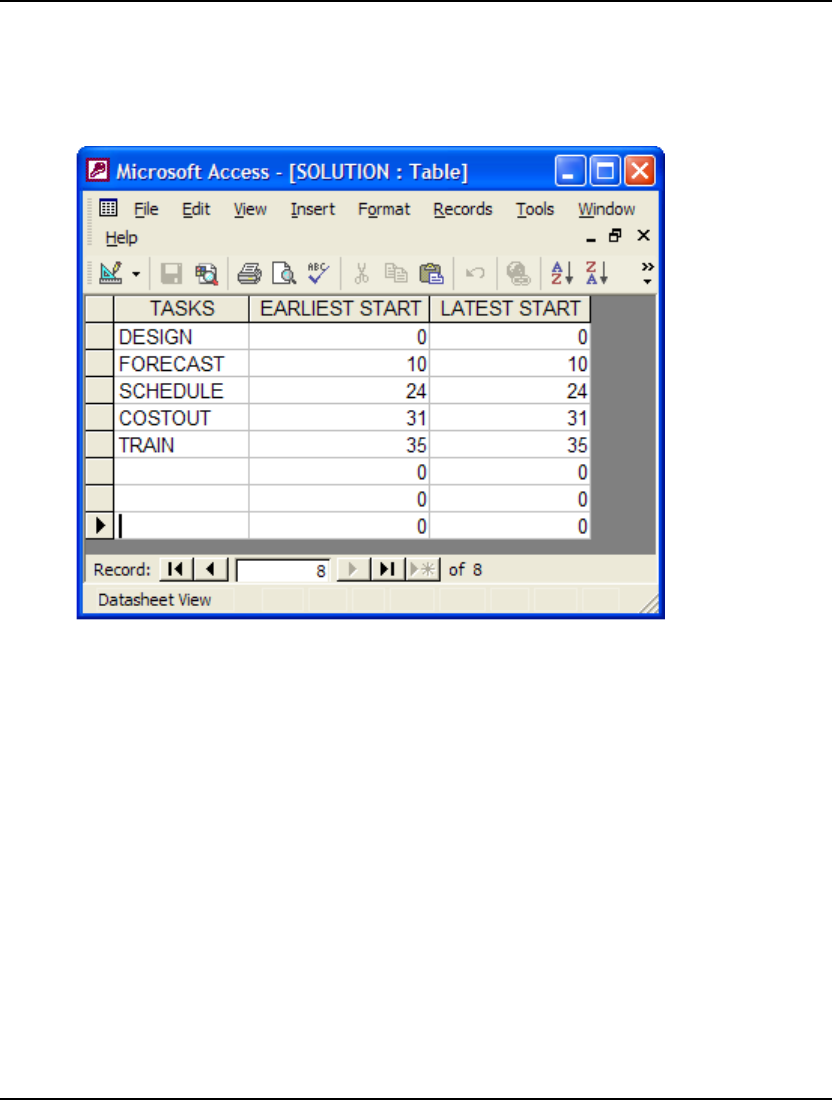
430 CHAPTER 10
We specify a conditional expression to test for the earliest start time equaling the latest start time,
thereby restricting the list of exported tasks to those that lie on the critical path. Note that if you limit
the number of output records there won't be enough records to completely fill our output table. We
can have LINGO fill out any extra fields with blanks and zeroes by enabling the Fill Out Ranges and
Tables option. Doing this, the solution table will resemble the following after solving the model:
Note that that LINGO nulled out all the extra records.
431
11 Interfacing with Other
Applications
Although LINGO has a convenient, interactive interface and a large library of callable functions that
make it easy to set up and solve models, there may be times when you would like to bundle LINGO's
functionality into your own applications, or call functions from within your LINGO models that were
written in an external programming language. LINGO makes use of the Dynamic Link Library (DLL)
standard under Windows to provide you with a “hook” to access LINGO's functionality from within
your own custom applications. This gives you the ability to build application specific front-ends to
LINGO that allow naïve users to input data and view solutions in a simple, familiar way without
having to worry about the details of LINGO modeling. Your application handles the details of driving
LINGO in the background, invisible to the user. LINGO also allows you to provide custom functions
in the DLL format that you can call from within any model with the @USER function.
In the following section, The LINGO Dynamic Link Library, we document how to call the LINGO
DLL in order to add LINGO's functionality to your own applications. Following this, in the section
User Defined Functions, we will show you how to build a function in an external programming
language and call it from a LINGO model with the @USER function.
The LINGO Dynamic Link Library
Windows versions of LINGO include a callable DLL. The ability to call a DLL is a standard feature of
all Windows development environments (e.g., Visual Basic, Delphi, and Visual C++). The LINGO
DLL is supplied in either 32-bit of 64-bit configurations and, thus, will run under all current releases of
Windows (Win32 and Win64). It is not callable under older 16-bit releases of Windows (e.g.,
Windows 3.x).
The interface to the LINGO DLL is relatively simple and gives you the ability to run a LINGO
command script from within your application. Given that you can access all the major features of
LINGO from a command script, the LINGO DLL interface is very powerful. You will, however, need
to familiarize yourself with LINGO's command language in order to build useful command scripts. For
more details on the commands available in the command language, see Command-line Commands. For
an example of a script file, see A Command Script Example.
432 CHAPTER 11
When LINGO is installed a number of examples on calling the DLL are installed, too. These
examples may be found in the Programming Samples folder below the main LINGO folder. You will
find examples for each of the following development environments:
♦ Visual C/C++
♦ Visual Basic
♦ Excel
♦ FORTRAN
♦ ASP .NET
♦ C# .NET
♦ VB .NET
♦ Delphi
♦ Java
In this chapter, we will walk through detailed examples on calling the LINGO DLL using both Visual
C/C++ and Visual Basic. Users of other development environments will also be interested in these
programming examples. Many of the ideas presented carry over to other development environments.
Staff-Scheduling Example Using the LINGO DLL
To illustrate interfacing with the LINGO DLL, we will again make use of the Pluto Dogs
staff-scheduling example introduced on page 54. We will create examples using both the Visual C++
and Visual Basic programming languages. We will construct a dialog box that resembles the
following:
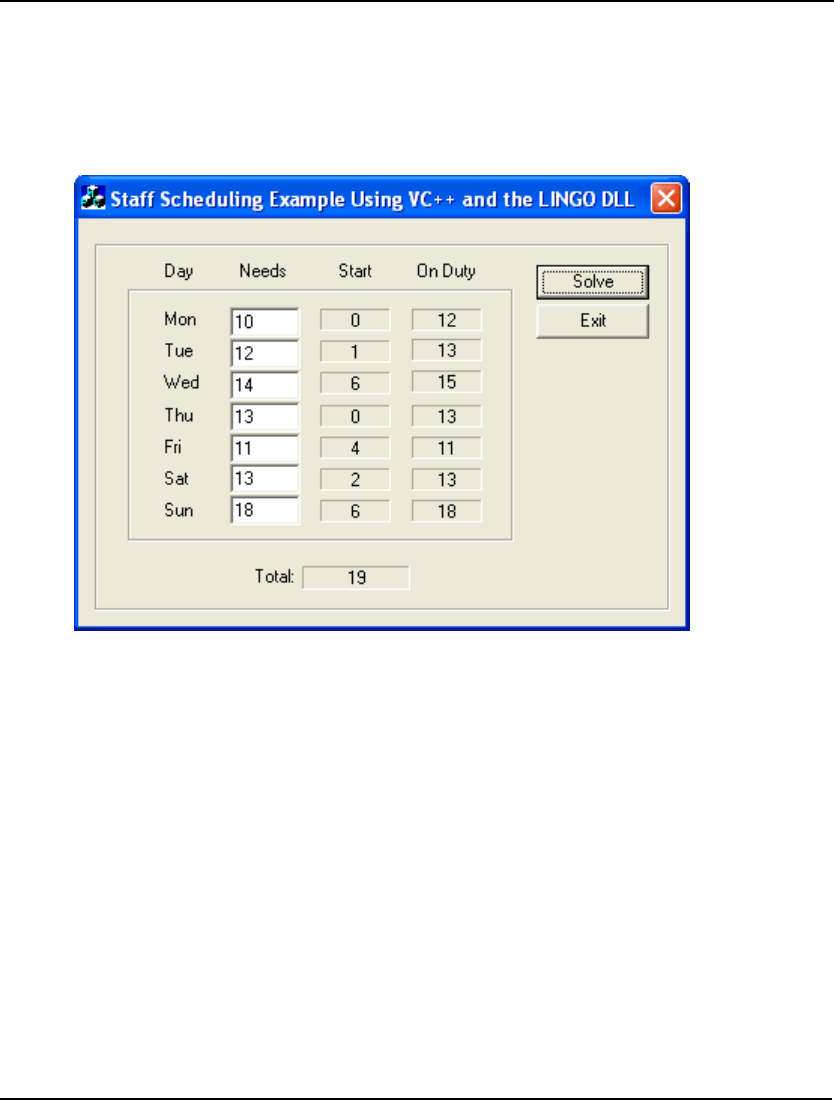
INTERFACING WITH OTHER APPLICATIONS 433
The user enters the staffing requirements in the cells of the Needs column and presses the Solve button.
The application then extracts the staffing requirements from the dialog box, passes them along with a
model to the LINGO DLL for solution, and places the results back into the dialog box for viewing.
Specifically, it shows the number of employees to start on each given day in the Start column, the
number of staff on duty in the On Duty column, and the total number of staff required in the Total cell.
As an example, here is how the dialog box will appear after a sample run:

434 CHAPTER 11
The Model
The model passed to LINGO to solve this problem is the familiar staffing model we’ve used before
with some modifications, and appears below with important changes in bold:
MODEL:
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/:
NEEDS, START, ONDUTY;
ENDSETS
[OBJECTIVE] MIN = @SUM(DAYS(I): START(I));
@FOR(DAYS(TODAY):
! Calculate number on duty;
ONDUTY(TODAY) =
@SUM(DAYS(D)| D #LE# 5:
START(@WRAP(TODAY - D + 1,
@SIZE(DAYS))));
! Enforce staffing requirement;
ONDUTY(TODAY) >= NEEDS(TODAY);
@GIN(START);
);
DATA:
NEEDS = @POINTER(1);
@POINTER(2) = START;
@POINTER(3) = ONDUTY;
@POINTER(4) = OBJECTIVE;
@POINTER(5) = @STATUS();
ENDDATA
END
Model: STAFFPTR
Since the LINGO script processor will read the model, it must begin with the MODEL: command and
end with the END command. The script processor treats all text between the MODEL: and END
keywords as model text, as opposed to script commands.
We have added the ONDUTY attribute to compute the number of employees on duty each day. We
compute these figures for the purpose of passing them back to the calling application, which, in turn,
posts them in the dialog box in the On Duty column.
We have named the objective row OBJECTIVE for the purpose of returning the objective’s value to
the calling application, so it may place the value in the Total cell.
The @POINTER Function
The @POINTER function in data, init and calc sections acts as direct memory link between the calling
application and the LINGO solver. This ability to do direct memory transfers of data in and out of
LINGO is very powerful. It allows for the fast transfer of data without the hassle of building and
parsing disk based files.
When you call the LINGO DLL, you can pass it a list of memory pointers. @POINTER( n) refers to
the n-th pointer in the passed pointer list. The @POINTER function only makes sense in a model when
accessing LINGO through the DLL or OLE interfaces.
INTERFACING WITH OTHER APPLICATIONS 435
If the @POINTER function appears on the right-hand side of a data statement, as in the case of the
following:
NEEDS = @POINTER( 1);
then LINGO will initialize the objects(s) on the left-hand side of the statement from the values in
memory beginning at the location referenced by the pointer on the right-hand side of the statement. On
the other hand, when the @POINTER function appears on the left-hand side of a data statement,
LINGO will export the values of the objects(s) on the right-hand side of the data statement to the
memory location referenced by the pointer on the left-hand side of the statement.
The @POINTER function reads and writes all numeric data (i.e., attribute values) using double
precision floating point format. BASIC and C/C++ developers know this as the double data type, while
FORTRAN developers refer to it as either REAL*8 or DOUBLE PRECISION. Set members are
passed as strings of ASCII text, with each member separated by a line feed character, with the list
being terminated with an null, or ASCII 0.
When setting aside memory locations for @POINTER, you must be sure to allocate adequate space.
LINGO assumes adequate space and/or supplied values are available at the passed memory locations.
If you do not allocate sufficient space or values, you may experience memory protection faults or, even
worse, erroneous results without warning.
So, reviewing the model's data section:
DATA:
NEEDS = @POINTER( 1);
@POINTER( 2) = START;
@POINTER( 3) = ONDUTY;
@POINTER( 4) = OBJECTIVE;
@POINTER( 5) = @STATUS();
ENDDATA
we see the staffing requirements attribute, NEEDS, is read from the first memory location. The START,
ONDUTY, and OBJECTIVE values are written to the second, third, and fourth memory locations,
respectively. Finally, the value for the @STATUS function is written to the fifth memory location.
See the following section for more details on the @STATUS function.

436 CHAPTER 11
The @STATUS Function
The @STATUS function returns the status of the solution process using the following codes:
@STATUS
Code Interpretation
0 Global Optimum - The optimal solution has been found.
1 Infeasible - No solution exists that satisfies all constraints.
2 Unbounded - The objective can be improved without
bound.
3 Undetermined - The solution process failed.
4 Feasible - A feasible solution was found that may, or may
not, be the optimal solution.
5 Infeasible or Unbounded - The preprocessor determined
the model is either infeasible or unbounded. Turn off
presolving and re-solve to determine which.
6 Local Optimum - Although a better solution may exist, a
locally optimal solution has been found.
7 Locally Infeasible - Although feasible solutions may
exist, LINGO was not able to find one.
8 Cutoff - The objective cutoff level was achieved.
9 Numeric Error - The solver stopped due to an undefined
arithmetic operation in one of the constraints.
In general, if @STATUS does not return a code of 0, 4, 6, or 8, the solution is of little use and should
not be trusted. In fact, if @STATUS does not return 0, 4, 6, or 8, in many cases LINGO will not even
export data to the @POINTER memory locations.
The @POINTER function reads and writes all data using double precision floating point format.
BASIC and C/C++ developers know this as the double data type, while FORTRAN developers refer to
it as either REAL*8 or DOUBLE PRECISION.
When setting aside memory locations for @POINTER, you must be sure to allocate adequate space.
LINGO assumes adequate space and/or supplied values are available at the passed memory locations.
If you do not allocate sufficient space or values, you may experience memory protection faults or, even
worse, erroneous results without warning.
Functions Exported by the LINGO DLL
The LINGO DLL exports twelve functions.The exported functions are contained in the file
Lingo12\Lingd12.Dll. The library file Lingo12\Programming Samples\Lingd12.lib may be used to
import these functions into your own custom application.
Below is a list of the functions exported by the LINGO DLL along with a brief description of each
routine’s functionality. The definitions are written using C language conventions. Refer to the
programming samples in the following sections for specific examples of the use of each of these
routines using Visual C and Visual Basic.

INTERFACING WITH OTHER APPLICATIONS 437
void LSclearPointersLng( pLSenvLINGO pL)
This clears out the list of @POINTER() pointers to user memory transfer areas established through
calls to LSsetPointerLng().
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
int LScloseLogFileLng( pLSenvLINGO pL)
This closes LINGO’s log file that was opened previously by a call to LSopenLogFileLng().
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.
pLSenvLINGO CALLTYPE LScreateEnvLng()
This creates a LINGO environment object. All other LINGO DLL routines require a valid pointer to a
LINGO environment object. You should free this object at the end of your application by calling
LSdeleteEnvLng(). LScreateEnvLng() will search the application's startup directory and the system
path for a valid LINGO license file. If you would prefer to pass LINGO the license key directly, refer
to the following function, LScreateEnvLicenseLNG().
Return Value:
Returns 0 if an error occurred, otherwise, a pointer to a LINGO environment object is
returned.
pLSenvLINGO CALLTYPE LScreateEnvLicenseLng( char* pcLicenseKey, int* pnErr)
This creates a LINGO environment object. All other LINGO DLL routines require a valid pointer to a
LINGO environment object. You should free this object at the end of your application by calling
LSdeleteEnvLng(). LScreateEnvLicenseLng() requires that you pass the license key directly. If you
would prefer to have LINGO search the application's startup directory and the system path for a valid
LINGO license file, refer to the previous function, LScreateEnvLng().

438 CHAPTER 11
Arguments:
pcLicenseKey Pointer to a text string containing a LINGO license key. The
license key may be found at the bottom of your LINGO license
file, typically stored in the main LINGO directory under the file
name LNDLNG??.LIC, where ?? is LINGO's version number.
The license key is delimited in the license file by a greater-than (>)
character.
pnError Pointer to an integer that returns 0 if no problem or an error code
listed in section LINGO DLL Error Codes.
Return Value:
Returns 0 if an error occurred, otherwise, a pointer to a LINGO environment object is
returned.
int LSdeleteEnvLng( pLSenvLINGO pL)
This deletes a LINGO environment object previously created through a call to LScreateEnvLng(),
which frees up the system memory allocated to the LINGO object.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.
int LSexecuteScriptLng( pLSenvLINGO pL, char* pcScript)
This routine is the main workhorse of the LINGO DLL that processes LINGO command scripts. The
script may be contained entirely in memory, or it may contain one or more TAKE commands to load
scripts from disk.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pcScript Pointer to a character string containing a LINGO command script.
Each line must be terminated with a linefeed character (ASCII 10),
and the entire script must be terminated with a NULL (ASCII 0).
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.
INTERFACING WITH OTHER APPLICATIONS 439
int LSgetCallbackInfoLng( pLSenvLINGO pL, int nObject, void* pResult)
You may establish a function in your application that the LINGO solver calls back to at regular
intervals to keep you abreast of its progress. We refer to this type of routine as being a callback
function and you may refer to section Callback Functions for more information. Your callback
function may then call LINGO through LSgetCallbackInfoLng() to request specific information from
the solver while it is processing a model.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
nObject Index of the information item you’re seeking. Current possibilities
are:
Index Name Type Information Item
0 LS_IINFO_VARIABLES_LNG Int Total number of
variables
1 LS_IINFO_VARIABLES_INTEGER_LNG Int Number of integer
variables
2 LS_IINFO_VARIABLES_NONLINEAR_LNG Int Number of
nonlinear variables
3 LS_IINFO_CONSTRAINTS_LNG Int Total number of
constraints
4 LS_IINFO_CONSTRAINTS_NONLINEAR_LNG Int Number of
nonlinear
constraints
5 LS_IINFO_NONZEROS_LNG Int Total nonzero
matrix elements
6 LS_IINFO_NONZEROS_NONLINEAR_LNG Int Number of
nonlinear nonzero
matrix elements
7 LS_IINFO_ITERATIONS_LNG Int Number of
iterations
8 LS_IINFO_BRANCHES_LNG Int Number of
branches (IPs only)
9 LS_DINFO_SUMINF_LNG Double Sum of
infeasibilities
10 LS_DINFO_OBJECTIVE_LNG Double Objective value
11 LS_DINFO_MIP_BOUND_LNG Double Objective bound
(IPs only)
12 LS_DINFO_MIP_BEST_OBJECTIVE_LNG Double Best objective
value found so far
(IPs only)
pResult Pointer to where you want LINGO to store the results of your
query. LINGO will place the result at this address. You must

440 CHAPTER 11
allocate four bytes of memory for ints and eight bytes of memory
for doubles beforehand.
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.
int LSgetCallbackVarPrimalLng( pLSenvLINGO pL, char* pcVarName, double*
pdPrimals)
You may establish a function in your application that the LINGO solver calls back to at regular
intervals to keep you abreast of its progress. We refer to this type of routine as being a callback
function, and you may refer to section Callback Functions for more information. Your callback
function may then call LINGO through LSgetCallbackVarPrimal() to request the current values for
attributes and/or scalar variables. This will allow you to keep your users posted on the values of the
model's variables in the current best solution found so far. This routine will only return values
successfully when solving integer models, or when solving models with the global solver.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pcVarName Pointer to a character string containing the name of the scalar variable or
attribute. The name must be terminated with either a blank or a NULL
(ASCII 0).
pdPrimals Points to where LINGO should write the variable value(s). You must
ensure that enough space is available for the full set of values to avoid
memory protection faults.
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed in section
LINGO DLL Error Codes is returned.
int LSopenLogFileLng( pLSenvLINGO pL, char *pcLogFile)
This creates a file for LINGO to write a log to while processing your script. In general, you should
always try to create a log file (at least in the early stages of your project) to assist with debugging. If an
error is occurring and you are not exactly sure why, then it is always a good idea to refer to the log file
for a clue.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pcLogFile Pointer to a character string containing the pathname for your log
file.
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.

INTERFACING WITH OTHER APPLICATIONS 441
int LSsetCallbackErrorLng( pLSenvLINGO pL, lngCBFuncError_t pcbf, void* pUserData)
Use this routine to specify a callback function that LINGO will call whenever an error is encountered.
This allows your application to keep close watch on any unusual conditions that might arise while
processing your script.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pcbf Pointer to your callback routine.
pUserData This is a user specified pointer. You may use it to point to any data
you might need to reference from your callback function. LINGO
merely passes the value of this pointer through to your callback
function. You may set this pointer to NULL if it is not required.
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.
The callback function you supply must use the standard call convention and must have the following
interface:
int MyErrCallback( pLSenvLINGO pL, void* pUserData, int nErrorCode, char*
pcErrorText);
Your computer will most likely crash if you don’t follow this interface specification exactly. The
LINGO error code is reported through the nErrorCode argument, along with the error text in
pcErrorText. You should set aside at least 200 bytes for the error text. The list of LINGO error codes
can be found in Appendix B, Error Messages.
int LSsetCallbackSolverLng( pLSenvLINGO pL, lngCBFuncError_t pcbf, void*
pUserData)
Use this routine to specify a callback function that LINGO will call at frequent intervals when solving
a model.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pcbf Pointer to your callback routine.
pUserData This is a user specified pointer. You may use it to point to any data
you might need to reference from your callback function. LINGO
merely passes the value of this pointer through to your callback
function. You may set this pointer to NULL if it is not required.
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.

442 CHAPTER 11
The callback function you supply must use the standard call convention and must have the following
interface:
int MySolverCallback( pLSenvLINGO pL, int nReserved, void* pUserData);
Your computer will most likely crash if you don’t follow this interface specification exactly. The
nReserved argument is reserved for future use and may be ignored.
int CALLTYPE LSsetPointerLng( pLSenvLINGO pL, double* pdPointer, int*
pnPointersNow)
Call this routine one or more times to pass a list of memory pointers to LINGO. These pointers are
used by LINGO’s @POINTER() function for moving data into and solutions out of the solver. In other
words, this allows you to have direct memory links with LINGO for fast and convenient data transfer.
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pdPointer Pointer to a memory transfer location to be used by an instance of
@POINTER().
pnPointersNow This is a pointer to an integer variable in which LINGO returns the
current number of entries in the @POINTER() pointer list. Thus,
on the first call to LSsetPointersLng(), this argument will return a
value of 1. The pointer list may be cleared at any time by a call to
LSclearPointersLng().
Return Value:
Returns 0 if no error occurred. Otherwise, one of the nonzero error codes listed below in
the section LINGO DLL Error Codes is returned.
LINGO DLL Error Codes
Most of the LINGO DLL functions return an error code. Below is a list of all possible codes:
Value Name Descriptions
0 LSERR_NO_ERROR_LNG No error.
1 LSERR_OUT_OF_MEMORY_LNG Out of dynamic system
memory.
2 LSERR_UNABLE_TO_OPEN_LOG_FILE_LNG Unable to open the log file.
3 LSERR_INVALID_NULL_POINTER_LNG A NULL pointer was passed
to a routine that was expecting
a non-NULL pointer.
4 LSERR_INVALID_INPUT_LNG An input argument contained
invalid input.
5 LSERR_INFO_NOT_AVAILABLE_LNG A request was made for
information that is not
currently available.
INTERFACING WITH OTHER APPLICATIONS 443
6 LSERR_UNABLE_TO_COMPLETE_TASK_LNG Unable to successfully
complete the specified task.
7 LSERR_INVALID_LICENSE_KEY_LNG The license key passed to
LScreateEnvLicenceLng()
was invalid.
8 LSERR_INVALID_VARIABLE_NAME_LNG A variable name passed to
LSgetCallbackVarPrimal()
was invalid.
1000 LSERR_JNI_CALLBACK_NOT_FOUND_LNG A valid callback function was
not found in the calling Java
application.
Supporting DLLs
The main LINGO DLL requires many additional component DLLs. All the required DLLs are
installed as part of the normal LINGO installation in the main LINGO folder. If you need a specific list
of all the supporting DLLs required by the LINGO DLL, then you can open Lingd12.Dll in the
Dependency Walker utility available at no charge from the following website:
http://www.dependencywalker.com. The Dependency Walker program is a useful tool that lists all the
required DLLs for an application, their current location on your system, and flags any DLLs that aren’t
currently available.
Staff Scheduling Using the LINGO DLL and Visual C++
In this section, we will illustrate the use of Microsoft Visual C/C++ to build an application that
interfaces with the LINGO DLL to solve the staff-scheduling problem presented above. This section
assumes the reader is well versed in the use of Visual C++. Visual Basic users may want to jump
ahead to the Visual Basic Example section.
If you would rather skip the details involved in constructing this project and would prefer to
experiment with the completed application, it can be found under the path
\LINGO12\Programming Samples\VC++\STAFF1\STAFF.EXE.
Building the Application in C++
We will be working from a code base generated using Visual C++’s AppWizard facility. The
generated code is for a dialog based application. In other words, the interface to the application will
consist of a single dialog box. This dialog box will be modified, so it resembles the one illustrated
above with fields for staffing requirements, daily employee starts, and so on.
444 CHAPTER 11
The source code for this project may be found in the Programming Samples\STAFF1 subdirectory or
you can create your own project using Visual C/C++ 6.0 as follows:
1. Start Visual C++ and issue the File|New command.
2. Select the Projects tab, give the project a name, select MFC
AppWizard(Exe) as the type of application, and click the OK button.
3. Click the dialog based radio button and then the Next button.
4. Clear the About box button, check the OLE Automation button, check the
OLE Controls button, and press the Next button. OLE support is required
for some of the features in the LINGO DLL.
5. Click the Next button again.
6. Click the Finish button.
After completing these steps, the following summary of the project should be shown:
Click the OK button, and AppWizard will generate the skeleton code base.
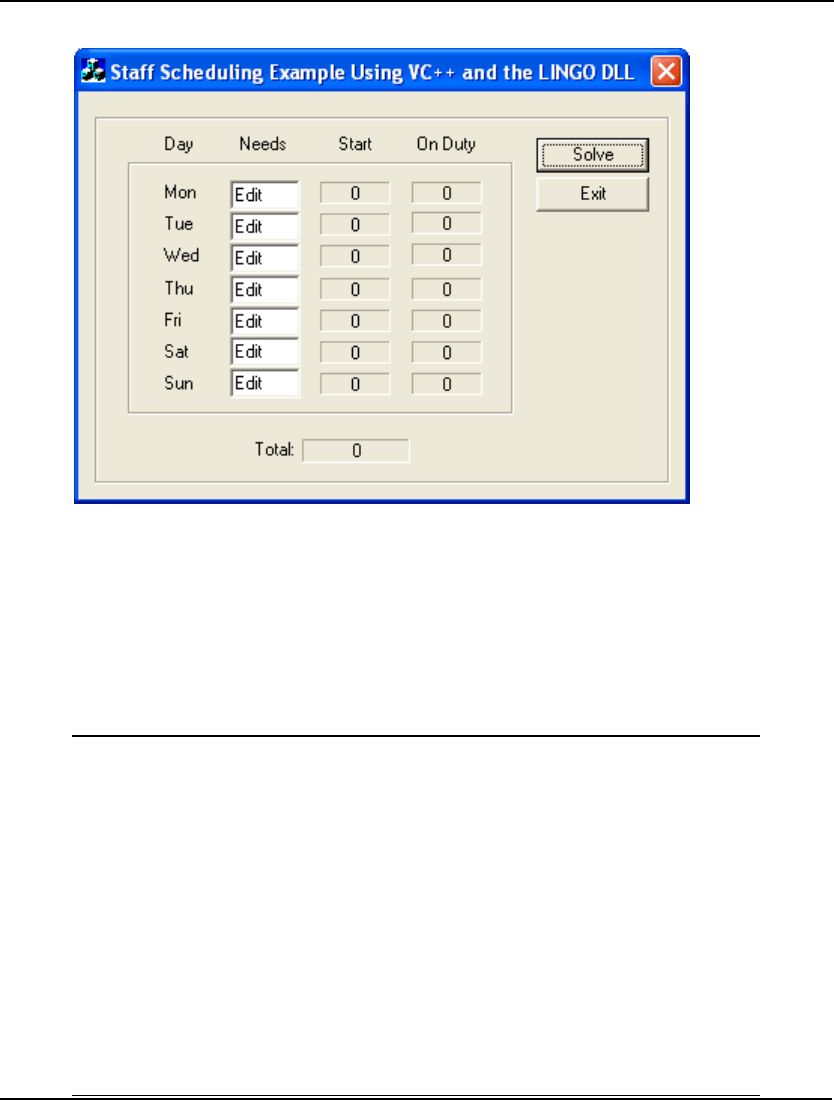
INTERFACING WITH OTHER APPLICATIONS 445
Use the resource editor to modify the application’s dialog box, so it resembles the following:
Next, use the ClassWizard in Visual C++ to associate member variables with each of the fields in the
dialog box. From the View menu, select the ClassWizard command and then select the Member
Variables tab.
At this point, the LINGO DLL import library must be added to the project in order to make the LINGO
DLL available to the code. Do this by running the Project|Add to Project|Files command and select the
file \LINGO12\Programming Samples\LINGD12.LIB for addition to the project.
After doing that, add the definitions of the LINGO DLL routines to the project. Simply include the
Lingd12.h header file at the top of the dialog class header file as follows (code changes listed in bold):
// staffDlg.h : header file
//
#include "lingd12.h"
#if
!defined(AFX_STAFFDLG_H__74D746B7_CA4D_11D6_AC89_00010240D2AE__INCLUD
ED_)
#define
AFX_STAFFDLG_H__74D746B7_CA4D_11D6_AC89_00010240D2AE__INCLUDED_
#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000
/////////////////////////////////////////////////////////////////////
////////
// CStaffDlg dialog
.
.
.

446 CHAPTER 11
All the groundwork has now been laid down and we’re ready to begin writing the actual code to call
LINGO to solve the staffing model. Go to the Resource View of the project, open the dialog box
resource, and then double click on the Solve button. You will be prompted to create a handler function
for the button, which should be named OnSolve. Now, edit the stub version of OnSolve, so it contains
the following code:
void CStaffDlg::OnSolve()
{
int nError, nPointersNow;
CString csScript, cs;
double dNeeds[7], dStart[7], dOnDuty[7], dStatus, dTotal;
// Get user's staffing requirements from our dialog box
UpdateData();
// Load staffing requirements into the LINGO transfer array.
// LINGO uses double precision for all values.
dNeeds[ 0] = (double) m_nNeedsMon;
dNeeds[ 1] = (double) m_nNeedsTue;
dNeeds[ 2] = (double) m_nNeedsWed;
dNeeds[ 3] = (double) m_nNeedsThu;
dNeeds[ 4] = (double) m_nNeedsFri;
dNeeds[ 5] = (double) m_nNeedsSat;
dNeeds[ 6] = (double) m_nNeedsSun;
// create the LINGO environment object
pLSenvLINGO pLINGO;
pLINGO = LScreateEnvLng();
if ( !pLINGO)
{
AfxMessageBox("Unable to create LINGO Environment");
return;
}
// Open LINGO's log file
nError = LSopenLogFileLng( pLINGO, "\\LINGO12\\LINGO.log");
if ( nError) goto ErrorExit;
// Pass memory transfer pointers to LINGO
// @POINTER(1)
nError = LSsetPointerLng( pLINGO, dNeeds, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(2)
nError = LSsetPointerLng( pLINGO, dStart, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(3)
nError = LSsetPointerLng( pLINGO, dOnDuty, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(4)
nError = LSsetPointerLng( pLINGO, &dTotal, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(5)
nError = LSsetPointerLng( pLINGO, &dStatus, &nPointersNow);
if ( nError) goto ErrorExit;

INTERFACING WITH OTHER APPLICATIONS 447
// Here is the script we want LINGO to run
csScript = "SET ECHOIN 1\n";
csScript = csScript +
"TAKE \\LINGO12\\SAMPLES\\STAFFPTR.LNG\n";
csScript = csScript +
"GO\n";
csScript = csScript +
"QUIT\n";
// Run the script
dStatus = -1.e0;
nError = LSexecuteScriptLng( pLINGO, (LPCTSTR) csScript);
// Close the log file
LScloseLogFileLng( pLINGO);
// Any problems?
if ( nError || dStatus)
{
// Had a problem
AfxMessageBox("Unable to solve!");
} else {
// Everything went ok ... load results into the dialog box
m_csStartMon.Format( "%d", (int) dStart[0]);
m_csStartTue.Format( "%d", (int) dStart[1]);
m_csStartWed.Format( "%d", (int) dStart[2]);
m_csStartThu.Format( "%d", (int) dStart[3]);
m_csStartFri.Format( "%d", (int) dStart[4]);
m_csStartSat.Format( "%d", (int) dStart[5]);
m_csStartSun.Format( "%d", (int) dStart[6]);
m_csOnDutyMon.Format( "%d", (int) dOnDuty[0]);
m_csOnDutyTue.Format( "%d", (int) dOnDuty[1]);
m_csOnDutyWed.Format( "%d", (int) dOnDuty[2]);
m_csOnDutyThu.Format( "%d", (int) dOnDuty[3]);
m_csOnDutyFri.Format( "%d", (int) dOnDuty[4]);
m_csOnDutySat.Format( "%d", (int) dOnDuty[5]);
m_csOnDutySun.Format( "%d", (int) dOnDuty[6]);
m_csCost.Format( "%g", dTotal);
UpdateData( FALSE);
}
goto Exit;
ErrorExit:
cs.Format( "LINGO Errorcode: %d", nError);
AfxMessageBox( cs);
return;
Exit:
LSdeleteEnvLng( pLINGO);
}
The first section of OnSolve is straightforward and deals with extracting the user’s staffing
requirements from the dialog box. Note that the data is stored in a double precision array rather than as
integers. This is because these values will be passed to LINGO, which only passes values in double
precision format.

448 CHAPTER 11
Our first call to LINGO creates the LINGO environment object with the following code:
// create the LINGO environment object
pLSenvLINGO pLINGO;
pLINGO = LScreateEnvLng();
if ( !pLINGO)
{
AfxMessageBox("Unable to create LINGO Environment");
return;
}
The pLSenvLINGO data type is defined in the LINGO header file, lingd11.h.
Then, a log file for LINGO is established with the following call:
// Open LINGO's log file
nError = LSopenLogFileLng( pLINGO, "\\LINGO.log");
if ( nError) goto ErrorExit;
As mentioned above, opening a log file for LINGO is good practice, at least when you’re debugging
the application. If something should go wrong, the log file will generally contain a helpful clue.
Our next step is to pass LINGO the physical addresses it will use to resolve the @POINTER() function
references used in the data section of the model (refer to the Staff Scheduling Example Using the
LINGO DLL section above for more details). This is done as follows:
// Pass memory transfer pointers to LINGO
// @POINTER(1)
nError = LSsetPointerLng( pLINGO, dNeeds, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(2)
nError = LSsetPointerLng( pLINGO, dStart, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(3)
nError = LSsetPointerLng( pLINGO, dOnDuty, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(4)
nError = LSsetPointerLng( pLINGO, &dTotal, &nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(5)
nError = LSsetPointerLng( pLINGO, &dStatus, &nPointersNow);
if ( nError) goto ErrorExit;
In summary, when LINGO is called to solve the model, the staffing needs are passed to LINGO in the
dNeeds array via the @POINTER( 1) reference. Solution information is passed from LINGO back to
the application in the dStart, dOnDuty, dTotal, and dStatus structures via @POINTER() references 2
through 5, respectively. If any of this is unfamiliar, review The @POINTER() Function section under
the Staff Scheduling Example Using the LINGO DLL section above.

INTERFACING WITH OTHER APPLICATIONS 449
Next, the following code is used to build the command script:
// Here is the script we want LINGO to run
csScript = "SET ECHOIN 1\n";
csScript = csScript +
"TAKE \\LINGO12\\SAMPLES\\STAFFPTR.LNG\n";
csScript = csScript +
"GO\n";
csScript = csScript +
"QUIT\n";
The script consists of four commands, which are each terminated with a new line character (ASCII
10). The end of the script is terminated with a NULL character (ASCII 0). These commands and their
functions are:
Command Function
SET ECHOIN 1 Causes LINGO to echo input to the log file. This is a useful feature
while building and debugging an application.
TAKE Loads the model from a disk file. The TAKE command may be used to
load model files, as in this example. It may also be used to run nested
command scripts contained in files.
GO Calls the solver to optimize the model.
QUIT Closes down LINGO’s script processor and returns control to the
calling application.
For more information on scripting commands, refer to Chapter 6, Command-line Commands.
At this point, the script is ready to be passed off to LINGO for processing with the following call:
// Run the script
dStatus = -1.e0;
nError = LSexecuteScriptLng( pLINGO, (LPCTSTR) csScript);
Note that dStatus is initialized to –1. LINGO returns the model status through memory transfer
location number 5 (i.e., @POINTER( 5)) to the dStatus variable. LINGO will only return a status value
if it was able to solve the model. If an unexpected error were to occur, LINGO might not ever reach
the solution phase. In that case, dStatus would never be set. Initializing dStatus to a negative value
tests for this situation. Given that LINGO returns only non-negative status codes, a negative status
code would indicate a problem. This method of error trapping is effective, but not particularly elegant.
Another method that involves specifying an error callback routine is demonstrated below.
Now, LINGO’s log file may be closed down by calling LScloseLogFileLng():
// Close the log file
LScloseLogFileLng( pLINGO);
Next, the following code tests to see if LINGO was able to find an optimal solution:
// Any problems?
if ( nError || dStatus)
// Had a problem
AfxMessageBox("Unable to solve!");
} else {

450 CHAPTER 11
Note that the code returned in nError pertains only to the mechanical execution of the script processor.
It has nothing to do with the status of the model’s solution, which is returned in dStatus via the use of
the @POINTER() and @STATUS() functions (see the Staff Scheduling Example Using the LINGO
DLL section above). A model may actually be infeasible or unbounded, and the error code returned by
LSexecuteScript() will give no indication. Thus, it is important to add a mechanism to return a
solution’s status to the calling application, as done here with the @STATUS() -> @POINTER(5) ->
dStatus link. The end result in the sample code is that “Unable to solve” is printed if either error
condition occurs. A more user-friendly application would offer more specific information regarding
the error condition.
As a final step, in order to avoid memory leaks in your application, remember to free up LINGO’s
environment when through:
Exit:
LSdeleteEnvLng( pLINGO);
If everything has been entered correctly, you should now be able to build and run the project.
Visual Basic Staff Scheduling Using the LINGO DLL
In this section, we will illustrate the use of Microsoft Visual Basic to build an application that
interfaces with the LINGO DLL to solve the staff-scheduling problem presented above. This section
assumes the reader is well versed in the use of Visual Basic.
If you would rather skip the details involved in constructing this project and would prefer to
experiment with the completed appliction, it can be found under the path
\LINGO12\Programming Samples\VBasic\STAFFVB.EXE.
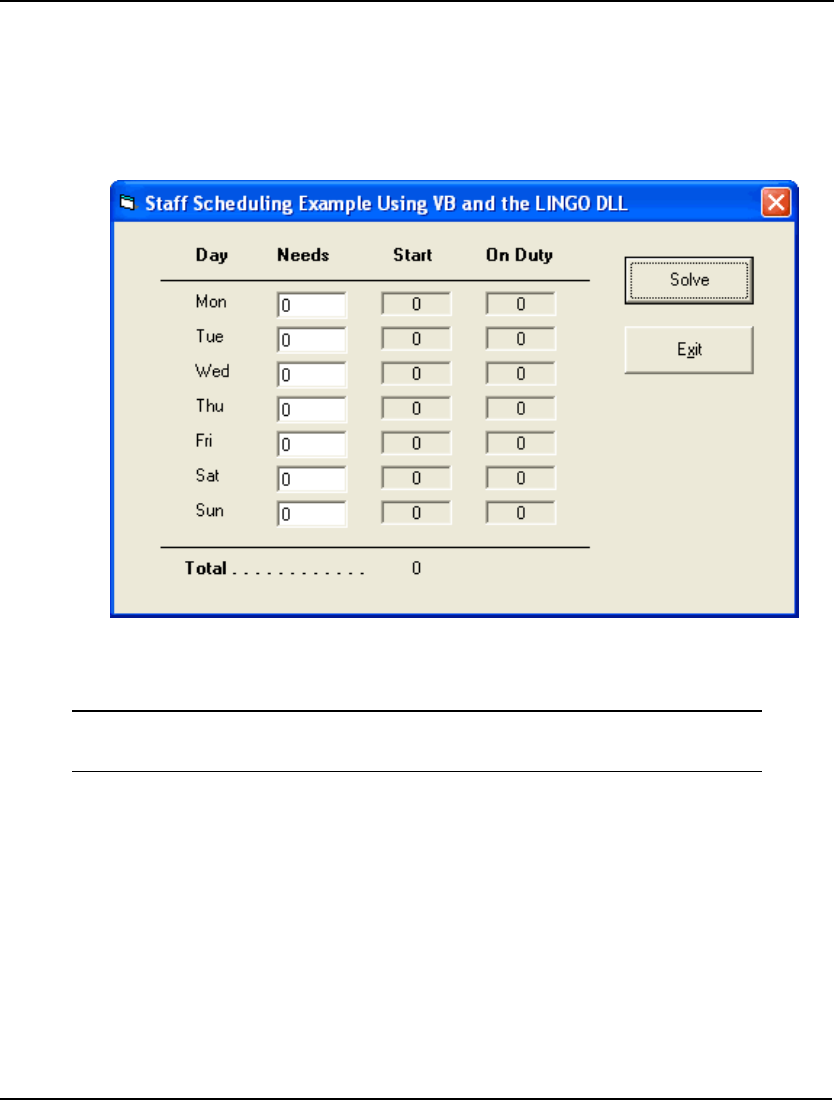
INTERFACING WITH OTHER APPLICATIONS 451
Building the Application
You can build the project as follows:
1. Start Visual Basic and then issue the File|NewProject command.
2. Select Standard Exe and click the OK button.
3. Use the resource editor to format the project’s form until it resembles the
following:
Now, add handler code for the two buttons in the form. The Exit button is easy. All the Exit button
does when the user clicks it is exit the application. So, double click on the Exit button and enter the
following code:
Private Sub Exit_Click()
End
End Sub
A little more work will be required to setup the Solve button. When the Solve button is pressed, the
application will retrieve the staffing requirements from the form, pass them along with the model to
the LINGO script processor (LGVBSCRIPT) to solve the model, retrieve the solution, and post the
solution in the form.

452 CHAPTER 11
First, we must declare the external LINGO functions. Do this by adding the
\LINGO12\Programming Samples\LINGD12.BAS module to the project using the Project|Add
Module command in VB. This module contains the definitions of all the exported function in the
LINGO DLL, and makes them available to our project.
Now, add the handler code for the Solve button. Go to the form, double click on the Solve button, and
enter the following code:
Private Sub Solve_Click()
' Calls the LINGO DLL to solve the staffing
' model in STAFFPTR.LNG. Staffing
' requirements are taken from the dialog
' box.
' Get the staffing needs from the dialog box
Dim dNeeds(7) As Double
For i = 1 To 7
dNeeds(i) = Needs(i - 1).Text
Next i
' Create the LINGO environment object
Dim pLINGO As Long
pLINGO = LScreateEnvLng()
If pLINGO = 0 Then
MsgBox ("Unable to create LINGO Environment.")
GoTo FinalExit
End If
' Open LINGO's log file
Dim nError As Long
nError = LSopenLogFileLng(pLINGO, "\LINGO.log")
If nError <> 0 Then GoTo ErrorExit
' Pass memory transfer pointers to LINGO
Dim dStart(7) As Double, dOnDuty(7) As Double
Dim dTotal As Double, dStatus As Double
' @POINTER(1)
nError = LSsetPointerLng(pLINGO, dNeeds(1), nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(2)
nError = LSsetPointerLng(pLINGO, dStart(1), nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(3)
nError = LSsetPointerLng(pLINGO, dOnDuty(1), nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(4)
nError = LSsetPointerLng(pLINGO, dTotal, nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(5)
nError = LSsetPointerLng(pLINGO, dStatus, nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' Build LINGO's command script (commands
' are terminated with an ASCII 10
Dim cScript As String

INTERFACING WITH OTHER APPLICATIONS 453
' Causes LINGO to echo input
cScript = "SET ECHOIN 1" & Chr(10)
' Read in the model file
cScript = cScript & _
"TAKE \LINGO12\SAMPLES\STAFFPTR.LNG" & Chr(10)
' Solve the model
cScript = cScript & "GO" & Chr(10)
' Quit LINGO DLL
cScript = cScript & "QUIT" & Chr(10)
' Mark end of script with a null byte
cScript = cScript & Chr(0)
' Run the script
dStatus = -1#
nError = LSexecuteScriptLng(pLINGO, cScript)
' Close the log file
LScloseLogFileLng (pLINGO)
' Problems?
If nError > 0 Or dStatus <> 0 Then
MsgBox ("Unable to solve!")
GoTo ErrorExit
End If
' Place Start values in dialog box
For i = 1 To 7
Start(i - 1).Caption = dStart(i)
Next i
' Place On Duty values in dialog box
For i = 1 To 7
OnDuty(i - 1).Caption = dOnDuty(i)
Next i
' Put Total staffing in dialog box
Total.Caption = dTotal
LSdeleteEnvLng (pLINGO)
GoTo FinalExit:
ErrorExit:
MsgBox ("LINGO Error Code: " & nError&)
LSdeleteEnvLng (pLINGO)
FinalExit:
End Sub
The first section of the Solve_Click procedure is straightforward and deals with extracting the user’s
staffing requirements from the dialog box. Note that the data is stored in a double precision array,
rather than as integers. This is because these values will be passed to LINGO, which only passes
numeric values in double precision format.

454 CHAPTER 11
The first call to LINGO creates the LINGO environment object with the following code:
' Create the LINGO environment object
Dim pLINGO As Long
pLINGO = LScreateEnvLng()
If pLINGO = 0 Then
MsgBox ("Unable to create LINGO Environment.")
GoTo FinalExit
End If
Next, a log file for LINGO is established with the call:
' Open LINGO's log file
Dim nError As Long
nError = LSopenLogFileLng(pLINGO, "\LINGO.log")
If nError <> 0 Then GoTo ErrorExit
As mentioned above, opening a log file for LINGO is good practice, at least when you’re debugging
the application. If something should go wrong, the log file will generally contain a helpful clue.
The next step is to pass LINGO the physical addresses it will use to resolve the @POINTER() function
references used in the data section of the model (refer to the Staff Scheduling Example Using the
LINGO DLL section above for more details). This is done as follows:
' Pass memory transfer pointers to LINGO
Dim dStart(7) As Double, dOnDuty(7) As Double
Dim dTotal As Double, dStatus As Double
' @POINTER(1)
nError = LSsetPointerLng(pLINGO, dNeeds(1), nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(2)
nError = LSsetPointerLng(pLINGO, dStart(1), nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(3)
nError = LSsetPointerLng(pLINGO, dOnDuty(1), nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(4)
nError = LSsetPointerLng(pLINGO, dTotal, nPointersNow)
If nError <> 0 Then GoTo ErrorExit
' @POINTER(5)
nError = LSsetPointerLng(pLINGO, dStatus, nPointersNow)
If nError <> 0 Then GoTo ErrorExit
In summary, when LINGO is called to solve the model, the staffing needs are passed to LINGO in the
dNeeds array via the @POINTER( 1) reference. Solution information is passed from LINGO back to
the application in the dStart, dOnDuty, dTotal, and dStatus structures via @POINTER() references 2
through 5, respectively. If any of this is unfamiliar, review The @POINTER() Function section under
the Staff Scheduling Example Using the LINGO DLL section above.
INTERFACING WITH OTHER APPLICATIONS 455
Next, the following code is used to build the command script:
' Build LINGO's command script (commands
' are terminated with an ASCII 10
Dim cScript As String
' Causes LINGO to echo input
cScript = "SET ECHOIN 1" & Chr(10)
' Read in the model file
cScript = cScript & _
"TAKE \LINGO12\SAMPLES\STAFFPTR.LNG" & Chr(10)
' Solve the model
cScript = cScript & "GO" & Chr(10)
' Quit LINGO DLL
cScript = cScript & "QUIT" & Chr(10)
' Mark end of script with a null byte
cScript = cScript & Chr(0)
The script consists of four commands, which are each terminated with a new line character (ASCII
10). The end of the script is terminated with a NULL character (ASCII 0). These commands and their
functions are:
Command Function
SET ECHOIN 1 Causes LINGO to echo input to the log file. This is a useful feature
while building and debugging an application.
TAKE Loads the model from a disk file. The TAKE command may be used to
load model files, as in this example. It may also be used to run nested
command scripts contained in files.
GO Calls the solver to optimize the model.
QUIT Closes down LINGO’s script processor and returns control to the
calling application.
At this point, the script is ready to be passed off to LINGO for processing with the following call:
' Run the script
dStatus = -1#
nError = LSexecuteScriptLng(pLINGO, cScript)
Note that dStatus is initialized to –1. LINGO returns the model status through memory transfer
location number 5 (i.e., @POINTER( 5)) to the dStatus variable. LINGO will only return a status
value, if it was able to solve the model. If an unexpected error were to occur, LINGO might not ever
reach the solution phase. In that case, dStatus would never be set. Initializing dStatus to a negative
value tests for this situation. Given that LINGO returns only non-negative status codes, a negative
status code would indicate a problem. This method of error trapping is effective, but not particularly
elegant. Another method that involves specifying an error callback routine is demonstrated below.
Now, LINGO’s log file may be closed down by calling LScloseLogFileLng():
' Close the log file
LScloseLogFileLng (pLINGO)

456 CHAPTER 11
Next, the following code tests to see if LINGO was able to find an optimal solution:
' Problems?
If nError > 0 Or dStatus <> 0 Then
MsgBox ("Unable to solve!")
GoTo ErrorExit
End If
Note that the code returned in nError pertains only to the mechanical execution of the script processor.
It has nothing to do with the status of the model’s solution, which is returned in dStatus via the use of
the @POINTER() and @STATUS() functions (see the Staff Scheduling Example Using the LINGO
DLL section above). A model may actually be infeasible or unbounded, and the error code returned by
LSexecuteScriptLng()will give no indication. Thus, it is important to add a mechanism to return a
solution’s status to the calling application, as done here with the @STATUS() -> @POINTER(5) ->
dStatus link. The end result in the sample code is that “Unable to solve” is printed if either error
condition occurs. A more user-friendly application would offer more specific information regarding
the error condition.
As a final step, in order to avoid a memory leak in the application, remember to free up LINGO’s
environment when through:
LSdeleteEnvLng (pLINGO)
GoTo FinalExit:
If everything has been entered correctly, you should now be able to run the project.
Passing Set Members with @POINTER
In the previous examples, when using the @POINTER function, we only passed attribute values back
and forth. You may also pass set members using @POINTER, with the primary difference being that
the set members are passed as ASCII text, as opposed to double precision numeric values. In addition,
each set member is separated by a line feed (ASCII 10), with the end of the list of set members
denoted with a null (ASCII 0) character.
In order to illustrate passing set members via @POINTER, we will modify the knapsack problem
discussed above in section Binary Integer Example - The Knapsack Problem. You will recall that the
data in a knapsack problem consists of the list of potential items to include in the knapsack, their
weight, their utility/value, and the knapsack's capacity. We will pass all this data to LINGO via the
@POINTER function, including the set of potential items. After solving the model, we will create a
new set, derived from the original set of items, which contains only those items that are included in the
optimal solution. Finally, we will use the @POINTER function to pass the optimal set of items back to
our calling program so that we can display them for the user.
We will develop this example using the C programming language, however, the concepts should carry
over in a straightforward manner to all other development environments. The code for this example
may be found in the Programming Samples\VC++\Knapsack folder off the main LINGO directory.

INTERFACING WITH OTHER APPLICATIONS 457
The Model
Here is a copy of the knapsack model our application will load into LINGO:
MODEL:
SETS:
ITEMS: INCLUDE, WEIGHT, RATING;
ENDSETS
DATA:
ITEMS = @POINTER( 1);
WEIGHT = @POINTER( 2);
RATING = @POINTER( 3);
KNAPSACK_CAPACITY = @POINTER( 4);
ENDDATA
SUBMODEL SACK:
MAX = @SUM( ITEMS: RATING * INCLUDE);
@SUM( ITEMS: WEIGHT * INCLUDE) <=
KNAPSACK_CAPACITY;
@FOR( ITEMS: @BIN( INCLUDE));
ENDSUBMODEL
CALC:
!keep output to a minimum;
@SET( 'TERSEO', 1);
!solve the model;
@SOLVE( SACK);
!fix the INCLUDE attribute to it's optimal value;
@FOR( ITEMS( I): INCLUDE( I) = INCLUDE( I));
ENDCALC
SETS:
!construct a set of the optimal items;
ITEMSUSED( ITEMS) | INCLUDE( &1) #GT# .5:;
ENDSETS
DATA:
!send optimal items set back to caller;
@POINTER( 5) = ITEMSUSED;
!along with the solver status;
@POINTER( 6) = @STATUS();
ENDDATA
END
Model: SACK
Note: Some of the model features in this example take advantage of the scripting capability in
LINGO models. Scripting in models is discussed in more detail in Chapter 13, Programming
LINGO.
In the model's sets section:
SETS:
ITEMS: INCLUDE, WEIGHT, RATING;
ENDSETS

458 CHAPTER 11
We define the ITEMS set, which will store the set of potential items for the knapsack. Each item has
the following attributes:
• INCLUDE ⎯ a binary variable indicating whether or not the item is to be included in the
optimal knapsack.
• WEIGHT ⎯ the item's weight
• RATING ⎯ the items utility, or value.
In the data section, we ask LINGO to import all the data for the model via the @POINTER function:
DATA:
ITEMS = @POINTER( 1);
WEIGHT = @POINTER( 2);
RATING = @POINTER( 3);
KNAPSACK_CAPACITY = @POINTER( 4);
ENDDATA
Note that in addition to strictly numeric values, we are also importing the set ITEMS. This set will be
passed from our calling application as an ASCII string.
Next, we have the actual knapsack model. We partition the model as a submodel within our main
model (the concept of submodels is discussed further in Chapter 13):
SUBMODEL SACK:
MAX = @SUM( ITEMS: RATING * INCLUDE);
@SUM( ITEMS: WEIGHT * INCLUDE) <=
KNAPSACK_CAPACITY;
@FOR( ITEMS: @BIN( INCLUDE));
ENDSUBMODEL
This submodel contains three expressions. First, there's the objective that maximizes total utility of the
selected items. Second, there is a constraint that forces total weight to not exceed capacity. Finally,
via the @BIN function, we force the INCLUDE attribute members to be either 0 or 1, given that
fractional solution do not make sense for this model.
The next section is a calc section where we perform three steps:
CALC:
!keep output to a minimum;
@SET( 'TERSEO', 1);
!solve the model;
@SOLVE( SACK);
!fix the INCLUDE attribute to it's optimal value;
@FOR( ITEMS( I): INCLUDE( I) = INCLUDE( I));
ENDCALC
The first step sets the TERSEO function to minimize output from LINGO. Next, we use the @SOLVE
function to solve the knapsack submodel. Finally,. we loop over the ITEMS set, fixing the INCLUDE
attribute members to their optimal values in the SACK submodel. The reason we need to fix their
values is that we will need them in the following sets section where we use a set membership condition
to generate the optimal set of items in the knapsack (set membership conditions will reject variables
that aren't fixed in value).
Next, we derive the set ITEMSUSED from the original set of all potential items, however, we only
include those items that have a nonzero value in the optimal solution:

INTERFACING WITH OTHER APPLICATIONS 459
SETS:
!construct a set of the optimal items;
ITEMSUSED( ITEMS) | INCLUDE( &1) #GT# .5:;
ENDSETS
As our last step, we construct a data section to send the set of optimal items back to the calling
program via @POINTER:
DATA:
!send optimal items set back to caller;
@POINTER( 5) = ITEMSUSED;
!along with the solver status;
@POINTER( 6) = @STATUS();
ENDDATA

460 CHAPTER 11
The Code
Here is a copy of the C code we will use to drive our application:
#include <stdlib.h>
#include <string.h>
#include "..\..\lingd12.h"
/*
Solves a simple knapsack problem, passing
all data to Lingo and retrieving the optimal
set of knapsack items for display
*/
void main()
{
// input data for model:
// potential items in knapsack
char pcItems[256] = "ANT_REPEL \n BEER \n BLANKET \n"
"BRATWURST \n BROWNIES \n FRISBEE \n SALAD \n"
"WATERMELON";
// and their weights
double pdItemWeight[8] = { 1, 3, 4, 3, 3, 1, 5,10};
// and their rankings
double pdItemRank[8] = { 2, 9, 3, 8,10, 6, 4,10};
// knapsack size
double dSackSize = 15;
// other declarations
int i, nPointersNow, nError;
double dStatus=-1.0;
char pcScript[256];
char pcItemsSolution[256];
// create the LINGO environment object
pLSenvLINGO pLINGO;
pLINGO = LScreateEnvLng();
if ( !pLINGO)
{
printf( "Can''t create LINGO environment!\n");
goto FinalExit;
}
// Open LINGO's log file
nError = LSopenLogFileLng( pLINGO, "LINGO.log");
if ( nError) goto ErrorExit;
// Pass memory transfer pointers to LINGO
// @POINTER(1) - Items set
nError = LSsetPointerLng( pLINGO, (void*) pcItems,
&nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(2) - Item weights

INTERFACING WITH OTHER APPLICATIONS 461
nError = LSsetPointerLng( pLINGO, (void*) pdItemWeight,
&nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(3) - Item ranks
nError = LSsetPointerLng( pLINGO, (void*) pdItemRank,
&nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(4) - Sack size
nError = LSsetPointerLng( pLINGO, (void*) &dSackSize,
&nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(5) - Output region for optimal items set
nError = LSsetPointerLng( pLINGO, (void*) pcItemsSolution,
&nPointersNow);
if ( nError) goto ErrorExit;
// @POINTER(6) - Variable to receive solution status
nError = LSsetPointerLng( pLINGO, &dStatus, &nPointersNow);
if ( nError) goto ErrorExit;
// Here is the script we want LINGO to run:
// Load the model, solve the model, exit.
strcpy( pcScript, "TAKE SACK.LNG \n GO \n QUIT \n");
// Run the script
nError = LSexecuteScriptLng( pLINGO, pcScript);
if ( nError) goto ErrorExit;
// display solution status
printf("\nSolution status (should be 0): %d\n", (int) dStatus);
// display items in optimal sack
printf("\nItems in optimal sack:\n%s\n", pcItemsSolution);
// Close the log file
LScloseLogFileLng( pLINGO);
// All done
goto NormalExit;
ErrorExit:
printf("LINGO Error Code: %d\n", nError);
NormalExit:
LSdeleteEnvLng( pLINGO);
FinalExit: ;
}
SACK.C
There are a couple of interesting features to note in this code pertaining to the passing of set members.
First off, there is the declaration of the original set members:

462 CHAPTER 11
// potential items in knapsack
char pcItems[256] = "ANT_REPEL \n BEER \n BLANKET \n"
"BRATWURST \n BROWNIES \n FRISBEE \n SALAD \n"
"WATERMELON";
The set members are merely listed as one long string, separated by line feeds (\n). We also added
blank spaces for readability, which LINGO strips out when it parses the names. Note, that since we
are working in C, there is an implicit null byte at the end of this string due to the use of double quotes.
This terminating null is important, because it lets LINGO know where the end of the list occurs.
We pass a pointer to the set to LINGO with the following call to LSsetPointerLng
// @POINTER(1) - Items set
nError = LSsetPointerLng( pLINGO, (void*) pcItems,
&nPointersNow);
if ( nError) goto ErrorExit;
We pass a pointer to the set to LINGO with the following call to LSsetPointerLng. For receiving the
optimal set of items back from LINGO we set aside the following text array: char
pcItemsSolution[256];
We let LINGO know to store the solution set in this array with the following call to LSLsetPointerLng:
// @POINTER(5) - Output region for optimal items set
nError = LSsetPointerLng( pLINGO, (void*) pcItemsSolution,
&nPointersNow);
Recall that this statement in the code pairs with the following statement in the model to establish the
link for receiving the optimal set of items:
!send optimal items set back to caller;
@POINTER( 5) = ITEMSUSED;
If you have Visual C/C++ 6.0 installed on your machine, you should be able to build the application by
going to the \LINGO\Programming Samples\VC++\Knapsack folder and issuing the NMAKE
command. Alternatively, you may simply go to the folder and run the sack.exe executable. After
running the application, you should see the following:
Solution status (should be 0): 0
Items in optimal sack:
ANT_REPEL
BEER
BLANKET
BRATWURST
BROWNIES
FRISBEE
From the solution we see that all items except the salad and watermelon are included in the optimal
solution.
Callback Functions
In many instances, solving a model can be a lengthy operation. Given this, it may be useful to provide
some device to keep the user posted as to the progress of the optimization. The standard interactive

INTERFACING WITH OTHER APPLICATIONS 463
version of LINGO displays a status window showing the iteration count, objective value, and various
other model statistics each time the solver is invoked. In addition, the user has the ability to interrupt
the solver by clicking on a button in the status window. You can provide similar functionality to users
through the LINGO DLL by supplying LINGO with a callback function—so named because the code
calls the LINGO solver, and the LINGO solver then calls back to the supplied callback routine.
In the next section, the calling sequences used in establishing a callback function are discussed. After
that, there are sample callback routines to the Visual C++ and Visual Basic staff scheduling examples
illustrated above.
Specifying a Callback Function
To specify a callback function, the LINGO exported routine LSsetCallbackSolverLng() needs to be
called before calling LINGO’s script processor. The callback function will be called frequently by the
LINGO solver.
You will recall from above the calling sequence for LSsetCallbackSolverLng:
int LSsetCallbackSolverLng( pLSenvLINGO pL, lngCBFuncError_t pcbf, void*
pUserData)
Arguments:
pL Pointer to a LINGO environment created by a previous call to
LScreateEnvLng().
pcbf Pointer to your callback routine.
pUserData This is a user specified pointer. You may use it to point to any data you might
need to reference from your callback function. LINGO merely passes the
value of this pointer through to your callback function. You may set this
pointer to NULL if it is not required.
Return Value:
Returns 0 if no error occurred. Otherwise, it returns one of the nonzero error codes listed
below in the section LINGO DLL Error Codes.
The callback function must use the standard call convention and must have the following interface:
int MySolverCallback( pLSenvLINGO pL, int nReserved, void* pUserData);
Your computer will most likely crash if this interface specification is not followed exactly. The
nReserved argument is reserved for future use and may be ignored.
Once the callback function has control, information regarding the solver’s status can be retrieved from
LINGO using the LSgetCallbackInfoLng()function. See the section Functions Exported by the LINGO
DLL above for more information on the LSgetCallbackInfoLng() interface.
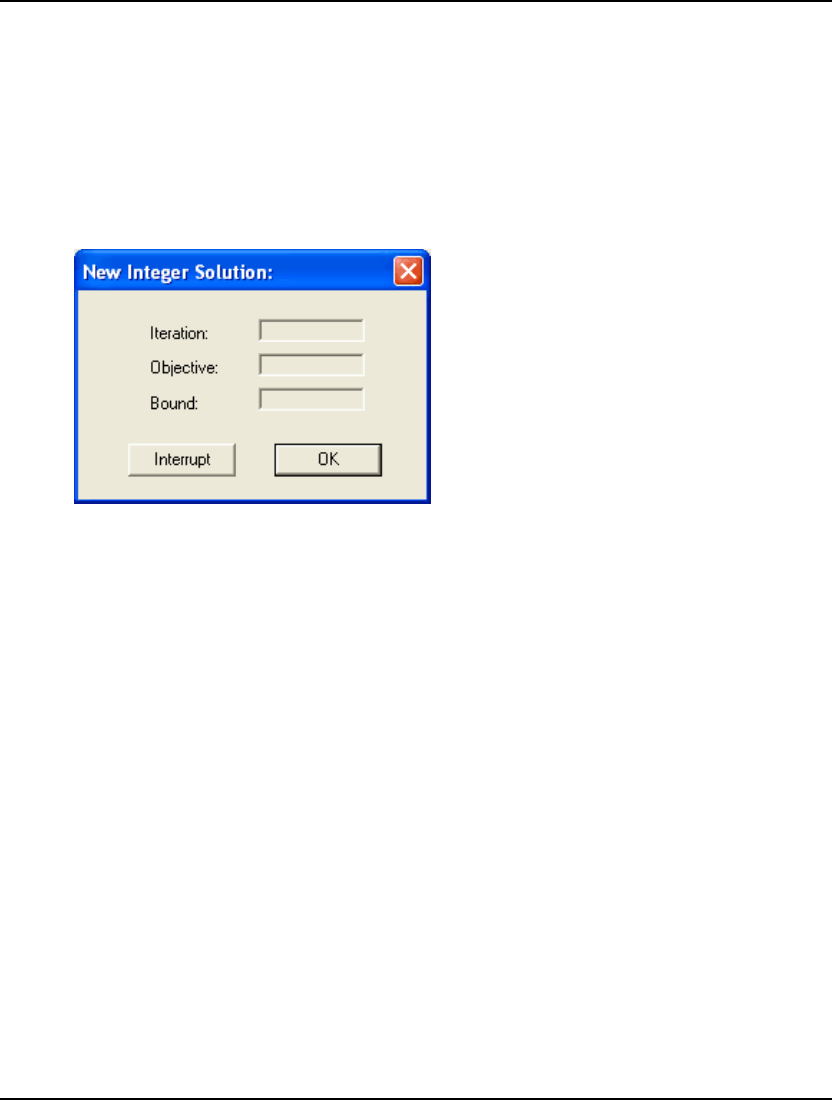
464 CHAPTER 11
A Visual C++ Callback Function
We will now extend the Visual C++ staffing example presented above by introducing a callback
function. The callback function in this example will post a small dialog box each time the solver finds
a better integer solution. The dialog box will display the solver’s iteration count, the objective value
for the new solution, the bound on the objective, and also include a button to allow the user to interrupt
the solver if they desire. You can find the complete project for this sample in the directory
LINGO12\Programming Samples\VC++\STAFF2.
The first step is to design the dialog box that we will post whenever a new integer solution is found.
Here is a look at the dialog box for this example:
The box has three edit fields for the iterations, objective, and bound. There are two buttons—one to
interrupt the solver and the other to clear the dialog box.

INTERFACING WITH OTHER APPLICATIONS 465
The next step is to use the ClassWizard to attach a handler class to the new dialog box. This class was
named CNewIPDlg. When a class has been attached to the dialog box, then the ClassWizard must be
used to assign member variables to handle the Iterations, Objective, and Bound edit fields. Once this is
done, the header file for the dialog box will resemble:
// NewIPDlg.h : header file
//
////////////////////////////////////////////////////////////////
// CNewIPDlg dialog
class CNewIPDlg : public CDialog
{
// Construction
public:
CNewIPDlg(CWnd* pParent = NULL); // standard constructor
// Dialog Data
//{{AFX_DATA(CNewIPDlg)
enum { IDD = IDD_NEW_IP_SOLUTION };
CString m_csBound;
CString m_csIteration;
CString m_csObjective;
//}}AFX_DATA
// Overrides
// ClassWizard generated virtual function overrides
//{{AFX_VIRTUAL(CNewIPDlg)
protected:
virtual void DoDataExchange(CDataExchange* pDX);
//}}AFX_VIRTUAL
// Implementation
protected:
// Generated message map functions
//{{AFX_MSG(CNewIPDlg)
// NOTE: the ClassWizard will add member functions here
//}}AFX_MSG
DECLARE_MESSAGE_MAP()
};
Callback Dialog Header File (NewIPDlg.h)

466 CHAPTER 11
Here is the code to handle events from the new dialog box:
// NewIPDlg.h : header file
//
/////////////////////////////////////////////////////////////////
// CNewIPDlg dialog
class CNewIPDlg : public CDialog
{
// Construction
public:
CNewIPDlg(CWnd* pParent = NULL); // standard constructor
// Dialog Data
//{{AFX_DATA(CNewIPDlg)
enum { IDD = IDD_NEW_IP_SOLUTION };
CString m_csBound;
CString m_csIteration;
CString m_csObjective;
//}}AFX_DATA
// Overrides
// ClassWizard generated virtual function overrides
//{{AFX_VIRTUAL(CNewIPDlg) protected:
virtual void DoDataExchange(CDataExchange* pDX);
//}}AFX_VIRTUAL
// Implementation
protected:
// Generated message map functions
//{{AFX_MSG(CNewIPDlg)
// NOTE: the ClassWizard will add member functions here
//}}AFX_MSG
DECLARE_MESSAGE_MAP()
};
Callback Dialog Handler (NewIPDlg.cpp)
The code in these two files was entirely generated by the ClassWizard, requiring no actual user input.

INTERFACING WITH OTHER APPLICATIONS 467
Next, the code for the callback function must be added. Here is a copy of the global routine that was
added for this purpose:
int __stdcall MyCallback( void* pModel, int nReserved,
void* pUserData)
{
// Callback function called by the LINGO solver
//
// return value: >= 0 if solver is to continue, else < 0 to interrupt
// Get current best IP
int nErr;
double dBestIP;
nErr = LSgetCallbackInfoLng( pModel,
LS_DINFO_MIP_BEST_OBJECTIVE_LNG, &dBestIP);
if ( nErr) return( 0);
// Get best IP value published in dialog box
double* pdBestIPShown = (double*) pUserData;
// Is current better than incumbent?
if ( dBestIP < *pdBestIPShown)
{
// Yes ... save its value
*pdBestIPShown = dBestIP;
// Get iteration count from LINGO
int nIterations;
LSgetCallbackInfoLng( pModel, LS_IINFO_ITERATIONS_LNG,
&nIterations);
// Get bound on solution
double dBound;
LSgetCallbackInfoLng( pModel, LS_DINFO_MIP_BOUND_LNG, &dBound);
// Create a dialog to show the current solution value
CNewIPDlg dlgNewIP;
// Initialize the fields of the dialog
dlgNewIP.m_csIteration.Format( "%d", nIterations);
dlgNewIP.m_csObjective.Format( "%d", (int) dBestIP);
dlgNewIP.m_csBound.Format( "%d", (int) dBound);
// Post the dialog and check for a user interrupt
if ( dlgNewIP.DoModal() == IDCANCEL) return( -1);
}
return( 0);
}
Callback Routine

468 CHAPTER 11
Of course, this routine has the same interface that was described in the previous section:
int __stdcall MySolverCallback( pLSenvLINGO pL, int nReserved, void* pUserData)
The following code uses the LSgetCallbackInfo routine to get the value of the current best integer
solution:
// Get current best IP
int nErr;
double dBestIP;
nErr = LSgetCallbackInfoLng( pModel,
LS_DINFO_MIP_BEST_OBJECTIVE_LNG, &dBestIP);
if ( nErr) return( 0);
The constant, LS_DINFO_MIP_BEST_OBJECTIVE, is defined in the LINGD11.H header file.
We then get the value for the best integer solution that we have currently posted in the dialog box with
the statement:
// Get best IP value published in dialog box
double* pdBestIPShown = (double*)pUserData;
Note that this statement references the user data pointer, pUserData. This pointer is passed to LINGO
when the callback function is established, and it is useful as a means of accessing the data from within
the callback function. In this particular case, a single variable is being pointing to. If needed, the
pointer could reference a large data structure containing whatever data desired.
Next, test to see if the latest integer solution is better than the incumbent solution with the statement:
// Is current better than incumbent?
if ( dBestIP < *pdBestIPShown)
If the new solution is better, then we get additional information from LINGO on the iteration count and
solution bound. Also, an instance of the callback dialog box to display the latest information in is
created with the line:
// Create a dialog to show the current solution value
CNewIPDlg dlgNewIP;
The new data is then loaded into the fields of the dialog box:
// Initialize the fields of the dialog
dlgNewIP.m_csIteration.Format( "%d", nIterations);
dlgNewIP.m_csObjective.Format( "%d", (int) dBestIP);
dlgNewIP.m_csBound.Format( "%d", (int) dBound);
As the final step in this callback routine, we display the dialog box, and if the user hits the interrupt
button we return a –1, indicating that the solver should stop and return with the best answer found so
far:
// Post the dialog and check for a user interrupt
if ( dlgNewIP.DoModal() == IDCANCEL) return( -1);

INTERFACING WITH OTHER APPLICATIONS 469
At this point, there is one more piece of code to add. We must make a call to the
LSsetCallbackSolverLng() routine to pass LINGO a pointer to our callback routine. A good place to
do this is right after creating the LINGO environment in the OnSolve() handler code for our Solve
button. The changes are listed below in bold type:
// create the LINGO environment object
pLSenvLINGO pLINGO;
pLINGO = LScreateEnvLng();
if ( !pLINGO)
{
AfxMessageBox("Unable to create LINGO Environment");
return;
}
// Pass LINGO a pointer to our callback function
nError = LSsetCallbackSolverLng( pLINGO, &MyCallback,
&dBestIPShown);
if ( nError) goto ErrorExit;
// Open LINGO's log file
nError = LSopenLogFileLng( pLINGO, "\\LINGO.log");
if ( nError) goto ErrorExit;
A Visual Basic Callback Function
We will now extend the Visual Basic staffing example presented above by introducing a callback
function. The callback function in this example will post a small dialog box each time the solver finds
a better integer solution. The dialog box will display the solver’s iteration count, the objective value
for the new solution, and the bound on the objective. You can find the complete project for this sample
in the directory LINGO12\Programming Samples\VBasic\STAFF2.
First, we need to construct a callback function and place it in a separate Module file (.bas file) . Here
are the contents of the callback function file Module1.bas:
Public Function MySolverCallback(ByVal pModel As Long, _
ByVal nReserved As Long, ByRef dBestIP As Double) As Long
' Callback function called by the LINGO DLL
' during model solution.
'
' Return value: >= 0 if solver is to continue,
' else < 0 to interrupt the solver
Dim nReturnVal As Long
nReturnVal = 0
' Get current best IP
Dim dObj As Double
Dim nError As Long
nError = LSgetCallbackInfoDoubleLng(pModel, _
LS_DINFO_MIP_BEST_OBJECTIVE_LNG, dObj)
' Check for any error
If (nError = LSERR_NO_ERROR_LNG) Then
' Is it better than the best one displayed so far?
If (dObj < dBestIP) Then
470 CHAPTER 11
' Yes ... display this solution
' Save the new best objective value
dBestIP = dObj
' Get the iteration count from LINGO
Dim nIterations As Long
nResult = LSgetCallbackInfoLongLng(pModel, _
LS_IINFO_ITERATIONS_LNG, nIterations)
' Get the objective bound from LINGO
Dim dBound As Double
nResult = LSgetCallbackInfoDoubleLng(pModel, _
LS_DINFO_MIP_BOUND_LNG, dBound)
' Display the information in a dialog box
Dim nButtonPressed
Dim cMessage As String
cMessage = "Objective:" + Str(dBestIP) _
+ Chr(10) + "Bound:" + Str(dBound) _
+ Chr(10) + "Iterations:" + Str(nIterations)
nButtonPressed = MsgBox(cMessage, vbOKCancel)
If (nButtonPressed = vbCancel) Then
nReturnVal = -1
End If
End If
End If
MySolverCallback = nReturnVal
End Function
VB Callback Module (Module1.bas)
Note: A VB callback function must be placed in a Module file (.bas file) . The callback function
will not work if it is placed in a Forms file (.frm file). Also, the callback function and the
module file must have different names. If the module file has the same name as the callback
function, then the VB AddressOf operator will not be able to return the address of the callback
function.
You will recall from the section Specifying a Callback Function above that the callback routine must
use the following calling sequence:
int __stdcall MySolverCallback( pLSenvLINGO pL, int nReserved, void* pUserData)
An equivalent function definition using VB code is:
Public Function MySolverCallback(ByVal pModel As Long, _
ByVal nReserved As Long, ByRef dBestIP As Double) As Long
VB uses the standard call (__stdcall) convention by default, so we need not specify this explicitly.
We will make use of the user data pointer to pass the value of the best objective displayed so far in the
dBestIP argument. This variable will hold the objective value of the best integer solution found so far.
We compare each new objective value to the best one found so far. If the latest is an improvement
over the incumbent, then we display a dialog box summarizing the new solution.

INTERFACING WITH OTHER APPLICATIONS 471
The following code uses the LSgetCallbackInfo routine to get the value of the current best integer
solution:
' Get current best IP
Dim dObj As Double
Dim nError As Long
nError = LSgetCallbackInfoDoubleLng(pModel, _
LS_DINFO_MIP_BEST_OBJECTIVE_LNG, dObj)
In the VB header file for LINGO (LINGD11.BAS), we created two aliases for the
LSgetCallbackInfoLng() function: LSgetCallbackInfoDoubleLng() and LSgetCallbackInfoLongLng().
These were for retrieving, respectively, double and long data from LINGO. This is required due to VB
not supporting the void data type found in C. We use LSgetCallbackInfoDoubleLng() to retrieve the
objective value given that it is a double precision quantity.
Next, we check for any errors in retrieving the objective value. If none occurred, we check to see if the
latest objective is better than the incumbent:
' Check for any error
If (nError = LSERR_NO_ERROR_LNG) Then
' Is it better than the best one displayed so far?
If (dObj < dBestIP) Then
If the new objective is better than the incumbent, then we save the new objective value, and retrieve
the iteration count and objective bound:
' Save the new best objective value
dBestIP = dObj
' Get the iteration count from LINGO
Dim nIterations As Long
nResult = LSgetCallbackInfoLongLng(pModel, _
LS_IINFO_ITERATIONS_LNG, nIterations)
' Get the objective bound from LINGO
Dim dBound As Double
nResult = LSgetCallbackInfoDoubleLng(pModel, _
LS_DINFO_MIP_BOUND_LNG, dBound)
We post a summary of the new solution in a dialog box:
' Display the information in a dialog box
Dim nButtonPressed
Dim cMessage As String
cMessage = "Objective:" + Str(dBestIP) _
+ Chr(10) + "Bound:" + Str(dBound) _
+ Chr(10) + "Iterations:" + Str(nIterations)
nButtonPressed = MsgBox(cMessage, vbOKCancel)

472 CHAPTER 11
If the user pressed the Cancel button, as opposed to the OK button, then we set the return value to –1
before returning, which will cause the LINGO solver to interrupt:
If (nButtonPressed = vbCancel) Then
nReturnVal = -1
End If
End If
End If
MySolverCallback = nReturnVal
End Function
At this point, there is one more piece of code to add. We must make a call to the
LssetCallbackSolverLng() routine to pass LINGO a pointer to our callback routine. This is
accomplished at the start of the Solve button handler routine with the call:
' Pass LINGO a pointer to the callback routine
Dim nError As Long
Dim dBestObj As Double
dBestObj = 1E+30
nError = LSsetCallbackSolverLng(pLINGO, _
AddressOf MySolverCallback, dBestObj)
Note the use of the VB AddressOf operator in the call to LSsetCallbackSolverLng(). This operator
may be used only in function calls to pass the address of routines contained in module files.
Note: The AddressOf operator was added to VB starting with release 5.0. Thus, earlier releases of
VB won’t be able to exploit the callback feature in LINGO. Also, Visual Basic for
Applications (VBA), the VB macro capability supplied with Microsoft Office, does not
support the AddressOf operator. Thus, VBA applications calling LINGO will also not be able
to establish callback routines.

INTERFACING WITH OTHER APPLICATIONS 473
Summary
The LINGO DLL has a very simple structure. You need only acquaint yourself with a handful of
functions in order to access the DLL and add the power of the LINGO solver to your applications.
We’ve given brief examples on calling the DLL from Visual Basic and Visual C++. Additional
examples are provided in the Programming Samples. Application developers working in other
environments should be able to access the LINGO DLL in a fashion similar to the examples given
here.
Finally, keep in mind that any application you build that makes use of the LINGO DLL is protected
under the LINGO License Agreement. Thus, you may not distribute such applications without explicit
permission from LINDO Systems. If you would like to make arrangements for distributing your
application, please feel free to contact LINDO Systems regarding available runtime licensing
arrangements.
User Defined Functions
The @USER function allows the use of custom functions of your own design in LINGO. In Windows
versions of LINGO, you provide a 32-bit Dynamic Link Library (DLL) that contains your @USER
function. Most programming languages that support Windows should allow you to build a DLL. For
platforms other than Windows, you provide LINGO with a compiled C or FORTRAN subroutine
containing your @USER function.
From the perspective of a LINGO modeler, an @USER function is a function that can take any number
of arguments, but must take at least one. It returns a result calculated by the user-written routine.
From the perspective of the programmer writing the custom function, an @USER function takes only
two input arguments and returns a single result. The two input arguments consist of:
1. an integer specifying the number of arguments encountered in the @USER
reference in the LINGO model, and
2. a vector containing the values of the arguments in the order that they were
encountered in the @USER reference in double precision format (i.e., an 8
byte floating point format).
In other words, although to the LINGO modeler an @USER function can appear to take any number of
arguments, to the programmer implementing the @USER function, only two input arguments are
passed.
It is possible to use multiple functions with @USER by writing and compiling each function as a
separate subroutine and taking an argument to @USER as the index number of the subroutine that you
want to branch to.

474 CHAPTER 11
Installing @USER Under Windows
When LINGO for Windows starts up, it searches for the DLL file called MYUSER.DLL. LINGO
searches for this file in your working directory first. If nothing is found in your working directory,
LINGO then searches the startup directory. The working directory is the directory where you store
your LINGO files. The startup directory is the directory where you installed the LINGO program. If
LINGO finds MYUSER.DLL, it loads the DLL into memory and calls the exported MYUSER routine
every time a model references an @USER function.
On platforms other than Windows, you must link a compiled FORTRAN or C subroutine with the
LINGO libraries in order to provide a customized @USER function. Refer to the README file for
your version of LINGO for technical information on how to link your custom routines with LINGO.
In the following section, we illustrate the details of building such a DLL using Microsoft Visual C++.
Visual C++ Example
In this section, we will use Microsoft Visual C/C++ to create a 32-bit DLL that contains an @USER
function to perform the square root function. This is very easy to do if we make use of the AppWizard
in Visual C++ to build the base code for the DLL. Or, you will find the code for this example in the
USER\VC++ subdirectory off of your main LINGO directory. To build the base code, start the Visual
C++ Developer Studio and do the following:
1. Issue the File|New command.
2. You should now see a New dialog box. Select the Project Workspace
options and then click OK.
3. You will now see a New Project Workspace dialog box. Give the project the
name sqroot. In the Type box, select the MFC AppWizard (dll) option. Click
on the Create button.
4. A new MFC AppWizard dialog box should appear. Simply click on the
Finish button.
INTERFACING WITH OTHER APPLICATIONS 475
5. You should now see a New Project Information box containing a summary
of the options selected for your project that resembles:
Click the OK button to finish creating the base code for our DLL.

476 CHAPTER 11
Now, edit the SQROOT.CPP file and add the modifications listed below in bold:
// sqroot.cpp : Defines the initialization
// routines for the DLL.
//
#include "stdafx.h"
#include "sqroot.h"
#ifdef _DEBUG
#define new DEBUG_NEW
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
#endif
/////////////////////////////////////////////////////
// CSqrootApp
BEGIN_MESSAGE_MAP(CSqrootApp, CWinApp)
//{{AFX_MSG_MAP(CSqrootApp)
//NOTE-the ClassWizard will add and
// remove mapping macros here.
// DO NOT EDIT what you see in these
// blocks of generated code!
//}}AFX_MSG_MAP
END_MESSAGE_MAP()
CSqrootApp::CSqrootApp()
{
// The constructor
// Remove next line for a "quiet" version
// of MyUser.DLL
AfxMessageBox("@USER DLL installed");
}
CSqrootApp theApp;
#include <math.h>
extern "C" __declspec(dllexport)
void MyUser(int* pnNumberOfArgs,
double* pdArgs, double* dResult)
{
// This is an @USER routine callable by LINGO. In
// this particular case we simply take the
// square root of the first argument.
*dResult = sqrt(*pdArgs);
}
File: SQROOT.CPP
INTERFACING WITH OTHER APPLICATIONS 477
You should now be able to build the DLL. When Visual C++ completes the build, copy the
SQROOT.DLL file to LINGO’s startup directory (the one where LINGO12.EXE is located) and rename
SQROOT.DLL to be MYUSER.DLL. Now, start LINGO and you should see the following dialog box
confirming the DLL was successfully loaded:
Input a small model to compute the square root of 9 and solve it to get the following results:
If you don’t have a copy of Visual C++, you may experiment with this @USER routine by copying the
DLL supplied with LINGO into your LINGO startup directory. You can find the SQROOT.DLL file in
the USER\VC++ subdirectory off the main LINGO directory.

479
12 Developing More
Advanced Models
In this chapter, we will walk through the development of models in a handful of different application
areas. The goal here is twofold. On the one hand, walking through a number of different models should
help hone your skills at building LINGO models. Secondly, by applying LINGO to an array of
different application areas, we hope to illustrate the potential benefits of mathematical modeling in
almost any business situation. Below is a list of the application areas we will be touching upon in this
chapter:
♦ Production Management
♦ Logistics
♦ Finance
♦ Queuing
♦ Marketing
The reader interested in additional examples of LINGO modeling should refer to Optimization
Modeling with LINGO, by Linus Schrage, published by LINDO Systems. This book contains an
exhaustive set of modeling examples from a wide array of application areas. In many cases, you should
be able to find a model that will suit your needs with only modest modifications. Interested readers
may also refer to Appendix A, Additional Examples of LINGO Modeling, to find additional samples of
LINGO models.
480 CHAPTER 12
Production Management Models
Blending Model Model Name: Blend
Background
In blending problems, two or more raw materials are to be blended into one or more finished goods
satisfying one or more quality requirements on the finished goods. Blending problems are of interest in
a number of different fields. Some examples include determining an optimal blend for animal feed,
finding the least costly mix of ores that produce an alloy with specified characteristics, or deciding on
the most efficient combination of advertising media purchases to reach target audience percentages.
The Problem in Words
As a production manager at a fuel processing plant, you would like to maximize profit from blending
the raw materials butane, catalytic reformate, and naphtha into the two finished products Regular and
Premium. These final products must satisfy quality requirements on octane, vapor pressure, and
volatility. Each raw material has a known limited availability and cost per unit. You know the
minimum required for each finished good, the maximum you will be able to sell, and the profit
contribution per unit.
The Model
MODEL:
TITLE BLEND;
SETS:
!Each raw material has an availability
and cost/unit;
RAWMAT/ BUTANE, CATREF, NAPHTHA/: AVAIL, COST;
!Each finished good has a min required,
max sellable, selling price,
and batch size to be determined;
FINGOOD/ REGULAR, PREMIUM/:
MINREQ, MAXSELL, PRICE, BATCH;
!Here is the set of quality measures;
QUALMES/ OCTANE, VAPOR, VOLATILITY/;
!For each combo of raw material and
quality measure there is a quality
level;
RXQ(RAWMAT, QUALMES): QLEVEL;
!For each combination of quality
measure and finished good there are
upper and lower limits on quality,
and a slack on upper quality to be
determined;
QXF(QUALMES, FINGOOD):
QUP, QLOW, QSLACK;
!For each combination of raw material
and finished good there is an amount
of raw material used to be solved for;
RXF(RAWMAT, FINGOOD): USED;

Developing More Advanced Models 481
ENDSETS
DATA:
!Raw material availability;
AVAIL = 1000, 4000, 5000;
!Raw material costs;
COST = 7.3, 18.2, 12.5;
!Quality parameters of raw
materials;
QLEVEL = 120, 60, 105,
100, 2.6, 3,
74, 4.1, 12;
!Limits on finished goods;
MINREQ = 4000, 2000;
MAXSELL = 8000, 6000;
!Finished goods prices;
PRICE = 18.4, 22;
!Upper and lower limits on
quality for each finished good;
QUP = 110, 110,
11, 11,
25, 25;
QLOW = 90, 95,
8, 8,
17, 17;
ENDDATA
!Subject to raw material availability;
@FOR(RAWMAT(R):
[RMLIM] @SUM(FINGOOD(F): USED(R, F))
<= AVAIL(R);
);
@FOR(FINGOOD(F):
!Batch size computation;
[BATCOMP] BATCH(F) =
@SUM(RAWMAT(R): USED(R, F));
!Batch size limits;
@BND(MINREQ, BATCH, MAXSELL);
!Quality restrictions for each
quality measure;
@FOR(QUALMES(Q):
[QRESUP] @SUM(RAWMAT(R):
QLEVEL(R, Q) * USED(R, F))
+ QSLACK(Q, F) = QUP(Q, F) *
BATCH(F);
[QRESDN] QSLACK(Q, F) <=
(QUP(Q, F) - QLOW(Q, F)) *
BATCH(F);
);
);
! We want to maximize the profit contribution;
[OBJECTIVE] MAX =

482 CHAPTER 12
@SUM(FINGOOD: PRICE * BATCH) -
@SUM(RAWMAT(R): COST(R) *
@SUM(FINGOOD(F): USED(R, F)));
END
Model: BLEND
The Sets
We have three primitive sets in this model ⎯ raw materials (RAWMAT), finished goods (FINGOOD),
and quality measures (QUALMES).
From these three primitive sets, we create three derived sets.
The first derived set, RXQ, is a dense derived set and is a cross on the raw materials set and the quality
measures set. We need this derived set in order to define an attribute to hold the quality values for the
raw materials.
The second derived set, QXF, is a cross on the quality measures and the finished goods. We need this
set because we will be concerned with the levels of the quality measures in the finished goods.
The final derived set, RXF, is a cross on the raw materials and finished goods. We need this set
because we need to compute the amount of raw material used in each finished good.
The Variables
The primary variable that drives this model is the amount of each raw material used in each finished
good (USED). We have also added two other variables for computation purposes. First, there is the
BATCH variable, which is used to compute the batch size of each finished good. There is also the
QSLACK variable, which computes the slack on the upper quality limit for each finished good and
each quality measure.
The Objective
The objective in this model is to maximize the total profit contribution. This is computed using the
following expression:
[OBJECTIVE] MAX =
@SUM(FINGOOD: PRICE * BATCH) -
@SUM(RAWMAT(R): COST(R) *
@SUM(FINGOOD(F): USED(R, F)));
Total profit, of course, is total revenue minus total expenses. Total revenue is the sum over the finished
goods of the price of each finished good multiplied by the batch size of each finished good, or, in
LINGO syntax:
@SUM(FINGOOD: PRICE * BATCH)
Total expenses are computed by taking the sum over the raw materials of the price of the raw material
multiplied by the amount of each raw material used. This is computed with the expression:
@SUM(RAWMAT(R): COST(R) *
@SUM(FINGOOD(F): USED(R, F))
The Constraints
There are four sets of constraints in this model. Two of them are merely computational.
Developing More Advanced Models 483
This first computational set of constraints computes the batch size of each finished good with the
following expression:
!Batch size computation;
[BATCOMP] BATCH(F) =
@SUM(RAWMAT(R): USED(R, F));
In words, the batch size of finished good F is the sum of all the raw materials used in the production of
the finished good.
The second set of computational constraints computes the slack on the upper quality limit for each
finished good and each quality measure as follows:
[QRESUP] @SUM(RAWMAT(R):
QLEVEL(R, Q) * USED(R, F))
+ QSLACK(Q, F) = QUP(Q, F) *
BATCH(F);
In words, the actual quality level plus the slack on the upper quality level is equal to the upper quality
level.
The first true constraint is on the finished products’ batch sizes, which must fall within minimum and
maximum levels. We use the @BND function to set this up as follows:
!Batch size limits;
@BND(MINREQ, BATCH, MAXSELL);
Note that we could have entered explicit constraints for the batch size limits, but the @BND function is
more efficient at handling simple bounds on variables.
The final constraint forces the quality level of each finished good for each quality measure to fall
within specifications. We do this with the following:
[QRESDN] QSLACK(Q, F) <=
(QUP(Q, F) - QLOW(Q, F)) *
BATCH(F);
In words, the slack must be less than the difference between the upper limit and the lower limit. If this
were not true, quality would be beneath the lower limit. The fact that the slack variable cannot be
negative guarantees we won’t exceed the quality limit.
The Solution
Rounding all solution values to the nearest whole integer, total profit is $44,905 with batch sizes of
4,000 Regular and 4,095 Premium. The following matrix shows the recommended quantities of each
raw material to use in the Regular and Premium blends:
Raw Material Regular Premium
Butane 534 466
Catalytic Reformate 1,516 2,484
Naphtha 1,950 1,146

484 CHAPTER 12
Material Requirements Planning Model: MRP
Background
Material Requirements Planning, or MRP, is used to generate production schedules for the
manufacture of complex products. MRP uses the demand schedule for a finished product, the lead
times to produce the finished product, and all the various subcomponents that go into the finished
product to work backwards and develop a detailed just-in-time production schedule that meets the
demand schedule.
MRP’s main focus is finding a feasible just-in-time production schedule to meet demand. MRP does
not, however, attempt to optimize the production schedule to minimize total production costs. In many
cases, the problems solved by MRP are so complex optimization would be prohibitive.
The Problem in Words
Suppose you are a manufacturer of human powered vehicles. You have a given schedule of demands
for finished products over time. You need to know when and how many of each component,
subcomponent, etc. is needed to meet demand.
Your final products are as follows:
1. Unicycles, made from a seat and a wheel,
2. Bicycles, made from a seat, two wheels, and a chain,
3. Tandems (bicycles built for two), made from two seats, two wheels, and
two chains.
Each product is assembled from a set of components. Each component in turn may be assembled from
other subcomponents. For simplicity and generality, we will refer to all products, components, and
subcomponents as parts.
The subcomponents are as follows:
1. Seats,
2. Wheels, made from a hub and 36 spokes,
3. Chains, made from 84 links,
4. Hubs,
5. Spokes, and
6. Links.
It takes a certain amount of time, called the lead-time, to produce each batch of parts. The component
parts for each part must be on hand when you begin production of a part.
The sales department has estimated demand for two months (eight weeks) in the future. According to
their findings, there will be a demand for 10 unicycles in week eight, and 20 bicycles and 20 tandems
in week nine.

Developing More Advanced Models 485
The Model
MODEL:
! Data for this model is read from MRP.LDT;
SETS:
! The set of parts;
PART: LT;
! LT(i) = Lead time to produce part i;
! The set of time periods;
TIME;
! A relationship called USES between pairs of parts;
USES( PART, PART): NEEDS;
! Parent part i needs NEEDS(i, j) units of
child part j;
! For each part and time period we're interested in;
PXT( PART, TIME): ED, TD;
! ED(i, j) = External demand for part i at time j;
! TD(i, j) = Total demand for part i at time j;
ENDSETS
DATA:
! Load the data from an external file;
! Parts list;
PART = @FILE( 'MRP.LDT');
! Time periods;
TIME = @FILE( 'MRP.LDT');
! Get the parent child relations and the
number of parts required;
USES, NEEDS = @FILE( 'MRP.LDT');
! Get the lead times from the file;
LT = @FILE( 'MRP.LDT');
! Get the external demands
over time for each part;
ED = @FILE( 'MRP.LDT');
ENDDATA
! Set NP = no. of time periods in the problem;
NP = @SIZE( TIME);
! For each part P and period T, the total demand =
external demand + demand generated by parents
one lead time in the future;
@FOR( PXT( P, T) | T + LT( P) #LE# NP :
TD( P, T) = ED( P, T + LT( P)) +
@SUM( USES( P2, P): TD( P2, T + LT( P)) *
NEEDS( P2, P));
);
DATA:

486 CHAPTER 12
! Display a table showing the production schedule;
@TEXT() = ' The production schedule:';
@TEXT() = @TABLE( TD);
ENDDATA
END
Model: MRP
The Data
An interesting feature of this model is all of the data is imported from an external text file using the
@FILE function (for more information on @FILE, see Chapter 8, Interfacing with External Files).
More specifically, @FILE reads all the data from a single file, MRP.LDT, that is pictured below:
! Parts list;
U, ! Unicycles;
B, ! Bicycles;
T, ! Tandems;
S, ! Seats;
W, ! Wheels;
C, ! Chains;
H, ! Hubs;
P, ! sPokes;
L~ ! Links;
! The set of periods;
1..9 ~
! The parent-child use relationships
(i.e., Unicycles use Seats, etc.)
The number of child parts required
in each parent- child relationship,
respectively (i.e, Unicycles use 1
Seat, Wheels use 36 sPokes, etc.);
U S 1, U W 1, B S 1, B W 2, B C 1,
T S 2, T W 2, T C 2, W H 1, W P 36,
C L 84~
! The lead times for each part;
1, 2, 1, 1, 3, 1, 1, 2, 2~
! The external demands or master schedule;
! Time period;
! 1 2 3 4 5 6 7 8 9;
! U; 0, 0, 0, 0, 0, 0, 0,10, 0,
! B; 0, 0, 0, 0, 0, 0, 0, 0,20,
! T; 0, 0, 0, 0, 0, 0, 0, 0,20,
! S; 0, 0, 0, 0, 0, 0, 0, 0, 0,
! W; 0, 0, 0, 0, 0, 0, 0, 0, 0,
! C; 0, 0, 0, 0, 0, 0, 0, 0, 0,
! H; 0, 0, 0, 0, 0, 0, 0, 0, 0,
! P; 0, 0, 0, 0, 0, 0, 0, 0, 0,
! L; 0, 0, 0, 0, 0, 0, 0, 0, 0
File: MRP.LDT
You will recall the tilde (~) is LINGO’s end-of-record mark. Whenever a tilde is encountered in a data
file, LINGO stops reading input from the data file and begins reading where it left off in the model
file.

Developing More Advanced Models 487
The Sets
We have two primitive sets in this model⎯the component parts (PARTS) and the time periods (TIME).
From these two primitive sets, we create two derived sets.
The first derived set, USES, is a sparse set derived from the cross of the PARTS set on itself. We use
this set to construct a data table, or input-output matrix (NEEDS), containing the parts usage data,
which tells us how many of each of the other parts are required to produce a given part. The set is
sparse because not all parts are required in the production of certain other parts (e.g., chains are not
required to produce a spoke).
The other derived set, PXT, is a dense set formed from the cross on the parts and time periods sets. We
need this set because we will be concerned with the demand for each part in each period and the
amount of each part to begin producing in each period.
The Variables
The only unknown in this model is the total demand (TD) attribute, where TD(p, t) is the total demand
for product p in period t. Total demand stems from two sources—external demand (ED) from
customers and internal demand for production requirements. We compute TD by incorporating the
part’s lead time. Thus, when TD is nonzero in a period, production must begin in that period.
The Formulas
The key computation in this model is:
! For each part P and period T, the total demand =
external demand + demand generated by parents
one lead time in the future;
@FOR(PXT(P, T) | T + LT(P) #LE# NP:
TD(P, T) = ED(P, T + LT(P)) +
@SUM(USES(P2, P): TD(P2, T + LT(P)) *
NEEDS(P2, P));
);
For each part in each time period, the amount of that part we must begin producing in the period is the
amount we will need one lead time away to satisfy 1) external demand, and 2) internal production
requirements. The subexpression that gives external demand is simply:
ED(P, T + LT(P))
The remainder of the expression:
@SUM(USES(P2, P): TD(P2, T + LT(P)) *
NEEDS(P2, P));
sums up the amount of the part needed for internal production of all other parts one lead time away.
Note, we place a logical condition on the outer @FOR loop in this calculation (shown here in bold):
@FOR(PXT(P, T) | T + LT(P) #LE# NP:
Without this condition, the calculation would extend beyond the final period in the TIME set.
488 CHAPTER 12
The Solution
Solving the model, we get the following nonzero values for TD:
Variable Value
TD(U, 7) 10.00000
TD(B, 7) 20.00000
TD(T, 8) 20.00000
TD(S, 6) 30.00000
TD(S, 7) 40.00000
TD(W, 4) 50.00000
TD(W, 5) 40.00000
TD(C, 6) 20.00000
TD(C, 7) 40.00000
TD(H, 3) 50.00000
TD(H, 4) 40.00000
TD(P, 2) 1800.000
TD(P, 3) 1440.000
TD(L, 4) 1680.000
TD(L, 5) 3360.000
Solution: MRP
Putting this solution in tabular form, we get the following production schedule:
2 3 4 5 6 7 8
Unicycles 10
Bicycles 20
Tandems 20
Seats 30 40
Wheels 50 40
Chains 20 40
Hubs 50 40
Spokes 1,800 1,440
Links 1,680 3,360
MRP Production Schedule
Note the use of the @TABLE output function in the data section at the end of the model that displays
the TD attribute in table form similar to the table above:
The production schedule:
1 2 3 4 5 6 7 8 9
U 0 0 0 0 0 0 10 0 0
B 0 0 0 0 0 0 20 0 0
T 0 0 0 0 0 0 0 20 0
S 0 0 0 0 0 30 40 0 0
W 0 0 0 50 40 0 0 0 0
C 0 0 0 0 0 20 40 0 0
H 0 0 50 40 0 0 0 0 0
P 0 1800 1440 0 0 0 0 0 0
L 0 0 0 1680 3360 0 0 0 0
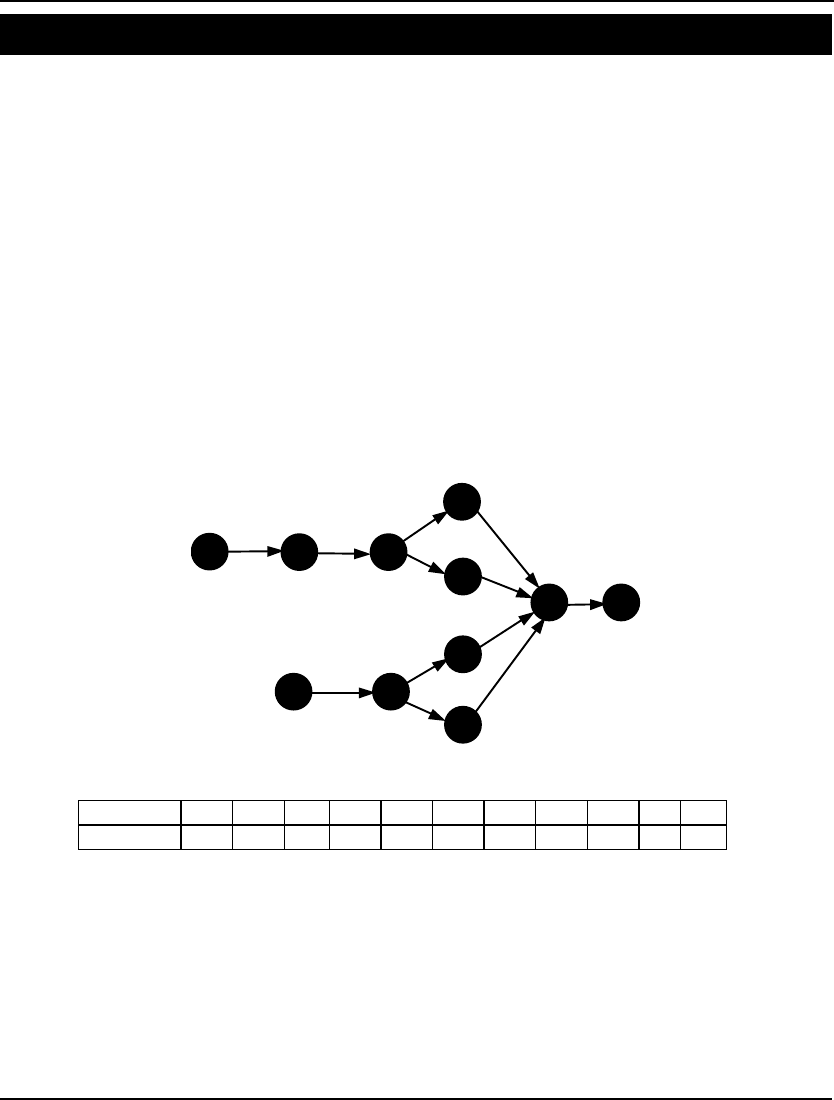
Developing More Advanced Models 489
Assembly Line Balancing Model: ASLBAL
Background
In the assembly line balancing problem, tasks are assigned to workstations on an assembly line, so the
line’s cycle time is minimized. An assembly line consists of a series of workstations, which each
perform one or more specialized tasks in the manufacture of a final product. The cycle time is the
maximum time it takes any workstation to complete its assigned tasks. The goal in balancing an
assembly line is to assign tasks to stations, so equal amounts of work are performed at each station.
Improperly balanced assembly lines will experience bottlenecks⎯workstations with less work are
forced to wait on preceding stations that have more work assigned.
The problem is complicated further by precedence relations amongst the tasks, where some tasks must
be completed before others may begin (e.g., when building a computer, installing the disk drives must
precede putting on the outer casing). The assignment of tasks to workstations must obey the
precedence relations.
The Problem in Words
For our example, we have eleven tasks (A through K) to assign to four stations (1 through 4). The task
precedence diagram looks like this:
A B C
D E
F
G
H
I
J K
The times to complete the various tasks are given in the table below:
Task: A B C D E F G H I J K
Minutes: 45 11 9 50 15 12 12 12 12 8 9
We need to find an assignment of tasks to workstations that minimize the assembly line's cycle time.

490 CHAPTER 12
The Model
MODEL:
! Assembly line balancing model;
!This model involves assigning tasks to stations in an
assembly line so bottlenecks are avoided. Ideally, each
station would be assigned an equal amount of work.;
SETS:
! The set of tasks to be assigned are A through
K, and each task has a time to complete, T;
TASK/ A B C D E F G H I J K/: T;
! Some predecessor,successor pairings must be
observed(e.g. A must be done before B, B
before C, etc.);
PRED(TASK, TASK)/ A,B B,C C,F C,G F,J G,J
J,K D,E E,H E,I H,J I,J /;
! There are 4 workstations;
STATION/1..4/;
TXS(TASK, STATION): X;
! X is the attribute from the derived set TXS
that represents the assignment. X(I,K) = 1
if task I is assigned to station K;
ENDSETS
DATA:
! Data taken from Chase and Aquilano, POM;
! There is an estimated time required for each
task:
A B C D E F G H I J K;
T = 45 11 9 50 15 12 12 12 12 8 9;
ENDDATA
! The model;
! *Warning* may be slow for more than 15 tasks;
! For each task, there must be one assigned station;
@FOR(TASK(I): @SUM(STATION(K): X(I, K)) = 1);
! Precedence constraints;
! For each precedence pair, the predecessor task
I cannot be assigned to a later station than
its successor task J;
@FOR(PRED(I, J):
@SUM(STATION(K):
K * X(J, K) - K * X(I, K)) >= 0);

Developing More Advanced Models 491
! For each station, the total time for the assigned tasks must
less than the maximum cycle time, CYCTIME;
@FOR(STATION(K):
@SUM(TXS(I, K): T(I) * X(I, K)) <= CYCTIME);
! Minimize the maximum cycle time;
MIN = CYCTIME;
! The X(I,J) assignment variables are
binary integers;
@FOR(TXS: @BIN(X));
END
Model: ASLBAL
The Sets
We have two primitive sets in this model⎯the tasks (TASK) and the workstations (STATION). From
these two primitive sets, we create two derived sets.
The first derived set, PRED, is a sparse derived set and is based on a cross of the TASK set on itself.
The members of this set are the precedence relations amongst the tasks. For instance, the first member
of this set is the pair (A,B), indicating task A must precede task B.
The other derived set, TXS, is a dense derived set formed by taking the cross of the task set on the
workstation set. We need this set because we will be determining what tasks get assigned to what
workstations.
The Variables
The decision variables in this model are the members of the X attribute that is defined in the TXS set.
X(t, s) is a binary variable that is 1 if task t is assigned to station s, otherwise 0. The X attribute is
forced to being binary in the expression:
! The X(I,J) assignment variables are
binary integers;
@FOR(TXS: @BIN(X));
We also introduce the scalar variable, CYCTIME, to represent the entire assembly line’s cycle time,
which is computed by taking the maximum cycle time over the workstations.
The Objective
The objective in this model is simply to minimize total cycle time for the line and is given as:
! Minimize the maximum cycle time;
MIN = CYCTIME;
The Constraints
We have the following three types of constraints in this model:
1. each task must be assigned to one station,
2. precedence relations must be observed amongst the tasks, and
3. the line cycle time variable, CYCTIME, must be greater-than-or-equal-to the
actual cycle time.

492 CHAPTER 12
The following expression sums up the assignment variable for each task, and sets the sum to equal 1:
! For each task, there must be one assigned station;
@FOR(TASK(I): @SUM(STATION(K): X(I, K)) = 1);
This forces each task to be assigned to a single station.
We use the following expression to enforce the precedence relationships amongst the tasks:
! Precedence constraints;
! For each precedence pair, the predecessor task
I cannot be assigned to a later station than its
successor task J;
@FOR(PRED(I, J):
@SUM(STATION(K):
K * X(J, K) - K * X(I, K)) >= 0);
Suppose task I is a predecessor to task J. If I were incorrectly assigned to a workstation later than J, the
sum of the terms K * X(I, K) would exceed the sum of the terms K * X(J, K) and the constraint would
be violated. Thus, this constraint effectively enforces the predecessor relations.
We restrain the cycle time using the following constraints:
! For each station, the total time for the
assigned tasks must be less than the maximum
cycle time, CYCTIME;
@FOR(STATION(K):
@SUM(TXS(I, K): T(I) * X(I, K)) <= CYCTIME);
The quantity:
@SUM(TXS(I, K): T(I) * X(I, K))
in this constraint computes the cycle time for station K. We use the @FOR statement to make the
CYCTIME variable greater-than-or-equal-to the cycle times for all the workstations. If we couple this
with the fact that we are minimizing CYCTIME in the objective, CYCTIME will be “squeezed” into
exactly equaling the maximum of the cycle times for the workstations.
By “squeezing” CYCTIME to the correct value, we avoid using the @MAX function. Had the @MAX
function been used, LINGO would have had to resort to its nonlinear solver to handle the piecewise
linear @MAX. Avoiding nonlinear models whenever possible is a critical modeling practice.
The Solution
Solving the model, we get the following nonzero values for the assignment X variable:
Variable Value
X(A, 2) 1.000000
X(B, 3) 1.000000
X(C, 4) 1.000000
X(D, 1) 1.000000
X(E, 3) 1.000000
X(F, 4) 1.000000
X(G, 4) 1.000000
X(H, 3) 1.000000
X(I, 3) 1.000000
X(J, 4) 1.000000
X(K, 4) 1.000000
Solution: ASLBAL
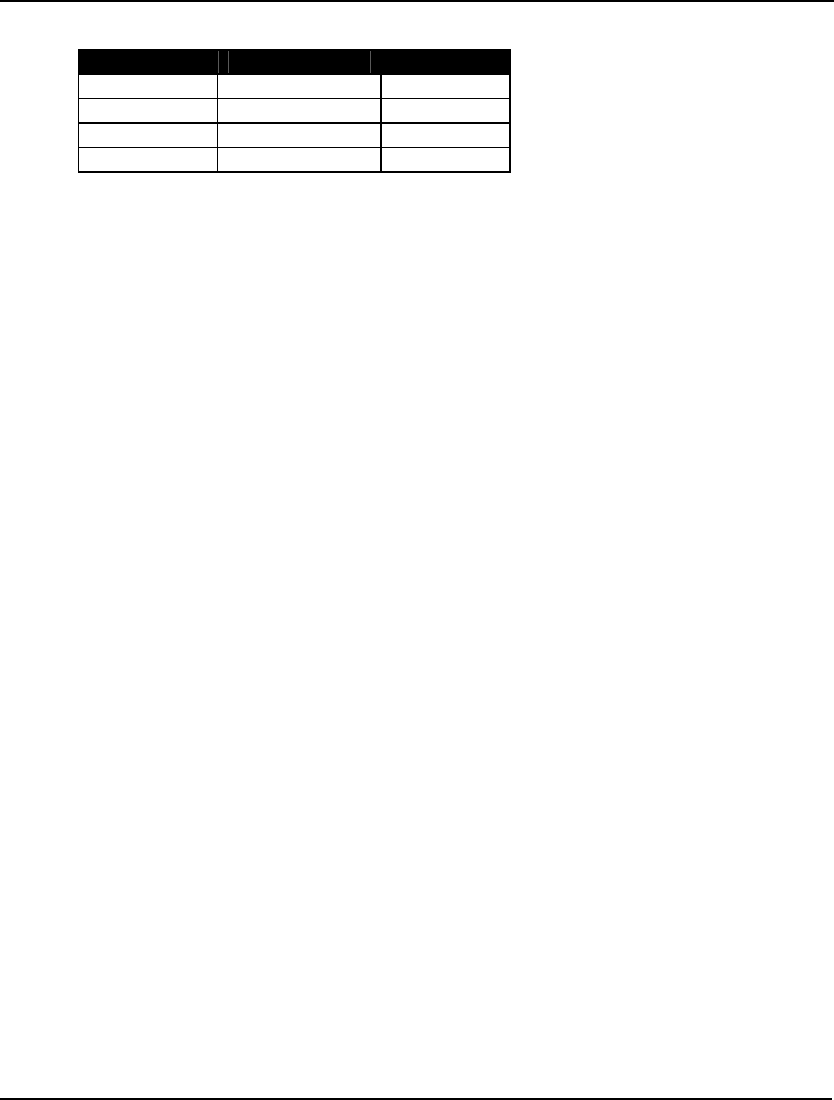
Developing More Advanced Models 493
Summarizing this solution, we have:
Workstation Assigned Tasks Cycle Time
1 D 50
2 A 45
3 B, E, H, I 50
4 C, F, G, J, K 50
The cycle time for the entire line is 50 minutes⎯the maximum of the cycle times across all the
workstations. We have a well-balanced line in that only workstation 2 has slack time totaling 5
minutes.

494 CHAPTER 12
Logistics Models
Capacitated Plant Location Model: CAPLOC
Background
The capacitated plant location model is a generalization of the transportation model we introduced in
Chapter 1, Getting Started with LINGO. The capacitated plant location problem allows greater latitude
of decision making in that the points of origin (plant locations) are variable. Manufacturers and
wholesale businesses are likely to encounter problems of this sort in matching existing customer
demand to product availability and minimizing transportation costs.
The Problem in Words
Your firm has a choice of three locations to operate a manufacturing facility in. Four customers exist
with a known demand for your product. Each potential plant location has an associated monthly
operating cost, and shipping routes to the demand cities have varying costs. In addition, each potential
plant will have a shipping capacity that must not be exceeded. You need to determine what plant(s) to
open and how much of a product to send from each open plant to each customer to minimize total
shipping costs and fixed plant operating costs.
The Model
MODEL:
! Capacitated Plant Location Problem;
SETS:
PLANTS: FCOST, CAP, OPEN;
CUSTOMERS: DEM;
ARCS( PLANTS, CUSTOMERS) : COST, VOL;
ENDSETS
DATA:
! The plant, their fixed costs
and capacity;
PLANTS, FCOST, CAP =
P1 91 39
P2 70 35
P3 24 31;
! Customers and their demands;
CUSTOMERS, DEM =
C1 15
C2 17
C3 22
C4 12;
! The plant to cust cost/unit
shipment matrix;
COST = 6 2 6 7
4 9 5 3
8 8 1 5;
ENDDATA
! The objective;
[TTL_COST] MIN = @SUM( ARCS: COST * VOL) +
@SUM( PLANTS: FCOST * OPEN);

Developing More Advanced Models 495
! The demand constraints;
@FOR( CUSTOMERS( J): [DEMAND]
@SUM( PLANTS( I): VOL( I, J)) >= DEM( J)
);
! The supply constraints;
@FOR( PLANTS( I): [SUPPLY]
@SUM( CUSTOMERS( J): VOL( I, J)) <=
CAP( I) * OPEN( I)
);
! Make OPEN binary(0/1);
@FOR( PLANTS: @BIN( OPEN));
END
Model: CAPLOC
The Sets
We have two primitive sets in this model⎯the plants (PLANTS) and the customers (CUSTOMERS).
From these two primitive sets, we create a dense derived set, ARCS, which is the cross of the plants
and customers sets. We use this set to represent the shipping arcs between the plants and customers.
The Variables
There are two sets of decision variables in this model. The VOL attribute, defined on the ARCS set,
represents the shipment volume from the plants to the customers along each arc. The OPEN attribute,
defined on the PLANTS set, is used to represent the plants that are open. Specifically, OPEN(p) is 1 if
plant p is opened, else it is 0. The members of the OPEN attribute are set to being binary using the
expression:
! Make OPEN binary(0/1);
@FOR(PLANTS: @BIN(OPEN));
The Objective
The objective in this model is to minimize total costs, which is the sum of the shipping costs and fixed
plant costs. This is computed using the following expression:
! The objective;
[TTL_COST] MIN = @SUM(ARCS: COST * VOL) +
@SUM(PLANTS: FCOST * OPEN);
The shipping cost component of the objective is computed with:
@SUM(ARCS: COST * VOL)
while the fixed plant costs component is given by:
@SUM(PLANTS: FCOST * OPEN)
The Constraints
There are two sets of constraints in the model:
1. each customer must be sent enough product to satisfy demand, and
2. each plant can’t supply more than its capacity.

496 CHAPTER 12
The following expression guarantees each customer receives the quantity of product demanded:
! The demand constraints;
@FOR(CUSTOMERS(J): [DEMAND]
@SUM(PLANTS(I): VOL(I, J)) >= DEM(J)
);
For each customer, we sum the amount being shipped to that customer and set it to be
greater-than-or-equal-to the customer’s demand.
To limit shipments from a plant to the plant’s capacity, we use:
! The supply constraints;
@FOR(PLANTS(I): [SUPPLY]
@SUM(CUSTOMERS(J): VOL(I, J)) <=
CAP(I) * OPEN(I)
);
For each plant, we sum up the amount being shipped from the plant and set this quantity to be
less-than-or-equal-to the plant’s capacity multiplied by the plant’s 0/1 OPEN indicator. Note that, in
order for the plant to be able to ship any quantity of product, the OPEN binary variable will be forced
to 1 by these constraints.

Developing More Advanced Models 497
The Solution
Solving the model, we get the following solution:
Global optimal solution found.
Objective value: 327.0000
Extended solver steps: 4
Total solver iterations: 25
Variable Value
OPEN(P1) 1.000000
OPEN(P3) 1.000000
VOL(P1, C1) 15.00000
VOL(P1, C2) 17.00000
VOL(P1, C4) 3.000000
VOL(P3, C3) 22.00000
VOL(P3, C4) 9.000000
Total costs are minimized at 327 by opening plants 1 and 3. From plant 1, we ship 15, 17, and 3 units
respectively to customers 1, 2, and 4. From plant 3, we ship 22 units to customer 3, and 9 units to
customer 4.
498 CHAPTER 12
Shortest Route Problem Model: DYNAMB
Background
In the shortest route problem, we want to find the shortest distance from point A to point B in a
network.
We will use an approach called dynamic programming (DP) to solve this problem. Dynamic
programming involves breaking a large, difficult problem up into a series of smaller, more manageable
problems. By solving the series of smaller problems, we are able to construct the solution to the initial
large problem. Typically, the most difficult aspect of DP is not the mathematics involved in solving the
smaller subproblems, but coming up with a scheme, or recursion, for decomposing the problem.
To find the distance of the shortest path through the network, we will use the following DP recursion:
F(i) = min [ D(i, j) + F(j)]
j
where F(i) is the minimal travel distance from point i to the final destination point, and D(i, j) is the
distance from point i to point j. In words, the minimal distance from node i to the terminal node is the
minimum over all points reachable along a single arc from i of the sum of the distance from i to the
adjoining node plus the minimal distance from the adjoining node to the terminal node.
The Problem in Words
Suppose we have the following network of cities:
110
9
8
7
6
5
4
3
2
Links are assumed to be one-way. The distances between the cities are given to us. We want to
determine the shortest distance between cities 1 and 10.

Developing More Advanced Models 499
The Model
SETS:
! Dynamic programming illustration (see
Anderson, Sweeney & Williams, An Intro to Mgt
Science, 6th Ed.). We have a network of 10
cities. We want to find the length of the
shortest route from city 1 to city 10.;
! Here is our primitive set of ten cities,
where F(i) represents the shortest path
distance from city i to the last city;
CITIES /1..10/: F;
! The derived set ROADS lists the roads that
exist between the cities (note: not all city
pairs are directly linked by a road, and
roads are assumed to be one way.);
ROADS(CITIES, CITIES)/
1,2 1,3 1,4
2,5 2,6 2,7
3,5 3,6 3,7
4,5 4,6
5,8 5,9
6,8 6,9
7,8 7,9
8,10
9,10/: D;
! D(i, j) is the distance from city i to j;
ENDSETS
DATA:
! Here are the distances that correspond to the
above links;
D =
1 5 2
13 12 11
6 10 4
12 14
3 9
6 5
8 10
5
2;
ENDDATA
! If you are already in City 10, then the cost
to travel to City 10 is 0;
F(@SIZE(CITIES)) = 0;
! The following is the classic dynamic
programming recursion. In words, the shortest
distance from City i to City 10 is the minimum
over all cities j reachable from i of the sum
of the distance from i to j plus the minimal
distance from j to City 10;
@FOR(CITIES(i)| i #LT# @SIZE(CITIES):
F(i) = @MIN(ROADS(i, j): D(i, j) + F(j))
);
Model: DYNAMB

500 CHAPTER 12
The Sets
We have the single primitive set, CITIES, which corresponds to the cities in the network. From this
primitive set, we form a single derived set, ROADS, to represent the links between the cities. We
specify the members of this set. Thus, ROADS is a sparse derived set.
The Variables
The F attribute defined on the CITIES set is used to store the distance from each city to the destination
city.
The Formulas
The recursion, discussed above, is entered in LINGO with the following statement:
@FOR(CITIES(i)| i #LT# @SIZE(CITIES):
F(i) = @MIN(ROADS(i, j): D(i, j) + F(j))
);
The Solution
Solving the model, we get the following values for F:
Variable Value
F(1) 19.00000
F(2) 19.00000
F(3) 14.00000
F(4) 20.00000
F(5) 8.000000
F(6) 7.000000
F(7) 12.00000
F(8) 5.000000
F(9) 2.000000
F(10) 0.000000
F(1), the shortest distance from city 1 to city 10, gives us the distance of the shortest path of 19. For
the curious reader, this distance corresponds to the path 1
→
3
→
5
→
8
→
10. Refer to model
DYNAMB2.LG4 to see how to extend this model to compute the actual path as well as its distance.

Developing More Advanced Models 501
Financial Models
Markowitz Portfolio Selection Model: GENPRT
Background
In the March, 1952 issue of Journal of Finance, Harry M. Markowitz published an article titled
Portfolio Selection. In the article, he demonstrates how to reduce the risk of asset portfolios by
selecting assets whose values aren’t highly correlated. At the same time, he laid down some basic
principles for establishing an advantageous relationship between risk and return. This has come to be
known as diversification of assets. In other words, don’t put all your eggs in one basket.
A key to understanding the Markowitz model is to be comfortable with the statistic known as the
variance of a portfolio. Mathematically, the variance of a portfolio is:
∑
i
∑
j Xi Xj
σ
i,j
where,
Xi is the fraction of the portfolio invested in asset i,
σ
i,j for i≠j: the covariance of asset i with asset j, and
for i=j: the variance of asset i.
Variance is a measure of the expected fluctuation in return—the higher the variance, the riskier the
investment. The covariance is a measure of the correlation of return fluctuations of one stock with the
fluctuations of another. High covariance indicates an increase in one stock’s return is likely to
correspond to an increase in the other. A covariance close to zero means the return rates are relatively
independent. A negative covariance means that an increase in one stock’s return is likely to correspond
to a decrease in the other.
The Markowitz model seeks to minimize a portfolio’s variance, while meeting a desired level of
overall expected return.
The Problem in Words
You’re considering investing in three stocks. From historical data, you have calculated an expected
return, the variance of the return rate, and the covariance of the return between the different stocks.
You want to reduce variability, or risk, by spreading your investment wisely amongst the three stocks.
You have a target growth rate of 12%. As an additional safety feature, you decide to invest no more
than 75% in any single asset. What percentages of your funds should you invest in the three stocks to
achieve this target and minimize the risk of the portfolio?

502 CHAPTER 12
The Model
! GENPRT: Generic Markowitz portfolio;
SETS:
ASSET/1..3/: RATE, UB, X;
COVMAT(ASSET, ASSET): V;
ENDSETS
DATA:
! The data;
! Expected growth rate of each asset;
RATE = 1.3 1.2 1.08;
! Upper bound on investment in each;
UB = .75 .75 .75;
! Covariance matrix;
V = 3 1 -.5
1 2 -.4
-.5 -.4 1;
! Desired growth rate of portfolio;
GROWTH = 1.12;
ENDDATA
! The model;
! Min the variance;
[VAR] MIN = @SUM(COVMAT(I, J):
V(I, J) * X(I) * X(J));
! Must be fully invested;
[FULL] @SUM(ASSET: X) = 1;
! Upper bounds on each;
@FOR(ASSET: @BND(0, X, UB));
! Desired value or return after 1 period;
[RET] @SUM(ASSET: RATE * X) >= GROWTH;
Model: GENPRT
The Sets
We define a single primitive set, ASSETS, corresponding to the three stocks in the model. From the
ASSETS set, we derive the dense set named COVMAT, which is the cross of the ASSETS set on itself.
We use the COVMAT set for defining the covariance matrix.
The Attributes
We define four attributes in this model.
The RATE, UB and V attributes are for storing data. RATE stores the expected return for each asset, UB
stores the upper bound on the fraction of the asset allowed in the portfolio, and V stores the covariance
matrix. (Note the covariance matrix is symmetric and larger portfolio models would benefit from
storing just half of the matrix, rather than the entire matrix as we have done here for simplicity
reasons.)
The final attribute, X, constitutes the decision variables for the model. Specifically, X(i) is the fraction
of the portfolio devoted to asset i.

Developing More Advanced Models 503
The Objective
The objective in this model is to minimize the portfolio’s risk. As we mentioned above, we use the
portfolio’s variance as a measure of risk in the following expression:
! Min the variance;
[VAR] MIN = @SUM(COVMAT(I, J):
V(I, J) * X(I) * X(J));
The Constraints
There are three forms of constraints in the model:
1. we must be fully invested,
2. we can’t invest too much in any one asset, and
3. expected return should meet, or exceed, our threshold level of 12%.
The following expression enforces the 100% investment requirement:
! Must be fully invested;
[FULL] @SUM(ASSET: X) = 1;
In words, the sum of all the weights of all the assets in the portfolio must equal 1. Without this
constraint, LINGO will tend to under invest in order to get a lower variance. You can confirm this by
dropping the constraint and running the model.
To keep the solution from investing too much in any one asset, we use the @BND function:
! Upper bounds on each;
@FOR(ASSET: @BND(0, X, UB));
As you recall, the @BND function is the most efficient method for placing simple bounds on variables.
We constrain the portfolio’s expected return to be greater-than-or-equal-to our target with the
expression:
! Desired value or return after 1 period;
[RET] @SUM(ASSET: RATE * X) >= GROWTH;
The left-hand side of this expression is the expected rate of return, and is the sum of the fractions
invested in each asset weighted by each asset’s return.

504 CHAPTER 12
The Solution
Solving the model, we get the following solution:
Local optimal solution found.
Objective value: 0.4173749
Total solver iterations: 13
Variable Value
X(1) 0.1548631
X(2) 0.2502361
X(3) 0.5949008
Row Slack or Surplus
VAR 0.4173749
FULL 0.0000000
RET 0.2409821E-01
Solution: GENPRT
Total variance is minimized at .4174 when we put 15.5% in asset 1, 25% in asset 2, and 59.5% in asset
3.

Developing More Advanced Models 505
Scenario Portfolio Selection Model: PRTSCEN
Background
Scenarios are outcomes of events with an influence on the return of a portfolio. Examples might
include an increase in interest rates, war in the Middle East, etc. In the scenario-based approach to
portfolio selection, the modeler comes up with a set of scenarios, each with a certain probability of
occurring during the period of interest. Given this set of scenarios and their probabilities, the goal is to
select a portfolio that minimizes risk, while meeting a target return level.
In the Markowitz portfolio model, presented above, we used a portfolio’s variance as a measure of
risk. As one might imagine, variance is not the only possible measure of risk. Variance is a measure of
the fluctuation of return above and below its average. As a statistic, variance weights a scenario that
returns 20% above average the same as a scenario that returns 20% below average. If you’re like most
investors, you’re probably more worried about the risk that return will be below average. In our
scenario-based model, we will expand our options by including two new measures of risk that focus on
returns below the target level—downside risk and semi-variance risk.
Both semi-variance and downside risk only consider the option that returns will be below the target.
Downside risk is a measure of the expected difference between the target and returns below the target,
while semi-variance is a measure of the squared expected difference between the target and returns
below the target. Therefore, semi-variance puts a relatively higher weight on larger shortfalls.
The Problem in Words
Again, you are considering investing in three stocks (ATT, GM, and USX). You have determined there
are 12 equally likely scenarios in the forthcoming period. You have come up with predicted rates of
return for the stocks under the twelve scenarios. You have a target growth rate of 15% for your
portfolio. Your goal is to construct optimal portfolios that minimize expected risk while meeting the
expected level of return using three different risk measures—variance, downside, and semi-variance.
The Model
! Scenario portfolio model;
SETS:
SCENE/1..12/: PRB, R, DVU, DVL;
STOCKS/ ATT, GMT, USX/: X;
SXI(SCENE, STOCKS): VE;
ENDSETS
DATA:
TARGET = 1.15;
! Data based on original Markowitz example;
VE =
1.300 1.225 1.149
1.103 1.290 1.260
1.216 1.216 1.419
0.954 0.728 0.922
0.929 1.144 1.169
1.056 1.107 0.965
1.038 1.321 1.133
1.089 1.305 1.732
1.090 1.195 1.021
1.083 1.390 1.131
506 CHAPTER 12
1.035 0.928 1.006
1.176 1.715 1.908;
! All scenarios happen to be equally likely;
PRB= .08333;
ENDDATA
! Compute expected value of ending position;
AVG = @SUM(SCENE: PRB * R);
! Target ending value;
AVG >= TARGET;
@FOR(SCENE(S):
! Compute value under each scenario;
R(S) = @SUM(STOCKS(J): VE(S, J) * X(J));
! Measure deviations from average;
DVU(S) - DVL(S) = R(S) - AVG
);
! Budget;
@SUM(STOCKS: X) = 1;
! Our three measures of risk;
[VARI] VAR = @SUM(SCENE: PRB * (DVU+DVL)^2);
[SEMI] SEMIVAR = @SUM(SCENE: PRB * (DVL) ^2);
[DOWN] DNRISK = @SUM(SCENE: PRB * DVL);
! Set objective to VAR, SEMIVAR, or DNRISK;
[OBJ] MIN = VAR;
Model: PRTSCEN
The Sets
We define two primitive sets⎯SCENE and STOCKS. The SCENE set corresponds to the set of 12
scenarios, while STOCKS is the set of three candidate stocks. We form a single dense derived set,
STXSC, which is the cross of these two sets. We need the STXSC set in order to establish the table of
returns for each stock under each scenario.
The Attributes
We define four attributes on the scenarios set⎯PRB, R, DVU, and DVL. PRB stores the probabilities
of the scenarios. R is the expected rate of return under each scenario for a given allocation amongst the
stocks. DVU is the deviation above average return for each scenario for a given stock allocation.
Finally, DVL is the deviation below average return for each scenario for a given stock allocation.
The X attribute is defined on the stocks set. X denotes the fraction of the portfolio allocated to each
stock. The members of X must be determined and constitute the decision variables of the model.
Finally, on the SXI set, we define the VE attribute, which stores the table containing the returns of each
stock under each scenario.

Developing More Advanced Models 507
The Objective
Once again, the objective in this model is to minimize the portfolio’s risk. The default version of the
objective minimizes variance as follows:
! Set objective to VAR, SEMIVAR, or DNRISK;
[OBJ] MIN = VAR;
To solve using the other two measures of risk, simply change the name of the variable from VAR to
either SEMIVAR or DNRISK.
The Formulas
There are six categories of formulas in this model:
1. computing the expected rate of return (AVG),
2. constraining the expected rate of return to exceed our target,
3. computing the expected rate of return under each scenario (R),
4. computing deviations from average return for each scenario (DVU and
DVL),
5. constraining the portfolio to be fully invested, and
6. computing the three measures of risk (VAR, SEMIVAR, and DNRISK).
The following expression computes the expected rate of return for the entire portfolio:
! Compute expected value of ending position;
AVG = @SUM(SCENE: PRB * R);
We do this by taking the sum of the expected returns for each scenario (R) weighted by the
probabilities of the scenarios (PRB).
We constrain expected return to be greater-than-or-equal-to our target using the constraint:
! Target ending value;
AVG >= TARGET;
The expected return under scenario S is computed using:
R(S) = @SUM(STOCKS(J): VE(S, J) * X(J));
This is just the sum of the return of each stock under the scenario weighted by the fraction of the
portfolio in each stock.
The deviations from average return for the scenarios are computed with:
DVU(S) - DVL(S) = R(S) - AVG
If the expected return from the scenario is greater than the average, DVU will be positive. If the
expected return is less than average, DVL will be positive. Given the fact that DVL and DVU impact
the objective, there will never be an optimal solution where both DVL and DVU are greater than 0. If
both are greater than 0, then a better solution can always be obtained by driving one of the two to zero.
By setting things up this way, we have partitioned the deviations into two parts. DVU represents
deviations above the average, which only the variance measure is concerned with. On the other hand,
DVL represents deviations below average, which both the downside risk and semi-variance measures
are computed from.
508 CHAPTER 12
The following constraint forces us to be fully invested and should be familiar from the discussion of
the Markowitz model:
! Budget;
@SUM(STOCKS: X) = 1;
We compute our three measures of risk using:
! Our three measures of risk;
[VARI] VAR = @SUM(SCENE: PRB * (DVU + DVL)^2);
[SEMI] SEMIVAR = @SUM(SCENE: PRB * (DVL) ^2);
[DOWN] DNRISK = @SUM(SCENE: PRB * DVL);
These are simply the sum of a measure of deviation across the scenarios weighted by the probabilities
of the scenarios. The variance measure takes the square of both the above and below average
deviations. The semi-variance measure squares just the below average deviation. While, the downside
risk measure uses the below average deviations without squaring.
The Solution
If we solve the model using the three risk measures in the objective, we get the following three
solutions:
Variance Semi-variance Downside Risk
ATT .530 .575 .511
GMT .357 .039 .489
USX .113 .386 .000
The fraction of the portfolio devoted to ATT is fairly consistent. However, the fractions of GMT and
USX can vary significantly when the risk measure changes.
Developing More Advanced Models 509
Options Pricing Model: OPTION
Background
A call option is a financial instrument that gives the holder the right to buy one share of a stock at a
given price (the exercise price) on or before some specified expiration date. A frequent question is,
“How much should one be willing to pay for such an option?” We can easily come up with some broad
bounds on what we would be willing to pay.
Suppose the stock price is $105 and we have a chance to buy an option with an exercise price of $100.
We should certainly be willing to pay up to $5 for the option, because, as a minimum, we could buy
the stock for $100 and immediately sell it for $105, realizing a profit of $5. Thus, when the stock price
exceeds the exercise price, we should be willing to pay at least the difference in the two prices.
When the exercise price exceeds the stock price, buying at the exercise price and selling at the market
price would not be an intelligent option. In this instance, we should be willing to “pay” at least $0.
In any case, the most we would ever be willing to pay for an option is the current price of the
underlying stock. Suppose the option price was more than the stock price. Then, we could get the same
expected return at a lower price by buying the stock.
The following graph illustrates these bounds on an option’s value as a function of the price of the
underlying stock:
Exercise
Price
Stock Price
Option
V
alue
P
Unfortunately, these bounds are not very tight. In reality, the option value function will resemble the
curve P in the graph. The exact shape of this curve is influenced by three additional factors. These are,
1) the time to expiration, 2) the volatility, or variance, in the price movements of the stock, and 3) the
interest rate. The underlying formula for curve P eluded researchers for many years until Fischer Black
and Myron Scholes derived it in 1973. A Nobel Prize was subsequently awarded for their work in
1997.

510 CHAPTER 12
The Problem in Words
You believe that the stock of National Semiconductor (symbol: NSM) is about to go up. To capitalize
on this belief, you would like to purchase call options on NSM. Checking the quotes on NSM options
with your online brokerage service, you find that NSM call options are trading at 6 5/8 per share.
These call options have an exercise price of $40, and expire in 133 days from today. The current price
of NSM shares is 40 3/4. Are the options trading at a fair price?
The Model
! Computing the value of an option using the Black
& Scholes formula (see "The Pricing of Options
and Corporate Liabilities", Journal of Political
Economy, May-June, 1973);
SETS:
! We have 27 weeks of prices P(t), LOGP(t) is log
of prices;
WEEK/1..27/: P, LOGP;
ENDSETS
DATA:
! Weekly prices of National Semiconductor;
P = 26.375, 27.125, 28.875, 29.625, 32.250,
35.000, 36.000, 38.625, 38.250, 40.250,
36.250, 41.500, 38.250, 41.125, 42.250,
41.500, 39.250, 37.500, 37.750, 42.000,
44.000, 49.750, 42.750, 42.000, 38.625,
41.000, 40.750;
! The current share price;
S = 40.75;
! Time until expiration of the option, expressed
in years;
T = .3644;
! The exercise price at expiration;
K = 40;
! The yearly interest rate;
I = .163;
ENDDATA
SETS:
! We will have one less week of differences;
WEEK1(WEEK)| &1 #LT# @SIZE(WEEK): LDIF;
ENDSETS
! Take log of each week's price;
@FOR(WEEK: LOGP = @LOG(P));
! and the differences in the logs;
@FOR(WEEK1(J): LDIF(J) =
LOGP(J + 1) - LOGP(J));
! Compute the mean of the differences;
MEAN = @SUM(WEEK1: LDIF)/ @SIZE(WEEK1);
! and the variance;
WVAR = @SUM(WEEK1: (LDIF - MEAN)^2)/
(@SIZE(WEEK1) - 1);

Developing More Advanced Models 511
! Get the yearly variance and standard deviation;
YVAR = 52 * WVAR;
YSD = YVAR^.5;
! The Black & Scholes option pricing formula;
Z = ((I + YVAR/2) *
T + @LOG(S/ K))/(YSD * T^.5);
! where VALUE is the expected value of the option;
VALUE = S *@PSN(Z) - K *@EXP(- I * T) *
@PSN(Z - YSD *T^.5);
! LDIF may take on negative values;
@FOR(WEEK1: @FREE(LDIF));
! The price quoted in the Wall Street Journal for
this option when there were 133 days left was $6.625;
Model: OPTION
The Sets and Attributes
In this model, there is a single primitive set, WEEK, which corresponds to the 27 weeks of price data.
We define the two attributes P and LOGP on this set. P stores the raw price data on NSM, while
LOGP stores the logarithm of the prices.
The Formulas
It is beyond the scope of this document to get into the theoretical details behind the Black & Scholes
pricing model. The interested reader should refer to Black and Scholes (1973) for the details. However,
we will briefly discuss some of the mechanics of the key formulas involved in the model.
In our model, we compute the option’s value in two key steps. First, we compute Z as follows:
Z = ((I + YVAR/2) * T + @LOG(S/ K))/(YSD * T^.5);
where,
I = the yearly interest rate,
YVAR = variance of the stock’s price,
T = time until expiration in years,
S = current share price,
K = exercise price, and
YSD = standard deviation on stock’s price.
We then use the value of Z in the following formula to determine the expected value of the option:
VALUE = S *@PSN(Z)-K *@EXP(- I * T) * @PSN(Z-YSD *T^.5);
where,
@PSN(Z) = returns the cumulative standard normal probability, and
@EXP(X) = returns ex.
The Solution
Solving the model, LINGO comes up with a value of $6.58 for the call option―not too far from the
quoted price of $6.63.
512 CHAPTER 12
Bond Portfolio Optimization Model: PBOND
Background
In certain situations, a business or individual may be faced with financial obligations over a future
number of periods. In order to defease (i.e., eliminate) this future debt, the debtor can determine a
minimal cost mix of current assets (e.g., cash and bonds) that can be used to cover the future stream of
payments. This problem is sometimes referred to as the cash flow matching problem or the debt
defeasance problem.
The Problem in Words
You are the head of your state’s lottery office. Lottery prizes are not paid out immediately, but are
parceled out over a 15 year period. You know exactly how much your office needs to pay out in prizes
over the next 15 years. You would like to set aside enough money from lottery receipts to invest in
secure government bonds to meet this future stream of payments. All remaining lottery receipts will be
turned over to the state’s treasurer to help fund the education system. You would like to turn over as
many of the receipts as possible to the treasurer, so your plan is to purchase a minimal cost mix of
bonds that just meets your future cash needs.
Here is the amount of cash you will need (in millions) to make future prize payments:
Year 0 1 2 3 4 5 6 7 8 9 10 11 12
Needs $10 $11 $12 $14 $15 $17 $19 $20 $22 $24 $26 $29 $31
There are two bonds currently being offered that you feel are of sufficient quality to guarantee the
future stream of prize payments. These bonds are listed below:
Bond Years to Maturity Price ($M) Coupon ($M)
A 6 .98 .06
B 13 .965 .065
If funds are not invested in bonds, they can be placed into short-term money market funds. You
conservatively estimate that short-term rates will be about 4% over the 15 year time horizon.
How many of each bond should you buy, and how much additional cash should you allocate to money
market funds to minimize your total outlay while still being able to meet all the future prize payments?

Developing More Advanced Models 513
The Model
! Bond portfolio/cash matching problem. Given cash
needs in a series of future periods, what
collection of bonds should we buy to meet these
needs?;
SETS:
BOND/A B/ :
MATAT, ! Maturity period;
PRICE, ! Price;
CAMNT, ! Coupon;
BUY; ! Amount to buy;
PERIOD/1..15/:
NEED, !Cash needed each period;
SINVEST; !Short term investment each period;
ENDSETS
DATA:
STRTE = .04; !Short term interest rate;
MATAT = 6, 13; !Years to maturity;
PRICE = .980, .965; !Bond purchase prices;
CAMNT = .060, .065; !Bond coupon amounts;
NEED = 10, 11, 12, 14, 15, 17, 19, 20, 22, 24,
26, 29, 31, 33, 36; ! Cash needs;
ENDDATA
!Minimize total investment required to generate
the stream of future cash needs;
MIN = LUMP;
! First period is slightly special;
LUMP = NEED(1) + SINVEST(1) +
@SUM(BOND: PRICE * BUY);
! For subsequent periods;
@FOR(PERIOD(I)| I #GT# 1:
@SUM(BOND(J)| MATAT(J) #GE# I:
CAMNT(J) * BUY(J)) +
@SUM(BOND(J)| MATAT(J) #EQ# I:
BUY(J)) +
(1 + STRTE) * SINVEST(I - 1) =
NEED(I) + SINVEST(I);
);
! Can only buy integer bonds;
@FOR(BOND(J): @GIN(BUY(J)));
Model: PBOND
The Sets
We define two primitive sets⎯BOND and PERIOD. The BOND set corresponds to the two bonds,
while PERIOD is the set of 15 years in the time horizon.
The Attributes
We define four attributes on the BONDS set⎯MATAT, PRICE, CAMNT, and BUY. MATAT stores the
bonds’ maturities, PRICE the price, CAMNT the coupon amount, and BUY the number of each bond to
buy.

514 CHAPTER 12
The NEED and SINVEST attributes are defined on the PERIOD set. NEED stores the cash needs in
each period and SINVEST stores the amount in short-term investments in each period.
The Objective
The objective of this model is to minimize the initial cash outlay. The initial cash outlay, or lump sum,
is stored in the LUMP variable. Thus, our objective is written simply as:
! Minimize the total investment required to generate
the stream of future cash needs;
MIN = LUMP;
The Formulas
There are three categories of formulas in this model:
1. computing the initial lump sum payment (LUMP),
2. sources=uses constraints, which enforce the condition that all sources of
cash in a period must equal uses for cash in a period, and
3. integer restrictions on the BUY variable limiting us to buying only whole
numbers of bonds.
The following expression computes the lump outflow of cash in the initial period:
LUMP = NEED(1) + SINVEST(1) +
@SUM(BOND: PRICE * BUY);
Cash is needed for three purposes in the initial period:
1. payment of lottery prizes (NEED(1)),
2. allocations to short-term money funds (SINVEST(1)), and
3. bond purchases (@SUM(BOND: PRICE * BUY)).
In the remaining 14 periods, sources of cash must equal uses of cash. We enforce this condition with:
! For subsequent periods;
@FOR(PERIOD(I)| I #GT# 1:
@SUM(BOND(J)| MATAT(J) #GE# I:
CAMNT(J) * BUY(J)) +
@SUM(BOND(J)| MATAT(J) #EQ# I:
BUY(J)) +
(1 + STRTE) * SINVEST(I - 1) =
NEED(I) + SINVEST(I);
);
The sources of cash in a period are threefold:
1. coupon receipts:
@SUM(BOND(J)| MATAT(J) #GE# I:
CAMNT(J) * BUY(J))
2. maturing bonds:
@SUM(BOND(J)| MATAT(J) #EQ# I:
BUY(J))

Developing More Advanced Models 515
3. maturing short-term investments from the previous period:
(1 + STRTE) * SINVEST(I - 1)
These sources must equal the following two uses:
1. lottery prize payments:
NEED(I)
2. new short-term investments:
SINVEST(I)
Finally, to force bond purchases to be whole numbers, we add:
! Can only buy integer bonds;
@FOR(BOND(J): @GIN(BUY(J)));
The Solution
If we solve the model, we get the following values:
Global optimal solution found.
Objective value: 195.7265
Extended solver steps: 4
Total solver iterations: 27
Variable Value
LUMP 195.7265
BUY(A) 96.00000
BUY(B) 90.00000
SINVEST(1) 4.796526
SINVEST(2) 5.598387
SINVEST(3) 5.432322
SINVEST(4) 3.259615
SINVEST(5) 0.000000
SINVEST(6) 90.61000
SINVEST(7) 81.08440
SINVEST(8) 70.17778
SINVEST(9) 56.83489
SINVEST(10) 40.95828
SINVEST(11) 22.44661
SINVEST(12) 0.1944784
SINVEST(13) 65.05226
SINVEST(14) 34.65435
SINVEST(15) 0.4052172E-01
Solution: PBOND
You have been able to cover a total future debt of $319 million with a lump payment of $195.73
million. To do this, you buy 96 A bonds, 90 B bonds, put $4.8 million into short-term investment
funds, and hold $10 million in cash to pay prizes in the initial period.

516 CHAPTER 12
Queuing Models
Erlang Queuing Models Model: EZQUEUE
Background
The telephone, communications, and computer industries have long used queuing models to estimate
the performance of a service system in the face of random demand. The two most frequently used
models are the Erlang loss and Erlang waiting models. In both cases, customers arrive randomly at a
number of identical servers. In the Erlang loss model, there is no queue, so any customer finding all
servers busy is lost. In the Erlang waiting model, there is an infinite queue space, so any customer
finding all servers busy waits until a server is free. In either case, the major measure of performance is
the fraction of customers that find all servers busy.
To compute a system’s performance, we must know the load placed on the system per unit of time and
the number of servers. The load is a unitless measure of the amount of work arriving per unit of time.
For example, if 20 customers arrive each hour and each requires ½ hour of work, then the arriving load
is 10 (20 customers per hour multiplied by ½ hour per customer).
The most crucial probabilistic assumption in both cases is the number of arrivals per unit of time is
Poisson distributed with a constant mean. The held case (with a queue) further requires that service
times be exponentially distributed. If the arriving load is denoted AL and the number of servers by NS,
then the expected fraction finding all servers busy is given in the loss case by @PEL(AL, NS) and in
the held case by @PEB(AL, NS).
The Problem in Words
You manage the customer service department of your business. Calls arrive at the rate of 25 customers
per hour. Each call requires an average of 6 minutes to process. How many service representatives
would be required for no more than 5% of customers to receive a busy signal?
The Model
! Arrival rate of customers/ hour;
AR = 25;
! Service time per customer in minutes;
STM = 6;
! Service time per customer in hours;
STH = STM/ 60;
! Fraction customers finding all servers busy;
FB = .05;
! The PEL function finds number of servers
needed, NS;
FB = @PEL(AR * STH, NS);
Model: EZQUEUE

Developing More Advanced Models 517
The Solution
Feasible solution found at step: 0
Variable Value
AR 25.00000
STM 6.000000
STH 0.1000000
FB 0.5000000E-01
NS 5.475485
Because we cannot have fractional servers, we need at least six servers to meet our requirement that no
more than 5% of customers find all servers busy.
Suppose you install a sufficient number of incoming lines, so customers finding all servers busy can
wait. Further, you will still use six servers. You want to find the following:
♦ the fraction of customers finding all servers busy,
♦ the average waiting time for customers who wait,
♦ the average overall waiting time, and
♦ the average number waiting.
The following variation on the previous model computes these four statistics:
! Arrival rate of customers/ hour;
AR = 25;
! Service time per customer in minutes;
STM = 6;
! Service time per customer in hours;
STH = STM/ 60;
! The number of servers;
NS = 6;
! The PEL function finds number of servers
needed, NS;
FB = @PEB(AR * STH, NS);
! The conditional wait time for those who wait;
WAITC = 1 / (NS / STH - AR);
! The unconditional wait time;
WAITU = FB * WAITC;
! The average number waiting;
NWAIT = AR * WAITU;
Note how we now use the @PEB function, rather than @PEL, to account for the presence of a queue
to hold callers finding all lines busy. The solution to the modified model is:
Variable Value
AR 25.00000
STM 6.000000
STH 0.1000000
NS 6.000000
FB 0.4744481E-01
WAITC 0.2857143E-01
WAITU 0.1355566E-02
NWAIT 0.3388915E-01
Remember the unit of time is an hour, so the expected waiting time for those who wait is
.2857 * 60 = 1.7 minutes.

518 CHAPTER 12
Machine Repairman Models Model: EZMREPAR
Background
Another queuing model illustrates service demand from a finite population of users. The underlying
assumption is, if a significant fraction of these users are already waiting for service, then the arrival
rate of further service demands decreases until more of the users are serviced and returned to the
calling community. Models of this class are referred to as Machine Repairman models because the
calling population can be viewed as a set of machines where individual machines occasionally break
down and need repair.
The @PFS ((Poisson Finite Source) function computes the expected number of customers either in
repair or waiting for repair, given the number of customers, number of repairmen, and the limiting load
of the queue. The following model illustrates the use of the @PFS function to model a computer
timesharing system. Each incoming port can be thought of as a customer. Usually, the number of
incoming ports is limited. Thus, the finite source assumption is appropriate.
The Problem in Words
You manage the accounting department in your company. You are contemplating installing a new
server to handle the growing computing needs of your department. However, you have your doubts as
to whether or not the system proposed by the computing services department will be adequate to meet
your current and future needs. Your department has 32 employees who will make continuous use of
the server throughout the day. You do some research and determine the mean time between server
requests is 40 seconds per user. On average, it will take the proposed server 2 seconds to process a user
request. Will the proposed server provide the horsepower needed by your department?

Developing More Advanced Models 519
The Model
! Model of a computer timesharing system;
! The mean think time for each user (more
generally, Mean Time Between Failures in a
repair system);
MTBF = 40;
! The mean time to process each compute request
(more generally, Mean Time To Repair in
seconds);
MTTR = 2;
! The number of users;
NUSER = 32;
! The number of servers/repairmen;
NREPR = 1;
! The mean number of users waiting or in service
(more generally, the mean number of machines
down);
NDOWN =
@PFS(MTTR * NUSER/ MTBF, NREPR, NUSER);
! The overall request for service rate (more
generally, overall failure rate), FR, must
satisfy;
FR = (NUSER - NDOWN)/ MTBF;
! The mean time waiting for or in service (more
generally, the mean time down), MTD, must
satisfy;
NDOWN = FR * MTD;
Model: EZMREPAR
The Solution
Variable Value
MTBF 40.00000
MTTR 2.000000
NUSER 32.00000
NREPR 1.000000
NDOWN 12.06761
FR 0.4983098
MTD 24.21707
Solution: EZMREPAR
This would probably be considered a heavily loaded system⎯on average, about 12 users are waiting
for a response from the server. Each request for processing requires an expected elapsed time of over
24 seconds, even though the average request is for only two seconds of processing. As a group, users
request service at the rate of almost one request every 2 seconds.

520 CHAPTER 12
Steady State Queuing Model Model: QUEUEM
Background
A useful approach for tackling general queuing models is to use the Rate In = Rate Out Principle
(RIRO) to derive a set of steady state equations for a queuing system. RIRO assumes a system can
reach a state of equilibrium. In equilibrium, the tendency to move out of a certain state must equal the
tendency to move towards that state. Given the steady state equations derived from this assumption,
we can solve for the probability that a system is in a given state at any particular moment.
The following example assumes a system with multiple servers and “customers” that arrive in batches.
The Problem in Words
You operate a motor rebuilding business that services auto repair shops throughout a several state area.
Motors arrive on trucks in batches of up to four motors per truck. On average, trucks arrive 1.5 times a
day. The probabilities that a truck contains 1, 2, 3 or 4 motors are, respectively, .1, .2, .3 and .4. You
presently have five workstations that can each rebuild two motors per day.
You would like to introduce a priority service that, in exchange for a higher fee, guarantees your
customers a one day turnaround. To do this effectively, at least one workstation must be free 90
percent of the time in order to begin immediate repair of any incoming priority job. Are your current
facilities adequate for this level of service?
The Model
! Model of a queue with arrivals in batches. In
this particular example, arrivals may show up in
batches of 1, 2, 3, or 4 units;
SETS:
! Look at enough states so P(i) for large i is
effectively zero, where P(i) is the steady state
probability of i-1 customers in the system;
STATE/ 1..41/: P;
! Potential batch sizes are 1, 2, 3 or 4 ,
customers and A(i) = the probability that an
arriving batch contains i customers;
BSIZE/ 1..4/: A;
ENDSETS
DATA:
! Batch size distribution;
A = .1, .2, .3, .4;
! Number of batches arriving per day;
LMDA = 1.5;
! Number of servers;
S = 5;
! Number of customers a server can
process per day;
MU = 2;
ENDDATA
! LAST = number of STATES;
LAST = @SIZE(STATE);

Developing More Advanced Models 521
! Balance equations for states where the number of
customers in the system is less than or equal to
the number of servers;
@FOR(STATE(N)| N #LE# S:
P(N) * ((N - 1)* MU + LMDA) =
P(N + 1) * MU * N +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I)
* P(N - I))
);
! Balance equations for states where number in
system is greater than the number of servers,
but less than the limit;
@FOR(STATE(N)| N #GT# S #AND# N #LT# LAST:
P(N) * (S * MU + LMDA) =
P(N + 1) * MU * S +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I) *
P(N - I))
);
! Probabilities must sum to 1;
@SUM(STATE: P) = 1;
Model: QUEUEM
The Formulas
The model computes the probabilities P(i), i = 1 to 41, where P(i) is the probability there are i - 1
motors in the system for repair. We have chosen to stop at 41 because the probability the system would
have more than 40 machines waiting for repair is effectively 0.
In order to solve for the 41 unknown P(i), we will need 41 equations. One of these equations comes
from the fact that the probabilities must all sum to 1:
! Probabilities must sum to 1;
@SUM(STATE: P) = 1;
The remaining 40 equations are derived from the steady state assumptions that the rate of movement
into any state must equal the rate out. We partition these balance equations into two types. In the first
case, there are the states where the number of motors in the system is less-than-or-equal-to the number
of servers. The balance equations in this case are:
@FOR(STATE(N)| N #LE# S:
P(N) * ((N - 1)* MU + LMDA) =
P(N + 1) * MU * N +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I)
* P(N - I))
);
For each state where the number of motors in the system is less-than-or-equal-to the number of
servers, we set the rate of flow out of the state:
P(N) * ((N - 1)* MU + LMDA)
equal to the rate of flow into the state:
P(N + 1) * MU * N +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I)
* P(N - I))

522 CHAPTER 12
The rate of flow out is the rate of flow to states with more motors, LMDA, plus the rate of flow to
lesser states, (N - 1) * MU, multiplied by the probability of being in the state, P(N). The rate of flow in
is the rate of flow in from higher states, P(N + 1) * MU * N, plus the expected rate of flow in from
lower states, LMDA * @SUM(BSIZE(I)| I #LT# N: A(I) * P(N - I)).
We generate equivalent balance equations for the higher states where the number of motors exceeds
the number of servers with the following:
@FOR(STATE(N)| N #GT# S #AND# N #LT# LAST:
P(N) * (S * MU + LMDA) =
P(N + 1) * MU * S +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I) *
P(N - I))
);
The Solution
An excerpt from the full solution report showing the first 10 values of P is listed below:
Variable Value
LMDA 1.500000
S 5.000000
MU 2.000000
LAST 41.00000
P(1) 0.2450015
P(2) 0.1837511
P(3) 0.1515947
P(4) 0.1221179
P(5) 0.9097116E-01
P(6) 0.5707410E-01
P(7) 0.4276028E-01
P(8) 0.3099809E-01
P(9) 0.2187340E-01
P(10) 0.1538003E-01
The probability at least one workstation is free is the probability that four or fewer motors are in the
system, in other words, the sum of the first five P(i). In this case, it works out that at least one
workstation will be free only about 70% of the time. Experimenting with the model by increasing the
number of servers reveals you will need at least seven workstations to provide the level of service
required by the new priority plan.
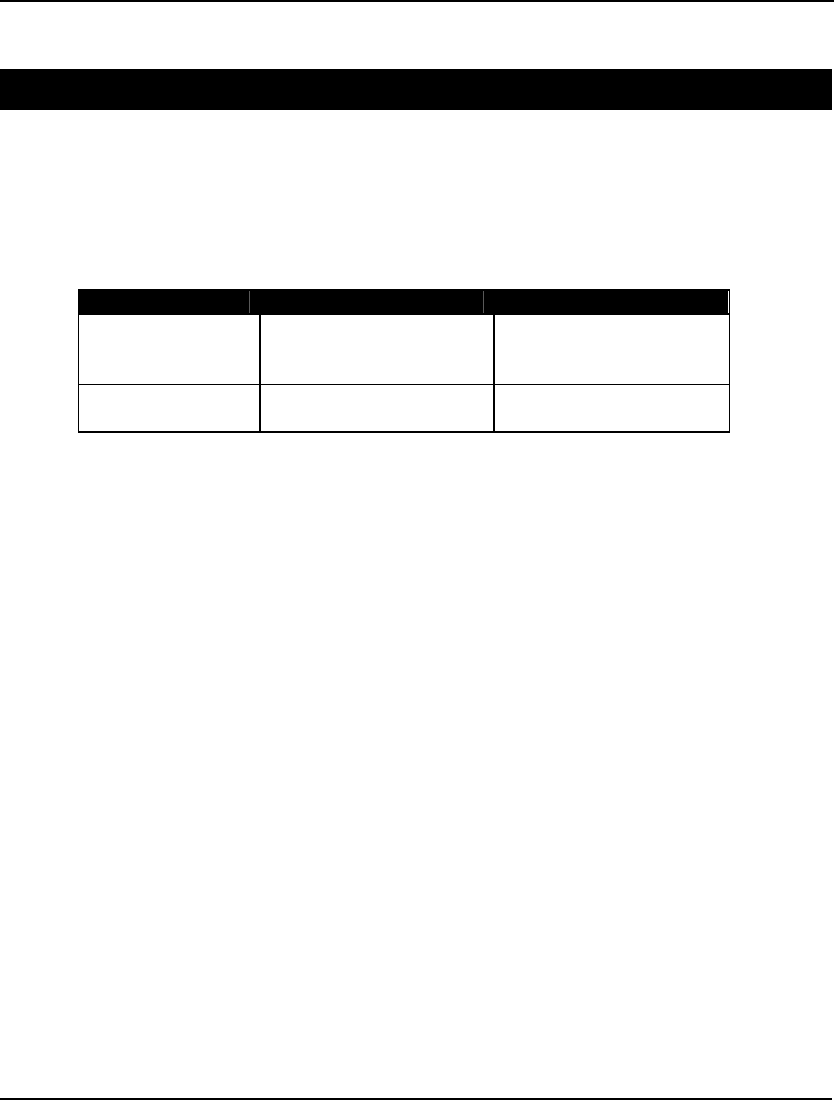
Developing More Advanced Models 523
Marketing Models
Markov Chain Model Model: MARKOV
Background
A standard approach used in modeling random variables over time is the Markov chain approach.
Refer to an operations research or probability text for complete details. The basic idea is to think of the
system as being in one of a discrete number of states at each point in time. The behavior of the system
is described by a transition probability matrix that gives the probability the system will move to a
specified other state from some given state. Some example situations are:
System States Cause of Transition
Consumer brand
switching
Brand of product most
recently purchased by
consumer
Consumer changes mind,
advertising
Inventory System Amount of inventory on
hand
Orders for new material,
demands
An interesting problem is to determine the long-term, steady state probabilities of the system. If we
assume the system can reach equilibrium, then it must be true the probability of leaving a particular
state must equal the probability of arriving in that state. You will recall this is the Rate In = Rate Out
Principle (RIRO) we used above in building the multi-server queuing model, QUEUEM. If we let:
π
i = the steady state probability of being in state i, and
pij = the transition probability of moving from state i to j,
then, by our RIRO assumption, for each state i:
∑
j
≠
i pj pji =
π
i (1 - pjj)
Rewriting the above, we get:
π
i =
∑
j
π
j pji
This gives us n equations to solve for the n unknown steady state probabilities. Unfortunately, it turns
out this system is not of full rank. Thus, there is not a unique solution. To guarantee a valid set of
probabilities, we must make use of one final condition—the sum of the probabilities must be 1.

524 CHAPTER 12
The Problem in Words
Your company is about to introduce a new detergent and you’re interested in whether it will clean up
in the market. It will be competing against three other existing brands. As a result of a small test
market and interviews with consumers familiar with all four detergents, we have derived the following
purchase transition matrix:
Next Purchase:
A B C D
A .75 .1 .05 .1
B .4 .2 .1 .3
C .1 .2 .4 .3
Previous
Purchase:
D .2 .2 .3 .3
Our new detergent is brand A in this matrix. The interpretation of the matrix is, for example, if
someone most recently purchased brand A, then with probability .75 his next purchase of this product
will also be brand A. Similarly, someone who most recently purchased brand B will next purchase
brand D with probability .3. An associate of yours who looked at this matrix said, “Aha, we should
expect to get 75% of the market in the long run with brand A.” Do you think your associate is correct?
The Model
! Markov chain model;
SETS:
! There are four states in our model and over
time the model will arrive at a steady state
equilibrium.
SPROB(J) = steady state probability;
STATE/ A B C D/: SPROB;
! For each state, there's a probability of moving
to each other state. TPROB(I, J) = transition
probability;
SXS(STATE, STATE): TPROB;
ENDSETS
DATA:
! The transition probabilities. These are proba-
bilities of moving from one state to the next
in each time period. Our model has four states,
for each time period there's a probability of
moving to each of the four states. The sum of
probabilities across each of the rows is 1,
since the system either moves to a new state or
remains in the current one.;
TPROB = .75 .1 .05 .1
.4 .2 .1 .3
.1 .2 .4 .3
.2 .2 .3 .3;
ENDDATA
! Steady state equations;
! Only need N equations, so drop last;
@FOR(STATE(J)| J #LT# @SIZE(STATE):
SPROB(J) = @SUM(SXS(I, J): SPROB(I) *
TPROB(I, J))
);

Developing More Advanced Models 525
! The steady state probabilities must sum to 1;
@SUM(STATE: SPROB) = 1;
! Check the input data, warn the user if the sum
of probabilities in a row does not equal 1.;
@FOR(STATE(I):
@WARN('Probabilities in a row must sum to 1.',
@ABS(1 - @SUM(SXS(I, K): TPROB(I, K)))
#GT# .000001);
);
Model: MARKOV
The Sets
The primitive STATE set represents the four states of purchasing detergents A, B, C, and D. We build
one derived set, SXS that is the cross of the STATE set on itself. The SXS set is used to establish the
state transition matrix.
The Attributes
We have two attributes. The first, SPROB, is defined on the STATES set and is used to store the steady
state probabilities of the system. We will be solving for the values of the SPROB attribute. The second
attribute, TPROB, is defined on the two-dimensional SXS set and is used to store the values of the state
transition matrix.
The Formulas
First off, to ensure data integrity, we use the @WARN function to verify the probabilities in each row
of the state transition matrix sum to 1 using:
! Check the input data, warn the user if the sum of
probabilities in a row does not equal 1.;
@FOR(STATE(I):
@WARN('Probabilities in a row must sum to 1.',
@ABS(1 - @SUM(SXS(I, K): TPROB(I, K)))
#GT# .000001);
Due to the potential for roundoff error, we allow for a modest transgression by using a tolerance factor
of .000001. If the probabilities in a row sum up to more than 1.000001 or less than .999999, the user
will receive a warning.
Next, the steady state probabilities must be exhaustive. We guarantee this by setting their sum to 1
with:
! The steady state probabilities must sum to 1;
@SUM(STATE: SPROB) = 1;
Finally, in addition to this last equation, we need an additional n-1 equations to solve for the n steady
state probabilities. We get these equations from the RIRO derivation above using:
! Steady state equations;
! Only need N equations, so drop last;
@FOR(STATE(J)| J #LT# @SIZE(STATE):
SPROB(J) = @SUM(SXS(I, J): SPROB(I) *
TPROB(I, J))
);

526 CHAPTER 12
The Solution
The solution is:
Variable Value
SPROB(A) 0.4750000
SPROB(B) 0.1525000
SPROB(C) 0.1675000
SPROB(D) 0.2050000
Solution: MARKOV
So, we see the long run share of our new brand A will only amount to about 47.5% of the market,
which is considerably less than the conjectured share of 75%.
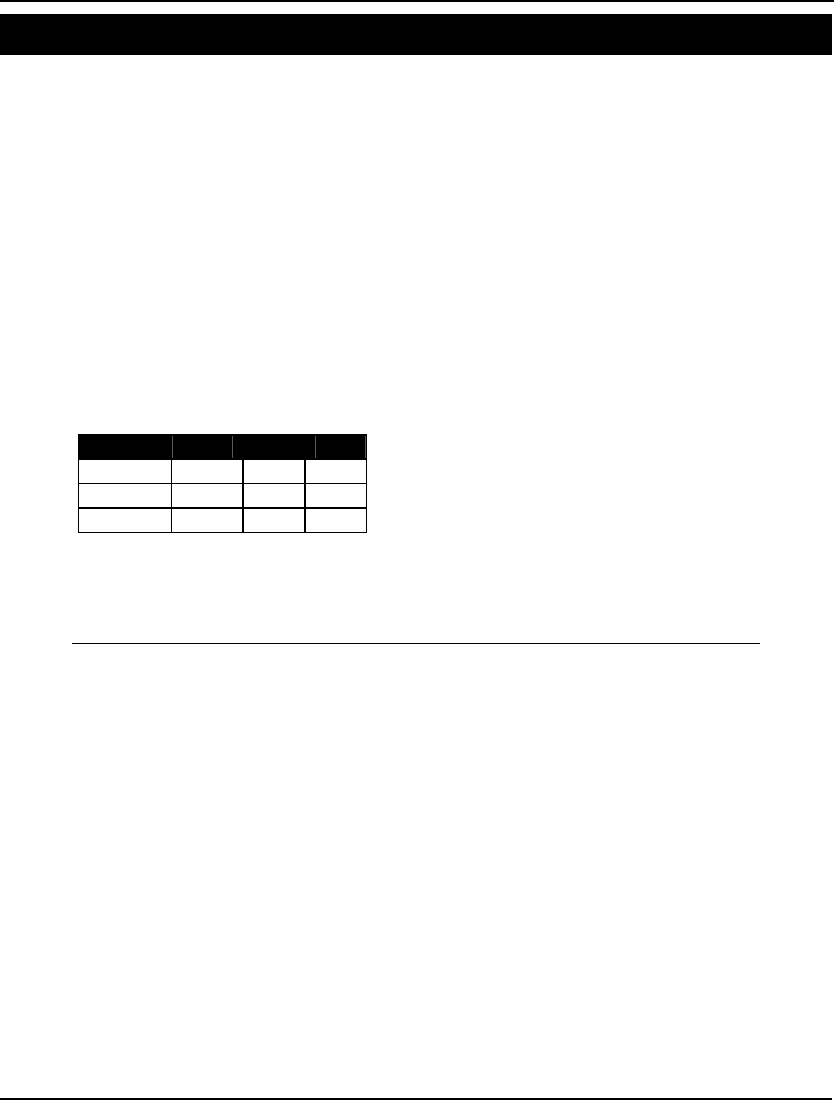
Developing More Advanced Models 527
Conjoint Analysis Model: CONJNT
Background
When designing a product, it is useful to know how much customers value various attributes of that
product. This allows us to design the product most preferred by consumers within a limited budget. For
instance, if we determine consumers place a very high value on a long product warranty, then we
might be more successful in offering a long warranty with fewer color options.
The basic idea behind conjoint analysis is, while it may be difficult to get consumers to accurately
reveal their relative utilities for product attributes, it’s easy to get them to state whether they prefer one
product configuration to another. Given these rank preferences, you can use conjoint analysis to work
backwards and determine the implied utility functions for the product attributes.
The Problem in Words
Your company is about to introduce a new vacuum cleaner. You have conducted customer surveys and
you determined the relative preferences for the following warranty/price product configurations (9
being the most preferred):
$129 $99 $79
2 Years 7 8 9
1 Year 3 4 6
None 1 2 5
In order to derive an optimal product configuration, you need to know the utility functions for
warranty length and price implied by the preferences in the table above.
The Model
! Conjoint analysis model to decide how much
weight to give to the two product attributes of
warranty length and price;
SETS:
! The three possible warranty lengths;
WARRANTY /LONG, MEDIUM, SHORT/ : WWT;
! where WWT(i) = utility assigned to warranty i;
! The three possible price levels (high,
medium, low);
PRICE /HIGH, MEDIUM, LOW/ : PWT;
! where PWT(j) = utility assigned to price j;
! We have a customer preference ranking for each
combination;
WP(WARRANTY, PRICE) : RANK;
ENDSETS
DATA:
! Here is the customer preference rankings running
from a least preferred score of 1 to the most
preferred of 9. Note that long warranty and low
price are most preferred with a score of 9,
while short warranty and high price are least
preferred with a score of 1;

528 CHAPTER 12
RANK = 7 8 9
3 4 6
1 2 5;
ENDDATA
SETS:
! The next set generates all unique pairs of
product configurations such that the second
configuration is preferred to the first;
WPWP(WP, WP) | RANK(&1, &2) #LT#
RANK(&3, &4): ERROR;
! The attribute ERROR computes the error of our
estimated preference from the preferences given
us by the customer;
ENDSETS
! For every pair of rankings, compute the amount
by which our computed ranking violates the true
ranking. Our computed ranking for the (i,j)
combination is given by the sum WWT(i) + PWT(j).
(NOTE: This makes the bold assumption that
utilities are additive!);
@FOR(WPWP(i, j, k, l): ERROR(i, j, k, l) >=
1 + (WWT(i) + PWT(j)) - (WWT(k) + PWT(l))
);
! The 1 is required on the right-hand-side of the
above equation to force ERROR to be nonzero in
the case where our weighting scheme incorrectly
predicts that the combination (i,j) is equally
preferred to the (k,l) combination.
Since variables in LINGO have a default lower
bound of 0, ERROR will be driven to zero when we
correctly predict (k,l) is preferred to (i,j).
Next, we minimize the sum of all errors in order
to make our computed utilities as accurate as possible;
MIN = @SUM(WPWP: ERROR);
Model: CONJNT
The Sets
We have two primitive sets in the model: WARRANTY is the set of warranty lengths and PRICE is the
set of prices. We form the derived set WP by taking the cross of WARRANTY and PRICE in order to
create an attribute to store the preferences for each (WARRANTY, PRICE) pair.
The interesting set in this model is the sparse derived set WPWP:
! The next set generates all unique pairs of product
configurations such that the second configuration
is preferred to the first;
WPWP(WP, WP) | RANK(&1, &2) #LT#
RANK(&3, &4): ERROR;
This set is derived from the cross of WP on itself. Each member of this set contains two product
configurations. Furthermore, we use a membership condition to limit the set to combinations of
product configurations where the first configuration is preferred to the second configuration. We need
this set because our model will be testing its proposed utility functions against all unique pairings of
configurations.

Developing More Advanced Models 529
Note that this set grows on the order of n2, where n is the number of product configurations. Thus, it
will tend to get big for large numbers of product configurations.
The Attributes
The model defines four attributes: WWT, PWT, RANK and ERROR. WWT and PWT are used to store
the utilities of the warranty and price configurations, respectively. The model will solve for values of
WWT and PWT that minimize total prediction error. These values will then give us the implied utility
functions for the two product attributes. RANK is used to store the customer preference rankings.
Finally, ERROR stores the error in predicting the preference of one configuration over another given
the implied utility values contained in WWT and PWT.
The Objective
The objective is quite simple⎯we want to minimize the total prediction error over all the unique
product configurations:
MIN = @SUM(WPWP: ERROR);
The Constraints
The model has just one class of constraints that computes the error term in predicting the preferences
over each product configuration:
@FOR(WPWP(i, j, k, l): ERROR(i, j, k, l) >=
1 + (WWT(i) + PWT(j)) -
(WWT(k) + PWT(l))
);
We need to add a 1 to the right-hand side of the constraint to account for the case where we predict
that configuration (i,j) is equally preferred to (k,l). Because of the way that we defined the WPWP set,
(i,j) will always be preferred to (k,l). Thus, it would be an error to predict they are equally preferred.
Note, also, because the lower bound on ERROR is 0 and we are also minimizing ERROR,
ERROR(i,j,k,l) will be driven to 0 when the model correctly predicts that (i,j) is preferred to (k,l).
The Solution
Portions of the solution are reproduced below:
Global optimal solution found at step: 35
Objective value: 0.000000
Variable Value
WWT(LONG) 7.000000
WWT(MEDIUM) 2.000000
WWT(SHORT) 0.000000
PWT(HIGH) 0.000000
PWT(MEDIUM) 1.000000
PWT(LOW) 4.000000
Solution: CONJNT
Short, medium and long warranties rate utilities of 0, 2, and 7, while high, medium and low prices rate
utilities of 0, 1, and 4. Note that, given the objective value of zero, this utility weighting scheme
exactly predicts preferences for each pair of product configurations.

531
13 Programming LINGO
Up to this point, we have primarily been concerned with self-contained models, which are solved once
and don’t receive input from, nor pass output to, other models. However, in many modeling situations,
there may be requirements for one, or more, models to be run in a sequence. Furthermore, the outputs
of one model may be required as inputs to a subsequent model. Such a series of models will typically
be run in a loop until some termination criterion is met. LINGO provides a number of programming
control structures to automate processing in situations where one has multiple, dependent models that
one must run in a sequence.
In the section immediately following, we will provide a brief introduction to the programming features
available in LINGO. We will then illustrate the use of these features in several models.
Programming Features
The programming capabilities in LINGO fall into seven categories:
♦ Model control
♦ Flow of control
♦ Model generation
♦ Output statements
♦ Setting parameters
♦ Stochastic Programming
♦ Utility functions
Model Control
In this category we have two types of statements. First are the SUBMODEL and ENDSUBMODEL
statements used to identify submodels, which are separate models contained within larger models. We
also have the @SOLVE statement for use in solving submodels.
SUBMODEL and ENDSUBMODEL:
These two statements are used to bracket a submodel within a larger, composite model. The
SUBMODEL statement must be followed immediately by a unique name of up to 32 characters that
follows the normal LINGO naming conventions. The name must then be followed by a colon. You
must also place a ENDSUBMODEL statement immediately after the last statement of your submodel.
Submodels may only exist in the model section and are not allowed in data, init and calc sections.

532 CHAPTER 13
As an example, the following illustrates a submodel for solving a knapsack type model:
SUBMODEL Pattern_Gen:
[R_OBJ] MAX = @SUM( FG(i): PRICE(i)* Y(i));
[R_WIDTH] @SUM( FG(i): WIDTH(i)*Y(i)) <= RMWIDTH;
@FOR( FG(i): @GIN(Y(i)));
ENDSUBMODEL
In this example, the submodel is titled Pattern_Gen and contains one objective, R_OBJ, one constraint,
R_WIDTH, and one @FOR loop to force the Y variables to be general integers via the @GIN function.
@DEBUG( [SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
Infeasible or unbounded submodels may be debugged in a calc section with the use of the @DEBUG
statement. Refer to the LINGO|Debug command for more information of model debugging.
If your model contains submodels, you can choose to debug a particular submodel by specifying its
name as an argument to @DEBUG. If desired, you may also specify more than one submodel name,
in which case, LINGO will simultaneously debug all the specified models as one combined model. If
a submodel name is omitted, LINGO will solve all model statements occurring before the @DEBUG
statement and not lying within a submodel section. It is the user’s responsibility to make sure the
submodels together make sense, e.g., at most one submodel in an @DEBUG invocation can have an
objective function.
In the following example, we solve a small submodel and then invoke the debugger if the solution is
found to be non-optimal:
MODEL:
SUBMODEL M:
MIN = X + Y;
X>4;
Y<3;
Y>X;
ENDSUBMODEL
CALC:
@SOLVE( M);
@IFC( @STATUS() #NE# 0: @DEBUG( M));
ENDCALC
END
Note: Submodels must be defined in the model prior to any references to them via the @DEBUG
statement.
PROGRAMMING LINGO 533
@SOLVE( [SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
Submodels may be solved in a calc section with the use of the @SOLVE statement. If your model
contains submodels, you can choose to solve a particular submodel by specifying its name as an
argument to @SOLVE. If desired, you may also specify more than one submodel name, in which case,
LINGO will simultaneously solve all the specified models as one combined model. If a submodel
name is omitted, LINGO will solve all model statements occurring before the @SOLVE statement and
not lying within a submodel section. It is the user’s responsibility to make sure the submodels together
make sense, e.g., at most one submodel in an @SOLVE can have an objective function.
As an example, to solve the submodel Pattern_Gen listed immediately above, you would add the
following statement to a calc section:
@SOLVE( Pattern_Gen);
Note: Submodels must be defined in the model prior to any references to them via the @SOLVE
statement.
Flow of Control
In a calc section, model statements are normally executed sequentially. Flow of control statements can
be used to alter the execution order of statements. In effect, this gives you a programming, or
scripting, capability within the LINGO environment.
@IFC and @ELSE
These statements provide you with conditional IF/THEN/ELSE branching capabilities. The syntax is as
follows:
@IFC( <conditional-exp>:
statement_1[; …; statement_n;]
[@ELSE
statement_1[; …; statement_n;]]
);
with the @ELSE block of statements being optional in case a pure if statement is desired.
Note: Be aware of the use of the letter ‘C’ in @IFC. This is to distinguish the flow of control if
statement (@IFC) from the arithmetic if (@IF).
To illustrate, the following sample code uses if/then/else blocks as part of a binary search for a key
value in an array:
@IFC( KEY #EQ# X( INEW):
LOC = INEW;
@ELSE
@IF( KEY #LT# X( INEW):
IE = INEW;
@ELSE
IB = INEW;
);
);

534 CHAPTER 13
@FOR
You’ve encountered the @FOR set looping statement previously as a way to generate constraints in
the model section. @FOR is also allowed in the calc section to perform looping. The main difference
is that @FOR does not generate constraints when used in the calc section. Instead, it immediately
executes any assignment statements contained within its scope. The following example shows a
@FOR loop extracted from a portfolio model. The loop is used to solve the portfolio model for a
number of different levels of desired return. For each level of return, the model minimizes variance,
and the variance is stored for later use.
@FOR( POINTS( I):
! Compute new return level;
RET_LIM = RET_MIN + (I-1)*INTERVAL;
! Re-solve the model;
@SOLVE();
! Store the return value;
YRET( I) = RET_LIM;
! Store the variance too;
XSTD( I) = VARIANCE^0.5;
);
@WHILE
The @WHILE statement is used for looping over a group of statements until some termination
criterion is met. The syntax is as follows:
@WHILE( <conditional-exp>: statement_1[; …; statement_n;]);
As long as the conditional expression is true, the @WHILE function will keep looping over its block of
statements.
As an example, the following code uses an @WHILE loop to search for a key value in an array as part
of a binary search procedure:
@WHILE( KEY #NE# X( LOC):
INEW = @FLOOR( ( IE + IB) / 2);
@IFC ( KEY #EQ# X( INEW):
LOC = INEW;
@ELSE
@IF ( KEY #LT# X( INEW):
IE = INEW - 1;
@ELSE
IB = INEW + 1;
);
);
);
In this case, the loop executes until the current value selected from the array, X(LOC), is equal to the
key value, KEY.

PROGRAMMING LINGO 535
@BREAK
The @BREAK statement is used to break out of the current loop. Execution resumes at the first
statement immediately following the end of the current loop. The @BREAK statement is valid only
within @FOR and @WHILE loops in calc sections and does not take any arguments. As an example,
we extend the @WHILE loop in the binary search example above to include an @BREAK statement
that will be executed when the key value can’t be found:
@WHILE( KEY #NE# X( LOC):
!exit loop if key can’t be found;
@IFC( IE – IB #LE# 1:
@PAUSE( 'Unable to find key!!!');
@BREAK;
);
INEW = @FLOOR( ( IE + IB) / 2);
@IFC ( KEY #EQ# X( INEW):
LOC = INEW;
@ELSE
@IF ( KEY #LT# X( INEW):
IE = INEW - 1;
@ELSE
IB = INEW + 1;
);
);
);
@STOP( [‘MESSAGE’])
The @STOP statement terminates execution of the current model. The @STOP statement is valid only
within calc sections and takes on optional text argument. When an @STOP is executed, LINGO will
display error message 258:
[Error Code: 258]
Model execution halted. STOP statement encountered.
If a text argument is included in the @STOP, then it will also be displayed as part of this error
message.
As an example, we extend the @WHILE loop in the binary search example above to include an
@STOP statement that will be executed when the key value can’t be found:
@WHILE( KEY #NE# X( LOC):
!exit if key can’t be found;
@IFC( IE –IB #LE# 1:
@STOP( 'Unable to find key!!!');
);
INEW = @FLOOR( ( IE + IB) / 2);
@IFC ( KEY #EQ# X( INEW):
LOC = INEW;
@ELSE

536 CHAPTER 13
@IF ( KEY #LT# X( INEW):
IE = INEW;
@ELSE
IB = INEW;
);
);
);
Model Generation
The commands in this category are related to the model generator, i.e., the component in LINGO that
translates your model’s statements into a format compatible with the solver.
@GEN( [SUBMODEL_NAME[, … SUBMODEL_NAME_N]])
The @GEN statement generates a model and displays the generated equations. @GEN converts the
model into the appropriate format for the solver engine; however, it does not actually call the solver.
You will primarily use @GEN for debugging your models.
@GEN produces a report showing all the equations in the expanded model. This report is identical to
the report created by the LINGO|Generate command. By default, the report will be sent to the
terminal output window. You may use the @DIVERT statement to route the report to a file.
The @GEN statement accepts an optional argument of one or more submodel names. If a submodel is
specified, LINGO will only generate the model contained within the specified submodel section. If
multiple submodel names are specified, LINGO will combine them all into a single, larger model. If
submodel names are omitted entirely, then LINGO will generate only those model statements
occurring before the @GEN statement and not contained in any submodels.
As an example, below is a small staffing model that uses the @GEN statement in a calc section:
MODEL:
SETS:
DAY / MON, TUE, WED, THU,
FRI, SAT, SUN/ :
NEED, START, COST;
ENDSETS
! Minimize total staffing costs;
[OBJ] MIN = @SUM( DAY( TODAY) :
START( TODAY) * COST( TODAY));
! Subject to meeting daily needs;
@FOR( DAY( TODAY): [CONS]
@SUM( DAY( COUNT)| COUNT #LE# 5:
START( @WRAP(TODAY - COUNT+1,
@SIZE( DAY)))) >= NEED( TODAY));
DATA:
NEED = 18 15 12 16 19 14 12;
COST = 400;

PROGRAMMING LINGO 537
ENDDATA
CALC:
@GEN();
ENDCALC
END
Running this sample model yields the following generated model report:
MODEL:
[OBJ] MIN= 400 * START_MON + 400 * START_TUE +
400 * START_WED + 400 * START_THU + 400 * START_FRI +
400 * START_SAT + 400 * START_SUN ;
[CONS_MON] START_MON + START_THU + START_FRI +
START_SAT + START_SUN >= 18 ;
[CONS_TUE] START_MON + START_TUE + START_FRI +
START_SAT + START_SUN >= 15 ;
[CONS_WED] START_MON + START_TUE + START_WED +
START_SAT + START_SUN >= 12 ;
[CONS_THU] START_MON + START_TUE + START_WED +
START_THU + START_SUN >= 16 ;
[CONS_FRI] START_MON + START_TUE + START_WED +
START_THU + START_FRI >= 19 ;
[CONS_SAT] START_TUE + START_WED + START_THU +
START_FRI + START_SAT >= 14 ;
[CONS_SUN] START_WED + START_THU + START_FRI +
START_SAT + START_SUN >= 12 ;
END
@GENDUAL( [SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
The @GENDUAL statement generates the dual formulation of a linear programming model and
displays the generated equations. Every linear programming model has a corresponding, mirror-image
formulation called the dual. If the original model has M constraints and N variables, then its dual will
have N constraints and M variables.
Some interesting properties of the dual are that any feasible solution to the dual model provides a
bound on the objective to the original, primal model, while the optimal solution to the dual has the
same objective value as the optimal solution to the primal problem. It's also true that the dual of the
dual model is, once again, the original primal model. You may wish to refer to any good linear
programming text for a further discussion of duality theory.
For instance, replacing the @GEN statement with an @GENDUAL statement in the staffing model
above, we’d have the following calc section:
CALC:
@GENDUAL();
ENDCALC
Running this sample model yields the following generated model report showing the original model's
dual formulation:
538 CHAPTER 13
MODEL:
MAX = 18 * CONS_MON + 15 * CONS_TUE + 12 * CONS_WED + 16 *
CONS_THU + 19 * CONS_FRI + 14 * CONS_SAT + 12 * CONS_SUN;
[ START_MON] CONS_MON + CONS_TUE + CONS_WED + CONS_THU
+
CONS_FRI <= 400;
[ START_TUE] CONS_TUE + CONS_WED + CONS_THU + CONS_FRI
+
CONS_SAT <= 400;
[ START_WED] CONS_WED + CONS_THU + CONS_FRI + CONS_SAT
+
CONS_SUN <= 400;
[ START_THU] CONS_MON + CONS_THU + CONS_FRI + CONS_SAT
+
CONS_SUN <= 400;
[ START_FRI] CONS_MON + CONS_TUE + CONS_FRI + CONS_SAT
+
CONS_SUN <= 400;
[ START_SAT] CONS_MON + CONS_TUE + CONS_WED + CONS_SAT
+
CONS_SUN <= 400;
[ START_SUN] CONS_MON + CONS_TUE + CONS_WED + CONS_THU
+
CONS_SUN <= 400;
END
Note that the dual is the transpose of the original linear program, with variables becoming the new row
names and row names becoming the new variable names.
@PIC( [SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
The @PIC statement works much like @GEN, with the exception that it displays a matrix picture
rather than the generated equations. For instance, replacing the @GEN statement with an @PIC
statement in the staffing model above, we’d have the following calc section:
CALC:
@PIC();
ENDCALC

PROGRAMMING LINGO 539
Running the modified model will generate the following matrix picture:
S S S S S S S
T T T T T T T
A A A A A A A
R R R R R R R
T T T T T T T
( ( ( ( ( ( (
M T W T F S S
O U E H R A U
N E D U I T N
) ) ) ) ) ) )
OBJ: C C C C C C C MIN
CONS(MON): 1 1 1 1 1 > B
CONS(TUE): 1 1' ' 1'1 1 > B
CONS(WED): 1 1 1 ' 1 1 > B
CONS(THU): 1 1 1 1 1 > B
CONS(FRI): 1 1'1 1 1' ' > B
CONS(SAT): ' 1 1 1 1 1 ' > B
CONS(SUN): ' 1 1 1 1 1 > B
Refer to the PICTURE command for a discussion on how to interpret matrix picture reports.
@SMPI( ‘FILE_NAME’[, SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
The @SMPI statement generates the model and then writes it to a specified file in MPI format. MPI is
a special format developed by LINDO Systems for representing all classes of mathematical programs:
linear, integer, and nonlinear. This format is not intended for permanent storage of your models.
LINDO API users may be interested in this format for exporting models to the LINDO API.
The @SMPI statement also accepts an optional argument of one or more submodel names. If a single
submodel is specified, LINGO will only generate and save the model contained within the specified
submodel section. If multiple submodel names are specified, LINGO will group them all together as
one larger, combined model before writing the MPI file. If no submodel name is specified, then only
the model statements occurring before the @GEN statement and not contained in any submodels will
be used in generating the MPI file.
As an example, we could write the staffing example listed above to an MPI file by modifying the calc
section to be:
CALC:
@SMPI( ’MYMPIFILE.MPI’);
ENDCALC
@SMPS( ‘FILE_NAME’[, SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
The @SMPS statement generates the model and then writes it to a specified file in MPS format file.
The MPS file format is an industry standard format developed by IBM, and is useful for passing
models from one solver or platform to another. LINDO API users may be interested in this format for
exporting models to the LINDO API.
540 CHAPTER 13
The @SMPS statement also accepts an optional argument of one or more submodel names. If a single
submodel is specified, LINGO will only generate and save the model contained within the specified
submodel section. If multiple submodel names are specified, LINGO will group them all together as
one larger, combined model before writing the MPS file. If no submodel name is specified, then only
the model statements occurring before the @GEN statement and not contained in any submodels will
be used in generating the MPI file.
As an example, we could write the staffing example listed above to an MPS file by modifying the calc
section to be:
CALC:
@SMPS( ’MYMPSFILE.MPS');
ENDCALC
Note 1: A model must be linear or quadratic to successfully export it in MPS format.
Note 2: When exporting an MPS file, LINGO truncates all variable names to 8 characters. For
instance, the two distinct LINGO names SHIP( WH1, C1) and SHIP( WH1, C2) would both
be truncated to the single 8 character name SHIPWH1C under MPS. Either choose names to
avoid collisions of truncated names, or enable the option for converting names to RC format
when doing MPS I/O. LINGO will display an error message if potential collisions exist.
Note 3: The MPS file format is intended primarily for exporting models to other applications or
platforms. The MPS format is purely scalar in nature—all set-based information is lost upon
converting a LINGO model to MPS format. Thus, when saving copies of a model on your
own machine, you should always use the File|Save command in order to preserve your model
in its entirety.
@STATS( [SUBMODEL_NAME[, …, SUBMODEL_NAME_N]])
The @STATS statement works much like @GEN, with the exception that it displays a report
containing summary statistics about the size of the generated model. Please refer to the
LINGO|Model Statistics command for more information on the fields of a STATS report.
@RELEASE( VARIABLE_NAME)
When a variable is assigned a value in a calc section, that variable is marked by LINGO as being
permanently fixed at the value, i.e., subsequent optimization via @SOLVE will not affect the variable’s
value. The @RELEASE statement is used to release such a fixed variable so that it may once again
become optimizable.
The following calc section, developed for the staff scheduling model presented above, will help to
illustrate the use of @RELEASE:

PROGRAMMING LINGO 541
CALC:
@SOLVE();
@FOR( DAY( D):
! Force starts to 0 for today;
START( D) = 0;
@SOLVE();
OBJ0( D) = OBJ;
! Allow START( D) to be optimizable again;
@RELEASE( START( D));
);
@FOR( DAY( D):
@WRITE( DAY( D), 10*' ', OBJ0( D), @NEWLINE( 1));
);
ENDCALC
This calc section loops through each day of the week and does the following:
1. Sets the number of employees starting on the day to zero: START( D) = 0
2. Solves for the low-cost staffing pattern given that the current day will have no starting
employees: @SOLVE()
3. Stores the objective for a later report: OBJ0( D) = OBJ
4. Releases the number of employee starts for the current day so that it can be optimized in
the next solve: RELEASE( DAY( D))
The last part of the calc section writes the following report summarizing the results:
MON 9800
TUE 9000
WED 8600
THU 9600
FRI 9200
SAT 8800
SUN 8600
Output Statements
The features in this section are for displaying output. In addition to the output functions discussed
here, all the reporting functions discussed in Chapter 7, Report Functions, for data and init sections are
also available for use in calc section scripts. The one exception is that the @TABLE function is only
available for use in data sections.
@SOLU( [0|1[, MODEL_OBJECT[, 'REPORT_HEADER']]])
The @SOLU statement mimics the functionality of the SOLU command-line command. If all
arguments are omitted, then @SOLU will display the default, LINGO solution report. All reports are
sent to the screen unless an @DIVERT (see below) command is in effect, routing output to a text file.
If the first argument to @SOLU is 0, then only nonzero variables and binding rows will be displayed.
If the first argument is 1, then all information will be displayed.
If you wish to narrow the scope of the solution report, then the optional MODEL_OBJECT argument
can be either an attribute or row name. In which case, the report will be restricted to the specified
object.

542 CHAPTER 13
The optional third argument, 'REPORT_HEADER', is used when you wish to place a header string on
the report.
You can refer to the LOOPOLE model in the Samples folder for an example of a model that uses the
@SOLU command
@WRITE( ‘TEXT1’|VALUE1[, …, ‘TEXTN’|VALUEN])
The @WRITE statement is the primary tool you’ll use for displaying output in calc sections. @WRITE
can display both text and variable values. Text strings are delimited with single or double-quotes. All
output will be directed to the screen unless @DIVERT (discussed below) is used to route output to a
file.
@WRITE is useful for both debugging your calc section code and for generating custom reports. As
an example, the following product mix model uses @WRITE statements in a calc section to construct a
custom report:
MODEL:
[PROFIT] MAX = 200 * WS + 300 * NC;
[CHASSIS1] WS <= 60;
[CHASSIS2] NC <= 40;
[DRIVES] WS + 2 * NC <= 120;
CALC:
@SOLVE();
@WRITE( 'Total profit = ', PROFIT, @NEWLINE( 1));
@WRITE( 'Production:', @NEWLINE( 1));
@WRITE( ' WS = ', WS, @NEWLINE( 1),
' NC = ', NC, @NEWLINE( 1),
'Total units = ', WS + NC,
@NEWLINE( 2)
);
@WRITE( 'Dual analysis:', @NEWLINE( 1),
' Chassis1: ', @DUAL( CHASSIS1),
@NEWLINE( 1),
' Chassis2: ', @DUAL( CHASSIS2),
@NEWLINE( 1),
' Drives: ', @DUAL( DRIVES),
@NEWLINE( 1)
);
ENDCALC
END
PROGRAMMING LINGO 543
Running this model will yield the following report:
Total profit = 21000
Production:
WS = 60
NC = 30
Total units = 90
Dual analysis:
Chassis1: 50
Chassis2: 0
Drives: 150
Note that in addition to the @WRITE statement, we also made use of both the @NEWLINE report
function to produce line feeds and the @DUAL report function to return the dual values, or shadow
prices, on the constraints. Additional information on these and other report functions may be found in
section Report Functions of Chapter 7.
@PAUSE( ‘TEXT1’|VALUE1[, …, ‘TEXTN’|VALUEN])
The @PAUSE statement has the same syntax as the @WRITE statement, however, @PAUSE causes
LINGO to pause execution and wait for a user response. For example, under Windows, the following
reference to @PAUSE:
CALC:
@PAUSE( 'An example of @PAUSE running on Windows.');
ENDCALC
will cause the following dialog box to be displayed:
The user has the option of pressing either the Resume button to continue normal processing, or the
Interrupt button to immediately terminate execution of the model. On platforms other than Windows,
the output will be routed to the terminal and LINGO will wait for the user to press the Enter key.

544 CHAPTER 13
@DIVERT( [‘FILE_NAME’])
By default, output generated by the @WRITE statement will be sent to the screen. However, you may
wish to capture this output in a file. @DIVERT allows you to do this. As an example, we modified the
product mix example from above to route its custom report to file MYREPORT.TXT as follows:
CALC:
@SOLVE();
@DIVERT( 'MYREPORT.TXT');
@WRITE( 'Total profit = ', PROFIT, @NEWLINE( 1));
@WRITE( 'Production:', @NEWLINE( 1));
@WRITE( ' WS = ', WS, @NEWLINE( 1),
' NC = ', NC, @NEWLINE( 1),
'Total units = ', WS + NC,
@NEWLINE( 2)
);
@WRITE( 'Dual analysis:', @NEWLINE( 1),
' Chassis1: ', @DUAL( CHASSIS1),
@NEWLINE( 1),
' Chassis2: ', @DUAL( CHASSIS2),
@NEWLINE( 1),
' Drives: ', @DUAL( DRIVES),
@NEWLINE( 1)
);
@DIVERT();
ENDCALC
Note the two occurrences of @DIVERT. In the first instance, we specify the file we want to open, and
subsequent @WRITE output is diverted to that file. The second reference to @DIVERT closes the file
and reverts output back to the terminal device.
@DIVERT also accepts an optional second argument of the letter ‘A’. If this argument is present,
LINGO will append output to the end of the file if it already exists. If the argument is omitted, LINGO
will overwrite the file if it already exists
Note: @DIVERT statements can be nested so that multiple levels of output files may be
simultaneously in use.
Setting Parameters
LINGO has many optional settings that can be controlled with the LINGO|Options command. At times, you
may find it necessary to alter these parameters dynamically in your model’s calc sections. For this reason,
LINGO provides the @SET statement, which gives you access to the entire set of system parameters. There
is also and additional function, @APISET, for setting more obscure parameters in the LINDO API
(LINGO’s solver library) that aren’t available through the standard LINGO options set.

PROGRAMMING LINGO 545
@SET( ‘PARAM_NAME’, PARAMETER_VALUE)
To change a parameter’s setting, @SET requires that you pass it a parameter name as a text string,
along with the parameter’s new value. For example, to set the integer solver’s relative optimality
tolerance to .05 we’d use:
@SET( ’IPTOLR’, .05);
A list of all the parameter names can be found in Chapter 6’s discussion of the SET command-line
command.
A parameter may be returned to its default value by omitting the parameter_value argument. For
instance,
@SET( ’IPTOLR’);
would return the IPTOLR parameter to its default value.
Use:
@SET( ’DEFAULT ’);
to return all parameters to their default settings:
Note: Parameters whose values have been changed with @SET in a calc section will be restored to
their original settings once the model run is completed.
@APISET( PARAM_INDEX, ‘INT|DOUBLE’, PARAMETER_VALUE)
LINGO uses the LINDO API solver library as its underlying solver engine. The LINDO API has a
wealth of parameters that may be set by the user. Many of these parameters would be of use only in
rare instances. Given this, LINGO does not provide direct access to all possible LINDO API
parameters. However, if you need access to certain API parameters that aren’t in the standard LINGO
set, you may do so with the @APISET command.
To change a parameter’s setting, @APISET requires that you pass it a parameter index, a text string of
either ‘INT’ or “DOUBLE’ indicating if the parameter is an integer or double precision quantity, along
with the parameter’s new value. You can refer to the LINDO API documentation (available on
LINDO Systems’ Web site) for a list of available parameters. A list of parameters and their indices is
also in the lindo.h file included as part of your LINGO installation.
As an example, the LINDO API adds cuts in the branch-and-bound tree every 10 nodes. If you would
like to add cuts more frequently, say every 5 nodes, then you could do so with the:
@APISET( 318, ‘INT’, 5);
You may also force all API parameters back to their default values with:
@APISET( ‘DEFAULT’);
Note: Parameters whose values have been changed with @APISET will be restored to their original
settings once the model run is completed.
546 CHAPTER 13
Stochastic Programming
LINGO 12.0 introduced a stochastic programming solver (SP) for multistage stochastic programs with
recourse. Details may be found in Chapter 14, Stochastic Programming. Some additional
programming features were also added for use with SP models. These additional programming
features are discussed delow.
@SPLOADSCENE( SCENARIO_INDEX)
This function loads the solution for scenario index SCENARIO_INDEX. The solution for this scenario
then becomes the current/active solution. As an example, the following would load the solution for
scenario 1:
@SPLOADSCENE( 1);
Suppose you have an SP model with an objective row call PROFIT_ROW. The following code will
compute the expected/average profit over each scenario:
I = 1;
EXP_PROFIT = 0;
@WHILE ( I #LE# @SPNUMSCENE()):
@SPLOADSCENE( I);
EXP_PROFIT = EXP_PROFIT + PROFIT_ROW;
I = I + 1;
);
EXP_PROFIT = EXP_PROFIT / @SPNUMSCENE();
@WRITE( 'Expected Profit = ', EXP_PROFIT);
@SPNUMSCENE()
Use @SPNUMSCENE to retrieve the total number of scenarios in the model. You can refer to the
code example immediately above for an example of using @SPNUMSCENE() to compute the
expected/average profit over each scenario in an SP model.
@SPPRBSCENE( SCENARIO_INDEX)
Use @SPPRBSCENE to retrieve the probability of a specified scenario index, SCENARIO_INDEX. In
the following example, we loop to display the probabilities for each scenario in the model:
CALC:
! Solve the SP;
@SOLVE();
! Loop to display scenario probabilities;
I = 1;
@WHILE( I #LE# @SPNUMSCENE():
@WRITE( ' Scenario: ', I, ' Probability: ',
@SPPRBSCENE( I), @NEWLINE( 1));
I = I + 1;
);
ENDCALC
The output from the loop is:

PROGRAMMING LINGO 547
Scenario: 1 Probability: 0.1666666666666667
Scenario: 2 Probability: 0.3333333333333333
Scenario: 3 Probability: 0.5
Utility Functions
RANKING_OF_ATTRIBUTE = @RANK( ATTRIBUTE_TO_BE_RANKED)
The @RANK function ranks the values of an attribute in ascending order. This can be a useful
function when you need to sort the members of an attribute. @RANK is available for use only in calc
sections.
As an example, consider the following small model:
model:
sets:
s1: x, rankx;
endsets
data:
x = 3.2 -1.1 5.7;
enddata
calc:
rankx = @rank( x);
endcalc
end
The @RANK function will place the following values into the RANKX attribute: 2, 1, 3, indicating that
X( 1) is the second from smallest value, X( 2) is the smallest, and X( 3) is the largest.

548 CHAPTER 13
The following is another illustration of the use of @RANK. Here, we generate a list of random
numbers and then sort them through the use of @RANK:
model:
! Generates 40,000 random numbers, ranks them
with @RANK(), and then moves them into sorted
order.;
sets:
s1 /1..40000/: xrand, xrank, xsort;
endsets
calc:
@set( 'terseo', 2);
seed = .5;
t0 = @time();
@for( s1( i):
xrand( i) = @rand( seed);
seed = xrand( i);
);
t1 = @time();
xrank = @rank( xrand);
t2 = @time();
@for( s1( i):
xsort( xrank( i)) = xrand( i);
);
t3 = @time();
@write(
' Time to generate: ', @format( t1 - t0, '8.2g'),
@newline( 1), ' Time to rank: ',
@format( t2 - t1, '8.2g'), @newline( 1),
' Time to move: ', @format( t3 - t2, '8.2g'),
@newline( 2)
);
endcalc
end
Model: SORTRAND
The following code generates the random numbers through the use of the @RAND function:
@for( s1( i):
xrand( i) = @rand( seed);
seed = xrand( i);
);
Then, we rank the random values via @RANK with:
PROGRAMMING LINGO 549
xrank = @rank( xrand);
The random values are then moved into sorted order with the loop:
@for( s1( i):
xsort( xrank( i)) = xrand( i);
);
Finally, we display the time these three operations used with the @WRITE statement:
@write(
' Time to generate: ', @format( t1 - t0, '8.2g'),
@newline( 1), ' Time to rank: ',
@format( t2 - t1, '8.2g'), @newline( 1),
' Time to move: ', @format( t3 - t2, '8.2g'),
@newline( 2)
);
Running the model in LINGO will yield a report similar to the following:
Time to generate: 0.07
Time to rank: 0.01
Time to move: 0.05
Programming Example: Binary Search
In this section we will illustrate some of LINGO’s programming features by developing a model to
perform a binary search. Binary searches are an efficient way to look up a key in a sorted list. In the
worst case, a binary search should perform no more than log2( n) comparisons to determine if a key is
on a sorted list, where n is the number of items on the list.
The basic idea behind a binary search is that you bracket the key in the list. You then iterate by
reducing the size of the bracket by a factor of 2 each pass. This process continues until you either find
the key, or conclude that the key is not on the list when the bracket size becomes 0.
Note: A binary search is not typically something you would do in LINGO, and we use it here
merely as an example of a simple algorithm for illustrative purposes.

550 CHAPTER 13
The Model
The following model is an example of implementing a binary search in LINGO:
MODEL:
! Illustrates programming looping
capabilities of LINGO by doing a
binary search;
SETS:
S1: X;
ENDSETS
DATA:
! The key for which we will search;
KEY = 16;
! The list (must be in sorted
increasing order);
X = 2 7 8 11 16 20 22 32;
ENDDATA
! Do a binary search for key;
CALC:
! Set begin and end points of search;
IB = 1;
IE = @SIZE( S1);
! Loop to find key;
@WHILE( IB #LE# IE:
! Cut bracket in half;
LOC = @FLOOR((IB + IE)/2);
@IFC( KEY #EQ# X(LOC):
@BREAK; ! Do no more loops;
@ELSE
@IFC( KEY #LT# X( LOC):
IE = LOC-1;
@ELSE
IB = LOC+1;
);
);
);
@IFC( IB #LE# IE)
! Display key's location;
@PAUSE( 'Key is at position: ', LOC);
@ELSE
! Key not in list;
@STOP( ' Key not on list!!!');
@ENDIF
ENDCALC
END
Model: LOOPBINS
The Details
Our first step is to define a set, S1, and give it the attribute X using the following sets section:
SETS:
S1: X;
ENDSETS
The X attribute will store the list that we will search for the key value. We populate X and input our
key in the data section:

PROGRAMMING LINGO 551
DATA:
! The key for which we will search;
KEY = 16;
! The list (must be in sorted
increasing order);
X = 2 7 8 11 16 20 22 32;
ENDDATA
Note that for the purposes of this example, the list of values must be input in sorted order. An
interesting exercise would be to extend this model so that it tests to determine if the data is sorted. Or,
if you are really ambitious, extend the model so that it will sort a list with arbitrary ordering.
Next comes the calc section, which contains our code to do the binary search. In the first part of the
calc section:
CALC:
! Set begin and end points of search;
IB = 1;
IE = @SIZE( S1);
we bracket the key by pointing to the beginning of the list, IB, and the end of the list, IE. Note that we
make use of the @SIZE function to dynamically compute the size of the list.
Next, we have the @WHILE loop to search for the key value:
! Loop to find key;
@WHILE( IB #LE# IE:
! Cut bracket in half;
LOC = @FLOOR((IB + IE)/2);
@IFC( KEY #EQ# X(LOC))
@BREAK; ! Do no more loops;
@ELSE
@IFC( KEY #LT# X( LOC):
IE = LOC-1;
@ELSE
IB = LOC+1;
);
);
);
The @WHILE loop tests if the candidate range has become empty at the start of each iteration:
@WHILE( IB #LE# IE:
If not, we continue by dissecting the bracket in half:
!cut bracket in half;
INEW = @FLOOR( ( IE + IB) / 2);
We then determine if the new bracket point resides above or below the key and set IB and IE
accordingly:
@IFC( KEY #EQ# X(LOC):
@BREAK; ! Do no more loops;
@ELSE
@IFC( KEY #LT# X( LOC):
IE = LOC-1;
@ELSE
IB = LOC+1;
552 CHAPTER 13
);
);
Finally, when we fall out of the @WHILE loop we display the result of our search:
@IFC( IB #LE# IE:
! Display key's location;
@PAUSE( 'Key is at position: ', LOC);
@ELSE
! Key not in list;
@STOP( ' Key not on list!!!');
);
If the eligible range is empty, then we did not find the key. Otherwise, the key was found and report
its location on the list.
If you run this model, LINGO should successfully find the key and display:
Programming Example: Markowitz Efficient
Frontier
In the March 1952 issue of Journal of Finance, Harry M. Markowitz published an article titled
Portfolio Selection. In the article, he demonstrates how to reduce the risk of asset portfolios by
selecting assets whose values aren't highly correlated. The concepts behind the Markowitz portfolio
model were discussed in detail in the previous chapter in section Markowitz Portfolio Selection Model.
The basic idea is that, given a desired level of expected return, one should select a basket of assets that
minimizes risk (i.e., variance in return). Any other basket of assets would be inefficient in that it
entails taking on extra risk without extra compensation.
The Markowitz model allows you to evaluate tradeoffs between risk and return. By running the model
for a series of different levels of return, you can see how portfolio risk must increase as desired return
increases. The return/risk tradeoff may be graphed, and this graph is known as the efficient frontier. If
we place risk on the vertical axis and return on the horizontal, then portfolios to the left of the efficient
frontier are inefficient. This is because portfolios exist with the same amount of return but less risk.
Conversely, all (return,risk) pairs that lie to the right of the curve cannot be achieved given the current
available asset pool. Finally, all portfolios with (return,risk) combinations that lie on the curve are
efficient—no portfolio can be found with the same level of return and lower risk.

PROGRAMMING LINGO 553
We will now demonstrate how you can use the programming capabilities in LINGO to generate points
along the efficient frontier by repeatedly solving the Markowitz model for a series of portfolio return
values.
The Model
Here’s the model we will use to generate points along the efficient frontier:
MODEL:
! Solves the generic Markowitz portfolio
model in a loop to generate the points
on the efficient frontier;
SETS:
ASSET: RATE, UB, X;
COVMAT( ASSET, ASSET): V;
POINTS: XRET, YVAR;
ENDSETS
DATA:
! Number of points on the
efficient frontier graph;
NPOINTS = 10;
POINTS = 1..NPOINTS;
! The stocks;
ASSET = GOOGLE, YAHOO, CISCO;
! Expected growth rate of each asset;
RATE = 1.3 1.2 1.08;
! Upper bound on investment in each;
UB = .75 .75 .75;
! Covariance matrix;
V = 3 1 -.5
1 2 -.4
-.5 -.4 1;
ENDDATA
! Below are the three objectives we'll use;
SUBMODEL SUB_RET_MAX:
[OBJ_RET_MAX] MAX = RETURN;
ENDSUBMODEL
SUBMODEL SUB_RET_MIN:
[OBJ_RET_MIN] MIN = RETURN;
ENDSUBMODEL
SUBMODEL SUB_MIN_VAR:
[OBJ_MIN_VAR] MIN =
@SUM( COVMAT( I, J): V( I, J) * X( I) * X( J));
ENDSUBMODEL
!and the constraints;
SUBMODEL SUB_CONSTRAINTS:
! Compute return;
RETURN = @SUM( ASSET: RATE * X);
! Must be fully invested;
@SUM( ASSET: X) = 1;
! Upper bounds on each;
@FOR( ASSET: @BND( 0, X, UB));
! Must achieve target return;

554 CHAPTER 13
RETURN >= RET_LIM;
ENDSUBMODEL
CALC:
! Set some parameters;
! Reset all params;
@SET( 'DEFAULT');
! Minimize output;
@SET( 'TERSEO', 1);
! Suppress status window;
@SET( 'STAWIN', 0);
! Capture unwanted output;
@DIVERT( 'LINGO.LOG');
! Solve to get maximum return;
RET_LIM = 0;
@SOLVE( SUB_RET_MAX, SUB_CONSTRAINTS);
! Save maximum return;
RET_MAX = OBJ_RET_MAX;
! Solve to get minimum return;
@SOLVE( SUB_RET_MIN, SUB_CONSTRAINTS);
! Save minimum return;
RET_MIN = OBJ_RET_MIN;
! Interval between return points;
INTERVAL =
( RET_MAX - RET_MIN) / ( NPOINTS-1);
! Loop over range of possible returns
minimizing variance;
RET_LIM = RET_MIN;
@FOR( POINTS( I):
@SOLVE( SUB_MIN_VAR, SUB_CONSTRAINTS);
XRET( I) = RET_LIM;
YVAR( I) = OBJ_MIN_VAR;
RET_LIM = RET_LIM + INTERVAL;
);
! Close log file;
@DIVERT();
! Display the results;
@WRITE( ' Return Variance', @NEWLINE( 1));
@FOR( POINTS: @WRITE( @FORMAT( XRET, '#12.6G'),
@FORMAT( YVAR, '#12.6G'), @NEWLINE( 1))
);
ENDCALC
END
Model: LOOPPORT

PROGRAMMING LINGO 555
The Details
First consider the sets section:
SETS:
ASSET: RATE, UB, X;
COVMAT( ASSET, ASSET): V;
POINTS: XRET, YVAR;
ENDSETS
It defines three sets: ASSET, COVMAT and POINTS.
The ASSET set will contain the set of assets available for investment. Each asset has an expected rate
of return (RETURN), an upper bound on the amount of the asset we’ll allow in the portfolio (UB), and
the fraction of the portfolio devoted to the asset (X). Note that the fraction of the portfolio devoted to
each asset, X, constitutes our decision variables.
The COVMAT set is a cross of the ASSET set on itself. We create this set for the attribute V, which
will store the covariance matrix for all the assets.
The POINTS set is used to represent the points on the efficient frontier that we will be generating. For
each point, we will determine its x-coordinate, XRET, and its y-coordinate, YVAR. Note that the x-
coordinate will represent risk, while the y-coordinate will represent return. What we intend to do is to
solve a portfolio model once for each member of the POINTS set to get a new point on the efficient
frontier. These points will be stored in XRET and YVAR. Once the loop is completed, the list of points
in XRET and YVAR will give us a glimpse of what the efficient frontier looks like.
Next we have the data section:
DATA:
! Number of points on the
efficient frontier graph;
NPOINTS = 10;
POINTS = 1..NPOINTS;
! The stocks;
ASSET = GOOGLE, YAHOO, CISCO;
! Expected growth rate of each asset;
RATE = 1.3 1.2 1.08;
! Upper bound on investment in each;
UB = .75 .75 .75;
! Covariance matrix;
V = 3 1 -.5
1 2 -.4
-.5 -.4 1;
ENDDATA
In this data section we are setting the number of points that we will generate along the efficient frontier
(NPOINTS) to 10. Once we have the number of points established, we dynamically create the POINTS
set. Next, we input the set of assets, their expected rate of return, their upper bounds, and their
covariance matrix.

556 CHAPTER 13
The next section of the model:
! Below are the three objectives we'll use;
SUBMODEL SUB_RET_MAX:
[OBJ_RET_MAX] MAX = RETURN;
ENDSUBMODEL
SUBMODEL SUB_RET_MIN:
[OBJ_RET_MIN] MIN = RETURN;
ENDSUBMODEL
SUBMODEL SUB_MIN_VAR:
[OBJ_MIN_VAR] MIN =
@SUM( COVMAT( I, J): V( I, J) * X( I) * X( J));
ENDSUBMODEL
makes use of the SUBMODEL and ENDSUBMODEL statements to establish three different objectives.
The first two objectives respectively maximize and minimize portfolio return, which are used later on
in the model to determine that maximum and minimum possible returns that can be generated with out
basket of available stocks. The third objective, SUB_MIN_VAR, minimizes portfolio risk as measured
by its variance.
Following the three submodels containing our various objectives, we have another submodel that
contains our three constraints:
!and the constraints;
SUBMODEL SUB_CONSTRAINTS:
! Compute return;
RETURN = @SUM( ASSET: RATE * X);
! Must be fully invested;
@SUM( ASSET: X) = 1;
! Upper bounds on each;
@FOR( ASSET: @BND( 0, X, UB));
! Must achieve target return;
RETURN >= RET_LIM;
ENDSUBMODEL
The first constraint of our constraint section computes portfolio return. The second constraint says that
we must invest 100 percent of our capital. The third constraint puts an upper bound on the percentage
of the portfolio invested in each asset. Finally, the fourth constraint forces total portfolio return to
achieve some desired level.
The next section, the calc section, is of primary interest. It contains the logic to solve the model
multiple times to generate and store the points on the efficient frontier. First, we make use of @SET to
set some parameter values:
! Set some parameters;
! Reset all params to their defaults; @SET( 'DEFAULT');
! Minimize output;
@SET( 'TERSEO', 1);
! Suppress status window;
@SET( 'STAWIN', 0);
The first call to @SET restores all parameters to their default values, the second call minimizes the
level of LINGO’s output to improve performance, while the third call suppresses the status window
that would normally pop up when solving a model. We suppress the status window so it does not
obscure the custom report we are creating at the end of the run.

PROGRAMMING LINGO 557
Next, we use @DIVERT to route LINGO’s output to a log file:
! Capture spurious output;
@DIVERT( 'LINGO.LOG');
We do this to capture the output LINGO would normally generate while it’s solving the various
portfolio models. We capture this output so it doesn’t distract from the custom report we will display
at the end of the run.
Our next task is to find out the possible range of portfolio returns. We want this information so that
we don’t try to run our model for returns lying outside this range, which would result in an infeasible
model. This requires two runs: one where we maximize return and one where we minimize return.
Here is the code that performs the runs:
! Solve to get maximum return;
RET_LIM = 0;
@SOLVE( SUB_RET_MAX, SUB_CONSTRAINTS);
! Save maximum return;
RET_MAX = OBJ_RET_MAX;
! Solve to get minimum return;
@SOLVE( SUB_RET_MIN, SUB_CONSTRAINTS);
! Save minimum return;
RET_MIN = OBJ_RET_MIN;
This is our first example of the the @SOLVE command. @SOLVE takes one or more submodel names
as arguments. It then combines the submodels into a single model and solves them. In this case, we
first solve submodel SUB_RET_MAX along with submodel SUB_CONSTRAINTS to get the maximum
return possible subject to our constraint set. We then do a similar solve to find the minimal return
subject to the constraints. Other items of interest are that we zero out RET_LIM, given that the
constraint on return is temporarily not required, and we store the two extreme objective values in
RET_MAX and RET_MIN for later use.
Our end goal is to solve the model for 10 values of portfolio return, with these values being equally
spaced from RET_MIN to RET_MAX. The next step in the model computes the distance, or interval,
between these points:
! Interval between return points;
INTERVAL =
( RET_MAX - RET_MIN) / ( NPOINTS-1);
Our next code segment is an @FOR loop that loops over each of the 10 return values and minimizes
portfolio variance subject to attaining the desired level of return:
! Loop over range of possible returns
minimizing variance;
RET_LIM = RET_MIN;
@FOR( POINTS( I):
@SOLVE( SUB_MIN_VAR, SUB_CONSTRAINTS);
XRET( I) = RET_LIM;
YVAR( I) = OBJ_MIN_VAR;
RET_LIM = RET_LIM + INTERVAL;
);

558 CHAPTER 13
We start by setting the desired level of return to RET_MIN and then increment this level of return each
pass through the loop by the interval amount. Note that the solve command now uses the submodel
containing the objective that minimizes return, SUB_MIN_VAR. Also, after each solve command, we
store the coordinates of the point on the efficient frontier in XRET and YRET.
Our next section of code creates a custom report:
! Close log file;
@DIVERT();
! Display the results;
@WRITE( ' Return Variance', @NEWLINE( 1));
@FOR( POINTS: @WRITE( @FORMAT( XRET, '#12.6G'),
@FORMAT( YVAR, '#12.6G'), @NEWLINE( 1))
);
Once again, we make use of @DIVERT, but this time we do not pass an argument. This results in
output once again going to the report window, which will allow us to view our report on screen. After
restoring terminal output with @DIVERT, we use the @WRITE command inside an @FOR loop to
write out the 10 points on the efficient frontier. If you run the model, you should see the following
report:
Return Variance
1.11000 0.417375
1.12833 0.417375
1.14667 0.418054
1.16500 0.462381
1.18333 0.575957
1.20167 0.758782
1.22000 1.01086
1.23833 1.33218
1.25667 1.72275
1.27500 2.18750
PROGRAMMING LINGO 559
In summary, returns range from 11% to a high of 27.5%, with portfolio variance ranging from .417 to
2.18. One final note, if you load this model from your Lingo samples folder you will find additional
Lingo code at the end devoted to graphing the frontier. We will not go into the details of that code at
this point; however, the generated graph is pictured below:
Risk
^
2.2 | *
|
|
|
|
| *
|
|
|
| *
|
|
|
| *
|
|
| *
|
| *
0.40 | * * * *
--------------------------------------------------------->
1.1 1.3
Model: LOOPPORT – Graph of Efficient Frontier
Programming Example: Cutting Stock
An optimization problem in the paper, steel, and wood industries is the cutting-stock problem. The
main feature of this problem is that finished goods of varying lengths are cut from larger raw material
pieces of varying lengths. The goal is to cut the raw materials using an efficient set of patterns to
minimize the total amount of raw materials required, while meeting demand for all finished products.
Examples would include sheet metal and paper manufacturers that take larger rolls of product and cut
them into smaller rolls for sale to customers.
As an example, suppose you are a steel fabricator that takes 45 foot steel beams and cuts them into 14,
12 and 7 foot beams for sale to construction firms. Cutting one 45 foot beam into one 14 foot piece,
two 12 foot pieces and one 7 foot piece would be very efficient in that it would exactly use up the 45
foot raw material piece with no trim waste. On the other hand, a pattern of one 14 foot piece, one 12
foot piece and two seven foot pieces would not be as efficient due to a 5 foot piece of trim waste.
A brute force method for attacking the cutting-stock problem would be to generate all possible
efficient patterns and run an optimization model to determine how may copies of each pattern to run to
satisfy demand at minimal cost. The drawback here is that the number of patterns grows exponentially
as the number of different finished good lengths increase. For all but the smallest problems, brute
force pattern generation will yield large, intractable models.

560 CHAPTER 13
Gilmore and Gomory published a paper in 1961 titled A Linear Programming Approach to the
Cutting-Stock Problem. In this paper they outline a two-stage, iterative approach for solving cutting-
stock problems that dramatically reduced the number of patterns one must generate to get good
solutions. The basic idea involves solving a master problem containing a limited number of patterns.
The dual prices on the finished goods are then passed to a small knapsack subproblem that selects a
new cutting pattern that maximizes the sum of the dual values of all the finished goods contained in the
pattern subject to not exceeding the length of the raw material. This pattern is then appended to the
previous master problem, which is then re-solved. This iterative process continues until no further
beneficial patterns can be generated by the knapsack subproblem. In which case, we have the optimal
solution to the original, linear cutting-stock problem. The remarkable feature of this algorithm is that
it typically takes relatively few passes to reach the optimal solution, thereby making it possible to
solve very large cutting-stock models in an extremely reasonable amount of time. This approach of
iteratively appending new columns to models is also referred to as column generation.
The Model
For our example, we will be cutting 45 foot wide rolls of paper into smaller rolls of widths: 34, 24, 15,
10 and 18. We use Lingo’s programming capability to iteratively solve the master and subproblem
until no further beneficial cutting patterns remain to be appended to the master problem.
MODEL:
! Uses Lingo’s programming capability to do
on-the-fly column generation for a
cutting-stock problem;
SETS:
PATTERN: COST, X;
FG: WIDTH, DEM, PRICE, Y, YIELD;
FXP( FG, PATTERN): NBR;
ENDSETS
DATA:
PATTERN = 1..20; ! Allow up to 20 patterns;
RMWIDTH = 45; ! Raw material width;
FG = F34 F24 F15 F10 F18;!Finished goods...;
WIDTH= 34 24 15 10 18;!their widths...;
DEM = 350 100 800 1001 377;!and demands;
BIGM = 999;
ENDDATA
SUBMODEL MASTER_PROB:
[MSTROBJ] MIN= @SUM( PATTERN( J)| J #LE# NPATS:
COST( J)*X( J));
@FOR( FG( I):
[R_DEM]
@SUM( PATTERN( J)| J #LE# NPATS:
NBR( I, J) * X( J)) >= DEM( I);
);
ENDSUBMODEL
SUBMODEL INTEGER_REQ:
@FOR( PATTERN: @GIN( X));
ENDSUBMODEL
SUBMODEL PATTERN_GEN:

PROGRAMMING LINGO 561
[SUBOBJ] MAX = @SUM( FG( I): PRICE( I)* Y( I));
@SUM( FG( I): WIDTH( I)*Y( I)) <= RMWIDTH;
@FOR( FG( I): @GIN(Y( I)));
ENDSUBMODEL
CALC:
! Send unwanted output to log file;
@DIVERT( 'LINGO.LOG');
! Set parameters;
@SET( 'DEFAULT');
@SET( 'TERSEO', 1);
@SET( 'STAWIN', 0);
! Max number of patterns we'll allow;
MXPATS = @SIZE( PATTERN);
! Make first pattern an expensive super pattern;
COST( 1) = BIGM;
@FOR( FG( I): NBR( I, 1) = 1);
! Loop as long as the reduced cost is
attractive and there is space;
NPATS = 1;
RC = -BIGM; ! Clearly attractive initially;
@WHILE( RC #LT# 0 #AND# NPATS #LT# MXPATS:
! Solve for current best pattern runs;
@SOLVE( MASTER_PROB);
! Copy dual prices to PATTERN_GEN submodel;
@FOR( FG( I): PRICE( I) = -@DUAL( R_DEM( I)));
! Generate the current most attractive pattern;
@SOLVE( PATTERN_GEN);
! Marginal value of current best pattern;
RC = 1 - SUBOBJ;
! Add the pattern to the Master;
NPATS = NPATS + 1;
@FOR( FG( I): NBR( I, NPATS) = Y( I));
COST( NPATS) = 1;
);
! Finally solve Master as an IP;
@SOLVE( MASTER_PROB, INTEGER_REQ);
! Redirect output back to terminal;
@DIVERT();
ENDCALC
END
Model: LOOPCUT
The Details
First, we have the sets section:
SETS:
PATTERN: COST, X;
FG: WIDTH, DEM, PRICE, Y, YIELD;
FXP( FG, PATTERN): NBR;
ENDSETS

562 CHAPTER 13
The PATTERN set is used to represent the cutting patterns we will be generating. Each pattern has a
cost, which, with one exception (discussed below), will be 1, i.e., each pattern uses 1 raw material
piece. We also assigned an attribute called X to the patterns set. X( p) will be used to store the
number of times each pattern p is to be cut and is one of the decision variables.
The FG set is used to represent the set of finished goods. As input, each finished good has a width and
customer demand. The PRICE attribute will be used to store the dual prices on the finished goods.
These prices will be updated each time we solve the master problem. Y will be an integer, decision
variable that we will use in the knapsack subproblem to represent the number of pieces of each
finished good to use in the next generated pattern. YIELD will be used to store the number of pieces of
each finished good that gets produced.
The derived set, FXP, is derived on the finished goods and patterns sets. The attribute NBR( i, j) will
store the number of finished goods I contained in pattern j.
Next, we have the data section
DATA:
PATTERN = 1..20; ! Allow up to 20 patterns;
RMWIDTH = 45; ! Raw material width;
FG = F34 F24 F15 F10 F18;!Finished goods...;
WIDTH= 34 24 15 10 18;!their widths...;
DEM = 350 100 800 1001 377;!and demands;
BIGM = 999;
ENDDATA
We initialize the pattern set to have 20 members. This will only allow for generation of up to 20
patterns; however, this should be more that adequate for this small example.
After inputting the raw material width of 45, we input the set of five finished goods and their widths.
After that, we input the demands for the finished goods. Finally, we input a parameter called BIGM,
the purpose of which is discussed below.
Next, we have our first submodel:
SUBMODEL MASTER_PROB:
[MSTROBJ] MIN= @SUM( PATTERN( J)| J #LE# NPATS:
COST( J)*X( J));
@FOR( FG( I):
[R_DEM]
@SUM( PATTERN( J)| J #LE# NPATS:
NBR( I, J) * X( J)) >= DEM( I);
);
ENDSUBMODEL
This is the master problem we’ve been mentioning. The objective states that we wish to minimize the
total cost of all the patterns used. The constraint says that we must meet, or exceed, demand for all the
finished goods.
The next submodel:
SUBMODEL INTEGER_REQ:
@FOR( PATTERN: @GIN( X));
ENDSUBMODEL

PROGRAMMING LINGO 563
will be used in conjunction with the master problem to force the variables to take on integer values.
Given that it’s not possible to cut a fractional number of a particular pattern, for our final solution we
need the X variables to be integer valued.
Our final submodel:
SUBMODEL PATTERN_GEN:
[SUBOBJ] MAX = @SUM( FG( I): PRICE( I)* Y( I));
@SUM( FG( I): WIDTH( I)*Y( I)) <= RMWIDTH;
@FOR( FG( I): @GIN(Y( I)));
ENDSUBMODEL
is the pattern-generation subproblem we’ve mentioned. This is a knapsack problem that finds the best
pattern that can be cut given the dual prices on the finished goods. Recall that we get the dual prices
on the finished goods from the demand constraints in the master problem.
We then enter the calc section, which contains the programming logic to coordinate the iterative
algorithm we’ve chosen. As with the previous Markowitz model, the start of the calc section is
devoted to diverting output to a file and setting of parameters. You may refer to the previous
Markowitz model for a discussion of why these steps are being performed.
One of the features of this model most likely to change in the future would be the maximum number of
patterns to generate. It’s probably not wise to assume that this number will always be fixed at 20
patterns. For this reason, we use the @SIZE function to get the current number of allowed patterns:
! Max number of patterns we'll allow;
MXPATS = @SIZE( PATTERN);
Next, we construct what we refer to as a “super pattern”:
! Make first pattern an expensive super pattern;
COST( 1) = BIGM;
@FOR( FG( I): NBR( I, 1) = 1);
The supper pattern is a device to jumpstart our algorithm by guaranteeing that the model will be
feasible from the start. We need the model to always be feasible in order to obtain a valid set of dual
prices to feed into the pattern generation submodel. The super pattern is an artificial pattern that can
create one piece of each finished good. In real life, such a pattern would not be possible because we
can’t physically fit one of each finished good on a single raw material piece. Given that the super
pattern is not physically possible, we assign it a high cost, BIGM, so it will not be used in the final
solution
Recall that NBR( i, j) represents the number of finished good i in pattern j. So, for our super pattern,
we use a for loop over all the finished goods i, setting NBR( i, 1) to 1 for each of the finished goods.
The second index of NBR is set at 1 given that the super pattern is the first pattern generated.
Next, the main loop that will alternate between solving the master and subproblem until an optimal
solution is found:

564 CHAPTER 13
! Loop as long as the reduced cost is
attractive and there is space;
NPATS = 1;
RC = -BIGM; ! Clearly attractive initially;
@WHILE( RC #LT# 0 #AND# NPATS #LT# MXPATS:
! Solve for current best pattern runs;
@SOLVE( MASTER_PROB);
! Copy dual prices to PATTERN_GEN submodel;
@FOR( FG( I): PRICE( I) = -@DUAL( R_DEM( I)));
! Generate the current most attractive pattern;
@SOLVE( PATTERN_GEN);
! Marginal value of current best pattern;
RC = 1 - SUBOBJ;
! Add the pattern to the Master;
NPATS = NPATS + 1;
@FOR( FG( I): NBR( I, NPATS) = Y( I));
COST( NPATS) = 1;
);
First, we set the pattern count, NPATS, to 1 for the one pattern already generated, i.e., the super
pattern. We will increment NPATS each time we generate a new pattern in our main loop.
Next, is the main @WHILE loop, which will execute until its condition evaluates false. We test two
things in the condition.
First, we see if the marginal impact of the current pattern, RC, is negative and will, therefore, reduce
the current cost. If the current pattern will reduce our cost, then this implies that we should continue
looping and generating patterns, because subsequent patterns may also be helpful. Once the marginal
benefit of the current best pattern goes to zero, generating subsequent patterns will be of no benefit; if
the current best pattern can’t help, subsequent patterns of less value will also be of no help. In which
case, we should exit our loop.
The second condition on the loop tests to see if we’ve generated the maximum allowed number of
patterns that we’ve allocated space for. If so, we must exit the loop.
Once in the loop, our first step is to invoke the @SOLVE command to solve the master problem. We
then use an @FOR loop to pass the dual values on the finished goods to the pattern generation
subproblem. We then solve the pattern generation subproblem and compute RC, the marginal rate of
decrease in the main objective using the new pattern. Finally, at the end of the loop we append the
new generated pattern to the master program for the next pass through the loop.
Once we can no longer find a cutting pattern that will further reduce our costs, we exit the loop and
solve the master problem one last time:
! Finally solve Master as an IP;
@SOLVE( MASTER_PROB, INTEGER_REQ);
The one difference is that we now include the integer restrictions on the pattern usage array, X. As
mentioned, cutting fractional quantities of a pattern is not physically possible, so we want our final
solution to be integral.
The version of this model in the samples folder has an additional calc section to prepare a tabular
report on the cutting patterns and their usage. We will not go into the details of this table-generating
code in this discussion. However, if you run the model, you should receive the following report:

PROGRAMMING LINGO 565
Total raws used: 985
Total feet yield: 43121
Total feet used: 44325
Percent waste: 2.7%
Pattern:
FG Demand Yield 1 2 3 4 5 6 7 8 9
=====================================================
F34 350 350 1 . . . 1 . . . .
F24 100 100 1 . . . . 1 . . 1
F15 800 801 1 . 3 . . . 1 1 .
F10 1001 1002 1 4 . . 1 2 1 3 .
F18 377 377 1 . . 2 . . 1 . 1
=====================================================
Usage: 0 0 133 0 350 0 277 125 100
A total of 985 raw materials were used, with only 2.7% of the raw material input lost to trim waste.
Note that only 9 patterns were needed to solve the model. Also note that Pattern 1, the super pattern, is
not used in the final solution as per our design.
Programming Example: Accessing Excel
In this example, we will solve the familiar staff scheduling model once again. However, to make
things interesting, we will solve several, independent models in a loop. Furthermore, the data for our
models will be contained in a single Excel workbook, with each tab in the workbook storing data for
an individual instance of the model. Solutions for each site will also be returned to their respective
tabs in the Excel workbook.
Suppose we have three hot dog stands: Pluto Dogs, Saturn Dogs and Mars Dogs. Each site has daily
staffing needs that vary throughout the week. We hire employees to work 5 continuous days in a row,
followed by two days off. As an example, an employee starting on Tuesday would be on duty Tuesday
through Saturday and off Sunday and Monday, while someone starting on Friday would work Friday
through Tuesday and be off Wednesday and Thursday. We need to know how many employees to
start on each day of the week at each site so as to minimize to total number of staff hired.
566 CHAPTER 13
The data for this model may be found in the DOGS.XLS workbook contained in the Samples folder off
the main LINGO folder. If you open this workbook, you'll see there are three tabs⎯Pluto, Saturn and
Mars. Each tab contains the data for its particular site. The tab for the Pluto site appears below:
DOGS.XLS

PROGRAMMING LINGO 567
Here we see that the Pluto site requires 10 people on Mondays, 12 on Tuesdays, and so on. The
staffing needs are also represented in the bar graph on the tab. Similar tabs for the remaining two sites
are also included in the workbook.
The Model
Here's our model loops over the three sites/tabs, solving each individual staffing model:
MODEL:
! Uses a loop to solve three staff scheduling
models, retrieving the data from and writing
the solution to an Excel workbook;
SETS:
SITES / PLUTO, MARS, SATURN/;
DAYS / MON TUE WED THU FRI SAT SUN/:
NEEDS, START, ONDUTY;
ENDSETS
SUBMODEL STAFF:
[OBJROW] MIN = @SUM( DAYS: START);
@FOR( DAYS( D):
ONDUTY( D) = @SUM( DAYS( D2) | D2 #LE# 5:
START( @WRAP( D - D2 + 1, @SIZE( DAYS))));
ONDUTY( D) >= NEEDS( D);
);
@FOR( DAYS: @GIN( START));
ENDSUBMODEL
CALC:
@SET( 'TERSEO', 2);
@FOR( SITES( S):
NEEDS = @OLE( '\LINGO12\SAMPLES\DOGS.XLS',
SITES( S)+'NEEDS');
@SOLVE( STAFF);
@SOLU( 0, ONDUTY, ' On Duty Report: ' + SITES( S));
@OLE( , SITES( S)+'START', SITES( S)+'ONDUTY',
SITES( S)+'TOTAL') = START, ONDUTY, OBJROW;
);
ENDCALC
END
Model: LOOPOLE
This model may also be found in the Samples folder of the main LINGO folder.
Note: Versions of this example staffing model that interface with an Access database or that
interface with text files are also available. Please see models LOOPODBC and LOOPTEXT.

568 CHAPTER 13
The Details
In the model's sets section:
SETS:
SITES / PLUTO, MARS, SATURN/;
DAYS / MON TUE WED THU FRI SAT SUN/:
NEEDS, START, ONDUTY;
ENDSETS
we declare two sets. The first set is our set of three sites followed by a set containing the days of the
week. The days of the week set has three associated attributes: NEEDS, START, and ONDUTY,
representing the staffing needs, the number of workers to start on each day of the week, and the total
number of workers on duty each day.
Next, we declare a submodel that contains the staffing model that will be applied to each of the three
sites:
SUBMODEL STAFF:
[OBJROW] MIN = @SUM( DAYS: START);
@FOR( DAYS( D):
ONDUTY( D) = @SUM( DAYS( D2) | D2 #LE# 5:
START( @WRAP( D - D2 + 1, @SIZE( DAYS))));
ONDUTY( D) >= NEEDS( D);
);
@FOR( DAYS: @GIN( START));
ENDSUBMODEL
The objective function minimizes the total number of employees hired at the site. This is then
followed by an @FOR loop over the days of the week that a) computes the number of employees on
duty each day, and b) requires the number on duty to equal, or exceed, the number required on each
day. We also require the number starting on each day to be an integer value using the @GIN
statement.
The following calc section:
CALC:
@SET( 'TERSEO', 2);
@FOR( SITES( S):
NEEDS = @OLE( '\LINGO12\SAMPLES\DOGS.XLS',
SITES( S)+'NEEDS');
@SOLVE( STAFF);
@SOLU( 0, ONDUTY, ' On Duty Report: ' + SITES( S));
@OLE( , SITES( S)+'START', SITES( S)+'ONDUTY',
SITES( S)+'TOTAL') = START, ONDUTY, OBJROW;
);
ENDCALC
starts off by restricting the amount of LINGO's output by setting the TERSEO parameter to 2, which
essentially eliminates all of LINGO"s output.

PROGRAMMING LINGO 569
Next, we construct an @FOR loop that loops over the three sites, allowing us to solve the submodel
STAFF for each site. The first statement in the loop is an @OLE statement that reads the staffing
requirements from the appropriate tab of the workbook and places the requirements into the NEEDS
attribute. If you look at the workbook closely, you'll see that there are three ranges named
"SaturnNeeds", "PlutoNeeds" and "MarsNeeds" that contain the staffing requirements for each of the
respective sites. We are building each of these range names via the SITES(S)+'NEEDS' argument in
the @OLE function call.
Once the staffing requirements are loaded, we invoke the @SOLVE command to solve the staffing
model for the current site. The @SOLU command prints out a small solution report to the screen
showing the number of workers on duty each day for each of the sites.
At the bottom of the calc section, the last @OLE call sends the solution back to the workbook. Note
that for each site there are three ranges titled "<site_name>START", "<Isite_name>ONDUTY" and
"<site_name>TOTAL", where we return the daily number of workers to start, the number on duty
each day, and the total number of employees required for the entire week. Note also that the workbook
name was omitted in the call. When the workbook name is omitted, LINGO simply uses the current
workbook in Excel. Given that we specified the workbook name in the original call to @OLE, it
should now be the current workbook, thereby allowing us to omit its name in the final call.
570 CHAPTER 13
If you solve the model, you'll see that the tab for each of the three sites contains the number of workers
to start each day, the total number on duty each day, and the total number of employees required. For
the Saturn site, the tab will resemble the following:

PROGRAMMING LINGO 571
Summary
There are many instances where you will need to solve a model multiple times and/or use the results of
one model as input into another. The programming capabilities in LINGO allow you to automate these
classes of problems. The three examples presented in this chapter introduce the programming
constructs available in LINGO.
In addition to the three examples presented in this chapter, several more examples of solving models in
a loop may be found in the samples folder of your LINGO installation. These additional examples
include:
Loopdea.lg4 – A Data Envelopment Analysis model with a loop over each of the decision-
making units to compute their individual efficiency scores.
Loopts.lg4 – A traveling salesman model that loops to append subtour breaking constraints to
the formulation, continuing until a complete tour of the cities is generated.
Loopttt.lg4 – A looping model that implements a game of ticktacktoe.
Finally, in addition to all the control structures and functions discussed in this chapter, all of the
functions and operators listed in Chapter 7, LINGO's Operators and Functions, are also available for
use in your calc section scripts, with the only exception being the variable domain functions. Variable
domain functions are restricted for use in model section only.

573
14 Stochastic
Programming
So far, we worked with deterministic mathematical programs where all model parameters (e.g.
coefficients, bounds, etc.) are known constants. A stochastic program (SP) is a mathematical program
(linear, nonlinear or mixed-integer) in which some of the model parameters are not known with
certainty, and the uncertainty can be expressed with known probability distributions. Applications
arise in a variety of industries:
♦ Financial portfolio planning over multiple periods for insurance and other financial
companies, in face of uncertain prices, interest rates, and exchange rates
♦ Exploration planning for petroleum companies,
♦ Fuel purchasing when facing uncertain future fuel demand,
♦ Fleet assignment: vehicle type to route assignment in face of uncertain route demand,
♦ Electricity generator unit commitment in face of uncertain demand,
♦ Hydro management and flood control in face of uncertain rainfall,
♦ Optimal time to exercise for options in face of uncertain prices,
♦ Capacity and Production planning in face of uncertain future demands and prices,
♦ Foundry metal blending in face of uncertain input scrap qualities,
♦ Product planning in face of future technology uncertainty,
♦ Revenue management in the hospitality and transport industries.
Multistage Decision Making Under Uncertainty
Stochastic programs fall into two major categories: a) multistage stochastic programs with recourse,
and b) chance-constrained programs. With version 12.0, LINGO's capabilities are extended to solve
models in the first category, namely multistage stochastic recourse models. Chance-constrained
models will be supported in future versions.
In this chapter, the term stochastic program (SP) refers to a multistage stochastic model with recourse.
The term stage is an important concept in this chapter. Usually it means the same as ‘time period’,
however there are situations where a stage may consist of several time periods. The terms random,
uncertain and stochastic are used interchangeably.
Multistage decision making under uncertainty involves making optimal decisions for a T-stage horizon
before uncertain events (random parameters) are revealed while trying to protect against unfavorable
outcomes that could be observed in the future.

574 CHAPTER 14
Note: A stage boundary is either a) the beginning of the problem, b) the end of the problem, or c) a
point just after a decision event but just before a random event. A stage is the sequence of
random events followed by decision events between two successive stage boundaries. Thus,
decisions made in stage k are based on all information revealed up to stage k, but no more.
In its most general form, a multistage decision process with T+1 stages follows an alternating sequence
of random events and decisions. Slightly more explicitly:
0.1) in stage 0, we make a decision x0, taking into account
that…
1.0) at the beginning of stage 1, “Nature” takes a set of
random decisions ω1, leading to realizations of all random
events in stage 1, and…
1.1) at the end of stage 1, having seen nature’s decision, as
well as our previous decision, we make a recourse decision
x1(ω1), taking into account that …
2.0) at the beginning of stage 2, “Nature” takes a set of
random decisions ω2, leading to realizations of all random
events in stage-2, and…
2.1) at the end of stage 2, having seen nature’s decision, as
well as our previous decisions, we make a recourse decision
x2(ω1, ω2), taking into account that …
.
.
.
T.0) At the beginning of stage T, “Nature” takes a random
decision, ωT, leading to realizations of all random events in
stage T, and…
T.1) at the end of stage T, having seen all of nature’s T
previous decisions, as well as all our previous decisions, we
make the final recourse decision xT(ω1,…,ωT).
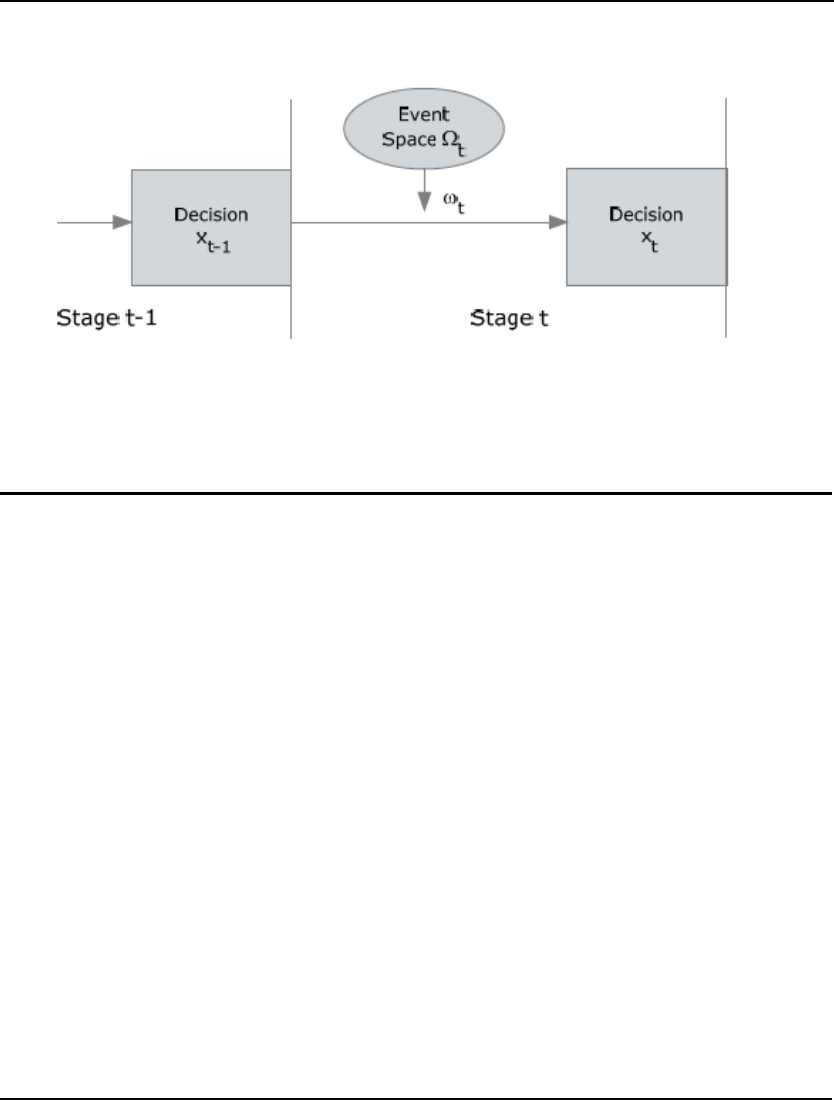
STOCHASTIC PROGRAMMING 575
This relationship between the decision variables and realizations of random data can be illustrated as
follows.
Each decision, represented with a rectangle, corresponds to an uninterrupted sequence of decisions
until the next random event. And each random observation corresponds to an uninterrupted sequence
of random events until the next decision point.
Recourse Models
The decision taken in stage 0 is called the initial decision, whereas decisions taken in succeeding
stages are called recourse decisions. Recourse decisions are interpreted as corrective actions that are
based on the actual values the random parameters realized so far, as well as the past decisions taken
thus far. Recourse decisions provide latitude for obtaining improved overall solutions by realigning
the initial decision with possible realizations of uncertainties in the best possible way.

576 CHAPTER 14
Restricting ourselves to linear multistage stochastic programs for illustration, we have the following
form for a multistage stochastic program with (T+1) stages.
Minimize (or maximize): c0x0 + E1[c1x1 + E2[c2x2 … + ET[cTxT ] … ]]
such that:
A00x0 ~ b0
A(
ω
1)10x0 + A(
ω
1)11x1
~ b(
ω
1)1
A(
ω
1,
ω
2)20x0 + A(
ω
1,
ω
2)21x1 + A(
ω
1,
ω
2)22x2 ~ b(
ω
1,
ω
2)2
… … … …
A(
ω
1,...,
ω
T)T0x0 + A(
ω
1,...,
ω
T)T1x1 + … + A(
ω
1,...,
ω
T)TTxT ~ b(
ω
1,...,
ω
T)T
L0 ≤ x0 ≤ U0
L(
ω
1)1 ≤ x1 ≤ U(
ω
1)1
… … …
L(
ω
1,...,
ω
T)T ≤ xT ≤ U(
ω
1,...,
ω
T)T
where,
(
ω
1,...,
ω
t) represents random outcomes from event space (
Ω
1,...,
Ω
t) up to stage-t,
A(
ω
1,...,
ω
t)tp is the coefficient matrix generated by outcomes up to stage-t for all p=1…t,
t=1…T,
c(
ω
1,...,
ω
t)t is the objective coefficients generated by outcomes up to stage-t for all t=1…T,
b(
ω
1,...,
ω
t)t is the right-hand-side values generated by outcomes up to stage-t for all t=1…T,
L(
ω
1,...,
ω
t)t and U(
ω
1,...,
ω
t)t are the lower and upper bounds generated by outcomes up to
stage-t for all t=1…T,
’~’ is one of the relational operators '≤', ‘=’, or ‘≥’ ; and
x0 and xt ≡ x(
ω
1,...,
ω
t)t are the decision variables (unknowns) for which optimal values are
sought. The expression being optimized is called the cost due to initial-stage plus the
expected cost of recourse.
Note: LINGO can solve linear, nonlinear and integer multistage stochastic programming problems.

STOCHASTIC PROGRAMMING 577
Scenario Tree
When the probability distributions for the random parameters (events) are discrete, there are only a
finite number of outcomes in each stage. With each random parameter fixed to one of its possible
outcomes, one can create a scenario representing one possible realization of the future. Enumeration of
all possible combinations of outcomes allows us to represent all scenarios in a tree, with each scenario
being a path from the root of the tree to one of its leaves. The nodes visited by each path correspond to
values assumed by random parameters in the model.
We illustrate the construction of a scenario tree with a stochastic version of the well-known
Newsvendor inventory problem. In this problem, we must decide how much to order initially and then
later, how much of any unsold product to return before the end of the planning horizon. There is a
shortage penalty when there are lost sales and a carrying cost for left over units. The decision process
takes place under uncertain demand and uncertain price per returned item:
1. In stage 0, the order quantity has to be decided (under uncertain demand).
2. In stage 1, at the beginning, the demand is revealed. A recourse decision, at the end of stage
1, is the number of units to be returned to the publisher (for an uncertain refund price)
3. In stage 2 at the beginning, the refund price is announced by the publisher. The price per
returned item can be either:
♦ Positive (i.e. publisher accepts them at a high price which covers the cost of shipping and
handling) or
♦ Negative (i.e. publisher accepts them at a low price which doesn’t cover the cost of
shipping and handling).
4. The objective is to maximize the total expected profit at the end of planning horizon (stage 2).
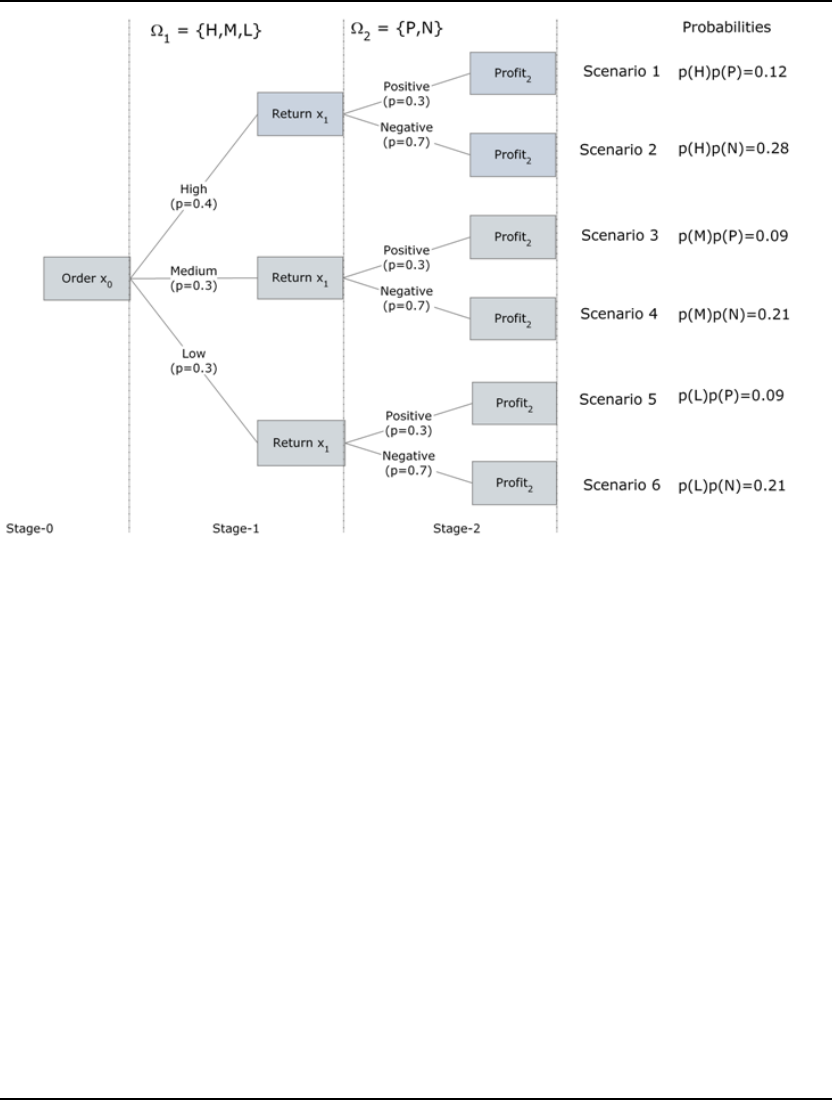
578 CHAPTER 14
In the scenario tree above, x0 represents the initial decision, or order size to be determined before
seeing any of the random outcomes. x1 represents the quantity to return to the publisher of any portion
of the unsold units. Profit2 represents the total profit collected at the end of planning horizon. The
notation
Ω
1 represents the event space for the unknown demand, for which there are three different
possible outcomes
Ω
1 = {Low, Medium, and High} with probabilities {0.4, 0.3, 0.3}, respectively.
Once we observe the demand
ω
1 ∈
Ω
1, we make a recourse decision x1 based upon which
ω
1 nature
chose and our previous decision x0. The notation
Ω
2 represents the event space for refund price per
unsold newspapers if returned to the publisher in stage 2. This event has two different outcomes
Ω
2 =
{Positive, Negative} with probabilities {0.7, 0.3}. Once the refund price
ω
2 ∈
Ω
2 in stage 2 is
observed, the total profit would be computed by the model as the final decision Profit2.
It should be clear from the scenario tree that,
♦ There are as many distinct scenarios in the SP as there are leaf-nodes.
♦ Each root-leaf path defines a scenario, induced by a full observation of all random
events.
♦ There is a one-to-one correspondence between the scenarios and the leaf-nodes in the
tree.
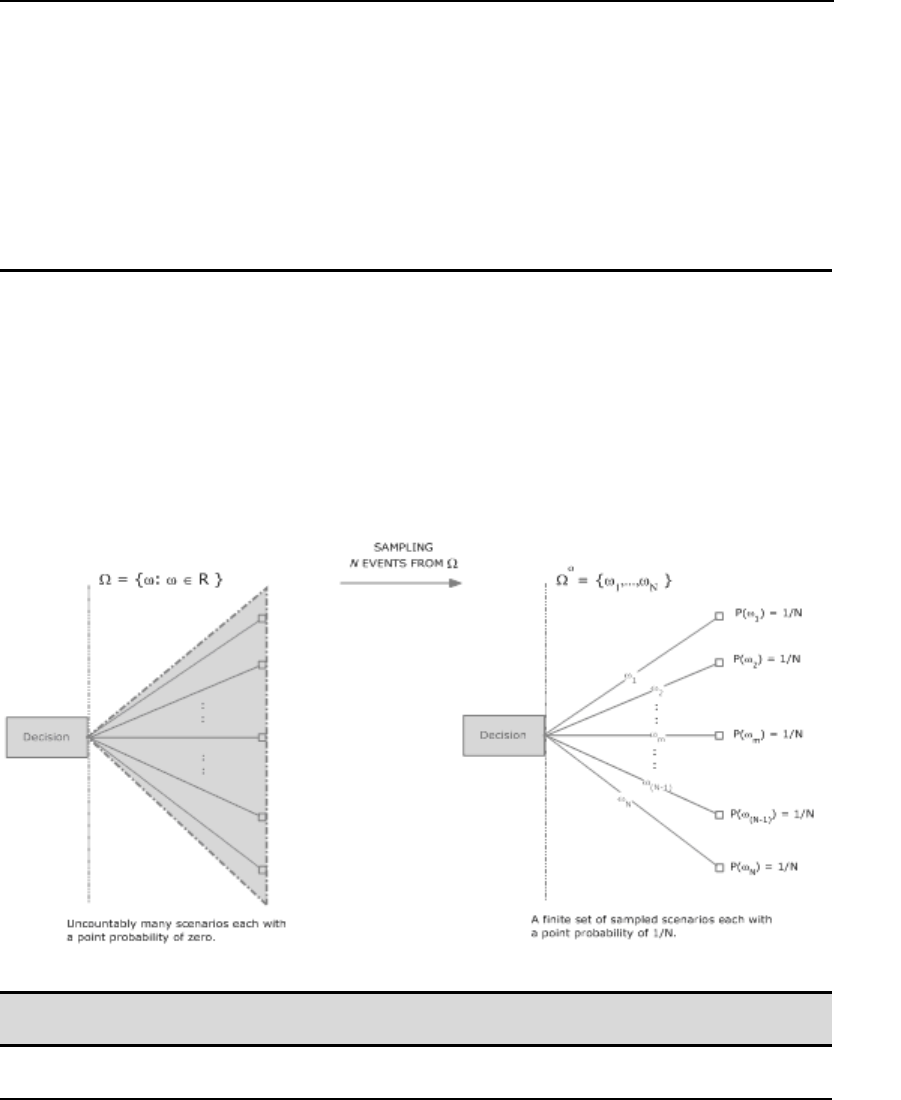
STOCHASTIC PROGRAMMING 579
♦ The unconditional probability of a node is computed by multiplying the conditional
probabilities of the nodes positioned on the path, which starts from the root and
terminates at that node.
♦ The unconditional probability of each leaf-node corresponds to the probability of the
associated scenario.
♦ Each node in the tree corresponds to a vector of random parameter with a particular
history up to that node in some scenario.
The branches out of each node enumerate all possible outcomes associated with random parameters
associated with it in order to construct the history of random parameters that belong to the next stage.
Monte Carlo Sampling
In stochastic programming (SP), when one or more random variables have a continuous (or discrete
but infinite) event space, it is obviously computationally impossible to explicitly account for the
infinite number of possible outcomes. For such cases, Monte Carlo sampling (also called pre-
sampling) can be used to approximate the problem using a finite scenario tree. As illustrated in the
figure below, if the model has a single stochastic parameter with a continuous distribution such as the
normal distribution, one can discretize the event space simply by generating N sample points and
thereby construct a finite and tractable scenario tree. This is also the case for discrete distributions
with infinite event spaces, such as the Poisson distribution.
Note: Since the point probability of each scenario in the original model is zero, it is customary to set
the probabilities of sampled scenarios to 1/N.
580 CHAPTER 14
Given the parametric distribution of each stochastic parameter, LINGO's sampling routines can be
used to efficiently generate univariate samples from these distributions. When sampling, LINGO uses
Latin-hyper-square techniques to reduce the sample variance. One may also specify a correlation
matrix for the continuous random variable, which the sampling routines will use to induce correlation
in the sample points. These sample points are then used to define discrete distributions, which
approximate the original distributions. Repeating this for all continuous stochastic parameters, LINGO
recasts the infinite event space model into an approximate model with a finite event space.
Setting up SP Models
There are four steps to setting up an SP model. Below is a list of these steps and the primary LINGO
functions that you will call to perform each step. Each of these steps will be illustrated in detail in the
example SP model later in this chapter.
Step Task Description How
1 Defining core model The core model is built just like any other
deterministic LINGO model. The random
variables are used directly in the core model's
expressions as if they were determinate.
Entered like any other
deterministic LINGO
model.
2 Identifying the
random variables
Each random variable must be identified along
with the stage of the model where it becomes
known.
@SPSTGRNDV
3 Identifying the initial
decision and recourse
variables
Each initial decision variable and each
recourse variable must be identified along
with the stage where it must be decided. The
initial decision variables are assigned stage 0,
while the subsequent recourse variables are
assigned to stages 1,2,... .
@SPSTGVAR

STOCHASTIC PROGRAMMING 581
4 Declaring
distributions
The probability distributions of the random
variables must be declared. The techniques
for doing so will depend on whether the
variable of interest has a distribution defined
by either a) a discrete outcome table, or b) a
parametric distribution.
An outcome table is a finite set of all possible
outcomes, their probabilities and values for
the random variable(s). Outcome tables may
be constructed using either scalar values or
attribute vectors.
A parametric distribution, on the other hand,
is defined by a particular type of probability
density function, e.g., the normal distribution.
Parametric distributions may have a finite or
infinite number of possible outcomes,
depending on the distribution type.
Outcome Tables:
Scalar-based:
@SPTABLESHAPE
@SPTABLEOUTC
@SPTABLEINST
@SPTABLERNDV
Vector-based:
@SPDISTTABLE
Parametic Distributions:
@SPDIST<TYPE>
@SPSAMPSIZE
@SPCORR<METHOD>
Language Features for SP Models
The primary features in the LINGO language used for building a stochastic programming model can
be partitioned into the following three categories, corresponding to steps 2-4 of the Setting up SP
Models section above:
1. Identifying random variables
2. Identifying initial decision and recourse variables
3. Declaring distributions
Each of the categories are discussed in the following five sections, which are primarily intended for
reference use. The reader may wish to jump directly to the first SP modeling example, Gas Buying
Example, in order to see LINGO's SP modeling features used in the context of an actual model.
There are additional SP language constructs available for use in calc sections for model's that exploit
LINGO's programming capability. These features are discussed in Chapter 13, Programming LINGO.
Identifying Random Variables
The fundamental component of any SP model is its set of random variables. The random variables are
the stochastic component of the model. Their values are not known with certainty beforehand,
however, their uncertainty can be expressed with known probability distributions. LINGO requires
each random variable to be explicitly identified. When we identify each random variable, we must also
provide the stage in the scenario tree where each variable's value is revealed. The @SPSTGRNDV
function is used for this purpose:

582 CHAPTER 14
@SPSTGRNDV( STAGE, VARIABLE_NAME)
This function takes two arguments: the random variable's name and the integer valued stage at which
the random variable's value is revealed. Note that this function merely flags a variable as being
random, and does not communicate any information regarding the actual distribution of the variable.
A distribution is associated with the random variable in the Binding random variables to distribution
instances, discussed below. Some examples follow:
Example 1: @SPSTGRNDV( 1, DEMAND);
Flags variable DEMAND as being a random variable in stage 1.
Example 2: @FOR( TIME_ASSET( T, A) | T #GT# 1:
@SPSTGRNDV( T - 1, RETURN( T, A)));
Flags RETURN( T, A) as being a random variable in stage T-1. Note that by using
@SPSTGRNDV in an @FOR loop, we are able to identify multiple variables as being random.
Identifying Initial Decision and Recourse Variables
After identifying the random variables, all the remaining variables in the model are either initial
decision variables or recourse variables. These are the variables that are in our control, as opposed to
being stochastic and in the control of Mother Nature. The initial decision variables are those variables
whose values must be determined at time 0, before nature has revealed values for any of the random
variables. The recourse variables are the variables whose values are decided at a later period in
response to outcomes for the random variables. Both initial decision and recourse variables are
identified with the @SPSTGVAR function, with initial decision variables being distinguished by a
stage of 0 and recourse variables by a stage >0. Row stages can be established using @SPSTGROW.
@SPSTGVAR( STAGE, VARIABLE_NAME)
This function takes two arguments: an integer value equal to the stage at which the variable's value
must be decided and the variable's name. Note that this function merely flags a variable as being
random, and does not communicate any information regarding the actual distribution of the variable.
A distribution must be associated with the random variable (see the following section: Declaring
Distributions). Some examples follow:
Example 1: @SPSTGVAR( 0, PURCHASE);
Flags variable PURCHASE as being an initial decision variable.
Example 2: @FOR( TIME_ASSET( T, A):
@SPSTGVAR( T - 1, INVEST( T, A)));
Flags INVEST( T, A) as being recourse variable in stage T-1 (or an initial decision variable when
T-1=0). Note that by using @SPSTGVAR in an @FOR loop, we are able to identify multiple
recourse variables.
Before an SP model can be passed to the SP solver engine, all initial and recourse variables must be
assigned stage values. Having to explicitly assign stage values to all these variables can be a tedious
and error-prone process. Fortunately, LINGO can deduce the stages for many of the variables based
on the user inputting a minimal set of stages for the variables. We refer to this process a stage
deduction and it is discussed more in section The Solution below of the Gas Buying Example.
Guidelines for determining the variables that require explicit stage identification are listed below.

STOCHASTIC PROGRAMMING 583
@SPSTGROW( VARIABLE_NAME, STAGE)
This function takes two arguments: an integer-valued stage at which the row's value becomes known
and the row's name. This function should generally not be required, in that LINGO can automatically
deduce all row stages. If you do use this function, you must name the rows whose stages you wish to
set. The syntax of assigning names to rows may be found in the Constraint Names section of Chapter
1.
Example:
@SPSTGROW( 4, CAPACITY);
Assigns row CAPACITY to stage 4.
Note: Guidelines for determining the variables and rows that must be explicitly staged are:
♦ All random variables must be assigned to a stage using @SPSTGRNDV.
♦ Any initial decision or recourse variable that belongs to stage N that does not depend either
directly, or indirectly, on another variable (random or otherwise) declared to be in stage N
must be explicitly assigned to stage N using @SPSTGVAR.
♦ If you are uncertain whether a particular variable must be explicitly assigned to a stage, or
not, then it doesn't hurt to assign it anyway using @SPSTGVAR.
♦ In general, stage assignment for rows should be left to LINGO. Each row will be assigned
to the stage equal to the maximum stage of the variables appearing in that row. However,
if you wish to explicitly specify a row’s stage, you may always do so using
@SPSTGROW.
Declaring Distributions
After identifying the random variables, you will need to assign them to appropriate probability
distributions. There are two classes of distributions: parametric distributions and outcome table
distributions, with each requiring different declarations. Declaring parametric distributions involves
declaring a particular type of probability density function (e.g., normal) and its parameters (e.g., mean
and standard deviation). Outcome table distributions may be declared using scalar values or, assuming
your model makes use of sets and attributes, they may also be declared very conveniently using
attribute vectors and matrices. In either case, you will need to identify all possible outcomes and their
respective probabilities.
Declaring Parametric Distributions
LINGO allows both independent and joint parametric probability distributions, as well as continuous
and discrete distributions. The functions used to declare these distributions are of the form
@SPDIST<TYPE>, where <TYPE> represents the type of distribution being declared. In addition,
there are the @SPSAMPSIZE and @SPCORR<METHOD> functions for, respectively, setting sample
sizes and inducing correlations, where <METHOD> refers to the particular method used to induce
correlation.

584 CHAPTER 14
@SPDIST<TYPE>( PARAM_1[, ... , PARAM_N], RANDOM_VAR)
This function is used to apply both continuous and discrete parametric probability distributions to
random variables. At least one distribution parameter argument will always be required. Additional
parameters may be required depending on the particular distribution. Parameter values are always
numeric. The random variable must be declared beforehand via @SPSTGRNDV.
Below is a list of supported continuous distributions.
Distribution Syntax Parameters
Beta @SPDISTBETA( A, B, RNDVAR) A = alpha > 0
B = beta > 0
Cauchy @SPDISTCACY( LOC, SCALE,
RNDVAR)
LOC = location
SCALE = scale > 0
Chi-Square @SPDISTCHIS( DF, RNDVAR) DF = degrees of freedom = a positive
integer
Exponential @SPDISTEXPO( LAMDA, RNDVAR) LAMDA = rate parameter > 0
F @SPDISTFDST( DF1, DF2, RNDVAR) DF1 = degrees of freedom 1 = a positive
integer
DF2 = degrees of freedom 2 = a positive
integer
Gamma @SPDISTGAMM( SHAPE, SCALE,
RNDVAR)
SHAPE = shape parameter > 0
SCALE = scale parameter > 0
Gumbel @SPDISTGMBL( LOC, SCALE,
RNDVAR)
LOC = location
SCALE = scale > 0
Laplace @SPDISTLAPL( LOC, SCALE,
RNDVAR)
LOC = location
SCALE = scale > 0
Logistic @SPDISTLGST( LOC, SCALE,
RNDVAR)
LOC = location
SCALE = scale > 0
Lognormal @SPDISTLOGN( MU, SIGMA,
RNDVAR)
MU = mu parameter
SIGMA = sigma parameter > 0
Normal @SPDISTNORM( MU, SIGMA,
RNDVAR)
MU = mean
SIGMA = standard deviation > 0
Pareto @SPDISTPRTO( SCALE, SHAPE,
RNDVAR)
SCALE = scale parameter > 0
SHAPE = shape parameter > 0
Student's t @SPDISTSTUT( DF, RNDVAR) DF = degrees of freedom = a positive
integer
Triangular @SPDISTTRIA( L, M, U, RNDVAR) L = lowest point
M = middle point
H = high point
Uniform @SPDISTUNIF( L, U, RNDVAR) L = lower point
U = upper point
Weibull @SPDISTWEIB( SHAPE, SCALE,
RNDVAR)
SHAPE = shape parameter > 0
SCALE = scale parameter > 0

STOCHASTIC PROGRAMMING 585
Example: @SPDISTNORM( 82.3, 18.1, RND_TEMP);
In this example, we apply a normal distribution to the random variable RND_TEMP, with a mean
of 82.3 inches and a standard deviation of 18.1.
Here's the list of discrete distributions currently supported:
Distribution Syntax Parameters
Binomial @SPDISTBINO( N, P, RNDVAR) N = population size = a non-negative integer
P = probability of success, 0 ≤ P ≤ 1
Geometric @SPDISTGEOM( P, RNDVAR) P = probability of success, 0 < P ≤ 1
Hypergeometric @SPDISTHYPG( N, NDEF, K,
RNDVAR)
N = population size = a non-negative integer
NDEF = number defective = a positive
integer ≤ N
K = sample size = positive integer ≤ N
Logarithmic @SPDISTLOGR( P, RNDVAR) P = P-factor, 0 < P < 1
Negative
Binomial
@SPDISTNEGB( R, P, RNDVAR) R = R-factor > 0
P = probability of success, 0 < P < 1
Poisson @SPDISTPOIS( LAMDA, RNDVAR) LAMDA = arrival rate > 0
Example: @SPDISTPOIS( 33, CUSTOMERS);
In this example, we apply a Poisson distribution with an arrival rate of 33 to the random variable
CUSTOMERS.
@SPSAMPSIZE( STAGE, SAMPLE_SIZE)
This function is used to set the sample size for probability distributions by stage. Most instances of
the parametric distributions listed in this section have a large, if not an infinite, number of outcomes.
Trying to incorporate all possible outcomes into the model would be impossible, therefore, LINGO
must sample from the parametric distributions. If a specific sample size is not set using
@SPSAMPSIZE, then LINGO defaults to a sample size equal to the Default Sample Size/Stage
parameter, which is typically set to 2. However, in some models you may wish to have different
sample sizes across stages, typically having larger samples in the more critical early stages, and less
sampling in the latter stages. @SPSAMPSIZE can enforce this type of sampling strategy.

586 CHAPTER 14
Example 1: @SPSAMPSIZE( 1, 8);
Here we set the sample size to 8 outcomes in stage 1.
Example 2: @FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPSAMPSIZE( P - 1, SAMP_SZ( P))
);
In this example, we set the sample size equal to SAMP_SZ( P) in periods 1 through N-1. Note that
by adding the conditional expression P #GT# @INDEX( P0) to the @FOR loop, the loop starts
with P0=2, and we avoid setting the sample size in stage 0. We do this because stage 0 never
contains random variables. Random variables first occur in stage 1, with stage 0 being reserved
for the initial decision variables. In this example, we have also not assigned a sample size to the
final stage, because we either want the final stage to use the default sample size, or the final stage
does not have random variables.
@SPCORR<METHOD>( RANDOM_VAR_1, RANDOM_VAR_2, RHO)
This function causes the sampling code to induce correlations between two random variables. The
ordering of the two variables is not significant. The correlation coefficient, RHO, must lie in the
interval [-1,1]. You must also choose between three methods available for inducing correlations:
Pearson, Kendall or Spearman. Only one correlation method is allowed per model. Some examples
follow:
Example 1: @SPCORPEARSON( X, Y, .9);
Here we set the correlation between random variables X and Y to be .9 using the Pearson method.
Example 2: @FOR( CORR_RNDM_PLANTS( P1, P2):
@SPCORRKENDALL( CAPACITY( P1), CAPACITY( P2), RHO( P1, P2));
);
In this example, we have a derived, two-dimensional set. CORR_RNDM_PLANTS, that contains
the pairs of electrical plants whose output capacities are correlated. We loop over these pairs,
setting each pair's correlation to RHO( P1, P2) using the Kendall method.

STOCHASTIC PROGRAMMING 587
Matrix Declarations of Outcome Table Distributions
LINGO allows probability density functions to be input as discrete outcome tables. You will need to
input the values for the random variables under each outcome, as well as the probability of each
outcome. Matrix-based declarations are considerably more concise than scalar-based declarations, in
that one simple function call can declare the outcome table, it's probabilities, as well as assign multiple
random variables to the distribution. The function used for vector-based outcome table declaration is
@SPDISTTABLE:
@SPDISTTABLE( OUTCOME_TABLE, RANDOM_VARIABLE_ATTR[,
PROBABILITY_ATTR])
This function identifies an outcome table, the random variables to be assigned to the outcome table,
and, optionally, probabilities for each of the outcomes. The first argument, or outcome table, must be
either a one or two-dimensional attribute containing the outcome values for the random variables. If it
is one-dimensional, then the random variable argument must be a scalar. If the outcome table is two-
dimensional, say M x N, then it must contain M outcomes, with each row being a single outcome for N
random variables. Also, in the two-dimensional case the random variable argument must be a one-
dimensional attribute of length N. If the probability argument is included, it must be a one-
dimensional attribute of length equal to the number of outcomes. If the probability argument is
omitted, then each outcome is assumed to be equally probable. Some examples follow:
Example 1: @SPDISTTABLE( DIST_RETURNS, RETURNS);
Declares an outcome table with the two-dimensional attribute DIST_RETURNS containing one
outcome per row for the random variables in the one-dimensional RETURNS attribute. The
number of columns in DIST_RETURNS must equal the number of elements in RETURNS. The
optional probability argument was omitted in this example, meaning that all outcomes are equally
likely.
Example 2: @SPDISTTABLE( DIST_SALES, SALES, PROB);
Declares an outcome table with the one-dimensional attribute DIST_SALES containing the
possible outcomes for the scalar random variable SALES. The PROB attribute is a one-
dimensional attribute of the same length as DIST_SALES that contains the probabilities of all the
outcomes.
Sample SP models installed with LINGO that utilize @SPDISTTABLE include: SPPUTOPT1,
SPNEWSDISC and SPHYDRO.
Scalar Declarations of Outcome Table Distributions
In the previous section, we discussed how to declare outcome tables using matrix-based declarations.
In general, the matrix form of declaration is the simplest and easiest to use. However, there may be
models that are not set based that would be unable to use matrix declarations. Also, there may be
instances when you only wish to declare portions of an attribute to be random. In these cases, you
will need to use scalar-based outcome table declarations. The scalar-based functions used to declare
outcome tables are: @SPTABLESHAPE, @SPTABLEOUTC., @SPTABLEINST and
@SPTABLERNDV.

588 CHAPTER 14
@SPTABLESHAPE( 'TABLE_NAME', NUMBER_OF_OUTCOMES,
NUMBER_OF_RANDOM_VARS)
This function initializes an outcome table and requires three arguments: a unique name for the
distribution table (entered as text), the number of possible outcomes, and the number of random
variables in the distribution. Some examples follow:
Example 1: @SPTABLESHAPE( 'WEATHER', 3, 1);
Declares an outcome table called WEATHER with 3 outcomes and 1 independent variable.
Example 2: @SPTABLESHAPE( 'RETURN', @SIZE( OUTCOMES), @SIZE( ASSETS));
Declares an outcome table called RETURN with the number of outcomes equal to the size of set
OUTCOMES and the number of jointly distributed variables equal to the size of set ASSETS.
@SPTABLEOUTC( 'TABLE_NAME', OUTC_PROB, OUTC_VAL1[ ,..., OUTC_VALN])
Once an outcome table has been declared with @SPTABLESHAPE, the next step is to load the table
with its set of outcome values and their probabilities. This is accomplished through calls to
@SPTABLEOUTC . @SPTABLEOUTC accepts a multiple number of arguments; however, there must
always be at least two arguments, with argument 1 always being the distribution name and the
remaining arguments being numeric values. The first numeric value passed will be taken as the
probability of outcome 1. Assuming the distribution has N variables, the next N arguments will be
taken as the values for variables 1 through N for outcome 1. This process repeats for each outcome
until a total of M * (N + 1) numeric values have been passed, where M is the number of outcomes.
These numeric values may be passed in as many calls as is convenient, but, again, the first argument of
each call must be the name of the relevant distribution. The following examples should help to
illustrate:
Example 1: @SPTABLEOUTC( 'WEATHER', .3, 56, .6, 77, .1, 92);
In this example, we have a 3-outcome, single-variable, outcome table named 'WEATHER'. We
make a single call to @SPTABLEOUTC to load all three outcomes. Outcome 1 has a probability
of .3 and a value of 56, outcome 2 has a .6 probability and a value of 77, while outcome 3 has a .1
probability and a value of 92.
Example 2: @FOR( OUTCOMES( O):
@SPTABLEOUTC( 'D1', 1 / @SIZE( OUTCOMES));
@FOR( ASSETS( A): @SPTABLEOUTC( 'D1', O_RETURN( O, A)));
);
Here we are making two calls to @SPTABLEOUTC for each member of the OUTCOMES set.
The first call passes the probability of the outcome, while the second call passes the outcomes for
each member of the ASSETS set. This example was taken from the SPCOLLEGEDISC.LG4
example, which you may wish to review for additional clarification.

STOCHASTIC PROGRAMMING 589
@SPTABLEINST( 'PARENT_TABLE_NAME', 'TABLE_INSTANCE_NAME')
In order to actually use an outcome table distribution in a model we must also declare an instance of
the relevant distribution. This allows us to use a particular distribution a multiple number of times in a
model, saving us from having to reenter the distribution's parameters each time. @SPTABLEINST is
the function for declaring distribution instances. This function takes two arguments: the parent
outcome table's name as established in the call to @SPTABLESHAPE, and a unique name to apply to
the new instance of the distribution. A particular outcome table may be used many times in a single
model, however, each particular instance requires a unique name. Some examples follow:
Example 1: @SPTABLEINST( 'WEATHER', 'WEATHER_1');
Declares an instance of the parent distribution 'WEATHER', giving it a name 'WEATHER_1'.
Example 2: @FOR( TIME( T):
@SPTABLEINST( 'D1', 'D1_' + TIME( T)));
Declares multiple instances of the parent distribution 'D1', assigning each one the name
'D1_'+TIME( T). In this case, TIME( T) is a primitive set member whose name gets appended to
the 'D1_' string to form the instance name. As an example, if set TIME has values T1..T12, then
the instance name for the first distribution would be 'D1_T1'.
@SPTABLERNDV( 'DIST_INSTANCE_NAME', RANDOM_VAR_1[, ... ,
RANDOM_VAR_N])
The final step in setting up an outcome table distribution is binding the random variables to the
distribution. This step associates specific random variables with the outcome table instance that was
defined as described above. The @SPTABLERNDV function is used for this purpose. This function
takes two, or more, arguments. The first argument is the distribution instance name, entered as text.
The second argument is the name of the random variable to bind to the distribution instance. If the
distribution has multiple variables, then you may include the additional variable names as arguments,
or you may call @SPTABLERNDV multiple times, until all relevant random variable names have been
assigned to the distribution instance. Some examples follow:
Example 1: @SPTABLERNDV( 'WEATHER_1', RV_WEATHER_1);
Binds random variable RV_WEATHER_1 to the 'WEATHER_1' distribution instance.
Example 2: @FOR( TIME( T): @FOR( ASSETS( A):
@SPTABLERNDV( 'D1_' + TIME( T), RETURN( T, A))));
Assuming the TIME set consists of members T1..T12, this example assigns one random for each
member of the ASSETS set to distribution instance 'D1_Ti', for i =1,...,12. Assuming the ASSETS
set has two members, then two random variables are assigned to each the 12 distribution instances.
Sample SP models installed with LINGO that utilize the above techniques include: SPGAS1 and
SPCOLLEGEDISC.

590 CHAPTER 14
Gas Buying Example
Our first example of how to formulate and solve an SP is a gas buying example. This example was
taken from the Committee on Stochastic Programming's (COSP) website:
http://stoprog.org/index.html?spintroduction.html. The complete LINGO model can be found in the
LINGO samples folder under the name SPGAS1.LG4.
A gas company must come up with a plan for its gas purchases under uncertain weather conditions.
The demand for the current period (period 1) is known and is 100 units. The demand for the upcoming
period is not known with certainty and will depend on how cold the weather is. There are three
possible outcomes for the weather: normal, cold and very cold. Each of these outcomes are equally
likely. The following table lists the costs and demands under the three outcomes:
Outcome Probability Gas Cost/Unit ($) Units Demand
Normal 1/3 5.0 100
Cold 1/3 6.0 150
Very Cold 1/3 7.5 180
Gas for the current period is bought now and delivered directly to the customers at a cost of $5 per
unit. Gas in the upcoming period can either be bought now and held in storage for period 2 use, or it
can be purchased in period 2 at a price that will depend on the weather as per the table above. Storing
gas bought in period 1 for use in period 2 costs the company $1 per unit. The question the company is
faced with is: How much gas should be bought in periods 1 and 2 to meet total customer demand at
minimal expected cost?
The Core Model
Step 1 - Defining the Core Model:
The core model is the same optimization model we would construct if all the random variables were
known with certainty. There is nothing in the core model that addresses the stochastic nature of the
model. The stochastic properties of the model will be introduced in a subsequent model section. For
our current example, the core model is formulated as follows:

STOCHASTIC PROGRAMMING 591
! Minimize Total Cost = Purchases + Holding;
[R_OBJ] MIN= PURCHASE_COST + HOLD_COST;
! Compute purchase cost;
[R_PC] PURCHASE_COST = 5 * PURCHASE_1 + COST_2 *
PURCHASE_2;
! Compute holding cost;
[R_HC] HOLD_COST = INVENTORY_1 + INVENTORY_2;
! Compute inventory levels;
[R_I1] INVENTORY_1 = PURCHASE_1 - 100;
[R_I2] INVENTORY_2 = INVENTORY_1 + PURCHASE_2 - DEMAND_2;
Core Model for Gas Buying Example
In the first expression:
! Minimize Total Cost = Purchases + Holding;
[R_OBJ] MIN= PURCHASE_COST + HOLD_COST;
we are saying that we want to minimize total cost, which consists of two components: the purchase
cost of buying gas in periods 1 and 2, as well as holding costs of buying gas in a current period for use
in a future period.
The following expression:
! Compute purchase cost;
[R_PC] PURCHASE_COST = 5 * PURCHASE_1 + COST_2 * PURCHASE_2;
calculates the total purchase cost, which is $5 per unit of gas purchased in period 1 plus the cost of gas
in period 2 (COST_2) multiplied by the number of units of gas purchased in period 2. Note that
COST_2 is stochastic and will depend on how the weather plays out. We will convey the probabilistic
nature of period 2 cost in the next section.
We next compute total holding costs, which, given the $1/unit holding cost, is simply the sum of units
held over in periods 1 and 2:
! Compute holding cost;
[R_HC] HOLD_COST = INVENTORY_1 + INVENTORY_2;
Finally, we compute the inventory levels for the two periods:
! Compute inventory levels;
[R_I1] INVENTORY_1 = PURCHASE_1 - 100 ;
[R_I2] INVENTORY_2 = INVENTORY_1 + PURCHASE_2 - DEMAND_2;
Period 1's inventory is the amount purchased in period 1 (PURCHASE_1) less the known demand in
period 1. While inventory in period 2 (INVENTORY_2) if equal to any inventory carried over from
period 2 plus the purchase in period 2 (PURCHASE_2) minus the demand in period 2 (DEMAND_2).
Once again, DEMAND_2 is not known with certainty. The uncertain nature of DEMAND_2 will be
established in the next section of the model - the stochastic declarations section.

592 CHAPTER 14
Stochastic Declarations
After the core model, the remainder of the model is the stochastic declarations section:
! *** STEP 2 *** - Define Random Variables;
!The random variables are period 2's demand and cost.;
@SPSTGRNDV( 1, COST_2);
@SPSTGRNDV( 1, DEMAND_2);
! *** STEP 3 *** - Define initial decision and recourse
variables;
!The initial decision is how much to purchase in period 1;
@SPSTGVAR( 0, PURCHASE_1);
!Period 2 purchases are a recourse variable after
the weather reveals itself;
@SPSTGVAR( 1, PURCHASE_2);
! *** STEP 4 *** - Assign distributions to the random
variables;
!Declare a discrete distribution called 'DST_DMD' with
three outcomes and two jointly distributed variables
(i.e., Demand and Cost);
@SPTABLESHAPE( 'DST_DMD', 3, 2);
!Load the three equally likely outcomes into 'DST_DMD';
!Dist Name Probability Cost Demand;
@SPTABLEOUTC( 'DST_DMD', 1/3, 5.0, 100);
@SPTABLEOUTC( 'DST_DMD', 1/3, 6.0, 150);
@SPTABLEOUTC( 'DST_DMD', 1/3, 7.5, 180);
!Declare a specific instance of the 'DST_DMD' distribution,
naming the instance 'DST_DMD_1';
@SPTABLEINST( 'DST_DMD', 'DST_DMD_1');
!Bind Period 2 Cost and Demand to the distribution instance;
@SPTABLERNDV( 'DST_DMD_1', COST_2, DEMAND_2);
Stochastic Declarations for Gas Buying Example
We use this section to identify all the random variables and their distributions. A detailed breakdown
of the stochastic declarations follows.
Step 2 - Identifying the Random Variables:
The next step in building our sample SP model is to identify the random variables. The random
variables are the variables that are stochastic by nature and whose values are not known before we
must make our initial decisions. The @SPSTGRNDV function is used to identify random variables.
@SPSTGRNDV accepts two arguments: the random variable's name and its stage.
In this example, there are two random variables, the second period cost and demand, and we identify
them via @SPSTGRNDV in the following to statements:

STOCHASTIC PROGRAMMING 593
!The random variables are period 2's demand and cost.;
@SPSTGRNDV( 1, COST_2);
@SPSTGRNDV( 1, DEMAND_2);
Note that we have indicated that the two variables are in stage 1. This may seem somewhat odd, in
that they are relevant to period 2. However, you will recall that the first set of random variables to
become known after our initial decision belong to stage 1. If this was a multiperiod model, period 3's
random variables would belong to stage 2, and so on.
Step 3 - Identifying the Initial Decision and Recourse Variables:
The next step is to identify the the initial decision variables and the recourse variables. Unlike the
random variables, which are under Mother Nature's control, the initial decision and recourse variables
are under our control. The initial decision variables occur at the very outset, before any of the random
variables become known, and are always assigned to stage 0. The recourse variables are the
subsequent decisions we make after learning of the outcomes of the random variables. Recourse
variables that are decided after the stage N random variables become known are assigned to stage N as
well.
The @SPSTGVAR function is used to identify initial decision and recourse variables. @SPSTGVAR
accepts two arguments: the variable's stage and its name.
In our example, there is one initial decision, which is PURCHASE_1, the amount of gas to purchase in
period 1. The weather then reveals itself and our recourse variable is PURCHASE_2, the amount to
purchase in period 2. We identify this information with the two statements:
!The initial decision is how much to purchase in period 1;
@SPSTGVAR( 0, PURCHASE_1);
!Period 2 purchases are a recourse variable after
the weather reveals itself;
@SPSTGVAR( 1, PURCHASE_2);
It turns out that before an SP model can be passed to the SP solver engine, all variables and rows must
be assigned stage values. You will note that we have not done this. Specifically, we have not assigned
stages to any of the rows nor to the variables: PURCHASE_COST, HOLD_COST, PURCHASE_2,
INVENTORY_1 and INVENTORY_2. The reason we have not made these stage assignments is that
LINGO can deduce the stages of the remaining rows and variables from the minimal stage information
we've already supplied. We will examine this stage deduction feature in more detail in the next
section. In the meantime, the following guidelines should suffice:

594 CHAPTER 14
Note: Guidelines for determining the variables and rows that must be explicitly staged are:
♦ All random variables must be assigned to a stage using @SPSTGRNDV.
♦ Any initial decision or recourse variable that belongs to stage N that does not depend either
directly, or indirectly, on another variable (random or otherwise) declared to be in stage N
must be explicitly assigned to stage N using @SPSTGVAR.
♦ If you are uncertain whether a particular variable must be explicitly assigned to a stage, or
not, then it doesn't hurt to assign it anyway using @SPSTGVAR.
♦ In general, stage assignment for rows should be left to LINGO. Each row will be assigned
to the stage equal to the maximum stage of the variables appearing in that row. However,
if you wish to explicitly specify a row’s stage, you may always do so using
@SPSTGROW.
Step 4 - Declare Distributions
Next, we need to declare the joint probability distribution for the random variables COST_2 and
DEMAMD_2. In this case, we will be using an outcome table distribution, and in order to declare our
distribution we will make use of the scalar-based functions: @SPTABLESHAPE and
@SPTABLEOUTC, @SPTABLEINST and @SPTABLERNDV.
@SPTABLESHAPE initializes the distribution with a name, number of outcomes and number of jointly
distributed variables, while @SPTABLEOUTC is called once for each outcome to load information
relevant to each outcome:
!Declare a discrete distribution called 'DST_DMD' with
three outcomes and two jointly distributed variables
(i.e., Demand and Cost);
@SPTABLESHAPE( 'DST_DMD', 3, 2);
!Load the three equally likely outcomes into 'DST_DMD';
! Dist Name Probability Cost Demand;
@SPTABLEOUTC( 'DST_DMD', 1/3, 5.0, 100);
@SPTABLEOUTC( 'DST_DMD', 1/3, 6.0, 150);
@SPTABLEOUTC( 'DST_DMD', 1/3, 7.5, 180);
@SPTABLESHAPE accepts three arguments: a name for the distribution, the number of outcomes and
the number of jointly distributed variables in the distribution. In this case, we've titled the distribution
'DST_DMD', and it has three outcomes along with two jointly distributed variables.
Now, to be able to actually apply the distribution to random variables we need to declare an instance of
the distribution. By doing things this way, it's possible to reuse the same outcome table on more than
one set of random variables. We declare an instance of a particular distribution using the
@SPTABLEINST function, which accepts two arguments - the name of the parent distribution and a
new name for the instance of the distribution. In the case of our example, we do the following:

STOCHASTIC PROGRAMMING 595
!Declare a specific instance of the 'DST_DMD' distribution,
naming the instance 'DST_DMD_1';
@SPTABLEINST( 'DST_DMD', 'DST_DMD_1');
Or, in words, we create an instance of the DST_DMD distribution,
which we name DST_DMD_1.
Our last step is to associate, or bind, the random variables to the instance of the distribution.
Specifically, we wish to bind the cost and demand random variables from period 2 to the DST_DMD_1
distribution instance. We do this with the following expression:
!Bind Period 2 Cost and Demand to the distribution instance;
@SPTABLERNDV( 'DST_DMD_1', COST_2, DEMAND_2);
Our SP model has now been fully set up and we are now ready to have LINGO solve the model.
The Solution
SP models are solved just like all other models by using the LINGO|Solve command. After solving
our sample gas buying model, SPGAS_SCALAR.LG4, you will see a solution report that begins with
the following section:
Global optimal solution found.
Objective value: 1400.000
Infeasibilities: 0.000000
Total solver iterations: 2
The first line tells us that the solver found a globally optimal solution. This solution status information
is critical. If the status is anything other than globally optimal, locally optimal, or feasible then the
solution will not be valid.
The objective value is the expected objective value of the objective over all the scenarios. Thus, in this
example, the gas companies expected cost over the three weather scenarios is $1400.
The infeasibilities figure measure the amount by which all constraints were violated in the
deterministic equivalent (DE) model. The amount of infeasibilities should always be a very small
number and should generally not exceed 1.e-7.
Total solver iterations lists the number of iterations, or passes, the solver required to solve the DE
model.
The next section of the solution report lists a number of expected values:
Expected value of:
Objective (EV): 1400.000
Wait-and-see model's objective (WS): 1326.667
Perfect information (EVPI = |EV - WS|): 73.33333
Policy based on mean outcome (EM): 1479.444
Modeling uncertainty (EVMU = |EM - EV|): 79.44444
These values are a guide as to how the stochastic nature of the model is impacting the objective value.
The following is a brief description of these expected values:

596 CHAPTER 14
Expected Value of Objective (EV)
-
is the expected value for the model's objective over all the
scenarios, and is the same as the reported objective value for the model.
Expected Value of Wait-and-See Model's Objective (WS)
-
reports the expected value of the
objective if we could wait and see the outcomes of all the random variables before making our
decisions. Such a policy would allow us to always make the best decision regardless of the
outcomes for the random variables, and, of course, is not possible in practice. For a minimization,
it's true that WS <= EV, with the converse holding for a maximization. Technically speaking, WS
is a relaxation of the true SP model, obtained by dropping the nonanticipativity constraints.
Expected Value of Perfect Information (EVPI)
-
is the absolute value of the difference between EV
and WS. This corresponds to the expected improvement to the objective were we to obtain perfect
information about the random outcomes. As such, this is a expected measure of how much we
should be willing to pay to obtain perfect information regarding the outcomes of the random
variables.
Expected Value of Policy Based On Mean Outcome (EM)
-
is an expected measure of the
objective if we were to follow a policy of assuming that the mean outcomes of the random
variables were always going to occur. EM is computed using a two-step process. First, the values
of all the random variables are fixed at their means, and the deterministic model is solved to yield
the optimal values for the stage 0 decision variables. Next, the stage 0 variables are fixed at their
optimal values from the previous step, while the random variables are freed up. At which point,
this SP is solved, with EM being equal to its objective value.
Expected Value of Modeling Uncertainty (EVMU)
-
is the absolute value of the difference between
EV and EM. As such, it's a measure of what we can expect to gain by incorporating uncertainty
into our modeling analysis, and not always assuming that we will be faced with mean outcomes.
This is sometimes also refered to as the Value of the Stochastic Solution (VSS).
Note: Computing these expected value statistics can be very time consuming for large models. If
speed is an issue, you may wish to disable this feature on the LINGO|Options|SP Solver tab.
STOCHASTIC PROGRAMMING 597
The next component of the solution lists various statistics regarding the class and size of the model:
Model Class: LP
Total scenarios/leaf nodes: 3
Total random variables: 2
Total stages: 1
Core Deteq
Total variables: 6 18
Nonlinear variables: 0 0
Integer variables: 0 0
Total constraints: 5 17
Nonlinear constraints: 0 0
Total nonzeros: 12 30
Nonlinear nonzeros: 0 0
Model class lists the DE's model class. In the case of our gas buying sample we have an LP, or linear
program. Possible model classes are detailed in the Solver Status Window section of Chapter 1.
Total scenarios/leaf nodes lists the total number of scenarios in the model. In this example, there are
three scenarios: Normal, Cold and Very Cold.
Note: The total number of scenarios will grow exponentially in the number of stages. For example,
suppose we have just one random variable with two possible outcomes in each of N stages,
then the number of scenarios will equal 2N. Thus, it doesn't take many stages before an SP
can become quite large.
Total random variables lists the number of random variables in the SP. In this example, we have just
two: COST_2 and PURCHASE_2.
The Total stages quantity is the model's stage count. In this case there is only one round of random
variable realizations and recourse decisions, giving a stage count of 1.
Next, LINGO displays statistics regarding the model's size. Statistics for both the core model and DE
are given. The more relevant statistics are the ones for the DE, which is the actual model that must be
solved. Definitions for these statistics may be found in the Solver Status Window section of Chapter 1.
The next section of the solution reports lists the stage-0 solution:
Stage 0 Solution
----------------
Variable Value
PURCHASE_1 200.0000
INVENTORY_1 100.0000
Row Slack or Surplus
R_I1 0.000000

598 CHAPTER 14
The stage-0 solution lists the values for all variables and rows that are part of the initial decision.
These values are of pressing importance, in that they must be implemented currently. For this reason,
they are displayed in their own separate section near the top of the report.
In the case of our gas company, the optimal initial decision to minimize expected cost is to purchase
200 units of gas in period 1, storing 100 units in inventory. If period 2 is normal the company can
fulfill demand entirely from inventory, otherwise it must make up the difference through additional
purchases in period 2.
Next, we have the Staging Report:
Staging Report
--------------
Random Variable Stage Distribution
COST_2 1 DST_DMD(DST_DMD_1,1)
DEMAND_2 1 DST_DMD(DST_DMD_1,2)
Variable Stage
PURCHASE_COST 1*
HOLD_COST 1*
PURCHASE_1 0
PURCHASE_2 1
INVENTORY_1 0*
INVENTORY_2 1*
Row Stage
R_OBJ 1*
R_PC 1*
R_HC 1*
R_I1 0*
R_I2 1*
(*) Stage was inferred
The staging report lists all variables and rows along with their stages. When an SP model is solved, all
variables and rows need to be assigned stage values before the model is passed to the SP solver
engine. We could have done this explicitly through the use of the @SPSTGVAR, @SPSTGROW and
@SPSTGRNDV functions; however, this can be a tedious process prone to errors - particularly for
large models. On the one hand, all random variables must be flagged using @SPSTGRNDV, but only
a minimal set of the recourse variables and the initial decision variables need to have their stages
explicitly assigned. The reason we only need to specify a minimal set is that LINGO can deduce the
stages of the remaining variables by tracing their dependency chains. We refer to this process as stage
deduction, and any variable or row whose stage has been deduced will be flagged with an asterisk in
the staging report. As an example, from the staging report we see that variable INVENTORY_1 was
deduced to be in stage 0. LINGO determined this from the following row:
[R_I1] INVENTORY_1 = PURCHASE_1 - 100;
Given that we declared PURCHASE_1 to be in stage 0, we can also compute INVENTORY_1's value
in stage 0. In which case, INVENTORY_1 can be deduced to be in stage 0. In turn, we can then use
this staging information for INVENTORY_1 in the following expression:

STOCHASTIC PROGRAMMING 599
[R_I2] INVENTORY_2 = INVENTORY_1 + PURCHASE_2 - DEMAND_2;
and deduce that INVENTORY_2 is in stage 1, by the fact that the maximum of the stages of all the
right-hand side variables is 1. LINGO continues in this fashion, iteratively tracing the dependencies in
the model and assigning stages to each remaining row and variable. Explicit stage assignments made
by the user are never overridden.
Guidelines for determining the variables and rows that require explicit staging were presented in
section, Identifying Initial Decision and Recourse Variables.
The next report is the Random Variable Distribution Report, which lists information on the
distribution assigned to each of the random variables:
Random Variable Stage Distribution
COST_2 1 DST_DMD(DST_DMD_1,1)
DEMAND_2 1 DST_DMD(DST_DMD_1,2)
From this, we can see that the random variable COST_2 is assigned to the first column of the
DST_DMD_1 instance of the tabular distribution DST_DMD.
The remainder of the solution report contains sub-reports for each of the scenarios. Information
regarding the each scenario's probability, objective value and variable values are displayed. The
values for the random variables for the scenario are contained in a separate section of the report. Here
we reproduce the report for scenario 1:
Scenario: 1 Probability: 0.3333333 Objective: 1100.000
----------------------------------------------------------
Random Variable Value
COST_2 5.000000
DEMAND_2 100.0000
Variable Value
PURCHASE_COST 1000.000
HOLD_COST 100.0000
PURCHASE_1 200.0000
PURCHASE_2 0.000000
INVENTORY_1 100.0000
INVENTORY_2 0.000000
Row Value
R_PC 0.000000
R_HC 0.000000
R_I1 0.000000
R_I2 0.000000

600 CHAPTER 14
Note: Moderate to large SP models can have a huge number of scenarios. In which case, the
standard solution report, with its detailed reporting of each scenario, can become unwieldy.
In which case, you may wish to reduce the amount of output by placing LINGO into Terse
output mode. You may then request more specific solution information using the
LINGO|Solution command or add output statements to your model (see SPCOLLEGE2.LG4
for an example of adding output statements to an SP model).
If you examine the reports for each of the three scenarios in this example, you will find that the costs
are as follows: $1,100 for Normal, $1,400 for Cold and $1,700 for Very Cold. This results in an
expected cost of $1,400 = (1/3) * $1100 + (1/3) * $1400 + (1/3) * $1700. The company buys 200 units
of gas in period 1, applying 100 units immediately to period 1 demand, while storing 100 units for
period 2. If period 2''s weather is normal, then period 2 demand is satisfied entirely from inventory. If
the period 2 turns out to be cold, an additional 50 units must be purchased in period 2. If the very cold
scenario occurs, then an additional 80 units must be purchased.
Stock Option Example
Here we will walk through a stochastic programming example of a six-period American put-option
model. The holder of an American put option has the right to sell a specified (underlying) stock at any
time (the feature of American options) between now and a specified expiration date at a specified
strike price. The holder makes a profit in the period of exercise if the strike price exceeds the market
price of the stock at the time of sale, otherwise the profit is 0. The objective will be to maximize the
expected present value of the option in period 0, which also corresponds to the maximum amount we
should be willing to pay for the option.
In this example, the underlying stock's initial price is $100, with the option's strike price equal to $99.
This initially places the option "out of the money" and make its value $0. However, should the stock's
price decline over subsequent periods to the point where it becomes less than the strike price, then the
option will have a positive value.
We will also use a risk free interest rate of 4% for discounting revenue back to the initial period.
The price behavior of the underlying stock is the stochastic element in this example. In any given
period, we have determined that there are four equally likely outcomes for the stock's price:
Return (%) Probability
+9.0 1/4
+3.0 1/4
-1.0 1/4
-8.0 1/4
Using the following reasoning, a casual observer might analyze the above data and declare the option
as being worthless:

STOCHASTIC PROGRAMMING 601
The stock is presently out of the money by $1. Before it will move into the money, the stock must
decline by at least $1. However, this seems highly unlikely given that the expected return in any
period is positive +0.75% = .25 * (9.0+3.0-1.0-8.0)%. On average, the stock will just go up in value,
and the option will never go into the money. Given this, we should not be willing to pay anything for
this option.
We will see below if our casual observer in on the right track or not.
The complete LINGO model can be found in the LINGO samples folder under the name
SPPUTOPT1.LG4.
The Core Model
Step 1 - Defining the Core Model:
First off, we have the data section containing the parameters we mentioned above, consisting of the
stock's initial price, the option's strike price and the risk free rate for discounting:
DATA:
INIT_PRICE = 100; !initial underlying stock price;
STRIKE_PRICE = 99; !option strike price;
RISK_FREE_RATE = .04; !risk free rate for discounting;
ENDDATA
Data Section
Unlike the previous gas-buying model, which was entirely scalar, we will make use of LINGO's set-
based modeling capabilities in this example. Any set-based model will have at least one sets section,
and for the core model for this example we have the following:
SETS:
PERIODS /P0..P5/: !six periods (1 initial and 5
recourse);
RETURN, !return of underlying stock, a r.v.;
PRICE, !current price of underlying stock;
SELL, !fraction of option position sold;
PV, !present value of option;
SAMP_SZ; !sample size;
ENDSETS
Sets Section
As mentioned, this is a six-period (one initial and five recourse) model. Across the six periods, we
have the following attributes:
♦ RETURN - the stock's return (fractional price change), a random variable
♦ PRICE - the current price of the stock (a function of the RETURN)
♦ SELL - a recourse variable indicating the fraction of the option position sold
♦ PV - the discounted present value of the option
♦ SAMP_SZ - the sample sizes used for sampling the distribution for RETURN.
Next, we have the core model's expressions. You will recall that the core model is the model we
would construct if the random variables were known with certainty.
602 CHAPTER 14
! Core Model -------------------------------------------+;
! Maximize the present value of the option in period 0;
[R_OBJ] MAX = PV( @INDEX( P0));
! Compute stock's price in each period;
[R_PRICE_INIT] PRICE( 1) = INIT_PRICE;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
[R_PRICE] PRICE( P) = PRICE( P - 1) * ( 1 + RETURN( P));
);
! Calculate the present value of the option in each period;
@FOR( PERIODS( P) | P #LT# @SIZE( PERIODS):
[R_PV] PV( P) = SELL( P) * ( STRIKE_PRICE - PRICE( P)) +
PV( P + 1) / ( 1 + RISK_FREE_RATE);
);
[R_PV_NPERIODS] PV( @SIZE( PERIODS)) =
SELL( @SIZE( PERIODS)) *
( STRIKE_PRICE - PRICE( @SIZE( PERIODS)));
! Can't sell more than we have;
[R_SELL_EQ_1] @SUM( PERIODS( P): SELL( P)) <= 1;
! Random variables not allowed in initial period;
[R_RETURN_P0] RETURN( @INDEX( P0)) = 0;
Core Model for Stock Option Example
As mentioned, our objective is to maximize the present value of the option in the initial period, which
will tell us the maximum we should be willing to pay for the option:
! Maximize the present value of the option in period 0;
[R_OBJ] MAX = PV( @INDEX( P0));
In the next expression:
! Compute stock's price in each period;
[R_PRICE_INIT] PRICE( 1) = INIT_PRICE;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
[R_PRICE] PRICE( P) = PRICE( P - 1) * ( 1 + RETURN( P));
);
we employ the RETURN random variable as if it were a known quantity so as to compute the stock's
price in each period. Specifically, the price in period t is equal to the price in period t-1 multiplied by
the quantity 1 plus the return in period t, or: PRICEt = PRICEt-1 * ( 1 + RETURNt).
The next two expressions compute the present value of the option in each period:

STOCHASTIC PROGRAMMING 603
! Calculate the present value of the option in each period;
@FOR( PERIODS( P) | P #LT# @SIZE( PERIODS):
[R_PV] PV( P) = SELL( P) * ( STRIKE_PRICE - PRICE( P)) +
PV( P + 1) / ( 1 + RISK_FREE_RATE);
);
[R_PV_NPERIODS] PV( @SIZE( PERIODS)) =
SELL( @SIZE( PERIODS)) *
( STRIKE_PRICE - PRICE( @SIZE( PERIODS)));
For periods prior to the final period, the option's present value is derived from two components. First,
there is any revenue from selling some, or all, of our option: SELLp * ( STRIKE_PRICE - PRICEp).
Second, there is a discounted component derived from the next periods present value: PVp+1 / ( 1 +
RISK_FREE_RATE). We include a special computation for the final period, where the present value
component is not relevant, and sales of the option are the only potential source of revenue.
Clearly, we can't sell more of full option position, so the sum of the SELL attribute across all periods
cannot exceed 1:
! Can't sell more than we have;
[R_SELL_EQ_1] @SUM( PERIODS( P): SELL( P)) <= 1;
Finally, you will recall that random variables are not allowed in the initial period. For this reason, we
set RETURN to 0 in the initial period:
! Random variables not allowed in initial period;
[R_RETURN_P0] RETURN( @INDEX( P0)) = 0;

604 CHAPTER 14
Stochastic Declarations
The remainder of the model after the core model is the stochastic declarations section:
! SP Related Declarations -----------------------------+;
! Returns are the random variables;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPSTGRNDV( P - 1, RETURN( P));
);
! Sell(P0) is the init decision,
Sell(P1..P5) are the recourse variables;
@FOR( PERIODS( P):
@SPSTGVAR( P - 1, SELL( P));
);
! Declare the outcome table distribution for returns;
SETS:
OUTCOMES: O_RETURN; !An outcome set with a single;
ENDSETS ! attribute of stock's return;
DATA:
SAMP_SZ = 0 4 4 2 2 2; !sample size/period;
O_RETURN = .09 .03 -.01 -.08; !4 outcomes for return;
ENDDATA
! Declare outcome table distribution for return;
@FOR( PERIODS( P)) | P #GT# @INDEX( PO):
@SPDISTTABLE( O_RETURN, RETURN( P));
);
! Set the sample sizes for the stages;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPSAMPSIZE( P - 1, SAMP_SZ( P));
);
END
Stochastic Declarations for Stock Option Example
Step 2 - Identifying the Random Variables:
As mentioned, the random variables in this example are the stock price returns, RETURN, for periods 1
through 5. We indicate this with the expression:
! Returns are the random variables;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPSTGRNDV( P - 1, RETURN( P));
);
Note that return in the initial period, P0, is not valid in this model and we zeroed it out above.

STOCHASTIC PROGRAMMING 605
Step 3 - Identifying the Initial Decision and Recourse Variables:
The initial decision is deciding whether or not to sell some, or all, of the option position in the initial
period. The recourse decisions are whether or not to sell some of our position in periods 1 through 5.
We set this up with the following:
! Sell(P0) is the initial decision,
Sell(P1..P5) are the recourse variables;
@FOR( PERIODS( P):
@SPSTGVAR( P - 1, SELL( P));
);
Step 4 - Declare Distributions:
We have a single discrete distribution for the returns on the underlying stock. As with the previous
gas-buying example, this distribution is represented by an outcome table. However, unlike the
previous example, we will make use of the matrix-based @SPDISTTABLE function for declaring our
outcome table and its random variables. The code in the model devoted to declaring this distribution
is:
! Declare the outcome table distribution for returns;
SETS:
OUTCOMES: O_RETURN; !An outcome set with a single;
ENDSETS ! attribute of stock's return;
DATA:
SAMP_SZ = 0 4 4 2 2 2; !sample size/period;
O_RETURN = .09 .03 -.01 -.08; !4 outcomes for return;
ENDDATA
! Declare outcome table distribution for return;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPDISTTABLE( O_RETURN, RETURN( P));
);
! Set the sample sizes for the stages;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPSAMPSIZE( P - 1, SAMP_SZ( P));
);
END
First, we define a set OUTCOMES with an attribute O_RETURN. O_RETURN will be used to hold the
four possible outcomes from the stock's return in a period. Next, we call @SPDISTTABLE to declare
the outcome table for each RETURN random variable in periods 1 through 5.
In the previous gas-buying example, we had only one stage and three outcomes, resulting in only three
possible scenarios. Given the small nature of the underlying SP, we decided not to sample the
distribution for weather and, instead, allowed LINGO to automatically generate a scenario for each
outcome. This current model has a much larger set of potential scenarios. There are 5 stages with 4
possible outcomes for return in each stage. This results in 45=1024 potential scenarios. In order to
keep the number of scenarios down to a more manageable size, we will chose to sample the
distribution in this example. In particular, we will chose a sample size of 4 in stages 1 and 2, and a
smaller sample size of 2 in stages 3 through 5. This cuts the number of scenarios in the underlying SP
model to 4*4*2*2*2=128 scenarios. This should help to dramatically cut the runtime, but at the
expense of potentially less accurate results.

606 CHAPTER 14
We set the samples sizes in the data section:
SAMP_SZ = 0 4 4 2 2 2; !sample size/period;
and then pass them to LINGO's SP solver in the @FOR loop:
! Set the sample sizes for the stages;
@FOR( PERIODS( P) | P #GT# @INDEX( P0):
@SPSAMPSIZE( P - 1, SAMP_SZ( P));
);
Note that a sample size is not relevant for the initial period, P0, given that no random variables are
permitted in the initial period. So, we have explicitly avoided passing a sample size for period P0.
The Solution
After solving the model, you'll find that the expected value of the option is $3.37:
Local optimal solution found.
Objective value: 3.370706
Infeasibilities: 0.000000
Total solver iterations: 11
Thus, it turns out that our casual observation of the option being worthless was incorrect. Even though
the option is initially out of the money, and, on average, is expected to go even further out of the
money as time passes, the option still has a positive expected value of $3.37. This is due to the
volatility in the stock price, which can temporarily send the stock price down, even though the long
run expectation is for the price to climb.
Based on our sample sizes of 4, 4, 2, 2 and 2 for the stages, there were a total of 128 scenarios. In
fully 70 of these scenarios, the option's value did prove to be worthless. However, in the remaining 58
scenarios the option had a positive value of as high as $13.28. Here's a histogram of the full range of
outcomes:
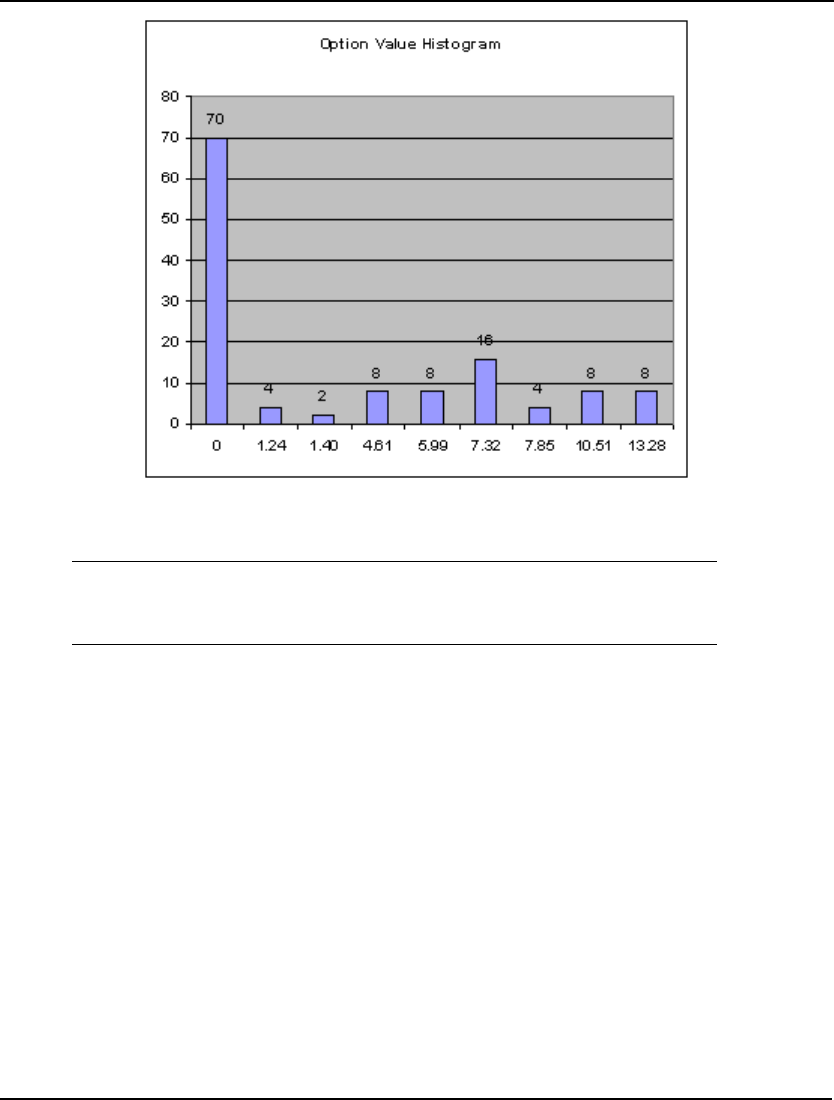
STOCHASTIC PROGRAMMING 607
The key initial decision was whether or not to sell the option. From the stage 0 (initial decision)
solution we see that the optimal decision is to not sell:
Stage 0 Solution
----------------
Variable Value
SELL( P0) 0.000000
Of course, we didn't really need LINGO to tell us not to sell in the first period - we could have
deduced this ourselves. The worst outcome we could experience is to gain $0. By selling in the initial
period, we lock in the $0 return, never allowing for the possibility of the stock to go down in price and
the option to come into the money. We will rely on LINGO's solution, however, to tell us the best
time to sell in subsequent periods. Here is a fragment of the solution report for scenario 1, which is
one of the scenarios with the maximum option value of $13.28:
608 CHAPTER 14
Scenario: 1 Probability: 0.7812500E-02 Objective:13.27663
-----------------------------------------------------------
Random Variable Value
RETURN( P1) -0.8000000E-01
RETURN( P2) -0.8000000E-01
RETURN( P3) -0.8000000E-01
RETURN( P4) 0.9000000E-01
RETURN( P5) 0.3000000E-01
Variable Value
RETURN( P0) 0.000000
PRICE( P0) 100.0000
SELL( P0) 0.000000
PV( P0) 13.27663
PRICE( P1) 92.00000
SELL( P1) 0.000000
PV( P1) 13.80769
PRICE( P2) 84.64000
SELL( P2) 1.000000
PV( P2) 14.36000
PRICE( P3) 77.86880
SELL( P3) 0.000000
PV( P3) 0.000000
PRICE( P4) 84.87699
Note that the stock goes down in the first three periods, but that we sold in period 2 for a gain of
$14.26, which discounted back to the initial period is equal to a gain of $13.28. Had we been
omniscient, we could of held on to the option for one more period for additional gains. But, of course,
we can't see the future, and we must base our decisions on maximizing the option's expected value
over all scenarios.
Investing Under Uncertainty Example
In the previous two examples, the random variable distributions were expressed as discrete outcome
tables. In this example, we will look at a model with distributions that are not discreet. In particular,
we will be using a normal distribution for our random variables. Given the infinite number of
outcomes in a normal distribution, we will also need to use @SPSAMPSIZE to declare the samples
sizes to be used by the SP solver. In addition, we will use @SPCORRPEARSON to input a correlation
coefficient for some of the random variables.
In this example, we are investing to fund a college education (Birge and Louveaux, 1997). We may
invest in either stocks or bonds, both of which are assumed to have returns that are normally
distributed as per the following table:
Asset Mean Return Standard Deviation
Bonds 12% 1%
Stocks 16% 10%

STOCHASTIC PROGRAMMING 609
It also turns out that the returns on stocks and bonds are correlated, with a correlation coefficient of .5.
Our initial wealth is $55,000, while our target at the end of four periods is $80,000. Our goal is to
maximize wealth at the end of the three periods, however, we will be very disappointed if we don't
meet our goal. For this reason, we penalize ourselves by a factor of four for each dollar that we are
short of our goal. We also have the option of readjusting our portfolio at the start of each period.
The complete LINGO model can be found in the LINGO samples folder under the name
SPCOLLEGENORM.LG4.

610 CHAPTER 14
The Core Model
The core model for our investing example follows:
! Core Model -------------------------------------------+;
SETS:
TIME;
ASSETS: MU, SIGMA;
AXT( ASSETS, TIME): INVEST, RETURN;
AXA( ASSETS, ASSETS) | &2 #GT# &1: RHO;
ENDSETS
DATA:
INITIAL = 55;
GOAL = 80;
PENALTY = 4;
TIME = T0..T3;
ASSETS, MU, SIGMA =
BONDS 1.12 .01
STOCKS 1.16 .10;
RHO = .5;
ENDDATA
MIN = PENALTY * UNDER - OVER;
@FOR( TIME( T) | T #GT# 1:
@SUM( ASSETS( A): RETURN( A, T) * INVEST( A, T - 1)) =
@SUM( ASSETS( A): INVEST( A, T))
);
FINAL = @SUM( ASSETS( A): INVEST( A, @SIZE( TIME)));
FINAL = GOAL + OVER - UNDER;
@SUM( ASSETS( A): INVEST( A, @INDEX( TIME, T0))) = INITIAL;
@FOR( ASSETS( A):
RETURN( A, @INDEX( TIME, T0)) = 0;
);
Core Model for College Investing Example
In the sets section, we have two primitive sets: TIME and ASSETS. The TIME set will be used to
represent our time periods and will have four members: T0 will represent the initial decision period,
while T1, T2 and T3 will represent the three time periods. The set ASSETS will contain two members:
BONDS and STOCKS.
We also define two derived sets in the sets section: AXT and AXA. The AXT set is a dense, 2-
dimensional set consisting of all (ASSETS,TIME) pairs. We define the two attributes INVEST and
RETURN on AXT. The INVESTa,t attribute is our decision variable of how much to invest in asset a in
period t, while RETURNa,t is a random variable representing the return of asset a in period t.

STOCHASTIC PROGRAMMING 611
Next, in the data section we input the following pieces of data:
♦ INITIAL - the initial wealth,
♦ GOAL - the final goal for wealth
♦ PENALTY - the penalty factor to apply to goal shortfalls
♦ TIME - the four members of the TIME set
♦ ASSETS,MU,SIGMA - the normal distribution data for returns on bonds and stocks, and
♦ RHO - the correlation coefficient between bond and stock returns
Getting into the model section, the first expression:
MIN = PENALTY * UNDER - OVER;
is the objective function, which can be viewed as a penalty function that we will be minimizing. For
each dollar under our goal (UNDER) we get penalized 4 units, while for each dollar over our goal
(OVER) we reduce the penalty by 1 unit. This will force the solver to more heavily weight solutions
that meet our goal, perhaps at the expense of maximizing total wealth.
In the next expression:
@FOR( TIME( T) | T #GT# 1:
@SUM( ASSETS( A): RETURN( A, T) * INVEST( A, T - 1)) =
@SUM( ASSETS( A): INVEST( A, T))
);
we are setting total investments in period t equal to total investments plus returns in period t-1. Note
that by formulating the investment flows in this manner, we are free to reallocate investments each
period.
The following two expressions are used to calculate the amount that we are either over (OVER) or
under (UNDER) goal:
FINAL = @SUM( ASSETS( A): INVEST( A, @SIZE( TIME)));
FINAL = GOAL + OVER - UNDER;
Next, we add a constraint to limit the initial investments to our initial wealth level:
@SUM( ASSETS( A): INVEST( A, @INDEX( TIME, T0))) = INITIAL;
Without this expression, the model would allow infinite investment, leading to an unbounded solution.
Finally, there are no investment returns in the initial decision period, so we zero out them out:
@FOR( ASSETS( A):
RETURN( A, @INDEX( TIME, T0)) = 0;
);

612 CHAPTER 14
Stochastic Declarations
After the core model, we enter the stochastic declarations identifying the stochastic features of the
model:
! SP Related Declarations -----------------------------+;
! The initial decision and recourse variables;
@FOR( AXT( A, T):
@SPSTGVAR( T - 1, INVEST( A, T));
);
@FOR( AXT( A, T) | T #GT# 1:
! Return is a random variable...;
@SPSTGRNDV( T - 1, RETURN( A, T));
! ...and it's normally distributed;
@SPDISTNORM( MU( A), SIGMA( A), RETURN( A, T))
);
@FOR( TIME( T)| T #GT# @INDEX( TIME, T0):
!Set a sample size for each period;
@SPSAMPSIZE( T-1, 8);
!Load the stock and bond correlation for the period;
@FOR( AXA( I, J):
@SPCORRPEARSON( RETURN( I, T), RETURN( J, T), RHO( I,
J))
);
);
Stochastic Declarations for College Investing Example
The initial decision variables in the model are how much to allocate to bonds and how much to allocate
to stocks in the initial time period, or variables INVEST( BONDS, T0) and INVEST( STOCKS, T0).
The recourse variables are how much to allocate to both assets in subsequent periods as the returns for
each period are observed, or INVEST( BONDS, T1), INVEST( STOCKS, T1), ..., INVEST( STOCKS,
T3). We identify these variables and assign them to their respective stages as follows:
! The initial decision recourse variables;
@FOR( AXT( A, T):
@SPSTGVAR( T - 1, INVEST( A, T));
);
In the following loop:
@FOR( AXT( A, T) | T #GT# 1:
! Return is a random variable...;
@SPSTGRNDV( T - 1, RETURN( A, T));
! ...and it's normally distributed;
@SPDISTNORM( MU( A), SIGMA( A), RETURN( A, T))
);
we declare the asset return variables as random variables and declare that they have a normal
distribution using the @SPDISTNORM function. Note that @SPDISTNORM requires the parameters
of the distribution, which, in the case of a normal distribution, are the mean and standard deviation.

STOCHASTIC PROGRAMMING 613
Finally, we set the sample size to 8 samples in each stage/period and load the correlation coefficient
between the two assets in each period in the loop:
@FOR( TIME( T)| T #GT# @INDEX( TIME, T0):
!Set a sample size for each period;
@SPSAMPSIZE( T-1, 8);
!Load the stock and bond correlation for the period;
@FOR( AXA( I, J):
@SPCORRPEARSON( RETURN( I, T), RETURN( J, T), RHO( I, J))
);
);
In this particular instance, we are using the Pearson method for inducing correlations in the sample
values. Other alternatives are the Kendall and Spearman methods.
The Solution
After solving the model, you'll find that the expected value of the penalty function is approximately
2.78:
Global optimal solution found.
Objective value: 2.775631
Infeasibilities: 0.000000
Total solver iterations: 1092
You will recall that the penalty function used in the model's objective is a weighted combination of 4
times the dollars under target minus the number of dollars over target. So, does the positive expected
objective value mean that we miss our target on average? Perhaps not, given that we weight the under
target dollars 4 times more than the over target dollars. To get a more meaningful result, a calc section
was added to the model:

614 CHAPTER 14
CALC:
@SET( 'TERSEO', 1);
@SOLVE();
I = 1;
NOVER = 0;
NUNDER = 0;
@WRITE( ' Surplus ');
@FOR( TIME( T) | T #GT# @INDEX( T0): @WRITE( '
', TIME( T)));
@WRITE( @NEWLINE( 1));
@WRITE( ' Scenario Return Prob');
@FOR( TIME( T) | T #GT# @INDEX( T0): @WRITE( ' Bond
Stock'));
@WRITE( @NEWLINE( 1));
X_SURPLUS = 0;
@WHILE( I #LE# @SPNUMSCENE():
@SPLOADSCENE( I);
@WRITE( @FORMAT( I, '10.0f'), @FORMAT( OVER - UNDER,
'15.3f'),
@FORMAT( @SPPRBSCENE( I), '10.3f')
);
@FOR( TIME( T) | T #GT# @INDEX( T0): @FOR( ASSETS(
A): @WRITE( ' ',
@FORMAT( 100*(RETURN( A, T) - 1), '4.1f'), '%')));
@WRITE( @NEWLINE( 1));
X_SURPLUS = X_SURPLUS + @SPPRBSCENE( I) * ( OVER -
UNDER);
I = I + 1;
@IFC( UNDER #LE# 1.E-8:
NOVER = NOVER + 1;
@ELSE
NUNDER = NUNDER + 1;
);
);
@WRITE( @NEWLINE( 1));
@WRITE( ' Expected surplus: ', @FORMAT( X_SURPLUS,
'15.3f'));
@WRITE( @NEWLINE( 1));
@WRITE( ' Scenarios over goal: ', @FORMAT( NOVER,
'12g'));
@WRITE( @NEWLINE( 1));
@WRITE( ' Scenarios under goal: ', @FORMAT( NUNDER,
'11g'));
@WRITE( @NEWLINE( 1));
@WRITE( ' Success ratio: ', @FORMAT(
NOVER/(NOVER+NUNDER), '18.3f'));
ENDCALC

STOCHASTIC PROGRAMMING 615
This calc section uses the scripting capabilities in LINGO to generate a custom report that displays
each of the 512 scenarios in the model, their return values and their expected surpluses of funds over
the goal. (More details on LINGO scripting capabilities may be found in Chapter 13, Programming
LINGO.) The report also lists summary information on the expected surplus dollars, along with the
number of scenarios over target and the number below target. Portions of this report follow:
Surplus T1 T2 T3
Scenario Return Prob Bond Stock Bond Stock Bond Stock
1 0.528 0.002 11.0% 35.4% 13.3% 7.7% 9.5% 0.3%
2 14.604 0.002 11.0% 35.4% 13.3% 7.7% 11.9% 17.9%
3 12.203 0.002 11.0% 35.4% 13.3% 7.7% 11.0% 14.9%
4 27.423 0.002 11.0% 35.4% 13.3% 7.7% 11.6% 33.9%
5 18.706 0.002 11.0% 35.4% 13.3% 7.7% 12.9% 23.0%
<...>
500 9.946 0.002 12.7% 23.3% 11.4% 0.5% 11.6% 33.9%
501 3.249 0.002 12.7% 23.3% 11.4% 0.5% 12.9% 23.0%
502 -7.809 0.002 12.7% 23.3% 11.4% 0.5% 12.3% 5.3%
503 -4.413 0.002 12.7% 23.3% 11.4% 0.5% 12.3% 10.8%
504 1.961 0.002 12.7% 23.3% 11.4% 0.5% 13.2% 20.9%
505 6.928 0.002 12.7% 23.3% 12.8% 27.7% 9.5% 0.3%
506 22.123 0.002 12.7% 23.3% 12.8% 27.7% 11.9% 17.9%
507 19.531 0.002 12.7% 23.3% 12.8% 27.7% 11.0% 14.9%
508 35.960 0.002 12.7% 23.3% 12.8% 27.7% 11.6% 33.9%
509 26.551 0.002 12.7% 23.3% 12.8% 27.7% 12.9% 23.0%
510 11.241 0.002 12.7% 23.3% 12.8% 27.7% 12.3% 5.3%
511 15.953 0.002 12.7% 23.3% 12.8% 27.7% 12.3% 10.8%
512 24.741 0.002 12.7% 23.3% 12.8% 27.7% 13.2% 20.9%
Expected surplus: 4.413
Scenarios over goal: 344
Scenarios under goal: 168
Success ratio: 0.672
Based on this report, we see that the expected surplus is $4,413, meaning that on average we can
expect to meet our goal by that amount. Furthermore, 344 of the 512 scenarios ended over target for a
success ratio of 67.2%.


15 On Mathematical
Modeling
When developing a model in LINGO, it helps to understand how the model is processed internally by
the LINGO solver. The relationships in your model influence the computation time, the solution
methods used by LINGO, and the type of answer returned. Here we’ll explain some of the different
types of relationships in a LINGO model and how each type affects the solution search. An
understanding of these topics is not required to use LINGO, but it can help you use the software more
effectively.
Solvers Used Internally by LINGO
LINGO has four solvers it uses to solve different types of models. These solvers are:
♦ a direct solver,
♦ a linear solver,
♦ a nonlinear solver, and
♦ a branch-and-bound manager.
The LINGO solvers, unlike solvers sold with other modeling languages, are all part of the same
program. In other words, they are linked directly to the modeling language. This allows LINGO to
pass data to its solvers directly through memory, rather than through intermediate files. Direct links to
LINGO’s solvers also minimize compatibility problems between the modeling language component
and the solver components.
When you solve a model, the direct solver first computes the values for as many variables as possible.
If the direct solver finds an equality constraint with only one unknown variable, it determines a value
for the variable that satisfies the constraint. The direct solver stops when it runs out of unknown
variables or there are no longer any equality constraints with a single remaining unknown variable.
Once the direct solver is finished, if all variables have been computed, LINGO displays the solution
report. If unknown variables remain, LINGO determines what solvers to use on a model by examining
its structure and mathematical content. For a continuous linear model, LINGO calls the linear solver. If
the model contains one or more nonlinear constraints, LINGO calls the nonlinear solver. When the
model contains any integer restrictions, the branch-and-bound manager is invoked to enforce them.
The branch-and-bound manager will, in turn, call either the linear or nonlinear solver depending upon
the nature of the model.

618 CHAPTER 15
The linear solver in LINGO uses the revised simplex method with product form inverse. A barrier
solver may also be obtained, as an option, for solving linear models. LINGO’s nonlinear solver
employs both successive linear programming (SLP) and generalized reduced gradient (GRG)
algorithms. Integer models are solved using the branch-and-bound method. On linear integer models,
LINGO does considerable preprocessing, adding constraint “cuts” to restrict the noninteger feasible
region. These cuts will greatly improve solution times for most integer programming models.
Type of Constraints
Through the use of the direct solver, LINGO substitutes out all the fixed variables and constraints from
the model. The remaining reduced set of constraints and variables are then classified as being either
linear or nonlinear. LINGO’s solver status window, which by default opens every time you solve a
model, gives a count of the linear and nonlinear variables and constraints in a model. If any nonlinear
variables or constraints are found in the model, the entire model is considered nonlinear and the
relatively slower nonlinear solver must be invoked in place of the linear solver.
Linear Constraints
If all the terms of a constraint are of the first order, the constraint is said to be linear. This means the
constraint doesn’t contain a variable squared, cubed, or raised to any power other than one, a term
divided by a variable, or variables multiplied by each other. Also, proportionality must exist. In other
words, for every unit increase or decrease in a variable, the value of the constraint increases or
decreases by a fixed amount.
Linear formulas are “straight line” relationships. The basic form of a linear formula is:
Y = m X + b
where m and b are constants.
For example, suppose you’re buying tomatoes for $1.50 per pound. The expression or function used to
calculate the cost (C) in terms of the amount of tomatoes purchased (T) is:
C = 1.5 * T.
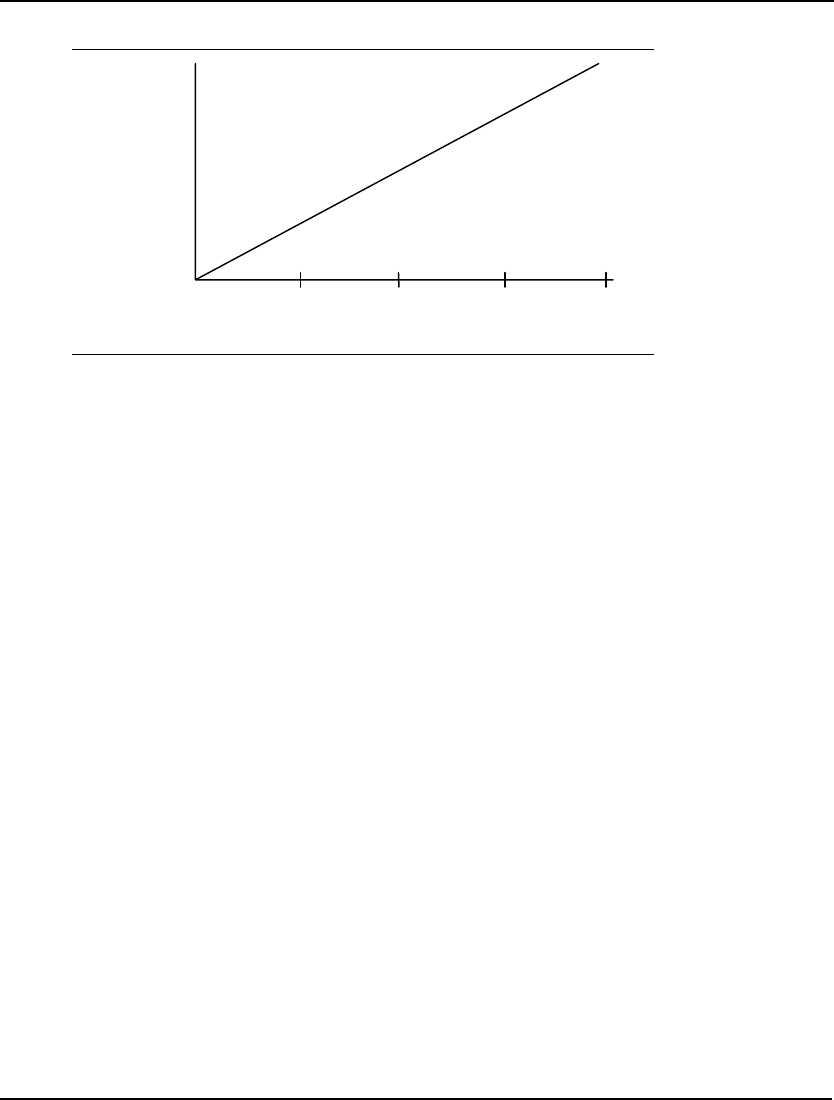
ON MATHEMATICAL MODELING 619
As you might expect, a graph of this function for cost is a straight line:
Tomatoes Purchased (lbs.)
Cost
$60
$50
$40
$30
$20
$10
$0
010 20 30 40
Linear expressions can have multiple variables. For example, if you added potatoes (P) at $0.75 per
pound and apples (A) at $1.25 per pound, your cost function would become:
C = 1.5 * T + 0.75 * P + 1.25 * A
This new cost expression is also linear. You could think of it as the sum of three simpler linear
expressions.
Because linear models can be solved much faster and with more accuracy than nonlinear models, it’s
preferable to formulate your models using linear expressions whenever possible. When the
LINGO|Solve command is issued, LINGO analyzes the relationships in the model. If all the
expressions are linear, LINGO will recognize and take advantage of this fact.
Relative to other types of models, problems expressed using exclusively linear relationships can be
solved quickly. If allowed to run to completion, LINGO will return the answer that yields the highest
value for a maximization objective, or the lowest value for a minimization objective.
One way to learn whether or not all expressions in your model are linear is to note the classification
statistics displayed during the solution process in the solver status window. The Nonlinear categories
of the Variables and Constraints boxes display the number of nonlinear relationships in the model. If
zeros appear in both these categories, the model is linear.
If LINGO displays a number greater than zero for the nonlinear relationships, you may want to
investigate whether the constraints and variables in your model could be reformulated in a linear
manner. For example, consider the following constraint:
X / Y = 10;
As written, this constraint is nonlinear because we are dividing by Y. By simply multiplying both sides
of the equation through by Y, we can convert it to the equivalent linear constraint:
X = 10 * Y;

620 CHAPTER 15
Nonlinear Constraints
By definition, all constraints that are not linear are nonlinear. Nonlinear expressions include
relationships with variables that are squared, cubed, taken to powers other than one, or multiplied or
divided by each other.
Models with nonlinear expressions are much more difficult to solve than linear models. Unlike linear
models, nonlinear models may prevent LINGO from finding a solution, though one exists. Or LINGO
may find a solution to a nonlinear model that appears to be the “best”, even though a better one may
exist. These results are obviously undesirable. For more on what you can do to help minimize the
occurrence of these undesirable results, see the Guidelines for Nonlinear Modeling section below.
Local Optima vs. Global Optima
When LINGO finds a solution to a linear optimization model, it is the definitive best solution—we say
it is the global optimum. Multiple optima may exist. However, a globally optimal solution is a feasible
solution with an objective value that is as good as or better than all other feasible solutions to the
model. The ability to obtain a globally optimal solution is attributable to certain properties of linear
models.
This is not the case for nonlinear optimization. Nonlinear optimization models may have several
solutions that are locally optimal. All gradient based nonlinear solvers converge to a locally optimal
point (i.e., a solution for which no better feasible solutions can be found in the immediate
neighborhood of the given solution). Additional local optimal points may exist some distance away
from the current solution. These additional locally optimal points may have objective values
substantially better than the solver's current local optimum. Thus, when a nonlinear model is solved,
we say the solution is merely a local optimum. The user should be aware that other local optimums
may, or may not, exist with better objective values. Conditions may exist where you may be assured
that a local optimum is in fact a global optimum. See the Convexity section below for more
information.
Consider the following small nonlinear model involving the highly nonlinear cosine function:
MIN = X * @COS( 3.1416 * X);
X < 6;
The following graph shows a plot of the objective function for values of X between 0 and 6. If you're
searching for a minimum, there are local optimal points at X values of 0, 1.09, 3.03, and 5.02 in the
"valleys." The global optimum for this problem is at X = 5.02, because it is the lowest feasible valley.
ON MATHEMATICAL MODELING 621
Graph of X * @COS( 3.1416 * X)
Imagine the graph as a series of hills. You're searching in the dark for the minimum or lowest
elevation. If you are at X = 2.5, every step towards 2 takes you uphill and every step towards 3 takes
you downhill. Therefore, you move towards 3 in your search for the lowest point. You'll continue to
move in that direction as long as it leads to lower ground.
When you reach X=3.03, you'll notice a small flat area (slope is equal to zero). Continuing begins to
lead uphill and retreating leads up the hill you just came down. You're in a valley, the lowest point in
the immediate neighborhood⎯a local optimum. However, is it the lowest possible point? In the dark,
you are unable to answer this question with certainty.
LINGO lets you enter initial values for variables (i.e., the point from which LINGO begins its search)
using an INIT section. A different local optimum may be reached when a model is solved with
different initial values for X. In this example, one might imagine that starting at a value of X=6 would
lead to the global optimum at X=5.02. Unfortunately, this is not guaranteed, because LINGO
approximates the true underlying nonlinear functions using linear and/or quadratic functions. In the
early stages of solving the model, these approximations can be somewhat rough in nature. Therefore,
the solver can be sent off to distant points, effectively passing over nearby local optimums to the true,
underlying model.
When "good" initial values for the variables are known, you should input these values in an INIT
section. Additionally, you may want to use the @BND function to bound the variables within a
reasonable neighborhood of the starting point. When you have no idea what the optimal solution to
your model is, you may find that observing the results of solving the model several times with different
initial values can help you find the best solution.
LINGO has several optional strategies to help overcome the problem of stalling at local optimal points.
The global solver employs branch-and-bound methods to break a model down into many convex sub-
regions. LINGO also has a multistart feature that restarts the nonlinear solver from a number of
intelligently generated points. This allows the solver to find a number of locally optimal points and
622 CHAPTER 15
report the best one found. Finally, LINGO can automatically linearize a number of nonlinear
relationships through the addition of constraints and integer variables so that the transformed linear
model is mathematically equivalent to the original nonlinear model. Keep in mind, however, that each
of these strategies will require additional computation time. Thus, whenever possible, you are always
better off formulating models to be convex so that they contain a single extreme point.
Convexity
The characteristic of an expression called convexity along with a closely related feature called
concavity are the most useful features of a model for guaranteeing that a local optimum is actually a
global optimum. Let’s consider the convexity property of a minimization problem. The mathematical
definition of a convex model is as follows:
f(y) ≤ a f(x) + (1-a) f(z), where y=a*x + (1-a)*z
In words, a function is convex if, for any two points on the function, a straight line connecting the two
points lies entirely on or above the function.
Determining the convexity of a multiple variable problem is no easy task. Mathematicians call a
function convex if the matrix of the second derivatives is positive definite or has positive Eigen values.
However, if you can identify your LINGO model as being convex for a minimization problem, you can
ensure that any solution you reach is a global optimum (including nonlinear models).
Strictly Convex
A strictly convex function with no constraints has a single global minimum. Therefore, minimizing a
strictly convex function will yield the unique global optimal solution regardless of the initial value of
the variables. The graph below shows a convex function of a single variable:
0
5000
10000
15000
20000
25000
30000
35000
40000
-300
-50
0
-100
-150
-200
-250
100
200
250
150
50
300
A Strictly Convex Function: .4*(x-3)2+.5
ON MATHEMATICAL MODELING 623
In this strictly convex function, the unique global minimum can be defined at the point on the function
where the variable x is equal to 3. Changing the value of x to be more or less than 3 will increase the
result of the function.
Loosely Convex
A loosely convex function with no constraints has multiple local minima, which are also global
minima. Therefore, minimizing a loosely convex function may yield different solutions for different
initial values of the variables. However, if you know the function is loosely convex, you will know the
solution is a global minimum. For example, note the flat section (i.e., slope is zero) from
approximately –200 to 150 in the following function that makes it loosely convex:
0
5000
10000
15000
20000
25000
30000
35000
40000
-300
-50
0
-100
-150
-200
-250
100
200
250
150
50
300
A Loosely Convex Function
In this loosely convex function, the global minimum of 3 can be found between about –200 through
just over 150 on the x-axis. Although variable values may vary, the result of the function will be the
same for all local minima.
Concavity
While convexity applies to minimization problems, concavity ensures the corresponding attribute of
global optimality in maximization problems. Concavity can be defined as the negative of convexity
(see above). In other words, a function is concave if, for any two points on the function, a straight line
connecting the two points lies entirely on or below the function.
624 CHAPTER 15
The following function is strictly concave:
-80000
0
-10000
-20000
-30000
-40000
-50000
-60000
-70000
0
-100
-50
-300
-250
-200
-150
50
300
250
200
150
100
-90000
A Strictly Concave Function: Graph of -(x2)
In this strictly concave function, the unique global maximum can be defined at the point on the
function where the variable x is equal to zero. Changing the value of the variable to be any more or
less than 0 will decrease the result of the function. A loosely concave function might look similar to
the negative of the loosely convex function shown in the previous section.
The only functions that are both convex and concave are straight lines (i.e., hyperplanes). Therefore
LINGO classifies the solutions to all linear optimization problems as globally optimal. Due to the
difficulty in determining convexity and concavity, LINGO classifies all nonlinear optimization models
as locally optimal. However, you can ensure you have a global optimum if you can determine that your
nonlinear optimization model is convex or concave, or you can reformulate it in such a way to make it
convex or concave.
On the other hand, if you can determine your nonlinear optimization model is definitely not convex or
concave, you know that it is a mixed function and multiple optima exist. It might be a good idea to try
solving with different starting values for the variables. See the section above Local Optima vs. Global
Optima for an example of a mixed function and more information on the strategies LINGO offers to
help overcome the problems with solving mixed functions.
ON MATHEMATICAL MODELING 625
Smooth vs. Nonsmooth Functions
Smooth functions have a unique defined first derivative (slope or gradient) at every point. Graphically,
a smooth function of a single variable can be plotted as a single continuous line with no abrupt bends
or breaks. All the examples you’ve seen so far in this chapter have been smooth.
Nonsmooth functions include nondifferentiable and discontinuous functions. Functions with first
derivatives with undefined regions are called nondifferentiable. Graphs of nondifferentiable functions
may have abrupt bends. The absolute value of a variable, @ABS(X), is an example of a
nondifferentiable expression, as illustrated in the following graph:
0
-100 -50 100 50
0
100
90
80
70
60
50
40
30
20
Graph of ABS(X)
Here, there is an abrupt bend in the graph at zero. This can dramatically increase solution times as well
as affect the accuracy of the solution. Additional nonsmooth functions are @MAX, @MIN, @SMAX,
@SMIN, and any of the probability functions that use linear interpolation to return results for
nonintegral arguments.
Perhaps even more confounding than functions with sharp bends are discontinuous functions that have
actual breaks in their graphs. Discontinuous functions in LINGO include @SIGN and @FLOOR.
In simplified terms, LINGO searches along the path of a function to find a maximum or minimum
point representing an optimal solution. As LINGO is searching along a function, it uses the function’s
derivatives to help guide the search. When derivatives vanish, as they do at sharp corners, LINGO is
“blinded” and is unable to “see” around the sharp corner. Thus, dealing with functions containing
breaks and sharp bends is considerably more difficult than dealing with smooth, continuous functions.
Where possible, nonsmooth functions should be replaced with linear constraints or some combination
of linear constraints and integer variables. As an example, refer to the assembly line balancing
example (ASLBAL.LNG) on page 629 to see how we constructed a model to avoid the use of the
@MAX function in order to maintain linearity.

626 CHAPTER 15
Guidelines for Nonlinear Modeling
As shown in the previous sections, nonlinear models can be extremely complex to solve. Spending a
little extra time to make sure the model is formulated in a way that is most efficient to solve can pay
off in terms of solution speed and reliability. This section gives some general guidelines to consider
when building and solving nonlinear models.
Supplying Bounds for Variables
Intelligent use of upper and lower bounds on variables can help make LINGO’s solution search as
efficient as possible. Supplying good bounds can keep LINGO from wasting time searching regions
unlikely to yield good solutions. For example, suppose you know that, even though the feasible range
for a particular variable is between 0 and 100, it is highly improbable the optimal value is outside the
range of 50 to 75. In this case, using the @BND function to specify a lower bound of 50 and an upper
bound of 75 could significantly reduce solution times.
Bounding can also help keep the solution search clear of mathematically troublesome areas like
undefined regions. For example, if you have a constraint with the term 1/X, it may be helpful to add a
lower bound on X, so it does not get too close to zero.
Supplying Initial Values for Variables
The initial values you provide for the variables in a model can affect the “path” LINGO takes to the
solution. Starting with values close to the optimal solution can noticeably reduce the solution time. In
many situations, you may not know “good” initial values. However, when you do know reasonable
ones, it may be to your benefit to use them in the INIT section.
Consider changing your supplied initial values and re-solving the model if you suspect: 1) there is an
answer better than the answer returned by LINGO, or 2) a feasible solution exists even though LINGO
returns the message “No feasible solution found”.
Scale the Model to a Reasonable Range of Units
Try to model your problem such that the units involved are of similar orders of magnitude. If the
largest number in the model is greater than 1000 times the smallest number in the model, LINGO may
encounter problems when solving the model. This may also affect the accuracy of the solution by
introducing rounding problems.
For example, consider a financial problem with equations expressing an interest rate of 8.5% (.085)
and budget constraints of $12,850,000. The difference in magnitude between these numbers is on the
order of 10^9 (1/100th compared to 10,000,000). A difference of 10^4 or less between the largest and
smallest units would be preferable. In this case, the budget could be expressed in units of millions of
dollars. That is, $12.85 would be used to represent $12,850,000. This lowers the difference in
magnitude of the units of these numbers to 10^4.

ON MATHEMATICAL MODELING 627
Simplify Relationships
When practical, use linear rather than nonlinear relationships. Some nonlinear expressions can be
reformulated in a linear manner. A simple example is a constraint on the ratio of two variables. Using
the example from earlier in the chapter, consider the following constraint:
X / Y < 10;
This constraint is nonlinear because we are dividing by Y. To linearize the constraint, you can multiply
both sides by Y. The equivalent, linear constraint becomes:
X < 10 * Y;
Avoid nonsmooth relationships when possible. Models with nonsmooth constraints are generally much
more difficult to solve. When possible, approximate the nonsmooth relationship with smooth
expressions and, perhaps, integer variables.
Reduce Integer Restrictions
Minimizing the use of integer restrictions can drastically reduce the solution time. In instances
involving larger variable values, you may find solving the model without integer restrictions and then
rounding yields acceptable answers in a fraction of the time required by the integer model. Be
forewarned, however, that rounding a solution will not necessarily yield a feasible or optimal solution.

629
Appendix A: Additional
Examples of LINGO
Modeling
In this Appendix, we list, in alphabetical order by model name, many of the models contained in the
SAMPLES directory off your main LINGO directory. Most of the models contain a brief background
discussion. Many have appeared in more detailed descriptions earlier in this manual and are
reproduced here for reference.
Assembly Line Balancing Model: ASLBAL
The following model illustrates how to balance an assembly line in order to minimize its total cycle
time. A detailed discussion of this model may be found in Chapter 12, Developing More Advanced
Models.
MODEL:
! Assembly line balancing model;
! This model involves assigning tasks to
stations in an assembly line so bottlenecks
are avoided. Ideally, each station would be
assigned an equal amount of work.;
SETS:
! The set of tasks to be assigned are A through
K, and each task has a time to complete, T;
TASK/ A B C D E F G H I J K/: T;
! Some predecessor,successor pairings must be
observed(e.g. A must be done before B, B
before C, etc.);
PRED(TASK, TASK)/ A,B B,C C,F C,G F,J G,J
J,K D,E E,H E,I H,J I,J /;
! There are 4 workstations;
STATION/1..4/;
TXS(TASK, STATION): X;
! X is the attribute from the derived set TXS
that represents the assignment. X(I,K) = 1
if task I is assigned to station K;
ENDSETS

630 APPENDIX A
DATA:
! Data taken from Chase and Aquilano, POM;
! Each task has an estimated time required:
A B C D E F G H I J K;
T = 45 11 9 50 15 12 12 12 12 8 9;
ENDDATA
! The model;
! *Warning* may be slow for more than 15 tasks;
! For each task, there must be one assigned
station;
@FOR(TASK(I): @SUM(STATION(K): X(I, K)) = 1);
! Precedence constraints;
! For each precedence pair, the predecessor task
I cannot be assigned to a later station than
its successor task J;
@FOR(PRED(I, J):
@SUM(STATION(K):
K * X(J, K) - K * X(I, K)) >= 0);
! For each station, the total time for the
assigned tasks must be less than the maximum
cycle time, CYCTIME;
@FOR(STATION(K):
@SUM(TXS(I, K): T(I) * X(I, K)) <= CYCTIME);
! Minimize the maximum cycle time;
MIN = CYCTIME;
! The X(I,J) assignment variables are binary integers;
@FOR(TXS: @BIN(X));
END
Model: ASLBAL

ADDITIONAL EXAMPLES 631
Bayes Rule; Conditional Probabilities Model: Bayes
MODEL:
SETS: ! Computing probabilities using Bayes rule;
ACTUAL/1..3/:MPA;!Marginal probability of actual;
FCAST/1..3/:MPF;!Marginal probability of forecast;
FXA(FCAST, ACTUAL): CAGF, !Conditional prob of actual given
forecast;
CFGA, !Conditional prob of forecast given actual;
JP; ! Joint probability of both;
ENDSETS
DATA:
!Conditional probability of forecast, given actual;
CFGA = .80 .15 .20
.10 .70 .20
.10 .15 .60;
! Marginal probabilities of actual;
MPA = .5 .3 .2;
ENDDATA
! The calculations;
! Marginal probabilities are the sum of
joint probabilities;
@FOR(ACTUAL(J):
MPA(J) = @SUM(FCAST(I): JP(I, J))
);
@FOR(FCAST(I):
MPF(I) = @SUM(ACTUAL(J): JP(I, J))
);
! Bayes rule relating joint to conditional
probabilities;
@FOR(FXA(I, J):
JP(I, J) = MPF(I) * CAGF(I, J);
JP(I, J) = MPA(J) * CFGA(I, J)
);
END
Model: BAYES

632 APPENDIX A
Blending of Ingredients I Model: BLEND
In blending problems, two or more raw materials are to be blended into one or more finished goods,
satisfying one or more quality requirements on the finished goods. A detailed discussion of this model
may be found in Chapter 12, Developing More Advanced Models.
MODEL:
TITLE BLEND;
SETS:
!Each raw material has an availability
and cost/unit;
RAWMAT/ BUTANE, CATREF, NAPHTHA/: AVAIL, COST;
!Each finished good has a min required,
max sellable, selling price,
and batch size to be determined;
FINGOOD/ REGULAR, PREMIUM/:
MINREQ, MAXSELL, PRICE, BATCH;
!Here is the set of quality measures;
QUALMES/ OCTANE, VAPOR, VOLATILITY/;
!For each combo of raw material and
quality measure there is a quality
level;
RXQ(RAWMAT, QUALMES): QLEVEL;
!For each combination of quality
measure and finished good there are
upper and lower limits on quality,
and a slack on upper quality to be
determined;
QXF(QUALMES, FINGOOD):
QUP, QLOW, QSLACK;
!For each combination of raw material
and finished good there is an amount
of raw material used to be solved for;
RXF(RAWMAT, FINGOOD): USED;
ENDSETS
DATA:
!Raw material availability;
AVAIL = 1000, 4000, 5000;
!Raw material costs;
COST = 7.3, 18.2, 12.5;
!Quality parameters of raw
materials;
QLEVEL = 120, 60, 105,
100, 2.6, 3,
74, 4.1, 12;
!Limits on finished goods;
MINREQ = 4000, 2000;
MAXSELL = 8000, 6000;
!Finished goods prices;
PRICE = 18.4, 22;
!Upper and lower limits on

ADDITIONAL EXAMPLES 633
quality for each finished good;
QUP = 110, 110,
11, 11,
25, 25;
QLOW = 90, 95,
8, 8,
17, 17;
ENDDATA
!Subject to raw material availability;
@FOR(RAWMAT(R):
[RMLIM] @SUM(FINGOOD(F): USED(R, F))
<= AVAIL(R);
);
@FOR(FINGOOD(F):
!Batch size computation;
[BATCOMP] BATCH(F) =
@SUM(RAWMAT(R): USED(R, F));
!Batch size limits;
@BND(MINREQ, BATCH, MAXSELL);
!Quality restrictions for each
quality measure;
@FOR(QUALMES(Q):
[QRESUP] @SUM(RAWMAT(R):
QLEVEL(R, Q) * USED(R, F))
+ QSLACK(Q, F) = QUP(Q, F) *
BATCH(F);
[QRESDN] QSLACK(Q, F) <=
(QUP(Q, F) - QLOW(Q, F)) *
BATCH(F);
);
);

634 APPENDIX A
! We want to maximize the profit contribution;
[OBJECTIVE] MAX =
@SUM(FINGOOD: PRICE * BATCH) -
@SUM(RAWMAT(R): COST(R) *
@SUM(FINGOOD(F): USED(R, F)));
END
Model: BLEND

ADDITIONAL EXAMPLES 635
Plant Location Model: CAPLOC
In this example, we build a model to help decide what plants to open and how much product to ship
from each plant to each customer. A detailed discussion of this model may be found in Chapter 12,
Developing More Advanced Models.
MODEL:
! Capacitated Plant Location Problem;
SETS:
PLANTS: FCOST, CAP, OPEN;
CUSTOMERS: DEM;
ARCS( PLANTS, CUSTOMERS) : COST, VOL;
ENDSETS
DATA:
! The plant, their fixed costs
and capacity;
PLANTS, FCOST, CAP =
P1 91 39
P2 70 35
P3 24 31;
! Customers and their demands;
CUSTOMERS, DEM =
C1 15
C2 17
C3 22
C4 12;
! The plant to cust cost/unit
shipment matrix;
COST = 6 2 6 7
4 9 5 3
8 8 1 5;
ENDDATA
! The objective;
[TTL_COST] MIN = @SUM( ARCS: COST * VOL) +
@SUM( PLANTS: FCOST * OPEN);
! The demand constraints;
@FOR( CUSTOMERS( J): [DEMAND]
@SUM( PLANTS( I): VOL( I, J)) >= DEM( J)
);
! The supply constraints;
@FOR( PLANTS( I): [SUPPLY]
@SUM( CUSTOMERS( J): VOL( I, J)) <=
CAP( I) * OPEN( I)
);

636 APPENDIX A
! Make OPEN binary(0/1);
@FOR( PLANTS: @BIN( OPEN));
END
Model: CAPLOC

ADDITIONAL EXAMPLES 637
Blending of Ingredients II Model: CHESS
In blending problems, two or more raw materials are to be blended into one or more finished goods,
satisfying one or more quality requirements on the finished goods. In this example, we blend mixed
nuts into four different brands with a goal of maximizing revenue. A detailed discussion of this model
may be found in Chapter 2, Using Sets.
MODEL:
SETS:
NUTS / PEANUTS, CASHEWS/: SUPPLY;
BRANDS / PAWN, KNIGHT, BISHOP, KING/:
PRICE, PRODUCE;
NCROSSB(NUTS, BRANDS): FORMULA;
ENDSETS
DATA:
SUPPLY = 750 250;
PRICE = 2 3 4 5;
FORMULA = 15 10 6 2
1 6 10 14;
ENDDATA
MAX = @SUM(BRANDS(I):
PRICE(I) * PRODUCE(I));
@FOR(NUTS(I):
@SUM(BRANDS(J):
FORMULA(I, J) * PRODUCE(J) / 16) <=
SUPPLY(I)
);
END
Model: CHESS

638 APPENDIX A
Chemical Equilibrium Model: CHMBL1
In a chemical equilibrium problem of a closed system (such as a sealed container), there are two or
more opposing processes, such as evaporation and condensation. The question is: at a given
temperature and pressure, what portion of the material will be found in each possible state—water and
vapor, for instance—at equilibrium. The typical equilibrium conditions are that the ratios of fractions
must equal known temperature and/or pressure-dependent constants. Note that, in many cases, the
numbers you will be dealing with in chemical equilibrium models will be infinitesimal. Such tiny
numbers will make it next to impossible to solve your model. Transforming values by taking their
logarithms is a useful strategy that is used here. This tends to result in a transformed model with more
manageable data.
MODEL:
!Chemical equilibrium problem of Peters, Hayes &
!Hieftje. Calculate concentrations of various
!components of phosphoric acid(H3PO4) with pH of 8
!and total phosphate concentration of .10. The
!equilibrium equations in obvious form look like:
!
! H2P * H/ H3P = .0075;
!
!However, for scale reasons it is better to take !logs thus;
LH2P + LH - LH3P = @LOG(.0075);
! Ditto for other equilibrium equations;
LHP + LH - LH2P = @LOG(6.2 * 10^-8);
LH + LP - LHP = @LOG(4.8 * 10^-13);
LH = @LOG(10 ^-8);
! Convert back to original variables;
H = @EXP(LH);
P = @EXP(LP);
HP = @EXP(LHP);
H2P = @EXP(LH2P);
H3P = @EXP(LH3P);
H3P + H2P + HP + P = .1;
! Must unconstrain log variables;
@FREE(LH2P); @FREE(LH); @FREE(LH3P);
@FREE(LHP); @FREE(LP);
! Solution should be: LH2P= -4.2767, LH= -18.4207,
LH3P= -17.8045, LHP= -2.4522, LP= -12.3965;
END
Model: CHMBL1

ADDITIONAL EXAMPLES 639
Conjoint Analysis Model: CONJNT
When designing a product, it’s useful to know how much customers value various attributes of that
product. This allows us to design the product most preferred by consumers within a limited budget. For
instance, if we determine consumers place a very high value on a long product warranty, then we
might be more successful in offering a long warranty with fewer color options.
The basic idea behind conjoint analysis is, while it may be difficult to get consumers to accurately
reveal their relative utilities for product attributes, it’s easy to get them to state whether they prefer one
product configuration to another. Given these rank preferences, we can use conjoint analysis to work
backwards and determine the implied utility functions for the product attributes. A detailed discussion
of this model may be found in Chapter 12, Developing More Advanced Models.
MODEL:
! Conjoint analysis model to decide how much
weight to give to the two product attributes of
warranty length and price;
SETS:
! The three possible warranty lengths;
WARRANTY /LONG, MEDIUM, SHORT/ : WWT;
! where WWT(i) = utility assigned to warranty i;
!The three possible price levels(high,medium,low);
PRICE /HIGH, MEDIUM, LOW/ : PWT;
! where PWT(j) = utility assigned to price j;
! We have a customer preference ranking for each
combination;
WP(WARRANTY, PRICE) : RANK;
ENDSETS
DATA:
! Here is the customer preference rankings running
from a least preferred score of 1 to the most
preferred of 9. Note that long warranty and low
price are most preferred with a score of 9,
while short warranty and high price are least
preferred with a score of 1;
RANK = 7 8 9
3 4 6
1 2 5;
ENDDATA
SETS:
! The next set generates all unique pairs of
product configurations such that the second
configuration is preferred to the first;
WPWP(WP, WP) | RANK(&1, &2) #LT#
RANK(&3, &4): ERROR;
! The attribute ERROR computes the error of our
estimated preference from the preferences given
us by the customer;
ENDSETS
! For every pair of rankings, compute the amount
by which our computed ranking violates the true
ranking. Our computed ranking for the (i,j)

640 APPENDIX A
combination is given by the sum WWT(i) + PWT(j).
(NOTE: This makes the bold assumption that
utilities are additive!);
@FOR(WPWP(i, j, k, l): ERROR(i, j, k, l) >=
1 + (WWT(i) + PWT(j)) -
(WWT(k) + PWT(l))
);
! The 1 is required on the right-hand-side of the
above equation to force ERROR to be nonzero in
the case where our weighting scheme incorrectly
predicts that the combination (i,j) is equally
preferred to the (k,l) combination.
Since variables in LINGO have a default lower
bound of 0, ERROR will be driven to zero when we
correctly predict that (k,l) is preferred to
(i,j).
Next, we minimize the sum of all errors in order
to make our computed utilities as accurate as
possible;
MIN = @SUM(WPWP: ERROR);
END
Model: CONJNT

ADDITIONAL EXAMPLES 641
Data Envelopment Analysis Model: DEAMOD
Data Envelopment Analysis (DEA) was developed to help compare the relative performance of
decision-making units. DEA generates an efficiency score between 0 and 1 for each unit, indicating
how effectively they are managing their resources. A compelling feature of DEA is it develops a
unique rating system for each unit designed to make them look their best. This should facilitate
acceptance of DEA within an organization. For more information on DEA, see Schrage (2006).
MODEL:
! Data Envelope Analysis of Decision Maker Efficiency;
SETS:
DMU/BL HW NT OP YK EL/: ! Six schools;
SCORE; ! Each decision making unit has a;
! score to be computed;
FACTOR/COST RICH WRIT SCIN/;
! There is a set of factors, input & output;
DXF(DMU, FACTOR): F; ! F(I, J) = Jth factor
of DMU I;
ENDSETS
DATA:
! Inputs are spending/pupil, % not low income;
! Outputs are Writing score and Science score;
NINPUTS = 2; ! The first NINPUTS factors are inputs;
! The inputs, the outputs;
F = 8939 64.3 25.2 223
8625 99 28.2 287
10813 99.6 29.4 317
10638 96 26.4 291
6240 96.2 27.2 295
4719 79.9 25.5 222;
ENDDATA
SETS:
! Weights used to compute DMU I's score;
DXFXD(DMU,FACTOR) : W;
ENDSETS
! Try to make everyone's score as high as possible;
MAX = @SUM(DMU: SCORE);
! The LP for each DMU to get its score;
@FOR(DMU(I):
SCORE(I) = @SUM(FACTOR(J)|J #GT# NINPUTS:
F(I, J)* W(I, J));
! Sum of inputs(denominator) = 1;
@SUM(FACTOR(J)| J #LE# NINPUTS:
F(I, J)* W(I, J)) = 1;
! Using DMU I's weights, no DMU can score better than 1;
@FOR(DMU(K):
@SUM(FACTOR(J)| J #GT# NINPUTS:
F(K, J) * W(I, J))
<= @SUM(FACTOR(J)| J #LE# NINPUTS:
F(K, J) * W(I, J))
)
);
! The weights must be greater than zero;
@FOR(DXFXD(I, J): @BND(.00001, X, 100000));
END
Model: DEAMOD

642 APPENDIX A
Generating Random Numbers Model: DEMRND
In cases where you are modeling under uncertainty, it is useful to have a random number generator to
help simulate a situation. LINGO supports the @RAND function, which can be used to generate
sequences of pseudo random numbers with uniform distribution between 0 and 1. By using the same
seed value, you can recreate a series of numbers. In this example, we generate 15 random numbers,
and then use them with the @PSN and @PTD functions to generate observations from both the unit
Normal and T distributions.
MODEL:
! Generate a series of Normal and T distributed
random variables ;
SETS:
SERIES/1..15/: U, ZNORM, ZT;
ENDSETS
! First uniform is arbitrary;
U(1) = @RAND(.1234);
! Generate the rest recursively;
@FOR(SERIES(I)| I #GT# 1:
U(I) = @RAND(U(I - 1))
);
! Generate some...;
@FOR(SERIES(I):
! Normal deviates...;
@PSN(ZNORM(I)) = U(I);
! and t deviates(2 degrees of freedom);
@PTD(2, ZT(I)) = U(I);
! ZNORM and ZT may take on negative values;
@FREE(ZNORM(I)); @FREE(ZT(I));
);
END
Model: DEMRND

ADDITIONAL EXAMPLES 643
Scenario-based Portfolio Model Model: DNRISK
In this model, we are attempting to come up with an optimal portfolio that meets a certain level of
return while minimizing downside risk. Downside risk is a measure of the risk of falling below our
target return. An additional feature of this model is it is scenario-based. More specifically, we have
seven scenarios that will each occur with a given probability. The model incorporates this distribution
of predicted outcomes in deriving the optimal portfolio.
MODEL: ! (dnrisk.lng);
! Downside risk portfolio model;
SETS:
ASSET: INVEST; ! Amount to invest in each asset;
SCENARIO:
TRETRN, ! Return under this scenario;
DRISK; ! Downside risk under this scenario;
TABLE( SCENARIO, ASSET):
ARETRN; ! Return in scenario I of asset J;
ENDSETS
DATA:
! Number of scenarios;
SCENARIO = 1..7;
! The available assets in which to invest;
ASSET = ATT GMC USX;
ARETRN =
-.071 .144 .169
.056 .107 -.035
.038 .321 .133
.089 .305 .732
.090 .195 .021
.083 .390 .131
.035 -.072 .006;
! Desired return;
DRETURN = .13;
! Threshold, below which we are unhappy;
THRESH = .11;
! Power to use for risk(1 or 2);
! When NPOW = 1, it is a linear program;
! When NPOW = 2 and threshold = desired return;
! it is the semi-variance;
NPOW = 2;
ENDDATA
NSCEN = @SIZE( SCENARIO);
! Minimize average downside risk;
MIN = @SUM( SCENARIO: DRISK ^ NPOW)/ NSCEN;
! Compute return for each scenario;
@FOR( SCENARIO( I):
TRETRN( I) = @SUM( ASSET( J):
ARETRN( I, J) * INVEST( J));
! .. and how much we fall short of threshold ;
DRISK( I) >= THRESH - TRETRN( I);
! Return in a period could be negative;

644 APPENDIX A
@FREE( TRETRN( I));
);
! Our budget constraint(divided by a billion);
[BUDGET] @SUM( ASSET: INVEST ) = 1;
! Our desired return;
[PRICER] @SUM( SCENARIO( I): TRETRN( I))/ NSCEN >= DRETURN;
END
Model: DNRISK

ADDITIONAL EXAMPLES 645
Staff Scheduling Model: STAFFDEM
This covering model assigns start days to employees to cover staffing needs, minimizing the total
number of staff, subject to the requirements that each staff member must have two consecutive days
off each week. A detailed discussion of this model may be found in Chapter 2, Using Sets.
MODEL:
SETS:
DAYS / MON TUE WED THU FRI SAT SUN/:
REQUIRED, START;
ENDSETS
DATA:
REQUIRED = 20 16 13 16 19 14 12;
ENDDATA
MIN = @SUM(DAYS(I): START(I));
@FOR(DAYS(J):
@SUM(DAYS(I) | I #LE# 5:
START(@WRAP(J - I + 1, 7)))
>= REQUIRED(J)
);
END
Model: STAFFDEM

646 APPENDIX A
Dynamic Programming Model: DYNAMB
Dynamic programming (DP) is a creative approach to problem solving that involves breaking a large,
difficult problem into a series of smaller, easy to solve problems. By solving this series of smaller
problems, we are able to assemble the optimal solution to the initial large problem. A detailed
discussion of this model may be found in Chapter 12, Developing More Advanced Models.
MODEL:
SETS:
! Dynamic programming illustration (see Anderson, Sweeney &
Williams, An Intro to Mgt Science, 6th Ed.). We have a network of
10 cities. We want to find the length of the shortest route from
city 1 to city 10.;
! Here is our primitive set of ten cities, where F(i) represents the
shortest path distance from city i to the last city;
CITIES /1..10/: F;
! The derived set ROADS lists the roads that exist between the
cities (note: not all city pairs are directly linked by a road,
and roads are assumed to be one way.);
ROADS(CITIES, CITIES)/
1,2 1,3 1,4
2,5 2,6 2,7
3,5 3,6 3,7
4,5 4,6
5,8 5,9
6,8 6,9
7,8 7,9
8,10
9,10/: D;
! D(i, j) is the distance from city i to j;
ENDSETS
DATA:
! The distances corresponding to the links;
D =
1 5 2
13 12 11
6 10 4
12 14
3 9
6 5
8 10
5
2;
ENDDATA
! If you are already in City 10, then the cost to travel to City 10
is 0;
F(@SIZE(CITIES)) = 0;
! The following is the classic dynamic programming recursion. In
words, the shortest distance from City i to City 10 is the minimum
over all cities j reachable from i of the sum of the distance from
i to j plus the minimal distance from j to City 10;
@FOR(CITIES(i)| i #LT# @SIZE(CITIES):
F(i) = @MIN(ROADS(i, j): D(i, j) + F(j))
);
END

ADDITIONAL EXAMPLES 647
Capacitated EOQ Model: EOQCAP
In this model, we have three products with known demand, production rates, setup costs, and holding
costs. The question is how much of each product should we produce to minimize total setup and
holding costs without exceeding the capacity of our production facility.
MODEL:
! Production capacity constrained EOQ;
! Demand rates for three products;
d1 = 400; d2 = 300; d3 = 300;
! Production rates;
p1 = 1300; p2 = 1100; p3 = 900;
! Setup costs for producing individual products;
sc1 = 10000; sc2 = 12000; sc3 = 13000;
! Per unit holding costs;
hc1 = 1; hc2 = 1.1; hc3 = 1.4;
! The model;
! Single machine capacity constraint; [CAP]
d1 / p1 + d2 / p2 + d3 / p3
+ 1.5 * (d1 / q1 + d2 / q2 + d3 / q3) <= 1;
! Minimize setup + holding costs;
min = setup + holding;
! Total setup costs;
setup = (sc1 * d1 / q1) + (sc2 * d2 / q2)
+ (sc3 * d3 / q3);
! Total holding costs;
holding = (hc1 * q1 * (1 - d1 / p1)
+ hc2 * q2 * (1 - d2 / p2)
+ hc3 * q3 * (1 - d3 / p3)) / 2;
!;
@BND(.01, Q1, 99999);
@BND(.01, Q2, 99999);
@BND(.01, Q3, 99999);
@FREE(SETUP);
@FREE(HOLDING);
END
Model: EOQCAP

648 APPENDIX A
Machine Repair Problem Model: EZMREPAR
This model analyzes a queuing system with a fixed population of members that periodically require
servicing. Although we model a computer timesharing system in this example, this model is typically
referred to as the machine repair problem, because one can think of it as applying to a group of
machines periodically requiring repair by a number of service personnel. A detailed discussion of this
model may be found in Chapter 12, Developing More Advanced Models.
MODEL:
! Model of a computer timesharing system;
! The mean think time for each user (more
generally, Mean Time Between Failures in a
repair system);
MTBF = 40;
! The mean time to process each compute request
(more generally, Mean Time To Repair in
seconds);
MTTR = 2;
! The number of users;
NUSER = 32;
! The number of servers/repairmen;
NREPR = 1;
! The mean number of users waiting or in service
(more generally, the mean number of machines
down);
NDOWN =
@PFS(MTTR * NUSER/ MTBF, NREPR, NUSER);
! The overall request for service rate (more
generally, overall failure rate), FR, must
satisfy;
FR = (NUSER - NDOWN)/ MTBF;
! The mean time waiting for or in service (more
generally, the mean time down), MTD, must
satisfy;
NDOWN = FR * MTD;
END
Model: EZMREPAR

ADDITIONAL EXAMPLES 649
Newsboy Problem Model: EZNEWS
A common inventory management problem occurs when the product in question has limited shelf life
(e.g., newspapers, produce, and computer hardware). There is a cost of over ordering, because the
product will shortly become obsolete and worthless. There is also an opportunity cost of under
ordering associated with forgone sales. Under such a situation, the question of how much of a product
to order to maximize expected profit is classically referred to as the newsboy problem. In this example,
we assume demand has a Poisson distribution. However, this is not mandatory. Refer to any operations
research textbook for a derivation of the formulas involved.
MODEL:
DATA:
! The average demand;
MU = 144;
! Opportunity cost of each unit of lost demand;
P = 11;
! Cost/unit of excess inventory;
H = 5;
ENDDATA
! Calculate the order-up-to point, S, using the
newsboy problem equation;
@PPS(MU, S) = P / (P + H);
! PS is the expected profit of being at S;
PS=P * MU - H * (S -MU) - (P + H) * @PPL(MU, S);
END
Model: EZNEWS

650 APPENDIX A
Simple Queuing Example Model: EZQUEUE
Given a queue with a certain arriving load and number of servers, the @PEL function determines the
fraction of customers lost due to all servers being busy. In this example, we use @PEL to solve for the
number of servers that limit customer loss to 5%.
MODEL:
! Arrival rate of customers/ hour;
AR = 25;
! Service time per customer in minutes;
STM = 6;
! Service time per customer in hours;
STH = STM/ 60;
! Fraction customers finding all servers busy;
FB = .05;
!The PEL function finds number of servers needed, NS;
FB = @PEL(AR * STH, NS);
END
Model: EZQUEUE

ADDITIONAL EXAMPLES 651
General Equilibrium of an Economy Model: GENEQ1
MODEL:
! General Equilibrium Model of an economy;
! Data based on Kehoe, Math Prog, Study 23(1985);
! Find clearing prices for commodities/goods and
equilibrium production levels for processes in
an economy;
SETS:
GOOD/1..4/: PRICE, H;
SECTOR/1..4/;
GXS(GOOD, SECTOR): ALPHA, W;
PROCESS/1..2/: LEVEL;
GXP(GOOD, PROCESS): MAKE;
ENDSETS
DATA:
! Demand curve parameter for each good and SECTOR;
ALPHA =
.5200 .8600 .5000 .0600
.4000 .1 .2 .25
.04 .02 .2975 .0025
.04 .02 .0025 .6875;
! Initial wealth of Good I by Market J;
W =
50 0 0 0
0 50 0 0
0 0 400 0
0 0 0 400;
! Amount produced of good I by process J;
MAKE =
6 -1
-1 3
-4 -1
-1 -1;
! Weights for price normalization constraint;
H = .25 .25 .25 .25;
ENDDATA
!————————————————————————————;
! Model based on Stone, Tech. Rep. Stanford OR(1988);
! Minimize the artificial variable;
MIN = V;
! Supply is >= demand;
@FOR(GOOD(G):
@SUM(SECTOR(M): W(G, M))
+ @SUM(PROCESS(P): MAKE(G, P) * LEVEL(P))
- @SUM(SECTOR(S):
ALPHA(G, S) * @SUM(GOOD(I): PRICE(I) *
W(I, S))/ PRICE(G)) + H(G) * V >= 0;
);
! Each process at best breaks even;
@FOR(PROCESS(P):
@SUM(GOOD(G): - MAKE(G, P) * PRICE(G)) >= 0;
);

652 APPENDIX A
! Prices scale to 1;
@SUM(GOOD(G): - H(G) * PRICE(G)) = -1;
END
Model: GENEQ1

ADDITIONAL EXAMPLES 653
Markowitz Portfolio Example Model: GENPRT
In the March, 1952 issue of Journal of Finance, Harry M. Markowitz published an article titled
Portfolio Selection. In the article, he demonstrates how to reduce the risk of asset portfolios by
selecting assets whose values aren’t highly correlated. The following model implements these ideas in
constructing a simple portfolio with three assets. A detailed discussion of this model may be found in
Chapter 12, Developing More Advanced Models.
MODEL:
! GENPRT: Generic Markowitz portfolio;
SETS:
ASSET/1..3/: RATE, UB, X;
COVMAT(ASSET, ASSET): V;
ENDSETS
DATA:
! The data;
! Expected growth rate of each asset;
RATE = 1.3 1.2 1.08;
! Upper bound on investment in each;
UB = .75 .75 .75;
! Covariance matrix;
V = 3 1 -.5
1 2 -.4
-.5 -.4 1;
! Desired growth rate of portfolio;
GROWTH = 1.12;
ENDDATA
! The model;
! Min the variance;
[VAR] MIN = @SUM(COVMAT(I, J):
V(I, J) * X(I) * X(J));
! Must be fully invested;
[FULL] @SUM(ASSET: X) = 1;
! Upper bounds on each;
@FOR(ASSET: @BND(0, X, UB));
! Desired value or return after 1 period;
[RET] @SUM(ASSET: RATE * X) >= GROWTH;
END
Model: GENPRT

654 APPENDIX A
Job Shop Scheduling Model: JOBSLT
In this model, there are six jobs that can be done on one machine. The machine can only work on one
job at a time. Each job has a due date. If we can’t complete a job by its due date, we do not take the
job. Our objective is to maximize the total value of the jobs selected.
Although we have based this model on a job shop scenario, the basic principles should be applicable in
any area where time is the limiting factor in deciding what projects to undertake.
MODEL:
! One machine job selection;
SETS:
!There are six jobs each of which has a Due Date,
Processing Time, Value, and a flag variable Y
indicating if the job has been selected.;
JOB/1..6/: ! Each job has a...;
DD, ! Due date;
PT, ! Processing time;
VAL, ! Value if job is selected;
Y; ! = 1 if job is selected, else 0;
ENDSETS
DATA:
VAL = 9 2 4 2 4 6;
DD = 9 3 6 5 7 2;
PT = 5 2 4 3 1 2;
ENDDATA
! Maximize the total value of the jobs taken;
MAX = TVAL;
TVAL = @SUM(JOB: VAL * Y);
! For the jobs we do, we do in due date order;
@FOR(JOB(J):
! Only jobs with earlier due dates can
precede job J, and jobs must be completed
by their due dates;
@SUM(JOB(I)| DD(I) #LT# DD(J) #OR#
(DD(I) #EQ# DD(J) #AND# I #LE# J):
PT(I) * Y(I)) <= DD(J);
! Make the Y's binary;
@BIN(Y);
);
END
Model: JOBSLT

ADDITIONAL EXAMPLES 655
Knapsack Model Model: KNAPSACK
In the knapsack model, one wants to select items to place into a knapsack to maximize a measure of
utility without exceeding the capacity of the knapsack. This model can be generalized to many other
areas such as truck loading, bin packing, choosing science experiments for the Space Shuttle, and so
on. An in-depth description of this model can be found in Chapter 3, Using Variable Domain
Functions.
SETS:
ITEMS / ANT_REPEL, BEER, BLANKET,
BRATWURST, BROWNIES, FRISBEE, SALAD,
WATERMELON/:
INCLUDE, WEIGHT, RATING;
ENDSETS
DATA:
WEIGHT RATING =
1 2
3 9
4 3
3 8
3 10
1 6
5 4
10 10;
KNAPSACK_CAPACITY = 15;
ENDDATA
MAX = @SUM(ITEMS: RATING * INCLUDE);
@SUM(ITEMS: WEIGHT * INCLUDE) <=
KNAPSACK_CAPACITY;
@FOR(ITEMS: @BIN(INCLUDE));
Model: KNAPSACK

656 APPENDIX A
Learning Curve Model: LEARNC
The cost, labor, and/or time it takes to perform a task will often decrease the more times it is
performed. A manufacturer may need to estimate the cost to produce 1,000 units of a product after
producing only 100. The average unit cost of the first 100 is likely to be considerably higher than the
average unit cost of the last 100. Learning curve theory assumes each time the quantity produced
doubles, the cost per unit decreases at a constant rate.
In our example, we wish to estimate the cost (in hours) to produce paper based on the cumulative
number of tons produced so far. The data is fitted to a curve of the form:
COST(i) = a * VOLUME(i) b
where COST is the dependent variable and VOLUME is the independent variable. By taking
logarithms, we can linearize the model:
ln[ COST(i)] = ln(a) + b * ln[ VOLUME(i)]
We can then use the theory of linear regression to find estimates of ln(a) and b that minimize the sum
of the squared prediction errors. Note that since the regression involves only a single independent
variable, the formulas for computing the parameters are straightforward. Refer to any theoretical
statistics text for a derivation of these formulas.
MODEL:
! Learning curve model;
! Assuming that each time the number produced
doubles, the cost per unit decreases by a
constant rate, predict COST per unit with
the equation:
COST(i) = A * VOLUME(i) ^ B;
SETS:
! The OBS set contains the data for COST
and VOLUME;
OBS/1..4/:
COST, ! The dependent variable;
VOLUME; ! The independent variable;
! The OUT set contains the outputs of the model.
Note: R will contain the output results.;
OUT/ A, B, RATE, RSQRU, RSQRA/: R;
ENDSETS
! Data on hours per ton, cumulative tons for a
papermill based on Balof, J. Ind. Eng.,
Jan. 1966;
DATA:
COST = .1666, .1428, .1250, .1111;
VOLUME = 8, 60, 100 190;
ENDDATA
! The model;
SETS:
! The derived set OBSN contains the set of
logarithms of our dependent and independent
variables as well the mean shifted values;
OBSN(OBS): LX, LY, XS, YS;
ENDSETS
NK = @SIZE(OBS);

ADDITIONAL EXAMPLES 657
! Take the logs;
@FOR(OBSN(I):
LX(I) = @LOG(VOLUME(I));
LY(I) = @LOG(COST(I)); );
! Compute means;
XBAR = @SUM(OBSN: LX)/ NK;
YBAR = @SUM(OBSN: LY)/ NK;
! Shift the observations by their means;
@FOR(OBSN:
XS = LX - XBAR;
YS = LY - YBAR);
! Compute various sums of squares;
XYBAR = @SUM(OBSN: XS * YS);
XXBAR = @SUM(OBSN: XS * XS);
YYBAR = @SUM(OBSN: YS * YS);
! Finally, the regression equation;
SLOPE = XYBAR/ XXBAR;
CONS = YBAR - SLOPE * XBAR;
RESID = @SUM(OBSN: (YS - SLOPE * XS)^2);
! The unadjusted/adjusted fraction of variance
explained;
[X1]R(@INDEX(RSQRU)) = 1 - RESID/ YYBAR;
[X2]R(@INDEX(RSQRA)) = 1 - (RESID/ YYBAR) *
(NK - 1)/(NK - 2);
[X3]R(@INDEX(A)) = @EXP(CONS);
[X4]R(@INDEX(B)) = - SLOPE;
[X5]R(@INDEX(RATE)) = 2 ^ SLOPE;
! Some variables must be unconstrained in sign;
@FOR(OBSN: @FREE(LY); @FREE(XS); @FREE(YS));
@FREE(YBAR); @FREE(XBAR); @FREE(SLOPE);
@FREE(XYBAR); @FREE(CONS);
END
Model: LEARNC

658 APPENDIX A
Markov Chain Model Model: MARKOV
A standard approach used in modeling random variables over time is the Markov chain approach. The
basic idea is to think of the system as being in one of a discrete number of states at each point in time.
The behavior of the system is described by a transition probability matrix, which gives the probability
the system will move to a specified other state from some given state. Some example situations are:
System States Cause of Transition
Consumer brand
switching
Brand of product most recently
purchased by consumer
Consumer changes mind,
advertising
Inventory System Amount of inventory on hand Orders for new material,
demands
In the following model, we use Markov chain analysis to determine the long-term, steady state
probabilities of the system. A detailed discussion of this model may be found in Chapter 12,
Developing More Advanced Models.
MODEL:
! Markov chain model;
SETS:
! There are four states in our model and over
time the model will arrive at a steady state
equilibrium.
SPROB(J) = steady state probability;
STATE/ A B C D/: SPROB;
! For each state, there's a probability of moving
to each other state. TPROB(I, J) = transition
probability;
SXS(STATE, STATE): TPROB;
ENDSETS
DATA:
! The transition probabilities. These are proba-
bilities of moving from one state to the next
in each time period. Our model has four states,
for each time period there's a probability of
moving to each of the four states. The sum of
probabilities across each of the rows is 1,
since the system either moves to a new state or
remains in the current one.;
TPROB = .75 .1 .05 .1
.4 .2 .1 .3
.1 .2 .4 .3
.2 .2 .3 .3;
ENDDATA
! The model;
! Steady state equations;
! Only need N equations, so drop last;
@FOR(STATE(J)| J #LT# @SIZE(STATE):
SPROB(J) = @SUM(SXS(I, J): SPROB(I) *
TPROB(I, J))
);
! The steady state probabilities must sum to 1;
@SUM(STATE: SPROB) = 1;
! Check the input data, warn the user if the sum
of probabilities in a row does not equal 1.;

ADDITIONAL EXAMPLES 659
@FOR(STATE(I):
@WARN('Probabilities in a row must sum to 1.',
@ABS(1 - @SUM(SXS(I, K): TPROB(I, K)))
#GT# .000001);
);
END
Model: MARKOV

660 APPENDIX A
Matching Model Model: MATCHD
Pair-matching problems require a number of objects be grouped into pairs subject to some criteria. The
objective may be to minimize cost, to group like objects, etc. As an example, the following matching
model pairs workers into offices to minimize total incompatibilities between paired individuals. A
detailed discussion of this model may be found in Chapter 2, Using Sets.
MODEL:
SETS:
ANALYSTS / 1..8/;
PAIRS(ANALYSTS, ANALYSTS) | &2 #GT# &1:
RATING, MATCH;
ENDSETS
DATA:
RATING =
9 3 4 2 1 5 6
1 7 3 5 2 1
4 4 2 9 2
1 5 5 2
8 7 6
2 3
4;
ENDDATA
MIN = @SUM(PAIRS(I, J):
RATING(I, J) * MATCH(I, J));
@FOR(ANALYSTS(I):
@SUM(PAIRS(J, K) | J #EQ# I #OR# K #EQ# I:
MATCH(J, K)) = 1
);
@FOR(PAIRS(I, J): @BIN(MATCH(I, J)));
END
Model: MATCHD

ADDITIONAL EXAMPLES 661
Computing Demand Backlog Model: METRIC
The METRIC model estimates the average number of backorders in a two level inventory system
composed of a single depot or distribution center and any number of outlets served by the depot.
Inventory policy at each location is described by a single number S. Whenever the sum of the amount
on hand and on order drops below S, an order is placed to bring inventory back up to S. This is an
evaluation model, rather than an optimization model. The user is prompted for the S values (SDEPOT
and SOUTLET).
MODEL:
! The two level METRIC inventory model. ;
SETS:
OUTLET/1..2/: ! Each outlet has a...;
ROUTLET, ! Resupply time from depot to outlet;
DEM, ! Demand rate at outlet;
SOUTLET, ! Stock level to use at outlet;
ERT, ! Effective resupply time to outlet;
AL; ! Average level of backlogged demand;
ENDSETS
DATA:
ROUTLET = 2 2;
DEM = .1 .1;
RDEPOT = 14;
! Get the stock levels from the user;
SDEPOT = ?;
SOUTLET = ?, ?;
ENDDATA
! Compute total demand;
DEM0 = @SUM(OUTLET: DEM);
! Effective expected wait at depot;
EWT0 = @PPL(DEM0 * RDEPOT, SDEPOT)/ DEM0;
@FOR(OUTLET(I):
! Estimate the resupply time including depot delay;
ERT(I) = ROUTLET(I) + EWT0;
! Expected demand on backorder;
AL(I) = @PPL(DEM(I) * ERT(I), SOUTLET(I));
);
! Total expected demand on backorder;
TBACK = @SUM(OUTLET: AL);
END
Model: METRIC

662 APPENDIX A
The Mexican Steel Problem Model: MEXICO
The following model is a production-planning model adapted from the GAMS documentation.
MODEL:
! The Mexican Steel problem;
SETS:
! Steel plants;
PLANT /AHMSA FUNDIDA SICARTSA HYLSA HYLSAP/:
RD2, MUE;
! Markets;
MARKET / MEXICO MONTE GUADA /: DD, RD3, MUV;
! Final products;
CF /STEEL/: PV, PE, EB;
! Intermediate products;
CI / SPONGE PIGIRON/;
! Raw materials;
CR /PELLETS COKE NATGAS ELECTRIC SCRAP/ : PD;
! Processes;
PR /PIGIRON1 SPONGE1 STEELOH STEELEL STEELBOF/;
! Productive units;
UNIT / BLASTFUR OPENHEAR BOF DIRECT ELECARC/;
! ;
CRXP(CR, PR) : A1; CIXP(CI, PR) : A2;
CFXP(CF, PR) : A3; UXP(UNIT, PR) : B;
UXI(UNIT, PLANT) : K;
PXM(PLANT, MARKET) : RD1, MUF;
PXI(PR, PLANT) : Z;
CFXPXM(CF, PLANT, MARKET) : X;
CRXI(CR, PLANT) : U; CFXI(CF, PLANT) : E;
CFXM(CF, MARKET) : D, V;
ENDSETS
! Demand equations;
@FOR(CFXM(C, J):
D(C,J) = 5.209 * (1 + 40/ 100) * DD(J)/100);
! Transport rate equations;
@FOR(PXM(I, J)| RD1(I, J) #GT# 0:
MUF(I, J) = 2.48 + .0084 * RD1(I, J));
@FOR(PXM(I, J)| RD1(I, J) #LE# 0:
MUF(I, J) = 0);
@FOR(PLANT(I)| RD2(I) #GT# 0:
MUE(I) = 2.48 + .0084 * RD2(I));
@FOR(PLANT(I)| RD2(I) #LE# 0: MUE(I) = 0);
@FOR(MARKET(J)| RD3(J) #GT# 0:
MUV(J) = 2.48 + .0084 * RD3(J));
@FOR(MARKET(J)| RD3(J) #LE# 0: MUV(J) = 0);
! For each plant I1;
@FOR(PLANT(I1):

ADDITIONAL EXAMPLES 663
! Sources >= uses, final products;
@FOR(CF(CF1): [MBF]
@SUM(PR(P1): A3(CF1, P1) * Z(P1, I1)) >=
@SUM(MARKET(J1): X(CF1, I1, J1)) +
E(CF1, I1));
! Intermediate products;
@FOR(CI(CI1): [MBI]
@SUM(PR(P1): A2(CI1, P1) *
Z(P1, I1)) >= 0);
! Raw materials;
@FOR(CR(CR1): [MBR]
@SUM(PR(P1): A1(CR1, P1) *
Z(P1, I1)) + U(CR1, I1) >= 0);
! Capacity of each productive unit M1;
@FOR(UNIT(M1): [CC]
@SUM(PR(P1): B(M1, P1) * Z(P1, I1)) <=
K(M1, I1));
);
! For each final product CF1;
@FOR(CF(CF1):
! Demand requirements for each market J1;
@FOR(MARKET(J1): [MR]
@SUM(PLANT(I1): X(CF1, I1, J1)) + V(CF1, J1)
>= D(CF1, J1));
! Upper limit on exports ;
[ME] @SUM(PLANT(I1): E(CF1, I1)) <= EB(CF1);
);
! Components of objective;
PHIPSI = @SUM(CR(CR1):
@SUM(PLANT(I1): PD(CR1) * U(CR1, I1)));
PHILAM = @SUM(CF(CF1):
@SUM(PLANT(I1): @SUM(MARKET(J1):MUF(I1,J1)*
X(CF1, I1, J1))) + @SUM(MARKET(J1):
MUV(J1) * V(CF1, J1)) + @SUM(PLANT(I1):
MUE(I1) * E(CF1, I1)));
PHIPI = @SUM(CFXM(CF1, I1):
PV(CF1) * V(CF1, I1));
PHIEPS = @SUM(CFXP(CF1, I1):
PE(CF1) * E(CF1, I1));
[OBJROW] MIN = PHIPSI + PHILAM + PHIPI - PHIEPS;

664 APPENDIX A
DATA:
A1= -1.58, -1.38, 0, 0, 0,
-0.63, 0, 0, 0, 0,
0, -0.57, 0, 0, 0,
0, 0, 0, -0.58, 0,
0, 0, -0.33, 0, -0.12;
A2= 1, 0, -0.77, 0, -0.95,
0, 1, 0, -1.09, 0;
A3= 0, 0, 1, 1, 1;
B = 1 0 0 0 0
0 0 1 0 0
0 0 0 0 1
0 1 0 0 0
0 0 0 1 0;
K = 3.25, 1.40, 1.10, 0, 0,
1.50, 0.85, 0, 0, 0,
2.07, 1.50, 1.30, 0, 0,
0, 0, 0, 0.98, 1,
0, 0, 0, 1.13, 0.56;
RD1= 1204 218 1125
1017 0 1030
819 1305 704
1017 0 1030
185 1085 760;
RD2 = 739, 521, 0, 521, 315;
RD3 = 428, 521, 300;
PD = 18.7, 52.17, 14, 24, 105;
PV = 150;
PE = 140;
EB = 1;
DD = 55, 30, 15;
ENDDATA
END
Model: MEXICO

ADDITIONAL EXAMPLES 665
Multiprod. Capac. Lot Sizing Model: MPSCHD
The following model is a production-planning model where multiple products compete for scarce
capacity. Each product has a setup time, setup cost, production time, production cost, and holding cost.
The question is how much of each product should we produce in each period to minimize total
production costs.
MODEL:
! Multiproduct Capacitated lot sizing;
SETS:
PROD/1..2/: ! Each product has a ...;
ST, ! Setup time;
VT, ! Production time per unit;
SC, ! Setup cost;
VC, ! Production cost per unit;
HC; ! Holding cost per unit per period;
TIME/1..6/:;
PXT(PROD, TIME):
! Each product in each period has...;
DEM, ! Demand;
MAKE, ! Amount to produce;
Y; ! = 1 if anything is produced;
ENDSETS
DATA:
CAP = 200; ! Capacity per period;
ST = 0 0; ! Setup times;
VT = 1 1; ! Production time per unit;
SC = 150 45; ! Setup costs;
VC = 7 4; ! Cost per unit to produce;
HC = 2 1; ! Holding cost per unit;
DEM = 40 60 130 0 100 200 ! Demands;
0 45 50 35 20 35;
ENDDATA
!——————————————————;
! The Eppen/Martin model;
SETS:
PXTXT(PROD, TIME, TIME)| &3 #GE# &2:
PCOF,
CCOF,
X;
ENDSETS
! Compute cost and production amounts for
various production runs;
@FOR(PROD(I):
@FOR(TIME(S):
PCOF(I, S, S) = DEM(I, S);
CCOF(I, S, S) = VC(I) * DEM(I, S);
@FOR(TIME(T)| T #GT# S:
PCOF(I, S, T) = PCOF(I, S, T - 1) +
DEM(I, T);
CCOF(I, S, T) = CCOF(I, S, T - 1) +
(VC(I) + HC(I) * (T - S)) * DEM(I, T);
)
)
);

666 APPENDIX A
! The objective;
MIN = TCOST;
TCOST = @SUM(PXTXT: CCOF * X) +
@SUM(PXT(I, S): SC(I) * Y(I, S));
@FOR(PROD(I):
! In period 1, some production run must be started;
! Note, watch out for periods without demand;
@SUM(PXTXT(I, S, T) | S #EQ# 1:
X(I, S, T)) = 1;
@FOR(TIME(K)| K #GT# 1:
! If we ended a run in period K - 1...;
@SUM(PXTXT(I, S, T)| T #EQ# K - 1:
X(I, S, K - 1))
! then we must start a run in period k;
= @SUM(PXTXT(I, K, T): X(I, K, T));
);
! Setup forcing;
@FOR(TIME(S):
Y(I, S) = @SUM(PXTXT(I, S, T)
: (PCOF(I, S, T) #GT# 0) * X(I, S, T));
! Calc amount made each period;
MAKE(I, S) = @SUM(PXTXT(I, S, T):
PCOF(I, S, T) * X(I, S, T))
)
);
! The capacity constraints;
@FOR(TIME(S):
@SUM(PROD(I): ST(I) * Y(I, S)) +
@SUM(PXTXT(I, S, T):
VT(I) * PCOF(I, S, T) * X(I, S, T)) <= CAP
);
! Make the Y's integer;
@FOR(PXT: @GIN(Y));
END
Model: MPSCHD

ADDITIONAL EXAMPLES 667
Machine Repair Model Model: MREPAR
This model illustrates the tradeoff between the cost of service people and the costs of machine
downtime. In our model, we have ten machines that have a tendency to break down randomly. It costs
$350/hour in lost production whenever a machine is broken. The question we need to answer is how
many service people should we hire to minimize the total cost of down time and salaries for service
people.
MODEL:
! Machine repair model;
SETS:
NREP/1..5/: !Consider 5 possible repair persons;
NDOWN, !Expected no. of down machines;
CPERHR,Expected cost/hour of down machines;
TCOST; !Total expected cost/hour;
ENDSETS
! The input data;
NMACH = 10;! No. machines subject to breakdown;
RTIME = 1; ! Average repair time;
UPTIME = 5;! Mean time between failures;
CR = 30; ! Hourly cost of a repair person;
CM = 350; ! Hourly cost of a down machine
! The machine repairman queuing model;
! For each case of 1 - 5 service people calculate
expected number of machines down, cost per hour
of down machines, and total cost per hour of
operations. @PFS calculates the Probability in
a Finite Source, in this case expected number
of machines under repair. ;
@FOR(NREP(I):
NDOWN(I) =
@PFS(NMACH * RTIME / UPTIME, I, NMACH);
CPERHR(I) = CM * NDOWN(I);
TCOST(I) = CPERHR(I) + CR * I
);
END
Model: MREPAR

668 APPENDIX A
Material Requirements Planning Model: MRP
Material Requirements Planning, or MRP, is used to generate production schedules for the
manufacture of complex products. MRP takes the demand schedule for a finished product and the lead
times to produce the finished product and all the various subcomponents that go into the finished
product, and then works backwards to come up with a detailed, just-in-time production schedule that
meets the demand schedule. A detailed discussion of this model may be found in Chapter 12,
Developing More Advanced Models.
MODEL:
! Data for this model is read from MRP.LDT;
SETS:
! The set of parts;
PART: LT;
! LT(i) = Lead time to produce part i;
! The set of time periods;
TIME;
! A relationship called USES between pairs of parts;
USES( PART, PART): NEEDS;
! Parent part i needs NEEDS(i, j) units of
child part j;
! For each part and time period we're interested in;
PXT( PART, TIME): ED, TD;
! ED(i, j) = External demand for part i at time j;
! TD(i, j) = Total demand for part i at time j;
ENDSETS
DATA:
! Load the data from an external file;
! Parts list;
PART = @FILE( 'MRP.LDT');
! Time periods;
TIME = @FILE( 'MRP.LDT');
! Get the parent child relations and the
number of parts required;
USES, NEEDS = @FILE( 'MRP.LDT');
! Get the lead times from the file;
LT = @FILE( 'MRP.LDT');
! Get the external demands
over time for each part;
ED = @FILE( 'MRP.LDT');
ENDDATA
! Set NP = no. of time periods in the problem;
NP = @SIZE( TIME);
! For each part P and period T, the total demand =
external demand + demand generated by parents
one lead time in the future;

ADDITIONAL EXAMPLES 669
@FOR( PXT( P, T) | T + LT( P) #LE# NP :
TD( P, T) = ED( P, T + LT( P)) +
@SUM( USES( P2, P): TD( P2, T + LT( P)) *
NEEDS( P2, P));
);
DATA:
! Display a table showing the production schedule;
@TEXT() = ' The production schedule:';
@TEXT() = @TABLE( TD);
ENDDATA
END
Model: MRP

670 APPENDIX A
Minimal Spanning Tree Model: MSPAN
In the minimal spanning tree, we need to find a set of links (a tree) in a network that connects all cities.
Furthermore, the sum of the distances over all the links in the tree should be minimized. Among other
things, this application is useful in constructing communications networks at minimal cost.
It turns out that this becomes a very difficult problem to solve using optimization as the number of
nodes grows. For large versions of this problem, the optimization techniques provided by LINGO are
not the appropriate tool. One would be wise to pursue alternatives such as heuristics or dynamic
programming.
MODEL:
!Given the number of nodes and the distance
between them, finding the shortest total distance
of links on the network to connect all the nodes
is the classic problem called minimal spanning tree (MST).
This model finds the (MST) connecting Atlanta,
Chicago, Cincinnati, Houston, LA, and Montreal so
that messages can be sent from Atlanta (base) to
other cities through the network at minimum cost;
SETS:
CITY / 1.. 6/: U; ! U(I) = level of city I;
! U(1) = 0;
LINK(CITY, CITY):
DIST, ! The distance matrix;
X; ! X(I, J) = 1 if we use link I, J;
ENDSETS
DATA: ! Distance matrix need not be symmetric;
! However, city 1 is base of the tree;
!to: Atl Chi Cin Hou LA Mon ;
DIST = 0 702 454 842 2396 1196 !from Atl;
702 0 324 1093 2136 764 !from Chi;
454 324 0 1137 2180 798 !from Cin;
842 1093 1137 0 1616 1857 !from Hou;
2396 2136 2180 1616 0 2900 !from LA;
1196 764 798 1857 2900 0; !from Mon;
ENDDATA
! The model size: Warning, may be slow for N >= 8;
N = @SIZE(CITY);
! Minimize total distance of the links;
MIN = @SUM(LINK: DIST * X);
! For city K, except the base, ... ;
@FOR(CITY(K)| K #GT# 1:
! It must be entered;
@SUM(CITY(I)| I #NE# K: X(I, K)) = 1;

ADDITIONAL EXAMPLES 671
! If there are 2 disjoint tours from 1 city to
another, we can remove a link without
breaking connections. Note: These are not
very powerful for large problems;
@FOR(CITY(J)| J #GT# 1 #AND# J #NE# K:
U(J) >= U(K) + X (K, J) -
(N - 2) * (1 - X(K, J)) +
(N - 3) * X(J, K); );
);
! There must be an arc out of city 1;
@SUM(CITY(J)| J #GT# 1: X(1, J)) >= 1;
! Make the X's 0/1;
@FOR(LINK: @BIN(X); );
! The level of a city except the base is at
least 1 but no more than N-1, and is 1 if it
links to the base;
@FOR(CITY(K)| K #GT# 1:
@BND(1, U(K), 999999);
U(K) <= N - 1 - (N - 2) * X(1, K); );
END
Model: MSPAN

672 APPENDIX A
Multilevel Distribution Model: MULLDC
In this model, we minimize shipping costs over a three tiered distribution system consisting of plants,
distribution centers, and customers. Plants produce multiple products that are shipped to distribution
centers. If a distribution center is used, it incurs a fixed cost. Customers are supplied by a single
distribution center.
MODEL:
! MULLDC;
! Multilevel DC location model, based on
Geoffrion/Graves, Man. Sci., Jan., 1974;
! Original LINGO model by Kamaryn Tanner;
SETS:
! Two products;
PRODUCT/ A, B/;
! Three plants;
PLANT/ P1, P2, P3/;
! Each DC has an associated fixed cost, F,
and an "open" indicator, Z.;
DISTCTR/ DC1, DC2, DC3, DC4/: F, Z;
! Five customers;
CUSTOMER/ C1, C2, C3, C4, C5/;
! D = Demand for a product by a customer.;
DEMLINK(PRODUCT, CUSTOMER): D;
! S = Capacity for a product at a plant.;
SUPLINK(PRODUCT, PLANT): S;
! Each customer is served by one DC,
indicated by Y.;
YLINK(DISTCTR, CUSTOMER): Y;
! C= Cost/ton of a product from a plant to a DC,
X= tons shipped.;
CLINK(PRODUCT, PLANT, DISTCTR): C, X;
! G= Cost/ton of a product from a DC to a customer.;
GLINK(PRODUCT, DISTCTR, CUSTOMER): G;
ENDSETS
DATA:
! Plant Capacities;
S = 80, 40, 75,
20, 60, 75;
! Shipping costs, plant to DC;
C = 1, 3, 3, 5, ! Product A;
4, 4.5, 1.5, 3.8,
2, 3.3, 2.2, 3.2,
1, 2, 2, 5, ! Product B;
4, 4.6, 1.3, 3.5,
1.8, 3, 2, 3.5;
! DC fixed costs;
F = 100, 150, 160, 139;
! Shipping costs, DC to customer;
G = 5, 5, 3, 2, 4, ! Product A;

ADDITIONAL EXAMPLES 673
5.1, 4.9, 3.3, 2.5, 2.7,
3.5, 2, 1.9, 4, 4.3,
1, 1.8, 4.9, 4.8, 2,
5, 4.9, 3.3, 2.5, 4.1, ! Product B;
5, 4.8, 3, 2.2, 2.5,
3.2, 2, 1.7, 3.5, 4,
1.5, 2, 5, 5, 2.3;
! Customer Demands;
D = 25, 30, 50, 15, 35,
25, 8, 0, 30, 30;
ENDDATA
!—————————————————————————;
! Objective function minimizes costs.;
[OBJ] MIN = SHIPDC + SHIPCUST + FXCOST;
SHIPDC = @SUM(CLINK: C * X);
SHIPCUST =
@SUM(GLINK(I, K, L):
G(I, K, L) * D(I, L) * Y(K, L));
FXCOST = @SUM(DISTCTR: F * Z);
! Supply Constraints;
@FOR(PRODUCT(I):
@FOR(PLANT(J):
@SUM(DISTCTR(K): X(I, J, K)) <= S(I, J))
);
! DC balance constraints;
@FOR(PRODUCT(I):
@FOR(DISTCTR(K):
@SUM(PLANT(J): X(I, J, K)) =
@SUM(CUSTOMER(L): D(I, L)* Y(K, L)))
);
! Demand;
@FOR(CUSTOMER(L):
@SUM(DISTCTR(K): Y(K, L)) = 1
);
Model: MULLDC

674 APPENDIX A
Network Equilibrium Model: NETEQ1
In this example, we have a network of pipelines capable of transporting either fluid or gas. There are a
total of eight nodes and 11 arcs between them. Two of the nodes are source nodes, while the remaining
nodes are net demanders of product. The pressures at the source nodes are given. The model
determines the flow of product down each arc and the pressures at each node.
MODEL:
! Network equilibrium NETEQ1:based on Hansen et.al., Math.
Prog. vol. 52, no.1;
SETS:
NODE/A, B, C, D, E, F, G, H/:
P; ! Pressure at this node;
ARC(NODE, NODE)/ B A, C A, C B, D C, E D,
F D, G D, F E, H E, G F, H F/ :
R, ! Resistance on this arc;
FLO; ! Flow on this arc;
SRC(NODE)/ G, H/:
PFIXED; ! Fixed pressure at source nodes;
DEST(NODE) | #NOT# @IN(SRC, &1):
DEMAND; ! Given demand at destination nodes;
ENDSETS
DATA:
PFIXED = 240, 240;
DEMAND = 1, 2, 4, 6, 8, 7;
R = 1, 25, 1, 3, 18, 45, 1, 12, 1, 30, 1;
! For incompressible fluids and electricity:
PPAM = 1, for gases: PPAM = 2;
PPAM = 1;
! For optimization networks: FPAM = 0
(for arcs withflow >= 0)
electrical networks: FPAM = 1
other fluids: 1.8 <= FPAM <= 2;
FPAM = 1.852;
ENDDATA
!Set the pressures for the source/reservoir nodes;
@FOR(SRC(I): P(I) = PFIXED(I));
! Conservation of flow at non-source nodes;
@FOR(DEST(J):
@SUM(ARC(I, J): FLO(I, J)) = DEMAND(J) +
@SUM(ARC(J, K): FLO(J, K)));
! Relate pressures at 2 ends of each arc;
@FOR(ARC(I, J):
P(I)^ PPAM - P(J)^ PPAM = R(I, J) *
FLO(I, J) ^ FPAM;);
END
Model: NETEQ1

ADDITIONAL EXAMPLES 675
Minimize Traffic Congestion Model: NLTRAZ
In this model, we have a network with seven nodes. Three of the nodes are source nodes and four of
the nodes are destination nodes. Each source node can ship to any of the destination nodes. The
problem is the more of a product you send down an arc, the longer it takes for it to arrive. This might
be the case if the underlying network were a railroad, for instance. We assume that shipping times
obey the following relationship:
Time = Rate / (1 - Flow / Limit)
where,
Time time to ship one unit of product down a route,
Rate time required to transport one unit down a route with no congestion
along the route,
Flow amount of product shipped down a route, and
Limit maximum limit of product flow down a route.
Based on this relationship, we see shipping times go to infinity as the capacity of an arc is approached.
The goal of the model is to determine how much of a product to ship from each source to each
destination so as to minimize total shipping times.
MODEL:
! Traffic congestion transportation problem.
Cost/unit increases to infinity as traffic on
link approaches its link capacity.
Truncated variation of an AMPL example;
SETS:
ORIG/ CHIC CINC ERIE/: SUPPLY;
DEST / HAM AKR COL DAY/ : DEMAND;
OXD(ORIG, DEST): RATE, LIMIT, TRAF;
ENDSETS
DATA:
SUPPLY = 1200 800 1400;
DEMAND = 1000 1200 700 500 ;
RATE = 39 14 11 14
27 9 12 9
24 14 17 13 ;
LIMIT = 500 1000 1000 1000
500 800 800 800
800 600 600 600 ;
ENDDATA
[TOTCOST] MIN =
@SUM(OXD: RATE * TRAF/(1 - TRAF/ LIMIT));
@FOR(ORIG(I):
@SUM(OXD(I, J): TRAF(I, J)) = SUPPLY(I));
@FOR(DEST(J):
@SUM(OXD(I, J): TRAF(I, J)) = DEMAND(J));
@FOR(OXD: @BND(0, TRAF, LIMIT););
END
Model: NLTRAZ

676 APPENDIX A
Newsboy with Fixed Order Charge Model: NUSBOY
In the simple newsboy model (EZNEWS), presented earlier in this chapter, we did not have a fixed
ordering charge to deal with. We add this minor complication to the model below. Assuming you
decide to order, the fixed charge is a sunk cost and you should therefore order up to the same quantity,
S, as in the standard newsboy model. However, there may be cases where preexisting inventory is of a
level close enough to S that the expected gains of a minimal increase in inventory are not outweighed
by the fixed order charge. The problem now is to not only determine S (or “big S”), but also to
determine the additional parameter, s (or “little s”), where when inventory exceeds s the optimal
decision is to not incur a fixed charge by foregoing an order for additional stock. Inventory strategies
such as this are referred to as “little s-big S”, or (s,S), policies.
One additional feature to note in this model is we now assume demand to be normally distributed. This
is acceptable because the newsboy model does not demand any particular form of demand distribution.
As with the EZNEWS model, we could have also used a Poisson distribution if we felt it was more
appropriate.
MODEL:
! Newsboy inventory model;
! This model calculates the optimal stock levels
for a product with normally distributed demand
and a fixed ordering cost;
ATA:
P = 11; ! Penalty/unit for not having enough;
H = 5; ! Holding cost/unit for excess;
MU = 144; ! Mean demand;
SIGMA = 25; ! Standard deviation in demand;
K = 15; ! Fixed cost of placing an order;
ENDDATA
! Compute reorder point, SLIL, and order up to
point, SBIG;
! Calculate the order up to point, SBIG, using
standard newsboy formula;
@PSN(ZBIG ) = P /(P + H);
ZBIG = (SBIG - MU)/ SIGMA;
! and the expected cost of being there, CSBIG;
CSBIG = SIGMA * @PSL(ZBIG) * (P+H) + H * (SBIG-MU);
! The expected cost at the reorder point should
differ from the expected cost at SBIG by the
fixed order cost, K;
CSLIL = K + CSBIG;
! Solve for SLIL;
CSLIL=SIGMA*@PSL(ZLIL)*(P+H)*H*(ZLIL*SIGMA);
ZLIL = (SLIL - MU)/ SIGMA;
END
Model: NUSBOY

ADDITIONAL EXAMPLES 677
Optimal Airline Overbooking I Model: OBOOKO
Closely related to the newsboy problem (in a mathematical sense) is the airline-overbooking problem.
Given that a certain percentage of fliers with reservations will not show up for a flight, airlines that
don’t overbook will be sending most planes up with empty seats. Assuming the penalty cost for
overbooking is not too high, an airline that hopes to maximize revenue should overbook its flights. The
following model determines the optimal number of reservations to allow on a flight, and assumes the
number of no-shows on a flight has a binomial distribution.
MODEL:
!
This overbooking model determines the number of
reservations, M, to allow on a flight if the
no-show distribution is binomial;
! Some available data ;
N = 16; ! total seats available;
V = 225; !Revenue from a sold seat;
P = 100; !Penalty for a turned down customer;
Q = .04; !Probability a customer is a no-show;
! The probability to turn down customers is
@PBN(Q, M, M - N), therefore the corresponding
expected loss due to imperfect information is:
(V + P) * @PBN(Q, M, M - N), and we want the
loss to equal the revenue V on the margin. So,
the break-even equation is:;
(V + P) * @PBN(Q, M, M - N) = V;
! Note, you should round up if M is fractional;
END
Model: OBOOKO

678 APPENDIX A
Optimal Airline Overbooking II Model: OBOOKT
For those of you uncomfortable with the previous overbooking example, we use a “brute force”
method here to compute the expected profits from overbooking 1 to 6 seats. Solving this model, you
will find the results agree with the previous—the overbooking level that maximizes expected revenue
is 1 passenger.
MODEL:
! A strategy for airlines to minimize loss from
no-shows is to overbook flights. Too little
overbooking results in lost revenue. Too much
overbooking results in excessive penalties.
This model computes expected profits for
various levels of overbooking.;
SETS:
SEAT/1..16/; ! seats available ;
EXTRA/1..6/: EPROFIT; ! expected profits from
overbooking 1-6 seats;
ENDSETS
! Available data;
V = 225; ! Revenue from a sold seat;
P = 100; ! Penalty for a turned down customer;
Q = .04; ! Probability customer is a no-show;
! No. of seats available;
N = @SIZE(SEAT);
! Expected profit with no overbooking;
EPROFIT0 = V * @SUM(SEAT(I):
(1 - @PBN(1- Q, N, I - 1)));
! Expected profit if we overbook by 1 is:
EPROFIT0 + Prob(he shows) * (V - (V + P) *
Prob(we have no room));
EPROFIT(1) = EPROFIT0 +
(1 - Q) * (V - (V + P) * @PBN(Q, N, 0));
! In general;
@FOR(EXTRA(I)| I #GT# 1:
EPROFIT(I) = EPROFIT(I - 1) +
(1 - Q) * (V - (V + P) *
@PBN(Q, N + I - 1, I - 1));
);
END
Model: OBOOKT

ADDITIONAL EXAMPLES 679
Black & Scholes Options Pricing Model: OPTION
A call option is a financial instrument that gives the holder the right to buy one share of a stock at a
given price (the exercise price) on or before some specified expiration date. A frequent question is,
“How much should one be willing to pay for such an option?” An exact answer to this question eluded
researchers for many years until Fischer Black and Myron Scholes derived an option pricing formula
in 1973. A Nobel Prize was subsequently awarded for their work in 1997. A detailed discussion of this
model may be found in Chapter 12, Developing More Advanced Models.
MODEL:
! Computing the value of an option using the Black
Scholes formula (see "The Pricing of Options and
Corporate Liabilities", Journal of Political
Economy, May-June, 1973);
SETS:
! We have 27 weeks of prices P(t), LOGP(t) is log of prices;
WEEK/1..27/: P, LOGP;
ENDSETS
DATA:
! Weekly prices of National Semiconductor;
P = 26.375, 27.125, 28.875, 29.625, 32.250,
35.000, 36.000, 38.625, 38.250, 40.250,
36.250, 41.500, 38.250, 41.125, 42.250,
41.500, 39.250, 37.500, 37.750, 42.000,
44.000, 49.750, 42.750, 42.000, 38.625,
41.000, 40.750;
! The current share price;
S = 40.75;
! Time until expiration of the option, expressed
in years;
T = .3644;
! The exercise price at expiration;
K = 40;
! The yearly interest rate;
I = .163;
ENDDATA
SETS:
! We will have one less week of differences;
WEEK1(WEEK)| &1 #LT# @SIZE(WEEK): LDIF;
ENDSETS
! Take log of each week's price;
@FOR(WEEK: LOGP = @LOG(P));
! and the differences in the logs;
@FOR(WEEK1(J): LDIF(J) =
LOGP(J + 1) - LOGP(J));
! Compute the mean of the differences;
MEAN = @SUM(WEEK1: LDIF)/ @SIZE(WEEK1);
! and the variance;
WVAR = @SUM(WEEK1: (LDIF - MEAN)^2)/
(@SIZE(WEEK1) - 1);

680 APPENDIX A
! Get the yearly variance and standard deviation;
YVAR = 52 * WVAR;
YSD = YVAR^.5;
! Here is the Black-Scholes option pricing formula;
Z = ((I + YVAR/2) *
T + @LOG(S/ K))/(YSD * T^.5);
! where VALUE is the expected value of the option;
VALUE = S *@PSN(Z) - K *@EXP(- I * T) *
@PSN(Z - YSD *T^.5);
! LDIF may take on negative values;
@FOR(WEEK1: @FREE(LDIF));
! The price quoted in the Wall Street Journal for
this option when there were 133 days left was
$6.625;
END
Model: OPTION

ADDITIONAL EXAMPLES 681
Binomial Options Pricing Model: OPTIONB
Compared to the Black & Scholes example above, we take a slightly different approach to options
pricing in this example. We now assume a stock’s return has a binomial distribution, and use dynamic
programming to compute the option’s value.
MODEL:
SETS:
! Binomial option pricing model: We assume that
a stock can either go up in value from one period
to the next with probability PUP, or down with
probability (1 - PUP). Under this assumption,
a stock's return will be binomially distributed.
In addition, the symmetric probabilities allow
us to build a dynamic programming recursion to
determine the option's value;
! No. of periods, e.g., weeks;
PERIOD /1..20/:;
ENDSETS
DATA:
! Current price of the stock;
PNOW = 40.75;
! Exercise price at option expiration;
STRIKE = 40;
! Yearly interest rate;
IRATE = .163;
! Weekly variance in log of price;
WVAR = .005216191 ;
ENDDATA
SETS:
! Generate our state matrix for the DP.
STATE(S, T) may be entered from STATE(S, T - 1)
if stock lost value, or it may be entered from
STATE(S - 1, T - 1) if stock gained;
STATE(PERIOD, PERIOD)| &1 #LE# &2:
PRICE, ! There is a stock price, and...;
VAL; ! a value of the option;
ENDSETS
! Compute number of periods;
LASTP = @SIZE(PERIOD);
! Get the weekly interest rate;
(1 + WRATE) ^ 52 = (1 + IRATE);
! The weekly discount factor;
DISF = 1/(1 + WRATE);
! Use the fact that if LOG(P) is normal with
mean LOGM and variance WVAR, then P has
mean EXP(LOGM + WVAR/2), solving for LOGM...;
LOGM = @LOG(1 + WRATE) - WVAR/ 2;
! Get the log of the up factor;
LUPF = (LOGM * LOGM + WVAR) ^ .5;
! The actual up move factor;
UPF = @EXP(LUPF);

682 APPENDIX A
! and the down move factor;
DNF = 1/ UPF;
! Probability of an up move;
PUP = .5 * (1 + LOGM/ LUPF);
! Initialize the price table;
PRICE(1, 1) = PNOW;
! First the states where it goes down every period;
@FOR(PERIOD(T) | T #GT# 1:
PRICE(1, T) = PRICE(1, T - 1) * DNF);
! Now compute for all other states S, period T;
@FOR(STATE(S, T)| T #GT# 1 #AND# S #GT# 1:
PRICE(S, T) = PRICE(S - 1, T - 1) * UPF);
! Set values in the final period;
@FOR(PERIOD(S):
VAL(S, LASTP) =
@SMAX(PRICE(S, LASTP) - STRIKE, 0));
! Do the dynamic programing;
@FOR(STATE(S, T) | T #LT# LASTP:
VAL(S, T) = DISF *
(PUP * VAL(S + 1, T + 1) +
(1 - PUP) * VAL(S, T + 1)));
! Finally, the value of the option now;
VALUE = VAL(1, 1);
END
Model: OPTION

ADDITIONAL EXAMPLES 683
Bond Portfolio Optimization Model: PBOND
In certain situations, a business or individual may be faced with financial obligations over a future
number of periods. In order to defease (i.e., eliminate) this future debt, the debtor can determine a
minimal cost mix of current assets (e.g., cash and bonds) that can be used to cover the future stream of
payments. This problem is sometimes referred to as the cash flow matching problem, or the debt
defeasance problem. A detailed discussion of this model may be found in Chapter 12, Developing
More Advanced Models.
MODEL:
!Bond portfolio/cash matching problem. Given cash
needs in a series of future periods, what
collection of bonds should we buy to meet needs?;
SETS:
BOND/A B/ :
MATAT, ! Maturity period;
PRICE, ! Price;
CAMNT, ! Coupon;
BUY; ! Amount to buy;
PERIOD/1..15/:
NEED, ! Cash needed each period;
SINVEST; !Short term investment each period;
ENDSETS
DATA:
STRTE = .04; ! Short term interest rate;
MATAT = 6, 13; ! Years to maturity;
PRICE = .980, .965; ! Bond purchase prices;
CAMNT = .060, .065; ! Bond coupon amounts;
NEED = 10, 11, 12, 14, 15, 17, 19, 20, 22, 24,
26, 29, 31, 33, 36; ! Cash needs;
ENDDATA
! Minimize the total investment required to
generate the stream of future cash needs;
MIN = LUMP;
! First period is slightly special;
LUMP = NEED(1) + SINVEST(1) +
@SUM(BOND: PRICE * BUY);
! For subsequent periods;
@FOR(PERIOD(I)| I #GT# 1:
@SUM(BOND(J)| MATAT(J) #GE# I:
CAMNT(J) * BUY(J)) +
@SUM(BOND(J)| MATAT(J) #EQ# I:
BUY(J)) + (1 + STRTE) * SINVEST(I - 1) =
NEED(I) + SINVEST(I);
);
! Can only buy integer bonds;
@FOR(BOND(J): @GIN(BUY(J)));
Model: PBOND

684 APPENDIX A
Simple Product-Mix Model: PC
In this example, we illustrate a simple product-mix model for deciding how many of two types of
computers to produce. Note, LINGO allows you to use scalar variables and forgo the use of sets, thus
allowing straightforward entry of simpler models.
MODEL:
! Total profit for the week;
MAX = 200 * WS + 300 * NC;
! The total number of Wordsmiths produced is
limited by the supply of graphics chips;
WS <= 60;
! The total number of Numbercrunchers produced
is limited by the supply of math
coprocessors;
NC <= 40;
! The total amount of memory used in all
machines manufactured for the week can't
exceed 120 Mb;
WS + 2 * NC <= 120;
END
Model: PC

ADDITIONAL EXAMPLES 685
Project Management Model: PERT
In this example, we will set up a PERT model to determine the critical path of tasks in a project
involving the roll out of a new product. For those not familiar, PERT stands for Project Evaluation
and Review Technique. PERT is a simple, but powerful, technique developed in the 1950s to assist
managers in tracking the progress of large projects. A detailed discussion of this model may be found
in Chapter 2, Using Sets.
MODEL:
SETS:
TASKS / DESIGN, FORECAST, SURVEY, PRICE,
SCHEDULE, COSTOUT, TRAIN/: TIME, ES, LS, SLACK;
PRED( TASKS, TASKS) /
DESIGN,FORECAST,
DESIGN,SURVEY,
FORECAST,PRICE,
FORECAST,SCHEDULE,
SURVEY,PRICE,
SCHEDULE,COSTOUT,
PRICE,TRAIN,
COSTOUT,TRAIN /;
ENDSETS
DATA:
TIME = 10, 14, 3, 3, 7, 4, 10;
ENDDATA
@FOR( TASKS( J)| J #GT# 1:
ES( J) = @MAX( PRED( I, J): ES( I) + TIME( I))
);
@FOR( TASKS( I)| I #LT# LTASK:
LS( I) = @MIN( PRED( I, J): LS( J) - TIME( I));
);
@FOR( TASKS( I): SLACK( I) = LS( I) - ES( I));
ES( 1) = 0;
LTASK = @SIZE( TASKS);
LS( LTASK) = ES( LTASK);
DATA:
!Use @TABLE() to display the precedence relations set, PRED;
@TEXT() = @TABLE( PRED);
END
Model: PERT

686 APPENDIX A
Proj. Management with Crashing Model: PERTC
In the previous example, PERT, it was assumed each task takes a fixed amount of time to complete.
However, if we allocated additional resources to a task, it is reasonable to assume that we could
complete that task in a shorter time period. This option of speeding up a task by spending more on it is
referred to as crashing. In this next model, we incorporate crashing as an option. The goal is to meet
the project’s due date, while minimizing total crashing costs.
MODEL:
! A PERT/CPM model with crashing;
! The precedence diagram is:
! /FCAST\—SCHED——COSTOUT\
! / \ \
! FIRST \ \
! \ \ \
! \SURVEY-PRICE—————————FINAL;
SETS:
TASK/ FIRST, FCAST, SURVEY, PRICE,
SCHED, COSTOUT, FINAL/:
TIME, ! Normal time for task;
TMIN, ! Min time at max crash;
CCOST, ! Crash cost/unit time;
EF, ! Earliest finish;
CRASH; ! Amount of crashing;
! Here are the precedence relations;
PRED(TASK, TASK)/ FIRST,FCAST FIRST,SURVEY,
FCAST,PRICE FCAST,SCHED SURVEY,PRICE,
SCHED,COSTOUT PRICE,FINAL COSTOUT,FINAL/;
ENDSETS
DATA:
TIME = 0 14 3 3 7 4 10; ! Normal times;
TMIN = 0 8 2 1 6 3 8; ! Crash times;
CCOST = 0 4 1 2 4 5 3; ! Cost/unit to crash;
DUEDATE = 31; ! Project due date;
ENDDATA
! The crashing LP model;
! Define earliest finish, each predecessor of a
task constrains when the earliest time the task
can be completed. The earliest the preceding
task can be finished plus the time required for
the task minus any time that could be reduced by
crashing this task.;
@FOR(PRED(I, J):
EF(J) >= EF(I) + TIME(J) - CRASH(J)
);
! For each task, the most it can be crashed is the
regular time of that task minus minimum time for
that task;
@FOR(TASK(J):
CRASH(J) <= TIME(J) - TMIN(J)
);
! Meet the due date;
! This assumes that there is a single last task;
EF(@SIZE(TASK)) <= DUEDATE;

ADDITIONAL EXAMPLES 687
! Minimize the sum of crash costs;
MIN = @SUM(TASK: CCOST * CRASH);
END
Model: PERTC

688 APPENDIX A
Product-Mix with Setup Costs Model: PRODMIX
In a product-mix model, the decision is how much of a number of different products should be
produced to maximize total revenue. Each product competes for a number of scarce resources. In this
example, we produce six different flying machines from six different raw materials. This model also
has the feature that, should we produce a given product, we incur a fixed setup cost.
MODEL:
SETS:
PLANES/ ROCKET, METEOR, STREAK,
COMET, JET, BIPLANE /:
PROFIT, SETUP, QUANTITY, BUILD;
RESOURCES /STEEL, COPPER, PLASTIC,
RUBBER, GLASS, PAINT/: AVAILABLE;
RXP(RESOURCES, PLANES): USAGE;
ENDSETS
DATA:
PROFIT SETUP =
30 35
45 20
24 60
26 70
24 75
30 30;
AVAILABLE =
800 1160 1780 1050 1360 1240;
USAGE = 1 4 0 4 2 0
4 5 3 0 1 0
0 3 8 0 1 0
2 0 1 2 1 5
2 4 2 2 2 4
1 4 1 4 3 4;
ENDDATA
MAX = @SUM(PLANES: PROFIT*QUANTITY - SETUP*BUILD);
@FOR(RESOURCES(I):
@SUM(PLANES(J):
USAGE(I,J) * QUANTITY(J)) <= AVAILABLE(I)
);
@FOR(PLANES:
QUANTITY <= 400 * BUILD;
@BIN(BUILD)
);
@FOR(PLANES:
@GIN(QUANTITY)
);
END
Model: PRODMIX

ADDITIONAL EXAMPLES 689
Scenario Portfolio Selection Model: PRTSCEN
Scenarios here refer to outcomes of events with an influence on the return of a portfolio. Examples
might include an increase in interest rates, war in the Middle East, etc. In the scenario-based approach
to portfolio selection, the modeler comes up with a set of scenarios, each with a certain probability of
occurring over the next period. Given this set of scenarios and their probabilities, the goal is to select a
portfolio that minimizes some measure of risk, while meeting a target return level. A detailed
discussion of this model may be found in Chapter 12, Developing More Advanced Models.
MODEL:
! Scenario portfolio model;
SETS:
SCENE/1..12/: PRB, R, DVU, DVL;
STOCKS/ ATT, GMT, USX/: X;
STXSC(SCENE, STOCKS): VE;
ENDSETS
DATA:
TARGET = 1.15;
! Data based on original Markowitz example;
VE =
1.300 1.225 1.149
1.103 1.290 1.260
1.216 1.216 1.419
0.954 0.728 0.922
0.929 1.144 1.169
1.056 1.107 0.965
1.038 1.321 1.133
1.089 1.305 1.732
1.090 1.195 1.021
1.083 1.390 1.131
1.035 0.928 1.006
1.176 1.715 1.908;
! All scenarios happen to be equally likely;
PRB= .08333;
ENDDATA
! Compute expected value of ending position;
AVG = @SUM(SCENE: PRB * R);
! Target ending value;
AVG >= TARGET;
@FOR(SCENE(S):
! Compute value under each scenario;
R(S) = @SUM(STOCKS(J): VE(S, J) * X(J));
! Measure deviations from average;
DVU(S) - DVL(S) = R(S) - AVG
);
! Budget;
@SUM(STOCKS: X) = 1;
! Our three measures of risk;
[VARI] VAR = @SUM(SCENE: PRB * (DVU + DVL)^2);
[SEMI] SEMIVAR = @SUM(SCENE: PRB * (DVL) ^2);
[DOWN] DNRISK = @SUM(SCENE: PRB * DVL);
! Set objective to VAR, SEMIVAR, or DNRISK;
[OBJ] MIN = VAR;
END
Model: PRTSCEN

690 APPENDIX A
Quadratic Assignment Model: QASGN
In this example, we need to assign airline flights to gates at a hub to minimize the distance traveled
from gate to gate by passengers transferring between flights. This model is called the quadratic
assignment model because we are assigning planes to gates, and a straightforward formulation would
involve the use of quadratic terms in the objective. By complicating things slightly through the
introduction of an additional variable (Y in this case), we are able to replace each quadratic objective
term with one of the new variables. The result of this substitution is a linear model, allowing us to
tackle much larger models.
MODEL:
! A quadratic assignment problem:
Given transfers between flights and distance between gates,
assign flights to gates to minimize total transfer distance;
SETS:
FLIGHT/1..3/; ! There are three flights;
GATE/1..4/; ! There are five gates;
FXG(FLIGHT, GATE): X; !Flight-gate assignment;
GXG(GATE, GATE): T; !Distance between gates;
FXF(FLIGHT, FLIGHT): N; !Transfers btwn flights;
ENDSETS
DATA:
N = 0 30 5 ! No. transfers between flights;
20 0 0
30 40 0 ;
T = 0 5 10 14 ! distance between gates;
5 0 5 10
10 4 0 6
15 10 5 0 ;
ENDDATA
SETS:
! Transfer between 2 flights must be required and related to
2 different gates. Warning: this set gets big fast.;
TGTG(FLIGHT, GATE, FLIGHT, GATE)|
&1 #LT# &3 #AND# ((N(&1, &3) #NE# 0) #AND#
(T(&2, &4) #NE# 0) #OR# (N(&3, &1) #NE# 0)
#AND# (T(&4, &2) #NE# 0)): Y;
ENDSETS
! Each flight, B, must be assigned to a gate;
@FOR(FLIGHT(B):
@SUM(GATE(J): X(B, J)) = 1);
! Each gate, J, can receive at most one flight;
@FOR(GATE(J):
@SUM(FLIGHT(B): X(B, J)) <= 1);
! Force Y(B,J,C,K)=1 if B assigned to J and C
assigned to K;
! Assumes the T and N matrices are nonnegative;
@FOR(TGTG(B, J, C, K):
Y(B, J, C, K) >= X(B, J) + X(C, K) - 1);
! Min the sum of transfers * distance;
MIN = @SUM(TGTG(B, J, C, K): Y(B, J, C, K) *
(N(B, C) * T(J, K) + N(C, B) * T(K, J)));
! Make the X's 0/1 (Y's will naturally be 0/1);
@FOR(FXG: @BIN(X));
END
Model: QASGN

ADDITIONAL EXAMPLES 691
Economic Order Quantity Model: QDISCX
The classic EOQ (Economic Order Quantity) inventory model detailed in every introductory
operations research text tells us the optimal order quantity of an item given its demand rate, unit
holding cost, and fixed order cost. A common situation not handled by the standard EOQ model is
quantity discounts. In this model, we extend the EOQ analysis by allowing for quantity discounts.
MODEL:
! Economic order quantity with quantity discounts;
! This model determines the optimal order quantity
for a product that has quantity discounts;
SETS:
! Each order size range has;
RANGE/1..4/:
B, ! An upper breakpoint;
P, ! A price/unit over this range;
H, ! A holding cost/unit over this range;
EOQ, ! An EOQ using this ranges H and K;
Q, ! An optimal order qty within this range;
AC; ! Average cost/year using this range's Q;
ENDSETS
DATA:
D = 40000; ! The yearly demand;
K = 90; ! The fixed cost of an order;
IRATE = .2; ! Yearly interest rate;
!The upper break points, B, and price per unit, P:
Range: 1 2 3 4;
B = 10000, 20000, 40000, 60000;
P = .35225, .34525, .34175, .33825;
ENDDATA
! The model;
! Calculate holding cost, H, and EOQ for each
range;
@FOR(RANGE:
H = IRATE * P;
EOQ = (2 * K * D/ H) ^.5;
);
! For the first range, the optimal order
quantity is equal to the EOQ ...;
Q(1) = EOQ(1)
! but, if the EOQ is over the first breakpoint,
lower it;
- (EOQ(1) - B(1) + 1) *
(EOQ(1) #GE# B(1));
@FOR(RANGE(J)| J #GT# 1:
! Similarly, for the rest of the ranges, Q = EOQ;
Q(J) = EOQ(J) +
! but, if EOQ is below the lower breakpoint,
raise it up;
(B(J-1) - EOQ(J)) *
(EOQ(J) #LT# B(J - 1))

692 APPENDIX A
! or if EOQ is above the upper breakpoint,
lower it down;
- (EOQ(J) - B(J) + 1) *
(EOQ(J) #GE# B(J));
);
! Calculate average cost per year, AC,
for each stage;
@FOR(RANGE: AC = P * D + H * Q/ 2 + K * D/ Q);
! Find the lowest average cost, ACMIN.;
ACMIN = @MIN(RANGE: AC);
! Select the Q that gives the lowest AC per year;
! Note: TRUE = 1, FALSE = 0;
QUSE = @SUM(RANGE: Q * (AC #EQ# ACMIN));
END
Model: QDISCX
An interesting feature to note in this model is the use of logical expressions as in the following:
QUSE = @SUM(RANGE: Q * (AC #EQ# ACMIN));
In this formula, we have the logical expression:
AC #EQ# ACMIN
Logical expressions will return the value 1 if they evaluate to TRUE, or 0 if they evaluate to FALSE.
As you know, expressions of this nature are discontinuous, and will make it very difficult for the
solver to find reliable answers to an optimization model. It turns out in this model, however, that all
the variables and formulas are fixed. When a formula is fixed in value, logical expressions contained in
the formula do not cause a problem.

ADDITIONAL EXAMPLES 693
Simple Queuing System Model: QMMC
In this simple queuing model, we use LINGO’s runtime prompt feature to prompt the user for the
arrival rate of service customers, the time required by a typical service call, and the number of
available servers. Once you enter these values, LINGO computes various statistics about the system
including using the Erlang busy function (@PEB) to compute the probability that a customer must wait
for service.
MODEL:
! Compute statistics for a multi-server system
with Poisson arrivals, exponential service time
distribution.
! We prompt the user for he system parameters;
DATA:
ARV_RATE = ?;
SRV_TIME = ?;
NO_SRVRS = ?;
ENDDATA
! The model;
! Average no. of busy servers;
LOAD = ARV_RATE * SRV_TIME;
! Probability a given call must wait;
PWAIT = @PEB(LOAD, NO_SRVRS);
!Conditional expected wait, i.e., given must wait;
WAITCND = SRV_TIME/(NO_SRVRS - LOAD);
! Unconditional expected wait;
WAITUNC = PWAIT * WAITCND;
END
Model: QMMC

694 APPENDIX A
Minimal Cost Queuing Model: QUEUEL
The objective of this model is to choose the number of servers in a queuing system that minimizes total
cost. If all servers are busy when a customer arrives, then the customer is lost. Total cost is composed
of the cost of hiring our servers plus the expected cost of lost customers. The @PEL function is used to
get the fraction of customers lost due to all servers being busy when they arrive.
MODEL:
! Model of a queuing system with N servers, each
of which costs $17/hour. Arrivals occur at a
rate of 70 per hour in a Poisson stream. Arrivals finding
all servers busy are lost. A lost customer costs
$35. The average time to process a customer is 5
minutes;
! Minimize total cost =
service costs + lost customer cost;
[COST] MIN = SCOST + LCOST ;
! Cost of servers;
SCOST = 17 * N ;
! Cost of lost customers;
LCOST = 35 * 70 * FLOST ;
! The fraction of customers lost;
FLOST = @PEL(70 * 5 / 60 , N);
END
Model: QUEUEL

ADDITIONAL EXAMPLES 695
Steady State Queuing Model Model: QUEUEM
A useful approach for tackling general queuing models is to use the Rate In = Rate Out Principle
(RIRO) to derive a set of steady state equations for a queuing system. RIRO assumes a system can
reach a state of equilibrium. In equilibrium, the tendency to move out of a certain state must equal the
tendency to move towards that state. Given the steady state equations derived from this assumption,
we can solve for the probability that a system is in a given state at any particular moment. A detailed
discussion of this model may be found in Chapter 12, Developing More Advanced Models.
MODEL:
! Model of a queue with arrivals in batches. In
this particular example, arrivals may show up in
batches of 1, 2, 3, or 4 units;
SETS:
! Look at enough states so that P(i) for large i
is effectively zero, where P(i) is the steady
state probability of i customers in the system;
STATE/ 1..41/: P;
! Potential batch sizes are 1, 2, 3 or 4 customers,
and A(i) = the probability that an arriving
batch contains i customers;
BSIZE/ 1..4/: A;
ENDSETS
DATA:
! Batch size distribution;
A = .1, .2, .3, .4;
! Number of batches arriving per day;
LMDA = 1.5;
! Number of servers;
S = 7;
! Number of customers a server can
process per day;
MU = 2;
ENDDATA
! LAST = number of STATES;
LAST = @SIZE(STATE);
! Balance equations for states where the number of
customers in the system is less than or equal to
the number of servers;
@FOR(STATE(N)| N #LE# S:
P(N) * ((N - 1)* MU + LMDA) =
P(N + 1) * MU * N +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I)
* P(N - I))
);
! Balance equations for states where number in system is
greater than the number of servers, but less than the limit;
@FOR(STATE(N)| N #GT# S #AND# N #LT# LAST:
P(N) * (S * MU + LMDA) =
P(N + 1) * MU * S +
LMDA * @SUM(BSIZE(I)| I #LT# N: A(I) *
P(N - I))
);

696 APPENDIX A
! Probabilities must sum to 1;
@SUM(STATE: P) = 1;
END
Model: QUEUEM

ADDITIONAL EXAMPLES 697
Designing a Computer Cabinet Model: BOX
In this example, we create a nonlinear optimization model to design the case for a computer.
MODEL:
! Design a box at minimum cost that meets area,
volume, marketing and aesthetic requirements;
[COST] min = 2*(.05*(d*w + d*h) +.1*w*h);
[SURFACE] 2*(h*d + h*w + d*w) >= 888;
[VOLUME] h*d*w >= 1512;
! These two enforce aesthetics;
[NOTNARRO] h/w <= .718;
[NOTHIGH] h/w >= .518;
! Marketing requires a small footprint;
[FOOTPRNT] d*w <= 252;
END
Model: BOX

698 APPENDIX A
Linear Regression Model: REGRES
Linear Regression is a forecasting technique used to predict the value of one variable (called the
dependent variable) based upon the value of one or more other variables (the independent variables).
Our example is a simple linear regression model with one independent variable. The data is fit to a
linear equation of the form:
Y(i) = CONS + SLOPE * X(i)
where Y is the dependent variable, X is the independent variable, CONS is the value of Y when X = 0,
and SLOPE is the rate of change in Y with a unit change in X.
For our example, the dependent variable, Y, is the number of annual road casualties and the
independent variable, X, is the number of licensed vehicles. We have 11 years of data.
MODEL:
! Linear Regression with one independent variable;
! Linear regression is a forecasting method that
models the relationship between a dependent
variable to one or more independent variable.
For this model we wish to predict Y with the equation:
Y(i) = CONS + SLOPE * X(i);
SETS:
! The OBS set contains the data points for
X and Y;
OBS/1..11/:
Y, ! The dependent variable (annual road
casualties);
X; ! The independent or explanatory variable
(annual licensed vehicles;
! The OUT set contains model output.;
OUT/ CONS, SLOPE, RSQRU, RSQRA/: R;
ENDSETS
! Our data on yearly road casualties vs. licensed
vehicles, was taken from Johnston, Econometric
Methods;
DATA:
Y = 166 153 177 201 216 208 227 238 268 268 274;
X = 352 373 411 441 462 490 529 577 641 692 743;
ENDDATA
SETS:
! The derived set OBS contains the mean
shifted values of the independent and
dependent variables;
OBSN(OBS): XS, YS;
ENDSETS

ADDITIONAL EXAMPLES 699
! Number of observations;
NK = @SIZE(OBS);
! Compute means;
XBAR = @SUM(OBS: X)/ NK;
YBAR = @SUM(OBS: Y)/ NK;
! Shift the observations by their means;
@FOR(OBS(I):
XS(I) = X(I) - XBAR;
YS(I) = Y(I) - YBAR);
! Compute various sums of squares;
XYBAR = @SUM(OBSN: XS * YS);
XXBAR = @SUM(OBSN: XS * XS);
YYBAR = @SUM(OBSN: YS * YS);
! Finally, the regression equation;
R(@INDEX(SLOPE)) = XYBAR/ XXBAR;
R(@INDEX(CONS)) = YBAR - R(@INDEX(SLOPE)) * XBAR;
RESID= @SUM(OBSN:(YS - R(@INDEX(SLOPE)) * XS)^2);
! A measure of how well X can be used to predict Y
- the unadjusted (RSQRU) and adjusted (RSQRA)
fractions of variance explained;
R(@INDEX(RSQRU)) = 1 - RESID/ YYBAR;
R(@INDEX(RSQRA)) = 1 - (RESID/ YYBAR) *
(NK - 1)/(NK - 2);
! XS and YS may take on negative values;
@FOR(OBSN: @FREE(XS); @FREE(YS));
END
Model: REGRES

700 APPENDIX A
Acceptance Sampling I Model: SAMPLE
In this example, we have a lot of 400 items. We take a sample of 100 items from the lot. We accept the
entire lot as being good if the sample has 2 or less defective items.
We use the hypergeometric distribution (@PHG) to determine the exact producer risk (probability of
rejecting a good lot), and the exact consumer risk (probability of accepting a bad lot). In the days
before computers were widely available, statisticians had to rely on published tables of the probability
distributions to compute probabilities such as these. Because the hypergeometric distribution is
specified by four parameters, it would have been unrealistic to carry around hypergeometric tables that
covered all possible scenarios. Instead, statisticians routinely used distributions of fewer parameters to
approximate the hypergeometric. So, in deference to the good old days, we make use of the binomial,
Poisson, and normal approximations to the hypergeometric to compute these same risk probabilities.
The interested reader can compare the accuracy of the various approximations.
MODEL:
! Acceptance sampling: taking one or more samples at random
from a lot, inspecting each of the items in the sample(s),
and deciding on the basis of inspection results whether to
accept or reject the entire lot. This Acceptance Sampling
model illustrates the effect choice of distribution.;
! From a lot of 400 items;
LOTSIZE = 400;
! We take a sample of size 100;
SAMPSIZE = 100;
! Producer considers the lot good if
the lot fraction defective is .0075 or less;
FGOOD = .0075;
! Consumer considers the lot bad if
the lot fraction defective is .025 or more;
FBAD = .025;
! We accept the lot if sample contains 2 or less;
ACCEPTAT = 2;
! The model;
! What is producer risk of rejecting a good lot;
!Using the (exact) hypergeometric distribution;
PGOODH = 1 - @PHG(LOTSIZE, LOTSIZE * FGOOD,
SAMPSIZE, ACCEPTAT);
! Using binomial approx. to the hypergeometric;
PGOODB = 1 - @PBN(FGOOD, SAMPSIZE, ACCEPTAT);
! Using the Poisson approx. to the binomial;
PGOODP = 1 - @PPS(FGOOD * SAMPSIZE, ACCEPTAT);
! Using Normal approximation;
PGOODN =
1 - @PSN((ACCEPTAT + .5 - MUG) / SIGMAG);
! where;
MUG = SAMPSIZE * FGOOD;
SIGMAG = (MUG * (1 - FGOOD)) ^ .5;
!What is the consumer risk of accepting a bad lot;
! Using the hypergeometric;

ADDITIONAL EXAMPLES 701
PBADH = @PHG(LOTSIZE, LOTSIZE * FBAD,
SAMPSIZE, ACCEPTAT);
! Binomial;
PBADB = @PBN(FBAD, SAMPSIZE, ACCEPTAT);
! Poisson;
PBADP = @PPS(FBAD * SAMPSIZE, ACCEPTAT);
! Using Normal approximation;
PBADN = @PSN((ACCEPTAT + .5 - MUB) / SIGMAB);
! where;
MUB = SAMPSIZE * FBAD;
SIGMAB = (MUB * (1 - FBAD)) ^ .5;
END
Model: SAMPLE

702 APPENDIX A
Stratified Sampling Design Model: SAMPLE2
In this model, we want to come up with a sampling strategy that yields a variance within a specified
target at minimal cost. We have four strata of a population that we will be querying on two topics.
There is a maximum variance limit on the two questions. We know the variance in responses for each
stratum on each question. How many respondents must you select from each stratum to meet your
maximal variance requirements at minimal cost?
MODEL:
! Stratified sampling plan design, taken from Bracken and McCormick.
Minimize the cost of sampling from 4 strata, subject to
constraints on the variances of the sample based estimates of two
categories;
SETS:
STRATUM/1..4/: SIZE, POP, COST, WEIGHT;
CATEGORY/1..2/: VARMAX, K2;
SXC(STRATUM, CATEGORY): VAR, K1;
ENDSETS
! POP = population of each stratum. COST = cost of sampling in each.
VARMAX = variance limits. VAR = variance for each category in each
stratum. CFIX = a fixed cost;
DATA:
POP = 400000, 300000, 200000, 100000;
COST = 1, 1, 1, 1;
VARMAX = .043, .014;
VAR = 25 1
25 4
25 16
25 64;
CFIX = 1;
ENDDATA
[OBJ] MIN = CFIX + @SUM(STRATUM: SIZE * COST);
! Compute some parameters;
TOTP = @SUM(STRATUM(I): POP(I));
@FOR(STRATUM(I):
! Weight given each stratum;
WEIGHT(I) = POP(I)/TOTP;
@GIN(SIZE(I));
);
@FOR(CATEGORY(J):
K2(J) =
@SUM(STRATUM(I): VAR(I, J)^2 *
WEIGHT(I)/ POP(I));
);
@FOR(SXC(I, J):
K1(I, J) = VAR(I, J)^2* WEIGHT(I)^2;
);
@FOR(CATEGORY(J):
@SUM(STRATUM(I): K1(I, J) / SIZE(I))
- K2(J) <= VARMAX(J)
);

ADDITIONAL EXAMPLES 703
@FOR(STRATUM(I):
@BND(0.0001, SIZE(I), POP(I) -1);
);
END
Model: SAMPLE2

704 APPENDIX A
Acceptance Sampling II Model: SAMSIZ
We are sampling items from a large lot. If the number of defectives in the lot is 3% or less, the lot is
considered “good”. If the defects exceed 8%, the lot is considered “bad”. We want a producer risk
(probability of rejecting a good lot) below 9% and a consumer risk (probability of accepting a bad lot)
below 5%. We need to determine N and C, where N is the minimal sample size, and C is the critical
level of defects such that, if defects observed in the sample are less-than-or-equal-to C, we accept the
lot.
MODEL:
! Acceptance sampling design. From a large lot, take a sample
of size N, accept if C or less are defective;
! Poisson approximation to number defective is used;
DATA:
AQL = .03; ! "Good" lot fraction defective;
LTFD = .08; ! "Bad" lot fraction defective;
PRDRISK = .09; ! Tolerance for rejecting good lot;
CONRISK = .05; ! Tolerance for accepting bad lot;
MINSMP = 125; ! Lower bound on sample size to help solver;
ENDDATA
[OBJ] MIN = N;
! Tolerance for rejecting a good lot;
1 - @PPS(N * AQL, C) <= PRDRISK;
! Tolerance for accepting a bad lot;
@PPS(N * LTFD, C) <= CONRISK;
! Give solver some help in getting into range;
N >= MINSMP; C>1;
! Make variables general integer;
@GIN(N); @GIN(C);
END
Model: SAMSIZ

ADDITIONAL EXAMPLES 705
Seasonal Sales Forecasting Model: SHADES
We have quarterly observations of sales for the last two years. We would like to estimate a base, trend,
and seasonal factors to form a sales forecasting function that minimizes the sum of squared prediction
errors when applied to the historical sales. A detailed discussion of this model may be found in
Chapter 3, Using Variable Domain Functions.
MODEL:
SETS:
PERIODS /1..8/: OBSERVED, PREDICT,
ERROR;
QUARTERS /1..4/: SEASFAC;
ENDSETS
DATA:
OBSERVED = 10 14 12 19 14 21 19 26;
ENDDATA
MIN = @SUM(PERIODS: ERROR ^ 2);
@FOR(PERIODS: ERROR = PREDICT - OBSERVED);
@FOR(PERIODS(P): PREDICT(P) = SEASFAC(@WRAP(P, 4))
* (BASE + P * TREND));
@SUM(QUARTERS: SEASFAC) = 4;
@FOR(PERIODS: @FREE(ERROR));
END
Model: SHADES

706 APPENDIX A
Exponential Smoothing Model: SIMXPO
Exponential smoothing is a technique that is relatively easy to implement, and yet has proven to be an
effective tool at forecasting sales. In its simplest form, this technique assumes, on average, sales are
constant, but include a random error term about the average. It is also assumed the underlying average
can drift from period to period. These assumptions lead to the following smoothing equation:
St =
α
Xt + (1 -
α
) St-1
where,
St = predicted sales, or signal, in period t,
Xt = observed sales in period t, and
α
= a constant term between 0 and 1.
From this equation, we can see the closer
α
is to 1, the more the current observation affects our signal
and, subsequently, the less “memory” our equation has. Frequently, a value for
α
is chosen in the
range of .01 to .3. In this example, we will solve for an
α
that minimizes the sum of the squared
prediction errors.
For more information on exponential smoothing, see Winston (1995).
MODEL:
SETS:
PERIODS /1..8/: OBSERVED, ERROR, PREDICT;
ENDSETS
DATA:
! The degree of the objective. N may be changed
to 1 to minimize absolute deviation;
N = 2;
! The observed values of the time series;
OBSERVED = 10 14 12 19 14 21 19 26;
ENDDATA
! Force Period 1 prediction to 10;
PREDICT(1) = 10;
! The objective function;
[OBJ] MIN= @SUM(PERIODS: @ABS(ERROR) ^ N);
! Calculate the forecasts;
@FOR(PERIODS(T) | T #GT# 1:
PREDICT(T) = ALPHA * OBSERVED(T - 1) +
(1 - ALPHA) * PREDICT(T - 1));
! Calculate forecast errors;
@FOR(PERIODS: ERROR = PREDICT - OBSERVED);
! Error terms may be negative as well as positive;
@FOR(PERIODS: @FREE(ERROR));

ADDITIONAL EXAMPLES 707
! Exclude meaningless Alphas of zero or one;
@BND(.01, ALPHA,.9999);
END
Model: SIMXPO

708 APPENDIX A
Placing Songs on a Cassette Tape Model: SONGS
In this model, we have seven songs, each with a different length, that must be placed on a cassette
tape. The goal is to maximize the number of songs on one side of the tape without exceeding half of
the total time of the music on the other side.
MODEL:
SETS:
SONG/1..7/: LENGTH, Y;
ENDSETS
! Maximize number of songs on short side;
MAX = @SUM(SONG: Y);
! It must contain at most half the music;
@SUM(SONG: LENGTH * Y) <= HALF;
! Compute half the length;
HALF = @SUM(SONG: LENGTH)/ 2;
! We want the Y's to be 0/1;
@FOR(SONG: @BIN(Y));
DATA:
LENGTH = 7, 5, 2, 2, 2, 2, 2;
ENDDATA
END
Model: SONGS

ADDITIONAL EXAMPLES 709
Computing Sort Order Model: SORTIN
This simple model sorts cities according to their distance from the equator.
MODEL:
! Compute sort order ;
SETS:
CITY: ! Some cities;
LAT, ! Their latitudes;
RANKLT, ! Compute rank in distance from equator;
RDRLIST; ! Store in this ordered list;
ENDSETS
DATA:
CITY = BEIJING LONDON PARIS NYC LA MOSCOW TOKYO;
LAT = 39.6 51.3 48.5 40.4 34.1 55.5 35.4;
ENDDATA
CALC:
! Minimize output;
@SET( 'TERSEO', 2);
! Compute rank of each city;
RANKLT = @RANK( LAT);
! Put the original indices in order in a list;
@FOR( CITY(i):
RDRLIST( RANKLT(i)) = i;
);
!Display them;
@WRITE(' The cities from closest to farthest from equator:',
@NEWLINE(1));
@WRITE(' Latitude City', @NEWLINE(1));
@FOR( CITY(i):
@WRITE(' ', LAT(RDRLIST(i)),' ', CITY(RDRLIST(i)),
@NEWLINE(1));
);
ENDCALC
END
Model: SORTIN

710 APPENDIX A
Traveling Salesman Problem Model: TSP
In the traveling salesman problem (TSP), we have a network of cities connected by roads. We need to
find a tour that visits each city exactly once, minimizing the total distance traveled.
As it turns, large TSP models are difficult to solve using optimization, and are best approached using
some form of heuristic (see Lin and Kernighan, 1973). The problem lies in the fact that solutions to
large models tend to contain subtours. A subtour is a tour of a subset of cities unconnected to the main
tour. One can add constraints to break the subtours, but the number of constraints required grows
dramatically as the number of cities increase.
MODEL:
! Traveling Salesman Problem for the cities of
Atlanta, Chicago, Cincinnati, Houston, LA,
Montreal;
SETS:
CITY / 1.. 6/: U; ! U(I) = sequence no. of city;
LINK(CITY, CITY):
DIST, ! The distance matrix;
X; ! X(I, J) = 1 if we use link I, J;
ENDSETS
DATA: !Distance matrix, it need not be symmetric;
DIST = 0 702 454 842 2396 1196
702 0 324 1093 2136 764
454 324 0 1137 2180 798
842 1093 1137 0 1616 1857
2396 2136 2180 1616 0 2900
1196 764 798 1857 2900 0;
ENDDATA
!The model:Ref. Desrochers & Laporte, OR Letters,
Feb. 91;
N = @SIZE(CITY);
MIN = @SUM(LINK: DIST * X);
@FOR(CITY(K):
! It must be entered;
@SUM(CITY(I)| I #NE# K: X(I, K)) = 1;
! It must be departed;
@SUM(CITY(J)| J #NE# K: X(K, J)) = 1;
!Weak form of the subtour breaking constraints;
!These are not very powerful for large problems;
@FOR(CITY(J)| J #GT# 1 #AND# J #NE# K:
U(J) >= U(K) + X (K, J) -
(N - 2) * (1 - X(K, J)) +
(N - 3) * X(J, K)
);
);
! Make the X's 0/1;
@FOR(LINK: @BIN(X));

ADDITIONAL EXAMPLES 711
! For the first and last stop we know...;
@FOR(CITY(K)| K #GT# 1:
U(K) <= N - 1 - (N - 2) * X(1, K);
U(K) >= 1 + (N - 2) * X(K, 1)
);
END
Model: TSP

712 APPENDIX A
The Log Gamma Function Model: EZCOUNT
The factorial function is used in many probability computations. Unfortunately, the factorial function
can generate some very large numbers that can exceed the fixed word size of most computers. A
common way around this is to use the Log Gamma function (@LGM), which returns the logarithm of
the factorial function. In the following model, we use @LGM to compute the number of possible poker
hands.
MODEL:
! This model computes the number of ways of
selecting 5 objects from a set of 52 objects;
! This is expressed by 52! / (5! * 47!). The
actual computation uses the log-gamma function;
WAYS = @EXP(@LGM(53) - @LGM(6) - @LGM(48));
! Note that the arguments of the @LGM functions
are one greater than the corresponding arguments
of the factorial functions, due to the
definition of the Gamma function;
END
Model: EZCOUNT

ADDITIONAL EXAMPLES 713
Vehicle Routing Problem Model: VROUTE
The vehicle routing problem occurs in many service systems such as delivery, customer pick-up, repair
and maintenance. A fleet of vehicles, each with fixed capacity, starts at a common depot and returns to
the depot after visiting locations where service is demanded. The objective is to minimize the total
distance of all the routes.
In general, it takes much longer to find the best routes as the number of locations grow. Large versions
of this model may have to be tackled using some form of heuristics.
In this particular example, we are delivering one product to seven cities with the depot at city 1.
MODEL:
! The Vehicle Routing Problem (VRP) occurs in many service systems
such as delivery, customer pick-up, repair and maintenance. A fleet
of vehicles, each with fixed capacity, starts at a common depot and
returns to the depot after visiting locations where service is
demanded. The objective is to minimize total routes.
In general it takes much longer time to find the best routes when the
number of locations become larger.
This model involves delivering the required amount of goods to seven
cities with depot at city 1 ;
SETS:
! Q(I) is the amount required at city I
U(I) is the accumulated delivers at city I ;
CITY/1..8/: Q, U;
! DIST(I,J) is the distance from city I to city J
X(I,J) is 0-1 variable: It is 1 if some vehicle travels from
city I to J, 0 if none ;
CXC(CITY, CITY): DIST, X;
ENDSETS
DATA:
! city 1 represent the common depot, i.e. Q(1) = 0;
Q = 0 6 3 7 7 18 4 5;
! distance from city I to city J is same from city J to city I
distance from city I to the depot is 0, since the vehicle has to
return to the depot ;
DIST = ! To City;
! Chi Den Frsn Hous KC LA Oakl Anah From;
0 996 2162 1067 499 2054 2134 2050! Chicago;
0 0 1167 1019 596 1059 1227 1055! Denver;
0 1167 0 1747 1723 214 168 250! Fresno;
0 1019 1747 0 710 1538 1904 1528! Houston;
0 596 1723 710 0 1589 1827 1579! K. City;
0 1059 214 1538 1589 0 371 36! L. A.;
0 1227 168 1904 1827 371 0 407! Oakland;
0 1055 250 1528 1579 36 407 0;! Anaheim;
! VCAP is the capacity of a vehicle ;
VCAP = 18;
ENDDATA
! The objective is to minimize total travel distance;
MIN = @SUM(CXC: DIST * X);
! for each city, except depot....;
@FOR(CITY(K)| K #GT# 1:

714 APPENDIX A
! a vehicle does not traval inside itself,...;
X(K, K) = 0;
! a vehicle must enter it,... ;
@SUM(CITY(I)| I #NE# K #AND# (I #EQ# 1 #OR#
Q(I) + Q(K) #LE# VCAP): X(I, K)) = 1;
! a vehicle must leave it after service ;
@SUM(CITY(J)| J #NE# K #AND# (J #EQ# 1 #OR#
Q(J) + Q(K) #LE# VCAP): X(K, J)) = 1;
! U(K) is at least amount needed at K but can't exceed capacity;
@BND(Q(K), U(K), VCAP);
! If K follows I, then can bound U(K) - U(I);
@FOR(CITY(I)| I #NE# K #AND# I #NE# 1: U(K) >=
U(I) + Q(K) - VCAP + VCAP*(X(K, I) + X(I, K))
- (Q(K) + Q(I)) * X(K, I);
) ;
! If K is 1st stop, then U(K) = Q(K);
U(K) <= VCAP - (VCAP - Q(K)) * X(1, K);
! If K is not 1st stop...;
U(K)>= Q(K)+ @SUM(CITY(I)| I #GT# 1: Q(I) * X(I, K));
);
! Make the X's binary;
@FOR(CXC(I, J): @BIN(X(I, J)) ;
);
! Minimum no. vehicles required, fractional and rounded;
VEHCLF = @SUM(CITY(I)| I #GT# 1: Q(I))/ VCAP;
VEHCLR = VEHCLF + 1.999 - @WRAP(VEHCLF - .001, 1);
! Must send enough vehicles out of depot;
@SUM(CITY(J)| J #GT# 1: X(1, J)) >= VEHCLR;
END
Model: VROUTE

ADDITIONAL EXAMPLES 715
Home Mortgage Calculation Model: WHATIF
This example models a home mortgage. The user is prompted for the monthly payment, the length of
the mortgage, and the interest rate. The model then solves for the value of the home that can be
purchased with the mortgage.
MODEL:
! A model of a home mortgage(WHATIF.LNG);
! The user is prompted for values for the
payment, years, and interest rate. The
face value of the mortgage (LUMP) is
solved for.;
DATA:
! User is prompted for these:
PAYMENT = ?; ! Monthly payment;
YEARS = ?; ! No. of years;
YRATE = ?; ! Interest rate;
ENDDATA
! Relate no. of months to no. of years;
MONTHS = YEARS * 12;
! Relate monthly interest rate to yearly rate;
(1 + MRATE) ^ 12 = 1 + YRATE;
! Relate lump sum to monthly payment, monthly
interest rate, and no. of months;
LUMP = PAYMENT * @FPA(MRATE, MONTHS);
END
Model: WHATIF

716 APPENDIX A
Transportation Problem Model: WIDGETS
In this example, we want to ship a product from warehouses to vendors at minimal cost. An in-depth
description of this model can be found in Chapter 1, Getting Started with LINGO.
MODEL:
! A 6 Warehouse 8 Vendor Transportation Problem;
SETS:
WAREHOUSES / WH1 WH2 WH3 WH4 WH5 WH6/: CAPACITY;
VENDORS / V1 V2 V3 V4 V5 V6 V7 V8/ : DEMAND;
LINKS(WAREHOUSES, VENDORS): COST, VOLUME;
ENDSETS
! The objective;
MIN = @SUM(LINKS(I, J):
COST(I, J) * VOLUME(I, J));
! The demand constraints;
@FOR(VENDORS(J):
@SUM(WAREHOUSES(I): VOLUME(I, J)) =
DEMAND(J));
! The capacity constraints;
@FOR(WAREHOUSES(I):
@SUM(VENDORS(J): VOLUME(I, J)) <=
CAPACITY(I));
! Here is the data;
DATA:
CAPACITY = 60 55 51 43 41 52;
DEMAND = 35 37 22 32 41 32 43 38;
COST = 6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
ENDDATA
END
Model: WIDGETS

717
Appendix B: Error
Messages
Listed below by code number are the error messages you may encounter when using LINGO.
Suggestions for overcoming the errors are also included.
0. THE MODEL GENERATOR RAN OUT OF MEMORY.
LINGO’s model generator ran out of working memory. The model generator converts the text
of your LINGO model to an expanded form suitable for an appropriate solver engine. On
most platforms, you can increase the amount of working memory allocated to the model
generator. Note that memory set aside for LINGO’s model generator will not be available to
LINGO’s various solver engines. Given this, you should not allocate an overly excessive
amount of memory to the generator.
In Windows versions, select the LINGO|Options command, then the General tab, and in the
Generator Memory Limit box increase the amount of working memory. Press the Save button
and then restart LINGO. You can verify the new memory allotment by issuing the Help|About
LINGO command.
On other platforms, use the following commands:
SET MAXMEMB n
FREEZE
where n is the new memory allotment in megabytes. Exit LINGO and restart. Once LINGO
restarts, you can verify the new memory allotment with the MEM command.
1. TOO MANY LINES OF TEXT IN THE MODEL.
There are too many lines in the model’s text. For all practical purposes, the limit on total lines
of text is large enough that this error message should never be encountered.
2. TOO MANY CHARACTERS IN THE MODEL TEXT.
There are too many characters in the model’s text. For all practical purposes, the limit on the
number of characters is large enough that this message should never be encountered.
3. OVERLENGTH LINE, CHARACTERS MAY HAVE BEEN LOST OFF END. USE
CARRIAGE RETURN TO BREAK UP OVER SEVERAL INPUT LINES.
Input lines are limited to 200 characters. You will need to break up long input lines into
shorter ones.
4. VALID LINES ARE 1 TO N. TYPE ‘ALL’ TO REFERENCE ALL LINES.
The LOOK command expects a range of row numbers. If the range is invalid, you will get this
message. Enter a new range with valid numbers.

718 APPENDIX B
5. THERE IS NO CURRENT MODEL.
Any command that makes sense only if there is a current model in memory will print this
message if invoked without the presence of a model. You need to load a model with the
File|Open command in Windows or the TAKE command on other platforms, or enter a new
model with the File|New command in Windows or the MODEL command on other platforms.
6. TOO MANY NESTED TAKE COMMANDS.
You have exceeded LINGO’s limit of ten nested TAKE commands within a command script.
If possible, try combining some commands into a single file.
7. UNABLE TO OPEN FILE: FILENAME.
The file you tried to read doesn’t exist, or you misspelled its name. Try opening the file again.
8. TOO MANY CONSECUTIVE COMMAND ERRORS. REVERT TO TERMINAL
INPUT.
LINGO prints this message after having encountered a number of consecutive errors in a
command script. LINGO assumes that something has gone seriously awry, closes the script
file, and returns you to command level.
9. NOT USED.
10. NOT USED.
11. INVALID INPUT. A SYNTAX ERROR HAS OCCURRED.
This is the generic error issued by the LINGO compiler when it detects a syntax error. In
Windows, when you close the error box, the cursor will be on the line where the error
occurred. Other versions of LINGO will try print out the general area where the error has
occurred, but LINGO cannot always pinpoint the exact line. Examine this area for any
obvious syntax errors. If you are unable to find any obvious errors, a useful technique is to
comment out small sections of the model until the error goes away. This should give you a
good idea of exactly where the error is occurring.
Syntax errors may also occur if you are not invoking the correct compiler in LINGO. Most
users will choose to build models using the native LINGO syntax, however, some users may
prefer building their models using LINDO syntax. LINGO can compile models written in
either native LINGO syntax or LINDO syntax. LINGO chooses the compiler based on a
model's file extension. LINGO models must have an extension of lg4 (the default) or lng.
LINDO models must have an ltx extension. The default model extension may be set by
clicking on: LINGO | Options | Interface | File Format. Each model window's title bar
displays whether it is a LINGO or LINDO model.
12. MISSING RIGHT PARENTHESIS.
A LINGO expression is missing at least one closing right parenthesis. LINGO will point to
the end of the expression where the error occurred. Count the number of parentheses in this
expression to verify if you have input the correct number, or, in Window use the Edit|Match
Parenthesis command to find the unmatched parenthesis.

ERROR MESSAGES 719
13. A SPECIFIED SPREADSHEET RANGE WAS NOT FOUND. RANGE_NAME.
You specified a spreadsheet range titled RANGE_NAME that LINGO was unable to find.
Check the spelling of the range name and be sure that the range is defined in the spreadsheet.
14. NOT ENOUGH TEMPORARY OPERATOR STACK SPACE.
LINGO uses a stack to temporarily hold operators and prefix functions during compilation of
an expression. It is possible, though unlikely, that this stack will overflow. If so, try breaking
up lengthy expressions, or adding parentheses to offending expressions.
15. NO RELATIONAL OPERATOR FOUND.
Each LINGO expression (with the exception of variable domain expressions) must contain
one relational operator (e.g., =, <, >). Check to be sure that all expressions contain relational
operators.
16. ALL MODEL OBJECTS MUST HAVE THE SAME PARENT SET FOR THIS
OPERATION.
You have attempted to use an import or export function in the data section that involves two
or more attributes from different parent sets. Break the function into multiple calls, so each
instance refers to attributes belonging to the same parent set.
17. NOT ENOUGH INDEX STACK SPACE.
LINGO uses a stack to keep track of indices referenced by set operators. It is possible, though
unlikely, that this stack will overflow. The only way to remedy this situation is to rewrite the
given expression, so it uses fewer indices.
18. OUT OF SET STACK SPACE.
LINGO uses a stack to keep track of sets referenced by set operators. This stack may
overflow, though it’s unlikely. The only way to remedy this situation is to rewrite the given
expression, so the maximum number of pending set operators is reduced.
19. INVALID USE OF @INDEX FUNCTION.
The @INDEX function expects an optional set name followed by a mandatory set number.
Check to see that your arguments comply with these restrictions.
20. IMPROPER USE OF SET NAME.
A set name has been used in an improper manner. For instance, you may have attempted to
set the name equal to a quantity. Check your model’s syntax.
21. IMPROPER USE OF ATTRIBUTE NAME.
This message is printed if an attribute name is used incorrectly. For instance, you may have
attempted to use it as a scalar (single value) variable. Check your model’s syntax.
22. TOO MANY INEQUALITY OR EQUALITY RELATIONS.
A constraint may have only one relational operator (i.e., =, <, or >). A two-sided constraint
such as 2 < X < 4 is not permitted. Instead, write it as two one sided constraints: X > 2; and X
< 4;.

720 APPENDIX B
23. IMPROPER NUMBER OF ARGUMENTS.
LINGO’s predefined functions generally expect a specific number of arguments. You’ll get
this message if you are passing an incorrect number of arguments. Check the syntax of the
function in question.
24. INVALID SET NAME.
If LINGO was expecting a set name and didn’t find it, you will get this message. Note that all
sets must be defined in a sets section before they are referenced in a model expression.
25. NOT USED.
26. IMPROPER NUMBER OF INDEX VARIABLES.
When using indices in conjunction with a set in a set operator function, LINGO checks to be
sure that you have specified the correct number of indices for the set. If not, it prints this
message.
27. THE FOLLOWING SPREADSHEET RANGE IS DISCONTINUOUS:
RANGE_NAME.
At present, LINGO only supports continuous ranges. Continuous ranges are simple,
rectangular ranges. Discontinuous ranges are unions of two, or more, continuous ranges. You
will need to break your discontinuous range up into a set of equivalent, continuous ranges.
28. INVALID USE OF A ROW NAME.
A row name may be input within brackets at the start of a constraint and may contain up to 32
characters. This error message indicates some improper use. Check your model’s syntax.
29. INVALID NUMBER OF INITIALIZATION VALUES IN A DATA/INIT/CALC
SECTION. THE REQUIRED NUMBER OF VALUES IS: N
When assigning values to an array, you must assign a value to every element in data, init and
calc statements. LINGO keeps track of the number of values you specified and checks this
against the length of each array being assigned. If the two numbers don’t agree, LINGO
prints this message along with the number of values that are required.
30. A GENERAL FAILURE OCCURRED WHILE ATTEMPTING A LINK TO EXCEL.
LINGO attempted to open an OLE link to Excel, but was unsuccessful. Be sure that Excel is
installed on your machine (version 5, or later). Also, if your machine is busy, this error
message can occur because it is taking an excessive amount of time to load Excel. In which
case, simply retry the action when the machine is less busy.
31. INVALID ARGUMENT LIST FOR AN @TEXT() FUNCTION CALL.
An instance of the @TEXT function has an invalid argument list. Check the documentation on
this function for the correct syntax.
32. ATTEMPT TO IMPORT A BLANK SET MEMBER NAME.
You have attempted to import a set member name that is entirely blank. All set member
names must conform to standard LINGO naming conventions and may not be blank. Assign a
nonblank name to the set member and retry.

ERROR MESSAGES 721
33. INVALID ARGUMENT LIST FOR AN @OLE() FUNCTION CALL.
Check the documentation on the @OLE function to determine the correct syntax.
34. RANGE LENGTHS MUST BE IDENTICAL WHEN IMPORTING DERIVED SETS.
You are importing a derived set from multiple ranges of varying lengths. When using
multiple ranges, each range must contain the same number of cells. Adjust the sizes of the
ranges so they agree and retry.
35. UNRECOGNIZED NAME IN AN OUTPUT FUNCTION.
You have attempted to use an output function (e.g., @OLE or @ODBC) to export the value of
a variable that does not exist. Check your output functions to see if all the variables exist and
that they are spelled correctly.
36. ATTEMPT TO IMPORT INVALID PRIMITIVE SET ELEMENT NAME: NAME.
A primitive set name imported from an external source is invalid. Make sure the name
conforms to normal LINGO naming standards.
37. NAME ALREADY IN USE: NAME. CHOOSE A DIFFERENT NAME.
A model can’t use duplicate names. Select a new, unique name.
38. THE ODBC SERVER RETURNED THE FOLLOWING ERROR MESSAGE:
MESSAGE-TEXT.
The ODBC server encountered an error. The text of the message will be displayed. In many
cases, the text of the message should help clarify the problem. Unfortunately, some ODBC
servers will not return an explanatory message for all error conditions, in which case, you
may need to experiment with the format of your data to determine the cause of the problem.
39. THE FOLLOWING SET ELEMENT WAS NOT DERIVED FROM ITS PARENT
PRIMITIVE SET: SET-ELEMENT.
When defining a sparse derived set, LINGO checks each set element against the parent set. If
the element is not found in the parent set, you will get this message. Please check the spelling
and ordering of the set elements in the sparse derived set you are defining.
40. INVALID NUMBER OF DERIVED SET INDEX ELEMENTS.
If a sparse derived set is formed from, say, three primitive sets, then there must be a multiple
of three primitive set element names in the explicit definition of the derived set. LINGO
checks this, and issues this message if there is not a match.
41. OUT OF ATTRIBUTE INDEX SPACE.
LINGO imposes a limit on the total number of primitive sets used in defining derived sets.
The current limit is quite large and should not pose a problem.
42. EXPLICIT VARIABLE IN A SET CONDITION FOR SET: SET_NAME.
When using a conditional expression to define the members of a derived set, you cannot
reference a variable that has not been fixed in a previous data statement. LINGO must be able
to completely evaluate these conditional expressions during compilation so it knows the size
of the set.

722 APPENDIX B
43. EXECUTOR ERROR IN SET CONDITION FOR SET: SET_NAME.
LINGO prints this message if an arithmetic error occurred when it was trying to evaluate a
conditional expression used to define the members of a derived set. Check all arithmetic
operations in the set definition in question.
44. UNTERMINATED CONDITION.
Each conditional expression placed on a set operator must be terminated with a colon (:).
LINGO prints this message if you fail to add one.
45. INVALID ARGUMENT LIST FOR AN @ODBC FUNCTION CALL.
You have a syntax error in an argument list of an @ODBC function call. Check the
documentation on the @ODBC function to determine the proper syntax.
46. INADMISSIBLE FILE NAME: FILENAME.
The file name is either too long or it contains characters not permitted on this platform. Use a
different file name and try again.
47. TOO MANY FILES OPEN: NAME_OF_LAST_FILE.
LINGO imposes a limit on the total number of files that can be opened simultaneously
through use of the @FILE command. You can try placing all the data in fewer files. Also,
avoid using the LINGO end-of-record mark (~) at the end of files. This allows LINGO to
“see” the end of the file, forcing it to close the file down, thus allowing for an additional open
file.
48. UNABLE TO OPEN FILE: FILENAME.
LINGO prints this message when it is unable to open a file. Check the spelling of the
filename. Be sure a copy of the file exists on your disk and that the file is not open in another
application.
49. ERROR READING FILE: FILENAME.
LINGO prints this message in case an error occurred while reading a file with the @FILE
function. Check the file to be sure it is not damaged. Another possibility is that you do not
have read access to the disk or directory where the file resides.
50. IMPROPER USE OF @FOR() FUNCTION.
LINGO prints this message if you’ve attempted to nest an @FOR function inside some other
set operator. You can nest @FOR functions within other @FORs, and other set operators
within @FORs, but nesting an @FOR inside any function other than another @FOR is not
permitted.
51. RAN OUT OF GENERATOR MEMORY COMPILING MODEL.
LINGO exhausted available generator memory compiling a model and was forced to halt. See
error message 0 for suggestions on increasing the model generator’s allotment of working
memory.
52. IMPROPER USE OF @IN() FUNCTION.
You passed incorrect arguments to the @IN function. Check the documentation on the @IN
function.

ERROR MESSAGES 723
53. UNABLE TO LOCATE RANGE NAME: RANGE_NAME.
You specified a range name in a spreadsheet interface function, which is either inadmissible
or was not found in the specified worksheet. Please check the worksheet file to be sure the
range name exists as spelled.
54. ERROR (N) READING FROM FILE.
LINGO was unable to read from the file FILE_NAME. Possible causes include the file being
locked by another user or the file being corrupted. Please check to see that the file is valid
and available for reading.
55. UNABLE TO OPEN @TEXT DATA FILE: FILENAME.
You have specified a file as part of the @TEXT function that could not be opened. Check to
see that the file exists and that you have spelled the name correctly.
56. ERROR READING FROM @TEXT DATA FILE: FILENAME.
A read error was encountered when LINGO attempted to read data from a file specified in an
@TEXT function. Check to be sure that the file is not corrupted.
57. INVALID INPUT ENCOUNTERED IN @TEXT DATA FILE: TEXT_STRING.
The @TEXT function may be used in the data section to read and write numeric values. This
error message results when nonnumeric data is encountered in a file being read with @TEXT.
If you need to import nonnumeric data from a text file, use the @FILE function.
58. NOT ENOUGH VALUES FOUND IN @TEXT DATA FILE: FILENAME.
N VALUES NEEDED.
M VALUES FOUND.
The @TEXT function may be used in the data section to read and write numeric values. This
error message results when an insufficient number of data points were found in a file being
read with @TEXT. Add enough data to the file to fully initialize the attributes of interest.
59. TOO MANY VALUES ENCOUNTERED IN @TEXT DATA FILE: FILENAME.
The @TEXT function may be used in the data section to read and write numeric values. This
error message results when too many data points were found in a file being read with
@TEXT. Remove data from the file until you have the exact number required to initialize the
attributes of interest.
60. FILE NAME REQUIRED IN AN @TEXT() INPUT OPERATION.
The @TEXT function may be used in the data section to read and write numeric values. This
error message results when an input file was not specified when attempting to read data points
from a file using @TEXT.
61. COMMAND DISREGARDED.
LINGO prints this message when it was unable to interpret a command you typed at the colon
prompt (:). Check the spelling of the command and that you are using correct syntax for the
command.
62. RAN OUT OF WORKSPACE IN MODEL GENERATION (N).
LINGO ran out of working memory generating your model. Refer to error message 0 for
strategies to increase the model generator’s working memory allotment.

724 APPENDIX B
63. MODEL IS ILL DEFINED. CHECK FOR UNDEFINED INDICES AND/OR
CONDITIONS IN EXPRESSION: EXPRESSION.
LINGO will print this message for one of two reasons: 1) a conditional expression used to
qualify a set operator function cannot be evaluated, or 2) a subscript expression cannot be
evaluated. When we say an expression cannot be evaluated, we mean that one or more
variables in the expression are not fixed. LINGO will report the expression number, or row
name (if used), where the fault occurred. Please be sure to add constraints or data statements
to fix all the variables in the conditional or subscript expression in question. Also, if you are
using primitive set member names in the model’s equations, you must use the @INDEX
function to get the index of the primitive set member. If you don’t use the @INDEX function,
LINGO will treat the primitive set member as if it is a new scalar variable. You can have
LINGO check for primitive set names that are in use in both the data and the model equations
by checking the Check for duplicate names in data and model box on the General Solver tab
of the LINGO|Options command dialog box (or the SET CHKDUP 1 command on other
platforms). Finally, if you would like to use primitive set names directly in your model’s
equations (a practice we don’t recommend), you can force LINGO to allow this by checking
the Allow unrestricted use of primitive set member names checkbox on the General Solver tab
(or the SET USEPNM 1 command on other platforms).
64. TOO MANY NESTED @FOR OPERATORS.
LINGO maintains a stack to keep track of pending nested @FOR functions. Too many nested
@FORs could cause this stack to overflow, although it would be an unusual model that
triggers this error. You can avoid nesting some @FORs by forming derived sets, and looping
over a single derived set as opposed to many primitive sets.
65. IMPROPER USE OF @WARN FUNCTION.
You have used the @WARN function incorrectly. Check the documentation on @WARN to
determine where you went wrong.
66. WARNING: TOTAL FIXED ROWS WITH NONUNIQUE ROOTS: N
When LINGO generates a model, it determines if a variable can be solved for directly and
substituted out of the model. These variables are referred to as being fixed, and the row in the
model used to solve for a fixed variable is referred to as a fixed row. When LINGO solves for
the value of a fixed variable in its fixed row, it will look around a neighborhood of the
variable’s value to determine if multiple roots exist, and display this message if any are
found. An example of an equation with such multiple roots would be: @SIGN(X ) = 1. All
non-negative values of X would satisfy this relation. LINGO will display the names of up to
three variables and their corresponding fixed rows with this symptom. LINGO will continue
to process the model, however. You should examine the model closely when this error occurs,
because it would be unusual to find a well formulated model displaying this characteristic.
Keep in mind that there might be a better solution involving a different value for the fixed
variable than was chosen by LINGO.
67. UNSUPPORTED STRING ARITHMETIC OPERATION.
You've attempted to perform an arithmetic operation on a text object.

ERROR MESSAGES 725
68. MULTIPLE OBJECTIVE FUNCTIONS IN MODEL.
The model contains more than one objective function. Possible solutions are to delete some
objectives, convert some objectives to constraints, or combine the multiple objectives into a
single objective using a weighting scheme.
69. UNDEFINED ARITHMETIC OPERATION IN CONSTRAINT: N.
LINGO ran into an undefined arithmetic operation during execution (e.g., 1/0). Check the
constraints to be sure all operations are defined.
70. SUBSCRIPT OUT OF RANGE ON ATTRIBUTE: ATTRIB.
While executing your model, LINGO found a subscript that was out of range. For example, if
you defined the attribute STAFF with the set /1..5/, then referencing STAFF(6) would result in
this error message. Nonintegral subscripts will also generate this message. Please be sure your
sets are defined across the intended range and that any subscript computations are correctly
specified.
71. IMPROPER USE OF A VARIABLE DOMAIN FUNCTION (E.G. , @GIN, @BIN,
@FREE, @BND).
This error results when the syntax of a variable domain function has been violated. Check the
model’s use of these functions.
72. UNABLE TO SOLVE FOR FIXED VARIABLE VAR_NAME IN CONSTRAINT
CONSTRAINT_NAME.
LINGO has determined that it should be able to solve for a particular variable in a given row.
The root finder was not able to converge on a solution. Be sure a solution exists for the row
(e.g., the expression: -1=x^.5, would have no real solution). If possible, rewrite the equation
in the form x = f(.), where x appears only once and is on the left-hand side of the expression.
LINGO is always able to solve expressions in this form, as long as the function is defined and
evaluates to a real number (e.g., x = @LOG(-3) evaluates to an imaginary number; and x/0 is
undefined). If this is not possible, then you might try solving the expression by some other
method, and enter the variable’s value as a constant in LINGO.
73. A USER INTERRUPT OCCURRED.
LINGO was interrupted before the solver completed its run.
74. MAGNITUDE OF BOUND EXCEEDS: 1.E+21 ON VARIABLE: VARIABLE_NAME.
You have entered a bound outside LINGO’s allowable limit. The magnitude of bounds input
using @BND may not exceed 1019.
75. CONFLICTING BOUNDS ON VARIABLE: VAR_NAME.
LINGO has detected a bound on the named variable that is outside of the range of another
bound. For instance, @BND(-6, X, 6), followed by @BND(-5, X, 5) would not yield this error.
However, following it with @BND(7, X, 9) would.
76. ERROR GENERATING MODEL.
LINGO was unable to pass the model to the optimizer. If this error occurs, contact LINDO
Systems technical support.

726 APPENDIX B
77. ARITHMETIC ERROR GENERATING MODEL.
LINGO was unable to generate the model due to an undefined arithmetic operation (e.g.,
division by zero). Remove all undefined arithmetic operations from your model.
78. SET SECTIONS NOT ALLOWED IN SUBMODELS.
Set sections can not be placed inside submodels. You can move the set section before the
relevant submodel to correct the problem.
79. NOT USED.
80. NOT ENOUGH WORK SPACE GENERATING MODEL.
LINGO ran out of working memory while trying to generate the model. Please refer to
message 0 for strategies to increase the model generator’s working memory.
81. NO FEASIBLE SOLUTION FOUND.
LINGO was unable to find a solution that simultaneously satisfies all the constraints. Check
the model’s consistency. Try dropping constraints until the problem goes away to get an idea
of where the trouble may lie. Also, check the solution report. Constraints contributing to the
infeasibility will have a nonzero dual price.
82. UNBOUNDED SOLUTION.
LINGO was able to increase the objective function without bound. Be sure that you have
added all constraints to your model and that they have been input correctly.
83. NOT USED.
84. @POINTER MAY NOT BE USED WITH @WRITE/@WRITEFOR IN CALC
SECTION.
Calc sections do not presently support the use of the @POINTER output operator in
conjunction with @WRITE/@WRITEFOR. In order to use @POINTER, you must pass
complete attributes as per the following example:
CALC:
@POINTER( 1) = X;
ENDCALC
85. STACK OVERFLOW. EXPRESSION TOO COMPLEX.
LINGO uses a stack to store temporary values while executing the expressions in a model.
The default stack size is quite large. Thus, this message should not occur. Should you receive
this message, contact LINDO Systems technical support.
86. ARITHMETIC ERROR IN CONSTRAINT: CONSTRAINT.
INSTRUCTION POINTER: N
An undefined arithmetic operation (e.g., 1/0 or @LOG(-1)) occurred while LINGO was
generating the model. If you have specified a row name for the constraint, LINGO will print
the name of the constraint. If you haven’t specified row names in your model, you may want
to add them to assist in tracking down this error. Check the referenced constraint for any
undefined operations.

ERROR MESSAGES 727
87. IMPROPER USE OF @IN FUNCTION.
You have specified improper arguments for the @IN function. Refer to the documentation on
this function for more details.
88. SOLUTION IS CURRENTLY UNDEFINED.
LINGO was not able to solve the model to completion for some reason. In which case, any
attempt to print out a solution will result in this message. Try re-solving the model and
determining the reason LINGO was unable to solve the model.
89. RUNTIME ERROR IN SOLVER ROUTINES. CONTACT LINDO SYSTEMS.
An unexpected runtime error has occurred in LINGO's solver routines. Please contact LINDO
Systems for assistance.
90. THE SOLVER TIME LIMIT WAS EXCEEDED.
The solver time limit was reached and the solution process was halted. If you believe that
there should be no time limit, then you should check to see what the current time limit is. In
Windows, check to see what the current setting is using the LINGO|Options command to
check the Time box on the General Solver tab. On other platforms, run the HELP SET
command to see what the setting is for the TIMLIM parameter.
91. INVALID RUNTIME PARAMETER VALUE.
At runtime, LINGO will prompt for any variable set to equal a question mark in the data
section. If LINGO receives an invalid value, you will get this error message. Correct your
data and try again.
92. WARNING: THE CURRENT SOLUTION MAY BE NONOPTIMAL/INFEASIBLE
FOR THE CURRENT MODEL.
If you’ve solved a model and brought another model window to the front, LINGO prints this
message to remind you that the solution you’ve asked for may not belong to the frontmost
model window. LINGO also prints this message whenever you attempt to examine a
nonoptimal solution. For instance, when you’ve interrupted the solver, or when LINGO
couldn’t find a feasible answer. In the latter case, correct any errors in the model and re-solve.
93. INVALID SWITCH IN COMMAND LINE.
Some LINGO commands accept switches, or modifiers. If there was an error in one of these
command-line modifiers, LINGO will print this message. Refer to the documentation on the
specific command to learn the available modifiers.
94. NOT USED.
95. NOT USED.

728 APPENDIX B
96. NOT USED.
97. NOT USED.
98. NOT USED.
99. NOT USED.
100. NOT USED.
101. NOT USED.
102. UNRECOGNIZED VARIABLE NAME: VARIABLE_NAME.
The model object name you have specified does not exist. Please check your spelling.
103. TEXT LITERALS NOT ALLOWED IN VECTOR-BASED, NON-TEXT OUTPUT
OPERATIONS.
When outputting solutions in vector format (i.e., passing an entire attribute at a time), text
literals may not be included in the list of output objects. For example, suppose you had the
following output statement in your model:
DATA:
@OLE( 'MYBOOK.XLS', 'HEADER', 'VOLUME') = 'SHIP=', VOLUME;
ENDDATA
In this case, VOLUME is an attribute containing multiple values, while 'SHIP=' is a single text
literal. This is a vector-based output statement in that we aren't embedding output objects in
@WRITE or @WRITEFOR statements. The use of text literals is not permitted in vector
based output. You will need to break the statement up into two statements, one using
@WRITE to output the text literal:
DATA:
@OLE( 'MYBOOK.XLS', 'HEADER') = @WRITE( 'SHIP=');
@OLE( 'MYBOOK.XLS', 'VOLUME') = VOLUME;
ENDDATA
104. MODEL NOT SOLVED YET, OR THE MODEL HAS BEEN SOLVED AND FOUND
TO CONTAIN NO CONSTRAINTS OR VARIABLES.
If the model has not already been solved then issue the SolveLINGO_Solve command. If the
model has been solved then it was found to be vacuous.
105. NOT USED.
106. MINIMUM AND MAXIMUM VALUES FOR WIDTH ARE: 68 800.
When changing terminal width using the WIDTH command, you must enter an integer
between 68 and 800.
107. INVALID @POINTER INDEX VALUE
Your model contains a reference to the @POINTER function with an invalid argument list.
The @POINTER function requires one argument that must be integer valued and greater-
than-or-equal-to 1.

ERROR MESSAGES 729
108. THE MODEL’S DIMENSIONS EXCEED THE CAPACITY OF THIS VERSION.
Your model is too large for your version of LINGO. Some versions of LINGO limit one or
more of the following model properties: total variables, integer variables, nonlinear variables,
and constraints. This error message displays the dimensions of the model and the limits of
your version. Refer to this information to determine the specific limit that is being exceeded.
You can also view the limits of your version of LINGO by issuing the Help|About command.
Nonlinear variables are allowed only if you have purchased the nonlinear option for your
LINGO system. If you aren't sure which parts of yout model, you can run the Generate |
Display nonlinear rows command to display the rows in the model containing nonlinearities.
It's possible that some or all of the nonlinear rows can be rewritten so that they become linear.
In general, you must either make your model smaller by simplifying it or upgrade to a larger
version of LINGO. If you are exceeding the limit on constraints and if you have simple
bounds entered as constraints, you should enter them with the @BND function. Constraints
entered using @BND don’t count against the constraint limit.
The limits for the various versions of LINGO are:
Version Total
Variables Integer
Variables Nonlinear
Variables
Constraints
Demo/Web 300 30 30 150
Solver Suite 500 50 50 250
Super 2,000 200 200 1,000
Hyper 8,000 800 800 4,000
Industrial 32,000 3,200 3,200 16,000
Extended Unlimited Unlimited Unlimited Unlimited
If your version of LINGO doesn't include the nonlinear option, then your models can't contain
any nonlinear variables.
109. THE SOLVER ITERATION LIMIT WAS EXCEEDED.
The solver iteration limit was reached and the solution process was halted. If you believe that
there should be no iteration limit, then you should check to see what the current iteration limit
is. In Windows, check to see what the current setting is using the LINGO|Options command
to check the Iterations box on the General Solver tab. On other platforms, run the HELP SET
command to see what the setting is for the ITRLIM parameter.
110. PASSWORDS ARE LIMITED TO 8 CHARACTERS.
The password associated with your HIDE command is too long.
111. COMMAND NOT AVAILABLE WHEN MODEL IS HIDDEN.
Any command that reveals the content of a model is not permitted when the model is hidden.
If you know the password to unhide the model, enter it with the HIDE command and try
again.

730 APPENDIX B
112. INCORRECT PASSWORD... MODEL REMAINS HIDDEN.
You have entered an incorrect password. The model may not be viewed without the correct
password.
113. LOOK/SAVE FAILED... THE FOLLOWING LINE IS TOO LONG: N. INCREASE
THE TERMINAL WIDTH.
An attempt to view a given line, all lines, or to save the model, has failed because a line is too
long. Lines can't exceed 200 characters in length. You will need to break each long line into
two or more shorter lines.
114. PASSWORD VERIFICATION FAILED... MODEL WILL NOT BE HIDDEN.
You must enter the same password twice to verify it.
115. NOT USED.
116. THE MAXIMUM NUMBER OF CHARACTERS IN A FILE NAME IS: N.
The maximum number of characters in a file name, including path, has been exceeded.
117. INVALID COMMAND. TYPE ‘COM’ TO SEE VALID COMMANDS.
You have entered a command that is not implemented in LINGO. Check the list of available
commands with the COMMANDS command to see whether you’ve misspelled a command.
118. AMBIGUOUS COMMAND. TYPE ‘COM’ TO SEE VALID COMMANDS.
You have probably typed an abbreviated command that can be interpreted in more than one
way. Spell out the command name completely.
119. TOO MANY CONSECUTIVE ERRORS IN BATCH MODE. LINGO WILL STOP.
When running a command script, LINGO will stop after the sixth consecutive error.
120. UNABLE TO WRITE CNF FILE TO STARTUP AND WORKING DIRECTORIES.
LINGO was unable to write its configuration file. You must have write permission for either
the working directory or the startup directory. If you’re connected to a network, check with
your network administrator to determine your disk privileges.
121. RANGE ANALYSIS NOT ALLOWED ON INTEGER PROGRAMMING MODELS.
Because they have no meaning in this context, range reports are not possible on IP models.
122. RANGE REPORTS NOT POSSIBLE WHEN RANGE ANALYSIS IS DISABLED.
Range computations are currently disabled. To enable range computations in Windows
versions of LINGO, run the LINGO|Options command, click the General Solver tab, and
select the Prices and Ranges option from the Dual Computations list box. To enable range
computations in command-line versions of LINGO, use the command: SET DUALCO 2. Be
aware that range computations will increase solution times.
123. MODELS MUST BE EITHER INFEASIBLE OR UNBOUNDED IN ORDER TO BE
DEBUGGED.
Debugging is permitted only on models that are either infeasible or unbounded.

ERROR MESSAGES 731
124. NATTEMPT TO INITIALIZE AN ATTRIBUTE OF A NULL SET.
You are attempting to assign values to an attribute of a null set. Given that the set is null,
each of its attributes also have no members, and, therefore, may not be assigned values.
Check the initialization of the attribute’s parent set to be sure it is being assigned at least one
member.
125. LINGO IS UNABLE TO DEBUG UNBOUNDED INTEGER MODELS.
The model debugger currently can’t debug unbounded integer models. You may want to
remove the integrality conditions and then debug the model. This should help you track down
the source of unboundedness
126. THE FOLLOWING VARIABLE NAME WAS NOT RECOGNIZED: VAR_NAME.
You have attempted to use an ODBC link to export an unknown variable to a database. Check
the spelling of the variable’s name and try again.
127. THE FOLLOWING VARIABLE IS OF A DIFFERENT DIMENSION: VAR_NAME.
You have attempted to use an ODBC link to export multiple variables of different dimensions
to a database. All variables being simultaneously exported must be of the same dimension.
128. THE PARAMETER INDEX MUST BE BETWEEN 1 AND N.
You have input an invalid parameter index as part of the SET command. Use the HELP SET
command to determine the valid indices.
129. THE PARAMETER VALUE IS NOT VALID.
You have input an invalid parameter value as part of the SET command. LINGO will print the
valid range of values. You should adjust the value of the parameter, so it falls within the valid
range, and reenter the command.
130. THE FOLLOWING PARAMETER NAME WAS NOT RECOGNIZED:
PARAMETER_NAME.
You have input an invalid parameter name as part of the SET command. Use the HELP SET
command to determine the valid parameter names.
131. UNABLE TO WRITE PARAMETERS TO CONFIGURATION FILE.
You have attempted to save LINGO’s current configuration using the FREEZE command.
LINGO was unable to write the parameter values to its configuration file (LINGO.CNF).
Perhaps you don’t have write access to the drive or the disk is full.
132. ONE OR MORE ERRORS OCCURRED WHILE READING THE
CONFIGURATION FILE.
LINGO was unable to successfully read its configuration file (LINGO.CNF). Perhaps the file
has become corrupted. Beware that some of the parameters you have set may revert back to
their default values.
133. UNABLE TO INITIALIZE WORKBOOK FOR OLE TRANSFERS.
You have attempted to link to a spreadsheet that LINGO was unable to load into Excel. Try
reading the file into Excel yourself, and check to be sure that some other user isn’t accessing
the file.

732 APPENDIX B
134. UNABLE TO COMPLETE ALL OUTPUT OPERATIONS.
You have attempted to use interface functions in the data section to export parts of the
solution. One or more of these operations failed. You will receive additional messages from
LINGO detailing the problem.
135. THE FOLLOWING FIXED VARIABLE VIOLATES ITS SEMICONTINUOUS
BOUNDS: VARIABLE.
You have specified semicontinuous bounds for the specified variable using the @SEMIC
function. The variable was determined to be fixed to a particular value that violates its
semicontinuous property. For example, if X were specified to be semicontinuous using the
statement @SEMIC( 5, X, 100), then X must be either 0 or lie within the range [5,100]. If the
model generator determines that X is fixed at some value other than this, you will receive this
error message. The most likely cause of this error is incorrect semicontinuous bounds, i.e., in
this example, the bounds of 5 and 100
136. ERROR PERFORMING @TEXT() OUTPUT OPERATION: N.
You have attempted to use the @TEXT interface function to export data to a text file. For
some reason, this operation has failed. Perhaps the disk is full or you don’t have write access
to the drive.
137. NOT USED.
138. TOO MANY NESTED DIVERT FILES.
LINGO allows you to nest DIVERT commands up to 10 levels deep. If you attempt to go
beyond 10 levels, you will get this error message.
139. DIVERT COMMAND FAILED. UNABLE TO OPEN FILE.
You have attempted to open a file for output using the DIVERT command. LINGO was
unable to open the files. Perhaps the disk is full or you don’t have write access to the drive.
140. DUAL VALUES WERE REQUESTED BUT DUAL COMPUTATIONS ARE
DISABLED.
You have attempted to export dual values when the solver is in primals only mode. In primals
only mode, dual values are not computed and, therefore, can't be exported. In Windows
versions of LINGO, to enable dual computations, run the LINGO|Options command, click the
General Solver Tab, and select the Prices option from the Dual Computations list box. To
enable range computations, as well as, dual computations, select the Prices & Ranges option
from the Dual Computations list box. In command-line versions of LINGO, enable dual
computations by using the command: SET DUALCO 1. To enable range computations, as
well as, dual computations, use the command: SET DUALCO 2.
141. RANGE VALUES WERE REQUESTED ON A ROW THAT WAS SUBSTITUTED
FROM THE MODEL.
You have attempted to export range values on a row that is fixed in value. LINGO substitutes
these rows from the model. Therefore, range values are not computed on these rows.
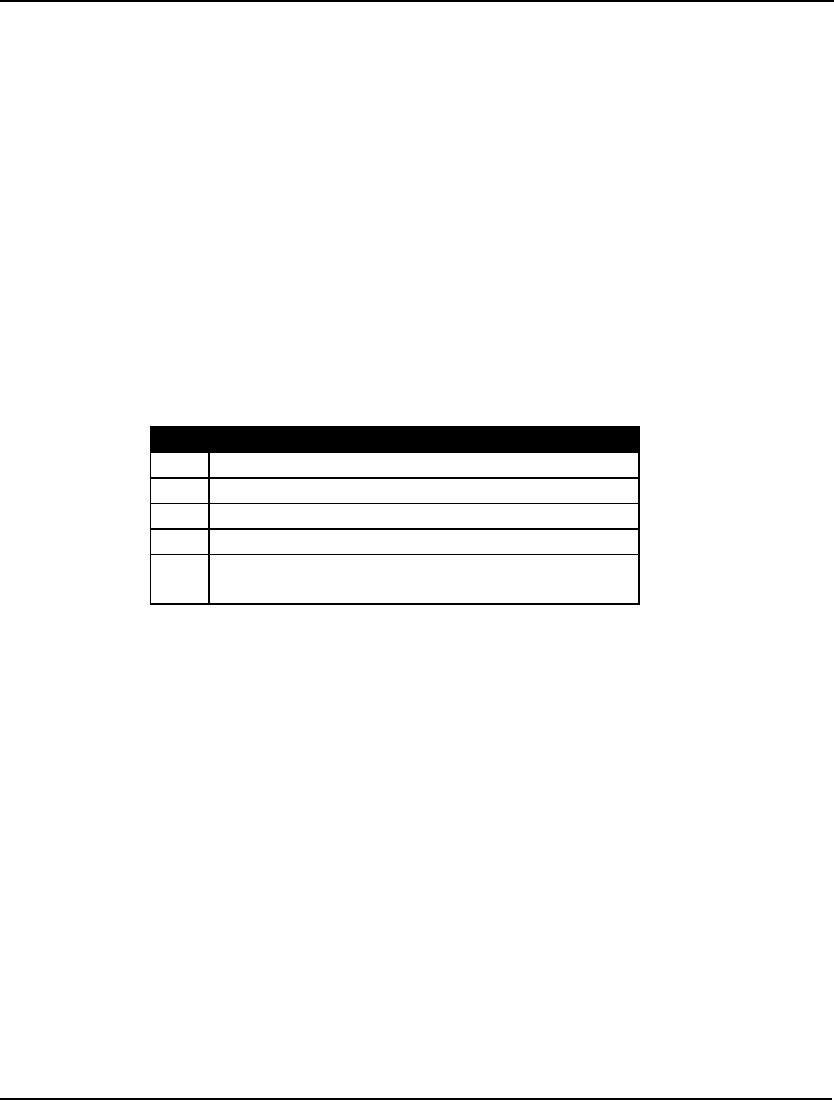
ERROR MESSAGES 733
142. AN UNEXPECTED ERROR OCCURRED. PLEASE CONTACT LINDO SYSTEMS
TECHNICAL SUPPORT.
In general, this error message should never occur. Should you receive this message, please
contact a technical support representative.
143. OUTPUT OPERATION FAILED. MODEL OBJECTS NOT OF SAME LENGTH.
You have attempted to use an interface function to export two or more model objects
simultaneously. This interface function requires all objects to be of the same dimension.
Break the output operation up into individual operations that all contain objects of the same
dimension.
144. INVALID ARGUMENT LIST FOR @POINTER FUNCTION.
The @POINTER function only accepts a single positive integer as an argument. Review the
documentation on the use of the @POINTER function.
145. ERROR N PERFORMING @POINTER OUTPUT OPERATION.
A @POINTER output function operation failed. Some of the values for N and their
interpretations are:
No. Interpretation
2 attempt to export an invalid variable
3 ran out of working memory
4 requested duals in primals only mode
5 range values were requested on fixed rows
6 unexpected error, call LINDO Systems Technical
Support
146. THE FOLLOWING NAMES APPEARED IN THE MODEL AND THE DATA:
NAME1 NAME2 NAME3.
If you go to the Model Generator tab on the LINGO|Options command’s dialog box, you will
see a Check for duplicates names in data and model checkbox. When this option is enabled,
LINGO will compare primal set member names to all the variable names used in the model’s
equations. If any duplicates are found, LINGO will print the first three and print this error
message. To enable this option in command-line versions, use the SET CHKDUP 1
command.
147. UNABLE TO EVALUATE ALL @WARN FUNCTIONS.
Conditional expressions contained in @WARN functions must contain fixed variables only.
When this is not the case, LINGO can’t evaluate the @WARN functions and you will receive
this error message.
148. @OLE FUNCTION NOT SUPPORTED ON THIS PLATFORM.
At present, the @OLE function is supported only in Windows versions of LINGO. If you
don’t have a Windows version of LINGO, you can export the data from your spreadsheet to a
file and use the @FILE function in your LINGO model to import the data.

734 APPENDIX B
149. TARGET RANGE NAMES CAN’T TAKE DEFAULT VALUES FOR INDEX
VARIABLE OUTPUT.
If you are outputting and index variable’s value to a workbook or database, you must
explicitly provide the name of the workbook range or the database column. LINGO cannot
provide default names in this instance.
150. ODBC INTERFACE NOT SUPPORTED ON THIS PLATFORM.
LINGO’s ODBC link to databases is supported only in Windows versions. If you don’t have a
Windows version of LINGO, you can use text files to move data in and out of LINGO. See
Chapter 8, Interfacing with External Files, for more details.
151. @POINTER NOT SUPPORTED ON THIS PLATFORM.
LINGO’s @POINTER function for interfacing with calling applications is supported only in
Windows versions. If you don’t have a Windows version of LINGO, you can use text files to
move data in and out of LINGO. See Chapter 8, Interfacing with External Files, for more
details.
152. COMMAND NOT SUPPORTED ON THIS PLATFORM.
You have selected a command that is not supported on your platform.
153. SET DEFINITIONS NOT ALLOWED IN INIT SECTIONS.
Sets can’t be initialized in an INIT section. You must change the model, so the set is
initialized in either a sets section or in a data section.
154. ATTEMPT TO REDEFINE A PREVIOUSLY DEFINED SET.
You have attempted to define a set twice in the same model. A set name can only be used
once. Choose a different name for the two sets and try again.
155. SET MEMBER NAMES MAY NOT BE OMITTED IN DATA STATEMENTS.
When initializing a set in a model’s data section, you must explicitly list each member. You
may not skip elements as you can with set attributes.
156. INCORRECT NUMBER OF ARGUMENTS IN A DATA SECTION.
ARGUMENT MUST BE A MULTIPLE OF: N
NUMBER OF ARGUMENTS FOUND: M
You have a data, init or calc statement in your model that doesn’t have the correct number of
values to initialize a specified list of attributes and/or sets. LINGO will let you know how
many values it found and what the number of arguments should be a multiple of. Add or
subtract values in the data statement and try again.
157. ATTEMPT TO USE @INDEX ON AN UNDEFINED SET.
LINGO can’t compile an instance of the @INDEX function without knowing of the existence
of the set that @INDEX is referencing. Move the expression with the @INDEX function after
the set definition to correct this problem.
158. A SET MEMBER NAME WAS EXPECTED.
You have used a function that was expecting a set member name as an argument. Correct the
arguments to the function and try again.

ERROR MESSAGES 735
159. THE FOLLOWING DERIVED SET MEMBER IS NOT CONTAINED IN ITS
PARENT SET.
You have specified a set member in a derived set that is not contained in the parent set. Each
member in a derived set must be derived from a member of its parent set(s). You have
probably misspelled the name of the derived set member. Check the spelling and try again.
160. ONLY ONE SET MAY BE DEFINED IN EACH DATA STATEMENT.
You have attempted to define more than one set in an individual data statement. Break the
data statement into multiple statements with no more that one set per statement.
161. INDEX VARIABLES MAY NOT SHARE NAMES WITH OTHER VARIABLES.
The index variables used in set looping functions may not use the same names as those used
by the structural variables in the model. For example, in the following model:
MODEL:
SETS:
S1/1..5/: X;
ENDSETS
MAX=I;
@SUM( S1( I): X( I)) <= 100;
END
the variable name i is used in the objective row for a structural variable. In the next to the last
statement in the model, the name i is also being used as an index variable, which will trigger
the error. In the case, you would need to change the name of either the variable in the
objective or the name of the index variable in the @SUM loop.
162. ATTEMPT TO INITIALIZE MIXED DATA TYPES (TEXT AND NUMERIC) FROM
A SINGLE WORKBOOK RANGE.
When specifying a single range for multiple model objects, all the objects must be of the
same data type—either text (set members) or numeric (set attributes). LINGO’s spreadsheet
interface can’t handle ranges with mixed data types. Break the data statement up into two—
one containing text model objects and the other containing numeric objects.
163. INVALID NUMBER OF DATA VALUES FOR OBJECT: OBJECT_NAME.
You have attempted to initialize a model object of known length with an incorrect number of
values. Check the initialization statement to be sure that the values are specified correctly.
164. INVALID LINGO NAME: NAME.
You have used a symbol name that doesn’t conform to LINGO’s naming conventions. Please
correct the name and try again.
165. SET EXPORTS NOT SUPPORTED WITH THIS FUNCTION.
Not all of LINGO’s export functions can handle set members. Switch to a different export
function and try again.

736 APPENDIX B
166. ATTEMPT TO OUTPUT OBJECTS OF VARYING LENGTHS TO A TABULAR
DEVICE.
LINGO requires output to be in tabular form for certain output devices (databases and text
files). You have constructed an output statement with two or more model objects of varying
length. In which case, it is not obvious how to transform the data into tabular form. Break the
output function call up into two or more function calls such that each call contains model
objects of identical length.
167. INCORRECT NUMBER OF RANGES SPECIFIED: N. NUMBER OF RANGES
REQUIRED: M.
You didn’t specify the correct number of ranges in an import/export function. In general, you
will need one range for each model object.
168. OUTPUT MODIFIERS NOT ALLOWED ON TEXT DATA.
When exporting set members, use of the @DUAL, @RANGEU, and @RANGED modifier
functions are not allowed. Remove the modifier function and try again.
169. RUNTIME INPUT OF SET MEMBERS NOT ALLOWED.
When initializing attributes in a data section, you can initialize all or part of an attribute with
a question mark. In which case, LINGO will prompt you for the values each time the model is
run. This is not the case with sets—all set members must be explicitly listed when initializing
a set in the data section.
170. LICENSE KEY WAS NOT FOUND OR IS INVALID.
LINGO did not recognize your license key. Please check to make sure you have entered it
correctly. If you received it as part of an email, then you may cut-and-paste it from the email
into LINGO's license dialog box.
171. LICENSE KEY IS INVALID.
Your license key is not recognized by LINGO. LINGO will continue to operate, but only in
demonstration mode.
172. INTERNAL SOLVER ERROR. CONTACT LINDO SYSTEMS.
LINGO’s solver encountered an unexpected error condition and was unable to continue.
Please contact LINDO Systems for assistance.
173. NUMERICAL ERROR IN THE SOLVER.
LINGO’s solver experienced numerical problems and was unable to continue. Scaling the
model’s coefficients so that they don’t cover as large a range may be helpful in eliminating
this error. Also, check for potentially undefined arithmetic operations in the model. If these
remedies fail, please contact LINDO Systems for assistance.
174. OUT OF MEMORY IN PREPROCESSOR.
LINGO’s solver ran out of memory during the preprocessor phase. Refer to error message
175 for possible remedies.

ERROR MESSAGES 737
175. NOT ENOUGH VIRTUAL SYSTEM MEMORY.
LINGO’s solver ran out of virtual system memory. LINGO’s solver accesses memory from
the system heap. Adding more memory to your machine may help. Note, also, that the
memory allocated to LINGO’s model generator is not available to the solver. Thus, if too
much memory is allocated to the generator there may not be enough left over for the solver. If
you are using a Windows version of LINGO, see the LINGO|Options command for
information on adjusting the generator memory level, otherwise, refer to the SET command.
176. OUT OF MEMORY DURING SOLVER POSTPROCESSING.
LINGO’s solver ran out of memory during the post-processing phase. Refer to error message
175 for possible remedies.
177. OUT OF MEMORY ALLOCATING SET: SET_NAME.
LINGO failed to allocate the internal data structures for a set due to lack of generator
memory. First, check to see that the set's dimensions are not unreasonably large, perhaps
indicating a typo in the model. If all appears well, then you will need to boost the available
generator memory, restart LINGO and try again.
178. OUT OF STACK SPACE ALLOCATING SET: SET_NAME.
When LINGO allocates the data structures for a set, it may find that the set is derived from
another set. If this parent set is also unallocated, LINGO must back track and allocate it, too.
In some rare instances, LINGO might have to backtrack many generations. As LINGO back
tracks, it keeps information on a stack. This error message is triggered when this stack runs
out of space. However, it would be a highly unusual model that causes this error.
179. THE MPS READER HAD TO PATCH NAMES TO MAKE THEM COMPATIBLE
VAR NAMES PATCHED: N
ROW NAMES PATCHED: M
This message occurs when LINGO imports an MPS file converting it to a LINGO model.
MPS format allows for variable and row names that aren’t entirely compatible with LINGO’s
syntax (e.g., spaces in names). In order to overcome this, LINGO will patch these names by
replacing inadmissible characters in the names with underscores and truncating names longer
than 32 characters. This can create problems because two or more unique MPS names may
get mapped into one LINGO name. A technique for avoiding this problem is to use R/C
naming conventions. Refer to the Use R/C format names for MPS I/O option for more
information.
180. UNABLE TO CREATE MODEL DATA STRUCTURE.
LINGO was unable to create the internal data structures required for transferring an MPS file.
The most likely cause of the problem is insufficient system memory. Try cutting back on
LINGO’s allotment of generator memory or using a machine with more memory.
181. ERROR EXTRACTING DATA FROM MODEL STRUCTURE.
LINGO was unable to extract model information from a data structure. The most likely cause
of the problem is insufficient system memory. Try cutting back on LINGO’s allotment of
generator memory, or try using a machine with more memory.

738 APPENDIX B
182. ERROR IN MPS OR MPI FILE ON LINE NUMBER: N
TEXT OF INVALID LINE: TEXT
LINGO encountered an error reading an MPS or MPI format file. Go to the line number in the
file, correct the error, and try again.
183. INVALID USE OF SP TABLE DECLARATION FUNCTION @SPDISTTABLE.
The @SPDISTTABLE function is a matrix oriented function that is uses in stochastic
programming models to declare outcome tables and assign to assign random variables to
those tables. Correct usage is:
@SPDISTTABLE( OUTCOME_TABLE_ATTR, RANDOM_VAR_VECTOR[,
PROBABILITY_VECTOR]);
The outcome table argument must be either one or two dimensions, with each row of the table
corresponding to an outcome of the random variable(s) in the random variable vector. The
number of elements in the random variable vector must equal the number of columns in the
outcome table argument. The third argument is optional, is used to pass the probabilities of
the outcomes, and must have one element for each row of the outcome table.
184. RANGE VALUES CAN'T BE REPORTED WHEN RANGE ANALYSIS IS
DISABLED.
You have attempted to reference range values while the solver is not set to compute ranges.
To enable range computations in Windows versions of LINGO, run the LINGO|Options
command, click the General Solver Tab, and select the Prices and Ranges option from the
Dual Computations list box. To enable dual and range computations in command-line
versions of LINGO use the command: SET DUALCO 2.
185. BARRIER SOLVER REQUESTED WITHOUT A LICENSE.
LINGO’s barrier solver capability is an additional option. To enable the option, contact
LINDO Systems for licensing information and fees.
186. SETS MAY NOT BE INITIALIZED WITH @QRAND.
The @QRAND function may be used for initializing attributes only. Set members can not be
initialized with this function.
187. ONLY ONE LHS ATTRIBUTE MAY BE INITIALIZED IN A @QRAND
STATEMENT.
You can initialize only one attribute at a time with the @QRAND function. For more
information, refer to the Probability Functions section in Chapter 7, Operators & Functions.
188. ATTRIBUTES INITIALIZED WITH @QRAND MUST BELONG TO DENSE SETS.
You can initialize only one attribute of dense sets with the @QRAND function. For more
information, refer to the Probability Functions section in Chapter 7, Operators & Functions.
189. INVALID SEED.
You have attempted to use an invalid seed value for a random number generating function.
Seed values must have non-negative, integer values.

ERROR MESSAGES 739
190. INVALID IMPLICIT SET DEFINITION.
LINGO allows you to express sets implicitly. An example would be Jan..Dec, which would
give you a set of 12 elements consisting of the months of the year. There are a number of
syntax rules required of implicit set definitions. For information on the specific rules, refer to
Chapter 2, Using Sets.
191. THE LINDO API RETURNED THE FOLLOWING ERROR CODE: N ERROR_TEXT.
The LINDO API is the core solver engine used by LINGO. On rare occasions, the LINDO
API may raise an unexpected error condition. LINGO will display a text message from the
API regarding the error. In most cases, this message should clarify the situation. If not, please
contact LINDO Systems technical support.
192. @WKX NO LONGER SUPPORTED…USE @OLE INSTEAD.
The @WKX function is no longer supported. You must now use the @OLE function to
interface with spreadsheets.
193. A SOLUTION IS NOT AVAILABLE FOR THIS MODEL.
There is no solution associated with the model. Either an error occurred while attempting to
solve the model, or the model has not been solved yet.
194. UNABLE TO CREATE ENVIRONMENT DATA STRUCTURE.
LINGO was not able to allocate some internal data structures. This is most likely due to
insufficient memory in your system’s dynamic memory pool. You can try running on a
machine with more memory, increasing Windows allotment of virtual memory, and/or
reducing the amount of generator memory allocated to LINGO’s model generator.
195. AN ERROR OCCURRED WHILE ATTEMPTING TO WRITE TO A FILE.
LINGO experienced problems writing to a file. Be sure your disk is not full and that you have
write access to the target file.
196. A DUAL SOLUTION DOES NOT EXIST FOR THIS MODEL.
The solver was unable to successfully compute the dual solution for the model. Given this,
the solution report will only display primal values. This is an unusual error. If possible, please
forward your model to LINDO Systems for evaluation.
197. THE MODEL CONTAINS ONE OR MORE VACUOUS @MAX OR @MIN
FUNCTIONS.
The model contains an @MAX or @MIN function that has no arguments. An example of
this situation is:
MODEL:
SETS:
S1/1..5/: X;
ENDSETS
THEMAX = @MAX( S1( I) | I #LT# 0: X( I));
END
Note that the index variable I will take on values 1, 2, 3, 4 and 5. In no case will I ever be
less than 0. This means that the condition (I #LT# 0) on the @MAX function will never be

740 APPENDIX B
satisfied, meaning that there are no explicit arguments to the @MAX function. Please check
that all the @MAX and @MIN functions in the model are correctly specified.
198. QUADRATIC MODEL IS NOT CONVEX.
Quadratic models must be convex in order for them to be solved by the quadratic solver. You
must disable the quadratic solver by turning off quadratic recognition and then re-solve. This
will cause the general purpose, nonlinear solver to be invoked.
199. A BARRIER SOLVER LICENSE IS REQUIRED FOR THE QUADRATIC SOLVER.
You will need a license for the barrier option to run the quadratic solver. You can proceed by
disabling quadratic recognition and re-solving. This will cause the general purpose, nonlinear
solver to be invoked.
200. UNABLE TO COMPUTE DUAL SOLUTION.
LINGO was unable to compute the dual values. You can proceed by turning off dual
calculations and re-solving.
201. THE MODEL IS LOCALLY INFEASIBLE.
The solver was unable to find a feasible solution within a local region. However, a feasible
solution may exist elsewhere. The global or multistart solvers may have more success.
202. THE NUMBER OF NONLINEAR VARIABLES IN THE MODEL: N1 EXCEEDS
THE GLOBAL SOLVER LIMIT IN THIS VERSION: N2
Some versions of LINGO impose a limit on the total number of nonlinear variables when
running the global solver. You will either need to reduce the number of nonlinear variables,
turn off the global solver, or upgrade to a larger version of LINGO.
203. THE GLOBAL SOLVER OPTION WAS REQUESTED WITHOUT A LICENSE.
LINGO WILL REVERT TO USING THE DEFAULT NONLINEAR SOLVER.
Your installation of LINGO does not have the global solver option enabled. The global solver
is an add-on option to LINGO. LINGO will use the standard nonlinear solver in upgrading
your license in order to enable this option.
204. THE MULTISTART OPTION WAS REQUESTED WITHOUT A LICENSE. LINGO
WILL REVERT TO USING THE DEFAULT NONLINEAR SOLVER.
Your installation of LINGO does not have the global solver option enabled. The multistart
solver is a component of the global solver add-on option. LINGO will use the standard
nonlinear solver in place of the multistart solver. You can contact LINDO Systems for
information on upgrading your license in order to enable this option.
205. THE MODEL IS POORLY SCALED AND MAY YIELD ERRATIC RESULTS. THE
UNITS OF THE ROWS AND VARIABLES SHOULD BE RESCALED SO THE
COEFFICIENTS COVER A MUCH SMALLER RANGE.
After LINGO generates a model, it checks all the nonzero coefficients in the model and
computes the ratio of the largest to smallest coefficients. This ratio is an indicator of how
well the model is scaled. When the ratio gets to be too high, scaling is considered to be poor,
and numerical difficulties may result during the solution phase. If the scaling ratio exceeds
the value of the SCALEW parameter, LINGO will display this error message. The default

ERROR MESSAGES 741
value for SCALEW is 1e9. Instead of simply increasing the SCALEW setting to eliminate
error 205, we strongly suggest that you attempt to rescale the units of your model so as to
reduce the largest-to-smallest coefficient ratio.
In some instances, changing the units of measure can be an easy way to improve a model’s
scaling. For instance, suppose we have a model with the following budget constraint in dollar
units:
1000000 * X + 2200000 * Y + 2900000 * Z <= 5000000;
This constraint introduces several large coefficients into the model. If we rewrote the
constraint so that it is in units of millions of dollars, then we would have:
X + 2.2 * Y + 2.9 * Z <= 5;
The coefficients in this new constraint are much less likely to present a problem.
As part of this error message, LINGO reports the values of the largest and smallest
coefficients, as well as where they appear in the model. This information should help in
tracking down the problem. You may also run the LINGO|Generate command to track down
other extreme coefficients. This Generate command displays the full, generated model and
specifically lists all the coefficients.
206. A MODEL MAY NOT BE SOLVED WITH LINEARIZATION AND THE GLOBAL
SOLVER SIMULTANEOUSLY ENABLED. LINEARIZATION WILL BE
TEMPORARILY DISABLED.
The linearization and global solver options may not be simultaneously selected when solving
a model. LINGO will default to using the global solver. You can set the linearization option
on the General tab of the LINGO|Options command, while the global solver option is
controlled on the Global Solver tab.
207. MISSING LEFT PARENTHESIS.
A unmatched right parenthesis was encountered in the model. Use the Edit|Match
Parenthesis command to help pair up parentheses.
208. @WRITEFOR() MAY ONLY APPEAR IN A DATA AND CALC SECTIONS.
The @WRITEFOR function is permitted only in the data and calc section of a model. You
will need to move the expression to a data or calc section.
209. RELATIONAL OPERATORS NOT ALLOWED IN @WRITEFOR() STATEMENTS.
The @WRITEFOR function is used to display output. Constraint relational operators may not
be used inside the @WRITEFOR function.
210. INVALID USAGE OF @WRITEFOR() FUNCTION.
The @WRITEFOR function is being used incorrectly. @WRITEFOR may only be used in the
data and calc sections for the purpose of creating reports. Refer to the documentation for the
correct usage of @WRITEFOR.

742 APPENDIX B
211. ARITHMETIC ERROR IN OUTPUT OPERATION.
The @WRITEFOR function is being used incorrectly. @WRITEFOR may only be used in the
data section for creating reports. Refer to the documentation for the correct usage of
@WRITEFOR.
212. SUBSCRIPT OUT OF RANGE ON SET NAME: SET_NAME
A subscript was found to be out of range while attempting to output a set member, . Check
all output operations that refer to the set SET_NAME for correctness.
213. TEXT OPERAND NOT PERMITTED HERE.
A text argument to a function was encountered where something other than text was
expected. Please check all function arguments to be sure they are correct.
214. DUPLICATE INITIALIZATION OF A VARIABLE.
A variable has been initialized more than one time in the model's data sections. Eliminate all
duplicate variable initializations.
215. OUTPUT MODIFIERS NOT ALLOWED HERE (E.G., @DUAL)
Output modifiers (e.g., @DUAL, @RANGEU, @RANGED) are not allowed here. Remove
them to continue.
216. PREFIX FUNCITON EXPECTED A TEXT ARGUMENT.
Output modifiers (e.g., @DUAL, @RANGEU, @RANGED) are not allowed here. Remove
them to continue.
217. PREFIX FUNCTION EXPECTED A NUMERIC ARGUMENT.
A function was expecting a numeric argument, but found something other than a numeric
value. Check all function arguments for correctness.
218. PREFIX FUNCITON EXPECTED A ROW OR VARIABLE INDEX ARGUMENT.
A function was expecting a variable or row name as an arguments but found something
different. Check all function arguments for correctness.
219. UNABLE TO FIND A SPECIFIED INSTANCE OF A ROW NAME.
You've requested the value of a row that does not exist in the model.
220. UNSUPPORTED OPERATION ON TEXT OPERAND.
You've attempted to perform an undefined operation on a text operand.
221. ARGUMENT OVERFLOW IN @WRITE() OR @WRITEFOR().
This error occurs when there are too many text objects being output within a single @WRITE
or @WRITEFOR function call. Reduce the size of any large arguments lists to these
functions.
222. A VARIABLE OR ROW REFERENCE WAS EXPECTED.
A variable or row reference was expected here.

ERROR MESSAGES 743
223. A DYNAMIC RANGE EXCEEDED BOUNDARY LIMITS WRITING TO RANGE:
RANGE_NAME
You attempted to write more values to a spreadsheet than it can actually hold. In general, this
means the dynamic range created by LINGO to receive all the values has overflowed the row
limit of the spreadsheet. An option is to specify the range yourself so that it stays within the
limits of the workbook.
224. THE FOLLOWING RANGE IS TOO SMALL TO RECEIVE ALL REQUESTED
OUTPUT: RANGE_NAME
You've specified a workbook range that is too small to receive all the exported values. You'll
need to increase the size of the range.
225. INVALID FORMAT FOR A CALC EXPRESSION.
A calc section is only for performing computations. Various functions are not permitted in
the calc section (e.g., @GIN and @FREE). Remove any disallowed functions to continue.
226. DEFAULT WORKBOOK NOT OPEN.
If all arguments are omitted to the @OLE spreadsheet interface function, then Excel must be
open with a workbook in memory (@OLE will default to using this open workbook). Open
Excel and then load the workbook containing the data for your model.
227. THE FOLLOWING RANGE: RANGE_NAME MUST HAVE A COLUMN COUNT
EQUAL TO THE NUMBER OF MODEL OBJECTS BEING
IMPORTED/EXPORTED.
When importing values from or exporting values to a workbook you need to consider the
number of model objects involved. When multiple objects are being either sent to or received
from a single range in a workbook, the number of columns in the range must coincide with
the number of model objects. Keep in mind that a derived set counts as more than one object
depending upon its dimension. You must either adjust the size of the workbook range to the
correct number of columns or edit the set of model objects involved in the interface statement.
228. INVALID API PARAMETER INDEX.
The parameter index you specified as part of the APISET command is not valid. Refer to the
LINDO API documentation for a list of valid parameter indices.
229. INVALID API PARAMETER TYPE.
The parameter type you specified as part of the APISET command is not valid. The
parameter type must be specified as either “int” for integer or “double” for double precision
floating point. Refer to the LINDO API documentation for a list of valid parameter indices
and their types.
230. INVALID API PARAMETER VALUE.
The parameter value you specified as part of the APISET command is not valid. Refer to the
LINDO API documentation for a list of valid parameter indices and their permissible values.

744 APPENDIX B
231. UNABLE TO SET LINDO API PARAMETER.
The parameter value you specified as part of the APISET command is not valid. Refer to the
LINDO API documentation for a list of valid parameter indices and their permissible values.
To clear all parameter values set with APISET enter the command: APISET DEFAULT.
232. RANGE ANALYSIS NOT AVAILABLE ON QUADRATIC PROGRAMS.
LINGO cannot currently perform range analysis on quadratic programs. You’ll need to
disable range analysis by running the LINGO|Options command, selecting the General Solver
tab, and set the Dual Computations option to disable range analysis. On platforms other than
Windows, you’ll need to set the DUALCO option to disable range analysis.
233. THE DEBUGGING PROCESS WAS INTERRUPTED.
You interrupted the model debugger, before it could complete its analysis. Given this, the
resulting report will be incomplete or empty.
234. N LARGE NUMBER(S) WERE TRUNCATED TO A VALUE OF:
<MACHINE_INFINITY>.
You attempted to input one or more numbers that are too large to be handled on your
hardware. LINGO reduced the numbers to your machine’s infinity. In general, you should
scale your models so that very large numbers are not required.
235. THE MODEL IS NONLINEAR AND MAY NOT BE GENERATED AS A LINEAR
PROGRAM
You have attempted to generate a nonlinear model with the Assume model is linear option
enabled. You will need to run the LINGO|Options command, select the Model Generator tab,
and disable this option. On platforms other than Windows, you will need to issue the SET
LINEAR 0 command.
236. INCORRECT @FORMAT USAGE IN AN OUTPUT STATEMENT.
The arguments to an @FORMAT() reference are not valid. @FORMAT() requires one
numeric argument (the numeric value to be formatted) and one text argument (the format
template). For example,
@FORMAT( X, ’14.5g’)
will cause X to be displayed using 5 significant digits in a field of 14 characters.
237. RANGE ANALYSIS NOT CURRENTLY AVAILABLE ON THIS MODEL.
LINGO does not have range analysis data available for the model. You’ll need to disable
range analysis by running the LINGO|Options command, selecting the General Solver tab,
and set the Dual Computations option to enable range analysis. You should then re-solve the
model.
238. OBJECTS DISPLAYED BY @TABLE() ARE LIMITED TO A DIMENSION OF: 16.
The @TABLE() function can be used to display sets and attributes in tabular format. At the
moment, these objects are limited to a maximum dimension of 16, which should be more than
adequate for most models.

ERROR MESSAGES 745
239. A TABLE IS TOO WIDE TO DISPLAY.
The @TABLE() function can be used to display setS and attributes in tabular format. You
have requested an @TABLE() report that is too wide for the current page width setting. You
will need to increase this setting by running the LINGO|Options command, selecting the
Interface tab and then increase the Width parameter in the Page Size Limits box. On
platforms other than Windows, you will need to adjust the line width parameter with the SET
LINLEN command.
240. INVALID USE OF @TABLE() OUTPUT FUNCTION.
The model contains an invalid reference to the @TABLE() function. The valid forms of
arguments lists for @TABLE() are:
1. @TABLE( AttrName|SetName)
2. @TABLE( AttrName|SetName, HzPrimSet)
3. @TABLE( AttrName|SetName, HzPrimSet1,…, HzPrimSetI)
4. @TABLE( AttrName|SetName, HzPrimSet1,…, HzPrimSetK)
5. @TABLE( AttrName|SetName, HzPrimSet1,…, HzPrimSetN, NHz)
Currently, @TABLE() output can only be routed to etiher the standard output device or text
files via the @TEXT() interface function.
241. @IFC STRUCTURE IS TOO DEEPLY NESTED.
Calc sections can use @IFC/@ELSE statements to implement conditional branching.
Presently, you may nest @IF statements up to 64 levels deep. You will receive this error
message if your model exceeds this limit.
242. INVALID USE OF @IFC CONSTRUCT.
Calc sections can use @IFC/@ELSE statements to implement conditional branching. You
will receive this error message if an @IFC is note being used correctly. An example would
be an @ELSE statement appearing before a corresponding @IFC. Refer to the
documentation on the use of @IFC for more information.
243. MULTIPLE @ELSE BLOCKS WERE FOUND.
Calc sections can use the @IFC/@ELSE statements to implement conditional branching.
You will receive this error message if a compound @IFC statement contained more than one
@ELSE branch.
244. @IFC CONTROL STRUCTURE ONLY ALLOWED IN CALC SECTIONS.
Calc sections can use the @IFC/@ELSE statements to implement conditional branching.
You have attempted to use these statements outside of a Calc section. You will need to either
move them to a Calc section or delete them.
245. AN UNTERMINATED @IFC STRUCTURE WAS FOUND.
Calc sections can use the @IFC/@ELSE statements to implement conditional branching. An
@IFC/@ELSE compound statement is terminated with a right parenthesis, which, in this
instance, is missing. You will need to add the terminating right parenthesis at the appropriate
place.

746 APPENDIX B
246. THE @SOLVE() FUNCTION IS ONLY VALID IN CALC SECTIONS.
A number of command functions are allowed only in Calc sections, one of which is the
@SOLVE() function for solving a model. You will need to either delete the function
reference or move it to a Calc section.
247. INVALID USE OF A SUBMODEL NAME.
LINGO allows you to define submodels within a main model. These submodels can be
solved using the @SOLVE() function in Calc sections. Your model has an invalid reference
to a submodel. You must remove this reference in order to proceed.
248. SUBMODEL NAMES MUST BE UNIQUE.
LINGO allows you to define submodels within a main model using the SUBMODEL
statement. These submodels can be solved using the @SOLVE() function in Calc sections.
You have attempted to use the same submodel name more that once. You must change the
names of the submodels so that all the names are unique.
249. SUBMODEL NOT VALID HERE.
LINGO allows you to define submodels within a main model using the SUBMODEL
statement. These submodels can be solved using the @SOLVE() function in Calc sections.
You have attempted to locate a submodel in an invalid section of the model. Please move the
submodel to the main part of the model, outside of all Data, Calc and Init sections.
250. SUBMODEL NOT DEFINED YET.
LINGO allows you to define submodels within a main model using the SUBMODEL
statement. These submodels can be solved using the @SOLVE() function in Calc sections.
You have referenced a submodel that has not been defined. Submodels must be defined in
the model before any occurrences of references to them. You may be able to solve this error
by moving the submodel in question to an earlier position in the model text.
251. MODEL CONTAINS AN UNTERMINATED SUBMODEL STATEMENT.
LINGO allows you to define submodels within a main model using the SUBMODEL
statement. These submodels can be solved using the @SOLVE() function in Calc sections.
Your model contains a submodel without a terminating ENDSUBMODEL statement.
252. A VARIABLE OR ROW REFERENCE WAS EXPECTED.
LINGO was expecting a reference to a row or variable name. You will need to correct the
problem to continue.
253. OPERATION ALLOWED ONLY IN CALC SECTIONS.
A number of operators are allowed only in Calc sections. An example would be the
@SOLVE() function. You will need to either delete the function reference or move it to a
Calc section.
254. INVALID PARAMETER ARGUMENT FOR @SET( PARAM, VALUE).
The @SET() function can be used in a Calc section to set any of LINGO’s parameters . You
must provide the parameter’s name as text, and a permissible value for the parameter. For
instance, to turn set the iteration limit to one million, you would use @SET( ‘ITRLIM’, 1.e6).

ERROR MESSAGES 747
You can refer to documentation on the SET command to learn all the parameters and their
names.
255. IMPROPER USE OF A CALC COMMAND FUNCTION.
You may include a Calc section in your model that contains a series of commands for LINGO
to execute. Examples would include the @SOLVE() and @WRITE() command functions.
This error is triggered when one of these command functions is used incorrectly. You should
refer to the documentation to learn the correct usage and syntax for the function.
256. @WHILE() ALLOWED ONLY IN CALC SECTION.
At present, the @WHILE() statement is allowed only in calc sections and may not appear in
the model section. You may be able to use the @FOR() statement instead.
257. INVALID ARGUMENT FOR @SET( ‘PARAM’, VALUE).
In order to set a parameter via the @SET command you must specify a correct parameter
name in quotes and a correct value. Please be sure you have spelled the parameter name
correctly and that you have placed it in quotes. Also, check that the specified value is
permissible for the parameter.
258. MODEL EXECUTION HALTED. STOP STATEMENT ENCOUNTERED.
LINGO encountered an @STOP() statement while processing a calc section. This terminates
execution of the current model. If a text string was specified in the reference to @STOP(),
then it will also be displayed as part of this message. @STOP is typically used in response to
some unexpected condition.
259. FILE NAME LENGTH EXCEEDS: N
You’ve specified a file name whose length exceeds the maximum length allowed of N
characters. You will need to shorten the length of the file name to continue.
260. @BREAK() MAY ONLY APPEAR IN @WHILE() AND @FOR() LOOPS INSIDE
CALC SECTIONS
The @BREAK() statement is used for unconditional breaks out of @FOR() and @WHILE()
loops. It may also only be used inside calc sections, and is not valid in the model section.
You will need to delete the reference to @BREAK() to continue.
261. INVALID ARGUMENT FOR @RELEASE(). ARGUMENTS MUST BE A SINGLE
VARIABLE REFERENCE, E.G., @RELEASE( X).
The @RELEASE() statement is used in calc sections to release a variable that was previously
fixed so it may once again become optimizable. To release an entire attribute, place the
@RELEASE() reference in an @FOR() loop, e.g., @FOR( SET( I): @RELEASE( X( I))).
262. INVALID ARGUMENT FOR @APISET( PARAM-ID, ‘INT|DOUBLE’, VALUE).
The @APISET() statement is used in calc sections to set options in the LINDO API
(LINGO’s solver engine) that aren’t available through the standard option set in LINGO. The
argument list consists of a parameter-id (an integer value), a string specifying if the parameter
is an integer or a double precision value, and the parameter value. More information on the
parameters available in the LINDO API may be found in the LINDO API documentation and
the Lindo.h header file included with your LINGO installation.

748 APPENDIX B
263. MODEL WAS FOUND TO BE FEASIBLE AND CANNOT BE DEBUGGED.
You have run the LINGO|Debug to find the infeasibilities in a model that was found to be
feasible. In which case the model debugger will stop its search for an infeasible subset of
constraints.
264. LINEARIZED MODEL TOO LARGE FOR THIS VERSION.
You have enabled LINGO's linearization option, which attempts to rewrite nonlinear models
in an equivalent, but linear, manner. This requires the addition of variables and constraints,
whose increased counts have exceeded the limits of your version. You will need to either
disable linearization or upgrade to a larger capacity version of LINGO.
265. DUPLICATE VARIABLES WERE FOUND IN THE SEMI-CONTINUOUS SET.
LINGO supports semi-continuous (SC) variables. SC variables are restricted to being either
0, or to lie within some non-negative range. Semi-continuous variables are declared using the
@SEMIC statement. A variable may only be declared semi-continuous once in a model.
You will receive this error message if one or more variables are declared semi-continuous
more than one time.
266. BOUNDS OUT OF RANGE ON A SEMI-CONTINUOUS VARIABLE.
LINGO supports semi-continuous (SC) variables. SC variables are restricted to being either
0, or to lie within some non-negative range. Semi-continuous variables are declared using the
@SEMIC statement. The syntax for @SEMIC is:
@SEMIC( lower_bound, variable, upper_bound)
You will receive this error whenever the variable bounds fall outside the range permitted by
LINGO.
267. @SOS OR @CARD SET LABEL EXCEEDS LIMIT OF: <N>
LINGO supports special ordered sets (SOS) of variables as well as cardinality sets of
variables. Each set is denoted by a unique name/label, which is limited to <N> characters in
length. You will need to choose a shorter label name for the variable set.
268. VARIABLE SET LABEL USED TO REPRESENT MORE THAN ONE SET TYPE.
LINGO supports special ordered sets (SOS) of variables as well as cardinality sets of
variables. Each set is denoted by a unique label/name. You have attempted to use the same
set label for different set types (e.g., SOS1 and SOS2). Check to be sure you've specified the
correct set name and/or set type.
269. THE FIRST ARGUMENT TO @SOS/@CARD MUST BE A STRING.
LINGO supports special ordered sets (SOS) of variables as well as cardinality sets of
variables. Each set is denoted by a unique label/name. The first argument to the @SOS and
@CARD functions must be a string representing the label name for the particular variable set.
Furthermore, the label name must be contained in single or double quotation marks.
270. THE SOS/CARD SET: <SET_NAME> CONTAINS THE FIXED VARIABLE:
<VAR_NAME>
LINGO supports special ordered sets (SOS) of variables as well as cardinality sets of
variables. All variables belonging to these sets must not be fixed, i.e., they must be

ERROR MESSAGES 749
optimizable decision variables. You will need to remove the fixed variable from the
designatged set.
271. NO CARDINALITY WAS SPECIFIED FOR @CARD SET: <SET_NAME>
LINGO supports cardinality sets of variables. All variables belonging to a particular
cardinality set must sum to a specified integer value. To form a cardinbality set for variable
X, Y and Z that sums to 2, you would specify the following in your model:
@CARD( 'MYSET', X);
@CARD( 'MYSET', Y);
@CARD( 'MYSET', Z);
@CARD( 'MYSET', 2);
You will receive this error message when the cardinality value, @CARD( 'MYSET', 2) in this
case, is omitted. You will need to add a cardinality value reference for the set.
272. DUAL FORMULATIONS MAY ONLY BE GENERATED FOR LINEAR
PROGRAMS.
LINGO can generate the dual formulation for linear programming models. You have
attempted to generate the dual for a model that is not a linear program, i.e., the model is either
nonlinear or it contains integer variables. If it is possible to rewrite the model so that it
becomes linear without any integer variables, then you should be able to generate the dual
formulation. Otherwise, it will not be possible to generate the dual formulation.
273. THE LICENSE MANAGER RETURNED THE FOLLOWING ERROR:
<LICENSE_ERROR>
LINGO's license manager was unable to find a valid license file. The license file is normally
located in your main LINGO subdirectory under the name: lndlng<version>.lic, where
<version> is the version number of your LINGO installation. You may want to examine this
file for any obvious errors or problems. The license manager will also return a brief string
with more specific information (e.g., "No dongle found"), which will be displayed as part of
this message. This additional information should help you narrow down the problem. If you
are still unable to resolve this problem, please contact LINDO Systems Technical Support for
assistance.
274. THE MODEL CONTAINS FUNCTIONS NOT SUPPORTED BY THE GLOBAL
SOLVER.
The model contains functions not supported by the global solver. You will need to either
remove these functions or disable the global solver options.
The global solver supports most of the functions of the LINGO language. However, there are
few that aren’t currently, or can’t be supported. You may refer the Use Global Solver section
of Chapter 5 for a listing of functions not supported by the global solver.
275. A BARRIER LICENSE IS REQUIRED TO RUN BARRIER IN A CORE.
LINGO can run multiple linear programming solvers in parallel on multi-core machines. You
have requested to run the barrier solver in parallel, but your installation does not have a

750 APPENDIX B
license for the barrier solver. You will need to run the LINGO|Options command, go to the
Linear Solver tab, and disable the request to run the barrier solver in parallel.
276. PRIMAL2 MAY NOT BE RUN WITHOUT BARRIER RUNNING IN PARALLEL.
LINGO can run multiple linear programming solvers in parallel on multi-core machines. You
have requested to run the Primal2 solver in parallel without also requesting the barrier solver.
You will need to run the LINGO|Options command, go to the Linear Solver tab, and either
enable the barrier solver to run parallel or disable Primal2 from running in parallel.
277. INCONSISTENT BOUNDS ON VARIABLE: <NAME> IN THE SOS/CARD SET:
<SET>
LINGO supports special ordered sets (SOS) of variables as well as cardinality sets of
variables. You have specified bounds on variables in the designated set that are inconsistent
with variables belonging to such a set. Check to be sure you've specified the bounds
correctly.
278. ERROR IN DYNAMIC SET DEFINITION FOR SET: SET_NAME.
In some instances, you may not need to explicitly define a set. Instead, you can have LINGO
infer the dimensions of the set from the number data points assigned to an attribute of the set
in the model's Data section. This is referred to as a dynamic set definition. It's not always
possible for LINGO to accurately deduce a set's dimension from a data statement, in which
case, you will receive this error message. A valid solution is to explicitly define the set in
question in the model's Sets section.
279. AN UNALLOCATED SET WAS REFERENCED: <SET_NAME>
You've referenced members of a set that has not been allocated. You must allocate sets in a
model before they can be referenced. Many times, all that is required is to move the set's
allocation to a point in the model that precedes any references to it. Set allocation refers to
the declaration of the set's members. Allocation is generally done in a sets section or in a data
section.
280. INVALID SYNTAX FOR A CALC SECTION I/O OPERATION.
You have incorrectly specified an I/O function (@TEXT, @OLE, @ODBC, @POINTER) in
a calc section. Please refer to the documentation for the correct usage of these functions.
281. I/O OPERATIONS MAY ONLY APPEAR IN CALC, DATA AND INIT SECTIONS.
You have attempted to us an I/O function (@TEXT, @OLE, @ODBC, @POINTER) in the
model section. These fucntions are available only in calc, data and init sections of a model.
Please refer to the documentation for the correct usage
282. SETS MAY ONLY BE INITIALIZED IN SETS AND DATA SECTIONS.
You have attempted to initialize a set outside of a set and data section. You will need to
move the initiation statement to the correct model section.
283. TEXT AND NUMERIC OBJECTS CAN'T BE COMBINED IN A SINGLE
@POINTER OPERATION.
You have attempted to reference both text and numeric objects in a single @POINTER
statement. A given reference to the @POINTER function can only import/export items of

ERROR MESSAGES 751
one type, i.e., text or numeric. You will need to split the statement up into two or more
statements, such that each new statement only references either text or only references
numeric objects.
284. INVALID @POINTER SET I/O OPERATION. @POINTER CAN ONLY
REFERENCE ONE SET AT A TIME.
You have attempted to reference both more than one set in a single @POINTER statement. A
given reference to the @POINTER function can only import/export one set at a time. You
will need to split the statement up into two or more statements, such that each new statement
only references no more than one set.
285. INCORRECT USAGE OF @RANK.
You used the @RANK sorting function incorrectly. Proper usage is:
ATTR_RANK = @RANK( ATTR1[,...,ATTRN);
where ATTR_RANK receives the ranking of attribute ATTR1, with ties being broken by the
optionally supplied attributes ATTR2 through ATTRN. In addition, @RANK is only valid in
calc sections. Please refer to the documentation on @RANK for more details.
286. INCORRECT USAGE OF @SOLU.
You used the @SOLU sorting solution report function incorrectly. This function displays the
standard LINGO solution report and may be called in calc sections. Proper usage is:
@SOLU( [0|1[, OBJECT_NAME[, ''HEADER_TEXT'']]]);
where the first argument is set to 1 if only nonzero variable values are desired (and binding
rows), OBJECT_NAME is the optional name of an object to report on (the entire report will
be generated otherwise), and the optionalHEADER_TEXT is a header line to display in the
report. Please refer to the documentation on @SOLU for more details.
287. INCORRECT USAGE OF @SPSTGVAR/@SPSTGRNDV/@SPSTGROW.
You used either the @SPSTGVAR, @SPSTGRNDV or @SPSTGROW function incorrectly.
Proper usage is:
@SPSTG[VAR | RNDV | ROW]( STAGE, VARIABLE_OR_ROW_NAME);
where the first argument is the stage of the variable or row and the second argument the name
of the variable or row.
288. INVALID STAGE VALUE.
An invalid stage value was specified. Stage values must be non-negative, integer values. In
addition, random variables must have stages of 1, or higher. Please correct the indicated stage
value and retry.
289. STOCHASTIC PROPERTIES MAY ONLY BE ASSIGNED ONCE.
You may assign stochastic properties to variable and rows one time only. Please remove
multiple declarations and retry.

752 APPENDIX B
290. INVALID DECLARATION OF A STOCHASTIC DISTRIBUTION.
A stochastic distribution declaration was incorrectly specified. Please refer to the Declaring
Distributions section of Chapter 12 for clarification.
291. NAME IS TOO LONG.
The indicated name in the model exceeds the maximum name length of 64 characters. You
must shorten the name to continue.
292. NAME ALREADY IN USE.
The indicated name is already in use. To continue, you will need to change the.name so that
it is unique.
293. INVALID DISTRIBUTION PARAMETER.
The indicated parameter is invalid for the chosen probability distribution. Please refer to the
Declaring Distributions section of Chapter 12 for clarification.
294. INVALID USE OF @SPTABLEOUTC.
The @SPTABLEOUTC function for declaring discrete distribution outcomes was used
incorrectly. The correct usage is:
@SPTABLEOUTC( 'DIST_NAME', OUTC_PROB, OUTC_VAL1[ ,...,
OUTC_VALN])
For more information, refer to the Declaring Distributions Using Outcome Tables in Chapter
14.
295. OUTCOME TABLE NAME NOT PREVIOUSLY DEFINED.
You have attempted to use the designated outcome table name before defining it. For more
information on defining outcome tables, please refer to the Declaring Outcome Tables
section of Chapter 14. Note that the declaration of an outcome table must occur before the
name is used for other purposes.
296. INCORRECT NUMBER OF OUTCOMES FOR OUTCOME TABLE.
When declaring an outcome table using @SPDISTTABLE you declare its total number of
outcomes. The number of outcomes loaded via @SPTABLEOUTC does not match this total
number for the specified table. Please check the declaration of the table and the calls to
@SPTABLEOUTC. For more information on defining outcome tables, please refer to the
Declaring Outcome Tables section of Chapter 14.
297. INVALID USE OF @SPTABLERNDV.
The @SPTABLERNDV is used to associate random variables with an instance of a discrete
outcome table. The format of @SPTABLERNDV is:
@SPTABLERNDV( 'DIST_INSTANCE_NAME', RANDOM_VAR_1[, ... ,
RANDOM_VAR_N]);
Please check to see that the arguments conform to this syntax. For more information on
defining outcome tables and using @SPTABLERNDV, please refer to the Declaring Outcome
Tables section of Chapter 14.

ERROR MESSAGES 753
298. INCORRECT NUMBER OF RANDOM VARIABLES ASSIGNED TO
DISTRIBUTION.
The @SPTABLERNDV is used to associate random variables with an instance of a discrete
outcome table. The format of @SPTABLERNDV is:
@SPTABLERNDV( 'DIST_INSTANCE_NAME', RANDOM_VAR_1[, ... ,
RANDOM_VAR_N]);
When the parent outcome table was defined using @SPDISTTABLE, the number of
associated random variables was also declared. The number of variables associated with the
specified outcome table instance does not match this declared number. For more information
on defining outcome tables and using @SPTABLERNDV, please refer to the Declaring
Outcome Tables section of Chapter 14.
299. VARIABLES ASSIGNED TO DISTRIBUTIONS MUST BE DESIGNATED AS
RANDOM VARIABLES.
All variables associated with a probability distribution must first be declared as random
variables using the @SPSTGRNDV function. For more information on identifying random
variables and associating them with distributions, please refer to the Language Features for
SP Models section in Chapter 14.
300. RANDOM VARIABLES CAN ONLY BE ASSIGNED TO ONE DISTRIBUTION.
Only one random variable may be associated with a probability distribution. For more
information on identifying random variables and associating them with distributions, please
refer to the Language Features for SP Models section in Chapter 14.
301. INVALID USE @SPTABLEINST.
The @SPTABLEINST function is used to declare a particular instance of an outcome table.
The syntax for @SPTABLEINST is as follows:
@SPTABLEINST( 'PARENT_TABLE_NAME', 'TABLE_INSTANCE_NAME')
The parent table must have already been declared using @SPDISTTABLE. For more
information on declaring outcome tables and using @SPTABLEINST, please refer to the
Declaring Outcome Tables section of Chapter 14.
302. INVALID USE @SPSAMPSIZE.
The @SPSAMPSIZE function is used to declare a sample size for a particular stage of a
stochastic programming model. The syntax for @SPSAMPSIZE is as follows:
@SPSAMPSIZE( STAGE, SAMPLE_SIZE)
For more information on using @SPSAMPSIZE, please refer to the Declaring Parametric
Distributions section of Chapter 14.
303. PROBABILITIES DO NOT SUM TO 1 FOR OUTCOME TABLE.
Outcome tables are loaded with outcomes and their respective probabilities using the
@SPDISTOUTC function. You will receive this error message if the sum of the probabilities
for all outcomes for the specified outcome table do not sum to 1. You should check the

754 APPENDIX B
probability values for the specified distribution. For more information on defining outcome
tables and using @SPTABLEOUTC, please refer to the Declaring Outcome Tables section of
Chapter 14.
304. NO OUTCOMES DECLARED FOR OUTCOME TABLE.
Outcome tables are loaded with outcomes and their respective probabilities using the
@SPDISTOUTC function. You will receive this error message if no outcomes were declared
for the specified outcome table. You will need to load at least one or more outcomes into the
specified table instance. For more information on defining outcome tables and using
@SPTABLEOUTC, please refer to the Declaring Outcome Tables section of Chapter 14.
305. NO RANDOM VARIABLES ASSIGNED TO STAGE.
Each stage other than stage 0 of a stochastic programming model must have at least one
random variable assigned to it. Random variables are assigned to stages using the
@SPSTGRNDV function, which has the following syntax:
@SPSTGRNDV( STAGE, VARIABLE_NAME);
You will need to assign a random variable to the specified stage or reduce the number of
stages in the model. For more information on identifying random variables and associating
them with distributions, please refer to the Language Features for SP Models section in
Chapter 14.
306. SP CORRELATION TYPES CAN'T BE MIXED IN THE SAME MODEL.
There are three methods available for inducing correlations between random variables -
Pearson, Kendall and Spearman. You may use only one method throughout an entire model.
Trying to use more than one particular method will trigger this error message.
307. STOCHASTIC PROGRAMS MUST HAVE AT LEAST TWO STAGES.
Stochastic programs must have two, or more, stages. The first stage, stage 0, is the initial
decision stage. The second stage, stage 1, is a recourse decision stage which occurs after the
stage 1 random variable values have been revealed. Subsequent rounds of random variable
revelations and recourse decisions are permitted but not required. For more information on
adding random variables and stages to an SP model, please refer to the Language Features for
SP Models section in Chapter 14.
308. LINEARIZATION OPTION NOT PERMITTED ON STOCHASTIC PROGRAMS.
LINGO has the capability to reformulate certain nonlinear expressions so that they become
linear, while maintaining mathematical equivalency to the original model. This linearization
option is only available on deterministic models. If you enable the linearization option on SP
models, you will receive this error message. An option is to enable the global solver instead
(assuming your license allows for this optional feature). If the SP model can be completely
linearized, the global solver will realize this and perform the linearization, thereby allowing
for a globally optimal solution.

ERROR MESSAGES 755
309. THE DETEQ MODEL GENERATED BY THE SP SOLVER EXCEEDS THE
CAPACITY OF THIS VERSION.
LINGO's SP solver generates a deterministic model to solve the original SP model. This
model is called the deterministic equivalent (deteq). Depending on the number of stages,
random variables and samples sizes, the deteq may get to be very large. In which case, there
is a possibility that it will exceed the capacity of your LINGO license. This can occur even
when the core model lies well within the capacity of your license. You will need to either
reduce the size of the model (by using fewer stages, less random variables or smaller sample
sizes), or upgrade to a license with more capacity.
310. INVALID SP CORRELATION MATRIX.
The correlation matrix entered for the random variables using @SPCORREL is not valid.
Please check the correlations to see that they lie within a range of [-1,+1]. Also check to see
that explicit correlation values lie within any implied range, e.g., CORR( X, Y) = .9 and
CORR( Y, Z) = .9 implies that CORR( X, Z) is at least .62.
311. ATTEMPT TO CORRELATE NON-RANDOM VARIABLES.
In a stochastic programming (SP) model, only random variable may be correlated via the
@SPCORREL function. In addition, the correlated variables must be flagged as random
variables using the @SPSTGRNDV function prior to inputting their correlation coefficient
using @SPCORREL.
312. INVALID CORRELATION COEFFICIENT.
You've input an invalid correlation coefficient that lies outside [-1,+1]. Please correct the
coefficient's value and try again.
313. SCENARIO INDICES MUST BE INTEGRAL.
In referring to a scenario, you've attempted to use an out-of-range index. In other words, the
index is either less than 1 or greater than the total number of scenarios. Please correct the
index and retry.
314. SCENARIO INDEX OUT OF RANGE.
The scenario index must be an integer greater-than-or-equal-to 1 and may not exceed the total
number of scenarios in the model.
315. THE FOLLOWING SET MEMBER: SET-MEMBER APPEARS MORE THAN ONCE
IN SET: SET-NAME.
The indicated set member, SET-MEMBER, appears more than one in its set SET-NAME.
Please correct the duplicated set members to continue.
316. UNABLE TO GENERATE DETERMINISTIC EQUIVALENT.
LINGO's SP solver generates a deterministic model to solve the original SP model. This
model is called the deterministic equivalent (deteq). Depending on the number of stages,
random variables and samples sizes, the deteq may get to be very large. There is a remote
chance that LINGO will not be able to generate the deteq. This would be a very unusual
situation. If there is no obvious reason for this problem, you may wish to contact LINDO
Systems Technical Support desk for assistance.

756 APPENDIX B
317. THE MODEL IS NOT A STOCHASTIC PROGRAM.
You've attempted to request information relevant only to stochastic programs while running a
deterministic model.
318. THIS OPERATION REQUIRES THE STOCHASTIC PROGRAMMING OPTION.
You're attempting to solve a stochastic program (SP) on a LINGO installation that does not
support the SP option. You will need to upgrade your license to include the option.
319. ONE OR MORE SP SCENARIO SOLUTIONS DO NOT EXIST.
LINGO was unable to generate solutions for all the models scenarios. This would be a very
unusual situation. If there is no obvious reason for this problem, you may wish to contact
LINDO Systems Technical Support desk for assistance.
320. @SPLOADSCEN() FAILED FOR SCENARIO: N.
LINGO was unable to load the solution for scenario N via the @SPLOADSCEN function.
This would be an unusual situation. If there is no obvious reason for this problem, you may
wish to contact LINDO Systems Technical Support desk for assistance.
321. UNABLE TO GENERATE INDIVIDUAL SCENARIO MODEL.
LINGO was unable to generate a requested individual scenario for an SP mode. This would
be an unusual situation. If there is no obvious reason for this problem, you may wish to
contact LINDO Systems Technical Support desk for assistance.
322. NO CONSTRAINTS WERE ASSIGNED TO STAGE: N
One or more stages in the stochastic program do not have any constraints. If this is an error,
then correct it and continue. If this is not an error, then you should fold the random variables
from the offending stage into the subsequent stage. This will reduce the total number of
stages in the model by one.
323. THE FOLLOWING RANDOM VARIABLE IS NOT ASSIGNED TO A STAGE.
Each random variable declared with @SPSTGRNDV must also be assigned to a stochastic
distribution. LINGO will display the name of the first unassigned random variable. You will
need to use either @SPDISTTABLE or @SPTABLERNDV to assign the variable to a
distribution.
324. THE FOLLOWING RANDOM VARIABLE ATTRIBUTE HAS ELEMENTS
BELONGING TO DIFFERENT STAGES.
The attribute in question was assigned to an outcome table using @SPDISTTABLE. All
elements of the attribute must be random variables and must all be assigned to the same stage
using the @SPSTGRNDV function. Please check to see that all the elements of the attribute
have been assigned to the correct and identical stage.
325. THE FOLLOWING PROBABILITY OR OUTCOME ATTRIBUTE CONTAINS
NON-CONSTANT ELEMENTS.
The attribute in question was used to construct an outcome table distribution using
@SPDISTTABLE. All elements of outcome and probability attributes must be constants and
may not be optimizable. Please assign appropriate values to each element of the attribute.

ERROR MESSAGES 757
326. THE SP SAMPLE SIZES ARE NOT LARGE ENOUGH TO GENERATE A
MEANINGFUL SAMPLE.
The sample sizes in your SP model are not large enough to allow for generation of a
meaningful sample of the random variables. Note that models that induce correlation between
random variable will require larger sample sizes. You will need to use the @SPSAMPSIZE
function to increase the sample sizes.
327. UNSUPPORTED MPI INSTRUCTION CODE: N
You are attempting to read an MPI format file that contains an instruction code not currently
supported by LINGO. LINGO supports most of the frequently used MPI instruction codes,
however, it does not support 100% of the codes offered by the MPI format. In order to
continue, you will need to either remove the unsupported function code or rewrite the
expression using supported instructions codes.
328-1000. UNUSED.
Note: Error messages 1001 through 1016 pertain only to the Windows version of LINGO.
1001. NO MATCHING PARENTHESIS WAS FOUND.
LINGO did not find a closing parenthesis for the selected parenthesis. Add a closing
parenthesis and try again.
1002. UNABLE TO SOLVE ... NO MODEL CURRENTLY IN MEMORY.
LINGO does not have the text of a model available to attempt to solve. Select a model
window and try solving again.
1003. LINGO IS BUSY AND CAN’T COMPLETE YOUR REQUEST RIGHT NOW. TRY
AGAIN LATER.
You have attempted an operation that is not possible because LINGO is currently solving a
model. To halt the solver, press the Interrupt Solver button on the solver status window.
1004. ERROR WRITING TO LOG FILE. PERHAPS THE DISK IS FULL?
LINGO can’t write any additional output from the command window to an open log file.
Check to see if there is any free space remaining on the disk.
1005. UNABLE TO OPEN LOG FILE.
LINGO could not open the log file that you requested. Does the path exist? Do you have write
access to the selected path?
1006. COULD NOT OPEN FILE: FILENAME.
LINGO could not open a requested file. Did you spell the file’s name correctly? Does the file
exist?
1007. NOT ENOUGH MEMORY TO COMPLETE COMMAND.
LINGO was unable to allocate additional system memory while attempting to execute a
command. Exit any other applications and try again. If the error still occurs, you may have set
the model generator’s working memory area to be too large. You can adjust the generator’s
memory allocation downward on the General tab of the LINGO|Options command's dialog
box.

758 APPENDIX B
1008. UNABLE TO CREATE A NEW WINDOW.
LINGO was unable to create a new window. This is probably caused by insufficient system
resources.
1009. UNABLE TO ALLOCATE ENOUGH MEMORY FOR SOLUTION REPORT.
LINGO could not allocate enough memory to store the solution report to the model. System
resources must be very low in order to receive this message. Exit any other applications and
try again. If the error still occurs, you may have set the model generator’s working memory
area to be too large. You can adjust the generator’s memory allocation downward on the
General tab of the LINGO|Options command's dialog box. If all else fails, you can use the
LINGO|Solution command to request smaller solution reports for individual variables.
1010. NOT USED.
1011. UNABLE TO COMPLETE GRAPHICS REQUEST.
LINGO was unable to generate a requested graph. Either LINGO is incorrectly installed or
there is not enough free memory to perform the operation. Try cutting back on the amount of
memory allocated to LINGO’s model generator using the LINGO|Options command. If this
doesn’t help, try reinstalling LINGO.
1012. NOT USED.
1013. NOT USED.
1014. NOT USED.
1015. EDIT COMMAND NOT SUPPORTED UNDER WINDOWS. USE THE FILE|OPEN
COMMAND INSTEAD.
The EDIT command is not supported in Windows versions of LINGO. If you need to edit the
file, use the File|Open command to load the file into a window for editing.
1016. COULD NOT SAVE FILE.
LINGO was unable to save the file. Check for a valid path name and sufficient disk space.
9999. OPTIMIZER FAILED DUE TO A SERIOUS ERROR. PLEASE REFER TO YOUR
DOCUMENTATION UNDER APPENDIX B, “ERROR MESSAGES”.
The optimizer was unable to continue due to a serious error. The most likely cause of this
error stems from a problem in evaluating the functions within your model. Not all functions
are defined for all values of their arguments. For example, @LOG(X – 1) is undefined for
values of X less-than-or-equal-to 1. You should check your model for any such functions, and
use the @BND function to place bounds on your variables to keep the optimizer from straying
into any regions where functions become undefined.
Another complicating factor can be nonlinear relations in a model. Linear models can be
solved much more reliably and quickly than nonlinear models of comparable size. If possible,
try to linearize your model by approximating nonlinear functions with linear ones, or by
eliminating nonlinear equations.

ERROR MESSAGES 759
Another possible remedy when dealing with nonlinear models is to attempt different starting
points. A starting point may be input in the model’s INIT section. Refer to Chapter 5,
Windows Commands, for more details.
If this problem persists after bounding any variables that could potentially lead to a problem,
removing any unnecessary nonlinearities, and attempting new starting points, please contact
LINDO systems for assistance.

761
Appendix C: Bibliography
and Suggested Reading
Anderson, Sweeney, and Williams, Introduction to Management Science, 8th ed. St. Paul, MN: West
Publishing, 1997.
_______________ , Quantitative Methods for Business, 6th ed. St. Paul, MN: West Publishing, 1991.
Birge, J., and F. Louveaux, Introduction to Stochastic Programming, Volume 57, Springer-Verlag New
York, Inc., 1997.
Black, F., and M. Scholes. (1973). “The Pricing of Options and Corporate Liabilities.”, Journal of
Political Economy, vol. 81, pp. 637-654.
Bradley, S.P., A.C. Hax, and T.L. Magnanti, Applied Mathematical Programming. Reading, MA :
Addison-Wesley Publishing Company, Inc., 1977.
Cochran, W.G., Sampling Techniques. 2nd ed. New York, NY : Wiley, 1963.
Conway, R.W., W.L. Maxwell, and L.W. Miller, Theory of Scheduling. Reading, MA :
Addison-Wesley Publishing Company, Inc.,1967.
Cox, John C. and Mark Rubinstein, Options Markets. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1985.
Dantzig, G.B., Linear Programming and Extensions. Princeton, N.J. : Princeton University Press,
1963.
Eppen, G.D., F.J. Gould, and Schmidt, C.P., Quantitative Concepts for Management: Decision Making
Without Algorithms, 3rd ed. Englewood Cliffs, N.J. : Prentice-Hall, Inc., 1989.
_______________ , Introductory Management Science, 4th ed. Englewood Cliffs, N.J. : Prentice-Hall,
Inc., 1993.
Gass, S., Decision Making, Models & Algorithms. New York: Wiley-Interscience, 1985.
_______________ , Linear Programming, 5th ed. New York: McGraw-Hill, 1985.
Geoffrion, A., The Theory of Structured Modeling, Western Management Science Institute, UCLA,
1987.
Hadley, G., and T.M. Whitin, Analysis of Inventory Systems. Englewood Cliffs, N.J. : Prentice-Hall,
Inc., 1963.
Hillier, F., and G.J. Lieberman, Introduction to Operations Research, 9th ed. New York :
McGraw-Hill, Inc., 2010.
Johnson, L., and D.C. Montgomery, Operations Research in Production Planning, Scheduling, and
Inventory Control. New York: John Wiley & Sons, Inc., 1974.

762 APPENDIX C
Knowles, T., Management Science. Homewood, IL: Irwin Publishing, 1989.
Lin, S., and B. Kernighan (1973), “An effective Heuristic Algorithm for the Traveling Salesman
Problem.”, Operations Research, vol. 10, pp. 463-471.
Markowitz, H. M., Portfolio Selection, Efficient Diversification of Investments, John Wiley & Sons,
1959.
Nemhauser, G., and L. Wolsey, Integer and Combinatorial Optimization. New York : John Wiley &
Sons, 1988.
Moder, Joseph J., and Salah E. Elmaghraby (editors), Handbook of Operations Research. New York:
Van Nostrand Reinhold Company, 1978.
Schrage, L., Optimization Modeling with LINDO, 5th. ed. Belmont, CA: Duxbury Press, 1997.
_______________, Optimization Modeling with LINGO, 6th. ed. Chicago, IL: LINDO Systems Inc.,
2006.
Wagner, H.M., Principles of Management Science with Applications to Executive Decisions, 2nd ed.
Englewood Cliffs, N.J. : Prentice-Hall, Inc., 1975.
_________, Principles of Operations Research, 2nd ed. Englewood Cliffs, N.J. : Prentice-Hall, Inc.,
1975.
Winston, Wayne L., Introduction to Mathematical Programming: Applications and Algorithms, 3rd
ed. Belmont, CA: Duxbury Press, 1995.
_____________, Operations Research: Applications and Algorithms, 2nd ed. Belmont, CA: Duxbury
Press, 1995.

INDEX 763
Index
!
!, 6, 332
~
~ (End-of-record mark), 363
A
About LINGO command, 38, 248
ABS function, 337, 629
ABSINT parameter, 297
Absolute Integrality, 203
Absolute integrality tolerance, 203, 297
Absolute optimality tolerance, 206, 298
Accelerator key, 118
Acceptance sampling, 708, 712
Access
datasources, 409–14
importing, 369, 417–19
interfacing, 149
ACOS function, 337
ACOSH function, 337
Administrator, ODBC, 409–14
Airline overbooking, 683
Algebraic formulation, 134, 275
Algebraic reformulation, 319
Algorithm
barrier
cold start, 205, 309
error messages, 746
options, 185
parameters, 305
warm start, 205, 309
branch-and-bound, 76, 202, 307
generalized reduced gradient, 622
simplex
cold start, 205, 309
options, 185
parameters, 305
warm start, 205, 309
Allowable Increase/Decrease, 156, 157, 281
ALTER command, 264, 284
Analysis
conjoint, 529, 643
data envelopment, 645
range, 746
regression, 662, 706
What If, 109
Analytical derivatives, 193, 629
Anderson, D., 497
Annuity, present value, 339
APISET, 548
APISET command, 253, 751
Append output checkbox, 131
Application drop-down box, 199
AppWizard, 439, 470
Arithmetic operators, 334, 730, 734
Arrange Icons command, 244
ASCII format, 26, 122, 274, 361, 363, 376
ASIN function, 337
ASINH function, 337
Assembly line balancing, 487, 633
Assume Model is Linear, 181
ATAN function, 337
ATAN2 function, 337
ATANH function, 337
Attributes
definition, 41
dynamic link library, 430
examples
marketing models, 527
portfolio models, 500, 513
production models, 61, 66, 531
exporting, 419
importing, 416
initializing, 107
names, 727
solution report, 34
AUTOLG.DAT, 137, 373
AutoUpdate command, 247
B
Backorders, 667
Balof, J., 662
Barrier algorithm
cold start, 205, 309

764 INDEX
error messages, 746
options, 185
parameters, 305
warm start, 205, 309
Barrier Crossover, 189
BAS file, 465, 466
BASCTS, 310
BASCTS parameter, 318
BASIC, 432
Basis cuts, 200, 310, 318
Bayes rule, 635
BCROSS parameter, 293, 322
Best bound, 208, 299
Best Obj field, 14
Beta distribution, 588
BigM Threshhold., 203
BIGMVL Paramater, 323
BIGMVL parameter, 293
BIN function
definition, 342
dual values, 93
example, 72
options, 201
syntax, 82
Binary
format, 377
operators, 334
Binary integer variables
examples, 489
functions, 75, 342
priority, 202, 308
syntax, 82–93
Binary Search, 552
Binding constraints, 25, 239, 270
Binomial distribution, 339, 589, 683, 687
Black & Scholes pricing model, 509, 685
Black, F., 507, 685
Blending problems, 61, 476, 636, 641
BND function
definition, 342
error messages, 733
examples, 479, 501
syntax, 99
BND(), 174
Bond portfolio optimization, 511, 689
Bounds
allowable limit, 733
conflicting, 733
objective, 14
variables
functions, 342
global, 319
guidelines for, 630
probing, 197
syntax, 99
Bracken, J., 710
Brahnc-and-bound
global solver, 214
Branch-and-bound
constraint cuts
options, 198, 201
parameters, 297, 310, 318
reports, 239
definition, 76, 533, 621
direction, 307, 319
heuristics, 197, 214, 318
optimality tolerance, 206, 298
solver, 13, 196
strategy, 202
BRANDPR parameter, 308
BRANDR parameter, 307
BREAK, 537
C
C# .NET, 428
C/C++, 428, 438–46
callback function, 460
pointer function, 432
user defined function, 469, 470
Calc Section, 112
Call option, 507, 685
Callable Library, 427–69
Callback functions, 435, 436, 437, 459–69, 465
Capacitated EOQ, 653
Capacitated lot sizing, 671
Capacitated Plant Location, 492, 639
Capacity, scarce, 671
Cartesian product, 47, 64
Cascade command, 244
Case sensitivity, 6
Cash flow matching, 511, 689
CAT command, 251, 253
Cauchy distribution, 588
Chemical equilibrium, 642
CHESS model, 61, 279, 283, 641
Chi-Square distribution, 588
Chi-squared distribution, 339
CHKDUP parameter, 303
Class of a model, 11
Classification statistics, 238, 269, 623
ClassWizard, 440, 461, 462
Clipboard, 139, 235
Close All command, 243

INDEX 765
Close command, 128
Coefficient reduction, 310
Coefficients
current, 156, 281
matrix of, 190, 234, 267
nonzeros, 10, 239, 270
objective, 24
objective ranges, 156, 281
reduction, 200, 310
right-hand side, 281
unity, 239, 270
COFCTS, 310
Cold start option, 205, 309
Colon prompt, 22, 251, 257
Coloring, 146, 166, 311
Column length, 424
COM command, 253, 738
Command scripts, 371–73
command-line, 257
DLL, 434, 445, 450
OLE automation
importing, 392–96
Windows, 131–34, 241
Command Window command, 167, 241, 302
Command-line interface, 21, 22, 131, 167
Commands
Command-line, 251–53, 253–332
Windows, 118–20, 121–249
Comments, 6, 332
Compiling the model
generating, 53
solving, 124, 151, 278
CompuQuick Corporation, 4, 15, 22, 77
Concavity, 627
loose, 628
strict, 628
Conditional qualifier, 50, 54, 72
Conjoint analysis, 529, 643
Constraints
binding, 25, 239, 270
cuts
options, 198, 201
parameters, 297, 310, 318
reports, 239
defining, 4, 5, 28
examples, 479, 494, 501, 531
fixed, 10
in solutions, 10
limits, 100
modeling language, 41
names, 35, 125
nonlinear, 10
options, 198
selective evaluation, 194, 305
two-sided, 727
types, 622–24
Constraints Cuts box, 198
Contacting LINDO, 39, 249
Continuous variables, 72
convexity, 214, 319
Convexity, 626
loose, 627
strict, 626
Copy command, 139, 361–62, 362
Correlation, 590
COS function, 337
COSH function, 337
Covariance, 499, 500
Covering model, 650
Crashing, 194, 304, 692
Create from File, 403
Critical path, 65, 69, 691
Cumulative distribution, 340
Current coefficients, 156, 281
Cut command, 139
CUTAPP parameter, 297
Cutoff level, 432
CUTOFF parameter, 308
Cuts
options, 198, 201, 310, 318
parameters, 297
reports, 239
Cutting Stock, 563
Cycle time, 487, 489
D
Dantzig pricing, 306
Data envelopment analysis, 645
Data independence, 26, 68, 86
Data section
definition, 26
error messages, 742
attributes, 727
exporting, 739
importing, 731
names, 731, 742
question marks, 735, 744
examples, 62, 364
syntax, 107–11
Data type, 467
Database User Info command, 137
Databases, 407–25
exporting

766 INDEX
functions, 419–25
reports, 287
importing, 380, 415–19
Datasources, 408–14
linking, 137, 147, 289
ODBC function, 147, 419
DBGCLD parameter, 321
DBGLVL parameter, 293
DBGLVL Parameter, 322
DBGWRM parameter, 321
DBPWD command, 137, 289
DBUID command, 137, 289
Debt defeasance, 511, 689
Debug command
command-line, 276
Windows, 236–38
Debugging, 234, 267
Decision variables
defining, 4
examples, 71, 489, 493, 504
ranges, 155, 280
DECOMP parameter, 318
Decomposition, 190
Default button, 159
Delay field, 166
DELETE command, 286
Delphi, 428
Demand backlog model, 667
Dense set, 45
Depth first, 208, 299
DERCMP parameter, 295
Derivatives, 193, 295, 626, 629
Derived sets
defining, 42, 45–48, 745
dense, 62
examples
blending models, 61–64, 478
financial models, 504
marketing models, 530
production models, 484, 489
exporting, 419
sparse, 64–69, 69–74
Designing a computer cabinet, 705
Desrochers, M., 718
Devex pricing, 187, 306
Direct solver, 533, 621
Direction box, 202
Disaggregation, 200, 310
DISCTS, 310
Display As Icon button, 148
Distribution, 340, 647
binomial, 339, 683, 687
Chi-squared, 339
cumulative, 340
hypergeometric, 340, 708
Multi-level, 678
Poisson, 340, 516, 655
Diversification, 499
DIVERT, 547
DIVERT command
error messages, 740
printing, 23
reverting, 274
syntax, 272
DLLs, 427–69
Domain functions, 72, 733
Double data type, 467
Downloading, 247
Downside risk, 234, 503, 506, 648
Dual computations box, 172
DUAL function, 347
Dual values, 25
enabling, 155, 172, 740
examples, 64
integer programming, 93
nonzeros, 734
ranges, 155, 157, 281
DUALCO, 306
DUALCO parameter, 280
DUALPR parameter, 306
Duplicate names, 182, 729, 741
DYNAMB model, 496
Dynamic Link Library, 427–69
functions, 432–37
Dynamic programming, 496, 651, 676, 687
E
Echo Input, 167
Echo to screen checkbox, 131
ECHOIN parameter, 303
Economic order quantity, 653, 699
Edit menu, 119, 138–50
Efficient Frontier, 556
Eigen values, 626
Elapsed Runtime, 10
ELSE, 535
Embedding files, 396–405
END command, 22
End-of-file, 366
End-of-record Mark (~), 363, 366, 484, 730
ENDSUBMODEL, 533
Entering a Model
Command-line, 21–23

INDEX 767
Windows, 3–21
Eppen/Martin model, 671
Equality relation, 25, 335
Equilibrium
network, 680
Erlang busy probability, 339, 701
Erlang loss probability, 340, 516, 656
ERRDLG parameter, 303
Error messages, 7, 125, 303, 436, 438, 725–66
Error Text box, 151
Errors In Dialogs, 161
EVMU, 600
EVPI, 600
Excel
exporting, 391
linking with LINGO, 141, 379, 433
OLE automation, 392–406
OLE function, 379, 390
TEXT function, 369
Exclamation point, 6, 332
Exercise price, 507, 685
Exit, 332
Exit command, 137
EXP function, 337
Expected rate of return, 505
Expected Value Statistics, 223
Explicit listing, 46, 64, 66
Exponential distribution, 588
Exponential smoothing, 516, 714
Export summary report
ODBC based, 424
OLE based, 391
Exporting
attributes, 419
databases
functions, 419–25
reports, 287
MPI files, 136, 274
MPS files, 134–36
pasting out, 362
spreadsheets
functions, 384–92
reports, 287
Expressions, 629
EXTEND command, 286
Extended Solver Status, 13
EZCOUNT model, 720
EZMREPAR model, 519, 654
EZNEWS model, 655
F
F distribution, 588
Factorial function, 720
Feasibility tolerances, 186, 192
Feasible solution, 186
Features, new, vii
File
data, 376
format
ASCII, 26, 122, 274, 361, 363, 376
BAS, 465, 466
binary, 377
LDT, 122, 376
LG4
definition, 122
linked objects, 149
saving, 17, 127, 376
LNG, 122, 376
LRP, 376
LTF, 122, 376
MPI, 136, 274
MPS
definition, 119
exporting, 134–35, 275
importing, 125, 254
header, 441, 464
importing, 124
log files, 765
names, 6, 35, 127
script files, 371–73
types, 122
FILE, 363
File Format box, 165
FILE function, 122, 346, 363–67
examples, 373, 483
File menu, 119, 121–37
FILFMT parameter, 302
FILOUT parameter, 322
Filter, 46, 69
Final linear feasibility tolerance, 186, 294
Final nonlinear feasibility tolerance, 192, 294
Financial models, 339, 499–515
Find/Find Next command, 144
Finite source, Poisson, 519
Fixed constraints, 10
Fixed costs, 88
Fixed MPS format, 254
Fixed ordering charge, 682
Fixed Var Reduction, 177
Fixed variables, 9, 157, 622, 732
FLFTOL parameter, 294

768 INDEX
Floating point operations, 186, 294
FLOOR function, 337
Flow Cover, 200, 310
Flow cuts, 310
FLWCTS, 310
FNFTOL parameter, 294
Font selecting, 146
FOR, 536
FOR function
constraints, 37, 53
error messages, 730, 732
nesting, 55, 145
sets, 43, 345
syntax, 50
variables, 81, 96
Forecasting, 65, 94, 706, 714
FORMAT function, 347
Formatting, 122
FORTRAN
pointer functions, 432
user defined functions, 469, 470
FPA function, 339
FPL function, 339
Fragmentation ratio, 254
Free MPS format, 254
Free variables, 94–99, 342
FREEZE command, 289, 296, 739
FRMPS command, 254
Functions, 41, 333–60
callback, 459–69
DLL, 432–37
factorial, 720
interface functions, 363, 740
non-differentiable, 629
pasting, 146
probability, 339–41
set-looping, 48–55, 345
user defined, 469–73
utility, 529
variable domain, 72, 733
G
Gamma distribution, 588
GCD cuts, 200, 310
GCDCTS, 310
GEN, 260, 538
GEN command, 53
GENDUAL, 540
General box, 161
General equilibrium of an economy, 657
General integer variables, 75, 76–81, 342
General Solver tab, 169–84
Generate command, 225
Generate command, 53
Generating a model, 178, 307
Generator Memory Limit Box, 176
Generator memory used, 10, 254
Geoffrion, A., 678
Geometric distribution, 589
GIN function
definition, 342
dual values, 93
examples, 77, 81
options, 201
syntax, 76
GLBBRN parameter, 319
GLBBXS parameter, 319
GLBDLT parameter, 319
GLBOPT parameter, 318
GLBREF parameter, 319
GLBUBD parameter, 319
GLBVBD parameter, 319
Global delta tolerance, 319
Global optimality tolerance, 318
Global optimum, 312, 432, 624, 626
Global solver, 13, 314, 748
Global Solver, 160, 194, 213, 214, 216, 218, 359,
749
Global Solver tab, 213
GO command, 23, 33, 278
Go To Line command, 145
GOMCTS, 310
Gomory, 310
Gomory cuts, 200, 310
Gradient, 192, 295, 622, 629
Graphic reports, 155
Graves, G., 678
Greatest common divisor, 310
Growth rate, 499
GUB cuts, 200, 239, 270, 310
GUBCTS, 310
Gumbel distribution, 588
H
Handle usage, 254
Hansen, P., 680
Hayes, J.M., 642
Header file, 441, 464
Heap compacts, 254
HELP command, 253
Help menu, 120, 244–49
Help Topics command, 245

INDEX 769
HEUCUT parameter, 331
HEURIS parameter, 297
Heuristics, 197, 318, 676, 718, 721
HIDE command, 264, 737
Hieftje, G.M., 642
Holding costs, 653, 671
Home mortgage calculation, 723
HUMNTM parameter, 318
Hurdle, 207
HURDLE parameter, 297
Hypergeometric distribution, 340, 589, 708
Hyperplanes, 628
I
IF function, 358
IFC, 535
ILFTOL parameter, 294
ILP, 11
Implicit set members, 746
Implied indexing, 51
Importing
attributes, 416
command scripts, 371–73
databases, 380, 415–19
FILE function, 122, 363–67
MPS files, 124–26, 254
pasting in, 361–62
set members, 181
spreadsheets, 379–84
IN function, 342, 730, 735
Include file, 366
Index, 266, 727, 728, 739
implied, 51
internal, 35, 157
placeholder, 46, 71
INDEX function
error messages, 727, 732
examples, 84
parameters, 304
set names, 181, 182
Inequality relation, 335
Infeasible model, 25, 236, 276, 432, 735
INFTOL parameter, 294
Init section, 111–15
importing, 380
Initial linear feasibility tolerance, 186, 294
Initial nonlinear feasibility tolerance, 192, 294
Initializing data
error messages, 746
variables, 630
INLP, 12
Insert New Object command, 147–49, 403
Installing LINGO
command-line, 21
Windows, 1
Integer pre-solver tab, 196–200
Integer programming, 738
branch-and-bound
constraint cuts
options, 198, 201
parameters, 297, 310, 318
reports, 239
definition, 76, 533, 621
direction, 307
heuristics, 197, 318
optimality tolerance, 206, 298
solver, 196
strategy, 202
dual values, 93
probing, 197
Integer Solver tab, 201–12
Integer variables
binary (0/1)
examples, 489
functions, 75, 342
priority, 202, 308
syntax, 82–93
examples, 480
general, 75, 76–81, 342
limits, 38
solutions, 9, 631
variable domain functions, 75–93
Integrality tolerance, 203, 294
Interest rate, 507
Interface functions, 363, 740
Interface tab, 161–68
Interfacing with other applications, 427–73
Interior point algorithm, 185, 305
Interrupting the solver, 8, 765
Invalid switch, 735
Inventory system
demand backlog, 667
newsboy model, 655, 682
PERT, 65, 417–19, 422–25, 691
IPTOLA parameter, 298
IPTOLR parameter, 298
IQP, 11
Iterations, 186
definition, 171, 295
dynamic link library, 461
limit, 295
max passes, 199
SLP direction, 195, 305

770 INDEX
steepest edge, 187, 195, 304, 306
ITERS function, 351
ITRLIM parameter, 295
ITRSLW parameter, 295
J
Job shop scheduling, 660
Just-in-time production, 481, 674
K
K-Best Solutions, 208
KBESTS Parameter, 293, 324
Kehoe, T.J., 657
Kendall correlation, 590
Kernighan, B., 718
KILLSC Paramater, 324
KILLSC Parameter, 293
Knapsack cover, 310
Knapsack cover cuts, 200, 310
Knapsack problem, 82–88, 285, 661
KNPCTS, 310
L
Labor supply, 5
Laplace distribution, 588
Laporte, G., 718
LATCTS, 310
Latin-hyper-square, 584
Lattice, 310
Lattice cuts, 200, 310
LCORE1 – LCORE4 parameters, 325
LCORES Parameter, 293, 324
LCRASH parameter, 293, 321
LDT format, 122, 376
Lead time, 481, 484
Learning curve, 662
LENPAG parameter, 299
LFTCTS, 310
LG4 format
definition, 122
linked objects, 149
saving, 17, 127, 376
LGM function, 338, 720
Libraries (DLL), 427–69
License key
global solver, 213
Windows, 136
Lift cuts, 310
Lifting cuts, 200, 310
Limits
BND function, 100, 733
constraints, 4, 5, 89
cuts, 310
integers, 199
iterations, 192, 295
line counts, 166, 167
page size, 168
runtimes, 171
sets, 26
software version, 38
Lin, S., 718
LINDO API, 136, 274
LINDO contact information, 39, 249
Line capacity, 5
Line count limits, 167
Line limit field, 166
Linear formula, 622
Linear loss function, Poisson, 340
Linear Optimality Tolerance, 189
LINEAR parameter, 293
LINEAR Parameter, 323
Linear regression, 662, 706
Linear solver, 184, 204, 533, 621
Linearization, 178, 316, 749
LINGO menu, 120, 151–240
LINGO.CNF, 739
Linking databases, 137, 147
Links command, 143, 150
LINLEN parameter, 299
Little s-big S policies, 682
LNBIGM parameter, 316
LNDLTA parameter, 316
LNG format, 122, 376
LNRISE parameter, 316
Local optimum, 214, 432, 624
Log files, 433, 436, 445, 765
LOG function, 112, 338
Log Output command, 131, 168
LOG10 function, 338
Logarithm, 509, 642, 662, 720
Logarithmic distribution, 589
Logical expressions
conditions, 69, 86
examples, 485, 700
operators, 46, 335
Logistic distribution, 588
Logistics models, 492–98
Lognormal distribution, 588
Long data type, 467
LOOK command, 240, 266, 725

INDEX 771
Loop Optimization, 182
Looping, 536
LOOPOP parameter, 330
LOPTOL parameter, 293
Lot sizing, 671
LOWMEM parameter, 322
LP, 11
LRP format, 376
LS_DINFO_MIP_BEST_OBJECTIVE_LNG, 435
LS_DINFO_MIP_BOUND_LNG, 435
LS_DINFO_OBJECTIVE_LNG, 435
LS_DINFO_SUMINF_LNG, 435
LS_IINFO_BRANCHES_LNG, 435
LS_IINFO_CONSTRAINTS_LNG, 435
LS_IINFO_CONSTRAINTS_NONLINEAR_LNG,
435
LS_IINFO_ITERATIONS_LNG, 435
LS_IINFO_NONZEROS_LNG, 435
LS_IINFO_NONZEROS_NONLINEAR_LNG,
435
LS_IINFO_VARIABLES_INTEGER_LNG, 435
LS_IINFO_VARIABLES_LNG, 435
LS_IINFO_VARIABLES_NONLINEAR_LNG,
435
LSclearPointersLng, 433
LScloseLogFileLng, 433, 451
LSdeleteEnvLng, 434
LSERR_INFO_NOT_AVAILABLE_LNG, 438
LSERR_INVALID_INPUT_LNG, 438
LSERR_INVALID_NULL_POINTER_LNG, 438
LSERR_NO_ERROR_LNG, 438
LSERR_OUT_OF_MEMORY_LNG, 438
LSERR_UNABLE_TO_OPEN_LOG_FILE_LNG,
438
LSexecuteScriptLng, 434, 451
LSgetCallbackInfoDoubleLng, 467
LSgetCallbackInfoLng, 435, 460
LSgetCallbackInfoLongLng, 467
LSopenLogFileLng, 436
LSsetCallbackErrorLng, 436
LSsetCallbackSolverLng, 437, 459
LSsetPointerLng, 437
LTF format, 122, 376
M
Machine repairman model, 519, 654, 673
Marketing models, 525–32
Markov chain model, 525, 664
Markowitz portfolio selection, 499, 503, 506, 659
Markowitz, H., 499, 659
Match Parenthesis command, 145, 166
Matching model, 70, 666
Material requirements planning, 481, 674
Mathematical functions, 337
Mathematical notation, 25–31
Matrix decomposition, 190, 318
Matrix Decomposition, 190
Matrix form, 234, 267, 526
MAX function, 5, 50, 52, 345, 490, 629
Max passes, 199
Max Scenarios limit, 223
MAXCTP parameter, 310
MAXCTR parameter, 318
McCormick, G., 710
MEM command, 254
Members of sets, 45
Membership filter, 46, 69, 71
Memory
allocated, 254, 296, 432
Memory Limit box, 170
usage, 10, 254
virtual, 297
working, 725, 730
Menu commands, 117, 118, 399
edit, 119, 138–50
file, 119, 121–37
help, 120, 244–49
LINGO, 120, 151–240
window, 120, 240–44
Menu tips, 118, 302
Method, Solution, 185
METRIC model, 667
Mexican steel model, 668
MIN function, 50, 52, 629
Minimal cost queuing, 702
Minimize Memory Usage, 182
MOD function, 338
MODEL command, 22, 257, 726
Model Generator Tab, 175
Model reduction, 185, 306
Model Statistics command, 120, 238
Modeling language, 25–31, 35–38, 41
Models
class, 11
entering, 3–21
infeasible, 25, 236, 276, 432, 735
nonlinear, 1, 111, 194, 314, 630–31
regenerating, 178, 307
titles, 37
types, 621
unbounded, 236, 276, 432, 734
More button, 168
Mortgage calculation, 723

772 INDEX
MPI files, 136, 274
MPS File
command, 119
definition, 119
exporting, 134–35, 174, 275
format, 745
importing, 124–26, 174, 254
MREGEN parameter, 307
Multi-Core, 187
Multilevel distribution, 678
Multiprod. capacitated lot sizing, 671
MULTIS, 311
Multistart solver, 13, 214, 311, 748
MultiStart Solver, 218
MXMEMB parameter, 296
MYUSER.DLL, 470
N
NAME function, 351
Naming conventions
constraints, 35, 728
duplicate names, 182, 741
file names, 127, 729
MPS files, 125, 174, 256
parameters, 307
sets, 181, 727, 729
variables, 6
NCRASH parameter, 304
Necessary set, 236, 276
Negative Binomial distribution, 589
Negative variables, 94–99, 342
Nemhauser, G., 200
Nesting, 55, 145
FOR functions, 732
TAKE command, 726
Network equilibrium, 680
New command, 122, 726
New features, vii
NEWLINE function, 351
Newsboy problem, 655, 682
NLP, 11
NLPVER Parameter, 321
Node selection, 208, 299
NODESL parameter, 299
Non-differentiable functions, 629
Nonlinear
constraints, 10
limits, 38
models, 1, 111, 214, 630–31
optimality tolerance, 192, 295
solver, 533, 621
variables, 9
Nonlinear models, 314
Nonlinear Solver, 193
Nonlinear Solver tab, 191–95
derivatives box, 193
NONNEF parameter, 293
NONNEG Parameter, 323
Nonoptimal solution, 735
NONZ command, 278–80
Nonzeros, 10, 239, 270
dual price, 734
reports, 33, 34, 154
NOPTOL parameter, 295
Normal distribution, 588, 647
NORMSINV function, 339
NSLPDR parameter, 305
NSTEEP parameter, 304
Numeric precision, 186, 190, 432
O
Obj Bound field, 14
OBJBND function, 351
OBJCTS, 310
OBJCTS parameter, 296
Object Linking and Embedding, 377
Object Properties command, 150
Object, Insert New, 147–49, 403
Objective coefficient ranges, 156, 281, 282
Objective coefficients, 24
Objective cuts, 310
Objective function
bounds, 14
cuts, 200, 310
definition, 4
developing, 5, 27
examples
financial models, 501, 505, 513
marketing models, 531
plant location, 493
production models, 478, 489
ODBC, 407–25
administrator, 409, 425
datasources
linking, 137, 147, 289
ODBC function, 147, 419
exporting, 419–25
importing, 415–19
ODBC function, 346
OLE automation
importing, 392–96
OLE function, 346

INDEX 773
exporting
reports, 391
syntax, 385–91
importing, 379–84
Omitting values, 110
One Page button, 130
On-line registration, 246
Open command, 123, 125, 726, 766
Open Data Base Connectivity, 407–25
Operators, 333–36, 727, 730, 734
Optimal solution, 312, 432, 624
Optimality tolerance, 192, 206
Optimization, 1, 4
Optimization Modeling with LINGO, 475
Options command, 159–240
Options pricing, 507, 687
Oracle, 414
OROUTE parameter, 302
Overbooking, Airline, 683
P
PAGE command, 280, 284, 287
Page size limits, 168
Parameters
error messages, 736, 739
pre-defined, 280, 288, 294–307
user defined, 108
Paren Match checkbox, 166
Parent sets, 45
Parentheses, 145, 166, 764
Pareto distribution, 588
Passwords
databases, 137, 289
error messages, 737
HIDE command, 264
Paste command, 139, 362
Paste Function command, 146
Paste Special command, 140
PAUSE, 546
PAUSE command, 287
PBN function, 339
PCX function, 339
Pearson correlation, 590
PEB function, 339, 701
PEL function, 340, 516, 656, 702
PERT, 65, 417–19, 422–25, 691
Peters, D.G., 642
PFD function, 340
PFS function, 340, 519
PHG function, 340, 708
PIC, 541
Picture command, 120, 234
PICTURE command, 267
PILP, 11
PINLP, 12
PIQP, 11
Plant location, 200, 310, 492, 639
Platforms, 251
PLOCTS, 310
pLSenvLINGO, 444
Pluto Dogs, 56, 79
POINTER function, 347
data section, 430, 432
DLL, 433, 437, 444
Poisson
finite source, 519
linear loss function, 340
probability distribution, 340, 516, 655
random variable, 340
Poisson distribution, 589
Polaris project, 65
Portfolio selection
Markowitz, 499, 503, 506, 659
scenario based, 648, 695
Portfolio Selection, Markowitz, 556
POW function, 338
Powerstation FORTRAN
pointer functions, 432
user defined functions, 469, 470
PPL function, 340
PPS function, 340
PRBLVL parameter, 305
Precedence relations, 487, 490
PRECIS parameter, 330
Precision, Numeric, 186
Present value, 339
Prices
Black & Scholes, 509, 685
computing, 172
options, 507, 687
strategies, 186, 306
Primal/dual interior point algorithm, 185, 305
Primitive set
defining, 42–44
examples, 42, 56–60, 61, 66
exporting, 419
names, 181, 729
PRIMPR parameter, 306
Print command, 17, 128
Print Preview command, 130
Print Setup command, 129
Priority option, 202, 308
PRNCLR parameter, 311

774 INDEX
Probabilities, 504
Probability distribution
binomial, 339, 683, 687
Erlang busy, 339, 701
Erlang loss, 340, 516, 656
Erlang queuing, 516
exponential, 516
hypergeometric, 340, 708
normal, 340, 647
Poisson, 340, 516, 519, 655
steady state, 525, 664
t distributions, 647
transition, 525
Probability functions, 339–41
Probing, 197, 305
PROD function, 345
Product form inverse, 622
Production, 671
planning, 671
product mix, 4, 88–93, 132, 690, 694
rates, 653
schedules, 481, 674
Production management models, 476–91
Programming Example
Binary Search, 552
Cutting Stock, 563
Markowitz Efficient Frontier, 556
Project Evaluation and Review Technique, 65, 417–
19, 422–25, 691
Prompts, 22, 251, 257
Properties command, 375
Proportionality, 622
PSL function, 340
PSN function, 340, 647
PTD function, 340, 647
Purchase transition matrix, 526
Q
QP, 11
QRAND function, 341, 746
Quadratic functions, 9, 697
Quadratic MPS format, 254
Quadratic recognition, 194
Quasi-random numbers, 341
Question mark prompt, 22, 257
Queuing models
examples
Erlang, 516–24, 656, 701–2
machine repairman, 654
steady state, 703
probabilities, 339, 340
QUIT command, 332
R
R/C format names
options, 126, 174
parameter, 256, 307
RAND function, 341, 647
Random Generator Seed, 222
Random numbers, 341, 647, 664, 746
Range
analysis, 746
bounding, 214
dual values, 155, 157, 281
names
defining, 390
exporting (OLE), 386
exporting (WKX), 392
importing (OLE), 384
OLE automation, 393
reports
command-line, 280
error messages, 738
Windows, 155
Range command, 25, 155
RANGE command, 280
RANGED function, 351
RANGEU function, 352
Rate of return, 501, 505
RCMPSN parameter, 307
RCTLIM parameter, 310
Read error, 731
Redirecting I/O, 376
Redo command, 138
REDUCE parameter, 306
Reduced cost, 24
examples, 64
ranges, 155, 157, 281
REFRAQ parameter, 326
Register command, 246
Regression Analysis, 662, 706
Relational operators, 335, 727
Relationships, 631
Relative Integrality, 203
Relative integrality tolerance, 203, 294
Relative limit box, 199
Relative optimality tolerance, 206, 298
RELEASE, 543
RELINT parameter, 294
REOPTB parameter, 309
REOPTX parameter, 309
Replace command, 144

INDEX 775
Reports, 302
export summary report
ODBC based, 424
OLE based, 391
generating, 272
graphic, 155
nonzeros only, 33, 154
range report
command-line, 280
error messages, 738
Windows, 155
send to command window, 167
solution report
command-line, 23, 278, 282
examples, 33, 64
exporting, 424
naming constraints, 37
tolerances, 186, 294, 308
width, 288
Windows, 153, 154
statistics, 120, 238, 269
Resource limits, 4, 5, 26, 89
Right-hand side
probing, 197
range report, 157, 282
Risk
downside risk, 234, 648
portfolio selection, 499–506, 659, 695
sampling, 708, 712
RMPS command, 254
Root filed, 199
Rounding, 75, 80, 190, 308
Row name, 34, 728
Runtime, 10, 206
Runtime Limits box, 171
RVRT command, 274
S
Sales forecasting, 713
Sample Continuous Only, 222
sample size, 589
Sampling, 341, 708, 710, 712
SAVE command, 24, 274
Save/Save As command, 17, 127
Scalar variables
examples, 26, 28, 489, 690
initializing, 108
Scale Model, 190
SCALEM parameter, 306
SCALEW parameter, 326
Scaling, 186, 294, 630, 748
Scaling Warning Threshold, 173
Scarce capacity, 671
Scenario portfolio selection, 503, 648, 695
SCENE command, 268
Scholes, M., 507, 685
Schrage, L., 93, 475, 645
SCLRDL parameter, 311
SCLRLM parameter, 311
Script files, 371–73, 450
command-line, 257
DLL, 434, 445
OLE automation
importing, 392–96
Windows, 131–34, 241
Script processor, 430
Scripting, 535
Second order derivatives, 193
SECORD parameter, 293
SECORD Parameter, 323
Seed value, 746
SELCON parameter, 305
Select All command, 144, 362
Select Font command, 146
Selective constraint evaluation, 194, 305
Semi-variance risk, 503, 506
Send To Back command, 243
SET, 548
SET command, 290, 739
Set-looping functions, 48–55, 345
Sets, 26–35, 41–74, 746
derived sets
defining, 42, 45–48, 745
dense, 62, 489, 746
examples
blending models, 61–64, 478
financial models, 504
marketing models, 530
production models, 484, 489
exporting, 419
sparse, 64–69, 69–74
errors, 744
implicit, 746
importing, 181
names, 727
necessary, 236, 276
primitive set
defining, 42–44
examples, 42, 56–60, 61, 66
exporting, 419
names, 729
sufficient, 236, 238, 276, 278
Sets section, 42–48, 364

776 INDEX
Setup cost, 653, 671
Shack4Shades, 94
Shadow prices, 25, 157, 281
Shipping problem, 26, 41, 492, 678
Shortcut, 374
Shortest route problem, 496
SHOWNL command, 273
SIGN function, 338
Simplex method, 622
cold start, 205, 309
options, 185
parameters, 305
warm start, 205, 309
SIN function, 338
SINH function, 338
SIZE function, 68, 344
Slack or Surplus, 25, 186, 294, 491
Slack variables, 239, 270, 479
Slope, 95, 629
Slow progress iteration limit, 192, 295
SLP directions, 195, 305
SMAX function, 338
SMIN function, 338
Smooth expressions, 516, 629, 714
SMPI, 542
SMPI command, 274
SMPS, 542
SMPS command, 275
SOLU, 282, 544
Solution command, 33, 154
SOLUTION command, 282
Solution report
command-line, 23, 278, 282
examples, 33, 64
exporting, 424
naming constraints, 37
tolerances, 186, 294, 308
width, 288
Windows, 153, 154
Solutions
feasible, 186
infeasible, 25, 236, 276, 432, 735
non-optimal, 735
optimal, 312, 432, 624
unbounded, 236, 276, 432, 734
undefined, 735
undetermined, 432
SOLVE, 535
Solve command, 7–16, 33, 124, 151, 243, 405
SOLVE Time-Limit box, 172
SOLVEL parameter, 305
Solver, 8, 533, 621
branch-and-bound
constraint cuts
options, 198, 201
parameters, 297, 310, 318
definition, 76, 533, 621
direction, 307
heuristics, 197, 318
optimality tolerance, 206
solver, 13, 196
strategy, 202
global, 13, 314
interrupting, 8, 765
linear, 184, 204, 533, 621
method, 305, 746
multistart, 13, 311
nonlinear, 533, 621
quadratic, 194
type, 14
Solver status window, 152
error messages, 765
field definitions, 8–15
model classification, 622, 623
options, 163, 301
SONGS model, 716
Sorting, 717
SOS
variables
syntax, 100
SP Sample Size/Stage, 221
SP Solver, 221
SP Solver Method, 223
SP Solver Tab, 221
Spanning tree model, 676
Sparse derived set, 64–69, 69–74, 729
Sparse set, 45
Spearman correlation, 590
Splash screen, 163, 301
SPLOADSCENE, 549
SPMAXS parameter, 329
SPMTHD parameter, 328
SPNUMSCENE, 549
SPPRBSCENE, 549
Spreadsheets
data section, 26
exporting
functions, 384–92
reports, 287
importing, 379–84
interfacing with, 141, 361, 363, 379–406
SPSCON parameter, 327
SPSEED parameter, 328
SPSMSZ parameter, 327

INDEX 777
SPXVAL parameter, 328
SQL, 414
SQR function, 338
SQRT function, 338
STABAR parameter, 302
Stack space, 727
Staff scheduling, 56, 368, 372, 438–55, 650
DLL, 427–47, 430
State of the model, 10, 12, 13, 734, 735
Statistics, 120, 238, 269, 623
STATS command, 269
Status bar, 3, 118, 162, 302
STATUS function, 353
Status Window command, 163, 243
STAWIN parameter, 301
Steady state, 523, 703
equations, 521
probability, 525, 664
queuing model, 521, 703
Steepest edge, 187, 195, 304, 306
Steps field, 15
Stochastic Programming
Declaring Distributions, 587
Gas Buying Core Model, 594
Gas Buying Example, 594
Introduction, 577
Investing Under, 614
Investing Under Uncertainty Example, 612
Language Features, 585
Monte Carlo Sampling, 583
Multistage Decision Making, 577
Recourse Models, 579
Scenario Tree, 581
Setting up SP Models, 584
Stock Option Core Model, 605
Stock Option Example, 604
Stock options, 507
STOP, 538
Straight line relationships, 622
Strategies, 194
Strategies box, 217
Stratified sampling design, 710
STRLEN function, 354
Strong branch, 208, 308
STRONG parameter, 308
Student t distribution, 588
SUBMODEL, 533
SUBOUT parameter, 320
Successive linear programming, 195, 305, 622
Sufficient set, 236, 238, 276, 278
SUM function, 50, 84, 345
Sum of a set, 345
Sum of squared prediction, 713
Sweeney, D., 497
Syntax, 6, 7, 107
coloring, 146, 166, 311
T
t distribution, 647
TABLE function, 354
Table of Contents, iii
TAKE command, 257
command scripts, 371
Take Commands command, 122, 131–34, 371
TAN function, 338
TANH function, 338
Tanner, K., 678
TATSLV Paramater, 324
TATSLV Parameter, 293
Technical support, 39
Terminal width parameter, 288, 736
TERSE command, 287
Terse output, 164
TERSEO parameter, 300
Text files, 26, 274, 361, 363, 376
TEXT function, 347
command scripts, 373
Tiered distribution, 678
Tile command, 244
TIM2RL parameter, 299
TIME command, 332
TIME function, 356
Time to relative tolerance, 206, 207, 299
Timesharing system, 519, 654
TIMLIM parameter, 296
TITLE command, 37
Tolerances, 186, 192, 203, 206
command-line, 253, 288, 290, 294–98
examples, 527
Tolerances box, 207, 217
Tool tips, 118, 302
Toolbar, 3, 117, 164, 242, 303, 399
TOOLBR parameter, 303
Traffic congestion, 681
Transfer method
command line, 391, 424
Transition probability, 525, 664
Transportation model, 724
datasources, 408
exporting, 389
importing, 382
linking, 140
sets, 26

778 INDEX
Traveling salesman problem, 718
Tree field, 199
Triangular distribution, 589
Truncating, 76, 135, 168, 276
Two-sided constraints, 727
U
Unary Minus Priority, 176
UNARYM parameter, 293
UNARYM Parameter, 322
Unbounded solution, 236, 276, 432, 734
Undefined arithmetic operation, 305, 733, 734
Undefined solution, 735
Undetermined solution, 432
Undo command, 138
Uniform distribution, 589
Unit normal linear loss, 340
Unity coefficients, 239, 270
Unix, 376
Update interval, 9, 163, 301
Updating LINGO, 247
Updating links, 150
Use RC Format Names, 174
USEPNM parameter, 304
USEQPR parameter, 314
User defined functions, 469–73
USER function, 360
User ID, 137, 289
User interrupt, 8, 765
Utility functions, 529
V
Values transferred
command-line, 392
Variable domain functions, 72, 733
Variable Upper Bound Box, 216
Variables
bounds, 319
functions, 342
guidelines for, 630
probing, 197
syntax, 99
continuous variables, 72
decision variables
defining, 4
examples, 71, 489, 493, 504
ranges, 155, 280
defining, 5, 27
fixed variables, 9, 157, 622, 732
free variables, 94–99, 342
initializing, 630
integer variables
binary
examples, 489
functions, 75, 342
priority, 202, 308
syntax, 82–93
examples, 480
general, 75, 76–81, 342
solutions, 9, 631
variable domain functions, 75–93
limits, 38
names, 6, 125, 256
negative, 94–99, 342
nonlinear, 1, 9
production models, 478, 484
random, 340
scalar
examples, 26, 28, 489, 690
initializing, 108
slack, 239, 270, 479
solver status window, 9
SOS
syntax, 100
transportation models, 498
Variables Assumed Non-Negative, 174
Variance, 499, 506, 507
Vehicle routing problem, 721
VERBOSE command, 287
Verbose output, 164
Virtual memory, 297
Visual Basic, 428, 446–47
callback function, 465
macros in Excel, 392, 395
Visual Basic .NET, 428
Visual C++, 428, 438–46
callback function, 460
user defined function, 470
Volatility, 507
VSS, 600
W
Warm start option, 204, 309
WARN function, 360, 527, 732, 741
Weibull distribution, 589
What If analysis, 109
WHILE, 536
WIDTH command, 288, 736
Williams, T., 497
Window menu, 120, 240–44

INDEX 779
Windows commands
in brief, 118–20
in depth, 121–249
Winston, W., 93, 714
Wireless Widgets
examples, 26
importing, 364, 382
sets, 42, 65
WNLINE parameter, 302
WNTRIM parameter, 302
Wolsey, E., 200
Working memory, 730
Workstations, 487, 521, 524
Worst bound, 208, 299
WRAP function, 96, 344
WRITE, 545
Write access, 739, 740, 765
WRITE function, 356
WRITEFOR function, 357
Writing to files, 367
X
XDETEQ command, 270
Z
Zoom, 235