MANUAL
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 6
BarrierTool Manual
Stergios Katsanoulis
Institute for Mechanical Systems, ETH Zürich, Leonhardstrasse 21, 8092 Zürich, Switzerland
In this brief manual the user is guided through the GUI of BarrierTool by means of an example. To launch the
GUI, the user needs to go to the folder “Main” and type the command “null_geo” in the command prompt.
1 Detection Method
The first thing the user has to decide is whether he wants to detect Lagrangian or Eulerian barriers. One should
select the former if he is interested in structures intrinsically tied to a specific finite time interval over which they
exert their influence on nearby trajectories and the latter if he is particularly interested in the short-term limit of
the former. In the following sections of this tutorial we present the Lagrangian case, as it is more general, and we
demonstrate an example of the Eulerian limit at the section 6.
In the Lagrangian setting one can look for Closed Diffusion Barriers or Elliptic Lagrangian Coherent Structures.
In principle, the distinction between the two lies on the different variational principles they should satisfy. These
principles are described in detail in [1] and [2], both of which are included in the folder “doc”. One should experiment
with both options to extract larger structures.
Once the detection method is chosen, the user has to select the range and number of values for T0or λ. In case of
lagrangian coherent structures, one needs also to specify the time interval on which they want to detect structures.
In the diffusive setting such a choice is extraneous since the underlying theory suggests that we use the time-averaged
version of the Cauchy-Green strain tensor for our computations.
Another thing that is worth mentioning is the admissible range of values for T0or λ. In every case that we tried
the default range of these values produced barriers. However, this does not preclude the existence of flows where
this range needs to be larger. This is why we suggest that the user experiment with this range.
2 Averaged Diffusive Cauchy-Green Tensor Field
The first step for the detection of barriers is the computation of the right Cauchy-Green strain tensor in case of
lagrangian coherent structures or its time-averaged version in the diffusive setting. To this end, the GUI accepts
as input a “.mat” file containg the velocity field. More specifically, this file must contain five variables, i.e., the
variables “time”, “vx”, “vy”, “xc” and “yc” corresponding to the time instances for which the velocity field is known,
the x and y components of the velocity field and the x and y coordinates of the grid on which the velocity field
is defined, respectively. In case of material diffusion barriers, the user needs to specify three additional variables,
i.e., “D11 ”, “D12 ” and “D22 ” corresponding to the components of the symmetric diffusive structure tensor. For
the majority of diffusive cases this tensor can be set to identity. One may find an example of the acceptable file
structure in the folder “data”, namely, in the file “ocean_velocity_example_diffusive.mat”.
To demostrate the use of GUI, we detected material diffusion barriers for the default set of T0values using the file
“ocean_velocity_example_diffusive.mat”. Once we selected this file, we used the values shown in Figure 1 for the
computation of the time-averaged Cauchy-Green strain tensor.
1
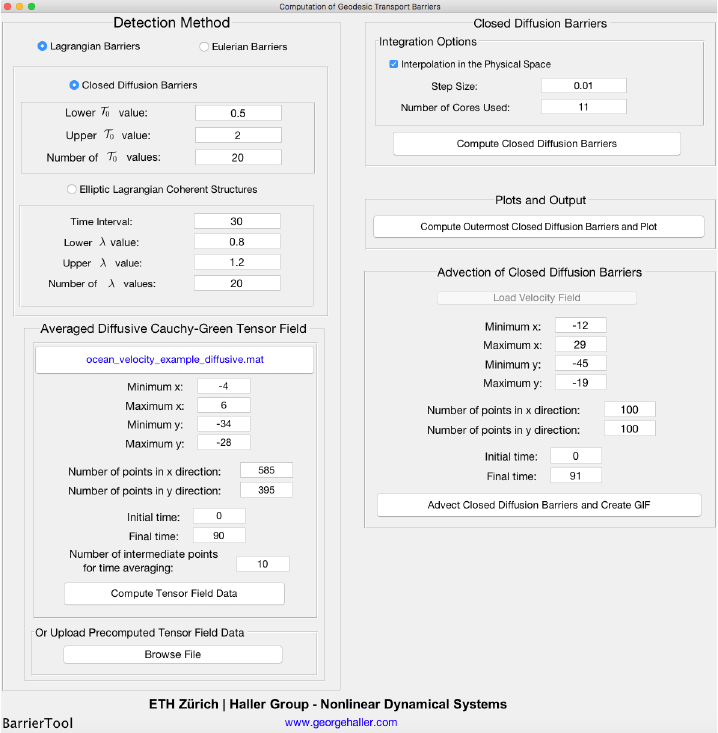
Figure 1: Set of values used for the computation of the time-averaged Cauchy-Green strain tensor.
Once the computation is finished, the results may be found in the file “TensorFieldData.mat” inside the folder
“Output”. This file can be used as input to the GUI in the field “Upload Precomputed Tensor Field Data” to avoid
the computationally expensive task of re-computing the Cauchy-Green tensor field at a later time.
The computational procedure to detect Elliptic Lagrangian Coherent Structures is exactly the same after the user
has selected the “Elliptic Lagrangian Coherent Structures”.
3 Closed Diffusion Barriers
Before being able to compute closed diffusion barriers, we need to specify the necessary integration options. These
comprise the fields “Integration in the Physical Space” and “Step Size”. The user may start with the default values
and then experiment with them to extract larger structures. Finally, the GUI automatically detects the number of
cores of the machine in which it is running and it sets the number of cores used for the computation to one less
than that. Once these selections are made, we press the button “Compute Closed Diffusion Barriers”.
4 Plots and Output
After the computation of closed diffusion barriers is completed, we press “Compute Outermost Closed Diffusion
Barriers and Plot”. This results in the creation of the files “NullGeodesics.fig” and “OutermostNullGeodesics.fig”
in the folder “Output” containg all and the outermost extracted material diffusion barriers, respectively, both
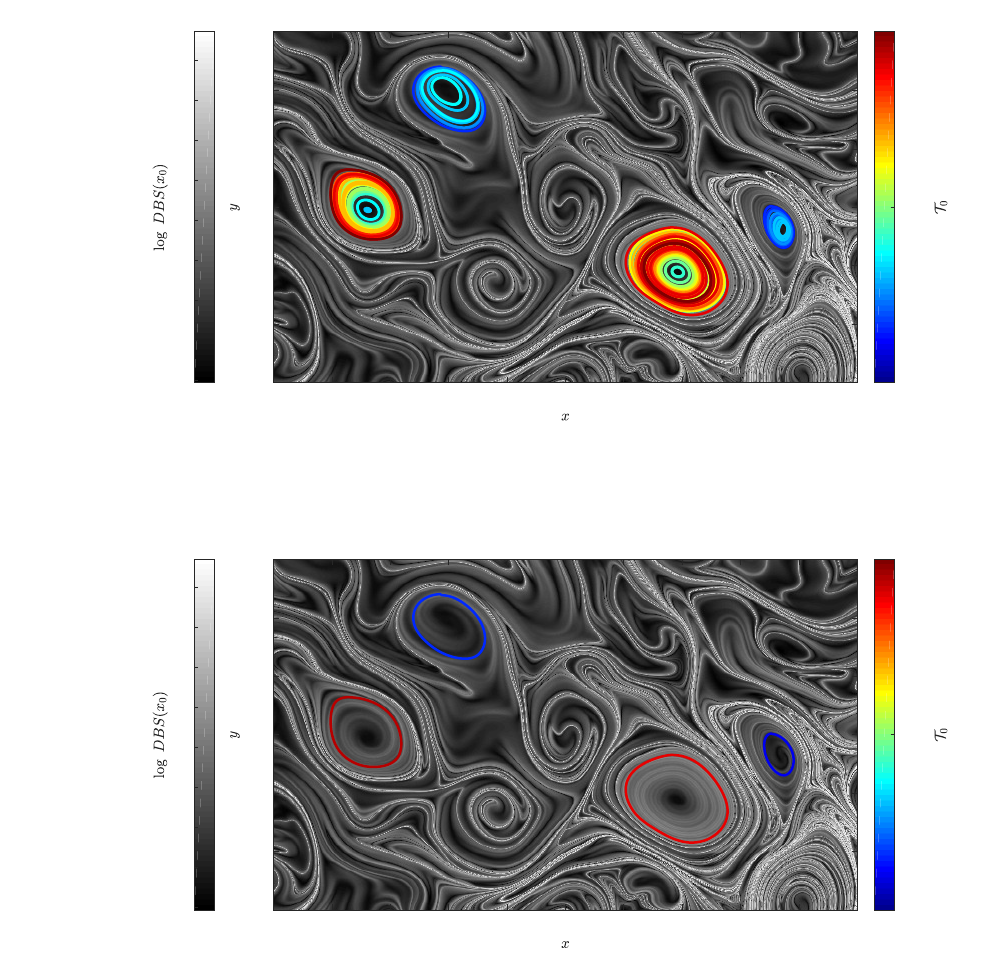
superimposed with the DBS field. The structures that we extracted using the values shown in Figure 1 are depicted
in Figures 2 and 3. Finally, in the folder “Output” the file “OutermostNullGeodesics.mat” contains the x and y
components of the outermost structures for post-processing.
2
Diffusion Barrier Strength field and Closed Diffusion Barriers
-4 -3 -2 -1 0 1 2 3 4 5 6
-34
-33
-32
-31
-30
-29
-28
0
2
4
6
8
10
12
14
16
0.50
1.25
2.00
Figure 2: Diffusion Barrier Strength field and Closed Diffusion Barriers for the values presented in Figure 1.
Diffusion Barrier Strength field and Outermost Closed Diffusion Barriers
-4 -3 -2 -1 0 1 2 3 4 5 6
-34
-33
-32
-31
-30
-29
-28
0
2
4
6
8
10
12
14
16
0.50
1.25
2.00
Figure 3: Diffusion Barrier Strength field and Outermost Closed Diffusion Barriers for the values presented in
Figure 1.
5 Advection of Closed Diffusion Barriers
The last feature of the GUI showcases the comparison of time evolution of random tracers and the outermost
material diffusion barriers. The tracers are placed in a uniform rectangular grid. In our example we used the values
presented in Figure 4 for the rectangular grid and the time interval, respectively. The button “Advect Material
Diffusion Barriers and Create GIF” creates the animation and saves it in the file “NullGeodesics.gif” inside the
folder “Output”.
3
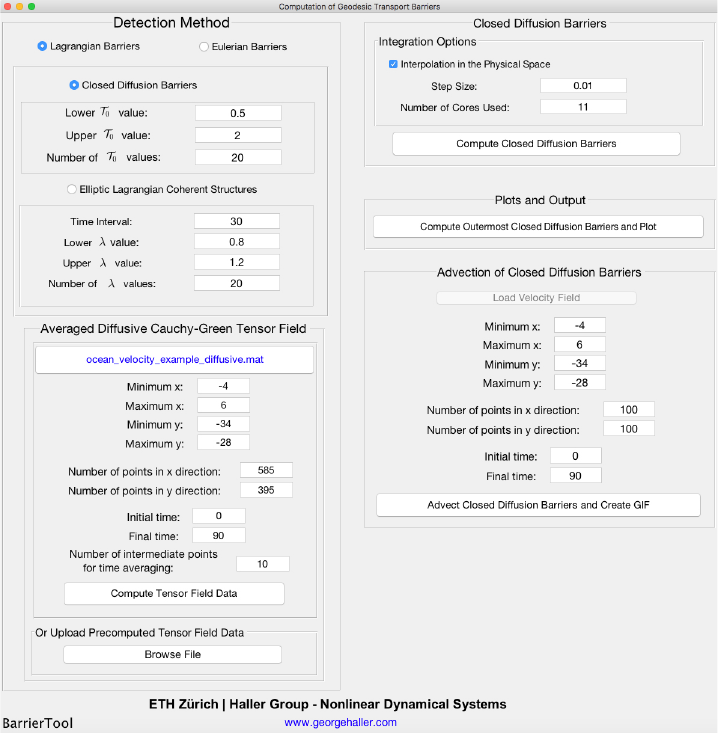
Figure 4: Set of values used for the computation of the advection of Closed Diffusion Barriers.
6 Eulerian Barriers
In case of Eulerian Barriers, the computational procedure is almost the same as in the Lagrangian setting. The
differences are highlighted in Figure 5. More specifically, following [3] included in the folder “doc”, the corresponding
tensor inherent to the underlying theory is the rate-of strain tensor. This tensor is not positive definite and thus,
the admissible range of λvalues is allowed to contain negative values. Finally, since it is a computation concerning
the instantaneous limit of the Lagrangian setting, the user can only specify one time, namely, the initial time.
The extracted Eulerian Barriers for the case presented in Figure 5 are depicted in Figure 6.
4
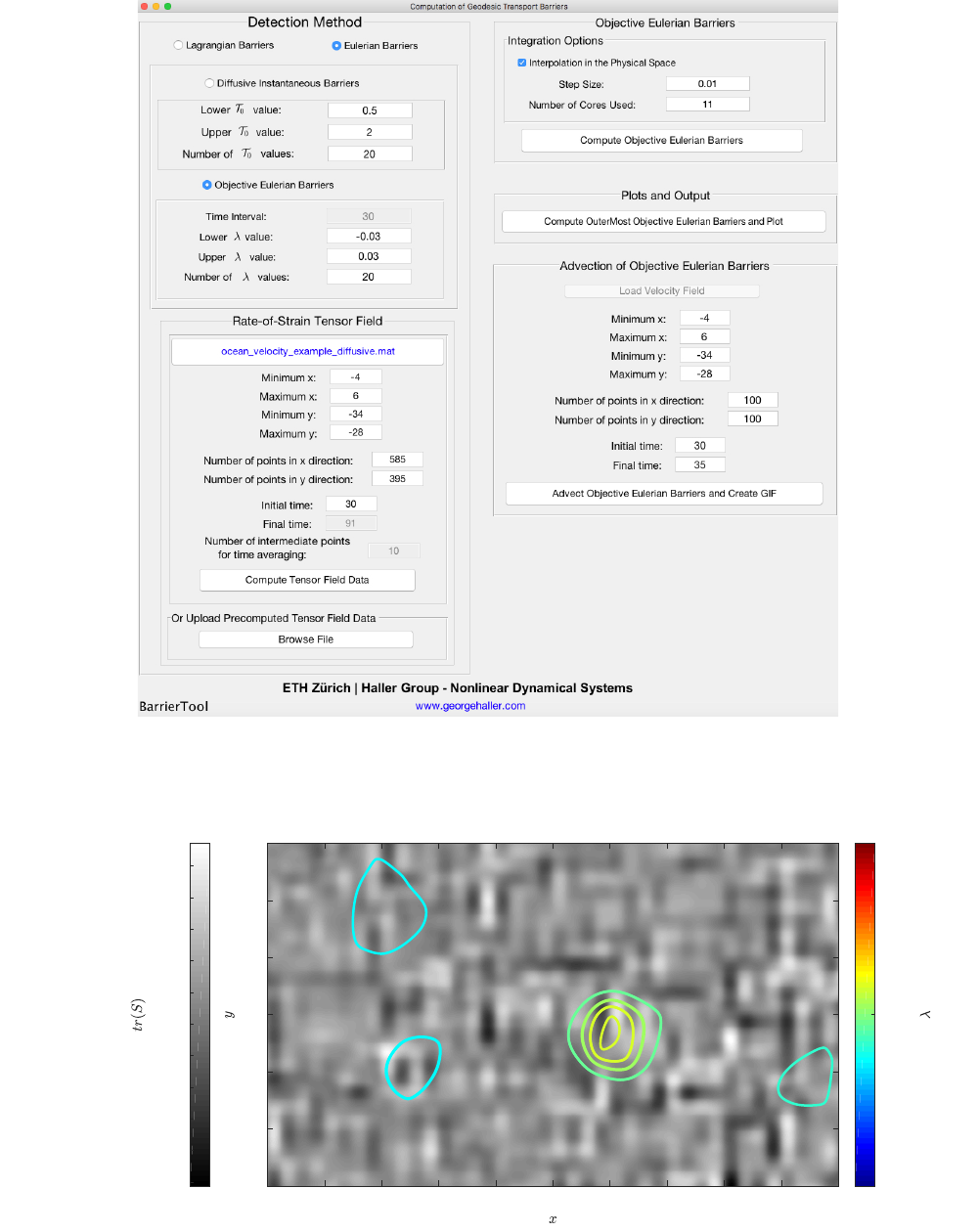
Figure 5: Set of values used for the computation of the Eulerian Barriers.
Trace of Rate-of-Strain tensor field and Eulerian Coherent Structures
-4 -3 -2 -1 0 1 2 3 4 5 6
-34
-33
-32
-31
-30
-29
-28
-0.06
-0.05
-0.04
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
-0.03
0.00
0.03
Figure 6: Extracted Eulerian Barriers for the values presented in Figure 5.
5
References
[1] G. Haller, D. Karrasch & F. Kogelbauer, Material barriers to diffusive and stochastic transport. Proc. Natl.
Acad. Sci. U.S.A. (2018).
[2] G. Haller & F.J. Beron-Vera, Coherent Lagrangian vortices: The black holes of turbulence. J. Fluid Mech. 731
(2013) R4.
[3] M. Serra & G. Haller, Objective Eulerian coherent structures. Chaos26 (2016).
6