MATPOWER Manual

MATPOWER-manual

User Manual:

Open the PDF directly: View PDF .
Page Count: 246 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Introduction
Getting Started
Modeling
Power Flow
Continuation Power Flow
Optimal Power Flow
Extending the OPF
Unit De-commitment Algorithm
Miscellaneous Matpower Functions
Acknowledgments
Appendix MIPS – Matpower Interior Point Solver
Appendix Data File Format
Appendix Matpower Options
- Mapping of Old-Style Options to New-Style Options
Appendix Matpower Files and Functions
Appendix Extras Directory
Appendix ``Smart Market'' Code
Appendix Optional Packages
Appendix Release History
References

MATP WER

User’s Manual

Version 7.0b1

Ray D. Zimmerman Carlos E. Murillo-S´anchez

October 31, 2018

Contents

1 Introduction 10

1.1 Background ................................ 10

1.2 License and Terms of Use ........................ 11

1.3 Citing Matpower ............................ 12

1.4 Matpower Development ........................ 12

2 Getting Started 13

2.1 System Requirements ........................... 13

2.2 Getting Matpower ........................... 14

2.2.1 Versioned Releases ........................ 14

2.2.2 Current Development Version .................. 14

2.3 Installation ................................ 16

2.4 Running a Simulation ........................... 18

2.4.1 Preparing Case Input Data .................... 18

2.4.2 Solving the Case ......................... 18

2.4.3 Accessing the Results ....................... 19

2.4.4 Setting Options .......................... 20

2.5 Documentation .............................. 20

3 Modeling 23

3.1 Data Formats ............................... 23

3.2 Branches .................................. 23

3.3 Generators ................................. 25

3.4 Loads ................................... 25

3.5 Shunt Elements .............................. 26

3.6 Network Equations ............................ 26

3.7 DC Modeling ............................... 27

4 Power Flow 30

4.1 AC Power Flow .............................. 30

4.2 DC Power Flow .............................. 32

4.3 Distribution Power Flow ......................... 32

4.3.1 Radial Power Flow ........................ 33

4.3.2 Current Summation Method ................... 34

4.3.3 Power Summation Method .................... 35

4.3.4 Admittance Summation Method ................. 35

4.3.5 Handling PV Buses ........................ 37

4.4 runpf ................................... 38

4.5 Linear Shift Factors ............................ 39

5 Continuation Power Flow 43

5.1 Parameterization ............................. 44

5.2 Predictor .................................. 44

5.3 Corrector ................................. 45

5.4 Step Length Control ........................... 45

5.5 Event Detection and Location ...................... 46

5.6 runcpf ................................... 47

5.6.1 CPF Callback Functions ..................... 50

5.6.2 CPF Example ........................... 53

6 Optimal Power Flow 56

6.1 Standard AC OPF ............................ 56

6.1.1 Cartesian vs. Polar Coordinates for Voltage .......... 57

6.1.2 Current vs. Power for Nodal Balance Constraints ....... 58

6.2 Standard DC OPF ............................ 59

6.3 Extended OPF Formulation ....................... 60

6.3.1 User-deﬁned Variables ...................... 61

6.3.2 User-deﬁned Constraints ..................... 61

6.3.3 User-deﬁned Costs ........................ 62

6.4 Standard Extensions ........................... 64

6.4.1 Piecewise Linear Costs ...................... 64

6.4.2 Dispatchable Loads ........................ 66

6.4.3 Generator Capability Curves ................... 68

6.4.4 Branch Angle Diﬀerence Limits ................. 69

6.5 Solvers ................................... 69

6.6 runopf ................................... 70

7 Extending the OPF 76

7.1 Direct Speciﬁcation ............................ 76

7.1.1 User-deﬁned Variables ...................... 76

7.1.2 User-deﬁned Constraints ..................... 76

7.1.3 User-deﬁned Costs ........................ 78

7.1.4 Additional Comments ...................... 79

7.2 Callback Functions ............................ 79

7.2.1 User-deﬁned Variables ...................... 80

7.2.2 User-deﬁned Costs ........................ 80

7.2.3 User-deﬁned Constraints ..................... 81

7.3 Callback Stages and Example ...................... 82

7.3.1 ext2int Callback ......................... 83

7.3.2 formulation Callback ...................... 84

7.3.3 int2ext Callback ......................... 88

7.3.4 printpf Callback ......................... 91

7.3.5 savecase Callback ........................ 93

7.4 Registering the Callbacks ......................... 95

7.5 Summary ................................. 97

7.6 Example Extensions ........................... 97

7.6.1 Fixed Zonal Reserves ....................... 97

7.6.2 Interface Flow Limits ....................... 99

7.6.3 DC Transmission Lines ...................... 100

7.6.4 OPF Soft Limits ......................... 103

8 Unit De-commitment Algorithm 110

9 Miscellaneous Matpower Functions 112

9.1 Input/Output Functions ......................... 112

9.1.1 loadcase ............................. 112

9.1.2 savecase ............................. 112

9.1.3 cdf2mpc .............................. 113

9.1.4 psse2mpc ............................. 113

9.1.5 save2psse ............................. 114

9.2 System Information ............................ 114

9.2.1 case info ............................. 114

9.2.2 compare case ........................... 114

9.2.3 find islands ........................... 115

9.2.4 get losses ............................ 115

9.2.5 margcost ............................. 116

9.2.6 isload ............................... 116

9.2.7 loadshed ............................. 116

9.2.8 printpf .............................. 116

9.2.9 total load ............................ 117

9.2.10 totcost .............................. 117

9.3 Modifying a Case ............................. 117

9.3.1 extract islands ......................... 117

9.3.2 load2disp ............................. 118

9.3.3 modcost .............................. 118

9.3.4 scale load ............................ 118

9.3.5 apply changes .......................... 119

9.3.6 savechgtab ............................ 122

9.4 Conversion between External and Internal Numbering ......... 123

9.4.1 ext2int,int2ext ......................... 123

9.4.2 e2i data,i2e data ........................ 123

9.4.3 e2i field,i2e field ...................... 124

9.5 Forming Standard Power Systems Matrices ............... 125

9.5.1 makeB ............................... 125

9.5.2 makeBdc .............................. 125

9.5.3 makeJac .............................. 125

9.5.4 makeLODF ............................. 126

9.5.5 makePTDF ............................. 126

9.5.6 makeYbus ............................. 126

9.6 Miscellaneous ............................... 127

9.6.1 define constants ........................ 127

9.6.2 feval w path ........................... 127

9.6.3 have fcn ............................. 127

9.6.4 mpopt2qpopt ........................... 128

9.6.5 mpver ............................... 129

9.6.6 nested struct copy ....................... 129

10 Acknowledgments 130

Appendix A MIPS – Matpower Interior Point Solver 131

A.1 Example 1 ................................. 133

A.2 Example 2 ................................. 135

A.3 Quadratic Programming Solver ..................... 137

A.4 Primal-Dual Interior Point Algorithm .................. 138

A.4.1 Notation .............................. 138

A.4.2 Problem Formulation and Lagrangian .............. 139

A.4.3 First Order Optimality Conditions ............... 140

A.4.4 Newton Step ........................... 141

Appendix B Data File Format 144

Appendix C Matpower Options 150

C.1 Mapping of Old-Style Options to New-Style Options .......... 166

Appendix D Matpower Files and Functions 170

D.1 Directory Layout and Documentation Files ............... 170

D.2 Matpower Functions .......................... 172

D.3 Example Matpower Cases ....................... 184

D.4 Automated Test Suite .......................... 187

Appendix E Extras Directory 191

Appendix F “Smart Market” Code 193

F.1 Handling Supply Shortfall ........................ 195

F.2 Example .................................. 195

F.3 Smartmarket Files and Functions .................... 200

Appendix G Optional Packages 201

G.1 BPMPD MEX – MEX interface for BPMPD .............. 201

G.2 CLP – COIN-OR Linear Programming ................. 201

G.3 CPLEX – High-performance LP and QP Solvers ............ 202

G.4 GLPK – GNU Linear Programming Kit ................ 203

G.5 Gurobi – High-performance LP and QP Solvers ............ 203

G.6 Ipopt – Interior Point Optimizer .................... 204

G.7 KNITRO – Non-Linear Programming Solver .............. 205

G.8 MINOPF – AC OPF Solver Based on MINOS ............. 206

G.9 MOSEK – High-performance LP and QP Solvers ........... 206

G.10 Optimization Toolbox – LP, QP, NLP and MILP Solvers . . . . . . . 207

G.11 PARDISO – Parallel Sparse Direct and Multi-Recursive Iterative Lin-

ear Solvers ................................. 207

G.12 SDP PF – Applications of a Semideﬁnite Programming Relaxation of

the Power Flow Equations ........................ 208

G.13 TSPOPF – Three AC OPF Solvers by H. Wang ............ 208

Appendix H Release History 210

H.1 Pre 1.0 – released Jun 25, 1997 ..................... 210

H.2 Version 1.0 – released Sep 17, 1997 ................... 210

H.3 Version 1.0.1 – released Sep 19, 1997 .................. 210

H.4 Version 2.0 – released Dec 24, 1997 ................... 211

H.5 Version 3.0 – released Feb 14, 2005 ................... 212

H.6 Version 3.2 – released Sep 21, 2007 ................... 213

H.7 Version 4.0 – released Feb 7, 2011 .................... 215

H.8 Version 4.1 – released Dec 14, 2011 ................... 218

H.9 Version 5.0 – released Dec 17, 2014 ................... 219

H.10 Version 5.1 – released Mar 20, 2015 ................... 224

H.11 Version 6.0 – released Dec 16, 2016 ................... 227

H.12 Version 7.0 – beta 1 released released Oct 31, 2018 ........... 232

References 240

List of Figures

3-1 Branch Model ............................... 24

4-1 Oriented Ordering ............................ 33

4-2 Branch Representation: branch kbetween buses i(sending) and k

(receiving) and load demand and shunt admittances at both buses . . 34

5-1 Nose Curve of Voltage Magnitude at Bus 9 ............... 53

6-1 Relationship of wito rifor di= 1 (linear option) ............ 63

6-2 Relationship of wito rifor di= 2 (quadratic option) ......... 64

6-3 Constrained Cost Variable ........................ 65

6-4 Marginal Beneﬁt or Bid Function .................... 66

6-5 Total Cost Function for Negative Injection ............... 67

6-6 Generator P-QCapability Curve .................... 68

7-1 Adding Constraints Across Subsets of Variables ............ 87

7-2 DC Line Model .............................. 101

7-3 Equivalent “Dummy” Generators .................... 101

7-4 Feasible Region for Branch Flow Violation Constraints ........ 104

List of Tables

4-1 Power Flow Results ............................ 39

4-2 Power Flow Options ........................... 40

4-3 Power Flow Output Options ....................... 41

5-1 Continuation Power Flow Results .................... 48

5-2 Continuation Power Flow Options .................... 49

5-3 Continuation Power Flow Callback Input Arguments ......... 51

5-4 Continuation Power Flow Callback Output Arguments ........ 52

5-5 Continuation Power Flow State ..................... 52

6-1 Optimal Power Flow Results ....................... 71

6-2 Optimal Power Flow Solver Options ................... 73

6-3 Other OPF Options ............................ 74

6-4 OPF Output Options ........................... 75

7-1 User-deﬁned Nonlinear Constraint Speciﬁcation ............ 78

7-2 Names Used by Implementation of OPF with Reserves ........ 83

7-3 Results for User-Deﬁned Variables, Constraints and Costs ....... 89

7-4 Callback Functions ............................ 97

7-5 Input Data Structures for Fixed Zonal Reserves ............ 98

7-6 Output Data Structures for Fixed Zonal Reserves ........... 98

7-7 Input Data Structures for Interface Flow Limits ............ 99

7-8 Output Data Structures for Interface Flow Limits ........... 100

7-9 Soft Limit Formulation .......................... 105

7-10 Input Data Structures for OPF Soft Limits ............... 106

7-11 Default Soft Limit Values ........................ 107

7-12 Possible Hard-Limit Modiﬁcations .................... 107

7-13 Output Data Structures for OPF Soft Limits .............. 108

9-1 Columns of chgtab ............................ 120

9-2 Values for CT TABLE Column ....................... 120

9-3 Values for CT CHGTYPE Column ...................... 121

9-4 Values for CT COL Column ........................ 121

A-1 Input Arguments for mips ........................ 132

A-2 Output Arguments for mips ....................... 133

A-3 Options for mips ............................. 134

B-1 Bus Data (mpc.bus)............................ 145

B-2 Generator Data (mpc.gen)........................ 146

B-3 Branch Data (mpc.branch)........................ 147

B-4 Generator Cost Data (mpc.gencost)................... 148

B-5 DC Line Data (mpc.dcline)....................... 149

C-1 Top-Level Options ............................ 152

C-2 Power Flow Options ........................... 153

C-3 Continuation Power Flow Options .................... 154

C-4 OPF Solver Options ........................... 155

C-5 General OPF Options .......................... 156

C-6 Power Flow and OPF Output Options ................. 157

C-7 OPF Options for MIPS .......................... 158

C-8 OPF Options for CLP .......................... 158

C-9 OPF Options for CPLEX ........................ 159

C-10 OPF Options for fmincon ........................ 160

C-11 OPF Options for GLPK ......................... 160

C-12 OPF Options for Gurobi ......................... 161

C-13 OPF Options for Ipopt ......................... 161

C-14 OPF Options for KNITRO ........................ 162

C-15 OPF Options for MINOPF ........................ 163

C-16 OPF Options for MOSEK ........................ 164

C-17 OPF Options for PDIPM ......................... 165

C-18 OPF Options for TRALM ........................ 165

C-19 Old-Style to New-Style Option Mapping ................ 166

D-1 Matpower Directory Layout and Documentation Files . . . . . . . 171

D-2 Top-Level Simulation Functions ..................... 172

D-3 Input/Output Functions ......................... 172

D-4 Data Conversion Functions ........................ 173

D-5 Power Flow Functions .......................... 173

D-6 Continuation Power Flow Functions ................... 174

D-7 OPF and Wrapper Functions ...................... 175

D-8 OPF Model Objects ........................... 176

D-9 Deprecated @opt model Methods ..................... 177

D-10 OPF Solver Functions .......................... 177

D-11 Other OPF Functions ........................... 178

D-12 OPF User Callback Functions ...................... 179

D-13 Power Flow Derivative Functions .................... 179

D-14 NLP, LP & QP Solver Functions .................... 180

D-15 Matrix Building Functions ........................ 181

D-16 Utility Functions ............................. 182

D-17 Other Functions .............................. 183

D-18 Small Transmission System Test Cases ................. 184

D-19 Small Radial Distribution System Test Cases .............. 184

D-20 ACTIV Synthetic Grid Test Cases .................... 185

D-21 Polish System Test Cases ......................... 185

D-22 PEGASE European System Test Cases ................. 186

D-23 RTE French System Test Cases ..................... 186

D-24 Automated Test Functions from MP-Test ................ 187

D-25 MIPS Tests ................................ 187

D-26 Test Data ................................. 188

D-27 Miscellaneous Matpower Tests ..................... 189

D-28 Matpower OPF Tests ......................... 190

F-1 Auction Types .............................. 194

F-2 Generator Oﬀers ............................. 196

F-3 Load Bids ................................. 196

F-4 Generator Sales .............................. 199

F-5 Load Purchases .............................. 199

F-6 Smartmarket Files and Functions .................... 200

MATP WER

1 Introduction

1.1 Background

Matpower [1] is a package of Matlab®M-ﬁles for solving power ﬂow and optimal

power ﬂow problems. It is intended as a simulation tool for researchers and educators

that is easy to use and modify. Matpower is designed to give the best performance

possible while keeping the code simple to understand and modify. The Matpower

website can be found at:

http://www.pserc.cornell.edu/matpower/

Matpower was initially developed by Ray D. Zimmerman, Carlos E. Murillo-

S´anchez and Deqiang Gan of PSerc1at Cornell University under the direction of

Robert J. Thomas. The initial need for Matlab-based power ﬂow and optimal power

ﬂow code was born out of the computational requirements of the PowerWeb project2.

Many others have contributed to Matpower over the years and it continues to be

developed and maintained under the direction of Ray Zimmerman.

Beginning with version 6, Matpower includes a framework for solving general-

ized steady-state electric power scheduling problems. This framework is known as

MOST, for Matpower Optimal Scheduling Tool [2,3].

MOST can be used to solve problems as simple as a deterministic, single pe-

riod economic dispatch problem with no transmission constraints or as complex as

a stochastic, security-constrained, combined unit-commitment and multiperiod op-

timal power ﬂow problem with locational contingency and load-following reserves,

ramping costs and constraints, deferrable demands, lossy storage resources and un-

certain renewable generation.

MOST is documented separately from the main Matpower package in its own

manual, the MOST User’s Manual.

1http://pserc.org/

2http://www.pserc.cornell.edu/powerweb/

1.2 License and Terms of Use

Beginning with version 5.1, the code in Matpower is distributed under the 3-clause

BSD license3[5]. The full text of the license can be found in the LICENSE ﬁle at

the top level of the distribution or at http://www.pserc.cornell.edu/matpower/

LICENSE.txt and reads as follows.

(PSERC) and individual contributors (see AUTHORS file for details).

Redistribution and use in source and binary forms, with or without

modification, are permitted provided that the following conditions

are met:

1. Redistributions of source code must retain the above copyright

notice, this list of conditions and the following disclaimer.

2. Redistributions in binary form must reproduce the above copyright

notice, this list of conditions and the following disclaimer in the

documentation and/or other materials provided with the distribution.

3. Neither the name of the copyright holder nor the names of its

contributors may be used to endorse or promote products derived from

this software without specific prior written permission.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS

"AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT

LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS

FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE

INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING,

BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES;

LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER

CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT

LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN

ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE

POSSIBILITY OF SUCH DAMAGE.

3Versions 4.0 through 5.0 of Matpower were distributed under version 3.0 of the GNU General

Public License (GPL) [6] with an exception added to clarify our intention to allow Matpower to

interface with Matlab as well as any other Matlab code or MEX-ﬁles a user may have installed,

regardless of their licensing terms. The full text of the GPL can be found at http://www.gnu.

org/licenses/gpl-3.0.txt.Matpower versions prior to version 4 had their own license.

Please note that the Matpower case ﬁles distributed with Matpower are not

covered by the BSD license. In most cases, the data has either been included with

permission or has been converted from data available from a public source.

1.3 Citing Matpower

While not required by the terms of the license, we do request that publications derived

from the use of Matpower explicitly acknowledge that fact by citing reference [1].

R. D. Zimmerman, C. E. Murillo-S´anchez, and R. J. Thomas, “Matpower: Steady-

State Operations, Planning and Analysis Tools for Power Systems Research and Ed-

ucation,” Power Systems, IEEE Transactions on, vol. 26, no. 1, pp. 12–19, Feb. 2011.

DOI: 10.1109/TPWRS.2010.2051168

Similarly, we request that publications derived from the use of MOST explicitly

acknowledge that fact by citing both the main Matpower reference above and

reference [2]:

C. E. Murillo-S´anchez, R. D. Zimmerman, C. L. Anderson, and R. J. Thomas, “Secure

Planning and Operations of Systems with Stochastic Sources, Energy Storage and

Active Demand,” Smart Grid, IEEE Transactions on, vol. 4, no. 4, pp. 2220–2229,

Dec. 2013.

DOI: 10.1109/TSG.2013.2281001

1.4 Matpower Development

Following the release of Matpower 6.0, the Matpower project moved to an open

development paradigm, hosted on the Matpower GitHub project page:

https://github.com/MATPOWER/matpower

The Matpower GitHub project hosts the public Git code repository as well

as a public issue tracker for handling bug reports, patches, and other issues and

contributions. There are separate GitHub hosted repositories and issue trackers for

Matpower, MOST, MIPS and the testing framework used by all of them, MP-Test,

all available from https://github.com/MATPOWER/.

2 Getting Started

2.1 System Requirements

To use Matpower 7.0b1 you will need:

•Matlab®version 7.3 (R2006b) or later4, or

•GNU Octave version 4 or later5

See Section 2.1 in the MOST User’s Manual for any requirements speciﬁc to

MOST.

For the hardware requirements, please refer to the system requirements for the

version of Matlab6or Octave that you are using. If the Matlab Optimization

Toolbox is installed as well, Matpower enables an option to use it to solve optimal

power ﬂow problems.

In this manual, references to Matlab usually apply to Octave as well. At the

time of writing, none of the optional MEX-based Matpower packages have been

built for Octave, but Octave does typically include GLPK.

4Matlab is available from The MathWorks, Inc. (http://www.mathworks.com/). Mat-

power 5 and Matpower 6 required Matlab 7 (R14), Matpower 4 required Matlab 6.5 (R13),

Matpower 3.2 required Matlab 6 (R12), Matpower 3.0 required Matlab 5 and Matpower 2.0

and earlier required only Matlab 4. Matlab is a registered trademark of The MathWorks, Inc.

5GNU Octave [4] is free software, available online at http://www.gnu.org/software/octave/.

Matpower 5 and Matpower 6 required Octave 3.4, Matpower 4 required Octave 3.2.

6http://www.mathworks.com/support/sysreq/previous_releases.html

2.2 Getting Matpower

You can either download an oﬃcial versioned release or you can obtain the current

development version, which we also attempt to keep stable enough for everyday use.

The development version includes new features and bug ﬁxes added since the last

versioned release.

2.2.1 Versioned Releases

•Download the ZIP ﬁle of the latest oﬃcial versioned release from the Mat-

power website7.

–Go to the Matpower website.

–Click the Download Now button.

2.2.2 Current Development Version

There are also two options for obtaining the most recent development version of

Matpower from the master branch on GitHub.

1. Clone the Matpower repository from GitHub.

•From the command line:

–git clone https://github.com/MATPOWER/matpower.git

•Or, from the Matpower GitHub repository page8:

–Click the green Clone or download button, then Open in Desk-

top.

Use this option if you want to be able to easily update to the current development

release, with the latest bug ﬁxes and new features, using a simple git pull

command, or if you want to help with testing or development. This requires

that you have a Git client9(GUI or command-line) installed.

2. Download a zip ﬁle of the Matpower repository from GitHub.

•Go to the Matpower GitHub repository page.

7http://www.pserc.cornell.edu/matpower/

8https://github.com/MATPOWER/matpower

9See https://git-scm.com/downloads for information on downloading Git clients.

•Click the green Clone or download button, then Download ZIP.

Use this option if you need features or ﬁxes introduced since the latest versioned

release, but you do not have access to or are not ready to begin using Git (but

don’t be afraid to give Git a try).10

See CONTRIBUTING.md for information on how to get a local copy of your own

Matpower fork, if you are interesting in contributing your own code or modiﬁca-

tions.

10A good place to start is https://git-scm.com.

2.3 Installation

Installation and use of Matpower requires familiarity with the basic operation of

Matlab or Octave. Make sure you follow the installation instructions for the version

of Matpower you are installing. The process was simpliﬁed with an install script

following version 6.0.

Step 1: Get a copy of Matpower as described above.

Clone the repository or download and extract the ZIP ﬁle of the Mat-

power distribution and place the resulting directory in the location of

your choice and call it anything you like.11 We will use <MATPOWER>

as a placeholder to denote the path to this directory (the one containing

install matpower.m). The ﬁles in <MATPOWER>should not need to be

modiﬁed, so it is recommended that they be kept separate from your own

code.

Step 2: Run the installer.

Open Matlab or Octave and change to the <MATPOWER>directory.

Run the installer and follow the directions to add the required directories

to your Matlab or Octave path, by typing:

install matpower

Step 3: That’s it. There is no step 3.

But, if you chose not to have the installer run the test suite for you in step 2,

you can run it now to verify that Matpower is installed and functioning

properly, by typing:12

test matpower

The result should resemble the following, possibly including extra tests,

depending on the availablility of optional packages, solvers and extras.

11Do not place Matpower’s ﬁles in a directory named 'matlab'or 'optim'(both case-

insensitive), as these can cause Matlab’s built-in ver command to behave strangely in ways that

aﬀect Matpower.

12The MOST test suite is run separately by typing test most. See the MOST User’s Manual for

details.

>> test_matpower

t_test_fcns.............ok

t_nested_struct_copy....ok

t_feval_w_path..........ok

t_mpoption..............ok

t_loadcase..............ok

t_ext2int2ext...........ok

t_jacobian..............ok

t_hessian...............ok

t_margcost..............ok

t_totcost...............ok

t_modcost...............ok

t_hasPQcap..............ok

t_mplinsolve............ok (6 of 44 skipped)

t_mips..................ok

t_mips_pardiso..........ok (60 of 60 skipped)

t_qps_matpower..........ok (288 of 360 skipped)

t_miqps_matpower........ok (240 of 240 skipped)

t_pf....................ok

t_pf_radial.............ok

t_cpf...................ok

t_islands...............ok

t_opf_model.............ok

t_opf_model_legacy......ok

t_opf_default...........ok

t_opf_mips..............ok (278 of 1296 skipped)

t_opf_dc_mips...........ok

t_opf_dc_mips_sc........ok

t_opf_userfcns..........ok

t_opf_softlims..........ok

t_runopf_w_res..........ok

t_dcline................ok

t_get_losses............ok

t_load2disp.............ok

t_makePTDF..............ok

t_makeLODF..............ok

t_printpf...............ok

t_vdep_load.............ok

t_total_load............ok

t_scale_load............ok

t_apply_changes.........ok

t_psse..................ok

t_off2case..............ok

t_auction_mips..........ok

t_runmarket.............ok

All tests successful (7961 passed, 872 skipped of 8833)

Elapsed time 29.39 seconds. 17

2.4 Running a Simulation

The primary functionality of Matpower is to solve power ﬂow and optimal power

ﬂow (OPF) problems. This involves (1) preparing the input data deﬁning the all of

the relevant power system parameters, (2) invoking the function to run the simulation

and (3) viewing and accessing the results that are printed to the screen and/or saved

in output data structures or ﬁles.

2.4.1 Preparing Case Input Data

The input data for the case to be simulated are speciﬁed in a set of data matrices

packaged as the ﬁelds of a Matlab struct, referred to as a “Matpower case” struct

and conventionally denoted by the variable mpc. This struct is typically deﬁned in a

case ﬁle, either a function M-ﬁle whose return value is the mpc struct or a MAT-ﬁle

that deﬁnes a variable named mpc when loaded13. The main simulation routines,

whose names begin with run (e.g. runpf,runopf), accept either a ﬁle name or a

Matpower case struct as an input.

Use loadcase to load the data from a case ﬁle into a struct if you want to make

modiﬁcations to the data before passing it to the simulation.

>> mpc = loadcase(casefilename);

See also savecase for writing a Matpower case struct to a case ﬁle.

The structure of the Matpower case data is described a bit further in Section 3.1

and the full details are documented in Appendix Band can be accessed at any time

via the command help caseformat. The Matpower distribution also includes many

example case ﬁles listed in Table D-18.

2.4.2 Solving the Case

The solver is invoked by calling one of the main simulation functions, such as runpf

or runopf, passing in a case ﬁle name or a case struct as the ﬁrst argument. For

example, to run a simple Newton power ﬂow with default options on the 9-bus system

deﬁned in case9.m, at the Matlab prompt, type:

>> runpf('case9');

13This describes version 2 of the Matpower case format, which is used internally and is the

default. The version 1 format, now deprecated, but still accessible via the loadcase and savecase

functions, deﬁnes the data matrices as individual variables rather than ﬁelds of a struct, and some

do not include all of the columns deﬁned in version 2.

If, on the other hand, you wanted to load the 30-bus system data from case30.m,

increase its real power demand at bus 2 to 30 MW, then run an AC optimal power

ﬂow with default options, this could be accomplished as follows:

>> define_constants;

>> mpc = loadcase('case30');

>> mpc.bus(2, PD) = 30;

>> runopf(mpc);

The define constants in the ﬁrst line is simply a convenience script that deﬁnes a

number of variables to serve as named column indices for the data matrices. In this

example, it allows us to access the “real power demand” column of the bus matrix

using the name PD without having to remember that it is the 3rd column.

Other top-level simulation functions are available for running DC versions of

power ﬂow and OPF, for running an OPF with the option for Matpower to shut

down (decommit) expensive generators, etc. These functions are listed in Table D-2

in Appendix D.

2.4.3 Accessing the Results

By default, the results of the simulation are pretty-printed to the screen, displaying

a system summary, bus data, branch data and, for the OPF, binding constraint

information. The bus data includes the voltage, angle and total generation and load

at each bus. It also includes nodal prices in the case of the OPF. The branch data

shows the ﬂows and losses in each branch. These pretty-printed results can be saved

to a ﬁle by providing a ﬁlename as the optional 3rd argument to the simulation

function.

The solution is also stored in a results struct available as an optional return value

from the simulation functions. This results struct is a superset of the Matpower

case struct mpc, with additional columns added to some of the existing data ﬁelds

and additional ﬁelds. The following example shows how simple it is, after running a

DC OPF on the 118-bus system in case118.m, to access the ﬁnal objective function

value, the real power output of generator 6 and the power ﬂow in branch 51.

>> define_constants;

>> results = rundcopf('case118');

>> final_objective = results.f;

>> gen6_output = results.gen(6, PG);

>> branch51_flow = results.branch(51, PF);

Full documentation for the content of the results struct can be found in Sec-

tions 4.4 and 6.6.

2.4.4 Setting Options

Matpower has many options for selecting among the available solution algorithms,

controlling the behavior of the algorithms and determining the details of the pretty-

printed output. These options are passed to the simulation routines as a Matpower

options struct. The ﬁelds of the struct have names that can be used to set the

corresponding value via the mpoption function. Calling mpoption with no arguments

returns the default options struct, the struct used if none is explicitly supplied.

Calling it with a set of name and value pairs modiﬁes the default vector.

For example, the following code runs a power ﬂow on the 300-bus example in

case300.m using the fast-decoupled (XB version) algorithm, with verbose printing of

the algorithm progress, but suppressing all of the pretty-printed output.

>> mpopt = mpoption('pf.alg', 'FDXB', 'verbose', 2, 'out.all', 0);

>> results = runpf('case300', mpopt);

To modify an existing options struct, for example, to turn the verbose option oﬀ

and re-run with the remaining options unchanged, simply pass the existing options

as the ﬁrst argument to mpoption.

>> mpopt = mpoption(mpopt, 'verbose', 0);

>> results = runpf('case300', mpopt);

See Appendix Cor type:

>> help mpoption

for more information on Matpower’s options.

2.5 Documentation

There are four primary sources of documentation for Matpower. The ﬁrst is

this manual, which gives an overview of Matpower’s capabilities and structure

and describes the modeling and formulations behind the code. It can be found in

your Matpower distribution at <MATPOWER>/docs/MATPOWER-manual.pdf and the

latest version is always available at: http://www.pserc.cornell.edu/matpower/

MATPOWER-manual.pdf.

Secondly, the MOST User’s Manual describes MOST and its problem formulation,

features, data formats and options. It is located at <MATPOWER>/docs/MOST-manual.pdf

in your Matpower distribution and the latest version is also available online at:

http://www.pserc.cornell.edu/matpower/MOST-manual.pdf.

The Matpower Online Function Reference is the third source of documen-

tation, allowing you to view not only the help text, but also the code itself for

each Matpower function directly from a web browser. It is available online at:

http://www.pserc.cornell.edu/matpower/docs/ref

Last, but certainly not least, is the built-in help command. As with Matlab’s

built-in functions and toolbox routines, you can type help followed by the name of

a command or M-ﬁle to get help on that particular function. Nearly all of Mat-

power’s M-ﬁles have such documentation and this should be considered the main

reference for the calling options for each individual function. See Appendix Dfor a

list of Matpower functions.

As an example, the help for runopf looks like:

>> help runopf

RUNOPF Runs an optimal power flow.

[RESULTS, SUCCESS] = RUNOPF(CASEDATA, MPOPT, FNAME, SOLVEDCASE)

Runs an optimal power flow (AC OPF by default), optionally returning

a RESULTS struct and SUCCESS flag.

Inputs (all are optional):

CASEDATA : either a MATPOWER case struct or a string containing

the name of the file with the case data (default is 'case9')

(see also CASEFORMAT and LOADCASE)

MPOPT : MATPOWER options struct to override default options

can be used to specify the solution algorithm, output options

termination tolerances, and more (see also MPOPTION).

FNAME : name of a file to which the pretty-printed output will

be appended

SOLVEDCASE : name of file to which the solved case will be saved

in MATPOWER case format (M-file will be assumed unless the

specified name ends with '.mat')

Outputs (all are optional):

RESULTS : results struct, with the following fields:

(all fields from the input MATPOWER case, i.e. bus, branch,

gen, etc., but with solved voltages, power flows, etc.)

order - info used in external <-> internal data conversion

et - elapsed time in seconds

success - success flag, 1 = succeeded, 0 = failed

(additional OPF fields, see OPF for details)

SUCCESS : the success flag can additionally be returned as

a second output argument

Calling syntax options:

results = runopf;

results = runopf(casedata);

results = runopf(casedata, mpopt);

results = runopf(casedata, mpopt, fname);

results = runopf(casedata, mpopt, fname, solvedcase);

[results, success] = runopf(...);

Alternatively, for compatibility with previous versions of MATPOWER,

some of the results can be returned as individual output arguments:

[baseMVA, bus, gen, gencost, branch, f, success, et] = runopf(...);

Example:

results = runopf('case30');

See also RUNDCOPF, RUNUOPF. 22

3 Modeling

Matpower employs all of the standard steady-state models typically used for power

ﬂow analysis. The AC models are described ﬁrst, then the simpliﬁed DC models. In-

ternally, the magnitudes of all values are expressed in per unit and angles of complex

quantities are expressed in radians. Internally, all oﬀ-line generators and branches

are removed before forming the models used to solve the power ﬂow or optimal power

ﬂow problem. All buses are numbered consecutively, beginning at 1, and generators

are reordered by bus number. Conversions to and from this internal indexing is done

by the functions ext2int and int2ext. The notation in this section, as well as Sec-

tions 4and 6, is based on this internal numbering, with all generators and branches

assumed to be in-service. Due to the strengths of the Matlab programming lan-

guage in handling matrices and vectors, the models and equations are presented here

in matrix and vector form.

3.1 Data Formats

The data ﬁles used by Matpower are Matlab M-ﬁles or MAT-ﬁles which deﬁne

and return a single Matlab struct. The M-ﬁle format is plain text that can be edited

using any standard text editor. The ﬁelds of the struct are baseMVA,bus,branch,gen

and optionally gencost, where baseMVA is a scalar and the rest are matrices. In the

matrices, each row corresponds to a single bus, branch, or generator. The columns

are similar to the columns in the standard IEEE CDF and PTI formats. The number

of rows in bus,branch and gen are nb,nland ng, respectively. If present, gencost

has either ngor 2ngrows, depending on whether it includes costs for reactive power

or just real power. Full details of the Matpower case format are documented

in Appendix Band can be accessed from the Matlab command line by typing

help caseformat.

3.2 Branches

All transmission lines14, transformers and phase shifters are modeled with a com-

mon branch model, consisting of a standard πtransmission line model, with series

impedance zs=rs+jxsand total charging susceptance bc, in series with an ideal

phase shifting transformer. The transformer, whose tap ratio has magnitude τand

14This does not include DC transmission lines. For more information the handling of DC trans-

mission lines in Matpower, see Section 7.6.3.

phase shift angle θshift, is located at the from end of the branch, as shown in Fig-

ure 3-1. The parameters rs,xs,bc,τand θshift are speciﬁed directly in columns BR R

(3), BR X (4), BR B (5), TAP (9) and SHIFT (10), respectively, of the corresponding row

of the branch matrix.15

The complex current injections ifand itat the from and to ends of the branch,

respectively, can be expressed in terms of the 2 ×2 branch admittance matrix Ybr

and the respective terminal voltages vfand vt

if

it=Ybr vf

vt.(3.1)

With the series admittance element in the πmodel denoted by ys= 1/zs, the branch

admittance matrix can be written

Ybr =ys+jbc

21

τ2−ys1

τe−jθshift

−ys1

τejθshift ys+jbc

2.(3.2)

Figure 3-1: Branch Model

If the four elements of this matrix for branch iare labeled as follows:

br =yi

ff yi

tf yi

tt (3.3)

then four nl×1 vectors Yff ,Yft,Ytf and Ytt can be constructed, where the i-th element

of each comes from the corresponding element of Yi

br. Furthermore, the nl×nbsparse

15A value of zero in the TAP column indicates that the branch is a transmission line and not a

transformer, i.e. mathematically equivalent to a transformer with tap ratio set to 1.

connection matrices Cfand Ctused in building the system admittance matrices can

be deﬁned as follows. The (i, j)th element of Cfand the (i, k)th element of Ctare

equal to 1 for each branch i, where branch iconnects from bus jto bus k. All other

elements of Cfand Ctare zero.

3.3 Generators

A generator is modeled as a complex power injection at a speciﬁc bus. For generator i,

the injection is

g=pi

g+jqi

g.(3.4)

Let Sg=Pg+jQgbe the ng×1 vector of these generator injections. The MW and

MVAr equivalents (before conversion to p.u.) of pi

gand qi

gare speciﬁed in columns

PG (2) and QG (3), respectively of row iof the gen matrix. A sparse nb×nggenerator

connection matrix Cgcan be deﬁned such that its (i, j)th element is 1 if generator j

is located at bus iand 0 otherwise. The nb×1 vector of all bus injections from

generators can then be expressed as

Sg,bus =Cg·Sg.(3.5)

A generator with a negative injection can also be used to model a dispatchable load.

3.4 Loads

Constant power loads are modeled as a speciﬁed quantity of real and reactive power

consumed at a bus. For bus i, the load is

d=pi

d+jqi

d(3.6)

and Sd=Pd+jQddenotes the nb×1 vector of complex loads at all buses. The

MW and MVAr equivalents (before conversion to p.u.) of pi

dand qi

dare speciﬁed in

columns PD (3) and QD (4), respectively of row iof the bus matrix. These ﬁelds can

also take on negative quantities to represent ﬁxed (e.g. distributed) generation.

Constant impedance and constant current loads are not implemented directly,

but the constant impedance portions can be modeled as a shunt element described

below. Dispatchable loads are modeled as negative generators and appear as negative

values in Sg.

3.5 Shunt Elements

A shunt connected element such as a capacitor or inductor is modeled as a ﬁxed

impedance to ground at a bus. The admittance of the shunt element at bus iis given

sh =gi

sh +jbi

sh (3.7)

and Ysh =Gsh +jBsh denotes the nb×1 vector of shunt admittances at all buses.

The parameters gi

sh and bi

sh are speciﬁed in columns GS (5) and BS (6), respectively,

of row iof the bus matrix as equivalent MW (consumed) and MVAr (injected) at a

nominal voltage magnitude of 1.0 p.u and angle of zero.

A shunt element can also be used to model a constant impedance load and, though

correctly, Matpower does not currently report these quantities as “load”.

3.6 Network Equations

For a network with nbbuses, all constant impedance elements of the model are

incorporated into a complex nb×nbbus admittance matrix Ybus that relates the

complex nodal current injections Ibus to the complex node voltages V:

Ibus =YbusV. (3.8)

Similarly, for a network with nlbranches, the nl×nbsystem branch admittance

matrices Yfand Ytrelate the bus voltages to the nl×1 vectors Ifand Itof branch

currents at the from and to ends of all branches, respectively:

If=YfV(3.9)

It=YtV. (3.10)

If [ ·] is used to denote an operator that takes an n×1 vector and creates the

corresponding n×ndiagonal matrix with the vector elements on the diagonal, these

system admittance matrices can be formed as follows:

Yf= [Yff ]Cf+ [Yf t]Ct(3.11)

Yt= [Ytf ]Cf+ [Ytt]Ct(3.12)

Ybus =Cf

TYf+Ct

TYt+ [Ysh].(3.13)

The current injections of (3.8)–(3.10) can be used to compute the corresponding

complex power injections as functions of the complex bus voltages V:

Sbus(V) = [V]I∗

bus = [V]Y∗

busV∗(3.14)

Sf(V) = [CfV]I∗

f= [CfV]Y∗

fV∗(3.15)

St(V) = [CtV]I∗

t= [CtV]Y∗

tV∗.(3.16)

The nodal bus injections are then matched to the injections from loads and generators

to form the AC nodal power balance equations, expressed as a function of the complex

bus voltages and generator injections in complex matrix form as

gS(V, Sg) = Sbus(V) + Sd−CgSg= 0.(3.17)

3.7 DC Modeling

The DC formulation [17] is based on the same parameters, but with the following

three additional simplifying assumptions.

•Branches can be considered lossless. In particular, branch resistances rsand

charging capacitances bcare negligible:

ys=1

rs+jxs≈1

jxs

, bc≈0.(3.18)

•All bus voltage magnitudes are close to 1 p.u.

vi≈ejθi.(3.19)

•Voltage angle diﬀerences across branches are small enough that

sin(θf−θt−θshift)≈θf−θt−θshift.(3.20)

Substituting the ﬁrst set of assumptions regarding branch parameters from (3.18),

the branch admittance matrix in (3.2) approximates to

Ybr ≈1

jxs1

τ2−1

τe−jθshift

−1

τejθshift 1.(3.21)

Combining this and the second assumption with (3.1) yields the following approxi-

mation for if:

if≈1

jxs

τ2ejθf−1

τe−jθshift ejθt)

jxsτ(1

τejθf−ej(θt+θshift)).(3.22)

The approximate real power ﬂow is then derived as follows, ﬁrst applying (3.19) and

(3.22), then extracting the real part and applying (3.20).

pf=<{sf}

=<vf·i∗

f

≈ <ejθf·j

xsτ(1

τe−jθf−e−j(θt+θshift))

=<j

xsτ1

τ−ej(θf−θt−θshift)

=<1

xsτsin(θf−θt−θshift) + j1

τ−cos(θf−θt−θshift)

≈1

xsτ(θf−θt−θshift) (3.23)

As expected, given the lossless assumption, a similar derivation for the power injec-

tion at the to end of the line leads to leads to pt=−pf.

The relationship between the real power ﬂows and voltage angles for an individual

branch ican then be summarized as

pf

pt=Bi

br θf

θt+Pi

shift (3.24)

where

br =bi1−1

−1 1 ,

shift =θi

shiftbi−1

1

and biis deﬁned in terms of the series reactance xi

sand tap ratio τifor branch ias

bi=1

sτi.

For a shunt element at bus i, the amount of complex power consumed is

sh =vi(yi

shvi)∗

≈ejθi(gi

sh −jbi

sh)e−jθi

=gi

sh −jbi

sh.(3.25)

So the vector of real power consumed by shunt elements at all buses can be approx-

imated by

Psh ≈Gsh.(3.26)

With a DC model, the linear network equations relate real power to bus voltage

angles, versus complex currents to complex bus voltages in the AC case. Let the

nl×1 vector Bff be constructed similar to Yff , where the i-th element is biand let

Pf,shift be the nl×1 vector whose i-th element is equal to −θi

shiftbi. Then the nodal

real power injections can be expressed as a linear function of Θ, the nb×1 vector of

bus voltage angles

Pbus(Θ) = BbusΘ + Pbus,shift (3.27)

where

Pbus,shift = (Cf−Ct)TPf,shift.(3.28)

Similarly, the branch ﬂows at the from ends of each branch are linear functions of

the bus voltage angles

Pf(Θ) = BfΘ + Pf,shift (3.29)

and, due to the lossless assumption, the ﬂows at the to ends are given by Pt=−Pf.

The construction of the system Bmatrices is analogous to the system Ymatrices

for the AC model:

Bf= [Bff ] (Cf−Ct) (3.30)

Bbus = (Cf−Ct)TBf.(3.31)

The DC nodal power balance equations for the system can be expressed in matrix

form as

gP(Θ, Pg) = BbusΘ + Pbus,shift +Pd+Gsh −CgPg= 0 (3.32)

4 Power Flow

The standard power ﬂow or loadﬂow problem involves solving for the set of voltages

and ﬂows in a network corresponding to a speciﬁed pattern of load and generation.

Matpower includes solvers for both AC and DC power ﬂow problems, both of

which involve solving a set of equations of the form

g(x) = 0,(4.1)

constructed by expressing a subset of the nodal power balance equations as functions

of unknown voltage quantities.

All of Matpower’s solvers exploit the sparsity of the problem and, except for

Gauss-Seidel, scale well to very large systems. Currently, none of them include any

automatic updating of transformer taps or other techniques to attempt to satisfy

typical optimal power ﬂow constraints, such as generator, voltage or branch ﬂow

limits.

4.1 AC Power Flow

In Matpower, by convention, a single generator bus is typically chosen as a refer-

ence bus to serve the roles of both a voltage angle reference and a real power slack.

The voltage angle at the reference bus has a known value, but the real power gen-

eration at the slack bus is taken as unknown to avoid overspecifying the problem.

The remaining generator buses are typically classiﬁed as PV buses, with the values

of voltage magnitude and generator real power injection given. These are speciﬁed

in the VG (6) and PG (3) columns of the gen matrix, respectively. Since the loads Pd

and Qdare also given, all non-generator buses are classiﬁed as PQ buses, with real

and reactive injections fully speciﬁed, taken from the PD (3) and QD (4) columns of

the bus matrix. Let Iref ,IPV and IPQ denote the sets of bus indices of the reference

bus, PV buses and PQ buses, respectively. The bus type classiﬁcation is speciﬁed in

the Matpower case ﬁle in the BUS TYPE column (2) of the bus matrix. Any isolated

buses must be identiﬁed as such in this column as well.

In the traditional formulation of the AC power ﬂow problem, the power balance

equation in (3.17) is split into its real and reactive components, expressed as functions

of the voltage angles Θ and magnitudes Vmand generator injections Pgand Qg, where

the load injections are assumed constant and given:

gP(Θ, Vm, Pg) = Pbus(Θ, Vm) + Pd−CgPg= 0 (4.2)

gQ(Θ, Vm, Qg) = Qbus(Θ, Vm) + Qd−CgQg= 0.(4.3)

For the AC power ﬂow problem, the function g(x) from (4.1) is formed by taking

the left-hand side of the real power balance equations (4.2) for all non-slack buses

and the reactive power balance equations (4.3) for all PQ buses and plugging in the

reference angle, the loads and the known generator injections and voltage magnitudes:

g(x) = "g{i}

P(Θ, Vm, Pg)

g{j}

Q(Θ, Vm, Qg)#∀i∈ IPV ∪ IPQ

∀j∈ IPQ.(4.4)

The vector xconsists of the remaining unknown voltage quantities, namely the volt-

age angles at all non-reference buses and the voltage magnitudes at PQ buses:

x=θ{i}

v{j}

m∀i /∈ Iref

∀j∈ IPQ.(4.5)

This yields a system of nonlinear equations with npv + 2npq equations and un-

knowns, where npv and npq are the number of PV and PQ buses, respectively. After

solving for x, the remaining real power balance equation can be used to compute

the generator real power injection at the slack bus. Similarly, the remaining npv + 1

reactive power balance equations yield the generator reactive power injections.

Matpower includes four diﬀerent algorithms for solving the general AC power

ﬂow problem.16 The default solver is based on a standard Newton’s method [8] using a

polar form and a full Jacobian updated at each iteration. Each Newton step involves

computing the mismatch g(x), forming the Jacobian based on the sensitivities of

these mismatches to changes in xand solving for an updated value of xby factorizing

this Jacobian. This method is described in detail in many textbooks.

Also included are solvers based on variations of the fast-decoupled method [9],

speciﬁcally, the XB and BX methods described in [10]. These solvers greatly reduce

the amount of computation per iteration, by updating the voltage magnitudes and

angles separately based on constant approximate Jacobians which are factored only

once at the beginning of the solution process. These per-iteration savings, however,

come at the cost of more iterations.

The fourth algorithm is the standard Gauss-Seidel method from Glimm and

Stagg [11]. It has numerous disadvantages relative to the Newton method and is

included primarily for academic interest.

By default, the AC power ﬂow solvers simply solve the problem described above,

ignoring any generator limits, branch ﬂow limits, voltage magnitude limits, etc. How-

ever, there is an option (pf.enforce q lims) that allows for the generator reactive

16Three more that are speciﬁc to radial networks typical of distribution systems are described in

Section 4.3.

power limits to be respected at the expense of the voltage setpoint. This is done

in a rather brute force fashion by adding an outer loop around the AC power ﬂow

solution. If any generator has a violated reactive power limit, its reactive injection is

ﬁxed at the limit, the corresponding bus is converted to a PQ bus and the power ﬂow

is solved again. This procedure is repeated until there are no more violations. Note

that this option is based solely on the QMAX and QMIN parameters for the generator,

from columns 4 and 5 of the gen matrix, and does not take into account the trape-

zoidal generator capability curves described in Section 6.4.3 and specifed in columns

PC1–QC2MAX (11–16). Note also that this option aﬀects generators even if the bus

they are attached to is already of type PQ.

4.2 DC Power Flow

For the DC power ﬂow problem [17], the vector xconsists of the set of voltage angles

at non-reference buses

x=θ{i},∀i /∈ Iref (4.6)

and (4.1) takes the form

Bdcx−Pdc = 0 (4.7)

where Bdc is the (nb−1) ×(nb−1) matrix obtained by simply eliminating from Bbus

the row and column corresponding to the slack bus and reference angle, respectively.

Given that the generator injections Pgare speciﬁed at all but the slack bus, Pdc can

be formed directly from the non-slack rows of the last four terms of (3.32).

The voltage angles in xare computed by a direct solution of the set of linear

equations. The branch ﬂows and slack bus generator injection are then calculated

directly from the bus voltage angles via (3.29) and the appropriate row in (3.32),

respectively.

4.3 Distribution Power Flow

Distribution systems are diﬀerent from transmission systems in a number of respects,

such as the xs/rsbranch ratio, magnitudes of xsand rsand most importantly the

typically radial structure. Due to these diﬀerences, a number of power ﬂow solu-

tion methods have been developed to account for the speciﬁc nature of distribution

systems and most widely used are the backward/forward sweep methods [12,13].

Matpower includes an additional three AC power ﬂow methods that are speciﬁc

to radial networks.

4.3.1 Radial Power Flow

When solving radial distribution networks it is practical to number branches with

numbers that are equal to the receiving bus numbers. An example is given in Fig-

ure 4-1, where branches are drawn black. Furthermore, the oriented branch ordering

[14] oﬀers a possibility for fast and eﬃcient backward/forward sweeps. All branches

are always oriented from the sending bus to the receiving bus and the only re-

quirement is that the sending bus number should be smaller than the receiving bus

number. This means that i<kfor branch i–k. The indices of the sending nodes of

branches are stored in vector Fsuch that i=fk.

Loop 1

Loop 2

011223

4477PV2

5PV1

Figure 4-1: Oriented Ordering

As usual, the supply bus (slack bus) is given index 1, meaning that branch indices

should go from 2 to nbwhich is the number of buses in the network. Introducing a

ﬁctitious branch with index 1 and zero impedance, given with dashed black line in

Figure 4-1, the number of branches nlbecomes equal to the number of buses nb.

For the example of Figure 4-1 vector Fis the following

F=0123324T,

and it oﬀers an easy way to follow the path between any bus and bus 0. If we

consider bus 4, the path to the slack bus consists of following branches: branch 4,

since considered bus is their receiving bus; branch 3, since f4= 3; branch 2, since

f3= 2; and branch 1, since f2= 1.

The representation of branch k, connecting buses iand k, is given in Figure 4-2,

where it is modeled with its serial impedance zk

s. At both ends there are load

demands si

dand sk

d, and shunt admittances yi

dand yk

dcomprised of admittances due

capacitance of all lines and shunt elements connected to buses iand k

d=jXbk

lines +Xbk

shunt.

isk

fzk

ssk

dyi

−

Figure 4-2: Branch Representation: branch kbetween buses i(sending) and k(re-

ceiving) and load demand and shunt admittances at both buses

4.3.2 Current Summation Method

The voltage calculation procedure with the Current Summation Method is performed

in 5 steps as follows [12,13].

1. Set all voltages to 1 p.u. (ﬂat start). Set iteration count ν= 1.

2. Set branch current ﬂow equal to the sum of current of the demand at receiving

end (sk

d) and the current drawn in the admittance (yk

d) connected to bus k

b=sk

vk∗

+yk

d·vk, k = 1,2, . . . , nb.(4.8)

3. Backward sweep: Perform current summation, starting from the branch with

the biggest index and heading towards the branch whose index is equal to 1.

The current of branch kis added to the current of the branch whose index is

equal to i=fk.

b,new =ji

b+jk

b, k =nl, nl−1,...,2 (4.9)

4. Forward sweep: The receiving end bus voltages are calculated with known

branch currents and sending bus voltages.

vk=vi−zk

s·jk

b, k = 2,3, . . . , nl(4.10)

5. Compare voltages in iteration νwith the corresponding ones from iteration

ν−1. If the maximum diﬀerence in magnitude is less than the speciﬁed toler-

ance

max

i=1...nbvν

i−vν−1

i< ε (4.11)

the procedure is ﬁnished. Otherwise go to step 2.

4.3.3 Power Summation Method

The voltage calculation procedure with the Power Summation Method is performed

in 5 steps as follows [14].

1. Set all voltages to 1 p.u. (ﬂat start). Set iteration count ν= 1.

2. Set receiving end branch ﬂow equal to the sum of the demand at receiving end

(sk

d) and the power drawn in the admittance (yk

d) connected to bus k

t=sk

d+yk

d∗

, k = 1,2, . . . , nb.(4.12)

3. Backward sweep: Calculate sending end branch power ﬂows as a sum of re-

ceiving end branch power ﬂows and branch losses via (4.13). Perform power

summation, starting from the branch with the biggest index and heading to-

wards the branch whose index is equal to 1. The sending power of branch kis

added to the receiving power of the branch whose index is equal to i=fkas

in (4.14).

f=sk

t+zk

s·

vk

k=nl, nl−1,...,2 (4.13)

t,new =si

t+sk

fk=nl, nl−1,...,2 (4.14)

4. Forward sweep: The receiving end bus voltages are calculated with known

sending powers and voltages.

vk=vi−zk

s· sk

vi!∗

k= 2,3, . . . , nl(4.15)

5. Compare voltages in iteration νwith the corresponding ones from iteration

ν−1, using (4.11). If the maximum diﬀerence in magnitude is less than the

speciﬁed tolerance the procedure is ﬁnished. Otherwise go to step 2.

4.3.4 Admittance Summation Method

For each node, besides the known admittance yk

d, we deﬁne the admittance yk

eas the

driving point admittance of the part of the network fed by node k, including shunt

admittance yk

d. We also deﬁne an equivalent current generator jk

efor the part of the

network fed by node k. The current of this generator consists of all load currents fed

by node k. The process of calculation of bus voltages with the admittance summation

method consists of the following 5 steps [15].

1. Set all voltages to 1 p.u. (ﬂat start). Set iteration count ν= 1. Set initial

values

e=yk

d, k = 1,2, . . . , nb.(4.16)

2. For each node k, calculate equivalent admittance yk

e. Perform admittance sum-

mation, starting from the branch with the biggest index and heading towards

the branch whose index is equal to 1. The driving point admittance of branch k

is added to the driving point admittance of the branch whose index is equal to

i=fkas in (4.18).

b=1

1 + zk

s·yk

k=nl, nl−1,...,2 (4.17)

e,new =yi

e+dk

b·yk

ek=nl, nl−1,...,2 (4.18)

3. Backward sweep: For each node kcalculate equivalent current generator jk

e, ﬁrst

set it equal to load current jk

dand perform current summation over equivalent

admittances using factor dk

bas in (4.17).

e=jk

d=sk

vk∗

k=nl, nl−1,...,2 (4.19)

e,new =ji

e+dk

b·jk

ek=nl, nl−1,...,2 (4.20)

4. Forward sweep: The receiving end bus voltages are calculated with known

equivalent current generators and sending bus voltages.

vk=dk

b·(vi−zk

s·jk

e)k= 2,3, . . . , nl(4.21)

5. Compare voltages in iteration νwith the corresponding ones from iteration

ν−1, using (4.11). If the maximum diﬀerence in magnitude is less than the

speciﬁed tolerance the procedure is ﬁnished. Otherwise go to step 3.

4.3.5 Handling PV Buses

The methods explained in the previous three subsections are applicable to radial

networks without loops and PV buses. These methods can be used to solve the

power ﬂow problem in weakly meshed networks if a compensation procedure based on

Thevenin equivalent impedance matrix is added [12,13]. In [14] a voltage correction

procedure is added to the process.

The list of branches is expanded by a set of npv ﬁctitious links, corresponding to

the PV nodes. Each of these links starts at the slack bus and ends at a corresponding

PV bus, thus forming a loop in the network. A ﬁctitious link going to bus kis

represented by a voltage generator with a voltage magnitude equal to the speciﬁed

voltage magnitude at bus k. Its phase angle is equal to the calculated phase angle

at bus k.

A loop impedance matrix Zlis formed for the loops made by the ﬁctitious links

and it has the following properties

•Element zmm

lis equal to the sum of branch impedances oﬀ all branches related

to loop m,

•Element zmk

lis equal to the sum of branch impedances of mutual branches of

loops mand k.

As an illustration, in Figure 4-1 there a two PV generators at buses 5 and 7. The

ﬁctitious links and loops orientation are drawn in red. The Thevenin matrix for this

case is

Zl=z2

b+z3

b+z5

bz2

b+z3

bz2

b+z3

b+z4

b+z7

b.

First column elements are equal to PV bus voltages when the current injection

at bus 5 is 1 p.u. and v1= 0. Bus voltages can be calculated with the current

summation method in a single iteration. By repeating the procedure for bus 7 one

can calculate the elements of second column.

By breaking all links the network becomes radial [13] and the three backward/forward

sweep methods are applicable. Since all link are ﬁctitious, only the injected reactive

power at their receiving bus mis determined [14] by the following equation

∆qm

pv = ∆dm

<{vm},(4.22)

which is practically an increment in reactive power injection of the corresponding

PV generator for the current iteration.

The incremental changes of the imaginary part of PV generator current ∆dm

pv can

be obtained by solving the matrix equation

={Zl} · ∆Dpv = ∆Epv,(4.23)

where

∆em

pv =vm

|vm|−1· <{vm}, m = 1,2, . . . , npv.(4.24)

In order to ensure 90◦phase diﬀerence between voltage and current at PV gen-

erators in [16] it was suggested to calculate the real part of PV generator current

∆cm

pv = ∆dm

pv ={vm}

<{vm}.(4.25)

In such a way the PV generator will inject purely reactive power, as it is supposed

to do. Its active power is added before as a negative load.

Before proceeding with the next iteration, the bus voltage corrections are cal-

culated. In order to do that, the radial network is solved by applying incremental

current changes ∆Ipv = ∆Cpv +j∆Dpv at the PV buses as excitations and setting

v1= 0. After the backward/forward sweep is performed with the current summation

method, the voltage corrections at all buses are known. They are added to the latest

voltages in order to obtain the new bus voltages, which are used in the next iteration

[14].

4.4 runpf

In Matpower, a power ﬂow is executed by calling runpf with a case struct or case

ﬁle name as the ﬁrst argument (casedata). In addition to printing output to the

screen, which it does by default, runpf optionally returns the solution in a results

struct.

>> results = runpf(casedata);

The results struct is a superset of the input Matpower case struct mpc, with some

additional ﬁelds as well as additional columns in some of the existing data ﬁelds.

The solution values are stored as shown in Table 4-1.

Additional optional input arguments can be used to set options (mpopt) and

provide ﬁle names for saving the pretty printed output (fname) or the solved case

data (solvedcase).

Table 4-1: Power Flow Results

name description

results.success success ﬂag, 1 = succeeded, 0 = failed

results.et computation time required for solution

results.iterations number of iterations required for solution

results.order see ext2int help for details on this ﬁeld

results.bus(:, VM)†bus voltage magnitudes

results.bus(:, VA) bus voltage angles

results.gen(:, PG) generator real power injections

results.gen(:, QG)†generator reactive power injections

results.branch(:, PF) real power injected into “from” end of branch

results.branch(:, PT) real power injected into “to” end of branch

results.branch(:, QF)†reactive power injected into “from” end of branch

results.branch(:, QT)†reactive power injected into “to” end of branch

†AC power ﬂow only.

>> results = runpf(casedata, mpopt, fname, solvedcase);

The options that control the power ﬂow simulation are listed in Table 4-2 and those

controlling the output printed to the screen in Table 4-3.

By default, runpf solves an AC power ﬂow problem using a standard Newton’s

method solver. To run a DC power ﬂow, the model option must be set to 'DC'. For

convenience, Matpower provides a function rundcpf which is simply a wrapper

that sets the model option to 'DC'before calling runpf.

Internally, the runpf function does a number of conversions to the problem data

before calling the appropriate solver routine for the selected power ﬂow algorithm.

This external-to-internal format conversion is performed by the ext2int function,

described in more detail in Section 7.3.1, and includes the elimination of out-of-service

equipment, the consecutive renumbering of buses and the reordering of generators

by increasing bus number. All computations are done using this internal indexing.

When the simulation has completed, the data is converted back to external format

by int2ext before the results are printed and returned.

4.5 Linear Shift Factors

The DC power ﬂow model can also be used to compute the sensitivities of branch

ﬂows to changes in nodal real power injections, sometimes called injection shift factors

(ISF) or generation shift factors [17]. These nl×nbsensitivity matrices, also called

Table 4-2: Power Flow Options

name default description

model 'AC'AC vs. DC modeling for power ﬂow and OPF formulation

'AC'– use AC formulation and corresponding alg options

'DC'– use DC formulation and corresponding alg options

pf.alg 'NR'AC power ﬂow algorithm:

'NR'– Newtons’s method

'FDXB'– Fast-Decoupled (XB version)

'FDBX'– Fast-Decouple (BX version)

'GS'– Gauss-Seidel

'PQSUM'– Power Summation (radial networks only)

'ISUM'– Current Summation (radial networks only)

'YSUM'– Admittance Summation (radial networks only)

pf.tol 10−8termination tolerance on per unit P and Q dispatch

pf.nr.max it 10 maximum number of iterations for Newton’s method

pf.nr.lin solver '' linear solver option for mplinsolve for computing Newton update step

(see mplinsolve for complete list of all options)

'' – default to '\'for small systems, 'LU3'for larger ones

'\'– built-in backslash operator

'LU'– explicit default LU decomposition and back substitution

'LU3'– 3 output arg form of lu, Gilbert-Peierls algorithm with

approximate minimum degree (AMD) reordering

'LU4'– 4 output arg form of lu, UMFPACK solver (same as

'LU')

'LU5'– 5 output arg form of lu, UMFPACK solver w/row scaling

pf.fd.max it 30 maximum number of iterations for fast-decoupled method

pf.gs.max it 1000 maximum number of iterations for Gauss-Seidel method

pf.radial.max it 20 maximum number of iterations for radial power ﬂow methods

pf.radial.vcorr 0 perform voltage correction procedure in distribution power ﬂow

0 – do not perform voltage correction

1 – perform voltage correction

pf.enforce q lims 0 enforce gen reactive power limits at expense of |Vm|

0 – do not enforce limits

1 – enforce limits, simultaneous bus type conversion

2 – enforce limits, one-at-a-time bus type conversion

power transfer distribution factors or PTDFs, carry an implicit assumption about

the slack distribution. If His used to denote a PTDF matrix, then the element in

row iand column j,hij , represents the change in the real power ﬂow in branch i

given a unit increase in the power injected at bus j,with the assumption that the

additional unit of power is extracted according to some speciﬁed slack distribution:

∆Pf=H∆Pbus.(4.26)

Table 4-3: Power Flow Output Options

name default description

verbose 1 amount of progress info to be printed

0 – print no progress info

1 – print a little progress info

2 – print a lot of progress info

3 – print all progress info

out.all -1 controls pretty-printing of results

-1 – individual ﬂags control what is printed

0 – do not print anything†

1 – print everything†

out.sys sum 1 print system summary (0 or 1)

out.area sum 0 print area summaries (0 or 1)

out.bus 1 print bus detail, includes per bus gen info (0 or 1)

out.branch 1 print branch detail (0 or 1)

out.gen 0 print generator detail (0 or 1)

out.force 0 print results even if success ﬂag = 0 (0 or 1)

out.suppress detail -1 suppress all output but system summary

-1 – suppress details for large systems (>500 buses)

0 – do not suppress any output speciﬁed by other ﬂags

1 – suppress all output except system summary section†

†Overrides individual ﬂags, but (in the case of out.suppress detail) not out.all = 1.

This slack distribution can be expressed as an nb×1 vector wof non-negative

weights whose elements sum to 1. Each element speciﬁes the proportion of the slack

taken up at each bus. For the special case of a single slack bus k,wis equal to the

vector ek. The corresponding PTDF matrix Hkcan be constructed by ﬁrst creating

the nl×(nb−1) matrix

Hk=e

Bf·B−1

dc (4.27)

then inserting a column of zeros at column k. Here e

Bfand Bdc are obtained from Bf

and Bbus, respectively, by eliminating their reference bus columns and, in the case

of Bdc, removing row kcorresponding to the slack bus.

The PTDF matrix Hw, corresponding to a general slack distribution w, can be

obtained from any other PTDF, such as Hk, by subtracting Hk·wfrom each column,

equivalent to the following simple matrix multiplication:

Hw=Hk(I−w·1T).(4.28)

These same linear shift factors may also be used to compute sensitivities of branch

ﬂows to branch outages, known as line outage distribution factors or LODFs [18].

Given a PTDF matrix Hw, the corresponding nl×nlLODF matrix Lcan be con-

structed as follows, where lij is the element in row iand column j, representing the

change in ﬂow in branch i(as a fraction of the initial ﬂow in branch j) for an outage

of branch j.

First, let Hrepresent the matrix of sensitivities of branch ﬂows to branch endpoint

injections, found by multplying the PTDF matrix by the node-branch incidence

matrix:

H=Hw(Cf−Ct)T.(4.29)

Here the individual elements hij represent the sensitivity of ﬂow in branch iwith

respect to injections at branch jendpoints, corresponding to a simulated increase in

ﬂow in branch j. Then lij can be expressed as

lij =





hij

1−hjj

i6=j

−1i=j.

(4.30)

Matpower includes functions for computing both the DC PTDF matrix and

the corresponding LODF matrix for either a single slack bus kor a general slack

distribution vector w. See the help for makePTDF and makeLODF and Sections 9.5.5

and 9.5.4, respectively, for details.

5 Continuation Power Flow

Continuation methods or branch tracing methods are used to trace a curve given an

initial point on the curve. These are also called predictor-corrector methods since

they involve the prediction of the next solution point and correcting the prediction

to get the next point on the curve.

Consider a system of nnonlinear equations g(x) = 0, x ∈Rn. By adding a

continuation parameter λand one more equation to the system, xcan be traced by

varying λ. The resulting system f(x, λ) = 0 has n+ 1 dimensions. The additional

equation is a parameterized equation which identiﬁes the location of the current

solution with respect to the previous or next solution.

The continuation process can be diagrammatically shown by (5.1).

xj, λjP redictor

−−−−−→ (ˆxj+1,ˆ

λj+1)Corrector

−−−−−→ xj+1, λj+1(5.1)

where, (xj, λj) represents the current solution at step j, (ˆxj+1,ˆ

λj+1) is the predicted

solution for the next step, and (xj+1, λj+1) is the next solution on the curve.

Continuation methods are employed in power systems to determine steady state

stability limits [19] in what is called a continuation power ﬂow17. The limit is de-

termined from a nose curve where the nose represents the maximum power transfer

that the system can handle given a power transfer schedule. To determine the steady

state loading limit, the basic power ﬂow equations

g(x) = P(x)−Pinj

Q(x)−Qinj = 0,(5.2)

are restructured as

f(x, λ) = g(x)−λb = 0 (5.3)

where x≡(Θ, Vm) and bis a vector of power transfer given by

b=Pinj

target −Pinj

base

Qinj

target −Qinj

base .(5.4)

The eﬀects of the variation of loading or generation can be investigated using the

continuation method by composing the bvector appropriately.

17Thanks to Shrirang Abhyankar, Rui Bo, and Alexander Flueck for contributions to Mat-

power’s continuation power ﬂow feature.

5.1 Parameterization

The values of (x, λ) along the solution curve can parameterized in a number of ways

[20,21]. Parameterization is a mathematical way of identifying each solution so that

the next solution or previous solution can be quantiﬁed. Matpower includes three

parameterization scheme options to quantify this relationship, detailed below, where

σis the continuation step size parameter.

•Natural parameterization simply uses λdirectly as the parameter, so the

new λis simply the previous value plus the step size.

pj(x, λ) = λ−λj−σj= 0 (5.5)

•Arc length parameterization results in the following relationship, where

the step size is equal to the 2-norm of the distance from one solution to the

next.

pj(x, λ) = X

(xi−xj

i)2+ (λ−λj)2−(σj)2= 0 (5.6)

•Pseudo arc length parameterization [23] is Matpower’s default pa-

rameterization scheme, where the next point (x, λ) on the solution curve is

constrained to lie in the hyperplane running through the predicted solution

(ˆxj+1,ˆ

λj+1) orthogonal to the tangent line from the previous corrected solution

(xj, λj). This relationship can be quantiﬁed by the function

pj(x, λ) = x

λ−xj

λjT

¯zj−σj= 0,(5.7)

where ¯zjis the normalized tangent vector at (xj, λj) and σjis the continuation

step size parameter.

5.2 Predictor

The predictor is used to produce an estimate for the next solution. The better the

prediction, the faster is the convergence to the solution point. Matpower uses a

tangent predictor for estimating the curve to the next solution. The tangent vector

zj=dx dλ j

Tat the current solution (xj, λj) is found by solving the linear

system fxfλ

pj−1

xpj−1

λzj=0

1.(5.8)

The matrix on the left-hand side is simply the standard power ﬂow Jacobian with an

additional column and row added. The extra column fλis simply the negative of the

power transfer vector band the extra row, required to make the system non-singular

and deﬁne the magnitude of zj, is the derivative of the the parameterization function

at the previous solution point pj−1.

The resulting tangent vector is then normalized

¯zj=zj

||zj||2

(5.9)

and used to compute the predicted approximation (ˆxj+1,ˆ

λj+1) to the next solution

(xj+1, λj+1) using ˆxj+1

λj+1 =xj

λj+σj¯zj,(5.10)

where σjis the continuation step size.

5.3 Corrector

The corrector stage ﬁnds the next solution (xj+1, λj+1) by correcting the approxi-

mation estimated by the predictor (ˆxj+1,ˆ

λj+1). Newton’s method is used to ﬁnd

the next solution by solving the n+ 1 dimensional system in (5.11), where one of

(5.5)–(5.7) has been added as an additional constraint to the parameterized power

ﬂow equations of (5.3). f(x, λ)

pj(x, λ)= 0 (5.11)

5.4 Step Length Control

Step length control is a key element aﬀecting the computational eﬃciency of a contin-

uation method. It aﬀects the continuation method with two issues: (1) speed – how

fast the corrector converges to a speciﬁed accuracy, and (2) robustness – whether

the corrector converges to a true solution given a predicted point. Matpower’s

continuation power ﬂow can optionally use adaptive steps, where the step size σis

adjusted by a scaling factor αwithin the limits speciﬁed.

σj+1 =αjσj, σmin ≤σj+1 ≤σmax (5.12)

This scaling factor αjfor step jis limited to a maximum of 2 and is calculated from

an error estimation between the predicted and corrected solutions γjas follows,

αj= 1 + βcpf cpf

γj−1, αj≤2,(5.13)

where βcpf is a damping factor, cpf is a speciﬁed tolerance, and γjis given by

γj=



xj+1, λj+1−ˆxj+1,ˆ

λj+1



∞.(5.14)

5.5 Event Detection and Location

A continuation power ﬂow event is triggered when the value of one of the elements

of an event function changes sign from one continuation step to the next. The

event occurs at the point where the corresponding value of the event function passes

through zero. Matpower provides event functions to detect the location at which

the continuation power ﬂow reaches the following:

•a speciﬁed target λvalue

•the nose point

•the end of a full trace

•a generator reactive power limit

•a generator active power limit

•a bus voltage magnitude limit

•a branch ﬂow limit

Each event function is registered with an event name, a ﬂag indicating whether

or not the location of the event should be pinpointed, and if so, to within what

tolerance. For events that are to be located, when an event interval is detected, that

is, when an element of the event function value changes sign, Matpower adjusts

the continuation step size via a False Position or Regula Falsi method until it locates

the point of the zero-crossing to within the speciﬁed tolerance.

The detection of an event zero, or even an event interval, can be used to trigger

further actions. The CPF callback function capability was extended in Matpower

6.x to include the ability to handle events by including information about any event

intervals or zeros detected. For example, Matpower includes a callback that ﬁxes

the reactive output of a generator and converts its bus from PV to PQ when the

corresponding event function indicates that its reactive power limit has been reached.

Another responds to the detection of the nose point by signaling the termination of

the continuation. In fact, continuation power ﬂow termination for nose point, target

lambda or full trace modes are all based on CPF callback functions in conjunction

with event detection.

While Matpower does include a mechanism for supplying user deﬁned callback

functions, it does not yet have a corresponding mechanism for user speciﬁed event

functions.

5.6 runcpf

In Matpower, a continuation power ﬂow is executed by calling runcpf with two

Matpower cases (case structs or case ﬁle names) as the ﬁrst two arguments,

basecasedata and targetcasedata, respectively. The ﬁrst contains the base load-

ing/generation proﬁle while the second contains the target loading/generation pro-

ﬁle. In addition to printing output to the screen, which it does by default, runcpf

optionally returns the solution in a results struct.

>> results = runcpf(basecasedata, targetcasedata);

Additional optional input arguments can be used to set options (mpopt) and

provide ﬁle names for saving the pretty printed output (fname) or the solved case

data (solvedcase).

>> results = runcpf(basecasedata, targetcasedata, mpopt, fname, solvedcase);

The results struct is a superset of the input Matpower case struct mpc, with

some additional ﬁelds as well as additional columns in some of the existing data

ﬁelds. In addition to the solution values included in the results for a simple power

ﬂow, shown in Table 4-1 in Section 4.4, the following additional continuation power

ﬂow solution values are stored in the cpf ﬁeld as shown in Table 5-1.

The options that control the continuation power ﬂow simulation are listed in

Table 5-2. All the power ﬂow options for Newton’s method (tolerance, maximum

iterations) and for controlling the output on the screen (see Tables 4-2 and 4-3) are

also available with the continuation power ﬂow.

Table 5-1: Continuation Power Flow Results

name description

results.cpf CPF output struct whose content depends on any user callback functions,

where default contains ﬁelds:

done msg string with message describing cause of continuation termination

events(eidx) a structure array of size ne, where neis the number of events located, with

ﬁelds:

kcontinuation step number at which event was located

name name of event

idx index(es) of critical elements in corresponding event function, e.g. index

of generator reaching VAr limit

msg descriptive text detailing the event

iterations nsteps, number of continuation steps performed

lam 1×nvector of λvalues from correction steps†

lam hat 1×nvector of λvalues from prediction steps†

max lam maximum value of λfound in results.cpf.lam

steps 1×nvector of step sizes for each continuation step performed†

Vnb×nmatrix of complex bus voltages from correction steps†

V hat nb×nmatrix of complex bus voltages from prediction steps†

†nis one more than the number of continuation steps, i.e. nsteps + 1, so the ﬁrst element corresponds to the

starting point.

Table 5-2: Continuation Power Flow Options

name default description

cpf.parameterization 3 choice of parameterization

1 — natural

2 — arc length

3 — pseudo arc length

cpf.stop at 'NOSE'determines stopping criterion

'NOSE'— stop when nose point is reached

'FULL'— trace full nose curve

λstop — stop upon reaching target λvalue λstop

cpf.enforce p lims 0 enforce gen active power limits

0 — do not enforce limits

1 — enforce limits

cpf.enforce q lims 0 enforce gen reactive power limits at expense of Vm

0 — do not enforce limits

1 — enforce limits

cpf.enforce v lims 0 enforce bus voltage magnitude limits

0 — do not enforce limits

1 — enforce limits

cpf.enforce flow lims 0 enforce branch MVA ﬂow limits

0 — do not enforce limits

1 — enforce limits

cpf.step 0.05 default value for continuation power ﬂow step size σ

cpf.step min 10−4minimum allowed step size, σmin

cpf.step max 0.2 maximum allowed step size, σmax

cpf.adapt step 0 toggle adaptive step size feature

0 — adaptive step size disabled

1 — adaptive step size enabled

cpf.adapt step damping 0.7 damping factor βcpf from (5.13) for adaptive step sizing

cpf.adapt step tol 10−3tolerance cpf from (5.13) for adaptive step sizing

cpf.target lam tol 10−5tolerance for target lambda detection

cpf.nose tol 10−5tolerance for nose point detection (p.u.)

cpf.p lims tol 10−2tolerance for generator active power limit detection

(MW)

cpf.q lims tol 10−2tolerance for generator reactive power limit detection

(MVAr)

cpf.v lims tol 10−4tolerance for bus voltage magnitude limit detection (p.u)

cpf.flow lims tol 0.01 tolerance for branch ﬂow limit detection (MVA)

cpf.plot.level 0 control plotting of nose curve

0 — do not plot nose curve

1 — plot when completed

2 — plot incrementally at each iteration

3 — same as 2, with pause at each iteration

cpf.plot.bus empty index of bus whose voltage is to be plotted

cpf.user callback empty string or cell array of strings with names of user callback

functions†

†See help cpf default callback for details. 49

5.6.1 CPF Callback Functions

Matpower’s continuation power ﬂow provides a callback mechanism to give the

user access to the iteration process for executing custom code at each iteration,

for example, to implement custom incremental plotting of a PV nose curve or to

handle a detected event. This callback mechanism is used internally to handle de-

fault plotting functionality as well as to handle the standard CPF events. The

cpf default callback function, for example, is used to collect the λand Vresults

from each predictor and corrector iteration and optionally plot the PV nose curve.

The prototype for a CPF callback function is

function [nx, cx, done, rollback, evnts, cb_data, results] = ...

cpf_user_callback(k, nx, cx, px, done, rollback, evnts, ...

cb_data, cb_args, results)

and the input and output arguments are described in Tables 5-3 through 5-5 and in

the help for cpf default callback. Each registered CPF callback function is called in

three diﬀerent contexts, distinguished by the value of the ﬁrst argument kas follows:

1. initial – called with k= 0, without results input/output arguments, after base

power ﬂow, before ﬁrst CPF step.

2. iterations – called with k>0, without results input/output arguments, at

each iteration, after predictor-corrector step

3. ﬁnal – called with k<0, with results input/output arguments, after exiting

predictor-corrector loop, inputs identical to last iteration call, except knegated

The user can deﬁne their own callback functions which take the same form and

are called in the same contexts as cpf default callback. User callback functions are

speciﬁed via the Matpower option cpf.user callback. This option can be a string

containing the name of the callback function, or a struct with the following ﬁelds,

where all but the ﬁrst are optional:

•fcn - string with name of callback function

•priority - numerical value specifying callback priority,18 default = 20

•args - arbitrary value (any type) passed to the callback as cb args each time

it is invoked

Multiple user callbacks can be registered by assigning a cell array of such strings

and/or structs to the cpf.user callback option.

18See cpf register callback for details.

Table 5-3: Continuation Power Flow Callback Input Arguments

name description

kcontinuation step iteration count

nx next CPF state*

, corresponding to proposed next step

cx current CPF state*

, corresponding to most recent successful step

px previous CPF state*

, corresponding to last successful step prior to cx

done struct, with ﬂag to indicate CPF termination and reason, with ﬁelds:

.flag termination ﬂag, 1 →terminate, 0 →continue

.msg string containing reason for termination

rollback scalar ﬂag to indicate that the current step should be rolled back and

retried with a diﬀerent step size, etc.

evnts struct array listing any events detected for this step‡

cb data struct containing static data§

, with the following ﬁelds (all based on internal

indexing):

.mpc base Matpower case struct of base case

.mpc target Matpower case struct of target case

.Sbusb handle of function returning nb×1 vector of complex base case bus injec-

tions in p.u. and derivatives w.r.t. |V|

.Sbust handle of function returning nb×1 vector of complex target case bus

injections in p.u. and derivatives w.r.t. |V|

.Ybus bus admittance matrix

.Yf branch admittance matrix, “from” end of branches

.Yt branch admittance matrix, “to” end of branches

.pv list of indices of PV buses

.pq list of indices of PQ buses

.ref list of indices of reference buses

.idx pmax vector of gen indices of gens at PMAX

.mpopt Matpower options struct

cb args arbitrary data structure containing user-provided callback arguments

results initial value of output struct to be assigned to cpf ﬁeld of results struct

returned by runcpf

*See Table 5-5 for details of the CPF state.

‡See cpf detect events for details of the evnts ﬁeld.

§Please note that any callback that modiﬁes the underlying problem is responsible to update the contents of

cb data accordingly. E.g. converting a bus from PV to PQ requires updates to mpc base,mpc target,Sbusb,

Sbust,pv,pq, and possibly ref. So, cb data should only be thought of as static for a ﬁxed base and target

case pair.

Table 5-4: Continuation Power Flow Callback Output Arguments

name description

All are updated versions of the corresponding input arguments, see Table 5-3 for more details.

nx next CPF state*

, user state (cb ﬁeld) should be updated here if rollback

is false

cx current CPF state*

, may contain updated this step or this parm values

to be used if rollback is true

done callback may have requested termination and set the msg ﬁeld

rollback callback can request a rollback step, even if it was not indicated by an

event function†

evnts msg ﬁeld for a given event may be updated‡

cb data this data should only be modiﬁed if the underlying problem has been

changed (e.g. generator limit reached), in which case it should always

be followed by a step of zero length, i.e. set nx.this step to 0§

results updated version of results input argument to be assigned to cpf ﬁeld of

results struct returned by runcpf

*See Table 5-5 for details of the CPF state.

†In this case, the callback should also modify the step size or parameterization to be used for the re-try, by

setting the this step or this parm ﬁelds in cx.

‡See cpf detect events for details of the evnts ﬁeld.

§It is the job of any callback modifying cb data to ensure that all data in cb data is kept consistent.

Table 5-5: Continuation Power Flow State

name description

lam hat value of λafter predictor step

V hat vector of complex bus voltages after predictor step

lam value of λafter corrector step

Vvector of complex bus voltages after corrector step

znormalized tangent predictor, ¯z

default step default step size

default parm default parameterization*

this step step size for this step only

this parm parameterization*for this step only

step current step size

parm current parameterization*

events event log

cb user state for callbacks†, a user-deﬁned struct containing any information

a callback function would like to pass from one invokation to the next

ef cell array of event function values

*Corresponding to the cpf.parameterization option in Table 5-2.

†Replaces cb state from Matpower 5.

5.6.2 CPF Example

The following is an example of running a continuation power ﬂow using a version of

the 9-bus system, looking at increasing all loads by a factor of 2.5. This example

plots the nose curve shown in Figure 5-1.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Voltage at Bus 9

Voltage Magnitude

Figure 5-1: Nose Curve of Voltage Magnitude at Bus 9

define_constants;

mpopt = mpoption('out.all', 0, 'verbose', 2);

mpopt = mpoption(mpopt, 'cpf.stop_at', 'FULL', 'cpf.step', 0.2);

mpopt = mpoption(mpopt, 'cpf.plot.level', 2);

mpcb = loadcase(t_case9_pfv2); % load base case

mpct = mpcb; % set up target case with

mpct.gen(:, [PG QG]) = mpcb.gen(:, [PG QG]) * 2.5; % increased generation

mpct.bus(:, [PD QD]) = mpcb.bus(:, [PD QD]) * 2.5; % and increased load

results = runcpf(mpcb, mpct, mpopt);

This should result in something like the following output to the screen.

MATPOWER Version 7.0b1, 31-Oct-2018 -- AC Continuation Power Flow

step 0 : lambda = 0.000, 4 Newton steps

step 1 : stepsize = 0.2 lambda = 0.181 2 corrector Newton steps

step 2 : stepsize = 0.2 lambda = 0.359 2 corrector Newton steps

step 3 : stepsize = 0.2 lambda = 0.530 2 corrector Newton steps

step 4 : stepsize = 0.2 lambda = 0.693 3 corrector Newton steps

step 5 : stepsize = 0.2 lambda = 0.839 3 corrector Newton steps

step 6 : stepsize = 0.2 lambda = 0.952 3 corrector Newton steps

step 7 : stepsize = 0.2 lambda = 0.988 3 corrector Newton steps

step 8 : stepsize = 0.2 lambda = 0.899 3 corrector Newton steps

step 9 : stepsize = 0.2 lambda = 0.776 3 corrector Newton steps

step 10 : stepsize = 0.2 lambda = 0.654 3 corrector Newton steps

step 11 : stepsize = 0.2 lambda = 0.533 2 corrector Newton steps

step 12 : stepsize = 0.2 lambda = 0.413 2 corrector Newton steps

step 13 : stepsize = 0.2 lambda = 0.294 2 corrector Newton steps

step 14 : stepsize = 0.2 lambda = 0.176 2 corrector Newton steps

step 15 : stepsize = 0.2 lambda = 0.060 2 corrector Newton steps

step 16a : stepsize = 0.2 lambda = -0.054 2 corrector Newton steps ^ ROLLBACK

step 16 : stepsize = 0.0604 lambda = 0.000 3 corrector Newton steps

CPF TERMINATION: Traced full continuation curve in 16 continuation steps

The results of the continuation power ﬂow are then found in the cpf ﬁeld of the

returned results struct.

>> results.cpf

ans =

V_hat: [9x17 double]

lam_hat: [1x17 double]

V: [9x17 double]

lam: [1x17 double]

steps: [1x17 double]

iterations: 16

max_lam: 0.9876

events: [1x1 struct]

done_msg: 'Traced full continuation curve in 16 continuation steps'

6 Optimal Power Flow

Matpower includes code to solve both AC and DC versions of the optimal power

ﬂow problem. The standard version of each takes the following form:

min

xf(x) (6.1)

subject to

g(x) = 0 (6.2)

h(x)≤0 (6.3)

xmin ≤x≤xmax .(6.4)

In both cases, the objective function f(x) consists of the polynomial cost of gener-

ator injections, the equality constraints g(x) are the power balance equations, the

inequality constraints h(x) are the branch ﬂow limits, and the xmin and xmax bounds

include reference bus angles, voltage magnitudes (for AC) and generator injections.

6.1 Standard AC OPF

The optimization vector xfor the standard AC OPF problem consists of the nb×1

vectors of voltage angles Θ and magnitudes Vmand the ng×1 vectors of generator

real and reactive power injections Pgand Qg.

x=









(6.5)

The objective function f(x) in (6.1) is simply a summation of individual polynomial

cost functions fi

Pand fi

Qof real and reactive power injections, respectively, for each

generator:

f(Pg, Qg) =

i=1

P(pi

g) + fi

Q(qi

g).(6.6)

The equality constraints in (6.2) are simply the full set of 2 ·nbnonlinear real and

reactive power balance equations from (4.2) and (4.3).

gP(Θ, Vm, Pg) = Pbus(Θ, Vm) + Pd−CgPg= 0 (6.7)

gQ(Θ, Vm, Qg) = Qbus(Θ, Vm) + Qd−CgQg= 0 (6.8)

The inequality constraints (6.3) consist of two sets of nlbranch ﬂow limits as non-

linear functions of the bus voltage angles and magnitudes, one for the from end and

one for the to end of each branch:

hf(Θ, Vm) = |Ff(Θ, Vm)| − Fmax ≤0 (6.9)

ht(Θ, Vm) = |Ft(Θ, Vm)| − Fmax ≤0.(6.10)

The ﬂows are typically apparent power ﬂows expressed in MVA, but can be real power

or current ﬂows, yielding the following three possible forms for the ﬂow constraints:

Ff(Θ, Vm) = 









Sf(Θ, Vm),apparent power

Pf(Θ, Vm),real power

If(Θ, Vm),current

(6.11)

where Ifis deﬁned in (3.9), Sfin (3.15), Pf=<{Sf}and the vector of ﬂow limits

Fmax has the appropriate units for the type of constraint. It is likewise for Ft(Θ, Vm).

The values used by Matpower’s OPF for the ﬂow limits Fmax are speciﬁed in the

RATE A column (6) of the branch matrix,19 and the selection of ﬂow constraint type

in (6.11) is determined by the opf.flow lim option.

The variable limits (6.4) include an equality constraint on any reference bus angle

and upper and lower limits on all bus voltage magnitudes and real and reactive

generator injections:

θref

i≤θi≤θref

i, i ∈ Iref (6.12)

vi,min

m≤vi

m≤vi,max

m, i = 1 . . . nb(6.13)

pi,min

g≤pi

g≤pi,max

g, i = 1 . . . ng(6.14)

qi,min

g≤qi

g≤qi,max

g, i = 1 . . . ng.(6.15)

The voltage reference angle θref

iand voltage magnitude bounds vi,max

mand vi,min

mare

speciﬁed in columns VA (9), VMAX (12) and VMIN (13), respectively, of row iof the bus

matrix. Similarly, the generator bounds qi,max

g,qi,min

g,pi,max

gand pi,min

gare specﬁed in

columns QMAX (4), QMIN (5), PMAX (9) and PMIN (10), respectively, of row iof the gen

matrix.

6.1.1 Cartesian vs. Polar Coordinates for Voltage

Another variation of the standard AC OPF problem represents the bus voltages

in cartesian, rather than polar, coordinates. That is, instead of Θ and Vm, the

19Setting the RATE A column (6) of branch to zero is the preferred way to indicate a completely

unconstrained line.

optimization vector xincludes the real and imaginary parts of the complex voltage,

denoted respectively by Uand W, where V=U+jW .

x=









(6.16)

The objective function remains unchanged, but the nodal power balance con-

straints (6.7) and (6.8) and branch ﬂow constraints (6.9) and (6.10) are implemented

as functions of Uand W.

gP(U, W, Pg) = Pbus(U, W ) + Pd−CgPg= 0 (6.17)

gQ(U, W, Qg) = Qbus(U, W ) + Qd−CgQg= 0 (6.18)

hf(U, W ) = |Ff(U, W )| − Fmax ≤0 (6.19)

ht(U, W ) = |Ft(U, W )| − Fmax ≤0.(6.20)

In this formulation, the voltage angle reference constraint (6.12) and voltage mag-

nitude limits (6.13) cannot be simply applied as bounds on optimization variables.

These constrained quantities also become functions of Uand W.

θref

i≤θi(ui, wi)≤θref

i, i ∈ Iref (6.21)

vi,min

m≤vi

m(ui, wi)≤vi,max

m, i = 1 . . . nb(6.22)

In Matpower setting the opf.v cartesian option to 1 (0 by default) selects the

cartesian representation for voltages when running an AC OPF.20

6.1.2 Current vs. Power for Nodal Balance Constraints

Another variation of the standard AC OPF problem uses current balance constraints

in place of the power balance constraints (6.7)–(6.8) or (6.17)–(6.18). If we let M

and Nrepresent the real and imaginary parts, respectively, of the current, we can

express the current balance functions for the polar form as

gM(Θ, Vm, Pg, Qg) = <{Ibus(Θ, Vm)+[V∗]−1(Sd−CgSg)∗}= 0 (6.23)

gN(Θ, Vm, Pg, Qg) = ={Ibus(Θ, Vm)+[V∗]−1(Sd−CgSg)∗}= 0 (6.24)

20This option only applies to solvers based on MIPS,fmincon,Ipopt and KNITRO.

and for the cartesian form as

gM(U, W, Pg, Qg) = <{Ibus(U, W )+[V∗]−1(Sd−CgSg)∗}= 0 (6.25)

gN(U, W, Pg, Qg) = ={Ibus(U, W )+[V∗]−1(Sd−CgSg)∗}= 0 (6.26)

where Sd=Pd+jQd,Sg=Pg+jQgand [V∗]−1is a diagonal matrix whose i-th

diagonal entry is 1/v∗

i, that is 1

mejθior 1/(ui−jwi).

In this formulation, which can be selected by setting the opf.current balance

option to 1,21 the objective function and other constraints are not aﬀected. This

option can be used in conjuntion with either the polar or cartesian representation of

bus voltages.

6.2 Standard DC OPF

When using DC network modeling assumptions and limiting polynomial costs to

second order, the standard OPF problem above can be simpliﬁed to a quadratic

program, with linear constraints and a quadratic cost function. In this case, the

voltage magnitudes and reactive powers are eliminated from the problem completely

and real power ﬂows are modeled as linear functions of the voltage angles. The

optimization variable is

x=Θ

Pg(6.27)

and the overall problem reduces to the following form.

min

Θ,Pg

i=1

P(pi

g) (6.28)

subject to

gP(Θ, Pg) = BbusΘ + Pbus,shift +Pd+Gsh −CgPg= 0 (6.29)

hf(Θ) = BfΘ + Pf,shift −Fmax ≤0 (6.30)

ht(Θ) = −BfΘ−Pf,shift −Fmax ≤0 (6.31)

θref

i≤θi≤θref

i, i ∈ Iref (6.32)

pi,min

g≤pi

g≤pi,max

g, i = 1 . . . ng(6.33)

21This option only applies to solvers based on MIPS,fmincon,Ipopt and KNITRO.

6.3 Extended OPF Formulation

Matpower employs an extensible OPF structure to allow the user to modify or

augment the problem formulation without rewriting the portions that are shared

with the standard OPF formulation described above. The standard formulation is

modiﬁed by introducing additional variables, user-deﬁned costs, and/or user-deﬁned

constraints. The full extended formulation can be written as follows:

min

ˆxf(x) + fu(ˆx) (6.34)

subject to

ˆg(ˆx) = 0 (6.35)

h(ˆx)≤0 (6.36)

ˆxmin ≤ˆx≤ˆxmax (6.37)

l≤Aˆx≤u(6.38)

The ﬁrst diﬀerence to note is that the optimization variable xfrom the standard

OPF formulation has been augmented with additional variables zto form a new

optimization variable ˆx, and likewise with the lower and upper bounds.

ˆx=x

zˆxmin =xmin

zmin ˆxmax =xmax

zmax (6.39)

Second, there is an additional user-deﬁned cost term fu(ˆx) in the objective function.

This cost consists of three pieces that will be described in more detail below.

fu(ˆx) = fq(ˆx) + fnln(ˆx) + flegacy(ˆx) (6.40)

Third, the nonlinear constraints gand hare augmented with user deﬁned additions

guand huto give ˆgand ˆ

ˆg(ˆx) = g(x)

gu(ˆx),ˆ

h(ˆx) = h(x)

hu(ˆx)(6.41)

And ﬁnally, a new set of linear constraints are included in (6.38).

Up through version 6.0 of Matpower, the OPF extensions were handled via op-

tional input parameters that deﬁne any additional variables,22 linear constraints,23

22Parameters zmin and zmax in (6.39).

23Parameters A,l,uin (6.38).

and costs of the pre-speciﬁed form deﬁned by flegacy.24 This preserved the ability to

use solvers that employ pre-compiled MEX ﬁles to compute all of the costs and con-

straints. This is referred to as Matpower’s legacy extended OPF formulation [24].

For the AC OPF, subsequent versions also include the general nonlinear con-

straints guand hu, and the quadratic and general nonlinear costs fqand fnln. The

new quadratic cost terms can be handled by all of Matpower’s AC OPF solvers,

but the general nonlinear costs and constraints require a solver that uses Matlab

code to implement the function, gradient and Hessian evaluations.25

Section 7describes the mechanisms available to the user for taking advantage of

the extensible formulation described here.

6.3.1 User-deﬁned Variables

The creation of additional user-deﬁned zvariables can be done explicitly or implicitly

based on the diﬀerence between the number of columns in Aand the dimension of

the standard OPF optimization variable x. The optional vectors zmin and zmax are

available to impose lower and upper bounds on z, respectively.

6.3.2 User-deﬁned Constraints

•Linear Constraints – The user-deﬁned linear constraints (6.38) are general

linear restrictions involving all of the optimization variables and are speciﬁed

via matrix Aand lower and upper bound vectors land u. These parameters

can be used to create equality constraints (li=ui) or inequality constraints

that are bounded below (ui=∞), bounded above (li=∞) or bounded on

both sides.

•Nonlinear Constraints – The user-deﬁned general nonlinear constraints take

the form

u(x)=0 ∀j∈ Gu(6.42)

u(x)≤0∀j∈ Hu,(6.43)

where Guand Huare sets of indices for user-deﬁned equality and inequality

constraint sets, respectively.

Each of these constraint sets is deﬁned by two M-ﬁle functions, similar to those

required by MIPS, one that computes the constraint values and their gradients

(Jacobian), and the other that computes Hessian values.

24Parameters H,C,N, ˆr,k,d,min (6.48)–(6.51).

25At the time of this writing, this includes solvers based on MIPS,fmincon,Ipopt and KNITRO.

6.3.3 User-deﬁned Costs

The user-deﬁned cost function fuconsists of three terms for three diﬀerent types of

costs: quadratic, general nonlinear, and legacy. Each term is a simple summation

over all of the cost sets of that type.

fq(ˆx) = Pjfj

q(ˆx) (6.44)

fnln(ˆx) = Pjfj

nln(ˆx) (6.45)

flegacy(ˆx) = Pjfj

legacy(ˆx) (6.46)

•Quadratic Costs for a cost set jare speciﬁed by parameters Qj,cjand kj

that deﬁne a quadratic function of the optimization variable ˆx.

q(ˆx) = ˆxTQjˆx+cj

Tˆx+kj(6.47)

•General Nonlinear Costs for a cost set jconsist of a cost function fj

nln(ˆx)

provided in the form of a function handle to an M-ﬁle function that evaluates

the cost and its gradients and Hessian for a given value of ˆx.

•Legacy Costs fj

legacy(ˆx) are speciﬁed in terms of parameters Hj,Cj,Nj, ˆrj,

kj,djand mj. For simplicity of presentation, we will drop the jsubscript for

the rest of this discussion. All of the parameters are nw×1 vectors except the

symmetric nw×nwmatrix Hand the nw×nˆxmatrix N. The legacy user cost

function takes the form

flegacy(ˆx) = 1

2wTHw +CTw(6.48)

where wis deﬁned in several steps as follows. First, a new vector uis created

by applying a linear transformation Nand shift ˆrto the full set of optimization

variables

u=Nˆx−ˆr, (6.49)

then a scaled function with a “dead zone” is applied to each element of uto

produce the corresponding element of w.

wi=





mifdi(ui+ki), ui<−ki

0,−ki≤ui≤ki

mifdi(ui−ki), ui> ki

(6.50)

Here kispeciﬁes the size of the “dead zone”, miis a simple scale factor and fdiis

a pre-deﬁned scalar function selected by the value of di. Currently, Matpower

implements only linear and quadratic options:

fdi(α) = α, if di= 1

α2,if di= 2 (6.51)

as illustrated in Figure 6-1 and Figure 6-2, respectively.

ˆri

Figure 6-1: Relationship of wito rifor di= 1 (linear option)

This form for flegacy provides the ﬂexibility to handle a wide range of costs, from

simple linear functions of the optimization variables to scaled quadratic penal-

ties on quantities, such as voltages, lying outside a desired range, to functions

of linear combinations of variables, inspired by the requirements of price coor-

dination terms found in the decomposition of large loosely coupled problems

encountered in our own research.

Some limitations are imposed on the parameters in the case of the DC OPF

since Matpower uses a generic quadratic programming (QP) solver for the

optimization. In particular, ki= 0 and di= 1 for all i, so the “dead zone” is

not considered and only the linear option is available for fdi. As a result, for

the DC case (6.50) simpliﬁes to wi=miui.

ˆri

Figure 6-2: Relationship of wito rifor di= 2 (quadratic option)

6.4 Standard Extensions

In addition to making this extensible OPF structure available to end users, Mat-

power also takes advantage of it internally to implement several additional capa-

bilities.

6.4.1 Piecewise Linear Costs

The standard OPF formulation in (6.1)–(6.4) does not directly handle the non-

smooth piecewise linear cost functions that typically arise from discrete bids and

oﬀers in electricity markets. When such cost functions are convex, however, they

can be modeled using a constrained cost variable (CCV) method. The piecewise lin-

ear cost function c(x) is replaced by a helper variable yand a set of linear constraints

that form a convex “basin” requiring the cost variable yto lie in the epigraph of the

function c(x).

Figure 6-3 illustrates a convex n-segment piecewise linear cost function

c(x) = 









m1(x−x1) + c1, x ≤x1

m2(x−x2) + c2, x1< x ≤x2

mn(x−xn) + cn, xn−1< x

(6.52)

deﬁned by a sequence of points (xj, cj), j= 0 . . . n, where mjdenotes the slope of

Figure 6-3: Constrained Cost Variable

the j-th segment

mj=cj−cj−1

xj−xj−1

, j = 1 . . . n (6.53)

and x0< x1<··· < xnand m1≤m2≤ ··· < mn.

The “basin” corresponding to this cost function is formed by the following n

constraints on the helper cost variable y:

y≥mj(x−xj) + cj, j = 1 . . . n. (6.54)

The cost term added to the objective function in place of c(x) is simply the variable y.

Matpower uses this CCV approach internally to automatically generate the

appropriate helper variable, cost term and corresponding set of constraints for any

piecewise linear costs on real or reactive generation. All of Matpower’s OPF

solvers, for both AC and DC OPF problems, use the CCV approach with the ex-

ception of two that are part of the optional TSPOPF package [25], namely the

step-controlled primal/dual interior point method (SCPDIPM) and the trust region

based augmented Lagrangian method (TRALM), both of which use a cost smoothing

technique instead [26].

Note that Matpower (in opf setup) automatically converts any single-segment

piecewise linear costs into polynomial (linear) form to avoid unnecessarily creating

extra variables and constraints. It is this modiﬁed cost, rather than the original

piecewise linear equivalent, that is returned in the gencost ﬁeld of the results struct.

6.4.2 Dispatchable Loads

A simple approach to dispatchable or price-sensitive loads is to model them as nega-

tive real power injections with associated negative costs. This is done by specifying

a generator with a negative output, ranging from a minimum injection equal to the

negative of the largest possible load to a maximum injection of zero.

Consider the example of a price-sensitive load whose marginal beneﬁt function is

shown in Figure 6-4. The demand pdof this load will be zero for prices above λ1,p1

for prices between λ1and λ2, and p1+p2for prices below λ2.

λ(marginal beneﬁt)

$/MW

λ1

λ2

p(load)

Figure 6-4: Marginal Beneﬁt or Bid Function

This corresponds to a negative generator with the piecewise linear cost curve

shown in Figure 6-5. Note that this approach assumes that the demand blocks can

be partially dispatched or “split”. Requiring blocks to be accepted or rejected in

their entirety would pose a mixed-integer problem that is beyond the scope of the

current Matpower implementation.

It should be noted that, with this deﬁnition of dispatchable loads as negative

generators, if the negative cost corresponds to a beneﬁt for consumption, minimizing

the cost f(x) of generation is equivalent to maximizing social welfare.

With an AC network model, there is also the question of reactive dispatch for

such loads. Typically the reactive injection for a generator is allowed to take on any

value within its deﬁned limits. Since this is not normal load behavior, the model used

2

1

p(injection)

c(total cost)

1p1

2p2

Figure 6-5: Total Cost Function for Negative Injection

in Matpower assumes that dispatchable loads maintain a constant power factor.

When formulating the AC OPF problem, Matpower will automatically generate

an additional equality constraint to enforce a constant power factor for any “negative

generator” being used to model a dispatchable load.

The power factor, which can be lagging or leading, is determined by the ratio of

reactive to active power for the load and is speciﬁed by the active and reactive limits

deﬁning the nominal load in the gen matrix. For all dispatchable loads, the value

in the PMIN column is negative and deﬁnes the nominal active power of the load.

And PMAX is zero, allowing the load to be fully curtailed depending on the price.

The reactive limits, QMIN and QMAX, depend on whether the power ﬂow is lagging

or leading. One deﬁnes the nominal reactive load and the other must be zero to

allow the load to be fully curtailed. The values of PG and QG must be deﬁned to be

consistent with the nominal power factor.

•Lagging Power Factor – The reactive injection is negative, meaning that

reactive power is consumed by the load. Hence, QMIN is negative, QMAX is zero,

and PG and QG must be set so that QG is equal to PG * QMIN/PMIN.

•Leading Power Factor – The reactive injection is positive, that is, reactive

power is produced by the load. Hence, QMAX is positive, QMIN is zero, and PG

and QG must be set so that QG is equal to PG * QMAX/PMIN.

6.4.3 Generator Capability Curves

The typical AC OPF formulation includes box constraints on a generator’s real and

reactive injections, speciﬁed as simple lower and upper bounds on p(pmin and pmax)

and q(qmin and qmax). On the other hand, the true P-Qcapability curves of phys-

ical generators usually involve some tradeoﬀ between real and reactive capability,

so that it is not possible to produce the maximum real output and the maximum

(or minimum) reactive output simultaneously. To approximate this tradeoﬀ, Mat-

power includes the ability to add an upper and lower sloped portion to the standard

box constraints as illustrated in Figure 6-6, where the shaded portion represents the

feasible operating region for the unit.

qmax

qmin

qmax

pmax

pmin

Figure 6-6: Generator P-QCapability Curve

The two sloped portions are constructed from the lines passing through the two

pairs of points deﬁned by the six parameters p1,qmin

1,qmax

1,p2,qmin

2, and qmax

If these six parameters are speciﬁed for a given generator in columns PC1–QC2MAX

(11–16), Matpower automatically constructs the corresponding additional linear

inequality constraints on pand qfor that unit.

If one of the sloped portions of the capability constraints is binding for genera-

tor k, the corresponding shadow price is decomposed into the corresponding µPmax

and µQmin or µQmax components and added to the respective column (MU PMAX,MU QMIN

or MU QMAX) in the kth row of gen.

6.4.4 Branch Angle Diﬀerence Limits

The diﬀerence between the bus voltage angle θfat the from end of a branch and

the angle θtat the to end can be bounded above and below to act as a proxy for a

transient stability limit, for example. If these limits are provided in columns ANGMIN

(12) and ANGMAX (13) of the branch matrix, Matpower creates the corresponding

constraints on the voltage angle variables.26

6.5 Solvers

Early versions of Matpower relied on Matlab’s Optimization Toolbox [27] to

provide the NLP and QP solvers needed to solve the AC and DC OPF problems,

respectively. While they worked reasonably well for very small systems, they did not

scale well to larger networks. Eventually, optional packages with additional solvers

were added to improve performance, typically relying on Matlab extension (MEX)

ﬁles implemented in Fortran or C and pre-compiled for each machine architecture.

Some of these MEX ﬁles are distributed as optional packages due to diﬀerences in

performance interior point BPMPD solver [29] for LP/QP problems. For the AC

OPF problem, the MINOPF [30] and TSPOPF [25] packages provide solvers suitable

for much larger systems. The former is based on MINOS [31] and the latter includes

the primal-dual interior point and trust region based augmented Lagrangian methods

described in [26]. Matpower version 4 and later also includes the option to use

the open-source Ipopt solver27 for solving both AC and DC OPFs, based on the

Matlab MEX interface to Ipopt28. It also includes the option to use CPLEX29 or

MOSEK30 for DC OPFs. Matpower 4.1 added the option to use KNITRO [32]31

26The voltage angle diﬀerence for branch kis taken to be unbounded below if branch(k, ANGMIN)

is less than or equal to −360 and unbounded above if branch(k, ANGMAX) is greater than or equal

to 360. If both parameters are zero, the voltage angle diﬀerence is unconstrained.

27Available from http://www.coin-or.org/projects/Ipopt.xml.

28See https://projects.coin-or.org/Ipopt/wiki/MatlabInterface.

29See http://www.ibm.com/software/integration/optimization/cplex-optimizer/.

30See http://www.mosek.com/.

31See http://www.ziena.com/.

for AC OPFs and the Gurobi Optimizer [33]32 for DC OPFs and Matpower 5

added GLPK [34] and 5.1 added CLP [35]. See Appendix Gfor more details on

these optional packages.

Beginnning with version 4, Matpower also includes its own primal-dual interior

point method implemented in pure-Matlab code, derived from the MEX implemen-

tation of the algorithms described in [26]. This solver is called MIPS (Matpower

Interior Point Solver) and is described in more detail in Appendix A. If no optional

packages are installed, MIPS will be used by default for both the AC OPF and

as the QP solver used by the DC OPF. The AC OPF solver also employs a unique

technique for eﬃciently forming the required Hessians via a few simple matrix opera-

tions [36–38]. This solver has application to general nonlinear optimization problems

outside of Matpower and can be called directly as mips. There is also a conve-

nience wrapper function called qps mips making it trivial to set up and solve LP and

QP problems, with an interface similar to quadprog from the Matlab Optimization

Toolbox.

6.6 runopf

In Matpower, an optimal power ﬂow is executed by calling runopf with a case

struct or case ﬁle name as the ﬁrst argument (casedata). In addition to printing

output to the screen, which it does by default, runopf optionally returns the solution

in a results struct.

>> results = runopf(casedata);

The results struct is a superset of the input Matpower case struct mpc, with

some additional ﬁelds as well as additional columns in some of the existing data

ﬁelds. In addition to the solution values included in the results for a simple power

ﬂow, shown in Table 4-1 in Section 4.4, the following additional optimal power ﬂow

solution values are stored as shown in Table 6-1.

32See http://www.gurobi.com/.

Table 6-1: Optimal Power Flow Results

name description

results.f ﬁnal objective function value

results.x ﬁnal value of optimization variables (internal order)

results.om OPF model object†

results.bus(:, LAM P) Lagrange multiplier on real power mismatch

results.bus(:, LAM Q) Lagrange multiplier on reactive power mismatch

results.bus(:, MU VMAX) Kuhn-Tucker multiplier on upper voltage limit

results.bus(:, MU VMIN) Kuhn-Tucker multiplier on lower voltage limit

results.gen(:, MU PMAX) Kuhn-Tucker multiplier on upper Pglimit

results.gen(:, MU PMIN) Kuhn-Tucker multiplier on lower Pglimit

results.gen(:, MU QMAX) Kuhn-Tucker multiplier on upper Qglimit

results.gen(:, MU QMIN) Kuhn-Tucker multiplier on lower Qglimit

results.branch(:, MU SF) Kuhn-Tucker multiplier on ﬂow limit at “from” bus

results.branch(:, MU ST) Kuhn-Tucker multiplier on ﬂow limit at “to” bus

results.mu shadow prices of constraints‡

results.g (optional) constraint values

results.dg (optional) constraint 1st derivatives

results.raw raw solver output in form returned by MINOS, and more‡

results.var.val ﬁnal value of optimization variables, by named subset‡

results.var.mu shadow prices on variable bounds, by named subset‡

results.nle shadow prices on nonlinear equality constraints, by named subset‡

results.nli shadow prices on nonlinear inequality constraints, by named subset‡

results.lin shadow prices on linear constraints, by named subset‡

results.cost ﬁnal value of user-deﬁned costs, by named subset‡

†See help for opf model and opt model for more details.

‡See help for opf for more details.

Additional optional input arguments can be used to set options (mpopt) and

provide ﬁle names for saving the pretty printed output (fname) or the solved case

data (solvedcase).

>> results = runopf(casedata, mpopt, fname, solvedcase);

Some of the main options that control the optimal power ﬂow simulation are listed

in Tables 6-2 and 6-3. There are many other options that can be used to control the

termination criteria and other behavior of the individual solvers. See Appendix C

or the mpoption help for details. As with runpf the output printed to the screen can

be controlled by the options in Table 4-3, but there are additional output options

for the OPF, related to the display of binding constraints that are listed Table 6-4,

along with an option that can be used to force the AC OPF to return information

about the constraint values and Jacobian and the objective function gradient and

Hessian.

For OPF problems, the preferred way to eliminate the ﬂow limit on a branch is

to set the RATE A column (6) of the corresponding row in the branch matrix to zero.

This indicates a completely unconstrained ﬂow (as opposed to zero ﬂow).

By default, runopf solves an AC optimal power ﬂow problem using a primal dual

interior point method. To run a DC OPF, the model option must be set to 'DC'. For

convenience, Matpower provides a function rundcopf which is simply a wrapper

that sets the model to 'DC'before calling runopf.

Internally, the runopf function does a number of conversions to the problem

data before calling the appropriate solver routine for the selected OPF algorithm.

This external-to-internal format conversion is performed by the ext2int function,

described in more detail in Section 7.3.1, and includes the elimination of out-of-service

equipment, the consecutive renumbering of buses and the reordering of generators

by increasing bus number. All computations are done using this internal indexing.

When the simulation has completed, the data is converted back to external format

by int2ext before the results are printed and returned. In addition, both ext2int

and int2ext can be customized via user-supplied callback routines to convert data

needed by user-supplied variables, constraints or costs into internal indexing.

Table 6-2: Optimal Power Flow Solver Options

name default description

opf.ac.solver 'DEFAULT'AC optimal power ﬂow solver:

'DEFAULT'– choose default solver, i.e. 'MIPS'

'MIPS'– MIPS, Matpower Interior Point Solver,

primal/dual interior point method†

'FMINCON'–Matlab Optimization Toolbox, fmincon

'IPOPT'–Ipopt*

'KNITRO'– KNITRO*

'MINOPF'– MINOPF*

, MINOS-based solver

'PDIPM'– PDIPM*

, primal/dual interior point method‡

'SDPOPF'– SDPOPF*

, solver based on semideﬁnite relax-

ation

'TRALM'– TRALM*

, trust region based augmented Lan-

grangian method

opf.dc.solver 'DEFAULT'DC optimal power ﬂow solver:

'DEFAULT'– choose default solver based on availability

in the following order: 'GUROBI','CPLEX',

'MOSEK','OT','GLPK'(linear costs only),

'BPMPD','MIPS'

'MIPS'– MIPS, Matpower Interior Point Solver,

primal/dual interior point method†

'BPMPD'– BPMPD*

'CLP'– CLP*

'CPLEX'– CPLEX*

'GLPK'– GLPK*(no quadratic costs)

'GUROBI'– Gurobi*

'IPOPT'–Ipopt*

'MOSEK'– MOSEK*

'OT'–Matlab Opt Toolbox, quadprog,linprog

*Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

†For MIPS-sc, the step-controlled version of this solver, the mips.step control option must be set to 1.

‡For SC-PDIPM, the step-controlled version of this solver, the pdipm.step control option must be set to 1.

Table 6-3: Other OPF Options

name default description

opf.current balance 0 use current, as opposed to power, balance formulation for

AC OPF, 0 or 1

opf.v cartesian 0 use cartesian, as opposed to polar, representation for volt-

ages for AC OPF, 0 or 1

opf.violation 5×10−6constraint violation tolerance

opf.use vg 0 respect generator voltage setpoint, 0 or 1†

0 – use voltage magnitude limits speciﬁed in bus, ig-

nore VG in gen

1 – replace voltage magnitude limits speciﬁed in bus

by VG in corresponding gen

opf.flow lim 'S'quantity to limit for branch ﬂow constraints

'S'– apparent power ﬂow (limit in MVA)

'P'– active power ﬂow (limit in MW)

'I'– current magnitude (limit in MVA at 1 p.u.

voltage)

'2'– same as 'P', but implemented using square

of active ﬂow, rather than simple max

opf.ignore angle lim 0 ignore angle diﬀerence limits for branches

0 – include angle diﬀerence limits, if speciﬁed

1 – ignore angle diﬀerence limits even if speciﬁed

opf.softlims.default 1 behavior of OPF soft limits for which parameters are not

explicitly provided

0 – do not include softlims if not explicitly speciﬁed

1 – include softlims with default values if not ex-

plicitly speciﬁed

opf.init from mpc*-1 specify whether to use the current state in Matpower

case to initialize OPF

-1 – Matpower decides based on solver/algorithm

0 – ignore current state in Matpower case‡

1 – use current state in Matpower case

opf.start 0 strategy for initializing OPF starting point

0 – default, Matpower decides based on solver,

(currently identical to 1)

1 – ignore current state in Matpower case‡

2 – use current state in Matpower case

3 – solve power ﬂow and use resulting state

opf.return raw der 0 for AC OPF, return constraint and derivative info in

results.raw (in ﬁelds g,dg,df,d2f)

*Deprecated. Use opf.start instead.

†Using a value between 0 and 1 results in the limits being determined by the corresponding weighted average of

the 2 options.

‡Only applies to fmincon,Ipopt, KNITRO and MIPS solvers, which use an interior point estimate; others use

current state in Matpower case, as with opf.start = 2.

Table 6-4: OPF Output Options

name default description

out.lim.all -1 controls constraint info output

-1 – individual ﬂags control what is printed

0 – do not print any constraint info†

1 – print only binding constraint info†

2 – print all constraint info†

out.lim.v 1 control output of voltage limit info

0 – do not print

1 – print binding constraints only

2 – print all constraints

out.lim.line 1 control output of line ﬂow limit info‡

out.lim.pg 1 control output of gen active power limit info‡

out.lim.qg 1 control output of gen reactive power limit info‡

†Overrides individual ﬂags.

‡Takes values of 0, 1 or 2 as for out.lim.v.

7 Extending the OPF

The extended OPF formulation described in Section 6.3 allows the user to modify the

standard OPF formulation to include additional variables, costs and/or constraints.

There are two primary mechanisms available for the user to accomplish this. The ﬁrst

is by directly constructing the full parameters for the addional costs or constraints

and supplying them either as ﬁelds in the case struct or directly as arguments to

the opf function. The second, and more powerful, method is via a set of callback

functions that customize the OPF at various stages of the execution. Matpower

includes several examples of using the latter method, for example to add a ﬁxed zonal

reserve requirement, to implement interface ﬂow limits, dispatchable DC transmission

lines, or branch ﬂow soft limits.

7.1 Direct Speciﬁcation

This section describes the additional ﬁelds that can be added to mpc (the Matpower

case struct) or, alternatively, the input parameters that can be passed directly to the

opf function. The former is the preferred approach, as it allows the normal use of

runopf and related functions.

7.1.1 User-deﬁned Variables

In the case of direct speciﬁcation, additional variables are created implicitly based on

the diﬀerence between the number of columns in Aand the number nxof standard

OPF variables. If Ahas more columns than xhas elements, the extra columns are

assumed to correspond to a new zvariable. The initial value and lower and upper

bounds for zcan also be speciﬁed in the optional ﬁelds or arguments, z0,zl and zu,

respectively.

7.1.2 User-deﬁned Constraints

•Linear Constraints can be added by specifying the A,land uparameters of

(6.38) directly as ﬁelds or arguments of the same names, A,land u, respectively,

where Ais sparse.

•Nonlinear Constraints for a constraint set j, that is, gj

u(x) or hj

u(x) from

(6.42) or (6.43), are implemented by deﬁning two M-ﬁle functions, similar to

those required by MIPS. The ﬁrst is a function to compute the constraint values

and their gradients (Jacobian),33 with calling syntax:

[g, dg] = my constraint fcn(x, <p1>, <p2>, ...)

Here <p1> and <p2> represent arbitrary optional input parameters that remain

constant for all calls to the function. The second is a function to compute the

Hessian of the corresponding term in the Lagrangian function, that is the term

corresponding to λTgj

u(x) or µThj

u(x). This function has the following calling

syntax:

d2G = my constraint hess(x, lambda, <p1>, <p2>, ...)

Once again this is similar to the form of the Hessian evaluation function ex-

pected by MIPS.34

In order to add a set of user-deﬁned nonlinear constraints to the formula-

tion through direct speciﬁcation, an entry must be added to the optional

user constraints.nle (nonlinear equality) or user constraints.nli (nonlin-

ear inequality) ﬁelds of the Matpower case struct. These ﬁelds are cell ar-

rays, in which each element (also a cell array) speciﬁes a constraint set of the

corresponding kind. The format is as follows, where the details are described

in Table 7-1.

mpc.user_constraints.nle = {

{name, N, g_fcn, hess_fcn, varsets, params},

...

};

There is an example in the OPF testing code (e.g. t opf mips) near the end,

that implements a nonlinear relationship between three diﬀerent generator out-

puts by adding the following line.

33The diﬀerences between this function and the one required by MIPS is that (1) this one repre-

sents a single set of equality constraints or inequality constraints, not both, (2) it returns in dg the

m×nJacobian (for mconstraints and nvariables), whereas MIPS expects the n×mtranspose,

(3) this function allows arbitrary additional parameters, and (4) xcan be a cell array of sub-vectors

of optimization variable ˆx(see varsets in Table 7-1).

34The diﬀerences between this function and the one required by MIPS is that (1) this one returns

the Hessian of a single term of the Lagrangian, not of the full Lagrangian, (2) the lambda argument

is a simple vector of multipliers (λor µ) corresponding just to this set of constraints, not a struct

containing the full λand µvectors, in ﬁelds eqnonlin and ineqnonlin, respectively, and (3) this

function allows arbitrary additional parameters, and (4) xcan be a cell array of sub-vectors of

optimization variable ˆx(see varsets in Table 7-1).

Table 7-1: User-deﬁned Nonlinear Constraint Speciﬁcation

name description

name string with name of constraint set, used to label multipliers in results struct

Nnumber of constraints, i.e. dimension of gj

u(x) (or hj

u(x) as the case may be)

g fcn string containing name of function to evaluate constraint and gradients (Jacobian)

hess fcn string containing name of function to evaluate Hessian of corresponding term of

Lagrangian

varsets cell array of variable set names, specifying sub-vectors of optimization vector ˆxto

be passed as inputs in x†

params cell array of optional, arbitrary parameters to pass to each call to the constraint and

Hessian evaluation functions

†If varsets is empty, xwill be the full optimization vector ˆx, otherwise it will be a cell array of sub-vectors of ˆxfor

the speciﬁed variable sets. Valid names include 'Va','Vm','Pg', and 'Qg'. It can include others depending on

the OPF extensions in use. See the variable names displayed by results.om for a complete list for your problem.

mpc.user_constraints.nle = {

{'Pg_usr', 1, 'opf_nle_fcn1', 'opf_nle_hess1', {'Pg'}, {}}

};

This adds a single constraint named 'Pg usr'as a function of the vector of

generator active injections (xwill be {Pg}, where Pg is a sub-vector of the

optimization vector ˆxcontaining only the generator active injections). The

constraints and gradients are evaluated by a function named 'opf nle fcn1'

and the Hessian of the corresponding term of the Lagrangian by a function

named 'opf nle hess1', neither of which expect any additional parameters.

7.1.3 User-deﬁned Costs

•Quadratic Costs by direct speciﬁcation are not currently supported.

•General Nonlinear Costs by direct speciﬁcation are not currently supported.

•Legacy Costs – To add legacy costs directly, the parameters H,C,N, ˆr,k,

dand mof (6.48)–(6.51) described in Section 6.3.3 are speciﬁed as ﬁelds or

arguments H,Cw,Nand fparm, respectively, where fparm is the nw×4 matrix

fparm =dˆr k m .(7.1)

When specifying additional costs, Nand Cw are required, while Hand fparm are

optional. The default value for His a zero matrix, and the default for fparm is

such that dand mare all ones and ˆrand kare all zeros, resulting in simple

linear cost, with no shift or “dead-zone”. Nand Hshould be speciﬁed as sparse

matrices.

7.1.4 Additional Comments

For a simple formulation extension to be used for a small number of OPF cases, this

method has the advantage of being direct and straightforward. While Matpower

does include code to eliminate the columns of Aand Ncorresponding to Vmand Qg

when running a DC OPF35, as well as code to reorder and eliminate columns appro-

priately when converting from external to internal data formats, this mechanism still

requires the user to take special care in preparing the Aand Nmatrices to ensure

that the columns match the ordering of the elements of the optimization vectors x

and z. All extra constraints and variables must be incorporated into a single set of

parameters that are constructed before calling the OPF. The bookkeeping needed to

access the resulting variables and shadow prices on constraints and variable bounds

must be handled manually by the user outside of the OPF, along with any pro-

cessing of additional input data and processing, printing or saving of the additional

result data. Making further modiﬁcations to a formulation that already includes

user-supplied costs, constraints or variables, requires that both sets be incorporated

into a new single consistent set of parameters.

7.2 Callback Functions

The second method, based on deﬁning a set of callback functions, oﬀers several

distinct advantages, especially for more complex scenarios or for adding a feature

for others to use, such as the zonal reserve requirement or the interface ﬂow limits

mentioned previously. This approach makes it possible to:

•deﬁne and access variable/constraint/cost sets as individual named blocks

•deﬁne constraints, costs only in terms of variables directly involved

•pre-process input data and/or post-process result data

•print and save new result data

•simultaneously use multiple, independently developed extensions (e.g. zonal

reserve requirements and interface ﬂow limits)

35Only if they contain all zeros.

With this approach the OPF formulation is modiﬁed in the formulation callback,

which is described and illustrated below in Section 7.3.2. The modiﬁcations to the

formulation are handled by adding variables, costs and/or constraints to the OPF

Model object (om) using one of the add * methods. Please see the documentation for

each of these methods for more details.

7.2.1 User-deﬁned Variables

Additional variables are added using the add var method.

om.add_var('myV', N, myV0, myV_min, myV_max);

Here myV is the name of the variable set, Nthe number of variables being added (i.e.

this is an N×1 vector being appended to the current optimization variable ˆx), and

myV0,myV min,myV max are vectors of initial values, lower bounds and upper bounds,

respectively.

7.2.2 User-deﬁned Costs

•Quadratic Costs are added using the add quad cost method.

om.add_quad_cost('myQcost', Q, c, k, varsets);

Here myQcost is the name of the cost set, Q,cand kare the Qj,cjand kj

parameters from (6.47), respectively, and var sets is an optional cell array of

variable set names. If var sets is provided, the dimensions of Qand cwill

correspond, not to the full optimization vector ˆx, but to the subvector formed

by stacking only the variable sets speciﬁed in var sets.

•General Nonlinear Costs are added using the add nln cost method.

om.add_nln_cost('myNonlinCost', 1, fcn, varsets);

Here myNonlinCost is the name of the cost set, fcn is a function handle and

var sets is an optional cell array of variable set names. The function handle

fcn must point to a function that implements the fj

nln(ˆx) function from (6.46),

returning the value of the function, along with its gradient and Hessian. This

function has a format similar to that required by MIPS for its cost function.

If var sets is provided, instead of the full optimization vector ˆx, the xpassed

to the function fcn will be a cell array of sub-vectors of ˆxcorresponding to the

speciﬁed variable sets.

•Legacy Costs are added using the add legacy cost method.

om.add_legacy_cost('myLegacyCost', cp, varsets);

Here myLegacyCost is the name of the cost set, cp is a struct containing the cost

parameters H,C,N, ˆr,k,dand mfrom (6.48)–(6.51) in ﬁelds H,Cw,N,rh,kk,

dd and mm, respectively, and var sets is an optional cell array of variable set

names. If var sets is provided, the number of columns in Nwill correspond,

not to the full optimization vector ˆx, but to the subvector formed by stacking

only the variable sets speciﬁed in var sets.

7.2.3 User-deﬁned Constraints

•Linear Constraints are added using the add lin constraint method.

om.lin_constraint('myLinCons', A, l, u, varsets);

Here myLinCons is the name of the constraint set, A,land ucorrespond to

additional rows to add to the A,land uparameters in (6.38), respectively, and

var sets is an optional cell array of variable set names. If var sets is provided,

the number of columns in Awill correspond, not to the full optimization vector

ˆx, but to the subvector formed by stacking only the variable sets speciﬁed in

var sets.

•Nonlinear Constraints are added using the add nln constraint method.

om.nln_constraint('myNonlinCons', N, iseq, fcn, hess, varsets);

Here myNonlinCons is the name of the constraint set, Nis the number of con-

straints being added, iseq is a true or false value indicating whether this is a set

of equality (or else inequality) constraints, fcn and hess are function handles

and var sets is an optional cell array of variable set names. The function han-

dle fcn must point to a function that implements the corresponding constraint

function gj

u(x) or hj

u(x) and its gradients, and hess to one that evaluates the

corresponding term in the Hessian of the Lagrangian function. This function

has a format similar to that required by MIPS for its cost function. See more

details in Section 7.1.2.

If var sets is provided, instead of the full optimization vector ˆx, the xpassed

to the function fcn will be a cell array of sub-vectors of ˆxcorresponding to the

speciﬁed variable sets.

7.3 Callback Stages and Example

Matpower deﬁnes ﬁve stages in the execution of a simulation where custom code

can be inserted to alter the behavior or data before proceeding to the next stage.

This custom code is deﬁned as a set of “callback” functions that are registered via

add userfcn for Matpower to call automatically at one of the ﬁve stages. Each

stage has a name and, by convention, the name of a user-deﬁned callback func-

tion ends with the name of the corresponding stage. For example, a callback for

the formulation stage that modiﬁes the OPF problem formulation to add reserve

requirements could be registered with the following line of code.

mpc = add_userfcn(mpc, 'formulation', @userfcn_reserves_formulation);

The sections below will describe each stage and the input and output arguments

for the corresponding callback function, which vary depending on the stage. An

example that employs additional variables, constraints and costs will be used for

illustration.

Consider the problem of jointly optimizing the allocation of both energy and

reserves, where the reserve requirements are deﬁned as a set of nrz ﬁxed zonal MW

quantities. Let Zkbe the set of generators in zone kand Rkbe the MW reserve

requirement for zone k. A new set of variables rare introduced representing the

reserves provided by each generator. The value ri, for generator i, must be non-

negative and is limited above by a user-provided upper bound rmax

i(e.g. a reserve

oﬀer quantity) as well as the physical ramp rate ∆i.

0≤ri≤min(rmax

i,∆i), i = 1 . . . ng(7.2)

If the vector ccontains the marginal cost of reserves for each generator, the user

deﬁned cost term from (6.34) is simply

fu(ˆx) = cTr. (7.3)

There are two additional sets of constraints needed. The ﬁrst ensures that, for

each generator, the total amount of energy plus reserve provided does not exceed the

capacity of the unit.

g+ri≤pi,max

g, i = 1 . . . ng(7.4)

The second requires that the sum of the reserve allocated within each zone kmeets

the stated requirements.

i∈Zk

ri≥Rk, k = 1 . . . nrz (7.5)

Table 7-2: Names Used by Implementation of OPF with Reserves

name description

mpc Matpower case struct

reserves additional ﬁeld in mpc containing input parameters for zonal reserves in

the following sub-ﬁelds:

cost ng×1 vector of reserve costs, cfrom (7.3)

qty ng×1 vector of reserve quantity upper bounds, ith element is rmax

zones nrz ×ngmatrix of reserve zone deﬁnitions

zones(k,j) =1 if gen jbelongs to reserve zone k(j∈Zk)

0 otherwise (j /∈Zk)

req nrz ×1 vector of zonal reserve requirements, kth element is Rkfrom (7.5)

om OPF model object, already includes standard OPF setup

results OPF results struct, superset of mpc with additional ﬁelds for output data

ng ng, number of generators

Rname for new reserve variable block, ith element is ri

Pg plus R name for new capacity limit constraint set (7.4)

Rreq name for new reserve requirement constraint set (7.5)

Table 7-2 describes some of the variables and names that are used in the example

callback function listings in the sections below.

7.3.1 ext2int Callback

Before doing any simulation of a case, Matpower performs some data conversion

on the case struct in order to achieve a consistent internal structure, by calling the

following.

mpc = ext2int(mpc, mpopt);

All isolated buses, out-of-service generators and branches are removed, along with

any generators or branches connected to isolated buses. The buses are renumbered

consecutively, beginning at 1, and the in-service generators are sorted by increasing

bus number. All of the related indexing information and the original data matrices

are stored in an order ﬁeld in the case struct to be used later by int2ext to perform

the reverse conversions when the simulation is complete.

The ﬁrst stage callback is invoked from within the ext2int function immediately

after the case data has been converted. Inputs are a Matpower case struct (mpc)

freshly converted to internal indexing, a Matpower options struct mpopt,36 and

36The mpopt may be empty if ext2int() is called manually without providing it.

any (optional) args value supplied when the callback was registered via add userfcn.

Output is the (presumably updated) mpc. This is typically used to reorder any input

arguments that may be needed in internal ordering by the formulation stage. The

example shows how e2i field can also be used, with a case struct that has already

been converted to internal indexing, to convert other data structures by passing in

2 or 3 extra parameters in addition to the case struct. In this case, it automatically

converts the input data in the qty,cost and zones ﬁelds of mpc.reserves to be

consistent with the internal generator ordering, where oﬀ-line generators have been

eliminated and the on-line generators are sorted in order of increasing bus number.

Notice that it is the second dimension (columns) of mpc.reserves.zones that is being

re-ordered. See the on-line help for e2i field and e2i data for more details on what

all they can do.

function mpc = userfcn_reserves_ext2int(mpc, mpopt, args)

mpc = e2i_field(mpc, {'reserves', 'qty'}, 'gen');

mpc = e2i_field(mpc, {'reserves', 'cost'}, 'gen');

mpc = e2i_field(mpc, {'reserves', 'zones'}, 'gen', 2);

This stage is also a good place to check the consistency of any additional input

data required by the extension and throw an error if something is missing or not as

expected.

7.3.2 formulation Callback

This stage is called at the end of opf setup after the OPF Model (om) object has been

initialized with the standard OPF formulation, but before calling the solver. This

is the ideal place for modifying the problem formulation with additional variables,

constraints and costs, using the add var,add lin constraint,add nln constraint,

add quad cost,add nln cost and add legacy cost methods of the OPF Model ob-

ject.37 Inputs are the om object, the Matpower options struct mpopt and any

(optional) args supplied when the callback was registered via add userfcn. Output

is the updated om object.

The om object contains both the original Matpower case data as well as all of

the indexing data for the variables and constraints of the standard OPF formulation.

37It is perfectly legitimate to register more than one callback per stage, such as when enabling

multiple independent OPF extensions. In this case, the callbacks are executed in the order they

were registered with add userfcn. E.g. when the second and subsequent formulation callbacks

are invoked, the om object will reﬂect any modiﬁcations performed by earlier formulation callbacks.

See the on-line help for opf model and opt model for more details on the OPF model

object and the methods available for manipulating and accessing it.

In the example code, a new variable block named Rwith ngelements and the

limits from (7.2) is added to the model via the add var method. Similarly, two linear

constraint blocks named Pg plus R and Rreq, implementing (7.4) and (7.5), respec-

tively, are added via the add lin constraint method. And ﬁnally, the add quad cost

method is used to add to the model a quadratic (actually linear) cost block corre-

sponding to (7.3).

Notice that the last argument to add lin constraint and add quad cost allows

the constraints and costs to be deﬁned only in terms of the relevant parts of the

optimization variable ˆx. For example, the Amatrix for the Pg plus R constraint

contains only columns corresponding to real power generation (Pg) and reserves (R)

and need not bother with voltages, reactive power injections, etc. As illustrated in

Figure 7-1, this allows the same code to be used with both the AC OPF, where

ˆxincludes Vmand Qg, and the DC OPF where it does not. This code is also

independent of any additional variables that may have been added by Matpower

(e.g. yvariables from Matpower’s CCV handling of piece-wise linear costs) or by

the user via previous formulation callbacks. Matpower will place the constraint

and cost matrix blocks in the appropriate place when it constructs the aggregated

constraint and cost matrices at run-time. This is an important feature that enables

independently developed Matpower OPF extensions to work together.

function om = userfcn_reserves_formulation(om, mpopt, args)

%% initialize some things

define_constants;

mpc = om.get_mpc();

r = mpc.reserves;

ng = size(mpc.gen, 1); %% number of on-line gens

%% variable bounds

Rmin = zeros(ng, 1); %% bound below by 0

Rmax = r.qty; %% bound above by stated max reserve qty ...

k = find(mpc.gen(:, RAMP_10) > 0 & mpc.gen(:, RAMP_10) < Rmax);

Rmax(k) = mpc.gen(k, RAMP_10); %% ... and ramp rate

Rmax = Rmax / mpc.baseMVA;

%% constraints

I = speye(ng); %% identity matrix

Ar = [I I];

Pmax = mpc.gen(:, PMAX) / mpc.baseMVA;

lreq = r.req / mpc.baseMVA;

%% cost

Cw = r.cost * mpc.baseMVA; %% per unit cost coefficients

%% add them to the model

om.add_var('R', ng, [], Rmin, Rmax);

om.add_lin_constraint('Pg_plus_R', Ar, [], Pmax, {'Pg', 'R'});

om.add_lin_constraint('Rreq', r.zones, lreq, [], {'R'});

om.add_quad_cost('Rcost', [], Cw, 0, {'R'});

A = 0A10 00 A2

A = 0A1 0A2

Ar = A1 A2

Va PgVm yQg R

Pg y R

AC OPF

DC OPF

Figure 7-1: Adding Constraints Across Subsets of Variables

7.3.3 int2ext Callback

After the simulation is complete and before the results are printed or saved, Mat-

power converts the case data in the results struct back to external indexing by

calling the following.

results = int2ext(results, mpopt);

This conversion essentially undoes everything that was done by ext2int. Generators

are restored to their original ordering, buses to their original numbering and all

out-of-service or isolated generators, branches and buses are restored.

This callback is invoked from int2ext immediately before the resulting case is

converted from internal back to external indexing. At this point, the simulation has

been completed and the results struct, a superset of the original Matpower case

struct passed to the OPF, contains all of the results. This results struct is passed to

the callback, along with the Matpower options struct mpopt,38 and any (optional)

args supplied when the callback was registered via add userfcn. The output of the

callback is the updated results struct. This is typically used to convert any results

to external indexing and populate any corresponding ﬁelds in the results struct.

The results struct contains, in addition to the standard OPF results, solution

information related to all of the user-deﬁned variables, constraints and costs. Ta-

ble 7-3 summarizes where the various data is found. Each of the ﬁelds listed in

the table is actually a struct whose ﬁelds correspond to the named sets created by

add var,add lin constraint,add nln constraint,add quad cost,add nln cost and

add legacy cost.

In the example code below, the callback function begins by converting the reserves

input data in the resulting case (qty,cost and zones ﬁelds of results.reserves) back

to external indexing via calls to i2e field. See the help for i2e field and i2e data

for more details on how they can be used.

38The mpopt may be empty if int2ext() is called manually without providing it.

Table 7-3: Results for User-Deﬁned Variables, Constraints and Costs

name description

results.var.val ﬁnal value of user-deﬁned variables

results.var.mu.l shadow price on lower limit of user-deﬁned variables

results.var.mu.u shadow price on upper limit of user-deﬁned variables

results.lin.mu.l shadow price on lower (left-hand) limit of linear constraints

results.lin.mu.u shadow price on upper (right-hand) limit of linear constraints

results.nle.lambda shadow price on nonlinear equality constraints

results.nli.mu shadow price on nonlinear inequality constraints

results.cost ﬁnal value of legacy user costs

results.nlc ﬁnal value of general nonlinear costs

results.qdc ﬁnal value of quadratic costs

Then the reserves results of interest are extracted from the appropriate sub-ﬁelds

of results.var,results.lin and results.cost, converted from per unit to per MW

where necessary, and stored with external indexing for the end user in the chosen

ﬁelds of the results struct.

function results = userfcn_reserves_int2ext(results, mpopt, args)

%%----- convert stuff back to external indexing -----

%% convert all reserve parameters (zones, costs, qty, rgens)

results = i2e_field(results, {'reserves', 'qty'}, 'gen');

results = i2e_field(results, {'reserves', 'cost'}, 'gen');

results = i2e_field(results, {'reserves', 'zones'}, 'gen', 2);

r = results.reserves;

ng = size(results.gen, 1); %% number of on-line gens (internal)

ng0 = size(results.order.ext.gen, 1); %% number of gens (external)

%%----- results post-processing -----

%% get the results (per gen reserves, multipliers) with internal gen indexing

%% and convert from p.u. to per MW units

[R0, Rl, Ru] = results.om.params_var('R');

R = results.var.val.R * results.baseMVA;

Rmin = Rl * results.baseMVA;

Rmax = Ru * results.baseMVA;

mu_l = results.var.mu.l.R / results.baseMVA;

mu_u = results.var.mu.u.R / results.baseMVA;

mu_Pmax = results.lin.mu.u.Pg_plus_R / results.baseMVA;

%% store in results in results struct

z = zeros(ng0, 1);

results.reserves.R = i2e_data(results, R, z, 'gen');

results.reserves.Rmin = i2e_data(results, Rmin, z, 'gen');

results.reserves.Rmax = i2e_data(results, Rmax, z, 'gen');

results.reserves.mu.l = i2e_data(results, mu_l, z, 'gen');

results.reserves.mu.u = i2e_data(results, mu_u, z, 'gen');

results.reserves.mu.Pmax = i2e_data(results, mu_Pmax, z, 'gen');

results.reserves.prc = z;

for k = 1:ng0

iz = find(r.zones(:, k));

results.reserves.prc(k) = sum(results.lin.mu.l.Rreq(iz)) / results.baseMVA;

end

results.reserves.totalcost = results.cost.Rcost;

7.3.4 printpf Callback

The pretty-printing of the standard OPF output is done via a call to printpf after

the case has been converted back to external indexing. This callback is invoked from

within printpf after the pretty-printing of the standard OPF output. Inputs are

the results struct, the ﬁle descriptor to write to, a Matpower options struct, and

any (optional) args supplied via add userfcn. Output is the results struct. This is

typically used for any additional pretty-printing of results.

In this example, the out.all ﬂag in the options struct is checked before printing

anything. If it is non-zero, the reserve quantities and prices for each unit are printed

ﬁrst, followed by the per-zone summaries. An additional table with reserve limit

shadow prices might also be included.

function results = userfcn_reserves_printpf(results, fd, mpopt, args)

%% define named indices into data matrices

[GEN_BUS, PG, QG, QMAX, QMIN, VG, MBASE, GEN_STATUS, PMAX, PMIN, ...

MU_PMAX, MU_PMIN, MU_QMAX, MU_QMIN, PC1, PC2, QC1MIN, QC1MAX, ...

QC2MIN, QC2MAX, RAMP_AGC, RAMP_10, RAMP_30, RAMP_Q, APF] = idx_gen;

%%----- print results -----

r = results.reserves;

ng = length(r.R);

nrz = size(r.req, 1);

if mpopt.out.all ~= 0

fprintf(fd, '\n=======================================================');

fprintf(fd, '\n| Reserves |');

fprintf(fd, '\n=======================================================');

fprintf(fd, '\n Gen Bus Status Reserves Price');

fprintf(fd, '\n # # (MW) ($/MW)');

fprintf(fd, '\n---- ----- ------ -------- --------');

for k = 1:ng

fprintf(fd, '\n%3d %6d %2d ', k, results.gen(k, GEN_BUS), ...

results.gen(k, GEN_STATUS));

if results.gen(k, GEN_STATUS) > 0 && abs(results.reserves.R(k)) > 1e-6

fprintf(fd, '%10.2f', results.reserves.R(k));

else

fprintf(fd, ' - ');

end

fprintf(fd, '%10.2f ', results.reserves.prc(k));

end

fprintf(fd, '\n --------');

fprintf(fd, '\n Total:%10.2f Total Cost: $%.2f', ...

sum(results.reserves.R(r.igr)), results.reserves.totalcost);

fprintf(fd, '\n');

fprintf(fd, '\nZone Reserves Price ');

fprintf(fd, '\n # (MW) ($/MW) ');

fprintf(fd, '\n---- -------- --------');

for k = 1:nrz

iz = find(r.zones(k, :)); %% gens in zone k

fprintf(fd, '\n%3d%10.2f%10.2f', k, sum(results.reserves.R(iz)), ...

results.lin.mu.l.Rreq(k) / results.baseMVA);

end

fprintf(fd, '\n');

%% print binding reserve limit multipliers ...

end

7.3.5 savecase Callback

The savecase is used to save a Matpower case struct to an M-ﬁle, for example,

to save the results of an OPF run. The savecase callback is invoked from savecase

after printing all of the other data to the ﬁle. Inputs are the case struct, the ﬁle

descriptor to write to, the variable preﬁx (typically 'mpc.') and any (optional) args

supplied via add userfcn. Output is the case struct. The purpose of this callback is

to write any non-standard case struct ﬁelds to the case ﬁle.

In this example, the zones,req,cost and qty ﬁelds of mpc.reserves are written

to the M-ﬁle. This ensures that a case with reserve data, if it is loaded via loadcase,

possibly run, then saved via savecase, will not lose the data in the reserves ﬁeld.

This callback could also include the saving of the output ﬁelds if present. The

contributed serialize function39 can be very useful for this purpose.

39http://www.mathworks.com/matlabcentral/fileexchange/1206

function mpc = userfcn_reserves_savecase(mpc, fd, prefix, args)

% mpc = userfcn_reserves_savecase(mpc, fd, mpopt, args)

% This is the 'savecase' stage userfcn callback that prints the M-file

% code to save the 'reserves' field in the case file. It expects a

% MATPOWER case struct (mpc), a file descriptor and variable prefix

% (usually 'mpc.'). The optional args are not currently used.

r = mpc.reserves;

fprintf(fd, '\n%%%%----- Reserve Data -----%%%%\n');

fprintf(fd, '%%%% reserve zones, element i, j is 1 iff gen j is in zone i\n');

fprintf(fd, '%sreserves.zones = [\n', prefix);

template = '';

for i = 1:size(r.zones, 2)

template = [template, '\t%d'];

end

template = [template, ';\n'];

fprintf(fd, template, r.zones.');

fprintf(fd, '];\n');

fprintf(fd, '\n%%%% reserve requirements for each zone in MW\n');

fprintf(fd, '%sreserves.req = [\t%g', prefix, r.req(1));

if length(r.req) > 1

fprintf(fd, ';\t%g', r.req(2:end));

end

fprintf(fd, '\t];\n');

fprintf(fd, '\n%%%% reserve costs in $/MW for each gen\n');

fprintf(fd, '%sreserves.cost = [\t%g', prefix, r.cost(1));

if length(r.cost) > 1

fprintf(fd, ';\t%g', r.cost(2:end));

end

fprintf(fd, '\t];\n');

if isfield(r, 'qty')

fprintf(fd, '\n%%%% max reserve quantities for each gen\n');

fprintf(fd, '%sreserves.qty = [\t%g', prefix, r.qty(1));

if length(r.qty) > 1

fprintf(fd, ';\t%g', r.qty(2:end));

end

fprintf(fd, '\t];\n');

end

%% save output fields for solved case ...

7.4 Registering the Callbacks

As seen in the ﬁxed zonal reserve example, adding a single extension to the standard

OPF formulation is often best accomplished by a set of callback functions. A typical

use case might be to run a given case with and without the reserve requirements

active, so a simple method for enabling and disabling the whole set of callbacks as a

single unit is needed.

The recommended method is to deﬁne all of the callbacks in a single ﬁle containing

a “toggle” function that registers or removes all of the callbacks depending on whether

the value of the second argument is 'on'or 'off'. The state of the registration of any

callbacks is stored directly in the mpc struct. In our example, the toggle reserves.m

ﬁle contains the toggle reserves function as well as the ﬁve callback functions.

function mpc = toggle_reserves(mpc, on_off)

%TOGGLE_RESERVES Enable, disable or check status of fixed reserve requirements.

% MPC = TOGGLE_RESERVES(MPC, 'on')

% MPC = TOGGLE_RESERVES(MPC, 'off')

% T_F = TOGGLE_RESERVES(MPC, 'status')

if strcmp(upper(on_off), 'ON')

% <code to check for required 'reserves' fields in mpc>

%% add callback functions

mpc = add_userfcn(mpc, 'ext2int', @userfcn_reserves_ext2int);

mpc = add_userfcn(mpc, 'formulation', @userfcn_reserves_formulation);

mpc = add_userfcn(mpc, 'int2ext', @userfcn_reserves_int2ext);

mpc = add_userfcn(mpc, 'printpf', @userfcn_reserves_printpf);

mpc = add_userfcn(mpc, 'savecase', @userfcn_reserves_savecase);

mpc.userfcn.status.dcline = 1;

elseif strcmp(upper(on_off), 'OFF')

mpc = remove_userfcn(mpc, 'savecase', @userfcn_reserves_savecase);

mpc = remove_userfcn(mpc, 'printpf', @userfcn_reserves_printpf);

mpc = remove_userfcn(mpc, 'int2ext', @userfcn_reserves_int2ext);

mpc = remove_userfcn(mpc, 'formulation', @userfcn_reserves_formulation);

mpc = remove_userfcn(mpc, 'ext2int', @userfcn_reserves_ext2int);

mpc.userfcn.status.dcline = 0;

elseif strcmp(upper(on_off), 'STATUS')

if isfield(mpc, 'userfcn') && isfield(mpc.userfcn, 'status') && ...

isfield(mpc.userfcn.status, 'dcline')

mpc = mpc.userfcn.status.dcline;

else

mpc = 0;

end

else

error('toggle_dcline: 2nd argument must be ''on'', ''off'' or ''status''');

end

Running a case that includes the ﬁxed reserves requirements is as simple as

loading the case, turning on reserves and running it.

mpc = loadcase('t_case30_userfcns');

mpc = toggle_reserves(mpc, 'on');

results = runopf(mpc);

7.5 Summary

The ﬁve callback stages currently deﬁned by Matpower are summarized in Ta-

ble 7-4.

Table 7-4: Callback Functions

name invoked . . . typical use

ext2int . . . from ext2int immediately after

case data is converted from external

to internal indexing.

Check consistency of input data, con-

vert to internal indexing.

formulation . . . from opf after OPF Model (om)

object is initialized with standard

OPF formulation.

Modify OPF formulation, by adding

user-deﬁned variables, constraints,

costs.

int2ext . . . from int2ext immediately before

case data is converted from internal

back to external indexing.

Convert data back to external index-

ing, populate any additional ﬁelds in

the results struct.

printpf . . . from printpf after pretty-printing

the standard OPF output.

Pretty-print any results not included

in standard OPF.

savecase . . . from savecase after printing all of

the other case data to the ﬁle.

Write non-standard case struct ﬁelds

to the case ﬁle.

7.6 Example Extensions

Matpower includes three OPF extensions implementing via callbacks, respectively,

the co-optimization of energy and reserves, interface ﬂow limits and dispatchable DC

transmission lines.

7.6.1 Fixed Zonal Reserves

This extension is a more complete version of the example of ﬁxed zonal reserve

requirements used for illustration above in Sections 7.3 and 7.4. The details of

the extensions to the standard OPF problem are given in equations (7.2)–(7.5) and

a description of the relevant input and output data structures is summarized in

Tables 7-5 and 7-6, respectively.

The code for implementing the callbacks can be found in toggle reserves. A

wrapper around runopf that turns on this extension before running the OPF is

Table 7-5: Input Data Structures for Fixed Zonal Reserves

name description

mpc Matpower case struct

reserves additional ﬁeld in mpc containing input parameters for zonal reserves in the

following sub-ﬁelds:

cost (ngor ngr†)×1 vector of reserve costs in $/MW, cfrom (7.3)

qty (ngor ngr†)×1 vector of reserve quantity upper bounds in MW, ith element is

rmax

zones nrz ×ngmatrix of reserve zone deﬁnitions

zones(k,j) =1 if gen jbelongs to reserve zone k(j∈Zk)

0 otherwise (j /∈Zk)

req nrz ×1 vector of zonal reserve requirements in MW, kth element is Rkfrom (7.5)

†Here ngr is the number of generators belonging to at least one reserve zone.

Table 7-6: Output Data Structures for Fixed Zonal Reserves

name description

results OPF results struct, superset of mpc with additional ﬁelds for output data

reserves zonal reserve data, with results in the following sub-ﬁelds:‡

Rreserve allocation ri, in MW

Rmin lower bound of riin MW from (7.2), i.e. all zeros

Rmax upper bound of riin MW from (7.2), i.e. min(rmax

i,∆i)

mu shadow prices on constraints in $/MW

lshadow price on lower bound of riin (7.2)

ushadow price on upper bound of riin (7.2)

Pmax shadow price on capacity constraint (7.4)

prc reserve price in $/MW, computed for unit ias the sum of the shadow prices of

constraints kin (7.5) in which unit iparticipates (k|i∈Zk)

‡All zonal reserve result sub-ﬁelds are ng×1 vectors, where the values are set to zero for units not participating

in the provision of reserves.

provided in runopf w res, allowing you to run a case with an appropriate reserves

ﬁeld, such as t case30 userfcns, as follows.

results = runopf_w_res('t_case30_userfcns');

See help runopf w res and help toggle reserves for more information. Exam-

ples of using this extension and a case ﬁle deﬁning the necessary input data can be

found in t opf userfcns and t case30 userfcns, respectively. Additional tests for

runopf w res are included in t runopf w res.

7.6.2 Interface Flow Limits

This extension adds interface ﬂow limits based on ﬂows computed from a DC network

model. It is implemented in toggle iflims. A ﬂow interface kis deﬁned as a set Bk

of branch indices iand a direction for each branch. If pirepresents the real power

ﬂow (“from” bus →“to” bus) in branch iand diis equal to 1 or −1 to indicate the

direction,40 then the interface ﬂow fkfor interface kis deﬁned as

fk(Θ) = X

i∈Bk

dipi(Θ),(7.6)

where each branch ﬂow piis an approximation calculated as a linear function of the

bus voltage angles based on the DC power ﬂow model from equation (3.29).

This extension adds to the OPF problem a set of nif doubly-bounded constraints

on these ﬂows.

Fmin

k≤fk(Θ) ≤Fmax

k∀k∈ If(7.7)

where Fmin

kand Fmax

kare the speciﬁed lower and upper bounds on the interface ﬂow,

and Ifis a the set indices of interfaces whose ﬂow limits are to be enforced.

The data for the problem is speciﬁed in an additional if ﬁeld in the Matpower

case struct mpc. This ﬁeld is itself a struct with two sub-ﬁelds, map and lims, used

for input data, and two others, Pand mu, used for output data. The format of this

data is described in detail in Tables 7-7 and 7-8.

Table 7-7: Input Data Structures for Interface Flow Limits

name description

mpc Matpower case struct

if additional ﬁeld in mpc containing input parameters for interface ﬂow limits

in the following sub-ﬁelds:

map (Pknk)×2 matrix deﬁning the interfaces, where nkis the number branches

that belong to interface k. The nkbranches of interface kare deﬁned by

nkrows in the matrix, where the ﬁrst column in each is equal to kand

the second is equal to the corresponding branch index imultiplied by di

to indicate the direction.

lims nif ×3 matrix of interface limits, where nif is the number of interface limits

to be enforced. The ﬁrst column is the index kof the interface, and the

second and third columns are Fmin

kand Fmax

k, the lower and upper limits

respectively, on the DC model ﬂow limits (in MW) for the interface.

40If di= 1, the deﬁnitions of the positive ﬂow direction for the branch and the interface are the

same. If di=−1, they are opposite.

Table 7-8: Output Data Structures for Interface Flow Limits

name description

results OPF results struct, superset of mpc with additional ﬁelds for output data

if additional ﬁeld in results containing output parameters for interface ﬂow

limits in the following sub-ﬁelds:

Pnif ×1 vector of actual ﬂow in MW across the corresponding interface (as

measured at the “from” end of associated branches)

mu.l nif ×1 vector of shadow prices on lower ﬂow limits (u/MW)†

mu.u nif ×1 vector of shadow prices on upper ﬂow limits (u/MW)†

†Here we assume the objective function has units u.

See help toggle iflims for more information. Examples of using this extension

and a case ﬁle deﬁning the necessary input data for it can be found in t opf userfcns

and t case30 userfcns, respectively. Note that, while this extension can be used for

AC OPF problems, the actual AC interface ﬂows will not necessarily be limited to the

speciﬁed values, since it is a DC ﬂow approximation that is used for the constraint.

Running a case that includes the interface ﬂow limits is as simple as loading the

case, turning on the extension and running it. Unlike with the reserves extension,

Matpower does not currently have a wrapper function to automate this.

mpc = loadcase('t_case30_userfcns');

mpc = toggle_iflims(mpc, 'on');

results = runopf(mpc);

7.6.3 DC Transmission Lines

Beginning with version 4.1, Matpower also includes a simple model for dispatchable

DC transmission lines. While the implementation is based on the extensible OPF

architecture described above, it can be used for simple power ﬂow problems as well,

in which the case the (OPF only) formulation callback is skipped.

A DC line in Matpower is modeled as two linked “dummy” generators, as shown

in Figures 7-2 and 7-3, one with negative capacity extracting real power from the

network at the “from” end of the line and another with positive capacity injecting

power into the network at the “to” end. These dummy generators are added by the

ext2int callback and removed by the int2ext callback. The real power ﬂow pfon

the DC line at the “from” end is deﬁned to be equal to the negative of the injection

of corresponding dummy generator. The ﬂow at the “to” end ptis deﬁned to be

equal to the injection of the corresponding generator.

100

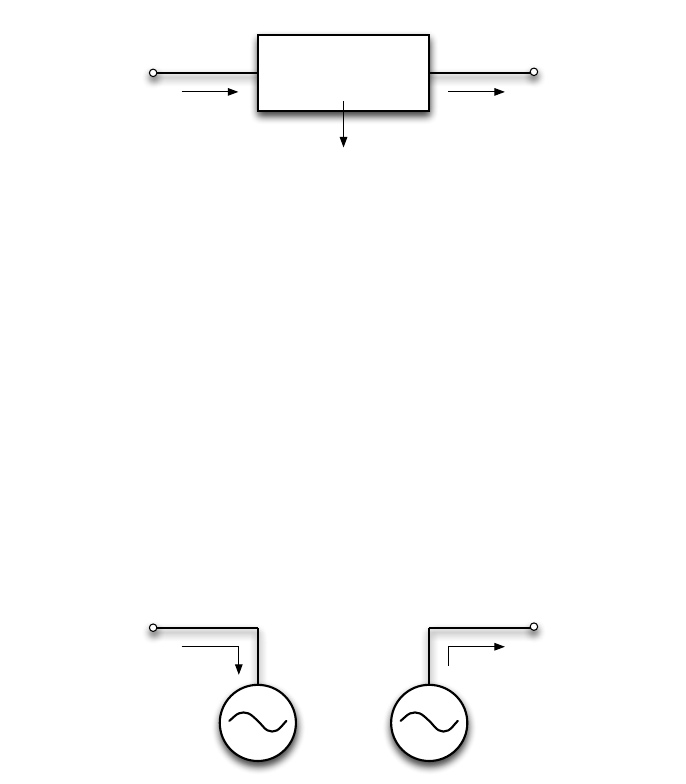
DC Line

“from”

bus

“to”

bus

ploss =l0+l1pf

Figure 7-2: DC Line Model

pt=(1−l1)pf−l0

“from”

bus

“to”

bus

Figure 7-3: Equivalent “Dummy” Generators

101

Matpower links the values of pfand ptusing the following relationship, which

includes a linear approximation of the real power loss in the line.

pt=pf−ploss

=pf−(l0+l1pf)

= (1 −l1)pf−l0(7.8)

Here the linear coeﬃcient l1is assumed to be a small (1) positive number. Ob-

viously, this is not applicable for bi-directional lines, where the ﬂow could go either

direction, resulting in decreasing losses for increasing ﬂow in the “to” →“from” di-

rection. There are currently two options for handling bi-directional lines. The ﬁrst

is to use a constant loss model by setting l1= 0. The second option is to create

two separate but identical lines oriented in opposite directions. In this case, it is

important that the lower limit on the ﬂow and the constant term of the loss model l0

be set to zero to ensure that only one of the two lines has non-zero ﬂow at a time.41

Upper and lower bounds on the value of the ﬂow can be speciﬁed for each DC

line, along with an optional operating cost. It is also assumed that the terminals of

the line have a range of reactive power capability that can be used to maintain a

voltage setpoint. Just as with a normal generator, the voltage setpoint is only used

for simple power ﬂow; the OPF dispatches the voltage anywhere between the lower

and upper bounds speciﬁed for the bus. Similarly, in a simple power ﬂow the input

value for pfand the corresponding value for pt, computed from (7.8), are used to

specify the ﬂow in the line.

Most of the data for DC lines is stored in a dcline ﬁeld in the Matpower

case struct mpc. This ﬁeld is a matrix similar to the branch matrix, where each

row corresponds to a particular DC line. The columns of the matrix are deﬁned in

Table B-5 and include connection bus indices, line status, ﬂows, terminal reactive

injections, voltage setpoints, limits on power ﬂow and VAr injections, and loss pa-

rameters. Also, similar to the branch or gen matrices, some of the columns are used

for input values, some for results, and some, such as PF can be either input or output,

depending on whether the problem is a simple power ﬂow or an optimal power ﬂow.

The idx dcline function deﬁnes a set of constants for use as named column indices

for the dcline matrix.

An optional dclinecost matrix, in the same form as gencost, can be used to

specify a cost to be applied to pfin the OPF. If the dclinecost ﬁeld is not present,

the cost is assumed to be zero.

41A future version may make the handling of this second option automatic.

102

Matpower’s DC line handling is implemented in toggle dcline and examples

of using it can be found in t dcline. The case ﬁle t case9 dcline includes some

example DC line data. See help toggle dcline for more information.

Running a case that includes DC lines is as simple as loading the case, turning

on the extension and running it. Unlike with the reserves extension, Matpower

does not currently have a wrapper function to automate this.

mpc = loadcase('t_case9_dcline');

mpc = toggle_dcline(mpc, 'on');

results = runopf(mpc);

7.6.4 OPF Soft Limits

Matpower includes an extension that replaces limits (such as branch ﬂow limits,

voltage magnitude bounds, generator limits, etc.) in an optimal power ﬂow with

soft limits, that is, limits that can be violated with some linear penalty cost. This

can be useful in identifying the cause of infeasibility in some optimal power ﬂow

problems. The extension is implemented in toggle softlims. A limited version for

branch ﬂow constraints in a DC model only, was introduced in Matpower 5.0, with

a generalization to all of the standard OPF limits added in Matpower 7.0. The soft

AC branch ﬂow limit implemention provides an example of user-deﬁned nonlinear

constraints.

In general, replacing a hard constraint of the form

hi(x)≤0 (7.9)

with a soft limit involves introducing a new non-negative variable sito represent the

violation of the original constraint. The original hard constraint (7.9) is replaced by

one in which this violation variable is used to “relax” the constraint by adding it to

the right-hand.

si≥0 (7.10)

hi(x)≤si.(7.11)

Finally, a penalty cost on violations is implemented via a linear cost coeﬃcient, ci

applied to each violation variable si, so that the additional user deﬁned cost term

from (6.47) for the set of soft limits looks like

fu(ˆx) = cv

Ts. (7.12)

103

Take, as an example, branch ﬂow limits. The ﬂow constraints in (6.9) and (6.10)

are rewritten by replacing the right hand side with a ﬂow violation variable si

rate a

rate a ≥0∀i(7.13)

f(Θ, Vm) = fi

f(Θ, Vm)−fi,max ≤si

rate a∀i(7.14)

t(Θ, Vm) = fi

t(Θ, Vm)−fi,max ≤si

rate a ∀i. (7.15)

In the case of AC ﬂow constraints, the ﬂow functions fi

fand fi

tare nonlinear and

can be either apparent power, active power, or current as shown in (6.11). In the case

of DC ﬂow constraints, where there are no losses, these ﬂows can be implemented in

terms of the ﬂow at the from end of the line and its negative, both linear functions

of the bus voltage angles, based on (6.30) and (6.31).

rate a ≥0∀i(7.16)

fΘ + pi

f,shift −pi,max

f≤si

rate a ∀i(7.17)

−Bi

fΘ−pi

f,shift −pi,max

f≤si

rate a ∀i. (7.18)

The feasible area for the DC case is illustrated in Figure 7-4.

rate a

−pi,max

fpi,max

−11

Figure 7-4: Feasible Region for Branch Flow Violation Constraints

Matpower implements soft limits for each of the types of constraints listed in

Table 7-9, where the formulation for each constraint type is shown.

The parameters for the problem are speciﬁed in an additional softlims ﬁeld in

the Matpower case struct mpc. This ﬁeld is itself a struct where each sub-ﬁeld

104

Table 7-9: Soft Limit Formulation

name hard-limit formulation soft-limit formulation

VMIN,VMAX†vi

m≥vi,min

m,vi

m≤vi,max

mvi

m+si

vmin ≥vi,min

m,vi

m−si

vmax ≤vi,max

RATE A‡fi

f(Θ, Vm)≤fi

max fi

f(Θ, Vm)−srate a ≤fi

max

fi

t(Θ, Vm)≤fi

max fi

t(Θ, Vm)−srate a ≤fi

max

PMIN,PMAX pi

g≥pi,min

g,pi

g≤pi,max

gpi

g+spmin ≥pi,min

g,pi

g−spmax ≤pi,max

QMIN,QMAX†qi

g≥qi,min

g,qi

g≤qi,max

gqi

g+sqmin ≥qi,min

g,qi

g−sqmax ≤qi,max

ANGMIN θi

f−θi

t≥∆θi,min θi

f−θi

t+sangmin ≥∆θi,min

ANGMAX θi

f−θi

t≤∆θi,max θi

f−θi

t−sangmax ≤∆θi,max

†Only applicable for the AC OPF.

‡Example of a user-deﬁned nonlinear constraint in the AC version.

corresponds to the name of one of the limits listed in Table 7-9. For each of the

limits, the input parameters are speciﬁed in the ﬁelds detailed in Table 7-10, with

defaults summarized in Table 7-11.

Depending on whether the original constraint in (7.10) is an upper bound or a

lower bound, it can be written as one of the following

hi(x) = (¯

hi(x)−hi,lim (upper bound)

hi,lim −¯

hi(x) (lower bound) (7.19)

where hi,lim is the actual value of the hard limit. When introducing a soft limit,

this original hard limit can be removed completely or modiﬁed to have a new value.

Matpower provides a several ways of modifying the original hard limit based on

ﬁelds hl mod (“hard limit modiﬁcation”) and hl val (“hard limit value”) in the re-

spective limit structures. This new hard limit is implemented via an upper bound on

the corresponding violation variable si. Table 7-12 summarizes the new hard limits

and the corresponding bounds on the violation variable as functions of the values of

hl mod and hl val.

Unspeciﬁed limits in the mpc.softlims input parameters are handled diﬀerently,

depending on the value of the Matpower option 'opf.softlims.default'(see Ta-

ble C-5).

•If the opf.softlims.default option is 1 (default), each limit not explicitly spec-

iﬁed, whether missing in mpc.softlims or present but empty, will be initialized

as in Table 7-11.

•If the opf.softlims.default option is 0, limits that are missing in mpc.softlims

are treated as though speciﬁed with hl mod ='none', that is, they are not

105

Table 7-10: Input Data Structures for OPF Soft Limits

name description

mpc Matpower case struct

softlims additional ﬁeld in mpc containing OPF soft limit input parameters for the pos-

sible limits, each of which is optional.*

<LIM> <LIM> refers to the name of the limit, i.e. one of the following: ANGMIN,ANGMAX,

RATE A,PMIN,PMAX,QMIN,QMAX,VMIN,VMAX. Each of these is a struct with input

parameters deﬁning the soft limits for this type of constraint in the following

optional ﬁelds (see Table 7-11 for defaults):

idx nsl ×1 vector of row indices for bus,branch or gen matrix, depending on <LIM>,

specifying the elements for which corresponding soft limits are to be applied†

busnum‡nsl ×1 vector of external bus numbers specifying the buses to which soft limits

are to be applied†

cost scalar or nsl ×1 vector cvof linear cost coeﬃcients for limit violation costs

hl mod§string indicating type of modiﬁcation to original hard limit:

'none'– do not add soft limit, no change to original hard limit

'remove'– add soft limit, relax hard limit by removing it completely

'replace'– add soft limit, relax hard limit by replacing original with value

speciﬁed in hl val

'scale'– add soft limit, relax hard limit by scaling original by value spec-

iﬁed in hl val

'shift'– add soft limit, relax hard limit by shifting original by value spec-

iﬁed in hl val

hl val§scalar or nsl ×1 vector value used to modify hard limit according to hl mod.

Ignored for 'none'and 'remove', required for 'replace', and optional, with

the following defaults, for 'scale'and 'shift':

'scale'– 2 for positive upper limits or negative lower limits, 0.5 otherwise

'shift'– 0.25 for VMAX and VMIN, 10 otherwise

*For ﬁelds not present, the value of the 'opf.softlims.defaults'option determines whether the corresponding

limit is unchanged (= 0) or converted (= 1, default) to a soft limit using default values from Table 7-11.

†For bus constraints, idx overrides busnum if both are provided.

‡Only applicable for bus constraints, i.e. <LIM> is VMIN or VMAX.

§Any new, relaxed hard limits are implemented via bounds on the violation variables. See Table 7-12 for details.

converted to soft limits at all. On the other hand, the default soft limits

of Table 7-11 are still applied to any limit that is present in mpc.softlims

but empty. For example, mpc.softlims.RATE A = struct() would result in the

default soft branch limits being applied.

Soft limit outputs, summarized in Table 7-13, include the amount and cost of

any overloads, that is, violations of the original hard limits. These can be found

as additional ﬁelds, overload and ov cost, under each limit in results.softlims.

The Kuhn-Tucker multipliers on the soft limit constraints are also included in the

106

Table 7-11: Default Soft Limit Values

name description

VMIN voltage magnitude lower bound

idx all buses

cost $100,000/p.u.†

hl mod 'replace'

hl val 0

VMAX voltage magnitude upper bound

idx all buses

cost $100,000/p.u.†

hl mod 'remove'

RATE A branch ﬂow limit

idx all on-line branches with bounded ﬂow limits

cost $1000/MVA, $1000/MW, or $1000/MA†depending on 'opf.flow lim'

hl mod 'remove'

PMIN generator active power lower bound

idx all on-line generators, excluding dispatchable loads

cost $1000/MW†

hl mod 'replace'

hl val 0 if Pi,min

g≥0, −∞ otherwise

PMAX,QMIN,QMAX generator active power upper bound, reactive power lower/upper bounds

idx all on-line generators, excluding dispatchable loads

cost $1000/MW or $1000/MVAr†

hl mod 'remove'

ANGMIN,ANGMAX branch angle diﬀerence lower/upper bounds

idx all on-line branches with angle diﬀerence limits, ∆θ, where |∆θ|<360◦

cost $1000/deg†

hl mod 'remove'

†Unless the maximum marginal cost at Pmax across all online generators, which we call cmax

g, exceeds

$1000/MWh, in which case the numerical value of the default cost is cmax

ginstead of 1000 (or 100 ·cmax

instead of 100,000, for VMIN or VMAX).

Table 7-12: Possible Hard-Limit Modiﬁcations

h mod new hard limit hi,lim

new upper bound on violation variable si

'remove'±∞†∞

'replace'hl val hl val −hi,lim

orig 

'scale'hl val ·hi,lim

orig (hl val −1) ·hi,lim

orig 

'shift'hi,lim

orig ±hl val†hl val

†Plus sign for upper bounds and minus sign for lower bounds.

107

usual columns of the corresponding matrix in the results, e.g. bus(:, MU VMAX),

branch(:, MU SF), etc. When there are no violations, these shadow prices are the

same as if hard limits were imposed. When there is a violation, they are equal to the

cost cvassociated with the violation variable, except in the case where a modiﬁed

hard limit is also binding, in which case it also reﬂects the shadow price on this

modiﬁed hard constraint.

Table 7-13: Output Data Structures for OPF Soft Limits

name description

results Matpower case struct

softlims additional ﬁeld in results containing OPF soft limit outputs for

each limit type

<LIM> <LIM> refers to the name of the limit, i.e. one of the following:

ANGMIN,ANGMAX,RATE A,PMIN,PMAX,QMIN,QMAX,VMIN,VMAX. Each

of these is a struct with the following output ﬁelds:

overload†nb/l/g ×1 vector of overload quantities for this limit (amount of

original hard limit violation)

ov cost†nb/l/g ×1 vector of overload penalty costs for this limit

branch(:, MU ANGMIN) Kuhn-Tucker multipliers on angle diﬀerence lower bounds‡

branch(:, MU ANGMAX) Kuhn-Tucker multipliers on angle diﬀerence upper bounds‡

branch(:, MU SF) Kuhn-Tucker multipliers on branch ﬂow limits (from end)‡

branch(:, MU ST) Kuhn-Tucker multipliers on branch ﬂow limits (to end)‡

gen(:, MU PMIN) Kuhn-Tucker multipliers on active gen lower bounds‡

gen(:, MU PMAX) Kuhn-Tucker multipliers on active gen upper bounds‡

gen(:, MU QMIN) Kuhn-Tucker multipliers on reactive gen lower bounds‡

gen(:, MU QMAX) Kuhn-Tucker multipliers on reactive gen upper bounds‡

bus(:, MU VMIN) Kuhn-Tucker multipliers on voltage magnitude lower bounds‡

bus(:, MU VMAX) Kuhn-Tucker multipliers on voltage magnitude upper bounds‡

†The dimensions of overload and ov cost correspond to all buses, branches or generators (depending on <LIM>),

not just those whose limits were converted to soft limits. Entries corresponding to those not included (implicitly

or explicitly) in idx are set to zero.

†For limits that have been converted to soft limits, these are the shadow prices on the soft limit constraints. When

there is no violation of the soft limit, this shadow price is the same as it would be for the original hard limit.

When there is a violation, it is equal to the corresponding user-supplied violation cost ci

v, unless an updated

hard constraint is also binding.

108

See help toggle softlims for more information on this extension. Examples of

using this extension can be found in t opf softlims. Running a case that includes

the default soft limits is as simple as loading the case, turning on the extension and

running it. Unlike with the reserves extension, Matpower does not currently have

a wrapper function to automate this.

mpc = loadcase('case2383wp');

mpc = toggle_softlims(mpc, 'on');

results = runopf(mpc, mpopt);

109

8 Unit De-commitment Algorithm

The standard OPF formulation described in the previous section has no mechanism

for completely shutting down generators which are very expensive to operate. Instead

they are simply dispatched at their minimum generation limits. Matpower includes

the capability to run an optimal power ﬂow combined with a unit de-commitment

for a single time period, which allows it to shut down these expensive units and ﬁnd

a least cost commitment and dispatch. To run this for case30, for example, type:

>> runuopf('case30')

By default, runuopf is based on the AC optimal power ﬂow problem. To run a DC

OPF, the model option must be set to 'DC'. For convenience, Matpower provides

a function runduopf which is simply a wrapper that sets the model option to 'DC'

before calling runuopf.

Matpower uses an algorithm similar to dynamic programming to handle the

de-commitment. It proceeds through a sequence of stages, where stage Nhas N

generators shut down, starting with N= 0, as follows:

Step 1: Begin at stage zero (N= 0), assuming all generators are on-line with all

limits in place.

Step 2: If the sum of the minimum generation limits for all on-line generators is less

than the total system demand, then go to Step 3. Otherwise, go to the next

stage, N=N+ 1, shut down the generator whose average per-MW cost of

operating at its minimum generation limit is greatest and repeat Step 2.

Step 3: Solve a normal OPF. Save the solution as the current best.

Step 4: Go to the next stage, N=N+ 1. Using the best solution from the previous

stage as the base case for this stage, form a candidate list of generators

with minimum generation limits binding. If there are no candidates, skip

to Step 6.

Step 5: For each generator on the candidate list, solve an OPF to ﬁnd the total

system cost with this generator shut down. Replace the current best solu-

tion with this one if it has a lower cost. If any of the candidate solutions

produced an improvement, return to Step 4.

Step 6: Return the current best solution as the ﬁnal solution.

110

It should be noted that the method employed here is simply a heuristic. It does

not guarantee that the least cost commitment of generators will be found. It is also

rather computationally expensive for larger systems and was implemented as a simple

way to allow an OPF-based “smart-market”, such as described in Appendix F, the

option to reject expensive oﬀers while respecting the minimum generation limits on

generators.

111

9 Miscellaneous Matpower Functions

This section describes a number of additional Matpower functions that users may

ﬁnd useful. The descriptions here are simply brief summaries, so please use the

Matlab help function to get the full details on each function.

9.1 Input/Output Functions

9.1.1 loadcase

mpc = loadcase(casefile)

The loadcase function provides the canonical way of loading a Matpower case

from a ﬁle or struct. It takes as input either a struct or the name of an M-ﬁle or

MAT-ﬁle in the Matlab path (casefile) and returns a standard Matpower case

struct (mpc). It can also convert from the older version 1 case ﬁle format to the

current format. This function allows a case to be loaded, and potentially modiﬁed,

before calling one of the main simulation functions such as runpf or runopf.

9.1.2 savecase

savecase(fname, mpc)

savecase(fname, mpc, version)

savecase(fname, comment, mpc)

savecase(fname, comment, mpc, version)

fname = savecase(fname, ...)

The savecase function writes out a Matpower case ﬁle, given a name for the

ﬁle to be created or overwritten (fname), and a Matpower case struct (mpc). If

fname ends with '.mat'it saves the case as a MAT-ﬁle, otherwise it saves it as an

M-ﬁle. Optionally returns the ﬁlename, with extension added if necessary. The

optional comment argument is either string (single line comment) or a cell array of

strings which are inserted as comments in the help section of the ﬁle. If the optional

version argument is '1'it will modify the data matrices to version 1 format before

saving.

112

9.1.3 cdf2mpc

mpc = cdf2mpc(cdf_file_name)

mpc = cdf2mpc(cdf_file_name, verbose)

mpc = cdf2mpc(cdf_file_name, mpc_name)

mpc = cdf2mpc(cdf_file_name, mpc_name, verbose)

[mpc, warnings] = cdf2mpc(cdf_file_name, ...)

The cdf2mpc function converts an IEEE Common Data Format (CDF) data ﬁle

into a Matpower case struct. Given an optional ﬁle name mpc name, it can save the

converted case to a Matpower case ﬁle. Warnings generated during the conversion

process can be optionally returned in the warnings argument.

Since the IEEE CDF format does not contain all of the data needed to run an

optimal power ﬂow, some data, such as voltage limits, generator limits and generator

costs are created by cdf2mpc. See help cdf2mpc for details.

9.1.4 psse2mpc

mpc = psse2mpc(rawfile_name)

mpc = psse2mpc(rawfile_name, verbose)

mpc = psse2mpc(rawfile_name, verbose, rev)

mpc = psse2mpc(rawfile_name, mpc_name)

mpc = psse2mpc(rawfile_name, mpc_name, verbose)

mpc = psse2mpc(rawfile_name, mpc_name, verbose, rev)

[mpc, warnings] = psse2mpc(rawfile_name, ...)

The psse2mpc function converts a PSS/E RAW data ﬁle into a Matpower case

struct. Given an optional ﬁle name mpc name, it can save the converted case to a

Matpower case ﬁle. Warnings generated during the conversion process can be

optionally returned in the warnings argument. By default, psse2mpc attempts to

determine the revision of the PSS/E RAW ﬁle from the contents, but the user can

specify an explicit revision number to use in the optional rev argument.

113

9.1.5 save2psse

save2psse(fname, mpc)

fname_out = save2psse(fname, mpc)

The save2psse function saves a Matpower case struct mpc as a PSS/E RAW

ﬁle. The fname parameter is a string containing the name of the ﬁle to be created or

overwritten. If fname does not include a ﬁle extension, codeq.raw will be added. Op-

tionally returns the, possibly updated, ﬁlename. Currently exports to RAW format

Rev 33.

9.2 System Information

9.2.1 case info

case_info(mpc)

case_info(mpc, fd)

[groups, isolated] = case_info(mpc)

The case info function prints out detailed information about a Matpower case,

including connectivity information, summarizing the generation, load and other data

by interconnected island. It can optionally print the output to an open ﬁle, whose

ﬁle identiﬁer (as returned by fopen) is speciﬁed in the optional second parameter fd.

Optional return arguments include groups and isolated buses, as returned by the

find islands function.

9.2.2 compare case

compare_case(mpc1, mpc2)

Compares the bus,branch and gen matrices of two Matpower cases and prints

a summary of the diﬀerences. For each column of the matrix it prints the maximum

of any non-zero diﬀerences.

114

9.2.3 find islands

groups = find_islands(mpc)

[groups, isolated] = find_islands(mpc)

The find islands function returns the islands in a network. The return value

groups is a cell array of vectors of the bus indices for each island. The second and

optional return value isolated is a vector of indices of isolated buses that have no

connecting branches.

9.2.4 get losses

loss = get_losses(results)

loss = get_losses(baseMVA, bus, branch)

[loss, chg] = get_losses(results)

[loss, fchg, tchg] = get_losses(results)

[loss, fchg, tchg, dloss_dv] = get_losses(results)

[loss, fchg, tchg, dloss_dv, dchg_dvm] = get_losses(results)

The get losses function computes branch series losses, and optionally reactive

injections from line charging, as functions of bus voltages and branch parameters,

using the following formulae for a branch, as described in Section 3.2, connecting

bus fto bus t:

lossi=vf

τejθshift −vt2

rs−jxs

(9.1)

fchg =vf

τejθshift 

2bc

2(9.2)

tchg =|vt|2bc

2(9.3)

It can also optionally compute the partial derivatives of the line losses and reactive

charging injections with respect to voltage angles and magnitudes.

115

9.2.5 margcost

marginalcost = margcost(gencost, Pg)

The margcost function computes the marginal cost for generators given a matrix

in gencost format and a column vector or matrix of generation levels. The return

value has the same dimensions as Pg. Each row of gencost is used to evaluate the cost

at the output levels speciﬁed in the corresponding row of Pg. The rows of gencost

can specify either polynomial or piecewise linear costs and need not be uniform.

9.2.6 isload

TorF = isload(gen)

The isload function returns a column vector of 1’s and 0’s. The 1’s correspond

to rows of the gen matrix which represent dispatchable loads. The current test is

Pmin <0 and Pmax = 0.

9.2.7 loadshed

shed = loadshed(gen)

shed = loadshed(gen, ild)

The loadshed function returns a column vector of MW curtailments of dispatch-

able loads, computed as the diﬀerence between the PG and PMIN values in the corre-

sponding rows of the gen matrix. The optional ild argument is a column vector of

generator indices to the dispatchable loads of interest.

9.2.8 printpf

printpf(results, fd, mpopt)

The printpf function prints power ﬂow and optimal power ﬂow results, as re-

turned to fd, a ﬁle identiﬁer which defaults to STDOUT (the screen). The details of

what gets printed are controlled by an optional Matpower options struct mpopt.

116

9.2.9 total load

Pd = total_load(mpc)

Pd = total_load(mpc, load_zone, opt, mpopt)

Pd = total_load(bus)

Pd = total_load(bus, gen, load_zone, opt, mpopt)

[Pd, Qd] = total_load(...)

The total load function returns a vector of total load in each load zone. The

opt argument controls whether it includes ﬁxed loads, dispatchable loads or both,

and for dispatchable loads, whether to use the nominal or realized load values. The

load zone argument deﬁnes the load zones across which loads will be summed. It

uses the BUS AREA column (7) of the bus matrix by default. The string value 'all'can

be used to specify a single zone including the entire system. The reactive demands

are also optionally available as an output.

9.2.10 totcost

totalcost = totcost(gencost, Pg)

The totcost function computes the total cost for generators given a matrix in

gencost format and a column vector or matrix of generation levels. The return value

has the same dimensions as Pg. Each row of gencost is used to evaluate the cost at

the output levels speciﬁed in the corresponding row of Pg. The rows of gencost can

specify either polynomial or piecewise linear costs and need not be uniform.

9.3 Modifying a Case

9.3.1 extract islands

mpc_array = extract_islands(mpc)

mpc_array = extract_islands(mpc, groups)

mpc_k = extract_islands(mpc, k)

mpc_k = extract_islands(mpc, groups, k)

mpc_k = extract_islands(mpc, k, custom)

mpc_k = extract_islands(mpc, groups, k, custom)

The extract islands function extracts individual islands in a network that is not

fully connected. The original network is speciﬁed as a Matpower case struct (mpc)

and the result is returned as a cell array of case structs, or as a single case struct.

Supplying the optional group avoids the need to traverse the network again, saving

117

time on large systems. A ﬁnal optional argument custom is a struct that can be used

to indicate custom ﬁelds of mpc from which to extract data corresponding to buses

generators, branches or DC lines.

9.3.2 load2disp

mpc = load2disp(mpc0)

mpc = load2disp(mpc0, fname)

mpc = load2disp(mpc0, fname, idx)

mpc = load2disp(mpc0, fname, idx, voll)

The load2disp function takes a Matpower case mpc0, converts ﬁxed loads to

dispatchable loads, curtailable at a speciﬁc price, and returns the resulting case

struct mpc. It can optionally save the resulting case to a ﬁle (fname), convert loads

only at speciﬁc buses (idx), and set the value of lost load (voll) to be used as the

curtailment price (default is $5,000/MWh).

9.3.3 modcost

newgencost = modcost(gencost, alpha)

newgencost = modcost(gencost, alpha, modtype)

The modcost function can be used to modify generator cost functions by shifting

or scaling them, either horizontally or vertically. The alpha argument speciﬁes the

numerical value of the modiﬁcation, and modtype deﬁnes the type of modiﬁcation

as a string that takes one of the following values: 'SCALE F'(default), 'SCALE X',

'SHIFT F', or 'SHIFT X'.

9.3.4 scale load

mpc = scale_load(load, mpc)

mpc = scale_load(load, mpc, load_zone)

mpc = scale_load(load, mpc, load_zone, opt)

bus = scale_load(load, bus)

[bus, gen] = scale_load(load, bus, gen, load_zone, opt)

[bus, gen, gencost] = ...

scale_load(load, bus, gen, load_zone, opt, gencost)

The scale load function is used to scale active (and optionally reactive) loads in

each zone by a zone-speciﬁc ratio, i.e. R(k) for zone k. The amount of scaling for

118

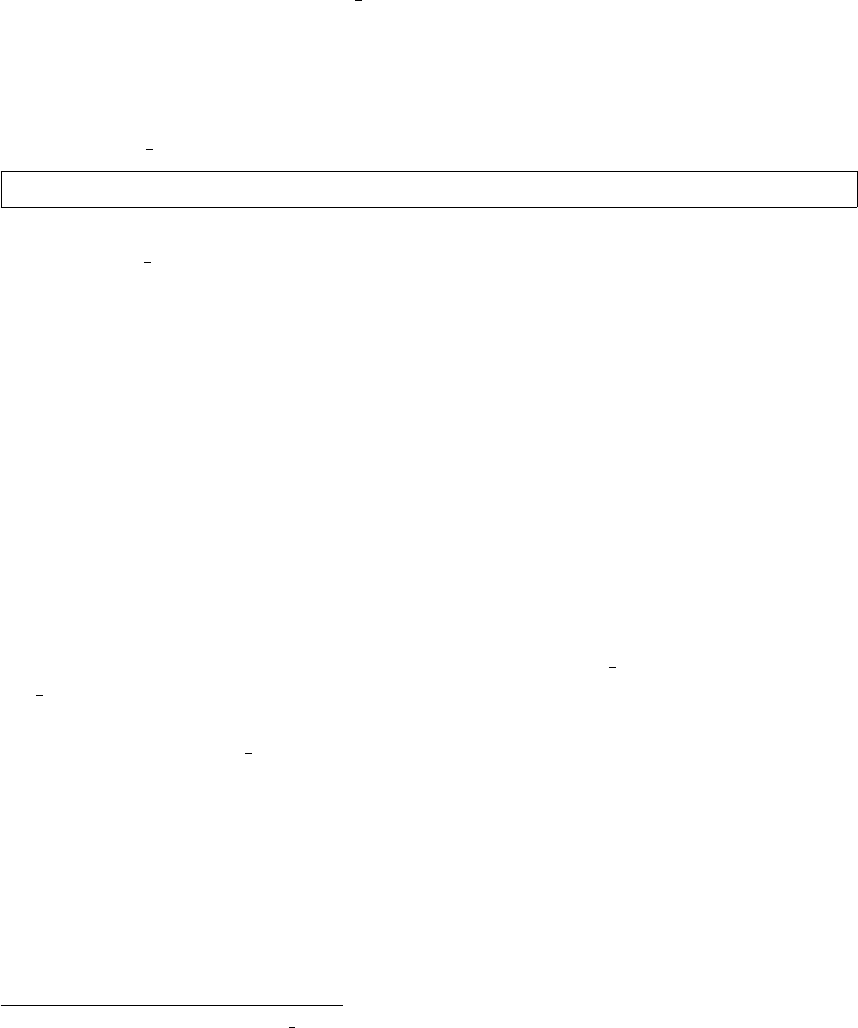
each zone, either as a direct scale factor or as a target quantity, is speciﬁed in load.

The load zones are deﬁned by load zone, and opt speciﬁes the type of scaling (factor

or target quantity) and which loads are aﬀected (active, reactive or both and ﬁxed,

dispatchable or both). The costs (gencost) associated with dispatchable loads can

also be optionally scaled with the loads.

9.3.5 apply changes

mpc_modified = apply_changes(label, mpc_original, chgtab)

The apply changes function implements a general mechanism to apply a set of

changes to a base Matpower case. This can be used, for example, to deﬁne and

apply a set of contingencies. There are three basic types of changes, those that

replace old values with new ones, those that scale old values by some factor, and

those that add a constant to existing values.

The change table matrix, chgtab, speciﬁes modiﬁcations to be applied to an

existing case. These modiﬁcations are grouped into sets, designated change sets,

that are always applied as a group. A change set consists of one or more changes,

each speciﬁed in a separate row in the chgtab, where the rows share a common label

(integer ID).

For example, ncchange sets can be used to deﬁne nccontingencies via a single

chgtab with many rows, but only ncunique labels. The chgtab also optionally speci-

ﬁes a probability πkof occurance associated with change set k. Table 9-1 summarizes

the meaning of the data in each column of chgtab. All of the names referenced in

Tables 9-1 through 9-4 are deﬁned as constants by the idx ct function. Type help

idx ct at the Matlab prompt for more details. Use of the named constants when

constructing a chgtab matrix is encouraged to improve readability.

The value in the CT TABLE column of chgtab deﬁnes which data table is to be

modiﬁed and the options are given in Table 9-2. With the exception of load and cer-

tain generator cost changes, each individual change record speciﬁes modiﬁcation(s)

to a single column of a particular data matrix, either bus,gen,branch or gencost.

Some are changes to that column for an individual row in the matrix (or all rows, if

the row index is set to 0), while others are area-wide changes that modify all rows

corresponding to the speciﬁed area.42

Load changes are special and may modify multiple columns of the bus and/or gen

tables. They oﬀer a more ﬂexible and convenient means of specifying modiﬁcations

42Areas are deﬁned by the BUS AREA column of the bus matrix.

119

Table 9-1: Columns of chgtab

name column description

CT LABEL 1 change set label, unique for each change set (integer)

CT PROB 2 change set probability (number between 0 and 1)†

CT TABLE 3 type of table to be modiﬁed (see Table 9-2 for possible values)

CT ROW 4 row index of data to be modiﬁed, 0 means all rows,

for area-wide changes this is the area index, rather than row index

CT COL 5 column index of data to be modiﬁed (see Table 9-4 for exceptions)

CT CHGTYPE 6 type of change, e.g. replace, scale or add (see Table 9-3 for details)

CT NEWVAL 7 new value used to replace or modify existing data

†The change set probability πkis taken from this column of the ﬁrst row for change set k.

to loads (ﬁxed, dispatchable, real and/or reactive) than directly including individ-

ual change speciﬁcations for each of the corresponding entries in the bus and gen

matrices. The row indices for load changes refer to bus numbers.

In addition to the normal direct modiﬁcations for generator cost parameters,

there is also the option to scale or shift an entire cost function, either vertically or

horizontally. This is often more convenient than manipulating the individual cost

parameters directly, especially when dealing with a mix of polynomial and piecewise

linear generator costs.

Table 9-2: Values for CT TABLE Column

name value description

CT TBUS 1bus table

CT TGEN 2gen table

CT TBRCH 3branch table

CT TAREABUS 4 area-wide change in bus table

CT TAREAGEN 5 area-wide change in gen table

CT TAREABRCH 6 area-wide change in branch table

CT TLOAD 7 per bus load change†

CT TAREALOAD 8 area-wide load change†

CT TGENCOST 9gencost table

CT TAREAGENCOST 10 area-wide change in gencost table

†Preferred method of modifying load, as opposed to manipulating bus and

gen tables directly.

Normally, the CT COL column contains the column index of the entry or entries in

the data tables to be modiﬁed. And the CT CHGTYPE and CT NEWVAL columns specify,

respectively, the type of change (replacement, scaling or adding) and the correspond-

120

ing replacement value, scale factor or constant to add, as shown in Table 9-3.

Table 9-3: Values for CT CHGTYPE Column

name value description

CT REP 1 replace old value by new one in CT NEWVAL column

CT REL 2 scale old value by factor in CT NEWVAL column

CT ADD 3 add value in CT NEWVAL column to old value

For load changes, the CT COL column is not a column index, but rather a code that

deﬁnes which loads at the speciﬁed bus(es) are to be modiﬁed, with the ability to

select ﬁxed loads only, dispatchable loads only or both, and for each whether or not

to include the reactive load in the change. Similarly, the CT COL column for generator

cost modiﬁcations can be set to a special code to indicate a scaling or shifting of the

entire corresponding cost function(s). The various options for the CT COL column are

summarized in Table 9-4.

Table 9-4: Values for CT COL Column

name value description

for CT TABLE column = CT TLOAD or CT TAREALOAD

CT LOAD ALL PQ 1 modify all (ﬁxed & dispatchable) loads, active and reactive

CT LOAD FIX PQ 2 modify ﬁxed loads, active and reactive

CT LOAD DIS PQ 3 modify dispatchable loads, active and reactive

CT LOAD ALL P 4 modify all (ﬁxed & dispatchable) loads, active power only

CT LOAD FIX P 5 modify ﬁxed loads, active power only

CT LOAD DIS P 6 modify dispatchable loads, active power only

for CT TABLE column = CT TGENCOST or CT TAREAGENCOST

CT MODCOST F -1 scales or shifts the cost function vertically†

CT MODCOST X -2 scales or shifts the cost function horizontally†

otherwise‡

nindex of column in data matrix to be modiﬁed

†Use CT CHGTYPE column = CT REL to scale the cost and CT ADD to shift the cost.

‡Can also be used for CT TGENCOST or CT TAREAGENCOST in addition to the special codes above.

121

For example, setting up a chgtab matrix for the following four scenarios could be

done as shown below.

1. Turn oﬀ generator 2 (10% probability).

2. Reduce the line rating of all lines to 95% of their nominal values (0.2% proba-

bility).

3. Scale all loads in area 2 (real & reactive, ﬁxed & dispatchable) up by 10%

(0.1% probability).

4. Decrease capacity of generator 3 and shift its cost function to the left both by

10 MW (5% probability).

chgtab = [ ...

1 0.1 CT_TGEN 2 GEN_STATUS CT_REP 0;

2 0.002 CT_TBRCH 0 RATE_A CT_REL 0.95;

3 0.001 CT_TAREALOAD 2 CT_LOAD_ALL_PQ CT_REL 1.1;

4 0.05 CT_TGEN 3 PMAX CT_ADD -10;

4 0.05 CT_TGENCOST 3 CT_MODCOST_X CT_ADD -10;

];

A change table can be used to easily create modiﬁed cases from an existing base

case with the apply changes function. Given the chgtab from the example above, a

new case with all lines derated by 5% can easily be created from an existing case mpc

with the following line of code.

mpc_new = apply_changes(2, mpc, chgtab);

9.3.6 savechgtab

savechgtab(fname, chgtab)

savechgtab(fname, chgtab, warnings)

fname = savechgtab(fname, ...)

This function can be used to save a change table matrix, chgtab, to a ﬁle speciﬁed

by fname. If the fname string ends with '.mat'it saves chgtab and warnings to a

MAT-ﬁle as the variables chgtab and warnings, respectively. Otherwise, it saves an

M-ﬁle function that returns the chgtab, with the optional warnings included in the

comments, where warnings is a cell array of warning messages such as those returned

by pssecon2chgtab.

122

9.4 Conversion between External and Internal Numbering

9.4.1 ext2int,int2ext

mpc_int = ext2int(mpc_ext)

mpc_int = ext2int(mpc_ext, mpopt)

mpc_ext = int2ext(mpc_int)

mpc_ext = int2ext(mpc_int, mpopt)

These functions convert a Matpower case struct from external to internal, and

from internal to external numbering, respectively. ext2int ﬁrst removes all isolated

buses, oﬀ-line generators and branches, and any generators or branches connected

to isolated buses. Then the buses are renumbered consecutively, beginning at 1,

and the generators are sorted by increasing bus number. Any 'ext2int'callback

routines registered in the case are also invoked automatically. All of the related

indexing information and the original data matrices are stored in an 'order'ﬁeld

in the struct to be used later by codeint2ext to perform the reverse conversions. If

the case is already using internal numbering it is returned unchanged. The optional

Matpower options struct (mpopt) input argument is only needed in conjunction

with callback routines that depend on it, e.g. when toggle softlims is on.

9.4.2 e2i data,i2e data

val = e2i_data(mpc, val, ordering)

val = e2i_data(mpc, val, ordering, dim)

val = i2e_data(mpc, val, oldval, ordering)

val = i2e_data(mpc, val, oldval, ordering, dim)

These functions can be used to convert other data structures from external to

internal indexing and vice versa. When given a case struct (mpc) that has already

been converted to internal indexing, e2i data can be used to convert other data

structures as well by passing in 2 or 3 extra parameters in addition to the case

struct. If the value passed in the second argument (val) is a column vector or cell

array, it will be converted according to the ordering speciﬁed by the third argument

(described below). If val is an n-dimensional matrix or cell array, then the optional

fourth argument (dim, default = 1) can be used to specify which dimension to reorder.

The return value in this case is the value passed in, converted to internal indexing.

The third argument, ordering, is used to indicate whether the data corresponds

to bus-, gen- or branch-ordered data. It can be one of the following three strings:

'bus','gen'or 'branch'. For data structures with multiple blocks of data, ordered

123

by bus, gen or branch, they can be converted with a single call by specifying ordering

as a cell array of strings.

Any extra elements, rows, columns, etc. beyond those indicated in ordering, are

not disturbed.

The function i2e data performs the opposite conversion, from internal back to

external indexing. It also assumes that mpc is using internal indexing, and the only

diﬀerence is that it also includes an oldval argument used to initialize the return

value before converting val to external indexing. In particular, any data correspond-

ing to oﬀ-line gens or branches or isolated buses or any connected gens or branches

will be taken from oldval, with val supplying the rest of the returned data.

9.4.3 e2i field,i2e field

mpc = e2i_field(mpc, field, ordering)

mpc = e2i_field(mpc, field, ordering, dim)

mpc = i2e_field(mpc, field, ordering)

mpc = i2e_field(mpc, field, ordering, dim)

These functions can be used to convert additional ﬁelds in mpc from external to

internal indexing and vice versa. When given a case struct that has already been

converted to internal indexing, e2i field can be used to convert other ﬁelds as well

by passing in 2 or 3 extra parameters in addition to the case struct.

The second argument (field) is a string or cell array of strings, specifying a

ﬁeld in the case struct whose value should be converted by a corresponding call to

e2i data. The ﬁeld can contain either a numeric or a cell array. The converted value

is stored back in the speciﬁed ﬁeld, the original value is saved for later use and the

updated case struct is returned. If field is a cell array of strings, they specify nested

ﬁelds.

The third and optional fourth arguments (ordering and dim) are simply passed

along to the call to e2i data.

Similarly, i2e field performs the opposite conversion, from internal back to ex-

ternal indexing. It also assumes that mpc is using internal indexing and utilizes the

original data stored by e2i field, calling i2e data to do the conversion work.

124

9.5 Forming Standard Power Systems Matrices

9.5.1 makeB

[Bp, Bpp] = makeB(mpc, alg)

[Bp, Bpp] = makeB(baseMVA, bus, branch, alg)

The makeB function builds the two matrices B0and B00 used in the fast-decoupled

power ﬂow. The alg, which can take values 'FDXB'or 'FDBX', determines whether the

matrices returned correspond to the XB or BX version of the fast-decoupled power

ﬂow. Bus numbers must be consecutive beginning at 1 (i.e. internal ordering).

9.5.2 makeBdc

[Bbus, Bf, Pbusinj, Pfinj] = makeBdc(mpc)

[Bbus, Bf, Pbusinj, Pfinj] = makeBdc(baseMVA, bus, branch)

The function builds the Bmatrices, Bdc (Bbus) and Bf(Bf), and phase shift in-

jections, Pdc (Pbusinj) and Pf,shift (Pfinj), for the DC power ﬂow model as described

in (3.29) and (4.7). Bus numbers must be consecutive beginning at 1 (i.e. internal

ordering).

9.5.3 makeJac

J = makeJac(mpc)

J = makeJac(mpc, fullJac)

[J, Ybus, Yf, Yt] = makejac(mpc)

The makeJac function forms the power ﬂow Jacobian and, optionally, the system

admittance matrices. Bus numbers in the input case must be consecutive beginning

at 1 (i.e. internal indexing). If the fullJac argument is present and true, it returns

the full Jacobian (sensitivities of all bus injections with respect to all voltage angles

and magnitudes) as opposed to the reduced version used in the Newton power ﬂow

updates.

125

9.5.4 makeLODF

PTDF = makePTDF(mpc)

LODF = makeLODF(mpc.branch, PTDF)

The makeLODF function forms the DC line outage distribution factor matrix for

a given PTDF. The matrix is nbr ×nbr, where nbr is the number of branches. See

Section 4.5 on Linear Shift Factors for more details.

9.5.5 makePTDF

H = makePTDF(mpc)

H = makePTDF(mpc, slack)

H = makePTDF(baseMVA, bus, branch)

H = makePTDF(baseMVA, bus, branch, slack)

The makePTDF function returns the DC PTDF matrix for a given choice of slack.

The matrix is nbr ×nb, where nbr is the number of branches and nbis the number

of buses. The slack can be a scalar (single slack bus) or an nb×1 column vector of

weights specifying the proportion of the slack taken up at each bus. If the slack is

not speciﬁed, the reference bus is used by default. Bus numbers must be consecutive

beginning at 1 (i.e. internal ordering). See Section 4.5 on Linear Shift Factors for

more details.

9.5.6 makeYbus

[Ybus, Yf, Yt] = makeYbus(mpc)

[Ybus, Yf, Yt] = makeYbus(baseMVA, bus, branch)

The makeYbus function builds the bus admittance matrix and branch admittance

matrices from (3.11)–(3.13). Bus numbers in the input case must be consecutive

beginning at 1 (i.e. internal indexing).

126

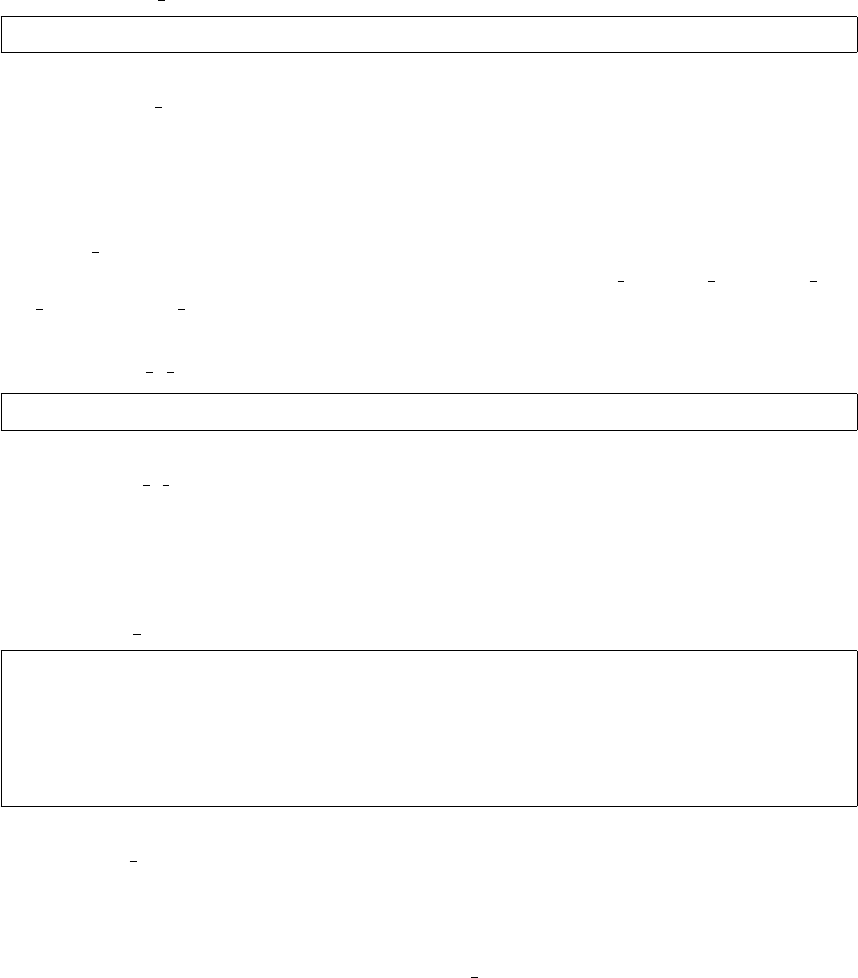
9.6 Miscellaneous

9.6.1 define constants

define_constants

The define constants script is a convenience script that deﬁnes a set of useful

constants, mostly to be used as named column indices into the bus,branch,gen

and gencost data matrices. The purpose is to avoid having to remember column

numbers and to allow code to be more robust against potential future changes to the

Matpower case data format. It also deﬁnes constants for the change tables used

by apply changes.

Speciﬁcally, it includes all of the constants deﬁned by idx bus,idx brch,idx gen,

idx cost and idx ct.

9.6.2 feval w path

[y1, ..., yn] = feval_w_path(fpath, f, x1, ..., xn)

The feval w path function is identical to Matlab’s own feval, except that the

function fneed not be in the Matlab path if it is deﬁned in a ﬁle in the path

speciﬁed by fpath. Assumes that the current working directory is always ﬁrst in the

Matlab path.

9.6.3 have fcn

TorF = have_fcn(tag)

TorF = have_fcn(tag, toggle)

ver_str = have_fcn(tag, 'vstr')

ver_num = have_fcn(tag, 'vnum')

rdate = have_fcn(tag, 'date')

info = have_fcn(tag, 'all')

The have fcn function provides a uniﬁed mechanism for testing for optional func-

tionality, such as the presence of certain solvers, or to detect whether the code is

running under Matlab or Octave. Since its results are cached they allow for a very

quick way to check frequently for functionality that may initially be a bit more costly

to determine. For installed functionality, have fcn also determines the installed ver-

sion and release date, if possible. The optional second argument, when it is a string,

deﬁnes which value is returned, as follows:

127

•empty – 1 if optional functionality is available, 0 if not available

•'vstr'– version number as a string (e.g. '3.11.4')

•'vnum'– version number as numeric value (e.g. 3.011004)

•'date'– release date as a string (e.g. '20-Jan-2015')

•'all'– struct with ﬁelds named av (for “availability”), vstr,vnum and date,

and values corresponding to each of the above, respectively.

Alternatively, the optional functionality speciﬁed by tag can be toggled OFF or

ON by calling have fcn with a numeric second argument toggle with one of the

following values:

•0 – turn OFF the optional functionality

•1 – turn ON the optional functionality (if available)

•−1 – toggle the ON/OFF state of the optional functionality

9.6.4 mpopt2qpopt

qpopt = mpopt2qpopt(mpopt)

qpopt = mpopt2qpopt(mpopt, model)

qpopt = mpopt2qpopt(mpopt, model, alg)

The mpopt2qpopt function returns an options struct suitable for qps matpower,

miqps matpower or one of the solver speciﬁc equivalents. It is constructed from the

relevant portions of mpopt, a Matpower options struct. The model argument spec-

iﬁes whether the problem to be solved is an LP, QP, MILP or MIQP problem to

allow for the selection of a suitable default solver. The ﬁnal alg argument allows

the solver to be set explicitly (in qpopt.alg). By default this value is taken from

mpopt.opf.dc.solver.

When the solver is set to 'DEFAULT', this function also selects the best available

solver that is applicable43 to the speciﬁc problem class, based on the following prece-

dence: Gurobi, CPLEX, MOSEK, Optimization Toolbox, GLPK, BPMPD, MIPS.

43GLPK is not available for problems with quadratic costs (QP and MIQP), BPMPD and MIPS

are not available for mixed integer problems (MILP and MIQP), and the Optimization Toolbox is

not an option for problems that combine the two (MIQP).

128

9.6.5 mpver

mpver

v = mpver

v = mpver('all')

The mpver function returns the current Matpower version number. With the

optional 'all'argument, it returns a struct with the ﬁelds 'Name','Version',

'Release'and 'Date'(all strings). Calling mpver without assigning the return value

prints the version and release date of the current installation of Matpower,Mat-

lab (or Octave), the Optimization Toolbox, MIPS and any optional Matpower

packages.

9.6.6 nested struct copy

ds = nested_struct_copy(d, s)

ds = nested_struct_copy(d, s, opt)

The nested struct copy function copies values from a source struct sto a desti-

nation struct din a nested, recursive manner. That is, the value of each ﬁeld in s

is copied directly to the corresponding ﬁeld in d, unless that value is itself a struct,

in which case the copy is done via a recursive call to nested struct copy. Certain

aspects of the copy behavior can be controled via the optional options struct opt,

including the possible checking of valid ﬁeld names.

129

10 Acknowledgments

The authors would like to acknowledge contributions from others who have helped

make Matpower what it is today. First we would like to acknowledge the input

and support of Bob Thomas throughout the development of Matpower. Thanks to

Chris DeMarco, one of our PSerc associates at the University of Wisconsin, for the

technique for building the Jacobian matrix. Our appreciation to Bruce Wollenberg

for all of his suggestions for improvements to version 1. The enhanced output func-

tionality in version 2.0 is primarily due to his input. Thanks also to Andrew Ward

for code which helped us verify and test the ability of the OPF to optimize reactive

power costs. Thanks to Alberto Borghetti for contributing code for the Gauss-Seidel

power ﬂow solver and to Mu Lin for contributions related to power ﬂow reactive

power limits. Real power line limits were suggested by Pan Wei. Thanks to Roman

Korab for data for the Polish system. Some state estimation code was contributed

by James S. Thorp and Rui Bo contributed additional code for state estimation and

continuation power ﬂow. Matpower was improved in various ways in response to

Doug Mitarotonda’s contributions and suggestions.

Thanks also to many others who have contributed code, testing time, bug reports

and suggestions over the years. And, last but not least, thanks to all of the many

users who, by using Matpower in their own work, have helped to extend the

contribution of Matpower to the ﬁeld of power systems far beyond what we could

do on our own.

130

Appendix A MIPS – Matpower Interior Point Solver

Beginning with version 4, Matpower includes a new primal-dual interior point

solver called MIPS, for Matpower Interior Point Solver. It is implemented in pure-

Matlab code, derived from the MEX implementation of the algorithms described

in [26,41].

This solver has application outside of Matpower to general nonlinear optimiza-

tion problems of the following form:

min

xf(x) (A.1)

subject to

g(x) = 0 (A.2)

h(x)≤0 (A.3)

l≤Ax ≤u(A.4)

xmin ≤x≤xmax (A.5)

where f:Rn→R,g:Rn→Rmand h:Rn→Rp.

The solver is implemented by the mips function, which can be called as follows,

[x, f, exitflag, output, lambda] = ...

mips(f_fcn, x0, A, l, u, xmin, xmax, gh_fcn, hess_fcn, opt);

where the input and output arguments are described in Tables A-1 and A-2, respec-

tively. Alternatively, the input arguments can be packaged as ﬁelds in a problem

struct and passed in as a single argument, where all ﬁelds except f fcn and x0 are

optional.

[x, f, exitflag, output, lambda] = mips(problem);

The calling syntax is nearly identical to that used by fmincon from Matlab’s

Optimization Toolbox. The primary diﬀerence is that the linear constraints are

speciﬁed in terms of a single doubly-bounded linear function (l≤Ax ≤u) as opposed

to separate equality constrained (Aeqx=beq) and upper bounded (Ax ≤b) functions.

Internally, equality constraints are handled explicitly and determined at run-time

based on the values of land u.

The user-deﬁned functions for evaluating the objective function, constraints and

Hessian are identical to those required by fmincon, with one exception described

131

Table A-1: Input Arguments for mips†

name description

f fcn Handle to a function that evaluates the objective function, its gradients and Hessian‡

for a given value of x. Calling syntax for this function:

[f, df, d2f] = f fcn(x)

x0 Starting value of optimization vector x.

A,l,uDeﬁne the optional linear constraints l≤Ax ≤u. Default values for the elements of

land uare -Inf and Inf, respectively.

xmin,xmax Optional lower and upper bounds on the xvariables, defaults are -Inf and Inf,

respectively.

gh fcn Handle to function that evaluates the optional nonlinear constraints and their gra-

dients for a given value of x. Calling syntax for this function is:

[h, g, dh, dg] = gh fcn(x)

hess fcn Handle to function that computes the Hessian‡of the Lagrangian for given values

of x,λand µ, where λand µare the multipliers on the equality and inequality

constraints, gand h, respectively. The calling syntax for this function is:

Lxx = hess fcn(x, lam, cost mult),

where λ=lam.eqnonlin,µ=lam.ineqnonlin and cost mult is a parameter used

to scale the objective function

opt Optional options structure with ﬁelds, all of which are also optional, described in

Table A-3.

problem Alternative, single argument input struct with ﬁelds corresponding to arguments

above.

†All inputs are optional except f fcn and x0.

‡If gh fcn is provided then hess fcn is also required. Speciﬁcally, if there are nonlinear constraints, the Hessian

information must provided by the hess fcn function and it need not be computed in f fcn.

below for the Hessian evaluation function. Speciﬁcally, f fcn should return fas the

scalar objective function value f(x), df as an n×1 vector equal to ∇fand, unless

gh fcn is provided and the Hessian is computed by hess fcn,d2f as an n×nmatrix

equal to the Hessian ∂2f

∂x2. Similarly, the constraint evaluation function gh fcn must

return the m×1 vector of nonlinear equality constraint violations g(x), the p×1

vector of nonlinear inequality constraint violations h(x) along with their gradients

in dg and dh. Here dg is an n×mmatrix whose jth column is ∇gjand dh is n×p,

with jth column equal to ∇hj. Finally, for cases with nonlinear constraints, hess fcn

returns the n×nHessian ∂2L

∂x2of the Lagrangian function

L(x, λ, µ, σ) = σf(x) + λTg(x) + µTh(x) (A.6)

for given values of the multipliers λand µ, where σis the cost mult scale factor for

the objective function. Unlike fmincon,mips passes this scale factor to the Hessian

evaluation function in the 3rd argument.

132

Table A-2: Output Arguments for mips

name description

xsolution vector

fﬁnal objective function value

exitflag exit ﬂag

1 – ﬁrst order optimality conditions satisﬁed

0 – maximum number of iterations reached

-1 – numerically failed

output output struct with ﬁelds

iterations number of iterations performed

hist struct array with trajectories of the following: feascond,

gradcond,compcond,costcond,gamma,stepsize,obj,alphap,

alphad

message exit message

lambda struct containing the Langrange and Kuhn-Tucker multipliers on the con-

straints, with ﬁelds:

eqnonlin nonlinear equality constraints

ineqnonlin nonlinear inequality constraints

mu l lower (left-hand) limit on linear constraints

mu u upper (right-hand) limit on linear constraints

lower lower bound on optimization variables

upper upper bound on optimization variables

The use of nargout in f fcn and gh fcn is recommended so that the gradients

and Hessian are only computed when required.

A.1 Example 1

The following code shows a simple example of using mips to solve a 2-dimensional

unconstrained optimization of Rosenbrock’s “banana” function44

f(x) = 100(x2−x2

1)2+ (1 −x1)2.(A.7)

First, create a Matlab function that will evaluate the objective function, its

gradients and Hessian, for a given value of x. In this case, the coeﬃcient of the ﬁrst

term is deﬁned as a paramter a.

44http://en.wikipedia.org/wiki/Rosenbrock_function

133

Table A-3: Options for mips†

name default description

opt.verbose 0 controls level of progress output displayed

0 – print no progress info

1 – print a little progress info

2 – print a lot of progress info

3 – print all progress info

opt.feastol 10−6termination tolerance for feasibility condition

opt.gradtol 10−6termination tolerance for gradient condition

opt.comptol 10−6termination tolerance for complementarity condition

opt.costtol 10−6termination tolerance for cost condition

opt.max it 150 maximum number of iterations

opt.step control 0 set to 1 to enable step-size control

opt.sc.red it 20 max number of step-size reductions if step-control is on

opt.cost mult 1 cost multiplier used to scale the objective function for improved

conditioning. Note: This value is also passed as the 3rd argu-

ment to the Hessian evaluation function so that it can appro-

priately scale the objective function term in the Hessian of the

Lagrangian.

opt.xi 0.99995 ξconstant used in αupdates in (A.46) and (A.47)

opt.sigma 0.1 centering parameter σused in γupdate in (A.52)

opt.z0 1 used to initialize elements of slack variable Z

opt.alpha min 10−8algorithm returns “Numerically Failed” if the αpor αdfrom

(A.46) and (A.47) become smaller than this value

opt.rho min 0.95 lower bound on ρtcorresponding to 1 −ηin Fig. 5 in [26]

opt.rho max 1.05 upper bound on ρtcorresponding to 1 + ηin Fig. 5 in [26]

opt.mu threshold 10−5Kuhn-Tucker multipliers smaller than this value for non-binding

constraints are forced to zero

opt.max stepsize 1010 algorithm returns “Numerically Failed” if the 2-norm of the New-

ton step ∆X

∆λfrom (A.45) exceeds this value

function [f, df, d2f] = banana(x, a)

f = a*(x(2)-x(1)^2)^2+(1-x(1))^2;

if nargout > 1 %% gradient is required

df = [ 4*a*(x(1)^3 - x(1)*x(2)) + 2*x(1)-2;

2*a*(x(2) - x(1)^2) ];

if nargout > 2 %% Hessian is required

d2f = 4*a*[ 3*x(1)^2 - x(2) + 1/(2*a), -x(1);

-x(1) 1/2 ];

end

134

Then, create a handle to the function, deﬁning the value of the paramter ato be

100, set up the starting value of x, and call the mips function to solve it.

>> f_fcn = @(x)banana(x, 100);

>> x0 = [-1.9; 2];

>> [x, f] = mips(f_fcn, x0)

x =

f =

A.2 Example 2

The second example45 solves the following 3-dimensional constrained optimization,

printing the details of the solver’s progress:

min

xf(x) = −x1x2−x2x3(A.8)

subject to

1−x2

2+x2

3−2≤0 (A.9)

1+x2

2+x2

3−10 ≤0.(A.10)

First, create a Matlab function to evaluate the objective function and its gra-

dients,46

45From http://en.wikipedia.org/wiki/Nonlinear_programming#3-dimensional_example.

46Since the problem has nonlinear constraints and the Hessian is provided by hess fcn, this

function will never be called with three output arguments, so the code to compute d2f is actually

not necessary.

135

function [f, df, d2f] = f2(x)

f = -x(1)*x(2) - x(2)*x(3);

if nargout > 1 %% gradient is required

df = -[x(2); x(1)+x(3); x(2)];

if nargout > 2 %% Hessian is required

d2f = -[0 1 0; 1 0 1; 0 1 0]; %% actually not used since

end %% 'hess_fcn' is provided

end

one to evaluate the constraints, in this case inequalities only, and their gradients,

function [h, g, dh, dg] = gh2(x)

h = [ 1 -1 1; 1 1 1] * x.^2 + [-2; -10];

dh = 2 * [x(1) x(1); -x(2) x(2); x(3) x(3)];

g = []; dg = [];

and another to evaluate the Hessian of the Lagrangian.

function Lxx = hess2(x, lam, cost_mult)

if nargin < 3, cost_mult = 1; end %% allows to be used with 'fmincon'

mu = lam.ineqnonlin;

Lxx = cost_mult * [0 -1 0; -1 0 -1; 0 -1 0] + ...

[2*[1 1]*mu 0 0; 0 2*[-1 1]*mu 0; 0 0 2*[1 1]*mu];

Then create a problem struct with handles to these functions, a starting value for x

and an option to print the solver’s progress. Finally, pass this struct to mips to solve

the problem and print some of the return values to get the output below.

function example2

problem = struct( ...

'f_fcn', @(x)f2(x), ...

'gh_fcn', @(x)gh2(x), ...

'hess_fcn', @(x, lam, cost_mult)hess2(x, lam, cost_mult), ...

'x0', [1; 1; 0], ...

'opt', struct('verbose', 2) ...

);

[x, f, exitflag, output, lambda] = mips(problem);

fprintf('\nf = %g exitflag = %d\n', f, exitflag);

fprintf('\nx = \n');

fprintf(' %g\n', x);

fprintf('\nlambda.ineqnonlin =\n');

fprintf(' %g\n', lambda.ineqnonlin);

136

>> example2

MATPOWER Interior Point Solver -- MIPS, Version 1.3, 30-Oct-2018

(using built-in linear solver)

it objective step size feascond gradcond compcond costcond

---- ------------ --------- ------------ ------------ ------------ ------------

0 -1 0 1.5 5 0

1 -5.3250167 1.6875 0 0.894235 0.850653 2.16251

2 -7.4708991 0.97413 0.129183 0.00936418 0.117278 0.339269

3 -7.0553031 0.10406 0 0.00174933 0.0196518 0.0490616

4 -7.0686267 0.034574 0 0.00041301 0.0030084 0.00165402

5 -7.0706104 0.0065191 0 1.53531e-05 0.000337971 0.000245844

6 -7.0710134 0.00062152 0 1.22094e-07 3.41308e-05 4.99387e-05

7 -7.0710623 5.7217e-05 0 9.84879e-10 3.41587e-06 6.05875e-06

8 -7.0710673 5.6761e-06 0 9.73527e-12 3.41615e-07 6.15483e-07

Converged!

f = -7.07107 exitflag = 1

x =

1.58114

2.23607

1.58114

lambda.ineqnonlin =

0.707107

More example problems for mips can be found in t mips.m.

A.3 Quadratic Programming Solver

A convenience wrapper function called qps mips is provided to make it trivial to set

up and solve linear programming (LP) and quadratic programming (QP) problems

of the following form:

min

2xTHx +cTx(A.11)

subject to

l≤Ax ≤u(A.12)

xmin ≤x≤xmax.(A.13)

Instead of a function handle, the objective function is speciﬁed in terms of the

paramters Hand cof quadratic cost coeﬃcients. Internally, qps mips passes mips

137

the handle of a function that uses these paramters to evaluate the objective function,

gradients and Hessian.

The calling syntax for qps mips is similar to that used by quadprog from the

Matlab Optimization Toolbox.

[x, f, exitflag, output, lambda] = qps_mips(H, c, A, l, u, xmin, xmax, x0, opt);

Alternatively, the input arguments can be packaged as ﬁelds in a problem struct and

passed in as a single argument, where all ﬁelds except H,c,Aand lare optional.

[x, f, exitflag, output, lambda] = qps_mips(problem);

Aside from Hand c, all input and output arguments correspond exactly to the same

arguments for mips as described in Tables A-1 and A-2.

As with mips and fmincon, the primary diﬀerence between the calling syntax

for qps mips and quadprog is that the linear constraints are speciﬁed in terms of a

single doubly-bounded linear function (l≤Ax ≤u) as opposed to separate equality

constrained (Aeqx=beq) and upper bounded (Ax ≤b) functions.

Matpower also includes another wrapper function qps matpower that provides

a consistent interface for all of the QP and LP solvers it has available. This interface

is identical to that used by qps mips with the exception of the structure of the opt

input argument. The solver is chosen according to the value of opt.alg. See the help

for qps matpower for details.

Several examples of using qps matpower to solve LP and QP problems can be

found in t qps matpower.m.

A.4 Primal-Dual Interior Point Algorithm

This section provides some details on the primal-dual interior point algorithm used

by MIPS and described in [26,41].

A.4.1 Notation

For a scalar function f:Rn→Rof a real vector X=x1x2··· xnT, we use

the following notation for the ﬁrst derivatives (transpose of the gradient):

fX=∂f

∂X =h∂f

∂x1

∂f

∂x2··· ∂f

∂xni.(A.14)

138

The matrix of second partial derivatives, the Hessian of f, is:

fXX =∂2f

∂X2=∂

∂X ∂f

∂X T

=





∂2f

∂x2

1··· ∂2f

∂x1∂xn

.....

∂2f

∂xn∂x1··· ∂2f

∂x2





.(A.15)

For a vector function F:Rn→Rmof a vector X, where

F(X) = f1(X)f2(X)··· fm(X)T(A.16)

the ﬁrst derivatives form the Jacobian matrix, where row iis the transpose of the

gradient of fi

FX=∂F

∂X =





∂f1

∂x1··· ∂f1

∂xn

.....

∂fm

∂x1··· ∂fm

∂xn





.(A.17)

In these derivations, the full 3-dimensional set of second partial derivatives of Fwill

not be computed. Instead a matrix of partial derivatives will be formed by computing

the Jacobian of the vector function obtained by multiplying the transpose of the

Jacobian of Fby a vector λ, using the following notation

FXX (λ) = ∂

∂X FX

Tλ.(A.18)

Please note also that [A] is used to denote a diagonal matrix with vector Aon

the diagonal and eis a vector of all ones.

A.4.2 Problem Formulation and Lagrangian

The primal-dual interior point method used by MIPS solves a problem of the form:

min

Xf(X) (A.19)

subject to

G(X) = 0 (A.20)

H(X)≤0 (A.21)

where the linear constraints and variable bounds from (A.4) and (A.5) have been

incorporated into G(X) and H(X). The approach taken involves converting the ni

139

inequality constraints into equality constraints using a barrier function and vector of

positive slack variables Z.

min

X"f(X)−γ

m=1

ln(Zm)#(A.22)

subject to

G(X) = 0 (A.23)

H(X) + Z= 0 (A.24)

Z > 0 (A.25)

As the parameter of perturbation γapproaches zero, the solution to this problem

approaches that of the original problem.

For a given value of γ, the Lagrangian for this equality constrained problem is

Lγ(X, Z, λ, µ) = f(X) + λTG(X) + µT(H(X) + Z)−γ

m=1

ln(Zm).(A.26)

Taking the partial derivatives with respect to each of the variables yields:

Lγ

X(X, Z, λ, µ) = fX+λTGX+µTHX(A.27)

Lγ

Z(X, Z, λ, µ) = µT−γeT[Z]−1(A.28)

Lγ

λ(X, Z, λ, µ) = GT(X) (A.29)

Lγ

µ(X, Z, λ, µ) = HT(X) + ZT.(A.30)

And the Hessian of the Lagrangian with respect to Xis given by

Lγ

XX (X, Z, λ, µ) = fXX +GXX (λ) + HXX (µ).(A.31)

A.4.3 First Order Optimality Conditions

The ﬁrst order optimality (Karush-Kuhn-Tucker) conditions for this problem are

satisﬁed when the partial derivatives of the Lagrangian above are all set to zero:

F(X, Z, λ, µ) = 0 (A.32)

Z > 0 (A.33)

µ > 0 (A.34)

140

where

F(X, Z, λ, µ) = 





Lγ

[µ]Z−γe

G(X)

H(X) + Z





=





T+GX

Tλ+HX

Tµ

[µ]Z−γe

G(X)

H(X) + Z





.(A.35)

A.4.4 Newton Step

The ﬁrst order optimality conditions are solved using Newton’s method. The Newton

update step can be written as follows:

FXFZFλFµ





∆X

∆Z

∆λ

∆µ





=−F(X, Z, λ, µ) (A.36)







Lγ

XX 0GX

THX

0 [µ] 0 [Z]

GX0 0 0

HXI0 0











∆X

∆Z

∆λ

∆µ





=−





Lγ

[µ]Z−γe

G(X)

H(X) + Z





.(A.37)

This set of equations can be simpliﬁed and reduced to a smaller set of equations

by solving explicitly for ∆µin terms of ∆Zand for ∆Zin terms of ∆X. Taking the

2nd row of (A.37) and solving for ∆µwe get

[µ] ∆Z+ [Z] ∆µ=−[µ]Z+γe

[Z] ∆µ=−[Z]µ+γe −[µ] ∆Z

∆µ=−µ+ [Z]−1(γe −[µ] ∆Z).(A.38)

Solving the 4th row of (A.37) for ∆Zyields

HX∆X+ ∆Z=−H(X)−Z

∆Z=−H(X)−Z−HX∆X. (A.39)

141

Then, substituting (A.38) and (A.39) into the 1st row of (A.37) results in

Lγ

XX ∆X+GX

T∆λ+HX

T∆µ=−Lγ

Lγ

XX ∆X+GX

T∆λ+HX

T(−µ+ [Z]−1(γe −[µ] ∆Z)) = −Lγ

Lγ

XX ∆X+GX

T∆λ

+HX

T(−µ+ [Z]−1(γe −[µ] (−H(X)−Z−HX∆X))) = −Lγ

Lγ

XX ∆X+GX

T∆λ−HX

Tµ+HX

T[Z]−1γe

+HX

T[Z]−1[µ]H(X) + HX

T[Z]−1[Z]µ+HX

T[Z]−1[µ]HX∆X=−Lγ

(Lγ

XX +HX

T[Z]−1[µ]HX)∆X+GX

T∆λ

+HX

T[Z]−1(γe + [µ]H(X)) = −Lγ

M∆X+GX

T∆λ=−N(A.40)

where

M≡ Lγ

XX +HX

T[Z]−1[µ]HX(A.41)

=fXX +GXX (λ) + HXX (µ) + HX

T[Z]−1[µ]HX(A.42)

and

N≡ Lγ

T+HX

T[Z]−1(γe + [µ]H(X)) (A.43)

=fX

T+GX

Tλ+HX

Tµ+HX

T[Z]−1(γe + [µ]H(X)).(A.44)

Combining (A.40) and the 3rd row of (A.37) results in a system of equations of

reduced size: M GX

GX0∆X

∆λ=−N

−G(X).(A.45)

The Newton update can then be computed in the following 3 steps:

1. Compute ∆Xand ∆λfrom (A.45).

2. Compute ∆Zfrom (A.39).

3. Compute ∆µfrom (A.38).

In order to maintain strict feasibility of the trial solution, the algorithm truncates

the Newton step by scaling the primal and dual variables by αpand αd, respectively,

142

where these scale factors are computed as follows:

αp= min ξmin

∆Zm<0−Zm

∆Zm,1(A.46)

αd= min ξmin

∆µm<0−µm

∆µm,1(A.47)

resulting in the variable updates below.

X←X+αp∆X(A.48)

Z←Z+αp∆Z(A.49)

λ←λ+αd∆λ(A.50)

µ←µ+αd∆µ(A.51)

The parameter ξis a constant scalar with a value slightly less than one. In MIPS,

ξis set to 0.99995.

In this method, during the Newton-like iterations, the perturbation parameter γ

must converge to zero in order to satisfy the ﬁrst order optimality conditions of the

original problem. MIPS uses the following rule to update γat each iteration, after

updating Zand µ:

γ←σZTµ

(A.52)

where σis a scalar constant between 0 and 1. In MIPS, σis set to 0.1.

143

Appendix B Data File Format

There are two versions of the Matpower case ﬁle format. Matpower versions 3.0.0

and earlier used the version 1 format internally. Subsequent versions of Matpower

have used the version 2 format described below, though version 1 ﬁles are still han-

dled, and converted automatically, by the loadcase and savecase functions.

In the version 2 format, the input data for Matpower are speciﬁed in a set of

data matrices packaged as the ﬁelds of a Matlab struct, referred to as a “Mat-

power case” struct and conventionally denoted by the variable mpc. This struct is

typically deﬁned in a case ﬁle, either a function M-ﬁle whose return value is the mpc

struct or a MAT-ﬁle that deﬁnes a variable named mpc when loaded. The ﬁelds of

this struct are baseMVA,bus,branch,gen and, optionally, gencost. The baseMVA ﬁeld

is a scalar and the rest are matrices. Each row in the data matrices corresponds to

a single bus, branch, or generator and the columns are similar to the columns in the

standard IEEE and PTI formats. The mpc struct also has a version ﬁeld whose value

is a string set to the current Matpower case version, currently '2'by default. The

version 1 case format deﬁnes the data matrices as individual variables rather than

ﬁelds of a struct, and some do not include all of the columns deﬁned in version 2.

Numerous examples can be found in the case ﬁles listed in Table D-18 in Ap-

pendix D. The case ﬁles created by savecase use a tab-delimited format for the data

matrices to make it simple to transfer data seamlessly back and forth between a text

editor and a spreadsheet via simple copy and paste.

The details of the Matpower case format are given in the tables below and

can also be accessed by typing help caseformat at the Matlab prompt. First,

the baseMVA ﬁeld is a simple scalar value specifying the system MVA base used

for converting power into per unit quantities. For convenience and code portability,

idx bus deﬁnes a set of constants to be used as named indices into the columns of the

bus matrix. Similarly, idx brch,idx gen and idx cost deﬁne names for the columns

of branch,gen and gencost, respectively. The script define constants provides a

simple way to deﬁne all the usual constants at one shot. These are the names that

appear in the ﬁrst column of the tables below.

144

The Matpower case format also allows for additional ﬁelds to be included in the

structure. The OPF is designed to recognize ﬁelds named A,l,u,H,Cw,N,fparm,z0,

zl and zu as parameters used to directly extend the OPF formulation as described

in Section 7.1. Additional standard optional ﬁelds include bus name,gentype and

genfuel.47 Other user-deﬁned ﬁelds may also be included, such as the reserves

ﬁeld used in the example code throughout Section 7.3. The loadcase function will

automatically load any extra ﬁelds from a case ﬁle and, if the appropriate 'savecase'

callback function (see Section 7.3.5) is added via add userfcn,savecase will also save

them back to a case ﬁle.

Table B-1: Bus Data (mpc.bus)

name column description

BUS I 1 bus number (positive integer)

BUS TYPE 2 bus type (1 = PQ, 2 = PV, 3 = ref, 4 = isolated)

PD 3 real power demand (MW)

QD 4 reactive power demand (MVAr)

GS 5 shunt conductance (MW demanded at V= 1.0 p.u.)

BS 6 shunt susceptance (MVAr injected at V= 1.0 p.u.)

BUS AREA 7 area number (positive integer)

VM 8 voltage magnitude (p.u.)

VA 9 voltage angle (degrees)

BASE KV 10 base voltage (kV)

ZONE 11 loss zone (positive integer)

VMAX 12 maximum voltage magnitude (p.u.)

VMIN 13 minimum voltage magnitude (p.u.)

LAM P†14 Lagrange multiplier on real power mismatch (u/MW)

LAM Q†15 Lagrange multiplier on reactive power mismatch (u/MVAr)

MU VMAX†16 Kuhn-Tucker multiplier on upper voltage limit (u/p.u.)

MU VMIN†17 Kuhn-Tucker multiplier on lower voltage limit (u/p.u.)

†Included in OPF output, typically not included (or ignored) in input matrix. Here we assume

the objective function has units u.

47All three of these are cell arrays of strings. See gentypes and genfuels for more information

on the corresponding ﬁelds.

145

Table B-2: Generator Data (mpc.gen)

name column description

GEN BUS 1 bus number

PG 2 real power output (MW)

QG 3 reactive power output (MVAr)

QMAX 4 maximum reactive power output (MVAr)

QMIN 5 minimum reactive power output (MVAr)

VG‡6 voltage magnitude setpoint (p.u.)

MBASE 7 total MVA base of machine, defaults to baseMVA

GEN STATUS 8 machine status, >0 = machine in-service

≤0 = machine out-of-service

PMAX 9 maximum real power output (MW)

PMIN 10 minimum real power output (MW)

PC1*11 lower real power output of PQ capability curve (MW)

PC2*12 upper real power output of PQ capability curve (MW)

QC1MIN*13 minimum reactive power output at PC1 (MVAr)

QC1MAX*14 maximum reactive power output at PC1 (MVAr)

QC2MIN*15 minimum reactive power output at PC2 (MVAr)

QC2MAX*16 maximum reactive power output at PC2 (MVAr)

RAMP AGC*17 ramp rate for load following/AGC (MW/min)

RAMP 10*18 ramp rate for 10 minute reserves (MW)

RAMP 30*19 ramp rate for 30 minute reserves (MW)

RAMP Q*20 ramp rate for reactive power (2 sec timescale) (MVAr/min)

APF*21 area participation factor

MU PMAX†22 Kuhn-Tucker multiplier on upper Pglimit (u/MW)

MU PMIN†23 Kuhn-Tucker multiplier on lower Pglimit (u/MW)

MU QMAX†24 Kuhn-Tucker multiplier on upper Qglimit (u/MVAr)

MU QMIN†25 Kuhn-Tucker multiplier on lower Qglimit (u/MVAr)

*Not included in version 1 case format.

†Included in OPF output, typically not included (or ignored) in input matrix. Here we assume the

objective function has units u.

‡Used to determine voltage setpoint for optimal power ﬂow only if opf.use vg option is non-zero (0

by default). Otherwise generator voltage range is determined by limits set for corresponding bus

in bus matrix.

146

Table B-3: Branch Data (mpc.branch)

name column description

F BUS 1 “from” bus number

T BUS 2 “to” bus number

BR R 3 resistance (p.u.)

BR X 4 reactance (p.u.)

BR B 5 total line charging susceptance (p.u.)

RATE A 6 MVA rating A (long term rating), set to 0 for unlimited

RATE B 7 MVA rating B (short term rating), set to 0 for unlimited

RATE C 8 MVA rating C (emergency rating), set to 0 for unlimited

TAP 9 transformer oﬀ nominal turns ratio, if non-zero (taps at “from”

bus, impedance at “to” bus, i.e. if r=x=b= 0, tap =|Vf|

|Vt|;

tap = 0 used to indicate transmission line rather than transformer,

i.e. mathematically equivalent to transformer with tap = 1)

SHIFT 10 transformer phase shift angle (degrees), positive ⇒delay

BR STATUS 11 initial branch status, 1 = in-service, 0 = out-of-service

ANGMIN*12 minimum angle diﬀerence, θf−θt(degrees)

ANGMAX*13 maximum angle diﬀerence, θf−θt(degrees)

PF†14 real power injected at “from” bus end (MW)

QF†15 reactive power injected at “from” bus end (MVAr)

PT†16 real power injected at “to” bus end (MW)

QT†17 reactive power injected at “to” bus end (MVAr)

MU SF‡18 Kuhn-Tucker multiplier on MVA limit at “from” bus (u/MVA)

MU ST‡19 Kuhn-Tucker multiplier on MVA limit at “to” bus (u/MVA)

MU ANGMIN‡20 Kuhn-Tucker multiplier lower angle diﬀerence limit (u/degree)

MU ANGMAX‡21 Kuhn-Tucker multiplier upper angle diﬀerence limit (u/degree)

*Not included in version 1 case format. The voltage angle diﬀerence is taken to be unbounded below if

ANGMIN ≤ −360 and unbounded above if ANGMAX ≥360. If both parameters are zero, the voltage angle

diﬀerence is unconstrained.

†Included in power ﬂow and OPF output, ignored on input.

‡Included in OPF output, typically not included (or ignored) in input matrix. Here we assume the

objective function has units u.

147

Table B-4: Generator Cost Data†(mpc.gencost)

name column description

MODEL 1 cost model, 1 = piecewise linear, 2 = polynomial

STARTUP 2 startup cost in US dollars*

SHUTDOWN 3 shutdown cost in US dollars*

NCOST 4 number of cost coeﬃcients for polynomial cost function,

or number of data points for piecewise linear

COST 5 parameters deﬁning total cost function f(p) begin in this column,

units of fand pare $/hr and MW (or MVAr), respectively

(MODEL = 1) ⇒p0, f0, p1, f1, . . . , pn, fn

where p0< p1<··· < pnand the cost f(p) is deﬁned by

the coordinates (p0, f0), (p1, f1), . . . , (pn, fn)

of the end/break-points of the piecewise linear cost

(MODEL = 2) ⇒cn, . . . , c1, c0

n+ 1 coeﬃcients of n-th order polynomial cost, starting with

highest order, where cost is f(p) = cnpn+··· +c1p+c0

†If gen has ngrows, then the ﬁrst ngrows of gencost contain the costs for active power produced by the

corresponding generators. If gencost has 2ngrows, then rows ng+ 1 through 2ngcontain the reactive

power costs in the same format.

*Not currently used by any Matpower functions.

148

Table B-5: DC Line Data*(mpc.dcline)

name column description

F BUS 1 “from” bus number

T BUS 2 “to” bus number

BR STATUS 3 initial branch status, 1 = in-service, 0 = out-of-service

PF†4 real power ﬂow at “from” bus end (MW), “from” →“to”

PT†5 real power ﬂow at “to” bus end (MW), “from” →“to”

QF†6 reactive power injected into “from” bus (MVAr)

QT†7 reactive power injected into “to” bus (MVAr)

VF 8 voltage magnitude setpoint at “from” bus (p.u.)

VT 9 voltage magnitude setpoint at “to” bus (p.u.)

PMIN 10 if positive (negative), lower limit on PF (PT)

PMAX 11 if positive (negative), upper limit on PF (PT)

QMINF 12 lower limit on reactive power injection into “from” bus (MVAr)

QMAXF 13 upper limit on reactive power injection into “from” bus (MVAr)

QMINT 14 lower limit on reactive power injection into “to” bus (MVAr)

QMAXT 15 upper limit on reactive power injection into “to” bus (MVAr)

LOSS0 16 coeﬃcient l0of constant term of linear loss function (MW)

LOSS1 17 coeﬃcient l1of linear term of linear loss function (MW/MW)

(ploss =l0+l1pf, where pfis the ﬂow at the “from” end)

MU PMIN‡18 Kuhn-Tucker multiplier on lower ﬂow limit at “from” bus (u/MW)

MU PMAX‡19 Kuhn-Tucker multiplier on upper ﬂow limit at “from” bus (u/MW)

MU QMINF‡20 Kuhn-Tucker multiplier on lower VAr limit at “from” bus (u/MVAr)

MU QMAXF‡21 Kuhn-Tucker multiplier on upper VAr limit at “from” bus (u/MVAr)

MU QMINT‡22 Kuhn-Tucker multiplier on lower VAr limit at “to” bus (u/MVAr)

MU QMAXT‡23 Kuhn-Tucker multiplier on upper VAr limit at “to” bus (u/MVAr)

*Requires explicit use of toggle dcline.

†Output column, value updated by power ﬂow or OPF (except PF in case of simple power ﬂow).

‡Included in OPF output, typically not included (or ignored) in input matrix. Here we assume the objective

function has units u.

149

Appendix C Matpower Options

Beginning with version 4.2, Matpower uses an options struct to control the many

options available. Earlier versions used an options vector with named elements.

Matpower’s options are used to control things such as:

•power ﬂow algorithm

•power ﬂow termination criterion

•power ﬂow options (e.g. enforcing of reactive power generation limits)

•continuation power ﬂow options

•OPF algorithm

•OPF termination criterion

•OPF options (e.g. active vs. apparent power vs. current for line limits)

•verbose level

•printing of results

•solver speciﬁc options

As with the old-style options vector, the options struct should always be created

and modiﬁed using the mpoption function to ensure compatibility across diﬀerent

versions of Matpower. The default Matpower options struct is obtained by

calling mpoption with no arguments.

>> mpopt = mpoption;

Individual options can be overridden from their default values by calling mpoption

with a set of name/value pairs as input arguments. For example, the following runs

a fast-decoupled power ﬂow of case30 with very verbose progress output:

>> mpopt = mpoption('pf.alg', 'FDXB', 'verbose', 3);

>> runpf('case30', mpopt);

For backward compatibility, old-style option names/values can also be used.

>> mpopt = mpoption('PF_ALG', 2, 'VERBOSE', 3);

150

Another way to specify option overrides is via a struct. Using the example above,

the code would be as follows.

>> overrides = struct('pf', struct('alg', 'FDXB'), 'verbose', 3);

>> mpopt = mpoption(overrides);

Finally, a string containing the name of a function that returns such a struct, can be

passed to mpoption instead of the struct itself.

>> mpopt = mpoption('verbose_fast_decoupled_pf_opts');

where the function verbose fast decoupled pf opts is deﬁned as follows:

function ov = verbose_fast_decoupled_pf_opts()

ov = struct('pf', struct('alg', 'FDXB'), 'verbose', 3);

To make changes to an existing options struct (as opposed to the default options

struct), simply include it as the ﬁrst argument. For example, to modify the previous

run to enforce reactive power limts, suppress the pretty-printing of the output and

save the results to a struct instead:

>> mpopt = mpoption(mpopt, 'pf.enforce_q_lims', 1, 'out.all', 0);

>> results = runpf('case30', mpopt);

This works when specifying the overrides as a struct or function name as well. For

backward compatibility, the ﬁrst argument can be an old-style options vector, fol-

lowed by old-style option name/value pairs.

The available options and their default values are summarized in the following

tables and can also be accessed via the command help mpoption. Some of the options

require separately installed optional packages available from the Matpower website.

151

Table C-1: Top-Level Options

name default description

model 'AC'AC vs. DC modeling for power ﬂow and OPF formulation

'AC'– use AC formulation and corresponding algs/options

'DC'– use DC formulation and corresponding algs/options

pf see Table C-2 power ﬂow options

cpf see Table C-3 continuation power ﬂow options

opf see Tables C-4,C-5 optimal power ﬂow options

verbose 1 amount of progress info printed

0 – print no progress info

1 – print a little progress info

2 – print a lot of progress info

3 – print all progress info

out see Table C-6 pretty-printed output options

mips see Table C-7 MIPS options

clp see Table C-8 CLP options*

cplex see Table C-9 CPLEX options*

fmincon see Table C-10 fmincon options†

glpk see Table C-11 GLPK options*

gurobi see Table C-12 Gurobi options*

ipopt see Table C-13 Ipopt options*

knitro see Table C-14 KNITRO options*

minopf see Table C-15 MINOPF options*

mosek see Table C-16 MOSEK options*

pdipm see Table C-17 PDIPM options*

tralm see Table C-18 TRALM options*

*Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

†Requires Matlab’s Optimization Toolbox, available from The MathWorks, Inc (http://www.mathworks.com/).

152

Table C-2: Power Flow Options

name default description

pf.alg 'NR'AC power ﬂow algorithm:

'NR'– Newtons’s method

'FDXB'– Fast-Decoupled (XB version)

'FDBX'– Fast-Decouple (BX version)

'GS'– Gauss-Seidel

'PQSUM'– Power Summation (radial networks only)

'ISUM'– Current Summation (radial networks only)

'YSUM'– Admittance Summation (radial networks only)

pf.tol 10−8termination tolerance on per unit P and Q dispatch

pf.nr.max it 10 maximum number of iterations for Newton’s method

pf.nr.lin solver '' linear solver option for mplinsolve for computing Newton update step

(see mplinsolve for complete list of all options)

'' – default to '\'for small systems, 'LU3'for larger ones

'\'– built-in backslash operator

'LU'– explicit default LU decomposition and back substitution

'LU3'– 3 output arg form of lu, Gilbert-Peierls algorithm with

approximate minimum degree (AMD) reordering

'LU4'– 4 output arg form of lu, UMFPACK solver (same as

'LU')

'LU5'– 5 output arg form of lu, UMFPACK solver w/row scaling

pf.fd.max it 30 maximum number of iterations for fast-decoupled method

pf.gs.max it 1000 maximum number of iterations for Gauss-Seidel method

pf.radial.max it 20 maximum number of iterations for radial power ﬂow methods

pf.radial.vcorr 0 perform voltage correction procedure in distribution power ﬂow

0 – do not perform voltage correction

1 – perform voltage correction

pf.enforce q lims 0 enforce gen reactive power limits at expense of |Vm|

0 – do not enforce limits

1 – enforce limits, simultaneous bus type conversion

2 – enforce limits, one-at-a-time bus type conversion

153

Table C-3: Continuation Power Flow Options

name default description

cpf.parameterization 3 choice of parameterization

1 — natural

2 — arc length

3 — pseudo arc length

cpf.stop at 'NOSE'determines stopping criterion

'NOSE'— stop when nose point is reached

'FULL'— trace full nose curve

λstop — stop upon reaching target λvalue λstop

cpf.enforce p lims 0 enforce gen active power limits

0 — do not enforce limits

1 — enforce limits

cpf.enforce q lims 0 enforce gen reactive power limits at expense of Vm

0 — do not enforce limits

1 — enforce limits

cpf.enforce v lims 0 enforce bus voltage magnitude limits

0 — do not enforce limits

1 — enforce limits

cpf.enforce flow lims 0 enforce branch MVA ﬂow limits

0 — do not enforce limits

1 — enforce limits

cpf.step 0.05 default value for continuation power ﬂow step size σ

cpf.step min 10−4minimum allowed step size, σmin

cpf.step max 0.2 maximum allowed step size, σmax

cpf.adapt step 0 toggle adaptive step size feature

0 — adaptive step size disabled

1 — adaptive step size enabled

cpf.adapt step damping 0.7 damping factor βcpf from (5.13) for adaptive step sizing

cpf.adapt step tol 10−3tolerance cpf from (5.13) for adaptive step sizing

cpf.target lam tol 10−5tolerance for target lambda detection

cpf.nose tol 10−5tolerance for nose point detection (p.u.)

cpf.p lims tol 10−2tolerance for generator active power limit detection

(MW)

cpf.q lims tol 10−2tolerance for generator reactive power limit detection

(MVAr)

cpf.v lims tol 10−4tolerance for bus voltage magnitude limit detection (p.u)

cpf.flow lims tol 0.01 tolerance for branch ﬂow limit detection (MVA)

cpf.plot.level 0 control plotting of nose curve

0 — do not plot nose curve

1 — plot when completed

2 — plot incrementally at each iteration

3 — same as 2, with pause at each iteration

cpf.plot.bus empty index of bus whose voltage is to be plotted

cpf.user callback empty string or cell array of strings with names of user callback

functions†

†See help cpf default callback for details. 154

Table C-4: OPF Solver Options

name default description

opf.ac.solver 'DEFAULT'AC optimal power ﬂow solver:

'DEFAULT'– choose default solver, i.e. 'MIPS'

'MIPS'– MIPS, Matpower Interior Point Solver,

primal/dual interior point method†

'FMINCON'–Matlab Optimization Toolbox, fmincon

'IPOPT'–Ipopt*

'KNITRO'– KNITRO*

'MINOPF'– MINOPF*

, MINOS-based solver

'PDIPM'– PDIPM*

, primal/dual interior point method‡

'SDPOPF'– SDPOPF*

, solver based on semideﬁnite relax-

ation

'TRALM'– TRALM*

, trust region based augmented Lan-

grangian method

opf.dc.solver 'DEFAULT'DC optimal power ﬂow solver:

'DEFAULT'– choose default solver based on availability

in the following order: 'GUROBI','CPLEX',

'MOSEK','OT','GLPK'(linear costs only),

'BPMPD','MIPS'

'MIPS'– MIPS, Matpower Interior Point Solver,

primal/dual interior point method†

'BPMPD'– BPMPD*

'CLP'– CLP*

'CPLEX'– CPLEX*

'GLPK'– GLPK*(no quadratic costs)

'GUROBI'– Gurobi*

'IPOPT'–Ipopt*

'MOSEK'– MOSEK*

'OT'–Matlab Opt Toolbox, quadprog,linprog

*Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

†For MIPS-sc, the step-controlled version of this solver, the mips.step control option must be set to 1.

‡For SC-PDIPM, the step-controlled version of this solver, the pdipm.step control option must be set to 1.

155

Table C-5: General OPF Options

name default description

opf.current balance 0 use current, as opposed to power, balance formulation for

AC OPF, 0 or 1

opf.v cartesian 0 use cartesian, as opposed to polar, representation for volt-

ages for AC OPF, 0 or 1

opf.violation 5×10−6constraint violation tolerance

opf.use vg 0 respect generator voltage setpoint, 0 or 1†

0 – use voltage magnitude limits speciﬁed in bus, ig-

nore VG in gen

1 – replace voltage magnitude limits speciﬁed in bus

by VG in corresponding gen

opf.flow lim 'S'quantity to limit for branch ﬂow constraints

'S'– apparent power ﬂow (limit in MVA)

'P'– active power ﬂow (limit in MW)

'I'– current magnitude (limit in MVA at 1 p.u.

voltage)

'2'– same as 'P', but implemented using square

of active ﬂow, rather than simple max

opf.ignore angle lim 0 ignore angle diﬀerence limits for branches

0 – include angle diﬀerence limits, if speciﬁed

1 – ignore angle diﬀerence limits even if speciﬁed

opf.softlims.default 1 default behavior of implicit soft limits, where parameters

are not explicitly provided

0 – do not include softlims if not explicitly speciﬁed

1 – include softlims with default values if not ex-

plicitly speciﬁed

opf.init from mpc*-1 specify whether to use the current state in Matpower

case to initialize OPF

-1 – Matpower decides based on solver/algorithm

0 – ignore current state in Matpower case‡

1 – use current state in Matpower case

opf.start 0 strategy for initializing OPF starting point

0 – default, Matpower decides based on solver,

(currently identical to 1)

1 – ignore current state in Matpower case‡

2 – use current state in Matpower case

3 – solve power ﬂow and use resulting state

opf.return raw der 0 for AC OPF, return constraint and derivative info in

results.raw (in ﬁelds g,dg,df,d2f)

*Deprecated. Use opf.start instead.

†Using a value between 0 and 1 results in the limits being determined by the corresponding weighted average of

the 2 options.

‡Only applies to fmincon,Ipopt, KNITRO and MIPS solvers, which use an interior point estimate; others use

current state in Matpower case, as with opf.start = 2.

156

Table C-6: Power Flow and OPF Output Options

name default description

verbose 1 amount of progress info to be printed

0 – print no progress info

1 – print a little progress info

2 – print a lot of progress info

3 – print all progress info

out.all -1 controls pretty-printing of results

-1 – individual ﬂags control what is printed

0 – do not print anything†*

1 – print everything†

out.sys sum 1 print system summary (0 or 1)

out.area sum 0 print area summaries (0 or 1)

out.bus 1 print bus detail, includes per bus gen info (0 or 1)

out.branch 1 print branch detail (0 or 1)

out.gen 0 print generator detail (0 or 1)

out.lim.all -1 controls constraint info output

-1 – individual ﬂags control what is printed

0 – do not print any constraint info†

1 – print only binding constraint info†

2 – print all constraint info†

out.lim.v 1 control output of voltage limit info

0 – do not print

1 – print binding constraints only

2 – print all constraints

out.lim.line 1 control output of line ﬂow limit info‡

out.lim.pg 1 control output of gen active power limit info‡

out.lim.qg 1 control output of gen reactive power limit info‡

out.force 0 print results even if success ﬂag = 0 (0 or 1)

out.suppress detail -1 suppress all output but system summary

-1 – suppress details for large systems (>500 buses)

0 – do not suppress any output speciﬁed by other ﬂags

1 – suppress all output except system summary section†

*This setting is ignored for pretty-printed output to ﬁles speciﬁed as FNAME argument in calls to runpf,runopf,

etc.

†Overrides individual ﬂags, but (in the case of out.suppress detail) not out.all = 1.

‡Takes values of 0, 1 or 2 as for out.lim.v.

157

Table C-7: OPF Options for MIPS

name default description

mips.linsolver '' linear system solver for update step

'' or '\'– built-in backslash \operator

'PARDISO'– PARDISO solver†

mips.feastol 0 feasibiliy (equality) tolerance

set to value of opf.violation by default

mips.gradtol 10−6gradient tolerance

mips.comptol 10−6complementarity condition (inequality) tolerance

mips.costtol 10−6optimality tolerance

mips.max it 150 maximum number of iterations

mips.step control 0 set to 1 to enable step-size control

mips.sc.red it‡20 maximum number of step size reductions per iteration

†Requires installation of the optional PARDISO package. See Appendix G.11 for details.

‡Only relevant when mips.step control is on.

Table C-8: OPF Options for CLP†

name default§description

clp.opts empty struct of native CLP options passed to clp options to override

defaults, applied after overrides from clp.opt fname‡

clp.opt fname empty name of user-supplied function passed as FNAME argument to

clp options to override defaults‡

†For opf.dc.solver option set to 'CLP'only. Requires the installation of the optional CLP package. See

Appendix G.2 for details.

‡For details, see help clp options or help clp.

158

Table C-9: OPF Options for CPLEX†

name default description

cplex.lpmethod 0 algorithm used by CPLEX for LP problems

0 – automatic; let CPLEX choose

1 – primal simplex

2 – dual simplex

3 – network simplex

4 – barrier

5 – sifting

6 – concurrent (dual, barrier, and primal)

cplex.qpmethod 0 algorithm used by CPLEX for QP problems

0 – automatic; let CPLEX choose

1 – primal simplex

2 – dual simplex

3 – network simplex

4 – barrier

cplex.opts empty struct of native CPLEX options (for cplexoptimset) passed to

cplex options to override defaults, applied after overrides from

cplex.opt fname‡

cplex.opt fname empty name of user-supplied function passed as FNAME argument to

cplex options to override defaults‡

cplex.opt 0 if cplex.opt fname is empty and cplex.opt is non-zero, the

value of cplex.opt fname is generated by appending cplex.opt

to 'cplex user options '(for backward compatibility with old

Matpower option CPLEX OPT)

†For opf.dc.solver option set to 'CPLEX'only. Requires the installation of the optional CPLEX package. See

Appendix G.3 for details.

‡For details, see help cplex options and the “Parameters of CPLEX” section of the CPLEX documentation

at http://www.ibm.com/support/knowledgecenter/SSSA5P.

159

Table C-10: OPF Options for fmincon†

name default description

fmincon.alg 4 algorithm used by fmincon in Matlab Opt Toolbox ≥4

1 – active-set‡

2 – interior-point, default “bfgs” Hessian approximation

3 – interior-point, “lbfgs” Hessian approximation

4 – interior-point, exact user-supplied Hessian

5 – interior-point, Hessian via ﬁnite-diﬀerences

6 – sqp, sequential quadratic programming‡

fmincon.tol x 10−4termination tolerance on x*

fmincon.tol f 10−4termination tolerance on f*

fmincon.max it 0 maximum number of iterations*

0⇒use solver’s default value

†Requires Matlab’s Optimization Toolbox, available from The MathWorks, Inc (http://www.mathworks.

com/).

‡Does not use sparse matrices, so not applicable for large-scale systems.

*Display is set by verbose,TolCon by opf.violation,TolX by fmincon.tol x,TolFun by fmincon.tol f,

and MaxIter and MaxFunEvals by fmincon.max it.

Table C-11: OPF Options for GLPK†

name default§description

glpk.opts empty struct of native GLPK options passed to glpk options to over-

ride defaults, applied after overrides from glpk.opt fname‡

glpk.opt fname empty name of user-supplied function passed as FNAME argument to

glpk options to override defaults‡

†For opf.dc.solver option set to 'GLPK'only. Requires the installation of the optional GLPK package. See

Appendix G.4 for details.

‡For details, see help glpk options or the “param” section of the GLPK documentation at http://www.gnu.

org/software/octave/doc/interpreter/Linear-Programming.html.

160

Table C-12: OPF Options for Gurobi†

name default§description

gurobi.method 0 algorithm used by Gurobi for LP/QP problems

0 – primal simplex

1 – dual simplex

2 – barrier

3 – concurrent (LP only)

4 – deterministic concurrent (LP only)

gurobi.timelimit ∞maximum time allowed for solver (secs)

gurobi.threads 0 (auto) maximum number of threads to use

gurobi.opts empty struct of native Gurobi options passed to gurobi options to

override defaults, applied after overrides from gurobi.opt fname‡

gurobi.opt fname empty name of user-supplied function passed as FNAME argument to

gurobi options to override defaults‡

gurobi.opt 0 if gurobi.opt fname is empty and gurobi.opt is non-zero,

the value of gurobi.opt fname is generated by appending

gurobi.opt to 'gurobi user options '(for backward compat-

ibility with old Matpower option GRB OPT)

†For opf.dc.solver option set to 'GUROBI'only. Requires the installation of the optional Gurobi package. See

Appendix G.5 for details.

§Default values in parenthesis refer to defaults assigned by Gurobi if called with option equal to 0.

‡For details, see help gurobi options and the “Parameters” section of the “Gurobi Optimizer Reference Manual”

at http://www.gurobi.com/documentation/6.0/refman/parameters.html.

Table C-13: OPF Options for Ipopt†

name default description

ipopt.opts empty struct of native Ipopt options (options.ipopt for ipopt)

passed to ipopt options to override defaults, applied after over-

rides from ipopt.opt fname‡

ipopt.opt fname empty name of user-supplied function passed as FNAME argument to

ipopt options to override defaults‡

ipopt.opt 0 if ipopt.opt fname is empty and ipopt.opt is non-zero, the

value of ipopt.opt fname is generated by appending ipopt.opt

to 'ipopt user options '(for backward compatibility with old

Matpower option IPOPT OPT)

†For opf.ac.solver or opf.dc.solver option set to 'IPOPT'only. Requires the installation of the optional

Ipopt package [49]. See Appendix G.6 for details.

‡For details, see help ipopt options and the options reference section of the Ipopt documentation at http:

//www.coin-or.org/Ipopt/documentation/.

161

Table C-14: OPF Options for KNITRO†

name default description

knitro.tol x 10−4termination tolerance on x

knitro.tol f 10−4termination tolerance on f

knitro.maxit 0 maximum number of iterations

0⇒use solver’s default value

knitro.opt fname empty name of user-supplied native KNITRO options ﬁle that overrides

other options‡

knitro.opt 0 if knitro.opt fname is empty and knitro.opt is a posi-

tive integer n, the value of knitro.opt fname is generated

as 'knitro user options n.txt'(for backward compatibility

with old Matpower option KNITRO OPT)

†For opf.ac.solver option set to 'KNITRO'only. Requires the installation of the optional KNITRO package [32].

See Appendix G.7 for details.

‡Note that KNITRO uses the opt fname option slightly diﬀerently from other optional solvers. Speciﬁcally, it is

the name of a text ﬁle processed directly by KNITRO, not a Matlab function that returns an options struct

passed to the solver.

162

Table C-15: OPF Options for MINOPF†

name default‡description

minopf.feastol 0 (10−3) primal feasibility tolerance

set to value of opf.violation by default

minopf.rowtol 0 (10−3) row tolerance

set to value of opf.violation by default

minopf.xtol 0 (10−4)xtolerance

minopf.majdamp 0 (0.5) major damping parameter

minopf.mindamp 0 (2.0) minor damping parameter

minopf.penalty 0 (1.0) penalty parameter

minopf.major it 0 (200) major iterations

minopf.minor it 0 (2500) minor iterations

minopf.max it 0 (2500) iteration limit

minopf.verbosity -1 amount of progress output printed by MEX ﬁle

-1 – controlled by verbose option

0 – do not print anything

1 – print only only termination status message

2 – print termination status & screen progress

3 – print screen progress, report ﬁle (usually fort.9)

minopf.core 0 memory allocation

defaults to 1200nb+ 2(nb+ng)2

minopf.supbasic lim 0 superbasics limit, defaults to 2nb+ 2ng

minopf.mult price 0 (30) multiple price

†For opf.ac.solver option set to 'MINOPF'only. Requires the installation of the optional MINOPF pack-

age [30]. See Appendix G.8 for details.

‡Default values in parenthesis refer to defaults assigned in MEX ﬁle if called with option equal to 0.

163

Table C-16: OPF Options for MOSEK†

name default§description

mosek.lp alg 0 solution algorithm used by MOSEK for continuous LP problems

(MSK IPAR OPTIMIZER)*

0 – automatic; let MOSEK choose

1 – interior point

3 – primal simplex

4 – dual simplex

5 – primal dual simplex

6 – automatic simplex (MOSEK chooses which simplex)

7 – network primal simplex

10 – concurrent

mosek.max it 0 (400) interior point maximum iterations

(MSK IPAR INTPNT MAX ITERATIONS)

mosek.gap tol 0 (10−8) interior point relative gap tolerance

(MSK DPAR INTPNT TOL REL GAP)

mosek.max time 0 (-1) maximum time allowed for solver (negative means ∞)

(MSK DPAR OPTIMIZER MAX TIME)

mosek.num threads 0 (1) maximum number of threads to use

(MSK IPAR INTPNT NUM THREADS)

mosek.opts empty struct of native MOSEK options (param struct normally passed

to mosekopt) passed to mosek options to override defaults, ap-

plied after overrides from mosek.opt fname‡

mosek.opt fname empty name of user-supplied function passed as FNAME argument to

mosek options to override defaults‡

mosek.opt 0 if mosek.opt fname is empty and mosek.opt is non-zero, the

value of mosek.opt fname is generated by appending mosek.opt

to 'mosek user options '(for backward compatibility with old

Matpower option MOSEK OPT)

†For opf.dc.solver option set to 'MOSEK'only. Requires the installation of the optional MOSEK package. See

Appendix G.9 for details.

§Default values in parenthesis refer to defaults assigned by MOSEK if called with option equal to 0.

*The values listed here correspond to those used by MOSEK version 7.x. Version 6.x was diﬀerent. It is probably

safer to write your code using the symbolic constants deﬁned by mosek symbcon rather than using explicit numerical

values.

‡For details, see help mosek options and the “Parameters” reference in “The MOSEK optimization toolbox for

MATLAB manual” at http://docs.mosek.com/7.1/toolbox/Parameters.html.

164

Table C-17: OPF Options for PDIPM†

name default description

pdipm.feastol 0 feasibiliy (equality) tolerance

set to value of opf.violation by default

pdipm.gradtol 10−6gradient tolerance

pdipm.comptol 10−6complementarity condition (inequality) tolerance

pdipm.costtol 10−6optimality tolerance

pdipm.max it 150 maximum number of iterations

pdipm.step control 0 set to 1 to enable step-size control

pdipm.sc.red it‡20 maximum number of step size reductions per iteration

pdipm.sc.smooth ratio‡0.04 piecewise linear curve smoothing ratio

†Requires installation of the optional TSPOPF package [25]. See Appendix G.13 for details.

‡Only relevant when pdipm.step control is on.

Table C-18: OPF Options for TRALM†

name default description

tralm.feastol 0 feasibiliy tolerance

set to value of opf.violation by default

tralm.primaltol 5×10−4primal variable tolerance

tralm.dualtol 5×10−4dual variable tolerance

tralm.costtol 10−5optimality tolerance

tralm.major it 40 maximum number of major iterations

tralm.minor it 100 maximum number of minor iterations

tralm.smooth ratio 0.04 piecewise linear curve smoothing ratio

†Requires installation of the optional TSPOPF package [25]. See Appendix G.13 for details.

165

C.1 Mapping of Old-Style Options to New-Style Options

AMatpower options struct can be created from an old-style options vector simply

by passing it to mpoption. The mapping of old-style options into the ﬁelds in the

option struct are summarized in Table C-19. An old-style options vector can also

be created from an options struct by calling mpoption with the struct and an empty

second argument.

mpopt_struct = mpoption(mpopt_vector);

mpopt_vector = mpoption(mpopt_struct, []);

Table C-19: Old-Style to New-Style Option Mapping

idx old option new option notes

1PF ALG pf.alg new option has string values

1→'NR'

2→'FDXB'

3→'FDBX'

4→'GS'

2PF TOL pf.tol

3PF MAX IT pf.nr.max it

4PF MAX IT FD pf.fd.max it

5PF MAX IT GS pf.gs.max it

6ENFORCE Q LIMS pf.enforce q lims

10 PF DC model new option has string values

0→'AC'

1→'DC'

11 OPF ALG opf.ac.solver new option has string values

0→'DEFAULT'

500 →'MINOPF'

520 →'FMINCON'

540 →'PDIPM'(and pdipm.step control = 0)

545 →'PDIPM'(and pdipm.step control = 1)

550 →'TRALM'

560 →'MIPS'(and mips.step control = 0)

565 →'MIPS'(and mips.step control = 1)

580 →'IPOPT'

600 →'KNITRO'

16 OPF VIOLATION opf.violation

17 CONSTR TOL X fmincon.tol x,

knitro.tol x

support for constr has been removed

18 CONSTR TOL F fmincon.tol f,

knitro.tol f

support for constr has been removed

19 CONSTR MAX IT fmincon.max it support for constr has been removed

continued on next page

166

Table C-19: Old-Style to New-Style Option Mapping – continued

idx old option new option notes

24 OPF FLOW LIM opf.flow lim new option has string values

0→'S'

1→'P'

2→'I'

25 OPF IGNORE ANG LIM opf.ignore angle lim

26 OPF ALG DC opf.dc.solver new option has string values

0→'DEFAULT'

100 →'BPMPD'

200 →'MIPS'(and mips.step control = 0)

250 →'MIPS'(and mips.step control = 1)

300 →'OT'

400 →'IPOPT'

500 →'CPLEX'

600 →'MOSEK'

700 →'GUROBI'

31 VERBOSE verbose

32 OUT ALL out.all

33 OUT SYS SUM out.sys sum

34 OUT AREA SUM out.area sum

35 OUT BUS out.bug

36 OUT BRANCH out.branch

37 OUT GEN out.gen

38 OUT ALL LIM out.lim.all

39 OUT V LIM out.lim.v

40 OUT LINE LIM out.lim.line

41 OUT PG LIM out.lim.pg

42 OUT QG LIM out.lim.qg

44 OUT FORCE out.force

52 RETURN RAW DER opf.return raw der

55 FMC ALG fmincon.alg

58 KNITRO OPT knitro.opt

60 IPOPT OPT ipopt.opt

61 MNS FEASTOL minopf.feastol

62 MNS ROWTOL minopf.rowtol

63 MNS XTOL minopf.xtol

64 MNS MAJDAMP minopf.majdamp

65 MNS MINDAMP minopf.mindamp

66 MNS PENALTY PARM minopf.penalty

67 MNS MAJOR IT minopf.major it

continued on next page

167

Table C-19: Old-Style to New-Style Option Mapping – continued

idx old option new option notes

68 MNS MINOR IT minopf.minor it

69 MNS MAX IT minopf.max it

70 MNS VERBOSITY minopf.verbosity

71 MNS CORE minopf.core

72 MNS SUPBASIC LIM minopf.supbasic lim

73 MNS MULT PRICE minopf.mult price

80 FORCE PC EQ P0 sopf.force Pc eq P0 for c3sopf (not part of Matpower)

81 PDIPM FEASTOL mips.feastol,

pdipm.feastol

82 PDIPM GRADTOL mips.gradtol,

pdipm.gradtol

83 PDIPM COMPTOL mips.comptol,

pdipm.comptol

84 PDIPM COSTTOL mips.costtol,

pdipm.costtol

85 PDIPM MAX IT mips.max it,

pdipm.max it

86 SCPDIPM RED IT mips.sc.red it,

pdipm.sc.red it

87 TRALM FEASTOL tralm.feastol

88 TRALM PRIMETOL tralm.primaltol

89 TRALM DUALTOL tralm.dualtol

90 TRALM COSTTOL tralm.costtol

91 TRALM MAJOR IT tralm.major it

92 TRALM MINOR IT tralm.minor it

93 SMOOTHING RATIO tralm.smooth ratio,

pdipm.sc.smooth ratio

95 CPLEX LPMETHOD cplex.lpmethod

98 CPLEX QPMETHOD cplex.qpmethod

97 CPLEX OPT cplex.opt

111 MOSEK LP ALG mosek.lp alg

112 MOSEK MAX IT mosek.max it

113 MOSEK GAP TOL mosek.gap tol

114 MOSEK MAX TIME mosek.max time

115 MOSEK NUM THREADS mosek.num threads

116 MOSEK OPT mosek.opt

continued on next page

168

Table C-19: Old-Style to New-Style Option Mapping – continued

idx old option new option notes

121 GRB METHOD gurobi.method

122 GRB TIMELIMIT gurobi.timelimit

123 GRB THREADS gurobi.threads

124 GRB OPT gurobi.opt

169

Appendix D Matpower Files and Functions

This appendix lists all of the ﬁles and functions that Matpower provides, with

the exception of those in the extras directory (see Appendix E). In most cases,

the function is found in a Matlab M-ﬁle of the same name in the lib directory

of the distribution, where the .m extension is omitted from this listing. For more

information on each, at the Matlab prompt, simply type help followed by the

name of the function. For documentation and data ﬁles, the ﬁlename extensions are

included.

D.1 Directory Layout and Documentation Files

Some of these ﬁles appear at the top level of the distribution and others in the docs

directory.

170

Table D-1: Matpower Directory Layout and Documentation Files

name description

data/ Matpower cases (see Section D.3)

docs/ Matpower documentation

MATPOWER-dev-guide.md Matpower Developer’s Guide

MATPOWER-manual.pdf Matpower User’s Manual†

relnotes/ Matpower release notes

src/ L

X source for Matpower User’s Manual

TN1-OPF-Auctions.pdf Matpower Technical Note 1 “Uniform Price

Auctions and Optimal Power Flow” [46]

TN2-OPF-Derivatives.pdf Matpower Technical Note 2 “AC Power Flows,

Generalized OPF Costs and their Derivatives us-

ing Complex Matrix Notation” [36]

TN3-More-OPF-Derivatives.pdf Matpower Technical Note 3 “Addendum to AC

Power Flows and their Derivatives using Complex

Matrix Notation: Nodal Current Balance” [37]

TN4-OPF-Derivatives-Cartesian.pdf Matpower Technical Note 4 “AC Power Flows

and their Derivatives using Complex Matrix No-

tation and Cartesian Coordinate Voltages” [38]

lib/ Matpower software (see Section D.2)

caseformat.m help ﬁle documenting Matpower case for-

mat (i.e. at the command prompt, type help

caseformat to see details)

t/ Matpower tests and examples (see Section D.4)

mips/ integrated MIPS distribution†

most/ integrated MOST distribution†

mptest/ integrated MP-Test distribution (see Table D-24)

AUTHORS list of Matpower authors

CHANGES.md Matpower change history

CONTRIBUTING.md Matpower Contributors Guide

LICENSE license ﬁle

README.md basic introduction to Matpower

†The MIPS User’s Manual and MOST User’s Manual are found in <MATPOWER>/mips/docs and

<MATPOWER>/most/docs, respectively.

171

D.2 Matpower Functions

All of the functions listed in this section are found in <MATPOWER>/lib, unless noted

otherwise.

Table D-2: Top-Level Simulation Functions

name description

runpf power ﬂow†

runcpf AC continuation power ﬂow

runopf optimal power ﬂow†

runuopf optimal power ﬂow with unit-decommitment†

rundcpf DC power ﬂow‡

rundcopf DC optimal power ﬂow‡

runduopf DC optimal power ﬂow with unit-decommitment‡

runopf w res optimal power ﬂow with ﬁxed reserve requirements†

most MOST, Matpower Optimal Scheduling Tool §

†Uses AC model by default.

‡Simple wrapper function to set option to use DC model before calling the cor-

responding general function above.

§MOST and its supporting ﬁles and functions in the most/ sub-directory are

documented in the MOST User’s Manual and listed in its Appendix A.

Table D-3: Input/Output Functions

name description

cdf2mpc converts power ﬂow data from IEEE Common Data Format (CDF) to

Matpower format

loadcase loads data from a Matpower case ﬁle or struct into data matrices or a

case struct

mpoption sets and retrieves Matpower options

printpf pretty prints power ﬂow and OPF results

psse2mpc converts power ﬂow data from PSS/E RAW format to Matpower format

save2psse exports Matpower case to PSS/E RAW format

savecase saves case data to a Matpower case ﬁle

172

Table D-4: Data Conversion Functions

name description

ext2int converts case from external to internal indexing

e2i data converts arbitrary data from external to internal indexing

e2i field converts ﬁelds in mpc from external to internal indexing

int2ext converts case from internal to external indexing

i2e data converts arbitrary data from internal to external indexing

i2e field converts ﬁelds in mpc from internal to external indexing

get reorder returns Awith one of its dimensions indexed

set reorder assigns Bto Awith one of the dimensions of Aindexed

Table D-5: Power Flow Functions

name description

calc v i sum implementation of current summation power ﬂow solver†

calc v pq sum implementation of power summation power ﬂow solver†

calc v y sum implementation of admittance summation power ﬂow solver†

dcpf implementation of DC power ﬂow solver

fdpf implementation of fast-decoupled power ﬂow solver

gausspf implementation of Gauss-Seidel power ﬂow solver

make vcorr calculate voltage corrections for radial power ﬂow†

make zpv form loop impedance for PV bus handling in radial power ﬂow†

newtonpf implementation of Newton-method power ﬂow solver

order radial performs oriented ordering of buses and branches for radial power ﬂow†

pfsoln computes branch ﬂows, generator reactive power (and real power for slack

bus), updates bus,gen,branch matrices with solved values

radial pf wrapper for backward/forward sweep power ﬂow solvers†

†For radial networks only.

173

Table D-6: Continuation Power Flow Functions

name description

cpf corrector computes Newton method corrector steps

cpf current mpc construct Matpower case struct for current continuation step

cpf default callback callback function that accumulates, and optionally plots, results

from each iteration

cpf detect events detects event intervals and zeros given previous and current event

function values

cpf flim event cb callback function to handle 'FLIM'events

cpf flim event event function for 'FLIM'events, to detect branch MVA ﬂow

limits

cpf nose event cb callback function to handle 'NOSE'events

cpf nose event event function for 'NOSE'events, to detect nose point of contin-

uation curve

cpf p jac computes partial derivatives of parameterization function

cpf p computes value of parameterization function at current solution

cpf plim event cb callback function to handle 'PLIM'events

cpf plim event event function for 'PLIM'events, to detect generator active

power limits

cpf predictor computes the predicted solution from the current solution and

tangent direction

cpf qlim event cb callback function to handle 'QLIM'events

cpf qlim event event function for 'QLIM'events, to detect generator reactive

power limits

cpf register callback registers a CPF callback function to be called by runcpf

cpf register event registers a CPF event function to be called by runcpf

cpf tangent computes the normalized tangent vector at the current solution

cpf target lam event cb callback function to handle 'TARGET LAM'events

cpf target lam event event function for 'TARGET LAM'events, to detect end of contin-

uation curve or other target λvalue

cpf vlim event cb callback function to handle 'VLIM'events

cpf vlim event event function for 'VLIM'events, to detect bus voltage magni-

tude limits

174

Table D-7: OPF and Wrapper Functions

name description

opf†the main OPF function, called by runopf

dcopf‡calls opf with options set to solve DC OPF

fmincopf‡calls opf with options set to use fmincon to solve AC OPF

mopf‡calls opf with options set to use MINOPF to solve AC OPF§

uopf‡implements unit-decommitment heuristic, called by runuopf

†Can also be used as a top-level function, run directly from the command line. It provides more calling

options than runopf, primarly for backward compatibility with previous versions of mopf from MINOPF,

but does not oﬀer the option to save the output or the solved case.

‡Wrapper with same calling conventions as opf.

§Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

175

Table D-8: OPF Model Objects

name description

@opf model/ OPF model object used to encapsulate OPF problem formulation

display called to display object when statement not ended with semicolon

get mpc returns the Matpower case struct

opf model constructor for the opf model class

@opt model/ optimization model object (@opf model base class)

add legacy cost adds a named subset of legacy user-deﬁned costs to the model

add lin constraint adds a named subset of linear constraints to the model

add named set†adds a named subset of costs, constraints or variables to the model

add nln constraint adds a named subset of nonlinear constraints to the model

add nln cost adds a named subset of general nonlinear costs to the model

add quad cost adds a named subset of quadratic costs to the model

add var adds a named subset of optimization variables to the model

describe idx identiﬁes variable, constraint or cost row indices

display called to display object when statement not ended with semicolon

eval legacy cost evaluates legacy user costs and derivatives

eval nln constraint returns full set of nonlinear equality or inequality constraints and

their gradients

eval nln constraint hess returns Hessian for full set of nonlinear equality or inequality con-

straints

eval nln cost evaluates general nonlinear costs and derivatives

eval quad cost evaluates quadratic costs and derivatives

get idx returns the idx struct for vars, lin/nln constraints, costs

get userdata returns values of user data stored in the model

getN returns the number of variables, constraints or cost rows‡

get returns the value of a ﬁeld of the object

init indexed name initializes dimensions for indexed named set of costs, constraints

or variables

opt model constructor for the opt model class

params lin constraint returns individual or full set of linear constraint parameters

params legacy cost returns individual or full set of legacy user cost coeﬃcients

params nln cost returns individual general nonlinear cost parameters

params quad cost returns individual or full set of quadratic cost coeﬃcients

params var returns initial values, bounds and variable type for optimimization

vector ˆx‡

valid named set type†returns label for given named set type if valid, empty otherwise

varsets cell2struct†converts variable set list from cell array to struct array

varsets idx returns vector of indices into opt vector ˆxfor variable set list

varsets len returns total number of optimization variables for variable set list

varsets x assembles cell array of sub-vectors of opt vector ˆxspeciﬁed by

variable set list

†Private method for internal use only.

‡For all, or alternatively, only for a named (and possibly indexed) subset.

176

Table D-9: Deprecated @opt model Methods

name description

@opt model/ optimization model object (@opf model base class)

add constraints use add lin constraint or add nln constraint instead†

add costs use add legacy cost,add nln cost or add quad cost instead†

add vars use add var instead†

build cost params no longer needed

compute cost use eval legacy cost instead

get cost params use params legacy cost instead

getv use params var instead

linear constraints use params lin constraint instead

†Or init indexed name if simply initializing the dimensions for an indexed named set.

Table D-10: OPF Solver Functions

name description

dcopf solver sets up and solves DC OPF problem

fmincopf solver sets up and solves OPF problem using fmincon,Matlab Opt Toolbox

ipoptopf solver sets up and solves OPF problem using Ipopt†

ktropf solver sets up and solves OPF problem using KNITRO†

mipsopf solver sets up and solves OPF problem using MIPS

mopf solver sets up and solves OPF problem using MINOPF†

tspopf solver sets up and solves OPF problem using PDIPM, SC-PDIPM or TRALM†

†Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

177

Table D-11: Other OPF Functions

name description

margcost computes the marginal cost of generation as a function of gener-

ator output

makeAang forms linear constraints for branch angle diﬀerence limits

makeApq forms linear constraints for generator PQ capability curves

makeAvl forms linear constraints for dispatchable load constant power fac-

tor

makeAy forms linear constraints for piecewise linear generator costs (CCV)

opf args input argument handling for opf

opf setup constructs an OPF model object from a Matpower case

opf execute executes the OPF speciﬁed by an OPF model object

opf branch ang fcn†evaluates AC branch angle diﬀerence limit constraints and

gradients‡

opf branch ang hess†evaluates Hessian of AC branch angle diﬀerence limit constraints‡

opf branch flow fcn†evaluates AC branch ﬂow limit constraints and gradients

opf branch flow hess†evaluates Hessian of AC branch ﬂow limit constraints

opf consfcn†evaluates function and gradients for AC OPF nonlinear con-

straints

opf costfcn†evaluates function, gradients and Hessian for AC OPF objective

function

opf current balance fcn†evaluates AC current balance constraints and gradients

opf current balance hess†evaluates Hessian of AC current balance constraints

opf gen cost fcn†evaluates polynomial generator costs and derivatives

opf hessfcn†evaluates the Hessian of the Lagrangian for AC OPF

opf legacy user cost fcn†evaluates legacy user-deﬁned costs and derivatives

opf power balance fcn†evaluates AC power balance constraints and gradients

opf power balance hess†evaluates Hessian of AC power balance constraints

opf veq fcn†evaluates voltage magnitude equality constraints and gradients‡

opf veq hess†evaluates Hessian of voltage magnitude equality constraints‡

opf vlim fcn†evaluates voltage magnitude limit constraints and gradients‡

opf vlim hess†evaluates Hessian of voltage magnitude limit constraints‡

opf vref fcn†evaluates reference voltage angle equality constraints and

gradients‡

opf vref hess†evaluates Hessian of reference voltage angle equality constraints‡

totcost computes the total cost of generation as a function of generator

output

update mupq updates generator limit prices based on the shadow prices on ca-

pability curve constraints

†Used by fmincon, MIPS, Ipopt and KNITRO for AC OPF.

‡Used with cartesian coordinate voltage representation only. I.e. opf.v cartesian option set to 1.

178

Table D-12: OPF User Callback Functions

name description

add userfcn appends a user callback function to the list of those to be called for a

given case

remove userfcn removes a user callback function from the list

run userfcn executes the user callback functions for a given stage

toggle dcline enable/disable or check the status of the callbacks implementing DC

lines

toggle iflims enable/disable or check the status of the callbacks implementing in-

terface ﬂow limits

toggle reserves enable/disable or check the status of the callbacks implementing ﬁxed

reserve requirements

toggle softlims enable/disable or check the status of the callbacks implementing DC

OPF branch ﬂow soft limits

Table D-13: Power Flow Derivative Functions

name description†

dIbr dV evaluates the partial derivatives of If|twith respect to V

dSbr dV evaluates the partial derivatives of Sf|twith respect to V

dAbr dV evaluates the partial derivatives of |Ff|t|2with respect to V

dImis dV evaluates the partial derivatives of Imis with respect to V

dSbus dV evaluates the partial derivatives of Sbus with respect to V

d2Ibr dV2 evaluates the 2nd derivatives of If|twith respect to V

d2Sbr dV2 evaluates the 2nd derivatives of Sf|twith respect to V

d2Abr dV2 evaluates the 2nd derivatives of |Ff|t|2with respect to V

d2AIbr dV2*evaluates the 2nd derivatives of |If|t|2with respect to V

d2ASbr dV2*evaluates the 2nd derivatives of |Sf|t|2with respect to V

d2Imis dV2 evaluates the 2nd derivatives of Imis with respect to V

d2Imis dVdSg evaluates the 2nd derivatives of Imis with respect to Vand Sg.

d2Sbus dV2 evaluates the 2nd derivatives of Sbus with respect to V

*Deprecated. Please use d2Abr dV2 instead.

†Vrepresents complex bus voltages, Sgthe complex generator power injections, If|tcomplex branch current

injections, Sf|tcomplex branch power injections, Imis complex bus current injections, Sbus complex bus power

injections and Ff|trefers to branch ﬂows, either If|tor Sf|t, depending on the inputs. The second derivatives

are all actually partial derivatives of the product of a ﬁrst derivative matrix and a vector λ. Please see

Matpower Technical Note 2 [36], Matpower Technical Note 3 [37] and Matpower Technical Note 4 [38] for

the detailed derivations of the formulas implemented by these functions.

179

Table D-14: NLP, LP & QP Solver Functions

name description

clp options default options for CLP solver†

cplex options default options for CPLEX solver†

glpk options default options for GLPK solver†

gurobi options default options for Gurobi solver†

gurobiver prints version information for Gurobi/Gurobi MEX

ipopt options default options for Ipopt solver†

mips Matpower Interior Point Solver – primal/dual interior point solver for NLP

mipsver prints version information for MIPS

miqps matpower Mixed-Integer Quadratic Program Solver for Matpower, wrapper function

provides a common MIQP solver interface for various MIQP/MILP solvers

miqps cplex common MIQP/MILP solver interface to CPLEX (cplexmiqp and

cplexmilp)†

miqps glpk common MILP solver interface to GLPK†

miqps gurobi common MIQP/MILP solver interface to Gurobi†

miqps mosek common MIQP/MILP solver interface to MOSEK (mosekopt)†

miqps ot common QP/MILP solver interface to Matlab Opt Toolbox’s intlinprog,

quadprog,linprog

mosek options default options for MOSEK solver†

mosek symbcon symbolic constants to use for MOSEK solver options†

mplinsolve common linear system solver interface, used by MIPS

mpopt2qpopt create mi/qps matpower options struct from Matpower options struct

qps matpower Quadratic Program Solver for Matpower, wrapper function

provides a common QP solver interface for various QP/LP solvers

qps bpmpd common QP/LP solver interface to BPMPD MEX†

qps clp common QP/LP solver interface to CLP†

qps cplex common QP/LP solver interface to CPLEX (cplexqp and cplexlp)†

qps glpk common QP/LP solver interface to GLPK†

qps gurobi common QP/LP solver interface to Gurobi†

qps ipopt common QP/LP solver interface to Ipopt-based solver†

qps mips common QP/LP solver interface to MIPS-based solver

qps mosek common QP/LP solver interface to MOSEK (mosekopt)†

qps ot common QP/LP solver interface to Matlab Opt Toolbox’s quadprog,

linprog

†Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

180

Table D-15: Matrix Building Functions

name description

makeB forms the fast-decoupled power ﬂow matrices, B0and B00

makeBdc forms the system matrices Bbus and Bfand vectors Pf,shift and Pbus,shift

for the DC power ﬂow model

makeJac forms the power ﬂow Jacobian matrix

makeLODF forms the line outage distribution factor matrix

makePTDF forms the DC PTDF matrix for a given choice of slack

makeSbus forms the vector of complex bus power injections

makeSdzip forms a struct w/vectors of nominal values for each component of ZIP load

makeYbus forms the complex bus and branch admittance matrices Ybus,Yfand Yt

181

Table D-16: Utility Functions

name description

apply changes modiﬁes an existing Matpower case by applying changes deﬁned

in a change table

bustypes creates vectors of bus indices for reference bus, PV buses, PQ buses

calc branch angle calcultes a vector of voltage angle diﬀerences for branches

case info checks a Matpower case for connectivity and prints a system

summary

compare case prints summary of diﬀerences between two Matpower cases

define constants convenience script deﬁnes constants for named column indices to

data matrices (calls idx bus,idx brch,idx gen and idx cost)

extract islands extracts islands in a network into their own Matpower case struct

feval w path same as Matlab’s feval function, except the function being eval-

uated need not be in the Matlab path

find islands ﬁnds islands and isolated buses in a network

genfuels list of standard values for generator fuel types, for mpc.genfuel

gentypes list of standard values for generator unit types, for mpc.gentype

get losses compute branch losses (and derivatives) as functions of bus voltage

hasPQcap checks for generator P-Q capability curve constraints

have fcn checks for availability of optional functionality

idx brch named column index deﬁnitions for branch matrix

idx bus named column index deﬁnitions for bus matrix

idx cost named column index deﬁnitions for gencost matrix

idx ct constant deﬁnitions for use with change tables and apply changes

idx dcline named column index deﬁnitions for dcline matrix

idx gen named column index deﬁnitions for gen matrix

isload checks if generators are actually dispatchable loads

load2disp converts ﬁxed loads to dispatchable loads

loadshed computes MW curtailments of dispatchable loads

mpver prints version information for Matpower and optional packages

modcost modiﬁes gencost by horizontal or vertical scaling or shifting

nested struct copy copies the contents of nested structs

poly2pwl creates piecewise linear approximation to polynomial cost function

polycost evaluates polynomial generator cost and its derivatives

pqcost splits gencost into real and reactive power costs

savechgtab saves a change table, such as used by apply changes, to a ﬁle

scale load scales ﬁxed and/or dispatchable loads by load zone

total load returns vector of total load in each load zone

182

Table D-17: Other Functions

name description

connected components returns the connected components of a graph

mpoption info clp option information for CLP

mpoption info cplex option information for CPLEX

mpoption info fmincon option information for FMINCON

mpoption info glpk option information for GLPK

mpoption info gurobi option information for Gurobi

mpoption info intlinprog option information for INTLINPROG

mpoption info ipopt option information for Ipopt

mpoption info knitro option information for KNITRO

mpoption info linprog option information for LINPROG

mpoption info mips option information for MIPS

mpoption info mosek option information for MOSEK

mpoption info quadprog option information for QUADPROG

psse convert converts data read from PSS/E RAW ﬁle to Matpower format

psse convert hvdc called by psse convert to handle HVDC data

psse convert xfmr called by psse convert to handle transformer data

psse parse parses data from a PSS/E RAW data ﬁle

psse parse line called by psse parse to parse a single line

psse parse section called by psse parse to parse an entire section

psse read reads data from a PSS/E RAW data ﬁle

183

D.3 Example Matpower Cases

All of the functions listed in this section are found in <MATPOWER>/data, unless

noted otherwise.

Table D-18: Small Transmission System Test Cases

name description

case4gs 4-bus example case from Grainger & Stevenson

case5 modiﬁed 5-bus PJM example case from Rui Bo

case6ww 6-bus example case from Wood & Wollenberg

case9 9-bus example case from Chow

case9Q case9 with reactive power costs

case9target modiﬁed case9, target for example continuation power ﬂow

case14 IEEE 14-bus case

case24 ieee rts IEEE RTS 24-bus case

case30 30-bus case, based on IEEE 30-bus case

case ieee30 IEEE 30-bus case

case30pwl case30 with piecewise linear costs

case30Q case30 with reactive power costs

case39 39-bus New England case

case57 IEEE 57-bus case

case RTS GMLC 96-machine, 73-bus Reliability Test System*

case118 IEEE 118-bus case

case145 IEEE 145-bus case, 50 generator dynamic test case

case300 IEEE 300-bus case

*Reliability Test System Grid Modernization Lab Consortium data from

https://github.com/GridMod/RTS-GMLC.

Table D-19: Small Radial Distribution System Test Cases

name description

case4 dist 4-bus example radial distribution system case

case18 18-bus radial distribution system from Grady, Samotyj and Noyola

case22 22-bus radial distribution system from Raju, Murthy and Ravindra

case33bw 33-bus radial distribution system from Baran and Wu

case69 69-bus radial distribution system from Das

case85 85-bus radial distribution system from Das, Kothari and Kalam

case141 141-bus radial distribution system from Khodr, Olsina, De Jesus and Yusta

184

Table D-20: ACTIV Synthetic Grid Test Cases

name description

case ACTIVSg200 200-bus Illinois synthetic model*

case ACTIVSg500 500-bus South Carolina synthetic model*

case ACTIVSg2000 2000-bus Texas synthetic model*

case ACTIVSg10k 10,000-bus US WECC synthetic model*

case ACTIVSg25k 25,000-bus US Northeast/Mid-Atlantic synthetic model*

case ACTIVSg70k 70,000-bus Eastern US synthetic model*

case SyntheticUSA 82,000-bus continental USA synthetic model*

contab ACTIVSg200 contingency table for case ACTIVSg200*

contab ACTIVSg500 contingency table for case ACTIVSg500*

contab ACTIVSg2000 contingency table for case ACTIVSg2000*

contab ACTIVSg10k contingency table for case ACTIVSg10k*

scenarios ACTIVSg200 one year of hourly zonal load scenarios for case ACTIVSg200*

scenarios ACTIVSg2000 one year of hourly area load scenarios for case ACTIVSg2000*

*These synthetic grid models are ﬁctitious representations that are designed to be statistically and functionally

similar to actual electric grids while containing no conﬁdential critical energy infrastructure information

(CEII). Please cite reference [42] when publishing results based on this data. More information about these

synthetic cases can be found at https://electricgrids.engr.tamu.edu.

Table D-21: Polish System Test Cases

name description

case2383wp Polish system - winter 1999-2000 peak*

case2736sp Polish system - summer 2004 peak*

case2737sop Polish system - summer 2004 oﬀ-peak*

case2746wop Polish system - winter 2003-04 oﬀ-peak*

case2746wp Polish system - winter 2003-04 evening peak*

case3012wp Polish system - winter 2007-08 evening peak*

case3120sp Polish system - summer 2008 morning peak*

case3375wp Polish system plus - winter 2007-08 evening peak*

*Contributed by Roman Korab.

185

Table D-22: PEGASE European System Test Cases

name description

case89pegase 89-bus portion of European transmission system from PEGASE project*

case1354pegase 1354-bus portion of European transmission system from PEGASE project*

case2869pegase 2869-bus portion of European transmission system from PEGASE project*

case9241pegase 9241-bus portion of European transmission system from PEGASE project*

case13659pegase 13659-bus portion of European transmission system from PEGASE project*

*Contributed by C´edric Josz and colleagues from the French Transmission System Operator. Please cite references

[43,44] when publishing results based on this data.

Table D-23: RTE French System Test Cases

name description

case1888rte 1888-bus snapshot of VHV French transmission system from RTE*

case1951rte 1951-bus snapshot of VHV French transmission system from RTE*

case2848rte 2848-bus snapshot of VHV French transmission system from RTE*

case2868rte 2868-bus snapshot of VHV French transmission system from RTE*

case6468rte 6468-bus snapshot of VHV and HV French transmission system from RTE*

case6470rte 6470-bus snapshot of VHV and HV French transmission system from RTE*

case6495rte 6495-bus snapshot of VHV and HV French transmission system from RTE*

case6515rte 6515-bus snapshot of VHV and HV French transmission system from RTE*

*Contributed by C´edric Josz and colleagues from the French Transmission System Operator. Please cite

reference [43] when publishing results based on this data.

186

D.4 Automated Test Suite

All of the functions and ﬁles listed in this section are found in <MATPOWER>/lib/t,

unless noted otherwise.

Table D-24: Automated Test Functions from MP-Test†

name description

mptest/lib/

t begin begin running tests

t end ﬁnish running tests and print statistics

t is tests if two matrices are identical to with a speciﬁed tolerance

t ok tests if a condition is true

t run tests run a series of tests

t skip skips a number of tests, with explanatory message

t/ MP-Test tests

test mptest runs full MP-Test test suite

t test fcns test t ok and t is

†These functions are part of MP-Test and are found in <MATPOWER>/mptest/lib.

Table D-25: MIPS Tests†

name description

mips/lib/

t/ MIPS tests

test mips runs full MIPS test suite

t mips runs tests for MIPS NLP solver

t mips pardiso runs tests for MIPS NLP solver, using PARDISO as linear solver

t mplinsolve tests for mplinsolve

t qps mips runs tests for qps mips

†These tests are part of MIPS and are found in <MATPOWER>/mips/lib/t.

187

Table D-26: Test Data

name description

opf nle fcn1.m user-deﬁned nonlinear equality constraint function for OPF tests

opf nle hess1.m user-deﬁned nonlinear equality constraint Hessian for OPF tests

pretty print acopf.txt pretty-printed output of an example AC OPF run

pretty print dcopf.txt pretty-printed output of an example DC OPF run

soln9 dcopf.mat solution data, DC OPF of t case9 opf

soln9 dcpf.mat solution data, DC power ﬂow of t case9 pf

soln9 opf ang.mat solution data, AC OPF of t case9 opfv2 w/only branch angle

diﬀerence limits (gen PQ capability constraints removed)

soln9 opf extras1.mat solution data, AC OPF of t case9 opf w/extra cost/constraints

soln9 opf Plim.mat solution data, AC OPF of t case9 opf w/opf.flow lim ='P'

soln9 opf PQcap.mat solution data, AC OPF of t case9 opfv2 w/only gen PQ capabil-

ity constraints (branch angle diﬀ limits removed)

soln9 opf vg.mat solution data, AC OPF of t case9 opf with option opf.use vg

soln9 opf.mat solution data, AC OPF of t case9 opf

soln9 pf.mat solution data, AC power ﬂow of t case9 pf

t auction case.m case data used to test auction code

t case ext.m case data used to test ext2int and int2ext, external indexing

t case info eg.txt example output from case info, used by t islands

t case int.m case data used to test ext2int and int2ext, internal indexing

t case9 dcline.m same as t case9 opfv2 with additional DC line data

t case9 opf.m sample case ﬁle with OPF data, version 1 format

t case9 opfv2.m sample case ﬁle with OPF data, version 2 format, includes addi-

tional branch angle diﬀ limits & gen PQ capability constraints

t case9 pf.m sample case ﬁle with only power ﬂow data, version 1 format

t case9 pfv2.m sample case ﬁle with only power ﬂow data, version 2 format

t case9 save2psse.m sample 9-bus case ﬁle used by t psse for testing save2psse

t case30 userfcns.m sample case ﬁle with OPF, reserves and interface ﬂow limit data

t chgtab.m sample change table data, used by t apply changes

t psse case.raw sample PSS/E format RAW ﬁle used to test conversion code

t psse case2.m result of converting t psse case2.raw to Matpower format

t psse case2.raw sample PSS/E format RAW ﬁle used to test conversion code

t psse case3.m result of converting t psse case3.raw to Matpower format

t psse case3.raw sample PSS/E format RAW ﬁle used to test conversion code

188

Table D-27: Miscellaneous Matpower Tests

name description

test matpower runs full Matpower test suite

test most‡runs full MOST test suite

t apply changes runs tests for apply changes

t auction minopf runs tests for auction using MINOPF†

t auction mips runs tests for auction using MIPS

t auction tspopf pdipm runs tests for auction using PDIPM†

t cpf runs tests for AC continuation power ﬂow

t cpf cb1 example CPF callback function for t cpf

t cpf cb2 example CPF callback function with cb args for t cpf

t dcline runs tests for DC line implementation in toggle dcline

t ext2int2ext runs tests for ext2int and int2ext

t get losses runs tests for get losses

t hasPQcap runs tests for hasPQcap

t hessian runs tests for 2nd derivative code

t islands runs test for find islands and extract islands

t jacobian runs test for partial derivative code

t load2disp runs tests for load2disp

t loadcase runs tests for loadcase

t makeLODF runs tests for makeLODF

t makePTDF runs tests for makePTDF

t margcost runs tests for margcost

t miqps matpower runs tests for miqps matpower

t modcost runs tests for modcost

t mpoption runs tests for mpoption

t nested struct copy runs tests for nested struct copy

t off2case runs tests for off2case

t opf model runs tests for opf model and opt model objects

t opf model legacy runs tests for opf model and opt model objects using legacy (dep-

recated) add constraints method

t printpf runs tests for printpf

t psse runs tests for psse2mpc and related functions

t qps matpower runs tests for qps matpower

t pf runs tests for AC and DC power ﬂow

t pf radial runs tests for AC power ﬂow for radial distribution systems

t runmarket runs tests for runmarket

t scale load runs tests for scale load

t total load runs tests for total load

t vdep load runs PF, CPF and OPF tests for voltage dependent (ZIP) loads

t totcost runs tests for totcost

†Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

‡While test most is listed here with other tests, it is actually located in <MATPOWER>/most/lib/t, not

<MATPOWER>/lib/t. MOST and its supporting ﬁles and functions in the most/ sub-directory are documented

in the MOST User’s Manual and listed in its Appendix A.

189

Table D-28: Matpower OPF Tests

name description

t opf dc bpmpd runs tests for DC OPF solver using BPMPD MEX†

t opf dc clp runs tests for DC OPF solver using CLP†

t opf dc cplex runs tests for DC OPF solver using CPLEX†

t opf dc glpk runs tests for DC OPF solver using GLPK†

t opf dc gurobi runs tests for DC OPF solver using Gurobi†

t opf dc ipopt runs tests for DC OPF solver using Ipopt†

t opf dc mosek runs tests for DC OPF solver using MOSEK†

t opf dc ot runs tests for DC OPF solver using Matlab Opt Toolbox

t opf dc mips runs tests for DC OPF solver using MIPS

t opf dc mips sc runs tests for DC OPF solver using MIPS-sc

t opf default runs tests for AC OPF solver using default solver

t opf fmincon runs tests for AC OPF solver using fmincon

t opf ipopt runs tests for AC OPF solver using Ipopt†

t opf knitro runs tests for AC OPF solver using KNITRO†

t opf minopf runs tests for AC OPF solver using MINOPF†

t opf mips runs tests for AC OPF solver using MIPS

t opf mips sc runs tests for AC OPF solver using MIPS-sc

t opf softlims runs tests for DC OPF with user callback functions for branch ﬂow

soft limits

t opf tspopf pdipm runs tests for AC OPF solver using PDIPM†

t opf tspopf scpdipm runs tests for AC OPF solver using SC-PDIPM†

t opf tspopf tralm runs tests for AC OPF solver using TRALM†

t opf userfcns runs tests for AC OPF with user callback functions for reserves

and interface ﬂow limits

t runopf w res runs tests for AC OPF with ﬁxed reserve requirements

†Requires the installation of an optional package. See Appendix Gfor details on the corresponding package.

190

Appendix E Extras Directory

For a Matpower installation in <MATPOWER>, the contents of <MATPOWER>/extras

contains additional Matpower related code, some contributed by others. Some of

these could be moved into the main Matpower distribution in the future with a

bit of polishing and additional documentation. Please contact the developers if you

are interested in helping make this happen.

maxloadlim An optimal power ﬂow extension, contributed by Camille Ha-

mon, for computing maximum loadability limits.48 Please see

extras/maxloadlim/manual/maxloadlim manual.pdf for details on

the formulation and implementation.

misc A number of potentially useful functions that are either not yet

fully implemented, tested, documented and/or supported. See the

help (and the code) in each individual ﬁle to understand what it

does.49

reduction A network reduction toolbox that performs a modifed Ward re-

duction and can be used to produce a smaller approximate equiv-

alent from a larger original system. Code contributed by Yu-

jia Zhu and Daniel Tylavsky. For more details, please see the

Network Reduction Toolbox.pdf ﬁle.

sdp pf Applications of a semideﬁnite programming programming relax-

ation of the power ﬂow equations. Code contributed by Dan

Molzahn. See Appendix G.12 and the documentation in the

<MATPOWER>/extras/sdp pf/documentation directory, especially

the ﬁle sdp pf documentation.pdf, for a full description of the

functions in this package.

se State-estimation code contributed by Rui Bo. Type test se,

test se 14bus or test se 14bus err to run some examples. See

se intro.pdf for a brief introduction to this code.

smartmarket Code that implements a “smart market” auction clearing mech-

anism based on Matpower’s optimal power ﬂow solver. See

Appendix Ffor details.

48Camille Hamon maintains a GitHub repository of this code at:

https://github.com/CamilleH/Max-Load-Lim-matpower

49For more information on qcqp opf, see [43]. For more information on plot mpc, see [45].

191

state estimator Older state estimation example, based on code by James S. Thorp.

192

Appendix F “Smart Market” Code

Matpower 3 and later includes in the extras/smartmarket directory code that

implements a “smart market” auction clearing mechanism. The purpose of this code

is to take a set of oﬀers to sell and bids to buy and use Matpower’s optimal

power ﬂow to compute the corresponding allocations and prices. It has been used

extensively by the authors with the optional MINOPF package [30] in the context of

PowerWeb50 but has not been widely tested in other contexts.

The smart market algorithm consists of the following basic steps:

1. Convert block oﬀers and bids into corresponding generator capacities and costs.

2. Run an optimal power ﬂow with decommitment option (uopf) to ﬁnd generator

allocations and nodal prices (λP).

3. Convert generator allocations and nodal prices into set of cleared oﬀers and

bids.

4. Print results.

For step 1, the oﬀers and bids are supplied as two structs, offers and bids,

each with ﬁelds Pfor real power and Qfor reactive power (optional). Each of these

is also a struct with matrix ﬁelds qty and prc, where the element in the i-th row

and j-th column of qty and prc are the quantity and price, respectively of the j-th

block of capacity being oﬀered/bid by the i-th generator. These block oﬀers/bids are

converted to the equivalent piecewise linear generator costs and generator capacity

limits by the off2case function. See help off2case for more information.

Oﬀer blocks must be in non-decreasing order of price and the oﬀer must cor-

respond to a generator with 0 ≤PMIN <PMAX. A set of price limits can be speci-

ﬁed via the lim struct, e.g. and oﬀer price cap on real energy would be stored in

lim.P.max offer. Capacity oﬀered above this price is considered to be withheld from

the auction and is not included in the cost function produced. Bids must be in non-

increasing order of price and correspond to a generator with PMIN <PMAX ≤0 (see

Section 6.4.2 on page 66). A lower limit can be set for bids in lim.P.min bid. See

help pricelimits for more information.

The data speciﬁed by a Matpower case ﬁle, with the gen and gencost matrices

modiﬁed according to step 1, are then used to run an OPF. A decommitment mech-

anism is used to shut down generators if doing so results in a smaller overall system

cost (see Section 8).

50See http://www.pserc.cornell.edu/powerweb/.

193

In step 3 the OPF solution is used to determine for each oﬀer/bid block, how

much was cleared and at what price. These values are returned in co and cb, which

have the same structure as offers and bids. The mkt parameter is a struct used to

specify a number of things about the market, including the type of auction to use,

type of OPF (AC or DC) to use and the price limits.

There are two basic types of pricing options available through mkt.auction type,

discriminative pricing and uniform pricing. The various uniform pricing options are

best explained in the context of an unconstrained lossless network. In this context,

the allocation is identical to what one would get by creating bid and oﬀer stacks

and ﬁnding the intersection point. The nodal prices (λP) computed by the OPF

and returned in bus(:,LAM P) are all equal to the price of the marginal block. This

is either the last accepted oﬀer (LAO) or the last accepted bid (LAB), depending

which is the marginal block (i.e. the one that is split by intersection of the oﬀer and

bid stacks). There is often a gap between the last accepted bid and the last accepted

oﬀer. Since any price within this range is acceptable to all buyers and sellers, we end

up with a number of options for how to set the price, as listed in Table F-1.

Table F-1: Auction Types

auction type name description

0 discriminative price of each cleared oﬀer (bid) is equal to the oﬀered (bid)

price

1 LAO uniform price equal to the last accepted oﬀer

2 FRO uniform price equal to the ﬁrst rejected oﬀer

3 LAB uniform price equal to the last accepted bid

4 FRB uniform price equal to the ﬁrst rejected bid

5 ﬁrst price uniform price equal to the oﬀer/bid price of the marginal

unit

6 second price uniform price equal to min(FRO, LAB) if the marginal unit

is an oﬀer, or max(FRB, LAO) if it is a bid

7 split-the-diﬀerence uniform price equal to the average of the LAO and LAB

8 dual LAOB uniform price for sellers equal to LAO, for buyers equal to

LAB

Generalizing to a network with possible losses and congestion results in nodal

prices λPwhich vary according to location. These λPvalues can be used to normalize

all bids and oﬀers to a reference location by multiplying by a locational scale factor.

For bids and oﬀers at bus i, this scale factor is λref

P/λi

P, where λref

Pis the nodal

price at the reference bus. The desired uniform pricing rule can then be applied to

the adjusted oﬀers and bids to get the appropriate uniform price at the reference

194

bus. This uniform price is then adjusted for location by dividing by the locational

scale factor. The appropriate locationally adjusted uniform price is then used for all

cleared bids and oﬀers.51 The relationships between the OPF results and the pricing

rules of the various uniform price auctions are described in detail in [46].

There are certain circumstances under which the price of a cleared oﬀer deter-

mined by the above procedures can be less than the original oﬀer price, such as

when a generator is dispatched at its minimum generation limit, or greater than

the price cap lim.P.max cleared offer. For this reason, all cleared oﬀer prices are

clipped to be greater than or equal to the oﬀer price but less than or equal to

lim.P.max cleared offer. Likewise, cleared bid prices are less than or equal to the

bid price but greater than or equal to lim.P.min cleared bid.

F.1 Handling Supply Shortfall

In single sided markets, in order to handle situations where the oﬀered capacity is

insuﬃcient to meet the demand under all of the other constraints, resulting in an

infeasible OPF, we introduce the concept of emergency imports. We model an import

as a ﬁxed injection together with an equally sized dispatchable load which is bid in

at a high price. Under normal circumstances, the two cancel each other and have

no eﬀect on the solution. Under supply shortage situations, the dispatchable load is

not fully dispatched, resulting in a net injection at the bus, mimicking an import.

When used in conjunction with the LAO pricing rule, the marginal load bid will not

set the price if all oﬀered capacity can be used.

F.2 Example

The case ﬁle lib/t/t auction case.m, used for this example, is a modiﬁed version of

the 30-bus system that has 9 generators, where the last three have negative PMIN to

model the dispatchable loads.

•Six generators with three blocks of capacity each, oﬀering as shown in Ta-

ble F-2.

•Fixed load totaling 151.64 MW.

•Three dispatchable loads, bidding three blocks each as shown in Table F-3.

51In versions of Matpower prior to 4.0, the smart market code incorrectly shifted prices instead

of scaling them, resulting in prices that, while falling within the oﬀer/bid “gap” and therefore

acceptable to all participants, did not necessarily correspond to the OPF solution.

195

Table F-2: Generator Oﬀers

Generator Block 1 Block 2 Block 3

MW @ $/MWh MW @ $/MWh MW @ $/MWh

1 12 @ $20 24 @ $50 24 @ $60

2 12 @ $20 24 @ $40 24 @ $70

3 12 @ $20 24 @ $42 24 @ $80

4 12 @ $20 24 @ $44 24 @ $90

5 12 @ $20 24 @ $46 24 @ $75

6 12 @ $20 24 @ $48 24 @ $60

Table F-3: Load Bids

Load Block 1 Block 2 Block 3

MW @ $/MWh MW @ $/MWh MW @ $/MWh

1 10 @ $100 10 @ $70 10 @ $60

2 10 @ $100 10 @ $50 10 @ $20

3 10 @ $100 10 @ $60 10 @ $50

To solve this case using an AC optimal power ﬂow and a last accepted oﬀer (LAO)

pricing rule, we use:

mkt.OPF = 'AC';

mkt.auction_type = 1;

196

and set up the problem as follows:

mpc = loadcase('t_auction_case');

offers.P.qty = [ ...

12 24 24;

12 24 24 ];

offers.P.prc = [ ...

20 50 60;

20 40 70;

20 42 80;

20 44 90;

20 46 75;

20 48 60 ];

bids.P.qty = [ ...

10 10 10;

10 10 10 ];

bids.P.prc = [ ...

100 70 60;

100 50 20;

100 60 50 ];

[mpc_out, co, cb, f, dispatch, success, et] = runmarket(mpc, offers, bids, mkt);

197

The resulting cleared oﬀers and bids are:

>> co.P.qty

ans =

12.0000 23.3156 0

12.0000 24.0000 0

>> co.P.prc

ans =

50.0000 50.0000 50.0000

50.2406 50.2406 50.2406

50.3368 50.3368 50.3368

51.0242 51.0242 51.0242

52.1697 52.1697 52.1697

52.9832 52.9832 52.9832

>> cb.P.qty

ans =

10.0000 10.0000 10.0000

10.0000 0 0

10.0000 10.0000 0

>> cb.P.prc

ans =

51.8207 51.8207 51.8207

54.0312 54.0312 54.0312

55.6208 55.6208 55.6208

198

In other words, the sales by generators and purchases by loads are as shown

summarized in Tables F-4 and Tables F-5, respectively.

Table F-4: Generator Sales

Generator Quantity Sold Selling Price

MW $/MWh

1 35.3 $50.00

2 36.0 $50.24

3 36.0 $50.34

4 36.0 $51.02

5 36.0 $52.17

6 36.0 $52.98

Table F-5: Load Purchases

Load Quantity Bought Purchase Price

MW $/MWh

1 30.0 $51.82

2 10.0 $54.03

3 20.0 $55.62

199

F.3 Smartmarket Files and Functions

Table F-6: Smartmarket Files and Functions

name description

extras/smartmarket/

auction clears set of bids and oﬀers based on pricing rules and OPF results

case2off generates quantity/price oﬀers and bids from gen and gencost

idx disp named column index deﬁnitions for dispatch matrix

off2case updates gen and gencost based on quantity/price oﬀers and bids

pricelimits ﬁlls in a struct with default values for oﬀer and bid limits

printmkt prints the market output

runmarket top-level simulation function, runs the OPF-based smart market

runmkt*top-level simulation function, runs the OPF-based smart market

smartmkt implements the smart market solver

SM CHANGES change history for the smart market software

*Deprecated. Will be removed in a subsequent version.

200

Appendix G Optional Packages

There are a number of optional packages, not included in the Matpower distribu-

tion, that Matpower can utilize if they are installed in your Matlab path. Each

of them is based on one or more MEX ﬁles pre-compiled for various platforms, some

distributed by PSerc, others available from third parties, and each with their own

G.1 BPMPD MEX – MEX interface for BPMPD

BPMPD MEX [28,29] is a Matlab MEX interface to BPMPD, an interior point

solver for quadratic programming developed by Csaba M´esz´aros at the MTA SZ-

TAKI, Computer and Automation Research Institute, Hungarian Academy of Sci-

ences, Budapest, Hungary. It can be used by Matpower’s DC and LP-based OPF

solvers and it improves the robustness of MINOPF. It is also useful outside of Mat-

power as a general-purpose QP/LP solver.

This MEX interface for BPMPD was coded by Carlos E. Murillo-S´anchez, while

he was at Cornell University. It does not provide all of the functionality of BPMPD,

however. In particular, the stand-alone BPMPD program is designed to read and

write results and data from MPS and QPS format ﬁles, but this MEX version does

not implement reading data from these ﬁles into Matlab.

The current version of the MEX interface is based on version 2.21 of the BPMPD

solver, implemented in Fortran.

Builds are available for Linux (32-bit), Mac OS X (PPC, Intel 32-bit) and Win-

dows (32-bit) at http://www.pserc.cornell.edu/bpmpd/.

When installed BPMPD MEX can be selected as the solver for DC OPFs by

setting the opf.dc.solver option to 'BPMPD'. It can also be used to solve general

LP and QP problems via Matpower’s common QP solver interface qps matpower

with the algorithm option set to 'BPMPD'(or 100 for backward compatibility), or by

calling qps bpmpd directly.

G.2 CLP – COIN-OR Linear Programming

The CLP [35] (COIN-OR Linear Programming) solver is an open-source linear pro-

gramming solver written in C++ by John Forrest. It can solve both linear program-

ming (LP) and quadratic programming (QP) problems. It is primarily meant to be

used as a callable library, but a basic, stand-alone executable version exists as well. It

is available from the COIN-OR initiative at http://www.coin-or.org/projects/

Clp.xml.

201

To use CLP with Matpower, a MEX interface is required52. For Microsoft

Windows users, a pre-compiled MEX version of CLP (and numerous other solvers,

such as GLPK and Ipopt) are easily installable as part of the OPTI Toolbox53 [47]

With the Matlab interface to CLP installed, it can be used to solve DC OPF

problems by setting the opf.dc.solver option equal to 'CLP'. The solution algo-

rithms and other CLP parameters can be set directly via Matpower’s clp.opts

option. A “CLP user options” function can also be speciﬁed via clp.opt fname to

override the defaults for any of the many CLP parameters. See help clp for details.

See Table C-8 for a summary of the CLP-related Matpower options.

CLP can also be used to solve general LP and QP problems via Matpower’s

common QP solver interface qps matpower with the algorithm option set to 'CLP',

or by calling qps clp directly.

G.3 CPLEX – High-performance LP and QP Solvers

The IBM ILOG CPLEX Optimizer, or simply CPLEX, is a collection of optimiza-

tion tools that includes high-performance solvers for large-scale linear programming

(LP) and quadratic programming (QP) problems, among others. More informa-

tion is available at http://www.ibm.com/software/integration/optimization/

cplex-optimizer/.

Although CPLEX is a commercial package, at the time of this writing the full

version is available to academics at no charge through the IBM Academic Initia-

tive program for teaching and non-commercial research. See http://www.ibm.com/

support/docview.wss?uid=swg21419058 for more details.

When the Matlab interface to CPLEX is installed, the CPLEX LP and QP

solvers, cplexlp and cplexqp, can be used to solve DC OPF problems by setting the

opf.dc.solver option equal to 'CPLEX'. The solution algorithms can be controlled

by Matpower’s cplex.lpmethod and cplex.qpmethod options. See Table C-9 for

a summary of the CPLEX-related Matpower options. A “CPLEX user options”

function can also be speciﬁed via cplex.opt fname to override the defaults for any

of the many CPLEX parameters. See help cplex options and the “Parameters of

52According to David Gleich at http://web.stanford.edu/~dgleich/notebook/2009/03/

coinor_clop_for_matlab.html, there was a Matlab MEX interface to CLP written by Jo-

han Lofberg and available (at some point in the past) at http://control.ee.ethz.ch/~joloef/

mexclp.zip. Unfortunately, at the time of this writing, it seems it is no longer available

there, but Davide Barcelli makes some precompiled MEX ﬁles for some platforms available here

http://www.dii.unisi.it/~barcelli/software.php, and the ZIP ﬁle linked as Clp 1.14.3 con-

tains the MEX source as well as a clp.m wrapper function with some rudimentary documentation.

53The OPTI Toolbox is available from http://www.i2c2.aut.ac.nz/Wiki/OPTI/.

202

CPLEX” section of the CPLEX documentation at http://www.ibm.com/support/

knowledgecenter/SSSA5P for details.

It can also be used to solve general LP and QP problems via Matpower’s com-

mon QP solver interface qps matpower, or MILP and MIQP problems via miqps matpower,

with the algorithm option set to 'CPLEX'(or 500 for backward compatibility), or by

calling qps cplex or miqps cplex directly.

G.4 GLPK – GNU Linear Programming Kit

The GLPK [34] (GNU Linear Programming Kit) package is intended for solving

large-scale linear programming (LP), mixed integer programming (MIP), and other

related problems. It is a set of routines written in ANSI C and organized in the form

of a callable library.

To use GLPK with Matpower, a MEX interface is required54. For Microsoft

Windows users, a pre-compiled MEX version of GLPK (and numerous other solvers,

such as CLP and Ipopt) are easily installable as part of the OPTI Toolbox55 [47].

When GLPK is installed, either as part of Octave or with a MEX interface for

Matlab, it can be used to solve DC OPF problems that do not include any quadratic

costs by setting the opf.dc.solver option equal to 'GLPK'. The solution algorithms

and other GLPK parameters can be set directly via Matpower’s glpk.opts option.

A “GLPK user options” function can also be speciﬁed via glpk.opt fname to override

the defaults for any of the many GLPK parameters. See help glpk options and the

parameters section the GLPK documentation at http://www.gnu.org/software/

octave/doc/interpreter/Linear-Programming.html for details. See Table C-11

for a summary of the GLPK-related Matpower options.

GLPK can also be used to solve general LP problems via Matpower’s common

QP solver interface qps matpower, or MILP problems via miqps matpower, with the

algorithm option set to 'GLPK', or by calling qps glpk or miqps glpk directly.

G.5 Gurobi – High-performance LP and QP Solvers

Gurobi [33] is a collection of optimization tools that includes high-performance solvers

for large-scale linear programming (LP) and quadratic programming (QP) problems,

54The http://glpkmex.sourceforge.net site and Davide Barcelli’s page http://www.dii.

unisi.it/~barcelli/software.php may be useful in obtaining the MEX source or pre-compiled

binaries for Mac or Linux platforms.

55The OPTI Toolbox is available from http://www.i2c2.aut.ac.nz/Wiki/OPTI/.

203

among others. The project was started by some former CPLEX developers. More

information is available at http://www.gurobi.com/.

Although Gurobi is a commercial package, at the time of this writing their is a

free academic license available. See http://www.gurobi.com/html/academic.html

for more details.

Beginning with version 5.0.0, Gurobi includes a native Matlab interface, which

is supported in Matpower version 4.2 and above.56

When Gurobi is installed, it can be used to solve DC OPF problems by setting

the opf.dc.solver option equal to 'GUROBI'. The solution algorithms can be con-

trolled by Matpower’s gurobi.method option. See Table C-12 for a summary of the

Gurobi-related Matpower options. A “Gurobi user options” function can also be

speciﬁed via gurobi.opt fname to override the defaults for any of the many Gurobi pa-

rameters. See help gurobi options and the “Parameters” section of the “Gurobi Op-

timizer Reference Manual” at http://www.gurobi.com/documentation/6.0/refman/

parameters.html for details.

It can also be used to solve general LP and QP problems via Matpower’s com-

mon QP solver interface qps matpower, or MILP and MIQP problems via miqps matpower,

with the algorithm option set to 'GUROBI'(or 700 for backward compatibility), or

by calling qps gurobi or miqps gurobi directly.

G.6 Ipopt – Interior Point Optimizer

Ipopt [49] (Interior Point OPTimizer, pronounced I-P-Opt) is a software package

for large-scale nonlinear optimization. It is is written in C++ and is released as

open source code under the Common Public License (CPL). It is available from the

COIN-OR initiative at http://www.coin-or.org/projects/Ipopt.xml. The code

has been written by Carl Laird and Andreas W¨achter, who is the COIN project

leader for Ipopt.

Matpower requires the Matlab MEX interface to Ipopt, which is included in

the Ipopt source distribution, but must be built separately. Additional information

on the MEX interface is available at https://projects.coin-or.org/Ipopt/wiki/

MatlabInterface. Please consult the Ipopt documentation, web-site and mailing

lists for help in building and installing the Ipopt Matlab interface. This inter-

face uses callbacks to Matlab functions to evaluate the objective function and its

gradient, the constraint values and Jacobian, and the Hessian of the Lagrangian.

56Matpower version 4.1 supported Gurobi version 4.x, which required a free third-party

Matlab MEX interface [48], available at http://www.convexoptimization.com/wikimization/

index.php/Gurobi_mex.

204

Precompiled MEX binaries for a high-performance version of Ipopt, using the

PARDISO linear solver [50,51], are available from the PARDISO project57. At the

time of this writing, these are the highest performing solvers available to Matpower

for very large scale AC OPF problems. For Microsoft Windows users, a pre-compiled

MEX version of Ipopt (and numerous other solvers, such as CLP and GLPK) are

easily installable as part of the OPTI Toolbox58 [47].

When installed, Ipopt can be used by Matpower to solve both AC and DC

OPF problems by setting the opf.ac.solver or opf.dc.solver options, respectively,

equal to 'IPOPT'. See Table C-13 for a summary of the Ipopt-related Matpower

options. The many algorithm options can be set by creating an “Ipopt user op-

tions” function and specifying it via ipopt.opt fname to override the defaults set

by ipopt options. See help ipopt options and the options reference section of the

Ipopt documentation at http://www.coin-or.org/Ipopt/documentation/ for de-

tails.

It can also be used to solve general LP and QP problems via Matpower’s

common QP solver interface qps matpower with the algorithm option set to 'IPOPT'

(or 400 for backward compatibility), or by calling qps ipopt directly.

G.7 KNITRO – Non-Linear Programming Solver

KNITRO [32] is a general purpose optimization solver specializing in nonlinear

problems, available from Ziena Optimization, LLC. As of version 9, KNITRO in-

cludes a native Matlab interface, knitromatlab59. More information is available at

http://www.ziena.com/ and http://www.ziena.com/knitromatlab.htm.

Although KNITRO is a commercial package, at the time of this writing there is

a free academic license available, with details on their download page.

When installed, KNITRO’s Matlab interface function, knitromatlab or ktrlink,

can be used by Matpower to solve AC OPF problems by simply setting the

opf.ac.solver option to 'KNITRO'. See Table C-14 for a summary of KNITRO-related

Matpower options. The knitromatlab function uses callbacks to Matlab func-

tions to evaluate the objective function and its gradient, the constraint values and

Jacobian, and the Hessian of the Lagrangian.

KNITRO options can be controlled directly by creating a standard KNITRO op-

57See http://www.pardiso-project.org/ for the download links.

58The OPTI Toolbox is available from http://www.i2c2.aut.ac.nz/Wiki/OPTI/.

59Earlier versions required the Matlab Optimization Toolbox from The MathWorks, which

includes an interface to the KNITRO libraries called ktrlink, but the libraries themselves still had

to be acquired directly from Ziena Optimization, LLC.

205

tions ﬁle in your working directory and specifying it via the knitro.opt fname (or,

for backward compatibility, naming it knitro user options n.txt and setting Mat-

power’s knitro.opt option to n, where nis some positive integer value). See the

KNITRO user manuals at http://www.ziena.com/documentation.htm for details

on the available options.

G.8 MINOPF – AC OPF Solver Based on MINOS

MINOPF [30] is a MINOS-based optimal power ﬂow solver for use with Matpower.

It is for educational and research use only. MINOS [31] is a legacy Fortran-based

software package, developed at the Systems Optimization Laboratory at Stanford

University, for solving large-scale optimization problems.

While MINOPF is often Matpower’s fastest AC OPF solver on small problems,

as of Matpower 4, it no longer becomes the default AC OPF solver when it is in-

stalled. It can be selected manually by setting the opf.ac.solver option to 'MINOPF'

(see help mpoption for details).

Builds are available for Linux (32-bit), Mac OS X (PPC, Intel 32-bit) and Win-

dows (32-bit) at http://www.pserc.cornell.edu/minopf/.

G.9 MOSEK – High-performance LP and QP Solvers

MOSEK is a collection of optimization tools that includes high-performance solvers

for large-scale linear programming (LP) and quadratic programming (QP) problems,

among others. More information is available at http://www.mosek.com/.

Although MOSEK is a commercial package, at the time of this writing there is a

free academic license available. See http://mosek.com/resources/academic-license/

for more details.

When the Matlab interface to MOSEK is installed, the MOSEK LP and QP

solvers can be used to solve DC OPF problems by setting the opf.dc.solver op-

tion equal to 'MOSEK'. The solution algorithm for LP problems can be controlled

by Matpower’s mosek.lp alg option. See Table C-16 for other MOSEK-related

Matpower options. A “MOSEK user options” function can also be speciﬁed via

mosek.opt fname to override the defaults for any of the many MOSEK parame-

ters. For details see help mosek options and the “Parameters” reference in “The

MOSEK optimization toolbox for MATLAB manual” at http://docs.mosek.com/

7.1/toolbox/Parameters.html. You may also ﬁnd it helpful to use the symbolic

constants deﬁned by mosek symbcon.

206

It can also be used to solve general LP and QP problems via Matpower’s com-

mon QP solver interface qps matpower, or MILP and MIQP problems via miqps matpower,

with the algorithm option set to 'MOSEK'(or 600 for backward compatibility), or by

calling qps mosek or miqps mosek directly.

G.10 Optimization Toolbox – LP, QP, NLP and MILP Solvers

Matlab’s Optimization Toolbox [27,52], available from The MathWorks, provides

a number of high-performance solvers that Matpower can take advantage of.

It includes fmincon for nonlinear programming problems (NLP), and linprog and

quadprog for linear programming (LP) and quadratic programming (QP) problems,

respectively. For mixed-integer linear programs (MILP), it provides intlingprog.

Each solver implements a number of diﬀerent solution algorithms. More information

is available from The MathWorks, Inc. at http://www.mathworks.com/.

When available, the Optimization Toolbox solvers can be used to solve AC or DC

OPF problems by setting the opf.ac.solver or opf.dc.solver options, respectively,

equal to 'OT'.

The solution algorithm used by fmincon for NLP problems can be controlled

by Matpower’s fmincon.alg option. See Table C-10 for other Matpower options

related to fmincon. For linprog,quadprog and intlingprog, the corresponding Mat-

power option can be used to pass in native Optimization Toolbox options directly

to the solver. For example, to set the LP solver to use a dual simplex method, simply

set Matpower’s 'linprog.Algorithm'option to 'dual-simplex'. For details on the

full set of Optimization Toolbox options, please refer to their documentation.60

The Optimization Toolbox can also be used to solve general LP and QP problems

via Matpower’s common QP solver interface qps matpower, or MILP problems

via miqps matpower, with the algorithm option set to 'OT', or by calling qps ot or

miqps ot directly.

G.11 PARDISO – Parallel Sparse Direct and Multi-Recursive

Iterative Linear Solvers

The PARDISO package is a thread-safe, high-performance, robust, memory eﬃcient

and easy to use software for solving large sparse symmetric and non-symmetric linear

systems of equations on shared-memory and distributed-memory multiprocessor sys-

tems [50,51]. More information is available at http://www.pardiso-project.org.

60See http://www.mathworks.com/help/optim/ and [52].

207

When the Matlab interface to PARDISO is installed, PARDISO’s solvers can

be used to replace the built-in \operator for solving for the Newton update step

in Matpower’s default primal-dual interior point solver (MIPS) by setting the

mips.linsolver option equal to 'PARDISO'. The mplinsolve function can also be

called directly to solve Ax =bproblems via PARDISO or the built-in solver, de-

pending on the arguments supplied. This interface also gives access to the full range

of PARDISO’s options. For details, see help mplinsolve and the PARDISO User’s

Manual at http://www.pardiso-project.org/manual/manual.pdf.

When solving very large AC optimal power ﬂow problems with MIPS, selecting

PARDISO as the linear solver can often dramtically improve both computation time

and memory use.

Also note that precompiled MEX binaries for a high-performance version of

Ipopt, using the PARDISO linear solver, are available. Refer to Section G.6 for

more details.

G.12 SDP PF – Applications of a Semideﬁnite Programming

Relaxation of the Power Flow Equations

This package is contributed by Dan Molzahn and is currently included with Mat-

power in the <MATPOWER>/extras/sdp pf directory. Complete documentation is

available in <MATPOWER>/extras/sdp pf/documentation directory, and especially in

the ﬁle sdp pf documentation.pdf.

G.13 TSPOPF – Three AC OPF Solvers by H. Wang

TSPOPF [25] is a collection of three high performance AC optimal power ﬂow solvers

for use with Matpower. The three solvers are:

•PDIPM – primal/dual interior point method

•SCPDIPM – step-controlled primal/dual interior point method

•TRALM – trust region based augmented Lagrangian method

The algorithms are described in [26,41]. The ﬁrst two are essentially C-language

implementations of the algorithms used by MIPS (see Appendix A), with the ex-

ception that the step-controlled version in TSPOPF also includes a cost smoothing

technique in place of the constrained-cost variable (CCV) approach for handling

piece-wise linear costs.

208

The PDIPM in particular is signiﬁcantly faster for large systems than any previ-

ous Matpower AC OPF solver, including MINOPF. When TSPOPF is installed,

the PDIPM solver becomes the default optimal power ﬂow solver for Matpower.

Additional options for TSPOPF can be set using mpoption (see help mpoption for

details).

Builds are available for Linux (32-bit, 64-bit), Mac OS X (PPC, Intel 32-bit, Intel

64-bit) and Windows (32-bit, 64-bit) at http://www.pserc.cornell.edu/tspopf/.

209

Appendix H Release History

The full release history can be found in docs/CHANGES or online at http://www.

pserc.cornell.edu/matpower/CHANGES.txt.

H.1 Pre 1.0 – released Jun 25, 1997

Work on Matpower began in 1996, with an optimal power ﬂow based on Matlab’s

constr function.

H.2 Version 1.0 – released Sep 17, 1997

The Matpower 1.0 User’s Manual is available online.61

New Features

•Successive LP-based optimal power ﬂow solver, by Deqiang Gan.

•Automatic conversion between possibly non-consecutive external bus numbers

and consecutive internal bus numbers.

•IEEE CDF to Matpower case conversion script, by Deqiang Gan.

Other Changes

•Top-level scripts converted to functions that take case ﬁle as input.

•Updated case ﬁle format. Generator costs moved to separate gencost table.

H.3 Version 1.0.1 – released Sep 19, 1997

Changes

•Bug ﬁxes.

61http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-1.pdf

210

H.4 Version 2.0 – released Dec 24, 1997

The Matpower 2.0 User’s Manual is available online.62

New Features

•greatly enhanced output options

•fast-decoupled power ﬂow

•optional costs for reactive power generation in OPF

•consolidated parameters in Matpower options vector

Other Changes

•optimized building of Ybus and Jacobian matrices (much faster on large systems,

especially in Matlab 5)

•highly improved unit decommitment algorithm

•completely rewritten LP-based OPF solver

•various bug ﬁxes

62http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-2.0.pdf

211

H.5 Version 3.0 – released Feb 14, 2005

The Matpower 3.0 User’s Manual is available online.63

New Features

•Compatibility with Matlab 7 and Optimization Toolbox 3.

•DC power ﬂow and DC OPF solvers added.

•Option to enforce generator reactive power limits in AC power ﬂow solution.

•Gauss-Seidel power ﬂow solver added.

•Support for MINOS-based OPF solver added (separate package, see

http://www.pserc.cornell.edu/minopf/ for more details)

•Multiple generators at a single bus.

•Saving of solved cases as M-ﬁles or MAT-ﬁles.

•Loading of input data from M-ﬁles, MAT-ﬁles, or structs.

•Improved decommitment algorithm.

•Added a very incomplete test suite.

•Handling of dispatchable loads in OPF, modeled as negative generators with

constant power factor constraint.

Bugs Fixed

•Phase shifters shifted the wrong direction.

•Minor ﬁxes to IEEE CDF to Matpower format conversion (reported by D.

Devaraj and Venkat)

•Flows on out-of-service lines were not being zeroed out. (reported by Ramazan

Caglar)

•Reported total inter-tie ﬂow values and area export values were incorrect.

•Several other bugs in solution printouts.

63http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-3.0.pdf

212

H.6 Version 3.2 – released Sep 21, 2007

The Matpower 3.2 User’s Manual is available online.64

New Features

•AC OPF formulation enhancements

–new generalized cost model

–piece-wise linear generator PQ capability curves

–branch angle diﬀerence constraints

–simpliﬁed interface for specifying additional linear constraints

–option to use current magnitude for line ﬂow limits (set OPF FLOW LIM to

2, fmincopf solver only)

•AC OPF solvers

–support for TSPOPF, a new optional package of three OPF solvers, im-

plemented as C MEX ﬁles, suitable for large scale systems

–ability to specify initial value and bounds on user variables z

•New (v. 2) case ﬁle format

–all data in a single struct

–generator PQ capability curves

–generator ramp rates

–branch angle diﬀerence limits

•New function makePTDF to build DC PDTF matrix

•Added 5 larger scale (>2000 bus) cases for Polish system (thanks to Roman

Korab).

•Improved identiﬁcation of binding constraints in printout.

•Many new tests in test suite.

64http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-3.2.pdf

213

Bugs Fixed

•Phase shifters shifted the wrong direction, again (v.2 had it right).

•Fixed bug in pfsoln which caused incorrect value for reactive generation when

Qmin =Qmax for all generators at a bus in power ﬂow solution.

Incompatible Changes

•User supplied Amatrix for general linear constraints in OPF no longer includes

columns for helper variables for piecewise linear gen costs, and now requires

columns for all x(OPF) variables.

•Changed the sign convention used for phase shifters to be consistent with PTI,

PowerWorld, PSAT, etc. E.g. A phase shift of 10 deg now means the voltage

at the “to” end is delayed by 10 degrees.

•Name of option 24 in mpoption changed from OPF P LINE LIM to OPF FLOW LIM.

214

H.7 Version 4.0 – released Feb 7, 2011

The Matpower 4.0 User’s Manual is available online.65

New Features

•Licensed under the GNU General Public License (GPL).

•Added compatibility with GNU Octave, a free, open-source Matlab clone.

•Extensive OPF enhancements:

–Generalized, extensible OPF formulation applies to all solvers (AC and

DC).

–Improved method for modifying OPF formulation and output via a new

user-deﬁned callback function mechanism.

–Option to co-optimize reserves based on ﬁxed zonal reserve requirements,

implemented using new callback function mechanism.

–Option to include interface ﬂow limits (based on DC model ﬂows), imple-

mented using new callback function mechanism.

•New high performance OPF solvers:

–MIPS (Matpower Interior Point Solver), a new a pure-Matlab im-

plementation of the primal-dual interior point methods from the optional

package TSPOPF. MIPS is suitable for large systems and is used as Mat-

power’s default solver for AC and DC OPF problems if no other optional

solvers are installed. To select MIPS explicitly, use OPF ALG = 560/565 and

OPF ALG DC = 200/250 for AC and DC OPF, respectively. MIPS can also

be used independently of Matpower as a solver for general nonlinear

constrained optimization problems.

–Support for the Ipopt interior point optimizer for large scale nonlinear

optimization. Use OPF ALG = 580 and OPF ALG DC = 400 for AC and DC

OPF, respectively. Requires the Matlab MEX interface for Ipopt, avail-

able from https://projects.coin-or.org/Ipopt/.

–Support for CPLEX to solve LP and QP problems. Set option OPF ALG DC = 500

to use CPLEX to solve the DC OPF. Requires the Matlab interface to

65http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-4.0.pdf

215

CPLEX, available from http://www.ibm.com/software/integration/

optimization/cplex-optimizer/. See help mpoption for more CPLEX

options.

–Support for MOSEK to solve LP and QP problems. Set option OPF ALG DC = 600

to use MOSEK to solve the DC OPF. Requires the Matlab interface to

MOSEK, available from http://www.mosek.com/. See help mpoption for

more MOSEK options.

–Updated support for MathWorks’ Optimization Toolbox solvers, fmincon(),

linprog() and quadprog().

•Improved documentation:

–New, rewritten User’s Manual (docs/manual.pdf).

–Two new Tech Notes, available from Matpower home page.

∗Uniform Price Auctions and Optimal Power Flow

∗AC Power Flows, Generalized OPF Costs and their Derivatives using

Complex Matrix Notation

–Help text updates to more closely match MathWorks conventions.

•New functions:

–load2disp() converts from ﬁxed to dispatchable loads.

–makeJac() forms the power ﬂow Jacobian. Optionally returns the system

admittance matrices too.

–makeLODF() computes line outage distribution factors.

–modcost() shifts/scales generator cost functions.

–qps matpower() provides a consistent, uniﬁed interface to all of Mat-

power’s available QP/LP solvers, serving as a single wrapper around

qps bpmpd(),qps cplex(),qps ipopt(),qps mips(), and qps ot() (Opti-

mization Toolbox, i.e. quadprog(),linprog()).

–scale load() conveniently modiﬁes multiple loads.

–total load() retreives total load for the entire system, a speciﬁc zone or

bus, with options to include ﬁxed loads, dispatchable loads or both.

•Option to return full power ﬂow or OPF solution in a single results struct,

which is a superset of the input case struct.

216

•Ability to read and save generalized OPF user constraints, costs and variable

limits as well as other user data in case struct.

•Numerous performance optimizations for large scale systems.

•Perl script psse2matpower for converting PSS/E data ﬁles to Matpower case

format.

•Deprecated areas data matrix (was not being used).

•Many new tests in test suite.

Bugs Fixed

•Auction code in extras/smartmarket in all previous versions contained a design

error which has been ﬁxed. Prices are now scaled instead of shifted when

modiﬁed according to speciﬁed pricing rule (e.g. LAO, FRO, LAB, FRB, split-

the-diﬀerence, etc.). Auctions with both real and reactive oﬀers/bids must be

type 0 or 5, type 1 = LAO is no longer allowed.

•Branch power ﬂow limits could be violated when using the option OPF FLOW LIM = 1.

Incompatible Changes

•Renamed functions used to compute AC OPF cost, constraints and hessian,

since they are used by more than fmincon:

costfmin →opf costfcn

consfmin →opf consfcn

hessfmin →opf hessfcn

•Input/output arguments to uopf() are now consistent with opf().

•dAbr dV() now gives partial derivatives of the squared magnitudes of ﬂows

w.r.t. V, as opposed to the magnitudes.

217

H.8 Version 4.1 – released Dec 14, 2011

The Matpower 4.1 User’s Manual is available online.66

New Features

•More new high performance OPF solvers:

–Support for the KNITRO interior point optimizer for large scale nonlin-

ear optimization. Use OPF ALG = 600 for to select KNITRO to solve the

AC OPF. Requires the Matlab Optimization Toolbox and a license for

KNITRO, available from http://www.ziena.com/. See help mpoption

for more KNITRO options.

–Support for Gurobi to solve LP and QP problems. Set option OPF ALG DC = 700

to use Gurobi to solve the DC OPF. Requires Gurobi (http://www.

gurobi.com/) and the Gurobi MEX interface (http://www.convexoptimization.

com/wikimization/index.php/Gurobi_mex). See help mpoption for more

Gurobi options.

–Updated for compatibility with CPLEX 12.3.

–Changed options so that fmincon uses its interior-point solver by default.

Much faster on larger systems.

•Support for basic modeling of DC transmission lines.

•New case ﬁles with more recent versions of Polish system.

•Power ﬂow can handle networks with islands.

Bugs Fixed

•Computation of quadratic user-deﬁned costs had a potentially fatal error.

Thanks to Stefanos Delikaraoglou for ﬁnding this.

•Calculation of reserve prices in toggle reserves() had an error.

Incompatible Changes

•Optional packages TSPOPF and MINOPF must be updated to latest versions.

66http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-4.1.pdf

218

H.9 Version 5.0 – released Dec 17, 2014

The Matpower 5.0 User’s Manual is available online.67

New Features

•Continuation power ﬂow with tangent predictor and Newton method corrector,

based on code contributed by Shrirang Abhyankar and Alex Flueck.

•SDP PF, a set of applications of a semideﬁnite programming relaxation of the

power ﬂow equations, contributed by Dan Molzahn (see extras/sdp pf):

–Globally optimal AC OPF solver (under certain conditions).

–Functions to check suﬃcient conditions for:

∗global optimality of OPF solution

∗insolvability of power ﬂow equations

•PSS/E RAW data conversion to Matpower case format (experimental) based

on code contributed by Yujia Zhu.

•Brand new extensible Matpower options architecture based on options struct

instead of options vector.

•Utility routines to check network connectivity and handle islands and isolated

buses.

•New extension implementing DC OPF branch ﬂow soft limits. See help toggle softlims

for details.

•New and updated support for 3rd party solvers:

–CPLEX 12.6

–GLPK

–Gurobi 5.x

–Ipopt 3.11.x

–KNITRO 9.x.x

–Optimization Toolbox 7.1

67http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-5.0.pdf

219

•Numerous performance enhancements.

•New functions:

–runcpf() for continuation power ﬂow.

–case info() for summarizing system information, including network con-

nectivity.

–extract islands() to extract a network island into a separate Mat-

power case.

–find islands() to detect network islands.

–@opt model/describe idx() to identify variable, constraint or cost row

indices to aid in debugging.

–margcost() for computing the marginal cost of generation.

–psse2mpc() to convert PSS/E RAW data into Matpower case format.

–get losses() to compute branch series losses and reactive charging injec-

tions and derivatives as functions of bus voltages.

–New experimental functions in extras/misc for computing loss factors,

checking feasibility of solutions, converting losses to negative bus injec-

tions and modifying an OPF problem to make it feasible.

•Added case5.m, a 5-bus, 5-generator example case from Rui Bo.

•New options:

–scale load() can scale corresponding gencost for dispatchable loads.

–makeJac() can return full Jacobian instead of reduced version used in

Newton power ﬂow updates.

–modcost() can accept a vector of shift/scale factors.

–total load() can return actual or nominal values for dispatchable loads.

–runpf(),runopf(), etc. can send pretty-printed output to ﬁle without

also sending it to the screen.

–out.suppress detail option suppresses all output except system summary

(on by default for large cases).

–opf.init from mpc option forces some solvers to use user-supplied starting

point.

220

–MIPS 1.1 includes many new user-settable options.

•Reimplementated @opf model class as sub-class of the new @opt model class,

which supports indexed named sets of variables, constraints and costs.

•Many new tests in test suite.

Bugs Fixed

•Running a power ﬂow for a case with DC lines but no gencost no longer causes

an error.

•Fixed a bug in runpf() where it was using the wrong initial voltage magnitude

for generator buses marked as PQ buses. Power ﬂow of solved case was not

converging in zero iterations as expected.

•Fixed fatal bug in MIPS for unconstrained, scalar problems. Thanks to Han

Na Gwon.

•Fixed a bug in int2ext() where converting a case to internal ordering before

calling runpf() or runopf() could result in a fatal error due to mismatched

number of columns in internal and external versions of data matrices. Thanks

to Nasiruzzaman and Shiyang Li for reporting and detailing the issue.

•DC OPF now correctly sets voltage magnitudes to 1 p.u. in results.

•Fixed a bug in MIPS where a near-singular matrix could produce an extremely

large Newton step, resulting in incorrectly satisfying the relative feasibility

criterion for successful termination.

•Improved the starting point created for Ipopt, KNITRO and MIPS for vari-

ables that are only bounded on one side.

•Fixed bug in savecase() where the function name mistakenly included the path

when the fname input included a path.

•Fixed bugs in runpf() related to enforcing generator reactive power limits when

all generators violate limits or when the slack bus is converted to PQ.

•Fixed crash when using KNITRO to solve cases with all lines unconstrained.

221

•Fixed memory issue resulting from nested om ﬁelds when repeatedly running an

OPF using the results of a previous OPF as input. Thanks to Carlos Murillo-

S´anchez.

•Fixed fatal error when uopf() shuts down all gens attempting to satisfy Pmin

limits.

•Reactive power output of multiple generators at a PQ bus no longer get re-

allocated when running a power ﬂow.

•Fixed a bug in savecase() where a gencost matrix with extra columns of zeros

resulted in a corrupted Matpower case ﬁle.

•Fixed bug in runpf() that caused a crash for cases with pf.enforce q lims

turned on and exactly two Q limit violations, one Qmax and one Qmin. Thanks

to Jose Luis Mar´ın.

Incompatible Changes

•Optional packages TSPOPF and MINOPF must be updated to latest versions.

•Renamed cdf2matp() to cdf2mpc() and updated the interface to be consistent

with psse2mpc().

•Removed ot opts ﬁeld, replaced with linprog opts and quadprog opts ﬁelds in

the opt argument to qps matpower() and qps ot().

•The name of the mips() option used to specify the maximum number of step-

size reductions with step control on was changed from max red to sc.red it

for consistency with other Matpower options.

•Removed max it option from qps matpower() (and friends) args. Use algorithm

speciﬁc options to control iteration limits.

•Changed behavior of branch angle diﬀerence limits so that 0 is interpreted as

unbounded only if both ANGMIN and ANGMAX are zero.

•In results struct returned by an OPF, the value of results.raw.output.alg

is now a string, not an old-style numeric alg code.

222

•Removed:

–Support for Matlab 6.x.

–Support for constr() and successive LP-based OPF solvers.

–Support for Gurobi 4.x/gurobi mex() interface.

–extras/cpf, replaced by runcpf().

–extras/psse2matpower, replaced by psse2mpc().

223

H.10 Version 5.1 – released Mar 20, 2015

The Matpower 5.1 User’s Manual is available online.68

New License

•Switched to the more permissive 3-clause BSD license from the previously used

GNU General Public License (GPL) v3.0.

New Case Files

•Added four new case ﬁles, ranging from 89 up to 9421 buses, representing

parts of the European high voltage transmission network, stemming from the

Pan European Grid Advanced Simulation and State Estimation (PEGASE)

project. Thanks to C´edric Josz and colleagues from the French Transmission

System Operator.

New Documentation

•Added an online function reference to the website at http://www.pserc.

cornell.edu/matpower/docs/ref/.

New Features

•Added support for using PARDISO (http://www.pardiso-project.org/) as

linear solver for computing interior-point update steps in MIPS, resulting in

dramatic improvements in computation time and memory use for very large-

scale problems.

•Added support for LP/QP solver CLP (COIN OR Linear Programming, http:

//www.coin-or.org/projects/Clp.xml). Use opf.dc.solver option 'CLP'or

qps clp().

•Added support for OPTI Toolbox (http://www.i2c2.aut.ac.nz/Wiki/OPTI/)

versions of CLP, GLPK and Ipopt solvers, providing a very simple installation

path for some free high-performance solvers on Windows platforms.

•Network reduction toolbox for creating smaller approximate network equiv-

alents from a larger original case ﬁle. Contributed by Yujia Zhu and Daniel

Tylavsky.

68http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-5.1.pdf

224

•Added uniﬁed interface to various solvers for mixed-integer linear and quadratic

programming (MILP/MIQP) problems.

•Major update to have fcn(), which now determines and caches version num-

bers and release dates for optional packages, and includes ability to toggle the

availability of optional functionality.

•New and updated support for 3rd party solvers:

–High-performance Ipopt-PARDISO solver builds from the PARDISO Project

http://www.pardiso-project.org (at time of release this is Matpower’s

highest performing solver for very large scale AC OPF problems)

–OPTI Toolbox versions of CLP, GLPK, Ipopt

–CLP

–Gurobi 6.x

–KNITRO 9.1

–MOSEK 7.1

–Optimization Toolbox 7.2

∗dual-simplex algorithm for linprog()

∗intlinprog() for MILP

•New functions:

–mplinsolve() provides uniﬁed interface for linear system solvers, including

PARDISO and built-in backslash operator

–miqps matpower() provides uniﬁed interface to multiple MILP/MIQP solvers.

–miqps clex() provides a uniﬁed MILP/MIQP interface to CPLEX.

–miqps glpk() provides a uniﬁed MILP interface to GLPK.

–miqps gurobi() provides a uniﬁed MILP/MIQP interface to Gurobi.

–miqps mosek() provides a uniﬁed MILP/MIQP interface to MOSEK.

–miqps ot() provides a uniﬁed MILP interface to intlingprog().

–mosek symbcon() deﬁnes symbolic constants for setting MOSEK options.

225

Other Improvements

•Cleaned up and improved consistency of output in printpf() for generation

and dispatchable load constraints.

•Modiﬁed runcpf() to gracefully handle the case when the base and target cases

are identical (as opposed to getting lost in an inﬁnite loop).

•Optional generator and dispatchable load sections in pretty-printed output now

include oﬀ-line units.

Bugs Fixed

•Fixed fatal bug in case info() for islands with no generation.

•Fixed fatal bug in toggle dcline() when pretty-printing results. Thanks to

Deep Kiran for reporting.

•Fixed sign error on multipliers on lower bound on constraints in qps clp() and

qps glpk().

•Fixed bug in handling of interface ﬂow limits, where multipliers on binding

interface ﬂow limits were oﬀ by a factor of the p.u. MVA base.

•Fixed minor bug with poly2pwl(), aﬀecting units with PMAX ≤0.

•Fixed error in qps mosek() in printout of selected optimizer when using MOSEK 7.

•Fixed bug in hasPQcap() that resulted in ignoring generator capability curves

for units whose reactive range increases as real power output increases. Thanks

to Irina Boiarchuk for reporting.

•Fixed several incompatibilities with Matlab versions <7.3.

226

H.11 Version 6.0 – released Dec 16, 2016

The Matpower 6.0 User’s Manual is available online.69

New Open Development Model

•Matpower development has moved to GitHub! The code repository is now

publicly available to clone and submit pull requests.70

•Public issue tracker for reporting bugs, submitting patches, etc.71

•Separate repositories for Matpower, MOST, MIPS, MP-Test, all available

from https://github.com/MATPOWER/.

•New developer e-mail list (MATPOWER-DEV-L) to facilitate communication

between those collaborating on Matpower-related development. Sign up at:

http://www.pserc.cornell.edu/matpower/mailinglists.html#devlist.

New Case Files

•Added 9 new case ﬁles, 8 cases ranging from 1888 to 6515 buses representing the

French system, and a 13,659-bus case representing parts of the of the European

high voltage transmission network, stemming from the Pan European Grid

Advanced Simulation and State Estimation (PEGASE) project. Thanks again

to C´edric Josz and colleagues from the French Transmission System Operator.

Please cite reference [43] when publishing results based on these cases.

•Added case145.m, IEEE 145 bus, 50 generator dynamic test case from the U

of WA Power Systems Test Case Archive72.

•Added case33bw.m, a 33-bus radial distribution system from Baran and Wu.

69http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-6.0.pdf

70https://github.com/MATPOWER/matpower

71https://github.com/MATPOWER/matpower/issues

72http://www.ee.washington.edu/research/pstca/dyn50/pg_tcadd50.htm

227

New Features

•Matpower Optimal Scheduling Tool (MOST) 1.0b1 is a major new fea-

ture, implementing a full range of optimal power scheduling problems, from

a simple as a deterministic, single period economic dispatch problem with no

transmission constraints to as complex as a stochastic, security-constrained,

combined unit-commitment and multiperiod OPF problem with locational con-

tingency and load-following reserves, ramping costs and constraints, deferrable

demands, lossy storage resources and uncertain renewable generation. See

docs/MOST-manual.pdf for details.

•General mechanism for applying modiﬁcations to an existing Matpower case.

See apply changes() and idx ct().

•Redesigned CPF callback mechanism to handle CPF events such as generator

limits, nose point detection, etc. Included event log in CPF results.

•Added options 'cpf.enforce p lims'and 'cpf.enforce q lims'to enforce gen-

erator active and reactive power limts in the continuation power ﬂow.

•Added OPF option 'opf.use vg'to provide a convenient way to have the OPF

respect the generator voltage setpoints speciﬁed in the gen matrix.

•Experimental foundation for handling of ZIP load models in power ﬂow (New-

ton, fast-decoupled only), continuation power ﬂow, and optimal power ﬂow

(MIPS, fmincon, KNITRO, Ipopt solvers only). Currently, ZIP loads can only

be speciﬁed on a system-wide basis using the experimental options

'exp.sys wide zip loads.pw'and 'exp.sys wide zip loads.qw'.

•Support for quadprog() under GNU Octave.

•New contributed extras:

–Plot electrically meaningful drawings of a Matpower case using plot mpc()

in extras/misc, contributed by Paul Cuﬀe.

–Find the maximum loadability limit of a system via an optimal power

ﬂow and dispatchable loads, using maxloadlim() in extras/maxloadlim,

contributed by Camille Hamon.

–Create a quadratically-constrained quadratic programming (QCQP) rep-

resentation of the AC power ﬂow problem using using qcqp opf() in

extras/misc, contributed by C´edric Josz and colleagues.

228

•New functions:

–apply changes() and idx ct() provide a general mechanism for applying

modiﬁcations to an existing Matpower case.

–feval w path() evaluates a function located at a speciﬁed path, outside

of the Matlab path.

–mpopt2qpopt() provides a common interface for creating options struct for

mi/qps matpower() from a Matpower options struct.

•New function options:

–Option to call makeB(),makeBdc(),makePTDF(),scale load(), and total load()

with full case struct (mpc) instead of individual data matrices (bus,branch,

etc.).

–total load(), which now computes voltage-dependent load values, accepts

the values 'bus'and 'area'as valid values for 'load zone'argument.

Other Improvements

•Changed default solver order for LP, QP, MILP, MIQP problems to move

Gurobi before CPLEX and BPMPD after Optimization Toolbox and GLPK.

•Added some caching to mpoption() and made minor changes to nested struct copy()

to greatly decrease the overhead added by mpoption() when running many

small problems.

•Added option 'cpf.adapt step damping'to control oscillations in adaptive step

size control for continuation power ﬂow.

•Added CPF user options for setting tolerances for target lambda detection and

nose point detection, 'cpf.target lam tol'and 'cpf.nose tol', respectively.

•Added support for Matlab Optimization Toolbox 7.5 (R2016b).

•Added support for MOSEK v8.x.

•Added tests for power ﬂow with 'pf.enforce q lims'option.

•Updated network reduction code to handle cases with radially connected ex-

ternal buses.

229

•Updated versions of qcqp opf() and qcqp opf() in extras/misc,from C´edric

Josz.

•Added “Release History” section to Appendix of manual.

•Many new tests.

Bugs Fixed

•Fixed bug in toggle dclines() that resulted in fatal error when used with OPF

with reactive power costs. Thanks to Irina Boiarchuk.

•Fixed fatal bug in update mupq() aﬀecting cases where QMIN is greater than or

equal to QC1MIN and QC2MIN (or QMAX is less than or equal to QC1MAX and QC2MAX)

for all generators. Thanks Jose Miguel.

•Copying a ﬁeld containing a struct to a non-struct ﬁeld with nested struct copy()

now overwrites rather than causing a fatal error.

•Fixed a bug in psse convert xfmr() where conversion of data for transformers

with CZ=3 was done incorrectly. Thanks to Jose Marin and Yujia Zhu.

•Fixed a fatal bug in psse convert xfmr() aﬀecting transformers with CW

and/or CZ equal to 1. Thanks to Matthias Resch.

•Fixed a crash in have fcn() caused by changes in OPTI Toolbox v2.15 (or

possibly v2.12)

•Commented out isolated bus 10287 in case3375wp.m.

•Added code to DC OPF to return success = 0 for cases where the matrix is

singular (e.g. islanded system without slack).

•Fixed problem in have fcn() where SeDuMi was turning oﬀ and leaving oﬀ all

warnings.

•Fixed shadow prices on variable bounds for AC OPF for fmincon,Ipopt, and

KNITRO.

•In savecase() single quotes are now escaped properly in bus names.

•Generator capability curve parameters that deﬁne a zero-reactive power line

no longer cause a fatal error.

230

•Bad bus numbers no longer cause a fatal error (after reporting the bad bus

numbers) in case info().

Incompatible Changes

•Removed fairmax() from the public interface by moving it inside uopf(), the

only place it was used.

•Removed 'cpf.user callback args'option and modiﬁed 'cpf.user callback'.

•Changed name of 'cpf.error tol'option to 'cpf.adapt step tol'.

231

H.12 Version 7.0 – beta 1 released released Oct 31, 2018

The Matpower 7.0b1 User’s Manual is available online.73

New Features

•New Matpower installer script install matpower() automatically updates

Matlab or Octave paths or optionally provides the commands required to so.

•Support for additional user-deﬁned general nonlinear constraints and costs in

AC OPF.

•Support for exporting Matpower case to PSS/E RAW data format.

•Three new variants of the standard AC OPF formulation, for a total of four,

including both nodal power and current balance constraints and both polar

and cartesian representations of voltage. See the new opf.current balance

and opf.v cartesian options. Thanks to Baljinnyam Sereeter.

•Three new power ﬂow algorithms for radial distribution systems selected via

the three new options for pf.alg, namely 'PQSUM','ISUM','YSUM'. Also in-

cludes new Matpower options pf.radial.max it and pf.radial.vcorr. See

Section 4.3 on “Distribution Power Flow” for details. Thanks to Mirko Todor-

ovski.

•Major update to OPF soft limit functionality, supporting soft limits on all AC

and DC OPF inequality constraints, including branch ﬂow constraints, bus

voltage bounds, generator active and reactive bounds, branch ﬂow and branch

angle diﬀerence limits. Thanks to Eran Schweitzer.

•New options:

–pf.nr.lin solver controls the linear solver used to compute the Newton

update step in the Newton-Raphson power ﬂow.

–pf.radial.max it and pf.radial.vcorr are options for the new radial

power ﬂow algorithms. Thanks to Mirko Todorovski.

–cpf.enforce flow lims and cpf.enforce v lims control enforcement of

branch ﬂow and bus voltage magnitude limits in the continuation power

73http://www.pserc.cornell.edu/matpower/docs/MATPOWER-manual-7.0b1.pdf

232

ﬂow and cpf.flow lims tol and cpf.v lims tol control the respective de-

tection tolerances. Thanks to Ahmad Sadiq Abubakar and Shrirang Ab-

hyankar.

–opf.current balance and opf.v cartesian control formulation used for

AC OPF. Thanks to Baljinnyam Sereeter.

–opf.softlims.default determines whether or not to include soft lim-

its on constraints whose parameters are not speciﬁed explicitly in the

mpc.softlims struct. For use with enhanced toggle softlims() function-

ality. Thanks to Eran Schweitzer.

–opf.start replaces deprecated opf.init from mpc and adds a new possi-

bility to automatically run a power ﬂow to initialize the starting state for

the OPF.

•New functions:

–calc branch angle calcultes voltage angle diﬀerences for branches.

–dImis dV() evaluates the partial derivatives of nodal current balance with

respect to bus voltages.

–d2Imis dV2() evaluates the 2nd derivatives of nodal current balance with

respect to bus voltages.

–d2Imis dVdSg() evaluates the 2nd derivatives of nodal current balance with

respect to bus voltages and generator injections.

–d2Abr dV2() evaluates the 2nd derivatives of squared branch ﬂows with

respect to bus voltages.

–gentypes() and genfuels provide list of standard generator unit types

and fuel types, respectively.

–install matpower() installs Matpower by automatically modifying or,

alternatively, showing needed modiﬁcations to Matlab or Octave path.

–loadshed() computes MW curtailments of dispatchable loads.

–opf branch ang fcn() evaluates AC branch ﬂow limit constraints and gra-

dients.

–opf branch ang hess() evaluates Hessian of AC branch ﬂow limit con-

straints.

–opf current balance fcn() evaluates AC current balance constraints and

gradients.

233

–opf current balance hess() evaluates Hessian of AC current balance con-

straints.

–opf veq fcn() evaluates voltage magnitude equality constraints and gra-

dients.

–opf veq hess() evaluates Hessian of voltage magnitude equality constraints.

–opf vlim fcn() evaluates voltage magnitude limit constraints and gradi-

ents.

–opf vlim hess() evaluates Hessian of voltage magnitude limit constraints.

–opf vref fcn() evaluates reference voltage angle equality constraints and

gradients.

–opf vref hess() evaluates Hessian of reference voltage angle equality con-

straints.

–opt model/add lin constraint() to add linear constraints to an optimiza-

tion model.

–opt model/add nln constraint() to add nonlinear constraints to an opti-

mization model.

–opt model/init indexed name() to initialize the indices for an indexed

name set of constraints, costs or variables.

–save2psse() to export a Matpower case to PSS/E RAW data format.

–savechgtab() to save change tables, such as those used by apply changes,

to a ﬁle.

234

New Case Files

•Seven new purely synthetic cases from the ACTIVSg team (ASU, Cornell,

Texas A&M, U of Illinois, and VCU - Synthetic grids), resulting from work

supported by the ARPA-E GRID DATA program. Thanks to Adam Birchﬁeld

and the ACTIVSg team.

–case ACTIVSg200 – 200-bus Illinois synthetic model

–case ACTIVSg500 – 500-bus South Carolina synthetic model

–case ACTIVSg2000 – 2000-bus Texas synthetic model

–case ACTIVSg10k – 10,000-bus US WECC synthetic model

–case ACTIVSg25k – 25,000-bus US Northeast/Mid-Atlantic synthetic model

–case ACTIVSg70k – 70,000-bus Eastern US synthetic model

–case SyntheticUSA – 82,000-bus continental USA synthetic model (ag-

gregation of case ACTIVSg70k,case ACTIVSg10k, and case ACTIVSg2000,

connected by 9 DC lines)

Some of these cases also include contingency tables and/or hourly load scenarios

for 1 year.

–contab ACTIVSg200

–contab ACTIVSg500

–contab ACTIVSg2000

–contab ACTIVSg10k

–scenarios ACTIVSg200

–scenarios ACTIVSg2000

•New RTS-GMLC case from https://github.com/GridMod/RTS-GMLC.

–case4 RTS GMLC

•Six new radial distribution system cases. Thanks to Mirko Todorovski.

–case4 dist

–case18

–case22

–case69

–case85

–case141

235

New Documentation

•Two new Tech Notes, available from Matpower home page.

–Matpower Technical Note 3 “Addendum to AC Power Flows and their

Derivatives using Complex Matrix Notation: Nodal Current Balance” [37]

–Matpower Technical Note 4 “AC Power Flows and their Derivatives

using Complex Matrix Notation and Cartesian Coordinate Voltages” [38]

•L

EX source code for Matpower User’s Manual included in docs/src, for

MIPS User’s Manual in mips/docs/src and for MOST User’s Manual in most/docs/src.

Other Improvements

•Update versions of included packages:

–MIPS 1.3.

–MOST 1.0.1.

–MP-Test 7.0b1.

•Continuous integration testing via GitHub and Travis-CI integration.

•Support added in core optimization model opt model for:

–general nonlinear constraints

–general nonlinear costs

–quadratic costs

•Refactor OPF code to take advantage of new opt model capabilities for nonlin-

ear constraints and quadratic and nonlinear costs.

•Derivative functions now support cartesian coordinates for voltage in addition

to polar coordinates.

•In the Newton power ﬂow, for larger systems use explicit LU decomposition

with AMD reordering and the 3 output argument form of lu (to select the

Gilbert-Peierls algorithm), resulting in up to a 2x speedup in Matlab, 1.1x

in Octave. Thanks to Jose Luis Mar´ın.

•Support plotting of multiple nose curves in CPF by allowing option cpf.plot.bus

to take on vector values.

236

•Add line for curtailed load to case info() output.

•Change default implementation of active power line ﬂow constraints (opf.flow lim

='P') to use ﬂow directly, rather than square of ﬂow, which is now a separate

option, namely opf.flow lim = '2'.Thanks to Nico Meyer-Huebner.

•Add genfuels and gentypes to establish standard set of values for optional

mpc.genfuel and mpc.gentype ﬁelds for generator fuel type and generator unit

type, respectively.

•Add support for gentype and genfuel ﬁelds of Matpower case struct in

extract islands,ext2int,int2ext,load2disp and savecase.

•Add support for bus name ﬁeld of Matpower case struct to extract islands,

ext2int and int2ext.

•Deprecated functions:

–d2AIbr dV2() – use dA2br dV2() instead.

–d2ASbr dV2() – use dA2br dV2() instead.

–opt model/add constraints() – use the corresponding one of the follow-

ing methods instead: add lin constraint(),add nln constraint(), or

init indexed name().

–opt model/add costs() – use the corresponding one of the following meth-

ods instead: add quad cost(),add nln cost(),add legacy cost(), or

init indexed name().

–opt model/linear constraints() – use opt model/params lin constraint()

instead.

–opt model/build cost params() – no longer needed, incorporated into

opt model/params legacy cost().

–opt model/get cost params() – use opt model/params legacy cost() in-

stead.

237

Bugs Fixed

•Fix bug in conversion of older versions of Matpower options.

•Fix bug #4 where some Q limits were not being respected by CPF when buses

were converted to PQ by initial power ﬂow run. Thanks to Shruti Rao.

•Fix fatal bug #8 when calling runcpf with base and target cases with identical

load and generation. Thanks to Felix.

•Fix fatal bug in get losses when computing derivatives of reactive branch

injections and ﬁx some related tests.

•Fix #11 fatal error encountered when running test matpower with SDP PF and

YALMIP installed, but no SDP solver. Now checks for availability of SeDuMi,

SDP3 or MOSEK before attempting to run SDP PF tests that require solving

an SDP. Thanks to Felix.

•Fix bug #12 where the CPF could terminate early when requesting trace of

the full curve with P or Q limits enforced, if a limit becomes binding at the

base case. Thanks to Felix.

•Fix bug #13 where setting all buses to type NONE (isolated) resulted in a fatal

error for ext2int,runpf,runcpf and runopf.Thanks to SNPerkin.

•Fix bug #21 where a continuation power ﬂow that failed the ﬁrst corrector

step would produce a fatal error. Thanks to Elis Nycander.

•Fix bug #23 where the continuation power ﬂow could switch directions unex-

pectedly when the operating point switched from stable to unstable manifold

or vice-versa after hitting a limit. Thanks to Elis Nycander and Shrirang Ab-

hyankar.

•Fix bug #26 where, in a continuation power ﬂow, a reactive limit at a bus

could be detected in error if multiple generators at the bus had reactive ranges

of very diﬀerent sizes. Thanks to Elis Nycander and Shrirang Abhyankar.

•Fix runpf handling of case where individual power ﬂow fails during Q limit

enforcement.

238

Incompatible Changes

•Move included Matpower case ﬁles to new data subdirectory.

•Turning soft limits on without specifying any parameters explicitly in mpc.softlims

now implements soft limits for all constraints, by default, not just branch ﬂow

limits. And the format of the input parameters in mpc.softlims has changed.

See help toggle softlims or Tables 7-9,7-10 and 7-11 for the details.

•Swap the order of the output arguments of dSbus dV()) for polar coordinate

voltages (angle before magnitude) for consistency.

•Correct signs of phase shifter angles in Polish system cases, since they were

based on the old sign convention used by Matpower prior to v3.2 (see change

on 6/21/07). Aﬀects the following cases:

–case2383wp

–case2736sp

–case2737sop

–case2746wop

–case2746wp

–case3375wp

Thanks to Mikhail Khokhlov and Dr. Artjoms Obusevs for reporting.

•Remove nln.mu.l.<name> and nln.mu.u.<name> ﬁelds from OPF results struct.

Use nle.lambda.<name> and nli.mu.<name> ﬁelds instead for nonlinear con-

straint multipliers.

•Modify order of default output arguments of opt model/get idx().

•Add mpopt to input args for OPF 'ext2int','formulation', and 'int2ext'

callbacks.

239

References

[1] R. D. Zimmerman, C. E. Murillo-S´anchez, and R. J. Thomas, “Matpower:

Steady-State Operations, Planning and Analysis Tools for Power Systems Re-

search and Education,” Power Systems, IEEE Transactions on, vol. 26, no. 1,

pp. 12–19, Feb. 2011. DOI: 10.1109/TPWRS.2010.2051168 1.1,1.3

[2] C. E. Murillo-S´anchez, R. D. Zimmerman, C. L. Anderson, and R. J. Thomas,

“Secure Planning and Operations of Systems with Stochastic Sources, Energy

Storage and Active Demand,” Smart Grid, IEEE Transactions on, vol. 4, no. 4,

pp. 2220–2229, Dec. 2013. DOI: 10.1109/TSG.2013.2281001 1.1,1.3

[3] A. J. Lamadrid, D. Mu˜noz- ´

Alvarez, C. E. Murillo-S´anchez, R. D. Zimmerman,

H. D. Shin and R. J. Thomas, “Using the Matpower Optimal Scheduling Tool

to Test Power System Operation Methodologies Under Uncertainty,” Sustainable

Energy, IEEE Transactions on, 2018. DOI: 10.1109/TSTE.2018.2865454 1.1

[4] John W. Eaton, David Bateman, Søren Hauberg, Rik Wehbring (2015). GNU

Octave version 4.0.0 manual: a high-level interactive language for numer-

ical computations. Available: http://www.gnu.org/software/octave/doc/

interpreter/.5

[5] The BSD 3-Clause License. [Online]. Available: http://opensource.org/

licenses/BSD-3-Clause.1.2

[6] GNU General Public License. [Online]. Available: http://www.gnu.org/

licenses/.3

[7] F. Milano, “An Open Source Power System Analysis Toolbox,” Power Systems,

IEEE Transactions on, vol. 20, no. 3, pp. 1199–1206, Aug. 2005.

[8] W. F. Tinney and C. E. Hart, “Power Flow Solution by Newton’s Method,”

IEEE Transactions on Power Apparatus and Systems, vol. PAS-86, no. 11,

pp. 1449–1460, November 1967. 4.1

[9] B. Stott and O. Alsa¸c, “Fast Decoupled Load Flow,” IEEE Transactions on

Power Apparatus and Systems, vol. PAS-93, no. 3, pp. 859–869, May 1974. 4.1

[10] R. A. M. van Amerongen, “A General-Purpose Version of the Fast Decoupled

Load Flow,” Power Systems, IEEE Transactions on, vol. 4, no. 2, pp. 760–770,

May 1989. 4.1

240

[11] A. F. Glimm and G. W. Stagg, “Automatic Calculation of Load Flows,” AIEE

Transactions (Power Apparatus and Systems), vol. 76, pp. 817–828, October

1957. 4.1

[12] D. Shirmohammadi, H. W. Hong, A. Semlyen, and G. X. Luo, “A compensation-

based power ﬂow method for weakly meshed distribution and transmission net-

works,” IEEE Transactions on Power Systems, vol. 3, no. 2, pp. 753–762, May

1988. DOI: 10.1109/59.192932 4.3,4.3.2,4.3.5

[13] G. X. Luo and A. Semlyen, “Eﬃcient load ﬂow for large weakly meshed net-

works,” IEEE Transactions on Power Systems, vol. 5, no. 4, pp. 1309–1316, Nov

1990. DOI: 10.1109/59.99382 4.3,4.3.2,4.3.5

[14] D. Rajiˇci´c, R. Ackovski, and R. Taleski, “Voltage correction power ﬂow,”

IEEE Transactions on Power Delivery, vol. 9, no. 2, pp. 1056–1062, Apr 1994.

DOI: 10.1109/61.296308 4.3.1,4.3.3,4.3.5,4.3.5

[15] D. Rajiˇci´c and R. Taleski, “Two novel methods for radial and weakly meshed

network analysis,” Electric Power Systems Research, vol. 48, no. 2, pp. 79–87,

1998. [Online]. Available: //www.sciencedirect.com/science/article/pii/

S0378779698000674 4.3.4

[16] D. Rajiˇci´c and A. Dimitrovski, “A new method for handling pv nodes in back-

ward/forward power ﬂow for radial and weakly meshed networks,” in 2001 IEEE

Porto Power Tech Proceedings (Cat. No.01EX502), vol. 3, 2001, 6 pp.

DOI: 10.1109/PTC.2001.964896 4.3.5

[17] A. J. Wood and B. F. Wollenberg, Power Generation, Operation, and Control,

2nd ed. New York: J. Wiley & Sons, 1996. 3.7,4.2,4.5

[18] T. Guler, G. Gross, and M. Liu, “Generalized Line Outage Distribution Fac-

tors,” Power Systems, IEEE Transactions on, vol. 22, no. 2, pp. 879–881, May

2007. 4.5

[19] V. Ajjarapu, C. Christy, “The Continuation Power Flow: A Tool for Steady

State Voltage Stability Analysis,” Power Systems, IEEE Transacations on,

vol. 7, no. 1, pp. 416–423, Feb. 1992. 5

[20] H.-D. Chiang, A. Flueck, K. Shah, and N. Balu, “CPFLOW: A Practical Tool

for Tracing Power System Steady-State Stationary Behavior Due to Load and

Generation Variations,” Power Systems, IEEE Transactions on, vol. 10, no. 2,

pp. 623–634, May 1995. 5.1

241

[21] S. H. Li and H. D. Chiang, “Nonlinear Predictors and Hybrid Corrector for

Fast Continuation Power Flow”, Generation, Transmission Distribution, IET,

2(3):341–354, 2008. 5.1

[22] A. J. Flueck, “Advances in Numerical Analysis of Nonlinear Dynamical Sys-

tems and the Application to Transfer Capability of Power Systems,” Ph. D.

Dissertation, Cornell University, August 1996.

[23] H. Mori and S. Yamada, “Continuation Power Flow with the Nonlinear Predictor

of the Lagrange’s Polynomial Interpolation Formula, ” In Transmission and

Distribution Conference and Exhibition 2002: Asia Paciﬁc. IEEE/PES, vol. 2,

pp. 1133–1138, Oct 6–10, 2002. 5.1

[24] R. D. Zimmerman, C. E. Murillo-S´anchez, and R. J. Thomas, “Mat-

power’s Extensible Optimal Power Flow Architecture,” Power and En-

ergy Society General Meeting, 2009 IEEE, pp. 1–7, July 26–30 2009.

DOI: 10.1109/PES.2009.5275967 6.3

[25] TSPOPF. [Online]. Available: http://www.pserc.cornell.edu/tspopf/.

6.4.1,6.5,C-17,C-18,G.13

[26] H. Wang, C. E. Murillo-S´anchez, R. D. Zimmerman, and R. J. Thomas, “On

Computational Issues of Market-Based Optimal Power Flow,” Power Systems,

IEEE Transactions on, vol. 22, no. 3, pp. 1185–1193, August 2007. 6.4.1,6.5,

A,A-3,A.4,G.13

[27] Optimization Toolbox, The MathWorks, Inc. [Online]. Available: http://www.

mathworks.com/products/optimization/.6.5,G.10

[28] BPMPD MEX. [Online]. Available: http://www.pserc.cornell.edu/bpmpd/.

6.5,G.1

[29] C. M´esz´aros, The Eﬃcient Implementation of Interior Point Methods for Linear

Programming and their Applications, Ph.D. thesis, E¨otv¨os Lor´and University of

Sciences, Budapest, Hungary, 1996. 6.5,G.1

[30] MINOPF. [Online]. Available: http://www.pserc.cornell.edu/minopf/.6.5,

C-15,F,G.8

[31] B. A. Murtagh and M. A. Saunders, MINOS 5.5 User’s Guide, Stanford Uni-

versity Systems Optimization Laboratory Technical Report SOL83-20R. 6.5,

G.8

242

[32] R. H. Byrd, J. Nocedal, and R. A. Waltz, “KNITRO: An Integrated Package for

Nonlinear Optimization”, Large-Scale Nonlinear Optimization, G. di Pillo and

M. Roma, eds, pp. 35–59 (2006), Springer-Verlag.

http://www.ziena.com/papers/integratedpackage.pdf 6.5,C-14,G.7

[33] Gurobi Optimization, Inc., “Gurobi Optimizer Reference Manual,” 2016. [On-

line]. Available: http://www.gurobi.com/.6.5,G.5

[34] GLPK. [Online]. Available: http://www.gnu.org/software/glpk/.6.5,G.4

[35] COIN-OR Linear Programming (CLP) Solver. [Online]. Available: http://www.

coin-or.org/projects/Clp.xml.6.5,G.2

[36] R. D. Zimmerman, AC Power Flows, Generalized OPF Costs and their Deriva-

tives using Complex Matrix Notation,Matpower Technical Note 2, Febru-

ary 2010. [Online]. Available: http://www.pserc.cornell.edu/matpower/

TN2-OPF-Derivatives.pdf 6.5,D-1,D-13

[37] B. Sereeter and R. D. Zimmerman, Addendum to AC Power Flows and their

Derivatives using Complex Matrix Notation: Nodal Current Balance,Mat-

power Technical Note 3, April 2018. [Online]. Available: http://www.pserc.

cornell.edu/matpower/TN3-More-OPF-Derivatives.pdf 6.5,D-1,D-13,

H.12

[38] B. Sereeter and R. D. Zimmerman, AC Power Flows and their Derivatives us-

ing Complex Matrix Notation and Cartesian Coordinate Voltages,Matpower

Technical Note 4, April 2018. [Online]. Available: http://www.pserc.cornell.

edu/matpower/TN4-OPF-Derivatives-Cartesian.pdf 6.5,D-1,D-13,H.12

[39] A. J. Lamadrid, S. Maneevitjit, T. D. Mount, C. E. Murillo-S´anchez,

R. J. Thomas, R. D. Zimmerman, “A ‘SuperOPF’ Framework”, CERTS

Report, December 2008. [Online]. Available: http://certs.lbl.gov/pdf/

superopf-framework.pdf

[40] C. E. Murillo-S´anchez, R. D. Zimmerman, C. L. Anderson, and R. J. Thomas,

“A Stochastic, Contingency-Based Security-Constrained Optimal Power Flow

for the Procurement of Energy and Distributed Reserve,” Decision Support Sys-

tems, Vol. 56, Dec. 2013, pp. 1–10. DOI: 10.1016/j.dss.2013.04.006

[41] H. Wang, On the Computation and Application of Multi-period Security-

constrained Optimal Power Flow for Real-time Electricity Market Operations,

243

Ph.D. thesis, Electrical and Computer Engineering, Cornell University, May

2007. A,A.4,G.13

[42] A.B. Birchﬁeld, T. Xu, K.M. Gegner, K.S. Shetye, T.J. Overbye, “Grid Struc-

tural Characteristics as Validation Criteria for Synthetic Networks,” Power

Systems, IEEE Transactions on, vol. 32, no. 4, pp. 3258–3265, July 2017.

DOI: 10.1109/TPWRS.2016.2616385 D-20

[43] C. Josz, S. Fliscounakis, J. Maeght, and P. Panciatici, “AC Power Flow Data

in Matpower and QCQP Format: iTesla, RTE Snapshots, and PEGASE.”

Available: http://arxiv.org/abs/1603.01533.D-22,D-23,49,H.11

[44] S. Fliscounakis, P. Panciatici, F. Capitanescu, and L. Wehenkel, “Contingency

Ranking With Respect to Overloads in Very Large Power Systems Taking Into

Account Uncertainty, Preventive, and Corrective Actions,” Power Systems,

IEEE Transactions on, vol. 28, no. 4, pp. 4909–4917, Nov. 2013. D-22

[45] P. Cuﬀe and A. Keane, “Visualizing the Electrical Structure of Power Sys-

tems,” IEEE Systems Journal, vol. 11, no. 3, pp. 1810–1821, Sept. 2017.

DOI: 10.1109/JSYST.2015.2427994 49

[46] R. D. Zimmerman, Uniform Price Auctions and Optimal Power Flow,Mat-

power Technical Note 1, February 2010. [Online]. Available: http://www.

pserc.cornell.edu/matpower/TN1-OPF-Auctions.pdf D-1,F

[47] J. Currie and D. I. Wilson,“OPTI: Lowering the Barrier Between Open Source

Optimizers and the Industrial MATLAB User,” Foundations of Computer-Aided

Process Operations, Georgia, USA, 2012. G.2,G.4,G.6

[48] Wotao Yin. Gurobi Mex: A MATLAB interface for Gurobi, URL:

http://convexoptimization.com/wikimization/index.php/gurobi_mex,

2009-2011. 56

[49] A. W¨achter and L. T. Biegler, “On the implementation of a primal-dual inte-

rior point ﬁlter line search algorithm for large-scale nonlinear programming,”

Mathematical Programming, 106(1):25—57, 2006. C-13,G.6

[50] O. Shenk and K. G¨artner, “Solving unsymmetric sparse systems of linear

equations with PARDISO,” Journal of Future Generation Computer Systems,

20(3):475–487, 2004. G.6,G.11

244

[51] A. Kuzmin, M. Luisier and O. Shenk, “Fast methods for computing selected

elements of the Greens function in massively parallel nanoelectronic device sim-

ulations,” in F. Wolf, B. Mohr and D. Mey, editors, Euro-Par 2013 Parallel Pro-

cessing, Vol. 8097, Lecture Notes in Computer Science, pp. 533—544, Springer

Berlin Heidelberg, 2013. G.6,G.11

[52] Optimization Toolbox Users’s Guide, The MathWorks, Inc., 2016. [On-

line]. Available: http://www.mathworks.com/help/releases/R2016b/pdf_

doc/optim/optim_tb.pdf.G.10,60

245

MATPOWER Manual

MATPOWER-manual

MATPOWER-manual

Navigation menu

Versions of this User Manual:

Views

Navigation