MOM5 Manual
MOM5_manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 645 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Introducing the Modular Ocean Model
- I Formulation of the ocean equations
- II Numerical formulations
- B and C grid discretizations
- Quasi-Eulerian algorithms for hydrostatic models
- Pressure and geopotential at tracer points
- Initialization issues
- Vertical dimensions of grid cells
- Summary of vertical grid cell increments
- Surface height and bottom pressure diagnosed
- Vertically integrated volume/mass budgets
- Compatibility between tracer and mass
- Diagnosing the dia-surface velocity component
- Vertically integrated horizontal momentum
- Time stepping schemes
- Split between fast and slow motions
- Time stepping the model equations as in MOM4.0
- Introduction to time stepping in MOM
- Basics of staggered time stepping in Boussinesq MOM
- Predictor-corrector for the barotropic system
- The Griffies (2004) scheme
- Algorithms motivated from predictor-corrector
- Algorithms enforcing compatibility
- Discrete space-time Coriolis force
- Time-implicit treatment of vertical mixing and bottom drag
- Mechanical energy conversions and advective mass transport
- Basic considerations
- Energetic conversions in the continuum
- How we make use of energetic conversions
- Thickness weighted volume and mass budgets
- Thickness and mass per area for the momentum
- B-grid Boussinesq pressure work conversions
- C-grid Boussinesq pressure work conversions
- B-grid non-Boussinesq pressure work conversions
- C-grid non-Boussinesq pressure work conversions
- Effective Coriolis force and mechanical energy
- B-grid kinetic energy advection
- C-grid kinetic energy advection
- Advection velocity and horizontal remapping for the B-grid
- Open boundary conditions for the B-grid
- III Subgrid scale parameterizations for vertical processes
- IV Subgrid scale parameterizations for lateral processes
- V Ad hoc subgrid scale parameterizations
- VI Diagnostic capabilities
- Methods for diagnosing mass transport
- Kinetic energy diagnostics
- Effective dianeutral diffusivity
- Spurious dissipation from numerical advection
- Dianeutral transport and associated budgets
- Introduction to the diagnostic methods
- Density layer mass budgets and watermass formation
- Pieces required to locally compute dianeutral transport
- The dianeutral transport
- Layer calculation of the watermass transformation G()
- Kinematic method to compute the material time derivative
- Process method to compute the material time derivative
- Finite volume estimate of the advective-form material time derivative
- Comments on the MOM diagnostic calculation
- Kinematic method diagnosed in MOM
- Process method diagnosed in MOM
- Budget for locally referenced potential density
- Diagnosing mass budgets for density layers
- Inferring transformation from surface buoyancy fluxes
- Specifying the density classes for layer diagnostics
- Known limitations
- Mixed layer depth diagnostics
- Subduction diagnostics
- Diagnosing the contributions to sea level evolution
- Mass conservation for seawater and tracers
- Kinematic equations for sea level evolution
- The non-Boussinesq steric effect
- Evolution of global mean sea level
- Vertical diffusion and global mean sea level
- Neutral diffusion and global mean sea level
- Parameterized quasi-Stokes transport and global mean sea level
- MOM sea level diagnostics: Version I
- MOM sea level diagnostics: Version II
- Gyre and overturning contributions to tracer transport
- Balancing the hydrological cycle in ocean-ice models
- Diagnosing the momentum budget
- Bibliography
Elements of the Modular Ocean Model (MOM)
2012 release with updates
Stephen M. Griffies
NOAA Geophysical Fluid Dynamics Laboratory
Princeton, USA
With Contributions from
NOAA/GFDL and Princeton University Scientists and Engineers
and the International MOM Community
!"#$%&'()'*++$,-'.&,+'/$%0,1&'1$%%&+2'/3&&45'$+"2/',%&'.'/6(7'8$-0'92%&,.'%&#":+'0:%';,<'=>?7(',+4'';@<'
=>?7A7'B,@%,4:%'9&,'%&#":+'0:%';1<'=>?7(',+4';4<'=>?7A7'*--'C,-$&/'3-:D&4',%&',++$,-'.&,+',C&%,#&/':C&%'
2E&'3&%":4':0'F&,%/'(G(6?GG':0'2E&'(HHG'1:+2%:-'%$+/7'
!"#$$
%&'()$
;,<'=>?7('
;@<'=>?7A'
;1<'
=>?7('
;4<'
=>?7A'
Elements of MOM4p1 (December 2011 release)
Stephen M. Griffies
NOAA Geophysical Fluid Dynamics Laboratory
Princeton, USA
With Contributions from
NOAA/GFDL and Princeton University Scientists and Engineers
and the International MOM Community
92 CHAPTER 4. QUASI-EULERIAN ALGORITHMS
tracer and mass budgets. To do so, recall the tracer budgets for the interior, bottom, and surface grid cells,
given by equations (2.153), (2.161), and (2.171)
∂t(dzρC)=dzρS(C) −∇
s·[dzρ(uC+F)]
−[ρ(w(z)C+F(s))]s=sk−1
+[ρ(w(z)C+F(s))]s=sk.
∂t(dzρC)=dzρS(C) −∇
s·[dzρ(uC+F)]
−ρ(w(z)C+F(s))s=skbot−1
+Q(C)
(bot)
∂t(dzρC)=dzρS(C) −∇
s·[dzρ(uC+F)]
+ρ(w(z)C+F(s))s=sk=1
+QmCm−Q(turb)
(C) .
Summing these budgets over a vertical column leads to
∂t
k
dzρC
=
k
dzρS(C) −∇
s·
k
dzρ(uC+F)
+QmCm−Q(turb)
(C) +Q(bott)
(C) .
(4.74)
As expected, the only contributions from vertical fluxes come from the top and bottom boundaries. Further-
more, by setting the tracer concentration to a uniform constant, all the turbulent flux terms vanish, in which
case the budget reduces to the vertically integrated mass budget discussed in Section 4.6.2. This compatiblity
between tracer and mass budgets must be carefully maintained by the discrete model equations.1
4.8 Diagnosing the dia-surface velocity component
The key distinction between Eulerian vertical coordinates and Lagrangian vertical coordinates is how they
treat the dia-surface velocity component
w(z)=∂z
∂s
ds
dt.(4.75)
The Lagrangian models prescribe it whereas Eulerian models diagnose it. The purpose of this section is
develop Eulerian algorithms for diagnosing the dia-surface velocity component for the depth based and
pressure based vertical coordinates of Chapter ??. As we will see, a crucial element for the utility of
these algorithms is that the specific thickness z,sis depth independent using depth based coordinates in
a Boussinesq fluid, and ρz,sis depth independent using pressure based coordinates in a non-Boussinesq
fluid.
1As discussed by Griffies et al. (2001), local conservation of an algorithm for tracer and volume/mass can readily be checked by
running a model with uniform tracer concentration and blowing winds across the ocean surface. Surface height undulations will
ensue, thus causing changes in volume for the grid cells. But the tracer concentration should remain uniform in the absence of surface
fluxes. Changes in tracer concentration will not occur if the volume/mass and tracer budgets are compatible in the sense defined in
this section.
98 CHAPTER 4. QUASI-EULERIAN ALGORITHMS
4.8.3 Comments about diagnosing the dia-surface velocity component
We emphasize again that a critical element in the Eulerian algorithms for diagnosing the vertical velocity
components is the ability to exploit the depth independence of the specific thickness z,sfor the depth based
coordinates for a Boussinesq fluid, and the density weighted specific thickness ρz,sfor the pressure based
coordinates for a non-Boussinesq fluid. These properties allow us to remove the time tendencies for surface
height and pressure from the respective diagnostic relations by substituting the depth integrated budgets
(4.63) for the depth based models, and (4.72) for the pressure based models. Absent the depth independence,
one would be forced to consider another approach, such as the time extrapolation approach to approximate
the time tendency proposed by Greatbatch et al. (2001) and McDougall et al. (2002) for implementing a
non-Boussinesq algorithm within a Boussinesq model.
4.9 Vertically integrated horizontal momentum
We now outline the split between the fast vertically integrated dynamics from the slower depth dependent
dynamics. This split forms the basis for the split-explicit method used in MOM to time step the momentum
equation. For this purpose, we formulate the budget for the vertically integrated momentum budget.
4.9.1 Budget using contact pressures on cell boundaries
Before proceedingwith a formulation directly relevant for MOM, we note the form of the vertically integrated
budget arising when we consider pressure acting on a cell as arising from the accumulation of contact
stresses. For this purpose, we vertically sum the momentum budgets given by equations (2.225), (2.228)
and (2.233), which leads to
(∂t+fˆz∧)(dzρu)=−ˆz∧(dzMρu)+∇s·[dzu(ρu)]
+−∇s(pdz)+dzρF
+[pa∇η+τwind +ρwQmum]
+[pb∇H−τbottom].
(4.124)
Contact pressures on the top and bottom of the grid cells cancel throughout the column, just as other
vertical fluxes from momentum and friction. The remaining contact pressures are from the bottom and
top of the ocean column and the vertically integrated contact pressures on the sides of the fluid column.
Correspondingly, if we integrate over the horizontal extent of the ocean domain, we are left only with
contact pressures acting on the solid boundaries and undulating free surface. Such is to be expected, since
the full ocean domain experiences a pressure force only from its contact with other components of the earth
climate system.
4.9.2 Budget using the pressure gradient body force
As discussed in Section 2.8.2, we prefer to formulate the contribution of pressure to the linear momentum
balance as a body force, whereby we exploit the hydrostatic balance. Hence, to develop the vertically
integrated horizontal momentum budget, we start from the form of the budget given by equations (3.19),
(3.20), and (3.21), rewritten here for the interior, bottom, and surface grid cells
[∂t+(f+M)ˆz∧] (dzρu)=ρdzS(u)−∇
s·[dzu(ρu)]
−dz(∇sp+ρ∇sΦ)+dzρF
−[ρ(w(z)u−κu,z)]
s=sk−1
+[ρ(w(z)u−κu,z)]
s=sk
(4.125)
m(new)
˙x(new)
dm
m
˙x
dm
m
˙x
dm
m(dstry)
m
˙x
m(new)
˙x(new)
dm
m
˙x
m(dstry)
˙x(dstry)
˙x
m
ˆz
ˆx, ˆy
Tracer cells T(i,j) with fluxes and land/sea masking
X=corner point
(=B-grid velocity point)
(=C-grid vorticity point)
j
i
X
T(1,4)
X
T(2,4)
X
T(3,4)
X
T(4,4)
X
X
T(1,3)
X
T(2,3)
X
T(3,3)
X
T(4,3)
X
X
T(1,2)
X
T(2,2)
X
T(3,2)
X
T(4,2)
X
X
T(1,1)
X
T(2,1)
X
T(3,1)
X
T(4,1)
X
This document is freely distributed. It provides information regarding the fundamentals and practices of
the Modular Ocean Model. This document should be referenced as the following.
Elements of the Modular Ocean Model (MOM) (2012 release with updates)
GFDL Ocean Group Technical Report No. 7
Stephen M. Griffies
NOAA/Geophysical Fluid Dynamics Laboratory
632 + xiii pages
Information about how to download and run MOM can be found at the GFDL Flexible Modeling System
(FMS) web site accessible from www.gfdl.noaa.gov/fms.
This document was prepared using L
A
T
EX as described by Lamport (1994) and Goosens et al. (1994).
Cover images
• Sea surface temperature anomalies over years 101-200 from the coupled climate model CM2.1 docu-
mented in Griffies et al. (2005), Gnanadesikan et al. (2006), Delworth et al. (2006), Wittenberg et al.
(2006), and Stouffer et al. (2006a). CM2.1 is provided as a test case with MOM.
• Annual mean surface current speed from the nominally one-degree ocean model used in CM2.1, and
the nomimally 1/4-degree ocean model used in CM2.5. This figure is taken after Delworth et al.
(2012).
• Finite volume based momentum and tracer equations forming the basis for MOM, and as derived in
Chapter 2.
• Schematic layout of tracer cells with fluxes crossing the cell faces. This layout is used for both the B-
grid and C-grid arrangements. The B-grid is standard in MOM, and the C-grid is under development.
See Chapters 9and 14 for details.
• Schematic of the interactions between the Lagrangian blob submodel available in MOM and bottom
topography, as may occur in an overflow situation (Bates et al.,2012a,b).

Section 0.0
MOM and this document
The Modular Ocean Model (MOM) is a hydrostatic generalized level coordinate numer-
ical ocean code with mass conserving non-Boussinesq or volume conserving Boussinesq
kinematics. The model equations are discretized with generalized horizontal coordinates
on the sphere using either an Arakawa B-grid or C-grid.1MOM has a broad suite of phys-
ical parameterizations, diagnostic features, test cases, and documentation. It has been
utilized for research and operations from the coasts to the globe. MOM is institution-
ally sanctioned by NOAA’s Geophysical Fluid Dynamics Laboratory (GFDL), where devel-
opment is centered. Additional development and use occurs through hundreds of inter-
national scientists and engineers comprising the MOM community. MOM is free software
distributed under GPLv2 and it is part of an open source community.
The 2014 release of MOM is the latest in a 50+ year history of numerical ocean codes developed at
GFDL. In addition to GFDL leadership, MOM code development and use occurs through a broad network
of scientists and engineers who contribute numerical algorithms, physical parameterizations, diagnostics,
bug fixes, test cases, documentation, and user feedback. The development and use of MOM thus comprises
a vital international open source community.
Ocean climate modeling has evolved tremendously over the years since Kirk Bryan first illustrated
the compelling nature of a nonlinear wind driven ocean circulation in Bryan (1963) using a numerical
model. We know far more about the ocean than in 1963, and we have far more realistic numerical tools
to investigate the ocean using some of the most powerful computers on the planet. Furthermore, the
problems associated with anthropogenic climate change prompt an increasing relevance and importance
to the results produced by ocean models. That is, climate science is not limited to the domain of curiousity
driven research. Instead, the science points to the nontrivial consequences of an ongoing uncontrolled
planetary-wide experiment. Hence, there has never been a more critical time for numerical models to be
fully detailed with rational and thorough descriptions, and supported by theory and observations.
Generations of ocean and climate scientists studied the ocean circulation by using the Cox code (Cox,
1984) in both idealized and realistic simulations. Cox’s code formed the basis for the first version of MOM
(Pacanowski et al.,1991) (see Section 1.1 for a brief history of MOM). Over the years since Cox (1984), the
name “MOM” has become synonymous with ocean climate models. The MOM release of 2014 is hence
the result of decades of contributions by hundreds of scientists and engineers. Each contribution, however
large or small, adds valuable experience and features that allows MOM to be a numerical tool worthy of the
trust and utility required to make it suitable for both research and operations. A trustworthy and useful
numerical tool is the result of robust numerical methods, a wide range of state-of-the-science physical
parameterizations, and extensive diagnostics, combined with thorough and pedagogical documentation, a
huge suite of proven applications, and decades of experience by generations of scientists and engineers. By
this definition, MOM is among the world’s most useful and valuable ocean codes.
This document provides an account of the theory and methods forming the fundamentals of MOM,
with a focus on the most recent release, MOM5. Further documentation is available as part of the MOM
distribution where details are given for how to configure the code for a particular model experiment. All
of this documentation aims to strengthen the intellectual basis for MOM as well as its practical usability.
It is with sincere humility and honor that I remain part of the MOM community, both as one interested
in the science resulting from its simulations, and as one who nurtures and supports the science forming
the foundations of the code itself. I hope that this document enables yet another generation of scientists
and engineers, young and old, new and experienced, to wrap their heads around a truly significant piece
of code, and in turn to offer feedback to support the integrity, transparency, utility, and evolution of MOM.
Stephen.Griffies@noaa.gov NOAA/GFDL, Princeton, USA
1The C-grid version of MOM5 is new as of June 2012, and not yet available for general use. It is thus anticipated that the C-grid
option in MOM will mature rapidly over 2012 and beyond, and become the standard choice, particularly for coastal and mesoscale
eddying applications.
Elements of MOM November 19, 2014 Page iii

Section 0.0
Elements of MOM November 19, 2014 Page iv
Contents
1Introducing the Modular Ocean Model 1
1.1 A brief history of MOM ...................................... 2
1.2 Releases of MOM since 2003 ................................... 4
1.3 The MOM6 Project ........................................ 5
1.4 Elements of MOM5 ........................................ 5
1.5 A flow diagram for the MOM algorithm ............................ 18
1.6 Papers and reports providing documentation of MOM .................... 21
1.7 Remainder of this document ................................... 22
I Formulation of the ocean equations 23
2Fundamental equations 25
2.1 Fluid kinematics ......................................... 26
2.2 Mass conservation and the tracer equation ........................... 37
2.3 Thermodynamical tracers .................................... 39
2.4 Material time changes over finite regions ........................... 42
2.5 Basics of the finite volume method ............................... 44
2.6 Mass and tracer budgets over finite regions .......................... 45
2.7 Special considerations for tracers ................................ 51
2.8 Forces from pressure ....................................... 53
2.9 Linear momentum budget .................................... 58
2.10 The Boussinesq budgets ..................................... 62
3The hydrostatic pressure force 65
3.1 Hydrostatic pressure forces at a point ............................. 65
3.2 Pressure gradient body force ................................... 66
3.3 Pressure gradient body force in B-grid MOM ......................... 71
3.4 Pressure gradient body force in C-grid MOM ......................... 74
4Parameterizations with generalized level coordinates 75
4.1 Friction ............................................... 75
4.2 Diffusion and skew diffusion .................................. 79
5Depth and pressure based vertical coordinates 85
5.1 Depth based vertical coordinates ................................ 85
5.2 Pressure based coordinates .................................... 92
v

Contents Section 0.0
6Equation of state and related quantities 97
6.1 Introduction ............................................ 97
6.2 Linear equation of state ..................................... 99
6.3 The two realistic equations of state ............................... 99
7Dynamical ocean equations with a nonconstant gravity field 103
7.1 Gravitational force: conventional approach .......................... 103
7.2 Gravitational force: general approach ............................. 105
8Tidal forcing from the moon and sun 109
8.1 Tidal consituents and tidal forcing ............................... 109
8.2 Formulation in non-Boussinesq models ............................ 110
8.3 Implementation in MOM ..................................... 110
II Numerical formulations 113
9B and C grid discretizations 115
9.1 B and C grids used in MOM ................................... 115
9.2 Describing the horizontal grid .................................. 117
9.3 The Murray (1996) tripolar grid ................................. 121
9.4 Specifying fields and grid distances within halos ....................... 123
10 Quasi-Eulerian algorithms for hydrostatic models 135
10.1 Pressure and geopotential at tracer points ........................... 136
10.2 Initialization issues ........................................ 139
10.3 Vertical dimensions of grid cells ................................. 139
10.4 Summary of vertical grid cell increments ........................... 141
10.5 Surface height and bottom pressure diagnosed ........................ 147
10.6 Vertically integrated volume/mass budgets .......................... 148
10.7 Compatibility between tracer and mass ............................ 150
10.8 Diagnosing the dia-surface velocity component ........................ 150
10.9 Vertically integrated horizontal momentum .......................... 156
11 Time stepping schemes 159
11.1 Split between fast and slow motions .............................. 160
11.2 Time stepping the model equations as in MOM4.0 ...................... 160
11.3 Introduction to time stepping in MOM ............................. 166
11.4 Basics of staggered time stepping in Boussinesq MOM .................... 167
11.5 Predictor-corrector for the barotropic system ......................... 167
11.6 The Griffies (2004) scheme .................................... 169
11.7 Algorithms motivated from predictor-corrector ........................ 169
11.8 Algorithms enforcing compatibility ............................... 174
12 Discrete space-time Coriolis force 177
12.1 The Coriolis force and inertial oscillations ........................... 177
12.2 Time stepping for the B-grid version of MOM ......................... 179
12.3 Time stepping for the C-grid version of MOM ......................... 182
13 Time-implicit treatment of vertical mixing and bottom drag 183
13.1 General form of discrete vertical diffusion ........................... 184
13.2 Discretization of vertical fluxes ................................. 184
13.3 A generic form: Part A ...................................... 185
13.4 A generic form with implicit bottom drag ........................... 186
Elements of MOM November 19, 2014 Page vi

Contents Section 0.0
14 Mechanical energy conversions and advective mass transport 189
14.1 Basic considerations ....................................... 190
14.2 Energetic conversions in the continuum ............................ 191
14.3 How we make use of energetic conversions .......................... 193
14.4 Thickness weighted volume and mass budgets ........................ 194
14.5 Thickness and mass per area for the momentum ....................... 195
14.6 B-grid Boussinesq pressure work conversions ......................... 196
14.7 C-grid Boussinesq pressure work conversions ......................... 203
14.8 B-grid non-Boussinesq pressure work conversions ...................... 206
14.9 C-grid non-Boussinesq pressure work conversions ...................... 210
14.10 Effective Coriolis force and mechanical energy ........................ 212
14.11 B-grid kinetic energy advection ................................. 214
14.12 C-grid kinetic energy advection ................................. 218
15 Advection velocity and horizontal remapping for the B-grid 221
15.1 General considerations ...................................... 221
15.2 Remapping operators for horizontal fluxes ........................... 222
15.3 Remapping operator for vertical fluxes ............................. 224
15.4 Remapping error ......................................... 225
15.5 Subtleties at the southern-most row .............................. 228
16 Open boundary conditions for the B-grid 229
16.1 Introduction ............................................ 230
16.2 Types of open boundary conditions ............................... 231
16.3 Implementation of sea level radiation conditions ....................... 234
16.4 OBC for tracers .......................................... 238
16.5 The namelist obc nml ...................................... 241
16.6 Topography generation - Preparation of boundary data ................... 243
III Subgrid scale parameterizations for vertical processes 247
17 Surface and penetrative shortwave heating 249
17.1 General considerations and model implementation ...................... 249
17.2 The Paulson and Simpson (1977) irradiance function ..................... 250
17.3 Shortwave penetration based on chlorophyll-a ........................ 251
17.4 Diagnosing shortwave heating in MOM ............................ 252
18 KPP for the surface ocean boundary layer (OBL) 255
18.1 Elements of the K-profile parameterization (KPP) ....................... 256
18.2 Surface ocean boundary momentum fluxes .......................... 261
18.3 Surface ocean boundary buoyancy fluxes ............................ 262
18.4 Surface layer and Monin-Obukhov similarity ......................... 268
18.5 Specifying the KPP parameterization .............................. 272
19 Vertical convective adjustment schemes 283
19.1 Introduction ............................................ 283
19.2 Summary of the vertical adjustment options .......................... 283
19.3 Concerning a double application of vertical adjustment ................... 284
19.4 Implicit vertical mixing ..................................... 284
19.5 Convective adjustment ...................................... 284
Elements of MOM November 19, 2014 Page vii

Contents Section 0.0
20 Mixing related to tidal energy dissipation 287
20.1 Formulation ............................................ 287
20.2 Mixing from internal wave breaking .............................. 288
20.3 Dianeutral diffusivities from bottom drag ........................... 292
21 Mixing related to specified minimum dissipation 295
21.1 Formulation ............................................ 295
22 Parameterization of form drag 297
22.1 Regarding the TEM approach .................................. 297
22.2 What is available in MOM .................................... 298
IV Subgrid scale parameterizations for lateral processes 299
23 Neutral Physics 301
23.1 Introduction ............................................ 303
23.2 Notation .............................................. 306
23.3 Discretization ........................................... 309
23.4 Implementation .......................................... 315
23.5 Diffusion and Skew-Diffusion Tensors ............................. 320
23.6 Tracer Gradients .......................................... 328
23.7 Quantities related to density gradients ............................. 329
23.8 Specification of the diffusivity .................................. 333
23.9 Summary of the notation ..................................... 342
24 Restratification by submesoscale eddies 347
24.1 Basics of the scheme ....................................... 347
24.2 Skew tracer flux components .................................. 349
24.3 Eddy induced transport ..................................... 350
24.4 Eddy advection implementation ................................. 352
24.5 Cautionary remarks on compute psi legacy ......................... 352
24.6 Horizontal diffusion associated with submesoscale processes ................ 353
25 Lateral friction methods 355
25.1 Introduction ............................................ 356
25.2 Lateral friction options in MOM ................................. 356
25.3 Continuum formulation for the friction operator ....................... 357
25.4 Lateral friction operator for B-grid MOM ........................... 359
25.5 Lateral friction operator for C-grid MOM ........................... 367
25.6 Boundary conditions ....................................... 371
26 Eddy-topography interaction via Neptune 373
26.1 Introduction ............................................ 373
26.2 Basics of the parameterization in MOM ............................ 374
26.3 Topostrophy diagnostic ...................................... 375
VAd hoc subgrid scale parameterizations 377
27 Overflow schemes 379
27.1 Motivation for overflow schemes ................................ 380
27.2 The sigma transport scheme ................................... 380
27.3 The Campin and Goosse (1999) scheme ............................ 385
27.4 Neutral depth over extended horizontal columns ....................... 389
Elements of MOM November 19, 2014 Page viii

Contents Section 0.0
27.5 Sigma friction ........................................... 391
28 River discharge into the ocean model 393
28.1 Introduction ............................................ 393
28.2 General considerations ...................................... 394
28.3 Steps in the algorithm ...................................... 395
29 Cross-land mixing 397
29.1 Introduction ............................................ 397
29.2 Tracer and mass/volume compatibility ............................. 398
29.3 Tracer mixing in a Boussinesq fluid with fixed boxes ..................... 398
29.4 Mixing of mass/volume ..................................... 399
29.5 Tracer and mass mixing ..................................... 401
29.6 Formulation with multiple depths ............................... 402
29.7 Suppression of B-grid null mode ................................ 404
30 Cross-land insertion 405
30.1 Introduction ............................................ 405
30.2 Algorithm details ......................................... 406
30.3 An example: insertion to three cells in MOM4.0 ....................... 407
30.4 An example: insertion to just the top cell in MOM4.0 .................... 409
30.5 Updates for generalized level coordinates ........................... 410
31 The B-grid computational mode 411
31.1 Checkerboard mode ....................................... 411
31.2 Filter for sea surface height ................................... 412
31.3 Filter for bottom pressure .................................... 412
VI Diagnostic capabilities 413
32 Methods for diagnosing mass transport 415
32.1 Brief on notation ......................................... 416
32.2 Meridional-overturning streamfunction ............................ 416
32.3 Mass transport through tracer cell faces ............................ 421
32.4 Vertically integrated transport .................................. 425
33 Kinetic energy diagnostics 427
33.1 Formulation of kinetic energy diagnostics ........................... 427
34 Effective dianeutral diffusivity 429
34.1 Potential energy and APE in Boussinesq fluids ........................ 430
34.2 Effective dianeutral mixing ................................... 431
34.3 Modifications for time dependent cell thicknesses ...................... 434
34.4 An example with vertical density gradients .......................... 435
34.5 An example with vertical and horizontal gradients ...................... 440
35 Spurious dissipation from numerical advection 449
35.1 Formulation of the method for Boussinesq fluid ........................ 449
35.2 Formulation for MOM ...................................... 451
35.3 Comparing to physical mixing .................................. 453
Elements of MOM November 19, 2014 Page ix

Contents Section 0.0
36 Dianeutral transport and associated budgets 455
36.1 Introduction to the diagnostic methods ............................ 458
36.2 Density layer mass budgets and watermass formation .................... 459
36.3 Pieces required to locally compute dianeutral transport ................... 464
36.4 The dianeutral transport ..................................... 470
36.5 Layer calculation of the watermass transformation G(γ)................... 472
36.6 Kinematic method to compute the material time derivative ................. 475
36.7 Process method to compute the material time derivative ................... 477
36.8 Finite volume estimate of the advective-form material time derivative ........... 480
36.9 Comments on the MOM diagnostic calculation ........................ 489
36.10 Kinematic method diagnosed in MOM ............................. 493
36.11 Process method diagnosed in MOM ............................... 502
36.12 Budget for locally referenced potential density ........................ 525
36.13 Diagnosing mass budgets for density layers .......................... 526
36.14 Inferring transformation from surface buoyancy fluxes ................... 534
36.15 Specifying the density classes for layer diagnostics ...................... 537
36.16 Known limitations ........................................ 539
37 Mixed layer depth diagnostics 541
37.1 The mixed layer depth ...................................... 541
37.2 Tracer budgets within the mixed layer ............................. 542
38 Subduction diagnostics 543
38.1 Kinematics of flow across a surface ............................... 543
38.2 MOM subduction diagnostic calculation ............................ 548
39 Diagnosing the contributions to sea level evolution 551
39.1 Mass conservation for seawater and tracers .......................... 553
39.2 Kinematic equations for sea level evolution .......................... 559
39.3 The non-Boussinesq steric effect ................................. 563
39.4 Evolution of global mean sea level ............................... 570
39.5 Vertical diffusion and global mean sea level .......................... 573
39.6 Neutral diffusion and global mean sea level .......................... 574
39.7 Parameterized quasi-Stokes transport and global mean sea level .............. 577
39.8 MOM sea level diagnostics: Version I .............................. 580
39.9 MOM sea level diagnostics: Version II ............................. 592
40 Gyre and overturning contributions to tracer transport 595
40.1 Formulation ............................................ 595
40.2 Enabling the diagnostic ..................................... 596
41 Balancing the hydrological cycle in ocean-ice models 599
41.1 Transfer of water between sea ice and ocean .......................... 599
41.2 Balancing the hydrological cycle ................................ 599
41.3 Water mass flux from salt mass flux ............................... 600
42 Diagnosing the momentum budget 603
42.1 A split-explicit algorithm to time step momentum ...................... 604
42.2 Momentum budget diagnostics ................................. 608
Bibliography 613
Elements of MOM November 19, 2014 Page x
List of Figures
1.1 Bipolar Arctic grid lines ....................................... 7
1.2 Bottom topography comparing full and partial cells ....................... 8
1.3 Comparing geopotential and z∗vertical coordinates ........................ 9
1.4 Schematic of Lagrangian blobs .................................... 12
1.5 Flow diagram for the MOM algorithm ............................... 19
2.1 Schematic of a generalized surface interior to the ocean ..................... 30
2.2 Schematic of the ocean bottom surface ............................... 33
2.3 Schematic of the ocean upper surface ................................ 36
2.4 Schematic of an ocean grid cell ................................... 47
2.5 Schematic of an ocean grid cell next to bottom ........................... 49
2.6 Schematic of an ocean grid cell next to ocean surface ....................... 50
2.7 Schematic of mass convergence-divergence ............................. 54
2.8 Schematic of pressure acting on a cube ............................... 54
2.9 Schematic of pressure in two dimensions .............................. 56
3.1 Illustrating grid cells in a vertical slice ............................... 72
4.1 Relation between slopes of surfaces ................................. 82
5.1 Comparison of partial step and full step topography ....................... 87
5.2 Constant depth surfaces with partial step ............................. 88
5.3 Constant sigma surfaces ....................................... 91
7.1 Coordinates on a sphere ....................................... 104
9.1 Placement of fields onto the B-grid ................................. 117
9.2 Placement of fields onto the C-grid ................................. 118
9.3 Four basic grid points for B and C grids .............................. 119
9.4 Grid cells with land-sea masking .................................. 120
9.5 Grid distances between points and vertices ............................. 122
9.6 Cell distances ............................................. 123
9.7 Distances between grid points .................................... 124
9.8 Bipolar grid lines ........................................... 125
9.9 Tracer and velocity cells on bipolar grid .............................. 125
9.10 North and east vectors on tracer cell faces within the bipolar grid ................ 126
9.11 Basic elements of halos ........................................ 127
9.12 Zonally periodic array ........................................ 128
9.13 Quarter-cell distances at the bipolar fold .............................. 131
xi

List of Figures Section 0.0
9.14 Tracer cell distances at the bipolar fold ............................... 133
9.15 Velocity cell distances at the bipolar fold .............................. 133
9.16 Grid distances between tracer points at the bipolar fold ..................... 134
10.1 Vertical column of tracer cells .................................... 138
11.1 Illustrating problems with leap-frog time stepping ........................ 165
14.1 Grid cells through a vertical slice with land-sea masking ..................... 195
14.2 Computation of discrete pressure .................................. 201
14.3 Tracer cell distances .......................................... 203
14.4 Velocity cell distances ......................................... 214
15.1 Schematic of the remapping function REMAP ET TO EU ...................... 224
15.2 Tracer and velocity cell quarter distances .............................. 225
15.3 Tracer and velocity cell spacings ................................... 226
15.4 Tracer cell distances .......................................... 226
15.5 Velocity cell distances ......................................... 227
16.1 Schematic of open boundary conditions .............................. 231
18.1 KPP boundary layer schematic .................................... 259
18.2 Figure 1 from Large et al. (1994) ................................... 261
18.3 Figure 2 from Large et al. (1994) ................................... 274
18.4 Figure B1 from Large et al. (1994) .................................. 275
18.5 Alternative similarity functions ................................... 276
20.1 Problems with MOM4 implementation of Lee et al. (2006) .................... 293
23.1 Stencils and indices for a centered triad group. .......................... 308
23.2 Stencils and indices for horizontal and vertical face centered triad groups. ........... 309
23.3 The sine taper function. ........................................ 321
23.4 the tanh taper function. ........................................ 323
23.5 Diffusivity module namelist parameters and their relationships. ................ 334
23.6 Illustrating the baroclinic zone for use in computing the diffusivity ............... 341
25.1 Stencil for the discrete frictional functional ............................ 361
25.2 Notation for the quadrants surrounding a velocity point ..................... 364
25.3 Array of C-grid velocity vectors ................................... 368
25.4 Stencil for ui,j and vi,j contributions to lateral C-grid friction .................. 369
25.5 C-grid layout for the deformation rates ............................... 372
27.1 Schematic of sigma transport pathways ............................... 381
27.2 Schematic of the Campin and Goosse overflow method ...................... 386
27.3 Specifying where a step occurs in the topography ......................... 388
27.4 Comparison of Campin and Goosse overflow method to Beckmann and D¨
oscher ....... 391
28.1 Schematic of river discharge algorithm ............................... 395
29.1 Schematic of cross-land mixing ................................... 399
30.1 Schematic of cross-land insertion .................................. 408
30.2 Example of cross-land insertion ................................... 410
32.1 Relating the overturning streamfunction to the transport .................... 419
Elements of MOM November 19, 2014 Page xii

List of Figures Section 0.0
34.1 Sample vertical density profile .................................... 435
34.2 Vertical diffusive flux ......................................... 436
34.3 Example of effective diffusivity ................................... 438
34.4 Example of effective diffusivity ................................... 439
34.5 Sorting a density profile ....................................... 441
34.6 Vertical diffusive flux and sorted density .............................. 442
34.7 Vertical diffusive flux and sorted density .............................. 443
34.8 Sorting the density and the potential energy ............................ 445
34.9 Sorting the density field and the effective diffusivity ....................... 447
36.1 Mass balance for a density layer ................................... 460
36.2 Surfaces of constant generalized vertical coordinate ........................ 467
36.3 Schematic of an ocean grid cell ................................... 476
38.1 Surfaces of constant generalized vertical coordinate ........................ 544
39.1 Schematic of an ocean basin and the processes impacting sea level ............... 561
39.2 Schematic ocean basin and the boundary and internal ocean processes impacting sea level . 568
39.3 Schematic of how the Gent et al. (1995) scheme impacts sea level ................ 579
Elements of MOM November 19, 2014 Page xiii

Chapter 1
Introducing the Modular Ocean Model
Contents
1.1 A brief history of MOM ..................................... 2
1.2 Releases of MOM since 2003 .................................. 4
1.2.1 First release of MOM4.0: October 2003 ........................... 4
1.2.2 First release of MOM4p1: Early 2007 ............................ 4
1.2.3 MOM4p1 release December 2009 .............................. 4
1.2.4 MOM5 release 2012 and afterward ............................. 4
1.3 The MOM6 Project ........................................ 5
1.4 Elements of MOM5 ........................................ 5
1.4.1 FMS and parallel programming ............................... 5
1.4.2 Features of the dynamical core ............................... 6
1.4.2.1 Generalized orthogonal horizontal coordinates ................. 6
1.4.2.2 Partial bottom steps ................................ 6
1.4.2.3 Generalized level coordinates ........................... 7
1.4.2.4 Explicit barotropic solver ............................. 10
1.4.2.5 Time stepping schemes .............................. 10
1.4.2.6 Pressure gradient calculation ........................... 11
1.4.3 Dynamically interacting Lagrangian parcels ........................ 11
1.4.4 Tracer features ......................................... 11
1.4.4.1 Equation of state .................................. 11
1.4.4.2 Conservative temperature ............................. 12
1.4.4.3 Freezing temperature for frazil .......................... 12
1.4.4.4 Tracer advection .................................. 12
1.4.4.5 Tracer packages ................................... 13
1.4.5 Subgrid scale parameterizations ............................... 14
1.4.5.1 Penetration of shortwave radiation ........................ 14
1.4.5.2 Horizontal friction ................................. 15
1.4.5.3 Convective adjustment schemes ......................... 15
1.4.5.4 Neutral physics ................................... 15
1.4.5.5 Restratification effects from submesoscale eddies ............... 16
1.4.5.6 Parameterization of form drag .......................... 16
1.4.5.7 Tidal mixing parameterizations .......................... 16
1.4.5.8 An array of vertical mixing schemes ....................... 16
1.4.5.9 Overflow schemes ................................. 17
1.4.6 Diagnostics and the FMS diagnostic manager ....................... 17
1

Chapter 1. Introducing the Modular Ocean Model Section 1.1
1.4.7 Open boundary conditions .................................. 17
1.4.8 Test cases ............................................ 17
1.5 A flow diagram for the MOM algorithm ............................ 18
1.6 Papers and reports providing documentation of MOM ................... 21
1.7 Remainder of this document .................................. 22
The Modular Ocean Model (MOM) is a numerical representation of the ocean’s hydrostatic primitive
equations employing either Boussinesq (volume conserving) or non-Boussinesq (mass conserving) kinemat-
ics. It is formulated using a quasi-Eulerian algorithm employing generalized level coordinate technology
that facilitates the use of a suite of vertical coordinates. It is designed primarily as a tool for studying the
ocean climate as well as regional and coastal phenomena. There is a wide array of subgrid scale parameteri-
zations (SGS) available for use in a variety of global to coastal applications. An extensive suite of diagnostic
capabilities allows the researcher to probe into mechanisms underlying simulation features. MOM is devel-
oped by an international team of ocean scientists and engineers participating in the MOM project, with the
main algorithm development and software engineering provided by NOAA’s Geophysical Fluid Dynamics
Laboratory (GFDL) in Princeton, USA. The model is freely available under the GNU General Public License
(http://www.gnu.org/licenses/gpl.html) and can be downloaded after registration at
http ://www.gfdl.noaa.gov/fms
The purpose of this document is to present a rationalized account of the theory and practice of MOM as
an ocean model tool for use in studying the ocean climate system. To achieve this purpose, this document
incorporates salient features of the following MOM related documents:
• The MOM3 Manual of Pacanowski and Griffies (1999)
• Fundamentals of Ocean Climate Models by Griffies (2004)
• A Technical Guide to MOM4.0 by Griffies et al. (2004)
There are additional elements in this document that are unique to more recent versions of MOM.
Note that MOM encompasses a relatively large body of code. Besides the code directly related to the
ocean model itself, there are allied codes required to support the use of MOM on various computational
platforms, including parallel machines; codes required to perform input/output operations; codes for cou-
pling to other component models, etc. The present document is concerned exclusively with that code
associated with the ocean equations.
1.1 A brief history of MOM
The Modular Ocean Model evolved from numerical ocean models developed in the 1960’s-1980’s by Kirk
Bryan and Mike Cox at GFDL. Most notably, the first internationally released and supported primitive
equation ocean model was developed by Mike Cox (Cox (1984)). Although somewhat common today, it
was actually quite revolutionary in 1984 to freely release, support, and document code for use in numerical
ocean modeling. The Cox-code provided scientists worldwide with a powerful tool to investigate basic
and applied questions about the ocean and its interactions with other components of the climate system.
Previously, rational investigations of such questions focused on idealized models and analytical methods.
Many researchers embraced the Cox-code, thus fostering a wide community of users and developers that
further enhanced the features and robustness of the code. This community approach has been fundamental
to all versions of the Cox-code and subequent releases of MOM, with the underlying assumption that the
scientific integrity of the code progresses more rapidly through input from a wide suite of researchers
employing the code for a variety of scientific and operational applications. Quite simply, the Cox-code
started what has today become a right-of-passage for every high-end numerical model of dynamical earth
systems.
Upon the untimely passing of Mike Cox in 1989 (Bryan,1991), Ron Pacanowski, Keith Dixon, and Tony
Rosati at GFDL rewrote the Cox-code with an eye on new ideas of modular programming using Fortran
Elements of MOM November 19, 2014 Page 2

Chapter 1. Introducing the Modular Ocean Model Section 1.1
77. The result was the first version of MOM (Pacanowski et al. (1991)). Version 2 of MOM (Pacanowski
(1995)) introduced the memory window idea, which was a generalization of the vertical-longitudinal slab
approach used in the Cox-code and MOM1. Both of these methods were driven by the desires of modelers
to run large experiments on machines with relatively small memories. The memory window provided
enhanced flexibility to incorporate higher order numerics, whereas slabs used in the Cox-code and MOM1
restricted the numerics to second order accuracy. MOM3 (Pacanowski and Griffies (1999)) even more fully
exploited the memory window with a substantial number of new physics and numerics options.
MOM4 has origins dating back to a transition from vector to parallel computers at GFDL, starting in
1999. Other related codes successfully made the transition some years earlier (e.g., The Los Alamos Par-
allel Ocean Program (POP) and the OCCAM model from Southampton, UK). New computer architectures
generally allow far more memory than previously available, thus removing many of the reasons for the
slabs and memory window approaches used in earlier versions of MOM. Additionally, the loop structure
can be quite opaque with the memory windows, making it relatively difficult to introduce new algorithms,
especially for the novice. Hence, for MOM4.0, the memory window was jettisoned in favor of a horizontal
2D domain decomposition. The project to convert MOM3 to MOM4.0 took roughly four years of coding
and testing.
After gaining some experience on parallel machines with MOM4.0, and after developing the IPCC AR4
coupled climate model CM2.1 at GFDL (Griffies et al.,2005;Delworth et al.,2006;Gnanadesikan et al.,
2006), development focused on a generalized level coordinate version of MOM, allowing the code to be
used with depth based Boussinesq vertical coordinates or pressure based non-Boussinesq vertical coordi-
nates. This effort led to the MOM4p1 project. During development and use of MOM4p1, a wide suite of
new diagnostics were developed in support of the evolving applications toward climate and biogeochem-
istry modeling. Additionally, MOM4p1 has incorporated tools required for use in regional and coastal
applications (Herzfeld et al.,2011).
MOM4p1 continued to evolve from its initial release in 2007 toward the end of 2011. The most recent
release took place in 2012, which represents the first release of MOM5. For many applications, the 2012
release of MOM is quite similar to the December 2009 release of MOM4p1. However, the 2012 MOM
release has two notable enhancements to the underlying model framework.
• The 2012 MOM release has a C-grid layout for the horizontal gridding of the discrete model fields.
The C-grid has many advantages for fine resolution models and for representing land/sea boundaries
(see Section 9.1). Hence, there is much interest at GFDL and within the MOM community to allow
MOM to support both the B-grid and C-grid. It is anticipated that the bulk of the fine resolution
modeling with MOM at GFDL will transition from the B-grid to the C-grid during late 2012 and
beyond. Note that that the C-grid available in the initial release of MOM5 is a proto-type, with
extensive testing remaining to be performed over the course of 2012 and beyond. Users intent on
applying the C-grid for their purposes should recognize the early stages of this code.
• The 2012 MOM release is coupled to a dynamically active Lagrangian submodel as documented by
Bates et al. (2012a,b). The interactive Lagrangian parcels provide a fundamentally new means to
represent/parameterize vertical convection and gravity driven downslope processes. It is anticipated
that much effort will be devoted over the next few years towards development and understanding of
the utility of solving a coupled set of Eulerian and Lagrangian equations that interact through the
exchange of mass, tracer, and momentum.
• Further work has continued to refine the many physical parameterizations in MOM.
• The 2012 MOM release has signficantly new diagnostic facilities allowing researchers to probe mech-
anisms for water mass transformation and steric changes to sea level, amongst the growing suite of
other diagnostic features.
The Cox-code and each version of MOM have an associated manual or user guide. Besides describing
elements of the code and its practical use, these manuals aim to rationalize model methods, algorithms, and
parameterizations. Absent such documentation, the code could present itself as a black box, thus greatly
hindering its utility to the curious and skeptical scientific researcher. As the code grows and evolves, it
is a nontrivial task to keep code and documentation consistent. Hence, visions for complete and updated
Elements of MOM November 19, 2014 Page 3

Chapter 1. Introducing the Modular Ocean Model Section 1.2
documentation are unrealized, with elements of the documentation incomplete and/or not fully consistent
with the code. Nonetheless, the present document, as well as the earlier MOM documents, should provide
ample opportunity to understand many details of the code, thus facilitating its use for simulating the ocean.
1.2 Releases of MOM since 2003
There have been many releases of MOM since the original MOM1 code in 1991. We focus here on the
releases of MOM4.
1.2.1 First release of MOM4.0: October 2003
When physical scientists aim to rewrite code based on software engineering motivations, more than soft-
ware issues are addressed. During the writing of MOM4, numerous algorithmic issues were also addressed,
which added to the development time. Hence, the task of rewriting MOM3 into MOM4.0 took roughly four
years to complete, taking place from 1999 to 2003. Such represents a very useful lesson. Namely, even
if one presumes from the start that the code will be rewritten only with an eye towards computational
architecture questions, such questions inevitably raise questions about fundamentals of algorithms and
parameterizations. When introducing such additional questions, the timeline for rewriting code grows ex-
tensively. There is a general rule in code/model development that must be honestly acknowledged when
scoping out the timelines for a project:
It always takes longer to develop code and model configurations than originally antici-
pated, even when understanding that it takes longer then anticipated.
This rule has been proven valid multiple times with the development of MOM versions, and various model
configurations, over its multiple decades of history.
1.2.2 First release of MOM4p1: Early 2007
Griffies spent much of 2005 in Hobart, Australia as a NOAA representative at the CSIRO Marine and At-
mospheric Research Laboratory, as well as with researchers at the University of Tasmania. This period saw
focused work to upgrade MOM4.0 to include certain features of generalized level coordinates. By allowing
for the use of a suite of vertical coordinates, MOM4p1 is algorithmically more flexible than any previous
version of MOM. This work, however, did not fundamentally alter the overall computational structure rel-
ative to the last release of MOM4.0 (the MOM4p0d release in May 2005). In particular, MOM4p1 is closer
in “look and feel” to MOM4p0d than MOM4p0a is to MOM3.1. Given this similarity, it was decided to
retain the MOM4 name for the MOM4p1 release, rather switch to MOM5.
1.2.3 MOM4p1 release December 2009
The MOM4p1 release of December 2009 represents a major upgrade to the code, especially those areas
related to open boundary conditions of use for regional applications (Chapter 16 and Herzfeld et al. (2011)),
various physical parameterizations, diagnostics, and computtional infrastructure. This public release also
provides the community with a test case consisting of the CM2.1 configuration used by GFDL for the IPCC
AR4 assessment, as documented by Griffies et al. (2005), Gnanadesikan et al. (2006), Delworth et al. (2006),
Wittenberg et al. (2006), and Stouffer et al. (2006a). Although CM2.1 for the AR4 assessement actually used
MOM4.0, the setup in the CM2.1-MOM4p1 test case is backwards compatibile, meaning that the climate
state is the same.
1.2.4 MOM5 release 2012 and afterward
The most recent release of MOM occurred in 2012, and it is referred to as MOM5. This code is released via
GitHub, with the source code continually updated. Hence, the user is able to access the most recent code
without having to await bundling the code into a formal release.
Elements of MOM November 19, 2014 Page 4

Chapter 1. Introducing the Modular Ocean Model Section 1.4
As noted earlier, MOM5 includes a C-grid option as well as a dynamically interacting Lagrangian sub-
model. It is notable that both the C-grid and Lagrangian submodel are less mature than other portions of
MOM. Hence, extensive further tests and development are required. Therefore, we offer the Lagrangian
code with the following caveat:
The Lagrangian blob submodel released with MOM remains in the early research/development
stage. It has not yet been ported to the C-grid. Furthermore, it is not fully supported for
production work.
The C-grid option released with MOM in 2012 remains in the early research/development
stage. It has not yet been fully tested.
1.3 The MOM6 Project
In addition to MOM, GFDL has supported the development of a generalized layer ocean model under
the leadership of Bob Hallberg and Alistair Adcroft. This project has been termed GOLD, for Generalized
Ocean Layer Dynamics. For certain applications, the choice for vertical coordinate needs to be more general
than that available with the generalized level capability of MOM5 and earlier. In particular, the questions
of spurious diapycnal mixing, first identified by Griffies et al. (2000b) and more recently summarized by
Ilicak et al. (2012), motivated much of the GOLD effort, as did difficulties representing gravity driven
downslope flows (Winton et al.,1998). GOLD has matured recently through development of an IPCC
class earth system model using isopycnal vertical coordinates (the ESM2G model documented in Dunne
et al. (2012,2013)). Arguably GOLD represents the state-of-the-science in isopycnal layer models, and its
dynamical core provides the framework for doing any vertical coordinate or hybrid coordinate.
Starting June 2012, Adcroft, Griffies and Hallberg have embarked on a major effort to merge key phys-
ical parameterizations and the dynamical core from GOLD into MOM. This project, known as MOM6, is
timely for many reasons. The key motivator is that GFDL is initiating development of an new climate
model, CM4, that includes a mesoscale eddy permitting ocean configuration. To ensure success of CM4,
GFDL is focusing its presently diverse climate model development pathways. Thus, all the ocean model
developers at GFDL will focus on a single ocean code trunk for use in the new climate model, as well as for
other applications.
Progress towards MOM6 will occur in stages. Much of the initial efforts involve an upgrade to the com-
putational framework in GOLD to facilitate merging in elements of MOM5’s physical parameterizations
and diagnostics. The associated code restructuring is relevant regardless of the merger with GOLD, given
the need for MOM6 to address elements of the changing paradigm in computational platforms appearing
on the near-term horizon. Throughout development towards MOM6, we will continue to support key ca-
pabilities of MOM5 as well as GOLD. At strategic points in this development, we will solicit input from
the MOM community to examine the code and to provide assistance in upgrading selected portions where
non-GFDL expertise is required. There will be frequent updates to the MOM community as development
progresses towards MOM6. At GFDL, we are incredibly excited about the prospects of working towards a
unified ocean model code base. We trust the community will be also be excited when the project matures.
1.4 Elements of MOM5
In this section, we outline certain features of MOM as of 2012. Note that much of the following discussion
holds also for MOM4.0 and earlier releases of MOM4p1.
1.4.1 FMS and parallel programming
The tools required for parallel programming with MOM are provided by the GFDL Flexible Modeling
System (FMS). FMS provides the foundation upon which MOM is coded. That is, MOM is based on FMS.
There are dozens of scientists and engineers at GFDL focused on meeting the evolving needs of climate
Elements of MOM November 19, 2014 Page 5

Chapter 1. Introducing the Modular Ocean Model Section 1.4
scientists pushing the envelope of computational tools for studying climate. This situation is favorable to
the oceanographer who is less interested in the computer science required to run a high-end model, and
more interested in coding his or her new idea into MOM in a manner that is clear, flexible, and robust
across various computational platforms.
One of the early decisions made towards porting MOM3 to MOM4.0 concerned the elimination of
the memory window in MOM3 and MOM2. Instead, MOM4.0 and later releases employ arrays ordered
(i,j,k) for straightforward processor domain decomposition over the horizontal (i,j) directions. This
array layout provides the orientation of data structures used to parallelize MOM and other codes based on
GFDL FMS.
For those unfamiliar with parallel programming, yet wish to code something new in MOM, it is rec-
ommended that study be placed on certain of the existing MOM modules. By doing so, one can garner a
working understanding of the methods used to pass data across processor boundaries, thus ensuring that
simulation results are independent of the details of processor layout.
1.4.2 Features of the dynamical core
This section outlines certain features of the dynamical core in MOM.
1.4.2.1 Generalized orthogonal horizontal coordinates
MOM4.0 and later releases are written using generalized horizontal coordinates, with the coordinates as-
sumed to be locally orthogonal. The formulation in this document follows this approach as well. For global
ocean climate modeling, MOM comes with test cases using the tripolar grid of Murray (1996).
Code for reading in the grid and defining MOM specific grid factors is found in the module
ocean core/ocean grids.
MOM comes with preprocessing code suitable for generating grid specification files of various complexity,
including the Murray (1996) tripolar grid that has a bipolar Arctic region (see Figure 1.1). Note that the
horizontal grid in MOM is static (time independent), whereas the vertical grid is generally time dependent.
Hence, there is utility in separating the horizontal from the vertical grids.
1.4.2.2 Partial bottom steps
MOM4.0 and later releases employ the partial bottom step technology of Pacanowski and Gnanadesikan
(1998) to facilitate the representation of bottom topography. Each of the generalized level coordinates in
MOM make use of this technology. Code associated with partial bottom steps is located in the module
ocean core/ocean topog.
It is common in older (those dating from before 1997) z-models for model grid cells at a given discrete
level to have the same thickness. In these models, it is difficult to resolve weak topographic slopes without
including uncommonly fine vertical and horizontal resolution. This limitation can have important impacts
on the model’s ability to represent topographically influenced advective and wave processes. The partial
step methods of Adcroft et al. (1997) and Pacanowski and Gnanadesikan (1998) have greatly remedied this
problem via the implementation of more realistic representations of the solid earth lower boundary. Here,
the vertical thickness of a grid cell at a particular discrete level does not need to be the same. This added
freedom allows for a smoother, and more realistic, representation of topography by adjusting the bottom
grid cell thickness to more faithfully contour the topography. Figure 1.2 illustrates the bottom realized with
the ocean component of CM2.1, CM3, and ESM2M along the equator. Also shown is a representation using
an older full step method with the same horizontal and vertical resolution. The most visible differences
between full step and partial step topography are in regions where the topographic slope is not large,
whereas the differences are minor in steeply sloping regions.
Elements of MOM November 19, 2014 Page 6
Chapter 1. Introducing the Modular Ocean Model Section 1.4
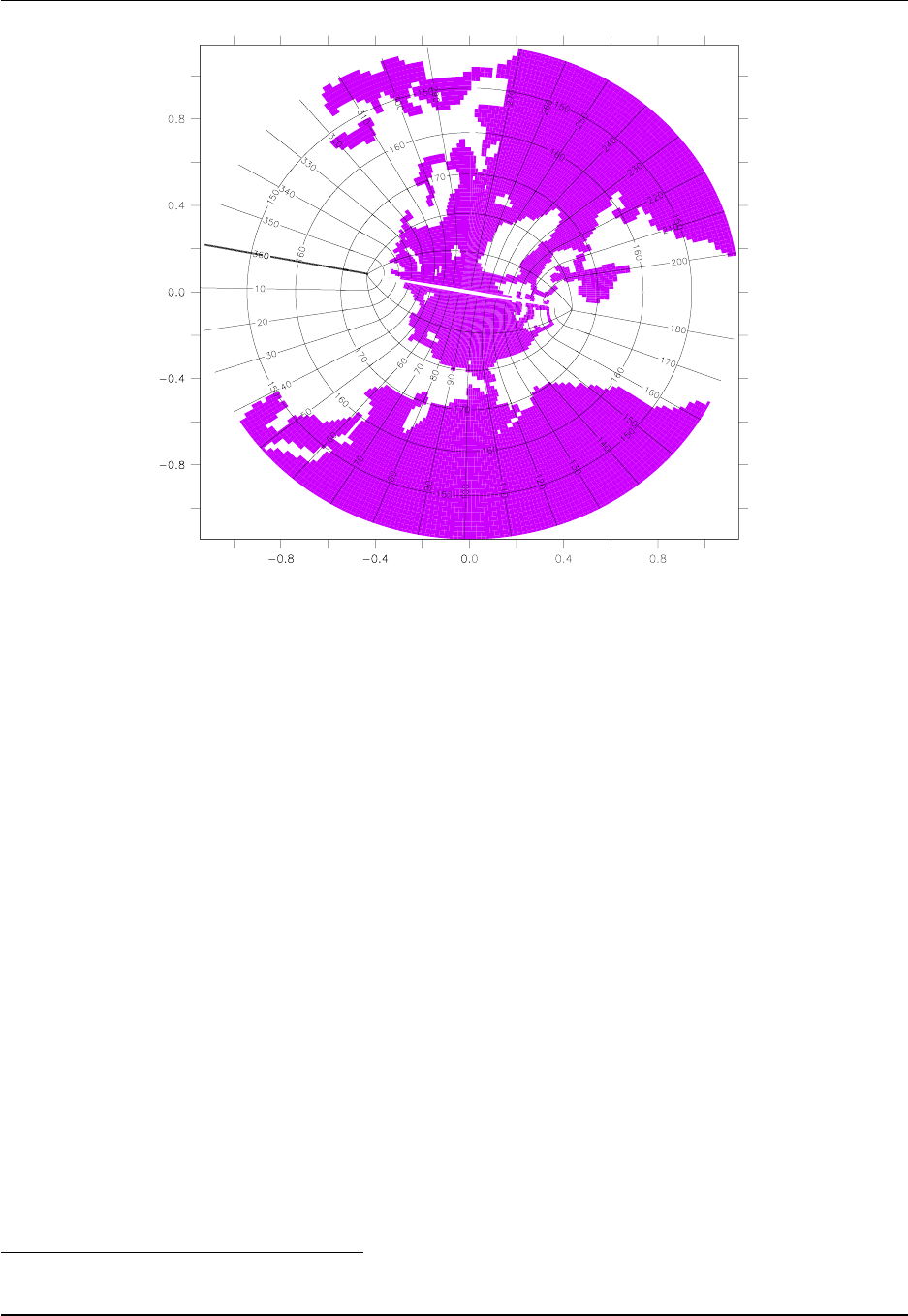
Figure 1.1: Illustration of the bipolar Arctic as prescribed by Murray (1996) (see his Figure 7) and realized
in the ocean component of CM2.1, CM3, and ESM2M. The transition from the bipolar Arctic to the spherical
grid occurs at 65◦N. We denote horizontal grid cells by (i,j) indices. As in the spherical coordinate region
of the grid, lines of constant i−index move in a generalized eastward direction within the bipolar region.
They start from the bipolar south pole at i= 0, which is identified with i=ni, where ni is the number
of points along a latitude circle and ni = 360 for a one degree horizontal resolution. The bipolar north
pole is at i=ni/2, which necessitates that ni be an even number. Both poles are centered at a velocity
point when using the B-grid in MOM. Lines of constant jmove in a generalized northward direction. The
bipolar prime-meridian is situated along the j-line with j=nj, where nj = 200 in OM3. This line defines
the bipolar fold that bisects the tracer grid. Care must be exercised when mapping fields across this fold.
As noted by Griffies et al. (2004), maintaining the exact identity of fields computed redundantly along the
fold is essential for model stability. Note that the cut across the bipolar fold is a limitation of the graphics
package, and does not represent a land-sea boundary in the model domain. This figure is taken after Figure
1ofGriffies et al. (2005).
1.4.2.3 Generalized level coordinates
Various vertical coordinates have been implemented in MOM. We have focused attention on vertical coor-
dinates based on functions of depth or pressure, which means in particualar that MOM does not support
thermodynamic or isopycnal based vertical coordinates.1
The following list summarizes vertical coordinates presently implemented in MOM. Extensions to other
vertical coordinates are straightforward, given the framework available for the coordinates already present.
Full details of the vertical coordinates are provided in Chapter 5.
• Geopotential coordinate as in MOM4.0, including the undulating free surface at z=ηand bottom
partial cells approximating the bottom topography at z=−H
s=z. (1.1)
1The Hallberg Isopycnal Model (HIM) is available from GFDL for those wishing to use layered models and it is available at
http://www.gfdl.noaa.gov/fms/.
Elements of MOM November 19, 2014 Page 7
Chapter 1. Introducing the Modular Ocean Model Section 1.4
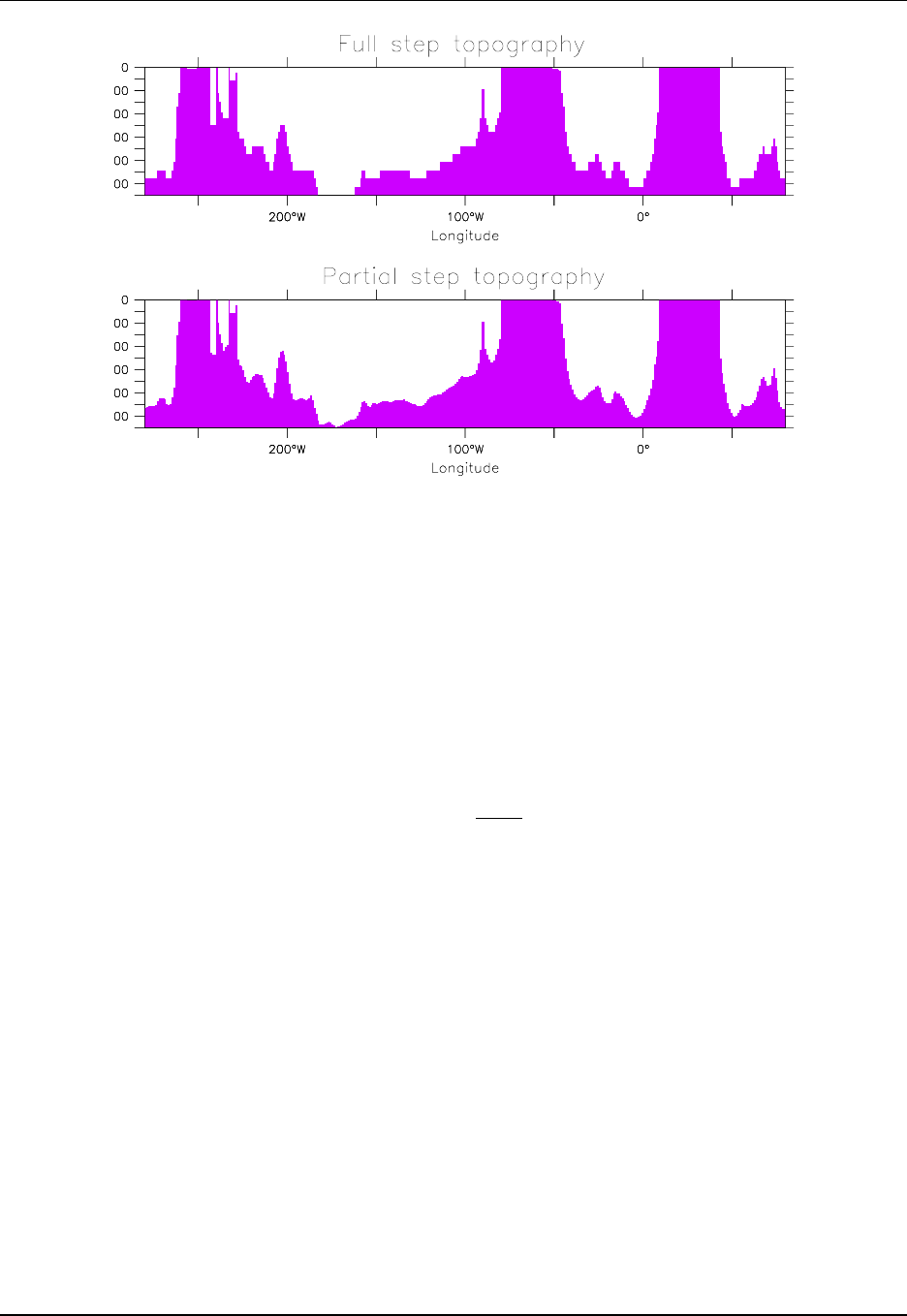
Figure 1.2: Bottom topography along the equator for the tracer cells. This figure illustrates the difference
between the older full step representation of the bottom topography (upper) and the partial step represen-
tation used in CM2.1, CM3, and ESM2M (lower). Note the large differences especially in regions where the
topographic slope is modest and small. This figure is taken after Figure 4 of Griffies et al. (2005).
This is the vertical coordinate used in the GFDL IPCC AR4 coupled climate model CM2.1 docu-
mented by Griffies et al. (2005); Delworth et al. (2006); Gnanadesikan et al. (2006).
• Quasi-horizontal rescaled height coordinate of Stacey et al. (1995) and Adcroft and Campin (2004)
s=z∗
=H z−η
H+η!.(1.2)
This is the vertical coordinate used in the ocean component of the GFDL IPCC AR5 coupled climate
model CM3 documented by Griffies et al. (2011) and Donner et al. (2011). It is also the vertical
coordinate used in the earth system model ESM2M documented by Dunne et al. (2012,2013). Note
that tests at GFDL indicate that CM2.1 with the z∗vertical coordinate exhibits the same climate as
CM2.1 with geopotential vertical coordinate.
In equation (1.2), z=η(x,y,t) is the deviation of the ocean free surface from a state of rest at z= 0,
and z=−H(x,y) is the ocean bottom. Whereas a geopotential ocean model places all free surface
undulations into the top model grid cell, a z∗model distributes the undulations throughout the ocean
column. All grid cells thus have a time dependent thickness with z∗. Surfaces of constant z∗differ
from geopotential surfaces according to the ratio η/H, which is generally quite small. Hence, surfaces
of constant z∗are quasi-horizontal, thus minimizing difficulties of accurately computing the horizon-
tal pressure gradient (see Griffies et al.,2000a, for a review). The z∗vertical coordinate is analogous
to the “eta” coordinate sometimes used for atmospheric models (Black,1994).
We chose z∗for CM3 and ESM2M because of the enhanced flexibility when considering two key ap-
plications of climate models. The first application concerns large surface height deviations associated
with tides and/or increased loading from sea ice (e.g., a global cooling simulation). The z∗model
allows for the free surface to fluctuate to values as large as the local ocean depth, |η|< H, whereas
the geopotential model is subject to the more stringent constraint |η|<∆z1, with ∆z1the thickness of
Elements of MOM November 19, 2014 Page 8
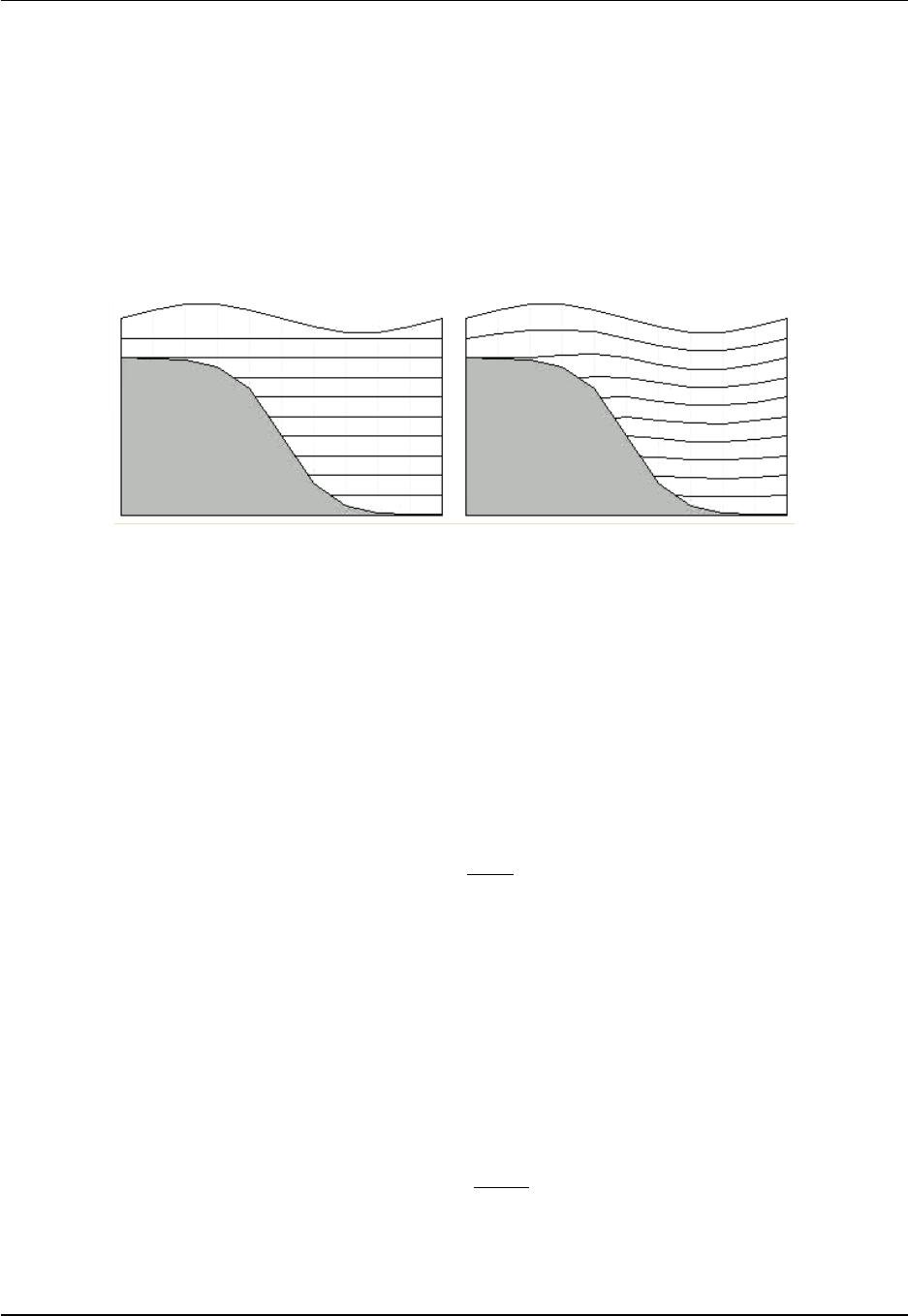
Chapter 1. Introducing the Modular Ocean Model Section 1.4
the top grid cell with a resting ocean. The ocean models in CM2.1 and CM3 set a minimum depth
to H≥40m, whereas ∆z1= 10m (note that there is no wetting and drying algorithm in MOM). This
flexibility with z∗is further exploited if considering even finer vertical grid resolution. Figure 1.3
illustrates this flexibility.
The second application where z∗is useful concerns increased land ice melt that adds substantially
to the sea level, as in the idealized studies of Stouffer et al. (2006b), Kopp et al. (2010), and Yin
et al. (2010b). Placing all of the surface expansion into the top model grid cell, as with the free
surface geopotential model, greatly coarsens the vertical grid resolution in this important portion of
the ocean, whereas the z∗model does not suffer from this problem since the expansion is distributed
throughout the column.
4
• AR4ClimateModelsCM2.0/CM2.1
• AR5Climate/EarthSystemModelsCM2M/ESM2M
• AR5DecadalVariability/PredictionCM2.1/CM2.4
• NCEPClimateForecastSystemv2
KeyNOAAApplicationsofMOM4
KeyNOAAApplicationsofMOM4
Figure 1.3: Illustrating the differences between geopotential vertical coordinate (left panel) and z∗vertical
coordinate (right panel). In the upper ocean grid cell, the free surface with the geopotential vertical coor-
dinate can generally penetrate through the bottom of the top cell lower boundary, in which case there is a
problem with the simulation. In contrast, for the z∗vertical coordinate, all vertical cells undulate in time,
with motion of the free surface spread throughout the ocean depth. Note that the undulations of the cell
interfaces with z∗are scaled according to η/H, which is generally quite small. The undulations shown in
this schematic are thus highly exaggerated for visualization purposes.
• Depth based terrain following “sigma” coordinate, popular for coastal applications (e.g., Blumberg
and Mellor,1987)
s=σ(z)
=z−η
H+η.(1.3)
This coordinate has not been for research applications by GFDL researchers.
• The pressure coordinate
s=p(1.4)
was shown by Huang et al. (2001), DeSzoeke and Samelson (2002), Marshall et al. (2004), and Losch
et al. (2004) to be a useful way to transform Boussinesq z-coordinate models into non-Boussinesq
pressure coordinate models.
• Quasi-horizontal rescaled pressure coordinate
s=p∗
=po
b p−pa
pb−pa!,(1.5)
where pais the pressure applied at the ocean surface from the atmosphere and/or sea ice, pbis the
hydrostatic pressure at the ocean bottom, and po
bis a time independent reference bottom pressure.
This coordinate is the pressure coordinate analog to the z∗coordinate.
Elements of MOM November 19, 2014 Page 9

Chapter 1. Introducing the Modular Ocean Model Section 1.4
• Pressure based terrain following coordinate
s=σ(p)
= p−pa
pb−pa!.(1.6)
This coordinate is the pressure coordinate analog to the σ(z)coordinate.
We now highlight the following points regarding these vertical coordinates.
• All depth based vertical coordinates implement the volume conserving, Boussinesq, ocean primitive
equations.
• All pressure based vertical coordinates implement the mass conserving, nonBoussinesq, ocean prim-
itive equations.
• There has little effort focused on reducing pressure gradient errors in the terrain following coordi-
nates (Section 3.2). Researchers intent on using terrain following coordinates may find it necessary
to implement one of the more sophisticated pressure gradient algorithms available in the literature,
such as that from Shchepetkin and McWilliams (2002).
• Use of neutral physics parameterizations (Section 4.2.3 and Chapter 23) with terrain following coor-
dinates is not recommended with the present implementation. There are formulation issues that have
not been addressed, since the main focus of neutral physics applications at GFDL centres on vertical
coordinates that are quasi-horizontal.
• Most of the vertical coordinate dependent code is in the module
ocean core/ocean thickness
where the thickness of a grid cell is updated according to the vertical coordinate choice. The developer
intent on introducing a new vertical coordinate may find it suitable to emulate the steps taken in this
module for other vertical coordinates. The remainder of the model code is generally transparent to
the specific choice of vertical coordinate, and such has facilitated a straightforward upgrade of the
code from MOM4.0 to later releases.
• The restart file for ocean core/ocean thickness is not compatible across vertical coordinates, given
particular distinctions between the various vertical coordinates. Hence, one should not modify the
vertical coordinate in the middle of a simulation without re-initializing the thickness module.
1.4.2.4 Explicit barotropic solver
MOM4.0 and later releases employ a split-explicit time stepping scheme where fast two-dimensional dy-
namics is sub-cycled within the slower three dimensional dynamics. The method follows ideas detailed in
Chapter 12 of Griffies (2004), which are based on Killworth et al. (1991) and Griffies et al. (2001). Chapter
10 presents the details for MOM, and the code is on the module
ocean core/ocean barotropic.
1.4.2.5 Time stepping schemes
The time tendency for tracer and baroclinic velocity can be discretized two ways.
1. The first approach uses the traditional leap-frog method for the inviscid/dissipationless portion of
the dynamics, along with a Robert-Asselin time filter. This method is available in MOM4.0. However,
its use is strongly discouraged given that it is unstable when used without time filters, and since the
time filters preclude conservation of tracer.2
2The method from Leclair and Madec (2009) aims to overcome the limitations of tracer conservation with a time filtered leap frog
scheme. Their method has not been implemented in MOM.
Elements of MOM November 19, 2014 Page 10

Chapter 1. Introducing the Modular Ocean Model Section 1.4
2. The preferred method discretizes the time tendency with a two-level forward step, which eliminates
the need to time filter. Tracer and velocity are staggered in time, thus providing second order accu-
racy in time. For certain model configurations, this scheme has been found to be twice as efficient
as the leap-frog based scheme since one can take twice the time step with the two-level approach.
Furthermore, without the time filtering needed with the leap-frog, the new scheme conserves total
tracer to within numerical roundoff. This scheme is discussed in Griffies et al. (2005) and Griffies
(2004) (see Chapter 12), as well as in Chapter 10 of this document.
The code implementing these ideas in MOM can be found in
ocean core/ocean velocity
ocean tracers/ocean tracer
As discussed in Chapter 12, there are various methods available for time stepping the Coriolis force in
MOM. The most commonly used method for global climate simulations with the B-grid version of MOM is
the semi-implicit approach in which half the force is evaluated at the present time and half at the future
time. An Adams-Bashforth scheme is used for the C-grid version of MOM.
1.4.2.6 Pressure gradient calculation
The pressure gradient calculation has been updated in MOM4p1 later releases to allow for the use of gen-
eralized vertical coordinates. A description of the formulation is given in Chapter 3, and the code is in the
module
ocean core/ocean pressure.
Notably, none of the sophisticated methods described by Shchepetkin and McWilliams (2002) are imple-
mented in MOM, and so terrain following vertical coordinates may suffer from unacceptably large pressure
gradients errors. Researchers are advised to perform careful tests prior to using these coordinates.
1.4.3 Dynamically interacting Lagrangian parcels
The one feature that most distinguishes the 2012 release of MOM relative to earlier releases is the abil-
ity to enable an interactive Lagrangian parcel scheme, whereby the parcels, or “blobs”, are dynamically
coupled to the traditional Eulerian grid cell properties. That is, the Lagrangian and Eulerian submodels
conservatively exchange seawater mass, tracer mass, and momentum. Figure 1.4 provides a schematic of
this coupled system.
There are two general physical applications that motivate considering the added degrees of freedom
afforded with a Lagrangian submodel, with both applications associated with vertically unstable water.
• Representation of convection in a hydrostatic model;
• Representation of gravitationally driven bottom downslope flows.
Bates et al. (2012a,b) presents the formulation of how the Lagrangian submodel is coupled to the traditional
Eulerian grid cells of MOM. The Lagrangian blobs comes with the following caveat:
The Lagrangian blob submodel released with MOM remains in the early research/development
stage.
1.4.4 Tracer features
In this section we outline features available for tracers in MOM.
1.4.4.1 Equation of state
As discussed in Chapter 6, the equation of state in MOM has been updated to TEOS-10 as detailed in IOC
et al. (2010). The code for computing density and related fields is found in the module
ocean core/ocean density.
Elements of MOM November 19, 2014 Page 11
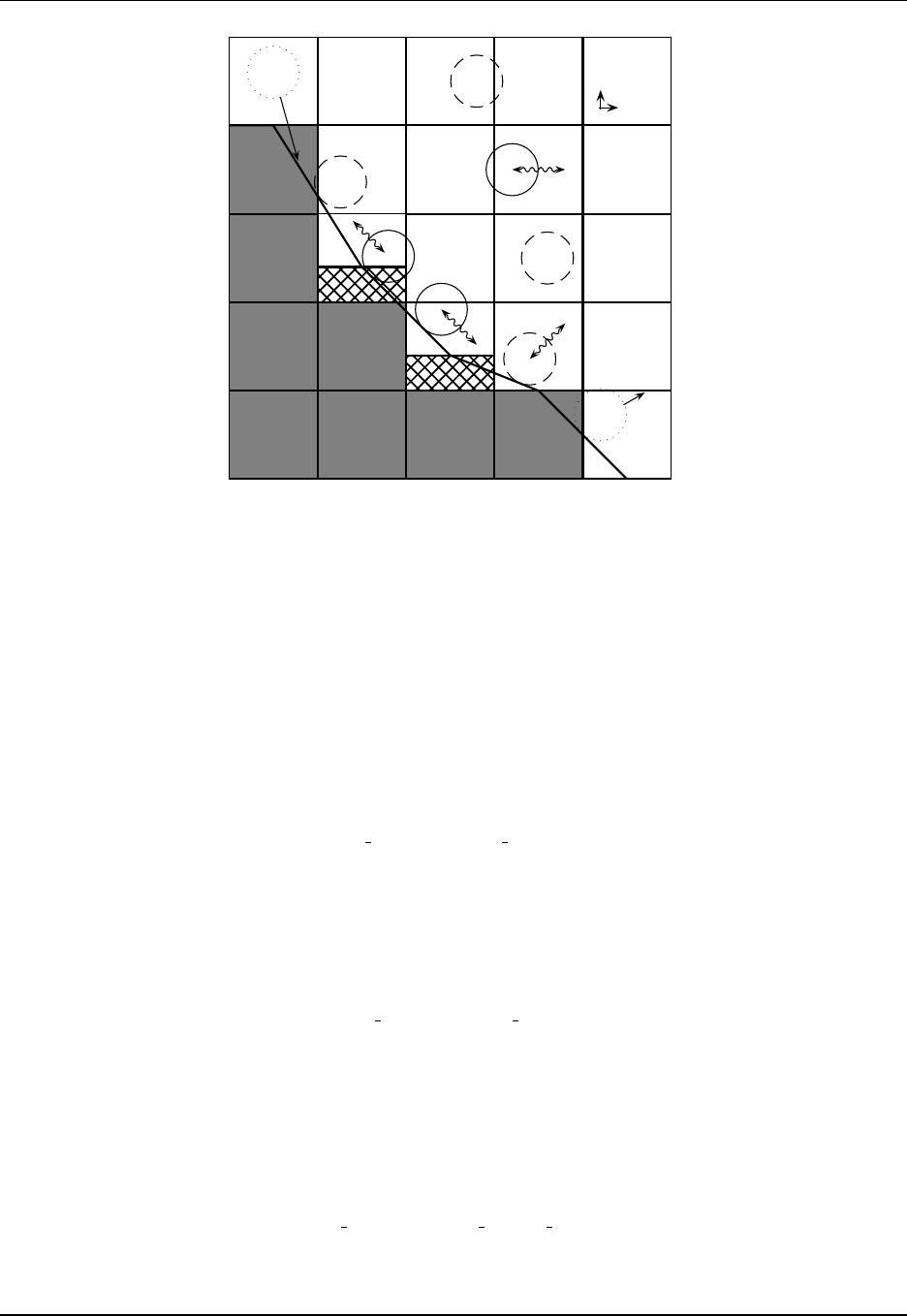
Chapter 1. Introducing the Modular Ocean Model Section 1.4
m(new)
˙x(new)
dmm
˙x
dm
m
˙x
dm
m(dstry)
m
˙x
m(new)
˙x(new)
dm
m
˙x
m(dstry)
˙x(dstry)
˙x
m
ˆz
ˆx, ˆy
Figure 1.4: A vertical-horizontal section near the ocean bottom to illustrate Lagrangian parcels or blobs
in MOM intereacting with Eulerian grid cell properties. The cross-hatched region denotes partial step
topography, and the entrainment and detrainment rates illustrate the decay and growth of a blob as it
moves downslope with an acceleration ˙
x.
1.4.4.2 Conservative temperature
MOM time steps the conservative temperature described by McDougall (2003) to provide a measure of
heat in the ocean (see Section 2.3.2). This variable is about 100 times more conservative than the tradi-
tional potential temperature variable. An option exists to set either conservative temperature or potential
temperature prognostic, with the alternative temperature variable carried as a diagnostic tracer. This code
for computing conservative temperature is within the module
ocean tracers/ocean tempsalt.
1.4.4.3 Freezing temperature for frazil
Accurate methods for computing the freezing temperature of seawater are provided by Jackett et al. (2006)
and IOC et al. (2010). These methods allow, in particular, for the computation of the freezing point at
arbitrary depth, which is important for ice shelf modelling. These methods have been incorporated into
the frazil module
ocean tracers/ocean frazil,
with heating due to frazil formation treated as a diagnostic tracer.
1.4.4.4 Tracer advection
MOM comes with the following array of tracer advection schemes. Note that centred schemes are stable only
for the leap-frog version of MOM. We thus partition the advection schemes according to the corresponding
time stepping schemes. The code for tracer advection schemes are in the module
ocean tracers/ocean tracer advect.
Examples of the advection scheme simulation features are provided in the Torus test case that comes with
the MOM distribution.
Elements of MOM November 19, 2014 Page 12
Chapter 1. Introducing the Modular Ocean Model Section 1.4
• Tracer advection schemes available for either time stepping method include the following.
1. First order upwind
2. Quicker scheme is third order upwind biased and based on the Leonard (1979). Holland et al.
(1998) and Pacanowski and Griffies (1999) discuss implementations in ocean climate models.
This scheme does not have flux limiters, so it is not monotonic.
3. Quicker-MOM3: The Quicker scheme in MOM4p1 differs slightly from that in MOM3, and so
the MOM3 algorithm has also been ported to MOM4p1 and later releases.
4. Multi-dimensional third order upwind biased approach of Hundsdorfer and Trompert (1994),
with Super-B flux limiters.3The scheme is available in MOM4p1 and later releases using either
time stepping scheme.
5. Multi-dimensional third order upwind biased approach of Hundsdorfer and Trompert (1994),
with flux limiters of Sweby (1984).4It is available in MOM4p1 and later releases with either time
stepping scheme. This scheme was used in the ocean component of the CM2.1 climate model
(Griffies et al.,2005;Delworth et al.,2006;Gnanadesikan et al.,2006).
6. The second moment scheme of Prather (1986) has been implemented in MOM . It is available
without limiters, or with the limiters of Prather (1986) and Merryfield and Holloway (2003).
7. The multi-dimensional piece-wise parabolic method (MDPPM) has been implemented in MOM.
5This is the scheme used for most of the newer (post 2010) climate models developed at GFDL
such as ESM2M (Dunne et al.,2012,2013).
Both the Super-B and Sweby schemes are non-dispersive, preserve shapes in three dimensions, and
preclude tracer concentrations from moving outside of their natural ranges in the case of a purely
advective process. They are modestly more expensive than the Quicker scheme, and it do not signif-
icantly alter the simulation relative to Quicker in those regions where the flow is well resolved. The
Sweby limiter code was used for the ocean climate model documented by Griffies et al. (2005). The
MDPPM scheme can likewise ensure montonicity with one of the three possible limiters.
• Tracer advection schemes available just for the leap-frog time stepping method include the following.
1. Second order centred differences
2. Fourth order centred differences: This scheme assumes the grid is uniformly spaced (in metres),
and so is less than fourth order accurate when the grid is stretched, in either the horizontal or
vertical.
3. Sixth order centred differences: This scheme assumes the grid is uniformly spaced (in metres),
and so is less than sixth order accurate when the grid is stretched, in either the horizontal or
vertical. This scheme is experimental, and so not supported for general use.
1.4.4.5 Tracer packages
MOM comes with an array of tracer packages of use for understanding water mass properties and for
building more sophisticated tracer capabilities, such as for ocean ecosystem models. Modules for these
tracers are in the directories
ocean tracers
ocean bgc
ocean shared/generic tracers.
Various of the tracer options include the following.
3This scheme was ported to MOM4.0 by Alistair Adcroft, based on his implementation in the MITgcm. The online documentation
of the MITgcm at http://mitgcm.org contains useful discussions and details about this advection scheme.
4This scheme was ported to MOM4.0 by Alistair Adcroft, based on his implementation in the MITgcm. The online documentation
of the MITgcm at http://mitgcm.org contains useful discussions and details about this advection scheme.
5This scheme was ported to MOM4p1 by Alistair Adcroft, based on his implementation in the MITgcm. The online documentation
of the MITgcm at http://mitgcm.org contains useful discussions and details about this advection scheme.
Elements of MOM November 19, 2014 Page 13

Chapter 1. Introducing the Modular Ocean Model Section 1.4
• Idealized passive tracer module with internally generated initial conditions. These tracers are ideal
for testing various advection schemes, for example, as well as to diagnose pathways of transport.
• An ideal age tracer, with various options for specifying the initial and boundary conditions.
• The OCMIP2 protocol tracers (CO2, CFC, biotic).
• iBGC: A simple ocean biogeochemistry model.
• BLING: An intermediate complexity ocean biogeochemistry model. This model has been written
in a generic format to allow for its use with both MOM and GFDL’s model code GOLD. BLING is
documented in the paper by Galbraith et al. (2011).
• TOPAZ: A comprehensive model of oceanic ecosystems and biogeochemical cycles is a state of the
art model that considers 22 tracers including three phytoplankton groups, two forms of dissolved or-
ganic matter, heterotrophic biomass, and dissolved inorganic species for C,N,P,Si,Fe,CaCO3and
O2cycling. The model includes such processes as gas exchange, atmospheric deposition, scavenging,
N2fixation and water column and sediment denitrification, and runoffof C,N,Fe,O2, alkalinity and
lithogenic material. The phytoplankton functional groups undergo co-limitation by light, nitrogen,
phosphorus and iron with flexible physiology. Loss of phytoplankton is parameterized through the
size-based relationship of Dunne et al. (2013). Particle export is described through size and temper-
ature based detritus formation and mineral protection during sinking with a mechanistic, solubility-
based representation alkalinity addition from rivers, CaCO3sedimentation and sediment preserva-
tion and dissolution. This model has been written in a generic format to allow for its use with both
MOM and GFDL’s isopycnal model GOLD. Further documentation of TOPAZ is provided by Dunne
et al. (2013).
1.4.5 Subgrid scale parameterizations
Simulations in the ocean require the use of subgrid scale (SGS) parameterizations to allow the impacts
from unresolved scales to impact the resolved scales. The development of robust and scientifically based
SGS parameterizations is an active area of theoretical oceanography. Given the large uncertainty associated
with parameterizations, MOM has chosen to implement a wide suite of methods so that researchers can
have access to a variety of approaches that may best fit the particular application. The downside of such
variety is that it requires knowledge by the user to best make use of the huge number of options. Some
guidance for the use of SGS parameterizations is available from the test cases that come with MOM, and
some is provided by querying the online MOM user community. Nonetheless, the best approach is for
the MOM researcher to penetrate into the literature in order to make well educated decisions about SGS
parameterizations for a particular application.
In this section we outline some features of the subgrid scale parameterizations available in MOM.
1.4.5.1 Penetration of shortwave radiation
Chapter 17 describes the computational method used in MOM for implementing the penetration of short-
wave radiation into the ocean. The following modules are available for determining the details of how
shortwave radiation penetrates into the ocean.
ocean param/sources/ocean shortwave
ocean param/sources/ocean shortwave csiro
ocean param/sources/ocean shortwave gfdl
ocean param/sources/ocean shortwave jerlov
Please refer to each module for full documentation. In brief, these modules provide the following options.
•ocean shortwave: This module drives the other shortwave modules.
Elements of MOM November 19, 2014 Page 14
Chapter 1. Introducing the Modular Ocean Model Section 1.4
•ocean shortwave csiro: This module implements an exponential decay for the penetrative short-
wave radiation. This module was prepared at CSIRO Marine and Atmospheric Research in Australia.
•ocean shortwave jerlov: This module implements yet another exponential decay formulation (ac-
tually, a double exponential) for the penetrative shortwave radiation.
•ocean shortwave gfdl: This module implements the optical model of Morel and Antoine (1994) as
well as that of Manizza et al. (2005).
–Sweeney et al. (2005) compile a seasonal climatology of chlorophyll based on measurements
from the NASA SeaWIFS satellite, and this climatology is available with the distribution of
MOM. They used this data to develop two parameterizations of visible light absorption based
on the optical models of Morel and Antoine (1994) and Ohlmann (2003). The two models yield
quite similar results when used in global ocean-only simulations, with very small differences in
heat transport and overturning.
–The Morel and Antoine (1994) method for attenuating shortwave radiation was employed in the
CM2 coupled climate model, as discussed by Griffies et al. (2005). MOM4p1 and later releases
have updated the implementation of this algorithm relative to MOM4.0 by including the time
dependent nature of the vertical position of a grid cell. The MOM4.0 implementation used the
vertical position appropriate only for the case of a static ocean free surface.
–In more recent model development, especially that associated with interactive biogeochemistry,
GFDL modelers have preferred the scheme from Manizza et al. (2005) rather than Morel and
Antoine (1994).
1.4.5.2 Horizontal friction
MOM has a suite of horizontal friction schemes, such as Smagorinsky laplacian and biharmonic schemes
described in Griffies and Hallberg (2000) and the anisotropic laplacian scheme from Large et al. (2001) and
Smith and McWilliams (2003). Code for these schemes is found in the modules
ocean param/lateral/ocean lapgen friction
ocean param/lateral/ocean bihgen friction.
1.4.5.3 Convective adjustment schemes
There are various convective methods available for producing a gravitationally stable column, with the
code found in the module
ocean param/vertical/ocean convect.
The scheme used most frequently at GFDL for idealized modeling is that due to Rahmstorf (1993). Chapter
19 details this scheme and other adjustment methods. Note that for realistic climate and regional modeling,
convective adjustment is not recommended. Instead, preference is given towards the use of a large verti-
cal diffusivity, such as that promoted by Klinger et al. (1996). Consequently, the convective adjustment
schemes remain in MOM largely for idealized simulations and legacy purposes.
1.4.5.4 Neutral physics
The parameterization of mesoscale eddies remains amongst the most active areas of theoretical research
impacting ocean models. MOM comes with a suite of options available for treating neutral physics in the
ocean interior as well as in boundary regions. A discussion of the methods is given in Chapter 23. The code
related to this material is available in the directory
ocean param/neutral.
Elements of MOM November 19, 2014 Page 15

Chapter 1. Introducing the Modular Ocean Model Section 1.4
1.4.5.5 Restratification effects from submesoscale eddies
There is an option available for parameterizing the restratification effects from submesoscale eddies, as
proposed by Fox-Kemper et al. (2008b) and Fox-Kemper et al. (2011). The MOM formulation is given in
Chapter 24, and the code is available in the module
ocean param/lateral/ocean submesoscale.
1.4.5.6 Parameterization of form drag
MOM has various options associated with the parameterization of form drag arising from unresolved
mesoscale eddies, as proposed by Greatbatch and Lamb (1990), Aiki et al. (2004), and Ferreira and Marshall
(2006). The code is available in the module
ocean param/vertical/ocean form drag,
and documentation is given in Chapter 22. The form drag parameterization schemes have not been thor-
oughly used at GFDL.
1.4.5.7 Tidal mixing parameterizations
The tidal mixing parameterization of Simmons et al. (2004) has been implemented as a means to parameter-
ize the diapycnal mixing effects from breaking internal gravity waves, especially those waves influenced by
rough bottom topography. Additionally, this scheme has been combined with that used by Lee et al. (2006),
who discuss the importance of barotropic tidal energy on shelves for dissipating energy and producing
tracer mixing. Chapter 20 presents the model formulation, and
ocean param/vertical/ocean vert tidal
contains the code.
1.4.5.8 An array of vertical mixing schemes
MOM comes with a wide array of vertical mixing schemes, including the following.
• Constant background diffusivity proposed by Bryan and Lewis (1979)
ocean param/vertical/ocean vert mix
• Richardson number dependent scheme from Pacanowski and Philander (1981)
ocean param/vertical/ocean vert pp
• The KPP scheme from Large et al. (1994)
ocean param/vertical/ocean vert kpp
ocean param/vertical/ocean vert kpp mom4p0
The module ocean vert kpp maintains code provides some code updates relative to MOM4.0, such
as to allow for the use of generalized vertical coordinates; features found useful in fresh inland seas;
and modifications introduced by Danabasoglu et al. (2006). The module ocean vert kpp mom4p0
maintains code compatibility with the implementation of MOM4.0 necessary to allow for backwards
compatiblity with the CM2.1 coupled model documented in Griffies et al. (2005).
•General Ocean Turbulence Model (GOTM): Coastal simulations require a suite of vertical mixing
schemes beyond those available in most ocean climate models. GOTM (Umlauf et al.,2005) is a public
domain Fortran90 free software used by a number of coastal ocean modellers
http ://www.gotm.net/
Elements of MOM November 19, 2014 Page 16

Chapter 1. Introducing the Modular Ocean Model Section 1.5
GOTM includes many sophisticated turbulence closure schemes, and is updated periodically. It thus
provides users of MOM4p1 and later releases access to most updated methods for computing vertical
diffusivities and vertical viscosities. GOTM has been coupled to MOM by scientists at CSIRO in
Australia in collaboration with German and GFDL scientists.
The MOM wrapper for GOTM is
ocean param/vertical/ocean vert gotm
with the GOTM source code in the directory
ocean param/gotm.
1.4.5.9 Overflow schemes
MOM comes with various methods of use for parameterizing, or at least facilitating the representation of,
dense water moving into the abyss. These schemes are documented in Chapter 27, with the following
modules implementing these methods
ocean param/lateral/ocean sigma transport
ocean param/lateral/ocean mixdownslope
ocean param/sources/ocean overflow
ocean param/sources/ocean overexchange.
1.4.6 Diagnostics and the FMS diagnostic manager
MOM has traditionally had a plethora of diagnostic features. Indeed, perhaps one of the most appealing
features of MOM is the exceptional range of online diagnostics available for help in understanding all
aspects of the simulation, from details of the subgrid scale parameterizations to water mass transformation
rates. A thorough discussion of various MOM diagnostic features is available in Part VI of this document.
The diagnostic manager is the central tool from the GFDL FMS code repository employed for writing
diagnostics in MOM. The diagnostic manager allows users to decide at runtime whether to save a particu-
lar diagnostic field, and what particular space and time sampling to use. To access the diagnostic manager
facility, the programmer must register a field to be sampled in the appropriate MOM location. This reg-
istration process is straightforward, with thousands of fields presently registered in MOM. But inevitably
there will be a need to add a new diagnostic field. In this case, it is trivial to register this new field by
emulating what has been done for other fields already in MOM. Furthermore, if the new field is deemed of
use to the broader MOM community, then please suggest that it be included in future MOM releases.
1.4.7 Open boundary conditions
Much of the appeal of recent MOM releases is related to its enhanced facilities for regional ocean modeling,
with Herzfeld et al. (2011) documenting a suite of tests that exercise these features. Central to this utility
is the open boundary condition module
ocean core/ocean obc
which is documented in Chapter 16 as well as Herzfeld et al. (2011).
1.4.8 Test cases
All of the test cases have been revised as well as the addition of some new tests. These test cases are
provided for computations and numerical evaluation, and as starting points for those wishing to design
and implement their own research models.
Elements of MOM November 19, 2014 Page 17

Chapter 1. Introducing the Modular Ocean Model Section 1.5
1.5 A flow diagram for the MOM algorithm
This document aims to provide a full rationalization of how MOM updates the ocean state. Prior to delving
into these extensive details, the reader may find it useful to see a coarse-grained perspective provided by
Figure 1.5. Note that the particular order for the calculations are in some cases quite important, as they
follow from the staggered time stepping methods detailed in Chapter 11. We now summarize the basic
steps used in the MOM algorithm.
• Drive MOM using either the
driver/ocean solo.F90
module when running MOM as an ocean-only model, or the module
coupler/coupler main.F90
when coupling MOM to another component, such as sea ice or the atmosphere.
• Initialize ocean related fields for the start of a new time step, with these initialization calls coordi-
nated by the module
ocean core/ocean model.F90.
Some of these fields are needed for prognostic calculations, and some are required for diagnostics.
• Accumulate surface and bottom boundary fluxes for use in forcing the ocean fluid. The surface fluxes
are computed in
ocean core/ocean sbc.F90
and the bottom fluxes are computed in
ocean core/ocean bbc.F90.
• Compute the vertical mixing coefficients associated with subgrid scale (SGS) parameterizations. These
coefficients are determined according to the chosen parameterization, and they are computed in mod-
ules contained in the directory
ocean param/.
• Compute any sources or sponge data for tracer fields using modules in the directories
ocean tracers/
ocean sources/.
If there are biogeochemical tracers, then further sources will be computed in the biogeochemical
modules contained in
ocean bgc/
ocean shared/generic tracers/.
• Compute tracer tendencies associated with the first suite of subgrid scale parameterizations. These
processes are computed using the ocean cell thicknesses as updated on the previous time step. Mod-
ules associated with this step are generally located in the directory
ocean param/.
• Accumulate mass sources for use in updating the sea level or bottom pressure. This task is handled
by code in
ocean core/ocean barotropic.F90
ocean core/ocean thickness.F90.
Elements of MOM November 19, 2014 Page 18

Chapter 1. Introducing the Modular Ocean Model Section 1.5
Algorithmic flow for a time step of MOM4p1
algorithmic task code
driver for ocean ocean solo.F90 or coupler.F90
initialize ocean related
prognostic &diagnostic fields
ocean model.F90
accumulate boundary fluxes ocean sbc.F90, ocean bbc.F90
vertical mixing coefficients ocean param/
tracer sources ocean tracers/, ocean param/sources/
ocean bgc, ocean shared/ocean generic/
tracer SGS tendencies part Aocean param/
mass and volume tendencies ocean barotropic.F90, ocean thickness.F90
advection velocity components ocean advection velocity.F90
update ηor bottom pressure ocean barotropic.F90
update T-cell thickness ocean thickness.F90
tracer SGS tendencies part Bocean param/
update ocean tracers,
density,and pressure
ocean tracers/ ocean density.F90
accumulate acceleration part Aocean velocity.F90
update barotropic system ocean barotropic.F90
accumulate acceleration part Bocean velocity.F90
update U-cell thickness ocean thickness.F90
update velocity ocean velocity.F90
compute diagnostic quantities ocean diag/
Figure 1.5: A flow diagram for the algorithm used in MOM to time step the ocean equations. Note that
there are a few more steps required when enabling interactive Lagrangian blobs, with these additional
steps detailed in Bates et al. (2012a,b).
• Diagnose the velocity components for use in tracer and velocity advection. The vertical component
is diagnosed through the continuity equation, whereas the horizontal components are based on inter-
polating the velocity components to the tracer and velocity cell faces. This task is handled by code
in
ocean core/ocean advection velocity.F90.
Elements of MOM November 19, 2014 Page 19

Chapter 1. Introducing the Modular Ocean Model Section 1.6
• Update the sea surface height η(for Boussinesq depth based vertical coordinates) or bottom pressure
(for non-Boussinesq pressure based vertical coordinates) to a new time step. This task is handled by
code in
ocean core/ocean barotropic.F90.
• Update the vertical elements to the tracer cell using code in
ocean core/ocean thickness.F90.
• Compute tracer tendencies associated with the second suite of subgrid scale parameterizations. These
processes are computed using the updated ocean cell thicknesses. Modules associated with this step
are generally located in
ocean param/.
• Update the tracer concentrations using tendencies associated with SGS processes, advection, and
boundary fluxes. Perform the update first using time-explicit processes, and then update vertical
and boundary processes using time-implicit methods. This task is handled by routines in
ocean tracers/ocean tracer.F90.
With the updated tracer concentrations, we then update the density in the module
ocean core/ocean density.F90
using the equation of state ρ=ρ(S(τ+1),Θ(τ+ 1),p(τ)), with the hydrostatic pressure computed from
the previous time step. Pressure and density derivatives are then updated using all fields consistently
at the τtime step.
• Accumulate the first portion of the acceleration, here associated with velocity advection, horizontal
pressure gradients, horizontal friction, momentum sources, and parameterized form drag. Each of
these acceleartions are computed in a time-explicit manner, and they are coordinated by a routine in
ocean core/ocean velocity.F90.
• Update the two-dimensional vertically integrated momentum by time stepping the forced shallow
water equations using routines in
ocean core/ocean barotropic.F90.
• Accumulate the second portion of the acceleration, here associated with time-explicit portion of the
Coriolis force and time-explicit portion of vertical friction. These calculations are coordinated by a
routine in
ocean core/ocean velocity.F90.
• Update the vertical elements to the velocity cell using code in
ocean core/ocean thickness.F90.
• Update the three dimensional velocity, including time implicit portions of the Coriolis forcing, verti-
cal friction, and boundary forcing. This calculation is located in
ocean core/ocean velocity.F90.
• Complete a time step by computing some optional diagnostic quantities, such as energey analyses,
global tracer budgets, etc. This calculation is coordinated by routines in the directory
ocean diag/.
• Return ocean fields to the driver, including in particular the surface ocean properties that are used to
compute boundary fluxes exchanged with the sea ice and atmosphere models.
Elements of MOM November 19, 2014 Page 20

Chapter 1. Introducing the Modular Ocean Model Section 1.7
1.6 Papers and reports providing documentation of MOM
The following is an incomplete list of documents that provide some further documentation of MOM than
that provided here. We list in particular those papers and reports that provide some details of use to help
understand aspects of the code and its use in applications.
•MOM manuals and ocean model monograph: As mentioned at the start of this chapter, the present
document aims to incorporate many of the salient features from previous MOM related technical
guides and monographs. The following lists these other documents.
–The MOM3 Manual of Pacanowski and Griffies (1999)
–Fundamentals of Ocean Climate Models by Griffies (2004)
–A Technical Guide to MOM4.0 by Griffies et al. (2004)
–Elements of MOM4p1 by Griffies (2009).
•IPCC AR4 related papers: The main application of MOM at GFDL relates to the study of global
climate. MOM4.0 is largely the product of developing the IPCC AR4 climate models CM2.0 and
CM2.1. MOM4p1 is largely the product of developing the IPCC AR5 models CM3 and ESM2M. The
following papers document these models, with much in these papers of use for understanding MOM.
–The paper by Griffies et al. (2005) provides a formulation of the ocean climate model used in
the GFDL CM2 climate model for the study of global climate variability and change. The ocean
code is based on MOM4.0.
–The paper by Gnanadesikan et al. (2006) describes the ocean simulation characteristics from the
coupled climate model CM2.
–The paper by Delworth et al. (2006) describes the coupled climate model CM2.
–The paper by Wittenberg et al. (2006) focuses on the tropical simulations in the CM2 coupled
climate model.
–The paper by Stouffer et al. (2006a) presents some idealized climate change simulations with the
coupled climate model CM2.
•IPCC AR5 related papers: Recent development of MOM at GFDL, in particular MOM4p1, is largely
associated with development of the IPCC AR5 models.
– ESM2M: Development of the earth system model ESM2M (Dunne et al.,2012,2013) prompted
many developments in MOM. It is anticipated that further papers will be written that focus on
physical aspects of the ocean component.
– CM3: The climate model CM3 was developed using MOM configured very similarly to the
CM2.1 ocean component. Nonetheless, the paper by Griffies et al. (2011) is of use to docu-
ment various aspects of the ocean simulation that may be of use to those wishing to understand
a bit more about MOM.
•Regional modeling: The paper by Herzfeld et al. (2011) documents the use of MOM for regional
modeling.
•Eddying global modeling: The paper by Delworth et al. (2012) documents the use of MOM as a
component to an eddying coupled climate model, with the ocean resolution no coarser than 25km
and the atmospheric resolution roughly 50km. Further development with this model is focused on
the C-grid aspects available in the 2012 release of MOM.
•Lagrangian submodeling: This work largely remains ongoing, with the most extensive documenta-
tion given by Bates (2011) as well as Bates et al. (2012a,b).
Elements of MOM November 19, 2014 Page 21

Chapter 1. Introducing the Modular Ocean Model Section 1.7
1.7 Remainder of this document
This document aims to provide the reader with a reasonably full accounting of the theoretical foundations
of MOM, along with a thorough understanding of its use as a tool to study the ocean system. This document
is split into chapters, with chapters in turn grouped into parts. An attempt is made to identify that portion
of the code associated with each of the chapters.
It is inevitable that certain topics will be either incomplete or totally absent. Such represents more a
limitation of those contributing to this document than a statement about the reletive importance of a topic.
We value all input on the document and will aim to improve the presentation with future drafts.
Elements of MOM November 19, 2014 Page 22
Formulation of the ocean equations
Descriptive methods provide a foundation for physical oceanography. Indeed, many observational oceanog-
raphers are masters at weaving a physical story of the ocean. Once a grounding in observations and exper-
imental science is established, it is the job of the theorist to rationalize the phenomenology. For physical
oceanography, these fundamentals largely rest in the classical mechanics of continuous fluids combined
with continuum linear irreversible thermodynamics. That is, for a fundamental understanding, it is neces-
sary to combine the descriptive, and more generally the experimental, approaches with theoretical methods
based on mathematical physics. Together, the descriptive/experimental and theoretical methods render
deep understanding of physical phenomena, and provide rational, albeit imperfect, predictions of unob-
served phenomena, including the state of future ocean climate.
Many courses in physics introduce the student to mathematical tools required to garner a quantative
understanding of physical phenomena. Mathematical methods add to the clarity, conciseness, and preci-
sion of our description of physical phenomena, and so enhance our ability to unravel the essential physical
processes involved with a phenomenon.
The purpose of this part is to mathematically formulate the fundamental equations providing the ratio-
nal basis of the MOM ocean code. It is assumed that the reader has a basic understanding of calculus and
fluid mechanics. Much of the presentation starts from first principles, and so should be accessible to those
unfamiliar with physical oceanography.
23

Section 1.7
Elements of MOM November 19, 2014 Page 24

Chapter 2
Fundamental equations
Contents
2.1 Fluid kinematics ......................................... 26
2.1.1 Mass conserving fluid parcels ................................ 26
2.1.2 Volume conserving fluid parcels ............................... 28
2.1.3 Mass conservation for finite domains ............................ 28
2.1.4 Dia-surface transport ..................................... 29
2.1.4.1 Basic formulation .................................. 29
2.1.4.2 Alternative expressions for the dia-surface velocity component ....... 31
2.1.5 Solid earth kinematic boundary condition ......................... 32
2.1.5.1 Orthogonal coordinates .............................. 32
2.1.5.2 Generalized vertical coordinates ......................... 33
2.1.6 Upper surface kinematic condition ............................. 35
2.1.6.1 Orthogonal coordinates .............................. 35
2.1.6.2 Generalized vertical coordinates ......................... 37
2.2 Mass conservation and the tracer equation .......................... 37
2.2.1 Eulerian form of mass conservation ............................. 37
2.2.2 Mass conservation for parcels ................................ 38
2.2.3 Mass conservation for constituents: the tracer equation ................. 39
2.3 Thermodynamical tracers .................................... 39
2.3.1 Potential temperature ..................................... 40
2.3.2 Potential enthalpy ....................................... 40
2.4 Material time changes over finite regions ........................... 42
2.5 Basics of the finite volume method .............................. 44
2.6 Mass and tracer budgets over finite regions ......................... 45
2.6.1 General formulation ..................................... 45
2.6.2 Budget for an interior grid cell ............................... 47
2.6.3 Cells adjacent to the ocean bottom ............................. 49
2.6.4 Cells adjacent to the ocean surface ............................. 50
2.7 Special considerations for tracers ............................... 51
2.7.1 Compatability between vertically integrated mass and tracer budgets ......... 51
2.7.2 Fresh water budget ...................................... 52
2.7.3 The ideal age tracer ...................................... 52
2.7.4 Budgets without dia-surface fluxes ............................. 53
2.8 Forces from pressure ....................................... 53
25

Chapter 2. Fundamental equations Section 2.1
2.8.1 The accumulation of contact pressure forces ........................ 55
2.8.2 Pressure gradient body force in hydrostatic fluids ..................... 57
2.9 Linear momentum budget .................................... 58
2.9.1 General formulation ..................................... 59
2.9.2 An interior grid cell ...................................... 59
2.9.3 Cell adjacent to the ocean bottom .............................. 60
2.9.4 Cell adjacent to the ocean surface .............................. 61
2.9.5 Horizontal momentum equations for hydrostatic fluids ................. 62
2.10 The Boussinesq budgets ..................................... 62
The purpose of this chapter is to formulate the kinematic and dynamic equations that form the basis for
MOM. Much of this material is derived from lectures of Griffies (2005) at the 2004 GODAE School on Op-
erational Oceanography. The proceedings of this school have been put together by Chassignet and Verron
(2005), and this book contains many pedagogical reviews of ocean modelling. Additional discussions can
be found in Griffies (2004), and Griffies and Adcroft (2008). The material here should be accessible to those
having some exposure to the basics of mathematical physics, yet there is little assumed about knowledge
of fluid mechanics.
2.1 Fluid kinematics
Kinematics is the study of the intrinsic properties of motion, without concern for dynamical laws. The
purpose of this section is to derive some of the basic equations of fluid kinematics applied to the ocean.
As considered here, fluid kinematics is concerned with balances of mass for infinitesimal fluid parcels or
finite regions of the ocean. It is also concerned with the behaviour of a fluid as it interacts with geometrical
boundaries of the domain, such as the land-sea and air-sea boundaries of an ocean basin.
2.1.1 Mass conserving fluid parcels
Consider an infinitesimal parcel of seawater contained in a volume of size1
dV= dxdydz(2.1)
with a mass given by
dM=ρdV . (2.2)
In these equations, ρis the in situ mass density of the parcel and x= (x,y,z) is the Cartesian coordinate
of the parcel with respect to an arbitrary origin. As the parcel moves through space-time, we measure its
velocity
v=dx
dt(2.3)
by considering the time changes in its position.2
The time derivative d/dtintroduced in equation (2.3) measures time changes of a fluid property as
one follows the parcel. That is, we place ourselves in the parcel’s moving frame of reference. This time
derivative is thus directly analogous to that employed in classical particle mechanics (Landau and Lifshitz,
1976;Marion and Thornton,1988). Describing fluid motion from the perspective of an observer moving
with fluid parcels affords us with a Lagrangian description of fluid mechanics. For many purposes, it is
1A parcel of fluid is macroscopically small yet microscopically large. That is, from a macroscopic perspective, the parcel’s thermo-
dynamic properties may be assumed uniform, and the methods of continuum mechanics are applicable to describing the mechanics
of an infinite number of these parcels. However, from a microscopic perspective, these fluid parcels contain many molecules, and so
it is safe to ignore the details of molecular interactions. Regions of a fluid with length scales on the order of 10−3cm satisfy these
properties of a fluid parcel. See Section 2.2 of Griffies (2004) for further discussion.
2The three dimensional velocity vector is written v= (u, w) throughout these notes, with u= (u,v) the horizontal components and
wthe vertical component.
Elements of MOM November 19, 2014 Page 26

Chapter 2. Fundamental equations Section 2.1
useful to take a complementary perspective in which we measure fluid properties from a fixed space frame,
and so allow fluid parcels to stream by the observer. The fixed space frame affords one with an Eulerian
description of fluid motion. To relate the time tendencies of scalar properties measured in the moving and
fixed frames, we perform a coordinate transformation, the result of which is (see Section 2.3.3 of Griffies
(2004) for details)
d
dt=∂t+v·∇,(2.4)
where
∂t=∂
∂t (2.5)
measures time changes at a fixed space point. The transport term
v·∇ =u·∇s+w(s)∂z(2.6)
reveals the fundamentally nonlinear character of fluid dynamics. In this relation, ∇sis the horizontal
gradient operator taken on surfaces of constant generalized vertical coordinate s, and w(s)measures the
transport of fluid crossing these surfaces. We provide further discussion of this expression in Section 2.1.4.
In general, the operator v·∇ is known as the advection operator in geophysical fluids, whereas it is often
termed convection in the classical fluids literature.3
It is convenient, and conventional, to formulate the mechanics of fluid parcels that conserve mass.
Choosing to do so allows many notions from classical particle mechanics to transfer over to continuum
mechanics of fluids, especially when formulating the equations of motion from a Lagrangian perspective.
We thus focus on kinematics satisfied by mass conserving fluid parcels. In this case, the mass of a parcel
changes only if there are sources within the continuous fluid, so that
d
dtln(dM) = S(M)(2.7)
where S(M)is the rate at which mass is added to the fluid, per unit mass. Mass sources are often assumed
to vanish in textbook formulations of fluid kinematics. However, they can be nonzero in certain cases
for ocean modelling in which mass is moved from one region to another through certain subgrid scale
parameterizations, such as the cross land schemes of Chapters 29 and 30. So it is convenient to carry mass
sources around in our formulation of the equations used by MOM.
Equation (2.7) expresses mass conservation for fluid parcels in a Lagrangian form. To derive the Eulerian
form of mass conservation, start by substituting the mass of a parcel given by equation (2.2) into the mass
conservation equation (2.7) to derive
d
dtln ρ=−∇·v+S(M).(2.8)
That is, the density of a parcel increases when the velocity field converges onto the parcel. To reach this
result, we first note the expression
d
dtln(dV) = ∇·v,(2.9)
which says that the infinitesimal volume of a fluid parcel increases in time if the velocity of the parcel
diverges from the location of the parcel. Imagine the parcel expanding in response to the diverging velocity
field.
Upon deriving the material evolution of density as given by equation (2.8), rearrangement renders the
Eulerian form of mass conservation
ρ,t +∇·(ρv) = ρS(M).(2.10)
A comma is used here as shorthand for the partial time derivative taken at a fixed point in space
ρ,t =∂ρ
∂t .(2.11)
3Convection in geophysical fluid dynamics generally refers to the rapid vertical motions that act to stabilize fluids that are gravita-
tionally unstable (e.g., Marshall and Schott,1999).
Elements of MOM November 19, 2014 Page 27

Chapter 2. Fundamental equations Section 2.1
We use an analogous notation for other partial derivatives throughout these notes. Rewriting mass conser-
vation in terms of the density time tendency
ρ,t =−∇·(ρv) + ρS(M),(2.12)
reveals that at each point in the fluid, the mass density increases if the linear momentum per volume of the
fluid parcel,
p=ρv,(2.13)
converges to the point.
2.1.2 Volume conserving fluid parcels
Fluids that are comprised of parcels that conserve their mass, as considered in the previous discussion,
satisfy non-Boussinesq kinematics. In ocean climate modelling, it has been traditional to exploit the large
degree to which the ocean fluid is incompressible, in which case the volume of fluid parcels is taken as
constant. These fluids are said to satisfy Boussinesq kinematics.
For the Boussinesq fluid, conservation of volume for a fluid parcel leads to
d
dtln(dV) = S(V),(2.14)
where S(V)is the volume source per unit volume present within the fluid. It is numerically the same as
the mass source S(M)defined in equation (2.7). This statetment of volume conservation is equivalent to the
mass conservation statement (2.7)if we assume the mass of the parcel is given by
dM=ρodV , (2.15)
where ρois a constant reference density.
Using equation (2.9) in the Lagrangian volume conservation statement (2.14) leads to the following
constraint for the Boussinesq velocity field
∇·v=S(V).(2.16)
Where the volume source vanishes, the three dimensional velocity field is non-divergent
∇·v= 0 for Boussinesq fluids with S(V)= 0.(2.17)
2.1.3 Mass conservation for finite domains
Now consider a finite sized region of ocean extending from the free surface at z=η(x,y,t) to the solid earth
boundary at z=−H(x,y), and allow the fluid within this region to respect the mass conserving kinematics
of a non-Boussinesq fluid. The total mass of fluid inside the region is given by
M=Zdxdy
η
Z
−H
ρdz. (2.18)
Conservation of mass for this region implies that the time tendency
∂tM=Zdxdy ∂t
η
Z
−H
dzρ(2.19)
changes due to imbalances in the flux of seawater passing across the domain boundaries, and from sources
within the region.4For a region comprised of a vertical fluid column, the only means of affecting the mass
are through fluxes crossing the ocean free surface, convergence of mass brought in by horizontal ocean
4We assume no water enters the domain through the solid-earth boundaries.
Elements of MOM November 19, 2014 Page 28

Chapter 2. Fundamental equations Section 2.1
currents through the vertical sides of the column, and sources within the column. These considerations
lead to the balance
∂tM=ZdxdyQm+
η
Z
−H
dzρ S(M)−∇·
η
Z
−H
dzρ u.(2.20)
The term Qmdxdyrepresents the mass flux of material (mass per unit time) crossing the free surface.5We
provide a more detailed accounting of this flux in Section 2.1.6. Equating the time tendencies given by
equations (2.19) and (2.20) leads to a mass balance within each vertical column of fluid
∂t
η
Z
−H
dzρ+∇·Uρ=Qm+
η
Z
−H
dzρ S(M),(2.21)
where
Uρ=
η
Z
−H
dzρ u(2.22)
is a shorthand notation for the vertically integrated horizontal momentum per volume.
Setting density factors in the mass conservation equation (2.21) to the constant reference density ρo
renders the volume conservation equation
∂tη+∇·U=Qm/ρo+
η
Z
−H
dzS(V)(2.23)
appropriate for a Boussinesq fluid, where fluid parcels conserve volume rather than mass. In this equation
U=
η
Z
−H
dzu(2.24)
is the vertically integrated horizontal velocity.
2.1.4 Dia-surface transport
A surface of constant generalized vertical coordinate, s, is of importance when establishing the balances of
mass, tracer, and momentum within a layer of fluid whose upper and lower bounds are determined by sur-
faces of constant s. Fluid transport through this surface is said to constitute the dia-surface transport. This
transport plays a fundamental role in generalized vertical coordinate models such as MOM. Additionally,
when considering the flow of fluid and tracer properties across the ocean surface and bottom, the notions
of dia-surface transport are useful.
Generalized vertical coordinates provide the ocean theorist and modeler with a powerful set of tools to
describe ocean flow, which in many situations is far more natural than the more traditional geopotential
coordinates (x,y,z) that we have been using thus far. Therefore, it is important for the student to gain some
exposure to the fundamentals of these coordinates, as they are ubiquitous in ocean modelling today.
2.1.4.1 Basic formulation
At an arbitrary point on a surface of constant generalized vertical coordinate (see Figure 2.1), the flux of
fluid in the direction normal to the surface is given by
seawater flux in direction ˆ
n=v·ˆ
n,(2.25)
5Water crossing the ocean surface is typically quite fresh, such as for precipitation or evaporation. However, rivers and ice melt can
generally contain a nonzero salinity. Additionally, for most climate model applications, the mass of salt particles exchanged across
the liquid ocean interface upon melting and freezing of sea ice is ignored when considering the mass balance of the liquid ocean fluid.
Elements of MOM November 19, 2014 Page 29
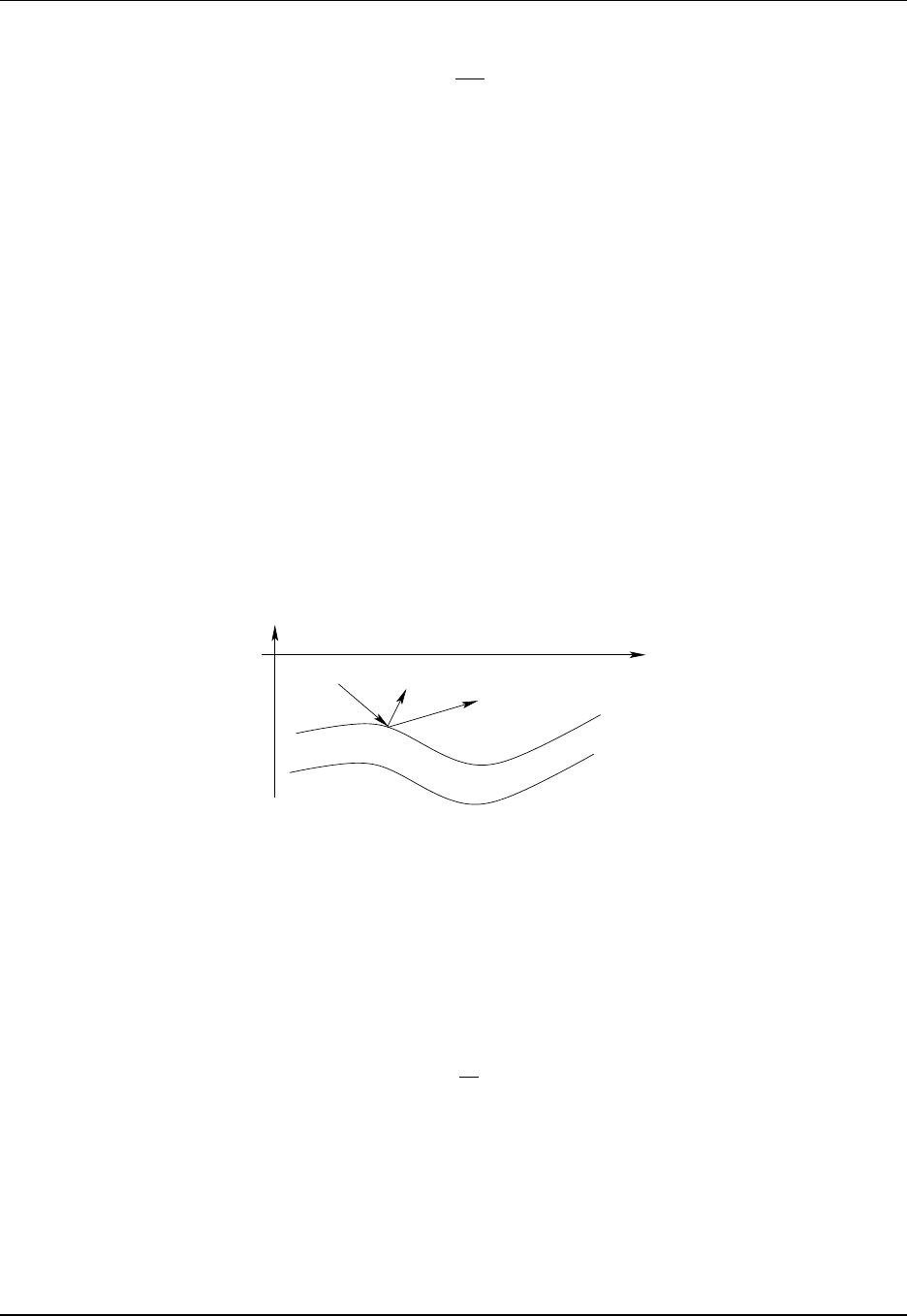
Chapter 2. Fundamental equations Section 2.1
with
ˆ
n=∇s
|∇s|(2.26)
the surface unit normal direction. Introducing the material time derivative ds/dt=s,t +v·∇sleads to the
equivalent expression
v·ˆ
n=|∇s|−1(d/dt−∂t)s. (2.27)
That is, the normal component to a fluid parcel’s velocity is proportional to the difference between the
material time derivative of the surface and its partial time derivative.
Since the surface is generally moving, the net flux of seawater penetrating the surface is obtained by
subtracting the velocity of the surface v(ref)in the ˆ
ndirection from the velocity component v·ˆ
nof the fluid
parcels. We thus define the dia-surface velocity component according to
w(s)≡flux of seawater through surface
=ˆ
n·(v−v(ref)).(2.28)
The velocity v(ref)is the velocity of a reference point fixed on the surface, which is defined so that
(∂t+v(ref)·∇)s= 0.(2.29)
Consequently,
ˆ
n·v(ref)=−s,t |∇s|−1,(2.30)
so that the normal component of the surface’s velocity vanishes when the surface is static.
z
n
^
s=constant
vvref
x,y
Figure 2.1: Surfaces of constant generalized vertical coordinate living interior to the ocean. An upward
normal direction ˆ
nis indicated on one of the surfaces. Also shown is the orientation of a fluid parcel’s
velocity vand the velocity v(ref)of a reference point living on the surface.
Expression (2.30) then leads to the following expression for the net flux of seawater crossing the surface
w(s)=ˆ
n·(v−v(ref))
=|∇s|−1(∂t+v·∇)s
=|∇s|−1ds
dt.
(2.31)
Hence, the material time derivative of the generalized surface vanishes if and only if no water parcels
cross it. This important result is used throughout ocean theory and modelling. It measures the volume of
seawater crossing a generalized surface, per time, per area. The area normalizing the volume flux is that
area dA(ˆ
n)of an infinitesimal patch on the surface of constant generalized vertical coordinate with outward
unit normal ˆ
n. When surfaces of constant generalized vertical coordinate are monotonically stacked in the
vertical, this area factor can be written (see equation (6.58) of Griffies (2004))
dA(ˆ
n)=|z,s ∇s|dA, (2.32)
Elements of MOM November 19, 2014 Page 30
Chapter 2. Fundamental equations Section 2.1
where
dA= dxdy(2.33)
is the horizontal projection of the area element. Hence, the volume per time of fluid passing through the
generalized surface is
(volume/time) through surface =ˆ
n·(v−v(ref))dA(ˆ
n)
=|z,s|(ds/dt)dxdy, (2.34)
and the magnitude of this flux is
|ˆ
n·(v−v(ref))dA(ˆ
n)|≡|w(z)|dxdy. (2.35)
We introduced the expression
w(z)=z,s
ds
dt,(2.36)
which measures the volume of fluid passing through the surface, per unit area dA= dxdyof the horizontal
projection of the surface, per unit time. That is,
w(z)≡ˆ
n·(v−v(ref))dA(ˆ
n)
dA
=(volume/time) of fluid through surface
area of horizontal projection of surface.
(2.37)
The quantity w(z)is the dia-surface velocity component that appears in the budget equations for mass,
tracer, and momentum in the generalized level formulation of MOM.
2.1.4.2 Alternative expressions for the dia-surface velocity component
To gain some experience with the dia-surface velocity component, it is useful to write it in the equivalent
forms
w(z)=z,s
ds
dt
=z,s ∇s·(v−v(ref))
= (ˆ
z−∇sz)·v−z,t
=w−(∂t+u·∇s)z
(2.38)
where the penultimate step used the identity (2.40), and where
S=∇sz
=−z,s ∇zs(2.39)
is the slope of the ssurface as projected onto the horizontal directions. For example, if the slope vanishes,
then the dia-surface velocity component measures the flux of fluid moving vertically relative to the motion
of the generalized surface. When the surface is static and flat, then the dia-surface velocity component is
simply the vertical velocity component w= dz/dt.
When interpreting the dia-surface velocity component below, we find it useful to note that relation
(2.30) leads to
z,s ∇s·v(ref)=z,t.(2.40)
To reach this result, we used the identity s,t z,s =−z,t, with z,t the time tendency for the depth of a particular
constant ssurface.
Elements of MOM November 19, 2014 Page 31

Chapter 2. Fundamental equations Section 2.1
The expression (2.36) for w(z)brings the material time derivative (2.4) into the following equivalent
forms
d
dt= ∂
∂t !z
+u·∇z+w ∂
∂z !(2.41)
= ∂
∂t !s
+u·∇s+ds
dt ∂
∂s !(2.42)
= ∂
∂t !s
+u·∇s+w(z) ∂
∂z !,(2.43)
where
∂s=z,s ∂z(2.44)
relates the vertical coordinate partial derivatives. The form given by equation (2.43) motivates some to
refer to w(z)as a vertical velocity component that measures the rate at which fluid parcels penetrate the
surface of constant generalized coordinate (see Appendix A to McDougall (1995)). Indeed, such is part
of the motivation for using the (z) superscript notation. However, we must be careful to distinguish w(z)
from the generally different vertical velocity component w= dz/dt, which measures the water flux crossing
constant geopotential surfaces.
We close with a few points of clarification for the case where no fluid parcels cross the generalized
surface. Such occurs, in particular, in the case of adiabatic flows with s=ρan isopycnal coordinate. In
this case, the material time derivative (2.43) only has a horizontal two-dimensional advective component
u·∇s. This result should not be interpreted to mean that the velocity of a fluid parcel is strictly horizontal.
Indeed, it generally is not, as the form (2.41) should make clear. Rather, it means that the transport of
fluid properties occurs along surfaces of constant s, and such transport is measured by the convergence of
horizontal advective fluxes as measured along surfaces of constant s. We revisit this point in Section 2.6.2
when discussing tracer transport (see in particular Figure 2.7).
2.1.5 Solid earth kinematic boundary condition
We now apply the discussion of dia-surface transport from Section 2.1.4 to perhaps the simplest surface;
namely, the time independent solid earth boundary. This surface is commonly assumed to be impenetrable
to fluid.6The expression for fluid transport at the lower surface leads to the solid earth kinematic boundary
condition. In addition to deriving the bottom kinematic boundary condition, we introduce some mathe-
matical techniques useful when working with non-orthogonal generalized vertical coordinates, as used in
many ocean models such as MOM.
2.1.5.1 Orthogonal coordinates
As there is no fluid crossing the solid earth lower boundary, a no-normal flow condition is imposed at the
solid earth boundary at the depth
z=−H(x,y).(2.45)
To develop a mathematical expression for the boundary condition, note that the outward unit normal
pointing from the ocean into the underlying rock is given by7(see Figure 2.2)
ˆ
nH=− ∇(z+H)
|∇(z+H)|!.(2.46)
Furthermore, we assume that the bottom topography can be represented as a continuous function H(x,y)
that does not possess “overturns.” That is, we do not consider caves or overhangs in the bottom boundary
6This assumption may be broken in some cases. For example, when the lower boundary is a moving sedimentary layer in a coastal
estuary, or when there is seeping ground water. We do not consider such cases here.
7The three dimensional gradient operator ∇= (∂x,∂y,∂z) reduces to the two dimensional horizontal operator ∇z= (∂x,∂y,0) when
acting on functions that depend only on the horizontal directions. To reduce notation clutter, we do not expose the zsubscript in cases
where it is clear that the horizontal gradient is all that is relevant.
Elements of MOM November 19, 2014 Page 32

Chapter 2. Fundamental equations Section 2.1
where the topographic slope becomes infinite. Such would make it difficult to consider the slope of the
bottom in our formulations. This limitation is common for ocean models.8
x,y
n
^H
z=−H(x,y)
z
Figure 2.2: Schematic of the ocean’s bottom surface with a smoothed undulating solid earth topography
at z=−H(x,y) and outward normal direction ˆ
nH. Undulations of the solid earth can reach from the ocean
bottom at 5000m-6000m to the surface over the course of a few kilometers (slopes on the order of 0.1 to 1.0).
These ranges of topographic variation are far greater than the surface height (see Figure 2.3). It is important
for simulations to employ numerics that facilitate an accurate representation of the ocean bottom.
A no-normal flow condition on fluid flow at the ocean bottom implies
v·ˆ
nH= 0 at z=−H(x,y).(2.47)
Expanding this constraint into its horizontal and vertical components yields
u·∇H+w= 0 at z=−H(x,y).(2.48)
Furthermore, introducing a material time derivative (2.4) allows us to write this boundary condition as
d(z+H)
dt= 0 at z=−H(x,y). (2.49)
Equation (2.49) expresses in a material or Lagrangian form the impenetrable nature of the solid earth lower
surface, whereas equation (2.48) expresses the same constraint in an Eulerian form.
2.1.5.2 Generalized vertical coordinates
We now consider the form of the bottom kinematic boundary condition in generalized vertical coordinates.
Chapter 6 of Griffies (2004) develops a calculus for generalized vertical coordinates. Experience with these
methods is useful to nurture an understanding for ocean modelling in generalized vertical coordinates.
Most notably, these coordinates, when used with the familiar horizontal coordinates (x,y), form a non-
orthogonal triad, and thus lead to some relationships that may be unfamiliar. To proceed in this section,
we present some salient results of the mathematics of generalized vertical coordinates, and reserve many
of the derivations for Griffies (2004).
When considering generalized vertical coordinates for ocean models, we assume that the surfaces in
question do not overturn on themselves. This constraint means that the Jacobian of transformation between
the generalized vertical coordinate
s=s(x,y,z,t) (2.50)
8For hydrostatic models, the solution algorithms rely on the ability to integrate vertically from the ocean bottom to the top,
uninterrupted by rock in between. Non-hydrostatic models do not employ such algorithms, and so may in principle allow for arbitrary
bottom topography, including overhangs.
Elements of MOM November 19, 2014 Page 33

Chapter 2. Fundamental equations Section 2.1
and the geopotential coordinate z, must be one signed. That is, the specific thickness
∂z
∂s =z,s (2.51)
is of the same sign throughout the ocean fluid. The name specific thickness arises from the property that
dz=z,s ds(2.52)
is an expression for the thickness of an infinitesimal layer of fluid bounded by two constant ssurfaces.
Deriving the bottom kinematic boundary condition in s-coordinates requires a relation between the ver-
tical velocity component used in geopotential coordinates, w= dz/dt, and the pseudo-velocity component
ds/dt. For this purpose, we refer to some results from Section 6.5.5 of Griffies (2004). As in that discussion,
we derive the isomorphic relations
˙
z= (∂t+u·∇s+˙
s∂s)z(2.53)
˙
s= (∂t+u·∇z+˙
z∂z)s, (2.54)
where
˙
z=dz
dt(2.55)
˙
s=ds
dt(2.56)
are useful shorthands for the vertical velocity components, motivated from similar notation used in classi-
cal particle mechanics. Note that the partial time derivative appearing in each of the expressions is taken
with the corresponding space variables held fixed. That is, ∂tin equation (2.53) is taken with sheld fixed,
whereas ∂tin equation (2.54) is taken with zheld fixed.
Rearrangement of equations (2.53) and (2.54) leads to
˙
z=z,s (d/dt−∂t−u·∇z)s. (2.57)
This expression is relevant when measurements are taken on surfaces of constant geopotential, or depth.
To reach this result, we made use of the triple product identities
z,t =−s,t z,s (2.58)
z,x =−s,x z,s (2.59)
z,y =−s,y z,s.(2.60)
A derivation of these identities is given in Section 6.5.4 of Griffies (2004). These relations should be famil-
iar to those having studied thermodynamics, where the analogous expressions are known as the Maxwell
relations (e.g., Callen,1985).
We now apply relation (2.57) to the ocean bottom, which is generally not a surface of constant depth. It
is thus necessary to transform the constant depth gradient ∇zto a horizontal gradient taken along the bot-
tom. To do so, proceed as in Section 6.5.3 of Griffies (2004) and consider the time-independent coordinate
transformation
(x,y,z,t)=(x,y,−H(x,y),t).(2.61)
The horizontal gradient taken on constant depth surfaces, ∇z, and the horizontal gradient along the bottom,
∇z, are thus related by
∇z=∇z−(∇H)∂z.(2.62)
Using this result in equation (2.57) yields
s,z (w+u·∇H) = (d/dt−∂t−u·∇z)sat z=−H. (2.63)
The left hand side vanishes due to the kinematic boundary condition (2.48), which then leads to
ds/dt= (∂t+u·∇z)sat s=s(x,y,z =−H(x,y),t).(2.64)
Elements of MOM November 19, 2014 Page 34

Chapter 2. Fundamental equations Section 2.1
The value of the generalized coordinate at the ocean bottom can be written in the shorthand form
sbot(x,y,t) = s(x,y,z =−H,t) (2.65)
which leads to d(s−sbot)
dt= 0 at s=sbot.(2.66)
This relation is analogous to equation (2.49) appropriate to z-coordinates. Indeed, it is actually a basic
statement of the impenetrable nature of the solid earth lower boundary, which is true regardless the vertical
coordinates.
The various mathematical steps that led to the very simple result (2.66) could have been dispensed with
if we already understood some notions of generalized vertical coordinates. Nonetheless, the steps intro-
duced some of the formalism required to work with generalized vertical coordinates, and as such provide
a useful testing ground for later manipulations where the answer is less easy to anticipate. This strategy
is highly recommended to the student working with new formalisms. That is, first test your mathematical
skills with problems where the answer is either known, or can be readily judged correct with basic phys-
ical understanding. After garnering experience and confidence, one may then approach genuinely new
problems using the methods.
2.1.6 Upper surface kinematic condition
To formulate budgets for mass, tracer, and momentum in the ocean, we consider the upper ocean surface
to be a time dependent permeable membrane through which precipitation, evaporation, ice melt, and river
runoff9pass. The expression for fluid transport at the upper surface leads to the upper ocean kinematic
boundary condition.
2.1.6.1 Orthogonal coordinates
To describe the kinematics of water transport into the ocean, it is useful to introduce an effective transport
through a smoothed ocean surface, where smoothing is performed via an ensemble average. We assume
that this averaging leads to a surface absent overturns or breaking waves, thus facilitating a mathematical
description analogous to the ocean bottom just considered. The value of the geopotential at the ocean
surface takes on the value
z=η(x,y,t) (2.67)
at this idealized ocean surface. Correspondingly, the mass flux of material crossing the ocean surface is
written
Qm=(mass/time) through free surface
horizontal area under free surface
=−
ρdA(ˆ
n)ˆ
n·(v−vref)
dAat z=η.
(2.68)
In this expression, the outward normal
ˆ
n= ∇(z−η)
|∇(z−η)|!at z=η(2.69)
points from the ocean surface at z=ηinto the overlying atmosphere (see Figure 2.3). The velocity vref is
taken from a point fixed on the free surface, so that
∂t(z−η) + vref ·∇(z−η)=0,(2.70)
9River runoffgenerally enters the ocean at a nonzero depth rather than through the surface. Many global models, however, have
traditionally inserted river runoffto the top model cell. Such can become problematic numerically and physically when the top grid
cells are refined to levels common in coastal modelling. Hence, more applications are now considering the input of runoffthroughout
a nonzero depth. Likewise, sea ice can melt at depth, thus necessitating a mass transport to occur within the ocean between the liquid
and solid water masses.
Elements of MOM November 19, 2014 Page 35
Chapter 2. Fundamental equations Section 2.1
or equivalently
wref = (∂t+∇·uref)η(2.71)
or
|∇(z−η)|ˆ
n·vref =∂tηat z=η. (2.72)
Finally, the area element dA(ˆ
n)measures an infinitesimal area element on the ocean surface z=η, and it is
given by (see Section 20.13.2 of Griffies (2004))
dA(ˆ
n)=|∇(z−η)|dAat z=η, (2.73)
where dA= dxdyis the horizontal area element. Use of these relations leads to the surface kinematic
boundary condition written in material form
ρd(z−η)
dt=−Qmat z=η. (2.74)
Contrary to the solid earth condition (2.49), where z+His materially constant, permeability of the ocean
surface leads to a nontrivial material evolution of z−η.
^
x,y
z
nη
^
nw
z=η
Figure 2.3: Schematic of the ocean’s upper surface with a smoothed undulating surface at z=η(x,y,t),
outward normal direction ˆ
nη, and normal direction ˆ
nworienting the passage of water across the surface.
Undulations of the surface height are on the order of a few metres due to tidal fluctuations in the open
ocean, and order 10m-20m in certain embayments (e.g., Bay of Fundy in Nova Scotia). When imposing
the weight of sea ice onto the ocean surface, the surface height can depress even further, on the order of
5m-10m, with larger values possible in some cases. It is important for simulations to employ numerical
schemes facilitating such wide surface height undulations.
As an alternative means to develop the surface kinematic boundary condition, return to the expression
(2.21) for mass conservation, rewritten here for completeness
∂t
η
Z
−H
dzρ+∇·
η
Z
−H
dzρ u=Qm+
η
Z
−H
dzρ S(M).(2.75)
Next, perform the derivative operations on the integrals, making use of Leibnitz’s Rule when differentiating
the integrals. The first step of the derivation leads to
[ρ(∂t+u·∇)η]z=η+ [ρ∇H·u]z=−H+
η
Z
−H
dz[ρ,t +∇·(ρu)] = Qm+
η
Z
−H
dzρ S(M).(2.76)
The Eulerian mass conservation relation (2.10) and bottom kinematic boundary condition (2.48) render the
Eulerian form of the surface kinematic boundary condition
ρ(∂t+u·∇)η=Qm+ρw at z=η. (2.77)
Elements of MOM November 19, 2014 Page 36

Chapter 2. Fundamental equations Section 2.2
2.1.6.2 Generalized vertical coordinates
To derive the s-coordinate surface kinematic boundary condition, we proceed as for the bottom boundary
condition in Section 2.1.5.2. Here, the coordinate transformation is time dependent
(x,y,z,t)=(x,y,η(x,y,t),t).(2.78)
The horizontal gradient and time derivative operators are therefore related by
∇z=∇z+ (∇η)∂z(2.79)
∂t=∂t+ (∂tη)∂z.(2.80)
Hence, the relation (2.57) between vertical velocity components takes the following form at the ocean sur-
face
w=z,s (d/dt−∂t−u·∇z)s+ (∂t+u·∇)ηat z=η. (2.81)
Substitution of the z-coordinate kinematic boundary condition (2.77) leads to
ρz,s (d/dt−∂t−u·∇z)s=−Qmat s=stop (2.82)
where stop =s(x,y,z =η,t) is the value of the generalized vertical coordinate at the ocean surface. Reorga-
nizing the result (2.82) leads to the material time derivative form
ρz,s d(s−stop)
dt!=−Qmat s=stop (2.83)
which is analogous to the z-coordinate result (2.74). Indeed, it can be derived trivially by noting that
dz/dt=z,s ds/dt. Even so, just as for the bottom kinematic boundary condition considered in Section
2.1.5.2, it is useful to have gone through these manipulations to garner experience and confidence with
the formalism.
2.2 Mass conservation and the tracer equation
We revisit here the mathematical description of a mass conserving fluid parcel for the purpose of introduc-
ing the evolution equation for trace material within a parcel. For brevity, we ignore the possibilities of mass
sources in this discussion, though note as in Section 2.1 that mass sources may be of use for implementing
certain subgrid scale schemes in MOM. This discussion here follows that in Section II.2 of DeGroot and
Mazur (1984), Section 8.4 of Chaikin and Lubensky (1995), and Section 3.3 of M¨
uller (2006). See also the
discussion in Warren (2009).
2.2.1 Eulerian form of mass conservation
Seawater consists of many material constituents, such as freshwater, salts and biogeochemical components,
with the possibility also for chemical reactions to take place. For brevity, we ignore chemical reactions,
though note that the following discussion can be generalized to such cases (see, for example, Section II-2
in DeGroot and Mazur,1984).
The mass density of each constituent within a parcel of seawater is given by
ρn=mass of component n
volume of seawater parcel,(2.84)
with the total density in a parcel given by the sum over all N constituents
ρ=
N
X
n=1 mass of component n
volume of seawater parcel!
=
N
X
n=1
ρn.
(2.85)
Elements of MOM November 19, 2014 Page 37

Chapter 2. Fundamental equations Section 2.2
Observe that the mass of a seawater parcel is the sum of individual constituent masses (numerator in
equation (2.85)), whereas the volume of the parcel is a complicated function of the temperature, pressure,
and material constituents.
For an arbitrary finite region within the fluid, conservation of mass for each constituent takes the form
∂t ZρndV!=−Zρnvn·dA,(2.86)
where
dA=ˆ
ndA(ˆ
n)(2.87)
is the area element on the region boundary, with ˆ
nthe outward normal, and vnis the velocity of constituent
n. Equation (2.86) says that the mass of each constituent within a region is affected by the flow of that
constituent through the region boundaries.
Now apply the mass budget (2.86) to a static volume, in which case we can bring the time derivative
inside the integral, and use Gauss’ Theorem on the boundary integral to render
ZdV(∂tρn+∇·(ρnvn))= 0.(2.88)
Since the volume is arbitrary, this relation leads to the local expression of mass balance for each constituent
∂tρn=−∇·(ρnvn).(2.89)
Summing over all constituents then leads to the familiar Eulerian expression of mass conservation
∂tρ=−∇·(ρv),(2.90)
where
v=ρ−1
N
X
n=1
ρnvn(2.91)
is the velocity for the center of mass of the parcel.
The density of seawater is often well approximated by
ρ≈ρsalt +ρfresh,(2.92)
where ρsalt is the mass of ocean “salt” per mass of seawater, and ρfresh is the mass of fresh water per mass
of seawater. Other material constituents occur in such small concentrations that their contributions to the
seawater density are generally ignored for purposes of ocean modeling.
2.2.2 Mass conservation for parcels
The material time derivative
d
dt=∂t+v·∇,(2.93)
measures time changes of a fluid property for an observer moving with the center of mass velocity v. Mass
conservation (2.90) in the moving, or Lagrangian, frame then takes the form
dρ
dt=−ρ∇·v,(2.94)
indicating that the density of a fluid parcel increases in regions where currents converge, and density
decreases where currents diverge.
Elements of MOM November 19, 2014 Page 38
Chapter 2. Fundamental equations Section 2.3
2.2.3 Mass conservation for constituents: the tracer equation
Introducing the material time derivative to the constituent mass balances (2.89) leads to the material budget
dρn
dt=−ρn∇·v−∇·[ρn(vn−v)].(2.95)
Now define the relative mass flux
Jn=ρn(vn−v) (2.96)
to render an expression for the material evolution of the density for each constituent
dρn
dt=−ρn∇·v−∇·Jn.(2.97)
The flux Jnis nonzero for those motions where the constituent nmoves relative to the parcel’s center of
mass. This motion can be caused by many effects, with molecular diffusion the canonical example, in
which case we parameterize Jnas a downgradient diffusive flux.10 Notably, the total mass flux vanishes
J=
N
X
n=1
Jn= 0,(2.98)
which follows since we choose to measure the parcel motion with respect to its center of mass. Hence, there
is no subgrid scale flux for the full density ρ; i.e., the mass conservation equation (2.90) is exact, even in the
presence of subgrid scale processes.
As a final step in our development of mass conservation, introduce the concentration of a material
constituent, defined by
Cn=mass of component n
mass of seawater parcel
=ρn
ρ.
(2.99)
Substituting this tracer concentration into the constituent density equation (2.97) leads to the material form
of the tracer equation
ρdCn
dt=−∇·Jn,(2.100)
with the Eulerian form given by
∂t(ρCn) = −∇·(ρvCn+Jn).(2.101)
This is the Eulerian form of the tracer equation implemented in MOM. It applies to both the material tracers
considered here, and the thermodynamical heat tracer described in Section 2.3.
2.3 Thermodynamical tracers
Heating and cooling of the ocean, as well as mass exchange, predominantly occur near the ocean surface.
In contrast, transport in the interior is nearly adiabatic and isohaline. Hence, the surface ocean experiences
irreversible processes that set characteristics of the water masses moving quasi-isentropically within the
ocean interior. Useful labels for these water masses maintain their values when moving within the largely
ideal ocean interior. Salinity is a good tracer for such purposes since it is altered predominantly by mixing
between waters of varying concentrations, and the resulting salinity after homogenization of two water
parcels is the mass weighted mean of the salinities of the individual parcels. These two properties are basic
to the material tracers considered in Section 2.2. We discuss here desirable properties of a thermodynamic
tracer that tags the heat within a water parcel and evolves analogously to material tracers. Much of this
material follows from Chapter 5 of Griffies (2004).
10For an ocean model, whose grid spacing is far greater than that appropriate for molecular diffusion, the relative motion of a
constituent is also affected by far larger subgrid scale processes, such as unresolved eddy advective and diffusive transport.
Elements of MOM November 19, 2014 Page 39

Chapter 2. Fundamental equations Section 2.3
2.3.1 Potential temperature
Vertical adiabatic and isohaline motion in the ocean changes a fluid parcel’s hydrostatic pressure, which
thus causes its in situ temperature to change in proportion to the adiabatic lapse rate as given by
dT=Γdp. (2.102)
Consequently, in situ temperature is not a useful thermodynamic variable to label water parcels of common
origin. Instead, it is more useful to remove the adiabatic pressure effects.
Removing adiabatic pressure effects from in situ temperature leads to the concept of potential tempera-
ture. Potential temperature is the in situ temperature that a water parcel of fixed composition would have
if it were isentropically transported from its in situ pressure to a reference pressure pr, with the reference
pressure typically taken at the ocean surface. Mathematically, the potential temperature θis the reference
temperature obtained via integration of dT=Γdpfor an isentropic in situ temperature change with respect
to pressure (e.g., Apel,1987):
T=θ(s,T ,pr) +
p
Z
pr
Γ(s,θ,p0) dp0,(2.103)
with Γthe lapse rate defined in terms of pressure changes. By definition, the in situ temperature Tequals
the potential temperature θat the reference pressure p=pr. Elsewhere, they differ by an amount deter-
mined by the adiabatic lapse rate. Beneath the diabatic surface mixed layer, a vertical profile of potential
temperature is far more constant than in situ temperature.
As shown in Section 5.6.1 of Griffies (2004), the potential temperature of a parcel is constant when the
parcel’s specific entropy ζand material composition are constant. Mathematically, this result follows by
noting that when entropy changes at a fixed pressure and composition, p=prso that temperature equals
potential temperature. Equation (5.41) of Griffies (2004) then leads to
dζ=Cpdlnθ, (2.104)
implying dζ= 0 if and only if dθ= 0.
2.3.2 Potential enthalpy
Potential temperature has proven useful for many oceanographic purposes. However, we have yet to ask
whether it is a convenient variable to mark the heat content in a parcel of seawater. Traditionally, it is the
potential temperature multiplied by the heat capacity that is used for this purpose. Bacon and Fofonoff
(1996) provide a review with suggestions for this approach. In contrast, McDougall (2003) argues that
potential temperature multiplied by heat capacity is less precise, by some two orders of magnitude, than
an alternative thermodynamic tracer called potential enthalpy.
To understand this issue from a mathematical perspective, consider the evolution equation for potential
temperature
ρdθ
dt=−∇·Jθ+Σθ,(2.105)
where Jθis a flux due to molecular diffusion, and Σθis a source. That potential temperature evolves in
this manner is ensured by its being a scalar field. Consider the mixing of two seawater parcels at the same
pressure where the parcels have different potential temperature and salinity. In the absence of the source
term, the equilibrated state consists of a single parcel with mass equal to the sum of the two separate
masses, and potential temperature and salinity determined by their respective mass weighted means. Does
this actually happen in the real ocean? That is, can source terms be ignored? Fofonoff(1962) and McDougall
(2003) note that it is indeed the case for salinity (and any other material tracer due to conservation of
matter), yet it is not the case for potential temperature. Instead, potential temperature contains source
terms that alter the mass weighted average equilibrated state. In contrast, potential enthalpy (discussed
below) maintains the desired conservative behavior when mixing at constant reference pressure, and nearly
maintains this behavior if mixing parcels at a different pressure. Hence, ocean models which set the source
term to zero upon mixing potential temperature are in error. McDougall (2003) quantifies this error.
Elements of MOM November 19, 2014 Page 40

Chapter 2. Fundamental equations Section 2.3
Potential enthalpy is defined analogously to potential temperature. What motivates the use of potential
enthalpy is the observation that the fundamental relation between thermodynamic state variables takes
a nearly conservative form when written in terms of potential enthalpy. To see this point, consider the
evolution of internal energy (see equation (5.94) in Griffies,2004), and introduce the enthalpy per mass
(specific enthalpy)
H=I+p/ρ (2.106)
leads to
ρdH
dt=−∇·Jq+dp
dt+ρ. (2.107)
Dropping the frictional dissipation term arising from molecular friction leads to the approximate statement
ρdH
dt−dp
dt≈ −∇·Jq.(2.108)
To proceed, the fundamental thermodynamic relation (see equation (5.31) Griffies,2004, in) becomes
dH=Tdζ+ρ−1dp+µdC(2.109)
in terms of enthalpy. Thus, enthalpy can be written as a function of entropy, salt concentration, and pres-
sure,
H=H(ζ,C,p).(2.110)
Transport of a seawater parcel without changing heat, salt, or momentum occurs without change in entropy,
thus rendering ∂H
∂p !ζ,C
=ρ−1.(2.111)
Keeping salinity and entropy fixed (or equivalently fixed salinity and potential temperature) leads to
H(θ,s,p) = Ho(θ,s,pr) +
p
Z
pr
ρ−1(θ,s,p0) dp0(2.112)
with Ho(θ,s,pr) defining the potential enthalpy of a parcel with potential temperature θand salinity s.
Taking the time derivative and using the approximate relation (2.108) yields
dHo
dt≈ −ρ−1∇·Jq+
pr
Z
p
dp0dρ−1(θ,s,p0)
dt.(2.113)
McDougall (2003) shows that for the ocean, the integral
pr
Z
p
dp0dρ−1(θ,s,p0)
dt=
pr
Z
p
dp0 ∂ρ−1
∂θ
dθ
dt+∂ρ−1
∂s
ds
dt!
=dθ
dt
pr
Z
p
dp0ρ−1α−ds
dt
pr
Z
p
dp0ρ−1β
(2.114)
has magnitude on the order of the ocean’s tiny levels of dissipation arising from molecular viscosity. These
expressions introduced the thermal expansion coefficient α=−∂lnρ/∂θ and saline contraction coefficient
β=∂lnρ/∂s. The time derivatives of potential temperature and salinity can be removed from the pressure
integrals, since they are each independent of pressure. Given the smallness of Rpr
pdp0dρ−1/dt, one can
write the approximate potential enthalpy equation
ρdHo
dt≈ −∇·Jq.(2.115)
Elements of MOM November 19, 2014 Page 41

Chapter 2. Fundamental equations Section 2.4
Hence, potential enthalpy is a state function that approximately specifies the heat in a parcel of seawater,
and it evolves analogously to a material tracer such as salinity. See McDougall (2003) for a proof that Ho
more accurately sets the heat for a parcel of seawater than does Cpθ. Given that it does, McDougall (2003)
suggests that conservative temperature
Θ≡Ho(θ,s,pr)
Co
p(2.116)
with pr= 0 is more appropriate than potential temperature as a thermodynamic tracer for use in an ocean
model, and generally for measuring heat in the ocean. In this equation
Co
p=H(θ= 25◦C,s = 35psu,pr= 0)
25◦C
= 3989.245Jkg−1◦K−1
(2.117)
is a heat capacity chosen to minimize the difference between Co
pθand potential enthalpy Ho(θ,s,pr) when
averaged over the sea surface.11
Conservative temperature of McDougall (2003) has been recommended by IOC et al. (2010) as the pre-
ferred means to measure heat content in a seawater parcel. MOM has the ability to use conservative tem-
perature as its prognostic temperature field. Conservative temperature is the preferred method rather than
the older potential temperature, with potential temperature retained for legacy purposes. In the remain-
der of these notes, we maintain the notation θto mean conservative temperature, but with all formulas
remaining unchanged if interpreted as potential temperature.
2.4 Material time changes over finite regions
In the following sections, we focus on the mass, tracer, and momentum budgets formulated over a finite
domain. The domain, or control volume, of interest is that of an ocean model grid cell. The budget for a
grid cell is distinct from budgets for infinitesimal mass conserving Lagrangian fluid parcels moving with
the fluid. Mass conserving fluid parcels form the fundamental system for which the budgets of mass, tracer,
momentum, and energy are generally formulated from first principles (see, for example, chapters 3-5 in
Griffies,2004). Grid cell budgets are then derived from the fundamental parcel budgets.
The grid cells of concern for MOM have vertical sides fixed in space-time, but with the top and bottom
generally moving. In particular, the top and bottom either represent the ocean top, ocean bottom, or a
surface of constant generalized vertical coordinate. We furthermore assume that at no place in the fluid do
the top or bottom surfaces of the grid cell become vertical. This assumption allows for a one-to-one relation
to exist between geopotential depth zand the generalized vertical coordinate sintroduced in Section 2.1.5.2
(i.e., the relation is invertible).
To establish the grid cell budget, we integrate the budget for mass conserving fluid parcels over the
volume of the cell. This section is focused on the mathematics required for integrating the density weighted
material time derivative acting on an arbitrary field ψ
ρdψ
dt= (ρψ),t +∇·(ρvψ).(2.118)
We start with the partial time derivative on the right hand side, and introduce Cartesian coordinates (x,y,z)
11The value quoted by McDougall (2003) is Co
p= 3989.24495292815Jkg−1◦K−1.
Elements of MOM November 19, 2014 Page 42

Chapter 2. Fundamental equations Section 2.5
for the purpose of performing the grid cell integral
$dV(ρψ),t =$dxdydz(ρ ψ),t
="dxdy
z2
Z
z1
dz(ρψ),t
="dxdy−(ρ ψ)2∂tz2+ (ρψ)1∂tz1+∂t
z2
Z
z1
dz(ρψ).
(2.119)
The second equality follows by noting that the horizontal extent of a grid cell remains static, thus allowing
for the horizontal integral to be brought outside of the time derivative. In contrast, the vertical extent has
a time dependence, which necessitates the use of Leibniz’s Rule. We now use equation (2.58)
z,t =−s,t z,s (2.120)
which relates time tendencies of the depth of a generalized surface to time tendencies of the surface itself.
Equation (2.30) is next used to write
z,t =−s,t z,s
=z,s |∇s|ˆ
n·v(ref),(2.121)
in which we introduced the reference velocity v(ref)for a point sitting on the generalized surface. Finally,
recall equation (2.32), which relates the area element on the surface to the horizontal projection dA= dxdy
of the surface
dA(ˆ
n)=|z,s ∇s|dA. (2.122)
Introducing this area then renders
z,t dA=ˆ
n·v(ref)dA(ˆ
n).(2.123)
This equation relates the time tendency of the depth of the generalized surface to the normal component
of the velocity at a point on the surface. The two are related through the ratio of the area elements. This
result is now used for the top and bottom boundary terms in relation (2.119), yielding
$dV(ρψ),t =∂t $ρdV ψ!−"dA(ˆ
n)ˆ
n·v(ref)(ρψ).(2.124)
Hence, the domain integrated Eulerian time tendency of the density weighted field equals the time ten-
dency of the density weighted field integrated over the domain, minus an integral over the domain bound-
ary associated with transport of material across that domain, with proper account taken for time depen-
dence of the domain boundary.
The next step needed for volume integrating the density weighted material time derivative in equation
(2.118) involves the divergence of the density weighted field
$dV∇·(ρvψ) = "dA(ˆ
n)ˆ
n·v(ρψ),(2.125)
which follows from Gauss’ Law. Combining this result with equation (2.124) leads to the relation
$ρdVdψ
dt=∂t $ρdV ψ!+"dA(ˆ
n)ˆ
n·(v−v(ref))(ρψ).(2.126)
Hence, the mass weighted grid cell integral of the material time derivative of a field is given by the time
derivative of the mass weighted field integrated over the domain, plus a boundary term that accounts for
the transport across the domain boundaries, with allowance made for moving domain boundaries. The
Elements of MOM November 19, 2014 Page 43

Chapter 2. Fundamental equations Section 2.5
manipulations leading to this result focused on an interior grid cell. The result, however, holds in general
for a cell that abuts either the ocean surface or ocean bottom. For the ocean bottom, the boundary term
vanishes since the bottom has a zero reference velocity, and there is no normal flow of fluid across the
bottom. For the ocean surface, we employ relation (2.68) that defines the dia-surface transport of mass
across the ocean surface in a manner analogous to the dia-surface transport (2.37) across an interior surface.
2.5 Basics of the finite volume method
The finite volume method for formulating the discrete equations of an ocean model has been incorporated
to the ocean modelling literature only since the late 1990’s. The work of Adcroft et al. (1997) is a canonical
example of how this method can be used to garner a better representation of the solid earth boundary.
In this section, we briefly outline the basis for this method. The interested reader may wish to look at
chapter 6 of the book by Hirsch (1988), or the chapter by Machenhauer et al. (2009) for a more thorough
introduction, or one of the growing number of monographs devoted exclusively to the method.
The general equations of fluid mechanics can be represented as conservation equations for scalar quan-
tities (e.g., seawater mass and tracer mass) and vector quantities (e.g., linear momentum). As just detailed
in Section 2.4, the conservation law for a scalar Ψover an arbitrary fluid region can be put in the form
∂t $ΨdV!=−"dA(ˆ
n)ˆ
n·F+$SdV . (2.127)
The volume integral is taken over an arbitrary fluid region, and the area integral is taken over the bounding
surface to that volume, with outward normal ˆ
n. The flux Fpenetrates the surface and acts to alter the scalar,
whereas internal sources Scontribute to changes in the scalar throughout the interior of the domain. The
budget for the vector linear momentum can be written in this form, with the addition of body forces that act
similar to the source term written here (see Section 2.9). Fundamental to the finite volume method is that
the fluxes contribute only at the boundary to the domain, and not within the interior as well. Hence, the
domain can be subdivided into arbitrary shapes, with budgets over the subdivisions summing to recover
the global budget.
A discrete finite volume analog to equation (2.127), for a region labeled with the integer J, takes the
form
∂t(VJΨJ) = −X
sides
(A(ˆ
n)ˆ
n·F) + VJSJ.(2.128)
Quantities with the integer Jsubscript refer to the discrete analogs to the continuum fields and the geo-
metric factors in equation (2.127). In particular, we define the discrete finite volume quantities
VJ≡$dV(2.129)
ΨJ≡#dVΨ
#dV(2.130)
SJ≡#dVS
#dV.(2.131)
Again, it is due to the conservation form of the fundamental fluid dynamic equation (2.127) that allows for
a straightforward finite volume interpretation of the discrete equations. Notably, once formulated as such,
the problem shifts from fundamentals to details, with details differing on how one represents the subgrid
scale behaviour of the continuum fields. This shift leads to the multitude of discretization methods avail-
able for such processes as transport, time stepping, etc. In the following, we endeavour to write the fluid
equations of the ocean in the conservation form (2.127). Doing so then renders a finite volume framework
for the resulting discrete or semi-discrete equations.
When working with non-Boussinesq budgets, the finite volume interpretation applies directly to the
tracer mass per volume, ρC, rather than to the tracer concentration C. The same applies to the linear
Elements of MOM November 19, 2014 Page 44

Chapter 2. Fundamental equations Section 2.6
momentum per volume, ρv, rather than to the velocity v. That is, the finite volume model carries the
discrete fields ρJ, (ρC)Jand (ρv)J, defined as
ρJ≡#dV ρ
#dV(2.132)
(ρC)J≡#dV ρC
#dV(2.133)
(ρv)J≡#dV ρv
#dV.(2.134)
As we will see in the discussions in Sections 2.6 and 2.9, we actually work with a slightly modified fi-
nite volume suite of variables, whereby the finite volume interpretation applies to the seawater mass per
horizontal area, the tracer mass per horizontal area and linear momentum per horizontal area
(dzρ)J≡!dARdzρ
!dA(2.135)
(dzρC)J≡!dARdzρC
!dA(2.136)
(dzρ v)J≡!dARdz ρ v
!dA,(2.137)
where dzis the thickness of a grid cell, and dA= dxdyis the horizontal projection of its area. The inclusion
of thickness facilitates the treatment of grid cells whose thickness is a function of time, such as in MOM.
Note that to reduce notational clutter, we employ the same symbol for the continuum field as for the
discrete, so we drop the Jsubscript in the following.
2.6 Mass and tracer budgets over finite regions
The purpose of this section is to extend the kinematics discussed in the previous sections to the case of
mass and tracer budgets for finite domains within the ocean fluid. In the formulation of ocean models,
these domains are thought of as discrete model grid cells.
2.6.1 General formulation
As described in Section 2.2, the tracer concentration Crepresents a mass of tracer per mass of seawater for
material tracers such as salt or biogeochemical tracers. Mathematically, this definition means that for each
fluid parcel,
C=mass of tracer
mass of seawater
=ρCdV
ρdV,
(2.138)
where ρCis the mass density of tracer within the fluid parcel. In addition to material tracers, we are
concerned with a thermodynamical tracer that measures the heat within a fluid parcel. In this case, Cis
typically taken to be the potential temperature. However, the work of McDougall (2003) prompts us to
consider a modified temperature known as conservative temperature, which more accurately measures the
heat within a fluid parcel and is transported, to within a very good approximation, in a manner directly
analogous to material tracers. We discussed these temperature variables in Section 2.3.
Elements of MOM November 19, 2014 Page 45

Chapter 2. Fundamental equations Section 2.6
Given these considerations, the total tracer mass within a finite region of seawater is given by the inte-
gral.
tracer mass in a region = $ρCdV
=$C ρdV .
(2.139)
Correspondingly, the evolution of tracer mass within a Lagrangian parcel of mass conserving fluid is given
by (see Section 5.1 of Griffies,2004)
ρdC
dt=−∇·J+ρS(C),(2.140)
where S(C)is a tracer source in the region, with units of tracer concentration per time. The tracer flux
Jarises from subgrid scale transport of tracer in the absence of mass transport. Such transport in MOM
consists of diffusion and/or unresolved advection. As discussed in Section 2.2.3, this flux is computed
with respect to the center of mass of a fluid parcel. It therefore vanishes when the tracer concentration is
uniform, in which case the tracer budget reduces to the mass budget (2.7).
We now develop a regional budget for tracer mass over a grid cell. For this purpose, apply the general
result (2.126) relating the material time derivative to a regional budget, to render
∂t $C ρdV!=$S(C)ρdV−"dA(ˆ
n)ˆ
n·[(v−vref)ρ C +J].(2.141)
Again, the left hand side of this equation is the time tendency for tracer mass within the finite sized grid cell
region. When the tracer concentration is uniform, the SGS flux vanishes, in which case the tracer budget
(2.141) reduces to the finite domain mass budget
∂t $ρdV!=$S(M)ρdV−"dA(ˆ
n)ˆ
n·[(v−vref)ρ].(2.142)
In addition to the tracer flux J, it is convenient to define the tracer concentration flux Fvia
J=ρF,(2.143)
where the dimensions of Fare velocity ×tracer concentration.
In a manner analogous to our definition of a dia-surface velocity component in Section 2.1.4, it is useful
to introduce the dia-surface SGS flux component. For this purpose, consider the tracer mass per time cross-
ing a surface of constant generalized vertical coordinate, where this transport arises from SGS processes.
Manipulations similar to those used to derive the dia-surface velocity component lead to
(SGS tracer mass through surface)/(time) = dA(ˆ
n)ˆ
n·J
=z,s ∇s·Jdxdy
= (ˆ
z−S)·Jdxdy,
(2.144)
where Sis the slope vector for the generalized surface defined in equation (2.39). We are therefore led to
introduce the dia-surface SGS tracer flux
J(z)≡dA(ˆ
n)ˆ
n·J
dA
=z,s ∇s·J
= (ˆ
z−S)·J,
(2.145)
where dA= dxdyis the horizontal cross-sectional area. In words, J(z)is the tracer mass per time per
horizontal area penetrating surfaces of constant generalized vertical coordinate via processes that are un-
resolved by the dia-surface velocity component w(z).
Elements of MOM November 19, 2014 Page 46

Chapter 2. Fundamental equations Section 2.6
Grid cell k x,y
z
s=s
s=s
k−1
k
Figure 2.4: Schematic of an ocean grid cell labeled by the vertical integer k. Its sides are vertical and
oriented according to ˆ
xand ˆ
y, and its horizontal position is fixed in time. The top and bottom surfaces are
determined by constant generalized vertical coordinates sk−1and sk, respectively. Furthermore, the top and
bottom are assumed to always have an outward normal with a nonzero component in the vertical direction
ˆ
z. That is, the top and bottom are never vertical. We take the convention that the discrete vertical label k
increases as moving downward in the column, and grid cell kis bounded at its upper face by s=sk−1and
lower face by s=sk.
2.6.2 Budget for an interior grid cell
Consider the budget for a region bounded away from the ocean surface and bottom, such as that shown in
Figure 2.4. We have in mind here a grid cell within a discrete numerical model. There are two assumptions
that define a grid cell for our purposes.
• The sides of the cell are vertical, so they are parallel to ˆ
zand aligned with the horizontal coordinate
directions (ˆ
x,ˆ
y). Their horizontal positions are fixed in time.
• The top and bottom of the cell are defined by surfaces of constant generalized vertical coordinate s=
s(x,y,z,t). The generalized surfaces do not overturn, which means that s,z is single signed throughout
the ocean.
These assumptions lead to the following results for the sides of the grid cell
tracer mass entering cell west face ="
x=x1
dydz(u ρC +ρ Fx) (2.146)
tracer mass leaving cell east face =−"
x=x2
dydz(u ρC +ρ Fx) (2.147)
Elements of MOM November 19, 2014 Page 47

Chapter 2. Fundamental equations Section 2.6
where x1≤x≤x2defines the domain boundaries for the east-west coordinates.12 Similar results hold for
the tracer mass crossing the cell in the north-south directions. At the top and bottom of the grid cell
tracer mass entering cell bottom face ="
s=sk
dxdy ρ(w(z)C+F(z)) (2.148)
tracer mass leaving cell top face =−"
s=sk−1
dxdy ρ(w(z)C+F(z)).(2.149)
To reach this result, we used a result from Section 2.1.4 to write the volume flux passing through the top
face of the grid cell
dA(ˆ
n)ˆ
n·(v−vref) = w(z)dxdy, (2.150)
with w(z)=z,s ds/dtthe dia-surface velocity component from Section 2.1.4. A similar relation holds for the
bottom face of the cell. The form of the SGS flux passing across the top and bottom is correspondingly
given by
dA(ˆ
n)ˆ
n·J=J(z)dxdy, (2.151)
which follows from the general expression (2.145) for the dia-surface tracer flux.
In a model using the generalized coordinate sfor the vertical, it is sometimes convenient to do the
vertical integrals over sinstead of z. For this purpose, recall that with z,s single signed, the vertical thickness
of a grid cell is given by equation (2.52), repeated here for completeness
dz=z,s ds. (2.152)
Bringing these results together, and taking the limit as the volume of the cell in (x,y,s) space goes to zero
(i.e., dxdyds→0) leads to
∂t(z,s ρC) = z,s ρS(C)−∇s·[z,s ρ(uC+F)] −∂s[ρ(w(z)C+F(z))] (2.153)
Notably, the horizontal gradient operator ∇sis computed on surfaces of constant s, and so it is distinct
generally from the horizontal gradient ∇ztaken on surfaces of constant z.
As indicated at the end of Section 2.5, we prefer to work with thickness weighted quantities, given
the general time dependence of a model grid cell in MOM. Hence, as an alternative to taking the limit
as dxdyds→0, consider instead the limit as the time independent horizontal area dxdygoes to zero,
thus maintaining the time dependent thickness dz=z,s dsinside the derivative operators. In this case, the
thickness weighted tracer mass budget takes the form
∂t(dzρC)=dz ρS(C)−∇s·[dzρ(uC+F)] −[ρ(w(z)C+F(z))]s=sk−1+ [ρ(w(z)C+F(z))]s=sk.(2.154)
Similarly, the thickness weighted mass budget is
∂t(dzρ)=dzρS(M)−∇s·(dzρ u)−(ρ w(z))s=sk−1+ (ρ w(z))s=sk.(2.155)
For clarity, note that the horizontal divergence operator acting on the mass transport takes the form
∇s·(dzρ u) = 1
dy
∂
∂x (dydzρu) + 1
dx
∂
∂y (dxdzρv).(2.156)
The mass source S(M)has units of inverse time that, for self-consistency, must be related to the tracer
source via
S(M)=S(C)(C= 1).(2.157)
12We use generalized horizontal coordinates, such as those discussed in Griffies (2004). Hence, the directions east, west, north, and
south may not correspond to the usual geographic directions. Nonetheless, this terminology is useful for establishing the budgets,
whose validity is general.
Elements of MOM November 19, 2014 Page 48
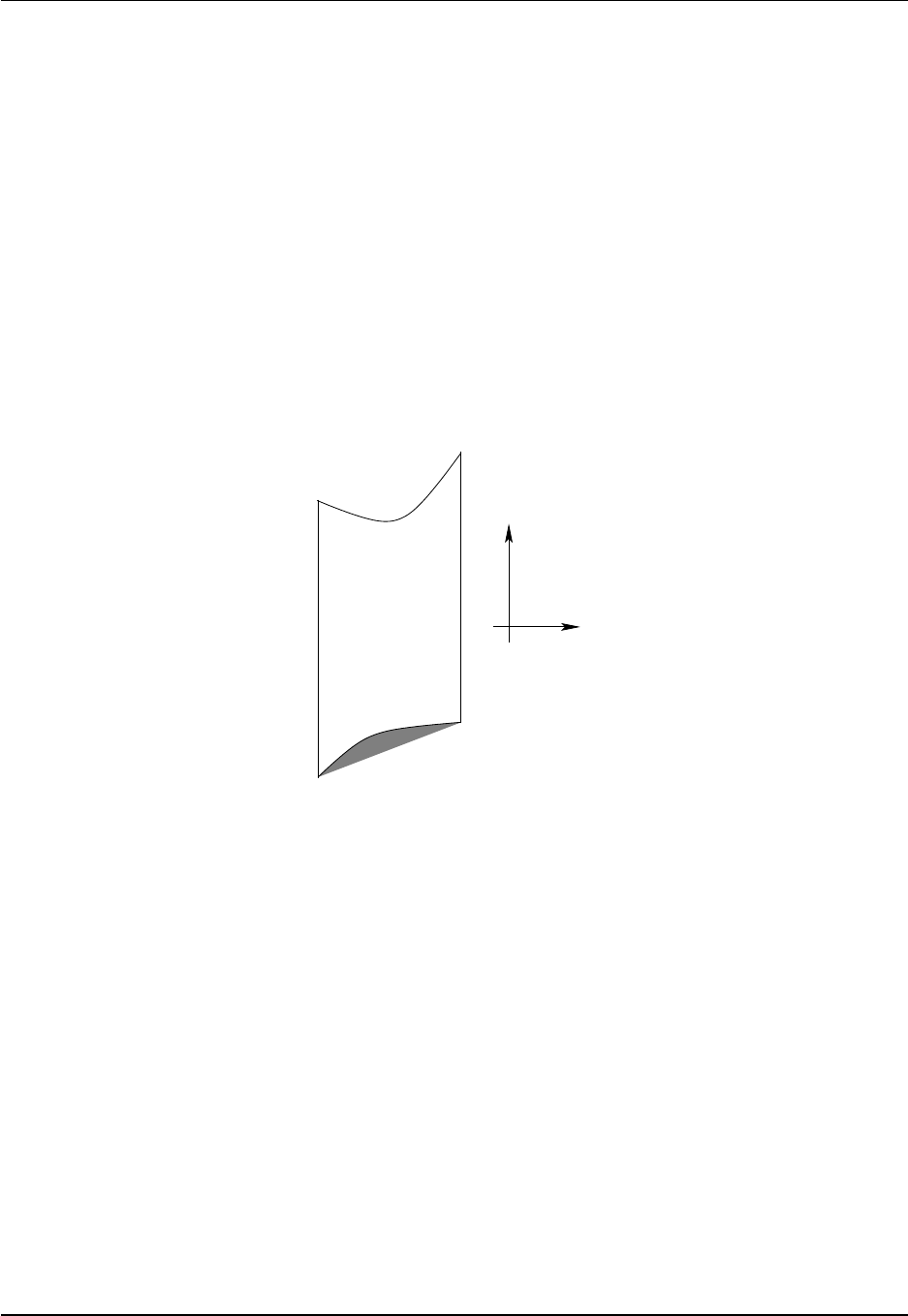
Chapter 2. Fundamental equations Section 2.6
Additionally, the SGS tracer flux vanishes with a uniform tracer
F(C= 1) = 0.(2.158)
Note that by setting the tracer concentration in equation (2.154) to a uniform constant, SGS transort fluxes
vanish, thus revealing the mass conservation budget. This procedure for deriving the mass budget from the
tracer budget follows trivially from the definition of the tracer concentration given by equation (2.138). It
represents a compatibility condition between the discrete budgets, and this condition is critical to maintain
within a numerical model in order to respect tracer and mass conservation in the simulation. We have more
to say about the compatibility condition in Section 2.7.1.
One reason that the thickness weighted budget given by equation (2.154) is more convenient than equa-
tion (2.153) is that equation (2.154) expresses the budget in terms of the grid cell thickness dz, rather than
the specific thickness z,s. Nonetheless, this point is largely one of style and convenience, as there is no
fundamental reason to prefer one form over the other for purposes of developing the discrete equations of
an ocean model.
2.6.3 Cells adjacent to the ocean bottom
z=−H
x,y
z
s=skbot−1
Grid cell k=kbot
bot
s=s
Figure 2.5: Schematic of an ocean grid cell next to the ocean bottom labeled by k=kbot. Its top face is a
surface of constant generalized vertical coordinate s=skbot−1, and the bottom face is determined by the
ocean bottom topography at z=−Hwhere sbot(x,y,t) = s(x,y,z =−H,t).
For a grid cell adjacent to the ocean bottom (Figure 2.5), we assume that just the bottom face of this cell
abuts the solid earth boundary. The outward normal ˆ
nHto the bottom is given by equation (2.46), and the
area element along the bottom is
dAH=|∇(z+H)|dxdy. (2.159)
Hence, the transport across the solid earth boundary is
−"dAHˆ
nH·(vρC +J) = "dxdy(∇H+ˆ
z)·(vρC +J).(2.160)
We assume that there is zero advective mass flux across the bottom, in which case the advective flux drops
out since v·(∇H+ˆ
z) = 0 (equation (2.48)). However, the possibility of a nonzero geothermal tracer transport
warrants a nonzero SGS tracer flux at the bottom, in which case the bottom tracer flux is written
Q(C)
(bot)= (∇H+ˆ
z)·J.(2.161)
The corresponding thickness weighted budget is given by
∂t(dzρC) = dz ρ S(C)−∇s·[dzρ(uC+F)] −hρ(w(z)C+z,s ∇s·F)is=skbot−1
+Q(C)
(bot),(2.162)
Elements of MOM November 19, 2014 Page 49
Chapter 2. Fundamental equations Section 2.6
and the corresponding mass budget is
∂t(dzρ)=dzρS(M)−∇s·(dzρ u)−(ρ ws))s=skbot−1+Q(M)
(bot),(2.163)
where Q(M)
(bot)allows for the possibility of mass entering through geothermal boundary sources. For brevity,
we drop this term in the following, since it generally is ignored for ocean climate modeling.
2.6.4 Cells adjacent to the ocean surface
Grid cell k=1
x,y
z
z=−H
s=s
k=1
s=stop z=η
Figure 2.6: Schematic of an ocean grid cell next to the ocean surface labeled by k= 1. Its top face is at z=η,
and the bottom is a surface of constant generalized vertical coordinate s=sk=1.
For a grid cell adjacent to the ocean surface (Figure 2.6), we assume that just the upper face of this cell
abuts the boundary between the ocean and the atmosphere or sea ice. The ocean surface is a time dependent
boundary with z=η(x,y,t). The outward normal ˆ
nηis given by equation (2.69), and its area element dAη
is given by equation (2.73).
As the surface can move, we must measure the advective transport with respect to the moving surface.
Just as in the dia-surface transport discussed in Section 2.1.4, we consider the velocity of a reference point
on the surface
vref =uref +ˆ
zwref.(2.164)
Since z=ηrepresents the vertical position of the reference point, the vertical component of the velocity for
this point is given by
wref = (∂t+uref ·∇)η(2.165)
which then leads to
vref ·∇(z−η) = η,t.(2.166)
Hence, the advective transport leaving the ocean surface is
"
z=η
dA(ˆ
n)ˆ
n·(v−vref)ρ C ="
z=η
dxdy(−η,t +w−u·∇η)ρC
=−"
z=η
dxdy QmC,
(2.167)
where the surface kinematic boundary condition (2.77) was used. The negative sign on the right hand side
arises from our convention that Qm>0 represents an input of mass to the ocean domain. In summary, the
Elements of MOM November 19, 2014 Page 50

Chapter 2. Fundamental equations Section 2.7
tracer flux leaving the ocean free surface is given by
"
z=η
dA(ˆ
n)ˆ
n·[(v−vref)ρ C +J] = "
z=η
dxdy(−QmC+∇(z−η)·J).(2.168)
In equation (2.168), we formally require the tracer concentration precisely at the ocean surface z=η.
However, as mentioned at the start of Section 2.1.6, it is actually a fiction that the ocean surface is a smooth
mathematical function. Furthermore, seawater properties precisely at the ocean surface, known generally
as skin properties, are generally not what an ocean model carries as its prognostic variable in its top grid
cell. Instead, the model carries a bulk property averaged over roughly the upper few tens of centimeters.
To proceed in formulating the boundary condition for an ocean climate model, we consider there to be
a boundary layer model that provides us with the total tracer flux passing through the ocean surface. De-
veloping such a model is a nontrivial problem in air-sea and ice-sea interaction theory and phenomenology.
For present purposes, we do not focus on these details, and instead just introduce this flux in the form
Q(C)=−QmCm+Q(C)
(turb)(2.169)
where Cmis the tracer concentration within the incoming water. The first term on the right hand side
represents the advective transport of tracer through the surface with the fresh water (i.e., ice melt, rivers,
precipitation, evaporation). The term Q(C)
(turb)arises from parameterized turbulence and/or radiative fluxes,
such as sensible, latent, shortwave, and longwave heating appropriate for the temperature equation. A
positive value for Q(C)
(turb)signals tracer leaving the ocean through its surface. In the special case of zero
fresh water flux, then
∇(z−η)·J=Q(C)
(turb)if Qm= 0.(2.170)
In general, it is not possible to make this identification. Instead, we must settle for the general expression
"
z=η
dA(ˆ
n)ˆ
n·[(v−vref)ρ C +J] = "
z=η
dxdy(−QmCm+Q(C)
(turb)).(2.171)
The above results lead to the thickness weighted tracer budget for the ocean surface grid cell
∂t(dzρC)=dz ρS(C)−∇s·[dzρ(uC+F)]
+hρ(w(z)C+z,s ∇s·F)is=sk=1
+ (QmCm−Q(turb)
(C)),(2.172)
and the corresponding mass budget
∂t(dzρ)=dzρS(M)−∇s·(dzρ u) + (ρ w(z))s=sk=1 +Qm.(2.173)
2.7 Special considerations for tracers
The purpose of this section is to describe some special considerations for tracers in a numerical ocean
model.
2.7.1 Compatability between vertically integrated mass and tracer budgets
In Section 2.6.2, we considered issues of compatibility between the tracer and mass budgets within a grid
cell. Such compatibility follows trivially from the definition of tracer concentration given in Section 2.6.1.
We briefly revisit compatibility here, by focusing on the vertically integrated tracer and mass budgets.
Elements of MOM November 19, 2014 Page 51

Chapter 2. Fundamental equations Section 2.7
Combining the surface tracer budget (2.173), the bottom budget (2.162), and interior budget (2.154),
renders the vertically integrated tracer budget
∂tX
k
dzρC=X
k
dzρ S(C)−∇s·X
k
dzρ (uC+F)
+QmCm−Q(turb)
(C)+Q(bott)
(C).
(2.174)
As expected, the only contributions from vertical fluxes come from the top and bottom boundaries. Fur-
thermore, by setting the tracer concentration to a uniform constant, in which case the SGS turbulent terms
vanish, the tracer budget reduces to the vertically integrated mass budget
∂tX
k
dzρ =X
k
dzρ S(M)−∇s·Uρ+Qm,(2.175)
where
Uρ=X
k
dzρ u(2.176)
is the discrete form of the vertically integrated horizontal momentum per volume defined by equation
(2.22). As for the individual grid cells, this vertically integrated compatiblity between tracer and mass
budgets must be carefully maintained by the space and time discretizations used in an ocean model. Oth-
erwise, conservation properties of the model will be compromised (Griffies et al.,2001).
2.7.2 Fresh water budget
Seawater is comprised of freshwater with a relatively fixed ratio of various salts. It is common to consider
the budget for the concentration of these salts, which is described by the tracer equation (2.154). As a
complement, it may be of interest to formulate a budget for freshwater. In this case, we consider the mass
of fresh water within a fluid parcel
mass of fresh water = mass of seawater −mass of salt
=ρdV(1 −S)
=ρdV W ,
(2.177)
where Sis the salinity (mass of salt per mass of seawater), and
W≡1−S(2.178)
is the mass of fresh water per mass of seawater. Results from the tracer budget considered in Section 2.6.2
allow us to derive the following budget for fresh water within an interior ocean model grid cell
∂t(dzρW)=dz ρ(S(M)−S(S))−∇s·[dz ρ (uW−F)]
−[ρ(w(z)W−F(z))]s=sk−1+ [ρ(w(z)W−F(z))]s=sk.(2.179)
In these relations, the SGS tracer flux components Fand F(z)are those for salt, and S(S)is the salt source.
Equation (2.179) is very similar to the tracer equation (2.154), with modified source term and negative
signs on the SGS flux components.
2.7.3 The ideal age tracer
Thiele and Sarmiento (1990) and England (1995) consider an ideal age tracer for Boussinesq fluids. We
consider the generalization here to non-Boussinesq fluids, in which
ρdA
dt+∇·J=ρS(A),(2.180)
Elements of MOM November 19, 2014 Page 52

Chapter 2. Fundamental equations Section 2.8
where the age tracer Ahas dimensions of time and it is initialized globally to zero. It is characterized by
the dimensionless clock source S(A), which takes the values
S(A)=(0 if z=η
1 if z < η,(2.181)
In a finite difference model, the boundary condition at z=ηis applied at the top grid cell k= 1. In MOM,
various age tracers can be defined that differ by the region that their boundary condition is set to zero.
Given these prescriptions, Ameasures the age, in units of time, that a water parcel has spent away from the
region where it was set to zero. Therefore, visual maps of Aare useful to deduce such physically interesting
properties as ventilation times.
From equation (2.154), the budget for tracer mass per area in a grid cell is given by
∂t(dzρA)=dz ρ S(A)−∇s·[dz ρ(uA+F)]
−[ρ(w(z)A+F(z))]s=sk−1+ [ρ(w(z)A+F(z))]s=sk.(2.182)
In practice, the clock source is added to the age tracer at the very end of the time step, so that it is imple-
mented as an adjustment process. In this way, we remove the ambiguity regarding the time step to evaluate
the ρdzfactor that multiplies the age source.
2.7.4 Budgets without dia-surface fluxes
To garner some experience with tracer budgets, it is useful to consider the special case of zero dia-surface
transport, either via advection or SGS fluxes, and zero tracer/mass sources. In this case, the thickness
weighted mass and tracer mass budgets take the simplified form
∂t(dzρ) = −∇s·(dz ρu) (2.183)
∂t(dzρC) = −∇s·[dz ρ (uC+F)].(2.184)
The first equation says that the time tendency of the thickness weighted density (mass per area) at a point
between two surfaces of constant generalized vertical coordinate is given by the horizontal convergence
of mass per area onto that point. The transport is quasi-two-dimensional in the sense that it is only a
two-dimensional convergence that determines the evolution. The tracer equation has an analogous inter-
pretation. We illustrate this situation in Figure 2.7. As emphasized in our discussion of the material time
derivative (2.43), this simplification of the transport equation does not mean that fluid parcels are strictly
horizontal. Indeed, such is distinctly not the case when the surfaces are moving.
A further simplification of the mass and tracer mass budgets ensues when considering adiabatic and
Boussinesq flow in isopycnal coordinates. We consider ρnow to represent the constant potential density of
the finitely thick fluid layer. In this case, the mass and tracer budgets reduce to
∂t(dz) = −∇ρ·(dzu) (2.185)
∂t(dzC) = −∇ρ·[dz(uC+F)].(2.186)
Equation (2.185) provides a relation for the thickness of the density layers, and equation (2.186) is the
analogous relation for the tracer within the layer. These expressions are commonly used in the construction
of adiabatic isopycnal models, which are often used in the study of geophysical fluid mechanics of the
ocean.
2.8 Forces from pressure
Pressure is a contact force per area that acts in a compressive manner on the boundary of a finite fluid
domain (e.g., see Figure 2.8). Mathematically, we have
Fpress =−"dA(ˆ
n)ˆ
np, (2.187)
Elements of MOM November 19, 2014 Page 53
Chapter 2. Fundamental equations Section 2.8
k−1
diverge
converge converge
s=sk
s=s
Figure 2.7: Schematic of the horizontal convergence of mass between two surfaces of constant generalized
vertical coordinates. As indicated by equation (2.183), when there is zero dia-surface transport, it is just
the horizontal convergence that determines the time evolution of mass between the layers. Evolution of
thickness weighted tracer concentration in between the layers is likewise evolved just by the horizontal
convergence of the thickness weighted advective and diffusive tracer fluxes (equation (2.184)). In this way,
the transport is quasi-two-dimensional when the dia-surface transports vanish. A common example of this
special system is an adiabatic ocean where the generalized surfaces are defined by isopycnals.
where pis the pressure (with units of a force per area) acting on the boundary of the domain with outward
normal ˆ
nand area element dA(ˆ
n). The minus sign accounts for the compressive behaviour of pressure. The
accumulation of contact pressure forces acting over the bounding area of the domain leads to a net pressure
force acting on the domain.
Through use of the Green-Gauss theorem of vector calculus, we can equivalently consider pressure to
exert a body force per area at each point within the domain, so that
Fpress =−$dV∇p, (2.188)
where dVis the volume element. That is, the volume integral of the pressure gradient body force over the
domain yields the net pressure force.
In the continuum, the two formulations (2.187) and (2.188) yield identical pressure forces. Likewise,
in a finite volume discretization, the two forms are identical (e.g., Section 6.2.2 of Hirsch,1988). But with
finite differences, as used in earlier versions of MOM for pressure forces, the two forms can lead to different
numerical methods. In the remainder of this section, we further explore the computation of pressure forces
according to the two different formulations. Further details of discrete expressions are presented in Chapter
3.
z
y
x
Figure 2.8: Schematic of a grid cell bounded at its top and bottom in general by sloped surfaces and vertical
side walls. The top and bottom surfaces can represent linear piecewise approximations to surfaces of
constant generalized vertical coordinates, with s=s1at the top surface and s=s2at the bottom surface.
They could also represent the ocean surface (for the top face) or the ocean bottom (for the bottom face).
The arrows represent the pressure contact forces that act in a compressive manner along the boundaries
of the grid cell and in a direction normal to the boundaries. These forces arise from contact between the
shown fluid volume and adjacent regions. Due to Newton’s Third Law, the pressure acting on an arbitrary
fluid parcel Adue to contact with a parcel Bis equal and opposite to the pressure acting on parcel Bdue to
contact with parcel A. If coded according to finite volume budgets, as in Lin (1997) or Adcroft et al. (2008),
this law extends to the pressure forces acting between grid cells in an ocean model.
Elements of MOM November 19, 2014 Page 54

Chapter 2. Fundamental equations Section 2.8
2.8.1 The accumulation of contact pressure forces
Pressure acts as a contact or interfacial stress on the sides of a finite region of fluid. In particular, the total
pressure force acting on the grid cell in Figure 2.8 is given by summing the pressure forces acting on the
six cell faces
Fpressure =Fx=x1+Fx=x2+Fy=y1+Fy=y2+Fs=s1+Fs=s2.(2.189)
The pressure acting on faces with a zonal normal can be written
Fx=x1=ˆ
xZdy
z1
Z
z2
dzpx=x1
(2.190)
Fx=x2=−ˆ
xZdy
z1
Z
z2
dzpx=x2
(2.191)
where the vertical integral extends from the bottom face at z2=z(x,y,s =s2,t) to the top face at z1=
z(x,y,s =s1,t). Likewise, the meridional pressure forces are
Fy=y1=ˆ
yZdx
z1
Z
z2
dzpy=y1
(2.192)
Fy=y2=−ˆ
yZdx
z1
Z
z2
dzpy=y2
.(2.193)
On the top face, the pressure force is given by
Fs=s1=− ZdyZdxpz,s ∇s!s=s1
=− ZdyZdxp (−∇sz+ˆ
z)!s=s1
.
(2.194)
Note the contribution from the generally non-horizontal top face as represented by the two dimensional
vector
∇sz=S,(2.195)
which is the slope of the surface of constant generalized vertical coordinate relative to the horizontal plane.
The pressure force on the bottom face has a similar appearance
Fs=s2= ZdyZdxp (−∇sz+ˆ
z)!s=s2
.(2.196)
If the top and bottom faces are horizontal, as for z-models, the pressure force acting at s=s1and s=s2acts
solely in the vertical direction. More generally, the pressure force per area on the top and bottom faces is
oriented according to the slope of the faces and so has a nontrivial projection into all three directions.
To garner a sense for how pressure acts on the face of a grid cell, consider the case where the top surface
of a grid cell rises to the east as shown in Figure 2.9. In this case, the pressure force per area in the x−z
plane takes the form
pressure force per area on top face =−p[ˆ
z−(∂z/∂x)sˆ
x].(2.197)
Since (∂z/∂x)s>0 for this example, the pressure force per area has a positive component in the ˆ
xdirection,
as indicated by the arrow normal to the top surface in Figure 2.9.
Elements of MOM November 19, 2014 Page 55

Chapter 2. Fundamental equations Section 2.8
x
A
B
C
D
p(x1,s)
p(x,s1)
p(x2,s)
p(x,s2)
z
Figure 2.9: The sides of the grid cell, with the slopes top and bottom surfaces more enhanced here than in
Figure 2.9. The corners are denoted A, B, C, and D, and oriented in a counterclockwise manner. This is the
orientation appropriate for performing a contour integral in order to compute the pressure force acting on
the area.
When the top surface represents the surface of the ocean at z=η, the pressure pis the applied pressure
paarising from any media above the ocean, such as the atmosphere and sea ice. In this case,
pressure force per area on ocean surface =−pa∇(z−η)
=−pa(ˆ
z−∇η),(2.198)
where ∇ηis the slope of the ocean surface. Likewise, if the bottom of the grid cell is bounded by the solid
earth boundary,
pressure force per area on ocean bottom =pb∇(z+H)
=pb(ˆ
z+∇H),(2.199)
where ∇His the bottom slope.
A sum of the pressure forces acting on the six faces of the grid cell determines the acceleration due to
pressure acting on a grid cell. Organizing the forces into the three directions leads to
Fx
pressure =Zdy
z1
Z
z2
dzpx=x1
−Zdy
z1
Z
z2
dzpx=x2
(2.200)
+Zdy
x2
Z
x1
dxz,x ps=s1
−Zdy
x2
Z
x1
dxz,x ps=s2
(2.201)
Fy
pressure =Zdx
z1
Z
z2
dzpy=y1
−Zdx
z1
Z
z2
dzpy=y2
(2.202)
+Zdx
y2
Z
y1
dy z,y ps=s1
−Zdx
y2
Z
y1
dy z,y ps=s2
(2.203)
Fz
pressure = "dxdy p!s=s2− "dxdy p!s=s1
.(2.204)
Making the hydrostatic approximation, whereby the vertical momentum equation maintains the inviscid
hydrostatic balance, allows us to note that the difference in pressure between the top and bottom surfaces
Elements of MOM November 19, 2014 Page 56

Chapter 2. Fundamental equations Section 2.8
of the region is determined by the weight of fluid between the surfaces,
"
s=s2
dxdy p −"
s=s1
dxdy p =gZρdV . (2.205)
It is notable that this expression relates the difference in contact forces acting on the domain boundaries to
the integral of a body force (the gravitational force) acting throughout the domain interior.
We now work on reformulating the horizontal pressure forces into a manner amenable to finite volume
discretization. Referring to Figure 2.9, we can write the horizontal forces in a manner than builds in the
orientation of pressure via a counterclockwise contour integral
Fx
pressure =−Zdy
z2
Z
z1
dzpx=x1
−Zdy
x2
Z
x1
dxz,x ps=s2
−Zdy
z1
Z
z2
dzpx=x2
−Zdy
x1
Z
x2
dxz,x ps=s1
=−Zdy
z2
Z
z1
dzpx=x1
−Zdy
x2
Z
x1
dzps=s2
−Zdy
z1
Z
z2
dzpx=x2
−Zdy
x1
Z
x2
dzps=s1
=−ZdyI
ABCD
dzp.
(2.206)
In the penultimate step, we set z,x dx= dz, which is an relation valid along the particular contour ABCD.
That is, in all the integrals, the differential increment dzis taken along the contour surrounding the cell.
The counter-clockwise orientation of the integral follows from the compressive nature of pressure. Since
the contour of integration is closed, we have the identity
Fx
pressure =−ZdyI
ABCD
pdz
=ZdyI
ABCD
zdp.
(2.207)
The contour integral form of the pressure force is key to providing a finite volume discretization that is
consistent with Newton’s Third Law (Lin,1997;Adcroft et al.,2008). What is needed next is an assumption
about the subgrid profiles for pressure and geopotential Φ=g z in order to evaluate the contour integral.
2.8.2 Pressure gradient body force in hydrostatic fluids
In the early finite difference formulations of the pressure force, modelers discretized the gradient of pres-
sure and performed certain grid averages so that the gradient occurs at the appropriate grid point. Guid-
ance to the discretization details was provided by concerns of energetic consistency (Chapter 14), whereby
work done by pressure in the discrete algorithm is balanced by buoyancy work (Bryan,1969). This general
philosophy still guides the formulation of the pressure force in MOM.
As with the contact forces formulation, in a hydrostatic fluid we are only concerned with horizontal
pressure gradients, since the vertical momentum equation is reduced to the inviscid hydrostatic balance.
Elements of MOM November 19, 2014 Page 57

Chapter 2. Fundamental equations Section 2.9
Hence, we are concerned with the horizontal acceleration arising from pressure differences in a hydrostatic
and non-Boussinesq fluid, and this acceleration can be written13
ρ−1∇zp=ρ−1(∇s−∇sz∂z)p
=ρ−1∇sp+g∇sz
=ρ−1∇sp+∇sΦ,
(2.208)
where the hydrostatic relation p,z =−ρg was used to reach the second equality, and
Φ=g z (2.209)
is the geopotential. To reach this result, we used the expression
∇z=∇s−∇sz∂z,(2.210)
which relates the lateral gradient operator acting on constant depth surfaces, ∇z, to the lateral operator
acting on surfaces of constant generalized vertical coordinate, ∇s.
Depending on the choice for the vertical coordiante s, discretizations of the pressure gradient body force
can result in both terms in equation (2.208) being large and of opposite sign in many regions. This issue
is especially pernicious for terrain following coordinates in regions of nontrivial topographic slope (e.g.,
Griffies et al.,2000a). Hence, this calculation exposes the discrete pressure gradient force to nontrivial
numerical truncation errors which can lead to spurious numerical pressure gradients and thus to incorrect
simulated currents. Significant effort has gone into reducing such pressure gradient errors, especially in ter-
rain following models where undulations of the coordinate surfaces can be large with realistic topography
(e.g., see Figure 5.3). Some of these issues are summarized in Section 2 of Griffies et al. (2000a).
The pressure gradient force acting at a point represents the infinitesimal limit of a body force. We see
this fact by multiplying the pressure gradient acceleration by the mass of a fluid parcel, which leads to the
pressure force acting at a point in the continuum
pressure gradient force =−(ρdV)ρ−1∇zp
=−dV∇zp
=−dV(∇sp+ρ∇sΦ).
(2.211)
Hence, the pressure force acting on a finite region is given by the integral over the extent of the region
pressure gradient force over region =−$(ρdV)ρ−1∇zp
=−$dV∇zp.
(2.212)
As stated earlier, a finite volume discretization of this force will take the same form as the finite volume
discretization of the pressure contact force discussed in Section 2.8.1, as it should due to the Green-Gauss
Theorem invoked to go from equation (2.187) to (2.188). However, these formulations generally do not
provide for a clear energetic interpretation as promoted by the finite difference formulation of Bryan (1969).
2.9 Linear momentum budget
The purpose of this section is to formulate the budget for linear momentum over a finite region of the
ocean, with specific application to ocean model grid cells. The material here requires many of the same
elements as in Section 2.6, but with added richness arising from the vector nature of momentum, and the
additional considerations of forces from pressure, friction, gravity, and planetary rotation. Note that we
initially formulate the equations using the pressure contact force, as this provides a general formulation.
Afterwards, we specialize to hydrostatic fluids, and thus write the pressure force as a gradient (Section
2.8.2), as commonly done in primitive equation ocean models
13For a Boussinesq fluid, equation (2.208) is modified by a factor of ρ/ρo.
Elements of MOM November 19, 2014 Page 58

Chapter 2. Fundamental equations Section 2.9
2.9.1 General formulation
The budget of linear momentum for a finite region of fluid is given by the following relation based on
Newton’s second and third laws
∂t $dV ρv!=$dVS(v)−"dA(ˆ
n)[ˆ
n·(v−vref)] ρv
+"dA(ˆ
n)(ˆ
n·τ−ˆ
np)−$dV ρ[gˆ
z+ (f+M)ˆ
z∧v].
(2.213)
The left hand side is the time tendency of the region’s linear momentum. The first term on the right hand
side, S(v), is a momentum source, with units momentum per volume per time. This term is nonzero if,
for example, the addition of mass to the ocean via a source occurs with a nonzero momentum. Often, it is
assumed that mass is added with zero velocity, and so does not appear as a momentum source. The second
term is the advective transport of linear momentum across the boundary of the region, with recognition
that the region’s boundaries are generally moving with velocity vref. The third term is the integral of the
contact stresses due to friction and pressure. These stresses act on the boundary of the fluid domain. We
already discussed the forces from pressure in Section 2.8. The stress tensor τis a symmetric second order
tensor that parameterizes subgrid scale transport of momentum. The final term on the right hand side is
the volume integral of body forces due to gravity and the Coriolis force.14 In addition, there is a body force
arising from the nonzero curvature of the spherical space. This curvature leads to the advection metric
frequency (see equation (4.49) of Griffies (2004))
M=v ∂xlndy−u ∂ylndx. (2.214)
In spherical coordinates where
dx= (rcosφ)dλ(2.215)
dy=rdφ, (2.216)
with rthe distance from the earth’s center, λthe longitude, and φthe latitude, the advective metric fre-
quency takes the form
M= (u/r) tanφ. (2.217)
The advection metric frequency arises since linear momentum is not conserved on the sphere.15 Hence, the
linear momentum budget picks up this extra term that is a function of the chosen lateral coordinates.
2.9.2 An interior grid cell
At the west side of a grid cell, ˆ
n=−ˆ
xwhereas ˆ
n=ˆ
xon the east side. Hence, the advective transport of
linear momentum entering through the west side of the grid cell and that which is leaving through the east
side are given by
transport entering from west ="
x=x1
dyds z,s u(ρv) (2.218)
transport leaving through east =−"
x=x2
dyds z,s u(ρv).(2.219)
14The wedge symbol ∧represents a vector cross product, also commonly written as ×. The wedge is typically used in the physics
literature, and is preferred here to avoid confusion with the horizontal coordinate x.
15Linear momentum is not conserved for ideal flow on a sphere. Instead, angular momentum is conserved for ideal fluid flow on
the sphere in the absence of horizontal boundaries (see Section 4.11.2 of Griffies (2004)).
Elements of MOM November 19, 2014 Page 59

Chapter 2. Fundamental equations Section 2.9
Similar results hold for momentum crossing the cell boundaries in the north and south directions. Momen-
tum crossing the top and bottom surfaces of an interior cell is given by
transport entering from the bottom ="
s=s2
dxdy w(z)(ρv) (2.220)
transport leaving from the top =−"
s=s1
dxdy w(z)(ρv).(2.221)
Forces due to the contact stresses at the west and east sides are given by
contact force on west side =−"
x=x1
dyds z,s (ˆ
x·τ−ˆ
xp) (2.222)
contact force on east side ="
x=x2
dyds z,s (ˆ
x·τ−ˆ
xp) (2.223)
with similar results at the north and south sides. At the top of the cell, dA(ˆ
n)ˆ
n=∇sdxdywhereas dA(ˆ
n)ˆ
n=
−∇sdxdyat the bottom. Hence,
contact force on cell top ="
s=sk−1
dxdy z,s (∇s·τ−p∇s) (2.224)
contact force on cell bottom =−"
s=sk
dyds z,s (∇s·τ−p∇s).(2.225)
Bringing these results together, and taking limit as the time independent horizontal area dxdy→0, leads
to the thickness weighted budget for the momentum per horizontal area of an interior grid cell
∂t(dzρ v)=dzS(v)−∇s·[dzu(ρv)] + (w(z)ρv)s=sk−(w(z)ρv)s=sk−1
+∂x[dz(ˆ
x·τ−ˆ
xp)] + ∂y[dz(ˆ
y·τ−ˆ
yp)]
+ [z,s (∇s·τ−p∇s)]s=sk−1−[z,s (∇s·τ−p∇s)]s=sk
−ρdz[gˆ
z+ (f+M)ˆ
z∧v].
(2.226)
Note that both the time and horizontal partial derivatives are for positions fixed on a constant generalized
vertical coordinate surface. Also, the pressure force as written here is a shorthand for the more complete
contour integral formulation provided in Section 2.8 (e.g., equation (2.207)). Additionally, we have yet to
take the hydrostatic approximation, so these equations are written for the three components of the velocity.
The first term on the right hand side of the thickness weighted momentum budget (2.226) is the mo-
mentum source, and the second is the convergence of advective momentum fluxes occurring within the
layer. We discussed the analogous flux convergence for the tracer and mass budgets in Section 2.7.4. The
third and fourth terms arise from the transport of momentum across the upper and lower constant sinter-
faces. The fifth and sixth terms arise from the horizontal convergence of pressure and viscous stresses. The
seventh and eigth terms arise from the frictional and pressure stresses acting on the constant generalized
surfaces. These forces provide an interfacial stress between layers of constant s. Note that even in the ab-
sence of frictional stresses, interfacial stresses from pressure acting on the generally curved ssurface can
transmit momentum between vertically stacked layers. The final term arises from the gravitational force,
the Coriolis force, and the advective frequency.
2.9.3 Cell adjacent to the ocean bottom
As for the tracer and mass budgets, we assume zero mass flux through the ocean bottom at z=−H(x,y).
However, there is generally a nonzero stress at the bottom due to both the pressure between the fluid
Elements of MOM November 19, 2014 Page 60

Chapter 2. Fundamental equations Section 2.9
and the bottom, and unresolved features in the flow which can correlate or anti-correlate with bottom
topographic features (Holloway (1999)). The area integral of the stresses lead to a force on the fluid at the
bottom
Fbottom =−"
z=−H
dxdy[∇(z+H)·τ−p∇(z+H)].(2.227)
Details of the stress term requires fine scale information that is generally unavailable. For present purposes
we assume that some boundary layer model provides information that is schematically written
τbot =∇(z+H)·τ(2.228)
where τbot is a vector bottom stress. Taking the limit as the horizontal area vanishes leads to the thickness
weighted budget for momentum per horizontal area of a grid cell next to the ocean bottom
∂t(dzρ v)=dzS(v)−∇s·[dzu(ρv)] −(w(z)ρv)s=skbot−1
+∂x[dz(ˆ
x·τ−ˆ
xp)] + ∂y[dz(ˆ
y·τ−ˆ
yp)]
+ [z,s (∇s·τ−p∇s)]s=skbot−1
−τbot +pb∇(z+H)
−ρdz[gˆ
z+ (f+M)ˆ
z∧v].
(2.229)
2.9.4 Cell adjacent to the ocean surface
There is a nonzero mass and momentum flux through the upper ocean surface at z=η(x,y,t), and contact
stresses are applied from resolved and unresolved processes involving interactions with the atmosphere
and sea ice. Following the discussion of the tracer budget at the ocean surface in Section 2.6.4 leads to the
expression for the transport of momentum into the ocean due to mass transport at the surface
−"dA(ˆ
n)ˆ
n·[(v−vref)ρv="
z=η
dxdy Qmv.(2.230)
The force arising from the contact stresses at the surface is written
Fcontact ="
z=η
dxdy[∇(z−η)·τ−p∇(z−η)].(2.231)
Bringing these results together leads to the force acting at the ocean surface
Fsurface ="
z=η
dxdy[∇(z−η)·τ−p∇(z−η) + Qmv].(2.232)
Details of the various terms in this force are generally unknown. Therefore, just as for the tracer at z=ηin
Section 2.6.4, we assume that a boundary layer model provides information about the total force, and that
this force is written
Fsurface ="
z=η
dxdy[τtop −pa∇(z−η) + Qmvm],(2.233)
where vmis the velocity of the water crossing the ocean surface. This velocity is typically taken to be equal
to the velocity of the ocean currents in the top cells of the ocean model, but such is not necessarily the case
when considering the different velocities of, say, river water and precipitation. The stress τtop is that arising
from the wind, as well as interactions between the ocean and sea ice. Letting the horizontal area vanish
Elements of MOM November 19, 2014 Page 61

Chapter 2. Fundamental equations Section 2.10
leads to the thickness weighted budget for a grid cell next to the ocean surface
∂t(dzρ v)=dzS(v)−∇s·[dzu(ρv)] + (w(z)ρv)s=sk=1
+∂x[dz(ˆ
x·τ−ˆ
xp)] + ∂y[dz(ˆ
y·τ−ˆ
yp)]
−[z,s (∇s·τ−p∇s)]s=sk=1
+ [τtop −pa∇(z−η) + Qmvm]
−ρdz[gˆ
z+ (f+M)ˆ
z∧v].
(2.234)
2.9.5 Horizontal momentum equations for hydrostatic fluids
We now assume the fluid to maintain a hydrostatic balance, which is the case for primitive equation ocean
general circulation models. In this case, we exploit the pressure gradient body force as discussed in Section
2.8.2. Specializing the momentum budgets from Sections 2.9.2,2.9.3, and 2.9.4 to use the hydrostatic
pressure gradient force (again, interpreted according to the finite volume form given in Section 2.8) leads
to the horizontal linear momentum budget for interior, bottom, and surface grid cells
[∂t+ (f+M)ˆ
z∧](ρdzu)=dzS(u)−∇s·[ dzu(ρu)]
−dz(∇sp+ρ∇sΦ)
+∂x(dzˆ
x·τ) + ∂y(dzˆ
y·τ)
−[w(z)ρu−z,s ∇s·τ]s=sk−1
+ [w(z)ρu−z,s ∇s·τ]s=sk.
(2.235)
[∂t+ (f+M)ˆ
z∧](ρdzu)=dzS(u)−∇s·[ dzu(ρu)]
−dz(∇sp+ρ∇sΦ)
+∂x(dzˆ
x·τ) + ∂y(dzˆ
y·τ)
−[w(z)ρu−z,s ∇s·τ]s=skbot−1
−τbottom
(2.236)
[∂t+ (f+M)ˆ
z∧](ρdzu)=dzS(u)−∇s·[ dzu(ρu)]
−dz(∇sp+ρ∇sΦ)
+∂x(dzˆ
x·τ) + ∂y(dzˆ
y·τ)
+ [τwind +Qmuw]
+ [w(z)ρu−z,s ∇s·τ]s=s1.
(2.237)
2.10 The Boussinesq budgets
We consider various depth-based vertical coordinates in Section 5.1. These coordinates are used to dis-
cretize the Boussinesq model equations where the volume of a parcel is conserved rather than the mass. A
detailed discussion of the interpretation of the Boussinesq equations in terms of density weighted fields is
given by McDougall et al. (2002) and Griffies (2004). For now, we gloss over those details by quoting the
Boussinesq equations for volume, tracer, and momentum as arising from setting all density factors to the
constant ρo, except when multiplied by the gravitational acceleration in the hydrostatic balance (i.e., for
calculation of pressure and geopotential, the full density is used). The density ρois a representative density
of the ocean fluid. In MOM4 we set
ρo= 1035kg/m3,(2.238)
although this value can be changed via altering a parameter statement and thus recompiling the code). For
much of the ocean, the in situ density deviates less than 3% from 1035kgm−3(see page 47 of Gill (1982)).
Elements of MOM November 19, 2014 Page 62

Chapter 2. Fundamental equations Section 2.10
The replacement of density in the mass, tracer, and linear momentum budgets over a grid cell in the
ocean interior leads to the following budgets for the hydrostatic model
∂t(dz)=dzS(V)−∇s·(dzu)−(w(z))s=sk−1+ (w(z))s=sk
∂t(dzC)=dzS(C)−∇s·[dz(uC+F)]
−(w(z)C+F(z))s=sk−1
+ (w(z)C+F(z))s=sk
[∂t+ (f+M)ˆ
z∧](ρodzu)=dzS(u)−∇s·[ dzu(ρou)]
−dz(∇sp+ρ∇sΦ)
+∂x(dzˆ
x·τ) + ∂y(dzˆ
y·τ)
−[w(z)ρou−z,s ∇s·τ]s=sk−1
+ [w(z)ρou−z,s ∇s·τ]s=sk.
(2.239)
The first equation reduces to a volume budget rather than a mass budget found for the non-Boussinesq
system. In this equation, S(V)is a volume source with units of inverse time. Likewise, S(u)is a velocity
source (with units of acceleration). The Boussinesq equations for a grid cell adjacent to the ocean bottom
are given by
∂t(dz)=dzS(V)−∇s·(dzu)−(w(z))s=skbot−1
∂t(dzC)=dzS(C)−∇s·[dz(uC+F)]
−(w(z)C+F(z))s=skbot−1
+Q(C)
(bot)
[∂t+ (f+M)ˆ
z∧](ρodzu)=dzS(u)−∇s·[ dzu(ρou)]
−dz(∇sp+ρ∇sΦ)
+∂x(dzˆ
x·τ) + ∂y(dzˆ
y·τ)
−[w(z)ρou−z,s ∇s·τ]s=skbot−1
−τbottom
(2.240)
and the equations for a cell next to the ocean surface are
∂t(dz)=dzS(V)−∇s·(dzu) + (w(z))s=sk=1 +Qm/ρo
∂t(dzC)=dzS(C)−∇s·[dz(uC+F)]
+ (w(z)C+F(z))s=sk=1
+ ((Qm/ρo)Cm−Q(turb)
(C))
[∂t+ (f+M)ˆ
z∧](ρodzu)=dzS(u)−∇s·[ dzu(ρou)]
−dz(∇sp+ρ∇sΦ)
+∂x(dzˆ
x·τ) + ∂y(dzˆ
y·τ)
+ [τwind +Qmuw]
+ [w(z)ρou−z,s ∇s·τ]s=s1.
(2.241)
Elements of MOM November 19, 2014 Page 63

Chapter 2. Fundamental equations Section 2.10
Elements of MOM November 19, 2014 Page 64

Chapter 3
The hydrostatic pressure force
Contents
3.1 Hydrostatic pressure forces at a point ............................. 65
3.2 Pressure gradient body force .................................. 66
3.2.1 Depth based vertical coordinates .............................. 67
3.2.1.1 Geopotential vertical coordinates ......................... 68
3.2.1.2 z∗and σ(z)vertical coordinate .......................... 69
3.2.2 A test case for zero cross-coordinate flow .......................... 69
3.2.3 Pressure based vertical coordinates ............................. 70
3.3 Pressure gradient body force in B-grid MOM ........................ 71
3.3.1 Depth based vertical coordinates .............................. 72
3.3.2 Pressure based vertical coordinates ............................. 73
3.4 Pressure gradient body force in C-grid MOM ........................ 74
3.4.1 Depth based vertical coordinates .............................. 74
3.4.2 Pressure based vertical coordinates ............................. 74
The purpose of this chapter is to detail issues related to computing the pressure force in hydrostatic
ocean models. Care is taken to split the pressure force into its slow and fast components, thus facilitating
a split of the momentum equation for use in an explicit time stepping scheme. Additional consideration is
given to the distinct needs of the B-grid and C-grid implementations available in MOM.
In Section 2.8, we encountered two formulations of the pressure force. The first computes the pressure
gradient body force (Section 2.8.2), and considers the pressure force to be acting at a point. This inter-
pretation follows from a finite difference interpretation of the velocity equation, following the energetic
approach of Bryan (1969) and all versions of MOM. The second formulation applies a finite volume inter-
pretation advocated in Chapter 2, with particular attention given to the contour integral form of pressure
as derived in Section 2.8.1. The finite volume approach does not lend itself to straightforward energetic
conversion arguments (Chapter 14). It is for this reason that we maintain the finite difference approach of
Bryan (1969) in MOM.
3.1 Hydrostatic pressure forces at a point
A hydrostatic fluid maintains the balance
∂p
∂z =−ρg. (3.1)
This balance means that the pressure at a point in a hydrostatic fluid is determined by the weight of fluid
above this point. This relation is maintained quite well in the ocean on horizontal spatial scales larger than
65

Chapter 3. The hydrostatic pressure force Section 3.2
roughly 1km. Precisely, when the squared ratio of the vertical to horizontal scales of motion is small, then
the hydrostatic approximation is well maintained. In this case, the vertical momentum budget reduces to
the hydrostatic balance, in which case vertical acceleration and friction are neglected. If we are interested
in explicitly representing such motions as Kelvin-Helmholtz billows and flow within a convective chimney,
vertical accelerations are nontrivial and so the non-hydrostatic momentum budget must be used.
The hydrostatic balance greatly affects the algorithms used to numerically solve the equations of motion.
Marshall et al. (1997) highlight these points in the context of developing an algorithm suited for both
hydrostatic and non-hydrostatic simulations. However, so far no long-term global climate simulations have
been run at resolutions sufficiently refined to require the non-hydrostatic equations. Additionally, many
regional and coastal models, even some with grid resolutions finer than 1km, still maintain the hydrostatic
approximation, and thus they must parameterize the unrepresented non-hydrostatic motions.
As discussed in Section 2.8.2, at a point in the continuum, the horizontal acceleration arising from
pressure differences in a hydrostatic and non-Boussinesq fluid can be written1
ρ−1∇zp=ρ−1(∇s−∇sz∂z)p
=ρ−1∇sp+g∇sz
=ρ−1(∇sp+ρ∇sΦ)
(3.2)
where the hydrostatic relation ∂zp=−ρg was used to reach the second equality, and
Φ=g z (3.3)
is the geopotential. The general expression for the horizontal pressure gradient to evaluate in an ocean
model is thus given by
∇zp=∇sp+ρ∇sΦ(3.4)
For cases where the density is constant on ssurfaces, we can combine the two terms on the right hand
side into the gradient of a scalar, thus rendering a horizontal pressure gradient force with a zero curl.
This special case holds for geopotential and pressure coordinates. It also holds for isopycnal coordinates
in the special case of an idealized linear equation of state. However, it does not hold in the more general
case, in which the difficulty of numerically computing the acceleration from pressure arises when there are
contributions from both terms. Generally, both terms can be large and of opposite sign in many regions. In
this case, the simulation is exposed to nontrivial numerical truncation errors that can, for example, lead to
spurious pressure gradients that spin up an unforced fluid with initially flat isopycnals. However, in certain
cases one term dominates, in which case an accurate pressure gradient is simpler to compute numerically.
Significant effort has gone into reducing such pressure gradient errors, especially in terrain following
models where undulations of the coordinate surfaces can be large with realistic bottom topography (e.g.,
see Figure 5.3). Some of these issues are summarized in Section 2 of Griffies et al. (2000a). Perhaps the most
promising approach is that proposed by Shchepetkin and McWilliams (2002). It is notable that difficulties
with pressure gradient errors have largely been responsible for the near absence of sigma models being
used for long term global ocean climate simulations.2
3.2 Pressure gradient body force
As stated above, the presence of both terms on the right hand side of equation (3.4) complicates the nu-
merical implementation of the horizontal pressure gradient force. The problem is that numerical errors
in one term are often not compensated by the other term, and such can lead to spurious flows. For the
quasi-horizontal depth based and pressure based coordinates supported by MOM (i.e., s=z,s=z∗,s=p,
or s=p∗; see Chapter 5), these errors are quite small. The reason is that these choices ensure that one of
the two terms appearing in equation (3.4) is significantly smaller than the other. Nonetheless, it is useful
to provide a formulation that even further reduces the potential for errors for both the quasi-horizontal
coordinates, as well as the terrain following coordinates σ(z)and σ(p)(Chapter 5).
1To obtain this result for a Boussinesq fluid, multiply both sides of equation (3.2) by ρ/ρo.
2The work of Diansky et al. (2002) is one example of a published global sigma model used for climate purposes.
Elements of MOM November 19, 2014 Page 66

Chapter 3. The hydrostatic pressure force Section 3.2
In addition to reducing errors associated with a numerical computation of the pressure gradient, we aim
to split the pressure gradient into two terms associated with the slowly evolving internal modes and the
faster external mode. Details of this split are a function of the vertical coordinate. This split in the pressure
gradient then facilitates our treatment of the vertically integrated momentum equations, as discussed in
Section 10.9.
In the following, we are motivated by the formulation of the pressure gradient commonly applied to
z-models. Adcroft and Campin (2004) extended this treatment to the z∗vertical coordinate. We take it one
more step in order to handle all vertical coordinates supported by MOM. Hallberg (1997) goes further by
treating the pressure gradient in isopycnal layered models using a realistic equation of state, and Adcroft
et al. (2008) present a more accurate approach for generlized vertical coordinate models.
3.2.1 Depth based vertical coordinates
As mentioned on page 47 of Gill (1982), in situ density in the bulk of the ocean deviates less than 3% from
the constant density
ρo= 1035kg/m3.(3.5)
The hydrostatic pressure associated with this constant density has no horizontal gradients, and so it does
not contribute to horizontal pressure gradient forces. For increased accuracy computing the horizontal
pressure gradient, it is useful to remove this term from the calculation of hydrostatic pressure. For this
purpose, we write the hydrostatic balance as
∂p
∂z =−g ρ
=−g(ρo+ρ0),
(3.6)
which has an associated split in the hydrostatic pressure field
p=pa+po(z) + p0(x,y,z,t).(3.7)
We can solve for the pressures by assuming
po(z=η) = 0 (3.8)
p0(z=η)=0,(3.9)
which leads to
po=−g ρo(z−η)
=−ρoΦ+g ρoη, (3.10)
and
p0=gZη
z
ρ0dz, (3.11)
and thus
p=pa+g ρoη−ρoΦ+p0.(3.12)
Splitting offthe free surface height is advantageous as it allows for a split of the pressure gradient
into its fast two dimensional barotropic contributions and slow three dimensional baroclinic contributions.
This split in pressure gradient facilitates the development of a split-explicit time stepping method for the
momentum equations considered in Section 10.9. Details of the split in pressure are dependent on the
vertical coordinate choice. We now discuss the three depth based vertical coordinates used in MOM.
Elements of MOM November 19, 2014 Page 67

Chapter 3. The hydrostatic pressure force Section 3.2
3.2.1.1 Geopotential vertical coordinates
We first consider the horizontal pressure gradient realized with geopotential vertical coordinates. We are
here motivated by the desire to split the dynamics into fast and slow portions, as approximated by depth
integrating the momentum equation (Section 10.9).
The anomalous pressure p0maintains a dependence on surface height through the upper limit on the
vertical integral in equation (3.11). When working with geopotential vertical coordinates, it is very conve-
nient to isolate this dependence by exploiting a very accurate approximation described below. This split
then allows us to exclusively place the surface height dependent pressure gradient into the vertically inte-
grated momentum equation. The slow component to the pressure gradient then has no dependence on the
surface height; it is instead just a function of the anomalous density. The slow pressure gradient component
thus vanishes when the density is horizontally unstratified; i.e., when there is no baroclinicity.
To facilitate the split described above, we proceed in the following manner
p0=gZη
z
ρ0dz
=gZ0
z
ρ0dz+gZη
0
ρ0dz
≈gZ0
z
ρ0dz+g η ρ0
surf
≡p0
clinic +p0
surf.
(3.13)
The approximation made in the third step remains good where density is well mixed between z= 0 and
z=η, and this is generally the case for large scale modelling. Here, density in the surface region of the
ocean is assumed to take on the value
ρsurf =ρo+ρ0
surf,(3.14)
which is a function of horizontal position and time. The anomalous pressure p0has therefore been separated
into two pressures, where the anomalous surface pressure
p0
surf =ρ0
surf g η (3.15)
is a function of the surface height and surface density, and the pressure
p0
clinic =gZ0
z
ρ0dz(3.16)
is the anomalous hydrostatic baroclinic pressure within the region from a depth z < 0 to z= 0. Again, the
baroclinic pressure is independent of the surface height, and so its horizontal gradients are only a function
of density.
This split of pressure thus renders the horizontal pressure gradient (equation (3.4))
(∇zp)approx =∇sp+ρ∇sΦ
=∇s(pa+g ρoη−ρoΦ+p0) + ρ∇sΦ
≈ ∇(pa+g ρoη+p0
surf) + ∇sp0
clinic + (ρ−ρo)∇sΦ
=∇(pa+g ρsurf η)
| {z }
fast
+∇sp0
clinic +ρ0∇sΦ.
| {z }
slow
(3.17)
In a geopotential vertical coordinate model, interior grid cells are discretized at levels of constant geopo-
tential. Hence, the gradient ∇sreduces to the constant geopotential gradient ∇z. In this case the horizontal
gradient of the geopotential vanishes, ∇zΦ= 0. At the bottom, however, MOM employs bottom partial
step topography (Pacanowski and Gnanadesikan,1998). The bottom cells are thus not discretized along a
constant geopotential. Hence, just at the bottom, there is a nontrivial gradient of the geopotential Φ(see
Figure 5.1). In general, note how the geopotential is multiplied by the anomalous density ρ0=ρ−ρo, thus
minimizing the impact of this term.
Elements of MOM November 19, 2014 Page 68

Chapter 3. The hydrostatic pressure force Section 3.2
3.2.1.2 z∗and σ(z)vertical coordinate
The new issue that arises when moving away from geopotential coordinates is that the geopotential Φ=g z
has a nonzero along coordinate gradient in the interior, whereas with geopotential coordinates it remains
nonzero only along the partial bottom stepped topography. The presence of Φgradients in the interior is
fundamental.
Following the discussion in Section 3.2.1, we are led to the following expressions for the horizontal
pressure gradient. The exact expression relevant for the z∗and σ(z)coordinates is given by
(∇zp)exact =∇sp+ρ∇sΦ
=∇s(pa+po+p0) + ρ∇sΦ
=∇s(pa−ρoΦ+g ρoη+p0) + ρ∇sΦ
=∇(pa+g ρoη)
| {z }
fast
+∇sp0+ρ0∇sΦ
| {z }
slow
.
(3.18)
Note that we have assumed that the geopotential falls inside the slow portion of the pressure gradient. This
assumption is made even though the depth of a grid point is a function of the undulating surface height.
The validity of this assumption can be assessed by the integrity and stability of the simulation.
To facilitate a unified treatment in subsequent manipulations, we define
psurf =ρsurf g η s =z
psurf =ρ0g η s =z∗,σ(z)(3.19)
and
p0=gR0
zρ0dz s =z
p0=gRη
zρ0dz s =z∗,σ(z).(3.20)
In both the exact and aproximated pressure gradient expressions, the geopotential gradient ∇sΦin the
ocean interior is weighted by the small density deviation ρ0=ρ−ρo. For quasi-horizontal depth-based
vertical coordinates supported in MOM (Section 5.1), the horizontal gradient of the geopotential is small,
and the ρ0weighting further reduces its contribution. For terrain following coordinates, the horizontal
gradient term is not small, and the ρ0weighting is essential to reduce its magnitude.
3.2.2 A test case for zero cross-coordinate flow
In the development of generalized vertical coordinates, a useful test case was suggested by Alistair Adcroft.
We focus here on the special case of s=z∗. In this test, initialize the density field as a function only of the
vertical coordinate z∗. The domain is flat bottomed and doubly periodic in the horizontal, thus precluding
pressure gradients due to side boundaries or topography. In a state of rest, there is no horizontal pressure
gradients, and so no motion. As a body force is applied to the barotropic equations, such as through an ideal
tidal forcing, there will now be a nontrivial surface height field ηas well as a nontrivial barotropic velocity.
Both pieces of the slow contribution to the horizontal pressure gradient (3.18) develop a nontrivial vertical
structure, and this will initiate baroclinic structure and thus a nonzero cross coordinate vertical velocity
w(s). This cross coordinate velocity will be much smaller in the s=z∗case than with s=z, given than z∗
follows the motion of the free surface.
In order to further test the integrity of the z∗implementation, we wish to truncate the pressure cal-
culation in this test so that there will be no slow pressure gradients developed when the tidal forcing is
applied, and hence there will be no cross coordinate motion. For this purpose, truncate the slow piece of
the horizontal pressure gradient (3.18) as
∇sp0+ρ0∇sΦ→ ∇sp0
truncate.(3.21)
In this truncation, we drop the geopotential term ρ0∇sΦ, as this term will produce nontrivial horizontal
gradients as the surface height undulates. We also introduce a truncated perturbation pressure determined
Elements of MOM November 19, 2014 Page 69

Chapter 3. The hydrostatic pressure force Section 3.2
by
p0=gZη
z
ρ0dz
=gZs(η)
s(z)
ρ0z,s ds
=g(1 + η/H)Z0
z∗ρ0dz∗
=p0
truncate + (g η/H)Z0
z∗ρ0dz∗.
(3.22)
To reach the penultimate step, we used z,s = (1 + η/H) for s=z∗. The coordinate increments used to de-
fine the pressure field p0
truncate are static in a model discretizing the vertical according to s=z∗. Hence,
∇sp0
truncate = 0 if the density is a function only of z∗. So when the model’s slow pressure field is comprised of
just p0
truncate, the ideal tidal test in the torus should maintain zero cross coordinate flow, wz∗= 0, even as the
surface height fluctuates. Testing to see that this property is maintained is a useful means for evaluating
the integrity of the algorithm.
3.2.3 Pressure based vertical coordinates
A complementary discussion to the above is now given for pressure based vertical coordinates. Since for
pressure based vertical coordinates we solve for the bottom pressure, it is useful to formulate the geopo-
tential in terms of the bottom pressure rather than the atmospheric pressure. For this purpose, consider
the following identities
Φ+g H =g
z
Z
−H
dz
=g
p
Z
pb
∂z
∂p dp
=−
p
Z
pb
ρ−1dp
=−
p
Z
pb
(ρ−1
o+ρ−1−ρ−1
o)dp
= (pb−p)/ρo+ρ−1
o
p
Z
pb
(ρ0/ρ) dp
= (pb−p)/ρo−(g/ρo)
z
Z
−H
ρ0dz.
(3.23)
We are thus led to the expression
ρoΦ=pb−p+ρo(Φb+Φ0),(3.24)
where
ρoΦ0=−g
z
Z
−H
ρ0dz(3.25)
Elements of MOM November 19, 2014 Page 70

Chapter 3. The hydrostatic pressure force Section 3.3
is an anomalous geopotential similar to the anomalous hydrostatic pressure introduced in Section 3.2.1,
and
Φb=−g H (3.26)
is the geopotential at the ocean bottom. The horizontal pressure force is therefore written
∇sp+ρ∇sΦ=∇sp+ (ρ/ρo)∇(pb+ρoΦb)−(ρ/ρo)∇sp+ρ∇sΦ0
= (ρ/ρo)∇(pb+ρoΦb)
| {z }
fast
+ρ∇sΦ0−(ρ0/ρo)∇sp
| {z }
slow
.(3.27)
Note that the three-dimensional pressure term (ρ0/ρo)∇spis weighted by the generallly very small density
deviation ρ0=ρ−ρo. For the non-terrain following quasi-horizontal pressure-based vertical coordinates
supported in MOM (Section 5.2), the horizontal gradient of the pressure is small, and the weighting by
(ρ0/ρo) further reduces its contribution. Also note that the fast contribution is here weighted by the density,
and so this term may appear to require further splitting into ρ=ρo+ρ0before identifying the fast two
dimensional contribution. However, as the non-Boussinesq formulation here considers momentum per
area, the baroclinic velocity includes density weighting (see equation (11.1)). This is how we are to split the
horizontal momentum equations into fast two dimensional motions and slow three dimensional motions
for purposes of time stepping. We consider these issues further in Sections 10.9 and 11.1.
During the testing of this formulation for the pressure gradient, we found it useful to write the anoma-
lous geopotential in the following form
−(ρo/g)Φ0=
z
Z
−H
ρ0dz
=
η
Z
−H
ρ0dz−
η
Z
z
ρ0dz
=pb−pa
g−ρo(H+η)−
η
Z
z
ρ0dz
=pb−pa−p0
g−ρo(H+η).
(3.28)
To reach this result, we used the hydrostatic balance for the full ocean column in the form
η
Z
−H
ρ0dz=pb−pa
g−ρo(H+η),(3.29)
as well as the definition (3.11) of the anomalous hydrostatic pressure
p0=g
η
Z
z
ρ0dz(3.30)
used in Section 3.2.1 for the depth based vertical coordinates. These results then lead to the identiy
pb+ρo(Φb+Φ0) = p0+pa+ρog η. (3.31)
3.3 Pressure gradient body force in B-grid MOM
We now detail how the pressure gradient body force is represented in the B-grid generalized level coordi-
nate version of MOM. As the pressure force acts to accelerate a fluid parcel, our aim is to determine the
Elements of MOM November 19, 2014 Page 71
Chapter 3. The hydrostatic pressure force Section 3.3
pressure force acting at the velocity cell point. Much in the derivation of the pressure force depends on
assumptions regarding where pressure is computed in the discrete model. For the B-grid and C-grid, hy-
drostatic pressure is coincident with the tracer fields as shown in Figure 2.9, which illustrates a typical case
where a grid cell is bounded by vertical sidewalls with generally nonhorizontal tops and bottoms.
As mentioned in Section 2.8.2, we prefer to discretize the pressure gradient body force as it facilitates
the splitting of the pressure force into fast and slow components. The result here is a derivation of the
Pacanowski and Gnanadesikan (1998) discrete pressure gradient body force as originally implemented
for the treatment of partial step bottom topography. Their discussion is relevant here, since the pressure
gradient force in the presence of partial step bottoms must account for the pressure between cells that live
at different depths. This is also the essential issue for the treatment of pressure with the generalized level
coordinates of MOM.
z
x
TT
T
T
x
y
U
Figure 3.1: Illustration of a vertical slice through a set of grid cells in the x-z plane for a generalized
level coordinate version of MOM. The center point in each cell is a tracer point. As the temperature and
salinity tracers, along with pressure, determine density, and as density determines hydrostatic pressure,
the hydrostatic pressure is coincident with tracer points.
3.3.1 Depth based vertical coordinates
The aim here is to discretize the pressure gradient body force written in the forms (3.18) and (3.17)
∇sp+ρ∇sΦ=∇(pa+psurf) + ∇sp0+ρ0∇sΦ,(3.32)
where psurf and p0are defined according to equations (3.19) and (3.20), respectively. Our focus here is
the slowly evolving three dimensional terms ∇sp0+ρ0∇sΦ. The first term is straightforward to discretize
according to the assumptions regarding the placement of pressure given in Figure 3.1. Pressure sits at
tracer points, which are at the corners of velocity cells. Hence, to approximate pressure at the west and
east faces of the cell, one can average the pressure found at the corners. A grid weighted average may be
appropriate, but the simplest method, which is energetically consistent (see Sections 14.6 and 14.8) is an
unweighted average in which
∇sp0≈ˆ
xFDX NT(FAY(p0)) + ˆ
yFDY ET(FAX(p0)) (3.33)
Elements of MOM November 19, 2014 Page 72

Chapter 3. The hydrostatic pressure force Section 3.4
The forward algebraic averaging operators are defined according to
FAX(A) = Ai
x=Ai+1 +Ai
2(3.34)
FAX(Y) = Aj
y=Aj+1 +Aj
2,(3.35)
with the second expression in each equation exposing the notation used in the ocean model code. Addi-
tionally, finite difference operators have been introduced
FDX NT(A) = Ai+1 −Ai
dxui,j .
FDY ET(A) = Aj+1 −Aj
dyui,j
.
(3.36)
These operators are used for fields that live at the north face and east face, respectively, of a tracer cell.
The geopotential contribution in (3.45) is computed using the geopotential values at the tracer points,
and so its gradient is located at the tracer cell faces. To have the density multiplier at the same point
requires that it be averaged prior to multiplying. Finally, an orthogonal spatial average is required to place
the product onto the velocity point. The result is given by
ρ0∇sΦ≈ˆ
x"FAY[δiΦFAX(ρ0)]/dxui,j #+ˆ
y"FAX[δjΦFAY(ρ0)]/dyui,j #.(3.37)
Exposing just the pressure gradient force, the corresponding zonal and meridional momentum equa-
tions for the B-grid Boussinesq fluid take the form
∂t(u ρodzu)pressure =−dzuFDX NT(FAY(pa+psurf +p0)) + FAY[δiΦFAX(ρ0)]/dxui,j(3.38)
∂t(v ρodzu)pressure =−dzuFDY ET(FAX(pa+psurf +p0)) + FAX[δjΦFAY(ρ0)]/dyui,j.(3.39)
3.3.2 Pressure based vertical coordinates
The aim is to discretize the pressure gradient body force written in the form (3.27)
∇sp+ρ∇sΦ= (ρ/ρo)∇(pb+ρoΦb) + ρ∇sΦ0−(ρ0/ρo)∇sp(3.40)
and to do so in a manner analogous to the Boussinesq case. In particular, we consider here the slow three
dimensional contribution ρ∇sΦ0−(ρ0/ρo)∇spand write for the pressure term
ρ0∇sp≈ˆ
x"FAY[δipFAX(ρ0)]/dxui,j #+ˆ
y"FAX[δjpFAY(ρ0)]/dyui,j #,(3.41)
which is analogous to the discrete ρ0∇sΦcontribution in equation (3.37). The geopotential term is dis-
cretized as
ρ∇sΦ0≈ˆ
xρFDX NT (FAY(Φ0)) + ˆ
yρFDY ET (FAX(Φ0)),(3.42)
which is analogous to the discrete version of ∇sp0in equation (3.33). Note that the density ρin equation
(3.42) is centered on the velocity cell.
Exposing just the pressure gradient force, the zonal and meridional momentum equations for the B-grid
non-Boussinesq fluid take the form
∂t(urho dzu)pressure =−rho dzu FDX NT(FAY(pb/ρo+Φb+Φ0)) + dzu FAY[δipFAX(ρ0/ρo)]/dxui,j (3.43)
∂t(vrho dzu)pressure =−rho dzu FDY ET(FAX(pb/ρo+Φb+Φ0)) + dzu FAX[δjpFAY(ρ0/ρo)]/dyui,j.(3.44)
Elements of MOM November 19, 2014 Page 73

Chapter 3. The hydrostatic pressure force Section 3.4
3.4 Pressure gradient body force in C-grid MOM
We now detail how the pressure gradient body force is represented in the C-grid generalized level coordi-
nate version of MOM.
3.4.1 Depth based vertical coordinates
The aim here is to discretize the pressure gradient body force written in the forms (3.18) and (3.17)
∇sp+ρ∇sΦ=∇(pa+psurf) + ∇sp0+ρ0∇sΦ,(3.45)
where psurf and p0are defined according to equations (3.19) and (3.20), respectively. Our focus here is
the slowly evolving three dimensional terms ∇sp0+ρ0∇sΦ. The first term is straightforward to discretize
according to the assumptions regarding the placement of pressure on a C-grid (Figure 9.2)
∇sp0≈ˆ
xFDX T(p0) + ˆ
yFDY T(p0),(3.46)
where the averaging operators required for the B-grid are absent. Additionally, finite difference operators
have been introduced
FDX T(A) = Ai+1 −Ai
dxtei,j
FDY T(A) = Aj+1 −Aj
dytni,j
,
(3.47)
where the grid distances are defined in Figure 9.7. These operators are used for fields that live at the tracer
point.
The geopotential contribution in (3.45) is computed using the geopotential values at the tracer points,
and so its gradient is located at the tracer cell faces. To have the density multiplier at the same point
requires that it be averaged prior to multiplying, so that
ρ0∇sΦ≈ˆ
xFAX(ρ0)FDX T(Φ) + ˆ
yFAY(ρ0)FDY T(Φ).(3.48)
Exposing just the pressure gradient force, the corresponding zonal and meridional momentum equa-
tions for the C-grid Boussinesq fluid take the form
∂t(u ρodzte)pressure =−dzteFDX T(pa+psurf +p0) + FAX(ρ0)FDX T(Φ)(3.49)
∂t(v ρodztn)pressure =−dztnFDY T(pa+psurf +p0) + FAY(ρ0)FDY T(Φ).(3.50)
3.4.2 Pressure based vertical coordinates
The aim is to discretize the pressure gradient body force written in the form (3.27)
∇sp+ρ∇sΦ= (ρ/ρo)∇(pb+ρoΦb) + ρ∇sΦ0−(ρ0/ρo)∇sp(3.51)
and to do so in a manner analogous to the Boussinesq case. In particular, we consider here the slow three
dimensional contribution ρ∇sΦ0−(ρ0/ρo)∇spand write for the pressure term
ρ0∇sp≈ˆ
xFAX(ρ0)FDX T(p) + ˆ
yFAY(ρ0)FDY T(p),(3.52)
which is analogous to the discrete ρ0∇sΦcontribution in equation (3.48). The geopotential term is dis-
cretized as
ρ∇sΦ0≈ˆ
xρFDX T (Φ0) + ˆ
yρFDY T (Φ0).(3.53)
Importantly, the density factor in each term is on the respective tracer cell faces.
Exposing just the pressure gradient force, the corresponding zonal and meridional momentum equa-
tions for the C-grid non-Boussinesq fluid take the form
∂t(urho dzte)pressure =−rho dzte FDX T(pb/ρo+Φb+Φ0) + dzte FAX(ρ0/ρo)FDX T(p) (3.54)
∂t(vrho dztn)pressure =−rho dztn FDY T(pb/ρo+Φb+Φ0) + dztn FAY(ρ0/ρo)FDY T(p).(3.55)
Elements of MOM November 19, 2014 Page 74

Chapter 4
Parameterizations with generalized
level coordinates
Contents
4.1 Friction .............................................. 75
4.1.1 Vertical friction ........................................ 76
4.1.2 A comment on nonlinear vertical friction ......................... 76
4.1.3 Lateral friction ......................................... 77
4.1.4 Bottom stress ......................................... 78
4.1.5 Summary of the linear momentum budget ......................... 78
4.2 Diffusion and skew diffusion .................................. 79
4.2.1 Vertical diffusion ....................................... 79
4.2.2 Horizontal diffusion ..................................... 79
4.2.3 Neutral physics ........................................ 79
4.2.3.1 The velocity field from Gent and McWilliams (1990) ............. 80
4.2.3.2 Neutral slopes ................................... 81
4.2.3.3 Fluxes for neutral diffusion ............................ 82
4.2.3.4 Fluxes for skew diffusion ............................. 83
4.2.3.5 Summary of the neutral fluxes .......................... 84
The parameterization of subgrid scale (SGS) processes is of fundamental importance to ocean models.
Details of how these processes are parameterized depend on the choice of vertical coordinates. The pur-
pose of this chapter is to describe how various SGS parameterizations are formulated with generalized level
coordinates of MOM. As we will see, by diagnosing the vertical grid cell thicknesses according to the meth-
ods described in Section 10.3, parameterizations implemented in the geopotential MOM4.0 code remain
algorithmically unaltered when converting to the generalized level coordinate MOM.
4.1 Friction
The convergence of frictional stress leads to a friction force acting on fluid parcels. The purpose of this
section is to detail the form of friction appearing in the generalized level coordinates of MOM. For this
purpose, we follow much of the discussion in Chapter 17 of Griffies (2004). In particular, Section 17.3.4
leads us to take the physical components to the frictional stress tensor in the form
τ=
τxx τxy ρκu,z
τxy −τxx ρκv,z
ρκu,z ρκv,z 0,(4.1)
75

Chapter 4. Parameterizations with generalized level coordinates Section 4.1
where κis a non-negative viscosity with units m2s−1. Taking τ33 = 0 is consistent with use of the hydrostatic
approximation, which reduces the vertical momentum equation to the inviscid hydrostatic balance. We
comment in Section 4.1.3 on the form of the two-dimensional transverse elements τxx and τxy . Further
details of lateral friction are given in Chapter 25.
4.1.1 Vertical friction
As the gravitational force is so critical to stratified fluids close to a hydrostatic balance, it is typical in ocean
modelling to single out the vertical direction. In particular, closures for the unresolved vertical exchange
of momentum are usually taken to be proportional to the vertical derivative, or shear, of the horizontal
velocity field. This argument leads to the form of the stress tensor given by equation (4.1). For a generalized
level coordinate model, the vertical shear elements take the form
ρκ u,z =ρκs,z u,s.(4.2)
In MOM, the left hand side of this expression is numerically evaluated for purposes of computing the
vertical shear. That is, vertical derivatives are computed for arbitrary vertical coordinates just as in geopo-
tential coordinates. This result follows by diagnosing the vertical grid cell thicknesses using the methods
described in Section 10.3, where we make use of the relation between vertical coordinates
dz=z,s ds. (4.3)
Now return to the thickness weighted momentum budget for a grid cell discussed in Section 2.9. The
above considerations lead us to write the frictional stress acting on a generalized surface as
z,s ∇s·τ= (ˆ
z−S)·τ
≈ˆ
z·τ
=ρκ u,z.
(4.4)
The second step used the small angle approximation to drop the extra slope term. Alternatively, we can
interpret the dia-surface frictional stress z,s ∇s·τas parameterized by ρκu,z. Either way, the result (4.4) is
the form that vertical frictional stress is implemented in MOM.
4.1.2 A comment on nonlinear vertical friction
As noted above, we choose in MOM to implement vertical friction, and vertical tracer diffusion (Section
4.2.1) just as in a geopotential coordinate model. This method is facilitated by diagnosing the vertical
thickness of a grid cell according to equation (4.3) (see Section 10.3), prior to computing vertical derivatives.
We now mention an alternative method, not implemented in MOM, since this method is often seen in
the literature. The alternative is to compute the vertical shear according to the right hand side of equation
(4.2). The density weighted inverse specific thickness ρ/z,s adds a nonlinear term to the vertical friction,
and this complicates the numerical treatment (Hallberg,2000). It is reasonable to approximate this factor
by a constant for the dimensionful quasi-horizontal coordinates considered in Sections 5.1 and 5.2.1For
the Boussinesq case with depth-based vertical coordinates, this approximation results in
ρκ/z,s ≈ρoκ, (4.5)
where z,s ≈1 follows from the results for all but the sigma coordinate in Table 5.1. The vertical friction
therefore becomes
(ρκ u,z),z ≈ρos,z (κs,z u,s),s
≈ρo(κu,s),s.(4.6)
Likewise, dimensionful pressure-based coordinates used for non-Boussinesq fluids have
ρκ/z,s ≈ −g ρ2
oκ, (4.7)
1Terrain following sigma coordinates, which are dimensionless, are notable exceptions to this result.
Elements of MOM November 19, 2014 Page 76

Chapter 4. Parameterizations with generalized level coordinates Section 4.1
as follows for all but the sigma coordinate in Table 5.2. The vertical friction therefore becomes
(ρκ u,z),z ≈ρo(g ρo)2(κu,s),s.(4.8)
The above approximations are well motivated physically since the value of the vertical viscosity is not
known to better than 10%, and the above approximations are well within this range for vertical coordinates
whose iso-surfaces are quasi-horizontal. Similar arguments were presented by Losch et al. (2004). Addi-
tionally, the approximations are very conveinent numerically since they allow us to continue implementing
vertical physical processes in a linear manner as traditionally handled in z-models. Such facilitates straight-
forward time implicit methods to stably handle large vertical viscosities. Without these approximations,
or without use of the geopotential-based approach described above in Section 4.1.1, vertical physical pro-
cesses are nonlinear. Arbitrarily stable numerical methods for such processes require an iterative scheme
such as that discussed by Hallberg (2000) employed in isopycnal models.
4.1.3 Lateral friction
There is no fundamental theory to prescribe the form of lateral friction at the resolutions available for large
scale ocean modelling. Indeed, many argue that the form commonly used in models is wrong (Holloway,
1992). We take the perspective that lateral friction in ocean models provides a numerical closure. This
perspective motivates us to prescribe friction in a manner that maintains basic symmetry properties of the
physical system, and which is convenient to implement.
The deformation rates are a basic element of the lateral frictional stress. Using generalized orthogonal
horizontal coordinates and zfor the vertical, the deformation rates given in Section 17.7.1 of Griffies (2004)
take the form
eT= (dy)(u/dy),x −(dx)(v/dx),y (4.9)
eS= (dx)(u/dx),y + (dy)(v/dy),x (4.10)
where dxand dyare the infinitesimal horizontal grid increments. Consistent with lateral friction being
considered a numerical closure, we place no fundamental importance on the horizontal derivatives being
taken on constant zsurfaces. Hence, we propose to use the same mathematical form for the deformation
rates regardless the vertical coordinate. That is, for the generalized level coordinates used in MOM, the
deformation rates are computed according to the lateral strains within surfaces of constant vertical coordi-
nate.
As shown in the Appendix to Griffies and Hallberg (2000), and further detailed in Section 17.10 of
Griffies (2004), the divergence of the thickness weighted lateral stress within a layer, ∇ · τ, leads to the
thickness weighted forces per volume acting in the generalized horizontal directions
dzρFx= (dy)−2[(dy)2dzτxx],x + (dx)−2[(dx)2dzτxy ],y
dzρFy= (dx)−2[(dx)2dzτyy],y + (dy)−2[(dy)2dz τxy],x.(4.11)
We extend the forms for the stress tensor given in Chapter 17 of Griffies (2004) by assuming that all hor-
izontal derivatives appearing in the stress tensor are taken along surfaces of constant generalized level
coordinate. Notably, the forms all have an overall density factor, such as the general form given by equa-
tion (17.119) in Griffies (2004)
τxx τxy
τxy −τxx !=ρ (AeT+D∆Rx
x) (AeS+D∆Rx
y)
(AeS+D∆Ry
x) (−AeT+D∆Ry
y)!,(4.12)
with Ra rotation matrix
R(m)
(n)= sin2θ−cos2θ
−cos2θ−sin2θ!,(4.13)
A≥0 is a non-negative viscosity weighting the isotropic stress tensor, and D≥0 is a non-negative viscosity
weighting the aniostropic stress tensor. For the Boussinesq fluid, the density factor in the stress tensor is
Elements of MOM November 19, 2014 Page 77

Chapter 4. Parameterizations with generalized level coordinates Section 4.1
set to the constant ρo. Furthermore, the specific thickness z,s is a depth independent function when using
the depth-based Boussinesq vertical coordinates (Table 5.1 in Section 5.1). For the mass conserving non-
Boussinesq pressure-based vertical coordinates (Table 5.2 in Section 5.2), the density weighted specific
thickness ρz,s is a depth independent function, which then simplifies the density weighted thickness of
a grid cell ρdz=ρz,s ds. These results are familiar from the analogous simplifications arising for other
terms in the scalar and momentum budgets discussed in Chapter 2. We consider the needs of spatial
discretization for the B-grid and C-grid in Chapter 25.
4.1.4 Bottom stress
We exposed the form of bottom stress in Section 2.9.3, and it generally leads to a bottom force given by
Fbottom =−"
z=−H
dxdy∇(z+H)·τ
=−"
z=−H
dxdyτbottom.
(4.14)
A common method to parameterize this force is to consider unresolved small scale processes to give rise to
a dissipative drag written in the form
Fbottom =−"
z=−H
dxdy[ρCDub(u2
b+u2
tide)1/2],(4.15)
where it is only the horizontal bottom force that appears in hydrostatic models. In this equation, CDis a
dimensionless drag coefficient with common values taken as
CD≈10−3.(4.16)
Because the precise value of CDis not well known, the product ρCDis approximated in MOM as
ρCD≈ρoCD.(4.17)
The velocity utide represents a residual horizontal velocity that is not resolved in models running without
tidal forcing. Hence, even with the bottom flow weak, the residual velocity keeps the drag nontrivial. A
common value for the residual velocity is
|utide| ≈ 0.05 ms−1.(4.18)
The velocity ubis formally the velocity within the bottom boundary layer, but it is commonly taken in
models as the velocity at the grid cell adjacent to the bottom. Note that our assumed form of the unresolved
bottom stresses take the form of a bottom drag. See Holloway (1999) for more general forms where the
unresolved bottom stresses may act to accelerate the resolved flow field.
4.1.5 Summary of the linear momentum budget
The horizontal linear momentum budgets for interior, bottom, and surface grid cells are given by equations
(2.226), (2.229), and (2.234). We rewrite them here for future reference, incorporating the more detailed
form for friction appropriate for hydrostatic models
[∂t+ (f+M)ˆ
z∧](dzρu) = ρdzS(u)−∇s·[dzu(ρu)]
−dz(∇sp+ρ∇sΦ) + dzρ F
−[ρ(w(s)u−κu,z)]s=sk−1
+ [ρ(w(s)u−κu,z) ]s=sk
(4.19)
Elements of MOM November 19, 2014 Page 78

Chapter 4. Parameterizations with generalized level coordinates Section 4.2
[∂t+ (f+M)ˆ
z∧](dzρu) = ρdzS(u)−∇s·[dzu(ρu)]
−dz(∇sp+ρ∇sΦ) + dzρ F
−[ρ(w(s)u−κu,z)]s=skbot−1
−τbottom
(4.20)
[∂t+ (f+M)ˆ
z∧](dzρu) = ρdzS(u)−∇s·[dzu(ρu)]
−dz(∇sp+ρ∇sΦ) + dzρ F
+ [τwind +Qmum]
+ [ρ(w(s)u−κu,z) ]s=sk=1 .
(4.21)
As discussed in Section 2.8.2, we prefer to work with the pressure gradient body force acting within the
grid cell of a primitive equation ocean model, rather than the accumulation of contact pressures acting at
the faces. This formulation in terms of body forces is convenient in a hydrostatic fluid as it facilitates a
numerical treatment of pressure in the discrete ocean climate model (Section 3.3).
4.2 Diffusion and skew diffusion
Some of the results for friction are also applicable for diffusion. However, neutral diffusion and skew
diffusion require some added considerations.
4.2.1 Vertical diffusion
Dianeutral tracer transport is often parameterized with a diffusive closure, and these closures require the
dianeutral derivative of tracer. For most parameterizations, dianeutral derivatives are computed with a
vertical derivative (see Section 7.4 of Griffies (2004)), and these derivatives are computed in MOM just
as done for the velocity shears for vertical friction described in Section 4.1.1. Hence, vertical diffusion of
tracer concentration is implemented by a direct computation of the finite differenced vertical derivative
(ρκC,z),z ≈δz(ρκC,z) (4.22)
where Cis the tracer concentration and κis the vertical diffusivity.
4.2.2 Horizontal diffusion
Horizontal diffusion is used infrequently in the interior regions of the ocean in climate simulations with
MOM4, since neutral physics is preferred for physical reasons. However, near the surface boundary, argu-
ments presented in Treguier et al. (1997), Ferrari et al. (2008), and Ferrari et al. (2010) motivate orienting
lateral diffusive processes along surfaces of constant generalized level coordinate when in the surface tur-
bulent boundary, and along topography following coordinates for the bottom turbulent boundary layer.
Hence, it is useful to consider the form that horizontal diffusion takes in generalized level coordinates.
When computing the horizontal fluxes as downgradient along surfaces of constant vertical coordinate
s, we consider
ρF=−ρA∇sC, (4.23)
with Aa horizontal diffusivity. The thickness weighted horizontal diffusion operator is therefore given by
Rhorz =−∇s·(dzρ F).(4.24)
4.2.3 Neutral physics
As for horizontal and vertical diffusion, we compute the tracer flux from neutral physics as ρF, where
Fis the tracer concentration flux formulated as in a Boussinesq model, and ρis the in situ density for a
non-Boussinesq model and ρofor a Boussinesq model. This approach requires a bit of justification for the
neutral skewsion from Gent and McWilliams (1990), and we provide such in this section. The bottomline
Elements of MOM November 19, 2014 Page 79

Chapter 4. Parameterizations with generalized level coordinates Section 4.2
is there are no nontrivial issues involved with implementing this scheme in a non-Boussinesq model. The
only issue arising with generalized level coordinates thus relates to the computation of neutral direction
slopes.
Neutral diffusion fluxes are oriented relative to neutral directions. Hence, the slope of the neutral
direction relative to the surface of constant vertical coordinate is required to construct the neutral diffusion
flux.
The scheme of Gent and McWilliams (1990) requires the slope of the neutral direction relative to the
geopotential surface, since this slope provides a measure of the available potential energy. For simplicity,
we use the same slope for both neutral diffusion and skew diffusion in MOM. Doing so facilitates a straight-
forward extension of the neutral physics technology employed in the z-model MOM4.0 to the generalized
coordinates supported for later versions of MOM. It however produces a modified Gent and McWilliams
(1990) scheme in which skew diffusion relaxes neutral directions toward surfaces of constant vertical co-
ordinate rather than constant geopontential surfaces. For surfaces of constant vertical coordinate that are
quasi-horizontal, the modified skew diffusion scheme should act in a manner quite similar to that in a
z-model. However, for the terrain following coordinates σ(z)and σ(p), novel issues arise which have have
not been considered in the MOM formulation of Gent and McWilliams (1990) skewsion. Hence, the use of
neutral physics parameterizations with terrain following vertical coordinates is not recommended in MOM.
4.2.3.1 The velocity field from Gent and McWilliams (1990)
As formulated by Gent et al. (1995), the parameterization of Gent and McWilliams (1990) is typically
considered from the perspective of a Boussinesq ocean model. For the purposes of advective transport of
tracer, we add a non-divergent velocity v∗=∇ ∧ Ψto the non-divergent resolved scale velocity v. The
parameterized vector streamfunction is given by
Ψ=−κS∧ˆ
z,(4.25)
where Sis the neutral slope and κ > 0 is a kinematic diffusivity. In this way, volume conservation remains
unchanged, thus removing the need to modify the model’s kinematic relations used to diagnose the vertical
velocity component w.
The above results can be seen from a finite volume perspective by considering the volume conservation
equation for an interior model grid cell (Section 2.10), in which
∂t(dz) = dzS(V)−∇s·(dzu)−(w(z))s=sk−1+ (w(z))s=sk,(4.26)
where S(V)is a volume source, and w(z)is the dia-surface velocity component defined in Section 2.1.4. Use
of the Gent et al. (1995) advective velocity
u∗=−∂z(κS) (4.27)
leads to the finite volume result zk−1
Z
zk
dzu∗=−(κS)k−1+ (κS)k,(4.28)
which renders
−∇s·
zk−1
Z
zk
dzu∗−w∗
k−1+w∗
k=∇s·(κS)k−1−∇s·(κS)k−w∗
k−1+w∗
k
= 0.
(4.29)
Hence, there is no modification of the volume in a grid cell from the Gent et al. (1995) velocity field.
We now extend the formulation to a non-Boussinesq fluid, in which case the mass conservation takes
the form (see equation (2.155) in Section 2.6.2)
∂t(dzρ)=dzρS(M)−∇s·(dzρ u)−(ρ w(z))s=sk−1+ (ρ w(z))s=sk,(4.30)
Elements of MOM November 19, 2014 Page 80

Chapter 4. Parameterizations with generalized level coordinates Section 4.2
with S(M)a mass source. Define a density weighted horizontal advection velocity according to
ρu∗=−∂z(ρκ S),(4.31)
in which case the vector streamfunction from the Boussinesq case is extended to the non-Boussinesq merely
by introducing a density weighting
ρΨ=−ρκ S∧ˆ
z.(4.32)
This result then leads to
−∇s·
zk−1
Z
zk
ρdzu∗−(ρw∗)s=sk−1+ (ρ w∗)s=sk=
∇s·(ρκ S)k−1−∇s·(ρ κ S)k−(ρw∗)s=sk−1+ (ρ w∗)s=sk
= 0,
(4.33)
which means there is no modification to the mass of a grid cell through the introduction of the non-
Boussinesq Gent et al. (1995) parameterization.
Note that in the continuum, the above finite volume results mean that the non-Boussinesq Gent et al.
(1995) velocity satisfies
∇s·(ρz,s u∗) + ∂s(ρ z,s w∗)=0,(4.34)
where sis the vertical coordinate. For the geopotential case with s=z, we have
∇z·(ρu∗) + ∂z(ρw∗)=0,(4.35)
which reduces to the familiar non-divergence condition
∇z·u∗+∂zw∗= 0 (4.36)
in the Boussinesq case.
4.2.3.2 Neutral slopes
A key to the implementation of neutral physics is the slope of a neutral direction relative to either the
geopotential or a surface of constant generalized level coordinate. Implicit in the following is the assump-
tion that the neutral slope is finite relative to each surface.
The neutral slope relative to the geopotential is
S(γ/z)=∇γz
=−z,γ ∇zγ(4.37)
with γthe locally referenced potential density. The (γ/z) subscript notation highlights that the neutral
slope is computed relative to a geopotential. The relation between this slope and the others can be seen by
noting that in generalized vertical coordinates, the horizontal gradient ∇zis computed using the transfor-
mation (6.33) in Griffies (2004) so that
S(γ/z)=−z,γ (∇s−S(s/z)∂z)γ
=S(γ/s)+S(s/z).(4.38)
This equation identifies the slope of the vertical coordinate surface relative to the geopotential
S(s/z)=∇sz
=−z,s ∇zs(4.39)
Elements of MOM November 19, 2014 Page 81
Chapter 4. Parameterizations with generalized level coordinates Section 4.2
and the slope of the neutral direction relative to the vertical coordinate surface
S(γ/s)=∇γs
=−z,γ ∇sγ
=−z,s s,γ ∇sγ.
(4.40)
In words, equation (4.38) says that the slope of the neutral direction relative to the geopotential equals
to the slope of the neutral direction relative to the vertical coordinate surface plus the slope of the verti-
cal coordinate surface relative to the geopotential. In isopycnal models, the slope S(γ/s)is very small for
much of the ocean. Except for the sigma coordinates, each of the depth-based and pressure-based vertical
coordinates discussed in Sections 5.1 and 5.2 have S(s/z)typically less than 10−4and S(γ/s)less than 10−2.
For sigma coordinates, both S(γ/s)and S(s/z)can be nontrivial in much of the model domain affected by
topography.
Figure 4.1 illustrates the relation (4.38) between slopes. This figure shows a particular zonal-vertical
slice, with slope given by the tangent of the indicated angle. That is, the x-component of the slope vectors
are given by
S(s/z)= tanα(s/z)
S(γ/z)= tan α(γ/z)
S(γ/s)= tan α(γ/s).
(4.41)
In this example, S(s/z)<0 whereas S(γ/z)>0. Note that the angle between the generalized surface and the
isopycnal surface, S(γ/s), is larger in absolute value for this example than S(γ/z). This case may be applicable
to certain regions of σ-models, whereas for isopycnal models S(γ/s)will generally be smaller than S(γ/z). The
generally nontrivial angle S(γ/s)found in sigma models is yet another reason we do not recommend the use
of neutral physics as implemented in MOM along with terrain following vertical coordinates. Significant
work is required to ensure a proper treatment of neutral physics with terrain following coordinates, and
we are not prepared to support such in MOM.
γ-surface
α(γ/z)
s-surface
α(s/z)α(γ/s)
x,y
z
Figure 4.1: Relationship between the slopes of surfaces of constant depth, constant generalized vertical
coordinate s, and locally referenced potential density γ. Shown here is a case where the slope is projected
onto a single horizontal direction, so that the slope is given by the tangent of the indicated angle.
4.2.3.3 Fluxes for neutral diffusion
The relative slope between the neutral direction and vertical coordinate is required to compute the neutral
diffusion flux. We assume here that this slope is small, thus allowing us to approximate the full diffusion
Elements of MOM November 19, 2014 Page 82

Chapter 4. Parameterizations with generalized level coordinates Section 4.2
tensor of Redi (1982) with the small slope approximated tensor of Gent and McWilliams (1990). To lend
mathematical support for these comments, we start with the neutral diffusion flux as written for the small
slope approximation in z-models. As discussed in Section 14.1.4 of Griffies (2004), this flux has horizontal
and vertical components given by
F(h)=−AI∇γC(4.42)
F(z)=−AIS(γ/z)·∇γC. (4.43)
Converting this flux to a form appropriate for general vertical coordinates requires a transformation of the
gradient operator
∇γ=∇z+S(γ/z)∂z
=∇s+ [S(γ/z)−S(s/z)]∂z
=∇s+S(γ/s)∂z.
(4.44)
The third equality used the slope relation (4.38).
As seen in Section 2.6, the thickness weighted tracer budget contains a contribution from the conver-
gence of a SGS flux in the form
R=−∇s·(dzγ F)−[γ z,s ∇s·F]s=sk−1+ [γ z,s ∇s·F]s=sk.(4.45)
We are therefore led to consider the dia-surface flux component
F(s)=z,s ∇s·F
= (ˆ
z−S(s/z))·F
=−AI(S(γ/z)−S(s/z))·∇γC
=−AIS(γ/s)·∇γC
=S(γ/s)·F(h).
(4.46)
This flux component, as well as the horizontal flux component, take forms isomorphic to those for the
specific case of s=zgiven by equations (4.42) and (4.43). This isomorphism follows from the need to only
have information about the relative slope between the generalized surfaces of constant sand the neutral
directions.
4.2.3.4 Fluxes for skew diffusion
An arbitrary tracer has a Gent and McWilliams (1990) skew flux in the form
F=Agm (S(γ/z)C,z −ˆ
zS(γ/z)·∇zC),(4.47)
where Agm is a non-negative skew diffusivity. The horizontal component of this flux is converted to general
coordinates via
F(h)=Agm (S(γ/s)+S(s/z))C,z
≈Agm S(γ/s)C,z.(4.48)
Consistent with this same approximation, we are led to the dia-surface component of the skew flux
z,s ∇s·F= (ˆ
z−S(s/z))·F
=−Agm (S(γ/z)·∇z+S(γ/z)·S(s/z)∂z)C
=−Agm S(γ/z)·(∇s−S(s/z)∂z)C−Agm S(γ/z)·S(s/z)∂zC
=−Agm S(γ/z)·∇sC
≈ −Agm S(γ/s)·∇sC.
(4.49)
Elements of MOM November 19, 2014 Page 83

Chapter 4. Parameterizations with generalized level coordinates Section 4.2
These approximations are reasonable where |S(s/z)|is much smaller than |S(γ/z)|if S(γ/z)is nontrivial. When
the neutral slope S(γ/z)vanishes, as for regions of zero baroclinicity, this approximation may not be valid
when s,z. However, in regions of vanishing baroclinicity, we expect the error to be of minimal conse-
quence to the simulation since either the zor sbased skew fluxes are close to zero. In general, approximat-
ing the slope as proposed here leads the modified Gent and McWilliams (1990) scheme to dissipate neutral
slopes as they deviate from surfaces of constant generalized vertical coordinate. So long as these surfaces
are quasi-horizontal, the modified scheme should perform in a physically relevant manner.
4.2.3.5 Summary of the neutral fluxes
The horizontal and dia-surface components to the small angle neutral diffusion flux take the form
F(h)=−AI(∇s+S(γ/s)∂z)C
F(s)=S(γ/s)·F(h)(4.50)
where the slope is given by
S(γ/s)=∇γs
=−z,γ ∇sγ. (4.51)
The horizontal and dia-surface skew flux components are approximated by
F(h)≈Agm S(γ/s)C,z
F(s)≈ −Agm S(γ/s)·∇sC. (4.52)
Each of these neutral fluxes are isomorphic to the fluxes used in the z-model MOM4.0. This isomorphism
enables us to transfer the neutral physics technology from MOM4.0 directly to the generalized level ver-
sions of MOM.
Elements of MOM November 19, 2014 Page 84

Chapter 5
Depth and pressure based vertical
coordinates
Contents
5.1 Depth based vertical coordinates ............................... 85
5.1.1 Depth coordinate ....................................... 86
5.1.2 An example of depth coordinates .............................. 87
5.1.3 Depth deviation coordinate ................................. 87
5.1.4 Zstar coordinate ........................................ 89
5.1.5 Depth sigma coordinate ................................... 90
5.1.6 Summary of the depth based vertical coordinates ..................... 91
5.2 Pressure based coordinates ................................... 92
5.2.1 Pressure coordinate ...................................... 92
5.2.2 Pressure deviation coordinate ................................ 93
5.2.3 Pstar coordinate ........................................ 93
5.2.4 Pressure sigma coordinate .................................. 94
5.2.5 Summary of the pressure based vertical coordinates ................... 94
The purpose of this chapter is to document issues related to the choice of vertical coordinates. In MOM,
only depth-based and pressure-based coordinates are supported. Isopycnal coordinates are not supported.
Furthermore, terrain following sigma coordinates are coded in MOM. However, more work is required in
MOM to reduce pressure gradient errors (Section 3.2) and consistently employ neutral physics (see Lemari´
e
et al. (2012b) for some intriguing results on these topics of terrain coordinate ocean models). Much in this
chapter is derived from lectures of Griffies (2005) at the 2004 GODAE School.
5.1 Depth based vertical coordinates
We use depth based vertical coordinates in this section to discretize the Boussinesq equations.1Depth based
coordinates are also known as volume based coordinates, since for a Boussinesq model that uses depth as the
vertical coordinate, the volume of interior grid cells is constant in the absence of sources. Correspondingly,
depth based coordinates are naturally suited for Boussinesq fluids.
1Greatbatch and McDougall (2003) discuss an algorithm for non-Boussinesq dynamics in a z-model. Their methods are imple-
mented in mom4p0a and mom4p0b of Griffies et al. (2004). This approach may be of special use for non-Boussinesq non-hydrostatic
z-models. However, when focusing on hydrostatic models as we do here, pressure based vertical coordinates discussed in Section 5.2
are more convenient to realize non-Boussinesq dynamics.
85

Chapter 5. Depth and pressure based vertical coordinates Section 5.1
5.1.1 Depth coordinate
With a free surface, the vertical domain over which the z-coordinate
s=z(5.1)
ranges is given by the time dependent interval
−H≤z≤η. (5.2)
Consequently, the sum of the vertical grid cell increments equals to the total depth of the column
X
k
dz=H+η. (5.3)
The trivial form of the specific thickness z,s = 1 greatly simplifies the Boussinesq budgets.
The depth coordinate is very useful for many purposes in global climate modelling, and models based
on depth are the most popular ocean climate models. Their advantages include the following.
• Simple numerical methods have been successfully used in this framework.
• For a Boussinesq fluid, the horizontal pressure gradient can be easily represented in an accurate
manner.
• The equation of state for ocean water can be accurately represented in a straightforward manner (e.g.,
Jackett et al. (2006)).
• The upper ocean mixed layer is well parameterized using a z-coordinate.
Unfortunately, these models have some well known disadvantages, which include the following.
• Representation of tracer transport within the quasi-adiabatic interior is cumbersome, with problems
becoming more egregious as mesoscale eddies are admitted (Griffies et al. (2000b)).
• Representation and parameterization of bottom boundary layer processes and flow are unnatural.
Grid cells have static vertical increments ds= dzwhen s=z, except for the top where ∂t(dz) = ∂tη. The
time dependent vertical range of the coordinate slightly complicates a numerical treatment of the surface
cell in z-models (see Griffies et al. (2001) for details of one such treatment).
Placing all changes in ocean thickness in the top gric cell exposes the free surface geopotential co-
ordinate models to two pesky problems. First, when adding fresh water to the ocean, such as for with
simulations of land ice melting, the top cell thickens, which means the representation of vertical processes
is coarsened. Conversely, the surface cell can be lost (i.e., can become dry) if the free surface depresses
below the depth of the top grid cell’s bottom face. This is a very inconvenient feature that limits the use
of z-coordinates.2In particular, the following studies may require very refined vertical resolution and/or
large undulations of the surface height, and so would not be accessible with a conventional free surface
z-model.
• Process studies of surface mixing and biological cycling may warrant very refined upper ocean grid
cell thickness, some as refined as 1m.
• Realistic tidal fluctuations in some parts of the World Ocean can reach 10m-20m.
• Coastal models tend to require refined vertical resolution to represent shallow coastal processes along
the continental shelves and near-shore.
• When coupled to a sea ice model, the weight of the ice will depress the ocean free surface.
2Linearized free surfaces, in which the budgets for tracer and momentum are formulated assuming a constant top cell thickness,
avoid problems with vanishing top cells. However, such models do not conserve total tracer or volume, and so are of limited use for
long term climate studies (see Griffies et al. (2001) and Campin et al. (2004) for discussion).
Elements of MOM November 19, 2014 Page 86
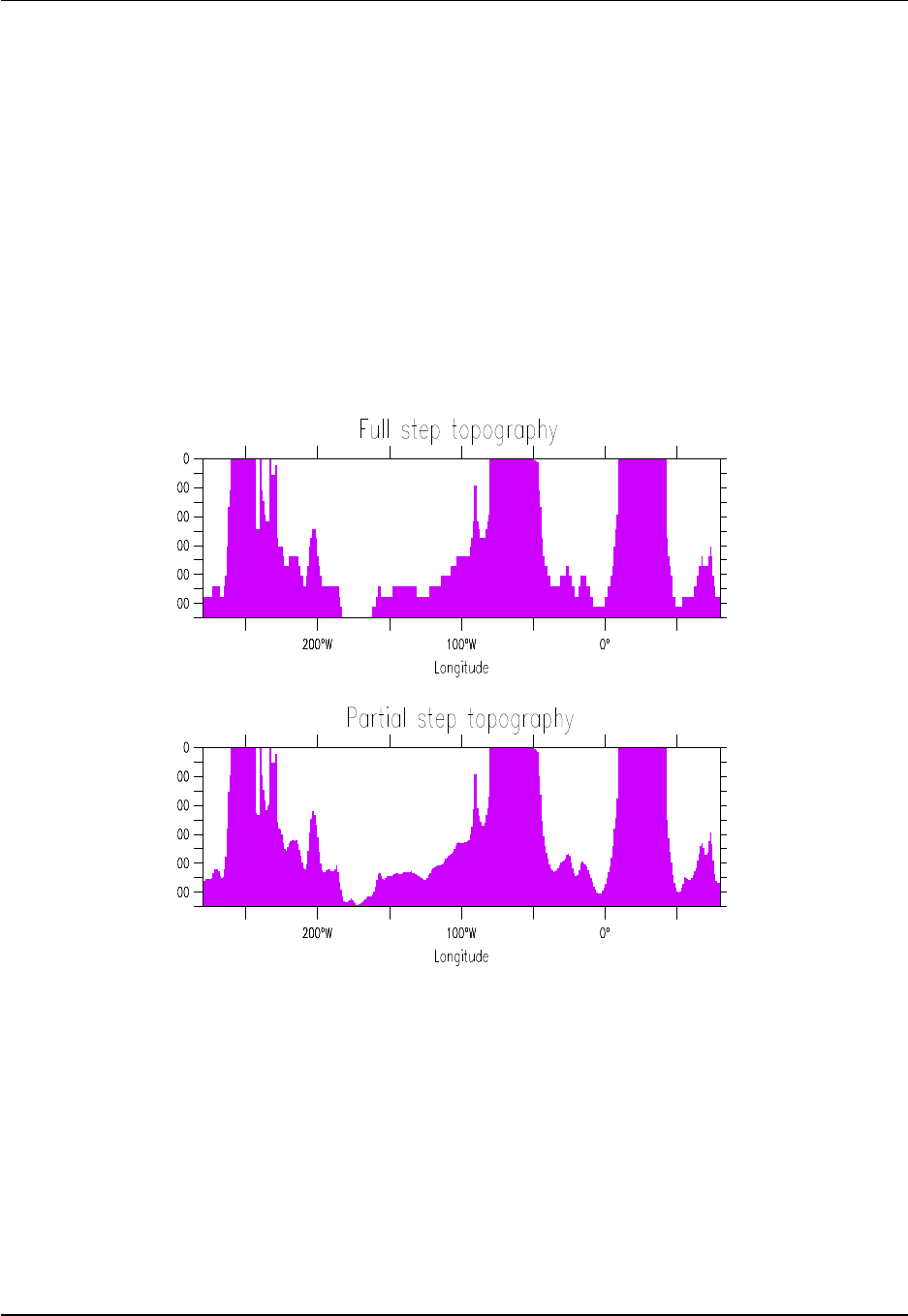
Chapter 5. Depth and pressure based vertical coordinates Section 5.1
5.1.2 An example of depth coordinates
In some of the following discussion, we illustrate aspects of vertical coordinates by diagnosing the values
for the coordinates from a realistic z-model run with partial step thicknesses. Partial steps have arbitrary
thickness set to accurately represent the bottom topography. The partial step technology was introduced
by Adcroft et al. (1997) in the C-grid MITgcm, and further discussed by Pacanowski and Gnanadesikan
(1998) for the B-grid Modular Ocean Model (MOM). Figure 5.1 compares the representation of topography
in a z-model using partial steps as realized in the MOM code of Griffies et al. (2004). Many z-models have
incorporated the partial step technology as it provides an important facility to accurately represent flow
and waves near topography.
Because of partial steps, the level next to the ocean bottom has grid cell centers that are generally at
different depths. Hence, the bottom cell in a partial step z-model computes its pressure gradient with
two terms: one due to gradients across cells with the same grid cell index k, and another due to slopes in
the bottom topography. Details of the pressure gradient calculation are provided in Chapter 3. All other
cells, including the surface, have grid cell centers that are at fixed depths. Figure 5.2 illustrates the lines of
constant partial step depth for this model.
Figure 5.1: Comparison of the partial step versus full step representation of topography as realized in the
z-model discussed by Griffies et al. (2005). This vertical section is taken along the equator. The model
horizontal grid has one degree latitudinal resolution. The main differences are in the deep ocean in regions
where the topographic slope is gradual. Steep sloped regions, and those in the upper ocean with refined
vertical resolution, show less distinctions.
5.1.3 Depth deviation coordinate
The depth deviation coordinate
s=z−η(5.4)
removes the restriction on upper ocean grid cell resolution present with s=z. That is, s= 0 is the time
independent coordinate value of the ocean surface, no matter how much the free surface depresses or
Elements of MOM November 19, 2014 Page 87
Chapter 5. Depth and pressure based vertical coordinates Section 5.1
Figure 5.2: This figure contours the depth of grid cell centers used in a modern geopotential ocean model.
Deviations from the horizontal occur next to the bottom due to use of a partial bottom step representation
of topography, as illustrated in Figure 5.1. In this case, the bottom cell has an arbitrary thickness according
to the methods of Adcroft et al. (1997) and Pacanowski and Gnanadesikan (1998). This technology is
common in modern geopotential ocean models, as it provides a more faithful and robust representation of
the ocean bottom. Shown here is a north-south section along 150◦W.
grows. Hence, no surface cells vanish so long as η > −H. If η < −H, the bottom topography is exposed,
in which case the model’s land-sea boundaries are altered. Such necessitates a model that can allow for
wetting and drying of grid cells. Alternatively, it requires a model where ocean is extended globally, with
infinitesimally thin ocean layers present over land. We do not have such features in MOM.
The depth deviation coordinate ranges between −(H+η)≤s≤0. The only time dependent interface
in s-space is at the bottom of the column. Consequently, by solving the problem at the ocean surface, the
deviation coordinate introduces a problem to the ocean bottom where bottom cells can now vanish. To see
this problem, discretize the deviation coordinate saccording to time independent values sk. For example,
the skvalues can be set as the depths of cells in a model with s=z. When ηevolves, depth zand s=z−η
become different, and so the depth of a grid cell must be diagnosed based on the time independent value
of skand the time dependent surface height
zk=sk+η. (5.5)
If the time dependent depth of the upper interface of a bottom grid cell is diagnosed to be deeper than
the actual bottom depth z=−H, then we know that the bottom grid cell has vanished and so there are
problems. To maintain nonvanishing cells requires a limit on how negative ηcan become. For example, if
the upper interface of a bottom cell is −5000m and the bottom interface (at the ocean bottom) is H= 5005m,
then the bottom cell is lost if η < −5m. This restriction is of some consequence when aiming to use partial
bottom steps (see Figure 5.1) along with tides and sea ice. In practice, if one is interested in allowing thick
sea ice and nontrivial tidal fluctuations, then it will be necessary to keep the bottom partial steps thicker
than roughly 10m-20m. This is arguably a less onerous constraint on the model’s vertical grid spacing than
the complementary problem at the ocean surface encountered with the traditional z-coordinate s=z.
Elements of MOM November 19, 2014 Page 88

Chapter 5. Depth and pressure based vertical coordinates Section 5.1
In summary, grid cells have static grid increments ds= dzfor all cells except the bottom. At the bottom,
∂t(dz) = ∂t(ds) = η,t. Hence, the thickness of the bottom cell grows when the surface height grows, and it
thins when the surface height becomes negative. The bottom cell can be lost if ηbecomes too negative. The
sum of the vertical increments yields the total depth of the column Pkds= (H+η). Because the surface
height fluctuations are so much smaller than changes in bottom topography, the depth deviation coordinate
appears nearly the same as the depth coordinate when viewed over the full depth range of a typical model
such as in Figure 5.2.
The author knows of no model routinely using the depth deviation coordinate. It does appear to have
advantages for certain applications over the depth coordinate. However, the zstar coordinate discussed next
resolves problems at both the top and bottom, and so is clearly preferable. The depth deviation coordinate
is not implemented in MOM for these reasons.
5.1.4 Zstar coordinate
To overcome problems with vanishing surface and/or bottom cells, we consider the zstar coordinate
z∗=H z−η
H+η!.(5.6)
This coordinate is closely related to the “eta” coordinate used in many atmospheric models (see Black (1994)
for a review of eta coordinate atmospheric models). It was originally used in ocean models by Stacey et al.
(1995) for studies of tides next to shelves, and it has been recently promoted by Adcroft and Campin (2004)
for global climate modelling.
The surfaces of constant z∗are quasi-horizontal. Indeed, the z∗coordinate reduces to zwhen ηis zero.
In general, when noting the large differences between undulations of the bottom topography versus undu-
lations in the surface height, it is clear that surfaces constant z∗are very similar to the depth surfaces shown
in Figure 5.2. These properties greatly reduce difficulties of computing the horizontal pressure gradient
relative to terrain following sigma models discussed next. Additionally, since z∗=zwhen η= 0, no flow is
spontaneously generated in an unforced ocean starting from rest, regardless the bottom topography.3This
behavior is in contrast to the case with sigma models, where pressure gradient errors in the presence of
nontrivial topographic variations can generate nontrivial spontaneous flow from a resting state, depend-
ing on the sophistication of the pressure gradient solver.4The quasi-horizontal nature of the coordinate
surfaces also facilitates the implementation of neutral physics parameterizations in z∗models using the
same techniques as in z-models (see Chapters 13-16 of Griffies (2004) for a discussion of neutral physics in
z-models, as well as Section 4.2.3 and Chapter 23 in this document for treatment in MOM).
The range over which z∗varies is time independent
−H≤z∗≤0.(5.7)
Hence, all cells remain nonvanishing, so long as the surface height maintains η > −H. This is a minor
constraint relative to that encountered on the surface height when using s=zor s=z−η.
Because z∗has a time independent range, all grid cells have static increments ds, and the sum of the
vertical increments yields the time independent ocean depth
X
k
ds=H. (5.8)
The z∗coordinate is therefore invisible to undulations of the free surface, since it moves along with the free
surface. This property means that no spurious vertical transport is induced across surfaces of constant z∗
by the motion of external gravity waves. Such spurious transport can be a problem in z-models, especially
those with tidal forcing. Quite generally, the time independent range for the z∗coordinate is a very conve-
nient property that allows for a nearly arbitrary vertical resolution even in the presence of large amplitude
fluctuations of the surface height, again so long as η > −H.
3Because of the use of partial bottom steps, there are two terms contributing to horizontal pressure gradients within the bottom
level when s=z. As discussed by Pacanowski and Gnanadesikan (1998), these two terms lead to modest pressure gradient errors.
These errors, however, are far smaller than those encountered with σcoordinates.
4Shchepetkin and McWilliams (2002) provide a thorough discussion of pressure gradient solvers along with methods for reducing
the pressure gradient error.
Elements of MOM November 19, 2014 Page 89

Chapter 5. Depth and pressure based vertical coordinates Section 5.1
5.1.5 Depth sigma coordinate
The depth-sigma coordinate
σ=z∗/H
= z−η
H+η!(5.9)
is the canonical terrain following coordinate. Figure 5.3 illustrates this coordinate in a realistic model. The
sigma coordinate has a long history of use in coastal modelling. For reviews, see Greatbatch and Mellor
(1999) and Ezer et al. (2002). Models based on the sigma coordinate have also been successfully extended
to basinwide studies (e.g., Lemari´
e et al.,2012b), as well as global work by Diansky et al. (2002).
Just as for z∗, the range over which the sigma coordinate varies is time independent. Here, it is given by
the dimensionless range
−1≤σ≤0.(5.10)
Hence, all cells have static grid increments ds, and the sum of the vertical increments yields unity
X
k
ds= 1.(5.11)
So long as the surface height is not depressed deeper than the ocean bottom (i.e., so long as η > −H), then
all cells remain nonvanishing.5
Some further key advantages of the sigma coordinate are the following.
• It provides a natural framework to represent bottom influenced flow and to parameterize bottom
boundary layer processes.
• Thermodynamic effects associated with the equation of state are well represented with this coordi-
nate.
However, some of the disadvantages are the following:
• As with the z-models, representation of the quasi-adiabatic interior is cumbersome due to numerical
truncation errors inducing unphysically large levels of spurious mixing, especially in the presence of
vigorous mesoscale eddies. Parameterization of these processes using neutral physics schemes may be
more difficult numerically than in the z-models. The reason is that neutral directions generally have
slopes less than 1/100 relative to the horizontal, but can have order unity slopes relative to sigma
surfaces. The larger relative slopes precludes the small slope approximation commonly made with z-
model implementations of neutral physics. The small slope approximation provides for simplification
of the schemes, and improves computational efficiency.
• Sigma models have difficulty accurately representing the horizontal pressure gradient in the presence
of realistic topography, where slopes are commonly larger than 1/100 (see Section 2.8 for a discussion
of the pressure gradient calculation).
Griffies et al. (2000a) notes that there are few examples of global climate models running with ter-
rain following vertical coordinates. Diansky et al. (2002) is the only exception known to the author. This
situation is largely due to problems representing realistic topography without incurring unacceptable pres-
sure gradient errors, as well as difficulties implementing parameterizations of neutral physical processes.
There are notable efforts to resolve these problems, such as the pressure gradient work of Shchepetkin and
McWilliams (2002). Continued efforts along these lines may soon facilitate the more common use of terrain
following coordinates for global ocean climate modelling. At present, the sterrain following igma coordi-
nate is coded in MOM in hopes that it will motivate researchers to further investigate its utility for ocean
modelling.
5If η < −H, besides drying up a region of ocean, the specific thickness z,s =H+ηchanges sign, which signals a singularity in the
vertical grid definition. The same problem occurs for the z∗coordinate.
Elements of MOM November 19, 2014 Page 90
Chapter 5. Depth and pressure based vertical coordinates Section 5.2
Figure 5.3: Constant sigma surfaces as diagnosed in a z-model. Shown here is a section along 150◦W, as in
Figure 5.2. Note the strong variations in the contours, as determined by changes in the bottom topography.
5.1.6 Summary of the depth based vertical coordinates
Depth based vertical coordinates are natural for Boussinesq equations. These coordinates and their specific
thicknesses z,s are summarized in Table 5.1. Notably, both the sigma and zstar coordinates have time
independent ranges, but time dependent specific thicknesses. In contrast, the depth and depth deviation
coordinates have time dependent depth ranges and time independent specific thicknesses. If plotted with
the same range as those given in Figure 5.2, surfaces of constant depth deviation and constant zstar are
indistinguishable from surfaces of constant depth. This result follows since the surface height undulations
are so much smaller than undulations in the bottom topography, thus making the depth deviation and zstar
coordinates very close to horizontal in most parts of the ocean.
coord definition range z,s
geopotential z−H≤z≤η1
z-deviation z0=z−η−(H+η)≤z0≤0 1
z-star z∗=H(z−η)/(H+η)−H≤z∗≤0 1 + η/H
z-sigma σ(z)= (z−η)/(H+η)−1≤σ≤0H+η
Table 5.1: Table of vertical coordinates based on depth. These coordinates are naturally used for discretiz-
ing the Boussinesq equations. Note that the specific thickness z,s is depth independent. This property
proves to be important for developing numerical algorithms in Section 10.8. The coordinates s=z,s=z∗,
and s=σ(z)are coded in MOM, whereas the depth deviation coordinate is not.
Elements of MOM November 19, 2014 Page 91

Chapter 5. Depth and pressure based vertical coordinates Section 5.2
5.2 Pressure based coordinates
The second class of vertical coordinates that we discuss is based on pressure. Pressure-based coordinates
are used to discretize the non-Boussinesq equations, and these coordinates are also known as mass based
coordinates. This name is based on noting that for a non-Boussinesq fluid using pressure, the mass of
interior grid cells is constant without sources (e.g., see equation (2.205)).
Pressure coordinates provide a straightforward way to generalize Boussinesq z-models to non-Boussinesq
pressure models (Huang et al.,2001;DeSzoeke and Samelson,2002;Marshall et al.,2004;Losch et al.,
2004). The reason is that there is an isomorphism between the Boussinesq equations written in depth based
coordinates and non-Boussinesq equations written in pressure based coordinates. The root of this isomor-
phism is the simplification of the density weighted specific thickness ρ z,s for pressure based coordinates.
We detail this point in the following discussions.
Pressure based vertical coordinates that we consider include the following:
s=ppressure (5.12)
s=p−papressure-deviation (5.13)
s= p−pa
pb−pa!pressure-sigma (5.14)
s=po
b p−pa
pb−pa!pressure-star. (5.15)
In these equations, pis the hydrostatic pressure at some depth within the ocean fluid, pais the pressure
applied at the ocean surface z=ηfrom any media above the ocean, such as the atmosphere and sea ice, pb
is the hydrostatic pressure at the solid-earth lower boundary arising from all fluid above the bottom (ocean
water and paabove the ocean), and po
bis a time independent reference pressure, usually taken to be the
bottom pressure in a resting ocean.6Since p,z =−ρg < 0 is single signed for the hydrostatic fluid, pressure
provides a well defined vertical coordinate. Strengths and weaknesses of the corresponding depth based
coordinates also hold for the pressure based coordinates, with the main difference being that pressure based
models are non-Boussinesq.
5.2.1 Pressure coordinate
With a free surface, the vertical domain over which the p-coordinate
s=p(5.16)
ranges is given by
pa≤p≤pb.(5.17)
Hence, the surface and bottom boundaries are time dependent, whereas the density weighted specific thick-
ness is constant
ρz,s =−g−1(5.18)
where the hydrostatic equation p,z =−ρg was used. Relation (5.18) is the root of the isomorphism between
Boussinesq depth based models and non-Boussinesq pressure based models.
The time dependent range for the pressure coordinate complicates the treatment of both the top and
bottom cells. In particular, if the bottom pressure is less than the time independent discrete pressure level
at the top interface of the lowest cell, then there is no mass within the bottom cell. Likewise, if the applied
pressure is greater than the discrete pressure level at the bottom interface of the top cell, then there is no
mass in the top cell. These results mean that grid cells have static vertical coordinate increments ds= dp
for all cells except the top and bottom. At the top, ∂t(ds) = ∂tpaand at the bottom ∂t(ds) = −∂tpb. The
6Note that equation (11.64) of Griffies (2004) used the time dependent pbrather than the time independent reference pressure
po
b. The former vertical coordinate has not been used in practice, and so we focus here on that coordinate defined with the reference
pressure po
b.
Elements of MOM November 19, 2014 Page 92

Chapter 5. Depth and pressure based vertical coordinates Section 5.2
associated mass per unit area in the cells evolves according to ∂t(ρdz) = −g−1∂tpaat the surface, and
∂t(ρdz) = g−1∂tpbat the bottom. Hence, the mass within the top cell decreases when the applied pressure
increases, and the mass in the bottom cell increases when the bottom pressure increases. Both the surface
and the bottom cells can therefore vanish depending on the applied and bottom pressures.
The sum of the vertical coordinate increments can be found by noting the total mass per area is given
by
g−1(pb−pa) = Xρdz
=Xρz,s ds
=−g−1Xds,
(5.19)
thus yielding the time dependent result
Xds=−(pb−pa).(5.20)
5.2.2 Pressure deviation coordinate
The pressure deviation coordinate
s=p−pa(5.21)
removes the restriction on upper ocean grid cell resolution since s= 0 is the time independent value of the
ocean surface. That is, this coordinate ranges between
0≤s≤pb−pa.(5.22)
This coordinate is isomorphic to the depth deviation coordinate s=z−ηdiscussed in Section 5.1.3, and
shares the same limitations which prompt us not to have this coordinate coded in MOM.
In summary, grid cells have static vertical coordinate increments dsfor all cells except the bottom. At
the bottom ∂t(ds) = −∂t(pb−pa). The associated mass per unit area in the bottom cell evolves according
to ∂t(ρdz) = g−1∂t(pb−pa). As for the pressure coordinate, the sum of the vertical coordinate increments
yields Xds=−(pb−pa).(5.23)
5.2.3 Pstar coordinate
The pstar coordinate is given by
p∗=po
b p−pa
pb−pa!,(5.24)
where po
bis a time independent reference pressure. Two possible choices for po
binclude
po
b=g
0
Z
−H
dzρinit,(5.25)
or the simpler case of
po
b=g ρoH. (5.26)
The p∗coordinate is isomorphic to the z∗coordinate, with p∗extending over the time independent range
0≤p∗≤po
b.(5.27)
Elements of MOM November 19, 2014 Page 93

Chapter 5. Depth and pressure based vertical coordinates Section 5.2
The sum of the vertical coordinate increments can be found by noting the total mass per area is given
by
g−1(pb−pa) = Xρdz
=Xρz,s ds
=− pb−pa
g po
b!Xds,
(5.28)
thus yielding the time independent result Xds=−po
b.(5.29)
5.2.4 Pressure sigma coordinate
The pressure-sigma terrain following coordinate
σ(p)= p−pa
pb−pa!(5.30)
is the pressure analog to the depth based sigma coordinate σ(z)= (z−η)/(H+η). This coordinate has been
used by Huang et al. (2001), and it shares the same advantages and disadvantages as the depth-based sigma
coordinate. Grid cells have static vertical coordinate increments dsfor all cells. The associated mass per
unit area never vanishes in any cell, so long as the bottom pressure is greater than the applied pressure.
The sum of the vertical coordinate increments can be found by noting the total mass per area is given
by
g−1(pb−pa) = Xρdz
=Xρz,s ds
=−g−1(pb−pa)Xds,
(5.31)
thus yielding the time independent result Xds=−1.(5.32)
5.2.5 Summary of the pressure based vertical coordinates
A technical reason that the pressure based coordinates considered here are so useful for non-Boussinesq
hydrostatic modelling is that ρz,s is either a constant or a two-dimensional field. In contrast, for depth
based models ρz,s is proportional to the three-dimensional in situ density ρ, thus necessitating special
algorithmic treatment for non-Boussinesq z-models (see Greatbatch and McDougall (2003) and Griffies
(2004)). Table 5.2 summarizes the pressure-based coordinates discussed in this section. The pressure and
pressure deviation coordinates have time dependent ranges but time independent specific thicknesses ρ z,s.
The sigma and pstar coordinates have time independent range but time dependent specific thickness.
As Table 5.2 reveals, the specific thickness z,s is negative for the pressure-based coordinates, whereas
it is positive for the depth-based coordinate (Table 5.1). The sign change arises since upward motion in a
fluid column increases the geopotential coordinate zyet decreases the hydrostatic pressure p. To establish
a convention, we assume that the thickness of a grid cell in zspace is always positive
dz=z,s ds > 0 (5.33)
as is the case in the conventional z-models. With z,s <0 for the pressure-based vertical coordinates, the
thickness of grid cells in sspace is negative
ds < 0 for pressure-based coordinates with z,s <0. (5.34)
Elements of MOM November 19, 2014 Page 94

Chapter 5. Depth and pressure based vertical coordinates Section 5.2
coord definition range g ρz,s
pressure p pa≤p≤pb−1
p-deviation p0=p−pa0≤p0≤pb−pa−1
pstar p∗=po
b(p−pa)/(pb−pa) 0 ≤p∗≤po
b−(pb−pa)/po
b
p-sigma σ(p)= (p−pa)/(pb−pa) 0 ≤σ≤1−(pb−pa)
Table 5.2: Table of vertical coordinates based on pressure. These coordinates are naturally used for non-
Boussinesq dynamics. Note that the density weighted specific thickness ρz,s is depth independent. This
property proves to be important for developing numerical algorithms in Section 10.8. The coordinates
s=p,s=p∗, and s=σ(p)are coded in MOM, whereas the pressure deviation coordinate is not.
Elements of MOM November 19, 2014 Page 95

Chapter 5. Depth and pressure based vertical coordinates Section 5.2
Elements of MOM November 19, 2014 Page 96

Chapter 6
Equation of state and related quantities
Contents
6.1 Introduction ............................................ 97
6.2 Linear equation of state ..................................... 99
6.3 The two realistic equations of state .............................. 99
6.3.1 The Jackett et al. (2006) equation of state .......................... 99
6.3.2 TEOS-10 equation of state .................................. 102
The purpose of this chapter is to present features of the equation of state used in MOM, with the dis-
cussion here an extension of that given in Griffies et al. (2004). The following summarizes the realistic
equations of state available in recent versions of MOM.
• MOM4.0 uses the McDougall et al. (2003) equation of state.
• MOM4p1 uses the Jackett et al. (2006) equation of state.
• MOM as of the 2012 release uses either of the Jackett et al. (2006) equation (retained for legacy
purposes) or the IOC et al. (2010) version recommended for new simulations.
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean density.F90
6.1 Introduction
It is important that the equation of state be accurate over the range of temperature, salinity, and pressure
values occurring in ocean simulations. Reasons for needing such accuracy include the following.
• Density is needed to compute the hydrostatic pressure, whose horizontal gradients drive ocean cur-
rents in the primitive equations.
• The locally referenced vertical derivative of density determines the static stability of a vertical fluid
column. This stability determines conditions for convective instability and is used to compute Richard-
son numbers necessary for mixing for such schemes as Pacanowski and Philander (1981), Chen et al.
(1994), Large et al. (1994), and Simmons et al. (2004).
97

Chapter 6. Equation of state and related quantities Section 6.2
• The locally referenced derivatives with respect to potential temperature and salinity
ρ,θ = ∂ρ
∂θ !p,s
(6.1)
ρ,s = ∂ρ
∂s !p,θ
(6.2)
are important for computing both the vertical stratification, and to compute the neutral slopes used
for sub-grid-scale tracer transport as in Griffies et al. (1998); Griffies (1998).
• The following combination of second derivatives is used to diagnose the potential for cabbeling to
occur in the ocean McDougall (1987b)
C=∂α
∂θ + 2α
β
∂α
∂S − α
β!2∂β
∂S
=−ρ−1ρ,θθ −2ρ,θS ρ,θ
ρ,S !+ρ,SS ρ,θ
ρ,S !2.
(6.3)
• The following combination of second derivatives is used to diagnose the potential for thermobaricity
and halobaricity to occur in the ocean McDougall (1987b)
T=β ∂p α
β!
=∂α
∂p −α
β
∂β
∂p
=−ρ−1"ρ,θp −ρ,pS ρ,θ
ρ,S !#.
(6.4)
Note that the name thermobaricity is generally used for this parameter, and we evaluate it as given
here. However, there are actually contributions from both halobaricity (dependency of haline con-
traction coefficient on the pressure) and thermobaricity (dependency of thermal expansion coefficient
on the pressure). But the thermal piece is generally far larger McDougall (1987b).
In early versions of MOM, density was computed according to the Bryan and Cox (1972) cubic poly-
nomial approximation to the UNESCO equation of state (Gill,1982). That approach was quite useful for
certain applications. Unfortunately, it has limitations that are no longer acceptable for global climate mod-
eling. First, the polynomials are fit at discrete depth levels. The use of partial cells makes this approach
cumbersome since with partial cells it is necessary to generally compute density at arbitrary depths. Sec-
ond, the cubic approximation is inaccurate for many regimes of ocean climate modeling, such as wide
ranges in salinity associated with rivers and sea ice. For these two reasons, a more accurate method is
desired.
Feistel (1993), Feistel and Hagen (1995), and Feistel (2003) studied the equilibrium thermodynamics
of seawater and produced a more accurate EOS than UNESCO by using more recent empirical data. Mc-
Dougall et al. (2003) produced a fit to Feistel and Hagen (1995) to render an expression convenient for use
in ocean models, and Jackett et al. (2006) updated this equation of state based on Feistel (2003). Finally,
IOC et al. (2010) presents a recent update to the equation of state that is the result of a SCOR working
group on the thermodynamics of seawater.
The following equations of state (EOS) are currently available in MOM for computing density.
• A linear equation of state whereby density is a linear function of potential temperature and salinity.
This EOS is relevant only for idealized simulations.
• The second EOS is that proposed by Jackett et al. (2006).
Elements of MOM November 19, 2014 Page 98

Chapter 6. Equation of state and related quantities Section 6.3
• The third is that recommended by IOC et al. (2010).
Either the Jackett et al. (2006) or IOC et al. (2010) equation of state are more accurate than the UNESCO
EOS due to the use of more accurate empirical data as reported in Feistel (1993), Feistel and Hagen (1995),
and Feistel (2003). Such equations of state are now standard in ocean climate modeling.
6.2 Linear equation of state
The default linear equation of state in MOM assumes that density is a linear function of potential tem-
perature and salinity. There is no pressure dependence. Due to the absence of pressure effects, the linear
equation of state leads to a density that is more precisely thought of as a potential density. The form used
for this equation of state is
ρ(x,t) = ρ0−˜
α θ(x,t) + ˜
β s(x,t).(6.5)
The default settings are
˜
α= 0.255(kg/m3)◦K−1(6.6)
˜
β= 0 (6.7)
ρ0= 1035kg/m3.(6.8)
Hence, the density partial derivatives are given by
ρ,θ =−˜
α(6.9)
ρ,s =˜
β. (6.10)
The cabbeling and thermobaric parameters vanish for this linear equation of state.
6.3 The two realistic equations of state
The equation of state for Jackett et al. (2006) has 25 terms, and the IOC et al. (2010) equation of state from
McDougall et al. (2012) has 48 terms. The form for both equations are motivated by that of Wright (1997)
and it takes the following form for the in situ density ρwritten in terms of pressure, salinity, and potential
or conservative temperature
ρ(s,θ,p) = Pn(s,θ,p)
Pd(s,θ,p),(6.11)
where pis the gauge pressure in units of decibars, θis the potential temperature referenced to zero pressure
in units of Celsius, and sis salinity in psu. Note the conversion between mks pressure and decibars is given
by
10−4db = 1Pa.(6.12)
The gauge pressure is given by
p=Pabsolute −10.1325dbars (6.13)
where the absolute pressure is the in situ pressure measured in the ocean.
For the Jackett et al. (2006) equation of state, salinity is measured in practical salinity units (psu).
For the IOC et al. (2010) equation of state available in MOM, salinity is measured in parts per thousand
appropriate for the absolute salinity or preformed salinity.
6.3.1 The Jackett et al. (2006) equation of state
The Jackett et al. (2006) equation of state has been fit over the range
0psu ≤s≤40psu (6.14)
−3◦C≤θ≤40◦C (6.15)
0db ≤p≤8000db.(6.16)
Elements of MOM November 19, 2014 Page 99
Chapter 6. Equation of state and related quantities Section 6.3
A check value for the density is ρ= 1033.213387kg.m−3with s= 35psu, θ= 20◦C, and p= 2000db =
2×107Pa. The coefficients anand bnare tabulated in Table A2 Jackett et al. (2006).
The polynomial functions Pnand Pdappearing in the 25-term equation of state (6.11)ofJackett et al.
(2006) are given by
Pn=ao+a1θ+a2θ2+a3θ3+a4s+a5sθ +a6s2
+a7p+a8pθ2+a9p s +a10 p2+a11 p2θ2(6.17)
Pd=bo+b1θ+b2θ2+b3θ3+b4θ4+b5s+b6sθ +b7s θ3+b8s3/2+b9s3/2θ2
+b10 p+b11 p2θ3+b12 p3θ. (6.18)
Rearrangement in order to reduce multiplications leads to
Pn=ao+θ(a1+θ(a2+a3θ)) + s(a4+a5θ+a6s)
+p(a7+a8θ2+a9s+p(a10 +a11 θ2)) (6.19)
Pd=bo+θ(b1+θ(b2+θ(b3+θ b4))) + s(b5+θ(b6+b7θ2) + s1/2(b8+b9θ2))
+p(b10 +p θ (b11 θ2+b12 p)).(6.20)
The first order partial derivatives of density for the 25 term equation of state are
∂ρ
∂θ !s,p
=ρ
1
Pn ∂Pn
∂θ !s,p −1
Pd ∂Pd
∂θ !s,p(6.21)
∂ρ
∂s !θ,p
=ρ
1
Pn ∂Pn
∂s !θ,p −1
Pd ∂Pd
∂s !θ,p(6.22)
∂ρ
∂p !θ,s
=ρ 1
Pn ∂Pn
∂p !θ,s −1
Pd ∂Pd
∂p !θ,s!.(6.23)
Since divisions are computationally more expensive than multiplications, we find it useful to rearrange
these results to ∂ρ
∂θ !s,p
= (Pd)−1 ∂Pn
∂θ !s,p −ρ ∂Pd
∂θ !s,p(6.24)
∂ρ
∂s !θ,p
= (Pd)−1 ∂Pn
∂s !θ,p −ρ ∂Pd
∂s !θ,p(6.25)
∂ρ
∂p !θ,s
= (Pd)−1" ∂Pn
∂p !θ,s −ρ ∂Pd
∂p !θ,s#(6.26)
where (Pd)−1can be saved in a temporary array, thus reducing the number of divisions.1
The second order density partial derivatives are
∂2ρ
∂θ2!s,p
= (Pd)−1"∂2Pn
∂θ2−2∂ρ
∂θ
∂Pd
∂θ −ρ∂2Pd
∂θ2#(6.27)
∂2ρ
∂s2!θ,p
= (Pd)−1"∂2Pn
∂s2−2∂ρ
∂s
∂Pd
∂s −ρ∂2Pd
∂s2#(6.28)
∂2ρ
∂s∂θ != (Pd)−1"∂2Pn
∂s∂θ −∂ρ
∂s
∂Pd
∂θ −∂ρ
∂θ
∂Pd
∂s −ρ∂2Pd
∂s∂θ #(6.29)
∂2ρ
∂s ∂p != (Pd)−1"∂2Pn
∂s∂p −∂ρ
∂p
∂Pd
∂s −∂ρ
∂s
∂Pd
∂p −ρ∂2Pd
∂s ∂p #(6.30)
∂2ρ
∂θ ∂p != (Pd)−1"∂2Pn
∂θ ∂p −∂ρ
∂p
∂Pd
∂θ −∂ρ
∂θ
∂Pd
∂p −ρ∂2Pd
∂θ ∂p #.(6.31)
1We thank Trevor McDougall for pointing out this simplification.
Elements of MOM November 19, 2014 Page 100
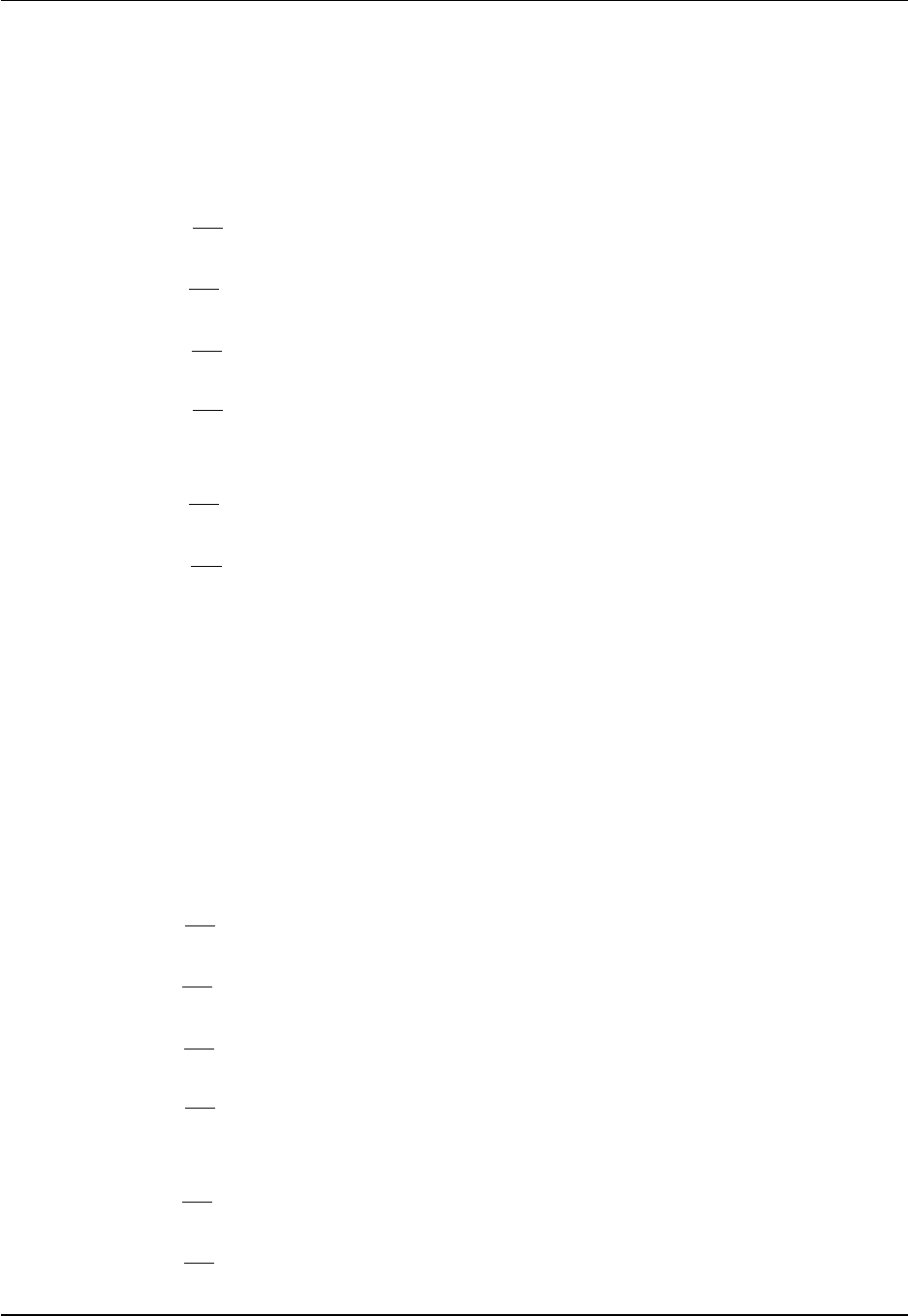
Chapter 6. Equation of state and related quantities Section 6.3
The first order partial derivatives of the equation of state functions are given by
∂Pn
∂θ !s,p
=a1+ 2a2θ+ 3a3θ2+a5s+ 2 a8pθ + 2a11 p2θ(6.32)
∂Pn
∂s !θ,p
=a4+a5θ+ 2a6s+a9p(6.33)
∂Pn
∂p !θ,s
=a7+a8θ2+a9s+ 2a10 p+ 2a11 p θ2(6.34)
∂Pd
∂θ !s,p
=b1+ 2b2θ+ 3b3θ2+ 4 b4θ3+b6s+ 3b7sθ2+ 2b9s3/2θ(6.35)
+ 3b11 p2θ2+b12 p3
∂Pd
∂s !θ,p
=b5+b6θ+b7θ3+ (3/2)b8s1/2+ (3/2)b9s1/2θ2(6.36)
∂Pd
∂p !θ,s
=b10 + 2b11 pθ3+ 3b12 p2θ(6.37)
with rearrangement leading to
∂Pn
∂θ !s,p
=a1+θ(2a2+ 3a3θ) + a5s+ 2 p θ (a8+a11 p) (6.38)
∂Pn
∂s !θ,p
=a4+a5θ+ 2a6s+a9p(6.39)
∂Pn
∂p !θ,s
=a7+a8θ2+a9s+ 2a10 p+ 2a11 p θ2(6.40)
∂Pd
∂θ !s,p
=b1+θ(2b2+θ(3b3+ 4 b4θ)) + s(b6+θ(3b7θ+ 2b9s1/2)) (6.41)
+p2(3b11 θ2+b12 p)
∂Pd
∂s !θ,p
=b5+θ(b6+b7θ2) + (3/2)s1/2(b8+b9θ2) (6.42)
∂Pd
∂p !θ,s
=b10 + 2b11 pθ3+ 3b12 p2θ. (6.43)
Elements of MOM November 19, 2014 Page 101

Chapter 6. Equation of state and related quantities Section 6.3
The second order partial derivatives of the equation of state functions are given by
∂2Pn
∂θ2= 2a2+ 6a3θ+ 2 a8p+ 2a11 p2(6.44)
∂2Pn
∂s2= 2 a6(6.45)
∂2Pn
∂s∂θ =a5(6.46)
∂2Pn
∂s∂p =a9(6.47)
∂2Pn
∂θ ∂p = 2a8θ+ 4a11 pθ (6.48)
∂2Pd
∂θ2= 2b2+ 6b3θ+ 12 b4θ2+ 6b7sθ + 2b9s3/2+ 6b11 p2θ(6.49)
∂2Pd
∂s2= (3/4) b8s−1/2+ (3/4)b9s−1/2θ2(6.50)
∂2Pd
∂s∂θ =b6+ 3b7θ2+ 3b9s1/2θ(6.51)
∂2Pd
∂s∂p = 0 (6.52)
∂2Pd
∂θ ∂p = 6b11 pθ2+ 3b12 p2.(6.53)
6.3.2 TEOS-10 equation of state
Documentation of the TEOS-10 equation of state relies on the work of IOC et al. (2010) and the paper by
McDougall et al. (2012) in preparation. The form of the equation of state is analogous to the 25 term form
of Section 6.3.1, with new polynomial terms needed to bettere account for a wider range of temperature
and salinity.
The TEOS-10 equation of state uses the following prognostic temperature and salinity fields:
•Conservative temperature: The conservative temperature variable of McDougall (2003).
•Preformed salinity: The preformed salinity variable detailed in IOC et al. (2010).
Although the salinity variable time stepped by the model is preformed salinity, there is a translation made
to absolute salinity before computing the density, since the equation of state is a function of absolute salin-
ity, not preformed salinity.
Caveat
Testing of the TEOS-10 equation of state, and in particular the use of preformed salinity, remains in-
complete. Additionally, some of the model diagnostics remain incomplete, such as the dianeutral transport
diagnostics detailed in Chapter 36.
Elements of MOM November 19, 2014 Page 102

Chapter 7
Dynamical ocean equations with a
nonconstant gravity field
Contents
7.1 Gravitational force: conventional approach .........................103
7.2 Gravitational force: general approach .............................105
7.2.1 Momentum equation ..................................... 105
7.2.2 Primitive equations ...................................... 107
7.2.3 Depth independent perturbed geopotential ........................ 107
The purpose of this chapter is to formulate the dynamical equations of the ocean in the presence of a
space and time dependent gravitational acceleration. This formulation has applications for the implemen-
tation of astronomical tide forcing (Chapter 8). In addition, inhomogeneities in mass distributions cause
the earth’s gravity field to be non-spherical. Of increasing interest to climate science is the study of how
the ocean responds to changes in mass distributions associated with melting land ice. Given the nontrivial
impact that melting land glaciers has on the earth’s geoid (Farrell and Clark (1976) and Mitrovica et al.
(2001)), we formulate the dynamical equations of a liquid ocean in the presence of a space-time dependent
gravity field.
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean barotropic.F90
7.1 Gravitational force: conventional approach
The effective gravitational force is noncentral due to the Earth’s rotation. Hence if the Earth were a homo-
geneous ideal fluid, matter would flow from the poles toward the equator, thus ensuring that the Earth’s
surface would everywhere be perpendicular to the effective gravitational acceleration, g. Indeed, the Earth
does exhibit a slight equatorial bulge. However, inhomogeneities in the Earth’s composition and surface
loading by continents, glaciers, and seawater make its shape differ from the ideal case.
Veronis (1973), Phillips (1973), and Gill (1982) discuss how the Earth’s geometry can be well approx-
imated by an oblate spheroid, with the equatorial radius larger than the polar due to centrifugal effects.
With this geometry, surfaces of constant geopotential are represented by surfaces with a constant oblate
spheroid radial coordinate (page 662 of Morse and Feshbach,1953). However, the oblate spheroidal metric
functions, which determine how to measure distances between points on the spheroid, are less convenient
to use for ocean modelling than the more familiar spherical metric functions.
103
Chapter 7. Dynamical ocean equations with a nonconstant gravity field Section 7.2
To provide a simpler form of the equations of motion on the Earth, Veronis (1973) and Gill (1982) (see
in particular page 91 of Gill) indicate that it is possible, within a high level of accuracy, to maintain the
best of both situations. That is, surfaces of constant radius rare interpreted as best fit oblate spheroidal
geopotentials, yet the metric functions used to measure distance between points in the surface are approx-
imated as spherical. As the metric functions determine the geometry of the surface, and hence the form of
the equations of motion, the equations are exactly those that result when using spherical coordinates on a
sphere. Hence, in global ocean climate modelling, one generally considers the geometry of the Earth to be
spherical as in Figure 7.1, yet the radial position rrepresents a surface of constant geopotential, which is
approximated by an oblate spheroid.
In summary, the gravitational field traditionally used for ocean climate modelling is an effective gravi-
tational field, which incorporates the effects from the centrifugal force. The effective gravitational field is
conservative, so that the gravitational acceleration of a fluid parcel can be represented as the gradient of a
scalar,
g=−∇Φ,(7.1)
with Φknown as the geopotential. With the mass of a fluid parcel written as ρdV, then
P= (ρdV)Φ(7.2)
is the gravitational potential energy of a parcel, thus making Φthe gravitational potential energy per mass
of a fluid parcel.
In this equation, ρis the in situ density and dVits volume. In most ocean modelling applications, the
local vertical direction is denoted by
z=r−R, (7.3)
with z= 0 the geopotential surface corresponding to a resting ocean. The geopotential in this case is given
by case
Φ≈Φ0=g z, (7.4)
with g≈9.8ms−2the typical value taken in ocean climate models for the acceleration due to gravity at the
earth’s surface.
x1
x2
1
x3
h
q
r
Figure 7.1: The position vector for a point in 3D Euclidean space can be represented in terms of many
sets of coordinates, such as the Cartesian coordinates (x1,x2,x3) or the spherical coordinates (λ,φ,r). In
a geophysical context, the angular coordinate 0 ≤λ≤2πis the longitude, with positive values measured
eastward from a meridian passing through Greenwich, England. The angular coordinate φis the latitude,
with values φ= 0 at the equator and φ=π/2(−π/2) at the north (south) poles. The radial distance ris
measured here with respect to the center of the sphere. The coordinate transformation between Cartesian
and spherical is given by (x1,x2,x3) = r(cosφcosλ,cosφsinλ,sin φ).
Elements of MOM November 19, 2014 Page 104

Chapter 7. Dynamical ocean equations with a nonconstant gravity field Section 7.2
7.2 Gravitational force: general approach
Absent changes to gravity and crustal rebound, the melting of Greenland would add about 7 m of water to
the ocean’s sea level. As shown by Farrell and Clark (1976) and Mitrovica et al. (2001), the melting of land
ice over Greenland, Antarctica, or mountain glaciers, creates a sizable perturbation to the present-day static
equilibrium sea level, which we refer to as the geoid in the following. For example, according to Farrell and
Clark (1976) and Mitrovica et al. (2001), if all of Greenland melted, much of the northern North Atlantic
and Arctic Ocean would see only a fraction of the 7 m rise, with some regions close to Greenland actually
seeing a reduction in sea level (see Figure 1A in Mitrovica et al.,2001), whereas other ocean regions, such
as the central and South Pacific, Indian, and South Atlantic, would see more than 7m sea level rise.
It is generally assumed by climate modellers that changes in the geoid can be used post facto to renor-
malize projections of sea level change from global climate models simulated with a fixed geoid. The results
from Farrell and Clark (1976) and Mitrovica et al. (2001) prompt us to question this assumption, especially
for dramatic changes associated with melting Greenland or Antarctica. Furthermore, changes in the geoid
associated with past glacial periods, such as ice ages, would likewise be a nontrivial modification to sea
level.
The study of Kopp et al. (2010) represents the first attempt to partially remove the constant geoid
assumption for purposes of global ocean climate. In that study, the prognostic sea level from an ocean
climate model was combined with an evolving equilibrium sea level determined as a function of changing
mass of seawater and land ice. The Kopp et al. (2010) study only partially addresses the main question
associated with this issues: namely, will the drastic and rapid changes in the geoid associated with land
ice melting have a nontrivial impact on ocean circulation? To address that question requires ocean climate
models to be run with an evolving gravity field. It is to this issue that we now turn.
Consider a generalized geopotential written in the form
Φ=Φ0(r) + Φ1(r,λ,φ,t),(7.5)
where Φ0(r) is the unperturbed geopotential given by equation (7.4), and Φ1incorporates perturbations to
the geopotential associated with changes in land ice cover. Within the ocean fluid, the radial dependence of
Φ1is generally quite weak, though it can be large for regions near the melting land ice. We thus maintain
this dependence for purposes of generality, though it will be dropped for certain specialized examples. The
calculation of ocean tides arising from astronomical forcing is formulated with a space-time dependent
geopotential as in equation (7.5), with the radial dependence of Φ1neglected (e.g., Section 9.8 in Gill,
1982). Arbic et al. (2004) provide a recent discussion of global tide modelling.
7.2.1 Momentum equation
The linear momentum of a fluid parcel is given by
P=vρdV , (7.6)
where again ρdVis the mass of the parcel. Through Newton’s Second Law of Motion, momentum changes
in time due to the influence of forces acting on the parcel. As recently reviewed by Griffies and Adcroft
(2008), the equation for linear momentum of a fluid parcel takes the form
ρdv
dt+2Ω∧ρv=−(∇p+ρ∇Φ) + ∇·τ.(7.7)
The left-hand side of this equation is the material time change for the linear momentum per volume of a
parcel, along with the Coriolis force, and the right-hand side is the sum of the pressure, gravitational, and
frictional forces.
In writing the momentum equation in the form of (7.7), we have chosen to retain an orientation af-
forded by the unperturbed geopotential surfaces, which correspond to surfaces of constant depth z. This
approach reflects that commonly used to study ocean tides. In the presence of a perturbed geopotential Φ1,
the “horizontal” directions defined by surfaces of constant zare no longer parallel to geopotential surfaces.
Elements of MOM November 19, 2014 Page 105

Chapter 7. Dynamical ocean equations with a nonconstant gravity field Section 7.2
We thus may interpret the sum ∇zp+ρ∇zΦas an orientation of the pressure gradient along surfaces of con-
stant geopotential, where the geopotential is determined by Φ=Φ0+Φ1, rather than just the unperturbed
geopotential Φ0. This result is familiar to those who have formulated ocean models in generalized vertical
coordinates (see, for example, Chapter 6 of Griffies,2004).
We next write the momentum equation in component form using spherical coordinates. For this pur-
pose, introduce the orthogonal unit vectors ˆ
λ,ˆ
φ, and ˆ
r, each moving with the rotating sphere (Figure
7.1). The vector ˆ
λpoints in the positive longitude direction, ˆ
φpoints in the positive latitude direction,
and ˆ
rpoints radially outward from the center of the sphere. In spherical coordinates, the angular rotation
velocity for the sphere takes the form
Ω=Ω(ˆ
rsinφ+ˆ
φcosφ),(7.8)
and the velocity of a fluid parcel is written
v=ˆ
λ(rcosλ)dλ
dt+rˆ
φdφ
dt+ˆ
rdr
dt
=uˆ
λ+vˆ
φ+wˆ
z,
(7.9)
where ˆ
z=ˆ
ris the radial/vertical unit vector, and
(u,v,w)=(rcos φdλ/dt,r dφ/dt,dr/dt) (7.10)
are spherical components to the velocity vector. Hence, the Coriolis force per mass is given by
2Ω∧v= 2Ω(wcosφ−vsin φ)ˆ
λ
+ 2Ωusinφˆ
φ−2Ωucosφˆ
r.(7.11)
Introducing the notation
f= 2Ωsinφ(7.12)
f∗= 2Ωcosφ, (7.13)
leads to the equation of motion
d
dt+ (ˆ
zf+ˆ
λf∗)∧!v=−(∇Φ+ρ−1∇p) + F(7.14)
which takes the component form
du
dt−v f +w f ∗=−(Φ,x +ρ−1p,x) + F(x)(7.15)
dv
dt+u f =−(Φ,y +ρ−1p,y) + F(y)(7.16)
dw
dt−u f ∗=−(Φ,z +ρ−1p,z) + F(z).(7.17)
In these equations, we defined
F=1
ρ∇·τ(7.18)
as the friction vector per unit mass, wrote
∂
∂x =1
rcosφ
∂
∂λ (7.19)
∂
∂y =1
r
∂
∂φ (7.20)
∂
∂z =∂
∂r (7.21)
as the three-dimensional gradient operator in spherical coordinates, and introduced a comma as a short-
hand for partial derivative.
Elements of MOM November 19, 2014 Page 106

Chapter 7. Dynamical ocean equations with a nonconstant gravity field Section 7.2
7.2.2 Primitive equations
Large-scale ocean general circulation models are typically based on the hydrostatic primitive equations.
Here, the vertical momentum equation is reduced to its static inviscid form with f∗= 0
∂zp=−ρ∂zΦ
=−ρ(g+∂zΦ1).(7.22)
This hydrostatic balance filters motions associated with strong vertical accelerations, such as may occur in
regions of gravitational instability. It also filters out the majority of acoustic modes, with only the Lamb
Wave remaining (see, for example, Griffies and Adcroft,2008, for further discussion). The hydrostatic
balance is modified from its traditional form for cases where the perturbation geopotential Φ1exhibits
nontrivial depth dependence. This extra term represents a potential significant modification to the usual
primitive equations of an ocean model.
Vertical integration of the hydrostatic balance (7.22) from the ocean surface to an arbitrary depth zleads
to the hydrostatic pressure
p(x,y,z,t) = pa+g
η
Z
z
ρdz+
η
Z
z
ρ∂zΦ1dz, (7.23)
where pais the pressure applied to the ocean surface from the media above the ocean (e.g., the overlying
atmosphere or ice).
Consistent with the hydrostatic balance, we drop the wf ∗term appearing in the zonal momentum
equations, thus reducing the momentum equation (7.14) to the primitive equation set
d
dt+ˆ
zf∧!u=−(∇zΦ1+ρ−1∇zp) + F(7.24)
∂zp=−ρ(g+∂zΦ1),(7.25)
where u= (u,v) is the horizontal velocity vector, and ∇z= (∂x,∂y,0) is the horizontal gradient taken on
surfaces of constant z. For a volume conserving Boussinesq fluid, such as used for CM2.1 and ESM2M we
make one final assumption for the pressure gradient, whereby the momentum equations become
d
dt+ˆ
zf∧!u=−ρ−1
o∇z(ρoΦ1+p) + F(7.26)
∂zp=−ρ(g+∂zΦ1),(7.27)
where ρois the constant reference density for a Boussinesq fluid. The Boussinesq form makes the addition
of a perturbed geopotential quite straightforward, in which it is gradients in ρoΦ1+pthat take the place of
gradients in pressure p.
7.2.3 Depth independent perturbed geopotential
The simplest case to consider is a depth independent perturbed geopotential
Φ1=Φ1(x,y,t).(7.28)
As stated earlier, this is precisely the form assumed for studies of ocean tides. In this form, we are motivated
to write the full geopotential as
Φ=g(z−h) (7.29)
where
Φ1=−g h (7.30)
introduces a perturbed geopotential height field h=h(x,y,t). Rather than z= 0, the zero of the geopotential
is now set by z=h. The impact of the perturbed geopotential is isolated to the depth integrated momentum
Elements of MOM November 19, 2014 Page 107

Chapter 7. Dynamical ocean equations with a nonconstant gravity field Section 7.2
equations, which for a Boussinesq fluid1takes the form (see Section 10.9)
ρo(∂t+fˆ
z∧)U=G−(H+η)∇(pa+psurf +ρoΦ1),(7.31)
where
U=
η
Z
−H
udz(7.32)
is the vertically integrated horizontal velocity, Gis the vertical integral of the depth dependent terms on
the right hand side of the momentum equation (7.24). Gembodies all contributions which are generally
evolving on a slower baroclinic time scale. The surface pressure is given by
psurf =g ρsurf η, (7.33)
and it represents the hydrostatic pressure at z= 0 associated with water in the region between z= 0 and
z=η. The applied pressure pais the pressure applied at the top of the ocean arising from media above the
ocean, such as the atmosphere and sea ice. To within a good approximation, we can combine the surface
pressure and geopotential terms to bring the momentum equation to the form
ρo(∂t+fˆ
z∧)U=G−(H+η)∇[pa+g ρsurf (η−h)].(7.34)
In this way, modifications to the geopotential, embodied by the perturbed geopotential height field h=
h(x,y,t), are isolated to their impacts on the horizontal pressure gradients acting on the vertically integrated
momentum field. As stated earlier, this formulation is identical to that associated with the study of ocean
tides, where in the case of tides, fluctuations in harise from astronomical perturbations to the earth’s gravity
field. For our present considerations, harises from perturbations in terrestrial masses, such as the melting
land ice on Greenland or Antarctica. In contrast to ocean tides, geoid perturbations associated with melting
land ice are not periodic. Furthermore, as evidenced by Figure 1 in Mitrovica et al. (2001), the amplitude
of geoid perturbations can be far greater than typical open ocean tide fluctuations.
Changes in the geoid associated with nontrivial h=h(x,y,t) will propagate throughout the vertically
integrated momentum field on a rapid barotropic time scale. Consequently, the ocean’s free surface will
adjust within a few days of geoid perturbations, just as it does for ocean tides. In contrast, it is unclear
how the depth dependent ocean circulation will adjust, with a general circulation model a useful tool for
considering the slower baroclinic adjustment processes.
We note that when coupling to a sea ice model, it is the effective sea level given by
ηeff=η+ pa
g ρsurf !−h(7.35)
that is to be passed from the ocean model to the sea ice model for the purpose of computing horizontal
pressure gradients acting on the ice.
1See Section 8.2 for the non-Boussinesq mass conserving form.
Elements of MOM November 19, 2014 Page 108

Chapter 8
Tidal forcing from the moon and sun
Contents
8.1 Tidal consituents and tidal forcing ..............................109
8.2 Formulation in non-Boussinesq models ............................110
8.3 Implementation in MOM ....................................110
The purpose of this chapter is to describe the formulation of lunar and solar tidal forcing implemented
in MOM. This chapter was written by Harper Simmons (hsimmons@iarc.uaf.edu) with some additions and
edits by Stephen.Griffies@noaa.gov.
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean barotropic.F90
8.1 Tidal consituents and tidal forcing
As formulated in Chapter 7(see also Marchuk and Kagan (1989)), tidal forcing appears in the momentum
equations as a depth independent acceleration. Consequently, tide dynamics can be isolated in the verti-
cally integrated momentum budget. As shown in Section 10.9.3, the equation for the vertically integrated
transport Uin a Boussinesq version of MOM takes the form (equation (10.137))
ρo(∂t+fˆ
z∧)X(dzu) = G−(H+η)∇(pa+psurf).(8.1)
In this equation, Gis the vertically integrated forcing arising from baroclinic effects, psis the pressure
associated with undulations of the surface height, pais the applied pressure from the atmosphere and sea
ice, His the depth of the ocean, and ηis the surface height deviation from a resting state with z= 0. Our
goal is to modify this equation to account for gravitational forcing that give rise to ocean tides.
Tidal forcing arising from the eight primary constituents (M2, S2, N2, K2, K1, O1, P1, Q1) (see Gill
(1982)) can be added to the forcing for Uin MOM. The formulation follows Marchuk and Kagan (1989),
by considering a tide generating potential (gηeq) with corrections due to both the earth tide (1 + k−h) and
self-attraction and loading (α). In this approach, the depth independent pressure gradient acceleration is
modified to the form
ρ−1
o∇(ps+pa)→ρ−1
o∇(ps+pa) + g∇hα η −(1 + k−h)ηeqi.(8.2)
The term ηeq is known as the equilibrium tide, and it arises from the astronomically derived gravity produc-
ing forces. It is modified by several factors. The Love numbers, kand h, named for the physicist A.L. Love,
account for the reduction of the ocean tide because of the deformation of the solid earth by tidal forces.
The Love numbers are frequency dependent, with 1 + k−hgenerally close to 0.7 (Wahr (1998)).
109

Chapter 8. Tidal forcing from the moon and sun Section 8.3
The term αin equation (8.2) accounts for a modification of the ocean’s tidal response as a result of self-
attraction and loading (SAL) (Hendershott (1972)). Self attraction is the modification of the tidal potential
as a result of the redistribution of the earth and ocean due to the equilibrium tidal forcing. Loading refers
to the depression of the earth’s crust by the mounding of tides. Calculation of the SAL term requires an
extremely cumbersome integration over the earth surface, rendering equation (8.2) an integro-differential
equation (Ray (1998)).
Instead of solving the integro-differential form of equation (8.2), MOM4 uses the scalar approximation
to SAL. We feel this is justified since our purpose in introducing tidal forcing is to study the effects of
tides on the general circulation, not the details of the tides themselves. The conjecture is that precise
calculation of the SAL term is not needed for to understand tidal effects on the general circulation. For the
scalar approximation, αis usually set between 0.940 −0.953. MOM4 uses α= 0.948. Limitations of the
scalar approximation to SAL are discussed by Ray (1998), who concluded that the scalar approximation
introduces phase errors of up to 30◦and amplitude errors of 10% into a global scale tidal simulation.
8.2 Formulation in non-Boussinesq models
The horizontal acceleration from pressure gradients is given by the two terms (see Section 10.9.4, where we
drop here the tilde notation used in that section)
ρ−1(∇zp)without tidal forcing =ρ−1∇sp+∇sΦ.(8.3)
In this equation, pis the hydrostatic pressure at a grid point, Φis the geopotential at this point, and sis the
generalized vertical coordinate. The ρ−1factor is set to ρ−1
ofor Boussinesq models, but remains nontrivial
for non-Boussinesq, pressure-based vertical coordinates in MOM. As noted in Section 8.1, gravitational
forces giving rise to ocean tides can be incorporated into MOM by adding a depth independent acceleration
throughout the water column. Following the approach used for the Boussinesq case, we add to the non-
Boussinesq pressure gradient a modification to the geopotential due to tidal acceleration
ρ−1(∇zp)with tidal forcing =ρ−1∇sp+∇sΦ+g∇hα η −(1 + k−h)ηeqi,(8.4)
where the tidal term is taken from equation (8.2). Inserting this modified acceleration into the vertically
integrated momentum equation (10.145) yields
(∂t+fˆ
z∧)X(dzρ u) = G−pb−pa
g ρo∇(pb+ρoΦb+g ρohtide),(8.5)
where
htide =α η −(1 + k−h)ηeq (8.6)
is shorthand for the tidal term, pbis the pressure at the ocean bottom, and Φb=−g H is the geopotential at
the bottom.
8.3 Implementation in MOM
The equilibrium tide is written for the nth diurnal tidal constituent as
ηeq,n =Hnsin2φcos(ωnt+λ),(8.7)
and for the nth semi-diurnal constituent as
ηeq,n =Hncos2φcos(ωnt+ 2λ),(8.8)
where φis latitude and λis longitude. Recognizing that equations (8.7) and (8.8) require the evaluation of
trigonometric functions at every grid point and every time-step, tidal forcing is introduced into MOM4 in
the following mathematically equivalent form. Making use of the identity
cos(A+B) = cos(A) cos(B)−sin(A) sin(B),(8.9)
Elements of MOM November 19, 2014 Page 110

Chapter 8. Tidal forcing from the moon and sun Section 8.3
constit name origin ω(1/day) 1 + k−h a (m)
1K1Luni-solar declinational 0.7292117 0.736 0.141565
2O1Principal lunar declinational 0.6759774 0.695 0.100661
3P1Principal solar declinational 0.7252295 0.706 0.046848
4Q1Larger lunar elliptic 0.6495854 0.695 0.019273
5M2Principal lunar 1.405189 0.693 0.242334
6S2Principal solar 1.454441 0.693 0.112743
7N2Largerl lunar elliptic 1.378797 0.693 0.046397
8K2Luni-solar declinational 1.458423 0.693 0.030684
Table 8.1: Frequencies, Love numbers, and amplitude functions for the eight principle constituents of tidal
forcing available in MOM4.
we can write the eight tidal forcing constituents as
ηeq =Σ4
n=1 hβnancos2φ[cos(ωnt)cos2λ−sin(ωnt) sin2λ]+
βn+4an+4 sin 2φ[cos(ωn+4t) cos2λ−sin(ωn+4t)sin2λ] ],(8.10)
which allows all the trigonometric functions of φand λto be precomputed. Note that we have written
βn= 1 + kn−hn. The frequencies (ωn), amplitudes (an) and Love numbers are listed in Table 8.1.
Elements of MOM November 19, 2014 Page 111

Chapter 8. Tidal forcing from the moon and sun Section 8.3
Elements of MOM November 19, 2014 Page 112
Numerical formulations
The purpose of this part of the document is to describe algorithms used to numerically solve the ocean
primitive equations in MOM. We address discretization issues for both space and time stepping the contin-
uum equations.
113

Section 8.3
Elements of MOM November 19, 2014 Page 114

Chapter 9
B and C grid discretizations
Contents
9.1 B and C grids used in MOM ...................................115
9.1.1 Variables on the B-grid .................................... 116
9.1.2 Variables on the C-grid .................................... 116
9.2 Describing the horizontal grid .................................117
9.2.1 Four basic grid points and corresponding cells ...................... 118
9.2.2 Horizontal layout of wet and dry cells ........................... 118
9.2.3 Computing the grid distances ................................ 119
9.2.4 Grid distances carried by the model ............................ 121
9.3 The Murray (1996) tripolar grid ................................121
9.4 Specifying fields and grid distances within halos ......................123
9.4.1 Interior domains ....................................... 123
9.4.2 Exterior domains ....................................... 126
9.4.2.1 Solid wall boundary conditions .......................... 126
9.4.2.2 Periodic boundary conditions ........................... 126
9.4.3 The bipolar Arctic grid .................................... 128
9.4.3.1 Fields defined at points T,U,N, and E ....................... 129
9.4.3.2 Grid distances for horizontal quarter-cells ................... 129
9.4.3.3 Grid distances for horizontal full cells ...................... 132
9.4.3.4 Summary of redundancies and halo mappings ................. 132
The purpose of this chapter is to detail the horizontal grids used in MOM as well as the specification of
field and grid values in halo regions. Details of the vertical discretization are presented in Section 10.1 (see
in particular Figure 10.1. This chapter builds from Chapter 4 in Griffies et al. (2004), with newer material
here concerned with the C-grid option now under development in MOM. Further information about the
MOM grids and topography can be found in Chapters 16 and 18 of the MOM3 Manual (Pacanowski and
Griffies,1999).
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean grid.F90
9.1 B and C grids used in MOM
The continuum partial differential equations of MOM are derived and discussed in Part I, as well as in
Griffies (2004). Bryan (1969) cast the discrete version of these equations on an Arakawa B-grid. As sum-
115

Chapter 9. B and C grid discretizations Section 9.1
marized in the review article by Griffies et al. (2000a), the B-grid allows for a reasonably accurate represen-
tation of geostrophic currents, even when running a coarse grid model. However, many recent applications
with other model codes such as GOLD, HYCOM, MITgcm, NEMO, and ROMs exploit the advantages of a
C-grid, with the following two advantages notable.
• At resolutions where the baroclinic radius is well resolved, the C-grid presents certain advantages for
rotating stratified flow over the B-grid (Section 3.2 of Griffies et al. (2000a)).1
• For coastal applications, details of the fractal land/sea boundary are critical. Use of the B-grid leads
to complexities associated with the need to distinguish between tracer and velocity cells. That is,
to have advective flow through a tracer cell requires two adjacent velocity cells. The net effect is
that narrow straights may need to be unphysically widened to facilitate advective transport. This
situation hinders the utility of the B-grid for representing complex land/sea regions, with particular
importance placed on such details for coastal modeling.
It is for these reasons that MOM, which has traditionally used exclusively a B-grid, will soon have a C-grid
option. The C-grid option is presently not available for general use, but development during late 2012 will
focus nearly exclusively on this layout, given the focus at GFDL on mesoscal eddy permitting and resolving
simulations.
9.1.1 Variables on the B-grid
Figure 9.1 illustrates the horizontal arrangement of prognostic model fields used with the B-grid. The B-
grid places both horizontal prognostic velocity components at the same point, the corner of the tracer cell.
This placement is natural when computing the Coriolis Force. However, it is unnatural for computation of
advective tracer transport or the horizontal pressure gradient force acting on velocity. The need to perform
an averaging operation when computing the horizontal pressure gradient leads to the computational mode
associated with gravity waves on the B-grid (see Section 31.1 and references cited there).
MOM follows a northeast convention, whereby the velocity is positioned at the northeast corner of the
corresponding tracer cell. With half-integer notation, the velocity U-point lives at (i+1/2,j+1/2) with
the T-point at (i,j). There are good reasons to employ the half-integer convention when representing
discrete quantities on a grid. However, we choose to avoid such notation, preferring instead to keep the
grid variable placements implied by use of the northeast convention.
The B-grid placement leads to the following placements for the discrete fields realized in MOM on the
grid.
• As density is a function of temperature, salinity, and pressure, density is naturally defined at the
tracer point. Correspondingly, so is hydrostatic pressure and the surface ocean height.
• For each tracer cell there is a corresponding velocity cell, as depicted in Figure 9.1. Fluxes through
the faces of the velocity cell are related to those through the faces of the tracer cell via remapping
operations as detailed in Chapter 15.
• The vertical velocity component is defined according to the requirements of continuity across the
tracer and velocity cells. Hence, the vertical velocity component lives at the bottom face of the corre-
sponding tracer or velocity cell. Once the horizontal grid placement is defined, the vertical position is
specified for both the grid point and the vertical velocity position. Chapter 16 of The MOM3 Manual
provides further details of the vertical grid.
9.1.2 Variables on the C-grid
Figure 9.2 illustrates the horizontal arrangement of prognostic model fields used with the C-grid. The C-
grid places the zonal velocity component on the zonal tracer cell face, and meridional velocity component
1As pointed out by Webb et al. (1998), there will potentially always be important unresolved baroclinic modes, such as in the
equatorial region. Hence, it will be very useful to have both B and C grid options in MOM to better examine the pros and cons for any
particular application.
Elements of MOM November 19, 2014 Page 116
Chapter 9. B and C grid discretizations Section 9.2
j
i
U(i,j,k)
T(i,j,k)
Figure 9.1: Illustration of how fields are placed on the horizontal B-grid used in MOM using a northeast
convention. Velocity points U(i,j,k) are placed to the northeast of tracer points T(i,j,k). Both horizontal
velocity components ui,j,k and vi,j,k are placed at the velocity point U(i,j,k). Both the tracer point and
velocity point have a corresponding grid cell region, denoted by the solid and dashed squares.
on the meridional tracer cell face. This placement is suited for computation of advective tracer transport. It
is also suited for computing the stress tensor and the horizontal pressure gradient force acting on velocity
components. However, it is not natural for computation of the Coriolis Force. The need to perform an
averaging operation to compute the Coriolis Force leads to the presence of a computational null mode
associated with geostrophically balanced flow (Adcroft et al.,1999).
Following a northeast convention, MOM places its zonal velocity component ui,j,k on the east face of
the tracer cell T(i,j), and the meridional velocity component vi,j,k at the north face of the same tracer
cell. With half-integer notation, the zonal velocity component ui,j,k lives at the (i+1/2,j) point whereas
the meridional velocity component vi,j,k lives at the (i,j+1/2) point. This C-grid convention leads to the
following placements for the discrete fields realized in MOM.
• As density is a function of temperature, salinity, and pressure, density is naturally defined at the
tracer point. Correspondingly, so is hydrostatic pressure and the surface ocean height. Indeed, all
tracer quantities from the B-grid are correspondingly on the same tracer cell using the C-grid. This
agreement means that nearly all processes associated with tracer transport have direct correspon-
dence across the B and C grids, without any changes required for the code.
• The vertical velocity component is defined according to the requirements of continuity across the
tracer cell. Hence, the vertical velocity component lives at the bottom face of the tracer cell. Addi-
tionally, it is necessary to prescribe a means to compute the vertical velocity used to advect zonal and
meridional velocity. This velocity component is prescribed in terms of averages of the corresponding
tracer grid vertical velocity component.
• The B-grid velocity point, which sits at the corner of the tracer cell, is the natural position for the
vertical component of vorticity
ζ=ˆ
z·(∇ ∧ v) = ∂v
∂x −∂u
∂y .(9.1)
When writing the velocity equation in a vector-invariant form (see Section 4.4.4 of Griffies (2004)), as
in GOLD, MITgcm, and NEMO, the vorticity point is also the natural location for defining the Coriolis
parameter, f, for use in computing the total vorticity ζ+f.
9.2 Describing the horizontal grid
With the use of generalized horizontal coordinates in MOM, there are many grid distances required to
compute discrete derivatives, integrals, and areas. When constructing the grid distances in MOM, we
Elements of MOM November 19, 2014 Page 117

Chapter 9. B and C grid discretizations Section 9.2
j
i
X
q(i,j,k)
T(i,j,k)
ui,j,k
vi,j,k
Figure 9.2: Illustration of how fields are placed on the horizontal C-grid used in MOM. As for the B-
grid, MOM’s convention is that the zonal velocity component ui,j,k sits at the east face of the tracer cell
T(i,j), and the meridional velocity component vi,j,k sits at the north face of the tracer cell T(i,j,k). This
convention follows the northeast convention also used for the B-grid. However, note that the notion of a
corresponding “velocity cell” that surrounds each velocity component is less tenable for the C-grid.
aimed to design a structure useful for both B and C-grids. It is with this goal in mind that the names for the
grid distances in the grid generator module are distinct from grid distances used in MOM’s grids module.
We note the mapping between the two grid conventions in the following.
9.2.1 Four basic grid points and corresponding cells
On both the B and C grids, it is useful to consider the tracer cell as the basic cell, and all other cells in
their relation to the tracer cell. Given this convention, there are four basic grid points and corresponding
grid cells that can be identified: T(i,j),E(i,j),C(i,j), and N(i,j). Figure 9.3 illustrates these points as
oriented according to the tracer cell.
•T(i,j) is the usual tracer point that is surrounded by a tracer cell region.
•C(i,j) sits at the northeast corner of the tracer cell, and so is equivalent to the B-grid velocity point
U(i,j) and the C-grid vorticity point q(i,j).
•E(i,j) sits at the east face of the tracer cell and so is where the zonal velocity component ui,j,k sits on
the C-grid.
•N(i,j) sits at the north face of the tracer cell and so is where the meridional velocity vi,j,k sits on the
C-grid.
The geographical coordinates of these four points is sufficient to place them on the discrete lattice.
9.2.2 Horizontal layout of wet and dry cells
The ocean land-sea boundary is fractal in nature, with each refinement in resolution introducing new
smaller scale features. The representation of the land-sea boundary is thus fundamental to the utility
of an ocean model for realistic simulations. We outline in this section the arrangement of grid variables on
both the B and C grids of MOM, with reference made to Figure 9.4.
Figure 9.4 depicts an array of tracer cells, each with a corresponding northeast corner point denoted by
an X. On the B-grid, the northeast corner is where both velocity components, ui,j,k and vi,j,k are located,
whereas for the C-grid this is where the vorticity ζi,j,k sits. Any corner point that touches a land cell will
have both components of the B-grid velocity set to zero. Arrows crossing the zonal and meridional faces
of a cell depict the tracer flux moving across the cell faces. There are no arrows drawn entering land, due
to the no-normal flow boundary condition. On the C-grid, arrows also represent the horizontal velocity
components. For both the B and C grids, arrows depict the advective and diffusive tracer flux components.
A fundamental distinction between the B and C grids is their treatment of narrow straights and through-
flows. We illustrate this distinction by examining the advective tracer transport through tracer cells T(3,2)
Elements of MOM November 19, 2014 Page 118

Chapter 9. B and C grid discretizations Section 9.2
j
i
C(i,j,k)
N(i,j,k)
T(i,j,k)
E(i,j,k)
Figure 9.3: The four basic grid points for the B and C grids that surround the fundamental tracer cell.
T(i,j,k) is the usual tracer point; C(i,j,k) is the corner point; E(i,j,k) is on the east side; and N(i,j,k)
is on the north side. The corner point is the position for the two horizontal velocity components for the
B-grid, whereas it is the vorticity position on the C-grid. The east and north points are the position of the
zonal and meridional velocity components on the C-grid.
and T(4,2). For these cells, the B-grid horizontal velocity components are zero, since the corner points
touch land. Hence, there is zero zonal advective flux through these cells for the B-grid. We conclude that
to allow advective tracer transport on the B-grid requires no less than two adjacent ocean tracer cells. In
contrast, the C-grid allows for advective tracer transport through a single tracer cell, and so has nonzero
advective tracer transport through tracer cells T(3,2) and T(4,2).
9.2.3 Computing the grid distances
To support a discrete calculus for casting the model equations on a grid, we must specify distances between
grid points and the grid cells. Knowing the geographical position of the four basic grid points as well as
the vertices of their corresponding grid cells is not sufficient. In addition, we need information regarding
the metric or stretching functions specific to the coordinate system used to tile the sphere.
The traditional approach is to use spherical coordinates for tiling the sphere. In this method, the dis-
tance between two points zonally displaced a finite distance from one another is given by the analytic
formula
∆x[a,b] = Rcosφ
λb
Z
λa
dλ= (Rcosφ)(λb−λa),(9.2)
and the distance between two points along a line of constant longitude is given by
∆y[a,b] = R
φb
Z
φa
dφ=R(φb−φa).(9.3)
Writing these expressions in a general manner leads to the generalized zonal and generalized meridional
distance given by
∆x[a,b] =
ξ(a)
1
Z
ξ(b)
1
h1dξ1(9.4)
∆y[a,b] =
ξ(a)
2
Z
ξ(b)
2
h2dξ2,(9.5)
Elements of MOM November 19, 2014 Page 119
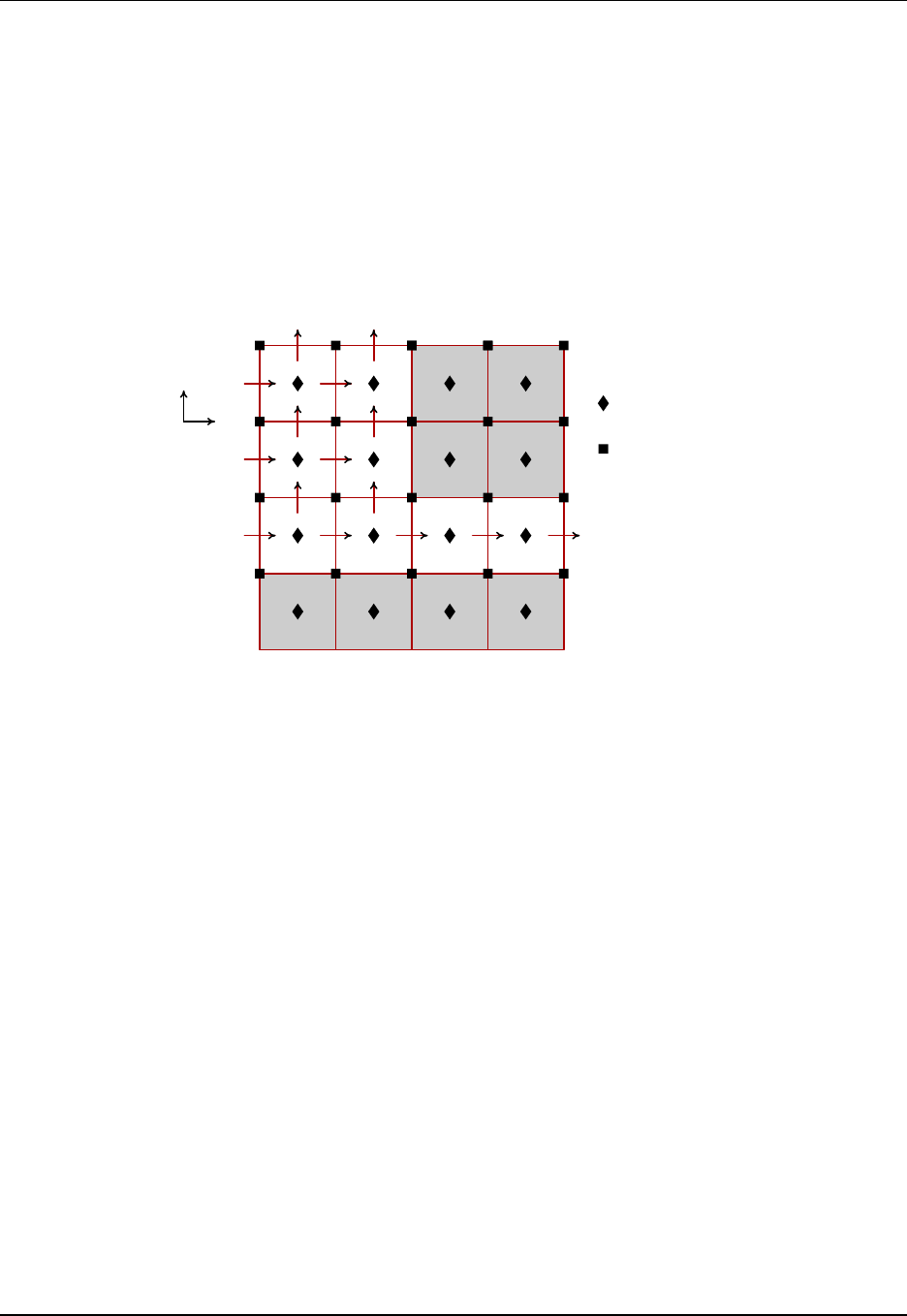
Chapter 9. B and C grid discretizations Section 9.2
Tracer cells T(i,j) with fluxes and land/sea masking
=corner point
=B-grid velocity
=C-grid vorticity
=tracer point
j
i
T(1,4) T(2,4) T(3,4) T(4,4)
T(1,3) T(2,3) T(3,3) T(4,3)
T(1,2) T(2,2) T(3,2) T(4,2)
T(1,1) T(2,1) T(3,1) T(4,1)
Figure 9.4: Shown here is a 4x4 region of a horizontal domain of tracer cells T(i,j), with ocean cells (un-
shaded) and land land cells (shaded). The notional tracer “point” is depicted by a solid triangle. Each
tracer cell has a corresponding northeast corner point depicted by a solid square. On the B-grid, the north-
east corner is where both velocity components are located. Any corner point that touches a land cell will
have the B-grid velocity set to zero. For the C-grid, the corner point is the vorticity location. It is also the
location of the shearing rate of strain eS(Chapter 25), which is set to zero for a free-slip C-grid model (Sec-
tion 25.6.2). Arrows crossing the zonal and meridional faces of a cell depict the tracer flux moving across
the cell faces. On the C-grid, these arrows are also where the horizontal velocity components are placed.
For both the B and C grids, the arrows depict the advective and diffusive tracer flux components. There
are no arrows drawn crossing into or from land cells, due to the no-normal flow boundary condition. For
tracer cells T(3,2) and T(4,2), the B-grid velocity components are zero, so there is zero zonal advective
flux through these cells on the B-grid. In contrast, the C-grid has advective transport through these cells.
This is a fundamental distinction between the B and C grids in their treatment of narrow straights and
throughflows.
Elements of MOM November 19, 2014 Page 120

Chapter 9. B and C grid discretizations Section 9.3
where (ξ1,ξ2) represent generalized orthogonal coordinates, and (h1,h2) are the stretching functions spe-
cific to the coordinate system. They determine the distance between two infinitesimally close points via the
line element formula
(ds)2= (h1dξ1)2+ (h2dξ2)2.(9.6)
With dx=h1dξ1and dy=h2dξ2, the line element formula takes the form of the usual Cartesian expression
(ds)2= (dx)2+ (dy)2.(9.7)
MOM makes use of dxand dy, with units of metre, to allow for cleaner expressions of length, area, and
volume.
It is not possible to perform the distance integrals analytically for an arbitrary general orthogonal co-
ordinate system. Therefore, approximations must be made. Indeed, in MOM3 the analytical form for the
zonal distance was actually approximated according to
∆x≈Rcosφ(9.8)
where φ= (φ1+φ2)/2 (see discussion in Section 39.6 of Pacanowski and Griffies (1999)). Assuming infor-
mation is available only at the grid points and at the cell vertices, MOM chooses to compute the distance
between two points along a generalized zonal direction (i−line) as
∆x[a,b] = ξ(a)
1−ξ(b)
1h(a)
1+h(b)
1/2.(9.9)
Likewise, the distance along a generalized meridional direction (j−line) is computed as
∆y[a,b] = ξ(a)
2−ξ(b)
2h(a)
2+h(b)
2/2.(9.10)
9.2.4 Grid distances carried by the model
Given coordinates for the grid points and grid vertices, as well as the stretching functions evaluated at these
points, we can use the approximate expressions (9.9) and (9.10) to compute distances between the T,U,N,
and E points. Figure 9.5 shows the notation for the grid distances that define four quarter-cells splitting up
each tracer and velocity cell. Shown is the notation used in the grid descriptor module as well as that used in
MOM. The full dimensions of the tracer and velocity cells are shown in Figure 9.6, where again the distances
computed in the grid descriptor module are translated into the grid distances used in MOM. Finally, Figure
9.7 shows the distances specifying the separation between adjacent tracer and velocity points.
9.3 The Murray (1996) tripolar grid
The Murray (1996) tripolar grid (see his Figure 7) has been a focus of ocean climate model development
with MOM and GOLD during 2001-2002. This grid is comprised of the usual spherical coordinate grid
southward of a chosen latitude circle, typically taken at 65◦N. This part of the grid has a single pole over
Antarctica, which is of no consequence to the numerical ocean climate model. In the Arctic region, the
Murray grid places a bipolar region with two poles situated over land, and so these poles are also of no
consequence to the numerical ocean model.
Figure 9.8 illustrates the grid lines used to discretize the ocean equations in the Arctic using Murray’s
grid. The placement of discrete model tracer and velocity points along the bipolar grid lines is schemati-
cally represented in Figure 9.9. The arrangement of northern and eastern vector components centered on
the tracer cell faces is shown in Figure 9.10. Details for how to transfer information across the bipolar prime
meridion located along the j=nj line are provided in Section 9.4.
Motivation for choosing the Murray (1996) grid includes the following:
• It removes the spherical coordinate singularity present at the geographical north pole.
Elements of MOM November 19, 2014 Page 121
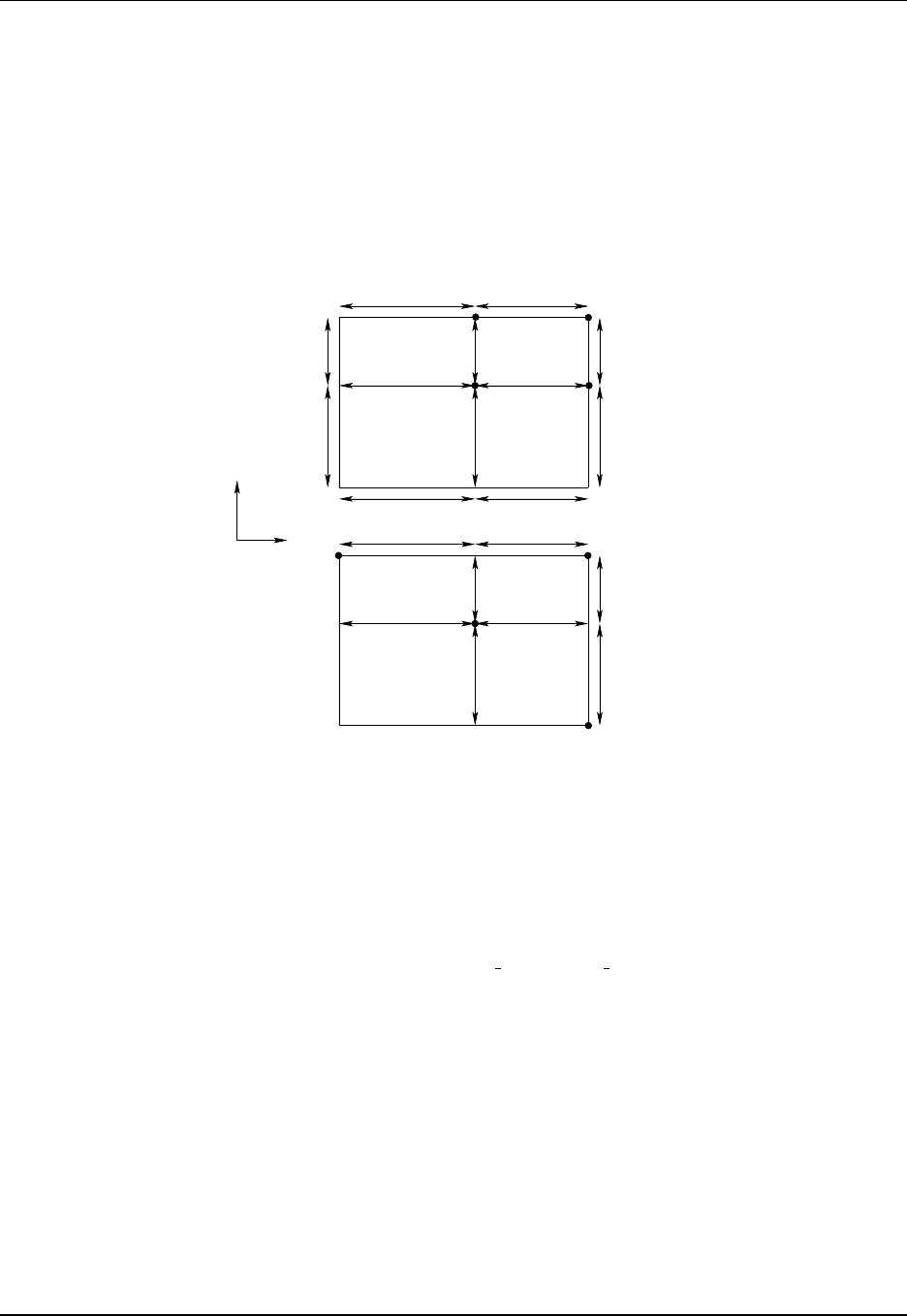
Chapter 9. B and C grid discretizations Section 9.3
dts(i,j)
dus(i,j)
dun(i,jï1)
duw(i,j)due(iï1,j)
T(i,j)
T(i,j)
C(i,j)
E(i,j)
dtw(i,j) dte(i,j)
i
j
(2,2)
(2,1)
ds_20_21_T
ds_21_22_T
ds_10_11_T
ds_11_12_T
ds_00_01_T
ds_01_02_T
ds_02_12_T ds_12_22_T
ds_01_11_T
ds_00_10_T ds_10_20_T
(1,1)
N(i,j)
(1,2)(0,2)
(0,0) (2,0)
(1,0)
(0,1)
ds_11_21_T
U(iï1,j)
dtn(i,j)
U(i,j)
U(i,jï1)
Figure 9.5: Upper panel: Grid distances used to measure the distance between the four fundamental grid
points shown in Figure 9.3. These distances are computed in the FMS grid descriptor module. The naming
convention is based on a Cartesian grid with the origin at the lower left corner of the tracer cell at (0,0),
the upper right hand corner is (2,2), the center at (1,1), and all other points set accordingly. The distances
are then named as distances between these grid points. Note that each tracer cell has a local Cartesian
coordinate set as here, and so there is redundancy in the various grid distances. Lower panel: when read
into MOM, the grid distances set the distance between the tracer and velocity points used in the model
(Figure 9.1) and the sides of the corresponding grid cells. A translation of the upper panel distance names
to those used in MOM is made within the module ocean core/ocean grid.F90. Note that the names in
the lower panel are chosen to correspond to a B-grid, though the lengths are used for both B and C grid
calculations.
Elements of MOM November 19, 2014 Page 122
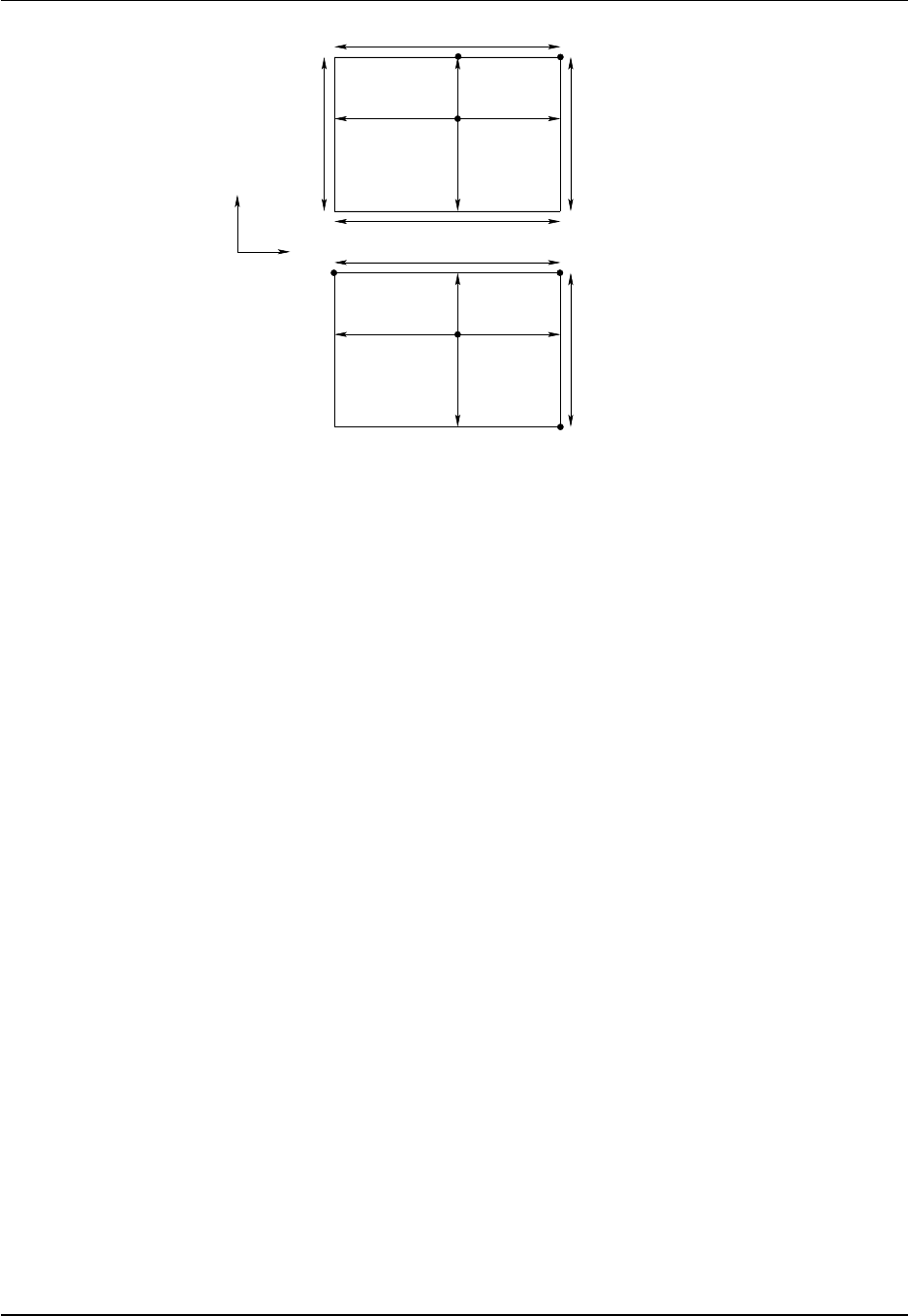
Chapter 9. B and C grid discretizations Section 9.4
C(i,j)
T(i,j)
T(i,j)
U(i,jï1)
dxt(i,j)
dyt(i,j)
dyte(i,j)=dyun(i,jï1)
dxtn(i,j) = dxue(iï1,j)
ds_02_22_T
i
j
(0,1)
ds_10_12_T
ds_01_21_T
(2,2)
(2,0)
(1,0)
ds_00_02_T ds_20_22_T
ds_00_20_T
(0,2)
(0,0)
(2,1)
(1,1)
(1,2)
U(iï1,j) U(i,j)
Figure 9.6: Grid cell distances used for computing the area of a grid cell. These dimensions are related
to the fundamental quarter-cell dimensions shown in Figure 9.5. Upper panel: distances computed in the
FMS grid descriptor module. Lower panel: names of the distances used in MOM. Note that the names in
the lower panel are chosen to correspond to a B-grid, though the lengths are used for both B and C grid
calculations.
• It maintains the usual spherical coordinate grid lines for latitudes southward of the Arctic region,
thus simplifying analysis.
• The grid resolution in the Arctic is more isotropic than the alternative approach of a displaced pole
used in simulations with POP (Smith et al.,1995), with isotropic grids generally preferred for numer-
ical accuracy.
• It is locally orthogonal, and so can be used with the MOM generalized horizontal coordinates.
• A similar global grid has been successfully run by the GOLD model code at GFDL (Dunne et al.,
2012), as well as the European NEMO modeling group (Madec and Imbard,1996).
9.4 Specifying fields and grid distances within halos
MOM has been designed to run on multiple parallel processors. The computation of finite derivative oper-
ators requires the passage of information across processor boundaries. In particular, the decomposition of
the model’s global domain into multiple local domains requires that fields and grid information from one
local domain be mapped to halos of adjacent local domains. For second order numerics, the calculation of
derivatives on the boundary of a local domain requires information within one grid row halo surrounding
the local domain. Higher order numerics require larger halos.
9.4.1 Interior domains
Within the interior of the ocean model, away from global boundaries, the mapping between domains is
performed using an FMS utility that fills the halo points for one local domain using information available
to another local domain. Figure 9.11 illustrates this basic point. Shown is a central processor, arbitrarily
labelled PE(0), and a surrounding hatched region representing halo points. The width of the halo is a
function of the numerics used in the model. For second order numerics, a halo width of a single point is
Elements of MOM November 19, 2014 Page 123
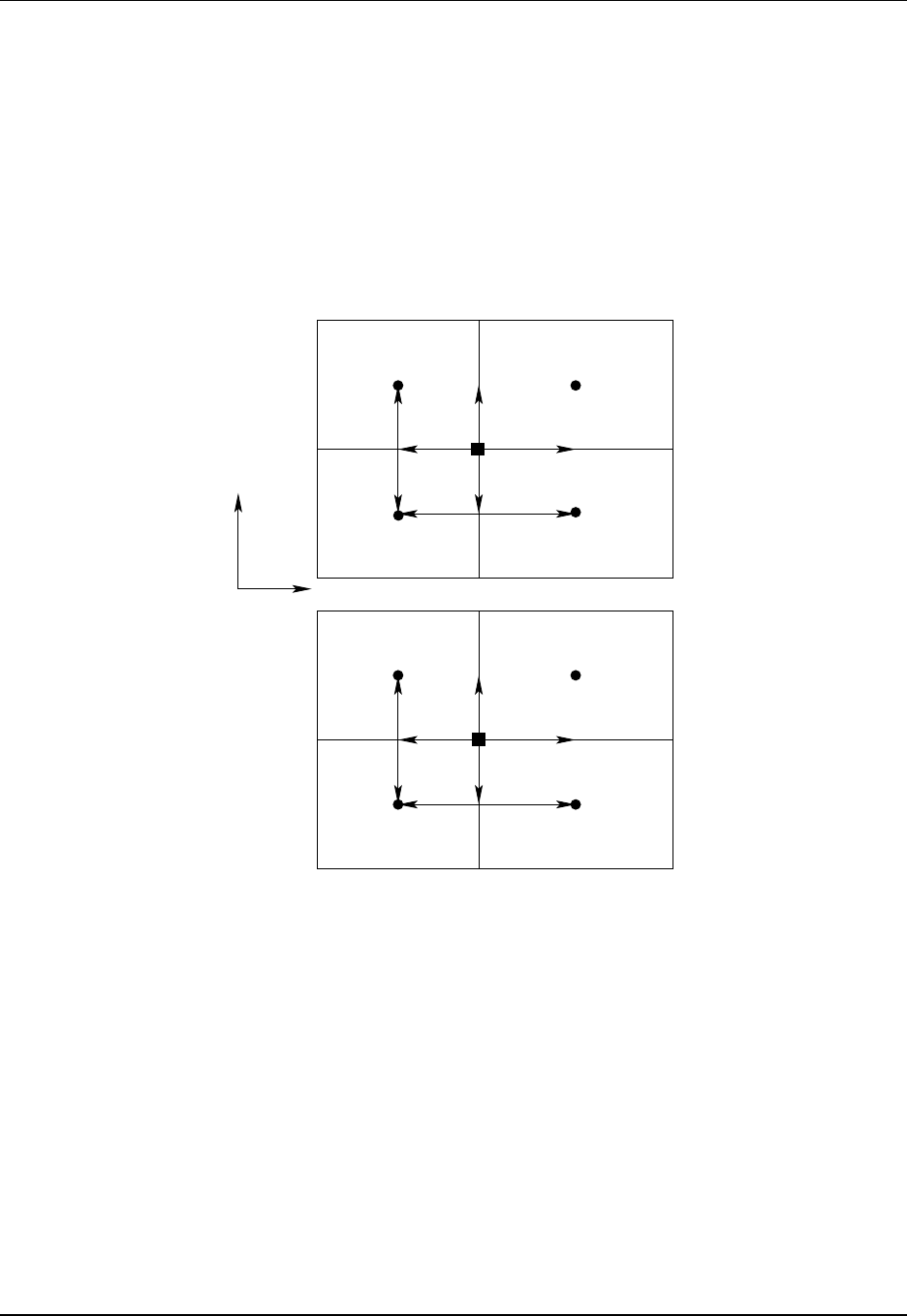
Chapter 9. B and C grid discretizations Section 9.4
T(i,j)
T(i+1,j+1)
T(i,j)
T(i+1,j+1)
dytn(i,j)
dxte(i,j)
dxu(i,j)
dyu(i,j)
C(i,j)
U(i,j)
T(i+1,j)
T(i,j+1)
T(i,j+1)
T(i+1,j)
j
i
ds_00_20_C
ds_00_02_C
Figure 9.7: Distances between fundamental grid points (upper panel) as computed by the grid descriptor
module. These distances are taken into MOM and used to set the distances between tracer and velocity
points (lower panel). Note that the names are chosen to correspond to a B-grid, though the lengths are used
for both B and C grid calculations.
Elements of MOM November 19, 2014 Page 124
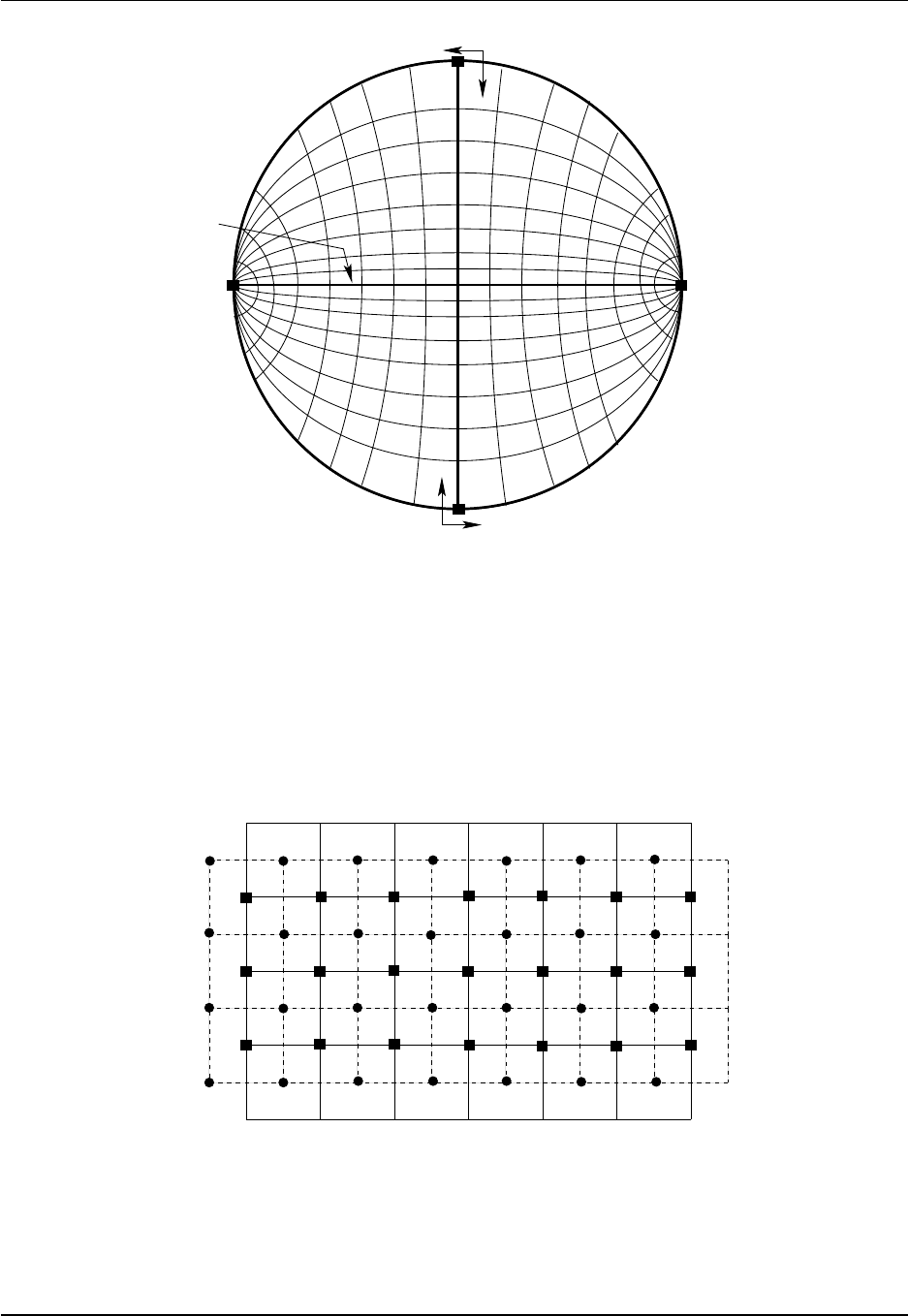
Chapter 9. B and C grid discretizations Section 9.4
j
i
j
i
i=0=ni
i=ni/4
i=3ni/4
j=nj
i=ni/2
Figure 9.8: Illustration of the grid lines forming the bipolar region in the Arctic. This figure is taken
after Figure 7 of Murray (1996). The thick outer boundary is a line of constant latitude in the spherical
coordinate grid. This latitude is typically at the latitude nearest to 65◦N. As in the spherical coordinate
region, lines of constant imove in a generalized eastward direction. They start from the bipolar south pole
at i= 0, which is identified with i=ni. The bipolar north pole is at i=ni/2. As shown in Figure 9.9,
the poles are centered at a velocity point. Lines of constant jmove in a generalized northward direction.
The bipolar prime-meridion is situated along the j-line with j=nj. This line defines the bipolar fold that
bisects the tracer grid. Its fold topology causes the velocity points centered along j=nj to have a two-fold
redundancy (see Figure 9.9 for more details).
T(ni,njï1)
T(niï1,njï1)
T(niï1,nj) T(ni,nj) T(nj,ni+1)
U(niï1,njï1) U(ni,njï1)
U(niï1,nj) U(ni,nj)
T(6,njï1)
T(5,njï1)T(4,njï1)
T(3,njï1)T(2,njï1)T(1,njï1)
T(6,nj)T(5,nj)
T(4,nj)
T(3,nj)
T(2,nj)
T(1,nj)
U(6,nj)
U(5,nj)U(4,nj)
U(3,nj)
U(2,nj)
U(1,nj)
U(6,njï1)U(5,njï1)
U(4,njï1)U(3,njï1)
U(2,njï1)
U(1,njï1)
T(10,nj)
T(9,nj)T(8,nj)
T(7,nj)
T(7,njï1) T(8,njï1) T(9,njï1) T(10,njï1)
U(10,njï1)U(9,njï1)U(8,njï1)U(7,njï1)
U(10,nj)
U(9,nj)
U(8,nj)
U(7,nj)
U(6,nj)
U(6,njï1)
T(njï1,ni+1
)
T(0,njï1)
T(0,nj)
U(0,njï1)
Figure 9.9: Schematic representation of the tracer and velocity cells on the bipolar grid shown in Figure
9.8. The global computational domain consists of ni = 12 i-points for this example. The j=nj line bisects
the tracer grid, which means there are redundant velocity points along this line. Along an i−line of velocity
points, velocity cells with i=ni/2 live at the bipolar north pole, whereas velocity cells with i= 0 = ni live
at the bipolar south pole.
Elements of MOM November 19, 2014 Page 125
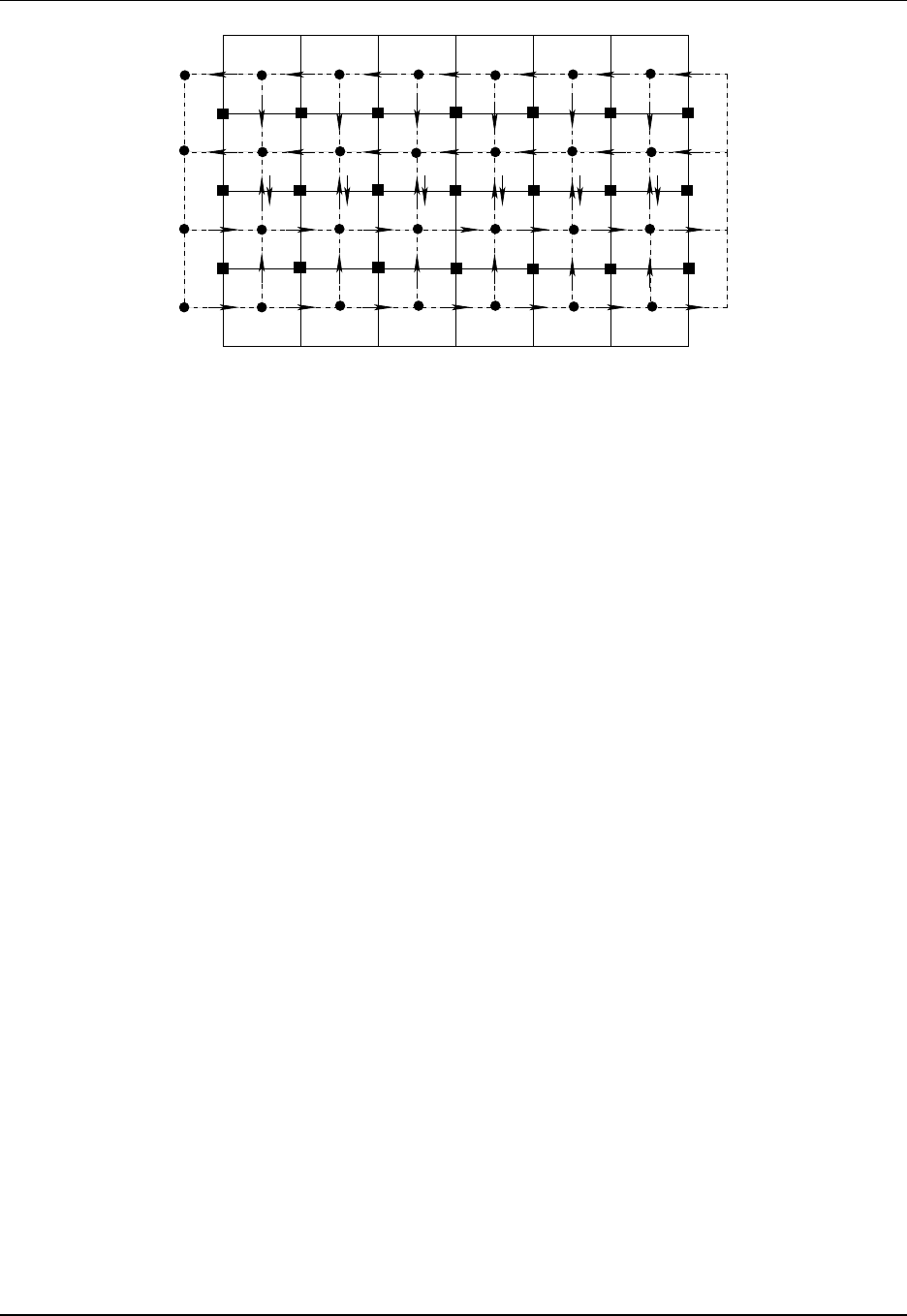
Chapter 9. B and C grid discretizations Section 9.4
E(0,njï1) E(1,njï1) E(2,njï1) E(3,njï1) E(4,njï1) E(5,njï1) E(6,njï1)
E(0,nj) E(1,nj) E(2,nj) E(3,nj) E(4,nj) E(5,nj) E(6,nj)
E(7,njï1) E(8,njï1) E(9,njï1) E(10,njï1) E(niï1,njï1) E(ni,njï1)E(6,njï1)
E(6,nj) E(7,nj) E(8,nj) E(9,nj) E(10,nj) E(niï1,nj) E(ni,nj)
N(1,njï1) N(2,njï1) N(3,njï1) N(4,njï1) N(5,njï1) N(6,njï1)
N(1,nj) N(2,nj) N(3,nj) N(4,nj) N(5,nj) N(6,nj)
N(7,nj) N(8,nj) N(9,nj) N(10,nj) N(niï1,nj) N(ni,nj)
N(8,njï1) N(10,njï1)N(9,njï1)N(7,njï1) N(niï1,njï1) N(ni,njï1)
Figure 9.10: Schematic representation of fields living at the north and east faces of the tracer cells as
configured using the bipolar grid shown in Figure 9.8. Typical fields of this sort are diffusive and advective
tracer flux components, and so they are components to a vector field, hence the vector notation. The global
computational domain consists of ni = 12 i-points for this example. The j=nj line bisects the tracer grid,
which means there are redundant velocity points along this line. Along an i−line of velocity points, velocity
cells with i=ni/2 live at the bipolar north pole, whereas velocity cells with i=0=ni live at the bipolar
south pole.
sufficient, whereas fourth order numerics requires two grid points in a halo. The values of fields and grid
factors within the halo are transmitted from the surrounding processors to PE(0) in order for PE(0) to time
step its portion of the ocean equations discretized on its local domain.
9.4.2 Exterior domains
For processors whose boundary touches the global model boundary, it is necessary to specify whether the
global boundary is a solid wall as in a sector model, periodic as in a zonal channel, or folded as in the
bipolar grid of Murray (1996). Each of these three topologies requires special consideration of the mpp code
used for transmitting information across processor boundaries. The information about grid topology is
defined in the grid specification file during the preprocessing step used to create the grid. We focus here on
the three common topologies supported by MOM. A fourth case, radiating open boundaries, is discussed
separately in chapter 16 (see also Herzfeld et al. (2011)).
9.4.2.1 Solid wall boundary conditions
For a solid wall boundary condition, all fluxes passing across the walls are zeroed out via masks, and fields
within the solid wall are either trivial or masked. Hence, no halo updates are necessary for fields and fluxes
at solid walls. However, it is important to specify self-consistent grid distances separating points within
the solid wall from those within the model’s computational domain. The reason is that various remapping
operators require grid distances be well defined for all points within the computational domain, including
those distances reaching into the halo. See Chapter 15 for details of remapping operators. For this reason,
we extend the grid into the solid wall halo so that resolution in this region is given by the resolution between
the two nearest interior points.
9.4.2.2 Periodic boundary conditions
Zonally periodic channels (x-cyclic) are commonly run for idealized studies. Additionally, for realistic
global domains, the zonal direction is periodic. Meriodionally periodic (y-cyclic) domains may also be of
interest for simulations on an f−plane or β-plane. For these reasons, we need to specify grid factors within
the halo assuming periodicity at the global domain boundary.
Elements of MOM November 19, 2014 Page 126
Chapter 9. B and C grid discretizations Section 9.4
halo for PE(0)
PE(2)
PE(1)
PE(0)
PE(4)
PE(5)
PE(3)
Figure 9.11: Elements of halos needed for computing finite difference operators on a local or computational
domain. The hatched region is comprised of halo points needed for the processor labelled PE(0) in order to
time step its equations. The halo values must be transmitted from the surrounding processors, since they
live outside of PE(0)’s local or computational domain. The union of the halo region plus the computational
domain defines the data domain. Fields that must be known in both the halo region and computational
domain have their array sizes set by the data domain. Most fields in MOM are routinely dimensioned over
the data domain, even if their halos values are never required.
Elements of MOM November 19, 2014 Page 127

Chapter 9. B and C grid discretizations Section 9.4
T(1,j) T(2,j) T(3,j) T(niï1,j) T(ni,j)
T(4,j)
U(1,j) U(2,j) U(3,j) U(4,j) U(niï1,j) U(ni,j)
T(ni+1,j)
U(0,j)
T(0,j)
Figure 9.12: A zonally periodic array of tracer and velocity (assuming B-grid placements) points with a
single halo point. In this example there are ni = 6 points in the global computational domain, and halo = 1
point in the surrounding halo region. The cyclic mapping leads us to specify halo points with values
Ti=0,j =Ti=ni,j ,Ti=ni+1,j =Ti=1,j , and Ui=0,j =Ui=ni,j.
We focus here on the needs of the more common zonally periodic boundary conditions, and refer to
Figure 9.12. The same considerations hold for y-cyclic conditions. For either case, we envision the grid
wrapped onto itself in the appropriate direction. With second order numerics, computation of the prog-
nostic tracer in grid cells Ti=1,j requires information regarding Ti=0,j. Likewise, Ti=ni,j requires information
about Ti=ni+1,j . Higher order numerics will need to reach out further.
First consider the eastern boundary of the domain where i=ni. For a single grid halo, we need to
specify values of fields living at the T,E,N, and Cpoints at i=ni + 1 (recall Figures 9.1 and 9.3 where the
Cpoint is equivalent to the B-grid Upoint). Zonal periodicity renders the equalities
Tni+1,j =T1,j (9.11)
Eni+1,j =E1,j (9.12)
Nni+1,j =N1,j (9.13)
Cni+1,j =C1,j .(9.14)
More generally, halo points with ni < i ≤ni +halo acquire the x-cyclic mapping
Ti,j =Ti−ni,j (9.15)
Ei,j =Ei−ni,j (9.16)
Ni,j =Ni−ni,j (9.17)
Ci,j =Ci−ni,j .(9.18)
At the western boundary, similar considerations lead to halo points 1 −halo ≤i < 1 mapped to interior
points according to
Ti,j =Ti+ni,j (9.19)
Ei,j =Ei+ni,j (9.20)
Ni,j =Ni+ni,j (9.21)
Ci,j =Ci+ni,j .(9.22)
9.4.3 The bipolar Arctic grid
The ideas considered for the cyclic case are now generalized to the more complex topology of the Murray
(1996) bipolar grid shown in Figures 9.8 and 9.9. In particular, Figures 9.9 and 9.10 allow us to deduce
the mappings between related points on the grid. We focus here on the B-grid naming conventions, and
assume that both horizontal velocity components both sit at the corner point C. However, C-grid relations
follow by placing the zonal velocity component at the east point, E, and meridional velocity component at
the north point, N.
Elements of MOM November 19, 2014 Page 128

Chapter 9. B and C grid discretizations Section 9.4
9.4.3.1 Fields defined at points T,U,N, and E
The generalized zonal direction (along a constant i-line) is treated with the x-cyclic conditions shown Figure
9.12. It is the bipolar prime meridion along the j−line with j=nj that introduces the most subtle issues.
This line bisects the tracer grid. Relating points across the prime meridion requires knowledge of the
tensorial nature of the field being considered. In particular, scalar fields map without a change in sign,
whereas components of a vector field have a sign change.
The U−points contain a two-fold redundancy of points along the j=nj line. For scalars living at these
points, such as some grid factors, we have the identity
Ui,nj =Uni−i,nj.(9.23)
Likewise, scalars living at the northern face of a tracer cell contain a two-fold redundancy of points along
the j=nj line so that
Ni,nj =Nni−i+1,nj .(9.24)
For vector components living at U−points, such as the B-grid horizontal velocity field, we associate transi-
tion across the j=nj meridion with a sign change
ui,nj =−uni−i,nj (9.25)
vi,nj =−vni−i,nj.(9.26)
This sign change takes the right handed orientation into a right handed orientation across the meridion.
Likewise, for components of vector fluxes living at the north face of a tracer cell, we have
Fn
Ni,nj =−Fn
Nni−i+1,nj .(9.27)
Note that numerical roundoffmay compromise these equalities in the model. Such compromise will gener-
ally make the model energetics appear to be larger than when running with the spherical grid, or with the
tripolar grid with the fold closed (debug tripolar =.true.).
Moving along a j-line, halo points for scalar fields with nj < j ≤nj +halo are evaluated according to the
following rules
Ti,j =Tni−i+1,2nj−j+1
Ui,j =Uni−i,2nj−j
Ni,j =Nni−i+1,2nj−j
Ei,j =Eni−i,2nj−j+1
for nj < j ≤nj +halo (9.28)
Vector components living at these points have the same index mapping along with a sign flip for the field
values.
9.4.3.2 Grid distances for horizontal quarter-cells
Grid distances must also be specified in halo points. Some distances also maintain redundancy relations.
Since grid distances are taken between T,U,N, or E points, their redundancy relations and halo mappings are
determined by those of their endpoints. We start by considering the grid factors defining the dimensions
of quarter-cells defined in Figure 9.5. These require the most care. Figure 9.13 illustrates the placement
of these factors on the bipolar grid. Immediately we see that the two-fold redundancy in the velocity cells
Ui,nj leads to the two-fold redundancy in grid cell distances
duei,nj =duwni−i,nj (9.29)
duwi,nj =dueni−i,nj (9.30)
duni,nj =dusni−i,nj (9.31)
dusi,nj =dunni−i,nj.(9.32)
Now consider the mappings needed to evaluate distances within halos. First consider the distances
associated with the tracer cells. By definition, dtei,jmeasures the distance between the tracer point Ti,j
Elements of MOM November 19, 2014 Page 129

Chapter 9. B and C grid discretizations Section 9.4
and its “eastern” neighbor Ei,j , and dtwi,jis the distance between Ti,j with its “western” neighbor Ei−1,j ,
where “eastern” and “western” are in a generalized sense. Mathematically, these distances are
∆x(Ti,j ,Ei,j) = dtei,j(9.33)
∆x(Ti,j ,Ei−1,j ) = dtwi,j(9.34)
where ∆x(A,B) is the distance between points Aand Bcomputed according to the generalized zonal distance
in equation (9.9). The question is how to map these distances across the bipolar fold. To do so, we note that
if we are in a halo region where nj < j ≤nj +halo, then the scalar mappings given by equation (9.28) lead to
∆x(Ti,j ,Ei,j) = ∆x(Tni−i+1,2nj−j+1,Eni−i,2nj−j+1) (9.35)
∆x(Ti,j ,Ei−1,j ) = ∆x(Tni−i+1,2nj−j+1,Eni−i+1,2nj−j+1).(9.36)
Comparison of these equalities with the definitions of dte and dtw then leads to the halo cell relations
dtei,j=dtwni−i+1,2nj−j+1
dtwi,j=dteni−i+1,2nj−j+1)for nj < j ≤nj +halo (9.37)
Distances to the northern and southern faces of the tracer cell, dtn and dts, are defined by
∆y(Ti,j ,Ni,j) = dtni,j(9.38)
∆y(Ti,j ,Ni,j−1) = dtsi,j(9.39)
where ∆yis the generalized meridional distance given by equation (9.10). Equation (9.28) indicate that
within the halo region nj < j ≤nj +halo,
∆y(Ti,j ,Ni,j) = ∆y(Tni−i+1,2nj−j+1,Nni−i+1,2nj−j) (9.40)
∆y(Ti,j ,Ni,j−1) = ∆y(Tni−i+1,2nj−j+1,Nni−i+1,2nj−j+1).(9.41)
Comparison of these equalities with the definitions of dtn and dts leads to the halo cell relations
dtni,j=dtsni−i+1,2nj−j+1
dtsi,j=dtnni−i+1,2nj−j+1)for nj < j ≤nj +halo (9.42)
Velocity cell distances are defined by
∆x(Ui,j ,Ni+1,j ) = duei,j(9.43)
∆x(Ui,j ,Ni,j) = duwi,j(9.44)
∆y(Ui,j ,Ei,j+1) = duni,j(9.45)
∆y(Ui,j ,Ei,j) = dusi,j(9.46)
Equation (9.28) indicate that within the halo region nj < j ≤nj +halo,
∆x(Ui,j ,Ni+1,j ) = ∆x(Uni−i,2nj−j,Nni−i,2nj−j) (9.47)
∆x(Ui,j ,Ni,j) = ∆x(Uni−i,2nj−j,Nni−i+1,2nj−j) (9.48)
∆y(Ui,j ,Ei,j+1) = ∆x(Uni−i,2nj−j,Eni−i,2nj−j) (9.49)
∆y(Ui,j ,Ei,j) = ∆x(Uni−i,2nj−j,Eni−i,2nj−j+1),(9.50)
which then leads to the halo cell relations
duei,j=duwni−i,2nj−j
duwi,j=dueni−i,2nj−j
duni,j=dusni−i,2nj−j
dusi,j=dunni−i,2nj−j
for nj < j ≤nj +halo (9.51)
Elements of MOM November 19, 2014 Page 130
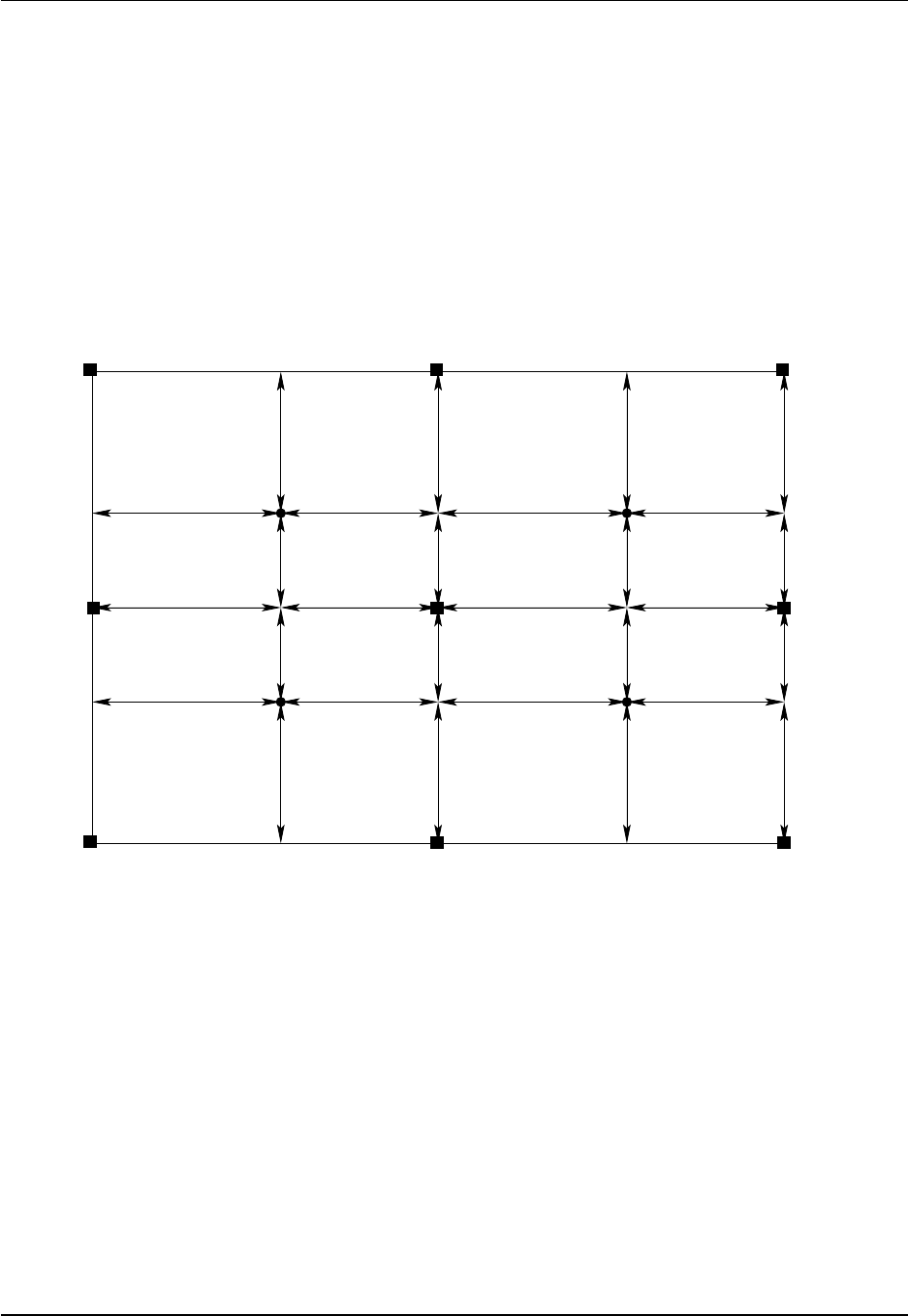
Chapter 9. B and C grid discretizations Section 9.4
T(1,nj)
dtn(1,nj)
U(1,njï1)
T(ni/2,nj)
U(ni/2,njï1)
U(1,nj)U(0,nj) due(0,nj) U(ni/2,nj)
U(0,njï1)
U(ni/2,nj) U(ni,nj)
T(ni,nj)
U(ni/2+1,njï1) U(ni,njï1)
U(ni/2,njï1)
dtn(ni/2,nj)
dtw(1,nj) dte(1,nj)
dus(1,nj)
dun(1,njï1)
dts(1,nj)
dte(ni/2,nj)dtw(ni/2,nj)
dts(ni/2,nj)
dus(ni/2,nj)
dtn(ni/2+1,nj)
dun(ni/2+1,njï1)dts(ni/2+1,nj)
dte(ni/2+1,nj)
T(ni/2+1,nj)
dtw(ni/2+1,nj)
dus(ni/2+1,nj)
dts(ni,nj)
dte(ni,nj)
dtw(ni,nj)
dtn(ni,nj)
duw(ni/2+1,nj) U(ni/2+1,nj) due(ni/2+1,nj) duw(ni,nj)
due(ni/2,nj)
dun(ni/2,njï1)
dus(ni/2,nj)
duw(ni/2,nj)
due(1,nj)
dun(ni/2,njï1)
dun(1,nj)
dun(ni/2+1,nj)
dun(ni/2,nj)
dun(ni/2,nj)
duw(1,nj)
Figure 9.13: Placement of quarter-cells distances at the bipolar fold. For this example, there are ni = 4
points in the generalized zonal computational domain. Equivalance of grid factors on the fold leads to the
two-fold redundancy for velocity cell distances duei,nj =duwni−i,nj and dusi,nj =dunni−i,nj.
Elements of MOM November 19, 2014 Page 131

Chapter 9. B and C grid discretizations Section 9.4
9.4.3.3 Grid distances for horizontal full cells
Inspection of Figures 9.6 and 9.7, with the definitions of grid points shown in Figure 9.3, leads to the
definitions of distances for full horizontal cells
∆x(Ei−1,j,Ei,j ) = dxti,j(9.52)
∆y(Ni,j−1,Ni,j) = dyti,j(9.53)
∆x(Ui−1,j,Ui,j ) = dxtni,j(9.54)
∆y(Ui,j ,Ui,j−1) = dytei,j(9.55)
∆x(Ti,j ,Ti+1,j ) = dxtei,j(9.56)
∆y(Ti,j ,Ti,j+1) = dytni,j(9.57)
∆x(Ni,j ,Ni+1,j ) = dxui,j(9.58)
∆y(Ei,j ,Ei,j+1) = dyui,j(9.59)
Figures 9.14,9.15, and 9.16 show these distances for regions surrounding the bipolar fold. To generate
the redundancy conditions and halo mappings, we again use the scalar mappings given by equation (9.28).
Using these relations we see that redundancy is satisfied by the distances
dxtni,nj =dxtnni−i+1,nj (9.60)
dytni,nj =dytnni−i+1,nj (9.61)
dxui,nj =dxuni−i,nj (9.62)
dyui,nj =dyuni−i,nj (9.63)
Equation (9.28) indicates that within the halo region nj < j ≤nj +halo,
∆x(Ei−1,j,Ei,j ) = ∆x(Eni−i+1,2nj−j+1,Eni−i,2nj−j+1) (9.64)
∆y(Ni,j−1,Ni,j) = ∆y(Nni−i+1,2nj−j+1,Nni−i+1,2nj−j) (9.65)
∆x(Ui−1,j,Ui,j ) = ∆x(Uni−i+1,2nj−j,Uni−i,2nj−j) (9.66)
∆y(Ui,j ,Ui,j−1) = ∆y(Uni−i,2nj−j,Uni−i,2nj−j+1) (9.67)
∆x(Ti,j ,Ti+1,j ) = ∆x(Tni−i+1,2nj−j+1,Tni−i,2nj−j+1) (9.68)
∆y(Ti,j ,Ti,j+1) = ∆y(Tni−i+1,2nj−j+1,Tni−i+1,2nj−j) (9.69)
∆x(Ni,j ,Ni+1,j ) = ∆x(Nni−i+1,2nj−j,Nni−i,2nj−j) (9.70)
∆y(Ei,j ,Ei,j+1) = ∆y(Eni−i,2nj−j+1,Eni−i,2nj−j) (9.71)
which then leads to to the halo cell relations
dxti,j=dxtni−i+1,2nj−j+1
dyti,j=dytni−i+1,2nj−j+1
dxtni,j=dxtnni−i+1,2nj−j
dytei,j=dyteni−i,2nj−j+1
dxtei,j=dxteni−i,2nj−j+1
dytni,j=dytnni−i+1,2nj−j
dxui,j=dxuni−i,2nj−j
dyui,j=dyuni−i,2nj−j
for nj < j ≤nj +halo (9.72)
9.4.3.4 Summary of redundancies and halo mappings
Table 9.1 summarizes the halo relations and redundancies realized at the bipolar fold. Notice that those
distances exhibiting a redundancy have their halo relations reduce to their redundancy relations for j=nj.
Additionally, the quarter-cell distances all transform from a right handed system to a right handed system.
In general, this table should be sufficient to deduce relations for any derived fields, fluxes, etc., computed
in the model.
Elements of MOM November 19, 2014 Page 132

Chapter 9. B and C grid discretizations Section 9.4
T(1,nj)
U(1,njï1)
T(ni/2,nj)
U(ni/2,njï1)
U(0,nj) U(ni/2,nj)
U(0,njï1)
U(ni/2,nj) U(ni,nj)
U(ni/2+1,njï1) U(ni,njï1)
U(ni/2,njï1)
dxt(1,nj)
dyt(1,nj)
dyte(1,nj)
dxt(ni/2,nj)
dyt(ni/2,nj)
dyte(ni/2,nj)
dyte(ni/2,nj)
T(ni/2+1,nj)
dxt(ni/2+1,nj)
dyt(ni/2+1,nj)
T(ni,nj)
dyt(ni,nj)
dxt(ni,nj)
dyte(ni/2+1,nj) dyte(ni,nj)
U(ni/2+1,nj)
U(1,nj)
dxtn(ni/2+1,nj)
dxtn(ni/2,nj)dxtn(1,nj)
dxtn(ni,nj)
Figure 9.14: Placement of tracer cell dimensions at the bipolar fold. For this example, there are ni = 4
points in the generalized zonal computational domain. Equivalance of grid factors on the fold leads to the
two-fold redundancy dxtni,nj =dxtnni−i+1,nj.
T(1,nj)
U(1,njï1)
T(ni/2,nj)
U(ni/2,njï1)
U(0,nj) U(ni/2,nj)
U(0,njï1)
U(ni/2,nj) U(ni,nj)
U(ni/2+1,njï1) U(ni,njï1)
U(ni/2,njï1)
T(ni,nj)
U(ni/2+1,nj)
U(1,nj)
T(ni/2+1,nj)
dyu(ni/2+1,nj)
dyu(1,nj)
dxu(ni/2+1,nj)
dxu(1,nj)
Figure 9.15: Velocity cell distances at the bipolar fold.
Elements of MOM November 19, 2014 Page 133
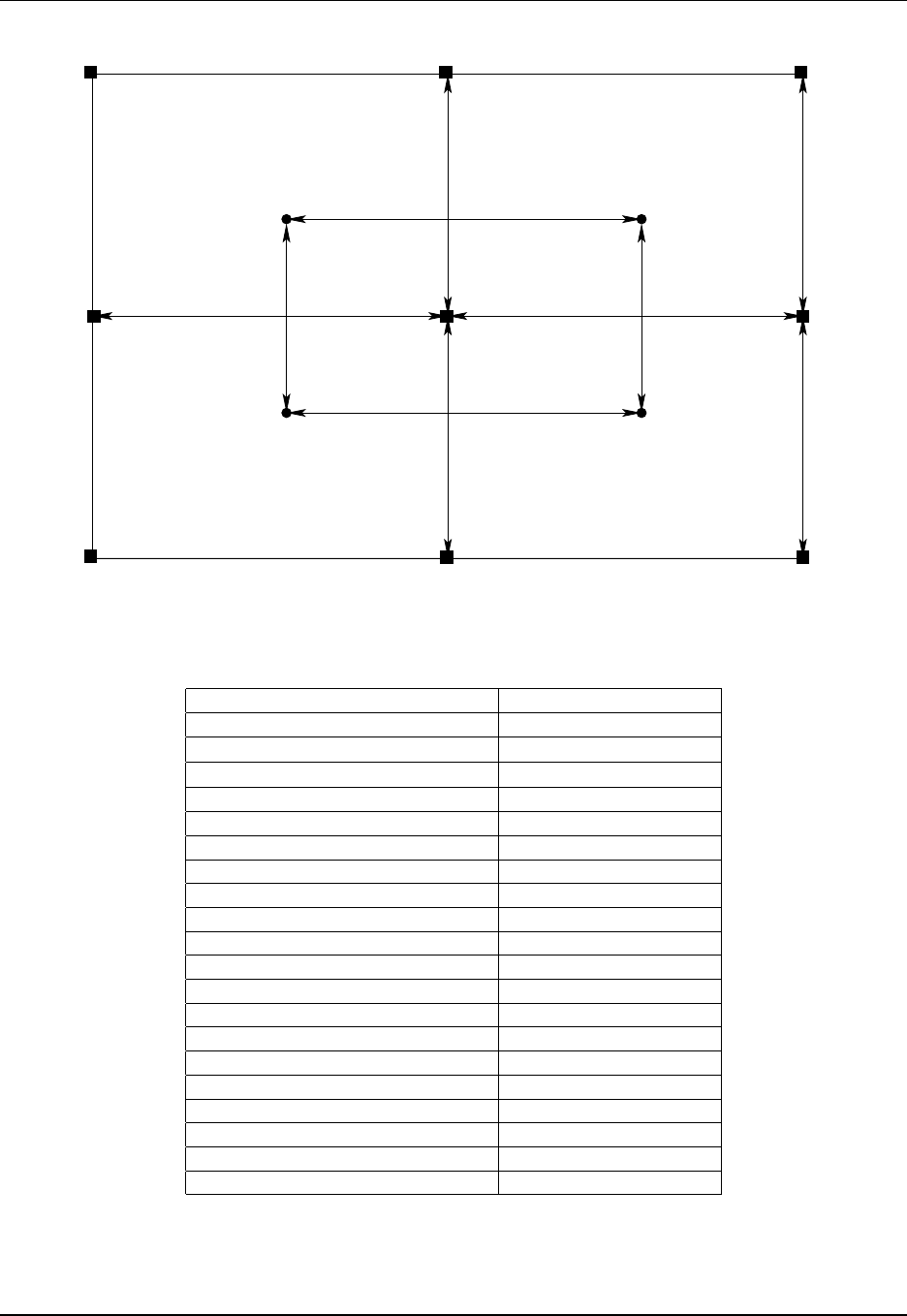
Chapter 9. B and C grid discretizations Section 9.4
T(1,nj)
U(1,njï1)
T(ni/2,nj)
U(ni/2,njï1)
U(0,nj) U(ni/2,nj)
U(0,njï1)
U(ni/2,nj) U(ni,nj)
U(ni/2+1,njï1) U(ni,njï1)
U(ni/2,njï1)
T(ni/2+1,nj) T(ni,nj)
U(ni/2+1,nj)
U(1,nj)
dytn(ni,nj)
dytn(1,nj)
dxte(1,nj)
dxte(ni/2+1,nj)
dytn(ni/2+1,nj)
dytn(ni/2,nj)
Figure 9.16: Grid distances for tracer points at the bipolar fold.
Halo relations (nj < j ≤nj +halo) Redundancy relations
Ui,j =ε Uni−i,2nj−jUi,nj =εUni−i,nj
Ti,j =ε Tni−i+1,2nj−j+1
Ni,j =ε Nni−i+1,2nj−jNi,nj =ε Nni−i+1,nj
Ei,j =ε Eni−i,2nj−j+1
dtei,j=dtwni−i+1,2nj−j+1
dtwi,j=dteni−i+1,2nj−j+1
dtni,j=dtsni−i+1,2nj−j+1
dtsi,j=dtnni−i+1,2nj−j+1
duei,j=duwni−i,2nj−jduei,nj =duwni−i,nj
duwi,j=dueni−i,2nj−jduwi,nj =dueni−i,nj
duni,j=dusni−i,2nj−jduni,nj =dusni−i,nj
dusi,j=dunni−i,2nj−jdusi,nj =dunni−i,nj
dxti,j=dxtni−i+1,2nj−j+1
dyti,j=dytni−i+1,2nj−j+1
dxtni,j=dxtnni−i+1,2nj−jdxtni,nj =dxtnni−i+1,nj
dytei,j=dyteni−i,2nj−j+1
dxtei,j=dxteni−i,2nj−j+1
dytni,j=dytnni−i+1,2nj−jdytni,nj =dytnni−i+1,nj
dxui,j=dxuni−i,2nj−jdxui,nj =dxuni−i,nj
dyui,j=dyuni−i,2nj−jdyui,nj =dyuni−i,nj
Table 9.1: Summary of the halo mappings and redundancies realized at the bipolar fold. The symbol εis 1
for scalar fields, and −1 for horizontal components of vector fields.
Elements of MOM November 19, 2014 Page 134

Chapter 10
Quasi-Eulerian algorithms for
hydrostatic models
Contents
10.1 Pressure and geopotential at tracer points ..........................136
10.1.1 Pressure at tracer point: energetic method ......................... 137
10.1.2 Pressure at a tracer point: finite volume considerations ................. 137
10.1.3 Discrete geopotential based on energetic considerations ................. 138
10.1.4 Discrete geopotential based on finite volume considerations ............... 138
10.2 Initialization issues .......................................139
10.2.1 Modification of dst ...................................... 139
10.2.2 Modification of the density field ............................... 139
10.2.3 Modification of the bottom topography ........................... 139
10.3 Vertical dimensions of grid cells ................................139
10.3.1 Thickness of a grid cell .................................... 140
10.3.2 Vertical distance between tracer points ........................... 140
10.3.2.1 Energetic based approach ............................. 141
10.3.2.2 Finite volume approach .............................. 141
10.4 Summary of vertical grid cell increments ...........................141
10.4.1 Geopotential vertical coordinate .............................. 141
10.4.2 z∗vertical coordinate ..................................... 142
10.4.3 Terrain following σ(z)vertical coordinate ......................... 142
10.4.4 Non-terrain following pressure vertical coordinate .................... 142
10.4.5 p∗vertical coordinate ..................................... 145
10.4.6 Steps to initialize pressure and p∗based models ...................... 145
10.4.7 Terrain following σ(p)coordinate .............................. 146
10.5 Surface height and bottom pressure diagnosed .......................147
10.5.1 Surface height diagnosed in pressure based models .................... 147
10.5.1.1 Concerning nonzero areal average ........................ 147
10.5.1.2 Concerning small scale features ......................... 147
10.5.2 Bottom pressure diagnosed in depth based models .................... 148
10.6 Vertically integrated volume/mass budgets .........................148
10.6.1 Vertically integrated volume budget ............................ 148
10.6.2 Vertically integrated mass budget .............................. 149
10.6.3 Summary of the vertically integrated volume/mass budgets ............... 149
135
Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.1
10.7 Compatibility between tracer and mass ............................150
10.8 Diagnosing the dia-surface velocity component .......................150
10.8.1 Depth based vertical coordinates .............................. 151
10.8.1.1 Depth coordinate .................................. 151
10.8.1.2 Depth deviation coordinate ............................ 151
10.8.1.3 Zstar coordinate .................................. 152
10.8.1.4 Depth-sigma coordinate .............................. 152
10.8.1.5 General expression for dia-surface velocity component ............ 152
10.8.2 Pressure based vertical coordinates ............................. 153
10.8.2.1 Pressure coordinate ................................ 153
10.8.2.2 Pressure deviation coordinate ........................... 154
10.8.2.3 Pstar coordinate .................................. 154
10.8.2.4 Pressure sigma coordinate ............................. 155
10.8.2.5 General expression for the dia-surface velocity component .......... 155
10.8.3 Comments about diagnosing the dia-surface velocity component ............ 155
10.9 Vertically integrated horizontal momentum .........................156
10.9.1 Budget using contact pressures on cell boundaries .................... 156
10.9.2 Budget using the pressure gradient body force ...................... 156
10.9.3 Depth based vertical coordinates .............................. 157
10.9.4 Pressure based vertical coordinates ............................. 158
Adcroft and Hallberg (2006) characterize two types of primitive equation ocean models. Eulerian ver-
tical coordinate algorithms, such as used in MOM, ROMS, and NEMO, diagnose the dia-surface velocity
component from the continuity equation. Lagrangian vertical coordinate algorithms, such as used in GOLD
and HYCOM, specify the dia-surface velocity component (e.g., zero diapycnal velocity in adiabatic simula-
tions with isopycnal coordinates). Eulerian in this context does not mean that a grid cell has a time constant
vertical position. Hence, the term quasi-Eulerian is used in this chapter.
In this chapter, we develop the semi-discrete budgets of a hydrostatic ocean model and present quasi-
Eulerian solution algorithms. Notably, as implemented in MOM, the quasi-Eulerian algorithms are formu-
lated assuming a time independent number of grid cells. That is, MOM does not allow for vanishing cell
thickness. This assumption simplifies the algorithms in many ways, but in turn limits the extent to which
this code can be used for simulations where water masses change in a nontrivial manner.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean advection velocity.F90
ocean core/ocean barotropic.F90
ocean core/ocean pressure.F90
ocean core/ocean thickness.F90
ocean core/ocean velocity.F90
ocean core/ocean velocity advect.F90
ocean tracers/ocean tracer.F90
ocean tracers/ocean tracer advect.F90
10.1 Pressure and geopotential at tracer points
We discussed the discrete pressure gradient body force appropriate for a finite difference discretization in
Sections 3.2 and 3.3. We require the anomalous hydrostatic pressure in the depth based models, and the
anomalous geopotential height in the pressure based models. That is, for depth based vertical coordinate
Elements of MOM November 19, 2014 Page 136

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.1
models, we need a discretization of the anomalous hydrostatic pressure (equation (3.20))
p0=gZ0
z
ρ0dzfor s=z(10.1)
p0=gZη
z
ρ0dzfor s=z∗,σ (z).(10.2)
For pressure based vertical coordinate models, we need a discretization of the anomalous geopotential
(equation (3.25))
Φ0=−(g/ρo)
z
Z
−H
ρ0dz. (10.3)
The vertical integrals involve some ambiguity for the finite difference formulation, since the tracer point
is not vertically centred within the tracer cell for the case of a vertically nonuniform grid. In this case, we
may choose to compute the pressure and geopotential at the tracer point using a more accurate vertical
integration that accounts for the non-centred placement of the tracer point.
The purpose of this section is to describe two methods used for the calculation of the pressure and
geopotential at the tracer grid point. Details of this discretization affect the manner used for diagnosing the
pressure conversion to buoyancy work, as described in Sections 14.6,14.7,14.8, and 14.9. The MOM code
provides both choices, with both producing analogous results for the surface height and bottom pressure.
10.1.1 Pressure at tracer point: energetic method
If the equation of state is linear, and both density and velocity are advected with second order centered
differences, then the conversion of pressure work to buoyancy work will balance potential energy changes.
This equality led Bryan (1969) to formulate the hydrostatic pressure calculation according to
p0
k+1 =p0
k+gdzwtkρ0
k
z.(10.4)
That is, anomalous hydrostatic pressure is computed given knowledge of the thicknesses dzwt and the
density ρ0
k. In this equation, primes refer to anomalies relative to the reference Boussinesq density
ρ0=ρ−ρo(10.5)
and
ρ0
k
z= (ρ0
k+ρ0
k+1)/2 (10.6)
is the simple vertical average of density. This average is the same as a finite volume average only if the
grid cell thicknesses are uniform. With stretched vertical grids, the simple average differs from the finite
volume average presented in Section 10.1.2. At the ocean surface, no average is available, so we use the
finite volume value for the pressure
p0
k=1 =gdzwtk=0 ρ0
k=1.(10.7)
Given this surface value, we then integrate downwards according to equation (10.4) to diagnose the anoma-
lous hydrostatic pressure at each discrete k-level.
10.1.2 Pressure at a tracer point: finite volume considerations
Although the finite volume method for computing the pressure force requires the pressure and geopotential
to be computed at the bottom of the tracer cells, we may choose to use a finite volume motivated approach
for computing the pressure and geopotential at the tracer point. Referring to the right hand panel in Figure
10.1, a finite volume motivated computation of hydrostatic pressure at a tracer point is given by
p0
k=1 =gdztupk=1 ρ0
k=1 (10.8)
p0
k+1 =p0
k+gdztlokρ0
k+gdztupk+1 ρ0
k+1.(10.9)
The pressure at k= 1 is the same as prescribed in the energetic method. However, for stretched vertical
grid cells, the interior cells have a different discrete pressure from that computed in the energetic method.
The finite volume approach is more accurate for stretched vertical grids.
Elements of MOM November 19, 2014 Page 137
Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.2
10.1.3 Discrete geopotential based on energetic considerations
Following in a manner analogous to the anomalous hydrostatic pressure in Section 10.1.1, we have the
discretized anomalous geopotential
Φ0
k=kbot =−(g/ρo)dzwtk=kbot ρ0
k=kbot (10.10)
Φ0
k=Φ0
k+1 −(g/ρo)dzwtkρ0
k
z.(10.11)
Iteration starts from the bottom at k=kbot using the finite volume expression, and moves upward in the
column towards the surface.
10.1.4 Discrete geopotential based on finite volume considerations
Following in a manner completely analogous to the anomalous hydrostatic pressure in Section 10.1.2, we
have the discretized anomalous geopotential
Φ0
k=kbot =−(g/ρo)dztlokbot ρ0
k=kbot (10.12)
Φ0
k=Φ0
k+1 −(g/ρo)dztupk+1ρ0
k+1 −(g/ρo)dztlokρ0
k.(10.13)
Iteration starts from the bottom at k=kbot using the finite volume expression, and moves upward in the
column towards the surface.
dztlo(k=kbot)
dzt(k=1)
dzt(k=2)
dzt(k=kbot)
dzwt(k=kbot)
dzwt(k=2)
dzwt(k=1)
dzwt(k=0) dztup(1)
dztlo(1)
dztup(2)
dztlo(2)
dztup(k=kbot)
Figure 10.1: A vertical column of three tracer cells and the corresponding vertical cell dimensions. In
MOM, the vertical spacing is related by dztk= (dzwtk−1+dzwtk)/2. With this specification, the average
tracer Tz= (Tk+Tk+1)/2 lives at the bottom of the tracer cell Tkand so is co-located with the dia-surface
velocity component w btk. The right column exposes the half-distances, which measure the distance from
the tracer cell point to the top and bottom faces of the tracer cell. The half-distances are used in the finite
volume formulation of pressure and geopotential computed at the tracer points (Sections 10.1.2 and 10.1.4),
whereas the grid spacing dzwt is used for the energetically based computation of pressure and geopotential
computed at the tracer points (Sections 10.1.1 and 10.1.3).
Elements of MOM November 19, 2014 Page 138

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.3
10.2 Initialization issues
When initializing a Boussinesq model, we place a fluid with initial in situ density ρinit onto a grid with
vertical increments dzt. Hence, both the density and volume of the grid cells are specified. The initial
mass of fluid is implied by this initialization method. Furthermore, by definition, the surface elevation ηis
zero.
For the non-Boussinesq model, we place a fluid with initial in situ density ρinit onto a grid with vertical
pressure increments dst. Hence, both the density and mass of the grid cells are specified. The initial
volume of fluid is thus implied from this initialization method. Furthermore, by definition, the bottom
pressure anomaly, pbot t −pbot0, is zero if we choose pbot0 as the initial bottom pressure.
The initialization methods are isomorphic. Notably, when initializing the Boussinesq model, there is
no guarantee that its bottom pressure anomaly will be intially zero. Likewise, there is no guarantee that
the surface elevation ηwill be zero with the non-Boussinesq initialization. For many applications, the
nonzero sea level may be of little concern, with the sea level adjusting rapidly on a barotropic time scale.
Nonetheless, we next outline three possible means to ensure a zero sea level results from initializing a
non-Boussinesq model. Such may be of interest for careful comparisons between Boussinesq and non-
Boussinesq simulations, such as considered by Losch et al. (2004).
10.2.1 Modification of dst
There are three general ways to approach non-Boussinesq initialization. First, we can modify the vertical
pressure increments dst of the grid cells to accomodate the initial density and to retain a zero surface
height. This approach generally requires nontrivial horizontal deviations in the dst array, so that it has
full grid dependence dst(i,j,k). Such dependence is generally acceptable for the bottom, where partial
cells introduce three-dimensional dependence to the vertical grid increments. However, with this added
dependence in the ocean interior, there is a possibility for introducing pressure gradient errors, depending
on the magnitude of the horizontal variations. If the variations are minor, then this approach may be
acceptable.
10.2.2 Modification of the density field
A second approach is to modify the initial density field. This approach, however, may fail after some time
integration, depending on the surface forcing. That is, over time the model may be forced towards a density
structure similar to the initial structure, in which case the possibility exists for losing the bottom cell in the
model if the evolved bottom pressure becomes lighter than the pressure at the top of the bottom cell.
10.2.3 Modification of the bottom topography
A third approach is motivated by one used with the MITgcm. Here, we deepen the bottom topography
so that the initial mass (as set by the pressure increments) and density result in vertical columns with
zero initial surface height. This approach may appear to be the least desirable, as we know the bottom
topography generally more accurately than the initial density. Yet depending on details of the initial density
field and the pressure increments, the changes in the bottom topography are often quite minor. We detail
this approach in Section 10.4.4.
10.3 Vertical dimensions of grid cells
The density weighted thickness of a grid cell is of fundamental importance in the formulation presented
in this document. In particular, density weighted thickness of a tracer cell is a basic ingredient and the
values on a velocity cell are diagnosed according to the minimum surrounding tracer cell values. Given
these fields, most of the equations for the ocean model retain the same appearance for arbitrary vertical
coordinates. The technology of generalized vertical coordinates then resides in the module specifying ρdz
Elements of MOM November 19, 2014 Page 139

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.3
coord definition cell thickness
geopotential zdz
zstar z∗=H(z−η)/(H+η) dz= (1 + η/H)dz∗
z-sigma σ(z)= (z−η)/(H+η) dz= (H+η)dσ(z)
pressure pdz=−(ρg)−1dp
pstar p∗=po
b(p−pa)/(pb−pa) dz=−[(pb−pa)/(ρg po
b)]dp∗
p-sigma σ(p)= (p−pa)/(pb−pa) dz=−[(pb−pa)/(ρg)]dσ(p)
Table 10.1: Table of vertical thicknesses dzfor grid cells as determined on the tracer grid using the vertical
coordinates discussed in Chapter 5. The vertical coordinate increments are specified, and the vertical
thicknesses dzare diagnosed.
(the MOM module ocean core/ocean thickness module), with extra work also needed for the pressure
and grid modules.
In addition to the density weighted thicknesses, we are in need of the depth of a grid cell center, depth of
the grid cell bottom, and vertical dimensions within the grid cell. Information is needed for these distances
both in depth space (z-coordinate), and coordinate space (s-coordinate). These needs introduce new time
dependent arrays that are updated and saved for restarts.
Figure 10.1 defines notation for the grid cell thicknesses used in MOM. Here, the left figure exposes the
vertical dimensions of the tracer grid cell, dzt and the distance between the T-cell points, dzwt. The right
figure exposes the half-distances, which measure the distance from the T-cell point to the upper face of the
cell, dztup, and the lower face, dztlo.
10.3.1 Thickness of a grid cell
The thickness of a grid cell is written
dz=z,s ds. (10.14)
For a tracer cell, this expression is written in the MOM codes as
dzt =dzt dst ∗dst.(10.15)
Inspection of the results from Tables 5.1 and 5.2 lead to the thicknesses given in Table 10.1, which are again
applied to the tracer grid. The corresponding velocity cell thicknesses are diagnosed based on the tracer
cell values.
For the finite volume approach to computing the pressure and geopotential, as discussed in Section
10.1.2, we need a method to compute the half-thicknesses. For this purpose, we assume the specific thick-
ness factor dzt dst is constant across the thickness of a tracer cell. We also assume knowledge of the
half-s-thicknesses dstlo and dstup, thus leading to
dztlo =dzt dst ∗dstlo (10.16)
dztup =dzt dst ∗dstup.(10.17)
The full cell thickness is then recovered by setting
dzt =dztlo +dztup,(10.18)
where
dst =dstlo +dstup.(10.19)
10.3.2 Vertical distance between tracer points
Through summation from the ocean surface, knowledge of the tracer cell thicknesses dztkwithin a vertical
column provides the depth of the bottom of any tracer cell within the column. For many purposes, it is also
Elements of MOM November 19, 2014 Page 140

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.4
important to know the depth where the tracer point is located. This information is obtained via vertical
summation from the distance between two vertically adjacent tracer cell points. As seen in Section 10.1
when discussing the hydrostatic pressure and the geopotential, the vertical distance between tracer points
is known as dzwt and the corresponding velocity cell vertical distance is dzwu.
10.3.2.1 Energetic based approach
For depth based vertical coordinates, dzwt is computed according to the results in Table 10.1 given the
corresponding coordinate thicknesses dswt. For pressure based vertical coordinates using the energetic
approach from Section 10.1.1, we are guided by the result (10.4) for the hydrostatic pressure computed in
a depth based vertical coordinate model. In general, this expression takes the form
ds= (s,z)zdz(10.20)
where az= (ak+ak+1)/2 is an unweighted discrete vertical average. Introducing model arrays leads to
dzwtk= 2
(s,z)k+ (s,z)k+1 !dswtk.(10.21)
For example, with s=p, this relation takes the form
dzwtk=− 2
g(ρk+ρk+1)!dswtk,(10.22)
where dswt is known and is negative, since pressure decreases upward, whereas geopotential increases
upward.
10.3.2.2 Finite volume approach
From the finite volume approach described in Section 10.3.1, we follow expressions (10.16) and (10.17) for
the thickness of a grid cell to write
dzwtk=0=dztupk=1(10.23)
dzwtk>1=dztlok−1+dztupk(10.24)
dzwtk=kbot =dztlok=kbot.(10.25)
10.4 Summary of vertical grid cell increments
We now summarize the results from Section 10.3 for the vertical coordinates z,z∗,σ(z),p,p∗, and σ(p). The
notation used in MOM is used to allow for direct comparison to the model code.
10.4.1 Geopotential vertical coordinate
The geopotential vertical coordinate has the following grid dimensions
dzt dst(i,j,k)=1
dzwt(i,j,k=0) = zt(k=1) + eta t(i,j)
dzt(i,j,k=1) = zw(k=1) + eta t(i,j).
(10.26)
The initial values of the depth of tracer points, depth zt, remain unchanged in time. However, the thick-
ness of the top cell is time dependent.
Elements of MOM November 19, 2014 Page 141

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.4
10.4.2 z∗vertical coordinate
The z∗coordinate has the grid dimensions
dzt dst(i,j,k) = 1+eta t(i,j)/ht(i,j)
dst(i,j,k) = dzt(i,j,k)|τ=0
dswt(i,j,k) = dzwt(i,j,k)|τ=0
dzt(i,j,k) = dzt dst(i,j,k)∗dst(i,j,k).
(10.27)
For the energetically based computation of hydrostatic pressure (Section 10.1.1), the distance between
tracer points is computed according to
dzwt(i,j,k=0) = dswt(i,j,k=0)
dst dzt(i,j,k=1)
dzwt(i,j,k=1,kmt −1) = 2dswt(i,j,k)
dst dzt(i,j,k) + dst dzt(i,j,k+1)
dzwt(i,j,k=kmt) = dswt(i,j,k=kmt)
dst dzt(i,j,k=kmt).
(10.28)
For the finite volume based computation of hydrostatic pressure (Section 10.1.2), the distance between
tracer points is computed according to equations (10.23)-(10.25). Notice how the s-grid increments are
constant in time, and are set by the z-grid increments at the initial model time step.
10.4.3 Terrain following σ(z)vertical coordinate
For the terrain following σ(z)coordinate, we proceed in a different manner than for the geopotential and z∗
coordinates. Here, a dimensionless partition of the σ(z)coordinate is prescribed during initialization, and
then the vertical grid dimensions deduced from knowledge of the depth field ht. The partitioning of σ(z)
can be chosen in many ways. We choose to base this partition on the vertical grid dimensions dzt(k) and
dzw(k) available in the Grid derived type. These are the full cell grid dimensions, which thus make dst and
dswt independent of horizontal position (i,j).
dzt dst(i,j,k) = ht(i,j) + eta t(i,j)
dst(i,j,k) = dzt(k)/zw(nk)
dswt(i,j,k) = dzw(k)/zw(nk)
dzt(i,j,k) = dzt dst(i,j,k)∗dst(i,j,k).
(10.29)
For the energetically based computation of hydrostatic pressure (Section 10.1.1), the distance between
tracer points is computed according to
dzwt(i,j,k=0) = dswt(i,j,k=0)
dst dzt(i,j,k=1)
dzwt(i,j,k=1,kmt −1) = 2∗dswt(i,j,k)
dst dzt(i,j,k) + dst dzt(i,j,k+1)
dzwt(i,j,k=kmt) = dswt(i,j,k=kmt)
dst dzt(i,j,k=kmt).
(10.30)
For the finite volume based computation of hydrostatic pressure (Section 10.1.2), the distance between
tracer points is computed according to equations (10.23)-(10.25).
10.4.4 Non-terrain following pressure vertical coordinate
As described in Section 10.2, initialization of the non-Boussinesq model must take place in a manner dif-
ferent from the Boussinesq model. That is, specifying the vertical grid increments with pressure vertical
Elements of MOM November 19, 2014 Page 142

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.4
coordinates introduces a fundamentally new consideration. Namely, the vertical grid dimensions dzt are a
function of the initial in situ density ρinit. However, with the present structure of MOM, we only know the
initial density after an initial grid structure is established. Furthermore, MOM does not allow for vanishing
layers. Hence, there is a possibility that a first guess at a vertical grid layout based on the bottom topog-
raphy and the initial density, will not provide for a realizable grid in a pressure model absent vanishing
layers. This point necessitates a multiple step process in the initialization of the pressure based model. We
clarify these points in the following discussion.
The first step of the initialization takes the initial temperature and salinity fields, and initial grid speci-
fication file, all generated using the familiar MOM4 preprocessing code that assumes geopotential vertical
coordinates. From this information, we compute a vertical density profile function
ρo(k) = Pi,j dati,jdzt0(i,j,k)ρinit
Pi,j dati,j dzt0(i,j,k).(10.31)
Here, the initial density ρinit is assumed to live on the initial grid specified by thicknesses dzt0(i,j,k) that
are created just as if the model vertical coordinate were geopotential (including bottom partial cells). The
model is run for a time step to allow for this function to be generated and written to a netCDF file. Then the
model is rerun, now reading in this function as an input file for use in subsequent steps of the initialization.
Note that the vertical density profile function ρo(k) takes account of the possibility for larger averaged
density in the deep ocean, in which case the vertical pressure increments increase at depth even moreso
than suggested by the generally larger vertical depth increments towards the deeper ocean. The utility of
the density profile for specifying the pressure levels is a function of many model details. For example, in
the global one degree model used for CM2.1 ( Griffies et al. (2005), Gnanadesikan et al. (2006), Delworth
et al. (2006), Wittenberg et al. (2006), and Stouffer et al. (2006a)) and ESM2M (Dunne et al. (2012)), using a
reference profile proved to be detrimental to the abyssal flow in the tropics. We hypothesize that the profile
produced a vertical grid spacing that was much coarser than otherwise provided with a depth basic vertical
coordinate. Another possibility is there is a bug with the nontrivial ρo(k) profile. Hence, we recommend
the trivial choice
ρo(k) = ρo.(10.32)
Other model configurations may find different profiles to be more useful.
We now proceed to generate the vertical grid increments dst. As the model is pressure-based, these
increments should be a function only of the vertical grid index k, with the only exception being at the
bottom where partial bottom steps allow for i,j dependence
dstlo(i,j,k) = −g ρo(k)dztlo0(i,j,k) (10.33)
dstup(i,j,k) = −g ρo(k)dztup0(i,j,k) (10.34)
dst(i,j,k) = dstlo(k) + dstup(k),(10.35)
where again
dzt0(i,j,k) = dztlo0(i,j,k) + dztup0(i,j,k) (10.36)
are generated by assuming the model is a geopotential model so that the i,j dependence arises just from
the bottom partial cell adjustments.
Now that we have the vertical pressure increments dst(i,j,k), dstlo(i,j,k), and dstup(i,j,k), and the
initial density ρinit, we recompute the vertical depth increments so that
dztlo1(i,j,k) = − dstlo(i,j,k)
g ρinit(i,j,k)!(10.37)
dztup1(i,j,k) = − dstup(i,j,k)
g ρinit(i,j,k)!(10.38)
dzt1(i,j,k) = dztlo(i,j,k) + dztup(i,j,k).(10.39)
The fundamental question is whether the above procedure allows for the same number of vertical grid
cells to exist in a column with the pressure coordinate model as for the analog geopotential model. A
Elements of MOM November 19, 2014 Page 143

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.4
general aim followed here is to include pressure coordinate models in MOM in a manner that represents an
overall modest adjustment to what is commonly done for initializing geopotential models. Given this aim,
we assume that both the geopotential model and pressure model have the same number of vertical grid
cells within each column. That is, the kmt(i,j) array computed for the geopotential model is the same as
for the pressure model. This assumption is self-consistent with the same bottom topography array ht(i,j)
only if
k=kmt(i,j)
X
k=1
dzt(i,j,k)≤ht(i,j).(10.40)
More stringently, we aim to allow for a nontrivial bottom cell thickness dztmin in the pressure model in
order to regularize the numerical calculations in this cell, so that
k=kmt(i,j)−1
X
k=1
dzt(i,j,k)≤ht(i,j)−dztmin.(10.41)
If this condition fails, then we are unable to initialize the pressure model with the same density distribu-
tion and bottom depths as in the geopotential model. There are two options: modify the density or modify
the bottom. Although not commonly applied at GFDL, the option of modifying the bottom has been fa-
cilitated in MOM, with documentation given in subroutine ocean thickness init adjust in the module
ocean core/ocean thickness.F90. Depending on details of the initial density and dztmin, modifications
of the bottom have been found to be modest, and mostly localized to shallow ocean shelf regions. There is
no general rule, and the researcher may wish to iterate somewhat to refine the choice of bottom topography
for use with the pressure model.
To appreciate the problem a bit more, we write the sum (10.41) in the form
k=kmt(i,j)−1
X
k=1
dzt(i,j,k) = −
k=kmt(i,j)−1
X
k=1
dst(i,j,k)
g ρinit(i,j,k)
=
k=kmt(i,j)−1
X
k=1
dzt0(i,j,k)ρo(k)
ρinit(i,j,k).
(10.42)
Thus, if we admit regions of the ocean where density is far less than the profile ρo(k), then the vertical
column will be relatively thick. Hence, in order to maintain the same number of vertical grid cells in
the pressure and geopotential model, we are forced to depress the bottom topography by some nonzero
amount.
Assuming the bottom topography is chosen according to one of the above conventions, we have the
following means for computing the grid increments with the pressure vertical coordinate model. Here are
the equations that summarize this step
dzt dst(i,j,k) = −(g∗rho(i,j,k))−1
dswt(i,j,k=1,kmt −1) = −g∗rho o(k)∗dzwt(i,j,k)|τ=0
dst(i,j,k=2,kmt −1) = −g∗rho o(k)∗dzt(i,j,k)|τ=0
dswt(i,j,k=0) = −st(i,j,k=1) + patm(i,j)
dswt(i,j,k=kmt) = st(i,j,k=kmt)−pbot(i,j)
dst(i,j,k=1) = −sw(i,j,k=1) + patm(i,j)
dst(i,j,k=kmt) = sw(i,j,k=kmt −1)−pbot(i,j)
dzt(i,j,k) = dzt dst(i,j,k)∗dst(i,j,k).
(10.43)
For the energetically based computation of hydrostatic pressure (Section 10.1.1), the distance between
Elements of MOM November 19, 2014 Page 144

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.4
tracer points is computed according to
dzwt(i,j,k=0) = dswt(i,j,k=0)
dst dzt(i,j,k=1)
dzwt(i,j,k=1,kmt −1) = 2∗dswt(i,j,k)
dst dzt(i,j,k) + dst dzt(i,j,k+1)
dzwt(i,j,k=kmt) = dswt(i,j,k=kmt)
dst dzt(i,j,k=kmt).
(10.44)
For the finite volume based computation of hydrostatic pressure (Section 10.1.2), the distance between
tracer points is computed according to equations (10.23)-(10.25).
10.4.5 p∗vertical coordinate
The same initialization procedure is followed for p∗as for pressure. Following the initialization, the model
employs the following equations for setting the vertical grid increments
dzt dst(i,j,k) = − pbot(i,j)−patm(i,j)
g∗rho(i,j,k)∗pbot0(i,j)!
dswt(i,j,k) = dswt(i,j,k)|τ=0
dst(i,j,k) = dst(i,j,k)|τ=0
dzt(i,j,k) = dzt dst(i,j,k)∗dst(i,j,k)
(10.45)
For the energetically based computation of hydrostatic pressure (Section 10.1.1), the distance between
tracer points is computed according to
dzwt(i,j,k=0) = dswt(i,j,k=0)
dst dzt(i,j,k=1)
dzwt(i,j,k=1,kmt −1) = 2∗dswt(i,j,k)
dst dzt(i,j,k) + dst dzt(i,j,k+1)
dzwt(i,j,k=kmt) = dswt(i,j,k=kmt)
dst dzt(i,j,k=kmt).
(10.46)
For the finite volume based computation of hydrostatic pressure (Section 10.1.2), the distance between
tracer points is computed according to equations (10.23)-(10.25).
10.4.6 Steps to initialize pressure and p∗based models
We now summarize the steps required to initialize the pressure and p∗based models.
• Determine dzt0(i,j,k) as z-model, with Pkmt(i,j)
k=1 dzt0(i,j,k) = ht(i,j)
• Determine the density profile function rho o(k) according to equation (10.31), with default rho o(k) =
ρo.
• Set the pressure increments according to
dstlo(i,j,k) = −grho o(k)dztlo0(i,j,k) (10.47)
dstup(i,j,k) = −grho o(k)dztup0(i,j,k) (10.48)
dst(i,j,k) = dstlo(k) + dstup(k),(10.49)
• Insert the initial temperature and salinity to the grid points (i,j,k) to then determine the initial den-
sity ρinit(i,j,k).
Elements of MOM November 19, 2014 Page 145

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.5
• Determine the modified thickness of the grid cells according to
dztlo1(i,j,k) = −dstlo(i,j,k)
g ρinit(i,j,k)(10.50)
dztup1(i,j,k) = −dstup(i,j,k)
g ρinit(i,j,k)(10.51)
dzt1(i,j,k) = dztlo(i,j,k) + dztup(i,j,k).(10.52)
• Determine if
k=kmt(i,j)−1
X
k=1
dzt(i,j,k)≤ht(i,j)−dztmin.(10.53)
If so, then make no modifications to the bottom topography. If not, then deepen the bottom topogra-
phy so that the following equality is satisfied
ht(i,j)mod =
k=kmt(i,j)−1
X
k=1
dzt(i,j,k) + dztmin.(10.54)
• Determine the bottom cell thickness according to
dzt(i,j,kmt) = ht(i,j)−
k=kmt(i,j)−1
X
k=1
dzt(i,j,k).(10.55)
10.4.7 Terrain following σ(p)coordinate
For the terrain following σ(p)coordinate, we use the same dimensionless partition as for the σ(z)coordinate
to initialize the grid arrangement. However, we have been unable to derive a self-consistent method to
incorporate the in situ density into the algorithm, since to compute the bottom pressure we must know
dzt, but to know dzt requires the bottom pressure. Hence, we expect there to be a large and spurious
deviation in surface height just after initialization for runs with σ(p)coordinate.
During the integration, we make use of the following grid increments
dzt dst(i,j,k) = − pbot(i,j)−patm(i,j)
g∗rho(i,j,k)!
dswt(i,j,k) = −dzw(k)/zw(nk)
dst(i,j,k) = −dzt(k)/zw(nk)
dzt(i,j,k) = dzt dst(i,j,k)∗dst(i,j,k)
(10.56)
For the energetically based computation of hydrostatic pressure (Section 10.1.1), the distance between
tracer points is computed according to
dzwt(i,j,k=0) = dswt(i,j,k=0)
dst dzt(i,j,k=1)
dzwt(i,j,k=1,kmt −1) = 2∗dswt(i,j,k)
dst dzt(i,j,k) + dst dzt(i,j,k+1)
dzwt(i,j,k=kmt) = dswt(i,j,k=kmt)
dst dzt(i,j,k=kmt).
(10.57)
For the finite volume based computation of hydrostatic pressure (Section 10.1.2), the distance between
tracer points is computed according to equations (10.23)-(10.25).
Elements of MOM November 19, 2014 Page 146

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.5
10.5 Surface height and bottom pressure diagnosed
The purpose of this section is to detail how the surface height and bottom pressure are diagnosed in non-
Boussinesq and Boussinesq models, respectively.
10.5.1 Surface height diagnosed in pressure based models
For models using a pressure based vertical coordinate, the surface height ηis diagnosed, whereas for depth
based models it is computed prognostically (Section 10.6). To diagnose the surface height, we use the
identity
η=−H+Xdz(10.58)
given the thickness dzof each cell determined via Table 10.1. This is the original calculation provided in
MOM for η, with the associated diagnostic table entry being
eta t =−H+Xdz. (10.59)
Another diagnostic method, identical in the continuum but differing numerically due to finite precision,
uses the following identity valid for the three pressure-based vertical coordinates supported in MOM
H+η= pb−pa
ρog!−
η
Z
−H ρ−ρo
ρo!dz. (10.60)
This alternative calculation separates the smaller density contribution arising from density anomaly ρ0=
ρ−ρo, from the larger bottom pressure contribution. This separation aims to facilitate a more precise
calculation by reducing numerical roundoff. However, in practice there is very little difference from the
original calculation in equation (10.58). The diagnostic table entry for the modified diagnostic is given by
eta t mod =pb−pa−ρog H
ρog−X ρ−ρo
ρo!dz. (10.61)
10.5.1.1 Concerning nonzero areal average
It is useful to note a common occurrance with pressure based models. Namely, the surface height will
generally have a nonzero areal average even in the absence of mass fluxes. Such should be expected since the
pressure based models conserve mass, not volume. For example, surface height can actually decrease even
when mass is added to a column, so long as the column density increases by a sufficient amount. Hence,
we are unable to make a general statement regarding the sign of the surface height without knowledge
of both the mass per area in the column (as determined by the bottom pressure) as well as the vertical
sum of the inverse density. Relatedly, the steric effect will cause the surface height to rise in regions of
heating/freshing and decrease in regions of cooling/evaporation.
10.5.1.2 Concerning small scale features
For a non-Boussinesq pressure-based simulation, the sea level is diagnosed through either equation (10.58)
or equation (10.60). The cell thickness, dz, appearing in these equations is a function of density and mass
in a cell. The density and mass change according to the flow, the temperature and salinity, and the cell
pressure. There are opportunities for relatively small scale features to appear in the diagnosed sea level
through the imprint of small scale features in the density and mass fields. Furthermore, adding the thick-
ness from small cells (e.g., thin bottom partial cells) to those from large cells offers an opportunity for
truncation errors, especially when later subtracting the summed depth of a resting ocean to compute the
sea level. For those familiar with the smoother sea level fields arising from a Boussinesq simulation, the
application of a smoothing operator to the diagnosed eta is a suitable approach to removing some of the
small scale features.
Elements of MOM November 19, 2014 Page 147

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.6
In summary, the prognosed sea level from a Boussinesq simulation is generally smoother than the di-
agnosed sea level in a non-Boussinesq pressure-based simulation. The physical reason is that the non-
Boussinesq sea level is impacted by the density and mass that sits within a fluid column, whereas the sea
level in a Boussinesq fluid is impacted by density only through the impacts on the convergence of depth
integrated currents.
10.5.2 Bottom pressure diagnosed in depth based models
For models using a depth based vertical coordinate, it is necessary to diagnose the bottom pressure pbusing
the following identity
pb=pa+gXρdz. (10.62)
Here, we use the in situ density ρand the thickness dzof each cell.
10.6 Vertically integrated volume/mass budgets
The vertically integrated mass and volume budgets determine, respectively, the bottom pressure and the
surface height. The purpose of this section is to derive these budgets for use with depth based and pressure
based vertical coordinates.
10.6.1 Vertically integrated volume budget
The budget for the volume per unit horizontal area for a Boussinesq fluid integrated over the depth of a
grid cell takes the following forms, depending on whether the cell is in the interior, the bottom, or the
surface
∂t(dz) = −∇s·(udz)−(w(z))s=sk−1+ (w(z))s=sk+S(V)dz(10.63)
∂t(dz) = −∇s·(udz)−(w(z))s=skbot−1+S(V)dz(10.64)
∂t(dz) = −∇s·(udz) + (w(z))s=sk=1 +Qm/ρo+S(V)dz(10.65)
We obtained these equations from the mass budgets (2.155), (2.163), and (2.173), with density set to the
constant Boussinesq reference value ρo, and with S(V)a volume source (with units of inverse time). The
vertical sum of these budgets leads to
∂t(H+η) = −∇·U+Qm/ρo+X
kS(V)dz, (10.66)
where we used X
k
dz=H+η, (10.67)
which is the total thickness of the water column, and we introduced the depth integrated horizontal velocity
X
k
udz=U.(10.68)
Since His the time independent ocean bottom, equation (10.66) provides a prognostic relation for the
surface height
∂tη=−∇·U+Qm/ρo+X
kS(V)dz. (10.69)
This is the free surface equation used for depth based vertical coordinate Boussinesq models.
Elements of MOM November 19, 2014 Page 148

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.7
10.6.2 Vertically integrated mass budget
The budget of the mass per unit horizontal area for a non-Boussinesq fluid integrated over the depth of
a grid cell takes the following forms, depending on whether the cell is in the interior, the bottom, or the
surface
∂t(ρdz) = −∇s·(uρdz)−(ρw(z))s=sk−1+ (ρw(z))s=sk+S(M)ρdz(10.70)
∂t(dzρ) = −∇s·(uρdz)−(ρw(z))s=skbot−1+S(M)ρdz(10.71)
∂t(dzρ) = −∇s·(uρdz) + (ρw(z))s=sk+Qm+S(M)ρdz. (10.72)
These are equations (2.155), (2.163), and (2.173). The vertical sum of these budgets lead to the vertically
integrated balance of mass per area for a column of fluid
∂tX
k
ρdz=−∇·X
k
uρdz+Qm+X
kS(M)ρdz. (10.73)
The vertical integral Pkρdzis the total mass per area in the fluid column. In a hydrostatic fluid, this mass
per area is equal to the difference in pressure between the bottom and top of the column
X
k
ρdz=g−1(pb−pa).(10.74)
Consequently, the mass budget generally takes the form
∂t(pb−pa) = −g∇·X
k
uρdz+g Qm+gX
kS(M)ρdz
=−g∇·Uρ+g Qm+gX
kS(M)ρdz
(10.75)
where
Uρ=X
k
uρdz(10.76)
is the vertically integrated density weighted horizontal velocity. Equivalently, it is the vertically integrated
horizontal momentum per horizontal area. The time tendency for the applied pressure could be provided
by another component model. Without this information, it can be approximated by, for example,
∂tpa≈pa(t)−pa(t−1)
∆t.(10.77)
For the vertical integral of the horizontal momentum per volume, ρu, note that z,s ρis depth independent
for either choice of pressure based coordinates given in Table 5.2. In summary, for the pressure based
coordinates in Table 5.2, the depth integrated mass balance (10.73) takes the form
∂t(pb−pa) = −g∇·Uρ+g Qm+gX
kS(M)ρdz. (10.78)
10.6.3 Summary of the vertically integrated volume/mass budgets
In summary, the vertically integrated volume and mass budgets take on the isomorphic form
∂tη=−∇·U+Qm/ρo+X
kS(V)dz
g−1∂t(pb−pa) = −∇·Uρ+Qm+X
kS(M)ρdz. (10.79)
These budgets provide prognostic relations for the surface height ηin the Boussinesq case, and the bottom
pressure pbin the non-Boussinesq case. The tendency for the applied pressure pamust be determined by
another component model, or approximated via equation (10.77).
Elements of MOM November 19, 2014 Page 149

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.8
10.7 Compatibility between tracer and mass
Although we do not time step the vertically integrated tracer budget in an ocean model, it is useful to write
it down for diagnostic purposes. Furthermore, it allows us to introduce a compatibility condition between
tracer and mass budgets. To do so, recall the tracer budgets for the interior, bottom, and surface grid cells,
given by equations (36.122), (2.162), and (2.172)
∂t(C ρdz) = S(C)ρdz−∇s·[ρdz(uC+F)]
−[ρ(w(z)C+F(s))]s=sk−1
+ [ρ(w(z)C+F(s))]s=sk.
∂t(C ρdz) = S(C)ρdz−∇s·[ρdz(uC+F)]
−hρ(w(z)C+F(s))is=skbot−1
+Q(C)
(bot)
∂t(C ρdz) = S(C)ρdz−∇s·[ρdz(uC+F)]
+hρ(w(z)C+F(s))is=sk=1
+QmCm−Q(turb)
(C).
Summing these budgets over a vertical column leads to
∂tX
k
C ρdz=X
kS(C)ρdz−∇s·X
k
ρdz(uC+F)
+QmCm−Q(turb)
(C)+Q(bott)
(C).
(10.80)
As expected, the only contributions from vertical fluxes come from the top and bottom boundaries. Fur-
thermore, by setting the tracer concentration to a uniform constant, all the turbulent flux terms vanish, in
which case the budget reduces to the vertically integrated mass budget discussed in Section 10.6.2. This
compatiblity between tracer and mass budgets must be carefully maintained by the discrete model equa-
tions.1
10.8 Diagnosing the dia-surface velocity component
The key distinction between Eulerian vertical coordinates and Lagrangian vertical coordinates is how they
treat the dia-surface velocity component
w(z)=∂z
∂s
ds
dt.(10.81)
The Lagrangian models prescribe it whereas Eulerian models diagnose it. The purpose of this section is
develop Eulerian algorithms for diagnosing the dia-surface velocity component for the depth based and
pressure based vertical coordinates of Chapter 5. As we will see, a crucial element for the utility of these
algorithms is that the specific thickness z,s is depth independent using depth based coordinates in a Boussi-
nesq fluid, and ρz,s is depth independent using pressure based coordinates in a non-Boussinesq fluid.
1As discussed by Griffies et al. (2001), local conservation of an algorithm for tracer and volume/mass can readily be checked by
running a model with uniform tracer concentration and blowing winds across the ocean surface. Surface height undulations will
ensue, thus causing changes in volume for the grid cells. But the tracer concentration should remain uniform in the absence of surface
fluxes. Changes in tracer concentration will not occur if the volume/mass and tracer budgets are compatible in the sense defined in
this section.
Elements of MOM November 19, 2014 Page 150

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.8
10.8.1 Depth based vertical coordinates
Rearrange the grid cell volume budgets (10.63)-(10.65) to express the dia-surface velocity component for
the top cell, interior cells, and bottom cell as
(w(z))s=sk=1 =∂t(dz)−S(V)dz+∇s·(udz)−Qm/ρo(10.82)
(w(z))s=sk=∂t(dz)−S(V)dz+∇s·(udz) + (w(z))s=sk−1(10.83)
0 = ∂t(dz)−S(V)dz+∇s·(udz) + (w(z))s=skbot−1.(10.84)
These equations are written from the surface to the bottom, with this order familiar from the z−coordinate
version of MOM4.0. Equation (10.84) indicates that there is no transport through the ocean bottom. In a
numerical model, this equation provides a useful diagnostic to check that dia-surface velocity components
in the cells above the bottom have been diagnosed correctly. A nonzero result at the bottom signals a code
bug.
We now detail how the dia-surface velocity component is diagnosed for the depth based vertical coor-
dinates discussed in Section 5.1. To do so, we determine diagnostic relations for the time tendency ∂t(dz)
of the grid cell thickness as a function of vertical coordinate. Because z,s is independent of depth for these
coordinates, we are able to express ∂t(dz) as a function of ∂tη, which in turn can be diagnosed using the
vertically integrated volume budget.
10.8.1.1 Depth coordinate
For s=z, the only grid cell that admits a non-zero ∂t(dz) is the surface cell, where ∂t(dz) = ∂tη. Also, in
MOM4.0 we assumed that there are no volume sources for k > 1. But this assumption is not fundamen-
tal. Indeed, volume sources throughout the column are not a problem, so long as their affects on volume
conservation for the cell are properly handled in the diagnosis of the vertical velocity component. These
results lead to the following expressions for the dia-surface velocity component w(z)= dz/dt=w
(w(z))z=zk=1 =∂tη−S(V)dz+∇z·(udz)−Qm/ρo(10.85)
(w(z))z=zk=−S(V)dz+∇z·(udz) + (w(z))z=zk−1(10.86)
0 = −S(V)dz+∇z·(udz) + (w(z))z=zkbot−1.(10.87)
The right hand side of the surface height equation (10.69) can be used to eliminate ∂tηin equation (10.85),
thus leading to a purely diagnostic set of equations
(w(z))z=zk=1 =−S(V)dz+∇z·(udz) + X
kS(V)dz−∇·U(10.88)
(w(z))z=zk=−S(V)dz+∇z·(udz) + (w(z))z=zk−1(10.89)
0 = −S(V)dz+∇z·(udz) + (w(z))z=zkbot−1.(10.90)
The algorithm starts at k= 1 given knowledge of the right hand side terms in equation (10.88). Movement
down the vertical column leads to the diagnosis of wfor the full column.
10.8.1.2 Depth deviation coordinate
For s=z−η, the only grid cell that admits a non-zero ∂t(dz) is the bottom cell where ∂t(dz) = ∂tη. The
dia-surface velocity component w(z)=w−dη/dtthus is diagnosed via
(w(z))s=sk=1 =−S(V)dz+∇s·(udz)−Qm/ρo(10.91)
(w(z))s=sk=−S(V)dz+∇s·(udz) + (w(z))s=sk−1(10.92)
0 = ∂tη−S(V)dz+∇s·(udz) + (w(z))s=skbot−1.(10.93)
Elements of MOM November 19, 2014 Page 151

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.8
As with the depth coordinate s=z, we use the surface height equation (10.69) to eliminate ∂tηin equation
(10.93) and so lead to a fully diagnostic set of equations
(w(z))s=sk=1 =−S(V)dz−Qm/ρo+∇z·(udz) (10.94)
(w(z))z=zk=−S(V)dz+ (w(z))z=zk−1+∇z·(udz) (10.95)
0 = −S(V)dz+ (w(z))z=zkbot−1+∇z·(udz)
+Qm/ρo−∇·U+X
kS(V)dz.(10.96)
10.8.1.3 Zstar coordinate
For s=z∗=H(z−η)/(H+η), all grid cells have time independent dssince the range for z∗is time indepen-
dent. However, the specific thickness z,s = 1 + η/H is time dependent. The dia-surface velocity component
is thus diagnosed via the equations
(w(z))s=sk=1 = dsH−1∂tη−S(V)dz+∇s·(udz)−Qm/ρo(10.97)
(w(z))s=sk= dsH−1∂tη−S(V)dz+∇s·(udz) + (w(z))s=sk−1(10.98)
0=dsH−1∂tη−S(V)dz+∇s·(udz) + (w(z))s=skbot−1.(10.99)
The surface height equation (10.69) is used to eliminate ∂tηfrom each of these equations. Note that in
verifying the correctness of these results, recall that Pkds=Hfor s=z∗.
10.8.1.4 Depth-sigma coordinate
For s=σ(z)= (z−η)/(H+η), all grid cells have constant dssince the range for σis time independent. How-
ever, it has a time dependent specific thickness z,s =H+η. These results lead to the following expressions
for the dia-surface velocity component
(w(z))s=sk=1 = ds∂tη−S(V)dz+∇s·(udz)−Qm/ρo(10.100)
(w(z))s=sk= ds∂tη−S(V)dz+∇s·(udz) + (w(z))s=sk−1(10.101)
0=ds∂tη−S(V)dz+∇s·(udz) + (w(z))s=skbot−1.(10.102)
The surface height equation (10.69) is used to eliminate ∂tηfrom each of these equations. In verifying the
correctness of these results, recall that Pkds= 1 for s=σ(z).
10.8.1.5 General expression for dia-surface velocity component
In summary, for depth based vertical coordinates, the dia-surface velocity component is diagnosed via
(w(z))s=sk=1 =∂t(dz)−S(V)dz+∇s·(udz)−Qm/ρo
(w(z))s=sk=∂t(dz)−S(V)dz+∇s·(udz) + (w(z))s=sk−1
0 = ∂t(dz)−S(V)dz+∇s·(udz) + (w(z))s=skbot−1
(10.103)
where the thickness of a grid cell evolves according to
∂t(dz) = δk,1∂tη s =z
∂t(dz) = δk,kbot ∂tη s =z−η
∂t(dz)=ds(∂tη/H)s=H(z−η)/(H+η)
∂t(dz)=ds∂tη s = (z−η)/(H+η).
(10.104)
Elements of MOM November 19, 2014 Page 152

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.8
The surface height evolution
∂tη=−∇·U+Qm/ρo+X
kS(V)dz(10.105)
embodies volume conservation for a Boussinesq fluid column. The right hand side of (10.105) is used in
equations (10.104) to produce a purely diagnostic expression for the dia-surface velocity components.
10.8.2 Pressure based vertical coordinates
We now diagnose the dia-surface velocity component for pressure based vertical coordinates. For this
purpose, rearrange the grid cell mass budgets (10.70)-(10.72) to express the vertical velocity component as
(ρw(z))s=sk=1 =∂t(ρdz)−S(M)ρdz+∇s·(uρdz)−Qm(10.106)
(ρw(z))s=sk=∂t(ρdz)−S(M)ρdz+∇s·(uρdz) + (ρ w(z))s=sk−1(10.107)
0 = ∂t(ρdz)−S(M)ρdz+∇s·(uρdz) + (ρ w(z))s=skbot−1.(10.108)
As for the depth based vertical coordinates, we write these equations from the surface to the bottom. Equa-
tion (10.108) indicates that there is no transport through the ocean bottom. In a numerical model, this
equation provides a useful diagnostic to check that velocity components in the cells above the bottom have
been diagnosed correctly. A nonzero result at the bottom signals a code bug.
We proceed as for depth based vertical coordinates by determining diagnostic relations for ∂t(ρdz) as
a function of the pressure based vertical coordinates discussed in Section 5.2. Because ρz,s is independent
of depth for these coordinates, we are able to express ∂t(ρdz) as a function of ∂tpaand ∂tpb. The time
tendency of the applied pressure is set according to other component models, or approximated as (10.77).
The time tendency for the bottom pressure is set according to the vertically integrated mass budget (10.78).
Finally, we note that it is the density weighted dia-surface velocity component ρ w(z)which is most naturally
diagnosed in this approach. Conveniently, it is ρw(z)that is required for the non-Boussinesq tracer and
momentum budgets discussed in Sections 2.6 and 2.9.
10.8.2.1 Pressure coordinate
For s=p, the density weighted specific thickness is a constant for all grid cells
ρz,s =−g−1,(10.109)
but both the surface and bottom grid cells admit a non-zero ∂t(ρdz). At the surface2,
ρdz=−g−1dp
=−g−1(pa−pbottom of cell k=1)(10.110)
which then leads to
∂t(ρdz) = −g−1∂tpa.(10.111)
That is, the top cell mass per area decreases when the applied pressure increases. This result follows since
the bottom face of the top cell has a fixed pressure, but the top face is at the applied pressure pa. As noted
in Section 5.2, if the applied pressure becomes greater than pbottom of cell k=1, then the top cell vanishes. For
the bottom cell,
ρdz=−g−1dp
=−g−1(ptop of cell k=kbot −pb),(10.112)
2Recall that our convention in equation (5.34) is that ds < 0 for pressure based vertical coordinates. At the surface with pressure
coordinates s=p, the coordinate increment is dp=pa−pbottom of cell k=1. This increment is negative since the applied pressure is
less than the pressure at the bottom interface to cell k= 1. For the bottom cell, dp=ptop of cell k=kbot −pb, which is negative when the
bottom pressure is greater than the pressure just above it.
Elements of MOM November 19, 2014 Page 153

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.8
and so
∂t(ρdz) = g−1∂tpb.(10.113)
Hence, the bottom cell thickness increases as the bottom pressure increases. If the bottom pressure de-
creases below ptop of cell k=kbot, then the bottom cell vanishes. These results lead to the following expressions
for the density weighted dia-surface velocity component
(ρw(z))s=sk=1 =∂tpa−dsS(M)+∇s·(dsu) + g Qm(10.114)
(ρw(z))s=sk=−dsS(M)+∇s·(dsu) + (ρw(z))s=sk−1(10.115)
0 = −∂tpb−dsS(M)+∇s·(dzu) + (ρw(z))s=skbot−1.(10.116)
As a check, a sum of these equations leads to the vertically integrated mass budget (10.78) written in
pressure coordinates. These equations are converted to diagnostic expressions for the dia-surface velocity
component by substituting the known time tendencies for the applied pressure ∂tpa(e.g., equation (10.77))
and the bottom pressure ∂tpbvia the column integrated mass budget (10.78).
10.8.2.2 Pressure deviation coordinate
For s=p−pa, the only grid cell that admits a non-zero ∂t(ρdz) is the bottom cell. At this cell,
ρdz=−g−1dp
=−g−1[ptop of cell k=kbot −(pb−pa)],(10.117)
and so
∂t(ρdz) = g−1∂t(pb−pa).(10.118)
The right hand side can be diagnosed via the column integrated mass budget (10.78). These results lead to
the following expressions for the dia-surface velocity component
(ρw(z))s=sk=1 =−dsS(M)+∇s·(dsu) + g Qm(10.119)
(ρw(z))s=sk=−dsS(M)+∇s·(dsu) + (ρw(z))s=sk−1(10.120)
0 = −∂t(pb−pa)−dzS(M)+∇s·(dsu) + (ρw(z))s=skbot−1.(10.121)
As a check, the sum of these equations recovers the vertically integrated mass budget (10.78) written in
pressure coordinates.
10.8.2.3 Pstar coordinate
For s=p∗with
p∗=po
b(p−pa)/(pb−pa),(10.122)
all grid cells have time independent constant ds. We are then led to the following mass per horizontal
volume of a grid cell
ρdz=ρz,s ds
=−(g po
b)−1(pb−pa)ds. (10.123)
The time tendency
∂t(ρdz) = −ds(g po
b)−1∂t(pb−pa) (10.124)
can be diagnosed via the column integrated mass budget (10.78). We then use these results in the general
expressions (10.106)-(10.108) to generate the algorithm for diagnosing the vertical velocity components.
As a check, the sum of these equations recovers the vertically integrated mass budget (10.78) written in
Elements of MOM November 19, 2014 Page 154

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.8
pressure coordinates. Note that in verifying this identity, it is important to note that Pkds=−po
bfor the
pstar coordinate, which results from the following identities
pb−pa=gX
k
ρdz
=gX
k
ρz,s ds
=− pb−pa
po
b!X
k
ds,
(10.125)
where we used the hydrstatic balance (10.74) for the first equality.
10.8.2.4 Pressure sigma coordinate
For s=σ(p)= (p−pa)/(pb−pa), all grid cells have time independent dssince the range for σis time inde-
pendent. However, this coordinate has a time dependent density weighted specific thickness, thus leading
to
ρdz=ρz,s ds
=−g−1(pb−pa)ds. (10.126)
We use these results in the general expressions (10.106)-(10.108) to generate the algorithm for diagnosing
the vertical velocity components. As a check, the sum of these equations recovers the vertically integrated
mass budget (10.78) written in pressure coordinates. In verifying this identity, it is important to note that
Pkds=−1 for s=σ(p).
10.8.2.5 General expression for the dia-surface velocity component
In summary, for pressure based vertical coordinates, the dia-surface velocity component is diagnosed via
(ρw(z))s=sk=1 =∂t(ρdz)−S(M)ρdz+∇s·(uρdz)−Qm
(ρw(z))s=sk=∂t(ρdz)−S(M)ρdz+∇s·(uρdz) + (ρ w(z))s=sk−1
0 = ∂t(ρdz)−S(M)ρdz+∇s·(uρdz) + (ρ w(z))s=skbot−1.
(10.127)
where the density weighted thickness of a grid cell evolves according to
g ∂t(ρdz) = −δk,1∂tpa+δk,kbot ∂tpbs=p
g ∂t(ρdz) = δk,kbot ∂t(pb−pa)s=p−pa
g ∂t(ρdz) = −(ds/po
b)∂t(pb−pa)s=po
b(p−pa)/(pb−pa)
g ∂t(ρdz) = −ds∂t(pb−pa)s= (p−pa)/(pb−pa)
(10.128)
and the bottom pressure evolution
∂t(pb−pa) = −g∇·Uρ+g Qm+gX
kS(M)ρdz(10.129)
embodies mass conservation for a non-Boussinesq fluid column.
10.8.3 Comments about diagnosing the dia-surface velocity component
We emphasize again that a critical element in the Eulerian algorithms for diagnosing the vertical velocity
components is the ability to exploit the depth independence of the specific thickness z,s for the depth
based coordinates for a Boussinesq fluid, and the density weighted specific thickness ρz,s for the pressure
Elements of MOM November 19, 2014 Page 155

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.9
based coordinates for a non-Boussinesq fluid. These properties allow us to remove the time tendencies for
surface height and pressure from the respective diagnostic relations by substituting the depth integrated
budgets (10.69) for the depth based models, and (10.78) for the pressure based models. Absent the depth
independence, one would be forced to consider another approach, such as the time extrapolation approach
to approximate the time tendency proposed by Greatbatch et al. (2001) and McDougall et al. (2002) for
implementing a non-Boussinesq algorithm within a Boussinesq model.
10.9 Vertically integrated horizontal momentum
We now outline the split between the fast vertically integrated dynamics from the slower depth dependent
dynamics. This split forms the basis for the split-explicit method used in MOM to time step the momentum
equation. For this purpose, we formulate the budget for the vertically integrated momentum budget.
10.9.1 Budget using contact pressures on cell boundaries
Before proceeding with a formulation directly relevant for MOM, we note the form of the vertically in-
tegrated budget arising when we consider pressure acting on a cell as arising from the accumulation of
contact stresses. For this purpose, we vertically sum the momentum budgets given by equations (2.226),
(2.229) and (2.234), which leads to
(∂t+fˆ
z∧)X(udzρ) = −X ˆ
z∧(Muρdz) + ∇s·[u(uρdz)]!
+X −∇s(pdz) + Fρdz!
+ [pa∇η+τwind +ρwQmum]
+ [pb∇H−τbottom].
(10.130)
Contact pressures on the top and bottom of the grid cells cancel throughout the column, just as other
vertical fluxes from momentum and friction. The remaining contact pressures are from the bottom and
top of the ocean column and the vertically integrated contact pressures on the sides of the fluid column.
Correspondingly, if we integrate over the horizontal extent of the ocean domain, we are left only with
contact pressures acting on the solid boundaries and undulating free surface. Such is to be expected, since
the full ocean domain experiences a pressure force only from its contact with other components of the earth
climate system.
10.9.2 Budget using the pressure gradient body force
As discussed in Section 2.8.2, we prefer to formulate the contribution of pressure to the linear momentum
balance as a body force, whereby we exploit the hydrostatic balance. Hence, to develop the vertically
integrated horizontal momentum budget, we start from the form of the budget given by equations (4.19),
(4.20), and (4.21), rewritten here for the interior, bottom, and surface grid cells
[∂t+ (f+M)ˆ
z∧](uρdz) = ρdzS(u)−∇s·[u(uρdz)]
−dz(∇sp+ρ∇sΦ) + Fρdz
−[ρ(w(z)u−κu,z)]s=sk−1
+ [ρ(w(z)u−κu,z) ]s=sk
(10.131)
[∂t+ (f+M)ˆ
z∧](uρdz) = S(u)ρdz−∇s·[u(uρdz)]
−dz(∇sp+ρ∇sΦ) + Fρdz
−[ρ(w(z)u−κu,z)]s=skbot−1
−τbottom
(10.132)
Elements of MOM November 19, 2014 Page 156

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.9
[∂t+ (f+M)ˆ
z∧](uρdz) = S(u)ρdz−∇s·[u(uρdz)]
−dz(∇sp+ρ∇sΦ) + Fρdz
+ [τwind +Qmum]
+ [ρ(w(z)u−κu,z) ]s=sk=1 .
(10.133)
A vertical sum of the momentum budgets leads to
(∂t+fˆ
z∧)X(uρdz) = XS(u)ρdz
−X ˆ
z∧(Muρdz) + ∇s·[u(uρdz)]!
+Xdz −∇sp−ρ∇sΦ+ρF!
+τwind −τbottom +Qmum.
(10.134)
Fluctuations in the surface height contribute both to fluctuations in the horizontal pressure gradient and
the geopotential gradient. These fluctuations lead to fast barotropic or external gravity waves, and so
they must be integrated with a small time step. In contrast, the slower baroclinic or internal motions can
be integrated with a larger time step, upwards of 100 times longer depending on details of the motions.
Hence, it is advantageous for ocean climate modeling to develop an algorithm that splits between the
motions when time stepping the equations. Details of this split depend on whether we work with a depth
based or pressure based vertical coordinate.
10.9.3 Depth based vertical coordinates
We follow the discussion in Section 3.2.1 where the pressure gradient is split according to either equation
(3.18) for s=z∗or s=σ(z), and equation (3.17) for s=z. For geopotential coordinates s=zthis split takes
the form
∇sp+ρ∇sΦ=∇(pa+psurf)
| {z }
fast
+∇sp0
clinic +ρ0∇sΦ
| {z }
slow
(10.135)
where psurf =ρ(z= 0)g η,ρ=ρo+ρ0and p0
clinic =gR0
zρ0dz. For zstar or sigma coordinates, this split takes
the form
∇sp+ρ∇sΦ=∇(pa+ρ0g η)
| {z }
fast
+∇sp0+ρ0∇sΦ
| {z }
slow
(10.136)
where p0=gRη
zρ0dzis the anomalous pressure field. The Boussinesq form of the vertically integrated
momentum budget (10.134) thus takes the form
ρo(∂t+fˆ
z∧)X(udz) = G−(H+η)∇(pa+psurf) (10.137)
for s=zcoordinates, and similarly for s=z∗and s=σ(z)coordinates. In either case, Gis the vertical integral
of the depth dependent terms on the right hand side of equation (10.134). Gembodies all contributions
that are generally evolving on the slower baroclinic time scale. This equation, along with the vertically
integrated volume budget discussed in Section 10.6, form the barotropic system for the Boussinesq fluid in
MOM. These equations are time stepped to resolve the fast waves using a predictor-corrector or leap-frog
scheme discussed in Chapter 12 of Griffies (2004) (see also Section 11.2), where Gis held fixed over the
course of the barotropic cycle. Note that the predictor-corrector is preferred due to its enhanced dissipation
of small spatial scale features, which are of some concern on the B-grid due to the gravity wave null mode
(Killworth et al.,1991;Griffies et al.,2001).
Elements of MOM November 19, 2014 Page 157

Chapter 10. Quasi-Eulerian algorithms for hydrostatic models Section 10.9
10.9.4 Pressure based vertical coordinates
We now follow the discussion in Section 3.2.3 where the pressure gradient is split according to equation
(3.27) into a slow three dimensional term and fast two dimensional term
∇sp+ρ∇sΦ=ρ∇sΦ0−(ρ0/ρo)∇sp
| {z }
slow
+(ρ/ρo)∇(pb+ρoΦb)
| {z }
fast
.(10.138)
where
Φ0=−(g/ρo)
z
Z
−H
ρ0dz. (10.139)
The vertically integrated pressure gradient can be written
Xdz(∇sp+ρ∇sΦ) = Xdz[ρ∇sΦ0−(ρ0/ρo)∇sp]
+∇(pb+ρoΦb)X(ρ/ρo) dz
=Xdz[ρ∇sΦ0−(ρ0/ρo)∇sp]
+ (g ρo)−1(pb−pa)∇(pb+ρoΦb),
(10.140)
where we used the hydrostatic balance to write
gXρdz=pb−pa(10.141)
The vertically integrated momentum budget (10.134) thus takes the form
(∂t+fˆ
z∧)X(uρdz) = G−(g ρo)−1(pb−pa)∇(pb+ρoΦb),(10.142)
where Gis the vertical integral of the depth dependent terms on the right hand side of equation (10.134),
including the slow contribution to the pressure gradient force. The time stepping of equation (10.145) then
proceeds as for the Boussinesq case discussed in Section 11.2. To help reduce errors in the calculation of
the pressure gradient, it is useful to consider the following split of the bottom pressure
pb=p0
b+ρog H, (10.143)
so that the vertically integrated mass and momentum budgets take the form
∂t(p0
b−pa) = −g∇·Uρ+g Qm+gX
kS(M)ρdz(10.144)
(∂t+fˆ
z∧)Uρ=G−(g ρo)−1(pb−pa)∇p0
b.(10.145)
The advantage of this formulation is that we remove the time independent bottom geopotential ρog H from
the pressure gradient contribution to the vertically integrated velocity. As this contribution is huge, its
removal enhances the numerical accuracy of the resulting pressure gradient.
Elements of MOM November 19, 2014 Page 158

Chapter 11
Time stepping schemes
Contents
11.1 Split between fast and slow motions .............................160
11.2 Time stepping the model equations as in MOM4.0 .....................160
11.2.1 The MOM4.0 scheme used in OM3.0 ............................ 161
11.2.2 Problems related to tracer conservation .......................... 162
11.2.3 The time staggered scheme used in OM3.1 ......................... 163
11.2.4 Sensitivity to the time stepping scheme .......................... 164
11.2.5 Dissipative aspects of the predictor-corrector ....................... 164
11.3 Introduction to time stepping in MOM ............................166
11.4 Basics of staggered time stepping in Boussinesq MOM ...................167
11.5 Predictor-corrector for the barotropic system ........................167
11.6 The Griffies (2004) scheme ...................................169
11.7 Algorithms motivated from predictor-corrector .......................169
11.7.1 Barotropic time stepping and surface height on integer time steps ........... 170
11.7.2 Surface height on half-integer time steps .......................... 170
11.7.3 Method A: U(τ+∆τ) = U................................... 172
11.7.3.1 Compatibile tracer concentration ......................... 172
11.7.3.2 Why this scheme is not closed .......................... 173
11.7.4 Method B: U(τ+∆τ/2) = U.................................. 173
11.7.4.1 Compatibile tracer concentration ......................... 173
11.7.4.2 Why this scheme is not closed .......................... 174
11.8 Algorithms enforcing compatibility ..............................174
11.8.1 Method I: Griffies (2004) ................................... 174
11.8.2 Method II: Algorithm based on barotropic predictor-corrector ............. 175
11.8.3 Method III: Modified Griffies (2004) ............................ 175
The purpose of this chapter is to detail various issues of time stepping the discrete equations of MOM. It
is written in two main parts, with the first part focusing on details of the scheme inherited from MOM4.0,
and successfully used for climate modelling. The second part revisits the MOM4.0 scheme, and pro-
poses some alternatives that are presently under investigation. The motivation for revisiting the MOM4.0
schemes is that they show problems when used with radiating open boundary conditions. Martin Schmidt
led the studies into these alternative time stepping schemes, with some details shared with the more sub-
stantial methods studied by Shchepetkin and McWilliams (2005).
159

Chapter 11. Time stepping schemes Section 11.2
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean barotropic.F90
ocean core/ocean velocity.F90
ocean tracers/ocean tracer.F90
11.1 Split between fast and slow motions
An algorithm of practical utility for climate modeling must split the fast and slow dynamics so that the
slow dynamics can be updated with a much longer time step than the fast dynamics. These algorithms are
known as split-explicit methods. Alternatives exist whereby the fast dynamics are time stepped implicitly
and so may use the same time step as the slow dynamics. We prefer split-explicit methods since they are
more efficient on parallel computers and arguably more straightforward (Griffies et al.,2001).
For a hydrostatic fluid, the fast motions can be approximated by the vertically integrated dynamics of
Section 10.9 and the vertically integrated mass or volume budgets of Section 10.6. The remainder consti-
tutes an approximation to the slower dynamics. Motions constituting the fast dynamics are embodied by
the barotropic or external mode, and the slower motions are embodied by advection as well as the baroclinic
or internal mode. Given the fundamental nature of the mass conserving non-Boussinesq flow, we formulate
the split between the fast and slow modes using density weighting. For the Boussinesq flow, the density
weighting reduces to an extra ρofactor that trivially cancels.
Following the discussion in Section 12.3.5 of Griffies (2004), we consider the following split of the
horizontal velocity field
u= u−Pkuρdz
Pkρdz!
| {z }
slow
+ Pkuρdz
Pkρdz!
| {z }
fast
≡ˆ
u+uz.
(11.1)
The fast barotropic velocity
uz=Uρ
Pkρdz(11.2)
is updated according to the vertically integrated momentum equation of Section 10.9. The slow baro-
clinic velocity ˆ
uhas zero density weighted vertical sum, and so its update is independent of any depth
independent forcing, such as fast fluctuations in the surface height associated with external gravity waves.
Therefore, we choose to update the slow dynamics using all pieces of the momentum equation forcing, ex-
cept contributions from the rapid pressure and geopotential fluctuations. This update produces a velocity
u0that is related to the baroclinic velocity via
ˆ
u=u0−Pku0ρdz
Pkρdz.(11.3)
A similar relation was discussed in Section 12.4.2 of Griffies (2004). For global climate simulations, the
time step available for the update of the slow dynamics is much larger (50 to 100 times larger) than the fast
dynamics. It is this large time split, and the attendant improved model efficiency, that motivate the added
complication arising from splitting the modes. Completing the updates of u0and Uρallows for an update
of the full horizontal velocity via
u= u0−Pku0ρdz
Pkρdz!+Uρ
Pkρdz.(11.4)
11.2 Time stepping the model equations as in MOM4.0
We present here some details of the time stepping schemes available in MOM. Much of this section is taken
from the paper Griffies et al. (2005) that documents two ocean climate models developed at GFDL; the
Elements of MOM November 19, 2014 Page 160

Chapter 11. Time stepping schemes Section 11.2
OM3.0 and OM3.1 models. Time stepping in OM3.0 is based on the standard MOM approach originating
from the work of Bryan (1969), and detailed for an explicit free surface by Killworth et al. (1991) and
Griffies et al. (2001). An alternative was developed for OM3.1.
The main motivation for developing an alternative was to address tracer non-conservation associated
with time filtering used to suppress the leap frog computational mode appearing in the older method. The
proposed time staggered method has much in common with that used by Hallberg (1997) for his isopyc-
nal model, as well as by Marshall et al. (1997) and Campin et al. (2004) for their hydrostatic and non-
hydrostatic z-coordinate models.
The purpose of this section is to detail features of the time stepping schemes employed in OM3.0 and
OM3.1. Further details are provided in Chapter 12 of Griffies (2004). We also refer the reader to the
pedagogical treatments of time stepping given by Mesinger and Arakawa (1976), Haltiner and Williams
(1980), and Durran (1999). For simplicity, we focus here on the Boussinesq system assuming z-coordinates
for the vertical. The more general case of arbitrary vertical coordinates with Boussinesq or non-Boussinesq
equations follows trivially from the discussions here. Additionally, the original implementation of these
ideas was based on the B-grid spatial discretization of MOM (Chapter 9). We include discussion here of
modifications required for the C-grid available in MOM.
11.2.1 The MOM4.0 scheme used in OM3.0
We start by describing the standard approach used in MOM4.0 for time stepping tracers and baroclinic
velocity. For the thickness weighted tracer equation, this update takes the form
(hT )τ+1 −(hT )τ−1
2∆τleap
=−∇z·[(hu)τTτ,τ−1+hτFτ−1]−δk[wτTτ,τ−1+Fτ+1
z].(11.5)
Here, his the time dependent thickness of a tracer cell and Tis the associated tracer concentration. Hor-
izontal and vertical advection velocity components are written (u,w), and (F,Fz) are the horizontal and
vertical SGS flux components. The horizontal gradient operator is written ∇z, and δkis the vertical finite
difference operator acting across a discrete level k. Prognostic fields are updated in time increments of
∆τleap. The thickness of a tracer cell is updated analogously to the tracer, as required to maintain compati-
blity between volume and tracer evolution (see Section 10.7 as well as Griffies et al. (2001)).
The time tendency in equation (11.5) has been aproximated with a centred in time discrete operator.
Skipping the central time step τintroduces a spurious computational mode, where even and odd time steps
decouple. We choose time filtering to suppress the associated instability, with hand Tdenoting the time
filtered thickness and tracer concentration. Absent time filtering, the discrete time tendency has a second
order global truncation error, whereas time filtering degrades the truncation error to first order (see Section
2.3.5 of Durran (1999)). We comment further on time filtering in the subsequent discussion, as it one of
the two main reasons we consider alternative time stepping schemes to be preferable.
Global ocean models generally employ anisotropic grids, with significantly more refined vertical spac-
ing than horizontal. When admitting realistically fast vertical mixing processes, parameterized by Fz,
a time implicit method is used to overcome the stringent time step constraints of an explicit approach.
Hence, Fzis evaluated at the future time τ+∆τleap. In contrast, coarser grid spacing in the horizontal gener-
ally allows for an explicit implementation of the horizontal SGS fluxes. Due to the dissipative nature of SGS
fluxes, stability considerations require them to be evaluated at the lagged time τ−∆τleap, with evaluation at
the central time τnumerically unstable. That is, the horizontal SGS fluxes are implemented with a forward
time step of size 2∆τleap.
In contrast to dissipative terms, numerical stability dictates that tracer concentration in the advection
operator be evaluated at the central time τif using central spatial differencing. As reviewed by Griffies
et al. (2000a), this approach was common in z-models for decades, particularly prior to around 2005. This
form of the time stepping gives rise to the commonly referred name leap frog applied to the older time
stepping method used in MOM4.0. However, it is important to note that leap frog in the tracer equation
is used only for advection, and only for central spatial discretizations of advection. Dissipative terms are
implemented with either a forward or an implicit time step as described above.
For purposes of ocean climate modeling with OM3.0, we found the dispersive errors from central dif-
ferenced tracer advection to be unacceptable, due to the introduction of spurious tracer extrema and large
Elements of MOM November 19, 2014 Page 161

Chapter 11. Time stepping schemes Section 11.2
levels of spurious dianeutral mixing when convective adjustment acts on dispersion errors (Griffies et al.,
2000b). To help remedy these problems, we chose a third order upwind biased scheme. As reviewed in
Durran (1999), upwind biasing introduces a damping or dissipative element to numerical advection. Con-
sequently, upwind biased fluxes must be evaluated at the lagged time τ−∆τleap just like the dissipative
horizontal SGS fluxes. A similar situation arises when implementing the Quicker advection scheme, in
which one separates a dissipative portion evaluated at the lagged time step from a non-dissipative piece
evaluated at τ(Holland et al.,1998;Pacanowski and Griffies,1999). This is the origin of the two time labels
placed on the tracer concentration for the advective flux in equation (11.5).
For the Sweby advection scheme used in OM3.0, the split into dissipative and non-dissipative terms is
not possible. The full advective flux is thus evaluated at the lagged time step τ−∆τleap. This result may
suggest increased levels of dissipation using Sweby relative to Quicker. Indeed, this is the case in regions
where dissipation is welcomed, such as near river mouths where Quicker was found to introduce unac-
ceptable tracer extrema. In other regions, we have seen negligible differences between the two advection
schemes.
An update of the thickness weighted baroclinic velocity using the leap-frog scheme on a B-grid takes
the form
hτ+1 uτ+1 −hτ−1uτ−1
2∆τ=−Mτˆ
z×hτuτ+ (wτuτ)k−(wτuτ)k−1−∇z·(hτuτuτ)
−hτ(fˆ
z×u)trapezoidal −hτ∇z(pτ/ρo) + hτ(Fu)(τ−1,τ+1).(11.6)
As for the tracer update, time filtering is applied to the lagged values of velocity and velocity cell thickness
to suppress time splitting. Central differences are used to spatially discretize velocity self-advection, thus
necessitating its evaluation at the central time step. Pressure is temporally evaluated likewise. The friction
operator (Fu)(τ−1,τ+1) arises from horizontal and vertical fluid deformations. Analogous to the treatment
of tracer SGS fluxes, horizontal deformations are evaluated at τ−∆τleap (forward time step) and vertical
deformations at τ+∆τleap (implicit time step).
Inertial energy is realistic in the coupled climate model CM2.0 since it includes a diurnal cycle of solar
insolation, and the atmosphere and sea ice fields passed to the ocean (wind stress, fresh water, turbulent
and radiative fluxes)1are updated every two hours. Inertial energy has important contributions to the
mixing coefficients determined by the model’s boundary layer scheme.
The model’s baroclinic time step ∆τleap = one hour is smaller than that needed to resolve inertial oscilla-
tions (e.g., Section 12.8.3 of Griffies (2004)). We nonetheless encountered an inertial-like instability in the
climate model’s Arctic sector when implementing the Coriolis force explicitly in time (see Chapter 12 for a
discussion of a discrete implementation of the Coriolis Force). This instability is presumably related to the
coupling between the ocean and sea ice, although the precise mechanism remains under investigation. The
climate model remained stable, however, when implementing the ocean’s Coriolis force with a trapezoidal
or semi-implicit method (Section 12.2). Hence, the semi-implicit method is employed in both OM3.0 and
OM3.1.2
11.2.2 Problems related to tracer conservation
Consider now the discrete time tracer equation in the abbreviated form
(hT )τ+∆τleap = (hT )τ−∆τleap + 2 ∆τ G, (11.7)
where Gsymbolizes the advective and diffusive terms as well as boundary fluxes (we ignore source/sink
terms for brevity). Thickness at the lagged time step results from a time average as described in Griffies
et al. (2001), whereas time filtering of tracer concentration is taken in the form suggested by Robert (1966)
1As recommended by Pacanowski (1987), wind stress applied to the ocean surface is computed using the relative velocity between
the atmospheric winds and the ocean currents.
2Recall that both OM3.0 and OM3.1 used the B-grid, which allows for an implicit implementation of the Coriolis force. See Sections
12.2 and 12.3 for details.
Elements of MOM November 19, 2014 Page 162

Chapter 11. Time stepping schemes Section 11.2
and Asselin (1972) (see also Section 2.3.5 of Durran (1999)).3Integrating equation (11.7) over the model
domain leads to the balance of total tracer content in the model. Total tracer at time τ+∆τleap is determined
by the input of tracer through boundaries during the 2∆τleap time step, plus the volume integrated product
of the time filtered thickness and tracer concentration, hT , at the lagged time τ−∆τleap. Notably, because
of time filtering, the model’s total tracer changes even in the case of zero boundary fluxes.
The magnitude of tracer change associated with time filtering can be negligible for many purposes, as
discussed in Griffies et al. (2001). However, we found the changes unacceptable when developing ecosys-
tem models, where precise conservation is desired. Additionally, filtering contributed to a globally aver-
aged heat non-conservation in the climate model on the order of ±0.03Wm−2. This non-conservative heat
flux is a few percent of the surface insolation change expected from doubling greenhouse gas concentrations
in the atmosphere. It is therefore of concern for our climate change simulations. Consequently, alternative
approaches were investigated.4
11.2.3 The time staggered scheme used in OM3.1
The alternative scheme we employ in OM3.1 discretizes the time derivative with a forward time step. That
is, it does not skip any time levels. Additionally, it staggers tracer and velocity fields by one-half time step
in a manner analogous to spatial staggering on Arakawa grids. We therefore refer to this method as a time
staggered scheme.
Forward time stepping does not admit time splitting, and so no time filters are needed. The alterna-
tive scheme therefore ensures tracer is conserved, which is our primary motivation for moving away from
the OM3.0 method involving the leap frog. There are other consequences of changing the time tendency
discretization, and the purpose of this section is to expose these issues.
A time staggered update of thickness weighted tracer is given by
(hT )τ+1/2−(hT )τ−1/2
∆τstag
=−∇z·[(hu)τTτ−1/2+hτ−1/2Fτ−1/2]−δk[wτTτ−1/2+Fτ+1/2
z].(11.8)
The two equations (11.5) and (11.8) become identical when the following holds:
• time steps are related by ∆τstag = 2∆τleap,
• time filtering in the OM3.0 leap frog method is not used,
• tracer advection employs an upwind biased scheme.
In effect, the time staggered method stays on just one of the two leap frog branches. This is the fundamental
reason that the two methods should be expected, for many purposes, to yield similar solutions.
We note the following points to keep in mind when transitioning to the staggered approach from the
leap-frog.
• Centred spatial differencing of advection is unstable with a forward time step. Hence, for tracer
advection we must employ an upwind biased advection scheme when using the staggered approach.
For our purposes with global ocean climate modelling, such advection schemes are motivated to
resolve problems with other schemes. Nonetheless, this consequence of changing the time stepping
scheme may be unacceptable for certain applications. An alternative method is to retain the ability
to discretize advection with centred spatial differences, but to alter the temporal evaluation of the
advection operator according to Adams-Bashforth methods (Durran,1999), or other schemes. In
particular, we chose a temporally third order accurate Adams-Bashforth method for velocity self-
advection, thus maintaining the traditional centred spatial differences of this operator. The third
order Adams-Bashforth method requires the advection operator at time steps τ,τ−1, and τ−2, thus
increasing memory requirements.
3We chose filtering for tracer over the alternative of periodically using a forward or backward time step, which was the method
used by Cox (1984). The use of a periodic forward or backward time step introduces an unphysical periodicity to the simulation, and
in particular was found by Marotzke (1991) to interact in unphysical ways with convective adjustment.
4Leclair and Madec (2009) propose a method to maintain conservation with the leap-frog scheme. We propose an alternative
staggered scheme for MOM discussed in Section 11.2.3.
Elements of MOM November 19, 2014 Page 163

Chapter 11. Time stepping schemes Section 11.2
• When choosing a forward time step for the tendency, the Coriolis force on the B-grid must be com-
puted using an implicit or semi-implicit approach, whereas on the C-grid we wrap the Coriolis force
into the momentum advection using a 3rd order Adams-Bashforth scheme (see Chapter 12 for details
of the Coriolis force). A time explicit approach is numerically unstable using a forward time step. In
contrast, the OM3.0 approach with the leap frog on the B-grid allows for an explicit leap frog time
stepping of the Coriolis force, as well as the semi-implicit or implicit.
• A leap frog discretization of the time tendency updates the ocean state by ∆τleap through taking a
2∆τleap step for the discrete time tendency. Consequently, gravity waves and dissipative operators
(i.e., diffusion, friction, and upwind biased advection) are time step constrained based on 2∆τleap. In
constrast, the staggered scheme updates the ocean state by ∆τstag and it employs ∆τstag to compute
tendencies. It is therefore time step constrained based on a ∆τstag time step. Hence, the staggered
time step ∆τstag can generally be twice that of the leap frog ∆τleap
∆τstag = 2∆τleap.(11.9)
The computational cost of OM3.1 with the staggered scheme is therefore one-half that of OM3.0 using
the older leap frog based scheme. There can be little argument that such an improvement in efficiency
is of great use for ocean modelling.
11.2.4 Sensitivity to the time stepping scheme
During the bulk of our development, the ocean model employed the older leap frog based time stepping
scheme for tracer, baroclinic, and barotropic equations. Upon developing the staggered time stepping
scheme for the tracer and baroclinic equations, we became convinced that the modified scheme has util-
ity for our climate modelling applications. The question arose whether switching time stepping schemes
would require retuning of the physical parameterizations.
Tests were run with the ocean and ice models using an annually repeating atmospheric forcing with
daily synoptic variability, again repeating annually. Runs using the staggered scheme had a two hour time
step for both tracer and baroclinic momentum, and a predictor-corrector scheme (e.g., Killworth et al.,
1991;Griffies,2004) for the barotropic equations with a 90s time step.5The comparison was made to
the older time stepping scheme using one hour time steps for the tracer and baroclinic equations, and
(3600/64)s for the leap frog barotropic equations.
Analysis of these solutions after 10 years revealed that regions with relatively high frequency temporal
variability, such as the equatorial wave guide, exhibit the most differences instantanously. Figure 11.1
illustrates the situation along the equator in the East Pacific. The older scheme exhibits substantial time
splitting, even with a nontrivial level of time filtering from a Robert-Asselin time filter. Moving just five
degrees north of the equator, however, reveals that the simulation has much less relative variability, and a
correspondingly negligible amount of time splitting. Even though the simulation along the equator showed
substantial time splitting, over longer periods of time, the large scale patterns and annual cycles showed
negligible differences between time stepping schemes. Indeed, time averaging, even over just a day, seems
sufficient to smooth over most of the instantaneous differences.
Tests were then run with the GFDL coupled climate models CM2.0 (using OM3.0 as the ocean compo-
nent) and CM2.1 (using OM3.1). Instantaneous differences were much larger, as expected due to the non-
trivial natural variability in the coupled system with a freely evolving atmospheric component. Nonethe-
less, differences for large scale patterns and seasonal or longer time averages were within levels expected
from the model’s natural variability.
11.2.5 Dissipative aspects of the predictor-corrector
The purpose of this section is to expose the dissipative aspects of the predictor-corrector scheme available
for use in the barotropic equations in MOM. A similar treatment is given in Section 12.8.1 of Griffies (2004).
5We found the predictor-corrector to be suitable for the barotropic equations due to our ability to increase the barotropic time
step beyond that of the leap frog. Additionally, it preferentially dissipates grid scale features, which are commonly found when
discretizing gravity waves on a B-grid (Killworth et al.,1991;Griffies et al.,2001). We present an analysis of the dissipative aspects
in Section 11.2.5.
Elements of MOM November 19, 2014 Page 164
Chapter 11. Time stepping schemes Section 11.2
Figure 11.1: Upper left panel: Instantaneous sea surface temperature over January 1 at (105◦W ,0◦N) as
realized in a simulation using the standard time stepping scheme with an hour tracer time step (noisy
time series) and the staggered scheme with a two hour tracer time step (smooth time series). Upper right
panel: Surface heating applied at (105◦W ,0◦N) from the Robert-Asselin time filter used to damp the leap
frog splitting. Lower left panel: Instantaneous sea surface temperature over a single day at (105◦W ,5◦N)
as realized in a simulation using the standard scheme with an hour tracer time step and the staggered
scheme with a two hour tracer time step. Note the width of the temperature range is set the same as at the
equator. In general, the agreement of the solution offthe equator, where the leap frog splitting is minimal,
is far greater than on the equator. Lower right panel: Surface heating applied at (105◦W ,5◦N) from the
Robert-Asselin filter. Note the much smaller magnitude relative to the values on the equator.
In two space dimensions, the predictor-corrector equations for an update of the surface height and
vertically integrated horizontal velocity in a Boussinesq model are
η∗−ηn
∆t=−γ∇·Un(11.10)
Un+1 −Un
∆t=−c2∇η∗(11.11)
ηn+1 −ηn
∆t=−∇·Un+1,(11.12)
where nsymbolizes the barotropic time step. For brevity we dropped the fresh water and source terms
appearing in the free surface equation (10.69), and we assumed an unforced linear shallow water system
with squared wave speed c2=g H. Setting the dimensionless dissipation parameter γ≥0 to zero recovers a
forward-backward scheme discussed by Killworth et al. (1991). Keeping γ > 0 was useful in our simulations
and was motivated by similar experiences in the Hallberg Isopycnal Model (Hallberg,1997).
Elements of MOM November 19, 2014 Page 165

Chapter 11. Time stepping schemes Section 11.4
Eliminating the predicted surface height η∗leads to
Un+1 −Un
∆t=−c2∇ηn+γ c2∆t∇[∇·Un] (11.13)
ηn+1 −ηn
∆t=−∇·Un+1.(11.14)
To directly see how the surface height evolves, eliminate Uto find
ηn+1 −2ηn+ηn−1
(∆t)2= (c∇)2ηn+γ(c∇)2ηn−ηn−1.(11.15)
Taking the limit ∆t→0, yet with γ∆tconstant, leads to a dissipative wave equation
(∂tt −c2∇2)η= (γ∆t)(c∇)2∂tη. (11.16)
A single spatial Fourier mode with wavenumber amplitude κthus satisfies
d2/dt2+γ∆t(cκ)2d/dt+ (cκ)2η= 0.(11.17)
This is the equation for a damped harmonic oscillator with inverse e-folding time (1/2)γ∆t(c κ)2. With
γ > 0, external gravity waves are selectively dissipated in regions where the surface height is changing in
time, and where the spatial scales are small. Faster waves are damped more readily than slower waves.
These properties are useful when aiming to suppress the B-grid computational null mode discussed in
Killworth et al. (1991) and Griffies et al. (2001).
11.3 Introduction to time stepping in MOM
For the remainder of this chapter, we step back from the OM3 simulations and revisit some of the basic
algorithmic details of the time stepping schemes used in MOM. For this purpose, it is sufficient to focus
on the Boussinesq version, where volume is conserved rather than mass. The exact same issues arise when
using mass conserving non-Boussinesq vertical coordinates.
To start, we summarize advantages of the staggered time stepping scheme employed by MOM and
introduced in Section 11.2.3 when discussing the OM3.1 model. For climate modelling, this scheme has
proven to be a great improvement over the traditional leap-frog based methods found in earlier GFDL
ocean codes, as well as many other ocean circulation models (Griffies et al. (2000a)). The improvements
include the following.
• There is no need to employ explicit time filters (e.g., Robert-Asselin filter) with the staggered scheme,
thus enhancing temporal accuracy over the time filtered leap-frog scheme.
• The time staggered scheme conserves seawater volume/mass and tracer mass to within numerical
roundoff, whereas the leap-frog based methods, due to the use of explicit time filtering, fail to con-
serve.
• The time staggered scheme updates the state of the ocean one time step by employing tendencies
based on that one time step. In contrast, leap-frog based schemes update the state over one time step
by using tendencies based on two time steps. Hence, the leap-frog based schemes have a CFL stability
constraint based on the two time step tendencies, and so can be run at only one-half the time step of
the staggered scheme. Thus, the staggered scheme is generally one half the computational cost of the
leap-frog based schemes.
The purpose of the following sections of this chapter is to expose salient points regarding the time
stepping algorithm that have been raised when developing the radiating open boundary condition.
Elements of MOM November 19, 2014 Page 166

Chapter 11. Time stepping schemes Section 11.5
11.4 Basics of staggered time stepping in Boussinesq MOM
Fundamental to the time staggered method is the need to provide a surface height ηat integer time steps
η(τ) as well as half integer time steps η(τ+∆τ/2). The surface height at integer time steps is needed
to couple to velocity variables, which are placed on integer time steps, whereas half integer time steps
provide a surface height for tracers. In addition, due to the split between barotropic and baroclinic modes,
the surface height is updated over the small barotropic time steps η(b)(τ,tn), where a raised (b) denotes a
field evaluated on the small barotropic time step. The first time label τdesignates which baroclinic branch
the cycle started, and
tn=τ+n∆t(11.18)
is the barotropic time step. The relation between the large time step ∆τand small time step ∆tis given by
2∆τ=N∆t. (11.19)
The barotropic time stepping procedes from the initial barotropic time t0=τto the final time tN=τ+2 ∆τ.
The integer Nis a function of the split between barotropic and baroclinic gravity waves, which can be
on the order of 100 in a global model. Deducing the connection between η(τ), η(τ+∆τ/2), and η(b)(τ,tn)
is a focus of these notes. Correspondingly, we require a connection between the barotropic time cycled
vertically integrated velocity U(b)and U(τ).
The barotropic cycle integrates over time 2∆τfor every ∆τupdate of the baroclinic system. Why the
doubling of the time integration? This method is based on experience with split-explicit time stepping
schemes, where we have found it important to provide sufficient time averaging to damp instabilities aris-
ing from the incomplete split between the fast and slow motions available with a vertical integration.
Longer time averaging is possible, though less convenient algorithmically, less accurate, and more expen-
sive.
A fundamental constraint of any time stepping scheme is that the tracer and volume/mass equations
must remain compatible. Compatibility means that the tracer concentration equation reduces to the vol-
ume or mass conservation equation when setting the tracer concentration to a constant. Without compati-
bility, tracer and volume/mass conservation are lost, and the algorithm is of limited use for ocean climate
modelling.
After completing the barotropic cycle, which extends from t0=τto tN=τ+ 2 ∆τ, we aim to have a
prescription for updating the vertically integrated velocity U(τ+∆τ), the free surface height η(τ+∆τ/2), as
well as η(τ+∆τ).
11.5 Predictor-corrector for the barotropic system
The preferred barotropic time stepping algorithm is the predictor-corrector scheme. The first step in the
algorithm “predicts” the surface height (again, we are focusing on the Boussinesq version of MOM) via
η(∗)(τ,tn+1)−η(b)(τ,tn)
γ∆t=−∇·U(b)(τ,tn) + E,(11.20)
where Eis the fresh water forcing or volume source, both of which are held constant over the course of the
barotropic cycle. We expose the time labels on these fields in later discussions. The raised (∗) denotes an
intermediate value of the surface height. This is the “predicted” value, to be later “corrected.” The nondi-
mensional parameter 0 ≤γacts to dissipate the small scales of motion (see Section 12.8 of Griffies (2004)).
Setting γ= 0 recovers a second order accurate forward-backward scheme, in which case the predictor step
(11.20) is eliminated. Larger values of γreduce the order of accuracy, yet provide effective damping. How-
ever, as shown in Section 12.8 of Griffies (2004), values of γlarger than 1/4 can compromise the scheme’s
stability. The value γ= 1/5 has been found useful for many purposes.
The predicted surface height η(∗)(τ,tn+1) is used to compute the surface pressure via
ρo˜
p(∗)
s(τ,tn+1) = g η(∗)(τ,tn+1)ρ(τ+1/2)
k=1 (11.21)
Elements of MOM November 19, 2014 Page 167

Chapter 11. Time stepping schemes Section 11.6
where the applied pressure pahas been dropped for brevity but can be trivially added. The surface pressure
is used to update the vertically integrated velocity
U(b)(τ,tn+1)−U(b)(τ,tn)
∆t="−fˆ
z∧U(b)(τ,tn) + U(b)(τ,tn+1)
2−D(τ)∇z˜
p(∗)
s(τ,tn+1) + G(τ)#.(11.22)
For the vertically integrated transport, the Coriolis force on the B-grid version of MOM is evaluated us-
ing the Crank-Nicholson semi-implicit time scheme in equation (11.22). Inverting the B-grid simi-implicit
approach provides an explicit update of the vertically integrated transport
U(b)(τ,tn+1) = [1 + (f∆t/2)2]−1[U(#)(τ,tn+1) + (f∆t/2)V(#)(τ,tn+1)] (11.23)
V(b)(τ,tn+1) = [1 + (f∆t/2)2]−1[V(#)(τ,tn+1)−(f∆t/2)U(#)(τ,tn+1)] (11.24)
where U(#)(τ,tn+1) is updated just with the time-explicit tendencies
U(#)(τ,tn+1)−U(b)(τ,tn)
∆t= (f /2)V(b)(τ,tn)−D(τ)∂x˜
p(∗)
s(τ,tn+1) + Gx(τ) (11.25)
V(#)(τ,tn+1)−V(b)(τ,tn)
∆t=−(f /2)U(b)(τ,tn)−D(τ)∂y˜
p(∗)
s(τ,tn+1) + Gy(τ).(11.26)
For the C-grid version of MOM, the Coriolis force is evaluated using an Adams-Bashforth scheme (see
Section 12.3).
The “corrector” part of the scheme steps the surface height using the updated transport
η(b)(τ,tn+1)−η(b)(τ,tn)
∆t=−∇·U(b)(τ,tn+1) + E.(11.27)
Note that η(b)(τ,tn+1) is used rather than the predicted height η(∗)(τ,tn+1), since η(∗)(τ,tn+1) is computed with
the altered time step γ∆t. Temporal dissipation is localized to the predictor portion of the time stepping,
with the corrector part hidden from this dissipation. Because of the predictor step, the convergence of
the vertically integrated transport is computed twice in the predictor-corrector scheme, thus increasing the
cost relative to a forward-backward approach where γ= 0. The payoffis an extra parameter that can be
used to tune the level of dissipation. Additionally, there is added stability towards representing gravity
waves so that ∆tcan be longer than when using the leap-frog method.
Let us detail how the barotropic steps accumulate over the course of a particular barotropic cycle. For
this purpose, write out the first and second corrector steps (11.27) for the surface height
η(b)(τ,tn=1)−η(b)(τ,tn=0)
∆t=F(tn=1) (11.28)
η(b)(τ,tn=2)−η(b)(τ,tn=1)
∆t=F(tn=2),(11.29)
where the right-hand side of equation (11.27) is abbreviated as F. Adding these two equations leads to
η(b)(τ,tn=2)−η(b)(τ,tn=0)
∆t=F(tn=1) + F(tn=2),(11.30)
where the intermediate value η(b)(τ,tn=1) has identically cancelled. This result easily generalizes, so that
η(b)(τ,tn=N)−η(b)(τ,tn=0)
N∆t=1
N
N
X
n=1
F(tn).(11.31)
This result does not hold for a leap-frog algorithm, since the intermediate values of the surface height do
not generally cancel completely, as they do here for the predictor-corrector.
Elements of MOM November 19, 2014 Page 168

Chapter 11. Time stepping schemes Section 11.7
11.6 The Griffies (2004) scheme
The only piece of the forcing F(tn) that changes during the barotropic cycle is the convergence of the ver-
tically integrated velocity. The result (11.31) then suggests that the time averaged vertically integrated
velocity should be given back to the baroclinic part of the model upon completion of the barotropic cycle.
To have this velocity centered on the integer time step τ+∆τ, it is necessary to run the barotropic cycle to
τ+ 2∆τ. Hence, upon reaching the last barotropic time step
tn=N=τ+ 2∆τ, (11.32)
the vertically integrated velocity is time averaged,
˜
U=1
N
N
X
n=1
U(b)(τ,tn).(11.33)
To produce the updated vertically integrated velocity at baroclinic time τ+∆τ, the vertically integrated
velocity U(τ+∆τ) is identified with this time averaged value,
U(τ+∆τ)≡˜
U.(11.34)
The surface height is needed at the integer time steps in order to specify the thickness of the velocity
cells. There are two options for updating the surface height to time step τ+∆τ. First, we could take the
instantaneous value from the barotropic portion of the cycle
η(τ+∆τ)≡η(b)(τ,tn=N/2).(11.35)
This approach has not been tried, since it likely leads to a meta-stable algorithm due to the absence of time
averaging, depending on the predictor-corrector dissipation parameter γ. In contrast, extensive experience
indicates that added stability is realized by using the time averaged surface height
η(τ+∆τ) = 1
N+ 1
N
X
n=0
η(b)(τ,tn).(11.36)
Notably, tracer and volume conservation is not compromised by this specification since it is only used to
define the surface height carried by the velocity cells. However, the surface height at half integer timesteps
needed for the tracer equation is diagnosed using equation (11.33),
η(τ+∆τ/2) −η(τ−∆τ/2)
∆τ=−∇·U(τ) + qw(τ) + S(η)(τ).(11.37)
As described in Section 11.7, this approach may cause divergence of sea level at integer and half integer
time steps.
11.7 Algorithms motivated from predictor-corrector
The previous algorithm makes a distinction between how the integer and half-integer surface heights are
updated. This distinction exposes the algorithm to possible time splitting between these surface heights.
The splitting has been found to be unacceptable for models with radiating open boundary conditions,
whereas other boundary conditions have shown no problem. Given the interest in radiating boundary
conditions, we consider here an alternative approach which is motivated from details of the barotropic
predictor-corrector method. It will turn out that the schemes developed here are not algorithmically closed.
However, approximations are considered in 11.8.2 to close the algorithms.
Elements of MOM November 19, 2014 Page 169

Chapter 11. Time stepping schemes Section 11.7
11.7.1 Barotropic time stepping and surface height on integer time steps
The predictor step in the predictor-corrector algorithm updates the surface height according to
η(b)(τ,tn+1)−η(b)(τ,tn) = ∆t F(tn+1).(11.38)
We now expose the time labels on all terms appearing in the forcing, whereby we set volume sources
F(tn+1) = −∇·U(b)(τ,tn+1) + qw(τ+∆τ/2) + S(η)(τ+∆τ/2).(11.39)
Only the convergence of the vertically integrated velocity U(b)(τ,tn+1) changes on each barotropic time step,
whereas the water forcing qw(τ+∆τ/2) and source S(η)(τ+∆τ/2) are held fixed.
To begin the barotropic integration of the surface height, it is necessary to prescribe an initial condition.
We choose to set
η(b)(τ,t0) = η(τ) (11.40)
for the surface height, and
U(b)(τ,t0) = U(τ) (11.41)
for the vertically integrated velocity. This choice of the starting point is essential for η, but different ap-
proximations are possible for the vertically integrated velocity. Here, η(τ) and U(τ) are centred at an integer
baroclinic time step, which again is the time step where the velocity field is centred using the MOM time
staggered method. These two prescriptions lead us to ask how to compute the updated surface height
η(τ+∆τ) and vertically integrated velocity U(τ+∆τ). Experience with various versions of the split-explicit
time stepping in MOM motivates us to take for the surface height a time average over the full suite of
barotropic surface heights according to
η(τ+∆τ) = 1
N+ 1
N
X
n=0
η(b)(τ,tn).(11.42)
We choose this simple form of time filtering, in which all terms within the barotropic time stepping con-
tribute equally. Although more sophisticated time filters are available, this one has been found suitable for
our purposes. Without time filtering, the algorithm can be very unstable and thus is unsuitable for large
scale modelling. As shown below, this time averaging for the surface height motivates a different form for
the time averaging of the vertically integrated velocity field.
11.7.2 Surface height on half-integer time steps
The fundamental prescription (11.42) for the integer time step surface height is readily extended to the
half-integer surface height by setting
η(τ+∆τ/2) ≡η(τ) + η(τ+∆τ)
2.(11.43)
This prescription couples the integer and half-integer time steps, and ensures that both are determined by
time averages over the barotropic cycle. The question then arises how to make this prescription compatible
with the time stepping for the tracer concentration. Compatibility is required for conservation of volume
and tracer, and so is of fundamental importance. Compatibility is also needed with the baroclinic veloc-
ity scheme, but keeping in mind the uncertainties of wind stress parameterisation, minor approximation
should be possible. Addressing these issues forms the remainder of this section.
To proceed, we first deduce the time stepping algorithm for the integer time steps which is implied
from the barotropic time stepping (11.38) and the time average (11.42). For this purpose, start by using the
initial condition (11.40) in the time average (11.42) to find
η(τ+∆τ) = 1
N+ 1
N
X
n=0
η(b)(τ,tn) (11.44)
=η(τ)
N+ 1 +1
N+ 1
N
X
n=1
η(b)(τ,tn).(11.45)
Elements of MOM November 19, 2014 Page 170

Chapter 11. Time stepping schemes Section 11.7
Iterating the barotropic time stepping equation (11.38) and using the initial condition (11.40) renders
η(b)(τ,tn) = η(τ) + ∆t
n
X
i=1
F(ti).(11.46)
Substitution of this result into equation (11.45) then leads to
η(τ+∆τ)−η(τ) = ∆t
N+ 1
N
X
n=1
n
X
i=1
F(ti).(11.47)
The double sum on the right hand side arises from the need to ensure that over the course of the barotropic
cycle, changes in volume correspond to changes in forcing; in particular, with changes in the convergence of
the depth integrated transport. To facilitate computing the double sum within the barotropic time stepping
scheme, we employ the following identity to reduce the double sum to a single sum
N
X
n=1
n
X
i=1
F(ti) =
N
X
n=1
(N−n+ 1)F(tn),(11.48)
which can be readily verified by induction.
The sum (11.48) does not represent a straightforward time average. It does, nonetheless, motivate
defining a “modified average” forcing that is implied by the barotropic cycle running from tn=0 =τto
tN=τ+2∆τ. In particular, the relation 2∆τ=N∆tbetween baroclinic and barotropic time steps motivates
the following definition for the averaged forcing
F≡2
N(N+ 1)
N
X
n=1
n
X
i=1
F(ti),
≡2
N(N+ 1)
N
X
n=1
(N−n+ 1)F(tn),
(11.49)
which renders η(τ+∆τ)−η(τ)
∆τ=F. (11.50)
Note that the average operator (11.49) reduces to the trivial result F=Fin the special case when each of
the barotropic time steps see a constant forcing F(ti)≡F. That is,
N
X
n=1
n
X
i=1
F(ti) = F
N
X
n=1
n(11.51)
=F(N/2)(N+ 1),(11.52)
where the last step used a common summation identity. This special case supports our definition of the
averaging operator, and furthermore checks the integrity of the manipulations. In particular, since the
fresh water and volume source are assumed to be constant over the barotropic time steps, we have
F=2
N(N+ 1)
N
X
n=1
n
X
i=1
F(ti) (11.53)
=−2
N(N+ 1)
N
X
n=1
n
X
i=1 ∇·U(b)(τ,ti) + qw(τ+∆τ/2) + S(η)(τ+∆τ/2) (11.54)
which leads to η(τ+∆τ)−η(τ)
∆τ=−∇·U+qw(τ+∆τ/2) + S(η)(τ+∆τ/2).(11.55)
Elements of MOM November 19, 2014 Page 171

Chapter 11. Time stepping schemes Section 11.7
So far, we have avoided placing a time label on the modified average operator. In particular, the question
arises how the averaged vertically integrated velocity
U=2
N(N+ 1)
N
X
n=1
n
X
i=1
U(b)(τ,ti) (11.56)
is related to the updated velocity U(τ+∆τ) or U(τ+∆τ/2). Absent the second summation, the resulting
average would be closely centred on the time step τ+∆τ, but the barycenter of the double sum is at τ+∆τ/2.
We now discuss algorithms based on both approximations.
11.7.3 Method A: U(τ+∆τ) = U
In this method, we consider U(τ+∆τ) = U, so that
U(τ+∆τ) = 2
N(N+ 1)
N
X
n=1
n
X
i=1
U(b)(τ,ti).(11.57)
Given this assumed time labelling of U, we are able to update the three dimensional velocity to the new time
step τ+∆τafter the baroclinic velocity is updated. The prescription (11.57) implies that the integer time
step surface height, which is computed as the time average in equation (11.42), also satisfies the following
time tendency equation
η(τ+∆τ)−η(τ)
∆τ=−∇·U(τ+∆τ) + qw(τ+∆τ/2) + S(η)(τ+∆τ/2).(11.58)
The definition (11.43) of the half-integer time step surface height then implies that it satisfies the tendency
equation
η(τ+∆τ/2) −η(τ−∆τ/2)
∆τ=−∇·U(τ+∆τ/2) + qw(τ) + S(η)(τ),(11.59)
where
U(τ+∆τ/2) = U(τ) + U(τ+∆τ)
2(11.60)
qw(τ) = qw(τ+∆τ/2) + qw(τ−∆τ/2)
2(11.61)
S(η)(τ) = S(η)(τ+∆τ/2) + S(η)(τ−∆τ/2)
2.(11.62)
11.7.3.1 Compatibile tracer concentration
For the surface height on half integer time steps, we must maintain compatibility with tracer concentration
fields, which are also centered on half-integer time steps. Compatibility means that time stepping the
surface height must take the identical form to time stepping tracer concentration, so that the two equations
agree in the special case of a constant tracer concentration. Without such compatibility, tracer and volume
are not conserved by the discrete model. This point was emphasized by Griffies et al. (2001) in the context
of the leap-frog based algorithm exclusively used in earlier versions of MOM.
Compatibility implies that the tracer concentration must be forced with the water source (11.61), the
volume source (11.62), and, because of equation (11.59), with the half-integer advection velocity. Given
these considerations, a compatible staggered time discretization of thickness weighted tracer, absent sub-
grid scale processes, takes the form (note the shorthand used for the time labels)
hτ+1/2Cτ+1/2−hτ−1/2Cτ−1/2
∆τ=−∇s·[(hu)τ+1/2Cτ−1/2] (11.63)
+ [wτ+1/2Cτ−1/2]k−[wτ+1/2Cτ−1/2]k−1,(11.64)
Elements of MOM November 19, 2014 Page 172
Chapter 11. Time stepping schemes Section 11.7
where the thickness weighted advection velocity on half-integer time steps is given by
(hu)τ+1/2=(hu)τ+1 + (hu)τ
2.(11.65)
11.7.3.2 Why this scheme is not closed
This algorithm is not closed, and so is not practical. The reason is that the compatible tracer equation
(11.64) requires the thickness weighted advection velocity (hu)τ+1/2. However, this velocity requires the
updated thickness weighted velocity (hu)τ+1, but the velocity at time uτ+1 is not known until the momen-
tum is updated.
11.7.4 Method B: U(τ+∆τ/2) = U
Since the barycenter of the double sum (11.48) is τ+∆τ/2, it is reasonable to prescribe U(τ+∆τ/2) = U, so
that
U(τ+∆τ/2) = 2
N(N+ 1)
N
X
n=1
n
X
i=1
U(b)(τ,ti).(11.66)
The prescription (11.57) implies that the integer time step surface height, which is computed as the time
average in equation (11.42), also satisfies the following time tendency equation
η(τ+∆τ)−η(τ)
∆τ=−∇·U(τ+∆τ/2) + qw(τ+∆τ/2) + S(η)(τ+∆τ/2).(11.67)
The definition (11.43) of the half-integer time step surface height then implies
η(τ+∆τ/2) −η(τ−∆τ/2)
∆τ=−∇·U(τ) + qw(τ) + S(η)(τ),(11.68)
where
U(τ) = U(τ+∆τ/2) + U(τ−∆τ/2)
2(11.69)
qw(τ) = qw(τ+∆τ/2) + qw(τ−∆τ/2)
2(11.70)
S(η)(τ) = S(η)(τ+∆τ/2) + S(η)(τ−∆τ/2)
2.(11.71)
11.7.4.1 Compatibile tracer concentration
Compatibility implies that in contrast to Section 11.7.3.1, the tracer concentration must be forced with the
water source (11.70), the volume source (11.71), and, because of Equation (11.68) with the integer advection
velocity. The compatible staggered time discretization of thickness weighted tracer, absent subgrid scale
processes, takes the form
hτ+1/2Cτ+1/2−hτ−1/2Cτ−1/2
∆τ=−∇s·[(hu)τCτ−1/2] (11.72)
+ [wτCτ−1/2]k−[wτCτ−1/2]k−1,(11.73)
where the thickness weighted advection velocity on integer time steps is given by
(hu)τ=(hu)τ+1/2+ (hu)τ−1/2
2.(11.74)
Elements of MOM November 19, 2014 Page 173

Chapter 11. Time stepping schemes Section 11.8
11.7.4.2 Why this scheme is not closed
This scheme is not closed algorithmically. That is, the velocity scheme cannot be completed after the
barotropic sequence is ready, because U(τ+∆τ) is still unknown. The compatible tracer equation (11.73)
requires also the thickness weighted advection velocity (hu)τ+1/2, which itself requires the updated thick-
ness weighted velocity (hu)τ+1. The velocity at time uτ+1, however, is not known until the momentum
is updated which in turn requres the barotropic scheme to be completed. Yet the momentum is updated
only after the tracer is updated. The repeated mapping between integer to half integer steps would reduce
accuracy. A significant rearrangement of the baroclinic and tracer equation may facilitate the use of this
algorithm. However, many attempts have failed.
11.8 Algorithms enforcing compatibility
We present three methods for time stepping the equations in MOM. Method I is that one discussed in
Section 11.6 based on Griffies (2004) and Griffies et al. (2005). Method III is a modification to Method I,
and Method II is a closed algorithm based on the barotropic predictor-corrector from Section 11.7. Methods
II and III each aim to provide a closed and compatible scheme that maintains stability with the radiating
open boundary condition. Methods I and II are implemented in MOM, with Method III remaining untested.
11.8.1 Method I: Griffies (2004)
We first summarize the method of Griffies (2004) and Griffies et al. (2005), as described in Section 11.6.
To produce an algorithm that maintains compatibility with tracer concentration, and is algorithmically
closed, we take the philosophy here that the fundamental fields are those which live on the baroclinic time
steps (including baroclinic velocity and tracer fields). The barotropic fields are coupled to the baroclinic
and tracer fields, but details of the barotropic algorithm do not dictate details of the baroclinic and tracer
algorithm. In particular, details of whether we use a barotropic leap-frog or predictor-corrector are unim-
portant, nor are details of the initial values used for the surface height and vertically integrated velocity
(so long as the initial values are reasonable). This philosophy is in contrast to that taken in Section 11.7,
and further described in Method III below, where the barotropic predictor-corrector motivated details of
the baroclinic and tracer updates.
The main steps of this scheme prescribe an updated vertically integrated velocity and updated surface
height, both as time averages over the barotropic time steps
U(τ+∆τ) = 1
N
N
X
n=1
U(b)(τ,tn) (11.75)
η(τ+∆τ) = 1
N+ 1
N
X
n=0
η(b)(τ,tn).(11.76)
The half-integer time step surface height is driven by the convergence of the time averaged vertically inte-
grated velocity, as well as surface boundary fluxes and interior volume sources
η(τ+∆τ/2) −η(τ−∆τ/2)
∆τ=−∇·U(τ) + qw(τ) + S(η)(τ).(11.77)
The compatible evolution equation for the tracer concentration follows from the update to the half-integer
surface height
hτ+1/2Cτ+1/2−hτ−1/2Cτ−1/2
∆τ=−∇s·[(hu)τCτ−1/2] (11.78)
+ [wτCτ−1/2]k−[wτCτ−1/2]k−1.(11.79)
There is a distinction in this method between η(τ+∆τ), which is based on a time average, and η(τ+∆τ/2),
which is based on a baroclinic forward time step. This dichotomy has been found to allow splitting between
the surface heights when using radiating open boundary conditions.
Elements of MOM November 19, 2014 Page 174

Chapter 11. Time stepping schemes Section 11.8
11.8.2 Method II: Algorithm based on barotropic predictor-corrector
We were led to the non-closed algorithms in Section 11.7 by aiming to treat the barotropic system in a
systematic manner, and by prescribing the use of a particular form of time averaging for the surface height.
Alternative methods can be found by altering the form of the time average, or by jettisoning time averaged
operators altogether. However, we are not in favour of jettisoning the time average, as past explorations of
this approach have led to unacceptably unstable schemes. Instead, we consider approximations described
in the following that close the algorithm.
To start, we follow the scheme proposed in Section 11.7.4, in which the integer time step surface height
is updated via a time average as in equation (11.76)
η(τ+∆τ) = 1
N+ 1
N
X
n=0
η(b)(τ,tn),(11.80)
and the half-integer time step surface height is also a time average via
η(τ+∆τ/2) ≡η(τ) + η(τ+∆τ)
2.(11.81)
Following the details of the barotropic predictor-corrector, we are led to the updated vertically integrated
velocity via the sum in equation (11.66) and using the barycenter for the time step placement as in Section
11.7.4
U(τ+∆τ/2) = 2
N(N+ 1)
N
X
n=1
n
X
i=1
U(b)(τ,ti)
=2
N(N+ 1)
N
X
n=1
(N−n+ 1)U(b)(τ,ti).
(11.82)
As described in Section 11.7.2, this sum arises from the need to maintain consistency with volume fluxes
passing across the radiating open boundaries, and thus for providing a stable scheme with radiating open
boundaries.
As noted in Section 11.7.4, the prescription (11.82) does not lead to a closed algorithm, since we need
to know the updated velocity U(τ+∆τ) at the end of the barotropic cycle in order to update the three
dimensional velocity field u(τ+∆τ). The following approximation which closes the algorithm has also
been found to lead to a stable scheme with radiating open boundaries
U(τ+∆τ)≈U(τ+∆τ/2).(11.83)
The half-integer time step surface height, which is defined by the time average (11.81), also satisfies the
time tendency equation
η(τ+∆τ/2) −η(τ−∆τ/2)
∆τ=−∇·U(τ) + qw(τ) + S(η)(τ).(11.84)
It follows that the compatible tracer equation is given by
hτ+1/2Cτ+1/2−hτ−1/2Cτ−1/2
∆τ=−∇s·[(hu)τCτ−1/2] (11.85)
+ [wτCτ−1/2]k−[wτCτ−1/2]k−1.(11.86)
The discrete tracer equation thus takes the same form as in Methods I and III.
11.8.3 Method III: Modified Griffies (2004)
To possibly resolve the problem of splitting between the integer and half-integer time steps encountered
with Method I in radiating open boundary problems, we consider here an alternative approach, whereby
Elements of MOM November 19, 2014 Page 175

Chapter 11. Time stepping schemes Section 11.8
the integer time step surface height is prescribed as the time average of the half-integer time step surface
height
2η(τ+∆τ) = η(τ+∆τ/2) + η(τ+ 3∆τ/2).(11.87)
That is, the integer time step surface height is no longer based on a time average, but instead evolves
according to
η(τ+∆τ)−η(τ)
∆τ=−∇·U(τ+∆τ/2) + qw(τ+∆τ/2) + S(η)(τ+∆τ/2),(11.88)
where
2U(τ+∆τ/2) = U(τ+∆τ) + U(τ) (11.89)
2qw(τ+∆τ/2) = qw(τ+∆τ) + qw(τ) (11.90)
2S(η)(τ+∆τ/2) = S(η)(τ+∆τ) + S(η)(τ).(11.91)
The problem with this prescription is that it is not closed, since the surface boundary condition module
only provides information about the surface forcing at the present time step. Likewise, we do not know the
updated volume source. Hence, to close the algorithm we make the following approximation
qw(τ+∆τ/2) ≈qw(τ) (11.92)
S(η)(τ+∆τ/2) ≈S(η)(τ),(11.93)
which amounts to saying that the boundary forcing and volume source term remain constant over the
course of a baroclinic time step; i.e., we cannot obtain information at higher frequency for these fields.
Hence, we are led to the following update for the integer time step surface height
η(τ+∆τ)−η(τ)
∆τ=−∇·U(τ+∆τ/2) + qw(τ) + S(η)(τ).(11.94)
Although of some interest, this scheme has not yet been coded in MOM. It thus remains untested.
Elements of MOM November 19, 2014 Page 176

Chapter 12
Discrete space-time Coriolis force
Contents
12.1 The Coriolis force and inertial oscillations ..........................177
12.1.1 B-grid considerations ..................................... 178
12.1.2 C-grid considerations ..................................... 178
12.2 Time stepping for the B-grid version of MOM ........................179
12.2.1 Explicit temporal discretization with a leap frog ..................... 179
12.2.2 Semi-implicit time discretization with a leap frog ..................... 180
12.2.3 Semi-implicit time discretization with a forward time step ............... 180
12.2.4 Discretization for the B-grid MOM ............................. 181
12.2.4.1 Algorithm in the code ............................... 181
12.2.4.2 Namelist parameters ................................ 182
12.2.5 Energy analysis ........................................ 182
12.3 Time stepping for the C-grid version of MOM ........................182
The purpose of this chapter is to present the methods used in MOM for discretizing the Coriolis force
in space and time. We pay particular attention to the distinct needs of a B-grid and C-grid implementation
(Section 9.1), as well as considering differences between forward time stepping (Section 11.4) and the older
leap frog (Section 11.2). Some of this material was presented in the MOM4 Guide of Griffies et al. (2004),
with new considerations here to handle the density and thickness weighting used in MOM.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean coriolis.F90
ocean core/ocean velocity.F90
12.1 The Coriolis force and inertial oscillations
The inviscid horizontal momentum equation in the absence of pressure gradient forces is given by
d
dt+fˆ
z∧!u= 0,(12.1)
which is equivalent to the second order free oscillator equation
d2
dt2+f2!u= 0.(12.2)
177

Chapter 12. Discrete space-time Coriolis force Section 12.1
Here, d/dtis the material time derivative relevant for Lagrangian observers. Motions which satisfy this
equation are termed inertial oscillations and they have period given by
Tinertial =2π
f=11.97
sinφhour (12.3)
where Ω= 7.292 ×10−5s−1is the earth’s angular speed. The period of inertial oscillations is smallest at
the North pole where φ=π/2 and Tsmallest ≈12 hour. An explicit temporal discretization of the inertial
oscillation equation (12.1) will be unstable if the time step is longer than some fraction of the inertial
period, where the fraction depends on details of the time stepping.
12.1.1 B-grid considerations
Coarse resolution models (models with resolutions on the order of 3 degrees or coarser) generally have
weak advection velocities. Hence, these models can have their baroclinic momentum equation partially
time step limited by inertial oscillations. To get around this limitation, a semi-implicit temporal treatment
has been traditionally considered, as in Bryan (1969). Temporally implicit treatment is available only for
the B-grid, where the two horizontal velocity components sit at the same grid point (Figure 9.1).
Additional issues with coupling to sea ice may warrant an implicit treatment even for ocean models
run with a momentum time step that well resolves the inertial period. In these cases, temporal details of
ocean-ice coupling have been found to cause enhanced energy at the inertial period. Semi-implicit time
stepping of the Coriolis force may assist in damping this energy.
It is for these reasons that MOM provides an option for implementing the Coriolis force on the B-grid
either explicitly in time or semi-implicitly for the baroclinic portion of the model. The namelist parameter
acor sets the level of implicitness, as described in Section 12.2.4.2. For the barotropic time stepping on the
B-grid, MOM generally uses a semi-implicit approach (Section 11.5).
12.1.2 C-grid considerations
Horizontal velocity components sit at different faces of the tracer cell (Figure 9.2). Hence, a spatial averag-
ing must be applied to bring the Coriolis force onto the proper position. Consider the Coriolis force acting
on the zonal velocity component ui,j sitting at the east face of the tracer cell T(i,j). There are various ways
to construct the averaging. We follow that used in GOLD for the energy conserving approach of Sadourny
(1975), in which the zonal Coriolis force per area acting to accelerate the zonal velocity ui,j is given by
(f v ρ dz)zonal Coriolis force ≈(1/4) hfi,j (v ρ dz)i,j +fi,j (v ρ dz)i+1,j +fi,j−1(v ρ dz)i,j−1+fi,j−1(v ρdz)i+1,j−1i
=hf(v ρdz)i−1
xij−1
y,(12.4)
where we introduced northeast grid averaging operators
Ax
i=Ai+Ai+1
2(12.5)
Ay
j=Aj+Aj+1
2.(12.6)
The discretization (12.4) computes the Coriolis parameter fat the vorticity point (northeast corner of the
tracer cell), which accords with the energy conserving method of Sadourny (1975) and GOLD. The normal-
ization by 1/4 holds regardless the land-sea mask, as such is required to maintain global energy conser-
vation from the Coriolis force. The meridional Coriolis force per area acting to accelerate the meridional
velocity vi,j follows similarly to the zonal Coriolis force
−(f u ρ dz)merid Coriolis force ≈ −(1/4) hfi−1,j (u ρ dz)i−1,j +fi−1,j (u ρdz)i−1,j+1 +fi,j (u ρ dz)i,j +fi,j (u ρ dz)i,j+1i
=−hf(u ρdz)j−1
yii−1
x.
(12.7)
Elements of MOM November 19, 2014 Page 178

Chapter 12. Discrete space-time Coriolis force Section 12.2
The spatial averaging used on the C-grid makes it impractical to compute the Coriolis force implicitly
in time.1Furthermore, the C-grid in MOM has been implemented solely for the staggered two-level time
scheme. To maintain temporal stability, we thus follow the approach used for the advection of momentum
(Section 11.2.3), in which a third order Adams-Bashforth method is used (Durran,1999).
12.2 Time stepping for the B-grid version of MOM
We now consider examples relevant to MOM of how the Coriolis force can be discretized in time for the
B-grid version of MOM.
12.2.1 Explicit temporal discretization with a leap frog
Consider now just the linear part of the inertial oscillation equation, where advection is dropped
(∂t+fˆ
z∧)u= 0.(12.8)
Following the time integration discussions in O’Brien (1986) and Bryan (1989) (see also Section 2.3 of
Durran (1999)), introduce the complex velocity
w=u+i v (12.9)
where i=√−1 and wshould not be confused with the vertical velocity component. In terms of w, equation
(12.8) takes the form
∂tw=−i f w (12.10)
which has an oscillatory solution
w=woeif t (12.11)
with period
Tinertial = 2π/f . (12.12)
Time discretizing equation (12.10) with a centered leap-frog scheme leads to
w(τ+∆τ) = w(τ−∆τ)−iλw(τ) (12.13)
with
λ= 2f∆τ(12.14)
a dimensionless number. We can write the finite difference solution in terms of an amplification factor
w(τ+∆τ) = Gw(τ).(12.15)
Substituting this ansatz into equation (12.13) leads to the quadratic equation
G2+i λG −1 = 0 (12.16)
whose solution is
G=−i λ ±√−λ2+ 4
2.(12.17)
If
λ/2 = f∆τ < 1,(12.18)
then |G|= 1, which means the two finite difference solutions are neutral and stable. One root is an unphys-
ical mode, known as the leap-frog computational mode, and the other corresponds to the physical solution.
If λ > 2 then |G|>1 which means both roots are unstable. Hence, stability requires a time step satisfying
∆τ < f −1.(12.19)
1It is practical to compute the Coriolis Force implicitly in time when time stepping the single-layer shallow water equations as in
(Adcroft et al.,1999).
Elements of MOM November 19, 2014 Page 179

Chapter 12. Discrete space-time Coriolis force Section 12.2
That is, Tinertial
∆τ=2π
f∆τ>2π, (12.20)
meaning the leap-frog scheme remains stable if there are at least 2πtime steps per inertial period. At the
North Pole, this constraint means
∆τ < 1.9 hours.(12.21)
For the baroclinic part of the model algorithm, ∆τ < 1.9hours can be the limiting time step for coarse
resolution global models, thus motivating an alternative approach discussed in Section 12.2.2.
12.2.2 Semi-implicit time discretization with a leap frog
To overcome the time-step constraint (12.21) on the baroclinic time step, we now consider a semi-implicit
time stepping scheme within the leap-frog portion of the baroclinic algorithm. As with any implicit ap-
proach, stability can be enhanced relative to explicit schemes. The price to pay is dissipation of the inertial
motions. See section 2.3 of Durran (1999) for discussion.
A semi-implicit treatment of the Coriolis force, within a leap-frog scheme, leads to
w(τ+∆τ)−w(τ−∆τ) = −i λ[(1 −γ)w(τ−∆τ) + γ w(τ+∆τ)] (12.22)
where
0≤γ≤1 (12.23)
is a dimensionless number whose value is set according to stability considerations. We can write w(τ+∆τ) =
Gw(τ−∆τ), with the semi-implicit scheme yielding the amplification factor
G=1−i λ(1 −γ)
1 + i λγ .(12.24)
The squared modulus |G|2is used to determine conditions for stability
|G|2=[1 −γ λ2(1 −γ)]2+λ2
[1 + (γ λ)2]2.(12.25)
For γ= 0, |G|>1 which leads to an unstable scheme. For γ= 1/2, |G|= 1 and so the scheme is neutral. With
1/2< γ ≤1, |G|<1, and so the scheme is unconditionally stable. Hence, we arrive at the stability range for
the semi-implicit parameter
1/2≤γ≤1,(12.26)
with γ= 1 yielding the most stable scheme. Section 2.3.2 of Durran (1999) details the impact on the phase
and amplitude of inertial waves depending on the value of γ. That analysis shows that γ= 1/2 is the most
accurate, with zero amplitude error and favorable phase errors relative to other methods.
12.2.3 Semi-implicit time discretization with a forward time step
As discussed in Section 12.8.3 of Griffies (2004) (see also page 51 of Durran (1999)), the Coriolis force with
a forward time step is unstable, and so an alternative must be considered. We apply here the semi-implicit
approach from Section 12.2.2 with a forward time step rather than the leap frog. Here, we consider
w(τ+∆τ)−w(τ) = −iΛ[(1 −γ)w(τ) + γ w(τ+∆τ)] (12.27)
where again 0 ≤γ≤1 is a dimensionless number whose value is set according to stability considerations.
The dimensionless parameter Λis given by
Λ=f∆τ. (12.28)
Note the factor of 2 needed for the leap frog scheme (equation (12.14)) is now absent for the forward
scheme. All of the analysis in Section 12.2.2 follows through, with the factor of 2 the only distinction.
Elements of MOM November 19, 2014 Page 180

Chapter 12. Discrete space-time Coriolis force Section 12.2
12.2.4 Discretization for the B-grid MOM
We now detail the treatment in MOM when employing the B-grid. Both an explicit and semi-implicit
treatment of the Coriolis force in the baroclinic equations are available when using leap frog tendencies.
However, the semi-implicit treatment is required when using the forward tendencies. For both cases, the
semi-implicit piece is handled at the end of a baroclinic time step, even after the implicit treatment of
vertical mixing. The logic used in the code can be a bit confusing, so it is useful to expose some details
here.
12.2.4.1 Algorithm in the code
Let us separate that portion of the Coriolis force proportional to the dimensionless parameter γ(see equa-
tion (12.23)) from the portion independent of γin order to ease coding for the case with a fully explicit
Coriolis force. We also expose the thickness and density weighting used in MOM. Since velocity is updated
first as the density and thickness weighted velocity, it is useful to introduce a shorthand
e
u≡(ρdz)u.(12.29)
We consider now three cases for handling the Coriolis force.
• An explicit treatment of the Coriolis force with the leap frog takes the form
−fˆ
z∧e
u→ −fˆ
z∧e
u(τ),(12.30)
• whereas a semi-implicit Coriolis force with the leap frog is
−fˆ
z∧e
u→ −fˆ
z∧[(1 −γ)e
u(τ−∆τ) + γe
u(τ+∆τ)]
=−fˆ
z∧e
u(τ−∆τ)−f γ ˆ
z∧[e
u(τ+∆τ)−e
u(τ−∆τ)],(12.31)
• and a semi-implicit Coriolis force with a forward time step is
−fˆ
z∧e
u→ −fˆ
z∧[(1 −γ)e
u(τ) + γe
u(τ+∆τ)]
=−fˆ
z∧e
u(τ)−f γ ˆ
z∧[e
u(τ+∆τ)−e
u(τ)].(12.32)
We now consider the remaining terms in the equations of motion. As stated earlier, when treating the
Coriolis force with an implicit piece (i.e., with γ > 0), this is handled last. We write those accelerations
independent of γin the form
δτe
u∗=F(12.33)
where Fincludes the thickness weighted and density weighted accelerations from velocity self-advection,
the horizontal pressure gradient force, friction force (both explicit and implicit), as well as that piece of the
Coriolis force independent of γ. If the Coriolis force is computed explicitly, then Fis the full time tendency
for the baroclinic velocity. For the semi-implicit treatment, we require those contributions proportional to
γ. For the leap frog, this leads to
e
u(τ+∆τ) = e
u(τ−∆τ) + 2∆τ δτe
u∗−λγ ˆ
z∧[e
u(τ+∆τ)−e
u(τ−∆τ)] (12.34)
where again λ= 2f∆τ. Writing out the components leads to
e
u(τ+∆τ) = e
u(τ−∆τ) + 2∆τ δτe
u∗+λγ [e
v(τ+∆τ)−e
v(τ−∆τ)] (12.35)
e
v(τ+∆τ) = e
v(τ−∆τ) + 2∆τ δτe
v∗−λγ [e
u(τ+∆τ)−e
u(τ−∆τ)],(12.36)
and solving for e
u(τ+∆τ) renders
e
u(τ+∆τ) = e
u(τ−∆τ) + 2∆τ δτe
u∗+λγ δτe
v∗
1 + (λγ)2!(12.37)
e
v(τ+∆τ) = e
v(τ−∆τ) + 2∆τ δτe
u∗−λγ δτe
u∗
1 + (λγ)2!.(12.38)
Elements of MOM November 19, 2014 Page 181

Chapter 12. Discrete space-time Coriolis force Section 12.3
The forward time stepping scheme is handled analogously, which leads to the update for the two compo-
nents
e
u(τ+∆τ) = e
u(τ) + ∆τ δτe
u∗+Λγ δτe
v∗
1 + (Λγ)2!(12.39)
e
v(τ+∆τ) = e
v(τ) + ∆τ δτe
u∗−Λγ δτe
u∗
1 + (Λγ)2!,(12.40)
where again Λ=f∆τ.
12.2.4.2 Namelist parameters
In the code,
∆τ= dtuv (12.41)
is the baroclinic time step, and
γ=acor (12.42)
is a namelist parameter setting the level of implicit treatment for the Coriolis force. The method for dis-
cretizing the Coriolis force in the baroclinic part of the model is set according to the value of acor, with
acor = 0 ⇒explicit Coriolis: only stable for leap frog (12.43)
1/2≤acor ≤1⇒semi-implicit Coriolis: required if using forward step.(12.44)
The vertically integrated part of the model algorithm typically uses a time step much smaller than f−1.
Hence, it is not necessary to discretize the Coriolis force semi-implicitly when time stepping the vertically
integrated equations with a leap frog algorithm. However, when using the predictor-corrector described in
Section 12.7 of Griffies (2004), 1/2≤γ≤1 is required for stability, and we choose γ= 1/2.
12.2.5 Energy analysis
In the continuum, the Coriolis force does no work on a fluid parcel since it is always directed orthogonal to
the flow direction
v·fˆ
z∧u= 0.(12.45)
This property is respected on the B-grid when we discretize the Coriolis force explicitly in time
v(τ)·fˆ
z∧u(τ)=0.(12.46)
However, the semi-implicit treatment does not respect this property since in general the product
v(τ)·fˆ
z∧[(1 −γ)u(τ−∆τ) + γu(τ+∆τ)] (12.47)
does not vanish unless the flow is in time independent steady state.
12.3 Time stepping for the C-grid version of MOM
As stated in Section 12.1.2, temporal stability is maintained using a forward time step on the C-grid if we
discretize the Coriolis force following the approach used for the advection of momentum (Section 11.2.3),
in which a third order Adams-Bashforth method is used (Durran,1999). The third order Adams-Bashforth
method requires the Coriolis force at time steps τ,τ−1, and τ−2, thus increasing memory requirements.
Spatial discretization is detailed in Section 12.1.2.
Elements of MOM November 19, 2014 Page 182
Chapter 13
Time-implicit treatment of vertical
mixing and bottom drag
Contents
13.1 General form of discrete vertical diffusion ..........................184
13.2 Discretization of vertical fluxes ................................184
13.3 A generic form: Part A ......................................185
13.3.1 Surface cells .......................................... 185
13.3.2 Interior cells .......................................... 185
13.3.3 Bottom cells .......................................... 185
13.3.4 Form appropriate for Numerical Recipes .......................... 186
13.4 A generic form with implicit bottom drag ..........................186
13.4.1 Surface cells .......................................... 187
13.4.2 Interior cells .......................................... 187
13.4.3 Bottom cells .......................................... 187
13.4.4 Form appropriate for Numerical Recipes .......................... 187
The purpose of this chapter is to detail the method used to time step vertical subgrid scale processes,
including bottom drag, using an implicit time stepping method. The material here is based on Section 9.5
of the MOM4.0 Guide (Griffies et al.,2004). There are some novel features discussed here arising from
the possibility of including bottom drag implicitly in MOM, which is useful when employing large bottom
drag coefficients.
When the MOM namelist aidif is set to unity, vertical mixing of momentum and tracers is time stepped
implicitly. When aidif = 0.0, vertical mixing is time stepped explicitly. Intermediate values give a semi-
implicit treatment, although at present MOM does not support semi-implicit treatments. An implicit treat-
ment of vertical mixing allows unrestrained values of the vertical mixing coefficients. An explicit treat-
ment, especially with fine vertical grid resolution, places an unreasonable limitation on the size of the time
step. The use of fine vertical resolution with sophisticated mixed layer and/or neutral physics schemes has
prompted the near universal implicit treatment of vertical mixing in ocean climate models.
The following MOM modules are directly connected to the material in this chapter:
ocean param/mixing/ocean vert mix.F90
ocean core/ocean util.F90
ocean core/ocean bbc.F90
183

Chapter 13. Time-implicit treatment of vertical mixing and bottom drag Section 13.2
13.1 General form of discrete vertical diffusion
We can write the vertical diffusion equation in the discrete form
∂t(φ ρdz)k=−(Jz
k−1−Jz
k),(13.1)
where Jz
kis the vertical SGS flux entering cell kthrough the bottom face of the cell, and Jz
k−1is the vertical
SGS flux leaving cell kthrough its top face. The field φcan be either a tracer concentration or a horizontal
velocity component. For an implicit treatment of either vertical diffusion (for tracers) or vertical friction
(for velocity), we have time stepped φusing all time explicit pieces, and thus produced a field φ∗(τ+ 1),
which is the updated field sans the time implicit contributions. So for the purpose of formulating the
implicit time stepping portion of the vertical physics, we write the time discrete vertical diffusion equation
(φ ρdz)k(τ+ 1) = (ρdz φ)∗
k(τ+ 1) −∆τaidif(Jz
k−1−Jz
k),(13.2)
where we assumed the preferred MOM forward time stepping scheme1, and exposed the dimensionless
time-implicit factor aidif. Again, for implicit time stepping, aidif = 1.0, which is the general case for a
simulation with nontrivial vertical physics. The mass per area of a grid cell is updated prior to the tracer
concentration or velocity components, thus allowing us to divide equation (13.2) by ρdzat time τ+ 1,
yielding
φk(τ+ 1) = φ∗
k(τ+ 1) −Γk(Jz
k−1−Jz
k),(13.3)
with
Γk=aidif∆τ
(ρdz)(τ+ 1).(13.4)
13.2 Discretization of vertical fluxes
The vertical flux Jz
kis located at the bottom of the kth tracer or velocity cell. A positive value for Jz
kleads
to an increase in φk(τ+ 1). Away from surface and bottom boundaries, we assume that this flux takes the
downgradient form
Jz
k=−ρoκk φk(τ+ 1) −φk+1(τ+ 1)
dzwtk!.(13.5)
The factors of φare evaluated at time τ+1 because of the implicit treatement. The vertical mixing coefficient
κkhas a general space-time dependence set by a vertical mixing scheme. As for the flux itself, the diffusivity
κkis situated at the bottom of the tracer or velocity cell, depending on whether φis a tracer field or velocity
component. The factor of ρois needed for dimensional consistency, and by our assumption that κis a
kinematic viscosity or diffusivity. The array dzwtkrepresents the vertical distance between tracer points at
time τ. For vertical mixing of velocity, dzwt becomes the distance between velocity points dzwu.
At the ocean surface, the vertical flux is given by the surface boundary condition sf lux placed on the
velocity or tracer. For a tracer,
Jz
k=0 =−stf,(13.6)
with stf MOM’s surface tracer flux array with units of velocity times density times tracer concentration.
The minus sign arises from the MOM convention that associates a positive stf with an increase in tracer
within the k= 1 cell. In contrast, the present discussion assumes a convention for the flux Jzwhereby a
positive Jz
k=0 is associated with a decrease in tracer within the k= 1 cell. For velocity,
Jz
k=0 =−smf,(13.7)
with smf the surface momentum flux with units of density times squared velocity. At the ocean bottom, a
similar condition leads to
Jz
k=kmt =−btf (13.8)
1For the leap-frog scheme, the ∆τfactor goes to 2∆τ.
Elements of MOM November 19, 2014 Page 184

Chapter 13. Time-implicit treatment of vertical mixing and bottom drag Section 13.3
for bottom tracer fluxes, and
Jz
k=kmu =−bmf (13.9)
for bottom momentum fluxes. The minus signs again represent a difference in convention between MOM
and the present discussion. In MOM, a negative btf represents the passage of tracer from solid rock into
the ocean domain, as in geothermal heating. For velocity, a positive bmf represents a drag on the ocean
momentum field due to SGS interactions with the solid earth.
13.3 A generic form: Part A
To develop the solution algorithm, it is necessary to put the vertical diffusion equation into a generic form.
For this purpose, let us consider in sequence the equation for surface cells k= 1, interior cells with k > 1,
and bottom cells with k=kmt.
13.3.1 Surface cells
For surface cells with k= 1 we have
φ∗
k(τ+ 1) = φk(τ+ 1) + Γk(τ)(Jz
k−1−Jz
k)
=φk(τ+ 1) −Γk(τ)(stf +Jz
k)
=φk(τ+ 1) −Γk(τ)stf +Γk(τ)ρoκk φk(τ+ 1) −φk+1(τ+ 1)
dzwtk!,(13.10)
which leads to
φ∗
k(τ+ 1) + Γk(τ)stf =φk(τ+ 1) 1 + Γk(τ)ρoκk
dzwtk!−φk+1(τ+ 1) Γk(τ)ρoκk
dzwtk!.(13.11)
For velocity mixing, stf becomes smf, and dzwt becomes dzwu.
13.3.2 Interior cells
For interior cells,
φ∗
k(τ+ 1) = φk(τ+ 1) + Γk(τ)(Jz
k−1−Jz
k)
=φk(τ+ 1) −Γk(τ)ρoκk−1 φk−1(τ+ 1) −φk(τ+ 1)
dzwtk−1!
+Γk(τ)ρoκk φk(τ+ 1) −φk+1(τ+ 1)
dzwtk!(13.12)
which leads to
φ∗
k(τ+ 1) = φk(τ+ 1) 1 + Γk(τ)ρoκk−1
dzwtk−1
+Γk(τ)ρoκk
dzwtk!
−φk−1(τ+ 1) Γk(τ)ρoκk−1
dzwtk−1!−φk+1(τ+ 1) Γk(τ)ρoκk
dzwtk!.(13.13)
13.3.3 Bottom cells
Bottom cells with k=kmt(i,j) have
φ∗
k(τ+ 1) = φk(τ+ 1) + Γk(τ)(Jz
k−1−Jz
k)
=φk(τ+ 1) + Γk(τ)(Jz
k−1+btf)
=φk(τ+ 1) + Γk(τ)btf −Γk(τ)ρoκk−1 φk−1(τ+ 1) −φk(τ+ 1)
dzwtk−1!,(13.14)
Elements of MOM November 19, 2014 Page 185

Chapter 13. Time-implicit treatment of vertical mixing and bottom drag Section 13.4
which leads to
φ∗
k(τ+ 1) −Γk(τ)btf =φk(τ+ 1) 1 + Γk(τ)ρoκk−1
dzwtk−1!−φk−1(τ+ 1) Γk(τ)ρoκk−1
dzwtk−1!.(13.15)
13.3.4 Form appropriate for Numerical Recipes
Introducing the notation
Ak=(−Γk(τ)ρoκk−1/dzwtk−1if k > 1
0 if k= 1 (13.16)
Ck=(−Γk(τ)ρoκk/dzwtkif k < kmt
0 if k=kmt (13.17)
Bk= 1 −Ak−Ck(13.18)
Φ∗
k=
φ∗
k(τ+ 1) + Γk(τ)stf if k= 1
φ∗
k(τ+ 1) if 1 < k < kmt
φ∗
k(τ+ 1) −Γk(τ)btf if k=kmt
(13.19)
renders
Φ∗
k=Akφk−1(τ+ 1) + Bkφk(τ+ 1) + Ckφk+1(τ+ 1).(13.20)
The solution is arrived at by performing a decomposition and forward substitution. The details are
taken from pages 42 and 43 of Press et al. (1992).
13.4 A generic form with implicit bottom drag
We deviate from the previous approach to present here the formulation assuming the bottom boundary
fluxes are computed implicitly. Such is important for the case of a bottom drag
Jz
k=kmu =−ρoCduqu2
res +u2,(13.21)
where a large bottom drag coefficient Cd, or large residual velocity ures require a time implicit solution
method. For the global one-degree class of models typically run at GFDL, Cd>0.002 generally requires
an implicit treatment of bottom drag. Implicit bottom drag is enabled in MOM by setting the appropriate
namelist logical inside ocean bbc nml.
To time step bottom drag implicitly requires a nonlinear solver. Rather than take that route, we take
the simpler approximate approach, also employed when the diffusivity or viscosity is a nonlinear function
of the flow. That is, we time discretize the bottom drag as
Jz
k=kmu =−ρoCdu(τ+ 1) qu2
res +u2(τ).(13.22)
Hence, for the purpose of formulating the time implicit algorithm, we write the bottom drag
Jz
k=kmu =−γu(τ+ 1),(13.23)
where
γ=ρoCdqu2
res +u2(τ) (13.24)
is a nonlinear function of velocity at time τ. We can now modify the steps detailed in Section 13.3, using the
nonlinear bottom drag (13.23). As this situation arises in practice for the momentum equation, we employ
velocity cell labels where appropriate.
Elements of MOM November 19, 2014 Page 186
Chapter 13. Time-implicit treatment of vertical mixing and bottom drag Section 13.4
13.4.1 Surface cells
For surface cells with k= 1 we have
φ∗
k(τ+ 1) = φk(τ+ 1) + Γk(τ)(Jz
k−1−Jz
k)
=φk(τ+ 1) −Γk(τ)(smf +Jz
k)
=φk(τ+ 1) −Γk(τ)smf +Γk(τ)ρoκk φk(τ+ 1) −φk+1(τ+ 1)
dzwuk!,(13.25)
which leads to
φ∗
k(τ+ 1) + Γk(τ)smf =φk(τ+ 1) 1 + Γk(τ)ρoκk
dzwuk!−φk+1(τ+ 1) Γk(τ)ρoκk
dzwuk!.(13.26)
13.4.2 Interior cells
For interior cells,
φ∗
k(τ+ 1) = φk(τ+ 1) + Γk(τ)(Jz
k−1−Jz
k)
=φk(τ+ 1) −Γk(τ)ρoκk−1 φk−1(τ+ 1) −φk(τ+ 1)
dzwuk−1!
+Γk(τ)ρoκk φk(τ+ 1) −φk+1(τ+ 1)
dzwuk!(13.27)
which leads to
φ∗
k(τ+ 1) = φk(τ+ 1) 1 + Γk(τ)ρoκk−1
dzwuk−1
+Γk(τ)ρoκk
dzwuk!
−φk−1(τ+ 1) Γk(τ)ρoκk−1
dzwuk−1!−φk+1(τ+ 1) Γk(τ)ρoκk
dzwuk!.(13.28)
13.4.3 Bottom cells
Bottom cells with k=kmu(i,j) have
φ∗
k(τ+ 1) = φk(τ+ 1) + Γk(τ)(Jz
k−1−Jz
k)
=φk(τ+ 1) + Γk(τ)(Jz
k−1+bmf)
=φk(τ+ 1) + Γk(τ)γ φk(τ+ 1) −Γk(τ)ρoκk−1 φk−1(τ+ 1) −φk(τ+ 1)
dzwuk−1!,(13.29)
which leads to
φ∗
k(τ+ 1) = φk(τ+ 1) 1 + γΓk(τ) + Γk(τ)ρoκk−1
dzwuk−1!−φk−1(τ+ 1) Γk(τ)ρoκk−1
dzwtk−1!.(13.30)
13.4.4 Form appropriate for Numerical Recipes
Introducing the notation
Ak=(−Γk(τ)ρoκk−1/dzwuk−1if k > 1
0 if k= 1 (13.31)
Ck=(−Γk(τ)ρoκk/dzwukif k < kmu
0 if k=kmu (13.32)
Bk=(1−Ak−Ckif k < kmu
1 + γΓk(τ)−Ak−Ckif k=kmu (13.33)
Φ∗
k=(φ∗
k(τ+ 1) + Γk(τ)smf if k= 1
φ∗
k(τ+ 1) if 1 < k ≤kmu (13.34)
Elements of MOM November 19, 2014 Page 187

Chapter 13. Time-implicit treatment of vertical mixing and bottom drag Section 13.4
renders
Φ∗
k=Akφk−1(τ+ 1) + Bkφk(τ+ 1) + Ckφk+1(τ+ 1).(13.35)
The solution is arrived at by performing a decomposition and forward substitution. The details are
taken from pages 42 and 43 of Press et al. (1992).
Elements of MOM November 19, 2014 Page 188

Chapter 14
Mechanical energy conversions and
advective mass transport
Contents
14.1 Basic considerations .......................................190
14.2 Energetic conversions in the continuum ...........................191
14.2.1 Pressure work conversions in Boussinesq fluids ...................... 191
14.2.2 Pressure work conversions in non-Boussinesq fluids ................... 192
14.2.3 Boussinesq kinetic energy advection conversion ...................... 192
14.2.4 Non-Boussinesq kinetic energy advection conversion ................... 193
14.3 How we make use of energetic conversions ..........................193
14.3.1 Conservation versus accuracy ................................ 193
14.3.2 Energy conservation, consistency, and conversion ..................... 194
14.3.3 A caveat regarding the tripolar grid in MOM ....................... 194
14.4 Thickness weighted volume and mass budgets .......................194
14.5 Thickness and mass per area for the momentum ......................195
14.5.1 B-grid momentum ...................................... 196
14.5.2 C-grid momentum ...................................... 196
14.6 B-grid Boussinesq pressure work conversions ........................196
14.6.1 The vertically integrated term P1.............................. 198
14.6.2 Advection velocity components for tracers ......................... 198
14.6.3 Divergence operator for surface height evolution ..................... 199
14.6.4 Completing the manipulations for P2............................ 200
14.6.4.1 Energetic approach ................................. 200
14.6.4.2 Finite volume approach .............................. 201
14.6.5 The geopotential gradient term P3............................. 202
14.6.6 Summary for the Boussinesq pressure conversion ..................... 202
14.7 C-grid Boussinesq pressure work conversions ........................203
14.7.1 Force from the horizontal pressure gradient ........................ 203
14.7.2 The vertically integrated term P1.............................. 204
14.7.3 Advection velocity components for tracers ......................... 205
14.7.4 Divergence operator for surface height evolution ..................... 205
14.7.5 The geopotential gradient term P3............................. 205
14.7.6 Summary for the Boussinesq pressure conversion ..................... 206
14.8 B-grid non-Boussinesq pressure work conversions .....................206
189

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.1
14.8.1 The vertically integrated term P1.............................. 207
14.8.2 Defining the advective mass transport ........................... 207
14.8.3 Completing the manipulations for P2............................ 208
14.8.3.1 Energetic approach ................................. 209
14.8.3.2 Finite volume approach .............................. 209
14.8.4 The pressure gradient term P3................................ 209
14.8.5 Summary for the non-Boussinesq pressure conversion .................. 210
14.9 C-grid non-Boussinesq pressure work conversions .....................210
14.9.1 The vertically integrated term P1.............................. 211
14.9.2 Defining the advective mass transport ........................... 211
14.9.3 The pressure gradient term P3................................ 212
14.9.4 Summary for the non-Boussinesq pressure conversion .................. 212
14.10 Effective Coriolis force and mechanical energy .......................212
14.10.1B-grid .............................................. 213
14.10.2C-grid ............................................. 213
14.10.3Comments ........................................... 214
14.11 B-grid kinetic energy advection ................................214
14.11.1B-grid momentum equation contribution from advection ................ 215
14.11.2Horizontal convergence ................................... 215
14.11.3Diagnosing the vertical transport for U-cells ........................ 215
14.11.4Discrete integration by parts on horizontal convergence ................. 216
14.11.5Discrete integration by parts on the vertical convergence ................ 217
14.11.6Final result for the Boussinesq case ............................. 217
14.11.7Non-Boussinesq kinetic energy advection ......................... 217
14.12 C-grid kinetic energy advection ................................218
14.12.1C-grid momentum equation contribution from advection ................ 218
14.12.2Energetic manipulations not generally useful ....................... 219
The purpose of this chapter is to discuss continuum and discrete mechanical energy balances. Mainte-
nance of such balances on the discrete grid have implications for spatial discretization of advective mass
transport. Both the B-grid and C-grid discretizations are considered.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean velocity.F90
ocean core/ocean advection velocity.F90
ocean core/ocean velocity advect.F90
ocean diag/ocean velocity diag.F90
14.1 Basic considerations
The following are the assumptions made for manipulations of this chapter.
• Choosing to maintain the integrity of certain energetic balances on the B-grid lattice prescribes the
form of the discrete advection velocity components located on the sides of tracer cells.
• Second order finite differenced advective fluxes are used for momentum. Tracer fluxes can remain
arbitrarily discretized.
• We choose a finite difference computation of the pressure gradient force, as described in Sections 3.1,
3.2, and 3.3. The finite volume method for computing the pressure force, as described in Section
2.8.1, does not lend itself to the results of this chapter.
Elements of MOM November 19, 2014 Page 190

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.2
• Details of the time stepping scheme play a role in determining the form of the energy diagnostics.
• Energy balance diagnostics are important for checking the integrity of certain finite difference al-
gorithms. Consequently, it is useful to provide a careful suite of energy diagnostics for algorithm
development purposes.
14.2 Energetic conversions in the continuum
In the continuum, the horizontal momentum equation for a shallow ocean fluid is given by (see chapter 4
of Griffies,2004)
(ρu),t +∇·(ρvu) + (f+M)(ˆ
z∧ρu) = −∇zp+ρF(14.1)
for the non-Boussinesq case, and
(u),t +∇·(vu) + (f+M)(ˆ
z∧u) = −∇z(p/ρo) + F(14.2)
for the Boussinesq case. The evolution of horizontal kinetic energy can be found by taking the scalar
product of horizontal velocity uwith the momentum equation. When globally integrating the kinetic
energy evolution, the forcing terms can be transformed into terms that highlight physically interesting
processes. These manipulations identify conversions between one form of energy and another. The form of
these conversions can be deduced from the momentum equations, boundary conditions, mass or volume
conservation, and integration by parts. Maintaining an analog of these energetic conversions on the discrete
lattice has been found to be very useful in the development of ocean model algorithms. The reason is
that these conversions provide the modeler with a powerful set of diagnostics to test the integrity of the
numerics.
There are three forms of energy conversion of interest in MOM. The first involves the pressure gradient
term, the second involves the advection term, and the third involves friction. We address only the inviscid
terms in this chapter. Part 5 of Griffies (2004) describes how friction dissipates kinetic energy in both the
continuous case and for a particular friction algorithm available in MOM.
14.2.1 Pressure work conversions in Boussinesq fluids
Let us first examine how pressure work is converted to other processes in Boussinesq fluids. For this
purpose, consider the following identities found using zfor the vertical coordinate
ZdVu·∇p=ZdV(v·∇p−wp,z)
=ZdV[∇·(vp)−wp,z]
=ZdA(ˆ
n)p(ˆ
n·v) + gZdV wρ
=ZdA(ˆ
n)p(ˆ
n·v) + ZdV ρ dΦ/dt
(14.3)
where dV= dxdydzis the volume element and dΦ/dtis the material time derivative of the geopotential
Φ=g z. To reach these results required volume conservation for a parcel in the form of the constraint
∇·v= 0, the hydrostatic relation p,z =−ρg, and the definitions
g w =gdz/dt
= dΦ/dt. (14.4)
Assuming no-normal flow at the solid boundaries leaves only the surface boundary at z=ηfor the surface
integral. The surface kinematic boundary condition, and volume conservation, lead to1
dA(ˆ
n)ˆ
n·v=−dxdy∇·U,(14.5)
1See Section 3.4 of Griffies (2004) for derivation.
Elements of MOM November 19, 2014 Page 191

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.2
and so ZdVu·∇p=−Z
z=η
dxdy pa∇·U+ZdV ρ dΦ/dt. (14.6)
In a rigid lid model, the first term vanishes. For the free surface model it represents the work done by
atmospheric pressure on the depth integrated flow. The second term is the volume integrated work done
by vertical currents against the buoyancy force. In generalized vertical coordinates, the buoyancy term
takes the form
dΦ/dt= (∂t+u·∇s+w(s)∂z)Φ
= (∂t+u·∇s)Φ+g w(s),(14.7)
where equation (6.72) of Griffies (2004) was used to express the material time derivative in general vertical
coordinates. Hence, the pressure conversion becomes
ZdVu·∇p=−Z
z=η
dxdy p∇·U+ZdV ρ [(∂t+u·∇s)Φ+g w(s)].(14.8)
Buoyancy contributions now comprise three terms instead of the one found with z-coordinates. This result
reflects the non-orthogonal nature of generalized vertical coordinates.
14.2.2 Pressure work conversions in non-Boussinesq fluids
For non-Boussinesq flows, pressure conversion takes the form
ZdVu·∇p=Z
z=η
pˆ
n·v+ZdV(ρdΦ/dt−p∇·v).(14.9)
The p∇·vterm represents pressure work on the changing volume of fluid parcels found in the compressible
non-Boussinesq fluid. The boundary condition
dA(ˆ
n)ˆ
n·v= dxdy(η,t −Qm/ρ) (14.10)
is discussed in Section 3.4.3 of Griffies (2004). The generalized vertical coordinate form of equation (14.9)
follows similarly to the Boussinesq case, where extra terms arise from expanding the material time deriva-
tive.
14.2.3 Boussinesq kinetic energy advection conversion
Just as for the pressure gradient term, the scalar product of the horizontal velocity and the advection of
momentum can be converted into alternative forms. To see this conversion in the continuum, write the
advection of horizontal velocity in the Boussinesq fluid as
A≡ −∇·(vu)−Mˆ
z∧v.(14.11)
The scalar product of Awith the horizontal currents leads to
u·A=−u·∇·(vu)
=−∇·(vK),(14.12)
where
K=u·u
2(14.13)
Elements of MOM November 19, 2014 Page 192

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.3
is the horizontal kinetic energy per mass. Integrating over the volume of the domain, and using the surface
and solid wall boundary conditions, leads to
A ≡ ZdVu·A
=Z
z=η
dxdyK∇·U.(14.14)
Consequently, the global integral of kinetic energy advection reduces to a boundary term, which vanishes
in the rigid lid model but remains nontrivial in a free surface model.
14.2.4 Non-Boussinesq kinetic energy advection conversion
For the non-Boussinesq fluid, we consider
A≡ −∇·(ρvu)−Mˆ
z∧ρv.(14.15)
The scalar product of Awith the horizontal currents leads to
u·A=−u·∇·(ρvu)
=−∇·(vK)−K∇·(ρv),(14.16)
and integrating over the volume of the domain yields
A ≡ ZdVu·A
=−Z
z=η
dA(ˆ
n)Kρˆ
n·v−ZdVK∇·(ρv)
=−Z
z=η
dxdyK(ρη,t −Qm)−ZdVK∇·(ρv),
(14.17)
where we used the surface boundary condition (14.10) for the last step.
14.3 How we make use of energetic conversions
We offer here some general comments regarding the utility of the energetic methods for deriving numerical
discretizations.
14.3.1 Conservation versus accuracy
Accuracy is often a primary consideration for numerical methods. Additionally, ease of analysis and in-
terpretation are also important. The presence of discrete analogs to continuous conservation properties
assists in the interpretation of the numerical simulation. Unfortunately, conservation and accuracy are
often incompatible.
Traditionally, climate modelers have chosen conservation properties over accuracy. For example, con-
servation of scalar properties are essential to ensure that mass/volume, heat and salt are conserved over
the course of a long climate integration. Another property that certain models claim is conservation of
mechanical energy. This claim, however, is unfounded for the space-time discrete equations in all mod-
els discussed in Griffies et al. (2000a). All ocean climate models break kinetic energy conservation when
discretizing in time. This point is explained below in the discussion of equation (14.18).
Elements of MOM November 19, 2014 Page 193

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.4
14.3.2 Energy conservation, consistency, and conversion
What is often meant by energy conservation statements is the more qualified property whereby certain
spatially discrete terms are discretized so they do not alter global kinetic energy in the absence of boundary
forcing. Deriving energetically consistent numerical schemes requires some care. In particular, ensuring
that pressure work transfers into vertical buoyancy work in the Boussinesq model necessitates a particular
form for the discrete advection velocity. We discuss this point in Sections 14.6 and 14.7.
When considering energetic issues using alternative time stepping schemes, one often encounters the
situation where certain terms, such as advection, the Coriolis force, and pressure gradients, are evaluated
at staggered time steps. Indeed, the preferred method discussed in Chapter 12 of Griffies (2004) and in
Chapter 11 in this document staggers the velocity and tracer one-half time step relative to one another,
and generally uses non-centred in-time methods for the advection and Coriolis force. Hence, pressure
gradients, whose temporal placement is set by density, is off-set in time from momentum advection, the
Coriolis force, and friction. These details are important when interpreting energetic balances of a space-
time discrete model. Often the more sophisticated the time stepping scheme (e.g., the three-time level
Adams-Bashforth method discussed in Chapter 12 of Griffies (2004)), the more difficult it is to maintain
energetic consistency and balances.
Energetic consistency is necessary but not sufficient for ensuring the discrete system conserves me-
chanical energy in the unforced inviscid limit. For example, time stepping according to the leap-frog
method, which possesses useful energy consistency properties, precludes mechanical energy conservation.
The Robert-Asselin time filter breaks energy conservation in a manner analogous to its corruption of global
tracer conservation (see Section 11.2.2 as well as Section 12.5.4 of Griffies (2004)). Furthermore, even
without time filtering, the continuum identity
2u·∂tu=∂t(u·u) (14.18)
is generally not satisfied by discrete time stepping schemes. As noted on page 158 of Durran (1999), trape-
zoidal time differencing allows for this property. Other schemes commonly used do not. As trapezoidal
time differencing is semi-implicit and not readily implemented for the primitive equations, it is not con-
sidered in the following.
14.3.3 A caveat regarding the tripolar grid in MOM
The tripolar grid (Section 9.3) is routinely used in global simulations with MOM in order to remove the
spherical coordinate singularity from the liquid ocean domain. Unfortunately, due to some limitations of
the energetic diagnostics, the energy conversion diagnostics are not precisely maintained when using the
tripolar grid. The issue is not related to a problem with the prognostic equations that time step the model
fields, but rather related to limitations with the diagnostic code. To resolve the diagnostic code requires
adding processor updates that have not been deemed important enough to warrant the potential model
slowdown.
14.4 Thickness weighted volume and mass budgets
We make use of the thickness weighted volume budgets for the Boussinesq fluid when deriving the discrete
energetic balances. The volume budgets are given by equations (10.82), (10.83), and (10.84). We expose
them here for completeness
(w(s))s=sk=1 =∂t(dz)−S(V)dz+∇s·(udz)−Qm/ρo(14.19)
(w(s))s=sk=∂t(dz)−S(V)dz+∇s·(udz) + (w(s))s=sk−1(14.20)
0 = ∂t(dz)−S(V)dz+∇s·(udz) + (w(s))s=skbot−1.(14.21)
Elements of MOM November 19, 2014 Page 194
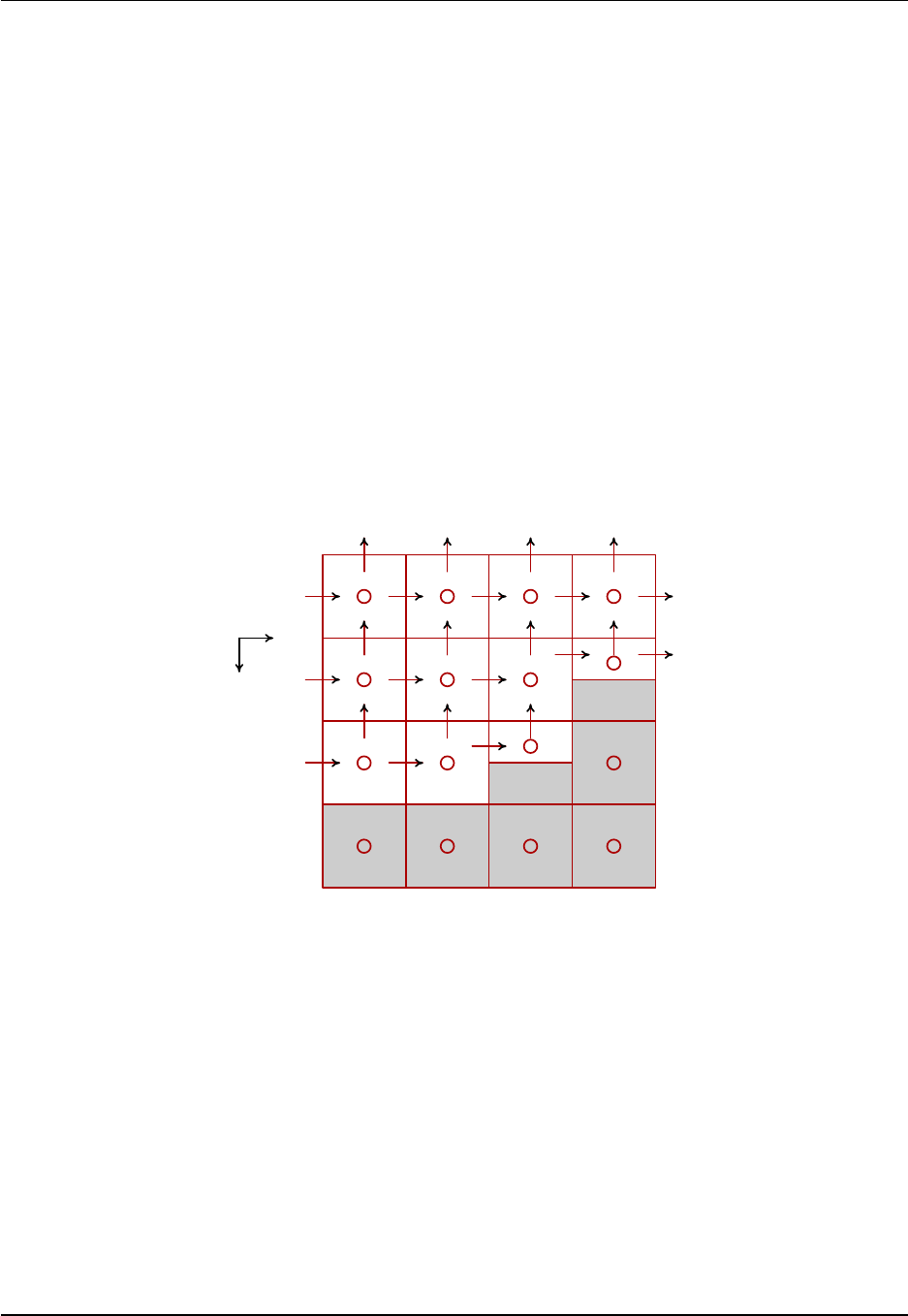
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.5
We also make use of the thickness weighted mass budgets for the non-Boussinesq case, given by equations
(10.106), (10.107), and (10.108). We expose them here for completeness
(ρw(s))s=sk=1 =∂t(ρdz)−S(M)ρdz+∇s·(uρdz)−Qm(14.22)
(ρw(s))s=sk=∂t(ρdz)−S(M)ρdz+∇s·(uρdz) + (ρ w(s))s=sk−1(14.23)
0 = ∂t(ρdz)−S(M)ρdz+∇s·(uρdz) + (ρ w(s))s=skbot−1.(14.24)
As described in Section 10.8.1, depth based vertical coordinates used in MOM (Section 5.1) allow for the
time derivative ∂t(dz) to be diagnosed from the vertically integrated volume budget. Likewise, the pressure
based vertical coordinates (Section 5.2) allow for the time derivative ∂t(ρdz) to be diagnosed from the
vertically integrated mass budget. These two properties are important to ensure the utility of the Eulerian
algorithms employed by MOM.
14.5 Thickness and mass per area for the momentum
We consider here the specification of various thickness or mass per horizontal area required for the B-grid
and C-grid.
k
i
T(1,1) T(2,1) T(3,1) T(4,1)
T(1,2) T(2,2) T(3,2)
T(4,2)
T(1,3) T(2,3)
T(3,3)
T(4,3)
T(1,4) T(2,4) T(3,4) T(4,4)
Figure 14.1: Shown here is a 4x4 region of a zonal-vertical domain of tracer cells T(i,k), with ocean cells
(unshaded) and land land cells (shaded). Note the partial bottom cells in cells T(3,3),T(4,3) and T(4,2).
For both the B-grid and C-grids, the advective transport through the zonal tracer cell face is depicted
by horizontal arrows, and vertical advective transport is depicted by vertical arrows. On the C-grid, the
thickness appearing in the discrete expression for the C-grid zontal momentum per area (u ρodz)i,j is taken
as the minimum thickness ρo(dzte)i,j =ρomin(dzti,j ,dzti+1,j) between the adjacent tracer cells. Likewise,
for a non-Boussinesq fluid, the mass per unit area appearing in the discrete expression for (u ρdz)i,j is
given by (ρdzte)i,j = min(ρdzti,j ,ρ dzti+1,j ). Similar expressions hold for the meridional cell face. The
minimum function ensures mass conservation when moving across cell faces where the adjacent cells have
distinct thicknesses, as when there is partial cell bottom topography or generalized level coordinates. That
is, the minimum function precludes too much mass entering or leaving the thinnest of the adjacent cells.
When considering a B-grid, where horizontal velocity components are co-located, it is the least massive
of the four surrounding tracer cells that provides the velocity cell mass per horizontal area (ρdzu)i,j =
min[(ρdzt)i,j ,(ρdzt)i+1,j,(ρdzt)i,j+1,(ρdzt)i+1,j+1].
Elements of MOM November 19, 2014 Page 195
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
14.5.1 B-grid momentum
The B-grid identifies a distinct control volume for the velocity cell and tracer cell (Figure 9.1). The mass
per unit area of the velocity cell is determined by the minimum of the surrounding four tracer cells
(rho dzu)i,j = min[(rho dzt)i,j,(rho dzt)i+1,j ,(rho dzt)i,j+1,(rho dzt)i+1,j+1],(14.25)
with the density factors set to the constant ρowhen making the Boussinesq approximation. Once the
momentum per horizontal area, urho dzu, is updated to a new time step, we divide by (rho dzu)i,j to
diagnose the updated B-grid velocity u.
The definition (14.25) follows the partial bottom cell considerations of Pacanowski and Gnanadesikan
(1998). Griffies et al. (2001) then applied this definition to the surface ocean in an explicit free surface
model with a geopotential vertical coordinate, where the top grid cells have a time dependent thickness.
Starting from MOM4p1, MOM follows that applyies the definition (14.25) throughout the fluid column for
all generalized level coordinates. Further discussion is given in the caption to Figure 14.1.
14.5.2 C-grid momentum
On the C-grid, there is no velocity control volume. Instead, there is a separate thickness or mass per unit
area associated with each momentum component, which are determined according to
(rho dzte)i,j = min[(rho dzt)i,j,(rho dzt)i+1,j ] (14.26)
(rho dztn)i,j = min[(rho dzt)i,j,(rho dzt)i,j+1].(14.27)
Motivation for these definitions is provided in Figure 14.1.
14.6 B-grid Boussinesq pressure work conversions
We now consider manipulations of the globally integrated discrete B-grid representation of u·∇zpfor the
Boussinesq case. In this section, discrete grid labels are exposed when needed, with many labels suppressed
to reduce clutter. Also, the horizontal velocity components are co-located on the northeast corners of the
tracer grid, as per the B-grid convention (Figure 9.1). The material in this Section is based on a similar
z-coordinate discussion given in Griffies et al. (2004), but it has been generalized to the arbitrary level
coordinates available in MOM.
Consider the domain integrated scalar product of
u·∇zp=u·(∇sp+ρ∇sΦ)
=u·∇(pa+psurf) + u·(∇sp0+ρ0∇sΦ).(14.28)
To reach this result we use equation (3.18) with s=z∗or s=σ(z), in which case
psurf =g ρoηwhen s=z∗or s=σ(z)(14.29)
is the rapidly fluctuating surface pressure term, and
p0=g
η
Z
z
ρ0dzwhen s=z∗or s=σ(z)(14.30)
is the slower fluctuating pressure anomaly where ρ0=ρ−ρ0. When s=zis the vertical coordinate, equation
(3.17) is used, in which case
psurf =g ρsurf ηwhen s=z(14.31)
and
p0=g
0
Z
z
ρ0dzwhen s=z. (14.32)
Elements of MOM November 19, 2014 Page 196

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
To determine the proper discrete form of the pressure conversion, recall from Section 3.3.1 the momen-
tum equations for a Boussinesq fluid on a B-grid with just the impacts from pressure acting
∂t(u ρodzu)pressure =−dzuFDX NT(FAY(pa+psurf +p0)) + FAY[δiΦFAX(ρ0)]/dxui,j(14.33)
∂t(v ρodzu)pressure =−dzuFDY ET(FAX(pa+psurf +p0)) + FAX[δjΦFAY(ρ0)]/dyui,j.(14.34)
The volume integrated pressure conversion
P=−Zu·∇zpdV , (14.35)
thus takes on the following discrete form on the B-grid
P ≡−X
i,j,k
dV(U)[uFDX NT(FAY(pa+psurf)) + vFDY ET(FAX(pa+psurf))]
−X
i,j,k
dV(U)[uFDX NT(FAY(p0)) + vFDY ET(FAX(p0))]
−X
i,j,k
dV(U)[uFAY(FAX(ρ0)δiΦ)/dxu +vFAX(FAY(ρ0)δjΦ)/dyu]
(14.36)
with
dV(U)=dau dzu (14.37)
the U-cell volume. The discrete expressions for the pressure gradient are based on the discussion in Section
3.3.1, where the horizontal pressure gradient body force is written for the B-grid. MOM employs the
following discrete forward derivative operators
FDX NT(A) = Ai+1 −Ai
dxui,j
(14.38)
FDY ET(A) = Aj+1 −Aj
dyui,j
,(14.39)
where the arguments of the derivatives live on the north and east faces, respectively, of a tracer cell. The
operators δiAand δjAcompute the forward difference
δiA=Ai+1 −Ai(14.40)
δjA=Aj+1 −Aj(14.41)
of a discrete field. MOM also employs the following forward averaging operators
FAX(A) = Ai+1 +Ai
2(14.42)
FAY(A) = Aj+1 +Aj
2.(14.43)
The first group of terms in equation (14.36) arises from applied pressure and surface geopotential acting
on the vertically integrated velocity. The second group represents the constant slateral pressure gradient
taken between cells living on the same discrete k-level. The third group arises from the use of generalized
vertical coordinates, where the depth of a k-level is generally a function of horizontal position.
The goal of the remainder of this section is to rearrange the discrete terms appearing in the pressure con-
version equation (14.36) to reveal an alternative, and physically sensible, form. In effect, we are performing
a discrete integration by parts. The MOM energy conversion diagnostic computes the unmanipulated form
of the pressure conversion and the manipulated form, and compares the two results: left hand side = right
hand side? Except for the caveat noted for the tripolar grid (Section 14.3.3), differences between the two
calculations can reveal basic algorithm mistakes.
Elements of MOM November 19, 2014 Page 197
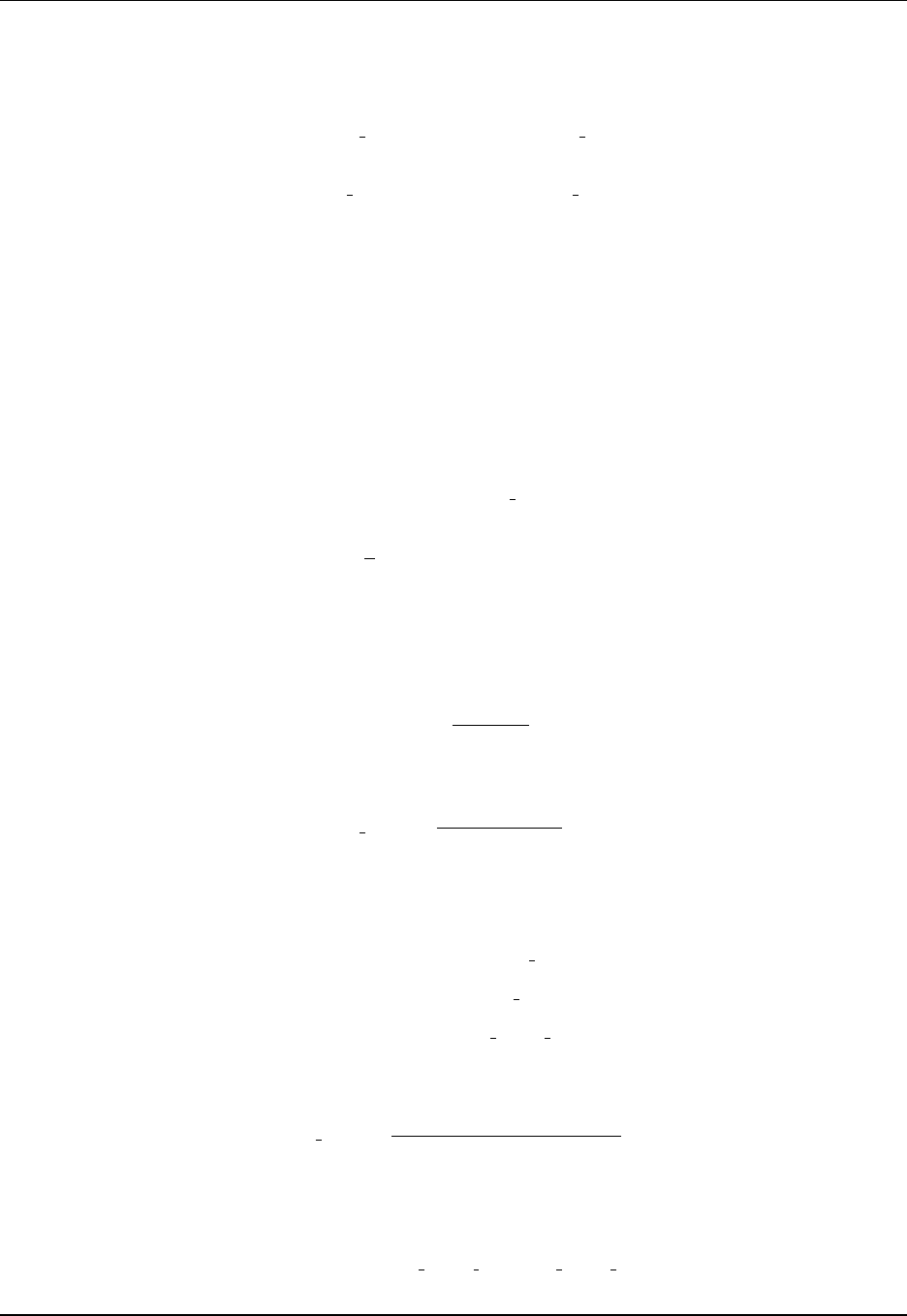
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
14.6.1 The vertically integrated term P1
The first term in equation (14.36) can be vertically integrated to yield
P1≡−X
i,j,k
dV(U)[uFDX NT(FAY(pa+psurf)) + vFDY ET(FAX(pa+psurf))]
=−X
i,j
dau [UFDX NT(FAY(pa+psurf)) + VFDY ET(FAX(pa+psurf))]
(14.44)
where
(U,V ) = X
k
dzu(u,v) (14.45)
is the vertically integrated horizontal velocity field. The P1term represents the work of applied pressure
and geopotential moving vertical columns of fluid.
14.6.2 Advection velocity components for tracers
Focus on the zonal piece of the baroclinic pressure term appearing in equation (14.36), in which
P2x≡−X
i,j,k
dau dzu uFDX NT(FAY(p0))
=−1
2Xdyu dzu u δi(p0
j+p0
j+1)
=−XBAY(dyu dzu u)δip0
j.
(14.46)
The boundary terms were dropped since they vanish for either periodic or solid wall conditions. We also
introduced the backward meridional average operator
BAY(A) = Aj+Aj−1
2.(14.47)
Now define the zonal thickness weighted advective transport velocity on the eastern face of a tracer cell as
uh eti,j,k =BAY(dyu dzu u)
dytei,j
,(14.48)
where dytei,j is the meridional width of the tracer cell’s east side (see Figure 14.3 for definitions of grid
distances). Doing so leads to
P2x=−Xδip0(dyte uh et)
=Xp0δi(dyte uh et)
=Xp0dat BDX ET(uh et),
(14.49)
where boundary terms vanish, and
BDX ET(A) = Ai,j dytei,j −Ai−1,j dytei−1,j
dati,j
(14.50)
is a backwards finite difference operator for fields defined on the east face of tracer cells. Similar manipu-
lations with the meridional term v ∂yp0leads to
P2=X
i,j,k
p0dat (BDX ET(uh et) + BDY NT(vh nt)),(14.51)
Elements of MOM November 19, 2014 Page 198

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
with
vh nti,j,k =BAX(dxu dzu v)
dxtni,j
(14.52)
the meridional tracer advective velocity on the north face of the tracer cell, and
BAX(A) = Ai+Ai−1
2(14.53)
defining the backward averaging operator. Finally,
BDY NT(A) = Ai,j dxtni,j −Ai,j−1dxtni,j−1
dati,j
(14.54)
is a backwards finite difference operator for fields defined on the north face of tracer cells.
The horizontal thickness weighted advective velocity components uh et and vh nt are defined at the
sides of the tracer cells, just like the C-grid velocity components (Figure 9.2 and 9.3)). They are the discrete
representation of the thickness weighted advective velocity components that transport tracer and volume
through the east and north cell faces. When fluid volume converges horizontally to a tracer cell, there is a
corresponding dia-surface velocity component and a generally nonzero time tendency for the cell thickness.
The thickness weighted volume budgets given by equations (14.19), (14.20), and (14.21) describe these
effects.
Given that the advective velocity components uh et and vh nt are defined at the sides of the tracer cells,
we are led to define a dia-surface velocity component w btkat the bottom of the cell. It can generally be
written by the discrete form of equation (14.20)
w btk=w btk−1+BDX ET(uh etk) + BDY NT(vh ntk) + ∂t(dztk)−S(V)dztk.(14.55)
Again, the time tendency on tracer cell thickness dztkis known in MOM from information about the
vertically integrated volume budget (Section 10.8.1.5). So equation (14.55) is indeed a diagnostic expression
for w btk, evaluated from the surface down to the bottom. At the ocean surface, the dia-surface velocity
component is determined by the input of water to the system
w btk=0 =−Qm/ρo.(14.56)
The minus sign is a convention, where positive w > 0 represents upward transport whereas positive Qm>0
represents downward transport of fresh water through the ocean surface into the ocean domain. Note that
in general, water can enter the ocean domain at any depth through the source term S(V). At the ocean
bottom, we are ensured of a proper discretization so long as
w btk=kbot = 0 (14.57)
is diagnosed to within numerical truncation. This statement is valid on either the B-grid or C-grid, since
the ocean bottom on tracer cells is flat. It is a useful diagnostic for verifying the integrity of volume conser-
vation discretization throughout a vertical column.
14.6.3 Divergence operator for surface height evolution
Integrating the continuity equation (14.55) vertically over an ocean column leads to
nk
X
k=1
(w btk−w btk−1)=
nk
X
k=1 BDX ET(uh etk) + BDY NT(vh ntk) + ∂t(dztk)−S(V)dztk.(14.58)
The time tendency for the thickness of an ocean column equals to that of the sea surface height, so that
∂tη=
nk
X
k=1
∂t(dztk).(14.59)
Elements of MOM November 19, 2014 Page 199

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
Use of the surface and bottom boundary conditions (14.56) and (14.57) thus lead to
∂tη=Qm/ρo−
nk
X
k=1
[BDX ET(uh etk) + BDY NT(vh ntk)]+
nk
X
k=1 S(V)dztk.(14.60)
We are thus led to introduce a finite difference operator for the divergence of the vertically integrated
transport
DIV UD(U,V ) =
nk
X
k=1
[BDX ET(uh etk) + BDY NT(vh ntk)].(14.61)
Use of the operator definitions (14.47), (14.50), (14.53), and (14.54), as well as the advection velocity com-
ponents (14.48) and (14.52) leads to the form relevant for the B-grid
DIV UD(U,V ) = [BAY(dyu U)]i,j −[BAY(dyu U)]i−1,j
dati,j !+ [BAX(dxu V)]i,j −[BAX(dxu V)]i,j−1
dati,j !,(14.62)
where (U,V ) is the vertically integrated horizontal velocity field defined by equation (14.45). Note that
this is the same divergence operator that is used for the bottom pressure evolution when implementing
the non-Boussinesq mass conserving form of MOM on a B-grid. The only difference is that the arguments
become the density-weighted horizontal velocity (see Section 14.8.2).
14.6.4 Completing the manipulations for P2
Substituting expression (14.55) for the vertical advective velocity component into equation (14.51) leads to
P2=X
i,j,k
p0
kdat w btk−w btk−1−∂t(dztk) + S(V)dztk.(14.63)
Now move the vertical difference operator from the dia-surface velocity to the hydrostatic pressure via the
following identity
kbot
X
k=1
p0
kdat (wbtk−w btk−1) = −p0
k=1 w btk=0 dat −
kbot
X
k=1
datw btk(p0
k+1 −p0
k),(14.64)
where we used the lower boundary condition p0
kbot+1 w btkbot = 0 to reach this result. The next step requires
us to specify how the hydrostatic pressure is computed. There are two ways, described in Sections 10.1.1
and 10.1.2.
14.6.4.1 Energetic approach
Section 10.1.1 noted that the older energetically based method specifies the hydrostatic pressure at the
tracer point depth (Figure 14.2) according to
p0
k=1 =gdztupk=1 ρ0
k=1 k= 1 (14.65)
p0
k+1 =p0
k+gdzwtkρ0
k
zk > 1,(14.66)
where
ρ0
k
z=ρ0
k+ρ0
k+1
2(14.67)
is the algebraically averaged density over the region between two tracer points Tkand Tk+1, and dzwtkis
the vertical distance between the tracer points (Section 10.3). Substituting this result into equation (14.64)
renders kbot
X
k=1
p0
kdat (w btk−w btk−1) = −p0
k=1 w btk=0 dat −g
kbot
X
k=1
dat dzwtkw btkρ0
k
z.(14.68)
Elements of MOM November 19, 2014 Page 200
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
dztlo(k=kbot)
dzt(k=1)
dzt(k=2)
dzt(k=kbot)
dzwt(k=kbot)
dzwt(k=2)
dzwt(k=1)
dzwt(k=0) dztup(1)
dztlo(1)
dztup(2)
dztlo(2)
dztup(k=kbot)
Figure 14.2: Left panel: schematic of the vertical grid cell arrangement used for computing the hydrostatic
pressure at a depth k+ 1 in terms of the pressure at depth kusing equations (14.65) and (14.66). The
vertical average of density is meant to account for the part of density within each of the two adjacent cells.
The factor of 1/2 used in the average operator yields an approximate average when vertical cells are non-
uniform. Yet the 1/2 factor is used for all vertical grid spacing since it renders a simple conversion of
discrete pressure work to discrete gravity work. Right panel: grid cell thicknesses used for computing the
finite volume hydrostatic pressure at depth k+ 1 (see equations (14.70) and (14.71)). Note that this figure
was also presented in Section 10.1 (see Figure 10.1).
This result then leads to
P2=−gX
i,j,k
dat dzwtkw btkρ0
k
z−X
i,j
dat p0
k=1 w btk=0 −X
i,j,k
dat p0
kh∂t(dztk)−S(V)dztki.(14.69)
14.6.4.2 Finite volume approach
Section 10.1.2 noted that a finite volume based method specifies the hydrostatic pressure at the tracer point
depth according to (see Figure 14.2)
p0
k=1 =gdztupk=1 ρ0
k=1 (14.70)
p0
k+1 =p0
k+gdztlokρ0
k+gdztupk+1 ρ0
k+1.(14.71)
Substituting this result into equation (14.64) renders
kbot
X
k=1
p0
kdat (w btk−w btk−1) = −p0
k=1 w btk=0 dat −g
kbot
X
k=1
dat w btk(dztlokρ0
k+gdztupk+1 ρ0
k+1).(14.72)
This result then leads to
P2=−gX
i,j,k
dat w btk(dztlokρ0
k+gdztupk+1 ρ0
k+1)−X
i,j
dat p0
k=1 w btk=0−X
i,j,k
dat p0
kh∂t(dztk)−S(V)dztki.
(14.73)
Elements of MOM November 19, 2014 Page 201

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.6
14.6.5 The geopotential gradient term P3
Now consider the zonal piece of the geopotential gradient from equation (14.36)
P3x=−X
i,j,k
dxu dyu dzu uFAY(FAX(ρ0)δiΦ)/dxu.(14.74)
Transferring the forward average FAY to a backward average BAY leads to
P3x=−XBAY(dyu dzu u)FAX(ρ0)δiΦ,(14.75)
where boundary terms vanish. Introducing the zonal thickness weighted advective transport velocity
(14.48) yields
P3x=−Xdyte uh et FAX(ρ0)δiΦ.(14.76)
Moving the difference operator δiΦ=Φi+1 −Φifrom the geopotential to the remaining terms gives
P3x=XΦδi(dyte FAX(ρ0)uh et)
=XΦdat BDX ET(FAX(ρ0)uh et),(14.77)
where boundary terms vanish. Similar manipulations with the meridional piece of P3lead to
P3=XΦdat [BDX ET(FAX(ρ0)uh et) + BDY NT(FAY(ρ0)vh nt)].(14.78)
14.6.6 Summary for the Boussinesq pressure conversion
In summary, for the energetically based method for computing hydrostatic pressure, the projection of the
horizontal velocity onto the downgradient pressure field is given by
P=−X
i,j
dau [UFDX NT(FAY(pa+psurf)) + VFDY ET(FAX(pa+psurf))]
−X
i,j
dat p0
k=1 w btk=0
−gX
i,j,k
dat dzwtkw btkρ0
k
z
−X
i,j,k
dat p0
kh∂t(dztk)−S(V)dztki
+X
i,j,k
Φdat [BDX ET(FAX(ρ0)uh et) + BDY NT(FAY(ρ0)vh nt)].
(14.79)
Within the MOM energy analysis diagnostic, the code computes the left hand side of equation (14.79) and
compares to the right hand side. Differences are due to coding errors. This diagnostic is very effective
because it involves advective velocities on the tracer cells, both tracer and velocity cell distances, the cal-
culation of pressure, and details of a partial step representation of the ocean bottom. Each requires precise
discretization to ensure an energy conversion error at the numerical roundofflevel. In a similar manner,
for the finite volume approach to computing hydrostatic pressure, we have the projection of the horizontal
Elements of MOM November 19, 2014 Page 202
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.7
T(i,j)
dxt(i,j) dyte(i,j)
dxtn(i,j)
dyt(i,j)
Figure 14.3: Time independent horizontal grid distances (meters) used for the tracer cell Ti,j in MOM. dxti,j
and dyti,j are the grid distances of the tracer cell in the generalized zonal and meridional directions, and
dati,j =dxti,j dyti,j is the area of the cell. The grid distance dxtni,j is the zonal width of the north face
of a tracer cell, and dytei,j is the meridional width of the east face. Note that the tracer point Ti,j is not
generally at the center of the tracer cell. Distances are functions of both iand jdue to the use of generalized
orthogonal coordinates.
velocity onto the downgradient pressure field is given by
P=−X
i,j
dau [UFDX NT(FAY(pa+psurf)) + VFDY ET(FAX(pa+psurf))]
−X
i,j
dat p0
k=1 w btk=0
−gX
i,j,k
dat w btk(dztlokρ0
k+gdztupk+1ρ0
k+1)
−X
i,j,k
dat p0
kh∂t(dztk)−S(V)dztki
+X
i,j,k
Φdat [BDX ET(FAX(ρ0)uh et) + BDY NT(FAY(ρ0)vh nt)].
(14.80)
14.7 C-grid Boussinesq pressure work conversions
We now consider pressure work conversions for the C-grid version of MOM. In this section, the horizontal
velocity components (u,v) are located on the zonal and meridional faces of the tracer cell, as per the C-grid
convention (Figure 9.2).
As for the B-grid in Section 14.6, the manipulations here lead to a consistent definition of the advective
transport crossing tracer cell faces. Again, the definition is specified by requiring a sensible discrete energy
conversion that reflects that found in the continuum. Once we define the advective transport uh et and
vh nt for the C-grid, all subsequent results for the pressure work conversion manipulations are identical
to those already considered for the B-grid.
14.7.1 Force from the horizontal pressure gradient
To start, consider the expressions given in Section 3.4.1 for the horizontal pressure gradient force acting
on the C-grid momentum. The zonal momentum per horizontal area, u ρodz, sits at the zonal face of the
Elements of MOM November 19, 2014 Page 203

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.7
tracer cell, and the meridional momentum per horizontal area, v ρodz, sits at the meridional face (Figure
9.2). Horizontal pressure gradients impart a force to the momentum according to
∂t(u ρodzte)pressure =−dzteFDX T(pa+psurf +p0) + FAX(ρ0)FDX T(Φ0)(14.81)
∂t(v ρodztn)pressure =−dztnFDY T(pa+psurf +p0) + FAY(ρ0)FDY T(Φ0).(14.82)
In these equations, derivative operators are defined by
FDX T(A) = Ai+1 −Ai
dxtei,j
FDY T(A) = Aj+1 −Aj
dytni,j
,
(14.83)
with the grid distances given in Figure 9.7. These operators are used for fields that live at the tracer point.
To compute the pressure work conversion
P=−Zu·∇zpdV(14.84)
on the discrete C-grid, we multiply the zonal momentum equation (14.129) by the thickness weighted zonal
velocity, udzte, and the meridional momentum equation (14.130) by the thickness weighted meridional
velocity, vdztn (see Section 14.5.2 for definition of thicknesses dzte and dztn), and integrate over the
tracer cells to render
P ≡−X
i,j,k
dat [udzte FDX T(pa+psurf) + vdztn FDY T(pa+psurf)]
−X
i,j,k
dat udzte FDX T(p0) + vdztn FDY T(p0)
−X
i,j,k
dat udzte FAX(ρ0)FDX T(Φ) + vdztn FAY(ρ0)FDY T(Φ).
(14.85)
Note the integration is over the area of the tracer cell, dat, which contrasts to the B-grid approach in Section
14.6, where integration is over the velocity cell area, dau. The reason for integrating here over the tracer
area is that there is no analogous velocity cell control volume for the C-grid.
14.7.2 The vertically integrated term P1
The first line in equation (14.85) can be vertically integrated to yield
P1≡−X
i,j,k
dat [udzte FDX T(pa+psurf) + vdztn FDY T(pa+psurf)]
=−X
i,j
dat [UFDX T(pa+psurf) + VFDY T(pa+psurf)]
(14.86)
where
(U,V ) = X
k
(udzte,v dztn)(14.87)
is the vertically integrated horizontal velocity field. The P1term represents the work of applied pressure
and geopotential moving vertical columns of fluid.
Elements of MOM November 19, 2014 Page 204
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.7
14.7.3 Advection velocity components for tracers
Focus on the zonal piece of the baroclinic pressure term appearing in equation (14.85), in which
P2x≡− X
i,j,k
dat udzte FDX T(p0)
=−Xdxt dyt udzte δip0
i
dxte !
=−Xδip0
idyte dxt
dxte dyt
dyte dzte u.
(14.88)
See Figure 14.3 for definitions of grid distances. Now define the zonal thickness weighted advective trans-
port velocity placed on the eastern face of a tracer cell as
uh eti,j,k =udzte dxt
dxte dyt
dyte ,(14.89)
which leads to
P2x=−Xδip0(dyte uh et).(14.90)
This is the exact same form as that arrived at for the B-grid in equation (14.49). All subsequent manipula-
tions performed on the B-grid in Sections 14.6.2 and 14.6.4 follow through with the modified form of the
advective transport given by equation(14.89), and the corresponding meridional transport
vh nti,j,k =vdztn dxt
dxtn dyt
dytn .(14.91)
In particular, the vertical transport w bt satisfies the same continuity equation (14.55) as for the B-grid.
14.7.4 Divergence operator for surface height evolution
We follow the discussion in Section 14.6.3 to develop the divergence operator for the C-grid sea level
evolution. For this purpose, we start from the general form of the finite difference divergence operator
(14.61)
DIV UD(U,V ) =
nk
X
k=1
[BDX ET(uh etk) + BDY NT(vh ntk)],(14.92)
with this form valid for either the B-grid or C-grid. Use of the operator definitions (14.50) and (14.54), as
well as the advection velocity components (14.89) and (14.91) leads to the form appropriate for the C-grid
DIV UD(U,V ) = dat
dxte Ui,j −dat
dxte Ui−1,j
dati,j +dat
dytn Vi,j −dat
dytn Vi,j−1
dati,j (14.93)
where (U,V ) is the vertically integrated horizontal velocity field defined by equation (14.87). Note that
this is the same divergence operator that is used for the bottom pressure evolution when implementing
the non-Boussinesq mass conserving form of MOM on a C-grid. The only difference is that the arguments
become the density-weighted horizontal velocity (see Section 14.9.2).
14.7.5 The geopotential gradient term P3
Now consider the zonal piece of the geopotential gradient from equation (14.85)
P3x=−X
i,j,k
dat dzte uFAX(ρ0)FDX T(Φ)
=−X
i,j,k udzte dxt
dxte
dyt
dyte dyte FAX(ρ0)δiΦ.
(14.94)
Elements of MOM November 19, 2014 Page 205
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.8
Introduce the zonal transport uh et given by equation (14.89) to render
P3x=−X
i,j,k
uh et dyte FAX(ρ0)δiΦ.(14.95)
This expression has the identical form as equation (14.76) derived for the B-grid. Consequently, all subse-
quent manipulations conducted for the B-grid now follow for the C-grid.
14.7.6 Summary for the Boussinesq pressure conversion
The summary for the C-grid pressure conversion terms is very similar to that for the B-grid given in Sec-
tion 14.6.6. For the energetically based method for computing hydrostatic pressure, the projection of the
horizontal velocity onto the downgradient pressure field is given by
P=−X
i,j
dat [UFDX T(pa+psurf) + VFDY T(pa+psurf)]
−X
i,j
dat p0
k=1 w btk=0
−gX
i,j,k
dat dzwtkw btkρ0
k
z
−X
i,j,k
dat p0
kh∂t(dztk)−S(V)dztki
+X
i,j,k
Φdat [BDX ET(FAX(ρ0)uh et) + BDY NT(FAY(ρ0)vh nt)].
(14.96)
In a similar manner, for the finite volume approach to computing hydrostatic pressure, we have the projec-
tion of the horizontal velocity onto the downgradient pressure field is given by
P=−X
i,j
dat [UFDX T(pa+psurf) + VFDY T(pa+psurf)]
−X
i,j
dat p0
k=1 w btk=0
−gX
i,j,k
dat w btk(dztlokρ0
k+gdztupk+1ρ0
k+1)
−X
i,j,k
dat p0
kh∂t(dztk)−S(V)dztki
+X
i,j,k
Φdat [BDX ET(FAX(ρ0)uh et) + BDY NT(FAY(ρ0)vh nt)].
(14.97)
14.8 B-grid non-Boussinesq pressure work conversions
Now consider manipulations of the globally integrated discrete B-grid representation of u· ∇zpfor the
non-Boussinesq case. Here, we are concerned with the domain integrated scalar product
u·∇zp=u·(∇sp+ρ∇sΦ)
= (ρ/ρo)u·∇(pb+ρoΦb) + u·[−(ρ0/ρo)∇sp+ρ∇sΦ0],(14.98)
where equation (3.27) was used for the pressure gradient as implemented in pressure based vertical coor-
dinate models. To determine the proper discrete form of the pressure conversion, recall from Section 3.3.2
Elements of MOM November 19, 2014 Page 206

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.8
the momentum equations for a non-Boussinesq fluid on a B-grid with just the impacts from pressure acting
∂t(urho dzu)pressure =−rho dzu FDX NT(FAY(pb/ρo+Φb+Φ0)) + dzu FAY[δipFAX(ρ0/ρo)]/dxui,j (14.99)
∂t(vrho dzu)pressure =−rho dzu FDY ET(FAX(pb/ρo+Φb+Φ0)) + dzu FAX[δjpFAY(ρ0/ρo)]/dyui,j.(14.100)
The pressure conversion
P=−Zu·∇zpdV(14.101)
for a non-Boussinesq fluid thus has the following discrete representation on the B-grid
ρoP ≡−X
i,j,k
dau rho dzu [uFDX NT(FAY(pb+ρoΦb)) + vFDY ET(FAX(pb+ρoΦb)) ]
−X
i,j,k
dau rho dzu uFDX NT(FAY(Φ0)) + vFDY ET(FAX(Φ0))
+X
i,j,k
dau dzu huFAY(FAX(ρ0)δip)/dxu +vFAX(FAY(ρ0)δjp)/dyu i.
(14.102)
We now consider these terms individually.
14.8.1 The vertically integrated term P1
The first term in equation (14.102) can be vertically integrated as
P1≡−X
i,j,k
dau rho dzu [uFDX NT(FAY(pb/ρo+Φb)) + vFDY ET(FAX(pb/ρo+Φb)) ]
=−X
i,j
dau [UρFDX NT(FAY(pb/ρo+Φb)) + VρFDY ET(FAX(pb/ρo+Φb))]
(14.103)
where
(Uρ,V ρ) = X
k
rho dzu(u,v) (14.104)
is the vertically integrated density weighted horizontal velocity field. Equivalently, it is the vertically inte-
grated horizontal momentum per horizontal area. The P1term represents the effects of applied pressure
and geopotential working on moving vertical columns of fluid.
14.8.2 Defining the advective mass transport
To motivate the definition of the advection velocity for the non-Boussinesq case, we focus on the zonal part
of the geopotential term
P2x≡−X
i,j,k
dau rho dzu uFDX NT(FAY(Φ0))
=−1
2Xdyu rho dzu u δi(Φ0
j+Φ0
j+1)
=−XBAY(dyu rho dzu u)δiΦ0
j.
(14.105)
The boundary terms were dropped since they vanish for either periodic or solid wall conditions. Now define
the thickness weighted and density weighted zonal advective transport on the eastern face of a tracer cell
uhrho eti,j,k =BAY(dyu rho dzu u)
dytei,j
.(14.106)
Elements of MOM November 19, 2014 Page 207

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.8
This definition of the non-Boussinesq advective mass transport leads to
P2x=−XδiΦ0(dyte uhrho et)
=XΦ0δi(dyte uhrho et)
=XΦ0dat BDX ET(uhrho et),
(14.107)
where boundary terms vanish. Similar manipulations with the meridional term v ∂yp, and reintroducing
the two-dimensional pieces, leads to
P2=XΦ0dat (BDX ET(uhrho et) + BDY NT(vhrho nt)),(14.108)
with
vhrho nti,j,k =BAX(dxu rho dzu v)
dxtni,j
(14.109)
the meridional density and thickness weighted advective tracer velocity on the north face of the tracer cell.
As for the Boussinesq case, the horizontal advective velocities uhrho et and vhrho nt are defined at
the sides of the tracer cells. They are the discrete representation of the thickness and density weighted
advective velocity transporting tracer and seawater mass through the east and north cell faces. When
mass converges horizontally to a tracer cell, there is a corresponding dia-surface velocity component and
a generally nonzero time tendency for the cell thickness. The thickness weighted mass budgets given by
equations (14.22), (14.23), and (14.24) describe these effects.
Given that the advective mass transport uhrho et and vhrho nt are defined at the sides of the tracer
cells, we are led to define a density weighted dia-surface velocity component wrho btkat the bottom of the
cell. It is determined by the discrete form of equation (14.23)
wrho btk=∂t(rho dzt)k−rho dzt S(M)+BDX ET(uhrho etk) + BDY NT(vhrho ntk) + wrho btk−1.(14.110)
For the non-Boussinesq versino of MOM, we use pressure-based vertical coordinates so that the tracer and
velocity cells maintain the identity
ρdz=ρ ∂z
∂s !ds(14.111)
where ρ ∂z/∂s is depth independent. The time tendency on density weighted tracer cell thickness (rho dzt)k
is known in MOM from information about the vertically integrated mass budget (Section 10.6.2). So equa-
tion (14.110) is indeed a diagnostic expression for wrho btk, evaluated from the surface down to the bottom.
At the ocean surface, the dia-surface velocity component is determined by the input of fresh water to the
system
wrho btk=0 =−Qm.(14.112)
At the ocean bottom, we are ensured of a proper discretization so long as
wrho btk=kbot = 0 (14.113)
is diagnosed.
14.8.3 Completing the manipulations for P2
Substituting expression (14.110) for the vertical advective velocity component into equation (14.108) leads
to
P2=XΦ0
kdat (wrho btk−wrho btk−1−∂t(rho dzt)k+rho dztkS(M)).(14.114)
Now move the vertical difference operator from the dia-surface velocity to the hydrostatic pressure via the
following identity
kbot
X
k=1
Φ0
kdat (wrho btk−wrho btk−1) = −dat Φ0
k=1 wrho btk=0 +
kbot
X
k=1
dat wrho btk(Φ0
k−Φ0
k+1),(14.115)
Elements of MOM November 19, 2014 Page 208

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.8
where we used the lower boundary condition Φ0
kbot+1 wrho btkbot = 0 to reach this result. The next step
requires us to specify how the anomalous geopotential height is computed. There are two ways, described
in Sections 10.1.3 and 10.1.4.
14.8.3.1 Energetic approach
In Section 10.1.3, we noted that the older energetically based method specifies the anomalous geopotential
height at the tracer point depth (Figure 14.2) according to
Φ0
k=Φ0
k+1 −(g/ρo)dzwtkρ0
k
z.(14.116)
In contrast to the hydrostatic pressure calculation in equations (14.65) and (14.66), the geopotential calcu-
lation procedes from the bottom upwards. Substituting equation (14.116) into equation (14.115) renders
kbot
X
k=1
Φ0
kdat (wrho btk−wrho btk−1) = −Φ0
k=1 wrho btk=0 dat −(g/ρo)
kbot
X
k=1
datdzwtkwrho btkρ0
k
z,(14.117)
which then leads to
P2=−(g/ρo)X
i,j,k
dat dzwtkwrho btkρ0
k
z−X
i,j
dat Φ0
k=1 wrho btk=0
+X
i,j,k
dat Φ0[(rho dzt)kS(M)−∂t(rho dzt)k].(14.118)
14.8.3.2 Finite volume approach
In Section 10.1.4, we noted that the finite volume based method specifies the anomalous geopotential height
at the tracer point depth (Figure 14.2) according to
Φ0
k=kbot =−(g/ρo)dztlokbot ρ0
k=kbot (14.119)
Φ0
k=Φ0
k+1 −(g/ρo)dztupk+1ρ0
k+1 −(g/ρo)dztlokρ0
k.(14.120)
Substituting equations (14.119) and (14.120) into equation (14.115) renders
kbot
X
k=1
Φ0
kdat (wrho btk−wrho btk−1) = −Φ0
k=1 wrho btk=0 dat−(g/ρo)
kbot
X
k=1
dat wrho btk(dztupk+1ρ0
k+1+dztlokρ0
k),
(14.121)
which then leads to
P2=−(g/ρo)X
i,j,k
dat wrho btk(dztupk+1ρ0
k+1 +dztlokρ0
k)−X
i,j
dat Φ0
k=1 wrho btk=0
+X
i,j,k
dat Φ0[(rho dzt)kS(M)−∂t(rho dzt)k].(14.122)
14.8.4 The pressure gradient term P3
Now consider the zonal piece of the geopotential gradient from equation (14.102)
ρoP3x=X
i,j,k
dxu dyu dzu uFAY(FAX(ρ0)δip)/dxu (14.123)
Transferring the forward average FAY to a backward average BAY leads to
ρoP3x=−XBAY(dyu dzu u)FAX(ρ0)δip, (14.124)
Elements of MOM November 19, 2014 Page 209

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.9
where boundary terms vanish. Further manipulations, analogous to the Boussinesq case in Section 14.6.5,
do not appear possible since the density weighted advection velocity will not appear. Instead, the ρ0
weighted velocity appears, and this is not relevant. So we simply write this term in its unmanipulated
form
ρoP3=X
i,j,k
dau dzu huFAY(FAX(ρ0)δip)/dxu +vFAX(FAY(ρ0)δjp)/dyu i.(14.125)
14.8.5 Summary for the non-Boussinesq pressure conversion
In summary, for the energetically based method for computing the anomalous geopotential, the projection
of the horizontal velocity onto the downgradient pressure field in the non-Boussinesq case is given by
P=−X
i,j
dau [UρFDX NT(FAY(pb/ρo+Φb)) + VρFDY ET(FAX(pb/ρo+Φb))]
−X
i,j
dat Φ0
k=1 wrho btk=0
−(g/ρo)X
i,j,k
dat dzwtkwrho btkρ0
k
z
−X
i,j,k
dat Φ0
k[∂t(rho dzt)k−ρdztkS(M)]
+ρ−1
oX
i,j,k
daudzu huFAY(FAX(ρ0)δip)/dxu +vFAX(FAY(ρ0)δjp)/dyui.
(14.126)
In a similar manner, for the finite volume approach to computing anomalous geopotential height, the
projection of the horizontal velocity onto the downgradient pressure field is given by
P=−X
i,j
dau [UρFDX NT(FAY(pb/ρo+Φb)) + VρFDY ET(FAX(pb/ρo+Φb))]
−X
i,j
dat Φ0
k=1 wrho btk=0
−(g/ρo)X
i,j,k
dat wrho btk(dztupk+1ρ0
k+1 +dztlokρ0
k)
−X
i,j,k
dat Φ0
k[∂t(rho dzt)k−rho dztkS(M)]
+ρ−1
oX
i,j,k
daudzu huFAY(FAX(ρ0)δip)/dxu +vFAX(FAY(ρ0)δjp)/dyui.
(14.127)
14.9 C-grid non-Boussinesq pressure work conversions
We now consider the discrete representation of the pressure conversion
P=−Zu·∇zpdV(14.128)
on the C-grid for a non-Boussinesq fluid. To start, consider the expressions given in Section 3.4.2 for the
horizontal pressure gradient force acting on the C-grid momentum in a non-Boussinesq fluid
∂t(urho dzte)pressure =−rho dzte FDX T(pb/ρo+Φb+Φ0) + dzte FAX(ρ0/ρo)FDX T(p) (14.129)
∂t(vrho dztn)pressure =−rho dztn FDY T(pb/ρo+Φb+Φ0) + dztn FAY(ρ0/ρo)FDY T(p).(14.130)
Elements of MOM November 19, 2014 Page 210

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.9
Recall that the zonal momentum per horizontal area, u ρdz, sits at the zonal face of the tracer cell, and
the meridional momentum per horizontal area, v ρdz, sits at the meridional face (Figure 9.2). The discrete
form of the pressure work conversion for a non-Boussinesq fluid on a C-grid is thus given by
P ≡−X
i,j,k
dat [urho dzte FDX T(pb/ρo+Φb) + vrho dztn FDY T(pb/ρo+Φb)]
−X
i,j,k
dat urho dzte FDX T(Φ0) + vrho dztn FDY T(Φ0)
+X
i,j,k
dat udzte FAX(ρ0/ρo)FDX T(p) + vdztn FAY(ρ0/ρo)FDY T(p).
(14.131)
Note the integration is over the area of the tracer cell, dat, which contrasts to the B-grid approach in Section
14.8, where integration is over the velocity cell area, dau. The reason for integrating here over the tracer
area is that there is no analogous velocity cell control volume for the C-grid.
14.9.1 The vertically integrated term P1
The first term in equation (14.131) can be vertically integrated as
P1≡−X
i,j,k
dat [urho dzte FDX T(pb/ρo+Φb) + vrho dztn FDY T(pb/ρo+Φb)]
=−X
i,j
dat [UρFDX T(pb/ρo+Φb) + VρFDY T(pb/ρo+Φb)]
(14.132)
where
(Uρ,V ρ) = X
k
(urho dzte,v rho dztn) (14.133)
is the vertically integrated density weighted horizontal velocity field for the C-grid. Equivalently, it is
the vertically integrated horizontal momentum per horizontal area. The P1term represents the effects of
applied pressure and geopotential working on moving vertical columns of fluid.
14.9.2 Defining the advective mass transport
To motivate the definition of the advection velocity for the non-Boussinesq case, we focus on the zonal part
of the geopotential term
P2x≡ − X
i,j,k
dat urho dzte FDX T(Φ0).(14.134)
We can immediately transfer the results from the Boussinesq case in equation (14.88) to render the advec-
tive mass transport for the C-grid non-Boussinesq fluid
uhrho eti,j,k =urho dzte dxt
dxte dyt
dyte ,(14.135)
which leads to
P2x=−XδiΦ0(dyte uhrho et).(14.136)
The corresponding meridional advective mass transport for the C-grid non-Boussinesq fluid is given by
vhrho nti,j,k =vrho dztn dxt
dxtn dyt
dytn ,(14.137)
These results place the C-grid results in line with that already considered in Section 14.8.2 for the B-grid.
All subsequent manipulations thus follow just as for the B-grid.
Elements of MOM November 19, 2014 Page 211

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.10
14.9.3 The pressure gradient term P3
As for the B-grid considerations in Section 14.8.4, we do not find manipulations of the pressure gradient
term in equation (14.131) to be possible, so we simply write the unmanipulated form as
ρoP3=X
i,j,k
dat udzte FAX(ρ0)FDX T(p) + vdztn FAY(ρ0)FDY T(p).(14.138)
14.9.4 Summary for the non-Boussinesq pressure conversion
In summary, for the energetically based method for computing the anomalous geopotential, the projection
of the horizontal velocity onto the downgradient pressure field in the non-Boussinesq C-grid case is given
by
P=−X
i,j
dat [UρFDX T(pb/ρo+Φb) + VρFDY T(pb/ρo+Φb)]
−X
i,j
dat Φ0
k=1 wrho btk=0
−(g/ρo)X
i,j,k
dat dzwtkwrho btkρ0
k
z
−X
i,j,k
dat Φ0
k[∂t(rho dzt)k−ρdztkS(M)]
+ρ−1
oX
i,j,k
dat udzte FAX(ρ0)FDX T(p) + vdztn FAY(ρ0)FDY T(p).
(14.139)
In a similar manner, for the finite volume approach to computing anomalous geopotential height, the
projection of the horizontal velocity onto the downgradient pressure field is given by
P=−X
i,j
dat [UρFDX T(pb/ρo+Φb) + VρFDY T(pb/ρo+Φb)]
−X
i,j
dat Φ0
k=1 wrho btk=0
−(g/ρo)X
i,j,k
dat wrho btk(dztupk+1ρ0
k+1 +dztlokρ0
k)
−X
i,j,k
dat Φ0
k[∂t(rho dzt)k−rho dztkS(M)]
+ρ−1
oX
i,j,k
dat udzte FAX(ρ0)FDX T(p) + vdztn FAY(ρ0)FDY T(p).
(14.140)
14.10 Effective Coriolis force and mechanical energy
In the continuum, the Coriolis force and the advection metric frequency combine to yield the effective
Coriolis force per volume (see equation (14.1))
Feff-coriolis =˜
f(ˆ
z∧ρu),(14.141)
where ˜
f=f+M(14.142)
is the effective Coriolis parameter, and (see equation (4.49) in Griffies (2004))
M=v ∂xdy
dy!−u ∂ydx
dx!(14.143)
Elements of MOM November 19, 2014 Page 212

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.10
is the advective metric frequency arising from the sphericity of the earth. The effective Coriolis force has
zero impact on mechanical energy, since it is directed perpendicular to the horizontal velocity
u·Feff-coriolis =u·˜
f(ˆ
z∧ρu)=0.(14.144)
However, assumptions about time and space discretizations generally compromise this continuum result.
14.10.1 B-grid
On the B-grid, the effective Coriolis force per horizontal area takes the form
Fx-eff-coriolis =−(f+M)vrho dzu (14.145)
Fy-eff-coriolis = (f+M)urho dzu,(14.146)
where the Coriolis parameter fis computed at the B-grid velocity point, as is the advective metric frequency
M=vdh2dx −udh1dy (14.147)
with
dh2dx =dyuei,j −dyuei−1,j
dxu dyu (14.148)
dh1dy =dxuni,j −dxuni,j−1
dxu dyu .(14.149)
(see Figure 14.4 for grid distances). Naively, the inner product of the horizontal velocity field, u(τ) and the
effective Coriolis force will vanish on the discrete B-grid. However, temporal staggering compromises this
result in the following cases.
• The Coriolis force on the B-grid is generally evaluated using a semi-implicit approach (Section 12.2).
We may also use an Adams-Bashforth approach, as for the momentum advection (Section 11.2.3 and
(Durran,1999)). Either approach leaves a nonzero contribution of the Coriolis force in the mechanical
energy budget. Only with the older, and nearly obsolete, leap-frog method with an explicit Coriolis
force will the Coriolis force vanish for the B-grid mechanical energy budget.
• The advection metric frequency is evaluated in MOM as part of the momentum advection operator.
With the leap-frog, this operator is evaluated at the present time step, and so the advection metric
frequency will drop out from the mechanical energy budget. However, using the staggered time
stepping preferred in MOM, the advection of momentum is temporally discretized using an Adams-
Bashforth scheme (Section 11.2.3 and (Durran,1999)), which means the advection metric frequency
will not drop out from the mechanical energy budget.
14.10.2 C-grid
We presented the C-grid form of the Coriolis force per area in Section 12.1.2. We add to that force the force
arising from the advective metric frequency to consider the effective Coriolis force per area
˜
f v ρ dzx-effcoriolis ≈(1/4) h˜
fi,j (v ρ dz)i,j +˜
fi,j (v ρ dz)i+1,j +˜
fi,j−1(v ρdz)i,j−1+˜
fi,j−1(v ρdz)i+1,j−1i(14.150)
−˜
f u ρ dzy-effcoriolis ≈ −(1/4) h˜
fi−1,j (u ρdz)i−1,j +˜
fi−1,j (u ρdz)i−1,j+1 +˜
fi,j (u ρ dz)i,j +˜
fi,j+1 (u ρdz)i,j+1i.
(14.151)
The the effective Coriolis parameter ˜
f(equation (14.142)) is evaluated at the B-grid velocity point, which
is the same as the C-grid vorticity point. For the advective metric frequency (14.147), we use the following
discrete expression evaluated at the B-grid velocity point
Mi,j =dh2dx vi+1,j +vi,j
2−dh1dyui,j+1 +ui,j
2.(14.152)
Elements of MOM November 19, 2014 Page 213
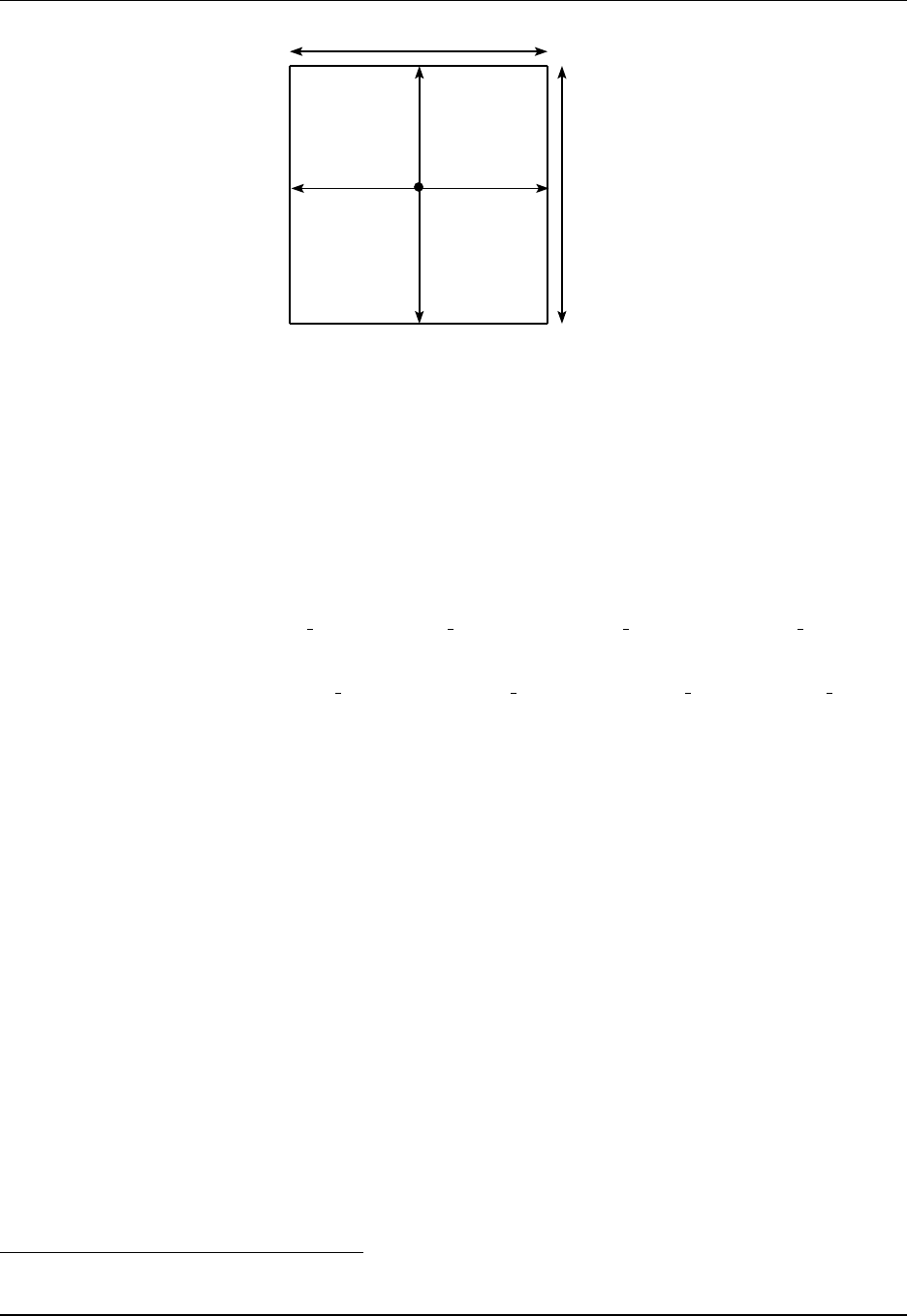
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.11
U(i,j)
dyu(i,j)
dxu(i,j)
dxun(i,j)
dyue(i,j)
Figure 14.4: Time independent horizontal grid distances (meters) used for the B-grid velocity cell Ui,j in
MOM. dxui,j and dyui,j are the grid distances of the velocity cell in the generalized zonal and meridional
directions, and daui,j =dxui,j dyui,j is the area of the cell. The grid distance dxuei,j is the zonal width of the
north face of a velocity cell, and dyuei,j is the meridional width of the east face. Note that the velocity point
Ui,j is not generally at the center of the velocity cell. Distances are functions of both iand jdue to the use
of generalized orthogonal coordinates.
We now introduce the C-grid advective mass transports (14.135) and (14.137) to write the C-grid Cori-
olis force per area as
˜
f v ρ dzx-effcoriolis ≈(1/4) h˜
fi,j vhrho nti,j +˜
fi,j vhrho nti+1,j +˜
fi,j−1vhrho nti,j−1+˜
fi,j−1vhrho nti+1,j−1i
(14.153)
−˜
f u ρ dzy-effcoriolis ≈ −(1/4) h˜
fi−1,j uhrho eti−1,j +˜
fi−1,j uhrho eti−1,j+1 +˜
fi,j uhrho eti,j +˜
fi,j uhrho eti,j+1i.
(14.154)
The Coriolis force and momentum advection for the C-grid in MOM are time discretized using the
Adams-Bashforth scheme. As for the B-grid, multi-time discretizations means that the Coriolis force con-
tributes to the discrete mechanical energy budget. Furthermore, the spatial averaging used in equations
(14.153) and (14.154) means that the effective Coriolis force contributes locally to the discrete C-grid me-
chanical energy, regardless how time is discretized. Note that if using a single time for the Coriolis force2,
there will in fact be no contribution to global mechanical energy from the effective Coriolis force for the
special case of spatially constant ρdzover each depth level. This property can be verified by shifting in-
dices.
14.10.3 Comments
It is unsatisfying that whenever the Coriolis force is discretized using more than a single time level, it
contributes to the discrete mechanical energy budget. Spatial averaging on the C-grid furthermore retains a
non-vanishing contribution to energy at each grid point, regardless how time is discretized. Such properties
of the discrete Coriolis force remain one of the many areas where discrete primitive equation modelling
could be made more elegant.
14.11 B-grid kinetic energy advection
We now consider how kinetic energy is advected in the discrete case. We start from the Boussinesq manip-
ulations, which are readily generalized to the non-Boussinesq.
2A single time for the Coriolis force is stable with a leap-frog, but unstable with MOM’s staggered time scheme. But the leap-frog
is not available for the C-grid in MOM.
Elements of MOM November 19, 2014 Page 214

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.11
There are two limitations of the manipulations presented here.
• Momentum advection is evaluated at a single time step, as is the case for a leap-frog version of MOM.
However, for the preferred time staggered scheme, momentum advection is implemented accord-
ing to a third order Adams-Bashforth (chapter 12 of Griffies,2004). In this case, the results here
are relevant when we take the scalar product of the horizontal velocity with just one of the three
Adams-Bashforth terms contributing to the advection tendency. Even though the energy conversion
properties are compromised, the utility of the kinetic energy conversion diagnostic remains. It is
for this reason that we present these manipulations, as the diagnostics are useful when developing
algorithms to identify numerical bugs.
• Velocity advection is discretized using second order centered advection. This is the original approach
used by Bryan (1969), and remains the default approach in MOM.
The following is a generalization of material presented in Griffies et al. (2004).
14.11.1 B-grid momentum equation contribution from advection
The contribution to the momentum time tendency arising from second order centered advection fluxes on
a B-grid is given by
∂t(uρodzu)i,j =−BDX EU [uh et FAX(u)]−BDY NU [vh nt FAY(u)]−w buk−1uk+uk−1
2−w bukuk+1 +uk
2.
(14.155)
The forward algebraic averaging operators FAX and FAY are given in equations (14.42) and (14.43). They
are used to estimate velocity on the velocity cell faces to construct the centered difference advective fluxes
of velocity. MOM also uses the backward derivative operators
BDX EU(A) = dyuei,j Ai,j −dyuei−1,j Ai−1,j
daui,j
(14.156)
BDY NU(A) = dxuei,j Ai,j −dxuei,j−1Ai,j−1
daui,j .(14.157)
These backward derivative operators act on fields defined at the east and north face of velocity cells, respec-
tively (see Figure 14.4 for definitions of grid distances). Note that the contribution from the momentum
advective frequency Mis discussed in Section 14.10.1. We focus in this section just with contributions
from advective flux components.
14.11.2 Horizontal convergence
To get started, we consdier the scalar product of the horizontal convergence term with the horizontal ve-
locity u, and integrate over the full ocean
Ahorz =−X
i,j,k
dau u·[BDX EU(uh eu FAX(u)) + BDY NU(vh nu FAY(u)) ].(14.158)
Note the use of thickness weighted advection velocity components uh eu and vh nu provides for the vertical
grid increment dzu needed for the discrete volume integral.
14.11.3 Diagnosing the vertical transport for U-cells
Thickness weighted horizontal advective velocities uh eu and vh nu are defined in MOM by remapping the
horizontal advective velocities uh et and vh nt, defined in Section 14.6.2, onto the velocity cell faces. The
satisfy volume conservation via a U-grid version of the T-grid result (14.55)
w buk=w buk−1+BDX EU(uh euk) + BDY NU(vh nuk) + ∂t(dzuk)−S(V)dzuk.(14.159)
Elements of MOM November 19, 2014 Page 215

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.11
In this equation, w bu is the dia-surface advective velocity component defined at the bottom face of a veloc-
ity cell, and the volume source S(V)and tendency ∂t(dzuk) have been mapped from their counterparts on
the tracer grid.
To diagnose the vertical transport w bu, we need to start at either the bottom or top of the ocean column,
given a boundary condition. On the B-grid, the bottom of the bottom-most U-cell does not live on the ocean
bottom, unless the ocean bottom is flat. Hence, a nontrivial mass or volume transport generally occurs
through the bottom of a velocity cell column. That is, in general
w buk=kbot ,0,(14.160)
which contrasts with the case on the T-cells (equations (14.57) and (14.113)).
A thorough discussion of this issue is provided in Section 22.3.3.2 of the MOM3 Manual (Pacanowski
and Griffies,1999). For present purposes, we note that it is sufficient to start the integration at the ocean
surface and integrate downwards, just as for the tracer cells. Equivalently, we can use MOM’s horizontal
remapping operator to map w btkto w buk. Either way, the continuity equation (14.159) is maintained.
14.11.4 Discrete integration by parts on horizontal convergence
We now perform the discrete analog of integration by parts. For this purpose, expand the backwards
derivative and average operators on the zonal flux terms, dropping the j,k labels for brevity
2X
i
dauui·BDX EU(uh eu FAX(u)) =
Xui·[dyueiuh euiui+1 +dyueiuh euiui
−dyuei−1uh eui−1ui−dyuei−1uh eui−1ui−1]
=Xui·ui(dyueiuh eui−dyuei−1uh eui−1)
+Xui·(dyueiuh euiui+1 −dyuei−1uh eui−1ui−1).(14.161)
Focus now on the second group of terms, where shifting sum labels leads to
nx
X
i=1
ui·ui+1 dyueiuh eui−
nx
X
i=1
ui·ui−1dyuei−1uh eui−1=
nx+1
X
i=2
ui−1·uidyuei−1uh eui−1−
nx
X
i=1
ui·ui−1dyuei−1uh eui−1
=unx ·unx+1 dyuenx uh eunx −u1·u0dyue0uh eu0.(14.162)
This result vanishes for either solid wall or periodic boundary conditions. Similar manipulations apply for
the meridional term, thus leading to
Ahorz =−XK(dyueiuh eui−dyuei−1uh eui−1)−XK(dxuejvh nuj−dxuej−1vh nuj−1)
=−Xdau K[BDX EU(uh eu) + BDY NU(vh nu)],(14.163)
where
Ki,j,k =1
2ui,j,k ·ui,j,k (14.164)
is the discrete kinetic energy per mass carried by the horizontal flow.
Elements of MOM November 19, 2014 Page 216

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.11
14.11.5 Discrete integration by parts on the vertical convergence
Now focus on the vertical advection term, which takes the form
2Avert =
kbot
X
k=1
dau uk·[−w buk−1(uk−1+uk) + w buk(uk+uk+1)]
=
kbot
X
k=1
dau uk·uk(wbuk−w buk−1) +
kbot
X
k=1
dau (w bukuk+1 ·uk−w buk−1uk·uk−1)
= 2
kbot
X
k=1
dau Kk(w buk−w buk−1)−Xdau w bu0(u0·u1) + Xdau w bukbot (ukbot+1 ·ukbot).
(14.165)
The horizontal velocity at k=kbot + 1 vanishes
ukbot+1 = 0,(14.166)
since k=kbot + 1 is interpreted as part of the solid earth. In contrast,
uk=0 =uw(14.167)
is the horizontal velocity of the fresh water. This velocity is often set equal to the surface ocean velocity
uw=u1, yet MOM retains the option of providing a different value. This result then leads to
2Avert = 2
kbot
X
k=1
dau Kk(w buk−w buk−1)−X
i,j
dau w bu0(u1·uw).(14.168)
14.11.6 Final result for the Boussinesq case
Combining the results for Ahorz and Avert renders
Ahorz +Avert =−(1/2) X
i,j
dau w bu0(u1·uw)−
nk
X
k=1
dau K[BDX EU(uh eu) + BDY NU(vh nu) + (w buk−1−w buk)]
=−(1/2) X
i,j
dau w bu0(u1·uw) + X
i,j,k
dau K[∂t(dzuk)−S(V)dzuk],
(14.169)
where we applied volume conservation over each U-cell as given by equation (14.159).
14.11.7 Non-Boussinesq kinetic energy advection
We now consider the conversion of kinetic energy advection in the discret non-Boussinesq discete. For this
purpose, consider
Ahorz =−X
i,j,k
dau dzu u·[BDX EU(uhrho eu FAX(u))/dzu +BDY NU(vhrho nu FAY(u))/dzu ].(14.170)
Thickness weighted and density weighted horizontal advective velocities uhrho eu and vhrho nu are de-
fined in MOM by remapping the horizontal advective velocities uhrho et and vhrho nt, defined by equa-
tions (14.106) and (14.109), onto the velocity cell faces. These horizontal transports satisfy continuity via a
U-grid version of the T-grid result (14.110)
wrho buk=wrho buk−1+BDX EU(uhrho euk) + BDY NU(vhrho nuk) + ∂t(rho dzu)k−S(M)rho dzuk(14.171)
Elements of MOM November 19, 2014 Page 217
Chapter 14. Mechanical energy conversions and advective mass transport Section 14.12
where the mass source has been mapped from the tracer to the velocity grid. In this equation, wrho bu is the
density weighted dia-surface advective velocity component defined at the bottom face of a velocity cell. As
in the Boussinesq case, this vertical transport is diagnosed using the continuity equation, or equivalently
via the MOM remap operator.
In general, results for the Boussinesq case transparently generalize to the non-Boussinesq case, which
allows us to write by inspection
A=−(1/2) Xdau wrho bu0(u1·uw)
−
nk
X
k=1
dau K[BDX EU(uhrho eu) + BDY NU(vhrho nu) + (wrho buk−1−wrho buk)]
=−(1/2) Xdau wrho bu0(u1·uw) + X
i,j,k
dau K[∂t(rho dzuk)−S(M)rho dzuk].
(14.172)
14.12 C-grid kinetic energy advection
The C-grid manipulations are similar to the B-grid, though we start from a slightly different form of the
momentum advection as appropriate for the C-grid.
14.12.1 C-grid momentum equation contribution from advection
The contribution to the zonal momentum time tendency arising from second order centered advection on
a C-grid is given by (see equation (55) of Blumberg and Mellor (1987))
∂t(u ρ dzte)i,j =−
F(x)(u)i,j,k −F(x)(u)i−1,j,k
dxtei,j −
F(y)(u)i,j,k −F(y)(u)i,j−1,k
dytei,j −F(z)(u)i,j,k−1−F(z)(u)i,j,k,
(14.173)
where the flux components are given by
F(x)(u)i,j,k =(uhrho eti+1,j +uhrho eti,j) (ui+1,j,k +ui,j,k)
4=FAX(uhrho et)FAX(u) (14.174)
F(y)(u)i,j,k =(vhrho nti,j +vhrho nti+1,j) (ui,j,k +ui,j+1,k)
4=FAX(vhrho nt)FAY(u) (14.175)
F(z)(u)i,j,k =(wrho bti,j,k +wrho bti+1,j,k) (ui,j,k +ui,j,k+1)
4=FAX(wrho bt)FAZ(u).(14.176)
We offer the following observations.
• We purposefully did not write the expression (14.173) in terms of MOM’s derivative operators, since
the indexing convention is slightly non-standard for MOM, given the MOM was originally written
solely for a B-grid.
• An alternative expression for the zonal flux is FAX(uhrho et u). But with uniform zonal resolution,
this form will lead to a time tendency proportional to (uhrho et u)i+1 −(uhrho et u)i−1, which skips
the central term (uhhro et u)i. Skipping the central term allows for a computational null mode in
which the even and odd grid terms decouple, and this behaviour is undesirable.
• The contribution from the momentum advective frequency Mis discussed in Section 14.10.2. We
focus in this section on contributions from advective flux components.
The meridional momentum tendency on the C-grid is given by (see equation (56) of Blumberg and
Mellor (1987))
∂t(v ρ dztn)i,j =−
G(x)(v)i,j,k −G(x)(v)i−1,j,k
dxtni,j −
G(y)(v)i,j,k −G(y)(v)i,j−1,k
dytni,j −G(z)(v)i,j,k−1−G(z)(v)i,j,k,
(14.177)
Elements of MOM November 19, 2014 Page 218

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.12
where the flux components are given by
G(x)(v)i,j,k =(uhrho eti,j +uhrho eti,j+1) (vi,j,k +vi+1,j,k)
4=FAY(uhrho et)FAX(v) (14.178)
G(y)(v)i,j,k =(vhrho nti,j +vhrho nti,j+1) (vi,j,k +vi,j+1,k)
4=FAY(vhrho nt)FAY(v) (14.179)
G(z)(v)i,j,k =(wrho bti,j,k +wrho bti,j+1,k) (vi,j,k +vi,j,k+1)
4=FAY(wrho bt)FAZ(v).(14.180)
14.12.2 Energetic manipulations not generally useful
We have attempted to follow the B-grid procedure using discrete integration by parts to reveal an analog to
the continuum results of Sections 14.2.3 and 14.2.4. However, in a manner similar to that encountered for
the Coriolis Force (Section 14.10.2), useful manipulations are available only when grid factors are assumed
horizontally constant. Given that such restrictions are rarely realized, we do not pursue the manipulations.
We have thus not been able to derive a suitable advection diagnostic for the C-grid.
Elements of MOM November 19, 2014 Page 219

Chapter 14. Mechanical energy conversions and advective mass transport Section 14.12
Elements of MOM November 19, 2014 Page 220

Chapter 15
Advection velocity and horizontal
remapping for the B-grid
Contents
15.1 General considerations .....................................221
15.1.1 Two main issues ........................................ 222
15.1.2 Constraints for discrete vertical velocities ......................... 222
15.2 Remapping operators for horizontal fluxes ..........................222
15.2.1 Uniformly distributed volume flux across a face ...................... 223
15.2.2 Lever-rule and the horizontal remapping operators .................... 223
15.3 Remapping operator for vertical fluxes ............................224
15.4 Remapping error .........................................225
15.4.1 Linear grids .......................................... 227
15.4.2 Nonlinear grids ........................................ 227
15.5 Subtleties at the southern-most row ..............................228
The purpose of this chapter is to discuss the computation of advection velocity components for the
advection of momentum on the B-grid. This material follows from that presented in Chapter 14 which de-
rived advection velocity components based on energetic arguments. Linear remapping operators provide
the means to compute the advection velocity components for the advection of momentum, and we detail
these operators in this chapter. In particular, these operators map tracer cell advection velocity compo-
nents, prescribed according to the arguments of Sections 14.6 and 14.8, to the B-grid velocity cell, as well
as to map selected other fields. The material in this chapter is taken largely from the MOM4.0 manual of
Griffies et al. (2004), which employs a Boussinesq formulation. Generalization to non-Boussinesq option
is trivial, with introduction of in situ density factors multiplying the thickness factor. Note that similar
treatments for C-grid advection of momentum is not needed, with the formulation given in Chapter 14
sufficient.
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean advection velocity.F90
15.1 General considerations
Advective fluxes are fundamental to the Eulerian evolution of tracer and momentum. How these fluxes are
discretized represents a basic problem in computational fluid dynamics. Notably, because of the interpre-
tation of model velocity discussed in Griffies (2004), there is no distinction between the advective fluxes
221
Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.2
for the Boussinesq and non-Boussinesq versions of MOM: they are computed using the same numerical
considerations detailed in this chapter.
15.1.1 Two main issues
There are two considerations required to compute advective fluxes of tracer or momentum. First, there is
the question of how to compute the advective velocity. Such is the focus of this chapter. For computing
fluxes across cell faces, the three components to the advective velocity must be known on the corresponding
face of the tracer and velocity cells. However, on the B-grid, both horizontal prognostic velocity components
are placed at the velocity cell point, not at the cell faces. Hence, an averaging operation must be prescribed
to diagnose the horizontal advective velocity components from the prognostic B-grid velocity. MOM com-
putes the horizontal components of the advection velocity on the faces of T-cells in a manner necessitated
by equating pressure work to buoyancy (see Chapter 14). The vertical advective velocity component is then
diagnosed at the bottom face of the tracer cell, based on the needs of volume or mass conservation across
the tracer cell (see Chapter 14 or Griffies (2004)). Computing the advective velocity on the faces of the
velocity cell remains to be determined, and that is the main technical subject of this chapter.
Once the advective velocity is computed on the cell faces, it remains to approximate the tracer and mo-
mentum values on these faces for use in constructing the advective tracer and momentum fluxes. There are
many different approaches available. As with previous versions of the GFDL ocean model, MOM chooses
to compute the advective flux of momentum according to the requirements of energetic consistency de-
scribed in Chapter 14. These constraints necessitate a second order centered approach, as in Bryan (1969).
The advective flux of tracer, however, is not so constrained and there are hence many options available,
some of which are detailed in The MOM3 Manual of Pacanowski and Griffies (1999).
15.1.2 Constraints for discrete vertical velocities
One important constraint for self-consistency of the discretization is that the vertical velocity at the T-cell
bottom topography must vanish: w bti,j,k=Nk = 0, since the T-cell top and bottom faces are horizontally
oriented. A vanising bottom velocity on T-cells is necessitated by the requirements of volume or mass
conservation (see Griffies (2004)). Many ocean models choose to set w bti,j,k=Nk = 0. However, MOM
chooses to start from the ocean surface and integrate the continuity equation downwards. Verification
that the computed w bti,j,k=Nk indeed vanishes has been found to be a very useful check on code integrity.
Relatedly, for a flat bottomed ocean w bui,j,k=Nk = 0. However, with topography, w bu is generally nonzero at
the bottom, since the bottom on velocity cells is not flat. Section 22.3 in The MOM3 Manual of Pacanowski
and Griffies (1999) details this point.
Furthermore, since the interior of the ocean domain uses constant cell thicknesses, in a Boussinesq
model volume should be conserved (the ocean surface conserves volume when also incorporating the pos-
sibly nonzero fresh water fluxes). Hence, integrating w bti,j,kacross a particular depth k > 1 should leave
no net volume flux upward or downward: Pi,j dxti,jdyti,jw bti,j,k= 0 for all levels k.
Finally, volume conservation warrants the MOM approach for diagnosing surface height on the U-cell,
ηu, according to an area weighted average of the surrounding T-cell heights ηt, instead of using the mini-
mum operation used in MOM3 and described in the Griffies et al. (2001) paper. This issue is relevant for
the Boussinesq and non-Boussinesq versions of MOM. We visit this issue in Section 15.3.
15.2 Remapping operators for horizontal fluxes
As stated in Section 15.1, MOM computes the horizontal components of the T-cell advection velocity in a
manner necessitated by equating pressure work to buoyancy (see Chapter 14). The vertical component is
diagnosed based the needs of continuity. Hence, we assume the T-cell advective velocity components are
known. We thus need to determine the corresponding advective velocity on the face of velocity cells.
Advective velocities represent fluxes of volume per unit area. There are three remapping operators that
take discrete volume fluxes defined at tracer points or sides of tracer cells, to discrete fluxes defined at
velocity points or sides of velocity cells. Although MOM is generally non-Boussinesq, we use the ideas of
volume conservation to generate algorithms for coupling advective velocities on the sides of tracer cells
Elements of MOM November 19, 2014 Page 222

Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.2
to those on the sides of velocity cells. Here, we describe the linear remapping operator taking horizontal
advective velocities centered on the face of a tracer cell to the corresponding face of a velocity cell.
15.2.1 Uniformly distributed volume flux across a face
Reference to Figure 15.1 reveals four eastward fluxes of volume per area leaving a tracer cell that surround
the single flux per volume leaving the corresponding velocity cell. The flux leaving a tracer cell is denoted
by Et in the figure, which is a shorthand for the model’s thickness weighted advective velocity uh et, with
the thickness factor dropped since we are concerned here with fluxes at a fixed depth. Eu denotes the
corresponding eastward flux leaving the velocity cell, and this flux is to be determined in terms of the
surrounding Et and appropriate grid distances.
We assume that along the face of a tracer cell, volume leaves through the face with a uniform distribu-
tion. Hence, the volume per unit length per time passing across the meridional face through the velocity
point Ui,j is given by
Et(i,j)dus(i,j) + Et(i,j + 1) dun(i,j),(15.1)
where the distances dus and dun are lengths along sides of the four quarter-cells comprising a single velocity
cell (Figure 15.2). Likewise, the volume per unit length per time passing across the meridional face through
the velocity point Ui+1,j is given by
Et(i+ 1,j)dus(i+1,j) + Et(i+ 1,j + 1)dun(i+1,j),(15.2)
and the volume per unit length per time passing across the eastern face of the velocity cell Ui,j is given by
Eu(i,j)dytn(i+1,j),(15.3)
where Eu is to be determined in terms of Et, and the grid distance dytn is the meridional distance between
tracer points, as defined in Figure 15.3.
15.2.2 Lever-rule and the horizontal remapping operators
We now employ linear interpolation, or a lever-rule average, to construct the volume per time passing
across the east face of the Ui,j cell, thus leading to
Eu(i,j)dytn(i+1,j)dxtn(i+1,j)=[Et(i,j)dus(i,j) + Et(i,j + 1)dun(i,j)]duw(i+1,j)
[Et(i+ 1,j)dus(i+1,j) + Et(i+ 1,j + 1)dun(i+1,j)]due(i,j),
where dxtn is the zonal distance along the north face of a tracer cell (Figure 15.4). Solving for Eu leads to
the remapping operator
Eu(i,j) = REMAP ET TO EU(Et)(i,j)
≡[Et(i,j)dus(i,j)duw(i+1,j) + Et(i,j + 1) dun(i,j)duw(i+1,j)
+Et(i+ 1,j)dus(i+1,j)due(i,j) + Et(i+ 1,j + 1)dun(i+1,j)due(i,j)]
datnr(i+1,j),(15.4)
where datnr is the reciprocal area at the north face of a T-cell given by
datnr(i,j) = 1
dxtn(i,j)dytn(i,j)(15.5)
Analogous considerations lead to the remapping operator that takes a volume flux Nt defined at the north
face of T-cells to a flux leaving the north face of U-cells
Nu(i,j) = REMAP NT TO NU(N t)(i,j)
≡[Nt(i,j)duw(i,j)dus(i,j+1) + Nt(i+ 1,j)due(i,j)dus(i,j+1)
+Nt(i,j + 1) duw(i,j+1)dun(i,j) + Nt(i+ 1,j + 1)due(i,j+1)dun(i,j)]
dater(i,j+1).(15.6)
Elements of MOM November 19, 2014 Page 223
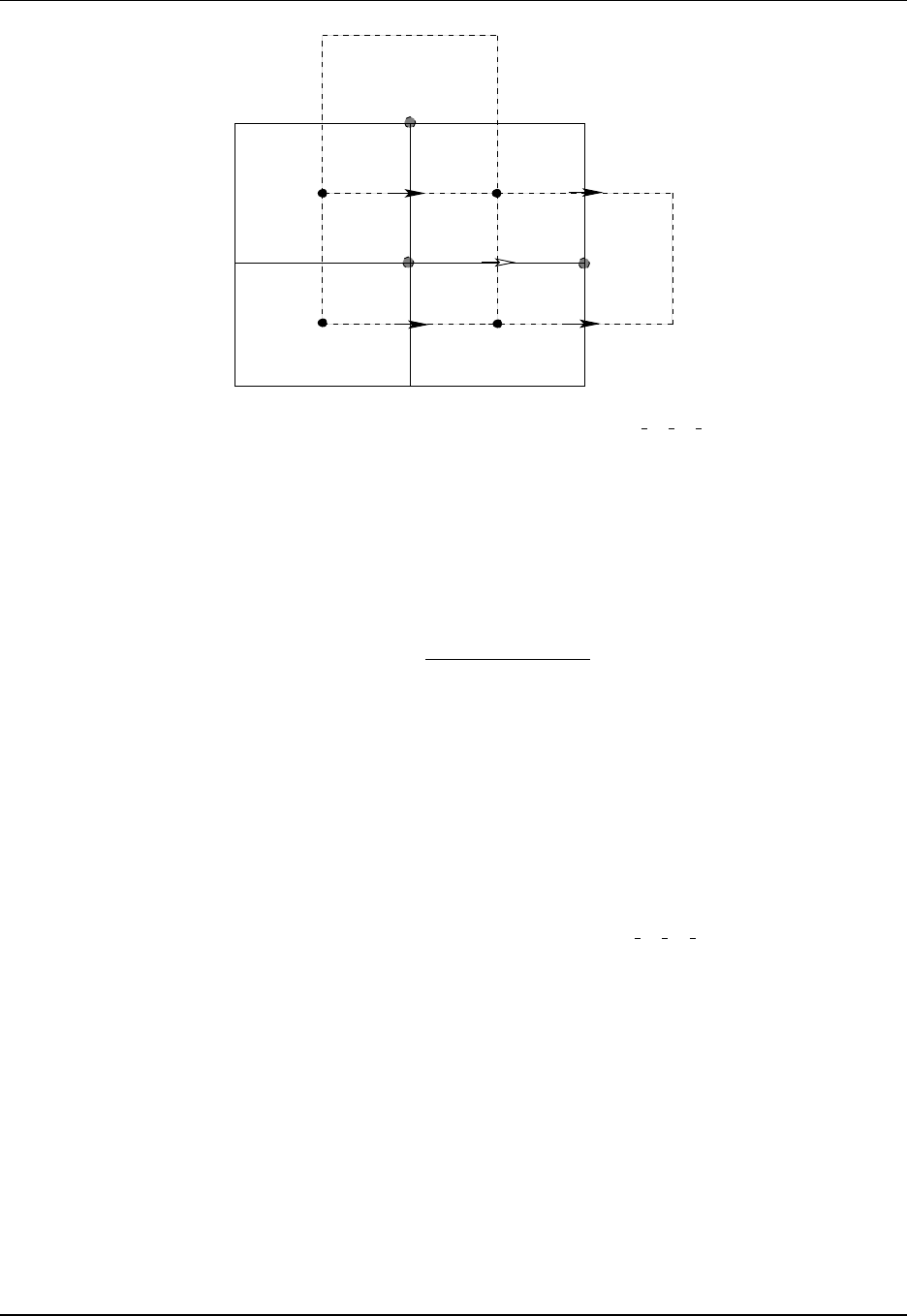
Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.3
U(i,j)
U(i,j+1)
T(i,j+1)
T(i,j)
U(i+1,j)
T(i+1,j+1)
T(i+1,j)
Et(i,j) Et(i+1,j)
Et(i+1,j+1)
Et(i,j+1)
Eu(i,j)
Figure 15.1: Schematic representation of the remapping function REMAP ET TO EU defined by equation
(15.4). This function is used to remap a horizontal flux of volume defined at the east face of T-cells (denoted
by Et in this figure) onto a horizontal flux of volume defined at the east face of U-cells (denoted by Eu in
this figure). The four fluxes Et(i,j), Et(i+ 1,j), Et(i,j + 1), and Et(i+ 1,j + 1) are used to construst the flux
Eu(i,j).
In this expression, dater is the reciprocal area at the east face of a T-cell given by
dater(i,j) = 1
dxte(i,j)dyte(i,j),(15.7)
dxte is the zonal distance between the T-cell points (Figure 15.3) and dyte is the meridional distance along
the east face of the T-cell (Figure 15.4).
15.3 Remapping operator for vertical fluxes
We now consider the remapping taking vertical volume fluxes passing across the bottom face of tracer cells
to the bottom face of velocity cells. This operator also maps surface height from T-cells to U-cells. This
remapping is distinguished from the horizontal remapping in that there is no analogous lever-rule step.
The distinction boils down to noting that the vertical remapping REMAP BT TO BU moves vertical fluxes
horizontally, whereas the east and north remapping operators move horizontal fluxes horizontally.
Reference to Figures 15.2 and 15.3, and again assuming fluxes are distributed uniformly across a cell
face, indicates that the vertical flux of volume per unit length passing across the southern face of the
velocity cell Ui,j is given by
Bt(i,j)dte(i,j) + Bt(i+ 1,j)dtw(i+1,j),(15.8)
the vertical flux of volume per unit length passing across the northern face of the velocity cell Ui,j is given
by
Bt(i,j + 1) dte(i,j+1) + Bt(i+ 1,j + 1)dtw(i+1,j+1),(15.9)
and the vertical flux of volume passing through the velocity cell is given by
Bu(i,j)dxu(i,j)dyu(i,j).(15.10)
Assuming that the total flux passing through the velocity cell is equivalent to that passing across the north-
Elements of MOM November 19, 2014 Page 224
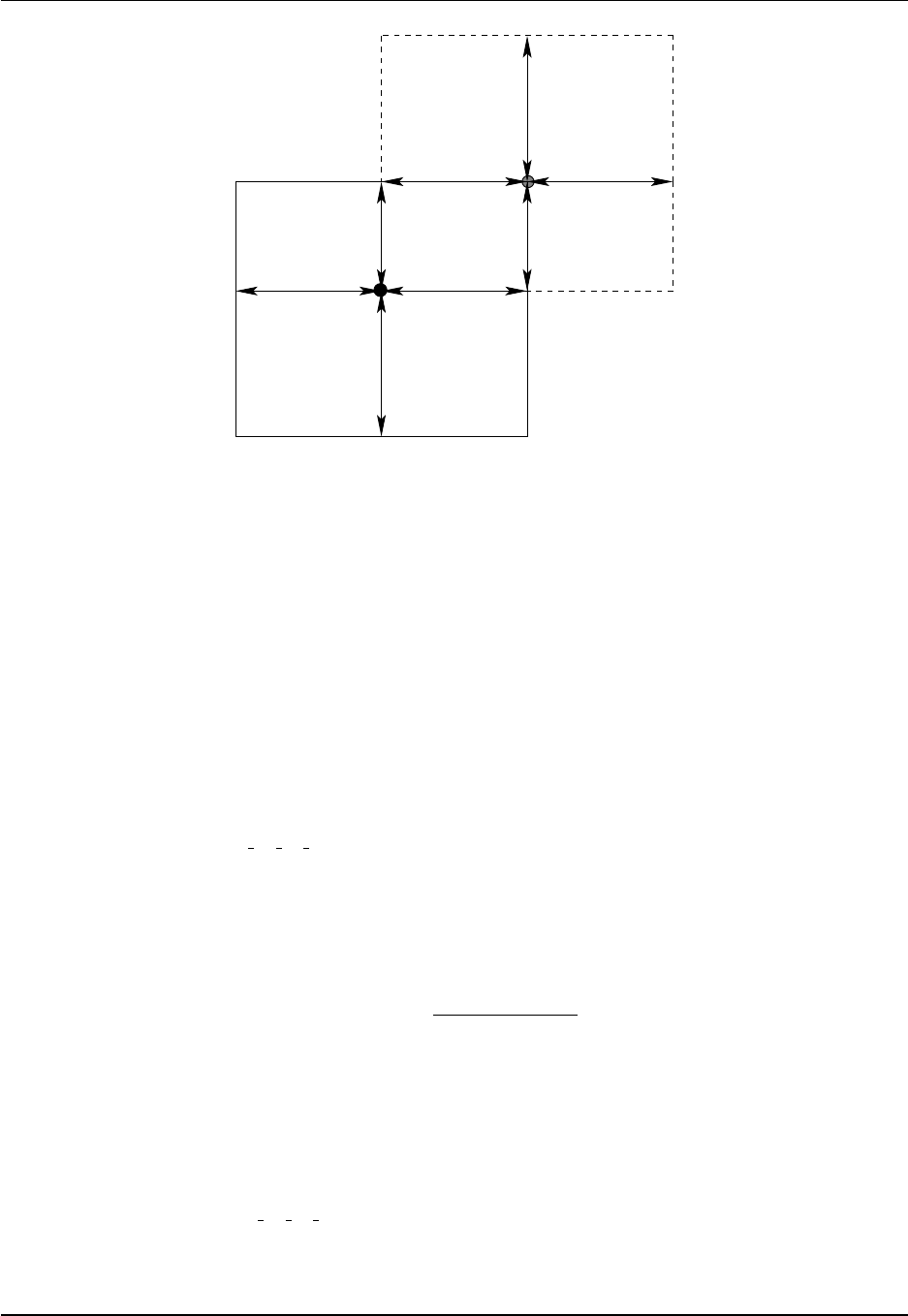
Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.4
dtw(i,j)
dtn(i,j)
dts(i,j)
T(i,j)
dte(i,j)
dun(i,j)
due(i,j)duw(i,j)
U(i,j)
dus(i,j)
Figure 15.2: Time independent horizontal grid distances (meters) used for the tracer cell Ti,j and velocity
cell Ui,j in MOM. These “quarter-cell” distances are refined relative to those shown in Figures 15.4 and 15.5,
and they are needed for the remapping between T and U cells when computing advection velocities. All dis-
tances are functions of both iand jdue to the use of generalized orthogonal coordinates. Comparing with
Figures 15.4 and 15.5 reveals the identities dtw(i,j) + dte(i,j) = dxt(i,j), dts(i,j) + dtn(i,j) = dyt(i,j),
duw(i,j) + due(i,j) = dxu(i,j), and dus(i,j) + dun(i,j) = dyu(i,j).
ern plus southern parts of the cell leads to
Bu(i,j)dxu(i,j)dyu(i,j)=[Bt(i,j)dte(i,j) + Bt(i+ 1,j)dtw(i+1,j)]dus(i,j)
+ [Bt(i,j + 1) dte(i,j+1) + Bt(i+ 1,j + 1)dtw(i+1,j+1)]dun(i,j).
Solving for Bu yields the vertical remapping operator
Bu(i,j) = REMAP BT TO BU(Bt)(i,j)
≡[Bt(i,j)dte(i,j)dus(i,j) + Bt(i+ 1,j)dtw(i+1,j)dus(i,j)
+Bt(i,j + 1) dte(i,j+1)dun(i,j) + Bt(i+ 1,j + 1)dtw(i+1,j+1)dun(i,j)]
daur(i,j) (15.11)
with daur the reciprocal area of the U-cell
daur(i,j) = 1
dxu(i,j)dyu(i,j)(15.12)
15.4 Remapping error
There are two ways to compute the vertical velocity on the velocity cell. The first method is to compute
this velocity according to the requirements of continuity over the velocity cell, using the convergence of
the remapped horizontal advective velocities entering the velocity cell. The second method is to use the
vertical remap operator REMAP BT TO BU to move the vertical velocity on the tracer cells to the velocity cells.
The result of these two approaches is identical when the tracer and velocity grids are related by a linear
average operator, as is the case for a spherical grid. The need to maintain a linear relation between the
tracer and velocity grids is based on the use of linear methods to derive the remapping operators.
Elements of MOM November 19, 2014 Page 225
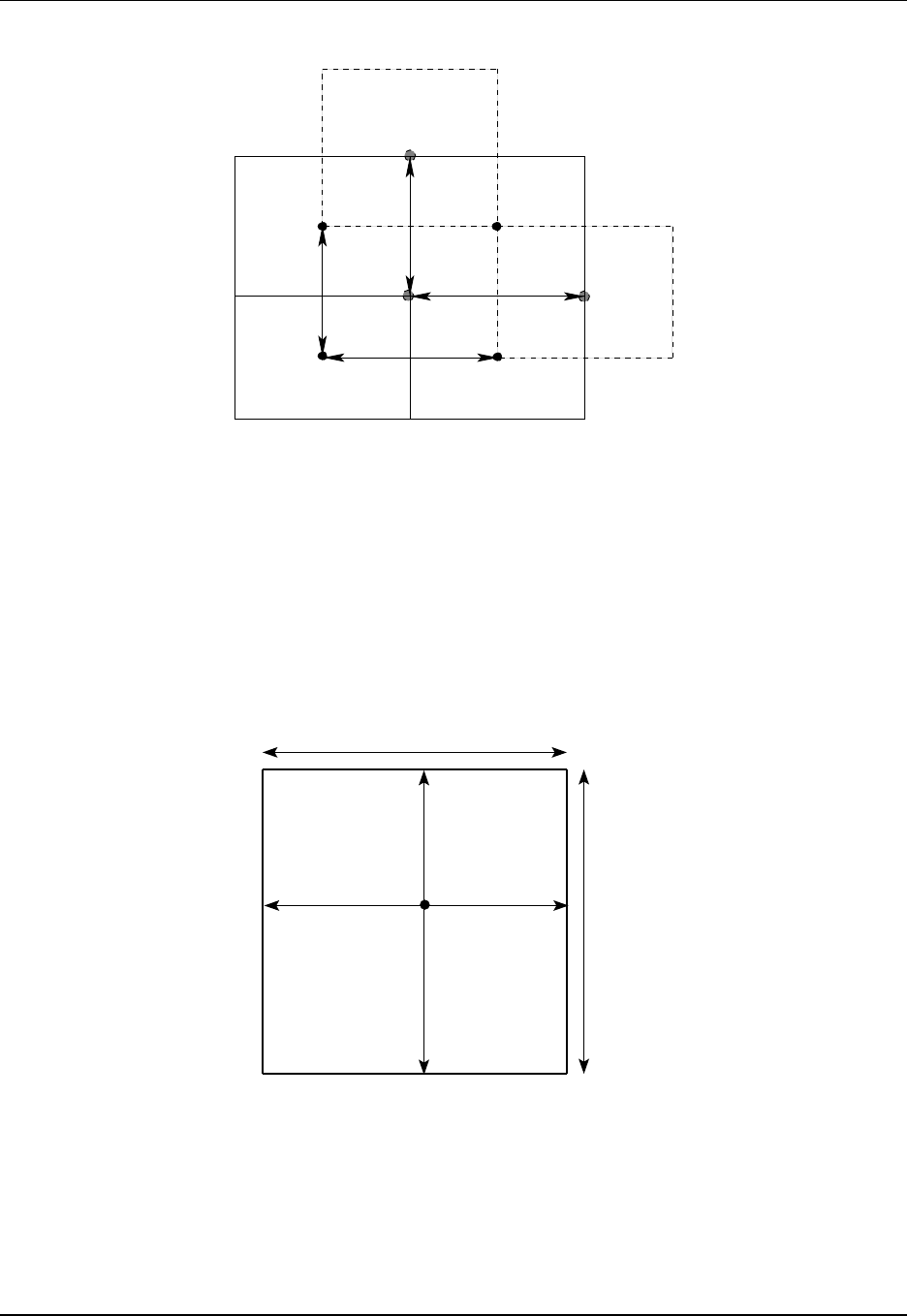
Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.4
U(i,j)
U(i,j+1)
T(i,j+1)
T(i,j)
U(i+1,j)
T(i+1,j+1)
T(i+1,j)
dyun(i,j)
dxte(i,j)
dytn(i,j) dxue(i,j)
Figure 15.3: Time independent horizontal grid distances (meters) setting the spacing between tracer and
velocity points in MOM. All distances are functions of both iand jdue to the use of generalized orthogonal
coordinates. When these distances are combined with those in Figures 15.4 and 15.5, and the quarter-cell
distances given in Figure 15.2, we then have full information about the discrete horizontal T and U cells on
the model grid. Note there is some redundancy with the distances defined in Figures 15.4 and 15.5, where
we have dytn(i,j) = dyue(i−1,j), dxte(i,j) = dxun(i,j−1), dxue(i,j) = dxtn(i+1,j), and dyun(i,j) = dyte(i,j+
1). Additionally, comparision with Figure 15.2 leads to the identities dyun(i,j) = dun(i,j) + dus(i,j + 1),
dxue(i,j) = due(i,j) + duw(i+ 1,j), dytn(i,j) = dtn(i,j) + dts(i,j + 1), and dxte(i,j) = dte(i,j) + dtw(i+ 1,j).
T(i,j)
dxt(i,j) dyte(i,j)
dxtn(i,j)
dyt(i,j)
Figure 15.4: Time independent horizontal grid distances (meters) used for the tracer cell Ti,j in MOM.
dxti,j and dyti,j are the grid distances of the tracer cell in the generalized zonal and meridional directions,
and dati,j =dxti,j dyti,j is the area of the cell. The grid distance dxtni,j is the zonal width of the north
face of a tracer cell, and dytei,j is the meridional width of the east face. Note that the tracer point Ti,j is not
generally at the center of the tracer cell. Distances are functions of both iand jdue to the use of generalized
orthogonal coordinates.
Elements of MOM November 19, 2014 Page 226
Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.5
U(i,j)
dyu(i,j)
dxu(i,j)
dxun(i,j)
dyue(i,j)
Figure 15.5: Time independent horizontal grid distances (meters) used for the velocity cell Ui,j in MOM.
dxui,j and dyui,j are the grid distances of the velocity cell in the generalized zonal and meridional direc-
tions, and daui,j =dxui,j dyui,j is the area of the cell. The grid distance dxuni,j is the zonal width of the
north face of a velocity cell, and dyuei,j is the meridional width of the east face. Note that the velocity point
Ui,j is not generally at the center of the velocity cell. Distances are functions of both iand jdue to the use
of generalized orthogonal coordinates.
15.4.1 Linear grids
MOM computes a diagnostic that examines the differences between the two approaches for computing
vertical advective velocities. It reports the difference as a “remapping error.” If the numerical discretization
is self-consistent, then the remapping error for a spherical grid will be roundoff, with values on the order
of 10−20m s−1common. Therefore, with a spherical grid, the remapping error provides a check on the
self-consistency of the grid distances and the remapping operators. Effectively, what is done is to check
that volume is conserved with the remapping operators. Even when running a non-Boussinesq model, the
remapping operators are constructed to respect volume conservation.
15.4.2 Nonlinear grids
For a grid defined via a nonlinear transformation of the spherical grid, such as the bipolar region of the
tripolar grid, the grid no longer maintains a linear relation between tracer and velocity cell distances. The
result is a nontrivial remapping error. This error can be reduced by defining new remapping operators that
account for a generally nonlinear relation between tracer and velocity grid distances. Such remains to be
done.
One consequence of the nonzero remapping error is that for a flat bottom model in regions where the
grid distances are nonlinearly related, w bui,j,k=Nk does not vanish, even though continuity is maintained
for all the grid cells. The problem is that w bui,j,k=0is defined by
w bui,j,k=0=REMAP BT TO BU(w bti,j,k=0).(15.13)
For nonlinear grids, the linear operator REMAP BT TO BU results in a slightly different value for w bui,j,k=0
than would result from an integration of the continuity equation upwards from the bottom, assuming
w bui,j,k=Nk = 0. Because the vertical advective flux at the ocean bottom is masked so that no momentum
will spuriously leak out the bottom of the ocean, having w bui,j,k=Nk slightly nonzero is of no consequence.
Nonetheless, it would be more satisfying to have a general remapping operator to clean-up this issue.
Elements of MOM November 19, 2014 Page 227

Chapter 15. Advection velocity and horizontal remapping for the B-grid Section 15.5
15.5 Subtleties at the southern-most row
Consider the special case of j= 0 in Figure 15.1. This row is strictly south of the southern-most latitude
comprising the computational domain of the model. However, there is a subtlety related to the treatment
of the eastward volume flux leaving the velocity cell Ui,j=0. That is, since this cell straddles the tracer cells
Ti,j=0 and Ti,j=1, it contains some portion that is within the computational domain. Thus, the eastward
volume flux leaving this cell is nonzero, as it is comprised of weighted average of the four surrounding
eastward fluxes leaving the tracer cells. Because the remapping function (15.4) is normalized with the area
datn =dxtndytn for j= 0, it is necessary to know the grid factors dxtni,j=0and dytni,j=0. In particular,
dytni,j=0is the distance between the computed tracer point Ti,j=1 and the tracer point Ti,j=0 that lives
outside the computational domain.
The need to know dytni,j=0presents a problem with the MOM method for computing grid specifica-
tions. Grids in MOM are computed in two steps. First, there is a preprocessing step whereby grid factors
are computed in a generic manner compatible with other models used at GFDL. This step knows nothing
about halo regions, so it only computes grid information over the computational domain. The result of this
step is a NetCDF grid specification file. The second step is to read the grid specification file into MOM and
translate the generic grid information into grid arrays used by MOM. Since there is no halo information
contained in the grid specification file, we cannot unambiguously specify values for the grid outside the
computational domain. And because we need dytni,j=0to be known consistently with the values for dytni,j
with j > 0, we cannot simply fill dytni,j=0with an arbitrary placeholder. If we do so, then the remapping
function used to compute the eastward flux leaving the velocity cell Ui,j=0 will be incorrect, thus compro-
mising the vertical velocity leaving Ui,j=0. The symptom will be most notable in spuriously large values of
the vertical velocity on the velocity cell at the computational row j= 1, as well as huge remapping errors at
j= 1.
There are three solutions to this problem. First, we could extend the definition of the grid within the
grid specification file to include the extra j= 0 row. This solution has been rejected since it adds an extra
calculation that is specific to the northeast B-grid used in MOM. As the grid specification file is designed
for use by all grid point models, it is not desirable to corrupt it with special cases. The second solution is
to require the southern-most row in MOM to be filled with land. This solution is arguably inelegant, and
it has indeed prompted some debate with the MOM developers. Yet this is the solution used in the GFDL
ice model, which is also on a B-grid, and so it has been the most popular solution thus far in MOM when
aiming to couple MOM to other models. The third solution is to extend the grid southward within MOM
after reading in the grid specification file. This solution is appropriate if we can assume a spherical grid in
the southern part of the domain, as true in most cases.
Elements of MOM November 19, 2014 Page 228

Chapter 16
Open boundary conditions for the
B-grid
Contents
16.1 Introduction ............................................230
16.2 Types of open boundary conditions ..............................231
16.2.1 Open boundaries in the Arakawa B-grid .......................... 231
16.2.1.1 Notation ....................................... 232
16.2.1.2 Boundary conditions for the sea level ...................... 232
16.2.1.3 Boundary conditions for tracers ......................... 232
16.2.1.4 Boundary conditions for velocity ......................... 232
16.2.2 Sommerfeld radiation condition ............................... 232
16.2.3 Clamped boundary conditions ................................ 233
16.2.4 No gradient boundary conditions .............................. 233
16.2.5 Interior cell no gradient boundary conditions ....................... 234
16.2.6 Enhanced friction and diffusion near the boundary .................... 234
16.3 Implementation of sea level radiation conditions ......................234
16.3.1 Sign convention for the phase speed ............................ 234
16.3.2 Gravity wave radiation condition for the phase speed .................. 234
16.3.3 Orlanski radiation condition for the phase speed ..................... 235
16.3.4 Camerlengo and O’Brien radiation condition ....................... 235
16.3.5 Radiation condition after Miller & Thorpe ......................... 235
16.3.6 Raymond and Kuo radiation condition ........................... 236
16.3.7 The IOW-radiation condition ................................ 236
16.3.8 Phase speed smoothing .................................... 237
16.3.9 Relaxation to data ....................................... 237
16.3.9.1 Relaxation towards prescribed profiles ..................... 237
16.3.9.2 Relaxation of the sea level average - conservation of geostrophic currents . . 238
16.3.9.3 Variable relaxation for incoming and outgoing waves ............. 238
16.4 OBC for tracers ..........................................238
16.4.1 Reduced tracer equations at open boundaries ....................... 238
16.4.2 Upstream advection of tracers near the boundary ..................... 239
16.4.3 Relaxation towards external data .............................. 240
16.4.4 Flow relaxation scheme of Martinsen and Engedahl ................... 240
16.4.5 Radiation conditions ..................................... 241
229

Chapter 16. Open boundary conditions for the B-grid Section 16.1
16.4.6 Vertical mixing and viscosity co-efficients ......................... 241
16.4.7 Enhanced horizontal mixing and viscosity co-efficients ................. 241
16.5 The namelist obc nml ......................................241
16.6 Topography generation - Preparation of boundary data ..................243
16.6.1 Topography generation with open boundaries ....................... 243
16.6.2 Preparation of input data files ................................ 243
16.6.3 Consistency of input data and model configuration .................... 245
16.6.3.1 The sea level in external data and the model zero level ............ 245
16.6.3.2 The sea level and the problem of air pressure .................. 245
The purpose of this chapter is to present the method used for the B-grid version of MOM to prescribe
open boundary conditions (OBCs), with further documentation and examples presented by Herzfeld et al.
(2011). The main point to take from this chapter, it is the following:
The numerical schemes for OBCs depend on details of the model setup. Hence, MOM has many
options.
This chapter was written by Mike Herzfeld, Martin Schmidt, and Stephen Griffies. The algorithm and
code developers for the MOM OBC are
Mike.Herzfeld@csiro.au
Martin.Schmidt@io-warnemuende.de
Zhi.Liang@noaa.gov
Matthew.Harrison@noaa.gov
Please email them directly for queries about the documentation or the OBC code.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean obc.F90
ocean core/ocean obc barotropic.F90
Caveat: As of May 2012, MOM’s open boundary condition has yet to be ported to the C-grid. Open
boundary conditions are only available using the B-grid option. Implementing the open boundary
conditions for the C-grid version of MOM is a high priority.
16.1 Introduction
Numerical circulation models of marginal seas with biological, chemical and sediment dynamic compo-
nents require a high model resolution and involve a large number of variables. Working with regional
models is one method to meet this challenge with a reasonable amount of computer resource consumption.
Mostly, the exchange of mass, heat, momentum and dissolved or suspended matter with the outer ocean is
important. At the model boundary an open boundary condition (OBC) must apply, which permits flux out
of - and into the model area.
This chapter describes the numerical schemes implemented for this purpose in MOM. They are de-
scribed in detail in the corresponding literature, in particular in Herzfeld et al. (2011). It seems, that an
universal open boundary condition suitable for all kinds of regional models does not exist. Hence, we have
chosen to implement several schemes, which can be selected and modified by namelist parameters.
Open boundary conditions for a regional model is a complex problem. To be more specific, consider
a large model ocean, subdivided by a virtual boundary into a western and an eastern sub-basin. Wind
forcing, heat flux or fresh water flux in the eastern subbasin drives elevation of the sea surface, currents
and changes in the density field as well. The information on such events in the eastern part is transmitted to
the west by waves, at large time scales also by advection. If the virtual boundary is replaced with the open
western boundary of a regional submodel of the eastern subbasin, the results of the regional submodel and
Elements of MOM November 19, 2014 Page 230
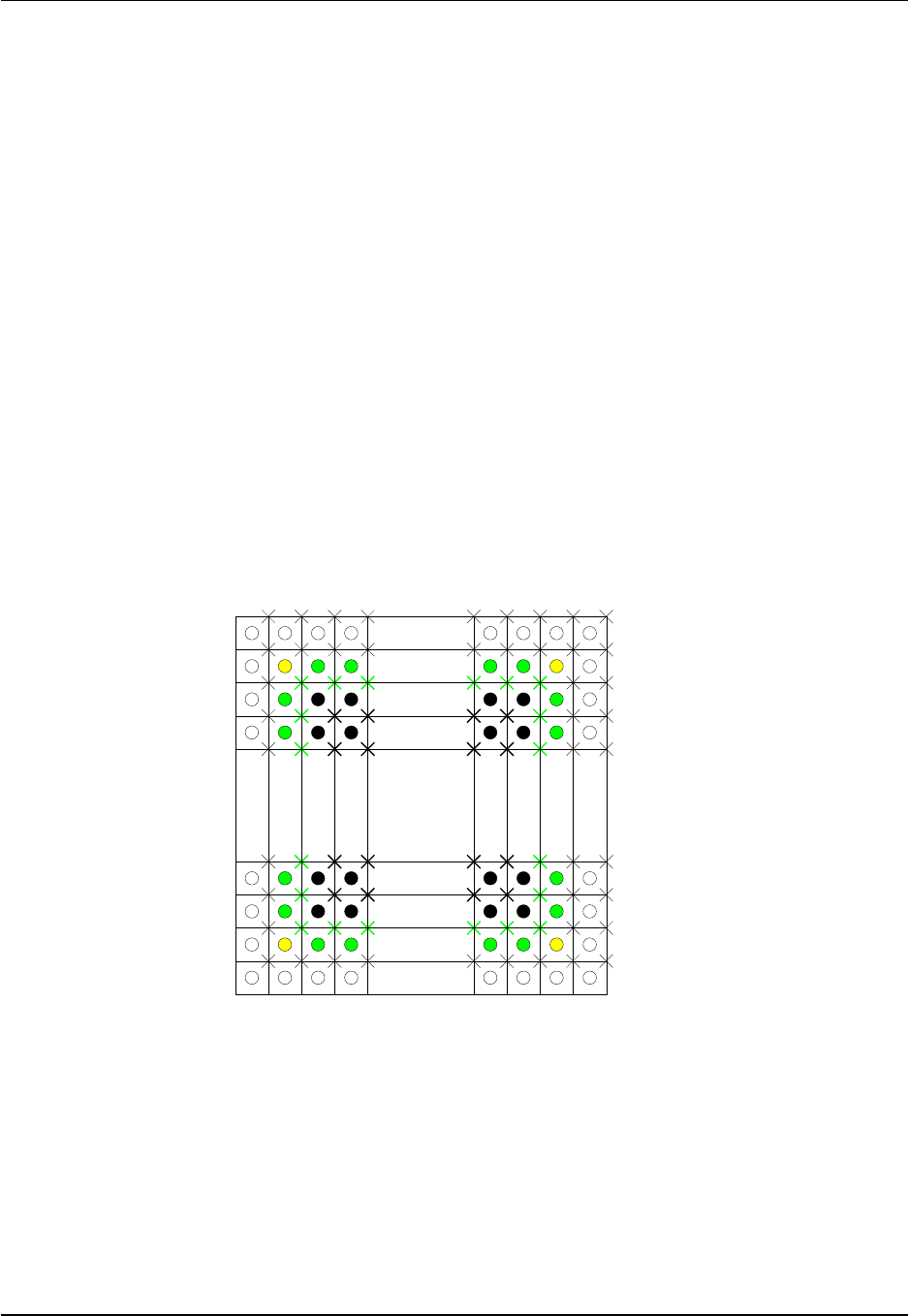
Chapter 16. Open boundary conditions for the B-grid Section 16.2
those of the larger model must be the same. Hence, waves generated in the eastern subbasin must be able
to pass an open boundary without reflection and refraction, just as if it was not there. In the same manner,
processes forced in the western subbasin influence the eastern part by waves too. If this is of importance
for the eastern model part, the western open boundary condition must generate these waves.
Hence, the required boundary condition is solution of the hydrodynamic equations at the boundary
itself and is basically unknown. Simplifying assumptions on the nature of the flow near the boundary are
needed to close the numerical schemes at the boundary. For ocean models many different methods are
known. Here we confine ourselves to methods, which combine a radiation condition, to facilitate outward
directed wave propagation through open boundaries in combination with relaxation to prescribed values of
ocean variables, to simulate the influences from outside the model domain. Relaxation of boundary values
helps also to eliminate numerical errors of the boundary scheme and to prevent the model from divergence
by the accumulation of numerical errors over longer model integration time.
16.2 Types of open boundary conditions
The purpose of this section is to describe the sorts of boundary conditions implemented in MOM. For realis-
tic applications the numerical solution near a boundary is always a superposition of outgoing and incoming
waves, which cannot be separated. Applying the radiation condition and relaxation of boundary values to
this complex variables, turns OBC into a mathematically ill-posed problem and there is no universally
perfect scheme for open boundary conditions. Hence, often the OBC configuration must be established by
trial and error on a case by case basis. So what may work fine in one application may not work if one alters
the bathymetry, geography, forcing, subgrid scale parameterizations, or numerical implementation of the
OBC.
B−1
B+1 B
B+1 B−1
B+1
BB
B+1
B−1
B−2 B−1
B−2
B−1
B
B+1
B
B−1
B+1
B+1BB−1 B+1BB−1B−2B
Figure 16.1: Open boundary conditions in the Arakawa B-grid. Circles mark tracer points, crosses velocity
points. Open boundary conditions apply at green points.
16.2.1 Open boundaries in the Arakawa B-grid
Because MOM uses the ARAKAWA B-grid, tracers and sea level points are the outmost points, where the
numerical scheme has to be closed by an open boundary condition. Velocity points are within the model
domain. At points adjacent to the boundary the non-linear advective terms and diffusion terms are unde-
fined. To close the numerical scheme for these terms, velocity points beyond the boundaries are defined
Elements of MOM November 19, 2014 Page 231

Chapter 16. Open boundary conditions for the B-grid Section 16.2
by appropriate extrapolation. The remaining terms in the momentum equations can be calculated using
pre-existing fields. This formulation of the open boundary conforms to a stencil originally proposed by
Stevens (1990),Stevens (1991). This approach effectively limits any error introduced by the OBC to the two
non-linear terms, thus preventing any error associated with the OBC from rapidly propagating into the
interior via the Coriolis terms.
16.2.1.1 Notation
Boundary points are marked with a capital B. The first points beyond the boundary outside the model
domain is B+ 1, the first internal point in the model domain is B−1. See also Figure 16.1!
16.2.1.2 Boundary conditions for the sea level
The boundary conditions presented here refer to circulation models which use explicit solvers for the sea
surface height where the variablity of the sea level is governed by waves. Hence, the boundary condition for
the sea level is based on the wave like properties of the solution and has the form of a radiation condition
for outgoing waves. Boundary conditions for the sea level apply at points marked with green circles in
Figure figure:grid.
16.2.1.3 Boundary conditions for tracers
The tracer propagation is described by an advection-diffusion equation, which does not have a wave like
solution itself. However, the underlying velocity field may be wave like. Hence, especially vertical tracer
advection, which is not well defined near an open boundary, can be approximated by a radiation condition.
The boundary condition used here combines a radiation condition, approximations for horizontal advection
and relaxation towards prescribed data. Boundary conditions for the tracers apply at points marked with
green circles in Figure 16.1.
16.2.1.4 Boundary conditions for velocity
Boundary conditions for velocity vectors apply at points marked with a green cross in Figure figure:grid.
At these points horizontal and vertical velocity advection is set to zero. An exception is the metric term,
which is well defined. Removing it implies horizontal inhomogeneity in the flow fields, which show up
especially in nearly uniform flow.
To get a well defined friction operator, velocity beyond the boundary must be defined too. This is done
with a no gradient condition. This condition applies at points marked with a this black cross in Figure 16.1.
For some application it may help, to take vertical advection of tracers at boundary points into consid-
eration. A no gradient condition for the tangential velocity enhances ±-structures, which are typical for
the Arakawa B-grid, and couples such structures into the tracer equations. Hence, the tangential velocity
at points beyond the boundary should be set to the value of the second interiour point, which prevents
infiltration of ±-structures from the velocity field into the tracer fields from the OBC.
16.2.2 Sommerfeld radiation condition
Most open boundary conditions are based on the Sommerfeld radiation condition (Sommerfeld,1949).
This kind of boundary condition was originally derived for the theory of electromagnetic waves to remove
incoming waves from the far field solution for an oscillating dipole antenna. The Sommerfeld radiation
condition takes the form:
η,t =−cη,x at x=xB.(16.1)
In this equation, η(x,t) is the space-time dependent free surface height, cis the wave phase speed de-
termined via a method discussed in Section 16.3,x=xBis the spatial position of the open boundary in
Elements of MOM November 19, 2014 Page 232

Chapter 16. Open boundary conditions for the B-grid Section 16.2
question. Finally, we use the shorthand notation
η,t =∂η
∂t
η,x =∂η
∂x
(16.2)
to denote partial derivatives. The performance of OBC’s based on the Sommerfeld condition (16.1) has
been extensively assessed in the literature (see, for example Chapman,1985;Roed and Cooper,1987;Tang
and Grimshaw,1996;Palma and Matano,1998,2001). Unfortunately, OBC’s based on the Sommerfeld
condition often exhibit inaccuracies. The key reason is that the model solution is a superposition of several
waves which have different phase speeds and which are dispersive (in contrast to the linear electromagnetic
waves that Sommerfeld was concerned). However, the Sommerfeld condition is based on just a single wave
condition. The OBC behaviour in practice is thus very sensitive to how the phase speed in equation (16.1)
is determined.
We can classify the boundary conditions as passive, in which case the OBC is determined solely from
information within the computational domain, or active, so that data is prescribed from an external source.
Since the behaviour of the model interior is rarely consistent with data prescribed at the boundary, the
model may become prone to errors due to under-specification (not enough information describing exter-
nal processes is provided) or over-specification (OBC information is incompatible with interior equations).
Marchesiello and Shchepetkin (2001) provide a thorough discussion of the active versus passive bound-
aries, and over versus under-specification of data.
To alleviate problems with over-specification, an active boundary condition may be rendered partially
passive by coupling to a radiation condition. This approach was used by Blumberg and Kantha (1985).
Here, relaxation towards externally prescribed data is performed with an associated relaxation timescale,
so that
η,t =−cη,x −(η−ηo)/τf.(16.3)
Here, ηois the prescribed data for the surface height, and τfis a timescale. Even with this prescription for
the OBC, the behaviour of the simulation can be sensitive to the choice of radiation condition and relaxation
timescale used.
Likewise a fresh water flux may be added, but its influence will most probably disappear behind the
relaxation term.
16.2.3 Clamped boundary conditions
A simple boundary condition is the clamped boundary condition, i.e., sea level or tracers are kept at a fixed
value. For the sea level no physical justification is given for using this condition. It is motivated solely from
the fact that it keeps the numerical scheme stable. For salinity and temperature it may be a reasonable
approximation. The clamped condition requires the user to supply a single time and space independent
value to be imposed on the boundary. This type of condition corresponds to a zero phase speed, c= 0,
in the Sommerfeld radiation condition (16.1). It creates many reflections at the boundary, which can be
undesirable.
In a modified form time and space dependent values for the sea level or tracers may be prescribed.
Keeping in mind, that most ocean flow is geostropically balanced, this defines the baroclinic and barotropic
geostrophic transport through the boundary. This may be desired, but implies also the possibility of un-
wanted numerical effects, which may corrupt the numerical solution in the model domain.
16.2.4 No gradient boundary conditions
This condition imposes a smooth solution near the boundary. The no-gradient OBC assumes that there
does not exist a gradient of a variable across the open boundary. It is sometimes referred to as a Neumann
boundary condition. This condition corresponds to setting the phase speed to infinity in the Sommerfeld
radiation condition (16.1). It is specified by setting the value at the open boundary equal to the value
immediately adjacent to the open boundary in the model interior, so that
η(t+ 1,xB) = η(t+ 1,xB−1).(16.4)
Elements of MOM November 19, 2014 Page 233

Chapter 16. Open boundary conditions for the B-grid Section 16.3
In this equation, t+ 1 is the updated time step, xBsignifies the spatial position of the open boundary, with
η(t+1,xB) is the surface height at that boundary. As shown in Figure 16.1 xB−1signifies the spatial position
of the nearest point interior from the open boundary, with the sign determined by the relative position of
the open boundary.
For velocity a no gradient boundary condition applies across the boundary, to get a defined viscosity
operator
u(t+ 1,xB+1) = u(t+ 1,xB).(16.5)
16.2.5 Interior cell no gradient boundary conditions
This condition is similar to the no-gradient boundary condition (16.4). However, instead of using the value
at the nearest interior grid cell, the boundary is set to the value at the next nearest interior (B−2) cell (i.e.,
two grid points away from the boundary)
η(t+ 1,xB) = η(t+ 1,xB−2).(16.6)
For the tangetial velocity a no gradient boundary condition across the boundary is used to get a defined
viscosity operator
u(t+ 1,xB+1) = u(t+ 1,xB−1).(16.7)
16.2.6 Enhanced friction and diffusion near the boundary
This method increases the dissipation from tracer diffusion and momentum friction in regions near the
open boundary. This approach acts to dissipate spurious reflections at the boundary. It also may be useful
to remove artificial currents near the boundary, which may grow to be large in some cases. However, this
approach has the detrimental effect of slowing cross boundary transport.
16.3 Implementation of sea level radiation conditions
In this section, we discuss various radiation conditions that are used to specify the phase speed. We also
discuss how to specify the tracers across the open boundary.
16.3.1 Sign convention for the phase speed
The phase speed is a vector quantity. Here it is always directed perpendicularly to the model boundary
and notation can simplified considerably by considering the projection of the phase speed onto the normal
vector of the model boundary. The sign of the phase speed is positive for eastward or northward travelling
waves and negative for westward or southward directed waves. However, the quantity of interest is the
projection of the phase speed onto the boundary normal vector. In all radiation conditions given below,
phase speed means this projection, which is positive for outgoing waves and negative for incoming waves.
16.3.2 Gravity wave radiation condition for the phase speed
This formulation computes a phase speed relevant for a flat bottom barotropic shallow water configuration,
so that
c=pg DB,(16.8)
where gis the acceleration from gravity, and DBis the depth at the boundary (Chapman,1985)). Hence,
in this approximation it is assumed, that processes near the boundary are always governed by outgoing
waves. The OBC is implemented in an implicit form, so that
η(t+ 1,xB) = η(t,xB) + µη(t+ 1,xB−1)
1 + µ,(16.9)
where
µ=c∆t
∆x,(16.10)
Elements of MOM November 19, 2014 Page 234

Chapter 16. Open boundary conditions for the B-grid Section 16.3
where ∆xis the horizontal grid spacing. That is, equation (16.9) is the implicit solution to equation (16.1)
using cas the gravity wave speed.
Note: phase speed is always positive for gravity wave radiation, implying that waves are always outgo-
ing. This means that outgoing relaxation ,τout, is always used when relaxing to data (see Section 16.3.9.3).
16.3.3 Orlanski radiation condition for the phase speed
We aim to account for the most important part of the wave spectrum. There are various means for doing
so, with the Orlanski radiation condition (Orlanski,1976) one of the most common. Here, the the phase
speed of disturbances approaching the boundary is diagnosed at every time-step from the distribution of
the interior values of the surface height near the boundary, so that
~c =−η,t/η,x.(16.11)
The Orlanski radiation condition theoretically has a zero reflection coefficient. This property is desired to
reduce spurious reflected waves at the open boundary. Unfortunately, in practice reflections occur due to
inaccuracies in the phase speed computation.
The form employed by MOM is the implicit formulation based on (Chapman,1985)
η(t+ 1,xB) = (1 −µ)η(t−1,xB) + 2µη(t,xB−1)
1 + µ.(16.12)
Here, the dimensionless parameter µis set according to
µ=
1 if C≥1
Cif 0 < C < 1
0 if C≤0,
(16.13)
where
C=η(t−1,xB−1)−η(t+ 1,xB−1)
η(t+ 1,xB−1) + η(t−1,xB−1)−2η(t,xB−2).(16.14)
16.3.4 Camerlengo and O’Brien radiation condition
Camerlengo and O’Brien (1980) suggested a modified form of the Orlanski radiation condition, where only
the extreme values of the phase speed, zero or h/t, so that;
η(t+ 1,xB) = (η(t,xB−1) if C > 0
η(t−1,xB) if C≤0,(16.15)
with Cgiven by equation (16.14).
16.3.5 Radiation condition after Miller & Thorpe
The Orlanski scheme is modified here so that time differences are evaluated using a forward scheme and
space differences with an upwind scheme (see equation 15 in Miller and Thorpe,1981)
η(t+ 1,xB) = η(t,xB)−µ(η(t,xB)−η(t,xB−1)).(16.16)
In this case, the dimensionless coefficient
µ=µ1+µ2+µ3,(16.17)
with
µ1=η(t+ 1,xB−1)−η(t,xB−1)
η(t,xB−2)−η(t,xB−1)(16.18)
µ2=η(t,xB)−η(t−1,xB)
η(t−1,xB−1)−η(t−1,xB)(16.19)
µ3=η(t,xB−1)−η(t−1,xB−1)
η(t−1,xB−2)−η(t−1,xB−1).(16.20)
Elements of MOM November 19, 2014 Page 235

Chapter 16. Open boundary conditions for the B-grid Section 16.3
The scheme is implemented in an explicit temporal form.
16.3.6 Raymond and Kuo radiation condition
This radiation condition was introduced by Raymond and Kuo (1984) and used in adaptive form by March-
esiello et al. (2001). This scheme calculates the phase velocity for multidimensional flows using a projection
of each coordinate direction, i.e. not just the normal component. The scheme is implemented in implicit
form. The Sommerfeld radiation condition takes the form:
η,t =−cxη,x −cyη,y (16.21)
where xand yare directions normal and tangential to the boundary respectively. The phase speeds cx
and cyare projections given by:
cx=−η,t
η,x
η2
,x +η2
,y
,(16.22)
cy=−η,t
η,y
η2
,x +η2
,y
.(16.23)
This is discretised following Marchesiello et al (2001);
η(t+ 1,xB,yB) = 1
1 + rx
(η(t,xB,yB) + rxη(t+ 1,xB−1,yB)−ry(η(t,xB,yB)−η(t,xB,yB−1))ry>0,
η(t,xB,yB) + rxη(t+ 1,xB−1,yB)−ry(η(t,xB,yB+1)−η(t,xB,yB))ry<0.
(16.24)
where:
rx=−∆ηt∆ηx
∆η2
x+∆η2
y
ry=−
∆ηt∆ηy
∆η2
x+∆η2
y
(16.25)
∆ηt=η(t+ 1,xB−1,yB)−η(t,xB−1,yB) (16.26)
∆ηx=η(t+ 1,xB−1,yB)−η(t+ 1,xB−2,yB) (16.27)
∆ηy=(η(t,xB−1,yB)−η(t,xB−1,yB−1) ifD > 0,
η(t,xB−1,yB+1)−η(t,xB−1,yB) if D < 0
D=∆ηt(η(t,xB−1,yB+1)−η(t+ 1,xB−1,yB−1))(16.28)
The adaptive for relaxation takes on a form similar to Equation (16.3),
η,t =−cxη,x −cyη,y −(η−ηo)/τf.(16.29)
where τf=τout if cx>0 and τf=τin with cx=cy= 0 if cx<0. The relaxation time scale τout τin
such that during outward phase propagation a weak relaxation exists to avoid boundary values drifting
excessively but also preventing problems of over-specification, while during inward phase propagation
stronger relaxation is applied that avoids shock issues.
16.3.7 The IOW-radiation condition
As for the gravity wave radiation condition an implicite scheme is used,
η(t+ 1,xB) = η(t,xB) + µη(t+ 1,xB−1)
1 + µ,(16.30)
Elements of MOM November 19, 2014 Page 236

Chapter 16. Open boundary conditions for the B-grid Section 16.3
where
µ=C∆t
∆x.(16.31)
The spatial and time derivative of ηare
∆η,x =η(t+ 1,xB−1)−η(t+ 1,xB−2)
∆x,(16.32)
∆η,t =η(ts,xB−1)−η(t+ 1,xB−1)
∆t.(16.33)
If the predictor-corrector scheme is used, the phase speed is calculated twice. In this case η(ts) denotes η
at the starting time step of this scheme. In the predictor step ∆tis the reduced time step ∆t=γdt. For the
leapfrog scheme ts=t−1 and ∆t= 2dt.
To ensure a well defined phase speed for small horizontal gradients this case is treated separately,
C(t+ 1) = (C∗(t+ 1) if ∆ηx> a,
0.99 e
C(t) if ∆ηx≤a, (16.34)
where ∆ηx=|η(t+ 1,xB−1)−η(t+ 1,xB−2)|and ais a small length, typically 10−8m. e
Cis the time smoothed
phase speed from the previous time step. The scheme allows to control the minium and maximum value
of the phase speed. For incoming waves, negative phase speed, positive values (or zero) are assumed,
C∗(t+ 1) =
Cinc if C+<0,
Cmin if C+< Cmin,
C+if Cmax > C+> Cmin,
Cmax if C+> Cmax.
(16.35)
C+(t+ 1) is calculated from the derivatives of η,
C+(t+ 1) = ∆η,t
∆η,x .(16.36)
Cmax,Cmin and Cinc are defined in terms of the gravity wave speed,
Cmax =cmax pg DB(16.37)
Cmin =cmin pg DB(16.38)
Cinc =cinc pg DB.(16.39)
The factors cmax,cmin and cinc can be modified via the namelist.
Relaxation is done as described in Section 16.3.9.
16.3.8 Phase speed smoothing
The diagnosed phase speed may be very noisy with altering sign every time step. A time smoother
e
C(t+ 1) = Fe
C(t) + (1−F)C(t+ 1),(16.40)
helps to reduce numerical noise. The default value is F= 0.7. The application of the smoother requires to
save e
Cin a restart file, to ensure reproducibility across model restarts.
16.3.9 Relaxation to data
16.3.9.1 Relaxation towards prescribed profiles
The radiation conditions may be coupled to prescribed data as described by Equation (16.3). This approach
is implemented implicitly as
η(t+ 1,xB) = e
η(t+ 1,xB) + ηo∆t
τf
1 + ∆t
τf
,(16.41)
Elements of MOM November 19, 2014 Page 237

Chapter 16. Open boundary conditions for the B-grid Section 16.4
where e
η(t+1,xB) is the solution on the boundary derived from the radiation conditions. τfis the time scale
for the relaxation process.
The relaxation may occur a given number of cells into the interior, in which case e
η(t+∆t,xB) is the
interior solution to the continuity equation.
16.3.9.2 Relaxation of the sea level average - conservation of geostrophic currents
If the model area is a semi-enclosed sea, which is connected to the ocean by a narrow channel, the open
boundary may be placed within this channel. By prescribing the sea level profile across the channel, one
defines also the geostrophic volume transport through this channel. In this case the incertitude of the
OBC may dominate the volume budget of the model. To overcome this serious shortcoming, an alternative
relaxation scheme may be used, which prescribes only the average sea level at the boundary. Doing so,
the geostropic transport defined by the cross channel sea level gradient is not affected by the relaxation.
Only the ageostropic flow may react to the prescribed sea level variation, geostrophic adjustment happens
through the internal model dynamics. The scheme works explicitly,
η(t+ 1,xB) = e
η(t+ 1,xB) + ∆t
τf
(ηo−e
η(t+ 1,xB))(16.42)
e
η(t+ 1,xB)is sea level averaged over the boundary.
16.3.9.3 Variable relaxation for incoming and outgoing waves
Likewise, the value of τfmay be different for prevailing incoming or outgoing waves,
τ−1
f=r τ−1
out + (1 −r)τ−1
in ,(16.43)
r(t) = e
C(t)
Cmax .(16.44)
16.4 OBC for tracers
16.4.1 Reduced tracer equations at open boundaries
The tracer equations in MOM are strongly linked with the sea level equation and tracers and sea level are
treated consistently. Because the radiation condition for the sea level is a rough approximation, a similar
consistency cannot be achieved for boundary points. Hence, the tracer equations at the boundaries are
simplified.
To avoid double coding, the normal code should be used at boundaries as far as possible. Tracers are
updated as
T(t+ 1)ρ(t+ 1)h(t+ 1) = T(t)ρ(t)h(t) + ∆tδ(h(t)ρ(t)T(t)) (16.45)
The time tendency of the vertically integrated tracer in the grid cell δ(ρT ) is the combined time tendency of
tracer concentration, density and cell thickness. It consists of an advective and diffusive contribution and
eventually of source terms from radiation and special convective schemes (kpp). We rewrite these terms in
such a manner, that for a constant tracer the sea level equation is retained. Especially for a uniform tracer
T= 1, δ(hρT ) must be the time tendency of the cell thickness, δ(hρ), i.e. δ(hρ1) →δ(hρ) = ∆hρ
∆t.
δ(hρT )k=−(∇s·hρ(uT+F))k−(ρ(wT +F(s)))k−1+ (ρ(wT +F(s)))k+ (hρST)k
δ(hρ)k=−(∇s·hρu)k−(ρw)k−1+ (ρw)k+ (hρSM)k(16.46)
Advection is rewritten to separate the different contributions to the time tendency,
Adv(T)k=−(∇s·hρuT)k−(ρwT )k−1+ (ρwT )k
=−(T∇s·hρu)k−(ρwT )k−1+ (ρwT )k−(hρu·∇sT)k.(16.47)
Elements of MOM November 19, 2014 Page 238

Chapter 16. Open boundary conditions for the B-grid Section 16.4
Applying approximations for open boundaries, the first three terms have to be kept consistent with the
equation for the level thickness. The level thickness is calculated from approximations only and it is ap-
propriate to express the convergence of the flow in terms of the level thickness time tendency. With of
−(∇s·hρu)k=δ(hρ)k+ (ρw)k−1−(ρw)k−(hρSM)k(16.48)
this renders to
δ(hρT )k=δ(hρ)kTk+ (hρ(ST−SMT))k+SGS
−(hρu·∇sT)k−(ρwT )k−1+ (ρwT )k+ ((ρw)k−1−(ρw)k)Tk.(16.49)
i.e., which ensures consistency between tracers and layer thickness for a uniform tracer. Also the approx-
imation of zero vertical advection and horizontal advection with an upwind scheme is consistent with the
thickness equation for cells of constant thickness. Diffusion and source terms apply unchanged and will
not be specified here.
For surface cells the vertical advection at the surface is expressed in terms of sea level variation, fresh
water flux and turbulent tracer flux,
δ(hρT )1= (δ(hρ)1T1+ρwqw(Tw−T1) + (hρ(ST−SMT))1−Qturb
T+SGS
−(hρu·∇sT)1+ (ρwT )1−(ρw)1T1.(16.50)
With this approximation the tracer concentration remains unchanged, if only the sea surface height is
undulating. If currents are zero, but fresh water flux and diffusion are present, a horizontally uniform
tracer distribution will not be disturbed near an open boundary. The consistency between sea level equation
and tracer equation is not broken, if approximations for the horizontal advection term are made, or if
radiation terms are added. Those terms vanish for horizontally uniform tracers especially for T= 1 and the
sea level time tendency is trivially retained.
Because vertical velocity is not well defined it is left out of consideration. It is replaced by a radiation
term, which accounts for the propagation of wave like undulations of internal interfaces from baroclinic
waves.
δ(hρT )k=δ(hρ)kTk+ (hρ(ST−SMT))k+SGS
−(hρu·∇sT)k+cρh∂Tk
∂x +ρh Tref −Tk
τf
(16.51)
δ(hρT )1≈(δ(hρ)1T1+ρwqw(Tw−T1) + (hρ(ST−SMT))1−Qturb
T+SGS
−(hρu·∇sT)1+cρh∂T1
∂x +ρh Tref −T1
τf.(16.52)
Implementation of the radiation condition and of the relaxation towards prescribed data is documented
below. Diagnostics of the phase speed is based on the tracer concentration, because the total tracer contend
may undulate rapidly from the barotropic mode in the cell thickness variability.
16.4.2 Upstream advection of tracers near the boundary
For advection across the open boundary, an upstream scheme with
T(xB+1) = T(xB) (16.53)
means that the incoming tracer has the same concentration as the tracer at the boundary point. This ap-
proximation may give poor results for long model runs and can cause model drifts.
After running a passive boundary over a long period, the tracer near the boundary will be determined
completely by processes in the model domain. As an example consider a marginal sea with a strong fresh
water surplus. There will be an estuarine circulation with a more or less permanent outflow of brackish
water in a surface layer and inflow near the bottom. However, the salinity of the inflowing water will be
Elements of MOM November 19, 2014 Page 239

Chapter 16. Open boundary conditions for the B-grid Section 16.4
reduced as well after some time by vertical mixing processes. The model results will suffer from underes-
timated stratification. To overcome this problem, information on the tracer concentration in the adjacent
sea must be provided for the model. The simple approximation
T(xB+1) = T(x0) (16.54)
where T0may stem from a database, improves the performance of the diffusion and the advection operators,
which in turn may invoke wave like processes spreading from the boundary into the model. Using an
upstream formulation for the tracer gradient in the advective term, this can switch on an inflow through
the open boundary. However, waves of a small amplitude but with a high phase speed may disturb this
scheme. Thus, the tracer source term STcan be used for a controlled restoring to prescribed boundary
values. The upstream advection condition is discretized as:
T(t+ 1,xB) = T(t,xB)
+∆t
∆x[(un−|un|)(T(t,xB−1)−T(t,xB)) + (un+|un|) (T(t,xB)−T(t,x0))](16.55)
where unis the velocity normal to the boundary times density and the cell height, T(xB) is the tracer on the
boundary, T(xB−1) is the tracer one cell into the interior and T(x0) is a tracer value that must be supplied
externally.
16.4.3 Relaxation towards external data
If external data are prescribed boundary values may be relaxed towards there data as
T(t+ 1,xB) = (T0−T(t,xB))∆t
τf.(16.56)
The relaxation time τfdepends on the flow direction near the boundary. If the sum of advection velocity
and phase speed at the boundary is directed inwards, one has τf=τin
fand τf=τout
fotherwise. τin
fand τout
f
can be specified in the namelist for each tracer and boundary separately.
16.4.4 Flow relaxation scheme of Martinsen and Engedahl
The flow relaxation scheme of Martinsen and Engedahl (1987) has been included to relax boundary data
to interior data. This is accomplished over a region NN cells wide (typically NN=10) where the tracer
variables are updated according to:
T=αiTB+ (1 −αi)TB±i(16.57)
where TBis the boundary specified value, TB±iare the interior variable values and αiis a relaxation param-
eter given by:
αiTB= 1 −tanh i−1
2i= 1,2,..NN (16.58)
Note that the flow relaxation scheme is used in conjunction with another boundary condition and TBmay
be obtained from the FILEIN or NOGRAD condition; whatever is specified on the boundary is relaxed to
the model integrated values over NN cells. The flow relaxation scheme is only implemented if UPSTRM is
included in the tracer obc. If TBis equal to zero (clamped boundary condition) then this flow relaxation
scheme acts as a sponge type condition. An example of the flow relaxation scheme implementation in the
namelist is given below:
obc_flow_relax(:,1) = 10, 1, 1
obc_flow_relax(:,2) = 10, 1, 1
Elements of MOM November 19, 2014 Page 240

Chapter 16. Open boundary conditions for the B-grid Section 16.5
16.4.5 Radiation conditions
If the velocity field near the boundary is wave like, vertical advection may result in a wave like tracer
motion. Hence, a radiation condition may improve the numerical scheme at the boundary.
The radiation condition for tracers is applied implicitly,
T(t+ 1,xB) = T(t,xB) + µT (t+ 1,xB−1)
1 + µ,(16.59)
where
µ=C∆t
∆x.(16.60)
The phase speed Cis set to zero for incoming waves and is limited by Cmax,
µ=
0 if C∗<0,
C∗if 0 < C∗< Cmax,
Cmax if C∗> Cmax.
(16.61)
C∗is calculated either bei the Orlanski scheme,
C∗=∆x
∆t
T(t−1,xB−1)−T(t+ 1,xB−1)
T(t+ 1,xB−1) + T(t−1,xB−1)−2T(t,xB−2),(16.62)
or by used in MOM-31 (IOW).
C∗=∆x
∆t
T(t−1,xB−1)−T(t+ 1,xB−1)
T(t,xB−1)−T(t,xB−2).(16.63)
For the time staggered scheme the index t−1 points to the same filed as t. The maximum phase speed,
Cmax, is given by the CFL-criterion,
Cmax =∆x
∆t.(16.64)
16.4.6 Vertical mixing and viscosity co-efficients
Vertical mixing at boundary points my be enabled or diabled. However, the mixing co-efficients at these
points are used to define viscosity at adjacent velocity points. The namelist parameter obc mix specifies,
how the mixing coefficient at boundary points is defined. Options are NOTHIN,NOGRAD,INGRAD and CLAMPD,
obc mix=NOGRAD is the default.
16.4.7 Enhanced horizontal mixing and viscosity co-efficients
To damp unwanted numerically generated flow patterns near open boundaries viscosity and diffusivity
may be enhanced within a stripe near the boundary.
16.5 The namelist obc nml
MOM requires that two components of velocity be prescribed on each open boundary (normal and tan-
gential velocities to the boundary) for both the 3D and 2D modes. Surface elevation and the values of any
tracers present are also required. Here are the flags that specify the various fields:
• Normal velocity: obc nor
• Tangential velocity: obc tan
• Sea level elevation: obc eta
• Tracers: obc tra(:).
Elements of MOM November 19, 2014 Page 241

Chapter 16. Open boundary conditions for the B-grid Section 16.6
The OBC specification is determined via text strings as listed in Table 16.1, where the variables these con-
ditions may be applied to are listed as un = normal velocity, ut = tangential velocity, η= surface elevation,
and T= tracers. The condition specified for velocities is used for both the 2D and 3D modes. Note that the
text identifier strings have have been truncated to the same length while attempting to describe the OBC
condition to accommodate neat alignment in the namelist.
Condition name Text identifier Applicable variables
Relaxation to data FILEIN η,T
Relaxation of mean MEANIN η
Clamped CLAMPD un,ut,η
No-gradient NOGRAD un,ut,η,T
Interior-gradient INGRAD un,ut
Linear extrapolation LINEAR un,ut
Gravity wave radiation GRAVTY η
Orlanski ORLANS η,T
Camerlengo and O-Brien CAMOBR η
Miller and Thorpe MILLER η
Raymond and Kuo RAYMND η
Schmidt MARTIN η,T
Upstream advection UPSTRM T
Table 16.1: Namelist settings for the OBC specification.
An example of open boundary specification for a domain containing three open boundaries and two
tracers is given below:
nobc = 3
direction =’west’, ’south’, ’north’
is = 2, 2, 2
ie = 2, 10, 10
js = 2, 2, 20
je = 20, 2, 20
obc_nor =’NOGRAD’, ’NOGRAD’, ’NOGRAD’
obc_tan =’INGRAD’, ’INGRAD’, ’INGRAD’
obc_eta =’GRAVTY’, ’FILEIN’, ’MEANIN|ORLANS’
obc_tra(:,1) =’UPSTRM|FILEIN’, ’UPSTRM|FILEIN’,’UPSTRM|FILEIN’
obc_tra(:,1) =’NOGRAD’, ’NOGRAD’,’UPSTRM|NOGRAD’
Note that by ’or-ing’ two conditions together then these two conditions will be invoked sequentially
(order is not important). Hence the condition UPSTRM|FILEIN will invoke an upstream advection condition,
using data from file when flow is into the domain. The condition UPSTRM|NOGRAD will invoke an upstream
advection condition, using the value one cell into the domain when flow is into the domain. A wave-like
contribution to the OBC can also be added for tracers, e.g. invoked by UPSTRM|FILEIN|ORLANS. This wave-
like contribution is added implicitly.
If partially passive conditions are to be used for elevation, then the FILEIN or MEANIN condition is
’or-ed’ with the desired radiation condition, e.g. using the Orlanski partially passive condition with data
prescribed from file use FILEIN|ORLANS. Note that in-going and out-coming relaxation timescales are also
required to be prescribed for these partially passive conditions.
Some compilers do not like the colon (:) syntax in field specifications. In this case each element must be
specified separately.
Elements of MOM November 19, 2014 Page 242

Chapter 16. Open boundary conditions for the B-grid Section 16.6
16.6 Topography generation - Preparation of boundary data
16.6.1 Topography generation with open boundaries
Open boundary conditions require modifications of the topography near the boundary. Gradients of the
depth normal to the boundary should be zero to avoid large vertical velocity in the boundary area. Because
vertical velocity usually is set to zero at boundary points, this approximation is less serious, if vertical
velocity is zero anyway.
The grid and topography generator ocean grid generator closes all model boundaries, if the model is nei-
ther cyclic or global. This has to be modified for open boundaries. Hence, open boundaries need to be
specified in this early stage of model preparation. This ensures, that initial fields and boundary values,
which may use the information in the grid specification file grid spec.nc, are fully consistent with the to-
pography used during model run time. For this purpose, the ocean grid generator ocean grid generator is
able to read those parts of the namelist obc nml, which define the open boundaries geographically. Here is
an example:
\&obc_nml
nobc = 3
direction = ’north’, ’south’, ’west’,
is = 2, 2, 2,
ie = 39, 63, 2,
js = 74, 2, 2,
je = 74, 2, 74,
name = ’northern’, ’southern’, ’western’
It is not recommended, to define the boundary conditions at outmost model points.
16.6.2 Preparation of input data files
Having the grid spec.nc file ready, one may proceed with preparing obc input data files. The grid of input
data files should match exactly the size of the open boundary. However, it is also possible, that the grid
of the input files may cover a larger area. In this case, those start and end index of the model grid, which
matches the first and the last index in the input file, must be specified in the namelist obc nml (but not for
ocean grid generator). The default is, that the input data files match the size of the boundary exactly. In the
example below, the input files for sea level and tracers have the same size as the model itself, 75 ×65. They
may be either preprocessed as decribed below, or used directly with help of namelist specifications:
\&obc_nml
nobc = 3
direction = ’north’, ’south’, ’west’,
is = 2, 2, 2,
ie = 39, 63, 2,
js = 74, 2, 2,
je = 74, 2, 74,
name = ’northern’, ’southern’, ’western’
iers = 1, 1, 2,
iere = 65, 65, 2,
jers = 2, 2, 1,
jere = 2, 2, 75,
itrs = 1, 1, 2,
itre = 65, 65, 2,
jtrs = 74, 2, 1,
jtre = 74, 2, 75,
It is supposed, that some data suitable for OBC are ready in netcdf-format. There are many tools to
process such files, here ferret is used. Alternatives may be grads and possibly matlab in combination with
Elements of MOM November 19, 2014 Page 243

Chapter 16. Open boundary conditions for the B-grid Section 16.6
the netcdf toolbox.Ferret is available from http://ferret.wrc.noaa.gov/Ferret. It is recommended to
use Ferret 6 or a later version, because previous versious do not permit full access to all netcdf attributes.
However, as long as the file are not to large, some fine tuning in the file structure could also be done with
a combination of the programs ncdump, a good editor, which can handle large files and ncgen.ncdump and
ncgen come with the netcdf library. Also the nco-tools are of great help.
Examples for ferret scripts are given below. For details of the syntax visit
http://ferret.wrc.noaa.gov/Ferret.
The following directory structure is assumed:
preprocessing/grid_spec.nc
preprocessing/OBCDATA
preprocessing/OBCDATA/1999/your_input.dta.nc
preprocessing/OBCDATA/2000/your_input.dta.nc
...
The working directory is for example
preprocessing/OBC/2000/
Then the following ferret commands should sufficient to generate the input file for the sea level at a
northern boundary at j=74:
SET MEMORY/SIZE=30
use "../../grid_spec.nc"
use "../OBCDATA/2000/your_input.dta.nc"
! the input file has units "cm", mom4 needs "m"
let/units=m/title=eta_t eta_t = eta[d=3,gx=wet[d=1,j=74]]/100
can axis/modulo ‘eta_t,return=xaxis‘
! add a calendar
SET AXIS/CALENDAR=JULIAN ‘eta_t,return=taxis‘
save/clobber/file=obc_trop_north.dta.nc/2:39 eta_t
It may happen, that the model landmask differs from the land mask in the input data. In this case one may
have land information from the input file at ocean points in the OBC input file, which would let the model
crash. In this case ferret functions could be used to fill these values with ocean data. Suitable tools are the
@fnr transformation or the new external function fill xy which is in the latest Ferret 6 release.
For depth dependent data as temperature and salinity more care is needed to avoid gaps in the in-
put data near the bottom. Most likely, topography representation in the model differes from topography
representation in the input data. So two things or needed, to organise the input data
- a mask, to define ocean points in your model
- an input data set, which covers all model ocean points with ocean data.
The mask can be derived from the grid spec.nc file:
SET MEMORY/SIZE=30
use "../../grid_spec.nc"
let mask_t=if k[gz=zb] le NUM_LEVELS then 1 else (-1)/0
save/clobber/file=tempfile.nc mask_t
For velocity data NUM LEV ELS C can be used in the same manner.
Extrapolation into the bottom should be mostly sufficient, to extend the input data, so that all model
ocean points are covered with input ocean data later:
use "../OBCDATA/2000/your_input.dta.nc"
let temp_n = temp[k=@fnr:5] ! 5 should sufficient
let salt_n = salinity[k=@fnr:5]
save/append/file=tempfile.nc temp_n, salt_n
Elements of MOM November 19, 2014 Page 244

Chapter 16. Open boundary conditions for the B-grid Section 16.6
The names of variables in the input file may be different. Saving into a temporary file is not needed in
any case, but it helps to avoid problems from ambiguous indecees in variables with different co-ordinate
definitions.
Now use tempfile.nc as new input file:
can data/all
can/var/all
!__________________________________________________________________
SET MEMORY/SIZE=55
use tempfile.nc
let/unit=Celsius/title=temperature temp = temp_n[g=mask_t]*mask_t[j=74]
let/unit=PSU/title=salinity salt = salt_n[g=mask_t]*mask_t[j=74]
save/clobber/file=obc_clin_north.dta.nc/2:39 temp, salt
Multiplying with the mask ensures, that only model ocean points contain tracer information. The grid
information is implicitely in mask t. Do not specify the range of the grid index for writing tempfile.nc. This
may disturb the horizontal interpolation.
16.6.3 Consistency of input data and model configuration
16.6.3.1 The sea level in external data and the model zero level
The models zero motion sea level is the average of the initial sea level. This value needs to be consistent
with boundary sea level data. If boundary and initial data come from a larger model, this should be the
trivially the case. Otherwise some adjustment is needed, because because even small artificial gradients
between boundaries and the model interiour may drive large currents, which would rapidly corrupt the
initial stratification. This requires an initial run, with advection of tracers switched off. This can be done
with the options zero tracer advect horz and zero tracer advect vert enabled in ocean tracer advect nml. The
resulting model sea level should be a reasonable choice for model initialisation. Eventually the procedure
could be repeated.
16.6.3.2 The sea level and the problem of air pressure
Air pressure gradients are part of geostrophic balance of current systems. If the air pressure gradients vary
only slowly, a corresponding negative sea level gradient develops, which may compensate its influence, so
that the currents calculated with and without air pressure are approximately the same. This is the reason,
why air pressure is often ommited in circulation models.
The sea level however may differ considerably in both cases. This has to be taken into account, if sea
level data are prescribed at open boundaries. MOM-4 permits the input of sea level air pressure, which is
added to the sea level elevation. Hence, after geostrophic adjustment air pressure gradients and sea level
gradients partially balance each other.
Elements of MOM November 19, 2014 Page 245

Chapter 16. Open boundary conditions for the B-grid Section 16.6
Elements of MOM November 19, 2014 Page 246
Subgrid scale parameterizations for
vertical processes
The purpose of this part of the manual is to describe certain of the subgrid scale (SGS) parameterizations
of physical processes used in MOM, with focus here on vertical and/or dianeutral processes.
247

Section 16.6
Elements of MOM November 19, 2014 Page 248

Chapter 17
Surface and penetrative shortwave
heating
Contents
17.1 General considerations and model implementation .....................249
17.2 The Paulson and Simpson (1977) irradiance function ...................250
17.3 Shortwave penetration based on chlorophyll-a .......................251
17.3.1 Solar penetration in the ocean ................................ 251
17.3.2 Morel and Antoine (1994) shortwave penetration model ................. 251
17.3.3 SeaWiFS based chlorophyll-a climatology ......................... 252
17.4 Diagnosing shortwave heating in MOM ............................252
The purpose of this chapter is to discuss the numerical implementation of shortwave heating. Sensitiv-
ity of the ocean solution to the penetration of shortwave radiation into the ocean column can be quite large.
This chapter, especially Section 17.3, benefitted from contributions by Colm Sweeney.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean sbc.F90
ocean param/sources/ocean shortwave.F90
ocean param/sources/ocean shortwave gfdl.F90
ocean param/sources/ocean shortwave csiro.F90
ocean param/sources/ocean shortwave jerlov.F90
Notably, the documentation here is somewhat out of date, with the code modules the best source for how
the various optical models have been implemented. In particular, the Morel and Antoine (1994) optical
scheme detailed in Section 17.3.2 has largely been supplanted at GFDL by the Manizza et al. (2005) scheme
available in MOM. Nonetheless, this chapter provides a useful overview of general methods for how short-
wave penetration is attentuated in MOM.
17.1 General considerations and model implementation
Solar penetration brings solar shortwave heating downward in the ocean column, thus providing a heating
at depth. The parameterization of the oceanic absorption of downward solar radiation is generally written
as
I(x,y,z) = I0−(x,y)F(z),(17.1)
249

Chapter 17. Surface and penetrative shortwave heating Section 17.3
where I0−, in units of W m−2, is the total shortwave downwelling radiative heating per unit area incident
at the earth surface, and F(z) is a dimensionless attenuation function. Note that the total downwelling
radiation I0−is to be distinguished from the total shortwave heating I0, where I0−= (1 −α)I0, with α≈0.06
the sea surface albedo.
Shortwave heating affects the heat budget locally according to
∂(ρΘ)
∂t =−(ρo/cp)∂z(cpFz−I).(17.2)
In this equation, Fzaccounts for vertical processes such as advection and diffusion, cpis the heat capacity
of seawater, ρis the in-situ density which for a Boussinesq fluid is set to the Boussinesq reference density
ρo. Finally, Θis the conservative temperature of McDougall (2003), which is commonly approximated by
potential temperature θ.
Shortwave heating leads to the following net heat flux over a column of ocean fluid
(ρo/cp)
η
Z
−H
dz∂zI= (ρo/cp)[I(η)−I(−H)].(17.3)
where I(η) is often approximated as I(0). We assume there is no shortwave heating of the solid rock under-
neath the ocean fluid, so I(z=−H) = 0 is appropriate, with this boundary condition set via masks in MOM.
Although the expression (17.5) suggests the upper boundary condition I(0) = I0−, we must be careful to not
double-count the shortwave source in since it is typically carried as part of the surface temperature flux ar-
ray stf and thus handled by the module ocean core/ocean sbc.F90. We now present the two approaches
available in MOM.
The vertical convergence of penetrative shortwave radiation, (ρo/cp)∂zI, is incorporated into MOM’s
potential temperature equation. Additionally, it is typical to include the total downwelling shortwave
heating I0−within the surface flux array stf, where other forms of heating such as those from latent and
long-wave affects are also incorporated. Hence, for proper accounting of the shortwave heating, the upper
boundary condition for the irradiance function must be specified as
I(η) = (0 if I0−is already included in stf
I0−(x,y) if I0−is NOT already included in stf.(17.4)
The typical practice at GFDL is to set I(η) = 0 since I0−is already included in stf. Care should be exercised
by those using the opposite convention.
17.2 The Paulson and Simpson (1977) irradiance function
Jerlov (1968) classified water into five types according to its optical properties, which determines the extent
that solar radiation penetrates into a vertical fluid column. For example, clear water allows for deeper
penetration, whereas mirky water, as occurs in the presence of active biology, more rapidly attenuates the
radiation. Studies by Paulson and Simpson (1977) then suggest a form for the attenuation function F(z)
based on the optical properties of water.
The parameterization of solar shortwave absorption of downwelling solar radiation used by Rosati and
Miyakoda (1988) is given by the Paulson and Simpson (1977) form
I(x,y,z) = I0−(x,y)[Rez/ζ1+ (1 −R)ez/ζ2],(17.5)
where I0−is the total shortwave downwelling radiative heating per unit area incident at the earth surface,
ζ1and ζ2are attentuation lengths and Ris an empirical constant dependent on the optical properties of
the water. In the Rosati and Miyakoda (1988) study, they chose R= 0.58, ζ1= 0.35m, and ζ2= 23m,
corresponding to Jerlov Type I water (clear water). This is the form of shortwave penetration originally
implemented in MOM. However, MOM4.0 and later releases implement the scheme discussed in Section
17.3.
Elements of MOM November 19, 2014 Page 250

Chapter 17. Surface and penetrative shortwave heating Section 17.3
17.3 Shortwave penetration based on chlorophyll-a
This Section was contributed by Colm Sweeney (cos@gfdl.noaa.gov).
Recent investigations with solar penetration have indicated a strong sensitivity of ocean simulations to
how light penetrates into the ocean and warms the upper few tens of meters. This section describes recent
work at GFDL whereby the use of a spatially and temporally dependent penetration depth is specified
according to climatological chlorophyll data. Although this data is taken from a climatology, its use is
believed to be preferable, even for climate change simulations, to the use of a space-time independent
optical type. Research into bio-optical influences on ocean climate remains an active area, and the methods
presented here remain under investigation by various groups.
17.3.1 Solar penetration in the ocean
Observations and models describing the distribution of solar radiation with depth in seawater have demon-
strated that nearly all (99.9%) of the downwelling infrared radiation (wavelengths of 750nm-2500nm) is
absorbed in the upper 2 meters of the ocean. While variability in the penetration depth of long wave
radiation has large implications for skin temperature and surface layer heat fluxes, this IR radiation has
little effect below the surface over the depths (roughly 10 m) used in present day ocean models (Morel and
Antoine (1994), Ohlmann and Siegel (2000)).
In contrast, attenuation of shortwave solar radiation (wavelengths <750nm) is both spatially and tem-
porally variable at scales important to ocean climate models. In waters with high particulate and dissolved
organic matter concentrations, the 1% light penetration depth can be less than 10 meters while in the clear,
biologically unproductive waters of the subtropical gyres, solar radiation can directly contribute to the heat
content at depths greater than 100 meters.
Previously, ocean climate models have parameterized the penetration of light into the ocean by identify-
ing six water types distinguished by the ”clarity” of the water (Paulson and Simpson (1977)). This method
is described in Section 17.2. More recently, the correlation between chlorophyll pigment concentrations
and short wave penetration depths has enabled us to parameterize shortwave penetration of solar radiation
with satellite observations of ocean color (Morel (1988), Morel and Antoine (1994), Ohlmann and Siegel
(2000)). By assimilating satellite observations of ocean color (e.g., SeaWiFS, OCTS, MODIS), it is possible
to more accurately simulate the spatial and temporal variability of penetrating radiation.
17.3.2 Morel and Antoine (1994) shortwave penetration model
Present modeling work at GFDL (Spring 2003) makes use of a parameterization developed by Morel and
Antoine (1994). This scheme was explicitly developed for large-scale ocean models with coarse depth
resolution (i.e., grids with ∆z > 5m). Morel and Antoine (1994) expand the exponential function used by
Denman (1973) into three exponentials to describe solar penetration into the water column.
The first exponential is for wavelengths >750nm (i.e., IIR) and assumes a single attenuation of 0.267meter
with a solar zenith angle θ= 0. At present we assume that the solar zenith angle stays constant throughout
the daily integration of the model. Thus, the resulting equation for the infared portion of the downwelling
radiation is:
IIR(x,y,z) = IIR−(x,y)e−z/(0.267cosθ)(17.6)
where again θ= 0. This relationship assumes z is the depth in meters and that IIR−(x,y) is a fraction, of the
total downwelling radiation, I0−such that
IIR−(x,y) = FIR I0−(17.7)
and
FIR +FV IS = 1 (17.8)
where FIR and FV IS are the fractions of infared (750nm to 2500nm) and visible (300nm to 750nm) radiation
downwelling from the surface ocean. Although Morel and Antoine (1994) note that water vapor, zenith
angle, and aerosol content each can effect the fraction of incoming radiation that is represented by infared
Elements of MOM November 19, 2014 Page 251

Chapter 17. Surface and penetrative shortwave heating Section 17.4
and visible light, in the present implementation we have chosen to keep these fractions constant such that
FIR = 0.46.
The second and third exponentials represent a parameterization of the attenuation function for down-
welling radiation in the visible range (300nm -750nm) in the following form:
IV I S (x,y,z) = IV IS−(x,y)(V1ez/ζ1+V2ez/ζ2).(17.9)
This form further partitions the visible radiation into long (V1) and short (V2) wavelengths assuming
V1+V2≡1.(17.10)
V1,V2,ζ1and ζ2are calculated from an empirical relationship as a function of chlorophyll-a concentration
using methods from Morel and Antoine (1994). Throughout most of the ocean V1<0.5 and V2>0.5. The e-
folding length scales ζ1and ζ2are the e-folding depths of the long (ζ1) and short visible and ultra violet (ζ2)
wavelengths. Based on the chlorophyll-a climatology used in the GFDL models, ζ1should not exceed 3m
while ζ2will vary between 30m in oligotrophic waters and 4m in coastal regions. All of these constants are
based on satellite estimates of chlorophyll-a plus Pheaophytin-a, as well as parameterizations which have
“nonuniform pigment profiles” (Morel and Antoine (1994)). The ”nonuniform pigment profiles” have been
proposed to account for deep chlorophyll maxima that are often observed in highly stratified oligotrophic
waters (Morel and Berthon (1989)).
17.3.3 SeaWiFS based chlorophyll-a climatology
A ”non- El Ni˜
no” chlorophyll-a climatology was produced from estimates of the Sea-viewing Wide Field-of-
view Sensor (SeaWiFS). The ”non - El-Ni˜
no” climatology is based on 8-day composites of SeaWiFS images
taken from 1999 to the end of 2001. The climatology calculates the weighted average chlorophyll-a con-
centration on the 15th day of each month considering all data 16 days before, and after the 15th day of
each month. Each 8-day composite is assigned a gaussian (alpha = 2.5) weight based on its proximity to the
15th day of each month. This data set is available from the GFDL NOMADS server where MOM datasets
are distributed.
17.4 Diagnosing shortwave heating in MOM
It is of interest to diagnose the impacts of shortwave heating on the ocean fluid, both at the surface and
beneath. As detailed here, there are two terms needed to fully diagnose the impacts of shortwave heating.
•surface net downward shortwave flux: This is the surface net downward shortwave flux I0−(x,y)
discussed in equation (17.1), and it is the shortwave heat flux entering through the top of the surface
ocean model grid cell. This heat flux is handled by ocean core/ocean sbc.F90, and it contributes to
the stf array as part of the temperature derived type.
The diagnostic table entry for I0−(x,y) is swflx, which is the surface net downward shortwave flux.
If there was zero penetrative shortwave radiation through the ocean column, then this flux would
represent the density and thickness weigthed convergence of shortwave flux impacting the surface
model grid cell. However, penetration is the norm, so there is another contribution to the net impacts
of shortwave radiation on the ocean.
•downward shortwave flux in seawater: This is the density and thickness weighted flux conver-
gence (units of W m−2) of shortwave heat that impacts a tracer grid cell, arising from the pene-
tration of shortwave radiation beneath the surface grid cell. This flux convergence is computed in
ocean param/sources/ocean shortwave.F90.
Because MOM typically includes the surface shortwave flux I0−(x,y) in the treatment of surface bound-
ary conditions (I(η) = 0 in equation (17.4)), the surface shortwave flux is excluded from the flux
convergence computed in ocean param/sources/ocean shortwave.F90 (equation (17.2)) in order to
avoid double counting. The diagnostic sw heat from ocean param/sources/ocean shortwave.F90
will thus have a negative flux convergence in the surface grid cell, since this convergence is computed
with a zero flux crossing the top of the surface grid cell.
Elements of MOM November 19, 2014 Page 252

Chapter 17. Surface and penetrative shortwave heating Section 17.4
•total impacts of shortwave radiation: Assuming the traditional MOM approach whereby surface
shortwave flux I0−(x,y) is included in the ocean core/ocean sbc.F90 module (I(η) = 0 in equation
(17.4)), to diagnose the full impacts of shortwave radiation requires the sum of two terms
net shortwave radiation heating at k=1=swflx +sw heat(k= 1).(17.11)
net shortwave radiation heating at k > 1 = sw heat(k > 1).(17.12)
Elements of MOM November 19, 2014 Page 253

Chapter 17. Surface and penetrative shortwave heating Section 17.4
Elements of MOM November 19, 2014 Page 254

Chapter 18
KPP for the surface ocean boundary
layer (OBL)
Contents
18.1 Elements of the K-profile parameterization (KPP) .....................256
18.1.1 Conventions .......................................... 257
18.1.2 General form of the parameterization ........................... 257
18.1.3 The vertical diffusivity .................................... 258
18.1.3.1 Boundary layer thickness ............................. 258
18.1.3.2 Measuring vertical distances within the OBL .................. 258
18.1.3.3 Vertical turbulent velocity scale wλ....................... 259
18.1.3.4 Non-dimensional vertical shape function Gλ(σ)................ 260
18.1.4 The non-local transport γλ.................................. 260
18.2 Surface ocean boundary momentum fluxes ..........................261
18.3 Surface ocean boundary buoyancy fluxes ...........................262
18.3.1 General features of buoyancy forcing ............................ 262
18.3.2 Temperature, salinity, and mass budget for a surface ocean model grid cell ...... 263
18.3.3 Salt fluxes from sea ice melt and formation ........................ 264
18.3.4 Salt and heat fluxes associated with water transport ................... 264
18.3.5 Non-penetrative surface heat fluxes ............................. 264
18.3.5.1 Longwave radiation ................................ 264
18.3.5.2 Latent heat fluxes .................................. 265
18.3.5.3 Sensible heat fluxes ................................ 265
18.3.5.4 Heating from frazil ................................. 265
18.3.6 Penetrative shortwave heating ................................ 265
18.3.7 Buoyancy budget for a surface ocean model grid cell ................... 265
18.3.8 Surface boundary terms contributing to ocean buoyancy evolution ........... 266
18.3.8.1 Heat carried by water transport .......................... 266
18.3.8.2 Salt carried by water transport .......................... 267
18.3.8.3 Penetrative radiation ................................ 267
18.3.8.4 Non-penetrative heating .............................. 267
18.3.8.5 Salt fluxes due to sea ice melt or formation ................... 267
18.3.9 Buoyancy forcing that acts on the OBL ........................... 268
18.4 Surface layer and Monin-Obukhov similarity ........................268
18.4.1 The surface layer ....................................... 269
255

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.1
18.4.2 Monin-Obukhov similarity theory ............................. 269
18.4.3 Similarity functions and length scale ............................ 270
18.5 Specifying the KPP parameterization .............................272
18.5.1 The turbulent vertical velocity scale wλ.......................... 272
18.5.1.1 Velocity scale with stable buoyancy forcing ................... 272
18.5.1.2 Velocity scale with unstable buoyancy forcing ................. 273
18.5.1.3 Summarizing properties of the turbulent velocity scale ............ 273
18.5.2 Similarity functions φΛ................................... 275
18.5.2.1 The Large et al. (1994) choices for unstable buoyancy forcing ........ 275
18.5.2.2 Alternative choices for unstable buoyancy forcing ............... 276
18.5.3 The shape function Gλ(σ).................................. 276
18.5.4 The non-local transport γλ.................................. 278
18.5.4.1 General features of γλwith the KPP parameterization ............. 278
18.5.4.2 Potential problems with the parameterized non-local transport ....... 279
18.5.5 The bulk Richardson number and the OBL thickness h.................. 279
18.5.5.1 Local gravitational stability ............................ 279
18.5.5.2 Non-local gravitational stability ......................... 281
18.5.5.3 The Ribcalculation ................................. 281
18.5.5.4 Unresolved shear Ut................................ 282
18.5.5.5 Restrictions on hunstable stable buoyancy forcing ............... 282
This chapter summarizes the KPP scheme originally proposed for the ocean surface boundary layer
by Large et al. (1994) as well as Large (1998). The material here forms the beginning of a community
research and development effort to merge elements of the KPP parameterization as implemented in MOM,
POP, and other codes. This community effort intends to remove some complications of the various KPP
implementations, introduce hooks for new physical features, and remove limitations and/or bugs in the
various codes.
The following MOM modules are directly connected to the material in this chapter:
ocean param/vertical/ocean vert kpp mom4p0.F90
ocean param/vertical/ocean vert kpp mom4p1.F90
ocean param/vertical/ocean vert kpp test.F90.
The modules ocean vert kpp mom4p0.F90 and ocean vert kpp mom4p1.F90 are frozen based on imple-
mentations in MOM4.0 and MOM4p1. The module ocean vert kpp test.F90 will be changing as a func-
tion of the ongoing research and development mentioned above. It is notable that the documentation is
somewhat further ahead than the code, in that some of the material presented in this chapter yet to be
implemented and tested.
18.1 Elements of the K-profile parameterization (KPP)
The ocean surface boundary layer (OBL) mediates the exchange of properties between the ocean and other
components of the climate system. Hence, parameterization of processes active in the OBL are fundamental
to the integrity of a climate simulation. The K-profile parameterization (KPP) is a widely used method for
parameterizing boundary layer processes in both the atmosphere and ocean. The paper by Large et al.
(1994) introduced this scheme to the ocean community for use in parameterizing processes in the surface
ocean boundary layer . The pedagogical lecture by Large (1998) provides added insight into the scheme
that complements some of the material in Large et al. (1994).
The KPP scheme has been used by many ocean climate studies for parameterizing mixing in the OBL,
with examples discussed in Large et al. (1997), Holland et al. (1998), Gent et al. (1998), Umlauf et al. (2005),
Elements of MOM November 19, 2014 Page 256
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.1
Li et al. (2001), Smyth et al. (2002),Durski et al. (2004), Chang et al. (2005)). We consider here only the
implementation of KPP for the surface ocean boundary layer, as implementations for the bottom do not
exist in MOM, nor are they well documented in the peer-review.
18.1.1 Conventions
We use the following conventions that are consistent with Large et al. (1994) and Large (1998).
• The fluid is assumed to be volume conserving Boussinesq, with extensions to a mass conserving non-
Boussinesq fluid trivial.
• The vertical direction, z, increases up with z= 0 defining the resting ocean surface. The ocean free
surface is defined by z=η(x,y,t) and the static ocean bottom is at z=−H(x,y).
• A lowercase λis used to denote a turbulent fluctuation of an arbitrary field within the surface ocean
boundary layer; e.g., a tracer such as potential or conservative temperature θand salinity s), or a
velocity component (u,v,w). Note that xis the notation used in Large et al. (1994) and Large (1998),
but we prefer the Greek letter λto avoid confusion with the horizontal spatial coordinate.
• An uppercase Λis used to denote the Eulerian mean of a tracer or velocity component within the
surface ocean boundary layer; e.g., potential or conservative temperature Θ, salinity S, or velocity
component (U,V ,W ). The Eulerian mean fields are time stepped by an ocean climate model within
the boundary layer, and correlations of turbulent variables must be parameterized to close the mean
field equations.
• The expression wλ is used to symbolize the Eulerian correlation of the fluctuating turbulent vertical
velocity and a fluctuating scalar or vector field. This correlation appears in the mean field time ten-
dency equation for Λin the Boussinesq primitive ocean equations (see equation (18.2)). KPP provides
a parameterization of this vertical turbulent flux within the surface ocean boundary layer.
• The mean and turbulent vertical velocity components, W ,w, are positive for upward motion. This
sign convention implies that
wλ > 0 =⇒turbulent flux for λtransported vertically upward.(18.1)
If λis the temperature, then a positive correlation at the ocean surface, w θ(η)>0, corresponds to
surface cooling.
18.1.2 General form of the parameterization
Ignoring all terms except vertical advective transport in the prognostic equation for the mean field Λ, its
time tendency is determined by
∂Λ
∂t =− ∂(WΛ)
∂z !− ∂(wλ)
∂z !.(18.2)
The advective flux by the mean vertical velocity, WΛ, is represented via a numerical advection operator. In
contrast, the turbulent correlation, wλ, is a subgrid scale flux that must be parameterized in order to close
the equation for Λ. Here, the overbar signifies an Eulerian averaging operator over unresolved turbulent
motions occurring within the OBL.
The KPP scheme provides a first order closure for wλ within the OBL. It does so by introducing two
terms in the following manner
wλ =−Kλ ∂Λ
∂z −γλ!.(18.3)
In effect, the KPP parameterization (18.3) splits the vertical turbulent flux into two terms
wλ =w λlocal +w λnon-local.(18.4)
Elements of MOM November 19, 2014 Page 257

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.1
The first term provides for the familiar downgradient vertical diffusion determined by a vertical diffusivity
and the local vertical derivative of the mean field. This term is referred to as the local portion of the
parameterization
wλlocal =−Kλ ∂Λ
∂z !,(18.5)
even though the diffusivity is a non-local function of boundary layer properties. The second term, γλ,
accounts for non-local transport that is not directly associated with local vertical gradients of Λ, in which
we have
wλnon-local =Kλγλ(18.6)
We next provide a general discussion of these two contributions to the KPP parameterization.
18.1.3 The vertical diffusivity
The vertical diffusivity arising from KPP in the OBL is determined as a non-local function of boundary
layer properties. It is written in the following form
Kλ(σ) = hwλ(σ)Gλ(σ).(18.7)
The diffusivity is a constructed as the product of three terms: the boundary layer thickness h, the vertical
turbulent velocity scale wλ(σ), and the vertical shape function Gλ(σ). Note that we introduce a dependence
of the shape function on the field diffused. As discussed in Section 18.5.3, this dependence arises from
matching to interior diffusivities, which generally differ as a function of λ.
18.1.3.1 Boundary layer thickness
The boundary layer thickness is denoted by
h≥0 is the boundary layer thickness.(18.8)
This is the thickness of the OBL prescribed by the KPP scheme, with details given in Section 18.5.5. The
direct dependence of the vertical diffusivity in equation (18.7) on the OBL thickness manifests the common
property of boundary layers, whereby thicker layers generally arise from stronger eddy motions and are
thus associated with more rapid mixing of tracer concentration and momentum.
Figure 18.1 provides a schematic of the KPP boundary layer, the Monin-Obukhov surface layer, and
the associated momentum, mass, and buoyancy fluxes impacting these layers. Details of this figure will be
explored in the following.
18.1.3.2 Measuring vertical distances within the OBL
When measuring distances within the boundary layer, it is the thickness of the water as measured from the
ocean surface that is important. Free surface undulations can be a nontrivial fraction of the boundary layer
thickness, particularly under conditions of stable buoyancy forcing. Hence, we make explicit note that the
ocean has an undulating free surface at z=η(x,y,t), which contrasts to Large et al. (1994) and Large (1998),
where it is assumed that z= 0 sets the upper ocean surface.
Following Large et al. (1994), we introduce the non-dimensional depth, σ, given by
σ=d
h.(18.9)
In this definition, d≥0 is the distance from the ocean surface at z=ηto a point within the boundary layer
d=−z+η. (18.10)
Likewise, h≥0 is the distance from the free surface to the bottom of the boundary layer
h=hobl +η, (18.11)
Elements of MOM November 19, 2014 Page 258
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.1
where hobl is the depth of the boundary layer as measured from z= 0. That is, his the thickness of the OBL,
and it is this thickness, not hobl , that is predicted by KPP (Section 18.5.5). Regions within the boundary
layer are given by the non-dimensional depth range
0≤σ≤1 within boundary layer, (18.12)
with σ= 0 the ocean surface and σ= 1 the bottom of the boundary layer.
air-sea or ice-sea interface:z=η
BR,Bf,τ,Qm
surface fluxes
penetrative
shortwave
h
KPP boundary
layer thickness:h
Monin-Obukhov surface layer
ocean bottom: z=−H
geothermal
Figure 18.1: Schematic of the upper ocean boundary layer regions associated with the KPP boundary layer
parameterization. The upper ocean is exposed to non-penetrative air-sea and ice-sea fluxes of momentum
τ(Section 18.2), mass Qm(Section 18.3), and buoyancy Bf(Section 18.3). In addition, there is penetra-
tive shortwave radiation, −w θR(Section 18.3), indicated by the exponentially decaying vertical sinusoidal.
The Monin-Obukhov surface layer (Section 18.4) has a thickness h, with ≈0.1. The surface layer is
where turbulence delivers fluxes to the molecular skin layer for transfer to the atmosphere or ice. The sur-
face layer starts from just beneath the surface roughness elements at the upper ocean interface. Since
neither these roughness elements, nor the molecular viscous sublayer, are resolved in ocean models, we
assume in practice that the Monin-Obukhov surface layer extends to the sea surface at z=η(x,y,t). The
KPP boundary layer includes the surface layer, and it has a thickness h(x,y,t)determined by the KPP pa-
rameterization (Section 18.5.5). The ocean bottom at z=−H(x,y)is rigid and is exposed to geothermal
heating. Presently, the KPP boundary layer scheme has not been implemented in MOM to parameterize
bottom boundary layer physics, though nothing fundamental precludes such. In fact, Durski et al. (2004)
provide just such an implementation.
18.1.3.3 Vertical turbulent velocity scale wλ
The velocity scale wλis a function of depth within the boundary layer, and a function of the field to which
it refers. We return to its specification in Section 18.5.1.
Elements of MOM November 19, 2014 Page 259

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.2
18.1.3.4 Non-dimensional vertical shape function Gλ(σ)
Non-dimensional vertical shape function Gλ(σ) is used to smoothly transition from the ocean surface to
the bottom of the boundary layer. Large et al. (1994) chose a cubic polynomial
Gλ(σ) = a0+a1σ+a2σ2+a3σ3.(18.13)
Since turbulent eddies do not cross the ocean surface at σ= 0, we should correspondingly have a vanishing
diffusivity at σ= 0. This constraint is satisfied by setting
a0= 0.(18.14)
We detail in Section later how to specify the remaining expansion coefficients a1,a2,a3. In particular, we
simplify the specification of Large et al. (1994), with their approach more complex than justified physically.
18.1.4 The non-local transport γλ
Section 2 of Large et al. (1994) notes the presence of many processes in the boundary layer that lead to
nonlocal transport. This behaviour leads to a diffusivity Kλthat is a function of the surface fluxes and
boundary layer thickness h. Furthermore, under convective forcing (negative surface buoyancy forcing;
Bf<0), fluxes can penetrate into stratified interior. This characteristic then motivates the introduction of a
non-local transport term γλto the KPP parameterization (equation (18.3)) when Bf<0. To further identify
the need for a non-local transport term γλ, we reproduce Figure 1 from Large et al. (1994), here shown
as Figure 18.2. The caption to Figure 18.2 explores the many facets of this figure used to help justify the
non-local term in KPP.
As part of the KPP parameterization, the non-local transport, γλ, aims to account for such processes as
boundary layer eddies whose transport may be unrelated to the local vertical gradient of the mean field, and
whose impacts may penetrate within the stratified ocean interior. In general, Large et al. (1994) prescribe
the following characteristics to γλ.
• Page 371 of (Large et al.,1994) notes that there is no theory for non-local momentum transport, and
so the non-local transport directly affects only the tracer fields:
γλ=(0 if λ= (u,v,w) a velocity component
,0 nonzero if λ=θ,s or another tracer. (18.15)
However, Smyth et al. (2002) consider a non-local term for momentum, thus motivating further re-
search to see whether it is suitable for climate modeling.
• The non-local transport is non-zero only within the OBL:
γλ=(0 if σ > 1
,0 if 0 ≤σ≤1. (18.16)
• The non-local transport is non-zero only in the presence of destabilizing negative surface ocean buoy-
ancy flux, whose presence gives rise to convective mixing:
γλ=(0 for positive (stabilizing) surface buoyancy forcing
,0 for negative (destabilizing) surface buoyancy forcing. (18.17)
• The non-local transport can give rise, under certain conditions, to either down-gradient or up-gradient
transport of the mean tracer field. Hence, it can either act to smooth gradients of mean fields (down-
gradient non-local fluxes) or enhance gradients (upgradient non-local fluxes).
In Section 18.5.4, we provide to the KPP parameterization of γλ.
Elements of MOM November 19, 2014 Page 260
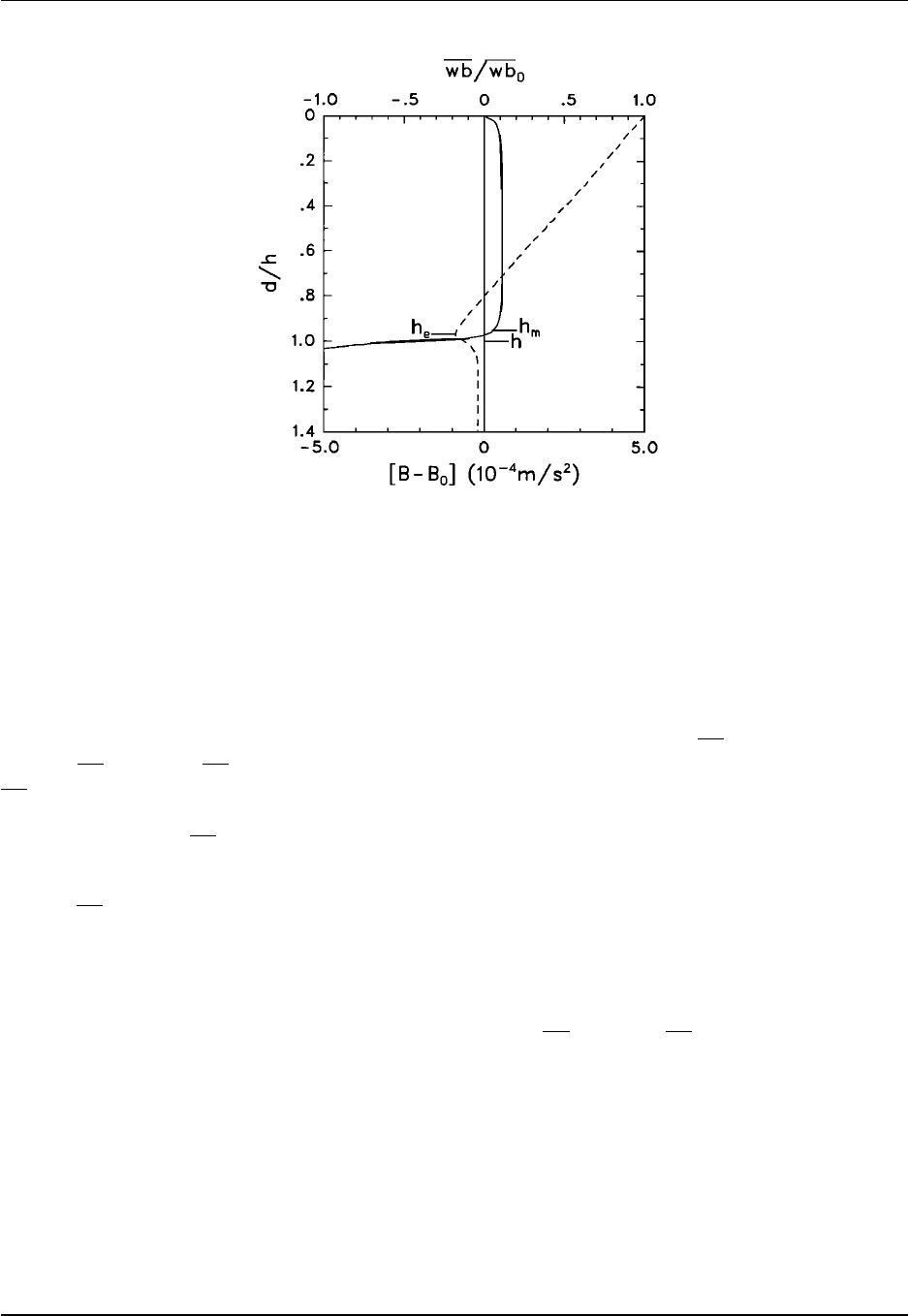
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.2
366 ß Large et al.' OCEANIC VERTICAL MIXING 32, 4 / REVIEWS OF GEOPHYSICS
-lO
o
.2
.4
.6
ß 8 -
1.0
1.2
1.4 '
-5.0
wb/•'b o
- .5 0 .5
, I '
/
,/
/
/
/
,/
h ///
e •'- _•h m
i i i i i
o
EB- Bo] (10-4m/s 2)
/
/
/
/
/
/
/
/
lO
5.0
Figure 1. Relative buoyancy (solid trace, bottom scale) and
buoyancy flux (dashed trace, top scale) profiles after 3.0
days of convective deepening into an initially uniformly
stratified water column of OzT = 0.1øC m -1, N = 0.016 s -1,
under the action of a steady cooling, Q t = -100 W m -2.
Axes have been normalized with a boundary layer depth, h
= 13.6 m and a surface buoyancy flux, wbo - 6.3 x 10- 8
m 2 s -3. Also shown are the entrainment depth, he, and the
mixed layer depth, h,n.
properties and gradients, local fluxes depend on
boundary layer parameters such as the surface fluxes
and h. Important characteristics of nonlocal behavior
are the coherent structures that can be detected in
PBLs [Mahr! and Gibson, 1992]. Coherent structures
identified in the turbulent ABL include buoyant verti-
cal plumes, convergence lines, sweeps, microbursts,
horizontal roll vortices, mesoscale cellular convective
elements, Kelvin-Helmholtz waves, and internal grav-
ity waves. Most of these structures are described by
Stull [1988]. After surface and internal gravity waves,
the most important coherent structures in the OBL are
thought to be Langmuir cells [Weller and Price, 1988].
These are near-surface, counterrotating vortices with
horizontal axes that are nearly aligned with the mean
wind. Their dynamics are not well understood, but in
the model of Craik and Leibovich [1976] they are
generated by the interaction between the surface grav-
ity wave induced current (Stokes drift) and the wind-
driven current. It is uncertain what role Langmuir
upward buoyancy flux • > 0 in locally stable or
neutral regions where the mean buoyancy increases or
remains constant with height. In general, such fluxes
can be present with any gradient, so nonlocal transport
[Holtslag and Boville, 1993] is a more general term
that also applies to passive scalar transports. This
feature of convection is generally observed throughout
the central 50% or more of both atmospheric and
laboratory boundary layers [Deardorff, 1966] and of
LES experiments [Deardorff, 1972b; Holtslag and
Moeng, 1991]. In Figure 1 it dominates the region 0.35
< d/h < 0.80. Different theoretical considerations
lead to the same result, namely, that the heat flux
should have a nonlocal convective transport in addi-
tion to the familiar local downgradient component.
Theoretical expressions for the countergradient heat
flux have been derived from the turbulent evolution
equation for 0tw0. Deardorff[ 1972b] finds that it arises
from the buoyant production term, while Holtslag and
Moeng [1991] find the turbulent transport term respon-
sible. Holtslag and Moeng [1991] use LES data to
evaluate both these possibilities and find that both give
similar nonlocal behavior throughout the central re-
gion of the boundary layer despite the differing phys-
ics.
Wyngaard and Brost [1984] suggest that another
fundamental property of convective boundary layers is
that the vertical diffusivity profile for passive scalars is
radically different depending on whether the property
fluxes are driven by entrainment or surface fluxes.
Because they were considering the ABL, entrainment-
driven diffusion was termed "top-down" and the more
familiar surface-driven diffusion was termed "bottom-
up." Furthermore, they attribute this peculiar behav-
ior to vertical asymmetry. An observed characteristic
of this asymmetry is that buoyant plumes are horizon-
tally narrower and have larger vertical velocities than
the more diffuse return flows. Wyngaard and Brost
[1984] present LES results that confirm that entrain-
ment-driven diffusivities are significantly smaller than
surface-driven diffusivities. An important implication
is that a single diffusivity defined for the total process
may be ill behaved but that the two processes can be
parameterized separately and later superimposed.
However, Holtslag and Moeng [1991] use the LES
data of Moeng and Wyngaard [1989] and obtain well-
behaved expressions by incorporating a nonlocal
transport term in the flux parameterizations. Entrain-
ment-driven diffusion may be very important in the
ci_r•ulatipn phys_in thepc•.an, but We!!er_et aL_[!984] ...... ocean,_. where it_.is__the_ prin_cipa!___sourc_.e.gf_. sglt and
suggest that it could be an important factor in trans-
porting properties that are not uniformly distributed
within the mixed layer.
Figure 1 illustrates expected profiles of buoyancy
and buoyancy flux in a convective oceanic boundary
layer. One manifestation of nonlocal behavior found in
such boundary layers is what is traditionally termed
countergradient heat flux. This flux is characterized by
nutrients to the OBL.
In the case of a purely convective boundary layer,
u* = 0 and Bf < 0, eroding into a region of stable
stratification (Figure 1), the entrainment depth he,
where the negative buoyancy flux is maximum, is less
than the boundary layer depth h. The mixed layer
depth hm can depend a great deal on definition [Lukas
and Lindstrom, 1991]. Here it is arbitrarily taken as
Figure 18.2: This is a reproduction of Figure 1 from Large et al. (1994). The figure is derived from a
one-dimensional simulation after 3 days of convective deepening (zero winds; negative surface buoyancy
forcing) into initially uniformly stratified water column. The vertical axis is vertical distance starting from
the ocean surface interface at z=ηand d= 0, extending down to d=h(h= 13.6m at this point of the
integration), which is the base of the boundary layer, and finally to d= 1.4h, which is beneath the boundary
layer.
The horizontal axis on the bottom is the mean buoyancy, B, relative to that at the surface, B0, and the
profile is depicted by the solid line. Positive values of B−B0indicate that the mean buoyancy at a point is
larger than at the surface, with B−B0>0expected under negative buoyancy forcing at the ocean surface.
The horizontal axis on the top is the ratio of the local turbulent buoyancy flux wb to the surface turbu-
lent flux wbη(denoted wb0by Large et al. (1994)). The dashed line depicts this ratio. Positive values of
wb represent upward turbulent buoyancy fluxes; e.g., upward fluxes of heat for the case where buoyancy
is determined by temperature, and the thermal expansion coefficient is positive.
Positive values for w b in regions between roughly 0.35 < d < 0.8represent upward turbulent buoyancy
fluxes in a region where the mean vertical gradient of Bis nearly zero, thus indicating non-local turbulent
transport. In shallower regions with d < 0.35, the mean gradient is negative, ∂zB < 0, and the fluxes are
positive, wb > 0, thus representing downgradient turbulent fluxes. Likewise, for d > 0.8, the turbulent fluxes
are downgradient.
The mixed layer depth is denoted by hm, though this depth is subject to arbitrary specification of the
density difference. The entrainment depth is he, with this depth taken where the buoyancy flux reaches a
negative extrema. Note that it is an empirical result that under pure convective forcing (τ= 0,Bf<0), the
turbulent entrainment flux is roughly 20% of the surface flux: w bd=he=−βTwbd=0, where βT= 0.2. This
situation is depicted in the figure.
18.2 Surface ocean boundary momentum fluxes
In this section and Section 18.3, we present features of how surface boundary fluxes force the upper ocean,
largely following Appendix A of Large et al. (1994). The aim is to identify how surface boundary fluxes
impact the upper ocean, with this characterization then used in Section 18.4 to help establish some basic
features of ocean boundary layers. These ideas are then used in Section 18.5 to specify the diffusivity and
Elements of MOM November 19, 2014 Page 261

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.3
non-local transport from the KPP parameterization.
Vertical exchange of momentum across the atmosphere-ocean or sea-ice-ocean boundary occurs largely
through turbulent processes. The resulting horizontal stress vector acting on the ocean, τ, is determined
through application of a bulk formula (e.g., see Appendix C of Griffies et al.,2009). For our purposes,
we assume τis given, thus yielding the ocean kinematic fluxes associated with the turbulent transport of
momentum across the ocean surface
−wuη= τ
ρ(η)!≈ τ
ρ0!.(18.18)
In this equation, ρ(η) is the surface ocean density, which is commonly approximated by the constant Boussi-
nesq reference density ρ0. A positive sign on a component of τacts to accelerate the flow in the respective
direction, whereas a positive sign to a component of wuηremoves momentum from the ocean. These sign
conventions give rise to the minus sign in the relation (18.18). In addition to defining the kinematic surface
fluxes, knowledge of τallows us to compute surface boundary layer velocity scales when working within
the Monin-Obukhov similarity theory (Section 18.4.2).
In addition to turbulent momentum transfer, momentum is also transported through mass exchange
across the ocean surface, since water transported across the ocean generally carries a nonzero momentum.
This advective momentum boundary exchange is typically ignored for climate models, though Kantha and
Clayson (2000) (see their page 431) make the case for including this effect, particularly when resolving
strong atmospheric storms. They also make the case for including this effect in computing the Monin-
Obukhov length scale defined by equation (18.65)) (see their equation (4.3.11)).
18.3 Surface ocean boundary buoyancy fluxes
Turbulent and advective fluxes of momentum and buoyancy are transferred across the upper ocean surface
boundary, with ocean processes such as advection and mixing then transporting the boundary momentum
and buoyancy laterally as well as into the ocean interior. In contrast, penetrative shortwave radiation is
absorbed into the ocean absent ocean transport processes, with such absorption a function of ocean op-
tical properties. In the unphysical case of perfectly transparent seawater, shortwave radiation penetrates
through the boundary layer and so has no influence on boundary layer processes. In realistic cases, much
of the shortwave radiation is absorbed in the boundary layer, with only a fraction leaking through to the
interior. In general, such non-turbulent and non-advective transport of buoyancy via penetrative radia-
tion represents a fundamentally novel aspect of ocean boundary layer physics relative to the atmosphere.
Namely, for the atmosphere, radiative absorption is far less relevant than in the upper ocean, since the
atmosphere is largely transparent to radiation. We therefore consider penetrative shortwave radiation as
distinct from other buoyancy fluxes when formulating how boundary fluxes impact the ocean.
18.3.1 General features of buoyancy forcing
The buoyancy of a fluid is commonly defined as (e.g., page 83 of Large (1998))
B=g ρ0−ρ
ρ0!,(18.19)
where gis the constant gravitational acceleration, and ρ0is a reference density, taken here to equal the
Boussinesq reference density. A reduction in density is associated with an increase in buoyancy; that is,
the water becomes more buoyant. Changes in buoyancy arise through changes in density associated with
temperature and salinity changes, since buoyancy changes are computed relative to a fixed pressure level.
In this way, buoyancy changes are directly related to processes that impact locally referenced potential
density.
Ocean buoyancy is affected through surface ocean heat, salt, and water fluxes.
• Turbulent processes transfer heat through latent and sensible heating.
• Longwave radiation cools the upper ocean, with this radiation affected by the upper ocean boundary
temperature.
Elements of MOM November 19, 2014 Page 262

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.3
• Penetrative shortwave radiation is absorbed in seawater.
• The transfer of salt occurs when sea ice melts and forms. This transfer is proportional to the water
mass flux and the difference in salinity between the liquid ocean and sea ice. More generally, we
simply consider this to be a salt flux between sea ice and ocean, with this flux operationally computed
as part of a sea ice model.
• Advective processes transfer heat and salt across the ocean surface through the transfer of water mass
across the interface.
We further detail these fluxes in the following.
18.3.2 Temperature, salinity, and mass budget for a surface ocean model grid cell
Buoyancy is not a prognostic variable in ocean models. So to develop a quantative understanding of how
buoyancy is impacted by surface fluxes, we consider the evolution of temperature, salinity, and mass in
an arbitrary top model grid cell, and focus exclusively on evolution arising from surface boundary fluxes.
We write these budgets in their finite volume sense (as implemented in MOM), which includes density and
thickness weighting
∂t(ρdzΘ) = QmΘm−Qnon-pen
θ+Qpen
θ(z=η)−Qpen
θ(z=−∆z)(18.20)
∂t(ρdzS) = QmSm−QS(18.21)
∂t(ρdz) = Qm.(18.22)
We now detail the terms appearing in these equations.
•ρdzis the mass per horizontal area of seawater in the grid cell. For a volume conserving Boussinesq
fluid, ρis set to the constant reference density ρ0.
•Θis the grid cell potential temperature or conservative temperature.
•Sis the grid cell salinity.
•Qmis the mass flux (kgm−2sec−1) of water crossing the ocean surface, with Qm>0 for water entering
the ocean (as when precipitation plus runoffexceeds evaporation).
•Θmis the temperature of water crossing the ocean surface, and CpQmΘmis the associated heat flux
(Wm−2). We further discuss this heat flux in Section 18.3.4.
•Smis the salinity of water crossing the ocean surface, and QmSmis the associated mass flux. Note that
Smis typically taken to be zero, as for precipitation and evaporation. However, rivers can contain a
nonzero salt concentration, so we keep Smfor the following formulation. We further discuss this salt
flux in Section 18.3.4.
•Cpis the seawater heat capacity at constant pressure (Jkg−1◦C−1). IOC et al. (2010) provides the most
precise value appropriate for an ocean with heat measured through conservative temperature.
•QSis the flux of salt (kgm−2sec−1) that leaves the ocean through the ocean surface. This flux arises in
the transfer of salt when sea ice forms and melts. We further discuss this salt flux in Section 18.3.3.
•CpQnon-pen
θis the non-penetrative surface heat flux associated with turbulent processes (latent and sen-
sible) and radiative longwave cooling (Wm−2). The sign convention is chosen so that Qnon-pen
θ>0 for
heat leaving the ocean surface (i.e., ocean cooling). We further discuss this heat flux in Section 18.3.5.
•CpQpen
θ(z=η) is the radiative shortwave heat flux (Wm−2) entering the ocean through its surface
at z=η, with Qpen
θ(η)>0 warming the ocean surface. Likewise, CpQpen
θ(z=−∆z) is the radiative
shortwave heat flux leaving the top cell through its bottom face. We further discuss this heat flux in
Section 18.3.6.
Elements of MOM November 19, 2014 Page 263

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.3
18.3.3 Salt fluxes from sea ice melt and formation
The mass flux of salt QS(kgm−2sec−1) is positive for salt leaving the ocean surface. There is transport
of salt across the ocean surface when sea ice forms and melts, due to the nonzero salt content in sea ice.
Otherwise, the surface salt flux is generally zero for the large scale ocean. For ocean models, however,
the salt flux can be nonzero when formulating the surface boundary in terms of virtual salt fluxes rather
than real water fluxes (Huang,1993;Griffies et al.,2001). This formulation is not recommended, as it is
distinctly unphysical and unnatural when using an explicit free surface or bottom pressure solver as in
MOM.
18.3.4 Salt and heat fluxes associated with water transport
In most cases, salinity in the water fluxed across the ocean surface is zero, so that Sm= 0. However, there are
some cases where rivers have a nonzero salinity so that Sm,0 and the product QmSmleads to an advective
transport of salt across the ocean surface.
Since water transported across the ocean has a nonzero heat content, this transport in turn affects the
net heat content in the upper ocean. One can either prescribe the temperature of this water, Θm, or the
product QmΘm. Consider the case where the product is specified for river water entering the ocean, which
is the case with the GFDL land model. In this case, the heat flux with respect to 0◦C(in units of W m−2) of
liquid river runoffHliquid runoffis given to the ocean from the land model, so that
QmΘm=Hliquid runoff
Cliquid runoff
p
,(18.23)
with Cliquid runoff
pthe heat capacity of the water coming in from the river runoff. Likewise, if the heat associated
with frozen runoff(e.g., calving land ice) is provided by the land model, then we have
QmΘm=Hsolid runoff
Csolid runoff
p,(18.24)
with Csolid runoff
pthe heat capacity of the solid runoff. These two heat capacities are typically provided by the
component model (i.e., the land model) used to compute the runofffields. Similar considerations hold for
transfer of water betwen sea ice models and the ocean.
18.3.5 Non-penetrative surface heat fluxes
The heat flux CpQnon-pen
θ(Wm−2) is defined with a sign so that it is positive for heat leaving the ocean. This
flux is comprised of the following contributions (see page 34 of Gill,1982)
CpQnon-pen
θ=Qlong +Qlatent +Qsens +Qfrazil.(18.25)
Longwave, latent, and sensible heat fluxes are typically deposited or withdrawn from the ocean surface
layer (Section 18.4). In practice, ocean models assume these fluxes are taken entirely from the surface grid
cell. Frazil is slightly different, as it represents the heat exchanged during the production of sea ice, and sea
ice can generally form at various levels in the upper ocean. Many ocean models assume frazil production
occurs just in the top grid cell. But that assumption is not fundamental, nor is it correct when models refine
their vertical grid spacing. We thus allow for frazil to have a depth dependence.
All of these fluxes are termed non-penetrative, since they are deposited or withdrawn from the liquid
ocean at a particular depth. Transport of the boundary buoyancy to another depth occurs only through
the action of ocean transport processes, such as advection or mixing. This behaviour contrasts to that of
penetrative shortwave radiation, which is transferred to depths as a function of seawater optics, so does not
depend on ocean transport. We now comment in a bit more detail on the various non-penetrative fluxes.
18.3.5.1 Longwave radiation
Qlong is the longwave radiation leaving the ocean in the form of the σSB T4Stefan-Boltzmann Law, so that
Qlong is typically positive, thus generally cooling the ocean surface.
Elements of MOM November 19, 2014 Page 264

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.3
18.3.5.2 Latent heat fluxes
Qlatent arises from phase changes whereby liquid seawater either evaporates, or it acts to melt frozen pre-
cipitation. When seawater evaporates, the latent heat lost by the ocean is determined by the latent heat of
vaporization for fresh water
Hvapor = 2.5×106Jkg−1,(18.26)
so that
Qevap =Hvapor Qevap
m(18.27)
where Qevap
mis the mass flux (kgm−2sec−1) of fresh water leaving the ocean due to evaporation. A similar
expression holds when seawater melts frozen precipitation (e.g., snow), in which case
Hfusion = 3.34 ×105Jkg−1,(18.28)
so that
Qmelt =Hfusion Qfrozen precip
m,(18.29)
where Qfrozen precip
mis the mass flux (kgm−2sec−1) of frozen precipitation falling onto the ocean surface. Both
Qevap and Qmelt are positive, indicating that they act to cool the ocean.
18.3.5.3 Sensible heat fluxes
Qsens is the sensible heat transfer proportional to the difference between atmosphere and ocean tempera-
tures. Sensible heating generally acts to cool the ocean, particularly near western boundary currents such
as the Gulf Stream, Kuroshio, and Agulhas.
18.3.5.4 Heating from frazil
As the temperature of seawater cools to the freezing point, sea ice is formed, initially through the produc-
tion of frazil ice. Operationally in an ocean model, liquid water can be supercooled at any particular time
step through surface fluxes and transport. An adjustment process is used in the models to heat the liquid
water back to the freezing point, with this positive heat flux Qfrazil >0 extracted from the ice model as frazil
sea ice is formed.
18.3.6 Penetrative shortwave heating
The penetrative shortwave radiative heat flux CpQpen
θ>0 arises from the net shortwave radiation entering
through the ocean surface and absorbed by seawater. This heat flux does not arise from turbulent or ad-
vective processes, which makes it distinct from other heat and salt fluxes impacting the ocean through its
upper boundary. This radiation is not generally deposited entirely within the ocean surface layer or the
top ocean model grid cell. Instead, a fraction of this radiation can penetrate to beneath the surface ocean
grid cell, with the fraction depending on the optical properties of seawater. Hence, we subtract a heat
flux CpQpen
θ(z=−∆z), which represents the radiative shortwave heat flux passing through the bottom of the
surface ocean cell at z=−∆z. It is the difference,
net shortwave heating of surface grid cell = CpQpen
θ(z=η)−Qpen
θ(z=−∆z)(18.30)
that stays in the surface grid cell. When considering the same budget for the surface ocean boundary layer,
we are interested in the shortwave flux that penetrates through the bottom of the boundary layer at z=−h.
18.3.7 Buoyancy budget for a surface ocean model grid cell
We now bring the previous fluxes together to form the budget for buoyancy in a surface grid cell due to the
impacts of surface fluxes. The resulting expression is then used to derive an expression for the buoyancy
forcing that acts on the ocean surface boundary layer. Buoyancy (equation (18.19)) has a time tendency
given by
− ρ0
g!∂B
∂t =ρ,Θ
∂Θ
∂t +ρ,S ∂S
∂t ,(18.31)
Elements of MOM November 19, 2014 Page 265

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.3
where we introduced the shorthand notation
ρ,Θ= ∂ρ
∂Θ!S,p
(18.32)
ρ,S = ∂ρ
∂S !Θ,p
(18.33)
for the partial derivatives of density with respect to conservative temperature and salinity, respectively,
each with pressure held constant. We wish to form an evolution equation for buoyancy at the ocean surface
grid cell just due to the effects of surface forcing. For this purpose, multiply the temperature equation
(18.20) by ρ,Θand add to the surface salinity equation (18.21) multiplied by ρ,S
ρ,Θ(ρdzΘ),t +ρ,S (ρdzS),t =Qm(ρ,ΘΘm+ρ,S Sm) + ρ,Θ−Qnon-pen
θ+δkQpen
θ−ρ,S QS,(18.34)
where we introduced the shorthand
δkQpen
θ=Qpen
θ(z=η)−Qpen
θ(z=−∆z).(18.35)
We now use the mass budget (18.22) and introduce the buoyancy tendency according to equation (18.31)
to realize an expression for the time tendency of the surface ocean buoyancy
(ρ0/g)ρdz ∂B
∂t !=Qmρ,Θ(Θ−Θm) + ρ,S (S−Sm)+ρ,ΘQnon-pen
θ−δkQpen
θ+ρ,S QS.(18.36)
Now introduce the thermal expansion and saline contraction coefficients
α=−1
ρ ∂ρ
∂Θ!S,p
(18.37)
β=1
ρ ∂ρ
∂S !Θ,p
(18.38)
to render
dz ∂B
∂t !=g
ρ0Qm[−α(Θ−Θm) + β(S−Sm)]+α(δkQpen
θ−Qnon-pen
θ) + β QS.(18.39)
18.3.8 Surface boundary terms contributing to ocean buoyancy evolution
We now summarize the various surface boundary terms appearing on the right hand side of the surface
buoyancy budget (18.39).
18.3.8.1 Heat carried by water transport
Assuming a positive thermal expansion coefficient, α > 0, the term −Qmα(Θ−Θm) reduces ocean buoyancy
when adding water Qm>0 to the ocean that is colder than the surface ocean temperature, Θ=Θk=1. The
opposite occurs in regions of cold fresh waters, such as the Baltic, where α < 0. In such cases, adding
water to the ocean that is colder than the sea surface temperature increases seawater buoyancy. We now
consider in turn the three cases evaporation, precipitation, and liquid river runoffand indicate how they
are typically treated in climate models.
• It is quite accurate to assume that evaporating water leaves the ocean at the sea surface temperature,
so that
Θevap =Θk=1,(18.40)
in which case there is no change to ocean buoyancy upon transfer of evaporating water across the
ocean surface. This is the approach taken by all ocean climate models.
Elements of MOM November 19, 2014 Page 266

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.3
• Precipitating liquid water need not fall on the ocean at the sea surface temperature, so that
Θprecip ,Θk=1 real world.(18.41)
Kantha and Clayson (2000) (see their page 429) discuss this difference, and the associated transfer of
heat across the ocean due to rain events, particularly in the West Pacific. However, we know of no
climate modeling application in which the atmospheric model component carries information about
the temperature of its condensed water, nor the heat content of that water. Hence, operationally all
climate modeling applications assume that
Θprecip =Θk=1 climate models,(18.42)
in which case there is no change in ocean buoyancy upon transfer of precipitating liquid water across
the ocean surface.
• Realistic river models carry the heat content of river water and pass this content to the ocean model
at river mouths. Following from the discussion surrounding equation (18.23), we may thus write the
river contribution to the buoyancy budget in the form
−Qmα(Θ−Θm) = α −QmΘ+Hliquid runoff
Cliquid runoff
p!.(18.43)
Depending on the heat content of liquid runoffrelative to the sea surface, ocean buoyancy may in-
crease or decrease when liquid runoffenters the ocean.
18.3.8.2 Salt carried by water transport
The haline contraction coefficient, β, is generally positive. Hence, the term Qmβ(S−Sm) increases ocean
buoyancy for those cases where the sea surface salinity, Sk=1, is greater than the salinity of the water trans-
ferred across the ocean surface. Most applications assume Sm= 0, such as for evaporation and precipitation
Sevap = 0 (18.44)
Sprecip = 0.(18.45)
However, river models sometimes consider a nonzero salinity of the runoff, in which case
Sliquid runoff,0.(18.46)
18.3.8.3 Penetrative radiation
Shortwave radiation is absorbed by seawater as it penetrates from the surface into the upper ocean. Hence,
δkQpen
θ>0 so that radiation increases the grid cell buoyancy.
18.3.8.4 Non-penetrative heating
Longwave, latent, and sensible heating generally cool the upper ocean, and so lead to a decrease in ocean
buoyancy. In contrast, frazil heating in sea ice regions increases buoyancy. The net effect from the non-
penetrative heat fluxes, Qnon-pen
θ, can be to either increase or decrease buoyancy.
18.3.8.5 Salt fluxes due to sea ice melt or formation
Salt is exchanged with the ocean when sea ice melts and forms, so that the term β QScan either increase
(when salt is removed from the liquid ocean) or decrease (when salt is added to the liquid ocean) buoyancy.
Elements of MOM November 19, 2014 Page 267
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.4
18.3.9 Buoyancy forcing that acts on the OBL
The expression (18.39) for the buoyancy forcing from surface fluxes acting on a surface grid cell is now ex-
tended to an expression for the buoyancy forcing on the OBL. The only subtle point concerns the treatment
of penetrative shortwave radiation. Rather than consider that radiation leaving the bottom of the surface
cell at z=−∆z, we are now concerned with that leaving the bottom of the boundary layer at z=−h. We also
multiply this penetrative flux by the thermal expansion coefficient at that depth, rather than the expansion
coefficient in the ocean surface cell. In this way we write the buoyancy forcing acting on the boundary layer
Bf=g
ρ0hQm[−α(Θ−Θm) + β(S−Sm)] −α Qnon-pen
θ+β QSi+α Qpen
θz=η−α Qpen
θz=−h.(18.47)
This expression for the net buoyancy forcing acting on the boundary layer can be written as the sum of two
terms
Bf=−wbη+BR.(18.48)
The first term takes the form of a kinematic turbulent flux at the ocean surface
−wbη=g
ρ0hQm[−α(Θ−Θm) + β(S−Sm)] −α Qnon-pen
θ+β QSi,(18.49)
where the minus sign on the left hand side accounts for the assumption that w > 0 for upward velocity. The
second term accounts for the penetrative radiation, which is neither a turbulent flux nor advective flux
BR=α Qpen
θz=η−α Qpen
θz=−h.(18.50)
The corresponding heat flux convergence onto the boundary layer is given by (see equation (A4) of Large
et al. (1994))
QR=Qpen
θz=η−Qpen
θz=−h.(18.51)
Notably, BR, and hence Bf, are two-dimensional functions of the boundary forcing, even though they de-
pend on the depth to which the penetrative radiation extends.
18.4 Surface layer and Monin-Obukhov similarity
The semi-empirical Monin-Obukhov similarity theory has proven quite useful in describing general fea-
tures of boundary layer turbulence active in the atmospheric planetary boundary layer (see, e.g., Section 3.3
of Kantha and Clayson,2000). One may thus choose to apply these ideas to the ocean planetary boundary
layer, particularly since the atmospheric boundary layer is far better measured than the ocean, and there
are certain features that are similar. However, before applying the Monin-Obukhov similarity theory to the
ocean, we acknowledge some characteristics of the ocean surface boundary layer that distinguish it from
atmospheric boundary layers.
• Surface ocean gravity waves can impact a nontrivial fraction of the ocean surface boundary layer,
whereas such waves only impact a small fraction of atmospheric boundary layers.
• The surface ocean velocity is generally the largest velocity in the ocean. In contrast, the surface
atmospheric velocity vanishes over land and is relatively small over the ocean.
• The surface ocean absorbs shortwave solar radiation, whereas the atmosphere is nearly transparent
to radiation.
Despite these basic distinctions between planetary boundary layers in the atmosphere and ocean, Large
et al. (1994) used the Monin-Obukhov similarity theory to introduce scales for turbulent fluctuations and
to identify non-dimensional similarity functions in the ocean surface layer.
Elements of MOM November 19, 2014 Page 268
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.4
18.4.1 The surface layer
A molecular layer exists within roughly a millimetre of the upper ocean interface, with this layer dominated
by molecular viscous and diffusive effects (Large,1998). Since it is dominated by molecular viscous effects,
this layer is not turbulent and thus leads to negligible mixing of tracer and momentum. It is the molecular
layer that ultimately transfers properties between the ocean and atmosphere or ice, including momentum
and buoyancy. The more this layer is “corrugated” through wave breaking and other turbulent action, the
faster properties are transferred across the surface ocean interface.
The ocean surface layer (Figure 18.1) is a turbulent layer whose turbulent fluxes are roughly independent
of distance from the upper boundary; i.e., the surface layer is nearly a constant flux layer. The surface layer
starts just beneath the molecular viscous layer. Turbulence within the surface layer delivers properties to
the molecular layer for transfer to the atmosphere or ice. Given that no ocean model resolves the molecular
sublayer, the upper ocean interface at z=η(x,y,t) in an ocean model operationally starts at the top of the
surface layer.
18.4.2 Monin-Obukhov similarity theory
The surface turbulent layer is of fundamental importance for determining the rate that properties are
transferred across the surface ocean interface. It thus plays a key role in how the ocean is forced. If
we needed to model all the details of this layer, then the problem of coupled modeling would perhaps
be intractable. Fortunately, the Monin-Obukhov similarity theory has proven to be quite useful in many
contexts, particularly for the atmosphere boundary layer. Following Large et al. (1994), we consider its use
for the ocean surface boundary layer.
Monin-Obukhov similarity theory assumes that the turbulent surface layer is a constant flux layer that
starts just beneath any roughness elements, and certainly beneath the the molecular sublayer. In the ab-
sence of breaking surface waves, roughness elements arise from capillary waves that allow the wind to
affect the otherwise smooth ocean surface, in which case the roughness length is on the order of centime-
tres. With breaking surface waves, the roughness length can increase to the order of a metre (e.g., see
concluding section to Craig and Banner,1994). Furthermore, the scalings from Monin-Obukhov are dis-
tinctly not correct with surface wave breaking (e.g., Craig and Banner,1994;Terray et al.,1996). Surface
gravity waves are ignored in the formulation of Large et al. (1994).
Even if the surface layer is not a constant flux layer, the following scalings are relevant so long as
the surface fluxes remain the dominant parameters determining properties of this layer (Tennekes,1973).
Within the surface layer, the relevant dimensional quantities are the distance dfrom the surface interface
at z=η, and the surface kinematic fluxes of momentum, tracer, scalars, and buoyancy
wuη= surface kinematic momentum flux (18.52)
ρoCpwθη= surface kinematic heat flux (18.53)
wsη= surface kinematic scalar (e.g., salt) flux (18.54)
wbη= surface kinematic buoyancy flux. (18.55)
We now introduce the following dimensional scales.
•friction velocity: From the surface kinematic momentum flux, we introduce the turbulent velocity
scale, also known as the friction velocity scale
u2
∗≡|wuη|.(18.56)
Use of the identity (18.18) provides a means to compute the surface friction velocity given the surface
momentum stress
ρ0u2
∗=|τ|.(18.57)
•temperature scale: From the surface kinematic heat flux and the surface kinematic momentum flux,
we define a scale for the surface turbulent temperature fluctuations
Θ∗=−wθη
p|wuη|=−w θη
u∗.(18.58)
Elements of MOM November 19, 2014 Page 269

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.4
The sign is chosen so that turbulent fluxes leading to surface ocean cooling, wθη>0, correspond to a
negative turbulent temperature scale, Θ∗<0.
•scalar scale: From the surface kinematic scalar flux and the surface kinematic momentum flux, we
define a scale for the surface turbulent scalar fluctuations
S∗=− wsη
u∗!.(18.59)
•buoyancy scale: From the surface kinematic buoyancy flux −wbη(equation (18.49)), and the pen-
etrative buoyancy flux BR(equation (18.50), we define a scale for the surface turbulent buoyancy
fluctuations
B∗= Bf
u∗!=−wbη+BR
u∗.(18.60)
18.4.3 Similarity functions and length scale
The Monin-Obukhov similarity theory assumes the vertical gradient of any mean field, Λ, within the sur-
face turbulent layer is a function of the scale Λ∗of its turbulent fluctuations, the buoyancy scale B∗, the
velocity scale u∗, and the vertical distance from the upper interface, d=−z+η(equation (18.10)). In this
case, we write ∂Λ
∂z =Ψ(d,u∗,B∗,Λ∗),(18.61)
where Ψis an unknown function. Although no exact analytical expression exists for Ψ, Monin-Obukhov
theory suggests that progress can be made by fitting data to the following form
∂Λ
∂z = Λ∗
κd !φΛ(ζ).(18.62)
In this expression,
κ≈0.4 (18.63)
is the von Karman constant, φΛ(ζ) is a dimensionless similarity function or flux profile that is dependent
only on the scaled distance
ζ≡d
L,(18.64)
and
L=u2
∗
κB∗
=u3
∗
κBf
=|τ/ρ0|3/2
κBf
(18.65)
is the Monin-Obukhov length scale determined by the ratio of the momentum forcing to buoyancy forcing.
The Monin-Obukhov length scale takes on the following values for the suite of available boundary
forcing
L=
0u∗= 0,B∗,0τ= 0,Bf,0 zero winds
∞u∗,0,B∗= 0 τ,0,Bf= 0 zero buoyancy forcing (neutral forcing)
>0u∗,0,B∗>0τ,0,Bf>0 stabilizing buoyancy forcing
<0u∗,0,B∗<0τ,0,Bf<0 destabilizing or convective buoyancy forcing.
(18.66)
Notably, Lis not the finite positive thickness of the surface turbulent layer (Figure 18.1), as evident since L
can be negative or infinite. Instead, Lis the depth scale at which buoyancy production of turbulent kinetic
energy is of the same magnitude as shear production. For depths shallower than L > 0, shear production
dominates due to the effects from mechanical forcing through momentum stress τ. The case L=∞is
trivially dominated by shear production since there is no buoyancy forcing. For depths deeper than L,
buoyancy production dominates the turbulence. The case of L < 0 (convection) is always dominated by
buoyancy production.
Elements of MOM November 19, 2014 Page 270

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
The similarity function φΛappearing in equation (18.62) satisfies the following limit case under neutral
forcing (zero buoyancy forcing)
φΛ(0) = 1 arising from Bf= 0 so that L=∞and ζ=d/L = 0. (18.67)
This limit reduces the more general Monin-Obukhov form for the vertical derivative (18.62) to the loga-
rithmic Law of the Wall form
∂Λ
∂z = Λ∗
κd !neutral forcing so φΛ= 1. (18.68)
In the general case of nonzero buoyancy forcing, we integrate the similarity form (18.62) to expose the
logrithmic Law of the Wall for neutral forcing, plus a term present with nonzero buoyancy forcing. For this
purpose, rewrite equation (18.62) in terms of the scaled Monin-Obukhov distance, ζ, to have
∂Λ
∂ζ =− Λ∗
κζ !φΛ(ζ),(18.69)
where we used the relation between vertical increments through
dζ=−Ldz(18.70)
using d=−z+η(equation (18.10)). We now vertically integrate equation (18.69) to have
Λ(ζ) = Λ(Zλ/L) + Λ∗
L!ζ
Z
Zλ/L (1 −φΛ)−1
ζ0!dζ0.(18.71)
In this expression,
Zλ= roughness length (18.72)
introduced the roughness length associated with each fluctuating field. Within a distance Zλor less from
the boundary at z=η, the kinematic fluxes are not expected to be constant due to the impacts from rough-
ness elements. Hence, we expect the Monin-Obukhov similarity theory to breakdown when getting closer
than the roughness length to the surface.
Integrating the right hand side of equation (18.71) from the roughness length to an arbitrary point
within the surface layer renders1
Λ(ζ) = Λ(Zλ/L)− Λ∗
L!ln(ζ L/Zλ) + Λ∗
L!ζ
Z
Zλ/L (1 −φΛ)
ζ0!dζ0.(18.73)
As expected, the first term exposes the logarithmic Law of the Wall behaviour occurring for neutral forcing
conditions (φΛ= 1). Deviations from Law of the Wall for non-neutral forcing are embodied in the integral
on the right hand side. Recall that values ζ < Zλ/L are within the roughness elements or molecular sublayer,
so the theory cannot be applied there.
Large et al. (1994) (see their page 365) use atmospheric boundary layer results from Tennekes (1973) to
set the surface layer thickness to (see Figure 18.1)
= 0.1 fraction of KPP boundary layer occupied by surface layer. (18.74)
Within the surface layer, atmospheric boundary layer studies indicate that turbulent fluxes are within 20%
of their surface values when reaching a distance d=h from the upper ocean interface at d= 0. The
value of = 0.1 has never been observed in the ocean, but there is no reason to believe it is fundamentally
incorrect. Hence, this is the value taken for the KPP scheme.
1The result (18.73) disagrees with equation (4) in Large et al. (1994) by a minus sign, with the origin of the minus sign the relation
(18.70) between infinitesimal changes in ζand infinitesimal changes in z.
Elements of MOM November 19, 2014 Page 271

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
18.5 Specifying the KPP parameterization
We are now ready to determine the KPP boundary layer depth, h, the diffusivity, Kλ, and non-local trans-
port, γλ, thus enabling a full parameterization of the turbulent flux wλ according to
wλ =−Kλ ∂Λ
∂z −γλ!,(18.75)
where the diffusivity is given by equation (18.7), rewritten here as
Kλ(σ) = hwλ(σ)Gλ(σ).(18.76)
Recall that
σ=d/h (18.77)
is the dimensionless distance from the upper surface normalized by the boundary layer thickness, with
d=−z+η(18.78)
the dimensionful distance.
18.5.1 The turbulent vertical velocity scale wλ
We now determine the turbulent vertical velocity scale wλappearing in equation (18.76).
18.5.1.1 Velocity scale with stable buoyancy forcing
Following page 370 of Large et al. (1994), we first specify the velocity scale within the Monin-Obukhov
surface layer, where σ=d/h < = 0.1. We also assume stable buoyancy forcing, so that the non-local term,
γλ, vanishes. We later extend these results to the full boundary layer for arbitrary buoyancy forcing.
The similarity result (18.62) holds in the surface layer, in which
∂Λ
∂z = Λ∗
κd !φΛ(ζ).(18.79)
We may eliminate the vertical gradient ∂Λ/∂z using the KPP parameterization (18.75) with a zero non-local
term under stable buoyancy forcing
φΛ=−κd
Λ∗ wλ
Kλ!.(18.80)
Substituting the turbulent scale Λ∗=−wλη/u∗from equation (18.59) yields
KλφΛ=κd u∗ w λ
wλη!.(18.81)
The KPP diffusivity expression (18.76) then renders
wλ(σ)σ−1Gλ(σ) = κu∗
φΛ(σ)!wλσ
wλη.(18.82)
Recalling that σ < = 0.1 in the surface layer yields the approximate linear relation
σ−1Gλ(σ)≈a1+a2σ, (18.83)
where we used expression (18.13) for the structure function Gλ(σ). Furthermore, within the surface layer,
turbulent fluxes for any fluctuating field, wλσ, are linearly proportional to their surface value, wλη. We
may thus use this result to specify a part of the structure function according to
a1+a2σ=wλσ
wλη.(18.84)
Elements of MOM November 19, 2014 Page 272

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
Note that as shown in Section 18.5.3, there is generally a dependence of a2on the field λ, whereas a1is
unity for all fields. With the specification (18.84), we are led to an expression for the turbulent velocity
scale within the surface layer
wλ(σ) = κ u∗
φΛ(σ h/L)for stable forcing Bf>0 and 0 < σ < . (18.85)
Troen and Mahrt (1986) assume this expression is valid throughout the stably forced boundary layer for
0< σ < 1, and Large et al. (1994) also make that assumption.
18.5.1.2 Velocity scale with unstable buoyancy forcing
For unstable buoyancy forcing conditions, Bf<0, the turbulent velocity scales within the surface layer are
assumed to be the same as the stable velocity scale (18.85), again within the surface layer. For unstable
forcing beneath the surface layer, < σ < 1, Large et al. (1994) cap the velocity scale to that evaluated at the
base of the surface layer at σ=.
18.5.1.3 Summarizing properties of the turbulent velocity scale
The net result for all conditions is that the turbulent vertical velocity scale is given by
wλ(σ) = κu∗
φ−1
Λ(σ h/L) stable forcing Bf>0 OBL 0 < σ < 1
φ−1
Λ(σ h/L) unstable forcing Bf<0 surface layer σ <
φ−1
Λ(h/L) unstable forcing Bf<0 OBL beneath surface layer < σ < 1.
(18.86)
We now summarize various properties of the velocity scale, with these properties reflected in Figure 18.3.
•stable forcing: The similarity functions φΛand velocity scales wλsatisfy the following properties
under positive buoyancy forcing, Bf>0.
–The similarity functions are increased so that the turbulent velocity scales are reduced.
–The similarity functions are the same for all scalars and momentum, so that the velocity scales
wλare the same.
•neutral forcing: with zero buoyancy forcing, Bf= 0, the similarity functions satisfy φΛ= 1, so that
wλ(σ) = κu∗.
•unstable forcing: The similarity functions φΛand velocity scales wλsatisfy the following properties
under negative buoyancy forcing, Bf<0.
–The similarity functions φΛare reduced so that the turbulent velocity scales wλare enhanced.
–The similarity functions for momentum are larger than those for scalars, so that the velocity
scales for momentum are smaller than for scalars: wm< ws.
–In the convective limit, for which u∗→0, the velocity scales behave according to
wλ∼w∗= (−Bfh)1/3.(18.87)
In order to satisfy this scaling, the similarity functions φΛmust have the form
φΛ= (aλ−cλζ)−1/3convective conditions with u∗→0, (18.88)
where ζ=d/L << 0, and the constants aλand cλare chosen to match the convective form (18.88)
to less unstable forms.
Elements of MOM November 19, 2014 Page 273
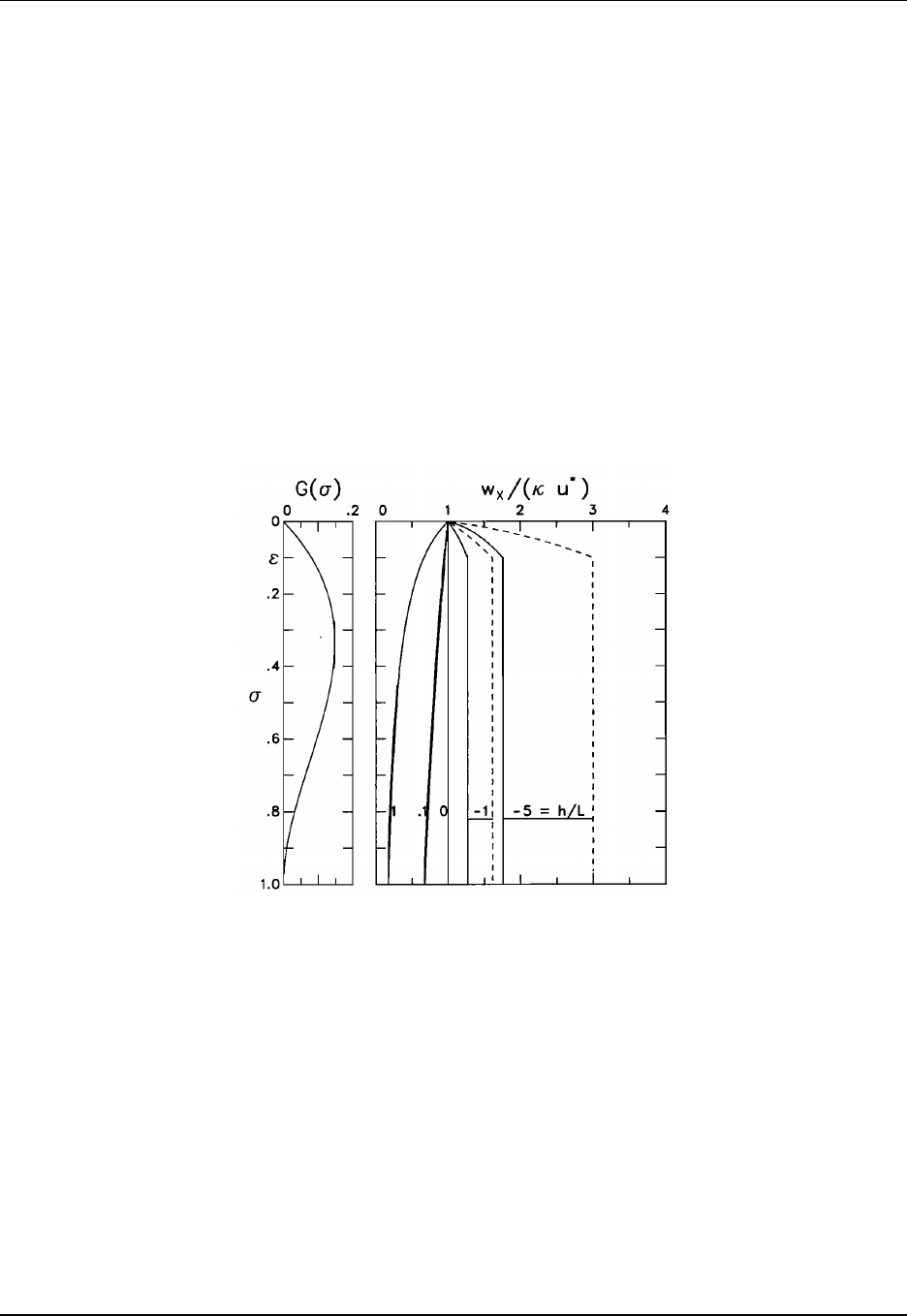
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
We now use the expression (18.88) within the unstable surface layer (σ < ) form in (18.86) to
render
wλ=κ(aλu3
∗−cλu3
∗ζ)1/3
=κ[aλu3
∗−cλu3
∗(hσ/L)]1/3
=κ(aλu3
∗−cλσ κhBf)1/3
=κ(aλu3
∗+cλσ κw3
∗)1/3
→κw∗(cλσ κ)1/3,
(18.89)
where the final limit case is for the convective limit with u∗→0. Likewise, outside the surface
layer ( < σ < 1) we have
wλ=κ(aλu3
∗+cλκw3
∗)1/3→κw∗(cλ κ)1/3,(18.90)
where again the final limit case is for the convective limit with u∗→0.
370 ß Large et al.: OCEANIC VERTICAL MIXING 32, 4 / REVIEWS OF GEOPHYSICS
G(•)
0 .2
0 •1 •
.2
.4
.6
.8
I
1.0
0 1 2 3 •
I
I I
I
I I --
I I
I I
I I i
I I
I I
I
I I I
I I
I I
I
i
I I
I I
I
I
I
-- I .1 0 -1Ii -5 : h/L ] -
I I
I
• I I I --
I I
I ,
Figure 2. (left) Vertical profile of the shape function G(cr),
where cr = d/h, in the special case of G(1) = 0,•G(1) = 0.
(right) Vertical profiles of the normalized turbulent velocity
scale, wx(o')/(Ku*), for the cases of h/L = 1, 0.1, 0, -1,
and -5. In unstable conditions, Ws(Cr) (dashed traces) is
greater than Wm(Cr) (solid traces) at all depths, but for stable
forcing h/L -> 0, the two velocity scales are equal at all
depths.
The problem of determining the vertical turbulent
fluxes of momentum and both active and passive sca-
lars in (1) throughout the OBL is closed by adding a
nonlocal transport term •/x to (5):
wx(a) = -gx(OzX- (9)
In practice, the external forcing is first prescribed,
then the boundary layer depth h is determined, and
finally profiles of the diffusivity and nonlocal transport
are computed. Here the depth determination is de-
scribed last because its formulation depends on the
form of the diffusivity. The external forcing is dis-
cussed in Appendix A.
Diffusivity and Nonlocal Transport
The profile of boundary layer diffusivity is ex-
pressed as the product of a depth dependent turbulent
velocity scale w x and a nondimensional vertical shape
function G(tr):
Kx(tr) = hwx(o')G(tr) (1 O)
where tr = d/h is a dimensionless vertical coordinate
that varies from 0 to 1 in the boundary layer. At all
depths, values of K x are directly proportional to h,
reflecting the ability of deeper boundary layers to
contain larger, more efficient turbulent eddies. Partic-
ular examples of G(tr) and Wx(tr) profiles are shown in
Figure 2. The shape function is assumed to be a cubic
polynomial [O'Brien, 1970],
G(tr) = a0 + a•tr + a2 0'2 q- a3 0'3 (11)
so that there are four coefficients with which to control
the diffusivities and their vertical derivatives at both
the top and bottom of the boundary layer.
Turbulent eddies do not cross the surface, so there
is no turbulent transport across d - 0. The implied
condition Kx(O) = 0 is imposed by setting ao = 0.
Molecular transport terms, in addition to (9), are re-
quired only if the very near surface, where molecular
processes dominate [Liu et al., 1979], is to be re-
solved.
In the surface layer • < e, where Monin-Obukhov
similarity theory applies, eliminating the property gra-
dient from (3) and (9) with •/x = 0 and then substituting
(10) for Kx with G(•r) -• ,(a• + a2{r) leads to
Wx(O')(al + a2o')= Lx(C)]x wxo / (12)
A sensible way of satisfying (12) is to equate the term
in square brackets to the turbulent velocity scales. As
was argued by Troen and Mahrt [1986], this formula-
tion is assumed to be valid everywhere in the stably
forced boundary layer. In unstable conditions the tur-
bulent velocity scales beyond the surface layer are
assumed to remain constant at their •r = e values.
Without this constraint, unstable W x values would be-
come very large (Figure 2), in the absence of any
supporting observational evidence. Therefore the gen-
eral expression for the velocity scales is
K/,/*
Wx(•r) = e < •r < 1 • < 0
q>x( eh/L )
nu* (13)
Wx(e) = otherwise
These scales are functions of [ = d/L = •rh/L, so
profiles of Wx(•r) are fixed functions of h/L, as is
shown in Figure 2.
The q>x functions (Appendix B, Figure B 1) are such
that the velocity scales equal nu* with neutral forcing
(h/L - 0 in Figure 2) and are enhanced and reduced in
unstable (h/L < 0) and stable (h/L > 0) conditions,
respectively. The turbulent velocities for momentum
and scalars are equal in stable forcing. The unstable
4)m is greater than 4)• (Figure B1), so W m becomes less
than the corresponding w• (dashed lines) in Figure 2.
In order for w x to scale with w* in the convective limit,
the q>x functions in very unstable (convective) condi-
tions of [ < Ix < 0.0 have the form
q>x = (ax - Cx[) -•/3 (14)
where the constants ax and Cx make (14) match less
unstable forms of q>x at [ = Ix (equation B1). Com-
bining (2), (6), (13), and (14) leads to
Figure 18.3: This is a reproduction of Figure 2 from Large et al. (1994). The vertical axis is the dimension-
less vertical coordinate σ=d/h within the KPP boundary layer 0≤σ≤1. The left panel shows the vertical
profile of the shape or structure function, Gλ(σ), used to scale the vertical diffusivity via equation (18.76).
The analytic form shown here is given by Gλ(σ) = σ(1 −σ)2, which corresponds to the Troen and Mahrt
(1986) form and which is independent of the quantity Λbeing diffused. Large et al. (1994) chose a more
general form, based on the need to match boundary layer diffusivities to interior diffusivities in which case
the shape function becomes a function of λ. We detail this approach in Section 18.5.3. The right panel
shows various examples of the normalized turbulent velocity scale wλ(called wxin Large et al. (1994)),
with the examples differing by the value of the dimensionless ratio h/L between the boundary layer depth,
h, and the Monin-Obukhov length scale L. For unstable buoyancy forcing, L < 0, the velocity scale for
scalars, ws(dashed lines), is greater than that for momentum, wm(solid lines). For stable forcing, L > 0,
and both scalar and momentum have the same turbulent velocity scales, ws=wm. In general, the turbu-
lent velocity scale is enhanced with unstable surface buoyancy forcing, and reduced with stable buoyancy
forcing.
Elements of MOM November 19, 2014 Page 274
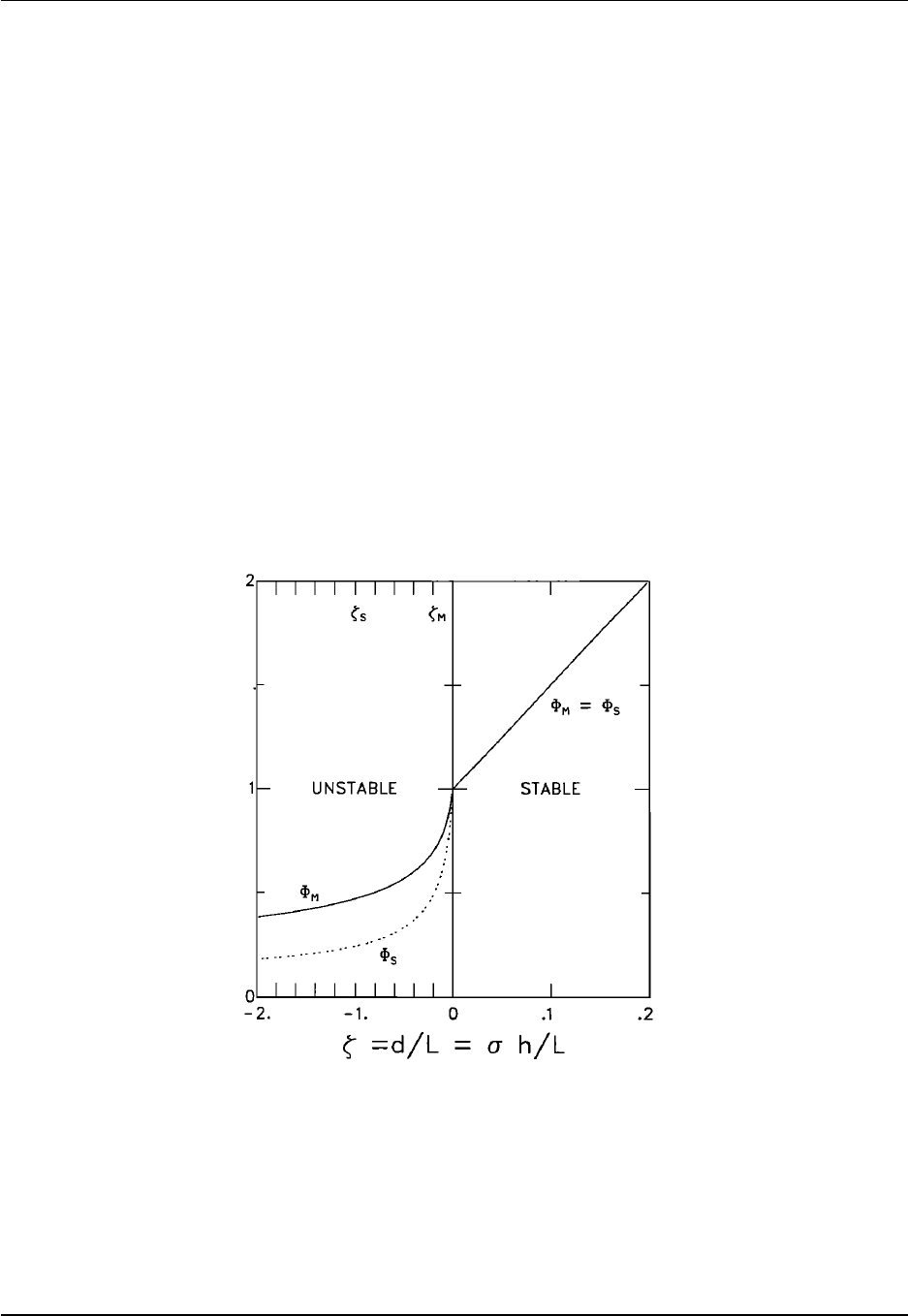
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
18.5.2 Similarity functions φΛ
The vertical velocity scales are functions of the similarity functions φΛ, also called the dimensionless flux
profiles. Appendix B of Large et al. (1994) present analytic forms for these functions, based on fits to
available data, with their Figure B1 (reproduced here as Figure 18.4) providing a summary of the choices
for the momentum function φmand the scalar function φs. Both functions agree for stable buoyancy
forcing, and they depend linearly on the dimensionless Monin-Obukhov length ζ=d/L =σ h/L.
18.5.2.1 The Large et al. (1994) choices for unstable buoyancy forcing
For unstable buoyancy forcing, where L < 0 and so ζ < 0, there are two regimes. The scalar function φsis
always less than the momentum function φm. Hence, for unstable forcing there is a larger turbulent velocity
scale for the scalars than momentum, and thus a larger vertical diffusivity for scalars. The turbulent Prandtl
number, P r, is given by the ratio of the flux functions
P r =Km/Ks=wm/ws=φm/φs.(18.91)
The choices made by Large et al. (1994) lead to a Prandtl number in the convective limit (ζ→ −∞) of
P r →(cm/cs)1/3= 0.44,(18.92)
where cmand csare parameters in the similarity functions φmand φs, respectively.
392 ß Large et al.' OCEANIC VERTICAL MIXING 32, 4 / REVIEWS OF GEOPHYSICS
1 - UNSTABLE
ß
ß
0 "
ß
ß
.
.
.
o
o.
.o
.............. •)$
I I I I I I I I I
-2. -1. 0
I
• = •s
(• -d/L - o- h/L
Figure BI. Plots of the nondimensional flux profiles for
momentum, 4)m, and for scalars, 4)s, as functions of the
stability parameter [. These functions become -1/3 power
laws for values of [ more negative than [m and Is, respec-
tively.
4)m -- 4)s -- 1 q- 5• 0 -< g (Bla)
4)m- (l -- 16•) -1/4 •m -< g < 0 (B lb)
4)rn: (am- Cm•) -1/3 • < gm (alc)
(bs = (1 - 16i•) -1/2 i• s --< g < 0 (Bld)
4)s = (as - Csg) -1/3 • < gs (Ble)
where the subscript s refers to all scalars. The con-
stants in (B 1) are prescribed as follows'
gs = -1.0 Cs = 98.96 as = -28.86 (B2)
gm= -0.20 Cm = 8.38 am = 1.26
where the ax and cx are chosen so that both 4)x and its
first derivative are continuous across g = gm and gs
(Figure B 1). This matching also ensures continuity of
w x and its first derivative. In stabilizing forcing nearly
all measurements have been for 0 < g < 1, and there is
general agreement on the linear form of (B1), though
the proportionality constant varies and sometimes dif-
fers for q>s and l•) m. The value of 5, used in (B1) and by
Troen and Mahrt [1986] for both, is common practice
[Panofsky and Dutton, 1984]. The restriction h -< L
precludes [ ever exceeding 1 in the boundary layer. In
unstable conditions near neutral, l•) m and q>s are the
most common Businger-Dyer forms [Panofsky and
Dutton, 1984]. These forms match the stable functions
at [ = 0 and are good fits to the available data
[H6gstr6m, 1988] for •m • • • 0 and •s --< • < O,
respectively.
In more unstable conditions there are no observa-
tions of (bx, but the data of Carl et al. [1973] suggest
the -1/3 dependency in (B1) and (14) for 4)m' This
dependency and a similar -1/3 dependency for (Ds is
also required in order to satisfy the theoretical result of
w x proportional to w* (equation (6)) in the convective
limit, as given in (15). The near-neutral Businger-Dyer
forms in (B1) do not lead to this result. In the Troen
and Mahrt [1986] formulation, only 4)m has a -1/3
power law dependency at large negative g.
The ratio of momentum to scalar diffusivity defines
the turbulent Prandtl number, Pt, which from (10) and
(13) becomes,
Pr = Km/Ks = Wm/Ws '- 4)s/4)m (B3)
Since there is no physical reason to expect the neutral
boundary layer to diffuse momentum differently than
scalars, the near-neutral functions (B 1) are equal at •
= 0 (Figure B 1), such that Pr = 1. The functions used
by Troen and Mahrt [1986] give Pr(• = 0) = 0.75 in
accord with some observations [Businger et al., 1971].
Beyond the surface layer, Wx is constant in the con-
vective limit, and (15) gives Wm = 0.28W* and Ws =
0.63w* and hence a finite Pr -• (Cm/Cs) 1/3 -- 0.44.
This value is just the limit of the ratio of the two curves
in Figure B 1 as [ becomes increasingly negative. Since
this figure shows l•)rn • l•) s for all [ < 0, convection
always mixes scalars, including buoyancy, more effi-
ciently than momentum.
APPENDIX C: KPP SENSITIVITY EXPERIMENTS
This appendix explores some sensitivities of the
KPP simulations in addition to those presented in
section 5. First, finite resolution is shown to produce
biases and oscillations in the model's boundary layer
depth, which are ameliorated numerically (Appendix
D). With these numerics the overall effect of entrain-
ment is shown to be well reproduced in a low-resolu-
tion convective simulation. Next, the sensitivity of the
stably forced LOTUS simulation is investigated.
These results are used to establish that the treatment
of solar radiation, through our values of hB and h•, is
reasonable. Finally, the sensitivity of the annual cycle
at OWS Papa is shown to be relatively insensitive to an
order of magnitude change in vertical resolution.
Finite Resolution
Any practical resolution of the upper ocean will not
always resolve the sharp gradients that occur near the
bottom of the boundary layer. The computational
problems that result are illustrated by a strongly wind-
forced case. Consider the idealized seasonal thermo-
cline shown in Figure Cl. The continuous buoyancy
and velocity profiles (solid lines) are constant down to
a depth h m = 17 m, below which the former has a
Figure 18.4: This is a reproduction of Figure B1 from Large et al. (1994). The vertical axis provides values
for the dimensionless flux profiles, φΛ, for momentum and scalars, and the horizontal axis gives the di-
mensionless Monin-Obukhov length scale ζ=d/L =σ h/L. There is a transition across the neutrally forced
value of ζ= 0. For stable buoyancy forcing (ζ > 0), both functions are the same, φs=φm, and are linear
functions of ζ. For unstable buoyancy forcing (ζ < 0), the scalar function is less than momentum, φs< φm,
with both functions falling offwith a negative fractional power. The analytic forms for the functions are
given by equations (B1) and (B2) in Large et al. (1994).
Elements of MOM November 19, 2014 Page 275
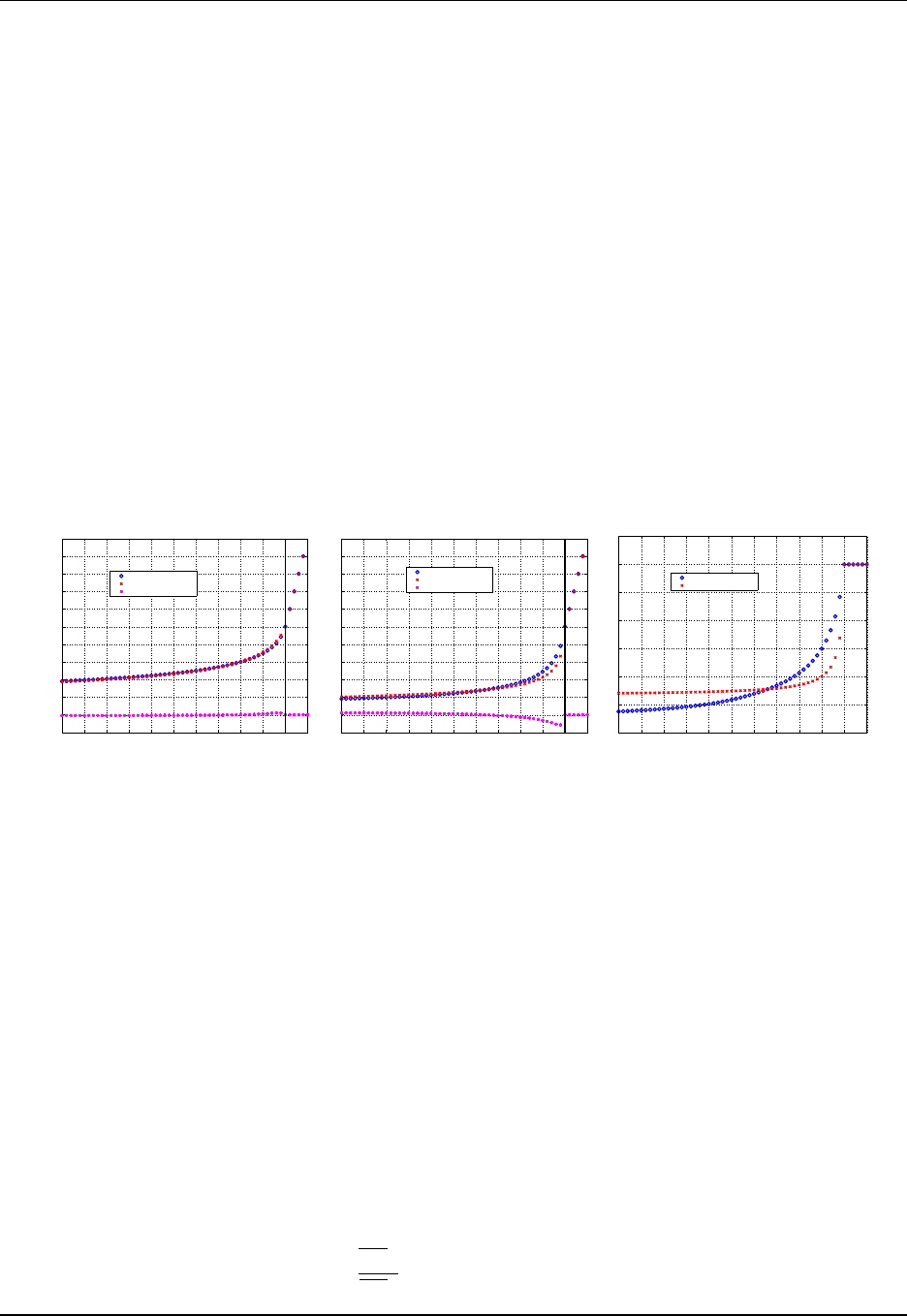
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
18.5.2.2 Alternative choices for unstable buoyancy forcing
Large et al. (1994) chose two regimes for the unstable buoyancy forced range, transitioning from different
fractional exponents near ζ= 0, to the same −1/3 power for larger negative ζ. The scalar function φsfalls
offfaster near ζ= 0, with a power −1/2, whereas the momentum function φmfalls offwith a −1/4 power.
This initial distinct fractional power falloffsets the scale for the Prandtl number in this portion of ζin the
weakly unstable regime.
Having two regimes for the negative buoyancy forcing adds complexity to the algorithm. We thus
consider how well the original two-regime forms for φmand φscan be fit using a single regime, using only
the fractional power −1/3. Tests suggest that the following forms may be suitable
φm(ζ) = (1 + 5ζ ζ > 0
(1 −9ζ)−1/3ζ < 0(18.93)
φs(ζ) = (1 + 5ζ ζ > 0
(1 −60ζ)−1/3ζ < 0.(18.94)
A comparison of the original forms from Large et al. (1994) to the alternative forms is shown in Figure 18.5.
Also shown is the ratio of these two functions which yields the turbulent Prandtl number according to
equation (18.91). The agreement between the original forms and the new forms is worse when considering
the Prandtl number.
−2 −1.8 −1.6 −1.4 −1.2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Two versions of φm
M−O dimensionless length ζ = d/L = σ h / L
dimensionless flux profile φm
3 regions from Large et al
2 regions
difference
−2 −1.8 −1.6 −1.4 −1.2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Two versions of φs
M−O dimensionless length ζ = d/L = σ h / L
dimensionless flux profile φs
3 regions from Large et al
2 regions
difference
−2 −1.8 −1.6 −1.4 −1.2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
Ratios of φs / φm for two versions of φm and φs
M−O dimensionless length ζ = d/L = σ h / L
dimensionless flux profile φs
3 regions from Large et al
2 regions
Figure 18.5: Shown here are alternative flux profiles given by equations (18.93) and (18.94), as well as their
ratio φs/φm, with this ratio defining the turbulent Prandtl number, or the ratio of the vertical momentum
viscosity to vertical tracer diffusivity.
18.5.3 The shape function Gλ(σ)
The vertical shape function Gλ(σ) is given by the cubic polynomial
Gλ(σ) = a0+a1σ+a2σ2+a3σ3.(18.95)
As already noted when introducing this cubic expression (equation (18.13)), turbulent eddies do not cross
the ocean surface at σ= 0, so the diffusivity should vanish at σ= 0. This constraint is satisfied by setting
a0= 0.(18.96)
We now discuss further constraints to specify the remaining coefficients.
We start by rewriting the expression (18.84) that expresses the ratio of turbulent fluxes within the sur-
face layer to those at the surface boundary
a1+a2σ=wλσ
wληsurface layer: 0 ≤σ≤. (18.97)
Elements of MOM November 19, 2014 Page 276

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
Satisfying this relation at the ocean surface, σ= 0, requires
a1= 1,(18.98)
so that
1 + a2σ=w λσ
wληsurface layer: 0 ≤σ≤. (18.99)
Now define the ratio
βλ=wλ
wλη,(18.100)
which is the ratio of the turbulent flux at the base of the surface layer, σ=, to the flux at the upper ocean
interface, z=η. For atmospheric boundary layers, Troen and Mahrt (1986) set
βλ= 2atmospheric boundary layers, (18.101)
with = 0.1. Troen and Mahrt (1986) further assume both the shape function and its first derivative vanish
at the base of the boundary layer, σ= 1. These assumptions lead to the cubic expression valid for all
fluctuating fields λ
G(σ) = σ(1 −σ)2atmospheric boundary layers, (18.102)
with this function exhibited in the left panel of Figure 18.3.
Large et al. (1994) also assume the surface layer is 10% of the boundary layer, so that
= 0.1 KPP scheme. (18.103)
However, they consider a more general approach for the remaining approach to deriving the shape func-
tion. The key reason to generalize the atmospheric approach of Troen and Mahrt (1986) is to admit the
possibility of ocean boundary layer turbulence to be impacted by interior mixing, with this mixing param-
eterized by downgradient vertical diffusion. Such diffusion generally introduces distinct diffusivities for
tracers (e.g., double diffusion) as well as for momentum (e.g., non-unit Prandtl number). For these reasons,
Large et al. (1994) insist that both the diffusivity and its vertical derivative match across the base of the
boundary layer at σ= 1. This matching condition leads to the constraints (18) given by Large et al. (1994),
which in turn leads to shape functions that are dependent on the field being transported.
Matching both the shape function and its vertical derivative across the boundary layer base adds com-
plexity to the KPP algorithm. Furthermore, it is unclear how accurate one can in fact satisfy both matching
conditions on a finite grid with potentially coarse vertical grid spacing at the boundary layer base. To sim-
plify the KPP algorithm, we drop the need to match the vertical derivative of the diffusivity. Instead, we
assume continuity of the diffusivity with a vanishing derivative at the boundary layer base, σ= 1. Setting
∂σG(σ) = 0 at σ= 1 leads to the relation
3a3=−(1 + 2a2).(18.104)
Matching diffusivities at σ= 1 between the boundary layer and interior value leads to
a2=−2 + 3Kλ(h)
hwλ(h)!,(18.105)
where the diffusivity Kλ(h) is determined by parameterizations of interior mixing. Substituting this expres-
sion for a2into equation (18.104) for a3leads to
a3= 1 − 2Kλ(h)
hwλ(h)!.(18.106)
Allowing for the interior mixing to influence the KPP boundary layer scheme suggests that the KPP calcu-
lation should be called after the various methods used to compute interior diffusivities.
Elements of MOM November 19, 2014 Page 277

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
18.5.4 The non-local transport γλ
We now consider the parameterization for the non-local transport (see Section 18.1.4) as suggested by Large
et al. (1994). Again, the KPP parameterization takes the form (equation (18.3))
wλ =−Kλ ∂Λ
∂z −γλ!,(18.107)
so that that non-local portion of the turbulent flux is parameterized according to
wλnon-local =Kλγλ,(18.108)
where Kλtakes the form in equation (18.76):
Kλ(σ) = hwλ(σ)Gλ(σ).(18.109)
For completeness, we repeat elements of the outline presented in Section 18.1.4.
18.5.4.1 General features of γλwith the KPP parameterization
•Smyth et al. (2002) consider a non-local term for momentum. Until their ideas have been fully tested
in climate models, we follow recommendations from (Large et al.,1994), who set the non-local mo-
mentum transport to zero:
γλ=(0 if λ= (u,v,w) a velocity component
,0 nonzero if λ=θ,s or another tracer. (18.110)
• The non-local transport is non-zero only within the OBL:
γλ=(0 if σ > 1
,0 if 0 ≤σ≤1. (18.111)
• The non-local transport is non-zero only in the presence of destabilizing negative surface ocean buoy-
ancy flux:
γλ=(0 for Bf>0
,0 for Bf<0. (18.112)
• The non-local transport for temperature and arbitrary scalars is given by the following form for desta-
bilizing negative surface ocean buoyancy fluxes:
γθ=Cs
wθη−QR/(ρ0Cp)
hwθ(σ)(18.113)
γs=Cs wsη
hws(σ)!,(18.114)
where
Cs=C∗κ(csκ)1/3,(18.115)
with
C∗= 10,(18.116)
and QRis the heat flux from penetrative radiation given by equation (18.51).
Combining the parameterizations (18.113) and (18.114) for the non-local term γλ, with that for the
vertical diffusivity Kλin equation (18.109) renders the non-local flux parameterization in the form
wθnon-local =Kθγθ=Gλ(σ)Csw θη−QR/(ρ0Cp)(18.117)
wsnon-local =Ksγs=Gs(σ)Cs(wsη).(18.118)
Notice how explicit dependence on both the turbulent velocity scale, wλ, and boundary layer depth,
h, drop out from the parameterization of the non-local flux.
Elements of MOM November 19, 2014 Page 278

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
18.5.4.2 Potential problems with the parameterized non-local transport
Experience has shown that there are cases when the parameteried non-local flux, (18.117) of (18.118), can
produce values larger than the surface flux. That is, one may realize cases when
Gλ(σ)Cs>1 non-local flux greater than surface flux. (18.119)
This situation arises particularly near the boundary layer base, σ= 1, when the interior diffusivity is large.
The matching conditions employed by Large et al. (1994) (Section 18.5.3) then lead to a very large value
for the shape function G(σ). In this case, one may be exposed to the production of extrema in the tracer
field. In the presence of sea-ice, problems may arise particularly in fresh water regions such as the Baltic
Sea where the thermal expansion coefficient is negative, α < 0 (Martin Schmidt, personal communication).
The following modifications to the original Large et al. (1994) scheme have been found useful to reduce
the potential for the non-local term to be problematic.
•interior gravitational instabilities: When the vertical stratification is unstable (N2<0), vertical
diffusivity is enhanced to remove the gravitational instability. Notably, it is not appropriate to en-
hance the diffusivity within the KPP boundary layer, beyond that already computed via the KPP
scheme, even when N2<0. On those occasions when the instabilities appear beneath the bound-
ary layer, diffusivities are enhanced. If one insisted that such diffusivities should match those in the
boundary layer, then the shape function G(σ) would indeed become quite large in magnitude. Hence,
NCAR recommends that one pull the “convective adjustment” portion of the mixing scheme outside
of the KPP portion of the algorithm. That is, the interior convective instability diffusivities should not
be matched to the KPP boundary layer diffusivities.
•simpler matching: As noted in Section 18.5.3, we propose to simplify the matching at the boundary
layer base, so that only the diffusivities match across the boundary layer base, rather than also insist-
ing on the derivative of the diffusivities as proposed by Large et al. (1994). The simplified matching
condition leads to less problems computing discrete vertical derivatives of the diffusivities, and in
turn produces more well regularized diffusivities and shape functions.
18.5.5 The bulk Richardson number and the OBL thickness h
Large et al. (1994) define the KPP boundary layer depth to be the first depth at which the bulk Richardson
number, Rib, equals to a critical Richardson number, Ric. The bulk Richardson number is computed using
bulk averaged buoyancy, Br, and horizontal velocity, Ur, over the surface layer, 0 ≤σ≤, so that
Rib(d) = d[Br−B(d)]
|Ur−U(d)|2+U2
t
.(18.120)
Recall the buoyancy was defined by equation (18.19) as
B=g ρ0−ρ
ρ0!,(18.121)
where ρis the in-situ density and ρ0is a constant reference density. In the denominator of the bulk Richard-
son number (18.120), Large et al. (1994) add the term U2
t, which is associated with parameterized unre-
solved vertical shears that may act to further reduce the bulk Richardson number.
The physics underlying the definition (18.120) is that boundary layer eddies with a suface layer buoy-
ancy Brand velocity Urmay penetrate to the full boundary layer h, at which point their turbulence is
suppressed by the reduced shear and increased buoyancy stratification. We now comment in turn on both
the specification of the buoyancy in the numerator, and the unresolved shear in the denominator.
18.5.5.1 Local gravitational stability
The flux Richardson number is defined by
Rif=N2
|∂zU|2,(18.122)
Elements of MOM November 19, 2014 Page 279
Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
where
N2=g α∂Θ
∂z −β∂S
∂z !(18.123)
is the buoyancy frequency. The denominator of the bulk Richardson number defined by equation (18.120)
represents a finite difference of the velocity averaged over the surface layer and that at a distance dbeneath
the ocean surface. The numerator is also reminiscient of a finite difference representation of the buoyancy
frequency, and so may represent a finite difference measure of gravitational stability. In the following, we
consider how this measure of gravitational stability for a fluid column arises from the more traditional
local methods in terms of local buoyancy frequency appearing in the flux Richardson number. In so doing,
we provide an equivalence between the method proposed by Large et al. (1994), and another method based
on vertically integrating the local buoyancy frequency. The alternative method may prove to be more
useful when kernalizing the KPP scheme so to remove the need to recompute the equation of state when
determining the boundary layer thickness.
To initiate the discussion, we start with some standard material on gravitational stability. Following
McDougall (1987a), introduce the notion of a neutrally stable direction by considering an infinitesimal
displacement dxof a fluid parcel. Under a general displacement, the in situ density is given to leading
order by
ρ(x+ dx) = ρ(x) + dρ(x),(18.124)
where
dρ(x) = ρdx· −α∇Θ+β∇S+1
ρc2
sound ∇p!,(18.125)
with the sound speed defined by
c2
sound = ∂p
∂ρ !S,Θ
,(18.126)
The ambient density, ρ(x+ dx), at the new point thus differs from density at the original point ρ(x) by an
amount dρaccording to
ρ(x+ dx) = ρ(x) + ρdx· −α∇Θ+β∇S+1
ρc2
sound ∇p!.(18.127)
Now instead of a general displacement that allows for temperature, salinity, and pressure to change,
consider instead a displacment restricted to adiabatic and isohaline conditions (i.e., no heat or salt ex-
changed during the parcel displacement). These sorts of fictitious displacements are physically interesting
since they occur in the absence of energy needed for mixing. The density change associated with an adia-
batic and isohaline displacement is determined just by pressure changes arising from the displacement, so
that
ρ(x+ dx)adiabatic/isohaline =ρ(x) + ρdx· 1
ρc2
sound ∇p!.(18.128)
The difference in density between a parcel undergoing an adiabatic and isohaline displacement, ρ(x+
dx)adiabatic/isohaline, and the density of the ambient environment, ρ(x+ dx), is thus given by
ρ(x+ dx)−ρ(x+ dx)adiabatic/isohaline =ρdx·(−α∇Θ+β∇S).(18.129)
If a parcel makes an adiabatic and isohaline excursion and finds itself in a region where the ambient density
is unchanged, then there are no buoyancy forces to resist that displacement. Directions defined by such
displacements are termed neutral directions (McDougall,1987a).
For the upper ocean boundary layer, we are concerned with vertical displacements and the resistence
from buoyancy stratification to such motions. In this case we have
ρ(z+dz)−ρ(z+dz)adiabatic/isohaline =ρdz"−α ∂Θ
∂z !+β ∂S
∂z !#=− ρdz
g!N2vertical displacements, (18.130)
where the second equality introduced the buoyancy frequency (18.123). To help further expose the physics
of this result, consider two cases of vertically downward parcel displacements, dz < 0.
Elements of MOM November 19, 2014 Page 280

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
•gravitationally stable: N2>0: In this case, a vertically downward displacement occurring without
heat or salt exchange will produce a parcel density that is less than the ambient density: ρ(z+dz)−ρ(z+
dz)adiabatic/isohaline >0. This particular adiabatic and isohaline displacement is hence resisted by buoyancy
forces. The vertical density profile is thus gravitationally stable.
•gravitationally unstable: N2<0: Now the downward adiabatic and isohaline displacement leads
to a greater density than the ambient environment: ρ(z+ dz)−ρ(z+ dz)adiabatic/isohaline <0. Hence, this
particular adiabatic and isohaline displacement is encouraged through buoyancy forces to deepen
even further. The vertical density profile is thus gravitationally unstable.
18.5.5.2 Non-local gravitational stability
We now extend the previous ideas to the finite depth of a surface boundary layer. That is, we develop a
means to compute the gravitational stability of seawater parcels that are a finite distance from one another.
The question fundamentally concerns the sign of the difference ρ(z+∆)−ρ(z+∆)adiabatic/isohaline, where zis an
arbitrary finite position in the ocean and ∆>0 is a finite distance.
Extending the result (18.130) to finite displacements upward in a water column leads to
ρ(z+∆)−ρ(z+∆)adiabatic/isohaline =−1
g
z+∆
Z
z
N2ρdz0.(18.131)
Correspondingly, downward displacements starting from the surface at z=ηlead to
ρ(−∆)−ρ(−∆)adiabatic/isohaline =1
g
η
Z
−∆
N2ρdz0.(18.132)
To check the signs in equation (18.132), note that for cases of N2>0 for a full water column, an adiabatic
and isohaline downward displacement always results in a less dense parcel than the surrounding water,
which is expected for a full column of gravitationally stable stratification. Operationally, the left hand side
of equation (18.132) is computed according to the following evaluations of the equation of state:
ρ(z=−∆) = ρ[Θ(z=−∆),S(z=−∆),p(z=−∆)](18.133)
ρ(z=−∆)adiabatic/isohaline =ρ[Θ(z=z1),S(z=z1),p(z=−∆)].(18.134)
That is, the adiabatic and isohaline density at z=−∆is computed using the temperature and salinity of the
origination depth z=z1, but the local pressure at z=−∆.
18.5.5.3 The Ribcalculation
The bulk Richardson number from Large et al. (1994) (equation (18.120)), is defined as the ratio of a buoy-
ancy difference to a squared shear of horizontal velocity. We now propose that the buoyancy difference
in the numerator should be replaced by the density difference (18.132), as we showed this density differ-
ence represents a measure of the gravitational stability of a finite depth water column. However, there is
one slight modification to equation (18.132), with the temperature and salinity at the origination depth
corresponding to values averaged over the surface layer Θr,Sr, so that
ρ(z=−∆)KPP
adiabatic/isohaline =ρ[Θr,Sr,p(z=−∆)].(18.135)
These results motivate the following definition for a bulk Richardson number
RiKPPa
b(z=−∆) = g∆
ρ0! ρ(z=−∆)−ρ(z=−∆)KPP
adiabatic/isohaline
|Ur−U(d)|2+U2
t!,(18.136)
with this definition according to that from Large et al. (1994) in equation (18.120). There are useful al-
gorithmic reasons to eschew recomputing the equation of state and determining a surface layer averaged
Elements of MOM November 19, 2014 Page 281

Chapter 18. KPP for the surface ocean boundary layer (OBL) Section 18.5
temperature and salinity profile. For that purpose, we propose the following alternative definition, based
on the right hand side of equation (18.132)
RiKPPb
b(z=−∆) = ∆
ρ0!
η
R
z=−∆
N2ρdz0
|Ur−U(d)|2+U2
t
.(18.137)
Since the definition RiKPPb
bdoes not require recomputation of the equation of state, it is more amenable to
kernalization, with the kernal given values of the buoyancy frequency, N2, from the calling model. On
the discrete grid, there will be differences between RiKPPa
band RiKPPb
b, but these differences are at the level of
numerical roundoff, and not physically meaningful.
18.5.5.4 Unresolved shear Ut
The shear, Ut/d, in the bulk Richardson number (18.120), or any of the alternatives such as (18.136) or
(18.137), is meant to acknowledge the potential presence of unresolved shears that can impact on the
boundary layer depth. Large et al. (1994) present an argument on page 372 for how to compute this shear
based on other parameters available from the KPP parameterization. Additional ongoing work suggests
modifications for unresolved Langmuir turbulence, such as the work of McWilliams and Sullivan (2001)
and Sullivan and McWilliams (2010).
18.5.5.5 Restrictions on hunstable stable buoyancy forcing
Large et al. (1994) suggest on page 372 that for stable buoyancy forcing, Bf>0, the boundary layer thick-
ness, h, should be no larger than either the Monin-Obukhov length scale, L, or the Ekman length scale,
hE= 0.7u∗/f , (18.138)
with fthe Coriolis parameter. The following reasons are noted to motivate these two restrictions.
•Monin-Obukhov: At depths deeper than L, buoyancy stratification suppresses the mechanically
forced turbulence, thus cutting offthe boundary layer.
•Ekman: The Ekman depth is the extent of the boundary layer in neutral stratification (N2= 0). With
stable buoyancy forcing, Bf>0, we then expect the boundary layer depth to be less than the Ekman
depth.
As noted in Large et al. (1994) and Large and Gent (1999), the restriction based on the Monin-Obukhov
has been dropped in the NCAR implementation of KPP, as it does not lead to favorable effects. Dropping
this constraint is also supported by the results from Shchepetkin (2005) and Lemari´
e et al. (2012b). Like-
wise, the constraint based on the Ekman depth is not used, as little sensitivity was seen with its use. Hence,
there are no restrictions for the maximum boundary layer depth under stable forcing imposed by the NCAR
implementation of KPP.
The key problem with the Monin-Obukhov length scale, L, relates to the question of how to include
penetrative shortwave heating in the calculation of the buoyancy forcing, Bf(Section 18.3.9). Depending
on the depth over which the penetrative heating is included (equation (18.50)), one can produce a positive
Monin-Obukhov length (if including sufficient shortwave heating) or negative (if including less heating).
Since there is no fundamental reason to choose a particular amount of the shortwave when considering
the total buoyancy forcing, there is no compelling reason to enforce the Lconstraint on boundary layer
thickness.
Elements of MOM November 19, 2014 Page 282

Chapter 19
Vertical convective adjustment schemes
Contents
19.1 Introduction ............................................283
19.2 Summary of the vertical adjustment options .........................283
19.3 Concerning a double application of vertical adjustment ..................284
19.4 Implicit vertical mixing .....................................284
19.5 Convective adjustment .....................................284
19.5.1 Comments on the convective adjustment schemes .................... 284
19.5.2 Coding of full convection by M. Eby ............................ 285
The purpose of this chapter is to present the vertical convective adjustment schemes available in MOM.
The following MOM modules are directly connected to the material in this chapter:
ocean param/vertical/ocean convect.F90.
ocean param/vertical/ocean vert mix.F90.
19.1 Introduction
The hydrostatic approximation necessitates the use of a parameterization of vertical overturning processes.
The original parameterization used by Bryan in the 1960’s was motivated largely from ideas then used for
modeling convection in stars (Bryan (1969)). Work by Marshall and collaborators (Klinger et al. (1996),
Marshall et al. (1997)) have largely supported the basic ideas of vertical adjustment for purposes of large-
scale ocean circulation.
The Cox (1984) implementation of convective adjustment (the “NCON” scheme) may leave columns
unstable after completing the code’s adjustment loop. Various full convective schemes have come on-line,
with that from Rahmstorf (1993) implemented in MOM. An alternative to the traditional form of convective
adjustment is to increase the vertical mixing coefficient to some large value (say ≥10m2s−1) in order to
quickly diffuse vertically unstable water columns. Indeed, it is this form recommended from the study of
Klinger et al. (1996), and it is the approach commonly used in mixed layer schemes such as Pacanowski
and Philander (1981) and Large et al. (1994).
19.2 Summary of the vertical adjustment options
The handling of gravitationally unstable water columns in MOM can happen in one of two basic ways.
283

Chapter 19. Vertical convective adjustment schemes Section 19.5
• Implicit vertical mixing: By setting the namelist parameter aidif = 1.0, all vertical diffusion is han-
dled implicitly. There are two approaches depending on the vertical mixing scheme used.
1. When using the constant vertical mixing module, the vertical diffusivity is set to a maximum
value determined by a namelist diff cbt limit upon reaching a gravitationally unstable situa-
tion. diff cbt limit = 10.0 m2sec−1is a typical value.
2. When using the Pacanowski and Philander, KPP, or Chen vertical mixing scheme, both the
vertical diffusivity and vertical viscosity are set to the namelist settings diff cbt limit and
visc cbu limit upon reaching a gravitationally unstable situation. diff cbt limit =visc cbu limit =
10.0 m2sec−1are typical values.
• Convective adjustment: There are two convective adjustment schemes in MOM. Both schemes act
only on tracers when mixing. The default is the full convect scheme of Rahmstorf (1993). The alter-
native scheme is the older one from Cox (1984) and is known colloquially as the “NCON scheme”.
The NCON scheme has been implemented in MOM4.0 and later releases for legacy purposes. It is
not recommended for new models, with preference given to the use of a large vertical diffusivity with
aidif = 1.0.
19.3 Concerning a double application of vertical adjustment
Whether solving the vertical diffusion equation implicitly (aidif = 1.0) or explicitly (aidif = 0.0), it is
possible to use convective adjustment. To avoid a double application of vertical adjustment, one should
keep in mind the following points.
When using neutral diffusion, it is necessary to have aidif = 1.0 for numerical stability. Hence, verti-
cal diffusion will be computed implicitly in time. For those wishing to have vertical adjustment applied
just via the convective adjustment scheme, then it will be necessary to set diff cbt limit =kappa h and
visc cbu limit =kappa m. If wishing to adjust via large vertical diffusivities, then set diff cbt limit to
a large value as described above, and set the namelist convective adjust =.false.
19.4 Implicit vertical mixing
When the namelist aidif is set to unity, vertical mixing of momentum and tracers is time stepped implic-
itly. When aidif = 0.0, vertical mixing is time stepped explicitly. Intermediate values give a semi-implicit
treatment, although at present MOM does not support semi-implicit treatments. An implicit treatment of
vertical mixing allows unrestrained values of the vertical mixing coefficients. Details of the time implicit
algorithm are given in Chapter 13.
An explicit treatment, especially with fine vertical grid resolution, places an unreasonable limitation on
the size of the time step. The use of fine vertical resolution with sophisticated mixed layer and/or neutral
physics schemes has prompted the near universal implicit treatment of vertical mixing in ocean climate
models.
19.5 Convective adjustment
This section provides a description of the NCON and full convective adjustment schemes.
19.5.1 Comments on the convective adjustment schemes
As detailed in Rahmstorf (1993) and Pacanowski and Griffies (1999), the NCON convection scheme takes
multiple passes through the water column, alternately looking for instability on odd and even model levels.
When an instability is found, tracers are mixed, with their means (weighted by cell thickness) preserved.
This process may induce further instability and therefore more than one pass through the water column
Elements of MOM November 19, 2014 Page 284

Chapter 19. Vertical convective adjustment schemes Section 19.5
may be needed to remove all instability. The number of passes through the water column is controlled by
the parameter ncon, hence the name of the scheme.
The NCON convection scheme has come under a lot of scrutiny. The discussion in Rahmstorf (1993),
Killworth (1989) and Marotzke (1991), provide some elaboration and motivation to not employ the NCON
scheme. Its presence in MOM4.0 is solely for legacy purposes so that modelers can attempt to reproduce
older results using the new code.
The question inevitably arises of whether to mix or not mix momentum during a vertical adjustment
process. When momentum is not mixed, it is thought that it is simply carried along through the effects on
the density field. Killworth (1989) supports this idea, so long as the purpose is large-scale ocean modeling.
Basically, through geostrophy, adjusting density appears sufficient. Also, the vertical thermal wind shears
in simulated convection regions were found by Killworth to not be too strong. Hence, mixing momentum
along with density did little to affect the overall solution. These ideas, however, appear less sound for
equatorial oceanography, and so the mixing of both momentum and tracers might be more important in
there.
19.5.2 Coding of full convection by M. Eby
In June 2000, Michael Eby (eby@uvic.ca) ported a coding of the Rahmstorf scheme to MOM3.1. His code
is a bit more efficient and modern than the original Rahmstorf code. In particular, there are no more
“goto” statements. This code was incorporated into MOM3.1 and then to MOM4. Tests reveal that the
results from the Eby code and the original Rahmstorf code are nearly identical. The researcher can uncom-
ment/comment out two lines highlighted in the code to get the exact same results as the original Rahmstorf
scheme, if one so desires.
Elements of MOM November 19, 2014 Page 285

Chapter 19. Vertical convective adjustment schemes Section 19.5
Elements of MOM November 19, 2014 Page 286

Chapter 20
Mixing related to tidal energy
dissipation
Contents
20.1 Formulation ............................................287
20.2 Mixing from internal wave breaking .............................288
20.2.1 Simmons etal (2004) scheme ................................. 288
20.2.2 Some considerations for testing the implementation ................... 290
20.2.2.1 Regularization of the diffusivity ......................... 290
20.2.2.2 Use of the scheme for all depths ......................... 291
20.2.2.3 Energetic balances ................................. 291
20.2.2.4 Further comments ................................. 291
20.3 Dianeutral diffusivities from bottom drag ..........................292
20.3.1 Formulation and model implementation .......................... 292
20.3.2 Caveats about spuriously large diffusivities ........................ 293
The purpose of this chapter is to summarize the MOM implementation of the dianeutral parameteriza-
tion of Simmons et al. (2004) and Lee et al. (2006). Both schemes are available in MOM. These schemes pro-
vide a physically based replacement for the vertical tracer diffusivity of Bryan and Lewis (1979). Through-
out this chapter, we assume that the mixing of interest occurs with a unit Prandtl number1, thus enhancing
both the dianeutral tracer diffusivity and momentum viscosity by equal amounts. This issue was not dis-
cussed in the work of Simmons et al. (2004).
Hyun-Chul Lee and Harper Simmons provided valuable comments and suggestions for this chapter.
The following MOM module is directly connected to the material in this chapter:
ocean param/vertical/ocean vert tidal.F90
20.1 Formulation
Dianeutral mixing of tracer and momentum arises when energy dissipates at the small scales. There are
two sources of energy dissipation considered here:
• breaking internal gravity waves, where the gravity wave energy source is from barotropic tidal energy
scattered into internal tidal energy occuring when tides interact with rough bottom topography,
1The Prandlt number is the ratio of viscosity to diffusivity.
287

Chapter 20. Mixing related to tidal energy dissipation Section 20.2
• frictional bottom drag as tides encounter continental shelves (whose depths are generally 500m or
less).
To resolve both of these dissipation processes explicitly in a numerical model requires grid resolution no
coarser than meters in the vertical (throughout the water column), and 1-10 kilometers in the horizontal.
This very fine resolution is not generally accessible to global climate models, in which case it is necessary
to consider a parameterization.
Bottom drag is typically parameterized as
Dbottom drag =CDu|u|,(20.1)
where CDis a dimensionless drag coefficient taken as 2.4×10−3by Lee et al. (2006). As discussed by
Lee et al. (2006), the velocity dominating this drag is associated with energy input to the ocean via the
barotropic tides as they encounter continental shelves and other shallow ocean regions. The energy dissi-
pation (W m−2) associated with this bottom drag is given by
Ebottom drag =CDρohu2i|u|(20.2)
where the angle bracket symbolizes a time or ensemble average. This energy dissipation represents en-
ergy taken out of the barotropic tide and into small scale dissipation within the ocean bottom boundary
layer. We assume that the dissipated energy due to bottom drag contributes to enhanced dianeutral mixing
locally, with a form for the dianeutral diffusivity described in Section 20.3.
A wave drag associated with breaking internal gravity waves is written by Jayne and St.Laurent (2001)
as
Dwave drag = (1/2) Nbκ h2u,(20.3)
where Nbis the buoyancy frequency at the ocean bottom, and (κ,h) are wavenumber and amplitude scales
for the topography. The product κ h2has dimensions of length and thus defines a roughness length
Lrough =κh2(20.4)
to be specified according to statistics of the observed ocean bottom topography.
The energy dissipation (W m−2) associated with breaking internal gravity waves is given by
Ewave drag = (ρo/2) NbLrough hu2i.(20.5)
In the Jayne and St.Laurent (2001) paper, they emphasize that κ, which sets the roughness length through
Lrough =κh2, is used as a tuning parameter, with the tide model tuned to give sea level values agreeing
with observations. Then, the energy dissipation can be diagnosed from the tide model. As with the bottom
drag, the wave drag energy dissipation represents energy taken out of the barotropic tides, with the energy
here transferred into the baroclinic tides. Some of the energy transferred into the baroclinic tides dissipates
locally due to local wave breaking, and this then leads to enhanced dianeutral mixing locally. The remain-
ing baroclinic energy propogates away (i.e., it is nonlocal). The ratio of local to nonlocal energy is not well
known, and is the focus of research.
20.2 Mixing from internal wave breaking
When mechanical energy is dissipated, it is associated with dianeutral mixing. The relation between energy
dissipation and mixing is not known precisely, though some empirical formulations have proven useful.
20.2.1 Simmons etal (2004) scheme
For energy dissipation due to breaking internal gravity waves, we follow Simmons et al. (2004), who com-
pute a tracer diffusivity2
κwaves =κ0+qΓEwaves(x,y)F(z)
ρN2,(20.6)
2As stated at the start of this chapter, we assume a unit Prandtl number. This assumption means the vertical viscosity is enhanced
along with the diffusivity when considering internal wave breaking. Simmons et al. (2004) do not discuss vertical viscosity in their
study.
Elements of MOM November 19, 2014 Page 288
Chapter 20. Mixing related to tidal energy dissipation Section 20.2
where Ewave drag is the wave energy flux from scattered barotropic to baroclinic waves, given by equation
(20.5). Vertical stratification as measured by the buoyancy frequency
ρN2=−g ∂ρ
∂z !p
=−g ∂ρ
∂θ
∂θ
∂z +∂ρ
∂S
∂S
∂z !(20.7)
acts to suppress vertical mixing, hence its presence in the denominator of equation (20.6). The energy flux
in equation (20.5) is evaluated as follows.
•Nbis computed from the model’s evolving buoyancy frequency at the top face of a bottom boundary
layer (often just the bottom-most tracer cell). Note that the buoyancy frequency at the bottom face of
the bottom-most cell is zero, by definition.
• The effective roughness length Lrough =κ h2requires an algorithm to compute hfrom observed bottom
topography, and tide model to tune κ. However, in practice what can be done is to take hgiven some
variance of topography within a grid cell, and then tune Ewave drag to be roughly 1TW in ocean deeper
than 1000m, with κas the tuning paramter.
The dimensionless parameter Γin equation (20.6) measures the efficiency that wave energy dissipation
translates into dianeutral mixing. It is often chosen as
Γ= 0.2 (20.8)
based on Osborn (1980). However, in regions of very weak stratification, the mixing efficiency tends to zero
according to
Γ= 0.2 N2
N2+Ω2!(20.9)
where
Ω=2π+ 2π/365.24
86400s
=π
43082s−1
= 7.2921 ×10−5s−1.
(20.10)
is the angular rotation rate of the earth about its axis and about the sun. This modified mixing efficiency
reduces the regions where spuriously large values of diffusivity may occur, especially next to the bottom,
where low values of N2may appear. There is little physical reason to believe the huge diffusivities diag-
nosed from regions with N2<Ω2.
Another dimensionless parameter, q, is used to measure the amount of energy dissipated locally, and
thus contributes to local dianeutral mixing. Simmons et al. (2004) chose
q= 1/3 (20.11)
based on the work of St.Laurent et al. (2002). The remaining 2/3 of the energy is assumed to propagate away
and be dissipated nonlocally. The nonlocal dissipation of internal tidal energy, as well as the dissipation
of internal energy from other sources (e.g., wind energy), are accounted for in an ad hoc manner via the
background diffusivity κ0(and background viscosity). A value within the range
κ0= (0.1−0.2) ×10−4m2s−1(20.12)
is recommended based on the measurements of Ledwell et al. (1993). Note that this value does not account
for mixing in a planetary boundary layer, such as that discussed by Large et al. (1994).
Elements of MOM November 19, 2014 Page 289

Chapter 20. Mixing related to tidal energy dissipation Section 20.2
Setting q= 1/3 globally is strictly incorrect. The actual value is related to the modal content of the ex-
cited internal tide, which is related to the roughness spectrum of topography. The redder the mode/roughness
spectrum, the lower q. For example, Hawaii has been modelled as a knife-edge by (St.Laurent et al.,2003).
This topography excites predominantly low modes, and these modes are stable, propogate quickly, and
have long interaction times. That is, they propagate to the far field. Klymak et al. (2005) argue that q= 0.1
for Hawaii from the Hawaiian Ocean Mixing Experiment (HOME) data. For the mid-Atlantic ridge, the use
of q= 1/3, as in Simmons et al. (2004), may be more suitable.
The bottom intensified vertical profile, or deposition function,F(z) is taken as
F=e−(D−h)/ζ
ζ(1 −e−D/ζ)
=eh/ζ
ζ(eD/ζ −1).
(20.13)
In this expression,
D=H+η(20.14)
is the time dependent thickness of water between the free surface at z=ηand the ocean bottom at z=−H,
and
h=−z+η(20.15)
is the time dependent distance from the free surface to a point within the water column.3The chosen form
of the deposition function is motivated by the microstructure measurements of St.Laurent et al. (2001) in
the abyssal Brazil Basin, and the continental slope measurements of Moum et al. (2002). This profile re-
spects the observation that mixing from breaking internal gravity waves, generated by scattered barotropic
tidal energy, is exponentially trapped within a distance ζfrom the bottom. An ad hoc decay scale of
ζ= 500m (20.16)
is suggested by Simmons et al. (2004) for use with internal gravity wave breaking in the abyssal ocean.
20.2.2 Some considerations for testing the implementation
We present some comments and details regarding the implementation and testing of the Simmons et al.
(2004) scheme.
20.2.2.1 Regularization of the diffusivity
The diffusivities resulting from this parameterization can reach levels upwards of the maximum around
20 ×10−4m2s−1seen in the Polzin et al. (1997) results. Due to numerical resolution issues, the scheme can
in practice produce even larger values. We need to consider the physical relevance of these large values.
The following lists some options that the modeller may wish to exercise.
• We may choose to limit the diffusivity to be no larger than a maximum value, defaulted to 50 ×
10−4m2s−1in MOM.
• Based on observations, the mechanical energy input from wave drag (equation (20.5)) should not
exceed roughly 0.1Wm−2at a grid point (Bob Hallberg, personal communication 2008). Depending
on details of the bottom roughness and tide velocity amplitude, a typical model implementation may
easily exceed this bound. Hence, it may be necessary to cap the mechanical energy input to be no
larger than a set bound.
• Use of the stratification dependent mixing efficiency (20.9) provides a physically based means to
regularize the regions where N2can get extremely small.
3We emphasize that with a free surface, Dand hare generally time dependent. Furthermore, with general vertical coordinates, h
is time dependent for all grid cells.
Elements of MOM November 19, 2014 Page 290

Chapter 20. Mixing related to tidal energy dissipation Section 20.2
20.2.2.2 Use of the scheme for all depths
Simmons et al. (2004) do not apply their scheme in waters with ocean bottom shallower than 1000m,
whereas Jayne (2009) applies the scheme for all depths. MOM has a namelist that allows for setting a cutoff
depth. For the continental shelves, the scheme of Lee et al. (2006) described in Section 20.3 dominates.
Hence, in principle, there is nothing wrong with using the Simmons et al. (2004) scheme all the way to
shallow waters. So one may wish to naively use q= 1/3 without a 1000m depth cutoff. Likewise, ζ= 500m
globally may be a reasonable choice. The structure function will do the right thing and integrate to unity,
whether or not the ocean depth His greater or less than ζ.
20.2.2.3 Energetic balances
One of the main reasons to formulate diffusivites based on energy input is that energy is exchanged in a
conservative manner. This conservation then leads to self-consistency tests for the model implementation.
In particular, the work done against stratification by dianeutral diffusion is given by
P ≡ ZdV κdianeutral ρ N 2.(20.17)
Use of equation (20.6) for the diffusivity with a constant mixing efficiency Γ= 0.2 yields
P=ZdV(κwave drag −κ0)ρN2
=qΓZdxdy Ewave drag(x,y)
(20.18)
assuming qΓconstant. Note that to reach this result, we set RF(z)dz= 1, which is a constraint that is
maintained by the model implementation. Equation (20.18) says that the energy deposited in the ocean
interior that works against stratification originates from that scattered from the ocean bottom. For the
general case of qΓspatially dependent, we have the balance
P=ZdV(κwave drag −κ0)ρN2
=Zdxdydzq ΓEwave drag(x,y)F(z),
(20.19)
which again is a statement of energy conservation between wave dissipation and mixing of density.
Although equation (20.19) is a trivial identity following from the definition of the closure, it is not
trivial to maintain in the ocean model. The main reason is that we work with diffusivities when integrating
the equations of an ocean model, and these diffusivities are often subjected to basic numerical consistency
criteria, such as the following.
• We may wish to have the diffusivities monotonically decay upwards in the column. Given the N−2
dependence of the diffusivity in equation (20.6), monotonicity is not necessary. Without an added
monotonicity constraint, the simulation can be subject to spurious instabilities in which intermediate
depths destratify, then producing larger diffusivities, and further reducing the stratification. Jayne
(2009) discovered this behaviour in his simulations.
• The diffusivities should be bounded by a reasonable number, such as 50 −100cm2sec−1.
Imposing constraints such as these on the diffusivity corrupts the identity (20.18). In general, the con-
straints remove energy from the interior, so that in practice RdV(κwave drag−κ0)ρ N 2<Rdxdydz q ΓEwave drag(x,y).
20.2.2.4 Further comments
Here are some further points to consider when setting some of the namelists for this scheme.
Elements of MOM November 19, 2014 Page 291

Chapter 20. Mixing related to tidal energy dissipation Section 20.3
• One means to ensure that the diffusivities are within a reasonable bound, without capping them after
their computation, is to artificially restrict the stratification used in the calculation to be no less than
a certain number. Simmons et al. (2004) chose the floor value N2≥10−8s−2. There is a great deal of
sensitivity to the floor value used. GFDL practice is to keep the floor value quite low so that N2
min <Ω2.
• If the maximum diffusivity realized by the scheme is allowed to be very large, say much greater than
as 1000cm2sec−1, then the near bottom stratification can become very small. In this case, Ewave drag can
dip below the canonical 1TW value. This process resembles a negative feedback in some manner,
though it has not been explored extensively.
20.3 Dianeutral diffusivities from bottom drag
The Lee et al. (2006) scheme provides a means to parameterize mixing from barotropic tides interacting
with the continental shelf regions. The purpose of this section is to detail the scheme and present some
discussion of its implementation in MOM.
20.3.1 Formulation and model implementation
Contrary to the energetic approach of Simmons et al. (2004), the Lee et al. (2006) scheme does not consider
energetic arguments for determining the diffusivity associated with barotropic tides dissipated by the bot-
tom boundary layer. Instead, it follows the older ideas of Munk and Anderson (1948), whereby a dianeutral
diffusivity is given by
κdrag =κmax (1 + σRi)−pexp−(D−h)/ztide ,(20.20)
where the dimensionless parameters σand phave the default values
σ= 3 (20.21)
p= 1/4.(20.22)
The Richardson number is given by
Ri = N2
|∂zu|2.(20.23)
Small Richardson numbers (e.g., regions of low stratification or strong vertical shear) will give larger ver-
tical diffusivities, with the maximum diffusivity set by κmax. Following Lee et al. (2006), we set the default
for the maximum diffusivity arising from bottom drag dissipation as
κmax = 5 ×10−3m2s−1.(20.24)
Since we do not generally resolve the bottom boundary layer in global models, we must approximate the
vertical shear to compute the Richardson number, and here we use the form
2|∂zu|2= ˜
Utide
D−h!2
,(20.25)
with the scaled tidal speed ˜
Utide given by
˜
Utide =Utide √Cd/κvon Karman.(20.26)
Here, Cd is the bottom drag coefficient, taken as Cd = 2.4×10−3by Lee et al. (2006),
κvon Karman = 0.41 (20.27)
is the von Karman constant, and Utide is the tidal speed taken from a barotropic tidal model. These speeds
are largest in the shallow regions.
Elements of MOM November 19, 2014 Page 292
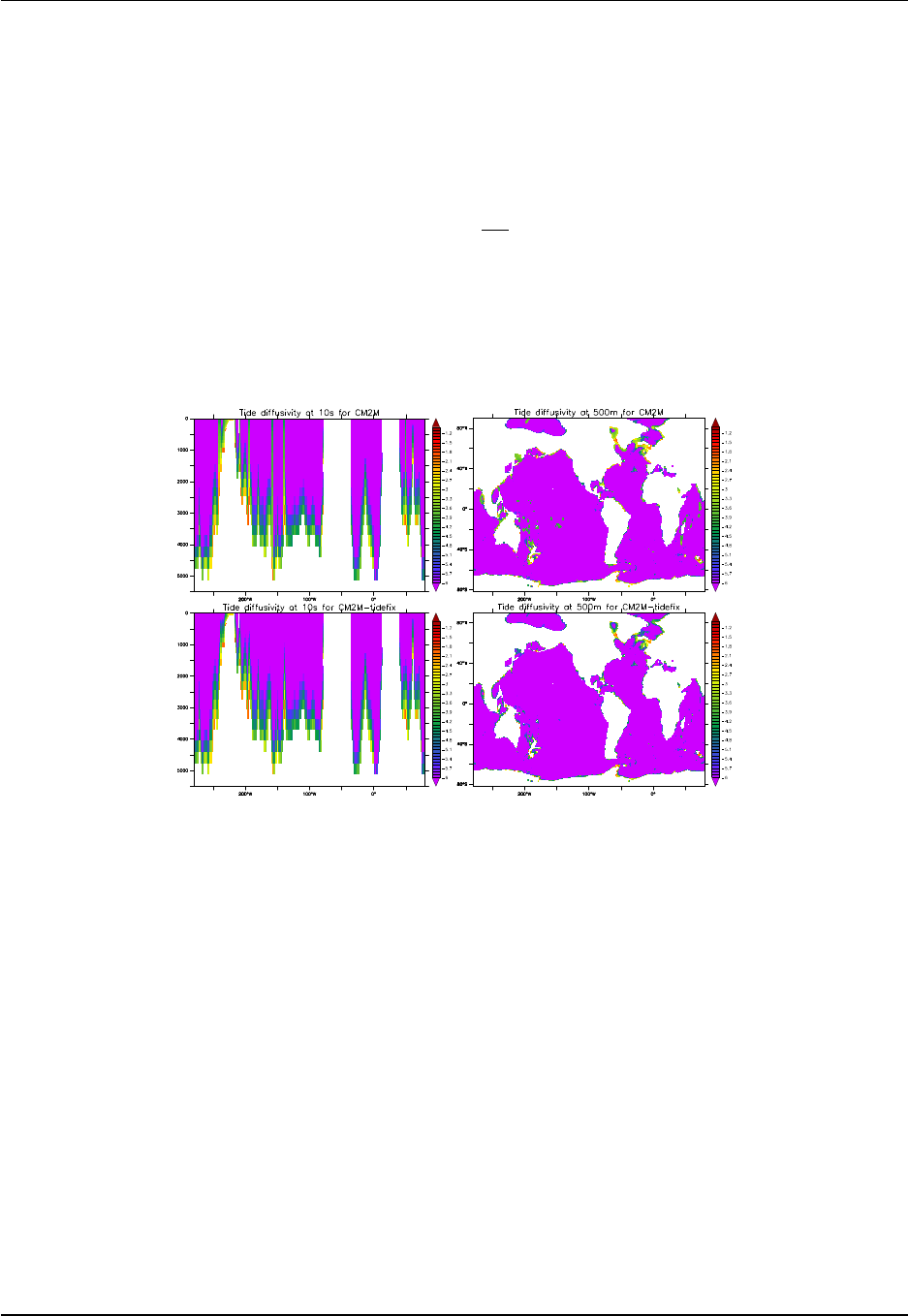
Chapter 20. Mixing related to tidal energy dissipation Section 20.3
20.3.2 Caveats about spuriously large diffusivities
The exponential decay appearing in equation (20.20) is not part of the original Lee et al. (2006) scheme,
nor was it part of the MOM4.0 and MOM4p1 implementations. However, it is an essential element added
for the MOM implementation as of 2012 that ensures diffusivities drop offexponentially when moving
away from the ocean bottom. Absent this exponential decay, regions of small Richardson number, leading
to large κdrag, can move upwards in a column, as revealed by the diffusivities in Figure 20.1. The chosen
exponential decay length scale is given by
ztide =˜
Utide
τtide
2π(20.28)
where
τtide = 12 ×3600 s,(20.29)
corresponding to the M2 tide period. Another means for removing the spurious diffusivities from the Lee
et al. (2006) scheme is to enable the scheme only in continental shelf regions, which is where it is physically
appropriate. Such is the default for the MOM implementation.
Figure 20.1: Shown here are the diffusivities resulting from the sum of the Simmons et al. (2004) and
Lee et al. (2006) schemes. The ocean component is taken from a coupled climate simulation forming the
basis for the ESM2M earth system model of Dunne et al. (2012), which uses a grid configured as in the
CM2.1 model documented by Delworth et al. (2006), Griffies et al. (2005) and Gnanadesikan et al. (2006),
but with updated numerics and physical parameterizations. Note in particular the nontrivial values in
certain “hot-spots” in the Pacific for the top row of figures. These regions arise from spurious treatment
of the original Lee et al. (2006) scheme, where the absence of an exponential decay exposes the scheme
to a positive feedback, whereby large diffusivities move upward in the column from regions where there
is a nontrivial barotropic tide. The bottom row of figures results from applying the exponential decay in
equation (20.20), which removes the spurious diffusivities. The result is a far more sensible diffusivity
profile that is bottom intensified and does not penetrate through the pycnocline from deep ocean regions.
Elements of MOM November 19, 2014 Page 293

Chapter 20. Mixing related to tidal energy dissipation Section 20.3
Elements of MOM November 19, 2014 Page 294

Chapter 21
Mixing related to specified minimum
dissipation
Contents
21.1 Formulation ............................................295
The purpose of this chapter is to summarize an option in MOM to specify the vertical tracer diffusivities
based on setting a floor to the power dissipation. The following MOM module is directly connected to the
material in this chapter:
ocean param/vertical/ocean vert mix.F90
21.1 Formulation
Vertical tracer diffusion is associated with a dissipation of power. Assuming temperature and salinity have
the same vertical diffusivities leads to the expression for power dissipation (W m−3)
=ρκN2
=−κg ∂ρ
∂z !p
=−κg ∂ρ
∂θ
∂θ
∂z +∂ρ
∂S
∂S
∂z !.
(21.1)
In these equations, κis the vertical tracer diffusivity, gis the gravitational acceleration, and the vertical
density derivative is locally referenced. When the temperature and salinity diffusivities differ, as occurs
with double diffusion, we compute the power dissipation via
=−κtemp g ∂ρ
∂θ
∂θ
∂z !−κsalt g ∂ρ
∂S
∂S
∂z !.(21.2)
We now compute a floor to the dissipation according to
floor =min +B|N|,(21.3)
where
min ∼10−6W m−3(21.4)
295

Chapter 21. Mixing related to specified minimum dissipation Section 21.1
is a specified minimum power dissipation (set according to a namelist),
B∼1.5×10−4J m−3(21.5)
is another namelist parameter, and |N|is the absolute value of the buoyancy frequency. The B|N|contribu-
tion to dissipation is motivated by the stratification dependent diffusivity proposed by Gargett (1984). We
establish a floor to the vertical diffusivity according to
κfloor =floor Γregularized
ρN2
≈0.2floor
ρo(N2+Ω2).
(21.6)
In this equation,
Γregularized =0.2N2
N2+Ω2(21.7)
is a regularized mixing efficiency, and
Ω= 7.2921 ×10−5s−1(21.8)
is the angular rotation rate of the earth about its axis and around the sun. The tracer diffusivity for tem-
perature, salinity, and passive tracers is not allowed to be smaller than κfloor.
Elements of MOM November 19, 2014 Page 296

Chapter 22
Parameterization of form drag
Contents
22.1 Regarding the TEM approach ..................................297
22.2 What is available in MOM ...................................298
This chapter is a placeholder for documentation of the form drag parameterizations available in MOM.
At present, MOM has implemented the schemes proposed by Greatbatch and Lamb (1990), Aiki et al.
(2004), and Ferreira and Marshall (2006). The following MOM module is directly connected to the material
in this chapter:
ocean param/vertical/ocean form drag.F90.
Notably, these schemes are experimental and have not been thoroughly used at GFDL.
22.1 Regarding the TEM approach
We comment here on the relevance of implementing the Gent and McWilliams (1990) scheme via the tracer
equation, as traditionally done in MOM as motivated by Gent et al. (1995) and Griffies (1998), versus the
alternative, which adds a vertical stress to the horizontal momentum equation, as recently implemented
in a global model by Ferreira and Marshall (2006). When adding a stress to the momentum equation,
the prognostic velocity variable is interpreted as the residual mean, or effective velocity, rather than the
traditional Eulerian mean velocity. This transformed Eulerian mean (TEM) interpretation is quite elegant,
since it is the residual mean velocity that advects tracers in a coarsely resolved (i.e., no mesoscale eddies)
z-model, not the Eulerian mean velocity. The elegance is maintained so long as one need not compute the
Eulerian mean velocity.
For many purposes, we do not require the Eulerian mean velocity, so the TEM momentum equation
provides all the variables required to run an ocean model. However, the following considerations point to
a need for the Eulerian mean velocity in cases of realistic ocean climate modeling.
• In computing the air-sea stress in realistic coupled climate models, it is important for many purposes
to include the velocity of the ocean currents according to the discussion in Pacanowski (1987). The
relevant currents for this calculation are the Eulerian mean currents, not the residual mean.
• When computing the Richardson number commonly required for mixed layer parameterizations, we
require the vertical shear of the Eulerian mean velocity, not the vertical shear of the residual mean
velocity.
There are two options that one may consider. First, one may choose to ignore the difference between the Eu-
lerian mean and the residual mean velocity. Alternatively, one may choose to diagnose the Eulerian mean
297

Chapter 22. Parameterization of form drag Section 22.2
from the residual mean. The Eulerian mean velocity is available within a TEM ocean model, given the
prognostic residual mean velocity plus a prescribed mesoscale eddy closure to compute the eddy induced
velocity. Its calculation requires derivatives of the quasi-Stokes streamfunction to obtain the eddy-induced
velocity, and one further derivative to compute the vertical shear. As discussed by Griffies (1998), this
calculation can produce a rather noisy eddy induced velocity, especially near boundaries. Furthermore,
there is no general principle guiding us in formulating a particular choice of discretization for the eddy
induced velocity from a streamfunction. A noisy eddy induced velocity produces a noisy diagnosed Eu-
lerian mean velocity, which then puts noise in the air-sea stress as well as the Richardson number. These
numerical sources of noise are unacceptable for realistic climate modeling, and represent a practical barrier
to making use of the TEM approach.
22.2 What is available in MOM
In addition to the practical limitations noted above, there are further theoretical concerns with the TEM
approach, as its formulation generally assumes a small Rossby number. Nonetheless, the idea is compelling
and as such it may be suitable for study, especially in idealized settings such as that of Ferreira and Marshall
(2006) and Zhao and Vallis (2008). Additionally, the scheme from Aiki et al. (2004) is quite novel, and may
present some interesting features of use for climate modeling. It is for these reasons that the form drag
approach has been implemented in MOM. Given the absence of extensive experience with the scheme at
GFDL, we recommend that it be used only by those who are focused on research related to the use of these
schemes.
Elements of MOM November 19, 2014 Page 298
Subgrid scale parameterizations for
lateral processes
The purpose of this part of the manual is to describe certain of the subgrid scale (SGS) parameterizations
of physical processes used in MOM, with focus here on lateral processes.
299

Section 22.2
Elements of MOM November 19, 2014 Page 300

Chapter 23
Neutral Physics
This chapter gives a description of a new implementation of the neutral physics component of MOM, with
the implemention coded by Tim.Leslie@gmail.com. The following MOM modules are directly connected to
the material in this chapter:
ocean param/neutral/ocean nphysics diff.F90
ocean param/neutral/ocean nphysics flux.F90
ocean param/neutral/ocean nphysics new.F90
ocean param/neutral/ocean nphysics skew.F90
ocean param/neutral/ocean nphysics tensor.F90
ocean param/neutral/ocean nphysics util new.F90
This new implementation breaks bitwise compatibility with the original code. However, it addresses some
issues while simplifying and clarifying much of the code. The original code is contained in the modules
ocean param/neutral/ocean nphysicsA.F90
ocean param/neutral/ocean nphysicsB.F90
ocean param/neutral/ocean nphysicsC.F90
ocean param/neutral/ocean nphysics.F90
ocean param/neutral/ocean nphysics util.F90
The original code is retained for legacy purposes, and as a means to carefully move forward with the new
code through testing various options.
This chapter was written by
tim.leslie@gmail.com
with help from
Stephen.Griffies@noaa.gov
There are many unfinished pieces to this chapter, reflecting the ongoing development, testing, and docu-
mentation of the new neutral physics code.
Caveat
Given the early stages of testing for the new implementation of neutral physics, we recommend that
the general user employ the original version of neutral physics, with these original options part of the MOM
test cases.
301

Chapter 23. Neutral Physics Section 23.0
Contents
23.1 Introduction ............................................303
23.1.1 Neutral diffusion and neutral skewsion .......................... 303
23.1.1.1 Advection-diffusion equations .......................... 304
23.1.1.2 Neutral Diffusion Parameterization ....................... 305
23.1.1.3 Skew Diffusion Parameterization ......................... 305
23.1.2 Overview of this chapter ................................... 306
23.2 Notation ..............................................306
23.2.1 Grid Points ........................................... 306
23.2.2 Tensors ............................................. 306
23.2.3 Cell Faces ........................................... 307
23.2.4 Spanning Pairs ......................................... 307
23.2.5 Triads .............................................. 307
23.2.6 Harmonic Mean ........................................ 308
23.3 Discretization ...........................................309
23.3.1 Functional ........................................... 309
23.3.2 Fluxes .............................................. 312
23.3.3 Skew flux discretization ................................... 314
23.4 Implementation .........................................315
23.4.1 Fluxes .............................................. 315
23.4.1.1 ............................................ 316
23.4.1.2 ............................................ 316
23.4.1.3 Tracer Limiting ................................... 316
23.4.1.4 ............................................ 317
23.4.1.5 ............................................ 319
23.4.1.6 Density Weighted Quarter-cell Volumes ..................... 319
23.5 Diffusion and Skew-Diffusion Tensors ............................320
23.5.1 Depth Taper .......................................... 320
23.5.2 Neutral Diffusion Tensor ................................... 321
23.5.2.1 Tapers ........................................ 322
23.5.3 Skew-Diffusion Tensor .................................... 323
23.5.3.1 Preliminaries .................................... 323
23.5.3.2 GM Skew-Diffusion Tensor ............................ 324
23.5.3.3 Baroclinic Modes .................................. 325
23.5.3.4 Boundary Value Problem ............................. 326
23.5.4 Vertical Boundary Tensor Values .............................. 328
23.6 Tracer Gradients .........................................328
23.7 Quantities related to density gradients ............................329
23.7.1 Gradient of locally referenced potential density ...................... 329
23.7.1.1 Optional adjustments of the vertical density derivative ............ 330
23.7.1.2 Diagnostics ..................................... 330
23.7.2 Neutral Slopes ......................................... 331
23.7.2.1 Neutral Slope Vector ................................ 331
23.7.2.2 Neutral Slope Magnitude ............................. 331
23.7.2.3 Diagnostics ..................................... 332
23.7.3 Buoyancy ............................................ 332
23.7.4 Baroclinic Gravity Wave Speed ............................... 332
23.7.5 Rossby Radius ......................................... 332
23.7.6 Neutral Boundary Layers ................................... 333
Elements of MOM November 19, 2014 Page 302

Chapter 23. Neutral Physics Section 23.1
23.7.7 Summary ............................................ 333
23.8 Specification of the diffusivity .................................333
23.8.1 Namelist Parameters ..................................... 334
23.8.2 Fixed GM Diffusivity ..................................... 335
23.8.3 Flow Dependent GM Diffusivity ............................... 335
23.8.3.1 Selecting a GM Diffusivity Closure ........................ 335
23.8.3.2 Diffusivity Postprocessing ............................. 335
23.8.3.3 Grid Scaling ..................................... 336
23.8.4 MICOM ............................................ 336
23.8.5 Buoyancy Scaling ....................................... 336
23.8.6 Rate Length Squared ..................................... 337
23.8.6.1 Growth Rate .................................... 337
23.8.6.2 Length ........................................ 340
23.8.6.3 Baroclinic Zone Width ............................... 341
23.8.7 Redi Diffusivity ........................................ 342
23.9 Summary of the notation ....................................342
23.9.1 General ............................................. 343
23.9.2 Tracer Gradients ........................................ 343
23.9.3 Density Calculations ..................................... 344
23.9.4 Neutral Boundary Layer ................................... 344
23.9.5 Diffusivity ........................................... 345
23.9.6 Tensors ............................................. 345
23.9.7 Fluxes .............................................. 346
23.1 Introduction
This chapter details the neutral physics parameterization as implemented in MOM. The two processes de-
scribed are neutral diffusion, which diffuses tracers along neutral directions, and skew diffusion or skew-
sion, which stirs tracers. These processes aim to parameterize the mixing and stirring effects of mesoscale
eddies. Both neutral and skew diffusion can be mathematically described in terms of a generalised trans-
port tensor, which in turn allows us to unify many aspects of the calculation (Griffies,1998).
The MOM implementation of neutral physics is limited to the use of quasi-horizontal coordinates z,z∗,
p, and p∗(see Chapter 5). As discussed in Section 4.2.3, when working with these coordinates, there is no
modification to the algorithm relative to that of the original geopotential implementation. However, terrain
following coordinates, which are not quasi-horizontal, require extra considerations, such as those detailed
in Lemari´
e et al. (2012b,a).
23.1.1 Neutral diffusion and neutral skewsion
Tracer prognostics within MOM are computed in terms of the non-Boussinesq thickness weighted tracer
concentration, dzρT . This quantity evolves according to a range of physical processes. We can therefore
write the tracer evolution equation as
∂
∂t (dzρT ) = X
processes
∂
∂t (dzρT ) (23.1)
where we sum over all the physical processes. When computing the neutral physics processes, we choose
to write the tracer evolution as
∂
∂t (dzρT )=dz∂
∂t (ρT )neutral +X
non-neutral
∂
∂t (dzρT ).(23.2)
Elements of MOM November 19, 2014 Page 303

Chapter 23. Neutral Physics Section 23.1
This chapter focuses on the first term in this equation, which we can write as dz(ρT )neutral
,t . We will param-
eterize the neutral processes with an advection-diffusion equations, so
(ρT )neutral
,t = (ρT )adv
,t + (ρT )diff
,t (23.3)
=−∇·(vρT −∇·(ρK∇T),(23.4)
where Kis a positive-semidefinite, symmetric diffusion tensor and
∇·(ρv)=0.(23.5)
We can write this equation in a number of equivalent forms. These different forms will help guide the
discritization used below.
23.1.1.1 Advection-diffusion equations
As shown in Griffies (1998), we can write both the advective and diffusive terms as the divergence of fluxes
which gives
(ρT )neutral
,t =−∇·ρ(Fadv +Fdiff),(23.6)
where
Fadv =vT(23.7)
Fdiff=−K∇T(23.8)
are tracer concentration fluxes. Since ρvis divergence free, it can be written as the curl of a stream
function plus the divergence of an arbitrary gauge field,
ρv=∇×(ρΨ+∇φ).(23.9)
We ignore the gauge function in the following, though our choice for Ψimplicitly assumes a choice. The
corresponding advective tracer flux is given by
ρFadv = (∇ × ρΨ)T(23.10)
=−∇T×ρΨ+∇ × (ρΨT).(23.11)
It follows that the advective portion of the tracer equation can be written as the convegence of a skew flux
(ρT )adv
,t =−∇·ρFskew (23.12)
where the skew flux is defined as
ρFskew =ρΨ× ∇T . (23.13)
We can write equation 23.3 as a generalised transport equation,
(ρT )neutral
,t =−∂m(ρFm) (23.14)
Fm=JmnT,n.(23.15)
Jmn is a transport tensor, and we have used tensor notation with repeated indices summed over their range,
and a comma denotes a partial derivative (see Griffies (2004) Chapter 20). The transport tensor can be
decomposed into symmetric and anti-symmetric terms, to give
Jmn =Kmn +Amn (23.16)
where
Kmn =Knm (23.17)
Amn =−Anm.(23.18)
Elements of MOM November 19, 2014 Page 304

Chapter 23. Neutral Physics Section 23.1
The symmetric tensor is identified as the neutral diffusion tensor Kin equation 23.4. The antisymmetric
tensor Acorresponds to the operator Ψ×in equation 23.13. We call Athe skew diffusion tensor, and it can
be written as
A=
0−ΨzΨy
Ψz0−Ψx
−ΨyΨx0.(23.19)
We can now define our neutral physics parameterization in terms of Kand Ψ.
23.1.1.2 Neutral Diffusion Parameterization
The neutral diffusion tensor parameterizes mixing from eddies according to a diffusion acting along neu-
tral directions. The small slope approximated form of this tensor Gent and McWilliams (1990); Griffies et al.
(1998) is given by
K=AR
1 0 Sx
0 1 Sy
SxSy|S|2,(23.20)
where
S= (Sx,Sy,0) (23.21)
is a horizontal vector measuring the slope of the neutral direction relative to the horizontal. We compute
this slope vector according to the following expression
S=− ρ,Θ∇sΘ+ρ,S ∇sS
ρ,Θ∂zΘ+ρ,S ∂zS!,(23.22)
where
ρ,Θ=∂ρ
∂Θ(23.23)
ρ,S =∂ρ
∂S (23.24)
are density partial derivatives with respect to conservative temperature and salinity. The lateral gradient
operator, ∇s, is taken along surfaces of constant vertical coordinates, s. The only vertical coordinates
in MOM that are supported for neutral physics are the quasi-horizontal coordinates z,z∗,p, and p∗(see
Chapter 5for a discussion of vertical coordinates). Hence, it is very accurate to compute the neutral slope
vector by taking lateral gradients along the constant vertical coordinate surfaces. The diffusivity ARsets
the overall magnitude of the neutral diffusion, with this diffusivity sometimes called the Redi diffusivity,
reflecting the work of Redi (1982) who formulated the kinematics of neutral diffusion. A discussion of
neutral diffusion, with details of how the MOM discretization is formulated, is given by Griffies et al. (1998)
and Griffies (2004).
23.1.1.3 Skew Diffusion Parameterization
The skew diffusion tensor parameterizes mesoscale eddy stirring, and it is given by
A=
0 0 Υx
0 0 Υy
−Υx−Υy0,(23.25)
where Υis the parameterized transport vector. Comparing this with equation 23.19 we note that
Υ=ˆ
z×Ψ.(23.26)
Elements of MOM November 19, 2014 Page 305

Chapter 23. Neutral Physics Section 23.2
We are able to make this choice due to the existance of the gauge term ∇φin equation 23.9. Most param-
eterizations of this transport vector are based on the Gent-McWilliams (GM) parameterization Gent and
McWilliams (1990); Griffies (1998),
ΥGM =−κS,(23.27)
which leads to the skew tensor
AGM =κ
0 0 −Sx
0 0 −Sy
SxSy0.(23.28)
However, Ferrari et al. (2010) propose an alternative to the traditional GM parameterization, with this al-
ternative also implemented in MOM. Indeed, it is the recommended approach, as the Ferrari et al. (2010)
method provides for an elegant treatment of weakly stratified regions, such as the surface and bottom
boundary layers.
23.1.2 Overview of this chapter
The remainder of this chapter details the discretization and parameterization of the equations described
above. Section 23.6 details the calculation of T,n for each of the tracers in the model. In Section 23.7
the calculation of the neutral slope vector Sis described, along with some other required quantities which
depend directly on the density gradients. The parameterization of the diffusivities ARand κare described
in Section 23.8. Having calculated these values, Section 23.5 outlines the calculation of the two tensors, K
and A. Finally, Section 23.3.2 describes the calculation of the flux vector Ffor each tracer, which allows us
to calculate the density-thickness weighted tendencies defined in Equations (23.3) and (23.4). Additionally,
Appendix A provides a summary of the values described in each section, along with the corresponding
variable names in the implementation.
23.2 Notation
The implementation of the neutral physics module requires the description of variables that are compo-
nents of a rank two tensor located on a two dimensional sub-grid at a point in three dimensional space.
Furthermore, these variables may be arranged in one of four configurations. This arrangement leads to
the requirement of some relatively advanced indexing notation, which we will describe here. We will also
describe how the indexing notation corresponds to variable naming conventions within the implementa-
tion.
23.2.1 Grid Points
Most variables are associated with a particular point in space. Within the model, these points correspond to
the tracer cell locations. Note that velocity cells are not used in this module, which means the treatment
of neutral physics is identical for B-grid and C-grid ocean models. Three dimensional fields have their
spatial location marked with the subscripts i,j,k, while two dimensional fields use i,j. These subscripts
correspond to array indices within the code. For example, the variable Amight be represented by the array
Ain the code, and the value Ai,j,k would correspond to A(i,j,k).
23.2.2 Tensors
The individual components of a rank two tensor are denoted by a pair of subscripts mn, where mis the row
and nis the column in the matrix representation of the tensor. For example a tensor Ahas components
A=
A11 A12 A13
A21 A22 A23
A31 A32 A33.(23.29)
Elements of MOM November 19, 2014 Page 306
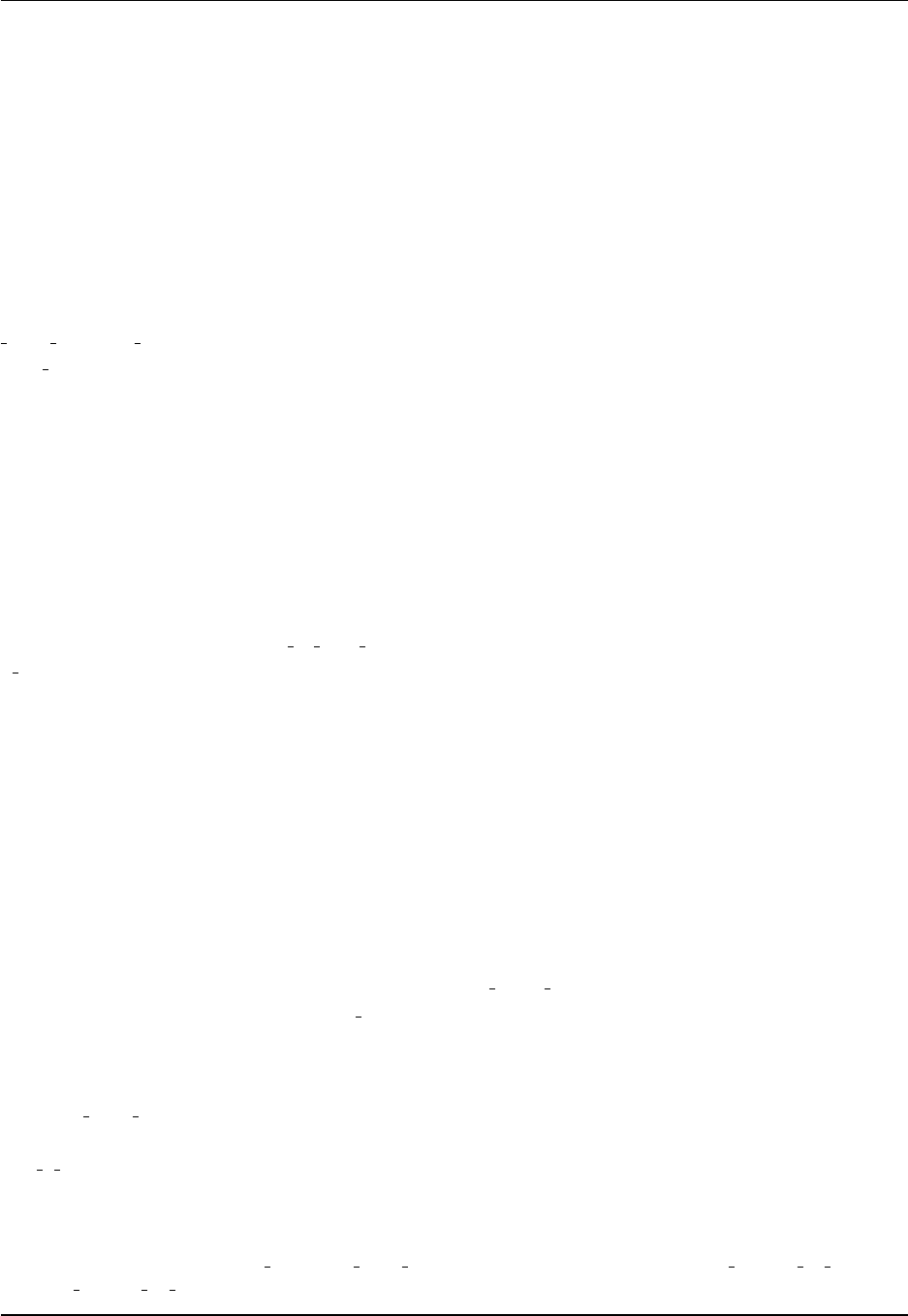
Chapter 23. Neutral Physics Section 23.2
To represent the value of a component at a grid point, parentheses are applied before the grid subscript,
giving e.g. (A23)i,j,k. In the code, separate variables are used for each component, with the component
label usually included in the name, e.g. A23(i,j,k).
23.2.3 Cell Faces
Some variables, such as the fluxes, are defined at the faces of the tracer cell, which is the appropriate
location when considering a finite volume interpretation of the tracer equation. By convention, we define
values at the eastern, northern and bottom faces in each of the directions respectively. Cell face variables
are thus indicated with a superscript of E,Nand brespectively. So for example, the flux through the
eastern face of the i,j,k tracer cell is written FE
i,j,k. In the code, such variables are denoted by appending
xte,ytn and ztb respectively to the variable names. So the flux FE
i,j,k is represented by the variable
flux xte(i,j,k).
23.2.4 Spanning Pairs
Some variables, such as gradients and cell widths, span multiple cells. A variable can span cells horizon-
tally to the left or right, or vertically up or down. These variables naturally occur as pairs, either hori-
zontally left-right or vertically up-down. To represent these variables, an additional superscript is added,
which takes the value zero or one (left/up = 0, right/down = 1). This index has the name ip,jq or kr for
the x,yor zdirections respectively. For example, a variable that spans horizontally to the left and right
in the xdirection is called A(ip)
i,j,k. The corresponding variable in the code is a four dimensional array and
the variable name has a suffix of x,yor zas appropriate. The variable A(ip)
i,j,k is therefore represented as
A x(i,j,k,ip).
23.2.5 Triads
When combining two variables that span different directions, there are four possible combinations to con-
sider, i.e. left-up, right-down, etc. These combinations use a three point stencil, and hence are called triads.
Figure 23.1 shows an example of a set of four triads with a common central point. When arranged in this
fashion the group is called a centred triad group. For a given point, the triads are indexed with a pair of
numbers as shown in the figure. When written as a variable, a parenthetical pair of superscripts are used
for these indexes. In the x−zplane they have the generic indices (ip,kr)while in the y−zplane indices
(jq,kr)are used. A variable in the x−zplane is therefore written as A(ip,kr)
i,j,k . In the code, such a variable is
represented with a five dimensional array, with the last two dimensions representing the ip and kr indices.
Furthermore, to indicate the plane being used, a suffix of xz or yz is appended to the variable. Therefore,
our variable A(ip,kr)
i,j,k is written in code as A xz(i,j,k,ip,kr).
As with regular variables, we will need to have groups of triads centred on the faces of tracer cells.
Figure 23.2 shows an example of such horizontal and vertical face centred triad groups. As with regular
variables, a face centred triad variable has an extra superscript of E,Nor b. In the code, an extra suffix
of either hor vis appended to indicate a horizontal or vertical face centred triad group. Hence, the
horizontal face centred triad group variable A, defined in the x−yplane, has indices AE(ip,kr)
i,j,k and is coded
as A h xz(i,j,k,ip,kr).
A variable defined over the centered triad group may be needed over the face centred triad group.
Mathematically we can indicate this shift implicitly by using a different indexing scheme. However, in the
code implementation, data must be copied from one array to another to accommodate the different index-
ing scheme. The module ocean nphysics util new provides the subroutines stencil centre to vert and
stencil centre to horiz to perform the appropriate copying actions. We do this shift mathematically by
Elements of MOM November 19, 2014 Page 307
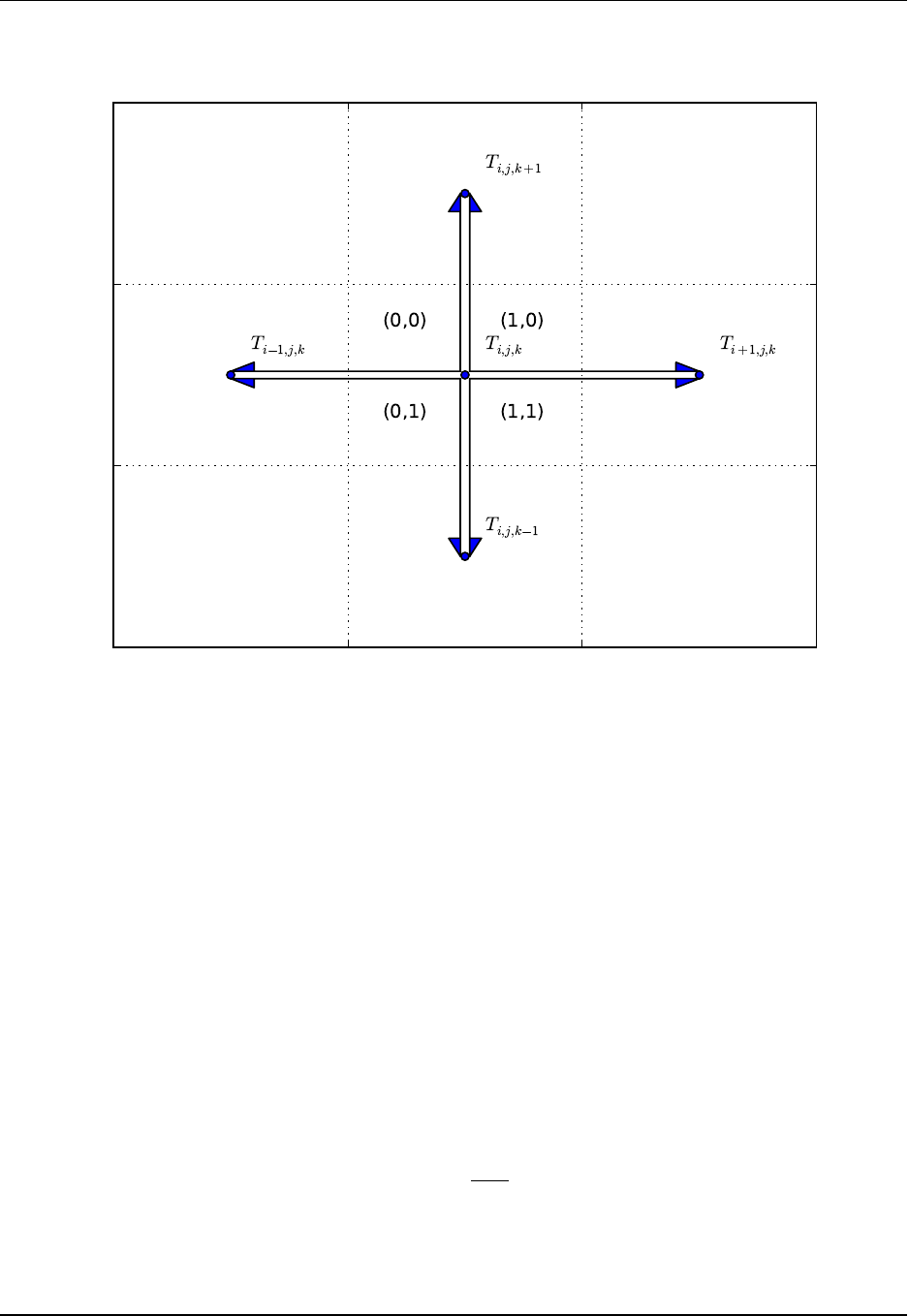
Chapter 23. Neutral Physics Section 23.3
Figure 23.1: Stencils and indices for a centered triad group.
the functions C2Vand C2Hrespectively, so the transformation of an array is written as
AE(ip,kr)
i,j,k =C2HA(ip,kr)
i,j,k (23.30)
AN(jq,kr)
i,j,k =C2HA(jq,kr)
i,j,k (23.31)
Ab(ip,kr)
i,j,k =C2VA(ip,kr)
i,j,k (23.32)
Ab(jq,kr)
i,j,k =C2VA(jq,kr)
i,j,k .(23.33)
23.2.6 Harmonic Mean
In a number of places a harmonic mean function is used to place a smooth but hard cap on the size of
certain values. This function is defined as
H(a,b) = 2ab
a+b.(23.34)
It has the useful property that
lim
a→∞H(a,b)=2b(23.35)
Elements of MOM November 19, 2014 Page 308
Chapter 23. Neutral Physics Section 23.3
Figure 23.2: Stencils and indices for horizontal and vertical face centered triad groups.
which means that in the transformation a→H(a,b),ais capped above by the value 2b, but approaches this
value smoothly.
23.3 Discretization
This section describes a discretization of the term −∇· ρFdiffin equation 23.6. The discretization of the
skew flux follows by direct analogy. A finite volume approach is used, however certain choices are made to
maintain key properties of the continuous equations.
The finite volume approximation can be written as
−∇·ρF≈ − 1
VZV∇·ρFdV (23.36)
=−1
VIS
ρF·ˆ
ndS, (23.37)
where the first integral is over the volume of a single tracer cells, and the second is over the faces of the
tracer cell, via the divergence theorem.
The above equation gives us a starting point for our discretization, however does not fully specify how
best to compute the fluxes at each face. To guide our choice of flux discretization, we have two key require-
ments which must be satisfied:
• Tracer variance must not increase.
• There must be zero flux of locally referenced potential density.
Proving that these conditions are satified by a given finite volume discretization is not easy. Using a
different formulation, based on functional calculus, a discretization can be developed which does meet
the requirements. This new discretization can be shown to be equivilent to a finite volume discretization,
which is how it is implemented.
23.3.1 Functional
The following discussion of the functiontal approach borrows heavily from Section 16.1 of Griffies (2004).
Certain results from that work are stated here without proof.
Elements of MOM November 19, 2014 Page 309
Chapter 23. Neutral Physics Section 23.3
We begin with the observation that the evolution of tracer variance can be written as
Vt=2ρ0
MZdV ∇T·F.(23.38)
We next define the functional
F=ZdV L(23.39)
=1
2ZdV F·∇T(23.40)
=M
2ρ0Vt.(23.41)
Therefore, if the functional is positive, then the tracer variance is non-increasing. Furthermore, we can
write the neutral diffusion equation at a given point as
(ρT )diff
,t (x) = −∇·ρF(23.42)
= (dx)−1∂F
∂T (x).(23.43)
As such, we would like to look at ways of discretizing the right hand side of these equation, while maintain-
ing our key requirements. We begin by writing equation 23.43 in discrete form:
(dx)−1∂F
∂T (x)≈1
Vi,j,k
∂F
∂Ti,j,k
(23.44)
If we consider for now the flux expressed in terms of the diffusion tensor, we can write the functional as
F=−1
2ZρdV ∇TK∇T(23.45)
=−1
2ZρdV AR((T,x −T,zSx)2+ (T,y −T,zSy)2) (23.46)
=Fx−z+Fy−z(23.47)
Fx−z=−1
2ZρdV AR(T,x −T,zSx)2.(23.48)
We will focus on the Fx−zterm, on the understanding that the Fy−zcan be handled symmetrically. We
now discretize the functional by breaking up each tracer cell into quarter cells and writing the continuous
equation in discrete form.
Fx−z=−1
2X
i,j,k X
ip,kr
ρi,j,kV(ip,kr)
i,j,k (AR)i,j,k (δxT)(ip)
i,j,k −(δzT)(kr)
i,j,k(Sx)(ip,kr)
i,j,k 2
(23.49)
=−1
2X
i,j,k X
ip,kr
C(ip,kr)
i,j,k L(ip,kr)
i,j,k 2
(23.50)
where
C(ip,kr)
i,j,k =ρi,j,kV(ip,kr)
i,j,k (AR)i,j,k (23.51)
L(ip,kr)
i,j,k = (δxT)(ip)
i,j,k −(δzT)(kr)
i,j,k(Sx)(ip,kr)
i,j,k .(23.52)
It is worth noting that this discretization maintains the sign-definite nature of the functional. It is this
property which ensures our tracer variance is non-increasing.
We now take the derivative of the functional with respect to the tracer. Care must be taken at this step
with the grid indices. The functional is a single value, resulting from an integral over the entire domain.
Elements of MOM November 19, 2014 Page 310
Chapter 23. Neutral Physics Section 23.3
We are now taking derivatives at each point. We use the indices (i0,j0,k0)to represent the point at which
the derivative is taken, and (i,j,k)in the summation for the functional.
δFx−z
δTi0,j0,k0=−X
i,j,k X
ip,kr C(ip,kr)
i,j,k L(ip,kr)
i,j,k
δL(ip,kr)
i,j,k
δTi0,j0,k0(23.53)
=−X
i,j,k X
ip,kr CL(ip,kr)
i,j,k
δL(ip,kr)
i,j,k
δTi0,j0,k0(23.54)
To make this simpler we will write
L(ip,kr)
i,j,k = (δxT)(ip)
i,j,k −(δzT)(kr)
i,j,k(Sx)(ip,kr)
i,j,k (23.55)
=Lx(ip)
i,j,k +Lz(ip,kr)
i,j,k (23.56)
and handle each term separately, so
δF(x−z)x
δTi0,j0,k0=−X
i,j,k X
ip,kr CL(ip,kr)
i,j,k
δLx(ip)
i,j,k
δTi0,j0,k0(23.57)
=−X
i,j,k X
ip,kr CL(ip,kr)
i,j,k
δ(δxT)(ip)
i,j,k
δTi0,j0,k0(23.58)
=−X
kr
CL(1,kr)
i0−1,j0,k0
(∆x)(1)
i0−1,j0,k0
+CL(0,kr)
i0,j0,k0
(∆x)(0)
i0,j0,k0
−X
kr −CL(1,kr)
i0,j0,k0
(∆x)(1)
i0,j0,k0−CL(0,kr)
i0+1,j0,k0
(∆x)(0)
i0+1,j0,k0(23.59)
=−GE
i0,j0,k0−GE
i0−1,j0,k0(23.60)
where
GE
i,j,k =−X
kr
CL(1,kr)
i,j,k
(∆x)(1)
i,j,k
+CL(0,kr)
i+1,j,k
(∆x)(0)
i+1,j,k .(23.61)
We note that in equation 23.59 the global summation disappears, as only those points horizontally adja-
cent to (or on) (i0,j0,k0)have non-zero derivatives. Likewise,
δF(x−z)z
δTi0,j0,k0=−X
i,j,k X
ip,kr CL(ip,kr)
i,j,k
δLz(ip,kr)
i,j,k
δTi0,j0,k0(23.62)
=X
i,j,k X
ip,kr CL(ip,kr)
i,j,k (Sx)(ip,kr)
i,j,k
δ(δzT)(kr)
i,j,k
δTi0,j0,k0(23.63)
=X
ip
CL(ip,1)
i0,j0,k0−1(Sx)(ip,1)
i0,j0,k0−1
(∆z)(1)
i0,j0,k0−1
+CL(ip,0)
i0,j0,k0(Sx)(ip,0)
i0,j0,k0
(∆z)(0)
i0,j0,k0(23.64)
+X
ip −CL(ip,1)
i0,j0,k0(S,x)(ip,1)
i0,j0,k0
(∆z)(1)
i0,j0,k0−CL(ip,0)
i0,j0,k0+1(Sx)(ip,0)
i0,j0,k0+1
(∆z)(0)
i0,j0,k0+1 (23.65)
=−Gb(x)
i0,j0,k0−Gb(x)
i0,j0,k0−1.(23.66)
Elements of MOM November 19, 2014 Page 311
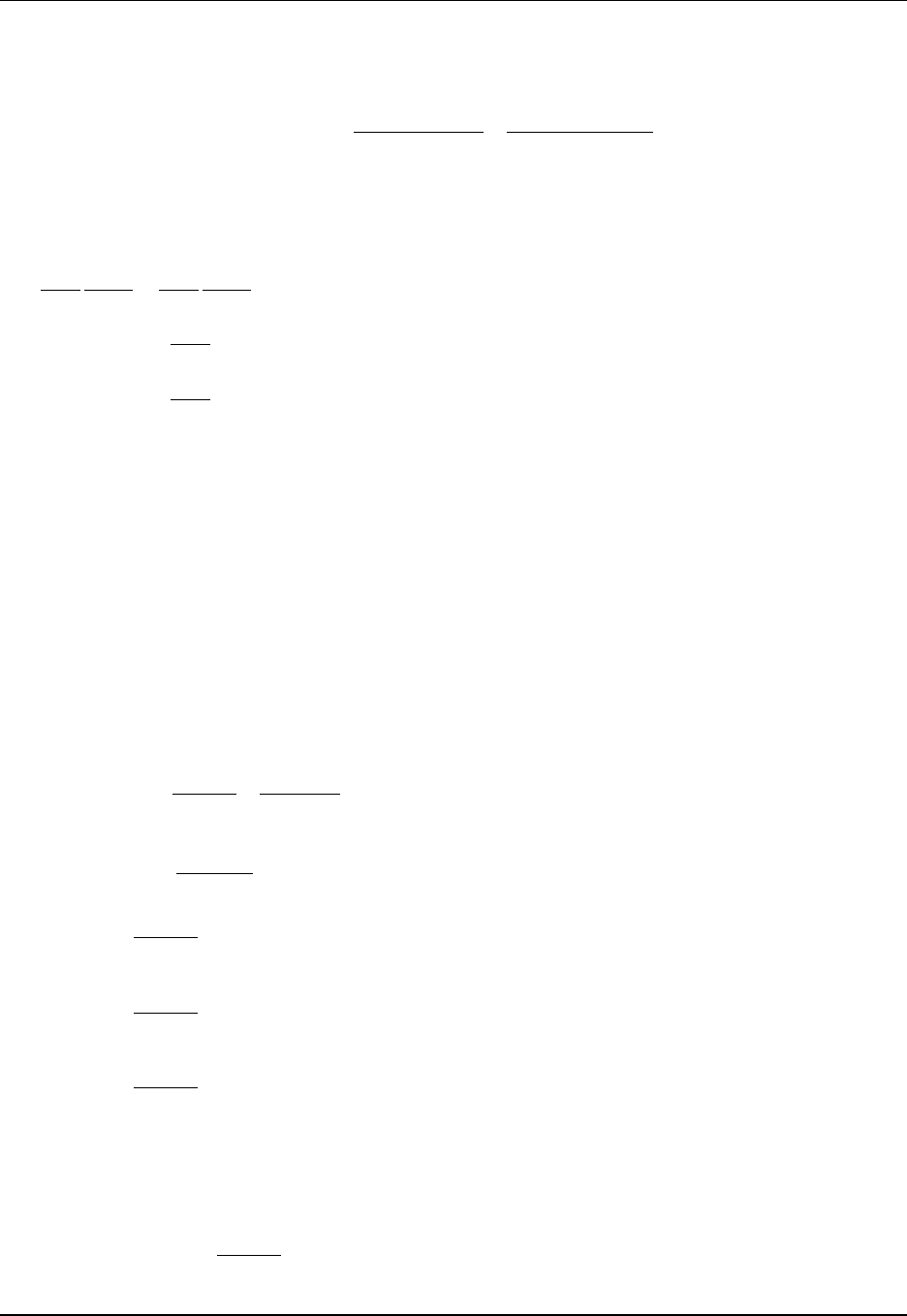
Chapter 23. Neutral Physics Section 23.3
where
Gb(x)
i,j,k =−X
ip
CL(ip,1)
i,j,k (Sx)(ip,1)
i,j,k
(∆z)(1)
i,j,k
+CL(ip,0)
i,j,k+1(Sx)(ip,0)
i,j,k+1
(∆z)(0)
i,j,k+1 .(23.67)
Invoking the symmetry mentioned above, we can now write our final discretization as
1
Vi,j,k
δF
δTi,j,k
=1
Vi,j,k
δ
δTi,j,k F(x−z)x+F(y−z)y+F(x−z)z+F(y−z)z(23.68)
=−1
Vi,j,k (GE
i,j,k −GE
i−1,j,k) + (GN
i,j,k −GN
i,j−1,k) + (Gb(x)
i,j,k −Gb(x)
i,j,k−1) + (Gb(y)
i,j,k −Gb(y)
i,j,k−1)(23.69)
=−1
Vi,j,k (GE
i,j,k −GE
i−1,j,k) + (GN
i,j,k −GN
i,j−1,k) + (Gb
i,j,k −(Gb
i,j,k−1))(23.70)
We notice that we have a Gterm defined at each face of the tracer cell. Each Gterm has the dimension of
a density times a flux times a surface area. We have thus derived exactly the finite volume flux formulation
we were after, however by deriving it from the functional approach, we can ensure our requirements are
satisfied.
23.3.2 Fluxes
We now have a discretization for our fluxes, which we can look at in detail. We begin with the xflux.
GE
i,j,k =−X
kr
CL(1,kr)
i,j,k
(∆x)(1)
i,j,k
+CL(0,kr)
i+1,j,k
(∆x)(0)
i+1,j,k (23.71)
=−X
ip,kr
CLE(ip,kr)
i,j,k
(∆x)E
i,j,k (23.72)
=−1
(∆x)E
i,j,k X
ip,kr
ρE(ip,kr)
i,j,k VE(ip,kr)
i,j,k (AR)E(ip,kr)
i,j,k (δxT)E
i,j,k + (δzT)E(ip,kr)
i,j,k (Sx)E(ip,kr)
i,j,k (23.73)
=−1
(∆x)E
i,j,k (δxT)E
i,j,k X
ip,kr
(ρV AR)E(ip,kr)
i,j,k +X
ip,kr
(ρV AR)E(ip,kr)
i,j,k (Sx)E(ip,kr)
i,j,k (δzT)E(ip,kr)
i,j,k (23.74)
=−1
(∆x)E
i,j,k (δxT)E
i,j,k (ρV AR)E
i,j,k +X
ip,kr
(ρV ARSx)E(ip,kr)
i,j,k (δzT)E(ip,kr)
i,j,k .(23.75)
By symmetry we also have
GN
i,j,k =−1
(∆y)N
i,j,k (δyT)N
i,j,k (ρV AR)N
i,j,k +X
jq,kr ρV ARSyN(jq,kr)
i,j,k (δzT)N(jq,kr)
i,j,k .(23.76)
Elements of MOM November 19, 2014 Page 312
Chapter 23. Neutral Physics Section 23.3
The xcomponent of the zflux can be written
Gb(x)
i,j,k =−X
ip
CL(ip,1)
i,j,k (Sx)(ip,1)
i,j,k
(∆z)(1)
i,j,k
+CL(ip,0)
i,j,k+1(Sx)(ip,0)
i,j,k+1
(∆z)(0)
i,j,k+1 (23.77)
=−X
ip,kr
CLb(ip,kr)
i,j,k (Sx)b(ip,kr)
i,j,k
(∆z)b
i,j,k (23.78)
=−1
(∆z)b
i,j,k X
ip,kr
ρb(ip,kr)
i,j,k Vb(ip,kr)
i,j,k (AR)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k + (δzT)b
i,j,k(Sx)b(ip,kr)
i,j,k (Sx)b(ip,kr)
i,j,k (23.79)
=−1
(∆z)b
i,j,k X
ip,kr
(ρV AR)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k (Sx)b(ip,kr)
i,j,k + (δzT)b
i,j,k Sx)b(ip,kr)
i,j,k 2!(23.80)
=−1
(∆z)b
i,j,k (δzT)b
i,j,k X
ip,kr ρV ARS2
xb(ip,kr)
i,j,k +X
ip,kr
(ρV ARSx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k (23.81)
=−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr ρV ARS2
xb(kr)
i,j,k +X
ip,kr
(ρV ARSx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k .(23.82)
Again, symmetry gives
Gb(y)
i,j,k =−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr ρV ARS2
yb(kr)
i,j,k +X
jq,kr ρV ARSyb(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k .(23.83)
Combining the two zflux terms we get
Gb
i,j,k =Gb(x)
i,j,k +Gb(y)
i,j,k (23.84)
=−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr ρV ARS2
xb(kr)
i,j,k +X
ip,kr
(ρV ARSx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k
+ (δzT)b
i,j,k X
kr ρV ARS2
yb(kr)
i,j,k +X
jq,kr ρV ARSyb(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k (23.85)
=−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr ρV ARS2
xb(kr)
i,j,k +ρV ARS2
yb(kr)
i,j,k
+X
ip,kr
(ρV ARSx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k +X
jq,kr ρV ARSyb(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k (23.86)
=−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr
(ρV ARS2)b(kr)
i,j,k
+X
ip,kr
(ρV ARSx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k +X
jq,kr ρV ARSyb(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k (23.87)
Elements of MOM November 19, 2014 Page 313

Chapter 23. Neutral Physics Section 23.3
Summarising all fluxes, we have
GE
i,j,k =−1
(∆x)E
i,j,k (δxT)E
i,j,k (ρV AR)E
i,j,k +X
ip,kr
(ρV ARSx)E(ip,kr)
i,j,k (δzT)E(ip,kr)
i,j,k (23.88)
GN
i,j,k =−1
(∆y)N
i,j,k (δyT)N
i,j,k (ρV AR)N
i,j,k +X
jq,kr ρV ARSyN(jq,kr)
i,j,k (δzT)N(jq,kr)
i,j,k (23.89)
Gb
i,j,k =−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr
(ρV ARS2)b(kr)
i,j,k
+X
ip,kr
(ρV ARSx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k +X
jq,kr ρV ARSyb(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k .(23.90)
Putting all these results together gives us the final discretized density weighted tracer tendency due to
diffusion,
dz(ρT )diff
,t i,j,k = dzi,j,k
1
Vi,j,k
∂F
∂Ti,j,k
(23.91)
=1
Ax−y
i,j,k (GE
i,j,k −GE
i−1,j,k) + (GN
i,j,k −GN
i,j−1,k) + (Gb
i,j,k −Gb
i,j,k−1).(23.92)
23.3.3 Skew flux discretization
We now need to discretize the skew flux term. This can be done by appealling to analogy with the diffusive
term. To distinguish between diffusive and skew terms we will employ dand ssuperscripts respectively. We
will look to write the skew-flux term as
dz(ρT )skew
,t i,j,k =1
Ax−y
i,j,k ((Gs)E
i,j,k −(Gs)E
i−1,j,k) + ((Gs)N
i,j,k −(Gs)N
i,j−1,k) + ((Gs)b
i,j,k −(Gs)b
i,j,k−1).(23.93)
The diffusive flux terms can be written with respect to the components of the diffusion tensor K,
(Gd)E
i,j,k =−1
(∆x)E
i,j,k (δxT)E
i,j,k (ρV K11)E
i,j,k +X
ip,kr
(ρV K13)E(ip,kr)
i,j,k (δzT)E(ip,kr)
i,j,k (23.94)
(Gd)N
i,j,k =−1
(∆y)N
i,j,k (δyT)N
i,j,k (ρV K22)N
i,j,k +X
jq,kr
(ρV K23)N(jq,kr)
i,j,k (δzT)N(jq,kr)
i,j,k (23.95)
(Gd)b
i,j,k =−1
(∆z)b
i,j,k (δzT)b
i,j,k X
kr
(ρV K33)b(kr)
i,j,k
+X
ip,kr
(ρV K31)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k +X
jq,kr
(ρV K32)b(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k .(23.96)
Elements of MOM November 19, 2014 Page 314

Chapter 23. Neutral Physics Section 23.4
Since the skew diffusion tensor only has the 13,23,31 and 32 terms as non-zero, the skew flux terms can
be written as
(Gs)E
i,j,k =−1
(∆x)E
i,j,k X
ip,kr
(ρV A13)E(ip,kr)
i,j,k (δzT)E(ip,kr)
i,j,k (23.97)
(Gs)N
i,j,k =−1
(∆y)N
i,j,k X
jq,kr
(ρV A23)N(jq,kr)
i,j,k (δzT)N(jq,kr)
i,j,k (23.98)
(Gs)b
i,j,k =−1
(∆z)b
i,j,k X
ip,kr
(ρV A31)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k +X
jq,kr
(ρV A32)b(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k ,(23.99)
or in terms of Υ,
(Gs)E
i,j,k =−1
(∆x)E
i,j,k X
ip,kr
(ρV Υx)E(ip,kr)
i,j,k (δzT)E(ip,kr)
i,j,k (23.100)
(Gs)N
i,j,k =−1
(∆y)N
i,j,k X
jq,kr ρV ΥyN(jq,kr)
i,j,k (δzT)N(jq,kr)
i,j,k (23.101)
(Gs)b
i,j,k =1
(∆z)b
i,j,k X
ip,kr
(ρV Υx)b(ip,kr)
i,j,k (δxT)b(ip,kr)
i,j,k +X
jq,kr ρV Υyb(jq,kr)
i,j,k (δyT)b(jq,kr)
i,j,k ,(23.102)
We have now derived the discrete formulation which forms the basis for the neutral physics modules within
MOM, based on the parameterizations of Redi and GM. The discritization does not yet include details of
how each of the terms in the given equations are computed. Various implementation details need to be
discussed to gain a full understanding of the handling of neutral physics within MOM.
23.4 Implementation
Having derived a discretization, we now turn to the implementation of this formulation within MOM. The
implementation is most easily understood from a top-down perspective, starting with the final result, and
progressively working down into the finer details.
The subroutine neutral physics new computes the value of dz(ρTn)neutral
,t for each tracer Tn. This
value is stored in the array total th tendency(:,:,:,n). Once calculated, this value it then added to
T prog(n)%th tendency.
23.4.1 Fluxes
The value of the tracer tendencies are computed in the subroutine flux calculations, in the module
ocean nphysics flux.F90.
Elements of MOM November 19, 2014 Page 315

Chapter 23. Neutral Physics Section 23.4
23.4.1.1
Within flux calculations, the subroutine update tendencies performs the calculations
dz(ρTn)diff
,t i,j,k =1
Ax−y
i,j,k ((Gd
n)E
i,j,k −(Gd
n)E
i−1,j,k)
+((Gd
n)N
i,j,k −(Gd
n)N
i,j−1,k) + ((Gd
n)b
i,j,k −(Gd
n)b
i,j,k−1)(23.103)
dz(ρTn)skew
,t i,j,k =1
Ax−y
i,j,k ((Gs
n)E
i,j,k −(Gs
n)E
i−1,j,k)
+((Gs
n)N
i,j,k −(Gs
n)N
i,j−1,k) + ((Gs
n)b
i,j,k −(Gs
n)b
i,j,k−1)(23.104)
dz(ρTn)neutral
,t i,j,k =dz(ρTn)diff
,t i,j,k +dz(ρTn)skew
,t i,j,k .(23.105)
The diffusive and skew-flux tendencies for each tracer can be diagnosed by the diagnostics diff th tendency(n)
and skew th tendency(n) respectively.
23.4.1.2
The flux terms are computed in the subroutine compute fluxes. These are computed according to the
equations
(Gd
n)E
i,j,k =−1
(∆x)E
i,j,k (δxTn)E
i,j,k (ρV K11)E
i,j,k +X
ip,kr
(ρV K13)E(ip,kr)
i,j,k (δzTn)E(ip,kr)
i,j,k (23.106)
(Gd
n)N
i,j,k =−1
(∆y)N
i,j,k (δyTn)N
i,j,k (ρV K22)N
i,j,k +X
jq,kr
(ρV K23)N(jq,kr)
i,j,k (δzTn)N(jq,kr)
i,j,k (23.107)
(Gd
n)b
i,j,k =−1
(∆z)b
i,j,k (δzTn)b
i,j,k ρV Kexp
33 b
i,j,k
+X
ip,kr
(ρV K31)b(ip,kr)
i,j,k (δxTn)b(ip,kr)
i,j,k +X
jq,kr
(ρV K32)b(jq,kr)
i,j,k (δyTn)b(jq,kr)
i,j,k (23.108)
for the diffusive flux, and
(Gs
n)E
i,j,k =−1
(∆x)E
i,j,k X
ip,kr
(ρV Υx)E(ip,kr)
i,j,k (δzTn)E(ip,kr)
i,j,k (23.109)
(Gs
n)N
i,j,k =−1
(∆y)N
i,j,k X
jq,kr ρV ΥyN(jq,kr)
i,j,k (δzTn)N(jq,kr)
i,j,k (23.110)
(Gs
n)b
i,j,k =1
(∆z)b
i,j,k X
ip,kr
(ρV Υx)b(ip,kr)
i,j,k (δxTn)b(ip,kr)
i,j,k +X
jq,kr ρV Υyb(jq,kr)
i,j,k (δyTn)b(jq,kr)
i,j,k (23.111)
for the skew flux.
23.4.1.3 Tracer Limiting
In regions of large tracer gradient, it may be desirable to resort to a purely horizontal diffusion, with no
vertical or skew terms. If the namelist parameter neutral physics limit .==. true then the following
procedure is applied for each each tracer. At those points where the mask T prog(n)%tmask limit(i,j,k)
Elements of MOM November 19, 2014 Page 316
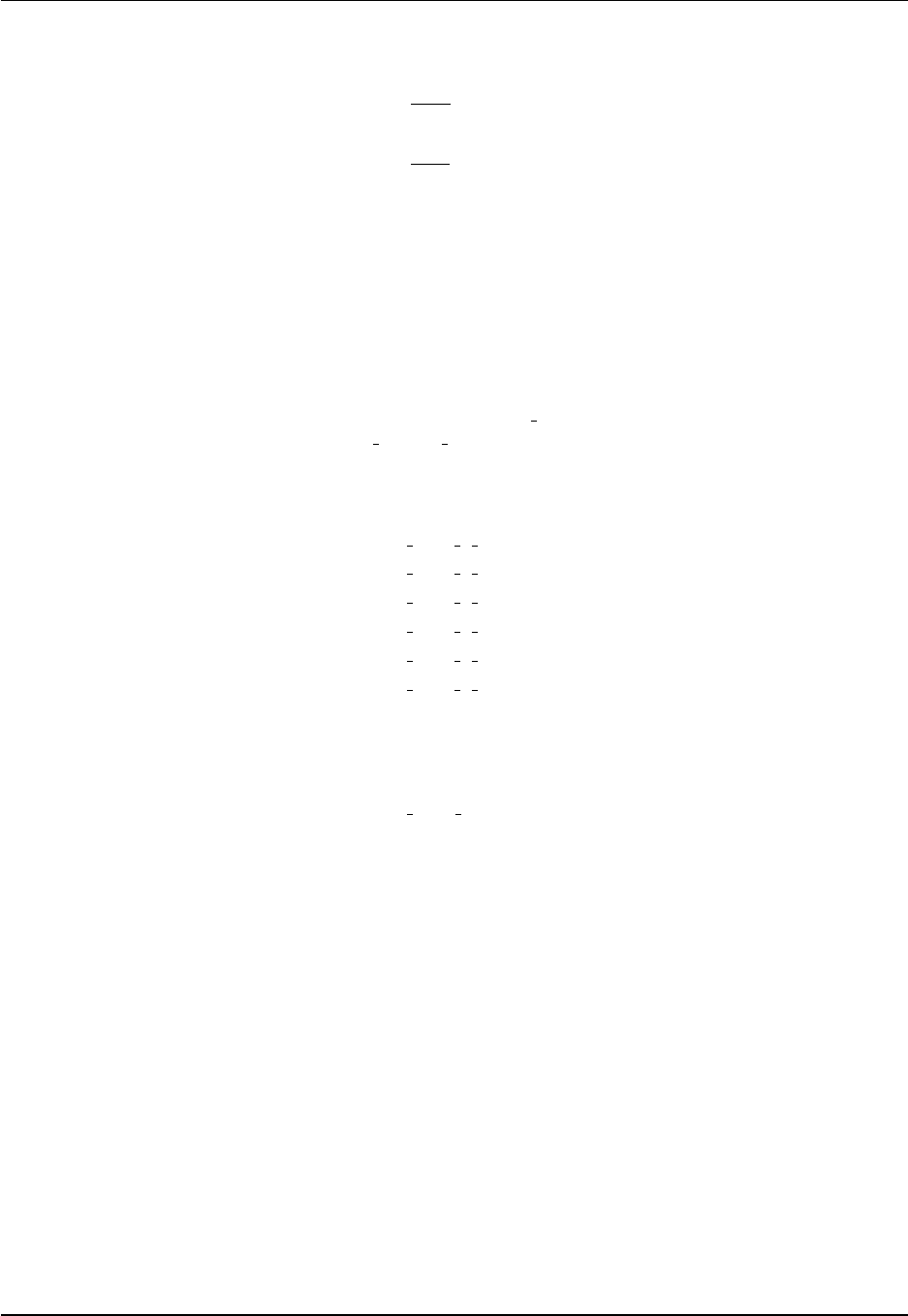
Chapter 23. Neutral Physics Section 23.4
== 1.0, the following transformations are applied,
(Gd
n)E
i,j,k → − 1
∆xE
i,j
(ρV K11)E
i,j,k (δxTn)E
i,j,k (23.112)
(Gd
n)N
i,j,k → − 1
∆yN
i,j
(ρV K22)N
i,j,k (δyTn)N
i,j,k (23.113)
(Gd
n)b
i,j,k →0.0 (23.114)
(Gs
n)E
i,j,k →0.0 (23.115)
(Gs
n)N
i,j,k →0.0 (23.116)
(Gs
n)b
i,j,k →0.0 (23.117)
ρKimp
33 n
i,j,k →0.0.(23.118)
The calculation of the mask is performed in the module ocean tracer, while the transformation described
above is performed in the subroutine apply tracer limits.
After the tracer limiting process has been applied, the fluxes are diagnosed. The quantities diagnosed
include a minus sign, i.e. −(Gd
n)E
i,j,k, to adhere to a legacy convention within MOM. The diagnostics used are
diff flux x xte(n)
diff flux y ytn(n)
diff flux z ztb(n)
skew flux x xte(n)
skew flux y ytn(n)
skew flux z ztb(n).
23.4.1.4
The terms incorporating the tensor components (e.g. (ρV K11)) have units of mass times diffusivity. These
terms are calculated in the subroutine compute mass diff. The diffusive terms are calculated as
(ρV K11)E
i,j,k =X
ip,kr
C2H(ρVx)(ip,kr)
i,j,k (AR)i,j,k(23.119)
(ρV K22)N
i,j,k =X
jq,kr
C2H(ρVy)(jq,kr)
i,j,k (AR)i,j,k(23.120)
(ρV K13)E(ip,kr)
i,j,k =C2H(ρV K13)(ip,kr)
i,j,k (23.121)
(ρV K23)N(jq,kr)
i,j,k =C2H(ρV K23)(jq,kr)
i,j,k (23.122)
(ρV K31)b(ip,kr)
i,j,k =C2V(ρV K13)(ip,kr)
i,j,k (23.123)
(ρV K32)b(jq,kr)
i,j,k =C2V(ρV K23)(jq,kr)
i,j,k (23.124)
(ρV K13)(ip,kr)
i,j,k = (ρVx)(ip,kr)
i,j,k (K13)(ip,kr)
i,j,k (23.125)
(ρV K23)(jq,kr)
i,j,k = (ρVy)(jq,kr)
i,j,k (K23)(jq,kr)
i,j,k (23.126)
(ρV K33)(kr)
i,j,k =X
ip
(ρVx)(ip,kr)
i,j,k (K33x)(ip,kr)
i,j,k +X
jq
(ρVy)(jq,kr)
i,j,k (K33y)(jq,kr)
i,j,k .(23.127)
Elements of MOM November 19, 2014 Page 317
Chapter 23. Neutral Physics Section 23.4
The skew terms are calculated as
(ρV Υx)E(ip,kr)
i,j,k =C2H(ρV Υx)(ip,kr)
i,j,k (23.128)
(ρV Υy)N(jq,kr)
i,j,k =C2H(ρV Υy)(jq,kr)
i,j,k (23.129)
(ρV Υx)b(ip,kr)
i,j,k =C2V(ρV Υx)(ip,kr)
i,j,k (23.130)
(ρV Υy)b(jq,kr)
i,j,k =C2V(ρV Υy)(jq,kr)
i,j,k (23.131)
(ρV Υx)(ip,kr)
i,j,k = (ρVx)(ip,kr)
i,j,k (Υx)(ip,kr)
i,j,k (23.132)
(ρV Υy)(jq,kr)
i,j,k = (ρVy)(jq,kr)
i,j,k (Υy)(jq,kr)
i,j,k .(23.133)
Three dimensional versions of each of these quantities are diagnosed. The diagnostics symm mass diff 11 xte
and symm mass diff 22 ytn diagnose the quantities in equations 23.119 and 23.120. The diagnostics
symm mass diff 13 h xz
symm mass diff 23 h yz
symm mass diff 31 v xz
symm mass diff 32 v yz
diagnose the terms
X
ip,kr
(ρV K13)E(ip,kr)
i,j,k (23.134)
X
jq,kr
(ρV K23)N(jq,kr)
i,j,k (23.135)
X
ip,kr
(ρV K31)b(ip,kr)
i,j,k (23.136)
X
jq,kr
(ρV K32)b(jq,kr)
i,j,k (23.137)
respectively. Likewise, the diagnostics
symm mass skew 13 h xz
symm mass skew 23 h yz
symm mass skew 31 v xz
symm mass skew 32 v yz
diagnose the terms
X
ip,kr
(ρV Υx)E(ip,kr)
i,j,k (23.138)
X
jq,kr
(ρV Υy)N(jq,kr)
i,j,k (23.139)
X
ip,kr
(ρV Υx)b(ip,kr)
i,j,k (23.140)
X
jq,kr
(ρV Υy)b(jq,kr)
i,j,k .(23.141)
Elements of MOM November 19, 2014 Page 318

Chapter 23. Neutral Physics Section 23.4
23.4.1.5
The ρV K33 term must be handled carefully. As discussed in Griffies (2004) Section 16.8.3, the vertical
diffusion from the 33-term is broken into an explicit and implicit component (Griffies (2004) Eqn 16.104),
K33 =Kexp
33 +Kimp
33 .(23.142)
The diffusivity is handled explicitly up to a critical threshold, above which the remainder is treated implicitly.
The critical diffusivity is given by (Griffies (2004) Eqn 16.105)
Kcrit
33 =(∆z)2
2∆tforward
(23.143)
The implementation of this decomposition is done in terms of mass weighted diffusivities, leading to a
critical value of
(ρV Kcrit
33 )(kr)
i,j,k =(µ(kr)
k∆zi,j,k)2
2∆τµ(kr)
k(ρ∆z)i,j,k∆Ai,j .(23.144)
The explicit component is then defined as
(ρV Kexp
33 )(kr)
i,j,k =
(ρV Kcrit
33 )(kr)
i,j,k if (ρV K33)(kr)
i,j,k >(ρV Kcrit
33 )(kr)
i,j,k
(ρV K33)(kr)
i,j,k otherwise.(23.145)
The implicit component is required at the tracer cell point, and so is given by
(ρV Kimp
33 )i,j,k =X
kr (ρV K33)(kr)
i,j,k −(ρV Kexp
33 )(kr)
i,j,k.(23.146)
Each tracer carries this value (as later steps apply tracer specific masks), with the volume term removed,
giving
ρKimp
33 n
i,j,k =(ρV Kimp
33 )i,j,k
∆zi,j,k∆Ai,j .(23.147)
This value is subsequently used by the module ocean vert mix to calculate the implicit component of
vertical diffusion.
Finally, the explicit component is calculated at the bottom of the tracer cell,
(ρV Kexp
33 )b
i,j,k = (ρV Kexp
33 )(1)
i,j,k + (ρV Kexp
33 )(0)
i,j,k+1.(23.148)
There is a namelist parameter which can be used to turn offthe above decomposition into explicit and
implicit parts. If diffusion all explicit == .true., then Equation (23.145) becomes
(ρV Kexp
33 )(kr)
i,j,k = (ρV K33)(kr)
i,j,k,(23.149)
which ensures that the implicit component is zero. These calculations are performed in the subroutine
compute 33 terms. The values of ρKimp
33 and (ρV Kexp
33 )bare diagnosed via the names m33 implicit and
m33 explicit ztb.
23.4.1.6 Density Weighted Quarter-cell Volumes
The geometric factor required is a density weighted volume for the quarter-cell associated with the triad
over which the diffusivity is defined. In the direction perpendicular to the triad plane the tracer cell width
is taken, while in the triad plane half cell widths are taken. For example, in the x−zplane, the density
weighted quarter-cell volume would be the product of the density, the width of the cell in the ydirection
and the half widths in the xand zdirections.
Elements of MOM November 19, 2014 Page 319

Chapter 23. Neutral Physics Section 23.5
An issue arises here in that the vertical thickness of adjacent cells may not be equal. As such, the
effective contact area of the two cells may not be equal when looked at from either side. It stands to
reason that the diffusive flux from each side of the cell faces should be calculated through the same area
from each side. As such, the minimum half-cell thickness between adjacent tracer cells is used in the
calculation of quarter-cell volumes. Further justification for this choice can be found in Griffies (2004)
Chapter 16.4.3.
The half-cell thicknesses at the eastern and northern faces are given by
(∆z0)E(kr)
i,j,k = minµ(kr)
k∆zi,j,k, µ(kr)
k∆zi+1,j,k(23.150)
(∆z0)N(kr)
i,j,k = minµ(kr)
k∆zi,j,k, µ(kr)
k∆zi,j+1,k.(23.151)
This leads to density weighted quarter-cell thicknesses defined as
(ρVx)(ip,kr)
i,j,k =ρi,j,k(∆z0)E(kr)
i−1+ip,j,k∆x(ip)
i,j ∆yi,j (23.152)
(ρVy)(jq,kr)
i,j,k =ρi,j,k(∆z0)N(kr)
i,j−1+jq,k ∆xi,j∆y(jq)
i,j (23.153)
where1
ρi,j,k =(ρ∆z)i,j,k
∆zi,j,k .(23.154)
These calculations are performed in the subroutine geometric terms.
23.5 Diffusion and Skew-Diffusion Tensors
We will now look at the parameterizations which are used to determine the values of the tensors Kand
A. As well as computing the expressions in equations (23.20) and (23.25), the parameterization must also
account for regions of steep neutral slope, which generally, but not always, occur within boundary layers.
In these regions, the basic equations require some modification due both to modifications of the physical
processes, and the need to maintain numerical regularity. The following computations are carried out in
the module ocean nphysics tensor.
23.5.1 Depth Taper
As discussed in Griffies (2004) Section 15.3.2, as the surface is approached, the transport due to neutral
physics must be modified. To do this, a taper function Tis calculated at each tracer point, which takes val-
ues between zero and one. This function is then multiplied by the appropriate components of the diffusion
tensors to ensure that the total transport behaves in a physically sensible manner.
The tapering is applied in regions where the vertical displacement due to the undulating density surface
is greater than the depth (Griffies (2004) Section 15.3.3). The vertical displacement is approximated by
ξ=λ1|S|. As per Large et al. (1997), the Rossby radius used in this calculation is restricted to lie within the
range [λmax,λmin]. This choice leads to the capped Rossby radius
λ0
1= max(λmin,min(λmax, λ1)).(23.155)
The limits are controlled by the namelist parameters rossby radius min and rossby radius max and have
default values of 15km and 100km respectively.
As well as considering the vertical displacement distance ξ, we also take into account the surface
boundary layer thickness, DBL, as calculated in the subroutine vert mix coeff in the ocean vert mix mod-
ule. Finally, the namelist parameter turb blayer min provides a minimum depth over which to taper the
1This computation is an implementation detail which eliminates the need for the Density variable in the neutral physics module.
Elements of MOM November 19, 2014 Page 320
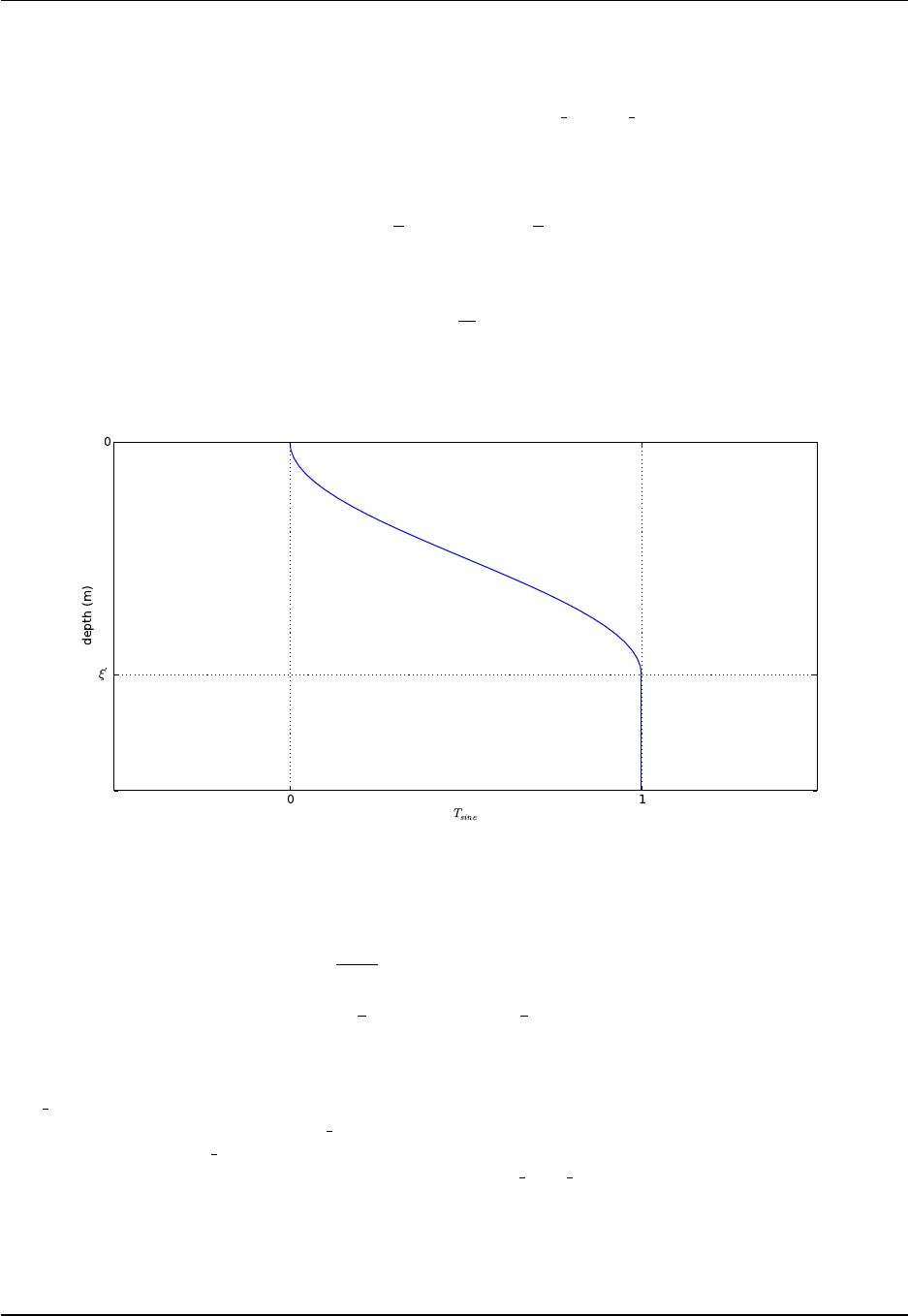
Chapter 23. Neutral Physics Section 23.5
neutral transport. Taking the deepest value of each of these depths, calculated at each tracer point, gives
us the adjusted displacement depth
ξ0
i,j,k = max(λ0
1)i,j |S|i,j,k ,(DBL)i,j,turb blayer min.(23.156)
In regions shallower than ξ0the taper goes as a sine function of the depth ratio r(Griffies (2004) equa-
tion (15.24))
Tsine =1
21 + sinπr−1
2,(23.157)
where (Griffies (2004) equation (15.22))
r=D
ξ0,(23.158)
as depicted in Figure 23.3.
Figure 23.3: The sine taper function.
This function is discretized as
ri,j,k =Di,j,k
ξ0
i,j,k
(23.159)
(Tsine)i,j,k =(1
21 + sinπri,j,k −1
2 if ri,j,k ≤1
1otherwise,(23.160)
where (Tsine)i,j,k is evaluated at the tracer points. This taper function is calculated in the subroutine
sine taper and is used in calculating both the diffusion tensor and the skew tensor. The depth taper
can be diagnosed via the name depth taper while the adjusted displacement depth can be diagnosed via
the name displacement depth. The tapering is used by default, however it can be turned off(i.e. Tsine set
to 1 everywhere) by setting the namelist parameter neutral sine taper to .false..
23.5.2 Neutral Diffusion Tensor
The tensor used to parameterize neutral diffusion is the small slope approximation of the Redi Diffusion
Tensor (Redi (1982), Gent and McWilliams (1990), Griffies (2004) equation (14.19)) with the term dropped
Elements of MOM November 19, 2014 Page 321

Chapter 23. Neutral Physics Section 23.5
from the (3,3) component,
K=AR
1 0 Sx
0 1 Sy
SxSyS2
x+S2
y(23.161)
To maintain physical and numerical consistency, the components of this tensor must be tapered near the
surface (as per Section 23.5.1) and also in regions of steep neutral slope. A neutral taper function TNis
calculated as a combination of Tsine and another taper function based on neutral slope. Those components
involving a slope term are multiplied by the neutral taper TN.This leads to the tensor
KR=AR
1 0 TNSx
0 1 TNSy
TNSxTNSyTN(S2
x+S2
y).(23.162)
Taking note of the symmetry of the system, the components of the matrix can be written as
K=
AR0K13
0ARK23
K13 K23 K33x+K33y,(23.163)
which leads to the discrete equations
(K13)(ip,kr)
i,j,k = (AR)i,j,k(TN)(kr)
i,j,k(Sx)(ip,kr)
i,j,k (23.164)
(K23)(jq,kr)
i,j,k = (AR)i,j,k(TN)(kr)
i,j,k(Sy)(jq,kr)
i,j,k (23.165)
(K33x)(ip,kr)
i,j,k = (AR)i,j,k(TN)(kr)
i,j,k (Sx)(ip,kr)
i,j,k 2
(23.166)
(K33y)(jq,kr)
i,j,k = (AR)i,j,k(TN)(kr)
i,j,k (Sy)(jq,kr)
i,j,k 2.(23.167)
The components of this tensor are computed in the subroutine diffusion tensor. The tensor values are
diagnosed by averaging over the triads, and are saved via the diagnostic table entries symm tensor33x,
symm tensor33y,symm tensor13 and symm tensor23.
23.5.2.1 Tapers
The tapers used in the above calculations must take into account both regions near the surface and also
regions of steep neutral slope (Griffies (2004) Section 15.1). Section 23.5.1 described the algorithm for
tapering based on depth. We now look at the slope based taper.
Exponential Tapering An exponential taper can be used to quickly and smoothly transition between 1.0
and 0.0 when the slope is above some critical value Smax (Danabasoglu and McWilliams (1995) Eqn A.7a).
The equation for the taper is given by
Ttanh =1
2 1 + tanh Smax −|S|
∆S!!,(23.168)
where ∆Stakes the value of the namelist parameter swidth and represents the half-width of the transition
region between the maximum and minimum values of the taper, as depicted in Figure 23.4. The discretiza-
tion of this equation is
(Ttanh)(kr)
i,j,k =1
21 + tanh
Smax −|S|(kr)
i,j,k
∆S.(23.169)
As noted in Griffies (2004) Section 15.1.4, this equation can be applied at all points, rather than having to
first test for those points above Smax.
Elements of MOM November 19, 2014 Page 322
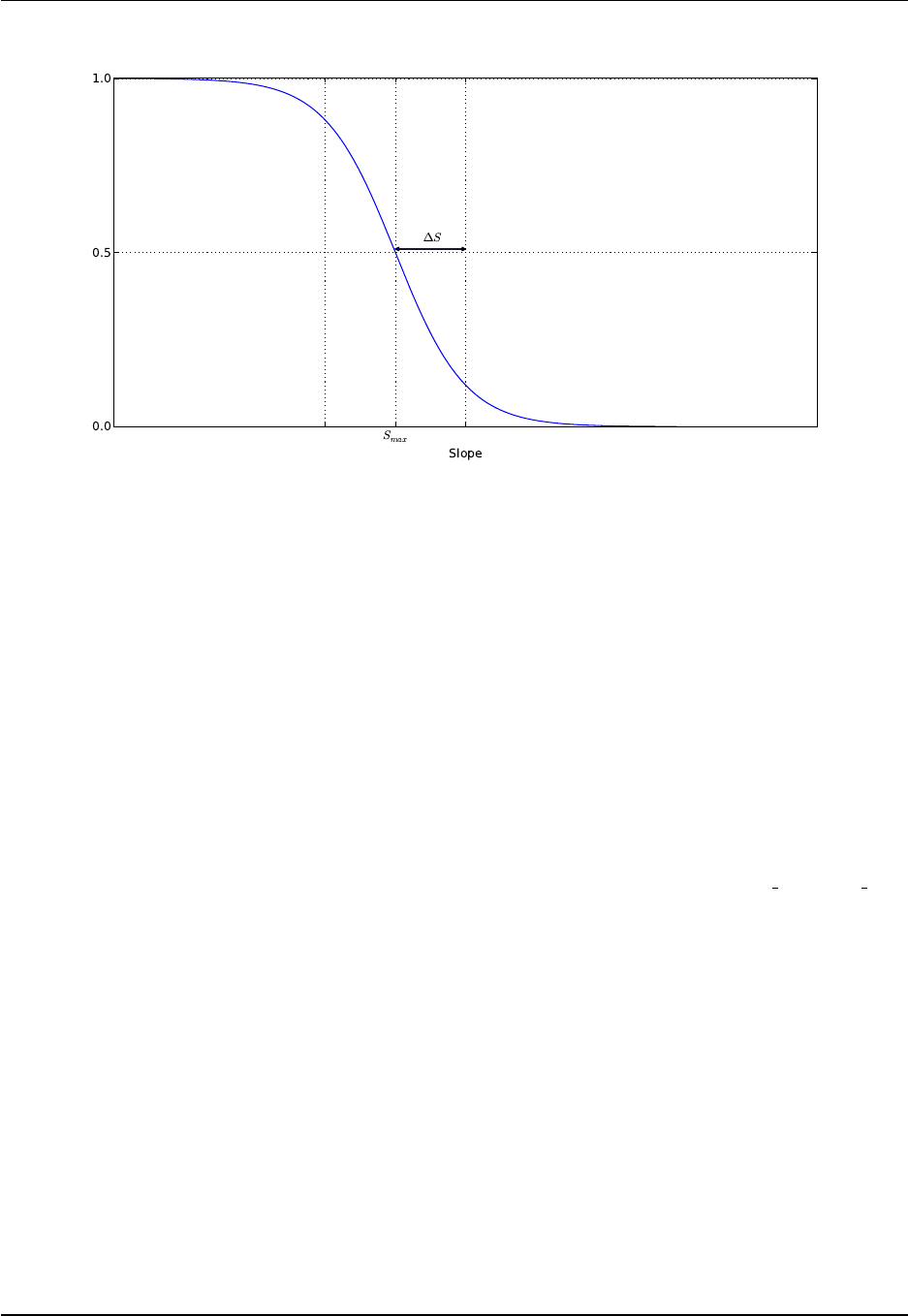
Chapter 23. Neutral Physics Section 23.5
Figure 23.4: the tanh taper function.
Neutral taper The neutral tapering function uses the product of the depth-based taper Tsine and the
slope-based taper Ttanh.
(TN)(kr)
i,j,k = (Ttanh)(kr)
i,j,k(Tsine)i,j,k.(23.170)
23.5.3 Skew-Diffusion Tensor
The stirring of tracers by mesoscale eddies is modeled by an anti-symmetric skew tensor, which combines
with the symmetric diffusion tensor to give the complete neutral transport tensor. The skew tensor can be
expressed in terms of the eddy-induced transport, Υ, to give (Ferrari et al. (2010) equation (52))
A=
0 0 Υx
0 0 Υy
−Υx−Υy0.(23.171)
The calculation of the transport, Υ, can be done in a number of ways. The module ocean nphysics skew
provides three different methods, which are described below. Each method computes a discretization of
Υover the centred triad grouping, giving Υ=(Υx)(ip,kr)
i,j,k ,(Υy)(jq,kr)
i,j,k . By averaging over the triads, these
values are diagnosable via the names upsilonx and upsilony.
23.5.3.1 Preliminaries
The following quantities are used in the calculations below, and their discretizations are given here for
completeness.
(κSx)(ip,kr)
i,j,k =κi,j,k(Sx)(ip,kr)
i,j,k (23.172)
(κSy)(jq,kr)
i,j,k =κi,j,k(Sy)(jq,kr)
i,j,k (23.173)
(N2∆z)(kr)
i,j,k = (N2)(kr)
i,j,k(∆z)(kr)
i,j,k (23.174)
(N2Sxκ∆z)(ip,kr)
i,j,k = (N2∆z)(kr)
i,j,k(κSx)(ip,kr)
i,j,k (23.175)
(N2Syκ∆z)(jq,kr)
i,j,k = (N2∆z)(kr)
i,j,k(κSy)(jq,kr)
i,j,k (23.176)
Elements of MOM November 19, 2014 Page 323

Chapter 23. Neutral Physics Section 23.5
It should be noted that the slope used here relates the density surface to the horizontal surface of con-
stant s, however the development of the GM tensor below is originally based on a slope vector relative to
surfaces of constant geopotential. As discussed in Section 4.2.3, using the generalized vertical coordinate
slope is usually a reasonable approximation to the geopotential slope, as long as the generalised vertical
coordinate is relatively horizontal. In situations where this is not the case, such as sigma models, the ap-
proximation may lead to spurious results. As stated in Section 23.1, neutral physics in MOM has not been
implemented for the terrain following vertical coordinate option.
23.5.3.2 GM Skew-Diffusion Tensor
The first technique for computing eddy-induced tracer-transport is based on the parameterization of Gent
and McWilliams (1990) and Gent et al. (1995). The implementation is based largely on that described in
Griffies (2004). This method is enabled by setting the namelist parameter gm transport = .true..
The skew-diffusion tensor which corresponds to the GM parameterization of eddy-induced tracer trans-
ports is defined as (Griffies (1998) equation (14).)
A=κ
0 0 −Sx
0 0 −Sy
SxSy0,(23.177)
which leads to the individual components being defined as (Ferrari et al. (2010) equation (9).)
ΥGM =−κS.(23.178)
As discussed in Griffies (2004), Section 15.3.4.3, the tensor must be tapered to zero at the surface. For
those points within the surface boundary layer, as defined in Section 23.7.6, a depth based linear tapering
scheme is applied. This reduces (κS)from (κS)max at the base of the boundary layer to zero at the surface.
The value of (κS)max is defined as
(κS)max =Smax
|S|0(κS)0,(23.179)
where primed variables indicate a value evaluated at the base of the boundary layer, i.e. at (i,j,k)for k=
ksurfi,j2. Including the linear taper, we obtain the following discretization for points (i,j,k)with k≤ksurfi,j:
(Υx)(ip,kr)
i,j,k =−Di,j,k
D0
i,j
Smax
|S|0
i,j
(κSx)0
i,j (23.180)
(Υy)(jq,kr)
i,j,k =−Di,j,k
D0
i,j
Smax
|S|0
i,j
(κSy)0
i,j .(23.181)
In those regions below the boundary layer, the depth based sine taper described in Section 23.5.1 is applied,
giving
(Υx)(ip,kr)
i,j,k =−(Tsine)i,j,k(κSx)(ip,kr)
i,j,k (23.182)
(Υy)(jq,kr)
i,j,k =−(Tsine)i,j,k(κSy)(jq,kr)
i,j,k .(23.183)
This calculation is performed in the subroutine gm tensor. The value of D0is diagnosed via the name
depth blayer base while the maximum slope vector is diagnosed via the names agm slopex max and
agm slopey max.
2This definition ensures that |(κS)max|=κ0Smax while maintaining the same orientation as S0. This definition is based on an
interpretation of the text in Sections 15.2 and 15.3.4.3 of Griffies (2004).
Elements of MOM November 19, 2014 Page 324

Chapter 23. Neutral Physics Section 23.5
23.5.3.3 Baroclinic Modes
The second technique involves writing the GM transport as a sum of baroclinic modes and taking only the
low mode-number terms. This method is described in Section 3.1 of Ferrari et al. (2010). This method
requires that the diffusivity κis depth independent, which is checked when the module is initially loaded,
based on the namelist parameters selected in the diffusivity module.
The baroclinic modes are defined as (Ferrari et al. (2010) equation (59))
Sm(z) = S0
msin 1
cmZz
−H
N(z0)dz0!(23.184)
=S0
msin(θm),(23.185)
subject to the normalization (Ferrari et al. (2010) equation (58c))
Z0
−HS2
mN2dz=g(23.186)
S0
m=sg
R0
−Hsin2(θm)N2dz.(23.187)
The GM transport can be now written as (Ferrari et al. (2010) equations (11) and (14))
ΥGM =∞
X
m=1 Sm(z)Υm(23.188)
=−1
ρ0
∞
X
m=1 Sm(z) Z0
−HSmκ∇zρdz0!(23.189)
which gives coefficients of
Υm=−1
ρ0 Z0
−HSmκ∇zρdz0!(23.190)
=−1
gZ0
−HSmκSN2dz. (23.191)
By considering only the baroclinic modes for m≤M, we can find the low baroclinic mode dominated trans-
port
ΥBC =
M
X
m=1 Sm(z)Υm.(23.192)
Implementation The subroutine compute transport modes implements this method. The baroclinic modes
are calculated for m= [1,M], where Mis set by the namelist parameter number bc modes, using the fol-
lowing discretizations
ci,j = max(cmin,(c1)i,j) (23.193)
θ(kr)
i,j,k =1
ci,j X
kX
kr
(N∆z)(kr)
i,j,k (23.194)
(sin(θm))(kr)
i,j,k = sinmθ(kr)
i,j,k(23.195)
(S0
m)i,j =sg
PkPkr(sin(θm))(kr)
i,j,k(N2∆z)(kr)
i,j,k
(23.196)
(Sm)(kr)
i,j,k = (S0
m)i,j (sin(θm))(kr)
i,j,k.(23.197)
Elements of MOM November 19, 2014 Page 325
Chapter 23. Neutral Physics Section 23.5
The value of cmin is set by the namelist parameter min bc speed. The tracer point averaged values of c,θ
and S1are diagnosed via the names bc speed,sine arg and bc mode 1. Having calculated the baroclinic
modes, the coefficients can then be determined, giving
(Υ(x)
m)(ip)
i,j =−1
gX
kX
kr
(Sm)(kr)
i,j,k(N2Sxκ∆z)(ip,kr)
i,j,k (23.198)
(Υ(y)
m)(jq)
i,j =−1
gX
kX
kr
(Sm)(kr)
i,j,k(N2Syκ∆z)(jq,kr)
i,j,k .(23.199)
Finally, the transport is calculated by taking the sum over the baroclinic modes,
(Υx)(ip,kr)
i,j,k =
M
X
m=1
(Sm)(kr)
i,j,k(Υ(x)
m)(ip)
i,j (23.200)
(Υy)(jq,kr)
i,j,k =
M
X
m=1
(Sm)(kr)
i,j,k(Υ(y)
m)(jq)
i,j .(23.201)
23.5.3.4 Boundary Value Problem
As a third option, the transport vector can be found as the solution to the one dimensional vertical boundary-
value problem (Ferrari et al. (2010) Eqn 16a,b)
c2
1
d2
dz2−N2!Υ(z) = g
ρ0
κ∇zρ(23.202)
=−N2
ρ,z κ∇zρ(23.203)
=N2κS(23.204)
Υ(η) = 0 (23.205)
Υ(−H)=0.(23.206)
The second order differential operator can be vertically discretized as
d2Υ
dz2=1
∆z d−
dzΥ−d+
dzΥ!(23.207)
=1
∆z Υ−−Υ0
∆z−−Υ0−Υ+
∆z+!(23.208)
=1
∆z Υ−
∆z−−Υ01
∆z−+1
∆z++Υ+
∆z+!.(23.209)
The left hand side of equation (23.202) thus becomes.
c2
1
d2
dz2−N2!Υ=c2
1
∆z Υ−
∆z−−Υ01
∆z−+1
∆z++Υ+
∆z+!−N2Υ0(23.210)
=c2
1Υ−
∆z∆z−−Υ0 N2+c2
1
∆z∆z−+c2
1
∆z∆z+!+c2
1Υ+
∆z∆z+.(23.211)
Finally, we can write down the vertically discretized boundary value problem as
c2
1Υ−
∆z∆z−−Υ0 N2+c2
1
∆z∆z−+c2
1
∆z∆z+!+c2
1Υ+
∆z∆z+=N2κS(23.212)
c2
1Υ−
∆z−−Υ0 N2∆z+c2
1
∆z−+c2
1
∆z+!+c2
1Υ+
∆z+=N2κS∆z, (23.213)
Elements of MOM November 19, 2014 Page 326

Chapter 23. Neutral Physics Section 23.5
which can be written as
aΥ−+bΥ0+cΥ+=r(23.214)
where
a=c2
1
∆z−(23.215)
b=− N2∆z+c2
1
∆z−+c2
1
∆z+!(23.216)
c=c2
1
∆z+(23.217)
r=N2κS∆z.
The boundary conditions given by equations (23.205) and (23.206) exist at the vertical faces of tracer
cells. As such, the following calculations are all performed on values at the bottom face of the tracer cells.
The right hand side term, ris discretized as
(rx)b(ip)
i,j,k = (N2Sxκ∆z)(ip,1)
i,j,k + (N2Sxκ∆z)(ip,0)
i,j,k+1 (23.218)
while the left hand side coefficients are given by
ai,j,k =(c1)i,j
∆zi,j,k
(23.219)
ci,j,k =(c1)i,j
∆zi,j,k+1
(23.220)
bi,j,k =−(N∆z)(1)
i,j,k +(N∆z)(0)
i,j,k+1+ai,j,k +ci,j,k(23.221)
Now, since Υ0=Υkmt = 0, the discretized one dimensional problem for a given column can be written
(omitting the i,j subscript) as
b1c1... 0
a2b2c2
..........
.
.
akbkck
.
.
..........
akmt−2bkmt−2ckmt−2
0... akmt−1bkmt−1
Υ1
Υ2
.
.
.
Υk
.
.
.
Υkmt−2
Υkmt−1
=
r1
r2
.
.
.
rk
.
.
.
rkmt−2
rkmt−1
.(23.222)
This result gives us the following matrix equation for the transport vector,
AΥ=r(23.223)
Υ=A−1r.(23.224)
When discretized, this result leads to values for Υevaluated at the base of the tracer cells.
(Υx)b(ip)
i,j,k =Ai,j−1·(rx)b(ip)
i,j k(23.225)
(Υy)b(jq)
i,j,k =Ai,j−1·(ry)b(jq)
i,j k(23.226)
For each column we need to solve a tridiagonal matrix problem using a single matrix and four different
right hand side vectors. This is done using a modified version of the invtri algorithm described in Press
et al. (1992), which is implemented as the subroutine invtri bvp. The modified algorithm vectorizes the
process across all columns and also saves use from inverting the same matrix multiple times for each
column.
Elements of MOM November 19, 2014 Page 327

Chapter 23. Neutral Physics Section 23.6
23.5.4 Vertical Boundary Tensor Values
The tapering processes applied above reduce the off-diagonal and (3,3) terms of the tensors towards zero
at the surface. Another option available to the user is to set the diffusivity tensors to be explicitly horizontal
at both the surface and bottom of the ocean. If the namelist parameter tmask neutral on == .true. then
the values of the tensors at the surface are modified to be
(K33x)(ip,kr)
i,j,1→0 (23.227)
K33y(jq,kr)
i,j,1→0 (23.228)
(K13)(ip,kr)
i,j,1→0 (23.229)
(K23)(jq,kr)
i,j,1→0 (23.230)
(Υx)(ip,kr)
i,j,1→0 (23.231)
Υy(jq,kr)
i,j,1→0 (23.232)
and at the ocean bottom are modified to be
(K33x)(ip,kr)
i,j,kmt →0 (23.233)
K33y(jq,kr)
i,j,kmt →0 (23.234)
(K13)(ip,kr)
i,j,kmt →0 (23.235)
(K23)(jq,kr)
i,j,kmt →0 (23.236)
(Υx)(ip,kr)
i,j,kmt →0 (23.237)
Υy(jq,kr)
i,j,kmt →0.(23.238)
23.6 Tracer Gradients
The gradients of tracer concentrations are fundamental to neutral physics calculations, as they define the
direction and magnitude of the physical processes being parameterized. The tracer flux is linearly related
to the tracer gradient, while the gradients of conservative temperature and salinity are also required to
calculate the neutral slopes (equation (23.22).
Finite difference approximations of the tracer gradient components are defined by the following equa-
tions (Griffies (2004) equation (16.58)),
∇Tn= (∇s+ˆ
z∂z)Tn(23.239)
→(δx+δy+δz)Tn
i,j,k (23.240)
(δxTn)E
i,j,k =Tn
i+1,j,k −Tn
i,j,k
∆xE
i,j
(23.241)
(δyTn)N
i,j,k =Tn
i,j+1,k −Tn
i,j,k
∆yN
i,j
(23.242)
(δzTn)b
i,j,k =Tn
i,j,k −Tn
i,j,k+1
∆zb
i,j,k
,(23.243)
Elements of MOM November 19, 2014 Page 328

Chapter 23. Neutral Physics Section 23.7
with vertical boundary conditions
(δzTn)b
i,j,0= 0 (23.244)
(δzTn)b
i,j,nk = 0.(23.245)
The gradients are calculated at all points on the grid for all tracers. The zgradient has an extra level
defined at k= 0 which serves to simplify notation in subsequent calculations. To account for points where
tracers are not defined (such as over land), each derivative is masked using the grid’s tracer mask, based
on those points used in each calculation.
(δxTn)E
i,j,k →Mi,j,k Mi+1,j,k (δzTn)E
i,j,k (23.246)
(δyTn)N
i,j,k →Mi,j,k Mi,j+1,k (δzTn)N
i,j,k (23.247)
(δzTn)b
i,j,k →Mi,j,k Mi,j,k+1 (δzTn)b
i,j,k.(23.248)
This masking ensures that the tracer derivatives are defined only across tracer cell faces when the tracer
exists on both sides of the cell face. The tracer gradients are computed in the subroutine tracer gradients.
The horizontal derivatives are calculated using the FDX T and FDY T functions. These functions come from
the ocean operators module.
Note that we may consider two calculations of the lateral tracer gradients. The first takes derivatives
along surfaces of constant vertical coordinate (constant k-level). This method follows the discretization
given above. The second method linearly maps tracers to a constant depth level before taking derivatives,
providing a horizontal derivative relative to a constant z-level. This approach can introduce spurious ex-
trema and so is not recommended, except perhaps for terrain following σ-models. As neutral physics has
not been implemented in MOM for sigma models (see Lemari´
e et al. (2012b,a) for a discussion), we do not
support the second derivative calculation in MOM.
23.7 Quantities related to density gradients
In this section, we detail the calculation of the density gradient, with this calculation used to compute
various density related quantities.
23.7.1 Gradient of locally referenced potential density
Components of the locally referenced potential density gradient ∇ρ= (∇s+ˆ
z∂z)ρare written as (Griffies
(2004) equation 13.36)
∂ρ
∂x =∂Θ
∂x ∂ρ
∂Θ!s,p
+∂S
∂x ∂ρ
∂S !Θ,p
(23.249)
∂ρ
∂y =∂Θ
∂y ∂ρ
∂Θ!s,p
+∂S
∂y ∂ρ
∂S !Θ,p
(23.250)
∂ρ
∂z =∂Θ
∂z ∂ρ
∂Θ!s,p
+∂S
∂z ∂ρ
∂S !Θ,p
,(23.251)
where Θis potential temperature or conservative temperature and Sis salinity. The spatial gradients of
temperature and salinity are available in the model as spanning variables, while the partial derivatives
of density are available at the tracer points (as components of the Dens model variable). The equations
above are therefore discretized as
δxρ(ip)
i,j,k = (δxΘ)E
i−1+ip,j,k(ρ,Θ)i,j,k + (δxS)E
i−1+ip,j,k(ρ,S )i,j,k (23.252)
δyρ(jq)
i,j,k = (δyΘ)N
i,j−1+jq,k (ρ,Θ)i,j,k + (δyS)N
i,j−1+jq,k (ρ,S )i,j,k (23.253)
δzρ(kr)
i,j,k = (δzΘ)b
i,j,k−1+kr (ρ,Θ)i,j,k + (δzS)b
i,j,k−1+kr (ρ,S )i,j,k.(23.254)
Elements of MOM November 19, 2014 Page 329
Chapter 23. Neutral Physics Section 23.7
These formulae are similar to those given in Griffies (2004) equations (16.64) and (16.65), however the
indexing scheme differs. The indexing scheme used here directly reflects that used in the code implemen-
tation.
Calculation of the density gradients are performed in the subroutine gradrho. After calculating the gra-
dient, various adjustments may be made to the vertical derivative δzρ(kr)
i,j,k to produce the adjusted vertical
density derivative.
23.7.1.1 Optional adjustments of the vertical density derivative
The following calculations are performed in the subroutine adjust drhodz. The first adjustment ensures
that the adjusted vertical derivative is always less than zero, i.e. it enforces a stable stratification. As per
equation (15.15) of Griffies (2004), the adjusted vertical density derivative is to set
δzρ(kr)
i,j,k →minδzρ(kr)
i,j,k ,−.(23.255)
This method guarantees that the adjusted derivative is always less than zero and thus prevents numerical
instabilities in subsequent calculations.
The second adjustment is a vertical smoothing process. If the namelist parameter drhodz smooth vert
== .true. then a simple 1-2-1 filter is applied to each point between k= 2 and k= kbot −2, i.e. all those
points on which the derivative is defined for the full three point stencil. The formula for this filter can be
written as
δzρ(kr)
i,j,k →δzρ(kr)
i,j,k−1+δzρ(kr)
i,j,k+1
4+δzρ(kr)
i,j,k
2.(23.256)
The vertical filtering is performed by the subroutine vert smooth in the module ocean nphysics util new.
This module has a namelist parameter num 121 passes, which controls how many times the vertical smooth-
ing process is performed. By default this value is set to 1, however larger values can be set to obtain an
even smoother vertical gradient.
The final adjustment made is a horizontal smoothing process. If the namelist parameter drhodz smooth horz
== .true. then the transformation
δzρ(kr)
i,j,k →δzρ(kr)
i,j,k +∆τ·LAP Tδzρ(kr)
i,j,k ,(κg)i,j(23.257)
is applied. The operator LAP T is defined in the module ocean operators and performs horizontal diffusive
smoothing. The diffusivity parameter is defined as
(κg)i,j =vg(Lg)i,j (23.258)
where vgis specified by the namelist parameter vel micom smooth and Lgis the grid length scale, defined
as
(Lg)i,j =H∆xT
i,j ,∆yT
i,j .(23.259)
The name “MICOM” is motivated by a suggestion by Eric Chassignet, in which he noted that this is how the
Miami Isopycnal Ocean Model based its diffusivities in the early 2000s.
23.7.1.2 Diagnostics
The density gradients are available as diagnostics via the names drhodx,drhody and drhodz. The diag-
nosed values are calculated at the tracer points as the average over the spanning variables, giving
δxρi,j,k =X
ip
δxρ(ip)
i,j,k (23.260)
δyρi,j,k =X
jq
δyρ(jq)
i,j,k (23.261)
δzρi,j,k =X
kr
δzρ(kr)
i,j,k.(23.262)
Elements of MOM November 19, 2014 Page 330

Chapter 23. Neutral Physics Section 23.7
23.7.2 Neutral Slopes
We now detail how neutral slopes are computed in MOM.
23.7.2.1 Neutral Slope Vector
The neutral slope vector
S=− ρ,Θ∇sΘ+ρ,S ∇sS
ρ,Θ∂zΘ+ρ,S ∂zS!(23.263)
(Griffies (2004) equation 13.42) is discretized by combining two spanning variables, which leads to the
slope vector components being defined over a centred triad group (see Section 23.2.5). By taking all avail-
able combinations of density gradients at the tracer point we obtain the following discretization
(Sx)(ip,kr)
i,j,k =−
δxρ(ip)
i,j,k
δzρ(kr)
i,j,k .(23.264)
To avoid dividing by zero, the slopes are only calculated over those grid points where the vertical density
derivative is well defined, based on the grid’s tracer mask. Since the vertical density gradient is not defined
through the surface or bottom boundaries, we set the slopes at these boundaries to their adjacent values,
(Sx)(ip,0)
i,j,1=(Sx)(ip,1)
i,j,1(23.265)
(Sx)(ip,1)
i,j,kmt =(Sx)(ip,0)
i,j,kmt .(23.266)
The yslope is computed in an identical manner, replacing xwith yand ip with jq.
23.7.2.2 Neutral Slope Magnitude
If we average over horizontal half cells of slope, we obtain the vertical half cell slope vector
(Sx)(kr)
i,j,k =1
2X
ip
(Sx)(ip,kr)
i,j,k (23.267)
Sy(kr)
i,j,k =1
2X
jq Sy(jq,kr)
i,j,k ,(23.268)
from which we can calculate the magnitude of the slope vector over the vertical half cells,
|S|(kr)
i,j,k =r(Sx)(kr)
i,j,k2
+Sy(kr)
i,j,k2.(23.269)
As well as calculating the magnitude of the slope vector over the vertical half cells, we also calculate
the average slope vector at each point, defined as
(Sx)i,j,k =1
4X
ip,kr
(Sx)(ip,kr)
i,j,k (23.270)
Syi,j,k =1
4X
jq,kr Sy(jq,kr)
i,j,k .(23.271)
This allows us to calculate the magnitude of the slope vector at the tracer point as
|S|i,j,k =r(Sx)2
i,j,k +Sy2
i,j,k.(23.272)
The subroutine neutral slopes returns the slope vector over the centered triad groups, (Sx)(ip.kr)
i,j,k ,(Sy)(jq.kr)
i,j,k ,
and the slope vector magnitudes |S|(kr)
i,j,k and |S|i,j,k.
Elements of MOM November 19, 2014 Page 331

Chapter 23. Neutral Physics Section 23.7
23.7.2.3 Diagnostics
The components of the slope vector and the slope vector magnitude are diagnosed at the tracer point
via the diagnostic table entries slopex,slopey and absslope. These diagnostics represent the values
calculated in equations (23.270), (23.271) and (23.272), respectively.
23.7.3 Buoyancy
The squared buoyancy frequency is defined as
N2=−g
ρ0
ρ,z.(23.273)
This equation is discretized directly in accordance with the vertical derivative of the locally referenced
potential density
N2(kr)
i,j,k =−g
ρ0ρ,z(kr)
i,j,k .(23.274)
The average over the vertical spans of this quantity is diagnosed via the diagnostic table entry N2.
A related quantity of interest is the product N∆zover the vertical half cells. This value is calculated as
(N∆z)(kr)
i,j,k =r(N2)(kr)
i,j,k∆z(kr)
i,j,k.(23.275)
Since calculation of the adjusted vertical density derivative is always negative, the term under the square
root is always positive.
23.7.4 Baroclinic Gravity Wave Speed
We also make use of the first baroclinic mode gravity wave speed (Griffies (2004) equation (14.83)), which
is approximated as
c1=1
πZ0
−H
Ndz. (23.276)
The discretization of this speed becomes
(c1)i,j =1
π
nk
X
k=1 X
kr
(N∆z)(kr)
i,j,k ,(23.277)
which is diagnosed via the diagnostic table entry gravity wave speed.
23.7.5 Rossby Radius
When calculating the Rossby radius, different equations apply depending on whether or not a point is near
the equator. The respective equations, given in Griffies (2004) equations (14.81) and (14.82) are
λnon-eq =c1
|f|(23.278)
λeq =rc1
2β.(23.279)
The Rossby radius is then defined as the smallest of these two values at any given point, leading to
λ1= min(λeq, λnon-eq).(23.280)
Elements of MOM November 19, 2014 Page 332

Chapter 23. Neutral Physics Section 23.8
The respective discretizations of these equations are
(λnon-eq)i,j =(c1)i,j
|f|i,j
(23.281)
(λeq)i,j =s(c1)i,j
2βi,j
(23.282)
(λ1)i,j = min((λeq)i,j,(λnon-eq)i,j ) (23.283)
Calculation of these values is performed in the subroutine compute rossby radius and the Rossby radius
is diagnosed via the diagnostic table entry rossby radius.
23.7.6 Neutral Boundary Layers
In regions near the surface of the ocean, the vertical stratification of density becomes weak, which leads
to a region of steep neutral slope. This neutral boundary layer can be defined as the region above which
the magnitude of the neutral slope vector is above some threshold Smax. More precisely, we can define the
index of the surface boundary layer as
ksurf i,j = max{0}∪nk:|S|i,j,k0> Smax if k0≤ko.(23.284)
This vertical index is calculated in the subroutine neutral blayer, using a vertical search algorithm from
the surface. The value of ksurf i,j is used in subsequent calculations related to the Ferrari et al. (2008)
and Danabasoglu et al. (2008) methods to obtain various values from the base of the surface boundary
layer. The boundary layer index is diagnosed via the diagnostic table entry ksurf blayer.
23.7.7 Summary
The density based calculations discussed above are all handled within the subroutine density calculations.
This routine returns values for
•slope vector:(Sx)(ip.kr)
i,j,k ,(Sy)(jq.kr)
i,j,k
•slope vector magnitude:|S|(kr)
i,j,k and |S|i,j,k
•buoyancy frequency:N2(kr)
i,j,k and (N∆z)(kr)
i,j,k
•gravity wave speed:(c1)i,j ; the Rossby radius, (λ1)i,j
•surface boundary layer index:(ksurf )i,j.
These density gradient based values will be used in subsequent calculations. It should be noted that at
this stage, the actual density gradient is no longer required, as these derived quantities are sufficient for
the remaining calculations.
23.8 Specification of the diffusivity
Equations (23.20) and (23.28) each feature a diffusivity, which must be computed according to some pre-
scription. The module ocean nphysics diff is responsible for this calculation, via its public interface
subroutine compute diffusivity. In this module, values are computed for the neutral diffusivity ARand
the skew or GM diffusivity κ. The final skew or GM diffusivity is diagnosed via the diagnostic table entry
agm array while the neutral diffusivity is diagnosed via the table entry aredi array.
Elements of MOM November 19, 2014 Page 333
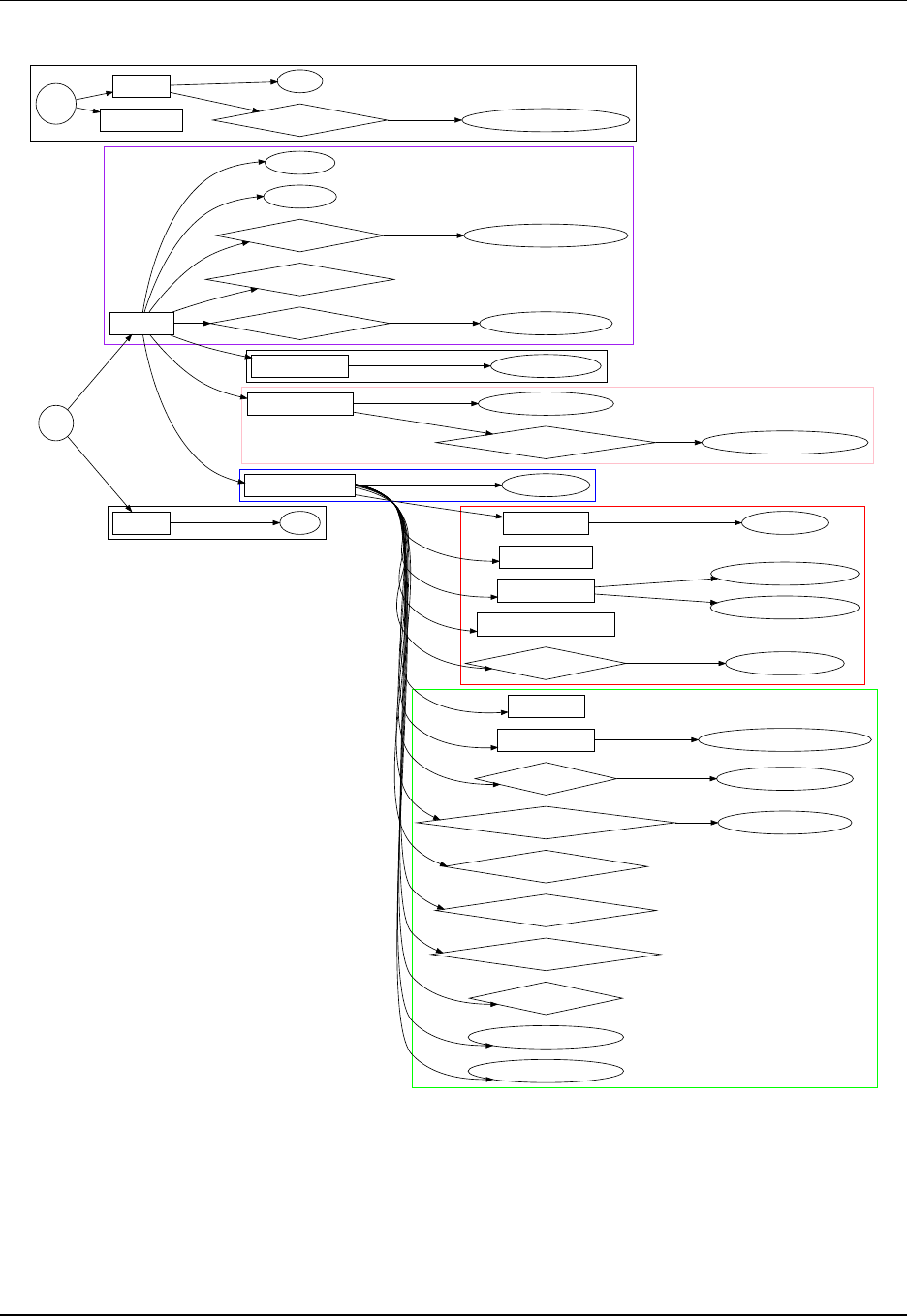
Chapter 23. Neutral Physics Section 23.8
GM
agm_closure
agm_const
Redi
aredi_equal_agm
aredi_fixed
agm_closure_micom agm_micom_vel
agm_closure_n2_scale
agm_n2_scale_nref_cst
agm_n2_scale_coeff
agm_closure_rate_len2
agm_length_fixed
agm_length_rossby
agm_length_bczone
agm_length_eden_greatbatch
agm_rate_eady
agm_rate_baroclinic
agm_length_cap
agm_rate_cap
agm_rate_eden_greatbatch
agm_rate_ave_mixed
agm_rate_smooth_vert
agm_rate_smooth_horiz
agm_rate_zave
agm_scaling
agm_rate_upper_depth
agm_rate_lower_depth
agm_length
agm_bczone_crit_rate
agm_bczone_max_pts
agm_smooth_time
agm_smooth_space
agm_grid_scaling
agm_max
agm_min
agm
aredi_grid_scaling
aredi
agm_rate_baro_buoy_freq
agm_n2_scale_buoy_freq
agm_length_max
agm_damping_time
agm_grid_scaling_power
agm_rate_cap_scale
agm_rate_eg_alpha
aredi_grid_scaling_power
Figure 23.5: Diffusivity module namelist parameters and their relationships.
23.8.1 Namelist Parameters
Specification of diffusivities for the neutral physics parameterization can be performed in many different
ways. MOM presently supports over 24,000 different combinations of boolean options. However, not all
Elements of MOM November 19, 2014 Page 334
Chapter 23. Neutral Physics Section 23.8
combinations are physically sensible. It is thus important to understand how the parameters fit together
to ensure that a physically meaningful set of options is selected. Figure 23.5 gives a visual representation
of all namelist parameters in the ocean nphysics diff module. Parameters are split into logical groups
according to their function and dependencies. The top level nodes, indicated by circles, are not actual pa-
rameters themselves, but serve to break the parameters into their main groups. Rectangular and diamond
nodes represent boolean options, while elliptical nodes represent numerical values.
More specifically, the diamond nodes indicate boolean switches that may be selected independently
from other options in their grouping. Rectangular nodes at the same level as each other indicate where
a selection of one particular option must be made. For example, in the “Redi” group, either aredi fixed
or aredi equal agm must be true. If a boolean node is set to false, then child nodes in the tree are not
considered. If a boolean node is set true, then its child nodes will be considered and must either be set to
an appropriate value, or rely on the default value. Users are advised to consult this graph to ensure that a
valid combination of namelist parameters is used. The subroutine check nml options verifies that a valid
combination of parameters has been chosen when the module is initialised. If an invalid combination is
picked then a fatal error is raised. However, the error checking evaluates only basic settings, so that if a
“valid” option is chosen, there is no guarantee that it will be physically sensible.
23.8.2 Fixed GM Diffusivity
The simplest method for setting the GM diffusivity is to use a fixed or constant diffusivity. If the namelist
parameter agm const == .true., then a space-time constant diffusivity value is used. This choice leads
to the result
κi,j,k =κ0,(23.285)
where κ0is set by the namelist parameter agm.
23.8.3 Flow Dependent GM Diffusivity
Research during the past decade has indicated that a more proper choise for the GM diffusivity is one that
is determined by the properties of the flow. These space-time dependent schemes come in many flavors,
with MOM offering many options.
23.8.3.1 Selecting a GM Diffusivity Closure
To enable one of the closure methods for a flow dependent GM diffusivity, one needs to set
agm closure == .true.
Figure 23.5 reveals three main options to choose:
•agm closure micom FIXME This option is not flow dependent; it is only slightly more complex than
constant agm. It should thus be allowed even if agm closure == .false.
•agm closure n2 ref
•agm closure rate len2.
Furthermore, if agm closure rate len2 is chosen, then one of four length scales and one of two growth
rate options must be chosen. Based on these options, a diffusivity will be calculated, giving a flow depen-
dent value for κi,j,k at each grid point.
23.8.3.2 Diffusivity Postprocessing
Each of the closure methods produces an array of diffusivities calculated at each grid point. A common
set of postprocessing techniques are subsequently applied. If agm grid scaling == .true. then the grid
scaling technique, described in Section 23.8.3.3, is applied to the diffusivity array. An upper and lower
Elements of MOM November 19, 2014 Page 335

Chapter 23. Neutral Physics Section 23.8
bound, as set by the namelist parameters agm max and agm min, is then applied to all elements of the array,
giving
κi,j,k →min(κmax,max(κmin, κi,j,k)).(23.286)
The value of κas calculated at this stage is diagnosed via the diagnostic table entry agm fast, as it repre-
sents the diffusivity before high-frequency components are filtered out below.
If agm smooth time == .true. then a low pass time filter is applied to the diffusivity. This filter is
calculated as
κi,j,k →κi,j,k(τ−1) −γ(κi,j,k(τ−1) −κi,j,k) (23.287)
where γ=∆τ
τκand τκis set to the namelist parameter agm damping time. Next, if agm smooth space ==
.true. then the diffusivity array is horizontally smoothed with the horz smooth function. Neither the
space nor time filter are typically used at GFDL, preferring instead to use the unfiltered value. Finally, the
diffusivity array is masked using the grid’s tracer mask to give
κi,j,k →Mi,j,kκi,j,k.(23.288)
23.8.3.3 Grid Scaling
The grid scaling of GM diffusivity is applied as a function of the grid length and the Rossby radius, so that
κi,j,k →1
1 + (λ1)i,j
(Lg)i,j γκi,j,k,(23.289)
where the value of γis set by the namelist parameter agm grid scaling power. This function serves to
decrease the diffusivity as the Rossby radius increases and the grid scale decreases. That is, the diffusivity
is decreased in regions where the grid scale is smaller than the Rossby radius. The intent is to reduce the
effects of the parameterization in regions where the flow field may otherwise be explicitly representing the
mesoscale eddies.
23.8.4 MICOM
If agm closure micom == .true. then the GM diffusivity is calculated as the product of a characteristic
velocity and length scale
κ=v0Lg.(23.290)
The length scale, Lg, is taken as the grid length, described in Section 23.7.1. The velocity v0is given by the
namelist parameter agm micom vel. This choice leads to the discretization
κi,j,k =v0Lgi,j.(23.291)
23.8.5 Buoyancy Scaling
Another method of computing the GM diffusivity is to take a fixed diffusivity and then scale it according to
the squared buoyancy frequency at each grid point. This method is selected by setting
agm closure n2 scale == .true..
The formula for the diffusivity is then
κ=κ0 N2
N2
ref !.(23.292)
The reference squared buoyancy frequency can either be taken to be a constant value or the computed
value at the base of the surface boundary layer. If agm n2 scale nref cst == .true. then the value of
Elements of MOM November 19, 2014 Page 336

Chapter 23. Neutral Physics Section 23.8
N2
ref is set by the square of the value of the namelist parameter agm n2 scale buoy freq. Otherwise the
discretization
(N2
ref)i,j =1
2X
kr
(N2)(kr)
i,j,ksurfi,j (23.293)
is used. This choise uses the boundary layer index calculated in Section 23.7.6. The reference squared
buoyancy frequency is diagnosed via the diagnostic table entry name N2 ref. The final discretization is
then given by
κi,j,k =κ0
1
2Pkr(N2)(kr)
i,j,k
(N2
ref)i,j
,(23.294)
where κ0is set by the namelist parameter agm n2 scale coeff. This diffusivity is depth dependent.
23.8.6 Rate Length Squared
By appealing to a dimensional argument it is clear that a diffusivity can be calculated from the product of
a squared length and divided by a time scale (Held and Larichev (1996), Visbeck et al. (1997))
κ=σL2.(23.295)
MOM allows for a number of different methods to calculate these characteristic scales. By setting
agm closure rate len2 == .true.,
in conjunction with appropriate rate and length parameters, this method is used to calculate the GM diffu-
sivity. The discretized diffusivity is given by
κi,j,k =ασi,j,k L2
i,j,k,(23.296)
where αis given by the namelist parameter agm scaling
23.8.6.1 Growth Rate
The growth rate term used by MOM is based on that used in Visbeck et al. (1997), which gives (Griffies
(2004) equation (14.80))
σ=f
DZ−Dt
−Db
Ri−1/2dz, (23.297)
where the Richardson number is (Griffies (2004) equation (14.88))
Ri = f
N|S|!2
.(23.298)
Equation (23.297) thus becomes
σ=1
DZ−Dt
−Db
N|S|dz. (23.299)
Raw Growth Rate We denote N|S|the raw growth rate, and can calculate it in two different ways. The
first simply uses the buoyancy frequency and neutral slope to give
N|S|=√N2|S|.(23.300)
This growth rate is equivalent to calculating the Eady growth rate Visbeck et al. (1997); Griffies (2004).
Elements of MOM November 19, 2014 Page 337

Chapter 23. Neutral Physics Section 23.8
The second method is to set the raw growth rate to be proportional to the baroclinicity, giving
N|S|∝∇zρ(23.301)
∝ρzsρ2
x+ρ2
y
ρ2
z
(23.302)
∝N2|S|(23.303)
=N2|S|
N0
,(23.304)
where N0is a constant frequency of proportionality. This corresponds to the method discussed in Griffies
(2004) Section 14.4.10, with a default value of N0= 0.004s−1. This method is also used in Farneti et al.
(2010).
If the namelist parameter agm rate eady == .true., then the first option from above is used and the
final discretization of the raw growth rate is
(N|S|)i,j,k =1
2X
kr r(N2)(kr)
i,j,k |S|(kr)
i,j,k ,(23.305)
where the two vertical stencils have been averaged over. Alternately, if agm rate baroclinic == .true.,
we have
(N|S|)i,j,k =1
2N0X
kr
(N2)(kr)
i,j,k |S|(kr)
i,j,k ,(23.306)
where N0is set by the namelist parameter agm rate baro buoy freq.
Adjusted Growth Rate Having calculated the raw growth rate, N|S|, a number of subsequent operations
can be performed on this value to obtain the inverse time scale σ.
If the namelist parameter agm rate cap == .true. then the growth rate has a harmonic scaling ap-
plied to give
(N|S|)i,j,k →H(N|S|)i,j,k,(σmax)i,j .(23.307)
The value of σmax is controlled by a combination of the Coriolis parameter (Griffies (2004) equation (4.14))
and the dimensionless namelist parameter α=agm rate cap scale, and is computed as
|f|i,j = 2Ωesin(φi,j)(23.308)
(σmax)i,j =α|f|i,j .(23.309)
where Ωeis the angular rotation rate of the earth, given by omega earth from the ocean parameters mod-
ule, and φi,j is the tracer grid point latitude.
If the namelist parameter agm rate ave mixed == .true. then the growth rate within the surface
mixed layer is set to the vertical average over this region. The depth of the mixed layer DMis calculated
by the subroutine calc mixed layer depth from the ocean tracer diag module and can be diagnosed via
the diagnostic table entry ml depth. The vertical averaged growth rate over this region is then given by
N|S|M=1
DMZ0
−DM
N|S|dz(23.310)
=R0
−DMN|S|dz
R0
−DMdz.(23.311)
Elements of MOM November 19, 2014 Page 338
Chapter 23. Neutral Physics Section 23.8
The discretization of the mixed layer averaged growth rate is given by
N|S|Mi,j =PkM
k=2(N|S|)i,j,k∆zi,j,k
PkM
k=2 ∆zi,j,k
(23.312)
where the lower boundary index is defined as
kMi,j = max{k:Di,j,k ≤(DM)i,j }.(23.313)
Note that the lower index in equation (23.312) is k= 2, rather than k= 1. This setting is because the growth
rate at the surface level k= 1 cannot be trusted. The mixed layer averaged growth rate is diagnosed via
the diagnostic table entry ave ml rate. Having calculated the average, those points within the mixed layer
are set to this value
N|S|i,j,k →N|S|Mi,j if Di,j,k <(DM)i,j.(23.314)
If the namelist parameter agm rate smooth vert == .true. then vertical smoothing is applied to N|S|,
using the vert smooth function described in Section 23.7.1.
If agm rate smooth horiz == .true then horizontal smoothing of N|S|is performed. This is done with
the S2D subroutine from the ocean operators module.
If the namelist parameter agm rate eden greatbatch == .true. then another growth rate cap ap-
plied. First, the Eden-Greatbatch rate is calculated as
σEG =αc1
λ1
,(23.315)
where αis a dimensionless scaling constant set by the namelist parameter agm rate eg alpha. The Eden-
Greatbatch rate is diagnosed via the name eg rate. The cap is then applied using the harmonic mean
function, leading to
N|S|i,j,k →H (N|S|)i,j,k, α (c1)i,j
(λ1)i,j !.(23.316)
Once all the caps and filters have been applied, the vertical average of N|S|is calculated, giving
N|S|=1
DZ−Dt
−Db
N|S|dz(23.317)
=R−Dt
−DbN|S|dz
R−Dt
−Dbdz.(23.318)
The values of Dtand Dbare set by the namelist parameters agm rate upper depth and agm rate lower depth
respectively. The default values for these bounds are set to Dt= 100m and Db= 2000m respectively. A
discussion on these choices can be found in Griffies (2004) Section 14.4.9.
The discretization of equation (23.318) is given by
N|S|i,j =Pkt
k=kb(N|S|)i,j,k ∆zi,j,k
Pkt
k=kb
∆zi,j,k
.(23.319)
where the upper and lower boundary indices are defined as
(kb)i,j = max{k:Di,j,k ≤Db}(23.320)
(kt)i,j = min{k:Di,j,k ≥Dt}.(23.321)
The calculation of N|S|is performed in the function vertical average.
Elements of MOM November 19, 2014 Page 339
Chapter 23. Neutral Physics Section 23.8
The final growth rate can now be determined. There are two available options, either the vertically
averaged growth rate can be used, or the unaveraged values of N|S|can be used. These options are
controlled by the namelist parameter agm rate zave. If true, then the growth rate is set to
σi,j,k =N|S|i,j,(23.322)
otherwise we have
σi,j,k = (N|S|)i,j,k.(23.323)
If the vertically averaged rate is not used then the diffusivity will be depth dependent.
The raw growth rate, N|S|; growth rate, σ; and vertically averaged growth rate, N|S|, are diagnosed via
the diagnostic table entries raw growth rate,growth rate and growth rate zave respectively.
23.8.6.2 Length
The length scale can be computed in a number of different ways. The length scale calculations are per-
formed in the subroutine compute length.
If a non-constant length is used (i.e. agm length fixed == .false.) then the computed length is
scaled against the grid length, Lg, using the harmonic mean function (Griffies (2004) equation (14.104)).
This choice gives
Li,j,k →HLi,j,k, Lgi,j.(23.324)
Once the length is calculated, an optional upper limit can be applied. If agm length cap == .true.
then
Li,j,k →min(Li,j,k, Lmax) (23.325)
where Lmax is set by the namelist parameter agm length max. The final length scale is diagnosed by the
name agm length.
The following options are available for computing the length scale.
Constant: If agm length fixed == .true. then the length scale is set to a constant value,
Li,j,k =Lconst,(23.326)
where Lconst is set by the namelist parameter agm length.
Rossby Radius: If agm length rossby == .true. then the length scale is set by the Rossby radius, as
defined in Section 23.7.5, which gives
Li,j,k = (λ1)i,j.(23.327)
Motivation for this choice is given in Griffies (2004) Section 14.4.4.
Baroclinic Zone Radius: If agm length bczone == .true. then the length scale is set by the width of
the baroclinic zone, as done in Visbeck et al. (1997). The algorithm used in MOM was first used in the
Hadley Centre model Gordon et al. (2000) and was first implemented in MOM in version 3 Pacanowski and
Griffies (1999).
The algorithm used to calculate the length scale Rbc is based on the vertically averaged growth rate
and is described in Section 23.8.6.3. The diffusivity calculation length scale is then given by
Li,j,k = (Rbc)i,j.(23.328)
Elements of MOM November 19, 2014 Page 340
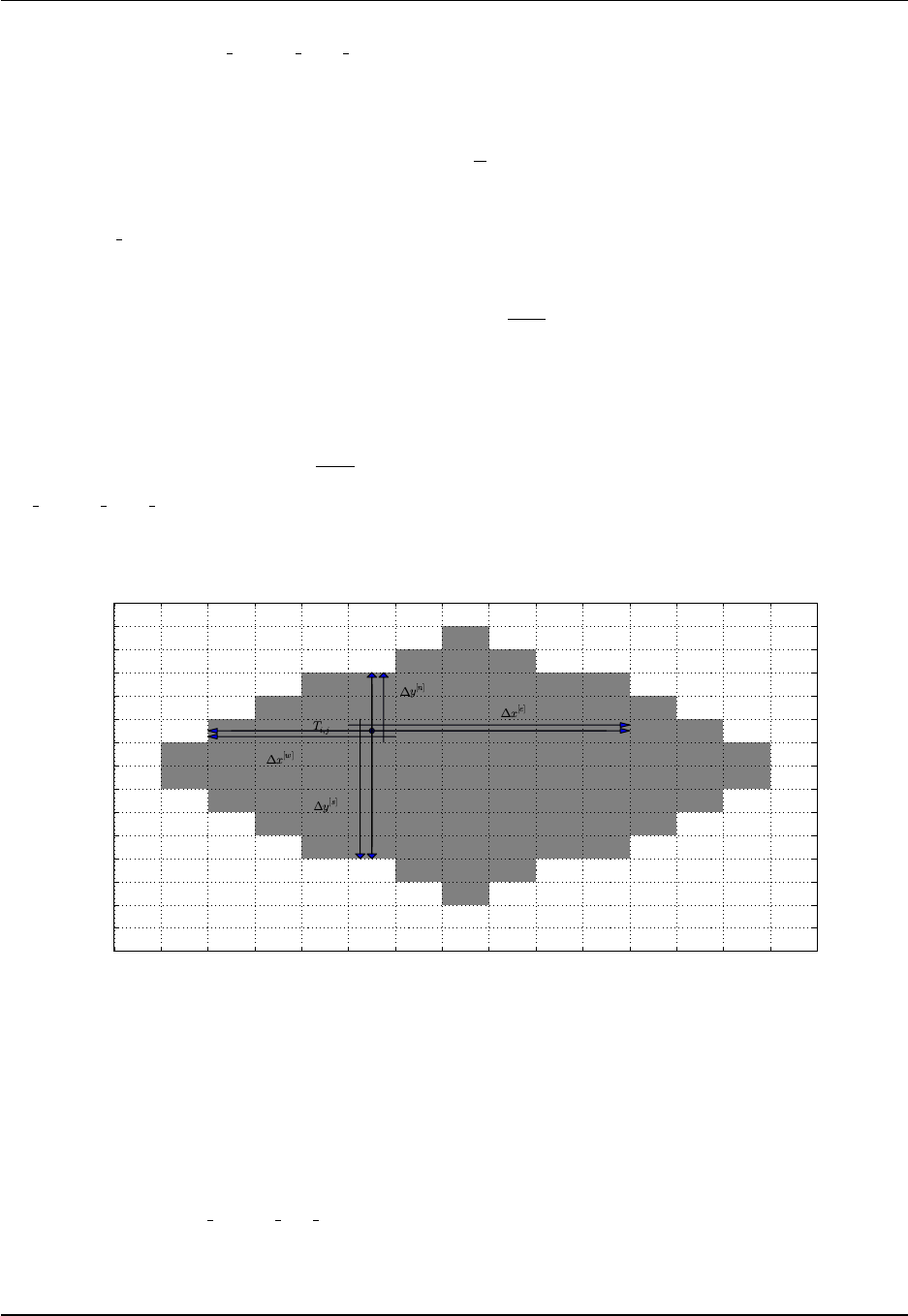
Chapter 23. Neutral Physics Section 23.8
Eden-Greatbatch: If agm length eden greatbatch == .true. then the length scale is set using the
method described in Eden et al. (2009). This takes the length scale as the minimum of the Rhines length
and the Rossby radius, where the Rossby radius is as calculated above and the Rhines length is a function
of the growth rate and is given by
LRhi =σ
β,(23.329)
where βis the beta plane parameter (Griffies (2004) Section 18.1.3). The value of LRhi is diagnosed via the
name rhines length. The discretized Eden-Greatbatch length is thus given by
βi,j = 2.28−11 cos(φi,j)(23.330)
Li,j,k = min (λ1)i,j,σi,j,k
βi,j !.(23.331)
Since this length scale is based on the growth rate, it introduces a depth dependence to the diffusivity.
23.8.6.3 Baroclinic Zone Width
A length scale can be defined as the width of the baroclinic zone. This region is defined as those grid
points with an average growth rate N|S|i,j above a certain threshold, as set by the namelist parameter
agm bczone crit rate. Those points outside of the baroclinic zone are set to have a length scale equal to
the grid length, Lg.
Figure 23.6: The grey region indicates where the baroclinic rate is above the threshold. The arrows indicate
the extant of the baroclinic region for the point Ti,j when the maximum number of points is set to 5.
For points inside the baroclinic zone, the length scale is calculated as a function of the distance to
the edge of the zone in each of the four directions, as shown in Figure 23.6. To find the width in each
direction from a given point, a search is performed in each direction. The search begins at the point and
then considers each point in the direction until either a point outside the baroclinic zone is reached, or
a maximum number of cells are considered. The maximum number of points to consider is set by the
namelist parameter agm bczone max pts. The directional width is then taken as the sum of the tracer cells
widths of all those points within the baroclinic zone in the given direction.
In Figure 23.6, the search is performed in each direction with the maximum number of points set to 5.
In the north, south and west directions, the search continues to the edge of the baroclinic zone, whilst to
Elements of MOM November 19, 2014 Page 341

Chapter 23. Neutral Physics Section 23.9
the east it reaches the maximum number of points. The directional widths, ∆x[E],∆x[W],∆y[N]and ∆y[S]
are indicated by the single headed arrows.
Having calculated the directional widths, the total widths can be calculated as
∆x[EW ]
i,j =∆x[E]+∆x[W]−∆xi,j (23.332)
∆y[NS]
i,j =∆y[N]+∆y[S]−∆yi,j ,(23.333)
where we have subtracted the tracer width of the cell to avoid double counting. These widths are indicated
by double headed arrows in Figure 23.6.
From this point, the baroclinic length scale is defined as the maximum of these total widths, scaled
according to how centred it is within the zone. This specification leads to the final equations
(Lbc)i,j =
min∆x[E]
i,j ,∆x[W]
i,j
max∆x[E]
i,j ,∆x[W]
i,j ∆x[EW ]
i,j if ∆x[EW ]
i,j ≥∆y[N S]
i,j (23.334)
(Lbc)i,j =
min∆y[N]
i,j ,∆y[S]
i,j
max∆y[N]
i,j ,∆y[S]
i,j ∆y[N S]
i,j otherwise.(23.335)
The value of Lbc is diagnosed via the name bczone radius.
23.8.7 Redi Diffusivity
The calculation of the Redi diffusivity is much simpler than that of the GM diffusivity. Either a constant
value is used, or the GM diffusivity is used. In most cases, one should choose to set the Redi diffusivity
equal to the GM diffusivity. However, tuning purposes may motivate taking different values.
If the namelist parameter aredi equal agm == .true. then the Redi diffusivity is set to be identical to
the GM diffusivity, giving
(AR)i,j,k =κi,j,k.(23.336)
If aredi fixed == .true. then a constant diffusivity is used, giving
(AR)i,j,k =A0,(23.337)
where A0is set by the namelist parameter aredi. In this case, grid scaling can also be applied to the
diffusivity. If aredi grid scaling == .true. then grid scaling is applied as described in Section 23.8.3.3,
giving
(AR)i,j,k →1
1 + (λ1)i,j
(Lg)i,j γ(AR)i,j,k,(23.338)
where in this case, γis set by the namelist parameter aredi grid scaling power.
23.9 Summary of the notation
This section summarizes the notation used in this chapter.
Elements of MOM November 19, 2014 Page 342

Chapter 23. Neutral Physics Section 23.9
23.9.1 General
Value Variable Units
∆xGrid%dxt m
∆yGrid%dyt m
∆zThickness%dzt m
∆xEGrid%dxte m
∆yNGrid%dytn m
∆zbThickness%dzwt m
∆x(0) Grid%dtw m
∆x(1) Grid%dte m
∆y(0) Grid%dts m
∆y(1) Grid%dtn m
∆z(0) Thickness%dztup m
∆z(1) Thickness%dztlo m
∆AGrid%dat m
DThickness%depth zt m
MGrid%tmask -
Lggrid length m
ggrav ms−2
ρ0rho0 kg m−3
πpi -
Ωeomega earth s−1
φGrid%phit rad
epsln context dependent
∆τTime steps%dtime t s
Smax smax -
23.9.2 Tracer Gradients
Value Variable Units
TnT prog(n)%field(:,:,:,Time%taum1) [Tn]
(δxTn)EdTdx(:,:,:,n) [Tn]m−1
(δyTn)NdTdy(:,:,:,n) [Tn]m−1
(δzTn)bdTdz(:,:,:,n) [Tn]m−1
Elements of MOM November 19, 2014 Page 343
Chapter 23. Neutral Physics Section 23.9
23.9.3 Density Calculations
Value Variable Units
(δxθ)EdTdx(:,:,:,index temp) Km−1
(δyθ)NdTdy(:,:,:,index temp) Km−1
(δzθ)bdTdz(:,:,:,index temp) Km−1
(δxS)EdTdx(:,:,:,index salt) psu m−1
(δyS)NdTdy(:,:,:,index salt) psu m−1
(δzS)bdTdz(:,:,:,index salt) psu m−1
ρ,θ Dens%drhodT kg m−3K−1
ρ,S Dens%drhodS kg m−3psu−1
δxρdrhodx x kg m−4
δyρdrhody y kg m−4
δzρdrhodz z kg m−4
κgsmooth diff m2s−1
Sxslope x -
Syslope y -
N2N2 s−2
Nbuoy freq s−1
c1gravity wave speed ms−1
λ1rossby radius m
Rraw rossby radius raw m
Rnon-eq rossby non equator m
Req rossby equator m
23.9.4 Neutral Boundary Layer
Value Variable Units
DEeddy depth m
DBL depth blayer base m
ksurf ksurf blayer -
Sbase slope blayer base -
Elements of MOM November 19, 2014 Page 344
Chapter 23. Neutral Physics Section 23.9
23.9.5 Diffusivity
Value Variable Units
κagm array m2s−1
ARaredi array m2s−1
Lagm length m
σgrowth rate ms−1
LRhi rhines length m
Rbc bczone radius m
Nref buoy ref s−1
NS raw growth rate ms−1
NS growth rate zave ms−1
σmax growth rate max ms−1
DMml depth m
NSMave ml rate ms−1
σEG eg rate ms−1
∆x[E]e zone m
∆x[W]w zone m
∆y[N]n zone m
∆y[S]s zone m
∆x[EW ]ewtot m
∆x[NS]nstot m
23.9.6 Tensors
Value Variable Units
1
∆ATGrid%datr m−2
|f|coriolis param s−1
βbeta param (ms)−1
Tsine depth taper -
Tx
tanh slope taper xz -
Ty
tanh slope taper yz -
Tx
Nneutral taper xz -
Ty
Nneutral taper yz -
Elements of MOM November 19, 2014 Page 345

Chapter 23. Neutral Physics Section 23.9
23.9.7 Fluxes
Value Variable Units
dz(ρTn)diff
,t diff th tendency(n) ρmT s−1
dz(ρTn)skew
,t skew th tendency(n) ρmT s−1
(Gd
n)Ediff flux x xte(n) T kgs−1
(Gd
n)Ndiff flux y ytn(n) T kgs−1
(Gd
n)bdiff flux z ztb(n) T kgs−1
(ρFn
x∆A)skew skew flux x xte T kgs−1
ρFn
y∆Askew skew flux y ytn T kgs−1
(ρFn
z∆A)skew skew flux z ztb T kgs−1
(ρV K11)symm mass diff 11 xz kgm2s−1
(ρV K22)symm mass diff 22 yz kgm2s−1
(ρV K33)symm mass diff 33 z kgm2s−1
(ρV K13)symm mass diff 13 xz kgm2s−1
(ρV K23)symm mass diff 23 yz kgm2s−1
(ρV A13)skew mass diff 13 xz kgm2s−1
(ρV A23)skew mass diff 23 yz kgm2s−1
(ρV K11)Esymm mass diff 11 xte kgm2s−1
(ρV K22)Nsymm mass diff 22 ytn kgm2s−1
(ρV K13)Esymm mass diff h xz kgm2s−1
(ρV K23)Nsymm mass diff h yz kgm2s−1
(ρV K31)bsymm mass diff v xz kgm2s−1
(ρV K32)bsymm mass diff v yz kgm2s−1
(ρV A13)Eskew mass diff h xz kgm2s−1
(ρV A23)Nskew mass diff h yz kgm2s−1
(ρV A31)bskew mass diff v xz kgm2s−1
(ρV A32)bskew mass diff v yz kgm2s−1
(ρV AR)Esimple mass diff 11 xte kgm2s−1
(ρV AR)Nsimple mass diff 22 ytn kgm2s−1
(ρVx)rho qcv xz kg
(ρVy)rho qcv yz kg
(∆z0)Emin dzt xte z m
(∆z0)Nmin dzt ytn z m
ρrho kgm−3
(ρV Kcrit
33 )m33 crit z kgm2s−1
(ρV Kexp
33 )m33 explicit z kgm2s−1
(ρV Kimp
33 )m33 implicit kgm2s−1
(ρV Kexp
33 )bm33 explicit ztb kgm2s−1
ρKimp
33 nT prog(n)%K33 implicit kgm−1s−1
Elements of MOM November 19, 2014 Page 346

Chapter 24
Restratification by submesoscale eddies
Contents
24.1 Basics of the scheme .......................................347
24.2 Skew tracer flux components ..................................349
24.3 Eddy induced transport .....................................350
24.3.1 Overturning circulation ................................... 350
24.3.2 Diagnosing the streamfunction in Ferret from MOM output ............... 351
24.3.3 Advective tracer fluxes .................................... 351
24.4 Eddy advection implementation ................................352
24.5 Cautionary remarks on compute psi legacy .........................352
24.6 Horizontal diffusion associated with submesoscale processes ...............353
This chapter documents the MOM implementation of the parameterization by Fox-Kemper et al. (2008b),
with further details discussed in Fox-Kemper et al. (2008a) and Fox-Kemper et al. (2011). This scheme pa-
rameterizes the restratification effects of submesoscale eddies in the ocean mixed layer. These effects
occur on a time scale much shorter than the mesoscale eddies parameterized via the neutral physics
scheme of Gent and McWilliams (1990) and Gent et al. (1995). The following MOM module is directly
connected to the material in this chapter:
ocean param/lateral/ocean submesoscale.F90.
24.1 Basics of the scheme
The parameterization is based on the calculation of a vector streamfunction Ψ(with units length2time−1)
Ψ=
Ceµh2g∆s
ρoLfpf2+τ−2ˆ
z∧ ∇γz.(24.1)
In this equation, we have
•0.06 ≤Ce≤0.08 is a dimensionless number;
•µ= [1 −(1 −2d/h)2][1 + 5/21 (1 −2d/h)2]is a non-negative vertical structure function 0≤µ≤1in the
mixed layer, with zero values outside the mixed layer where d≥hand d≤0;
•d=−z+ηis the depth of seawater, defined as the vertical distance from the ocean free surface;
•ηis the deviation of the ocean free surface from the resting state at z= 0;
347

Chapter 24. Restratification by submesoscale eddies Section 24.2
•gis the gravitational acceleration;
•his the mixed layer thickness;
•∇γzis the mixed layer averaged horizontal gradient of locally referenced potential density;
•fis the Coriolis parameter;
•τis a time scale for the submesoscale eddies (order few days);
•Lfis a length scale for the width of the submesoscale eddies (order 5km);
•∆sis the horizontal grid spacing;
•ρois the constant Boussinesq density.
Written in components, the streamfunction is given by
Ψ=Γµ(−γ,yz,γ,xz,0),(24.2)
where
Γ=Ceh2g∆s
ρoLfpf2+τ−2(24.3)
is shorthand for the non-negative dimensionful scalar contributions, with physical dimensions m6/(sec kg).
The dimensionless function µ(z)carries the only vertical dependence of the streamfunction Ψ. We make
the following observations.
• The formulation of Fox-Kemper et al. (2008b) is in terms of the mixed layer depth, rather than the
planetary boundary layer depth. The reasoning is that the planetary boundary layer can be very
small under stable buoyancy forcing. However, the submesoscale eddies remain even in these situ-
ations, so long as the mixed layer depth is nontrivial. MOM has an option for setting haccording to
either the mixed layer depth or the planetary boundary layer depth, with the mixed layer depth the
recommended choice.
•Fox-Kemper et al. (2008b) pose the parameterization in terms of the horizontal buoyancy gradient,
which is related to the gradient of the locally referenced potential density via
−ρo∇b=g∇γ(24.4)
=g(γ,θ ∇θ+γ,S ∇S),(24.5)
where θis the potential temperature, Sis the salinity, and
γ,θ =∂γ
∂θ (24.6)
γ,S =∂γ
∂S (24.7)
are the density partial derivatives.
• The front length can either be a constant, or computed according to the first baroclinic Rossby radius
over the mixed layer
Lf=hNz
f(24.8)
with Nzthe buoyancy frequency averaged over the depth of the mixed layer, and his the mixed layer
thickness. Substitution of the front length (24.8) into the streamfunction (24.1) leads to
Ψ=
Ceµhg∆s
ρoNzf
pf2+τ−2ˆ
z∧ ∇γz.(24.9)
In this way, the streamfunction goes to zero as the equator is approached.
Elements of MOM November 19, 2014 Page 348

Chapter 24. Restratification by submesoscale eddies Section 24.3
24.2 Skew tracer flux components
A method for implementing the effects of the streamfunction (24.1) on tracer concentration is to do so
via a skew diffusion, as motivated by the Griffies (1998) method for the Gent et al. (1995) scheme. Skew
diffusion for the submesoscale restratification parameterization is defined by an anti-symmetric stirring
tensor
A=Γµ
0 0 −γ,xz
0 0 −γ,y z
γ,xzγ,yz0(24.10)
acting on the gradient of the tracer concentration, so that
Fi=−Aij ∂C
∂xj!,(24.11)
with summation over j= 1,2,3implied on the right hand side. Components to the skew tracer flux are given
by
F(x)=Γµ γ,xzC,z (24.12)
F(y)=Γµ γ,yzC,z (24.13)
F(z)=−Γµ∇γz·∇C, (24.14)
which can be written in terms of the vector streamfunction
F(x)=Ψ(y)C,z (24.15)
F(y)=−Ψ(x)C,z (24.16)
F(z)=−Ψ(y)C,x +Ψ(x)C,y.(24.17)
It is revealing to consider the special case of potential temperature for a linear equation of state
γ=ρo−α θ, (24.18)
with α > 0constant. In this case, the skew temperature flux components are given by
F(h)=−Γµα θ,z ∇θz(24.19)
F(z)=Γµα ∇θ·∇θz.(24.20)
With a stable stratification where θ,z >0, the horizontal flux is directed opposite to the vertically averaged
horizontal temperature gradient: Fh∝ −∇θz, and so is downgradient in this sense.
The technology for discretizing the neutral physics operators (e.g., neutral diffusion as in Griffies et al.
(1998), and skew diffusion from Gent et al. (1995)asinGriffies (1998)) is useful for rotated diffusion and
skew diffusion. We can thus make use of this technology for discretizing the submesoscale closure of Fox-
Kemper et al. (2008b). The full tracer transport tensor, which is the sum of neutral diffusion plus Gent et al.
(1995) skew diffusion plus submesoscale restratification, is given by
J=
AI0 (AI−κ)S(x)−Γµγ,xz
0AI(AI−κ)S(y)−Γµγ,yz
(AI+κ)S(x)+Γµγ,xz(AI+κ)S(y)+Γµγ,yzAIS2(24.21)
=
AI0 (AI−κ)S(x)−Ψ(y)
0AI(AI−κ)S(y)+Ψ(x)
(AI+κ)S(x)+Ψ(y)(AI+κ)S(y)−Ψ(x)AIS2,(24.22)
where AIis the neutral diffusivity, κis the GM-diffusivity, and Sis the neutral slope vector. It is straight-
forward to incorporate the submesoscale closure into the neutral physics module. If doing so, one would
Elements of MOM November 19, 2014 Page 349

Chapter 24. Restratification by submesoscale eddies Section 24.3
then implement the full transport tensor (24.22). However, there are occassions where one does not wish
to turn on the neutral physics parameterizations. For example, in mesoscale eddying simulations, one may
choose to remove the neutral physics closure, but retain the submesoscale closure. We thus prefer to de-
velop a separate module for the submesoscale closure, taking only what we need from the neutral physics
module.
24.3 Eddy induced transport
The vector streamfunction (24.1) gives rise to an eddy induced velocity
v∗=∇ ∧ Ψ
= (−∂zΨ(y),∂zΨ(x),∂xΨ(y)−∂yΨ(x))(24.23)
and an associated volume transport within the mixed layer. There is zero net horizontal volume transport
Zη
−H
dzu∗= 0,(24.24)
since the vector streamfunction vanishes at the ocean surface and at the base of the mixed layer. A zero
net volume transport is also the case for the eddy induced transport from the Gent et al. (1995) mesoscale
parameterization, where the Gent et al. (1995) quasi-Stokes streamfunction vanishes at the ocean surface
and bottom (McDougall and McIntosh,2001).
24.3.1 Overturning circulation
For a vertical position zwithin the mixed layer, the meridional volume transport passing beneath this depth
z, zonally integrated within a basin or over the globe, is computed by the integral (see Section 32.2.3)
T(y)(y,z,t) = −ZdxZz
−H
dz0v∗
=−ZdxZz
−h
dz0∂z0Ψ(x)
=−ZdxΨ(x)(x,y,z,t)
=ZdxΓµγ,yz
(24.25)
since the streamfunction vanishes at z≤ −h(beneath the mixed layer). Likewise, the zonal transport within
the mixed layer is
T(x)(x,z,t) = −ZdyZz
−H
dz0u∗
=ZdyZz
−h
dz0∂z0Ψ(y)
=ZdyΨ(y)(x,y,z,t)
=ZdyΓµγ,xz.
(24.26)
Since Γµis single signed within the mixed layer, the sign of the horizontal transport in the mixed layer is
given by the sign of −∇γz. For example, with denser water towards the north, so that γ,yz>0, the meridional
transport passing beneath a depth zwithin the mixed layer will be negative, T(y)(y,z,t)<0. This property of
the transport provides a useful check that the scheme has been implemented in the model with the proper
sign.
Elements of MOM November 19, 2014 Page 350

Chapter 24. Restratification by submesoscale eddies Section 24.4
It is instructive to compare the volume transport from the submesoscale parameterization to that in-
duced by the Gent et al. (1995) mesoscale scheme. For Gent et al. (1995), the horizontal component of the
eddy-induced velocity is
ugm =−∂z(κS),(24.27)
with S=−∇γ/γ,z the neutral slope vector, and κ > 0a diffusivity. The meridional transport is given by
T(y)
gm =−ZdxZz
−H
dz0vgm
=−Zdx κγ,y
γ,z !,
(24.28)
where we set the streamfunction to zero at the ocean bottom. For a stable stratification with γ,z <0, the
volume transport is directed in the sign of the meridional density gradient, which is analogous to the case
for the submesoscale transport (24.25).
24.3.2 Diagnosing the streamfunction in Ferret from MOM output
To evaluate the overturning streamfunction when implementing the submesoscale closure using skew
fluxes, we perform the following step in Ferret
T(y)(y,z,t) = ty trans submeso[i= @sum]skew fluxes,(24.29)
which is just as for the skew flux implementation of Gent et al. (1995). Note that by definition, the vertically
integrated transport from the submesoscale parameterization scheme vanishes. So there is no contribu-
tion from this scheme to the column integrated transport through straits and throughflows.
If implementing the submesoscale closure using advective fluxes (still under testing so not the default
method), then the overturning should be computed in Ferret using the commands
T(y)(y,z,t) = ty trans submeso[i= @sum,k= @rsum]−ty trans submeso[i= @sum,k= @sum]advective fluxes,
(24.30)
which is just as for computing the streamfunction based on the resolved Eulerian flow (Section 32.2.6).
Subtraction of the depth integral in equation (24.30) is necessary since Ferret starts the vertical sum from
the surface (k=1) rather than from the bottom.
24.3.3 Advective tracer fluxes
Components to the advective tracer flux are given by
F(x)=u∗C(24.31)
F(y)=v∗C(24.32)
F(z)=w∗C, (24.33)
which can be written in terms of the vector streamfunction
F(x)=− ∂Ψ(y)
∂z !C(24.34)
F(y)= ∂Ψ(x)
∂z !C(24.35)
F(z)= ∂Ψ(y)
∂x −∂Ψ(x)
∂y !C. (24.36)
Comparison should be made to the corresponding skew flux components given by equations (24.15)–
(24.17). Note that the vertical structure for the horizontal advective transport velocity components is
given by the vertical derivative of the structure function
∂µ
∂z =− 1−2d/H
21H!64 + 40(1 −2d/H)2,(24.37)
Elements of MOM November 19, 2014 Page 351

Chapter 24. Restratification by submesoscale eddies Section 24.5
where again d=−z+ηand His the mixed layer depth.
24.4 Eddy advection implementation
The skew flux approach in Section 24.2 is the standard method used in MOM, as documented and il-
lustrated in Fox-Kemper et al. (2011). However, the skew flux suffers from a lack of monotonicity con-
straints, with such allowing for the introduction of spurious extrema. There are some cases when this
non-monotonicity may become a problem, especially with finer resolution simulations where gradients are
stronger.
We have not pursued the development of monotinicity constraints for skew fluxes. Instead, we have
provided an option in MOM to compute the advective flux using a monotonic advection scheme. For this
purpose, it is necessary to compute the eddy induced transport at the tracer cell faces, with the continuum
form given in Section 24.3.3. To compute the vertical derivative of the vector streamfunction, we perform
the analytical derivative of the vertical structure function and evaluate that derivative at the model depths.
Use of the continuity equation, as for the resolved Eulerian mass transport, then allows for the vertical
component to be diagnosed.
Once all three advective mass transport components are known, one can then use the transports to
compute tracer flux components via an advection scheme. The first order upwind scheme is presently the
only working scheme implemented in MOM for the submesoscale parameterization. Tests with the Sweby
scheme are incomplete. Either way, the use of a dissipative advection implementation of the submesoscale
parameterization introduces some mixing that is absent when using the skew flux approach. There are two
reasons we favour the introduction of enhanced mixing for this parameterization.
• The submesoscale parameterization in theory adds an extra advective transport to the tracer fields
in the mixed layer. It is arguable (Baylor Fox-Kemper, personal communication, 2011) that the param-
eterization should also provide some added lateral mixing in the mixed layer. The use of dissipative
advection schemes acts, through numerical truncation errors, to add such mixing.
• Because the submesoscale parameterization acts only in the mixed layer, there is little concern that
adding mixing through dissipative advection will adversely compromise the simulation. Indeed, given
the many sources for grid noise arising from this scheme, the addition of mixing from dissipative
advection in many ways enhances the physical integrity of the scheme.
There are many issues remaining to be resolved with the advective approach. Notably, in the presence
of topography, the approach has been found to produce some rather large tendencies near topography.
We have implemented a masking scheme to remove the fluxes at cells next to land. But that scheme does
not fully remove the problems. It is unclear whether this issue is a “bug” or a “feature” of the advective
implementation.
24.5 Cautionary remarks on compute psi legacy
The preferred organization of the numerical implementation of the submesoscale parameterization is as
follows:
• Compute the depth-independent portion of the vector streamfunction. Perform any desired smooth-
ing or limiting directly on this depth-independent portion.
• Project the depth-independent portion vertically by multiplying by the vertical structure function µ(z).
This is the overall philosophy taken with the MOM code as of Feb 2012. Unfortunately, earlier implemen-
tations computed the three-dimensional streamfunction and applied limiters and smoothers to the three-
dimensional streamfunction. The problem with this approach is that the analytical properties of the ver-
tical structure are generally corrupted when smoothing or limiting on the full three-dimensional stream-
function. Namely, both limiting and smoothing can produce multiple extrema in the vertical, as opposed to
the desired unimodal structure. Here are more details of the problems.
Elements of MOM November 19, 2014 Page 352
Chapter 24. Restratification by submesoscale eddies Section 24.6
•problems with smooth psi: A numerical calculation of the vector streamfunction can at times intro-
duce noise in the horizontal directions, so that a horizontal smoothing operator is motivated. How-
ever, examples have been found where smoothing the three-dimensional streamfunction produces
multiple extrema in the vertical, rather than a single extrema designed into the analytical unimodal
structure function µ(z). The problem of multiple extrema arises from horizontal smoothing of the
vector streamfunction, via smooth psi, across regions of different mixed layer depths. This lateral
smoothing mixes across the different structure functions, resulting in the potential for multiple ex-
trema.
•problems with limit psi legacy: The vector streamfunction can at times become quite large. If the
vertical gradient is correspondingly large, the model can be prone to instabilities. MOM provides the
following means to limit the value of the streamfunction magnitude
Ψlimited =sign(Ψ) min[vmax ∆z,abs(Ψ)],(24.38)
where vmax is a namelist-specified velocity scale on the order of 1m/sec, and ∆zis the grid cell thick-
ness. This limiter is not appropriate, since it is not the magnitude of the streamfunction that is prob-
lematic, it is instead the vertical derivative. Nonetheless, it is what was originally coded.
Consistent with this limiter being naive, it can introduce some rather unphysical side-effects. Depend-
ing on the value of vmax and ∆z, examples have been found where limit psi sets the streamfunction
to a vertical constant in the upper ocean where the vertical grid is fine (i.e., small ∆z), yet returns the
streamfunction to its normal values in the region where vertical thickness coarsens (larger ∆z). In
effect, this corrupted streamfunction places all restratification effects into the deeper ocean region
where the streamfunction has a jump, and removes restratification from the upper ocean where the
streamfunction is a vertical constant. Both effects are in fact opposite the theoretical intention of
the Fox-Kemper et al. (2008b) scheme, so that limit psi can be particularly egregious at corrupting
the submesoscale scheme.
For the above reasons, compute psi legacy should be avoided if one also aims to use the limit psi
or smooth psi options. A far more sensible approach is in the newer compute psi routine, where lim-
iters and smoothers are first applied to the depth independent portion of the streamfunction. After all
such operations are performed, the vertical structure function is applied to render the three-dimensional
streamfunction. In this manner, the proper analytic properties of the streamfunction are maintained, so
there are no spurious jumps in the vertical derivative.
24.6 Horizontal diffusion associated with submesoscale processes
We raised some issues in Sections 24.4 and 24.5 regarding the potential for the submesoscale parameter-
ization to introduce spurious extrema. The presence of these extrema raises the issue whether the param-
eterization should also include a mixing parameterized as downgradient diffusion. Adding such mixing will
in principle suppress the occurrances of spurious dispersion that create extrema. It also acknowledges
that the submesoscale processes create both an advective restratification as well as a lateral diffusive
effect, both within the upper ocean mixed layer. Such arguments are analogous to those used by Treguier
et al. (1997), Ferrari et al. (2008), and Ferrari et al. (2010) for parameterizing mesoscale eddy processes in
the upper ocean boundary layer, in which an additional horizontal diffusion is added to the eddy-induced
advection.
For the above reasons, MOM has an option within the submesoscale module that provides for a nonzero
horizontal tracer diffusion in addition to the eddy-induced advection from the vector streamfunction. This
option, submeso horz diffuse, is implemented using the magnitude of the vector streamfunction (units of
m2sec−1) to specify an effective diffusivity, in which case the downgradient horizontal diffusive flux for all
tracers is given by
F(submeso)=−ργ |Ψ|∇sC, (24.39)
where γis a dimensionless scaling parameter that can be used to increase or decrease the diffusivity
beyond that set by |Ψ|.
Elements of MOM November 19, 2014 Page 353

Chapter 24. Restratification by submesoscale eddies Section 24.6
Elements of MOM November 19, 2014 Page 354

Chapter 25
Lateral friction methods
Contents
25.1 Introduction ............................................356
25.2 Lateral friction options in MOM ................................356
25.2.1 Older options just for the B-grid .............................. 356
25.2.2 Laplacian and biharmonic modules for the B and C grids ................ 357
25.3 Continuum formulation for the friction operator ......................357
25.3.1 Laplacian friction ....................................... 357
25.3.2 Biharmonic friction ...................................... 358
25.4 Lateral friction operator for B-grid MOM ...........................359
25.4.1 Discrete dissipation functional for the B-grid ....................... 359
25.4.2 Grid cell distances and subcell volumes .......................... 360
25.4.3 Derivative operators ..................................... 360
25.4.4 Tension and strain for the subcells ............................. 360
25.4.5 Functional derivative of eTand eS.............................. 363
25.4.6 Tidy form for the discretized friction ............................ 364
25.4.7 Tension and strain in the quadrants ............................. 365
25.4.8 Comments ........................................... 366
25.4.9 Discretized Smagorinsky viscosity ............................. 366
25.5 Lateral friction operator for C-grid MOM ...........................367
25.5.1 Discrete functional derivative and the grid stencil .................... 367
25.5.2 Deformation rates ....................................... 367
25.5.3 Stress tensor components ................................... 368
25.5.4 Orientation angle ....................................... 369
25.5.5 Viscosities ........................................... 370
25.5.6 Volumes ............................................ 370
25.5.7 Discrete C-grid friction operators .............................. 370
25.6 Boundary conditions .......................................371
25.6.1 B-grid .............................................. 371
25.6.2 C-grid ............................................. 371
The purpose of this chapter is to summarize methods for implementing lateral viscous friction in MOM.
355

Chapter 25. Lateral friction methods Section 25.2
The following MOM modules are directly connected to the material in this chapter:
ocean param/lateral/ocean lapcst friction.F90
ocean param/lateral/ocean lapgen friction.F90
ocean param/lateral/ocean lapcgrid friction.F90
ocean param/lateral/ocean bihcst friction.F90
ocean param/lateral/ocean bihgen friction.F90
ocean param/lateral/ocean bihcgrid friction.F90
Some of the material in this chapter can also be found in Part 5 of Griffies (2004).
25.1 Introduction
Ocean models require some form of viscous friction for numerical reasons. One way to understand the
numerical need is that the Reynolds number for traditional advection schemes should be kept less than
unity, with a length scale given by the model grid scale used to set the Reynolds number. With grid scales
of many kilometers rather than the millimeters corresponding to the ocean’s Kolmogorov scale, numer-
ical viscosity must be increased accordingly. For the most part, ocean modelers employ lateral viscous
friction as a numerical closure. As a numerical closure, the aim is to reduce friction to low levels while sup-
pressing numerical instabilities and/or noise. Hence, lateral friction is generally tuned. Experience with
global models reveals a nontrivial sensitivity to details of friction. For example, friction affects transport
through frictionally controlled passages, modifies the Gulf Stream separation point (Chassignet and Gar-
raffo,2001), strongly influences the equatorial undercurrent strength (Large et al.,2001), and changes
poleward heat transport by altering transport in boundary currents and gyres. In practice, friction tuning
can be one of the least satisfying aspects of ocean climate model construction.
Given the need to apply friction for numerical reasons, is it necessary to damp toward a state of zero
kinetic energy? Certainly that is what molecular viscosity does, but the ocean models are so far from
resolving the Kolmogorov scale that analogies to molecular friction are unwarranted. Nonetheless, damp-
ing toward rest is the common approach. There are, however, arguments that suggest dissipation should
instead damp the solution toward a nonzero flow state. Holloway (1992) proposes a practical means to
realize this approach, with Chapter 26 detailing the MOM implementation.
25.2 Lateral friction options in MOM
MOM has both Laplacian and biharmonic friction operator options. Both operators can be employed at the
same time, such as used in the one-degree global model documented by Dunne et al. (2012) and Dunne
et al. (2013). Most applications with finer resolution simulations choose just the biharmonic operator,
such as in Farneti et al. (2010) and Delworth et al. (2012). Nonetheless, there are exceptions, such as the
combined Laplacian and biharmonic approaches used for the mesoscale eddying simulations described by
Hecht et al. (2008).
25.2.1 Older options just for the B-grid
The Laplacian and biharmonic friction modules
•ocean param/lateral/ocean lapcst friction.F90
•ocean param/lateral/ocean bihcst friction.F90
are based on the discretization method used in MOM prior to the year 2000. These two modules are largely
frozen, with minimal support for further development, and they are supported only for use with the B-grid
option in MOM. Consequently, options for computing the viscosity are somewhat limited when using these
two modules.
Elements of MOM November 19, 2014 Page 356
Chapter 25. Lateral friction methods Section 25.3
25.2.2 Laplacian and biharmonic modules for the B and C grids
The friction modules
•ocean param/lateral/ocean lapgen friction bgrid.F90
•ocean param/lateral/ocean bihgen friction bgrid.F90
•ocean param/lateral/ocean lapgen friction cgrid.F90
•ocean param/lateral/ocean bihgen friction cgrid.F90
employ the B-grid and C-grid discretization methods of Griffies and Hallberg (2000). The B-grid methods
are detailed in Chapter 19 of Griffies (2004) as well as Section 25.4 below. The C-grid methods are detailed
in Section 25.5.
Each of the Laplacian and biharmonic modules support the following suite of options for computing the
viscosity.
• The deformation dependent viscosity scheme of Smagorinsky (1963,1993), as detailed by Griffies
and Hallberg (2000) (see also Chapter 18 of Griffies (2004)) is available, and used quite frequently
at GFDL.
• The anisotropic Laplacian and biharmonic scheme of Large et al. (2001); Smith and McWilliams
(2003) (also see Chapter 17 of Griffies (2004)) has been used for the AR4 climate models at GFDL
(Griffies et al.,2005).
• The Neptune scheme of Holloway (1992), in the form implemented by Maltrud and Holloway (2008)
(see Chapter 26), is available. Tests with this scheme are sparse at GFDL, though many groups make
use of it, particularly in the Arctic.
• The side-drag scheme from Deremble et al. (2012) introduces a side-wall drag scheme following from
the drag coefficient used for computing bottom drag. It has been implemented for both the MOM B-
grid and C-grid. Incomplete tests with this scheme on a B-grid indicate some sensitivity of western
boundary current separation.
• Various static viscous profiles, in particular a method to enhance the viscosity next to western bound-
aries, have been implemented, and are readily modified for specific purposes. In particular, one may
read in a static background viscosity from a file.
25.3 Continuum formulation for the friction operator
We summarize here the continuum formulation for Laplacian and biharmonic friction.
25.3.1 Laplacian friction
As shown in Section 17.8.4 of Griffies (2004), the components to the horizontal friction operator, F(a), are
proportional to the functional derivative of the dissipation functional
ρF(a)=−1
2dV ∂S
∂u(a)!,(25.1)
where a= 1,2label the horizontal directions, dVis the volume element, and (u(1),u(2)) = (u,v)is the hori-
zontal velocity. The dissipation functional Sis given by the volume integral (equation (17.130) of Griffies
(2004))
S=ZhA(e2
T+e2
S)−2D∆2iρdV , (25.2)
Elements of MOM November 19, 2014 Page 357

Chapter 25. Lateral friction methods Section 25.3
where Ais the lateral isotropic viscosity, D < 2A(equation (17.105) of Griffies (2004)) is the lateral
anisotropic viscosity, and
2∆=eScos2θ−eTsin2θ(25.3)
orients the friction operator relative to an angle θand an orientation unit vector ˆ
s= (cosθ,sin θ)(see
equations (17.99) and (17.101) of Griffies (2004)). Fundamental to the calculation of lateral friction are
the horizontal tension and shear deformation rates
eT= dy ∂(u/dy)
∂x !−dx ∂(v/dx)
∂y !(25.4)
eS= dx ∂(u/dx)
∂y !+ dy ∂(v/dy)
∂x !,(25.5)
with the grid factors dxand dygenerally non-constant on the sphere. After some manipulations (see
Section 17.20.3 of Griffies (2004)), we are led to the friction operator arising from lateral shears on the
sphere
ρFx=1
(dy)2 ∂[(dy)2τxx]
∂x !+1
(dx)2"∂[(dx)2τxy ]
∂y !(25.6)
ρFy=1
(dx)2 ∂[(dx)2τyy ]
∂y !+1
(dy)2 ∂[(dy)2τxy ]
∂x !.(25.7)
The symmetric and trace-free friction stress tensor, associated with lateral shears, has components given
by (equations (19.7) and (19.8) of Griffies (2004))
τxx =ρ(AeT+D∆sin2θ) (25.8)
τxy =ρ(AeS−D∆cos2θ) (25.9)
τyy =−τxx (25.10)
τyx =τxy.(25.11)
25.3.2 Biharmonic friction
The general formulation of biharmonic friction is a straightforward extension of the Laplacian friction.
What is done is to iterate twice on the Laplacian approach. More precisely, the components Fm
Bof the
biharmonic friction vector are derived from the covariant divergence1
ρFm
B=Θmn
;n(25.12)
where
Θmn =−ρB(2Emn −gmn Ep
p),(25.13)
B > 0has units of L2t−1/2. As shown in Section 17.9.2 of Griffies (2004), use of this “square root” bihar-
monic viscosity is prompted by the desire to dissipate kinetic energy. This detail matters for cases with
a nonconstant viscosity. Θmn has the same form as the stress tensor used for the isotropic Laplacian
friction, except with a minus sign. Components of the symmetric “strain” tensor are given by
Emn = (Fm;n+Fn;m)/2.(25.14)
Fmare components to the friction vector determined through the covariant divergence of the Laplacian
frictional stress tensor
ρFm=τmn
;n
= [Bρ(2emn −gmn ep
p)];n(25.15)
1All labels in this section run over m,n,p = 1,2. The semi-colon represents a covariant derivative. Full details are given in Chapter
17 of Griffies (2004).
Elements of MOM November 19, 2014 Page 358

Chapter 25. Lateral friction methods Section 25.4
as derived in the previous sections, where the only difference is that the viscosity used for computing the
stress tensor τmn is now set to B, and the dimensions on Fmare Lt−3/2.
This approach ensures that the biharmonic friction is derived from the divergence of a symmetric tensor
Θmn, hence ensuring a proper angular momentum budget. Additionally, the computational work necessary
to compute the Laplacian friction is directly employed for the biharmonic friction. Finally, as shown in the
next subsection, this form for biharmonic friction also dissipates kinetic energy.
25.4 Lateral friction operator for B-grid MOM
Chapter 19 in Griffies (2004) provides a detailed derivation of the discrete friction operator for the B-grid.
We present here a summary of that material.
25.4.1 Discrete dissipation functional for the B-grid
The discrete dissipation functional takes the form
S=X
i,j
12
X
n=1
V(n)[A(n)(e2
T(n) + e2
S(n)) −2D(n)∆2(n)]
≡X
i,j Si,j .
(25.16)
Figure 25.1 illustrates the nearest neighbor stencil used for discretizing the dissipation functional using
second order numerics. The summation n= 1,12 arises from the 12 subcells to which the velocity point
Ui,j contributes when discretizing the functional on a B-grid. V(n)are the volumes of each of the subcells,
A(n)are the viscosities, and eT(n),eS(n), and ∆(n)are the corresponding tensions, strains, and anisotropic
contributions, respectively.
The physical component of the friction vector acting at the velocity cell Ui,j,k is given by the discrete
functional derivative
−F(b)
i,j =1
2VU
i,j
∂Si,j
∂(u(b))i,j
=1
VU
i,j
12
X
n=1
V(n)A(n)eT(n)∂eT(n)
∂(u(b))i,j
+A(n)eS(n)∂eS(n)
∂(u(b))i,j −2D(n)∆(n)∂∆(n)
∂(u(b))i,j
=1
ρoVU
i,j
12
X
n=1
V(n)∂eT(n)
∂(u(b))i,j
τxx(n) + ∂eS(n)
∂(u(b))i,j
τxy (n).(25.17)
In this equation, b= 1,2labels the generalized zonal and meridional directions, the discrete depth label k
was dropped since all points are at the same level,
(u(1))i,j,(u(2))i,j= (ui,j,vi,j ) (25.18)
are physical components of the velocity vector,
VU
i,j,k =dxui,j dyui,j dzui,j,k (25.19)
is the velocity cell volume,
τxx(n) = ρ[A(n)eT(n) + D(n)∆(n) sin2θ] (25.20)
τxy (n) = ρ[A(n)eS(n)−D(n)∆(n) cos2θ] (25.21)
are the stress tensor components, and the orientation angle θdetermines the orientation of the friction
(equation (25.3)) . The remainder of this section is devoted to performing the discrete functional deriva-
tives and then manipulating the results into a tidy expression for the discrete friction operator.
Elements of MOM November 19, 2014 Page 359

Chapter 25. Lateral friction methods Section 25.4
25.4.2 Grid cell distances and subcell volumes
Enumerating the 12 quarter cell volumes constitutes an important part of the discretization. Assume
knowledge of the distance along each of the four sides of a velocity and tracer cell, as well as the distance
from the velocity and tracer points to the sides of their respective cells. Although nonuniform grids with
general coordinates do not allow an exact (i.e., analytically exact) area calculation, the horizontal area
of the quarter cells is well approximated using this information. Even so, for the purpose of discretizing
friction, there is no reason to take pains to compute a very accurate quarter cell area. Indeed, the aim
is to realize the dissipative property of friction with minimal computational expense. Hence, make the
simplification that the volume of a quarter cell is equal to one-quarter the volume of the corresponding
velocity cell. In summary, we employ the following grid information (refer to Figure 25.1):
• The longitudinal spacing, in meters, between Ui,j and Ui+1,j is dxuei,j. The latitudinal spacing, in
meters, between Ui,j and Ui,j+1 is dyuni,j.
• The volume of a quarter cell is taken equal to one-quarter the volume of the velocity cell where the
quarter cell lives. For example, quarter cells 1, 2, 3, and 4 live inside velocity cell Ui,j,k and so have
volume
(1/4)VU
i,j,k = (1/4)dxui,j dyui,j dzui,j,k,(25.22)
whereas quarter cells 5 and 6 live inside velocity cell Ui+1,j,k and so have volume
(1/4)VU
i+1,j,k = (1/4) dxui+1,j dyui+1,j dzui+1,j,k.(25.23)
In summary, the volumes of the 12 quarter cells are taken to be
V(1) = V(2) = V(3) = V(4) = (1/4)VU
i,j,k
V(5) = V(6) = (1/4)VU
i+1,j,k
V(7) = V(8) = (1/4)VU
i−1,j,k
V(9) = V(10) = (1/4)VU
i,j+1,k
V(11) = V(12) = (1/4)VU
i,j−1,k.
(25.24)
25.4.3 Derivative operators
We use the second order finite difference approximations to the derivative of velocity fields
δxui,j =ui+1,j −ui,j
dxuei,j
(25.25)
δyui,j =ui,j+1 −ui,j
dyuni,j
.(25.26)
The distances dxuei,j and dyuni,j represent the zonal and meridional distances between the velocity points
(Figure 9.6). All metric stretching factors are absorbed into these grid distances according to the discus-
sion in Section 21.12.4 of Griffies (2004).
25.4.4 Tension and strain for the subcells
A decision must be made regarding the form of tension and strain to discretize. The goal here is to work
with a discretization involving the least amount of grid factors in order to minimize computational expense.
The first forms of tension and strain are more symmetric,
eT= dy(u/dy),x −dx(v/dx),y (25.27)
eS= dx(u/dx),y + dy(v/dy),x (25.28)
Elements of MOM November 19, 2014 Page 360

Chapter 25. Lateral friction methods Section 25.4
5
7
Ui-1,j Ui+1,j
Ui-1,j-1
Ui+1,j+1
Ti,j
Ui+1,j-1
Ti,j+1 Ti+1,j+1
x
Ui-1,j+1 x
xx
xx
Ti+1,j
Ui,j
11 12
x
x
Ui,j-1
x
Ui,j+1
12
10
9
46
83
Figure 25.1: Stencil for the discrete horizontal friction functional. The 12 quarter cells each contain contri-
butions to the functional from the central velocity point Ui,j . The tracer points Ti,j are oriented according
to the B-grid (see Figure 9.1). This figure is taken after Figure 19.2 of Griffies (2004).
and lead to a compact form for the discretized friction operator (see below), directly analogous to the
continuum form given by equations (25.6) and (25.7). The second forms isolate the Cartesian expression
eT=u,x −v,y +v ∂ylndx−u ∂xlndy(25.29)
eS=u,y +v,x −u ∂ylndx−v ∂xlndy. (25.30)
The second forms require less computation, since the metric terms
(MT)i,j =−ui,j (∂xln dy)i,j +vi,j (∂ylndx)i,j (25.31)
(MS)i,j =−ui,j (∂yln dx)i,j −vi,j (∂xlndy)i,j (25.32)
are common to each of the four surrounding triads, and the grid factors
dh1dyi,j = (∂ylndx)i,j (25.33)
dh2dxi,j = (∂xlndy)i,j (25.34)
can be computed at the start of the integration. Hence, we choose the first form of the deformation rates
to develop the discrete friction, and the second form to evaluate the deformation rates within the discrete
friction. For purposes of completeness, both discrete forms of the deformation rates are displayed in the
following.
Elements of MOM November 19, 2014 Page 361

Chapter 25. Lateral friction methods Section 25.4
The first form for tension in the 12 subcells is
eT(1) = dyuei−1,j δx(ui−1,j /dyui−1,j )−dxuni,j δy(vi,j/dxui,j ) (25.35)
eT(2) = dyuei,j δx(ui,j /dyui,j )−dxuni,j δy(vi,j /dxui,j ) (25.36)
eT(3) = dyuei−1,j δx(ui−1,j /dyui−1,j )−dxuni,j−1δy(vi,j−1/dxui,j−1) (25.37)
eT(4) = dyuei,j δx(ui,j /dyui,j )−dxuni,j−1δy(vi,j−1/dxui,j−1) (25.38)
eT(5) = dyuei,j δx(ui,j /dyui,j )−dxuni+1,j δy(vi+1,j/dxui+1,j ) (25.39)
eT(6) = dyuei,j δx(ui,j /dyui,j )−dxuni+1,j−1δy(vi+1,j−1/dxui+1,j−1) (25.40)
eT(7) = dyuei−1,j δx(ui−1,j /dyui−1,j )−dxuni−1,j δy(vi−1,j /dxui−1,j) (25.41)
eT(8) = dyuei−1,j δx(ui−1,j /dyui−1,j )−dxuni−1,j−1δy(vi−1,j−1/dxui−1,j−1) (25.42)
eT(9) = dyuei−1,j+1 δx(ui−1,j+1/dyui−1,j+1)−dxuni,j δy(vi,j /dxui,j ) (25.43)
eT(10) = dyuei,j+1 δx(ui,j+1/dyui,j+1)−dxuni,j δy(vi,j /dxui,j ) (25.44)
eT(11) = dyuei−1,j−1δx(ui−1,j−1/dyui−1,j−1)−dxuni,j−1δy(vi,j−1/dxui,j−1) (25.45)
eT(12) = dyuei,j−1δx(ui,j−1/dyui,j−1)−dxuni,j−1δy(vi,j−1/dxui,j−1) (25.46)
and the first form for strain is
eS(1) = dxuni,j δy(ui,j /dxui,j ) + dyuei−1,j δx(vi−1,j/dyui−1,j ) (25.47)
eS(2) = dxuni,j δy(ui,j /dxui,j ) + dyuei,j δx(vi,j /dyui,j ) (25.48)
eS(3) = dxuni,j−1δy(ui,j−1/dxui,j−1) + dyuei−1,j δx(vi−1,j /dyui−1,j) (25.49)
eS(4) = dxuni,j−1δy(ui,j−1/dxui,j−1) + dyuei,j δx(vi,j/dyui,j ) (25.50)
eS(5) = dxuni+1,j δy(ui+1,j/dxui+1,j ) + dyuei,j δx(vi,j/dyui,j ) (25.51)
eS(6) = dxuni+1,j−1δy(ui+1,j−1/dxui+1,j−1) + dyuei,j δx(vi,j/dyui,j) (25.52)
eS(7) = dxuni−1,j δy(ui−1,j/dxui−1,j ) + dyuei−1,j δx(vi−1,j /dyui−1,j) (25.53)
eS(8) = dxuni−1,j−1δy(ui−1,j−1/dxui−1,j−1) + dyuei−1,j δx(vi−1,j /dyui−1,j) (25.54)
eS(9) = dxuni,j δy(ui,j /dxui,j ) + dyuei−1,j+1 δx(vi−1,j+1/dyui−1,j+1) (25.55)
eS(10) = dxuni,j δy(ui,j /dxui,j ) + dyuei,j+1 δx(vi,j+1/dyui,j+1) (25.56)
eS(11) = dxuni,j−1δy(ui,j−1/dxui,j−1) + dyuei−1,j−1δx(vi−1,j−1/dyui−1,j−1) (25.57)
eS(12) = dxuni,j−1δy(ui,j−1/dxui,j−1) + dyuei,j−1δx(vi,j−1/dyui,j−1).(25.58)
The second forms for tension and strain are
eT(1) = δxui−1,j −δyvi,j + (MT)i,j eS(1) = δyui,j +δxvi−1,j + (MS)i,j (25.59)
eT(2) = δxui,j −δyvi,j + (MT)i,j eS(2) = δyui,j +δxvi,j + (MS)i,j (25.60)
eT(3) = δxui−1,j −δyvi,j−1+ (MT)i,j eS(3) = δyui,j−1+δxvi−1,j + (MS)i,j (25.61)
eT(4) = δxui,j −δyvi,j−1+ (MT)i,j eS(4) = δyui,j−1+δxvi,j + (MS)i,j (25.62)
eT(5) = δxui,j −δyvi+1,j + (MT)i+1,j eS(5) = δyui+1,j +δxvi,j + (MS)i+1,j (25.63)
eT(6) = δxui,j −δyvi+1,j−1+ (MT)i+1,j eS(6) = δyui+1,j−1+δxvi,j + (MS)i+1,j (25.64)
eT(7) = δxui−1,j −δyvi−1,j + (MT)i−1,j eS(7) = δyui−1,j +δxvi−1,j + (MS)i−1,j (25.65)
eT(8) = δxui−1,j −δyvi−1,j−1+ (MT)i−1,j eS(8) = δyui−1,j−1+δxvi−1,j + (MS)i−1,j (25.66)
eT(9) = δxui−1,j+1 −δyvi,j + (MT)i,j+1 eS(9) = δyui,j +δxvi−1,j+1 + (MS)i,j+1 (25.67)
eT(10) = δxui,j+1 −δyvi,j + (MT)i,j+1 eS(10) = δyui,j +δxvi,j+1 + (MS)i,j+1 (25.68)
eT(11) = δxui−1,j−1−δyvi,j−1+ (MT)i,j−1eS(11) = δyui,j−1+δxvi−1,j−1+ (MS)i,j−1(25.69)
eT(12) = δxui,j−1−δyvi,j−1+ (MT)i,j−1eS(12) = δyui,j−1+δxvi,j−1+ (MS)i,j−1.(25.70)
Elements of MOM November 19, 2014 Page 362

Chapter 25. Lateral friction methods Section 25.4
25.4.5 Functional derivative of eTand eS
Choosing to work with the discretized first form of tension (equation (25.27)) leads to the functional deriva-
tive of the tension within the central four subcells
∂eT(1)
∂(u(b))i,j
=dyuei−1,j
dxuei−1,j
δ1
b
dyui,j
+dxuni,j
dyuni,j
δ2
b
dxui,j
(25.71)
∂eT(2)
∂(u(b))i,j
=−dyuei,j
dxuei,j
δ1
b
dyui,j
+dxuni,j
dyuni,j
δ2
b
dxui,j
(25.72)
∂eT(3)
∂(u(b))i,j
=dyuei−1,j
dxuei−1,j
δ1
b
dyui,j −dxuni,j−1
dyuni,j−1
δ2
b
dxui,j
(25.73)
∂eT(4)
∂(u(b))i,j
=−dyuei,j
dxuei,j
δ1
b
dyui,j −dxuni,j−1
dyuni,j−1
δ2
b
dxui,j
(25.74)
and to the strain within the same cells
∂eS(1)
∂(u(b))i,j
=−dxuni,j
dyuni,j
δ1
b
dxui,j
+dyuei−1,j
dxuei−1,j
δ2
b
dyui,j
(25.75)
∂eS(2)
∂(u(b))i,j
=−dxuni,j
dyuni,j
δ1
b
dxui,j −dyuei,j
dxuei,j
δ2
b
dyui,j
(25.76)
∂eS(3)
∂(u(b))i,j
=dxuni,j−1
dyuni,j−1
δ1
b
dxui,j
+dyuei−1,j
dxuei−1,j
δ2
b
dyui,j
(25.77)
∂eS(4)
∂(u(b))i,j
=dxuni,j−1
dyuni,j−1
δ1
b
dxui,j −dyuei,j
dxuei,j
δ2
b
dyui,j
.(25.78)
The functional derivatives for tension and strain in the other eight cells are given by
∂eT(5)
∂(u(b))i,j
=−dyuei,j
dxuei,j
δ1
b
dyui,j
∂eS(5)
∂(u(b))i,j
=−dyuei,j
dxuei,j
δ2
b
dyui,j
(25.79)
∂eT(6)
∂(u(b))i,j
=−dyuei,j
dxuei,j
δ1
b
dyui,j
∂eS(6)
∂(u(b))i,j
=−dyuei,j
dxuei,j
δ2
b
dyui,j
(25.80)
∂eT(7)
∂(u(b))i,j
=dyuei−1,j
dxuei−1,j
δ1
b
dyui,j
∂eS(7)
∂(u(b))i,j
=dyuei−1,j
dxuei−1,j
δ2
b
dyui,j
(25.81)
∂eT(8)
∂(u(b))i,j
=dyuei−1,j
dxuei−1,j
δ1
b
dyui,j
∂eS(8)
∂(u(b))i,j
=dyuei−1,j
dxuei−1,j
δ2
b
dyui,j
(25.82)
∂eT(9)
∂(u(b))i,j
=dxuni,j
dyuni,j
δ2
b
dxui,j
∂eS(9)
∂(u(b))i,j
=−dxuni,j
dyuni,j
δ1
b
dxui,j
(25.83)
∂eT(10)
∂(u(b))i,j
=dxuni,j
dyuni,j
δ2
b
dxui,j
∂eS(10)
∂(u(b))i,j
=−dxuni,j
dyuni,j
δ1
b
dxui,j
(25.84)
∂eT(11)
∂(u(b))i,j
=−dxuni,j−1
dyuni,j−1
δ2
b
dxui,j
∂eS(11)
∂(u(b))i,j
=dxuni,j−1
dyuni,j−1
δ1
b
dxui,j
(25.85)
∂eT(12)
∂(u(b))i,j
=−dxuni,j−1
dyuni,j−1
δ2
b
dxui,j .∂eS(12)
∂(u(b))i,j
=dxuni,j−1
dyuni,j−1
δ1
b
dxui,j .(25.86)
Elements of MOM November 19, 2014 Page 363

Chapter 25. Lateral friction methods Section 25.4
25.4.6 Tidy form for the discretized friction
Focus first on the zonal friction with b= 1. Using the volumes enumerated in Section 25.4.2, and dropping
the vertical label ksince it is the same for all terms, yields for the tension
−
12
X
n=1
V(n)τxx(n)∂eT(n)
∂(u(1))i,j
= dyuei,j
4dxuei,j dyui,j ! [τxx(5) + τxx(6)]VU
i+1,j + [τxx(2) + τxx(4)]VU
i,j !
− dyuei−1,j
4dxuei−1,j dyui−1,j ! [τxx(1) + τxx(3)]VU
i,j + [τxx(7) + τxx(8)]VU
i−1,j!.(25.87)
Figure 25.1 indicates that a velocity point Ui,j is associated with four triads, each of which is used to
construct a tension and strain along with a viscosity. This arrangement motivates the following notation
(see Figure 25.2):
(1,1) = northeast triad
(0,1) = northwest triad
(0,0) = southwest triad
(1,0) = southeast triad.
(25.88)
(1,1)(0,1)
(0,0) (1,0)
y
x
Figure 25.2: Notation for the quadrants surrounding a velocity point.
With this notation,
−
12
X
n=1
V(n)τxx(n)∂eT(n)
∂(u(1))i,j
= dyuei,j
4dxuei,j dyui,j !1
X
ip=0
VU
i+ip,j
1
X
jq=0
(τxx)(1−ip,jq)
(i+ip,j)(25.89)
− dyuei−1,j
4dxuei−1,j dyui,j !1
X
ip=0
VU
i−1+ip,j
1
X
jq=0
(τxx)(1−ip,jq)
(i−1+ip,j).
The two terms on the right-hand side are centered on the east and west faces, respectively, of the Ui,j
velocity cell. Consequently, introduce the finite difference derivative operator to yield
−
12
X
n=1
V(n)τxx(n)∂eT(n)
∂(u(1))i,j
= dxui,j
4dyui,j !δx"dyuei−1,j
dxuei−1,j
1
X
ip=0
VU
i−1+ip,j
1
X
jq=0
(τxx)(1−ip,jq)
(i−1+ip,j)#.(25.90)
Dividing by the velocity cell volume VU
i,j =dxui,j dyui,j dzui,j leads to
−
1
VU
i,j
12
X
n=1
V(n)τxx(n)∂eT(n)
∂(u(1))i,j
= 1
4dzui,j (dyui,j )2!δx"dyuei−1,j
dxuei−1,j
1
X
ip=0
VU
i−1+ip,j
1
X
jq=0
(τxx)(1−ip,jq)
(i−1+ip,j)#.(25.91)
Elements of MOM November 19, 2014 Page 364

Chapter 25. Lateral friction methods Section 25.4
Similar manipulations apply for the strain terms, thus yielding
−
1
VU
i,j
12
X
n=1
V(n)τxy (n)∂eS(n)
∂(u(1))i,j
= 1
4dzui,j (dxui,j )2!δy"dxuni,j−1
dyuni,j−1
1
X
jq=0
VU
i,j−1+jq
1
X
ip=0
(τxy )(ip,1−jq)
(i,j−1+jq)#.(25.92)
Bringing the two pieces together leads to the zonal friction acting at the velocity cell Ui,j
ρoF(x)
i,j = 1
4dzui,j (dyui,j )2!δx"dyuei−1,j
dxuei−1,j
1
X
ip=0
VU
i−1+ip,j
1
X
jq=0
(τxx)(1−ip,jq)
(i−1+ip,j)#
+ 1
4dzui,j (dxui,j )2!δy"dxuni,j−1
dyuni,j−1
1
X
jq=0
VU
i,j−1+jq
1
X
ip=0
(τxy )(ip,1−jq)
(i,j−1+jq)#.(25.93)
By inspection, the meridional friction is given by
ρoF(y)
i,j = 1
4dzui,j (dyui,j )2!δx"dyuei−1,j
dxuei−1,j
1
X
ip=0
VU
i−1+ip,j
1
X
jq=0
(τxy )(1−ip,jq)
(i−1+ip,j)#
− 1
4dzui,j (dxui,j )2!δy"dxuni,j−1
dyuni,j−1
1
X
jq=0
VU
i,j−1+jq
1
X
ip=0
(τxx)(ip,1−jq)
(i,j−1+jq)#.(25.94)
Comparison with the continuum friction components given by equations (25.6) and (25.7) indicates that
the discretization is consistent, that is, the discrete friction reduces to the continuum friction as the grid
size goes to zero.
25.4.7 Tension and strain in the quadrants
There are four tensions and strains corresponding to the four triads surrounding each velocity point. Re-
ferring to Figure 25.2, assuming the central point is Ui,j , discretize the tensions and strains starting from
the second form of the continuous tension and strain (equations (25.29) and (25.30)) to find
(eT)i,j,(0,1) =δxui−1,j −δyvi,j + (MT)i,j (25.95)
(eT)i,j,(1,1) =δxui,j −δyvi,j + (MT)i,j (25.96)
(eT)i,j,(0,0) =δxui−1,j −δyvi,j−1+ (MT)i,j (25.97)
(eT)i,j,(1,0) =δxui,j −δyvi,j−1+ (MT)i,j (25.98)
(eS)i,j,(0,1) =δyui,j +δxvi−1,j + (MS)i,j (25.99)
(eS)i,j,(1,1) =δyui,j +δxvi,j + (MS)i,j (25.100)
(eS)i,j,(0,0) =δyui,j−1+δxvi−1,j + (MS)i,j (25.101)
(eS)i,j,(1,0) =δyui,j−1+δxvi,j + (MS)i,j.(25.102)
In general, the four tensions can be written
(eT)i,j,(ip,jq)=δxui+ip−1,j −δyvi,j+jq−1+ (MT)i,j (25.103)
and the four strains can be written
(eS)i,j,(ip,jq)=δyui,j+jq−1+δxvi+ip−1,j + (MS)i,j (25.104)
where ip = 0,1and jq = 0,1. Notably, the metric terms
(MT)i,j =−ui,j (∂xln dy)i,j +vi,j (∂ylndx)i,j (25.105)
(MS)i,j =−ui,j (∂yln dx)i,j −vi,j (∂xlndy)i,j (25.106)
Elements of MOM November 19, 2014 Page 365

Chapter 25. Lateral friction methods Section 25.5
are common to the four triads, and so only need be computed once per velocity point. Generally, the four
tensions and strains are computed in the model and are then used to compute the friction operator. When
the Smagorinsky viscosity scheme (Section 25.2 as well as Section 19.3.10 of Griffies (2004)) is enabled,
they are used to compute the Smagorinsky viscosity as well.
25.4.8 Comments
Note a few points here related to the proposed discretization.
• The tension and strain for ocean points next to land contain a contribution from a velocity living at
the land-sea interface. This velocity, due to the no-slip condition used in B-grid ocean models, has a
zero value. In order to provide a full accounting of the generally strong shears next to no-slip walls
present in the B-grid ocean models, it is important to include such contributions rather than masking
them out.
• In the special case of a uniform Cartesian grid, a constant isotropic viscosity, and a zero anisotropic
viscosity, the functionally derived discrete friction operator reduces to the 5-point discrete Laplacian.
• Practical experience has revealed problems with discretization for bottom grid cells when these cells
are thin partial cells that are surrounded by thicker partial cells. The problem is that contributions
from surrounding thick cells are then normalized by the thin dzt of the central cell. To alleviate this
problem, it is effective to use the traditional 5-point Laplacian operator for computing friction in the
bottom grid cells.
25.4.9 Discretized Smagorinsky viscosity
The nonlinear Smagorinsky viscosity coefficient is determined in terms of the deformation rates eTand eS
as well as the grid spacing. Since eTand eSinvolve terms with derivatives in both horizontal directions, an
averaging must be performed to place them at a common grid position.
Pacanowski et al. (1991) defined both deformation rates at the north face of the U-cell. This is the
natural position for the meridional derivative terms. However, to get the zonal derivative terms defined at
the north face, it is necessary to average over the four zonal derivatives surrounding the north face. The
problem with such “4 point” averages on the B-grid is that they can introduce computational modes. Com-
putational modes are not always problematical if there are other processes that can suppress the growth
of the modes. The problem with the computational modes in the Smagorinsky scheme is that they allow
nontrivial field configurations yielding a zero deformation rate. Hence, they produce a zero Smagorinsky
viscosity and so are not dissipated. Furthermore, these modes represent grid scale waves, which are the
waves an ideal implementation of the Smagorinsky scheme should dissipate the most. Therefore, it is not
acceptable to allow these modes in the discretized Smagorinsky scheme. Another approach is necessary.
The functional discretization described in this chapter eliminates the computational modes. For each
velocity triad, there is a corresponding Smagorinsky viscosity. In particular, referring to the deformation
rates defined in equation (25.102) yields the corresponding Smagorinsky diffusivities
Ai,j,(ip,jq)= (Υ ∆s/π)2|E|i,j,(ip,jq)(25.107)
where ip = 0,1,jq = 0,1are the triad labels, and
[Ei,j,(ip,jq)]2= [(eT)i,j,(ip,jq)]2+ [(eS)i,j,(ip,jq)]2(25.108)
is the discrete total deformation rate. As mentioned earlier, one advantage of the functional approach
over the “Laplacian plus metric” approach (see Section 19.4 of Griffies (2004)) is the exploitation of the
deformation rates for computing both the Smagorinsky viscosity and the friction operator.
Elements of MOM November 19, 2014 Page 366

Chapter 25. Lateral friction methods Section 25.5
25.5 Lateral friction operator for C-grid MOM
The purpose of this section is to formulate a discrete lateral friction operator for the C-grid. We follow the
B-grid approach by establishing a formalism based on taking the functional derivative of the dissipation
functional. Given the different layout of velocity, the C-grid has a somewhat simpler stencil for the friction
operator than the B-grid.
25.5.1 Discrete functional derivative and the grid stencil
The general approach used to derive a discrete friction operator is to first discretize the dissipation func-
tion, S, and then to perform a discrete version of a functional derivative. The discrete functional derivative
is merely a partial derivative of the discrete functional with respect to the discrete velocity components
ui,j and vi,j .
We start from the expression for the discrete friction operator (equation (25.17) as well as equation
(19.4) of Griffies (2004))
−ρFx
i,j =1
2V(u)
i,j
∂Si,j
∂ui,j
=1
V(u)
i,j X
n
V(n) ∂eT(n)
∂ui,j τxx(n) + ∂eS(n)
∂ui,j τxy (n)!(25.109)
−ρFy
i,j =1
2V(v)
i,j
∂Si,j
∂vi,j
=1
V(v)
i,j X
n
V(n) ∂eT(n)
∂vi,j τxx(n) + ∂eS(n)
∂vi,j τyx(n)!.(25.110)
The sum in these expressions extends over the stencil whereby the central velocity components ui,j and
vi,j contribute to a non-zero functional derivative. For the B-grid, the stencil extends over 12 sub-regions,
each with their own viscosity, volume V(n), deformation rates, and stresses (Figure 25.1). The stencil is
simpler for the C-grid.
To determine the stencil for the C-grid friction operator, consider the C-grid layout in Figure 25.3 and
focus on the zonal velocity component ui,j. This component participates in the calculation of the defor-
mation rates eTand eSthrough both its zonal and meridional derivatives. Figure 25.4 exposes the points
contributing to eTand eSwhere ui,j contributes. Note the 5-point stencil for the participating zonal velocity
components, and the 4-point stencil for the participating meridional velocity components. The comple-
ment situation holds for the points where vi,j participates (second panel of Figure 25.4). It is notable that
this stencil is smaller than the corresponding B-grid stencil shown in Figure 25.1.
25.5.2 Deformation rates
We now present details for deriving the discrete zonal friction operator on a C-grid. For this purpose, focus
on the left panel of Figure 25.4, in which we identify the deformation rates that include a contribution from
ui,j
ei,j
T= dyti,j
dxti,j ! ui,j
dytei,j −ui−1,j
dytei−1,j !− dxti,j
dyti,j ! vi,j
dxtni,j −vi,j−1
dxtni,j−1!(25.111)
ei+1,j
T= dyti+1,j
dxti+1,j ! ui+1,j
dytei+1,j −ui,j
dytei,j !− dxti+1,j
dyti+1,j ! vi+1,j
dxtni+1,j −vi+1,j−1
dxtni+1,j−1!(25.112)
ei,j
S= dxui,j
dyui,j ! ui,j+1
dxtei,j+1 −ui,j
dxtei,j !+ dyui,j
dxui,j ! vi+1,j
dytni+1,j −vi,j
dytni,j !(25.113)
ei,j−1
S= dxui,j−1
dyui,j−1! ui,j
dxtei,j −ui,j−1
dxtei,j−1!+ dyui,j−1
dxui,j−1! vi+1,j−1
dytni+1,j−1−vi,j−1
dytni,j−1!.(25.114)
Elements of MOM November 19, 2014 Page 367
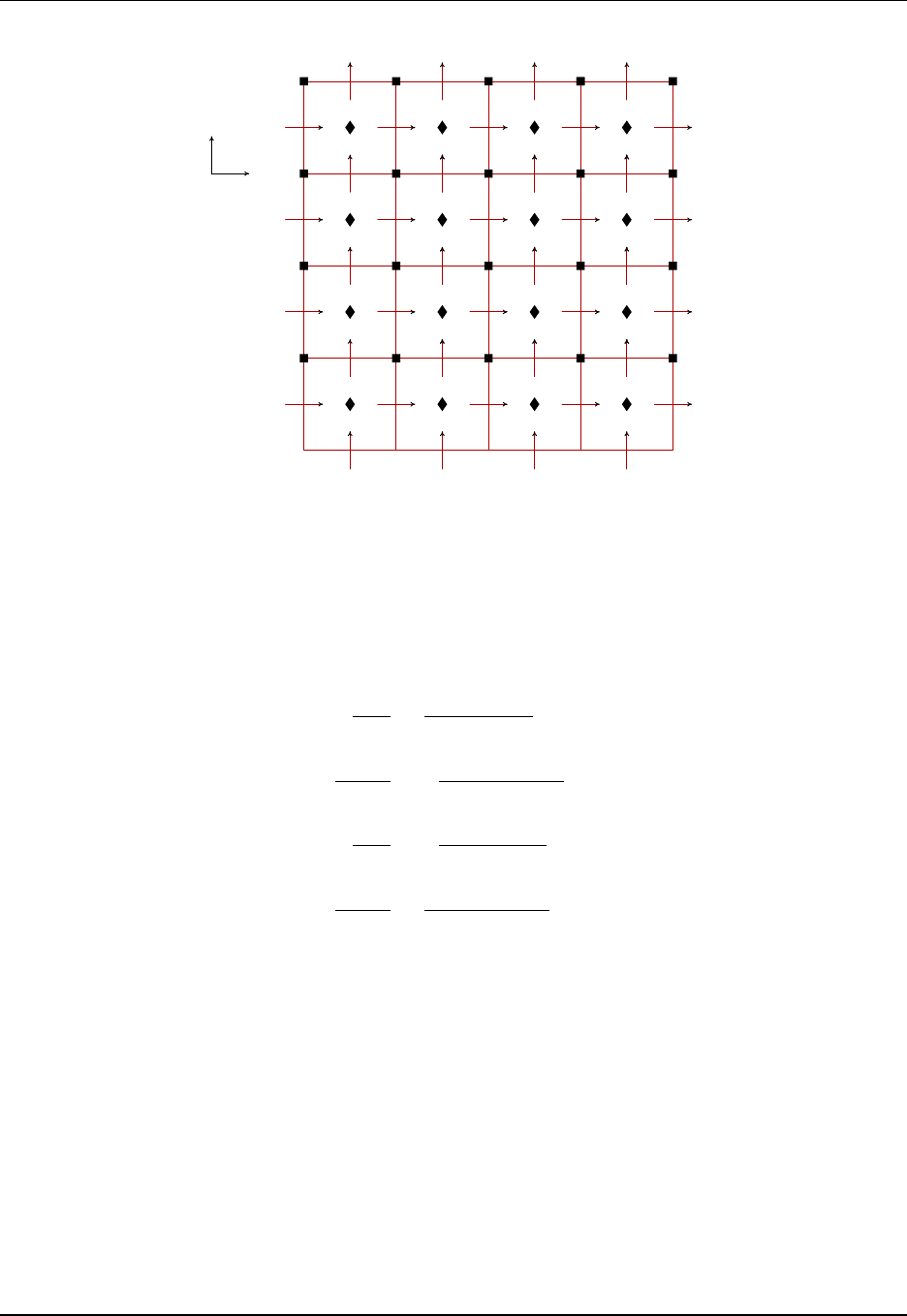
Chapter 25. Lateral friction methods Section 25.5
C-grid layout of horizontal velocity
j
i
u(i-2,j+1) u(i-1,j+1) u(i,j+1) u(i+1,j+1) u(i+2,j+1)
v(i-1,j+1) v(i,j+1) v(i+1,j+1) v(i+2,j+1)
u(i-2,j) u(i-1,j) u(i,j) u(i+1,j) u(i+2,j)
v(i-1,j) v(i,j) v(i+1,j) v(i+2,j)
u(i-2,j-1) u(i-1,j-1) u(i,j-1) u(i+1,j-1) u(i+2,j-1)
v(i-1,j-1) v(i,j-1) v(i+1,j-1) v(i+2,j-1)
u(i-2,j-2) u(i-1,j-2) u(i,j-2) u(i+1,j-2) u(i+2,j-2)
v(i-1,j-2) v(i,j-2) v(i+1,j-2) v(i+2,j-2)
v(i-1,j-3) v(i,j-3) v(i+1,j-3) v(i+2,j-3)
Figure 25.3: Array of C-grid velocity vectors, used to help deduce the friction operator stencil. The solid
diamonds are the tracer points, which are also points where the deformation rate eTis located on the C-grid.
The solid squares are the vorticity points, which are also points where the deformation rate eSis located on
the C-grid. Figure 25.4 provides more details for the discrete version of eTand eS.
The corresponding discrete functional derivatives are given by
∂ei,j
T
∂ui,j
= dyti,j
dxti,j dytei,j !(25.115)
∂ei+1,j
T
∂ui,j
=− dyti+1,j
dxti+1,j dytei,j !(25.116)
∂ei,j
S
∂ui,j
=− dxui,j
dyui,j dxtei,j !(25.117)
∂ei,j−1
S
∂ui,j
= dxui,j−1
dyui,j−1dxtei,j !.(25.118)
25.5.3 Stress tensor components
For discretization of the zonal friction ρFx
i,j , we need discrete versions of the stress tensor components
(equations (25.8) and (25.9))
τxx = (ρ/2)[2AeT+D(eScos2θ−eTsin2θ) sin 2θ] (25.119)
τxy = (ρ/2)[2AeS−D(eScos2θ−eTsin2θ) cos 2θ).(25.120)
The case of zero anisotropy in the viscosity tensor (D= 0) is simplest, in which case τxx is centered on the
grid according to the discretization of eT(solid diamonds on Figure 25.4), and τxy is centered according to
the discretization of eS(solid squard on Figure 25.4). When anisotropy is present, both eTand eScontribute
to each of the stress tensor components. This situation is awkward on the discrete C-grid since eTand eS
are not co-located. We could choose a spatial averaging to define co-located deformation rates, but such
averaging comes at the cost of a wider grid stencil. So instead of averaging, we choose to keep the same
Elements of MOM November 19, 2014 Page 368
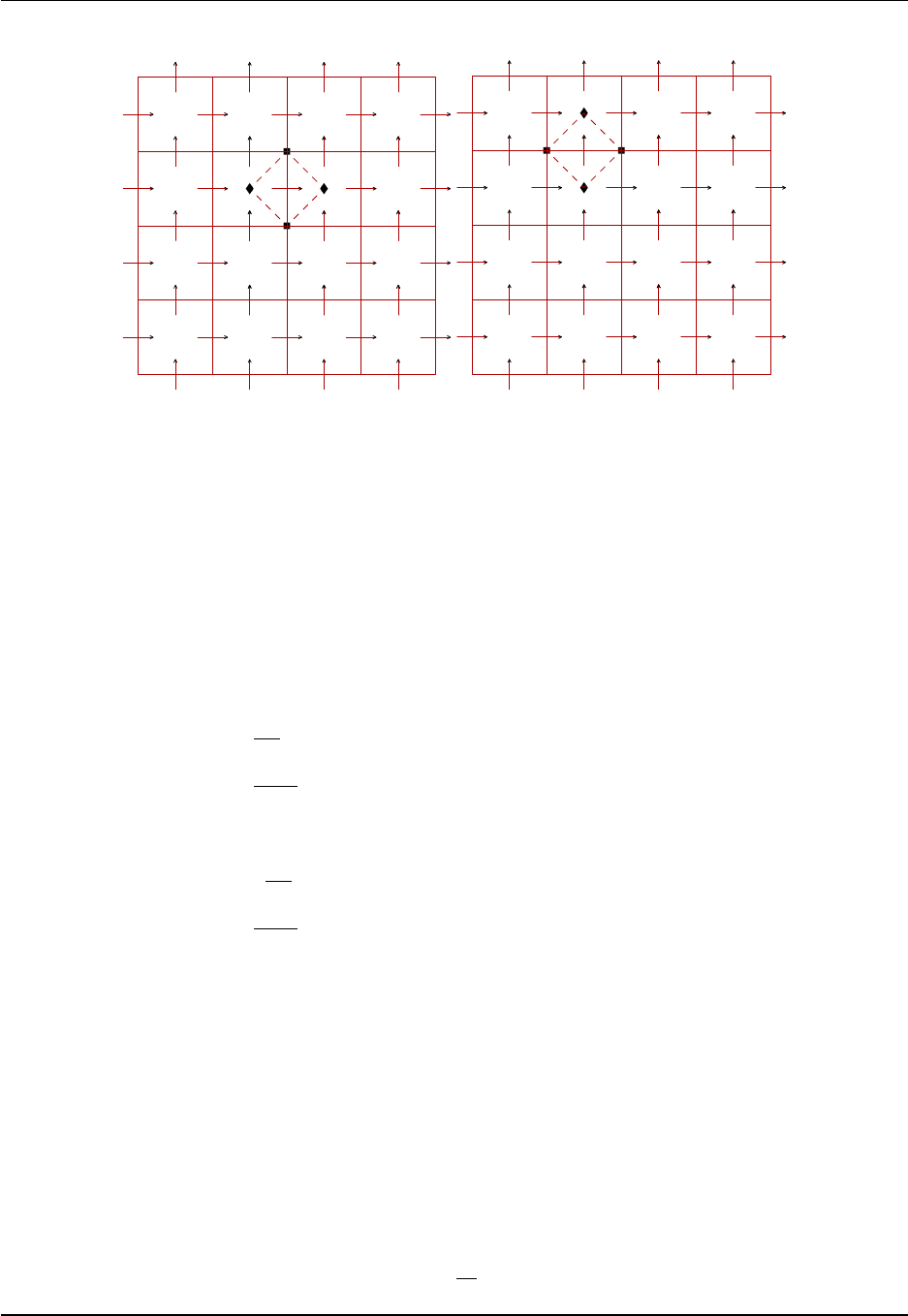
Chapter 25. Lateral friction methods Section 25.5
Stencil for ∂S/∂ui,j
eT(i,j) eT(i+1,j)
eS(i,j)
eS(i,j-1)
u(i,j+1)
u(i-1,j) u(i,j) u(i+1,j)
v(i,j) v(i+1,j)
u(i,j-1)
v(i,j-1) v(i+1,j-1)
Stencil for ∂S/∂vi,j
eT(i,j)
eT(i,j+1)
eS(i,j)eS(i-1,j)
u(i-1,j+1) u(i,j+1)
v(i,j+1)
u(i-1,j) u(i,j)
v(i-1,j) v(i,j) v(i+1,j)
v(i,j-1)
Figure 25.4: Left panel: stencil for the ui,j contribution to the lateral C-grid friction. Right panel: sten-
cil for the vi,j contribution to the lateral C-grid friction. The solid diamonds denote the central point
for the discrete version of eT= dy(u/dy),x −dx(v/dx),y (equation (25.27)), and the solid squares are for
eS= dx(u/dx),y + dy(v/dy),x (equation 25.28)). We identify a dashed diamond region that connects the
deformation rates used to compute the friction acting on the respective velocity components. In total,
there are 5u + 4v velocity points impacting the zonal friction, and 5v + 4u velocity points impacting the
meridional friction. Note the presence of a central 5-point stencil, which is typical of a discrete Laplacian
operator. This stencil should be compared to the larger stencil required for the B-grid (see Figure 25.1).
stencil and to associate ei,j
Tand ei,j
Sas a pair, and ei,j−1
Sand ei+1,j
Tas another pair. In this way, the discrete
ρFx
i,j will make use of the stress tensor elements
τxx
i,j =ρi,j
22Aei,j
T+Dsin2θei,j
Scos2θ−ei,j
Tsin2θ (25.121)
τxy
i,j−1=ρi+1,j
22Aei,j−1
S−Dcos2θei,j−1
Scos2θ−ei+1,j
Tsin2θ.(25.122)
Likewise, the meridional friction ρ Fy
i,j uses
τyy
i,j =−ρi,j
22Aei,j
T+Dsin2θei,j
Scos2θ−ei,j
Tsin2θ (25.123)
τyx
i−1,j =ρi,j+1
22Aei−1,j
S−Dcos2θei−1,j
Scos2θ−ei,j+1
Tsin2θ.(25.124)
Note that this prescription maintains the continuum symmetry of the stress tensor components
τxx
i,j =−τyy
i,j (25.125)
τxy
i,j =τyx
i,j .(25.126)
We detail choices for the orientation angle θin Section 25.5.4, and the viscosities in Section 25.5.5, with
these prescriptions maintaining the above symmetry. Yet note that the use of partial slip side boundaries
generally breaks the symmetry τxy
i,j =τyx
i,j (Section 25.6).
25.5.4 Orientation angle
As discussed by Smith and McWilliams (2003), the orientation angle θis often prescribed according to the
direction of the horizontal velocity field (equation (17.81) of Griffies (2004))
ˆ
s=u
|u|.(25.127)
Elements of MOM November 19, 2014 Page 369

Chapter 25. Lateral friction methods Section 25.6
It is awkward to compute this directional vector on the C-grid, given that the velocity components are no
co-located. Rather than perform a spatial average, we ignore the offset and so compute
sx
i,j =ui,j
|u|(25.128)
sy
i,j =vi,j
|u|(25.129)
u2
i,j =u2
i,j +v2
i,j .(25.130)
25.5.5 Viscosities
The isotropic viscosity, A, and anisotropic viscosity, D, are needed to compute the stress tensor. When
choosing a Smagorinsky approach (Section 25.4.9), we need to determine which deformation rates to use.
Following from that used for discretizing the stress tensor components in Section 25.5.3, we make the
following choices
• For the diagonal components τxx
i,j =−τyy
i,j , we choose A,D to be proportional to the deformation rates
ei,j
Tand ei,j
S.
• For the off-diagonal components τxy
i,j =τyx
i,j , we choose A,D to be proportional to the deformation
rates ei+1,j+1
Tand ei,j
S.
25.5.6 Volumes
We must now choose the volume factors appearing in expression (25.109) for the zonal friction. As for
the B-grid calculation in Section 25.4.2 (see also Section 19.3.3 of Griffies (2004)), we simplify the volume
expressions to simplify the resulting friction operator. For this purpose, we take all volume factors to be
equal to the volume of a cell in which ui,j is at the center
V(u)
i,j =V(1) = V(2) = dxtei,j dytei,j dztei,j .(25.131)
25.5.7 Discrete C-grid friction operators
Using this expression for the volume factors in equation (25.109), along with the functional derivatives
(25.111)-(25.114), leads to
−ρFx
i,j = dyti,j
dxti,j dytei,j !τxx
i,j − dyti+1,j
dxti+1,j dytei,j !τxx
i+1,j − dxui,j
dyui,j dxtei,j !τxy
i,j + dxui,j−1
dyui,j−1dxtei,j !τxy
i,j−1
(25.132)
Rearrangement renders for the zonal friction operator
ρFx
i,j = dxtei,j
dytei,j !
dyti+1,j
dxti+1,j τxx
i+1,j −dyti,j
dxti,j τxx
i,j
dxtei,j + dytei,j
dxtei,j !
dxui,j
dyui,j τxy
i,j −dxui,j−1
dyui,j−1τxy
i,j−1
dytei,j (25.133)
= dxtei,j
dytei,j !δx dyti,j
dxti,j τxx
i,j !+ dytei,j
dxtei,j !δy dxui,j−1
dyui,j−1
τxy
i,j−1!.(25.134)
Similar manipulations yield for the meridional friction operator
ρFy
i,j = dytni,j
dxtni,j !δy dxti,j
dyti,j
τyy
i,j !+ dxtni,j
dytni,j !δx dyui−1,j
dxui−1,j τyx
i−1,j!,(25.135)
where again τyy =−τxx. Also, τxy =τyx, with the exception of partial-slip side boundaries, as discussed in
Section 25.6.
Elements of MOM November 19, 2014 Page 370

Chapter 25. Lateral friction methods Section 25.6
25.6 Boundary conditions
The natural treatment of friction next to side boundaries is complementary between the B-grid and C-grid.
We summarize these issues in this section.
25.6.1 B-grid
Land cells in MOM are defined through the tracer cells. A velocity point that sits at the corner of a land
tracer cell, as per a B-grid, is given an identically zero value. It is for this reason that the B-grid MOM is
said to use a no-slip side boundary condition.
There are very special cases where one may specify a free-slip boundary, but these cases make unre-
alistic assumptions about the land-sea masking, such as for a zonally periodic channel. MOM does not
make these assumptions, which means that all B-grid simulations with MOM utilize a no-slip side boundary
condition.
25.6.2 C-grid
Since land cells in MOM are defined through the tracer cells, it is possible for there to be a nonzero C-grid
velocity crossing some of the faces of a grid cell adjacent to land. For example, consider the configuration
in Figure 25.5. Rather than velocity sitting at the tracer cell corner, it is the deformation rate eS. The
following choices are available in MOM.
•Free-slip: A simple choice for how to specify eSfor corner points adjacent to land is to set eS= 0. This
specification amounts to a free-slip condition. This is the default setting in MOM with the C-grid, with
this specification provided by masking with the B-grid velocity mask. Partial slip conditions can also
be specified, though further work is required with the code.
•Free-slip with anisotropic viscosity: When using the anisotropic viscosity scheme (Section 25.3),
the stress tensor τxy generally has contributions from both eSand eT(equation (25.9)). To remain
consistent with the free-slip side wall condition, we set τxy = 0 on the land corner points, even when
using anisotropic viscosity.
•Biharmonic operator: For the biharmonic operator, we set both eSto zero on land corner points, as
well as the strain associated with the Laplacian friction operator (equation (25.14)).
•Side drag: The side-drag scheme from Deremble et al. (2012) is implemented on the C-grid by setting
τxy =−ρ Cd|u|ufor Fx(25.136)
τyx =−ρ Cd|v|vfor Fy,(25.137)
where the uand vused in the respective stresses are taken from the value just in from the land
boundary.
Elements of MOM November 19, 2014 Page 371
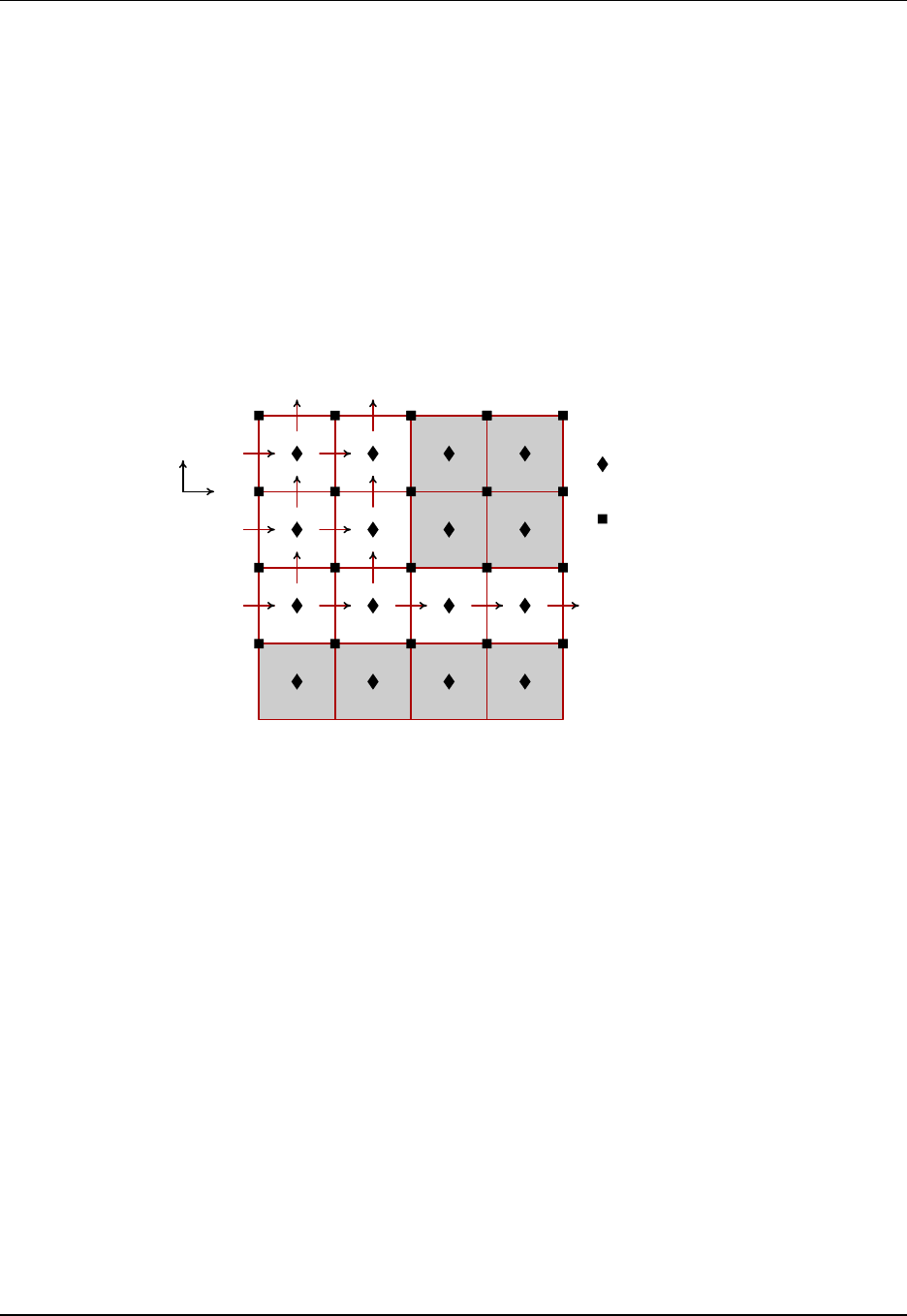
Chapter 25. Lateral friction methods Section 25.6
C-grid layout for the deformation rates eTand eS
=corner point
=C-grid vorticity
=C-grid eS
=tracer point
=C-grid eT
j
i
T(1,4) T(2,4) T(3,4) T(4,4)
T(1,3) T(2,3) T(3,3) T(4,3)
T(1,2) T(2,2) T(3,2) T(4,2)
T(1,1) T(2,1) T(3,1) T(4,1)
Figure 25.5: Land-sea example for the C-grid, with land cells shaded. The deformation rate eTis centred at
a tracer point (solid diamond), and the deformation rate eSis at the solid squares, on the northeast corner of
the tracer cell. The specification of eS, or more generally τxy, determine how friction next to side boundaries
impact the interior flow. The default for the C-grid MOM is a free-slip side wall condition, whereby eS= 0
when it is located on a land cell corner. Operationally, this boundary condition is directly analogous to
setting the B-grid velocity to zero at the same points. Physically, the impact on the interior flow is the
opposite, with the C-grid specification of eS= 0 leads to a free-slip whereas the B-grid specification u= 0
leads to a no-slip.
Elements of MOM November 19, 2014 Page 372

Chapter 26
Eddy-topography interaction via
Neptune
Contents
26.1 Introduction ............................................373
26.2 Basics of the parameterization in MOM ............................374
26.2.1 The Eby and Holloway (1994) approach .......................... 374
26.2.2 Maltrud and Holloway (2008) approach .......................... 374
26.2.3 Specifying the length scale .................................. 375
26.3 Topostrophy diagnostic .....................................375
The purpose of this chapter is to present a method for parameterizing the interactions between un-
resolved mesoscale eddies and topography. The following MOM modules are directly connected to the
material in this chapter:
ocean param/lateral/ocean lapgen friction.F90
ocean param/lateral/ocean bihgen friction.F90
ocean param/lateral/ocean lapcgrid friction.F90
ocean param/lateral/ocean bihcgrid friction.F90
26.1 Introduction
Based on statistical mechanics arguments, Holloway (1992) proposed that interactions between mesoscale
eddies and topography result in a stress on the ocean with two important consequences: (1) the ocean is
not driven toward a state of rest, (2) the resulting motion may have scales much larger than the eddy
scales. That is, eddy-topography interactions can generate coherent mean flows on the scale of the to-
pography. When Holloway described coastal currents that persistently flow against both the wind forcing
and pressure gradient, the response was that it must be due to Neptune. Who else? Hence, the effect
is referred to colloquially as the Neptune effect. The magnitude of the associated topographic stress is
dependent on the correlation between pressure pand topographic gradients ∇H, and this correlation is
largely unknown. But even if it is no larger than 0.1, the resulting topographic stress could be comparable
in magnitude to that from the surface wind.
Kinetic energy input via a sub-grid scale (SGS) parameterization is perhaps the central weakness of the
Neptune parameterization, where a more complete theory provides for total energy conservation (forcing
and dissipation) at the SGS. Notably, no such SGS theory presently exists. Instead, numerical modelers
373

Chapter 26. Eddy-topography interaction via Neptune Section 26.2
traditionally employ energy sinks via frictional dissipation toward a state of rest, as well as thickness diffu-
sion to a state of zero available potential energy, both with no corresponding source except that available
via forcing by surface momentum and buoyancy fluxes. Holloway (1992) argues that such is not an appro-
priate modeling practice, thus motivating the use of Neptune as a interim approach until a more complete
theory is available.
There is concern about the stepwise representation of bottom topography in z-coordinate models. The
use of partial cells in MOM enhances the model’s ability to represent the topographic slope in a more
faithful manner than with full cells. In general, however, the Neptune parameterization is an attempt to
instruct the simulation about physical consequences due to eddy-topography interactions. The hope is
that if the model can be suitably informed about these effects, it matters little that topography is only
approximately represented.
The Neptune parameterization is implemented in MOM for both Laplacian friction and biharmonic fric-
tion. Neptune systematically damps the deformation rates towards a state of approximate maximum en-
tropy. Notably, Neptune increases the kinetic energy as it damps the flow toward its maximum entropy
state. Such occurs even for flows at rest experiencing no external forcing. As a result. Neptune spins-up
the flow with shallow depths to the right of the downstream direction.
26.2 Basics of the parameterization in MOM
If the view is taken that equations of motion are solved for moments of probable flow, then those mo-
ments are forced in part by derivatives of the entropy distribution with respect to the realized moments.
The entropy gradient is estimated as proportional to a departure of the realized moments from a state
in which the entropy gradient is weak. This latter state is approximated by a depth-integrated transport
streamfunction ψnep (units of volume per time) and maximum entropy velocity unep.
26.2.1 The Eby and Holloway (1994) approach
An early suggestion for the streamfunction was given by Eby and Holloway (1994), who wrote
ψnep =−f L2H(26.1)
unep =ˆ
z∧H−1∇ψnep (26.2)
where fis the Coriolis parameter, His the ocean depth, and Lis an adjustable length scale on the or-
der of 10 km. If model resolution is coarse relative to the first deformation radius, unep is roughly depth
independent. Depth independence is assumed in the MOM implementation of Neptune. To parameterize
the unresolved driving of the mean flow by eddy-topography interactions, the Neptune parameterization
drives flow towards towards unep using an eddy stress proportional to (unep −u). The Eby and Holloway (1994)
method is implemented in MOM just for the Laplacian friction operator.
26.2.2 Maltrud and Holloway (2008) approach
For the biharmonic implementation of neptune, we follow the approach of Maltrud and Holloway (2008), in
which
unep =− f L2
H+Hmin !ˆ
z∧∇H. (26.3)
Contrary to the Eby and Holloway (1994) implementation, there is no gradient acting on the Coriolis pa-
rameter in the Maltrud and Holloway (2008) approach. The minimum depth Hmin regularizes the scheme so
that the velocity unep does not get too large in very shallow water.
Elements of MOM November 19, 2014 Page 374

Chapter 26. Eddy-topography interaction via Neptune Section 26.3
26.2.3 Specifying the length scale
As in Eby and Holloway (1994) and Maltrud and Holloway (2008), MOM provides the following specification
for the length scale Lin both of the above approaches
L=γneptune scaling "Lpole + (Lequator −Lpole) 1 + cos2φ
2!#,(26.4)
where Lpole is the polar length scale, Lequator is the equatorial length scale, φis the latitude, and γneptune scaling is a
dimensionless scaling coefficient used for further tuning. The tuning coefficient γneptune scaling was set to unity
in Maltrud and Holloway (2008), though they provided an extensive suite of smoothing operations on the
bottom slope.
26.3 Topostrophy diagnostic
The obvious means for diagnosing the impacts of Neptune are to directly compare the simulated velocity
field with versus without the parameterization. However, as noted by Holloway et al. (2007); Merryfield
and Scott (2007); Maltrud and Holloway (2008); Holloway (2008), it is simpler to consider a scalar field,
known as topostrophy, that directly measures the orientation of the velocity relative to the gradient of the
topography
Ttopostrophy =f(ˆ
z∧u)·∇H. (26.5)
This diagnostic is coded in MOM within the ocean velocity diag.F90 module. The neptune parameteriza-
tion tends to increase the topostrophy, with the trend consistent with topostrophy in eddying simulations
and observations (Holloway et al.,2007;Merryfield and Scott,2007;Maltrud and Holloway,2008;Hol-
loway,2008).
Elements of MOM November 19, 2014 Page 375

Chapter 26. Eddy-topography interaction via Neptune Section 26.3
Elements of MOM November 19, 2014 Page 376
Ad hoc subgrid scale parameterizations
The purpose of this part of the manual is to describe certain of the subgrid scale (SGS) parameterizations
of physical processes used in MOM, with the focus here on certain ad hoc approaches.
377

Section 26.3
Elements of MOM November 19, 2014 Page 378

Chapter 27
Overflow schemes
Contents
27.1 Motivation for overflow schemes ................................380
27.2 The sigma transport scheme ..................................380
27.2.1 Sigma diffusion ........................................ 380
27.2.2 Sigma advection ........................................ 381
27.2.2.1 Sigma velocity derived from resolved velocity ................. 382
27.2.2.2 Sigma velocity from a parameterization ..................... 382
27.2.2.3 Maintaining mass conservation .......................... 383
27.2.2.4 Dia-sigma transport ................................ 383
27.2.2.5 Mass sources .................................... 384
27.2.2.6 Undulating sigma layer thickness ........................ 384
27.2.2.7 Problems with the sigma advection scheme ................... 384
27.2.3 Implementation of sigma transport ............................. 385
27.3 The Campin and Goosse (1999) scheme ............................385
27.3.1 Finding the depth of neutral buoyancy ........................... 386
27.3.2 Prescribing the downslope flow ............................... 387
27.3.3 Mass conservation and tracer transport ........................... 387
27.3.4 Implementation in MOM ................................... 388
27.3.4.1 Start of the integration ............................... 388
27.3.4.2 During a time step ................................. 388
27.4 Neutral depth over extended horizontal columns ......................389
27.5 Sigma friction ...........................................391
The purpose of this chapter is to detail various methods available in MOM for enhancing the transport
of dense water downslope. Some of methods are implementations of schemes from the literature, some
are unique to MOM, and some remain incomplete methods which are part of MOM only for use by those
actively pursuing research into overflow algorithms. We present our prejudices in Section 27.4, though the
user should recognize that much research still is underway towards finding a suitable overflow scheme for
global ocean climate modelling.
There are four methods implemented in MOM described in this chapter, with the following modules
containing the code:
ocean param/lateral/ocean sigma transport.F90
ocean param/lateral/ocean mixdownslope.F90
ocean param/sources/ocean overflow.F90
ocean param/sources/ocean overexchange.F90.
379

Chapter 27. Overflow schemes Section 27.2
27.1 Motivation for overflow schemes
As described by Winton et al. (1998), coarse resolution z-coordinate models generally have difficulty mov-
ing dense water from shallow to deep regions. The key problem is that too much dense water spuriously
entrains with the ambient lighter fluid. Only when the topographic slope is resolved so that the grid spacing
satisfies
|∇H| ≤ ∆z
∆s,(27.1)
does the simulation begin to reach negligible levels of spurious entrainment. Resolving a slope of 1/100
with vertical resolution of ∆z= 20m thus requires horizontal grid spacing ∆s≈2km. This resolution is
one or two orders finer than the typical resolution of the 1-2 degree ocean climate models commonly
used today. Furthermore, refined vertical resolution, desired for representing vertical physical processes,
requires one to further refine the horizontal resolution required to resolve the slope. Notably, there is
little difference between the representation of steeply sloping features via either full or partial steps in z-
models (Section 5.1.2). Hence, steep “cliff” features remain ubiquitous in the typical ocean climate model
using vertical coordinates with quasi-horizontal isosurfaces. Short of respecting the constraint (27.1),
traditional tracer transport schemes (i.e., vertical convection; horizontal and vertical diffusion; and hori-
zontal and vertical advection) are generally unable to transport dense waters into the abyss to the extent
observed in Nature. This problem with spurious entrainment is shared by the quasi-horizontal vertical
coordinates such as those discussed in Chapter 5.
In an attempt to resolve the spurious entrainment problem, modelers have formulated ways to embed
terrain following transport schemes into geopotential or pressure coordinate models. These schemes
generally assume the bottom ocean region is turbulent, and so well mixed and not subject to geostrophy.
The resulting dynamics act to bring water downslope, eventually being entrained at a neutral buoyancy
depth.
Some approaches aim to modify both the momentum and tracer equations, with Killworth and Edwards
(1999) documenting a most promising approach. Unfortunately, when modifying the momentum equation
so that pressure gradients are computed within the bottom boundary layer, difficulties handling this cal-
culation have resulted in nontrivial problems with spurious transport, especially near the equator. It is for
this reason that no global ocean climate model presently employs the Killworth and Edwards (1999), or
analogous, scheme. Motivated by this difficulty, we do not consider any scheme in MOM that modifies the
momentum equation. Instead, we focus exclusively on methods restricted to the tracer equation.
27.2 The sigma transport scheme
This section documents the scheme available in the module
ocean param/mixing/ocean sigma transport.F90
The papers by Beckmann and D¨
oscher (1997) and D¨
oscher and Beckmann (2000) propose a method to
incorporate a rudimentary terrain following turbulent layer in z-models, or more generally into any model
with vertical coordinates having quasi-horizontal isosurfaces (e.g., pressure based vertical coordinates).
They prescribe changes only to the tracer equation, in which there is advection and diffusion within a
bottom turbulent layer. We term these transport mechanisms sigma diffusion and sigma advection, since
the sigma vertical coordinate (Section 5.1.5) is terrain following.
By enabling a terrain oriented route for tracer transport, in addition to the usual grid oriented transport,
the quasi-horizontal vertical coordinate models are now afforded an extra pathway for transporting dense
water into the abyss.
27.2.1 Sigma diffusion
Diffusion oriented according to the bottom topography is referred to as sigma diffusion in the following.
The diffusive flux between two adjacent cells living at the ocean bottom is given by
Fσ=−A∇σT , (27.2)
Elements of MOM November 19, 2014 Page 380

Chapter 27. Overflow schemes Section 27.2
horz
vert
Figure 27.1: Schematic of the along-topography pathway for tracer transport afforded by the sigma trans-
port scheme in MOM. Darkened regions denote land cells, and lightly hatched regions are within the bot-
tom turbulent boundary region. This boundary layer generally can fit within a single bottom cell, as in the
left turbulent boundary region; occupy a full cell, as in the middle region; or require more than one of the
bottom cells, as in the right region. Tracers communicate with their grid aligned horizontal and vertical
neighbors via the usual advection, diffusion, and convective processes. Tracers in the bottom turbulent
layer can additionally communicate with their neighbors within the turbulent region via sigma diffusion
and sigma advection.
with ∇σthe horizontal gradient operator taken between cells in the sigma layer. Note that this flux van-
ishes if the tracer concentration is the same between two adjacent cells within the sigma layer. We follow
the approach of D¨
oscher and Beckmann (2000) in which sigma diffusion is strong when densities of the
participating cells favors downslope motion. That is, the following diffusivity is used
A=(Amax if ∇σρ·∇H < 0
Amin if ∇σρ·∇H≥0,(27.3)
where z=−H(x,y)is the bottom depth. Note that in practice, this constraint is applied separately in the
two horizontal directions. That is, the zonal diffusivity is large if ρ,x H,x <0and the meridional diffusivity is
large if ρ,y H,y <0. A ratio of the two diffusivities Amax/Amin is a namelist parameter in MOM, with ≈106the
default value as suggested by D¨
oscher and Beckmann (2000).
An additional velocity dependent diffusion was also found by D¨
oscher and Beckmann (2000) to be of
use. In this case, an added sigma-diffusive flux in the zonal direction is computed using the diffusivity
A=(|u|∆xif ρ,x H,x <0and u H,x >0
Amin otherwise.(27.4)
In this expression, |u|is the magnitude of the model’s resolved zonal velocity component within the sigma
layer, and ∆xis the zonal grid spacing. An analogous meridional flux is computed as well.
Sigma diffusion can be specified to occur over an arbitrary layer thickness, even if this layer encom-
passes a non-integer number of bottom cells. If sigma diffusion is enabled without sigma advection, then
this bottom layer is time independent.
27.2.2 Sigma advection
In addition to sigma diffusion, MOM allows for an advective contribution to the bottom boundary layer flow.
This portion of the algorithm is experimental, and so it is not recommended for general use. We present
the discussion here only to expose some initial thoughts on a possible new method, but recognize that
the method as discussed here is incomplete. Note that the sigma advection scheme discussed here is
distinct from the method proposed by Beckmann and D¨
oscher (1997). Instead, the Campin and Goosse
Elements of MOM November 19, 2014 Page 381

Chapter 27. Overflow schemes Section 27.2
(1999) scheme discussed in Section 27.3 employs an analogous advective transport method which has
been implemented in MOM.
In the sigma advection scheme in MOM, there are two ways to determine the advective velocity compo-
nents acting on tracers within the sigma layer. In both cases, if the deeper parcel within the sigma layer is
denser than the shallower parcel, then the sigma advective transport is set to zero. Otherwise, it is active
and thus contributes to the downslope tracer transport. This criteria translates into the constraint
∇σρ·∇H < 0for density driven downslope flow, (27.5)
where ρis the density within the bottom sigma layer. This constraint is the same as used to determine the
value for the diffusivity discussed in Section 27.2.1.
27.2.2.1 Sigma velocity derived from resolved velocity
Beckmann and D¨
oscher (1997) and D¨
oscher and Beckmann (2000) determine the advective velocity com-
ponents acting in the sigma layer from the model’s resolved velocity components. In MOM, these veloc-
ity components are found by integrating the model’s resolved horizontal advective velocity components
within the bottom turbulent sigma layer.
27.2.2.2 Sigma velocity from a parameterization
Campin and Goosse (1999) suggest an additional approach to enhance the horizontal velocity available
for downslope flow. In MOM, we add this velocity to the resolved velocity within the sigma layer determine
as above.
Following Campin and Goosse (1999), assume the dense shallow parcel has a subgrid scale momentum
associated with its downslope motion. The zonal momentum is assumed to be proportional to the topo-
graphic slope, H,x, the acceleration from gravity, g, the amount of fluid within the cell participating in the
downslope flow,
0≤δ≤1,(27.6)
and the density difference
∆ρ= dx ∂ρ
∂x !σ
(27.7)
as measured in the zonal direction within the sigma layer. The momentum is retarded by frictional dissi-
pation, µ(with units of inverse time). These considerations then lead to the momentum balance
ρV (t)µuslope =−g δ V (t)∆ρ H,x sign(H,x) (27.8)
where
V(t)=dxt ∗dyt ∗dztσ(27.9)
is the volume of the dense parcel within the sigma layer, we assume ∆ρ H,x <0, as required for density
favorable downslope flow (equation (27.5)), and sign(H,x)sets the sign for the downslope velocity. Equa-
tion (27.8) is also used to determine a meridionally directed downslope transport, with the meridional
topographic slope H,y replacing H,x, and ∆ρ= dyρ,y the density difference between meridionally adjacent
parcels.
Solving equation (27.8) for the velocity component uslope yields
ρdztσuslope =− g δ
µ!H,x ∆ρdztσsign(H,x).(27.10)
With the depth Hrefering to the depth of a tracer cell, the slope H,x is defined at the zonal face of the
tracer cell. Hence, the velocity component uslope is likewise positioned at the zonal face. This is the desired
position for the zonal advective tracer transport velocity component.
Campin and Goosse (1999) suggest the values for frictional drag
µ= 10−4sec−1(27.11)
Elements of MOM November 19, 2014 Page 382

Chapter 27. Overflow schemes Section 27.2
and fraction of a cell participating in the transport
δ= 1/3.(27.12)
These parameters are namelists in MOM4. Using these numbers, with an absolute topographic slope of
|H,x| ≈ 10−3and density difference ∆ρ≈1kg m−3, leads to
uslope ≈.03m sec−1(27.13)
and the associated volume transport
Uslope =uslope ×thickness sigma ×dyt,(27.14)
where thickness sigma is the thickness of the sigma layer. With uslope ≈.03m s−1corresponding to the
speed of fluid within a sigma layer that is one-degree in width and 50m in thickness, we have a volume
transport Uslope ≈0.2Sv. Larger values are realized for steeper slopes, larger density differences, larger
grid cells, and thicker sigma layers.
27.2.2.3 Maintaining mass conservation
Introducing horizontal advection within the sigma layer necessitates the consideration of mass conserva-
tion within this layer. Our focus here is just on the additional mass conservation issues arising from sigma
advective transport.
The balance of mass within an arbitrary layer is detailed in Section 10.8. Assuming there is no trans-
port through the bottom of the sigma layer into rock, we are led to the mass budget for the sigma layer
(equation (10.108))
0 = ∂t(dz ρ)−dz ρ S(M)+∇σ·(dz ρu) + (ρw(σ))top of sigma layer.(27.15)
Again, each term in this equation is associated just with the sigma transport process. Hence, the hor-
izontal velocity uas that obtained from the considerations given earlier in this section. However, the
remaining terms have not been specified yet, and so must be set according to physical arguments and/or
convenience.
27.2.2.4 Dia-sigma transport
First, consider the case of zero mass source arising from sigma transport, and a zero time tendency term
∂t(dz ρ)(such as occurs in the Boussinesq case assuming a constant sigma layer thickness). The mass
budget within the sigma layer is thus closed by a dia-sigma transport
(ρw(σ))top of sigma layer =−∇σ·(dz ρ u).(27.16)
This transport measures the amount of water that crosses the sigma layer from the surrounding fluid. This
choice was taken by Beckmann and D¨
oscher (1997) and D¨
oscher and Beckmann (2000), and it was also
employed by Campin and Goosse (1999).
Furthermore, Beckmann and D¨
oscher (1997) suggest that to reduce the spurious entrainment associ-
ated with tracer advection aligned with the model’s grid, it is appropriate to reduce, or remove, this advec-
tive transport within the sigma layer in favour of the sigma advection transport. Tang and Roberts (2005)
also take this approach. Nonetheless, we do not follow this suggestion for the following reasons. First, it
complicates the treatment of the advection operator by introducing an ad hoc parameter that partitions
between sigma advection and grid aligned advection. Second, and primarily, we take the perspective that
the sigma advection process is subgrid scale. Hence, it should act only in those cases where the resolved,
grid aligned, velocity is unable to provide a sufficient downslope transport. We should thus not remove the
grid aligned advective transport using an ad hoc specification. That is, we do not aim to remedy spurious
entrainment arising from grid aligned advective transport by removing this transport altogether.
Given these objections, we do not pursue this approach further in MOM.
Elements of MOM November 19, 2014 Page 383

Chapter 27. Overflow schemes Section 27.2
27.2.2.5 Mass sources
Next, consider the case where all mass is advected downslope within the sigma layer, with a zero time
tendency term ∂t(dz ρ)and zero dia-sigma transport.1This assumption then leads to the sigma layer
mass budget
dz ρS(M)=∇σ·(dz ρ u).(27.17)
That is, the divergent horizontal advective transport within the sigma layer is balanced by a nonzero mass
source. The horizontal integral of the mass source over the sigma layer vanishes, since the sigma ad-
vection velocity satisfies either the no-normal boundary condition at land/sea interfaces, or periodicity.
Hence, the introduction of the nonzero mass source does not corrupt global mass conservation. It does,
however, come at the cost of also requiring nonzero tracer sources; the introduction of new fluid locally
requires also the introduction of nonzero tracer locally, since the fluid has some tracer content (e.g., a
temperature). These tracer sources do not necessarily lead to a zero global net introduction of tracer.
This approach is thus unacceptable.
27.2.2.6 Undulating sigma layer thickness
The time tendency ∂t(dz ρ)represents changes in the density weighted sigma layer thickness. It vanishes
for a Boussinesq case if the sigma layer has constant thickness. However, if the sigma layer can inflate
or deflate, this term remains nonzero. That is, without mass sources or without dia-sigma transport, the
mass budget within the sigma layer takes the form
∂t(dz ρ) = −∇σ·(dz ρ u).(27.18)
Hence, the sigma layer undulates according to the convergence or divergence of mass advected within the
layer. Its undulations are of just the magnitude needed to keep a zero dia-sigma transport. So the picture
is of a blob of heavy fluid moving downslope, causing the sigma layer to undulate in order to accomodate
the fluid motion. See Figure 2.7 for an illustration of this fluid motion. This approach is available only for
models such as MOM that allow an arbitrary time dependent thickness for the sigma layer.
During some initial research, we have favoured this approach in MOM as it avoids objections raised
about the previous alternatives. We do make some simplifications, and note that the approach has only
recently (as of 2006) been tested, with some unfortunate problems discussed below. Here are some things
to note.
• For the nonBoussinesq case, we replace the in situ density appearing in the time tendency with the
constant Boussinesq density ρo. Given uncertainties in many of the scheme’s parameters, this re-
placement is justified.
• The sigma layer thickness is bounded from above and below by user specified values. Allowing the
thickness to vary too far can lead to noisy behaviour. Settings bounds amounts to an implicit specifi-
cation of detrainment whenever the thickness gets too large, and entrainment when it gets to small.
• It has proven useful to smooth the sigma layer thickness. An option is available to smooth the layer
thickness with a Laplacian diffusion operator.
27.2.2.7 Problems with the sigma advection scheme
The most fundamental problem with the sigma advection scheme, as implemented according to equation
(27.18), is that as mass converges to a region to thus expand the sigma layer, there is no corresponding
dynamical mechanism to carry this perturbation away, and thus allow for an adjustment process. Instead,
by only considering the mass conservation equation, with no dynamical equations, the sigma layer will
generally grow without bound in regions where mass converges, or disapper in regions of divergence. This
situation is not encountered in an isopycnal model, since these models have dynamical processes to adjust
the fluctuating thicknesses.
1Grid aligned advection generally leads to transport across the sigma layer.
Elements of MOM November 19, 2014 Page 384

Chapter 27. Overflow schemes Section 27.3
Absent a dynamical mechanism for the adjustment, the sigma advection scheme must employ artificial
limits on the layer thickness. These limiters impose, in effect, a detrainment or entrainment process to keep
the layer thickness within the specified bounds. Such processes, however, have not yet been implemented
in MOM, so the present scheme is incomplete. Without the entrainment and detrainment processes, the
artificial limits, when imposed, allow for the tracer to realize extrema, since its time tendency is artificially
altered. This is unacceptable, and so the scheme as presently implemented is unusable.
27.2.3 Implementation of sigma transport
Consistent with Beckmann and D¨
oscher (1997), the turbulent bottom layer momentum equations remain
the same as interior k-level cells. We now just allow tracers in the bottom turbulent layer to be affected by
transport with their “sigma-neighbors” in addition to their horizontal and vertical neighbors. Figure 27.1
provides a schematic of the extra pathway available with sigma tracer transport.
The bottom turbulent sigma layer in MOM3 was appended to the very bottom of the model, and so
effectively lived beneath the deepest rock. This approach is inconvenient for the following reasons.
• It makes for awkward analyses.
• It precludes direct comparison between models run with and without sigma-physics since the grid
used by the two models is different.
• It makes it difficult to consider convergence when refining the grid mesh.
For these reasons, the bottom turbulent layer in MOM4 is included within the regular model domain. This
is the approach used by Beckmann and D¨
oscher (1997) (e.g., see their Figures 1 and 2).
The disadvantage of the MOM4p0 approach is that the bottom turbulent layer thickness thickness sigma
has a generally non-constant thickness and is determined by the thickness of the grid cell next to topog-
raphy. In particular, with partial bottom steps, the effective turbulent layer thickness could be very thin, in
which case thin cells act as a bottle-neck bo bottom transport. This implementation is inconvenient.
In MOM, we allow for an arbitrarily thick bottom turbulent layer. We do so by incorporating the required
grid cells into the bottom turbulent sigma layer. This approach requires some added accounting, but it is
straightforward. In particular, the tracer concentration within the bottom turbulent layer is computed by
Tsigma =Psigma ρdztT
Psigma ρdzt ,(27.19)
where the sum extends over the cells, including cell fractions, contained in the bottom turbulent layer.
A time tendency is computed for sigma transport of Tsigma within the bottom turbulent sigma layer. The
relative fraction of a grid cell participating in the bottom turbulent layer determines the magnitude of the
tracer time tendency added to this cell.
27.3 The Campin and Goosse (1999) scheme
This section documents the scheme available in the module
ocean param/sources/ocean overflow.F90.
Consider a heavy water parcel sitting on top of a shelf/cliffthat is horizontally adjacent to a lighter
parcel sitting over a deeper water column. We may expect that the dense parcel will move offthe shelf,
down the slope, and into the deep. Along the way, entrainment will occur, with many important processes
determining the details of the final water mass. This is indeed a cartoon of an important oceanic process
forming much of the deep and intermediate waters in the ocean. Unfortunately, without some extra “en-
gineering” help, Winton et al. (1998) show that coarse resolution z-models are incapable of providing the
proper dynamical pathways for this transfer of dense shelf water into the deep. Beckmann and D ¨
oscher
(1997) suggest one means to enhance the representation of this process, and we discussed this scheme
in Section 27.2.Campin and Goosse (1999) propose yet another, which we detail in this section. Both
schemes only affect the tracer equation.
Elements of MOM November 19, 2014 Page 385
Chapter 27. Overflow schemes Section 27.3
5
4
3
ρ(
ρ(
ρ(
kdw−1
kdw+1
kup
)
)
)
do
do
do
deep ocean(do)
shallow ocean(so)
ρ(
so
ρ(
so
ρ(
so
ρ(
so
kup,kdw)>ρ(
do
kdw)
kup,kdw+1)<ρ(
do
kdw+1)
kup,kdw−1 >ρ(
do
kdw−1
)
kup,kup)>ρ(
do
kup)
i,j
k
)
so
ρ(kup,kup)
2
1
ρ(
do
kdw)
Figure 27.2: Schematic of the Campin and Goosse (1999) overflow method in the horizontal-vertical plane.
The darkly filled region represents bottom topography using MOM4’s full cells. The lightly filled region
represents topography filled by a partial cell. Generally, the thickness of a cell sitting on top of a topo-
graphic feature, as the k= 2 cell in the “so” column, is thinner than the corresponding cell in the deep-
ocean column (the k= 2 cell in the “do” column). Shown are tracer cells, with arrows representing the
sense of the scheme’s upstream advective transport. This figure is based on Figure 1 of Campin and Goosse
(1999).
27.3.1 Finding the depth of neutral buoyancy
Figure 27.2 illustrates a typical situation in a horizontal-vertical plane. Here, we see a heavy parcel of in
situ density ρso(k=kup)sitting horizontally adjacent to a lighter parcel of in situ density ρdo(k=kup). The
superscript “so” refers to water in the “shallow ocean” column, whereas “do” refers to water in the “deep
ocean” column.
If the heavy parcel is allowed to adiabatically move offthe shelf and then vertically within the deep
column, it will equilibrate at its depth of neutral buoyancy. To compute the depth of neutral buoyancy, we
evaluate the in situ density for the parcel taken at the local value for the in situ pressure of the environment
where it may potentially equilibrate. For the example shown in Figure 27.2, with (i,j)setting the horizontal
position of the shelf parcel and (i+ 1,j)setting the horizontal position of the deep column, we have
ρso(kup,kup) = ρ(si,j,kup,θi,j,kup,pi,j,kup) (27.20)
ρso(kup,kdw −1) = ρ(si,j,kup,θi,j,kup,pi+1,j,kdw−1) (27.21)
ρso(kup,kdw) = ρ(si,j,kup,θi,j,kup,pi+1,j,kdw) (27.22)
ρso(kup,kdw + 1) = ρ(si,j,kup,θi,j,kup,pi+1,j,kdw+1).(27.23)
That is, we compute the density at the salinity and potential temperature of the shallow ocean parcel,
(si,j,kup,θi,j,kup), but at the in situ pressure for the respective grid cell in the deep column. The density is
then compared to the density of the parcel at the in situ salinity, temperature, and pressure of the cells in
the deep ocean column.
Elements of MOM November 19, 2014 Page 386

Chapter 27. Overflow schemes Section 27.3
27.3.2 Prescribing the downslope flow
Following Campin and Goosse (1999), we assume that the dense parcel has a downslope momentum im-
parted to it. This momentum is proportional to the topographic slope, H,x, the acceleration from gravity,g,
the amount of fluid within the cell participating in the downslope flow,
0≤δ≤1,(27.24)
and the positive density difference
∆ρ=ρso(kup,kup)−ρdo(kup)>0.(27.25)
The momentum is retarded by frictional dissipation, µ(in units of inverse time). These considerations then
lead to the momentum balance
ρoV(t)µuslope =g δV (t)∆ρ|H,x|(27.26)
where
V(t)=dxt ∗dyt ∗dzt (27.27)
is the volume of the dense parcel’s tracer cell. Equation (27.26) is also used to determine a meridionally di-
rected downslope transport, with the meridional topographic slope ∂yHreplacing ∂xH, and ∆ρthe density
difference between meridionally adjacent parcels.
Solving equation (27.26) for the speed uslope yields
uslope = g δ
ρoµ!|∂xH|∆ρ. (27.28)
If the depth Hrefers to the depth of a tracer cell, then the absolute slope |∂xH|is naturally defined at the
zonal face of the tracer cell. Hence, the speed, uslope, is likewise positioned at the zonal face. This is the
desired position for an advective tracer transport velocity.
Campin and Goosse (1999) suggest the values µ= 10−4sec−1and δ= 1/3. These parameters are set as
namelists in MOM4. Using these numbers, with an absolute topographic slope of |H,x| ≈ 10−3and density
difference ∆ρ≈1kgm−3, leads to the speed
uslope ≈.03msec−1.(27.29)
Associated with this downslope speed is a volume transport of fluid leaving the cell
Uslope =uslope dztmin dyt.(27.30)
In this equation, dztmin is the minimum thickness of the shelf cell and the adjacent cell. This minimum
operation is necessary when considering MOM4’s bottom partial cells, whereby the bottom-most cell in
a column can have arbitrary thickness (Figure 27.2). With uslope ≈.03ms−1corresponding to the speed
of fluid leaving a grid cell that is one-degree in width and 50m in depth, we have a volume transport
Uslope ≈0.2Sv. Larger values are easily realized for steeper slopes, larger density differences, and larger
grid cells.
27.3.3 Mass conservation and tracer transport
To conserve mass throughout the system, the mass flux exiting the shelf cell and entering the deep cell
must itself be returned from the adjacent cell. This situation then sets up a mass flux throughout the
participating cells, where there is zero convergence of the flux and so zero net increase or decrease in
mass. For the Boussinesq fluid, mass conservation is replaced by volume conservation. This redirected
plumbing is shown in Figure 27.2.
The convergence-free seawater mass flux carries with it tracer mass. If there are differences in the
tracer content of the cells, then the tracer flux will have a nonzero convergence, and so it moves tracer
throughout the system. We use first-order upstream advective transport as a discretization of this process.
First-order upstream advection is the simplest form of advection. Its large level of numerical diffusion is
consistent with our belief that the bottom layer flows in the real ocean near steep topography are quite
turbulent. Hence, although inappropriate for interior flows, we are satisfied with the use of upstream ad-
vection for the overflow scheme.
Elements of MOM November 19, 2014 Page 387
Chapter 27. Overflow schemes Section 27.3
27.3.4 Implementation in MOM
This section details the implementation of the Campin and Goosse (1999) scheme in MOM.
27.3.4.1 Start of the integration
At the start of the model integration, it is necessary to determine those grid points where it is possible
to have a downslope flow. For this purpose, we introduce the array topog step(i,j,m), with m= 1,2,3,4
specifying in a counter-clockwise direction the four surrounding columns whose depths are to be compared
to that at the central (i,j)point. Figure 27.3 illustrates this notation. If the adjacent column is deeper than
the central point, thus representing a possible direction for downslope flow, then topog step(i,j,m) for
this value of mis set to unity. Otherwise, topog step(i,j,m) for this mis zero. Note that with partial
bottom cells, it is possible for an adjacent column to be deeper yet for the number of vertical cells to be
the same in both columns. To initiate the downslope scheme of Campin and Goosse (1999), we insist that
there be at least one more grid cell in the adjacent column.
(i,j,3) (i,j,1)
(i,j,2)
(i,j,4)
i
j
T(i,j)
Figure 27.3: Plan view (x-y plane) of a tracer grid cell at (i,j) and its horizontally adjacent tracer cells. We
label the adjacent cells (i+ 1,j),(i,j + 1),(i−1,j),(i,j −1) as m= 1,2,3,4. Notice that we do not consider
downslope flow along a diagonal direction.
27.3.4.2 During a time step
During each time step, we locate where downslope flow is favorable for points sitting on the ocean bottom
at (i,j,kmt(i,j)). For each of the four directions (m= 1,2,3,4) where topog step(i,j,m)=1, we check the
density difference between the central point and the adjacent point. If the density of the central point
is larger, then the Campin and Goosse (1999) scheme is used to initiate downslope transport. For these
directions, we locate the depth of neutral buoyancy for the central point according to the discussion in
Section 27.3.1, and so specify the number of vertical cells, kdw, participating in the transport. Note that
we allow for downslope transport to occur in more than one direction, as occurs in those cases for a fixed
(i,j)where topog step(i,j,m) has more than a single nonzero element.
Our prescription is mindful of the possibility for the shallow-cell to be a partially filled cell sitting on the
topography. For this reason, the convergence-free volume transport associated with the downslope flow
is weighted by the minimum vertical thickness of the two cells (equation (27.30)). Otherwise, it would be
possible to flood a thin partial cell with a huge amount of tracer (e.g., heat).
We incorporate effects from the Campin and Goosse (1999) overflow scheme into MOM’s tracer time
tendency array. To derive the tendency, we proceed as for the river-mixing and cross-land mixing formula-
tions discussed in Griffies et al. (2004) by focusing on the time evolution due to just the overflow process.
Elements of MOM November 19, 2014 Page 388

Chapter 27. Overflow schemes Section 27.4
For the particular zonal-vertical case illustrated in Figure 27.3, we prescribe
∂t(V(t)ρC)so
i,j,kup =ρ Uslope (Cdo
i+1,j,kup −Cso
i,j,kup) (27.31)
∂t(V(t)ρC)do
i+1,j,kup =ρ Uslope (Cdo
i+1,j,kdw−1−Cdo
i+1,j,kup) (27.32)
∂t(V(t)ρC)do
i+1,j,kdw−1=ρUslope (Cdo
i+1,j,kdw −Cdo
i+1,j,kdw−1) (27.33)
∂t(V(t)ρC)do
i+1,j,kdw =ρUslope (Cso
i,j,kup −Cdo
i+1,j,kdw),(27.34)
where
ρUslope =uslope rho dztmin dyt,(27.35)
with
rho dzt(min)= min(rho dzti,j,kup,rho dzti+1,j,kup) (27.36)
the minimum density weighted thickness of the two cells at k=kup. For the Boussinesq case, ρfactors
are set to the constant reference density ρo. Setting the tracer concentration to the same uniform value
leads to vanishing time tendencies in each cell, thus reflecting volume/mass conservation. Additionally,
summing these four equations leads to a vanishing right hand side, thus reflecting conservation of total
tracer in the system. Since the downslope mixing has the form of an upstream advection, we discretize
temporally by evaluating the tracer and density on the right hand side at the lagged time τ−1.
27.4 Neutral depth over extended horizontal columns
Both Campin and Goosse (1999) and Beckmann and D¨
oscher (1997) provide quasi-physical approaches
to the problem of simulating deep water formation near topography. Each provides plumbing routes be-
yond the local horizontal-vertical routes available in geopotential or pressure models. In this way, these
methods afford a new means for representing the flows. Questions such as parameterizing the rates of
entrainment, volume flux, etc. (e.g., Killworth and Edwards (1999)) are not directly addressed by these
schemes, although the present schemes can be extended a bit to include such details.
Climate modelers generally gauge the utility of overflow schemes on the overall results. Namely, do
the schemes provide a route for deep water formation near topographic gradients in a manner expected
from observations? Details of the transport are often not the first priority. This situation is unsatisfying
from a process physics perspective. It may, nonetheless, be the best available for many coarse resolution
models.
In this section, we discuss our prejudices with MOM development. To start, consider the density struc-
ture in Figure 27.4. This figure illustrates a case where the sigma transport scheme of Section 27.2 does
not prescribe enhanced downslope transport. The reason is that the sigma transport scheme only works
with density within the bottom “sigma layer”. For this example, density at the bottom of the deeper col-
umn is greater than that on the shelf, and so there is no enhanced transport prescribed. In contrast, the
Campin and Goosse (1999) scheme prescribes a downslope transport, with the dense shelf water moving
to its neutral buoyancy depth. It is for this reason that we favour in MOM those downslope schemes where
the depth of neutral buoyancy is determined, with this depth possibly above the ocean bottom.
Even within this example, however, there remain limitations of the Campin and Goosse (1999) scheme.
The limitation is that their scheme only reaches out one grid box in the horizontal. That is, although the
scheme is non-local in the vertical, it remains local in the horizontal. What can happen is the dense parcel
will find itself denser than any parcel in the adjacent column, and so its resting place, with the Campin and
Goosse (1999) algorithm, is at the bottom of the adjacent column, rather than at a neutral buoyancy depth.
If given the opportunity to exchange with columns further removed from the central column, the parcel is
afforded the opportunity to find a more suitable neutral buoyancy layer. This general result motivates us
to consider two experimental schemes, whereby the notions of a neutral buoyancy level motivated from
Campin and Goosse (1999) are extended to columns removed from the central column. As the parcel finds
a more suitable resting place, it is assumed to exchange properties with the intermediate parcels, in a
manner meant to represent entrainment as it moves downslope. The rates of transport remain a function
of the topographic slope and the difference in density, just like the Campin and Goosse (1999) scheme.
Elements of MOM November 19, 2014 Page 389

Chapter 27. Overflow schemes Section 27.5
There are two methods available in MOM for realizing these ideas. The first is implemented in the
module
ocean param/sources/ocean overexchange.F90.
In this scheme, a dense shallow parcel is allowed to be transported horizontally over more than a single
column, so long as it continues to remain on the bottom of the adjacent columns, thus affording it more
opportunity to find its neutral buoyancy level. The exchange results in no net mass exchange between
parcels, and so there is no need for an advective replumbing to be implemented, in contrast to the Campin
and Goosse (1999) scheme. Here, the resolved dynamics adjust based on mixing of the water masses
and the associated changes in density structure. This process then becomes directly analogous to the
cross-land mixing formulation discussed in Griffies et al. (2004) and in Chapter 29. That is, we remove the
intermediate cells from the process described in Section 27.3.4.2, and just focus on the single shallow and
deep cell, thus leading to
∂t(V(t)ρC)so
i,j,kup =ρ Uslope (Cdo
i+1,j,kdw −Cso
i,j,kup) (27.37)
∂t(V(t)ρC)do
i+1,j,kdw =ρUslope (Cso
i,j,kup −Cdo
i+1,j,kdw),(27.38)
This parameterization is simpler to implement than the Campin and Goosse (1999) scheme, since we omit
the intermediate cells from the process. This approach also does not rely on assumptions of a flow that
may be set up in response to the exchange of fluid.
The second method is implemented in the module
ocean param/mixing/ocean mixdownslope.F90.
In this scheme, exchange of tracer occurs as a partial convective mixing process. We assume that a part
of the shallow dense cell is transported downslope, and this then mixes with the intermediate cells with
an efficiency proportional to the topographic slope and the density difference. In equations, we compute a
combined mass of the mixed water according to
Msum =M(s) + M(d),(27.39)
where
M(s) = γrho dzt(s)dat(s) (27.40)
is the mass of water in the shallow dense cell participating in the exchange, and
M(d) = δrho dzt(d)dat(d) (27.41)
is the mass of deep cell participating. In these equations, dat is the horizontal area of the cells, γis
the fraction of the shallow dense cell that is assumed to take part in the downslope transport, and δis
proportional to the topographic slope and the density difference between the shallow and deep parcel. If
assumed to mix completely over a time step, then the resulting tracer concentration Cmix would be given
by
Msum Cmix =γrho dzt(s)dat(s)C(s) + δrho dzt(d)dat(d)C(d).(27.42)
Instead of mixing completely, which would require an adjustment process as in convection, we use the
tracer concentration Cmix to deduce the following time tendencies which drive the cells toward the mixed
concentration
dat(s)tend(s) = M(s)γ
∆t!(Cmix −C(s)) (27.43)
dat(d)tend(d) = M(d)δ
∆t!(Cmix −C(d)).(27.44)
Given the mixed tracer concentration (27.42), we have
dat(s)tend(s) + dat(d)tend(d)=0,(27.45)
which reflects the conservation of tracer.
Elements of MOM November 19, 2014 Page 390
Chapter 27. Overflow schemes Section 27.5
ρ=
ρ=
ρ=
ρ=
1033
1034
1036
1037
3
4
5
2
1
k
i,j
ρ=1035
ρ=1035
Figure 27.4: Schematic of a situation where a dense parcel sits on a shelf next to a column whose upper
portion is light, but whose deeper portion is denser than the shelf. For this case, the Campin and Goosse
(1999) scheme prescribes a transport between the shelf water at level 1 and the deeper water at level 3,
with water bubbling upward to conserve mass as shown in Figure 27.2. In contrast, the sigma transport
scheme will not prescribe any enhanced transport, since here the bottom of the deep column is denser than
the shelf.
27.5 Sigma friction
The previous schemes introduce a new transport pathway for tracers. Nothing is done to the momentum
equation. Another idea is to consider an enhancement of the vertical friction acting near to the bottom,
with the friction introduced via a vertical viscosity. The effects of vertical friction are related, through
geostrophy, to those from Gent et al. (1995), whereby density slopes are reduced without mixing of density
classes (Greatbatch and Lamb,1990). Alternatively, enhancing the vertical viscosity next to the bottom
increases the Ekman layer thickness next to the bottom, and this breaks geostrophy, thus allowing for an
easier downslope transit of the fluid. The scheme described in this section is not available in MOM. We
mention it, nonetheless, as it may prove to be of use for some applications.
Following the scaling from Campin and Goosse (1999) discussed in Section 27.3.2, we define a vertical
viscosity according to equation (27.26)
κσ=dztσuslope
=− g δ
µρ !H,x ∆ρdztσsign(H,x).(27.46)
Using the parameters from Section 27.3.2 leads to a vertical visosity of
κσ= 0.15ms−2,(27.47)
with larger values for steeper topographic slopes and stronger density contrasts. We propose to introduce
this viscosity throughout the sigma layer, and exponentially decrease it above the layer, with a relatively
short decay scale
κσ
decay = 10m.(27.48)
Elements of MOM November 19, 2014 Page 391

Chapter 27. Overflow schemes Section 27.5
We suggest computing this viscosity separately for the two horizontal directions, and take the maximum
of the two for the parameterization.
Elements of MOM November 19, 2014 Page 392

Chapter 28
River discharge into the ocean model
Contents
28.1 Introduction ............................................393
28.2 General considerations .....................................394
28.3 Steps in the algorithm ......................................395
This chapter presents a method to distribute river runoffthroughout a vertical column comprised of
more than a single ocean model grid cell. This issue is most important for ocean models with fine vertical
grid resolution. Care is taken to account for the needs to conserve properties using the constraints of a
Boussinesq z-model where only the top cell is allowed to change its volume. The algorithm presented here
is based on discussions with Mike Winton (Michael.Winton@noaa.gov).
We formulate the river mixing process in terms of tendencies added to the tracer concentration equa-
tions. Changes in the free surface height are handled just as for other forms of fresh water, such as pre-
cipitation and evaporation. This scheme was originally implemented in the Boussinesq z-model MOM4.0.
It has been ported to the generalized level coordinate MOM4p1 and later MOM releases, only so far as
adding the appropriate vertical grid factors. No more modifications have been made to exploit the added
flexibility available with a generalized level model. Hence, the scheme is basically the same as that origi-
nally implemented in MOM4.0.
The following MOM module is directly connected to the material in this chapter:
ocean param/sources/ocean rivermix.F90
28.1 Introduction
Coupling rivers to an ocean model is necessary when building fully coupled climate models. For z-models,
river discharge is typically given fully to the top model grid cell. Depending on the model resolution, dump-
ing all the river properties to the top grid cell can cause problems. Notably, without enhanced mixing, a
strong halocline can arise, with associated problems appearing due to noise from vertical advection across
the strong front. This problem is enhanced in models with relatively fine vertical resolution, such as the
10m now common for the top grid cell in ocean climate models.
In the real world, there are two reasons that the halocline at river mouths is somewhat weaker than can
occur in ocean climate models. First, river water does not generally fill only a single layer of some 10m
depth. Instead, rivers discharge into the ocean over a vertical column whose depth can be deeper than
10m. Second, and more generally, river properties are mixed through a vertical column due to waves and
tides near the coasts.
Two methods to relieve numerical problems can be considered. First, we can enhance vertical mixing
of tracers in the region next to river mouths. This approach is straightforward and is available in MOM. In
393

Chapter 28. River discharge into the ocean model Section 28.3
detail, the enhanced mixing is strongest near the surface and tapers to zero at a specified depth. Such is
the only method available to rigid lid ocean models for handling enhanced mixing at river mouths. Another
method is to distribute the river water, along with its tracer content, over a pre-defined vertical column.
Since the top model grid cell in the z-coordinate MOM4.0 is the only one capable of changing its volume
through changes in the surface height, distributing river water into deeper cells must be done carefully. In
the remainder of this chapter, we detail such a method. Its generalization to MOM4p1 and later releases
is minimal, in that only the added vertical grid elements have been updated.
Note that we typically do not alter the transfer of momentum from the river to the ocean. Instead, we
assume that river horizontal momentum is the same as the corresponding ocean cell, thus leading to no
change in the ocean momentum associated with river discharge. This assumption may require modifica-
tions for careful studies of coastal processes, but it should be sufficient for ocean climate modeling.
28.2 General considerations
Consider a column of discrete ocean with kr cells in the vertical over which we aim to discharge river water:
kr =# of vertical ocean cells into which river water is discharged. (28.1)
Allow the river to be discharging at a volume per area per time given by R, which has units of a velocity:
R=volume per area per time of river water discharge. (28.2)
The river water flux Ris distinguished in MOM from fresh water associated with evaporation and precipita-
tion.
The tracer concentration within the river water is given by Criver :
Criver =tracer concentration within river water. (28.3)
Criver is distinguished in MOM from the tracer concentration associated with evaporation and precipita-
tion. What tracer concentration should be taken for the river water? Typically, we think of rivers at their
discharge point as having tracers of uniform concentration. More information about tracer profiles re-
quires a river model, and even so we may wish to summarize the river information prior to passing it into
the ocean. Assuming a single uniform value for the river tracer concentrations, and absent a river model,
it is typical to assume the following river tracer concentration
θriver =θk=1
ocean (28.4)
sriver = 0 (28.5)
Triver =Tk=1
ocean (28.6)
where k= 1 is the top cell of the ocean column into which the river water is discharged, θis the potential
temperature, which equals the in situ temperature at the ocean surface, sriver is the zero salinity of the
fresh water river, and Triver is the concentration of a passive tracer in the river. By assuming θriver =θk=1
ocean,
vertically distributing river water acts to warm the ocean column in regions where the ocean surface is
warmer than depth. In contrast, rivers with zero salinity do not alter the ocean salt content, yet they do
reduce the salinity.
Over a leap-frog tracer time step 2dtts, a thickness Hriver =R∗2dtts of river water is to be distributed
throughout the vertical ocean column:
Hriver =R∗2dtts =river water thickness discharged per tracer leap-frog. (28.7)
Along with this distribution of river water into the ocean column, we distribute the tracer content of the
river into the ocean column:
Criver Hriver =river tracer content discharged per tracer leap-frog. (28.8)
Elements of MOM November 19, 2014 Page 394
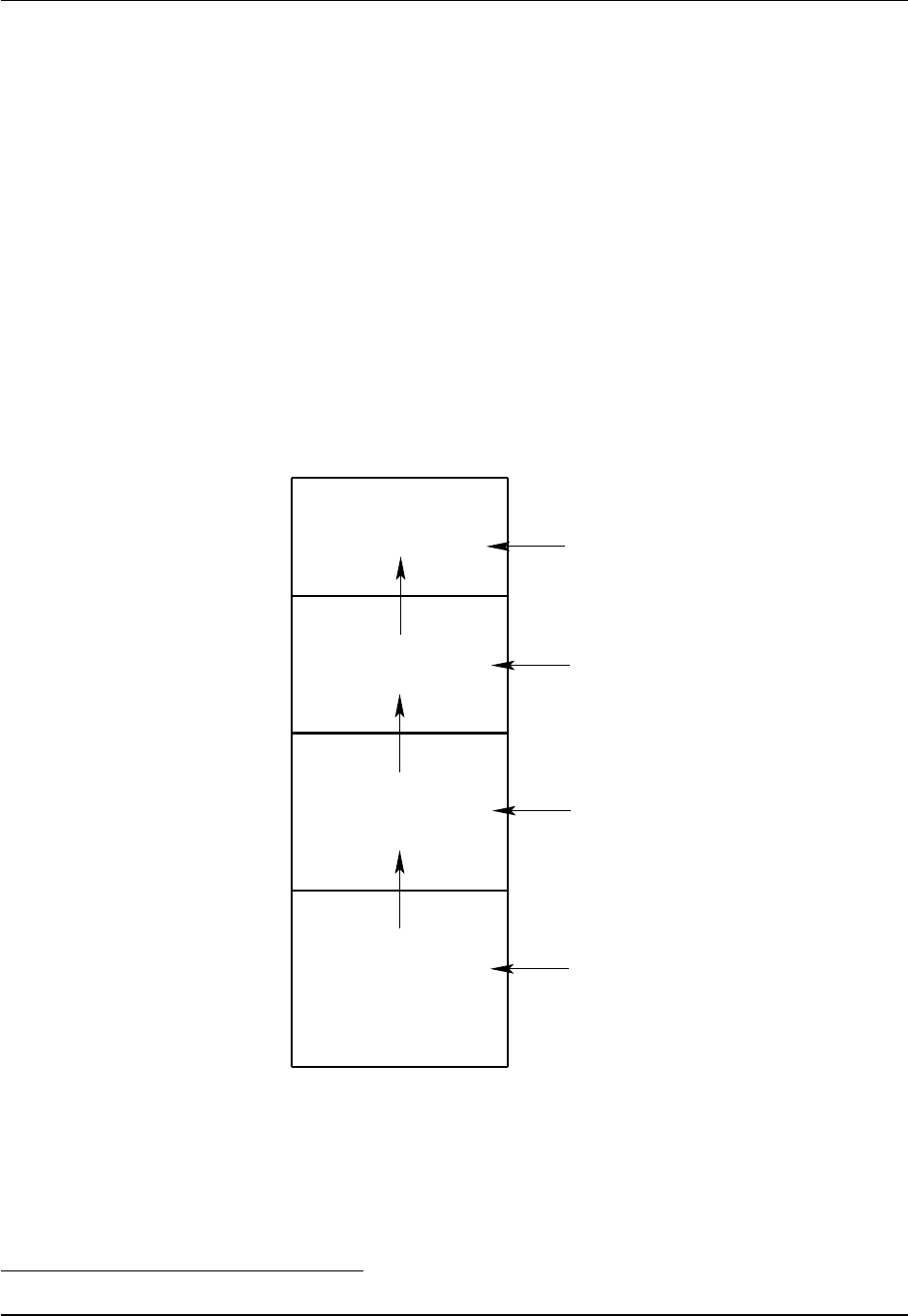
Chapter 28. River discharge into the ocean model Section 28.3
28.3 Steps in the algorithm
We derive the algorithm by considering the conservation equations for tracer in a vertical column of ocean
model grid cells. To isolate effects from river discharge, we ignore all horizontal processes. Without dis-
tributing river runoffwith depth, tracer conservation is given by
∂t(V ρC)k=1 =ρoARCriver
∂t(V ρC)k>1= 0 (28.9)
where V=Ah is the volume of a grid cell, Cis the tracer concentration, ρis the in situ density, Ris the river
discharge rate, and Criver is the concentration of tracer in the river. As the horizontal area Ais constant,
it can be dropped from the discussion. Conservation of total tracer in the four-box system is manifest by
∂t
kr
X
k=1
(hρC) = ρoRCriver .(28.10)
Whatever is done to redistribute river runoffwith depth, this conservation law must be preserved.1
R C water
R C water
R C water
R C water
R C
R C
R C 2
3
4
b
b
b
b
b
b
b
1
2
3
4
4
3
2
k=4
k=3
k=2
k=1
Figure 28.1: Schematic of river discharge algorithm for the case with kr = 4.We insert a fraction of the
river water into grid cells throughout the column, with a corresponding amount leaving each cell bubbling
upwards in order to conserve water mass/volume in the original implementation of MOM4.0, where grid
cells cannot change volume and there are no source terms.
To derive the algorithm, we refer to Figure 28.1. Here, we prescribe that a fraction of the river water
1The appearance of ρoon the right hand side, rather than ρriver , is described in Chapter 2as well as Griffies (2004).
Elements of MOM November 19, 2014 Page 395

Chapter 28. River discharge into the ocean model Section 28.3
and its tracer content is inserted into each of the cells within the column, where the fractions sum to unity
kr
X
k=1
δk= 1.(28.11)
We choose the fractions according to the grid cell thickness
δk=hk
Pkr
k=1 hk
(28.12)
where hkis the tracer cell thickness, and is known as dzti,j,kin the MOM code.
Because the interior cell volumes remain constant in MOM4.0, the same amount of water that entered
the cell via the river water must then leave. We assume that it leaves with the tracer concentration of
the cell prior to the insertion of the river water. That is, by inserting some of the river water into the cell
at tracer concentration Criver , we then displace the same amount of water but at concentration Ck. This
displaced water is bubbled upwards towards the surface cell. Conservation equations for this algorithm
take the form
∂t(hρC)1=R[(δρC)2+δ1ρoCriver ]
∂t(hρC)k=R[(δρC)k+1 −(δρC)k+δkρoCriver ]
∂t(hρC)kr =R[−(δρC)kr +δkr ρoCriver ]
(28.13)
where the first equation is for k= 1, the second for 1< k < kr, and the third for k=kr. The algorithm has
the appearance of upwind advection throughout the column. Hence, conservation of total tracer for the
column is trivially verified. Formulation as a thickness-weighted tracer source leads to
ρodzt ·tracer-source1=R[(δρC)2+δ1ρoCriver]
ρodzt ·tracer-sourcek=R[(δρC)k+1 −(δρC)k+δkρoCriver ]
ρodzt ·tracer-sourcekr =R[−(δρC)kr +δkr ρoCriver]
(28.14)
For kr = 1, the method reduces to the default discharge of river into the top cell.
Elements of MOM November 19, 2014 Page 396

Chapter 29
Cross-land mixing
Contents
29.1 Introduction ............................................397
29.2 Tracer and mass/volume compatibility ............................398
29.3 Tracer mixing in a Boussinesq fluid with fixed boxes ....................398
29.4 Mixing of mass/volume .....................................399
29.4.1 Instantaneous and complete mixing ............................ 400
29.4.2 A finite time incomplete mixing ............................... 400
29.4.3 A finite time incomplete mixing for surface cells ..................... 401
29.5 Tracer and mass mixing .....................................401
29.6 Formulation with multiple depths ...............................402
29.6.1 MOM1 formulation of cross-land tracer mixing ...................... 402
29.6.2 Generalizing to free surface and non-Boussinesq ..................... 403
29.7 Suppression of B-grid null mode ................................404
The purpose of this chapter is to present the method used in MOM for mixing tracers and mass/volume
across land separated points, such as across an unresolved Strait of Gibraltar. The material here is taken
from the MOM4 Technical Guide of Griffies et al. (2004), with slight modifications to account for generalized
vertical coordinates used in MOM.
The following MOM module is directly connected to the material in this chapter:
ocean param/sources/ocean xlandmix.F90.
29.1 Introduction
In climate modeling, it is often necessary to allow water masses that are separated by land to exchange
properties. This situation arises in models when the grid mesh is too coarse to resolve narrow passage-
ways that in reality provide crucial connections between water masses. For example, coarse grid spacing
typically closes offthe Mediterranean from the Atlantic at the Straits of Gibraltar. In this case, it is impor-
tant for climate models to include the effects of salty water entering the Atlantic from the Mediterranean.
Likewise, it is important for the Mediterranean to replenish its supply of water from the Atlantic to balance
the net evaporation occurring over the Mediterranean region.
We describe here a method used in MOM to establish communication between bodies of water sep-
arated by land. The communication consists of mixing tracers and mass/volume between non-adjacent
water columns. Momentum is not mixed. The scheme conserves total tracer content, total mass or volume
397

Chapter 29. Cross-land mixing Section 29.3
(depending on whether using the non-Boussinesq or Boussinesq versions of MOM), and maintains compat-
ibility between the tracer and mass/volume budgets. It’s only restriction is that no mixing occur between
cells if their time independent thicknesses differ. This constraint is of little practical consequence.
29.2 Tracer and mass/volume compatibility
Consider two boxes with fluid masses M(1) =ρ(1) V(1) and M(2) =ρ(2) V(2) and tracer concentrations (tracer
mass per mass of fluid) T(1) and T(2) (for a Boussinesq fluid, the density is set to the constant Boussinesq
density ρo). A mixing process that conserves total tracer mass and total fluid mass must satisfy
∂t(T(1) ρ(1) V(1) +T(2) ρ(2) V(2)) = 0 (29.1)
∂t(ρ(1) V(1) +ρ(2) V(2))=0.(29.2)
Notably, mass conservation can be considered a special case of total tracer conservation when the tracer
concentration is uniform and constant: T≡1. This result provides an important compatibility constraint
between the discrete tracer and mass/volume budgets. For constant volume boxes with a Boussinesq
fluid, such as considered in rigid lid models, compatibility is trivial. For boxes which change in time, such
as the top cells in MOM4.0 free surface or any box in the generalized vertical coordinates of later versions,
then compatibility provides an important constraint on the methods used to discretize the budgets for
mass/volume and tracer. The remainder of this chapter incorporates these ideas into the proposed cross-
land mixing scheme.
29.3 Tracer mixing in a Boussinesq fluid with fixed boxes
To start in our formulation of cross-land mixing, let us consider mixing of two volumes of Boussinesq fluid,
where the separate volumes remain constant in time
∂tV(1) =∂tV(2) = 0.(29.3)
An example is the mixing between two constant volume grid cells. If the mixing takes place instantaneously
and between the full contents of both boxes, as in convective adjustment, then the final tracer concentra-
tion in both boxes is given by
Tf inal =T(1) V(1) +T(2) V(2)
V(1) +V(2) .(29.4)
It is assumed in convective mixing that the volumes of the two boxes remains unchanged. The picture is of
an equal volume of water rapidly mixing from one box to the other, without any net transport between the
boxes.
Instead of instantaneous and complete convective mixing, consider mixing of the two boxes at a volume
rate U. That is, Urepresents an equal volume per time of water mixing between the boxes, with no net
transport. As shown in Figure 29.1,Uis chosen based on the observed amount of water exchanged through
the passageway. Just as for convective adjustment, the volumes of the two boxes remains fixed. But the
tracer concentrations now have a time tendency. One form for this tendency relevant for constant volume
cells is given by
∂t(V(1) T(1)) = U(T(2) −T(1)) (29.5)
∂t(V(2) T(2)) = U(T(1) −T(2)).(29.6)
Since the volumes are constant, we can write these budgets in the form
∂tT(1) =U
V(1) (T(2) −T(1)) (29.7)
∂tT(2) =U
V(2) (T(1) −T(2)),(29.8)
Elements of MOM November 19, 2014 Page 398
Chapter 29. Cross-land mixing Section 29.4
This is the form of cross-land tracer mixing used in the rigid lid full cell MOM1.
In the real world, transport is often comprised of stacked flows where deep water flows one way and
shallow water oppositely (e.g., see Figure 29.1). Hence, a more refined form of cross-land mixing may con-
sist of upwind advective fluxes acting between non-local points in the model, where the advective velocity
is specified based on observations. Such sophistication, however, is not implemented in MOM. Indeed, it is
arguable that one may not wish to have more details than provided by the simpler form above, since more
details also further constrain the solution.
kbot kbot
ktop ktop
U1
U2
Figure 29.1: Schematic of cross-land mixing. The model’s grid mesh is assumed too coarse to explicitly
represent the lateral exchange of water masses. For this schematic, we consider an observed sub-grid scale
transport U1moving in one direction, and U2in another. To represent the mixing effects on tracers by
these transports, we suggest taking the exchange rate Uin MOM’s cross-land mixing to be the average of
the transports U= (U1+U2)/2. Cross-land mixing occurs between the user-specified depth levels k=ktop
and k=kbot. If ktop = 1, then cross-land mixing of volume in the top cell must be considered, in addition to
tracer transport, in order to maintain compatibility between volume and tracer budgets.
29.4 Mixing of mass/volume
In a model with a coarse mesh, the Mediterranean is typically land-locked. Hence, the net evaporation ex-
perienced over the Mediterranean region will cause the simulated ocean volume in this region to decrease
without bound. In a model resolving the Straits of Gibraltar, there is a transfer of mass across the Strait
from the Atlantic. This mass transfer creates a change in the height of the free surface.
Our goal is to have a parameterized mass transfer associated just with a difference in the free surface
height. That is, if the densities are different yet the free surface heights are equal, then there is no mixing.
By transferring masses of water, we must also recognize that the water contains tracer. Hence, mass and
tracer mixing must maintain the compatibility mentioned in Section 29.2. In this section, however, we only
introduce a basic form for mass transfer. Full compatibility with tracer transfer is achieved in Section 29.5
Elements of MOM November 19, 2014 Page 399

Chapter 29. Cross-land mixing Section 29.4
29.4.1 Instantaneous and complete mixing
To start by considering what form for mixing is appropriate, consider a convective analog whereby a com-
plete mixing of masses ρ(1) A(1) h(1) and ρ(2) A(2) h(2) leaves the final mass per area in both cells given by
(ρh)f inal =ρ(1) A(1) h(1) +ρ(2) A(2) h(2)
A(1) +A(2) ,(29.9)
where A(1) and A(2) are the temporally constant horizontal areas of the two grid cells and h(1) and h(2) are
their generally time dependent thicknesses.
There are two problems with this mixing. First, it is too rapid and too complete. We prefer a method that
allows for some control in the rate of mixing. Second, it changes the mass within a grid cell in cases where
the initial masses per area are equal yet the constant horizontal areas of the cells differ.
29.4.2 A finite time incomplete mixing
A finite time and incomplete mixing is analogous to that taken for the tracers in Section 29.3. Here, we
consider the time tendencies for the mass per area within a cell
∂t(ρ(1) h(1)) = γ(1) (ρ(2) h(2) −ρ(1) h(1)) (29.10)
∂t(ρ(2) h(2)) = γ(2) (ρ(1) h(1) −ρ(2) h(2)),(29.11)
where γ(1) and γ(2) are inverse damping times. This proposed mixing results in a transfer of mass only
when the mass per area within the two boxes differs. The total mass of the two-box system is conserved if
the following constraint is satisfied
∂t[(ρhA)(1) + (ρhA)(2)]=(A(1) γ(1) −A(2) γ(2)) (ρ(2) h(2) −ρ(1) h(1))=0.(29.12)
This relation places a constraint on the inverse damping times γ(1) and γ(2)
A(1) γ(1) =A(2) γ(2) (29.13)
which is easily satisfied.
The problem with the mixing prescribed by equations (29.10) and (29.11) is that mixing will ensue in the
following two undesirable cases. First, if the densities of the two cells are initially the same ρ(1) =ρ(2) =
ρ, yet the cells have different thicknesses, then density change is driven solely by the difference in cell
thicknesses
h(1) ∂tρ(1) =ργ(1) (h(2) −h(1)) (29.14)
h(2) ∂tρ(2) =ργ(2) (h(1) −h(2)).(29.15)
Such is acceptable in our scheme only for the surface ocean grid cell.
Another problem with the mixing prescribed by equations (29.10) and (29.11) is seen by considering
the situation whereby two top model grid cells have initially equal thicknesses h(1) =h(2) =hyet different
densities. The model grid cell thickness will evolve because of the difference in densities
ρ(1) ∂th(1) =hγ(1) (ρ(2) −ρ(1)) (29.16)
ρ(2) ∂th(2) =hγ(2) (ρ(1) −ρ(2)).(29.17)
However, as stated at the beginning of this section, we aim to prescribe a mixing process that occurs
only when the tracer concentration and/or free surface heights differ. Therefore, we must consider an
alternative to equations (29.10) and (29.11)
Elements of MOM November 19, 2014 Page 400

Chapter 29. Cross-land mixing Section 29.5
29.4.3 A finite time incomplete mixing for surface cells
We consider the following prescription for the surface grid cells, in which mixing occurs only when the
surface heights differ
∂t(ρ(1) h(1)) = γ(1) ρ(h(2) −h(1)) (29.18)
∂t(ρ(2) h(2)) = γ(2) ρ(h(1) −h(2)).(29.19)
When considered over interior model grid cells, then we prescribe no mass transfer. The density factor ρ
can be given by anything convenient, such as
ρ=ρ(1) +ρ(2)
2,(29.20)
or the even simpler prescription
ρ=ρo.(29.21)
29.5 Tracer and mass mixing
The general case of mixing tracers and mass is now considered. The following are the aims of the formu-
lation.
• Total fluid mass in the two boxes is conserved.
• Total tracer mass in the two boxes is conserved.
• In the rigid lid Boussinesq full cell case, the tracer tendency reduces to equations (29.7) and (29.8)
used in MOM1.
• Mass is exchanged only between top grid cells, in which case if the tracer concentration in the two
boxes is the same yet the mass differs, then mixing of mass will leave the tracer concentrations
unchanged.
• The time tendency for the mass exchange in the top cells is proportional to the difference in sur-
face height eta t between the cells, rather than the generally smaller difference between the cell
thickness dzt.
Mixing that satisfies these constraints is given by the following for the surface grid cells with k= 1
∂t(ρ(1) h(1) T(1)) = 2U ρo
A(1) (H(1) +H(2))!(h(2) T(2) −h(1) T(1)) (29.22)
∂t(ρ(2) h(2) T(2)) = 2U ρo
A(2) (H(1) +H(2))!(h(1) T(1) −h(2) T(2)) (29.23)
∂t(ρ(1) h(1)) = 2U ρo
A(1) (H(1) +H(2))!(h(2) −h(1)) (29.24)
∂t(ρ(2) h(2)) = 2U ρo
A(2) (H(1) +H(2))!(h(1) −h(2)) (29.25)
Likewise, for interior cells with k > 1, we prescribe
∂t(ρ(1) h(1) T(1)) = 2Urho dzt
A(2) (H(1) +H(2))!(T(2) −T(1)) (29.26)
∂t(ρ(2) h(2) T(2)) = 2Urho dzt
A(2) (H(1) +H(2))!(T(1) −T(2)) (29.27)
∂t(ρ(1) h(1)) = 0 (29.28)
∂t(ρ(2) h(2))=0.(29.29)
Elements of MOM November 19, 2014 Page 401

Chapter 29. Cross-land mixing Section 29.6
In these equations, His the depth of a column with a resting ocean surface. For the k > 1equations,
rho dzt is the averaged thickness weighted density for the two cells. For the k= 1 equations,
h(k= 1) = Grd%dztk=1+eta t (29.30)
is the thickness of the top cell for the case of a geopotential vertical coordinate. The general Thickness%dzti,j,k=1
thickness varies much less rapidly in the horizontal when employing zstar or pstar as the vertical coordi-
nate. In order to employ similar mixing rates for the geopotential model as for the general vertical co-
ordinate models, we prefer the more restricted definition (29.30) of thickness based on the geopotential
model. The mass per area equations (29.24) and (29.25) result from the tracer equations (29.22) and
(29.23) upon setting the tracer concentrations to a constant, as required for compatible budgets.
29.6 Formulation with multiple depths
We now consider the case where there are multiple boxes in the vertical. We restrict attention to situations
where mixing occurs between boxes at the same vertical level, as shown in Figure 29.1.
29.6.1 MOM1 formulation of cross-land tracer mixing
In MOM1, the vertical cells all have time independent thicknesses (i.e., rigid lid geopotential coordinate
model), and the fluid is Boussinesq. It is useful to start with this case prior to considering the more general
case.
In the full cell rigid lid case, we follow the approach given by equations (29.7) and (29.8), where the
relevant volume now becomes that for the respective column. The volumes for the two columns lx = 1,2
are given by
V(lx)=A(lx)
ktop
X
k=kbot
dztk=A(lx)H(lx),(29.31)
where
A(lx)=dxti,j(lx)dyti,j(lx)(29.32)
are the generally different horizontal cross-sectional areas of the tracer cells in the two columns, and
H(1) =H(2) is the vertical thickness of the two columns. The top and bottom k-levels for the columns are
set by k=ktop and k=kbot. As mentioned earlier, the formulation here allows for mixing only between
boxes that live on the same k-level, so k=ktop and k=kbot are the same for both columns lx = 1,2.
Use of these volumes in equations (29.7) and (29.8) leads to the tracer time tendencies for a particular
k-level
∂tT(1)
k=B(1) (T(2)
k−T(1)
k) (29.33)
∂tT(2)
k=B(2) (T(1)
k−T(2)
k),(29.34)
where
B(lx)=U
V(lx)(29.35)
represents the rate (B(lx)has units of inverse time) at which the two columns participate in the mixing. Con-
servation of total tracer is maintained between two horizontally adjacent boxes within the two columns. We
see such conservation via multiplying the above tendencies by the respective time independent volumes
of the two cells, and adding
∂t(V(1)
kT(1)
k+V(2)
kT(2)
k)=(T(2)
k−T(1)
k)(A(1) B(1) h(1)
k−A(2) B(2) h(2)
k)=0,(29.36)
where
A(1) B(1) h(1)
k=U(h(1)
k/H(1))
=U(h(2)
k/H(2))
=A(2) B(2) h(2)
k
(29.37)
Elements of MOM November 19, 2014 Page 402

Chapter 29. Cross-land mixing Section 29.6
was used.
29.6.2 Generalizing to free surface and non-Boussinesq
We now generalize to the case of time varying grid cells with generalized vertical coordinates. Based on
the considerations of Section 29.5 and the form used in MOM1, we write for the general case for a surface
grid cell with k= 1
∂t(ρ(1)
kh(1)
kT(1)
k) = 2U ρo
A(1) (H(1) +H(2))!(h(2)
kT(2)
k−h(1)
kT(1)
k) (29.38)
∂t(ρ(2)
kh(2)
kT(2)
k) = 2U ρo
A(2) (H(1) +H(2))!(h(1)
kT(1)
k−h(2)
kT(2)
k),(29.39)
where again H(1) and H(2) are the generally different static resting depths of the two columns, and
h(k= 1) = Grd%dztk=1+eta t (29.40)
according to our prescription given by equation (29.30). Setting the tracers to uniform constants leads to
the transfer of mass per area between two surface cells
∂t(ρ(1)
kh(1)
k) = 2U ρo
A(1) (H(1) +H(2))!(h(2)
k−h(1)
k) (29.41)
∂t(ρ(2)
kh(2)
k) = 2U ρo
A(2) (H(1) +H(2))!(h(1)
k−h(2)
k),(29.42)
For interior cells with k > 1, we prescribe
∂t(ρ(1)
kh(1)
kT(1)
k) = 2Urho dztk
A(1) (H(1) +H(2))!(T(2)
k−T(1)
k) (29.43)
∂t(ρ(2)
kh(2)
kT(2)
k) = 2Urho dztk
A(2) (H(1) +H(2))!(T(1)
k−T(2)
k),(29.44)
where
rho dztk=rho dzt(1)
k+rho dzt(2)
k
2(29.45)
is the average thickness weighted density of the adjacent cells, and
h=Thickness%dzti,j,k(29.46)
is the general thickness of the tracer cell. By inspection, for each k-level this formulation conserves total
tracer mass and total fluid mass (recall Section 29.4). Setting the tracers to uniform constants leads to a
zero transfer of mass per area between two interior cells.
These budgets can be written in a form familiar from other damping processes, in which for k= 1 we
have
∂t(ρ(1) h(1) T(1)) = γ(1) ρo(h(2) T(2) −h(1) T(1)) (29.47)
∂t(ρ(2) h(2) T(2)) = γ(2) ρo(h(1) T(1) −h(2) T(2)) (29.48)
∂t(ρ(1) h(1)) = γ(1) ρo(h(2) −h(1)) (29.49)
∂t(ρ(2) h(2)) = γ(2) ρo(h(1) −h(2)) (29.50)
where the depth label kwas omitted for brevity, and
γ(1) =2U
A(1) (H(1) +H(2))(29.51)
γ(2) =2U
A(2) (H(1) +H(2))(29.52)
Elements of MOM November 19, 2014 Page 403

Chapter 29. Cross-land mixing Section 29.7
defines the damping coefficients. For interior cells, only tracer concentration is mixed, in which case
∂t(ρ(1) h(1) T(1)) = γ(1) rho dzt (T(2) −T(1)) (29.53)
∂t(ρ(2) h(2) T(2)) = γ(2) rho dzt (T(1) −T(2)),(29.54)
with γ(1) and γ(2) as for the surface cell.
The damping coefficients (29.51) and (29.52) are generally time dependent for cases with mixing in
the top cell and where the free surface height is included when computing the column thicknesses H(1)
and H(2). One may alternatively be motivated to keep the damping coefficients constant in time by setting
H(1) and H(2) to be the time independent depth of the respective columns. This choice is appropriate
when using cross-land mixing between columns in shallow regions where the free surface height is some
nontrivial fraction of the full column depth. MOM generally sets the thicknesses to the time independent
depths.
To get a sense for the strength of the mixing, consider the case of a one-degree horizontal grid mesh
where the upper thousand meters of the water column is mixed across Gibraltar with U= 1.75×106m3s−1,
which is a reasonable value. With H(1) =H(2) ≈1000mwe have
V(1) ≈V(2) ≈1.2×1013m3,(29.55)
and to the damping coefficient
γ(1) ≈γ(2) =U
V≈1.5×10−7s−1≈77 days−1.(29.56)
Just as for any other form of mixing, if the damping coefficients are too large, then it is possible for there
to be numerical instabilities. MOM provides a check so that no more than one-half of a particular grid cell
is mixed per model time step.
29.7 Suppression of B-grid null mode
When mixing the free surface height across an unresolved strait, it has been found essential to mix be-
tween two pairs of adjacent columns in order to suppress the checkerboard null mode present when using
the B-grid version of MOM (see Chapter 26 of Griffies et al. (2004)). For the Mediterranean example, this
means choosing any two adjacent points on each side of Gibraltar and setting the volume transport for
each column to U= (1/2)1.75 ×106m3s−1.
Elements of MOM November 19, 2014 Page 404

Chapter 30
Cross-land insertion
Contents
30.1 Introduction ............................................405
30.2 Algorithm details .........................................406
30.3 An example: insertion to three cells in MOM4.0 .......................407
30.4 An example: insertion to just the top cell in MOM4.0 ...................409
30.5 Updates for generalized level coordinates ..........................410
The purpose of this chapter is to present the method used in MOM for adjusting volume/mass and
tracers across land separated points, such as across an unresolved Strait of Gibraltar, in a way that aims
to reduce the difference between the surface heights. The method is a hybrid between the river discharge
process in Chapter 28 and the cross-land mixing process of Chapter 29.
Both the cross-land insertion and river discharge schemes were originally implemented in MOM4.0, in
which there is no interior volume sources, and the interior grid cells maintain constant volume. It is only
the top model grid cell can modify its volume. This constraint leads to an extra step to conserve volume
when moving volume from a surface cell to an interior cell. The result of this constraint is illustrated in
Figure 30.1.
The following MOM module is directly connected to the material in this chapter:
ocean param/sources/ocean xlandinsert.F90.
30.1 Introduction
In Nature, marginal seas such as the Mediterranean have a nontrivial connection to the World Ocean.
Hence, depletion of water in marginal seas by more than a few meters, or over-flowing water, is unlikely in
a century scale climate change scenario, even in cases where the net moisture budget over the regions
surrounding the marginal sea experience nontrivial changes. That is, the sea levels in marginal seas are
roughly in equilibrium with that in the World Ocean.
In many coarse climate models, the connection between marginal seas and the World Ocean is unre-
solved. The cross-land mixing process discussed in Chapter 29 specifies an a priori rate for mixing water
masses on the opposite sides of an unresolved straight. This method works fine for simulations where
surface forcing is reasonably steady in time. Hence, the sea level in the marginal sea cannot deviate
drastically from that in the World Ocean to which it mixes.
Problems arise in a climate change simulation where in general the net moisture balance over regions
may experience a trend. Hence, a constant cross-land mixing rate may prove insufficient to ensure that
the marginal sea grid cells do not either dry out or become overly full. As MOM cannot numerically run
405

Chapter 30. Cross-land insertion Section 30.2
with a dry top grid cell, it is necessary for numerical purposes to ensure that these cells remain wet. We are
therefore motivated to provide a mechanism for the coarse numerical model to retain water levels within
enclosed seas that are roughly in equilibrium with the corresponding levels in the adjacent World Ocean.
The cross-land insertion process described in this chapter is a hybrid between the river discharge pro-
cess in Chapter 28 and the cross-land mixing process of Chapter 29. Cross-land insertion computes the
difference in surface height between two grid columns separated by an unresolved straight. The surface
height difference defines a volume of seawater that is taken from the thicker cell and inserted into the
column with the thinner surface height. The insertion occurs over a depth set by the user, and is realized
via an upwind advection scheme just as in the river discharge method. The time scale for the insertion is
set according to a user specified delay time.
For cases in practice at GFDL, insertion occurs just from top cell to top cell. In this case, the cross-land
insertion process has the same mathematical form as the cross-land mixing process. Importantly, the rate
of mixing between the two cells with the cross-land insertion process is proportional to the surface height
difference. In contrast, for the cross-land mixing process, the rate of mixing is constant in time.
30.2 Algorithm details
Consider two columns of a Boussinesq fluid. Let the horizontal cross-sectional area of the two columns be
A1and A2, respectively, and let the vertical thickness of their top cells be h1and h2. The total volume of
seawater in the two top cells is
V=A1h1+A2h2.(30.1)
The cross-land insertion process must keep this volume constant. In particular, if the two top cells are
allowed to freely exchange fluid and reach an equilibrium, then the top cells would each have the same
final thickness hgiven by
h=V
A1+A2
.(30.2)
This result follows from volume conservation, which requires
A1h1+A2h2=A1h+A2h. (30.3)
We prescribe a mechanism to exchange fluid over a finite time so that the exchange nudges the top cells
toward the same thickness h.
To illustrate the algorithm, assume at the initial time that the free surface elevations satisfy η1> η2.
Upon full exchange (after an infinite time), the amount of water transferred from the thicker column to the
thinner column is
(h1−h)A1= (h−h2)A2.(30.4)
This exchange leads to the final volume in the two cells
h1A1−(h1−h)A1=hA1(30.5)
h2A2+ (h−h2)A1=hA2.(30.6)
Now assume that water is removed just from the surface cell from the thicker column and inserted into the
adjacent thinner column over its upper few cells. Figure 30.1 illustrates the algorithm.
If the transfer is assumed to occur at a finite rate set by a time constant τ, then one can identify an
effective rate of volume that leaves the thicker cell
Rthick A1=A1(h1−h)/τ. (30.7)
The corresponding rate of volume that enters the thinner cell is
Rthin A2=A2(h−h2)/τ. (30.8)
The volumes rates are the same, but the area normalized rates Rthick and Rthin differ when the horizontal
areas are different. Importantly, the rates of transfer are functions of the difference in surface heights.
Elements of MOM November 19, 2014 Page 406

Chapter 30. Cross-land insertion Section 30.3
This characteristic of the cross-land insertion process is fundamentally distinct from the cross-land mixing
process of Chapter 29. It is this property that makes the cross-land insertion process of use for climate
change situations.
The area normalized rates Rthick and Rthin are analogous to the river discharge rate considered in
Chapter 28. Consequently, it is anticipated that their magnitudes correspond roughly to that of river runoff,
whose values are on the order of a vertical velocity. This observation prescribes a time scale τon the order
of a day. A faster time scale may lead to numerical instability since it will force an overly strong tendency
in the surface height equation. As in Chapter 28, fluid from the thicker column is inserted into the adjacent
smaller column. Tracer conservation requires that we recognize that transferred seawater has a tracer
concentration of the surface cell in the thicker column.
Ignoring all other processes, the free surface and tracer equations for the two columns take the follow-
ing form. For the thicker column, just the top grid cell is affected
∂tηthick =−Rthick (30.9)
∂t(ρhC)thick
1=−Rthick Cthick
1ρo(30.10)
with ρ→ρofor the Boussinesq case. Note that for the tracer concentration in the Boussinesq case, we
have
∂tCthick
1=Cthick
1(−Rthick +Rthick)=0.(30.11)
This result holds so long as Cthick is evaluated to the τtime level when computing the tendency term in
the tracer equation. It is the expected result, since by transferring water with a concentration Cthick, we
should have left behind water of the same concentration (but less total tracer mass).
For the thinner column, all cells within the specified range 1≤k≤kr are affected
∂tηthin =Rthin
∂t(hρC)thin
1=Rthin [(δρC)thin
2+δ1ρoCthick
1]
∂t(hρC)thin
k=Rthin [(δρC)thin
k+1 −(δρC)thin
k+δkρoCthick
1]
∂t(hρC)thin
kr =Rthin [−(δρC)thin
kr +δkr ρoCthick
1]
(30.12)
30.3 An example: insertion to three cells in MOM4.0
It is useful to work through an explicit example to get a sense for how the scheme is expected to work.
For this purpose, consider the initial configuration shown in Figure 30.2, in which the thick column has an
excess surface height H. For simplicity, we take this excess height to also equal to the thickness of the
cells with a resting ocean surface. Assume that the horizontal cross-sectional area of the cells is all the
same. Hence, the rate of water transfer, R, is the same for the two columns, and is given by
R=H/τ (30.13)
with τthe damping time. Three cells in the vertical into which to transfer the water yields the fraction
δ= 1/3.(30.14)
The conservation equations for the top cell in the thick column are
∂tηthick =−R(30.15)
∂t(hC)thick
1=−RCthick
1(30.16)
where his the time dependent thickness of the thick upper cell, and we assumed a Boussinesq fluid for
simplicity. Note that the concentration on the right hand side of the tracer equation is evaluated at the
Elements of MOM November 19, 2014 Page 407
Chapter 30. Cross-land insertion Section 30.3
R C
R C
R C
R C
R C
R C
R C2
3
4
δ
δ
δ
δ
δ
δ
δ
1
2
3
4
4
3
2
k=4
k=3
k=2
k=1
thick
thick
thick
thick
k=4
k=3
k=2
Cthick
k=1
Figure 30.1: Schematic of the cross-land insertion algorithm. An amount of seawater is extracted from
the surface cell in a column with greater surface height. This water is inserted into the adjacent column
with smaller surface height. As implemented in MOM4.0, Insertion to cells with k > 1 requires a bubbling
upwards of water in order to conserve volume, since only the top cell can change its volume and MOM4.0
has no interior volume sources or sinks. This figure is directly analogous to Figure 28.1 which illustrates
the method used to discharge river water at depth. Note that insertion from the top cell to the top cell is
often used in practice. An example is provided in Section 30.4.
present time step, τ. As noted in Section 30.2, the tracer concentration remains unchanged in the top thick
cell, since
h∂tCthick
1=−RCthick
1−Cthick
1∂tηthick
=Cthick
1(−R+R)
= 0.
(30.17)
Conservation equations for the three cells in the thin column are
∂tηthin =R(30.18)
∂t(hC)thin
1=Rδ(Cthin
2+Cthick
1) (30.19)
∂t(H C)thin
2=Rδ(Cthin
3−Cthin
2+Cthick
1) (30.20)
∂t(H C)thin
3=Rδ(−Cthin
3+Cthick
1).(30.21)
Using ∂ththin =Rin the first tracer equation leads to
h∂tCthin
1=R(δCthin
2+δCthick
1−Cthin
1).(30.22)
The deep cells have time independent thickness h=H. For the surface cell, its thickness is assumed
to initially have the same value, hthin(τ) = H. Bringing these results together leads to the three tracer
Elements of MOM November 19, 2014 Page 408

Chapter 30. Cross-land insertion Section 30.4
concentration equations
∂tCthin
1=τ−1(δCthin
2+δCthick
1−Cthin
1) (30.23)
∂tCthin
2=τ−1δ(Cthin
3−Cthin
2+Cthick
1) (30.24)
∂tCthin
3=τ−1δ(−Cthin
3+Cthick
1).(30.25)
Now consider the initial tracer concentration values of
Cthin
k(τ) = 24 (30.26)
Cthick
1(τ) = 36,(30.27)
where the units are, for example, psu if the tracer represents salt. The first time step with these initial
conditions leads to the following budgets for tracer concentration. The top cell has the budget
τ ∂tCthin
1= (24δ+ 36δ−24)
=−4.(30.28)
The second cell’s budget is
τ ∂tCthin
2=δ(24 −24 + 36)
= 12.(30.29)
The third cell’s budget is
τ ∂tCthin
3=δ(−24 + 36)
= 4.(30.30)
Notice how the surface cell in the thin column has a negative tendency for its concentration, whereas
the surface thick cell has its concentration remain unchanged. The surface cell in the thin column has its
concentration reduced since its surface height increases by the amount of fluid that is moved from the
thick cell. This result may appear counter-intuitive since we are moving water with high tracer concentra-
tion from the thick column to the thin column. Additionally, only a fraction of the tracer that left the thick
cell is bubbled up to the top of the thin column. Hence, the negative tendency for the top cell in the thin
column can change to a positive tendency if the ratio δbecomes large enough. That is, when we insert
into fewer cells. The example in Section 30.4 considers this point further.
30.4 An example: insertion to just the top cell in MOM4.0
Consider now the case where the transfer is from the top cell of the thick column to just the top cell of the
thin column. Here, the surface height tendencies are the same, and the tracer budget for the thick cell is
the same. For the thin column, only the top cell is affected. The budget equations are thus given by
∂tηthick =−R(30.31)
∂t(hC)thick
1=−RCthick
1(30.32)
∂tηthin =R(30.33)
∂t(hC)thin
1=RCthick
1.(30.34)
Converting the tracer equations to tracer concentration equations leads to
∂tCthick
1= 0 (30.35)
∂tCthin
1= (R/h)(Cthick
1−Cthin
1).(30.36)
Elements of MOM November 19, 2014 Page 409
Chapter 30. Cross-land insertion Section 30.5
ThickThin
3
1
2
3
2
excess
H
H
H
H
1
Figure 30.2: Example for how the cross-land insertion method works. In the thicker column, we assume an
initial excess of water equal to the amount of water in one of the equally sized interior cells. This excess is
transported into the thinner column.
With Cthick
1= 36 and Cthin
1= 24, the tendency for Cthin
1is 12/τ, whereas it was −4/τ in the 3-cell insertion
example discussed in Section 30.3.
In general, recall that the rate of transfer, R, is a function of the difference in surface heights. For larger
surface height differences, the rate increases. This example provides a clear illustration of the difference
between the cross-land insertion process and the cross-land mixing of Chapter 29. Namely, when mixing
from top cell to top cell, the cross-land mixing process does so at a rate that is fixed. For the cross-land
insertion process, this rate changes as the surface height between the two columns changes.
30.5 Updates for generalized level coordinates
The generalized level coordinate model code in MOM allows for two modifications relevant for the cross
land insertion scheme. First, each grid cell can have a volume or mass source, thus allowing for water to
be arbitrarily moved from cell to cell, without requiring an a priori means to re-plumb the flow as in Figure
30.1 to conserve mass/volume. Second, each grid cell has a generally time dependent thickness, even in
the interior.
We have not generalized the formulation of cross-land insertion in a manner to exploit the added flex-
ibility of MOM. Instead, we have merely updated the algorithm to facilitate use of generalized level coor-
dinates and retain the basics of the MOM4.0 implementation. Given that the scheme is ad hoc anyhow, we
decided that there was little motivation to present a more rigorous or general formulation.
Elements of MOM November 19, 2014 Page 410

Chapter 31
The B-grid computational mode
Contents
31.1 Checkerboard mode .......................................411
31.2 Filter for sea surface height ...................................412
31.3 Filter for bottom pressure ....................................412
The purpose of this chapter is to detail the methods used in MOM to suppress the B-grid computational
mode associated with gravity waves. The following MOM module is directly connected to the material in
this chapter:
ocean core/ocean barotropic.F90
31.1 Checkerboard mode
As discussed by Mesinger (1973), Killworth et al. (1991), Pacanowski and Griffies (1999), Griffies et al.
(2001), and Section 12.9 of Griffies (2004), there is a ubiquitous problem with B-grid models due to a null
mode present when discretizing inviscid gravity waves. This mode is absent on the C-grid, though there
is another mode on the C-grid associated with the Coriolis force (Adcroft et al.,1999). The B-grid null
mode manifests in the velocity field when using a relatively small viscosity. Additionally, it manifests in the
surface height or bottom pressure, especially in coarsely represented enclosed or semi-enclosed embay-
ments where waves tend to resonate rather than to propagate. The pattern is stationary1and appears
as a plus-minus pattern; i.e., as a checkerboard. As there is generally no dissipation in the surface height
budget
∂tη=∇·U+qw,(31.1)
suppression of the null mode requires some form of artificial dissipation. An anlogous situation exists with
the bottom pressure equation in a pressure based vertical coordinate model.
Various methods have been described in the literature (e.g., Killworth et al.,1991;Griffies et al.,2001)
to address this problem. The following constraints guide how we specify the filter.
• For the Boussinesq fluid, the tracer and surface height budgets must remain compatible in the sense
defined in Section 10.7. Hence, if a filter is added to the surface height equation, one must corre-
spondingly be added to the tracer equation. Likewise, the non-Boussinesq tracer equation must have
a filter added if the bottom pressure equation has a filter.
• The filter should be zero in the case that the surface height is locally a constant, or if the bottom
pressure remains locally the same as the reference bottom pressure.
1Hence the term null, thus indicating it has a zero eigenvalue and zero phase speed.
411

Chapter 31. The B-grid computational mode Section 31.3
31.2 Filter for sea surface height
The following filter for the surface height in a depth based vertical coordinate model has been found suit-
able for suppressing noise2in the model of Griffies et al. (2004), and a variant on this form sufficient for
geopotential vertical coordinates was described in Section 12.9 of Griffies (2004)
∂tη= [∂tη]no filter +∇·(A∇η∗)δ∇η(31.2)
∂t(dztT)=[∂t(dzt T)]no filter +δk,1∇·[A∇(η∗T)] δ∇η.(31.3)
In these equations, A > 0is a diffusivity, δ∇ηvanishes if the surface height is locally constant, and δk,1
vanishes for all but the surface grid cell at k= 1. The surface height η∗is defined by
η∗=η+|ηmin|+ηoff(31.4)
where ηmin is the global minimum of the surface height, and ηoffis a nonzero offset. The use of η∗rather
than ηdoes not alter the filter acting on the surface height, since ∇η∗=∇η. However, η∗is important for
the tracer, since it ensures that η∗Thas the same sign as T. If we instead diffused η T , regions where η < 0
could lead to negative diffusion, which results in tracer extrema and potential instabilities. The alternative
δk,1∇·[A∇(dztT)] is not desirable for z∗and σvertical coordinates, in which case the bottom topography
potentially adds a nontrivial level of smoothing even when the surface height is a uniform constant.
Global conservation of volume and tracer is ensured by using no-flux conditions at the side boundaries.
Local conservation is ensured since the tracer and volume equations are compatible, as evidenced by
setting the tracer concentration to unity in the tracer equation which, upon vertical integration, recovers
the surface height equation (see Section 10.7). Note that a more conventional treatment of the filter in the
tracer equation is given by the convergence of the thickness weighted flux −η A∇T. However, ∇·(η A∇T)
is not compatible with the filter applied to the surface height, and so this alternative approach will lead to
local non-conservation.
31.3 Filter for bottom pressure
For pressure based vertical coordinates, we use the following filter
∂tpb= [∂tpb]no filter +∇·(A∇p∗
b)δ∇p∗
b(31.5)
∂t(ρdztT)=[∂t(ρdzt T)]no filter +δk,kb ∇·[A∇(g−1p∗
bT)]δ∇p∗
b,(31.6)
where δ∇p∗
bvanishes where ∇p∗
bvanishes. The modified bottom pressure p∗
b>0is defined by
p∗
b=pb−po
b+|min(pb−po
b)|+poff
b,(31.7)
where poff
bis a nonzero offset pressure. The positive pressure p∗
bis defined in a manner analogous to
the definition of η∗given by equation (31.4). Note that subtracting out the reference bottom pressure po
bis
useful prior to performing the Laplacian operations. Doing so ensures that the filter does not overly smooth
the bottom pressure in regions where its undulations arise from variations in the bottom topography. Such
variations are physical, and do not reflect a problem with the B-grid and so should not be filtered. The term
g−1p∗
bappearing in the tracer equation acts like an effective mass per area
(ρdzt)eff≡g−1p∗
b,(31.8)
which is positive since p∗
b>0. That is, the filter on the bottom pressure equation acts like a mass source
in the bottom cell. Hence, tracer must be rearranged in the bottom cell in order to maintain compatibility
(see Section 10.7). This filter satisfies the global and local conservation constraints, while adding a level
of filtering needed to smooth the bottom pressure.
2For added scale selectivity, it is sometimes useful to employ a biharmonic operator instead of a Laplacian. However, much
care should be exercised when using the biharmonic, as it is not positive definite and so can lead to negative tracer concentrations.
Therefore, the biharmonic, although present in the MOM codes, is not recommended for general use.
Elements of MOM November 19, 2014 Page 412
Diagnostic capabilities
To rationalize a numerical simulation with MOM, one must perform a suite of analyses to connect the
model results to those from theory and observations. This facet of numerical oceanography has long
been fundamental to the utility of MOM, since it is distributed with great deal of analysis or diagnostic
capabilities. In this part of the manual, we describe some of these features of MOM. The MOM developers
encourage contributions of further diagnostic features from the broader MOM community as they may
arise from various applications.
A question that is often asked: “Is there a tabulation of all diagnostics available in MOM?” There is
unfortunately, no such tabulation. One means of obtaining a listing of diagnostics is through the following
Unix command:
grep -whr -e "OO\|\(register_diag_field[[:blank:]]\{0,\}(\)" . | sed -e "s/ˆ[ˆ/]*register_diag_field[[:blank:]]\{0,\}(//" | uniq > diag_fields
413

Section 31.3
Elements of MOM November 19, 2014 Page 414

Chapter 32
Methods for diagnosing mass transport
Contents
32.1 Brief on notation .........................................416
32.2 Meridional-overturning streamfunction ...........................416
32.2.1 Summary of mass conservation for a finite region ..................... 416
32.2.2 Zonally integrated mass transport ............................. 416
32.2.3 Mass transport streamfunction ............................... 417
32.2.4 Transport beneath an arbitrary surface ........................... 419
32.2.5 Transport from GM90 .................................... 420
32.2.5.1 Boussinesq geopotential coordinates ....................... 420
32.2.5.2 Non-Boussinesq pressure coordinates ...................... 420
32.2.6 Diagnosing the streamfunction in Ferret from MOM output ............... 421
32.3 Mass transport through tracer cell faces ...........................421
32.3.1 Tracer cell mass transport from parameterized mesoscale and submesocale eddies . . 422
32.3.2 Summary of the mass transport diagnostics ........................ 423
32.3.3 A caveat about masking for the GM and submesoscale streamfunctions ........ 424
32.4 Vertically integrated transport .................................425
32.4.1 Summary of the rigid lid case ................................ 425
32.4.2 General case of divergent flow in non-Boussinesq fluids ................. 425
32.4.3 Vertically integrated transport from eddy parameterizations .............. 426
The purpose of this chapter is to present the various methods available in MOM to diagnose mass
transport. We give particular attention to the mathematical formulation of streamfunctions commonly
used to summarize the overturning circulation as well as the vertically integrated circulation. This chapter
is updated from that presented in the MOM4.0 manual of Griffies et al. (2004).
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean barotropic.F90
ocean diag
ocean param/neutral
ocean param/mixing/ocean submesoscale.F90
415

Chapter 32. Methods for diagnosing mass transport Section 32.2
32.1 Brief on notation
In this chapter, we employ generalized orthogonal coordinates, in which the horizontal grid increments are
given by
dx=h1dξ1(32.1)
dy=h2dξ2.(32.2)
The stretching functions h1and h2are generally dependent on the horizontal position on the sphere, but
independent of vertical position and independent of time. In spherical coordinates,
dx=Rcosφdλ(32.3)
dy=Rdφ, (32.4)
with Rthe earth’s radius, λthe longitude, and φthe latitude.
32.2 Meridional-overturning streamfunction
The meridional overturning streamfunction is commonly used to diagnose features of the thermohaline
circulation. The purpose of this section is to formulate an expression for this streamfunction, and in turn
to highlight its limitations.
32.2.1 Summary of mass conservation for a finite region
In Section 2.6, we developed the conservation equations for scalar fields over a finite size region, such as
a model grid cell. In particular, the mass budget for a grid cell (equation (2.155)) is written
∂t(dzρ)=dzρS(M)−∇s·(dzρ u)−(ρ w(s))s=sk−1+ (ρ w(s))s=sk.(32.5)
In the following, we neglect mass sources S(M)for brevity, but they may be easily reintroduced if present as
part of a model’s subgrid scale parameterization.1As noted by equation (2.156), the divergence operator
acting on the flux of mass per unit horizontal area takes the form
∇s·(dzρ u) = 1
dy
∂
∂x (dydzρu) + 1
dx
∂
∂y (dxdzρv),(32.6)
which leads to the expanded form of mass conservation
∂t(dxdydzρ) = −dx∂
∂x (dydzρu)−dy∂
∂y (dxdzρv)
−(dxdy ρw(s))s=sk−1+ (dxdy ρw(s))s=sk.
(32.7)
This result follows by assuming the horizontal area dxdyof a grid cell is independent of time and depth.
32.2.2 Zonally integrated mass transport
We now consider the integrated mass transports
V=
ξ1
b
Z
ξ1
a
dx(v ρdz) (32.8)
W=
ξ1
b
Z
ξ1
a
dx(wρ dy),(32.9)
1For example, the cross land scheme of Chapter 29 and the cross-land insertion scheme of Chapter 30 introduce mass source and
sink terms.
Elements of MOM November 19, 2014 Page 416

Chapter 32. Methods for diagnosing mass transport Section 32.2
which provide the meridional and vertical transport of mass (kg/sec) integrated along a line of constant
generalized zonal coordinate ξ1. Integration endpoints ξ1
aand ξ1
bare assumed to be at land-sea bound-
aries, where uvanishes, or over a periodic domain. As in the spherical coordinate case, we refer to Vas
the generalized meridional transport, though the generalized coordinates need not be aligned with the
geographical latitude/longitude coordinates.
Now consider the meridional derivative of the meridional transport
∂yV=∂
∂y
ξ1
b
Z
ξ1
a
dx(v ρdz)
=1
h2∂ξ2
ξ1
b
Z
ξ1
a
dx(v ρdz)
=1
h2
ξ1
b
Z
ξ1
a
∂
∂ξ2(dxv ρdz).
(32.10)
In the last step, we alllowed for the partial derivative operator ∂/∂ξ2to commute with integration over
paths with constant generalized zonal coordinate ξ1. This result follows since the generalized horizontal
coordinates (ξ1,ξ2)are independent. Correspondingly, we may introduce the increment dξ2inside and
outside of the integral to render
∂yV=1
dy
ξ1
b
Z
ξ1
a
dy∂
∂y (dxv ρ dz).(32.11)
We now use the mass conservation equation (32.7) to find
∂yV=1
dy
ξ1
b
Z
ξ1
a −∂t(dxdydzρ)−(dxdy ρw(s))s=sk−1+ (dxdy ρ w(s))s=sk!,(32.12)
where we cancelled the zonal transport term u ρ dydz, since it either vanishes at the zonal boundaries
(ξ1
b,ξ1
a), or exhibits periodicity. Introducing the vertical transport (32.9) yields
dy ∂yV+δkW=−
ξ1
b
Z
ξ1
a
∂t(dxdydzρ) (32.13)
with
δkW=Wk−1−Wk(32.14)
the vertical finite increment of the vertical transport.
Equation (32.13) is a direct result of the mass conservation equation (32.7) applied to a zonal integral.
It says that the divergence of the zonally integrated meridional and vertical transport equals to the zonally
integrated tendency of mass. This result is the basis for our next step, which is to define a streamfunction.
32.2.3 Mass transport streamfunction
A streamfunction can be defined for any non-divergent transport. For the zonally integrated mass trans-
port, equation (32.13) says there is zero divergence if the zonal integral of the time tendency of mass
Elements of MOM November 19, 2014 Page 417
Chapter 32. Methods for diagnosing mass transport Section 32.2
vanishes. Zero time tendency arises if the top and bottom grid cell boundaries are set according to con-
stant hydrostatic pressure surfaces, so that ρdz=−g−1dp. In this case, the mass within a cell is constant
in time. Analogously, there is also a zero divergence of the volume transport for a Boussinesq fluid using
geopotential vertical coordinates, in which case the volume of fluid in a cell is constant. In more general
cases, however, there is no guarantee that the mass within a cell is constant. Additionally, in the pres-
ence of water crossing the ocean boundaries, mass will change, again leading to a nonzero divergence.
Even with these caveats, the streamfunction defined below provides a very useful measure of the zonally
integrated mass transport, thus motivating its near ubiquitous use as a model diagnostic.
In the case of a non-divergent zonally integrated mass transport, a mass transport streamfunction Ψ
can be introduced according to the following specifications2
V=−δkΨ(32.15)
W=Ψ,y.(32.16)
The streamfunction has dimensions mass/time, just as the meridional and vertical transports Vand W.
The typical oceanographic dimension for these transports is Sverdrup, where 1Sv = 109kgsec−1.
To derive a diagnostic expression for the streamfunction, we may start from either of the expressions
(32.15) or (32.16). Integration and the use of boundary conditions then leads to expressions for Ψ, with the
two expressions equivalent if the zonally integrated mass transport is non-divergent. In many simulations,
the meridional transport Vis more easily computed than the vertical transport W, making the specification
V=−δkΨthe most common starting point. From a finite volume perspective, the relation V=−δkΨsays
that the discretized streamfunction should be computed at the top and bottom interfaces of grid cells,
so that its vertical difference across the cells then leads to the meridional transport through the cell’s
vertical side walls (see Figure 32.1). Correspondingly, the streamfunction is horizontally co-located with
the meridional transport V.3
The relation V=−δkΨremains valid if we modify Ψby any function of horizontal position, since the
vertical difference eliminates the arbitrary function.4We choose to exploit this ambiguity by specifying the
arbitrary function so that the streamfunction has a zero value at the ocean bottom. We are motivated to
take this choice since for most oceanographic purposes, there is no mass transport considered between
the liquid ocean and solid earth. Consequently, the solid earh boundary condition is time independent, and
for convenience we specify that it vanishes.
Let us now develop the streamfunction, starting from the ocean bottom using the definition V=−δkΨ.
For the top surface of the bottom-most cell with k=kmt, we have
Ψkmt−1= 0 −Vkmt ,(32.17)
where 0 = Ψkmt is inserted as a place-holder for the next iteration, and Vkmt is the meridonal transport
leaving the vertical side walls within the bottom-most cell. For the next cell up in the column, we have
Ψkmt−2=Ψkmt−1−Vkmt−1
=−Vkmt −Vkmt−1.(32.18)
Induction leads to the result
ΨK=−
kmt
X
k=K+1 Vk
=−
kmt
X
k=K+1
xb
Z
xa
dx(v ρdz)k
,
(32.19)
2This definition of Ψhas an associated sign convention, with the opposite convention just as valid mathematically, but chosen less
frequently in practice.
3We are led to an alternative grid placement for Ψif starting from the relation W=Ψ,y.
4This ambiguity represents a gauge symmetry, which can be exploited in whatever manner is most convenient.
Elements of MOM November 19, 2014 Page 418
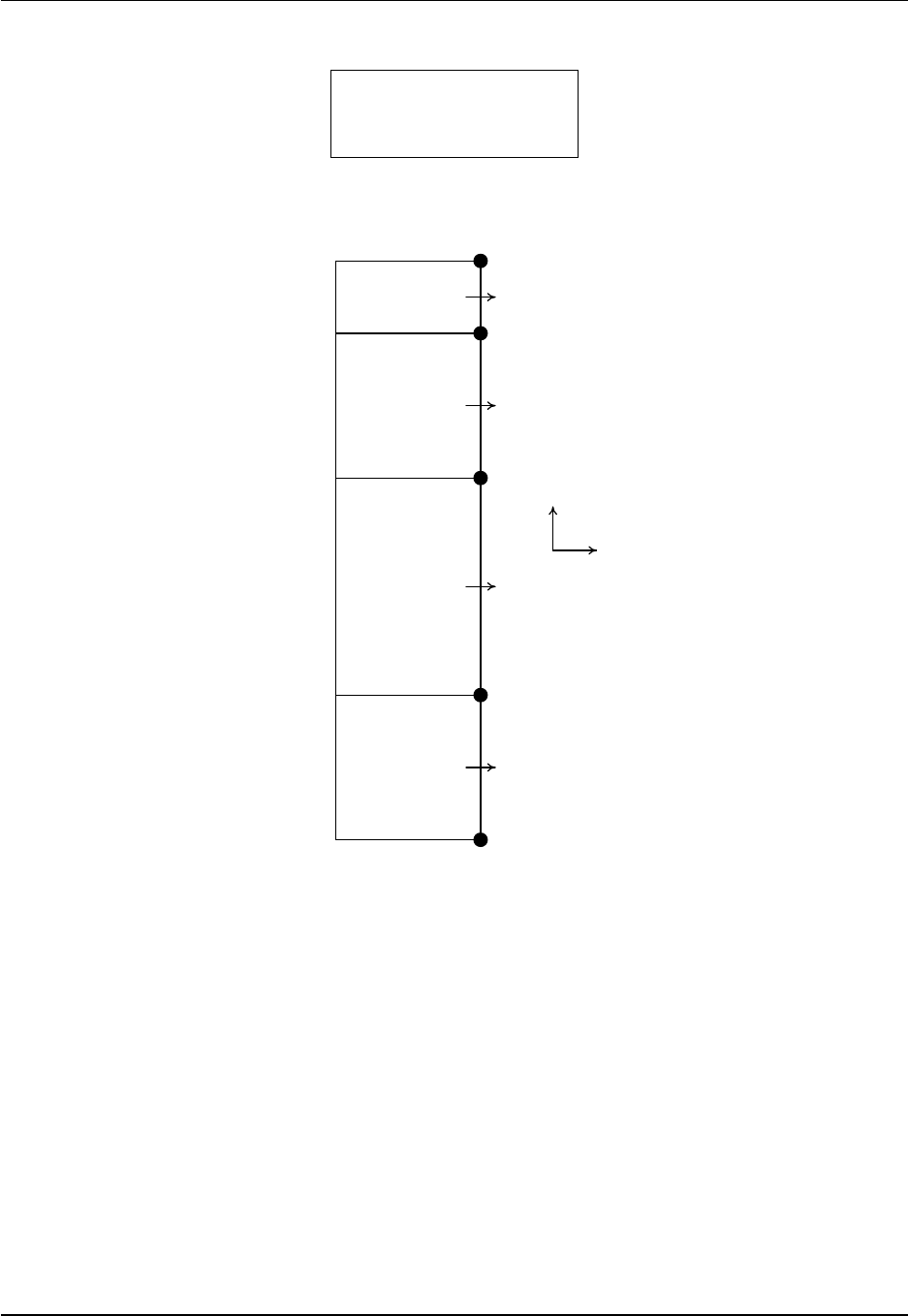
Chapter 32. Methods for diagnosing mass transport Section 32.2
with a continuous expression given by
Ψ(y,z,t) = −
xb
Z
xa
dx
z
Z
−H
v ρdz0.(32.20)
In the continuous expression, it is important to perform the vertical integral first, since the bottom topog-
raphy z=−H(x,y)is a function of the horizontal position.
STREAMFUNCTIONS 293
In the continuous expression, it is important to perform the vertical integral first,
since the bottom topography z=−H(x,y)is a function of the horizontal position.
Ψkmt =0
Vkmt
Ψkmt−1
Vkmt−1
Ψk=2
Vk=2
Ψk=1
Vk=1
Ψk=0
y
z
Figure 21.1 This figure illustrates the relation between the meridional-overturning stream-
function Ψand the meridional transport V, for the particular case of kmt =4
vertical grid cells. The streamfunction is evaluated on the interfaces between
the vertical cells, whereas the transport measures the mass leaving the cell in
the meridional direction. Note the relatively think bottom cell can arise from
the use of bottom partial step representation of topography as used in MOM4.
21.2.4 Transport beneath an arbitrary surface
As shown in Section 40.9 of Pacanowski and Griffies (1999), we can extend the
above considerations to the case of generalized vertical coordinates. In this case,
we are concerned with the meridional transport of fluid beneath some generalized
vertical coordinate surface. It is a straightforward matter to extend the definition of
the overturning streamfunction to this case, where
Ψ(y,s,t)=−
xb
Z
xa
dx
s(z)
Z
s(−H)
vρdz0,(21.21)
with s=s(x,y,z,t)the generalized vertical coordinate (see Griffies (2004) for de-
tails). Surfaces that are physically of interest include various potential density sur-
faces, which are especially relevant when the flow is adiabatic. See Section 40.9
of Pacanowski and Griffies (1999) for more discussion.
Figure 32.1: This figure illustrates the relation between the meridional-overturning streamfunction Ψand
the meridional transport V, for the particular case of kmt = 4 vertical grid cells. The streamfunction is
evaluated on the interfaces between the vertical cells, whereas the transport measures the mass leaving the
cell in the meridional direction. Note the relatively thin bottom cell can arise from the use of bottom partial
step representation of topography as used in MOM.
32.2.4 Transport beneath an arbitrary surface
As shown in Section 40.9 of Pacanowski and Griffies (1999), we can extend the above considerations to
the case of generalized vertical coordinates. In this case, we are concerned with the meridional transport
of fluid beneath some generalized vertical coordinate surface. It is a straightforward matter to extend the
definition of the overturning streamfunction to this case, where
Ψ(y,s,t) = −
xb
Z
xa
dx
s(z)
Z
s(−H)
v ρdz0,(32.21)
Elements of MOM November 19, 2014 Page 419

Chapter 32. Methods for diagnosing mass transport Section 32.2
with s=s(x,y,z,t)the generalized vertical coordinate (see Griffies (2004) for details). Surfaces that are
physically of interest include various potential density surfaces, which are especially relevant when the
flow is adiabatic. See Section 40.9 of Pacanowski and Griffies (1999) for more discussion.
32.2.5 Transport from GM90
The parameterization of Gent and McWilliams (1990) and Gent et al. (1995) provides a volume transport in
addition to the resolved scale Eulerian mean transport. The total meridional-overturning streamfunction
takes the form
Ψ(tot)(y,z,t) = −
xb
Z
xa
dx
z
Z
−H
dz0ρ(v+vgm).(32.22)
We consider now special cases for the eddy-induced velocity vgm.
32.2.5.1 Boussinesq geopotential coordinates
In the Boussinesq case with geopotential vertical coordinates, the meridional eddy-induced velocity is
given by
vgm =−∂z(κSy) (32.23)
with Sy=−∂yρ/∂zρthe neutral slope in the y-direction and κ > 0a kinematic diffusivity. Performing the
vertical integral on the GM90 piece leads to
Ψ(tot)(y,z,t) = Ψ(y,z,t) + Ψgm(y,z,t) (32.24)
where
Ψgm(y,z,t) = ρ0
xb
Z
xa
dx(κSy) (32.25)
with κSy= 0 at z=−H, and ρ0the reference density for the Boussinesq fluid. Hence, the Gent et al. (1995)
parameterization adds a contribution that scales linearly with basin size, isopyncal slope, and diffusivity
Ψgm ∼ρ0LS κ. (32.26)
As an example, let κ= 103m2s−1,S= 10−3, and L= 107m, which yields T ≈ 10Sv. Such transport can
represent a nontrivial addition to that from the resolved scale velocity field.
32.2.5.2 Non-Boussinesq pressure coordinates
In the hydrostatic non-Boussinesq case with pressure vertical coordinates, the meridional eddy-induced
velocity is given by
vgm =∂p(g ρκ Sy) (32.27)
with Sy=−∂yρ/∂zρthe neutral slope in the y-direction relative to constant pressure surfaces. Performing
the vertical integral for the GM90 streamfunction leads to
Ψgm(y,z,t) =
xb
Z
xa
dx(ρκSy).(32.28)
Elements of MOM November 19, 2014 Page 420

Chapter 32. Methods for diagnosing mass transport Section 32.3
32.2.6 Diagnosing the streamfunction in Ferret from MOM output
In MOM, there are two key diagnostics computed on-line that should be saved in order to determine an
accurate expression for the streamfunction:
ty trans = dx(v ρ dz) (32.29a)
ty trans gm = dx(ρκSy) (32.29b)
Computing the Eulerian streamfunction (32.20) requires the following operations
Ψ(y,z,t) = −
xb
Z
xa
dx
z
Z
−H
v ρdz0
=−
xb
Z
xa
dx
η
Z
−H
v ρdz0+
xb
Z
xa
dx
η
Z
z
v ρdz0
=−ty trans[i=@sum,k=@sum] +ty trans[i=@sum,k=@rsum].
(32.30)
We must compute the streamfunction in this manner since Ferret’s relative sum k=@rsum starts from
an assumed zero value at the surface and integrates downward, whereas the streamfunction has a zero
boundary condition on the ocean bottom. Hence, without subtracting the term ty trans[i=@sum,k=@sum],
the diagnosed streamfunction will incorrectly have nonzero values at the bottom. A nonzero value for
ty trans[i=@sum,k=@sum] arises from net vertically integrated mass transport through a section. For a
rigid lid model, this net transport vanishes. However, for a model with real water fluxes, this net transport
will generally be nonzero.
The GM-streamfunction is simpler to compute, whereby
Ψgm(y,z,t) = ty trans gm[i=@sum].(32.31)
There is no vertical sum, since the vertical integral has already been performed analytically (equations
(32.25) and (32.28)). In particular, Ψgm (y,z,t)in the ocean surface cell equals ty trans gm[i=@sum,k=1].
Since the vertical integral of the GM-streamfunction vanishes, ty trans gm[i=@sum,k=0] is zero, by defi-
nition, although this level is not explictly saved in the output.
In a similar manner, the streamfunction from a skew flux implementation of the submesoscale eddy
parameterization of Fox-Kemper et al. (2008b), Fox-Kemper et al. (2008a) and Fox-Kemper et al. (2011)
(see Chapter 24) is computed as
Ψsubmeso(y,z,t) = ty trans submeso[i=@sum].(32.32)
There is no vertical sum required, since the vertical integral has already been performed analytically just
as for the GM-streamfunction (see Section 24.3.2). Furthermore, as for the GM-streamfunction, the subme-
soscale transport vanishes when integrated over the full ocean depth, so that ty trans submeso[i=@sum,k=0]
is zero, by definition, although this level is not explictly saved in the output.
32.3 Mass transport through tracer cell faces
MOM has diagnostics for the following three components to the mass transport from resolved flow passing
through the tracer cell
tx trans =u ρ dzdytracer cell zonal face (32.33a)
ty trans =v ρ dzdxtracer cell meridional face (32.33b)
tz trans =w ρ dxdytracer cell bottom face.(32.33c)
We note in these equations where the mass transport is centred on the tracer cell face. These fields are
saved in units of either mass-Sverdrup (109kg s−1or mass transport kg s−1.
Elements of MOM November 19, 2014 Page 421

Chapter 32. Methods for diagnosing mass transport Section 32.3
32.3.1 Tracer cell mass transport from parameterized mesoscale and submesocale ed-
dies
MOM5 generally employs the skew flux approach of Griffies (1998), which means we generally do not diag-
nose the mass transport crossing a cell face associated with subgrid scale parameterizations. Instead, we
diagnose a vertically integrated streamfunction for use in mapping overturning circulation. We diagnose a
similar overturning streamfunction for the submesoscale scheme from Fox-Kemper et al. (2011). For many
purposes, it is useful to diagnose the mass transport crossing through a cell face, which requires taking a
vertical difference as per the schematic shown in Figure 32.1. We detail this diagnostic calculation here.
The overturning diagnostic fields saved for the mesoscale parameterization schemes (e.g., Gent et al.
(1995)) are the following
tx trans gm (32.34a)
ty trans gm (32.34b)
whereas for the Fox-Kemper et al. (2011) scheme we use
tx trans submeso (32.35a)
ty trans submeso.(32.35b)
Each of these arrays extends from k= 1 to k=nk, with nk the total number of vertical grid cells. For a
vertical level k, the zonal fields are located at the bottom of a tracer cell and at the zonal face, whereas
the meridional fields are located at the bottom of a tracer cell and at the meridional face (see Figure 32.1).
The k= 0 field vanishes, so it is not diagnosed. Likewise, bottom cell (at k=kmt) transport vanishes,
though it is written in the diagnosed field.
To develop the algorithm to diagnose the eddy-induced velocity, we note the Gent et al. (1995) merid-
ional overturning diagnostic is given by
ty trans gm =ρdx κ S(y),(32.36)
where κis the diffusivity and S(y)is the meridional slope of the neutral direction. The corresponding merid-
ional eddy-induced velocity is
vgm =−∂z(κS(y)).(32.37)
A diagnostic calculation of the meridional eddy-induced velocity is thus given by
vgm[k] = − ty trans gm[k−1] −ty trans gm[k]
dxnt rho dzt !,(32.38)
where vgm[k]is centred on the north face of the tracer cell, and dxnt is the zonal width (in meters) of the
tracer grid cell at the northern face. More simply, we diagnose a meridional mass transport by taking the
vertical difference
(vgm ρdxdz)[k] = −(ty trans gm[k−1] −ty trans gm[k]).(32.39)
This transport corresponds directly to the mass transport component ty trans diagnosed for the resolved
velocity (equation (32.33b)).
We extend the above diagnostic results to the zonal component as well as to the submesoscale scheme.
A summary of these diagnostic results for the eddy-induced velocity components is the following.
ugm[k] = − tx trans gm[k−1] −tx trans gm[k]
dyet rho dzt !(32.40a)
vgm[k] = − ty trans gm[k−1] −ty trans gm[k]
dxnt rho dzt !(32.40b)
usubmeso[k] = − tx trans submeso[k−1] −tx trans submeso[k]
dyet rho dzt !(32.40c)
vsubmeso[k] = − ty trans submeso[k−1] −ty trans submeso[k]
dxnt rho dzt !,(32.40d)
Elements of MOM November 19, 2014 Page 422

Chapter 32. Methods for diagnosing mass transport Section 32.3
where dyet is the meridional width (in meters) of the tracer cell at its eastern face. The corresponding
mass transport is given by
(ugm ρdydz)[k] = −(tx trans gm[k−1] −tx trans gm[k]) (32.41a)
(vgm ρdxdz)[k] = −(ty trans gm[k−1] −ty trans gm[k]) (32.41b)
(usubmeso ρdydz)[k] = −(tx trans submeso[k−1] −tx trans submeso[k]) (32.41c)
(vsubmeso ρdxdz)[k] = −(ty trans submeso[k−1] −ty trans submeso[k]).(32.41d)
As for the resolved mass transport diagnosed in tx trans and ty trans, these parameterized mass trans-
ports are centered on the corresponding zonal and meridional tracer cell face.
The vertical component to the parameterized mass transport is derived through continuity, in which
the mass entering a cell from the parameterized scheme equals the mass leaving a cell. We start from the
ocean bottom and move upwards in a column to derive the following expressions
(wgm ρdxdy)[i,j,k −1] = (wgm ρdxdy)[i,jk] + (ugm ρdydz)[i−1,j,k]−(ugm ρdydz)[i,j,k] (32.42a)
+ (vgm ρdxdz)[i,j −1,k]−(vgm ρdxdz)[i,j,k]
(wsubmeso ρdxdy)[i,j,k −1] = (wsubmeso ρdxdy)[i,j,k] + (usubmeso ρdydz)[i−1,j,k]−(usubmeso ρdydz)[i,j,k]
(32.42b)
+ (vsubmeso ρdxdz)[i,j −1,k]−(vsubmeso ρdxdz)[i,j,k]
The vertical transport from subgrid scale transport vanishes for the bottom of the bottom-most cell, and
for the surface of the ocean surface cell.
32.3.2 Summary of the mass transport diagnostics
We now summarize the mass transport diagnostics available from the MOM CORE-II simulation. All trans-
ports are diagnosed in the respective face of the tracer cell
zonal transport[i] = x-transport on east face of tracer cell (32.43a)
meridional transport[j] = y-transport on north face of tracer cell (32.43b)
vertical transport[k] = z-transport on bottom face of tracer cell.(32.43c)
Each diagnostic field has units of mass-Sverdrup (109kg s−1). As the model is configured using the Boussi-
nesq kinematics, division by the constant reference density
ρo= 1035 kg m−3(32.44)
brings the mass transports into volume-Sverdrup units (106m3s−1).
The following summarizes the diagnostics needed for the resolved mass transport through a tracer cell
face
tx trans =u ρ dzdy(32.45a)
ty trans =v ρ dzdx(32.45b)
tz trans =w ρ dxdy(32.45c)
For the GM advective mass transport, we diagnose the advective mass transports
tx trans gm adv = (ugm ρdydz)[i,j,k] (32.46a)
ty trans gm adv = (vgm ρdxdz)[i,j,k] (32.46b)
tz trans gm adv = (wgm ρdxdy)[i,j,k] (32.46c)
Elements of MOM November 19, 2014 Page 423
Chapter 32. Methods for diagnosing mass transport Section 32.3
using the following algorithm
tx trans gm adv[i,j,k] = −tx trans gm[i,j,k −1] + tx trans gm[i,j,k] (32.47a)
ty trans gm adv[i,j,k] = −ty trans gm[i,j,k −1] + ty trans gm[i,j,k] (32.47b)
tz trans gm adv[i,j,k −1] = tz trans gm adv[i,j,k] (32.47c)
+tx trans gm adv[i−1,j,k]−tx trans gm adv[i,j,k]
+ty trans gm adv[i,j −1,k]−ty trans gm adv[i,j,k].
For the vertical transport, we set the bottom boundary condition
tz trans gm adv[i,j,k =kbot]=0.(32.48)
The top boundary condition
tz trans gm adv[i,j,k = 0] = 0,(32.49)
should be checked by determining whether
0≈tz trans gm adv[i,j,k = 1] + tx trans gm adv[i−1,j,k = 1] −tx trans gm adv[i,j,k = 1] (32.50)
+ty trans gm adv[i,j −1,k = 1] −ty trans gm adv[i,j,k = 1].
For the parameterized submesoscale advective mass transport, we diagnose the advective mass trans-
ports
tx trans submeso adv = (usubmeso ρdydz)[i,j,k] (32.51a)
ty trans submeso adv = (vsubmeso ρdxdz)[i,j,k] (32.51b)
tz trans submeso adv = (wsubmeso ρdxdy)[i,j,k] (32.51c)
using the following algorithm
tx trans submeso adv[i,j,k] = −tx trans submeso[i,j,k −1] + tx trans submeso[i,j,k] (32.52a)
ty trans submeso adv[i,j,k] = −ty trans submeso[i,j,k −1] + ty trans submeso[i,j,k] (32.52b)
tz trans submeso adv[i,j,k −1] = tz trans submeso adv[i,j,k] (32.52c)
+tx trans submeso adv[i−1,j,k]−tx trans submeso adv[i,j,k]
+ty trans submeso adv[i,j −1,k]−ty trans submeso adv[i,j,k].
For the vertical transport, we set the bottom boundary condition
tz trans submeso adv[i,j,k =kmxl]=0,(32.53)
where kmxl is the cell at the mixed layer base. The top boundary condition
tz trans submeso adv[i,j,k = 0] = 0,(32.54)
should be checked by determining whether
0≈tz trans submeso adv[i,j,k = 1] + tx trans submeso adv[i−1,j,k = 1] −tx trans submeso adv[i,j,k = 1]
(32.55)
+ty trans submeso adv[i,j −1,k = 1] −ty trans submeso adv[i,j,k = 1].
32.3.3 A caveat about masking for the GM and submesoscale streamfunctions
As shown in Figure 32.1, the discrete streamfunction Ψi,j,k sits on the bottom corner of a tracer cell. As
mentioned in the caption to this figure, Ψi,j,k vanishes for points where there is land just beneath either
adjacent ocean column. Unfortunately, the diagnostics in MOM5 do not properly account for the mask-
ing required to set the parameterized mesoscale or submesoscale streamfunctions to zero in such cases
Elements of MOM November 19, 2014 Page 424

Chapter 32. Methods for diagnosing mass transport Section 32.4
where there is land at k=kmt in one column but not in the other. To properly account for this mistake
requires the offline masking to be applied to the following streamfunctions
tx trans gm[i,j,k]→tx trans gm[i,j,k]∗tmask[i,j,k + 1] ∗tmask[i+ 1,j,k + 1] (32.56a)
ty trans gm[i,j,k]→ty trans gm[i,j,k]∗tmask[i,j,k + 1] ∗tmask[i,j + 1,k + 1] (32.56b)
tx trans submeso[i,j,k]→tx trans submeso[i,j,k]∗tmask[i,j,k + 1] ∗tmask[i+ 1,j,k + 1] (32.56c)
ty trans submeso[i,j,k]→ty trans submeso[i,j,k]∗tmask[i,j,k + 1] ∗tmask[i,j + 1,k + 1].(32.56d)
32.4 Vertically integrated transport
When the vertically integrated transport is non-divergent, it may be described by a streamfunction, which
is often termed the barotropic streamfunction. This situation generally holds for a Boussinesq rigid lid model
in the absence of surface water fluxes. However, MOM is no longer a rigid lid model, so one requires both
a streamfunction and stream potential to describe the vertically integrated transport. Nonetheless, since
for many purposes the vertically integrated transport is nearly non-divergent on annual and longer time
scales, even in the presence of surface water fluxes, the quasi-streamfunction defined in the following is
quite useful as an approximation to the vertically integrated transport.
32.4.1 Summary of the rigid lid case
With the rigid lid method of Bryan (1969), it is assumed that the vertically integrated velocity in a Boussi-
nesq fluid is non-divergent ∇·U= 0. Hence, it can be described via a scalar streamfunction U=ˆ
z∧∇ ˜
ψ. In
this case, the vertically integrated advective mass transport between two points is given by
Tab =ρ0Zb
a
dl ˆ
n·Z0
−H
dzu=ρ0˜
ψa−˜
ψb,(32.57)
where dl is the line element along any path connecting the points aand b, and ˆ
nis a unit vector pointing
perpendicular to the path in a rightward direction when facing the direction of integration. As written, Tab
has units of mass per time, and so it represents a mass transport (Bryan,1969). Therefore, the difference
between the streamfunction at two points represents the vertically integrated mass transport between the
two points. It is for this reason that the streamfunction is sometimes called the mass transport stream-
function.
32.4.2 General case of divergent flow in non-Boussinesq fluids
The vertically integrated horizontal mass transport
Uρ=
η
Z
−H
ρu(32.58)
generally has a non-zero divergence due to fluctuations of mass within the vertical column, as seen by the
column integrated mass balance (equation (2.21))
∂t
η
Z
−H
dzρ+∇·Uρ=Qw+
η
Z
−H
dzρ S(M).(32.59)
As for the overturning transport, we ignore mass sources in the following, thus considering
∇·Uρ=−∂t
η
Z
−H
dzρ+Qw.(32.60)
Elements of MOM November 19, 2014 Page 425

Chapter 32. Methods for diagnosing mass transport Section 32.4
In either case, the presence of a nonzero divergence requires the introduction of a streamfunction ˜
ψand
a velocity potential χ
Uρ=ˆ
z∧∇ ˜
ψ+∇χ. (32.61)
Only for a Boussinesq rigid-lid model with zero fresh water flux will χvanish. Hence, to compute the precise
vertically integrated mass transport passing between two points, a direct evaluation of the integral
Tab =Zb
a
dl ˆ
n·Uρ(32.62)
is given. Although accurate and complete, this integral does not readily provide a horizontal map of trans-
port, and so it looses much of the appeal associated with the transport streamfunction used with a rigid
lid.
However, for many practical situations, maps of the function
ψ(x,y,t) = −Zy
yo
dy0Uρ(x,y0,t) (32.63)
are quite useful, where the lower limit yois taken at the southern boundary of the domain, generally given
by a solid wall for ocean climate models. By its definition, the meridional derivative of ψyields the zonal
mass transport
ψ,y =Uρ.(32.64)
The zonal derivative, however, does not yield the meridional mass transport due to the divergent nature
of the vertically integrated flow. It is for this reason that we denote ψaquasi-streamfunction. Notably, for
many cases, especially with long time averages, the divergence is small, thus allowing ψto present a good
indication of the path and intensity of the vertically integrated mass transport.
By construction, ψreduces to the transport streamfunction in the case of a rigid lid where ∇·U= 0.
However, this is not a unique choice and alternatives do exist. For example,
ψ∗(x,y,t) = ψ(xo,y,t) + Zx
xo
dx0Vρ(x0,y,t),(32.65)
gives
Vρ=ψ∗
,x.(32.66)
ψ∗has the advantage that zonal derivatives give the exact meridional transport, yet the meridional deriva-
tive in general deviates from the zonal transport. Comparing maps of ψand ψ∗reveals the degree to which
the vertically integrated mass transport is non-divergent. For most purposes of climate modeling at GFDL,
we map the streamfunction ψ=−Ry
yody0Uρ, as deviations from ψ∗are modest for most applications.
32.4.3 Vertically integrated transport from eddy parameterizations
As mentioned above, the vertically integrated transport from both the Gent et al. (1995) mesoscale eddy
closure and the submesoscale scheme of Fox-Kemper et al. (2008b) vanish. Hence, the transport from
these schemes add zero to the net vertically integrated transport through any ocean column.
Elements of MOM November 19, 2014 Page 426

Chapter 33
Kinetic energy diagnostics
Contents
33.1 Formulation of kinetic energy diagnostics ..........................427
The purpose of this chapter is to present the formulation of various kinetic energy diagnostics available
in MOM.
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean velocity diag.F90
33.1 Formulation of kinetic energy diagnostics
The kinetic energy of the fluid in a grid cell for a discrete hydrostatic fluid is determined by the horizontal
components
Ekinetic =1
2ρdVu·u(33.1)
where M=ρdVis the mass of fluid in the grid cell. Note that the in situ density ρreduces in the Boussinesq
case to the constant Boussinesq reference density ρo. The horizontal velocity vector is written as
u= (u,v) (33.2)
The SI unit for kinetic energy is Joule.
We often find it useful to split the kinetic energy into that determined by the barotropic, or vertically
averaged flow, and that determined by the baroclinic flow. For this purpose, define the vertically averaged
velocity according to
uz=
nk
P
k=1
uρdz
nk
P
k=1
ρdz
.(33.3)
The deviation from this vertical average approximates the baroclinic velocity
ˆ
u=u−uz.(33.4)
We thus introduce the baroclinic kinetic energy
Eclinic =1
2ρdVˆ
u·ˆ
u(33.5)
427

Chapter 33. Kinetic energy diagnostics Section 33.1
and the barotropic kinetic energy
Etropic =1
2uz·uz
nk
X
k=1
ρdV.(33.6)
Note that it is only when vertically integrating that we have the identity
nk
X
k=1
Ekinetic =Etropic +
nk
X
k=1
Eclinic.(33.7)
Elements of MOM November 19, 2014 Page 428

Chapter 34
Effective dianeutral diffusivity
Contents
34.1 Potential energy and APE in Boussinesq fluids .......................430
34.2 Effective dianeutral mixing ...................................431
34.2.1 Global effective dianeutral diffusivity ............................ 431
34.2.2 Finite difference approximation ............................... 432
34.2.3 Relevant vertical stratification range ............................ 433
34.2.4 A useful test case ....................................... 433
34.2.5 Computational precision ................................... 433
34.2.6 Negative κef f ......................................... 434
34.2.7 A comment on convection .................................. 434
34.2.8 The experimental design ................................... 434
34.3 Modifications for time dependent cell thicknesses .....................434
34.4 An example with vertical density gradients .........................435
34.4.1 Evolution of the unsorted state ............................... 436
34.4.2 Evolution of the sorted state ................................. 437
34.4.3 Caveat about weakly stratified regions ........................... 440
34.5 An example with vertical and horizontal gradients .....................440
34.5.1 Vertical diffusion ....................................... 440
34.5.1.1 Evolution of the unsorted state .......................... 440
34.5.1.2 Evolution of the sorted state ........................... 441
34.5.2 Horizontal diffusion ..................................... 444
34.5.2.1 Evolution of the unsorted state .......................... 444
34.5.2.2 Evolution of the sorted state ........................... 444
The purpose of this chapter is to detail a method to quantify water mass mixing in MOM without detailed
knowledge of the numerical transport scheme. The method is restricted to experiments configured with
the following:
• Boussinesq fluid;
• linear free surface, so that the thickness of a grid cell remains constant in time; alternatively, to the
use of z∗vertical coordinate, where each cell has a time independent spacing in z∗-space;
• flat bottom ocean;
• linear equation of state;
429

Chapter 34. Effective dianeutral diffusivity Section 34.1
• each grid cell has the same volume in x−y−sspace, with sthe general vertical coordinate;
• zero buoyancy forcing.
Relaxing some of these assumptions is possible, yet not implemented. Momentum forcing via winds is al-
lowed. Much of the fundamentals in this chapter are guided by the work of Winters et al. (1995) and Winters
and D’Asaro (1995). Griffies et al. (2000b) applied these methods to various idealized model configurations
in a rigid lid version of MOM3.
We assume the linear equation of state for an incompressible fluid is written in the form
ρ=ρ0(1 −α θ),(34.1)
where θis potential temperature, ρois a constant density associated with the Boussinesq approximation,
and αis a constant thermal expansion coefficient. The system is open to momentum fluxes yet closed to
buoyancy fluxes.
The following MOM module is directly connected to the material in this chapter:
ocean diag/ocean tracer diag.F90
34.1 Potential energy and APE in Boussinesq fluids
The purpose of this section is to introduce the notion of a sorted density profile in the context of potential
energy and available potential energy (APE). This profile is of particular relevance when considering the
effective mixing occuring throughout a column of sorted fluid in Section 34.2.
Potential energy of the ocean is given by
Ep=ZdV ρP,(34.2)
where
P=g z (34.3)
is the potential energy per mass of a fluid parcel, gis the acceleration of gravity, zis the vertical position
of a fluid parcel, and ρdV=ρdxdydzis the parcel mass.
Available potential energy (APE) is the difference between the potential energy of the fluid in its natural
state, and the potential energy of a corresponding stably stratified reference state. The reference state is
reached by adiabatically rearranging the fluid to a state of minimum potential energy, which is a state that
contains zero horizontal gradients. This rearrangement, or sorting, provides a non-local mapping between
the unsorted fluid density and the sorted density
ρ(x,t) = ρ(z∗(x,t),t).(34.4)
The sorting map determines a vertical position field z∗(x,t)which is the vertical height in the sorted state
occupied by a parcel at (x,t)in the unsorted state. Due to the monotonic arrangement of density in the
sorted state, z∗(x,t)is a monotonic function of density ρ(x,t).
It is convenient to set the origin of the vertical coordinate at the ocean bottom so to keep potential
energy of the unsorted state non-negative. This convention also allows for z∗(x,t)to be defined as a mono-
tonically decreasing function of density. That is,
ρ(x1,t)< ρ(x2,t)⇒z∗(x1,t)> z∗(x2,t).(34.5)
Conservation of volume in a flat bottom ocean implies that the sorted fluid state has the same vertical
extent as the unsorted fluid, which renders
0≤z,z∗≤H, (34.6)
where His the ocean depth.
Elements of MOM November 19, 2014 Page 430

Chapter 34. Effective dianeutral diffusivity Section 34.2
In the following, it proves convenient to denote the density profile in the sorted reference state using
the symbols
ρ(z∗,t) = ρref (z=z∗,t).(34.7)
Given this notation, the non-local sorting map between the unsorted and sorted fluid states provides the
equivalence
ρ(x,t) = ρ(z∗(x,t),t) = ρref (z=z∗,t).(34.8)
In turn, potential energy for the sorted fluid state can be written in two equivalent manners
Eref =gZdV zρref (z,t) (34.9)
=gZdV z∗(x,t)ρ(x,t).(34.10)
Equation (34.9) represents an integral over the sorted fluid state, in which the density of this state is a
function only of the depth. The horizontal area integral is thus trivial to perform. Equation (34.10) repre-
sents an integral over the unsorted fluid state, where the density ρ(x,t)of an unsorted parcel is weighted
by the vertical position z∗(x,t)that the parcel occupies in the sorted state. It follows that the APE can be
written in two equivalent ways
EAP E =gZdV z [ρ(x,t)−ρref (z,t)] (34.11)
=gZdV ρ(x,t) [z−z∗(x,t)].(34.12)
34.2 Effective dianeutral mixing
In this section we formulate a method to empirically quantify the effects on water masses arising from
various simulated tracer transport processes. A similar application was advocated by Winters et al. (1995)
and Winters and D’Asaro (1995) for the purpose of diagnosing mixing in direct numerical simulations of
unstable fluid flows. Their focus was on physically motivated mixing such as that occuring with breaking
waves. The main focus here is on spurious mixing due to numerical errors. The procedure is identical,
however, in that for each case, one considers the evolution of the reference density profile, ρref (z,t), in a
fluid system closed to buoyancy fluxes
∂tρref =∂z∗(κef f ∂z∗ρref ).(34.13)
Again, in this equation z∗is the vertical position in the sorted fluid state. Therefore, constant z∗surfaces
represent constant density surfaces in the unsorted state. As such, the effective diffusivity κef f summa-
rizes the total amount of mixing across constant density surfaces. If the simulation does not change the
water mass distribution, then Dρ/Dt = 0, the sorted reference density is static ∂tρref = 0, and the effective
diffusivity is zero. In turn, any temporal change in the reference density represents changes in the water
mass distribution. These changes are the result of dianeutral mixing, and so have an associated non-zero
κef f (z∗,t). This is the basic idea that is pursued in the following sections.
34.2.1 Global effective dianeutral diffusivity
In addition to the diffusivity κef f (z∗,t), which is local in density space, it is useful to garner a summary of
the overall dianeutral mixing occuring in an ocean model. A vertical integral of κef f (z∗,t)would provide
such information. A quicker computation of a global effective dianeutral diffusivity can be obtained by
inverting the variance equation for the sorted density
∂tZdV ρ2
ref =−2ZdV κef f (∂zρref )2.(34.14)
Elements of MOM November 19, 2014 Page 431

Chapter 34. Effective dianeutral diffusivity Section 34.2
This result, derived for a closed fluid system, suggests the introduction of a global effective diffusivity
κglobal (t) = −
∂tRdV ρ2
ref
2RdV(∂zρref )2.(34.15)
This diffusivity provides one number that can be used to represent the total amount of dianeutral diffusion
acting over the full model domain. It vanishes when the simulation is adiabatic, as does the effective
diffusivity κef f (z∗,t). However it is generally different from the vertical average of κef f (z∗,t).
34.2.2 Finite difference approximation
In the following, assume that the discrete sorted density is equally spaced in the vertical with a separation
∆z∗, and let the vertical coordinate increase upwards from zero at the flat bottom ocean floor. Note that in
general, ∆z∗<< ∆z, where ∆zis the ocean model’s grid spacing. The reason is that all the Nx×Ny×Nzgrid
points in the ocean model are sorted into the reference vertical profile, which has a vertical range over the
same extent as the ocean model: 0≤z,z∗≤H. As a consequence, the vertical resolution of the sorted
profile is Nx×Nytimes finer than the Nzpoints resolving the profile at a particular horizontal position in
the unsorted state.
On the discrete lattice, the vertical diffusive flux of the sorted density
Fz∗(z∗,t) = −κef f (z∗,t)∂z∗ρref (z∗,t) (34.16)
is naturally defined at the top face of the density cell whose center is at z∗. As such, the diffusion operator
at the lattice point z∗, which is constructed as the convergence of the diffusive flux across a density grid
cell, takes the discrete form
−(∂z∗Fz∗)(z∗,t)≈ − Fz∗(z∗,t −∆t)−Fz∗(z∗−∆z∗,t −∆t)
∆z∗!.(34.17)
The time lag is necessary to provide for a stable discretization of the diffusion equation. The discretization
of the flux is given by
Fz∗(z∗,t) = −κef f (z∗,t)∂z∗ρref (z∗,t)
≈ −κef f (z∗,t) ρref (z∗+∆∗z,t)−ρref (z∗,t)
∆z∗!.(34.18)
Since the flux is located at the top face of the density grid cell whose center is at the position z∗, the
effective diffusivity is located at this face as well. Each of these difference operators is consistent with
those used in MOM when discretizing the diffusion equation for the unsorted fluid.
As with the unsorted tendency, the time derivative in the effective diffusion equation can be approxi-
mated using a leap-frog differencing:
∂tρref (z∗,t)≈ρref (z∗,t +∆t)−ρref (z∗,t −∆t)
2∆t.(34.19)
Piecing these results together yields the expression for the vertical flux at the top of the density cell
z∗+∆z∗
Fz∗(z∗,t −∆t) = Fz∗(z∗−∆z∗,t −∆t)−∆z∗
2∆t[ρref (z∗,t +∆t)−ρref (z∗,t −∆t)].(34.20)
This flux can be determined starting from the ocean bottom, where is vanishes, and working upwards.
Without surface buoyancy fluxes, it also vanishes at the top of the water column, resulting in conservation
of Rdz∗ρref (z∗,t). After diagnosing the flux from the tendency, the effective diffusivity can be diagnosed
from
κef f (z∗,t) = −Fz∗(z∗,t) ∆z∗
ρref (z∗+∆z∗,t)−ρref (z∗,t)!.(34.21)
The issues of what to do when the density gradient becomes small, as in weakly stratified regions, is
discussed in Sections 34.2.3 and 34.2.5.
Elements of MOM November 19, 2014 Page 432

Chapter 34. Effective dianeutral diffusivity Section 34.2
34.2.3 Relevant vertical stratification range
In the stratified portions of the upper ocean, periods 2π/N for buoyancy oscillations are roughly 10-30
minutes, smaller in the pycnocline, and in the deep ocean periods are roughly 5-6 hours (see pages 55-56
of Pickard and Emery (1990)). The squared buoyancy frequency for the sorted reference state is given by
N2
∗=−g
ρo
dρref
dz∗
=−g
1000ρo
dσref
dz∗,(34.22)
where σref = 1000 (ρref −1) is the sigma value for the sorted density ρref (g/cm3). Working with σref is
desirable for accuracy reasons. The observed range in buoyancy periods provides a range over the sorted
vertical profile’s stratification for which a calculation of the model’s effective diffusivity will be performed:
dρref
dz∗=−1.035g/cm3
980cm/sec2
4π2
T2,(34.23)
where T(sec)is the period. With 1×60secs < T < 6×60×60secs defining the period range, the corresponding
vertical density gradient range is
10−10g/cm4≤
dρref
dz ≤10−5g/cm4,(34.24)
and the corresponding range for the sigma gradient is
10−7g/cm4≤
dσref
dz ≤10−2g/cm4.(34.25)
34.2.4 A useful test case
When coding the effective diffusivity algorithm, it has been found useful to compare results with those from
a different approach. Here, we horizontally average (i.e., homogenize) the density field along a particular
depth surface. In a model with stable stratification, rigid lid, flat bottom, no-flux boundary, potential density
evolution takes the form
∂thρix,y =−∂zhw ρix,y +∂zhκ ρ,zix,y (34.26)
where κis a vertical diffusivity and the angled-brackets indicate horizontally averaged quantities. With
zero advection, evolution occurs solely via vertical diffusion. Hence, backing out an effective diffusivity for
this horizontally homogenized system yields κ, regardless the horizontal/vertical stratification. It turns
out that this algorithm is far simpler to implement numerically, since it does not require sorting nor inter-
polation to a prespecified sorted coordinate z∗. Its results are in turn more robust. Yet, importantly, they
are relevant only for the case of no-advection, which is not so interesting in general yet serves as a good
check for specific cases.
34.2.5 Computational precision
Models run with pure horizontal and/or vertical diffusion theoretically show κef f ≥0(see Winters and
D’Asaro (1995) and Griffies et al. (2000b)). However, if the stratification range given by equations (34.24) or
(34.25) is violated by more than roughly an order of magnitude, then spurious values of κef f tend to arise.
These spurious values include unreasonably large values for κef f in regions of very low stratification,
and negative values in regions of very large stratification. However, within the range given by equations
(34.24) or (34.25), the computation yields reasonable values. For stratification outside this range, κef f is
arbitrarily set to zero.
Another point to consider is that the stratification of ρref shows much fine-scale step-liked structure.
Computing an effective diffusivity based on such a profile will in turn show lots of noise. Averaging over
Elements of MOM November 19, 2014 Page 433

Chapter 34. Effective dianeutral diffusivity Section 34.4
the fine scales is therefore necessary to garner robust answers. That is, the spurious mixing diagnostic
is smoother when having coarser vertical resolution. An objective means of averaging is to average ρref
vertically onto the same vertical grid used by the forward model in computing the unsorted density state.
If this vertical stratification is itself very fine, then spurious values of κef f may still result, again due to not
enough points of ρref averaged into a single layer.
34.2.6 Negative κef f
Those advection schemes which contain dispersion, such as centered differenced advection, have leading
order error terms that are not second order, but rather third order differential operators. Hence, the di-
agnosis of κef f for these schemes will likely to contain a fair amount of negative values. In turn, negative
κef f may be interpreted as a sign of dispersion errors, which can create or destroy water masses. Upon
introducing convection into the model, much of these undershoots and overshoots created by dispersion
are rapidly mixed. In turn, the resulting κef f should become positive upon introducing convection.
Another source of negative κef f apparently can arise simply due to the finite sampling time and discrete
grid, even in the case of pure diffusion. For example, if there is a mixing event, and if this event is under-
sampled in time, it is possible that the sorted state may have density appear in a non-local manner. Such
mixing events will lead to negative κef f . The ability to realize such values for κef f motivates a sampling
time ∆tequal to time step used to evolve the unsorted density.
34.2.7 A comment on convection
Although the relaxation experiments allow for a focus on adiabatic physics, in a z-coordinate model there
is no guarantee that an experiment will remain vertically stable, especially if running with a nonzero wind
stress. If convective adjustment is then allowed, water mass mixing will occur. Hence, the experiments
which focus on advection must remove convective adjustment. In turn, the presence of convection is
actually quite an important element in determining the effective amount of spurious water mass mixing
occuring in the model. The reason is that certain advection schemes, through dispersion errors, introduce
unstable water which is then mixed-out through convection. After determining the effective diffusivity
from the pure advection experiments, it is appropriate to then allow convection to occur and to compare
the amount of convection appearing with the various advection discretizations.
34.2.8 The experimental design
The framework developed in this section applies most readily to an ocean model with a linear equation
of state run without any buoyancy forcing. Since the model is to be run with zero buoyancy forcing, it is
necessary to spin-up to some interesting state and perform various relaxation experiments. An interesting
alternative is to run with zero buoyancy forcing but nonzero wind forcing, such as in a wind driven gyre.
As a test of the implementation for the algorithm to compute κef f , it is useful to run a set of tests with
pure horizontal and vertical diffusion; no advection or convection. These experiments are necessary to
establish a baseline for later comparison. After being satisfied, a set of relaxation experiments should be
run with advection and/or other transport processes enabled.
34.3 Modifications for time dependent cell thicknesses
There is presently no formulation of this diagnostic for the general case of a time dependent cell thickness.
The problem is that the one-dimensional effective diffusion equation, written as
∂t(∆z∗ρref ) = Fz∗
n−Fz∗
n+1 (34.27)
to account for time dependent thicknesses, no longer satisfies the compatibility condition of Griffies et al.
(2001). That is, for cases with all fluxes vanishing in the unsorted state, there is no guarantee that fluxes
likewise vanish in the sorted state, since the evolution of ∆z∗is no longer tied properly to its neighbor.
Elements of MOM November 19, 2014 Page 434
Chapter 34. Effective dianeutral diffusivity Section 34.4
34.4 An example with vertical density gradients
It is useful to present some examples which can be readily worked through by hand. These examples
highlight many of the points raised in the previous discussion, and provide guidance for interpreting the
three-dimensional MOM results. Each of these examples considers the dynamics of the unsorted and
sorted density fields when the unsorted field is affected by vertical and horizontal diffusion. For simplicity,
we assume the thickness of all grid cells remains time independent. Extensions to the more general case
were discussed in Section 34.3. We also assume a leap frog time stepping, though the analysis follows
trivially for a forward time step, with τ−∆τconverted to τ, and 2∆τconverted to ∆τ.
The first example considers the initial density field shown in Figure 34.1. There are a total of N=
NxNyNz= (4 ×1) ×3grid cells in this two-dimensional example. The density field has zero baroclinicity. So
the question is: How does this state, and the corresponding sorted density state, evolve under the effects
of vertical diffusion? Note the grid dimensions for the two states are related through
∆z= 4∆z∗,(34.28)
where zis the vertical coordinate for the unsorted state, and z∗is the vertical coordinate for the sorted
state. For the following, it is convenient to define this state as that at time (t−∆t). The potential energies
of the unsorted and sorted states are easily computed to be
Ep(t−∆t) = 56ρog∆zV (34.29)
Eref (t−∆t) = 56ρog∆zV (34.30)
EAP E(t−∆t) = 0 (34.31)
where Vis the volume of the grid cells, and ρois the density scale. The zero APE is due to the absence of
horizontal density gradients.
6 6 6 6
2
3 ∆z12
∆z* 3
∆z=
2
2
2
4
4
4
4
6
6
6
6
2 2 2 2
4 4 4 4
Figure 34.1: The initial density field for the first example. The number in each box represents the density,
given in units of ρo. The left panel shows the density ρ(x,z,t −∆t) in the unsorted fluid state, and the right
panel shows the density ρref (z∗,t −∆t) in the sorted state. Note that the vertical scale ∆z∗=∆z/4 for the
sorted state has been expanded for purposes of display.
Elements of MOM November 19, 2014 Page 435
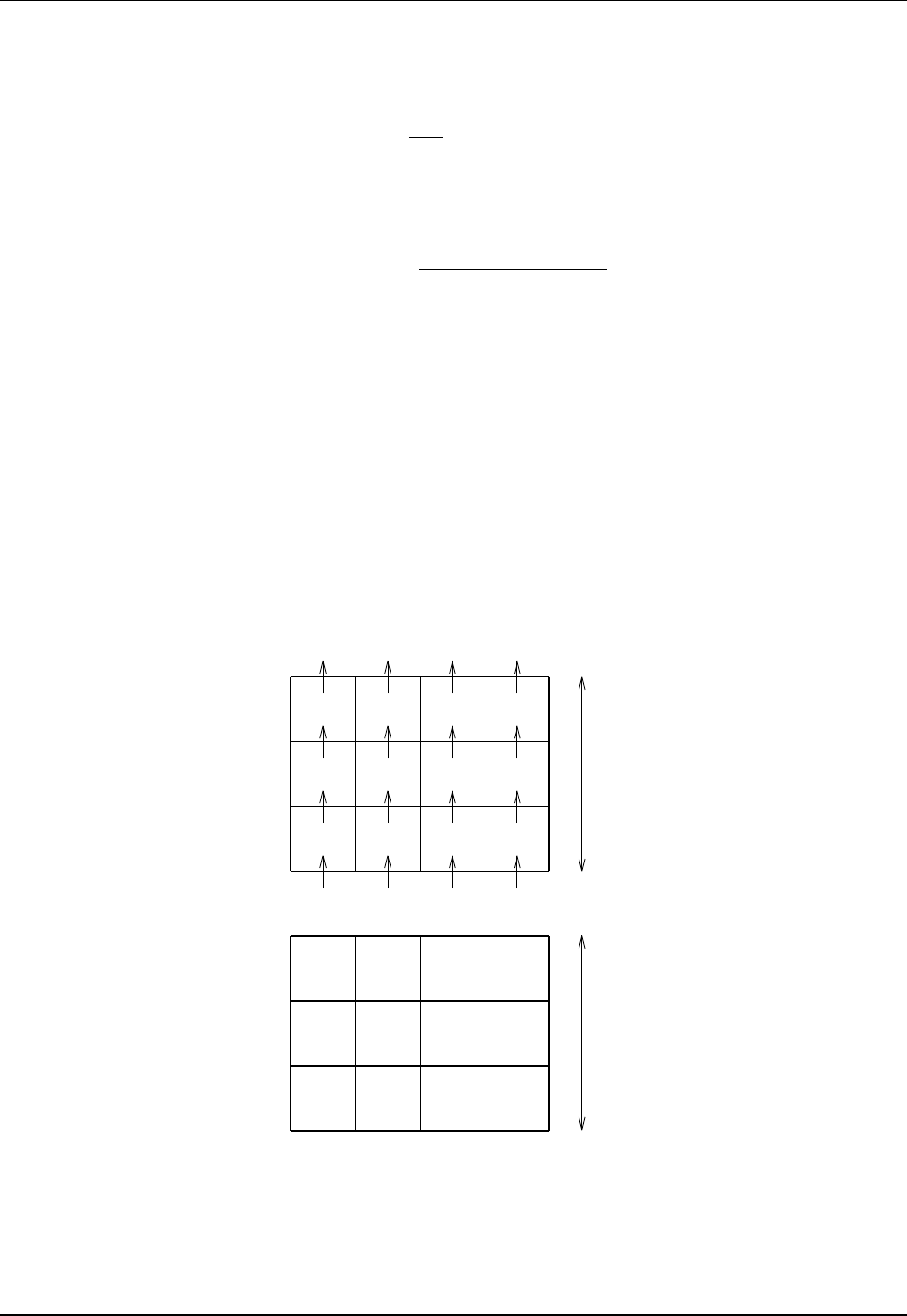
Chapter 34. Effective dianeutral diffusivity Section 34.4
34.4.1 Evolution of the unsorted state
Evolution of the unsorted density is given by the discrete equation
ρ(x,z,t +∆t) = ρ(x,z,t −∆t)− 2∆t
∆z![Fz(x,z,t −∆t)−Fz(x,z −∆z,t −∆t)],(34.32)
where the vertical diffusive flux is given by
Fz(x,z,t) = −κ δzρ(x,z,t)
≈ −κ ρ(x,z +∆z,t)−ρ(x,z,t)
∆z!.(34.33)
Fz(x,z,t)is defined at the top face of the density grid cell whose center has position (x,z). In the following,
it is useful to introduce the dimensionless quantity
δ(v)= 2κ∆t/(∆z)2.(34.34)
This number arises from the chosen discretization of the diffusion equation. For linear stability of the
discretization, δ(v)<1must be maintained.
The top panel of Figure 34.2 shows the vertical diffusive flux through the cell faces at time t−∆t, and
the bottom panel shows the resulting density ρ(z,z,t +∆t). Density in the middle row does not change,
whereas the upper row density increases and the lower row density decreases. The potential energy of
this state is
Ep(t+∆t) = ρog∆zV (56 + 8δ(v)).(34.35)
This increase in potential energy is a result of the raised center of mass arising from the vertical diffusive
fluxes.
δ
0
2
2
0 0 0
2 2
2 2
00
2
2
0
0
6-
4
2+ δ
3∆z
3∆z
δ
2+ 2+ 2+
δδ δ
4 4 4
6- 6- 6-
δδ
Figure 34.2: Top panel: The vertical diffusive flux Fz(x,z,t −∆t), in units of ρoκ/∆z, passing through the
faces of the unsorted density grid cells. Bottom panel: The unsorted density field ρ(x,z,t +∆t), in units of
ρo, where the dimensionless increment δis given by δ= 2δ(v)= 4κ∆t/(∆z)2. This density field results from
the vertical convergence of the flux Fz(x,z,t −∆t).
Elements of MOM November 19, 2014 Page 436

Chapter 34. Effective dianeutral diffusivity Section 34.4
34.4.2 Evolution of the sorted state
Corresponding to the evolution of the unsorted density, there is an evolution of the sorted density
ρref (z∗,t +∆t) = ρref (z∗,t −∆t)− 2∆t
∆z∗![Fz∗(z∗,t −∆t)−Fz∗(z∗−∆z∗,t −∆t)].(34.36)
The dianeutral diffusive flux is
Fz∗(z∗,t) = −κef f (z∗,t)δz∗ρref (z∗,t)
≈ −κef f (z∗,t) ρref (z∗+∆z∗,t)−ρref (z∗,t)
∆z∗!,(34.37)
where ρref (z∗,t)is the sorted state’s density. Fz∗(z∗,t)is defined at the top face of the sorted density grid
cell whose center has height z∗. Given the time tendency for the sorted state, the flux is diagnosed through
Fz∗(z∗,t −∆t) = Fz∗(z∗−∆z∗,t −∆t)− ∆z∗
2∆t![ρref (z∗,t +∆t)−ρref (z∗,t −∆t)].(34.38)
The left panel of Figure 34.3 shows the sorted density field ρref (z∗,t +∆t), and the second panel shows
the diagnosed vertical diffusive flux Fz∗(z∗,t −∆t). The third panel shows the vertical density gradient
[ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)]/∆z∗. The fourth panel shows the effective diffusivity κef f (z∗,t −∆t),
which is diagnosed from the relation
κef f (z∗,t −∆t) = −Fz∗(z∗,t −∆t) ∆z∗
ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)!.(34.39)
The units for κef f (z∗,t −∆t)are (∆z∗)2/∆t. Hence, a value for κef f (z∗,t −∆t)of 2δin Figure 34.3 indicates a
dimensional value of
κef f (z∗,t −∆t)=2δ(∆z∗)2
∆t
=κ4∆t
(∆z)2
(∆z∗)2
∆t
=κ/4.
(34.40)
This example illustrates a problem with unstratified parts of the sorted profile. As evident from Figures
34.1 and 34.3, the 12 sorted boxes are actually three larger homogeneous boxes, and so the calculation
should compute fluxes and diffusivities for these three boxes rather than for the 12 boxes. Figure 34.4
shows such a combined system, where there are three boxes each of height ∆zcomprising the sorted
state. Repeating the previous calculation for this configuration recovers the expected κef f =κon the
two interior interfaces. Note that there is no ad hoc setting to zero certain values of κef f associated with
unstratified portions of the profile.
As a final note, the potential energy of the sorted state at time t+∆tis
Eref (t+∆t) = ρog∆zV (56 + 16δ(v)),(34.41)
which is higher than the initial potential energy as a result of the raised center of mass. The APE remains
unchanged
EAP E(t+∆t)=0,(34.42)
as it should since there remains zero baroclinicity in the final state.
Elements of MOM November 19, 2014 Page 437
Chapter 34. Effective dianeutral diffusivity Section 34.4
δ
2 + δ
0
0
0
0
0
0
0
0
0
δ
0
0
0
0
0
2 +
2 +
2 +
δ
δ
δ
444
4
4
4
6 -
6 -
6 -
6 -
δ
δ
δ
2
3
4
4
4
4
4
3
2
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
0
0
-2
0
0
-2
0
0
0
2δ
0
0
2δ
0
Figure 34.3: First panel (left): The sorted density field ρref (z∗,t +∆t), in units of ρo. Second panel: The
vertical diffusive flux Fz∗(z∗,t −∆t), in units of ρo∆z∗/(2∆t), passing through the faces of the sorted density
grid cells. Third panel: The vertical density gradient [ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)]/∆z∗in units of
ρo/∆z∗. Fourth panel: The effective diffusivity κef f (z∗,t −∆t) in units of (∆z∗)2/∆t.
Elements of MOM November 19, 2014 Page 438
Chapter 34. Effective dianeutral diffusivity Section 34.4
z
4
- 2
- 2
δ
δ
2+
δ
δ
4
6−
2
6
0
0
0
0
κ
κ
0
0
3∆
Figure 34.4: First panel (far left): The initial density field ρref (z∗,t −∆t), consisting of the combination
of the three groups of four homogeneous cells. The values are given in units of ρo. In this recombined
arrangement, ∆z∗=∆z. Second panel: The vertical density gradient [ρref (z∗+∆z∗,t−∆t)−ρref (z∗,t−∆t)]/∆z∗,
in units of ρo/∆z∗. Third panel: The density ρref (z∗,t +∆t) in units of ρo. Fourth panel: The diffusive flux
Fz∗(z∗,t −∆t). Fifth panel (far right): The effective diffusivity κef f (z∗,t −∆t).
Elements of MOM November 19, 2014 Page 439

Chapter 34. Effective dianeutral diffusivity Section 34.5
34.4.3 Caveat about weakly stratified regions
Note that in this example, the same set of boxes are perfectly homogenized at each time step. As such,
it is straightforward to combine the boxes in order to derive their effective diffusivities. In general, this
simple situation will not be true, and so the effective height of the combined boxes will differ. Furthermore,
most cases of homogenization are approximate (Sections 34.2.3 and 34.2.5), which introduces even more
time dependence to the interfaces between effectively homogeneous boxes. In order to compute an effec-
tive diffusivity, however, our algorithm needs to evaluate all quantities at the same depth level z∗. Time
dependent z∗is problematical.
The current example suggestes that one possibile way to account for homogenization is to count the
number of nearly homogeneous boxes occuring in a particular section of the sorted column. When the
first interface is reached that has a nontrivial stratification, then the effective diffusivity computed for this
interface is multiplied by the number of trailing boxes which are homogeneous. This trick works for the
example just considered (κ/4×4 = κ). However, in the example considered in Section 34.5.2, it leads to
an effective diffusivity which can be larger than the horizontal diffusivity. Such is not possible, and so one
is led to reject the proposed patch. A clean way to proceed is to try to resolve as best as possible the
stratification within the sorted fluid state. For those regions which are simply too weakly stratified, it must
be recognized that the computed effective diffusivity might be smaller than a more refined computation.
An alternative approach is to average the sorted density field onto the discrete levels realized in the
unsorted state. Indeed, this resolution of the sorted state is arguably that which is relevant for diagnosing
the effective diffusivity. This is the approach taken with the MOM experiments documented in Griffies et al.
(2000b).
34.5 An example with vertical and horizontal gradients
This example considers the initial unsorted density configuration is shown in Figure 34.5. There are three
rows of four boxes stacked on top of one another, and there are both vertical and horizontal density gra-
dients. Also shown is the corresponding sorted state. As with the example in Section 34.4, the grid dimen-
sions for the two states are related through ∆z= 4∆z∗, where zis the vertical coordinate for the unsorted
state, and z∗is the vertical coordinate for the sorted state. The potential energies are
Ep(t−∆t) = 110ρog∆zV (34.43)
Eref (t−∆t) = 98ρog∆zV (34.44)
EAP E(t−∆t) = 12ρog∆zV , (34.45)
where Vis the volume of the boxes and ρois the density scale.
34.5.1 Vertical diffusion
Consider first just vertical diffusion acting on the unsorted state. The vertical diffusivity κacting on the
unsorted state is assumed to be uniform and constant.
34.5.1.1 Evolution of the unsorted state
Evolution of the unsorted density is given by the discrete equation
ρ(x,z,t +∆t) = ρ(x,z,t −∆t)− 2∆t
∆z![Fz(x,z,t −∆t)−Fz(x,z −∆z,t −∆t)],(34.46)
where the vertical diffusive flux is given by
Fz(x,z,t) = −κ δzρ(x,z,t)
≈ −κ ρ(x,z +∆z,t)−ρ(x,z,t)
∆z!.(34.47)
Elements of MOM November 19, 2014 Page 440
Chapter 34. Effective dianeutral diffusivity Section 34.5
=
2
4
4
6
6
6
8
8
8
10
10
12
2 4 6 8
4 6 8 10
6 8 10 12
3 ∆z12
∆z* 3
∆z
Figure 34.5: The initial density field for the horizontal and vertical diffusion examples. The number in
each box represents the density, given in units of ρo. The left panel shows the density ρ(x,z,t −∆t) in the
unsorted fluid state, and the right panel shows the density ρref (z∗,t −∆t) in the sorted state. Note that the
vertical scale ∆z∗=∆z/4 for the sorted state has been expanded for purposes of display.
Fz(x,z,t)is defined at the top face of the density grid cell whose center has height z. The top panel of
Figure 34.6 shows the vertical diffusive flux through these faces at time t−∆t, and the bottom panel shows
the resulting density field ρ(x,z,t +∆t). Density in the middle row does not change, whereas the upper row
density increases and the lower row density decreases. The potential energy of this state is
Ep(t+∆t) = ρog∆zV (110 + 16δ(v)),(34.48)
which is higher than the initial potential energy as a result of the raised center of mass.
34.5.1.2 Evolution of the sorted state
Corresponding to the evolution of the unsorted density, there is an evolution of the sorted density which is
given by
ρref (z∗,t +∆t) = ρref (z∗,t −∆t)− 2∆t
∆z∗![Fz∗(z∗,t −∆t)−Fz∗(z∗−∆z,t −∆t)].(34.49)
The dianeutral diffusive flux is given by
Fz∗(z∗,t) = −κef f (z∗,t)δz∗ρref (z∗,t)
≈ −κef f (z∗,t) ρref (z∗+∆z∗,t)−ρref (z∗,t)
∆z∗!,(34.50)
where ρref (z∗,t)is the sorted state’s density. Fz∗(z∗,t)is defined at the top face of the sorted density grid
cell whose center has height z∗. Given the time tendency for the sorted state, the flux is diagnosed through
Fz∗(z∗,t −∆t) = Fz∗(z∗−∆z∗,t −∆t)− ∆z∗
2∆t![ρref (z∗,t +∆t)−ρref (z∗,t −∆t)].(34.51)
The left panel of Figure 34.7 shows the sorted density field ρref (z∗,t +∆t), and the second panel shows
the diagnosed vertical diffusive flux Fz∗(z∗,t −∆t). The third panel shows the vertical density gradient
Elements of MOM November 19, 2014 Page 441
Chapter 34. Effective dianeutral diffusivity Section 34.5
z
0
2
2
0 0 0
2 2
2 2
00
2
2
0
0
6- 8- 10- 12-
8
6
4
2+ 4+ 6+ 8+
10
δδ
δ
δ
δδ δ δ
3∆z
3∆
Figure 34.6: Top panel: The vertical diffusive flux Fz(x,z,t −∆t), in units of ρoκ/∆z, passing through the
faces of the unsorted density grid cells. Bottom panel: The unsorted density field ρ(x,z,t +∆t), in units of
ρo, where δ= 2 δ(v)= 4κ∆t/(∆z)2. This is the density field resulting from the vertical convergence of the
flux Fz(x,z,t −∆t). The potential energy of this field is Ep(t+∆t) = ρog∆zV (110 + 16δ(v)).
[ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)]/∆z∗. Note the regions of zero stratification. The fourth panel shows
the effective diffusivity κef f (z∗,t −∆t), which is diagnosed from the relation
κef f (z∗,t −∆t) = −Fz∗(z∗,t −∆t) ∆z∗
ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)!.(34.52)
The units for κef f (z∗,t −∆t)are (∆z∗)2/∆t. In addition, consistent with the discussion in Section 34.4.2, the
effective diffusivity for the interfaces on top of unstratified water are multiplied by the number of unstrati-
fied boxes. A value for κef f (z∗,t −∆t)of δin Figure 34.7 indicates a dimensional value of
κef f (z∗,t −∆t) = δ(∆z∗)2
∆t
=κ4∆t
(∆z)2
(∆z∗)2
∆t
=κ/4.(34.53)
As a final note, the potential energy of the sorted state at time t+∆tis
Eref (t+∆t) = ρog∆zV (98 + 7δ(v)),(34.54)
which is higher than the initial potential energy as a result of the raised center of mass. The APE is there-
fore given by
EAP E(t+∆t) = ρog∆z V (12 + 11 δ(v)),(34.55)
which is larger than EAP E(t−∆t)given in equation (34.45).
Elements of MOM November 19, 2014 Page 442
Chapter 34. Effective dianeutral diffusivity Section 34.5
δ
2 + δ
4
4 + δ
6 - δ
6
6 + δ
8 - δ
8
8 +
10 - δ
10
12 - δ
δ
0
δ
2δ
δ
δ
2δ
δ
δ
2δ
δ
δ
0
0
-2
0
-2
0
0
-2
0
0
-2
0
-2
0
0
δ δ/2
0
δ
0
0
δ
0
0
δ
0
δ/2
0
2
δ
3
3δ
δ
Figure 34.7: Left panel: The sorted density field ρref (z∗,t +∆t), in units of ρo. Second panel: The vertical
diffusive flux Fz∗(z∗,t −∆t), in units of ρo∆z∗/∆t, passing through the faces of the sorted density grid cells.
Third panel: The vertical density gradient [ρref (z∗+∆z∗,t−∆t)−ρref (z∗,t−∆t)]/∆z∗in units of ρo/∆z∗. Fourth
panel: The effective diffusivity κef f (z∗, t −∆t) in units of (∆z∗)2/∆t. The four κef f values which are on top of
unstratified portions of the ρref (z∗,t −∆t) profile have been multiplied by the number of unstratified boxes
which lie directly beneath it.
Elements of MOM November 19, 2014 Page 443

Chapter 34. Effective dianeutral diffusivity Section 34.5
34.5.2 Horizontal diffusion
Consider now just horizontal diffusion acting on the unsorted state. The horizontal diffusivity Aacting on
the unsorted state is assumed to be uniform and constant.
34.5.2.1 Evolution of the unsorted state
Evolution of the unsorted density is given by the discrete equation
ρ(x,z,t +∆t) = ρ(x,z,t −∆t)− 2∆t
∆x![Fx(x,z,t −∆t)−Fx(x−∆x,z,t −∆t)],(34.56)
where the horizontal diffusive flux is given by
Fx(x,z,t) = −A δxρ(x,z,t)
≈ −A ρ(x+∆x,z,t)−ρ(x,z,t)
∆x!.(34.57)
Fx(x,z,t)is defined at the east face of the density grid cell whose center has position (x,z). The top panel
of Figure 34.8 shows the horizontal diffusive flux through these faces at time t−∆t, and the bottom panel
shows the resulting density field ρ(x,z,t +∆t). The potential energy of this state is the same as the initial
potential energy, since the horizontal fluxes are parallel to the geopotential
Ep(t+∆t) = Ep(t−∆t) = 110ρog∆zV . (34.58)
34.5.2.2 Evolution of the sorted state
Corresponding to the evolution of the unsorted density, there is an evolution of the sorted density which is
given by
ρref (z∗,t +∆t) = ρref (z∗,t −∆t)− 2∆t
∆z∗![Fz∗(z∗,t −∆t)−Fz∗(z∗−∆z,t −∆t)].(34.59)
The dianeutral diffusive flux is given by
Fz∗(z∗,t) = −κef f (z∗,t)δz∗ρref (z∗,t)
≈ −κef f (z∗,t) ρref (z∗+∆z∗,t)−ρref (z∗,t)
∆z∗!,(34.60)
where ρref (z∗,t)is the sorted state’s density. Fz∗(z∗,t)is defined at the top face of the sorted density grid
cell whose center has height z∗. Given the time tendency for the sorted state, the flux is diagnosed through
Fz∗(z∗,t −∆t) = Fz∗(z∗−∆z∗,t −∆t)− ∆z∗
2∆t![ρref (z∗,t +∆t)−ρref (z∗,t −∆t)].(34.61)
The left panel of Figure 34.5.2.2 shows the sorted density field ρref (z∗,t +∆t), and the second panel shows
the diagnosed vertical diffusive flux Fz∗(z∗,t −∆t). The third panel shows the vertical density gradient
[ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)]/∆z∗. Note the regions of zero stratification. The fourth panel shows
the effective diffusivity κef f (z∗,t −∆t), which is diagnosed from the relation
κef f (z∗,t −∆t) = −Fz∗(z∗,t −∆t) ∆z∗
ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)!.(34.62)
Elements of MOM November 19, 2014 Page 444
Chapter 34. Effective dianeutral diffusivity Section 34.5
δ
3∆z
3∆z
0
0
0 δ
δ
δ
δ
δ
δ
δ
δ
δ
0
0
0
68
2+ δ4 6 8 -
10 -
12 -
810
6 +
4 + δ
δ
δ
δ
Figure 34.8: Top panel: The horizontal diffusive flux Fx(x,z,t −∆t), in units of ρoA/∆x, passing through
the faces of the unsorted density grid cells. Bottom panel: The unsorted density field ρ(x,z,t +∆t), in units
of ρo, where δ= 2δ(h)= 4A∆t/(∆x)2. This is the density field resulting from the vertical convergence of the
flux Fx(x,z,t −∆t). The potential energy of this field is Ep(t+∆t) = 110ρog∆z V .
Elements of MOM November 19, 2014 Page 445

Chapter 34. Effective dianeutral diffusivity Section 34.5
The units for κef f (z∗,t −∆t)are (∆z∗)2/∆t. For example, a value for κef f (z∗,t −∆t)of 3δ/2in Figure 34.5.2.2
indicates a dimensional value of
κef f (z∗,t −∆t) = (3δ/2) (∆z∗)2
∆t
= 6A∆t
(∆x)2
(∆z∗)2
∆t
= 6A ∆z∗
∆x!2
.
(34.63)
For the special case of ∆x=∆z= 4∆z∗, the effective diffusivity is 3A/8. Note that if the patch proposed
in Section 34.4.3 is used, then the 3δ/2diffusivity would become 9δ/2, leading to the possibility for an
effective diffusivity of 9A/8, which is impossible.
As a final note, the potential energy of the sorted state at time t+∆tis
Eref (t+∆t) = ρog∆zV (98 + 19δ(h)/2),(34.64)
which is higher than the initial potential energy as a result of the raised center of mass. The APE is given
by
EAP E(t+∆t) = ρog∆z V (12 −19 δ(h)/2),(34.65)
which is smaller than EAP E(t−∆t)given in equation (34.45).
Elements of MOM November 19, 2014 Page 446
Chapter 34. Effective dianeutral diffusivity Section 34.5
δ
2 + δ
4
4 + δ
6
8 - δ
8
10 - δ
10
12 - δ0
δ
2δ
δ
δ
δ
δ
0
0
-2
0
-2
0
0
-2
0
0
-2
0
-2
0
0
δ δ/2
0
δ
0
0
0
0
δ
0
δ/2
0
6
8
δ2
δ
2
3
δ2
δ2
2
3δ/2
6 +
Figure 34.9: First panel (far left): The sorted density field ρref (z∗,t +∆t) in units of ρo. Second panel: The
vertical diffusive flux Fz∗(z∗,t −∆t), in units of ρo∆z∗/∆t, passing through the faces of the sorted density
grid cells. Third panel: The vertical density gradient [ρref (z∗+∆z∗,t −∆t)−ρref (z∗,t −∆t)]/∆z∗in units of
ρo/∆z∗. Fourth panel: The effective diffusivity κef f (z∗,t −∆t) in units of (∆z∗)2/∆t. The four κef f values
which are on top of unstratified portions of the ρref (z∗,t −∆t) profile have been multiplied by the number
of unstratified boxes which lie directly beneath it.
Elements of MOM November 19, 2014 Page 447

Chapter 34. Effective dianeutral diffusivity Section 34.5
Elements of MOM November 19, 2014 Page 448

Chapter 35
Spurious dissipation from numerical
advection
Contents
35.1 Formulation of the method for Boussinesq fluid ......................449
35.2 Formulation for MOM ......................................451
35.3 Comparing to physical mixing .................................453
The purpose of this chapter is to detail a method to locally quantify the level of dissipation (either
positive or negative) associated with discretization errors in numerical tracer advection. This method
was introduced by Burchard and Rennau (2008), and it provides a valuable complement to the effective
dianeutral diffusivity diagnostic detailed in Chapter 34. In particular, the Burchard and Rennau (2008)
method can provide a local quantification of the dissipation for any three dimensional model simulation. It
cannot, however, generally translate that mixing into a dianeutral diffusivity, since there is no knowledge
of neutral directions built into the diagnostic.
The following MOM module is directly connected to the material in this chapter:
ocean tracers/ocean tracer advect.F90
35.1 Formulation of the method for Boussinesq fluid
Consider a continuous Boussinesq fluid in the absence of mixing, subgrid-scale fluxes, or sources, in which
case the tracer concentration is affected only by advection
∂tC=−∇·(vC).(35.1)
Likewise, the squared tracer concentration (indeed, the tracer concentration raised to any power) satisfies
the same equation
∂tC2=−∇·(vC2).(35.2)
Now consider a space-time discretization of the tracer concentration equation (35.1)
Cn+1 =Cn−D(C) (35.3)
where we assume an explicit two-time level update of the tracer concentration onto discrete time levels
τn=τo+n∆τ. This is the preferred time stepping method in MOM (see Chapter 11). The discrete operator
D(C)≈∆τ∇·(vC) (35.4)
449

Chapter 35. Spurious dissipation from numerical advection Section 35.1
symbolizes one of the many possible methods used to discretize tracer advection. For later purposes, it is
useful to define the right hand side of equation (35.3) as the operator A(C), so that
A(C) = Cn−D(C).(35.5)
Given the discrete expression (35.3), we can form the square of the updated tracer concentration
[(Cn+1)2](a)= [A(C)]2
= (Cn)2+ [D(C)]2−2CnD(C).(35.6)
Additionally, another means for computing the updated squared tracer concentration is to discretize the
continuous equation for C2, given by equation (35.2), in which the updated squared tracer concentration
is given by
[(Cn+1)2](b)= (Cn)2−D(C2).(35.7)
Following the definition of the operator A(C)in equation (35.5), we have
[(Cn+1)2](b)=A(C2).(35.8)
The fundamental question that this diagnostic asks is how well the two approximations for (Cn+1)2
agree. To answer this question, we simply take the difference
[(Cn+1)2](a)−[(Cn+1)2](b)= [A(C)]2−A(C2)
= [D(C)]2−2CnD(C) + D(C2).(35.9)
A nonzero value for this difference results from nonzero spurious mixing or unmixing due to truncation
errors in the advection scheme. Computing this difference requires an evaluation of the advection operator
on both the tracer concentration and the squared tracer concentration.
To associate mixing with a particular sign of the difference (35.9), we consider the special case of
one-dimensional advection with a constant advection velocity u > 0, discretized with first order upstream
spatial differences on a uniform grid with spacing ∆x. In this case
[(Cn+1)2](a)≡ A(C)2
= (1 −γ)2(Cn
i)2+γ2(Cn
i−1)2+ 2γ(1 −γ)Cn
iCn
i−1
(35.10)
and
[(Cn+1)2](b)≡ A(C2)
= (1 −γ)(Cn
i)2+γ(Cn
i−1)2,(35.11)
where γ=u∆τ/∆xis the Courant number, and the discrete advection equation is stable so long as 0≤γ≤
1. With this chosen discretization, the difference (35.9) takes the form
[A(C)]2−A(C2)
∆τ=− γ(1 −γ)
∆τ!(Cn
i−Cn
i−1)2
=− γ(1 −γ)(∆x)2
∆τ! Cn
i−Cn
i−1
∆x!2
≈ −κeff(∂xC)2
≤0,
(35.12)
where we identified (Ci−Ci−1)/∆xas a discrete approximation to ∂xC, and defined an effective diffusivity
κeff= γ(1 −γ)(∆x)2
∆τ!.(35.13)
Elements of MOM November 19, 2014 Page 450

Chapter 35. Spurious dissipation from numerical advection Section 35.2
Hence, the difference between the two approximations to the updated squared tracer concentration takes
the form of a discrete dissipation of tracer variance, thus exemplefying the well known dissipative property
of first order upwind advection. The effective diffusivity that sets the scale of this dissipation vanishes
when the Courant number is either zero, which is the trivial case of no advective transport, or unity, in
which case the full contents of cell i−1are transported into cell iover a single time step.
Burchard and Rennau (2008) take the previous result as motivation to define a numerically induced
dissipation rate for any advection scheme. We follow their definition, yet introduce a division by (∆τ)−2
rather than their use of ∆τ
Σ≡A(C2)−[A(C)]2
(∆τ)2
=2CnD(C)−[D(C)]2−D(C2)
(∆τ)2.
(35.14)
The extra ∆τfactor is motivated by dimensional arguments given in the discussion following the more
general result given by equation (35.29). Again motivated by the one-dimensional upwind advection case,
Burchard and Rennau (2008) propose the following identifications
Σ>0⇒positive dissipation through mixing (35.15)
Σ<0⇒negative dissipation through unmixing (35.16)
Σ= 0 ⇒zero dissipation.(35.17)
Regardless whether these identifications are rigorous, they are suggestive and allow one to stratify differ-
ent advection schemes according to their values of Σ. In general, a key goal of an advection scheme is to
have Σfrom advection much smaller than the corresponding physically induced dissipation from subgrid
scale mixing.
35.2 Formulation for MOM
The previous formulation was based on finite differences applied to a Boussinesq fluid. MOM is based
on a finite volume formulation of the non-Boussinesq fluid. In this section, we generalize the previous
considerations to that appropriate for MOM.
For a non-Boussinesq fluid, mass conservation takes the form
∂tρ=−∇·(ρv).(35.18)
Likewise, tracer conservation in the absence of subgrid scale fluxes is given by
∂t(ρC) = −∇·(ρvC),(35.19)
and the corresponding budget for squared tracer concentration is
∂t(ρC2) = −∇·(ρvC2).(35.20)
MOM time steps a finite volume tracer budget for a non-Boussinesq fluid using generalized level coordi-
nates, in which case the budget for tracer mass per horizontal area is time stepped. As detailed in Section
2.6, this approach leads to the following tracer advection equation for an interior grid cell
∂t(C ρdz) = −∇s·(uC ρ dz)−(ρ w(s)C)s=sk−1+ (ρ w(s)C)s=sk,(35.21)
with w(s)the dia-surface velocity component. Following the notation from Section 35.1, we discretize this
budget as
(C ρdz)n+1 = (C ρ dz)n−E(C)
≡ B(C),(35.22)
Elements of MOM November 19, 2014 Page 451

Chapter 35. Spurious dissipation from numerical advection Section 35.3
where the discrete advection operator is written
E(C)/∆τ≈ ∇s·(uC ρdz) + (ρ w(s)C)s=sk−1−(ρw(s)C)s=sk.(35.23)
Likewise, the discretized budget for the mass weighted squared tracer concentration is
(C2ρdz)n+1 = (C2ρdz)n−E(C2)
≡ B(C2),(35.24)
where B(C2)has dimensions of squared tracer concentration times mass per area.
We follow the steps considered in Section 35.1 to derive an operator that identifies the dissipation due
to truncation errors with tracer advection. For this purpose, we consider the square of equation (35.22) as
one approximation to the updated squared mass per area of a tracer
[(C ρdz)n+1]2
(a)= [B(C)]2
= [(C ρdz)n]2+ [E(C)]2−2E(C)(C ρdz)n.(35.25)
An alternative approximation is obtained from equation (35.24), in which
[(C ρdz)n+1]2
(b)= (ρdz)n+1 B(C2)
= (ρdz)n+1 (ρdz)n(Cn)2−(ρdz)n+1 E(C2).(35.26)
The difference between these two approximations is given by
[B(C)]2−(ρdz)n+1 B(C2)=(C2ρdz)n[(ρdz)n−(ρdz)n+1]
+ [E(C)]2−2(C ρdz)nE(C) + (ρdz)n+1 E(C2).(35.27)
The first term arises from time tendencies in the mass per area of a grid cell
(ρdz)n−(ρdz)n+1
∆τ≈ −∂t(ρdz),(35.28)
and this term has nothing to do with errors in the advection scheme. Notably, it vanishes in two special
cases:
• Boussinesq fluid with z-coordinates, in which case the cell thickness dzis time independent. The only
exception is the top level, where the thickness changes due to time tendencies in the free surface
height.
• Non-Boussinesq fluid with pressure coordinates, in which case the cell mass per area ρdzis time
independent. The only exception is the bottom cell, where the mass per area changes due to time
tendencies in the bottom pressure.
To remove these effects from temporal changes in mass per area of a grid cell, we define the generalized
advection dissipation operator
Σgeneral ≡2(C ρdz)nE(C)−[E(C)]2−(ρdz)n+1 E(C2)
(∆τ)2.(35.29)
This definition corresponds to the operator Σdefined by equation (35.14). Even though we have ignored
the ∂t(ρdz)term, the operator (35.29) can still be nonzero even if the advection operators are perfect, as
occurs when ρdzhas horizontal spatial variations or time variations. Hence, this operator provides insight
towards the advection truncation errors only for the special cases listed in the above two bullet points.
Indeed, if the mass per area is the same temporal constant on a k-level (as for geopotential coordinates
below the surface cell, and pressure coordinates above the bottom cell), we have
Σgeneral = (ρdz)Σif ∇s(ρdz)=0,and ∂t(ρdz)=0,(35.30)
Elements of MOM November 19, 2014 Page 452

Chapter 35. Spurious dissipation from numerical advection Section 35.3
where the dissipation operator Σis defined by equation (35.14).
The extra ∆τfactor in the denominator of (35.29), relative to Burchard and Rennau (2008), provides
sensible units for the tracer dissipation. In particular, for tracer C=Cpθbeing the heat capacity times
potential temperature, Σgeneral has dimensions of (Watt/m2)2. For C= 1000 Sthe mass of salt per mass of
seawater, Σgeneral has dimensions of (kgm−2s−1)2.
35.3 Comparing to physical mixing
As a means to gauge the levels of Σgeneral, we may compare it to tracer dissipation arising from physically
motivated subgrid scale mixing processes. For this purpose, we introduce a subgrid scale flux J, so that the
tracer concentration and squared tracer concentration satisfy the following equations
∂t(ρC) + ∇·(ρvC) = −∇·J(35.31)
∂t(ρC2) + ∇·(ρvC2) = −C∇·J.(35.32)
For the squared tracer, write the right hand side in the following manner
∂t(ρC2) + ∇·(ρvC2) = −C∇·J
=−∇·(CJ) + ∇C·J.(35.33)
Considering a tensor formulation for the subgrid scale tracer flux
J=−ρK·∇C(35.34)
leads to
∂t(ρC2) + ∇·(ρvC2) = −∇·(CJ)−ρ∇C·K·∇C. (35.35)
For a symmetric diffusion tensor,
ρ∇C·K·∇C > 0,(35.36)
in which case the mass weighted squared tracer concentration is dissipated by the sink −ρ∇C·K·∇C. For
the special case of vertical diffusion with diffusivity κ > 0,
ρ∇C·K·∇C=ρκ(∂zC)2.(35.37)
A finite volume formulation of the squared tracer equation, focusing just on the dissipation from vertical
diffusion, leads to
(C2ρdz)n+1 = (C2ρdz)n−∆τ[ρdzκ (∂zC)2]n,(35.38)
which leads to
[(C ρdz)n+1]2= (ρdz)n+1 (C2ρdz)n−∆τ(ρdz)n+1 [ρdz κ(∂zC)2]n.(35.39)
We are thus led to identify the dissipation operator for vertical diffusion
Σvert-diff= (ρdz)n+1 (ρdz)n[κ(∂zC)2]n
∆τ.(35.40)
The dissipation operator Σvert-diffhas the same dimensions as Σgeneral defined for advection in equation
(35.29). Importantly, Σgeneral accounts for dissipation from the three dimensional advection operator,
whereas Σvert-diffaccounts for dissipation just from vertical diffusion. That is, the operator Σgeneral is un-
able to generally isolate advection induced dissipation associated any particular direction, with the most
physically relevant direction being the dianeutral. Furthermore, many of the more promising advection
operators are three dimensional, and so we cannot isolate any one of the directions to ascribe a particular
effective diffusivity.
Nonetheless, the following are two notable cases where the dissipation operators from advection and
diffusion can be directly compared.
Elements of MOM November 19, 2014 Page 453

Chapter 35. Spurious dissipation from numerical advection Section 35.3
• One-dimensional advection-diffusion, which is a rather trivial case, but very useful for prototype
development;
• A three-dimensional simulation with just advection and vertical diffusion, using a linear equation of
state with density directly proportional to temperature; in this case, the dissipation operators Σgeneral
and Σvert-difffor temperature are directly comparable.
Elements of MOM November 19, 2014 Page 454

Chapter 36
Dianeutral transport and associated
budgets
Contents
36.1 Introduction to the diagnostic methods ............................458
36.1.1 Two analysis methods ..................................... 458
36.1.2 A comment on terminology ................................. 459
36.2 Density layer mass budgets and watermass formation ...................459
36.2.1 Mass budget within a layer .................................. 461
36.2.2 Watermass transformation and formation ......................... 461
36.2.3 Accumulating the formation from the bottom to an arbitrary density ......... 462
36.2.4 Meridional overturning streamfunction .......................... 463
36.3 Pieces required to locally compute dianeutral transport ..................464
36.3.1 Neutral tangent plane and neutral density ......................... 464
36.3.2 The dia-surface velocity component ............................ 465
36.3.3 Resolved and parameterized tracer advection ....................... 469
36.4 The dianeutral transport ....................................470
36.5 Layer calculation of the watermass transformation G(γ)..................472
36.5.1 An expression for G(γ) via Leibniz’s Rule ......................... 472
36.5.2 Neutral density versus locally referenced potential density ............... 473
36.5.3 The discrete approximation ................................. 474
36.6 Kinematic method to compute the material time derivative ................475
36.6.1 Principles of the kinematic method ............................. 475
36.6.2 Finite volume considerations ................................ 475
36.6.3 Distinguishing material evolution from local time evolution .............. 477
36.7 Process method to compute the material time derivative ..................477
36.7.1 Neutral diffusion, cabbeling, and thermobaricity ..................... 477
36.7.2 Dianeutral diffusion ..................................... 479
36.7.3 Sources ............................................. 479
36.8 Finite volume estimate of the advective-form material time derivative .........480
36.8.1 A transport theorem for grid cells .............................. 480
36.8.2 Tracer and mass budgets for an interior grid cell ..................... 482
36.8.2.1 Semi-discrete flux-form expression ........................ 482
36.8.2.2 Advective-form expression ............................ 483
36.8.3 Material time derivative of locally referenced potential density for an interior cell . . 483
455

Chapter 36. Dianeutral transport and associated budgets Section 36.0
36.8.4 Tracer and mass budgets for a bottom grid cell ...................... 483
36.8.5 Material time derivative of locally referenced potential density for a bottom cell . . . 484
36.8.6 Tracer and mass budgets for a surface grid cell ...................... 485
36.8.6.1 Kinematic formulation ............................... 485
36.8.6.2 Process formulation and the boundary layer .................. 486
36.8.6.3 Advective form ................................... 487
36.8.6.4 Comments ...................................... 487
36.8.7 Material time derivative of locally referenced potential density for a surface cell . . . 488
36.8.7.1 Surface buoyancy forcing ............................. 489
36.8.7.2 Further comments on surface buoyancy fluxes ................. 489
36.9 Comments on the MOM diagnostic calculation .......................489
36.9.1 Sampling ............................................ 489
36.9.2 Accounting for time-explicit and time-implicit processes ................ 490
36.9.2.1 Explicit plus implicit time stepping ....................... 490
36.9.2.2 What if we diagnosed vertical processes in series? ............... 490
36.9.2.3 A priori and a posteriori diagnostics ........................ 491
36.9.3 Splitting physics into flux convergence plus thermodynamic source .......... 492
36.9.4 Cabbeling, thermobaricity, and neutral diffusion ..................... 492
36.9.5 Concerning spurious dianeutral transport ......................... 493
36.10 Kinematic method diagnosed in MOM ............................493
36.10.1Eulerian time tendency .................................... 495
36.10.2Advection by resolved flow ................................. 496
36.10.3Gent-McWilliams transport ................................. 496
36.10.4Submesoscale transport ................................... 497
36.10.5Precipitation minus evaporation: flux-form ........................ 497
36.10.6Precipitation minus evaporation: advective-form ..................... 498
36.10.7Liquid plus solid river runoff: flux-form .......................... 498
36.10.8Liquid plus solid river runoff: advective-form ....................... 499
36.10.9Liquid river runoff: flux-form ................................ 499
36.10.10Liquid river runoff: advective-form ............................. 500
36.10.11Solid calving land ice: flux-form .............................. 500
36.10.12Solid calving runoff: advective-form ............................ 501
36.10.13Summary of the kinematic method ............................. 501
36.10.13.1Material time derivative .............................. 501
36.10.13.2Dianeutral transport from wdian diagnostics .................. 502
36.10.13.3Dianeutral transport from tform diagnostics .................. 502
36.11 Process method diagnosed in MOM ..............................502
36.11.1Boundary fluxes of heat and salt through the vertical mixing operator ......... 504
36.11.1.1Surface boundary heat fluxes ........................... 504
36.11.1.2Surface boundary salt fluxes ........................... 504
36.11.1.3Net surface boundary heat and salt fluxes .................... 505
36.11.1.4Bottom boundary heat flux ............................ 505
36.11.1.5Penetrative shortwave radiation ......................... 505
36.11.2Boundary fluxes of buoyancy arising from mass transport ................ 505
36.11.2.1Precipitation minus evaporation ......................... 506
36.11.2.2Liquid plus solid river runoff........................... 507
36.11.2.3Liquid river runoff................................. 508
36.11.2.4Solid calving runoff................................ 509
36.11.3Vertical mixing processes ................................... 509
36.11.3.1Vertical diffusion and boundary fluxes ...................... 509
Elements of MOM November 19, 2014 Page 456

Chapter 36. Dianeutral transport and associated budgets Section 36.0
36.11.3.2Vertical diffusion from net vertical diffusivity ................. 510
36.11.3.3Vertical diffusion from static background vertical diffusivity ......... 511
36.11.3.4Vertical diffusion from internal tide mixing vertical diffusivity ........ 511
36.11.3.5Vertical diffusion from coastal tide mixing vertical diffusivity ........ 512
36.11.3.6Vertical diffusion from leewave induced vertical diffusivity .......... 513
36.11.3.7Vertical diffusion from K33-implicit ....................... 514
36.11.3.8Vertical diffusion from dianeutral mixing plus K33-implicit ......... 514
36.11.3.9Vertical mixing from convective adjustment schemes ............. 515
36.11.3.10Nonlocal KPP transport .............................. 515
36.11.3.11Diagnostic checks for vertical processes ..................... 516
36.11.4Neutral diffusion ....................................... 516
36.11.4.1Neutral diffusion operator: time-explicit piece ................. 516
36.11.4.2Cabbeling in the ocean interior .......................... 517
36.11.4.3Thermobaricity in the ocean interior ....................... 517
36.11.4.4Diagnostic checks for neutral diffusion ..................... 517
36.11.5Submesoscale horizontal diffusion ............................. 517
36.11.6Quasi-physical parameterizations of overflow and marginal sea exchange ....... 518
36.11.6.1Over-exchange scheme ............................... 519
36.11.6.2Overflow scheme .................................. 519
36.11.6.3Overflow scheme from NCAR ........................... 520
36.11.6.4Mixdownslope scheme ............................... 520
36.11.6.5Sigma diffusion scheme .............................. 521
36.11.6.6Cross land mixing scheme ............................. 521
36.11.6.7Cross land insertion scheme ............................ 522
36.11.7Miscellaneous schemes .................................... 522
36.11.7.1Frazil heating of ocean liquid ........................... 522
36.11.7.2Free surface or bottom pressure smoothing ................... 523
36.11.8Summary of the process method for the ESM2M ocean .................. 523
36.11.8.1Material time derivative .............................. 523
36.11.8.2Dianeutral transport from wdian diagnostics .................. 524
36.11.8.3Dianeutral transport from tform diagnostics .................. 524
36.12 Budget for locally referenced potential density .......................525
36.13 Diagnosing mass budgets for density layers .........................526
36.13.1Time tendency for layer mass, M(γ)............................ 526
36.13.1.1Time averaging the time tendency ........................ 526
36.13.1.2Noise in the tendency of binned mass ...................... 527
36.13.1.3A smoothed mass tendency ............................ 527
36.13.1.4Estimating layer mass via interpolation ..................... 528
36.13.1.5Binning the mass of a tracer cell to neutral density layers ........... 529
36.13.1.6Binning the time tendency for the mass per area (not recommended) . . . . 529
36.13.1.7Regarding water fluxes and vertical coordinates ................ 529
36.13.2Surface mass transport, E(γ)................................. 530
36.13.3Overturning streamfunction, Ψ†(γ) = −Rγb
γV†...................... 531
36.13.4watermass transformation, G(γ)............................... 533
36.14 Inferring transformation from surface buoyancy fluxes ..................534
36.14.1Density forcing associated with surface water fluxes ................... 534
36.14.2Density forcing associated with surface heat and salt fluxes ............... 535
36.15 Specifying the density classes for layer diagnostics .....................537
36.15.1Online calculation of neutral density ............................ 537
36.15.2Defining the density bins ................................... 537
Elements of MOM November 19, 2014 Page 457

Chapter 36. Dianeutral transport and associated budgets Section 36.1
36.15.3Convention for the binning ................................. 538
36.15.4Binning versus remapping .................................. 538
36.16 Known limitations ........................................539
36.16.1Disagreements between wdian and tform ......................... 539
36.16.2Inserting river water into the ocean ............................. 539
36.16.3Difficulty closing the mass budgets ............................. 539
The purpose of this chapter is to detail diagnostic methods available online in MOM to compute the
rate that seawater is transported across locally defined potential density surfaces, along with budgets for
locally referenced potential density. There are two general methods detailed: (A) The layer method based on
extensions of the Walin (1982) isopycnal mass budget approach, with this method fundamentally based on
balances within density layers. (B) A local method that calculates the dianeutral transport at each model
grid cell, with this transport mapped either in the native model coordinates or binned to density layers.
Each method in turn has an equivalent kinematic formulation and a process formulation. The layer and
direct methods are identical in the continuum, but differ in practice due to numerical truncation.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean sbc.F90
ocean core/ocean bbc.F90
ocean tracers/ocean tracer advect.F90
as well as various other modules associated with parameterized physical processes.
Caveat
Section 36.16 summarizes the many known limitations of this diagnostic scheme. Ongoing research is
aimed at resolving these limitations.
36.1 Introduction to the diagnostic methods
The purpose of this chapter is to detail two diagnostic methods available in MOM to compute the mass
flux crossing density surfaces. That is, we develop a diagnostic methodology that identifies and quantifies
the boundary and interior physical processes contributing to watermass transformation occurring in a
simulation. Quantifying and mapping such dianeutral mass transport, identifying the processes giving rise
to such transport, and quantifying the associated budgets for locally referenced potential density, is a
central piece required to answer oceanographic questions regarding the transformation of fluid between
density classes.
36.1.1 Two analysis methods
To deductively obtain information about density transformation from observations is nearly impossible,
given the need to have full information about ocean mixing processes. However, there is a powerful in-
ferential method, first introduced by Walin (1982), that offers many useful conclusions based on surface
buoyancy and mass fluxes, along with a steady state assumption and mass balance within density layers
(or volume balance for Boussinesq fluids). The Walin (1982) method has been further explored, general-
ized, and applied in such studies as Tziperman (1986), Speer and Tziperman (1992), Marshall et al. (1999),
Vi ´
udez (2000), Large and Nurser (2001), Maze et al. (2009), Iudicone et al. (2008), and Downes et al. (2011).
Given the far more detailed information available in an ocean model, we apply this method throughout the
ocean column, thus allowing for deductive statements to be made about the causes of simulated water-
mass transformation from the ocean surface to bottom. We refer the Walin (1982) based approach as the
layer method.
Elements of MOM November 19, 2014 Page 458

Chapter 36. Dianeutral transport and associated budgets Section 36.2
The layer method requires the specification of layer bounding surfaces that have a simply connected
topology. However, McDougall and Jackett (1988) showed that there is no simply connected surface in
the ocean whose tangents are equal to neutral directions, with neutral directions those most relevant
for orienting mixing processes (McDougall,1987a). Approximate simply connected surface are available,
such as the neutral density γnof Jackett and McDougall (1997). Neutral density is useful in certain parts
of the World Ocean, especially when considering limited geographical and/or density ranges. However,
isosurfaces of neutral density are a poor approximation to neutral directions when water properties deviate
from the climatology used to define the γn. Additionally, γngenerally has troubles in the Southern Ocean,
where the effects of the nonlinear equation of state are substantial. Iudicone et al. (2008) encountered
these issues in their analysis of the Southern Ocean, and presented a partial solution whose generality
and robustness are not well established.
A second limitation in practice with the layer method is that it requires the binning of transports into
density classes. Binning level model information to layer space can introduce a nontrivial level of noise to
the diagnostic, with this noise a function of the subjectively defined density classes. Such noise can often
be overcome with sufficient sampling through spatial and temporal averaging. But it remains a definite
concern for any diagnostic method aiming to be quantitatively robust.
As a means to add robustness to the diagnosed watermass transformation, and to avoid some of the
limitations of the layer approach, we introduce a second analysis method. The direct method for diagnosing
dianeutral transport computes the dianeutral transport at each point in the generalized level coordinate
ocean model, rather than through formulating a layer mass balance as in the layer method. Consequently,
the method is more “direct” than the layer method. Furthermore, the direct method allows one to map
the dianeutral transport on the native model grid, thus avoiding problems with density binning. Nonethe-
less, to directly compare to the layer method, and to thus provide a quantitative measure of watermass
transformation according to density classes, one may also bin according to density layers.
For those interested solely in applications of the two analyses methods, the differences in their formu-
lation are far less interesting than the fact that two methods exist, and that they agree in the continuum. In
practice, differences arise from discretization errors. Such errors are ubiquitous in numerical modelling, so
that having two methods offers added robustness to any results, especially results that aim at quantitative
precision. This chapter exposes the mathematical formulation as well as the numerical implementation
details required to garer a full understanding of the MOM watermass transformation diagnostic
36.1.2 A comment on terminology
Consistent with the usage in the Walin (1982) inspired watermass transformation literature, we consider
a “watermass” to be specified by its density class. The transformation of a watermass is thus associated
with processes leading to a material change in the locally referenced potential density. However, a more
general definition of watermass is found Sve (????), where on page 141 they state the following.
Watermasses can be classified on the basis of their temperature-salinity characteristics, but
density cannot be used for classification because two watermasses of different temperatures
and salinities may have the same density.
Changes in density arise through changes in temperature and salinity. Hence, changes in the “watermass”
as defined in the density-based methods lead to watermass changes in the sense of Sve (????). However,
the converse does not generally hold. Namely, there are physically interesting changes in temperature and
salinity that leave density unchanged. A more general watermass transformation equation, that incorpo-
rates both density changing and density compensated effects, has been discussed by McDougall (1987b),
and further explored by Zika et al. (2010). Nonetheless, for the purposes of the present chapter, we follow
the Walin (1982) inspired usage, in which watermasses are altered by material changes to density.
36.2 Density layer mass budgets and watermass formation
The purpose of this section is to introduce certain of the ideas used for density based watermass trans-
formation analysis. This discussion sets the theoretical stage for the diagnostic method detailed in later
Elements of MOM November 19, 2014 Page 459
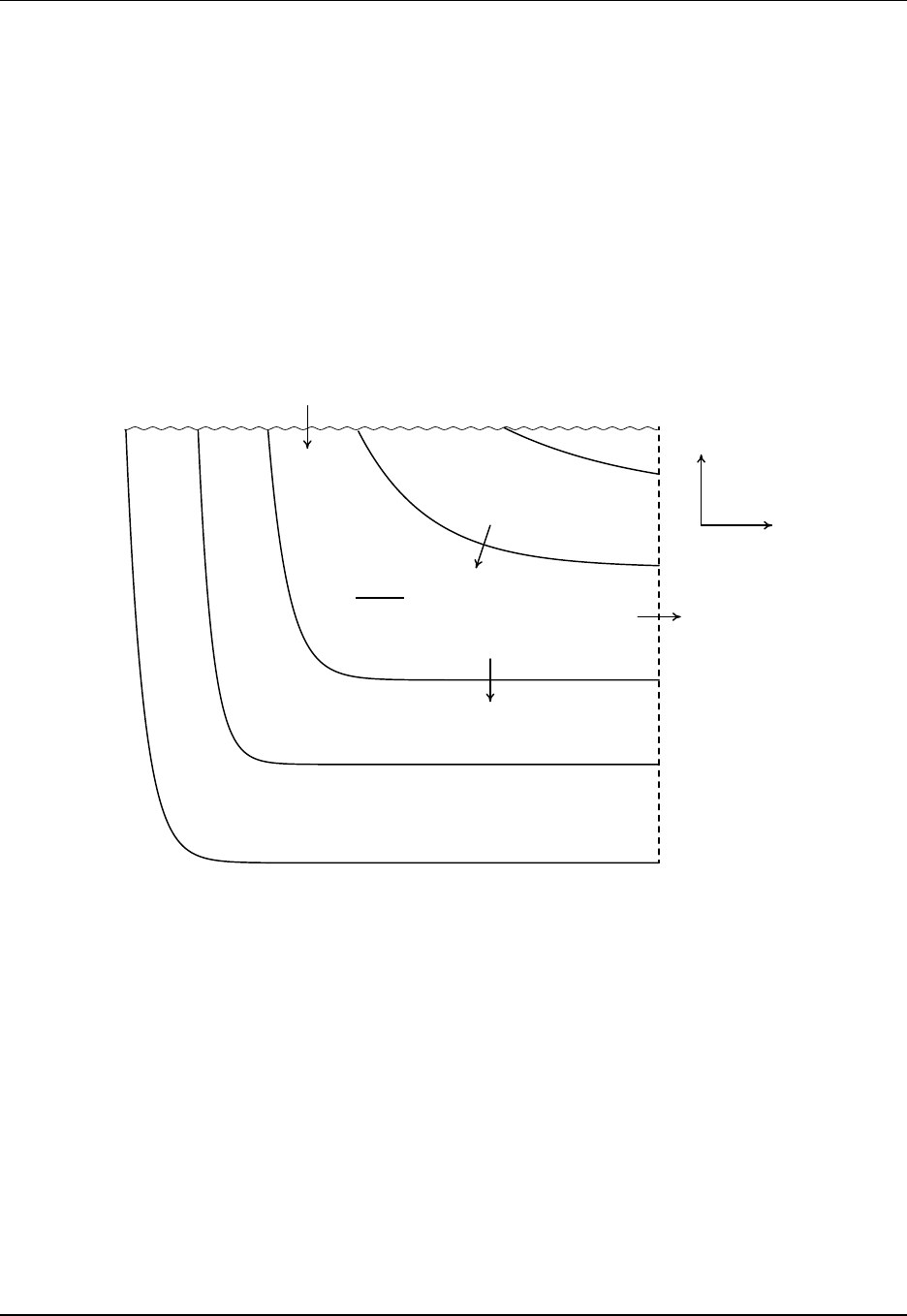
Chapter 36. Dianeutral transport and associated budgets Section 36.2
sections. We then return in Section 36.13 to summarize the diagnostic calculation of the layer mass bud-
get as available in MOM.
Figure 36.1 illustrates the geometry considered when formulating the mass budget for a layer of fluid
labelled by a density variable γ, bounded above and below by densities γ−δγ/2and γ+δγ/2, respectively.
We may choose an arbitrary region to establish the formalism, but our particular example of the Southern
Ocean is of great interest within the research community (e.g., Iudicone et al.,2008), so we consider it to
help ground the formalism in a particular application.
As for discrete isopycnal models, properties within a chosen layer are assumed to be uniform. We
specify a watermass according to the locally referenced potential density, γ. However, since surfaces
of constant γexhibit a nontrivial topology in an ocean with a realistic equation of state (McDougall and
Jackett,1988), we will ultimately consider the case of neutral density, following the ideas of Iudicone
et al. (2008). For the main portion of the formulation, we discount the limitations associated with locally
referenced potential density. We return to neutral density in Section 36.5.2.
z=η
y
z
φ=φnorth
G(γ−δγ/2)
G(γ+δγ/2)
∂M(γ)
∂t
E(γ)
V†(γ)
Figure 36.1: Illustration of seawater layers, oriented here according to that in the Southern Ocean where
dense water outcrops to the south. We formulate a mass budget for a layer of fluid, shown here labelled by
locally referenced potential density γwith layer boundaries at densities γ±δγ/2. The mass of this layer,
M(γ), will evolve according to mass fluxes (with units of kg s−1) crossing the layer boundaries. At the ocean
surface, precipitation minus evaporation plus runoffand ice melt contribute to a mass flux E(γ), with this
flux considered positive for water entering the layer. At the northern boundary, water can cross the bound-
ary at a rate V†(γ), with V†(γ)>0 taken for flow moving northward thus depleting mass in the layer. The
transport V†(γ) is computed as the residual mean transport, which includes the mean transport explicitly
represented by the model advection, plus the quasi-Stokes transport often parameterized according to Gent
et al. (1995) for the mesoscale or Fox-Kemper et al. (2008b) for the submesoscale. Finally, water can cross
the layer boundaries at a rate G(γ−δγ/2) from the lighter layer, and G(γ+δγ/2) into the denser layer. We
choose signs so that G(γ±δγ/2) >0 for water flowing from a light layer to a denser layer; i.e., for water
flowing downwards in a stably stratified fluid. Convergence of fluid transport across surfaces of constant
γ±δγ/2, associated with a nonzero transport G(γ±δγ/2), will inflate or deflate the constant γlayer, which
in turn leads to motion of the bounding surfaces γ±δγ/2.
Elements of MOM November 19, 2014 Page 460

Chapter 36. Dianeutral transport and associated budgets Section 36.2
36.2.1 Mass budget within a layer
Following the conventions defined by Figure 36.1, the mass budget for a layer of fluid specified by γis given
by
∂M(γ)
∂t =E(γ)−V†(γ) + G(γ−δγ/2) −G(γ+δγ/2).(36.1)
All terms on the right hand side denote the integrated mass transports (units of mass per time) across the
bounding interfaces of a particular density layer. The budget is posed over a fluid region whose bounding
surfaces are dynamic. For example, a layer accumulating mass will inflate, with inflation associated with
the motion of the surfaces. Each term in the mass budget (36.1) is straightforward to conceptualize; they
are merely transports across the layer interfaces, or tendencies associated with transients. Nonetheless,
the diagnostic calculation of each term requires care, with special care given to calculating the accumu-
lated dianeutral mass transport, G, also termed here the watermass transformation. Much of the formalism
developed in this chapter concerns methods to diagnose G, and in particular how to partition its contribu-
tions according to physical processes.
36.2.2 Watermass transformation and formation
We introduce some of the terminology of watermass transformation literature (e.g., Large and Nurser,
2001) by defining the watermass formation rate, F(γ)δγ, given by
F(γ)δγ ≡∂M(γ)
∂t +V†(γ).(36.2)
The quantity F(γ)is termed the formation rate per unit density. It measures the mass per time per density
class of water formed within the density interval
δγ > 0.(36.3)
Formation is associated with temporal changes in the mass of a layer, often termed the drift or secular
term, or through mass entering or exiting through the latitudinal domain boundary. In the steady state,
formation of water within a particular density class is balanced by export of water outside of the chosen
domain. That is,
F(γ)δγ =V†(γ)steady state.(36.4)
Therefore, in the steady state, measurements of mass transport within a particular density class that is
exiting a domain, V†(γ), is a direct reflection of formation of water with this density somewhere inside the
domain. Conversely, if there is no formation of water within a particular density class, then there can be
no export of that water through the domain boundaries. These statements are rather trivial conceptu-
ally. However, it is important to keep the language clear, and to precisely associate the language with a
mathematical expression. Confusion can arise without such care with the language and mathematics.
As seen from the mass budget (36.1), watermass formation arises from the input of water through the
ocean surface, or passage of water across the boundaries of the layer
F(γ)δγ =E(γ)−δγ ∂G
∂γ !.(36.5)
In this equation, we introduced the following approximation for the convergence of mass crossing γsur-
faces
−∂G
∂γ ≈ − G(γ+δγ/2) −G(γ−δγ/2)
δγ !.(36.6)
We term the cross layer transport G(γ)the rate of watermass transformation from one density class to
another. Through the relation (36.5), there is a nonzero watermass formation rate F(γ)δγ for a particular
density class so long as there is a nonzero mass flux entering the ocean through the upper boundary, as
measured by E(γ), or a nonzero convergence of the watermass transformation into the density layer, as
measured by −∂G/∂γ.
Elements of MOM November 19, 2014 Page 461

Chapter 36. Dianeutral transport and associated budgets Section 36.2
36.2.3 Accumulating the formation from the bottom to an arbitrary density
Rather than considering the watermass formation rate for a single density class, F(γ)δγ, it is generally
more convenient, and less noisy when diagnosing the formation in a level model, to perform a vertical
integral from the ocean bottom up to a particular density class in a manner that is directly analogous
to the treatment of an overturning streamfunction. We thus refer to the vertically integrated watermass
formation rate as the watermass formation streamfunction
Φ(γ)≡
γb
Z
γF(γ)δγ. (36.7)
The integration limits start from an arbitrary density γand then increase (δγ > 0) to the ocean bottom, γb,
with γb> γ for a stably stratified fluid. Note that Φ(γ)is in fact a streamfunction only in the steady state
case where mass in the layer is time independent. We nonetheless use the common “streamfunction”
terminology even in the time dependent case.
It follows from the definitions of watermass formation rate (36.2) and (36.5) that the formation stream-
function can be written in the following equivalent manners
Φ(γ)≡
γb
Z
γF(γ)δγ.
=
γb
Z
γ V†+∂M
∂t !
=
γb
Z
γ −δγ ∂G
∂γ !+E(γ)!
=G(γ)−G(γb) +
γb
Z
γE.
(36.8)
In order to compute the mass tendency for the layer, ∂M/∂t, the mass flux through the surface, E, and the
transformation G(γ)−G(γb), we must sum the grid-point contributions for each γlayer both zonally around
the domain, and meridionally from the southern boundary (e.g., the Antarctic continent) northward to the
chosen latitude. This step is assumed in the following discussion.
The accumulated formation equation (36.8) results just from considerations of mass balance for a
region with density greater than γ. Consequently, it has some very general implications. To help better
understand the implications, and to further solidify how the language of watermass transformation maps
to the mathematics, consider the following special cases.
•E= 0 and G(γb)=0: Consider the case with zero mass flux through the ocean surface, so that E= 0,
and zero geothermal heating, so that G(γb)=0. The accumulated formation equation (36.8) reduces
to
Φ(γ) = G(γ)when E= 0 and G(γb)=0.(36.9)
Hence, the formation of water with density greater than γ(left hand side) equals to the rate that
water transfers across the γsurface (right hand side). Reference to Figure 36.1 makes this rela-
tion manifest. This situation may be familiar to those having studied watermass transformation in
simulations with virtual salt fluxes, in which E= 0, as well as with zero geothermal heating. Hence,
formation equals transformation in this special case.
•∂M/∂t = 0: Consider now the steady state, in which the mass within each density layer remains
constant with time. Such may be a useful approximation when time averaging over many years. In
Elements of MOM November 19, 2014 Page 462

Chapter 36. Dianeutral transport and associated budgets Section 36.3
this case, the accumulated formation equation (36.8) reduces to
Φ(γ) =
γb
Z
γV†when ∂M/∂t = 0.(36.10)
Thus, in the steady state, the net formation of water with density greater than γequals to the water
leaving through the northern boundary with density greater than γ. Again, reference to Figure 36.1
makes this result quite clear. Further use of the accumulated formation equation (36.8) leads to
γb
Z
γV†=G(γ)−G(γb) +
γb
Z
γE(γ)when ∂M/∂t = 0.(36.11)
Hence, in the steady state, mass of water leaving through the northern boundary with density greater
than γ(left hand side), is balanced by water converging into the density layer across the density
interfaces, plus the mass of water crossing the ocean surface into this region (right hand side).
•E= 0,G(γb) = 0, and ∂M/∂t = 0: The simplest case is the steady state with zero surface mass flux
and zero geothermal heating. The accumulated formation equation (36.8) then reduces to
γb
Z
γV†=G(γ)when E= 0,G(γb)=0, and ∂M/∂t = 0.(36.12)
Steady state simulations with no surface water fluxes, no geothermal heating, and no irreversible
processes creating cross-density transport have zero residual mean circulation. As a corollary, for an
ocean with zero interior dianeutral transport and zero boundary water fluxes, steady state circulation
is restricted to density classes that intersect boundary regions with nonzero mixing. Conversely, if
there is a steady state circulation for regions denser than a particular density class γ, and there is
no surface mass flux E(γ)nor geothermal heating impacting this particular density, then we can infer
the presence of a nonzero cross density transport G(γ).
36.2.4 Meridional overturning streamfunction
The overturning streamfunction is generally defined according to
Ψ†(y,γ) = −Zdx
z=z(γ)
Z
z=−H
ρv†(x,y,z)dz, (36.13)
where z=−H(x,y)is the depth at the ocean bottom, z=z(γ)is the depth of the γsurface, and v†is the
meridional component of the residual mean velocity. The zonal integration occurs over a specified periodic
or closed domain, such as the full longitudinal extent of the Southern Ocean or the region between two
continents such as in the North Atlantic. Ψ†(y,γ)provides a means to display the mass flux of fluid moving
across a latitude line from the ocean bottom up to a chosen density layer γb.
The minus sign in equation (36.13) represents the most common convention used for defining an over-
turning streamfunction. Consider a stably stratified case in which there is a net northward movement
of mass for water denser than γ. That is, V†(y)>0in these regions, meaning that mass is leaving the
northern boundary of the domain (Figure 36.1). In this case, the streamfunction Ψ†(y,γ)is negative. Con-
versely, if water denser than γis accumulating into the region, so that V†(y)<0for the dense layers, then
the streamfunction is positive. From this definition, we have the following relation
Ψ†(y,γ) = −
γb
Z
γV†(y).(36.14)
This minus sign is important to keep in mind when performing watermass transformation diagnostics.
Elements of MOM November 19, 2014 Page 463

Chapter 36. Dianeutral transport and associated budgets Section 36.3
36.3 Pieces required to locally compute dianeutral transport
We are concerned with processes that contribute to transport across a locally defined potential density
surface. That is, we wish to compute the dianeutral transport, which in turn can be integrated over a density
layer to yield G(γ)appearing in the layer mass equation (36.1). As shown in this section, such transport is
directly related to material changes in the locally referenced potential density. The following represents a
summary of such processes.
• Boundary (surface and bottom) fluxes of buoyancy, including penetrative shortwave radiation;
• Dianeutral mixing, as typically parameterized by vertical diffusion, is the canonical example of a
process contributing to interior dianeutral transport.
• Nonlocal dianeutral mixing, which appears in certain boundary layer schemes such as KPP Large
et al. (1994), can also be an important source for dianeutral transport.
• Neutral diffusion coupled to the ocean’s nontrivial equilibrium thermodynamics, which is captured by
the seawater equation of state (IOC et al.,2010), leads to cabbeling, thermobaricity, and halobaricity
(McDougall,1987b).
In the remainder of this section, we introduce the three pieces of a framework used to formulate the
dianeutral transport.
36.3.1 Neutral tangent plane and neutral density
Under an infinitesimal displacement dx, the in situ density changes according to
dρ=ρdx· −α∇Θ+β∇S+1
ρc2
s∇p!(36.15)
where the thermal expansion coefficient is
α=−1
ρ ∂ρ
∂Θ!,(36.16)
the haline contraction coefficient is
β=1
ρ ∂ρ
∂S !,(36.17)
the inverse squared sound speed is
c−2
s= ∂ρ
∂p !,(36.18)
Sis the salinity, and Θis the conservative temperature. Under adiabatic and isohaline motions, the density
change is associated just with pressure changes
(dρ)adiabic/isohaline =ρdx· 1
ρc2
s∇p!.(36.19)
Therefore, if we consider an adiabatic and isohaline displacement of a fluid parcel, the difference in density
between the parcel and the surrounding environment is given by
dρ−(dρ)adiabatic/isohaline =ρdx·(−α∇Θ+β∇S)
=ρdx·ˆ
n(γ)|−α∇Θ+β∇S|,(36.20)
where the dianeutral unit vector is defined by
ˆ
n(γ)≡ρ,Θ∇Θ+ρ,S ∇S
|ρ,Θ∇Θ+ρ,S ∇S|
=−α∇Θ+β∇S
|−α∇Θ+β∇S|,
(36.21)
Elements of MOM November 19, 2014 Page 464

Chapter 36. Dianeutral transport and associated budgets Section 36.3
with the shorthand notation
ρ,Θ=∂ρ
∂Θ(36.22)
ρ,S =∂ρ
∂S .(36.23)
At each point in the fluid, the accumulation of displacements that are orthogonal to ˆ
n(γ)define the neutral
tangent plane.
Our goal is to quantify the rate that fluid moves across the neutral tangent plane, with such motion
termed the dianeutral mass transport. Additionally, we wish to realize this goal regardless the vertical strat-
ification, as measured by the squared buoyancy frequency
N2=−g α∂Θ
∂z −β∂S
∂z !.(36.24)
We are able to realize this goal locally at each grid point in a level coordinate model, which is a powerful
aspect of the diagnostic method detailed in this chapter. For many purposes, it is additionally of interest to
bin the dianeutral transport according to a scalar density-like field defined so that its iso-surfaces are par-
allel to neutral tangent planes. However, as noted by McDougall and Jackett (1988), the locus of neutral
tangent planes does not form a simply connected surface in the presence of a non-zero helicity
H=βT ∇p·(∇S∧ ∇Θ),(36.25)
where
T=β ∂(α/β)
∂p !(36.26)
is the thermobaricity parameter. Non-simply connected surfaces are not very useful for binning seawater
properties or transports, since there is no unique method to define this binning operation. Hence, our de-
sire to bin dianeutral transport into density-like classes is not generally possible. Various simply connected
surfaces have been proposed, with these surfaces aiming to balance, in a subjectively defined optimum
sense, the incompatible desires of maintaining a simply connected topology whilst having iso-surfaces
parallel the neutral tangent plane.
The standard simply connected density surface used to map seawater properties is the neutral density
field, γn, of Jackett and McDougall (1997). Neutral density has become a common tool for analysis of
model and observational data. However, a nontrivial limitation of the γnfield is that it relies on a static
observationally based climatology, such as that from Levitus (1982). This approach is not convenient for
many modeling applications, such as climate change simulations, and a more general approach is under
development based on work of Klocker et al. (2009). As an interim method, we haved tested the polyno-
mial equation for neutral density given in the appendix to McDougall and Jackett (2005). Although the
polynomial is only an approximation to the neutral density coordinate of Jackett and McDougall (1997),
it is more convenient to use in a simulation than the software package of Jackett and McDougall (1997).
However, we are presently favoring the use of potential density, since the McDougall and Jackett (2005)
can in fact be somewhat misleading (Trevor McDougall, personal communication 2011). A more general
method, also based on a polynomial expression, is under development (Trevor McDougall, personal com-
munication 2011).
36.3.2 The dia-surface velocity component
How do we measure the rate that seawater moves in an arbitrary direction, where the direction is generally
a function of space and time? To help answer this question, we generalize a geometric presentation given
in Section 6.7 of Griffies (2004), as well as Section 2.2 of Griffies and Adcroft (2008). The material here
can also be found in Vi ´
udez (2000).
The most fundamental geometric object in our considerations is a normal vector, ˆ
n, where ˆ
nis gen-
erally a function of space and time. If we can measure how fluid motion is oriented according to ˆ
n, then
Elements of MOM November 19, 2014 Page 465

Chapter 36. Dianeutral transport and associated budgets Section 36.3
we can answer the question posed above. A familiar expression for ˆ
narises when we specify a simply
connected smooth surface using a function s=s(x,y,z,t), such as a generalized vertical coordinate (see
Figure 36.2). In this case, we orient the surface with its outward normal vector,
ˆ
n(s) = ∇s
|∇s|(36.27)
which points in the direction of increasing s. For many oceanographic situations, we are interested in the
rate that seawater crosses surfaces of constant potential density in a stably stratified region of the ocean,
in which case sis chosen as potential density. In more general cases, we may be interested in normal
vectors defined only locally, such as the dianeutral unit vector ˆ
n(γ)defined by equation (36.21).
With a static normal vector, the rate that seawater moves in the direction of ˆ
nis proportional to v·ˆ
n,
where vis the three dimensional velocity vector of a seawater parcel. With a more general moving normal
vector, we measure the projection of the seawater velocity relative to the moving normal vector, in which
case we write this projection as
ˆ
n·∆v=ˆ
n·(v−v(ref)) (36.28)
where v(ref)is the velocity describing the motion of the moving normal vector. When the normal vector is
described according to a function sas in equation (36.27), then the projection of the reference velocity
v(ref)onto the normal vector is given by
ˆ
n(s)·v(ref)=− ∂s/∂t
|∇s|!(36.29)
Note that we only need to specify the normal component of the velocity v(ref)for our purposes. With the
definition (36.29) we have
ˆ
n(s)·∆v=v·∇s+∂ts
|∇s|
=1
|∇s|
ds
dt,
(36.30)
where ds/dtis the material time derivative of the surface. The result (36.30) is of fundamental importance
for describing fluid motion in the ocean. It states that fluid moving with a velocity vpenetrates an arbitrary
moving surface at a rate directly proportional to the material time derivative of the defining surface s=
s(x,y,z,t)itself, with proportionality determined by the inverse magnitude of the surface gradient.
The result (36.30) is enshrined by defining the dia-surface velocity component according to
w(s)≡ˆ
n(s)·(v−v(ref))
=1
|∇s|
ds
dt
=(volume/time) fluid penetrating surface, in direction of increasing s
local surface area .
(36.31)
In words, w(s)measures the volume per time of fluid penetrating a locally defined surface or tangent plane,
as defined by the normal vector ˆ
n(s), divided by the local area on that surface. Positive w(s)indicates fluid
moving across the surface in the direction of ˆ
n(s); e.g., into denser regions for the case where sis locally
referenced potential density. If we introduce the following symbol for the surface area element
dA(s)≡local surface area element,(36.32)
then we have
w(s)dA(s)=(volume/time) fluid penetrating surface, in direction of increasing s. (36.33)
Likewise, introducing the in situ density yields the dia-surface mass transport
ρw(s)dA(s)=(mass/time) fluid penetrating surface, in direction of increasing s. (36.34)
Elements of MOM November 19, 2014 Page 466

Chapter 36. Dianeutral transport and associated budgets Section 36.3
Equation (36.34) provides a definition of the mass flux of seawater penetrating a surface. Calculation of
this mass flux requires knowledge of the local dia-surface velocity component, w(s), and the local area
element, dA(s). We now consider these terms in some detail in order to provide practical methods for their
computation in an ocean model.
z
n
^
s=constant
vvref
x,y
Figure 36.2: Surfaces of constant generalized vertical coordinate living interior to the ocean. A normal
direction ˆ
nis indicated on one of the surfaces. Also shown is the orientation of the velocity of a fluid parcel
vand the velocity v(ref)of a reference point living on the surface. Note that the normal direction ˆ
nis drawn
here assuming increasing values of sare parallel to the vertical direction ˆ
z. Such is the case with many
vertical coordinates used for modeling the ocean, such as z∗=H(z−η)/(H+η). However, the opposite
sense holds when sis taken as the locally referenced potential density γ, where stably stratified water has
γincreasing downward.
For any particular orientation of the normal direction ˆ
n(s), it is possible to project the local area element
dA(s)onto at least one of the three coordinate planes perpendicular to the three unit directions ˆ
x,ˆ
y, and
ˆ
z. This projection provides the means for a practical calculation of the area element. For example, if sis a
density-like field, then in the stratified ocean interior, |∂zs|is nonzero. Indeed, it generally has the largest
magnitude of the three spatial derivatives (∂xs,∂ys,∂zs). In this case, ˆ
n(s)≈ −ˆ
z, so the area element dA(s)
is nearly equal to
dA(z)= dxdy, (36.35)
which is the area element in the plane perpendicular to the vertical direction ˆ
z. Our intuition based on this
common case in the ocean interior can be made precise by an expression from differential geometry that
relates two area elements. For this purpose, make use of the equation (6.58) in Griffies (2004), in which we
have the exact relation
dA(s)=|∂sZ||∇s|dA(z).(36.36)
In this equation, we introduced the depth of a s-surface, which has the following functional dependence
Z=Z(x,y,s,t).(36.37)
We choose the capital Zto denote this depth to distinguish it from the depth zof an arbitrary position in
the ocean. However, note that the inverse function is given by
∂s
∂z =1
∂Z/∂s .(36.38)
Again, for the highly stratified ocean interior with schosen as a density-like field,
|∇s|≈|∂zs|=|∂Z/∂s|−1,(36.39)
thus making dA(s)≈dA(z). The relation (36.36) holds in general, so long as the vertical derivative ∂zs
remains nonzero. It thus provides for a general method to compute the area element dA(s)in regions of
nonzero vertical stratification of siso-surfaces.
In regions where ∂zsis tiny, such as in the surface boundary layer using sas a density-like variable, we
cannot make use of expression (36.36). Instead, an alternative is needed based on assuming there is a
Elements of MOM November 19, 2014 Page 467

Chapter 36. Dianeutral transport and associated budgets Section 36.3
nontrivial stratification in at least one of the two horizontal directions. For example, consider a nontrivial
zonal stratification, and let
X=X(y,z,s,t) (36.40)
be the zonal position of the sisosurface, which we assume to be monotonic in a local patch. Then we may
project the area element dA(s)onto a plane perpendicular to the ˆ
xdirection, in which case
dA(s)=|∂sX||∇s|dA(x)(36.41)
where
dA(x)= dydz(36.42)
is the area element in the plane perpendicular to the ˆ
xdirection. Likewise, with a nontrivial meridional
stratification, the area element can be computed using
dA(s)=|∂sY||∇s|dA(y)(36.43)
where
dA(y)= dzdx(36.44)
is the area element in a plane perpendicular to ˆ
y, and
Y=Y(x,z,s,t) (36.45)
is the meridional position of the sisosurface. Either expression (36.41) or (36.43) are suitable when ∂zs
is tiny, so long as ∂xsand ∂ysare nonzero. In general, a useful approach algorithmically is to choose the
largest in magnitude from amongst the three derivatives (∂xs,∂ys,∂zs)to determine which identity (36.36),
(36.41), or (36.43) to use for computing the area element dA(s). Implicit in this approach is that the ocean
fluid has some nonzero stratification in at least one of the three coordinate directions. If this assumption
is not satisfied, then the notion of dianeutral transport becomes meaningless, since we cannot determine
a neutral direction, in which case the mathematical framework breaks down.
In most parts of the ocean with sa density-like vertical coordinate, the vertical derivative ∂zsis far
larger than either of the horizontal derivatives, so that the constant ssurface is more highly stratified in
the vertical direction. However, for a hydrostatic ocean, even when ∂zsmay be larger than the horizontal
derivatives ∂xsand ∂ys, we may still be in a situation where the slope of the constant ssurfaces is nearly
vertical in so far as physical processes are concerned. Indeed, for the neutral diffusion scheme detailed
in Section 36.7.1, if the slope of the neutral surface is greater than a parameter Smax ∼1/100, the neutral
diffusion scheme exponentially transitions to horizontal diffusion in recognition of the distinctly horizontal
processes active in such weakly stratified regions (Treguier et al.,1997;Ferrari et al.,2008,2010). More
generally, the aspect ratio of the discrete ocean model grid generally has the vertical spacing, ∆z, far
smaller than horizontal spacings ∆xand ∆y. Consequently, the largest coordinate surface slope that is
resolvable by the discrete grid is given by
Sresolvable =∆z
∆h,(36.46)
where ∆his some measure of the horizontal grid spacing, such as the geometric mean
∆h=2∆x∆y
∆x+∆y.(36.47)
Consequently, for a discrete ocean model, we can consider the vertical stratification to be the largest
stratification only so long as the coordinate surface slope is less than the grid aspect ratio
∂hs
∂zs<∆z
∆h,(36.48)
or equivalently if
Sresolvable ∂zs > ∂hs. (36.49)
Elements of MOM November 19, 2014 Page 468

Chapter 36. Dianeutral transport and associated budgets Section 36.3
The above discussion can be summarized by the following algorithmic approach to computing the dia-
surface volume transport. In regions of nontrivial vertical stratification where Sresolvable ∂zsis larger than
either of the two horizontal derivatives ∂xsand ∂ys, we compute the volume transport according to
w(s)dA(s)=1
|∇s|
ds
dtdA(s)
=
∂Z
∂s
ds
dtdA(z)
=w(z)dA(z),
(36.50)
where we defined the dia-surface velocity component1
w(z)=
∂Z
∂s
ds
dt.(36.51)
Likewise, in regions where ∂xsprovides the largest derivative of the surface s, we compute the volume
transport according to
w(s)dA(s)=1
|∇s|
ds
dtdA(s)
=
∂X
∂s
ds
dtdA(x)
=w(x)dA(x),
(36.52)
where
w(x)=
∂X
∂s
ds
dt.(36.53)
Finally, in regions where ∂ysprovides the largest derivative, we compute the volume transport according
to
w(s)dA(s)=1
|∇s|
ds
dtdA(s)
=
∂Y
∂s
ds
dtdA(y)
=w(y)dA(y),
(36.54)
where
w(y)=
∂Y
∂s
ds
dt.(36.55)
Table 36.1 summarizes this algorithm for the case where sis the locally referenced potential density.
36.3.3 Resolved and parameterized tracer advection
The third concept required to compute dianeutral transport concerns the appropriate velocity to use to
measure the motion of fluid perpendicular to a neutral direction. In the absence of surface forcing, interior
mixing, and with a simplified equilibrium thermodynamics, fluid transport occurs just through advection.
In this idealized situation, advection leads to no irreversible transport. That is, water parcels are merely
rearranged, and no fluid moves across a potential density surface, since potential density is materially
conserved. When simulating such flow, we must acknowledge that some scales of motion will not be re-
solved. Since the seminal work of Gent and McWilliams (1990), ocean models, especially coarsely resolved
1Note that in treatments of dianeutral velocity component, or dianeutral advection (e.g., McDougall (1987b) or Section 6.7 of
Griffies (2004)), in which case sis the locally defined potential density, the absolute value operation is not applied to the vertical
derivative on the right hand side of equation (36.51). In that case, w(z)has the opposite sign to w(s). We choose the convention
common in the watermass transformation literature, whereby positive w(z)indicates downward motion.
Elements of MOM November 19, 2014 Page 469

Chapter 36. Dianeutral transport and associated budgets Section 36.4
global climate models, generally include advective tracer transport from both the resolved motions, cap-
tured by the model’s resolved fluid velocity v, as well as a parameterization of unresolved motion, often
termed an eddy-induced or quasi-Stokes velocity v∗. Consequently, it is the effective velocity, also termed the
residual mean velocity,
v†=v+v∗(36.56)
that is relevant for considerations of dianeutral transport. Namely, the relevant fluid velocity must include
both the resolved velocity of any particular model simulation, v, as well as any parameterized subgrid
scale velocity, v∗such as arises from Gent et al. (1995)orFox-Kemper et al. (2008b). Consequently, the
material time derivative takes the form
d†
dt=∂
∂t +v†·∇.(36.57)
We now expose some general properties of the quasi-Stokes velocity v∗that will be useful in the follow-
ing. We are in particular interested in a formulation of the dianeutral velocity component that is appropri-
ate for both Boussinesq and non-Boussinesq fluids. As the Gent et al. (1995) paper focuses on Boussinesq
fluids, we make a few comments here concerning its non-Boussinesq generalization. These points apply
to any other quasi-Stokes velocity, such as that proposed by Fox-Kemper et al. (2008b) to parameterize
submesoscale transport. For non-Boussinesq fluids, the parameterized advection velocity v∗is assumed
to satisfy the following constraint
∇·(ρv∗)=0 non-Boussinesq,(36.58)
which ensures that seawater mass locally remains unaffected by the parameterization. This condition
ensures the existence of a vector streamfunction so that
ρv∗=∇ ∧ (ρΨ)non-Boussinesq.(36.59)
For Boussinesq models, the constraint (36.58) reduces to the familiar non-divergence condition
∇·v∗= 0 Boussinesq,(36.60)
so that volume is locally unaffected, and the relation (36.59) reduces to
v∗=∇ ∧ ΨBoussinesq.(36.61)
Notably, it is the vector streamfunction that is often employed in ocean models via the use of skew diffusive
tracer fluxes rather than advection fluxes (Griffies,1998). Regardless whether one uses a skew diffusive or
an advection formulation of Gent et al. (1995) (or any other scheme parameterized as an eddy advection
such as Fox-Kemper et al. (2008b)), for quantifying dianeutral transport, the quasi-Stokes transport should
be considered within a modified material time derivative operator (36.57).
36.4 The dianeutral transport
We now bring together the ideas from Section 36.3 to render the following definition of dianeutral velocity
component
w(γ)≡ˆ
n(γ)·(v†−v(ref)) (36.62)
=(volume/time) fluid through γ-surface in direction of increasing γ
local surface area .(36.63)
In this equation v(ref)is the velocity of a point taken on a locally defined potential density surface, whose
normal projection is given by
ˆ
n(γ)·v(ref)=− ρ,Θ∂tΘ+ρ,S ∂tS
|ρ,Θ∇Θ+ρ,S ∇S|!
=− −α ∂tΘ+β ∂tS
|−α∇Θ+β∇S|!,
(36.64)
Elements of MOM November 19, 2014 Page 470
Chapter 36. Dianeutral transport and associated budgets Section 36.4
with ˆ
n(γ)is the dianeutral unit vector given by equation (36.21) that points in the direction of increasing
locally referenced potential density. Inserting these expressions into the definition (36.63) renders
w(γ)=1
|ρ,Θ∇Θ+ρ,S ∇S| ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!
=1
|−α∇Θ+β∇S| −αd†Θ
dt+βd†S
dt!,
(36.65)
where again the material time derivative
d†
dt=∂
∂t +v†·∇ (36.66)
is determined by the effective or residual mean velocity
v†=v+v∗(36.67)
according to equation (36.57), with v∗determined by a SGS parameterization, such as Gent et al. (1995)
and/or Fox-Kemper et al. (2008b). Using the results from Section 36.3.2, we arrive at the algorithm summa-
rized in Table 36.1 to compute the dianeutral volume and mass transports, as a function of which spatial
direction provides the largest stratification.
largest derivative volume transport w-expression area element
|−α ∂xΘ+β ∂xS|w(γ)dA(γ)=w(x)dA(x)w(x)=|−α ∂xΘ+β ∂xS|−1(−αd†Θ/dt+βd†S/dt) dA(x)= dydz
|−α ∂yΘ+β ∂yS|w(γ)dA(γ)=w(y)dA(y)w(y)=|−α ∂yΘ+β ∂yS|−1(−αd†Θ/dt+βd†S/dt) dA(y)= dzdx
Sresolvable |−α ∂zΘ+β ∂zS|w(γ)dA(γ)=w(z)dA(z)w(z)=|−α ∂zΘ+β ∂zS|−1(−αd†Θ/dt+βd†S/dt) dA(z)= dxdy
Table 36.1: A summary of the algorithm proposed to compute the dianeutral volume transport w(γ)dA(γ)as
a function of the magnitude of the spatial derivative of the locally referenced potential density. We choose
to use the expression listed according to the magnitude of the derivatives in order to ensure an accurate
calculation in regions where stratification is absent in a particular direction. The slope Sresolvable is set
according to the model grid aspect ratio (equation (36.46)). The material time derivative is d†/dt=∂t+v†·∇,
as given by equation (36.57). Note that the volume transport w(γ)dA(γ)is trivially converted to a mass
transport ρw(γ)dA(γ)through multipication by the in situ density ρ.
Calculation of the material time derivative
∂ρ
∂Θ
d†Θ
dt+∂ρ
∂S
d†S
dt=−α ρd†Θ
dt!+β ρd†S
dt!(36.68)
is fundamental to the calculation of dianeutral transport. We consider two independent methods to evalu-
ate the material time derivatives. The kinematic method evaluates the material time derivative by diagnos-
ing the Eulerian time derivative plus the residual mean transport. This method provides a straightforward
means to answer the question: What is the dianeutral transport? Its calculation in MOM is detailed in Sec-
tion 36.6. The second method, termed the process method, allows us to answer the question: What physical
processes and boundary fluxes cause the dianeutral transport? This method is detailed in Section 36.7, and it
amounts to a diagnosis of each boundary and physical process contributing to the material evolution of
locally referenced potential density.
The kinematic and process methods represent two equivalent accountings of the same material time
derivative. Hence, they render the same value. In general, making such agreement manifest in a numerical
simulation is nontrivial, as doing so involves many diagnostic steps and the storage of intermediate terms
that are generally not considered when writing a prognostic model algorithm. MOM has the diagnostic
code modifications facilitating an accounting of both the kinematic and process methods. Assuming all
terms are properly saved in a particular simulation, the kinematic and process methods agree to within
numerical roundoff. Given the sometimes difficult numerical issues associated with diagnosing some of
the terms giving rise to dianeutral water transformation, it is prudent to exploit both methods in order to
develop confidence and robustness in the results.
Elements of MOM November 19, 2014 Page 471

Chapter 36. Dianeutral transport and associated budgets Section 36.5
Once we have a diagnostic computation of w(γ)dA(γ)according to the algorithm in Table 36.1, we may
choose to remap it to its corresponding density surface, and then integrate over that density surface to
obtain the watermass transformation
G(γ) = Z
A(γ)
ρw(γ)dA(γ).(36.69)
We thus have all terms available for the density layer mass budget (36.1). Sections 36.6 and 36.7 detail two
methods available for computing w(γ)dA(γ), thus providing information regarding the processes giving rise
to cross-density mass transport. Before doing so, we consider an alternative calculation of the watermass
transformation.
36.5 Layer calculation of the watermass transformation G(γ)
The purpose of this section is to detail an alternative method for computing the watermass transformation
G(γ). This method is formulated in density coordinates, and so it is fundamentally a density-based or layer
approach.
36.5.1 An expression for G(γ)via Leibniz’s Rule
There is an expression for G(γ)that has proven fundamental to the practical calculation of the transfor-
mation rate using the layered approach pioneered by Walin (1982). The expression makes use of Leibniz’s
Rule from calculus, in which we write the watermass transformation rate in the form
G(γ) = ∂
∂γ
γ
Z
γo
G(σ)dσ
=∂
∂γ
γ
Z
γo
dσZ
A(σ)
ρw(σ)dA(σ)
(36.70)
where γois an arbitrary reference density, σis a dummy variable of integration, and we substituted ex-
pression (36.69) for the watermass transformation G(σ). The integral represents the accumulation of dia-
neutral mass transport over the finite volume of the density layer γo≤σ≤γ. After computing the integral,
we take the derivative with respect to the density γ. Now temporarily assume the vertical stratification is
stable, so that (see equation (36.50))
w(σ)dA(σ)dσ=w(z)dA(z)dσ
=
∂σ
∂z w(z)dV
= ∂σ
∂Θ
d†Θ
dt+∂σ
∂S
d†S
dt!dV
(36.71)
where dVis the three-dimensional volume of the region within the density layer. This result then leads to
the general expression, applicable for an arbitrary statification,
G(γ) = ∂
∂γ Z
V(γ,γo)
dV ρ d†σ
dt,(36.72)
where V(γ,γo)is the volume of the density layer bounded by γand γo, and we introduced the shorthand
d†σ
dt=∂σ
∂Θ
d†Θ
dt+∂σ
∂S
d†S
dt(36.73)
Elements of MOM November 19, 2014 Page 472
Chapter 36. Dianeutral transport and associated budgets Section 36.5
for the material derivative of the locally referenced potential density. For a vertically stratified fluid, this
result takes the form
G(γ) = ∂
∂γ Zdxdy
z(γ)
Z
z(γo)
dz ρ d†σ
dt
vertically stable stratification,(36.74)
where z(γ)is the depth of the γdensity surface.
We next develop a finite difference approximation, in which the right hand side of equation (36.72) takes
the form (see also equation (4) in Maze et al. (2009))
G(γ) = ∂
∂γ Z
V(γ,γo)
dV ρ d†σ
dt
≈1
δγ Z
V(γ+δγ/2,γo)
dV ρ d†σ
dt−Z
V(γ−δγ/2,γo)
dV ρ d†σ
dt
=1
δγ Z
V(γ+δγ/2,γ−δγ/2)
dV ρ d†σ
dt.
(36.75)
Notice how the reference density γodropped out, so that the final expression is an integral over the volume
bounded by the two density surfaces γ−δγ/2≤σ≤γ+δγ/2. The integrand is the density weighted
material time derivative of the locally referenced potential density. Again, it is useful to touch base with
the vertically stratified case, in which the previous result takes the form
G(γ) = ∂
∂γ Z
V(γ,γo)
dV ρ d†σ
dt
=∂
∂γ Zdxdy
z(γ)
Z
z(γo)
dz ρ d†σ
dt
≈1
δγ Zdxdy
z(γ+δγ/2)
Z
z(γo)
dz ρ d†σ
dt−Zdxdy
z(γ−δγ/2)
Z
z(γo)
dz ρ d†σ
dt
=1
δγ Zdxdy
z(γ+δγ/2)
Z
z(γ−δγ/2)
dz ρ d†σ
dt.
(36.76)
This result, or rather the more general version given by equation (36.75), forms the basis for the watermass
transformation diagnostics appearing in such studies as Iudicone et al. (2008) and Maze et al. (2009).
36.5.2 Neutral density versus locally referenced potential density
In an attempt to exploit the watermass transformation formalism using neutral density, Iudicone et al.
(2008) introduce the scale factor
B ≡ |∇γn|
|ρ,Θ,∇Θ+ρ,S ∇S|,(36.77)
that approximately accounts for the differences between the evolution of neutral density γn(McDougall
and Jackett,2005) and locally referenced potential density. Regions where Bdeviates from unity include,
Elements of MOM November 19, 2014 Page 473

Chapter 36. Dianeutral transport and associated budgets Section 36.6
in particular, the Southern Ocean. We have had mixed results using the Bfactor for online diagnostics. The
problem arises in regions where the ratio can become unreasonably large, which is available for various
physical and numerical reasons. It is for this reason that we generally apply the watermass diagnostics
with the layer method based on potential density rather than neutral density.
As shown by Iudicone et al. (2008), the watermass transformation equation (36.72) using neutral den-
sity surfaces takes on the form
G(γn) = ∂
∂γnZ
V(γn,γo)
dV ρBd†γ
dt,(36.78)
with the finite difference approximation (36.75) given by
G(γn) = 1
δγnZ
V(γn+δγn/2,γn−δγn/2)
dV ρBd†γ
dt.(36.79)
The introduction of Ballows for an extension of the water mass transformation formalism to neu-
tral density framework. Unfortunately, the calculation of Bis not well posed. Namely, in any particular
simulation there may be points or regions where Bcan obtain very large or very small values. However,
fundamental to its use is the assumption that γand γnsurfaces deviate only modestly at any given point.
However, as the ratio of two numbers, each of which are subject to numerical truncation errors, there is
no guarantee that Bin a numerical simulation will remain well bounded within its physically reasonable
range. Indeed, what constitutes a physically reasonable range is a difficult question to answer in general.
Our experience has therefore been that the online calculation of Bis not robust. This behaviour suggests
that further research is required to bring about a more appropriate generalization of the watermass trans-
formation formalism.
Given the above noted difficulties with B, we provide various options in MOM. First, we may set Bto
unity everywhere, which returns the calculation to the traditional locally referenced potential density ap-
proach. Second, we provide options to bound B, with values ranging from 1/2 to 2 considered physically
reasonable. The alternative approach from Iudicone et al. (2008), who computed Bbased on a climatology,
is not generally appropriate for the MOM diagnostic. Namely, our aim is to use the diagnostic online, with
watermass transformation fields computed each time step during a simulation.
36.5.3 The discrete approximation
Equation (36.79) provides a method to compute the net watermass transformation associated with a neu-
tral density surface γn. A finite difference calculation of the volume integral takes the form
G(γn) = 1
δγnZ
V(γn+δγn/2,γn−δγn/2)
dV ρBd†γ
dt
≈1
δγnX
i,j,k
dVBρd†γ
dtΠ(γn±δγn/2).
(36.80)
The dimensionless function Πacts as a binning operator that vanishes when the density at a particular
i,j,k grid box is outside of the chosen density layer, and unity when inside the layer. The integrand is com-
puted at each grid point in the level model, and then a density binning is performed to approximate the
volume integral. Both sides of equation (36.80) have the physical dimensions of mass per time. The right
hand side is diagnosed in MOM, where the material time derivative is expanded into its various contribu-
tions. From this diagnostic, one can then diagnose terms in the mass equation (36.1).
Elements of MOM November 19, 2014 Page 474
Chapter 36. Dianeutral transport and associated budgets Section 36.6
36.6 Kinematic method to compute the material time derivative
The purpose of this section is to introduced the kinematic method used to compute the material time
derivative of locally referenced potential density. More details are provided in Section 36.8.
36.6.1 Principles of the kinematic method
The kinematic method works directly with the Eulerian time tendency and advection tendency (arising from
both resolved and parameterized advection) of potential temperature and salinity in order to diagnose
their material time derivatives. To unpack the terms required for this approach, we write the material time
derivative d†/dtas
d†
dt=d
dt+v∗·∇.(36.81)
Again, v∗is a parameterized eddy-induced transport velocity that satisfies the non-divergence constraint
(36.58) for a non-Boussinesq fluid, or the constraint (36.60) for a Boussinesq fluid. Expanding the deriva-
tives leads to
ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!=ρ,Θ ρdΘ
dt+ρv∗·∇Θ!+ρ,S ρdS
dt+ρv∗·∇S!
=ρ,Θ ρdΘ
dt+∇·(ρv∗Θ)!+ρ,S ρdS
dt+∇·(ρv∗S)!(36.82)
where we used the non-divergence condition (36.58) for the last step. We now expand the material time
derivative acting on Θand S. For this purpose, we expose a detail concerning the model’s generalized level
coordinates, in which a smooth function s=s(x,y,z,t)defines surfaces of constant generalized vertical
coordinate.2In this case, we choose to write the material time derivative from the resolved motions in the
form
d
dt=∂
∂t !s
+u·∇s+w(s)∂z(36.83)
where the time and horizontal derivative operators are taken on surfaces of constant s,uis the horizontal
velocity component, and w(s)is the model’s dia-surface velocity component defined according to equation
(36.31). Furthermore, we note that the generalized vertical coordinate form of mass conservation is given
by
∂t(z,s ρ) + ∇s·(z,s ρu) + ∂s(ρw(s))=0.(36.84)
These results then lead to the following form for the in situ density weighted material time derivative of
locally referenced potential density
ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!=ρ,Θ ρdΘ
dt+∇·(ρv∗Θ)!+ρ,S ρdS
dt+∇·(ρv∗S)!
=ρ,Θ∂t(z,s ρΘ) + ∇s·(z,s ρΘu) + ∂s(ρΘw(s)) + ∇·(ρv∗Θ)
+ρ,S ∂t(z,s ρS) + ∇s·(z,s ρS u) + ∂s(ρ S w(s)) + ∇·(ρv∗S).
(36.85)
The second equality writes the material derivative as the sum of two flux-form derivatives, each weighted
by their respective density partial derivatives.
36.6.2 Finite volume considerations
In developing diagnostic methods to measure dianeutral transport, it is useful to closely follow the numer-
ical methods used to time step the prognostic model variables. For this purpose, we briefly recall salient
elements of the tracer budget as discretized in MOM. More details are provided in Section 36.8.
2Be careful not to confuse the general vertical coordinate swith the salinity S.
Elements of MOM November 19, 2014 Page 475
Chapter 36. Dianeutral transport and associated budgets Section 36.6
s=sk−1
grid cell k
s=sk
z
Figure 36.3: Schematic of an ocean grid cell labeled by the vertical integer k. Its sides are vertical and
oriented according to ˆ
xand ˆ
y, and its horizontal position is fixed in time. The top and bottom surfaces are
determined by constant generalized vertical coordinates sk−1and sk, respectively. Furthermore, the top and
bottom are assumed to always have an outward normal with a nonzero component in the vertical direction
ˆ
z. That is, the top and bottom are never vertical. We take the convention that the discrete vertical label k
increases as moving downward in the column, and grid cell kis bounded at its upper face by s=sk−1and
lower face by s=sk.
Grid cells in MOM are bounded on the sides by surfaces of constant horizontal coordinates (x,y), and
the vertical by surfaces of constant generalized vertical coordinate s(see Figure 36.3). The continuous
expression for the material time derivative of tracer
ρd†C
dt=ρdC
dt+∇·(ρv∗C) (36.86)
takes the following semi-continuous form when integrated vertically over the extent of a grid cell
zk−1
Z
zk ρd†C
dt!dz=∂t(ρC dz) + ∇s·(ρ C u†dz) + ∆k(ρ C w(s)†).(36.87)
In equation (36.87), Cis the tracer concentration (tracer mass per seawater mass) within the grid cell; ρdz
is the seawater mass per horizontal area; dzρCu†is the horizontal flux of tracer mass associated with
residual mean advection with
u†=u+u∗(36.88)
the horizontal component of the residual mean velocity. The flux crossing the vertical interfaces of the grid
cell is given by ρC w(s)†, and the difference of these fluxes across the top and bottom of the cell is denoted
by the operator
∆kA=Ak−1−Ak,(36.89)
with ka discrete label for the vertical level. For Boussinesq vertical coordinates (e.g., geopotential, z∗),
the density factors are cancelled, whereas they remain for the non-Boussinesq pressure based vertical
coordinates.
It is the expression (36.87) that forms the basis for numerically integrating the tracer budgets in MOM.
Therefore, we use this expression as the basis for the diagnostic calculation of the material time derivative
of temperature and salinity in a model grid cell
zk−1
Z
zk
dz"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#=ρ,Θ∂t(ρΘdz) + ∇s·(ρΘu†dz) + ∆k(ρΘw(s)†)
+ρ,S ∂t(ρS dz) + ∇s·(ρ S u†dz) + ∆k(ρ S w(s)†).
(36.90)
Elements of MOM November 19, 2014 Page 476

Chapter 36. Dianeutral transport and associated budgets Section 36.7
The result (36.90) represents a semi-discrete analog to the continuum kinematic expression (36.85). Its
evaluation requires the time tendency for (Θρdz)and (S ρdz), and the corresponding tendencies arising
from the residual mean advection. Note that the material time derivative of locally referenced potential
density does not allow for a fully finite volume expression, since ρ,Θand ρ,S are generally functions of
space and time. We choose to evaluate these density derivatives at the grid cell center.
36.6.3 Distinguishing material evolution from local time evolution
When contemplating various test problems to ensure robustness of the diagnostics, one may encounter
a conundrum that is resolved when remaining mindful of the distinction between material time evolution
and local time evolution. For example, a grid cell may change its heat and/or temperature through the
convergence of an advective heat flux into the cell, which in turn will change the grid cell density. But if the
grid cell change arises solely from advection by the residual mean velocity, then there is no corresponding
material time evolution of temperature or density in the grid cell. In this situation, there is no penetration
of the moving neutral tangent plane, so that there is no dianeutral transport. This situation is fundamental
to the formulation of dia-surface transport in Sections 36.3.2 and 36.4. In short, it is only when the grid
cell evolution of heat and salt has an associated irreversible component will there be a nonzero material
evolution, which in turn will lead to nonzero dianeutral transport.
36.7 Process method to compute the material time derivative
The second method for diagnosing the material time derivative informs us how boundary fluxes of buoy-
ancy and physical processes individually impact material evolution, and thus dianeutral transport. We
term this the process method, as it identifies those processes, including boundary fluxes, that give rise to
irreversible mixing of water masses. In this approach, we note that the material time derivatives of conser-
vative temperature and salinity are driven by physical processes that are parameterized either by a local
flux convergence, or a source. The tracer equation then takes the continuum form
ρd†Θ
dt=−∇·JΘ+ρSΘ(36.91)
ρd†S
dt=−∇·JS+ρSS,(36.92)
where again Jconsists of SGS fluxes arising from lateral and dia-surface mixing processes. The local
source/sink terms SΘand SSimpact conservative temperature and salinity in a non-flux convergence
manner, with the nonlocal transport term from KPP (Large et al.,1994) an important example. These
forms for the tracer equations lead to
"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#=ρ,Θ(−∇·JΘ+ρSΘ) + ρ,S (−∇·JS+ρSS).(36.93)
We evaluate this expression using the same convention taken for the kinematic method, in which ρ,Θand
ρ,S are evaluated at a grid cell center and then multiply the finite volume integrated expressions for the
flux convergence and sources, so that
dz"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#=ρ,Θ∇s·(JΘdz) + ∆k(J(s)
Θ)+ρ,S ∇s·(JSdz) + ∆k(J(s)
S)+ρdz(ρ,ΘSΘ+ρ,S SS).
(36.94)
The remaining subsections identify particular processes contributing to the right hand side.
36.7.1 Neutral diffusion, cabbeling, and thermobaricity
The diagnosis of the dianeutral transport utilizes the numerical methods of MOM, which are based on finite
volume techniques applied to the scalar tracer equations. However, these techniques are not precisely
Elements of MOM November 19, 2014 Page 477

Chapter 36. Dianeutral transport and associated budgets Section 36.7
compatible with certain results arising from a continuum representation; in particular, with the manipu-
lations required to isolate the impacts from thermobaricity and cabbeling. That is, thermobaricity and
cabbeling result from manipulating the conservative temperature and salinity equations to expose the
specific nature of the nonlinear equation of state and its impacts on locally referenced potential density.
However, those manipulations are not respected precisely by the discrete equations. We therefore diag-
nose thermobaricity and cabbeling as a discrete representation of the analytical results presented in this
section.
Consider the material time evolution of conservative temperature and salinity associated with neutral
diffusion, and write this evolution in the form
"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#ndiffuse
=−ρ,Θ∇·JΘ−ρ,S ∇·JS
=−∇·(ρ,ΘJΘ+ρ,S JS) + ∇ρ,Θ·JΘ+∇ρ,S ·JS
=∇ρ,Θ·JΘ+∇ρ,S ·JS,
(36.95)
where we set
ρ,ΘJΘ+ρ,S JS= 0 neutral diffusive fluxes. (36.96)
for neutral diffusion fluxes, which is a property revealed by the specific form of neutral diffusion fluxes
detailed below (see, for example Griffies et al.,1998).
In the presence of neutral diffusion, the horizontal and vertical tracer flux components take the form
Jh=−Anρ∇nC(36.97)
Jz=−AnρS·∇nC, (36.98)
with An>0the neutral diffusivity, Sthe neutral slope vector relative to the horizontal, and
∇n=∇z+S∂z(36.99)
the horizontal gradient operator oriented along neutral directions. Note that we are assuming for the
meantime that the vertical coordinate is geopotential. However, as we will see, the final result of our
manipulations will be coordinate invariant, thus facilitating evaluation with any vertical coordinate.
With the flux components (36.97) and (36.98), one may indeed show that there is no flux of locally
referenced potential density, as per equation (36.96). However, in the presence of realistic seawater equi-
librium thermodynamics, the non-flux terms in equation (36.95) give rise to cabbeling, thermobaricity, and
halobaricity (McDougall,1987b). A series of straightforward manipulations (e.g., Section 14.1.7 of Griffies,
2004) render
JΘ·∇ρ,Θ+JS·∇ρ,S =Anρ2C|∇nΘ|2+T ∇np·∇nΘ,(36.100)
where
T=β ∂p α
β!
=∂α
∂p −α
β
∂β
∂p
=−ρ−1ρ,S ∂p ρ,Θ
ρ,S !
=−ρ−1"ρ,Θp−ρ,pS ρ,Θ
ρ,S !#
(36.101)
is the thermobaricity parameter (units of inverse temperature times inverse pressure), and
C=∂α
∂Θ+ 2α
β
∂α
∂S − α
β!2∂β
∂S
=−ρ−1ρ,ΘΘ −2ρ,ΘS ρ,Θ
ρ,S !+ρ,SS ρ,Θ
ρ,S !2
(36.102)
Elements of MOM November 19, 2014 Page 478

Chapter 36. Dianeutral transport and associated budgets Section 36.7
is the cabbeling parameter (units of squared inverse temperature). Empirically, the cabbeling parameter is
strictly positive for seawater, thus leading to an increase in density through cabbeling. The thermobaric-
ity parameter is predominantly positive. However, the product ∇np·∇nΘneed not be sign-definite, thus
allowing for thermobaricity to either increase or decrease density. Use of the expression (36.100) in the
material time derivative in equation (36.95) leads to the material time derivative arising from cabbeling
and thermobaricity
"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#ndiffuse
=Anρ2C|∇nΘ|2+T ∇np·∇nΘcabbeling and thermobaricity.
(36.103)
The right hand side is discretized for the cabbeling and thermobaricity diagnostic in MOM.
36.7.2 Dianeutral diffusion
Dianeutral diffusion of tracer is generally parameterized using a downgradient vertical diffusive flux (see
Section 7.4.3 of Griffies (2004) for discussion)
JΘ=JΘˆ
z(36.104)
JS=JSˆ
z(36.105)
where
JΘ=−D(Θ)ρ∂zΘ(36.106)
JS=−D(S)ρ∂zS, (36.107)
with eddy diffusivities D(Θ)>0and D(S)>0for potential temperature and salinity, respectively. The corre-
sponding material evolution is given by
"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#vdiffuse
=ρ,Θ
∂
∂z ρD(Θ)∂Θ
∂z !+ρ,S ∂
∂z ρD(S)∂S
∂z !vertical diffusion. (36.108)
We identify the following regimes for which vertical diffusion acts to produce a nonzero dianeutral trans-
port.
• In the ocean interior, D≈10−6m2s−1at the equator beneath the region of strong vertical shear
associated with the equatorial undercurrent (Gregg et al.,2003), and D≈10−5m2s−1in the mid-
dle latitudes (Ledwell et al.,1993,2011), with far larger values near rough topography and other
boundary regions (Polzin et al.,1997;Naveira-Garabato et al.,2004).
• The diffusivity can be set to a very large value in gravitationally unstable regions.
• The diffusivity for conservative temperature and salinity differ in regions where double diffusive pro-
cesses occur (Schmitt,1994;Large et al.,1994).
• The upper and lower ocean boundary conditions for the vertical tracer diffusive flux are Neumann
conditions, whereby the temperature and salt fluxes are specified through boundary interactions with
other components of the climate system. Hence, the vertical diffusion operator serves as the conduit
through which the boundary fluxes are fed into the tracer equations. There will be a correspondingly
very large dianeutral velocity component in the surface grid cell, and potentially nontrivial dianeutral
velocity component at the ocean bottom if geothermal heating is applied.
36.7.3 Sources
The sources appearing in equation (36.95) are evaluated in the model to determine the following dianeu-
tral velocity component
"ρ,Θ ρd†Θ
dt!+ρ,S ρd†S
dt!#sources
=ρρ,ΘSΘ+ρ,S SS.(36.109)
We consider the following sources that arise in ocean climate models.
Elements of MOM November 19, 2014 Page 479

Chapter 36. Dianeutral transport and associated budgets Section 36.8
• Penetrative shortwave radiation provides a heating source SΘthat extends over the upper 50m-
100m of the ocean, depending on optical properties. Iudicone et al. (2008) emphasized the impor-
tance of this term for dianeutral transport within the Walin (1982) framework. However, in MOM, the
shortwave heating is implemented as a flux convergence, as detailed in Section 17.1. So shortwave
penetration is in fact not formulated as a source term.
• The mixed layer parameterization of Large et al. (1994) includes a nonlocal transport term, whose
form appears as a source to the potential temperature and salinity equations. The importance of this
term for dianeutral transport remains unexplored in the literature.
• There are potentially other source terms that may arise in any particular simulation, such as those
associated with nonlocal mixing across land locked marginal seas (Griffies et al.,2005).
36.8 Finite volume estimate of the advective-form material time deriva-
tive
Diagnosis of the dianeutral transport must confront the need to estimate a material flux across a moving
surface using finite volume budget equations of a quasi-Eulerian ocean model. Namely, we must estimate
a material time derivative, written in advective-form, based on finite volume flux-form computations of the
temperature and salinity changes. We expose here the choices made for the diagnostics available in MOM,
with the following representing an outline of the approach.
• Formulate the finite-volume flux-form budgets for temperature and salinity;
• Multiply the budgets by ρ,Θand ρ,S to obtain a finite-volume budget for locally referenced potential
density;
• Expose the advective-form material time derivative of locally referenced potential density that is
implied by the flux-form finite volume discretization;
• Isolate the advective-form material time derivative and identify various contributions to both the
kinematic method and process method.
36.8.1 A transport theorem for grid cells
The starting point of the finite volume formulation is development of an expression for the material time
derivative of tracer, ψ, evaluated over a finite size grid cell in an ocean model, with the continuum form of
the material evolution written in the flux-form
ρd†ψ
dt=∂t(ρψ) + ∇·(ρv†ψ).(36.110)
Grid cells of concern with generalized level models, such as MOM, have static vertical side boundaries.
However, the top and bottom boundaries undulate in time, with these surfaces specified by a value of
the general vertical coordinate s. The manipulations in this section require methods of vector calculus,
with elements reviewed in Section 6.7 of Griffies (2004) and Section 2.2 of Griffies and Adcroft (2008).
The resulting equation (36.118) is a transport theorem for a grid cell, with this theorem similar to the
Reynolds Transport Theorem appropriate for a volume moving with the fluid motion (e.g., Aris,1962;Batch-
elor,1967). Those uninterested in the mathematical details can safely skip to the final result (36.118), as
that result is quite intuitive.
The most complex part of the derivation concerns the partial time derivative on the right hand side of
Elements of MOM November 19, 2014 Page 480

Chapter 36. Dianeutral transport and associated budgets Section 36.8
equation (36.110). We integrate this term over a grid cell by introducing Cartesian coordinates (x,y,z)
ZdV(ρψ),t =Zdxdydz(ρ ψ),t
=Zdxdy
z2
Z
z1
dz(ρψ),t
=Zdxdyh−(ρψ)|z2∂tz2+ (ρ ψ)|z1∂tz1i+∂t ZdV(ρ ψ)!.
(36.111)
The second equality follows by noting that the horizontal extent of a grid cell remains static, thus allowing
for the horizontal integral to be brought outside of the time derivative. In contrast, the vertical extents of
the cell, z1(x,y,t)≤z≤z2(x,y,t), are generally functions of space and time, which necessitates the use of
Leibniz’s Rule.
We next seek to relate the time derivatives of the depth of the generalized levels ∂tzto the velocity of
a point on that surface. For this purpose, first relate ∂tzto time tendencies ∂tsof the surface itself, making
use of the identity (see, for example, Section 6.5.4 of Griffies,2004)
∂z
∂t !s
=−∂z
∂s
∂s
∂t .(36.112)
Next, make use of the kinematics associated with dia-surface transport, as formulated in Section 6.7 of
Griffies (2004) or Section 2.2 of Griffies and Adcroft (2008), to write
∂tz=∂sz|∇s|ˆ
n·v(ref),(36.113)
where v(ref)is the three dimensional velocity vector for a point attached to the generalized level surface.
As a final step, relate the area element on the generalized surface to the horizontal projection dA= dxdy
of that surface
dA(ˆ
n)=|∂sz∇s|dA, (36.114)
which then renders
∂tzdA=ˆ
n·v(ref)dA(ˆ
n).(36.115)
This equation relates the time tendency of the depth of the generalized surface to the normal component
of the velocity at a point on the surface. The two are related through the ratio of the area elements. This
result is now used for the top and bottom boundary terms in relation (36.111), yielding
ZdV(ρψ),t =∂t ZρdV ψ!−ZdA(ˆ
n)ˆ
n·v(ref)(ρψ).(36.116)
Hence, the domain integrated Eulerian time tendency of the density weighted field equals the time ten-
dency of the density weighted field integrated over the domain, minus an integral over the domain bound-
ary associated with motion of the domain. If the domain boundary has zero velocity, as for a geopotential
coordinate model with fixed vertical grid spacing, then the second term in equation (36.116) vanishes.
The next step needed for volume integrating the density weighted material time derivative in equation
(36.110) involves the divergence of the density weighted field
ZdV∇·(ρv†ψ) = ZdA(ˆ
n)ˆ
n·v†(ρψ),(36.117)
which follows from Gauss’ Law. Combining this relation with equation (36.116) leads to the desired result
ZρdVdψ
dt=∂t ZρdV ψ!+ZdA(ˆ
n)ˆ
n·(v†−v(ref))(ρ ψ).(36.118)
Elements of MOM November 19, 2014 Page 481

Chapter 36. Dianeutral transport and associated budgets Section 36.8
Hence, the mass weighted grid cell integral of the material time derivative of a field is given by the time
derivative of the mass weighted field integrated over the domain, plus a boundary term that accounts for
the transport across the domain boundaries, with allowance made for moving domain boundaries.
In the case of a grid cell of concern here, the moving domain boundaries are only those at the top and
bottom of the cell, with motion associated with time dependence of the generalized vertical coordinate s.
It is for these surfaces that the reference velocity v(ref)is nonzero. Special interest arises for the ocean
surface boundary, where mass and buoyancy fluxes enter or leave the ocean. The bottom boundary allows
for geothermal heat fluxes to warm the deep ocean layers. Notably, the ocean bottom is kinematically
simpler than the ocean top surface, since the interface between the liquid ocean bottom and solid earth
is assumed to be static for our purposes. Hence, v(ref)= 0 for the ocean bottom. Finally, the vertical side
boundaries of all grid cells are static, which means v(ref)= 0 for these surfaces as well.
36.8.2 Tracer and mass budgets for an interior grid cell
We now apply the transport theorem (36.118) to derive budgets of seawater mass and tracer mass in a
grid cell, with applications then made to the semi-discrete budgets of a generalized level coordinate ocean
model. We start from the general expression for the material time derivative of a tracer
ρd†ψ
dt=−∇·J+ρSψ(36.119)
and use the transport theorem (36.118) to render a budget for the total tracer mass within a grid cell
∂t Zψ ρ dV!+ZdA(ˆ
n)ˆ
n·[(v†−vref)ρ ψ] = −ZdA(ˆ
n)ˆ
n·J+ZSψρdV . (36.120)
The left hand side of this tracer budget is the finite volume expression of the kinematic material time
derivative of the tracer, whereas the right hand side is the process version. It is useful to keep the kinematic
and process versions of the material time derivative distinct for purposes of attributing terms in the budget
for locally referenced potential density. When the tracer concentration is uniform, the subgrid scale flux
Jvanishes. Additionally, the eddy-induced velocity generally satisfies ∇ · (ρv∗) = 0. The resulting finite
domain mass budget takes the form
∂t ZρdV!+ZdA(ˆ
n)ˆ
n·[(v−vref)ρ] = ZSρρdV , (36.121)
where Sρis a mass source tendency (units of inverse time). For brevity in the following, we assume Sρ= 0.
36.8.2.1 Semi-discrete flux-form expression
Taking the limit as the time independent horizontal area dxdygoes to zero leads, after some steps, to the
semi-discrete flux-form tracer budget
∂t(dzρψ) + ∇s·(dz ρ u†ψ) + ∆k(ρw(s)†ψ) = −∇s·(dzJ)−∆k(J(s)) + ρdzSψ,(36.122)
where again
∆kA=Ak−1−Ak(36.123)
is a discrete operator acting in the vertical. In equation (36.122), w(s)†measures the volume flux crossing
the surfaces of constant generalized vertical coordinates due to the residual-mean transport velocity, and
J(s)is the corresponding subgrid scale tracer flux. Both w(s)†and J(s)are straightforward generalizations
of their geopotential coordinate model forms. Again, the left hand side of the tracer budget (36.122) is a
semi-discrete flux-form kinematic expression for the material time derivative, whereas the right hand side
is flux-form process version of the material time derivative. By setting the tracer concentration in equation
(36.122) to a uniform constant we recover the mass budget for a grid cell
∂t(dzρ) + ∇s·(dzρu†) + ∆k(ρ w(s)†)=0.(36.124)
Since the quasi-Stokes transport satisfies ∇·(ρv∗)=0, we could just as well write
∂t(dzρ) + ∇s·(dzρu) + ∆k(ρ w(s))=0.(36.125)
Elements of MOM November 19, 2014 Page 482

Chapter 36. Dianeutral transport and associated budgets Section 36.8
36.8.2.2 Advective-form expression
Equations (36.122) and (36.125)-(36.124) are the semi-discrete grid cell budgets for tracer mass and sea-
water mass that correspond directly to the flux-form discrete equations implemented in MOM. These equa-
tions are the basis for the diagnostic budgets developed for locally referenced potential density. However,
to diagnose the dianeutral transport, we need the advective-form of the material time derivative. We thus
wish to derive the semi-discrete expression for the advective-form of the material time derivative implied
by the flux-form. For this purpose, expand the time and horizontal space derivatives on the left hand side
of the flux-form tracer equation (36.122) to yield
∂t(dzρψ) + ∇s·(dz ρ u†ψ) + ∆k(ρw(s)†ψ) = ρdz∂tψ+u†·∇sψ+ψ∂t(dz ρ) + ∇s·(dz ρ u†)+∆k(ρ w(s)†ψ)
=ρdz∂tψ+u†·∇sψ−ψ∆k(ρw(s)†) + ∆k(ρw(s)†ψ)
=ρdz ∂tψ+u†·∇sψ+∆k(ρw(s)†ψ)−ψ∆k(ρw(s)†)
dz!,
(36.126)
where the mass balance (36.124) was used to reach the second equality. In the continuum limit, the right
hand side indeed reduces to a density and thickness weighted estimate for the material time derivative.
Hence, dividing the flux-form expression by ρdzyields a consistent estimate for the advective-form mate-
rial time derivative in an interior grid cell.
36.8.3 Material time derivative of locally referenced potential density for an interior
cell
We use the previous results to derive an expression for the material time derivative of locally referenced
potential density as integrated over an interior model grid cell. The kinematic version of the material time
derivative yields
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ) + (ρw(s)†Θ)k−1−(ρ w(s)†Θ)k!
+ dAρ,S ∂t(ρdzS) + ∇s·(ρdzu†S) + (ρw(s)†S)k−1−(ρ w(s)†S)k!.
(36.127)
It is common to represent the tracer effects from a quasi-Stokes transport velocity v∗from Gent and
McWilliams (1990) as a skew tracer diffusion rather than as an advection process (Griffies,1998). Do-
ing so does not alter the association of the skew tracer transport with the kinematic form of the material
time derivative. That is, just because skew diffusion might be computed along with neutral diffusion, the
skew diffusion should not be associated with the process version of the material time derivative.
The finite-volume process version of the material time derivative is given by
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ −∇s·(dzJΘ)−(J(s)Θ)s=sk−1+ (J(s)Θ)s=sk+ρdzSΘ!
+ dAρ,S −∇s·(dzJS)−(J(s)S)s=sk−1+ (J(s)S)s=sk+ρdzSS!.
(36.128)
Again, the fluxes JΘand JSarise from non-advective subgrid scale processes active in the ocean interior, as
well as penetrative boundary fluxes from solar radiation (which contributes just to the temperature flux).
36.8.4 Tracer and mass budgets for a bottom grid cell
We now apply the tracer budget (36.120) for a grid cell adjacent to the ocean bottom, where we assume
that just the bottom face of the cell abuts the solid earth boundary. The advective term vanishes
ZdA(ˆ
n)ˆ
n·[(v†−vref)ρ ψ] = 0 (36.129)
Elements of MOM November 19, 2014 Page 483

Chapter 36. Dianeutral transport and associated budgets Section 36.8
since there is no normal flow at the static ocean bottom with vref = 0
ˆ
n·v†= 0 =⇒w(s)†= 0 at z=−H(x,y).(36.130)
For the subgrid scale flux J, we note that the outward normal at the bottom is given by
ˆ
nH=− ∇(z+H)
|∇(z+H)|!at z=−H(x,y),(36.131)
and the area element along the bottom is (see Section 20.13.2 of Griffies (2004))
dAH=|∇(z+H)|dA, (36.132)
with dA= dxdythe horizontal area element. Hence, tracer transport across the solid earth boundary is
−ZdAHˆ
nH·J=ZdA(∇H+ˆ
z)·J.(36.133)
We allow for the possibility of a nonzero geothermal tracer transport, which renders
Qbott = (∇H+ˆ
z)·J=−J(s)Θ,(36.134)
with Qbott >0indicating an input of heat to the ocean through the bottom. The corresponding thickness
weighted budget for a grid cell next to the ocean bottom is given by
∂t(dzρψ) + ∇s·(dz ρ u†ψ) + (ρw(s)†ψ)s=skb−1=−∇s·(dzJ)−(J(s))s=skb−1+Qbott (36.135)
where kb is the number of vertical grid cells in a fluid column. The corresponding budget for mass in the
bottom cell is given by
∂t(dzρ) + ∇s·(dzρu) + (ρ w(s))s=skb−1= 0,(36.136)
assuming zero mass flux of seawater through the ocean bottom.
As for the discussion in Section 36.8.2, we may rewrite the kinematic (left hand side) of the tracer
budget (36.135) in the advective-form
∂t(dzρψ) + ∇s·(dz ρ u†ψ) + ∆k(ρw(s)†ψ) = ρdz ∂tψ+u†·∇sψ+∆k(ρ w(s)†ψ)−ψ∆k(ρ w(s)†)
dz!,(36.137)
which follows from equation (36.126) using the bottom no-flow kinematic boundary condition (36.130). So
just as for an interior cell, we estimate the advective-form of the material time derivative via division of the
flux-form by ρdz.
36.8.5 Material time derivative of locally referenced potential density for a bottom
cell
For a bottom ocean grid cell, the kinematic version of the material time derivative of locally referenced
potential density is given by
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ) + (ρw(s)†Θ)k−1!
+ dAρ,S ∂t(ρdzS) + ∇s·(ρdzu†S) + (ρw(s)†S)k−1!.
(36.138)
The process version of the material time derivative yields
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ −∇s·(dzJΘ)−(J(s)Θ)s=sk−1−Qbott +ρdzSΘ!
+ dAρ,S −∇s·(dzJS)−(J(s)S)s=sk−1+ρdzSS!.
(36.139)
This expression has assumed a zero flux of salt through the ocean bottom. As noted by equation (36.137),
an estimate for the advective-form of the material time derivative in a bottom grid cell is obtained through
dividing the flux-form by ρdz.
Elements of MOM November 19, 2014 Page 484

Chapter 36. Dianeutral transport and associated budgets Section 36.8
36.8.6 Tracer and mass budgets for a surface grid cell
Transport across the ocean surface occurs when water parcels enter or leave the ocean domain. As water
parcels generally carry tracer content (e.g., heat and salt), their cross boundary transport changes tracer
content of the ocean domain. The boundary transport of matter appears as an added term in the kine-
matic boundary condition for mass conservation. Additionally, cross boundary matter transfer involves an
irreversible mixing process to bring a parcel across the skin layer of the boundary and to incorporate the
matter into the liquid ocean. Details of the mixing that occurs when matter crosses the ocean surface are
not easily deduced, and such mixing is fundamental to boundary layer turbulence schemes and formula-
tion of flux relations (e.g., bulk formulae for heat transport; gas exchange formulae for biogeochemical
transport).
For the interior and bottom grid cells, there is no distinction between the flux-form and advective-form
of the material time derivative. However, for surface grid cells, there is a difference, with this difference
arising from the open nature of the surface boundary, in which mass is transported across the boundary.
Formulating the advective-form of the material time derivative in a surface cell thus proves to be more
subtle relative to the interior and bottom cells. We expose the necessary details in this section.
36.8.6.1 Kinematic formulation
For a grid cell adjacent to the ocean surface, assume that just the upper face of this cell abuts the boundary
between the ocean and the atmosphere or ice. The ocean surface is a time dependent boundary z=
η(x,y,t), with an outward normal
ˆ
nη=∇(z−η)
|∇(z−η)|at z=η(x,y,t),(36.140)
pointing from the ocean surface into the overlying media. We restrict attention to those free surface
undulations where ˆ
nηhas a positive projection in the vertical. That is, we do not consider overturning
or breaking surface waves, which is an assumption appropriate for hydrostatic ocean models. The area
element dAηmeasures an infinitesimal area on the ocean surface z=η, and it is related to the horizontal
area element dAvia
dAη=|∇(z−η)|dA. (36.141)
As the ocean free surface can move, the advective transport across this surface must be measured
with respect to the moving surface. We formulate the advective transport across this boundary just as
for the dia-surface transport crossing a moving generalized vertical coordinate surface. For this purpose,
consider the velocity of a reference point on the surface
vref =uref +ˆ
zwref.(36.142)
Since z=ηrepresents the vertical position of the reference point, the vertical component of the velocity
for this point is given by
wref = (∂t+uref ·∇)η(36.143)
which then leads to
vref ·∇(z−η) = η,t.(36.144)
Hence, the advective transport leaving the ocean surface is
Z
z=η
dA(ˆ
n)ˆ
n·(v†−vref)ρ ψ =Z
z=η
dA(−η,t +w−u·∇η)ρψ
=−Z
z=η
dAQmψ.
(36.145)
For the first equality, we noted that the eddy induced velocity satisfies the no normal flow condition at all
ocean boundaries
ˆ
n·v∗= 0 at boundaries. (36.146)
Elements of MOM November 19, 2014 Page 485

Chapter 36. Dianeutral transport and associated budgets Section 36.8
For the second equality, we made use of the surface kinematic boundary condition, which can be written in
its Lagrangian form
ρ d(z−η)
dt!=−Qmat z=η(x,y,t) (36.147)
or Eulerian form
∂tη+u·∇η=ρw +Qmat z=η(x,y,t).(36.148)
The mass flux Qmmeasures the mass per time per horizontal area of mass crossing the ocean surface,
with a sign chosen so that Qm>0represents an input of mass to the ocean domain. We can summarize
the result (36.145) with the local relation
Qm=(mass/time) through free surface
horizontal area under free surface
=− ρdA(ˆ
n)ˆ
n·(v−vref)
dA!at z=η.
(36.149)
36.8.6.2 Process formulation and the boundary layer
In summary, the tracer flux leaving the ocean free surface is given by
Z
z=η
dA(ˆ
n)ˆ
n·[(v†−vref)ρ ψ +J] = Z
z=η
dxdy(−Qmψ+J(s)).(36.150)
To evaluate right hand side requires, it seems, the tracer concentration and tracer flux J(s)precisely at the
ocean surface z=η. How literal should we interpret this kinematic result? Seawater properties precisely
at the ocean surface are not what an ocean model carries as its prognostic variable in its top grid cell.
Instead, the model carries a bulk property averaged over the upper finite sized grid cell, which averages
over many regions that occur at the microscale next to the ocean surface (e.g., Robinson,2005). Addition-
ally, within the surface skin region of the ocean, irreversible mixing supports the passage of a fluid parcel
across the boundary, either into the ocean interior (e.g., river runoffand precipitation) or away from the
ocean domain (e.g., evaporation).
To proceed, we assume there to be a boundary layer model that renders the total tracer flux passing
through the ocean surface. Developing such a model is a nontrivial problem in air-sea and ice-sea interac-
tion theory and phenomenology. For present purposes, we are not concerned with details of such models.
Instead, just introduce this boundary flux in the form
−Qmψ+J(s)z=η=−Qmψm−Qpbl,(36.151)
where ψmis the tracer concentration within the incoming mass flux Qm. The first term on the right hand
side of equation (36.151) represents a first order upwind represented advective transport of tracer through
the surface with the water (i.e., ice melt, rivers, precipitation, evaporation). The term Qpbl arises from
parameterized turbulence and/or radiative fluxes within the surface planetary boundary layer, such as
sensible, latent, shortwave, and longwave heating appropriate for the temperature equation. A positive
value for Qpbl signals tracer entering the ocean through its surface.
Using the result (36.151) in expression (36.150) leads to
Z
z=η
dA(ˆ
n)ˆ
n·[(v†−vref)ρ ψ +J] = −Z
z=η
dxdy(Qmψm+Qpbl),(36.152)
which renders the flux-form finite volume tracer budget for a surface ocean grid cell
∂t(dzρψ) + ∇s·(dz ρ u†ψ)−(ρw(s)†ψ)s=sk=1 −Qmψm=−∇s·(dzJ) + (J(s))s=sk=1 +Qpbl .(36.153)
The corresponding mass budget is given by
∂t(dzρ) + ∇s·(dzρu†)−(ρ w(s)†)s=sk=1 −Qm= 0,(36.154)
Elements of MOM November 19, 2014 Page 486

Chapter 36. Dianeutral transport and associated budgets Section 36.8
or the equivalent expression
∂t(dzρ) + ∇s·(dzρu)−(ρ w(s))s=sk=1 −Qm= 0,(36.155)
which follows since ∇·(ρv∗)=0.
36.8.6.3 Advective form
Following from our discussion of the interior and bottom grid cells (see equations (36.126) and (36.137)),
we rewrite the finite volume flux-form of the tracer equation (36.153) in the advective-form via the following
steps
∂t(dzρψ) + ∇s·(dz ρ u†ψ)−(ρw(s)†ψ)s=sk=1 −Qmψm= (ρdz) (∂t+u†·∇s)ψ−(ρw(s)†ψ)s=sk=1 −Qmψm
+ψ ∂t(dzρ) + ∇s·(dzρu†)!
= (ρdz)∂tψ+u†·∇sψ+ψ(w(s)†)s=sk=1 −(ψ w(s)†)s=sk=1
dz
+Qm(ψ−ψm),
(36.156)
where the last step used the finite volume flux-form of the mass budget (36.154). The large bracketed term
in the final step of equation (36.156) reduces to the advective-form of the material time derivative in the
continuum limit. Rearrangement then leads to the identity
(ρdz)∂tψ+u†·∇sψ+ψ(w(s)†)s=sk=1 −(ψ w(s)†)s=sk=1
dz=∂t(dzρψ) + ∇s·(dz ρu†ψ)−(ρw(s)†ψ)s=sk=1 −Qmψ
=−∇s·(dzJ) + (J(s))s=sk=1 +Qm(ψm−ψ) + Qpbl.
(36.157)
where we used equation (36.153) to introduce the process form of the tracer budget.
The result (36.157) suggests that we define the following surface boundary flux forcing that impacts
the advective-form of the material evolution of tracer
Γψ
advective =Qm(ψm−ψ) + Qpbl.(36.158)
For many numerical implementations, the value for ψis taken as the concentration ψk=1 in the surface grid
cell. In this case, the boundary term Qm(ψm−ψ)vanishes if the tracer concentration ψmequals ψk=1. That
is, tracer concentration in a surface grid cell is unchanged by the passage of tracer across the surface
boundary, if the tracer concentration in the boundary flux is the same as in the ocean surface grid cell.
Taking ψm=ψk=1 is commonly assumed for temperature. However, for salinity it is more appropriate to
assume Sm= 0, which leads to a change in surface ocean salinity as fresh water crosses the surface ocean
boundary; e.g., precipitating water reduces ocean salinity whereas evaporating water increases salinity.
Other material tracers (e.g., biogeochemical tracers) generally have concentrations in river water that are
distinct from open ocean seawater.
36.8.6.4 Comments
MOM is formulated using finite volume flux-form budgets for tracers, as in the flux-form tracer equation
(36.153). One key advantage of flux-form is that it facilitates tracer conservation to within numerical
roundoff, whereas advective form tracer budgets cannot ensure such accuracy. Hence, the advective form
of the material time derivative is typically not used to formulate the equations of an ocean model.
However, the advective form, as derived for the surface cell in equation (36.157), is the appropriate
form to estimate the material time evolution of tracer, which in turn is what we need for the dianeutral
Elements of MOM November 19, 2014 Page 487

Chapter 36. Dianeutral transport and associated budgets Section 36.8
mass transport diagnostic. In particular, in an ocean with constant salinity, there is no watermass trans-
formation induced by surface boundary fluxes if a boundary flux of freshwater is added with the same
temperature as the sea surface temperature. However, the ocean heat content does change. An ocean
model should be based on an evolution equation for heat content, as it is heat that is conserved. Yet water-
mass diagnostic as determined by dianeutral mass transport should be based on advective-form material
changes in temperature (and salinity), which in this trivial example does not change (at least through the
boundary fluxes). It is therefore the analog of Γψ
advective (equation (36.157)) that we require to deduce how sur-
face buoyancy fluxes impact watermass transformation. We detail these considerations in Section 36.8.7.
36.8.7 Material time derivative of locally referenced potential density for a surface
cell
The kinematic expression of the material time derivative of locally referenced potential density, for a sur-
face ocean grid cell (k= 1), is written in the flux-form as
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ)−(ρw(s)†Θ)s=sk−QmΘm!
+ dAρ,S ∂t(ρdzS) + ∇s·(ρdzu†S)−(ρw(s)†S)s=sk−QmSm!.
(36.159)
Following the steps considered in Section 36.8.6.3 exposes the advective-form
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ (ρdz)∂tΘ+u†·∇sΘ+
Θ(w(s)†)s=sk−(Θw(s)†)s=sk
dz+Qm(Θ−Θm)!
+ dAρ,S (ρdz)∂tS+u†·∇sS+S(w(s)†)s=sk−(S w(s)†)s=sk
dz+Qm(S−Sm)!.
(36.160)
Likewise, the process version of the material time derivative for a surface grid cell (k= 1) is given by
ZdV ρ ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!= dAρ,Θ −∇s·(dzJΘ) + (J(s)Θ)s=sk=1 +QΘ
pbl +ρdzSΘ!
+ dAρ,S −∇s·(dzJS) + (J(s)S)s=sk=1 +QS
pbl +ρdzSS!.
(36.161)
As in Section 36.8.6.3, we isolate the advective-form of the kinematic expression (36.160) to render the
identity
ρ,Θ (ρdz)∂tΘ+u†·∇sΘ+
Θ(w(s)†)s=sk=1 −(Θw(s)†)s=sk=1
dz!
+ρ,S (ρdz)∂tS+u†·∇sS+S(w(s)†)s=sk=1 −(S w(s)†)s=sk=1
dz!
=ρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ)−(ρw(s)†Θ)s=sk=1 −QmΘ!
+ρ,S ∂t(ρdzS) + ∇s·(ρdzu†S)−(ρw(s)†S)s=sk=1 −QmS!
=ρ,Θ −∇s·(dzJΘ) + (J(s)Θ)s=sk=1 +QΘ
pbl +Qm(Θm−Θ) + ρdzSΘ!
+ρ,S −∇s·(dzJS) + (J(s)S)s=sk=1 +QS
pbl +Qm(Sm−S) + ρdzSS!.
(36.162)
Either the kinematic expression (first equality) or process expression (second equality) can be used to
estimate the advective-form material time derivative.
Elements of MOM November 19, 2014 Page 488

Chapter 36. Dianeutral transport and associated budgets Section 36.9
36.8.7.1 Surface buoyancy forcing
Based on the result (36.162), we introduce the following surface mass flux associated with surface buoy-
ancy fluxes
Γρ= ρdA
∆γn!h−αQΘ
pbl + (Θm−Θ)Qm+βQS
pbl + (Sm−S)Qmi kg s−1,(36.163)
which is directly analogous to the forcing Γψ
advective affecting tracer concentration according to equation
(36.158). The division by ∆γnis relevant when binning the surface buoyancy flux into density classes
(Section 36.15). If Γρ>0, then density increases, and the opposite occurs for Γρ<0. A special case is
worth mentioning, in which we are away from sea ice, so that the salt flux vanishes QS
pbl = 0; the surface
temperature equals to the temperature in the boundary flux, Θk=1 =Θm; and the boundary concentration
of salt is zero, Sm= 0. In this case, the density forcing takes the form
Γρ=− ρdA
∆γn!α QΘ
pbl +β S QmΘk=1 =Θm,Sm= 0,QS
pbl = 0.(36.164)
This form is more familiar (e.g., Large and Nurser,2001) than the more general expression (36.163). As
noted in Section 36.6.3, the transport of water across the ocean surface is, by itself, not sufficient for water-
mass transformation to occur. There must also be mixing of the boundary flux with the ocean. Therefore,
by identifying the density forcing (36.163) as a mechanism of watermass transformation, we are assum-
ing that such mixing will occur. This assumption is generally quite good, since the upper ocean is very
turbulent and boundary fluxes are readily incorporated to the ocean mixed layer.
36.8.7.2 Further comments on surface buoyancy fluxes
Consider surface water and buoyancy fluxes passing into a uniform ocean, or equivalently an ocean com-
prised of a single grid cell. In this case, we drop all lateral and vertical advection, as well as all subgrid
scale and source terms, so that equation (36.162) for the material time derivative reduces to
ρdz ρ,Θ∂tΘ+ρ,S ∂tS!=ρ,Θ ∂t(ρdzΘ)−QmΘ!+ρ,S ∂t(ρdzS)−QmS!
=ρ,Θ Qm(Θm−Θ) + QΘ
pbl!+ρ,S Qm(Sm−S) + QS
pbl!,
(36.165)
where we cancelled the common factor of dAfrom each term. If there are no other physical processes
impacting temperature or salinity, then
∂t(ρΘdz) = QmΘm+QΘ
pbl (36.166)
∂t(ρS dz) = QmSm+QS
pbl (36.167)
∂t(ρdz) = Qm,(36.168)
which makes the two expressions in equation (36.165) consistent.
36.9 Comments on the MOM diagnostic calculation
The following represent some issues regarding the diagnostic calculation of a budget for locally referenced
potential density, and the associated dianeutral transport diagnostic.
36.9.1 Sampling
All of the diagnostics saved in relation to the budget of locally referenced potential density and the di-
aneutral transport are sampled at each model time step. Additionally, the rebinning into density layers
is performed at each model time step. Sampling at each model time step ensures there are no aliasing
issues, or problems related to poor sampling of seasonal and/or diurnal cycling in the upper ocean. How-
ever, there can be some noise, especially for the rebinned fields. Thus, it is best to allow for a thorough
sampling of density space as arrived at through multiple seasonal cycles.
Elements of MOM November 19, 2014 Page 489
Chapter 36. Dianeutral transport and associated budgets Section 36.9
36.9.2 Accounting for time-explicit and time-implicit processes
MOM is based on a finite volume time stepping of the mass of tracer per unit area within a grid cell. There
are two basic sub-steps involved in the update of a single time step. The first sub-step accumulates time-
explicit contributions, with the associated time tendencies computed based on the present state of the
concentration C(τ). Upon accumulating all time-explicit tendencies, the tracer concentration is updated to
C#(τ+ 1). The second sub-step updates based on the time-implicit processes, starting incrementally from
the concentration C#(τ+ 1). Time-implicit processes are generally associated with fast vertical processes,
such as surface boundary fluxes and gravitationally unstable columns. Upon updating the implicit pieces
yields the new tracer concentration C(τ+ 1).
36.9.2.1 Explicit plus implicit time stepping
A schematic update for the explicit time stepping for tracer concentration takes the form
ρdz(τ+ 1)C#(τ+ 1) = ρdz(τ)C(τ) + ∆τ δ(ρdz C)
δτ !expl
,(36.169)
where ∆τis the time step, ρdzis the mass per area of a grid cell. The term δ(ρdzC)/δτ is the time ten-
dency associated with time-explicit processes such as advection and lateral physical parameterizations.
Diagnosing the time tendencies associated with the time-explicit portion of the time step is straitforward,
as these time tendencies are computed directly, and so can be saved as desired. The tracer concentration
C#(τ+ 1) results from this portion of the time stepping.
The second portion of a MOM time step of tracer involves the time-implicit sub-step, which takes the
following schematic form
C(τ+ 1) = C#(τ+ 1) + ∆τδ C
δτ impl
.(36.170)
Combining this step with the time-explicit step (36.169) leads to the expression
ρdz(τ+ 1)C(τ+ 1) −ρdz(τ)C(τ)
∆τ= δ(ρdzC)
δτ !expl
+ρdz(τ+ 1)δC
δτ impl
.(36.171)
The time-implicit step (36.170) includes a single inversion of a tridiagonal solver, with the inversion wrap-
ping together the surface boundary fluxes, the bottom boundary fluxes, and the interior vertical diffusivity.
We can unambiguously identify a tendency associated with surface boundary fluxes and bottom boundary
fluxes, merely by inverting the tridiagonal matrix with the diffusivities set to zero but with the boundary
fluxes retained. However, tendencies from interior mixing that arise from a number of physical processes
(e.g., parameterized tide mixing; shear mixing; gravitationally unstable columns) must be diagnosed in an-
other manner. The reason is that the inversion process for the net of interior diffusion does not equal to
separate inversions of the processes. Alternatively, the single inversion does not equal to an incremental
update of the tracer concentration that would result from a series of inversions (see Section 36.9.2.2).
However, since we know the updated tracer C(τ+1) at the end of the single inversion, we can diagnose the
individual contributions as if they were computed explicitly in time, but using the updated concentration
C(τ+ 1). We detail the MOM diagnostic method in Section 36.9.2.3.
36.9.2.2 What if we diagnosed vertical processes in series?
Consider the case of vertical processes in which temperature or salinity are updated implicitly in time with
a surface boundary flux, a vertical diffusivity, an implicit piece of the K33 neutral diffusion tensor, and the
bottom boundary flux (i.e., geothermal heating for the temperature equation). Again, MOM handles these
processes using a single call to a combined time-implicit step. However, consider instead an update of
vertical processes occurring in series, with each step invoking a tridiagonal inversion and thus updating
tracer concentration in a piecewise or incremental manner. In that case, we would write the various time-
implicit pieces on the right hand side of equation (36.170) in the form
C(τ+ 1) = C#(τ+ 1) + ∆τδ C
δτ impl
sbc
+∆τδC
δτ impl
diffcbt
+∆τδC
δτ impl
K33
+∆τδC
δτ impl
bbc .(36.172)
Elements of MOM November 19, 2014 Page 490

Chapter 36. Dianeutral transport and associated budgets Section 36.9
Importantly, when computed in series, each of the interior mixing process acts on a different intermediate
tracer state that depend on which processes occurred earlier in the series. Hence, we cannot unambigu-
ously attribute a tendency to a separate mixing process, since the tendencies depend on the arbitrary
order that the mixing processes are computed. It is for this reason that an incremental update of interior
diffusive processes is not sensible, since there is no fundamental reason to apply one piece of the vertical
diffusivity prior to another piece. Contributions from the surface and bottom boundary fluxes are not sub-
ject to this ambiguity, since their tendencies are determined solely from the flux itself, which is computed
based on the concentration C(τ)and atmospheric conditions.
Let us nonetheless pursue the next step that would be required to assign a tendency to a process by
assuming the above ordering, so that
Csbc(τ+ 1) = C#(τ+ 1) + ∆τδC
δτ impl
sbc
(36.173)
Cdiffcbt(τ+ 1) = Csbc(τ+ 1) + ∆τδ C
δτ impl
diffcbt
(36.174)
CK33(τ+ 1) = Cdiffcbt(τ+ 1) + ∆τδ C
δτ impl
K33
(36.175)
Cbbc(τ+ 1) = CK33(τ+ 1) + ∆τδ C
δτ impl
bbc
(36.176)
C(τ+ 1) = Cbbc(τ+ 1).(36.177)
Intermediate values of the tracer concentration are required to diagnose time tendencies via the following
steps
δC
δτ impl
sbc
=Csbc(τ+ 1) −C#(τ+ 1)
∆τ(36.178)
δC
δτ impl
diffcbt
=Cdiffcbt(τ+ 1) −Csbc(τ+ 1)
∆τ(36.179)
δC
δτ impl
K33
=CK33(τ+ 1) −Cdiffcbt(τ+ 1)
∆τ(36.180)
δC
δτ impl
bbc
=Cbbc(τ+ 1) −CK33(τ+ 1)
∆τ.(36.181)
36.9.2.3 A priori and a posteriori diagnostics
What we wish is to unravel the tendency (δ C/δτ)impl in equation (36.170) to identify how individual mixing
processes impact this term. We take the following approach for individual mixing processes, whereby the
updated tracer concentration C(τ+ 1) is used to diagnose the tendencies. That is, we diagnose
tendency =∆k(ρoD ∂zC(τ+ 1)),(36.182)
where Dis the diffusivity associated with the particular process of interest. This operator is just like a
time-explicit calculation of vertical diffusion. To within time truncation errors, the sum of the individually
diagnosed tendencies will equal to that arising from the time-implicit tendency.
Based on the above considerations, the following diagnostic suite has been implemented in MOM.
• Bottom and surface flux tendency contributions are split from mixing contributions. This split is un-
ambiguous, since the tendencies from the boundary fluxes are due solely to the boundary fluxes. We
diagnose these contributions by calling the tridiagonal inversion with just the boundary fluxes. This
call to the tridiagonal solver is trivial, since with zero interior mixing, there is no inversion required.
• The contribution from the diff cbt vertical diffusivity is computed based on the diagnostic equation
(36.182).
Elements of MOM November 19, 2014 Page 491

Chapter 36. Dianeutral transport and associated budgets Section 36.9
• The contribution from the time-implicit piece of K33 is is computed based on the diagnostic equation
(36.182).
• The contribution from the combined diff cbt vertical diffusivity and time-implicit piece of K33 is
computed based on an intermediate update to the tracer fields based solely on the surface and
bottom boundary fluxes, and the diagnostic calls the tridiagonal inversion.
The resulting diagnostic fields should satisfy the following equalities
• total tendency from vertical processes = surface boundary + bottom boundary + combined interior
mixing (combined diff cbt + time-implicit K33). For example, we have
neut rho vdiffuse =neut rho sbc +neut rho bbc
+neut rho diff cbt +neut rho k33,(36.183)
with similar equalities holding for wdian rho and tform rho diagnostics mapped onto levels or binned
to density layers (see Sections 36.10 and 36.11).
• tendency from combined interior mixing (diff cbt + K33-implicit) equals to the separate calculation
of tendency from diff cbt + tendency from K33-implicit. For example, we have
neut rho vmix = +neut rho diff cbt +neut rho k33,(36.184)
with similar equalities holding for wdian rho and tform rho diagnostics mapped onto levels or binned
to density layers (see Sections 36.10 and 36.11).
36.9.3 Splitting physics into flux convergence plus thermodynamic source
In Section 36.7.1, we split the contributions from physical processes into the convergence of a subgrid
scale flux plus a thermodynamic source. This split then facilitated our deducing properties satisfied by
various of the subgrid scale processes, in particular where neutral diffusion reduced to cabbeling and ther-
mobaricity. However, in the discussion of dianeutral diffusion in Section 36.7.2, we chose not to consider
this split as it leads there to no new physical insights.
As MOM time steps the temperature and salinity equations, rather than the locally referenced potential
density equation, there is no guarantee that the discrete equations can be exactly split according to the
decomposition given in Section 36.7.1. Correspondingly, when diagnosing the contributions to the material
evolution, we do not artificially introduce the split to the diagnostic routines. Instead, we diagnose the
terms from the temperature and salinity equations just as computed by MOM. We therefore expect that
the split given in Section 36.7.1 will only hold approximately in the diagnostic calculation.
36.9.4 Cabbeling, thermobaricity, and neutral diffusion
We highlight here an issue related to the contribution from neutral diffusion to the dianeutral velocity com-
ponent. First, as just mentioned in Section 36.9.3, split of the flux convergence discussed in Section 36.7.1
may not be precisely reflected in the numerical model. Hence, the contribution from neutral diffusion,
given by the cabbeling and thermobaricity expressions in equation (36.103), may not be fully reflected in
model diagnostics computed according to equation (36.95). To assess the agreement, we separately eval-
uated these two expressions, and have found that, in regions where the neutral slopes are less than the
pre-defined maximum slope, the quantitative and qualitative features are reflected in both approaches.
This result serves as a useful cross-check on the diagnostic code.
In regions where the neutral slopes are steep, the two approaches differ for the following reasons. The
expressions for cabbeling and thermobaricity given by equation (36.103) assume that the lateral diffusion
of temperature and salinity occurs along neutral directions in regions of vertically stable stratification, and
that the neutral diffusion fluxes for temperature and salinity satisfy the balance (36.96). However, when
the neutral slopes steepen greater than a numerically specified value Smax, the numerical implementation
of neutral diffusion exponentially transitions to horizontal diffusion aligned parallel to iso-surfaces of the
Elements of MOM November 19, 2014 Page 492

Chapter 36. Dianeutral transport and associated budgets Section 36.10
vertical coordinate. Furthermore, the horizontal diffusion fluxes no longer satisfy the balance (36.96).
The transition to horizontal diffusion is physically motivated by the work of Treguier et al. (1997) and
Ferrari et al. (2008), who note the presence of increased mixing of watermasses in boundary layer regions
typically associated with steep neutral directions. That is, when neutral directions approach the vertical,
dianeutral diffusion becomes lateral diffusion. There can be a large contribution to dianeutral transport
associated with horizontal diffusion in regions of steep neutral directions. Yet such mixing processes are
not associated with the traditional notion of cabbeling and thermobaricity, and so they are removed when
diagnosing equation (36.103).
36.9.5 Concerning spurious dianeutral transport
Thus far in our formulation, there has been an assumption that the numerically diagnosed expressions
for the dianeutral transport correspond, at least qualitatively, to the continuum forms, with quantitative
differences arising from truncation errors. We identify here some caveats to this assumption.
For the case of a linear equation of state with zero vertical diffusion, zero sources, and zero boundary
fluxes, we should diagnose a vanishing material evolution of both temperature and salinity, and an asso-
ciated vanishing w(γ), since there will be zero dianeutral transport in the continuum fluid. Indeed, such will
be the case by definition of the kinematic method (equation (36.90)), since the method uses the diagnosed
time tendency and advection tendencies, which will be equal and opposite when there are no boundary
fluxes nor physical mixing processes. The question arises whether this result is a correct accounting of
the dianeutral transport occurring in the numerical simulation.
In a discrete model, there are generally nonzero levels of spurious mixing that arise from the numerical
discretization of advection, either resolved advection or parameterized subgrid scale advection (Griffies
et al.,2000b;Ilicak et al.,2012). If we could extract these spurious effects from the numerical advection
operator, the associated mixing (or unmixing) could be isolated and mapped. However, an explicit diagno-
sis of truncation errors that create spurious dianeutral mixing is generally not possible, given the many
sophisticated expressions for the numerical treatment of either resolved or parameterized advection.
Hence, even with zero physical subgrid scale fluxes, the spurious numerical fluxes do not generally
vanish. The expressions for the diagnosed dianeutral transport considered in the MOM diagnostic detailed
in this chapter fail to account for these spurious terms, since we do not know how to generally incorporate
them into the diagnostic framework. However, one may wish the diagnostic to behave just in this manner,
so that it focuses on the physical aspects of the simulation. Nonetheless, one must be careful not to over
interpret the results from this diagnostic, since there may be more dianeutral transport actually occurring
in the simulation than might be diagnosed via w(γ). So in practice, one can be confident in the diagnosed
form of w(γ)only in those cases that the spurious levels of mixing are smaller than the physical levels.
36.10 Kinematic method diagnosed in MOM
We now summarize the MOM diagnostics computed online in support of the kinematic method used to es-
timate the dianeutral transport as well as the associated budgets for locally referenced potential density.
For this approach, we diagnose all terms contributing to the advective-form of the material time evolution
of temperature and salinity according to the discussion in Section 36.8. For completeness, we repeat here
the salient equations from that section.
•Surface grid cell: The kinematic portion of equation (36.162) yields
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic ≈
ρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ)−(ρw(s)†Θ)s=sk=1 −QmΘ!
ρdz
+
ρ,S ∂t(ρdzS) + ∇s·(ρdzu†S)−(ρw(s)†S)s=sk=1 −QmS!
ρdz.
(36.185)
Elements of MOM November 19, 2014 Page 493

Chapter 36. Dianeutral transport and associated budgets Section 36.10
•Interior grid cell: equation (36.127) yields
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic ≈
ρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ) + ∆k(ρw(s)†Θ)!
ρdz
+
ρ,S ∂t(ρdzS) + ∇s·(ρdzu†S) + ∆k(ρw(s)†S)!
ρdz.
(36.186)
•Bottom grid cell: equation (36.138) yields
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic ≈
ρ,Θ ∂t(ρdzΘ) + ∇s·(ρdzu†Θ) + (ρw(s)†Θ)k−1!
ρdz
+
ρ,S ∂t(ρdzS) + ∇s·(ρdzu†S) + (ρw(s)†S)k−1!
ρdz.
(36.187)
Notice the division by the mass per horizontal area, (ρdz), which renders an expression for the density
evolution in units of (kg m−3)s−1.
We identify a suite of diagnostics in the following, where “name” refers to the name of a particular
physical process.
•neut rho name = contribution to the material time derivative of locally referenced potential density,
given in units of (kg m−3)s−1.
•neut rho name on nrho = result of binning neutral rho name into neutral density classes.
•wdian rho name = contribution to the dianeutral mass transport computed according to the algo-
rithm summarized in Table 36.1. It is given in units of kg s−1. It is computed according to
wdian rho name =neut rho name ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.188)
where his one of the coordinates x,y,z according to the algorithm in Table 36.1.
•wdian rho name on nrho = is the result of binning wdian rho name into neutral density classes.
•tform rho name = the contribution to the watermass transformation according to the discrete ap-
proximation (36.80), which is based on the layer approach of Walin (1982). It is computed according
to
tform rho name =neut rho name BρdV
∆γn!,(36.189)
where ρdVis the mass within a grid cell, and ∆γnis the specified density bins detailed in Section
36.15. Note that because of the division by ∆γn, this diagnostic makes more sense when binned into
neutral density classes, as per the diagnostic tform rho name on nrho. Nonetheless, we provide for
the diagnostic tform rho name as a direct analog to wdian rho name.
•tform rho name on nrho = is the result of binning tform rho name into neutral density classes.
Each contributing term is diagnosed as an Eulerian time tendency, using the same numerical operations
as used for the prognostic equations of conservative temperature and salinity. The motivation for doing
so is to facilitate a straightforward budget diagnostic for the locally referenced potential density of a grid
cell. In particular, the advection contribution is written as a convergence rather than divergence. This
Elements of MOM November 19, 2014 Page 494
Chapter 36. Dianeutral transport and associated budgets Section 36.10
point is critical to keep in mind when forming the material time derivative for computing the dianeutral
mass transport.
It is also of interest to separate out the temperature and salinity contributions for many of the diag-
nosed terms, as a means to uncover whether it is salinity or temperature that dominates in any particular
region. We focus only on those pieces that are written in advective form, as they are used to compute the
dianeutral transport. For these terms we introduce the following diagnostic fields
•neut temp name
•neut salt name
•wdian temp name
•wdian salt name
•tform temp name
•tform salt name
•neut temp name on nrho
•neut salt name on nrho
•wdian temp name on nrho
•wdian salt name on nrho
•tform temp name on nrho
•tform salt name on nrho
36.10.1 Eulerian time tendency
neut rho tendency =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!(36.190)
neut temp tendency =1
ρdz ρ,Θ∂t(Θρdz)!(36.191)
neut salt tendency =1
ρdz ρ,S ∂t(S ρdz)!(36.192)
wdian rho tendency =neut rho tendency ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!.(36.193)
wdian temp tendency =neut temp tendency ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!.(36.194)
wdian salt tendency =neut salt tendency ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!.(36.195)
tform rho tendency =neut rho tendency BρdV
∆γn!.(36.196)
tform temp tendency =neut temp tendency BρdV
∆γn!.(36.197)
tform salt tendency =neut salt tendency BρdV
∆γn!.(36.198)
This term represents the time tendency at a grid cell due to all processes impacting temperature and
salinity.
Elements of MOM November 19, 2014 Page 495
Chapter 36. Dianeutral transport and associated budgets Section 36.10
36.10.2 Advection by resolved flow
neut rho advect =− 1
ρdz! ρ,Θ[∇s·(Θuρdz) + ∆k(Θw(s)ρ)] + ρ,S [∇s·(Suρdz) + ∆k(S w(s)ρ)]!
(36.199)
neut temp advect =− 1
ρdz! ρ,Θ[∇s·(Θuρdz) + ∆k(Θw(s)ρ)]]!(36.200)
neut salt advect =− 1
ρdz! ρ,S [∇s·(Suρdz) + ∆k(S w(s)ρ)]!(36.201)
wdian rho advect =neut rho advect ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.202)
wdian temp advect =neut temp advect ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.203)
wdian salt advect =neut salt advect ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.204)
tform rho advect =neut rho advect BρdV
∆γn!.(36.205)
tform temp advect =neut temp advect BρdV
∆γn!.(36.206)
tform salt advect =neut salt advect BρdV
∆γn!.(36.207)
36.10.3 Gent-McWilliams transport
If enabling the mesoscale parameterization of Gent and McWilliams (1990) and Gent et al. (1995), we may
evaluate the following contribution
neut rho gm =− 1
ρdz! ρ,Θ[∇s·(Θugm ρdz) + ∆k(Θwgm ρ)] + ρ,S [∇s·(Sugm ρdz) + ∆k(S wgm ρ)]!
(36.208)
neut temp gm =− 1
ρdz! ρ,Θ[∇s·(Θugm ρdz) + ∆k(Θwgm ρ)]]!(36.209)
neut salt gm =− 1
ρdz! ρ,S [∇s·(Sugm ρdz) + ∆k(S wgm ρ)]!(36.210)
wdian rho gm =neut rho gm ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.211)
wdian temp gm =neut temp gm ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.212)
wdian salt gm =neut salt gm ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.213)
tform rho gm =neut rho gm BρdV
∆γn!.(36.214)
tform temp gm =neut temp gm BρdV
∆γn!.(36.215)
tform salt gm =neut salt gm BρdV
∆γn!.(36.216)
Elements of MOM November 19, 2014 Page 496
Chapter 36. Dianeutral transport and associated budgets Section 36.10
Note that we have written the Gent-McWilliams contribution as an eddy advection term. However, this term
may instead be evaluated according to the skew flux approach of Griffies (1998). Additionally, the modified
form of GM transport proposed by Ferrari et al. (2010) is also diagnosed in this field.
36.10.4 Submesoscale transport
If enabling the submesoscale parameterization of Fox-Kemper et al. (2008b), we may evaluate the following
contribution
neut rho submeso =− 1
ρdz! ρ,Θ[∇s·(Θusub ρdz) + ∆k(Θwsub ρ)] + ρ,S [∇s·(Susub ρdz) + ∆k(S wsub ρ)]!
(36.217)
neut temp submeso =− 1
ρdz! ρ,Θ[∇s·(Θusub ρdz) + ∆k(Θwsub ρ)]]!(36.218)
neut salt submeso =− 1
ρdz! ρ,S [∇s·(Susub ρdz) + ∆k(S wsub ρ)]!(36.219)
wdian rho submeso =neut rho submeso ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.220)
wdian temp submeso =neut temp submeso ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.221)
wdian salt submeso =neut salt submeso ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.222)
tform rho submeso =neut rho submeso BρdV
∆γn!.(36.223)
tform temp submeso =neut temp submeso BρdV
∆γn!.(36.224)
tform salt submeso =neut salt submeso BρdV
∆γn!.(36.225)
Note that we have written the submesoscale contribution as an eddy advection term. However, this term
may instead be evaluated according to the skew flux approach of Griffies (1998).
36.10.5 Precipitation minus evaporation: flux-form
The form that precipitation minus evaporation appears in the finite volume flux-form budget for tracer
(Section 36.8.6) is diagnosed as
neut rho pme =pme
ρdz ρ,ΘΘpme +ρ,S Spme!(36.226)
wdian rho pme =neut rho pme ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.227)
tform rho pme =neut rho pme BρdV
∆γn!.(36.228)
In this expression, pme is the mass flux of precipitation minus evaporation that “advects” temperature and
salinity across the ocean surface, with Θpme and Spme the temperature and salinity of the precipitation
minus evaporation.
Elements of MOM November 19, 2014 Page 497
Chapter 36. Dianeutral transport and associated budgets Section 36.10
36.10.6 Precipitation minus evaporation: advective-form
According to equation (36.185), the manner that precipitation minus evaporation impacts the surface grid
cell advective-form material time derivative is diagnosed according to
neut rho pbl pme kn =−pme
ρdz ρ,ΘΘk=1 +ρ,S Sk=1!(36.229)
neut temp pbl pme kn =−pme
ρdz ρ,ΘΘk=1!(36.230)
neut salt pbl pme kn =−pme
ρdz ρ,S Sk=1!(36.231)
wdian rho pbl pme kn =neut rho pbl pme kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.232)
wdian temp pbl pme kn =neut temp pbl pme kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.233)
wdian salt pbl pme kn =neut salt pbl pme kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.234)
tform rho pbl pme kn =neut rho pbl pme kn BρdV
∆γn!.(36.235)
tform temp pbl pme kn =neut temp pbl pme kn BρdV
∆γn!.(36.236)
tform salt pbl pme kn =neut salt pbl pme kn BρdV
∆γn!.(36.237)
36.10.7 Liquid plus solid river runoff: flux-form
The form that liquid plus solid river mass flux enters the ocean appears in the finite volume flux-form
budget for tracer is diagnosed as
neut rho rivermix =river
ρdz ρ,ΘΘriver +ρ,S Sriver!(36.238)
wdian rho rivermix =neut rho rivermix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.239)
tform rho rivermix =neut rho rivermix BρdV
∆γn!(36.240)
In this expression, river is the mass flux that “advects” temperature and salinity across the ocean surface
due to liquid plus solid river runoff, with Θriver and Sriver the conservative temperature and salinity of the
river water, respectively. This diagnostic is used when the liquid plus solid (i.e., calving land ice) river runoff
is combined into one field. Note that we generally insert the river runoffover a few of the upper ocean
model grid cells, so that river runoffwill appear over more than just the top model grid cell.
Elements of MOM November 19, 2014 Page 498

Chapter 36. Dianeutral transport and associated budgets Section 36.10
36.10.8 Liquid plus solid river runoff: advective-form
According to equation (36.185), the manner that liquid plus solid river mass flux impacts the advective-
form material time derivative is diagnosed as
neut rho pbl riv kn =−river
ρdz ρ,ΘΘk=1 +ρ,S Sk=1!(36.241)
neut temp pbl riv kn =−river
ρdz ρ,ΘΘk=1!(36.242)
neut salt pbl riv kn =−river
ρdz ρ,S Sk=1!(36.243)
wdian rho pbl riv kn =neut rho pbl riv kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.244)
wdian temp pbl riv kn =neut temp pbl riv kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.245)
wdian salt pbl riv kn =neut salt pbl riv kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.246)
tform rho pbl riv kn =neut rho pbl riv kn BρdV
∆γn!.(36.247)
tform temp pbl riv kn =neut temp pbl riv kn BρdV
∆γn!.(36.248)
tform salt pbl riv kn =neut salt pbl riv kn BρdV
∆γn!.(36.249)
36.10.9 Liquid river runoff: flux-form
The form that liquid river mass flux enters the ocean appears in the finite volume flux-form budget for
tracer is diagnosed as
neut rho runoffmix =runoff
ρdz ρ,ΘΘrunoff+ρ,S Srunoff!(36.250)
wdian rho runoffmix =neut rho runoffmix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.251)
tform rho runoffmix =neut rho runoffmix BρdV
∆γn!.(36.252)
In this expression, runoff is the mass flux that “advects” temperature and salinity across the ocean sur-
face due to liquid river runoff, with Θrunoffand Srunoffthe temperature and salinity of the liquid river runoff.
Note that we generally insert the river runoffover a few of the upper ocean model grid cells, so that river
runoffwill appear over more than just the top model grid cell.
Elements of MOM November 19, 2014 Page 499

Chapter 36. Dianeutral transport and associated budgets Section 36.10
36.10.10 Liquid river runoff: advective-form
According to equation (36.185), the manner that liquid river mass flux impacts the advective-form material
time derivative is diagnosed as
neut rho pbl rn kn =−runoff
ρdz ρ,ΘΘk=1 +ρ,S Sk=1!(36.253)
neut temp pbl rn kn =−runoff
ρdz ρ,ΘΘk=1!(36.254)
neut salt pbl rn kn =−runoff
ρdz ρ,S Sk=1!(36.255)
wdian rho pbl rn kn =neut rho pbl rn kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.256)
wdian temp pbl rn kn =neut temp pbl rn kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.257)
wdian salt pbl rn kn =neut salt pbl rn kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.258)
tform rho pbl rn kn =neut rho pbl rn kn BρdV
∆γn!.(36.259)
tform temp pbl rn kn =neut temp pbl rn kn BρdV
∆γn!.(36.260)
tform salt pbl rn kn =neut salt pbl rn kn BρdV
∆γn!.(36.261)
36.10.11 Solid calving land ice: flux-form
The form that solid mass flux (i.e., calving) enters the ocean appears in the finite volume flux-form budget
for tracer is diagnosed as
neut rho calvingmix =calving
ρdz ρ,ΘΘcalving +ρ,S Scalving!(36.262)
wdian rho calvingmix =neut rho calvingmix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.263)
tform rho calvingmix =neut rho calvingmix BρdV
∆γn!.(36.264)
In this expression, calving is the mass flux that “advects” temperature and salinity across the ocean
surface due to solid calving land ice, with Θcalving and Scalving the temperature and salinity of the land ice.
Elements of MOM November 19, 2014 Page 500

Chapter 36. Dianeutral transport and associated budgets Section 36.10
36.10.12 Solid calving runoff: advective-form
According to equation (36.185), the form that solid calving mass flux impacts the advective-form material
time derivative is diagnosed as
neut rho pbl cl kn =−calving
ρdz ρ,ΘΘk=1 +ρ,S Sk=1!(36.265)
neut temp pbl cl kn =−calving
ρdz ρ,ΘΘk=1!(36.266)
neut salt pbl cl kn =−calving
ρdz ρ,S Sk=1!(36.267)
wdian rho pbl cl kn =neut rho pbl cl kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.268)
wdian temp pbl cl kn =neut temp pbl cl kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.269)
wdian salt pbl cl kn =neut salt pbl cl kn ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.270)
tform rho pbl cl kn =neut rho pbl cl kn BρdV
∆γn!.(36.271)
tform temp pbl cl kn =neut temp pbl cl kn BρdV
∆γn!.(36.272)
tform salt pbl cl kn =neut salt pbl cl kn BρdV
∆γn!.(36.273)
36.10.13 Summary of the kinematic method
We take the convention that each term is diagnosed as an Eulerian time tendency, using the same numer-
ical operations as used for the prognostic equations of conservative temperature and salinity. This point
explains the minus signs in front of the advection and surface water flux terms appearing below in equa-
tion (36.274), with these signs required to form the material time derivative for computing the dianeutral
mass transport.
36.10.13.1 Material time derivative
The finite volume estimate of the advective-form of the kinematic material time derivative is given by
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic level ≈neut rho tendency −neut rho advect
−neut rho gm −neut rho submeso
+neut rho pbl pme kn
+neut rho pbl rn kn +neut rho pbl cl kn
(36.274)
where we assumed liquid plus solid runoffare split into their own separate arrays, as per a realistic climate
model with a liquid runoffand solid calving scheme. If these terms are combined, as commonly done in
ocean-ice models, we should instead diagnose
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic level ≈neut rho tendency −neut rho advect
−neut rho gm −neut rho submeso
+neut rho pbl pme kn
+neut rho pbl riv kn.
(36.275)
Elements of MOM November 19, 2014 Page 501

Chapter 36. Dianeutral transport and associated budgets Section 36.11
The same relations also hold for the density binned form
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic layer ≈neut rho tendency on nrho −neut rho advect on nrho
−neut rho gm on nrho −neut rho submeso on nrho
+neut rho pbl pme kn on nrho
+neut rho pbl rn kn on nrho +neut rho pbl cl kn on nrho.
(36.276)
36.10.13.2 Dianeutral transport from wdian diagnostics
The dianeutral mass transport, in units of kgs−1, can be estimated using wdian both on levels and binned
to neutral density layers. Following from the neutral rho diagnostics above, we have
ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|! ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic level ≈wdian rho tendency −wdian rho advect
−wdian rho gm −wdian rho submeso
+wdian rho pbl pme kn
+wdian rho pbl rn kn +wdian rho pbl cl kn.
(36.277)
The same relations also hold for the density binned dianeutral mass transport
ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|! ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic layer ≈wdian rho tendency on nrho −wdian rho advect on nrho
−wdian rho gm on nrho −wdian rho submeso on nrho
+wdian rho pbl pme kn on nrho
+wdian rho pbl rn kn on nrho +wdian rho pbl cl kn on nrho.
(36.278)
36.10.13.3 Dianeutral transport from tform diagnostics
The dianeutral mass transport, in units of kgs−1, can also be estimated using tform diagnostics. Here, the
results are only sensible when binned to neutral density layers. Following from the wdian rho diagnostics
above, we have
BρdV
∆γn! ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic layer ≈tform rho tendency on nrho −tform rho advect on nrho
−tform rho gm on nrho −tform rho submeso on nrho
+tform rho pbl pme kn on nrho
+tform rho pbl rn kn on nrho +tform rho pbl cl kn on nrho.
(36.279)
36.11 Process method diagnosed in MOM
We now summarize the MOM diagnostics computed online in support of the process method used to esti-
mate the dianeutral transport as well as the associated budgets for locally referenced potential density.
For this approach, we diagnose all terms contributing to the advective-form of the material time evolution
of temperature and salinity according to the discussion in Section 36.8. For completeness, we repeat here
the salient equations from that section.
Elements of MOM November 19, 2014 Page 502

Chapter 36. Dianeutral transport and associated budgets Section 36.11
•Surface grid cell: The process portion of equation (36.162) yields
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic ≈
ρ,Θ −∇s·(dzJΘ) + (J(s)Θ)s=sk=1 +QΘ
pbl +Qm(Θm−Θ) + ρdzSΘ!
ρdz
+
ρ,S −∇s·(dzJS) + (J(s)S)s=sk=1 +QS
pbl +Qm(Sm−S) + ρdzSS!
ρdz.
(36.280)
•Interior grid cell: equation (36.128) yields
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic ≈
ρ,Θ −∇s·(dzJΘ)−(J(s)Θ)s=sk−1+ (J(s)Θ)s=sk+ρdzSΘ!
ρdz
+
ρ,S −∇s·(dzJS)−(J(s)S)s=sk−1+ (J(s)S)s=sk+ρdzSS!
ρdz.
(36.281)
•Bottom grid cell: equation (36.139) yields
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!kinematic
=
ρ,Θ −∇s·(dzJΘ)−(J(s)Θ)s=sk−1−Qbott +ρdzSΘ!
ρdz
+
ρ,S −∇s·(dzJS)−(J(s)S)s=sk−1+ρdzSS!
ρdz.
(36.282)
As for the kinematic method in Section 36.10, we identify a suite of diagnostics in the following, where
“name” refers to the name of a particular physical process:
•neut rho name = contribution to the material time derivative of locally referenced potential density
in units of (kg m−3)s−1.
•neut rho name on nrho = result of binning neutral rho name into neutral density classes.
•wdian rho name = contribution to the dianeutral mass transport computed according to the algo-
rithm summarized in Table 36.1. It is given in units of kg s−1. It is computed according to
wdian rho name =neut rho name ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.283)
where his one of the coordinates x,y,z according to the algorithm in Table 36.1.
•wdian rho name on nrho = is the result of binning wdian rho name into neutral density classes.
•tform rho name = the contribution to the watermass transformation according to the discrete ap-
proximation (36.80), which is based on the layer approach of Walin (1982). It is computed according
to
tform rho name =neut rho name BρdV
∆γn!,(36.284)
where ρdVis the mass within a grid cell, and ∆γnis the specified density bins detailed in Section
36.15. Note that because of the division by ∆γn, this diagnostic makes more sense when binned into
neutral density classes, as per the diagnostic tform rho name on nrho. Nonetheless, we provide for
the diagnostic tform rho name as a direct analog to wdian rho name.
Elements of MOM November 19, 2014 Page 503
Chapter 36. Dianeutral transport and associated budgets Section 36.11
•tform rho name on nrho = is the result of binning tform rho name into neutral density classes.
As for the kinematic approach, our convention is to diagnose each term as a time tendency. Additionally,
we decompose the terms into temperature and salinity contributions, thus allowing for further refined
diagnostics to quantify the separate impacts from salinity and temperature.
36.11.1 Boundary fluxes of heat and salt through the vertical mixing operator
This suite of diagnostics computes the contribution to the material time derivative of locally referenced
potential density arising from boundary buoyancy fluxes associated with heat and salt fluxes. All of these
diagnostics are computed in the module
ocean param/mixing/ocean vert mix.F90
as per the model implementation of boundary fluxes as part of the time-implicit vertical mixing operator.
We diagnose these contributions according to the incremental methods detailed in Section 36.9.2.
There is some redundancy here with the diagnostic for vertical mixing discussed in Section 36.11.3.1.
As mentioned in Section 36.11.3.11, this redundancy allows for a double-check on the integrity of the
diagnostics.
36.11.1.1 Surface boundary heat fluxes
The following diagnostic accounts for the contribution from surface boundary fluxes of heat. In a coupled
model, or a model using the CORE protocol of Griffies et al. (2009), this heat flux is associated with short-
wave, longwave, latent (both latent heat of vaporization and latent heat of fusion), and sensible heating.
In a model that has a surface restoring boundary flux, then the restoring flux is included in this diagnostic.
Note that there is a conversion between a heat flux and conservative temperature flux according to
QΘ=Qheat
Cp
(36.285)
where
Cp= 3992.103 J kg−1C−1(36.286)
is the seawater heat capacity and Qheat is the surface heat flux (in units of W m−2).
neut rho sbc temp =1
ρdz ρ,Θ(QΘ
sw +QΘ
lw +QΘ
latent +QΘ
sensible)!(36.287)
wdian rho sbc temp =neut rho sbc temp ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.288)
tform rho sbc temp =neut rho sbc temp BρdV
∆γn!.(36.289)
36.11.1.2 Surface boundary salt fluxes
The following diagnostic field accounts for the contribution from surface boundary fluxes of salt associated
with melting and forming of sea ice. Additionally, in an ocean-ice model, there may be a salt flux associated
with surface salinity restoring towards a climatology. Such surface restoring fluxes will also be accounted
for in this diagnostic field.
neut rho sbc salt =1
ρdz ρ,S QS!(36.290)
wdian rho sbc salt =neut rho sbc salt ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.291)
tform rho sbc salt =neut rho sbc salt BρdV
∆γn!.(36.292)
Elements of MOM November 19, 2014 Page 504

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.1.3 Net surface boundary heat and salt fluxes
The following diagnostic field accounts for the contribution from the combined surface boundary fluxes of
heat and salt.
neutral rho sbc =1
ρdz ρ,Θ(QΘ
sw +QΘ
lw +QΘ
latent +QΘ
sensible) + ρ,S QS!(36.293)
wdian rho sbc =neut rho sbc ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.294)
tform rho sbc =neut rho sbc BρdV
∆γn!.(36.295)
36.11.1.4 Bottom boundary heat flux
The following diagnostic field accounts for the contribution from bottom boundary fluxes of heat associ-
ated with geothermal heating.
neut rho bbc temp =1
ρdz ρ,ΘQΘ
geothermal!(36.296)
wdian rho bbc temp =neut rho bbc temp ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.297)
tform rho bbc temp =neut rho bbc temp BρdV
∆γn!.(36.298)
36.11.1.5 Penetrative shortwave radiation
neut rho sw =1
ρdz ρ,Θ∂t(Θρdz)!sw
(36.299)
wdian rho sw =neut rho sw ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.300)
tform rho sw =neut rho sw BρdV
∆γn!.(36.301)
This contribution arises from penetrative shortwave radiation. This term only impacts temperature.
Note that the contribution at model grid level k= 1 appears to be a large cooling. This is because the
flux entering through the top of the top level is set to zero in the shortwave penetration module, since the
model has already incorporated this flux through the surface boundary condition module ocean sbc.F90.
This approach avoids double counting the impact of shortwave radiation. Full details of this issue are
given in Chapter 8 of Griffies et al. (2004). To get the full impact from shortwave radiation on watermass
transformation requires adding the two diagnostic terms. In particular, for tform, we need
full impacts from shortwave =tform rho sw on nrho +tform rho pbl sw on nrho,(36.302)
where the diagnostic term tform rho pbl sw on nrho is presented in Section 36.14.2.
36.11.2 Boundary fluxes of buoyancy arising from mass transport
This suite of diagnostics computes the contribution to the material time derivative of locally referenced
potential density arising from boundary buoyancy fluxes associated with mass fluxes. These diagnostics
are computed in the modules
ocean core/ocean sbc.F90
ocean tracers/ocean tracer.F90
ocean param/sources/ocean rivermix.F90
Elements of MOM November 19, 2014 Page 505
Chapter 36. Dianeutral transport and associated budgets Section 36.11
We base these diagnostics on expressions given in equation (36.162) (see also equation (36.280)).
36.11.2.1 Precipitation minus evaporation
According to equation (36.280), the form that precipitation minus evaporation impacts the surface grid
cell process version of the material time derivative is diagnosed according to
neut rho pbl pme pr =pme
ρdz ρ,Θ(Θm−Θk=1) + ρ,S (Sm−Sk=1)!(36.303)
neut temp pbl pme pr =pme
ρdz ρ,Θ(Θm−Θk=1)!(36.304)
neut salt pbl pme pr =pme
ρdz ρ,S (Sm−Sk=1)!(36.305)
wdian rho pbl pme pr =neut rho pbl pme pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.306)
wdian temp pbl pme pr =neut temp pbl pme pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.307)
wdian salt pbl pme pr =neut salt pbl pme pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.308)
tform rho pbl pme pr =neut rho pbl pme pr BρdV
∆γn!(36.309)
tform temp pbl pme pr =neut temp pbl pme pr BρdV
∆γn!(36.310)
tform salt pbl pme pr =neut salt pbl pme pr BρdV
∆γn!.(36.311)
Elements of MOM November 19, 2014 Page 506

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.2.2 Liquid plus solid river runoff
According to equation (36.280), the form that liquid plus solid water mass impacts the surface grid cell
process version of the material time derivative is diagnosed according to
neut rho pbl rv pr =river
ρdz ρ,Θ(Θm−Θk=1) + ρ,S (Sm−Sk=1)!(36.312)
neut temp pbl rv pr =river
ρdz ρ,Θ(Θm−Θk=1)!(36.313)
neut salt pbl rv pr =river
ρdz ρ,S (Sm−Sk=1)!(36.314)
wdian rho pbl rv pr =neut rho pbl rv pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.315)
wdian temp pbl rv pr =neut temp pbl rv pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.316)
wdian salt pbl rv pr =neut salt pbl rv pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.317)
tform rho pbl rv pr =neut rho pbl rv pr BρdV
∆γn!(36.318)
tform temp pbl rv pr =neut temp pbl rv pr BρdV
∆γn!(36.319)
tform salt pbl rv pr =neut salt pbl rv pr BρdV
∆γn!.(36.320)
In this expression, river is the mass flux that “advects” temperature and salinity across the ocean surface
due to liquid plus solid river runoff, with Θriver and Sriver the conservative temperature and salinity of the
river water, respectively. This diagnostic is used when the liquid plus solid (i.e., calving land ice) river runoff
is combined into one field. Note that we generally insert the river runoffover a few of the upper ocean
model grid cells, so that river runoffwill appear over more than just the top model grid cell. However,
this diagnostic assumes all the water enters the top cell, thus providing an approximate expression for the
impacts from river water.
Elements of MOM November 19, 2014 Page 507
Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.2.3 Liquid river runoff
According to equation (36.280), the form that liquid river runoffimpacts the process version of the material
time derivative is diagnosed according to
neut rho pbl rn pr =runoff
ρdz ρ,Θ(Θrunoff−Θk=1) + ρ,S (Srunoff−Sk=1)!(36.321)
neut temp pbl rn pr =runoff
ρdz ρ,Θ(Θrunoff−Θk=1)!(36.322)
neut salt pbl rn pr =runoff
ρdz ρ,S (Srunoff−Sk=1)!(36.323)
wdian rho pbl rn pr =neut rho pbl rn pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.324)
wdian temp pbl rn pr =neut temp pbl rn pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.325)
wdian salt pbl rn pr =neut salt pbl rn pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.326)
tform rho pbl rn pr =neut rho pbl rn pr BρdV
∆γn!(36.327)
tform temp pbl rn pr =neut temp pbl rn pr BρdV
∆γn!(36.328)
tform salt pbl rn pr =neut salt pbl rn pr BρdV
∆γn!.(36.329)
In this expression, runoff is the mass flux that “advects” temperature and salinity across the ocean sur-
face due to liquid river runoff, with Θrunoffand Srunoffthe temperature and salinity of the liquid river runoff.
Note that we generally insert the river runoffover a few of the upper ocean model grid cells, so that river
runoffwill appear over more than just the top model grid cell. However, this diagnostic assumes all the
water enters the top cell, thus providing an approximate expression for the impacts from river water.
Elements of MOM November 19, 2014 Page 508

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.2.4 Solid calving runoff
According to equation (36.280), the form that solid river runoff, or calving, impacts the process version of
the material time derivative is diagnosed according to
neut rho pbl cl pr =calving
ρdz ρ,Θ(Θcalve −Θk=1) + ρ,S (Scalve −Sk=1)!(36.330)
neut temp pbl cl pr =calving
ρdz ρ,Θ(Θcalve −Θk=1)!(36.331)
neut salt pbl cl pr =calving
ρdz ρ,S (Scalve −Sk=1)!(36.332)
wdian rho pbl cl pr =neut rho pbl cl pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.333)
wdian temp pbl cl pr =neut temp pbl cl pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.334)
wdian salt pbl cl pr =neut salt pbl cl pr ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.335)
tform rho pbl cl pr =neut rho pbl cl pr BρdV
∆γn!(36.336)
tform temp pbl cl pr =neut temp pbl cl pr BρdV
∆γn!(36.337)
tform salt pbl cl pr =neut salt pbl cl pr BρdV
∆γn!.(36.338)
In this expression, calving is the mass flux that “advects” temperature and salinity across the ocean
surface due to liquid river runoff, with Θcalve and Scalve the temperature and salinity of the liquid river
runoff. Note that we generally insert the river runoffover a few of the upper ocean model grid cells, so that
river runoffwill appear over more than just the top model grid cell. However, this diagnostic assumes all
the water enters the top cell, thus providing an approximate expression for the impacts from river water.
36.11.3 Vertical mixing processes
This suite of diagnostics computes the contribution to d†γ/dtdue to vertical mixing processes, including
diffusion, boundary fluxes, and parameterized vertical convection. All of these diagnostics are computed
in the module
ocean param/ocean vert mix.F90
36.11.3.1 Vertical diffusion and boundary fluxes
neut rho vdiffuse =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!vdiffuse
(36.339)
wdian rho vdiffuse =neut rho vdiffuse ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.340)
tform rho vdiffuse =neut rho vdiffuse BρdV
∆γn!.(36.341)
This contribution arises from the vertical diffusion operator acting on temperature and salinity. It includes
both the mixing from vertical diffusivity, as well as that from boundary fluxes. Note that the vertical diffu-
sivity may be large in the boundary regions in order to stabilize gravitationally unstable columns.
Elements of MOM November 19, 2014 Page 509
Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.3.2 Vertical diffusion from net vertical diffusivity
We estimate the contribution from dianeutral mixing due to the net vertical diffusivity in a manner dis-
cussed in Section 36.9.2.3. The following diagnostics are related to this contribution.
neut rho diff cbt =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!diffcbt
(36.342)
neut temp diff cbt =1
ρdz ρ,Θ∂t(Θρdz)!diffcbt
(36.343)
neut salt diff cbt =1
ρdz ρ,S ∂t(S ρdz)!diffcbt
(36.344)
wdian rho diff cbt =neut rho diff cbt ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.345)
wdian temp diff cbt =neut temp diff cbt ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.346)
wdian salt diff cbt =neut salt diff cbt ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.347)
tform rho diff cbt =neut rho diff cbt BρdV
∆γn!(36.348)
tform temp diff cbt =neut temp diff cbt BρdV
∆γn!(36.349)
tform salt diff cbt =neut salt diff cbt BρdV
∆γn!.(36.350)
This contribution arises from dianeutral mixing acting on temperature and salinity, and it excludes the
contribution from boundary fluxes. Note that vertical diffusivity may be large in the boundary regions in
order to stabilize gravitationally unstable columns.
Elements of MOM November 19, 2014 Page 510
Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.3.3 Vertical diffusion from static background vertical diffusivity
We estimate the contribution from dianeutral mixing due to background static vertical diffusivity in a man-
ner discussed in Section 36.9.2.3. The following diagnostics are related to this contribution.
neut rho diff back =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!diffcbt back
(36.351)
neut temp diff back =1
ρdz ρ,Θ∂t(Θρdz)!diffcbt back
(36.352)
neut salt diff back =1
ρdz ρ,S ∂t(S ρdz)!diffcbt back
(36.353)
wdian rho diff back =neut rho diff back ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.354)
wdian temp diff back =neut temp diff back ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.355)
wdian salt diff back =neut salt diff back ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.356)
tform rho diff back =neut rho diff back BρdV
∆γn!(36.357)
tform temp diff back =neut temp diff back BρdV
∆γn!(36.358)
tform salt diff back =neut salt diff back BρdV
∆γn!.(36.359)
This contribution arises from dianeutral mixing acting on temperature and salinity.
36.11.3.4 Vertical diffusion from internal tide mixing vertical diffusivity
We estimate the contribution from dianeutral mixing due to the internal tide mixing parameterization of
Simmons et al. (2004) (see Chapter 20), with the diagnostic method following that discussed in Section
Elements of MOM November 19, 2014 Page 511
Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.9.2.3. The following diagnostics are contained in this contribution.
neut rho diff wave =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!diffcbt wave
(36.360)
neut temp diff wave =1
ρdz ρ,Θ∂t(Θρdz)!diffcbt wave
(36.361)
neut salt diff wave =1
ρdz ρ,S ∂t(S ρdz)!diffcbt wave
(36.362)
wdian rho diff wave =neut rho diff wave ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.363)
wdian temp diff wave =neut temp diff wave ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.364)
wdian salt diff wave =neut salt diff wave ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.365)
tform rho diff wave =neut rho diff wave BρdV
∆γn!(36.366)
tform temp diff wave =neut temp diff wave BρdV
∆γn!(36.367)
tform salt diff wave =neut salt diff wave BρdV
∆γn!.(36.368)
This contribution arises from dianeutral mixing acting on temperature and salinity.
36.11.3.5 Vertical diffusion from coastal tide mixing vertical diffusivity
We estimate the contribution from dianeutral mixing due to the coastal tide mixing parameterization of
Lee et al. (2006) (see Chapter 20), with the diagnostic method following that discussed in Section 36.9.2.3.
The following diagnostics are contained in this contribution.
neut rho diff drag =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!diffcbt drag
(36.369)
neut temp diff drag =1
ρdz ρ,Θ∂t(Θρdz)!diffcbt drag
(36.370)
neut salt diff drag =1
ρdz ρ,S ∂t(S ρdz)!diffcbt drag
(36.371)
wdian rho diff drag =neut rho diff drag ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.372)
wdian temp diff drag =neut temp diff drag ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.373)
wdian salt diff drag =neut salt diff drag ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.374)
tform rho diff drag =neut rho diff drag BρdV
∆γn!(36.375)
tform temp diff drag =neut temp diff drag BρdV
∆γn!(36.376)
tform salt diff drag =neut salt diff drag BρdV
∆γn!.(36.377)
This contribution arises from dianeutral mixing acting on temperature and salinity.
Elements of MOM November 19, 2014 Page 512

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.3.6 Vertical diffusion from leewave induced vertical diffusivity
We estimate the contribution from dianeutral mixing due to a preliminary implementation of the leewave
induced mixing scheme of Nikurashin and Ferrari (2010), with the diagnostic method following that dis-
cussed in Section 36.9.2.3. The following diagnostics are contained in this contribution.
neut rho diff lee =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!diffcbt leewave
(36.378)
neut temp diff lee =1
ρdz ρ,Θ∂t(Θρdz)!diffcbt leewave
(36.379)
neut salt diff lee =1
ρdz ρ,S ∂t(S ρdz)!diffcbt leewave
(36.380)
wdian rho diff lee =neut rho diff lee ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.381)
wdian temp diff lee =neut temp diff lee ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.382)
wdian salt diff lee =neut salt diff lee ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.383)
tform rho diff lee =neut rho diff lee BρdV
∆γn!(36.384)
tform temp diff lee =neut temp diff lee BρdV
∆γn!(36.385)
tform salt diff lee =neut salt diff lee BρdV
∆γn!.(36.386)
This contribution arises from dianeutral mixing acting on temperature and salinity.
Elements of MOM November 19, 2014 Page 513

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.3.7 Vertical diffusion from K33-implicit
We estimate the contribution from the time-implicit K33 term in a manner discussed in Section 36.9.2.3,
with the following diagnostics containing this contribution.
neut rho k33 =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!k33
(36.387)
neut temp k33 =1
ρdz ρ,Θ∂t(Θρdz)!k33
(36.388)
neut salt k33 =1
ρdz ρ,S ∂t(S ρdz)!k33
(36.389)
wdian rho k33 =neut rho k33 ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.390)
wdian temp k33 =neut temp k33 ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.391)
wdian salt k33 =neut salt k33 ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.392)
tform rho k33 =neut rho k33 BρdV
∆γn!(36.393)
tform temp k33 =neut temp k33 BρdV
∆γn!(36.394)
tform salt k33 =neut salt k33 BρdV
∆γn!.(36.395)
This field can be somewhat noisy in appearance. However, when combined the time-explicit portion of the
neutral diffusion operator (see Section 36.11.4.1), their sum is far smoother. See Section 36.11.4 for more
discussion about neutral diffusion. Nonetheless, we provide the vmix diagnostic as a means to check that
the individual diagnostics of K33 and diff cbt are correct.
36.11.3.8 Vertical diffusion from dianeutral mixing plus K33-implicit
We estimate the combined contribution from dianeutral mixing and K33-implicit in a manner discussed in
Section 36.9.2.3, with the following diagnostics containing this contribution.
neut rho vmix =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!vmix
(36.396)
wdian rho vmix =neut rho vmix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.397)
tform rho vmix =neut rho vmix BρdV
∆γn!.(36.398)
Physically, these two diffusion processes are not related. Instead, the K33-implicit term is associated with
neutral diffusion. It should therefore be diagnosed alone and then added to the time-explicit portion of the
neutral diffusion operator as discussed in Section 36.11.4.
Elements of MOM November 19, 2014 Page 514

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.3.9 Vertical mixing from convective adjustment schemes
neut rho convect =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!convect adjust
(36.399)
neut temp convect =1
ρdz ρ,Θ∂t(Θρdz)!convect adjust
(36.400)
neut salt convect =1
ρdz ρ,S ∂t(S ρdz)!convect adjust
(36.401)
wdian rho diff convect =neut rho diff convect ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.402)
wdian temp diff convect =neut temp diff convect ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.403)
wdian salt diff convect =neut salt diff convect ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.404)
tform rho convect =neut rho convect BρdV
∆γn!(36.405)
tform temp convect =neut temp convect BρdV
∆γn!(36.406)
tform salt convect =neut salt convect BρdV
∆γn!.(36.407)
This contribution arises from the vertical mixing associated with convective adjustment schemes, such as
that of Rahmstorf (1993).
36.11.3.10 Nonlocal KPP transport
neut rho kpp nloc =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!kpp nonlocal
(36.408)
neut temp kpp nloc =1
ρdz ρ,Θ∂t(Θρdz)!kpp nonlocal
(36.409)
neut salt kpp nloc =1
ρdz ρ,S ∂t(S ρdz)!kpp nonlocal
(36.410)
wdian rho kpp nloc =neut rho kpp nloc ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.411)
wdian temp kpp nloc =neut temp kpp nloc ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.412)
wdian salt kpp nloc =neut salt kpp nloc ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.413)
tform rho kpp nloc =neut rho kpp nloc BρdV
∆γn!(36.414)
tform temp kpp nloc =neut temp kpp nloc BρdV
∆γn!(36.415)
tform salt kpp nloc =neut salt kpp nloc BρdV
∆γn!.(36.416)
This contribution arises from the nonlocal transport portion from KPP (Large et al.,1994).
Elements of MOM November 19, 2014 Page 515
Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.3.11 Diagnostic checks for vertical processes
In all ocean regions, we should have the following results respected to within numerical truncation errors
neut rho sbc =neut rho sbc temp +neut rho sbc salt (36.417)
neut rho vdiffuse =neut rho vmix +neut rho sbc +neut rho bbc temp (36.418)
neut rho vmix =neut rho diff cbt +neut rho k33,(36.419)
with the same equalities also holding when binned to density layers. Additionally, the same relations hold
for the wdian and tform diagnostics, again both on model levels and binned to density layers.
36.11.4 Neutral diffusion
This suite of diagnostics arises from the time-explicit portion of the neutral diffusion operator and various
versions of this operator. To get the full effects from neutral diffusion, we should in addition add the time-
implicit portion detailed in Section 36.11.3.7.
36.11.4.1 Neutral diffusion operator: time-explicit piece
neut rho ndiff =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!ndiffuse
(36.420)
neut temp ndiff =1
ρdz ρ,Θ∂t(Θρdz)!ndiffuse
(36.421)
neut salt ndiff =1
ρdz ρ,S ∂t(S ρdz)!ndiffuse
(36.422)
wdian rho ndiff =neut rho ndiff ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.423)
wdian temp ndiff =neut temp ndiff ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.424)
wdian salt ndiff =neut salt ndiff ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.425)
tform rho ndiff =neut rho ndiff BρdV
∆γn!(36.426)
tform temp ndiff =neut temp ndiff BρdV
∆γn!(36.427)
tform salt ndiff =neut salt ndiff BρdV
∆γn!.(36.428)
This contribution arises from the time-explicit portion of neutral diffusion. In the ocean interior, neutral
diffusion contributes to the evolution of locally referenced potential density via cabbeling and thermo-
baricity (Section 36.7.1). In regions of steep neutral directions, MOM generally converts neutral diffusion
to horizontal diffusion as per the recommendations of Treguier et al. (1997); Ferrari et al. (2008,2010).
Horizontal diffusion next to boundaries generally contributes to significant dianeutral transport, with this
transport leading to either an increase or descrease in density, depending on local gradients. The full ef-
fects from the neutral diffusion operator are obtained by adding the ndiff diagnostic to the k33 diagnostic
detailed in Section 36.11.3.7.
Elements of MOM November 19, 2014 Page 516

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.4.2 Cabbeling in the ocean interior
neut rho cabbeling =ρ AnC|∇nΘ|2(36.429)
wdian cabbeling =ρdzdA
dz(ρ,ΘΘ,z +ρ,S S,z) ρAnC|∇nΘ|2!(36.430)
tform rho cabbel on nrho = BρdV
∆γ!AnρC|∇γΘ|2.(36.431)
The diagnostics neut rho cabbeling on nrho and wdian cabbeling on nrho are obtained by binning into
neutral density classes. In general, this diagnostic computes the contribution from cabbeling in the ocean
interior according to the analytical manipulations provided in Section 36.7.1, in particular equation (36.100).
Regions of steep neutral slope and boundaries are omitted, since it is here that neutral diffusion transfers
into horizontal diffusion.
36.11.4.3 Thermobaricity in the ocean interior
neut rho thermob =ρ AnT ∇np·∇nΘ(36.432)
wdian thermob =ρdzdA
dz(ρ,ΘΘ,z +ρ,S S,z) ρAnT ∇np·∇nΘ!(36.433)
tform rho thermb on nrho = BρdV
∆γ!AnρT ∇γp·∇γΘ.(36.434)
The diagnostics neut rho thermob on nrho and wdian thermob on nrho are obtained by binning into neu-
tral density classes. In general, this diagnostic computes the contribution from thermobaricity in the ocean
interior according to the manipulations provided in Section 36.7.1, in particular equation (36.100). Regions
of steep neutral slope and boundaries are omitted, since it is here that neutral diffusion transfers into hor-
izontal diffusion.
36.11.4.4 Diagnostic checks for neutral diffusion
In regions away from steep neutral slopes, we should have the approximate relations
neut rho cabbeling +neut rho thermob ≈neut rho ndiff (36.435)
wdian cabbeling +wdian thermob ≈wdian rho ndiff.(36.436)
These relations fail in regions of steep neutral slopes since the neutral diffusion process switches to hori-
zontal diffusion in these regions. In steep neutral slope regions, the diagnostic terms neut rho cabbeling,
neut rho thermob,wdian cabbeling, and wdian thermob are set to zero.
Splitting the neutral diffusion operator into a time-explicit piece and time-implicit piece makes diag-
nosing the net effects of this operator cumbersome. It is with this caveat in mind that the total effects of
neutral diffusion, plus horizontal mixing in the steep sloped regions, is approximated via
neutral diffusion plus steep slope horiz diffusion ≈neutral rho ndiff +neut rho k33.(36.437)
Besides being approximate due to the time splitting of the neutral diffusion operator, this is an approximate
relation due to splitting the K33 piece from other pieces of the time-implicit inversion (Section 36.9.2).
Nonetheless, experience has shown that both time truncation errors are not critical to the use of this
diagnostic.
36.11.5 Submesoscale horizontal diffusion
If enabling the submesoscale parameterization of Fox-Kemper et al. (2008b), and enabling the horizontal
diffusive component to this parameterization as detailed in Section 24.6, we may evaluate the following
Elements of MOM November 19, 2014 Page 517

Chapter 36. Dianeutral transport and associated budgets Section 36.11
contribution
neut rho subdiff =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!submeso diffuse
(36.438)
neut temp subdiff =1
ρdz ρ,Θ∂t(Θρdz)!submeso diffuse
(36.439)
neut salt subdiff =1
ρdz ρ,S ∂t(S ρdz)!submeso diffuse
(36.440)
wdian rho subdiff =neut rho subdiff ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.441)
wdian temp subdiff =neut temp subdiff ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.442)
wdian salt subdiff =neut salt subdiff ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.443)
tform rho subdiff =neut rho subdiff BρdV
∆γn!(36.444)
tform temp subdiff =neut temp subdiff BρdV
∆γn!(36.445)
tform salt subdiff =neut salt subdiff BρdV
∆γn!.(36.446)
The same equalities also hold when binning the diagnostics to density layers. Additionally, the same rela-
tions hold for the wdian and tform diagnostics, again both on model levels and binned to density layers.
36.11.6 Quasi-physical parameterizations of overflow and marginal sea exchange
This suite of diagnostics arises from the the various means of representing/parameterizing overflow pro-
cesses and to connect the open ocean with spuriously land-locked marginal seas.
Elements of MOM November 19, 2014 Page 518

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.6.1 Over-exchange scheme
neut rho overex =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!overexch
(36.447)
neut temp overex =1
ρdz ρ,Θ∂t(Θρdz)!overexch
(36.448)
neut salt overex =1
ρdz ρ,S ∂t(S ρdz)!overexch
(36.449)
wdian rho overex =neut rho overex ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.450)
wdian temp overex =neut temp overex ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.451)
wdian salt overex =neut salt overex ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.452)
tform rho overex =neut rho overex BρdV
∆γn!(36.453)
tform temp overex =neut temp overex BρdV
∆γn!(36.454)
tform salt overex =neut salt overex BρdV
∆γn!.(36.455)
This contribution arises from one of the schemes available in MOM to parameterize processes associated
with deep overflows.
36.11.6.2 Overflow scheme
neut rho overfl =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!overflow
(36.456)
neut temp overfl =1
ρdz ρ,Θ∂t(Θρdz)!overflow
(36.457)
neut salt overfl =1
ρdz ρ,S ∂t(S ρdz)!overflow
(36.458)
wdian rho overfl =neut rho overfl ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.459)
wdian temp overfl =neut temp overfl ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.460)
wdian salt overfl =neut salt overfl ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.461)
tform rho overfl =neut rho overfl BρdV
∆γn!(36.462)
tform temp overfl =neut temp overfl BρdV
∆γn!(36.463)
tform salt overfl =neut salt overfl BρdV
∆γn!.(36.464)
This contribution arises from one of the schemes available in MOM to parameterize processes associated
with deep overflows.
Elements of MOM November 19, 2014 Page 519

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.6.3 Overflow scheme from NCAR
neut rho overofp =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!overflow ofp
(36.465)
neut temp overofp =1
ρdz ρ,Θ∂t(Θρdz)!overflow ofp
(36.466)
neut salt overofp =1
ρdz ρ,S ∂t(S ρdz)!overflow ofp
(36.467)
wdian rho overofp =neut rho overofp ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.468)
wdian temp overofp =neut temp overofp ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.469)
wdian salt overofp =neut salt overofp ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.470)
tform rho overofp =neut rho overofp BρdV
∆γn!(36.471)
tform temp overofp =neut temp overofp BρdV
∆γn!(36.472)
tform salt overofp =neut salt overofp BρdV
∆γn!.(36.473)
This contribution arises from one of the schemes available in MOM to parameterize processes associated
with deep overflows. It is based on the overflow scheme of Danabasoglu et al. (2010).
36.11.6.4 Mixdownslope scheme
neut rho mixdown =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!mixdown
(36.474)
neut temp mixdown =1
ρdz ρ,Θ∂t(Θρdz)!mixdown
(36.475)
neut salt mixdown =1
ρdz ρ,S ∂t(S ρdz)!mixdown
(36.476)
wdian rho mixdown =neut rho mixdown ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.477)
wdian temp mixdown =neut temp mixdown ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.478)
wdian salt mixdown =neut salt mixdown ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.479)
tform rho mixdown =neut rho mixdown BρdV
∆γn!(36.480)
tform temp mixdown =neut temp mixdown BρdV
∆γn!(36.481)
tform salt mixdown =neut salt mixdown BρdV
∆γn!.(36.482)
This contribution arises from one of the schemes available in MOM to parameterize processes associated
with deep overflows.
Elements of MOM November 19, 2014 Page 520

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.6.5 Sigma diffusion scheme
neut rho sigma =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!sigma
(36.483)
neut temp sigma =1
ρdz ρ,Θ∂t(Θρdz)!sigma
(36.484)
neut salt sigma =1
ρdz ρ,S ∂t(S ρdz)!sigma
(36.485)
wdian rho sigma =neut rho sigma ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.486)
wdian temp sigma =neut temp sigma ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.487)
wdian salt sigma =neut salt sigma ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.488)
tform rho sigma =neut rho sigma BρdV
∆γn!(36.489)
tform temp sigma =neut temp sigma BρdV
∆γn!(36.490)
tform salt sigma =neut salt sigma BρdV
∆γn!.(36.491)
This contribution arises from one of the schemes available in MOM to parameterize processes associated
with deep overflows. It is based on the diffusive portion of the Beckmann and D¨
oscher (1997) scheme.
36.11.6.6 Cross land mixing scheme
neut rho xmix =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!xmix
(36.492)
neut temp xmix =1
ρdz ρ,Θ∂t(Θρdz)!xmix
(36.493)
neut salt xmix =1
ρdz ρ,S ∂t(S ρdz)!xmix
(36.494)
wdian rho xmix =neut rho xmix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.495)
wdian temp xmix =neut temp xmix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.496)
wdian salt xmix =neut salt xmix ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.497)
tform rho xmix =neut rho xmix BρdV
∆γn!(36.498)
tform temp xmix =neut temp xmix BρdV
∆γn!(36.499)
tform salt xmix =neut salt xmix BρdV
∆γn!.(36.500)
This contribution arises from the parameterization of mixing across land-locked marginal seas (Griffies
et al.,2005), where the land-locking arises from the coarse resolution of the model grid.
Elements of MOM November 19, 2014 Page 521

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.6.7 Cross land insertion scheme
neut rho xinsert =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!xinsert
(36.501)
neut temp xinsert =1
ρdz ρ,Θ∂t(Θρdz)!xinsert
(36.502)
neut salt xinsert =1
ρdz ρ,S ∂t(S ρdz)!xinsert
(36.503)
wdian rho xinsert =neut rho xinsert ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.504)
wdian temp xinsert =neut temp xinsert ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.505)
wdian salt xinsert =neut salt xinsert ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.506)
tform rho xinsert =neut rho xinsert BρdV
∆γn!(36.507)
tform temp xinsert =neut temp xinsert BρdV
∆γn!(36.508)
tform salt xinsert =neut salt xinsert BρdV
∆γn!.(36.509)
This contribution arises from the parameterization of mixing across land-locked marginal seas (Griffies
et al.,2005), where the land-locking arises from the coarse resolution of the model grid.
36.11.7 Miscellaneous schemes
The following diagnostics are associated with miscellaneous processes.
36.11.7.1 Frazil heating of ocean liquid
As liquid seawater in MOM is influenced by surface boundary fluxes and transport, it may become colder
than the freezing point of ice. In this case, the seawater is warmed back to the freezing point, with the heat
required for this warming provided by the ice model. This adjustment process is known as frazil formation,
as that is what the ice model does to the super-cooled seawater. From the ocean model perspective, the
formation of frazil ice is a warming. Alternatively, it can be thought of as a re-partitioning of the surface
boundary fluxes (cooling fluxes in this case) between the liquid ocean and sea ice.
neut rho frazil =1
ρdz ρ,Θ∂t(Θρdz)!frazil
(36.510)
wdian rho frazil =neut rho frazil ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.511)
tform rho frazil =neut rho frazil BρdV
∆γn!.(36.512)
Elements of MOM November 19, 2014 Page 522

Chapter 36. Dianeutral transport and associated budgets Section 36.11
36.11.7.2 Free surface or bottom pressure smoothing
neut rho smooth =1
ρdz ρ,Θ∂t(Θρdz) + ρ,S ∂t(S ρdz)!smooth
(36.513)
neut temp smooth =1
ρdz ρ,Θ∂t(Θρdz)!smooth
(36.514)
neut salt smooth =1
ρdz ρ,S ∂t(S ρdz)!smooth
(36.515)
wdian rho smooth =neut rho smooth ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.516)
wdian temp smooth =neut temp smooth ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.517)
wdian salt smooth =neut salt smooth ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|!(36.518)
tform rho smooth =neut rho smooth BρdV
∆γn!(36.519)
tform temp smooth =neut temp smooth BρdV
∆γn!(36.520)
tform salt smooth =neut salt smooth BρdV
∆γn!.(36.521)
This contribution arises from the process of smoothing either the free surface (for Boussinesq simulations)
or bottom pressure (for non-Boussinesq simulations) in order to reduce the B-grid checkerboard noise (see,
e.g., Killworth et al. (1991) and Griffies et al. (2001)).
36.11.8 Summary of the process method for the ESM2M ocean
As for the kinematic method summarized in Section 36.10.13, we take the convention that each term is
diagnosed as an Eulerian time tendency, using the same numerical operations as used for the prognostic
equations of conservative temperature and salinity. We present here a specific example based on the
ocean component of the ESM2M earth system model documented by Dunne et al. (2012,2013).
36.11.8.1 Material time derivative
The finite volume estimate of the advective-form of the process material time derivative is given by
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!process level ≈
neut rho pbl pme pr +neut rho pbl rn pr +neut rho pbl cl pr
+neut rho sw +neut rho sbc temp +neut rho sbc salt
+neut rho diff cbt +neutral rho kpp nloc
+neut rho ndiff +neut rho k33
+neut rho mixdown +neut rho sigma
+neut rho xmix +neut rho xinsert
+neut rho smooth +neut rho frazil
+neut rho bbc temp
(36.522)
where we assumed liquid plus solid runoffare split into their own separate arrays, as per a realistic climate
model with a liquid runoffand solid calving scheme. If these terms are combined, as commonly done in
Elements of MOM November 19, 2014 Page 523
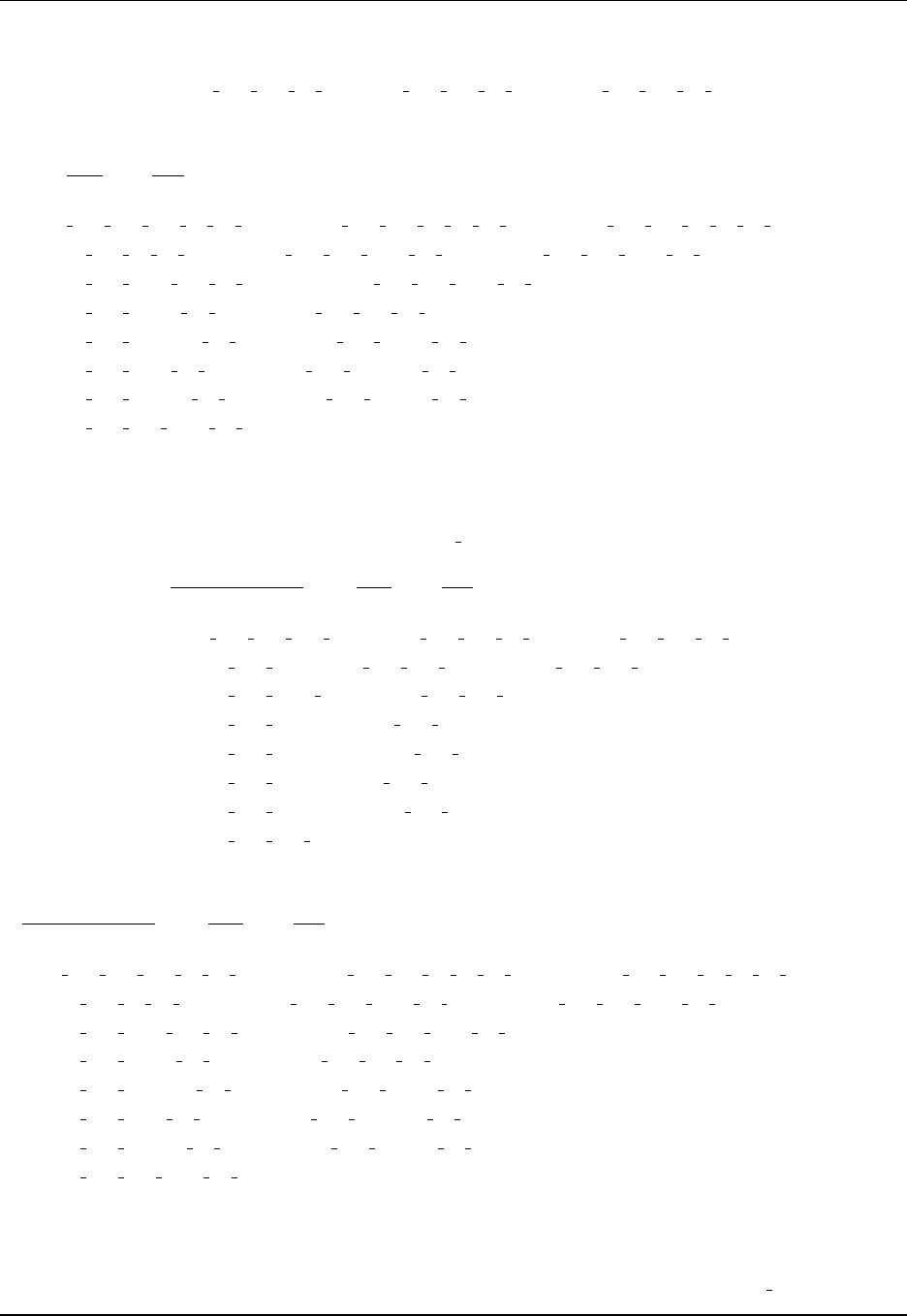
Chapter 36. Dianeutral transport and associated budgets Section 36.11
ocean-ice models, we should instead diagnose
neut rho pbl rn pr +neut rho pbl cl pr →neut rho pbl rv pr.(36.523)
The same relations also hold for the density binned form
ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!process layer ≈
neut rho pbl pme pr on nrho +neut rho pbl rn pr on nrho +neut rho pbl cl pr on nrho
+neut rho sw on nrho +neut rho sbc temp on nrho +neut rho sbc salt on nrho
+neut rho diff cbt on nrho +neutral rho kpp nloc on nrho
+neut rho ndiff on nrho +neut rho k33 on nrho
+neut rho mixdown on nrho +neut rho sigma on nrho
+neut rho xmix on nrho +neut rho xinsert on nrho
+neut rho smooth on nrho +neut rho frazil on nrho
+neut rho bbc temp on nrho.
(36.524)
36.11.8.2 Dianeutral transport from wdian diagnostics
The dianeutral mass transport, in units of kgs−1, can be estimated using wdian both on levels and binned
to neutral density layers. Following from the neutral rho diagnostics above, we have
ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|! ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!process level ≈
wdian rho pbl pme pr +wdian rho pbl rn pr +wdian rho pbl cl pr
+wdian rho sw +wdian rho sbc temp +wdian rho sbc salt
+wdian rho diff cbt +wdian rho kpp nloc
+wdian rho ndiff +wdian rho k33
+wdian rho mixdown +wdian rho sigma
+wdian rho xmix +wdian rho xinsert
+wdian rho smooth +wdian rho frazil
+wdian rho bbc temp.
(36.525)
The same relations also hold for the density binned dianeutral mass transport
ρdA(h)
|ρ,ΘΘ,h +ρ,S S,h|! ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!process layer ≈
wdian rho pbl pme pr on nrho +wdian rho pbl rn pr on nrho +wdian rho pbl cl pr on nrho
+wdian rho sw on nrho +wdian rho sbc temp on nrho +wdian rho sbc salt on nrho
+wdian rho diff cbt on nrho +wdian rho kpp nloc on nrho
+wdian rho ndiff on nrho +wdian rho k33 on nrho
+wdian rho mixdown on nrho +wdian rho sigma on nrho
+wdian rho xmix on nrho +wdian rho xinsert on nrho
+wdian rho smooth on nrho +wdian rho frazil on nrho
+wdian rho bbc temp on nrho.
(36.526)
36.11.8.3 Dianeutral transport from tform diagnostics
The dianeutral mass transport, in units of kgs−1, can also be estimated using tform diagnostics. Here, the
results are only sensible when binned to neutral density layers. Following from the wdian rho diagnostics
Elements of MOM November 19, 2014 Page 524

Chapter 36. Dianeutral transport and associated budgets Section 36.13
above, we have
BρdV
∆γn! ρ,Θ
d†Θ
dt+ρ,S
d†S
dt!process layer ≈
tform rho pbl pme pr on nrho +tform rho pbl rn pr on nrho +tform rho pbl cl pr on nrho
+tform rho sw on nrho +tform rho sbc temp on nrho +tform rho sbc salt on nrho
+tform rho diff cbt on nrho +tform rho kpp nloc on nrho
+tform rho ndiff on nrho +tform rho k33 on nrho
+tform rho mixdown on nrho +tform rho sigma on nrho
+tform rho xmix on nrho +tform rho xinsert on nrho
+tform rho smooth on nrho +tform rho frazil on nrho
+tform rho bbc temp on nrho.
(36.527)
36.12 Budget for locally referenced potential density
The diagnostics detailed in Sections 36.10 and 36.11 were used to obtain estimates of the advective-
form for the material time derivative of locally referenced potential density, along with the associated
dianeutral transport. Additionally, we have the kinematic formulation diagnosed in its flux-form (as used
for the prognostic model equations), which is distinct from the advective-form in the surface grid cell (see
Sections 36.10.5,36.10.7,36.10.9,36.10.11). We may thus obtain the budget (i.e., time tendency) for
locally referenced potential density. The following expression holds for the ESM2M coupled climate model
where river water is split into liquid runoffand solid calving
neut rho tendency =neut rho advect +neut rho gm +neut rho submeso
+neut rho pme +neut rho runoffmix +neut rho calvingmix
+neut rho sw +neut rho sbc temp +neut rho sbc salt
+neut rho diff cbt +neutral rho kpp nloc
+neut rho ndiff +neut rho k33
+neut rho mixdown +neut rho sigma
+neut rho xmix +neut rho xinsert
+neut rho smooth +neut rho frazil
+neut rho bbc temp.
(36.528)
This budget is also availalbe binned to neutral density classes through the on nrho version of the above
terms.
Elements of MOM November 19, 2014 Page 525

Chapter 36. Dianeutral transport and associated budgets Section 36.13
36.13 Diagnosing mass budgets for density layers
The purpose of this section is to detail the diagnostic methods available in MOM calculation of the accu-
mulated formation equation (36.8), repeated here for convenience
Φ(γ)≡
γb
Z
γF(γ)δγ.
=
γb
Z
γ V†+∂M
∂t !
=G(γ)−G(γb) +
γb
Z
γE.
(36.529)
Note that the caveats regarding neutral density given in Section 36.5.2 are relevant for general density
mass budgets. We ignore those details here. However, such details, as well as the more leading order
issues of just how to define the binning operation (detailed in this section), make the layer diagnostics far
less robust than the level diagnostics.
36.13.1 Time tendency for layer mass, M(γ)
Once the mass of a layer is estimated, the time tendency can be computed as the difference across a
chosen time step. It turns out that this calculation can be the source of some noise. As detailed in Sec-
tion 36.13.1, the noise can be ameliorated in two different manners. First, we diagnose the tendency by
taking the time mean of all forcing terms acting on the right hand side of the mass equation (36.1), and
interpreting the masses as living on the temporal interface of the time average period. That is, the masses
comprising the diagnosed time tendency live at half-integer time steps. The second means for comput-
ing the time tendency is to take the difference in the time averaged later mass (e.g., difference in annual
means). The second difference will result in a tendency that is offset by a half-integer from the forcing
terms. In a quasi-steady state, both tendencies will agree, and be small.
In general, the layer mass will evolve in time. Only by considering long time means in a simulation with
modest drift will the mass of each layer remain close to constant. So when diagnosing the mass balance
(36.1), or the streamfunction (36.7), it is important to determine how large the mass tendency is relative
to the other terms.
There are two general approaches for estimating the mass of a layer, M(γ). Briefly, the first approach
estimates, via linear interpolation, the lower and upper interfaces of the layer. The second approach bins
the mass of a grid cell according to its neutral density class. Multiplication by the horizontal area yields the
volume of that portion of the layer, and summing over the horizontal region within the domain of interest
then leads to the total volume for the layer. If working in a pressure based non-Boussinesq model, the
thickness of concern is actually the mass per area of the layer. The two aproaches agree quite well, with
differences arising in the case of unstably stratified waters, since the interpolation approach assumes
stable stratification. We detail these methods in this section. We also expose a limitation of the binning
approach used to measure layer masses, and propose a means to reduce the problems associated with
this limitation.
36.13.1.1 Time averaging the time tendency
We start by noting a trivial point relevant for diagnosing the time tendency of layer mass. Namely, the time
average of the layer mass time tendency is the difference in layer mass between the initial time step and
the final time step
1
T
T /2
Z
−T /2
dt ∂M(γ)
∂t !=M(γ,T /2) −M(γ,−T /2)
T,(36.530)
Elements of MOM November 19, 2014 Page 526

Chapter 36. Dianeutral transport and associated budgets Section 36.13
where Tis the length of the time interval, M(γ,±T /2) is the mass of the γlayer at time steps ±T /2. The
resulting time averaged tendency thus measures the mass difference between final and initial time steps.
Depending on the layer population, this diagnosed time tendency can be very noisy. Indeed, it can be so
noisy as to be of little use. The noise arises since computing the difference in the mass of a bin, where
the bin class is constant in time, is an intrinsically noisy procedure, whereby mass moves around in bin
space in a discrete manner subject to the arbitrary choice of bin classes. In particular, when filling an
empty bin, there is a huge change in the mass over just a small time step, and this change corresponds
to unphysically huge mass transport. Such huge jumps in mass arise solely from the arbitrary fixed bin
classes, and do not reflect a physically relevantn transfer of water into different layers.
36.13.1.2 Noise in the tendency of binned mass
Consider the layer mass equation (36.1), rewritten here in the generic form
∂M(t)
∂t =H(t),(36.531)
where His shorthand for the forcing terms on the right hand side of equation (36.1). Because of the identity
(36.530), the time averaged forcing, H(τ), forces a difference in the instantaneous layer mass. However,
computation of the difference in the instantaneous layer mass using fixed density bins generally results in
very noisy results for the left hand side to equation (36.531). In contrast, the right hand side forcing, H(τ),
is generally far smoother. Hence, one cannot expect the time average of both sides to equation (36.531)
to be equal when one uses fixed bins to diagnose both sides.
Fundamental to the problem of noise for the left hand side to equation (36.531) is that the mass con-
tained within a particular density bin will jump when using fixed density bins. For example, if a bin originally
was empty, the smooth diffusive transport of mass into that bin will result, at a particular time step, in a
huge jump in the bin mass over a single time step. Taking the temporal difference of the bin mass will
then lead to a huge jump in the mass tendency. Such jumps have no relevance to the otherwise smooth
rearrangement of mass between layers. Instead, it arises as an artifact of the use of fixed density bins.
Nonetheless, we wish to use fixed bins in order to allow for the online watermass diagnostic to be useful
across a wide suite of model processes. We thus need a means to smooth the binning noise. We choose a
temporal averaging operator for this purpose, with the approach motivated from that used in the barotropic
time stepping scheme used in MOM4 (see, for example, Section 12.7 of Griffies (2004)).
36.13.1.3 A smoothed mass tendency
Introduce the symbol ∆tto denote the time step used for an update tol model prognostic fields (i.e., the
prognostic model tracer time step), with tthe associated time label. Distinguish the model time step ∆t
from the generally longer time step ∆τ≥∆tassociated with time averaged diagnostics, which are typically
taken as daily, monthly, annual, or longer time means. The relation between the model time step and the
diagnostic time step is given by
tn=τ+n∆t, (36.532)
where n= 0,N is the discrete model time step, Nis the number of model time steps per diagnostic time
step, and τis the diagnostic time label. With these conventions, introduce the time averaged forcing term
appearing on the right hand side to equation (36.531)
H(τ+∆τ) = 1
N
N
X
n=1 H(τ+n∆t),(36.533)
where the time average is performed according to the specified diagnostic time step; i.e., day, month, year,
etc. Next, we define a diagnostic layer mass centered on a half integer diagnostic time step, f
M(τ+∆τ/2),
according to
f
M(τ+∆τ/2) −f
M(τ−∆τ/2)
∆τ≡ H(τ).(36.534)
Elements of MOM November 19, 2014 Page 527

Chapter 36. Dianeutral transport and associated budgets Section 36.13
That is, the half integer diagnostic layer mass f
M(τ+∆τ/2) is forced by the time averaged forcing H(τ).
Given the time averaged forcing H(τ), and an initial condition, we can time step the half integer layer
mass if so desired. A useful initial condition is given by setting the initial half-integer mass equal to the
integer mass at the first diagnostic time step. Note that since the forcing H(τ)is smooth, so too is the time
tendency (f
M(τ+∆τ/2) −f
M(τ−∆τ/2)/∆τ.
A check that the prescription (36.534) produces a sensible result is to compare the tendency to that
obtained by taking the difference between integer time step mean layer masses according to
M(τ+∆τ)−M(τ)
∆τ≡e
H(τ+∆τ/2),(36.535)
where
M(τ+∆τ) = 1
N
N
X
n=1 M(τ+n∆t),(36.536)
is the time averaged mass, and the right hand side of equation (36.535) defines a half integer diagnostic
forcing. In a steady state, the tendencies (36.534) and (36.535) will be the same. In the more general case,
they will differ according to the evolution of mass within a layer class.
The prescription (36.534) provides an indirect means to the calculation of the layer mass tendency.
That is, we infer the mass tendency through diagnosing the time mean forcing. The self-consistency of
this inference is examined by checking that it is consistent with the tendency (36.535) deduced from the
difference in time mean layer masses. In brief, we jettison the use of the difference in the instantaneous
layer mass given by equation (36.530), as that tendency is far to noisy for diagnostic use.
In the following, we detail two approaches available for computing the instantaneous layer mass, M(t).
Either approach can be used to compute the time averaged mass (36.536), whose tendency (36.536)
should correspond, though not generally equal, to the tendency of the half integer mass (36.534).
36.13.1.4 Estimating layer mass via interpolation
One approach to computing the mass tendency is to estimate the layer thickness via interpolation to deter-
mine the lower and upper interfaces of the layer, upon which multiplication by the horizontal area of a grid
cell yields the volume of that portion of the layer. Summing over the horizontal region within the domain of
interest then leads to the total volume for the layer. If working in a pressure based non-Boussinesq model,
the thickness of concern is actually the mass per area of the layer. Once the thickness is estimated, the
time tendency is computed as the difference in mass of the layer across a model time step.
The following diagnostics are related to computing M(γ)and ∂tM(γ), with each diagnostic computed
inside the ocean tracer.F90 module.
•mass nrho layer: estimate of M(γ)(units of kg). This diagnostic computes the time mean of the
layer mass, allowing for offline calculations to be used for computing time tendencies based on dif-
ferences of the time means (e.g., save annual mean mass nrho layer and compute the time tendency
by differencing annual mean masses).
•mass nrho tendency layer: estimate of ∂tM(γ)(units of kg s−1). This diagnostic computes the time
tendency at each time step and then performs a time average of the tendency. Because of the identity
(36.530), this time tendency can be very noisy, so it is not very useful. Instead, the time tendencies
(36.534 and (36.535) are more useful.
We offer the following comments regarding this diagnostic.
•Pro A: This algorithm appears to produce results that have little sensitivity to details of the pre-
defined density classes, with finer density bins producing cleaner results.
•Pro B: When the neutral density is stably stratified, the vertical sum of mass nrho tendency layer
equals to the mass entering through the boundaries. So this diagnostic respects mass conservation
for stably stratified columns.
Elements of MOM November 19, 2014 Page 528
Chapter 36. Dianeutral transport and associated budgets Section 36.13
•Con A: The algorithm is based on a linear interpolation that is sensible only when the diagnosed
neutral density layers are monotonically stacked in the vertical. In particular, the algorithm does not
guarantee mass conservation when there are unstably stratified regions.
36.13.1.5 Binning the mass of a tracer cell to neutral density layers
A second method for computing the mass tendency of a density layer is to bin the mass of a tracer cell (or
ρ0times the volume when working with a Boussinesq fluid) into neutral density classes. The evolution of
this binned mass then determines the mass tendency for the layer. This method is not equivalent to the
first method, since the binning approach is not equivalent to linear interpolation. The diagnostics available
with this method include the following.
•mass t: this is the mass of a tracer grid cell.
•mass t on nrho: this is the mass of a tracer cell binned into neutral density layers. It thus provides
an estimate of the mass of neutral density layers.
•mass t tendency on nrho: This is the time tendency of the layer mass, computed as the tendency of
mass t on nrho. This diagnostic computes the time tendency at each time step and then performs a
time average of the tendency. Because of the identity (36.530), this time tendency can be very noisy,
so it is not very useful. Instead, the time tendencies (36.534 and (36.535) are more useful.
We offer the following comments regarding this diagnostic approach.
•Pro A: Since we are binning the mass of a tracer cell according to density layers, the method works
for arbitrary density stratification.
•Pro B: The vertical sum of mass t tendency on nrho equals to the mass entering through the bound-
aries. So this diagnostic respects mass conservation.
•Con: Binning generally produces noisy results when the density classes are sporadically populated,
with finer density bins generally producing more noisy results. The results are therefore a function of
the pre-defined density classes. However, performing a vertical indefinite integral, as when forming
an accumulated formation streamfunction as in equation (36.8), will generally smooth the results.
36.13.1.6 Binning the time tendency for the mass per area (not recommended)
A spurious approach was discovered when working with the field rho dzt tendency. When multipled by
area of a grid cell, rho dzt tendency provides a measure of the mass tendency for a grid cell, with a
nonzero tendency associated with mass convergence and divergence into the cell. However, this tendency
is notably not what we aim to diagnose for the purpose of watermass transformation analysis. Indeed,
rho dzt tendency is identically zero in a rigid lid geopotential model, whereas the neutral density layers
certainly can evolve in such models. So again, it is inappropriate to consider mapping the area weigthed
rho dzt tendency to neutral density classes for the watermass transformation diagnostics.
36.13.1.7 Regarding water fluxes and vertical coordinates
An unsettling issue with the diagnosis of layer mass was uncovered when developing the diagnostics de-
tailed in this section. Namely, consider the transfer of water across the ocean surface, absent interior
mixing. In the case of a non-geopotential vertical coordinate, a water flux at the ocean surface will alter
interior tracer concentrations, including salinity and temperature, even in the absence of mixing, so long
as there is a nontrivial vertical stratification of the tracer concentration. This alteration of tracer concen-
tration results from rearrangement (expansion or contraction) of the vertical coordinate surfaces due to
changes in the surface height or bottom pressure.
A one-dimensional test case is sufficient to illustrate the issue. Consider for this purpose horizontally
flat temperature surfaces with stable vertical stratification. Allow salinity to be uniform and the equation
of state linear with just a temperature dependence. When passing water across the ocean surface, sea
Elements of MOM November 19, 2014 Page 529

Chapter 36. Dianeutral transport and associated budgets Section 36.13
level will change. For the geopotential vertical coordinate, it is just the surface grid cell that feels the sea
level change. However, for all other MOM4 vertical coordinates, each cell at depth will experience the sea
level change as well. In particular, as sea level changes, so too does the mass per area (non-Boussinesq)
or volume per area (Boussinesq). A nonzero vertical velocity will be established to conserve mass for each
grid cell. This vertical velocity will in turn advect tracer. As the salinity is uniform to begin with, there is no
change in salinity concentration throughout the vertical, except for the top grid cell, where the impacts of
the surface water flux impact the surface salinity. However, with a nonzero stratification in temperature,
there will be advective transport of temperature, and so the temperature field will be modified.
There are various unsettling aspects to this test case. Notably, the temperature stratification has been
modified throughout the full depth, yet we have no interior mixing. This alteration of temperature is un-
related to the spurious mixing from numerical advection described in Griffies et al. (2000b), where advec-
tive truncation errors generally become more egregious as eddy activity is enhanced. Instead, all that
has occurred is to transfer fresh water across the ocean surface in this one-dimensional test case. The
stratification change arises from motion of the coordinate surfaces, and the associated nonzero vertical
advection velocity developed to conserve mass within each grid cell. The vertical velocity then leads to a
nonzero advective temperature convergences, and hence to changes in temperature.
We acknowldege the somewhat unphysical nature to the above test case. Namely, the absence of mix-
ing is unrealistic. Motion of water across the ocean surface generally occurs in the presence of nontrivial
vertical mixing in the upper ocean. In particular, phase change for evaporating water and mixing of pre-
cipitating fresh water into a salty ocean are both irreversible. So the case of a geopotential model with
its upper grid cell remaining isolated from static deeper cells becomes unphysical, especially in the case
of a very fine upper cell thickness. Nonetheless, given these caveats, the test case presents an unsettling
example of how the choice of vertical coordinates can directly impact the level of effective tracer mixing
within a simulation, even when the flow regime is trivially laminar.
36.13.2 Surface mass transport, E(γ)
The transport of water crossing the ocean surface, E(γ), is determined according to a binning of the
surface water transport according to density classes. The following diagnostics are computed in the
ocean sbc.F90 module.
•mass pmepr on nrho: density binned net mass transport (units of kg s−1) of water that crosses the
ocean surface. A positive value indicates water enters the ocean.
•mass precip on nrho: density binned mass transport (units of kg s−1) of precipitating liquid plus
precipitating frozen water crossing the ocean surface, including water exchanged with sea ice (i.e.,
melt). A positive value indicates water enters the ocean.
•mass evap on nrho: density binned mass transport (units of kg s−1) of evaporating vapor or condens-
ing liquid water crossing the ocean surface. A positive value indicates water enters the ocean.
•mass river on nrho: density binned mass transport (units of kg s−1) of liquid river runoffand solid
calving land ice entering the ocean. A positive value indicates water enters the ocean.
•mass melt on nrho: density binned mass transport (units of kg s−1) of water exchanged with the sea
ice model through melting or forming sea ice. A positive value indicates water enters the ocean.
Again, note that melt is also included as part of precipitation.
In general, the full mass flux into a density layer through the ocean surface is given by
E=mass pmepr on nrho (36.537)
and note that the following identity holds for these diagnostics:
mass pmepr on nrho =mass precip on nrho +mass evap on nrho +mass river on nrho,(36.538)
where, again, ice melt is included as part of precipitation.
Elements of MOM November 19, 2014 Page 530

Chapter 36. Dianeutral transport and associated budgets Section 36.13
36.13.3 Overturning streamfunction, Ψ†(γ) = −Rγb
γV†
The overturning streamfunction is a diagnostic that is commonly computed in ocean simulations. Indeed,
analysis of Ψ†as computed on model levels as well as binned into density layers is becoming quite com-
mon, as the two perspectives provide useful complementary information. There are presently three terms
that contribute to the overturning streamfunction in MOM, with the two terms associated with eddy in-
duced transport treated differently than the one term associated with the model resolved Eulerian trans-
port. When computing terms in the accumulated watermass formation equation (36.8), it is important to
recall the minus sign relation (36.14)
Ψ†(y,γ) = −
γb
Z
γV†(y).(36.539)
We start the diagnostic calculation by considering the level space specification of the meridional stream-
function Ψ†, which takes the form
Ψ†(s) = −Z
zonal range
dx
z(s)
Z
−H
dzρ (v+v∗
gm +v∗
submeso).(36.540)
In this equation, the zonal integration occurs over a specified periodic or closed domain, such as the full
longitudinal extent of the Southern Ocean or the region between two continents. Vertical integration oc-
curs from the ocean bottom at a position z=−H(x,y), up to the depth of the coordinate surface z(s),
where sis the value of the generalized level for each model level. The in situ density factor ρrenders a
mass transport for mass conserving non-Boussinesq simulations, and it becomes the constant reference
density ρofor volume conserving Boussinesq simulations. The meridional velocity component vis part of
the model’s resolved horizontal velocity field u. We are most interested in meridional transport, but the
overturning streamfunction can also be defined for zonal transport, in which case ureplaces v.
There are two eddy induced velocity fields displayed in equation (36.540), with u∗
gm associated with the
Gent et al. (1995) parameterization of mesoscale eddies, and u∗
submeso associated with the Fox-Kemper et al.
(2008b) parameterization of mixed layer submesoscale eddies. Both eddy induced velocity fields can be
written as the vertical derivative of an eddy induced transport Υ(units of m2s−1), so that
ρu∗
gm =∂z(ρΥgm)
ρu∗
submeso =∂z(ρΥsubmeso),(36.541)
where the ρfactors reduce to the constant reference density ρofor Boussinesq fluids. Hence, the contri-
bution from the eddy induced transport to the overturning streamfunction takes the form
Ψeddy(s) = −Z
zonal range
dx
z(s)
Z
−H
dzρ (v∗
gm +v∗
submeso)
=−Z
zonal range
dx
z(s)
Z
−H
dz∂zρΥ(y)
gm +ρΥ(y)
submeso
=−Z
zonal range
dxρΥ(y)
gm +ρΥ(y)
submesoz=z(s).
(36.542)
In this equation, we wrote Υ(y)for the meridional component of the eddy induced transport. This transport
vanishes at the ocean bottom (and surface), thus leaving just the contribution from the interior transport
at a depth z=z(s). Given these results, we may write the full overturning streamfunction (36.540) in the
form
Ψ†(s) = −Z
zonal range
dx
z(s)
Z
−H
dzρv−Z
zonal range
dxρΥ(y)
gm +ρΥ(y)
submesoz=z(s).(36.543)
Elements of MOM November 19, 2014 Page 531

Chapter 36. Dianeutral transport and associated budgets Section 36.13
The following diagnostics are computed in the module ocean adv vel diag.F90 for the overturning
due to the Eulerian velocity.
•tx trans nrho: zonal mass transport through a grid cell, ρdydz u (units of kg s−1) binned according
to neutral density classes.
•ty trans nrho: meridional mass transport through a grid cell ρdxdzv (units of kg s−1) binned ac-
cording to neutral density classes.
The following diagnostics are computed in the module ocean nphysics util.F90 for the overturning due
to the Gent et al. (1995) eddy induced velocity.
•tx trans nrho gm: zonal eddy induced mass transport through a grid cell ρdyΥ(x)
gm (units of kg s−1)
mapped according to neutral density classes.
•ty trans nrho gm: meridional eddy induced mass transport through a grid cell ρdxΥ(y)
gm (units of
kg s−1) mapped according to neutral density classes.
The following diagnostics are computed in the module ocean submesoscalel.F90 for the overturning due
to the Fox-Kemper et al. (2008b) eddy induced velocity.
•tx trans nrho submeso: zonal eddy induced mass transport through a grid cell ρdyΥ(x)
submeso (units of
kg s−1) mapped according to neutral density classes.
•ty trans nrho submeso: meridional eddy induced mass transport through a grid cell ρdxΥ(y)
submeso (units
of kg s−1) mapped according to neutral density classes.
A calculation of the full meridional overturning streamfunction in Ferret takes the form
Ψ†(γ) = ty trans nrho[k= @rsum,i= @sum]−ty trans nrho[k= @sum,i= @sum]
+ty trans nrho gm[i= @sum] + ty trans nrho submeso[i= @sum]
Ψ†(y,γ) = −
γb
Z
γV†(y).
(36.544)
Note that absence of a vertical sum for the two eddy induced transports, since their respective vertical
integrals have been performed analytically according to equation (36.542). Subtracting the term
ty trans nrho[k= @sum,i= @sum] (36.545)
accounts for the convention in Ferret whereby it integrates from the surface downward, rather than from
the bottom upward. This step is required to ensure that the diagnosed streamfunction psi vanishes at the
ocean bottom. Other analysis software, such as Matlab, may not require this added step, so long as the
integration starts from zero at the bottom and goes from the bottom upwards.
We have had mixed success with the structure of the transports ty trans nrho gm and ty trans nrho submeso
resulting from the MOM diagnostic calculation. One may find the following Ferret command as a useful al-
ternative for either the Gent et al. (1995)orFox-Kemper et al. (2008b) transport computed from MOM:
let ty trans nrho gm new =ZAXREPLACE(ty trans gm,neutral rho,ty trans nrho),(36.546)
where ty trans gm is the level-space version of the Gent et al. (1995) transport, neutral rho is the di-
agnosed neutral density at each model grid point, and ty trans nrho provides Ferret with the density
classes upon which to remap ty trans gm. The Ferret function ZAXREPLACE replaces the vertical axis of
ty trans gm with the vertical axis from ty trans nrho according to the neutral density values in neutral rho.
There will be differences between ty trans nrho gm new and ty trans nrho gm due to sampling. But in
principle they should look quite simple. In practive, however, they may differ depending on other details
that are not clear. It is thus useful to compare the two versions of the eddy induced overturning.
Elements of MOM November 19, 2014 Page 532
Chapter 36. Dianeutral transport and associated budgets Section 36.13
36.13.4 watermass transformation, G(γ)
By definition, the transport crossing a density class is given by the surface integral (see equation (36.69))
G(γ) = Z
A(γ)
ρw(γ)dA(γ).(36.547)
The area integral extends over the density surface γfor the region south of the chosen latitude (see Figure
36.1). The algorithm detailed by Table 36.1 provides the means to compute the integral on the right hand
side of equation (36.547).
Following the form given by equation (36.529), we need to compute the
G(γ)−G(γb) = Z
A(γ)
ρw(γ)dA(γ)−Z
A(γb)
ρw(γb)dA(γb).(36.548)
Either the kinematic or process methods can be used to compute contributions to this integral, thus facili-
tating physical interpretations of the causes for the transformation. For a realistic global model with a full
suite of parameterizations, we have the following identity for arbitrary density interfaces, as represented
using the kinematic approach (see Section 36.10.13)
ρw(γ)dA(γ)−ρw(γb)dA(γb)kinematic ≈
wdian rho tendency on nrho −wdian rho advect on nrho
−wdian rho gm on nrho −wdian rho submeso on nrho
+wdian rho pbl pme kn on nrho
+wdian rho pbl rn kn on nrho +wdian rho pbl cl kn on nrho
−wdian rho bbc temp on nrho.
(36.549)
Note the subtraction of the geothermal heating term, which arises from the accumulated formation (see
equation (36.529)). The equivalent process version, again for the ESM2M ocean component (Dunne et al.,
2012,2013) discussed in Section 36.11.8, is given by
ρw(γ)dA(γ)−ρw(γb)dA(γb)process ≈
wdian rho pbl pme pr on nrho +wdian rho pbl rn pr on nrho +wdian rho pbl cl pr on nrho
+wdian rho sw on nrho +wdian rho sbc temp on nrho +wdian rho sbc salt on nrho
+wdian rho diff cbt on nrho +wdian rho kpp nloc on nrho
+wdian rho ndiff on nrho +wdian rho k33 on nrho
+wdian rho mixdown on nrho +wdian rho sigma on nrho
+wdian rho xmix on nrho +wdian rho xinsert on nrho
+wdian rho smooth on nrho +wdian rho frazil on nrho.
(36.550)
Note the absence of the geothermal heating term, since it is subtracted through the accumulated for-
mation (see equation (36.529)). Another estimate of these transformations can be obtained through the
tform diagnostic, in which case we have the kinematic expression
ρw(γ)dA(γ)−ρw(γb)dA(γb)kinematic ≈
tform rho tendency on nrho −tform rho advect on nrho
−tform rho gm on nrho −tform rho submeso on nrho
+tform rho pbl pme kn on nrho
+tform rho pbl rn kn on nrho +tform rho pbl cl kn on nrho
−tform rho bbc temp on nrho
(36.551)
Elements of MOM November 19, 2014 Page 533

Chapter 36. Dianeutral transport and associated budgets Section 36.14
as well as the process expression
ρw(γ)dA(γ)−ρw(γb)dA(γb)process ≈
tform rho pbl pme pr on nrho +tform rho pbl rn pr on nrho +tform rho pbl cl pr on nrho
+tform rho sw on nrho +tform rho sbc temp on nrho +tform rho sbc salt on nrho
+tform rho diff cbt on nrho +tform rho kpp nloc on nrho
+tform rho ndiff on nrho +tform rho k33 on nrho
+tform rho mixdown on nrho +tform rho sigma on nrho
+tform rho xmix on nrho +tform rho xinsert on nrho
+tform rho smooth on nrho +tform rho frazil on nrho.
(36.552)
36.14 Inferring transformation from surface buoyancy fluxes
Many applications of the Walin (1982) layer transformation method have focused on the surface buoy-
ancy fluxes, binned into density classes, and using these binned fluxes as a means to infer the interior
watermass transformation (Large and Nurser,2001). Returning to the layer mass equation (36.1), this
approach is based on diagnosing the mass tendency ∂M(γ)/∂t (usually assumed to be negligible in most
applications); the surface mass flux E(γ)arising from precipitation, evaporation, runoffand ice melt; and
contributions to the transformation G(γ)associated with surface buoyancy fluxes. From this information,
one may infer interior values for the watermass transformation G(γ).
The inferential approach is unnecessary when using the deductive methods detailed in the previous
sections, whereby explicit formulae for G(γ)were presented. However, the deductive approach is not avail-
able with observational data, where interior transport processes are not diagnosed to the degree required
to perform a fully deductive watermass transformation analysis. Additionally, the inferential approach is
a useful means for checking the integrity of the deductive diagnostics. Hence, we provide in this section a
discussion of the boundary flux approach, and detail the MOM diagnostics available with this method.
This section summarizes the diagnostics available in MOM to determine how surface buoyancy fluxes
affect a material change in density, when formulating the material change in the advective-form and using
the process perspective. We are concerned here with fluxes binned according to neutral density classes,
since we are interested in how the density census is modified through surface fluxes. All of these diagnos-
tics are named
tform rho pbl name on nrho,(36.553)
where name denotes the associated flux, and pbl signifies that these terms are associated with the sur-
face planetary boundary layer. Buoyancy fluxes associated with surface mass fluxes have already been
introduced in Section 36.11.2. They are also included here for completeness.
36.14.1 Density forcing associated with surface water fluxes
The following diagnostics are associated with surface buoyancy fluxes arising from the passage of water
across the ocean boundary. As water transported across the boundary carries both heat and salt (usually
zero salinity), it contributes a nonzero buoyancy flux. The diagnostics are each computed in the modules
ocean tracers/ocean tracer.F90
ocean param/sources/ocean rivermix.F90
•tform rho pbl pme pr on nrho: This diagnostic, computed in the module ocean tracer.F90, pro-
vides the process form contribution (see Section 36.11.2) due to the precipitation (liquid and frozen)
Elements of MOM November 19, 2014 Page 534

Chapter 36. Dianeutral transport and associated budgets Section 36.14
minus evaporation (units of kg s−1). It is also presented in Section 36.11.2.1.
tform rho pbl pme pr on nrho = BdA
∆γn! ρ,Θ(Θpme −Θk=1) + ρ,S (Spme −Sk=1)!Qpme (36.554)
tform temp pbl pme pr on nrho = BdA
∆γn! ρ,Θ(Θpme −Θk=1)!Qpme (36.555)
tform salt pbl pme pr on nrho = BdA
∆γn! ρ,S (Spme −Sk=1)!Qpme (36.556)
•tform rho pbl rv pr on nrho: This diagnostic, computed in the module ocean rivermix.F90, pro-
vides the process contribution (see Section 36.11.2) due to liquid river runoffplus solid calving land
ice (units of kg s−1). It is also presented in Section 36.11.2.2.
tform rho pbl rv pr on nrho = BdA
∆γn! ρ,Θ(Θriver −Θk=1) + ρ,S (Sriver −Sk=1)!Qriver (36.557)
tform temp pbl rv pr on nrho = BdA
∆γn! ρ,Θ(Θriver −Θk=1)!Qriver (36.558)
tform salt pbl rv pr on nrho = BdA
∆γn! ρ,S (Sriver −Sk=1)!Qriver.(36.559)
•tform rho pbl rn pr on nrho: This diagnostic, computed in the module ocean rivermix.F90, pro-
vides the process contribution (see Section 36.11.2) due to liquid river runoff(units of kg s−1). It is
also presented in Section 36.11.2.3.
tform rho pbl rn pr on nrho = BdA
∆γn! ρ,Θ(Θrunoff−Θk=1) + ρ,S (Srunoff−Sk=1)!Qrunoff(36.560)
tform temp pbl rn pr on nrho = BdA
∆γn! ρ,Θ(Θrunoff−Θk=1)!Qrunoff(36.561)
tform salt pbl rn pr on nrho = BdA
∆γn! ρ,S (Srunoff−Sk=1)!Qrunoff.(36.562)
•tform rho pbl cl pr on nrho: This diagnostic, computed in the module ocean rivermix.F90, pro-
vides the process contribution (see Section 36.11.2) due to solid calving land ice (units of kg s−1). It
is also presented in Section 36.11.2.4.
tform rho pbl cl pr on nrho = BdA
∆γn! ρ,Θ(Θcalving −Θk=1) + ρ,S (Scalving −Sk=1)!Qcalving (36.563)
tform temp pbl cl pr on nrho = BdA
∆γn! ρ,Θ(Θcalving −Θk=1)!Qcalving (36.564)
tform salt pbl cl pr on nrho = BdA
∆γn! ρ,S (Scalving −Sk=1)!Qcalving.(36.565)
36.14.2 Density forcing associated with surface heat and salt fluxes
The following diagnostics are associated with surface buoyancy fluxes arising from the passage of salt
and heat across the ocean. All fluxes are positive when entering the ocean (positive heat flux adds heat to
the ocean; positive salt flux adds salt to the ocean). Each of the following diagnostics are computed inside
the module
ocean core/ocean sbc.F90
Elements of MOM November 19, 2014 Page 535

Chapter 36. Dianeutral transport and associated budgets Section 36.14
•tform rho pbl flux on nrho: This diagnostic, computed in the module ocean sbc.F90, provides the
contribution due to the net surface radiative and turbulent heat fluxes, plus salt fluxes due to sea ice
interactions (units of kg s−1)
tform rho pbl flux on nrho = BdA
∆γn! ρ,Θ(QΘ
sw +QΘ
lw +QΘ
latent +QΘ
sensible) + ρ,S QS
sea ice!.(36.566)
This diagnostic is equivalent to tform rho sbc on nrho detailed in Section 36.11.1.3
tform rho pbl flux on nrho =tform rho sbc on nrho.(36.567)
•tform rho pbl heat on nrho: This diagnostic provides the contribution due to the net surface radia-
tive and turbulent heat fluxes (units of kg s−1)
tform rho pbl heat on nrho = BdA
∆γn! ρ,Θ(QΘ
sw +QΘ
lw +QΘ
latent +QΘ
sensible)!.(36.568)
This diagnostic is equivalent to tform rho sbc temp on nrho detailed in Section 36.11.1.1
tform rho pbl heat on nrho =tform rho sbc temp on nrho.(36.569)
•tform rho pbl salt on nrho: This diagnostic, computed in the module ocean sbc.F90, provides the
contribution due to the net surface salt fluxes due to sea ice interactions (units of kg s−1)
tform rho pbl salt on nrho = BdA
∆γn! ρ,S QS
sea ice!.(36.570)
This diagnostic is equivalent to tform rho sbc temp on nrho detailed in Section 36.11.1.2
tform rho pbl salt on nrho =tform rho sbc salt on nrho.(36.571)
•tform rho pbl lw on nrho: This diagnostic, computed in the module ocean sbc.F90, provides the
contribution due to the net longwave radiation crossing the ocean surface (units of kg s−1).
tform rho pbl lw on nrho = BdA
∆γn! ρ,ΘQΘ
lw !.(36.572)
•tform rho pbl lat on nrho: This diagnostic, computed in the module ocean sbc.F90, provides the
contribution due to latent heating (due to liquid-vapor and solid-liquid phase changes) crossing the
ocean surface (units of kg s−1). Note that in some regions, the air temperature may drop below
the wet bulb temperature, thus giving condensation rather than evaporation, and so causing latent
heating to not be sign definite.
tform rho pbl lat on nrho = BdA
∆γn! ρ,ΘQΘ
lat !.(36.573)
•tform rho pbl sens on nrho: This diagnostic, computed in the module ocean sbc.F90, provides the
contribution due to latent heating (due to liquid-vapor and solid-liquid phase changes) crossing the
ocean surface (units of kg s−1).
tform rho pbl sens on nrho = BdA
∆γn! ρ,ΘQΘ
sens!.(36.574)
•tform rho pbl sw on nrho: This diagnostic, computed in the module ocean sbc.F90, provides the
contribution due to the net solar shortwave crossing the ocean surface (units of kg s−1). This diag-
nostic does not consider penetrative shortwave effects
tform rho pbl sw on nrho = BdA
∆γn! ρ,ΘQΘ
sw !.(36.575)
Elements of MOM November 19, 2014 Page 536

Chapter 36. Dianeutral transport and associated budgets Section 36.15
•tform rho pbl adjheat on nrho: This diagnostic, computed in the module ocean sbc.F90, provides
the contribution due to the net surface temperature restoring fluxes (units of kg s−1)
tform rho pbl adjheat on nrho = BdA
∆γn! ρ,ΘQΘ
restore!.(36.576)
•tform rho pbl adjsalt on nrho: This diagnostic, computed in the module ocean sbc.F90, provides
the contribution due to the net surface salt restoring fluxes (units of kg s−1)
tform rho pbl adjsalt on nrho = BdA
∆γn! ρ,S QS
restore!.(36.577)
36.15 Specifying the density classes for layer diagnostics
All diagnostics presented in “neutral density” classes are binned according to the user specified density
layers. The neutral density at a model grid point is then used to determine where to bin the associated
properties into neutral density space. The purpose of this subsection is to detail how the bins are deter-
mined and how the binning occurs.
36.15.1 Online calculation of neutral density
The neutral density computed online for the dianeutral transport diagnostic can be computed in one of
the following ways.
• In early implementations of this diagnostic, the default approach followed the polynomial approxima-
tion given in the appendix to McDougall and Jackett (2005). This polynomial approximation is very
convenient to use for an online model diagnostic. However, it suffers from inaccuracies that limit
its utility. Under strong recommendation from Trevor McDougall, the MOM diagnostic presently de-
faults to potential density computed relative to 2000dbar as an approximation to the neutral density
coordinate. Ongoing work aims to provide a more sensible global approximation to neutral density
that is computable online without requiring a climatology.
• Another approach is to use potential density, which may be enabled by setting neutral density potrho
= .true. and neutral density mj = .false. in the module ocean density.F90. The pressure ref-
erence value is potrho press, which is also a namelist in ocean density.F90.
It remains a research question to determine an optimal online method for computing neutral density
for dianeutral transport diagnostics. In particular, we are exploring the approach of Klocker et al. (2009).
36.15.2 Defining the density bins
The model provides a namelist in ocean density nml for the maximum and minimum value for the den-
sity class, and the number of bins included between these range boundaries. The following details these
namelists.
•neutralrho min: minimum neutral density for the binning (units kg m−3)
•neutralrho max: maximum neutral density for the binning (units kg m−3)
•layer nk: number of bins used for defining the neutral density classes.
These namelist settings are then used to setup layer nk neutral density bins, whose boundaries or edges
are denoted by γbound. The boundaries γbound correspond to the intervals δγ/2shown in Figure 36.1. The
layer nk+1 boundaries of the layer nk bins are determined according to
γbound(kγ= 1) = neutralrho min (36.578)
γbound(kγ) = γbound (kγ−1) + neutralrho max −neutralrho min
layer nk for kγ= 2,layer nk+1.(36.579)
Elements of MOM November 19, 2014 Page 537
Chapter 36. Dianeutral transport and associated budgets Section 36.16
For example, the CM2 climate models run at GFDL using MOM have 50 vertical grid levels. When binning
according to σ2000, we choose the following for its density bins
•neutralrho min =1028 kg m−3
•neutralrho max =1038 kg m−3
•layer nk = 80.
Many choices for density range will not resolve processes that occur in certain inland seas (e.g., Baltic Sea
or Hudson Bay) where fresh water makes the neutral density lighter than 1028 kg m−3. It may also miss
certain deep processes with neutral density larger than 1038 kg m−3. So the user should choose the range
based on the region of interest for the analysis.
The use of refined density classes will allow for finer resolution of transport in density space. But adding
bins comes with a price. Furthermore, at some point there are reduced if not negative benefits. The cost
is associated with the memory required for the online calculation (i.e., more bins means more memory
to hold the binned fields) and archive storage for the binned output. The reduced and possibly negatie
benefits arise since adding more bins will reduce the population of any particular density class. At some
point, with too many bins, the reduced population leads to noisy results.
36.15.3 Convention for the binning
The fields available in neutral density layers are a function of density, and written in the form F(γ). The
discrete version of F(γ)is determined at each model time step according to the following binning proce-
dure
F(i,j,kγ) = X
kF(i,j,k)Π[γbound(kγ)≤γ(i,j,k)< γbound (kγ+ 1)] (36.580)
where Πis a binning function that is unity when γ(i,j,k)is inside the specified range, and vanishes when
outside. There are two choices we may make for densities γ(i,j,k)that fall outside of the maximum and
minimum of the predefined density range.
• Populate the nearest bin. That is, if γ(i,j,k)< γbound (kγ= 1) (i.e., neutral density is lighter than any
predefined density class), then F(i,j,kγ= 1) is populated. If γ(i,j,k)> γbound(kγ=layer nk)(i.e.,
neutral density is denser than any predefined density class), then F(i,j,kγ=layer nk)is populated.
• Ignore points outside of the predefined density range.
We choose the first method, where all cells are binned, even if falling outside of the bin range. This choice
is consistent with the traditional approach used to bin transport in MOM, where it is important to bin all of
the transport, including that which may occur for classes outside of the predefined range. However, this
approach can lead to an overpopulation of the lightest or densest density class when there are waters
that sit outside of the range. It is for this reason that we recommended that the maximum and minimum
density bins both be removed from an analysis of the dianeutral transport diagnostic.
36.15.4 Binning versus remapping
When examining the results from transport binning, it is important to understand that binning is not the
same as remapping. For example, consider a nonzero transport that has no depth dependence. When
remapped to density space, the transport value will remain the same and there will be no density depen-
dence, regardless of how the density layers are stratified. In contrast, when binned to density space, the
binned transport will be a function of the density stratification. Namely, there will be more contribution
to density bins that occupy a larger depth range, such as weakly stratified layers, and less contribution to
those layers that are within a strongly stratified region. The result from binning is relevant when measuring
the net mass transport within a particular density class.
Elements of MOM November 19, 2014 Page 538

Chapter 36. Dianeutral transport and associated budgets Section 36.16
36.16 Known limitations
The following summarizing some of the known limitations of this diagnostic framework.
36.16.1 Disagreements between wdian and tform
There are two general ways proposed in this chapter for diagnosing the dianeutral transformation of wa-
ter: the wdian approach of Section 36.4 and the tform method of Section 36.5. Both approach should
agree, as they do in the continuum. However, discrete numerical truncations preclude agreement in the
model. The disagreements can be quite large especially in regions of weak stratification, in which case the
division by the density gradient required for the wdian approach can lead to unphysically large values of
the associated transformation diagnostics. One means to regularize the wdian diagnostics is to smooth
the stratification prior to computing the diagnostics. Such smoothing is indeed fundamental to how one
estimates vertical mixing processes from observed data. Pursuit of such smoothing operations remains
incomplete for the MOM wdian diagnostics.
In contrast, the tform method appears to be more robust than the wdian diagnostics, since there is
no need to divide by the density gradient. Furthermore, agreement between the tform approach and the
traditional overturning streamfunction Ψ(Section 36.2.4) is far better using the tform approach than the
wdian approach. Consequently, in general we make more use of the tform diagnostics when aiming to
perform quantitative estimates of water mass transformation and to close the mass budget detailed in
Section 36.2.
36.16.2 Inserting river water into the ocean
Liquid runoffand solid calving are generally inserted into the upper few grid cells of a realistic ocean
model. For example, in the ESM2M ocean component of Dunne et al. (2012,2013), as well as the earlier
CM2.1 ocean component of Delworth et al. (2006), the liquid and solid runoffis inserted into the top four
model grid cells as detailed in Section 3.6 of Griffies et al. (2005). However, the kinematic formulation of
the advective form, as presented in Sections 36.10.8,36.10.10,36.10.12, assumes all of the liquid and
solid runoffare inserted to the top model grid cell. This assumption precludes the kinematic and process
versions of the dianeutral transport from agreeing to numerical roundoffin those cells where runoffis
actually inserted. Since the process diagnostic computes liquid and solid runoffcontributions correctly, it
is the preferred method for computing contributions to watermass transformation arising from runoff.
36.16.3 Difficulty closing the mass budgets
Section 36.13 summarizes the requirements for computing the mass budget according to density classes.
Our attempts to close the mass budget remain unsuccessful. That is, the diagnostic of the mass trans-
port does not agree with the diagnostic of the transformation. The following possible reasons for this
disagreement require further research to gain clarity on the issues.
• The polynomial computation of neutral density is problematic. Even if it was perfect, there is a fun-
damental difference between locally referenced potential density and a polynomial neutral density
variable. The differences necessitate the introduction of the Bfactor in equation (36.77). We have
yet to fully explore this approach. As discussed in Iudicone et al. (2008), details of the density binning
can be of leading order importance, especially in the Southern Ocean.
• An alternative to neutral density is to simply use the potential density referenced to a chosen pres-
sure level. We have pursued this approach, preferring 2000dbar reference level. Again, this choice
leads to problems in the Southern Ocean, with those problems impacting all regions to the north.
Elements of MOM November 19, 2014 Page 539

Chapter 36. Dianeutral transport and associated budgets Section 36.16
Elements of MOM November 19, 2014 Page 540

Chapter 37
Mixed layer depth diagnostics
Contents
37.1 The mixed layer depth ......................................541
37.2 Tracer budgets within the mixed layer ............................542
The purpose of this chapter is to detail MOM5 diagnostics used to compute the mixed layer depth and
budgets for tracers within the mixed layer. The following MOM module is directly connected to the material
in this chapter:
ocean diag/ocean tracer diag.F90
37.1 The mixed layer depth
The mixed layer depth is based on measuring the ocean stability in a manner similar to that used for the
KPP boundary layer scheme (see Section 18.5.5). To determine whether vertical transfer is favored requires
a thought experiment, in which a surface ocean fluid parcel is displaced downward without changing its
temperature or salinity, but feeling the local in situ pressure. If the density of this displaced parcel is suffi-
ciently far from the local in situ density, then the displacement is not favored, and we are thus beneath the
mixed layer and into the stratified interior. What determines “sufficiently far” is subjective, with convention
determining the precise value.
Mathematically, we compute the difference between the following two densities
ρdisplaced from surface =ρ[S(k= 1),Θ(k= 1),p(k)] (37.1a)
ρlocal =ρ[S(k),Θ(k),p(k)],(37.1b)
and convert that density difference to a buoyancy difference
δB =− g(ρdisplaced from surface −ρlocal)
ρlocal !.(37.2)
This buoyancy difference is computed from the surface down to the first depth at which δB > ∆Bcrit , where
the MOM5 default is
∆Bcrit = 0.0003 m s−2,(37.3)
with this value also used in Conkright et al. (2002). The mixed layer depth, Hmld is then approximated by
interpolating between the depth where δB > ∆Bcrit and the shallower depth.
For purposes of computing budgets for tracers within the mixed layer, we compute the grid level where
the mixed layer depth sits. Doing so provides a discrete approximation, Kmld, to the continuous mixed layer
depth.
541

Chapter 37. Mixed layer depth diagnostics Section 37.2
37.2 Tracer budgets within the mixed layer
Elements of MOM November 19, 2014 Page 542

Chapter 38
Subduction diagnostics
Contents
38.1 Kinematics of flow across a surface ..............................543
38.1.1 General form of the dia-surface mass transport ...................... 543
38.1.2 Surface area elements ..................................... 544
38.1.3 Oceanographic examples of surfaces ............................ 545
38.1.4 The dia-surface mass transport and dia-surface velocity component .......... 546
38.1.5 Oceanographic examples of dia-surface mass transport ................. 546
38.2 MOM subduction diagnostic calculation ...........................548
38.2.1 Algorithm for subduction diagnostic ............................ 548
38.2.2 Available diagnostics ..................................... 549
The purpose of this chapter is to detail diagnostic methods available online in MOM to compute the rate
that seawater is transported across the mixed layer base, with notable applications of these methods to
quantifying rates that water is transferred across the mixed layer base. The subduction rate is computed
as in Cushmin-Roisin (1987), along with the option to bin this instantaneous rate into density classes as
recommended by Kwon et al. (2013).
The following MOM module is directly connected to the material in this chapter:
ocean diag/ocean tracer diag.F90
38.1 Kinematics of flow across a surface
Following the discussion of dia-surface transport in Section 36.3.2, we develop a kinematic framework to
measure the rate that seawater crosses a surface, where the surface is generally moving. The surface
of interest in this chapter is the mixed layer base, whereas in Chapter 36 we were concerned with density
surfaces. The kinematic formulation is identical, so we follow the geometric presentation given in Section
6.7 of Griffies (2004), as well as Section 2.2 of Griffies and Adcroft (2008). Some of the material here can
also be found in Vi ´
udez (2000).
38.1.1 General form of the dia-surface mass transport
We assume that surfaces of interest can be specified, at least locally, by a function s=s(x,y,z,t)(see Figure
38.1). An orientation for the surface is specified by computing a normal direction
ˆ
n(s) = ∇s
|∇s|,(38.1)
543
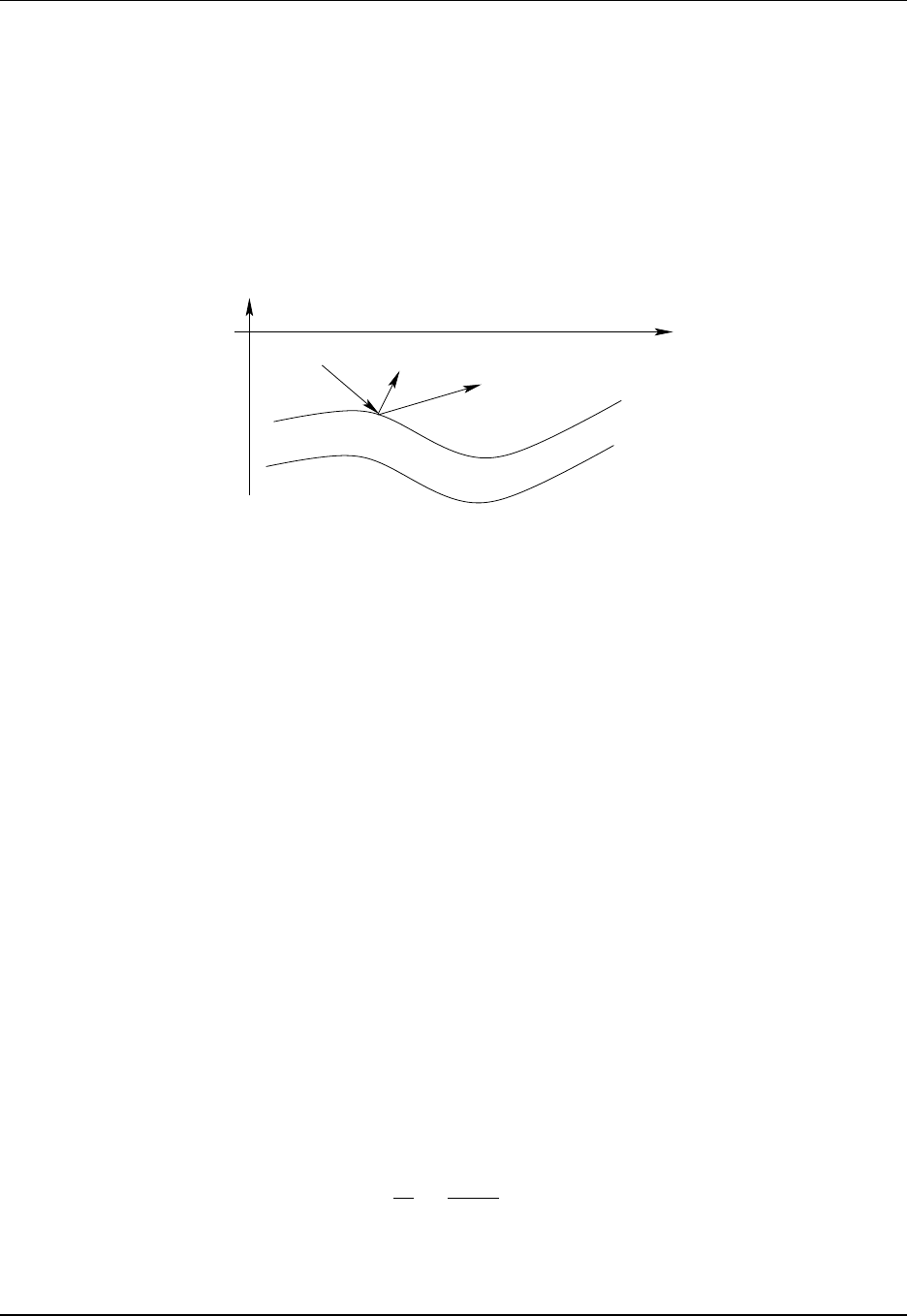
Chapter 38. Subduction diagnostics Section 38.1
which points in the direction of increasing s. Given the velocity of a fluid parcel,
v= (u,w),(38.2)
the in situ density ρ, and the velocity of a point on the surface, v(ref), we measure the mass per time of fluid
moving across a surface by computing
mass per time of fluid across surface =ρdA(s)ˆ
n(s)·(v−v(ref)),(38.3)
where dA(s)is an infinitesimal area element on the surface. This fundamental definition provides a baseline
from which to develop diagnostics for subduction (this chapter) and dianeutral transport (Chapter 36).
z
n
^
s=constant
vvref
x,y
Figure 38.1: A schematic of an undulating surface, with normal direction ˆ
nindicated on one of the surfaces.
Also shown is the orientation of the velocity of a fluid parcel vand the velocity v(ref)of a reference point
living on the surface.
38.1.2 Surface area elements
For any particular orientation of the normal direction ˆ
n(s), it is possible to project the local area element
dA(s)onto at least one of the three coordinate planes perpendicular to the three unit directions ˆ
x,ˆ
y, and ˆ
z.
This projection provides the means for a practical calculation of the area element. For example, if the field
sis a density-like field that exhibits a stable vertical stratification, then |∂zs|is nonzero. Indeed, it generally
has the largest magnitude of the three spatial derivatives (∂xs,∂ys,∂zs). In this case, ˆ
n(s)≈ −ˆ
z(density
increasing downward), so the area element dA(s)is nearly equal to
dA(z)= dxdy, (38.4)
which is the area element in the plane perpendicular to the vertical direction ˆ
z. Our intuition based on this
common case in the ocean interior can be made precise by an expression from differential geometry that
relates two area elements. For this purpose, make use of the equation (6.58) in Griffies (2004), in which we
have the exact relation
dA(s)=|∂sZ||∇s|dA(z).(38.5)
In this equation, we introduced the depth of an s-surface, which has the following functional dependence
Z=Z(x,y,s,t).(38.6)
We choose the capital Zto distinguish the depth of a particular surface of constant sfrom the depth zof
an arbitrary position in the ocean. Nonetheless, note that the inverse function is given by
∂s
∂z =1
∂Z/∂s .(38.7)
Again, for the highly stratified ocean interior with schosen as a density-like field,
|∇s|≈|∂zs|=|∂Z/∂s|−1,(38.8)
Elements of MOM November 19, 2014 Page 544

Chapter 38. Subduction diagnostics Section 38.1
thus making dA(s)≈dA(z). The relation (38.5) holds in general, so long as the vertical derivative ∂zsre-
mains nonzero. It thus provides for a general method to compute the area element dA(s)in regions of
nonzero vertical stratification of siso-surfaces.
In regions where ∂zsbecomes tiny, such as the surface mixed layer for sbased on density, then alterna-
tive measures for the area element must be used. We detail such cases in Section 36.3.2. The bottomline is
one merely needs to consider area elements in such cases that are projected onto either of the two vertical
planes spanned by the unit vectors (ˆ
x,ˆ
z)or (ˆ
y,ˆ
z), rather than the horizontal plane spanned by (ˆ
x,ˆ
y).
38.1.3 Oceanographic examples of surfaces
Consider the following examples of surfaces and their geometric specification.
•ocean bottom: Let Z=−h(topo)(x,y)represent the ocean bottom depth, which is assumed to be static
and to possess no overturns. The bottom is geometrically specified through the relation
s(x,y,z) = z+h(topo)(x,y)=0.(38.9)
The corresponding normal vector is given by
ˆ
n(topo)=∇(z+h(topo))
|∇(z+h(topo))|,(38.10)
and the area element is (with ∂sZ= 1 in equation (38.5))
dA(topo)=|∇(z+h(topo)(x,y))|dA(z).(38.11)
•free surface: Let Z=η(x,y,t)represent the deviation of the ocean surface from a resting state
at Z= 0. Writing the ocean surface as this function of horizontal position and time presumes an
averaging has occurred to remove the more general overturns and breaking waves present on the
real ocean surface. Having made this assumption, we can geometrically specify the free surface by
the relation
s(x,y,z,t) = z−η(x,y,t)=0.(38.12)
The corresponding normal vector is given by
ˆ
n(η)=∇(z−η)
|∇(z−η)|,(38.13)
and the area element is
dA(η)=|∇(z−η)|dA(z).(38.14)
•mixed layer base: Let Z=−h(mld)(x,y,t)represent the depth at the mixed layer base, determined,
for example, by a density threshold criteria. As for the ocean free surface, the mixed layer base is
geometrically specified by the relation
s(x,y,z,t) = z+h(mld)(x,y,t)=0.(38.15)
The corresponding normal vector is given by
ˆ
n(mld)=∇(z+h(mld))
|∇(z+h(mld))|,(38.16)
and the area element is
dA(mld)=|∇(z+h(mld))|dA(z).(38.17)
Elements of MOM November 19, 2014 Page 545

Chapter 38. Subduction diagnostics Section 38.1
•isopycnal depth: Now let Z=−h(x,y,γ,t)represent the depth of an isopycnal surface specified by
a density γ. As a shorthand, we write h(x,y,γ,t) = h(γ). As for the mixed layer base, an isopycnal
surface is geometrically specified by the relation
s(x,y,z,t) = z+h(x,y,γ,t)=0.(38.18)
The corresponding normal vector is given by
ˆ
n(γ)=∇(z+h(γ))
|∇(z+h(γ))|,(38.19)
and the area element is
dA(γ)=|∇(z+h(γ))|dA(z).(38.20)
38.1.4 The dia-surface mass transport and dia-surface velocity component
We now have an understanding of how to compute the area element dA(s)appearing in equation (38.3).
Next, consider the normal projection of the surface reference velocity, which is given by (see Section 6.7 of
Griffies (2004), as well as Section 2.2 of Griffies and Adcroft (2008))
ˆ
n(s)·v(ref)=− ∂s/∂t
|∇s|!.(38.21)
That is, the normal projection is nonzero so long as there is a time dependence of the surface itself.
Combining the result (38.21) with the expression (38.5) for the area element dA(s), and (38.1) for the
normal direction ˆ
n(s), leads to the mass transport expression
mass per time of fluid across surface =ρdA(s)ˆ
n(s)·(v−v(ref))
=ρdA(z)
∂Z
∂s
ds
dt.(38.22)
This equation provides an explicit expression for the mass per time of fluid penetrating a locally defined
surface or tangent plane. Again, this surface can generally be moving (i.e., v(ref)can generally be nonzero).
Positive mass transport indicates fluid moving across the surface in the direction of ˆ
n(s); e.g., into denser
regions for the case where sis locally referenced potential density. Following from the discussion in Section
36.3.2, we find it convenient to define the dia-surface velocity component according to
w(z)=
∂Z
∂s
ds
dt
=(volume/time) fluid penetrating surface, in direction of increasing s
horizontal surface area in x-y plane .
(38.23)
In words, w(z)measures the volume per time of fluid penetrating a locally defined surface or tangent plane,
as defined by the normal vector ˆ
n(s), divided by the horizontal projection of the local area on that surface.
Positive w(z)indicates fluid moving across the surface in the direction of ˆ
n(s); e.g., into denser regions for
the case where sis locally referenced potential density. Given this definition of w(z), the dia-surface mass
transport is given by the tidy expression
mass per time of fluid across surface =ρdA(z)w(z).(38.24)
38.1.5 Oceanographic examples of dia-surface mass transport
We return now to the examples from Section 38.1.3 to exhibit specific forms of the dia-surface mass trans-
port.
Elements of MOM November 19, 2014 Page 546

Chapter 38. Subduction diagnostics Section 38.2
•ocean bottom: The ocean bottom with Z=−h(topo)(x,y)is generally assumed to allow zero flow
through the solid earth boundary. Hence, the dia-surface transport reduces to the no-normal flow
boundary condition
ˆ
n(topo)·v= 0 at z=−H(x,y),(38.25)
which takes on the following familiar form
u·∇H+w= 0 at z=−H(x,y).(38.26)
•free surface: At the ocean free surface with s(x,y,z,t) = z−η(x,y,t)=0, the dia-surface mass trans-
port takes the form
−Qm≡ρdA(z) d(z−η)
dt!at z=η(x,y,t),(38.27)
where the surface mass transport Qm(dimensions of mass per time), arising from precipitation, evap-
oration, and runoff, is defined to be positive for mass entering the ocean. Rearrangement of this
result leads to a more familiar expression for the surface kinematic boundary condition
(∂t+u·∇)η=w+Qm
ρdA(z)
at z=η(x,y,t).(38.28)
•mixed layer base: At the base of the mixed layer with s(x,y,z,t) = z+h(mld)(x,y,t)=0, the dia-surface
mass transport takes the form
−S(subduction)≡ρdA(z) d(z+h(mld))
dt!at z=−h(mld)(x,y,t),(38.29)
where the mass transport S(subduction)(dimensions of mass per time) is positive for fluid moving down-
ward beneath the mixed layer base into the pycnocline (subduction) and negative for water moving
into the mixed layer (obduction). Expanding the material time derivative leads to
− S(subduction)
ρdA(z)!=w+(∂t+u·∇)h(mld)at z=−h(mld)(x,y,t),(38.30)
where again we define
S(subduction)>0subduction (38.31)
S(subduction)<0obduction. (38.32)
This definition of subduction rate corresponds to that given by Cushmin-Roisin (1987).
•isopycnal depth : At the depth of an isopycnal with s(x,y,z,t) = z+h(γ)= 0, the dia-surface mass
transport takes the form
−S(γ)≡ρdA(z) d(z+h(γ))
dt!at z=−h(x,y,γ,t),(38.33)
where the mass transport S(γ)(dimensions mass per time) is positive for fluid moving downward
beneath the isopyncal depth z=−h(γ). Expanding the material time derivative leads to
− S(γ)
ρdA(z)!=w+∂h(γ)
∂t +u·∇h(γ)at z=−h(x,y,γ,t).(38.34)
This definition of mass transport corresponds to the kinematic expresion for dia-surface mass trans-
port detailed in Chapter 36, where we are interested in transport across a locally referenced potential
density surface (see also equation (6.73) in Griffies (2004)).
Elements of MOM November 19, 2014 Page 547

Chapter 38. Subduction diagnostics Section 38.2
38.2 MOM subduction diagnostic calculation
The subduction diagnostic in MOM is based on the definition (38.30). In this section, we outline the code
algorithm and the available diagnostic fields.
38.2.1 Algorithm for subduction diagnostic
In brief, the algorithm consists of the following steps.
• Compute the mixed layer depth, h(mld)(x,y,t), based on some density increment criteria, with the in-
crement set according to a namelist. The depth is naturally placed at the tracer point.
• Optionally smooth the diagnosed mixed layer depth. Note that smoothing is enabled via a namelist
option; it incurs a trivial computational cost.
• Compute the time tendency ∂th(mld)based on the discrete time step difference between mixed layer
depth
∂h(mld)
∂t ≈h(mld)(t+∆t)−h(mld)(t)
∆t,(38.35)
with ∆tthe model tracer time step.
• Compute the horizontal gradient of the mixed layer depth, ∇h(mld). The zonal derivative is placed on
the zonal face of a tracer cell, and the meridional derivative at the meridional position.
• Horizontally interpolate the zonal velocity component to the zonal tracer cell face, and the merid-
ional velocity component to the meridional tracer cell face, both interpolations requiring two point
averages on the B-grid (see Figure 9.5). The result is an estimate for the horizontal C-grid velocity
components
ueast(i,j,k) = u(i,j,k)dun(i,j−1) + u(i,j−1,k)dus(i,j)
dus(i,j) + dun(i,j−1)(38.36)
vnorth(i,j,k) = v(i−1,j,k)duw(i,j) + v(i,j,k)due(i−1,j)
duw(i,j) + due(i−1,j).(38.37)
• Vertically interpolate the velocity (ueast,vnorth,w)to the mixed layer base to determine (umld
east,vmld
north,wmld ).
There are various conditional cases to consider.
–If h(mld)(i,j)≤depth zt(i,j,k=1), then no interpolation needed:
(umld
east,vmld
north,wmld )(i,j)=(ueast,vnorth,w)(i,j,k=1)if h(mld)(i,j)≤depth zt(i,j,k=1).(38.38)
–If h(mld)=depth zt(i,j,k)then no interpolation needed:
(umld
east,vmld
north,wmld )(i,j)=(ueast,vnorth,w)(i,j,k)if h(mld)(i,j)≤depth zt(i,j,k).(38.39)
–If depth zt(i,j,k−1)< h(mld)<depth zt(i,j,k)then vertical interpolation for each velocity com-
ponent
ψmld(i,j) = ψ(i,j,k−1)dzup(i,j,k) + ψ(i,j,k)dztlo(i,j,k−1)
dzup(i,j,k) + dztlo(i,j,k−1)(38.40)
–If h(mld)(i,j)≥depth zt(i,j,k=kmt(i,j)), then no interpolation needed:
(umld
east,vmld
north,wmld )(i,j)=(ueast,vnorth,w)(i,j,k=kmt)if h(mld)(i,j)≥depth zt(i,j,k=kmt).
(38.41)
Elements of MOM November 19, 2014 Page 548

Chapter 38. Subduction diagnostics Section 38.2
• Estimate horizontal advection of the mixed layer base via
u·∇h(mld)≈umld
east h(mld)(i+1,j)−h(mld)(i,j)
dxte(i,j)!+vmld
north h(mld)(i,j+1)−h(mld)(i,j)
dytn(i,j)!.(38.42)
• Compute the subduction mass flux rate via an estimate of equation (38.30)
S(subduction)(i,j)≈ −ρmld dxt(i,j)dyt(i,j) wmld +∂h(mld)
∂t +u(mld)·∇h(mld)!(i,j),(38.43)
where we use the estimate (38.35) for the time derivative, and equation (38.42) for the horizontal
advection. The density ρmld =ρofor a Boussinesq fluid, whereas it equals the vertically interpolated
in situ density for a non-Boussinesq fluid.
• A final step is the optional binning of S(subduction)(i,j)according to a chosen density classification, so
to record the subduction as a function of density class in a manner similar to the binning of surface
fluxes into density bins discussed in Section 36.14. This binning then allows for the diagnostic to be
computed according to the recommendations of Kwon et al. (2013).
38.2.2 Available diagnostics
The following diagnostics are available related to the subduction calculation
subduction =S(subduction)(38.44)
subduction dhdt =−ρmld dxt(i,j)dyt(i,j) ∂h(mld)
∂t !(38.45)
subduction horz =−ρmld dxt(i,j)dyt(i,j)u(mld)·∇h(mld)(38.46)
subduction vert =−ρmld dxt(i,j)dyt(i,j)wmld.(38.47)
Each of these fields has a corresponding diagnostic produced according to binning into neutral density
classes
subduction nrho =rebin onto rho (subduction)(38.48)
subduction dhdt nrho =rebin onto rho (subduction dhdt)(38.49)
subduction horz nrho =rebin onto rho (subduction horz)(38.50)
subduction vert nrho =rebin onto rho (subduction vert)(38.51)
Elements of MOM November 19, 2014 Page 549

Chapter 38. Subduction diagnostics Section 38.2
Elements of MOM November 19, 2014 Page 550

Chapter 39
Diagnosing the contributions to sea
level evolution
Contents
39.1 Mass conservation for seawater and tracers .........................553
39.1.1 Continuum fluid ....................................... 553
39.1.2 Kinematic boundary conditions ............................... 553
39.1.2.1 Bottom kinematic boundary condition ...................... 554
39.1.2.2 Surface kinematic boundary condition ...................... 554
39.1.3 Averaged mass and tracer equations ............................ 555
39.1.3.1 Form implied by mathematical correspondence ................ 556
39.1.3.2 Residual mean velocity and quasi-Stokes velocity ............... 556
39.1.3.3 Comments on particular averaging methods .................. 558
39.1.3.4 Notation convention for remainder of chapter ................. 558
39.1.4 Material changes of in situ density ............................. 558
39.1.5 General and simplified forms of the ocean equilibrium thermodynamics ....... 559
39.2 Kinematic equations for sea level evolution .........................559
39.2.1 Kinematic sea level equation: Version I ........................... 560
39.2.2 Kinematic sea level equation: Version II .......................... 560
39.2.3 How we make use of the kinematic sea level equations .................. 563
39.3 The non-Boussinesq steric effect ................................563
39.3.1 Defining the non-Boussinesq steric effect .......................... 563
39.3.2 Vertical motion across pressure surfaces .......................... 564
39.3.3 An expanded form of the kinematic sea level equation .................. 565
39.3.3.1 Exposing the boundary fluxes of temperature and salinity .......... 566
39.3.3.2 Expanded form of the kinematic sea level equation .............. 567
39.3.3.3 Buoyancy fluxes and mass fluxes ......................... 567
39.3.3.4 Interior sources ................................... 568
39.3.3.5 Concerning the absence of advective temperature and salt fluxes ...... 568
39.3.4 Boundary fluxes of heat and salt ............................... 569
39.3.4.1 Boundary heat fluxes ................................ 569
39.3.4.2 Boundary salt fluxes and sea ice ......................... 570
39.4 Evolution of global mean sea level ...............................570
39.4.1 Preliminaries ......................................... 571
39.4.2 Global mean sea level and the non-Boussinesq steric effect ............... 571
551

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
39.4.3 Global mean sea level and the global steric effect ..................... 572
39.4.4 Relating global steric to non-Boussinesq steric ...................... 573
39.5 Vertical diffusion and global mean sea level .........................573
39.5.1 Contributions from vertical diffusion ............................ 574
39.6 Neutral diffusion and global mean sea level .........................574
39.6.1 Neutral directions and neutral tangent plane ....................... 574
39.6.2 Fluxes computed with locally orthogonal coordinates .................. 575
39.6.3 Fluxes computed with projected neutral coordinates ................... 575
39.6.4 Compensating neutral diffusive fluxes of temperature and salinity ........... 576
39.6.5 The cabbeling and thermobaricity parameters ....................... 576
39.6.6 Physical aspects of cabbeling ................................ 576
39.6.7 Physical aspects of thermobaricity ............................. 577
39.7 Parameterized quasi-Stokes transport and global mean sea level .............577
39.7.1 Formulation with buoyancy impacted by quasi-Stokes transport ............ 577
39.7.2 Effects on global mean sea level ............................... 579
39.8 MOM sea level diagnostics: Version I .............................580
39.8.1 Surface buoyancy fluxes ................................... 580
39.8.2 Surface mass fluxes ...................................... 581
39.8.3 Bottom heat flux ........................................ 583
39.8.4 River insertion of liquid and solid water .......................... 583
39.8.5 River insertion of liquid water ................................ 583
39.8.6 River insertion of solid water ................................ 584
39.8.7 Heating of liquid ocean due to frazil formation ...................... 584
39.8.8 Motion across pressure surfaces ............................... 584
39.8.9 Mixing associated with vertical diffusion .......................... 585
39.8.10Mixing associated with neutral diffusion .......................... 585
39.8.11Parameterized eddy advection from GM .......................... 587
39.8.12Parameterized eddy advection from submesoscale parameterization .......... 588
39.8.13Parameterized horizontal diffusion from submesoscale parameterization ....... 589
39.8.14Penetrative shortwave radiation ............................... 589
39.8.15Sigma transport ........................................ 590
39.8.16Mixdownslope ......................................... 590
39.8.17KPP nonlocal mixing ..................................... 590
39.8.18Cross land mixing ....................................... 591
39.8.19Cross land insertion ...................................... 591
39.8.20Smoothing of free surface or bottom pressure ....................... 591
39.9 MOM sea level diagnostics: Version II ............................592
The purpose of this chapter is to discuss the suite of diagnostics in MOM to quantify how various terms
contribute to sea level evolution. The discussion here is an abbreviated version of that given by Griffies
and Greatbatch (2012). Some of this material repeats similar discussions in Chapter 2. However, we find it
useful to include such duplication here to enable the present chapter to be self-contained.
The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean barotropic.F90
ocean core/ocean sbc.F90
ocean core/ocean bbc.F90
as well as many other modules associated with parameterized subgrid scale physical processes.
Elements of MOM November 19, 2014 Page 552

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
39.1 Mass conservation for seawater and tracers
The purpose of this section is to formulate the equations for conservation of seawater mass and tracer
mass. The seawater mass conservation equation is the basis for the kinematic equations derived in Sec-
tion 39.2 for sea level. The tracer mass conservation equation describes the evolution of scalar trace
constituents in seawater such as salt and biogeochemical tracers. Additionally, the evolution equation for
conservative temperature satisfies the mathematically identical advection-diffusion equation (McDougall,
2003).
39.1.1 Continuum fluid
Eulerian expressions for the conservation of seawater mass and tracer mass are given by
∂ρ
∂t =−∇·(ρv) (39.1)
∂(ρC)
∂t =−∇·(ρvC+Jmdiff),(39.2)
which have equivalent Lagrangian expressions
dρ
dt=−ρ∇·v(39.3)
ρdC
dt=−∇·Jmdiff.(39.4)
In these equations,
d
dt=∂
∂t +v·∇ (39.5)
is the material time derivative computed by an observer moving with the fluid parcel’s center of mass
velocity v, whereas ∂tis the Eulerian time derivative computed at a fixed spatial point. The tracer concen-
tration, C, is the mass of a trace constituent within a fluid parcel, per mass of seawater within the parcel.
Consequently, the product ρC is the mass of tracer per volume of seawater, with ρthe in situ seawater
mass density. The flux Jmdiffarises from local gradients in the tracer field being acted upon by a nonzero
molecular diffusivity. For passive tracers (those tracers not impacting density), this molecular diffusion flux
vanishes when the tracer concentration is uniform, in which case the expression for tracer mass conserva-
tion (39.2) reduces to the seawater mass conservation (39.1). This compatibility condition is fundamental
to the continuum mass and tracer equations, and it follows since we choose to measure the motion of fluid
parcels using the parcel’s center of mass velocity v(e.g., see Section II.2 of DeGroot and Mazur (1984),
Section 8.4 of Chaikin and Lubensky (1995), or Section 3.3 of M¨
uller (2006)). For the active tracers (those
tracers impacting density) temperature and salinity, there is generally a nonzero molecular flux of each
field arising from gradients in the other field, with this process known the Soret and Dufour effect (Lan-
dau and Lifshitz,1987). As this cross-diffusion effect is swamped by larger eddy fluxes considered in the
following, we do not consider it further.
39.1.2 Kinematic boundary conditions
Kinematic boundary conditions arise from the geometric constraints imposed by the ocean bottom and
surface, with such constraints impacting the budgets of mass over a column of seawater. In formulating
the kinematic boundary conditions, we assume the ocean bottom to be static and impermeable (i.e., closed
to mass fluxes), whereas the ocean surface is dynamic and open to mass fluxes. We provide some detail re-
garding the derivation of these boundary conditions since they expose issues essential for understanding
the evolution of global mean sea level.
Elements of MOM November 19, 2014 Page 553

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
39.1.2.1 Bottom kinematic boundary condition
At the rigid ocean bottom, the kinematic boundary condition states that the geometric expression for the
ocean bottom
z+H(x,y)=0 ocean bottom, (39.6)
remains fixed in time for all parcels situated at the bottom, so that
d(z+H)
dt= 0 at z=−H(x,y),(39.7)
where the coordinates x,y denote the lateral position of a fluid parcel in the ocean. An equivalent state-
ment is that there is no normal flow of fluid at the ocean bottom, so that v·ˆ
n= 0, with the outward normal
given by
ˆ
n=− ∇(z+H)
|∇(z+H)|!at z=−H(x,y).(39.8)
In either case, we may write the bottom kinematic boundary condition as
w+u·∇H= 0 at z=−H(x,y),(39.9)
where
v= (u,w) (39.10)
is the fluid velocity field, with uthe horizontal velocity.
39.1.2.2 Surface kinematic boundary condition
We assume that the ocean surface can be written geometrically as
z−η(x,y,t)=0 ocean surface, (39.11)
which means that there are no overturns; i.e., we filter out breaking surface waves. The mass per time of
material crossing the surface is written as
mass per time through surface =QmdAη,(39.12)
where dAηis the infinitesimal area element on the ocean surface, and Qmis the mass per time per surface
area of material crossing the surface. This mass flux can be equivalently written as the normal projection
of the relative velocity at the ocean surface, multiplied by the surface density
QmdAη=ρ(v−vη)·ˆ
ndAηat z=η,(39.13)
where
ˆ
n=∇(z−η)
|∇(z−η)|at z=η(39.14)
is the outward normal at the ocean surface, and
vη·ˆ
n=∂tη
|∇(z−η)|at z=η(39.15)
is the normal velocity of a material point fixed to the ocean surface. The surface kinematic boundary con-
dition given by equation (39.13) says there is a nonzero projection of the relative velocity onto the surface
outward normal, (v−vη)·ˆ
n, only when there is a nonzero mass flux through the undulating surface. This
equation is written in a manner to expose the geometric nature of the boundary condition. The following
develops a related form that is somewhat more familiar.
Given that the surface has no overturns, we can equivalently write the mass flux in the more convenient
form
mass per time through surface =QmdA, (39.16)
Elements of MOM November 19, 2014 Page 554

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
where dAis the horizontal area element obtained by projecting the surface area element dAηonto the
horizontal plane, and Qmis the mass per time per horizontal area of material crossing the surface. The
two area elements are related by the expression (see Section 20.13.2 of Griffies (2004))
dAη=|∇(z−η)|dA. (39.17)
We now return to the boundary condition (39.13), yet replace the mass flux Qmwith Qm, use the area
relation (39.17), and write the normal material velocity at the ocean surface in the form (39.15), with these
steps yielding the kinematic boundary condition (e.g., Section 3.4 of Griffies (2004))
ρ(∂t+u·∇)η=Qm+ρw at z=η(39.18)
or the equivalent Lagrangian expression
ρ d(z−η)
dt!=−Qmat z=η.(39.19)
As a self-consistency check, note that the mass per horizontal area in a fluid column,
mass per horizontal area =
η
Z
−H
ρdz, (39.20)
is altered by the convergence of mass to the column via ocean currents, and mass entering through the
ocean surface, so that
∂t
η
Z
−H
ρdz+∇·
η
Z
−H
ρudz=Qm.(39.21)
Leibniz’s Rule can be used to move the time and space derivatives across the integral sign, with the bottom
kinematic boundary condition (39.9) and Eulerian form of the mass continuity equation (39.1) recovering
the surface kinematic boundary condition (39.18).
Matter entering the ocean is predominantly in the form of fresh water plus trace constituents, such as
salt and biogeochemical matter,
Qm=Qw+Q(S)(39.22)
where Qwis the mass flux of fresh water, and Q(S)is the mass flux of salt or other trace constituents. A
nonzero salt flux for climate purposes is generally limited to regions under sea ice. In general, the salt and
trace constituent surface mass flux is far smaller than the mass flux from fresh water. Hence, the matter
flux is often approximated just with the fresh water flux. In this way, the exchange of tracer mass across the
ocean surface generally does not impact the ocean mass in climate models. More realistic river models,
and sea ice models that carry the mass of tracers, will necessitate removing this assumption from ocean
models.
The surface kinematic boundary condition can be rearranged into a prognostic equation for sea level
∂tη=Qm/ρ + ( ˆ
n·v)|∇(z−η)|at z=η.(39.23)
Hence, mass entering through the free surface (Qm>0) contributes to a positive sea level tendency, as
does a three dimensional velocity that has a nonzero projection “upwards” ( ˆ
n·v>0). The expression
(39.23), though useful geometrically, does not provide the necessary means for partitioning sea level
evolution into physical processes. For this purpose, we pursue the development of alternative sea level
equations in Section 39.2.
39.1.3 Averaged mass and tracer equations
The seawater mass conservation equation (39.1), and the tracer mass conservation equation (39.2), arise
from a continuum formulation of fluid mechanics (e.g., Batchelor (1967) and Landau and Lifshitz (1987)).
Elements of MOM November 19, 2014 Page 555

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
The finite sized grid (or, less commonly, a finite spectral representation) used in a numerical ocean model
introduces a cutoffscale absent from the continuum. Formulating the equations discretized by an ocean
model requires an averaging operation in which the continuum equations are averaged over scales smaller
than the grid. A discrete ocean model then provides an approximation to the averaged equations by using
various methods from computational physics. When averaging nonlinear products, such as ρvC, correla-
tions appear between space and time fluctuations that are unresolved by the grid. Ideally, these correla-
tions can be organized into the form of a subgrid scale flux divergence. Parameterizing the subgrid scale
flux divergence is nontrivial, with no universal approach available.
39.1.3.1 Form implied by mathematical correspondence
We only require general properties of subgrid scale fluxes, rather than formulations specific to a particular
physical process. A very convenient property we desire is that the averaged mass and tracer equations
are written in the same mathematical form as the corresponding continuum equations. More precisely,
the terms appearing in the averaged equations correspond to, though are generally distinct from, their
continuum analogs. In turn, we insist that the compatibility condition between the continuum budgets for
seawater mass and tracer mass be maintained for the averaged equations. Maintaining this direct cor-
respondence between continuum and averaged equations facilitates straightforward physical interpreta-
tions of the averaged equations, which follow from the interpretation of the continuum equations.
Maintenance of the same mathematical form as the continuum mass conservation equation (39.1)
and tracer conservation equation (39.2) allows us to write the averaged mass and tracer conservation
equations in the form
∂ρa
∂t =−∇·(ρav†) (39.24)
∂(ρaCa)
∂t =−∇·(ρav†Ca+Jeddydiff),(39.25)
or the equivalent Lagrangian expressions
d†ρa
dt=−ρa∇·v†(39.26)
ρa
d†Ca
dt=−∇·Jeddydiff,(39.27)
where the “a” subscript signifies an averaged quantity. In ocean circulation models, the subgrid scale
eddy tracer diffusive flux, Jeddydiff, is generally far larger than the corresponding molecular flux, Jmdiffuse.
Nonetheless, as for the molecular flux, compatibility between the averaged mass and tracer equations
is maintained so long as the eddy flux vanishes when the tracer concentration, Ca, is spatially uniform.
Compatibility is maintained by the commonly used flux-gradient relation for the parameterized subgrid
scale tracer diffusive flux.
39.1.3.2 Residual mean velocity and quasi-Stokes velocity
Along with an eddy diffusive flux, Jeddydiff, we introduced to the averaged equations the residual mean velocity,
v†, which advects seawater mass and tracer mass, thus bringing the material time derivative to the form
d†
dt=∂
∂t +v†·∇.(39.28)
The residual mean velocity is generally partitioned into two pieces
v†=va+v∗,(39.29)
where vais the averaged velocity directly represented by the numerical model, and v∗is an eddy induced or
quasi-Stokes velocity that requires a parameterization before being represented by the model. Proposed
parameterizations of v∗used by ocean circulation models (e.g., Gent and McWilliams (1990), Gent et al.
Elements of MOM November 19, 2014 Page 556

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
(1995), McDougall and McIntosh (2001), Fox-Kemper et al. (2008b)) all satisfy the non-divergence property
in the ocean interior
∇·(ρav∗)=0 ocean interior (39.30)
and the no-normal flow condition at ocean boundaries
ˆ
n·v∗= 0 ocean boundaries. (39.31)
The non-divergence condition (39.30) means that the quasi-Stokes mass transport can be written as
the curl of a vector streamfunction
ρav∗=∇∧ρaΨ,(39.32)
so that the tracer equation (39.27) can be written as
ρa
dCa
dt=−∇·(Jeddydiff+Jskew).(39.33)
In this equation,
Jskew =−∇Ca∧ρaΨ(39.34)
is a skew tracer flux, which differs from the advective tracer flux through a non-divergent curl
ρav∗Ca=−∇Ca∧ρaΨ+∇ ∧ (ρaΨCa),(39.35)
thus making the divergence of the advective flux equal to the divergence of the skew flux
∇·(ρav∗Ca) = −∇·(∇Ca∧ρaΨ).(39.36)
The following presents three more implications of the non-divergence and no-normal flow properties
(39.30) and (39.31) that will be utilized in this paper.
•The averaged seawater mass continuity equations hold whether one uses the residual mean velocity
v†, as in equations (39.24) and (39.26), or the mean velocity va
∂ρa
∂t =−∇·(ρava) (39.37)
dρa
dt=−ρa∇·va.(39.38)
•The kinematic boundary conditions from Section 39.1.2 remain identical whether using v†or va.
•Vertical integration of the non-divergence condition (39.30) over a seawater column, and use of the
no-flux boundary condition (39.31), yields
∇·
η
Z
−H
dz ρau∗= 0,(39.39)
where u∗is the horizontal component to the eddy induced velocity. The Gent et al. (1995) mesoscale
eddy parameterization and the Fox-Kemper et al. (2008b) submesoscale eddy parameterization achieve
this property by satisfying Rη
−Hdz ρau∗= 0. The eddy induced mass transport for these parameteriza-
tions thus has zero vertically integrated component.
These three properties mean that it is a matter of convenience what form of the mass conservation equa-
tion we choose when formulating the kinematic sea level equations in Section 39.2. We prefer the starting
point offered by equations (39.37) and (39.38), in which the quasi-Stokes velocity is absent. This choice
then places impacts of the quasi-Stokes transport directly onto buoyancy, as detailed in Section 39.7,
rather than on the material evolution of pressure (Section 39.3.2).
Elements of MOM November 19, 2014 Page 557

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.1
39.1.3.3 Comments on particular averaging methods
Although we are not concerned with details of the averaging required to reach equations (39.24) and
(39.25), it is important to note that methods exist to write the averaged scalar equations in precisely these
forms. Examples include the density weighted averaging of Hesselberg (1926) (see also McDougall et al.
(2002) and Chapter 8 of Griffies (2004)); the isopycnal thickness weighted methods of DeSzoeke and Ben-
nett (1993) and McDougall and McIntosh (2001) (see also Chapter 9 of Griffies (2004)); and the combined
density and thickness weighted methods of Greatbatch and McDougall (2003). In contrast, the approach
of Eden et al. (2007) leads to different averaged mass and tracer equations than (39.24) and (39.25), since
they introduce a different eddy induced velocity for each tracer. However, so long as the eddy induced
velocity for each tracer satisfies the non-divergence condition (39.30) and the no-normal flow boundary
condition (39.31), their approach should maintain the compatibility condition between mass and tracer
equations, and thus it falls within the framework of the present considerations.
39.1.3.4 Notation convention for remainder of chapter
Now that we have introduced a convention for the model fields, which are the result of a particular aver-
aging procedure, we dispense with the “a” subscript in order to reduce notational clutter. In subsequent
discussions, all equations and fields will refer to their averaged forms.
39.1.4 Material changes of in situ density
The in situ density, ρ, is a function of three intensive fluid properties
ρ=ρ(Θ,S,p),(39.40)
with Θthe conservative temperature (McDougall,2003;IOC et al.,2010), Sthe salinity, and pthe pres-
sure. We prefer the conservative temperature as it reflects more accurately on the conservative nature of
enthalpy transport in the ocean as compared to the alternative potential temperature.
The equation of state (39.40) leads to the material time evolution of in situ density
dρ
dt=∂ρ
∂Θ
dΘ
dt+∂ρ
∂S
dS
dt+∂ρ
∂p
dp
dt
=−(ρα)dΘ
dt+ (ρβ)dS
dt+1
c2
sound
dp
dt.
(39.41)
These equations introduced the thermal expansion coefficient,
α=−1
ρ ∂ρ
∂Θ!p,S
(39.42)
the haline contraction coefficient
β=1
ρ ∂ρ
∂S !p,Θ
(39.43)
and the squared speed of sound
c2
sound = ∂p
∂ρ !S,Θ
.(39.44)
The material evolution of density is thus partitioned into the evolution of buoyancy (via changes in tem-
perature and salinity) and the evolution of pressure. Buoyancy remains unchanged by processes that are
both adiabatic and isohaline, as well as processes where diabatic and non-isohaline effects perfectly can-
cel. Pressure evolution arises from vertical motion across pressure surfaces which, in a hydrostatic fluid,
is equivalent to the vertical motion of mass.
Mass conservation in the form of equation (39.3), along with material evolution of density (39.41),
render the balance
−ρ∇·v=−(ρα)dΘ
dt+ (ρβ)dS
dt+1
c2
sound
dp
dt.(39.45)
Elements of MOM November 19, 2014 Page 558

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.2
To help further develop our understanding of this result, consider the mass of a fluid parcel of volume δV
written in the form M=ρ δV . Mass conservation for this parcel means that as the parcel volume increases,
the density must decrease, so that
1
ρ
dρ
dt=−1
δV
dδV
dt.(39.46)
Correspondingly, from the mass continuity equation (39.3), the volume of a fluid parcel increases when
moving through regions of fluid with a divergent velocity field
1
δV
dδV
dt=∇·v.(39.47)
Substitution into equation (39.45) then yields
−ρ
δV
dδV
dt=−(ρα)dΘ
dt+ (ρβ)dS
dt+1
c2
sound
dp
dt.(39.48)
This balance states that the volume of a fluid parcel increases (negative left hand side) as the buoyancy
of the parcel increases, such as occurs with heating in regions of α > 0, or freshening in regions of β > 0.
Volume also increases as the pressure of the parcel decreases (dp/dt < 0). We have many opportunities
to return to this balance, and its relatives, in the subsequent development of sea level equations, which
represent the accumulation of volume changes throughout a seawater column.
39.1.5 General and simplified forms of the ocean equilibrium thermodynamics
The thermal expansion coefficient α, haline contraction coefficient β, and squared speed of sound c2
sound
are properties of the equilibrium thermodynamics of seawater, with IOC et al. (2010) summarizing the
state of the science. In the ocean, these fields are nonlinear functions of the conservative temperature,
salinity, and pressure, and this dependence leads to the processes of cabbeling and thermobaricity, in
which parcels move dianeutrally (McDougall,1987b). Elements of these processes are described in Section
39.6, where we illustrate how they impact on global mean sea level through the non-Boussinesq steric
effect. Additionally, as shown in Section 39.3, the values for α,β, and c2
sound introduce scales that further
influence how physical processes and boundary fluxes impact global mean sea level through the non-
Boussinesq steric effect.
Under certain idealized situations, we may approximate α,β, and ρ c2
sound to be constants independent of
the ocean state. This approximation simplifies the equilibrium thermodynamics to help characterize where
the more general ocean thermodynamics is fundamental. In particular, as shown in Section 39.6, the
simplified thermodynamics associated with constant α,β, and ρc2
sound eliminates the processes of cabbeling
and thermobaricity. Furthermore, with constant α,β, and ρ c2
sound, mass conservation in the form of equation
(39.48) indicates that the material evolution for the volume of a fluid parcel is a linear function of material
changes in conservative temperature, salinity, and pressure. In the special case where density is a function
just of conservative temperature, a constant α=−ρ−1∂ρ/∂Θleads to ρ(Θ) = ρoe−α(Θ−Θo), where ρo=
ρ(Θo). For conservative temperatures near to the reference value Θo, density is given by the linear equation
of state
ρ(Θ)≈ρo[1 −α(Θ−Θo)].(39.49)
In turn, a constant αwith a linear equation of state corresponds to α=−ρ−1
o∂ρ/∂Θ.
39.2 Kinematic equations for sea level evolution
We formulate here the kinematic evolution equations for sea level, again under the assumptions of (1)
fixed geoid and ocean bottom, (2) constant horizontal area of the ocean, (3) space-time independent grav-
itational acceleration. All mathematical symbols refer to the averaged quantities appropriate for an ocean
model.
Elements of MOM November 19, 2014 Page 559
Chapter 39. Diagnosing the contributions to sea level evolution Section 39.2
39.2.1 Kinematic sea level equation: Version I
Integrating the material or Lagrangian form of the mass continuity equation (39.38) over the depth of
the ocean, using the kinematic boundary conditions (Section 39.1.2), and Leibniz’s rule for moving the
derivative operator across an integral, yields Version I of the kinematic sea level equation
∂η
∂t =Qm
ρ(η)−∇·U−
η
Z
−H
dz1
ρ
dρ
dt,(39.50)
with
U=
η
Z
−H
udz(39.51)
the vertically integrated horizontal velocity, and
ρ(η) = ρ(x,y,z =η(x,y,t),t) (39.52)
the ocean density at the free surface. Equation (39.50) partitions the evolution of sea level into the follow-
ing three physical processes, with Figure 39.1 providing a schematic.
1. Boundary mass fluxes: The transport of mass across the ocean surface is converted to a volume flux
through multiplication by the specific volume ρ(η)−1at the ocean surface. Transport of mass across
the ocean surface in regions of large surface specific volume ρ(η)−1(e.g., warm and freshwater) leads
to greater sea level tendencies than the transport in regions of small surface specific volume (e.g.,
cold and salty regions).
2. Dynamic: The convergence of vertically integrated horizontal currents onto a fluid column redis-
tributes ocean volume, and as such it imparts a sea level tendency. To help understand how flow
convergence arises, decompose the vertically integrated velocity as U=duz, where d=H+ηis
the thickness of the fluid column, and uzis the vertically averaged horizontal velocity. Converg-
ing flow in a flat bottom ocean is equivalent to convergence of the vertically averaged flow, so that
−∇·U=−d∇·uz>0. Flow convergence occurs also when the vertically averaged flow slows down
when approaching a region in the fluid, or flow convergence occurs when vertically constant flow
impinges on a shoaling bottom, so that −∇·U=−∇(d)·uz>0.
Globally integrating the sea level equation (39.50) eliminates the effects of ocean volume transport.
Hence, in this formulation of the sea level equation, ocean currents redistribute ocean volume, yet
do not directly impact global mean sea level. We find this property of the sea level equation (39.50)
especially convenient for studying the evolution of global mean sea level.
3. non-Boussinesq steric: Material time changes of the in situ density integrated over a column of
seawater lead to the expansion or contraction of the fluid column. Material changes in density arise
from buoyancy fluxes at the ocean boundaries, convergence of buoyancy fluxes in the ocean interior,
and processes associated with the equilibrium thermodynamics of the ocean as embodied by the
equation of state (equation (39.40)).
39.2.2 Kinematic sea level equation: Version II
The second version of the kinematic sea level equation is formulated from the mass budget for a fluid
column, rearranged to the form
∂t
η
Z
−H
ρdz=Qm−∇·
η
Z
−H
ρudz.(39.53)
The left hand side of this equation expresses the time tendency for the mass per unit horizontal area in the
column, with this tendency affected by mass transported across the ocean surface, and mass transported
Elements of MOM November 19, 2014 Page 560

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.2
z=η
z=−H
Qm
z
x,y
−∇ ·
η
R
−H
dzu
−
η
R
−H
dz1
ρ
dρ
dt
Figure 39.1: Shown here is a schematic ocean basin illustrating the ocean fluid dynamic and boundary pro-
cesses that impact sea level according to the kinematic sea level equation (39.50). The surface mass flux Qm
arises from exchange of mass across the permeable sea surface z=η(x,y,t) via precipitation, evaporation,
runoff, and melt. This mass flux is converted to a volume flux through dividing by the surface ocean den-
sity ρ(z=η). The non-Boussinesq steric effect, −Rη
−Hρ−1dρ/dt, arises from material changes in the in situ
density, as integrated from the impermeable bottom at z=−H(x,y) to the ocean surface. Both the surface
mass flux and non-Boussinesq steric effect can change the net global mean sea level. The third process
impacting sea level arises from the convergence of depth integrated currents, −∇ ·U, which redistributes
volume without impacting global mean sea level.
into the column by ocean currents. This mass budget can be written in a modified form by introducing the
column averaged density
ρz=1
H+η
η
Z
−H
ρdz,(39.54)
and the column integrated horizontal mass transport
Uρ=
η
Z
−H
ρudz, (39.55)
in which case the mass budget becomes
∂t[(H+η)ρz] = Qm−∇·Uρ.(39.56)
Expanding the time derivative renders Version II of the sea level equation
∂η
∂t =Qm−∇·Uρ−(H+η)∂ρz/∂t
ρz.(39.57)
Equation (39.57) is mathematically equivalent to Version I of the sea level equation (39.50). However,
there is a difference in emphasis that provides some complement to Version I. We thus find it useful to
again discuss the three physical processes that impact sea level as revealed by equation (39.57).
1. Boundary fluxes: As for Version I, the boundary contribution arises from mass fluxes crossing the
ocean boundaries. However, for Version II, the conversion of mass to volume flux occurs through the
column mean density, ρz, rather than the surface density ρ(η).
2. Dynamic: Version I considers the dynamic effects from the transport of volume by the vertically
integrated currents. Version II considers the transport of mass by the vertically integrated currents,
which is then converted to a sea level tendency through dividing by the vertically averaged density.
Since the mass flux must be converted to a volume flux through division by the spatially dependent
depth mean density, ρz, a global area integral of the sea level equation (39.57) does not identically
remove the effects on sea level from mass transport by ocean currents. Instead, the effects are only
approximately removed, to the extent that the vertical mean density is horizontally constant.
Elements of MOM November 19, 2014 Page 561

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.2
3. Local steric: Version II of the sea level equation (39.57) exposes an Eulerian time derivative acting
on the vertically averaged density, rather than the vertical integral of the material time derivative
present in Version I. In so doing, we see how sea level is directly affected through the local changes
to the column mean density. As the column mean density decreases, the column expands and this in
turn contributes a positive tendency to sea level evolution. We refer to this steric contribution as the
local steric effect to contrast it with the non-Boussinesq steric term introduced in Section 39.2.1.
Although we focus in the remainder of this paper on Version I of the kinematic sea level equation
(39.50), it is useful to here make a connection between the kinematic sea level equation (39.57) and the
analogous sea level equation proposed by Gill and Niiler (1973) for a hydrostatic fluid. First, note that the
sea level evolution in equation (39.57) can be partitioned into a contribution from mass changes and a
contribution from local steric changes
∂η
∂t =Qm−∇·Uρ
ρz
| {z }
mass
−(H+η)∂ρz/∂t
ρz
| {z }
local steric
.(39.58)
It is just this decomposition that was promoted by Gill and Niiler (1973) for a hydrostatic fluid. Notably,
equation (39.58) follows solely from the kinematics of a mass conserving fluid and so holds for both hy-
drostatic and non-hydrostatic fluids.
To further make the connection to Gill and Niiler (1973), introduce the hydrostatic approximation, in
which the difference between hydrostatic pressure at the ocean bottom, pb, and pressure applied to the
ocean surface, pa, is given by
pb−pa=g
η
Z
−H
ρdz, (39.59)
where gis the gravitational acceleration. Use of the column integrated mass balance (39.53) thus leads
to the kinematic evolution equation
g−1∂t(pb−pa) = Qm−∇·Uρ.(39.60)
This equation says that mass per area within a column of seawater changes according to the surface mass
flux and the convergence of the vertically integrated mass transport. Substituting this result into the sea
level equation (39.57) leads to
∂η
∂t =∂t(pb−pa)
g ρz
| {z }
mass
−(H+η)∂ρz/∂t
ρz
| {z }
local steric
.(39.61)
As for the expression (39.58), we see that sea level experiences a positive tendency in those regions where
mass locally increases and where the vertically averaged density decreases. As noted by Gill and Niiler
(1973), and further supported by model analyses from Landerer et al. (2007), Yin et al. (2009), and Yin et al.
(2010a), there are many useful physical insights concerning regional sea level garnered when performing
this kinematic partitioning of sea level evolution into mass and local steric changes, with local steric effects
further partitioned into thermal (thermosteric) and haline (halosteric) effects. The particular form of this
partition as proposed by Gill and Niiler (1973) arises from taking the time derivative of the hydrostatic
balance (39.59), which leads after rearrangement to
∂η
∂t =∂t(pb−pa)
g ρ(η)
| {z }
mass
−Rη
−H(∂ρ/∂t)dz
ρ(η)
| {z }
steric
.(39.62)
The two expressions (39.61) and (39.62) have the same physical content, though the terms on the right
hand side slightly differ quantitatively.
Elements of MOM November 19, 2014 Page 562

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
39.2.3 How we make use of the kinematic sea level equations
The kinematic sea level equations (39.50) and (39.57) arise just from mass balance and the kinematic
boundary conditions, which lends great generality to their applicability; e.g., they are valid for both hy-
drostatic and non-hydrostatic fluids. At each point in the ocean, sea level tendencies must respect these
fundamental kinematic results. Hence, equations (39.50) and (39.57) offer a means for partitioning the
evolution of sea level into various physical processes. However, there are questions that kinematics can-
not answer absent dynamical principles (e.g., Lowe and Gregory,2006). That is, the kinematic approach
provides a useful diagnostic framework, but it does not, alone, produce a complete predictive framework.
For example, a kinematic approach alone cannot uncover how sea level adjusts in the presence of
forcing, or the time scales over which low frequency patterns emerge. For example, should we expect
low frequency (order monthly or longer) sea level patterns to exhibit high values under regions of net
precipitation and low values under regions of net evaporation? At any instant of time, net precipitation will
contribute a positive tendency to the sea level, and net evaporation will contribute a negative tendency, as
revealed by the kinematic sea level equations (39.50) and (39.57). However, the low frequency sea level
patterns are not generally correlated with patterns of evaporation minus precipitation.
The reason for the decorrelation is that there is a dynamical adjustment occurring on a barotropic
time scale (a few days) that causes perturbations from boundary mass fluxes, as well as from the non-
Boussinesq steric effect, to be transmitted globally through gravity wave adjustments (Greatbatch,1994).
Consequently, these perturbations rapidly impact global mean sea level, but generally leave little imprint
on regional low frequency sea level patterns. That is, the perturbations can be considered barotropic
wavemakers. Additional impacts from the input of freshwater and buoyancy to the ocean alter regional
sea level patterns through baroclinic adjustments captured by both volume conserving Boussinesq and
mass conserving non-Boussinesq ocean models (see, e.g., Hsieh and Bryan (1996), Bryan (1996), Landerer
et al. (2007), Stammer (2008), Yin et al. (2009), and Yin et al. (2010a), Lorbacher et al. (2012)).
39.3 The non-Boussinesq steric effect
The non-Boussinesq steric effect and the boundary mass flux are the only two means, within the kinematic
sea level equation (39.50), to impact global mean sea level. Impacts from the convergence of vertically
integrated ocean currents exactly vanish in the global mean and so are of no direct relevance to global
sea level.
Certainly ocean currents are important for global mean sea level. In particular, they impact on turbu-
lent mixing, which in turn modifies the way heat irreversibly penetrates into the ocean. So in that regard
ocean dynamics is of fundamental importance for global sea level. But it is through the non-Boussinesq
steric effect that mixing impacts global mean sea level. It is also through the non-Boussinesq steric effect
that boundary fluxes of buoyancy impact global mean sea level. Consequently, to understand mechanisms
for changes to global mean sea level requires a framework to explore the non-Boussinesq steric effect.
39.3.1 Defining the non-Boussinesq steric effect
Version I of the sea level equation (39.50), repeated here for completeness,
∂η
∂t =Qm
ρ(η)−∇·U−
η
Z
−H
dz1
ρ
dρ
dt,(39.63)
provides a means to kinematically partition various physical processes impacting sea level evolution. We
are particularly interested in the time tendency
∂η
∂t !non-bouss steric ≡ −
η
Z
−H
dz1
ρ
dρ
dt,(39.64)
Elements of MOM November 19, 2014 Page 563

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
which we refer to as the non-Boussinesq steric effect, since it is absent in Boussinesq fluids (Greatbatch,
1994). The time derivative acting on in situ density in the non-Boussinesq steric effect (39.64) is a material
derivative, rather than an Eulerian tendency. This detail is fundamental to the formulation given in the
following, and we return to its implications throughout this paper.
39.3.2 Vertical motion across pressure surfaces
To initiate a discussion of the non-Boussinesq steric effect, we use the material evolution of in situ density
in the form of equation (39.41) to write
−1
ρ
dρ
dt=αdΘ
dt−βdS
dt−1
ρc2
sound
dp
dt.(39.65)
The material evolution of in situ density is thus affected by the material evolution of buoyancy, through ma-
terial changes in temperature and salinity, and by material evolution of pressure, with pressure evolution
the focus of this subsection.
To garner some exposure to the physics of dp/dtas it appears in equation (39.65), consider the special
case of a hydrostatic fluid, where the volume per time per horizontal area of fluid crossing a surface of
constant hydrostatic pressure is given by (see Section 6.7 of Griffies (2004))
w(p)=∂z
∂p
dp
dt
=−(ρg)−1dp
dt.
(39.66)
The transport measured by w(p)is the pressure-coordinate analog of the vertical velocity component
w= dz/dtin a geopotential coordinate representation of the vertical direction. To the extent that pres-
sure surfaces are well approximated by depth surfaces, w(p)≈w. Fluid moving into regions of increasing
hydrostatic pressure (dp/dt > 0) represents downward movement of fluid, with w(p)<0in this case. Con-
versely, motion into decreasing hydrostatic pressure represents upward motion, with w(p)>0.
We may identify the following contribution to the non-Boussinesq steric effect associated with vertical
motion across hydrostatic pressure surfaces
∂η
∂t !dp/dt≡ −
η
Z
−H
dz1
ρc2
sound
dp
dt
=g
η
Z
−H
dzw(p)
c2
sound
=g(H+η) w(p)
c2
sound !z
(39.67)
where we introduced the vertical average operator for an ocean column. In columns where the vertically
averaged vertical motion is upward, the column stretches, thus imparting a positive sea level tendency.
The opposite occurs for vertically averaged downward fluid motion. Fluid generally moves across pressure
surfaces under adiabatic and isohaline parcel motions, as in the presence of gravity or planetary waves.
Additionally, dianeutral mixing generally gives rise to vertical transport, for example as seen in the case
of a horizontally unstratified fluid in the presence of vertical diffusion. Diagnosing the term (39.67) does
not identify the cause of the dia-pressure motion; it merely quantifies the effects of this motion on global
mean sea level.
To gain a sense for the scale of the term (39.67), approximate the shallow water gravity wave speed as
c2
grav ≈g(H+η),(39.68)
Elements of MOM November 19, 2014 Page 564
Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
thus leading to
∂η
∂t !dp/dt≈w(p)(cgrav/csound)2z,(39.69)
where (cgrav/csound )2≤10−2.
The contribution (equation (39.67)) to the non-Boussinesq steric effect possesses a higher wave num-
ber structure and larger magnitude locally than contributions from surface water fluxes and from the
convergence of column integrated mass transport. We expect the high wave number power to increase
in simulations with refined resolutions and realistic diurnal and astronomical (tidal) forcing (absent in this
simulation), such that internal gravity wave activity is further promoted. In this way, dynamically active re-
gions, such as the Southern Ocean, act as a barotropic wavemaker through vertical motion. As explained
in Section 39.2.3 and Greatbatch (1994), contributions to the non-Boussinesq steric effect act dynamically
in a manner analogous to mass forcing, leaving a regional low frequency field that is smoother than forc-
ing from the non-Boussinesq steric effect. We thus do not generally see an imprint of the non-Boussinesq
steric effect on low frequency (i.e., longer than monthly) regional sea level.
39.3.3 An expanded form of the kinematic sea level equation
We now focus on how material changes in temperature and salinity contribute to the non-Boussinesq steric
effect. To do so, assume that the material evolution of conservative temperature and salinity is given by
the convergence of a subgrid scale flux plus a source term
ρdΘ
dt=−∇·J(Θ)+ρSθ(39.70)
ρdS
dt=−∇·J(S)+ρSS.(39.71)
The conservative temperature flux J(Θ)and the salt flux J(S)include their respective diffusive and skew
fluxes, as formulated by equation (39.33). Note that the temperature flux J(Θ)may also include the ef-
fects from penetrative shortwave radiation (e.g., Iudicone et al.,2008). The forms for the conservative
temperature and salinity equations (39.70) and (39.71) lead to (see equation (39.65))
−αdΘ
dt+βdS
dt= ∂ν
∂Θ!∇·J(Θ)+ ∂ν
∂S !∇·J(S)−αSθ+βSS
=∇· ∂ν
∂ΘJ(Θ)+∂ν
∂S J(S)!−J(Θ)·∇ ∂ν
∂Θ!−J(S)·∇ ∂ν
∂S !−αSθ+βSS
(39.72)
where
ν=ρ−1(39.73)
is the specific volume, and its derivatives are given by
∂ν
∂Θ=α
ρ,(39.74)
∂ν
∂S =−β
ρ,(39.75)
Elements of MOM November 19, 2014 Page 565

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
where α=−ρ−1∂ρ/∂Θand β=ρ−1∂ρ/∂S are the thermal expansion and haline contraction coefficients
introduced in Section 39.1.4. Bringing these results together leads to
∂η
∂t !non-bouss steric
=−
η
Z
−H
dz∇·h(α/ρ)J(Θ)−(β/ρ)J(S)i
+
η
Z
−H
dzαSθ−βSS
+
η
Z
−H
dz J(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)−1
ρc2
sound
dp
dt!.
(39.76)
39.3.3.1 Exposing the boundary fluxes of temperature and salinity
We expose the surface and bottom boundary fluxes through use of the following identity
η
Z
−H
dz∇·(α/ρ)J(Θ)−(β/ρ)J(S)=∇z·
η
Z
−H
dzh(α/ρ)J(Θ)−(β/ρ)J(S)i
+∇(z−η)·h(α/ρ)J(Θ)−(β/ρ)J(S)iz=η
−∇(z+H)·h(α/ρ)J(Θ)−(β/ρ)J(S)iz=−H.
(39.77)
Tracer fluxes through the ocean bottom z=−H(x,y)are written as
Q(C)=J(C)·ˆ
n dAˆ
n
dA!
=J(C)·∇(z+H),
(39.78)
where ˆ
n=−∇(z+H)/|∇(z+H)|is the bottom normal vector, and we used the relation (see Section 20.13.2
of Griffies (2004))
dAˆ
n=|∇(z+H)|dAat z=−H(x,y) (39.79)
between the area element dAˆ
non the ocean bottom, and its horizontal projection dA. Hence, the conser-
vative temperature and salt fluxes through the ocean bottom are given by
Q(Θ)=J(Θ)·∇(z+H)at z=−H(39.80)
Q(S)=J(S)·∇(z+H)at z=−H.(39.81)
The flux
enthalpy flux =cpQ(Θ)(39.82)
is the heat, or more precisely the enthalpy, per time per horizontal area entering the ocean through the
bottom, with
cp≈3992.1J kg−1K−1(39.83)
the heat capacity for seawater at constant pressure, with the value given by IOC et al. (2010) the most pre-
cise. Geothermal heating is quite small relative to surface heat fluxes. However, the work of Adcroft et al.
(2001) and Emile-Geay and Madec (2009) motivate retaining this contribution to the temperature equa-
tion, as there are some systematic impacts from geothermal heating over long periods. For climatological
purposes, the introduction of salt to the ocean through the sea floor is negligible, in which case
Q(S)= 0 at z=−H.(39.84)
Elements of MOM November 19, 2014 Page 566

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
Likewise, water may enter through the sea floor, but we know of no recommended dataset for doing so.
Thus, we set Qm= 0 at the bottom.
As for the ocean bottom, tracer fluxes through the ocean surface z=η(x,y,t)are written as
Q(C)=−J(C)·ˆ
n dAˆ
n
dA!
=−J(C)·∇(z−η),
(39.85)
where ˆ
n=∇(z−η)/|∇(z−η)|is the surface outward normal vector, and we used the relation (see Section
20.13.2 of Griffies (2004))
dAˆ
n=|∇(z−η)|dAat z=η(39.86)
between the area element dAˆ
non the ocean surface, and its horizontal projection dA. The sign convention
is chosen so that Q(C)>0signals the addition of tracer to the ocean. Hence, the conservative temperature
and salt fluxes through the ocean surface take the form
Q(Θ)=−J(Θ)·∇(z−η)at z=η(39.87)
Q(S)=−J(S)·∇(z−η)at z=η. (39.88)
Again, the sign convention is chosen so that positive flux Q(Θ)adds heat to the ocean, and positive flux
Q(S)adds salt to the ocean. There is near zero salt flux through the ocean surface, except for the small
exchange during the formation and melt of sea ice. We further discuss surface fluxes in Section 39.3.4.
39.3.3.2 Expanded form of the kinematic sea level equation
Bringing these results together leads to an expanded form of the kinematic sea level equation
∂η
∂t =−∇z·
η
Z
−H
dz(αJ(Θ)−βJ(S)+ρu)
ρ
+
η
Z
−H
dzαSθ−βSS
+
η
Z
−H
dz J(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)−1
ρc2
sound
dp
dt!
+ α Q(Θ)−β Q(S)+Qm
ρ!z=η
+ α Q(Θ)
ρ!z=−H
.
(39.89)
This expression provides a precise measure of how physical processes and boundary fluxes determine the
kinematic evolution of sea level. In particular, this equation suggests the following physical interpretations,
with reference made to Figure 39.2 for a schematic.
39.3.3.3 Buoyancy fluxes and mass fluxes
The first integral in the kinematic sea level equation (39.89) is the convergence of vertically integrated
lateral subgrid scale flux of buoyancy (arising from the non-Boussinesq steric effect), along with the lateral
advective flux of mass. When integrated over the global ocean, this convergence vanishes exactly. Hence,
this term moves mass and buoyancy around in the ocean without altering the global mean sea level.
The combination α Q(Θ)−β Q(S)represents the buoyancy flux crossing the ocean surface at z=η(x,y,t).
Boundary fluxes that increase net buoyancy of the global ocean increase global mean sea level. In par-
ticular, it is precisely through this effect that surface ocean warming acts to increase global mean sea
level. These boundary buoyancy fluxes act in concert with the boundary mass flux Qmto impact sea level
through interactions at the ocean surface.
Elements of MOM November 19, 2014 Page 567

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
39.3.3.4 Interior sources
The second integral in equation (39.89) arises from the interior source of temperature and salinity, such
as may arise from such parameterized processes as non-local mixing in the KPP boundary layer scheme
(Large et al.,1994). The third integral in equation (39.89) is another source, which arises from the non-
Boussinesq steric effect
source =J(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)−1
ρc2
sound
dp
dt,(39.90)
with the source having units of inverse time. There are three terms contributing to the source, the third
of which we discussed in Section 39.3.2 relates to vertical motion across pressure surfaces. The first
and second terms relate to the orientation of temperature and salinity subgrid scale fluxes in relation to
thermodynamic properties of the fluid and geometric properties of the density surface. We consider spe-
cial cases of the source term in Section 39.5 for dianeutral diffusion, approximated as vertical diffusion;
Section 39.6 for neutral diffusion, where it is shown how cabbeling and thermobaricity, arising from pa-
rameterized mixing effects from mesoscale eddies along neutral directions, impact global mean sea level;
and Section 39.7 for quasi-Stokes transport from mesoscale eddies as parameterized according to Gent
and McWilliams (1990).
39.3.3.5 Concerning the absence of advective temperature and salt fluxes
It is notable that the expanded kinematic sea level equation (39.89) only involves the subgrid scale fluxes
of temperature and salt, as well as their non-advective boundary fluxes. There are no interior nor boundary
advective fluxes of buoyancy that directly impact sea level. This absence relates to our choice to focus on
Version I of the sea level equation (39.50), in which the time derivative acting on in situ density is a material
or Lagrangian derivative, not an Eulerian derivative. This point is of fundamental importance to how we
identify physical processes impacting global mean sea level in Section 39.4 and further considered in Sec-
tions 39.5,39.6, and 39.7. Hence, buoyancy changes impact global mean sea level only through processes
that render a nonzero material change to in situ density, with such changes occurring through boundary
fluxes, interior mixing, nonlinear equation of state effects, and subgrid scale eddy induced advection.
z=η
z=−H
αQθ
ρ(−H)
αQθ−βQS+Qm
ρ(η)
η
R
−H
dz(source) − ∇z·
η
R
−H
dzαJθ−βJS+ρu
ρ
Figure 39.2: A schematic ocean basin as in Figure 39.1, but now illustrating the various boundary and
internal processes that impact sea level according to the unpacked kinematic sea level equation (39.89). The
surface mass flux, Qm, is combined here with a surface buoyancy flux to yield the surface boundary forcing
ρ(η)−1α Q(Θ)−β Q(S)+Qm. Likewise, the bottom boundary forcing arises from geothermal heating in the
form α Q(Θ)/ρ(−H), which is a small, but always positive, contribution to global mean sea level evolution.
In the ocean interior, the convergence of mass and buoyancy, along with a source term (equation (39.90)),
yield the forcing Rη
−Hdz(source) −∇z·Rη
−Hdzρ−1αJ(Θ)−βJ(S)+ρu.
Elements of MOM November 19, 2014 Page 568

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.3
39.3.4 Boundary fluxes of heat and salt
We now detail how boundary fluxes of heat, salt, and freshwater impact the non-Boussinesq steric effect
appearing in equation (39.89). The global integral of these fluxes impact on the global mean sea level
(Section 39.4). Start by noting that the contribution from the surface buoyancy flux,
∂η
∂t !surface buoyancy
=α Q(Θ)−β Q(S)
ρ(η),(39.91)
is determined both by the boundary fluxes of heat and salt, as well as the boundary values for the thermal
expansion coefficient, haline contraction coefficient, and density.
39.3.4.1 Boundary heat fluxes
The non-advective heat flux crossing the surface ocean boundary consists of the following contributions
(in units of W m−2),
Qsurface =QSW +QLW +Qsens +Qlat +Qfrazil (39.92)
with a sign convention chosen so that positive fluxes add heat to the liquid seawater. What appears in
the sea level equation is actually the surface flux of temperature, not heat. So it is necessary to convert
between heat and temperature fluxes when considering the impacts on sea level. As noted by McDougall
(2003), to convert from heat fluxes to fluxes of potential temperature requires the use of a non-constant
specific heat capacity, which varies by roughly 5% over the globe. In contrast, converting between heat
fluxes and conservative temperature fluxes is done with a constant specific heat capacity
Qsurface =cpQ(Θ)
surface,(39.93)
thus serving to further promote the use of conservative temperature.
We now summarize the various contributions to surface ocean heating.
•Shortwave: The dominant heating occurs through the shortwave contribution QSW >0. Shortwave
radiation penetrates on the order of 10m to 100m into the ocean interior, with the distance depending
on optical properties of seawater (see, e.g., Sweeney et al.,2005, and cited references).
•Longwave: The longwave contribution QLW <0represents the net longwave energy that is re-radiated
back to the atmosphere. Even though there are many occasions for backscattering, the net effect of
longwave radiation is to cool the ocean.
•Sensible: Sensible heating Qsens arises from turbulent exchange with the atmosphere, and is generally
parameterized by turbulent bulk formula. The sensible heat term typically cools the ocean surface.
•Latent: Latent heating Qlat cools the ocean, as it is the energy extracted from the ocean to vaporize
liquid water that enters the atmosphere. Additionally, the latent heating term includes heat extracted
from the ocean to melt solid runoff(i.e., calving land ice) or snow entering the liquid ocean. These
latent heat terms are thus related to mass transport across the ocean surface according to
Qvapor
lat =Hvapor Qevap
m(39.94)
Qmelt
lat =Hfusion (Qcalving
m+Qsnow
m),(39.95)
where Hvapor ≈2.5×106J kg−1is the latent heat of vaporization, Qevap
mis the evaporative mass flux in
units of kg m−2s−1,Hfusion ≈3.34 ×105J kg−1is the latent heat of fusion, Qcalving
mis the mass flux of
calving land ice entering the ocean, and Qsnow
mis the mass flux of frozen precipitation falling on the
ocean surface.
•Frazil: As the temperature of seawater cools to the freezing point, sea ice is formed, initially through
the production of frazil. Operationally in an ocean model, liquid water can be supercooled at any
particular time step through surface fluxes and transport. An adjustment process heats the liquid
water back to the freezing point, with this positive heat flux Qfrazil extracted from the ice model as
frazil sea ice is formed.
Elements of MOM November 19, 2014 Page 569

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.4
In addition to the above listed heat fluxes, there is a heat flux associated with the heat content of water
transferred across the ocean surface. However, this flux represents an advective (or mass transport) heat
flux that is captured by the advective term in the material time derivative.
The total non-advective boundary flux of heat affecting ocean heat content is the sum of the surface
flux detailed above, and the bottom flux arising from geothermal heating
Qheat =Qsurface +Qgeothermal.(39.96)
The geothermal contribution to heating is quite small (less than 0.1W m−2locally), and so contributes only
a very small amount to the global sea level evolution.
39.3.4.2 Boundary salt fluxes and sea ice
For most purposes of ocean climate modelling, the mass flux of salt into the liquid ocean is limited to
exchanges associated with the formation and melt of sea ice
Q(S)=Qice-ocean salt exchange ,(39.97)
which arises since the salinity of sea ice is nonzero (on the order of 5 parts per thousand). Hence, as sea
ice forms, it extracts a small amount of salt from the liquid ocean, and a larger amount of liquid freshwater.
The converse happens upon melting sea ice.
So how does the formation and melt of sea ice impact global mean sea level? First, there is a transfer
of mass between the solid and liquid phases. In particular, salt and freshwater transfer affect the mass of
the liquid ocean through the mass flux Qmappearing in equation (39.89) in the form
∂η
∂t !sea ice mass exchange
=Q(S)+Qw
ρ(η),(39.98)
with Qwthe mass flux from freshwater. As salt and freshwater are added to the ocean through sea ice
melt, they raise the global mean liquid sea level according to this expression. However, the transfer of
mass from the solid to liquid phase leads to near zero net change in the effective sea level, since the liquid
ocean response to sea ice loading is consistent with an inverse barometer. This mass transfer includes the
transfer of both freshwater and salt. However, most ocean and sea ice models used for climate studies
ignore the mass of salt when computing the liquid ocean mass and solid sea ice mass. So in practice, the
mass transfer referred to here occurs only through the transfer of freshwater.
In addition to exchanging mass, there is an exchange of buoyancy as salt is moved between the solid
and liquid phases. Changing buoyancy at the ocean surface impacts the non-Boussinesq steric effect
according to
∂η
∂t !surface salt buoyancy ≡ − β Q(S)
ρ!.(39.99)
As salt is added to the upper ocean through ice melt, this process removes buoyancy.
39.4 Evolution of global mean sea level
Global mean sea level is of great interest for climate studies. Indeed, it is often the only field that climate
models report when considering projections for sea level changes due to human-induced global warming.
The purpose of this section is to formulate evolution equations for the global mean sea level which, in an
ocean with constant horizontal area, are equivalent to equations for global ocean volume.
Elements of MOM November 19, 2014 Page 570

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.4
39.4.1 Preliminaries
We begin by establishing some notation and restating assumptions. For this purpose, write the volume of
liquid seawater in the global ocean in the following equivalent manners
V=Z
globe
dA
η
Z
−H
dz
=Z
globe
dA(η+H)
=A(H+η).
(39.100)
In the final step, we introduced the global ocean surface area
A=Z
globe
dA=Z
globe
dxdy, (39.101)
the global mean sea level
η=A−1Z
globe
ηdA, (39.102)
and the global mean ocean depth beneath a resting sea surface at z= 0
H=A−1Z
globe
HdA. (39.103)
We assume throughout this paper that the ocean surface area remains constant in time. That is, we do not
consider changes in sea level associated with shoreline changes. We also assume that the ocean depth
z=−H(x,y)remains constant in time. An evolution equation for the global ocean volume is therefore
equivalent to an evolution equation for global mean sea level
∂tV=A∂tη. (39.104)
39.4.2 Global mean sea level and the non-Boussinesq steric effect
The first version of the global mean sea level equation is formulated starting from Version I of the kinematic
sea level equation (39.50), rewritten here for completeness
∂η
∂t =Qm
ρ(η)−∇·U−
η
Z
−H
dz1
ρ
dρ
dt.(39.105)
A global integration, with no-flux side walls or periodic domains, leads to
∂tη= Qm
ρ(η)!−V
A*1
ρ
dρ
dt+,(39.106)
where
hψi=V−1Z
globe
dA
η
Z
−H
ψdz(39.107)
is the global volume mean of a field. The relation (39.106) says that the global mean sea level changes in
time according to (A) the area mean of the mass flux multiplied by the specific volume of seawater at the
ocean surface, and (B) the global mean of the non-Boussinesq steric effect.
Elements of MOM November 19, 2014 Page 571

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.4
To uncover some of the physical processes that impact global sea level, consider the unpacked version
of equation (39.106), obtained by taking a global area integral of the sea level equation (39.89)
A∂tη=Z
globe(z=η)
dA Qm+α Q(Θ)−β Q(S)
ρ!+Z
globe(z=−H)
dA α Q(Θ)−β Q(S)
ρ!
+Z
globe J(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)−1
ρc2
sound
dp
dt!dV
+Z
globe αSθ−βSSdV .
(39.108)
To reach this result required the following steps:
1. The direct impacts of ocean currents drop out from a global area integral of equation (39.89), due to
the no-normal flow solid earth boundary condition, or periodic boundary condition.
2. We assume zero water fluxes entering the ocean through the solid earth boundary.
3. There may be nonzero boundary heat or salt fluxes, though as noted in Section 39.3.4.2, salt ex-
changed through ocean boundaries is generally limited to a small exchange associated with sea ice
formation and melt. Correspondingly, we drop the bottom salt flux.
39.4.3 Global mean sea level and the global steric effect
Equation (39.106), and its unpacked version (39.108), help us to understand how physical processes and
boundary effects impact the global mean sea level. However, if one is only interested in the net effect on
sea level, then an alternative formulation is appropriate. This second version of the evolution equation for
global mean sea level is developed by introducing the following relation between the total mass of liquid
seawater, total volume of seawater, and global mean seawater density,
M=V hρi.(39.109)
In this relation,
M=Z
globe
dA
η
Z
−H
ρdz(39.110)
is the global liquid seawater mass, and Vis the global volume of seawater (equation (39.100)). It follows
that
∂tM=V∂thρi+hρi∂tV.(39.111)
An area integration of the mass budget (39.53) indicates that total seawater mass changes if there is a
nonzero mass flux across the ocean surface
∂tM=AQm(39.112)
where
Qm=A−1Zglobe
QmdA(39.113)
is the global mean mass per horizontal area per time crossing the ocean boundaries. Bringing these results
together, and recalling that ∂tV=A∂tη(equation (39.104)) leads to the second evolution equation for the
global mean sea level
∂tη=Qm
hρi−V
A∂thρi
hρi.(39.114)
As in the formulation given in Section 39.4.2, there is no direct contribution from ocean currents, since
they act to redistribute volume without changing the total volume. The first term on the right hand side
Elements of MOM November 19, 2014 Page 572
Chapter 39. Diagnosing the contributions to sea level evolution Section 39.5
of equation (39.114) alters sea level by adding or subtracting volume from the ocean through the surface
boundary, and the second term arises from temporal changes in the global mean density. We refer to the
second term as the global steric effect to make a distinction from the global mean of the non-Boussinesq
steric effect discussed in Section 39.4.2. Both terms on the right hand side of equation (39.114) are readily
diagnosed from a model simulation, thus providing a means to partition the change in global mean sea
level into a contribution from boundary fluxes and one from global steric changes.
We comment here on the dominance of changes in global mean temperature on the global steric effect
in equation (39.114). For this purpose, write the time tendency of global mean density in the form
∂tlnhρi=−αbulk ∂thΘi+βbulk ∂thSi+1
(ρc2
sound)bulk
∂thpi.(39.115)
This equation defines αbulk as a bulk, or effective, thermal expansion coefficient, βbulk as a bulk haline con-
traction coefficient, and (ρ c2
sound)bulk as a bulk density times the squared sound speed. These coefficients can
be thought of as best fit parameters for the linear relation (39.115) connecting changes in global mean
sea level to global mean temperature, salinity, and pressure. For the case that the global mean salinity
remains constant, which is roughly the case for most climate purposes (see Section 39.3.4.2), and when
changes in pressure are sub-dominant, as they generally are, then global mean density changes are dom-
inated by global mean temperature changes. Hence, the global mean sea level equation (39.114) takes on
the approximate form
∂tη≈Qm
hρi+Vαbulk
A∂thΘi.(39.116)
This approximate result provides a very good indicator of the 20th century global mean sea level rise
associated with ocean warming (Church and Gregory,2001;Nicholls and Cazenave,2010).
39.4.4 Relating global steric to non-Boussinesq steric
Equating the two equations (39.106) and (39.114) for global mean sea level yields the identity
Qm
ρ(η)!−V
A*1
ρ
dρ
dt+=Qm
hρi−V
A∂thρi
hρi.(39.117)
In the special case of zero surface boundary fluxes of mass, the global mean of the non-Boussinesq steric
effect is equal to the global steric effect
*1
ρ
dρ
dt+=∂thρi
hρiif Qm= 0.(39.118)
This result motivates a commonly used method to adjust the sea level in Boussinesq models, even in the
presence of nonzero boundary fluxes of mass.
39.5 Vertical diffusion and global mean sea level
This section is the first of three to further explore the non-Boussinesq steric effect discussed in Sections
39.3 and 39.4. The focus here is on how subgrid scale fluxes of conservative temperature and salinity
arising from vertical diffusion in the ocean interior determine patterns of the non-Boussinesq steric effect.
Vertical diffusion is the method used by global ocean climate models to parameterize the impacts from
dianeutral mixing processes. Section 39.6 considers the same questions for neutral diffusion, and Section
39.7 considers parameterized quasi-Stokes transport. By exposing patterns of the non-Boussinesq steric
effect associated with these parameterizations, we provide a framework to explore where the global mean
sea level in ocean climate models is impacted by subgrid scale physical parameterizations.
Elements of MOM November 19, 2014 Page 573

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.6
39.5.1 Contributions from vertical diffusion
Recall that we have already discussed in Sections 39.3.3 and 39.3.4 those contributions from boundary
fluxes of buoyancy. Hence, the impacts of concern here from vertical diffusion involve just contributions to
the source term (equation (39.90))
J(Θ)·∇(α/ρ)−J(S)·∇(β/ρ) = −ρhDΘ∂zΘ∂z(α/ρ)−DS∂zS ∂z(β/ρ)i.(39.119)
Here, we consider the tracer flux to equal that arising from downgradient vertical diffusion
J(Θ)=−ρDΘ∂zΘˆ
z(39.120)
J(S)=−ρDS∂zSˆ
z,(39.121)
with eddy diffusivities for conservative temperature and salinity, DΘ>0and DS>0. This flux is meant
to parameterize mixing arising from dianeutral processes (see Section 7.4.3 of Griffies (2004) for discus-
sion). In the ocean interior, the diffusivities have values D≈10−6m2s−1at the equator, beneath the
regions of strong vertical shears associated with the equatorial undercurrent (Gregg et al.,2003), and
D≈10−5m2s−1in the middle latitudes (Ledwell et al.,1993,2011), with far larger values near rough to-
pography and other boundary regions (Polzin et al.,1997;Naveira-Garabato et al.,2004). Additionally, D
can be set to a very large value in gravitationally unstable regions. Finally, differences in the temperature
and salinity diffusivities arise from double diffusive processes (Schmitt,1994).
39.6 Neutral diffusion and global mean sea level
Mesoscale eddy motions impact the large-scale ocean temperature and salinity distributions in important
and nontrivial ways, with their parameterization in coarsely resolved climate models a longstanding focus
of theoretical physical oceanography. Amongst the common means for parameterizing these effects is to
prescribe a diffusion of temperature and salinity oriented according to the planes tangent to locally refer-
enced potential density surfaces (Solomon,1971;Redi,1982;Olbers et al.,1985;McDougall and Church,
1986;Cox,1987;Gent and McWilliams,1990;Griffies et al.,1998). The purpose of this section is to detail
how such neutral diffusion of temperature and salinity affects the non-Boussinesq steric effect.
To expose how neutral diffusion impacts sea level first requires the establishment of salient properties
of neutral diffusion. Thereafter, we describe how the physical processes of cabbeling and thermobaric-
ity impact global mean sea level. Note that following McDougall (1987b) (see also Klocker and McDougall
(2010a), Klocker and McDougall (2010b), and IOC et al. (2010)), we are concerned with cabbeling and ther-
mobaricity as dianeutral transport processes that arise from a coarse-grained perspective of the mixing
of fluid parcels by mesoscale eddies along neutral directions. We are not concerned with how molecu-
lar diffusion or vertical diffusion can be formulated in terms of micro-scale cabbeling and thermobaricity
processes.
39.6.1 Neutral directions and neutral tangent plane
Following McDougall (1987a), we introduce the notion of a neutral direction by considering an infinitesimal
displacement dx, in which the in situ density changes according to
dρ=ρdx· −α∇Θ+β∇S+1
ρc2
s∇p!.(39.122)
Under adiabatic and isohaline motions, the density change is associated just with pressure changes
(dρ)adiabic/isohaline =ρdx· 1
ρc2
s∇p!.(39.123)
Elements of MOM November 19, 2014 Page 574

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.6
Therefore, if we consider an adiabatic and isohaline displacement, the difference in density between the
parcel and the surrounding environment is given by
dρ−(dρ)adiabatic/isohaline =ρdx·(−α∇Θ+β∇S)
=ρdx·ˆ
γ|−α∇Θ+β∇S|,(39.124)
where the dianeutral unit vector is defined by
ˆ
γ=−α∇Θ+β∇S
|−α∇Θ+β∇S|.(39.125)
At each point in the fluid, displacements orthogonal to ˆ
γdefine neutral directions, and the accumulation
of such displacements define a neutral tangent plane.
39.6.2 Fluxes computed with locally orthogonal coordinates
There are two means to write the neutral diffusion fluxes for a tracer. The first way follows from Redi
(1982), who considers the three dimensional fluxes computed parallel to the local neutral direction. This is
an approach that arises naturally if working in local orthogonal coordinates (Griffies et al.,1998;Griffies,
2004)
J(Θ)=−ρAn[∇Θ−ˆ
γ(ˆ
γ·∇Θ)] (39.126)
J(S)=−ρAn[∇S−ˆ
γ(ˆ
γ·∇S)].(39.127)
In this equation, An>0is a diffusivity (units of squared length per time) setting the magnitude of the
neutral diffusive fluxes. Geometrically, the neutral diffusive fluxes of conservative temperature, J(Θ), and
salinity, J(S), are proportional to that portion of the tracer gradient parallel to the neutral directions. Hence,
by construction,
J(Θ)·ˆ
γ= 0 (39.128)
J(S)·ˆ
γ= 0.(39.129)
39.6.3 Fluxes computed with projected neutral coordinates
The second means for computing neutral diffusive fluxes follows from Gent and McWilliams (1990), whereby
we employ the projected coordinates used in generalized vertical coordinate models (see Starr (1945),
Bleck (1978), McDougall (1995), or Chapter 6 of Griffies (2004)), here applied to the locally defined neutral
tangent plane as in McDougall (1987a). To use this framework requires a vertically stable stratification.
Here, lateral gradients of a tracer are computed along the neutral direction, but the lateral distance used
to compute the gradient is taken as the distance on the horizontal plane resulting from projecting the neu-
tral slope onto the constant depth surfaces (see, for example, Figure 6.4 in Griffies,2004). For this case,
the horizontal and vertical components of the neutral diffusion tracer fluxes take the form
Jh=−Anρ∇nC(39.130)
Jz=−AnρS·∇nC, (39.131)
where the projected lateral gradient operator is given by
∇n=∇z+S∂z.(39.132)
Just as for the fluxes associated with orthogonal coordinates, we have J·ˆ
γ= 0, which ensures that the
fluxes are indeed aligned with neutral directions. Furthermore, these flux components are equal to the
Redi (1982) flux components in the limit that the magnitude of the neutral slope
S=− −α∇zΘ+β∇zS
−α ∂zΘ+β ∂zS!(39.133)
Elements of MOM November 19, 2014 Page 575

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.6
becomes small. Because of this connection, the neutral diffusion fluxes associated with projected neutral
coordinates are known as the small slope fluxes. However, there is no approximation involved with using
the small slope fluxes, so long as the vertical stratification is stable. Rather, their use represents a choice
associated with how we measure lateral distances when computing gradients. Since the small slope fluxes
are directly related to those along-isopycnal fluxes used in isopycnal models, they are more commonly
used in level models than the fluxes implied by Redi (1982). The small slope fluxes are also simpler to
compute, as they involve fewer terms.
39.6.4 Compensating neutral diffusive fluxes of temperature and salinity
It is straightforward to show that either of the neutral diffusive fluxes defined in Sections 39.6.2 or 39.6.3
satisfy the identity
αJ(Θ)−βJ(S)= 0.(39.134)
That is, each component of the neutral diffusive flux of buoyancy vanishes, by definition. This is a key
property of neutral diffusion, which in particular means that neutral diffusion directly contributes to the
non-Boussinesq steric effect only through the source term defined by equation (39.90).
39.6.5 The cabbeling and thermobaricity parameters
To help further elucidate how neutral diffusion impacts the non-Boussinesq steric effect, and hence global
mean sea level, we massage the source term (39.90) for the case of neutral diffusive fluxes, with the final
result being
J(Θ)·∇(α/ρ)−J(S)·∇(β/ρ) = ρ−1J(Θ)·(T ∇p+C∇Θ).(39.135)
The cabbeling parameter Cand thermobaricity parameter Tare given by equations (39.136) and (39.141)
discussed in the following. We now consider some of the physical implications of this result.
39.6.6 Physical aspects of cabbeling
Consider the mixing of two water parcels along a neutral direction through the action of mesoscale ed-
dies. Let the parcels separately have distinct conservative temperature and/or salinity, but equal locally
referenced potential density. If the equation of state were linear (Section 39.1.5), then the resulting mixed
parcel would have the same density as the unmixed separate parcels. Due to the more general equilib-
rium thermodynamics in the ocean, in which there is a dependence of density on temperature, salinity, and
pressure, the mixed parcel actually has a different density. Furthermore, the density of the mixed parcel is
greater than the unmixed parcels. This densification upon mixing is a physical process known as cabbeling
(McDougall,1987b).
The sign definite nature of cabbeling (i.e., cabbeling always results in denser parcels after mixing) is a
direct result of the geometry of the locally referenced potential density surface when viewed in conserva-
tive temperature and salinity space. This property in turn manifests with the following inequality for the
cabbeling parameter
C=∂α
∂Θ+ 2α
β
∂α
∂S − α
β!2∂β
∂S ≥0,(39.136)
which is an empirical property of the ocean’s equilibrium thermodynamics (IOC et al.,2010).
Downgradient neutral diffusion is meant to parameterize the mesoscale eddy induced mixing of tracers
along neutral directions. We verify that the neutral diffusive flux considered thus far is indeed downgradi-
ent by considering the small slope neutral diffusive flux (equations (39.130) and (39.131)) to render
∇Θ·J(Θ)=−Anρ(∇nΘ)2≤0.(39.137)
Likewise, the neutral diffusive flux (39.126) from Redi (1982) yields
∇Θ·J(Θ)=−Anρ[(∇Θ)2−(ˆ
γ·∇Θ)2]≤0.(39.138)
Elements of MOM November 19, 2014 Page 576

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.7
Given this downgradient nature of the neutral diffusive fluxes, we have
ρ−1CJ(Θ)·∇Θ≤0,(39.139)
thus providing a mathematical expression for the cabbeling process. That is, cabbeling results in a positive
material evolution of density; i.e., density increases due to cabbeling, and this process can be interpreted
as a downward or negative dianeutral transport (McDougall,1987b).
An increase in density through cabbeling results in the reduction of sea level due to the compression
of the fluid column as manifest in the non-Boussinesq steric effect
∂η
∂t !cab
=−
η
Z
−H
dzCAn(∇nΘ)2<0.(39.140)
39.6.7 Physical aspects of thermobaricity
The thermobaricity parameter
T=β ∂p α
β!(39.141)
is nonzero due to pressure dependence of the ratio of thermal expansion coefficient to haline contraction
coefficient. As both thermal and haline effects are present, the parameter Tis more precisely split into
two terms
T=∂α
∂p −α
β
∂β
∂p .(39.142)
Thermobaricity is the common name for the sum, since pressure variations in the thermal expansion co-
efficient dominate those of the haline contraction coefficient. Since the thermal expansion coefficient
generally increases as pressure increases, the thermobaricity parameter is typically positive. Since neu-
tral diffusive fluxes need not be oriented in a special manner relative to the pressure gradient, there is no
sign-definite nature to the thermobaricity source term
ρ−1J(Θ)·T ∇p=−AnT(∇nΘ+ˆ
zS·∇nΘ)·∇p
=−AnT ∇nΘ·∇np. (39.143)
Thus, thermobaricity can either increase or decrease density. However, for the bulk of the ocean, thermo-
baricity tends to increase density, just as cabbeling.
The tendency for the non-Boussinesq steric effect from thermobaricity in an ocean climate model is
determined according to
∂η
∂t !thermob
=−
η
Z
−H
dzTAn∇np·∇nΘ.(39.144)
39.7 Parameterized quasi-Stokes transport and global mean sea level
We now consider how the parameterization of quasi-Stokes transport impacts on the non-Boussinesq
steric effect with a focus on its contribution to global mean sea level.
39.7.1 Formulation with buoyancy impacted by quasi-Stokes transport
To start, we make use of the non-divergent condition ∇·(ρv∗) = 0 (see equation (39.30)) satisfied by the
parameterized eddy-induced velocity v∗to write the contribution to the non-Boussinesq steric term from
Elements of MOM November 19, 2014 Page 577

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.7
quasi-Stokes advection
− 1
ρ
dρ
dt!quasi-Stokes
= αdΘ
dt−βdS
dt!quasi-Stokes
=1
ρ(−α∇·(ρv∗Θ) + β∇·(ρv∗S))
=v∗·(−α∇Θ+β∇S),
(39.145)
with the final expression in the form of an advection of buoyancy by the quasi-Stokes velocity. We now
introduce the vector streamfunction for the quasi-Stokes mass transport
ρv∗=∇∧ρΨ
=∂z(ρΥ)−ˆ
z∇z·(ρΥ),(39.146)
where Ψ=Υ∧ˆ
zis the quasi-Stokes vector streamfunction, and Υis the eddy induced transport (see
Section 39.1.3.2), which then leads to
− 1
ρ
dρ
dt!quasi-Stokes
=∂z(ρΥ)· −α∇zΘ+β∇zS
ρ!−∇z·(ρΥ) −α ∂zΘ+β ∂zS
ρ!.(39.147)
We specialize this result to the case of a stable vertical stratification (i.e., the buoyancy frequency N2>0),
in which case
− 1
ρ
dρ
dt!quasi-Stokes
= N2
ρg !∇n·(ρΥ),(39.148)
where ∇n=∇z+S∂zis the projected neutral gradient operator introduced by equation (39.132), N2is the
squared buoyancy frequency given by equation, and Sis the neutral slope given by equation (39.133). The
special case of the Gent et al. (1995) parameterization is revealing and most pertinent given its ubiquitous
use in ocean climate modelling to parameterize quasi-Stokes transport from mesoscale eddies. Here, we
set the quasi-Stokes transport to
Υgm =−Agm S=−Agm ∇nz, (39.149)
where Agm >0is a diffusivity, and
S=∇nz(39.150)
is an alternative expression for the neutral slope, written here in terms of the projected lateral gradient of
the depth of the neutral tangent plane (e.g., equation (6.6) of Griffies,2004). These expressions for the
parameterized quasi-Stokes transport yield
− 1
ρ
dρ
dt!gm
=− N2
ρg !∇n·(ρ Agm ∇nz).(39.151)
The operator on the right hand side represents a neutral diffusion of the depth of a neutral tangent plane.
We can make this correspondence precise through introducing the inverse infinitesimal thickness between
two neutral tangent planes1
h= dz= ρN2
g!−1
dγ, (39.152)
where dγis the density increment between the two tangent planes. This substitution leads to
− 1
ρ
dρ
dt!gm
=− 1
ρ2hg !∇n·N2Agm ρ2h∇nz.(39.153)
When surfaces of constant buoyancy bow downwards, as in a warm core eddy (see Figure 39.3), this
configuration represents a local minimum in the height of the buoyancy surface (or maximum in the depth).
1For example, see equation (9.70) in Griffies (2004) for the isopycnal diffusion operator in isopycnal coordinates.
Elements of MOM November 19, 2014 Page 578
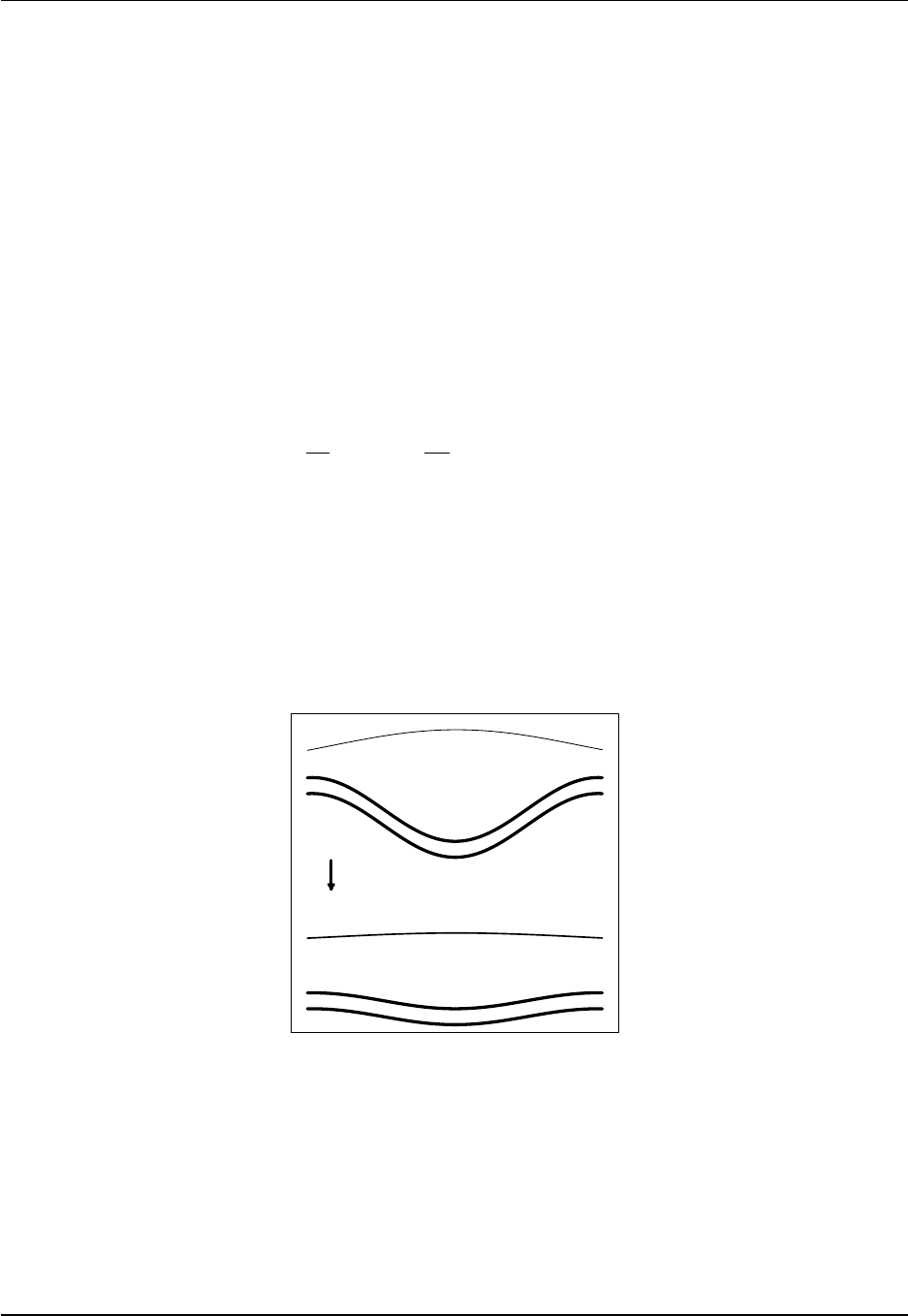
Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
The curvature of this surface is negative, so that the diffusion operator (39.151) is positive. The Gent
et al. (1995) scheme acts to dissipate the negative curvature by transporting light water away from the
anomalously light region, thus raising the depth maxima. That is, heat is transported away from a warm
core eddy. This physical interpretation of Gent et al. (1995) accords with its implementation in isopycnal
coordinate ocean models, where it appears as an isopycnal layer depth diffusion rather than an isopycnal
layer thickness diffusion (see Section 11.3.2 of Griffies et al. (2000a)). The common interpretation as a
thickness diffusion is only valid when the diffusivity is depth independent (see Section 9.5.4 of Griffies,
2004), and the ocean bottom is flat (see Section 11.3.2 of Griffies et al. (2000a)).
39.7.2 Effects on global mean sea level
So how does diffusion of the depth of a neutral tangent plane contribute to the global mean sea level
through the non-Boussinesq steric effect? This question is answered by taking the vertical integral of the
GM effect in equation (39.151) to find
∂η
∂t !gm
=−
η
Z
−H N2
ρg !∇n·(ρ Agm ∇nz)dz. (39.154)
Hence, the parameterized quasi-Stokes transport of buoyancy acts to erode depth maxima by raising
buoyancy surfaces, which in turn renders a negative tendency to global mean sea level through the non-
Boussinesq steric effect (see Figure 39.3). Conversely, the global mean sea level is raised on the flanks of
sea level maxima.
The behaviour exhibited in Figure 39.3 reflects the compensation between downward bowing buoyancy
surfaces and upward bowing sea level in a baroclinic ocean respecting hydrostatic balance (e.g., Tomczak
and Godfrey,1994). Figure 39.3 depicts the effect of Gent et al. (1995) for a 1.5 layer ocean.
z=η
isopycnals
GM effect
z=η
Figure 39.3: Schematic to illustrate the impact of the Gent et al. (1995) parameterization on isopycnals
(dark curves) and sea level (through the non-Boussinesq steric effect), assuming the idealized case of a 1.5
layer ocean. Note that the slope of the pycnocline is about 100-300 times larger than the sea level (Rule 1a of
Tomczak and Godfrey,1994). As the Gent et al. (1995) scheme shoals the depth of the depressed pycnocline
(moving from the top portion of the panel to the lower portion), it also lowers sea level. The opposite
follows for the case of a raised pycnocline, in which the depressed sea level is raised as the pycnocline is
lowered. In particular, as warm water is transported away from the core of a warm eddy, sea level is lowerd
through the non-Boussinesq steric effect.
Elements of MOM November 19, 2014 Page 579

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
39.8 MOM sea level diagnostics: Version I
Here we summarize diagnostics related to Version I of the kinematic sea level equation as detailed in Sec-
tion 39.2.1. As discussed in Griffies and Greatbatch (2012), these diagnostics are most useful in assessing
how various terms contribute to the evolution of global mean sea level.
39.8.1 Surface buoyancy fluxes
Each of the following diagnostics are computed inside the module
ocean core/ocean sbc.F90
Each term has units of m s−1. Additionally, note that the thermal expansion and haline contraction coeffi-
cients are evaluated in MOM according to equations (39.42) and (39.43).
•eta tend sw: This diagnostic measures the contribution due to the net surface shortwave radiation
eta tend sw = α Qsw
cpρ!k=1
,(39.155)
where Qsw is the shortwave heat flux crossing through the ocean surface. The global area mean of
eta tend sw is saved in eta tend sw glob.
•eta tend lw: This diagnostic measures the contribution due to the net surface longwave radiation
eta tend lw = α Qlw
cpρ!k=1
,(39.156)
where Qlw is the longwave heat flux crossing through the ocean surface. The global area mean of
eta tend lw is saved in eta tend lw glob.
•eta tend sens: This diagnostic measures the contribution due to the net surface sensible heating
eta tend sens = α Qsens
cpρ!k=1
,(39.157)
where Qsens is the sensible heat flux crossing through the ocean surface. The global area mean of
eta tend sens is saved in eta tend sens glob.
•eta tend evap heat: This diagnostic measures the contribution due to the net surface latent heat of
vaporization acting to cool the upper ocean
eta tend evap heat = α Qvaporization
cpρ!k=1
,(39.158)
where Qvaporization is the latent heat of vaporization impacting the surface ocean. The global area mean
of eta tend evap heat is saved in eta tend evap heat glob.
•eta tend fprec melt: This diagnostic measures the contribution due to the net latent heat of fusion
from frozen precipitation acting to cool the upper ocean
eta tend fprec melt = α Qfprec fusion
cpρ!k=1
,(39.159)
where Qfprec fusion is the latent heat of fusion from frozen precipitation impacting the surface ocean. The
global area mean of eta tend fprec melt is saved in eta tend fprec melt glob.
Elements of MOM November 19, 2014 Page 580

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
•eta tend iceberg melt: This diagnostic measures the contribution due to the net latent heat of
fusion from solid land ice or icebergs that act to cool the upper ocean
eta tend iceberg melt = α Qiceberg fusion
cpρ!k=1
,(39.160)
where Qiceberg fusion is the latent heat of fusion from icebergs that impacting the surface ocean. The
global area mean of eta tend iceberg melt is saved in eta tend fprec iceberg melt glob.
•eta tend heat coupler: This diagnostic measures the contribution due to the total surface heating
on the ocean surface
eta tend heat coupler = α Qcoupler heat
cpρ!k=1
,(39.161)
where Qcoupler heat is the surface ocean heat that enters through the coupler. This heat includes short-
wave, longwave, sensible, and latent heating, so that we have the identity
eta tend heat coupler =eta tend sw +eta tend lw +eta tend sens
+eta tend evap heat +eta tend fprec melt +eta tend iceberg melt.
(39.162)
The global area mean of eta tend heat coupler is saved in eta tend fprec heat coupler glob.
•eta tend heat restore: This diagnostic measures the contribution due to the heat input to the
ocean through surface restoring, as may occur in idealized simulations
eta tend heat restore = α Qheat restoring
cpρ!k=1
,(39.163)
where Qheat restoring is the heat input through surface restoring. The global area mean of eta tend heat restore
is saved in eta tend fprec heat restore glob.
•eta tend salt coupler: This diagnostic measures the contribution due to the salt input to the ocean
through the coupler, with such salt generally limited to regions of sea ice (see Section 39.3.4.2)
eta tend salt coupler =− β Qsalt coupler
cpρ!k=1
,(39.164)
where Qsalt coupler is the salt flux entering through the surface ocean. The global area mean of eta tend salt coupler
is saved in eta tend fprec salt coupler glob.
•eta tend salt restore: This diagnostic measures the contribution due to the salt input to the ocean
through surface restoring, as may occur in idealized simulations
eta tend salt restore =− β Qsalt restoring
cpρ!k=1
,(39.165)
where Qsalt restoring is the salt input through surface restoring. The global area mean of eta tend salt restore
is saved in eta tend fprec salt restore glob.
39.8.2 Surface mass fluxes
Each of the following diagnostics are computed inside the module
ocean core/ocean sbc.F90
Each term has units of m s−1.
Elements of MOM November 19, 2014 Page 581

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
•eta tend evap: This diagnostic measures the contribution due to the mass of water exchanged due
to evaporation or condensation at the ocean surface
eta tend evap = Qevaporation
ρ!k=1
,(39.166)
where Qevaporation is the mass exchanged due to evaporation or condensation. The global area mean of
eta tend evap is saved in eta tend evap glob.
•eta tend lprec: This diagnostic measures the contribution due to the mass of water exchanged due
to liquid precipitation at the ocean surface
eta tend lprec = Qliquid precip
ρ!k=1
,(39.167)
where Qliquid precip is the mass exchanged due to liquid precipitation. The global area mean of eta tend lprec
is saved in eta tend lprec glob.
•eta tend fprec: This diagnostic measures the contribution due to the mass of water exchanged due
to frozen precipitation at the ocean surface
eta tend fprec = Qfrozen precip
ρ!k=1
,(39.168)
where Qfrozen precip is the mass exchanged due to frozen precipitation (i.e., snow). The global area mean
of eta tend fprec is saved in eta tend fprec glob.
•eta tend runoff: This diagnostic measures the contribution due to the mass of water exchanged
due to liquid river runoffat the ocean surface
eta tend runoff = Qliquid runoff
ρ!k=1
,(39.169)
where Qliquid runoffis the mass exchanged due to liquid river runoff. The global area mean of eta tend runoff
is saved in eta tend runoff glob.
•eta tend iceberg: This diagnostic measures the contribution due to the mass of water exchanged
due to solid river runoff(i.e., icebergs) at the ocean surface
eta tend iceberg = Qiceberg
ρ!k=1
,(39.170)
where Qiceberg is the mass exchanged due to solid river runoff. The global area mean of eta tend iceberg
is saved in eta tend iceberg glob.
•eta tend water coupler: This diagnostic measures the net contribution due to the mass of water
exchanged through the coupler at the ocean surface
eta tend water coupler = Qwater coupler
ρ!k=1
,(39.171)
where Qwater coupler is the mass exchanged due to all water crossing the ocean surface as mediated by
the coupler. This tendency is equal to
eta tend water coupler =eta tend evap +eta tend lprec +eta tend fprec
+eta tend runoff +eta tend iceberg.(39.172)
The global area mean of eta tend water coupler is saved in eta tend water coupler glob.
Elements of MOM November 19, 2014 Page 582

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
39.8.3 Bottom heat flux
The following diagnostic is computed inside the module
ocean core/ocean bbc.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend geoheat: This diagnostic measures the contribution due to the net bottom geothermal
heating
eta tend geoheat = α Qgeoheat
cpρ!k=kmt
,(39.173)
where Qgeoheat is the geothermal heat flux crossing through the ocean bottom, and k=kmt is the bottom
grid cell. The global area mean of eta tend geoheat is saved in eta tend geoheat glob.
39.8.4 River insertion of liquid and solid water
The following diagnostic is computed inside the module
ocean param/sources/ocean rivermix.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend rivermix: This diagnostic measures the contribution due to the insertion of river water
(solid plus liquid) into the ocean (see Chapter 28)
eta tend rivermix =−X
k" dz
ρ!neut rho rivermix#,(39.174)
where neut rho rivermix is the time tendency for locally reference potential density, with this diag-
nostic detailed in Section 36.10.7. The global area mean of eta tend rivermix is saved in eta tend rivermix glob.
39.8.5 River insertion of liquid water
The following diagnostic is computed inside the module
ocean param/sources/ocean rivermix.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend runoffmix: This diagnostic measures the contribution due to the insertion of river water
(solid plus liquid) into the ocean (see Chapter 28)
eta tend runoffmix =−X
k" dz
ρ!neut rho runoffmix#,(39.175)
where neut rho runoffmix is the time tendency for locally reference potential density, with this
diagnostic detailed in Section 36.10.9. The global area mean of eta tend runoffmix is saved in
eta tend runoffmix glob.
Elements of MOM November 19, 2014 Page 583
Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
39.8.6 River insertion of solid water
The following diagnostic is computed inside the module
ocean param/sources/ocean rivermix.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend calvingmix: This diagnostic measures the contribution due to the insertion of river water
(solid plus liquid) into the ocean (see Chapter 28)
eta tend calvingmix =−X
k" dz
ρ!neut rho calvingmix#,(39.176)
where neut rho calvingmix is the time tendency for locally reference potential density, with this
diagnostic detailed in Section 36.10.11. The global area mean of eta tend calvingmix is saved in
eta tend calvingmix glob.
39.8.7 Heating of liquid ocean due to frazil formation
The following diagnostic is computed inside the module
ocean tracers/ocean tracer.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend frazil: This diagnostic measures the contribution due to the heating of liquid water due
to frazil formation (see Section 39.3.4.1)
eta tend frazil =−X
k" dz
ρ!neut rho frazil#,(39.177)
where neut rho frazil is the time tendency for locally reference potential density, with this diagnos-
tic detailed in Section 36.11.7.1. The global area mean of eta tend frazil is saved in eta tend frazil glob.
39.8.8 Motion across pressure surfaces
The following diagnostic is computed inside the module
ocean core/ocean advection velocity.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend press: This diagnostic measures the contribution due to the motion across pressure sur-
faces (see Section 39.3.2 and equation (39.67))
eta tend press =g(H+η) w(p)
c2
sound !z
.(39.178)
The global area mean of eta tend press is saved in eta tend press glob. Note that even if not using
pressure as the vertical coordinate, the vertical velocity component across pressure surfaces, w(p),
is very well approximated by the vertical velocity component across geopotential, z∗, or p∗surfaces.
Elements of MOM November 19, 2014 Page 584

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
39.8.9 Mixing associated with vertical diffusion
The following diagnostic is computed inside the module
ocean param/mixing/ocean vert mix.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
There are two forms computed for this diagnostic. The first is based on the integration by parts manipu-
lations considered in Section 39.3.3. Here, we expose the product between flux components and gradients
of α/ρ and β/ρ, which then leads to the interior source term given by the third term in equation (39.89).
The second approach is based directly on equation (39.72) prior to any integration by parts manipulations.
Both approaches are equivalent in the continuum for processes those that have zero boundary fluxes. The
second approach is simpler to diagnose, since it works directly on tendencies rather than requiring the
product of flux components with the gradients of α/ρ and β/ρ. However, the first form is more directly
related to physical interpretations, as it exposes flux components.
•eta tend diff cbt flx: This diagnostic measures the contribution due to vertical diffusion (see
Section 39.5 and equation (39.119)) just associated with the dianeutral diffusivities diff cbt t and
diff cbt s
eta tend diff cbt flx =−
η
Z
−H
dz ρ hDΘ∂zΘ∂z(α/ρ)−DS∂zS ∂z(β/ρ)i.(39.179)
The global area mean of eta tend diff cbt flx is saved in eta tend diff cbt flx glob.
•eta tend diff cbt tend: This diagnostic measures the contribution due to vertical diffusion just
arising from the dianeutral diffusivity diff cbt t and diff cbt s (see Section 39.5 prior to exposing
the flux components
eta tend diff cbt tend =−X
k" dz
ρ!neut rho diff cbt#,(39.180)
where neut rho diff cbt is the time tendency for locally reference potential density, with this diag-
nostic detailed in Section 36.11.3.2. The global area mean of eta tend diff cbt tend is saved in
eta tend diff cbt tend glob.
39.8.10 Mixing associated with neutral diffusion
The following diagnostic is computed inside the module
ocean param/neutral/ocean nphysics util.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
There are two general approaches to this diagnostic:
•numerical method: This approach computes the contribution to sea level tendency associated with
the full neutral diffusion operator, including the portion within the upper ocean boundary layer where
neutral diffusion exponentially transforms into horizontal diffusion as per the recommendations from
Treguier et al. (1997), Ferrari et al. (2008), and Ferrari et al. (2010).
Within this method there are also two approaches:
–The first is based on the integration by parts manipulations considered in Section 39.3.3. Here,
we expose the product between flux components and gradients of α/ρ and β/ρ, which then leads
to the interior source term given by the third term in equation (39.89).
Elements of MOM November 19, 2014 Page 585

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
–The second approach is based directly on equation (39.72) prior to any integration by parts
manipulations.
Both approaches are equivalent in the continuum for processes such as neutral diffusion that have
zero boundary fluxes. The second approach is simpler to diagnose, since it works directly on tenden-
cies rather than requiring the product of flux components with the gradients of α/ρ and β/ρ. However,
the first form is more directly related to physical interpretations, as it exposes flux components.
•analytical method: This approach computes the contribution to cabbeling and thermobaricity ac-
cording to the analytical manipulations detailed in Sections 39.6.6 and 39.6.7.
An approximate means to isolate the effects of horizontal diffusion is found by subtracting the cabbeling
and thermobaricity pieces from the full neutral diffusion operator.
•eta tend ndiff flx: This diagnostic measures the contribution due to the neutral diffusion operator
(see Section 39.6), including all contributions to the horizontal and vertical flux components
eta tend ndiff flx =
η
Z
−H
dzhJ(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)i,(39.181)
where the three-dimensional temperature and salinity fluxes are computed according to the neu-
tral diffusion operator. Note that we incorporate all pieces of the flux components, including the
implicit-in-time piece of the vertical flux. The global area mean of eta tend ndiff flx is saved in
eta tend ndiff flx glob. This diagnostic has been implemented only for the
ocean param/nphysics/ocean nphysicsC.F90
module.
•eta tend ndiff tend: This diagnostic measures the contribution due to neutral diffusion prior to
exposing the flux components, and without including the time-implicit portion of the K33 term
eta tend ndiff tend =−X
k" dz
ρ!neut rho ndiff#,(39.182)
where neut rho ndiff is the time tendency for locally reference potential density, with this diag-
nostic detailed in Section 36.11.4.1. The global area mean of eta tend ndiff tend is saved in
eta tend ndiff tend glob.
•eta tend k33 tend: This diagnostic measures the contribution due to time-implicit portion of the K33
term from neutral diffusion
eta tend k33 tend =−X
k" dz
ρ!neut rho k33#,(39.183)
where neut rho k33 is the time tendency for locally reference potential density, with this diagnostic
detailed in Section 36.11.3.7. The global area mean of eta tend k33 tend is saved in eta tend k33 tend glob.
Combining with the diagnostic eta tend ndiff tend yields an approximation to the full neutral dif-
fusion operator. Hence, when globally integrated, this result should approximate that from the diag-
nostic eta tend ndiff flx glob:
eta tend ndiff tend glob +eta tend k33 tend glob ≈eta tend ndiff flx glob.(39.184)
•cabbeling tend intz: This diagnostic measures the contribution due to cabbeling (see Section 39.6.6
and equation (39.140))
cabbeling tend intz =
η
Z
−H
dzCAn(∇nΘ)2.(39.185)
Elements of MOM November 19, 2014 Page 586

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
The global area mean of cabbeling tend intz is saved in cabbeling tend intz glob. To compute
the contribution to sea level requires a minus sign
sea level tendency from cabbeling =−cabbeling tend intz.(39.186)
•thermobaric tend intz: This diagnostic measures the contribution due to thermobaricity (see Sec-
tion 39.6.7 and equation (39.144))
thermobaric tend intz =
η
Z
−H
dzTAn∇np·∇nΘ.(39.187)
The global area mean of thermobaric tend intz is saved in thermobaric tend intz glob. To com-
pute the contribution to sea level requires a minus sign
sea level tendency from thermobaricity =−thermobaric tend intz.(39.188)
39.8.11 Parameterized eddy advection from GM
The following diagnostic is computed inside the module
ocean param/neutral/ocean nphysics util.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43). There are two general approaches to this
diagnostic:
•numerical method: This approach computes the contribution to sea level tendency associated with
the full mesoscale eddy induced quasi-Stokes transport operator. Within this method there are also
two approaches:
–The first is based on the integration by parts manipulations considered in Section 39.3.3. Here,
we expose the product between flux components and gradients of α/ρ and β/ρ, which then leads
to the interior source term given by the third term in equation (39.89).
–The second approach is based directly on equation (39.72) prior to any integration by parts
manipulations.
Both approaches are equivalent in the continuum for processes those that have zero boundary fluxes.
The second approach is simpler to diagnose, since it works directly on tendencies rather than requir-
ing the product of flux components with the gradients of α/ρ and β/ρ. However, the first form is more
directly related to physical interpretations, as it exposes flux components.
•analytical method: This approach computes the contribution to cabbeling and thermobaricity ac-
cording to the analytical manipulations detailed in Section 39.7.
•eta tend gm flx: This diagnostic measures the contribution due to the eddy-induced transport from
either Gent et al. (1995)orFerrari et al. (2010) (see Section 39.7)
eta tend gm flx =
η
Z
−H
dzhJ(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)i,(39.189)
where the three-dimensional temperature and salinity fluxes are computed according to the quasi-
Stokes transport operator. The global area mean of eta tend gm flx is saved in eta tend gm flx glob.
This diagnostic has been implemented only for the
ocean param/nphysics/ocean nphysicsC.F90
module.
Elements of MOM November 19, 2014 Page 587

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
•eta tend gm tend: This diagnostic measures the contribution due to parameterized quasi-Stokes
transport (see Section 39.7) prior to exposing the flux components
eta tend gm tend =−X
k" dz
ρ!neut rho gm#,(39.190)
where neut rho gm is the time tendency for locally reference potential density, with this diagnostic
detailed in Section 36.10.3. The global area mean of eta tend gm tend is saved in eta tend gm tend glob.
•eta tend gm90: This diagnostic measures the contribution due to the Gent and McWilliams (1990)
parameterization of eddy advection (see Section 39.7 and equation (39.154)), which is written in the
following analytic form
eta tend gm90 =−
η
Z
−H N2
ρg !∇n·(ρ Agm ∇nz)dz. (39.191)
The global area mean of eta tend gm90 is saved in eta tend gm90 glob. As this diagnostic computes
the contribution based on an analytic form, it is generally not as precise as the diagnostic computed
from the actual numerical implementation. For this reason, we recommend eta tend gm flx for more
precise calculations required for sea level budgets.
39.8.12 Parameterized eddy advection from submesoscale parameterization
The following diagnostic is computed inside the module
ocean param/mixing/ocean submesoscale.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
There are two forms computed for this diagnostic. The first is based on the integration by parts manipu-
lations considered in Section 39.3.3. Here, we expose the product between flux components and gradients
of α/ρ and β/ρ, which then leads to the interior source term given by the third term in equation (39.89).
The second approach is based directly on equation (39.72) prior to any integration by parts manipulations.
Both approaches are equivalent in the continuum for processes those that have zero boundary fluxes. The
second approach is simpler to diagnose, since it works directly on tendencies rather than requiring the
product of flux components with the gradients of α/ρ and β/ρ. However, the first form is more directly
related to physical interpretations, as it exposes flux components.
•eta tend submeso flx: This diagnostic measures the contribution due to the Fox-Kemper et al. (2008b)
submesoscale eddy parameterization
eta tend submeso flx =
η
Z
−H
dzhJ(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)i,(39.192)
where the three-dimensional temperature and salinity fluxes are computed according to the quasi-
Stokes transport operator according to the Fox-Kemper et al. (2008b) scheme. The global area mean
of eta tend submeso flx is saved in eta tend submeso flx glob.
•eta tend submeso tend: This diagnostic measures the contribution due to parameterized quasi-
Stokes transport from submesoscale processes according to Fox-Kemper et al. (2008b), with this
diagnostic computed prior to exposing the flux components
eta tend submeso tend =−X
k" dz
ρ!neut rho submeso#,(39.193)
where neut rho submeso is the time tendency for locally referenced potential density, with this di-
agnostic detailed in Section 36.10.4. The global area mean of eta tend submeso tend is saved in
eta tend submeso tend glob.
Elements of MOM November 19, 2014 Page 588
Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
39.8.13 Parameterized horizontal diffusion from submesoscale parameterization
The following diagnostic is computed inside the module
ocean param/mixing/ocean submesoscale.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
There are two forms computed for this diagnostic. The first is based on the integration by parts manipu-
lations considered in Section 39.3.3. Here, we expose the product between flux components and gradients
of α/ρ and β/ρ, which then leads to the interior source term given by the third term in equation (39.89).
The second approach is based directly on equation (39.72) prior to any integration by parts manipulations.
Both approaches are equivalent in the continuum for processes those that have zero boundary fluxes. The
second approach is simpler to diagnose, since it works directly on tendencies rather than requiring the
product of flux components with the gradients of α/ρ and β/ρ. However, the first form is more directly
related to physical interpretations, as it exposes flux components.
•eta tend subdiff flx: This diagnostic measures the contribution due to the horizontal diffusive as-
pects motivated by the Fox-Kemper et al. (2008b) submesoscale eddy parameterization (see Section
24.6)
eta tend subdiff flx =
η
Z
−H
dzhJ(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)i,(39.194)
where the two-dimensional horizontal temperature and salinity diffusive fluxes are computed accord-
ing to Section 24.6. The global area mean of eta tend subdiff flx is saved in eta tend subdiff flx glob.
•eta tend subdiff tend: This diagnostic measures the contribution due to the horizontal diffusive
aspects motivated by the Fox-Kemper et al. (2008b) submesoscale eddy parameterization (see Sec-
tion 24.6), with this diagnostic computed prior to exposing the flux components
eta tend subdiff tend =−X
k" dz
ρ!neut rho subdiff#,(39.195)
where neut rho subdiff is the time tendency for locally referenced potential density. The global
area mean of eta tend submeso tend is saved in eta tend submeso tend glob.
39.8.14 Penetrative shortwave radiation
The following diagnostic is computed inside the module
ocean param/sources/ocean shortwave.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend sw pen: This diagnostic measures the contribution due to the penetrative shortwave radi-
ation (see Chapter 17).
eta tend sw pen =
η
Z
−H
dzhJ(Θ)·∇(α/ρ)−J(S)·∇(β/ρ)i,(39.196)
where the three-dimensional temperature and salinity fluxes are computed according to the short-
wave penetration scheme. All components of the salt flux are zero, as are the horizontal tempera-
ture flux components. The vertical temperature flux component is diagnosed given the temperature
Elements of MOM November 19, 2014 Page 589

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.8
tendency from the shortwave scheme, and assuming the surface shortwave flux component is com-
puted from the surface flux module and thus contained in eta tend sw (see Section 39.8.1). That is,
we compute
J(θ)(k) = J(θ)(k−1) + th tendency(k),(39.197)
where J(θ)(k= 0) = 0, and th tendency(k) is the thickness and density weighted temperature ten-
dency from the penetrative shortwave scheme. The global area mean of eta tend sw pen is saved in
eta tend sw pen glob.
39.8.15 Sigma transport
The following diagnostic is computed inside the module
ocean param/mixing/ocean sigma transport.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend sigma: This diagnostic measures the contribution from sigma transport scheme. Since this
scheme is not implemented as a traditional flux-form, we diagnose its contribution just based on its
tendency
eta tend sigma =−X
k" dz
ρ!neut rho sigma#,(39.198)
where neut rho sigma is the time tendency for locally referenced potential density, with this diagnos-
tic detailed in Section 36.11.6.5. The global area mean of eta tend sigma is saved in eta tend sigma glob.
39.8.16 Mixdownslope
The following diagnostic is computed inside the module
ocean param/mixing/ocean mixdownslope.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend mixdown: This diagnostic measures the contribution from mixdown transport scheme. Since
this scheme is not implemented as a traditional flux-form, we diagnose its contribution just based on
its tendency
eta tend mixdown =−X
k" dz
ρ!neut rho mixdown#,(39.199)
where neut rho mixdown is the time tendency for locally referenced potential density, with this diag-
nostic detailed in Section 36.11.6.4. The global area mean of eta tend mixdown is saved in eta tend mixdown glob.
39.8.17 KPP nonlocal mixing
The following diagnostic is computed inside the module
ocean param/mixing/ocean vert kpp.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
Elements of MOM November 19, 2014 Page 590

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.9
•eta tend kpp nloc: This diagnostic measures the contribution from nonlocal KPP transport scheme
Large et al. (1994). Since this scheme is not implemented as a traditional flux-form, we diagnose its
contribution just based on its tendency
eta tend kpp nloc =−X
k" dz
ρ!neut rho kpp nloc#,(39.200)
where neut rho kpp nloc is the time tendency for locally referenced potential density, with this di-
agnostic detailed in Section 36.11.3.10. The global area mean of eta tend kpp nloc is saved in
eta tend kpp nloc glob.
39.8.18 Cross land mixing
The following diagnostic is computed inside the module
ocean param/sources/ocean xlandmix.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend xmix: This diagnostic measures the contribution from cross land mixing scheme. Since this
scheme is not implemented as a traditional flux-form, we diagnose its contribution just based on its
tendency
eta tend xmix =−X
k" dz
ρ!neut rho xmix#,(39.201)
where neut rho xmix is the time tendency for locally referenced potential density, with this diagnos-
tic detailed in Section 36.11.6.6. The global area mean of eta tend xmix is saved in eta tend xmix glob.
39.8.19 Cross land insertion
The following diagnostic is computed inside the module
ocean param/sources/ocean xlandinsert.F90
It has units of m s−1. Additionally, note that the thermal expansion and haline contraction coefficients are
evaluated in MOM according to equations (39.42) and (39.43).
•eta tend xinsert: This diagnostic measures the contribution from cross land mixing scheme. Since
this scheme is not implemented as a traditional flux-form, we diagnose its contribution just based on
its tendency
eta tend xinsert =−X
k" dz
ρ!neut rho xinsert#,(39.202)
where neut rho xinsert is the time tendency for locally referenced potential density, with this diag-
nostic detailed in Section 36.11.6.7. The global area mean of eta tend xinsert is saved in eta tend xinsert glob.
39.8.20 Smoothing of free surface or bottom pressure
•eta tend smooth: This diagnostic measures the contribution from the smoothing of either the sur-
face height or bottom pressure. Since this scheme is not implemented as a traditional flux-form, we
diagnose its contribution just based on its tendency
eta tend smooth =−X
k" dz
ρ!neut rho smooth#,(39.203)
where neut rho smooth is the time tendency for locally referenced potential density, with this diag-
nostic detailed in Section 36.11.7.2. The global area mean of eta tend smooth is saved in eta tend smooth glob.
Elements of MOM November 19, 2014 Page 591

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.9
39.9 MOM sea level diagnostics: Version II
Here we summarize diagnostics related to Version II of the kinematic sea level equation as detailed in Sec-
tion 39.2.2 (see equation (39.58)). As discussed in Griffies and Greatbatch (2012), these diagnostics are
often used in assessing how various terms contribute to the evolution of regional sea level. The diagnos-
tics are approximate when using the volume conserving Boussinesq form of MOM, and more accurate when
using the mass conserving non-Boussinesq form. Each diagnostic field is computed inside the module
ocean core/ocean barotropic.F90
The tendencies are in units of m s−1and the sealevel has units of meter.
•eta nonbouss tend: This diagnostic measures the contribution due to the evolution of the mass
conserving non-Boussinesq sea level according to equation (39.57)
eta nonbouss tend =Qm−∇·Uρ−(H+η)∂ρz/∂t
ρz+sources.(39.204)
Contributions from sources are associated with such non-local processes as cross-land mixing and
insertion (Chapters 29 and 30). Sources are also accounting for numerically motivated smooth-
ing the free surface, which optionally occurs to suppress the checker-board null mode present for
gravity waves on a B-grid (Section 31.1). The global area mean of eta nonbouss tend is saved in
eta nonbouss tend global.
•eta nonbouss: This diagnostic time steps the sea level as forced by eta nonbouss tend. Accordingly,
for a Boussinesq model it approximates the non-Boussinesq sea level. For a non-Boussinesq model,
eta nonbouss should agree quite closely to the actual eta t field.
eta nonbouss(τ+ 1) = eta nonbouss(τ) + ∆τeta nonbouss tend.(39.205)
The global area mean of eta nonbouss is saved in eta nonbouss global.
•eta dynamic tend: This diagnostic measures the contribution from the convergence of the depth
integrated mass transport in equation (39.57)
eta dynamic tend =− ∇·Uρ
ρz!.(39.206)
When using the Boussinesq version of MOM, we approximate this term using
eta dynamic tend ≈ −∇·UBoussinesq.(39.207)
The global area mean of eta dynamic tend is saved in eta dynamic tend global.
•eta water tend: This diagnostic measures the contribution from the mass fluxes crossing the ocean
surface (see equation 39.57))
eta water tend =Qm
ρz.(39.208)
When using the Boussinesq version of MOM, we approximate this diagnostic using
eta water tend ≈Qm
ρo
Boussinesq.(39.209)
The global area mean of eta water tend is saved in eta water tend global.
Elements of MOM November 19, 2014 Page 592

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.9
•eta nonsteric tend: This diagnostic measures the contribution due to the terms not associated
with the steric effect (see equation (39.57))
eta nonsteric tend =Qm−∇·Uρ
ρz+sources.(39.210)
When using the Boussinesq version of MOM, we approximate this diagnostic using
eta nonsteric tend ≈Qm
ρo−∇·U+sources.Boussinesq.(39.211)
The global area mean of eta nonsteric tend is saved in eta nonsteric tend global.
•eta source tend: This diagnostic measures the contribution due to the source terms associated
with such non-local processes as cross-land mixing and insertion (Chapters 29 and 30). Sources are
also accounting for numerically motivated smoothing the free surface, which optionally occurs to
suppress the checker-board null mode present for gravity waves on a B-grid (Section 31.1).
eta source tend =sources.(39.212)
The global area mean of eta source tend is saved in eta source tend global.
•eta steric tend: This diagnostic measures the contribution due to the term associated with the
local steric effect (see equation (39.57))
eta steric tend =− (H+η)∂ρz/∂t
ρz!.(39.213)
The global area mean of eta steric tend is saved in eta steric tend global.
Elements of MOM November 19, 2014 Page 593

Chapter 39. Diagnosing the contributions to sea level evolution Section 39.9
Elements of MOM November 19, 2014 Page 594

Chapter 40
Gyre and overturning contributions to
tracer transport
Contents
40.1 Formulation ............................................595
40.2 Enabling the diagnostic .....................................596
The purpose of this chapter is to discuss the diagnostic in MOM that computes the contribution to ad-
vective tracer transport in the j-direction (generalized meridional) associated with gyre and overturning
components of the flow. Bryan and Lewis (1979) were amongst the first to make use of this diagnostic,
and Peixoto and Oort (1992) (page 342) describe the decomposition in more detail. The gyre component
has traditionally been associated with wind driven processes, and overturning associated with thermoha-
line processes. However, this physical association is not clean, as it is generally not possible to split the
transport into two distinct physical processes. For example, removing wind forcing does not necessarily
mean the gyre contribution is zero. Nonetheless, this decomposition is commonly performed, and such
has provided some physical insight into the flow characteristics.
Note that in the present implementation, only the resolved advective transport is included in the gyre
and overturning diagnostic. A more complete implementation should include eddy induced transport as-
sociated with mesoscale closure of Gent et al. (1995) (Chapter 23) and the submesoscale scheme of Fox-
Kemper et al. (2008b) (Chapter 24).
The following MOM module is directly connected to the material in this chapter:
ocean tracers/ocean tracer advect.F90
40.1 Formulation
The meridional advective transport of a tracer within a particular ocean basin is given by the integral
H(y,t) =
x2
Z
x1
dx
η
Z
−H
dzρ C v, (40.1)
where vis the meridional velocity component, ρis the in situ density, Cis the tracer concentration,
z=−H(x,y)is the ocean bottom, z=η(x,y,t)is the ocean surface, and x1and x2are the longitudinal
boundaries of the basin or global ocean. With the generalized horizontal coordinates in MOM, the coordi-
nate yis assumed to be aligned with the jgrid lines. For the purposes of this diagnostic, we do not perform
595

Chapter 40. Gyre and overturning contributions to tracer transport Section 40.2
a rotation of the flow to the geographical longitude and latitude. For the tripolar grid commonly used for
global modeling with MOM, generalized zonal integrals along i-lines yield j-transport, and this is sufficient
for most diagnostic purposes. Note the term north will continue to be used, with this generally denoting
the j-direction, which corresponds to the geographical north when j-lines are parallel to longitudes.
In MOM, the density and thickness weighted advective velocity component
V=v ρdz(40.2)
is computed and held in the array vhrho nt, where ρreduces to the constant Boussinesq density ρofor the
Boussinesq version of MOM, but it remains the in situ density for the nonBoussinesq version. The product
dxVmeasures the mass per time of seawater leaving the north face of the grid cell, with dxVCthus mea-
suring the mass per time of tracer leaving the north face. We now consider the following decomposition of
this transport by defining the zonal average transport and zonal average tracer concentration as follows
[V] = PidxV
Pidx(40.3)
[C] = Pidx C
Pidx,(40.4)
along with the deviations from zonal average
V= [V] + V∗(40.5)
C= [C] + C∗.(40.6)
The discrete i-sum extends over the basin or global domain of interest, so that PidxVis the total merid-
ional transport of seawater at this zonal band at a particular k-level. The resulting meridional tracer trans-
port becomes
H(y,t) = X
iX
k
dxVC(40.7)
=X
iX
k
dx([V][C] + V∗C∗),(40.8)
where the ksum extends over the depth of a column.
We identify three components in the code:
merid flux advect =X
iX
k
dxVC(40.9)
merid flux over =X
iX
k
dx[V][C] (40.10)
merid flux gyre =X
iX
k
dxV∗C∗.(40.11)
Note that
merid flux gyre =merid flux advect −merid flux over.(40.12)
This identity follows very simply when the advective flux takes on the simple form of either first order
upwind or second order centered differences. It becomes more involved when considering higher order, or
flux limited, advection schemes. Nonetheless, we use this as a defintion of the gyre component, so that
the advective flux is built from the advection scheme used in the model.
40.2 Enabling the diagnostic
The following is necessary to enable this diagnostic.
Elements of MOM November 19, 2014 Page 596

Chapter 40. Gyre and overturning contributions to tracer transport Section 40.2
• Set any of the following within the diagnostic table:
“tracer00 merid flux advect 00basin00
“tracer00 merid flux over 00basin00
“tracer00 merid flux gyre 00basin00
where “tracer” is the MOM shortname for the tracer (e.g., “temp” or “salt”), and “basin” is one of the
names “global”, “southern”,“atlantic”, “pacific”, “arctic”, or “indian”.
• To get the transport diagnostic partitioned into basins in the World Ocean, it is necessary to read
in a netCDF basin mask. A sample mask is provided with the CORE test case based on the global
one-degree ocean used for CM2.1 (Griffies et al. (2005), Gnanadesikan et al. (2006), Delworth et al.
(2006), Wittenberg et al. (2006), and Stouffer et al. (2006a)). The logical to read in this mask is
read basin mask =.true.
The convention is that the basins are defined by the following values in the mask:
Southern = 1.0
Atlantic = 2.0
Pacific = 3.0
Arctic = 4.0
Indian = 5.0.
Elements of MOM November 19, 2014 Page 597

Chapter 40. Gyre and overturning contributions to tracer transport Section 40.2
Elements of MOM November 19, 2014 Page 598

Chapter 41
Balancing the hydrological cycle in
ocean-ice models
Contents
41.1 Transfer of water between sea ice and ocean .........................599
41.2 Balancing the hydrological cycle ................................599
41.3 Water mass flux from salt mass flux ..............................600
The purpose of this chapter is to discuss issues of how to balance the hydrological cycle in ocean-ice
simulations using MOM and the FMS coupler. In particular, we detail how the liquid water flux transferred
between sea ice and liquid ocean is diagnosed in MOM, given the salt mass flux transferred between the
media.
The following MOM module is directly connected to the material in this chapter:
ocean core/ocean sbc.F90
41.1 Transfer of water between sea ice and ocean
As sea ice forms, water is extracted from the liquid ocean and passed to the solid sea ice. Additionally,
there is generally a nonzero salt mass transferred from ocean to ice, thus producing a nonzero salinity for
sea ice. Conversely, as sea ice melts, liquid water and salt are added to the ocean.
The GFDL Sea Ice Simulator (SIS) generally simulates sea ice with a nonzero salt content. For example,
in the coupled climate model simulations discussed by Delworth et al. (2006), sea ice is assumed to have
a salinity
S ice =kg salt in sea ice
kg sea ice (41.1)
of S ice = 0.005 (five parts per thousand).
41.2 Balancing the hydrological cycle
When running ocean-ice simulations, we are not explicitly representing land processes, such as rivers,
catchment areas, snow accumulation, etc. However, to reduce model drift, it is important to balance the
hydrological cycle in ocean-ice models. We thus need to prescribe some form of global normalization to
the precipitation minus evaporation plus river runoff. The result of the normalization should be a global
integrated zero net water input to the ocean-ice system over a chosen time scale.
599

Chapter 41. Balancing the hydrological cycle in ocean-ice models Section 41.3
How often the normalization is done is a matter of choice. In MOM, we choose to do so at each model
time step, so that there is always a zero net input of water to the ocean-ice system. Others choose to
normalize over an annual cycle, in which case the net imbalance over an annual cycle is used to alter the
subsequent year’s water budget in an attempt to damp the annual water imbalance. Note that the annual
budget approach may be inappropriate with interannually varying precipitation forcing.
When running ocean-ice coupled models, it is incorrect to include the water transport between the
ocean and ice models when aiming to balance the hydrological cycle. The reason is that it is the sum of
the water in the ocean plus ice that should be balanced when running ocean-ice models, not the water in
any one subcomponent. As an extreme example to illustrate the issue, consider an ocean-ice model with
zero initial sea ice. As the ocean-ice model spins up, there should be a net accumulation of water in the
growing sea ice, and thus a net loss of water from the ocean. The total water contained in the ocean plus
ice system is constant, but there is an exchange of water between the subcomponents. This exchange
should not be part of the normalization used to balance the hydrological cycle in ocean-ice models.
41.3 Water mass flux from salt mass flux
Balancing the hydrological cycle in an ocean-ice model run with the FMS coupler requires an indirect
method. The reason is that melt water from the ice model is added to the precipitation field prior to being
added to the ocean model. So prior to balancing the water fluxes, we must remove the ice melt from the
precipitation. The namelist option for performing this normalization is
zero net water coupler
found in the module
ocean core/ocean sbc mod.
An alternative namelist option is
zero net water couple restore
which balances the water due to precipitation minus evaporation plus runoffplus restoring flux water.
Note that in MOM4p0, ice melt was not removed from precipitation prior to computing the water normal-
ization using zero net water coupler. This bug compromised the integrity of the ocean-ice models run
with MOM4p0 which used the option zero net water coupler.
To obtain the water mass flux between sea ice and ocean, we could consider two approaches. First,
we could alter the FMS sea ice code so that it carries explicit information about the water flux in question.
This approach requires modifying code that lives outside of MOM, and so is not desirable from a MOM
perspective. Alternatively, we can make use of the salt mass flux passed between the ocean and sea ice.
This approach is limitated to cases where the ice is assumed to have a uniform bulk salinity, as presently
assumed in the GFDL sea ice model.
In MOM, we have access to the following salt flux
salt flux to ice =Sice ρsea ice Tice melt
∆t.(41.2)
In this equation, ρsea ice is the density of sea ice, taken as ρsea ice = 905kgm−3in the GFDL ice model, and
Tice melt/∆tis the thickness (in meters) of ice that melts over the time step (in seconds) of the ice model.
By convention, this salt flux is positive when there is growth in sea ice, thus representing a passage of salt
from the liquid ocean into the sea ice. Correspondingly, this flux is positive when there is a mass flux of
water to the sea ice. Since we are here working from an ocean perspective, we prefer to measure the flux
of salt entering the ocean from the melting sea ice
salt flux to ocean =−salt flux to ice.(41.3)
Elements of MOM November 19, 2014 Page 600

Chapter 41. Balancing the hydrological cycle in ocean-ice models Section 41.3
Dividing the salt flux by the salinity of sea ice yields the mass flux of water that melts (i.e., mass flux of
water transferred from sea ice to the ocean)
mass melt =salt flux to ocean
S ice
= kg ice melt
area sea ice ×Tice melt !Tice melt
∆t
=kg ice melt
area sea ice ×∆t.
(41.4)
This mass of melting sea ice represents a gain of liquid water for the ocean.
Elements of MOM November 19, 2014 Page 601

Chapter 41. Balancing the hydrological cycle in ocean-ice models Section 41.3
Elements of MOM November 19, 2014 Page 602

Chapter 42
Diagnosing the momentum budget
Contents
42.1 A split-explicit algorithm to time step momentum .....................604
42.1.1 Splitting the velocity field .................................. 604
42.1.2 Details of the semi-discrete momentum equation ..................... 605
42.1.2.1 Split of the pressure gradient force with pressure-based vertical coordinates 607
42.1.2.2 Split of the pressure gradient force with depth-based vertical coordinates . 607
42.2 Momentum budget diagnostics .................................608
42.2.1 Decomposing the momentun budget ............................ 608
42.2.2 MOM5 diagnostics for the momentum budget ....................... 609
42.2.2.1 Net change in grid cell momentum per area .................. 609
42.2.2.2 Coriolis force per area ............................... 609
42.2.2.3 Momentum source/sink .............................. 609
42.2.2.4 Momentum advection ............................... 609
42.2.2.5 Slow/baroclinic pressure gradient force per area ................ 610
42.2.2.6 Fast/barotropic pressure gradient force per area ................ 610
42.2.2.7 Horizontal viscous friction from Laplacian and biharmonic operators . . . . 611
42.2.2.8 Vertical viscous friction, bottom drag, and surface stress ........... 611
42.2.2.9 Summary of the momentum diagnostic terms ................. 612
The purpose of this chapter is to detail the methods required to diagnose the momentum budget in
603

Chapter 42. Diagnosing the momentum budget Section 42.1
MOM5. The following MOM modules are directly connected to the material in this chapter:
ocean core/ocean barotropic.F90
ocean core/ocean bbc.F90
ocean core/ocean coriolis.F90
ocean core/ocean pressure.F90
ocean core/ocean sbc.F90
ocean core/ocean velocity.F90
ocean core/ocean velocity advect.F90
ocean param/lateral/ocean bihcgrid friction.F90
ocean param/lateral/ocean bihcst friction.F90
ocean param/lateral/ocean bihgen friction.F90
ocean param/lateral/ocean lapcgrid friction.F90
ocean param/lateral/ocean lapcst friction.F90
ocean param/lateral/ocean lapgen friction.F90
ocean param/vertical/ocean vert mix.F90
ocean param/sources/ocean momentum source.F90
42.1 A split-explicit algorithm to time step momentum
In this section, we summarize elements of the split-explicit algorithm used to time step the momentum
equations. Although essential for practical reasons, the split-explicit methods introduce a level of com-
plexity to the model algorithms that can be frustrating, particularly when aiming to cleanly diagnose terms
contributing to the momentum budget. This section may be readily skipped for those merely interested in
the momentum budget diagnostics, which are summarized in Section 42.2.
As discussed in Section 11.1, an algorithm of practical utility for climate modeling must split the fast
and slow dynamics so that the slow dynamics can be updated with a much longer time step than the
fast dynamics. These algorithms are known as split-explicit methods. For a hydrostatic fluid, the fast
motions can be approximated by the vertically integrated dynamics of Section 10.9 and the vertically
integrated mass or volume budgets of Section 10.6. The remainder constitutes an approximation to the
slower dynamics. Motions constituting the fast dynamics are embodied by the barotropic or external mode,
and the slower motions are embodied by advection as well as baroclinic or internal waves.
42.1.1 Splitting the velocity field
We formulate the split between the fast and slow modes using density weighting within the mass-conserving
non-Boussinesq framework. For Boussinesq equations, the density weighting reduces to a constant ρoref-
erence density factor that trivially cancels from the equations.
Following the discussion in Section 12.3.5 of Griffies (2004), we split of the horizontal velocity field
according to
u= u−Pkuρdz
Pkρdz!
| {z }
slow
+ Pkuρdz
Pkρdz!
| {z }
fast
(42.1a)
≡ˆ
u+uz,(42.1b)
where the vertical sum includes all grid cells within a column of fluid. The vertically averaged velocity is
Elements of MOM November 19, 2014 Page 604

Chapter 42. Diagnosing the momentum budget Section 42.1
given by
uz=Pkuρdz
Pkρdz(42.2a)
=Uρ
Pkρdz.(42.2b)
The vertically averaged velocity is updated according to the vertically integrated momentum equation of
Section 10.9. The slower depth dependent velocity, ˆ
u, has zero density weighted vertical sum. Therefore,
its time tendency is independent of any depth independent forcing. A relevant depth independent forcing
of concern arises from fast fluctuations in the surface height or bottom pressure associated with external
gravity waves. We thus choose to update the slow dynamics using all pieces of the momentum forcing,
except contributions from the rapid pressure and geopotential fluctuations contributing to the horizontal
pressure gradient. This update produces a velocity u0that is related to ˆ
uvia
ˆ
u=u0− Pku0ρdz
Pkρdz!.(42.3)
A similar relation was discussed in Section 12.4.2 of Griffies (2004). Completing the updates of u0and Uρ
to a new time level, τ+ 1, allows for an update of the full horizontal velocity via the identity
u=ˆ
u+uz(42.4a)
= u0−Pku0ρdz
Pkρdz!+Uρ
Pkρdz(42.4b)
=u0+Pk(u−u0)ρdz
Pkρdz.(42.4c)
42.1.2 Details of the semi-discrete momentum equation
From Section 4.1.5, the horizontal linear momentum budgets for interior, bottom, and surface grid cells
are given by
[∂t+ (f+M)ˆ
z∧](uρdz) = ρdzS(u)−∇s·[dzu(ρu)] −dz(∇sp+ρ∇sΦ) + dz ρF
−[ρ(w(s)u−κu,z)]s=sk−1+ [ ρ(w(s)u−κu,z)]s=sk
(42.5)
[∂t+ (f+M)ˆ
z∧](uρdz) = ρdzS(u)−∇s·[dzu(ρu)] −dz(∇sp+ρ∇sΦ) + dz ρF
−[ρ(w(s)u−κu,z)]s=skbot−1−τbottom (42.6)
[∂t+ (f+M)ˆ
z∧](uρdz) = ρdzS(u)−∇s·[dzu(ρu)] −dz(∇sp+ρ∇sΦ) + dz ρF
+ [τwind +Qmum] + [ρ(w(s)u−κu,z)]s=sk=1 .(42.7)
See Section 4.1.5 for definitions of the various terms in these equations. Equations (42.5)-(42.7) provide
prognostic expressions for the linear momentum per unit area of a grid cell
uρdz=linear momentum per horizontal area (kg m−1s−1),(42.8)
which is determined by the horizontal velocity, u, multiplied by the mass per unit area of a grid cell
dzρ =mass per unit horizontal area (kg m−2).(42.9)
If the mass per unit area is time independent, the linear momentum budget reduces to a budget for the
horizontal velocity. However, such grid cells are not the norm. More generally, the mass per unit area is
a function of time, since the volume and mass of a grid cell changes. Hence, in this more general case, it
is critical to formulate the semi-discrete momemtum equations using finite volume formulations. Doing so
ensures a conservation-based budget for the momentum in a grid cell.
Elements of MOM November 19, 2014 Page 605

Chapter 42. Diagnosing the momentum budget Section 42.1
Introducing a forward time step for the time tendency in equations (42.5)-(42.7) renders
(uρdz)τ+1 −(uρdz)τ
∆τ=−fˆ
z∧(uρdz) + ρdzS(u)− ∇s·[dzu(ρu)] + Mˆ
z∧(uρdz)!
−dz(∇sp+ρ∇sΦ) + dzρ F−[ρ(w(s)u−κu,z)]s=sk−1+ [ρ(w(s)u−κu,z)]s=sk
(42.10)
(uρdz)τ+1 −(uρdz)τ
∆τ=−fˆ
z∧(uρdz) + ρdzS(u)− ∇s·[dzu(ρu)] + Mˆ
z∧(uρdz)!
−dz(∇sp+ρ∇sΦ) + dzρ F−[ρ(w(s)u−κu,z)]s=skbot−1−τbottom
(42.11)
(uρdz)τ+1 −(uρdz)τ
∆τ=−fˆ
z∧(uρdz) + ρdzS(u)− ∇s·[dzu(ρu)] + Mˆ
z∧(uρdz)!
−dz(∇sp+ρ∇sΦ) + dzρ F+ [τwind +Qmum] + [ρ(w(s)u−κu,z) ]s=sk=1 .
(42.12)
We separated the term (f+M)ˆ
z∧(uρdz)into two parts to correspond to the code implementation. That
is, in MOM5, the Coriolis term
Coriolis force per area =−fˆ
z∧(uρdz) (42.13)
is handled separately from the advection metric term
advection metric =−Mˆ
z∧(uρdz).(42.14)
The advection metric term is combined with the horizontal advection operator
horizontal advection =−∇s·[ dzu(ρu)],(42.15)
whereas the Coriolis force is time stepped semi-implicitly when using the B-grid option (see Section 12.2),
or with an Adams-Bashforth scheme when using the C-grid (see Section 12.3).
As already stated in Section 42.1.1, the full momentum equations (42.10)-(42.12) are stable only if
taking a small time step sufficient to resolve fast barotropic wave motions. The split-explicit method is
realized by splitting the pressure gradient body force into a fast and a slow piece
∇sp+ρ∇sΦ= (∇sp+ρ∇sΦ)fast + (∇sp+ρ∇sΦ)slow.(42.16)
Expressions for the fast and slow components of the pressure gradient depend on the choice for vertical
coordinate, to which we return to in Sections 42.1.2.1 and 42.1.2.2. The slow portion of the split-explicit
method time steps a primed velocity, u0. Forcing for u0is identical to the full momentum, sans the fast
component of the pressure gradient in equations (42.10)-(42.12), so that
(uρdz0)τ+1 −(uρdz)τ
∆τ=−fˆ
z∧(uρdz) + ρdzS(u)−∇s·[dzu(ρu)] −Mˆ
z∧(uρdz)
−dz(∇sp+ρ∇sΦ)slow + dzρ F−[ρ(w(s)u−κu,z)]s=sk−1+ [ρ(w(s)u−κu,z)]s=sk
(42.17)
(uρdz0)τ+1 −(uρdz)τ
∆τ=−fˆ
z∧(uρdz) + ρdzS(u)−∇s·[dzu(ρu)] −Mˆ
z∧(uρdz)
−dz(∇sp+ρ∇sΦ)slow + dzρ F−[ρ(w(s)u−κu,z)]s=skbot−1−τbottom
(42.18)
(uρdz0)τ+1 −(uρdz)τ
∆τ=−fˆ
z∧(uρdz) + ρdzS(u)−∇s·[dzu(ρu)] −Mˆ
z∧(uρdz)
−dz(∇sp+ρ∇sΦ)slow + dzρ F+ [τwind +Qmum] + [ρ(w(s)u−κu,z) ]s=sk=1 .
(42.19)
All terms on the right hand side of equations (42.17)-(42.19) make use of the full velocity field u, rather
than the primed velocity field, u0. Hence, the difference between the updated full velocity and the updated
primed velocity is just due to the fast portion of the pressure gradient
(uρdz)τ+1 −(uρdz0)τ+1
∆τ=−dz(∇sp+ρ∇sΦ)fast.(42.20)
This identity holds only approximately in the model implementation, given that the fast pressure gradient
is diagnosed as a time average over the small time steps of the barotropic cycle (see Section 11.3).
Elements of MOM November 19, 2014 Page 606

Chapter 42. Diagnosing the momentum budget Section 42.2
42.1.2.1 Split of the pressure gradient force with pressure-based vertical coordinates
When making use of pressure-based vertical coordinates in MOM5, equation (3.27) from Section 3.2 allows
us to decompose the pressure gradient as
∇sp+ρ∇sΦ= (ρ/ρo)∇(pb+ρoΦb)
| {z }
fast
+ρ∇sΦ0−(ρ0/ρo)∇sp
| {z }
slow
.(42.21)
Substitution of this expression in equation (42.20) yields
u=ˆ
u+uz(42.22a)
= u0−Pku0ρdz
Pkρdz!+Uρ
Pkρdz(42.22b)
=u0+Pk(u−u0)ρdz
Pkρdz(42.22c)
=u0−∆τ Pkρdz∇(pb+ρoΦb)
ρoPkρdz!(42.22d)
=u0−∆τ ∇(pb+ρoΦb)
ρo!.(42.22e)
The final equality results from noting that
pb+ρoΦb=pb−ρog H (42.23)
is depth independent, where
Φb=−g H(x,y) (42.24)
is the geopotential at the ocean bottom.
42.1.2.2 Split of the pressure gradient force with depth-based vertical coordinates
When making use of depth-based vertical coordinates in MOM5, equation (3.18) from Section 3.2 allows
us to decompose the pressure gradient as
∇sp+ρ∇sΦ=∇(pa+g ρoη)
| {z }
fast
+∇sp0+ρ0∇sΦ
| {z }
slow
.(42.25)
Substitution of this expression in equation (42.20), along with setting ρdz=ρodzfor the Boussinesq fluid,
yields
u=ˆ
u+uz(42.26a)
= u0−Pku0ρdz
Pkρdz!+Uρ
Pkρdz(42.26b)
=u0+Pk(u−u0)ρdz
Pkρdz(42.26c)
=u0−∆τ Pkρdz∇(pa+g ρoη)
ρoPkρdz!(42.26d)
=u0−∆τ ∇(pa+g ρoη)
ρo!.(42.26e)
The final equality results from noting that pa+g ρoηis depth independent.
Elements of MOM November 19, 2014 Page 607

Chapter 42. Diagnosing the momentum budget Section 42.2
42.2 Momentum budget diagnostics
In this section, we develop the necessary diagnostic terms required to evaluate terms appearing in the mo-
mentum budget. Approximations are inherent in this diagnostic due to the split-explicit algorithm, whereby
the fast dynamics is separately time stepped from the slow dynamics. We nonetheless detail the diagnos-
tics assuming these time truncation errors do not damage the physical integrity of the diagnostics.
42.2.1 Decomposing the momentun budget
In Section 42.1.2, we wrote the semi-discrete momentum budget (42.10)-(42.12). We rewrite here that
budget, decomposing forcing terms according to how they are evaluated in MOM5
(uρdz)τ+1 −(uρdz)τ
∆τ
| {z }
net time tendency
=−fˆ
z∧(uρdz)
| {z }
Coriolis
+ρdzS(u)
| {z }
source
− ∇s·[dzu(ρu)] + Mˆ
z∧(uρdz) + [ρw(s)u]s=sk−1−[ρ w(s)u]s=sk!
| {z }
horizontal + vertical advection
−dz(∇sp+ρ∇sΦ)
| {z }
baroclinic press force
−dz(∇sp+ρ∇sΦ)
| {z }
time averaged fast press force
+ dzρ F
|{z}
horizontal friction
−[(ρκu,z)s=sk−(ρκu,z)s=sk−1]
| {z }
vertical friction
(42.27)
(uρdz)τ+1 −(uρdz)τ
∆τ
| {z }
net time tendency
=−fˆ
z∧(uρdz)
| {z }
Coriolis
+ρdzS(u)
| {z }
source
− ∇s·[dzu(ρu)] + Mˆ
z∧(uρdz) + [ρw(s)u]s=skbot−1!
| {z }
horizontal + vertical advection
−dz(∇sp+ρ∇sΦ)
| {z }
baroclinic press force
−dz(∇sp+ρ∇sΦ)
| {z }
time averaged fast press force
+ dzρ F
|{z}
horizontal friction
−τbottom −(ρκu,z)s=skbot−1
| {z }
vertical friction and bottom drag
(42.28)
(uρdz)τ+1 −(uρdz)τ
∆τ
| {z }
net time tendency
=−fˆ
z∧(uρdz)
| {z }
Coriolis
+ρdzS(u)
| {z }
source
− ∇s·[dzu(ρu)] + Mˆ
z∧(uρdz)−[ρw(s)u]s=sk=1 −Qmum!
| {z }
horizontal + vertical advection
−dz(∇sp+ρ∇sΦ)
| {z }
baroclinic press force
−dz(∇sp+ρ∇sΦ)
| {z }
time averaged fast press force
+ dzρ F
|{z}
horizontal friction
−(ρκ u,z)s=sk=1 −τwind
| {z }
vertical friction and surf stress
.
(42.29)
Elements of MOM November 19, 2014 Page 608

Chapter 42. Diagnosing the momentum budget Section 42.2
Note how the bottom drag, τbottom, and surface stress, τwind, are both wrapped into the vertical friction
terms. That is because bottom drag and surface stress are introduced to the model as boundary conditions
for the vertical momentum friction equation. If desired, these terms can be separately diagnosed.
42.2.2 MOM5 diagnostics for the momentum budget
The following MOM5 diagnostics are available for the momentum budget.
42.2.2.1 Net change in grid cell momentum per area
The net change in grid cell momentum per horizontal cell area is diagnosed by
momentum change u =(u ρ dz)τ+1 −(u ρdz)τ
∆τ(42.30a)
momentum change v =(v ρ dz)τ+1 −(v ρdz)τ
∆τ,(42.30b)
with units of N m−2. These diagnostics are evaluated at the end of a time step, once the full update for the
new momentum per area, (uρdz)τ+1, is available. Again, for a Boussinesq model, the in situ density factor,
ρ, is set to the constant Boussinesq reference density, ρo.
This diagnostic has not yet been coded in MOM5. Code is needed inside ocean core/ocean velocity.F90.
42.2.2.2 Coriolis force per area
The Coriolis force per horizontal grid cell area is diagnosed by the two terms
hrho cor u +ucori impl =f(v ρdz) (42.31a)
hrho cor v +vcori impl =−f(u ρdz),(42.31b)
with units of N m−2. As detailed in Chapter 12, the Coriolis force is discretized in time in one of the following
manners:
• B-grid: via a semi-implicit method;
• C-grid: via a third order Adams-Bashforth method, in which case ucori impl and vcori impl are
zero.
For a Boussinesq model, the in situ density factor, ρ, is set to the constant Boussinesq reference density,
ρo.
42.2.2.3 Momentum source/sink
The source/sink term for momentum is diagnosed by
rayleigh drag u =ρdzS(u)(42.32a)
rayleigh drag v =ρdzS(v)(42.32b)
with units of N m−2. This particular example of a source/sink term concerns the effects from dissipation
parameterized as Rayleigh drag.
42.2.2.4 Momentum advection
For interior grid cells, momentum advection is diagnosed by
momentum advect u =− ∇s·[u(uρdz)] −M(v ρ dz) + [ρ w(s)u]s=sk−1−[ρw(s)u]s=sk!(42.33a)
momentum advect v =− ∇s·[v(uρdz)] + M(u ρ dz) + [ρ w(s)v]s=sk−1−[ρ w(s)v]s=sk!(42.33b)
Elements of MOM November 19, 2014 Page 609

Chapter 42. Diagnosing the momentum budget Section 42.2
with units of N m−2. For bottom grid cells, momentum advection is diagnosed by
momentum advect u =− ∇s·[u(uρdz)] −M(v ρ dz) + [ρ w(s)u]s=skbot−1!(42.34a)
momentum advect v =− ∇s·[v(uρdz)] + M(u ρ dz) + [ρ w(s)v]s=sk−1!(42.34b)
with units of N m−2. For surface grid cells, momentum advection is diagnosed by
momentum advect u =− ∇s·[u(uρdz)] −M(v ρ dz)−[ρw(s)u]s=sk=1 −Qmum!(42.35a)
momentum advect v =− ∇s·[v(uρdz)] + M(u ρ dz)−[ρw(s)v]s=sk=1 −Qmvm!,(42.35b)
with units of N m−2. As discussed in Section 11.2.3, the time discretization of momentum advection is
generally handled via a third-order Adams-Bashforth method. The third order Adams-Bashforth method is
an explicit scheme that requires the advection operator to be evaluated at time steps τ,τ−1, and τ−2.
This diagnostic has not yet been coded in MOM5. Code is needed inside ocean core/ocean velocity.F90.
42.2.2.5 Slow/baroclinic pressure gradient force per area
According to Section 42.1.2.1, the slow/baroclinic pressure gradient force for pressure-based vertical co-
ordinates is diagnosed by
press baroclinic force u =−dz"ρ ∂Φ0
∂x !s−(ρ0/ρo) ∂p
∂x !s#(42.36a)
press baroclinic force v =−dz"ρ ∂Φ0
∂y !s−(ρ0/ρo) ∂p
∂y !s#(42.36b)
with units of N m−2=Pa. For depth-based vertical coordinates, we follow the details in Section 42.1.2.2 to
have the slow pressure gradient force diagnosed as
press baroclinic force u =−dz" ∂p0
∂x !s
+ρ0 ∂Φ
∂x !s#(42.37a)
press baroclinic force v =−dz" ∂p0
∂y !s
+ρ0 ∂Φ
∂y !s#.(42.37b)
This diagnostic has a different name in MOM5; the “baroclinic” portion of the name is missing. We
need to make the name change to better align this diagnostic with that for the fast/barotropic pressure
gradient. Code modification is needed inside ocean core/ocean pressure.F90.
42.2.2.6 Fast/barotropic pressure gradient force per area
According to Section 42.1.2.1, the fast/barotropic pressure gradient force for pressure-based vertical co-
ordinates is diagnosed by
press barotropic force u =−(ρdz/ρo)"∂pb
∂x +ρo∂Φb
∂x #(42.38a)
press barotropic force v =−(ρdz/ρo)"∂pb
∂y +ρo∂Φb
∂y #(42.38b)
Elements of MOM November 19, 2014 Page 610
Chapter 42. Diagnosing the momentum budget Section 42.2
with units of N m−2=Pa. For depth-based vertical coordinates, we follow the details in Section 42.1.2.2 to
have the fast/barotropic pressure gradient force diagnosed as
press barotropic force u =−dz"∂pa
∂x +g ρo
∂η
∂x #(42.39a)
press barotropic force v =−dz"∂pa
∂y +g ρo
∂η
∂y #.(42.39b)
This diagnostic has not yet been coded in MOM5. Code is needed inside ocean core/ocean barotropic.F90.
42.2.2.7 Horizontal viscous friction from Laplacian and biharmonic operators
The horizontal viscous friction from a Laplacian and/or a biharmonic operator is diagnosed by
bih fric u +lap fric u = dzρF(u)
| {z }
horizontal friction
(42.40a)
bih fric v +lap fric v = dzρF(v)
| {z }
horizontal friction
(42.40b)
with units of N m−2.
The Laplacian diagnostic code appears to have a bug; the diagnostic is spuriously called twice. Code
modificatio is needed inside ocean param/lateral/ocean lapgen friction.F90.
42.2.2.8 Vertical viscous friction, bottom drag, and surface stress
The vertical viscous friction in the ocean interior contains the following term
vfrict impl u =− ρκ ∂u
∂z !s=sk− ρκ ∂u
∂z !s=sk−1(42.41a)
vfrict impl v =− ρκ ∂v
∂z !s=sk− ρκ ∂v
∂z !s=sk−1(42.41b)
with units of N m−2. This term is generally time discretized using implicit methods, hence the name for the
diagnostic. For ocean surface cells, we absorb the surface stress into this diagnostic, thus yielding
vfrict impl u =− ρκ ∂u
∂z !s=sk=1 −τwind
(x)(42.42a)
vfrict impl v =− ρκ ∂v
∂z !s=sk=1 −τwind
(y)(42.42b)
For bottom ocean cells, we absorb the bottom drag into this diagnostic, thus yielding
vfrict impl u =−τdrag
(x)− ρκ ∂u
∂z !s=skbot=1 (42.43a)
vfrict impl v =−τdrag
(y)− ρκ ∂v
∂z !s=skbot=1 .(42.43b)
We can separately diagnose the surface and bottom stress via the following diagnostics
bmf u =−τdrag
(x)(42.44a)
bmf v =−τdrag
(y)(42.44b)
tau x =τwind
(x)(42.44c)
tau y =τwind
(y).(42.44d)
Elements of MOM November 19, 2014 Page 611

Chapter 42. Diagnosing the momentum budget Section 42.2
42.2.2.9 Summary of the momentum diagnostic terms
In summary, the following terms contribute to the budget for the momentum per horizontal area of a grid
cell
momentum change u =hrho cor u +ucori impl +momentum advect u
+press baroclinic force u +press barotropic force u
+bih fric u +lap fric u +vfrict impl u +rayleigh drag u
(42.45)
momentum change v =hrho cor v +vcori impl +momentum advect v
+press baroclinic force v +press barotropic force v
+bih fric v +lap fric v +vfrict impl v +rayleigh drag v.
(42.46)
Every term in these equations has units of N m−2. Multiplication by the grid cell area yields the force acting
on a grid cell due to the respective terms.
Elements of MOM November 19, 2014 Page 612
Bibliography
, ????
Adcroft, A., Campin, J.-M., 2004. Rescaled height coordinates for accurate representation of free-surface
flows in ocean circulation models. Ocean Modelling 7, 269–284.
Adcroft, A., Hallberg, R., Harrison, M., 2008. A finite volume discretization of the pressure gradient force
using analytic integration. Ocean Modelling 22, 106–113.
Adcroft, A., Hallberg, R. W., 2006. On methods for solving the oceanic equations of motion in generalized
vertical coordinates. Ocean Modelling 11, 224–233.
Adcroft, A., Hill, C., Marshall, J., 1997. Representation of topography by shaved cells in a height coordinate
ocean model. Monthly Weather Review 125, 2293–2315.
Adcroft, A., Hill, C., Marshall, J., 1999. A new treatment of the coriolis terms in c-grid models at both high
and low resolutions. Monthly Weather Review 127, 1928–1936.
Adcroft, A., Scott, J. R., Marotzke, J., 2001. Impact of geothermal heating on the global ocean circulation.
Geophysical Research Letters 28, 1735–1738.
Aiki, H., Jacobson, T., Yamagata, T., 2004. Parameterizing ocean eddy transports from surface to bottom.
Journal of Geophysical Research 31, L19 302, doi:10.1029/2004GL020703.
Apel, J. R., 1987. Principles of Ocean Physics. Vol. 38 of International Geophysics Series. Academic Press,
London.
Arbic, B., Garner, S. T., Hallberg, R. W., Simmons, H. L., 2004. The accuracy of surface elevations in forward
global barotropic and baroclinic tide models. Deep Sea Research 51, 3069–3101.
Aris, R., 1962. Vectors, Tensors and the Basic Equations of Fluid Mechanics. Dover Publishing, New York.
Asselin, R., 1972. Frequency filter for time integrations. Monthly Weather Review 100, 487–490.
Bacon, S., Fofonoff, N. P., 1996. Oceanic heat flux calculation. Journal of Atmospheric and Oceanic Tech-
nology 13, 1327–1329.
Batchelor, G. K., 1967. An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge, England.
Bates, M., 2011. Lagrangian blobs embedded in Eulerian models: a framework to parameterise vertical
and downslope motion of gravitationally unstable water parcels. University of New South Wales, Sydney,
Australia.
Bates, M., Griffies, S. M., England, M., 2012a. A dynamic, embedded Lagrangian model for ocean climate
models, Part I: Theory and implementation. Ocean Modelling 59-60, 41–59.
613

Bibliography Section 42.2
Bates, M., Griffies, S. M., England, M., 2012b. A dynamic, embedded Lagrangian model for ocean climate
models, Part II: Idealised overflow tests. Ocean Modelling 59-60, 60–76.
Beckmann, A., D¨
oscher, R., 1997. A method for improved representation of dense water spreading over
topography in geopotential-coordinate models. Journal of Physical Oceanography 27, 581–591.
Black, T. L., 1994. The new NMC mesoscale eta model: description and forecast examples. Weather and
Forecasting 9, 265–278.
Bleck, R., 1978. Finite difference equations in generalized vertical coordinates. Part I: Total energy conser-
vation. Contributions to Atmospheric Physics 51, 360–372.
Blumberg, A., Kantha, L., 1985. Open boundary condition for circulation models. Journal of Hydraulic En-
gineering 111, 237–255.
Blumberg, A. F., Mellor, G. L., 1987. A description of a three-dimensional coastal ocean circulation model.
In: Heaps, N. (Ed.), Three-Dimensional Coastal Ocean Models. Vol. 4 of Coastal and Estuarine Series.
American Geophysical Union.
Bryan, K., 1963. A numerical investigation of a nonlinear model of a wind-driven ocean. Journal of Atmo-
spheric Sciences 20, 594–606.
Bryan, K., 1969. A numerical method for the study of the circulation of the world ocean. Journal of Com-
putational Physics 4, 347–376.
Bryan, K., 1989. The design of numerical models of the ocean circulation. In: Anderson, D. L., Willebrand, J.
(Eds.), Oceanic Circulation Models: Combining Data and Dynamics. Vol. 284 of NATO ASI Series. Series
C. Kluwer Academic Publishers, pp. 465–511.
Bryan, K., 1991. Michael cox (1941-1989): his pioneering contributions to ocean circulation modeling.
Journal of Physical Oceanography 21, 1259–1270.
Bryan, K., 1996. The steric component of sea level rise associated with enhanced greenhouse warming: a
model study. Climate Dynamics 12, 545–555.
Bryan, K., Cox, M. D., 1972. An approximate equation of state for numerical models of the ocean circulation.
Journal of Physical Oceanography 4, 510–514.
Bryan, K., Lewis, L. J., 1979. A water mass model of the world ocean. Journal of Geophysical Research 84,
2503–2517.
Burchard, H., Rennau, H., 2008. Comparative quantification of physically and numerically induced mixing
in ocean models. Ocean Modelling 20, 293–311.
Callen, H. B., 1985. Thermodynamics and an Introduction to Thermostatics. John Wiley and Sons, New
York, 493 + xvi pp.
Camerlengo, A., O’Brien, J., 1980. Open boundary condition in rotating fluids. Journal of Computational
Physics 35, 12–35.
Campin, J.-M., Adcroft, A., Hill, C., Marshall, J., 2004. Conservation of properties in a free-surface model.
Ocean Modelling 6, 221–244.
Campin, J.-M., Goosse, H., 1999. Parameterization of density-driven downsloping flow for a coarse-
resolution ocean model in z-coordinate. Tellus 51A, 412–430.
Chaikin, P. M., Lubensky, T. C., 1995. Principles of Condensed Matter Physics. Cambridge University Press,
Cambridge, United Kingdom.
Elements of MOM November 19, 2014 Page 614

Bibliography Section 42.2
Chang, Y. S., Xu, X., ¨
Ozg¨
okmen, T. M., Chassignet, E. P., Peters, H., Fischer, P. F., 2005. Comparison of gravity
current mixing parameterizations and calibration using a high-resolution 3d nonhydrostatic spectral
element model. Ocean Modelling 3-4, 342–368.
Chapman, D., 1985. Numerical treatment of cross-shelf boundaries in a barotropic coastal ocean model.
Journal of Physical Oceanography 103(C1), 1060–1075.
Chassignet, E. P., Garraffo, Z., 2001. Viscosity parameterization and the Gulf Stream separation. In: M ¨
uller,
P., Henderson, D. (Eds.), From Stirring to Mixing in a Stratified Ocean. Proceedings of the 12th ’Aha Hu-
liko’a Hawaiian Winter Workshop. University of Hawaii at Manoa, pp. 37–41.
Chassignet, E. P., Verron, J., 2005. Ocean Weather Forecasting: an Integrated View of Oceanography.
Springer Publishers.
Chen, D., Rothstein, L., Busalacchi, A., 1994. A hybrid vertical mixing scheme and its application to tropical
ocean models. Journal of Physical Oceanography 24, 2156–2179.
Church, J., Gregory, J., 2001. Changes in sea level. In: Climate Change 2001: The Scientific Basis. Cam-
bridge University Press, Cambridge UK, pp. 639–693.
Conkright, M., Antonov, J., Baranova, O., Boyer, T., Garcia, H., Gelfeld, F., Johnson, D., Locarnini, R., Murphy,
P., O’Brien, T., Smolyar, I., Stephens, C., 2002. World Ocean Database 2001, Volume 1: Introduction.
NOAA Atlas NESDIS 42, U.S. Government Printing Office 13, NOAA, Washington, D.C., 167 pp.
Cox, M. D., 1984. A Primitive Equation, 3-Dimensional Model of the Ocean. NOAA/Geophysical Fluid Dy-
namics Laboratory, Princeton, USA.
Cox, M. D., 1987. Isopycnal diffusion in a z-coordinate ocean model. Ocean Modelling 74, 1–5.
Craig, P., Banner, M., 1994. Modeling wave-enhanced turbulence in the surface ocean layer. Journal of
Physical Oceanography 24, 2546–2559.
Cushmin-Roisin, B., 1987. Subduction. In: Dynamics of the oceanic surface mixed-layer. Hawaii Institude of
Geophysical Special Publications, pp. 181–196.
Danabasoglu, G., Ferrari, R., McWilliams, J., 2008. Sensitivity of an ocean general circulation model to a
parameterization of near-surface eddy fluxes. Journal of Climate 21, 1192–1208.
Danabasoglu, G., Large, W., Briegleb, B., 2010. Climate impacts of parameterized nordic sea overflows.
Journal of Geophysical Research 115, C11005, doi:10.1029/2010JC006243.
Danabasoglu, G., Large, W. G., Tribbia, J. J., Gent, P. R., Briegleb, B. P., McWilliams, J. C., 2006. Diurnal
coupling in the tropical oceans of CCSM3. Journal of Climate 19, 2347–2365.
Danabasoglu, G., McWilliams, J. C., 1995. Sensitivity of the global ocean circulation to parameterizations
of mesoscale tracer transports. Journal of Climate 8, 2967–2987.
DeGroot, S. R., Mazur, P., 1984. Non-Equilibrium Thermodynamics. Dover Publications, New York, 510 pp.
Delworth, T. L., Broccoli, A. J., Rosati, A., Stouffer, R. J., Balaji, V., Beesley, J. A., Cooke, W. F., Dixon, K. W.,
Dunne, J., Dunne, K. A., Durachta, J. W., Findell, K. L., Ginoux, P., Gnanadesikan, A., Gordon, C., Griffies,
S. M., Gudgel, R., Harrison, M. J., Held, I. M., Hemler, R. S., Horowitz, L. W., Klein, S. A., Knutson, T. R.,
Kushner, P. J., Langenhorst, A. L., Lee, H.-C., Lin, S., Lu, L., Malyshev, S. L., Milly, P., Ramaswamy, V., Russell,
J., Schwarzkopf, M. D., Shevliakova, E., Sirutis, J., Spelman, M., Stern, W. F., Winton, M., Wittenberg, A. T.,
Wyman, B., Zeng, F., Zhang, R., 2006. GFDL’s CM2 global coupled climate models - Part 1: Formulation
and simulation characteristics. Journal of Climate 19, 643–674.
Delworth, T. L., Rosati, A., Anderson, W., Adcroft, A. J., Balaji, V., Benson, R., Dixon, K., Griffies, S. M., Lee,
H.-C., Pacanowski, R. C., Vecchi, G. A., Wittenberg, A. T., Zeng, F., Zhang, R., 2012. Simulated climate
and climate change in the GFDL CM2.5 high-resolution coupled climate model. Journal of Climate 25,
2755–2781.
Elements of MOM November 19, 2014 Page 615

Bibliography Section 42.2
Denman, K., 1973. A time-dependend model of the upper ocean. Journal of Physical Oceanography 3,
173–184.
Deremble, B., Hogg, A. M., Berloff, P., Dewar, W., 2012. On the application of no-slip lateral boundary condi-
tions to ‘coarsely’ resolved ocean models. Ocean Modelling, doi:10.1016/j.ocemod.2011.05.002.
DeSzoeke, R. A., Bennett, A. F., 1993. Microstructure fluxes across density surfaces. Journal of Physical
Oceanography 23, 2254–2264.
DeSzoeke, R. A., Samelson, R. M., 2002. The duality between the Boussinesq and non-Boussinesq hydro-
static equations of motion. Journal of Physical Oceanography 32, 2194–2203.
Diansky, N., Bagno, A., Zalensy, V., 2002. Global ocean circulation sigma-model and its sensitivity to the
wind stress forcing. Izvestia, Atmospheric and Oceanic Physics 38, 477–494.
Donner, L. J., Wyman, B. L., Hemler, R. S., Horowitz, L. W., Ming, Y., Zhao, M., Golaz, J.-C., Ginoux, P., Lin, S.-J.,
Schwarzkopf, M. D., Austin, J., Alaka, G., Cooke, W. F., Delworth, T. L., Freidenreich, S. M., Gordon, C. T.,
Griffies, S. M., Held, I. M., Hurlin, W. J., Klein, S. A., Knutson, T. R., Langenhorst, A. R., Lee, H.-C., Lin, Y.,
Magi, B. I., Malyshev, S. L., Milly, P., Naik, V., Nath, M. J., Pincus, R., Ploshay, J. J., Ramaswamy, V., Seman,
C. J., Shevliakova, E., Sirutis, J. J., Stern, W. F., Stouffer, R. J., Wilson, R. J., Winton, M., Wittenberg, A. T.,
Zeng, F., 2011. The dynamical core, physical parameterizations, and basic simulation characteristics of
the atmospheric component of the GFDL global coupled model CM3. Journal of Climate 24, 3484–3519.
D¨
oscher, R., Beckmann, A., 2000. Effects of a bottom boundary layer parameterization in a coarse-
resolution model of the North Atlantic Ocean. Journal of Atmospheric and Oceanic Technology 17, 698–
707.
Downes, S. M., Gnanadesikan, A., Griffies, S. M., Sarmiento, J., 2011. Water mass exchange in the Southern
Ocean in coupled climate models. Journal of Physical Oceanography 41, 1756–1771.
Dunne, J. P., John, J. G., Hallberg, R. W., Griffies, S. M., Shevliakova, E. N., Stouffer, R. J., Krasting, J. P.,
Sentman, L. A., Milly, P. C. D., Malyshev, S. L., Adcroft, A. J., Cooke, W., Dunne, K. A., Harrison, M. J., Levy,
H., Samuels, B. L., Spelman, M., Winton, M., Wittenberg, A. T., Phillips, P. J., Zadeh, N., 2012. GFDLs ESM2
global coupled climate-carbon Earth System Models Part I: Physical formulation and baseline simulation
characteristics. Journal of Climate 25, 6646–6665.
Dunne, J. P., John, J. G., Hallberg, R. W., Griffies, S. M., Shevliakova, E. N., Stouffer, R. J., Krasting, J. P.,
Sentman, L. A., Milly, P. C. D., Malyshev, S. L., Adcroft, A. J., Cooke, W., Dunne, K. A., Harrison, M. J., Levy,
H., Wittenberg, A., Phillips, P., Zadeh, N., 2013. GFDLs ESM2 global coupled climate-carbon Earth System
Models Part II: Carbon system formulation and baseline simulation characteristics. Journal of Climate
26, 2247–2267.
Durran, D. R., 1999. Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. Springer Verlag,
Berlin, 470 pp.
Durski, S. M., Glenn, S. M., Haidvogel, D. B., 2004. Vertical mixing schemes in the coastal ocean: Compari-
son of the level 2.5 Mellor-Yamada scheme with an enhanced version of the K profile parameterization.
Journal of Geophysical Research 109, doi:10.1029/2002JC001702.
Eby, M., Holloway, G., 1994. Sensitivity of a large scale ocean model to a parameterization of topographic
stress. Journal of Physical Oceanography 24, 2577–2588.
Eden, C., Greatbatch, R., Olbers, D., 2007. Interpreting eddy fluxes. Journal of Physical Oceanography 37,
1282–1296.
Eden, C., Jochum, M., Danabasoglu, G., 2009. Effects of different closures for thickness diffusivity. Ocean
Modelling 26, 47–59.
Emile-Geay, J., Madec, G., 2009. Geothermal heating, diapycnal mixing and the abyssal circulation. Ocean
Science 5 (2), 203–217.
Elements of MOM November 19, 2014 Page 616

Bibliography Section 42.2
England, M. H., 1995. The age of water and ventilation timescales in a global ocean model. Journal of
Physical Oceanography 25, 2756–2777.
Ezer, T., Arango, H., Shchepetkin, A. F., 2002. Developments in terrain-following ocean models: Intercom-
parisons of numerical aspects. Ocean Modelling 4, 249–267.
Farneti, R., Delworth, T., Rosati, A., Griffies, S. M., Zeng, F., 2010. The role of mesoscale eddies in the rec-
tification of the Southern Ocean response to climate change. Journal of Physical Oceanography 40,
1539–1557.
Farrell, W., Clark, J., 1976. On postglacial sea level. Geophysical Journal of the Royal Astronomical Society
46, 646–667.
Feistel, R., 1993. Equilibrium thermodynamics of seawater revisited. Progress in Oceanography 31, 101–
179.
Feistel, R., 2003. A new extended Gibbs thermodynamic potential of seawater. Progress in Oceanography
58, 43–114.
Feistel, R., Hagen, E., 1995. On the Gibbs thermodynamic potential of seawater. Progress in Oceanography
36, 249–327.
Ferrari, R., Griffies, S. M., Nurser, A. J. G., Vallis, G. K., 2010. A boundary-value problem for the parameterized
mesoscale eddy transport. Ocean Modelling 32, 143–156.
Ferrari, R., McWilliams, J. C., Canuto, V. M., Dubovikov, M., 2008. Parameterization of eddy fluxes near
oceanic boundaries. Journal of Climate 21, 2770–2789.
Ferreira, D., Marshall, J., 2006. Formulation and implementation of a residual-mean ocean circulation
model. Ocean Modelling 13, 86–107.
Fofonoff, N. P., 1962. Physical properties of seawater. In: Hill, M. N. (Ed.), The Sea. Vol. 1. Wiley-Interscience,
pp. 3–30.
Fox-Kemper, B., Danabasoglu, G., Ferrari, R., Griffies, S. M., Hallberg, R. W., Holland, M., Peacock, S., Samuels,
B., 2011. Parameterization of mixed layer eddies. III: Global implementation and impact on ocean climate
simulations. Ocean Modelling 39, 61–78.
Fox-Kemper, B., Danabasoglu, G., Ferrari, R., Hallberg, R. W., 2008a. Parameterizing submesoscale physics
in global models. CLIVAR Exchanges 13, 3–5.
Fox-Kemper, B., Ferrari, R., Hallberg, R., 2008b. Parameterization of mixed layer eddies. I: Theory and diag-
nosis. Journal of Physical Oceanography 38, 1145–1165.
Galbraith, E., Gnanadesikan, A., Griffies, S. M., Dunne, J., Wittenberg, A., Held, I., Kwon, E.-Y., Rodgers, K.,
Bianchi, D., Sarmiento, J., Slater, R., Simeon, J., 2011. The impact of climate variability on the distribution
of radiocarbon in CM2Mc, a new earth system model. Journal of Climate 24, 4230–4254.
Gargett, A. E., 1984. Vertical eddy diffusivity in the ocean interior. Journal of Marine Research 42, 359–393.
Gent, P., Bryan, F., Danabasoglu, G., Doney, S., Holland, W., Large, W., McWilliams, J., 1998. The NCAR
climate system model global ocean component. Journal of Climate 11, 1287–1306.
Gent, P. R., McWilliams, J. C., 1990. Isopycnal mixing in ocean circulation models. Journal of Physical
Oceanography 20, 150–155.
Gent, P. R., Willebrand, J., McDougall, T. J., McWilliams, J. C., 1995. Parameterizing eddy-induced tracer
transports in ocean circulation models. Journal of Physical Oceanography 25, 463–474.
Gill, A., 1982. Atmosphere-Ocean Dynamics. Vol. 30 of International Geophysics Series. Academic Press,
London, 662 + xv pp.
Elements of MOM November 19, 2014 Page 617

Bibliography Section 42.2
Gill, A. E., Niiler, P., 1973. The theory of the seasonal variability in the ocean. Deep-Sea Research 20 (9),
141–177.
Gnanadesikan, A., Dixon, K. W., Griffies, S. M., Balaji, V., Beesley, J. A., Cooke, W. F., Delworth, T. L., Gerdes,
R., Harrison, M. J., Held, I. M., Hurlin, W. J., Lee, H.-C., Liang, Z., Nong, G., Pacanowski, R. C., Rosati, A.,
Russell, J., Samuels, B. L., Song, S. M., , Spelman, M. J., Stouffer, R. J., Sweeney, C. O., Vecchi, G., Winton,
M., Wittenberg, A. T., Zeng, F., Zhang, R., 2006. GFDL’s CM2 global coupled climate models-Part 2: The
baseline ocean simulation. Journal of Climate 19, 675–697.
Goosens, M., Mittelbach, F., Samarin, A., 1994. The L
A
T
E
XCompanion. Addison-Wesley, Reading, Mas-
sachusetts, 528 pp.
Gordon, C., Cooper, C., Senior, C. A., Banks, H., J. M. Gregory, T. C. J., Mitchell, J. F. B., Wood, R. A., 2000. The
simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled
model without flux adjustments. Climate Dynamics 16, 147–168.
Greatbatch, R. J., 1994. A note on the representation of steric sea level in models that conserve volume
rather than mass. Journal of Geophysical Research 99, 12767–12771.
Greatbatch, R. J., Lamb, K. G., 1990. On parameterizing vertical mixing of momentum in non-eddy resolving
ocean models. Journal of Physical Oceanography 20, 1634–1637.
Greatbatch, R. J., Lu, Y., Cai, Y., 2001. Relaxing the Boussinesq approximation in ocean circulation models.
Journal of Atmospheric and Oceanic Technology 18, 1911–1923.
Greatbatch, R. J., McDougall, T. J., 2003. The non-Boussinesq temporal-residual-mean. Journal of Physical
Oceanography 33, 1231–1239.
Greatbatch, R. J., Mellor, G. L., 1999. An overview of coastal ocean models. In: Mooers, C. (Ed.), Coastal
Ocean Prediction. Vol. 56 of Coastal and Estuarine Studies. American Geophysical Union, pp. 31–57.
Gregg, M., Sanford, T., Winkel, D., 2003. Reduced mixing from the breaking of internal waves in equatorial
waters. Nature 422, 513–515.
Griffies, S. M., 1998. The Gent-McWilliams skew-flux. Journal of Physical Oceanography 28, 831–841.
Griffies, S. M., 2004. Fundamentals of Ocean Climate Models. Princeton University Press, Princeton, USA,
518+xxxiv pages.
Griffies, S. M., 2005. Some ocean model fundamentals. In: Chassignet, E. P., Verron, J. (Eds.), GODAE Sum-
mer School. Springer/Kluwer, pp. 19–74.
Griffies, S. M., 2009. Elements of MOM4p1: GFDL Ocean Group Technical Report No. 6. NOAA/Geophysical
Fluid Dynamics Laboratory, Princeton, USA, 444 pp.
Griffies, S. M., Adcroft, A. J., 2008. Formulating the equations for ocean models. In: Hecht, M., Hasumi,
H. (Eds.), Ocean Modeling in an Eddying Regime. Geophysical Monograph 177. American Geophysical
Union, pp. 281–317.
Griffies, S. M., Biastoch, A., B¨
oning, C. W., Bryan, F., Danabasoglu, G., Chassignet, E., England, M. H., Gerdes,
R., Haak, H., Hallberg, R. W., Hazeleger, W., Jungclaus, J., Large, W. G., Madec, G., Pirani, A., Samuels,
B. L., Scheinert, M., Gupta, A. S., Severijns, C. A., Simmons, H. L., Treguier, A. M., Winton, M., Yeager, S.,
Yin, J., 2009. Coordinated Ocean-ice Reference Experiments (COREs). Ocean Modelling 26, 1–46.
Griffies, S. M., B¨
oning, C. W., Bryan, F. O., Chassignet, E. P., Gerdes, R., Hasumi, H., Hirst, A., Treguier, A.-M.,
Webb, D., 2000a. Developments in ocean climate modelling. Ocean Modelling 2, 123–192.
Griffies, S. M., Gnanadesikan, A., Dixon, K. W., Dunne, J. P., Gerdes, R., Harrison, M. J., Rosati, A., Russell,
J., Samuels, B. L., Spelman, M. J., Winton, M., Zhang, R., 2005. Formulation of an ocean model for global
climate simulations. Ocean Science 1, 45–79.
Elements of MOM November 19, 2014 Page 618

Bibliography Section 42.2
Griffies, S. M., Gnanadesikan, A., Pacanowski, R. C., Larichev, V., Dukowicz, J. K., Smith, R. D., 1998. Isoneu-
tral diffusion in a z-coordinate ocean model. Journal of Physical Oceanography 28, 805–830.
Griffies, S. M., Greatbatch, R. J., 2012. Physical processes that impact the evolution of global mean sea
level in ocean climate models. Ocean Modelling 51, 37–72.
Griffies, S. M., Hallberg, R. W., 2000. Biharmonic friction with a Smagorinsky viscosity for use in large-scale
eddy-permitting ocean models. Monthly Weather Review 128, 2935–2946.
Griffies, S. M., Harrison, M. J., Pacanowski, R. C., Rosati, A., 2004. A Technical Guide to MOM4.
NOAA/Geophysical Fluid Dynamics Laboratory, Princeton, USA, 337 pp.
Griffies, S. M., Pacanowski, R., Schmidt, M., Balaji, V., 2001. Tracer conservation with an explicit free surface
method for z-coordinate ocean models. Monthly Weather Review 129, 1081–1098.
Griffies, S. M., Pacanowski, R. C., Hallberg, R. W., 2000b. Spurious diapycnal mixing associated with advec-
tion in a z-coordinate ocean model. Monthly Weather Review 128, 538–564.
Griffies, S. M., Winton, M., Donner, L. J., Downes, S. M., Farneti, R., Gnanadesikan, A., Horowitz, L. W., Hurlin,
W. J., Lee, H.-C., Liang, Z., Palter, J. B., Samuels, B. L., Wittenberg, A. T., Wyman, B. L., Yin, J., Zadeh, N. T.,
2011. GFDL’s CM3 coupled climate model: Characteristics of the ocean and sea ice simulations. Journal
of Climate 24, 3520–3544.
Hallberg, R. W., 1997. Stable split time stepping schemes for large-scale ocean modeling. Journal of Com-
putational Physics 135, 54–65.
Hallberg, R. W., 2000. Time integration of diapycnal diffusion and Richardson number-dependent mixing in
isopycnal coordinate ocean models. Monthly Weather Review 128, 1402–1419.
Haltiner, G. T., Williams, R. T., 1980. Numerical Prediction and Dynamic Meteorology. John Wiley and Sons,
New York, USA.
Hecht, M., Peterson, M., Wingate, B., Hunke, E., Maltrud, M., 2008. Lateral mixing in the eddying regime and
a new broad-ranging formulation. In: Hecht, M., Hasumi, H. (Eds.), Ocean Modeling in an Eddying Regime.
Geophysical Monograph 177. American Geophysical Union, pp. 339–352.
Held, I. M., Larichev, V. D., 1996. A scaling theory for horizontally homogeneous baroclinically unstable flow
on a beta plane. Journal of Atmospheric Sciences 53, 946–952.
Hendershott, M., 1972. The effects of solid earth deformation on global ocean tide. Geophysical Journal of
the Royal Astronomical Society 29, 389–402.
Herzfeld, M., Schmidt, M., Griffies, S. M., Liang, Z., 2011. Realistic test cases for limited area ocean mod-
elling. Ocean Modelling 37, 1–34.
Hesselberg, T., 1926. Die Gesetze der ausgeglichenen atmosphaerischen Bewegungen. Beitr¨
ageder Physik
der freien Atmosphere 12, 141–160.
Hirsch, C., 1988. Numerical Computation of Internal and External Flows. John Wiley and Sons.
Holland, W., Chow, J., Bryan, F., 1998. Application of a third-order upwind scheme in the NCAR ocean model.
Journal of Climate 11, 1487–1493.
Holloway, G., 1992. Representing topographic stress for large-scale ocean models. Journal of Physical
Oceanography 22, 1033–1046.
Holloway, G., 1999. Moments of probable seas: statistical dynamics of Planet Ocean. Physica D 133, 199–
214.
Holloway, G., 2008. Observing global ocean topostrophy. Journal of Geophysical Research 113-C07054,
doi:10.1029/2007JC004635.
Elements of MOM November 19, 2014 Page 619

Bibliography Section 42.2
Holloway, G., Dupont, F., Golubeva, E., Ha¨
kkinen, S., Hunke, E., Jin, M., Karcher, M., Kauker, F., Maltrud, M.,
Morales-Maqueda, M. A., Maslowski, W., Platov, G., Stark, D., Steele, M., Suzuki, T., Wang, J., Zhang, J.,
2007. Water properties and circulation in Arctic Ocean models. Journal of Geophysical Research 112-
C04S03, doi:10.1029/2006JC003642.
Hsieh, W., Bryan, K., 1996. Redistribution of sea level rise associated with enhanced greenhouse warming:
a simple model study. Climate Dynamics 12, 535–544.
Huang, R. X., 1993. Real freshwater flux as a natural boundary condition for the salinity balance and ther-
mohaline circulation forced by evaporation and precipitation. Journal of Physical Oceanography 23,
2428–2446.
Huang, R. X., Jin, X., Zhang, X., 2001. An oceanic general circulation model in pressure coordinates. Ad-
vances in Atmospheric Physics 18, 1–22.
Hundsdorfer, W., Trompert, R., 1994. Method of lines and direct discretization: a comparison for linear
advection. Applied Numerical Mathematics, 469–490.
Ilicak, M., Adcroft, A. J., Griffies, S. M., Hallberg, R. W., 2012. Spurious dianeutral mixing and the role of
momentum dissipation. Ocean Modelling 45–46, 37–58.
IOC, SCOR, IAPSO, 2010. The international thermodynamic equation of seawater-2010: calculation and
use of thermodynamic properties. Intergovernmental Oceanographic Commission, Manuals and Guides
No. 56, UNESCO, available from http://www.TEOS-10.org, 196pp.
Iudicone, D., Madec, G., McDougall, T. J., 2008. Water-mass transformations in a neutral density framework
and the key role of light penetration. Journal of Physical Oceanography 38, 1357–1376.
Jackett, D. R., McDougall, T. J., 1997. A neutral density variable for the worlds oceans. Journal of Physical
Oceanography 27, 237–263.
Jackett, D. R., McDougall, T. J., Feistel, R., Wright, D. G., Griffies, S. M., 2006. Algorithms for density, potential
temperature, conservative temperature, and freezing temperature of seawater. Journal of Atmospheric
and Oceanic Technology 23, 1709–1728.
Jayne, S., 2009. The impact of abyssal mixing parameterizations in an ocean general circulation model.
Journal of Physical Oceanography 39, 1756–1775.
Jayne, S., St.Laurent, L. C., 2001. Parameterizing tidal dissipation over rough topography. Geophysical
Research Letters 28, 811–814.
Jerlov, N. G., 1968. Optical Oceanography. Elsevier.
Kantha, L. H., Clayson, C. A., 2000. Small Scale Processes in Geophysical Fluid Flows. Academic Press, New
York, USA, 883 pp.
Killworth, P., 1989. On the parameterisation of deep convection in ocean models. In: M ¨
uller, P., Holloway, G.
(Eds.), Parameterizing small scale processes in the ocean. Proceeding of the 5th ’Aha Huliko’a Hawaiian
Winter Workshop. University of Hawaii at Manoa, pp. 59–74.
Killworth, P. D., Edwards, N., 1999. A turbulent bottom boundary layer code for use in numerical ocean
models. Journal of Physical Oceanography 29, 1221–1238.
Killworth, P. D., Stainforth, D., Webb, D. J., Paterson, S. M., 1991. The development of a free-surface Bryan-
Cox-Semtner ocean model. Journal of Physical Oceanography 21, 1333–1348.
Klinger, B. A., Marshall, J., Send, U., 1996. Representation of convective plumes by vertical adjustment.
Journal of Geophysical Research 101, 18175–18182.
Klocker, A., McDougall, T. J., 2010a. Influence of the nonlinear equation of state on global estimates of
dianeutral advection and diffusion. Journal of Physical Oceanography 40, 1690–1709.
Elements of MOM November 19, 2014 Page 620

Bibliography Section 42.2
Klocker, A., McDougall, T. J., 2010b. Quantifying the consequences of the ill-defined nature of neutral
surfaces. Journal of Physical Oceanography 40, 1866–1880.
Klocker, A., McDougall, T. J., Jackett, D. R., 2009. A new method for forming approximately neutral surfaces.
Ocean Science 5, 155–172.
Klymak, J., Moum, J., Nash, J., Kunze, E., Girton, J., Carter, G., Lee, C., Sanford, T., Gregg, M., 2005. An
estimate of tidal energy lost to turbulence at the hawaiian ridge. Journal of Physical Oceanography
submitted.
Kopp, R. E., Mitrovica, J. X., Griffies, S. M., Yin, J., Hay, C. C., Stouffer, R. J., 2010. The impact of Greenland
melt on regional sea level: a preliminary comparison of dynamic and static equilibrium effects. Climatic
Change Letters 103, 619–625.
Kwon, E., Downes, S., Sarmiento, J., Farneti, R., Deutsch, C., 2013. Role of the seasonal cycle in the subduc-
tion rates of Upper-Southern Ocean mode waters. Journal of Physical Oceanography 43, 1096–1113.
Lamport, L., 1994. L
A
T
E
X: A Documentation Preparation System User’s Guide and Reference Manual.
Addison-Wesley, Reading, Massachusetts, 272 pp.
Landau, L. D., Lifshitz, E. M., 1976. Mechanics. Pergamon Press, Oxford, UK, 170 pp.
Landau, L. D., Lifshitz, E. M., 1987. Fluid Mechanics. Pergamon Press, Oxford, UK, 539 pp.
Landerer, F., Jungclaus, J., Marotzke, J., 2007. Regional dynamic and steric sea level change in response
to the IPCC-A1B Scenario. Journal of Physical Oceanography 37, 296–312.
Large, W., 1998. Modeling the oceanic boundary layer. In: Chassignet, E. P., Verron, J. (Eds.), Ocean Model-
ing and Parameterization. Vol. 516 of NATO ASI Mathematical and Physical Sciences Series. Kluwer, pp.
81–120.
Large, W., Gent, P., 1999. Validation of vertical mixing in an equatorial ocean model using large eddy simu-
lations and observations. Journal of Physical Oceanography 29, 449–464.
Large, W., McWilliams, J., Doney, S., 1994. Oceanic vertical mixing: a review and a model with a nonlocal
boundary layer parameterization. Reviews of Geophysics 32, 363–403.
Large, W. B., Nurser, A. G., 2001. Ocean surface water mass transformation. In: Seidler, G., Church, J.,
Gould, J. (Eds.), Ocean Circulation and Climate. Vol. 77 of International Geophysics Series. Academic
Press, San Diego, pp. 317–336.
Large, W. G., Danabasoglu, G., Doney, S. C., McWilliams, J. C., 1997. Sensitivity to surface forcing and
boundary layer mixing in a global ocean model: annual-mean climatology. Journal of Physical Oceanog-
raphy 27, 2418–2447.
Large, W. G., Danabasoglu, G., McWilliams, J. C., Gent, P. R., Bryan, F. O., 2001. Equatorial circulation of a
global ocean climate model with anisotropic horizontal viscosity. Journal of Physical Oceanography 31,
518–536.
Leclair, M., Madec, G., 2009. A conservative leapfrog time-stepping method. Ocean Modelling 30, 88–94.
Ledwell, J. R., St.Laurent, L., Girton, J., Toole, J., 2011. Diapycnal mixing in the Antarctic Circumpolar Cur-
rent. Journal of Physical Oceanography 41, 241–246.
Ledwell, J. R., Watson, A. J., Law, C. S., 1993. Evidence for slow mixing across the pycnocline from an
open-ocean tracer-release experiment. Nature 364, 701–703.
Lee, H.-C., Rosati, A., Spelman, M., 2006. Barotropic tidal mixing effects in a coupled climate model:
Oceanic conditions in the northern Atlantic. Ocean Modelling 3-4, 464–477.
Elements of MOM November 19, 2014 Page 621

Bibliography Section 42.2
Lemari´
e, F., Debreu, L., Shchepetkin, A. F., McWilliams, J. C., 2012a. On the stability and accuracy of the
harmonic and biharmonic isoneutral mixing operators in ocean models. Ocean Modelling 52-53, 9–35.
Lemari´
e, F., Kurian, J., Shchepetkin, A. F., Molemaker, M. J., Colas, F., McWilliams, J. C., 2012b. Are there
inescapable issues prohibiting the use of terrain-following coordinates in climate models? Ocean Mod-
elling 42, 57–79.
Leonard, B. P., 1979. A stable and accurate convective modelling procedure based on quadratic upstream
interpolation. Computer Methods in Applied Mechanics and Engineering 19, 59–98.
Levitus, S., 1982. Climatological atlas of the world ocean. U.S. Government Printing Office 13, NOAA, Wash-
ington, D.C., 163 pp.
Li, X., Chao, Y., McWilliams, J. C., Fu, L. L., 2001. A comparison of two vertical-mixing schemes in a Pacific
ocean general circulation model. Journal of Climate 14, 1377–1398.
Lin, S. J., 1997. A finite volume integration method for computing pressure gradient force in general verti-
cal coordinates. Quarterly Journal of the Royal Meteorological Society 123, 1749–1762.
Lorbacher, K., Marsland, S. J., Church, J. A., Griffies, S. M., Stammer, D., 2012. Rapid barotropic sea-level
rise from ice-sheet melting scenarios. Journal of Geophysical Research 117, C06003.
Losch, M., Adcroft, A., Campin, J.-M., 2004. How sensitive are coarse general circulation models to funda-
mental approximations in the equations of motion? Journal of Physical Oceanography 34, 306–319.
Lowe, J. A., Gregory, J. M., 2006. Understanding projections of sea level rise in a hadley centre coupled
climate model. Journal of Geophysical Research: Oceans 111 (C11), n/a–n/a.
URL http://dx.doi.org/10.1029/2005JC003421
Machenhauer, B., Kaas, E., Lauritzen, P., 2009. Finite-volume methods in meteorology. In: Temam, R., Trib-
bia, J. (Eds.), Computational Methods for the Atmosphere and the Oceans. Elsevier, Amsterdam, p. 761.
Madec, G., Imbard, M., 1996. A global ocean mesh to overcome the North Pole singularity. CD 12, 381–388.
Maltrud, M., Holloway, G., 2008. Implementing biharmonic neptune in a global eddying ocean model. Ocean
Modelling 21, 22–34.
Manizza, M., Le Quere, C., Watson, A., Buitenhuis, E., 2005. Bio-optical feedbacks among phyto-
plankton, upper ocean physics and sea-ice in a global model. Geophysical Research Letters 32,
doi:10.1029/2004GL020778.
Marchesiello, J. M. P., Shchepetkin, A., 2001. Open boundary conditions for long-term integration of re-
gional oceanic models. Ocean Modelling 3, 1–20.
Marchuk, Kagan, 1989. Dynamics of Ocean Tides. Kluwer Academic.
Marion, J. B., Thornton, S. T., 1988. Classical Dynamics of Particles and Systems. Harcourt Brace Jo-
vanovich, San Diego, USA, 602 pp.
Marotzke, J., 1991. Influence of convective adjustment on the stability of the thermohaline circulation.
Journal of Physical Oceanography 21, 903–907.
Marshall, J., Adcroft, A., Campin, J.-M., Hill, C., White, A., 2004. Atmosphere-ocean modeling exploiting fluid
isomorphisms. Monthly Weather Review 132, 2882–2894.
Marshall, J., Hill, C., Perelman, L., Adcroft, A., 1997. Hydrostatic, quasi-hydrostatic, and nonhydrostatic
ocean modeling. Journal of Geophysical Research 102, 5733–5752.
Marshall, J., Jamous, D., Nilsson, J., 1999. Reconciling thermodynamic and dynamic methods of computa-
tion of water-mass transformation rates. Deep-Sea Research I 46, 545–572.
Elements of MOM November 19, 2014 Page 622

Bibliography Section 42.2
Marshall, J., Schott, F., 1999. Open-ocean convection: observations, theory, and models. Reviews of Geo-
physics 37, 1–64.
Martinsen, E., Engedahl, H., 1987. Implementation and testing of a lateral boundary scheme as an open
boundary condition in a barotropic ocean model. Coastal Engineering 11, 603–627.
Maze, G., Forget, G., Buckley, M., Marshall, J., Cerovecki, I., 2009. Using transformation and formation maps
to study the role of air-sea heat fluxes in the North Atlantic eighteen degree water formation. Journal of
Physical Oceanography 39, 1818–1835.
McDougall, T. J., 1987a. Neutral surfaces. Journal of Physical Oceanography 17, 1950–1967.
McDougall, T. J., 1987b. Thermobaricity, cabbeling, and water-mass conversion. Journal of Geophysical
Research 92, 5448–5464.
McDougall, T. J., 1995. The influence of ocean mixing on the absolute velocity vector. Journal of Physical
Oceanography 25, 705–725.
McDougall, T. J., 2003. Potential enthalpy: a conservative oceanic variable for evaluating heat content and
heat fluxes. Journal of Physical Oceanography 33, 945–963.
McDougall, T. J., Barker, P., Feistel, R., Jackett, D., 2012. A computationally efficient 48-term expression for
the density of seawater in terms of conservative temperature, and related properties of seawater. Ocean
Science in preparation.
McDougall, T. J., Church, J. A., 1986. Pitfalls with numerical representations of isopycnal and diapycnal
mixing. Journal of Physical Oceanography 16, 196–199.
McDougall, T. J., Greatbatch, R., Lu, Y., 2002. On conservation equations in oceanography: How accurate
are Boussinesq ocean models? Journal of Physical Oceanography 32, 1574–1584.
McDougall, T. J., Jackett, D. R., 1988. On the helical nature of neutral trajectories in the ocean. Progress in
Oceanography 20, 153–183.
McDougall, T. J., Jackett, D. R., 2005. The material derivative of neutral density. Journal of Marine Research
63, 159–185.
McDougall, T. J., Jackett, D. R., Wright, D. G., Feistel, R., 2003. Accurate and computationally efficient algo-
rithms for potential temperature and density of seawater. Journal of Atmospheric and Oceanic Technol-
ogy 20, 730–741.
McDougall, T. J., McIntosh, P. C., 2001. The temporal-residual-mean velocity. Part II: isopycnal interpretation
and the tracer and momentum equations. Journal of Physical Oceanography 31, 1222–1246.
McWilliams, J. C., Sullivan, P., 2001. Vertical mixing by Langmuir circulations. Spill Science and Technology
Bulletin 6, 225–237.
Merryfield, W. J., Holloway, G., 2003. Application of an accurate advection algorithm to sea-ice modelling.
Ocean Modelling 5, 1–15.
Merryfield, W. J., Scott, R., 2007. Bathymetric influence on mean currents in two high resolution near-global
ocean models. Ocean Modelling 16, 76–94.
Mesinger, F., 1973. A method for construction of second-order accurate difference schemes permitting no
false two-grid-interval waves in the height field. Tellus 25, 444–457.
Mesinger, F., Arakawa, A., 1976. Numerical methods used in atmospheric models. In: GARP Publication
Series. Vol. 1. p. 66 pages.
Miller, M., Thorpe, A., 1981. Radiation conditions for the lateral boundaries of limited-area numerical mod-
els. Quarterly Journal of the Royal Meteorological Society 107, 615–628.
Elements of MOM November 19, 2014 Page 623

Bibliography Section 42.2
Mitrovica, J. X., Tamisiea, M. E., Davis, J. L., Milne, G. A., 2001. Recent mass balance of polar ice sheets
inferred from patterns of global sea-level change. Nature 409, 1026–1029.
Morel, A., 1988. Optical modeling of the upper ocean in relation to its biogenous matter content (case-i
waters). JGR 93, 10749–10768.
Morel, A., Antoine, D., 1994. Heating rate within the upper ccean in relation to its bio-optical state. Journal
of Physical Oceanography 24, 1652–1665.
Morel, A., Berthon, J.-F., 1989. Surface pigments, algal biomass profiles, and potential production of
the euphotic layer: relationship reinvestigated in view of remote-sensing applications. Limnology and
Oceanography 34, 1542–1562.
Morse, P. M., Feshbach, H., 1953. Methods of Theoretical Physics Part I and II. McGraw-Hill Book Company,
New York.
Moum, J., Caldwell, D., Nash, J., Gunderson, G., 2002. Observations of boundary mixing over the continen-
tal slope. Journal of Physical Oceanography 32, 2113–2130.
M¨
uller, P., 2006. The Equations of Oceanic Motions, 1st Edition. Cambridge University Press, Cambridge,
302pp.
Munk, W., Anderson, E., 1948. Notes on a theory of the thermocline. Journal of Marine Research 3, 276–
295.
Murray, R., 1996. Explicit generation of orthogonal grids for ocean models. Journal of Computational
Physics 126, 251–273.
Naveira-Garabato, A., Polzin, K., King, B., Heywood, K., Visbeck, M., 2004. Widspread intense turbulent
mixing in the Southern Ocean. Science 303, 210–213.
Nicholls, R., Cazenave, A., 2010. Sea-level rise and its impact on coastal zones. Science 328, 1517–1520.
Nikurashin, M., Ferrari, R., 2010. Radiation and dissipation of internal waves generated by geostrophic
motions impinging on small-scale topography: Application to the Southern Ocean. Journal of Physical
Oceanography 40, 2025–2042.
O’Brien, J. J., 1986. Advanced Physical Oceanographic Numerical Modelling. D. Reidel Publishing Company.
Ohlmann, J., 2003. Ocean radiant heating in climate models. JOC 16, 1337–1351.
Ohlmann, J., Siegel, D., 2000. Ocean radiant heating. Part i: Optical influences. JPO 30, 1833–1848.
Olbers, D. J., Wenzel, M., Willebrand, J., 1985. The inference of North Atlantic circulation patterns from
climatological hydrographic data. Reviews of Geophysics 23, 313–356.
Orlanski, I., 1976. A simple boundary condition for unbounded hyberbolic flows. Journal of Computational
Physics 21, 251–269.
Osborn, T. R., 1980. Estimates of the local rate of vertical diffusion from dissipation measurements. Journal
of Physical Oceanography 10, 83–89.
Pacanowski, R. C., 1987. Effect of equatorial currents on surface stress. Journal of Physical Oceanography
17, 833–838.
Pacanowski, R. C., 1995. MOM2 Documentation, User’s Guide, and Reference Manual. NOAA/Geophysical
Fluid Dynamics Laboratory, Princeton, USA, 216 pp.
Pacanowski, R. C., Dixon, K., Rosati, A., 1991. The GFDL Modular Ocean Model User Guide.
NOAA/Geophysical Fluid Dynamics Laboratory, Princeton, USA, 16 pp.
Elements of MOM November 19, 2014 Page 624

Bibliography Section 42.2
Pacanowski, R. C., Gnanadesikan, A., 1998. Transient response in a z-level ocean model that resolves to-
pography with partial-cells. Monthly Weather Review 126, 3248–3270.
Pacanowski, R. C., Griffies, S. M., 1999. The MOM3 Manual. NOAA/Geophysical Fluid Dynamics Laboratory,
Princeton, USA, 680 pp.
Pacanowski, R. C., Philander, G., 1981. Parameterization of vertical mixing in numerical models of the trop-
ical ocean. Journal of Physical Oceanography 11, 1442–1451.
Palma, E., Matano, R., 1998. On the implementation of passive open boundary conditions for a general
circulation model: The barotropic mode. Journal of Geophysical Research 103(C1), 1319–1341.
Palma, E., Matano, R., 2001. Dynamical impacts associated with radiation boundary conditions. Journal of
Sea Research 46, 117–132.
Paulson, E. A., Simpson, J. J., 1977. Irradiance measurements in the upper ocean. Journal of Physical
Oceanography 7, 952–956.
Peixoto, J. P., Oort, A. H., 1992. Physics of Climate. American Institute of Physics, 520 + xxxix pp.
Phillips, N., 1973. Principles of large-scale numerical weather prediction. In: Morel, P. (Ed.), Dynamic Mete-
orology. Riedel, pp. 1–96.
Pickard, G. L., Emery, W. J., 1990. Descriptive Physical Oceanography, 5th Edition. Pergamon Press, Oxford.
Polzin, K. L., Toole, J. M., Ledwell, J. R., Schmitt, R. W., 1997. Spatial variability of turbulent mixing in the
abyssal ocean. Science 276, 93–96.
Prather, M., 1986. Numerical advection by conservation of second-order moments. Journal of Geophysical
Research 91, 6671–6681.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., Flannery, B. P., 1992. Numerical Recipes in FORTRAN: The Art
of Scientific Computing, 2nd Edition. Cambridge University Press, Cambridge, 963 + xxvi pp.
Rahmstorf, S., 1993. A fast and complete convection scheme for ocean models. Ocean Modelling 101,
9–11.
Ray, R. D., 1998. Ocean self-attraction and loading in numerical tidal models. Marine Geodesy 21, 181–192.
Raymond, W., Kuo, H., 1984. A radiation boundary condition for multidimensional flows. Quaterly Journal
of the Royal Meterological Society 110, 535–551.
Redi, M. H., 1982. Oceanic isopycnal mixing by coordinate rotation. Journal of Physical Oceanography 12,
1154–1158.
Robert, A., 1966. The integration of a low order spectral form of the primitive meteorological equations.
Journal of the Meteorological Society of Japan 44, 237–244.
Robinson, I., 2005. Satellite oceanography. In: Chassignet, E. P., Verron, J. (Eds.), GODEA Summer School.
Springer/Kluwer.
Roed, L., Cooper, C., 1987. A study of various open boundary conditions for wind-forced barotropic numer-
ical ocean models. In: Nihoul, J., Jamart, B. (Eds.), Three-dimensional Models of marine and Estuarine
Dynamics. Elsevier, pp. 305–335.
Rosati, A., Miyakoda, K., 1988. A general circulation model for upper ocean simulation. Journal of Physical
Oceanography 18, 1601–1626.
Sadourny, R., 1975. The dynamics of finite-difference models of the shallow-water equations. Journal of
Atmospheric Sciences 32, 680–689.
Elements of MOM November 19, 2014 Page 625

Bibliography Section 42.2
Schmitt, R. W., 1994. Double diffusion in oceanography. Annual Review of Fluid Mechanics 26, 255–285.
Shchepetkin, A., McWilliams, J., 2002. A method for computing horizontal pressure-gradient force in an
ocean model with a non-aligned vertical coordinate. Journal of Geophysical Research 108, 35.1–35.34.
Shchepetkin, A., McWilliams, J., 2005. The regional oceanic modeling system (ROMS): a split-explicit, free-
surface, topography-following-coordinate oceanic model. Ocean Modelling 9, 347–404.
Shchepetkin, A. F., 2005. If-less kpp. ROMS/TOMS Workshop: Adjoint Modeling and Applications.
Simmons, H. L., Jayne, S. R., St.Laurent, L. C., Weaver, A. J., 2004. Tidally driven mixing in a numerical
model of the ocean general circulation. Ocean Modelling 6, 245–263.
Smagorinsky, J., 1963. General circulation experiments with the primitive equations: I. The basic experi-
ment. Monthly Weather Review 91, 99–164.
Smagorinsky, J., 1993. Some historical remarks on the use of nonlinear viscosities. In: Galperin, B., Orszag,
S. A. (Eds.), Large Eddy Simulation of Complex Engineering and Geophysical Flows. Cambridge University
Press, pp. 3–36.
Smith, R. D., Kortas, S., Meltz, B., 1995. Curvilinear coordinates for global ocean models. Los Alamos
preprint LA-UR-95-1146.
Smith, R. D., McWilliams, J. C., 2003. Anisotropic horizonal viscosity for ocean models. Ocean Modelling 5,
129–156.
Smyth, G. C. W. D., Skyllingstad, E. D., Wijesekera, H., 2002. Nonlocal fluxes and Stokes drift effects in the
K-profile parameterization. Ocean Dynamics 52, 104–115.
Solomon, H., 1971. On the representation of isentropic mixing in ocean models. Journal of Physical
Oceanography 1, 233–234.
Sommerfeld, A., 1949. Partial differential equations. Lectures in Theoretical Physics 6. Academic Press,
New York.
Speer, K., Tziperman, E., 1992. Rates of water mass formation in the North Atlantic Ocean. Journal of
Physical Oceanography 22, 2444–2457.
Stacey, M. W., Pond, S., Nowak, Z. P., 1995. A numerical model of the circulation in Knight Inlet, British
Columbia, Canada. Journal of Physical Oceanography 25, 1037–1062.
Stammer, D., 2008. Response of the global ocean to Greenland and Antarctic ice melting. Journal of Geo-
physical Research 113, doi:10.1029/2006JC004079.
Starr, V. P., 1945. A quasi-Lagrangian system of hydrodynamical equations. Journal of Meteorology 2, 227–
237.
Stevens, D. P., 1990. On open boundary conditions for three dimensional primitive equation ocean circula-
tion models. Geophysical and Astrophysical Fluid Dynamics 51, 103–133.
Stevens, D. P., 1991. The open boundary conditions in the united kingdom fine-resolution antarctic model.
Journal of Physical Oceanography 21, 1494–1499.
St.Laurent, L. C., Simmons, H., Jayne, S., 2002. Estimating tidally driven energy in the deep ocean. Geo-
physical Research Letters 29, 2106–2110.
St.Laurent, L. C., Stringer, S., Garrett, C., Perrault-Joncas, D., 2003. The generation of internal tides at
abrupt topography. Deep-Sea Research 50, 987–1003.
St.Laurent, L. C., Toole, J., Schmitt, R., 2001. Buoyancy forcing by turbulence above rough topography in
the abyssal brazil basin. Journal of Physical Oceanography 31, 3476–3495.
Elements of MOM November 19, 2014 Page 626

Bibliography Section 42.2
Stouffer, R. J., Broccoli, A., Delworth, T., Dixon, K., Gudgel, R., Held, I., Hemler, R., Knutsn, T., Lee, H.-C.,
Schwarzkopf, M., Soden, B., Spelman, M., Winton, M., Zeng, F., 2006a. GFDL’s CM2 global coupled climate
models: Part 4: idealized climate response. Journal of Climate 19, 723–740.
Stouffer, R. J., Dixon, K., Spelman, M., Hurlin, W., Yin, J., Gregory, J., Weaver, A., Eby, M., Flato, G., Robitaille,
D., Hasumi, H., Oka, A., Hu, A., Jungclaus, J., Kamenkovich, I., Levermann, A., Montoya, M., Murakami,
S., Nawrath, S., Peltier, W., Vettoretti, G., Sokolov, A., Weber, S., 2006b. Investigating the causes of the
response of the thermohaline circulation to past and future climate changes. Journal of Climate 19,
1365–1387.
Sullivan, P. P., McWilliams, J. C., 2010. Dynamics of winds and currents coupled to surface waves. Annual
Review of Fluid Mechanics 42, 19–42.
Sweby, P., 1984. High-resolution schemes using flux limiters for hyperbolic conservation-laws. SIAM Journal
of Numerical Analysis 21, 995–1011.
Sweeney, C., Gnanadesikan, A., Griffies, S. M., Harrison, M., Rosati, A., Samuels, B., 2005. Impacts of
shortwave penetration depth on large-scale ocean circulation and heat transport. Journal of Physical
Oceanography 35, 1103–1119.
Tang, Y., Grimshaw, R., 1996. Radiation boundary conditions in barotropic coastal ocean numerical models.
Journal of Computational Physics 123, 96–110.
Tang, Y., Roberts, M., 2005. The impact of a bottom boundary layer scheme on the North Atlantic Ocean in
a global coupled climate model. Journal of Physical Oceanography 35, 202–217.
Tennekes, H., 1973. The logarithmic wind profile. Journal of Atmospheric Sciences 30, 558–567.
Terray, E., Donelan, M., Agrawal, Y., Drennan, W., Kahma, K., Williams, A., Hwang, P., Kitaigorodskii, S., 1996.
Estimates of kinetic energy dissipation under breaking waves. Journal of Physical Oceanography 26,
792–807.
Thiele, G., Sarmiento, J. L., 1990. Tracer dating and ocean ventilation. Journal of Geophysical Research
95, 9377–9391.
Tomczak, M., Godfrey, J. S., 1994. Regional Oceanography: An Introduction. Pergamon Press, Oxford, Eng-
land, 422 + vii pp.
Treguier, A. M., Held, I. M., Larichev, V. D., 1997. On the parameterization of quasi-geostrophic eddies in
primitive equation ocean models. Journal of Physical Oceanography 27, 567–580.
Troen, I. B., Mahrt, L., 1986. A simple model of the atmospheric boundary layer: sensitivity to surface
evaporation. Boundary Layer Meteorology 37, 129–148.
Tziperman, E., 1986. On the role of interior mixing and air-sea fluxes in determining the stratification and
circulation in the oceans. Journal of Physical Oceanography 16, 680–693.
Umlauf, L., Burchard, H., Bolding, K., 2005. GOTM: source code and test case documentation: version 3.2.
231pp.
Veronis, G., 1973. Large scale ocean circulation. Advances in Applied Mechanics 13, 2–92.
Visbeck, M., Marshall, J. C., Haine, T., Spall, M., 1997. Specification of eddy transfer coefficients in coarse
resolution ocean circulation models. Journal of Physical Oceanography 27, 381–402.
Vi ´
udez, A., 2000. Volume and mass transport across isosurfaces of a balanced fluid property. Journal of
Physical Oceanography 30, 1478–1485.
Wahr, J., 1998. Body tides on an elliptical, rotating, elastic and oceanless earth. Geophysical Journal of
the Royal Astronomical Society 64, 677–703.
Elements of MOM November 19, 2014 Page 627

Bibliography Section 42.2
Walin, G., 1982. On the relation between sea-surface heat flow and thermal circulation in the ocean. Tellus
34, 187–195.
Warren, B., 2009. Note on the vertical velocity and diffusive salt flux induced by evaporation and precipita-
tion. Journal of Physical Oceanography 39, 2680–2682.
Webb, D. J., Coward, A. C., de Cuevas, B. A., Gwilliam, C. S., 1998. The first main run of the OCCAM global
ocean model. Internal Document No. 34. Southampton Oceanography Centre, Southampton, England.
Winters, K. B., D’Asaro, E. A., 1995. Diascalar flux and the rate of fluid mixing. Journal of Fluid Mechanics
317, 179–193.
Winters, K. B., Lombard, P. N., Riley, J. J., D’Asaro, E. A., 1995. Available potential energy and mixing in
density-stratified fluids. Journal of Fluid Mechanics 289, 115–128.
Winton, M., Hallberg, R., Gnanadesikan, A., 1998. Simulation of density-driven frictional downslope flow in
z-coordinate ocean models. Journal of Physical Oceanography 28, 2163–2174.
Wittenberg, A., Rosati, A., Lau, G., Ploshay, J., 2006. GFDL’s CM2 global coupled climate models - Part 3:
Tropical Pacific climate and ENSO. Journal of Climate 19, 698–722.
Wright, D. G., 1997. An equation of state for use in ocean models: Eckart’s formula revisited. Journal of
Atmospheric and Oceanic Technology 14, 735–740.
Yin, J., Griffies, S. M., Stouffer, R., 2010a. Spatial variability of sea-level rise in 21st century projections.
Journal of Climate 23, 4585–4607.
Yin, J., Schlesinger, M., Stouffer, R., 2009. Model projections of rapid sea-level rise on the northeast coast
of the United States. Nature Geosciences 2, 262–266.
Yin, J., Stouffer, R., Spelman, M. J., Griffies, S. M., 2010b. Evaluating the uncertainty induced by the virtual
salt flux assumption in climate simulations and future projections. Journal of Climate 23, 80–96.
Zhao, R., Vallis, G. K., 2008. Parameterizing mesoscale eddies with residual and eulerian schemes, and a
comparison with eddy-permitting models. Ocean Modelling 23, 1–12.
Zika, J., McDougall, T., Sloyan, B., 2010. A tracer-contour inverse method for estimating ocean circulation
and mixing. Journal of Physical Oceanography 40, 26–47.
Elements of MOM November 19, 2014 Page 628
Index
Adcroft and Campin (2004), 8,67,89,613
Adcroft and Hallberg (2006), 136,613
Adcroft et al. (1997), 6,44,87,88,613
Adcroft et al. (1999), 117,179,411,613
Adcroft et al. (2001), 566,613
Adcroft et al. (2008), 54,57,67,613
Aiki et al. (2004), 16,297,298,613
Apel (1987), 40,613
Arbic et al. (2004), 105,613
Aris (1962), 480,613
Asselin (1972), 163,613
Bacon and Fofonoff(1996), 40,613
Batchelor (1967), 480,555,613
Bates et al. (2012a), ii,3,11,19,21,613
Bates et al. (2012b), ii,3,11,19,21,613
Bates (2011), 21,613
Beckmann and D¨
oscher (1997), 380–383,385,389,
521,614
Black (1994), 8,89,614
Bleck (1978), 575,614
Blumberg and Kantha (1985), 233,614
Blumberg and Mellor (1987), 9,218,614
Bryan and Cox (1972), 98,614
Bryan and Lewis (1979), 16,287,595,614
Bryan (1963), iii,614
Bryan (1969), 57,58,65,115,137,161,178,215,
222,283,425,614
Bryan (1989), 179,614
Bryan (1991), 2,614
Bryan (1996), 563,614
Burchard and Rennau (2008), 449,451,453,614
Callen (1985), 34,614
Camerlengo and O’Brien (1980), 235,614
Campin and Goosse (1999), 381–383,385–391,614
Campin et al. (2004), 86,161,614
Chaikin and Lubensky (1995), 37,553,614
Chang et al. (2005), 257,614
Chapman (1985), 233–235,615
Chassignet and Garraffo (2001), 356,615
Chassignet and Verron (2005), 26,615
Chen et al. (1994), 97,615
Church and Gregory (2001), 573,615
Conkright et al. (2002), 541,615
Cox (1984), iii,2,163,283,284,615
Cox (1987), 574,615
Craig and Banner (1994), 269,615
Cushmin-Roisin (1987), 543,547,615
Danabasoglu and McWilliams (1995), 322,615
Danabasoglu et al. (2006), 16,615
Danabasoglu et al. (2008), 333,615
Danabasoglu et al. (2010), 520,615
DeGroot and Mazur (1984), 37,553,615
DeSzoeke and Bennett (1993), 558,616
DeSzoeke and Samelson (2002), 9,92,616
Delworth et al. (2006), ii,3,4,8,13,21,143,293,
539,597,599,615
Delworth et al. (2012), ii,21,356,615
Denman (1973), 251,615
Deremble et al. (2012), 357,371,616
Diansky et al. (2002), 66,90,616
Donner et al. (2011), 8,616
Downes et al. (2011), 458,616
Dunne et al. (2012), 5,8,13,21,123,143,293,356,
523,533,539,616
Dunne et al. (2013), 5,8,13,14,21,356,523,533,
539,616
Durran (1999), 161–163,179,180,182,194,213,
616
Durski et al. (2004), 257,259,616
D¨
oscher and Beckmann (2000), 380–383,616
Eby and Holloway (1994), 374,375,616
Eden et al. (2007), 558,616
Eden et al. (2009), 341,616
Emile-Geay and Madec (2009), 566,616
England (1995), 52,616
Ezer et al. (2002), 90,617
Farneti et al. (2010), 338,356,617
Farrell and Clark (1976), 103,105,617
Feistel and Hagen (1995), 98,99,617
Feistel (1993), 98,99,617
Feistel (2003), 98,99,617
Ferrari et al. (2008), 79,333,353,468,493,516,
585,617
629

Index Section 42.2
Ferrari et al. (2010), 79,306,323–326,353,468,
497,516,585,587,617
Ferreira and Marshall (2006), 16,297,298,617
Fofonoff(1962), 40,617
Fox-Kemper et al. (2008a), 347,421,617
Fox-Kemper et al. (2008b), 16,347–349,353,421,
426,460,470,471,497,517,531,532,
557,588,589,595,617
Fox-Kemper et al. (2011), 16,347,352,421,422,
617
Galbraith et al. (2011), 14,617
Gargett (1984), 296,617
Gent and McWilliams (1990), 79,80,83,84,297,
305,306,321,324,347,420,469,483,
496,556,568,574,575,588,617
Gent et al. (1995), xiii,80,81,297,324,347,349–
351,391,420,422,426,460,470,471,
496,531,532,556,557,578,579,587,
595,617
Gent et al. (1998), 256,617
Gill and Niiler (1973), 562,617
Gill (1982), 62,67,98,103–105,109,264,617
Gnanadesikan et al. (2006), ii,3,4,8,13,21,143,
293,597,618
Goosens et al. (1994), ii,618
Gordon et al. (2000), 340,618
Greatbatch and Lamb (1990), 16,297,391,618
Greatbatch and McDougall (2003), 85,94,558,618
Greatbatch and Mellor (1999), 90,618
Greatbatch et al. (2001), 156,618
Greatbatch (1994), 563–565,618
Gregg et al. (2003), 479,574,618
Griffies and Adcroft (2008), 26,105,107,465,480,
481,543,546,618
Griffies and Greatbatch (2012), 552,580,592,619
Griffies and Hallberg (2000), 15,77,357,619
Griffies et al. (1998), 98,305,349,478,574,575,
618
Griffies et al. (2000a), 8,58,66,90,116,161,166,
193,579,618
Griffies et al. (2000b), 5,86,162,430,433,440,
493,530,619
Griffies et al. (2001), 10,52,86,150,157,160–164,
166,172,196,222,264,411,434,523,
619
Griffies et al. (2004), 2,7,21,85,87,97,115,177,
183,196,215,221,388,390,397,404,
412,415,505,619
Griffies et al. (2005), ii,3,4,7,8,11,13,15,16,21,
87,143,160,174,293,357,480,521,522,
539,597,618
Griffies et al. (2009), 262,504,618
Griffies et al. (2011), 8,21,619
Griffies (1998), 98,297,298,303,304,306,324,
349,422,470,483,497,618
Griffies (2004), 2,10,11,21,26,27,30,33,34,36,
39–42,46,48,59,62,75,77,79,81,83,
89,92,94,106,115,117,157,160–162,
164,167,174,180,182,191,192,194,
212,215,221,222,304,305,309,319–
322,324,328–332,337–341,356–361,366,
367,369,370,395,411,412,420,465,
467,469,478–481,484,527,543,544,546,
547,555,558,564,566,567,574,575,
578,579,604,605,618
Griffies (2005), 26,85,618
Griffies (2009), 21,618
Hallberg (1997), 67,161,165,619
Hallberg (2000), 76,77,619
Haltiner and Williams (1980), 161,619
Hecht et al. (2008), 356,619
Held and Larichev (1996), 337,619
Hendershott (1972), 110,619
Herzfeld et al. (2011), 3,4,17,21,126,230,619
Hesselberg (1926), 558,619
Hirsch (1988), 44,54,619
Holland et al. (1998), 13,162,256,619
Holloway et al. (2007), 375,619
Holloway (1992), 77,356,357,373,374,619
Holloway (1999), 61,78,619
Holloway (2008), 375,619
Hsieh and Bryan (1996), 563,620
Huang et al. (2001), 9,92,94,620
Huang (1993), 264,620
Hundsdorfer and Trompert (1994), 13,620
Ilicak et al. (2012), 5,493,620
Iudicone et al. (2008), 458–460,473,474,480,539,
565,620
Jackett and McDougall (1997), 459,465,620
Jackett et al. (2006), 12,86,97–100,620
Jayne and St.Laurent (2001), 288,620
Jayne (2009), 291,620
Jerlov (1968), 250,620
Kantha and Clayson (2000), 262,267,268,620
Killworth and Edwards (1999), 380,389,620
Killworth et al. (1991), 10,157,161,164–166,411,
523,620
Killworth (1989), 285,620
Klinger et al. (1996), 15,283,620
Klocker and McDougall (2010a), 574,620
Klocker and McDougall (2010b), 574,620
Klocker et al. (2009), 465,537,621
Klymak et al. (2005), 290,621
Kopp et al. (2010), 9,105,621
Kwon et al. (2013), 543,549,621
Lamport (1994), ii,621
Landau and Lifshitz (1976), 26,621
Elements of MOM November 19, 2014 Page 630

Index Section 42.2
Landau and Lifshitz (1987), 553,555,621
Landerer et al. (2007), 562,563,621
Large and Gent (1999), 282,621
Large and Nurser (2001), 458,461,489,534,621
Large et al. (1994), xii,16,97,256–258,260,261,
268,269,271–283,289,464,477,479,480,
515,568,591,621
Large et al. (1997), 256,320,621
Large et al. (2001), 15,356,357,621
Large (1998), 256–258,262,269,621
Leclair and Madec (2009), 10,163,621
Ledwell et al. (1993), 289,479,574,621
Ledwell et al. (2011), 479,574,621
Lee et al. (2006), xii,16,287,288,291–293,512,
621
Lemari´
e et al. (2012a), 303,329,621
Lemari´
e et al. (2012b), 85,90,282,303,329,622
Leonard (1979), 13,622
Levitus (1982), 465,622
Li et al. (2001), 257,622
Lin (1997), 54,57,622
Lorbacher et al. (2012), 563,622
Losch et al. (2004), 9,77,92,139,622
Lowe and Gregory (2006), 563,622
M¨
uller (2006), 37,553,624
Machenhauer et al. (2009), 44,622
Madec and Imbard (1996), 123,622
Maltrud and Holloway (2008), 357,374,375,622
Manizza et al. (2005), 15,249,622
Marchesiello and Shchepetkin (2001), 233,622
Marchuk and Kagan (1989), 109,622
Marion and Thornton (1988), 26,622
Marotzke (1991), 163,285,622
Marshall and Schott (1999), 27,622
Marshall et al. (1997), 66,161,283,622
Marshall et al. (1999), 458,622
Marshall et al. (2004), 9,92,622
Martinsen and Engedahl (1987), 623
Maze et al. (2009), 458,473,623
McDougall and Church (1986), 574,623
McDougall and Jackett (1988), 459,460,465,623
McDougall and Jackett (2005), 465,473,537,623
McDougall and McIntosh (2001), 350,557,558,623
McDougall et al. (2002), 62,156,558,623
McDougall et al. (2003), 97,98,623
McDougall et al. (2012), 99,102,623
McDougall (1987a), 280,459,574,575,623
McDougall (1987b), 98,459,464,469,478,559,
574,576,577,623
McDougall (1995), 32,575,623
McDougall (2003), 12,40–42,45,102,250,553,
558,569,623
McWilliams and Sullivan (2001), 282,623
Merryfield and Holloway (2003), 13,623
Merryfield and Scott (2007), 375,623
Mesinger and Arakawa (1976), 161,623
Mesinger (1973), 411,623
Miller and Thorpe (1981), 235,623
Mitrovica et al. (2001), 103,105,108,623
Morel and Antoine (1994), 15,249,251,252,624
Morel and Berthon (1989), 252,624
Morel (1988), 251,624
Morse and Feshbach (1953), 103,624
Moum et al. (2002), 290,624
Munk and Anderson (1948), 292,624
Murray (1996), 6,7,121,125,126,128,624
Naveira-Garabato et al. (2004), 479,574,624
Nicholls and Cazenave (2010), 573,624
Nikurashin and Ferrari (2010), 513,624
O’Brien (1986), 179,624
Ohlmann and Siegel (2000), 251,624
Ohlmann (2003), 15,624
Olbers et al. (1985), 574,624
Orlanski (1976), 235,624
Osborn (1980), 289,624
Pacanowski and Gnanadesikan (1998), 6,68,72,87–
89,196,624
Pacanowski and Griffies (1999), 2,3,13,21,115,
121,162,216,222,284,340,411,419,
420,625
Pacanowski and Philander (1981), 16,97,283,625
Pacanowski et al. (1991), iii,3,366,624
Pacanowski (1987), 162,297,624
Pacanowski (1995), 3,624
Palma and Matano (1998), 233,625
Palma and Matano (2001), 233,625
Paulson and Simpson (1977), 250,251,625
Peixoto and Oort (1992), 595,625
Phillips (1973), 103,625
Pickard and Emery (1990), 433,625
Polzin et al. (1997), 290,479,574,625
Prather (1986), 13,625
Press et al. (1992), 186,188,327,625
Rahmstorf (1993), 15,283–285,515,625
Raymond and Kuo (1984), 625
Ray (1998), 110,625
Redi (1982), 83,305,321,574–576,625
Robert (1966), 162,625
Robinson (2005), 486,625
Roed and Cooper (1987), 233,625
Rosati and Miyakoda (1988), 250,625
Sadourny (1975), 178,625
Schmitt (1994), 479,574,625
Shchepetkin and McWilliams (2002), 10,11,66,89,
90,626
Shchepetkin and McWilliams (2005), 159,626
Shchepetkin (2005), 282,626
Simmons et al. (2004), 16,97,287–293,511,626
Elements of MOM November 19, 2014 Page 631

Index Section 42.2
Smagorinsky (1963), 357,626
Smagorinsky (1993), 357,626
Smith and McWilliams (2003), 15,357,369,626
Smith et al. (1995), 123,626
Smyth et al. (2002), 257,260,278,626
Solomon (1971), 574,626
Sommerfeld (1949), 232,626
Speer and Tziperman (1992), 458,626
St.Laurent et al. (2001), 290,626
St.Laurent et al. (2002), 289,626
St.Laurent et al. (2003), 290,626
Stacey et al. (1995), 8,89,626
Stammer (2008), 563,626
Starr (1945), 575,626
Stevens (1990), 232,626
Stevens (1991), 232,626
Stouffer et al. (2006a), ii,4,21,143,597,626
Stouffer et al. (2006b), 9,627
Sullivan and McWilliams (2010), 282,627
Sve (????), 459,613
Sweby (1984), 13,627
Sweeney et al. (2005), 15,569,627
Tang and Grimshaw (1996), 233,627
Tang and Roberts (2005), 383,627
Tennekes (1973), 269,271,627
Terray et al. (1996), 269,627
Thiele and Sarmiento (1990), 52,627
Tomczak and Godfrey (1994), 579,627
Treguier et al. (1997), 79,353,468,493,516,585,
627
Troen and Mahrt (1986), 273,274,277,627
Tziperman (1986), 458,627
Umlauf et al. (2005), 16,256,627
Veronis (1973), 103,104,627
Vi ´
udez (2000), 458,465,543,627
Visbeck et al. (1997), 337,340,627
Wahr (1998), 109,627
Walin (1982), 458,459,472,480,494,503,534,
627
Warren (2009), 37,628
Webb et al. (1998), 116,628
Winters and D’Asaro (1995), 430,431,433,628
Winters et al. (1995), 430,431,628
Winton et al. (1998), 5,380,385,628
Wittenberg et al. (2006), ii,4,21,143,597,628
Wright (1997), 99,628
Yin et al. (2009), 562,563,628
Yin et al. (2010a), 562,563,628
Yin et al. (2010b), 9,628
Zhao and Vallis (2008), 298,628
Zika et al. (2010), 459,628
IOC et al. (2010), 11,12,42,97–99,102,263,464,
558,559,566,574,576,620
Elements of MOM November 19, 2014 Page 632