Manual 1

Published by Inspiration Books, 2009,

Kensglen, Nr Carsphairn, Castle Douglas, DG7 3TE, Scotland, U.K.

ISBN 978-1-902517-16-2

First published in 2002 by Inspiration Books.

Revised edition 2009.

PREFACE

This Manual is the first of three self-contained Manuals (Elementary,

Intermediate and Advanced) which are designed for adults with a basic

understanding of mathematics to learn or teach the Vedic system. So teachers

could use it to learn Vedic Mathematics, though it is not suitable as a text for

children (for that the Cosmic Calculator Course is recommended). Or it could be

used to teach a course on Vedic Mathematics. This Manual is suitable for

teachers of children in grades 3 to 7.

The sixteen lessons of this course are based on a series of one week summer

courses given at Oxford University by the author to Swedish mathematics

teachers between 1990 and 1995. Those courses were quite intensive consisting

of eighteen, one and a half hour, lessons.

All techniques are fully explained and proofs are given where appropriate, the

relevant Sutras are indicated throughout (these are listed at the end of the

Manual) and, for convenience, answers are given after each exercise. Cross-

references are given showing what alternative topics may be continued with at

certain points.

It should also be noted that in the Vedic system a mental approach is preferred

so we always encourage students to work mentally as long as it is comfortable.

In the Cosmic Calculator Course pupils are given a short mental test at the start

of most or all lessons, which makes a good start to the lesson, revises previous

work and introduces some of the ideas needed in the current lesson. In the

Cosmic Calculator course there are also many games that help to establish and

promote confidence in using the Vedic system.

Some topics will be found to be missing in this text: for example, there is no

section on area, only a brief mention. This is because the actual methods are the

same as currently taught so that the only difference would be to give the relevant

Sutra(s).

CONTENTS

PREFACE iii

LESSON 1 COMPLETING THE

WHOLE 1

1.1 INTRODUCTION 1

1.2 THE TEN POINT CIRCLE 3

1.3 MULTIPLES OF TEN 4

1.4 DEFICIENCY FROM TEN 5

DEFICIENCY AND COMPLETION

TOGETHER 5

1.5 MENTAL ADDITION 6

COMPLETING THE WHOLE 7

COLUMNS OF FIGURES 9

1.6 BY ADDITION AND BY

SUBTRACTION 11

SUBTRACTING NUMBERS NEAR A

BASE 12

LESSON 2 DOUBLING AND

HALVING 14

2.1 DOUBLING 14

MULTIPLYING BY 4, 8 16

2.2 HALVING 17

SPLITTING NUMBERS 18

DIVIDING BY 4, 8 18

2.3 EXTENDING YOUR TABLES 19

2.4 MULTIPLYING BY 5, 50, 25 20

2.5 DIVIDING BY 5, 50, 25 21

DIVIDING BY 5 21

DIVIDING BY 50, 25 22

LESSON 3 DIGIT SUMS 24

3.1 ADDING DIGITS 24

3.2 THE NINE POINT CIRCLE 26

3.3 CASTING OUT NINES 26

3.4 DIGIT SUM PUZZLES 29

MORE DIGIT SUM PUZZLES 30

3.5 THE DIGIT SUM CHECK 31

MULTIPLICATION CHECK 33

3.6 THE VEDIC SQUARE 34

3.7 PATTERNS FROM THE VEDIC

SQUARE 36

3.8 NUMBER NINE 37

LESSON 4 LEFT TO RIGHT 40

4.1 ADDITION: LEFT TO RIGHT 40

4.2 MULTIPLICATION: LEFT TO RIGHT 42

4.3 DOUBLING AND HALVING 43

4.4 SUBTRACTION: LEFT TO RIGHT 44

4.5 CHECKING SUBTRACTION SUMS 45

4.6 MORE SUBTRACTIONS 46

LESSON 5 ALL FROM 9 AND THE

LAST FROM 10

5.1 APPLYING THE FORMULA 48

5.2 SUBTRACTION 49

ADDING ZEROS 50

ONE LESS 51

ONE MORE 51

ONE LESS AGAIN 52

5.3 MONEY 53

LESSON 6 NUMBER SPLITTING 54

6.1 ADDITION 54

6.2 SUBTRACTION 55

6.3 MULTIPLICATION 56

6.4 DIVISION 57

LESSON 7 BASE

MULTIPLICATION 59

7.1 TIMES TABLES 59

7.2 NUMBERS JUST OVER TEN 61

7.3 MULTIPLICATION TABLE

PATTERNS 62

RECURRING DECIMALS 64

7.4 NUMBERS CLOSE TO 100 65

MENTALLY 67

NUMBERS OVER 100 68

MENTAL MATHS 69

RUSSIAN PEASANT MULTIPLICATION 69

7.5 LARGER NUMBERS 70

NUMBERS ABOVE THE BASE 71

7.6 PROPORTIONATELY 71

ANOTHER APPLICATION OF

PROPORTIONATELY 73

7.7 MULTIPLYING NUMBERS NEAR

DIFFERENT BASES 74

7.8 SQUARING NUMBERS NEAR A BASE 75

7.9 A SUMMARY 77

LESSON 8 CHECKING AND

DIVISIBILITY 78

8.1 DIGIT SUM CHECK FOR DIVISION 78

8.2 THE FIRST BY THE FIRST AND

THE LAST BY THE LAST 79

THE FIRST BY THE FIRST 79

THE LAST BY THE LAST 81

8.3 DIVISIBILITY BY 4 81

8.4 DIVISIBILITY BY 11 82

REMAINDER AFTER DIVISION BY 11 83

ANOTHER DIGIT SUM CHECK 84

LESSON 9 BAR NUMBERS 85

9.1 REMOVING BAR NUMBERS 85

ALL FROM 9 AND THE LAST FROM

10 87

9.2 SUBTRACTION 88

9.3 CREATING BAR NUMBERS 89

9.4 USING BAR NUMBERS 91

LESSON 10 SPECIAL

MULTIPLICATION 92

10.1 MULTIPLICATION BY 11 92

CARRIES 94

LONGER NUMBERS 94

10.2 BY ONE MORE THAN THE ONE

BEFORE 96

10.3 MULTIPLICATION BY NINES 97

10.4 THE FIRST BY THE FIRST AND

THE LAST BY THE LAST 98

10.5 USING THE AVERAGE 99

10.6 SPECIAL NUMBERS 101

REPEATING NUMBERS 101

PROPORTIONATELY 102

DISGUISES 102

LESSON 11 GENERAL

MULTIPLICATION 105

11.1 REVISION 105

11.2 TWO-FIGURE NUMBERS 106

CARRIES 107

11.3 MOVING MULTIPLIER 109

11.4 EXTENSION 111

11.5 MULTIPLYING BINOMIALS 112

11.6 MULTIPLYING 3-FIGURE

NUMBERS 114

11.7 WRITTEN CALCULATIONS 116

CONTENTS

LESSON 12 SQUARING 119

12.1 SQUARING NUMBERS THAT END IN

5 119

12.2 SQUARING NUMBERS NEAR 50 120

12.3 GENERAL SQUARING 121

THE DUPLEX 121

12.4 NUMBER SPLITTING 123

12.5 ALGEBRAIC SQUARING 124

12.6 DIGIT SUMS OF SQUARES 125

12.7 SQUARE ROOTS OF PERFECT

SQUARES 126

12.8 3 AND 4 FIGURE NUMBERS 128

LESSON 13 EQUATIONS 130

13.1 ONE-STEP EQUATIONS 130

13.2 TWO-STEP EQUATIONS 131

13.3 THREE-STEP EQUATIONS 132

LESSON 14 FRACTIONS 134

14.1 VERTICALLY AND CROSSWISE 134

14.2 A SIMPLIFICATION 136

14.3 COMPARING FRACTIONS 137

14.4 UNIFICATION OF OPERATIONS 138

LESSON 15 SPECIAL DIVISION 139

15.1 DIVISION BY 9 139

LONGER NUMBERS 141

CARRIES 142

A SHORT CUT 142

15.2 DIVISION BY 8 ETC. 143

15.3 DIVISION BY 99, 98 ETC. 145

15.4 DIVISOR BELOW A BASE NUMBER 146

TWO-FIGURE ANSWERS 148

15.5 DIVISOR ABOVE A BASE NUMBER 150

LESSON 16 THE CROWNING GEM 152

16.1 SINGLE FIGURE ON THE FLAG 152

16.2 SHORT DIVISION DIGRESSION 153

16.3 LONGER NUMBERS 155

16.4 NEGATIVE FLAG DIGITS 157

16.5 DECIMALISING THE REMAINDER 159

SUTRAS AND SUB-SUTRAS 160

9-POINT CIRCLES 162

REFERENCES 163

INDEX OF THE VEDIC FORMULAE 164

INDEX 166

SUMMARY

1.1 Introduction - background information about Vedic Mathematics.

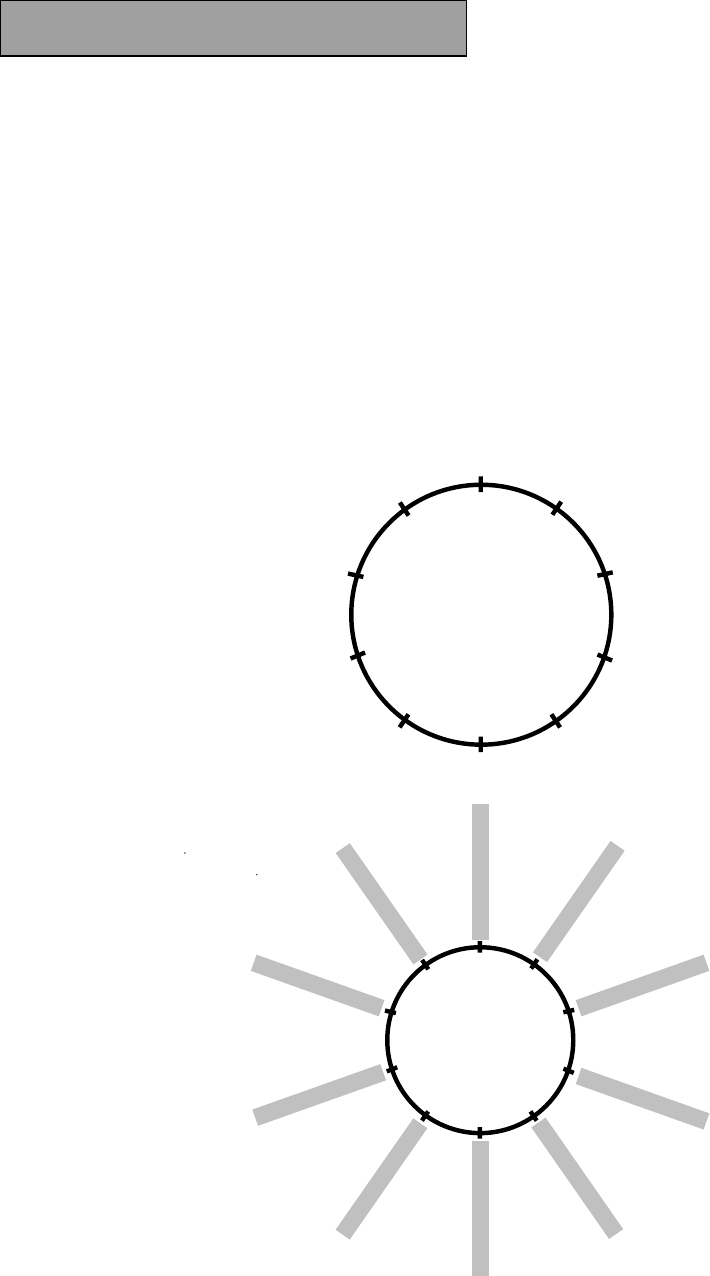
1.2 The Ten Point Circle – representing numbers on a circle.

1.3 Multiples of Ten

1.4 Deficiency from Ten – relating numbers to multiples of ten.

1.5 Mental Addition

1.6 By Addition and By Subtraction – of numbers near a multiple of ten.

Vedic Mathematics is the ancient system of mathematics which was rediscovered early last

century by Sri Bharati Krsna Tirthaji (henceforth referred to as Bharati Krsna).

The Sanskrit word “Veda” means “knowledge”. The Vedas are ancient writings whose date is

disputed but which date from at least several centuries BC. According to Indian tradition the

content of the Vedas was known long before writing was invented and was freely available to

everyone. It was passed on by word of mouth. The writings called the Vedas consist of a huge

number of documents (there are said to be millions of such documents in India, many of

which have not yet been translated) and these have recently been shown to be highly

structured, both within themselves and in relation to each other (see Reference 2). Subjects

covered in the Vedas include Grammar, Astronomy, Architecture, Psychology, Philosophy,

Archery etc., etc.

A hundred years ago Sanskrit scholars were translating the Vedic documents and were

surprised at the depth and breadth of knowledge contained in them. But some documents

headed “Ganita Sutras”, which means mathematics, could not be interpreted by them in terms

of mathematics. One verse, for example, said “in the reign of King Kamse famine, pestilence

and unsanitary conditions prevailed”. This is not mathematics they said, but nonsense.

Bharati Krsna was born in 1884 and died in 1960. He was a brilliant student, obtaining the

highest honours in all the subjects he studied, including Sanskrit, Philosophy, English,

Mathematics, History and Science. When he heard what the European scholars were saying

about the parts of the Vedas which were supposed to contain mathematics he resolved to

study the documents and find their meaning. Between 1911 and 1918 he was able to

reconstruct the ancient system of mathematics which we now call Vedic Mathematics.

LESSON 1

COMPLETING THE WHOLE

1.1 INTRODUCTION

VEDIC MATHEMATICS MANUAL 1

2

He wrote sixteen books expounding this system, but unfortunately these have been lost and

when the loss was confirmed in 1958 Bharati Krsna wrote a single introductory book entitled

“Vedic Mathematics”. This is currently available and is a best-seller (see Reference 1).

The present author came across the book “Vedic Mathematics” in 1971 and has been

developing the content of that book, and applying the system in other areas not covered by

Bharati Krsna, since then. Anything in this book which is not in “Vedic Mathematics” has

been developed independently by the author in this way.

There are many special aspects and features of Vedic Mathematics which are better discussed

as we go along rather than now because you will need to see the system in action to appreciate

it fully. But the main points for now are:

1) The system rediscovered by Bharati Krsna is based on sixteen formulae (or Sutras) and

some sub-formulae (sub-Sutras). These Sutras are given in word form: for example By One

More than the One Before and Vertically and Crosswise. In this text they are indicated by

italics. The Sutras can be related to natural mental functions such as completing a whole,

noticing analogies, generalisation and so on.

2) Not only does the system give many striking general and special methods, previously

unknown to modern mathematics, but it is far more coherent and integrated as a system.

3) Vedic Mathematics is a system of mental mathematics (though it can also be written

down).

Many of the Vedic methods are new, simple and striking. They are also beautifully

interrelated so that division, for example, can be seen as an easy reversal of the simple

multiplication method (similarly with squaring and square roots). This is in complete contrast

to the modern system. Because the Vedic methods are so different to the conventional

methods, and also to gain familiarity with the Vedic system, it is best to practice the

techniques as you go along.

“The Sutras (aphorisms) apply to and cover each an

d

every part of each and every chapter of each and ever

y

branch of mathematics (including arithmetic, algebra,

geometry – plane and solid, trigonometry – plane an

d

spherical, conics- geometrical and analytical,

astronomy, calculus – differential and integral etc., etc.

I

n fact, there is no part of mathematics, pure o

r

applied, which is beyond their jurisdiction”

From “Vedic Mathematics”, Page xvi.

1: COMPLETING THE WHOLE

3

1 2 3 4 5 6 7 8 9 10 . . .

Numbers start with number one.

Then comes number two, then three and so on.

The Sutra By One More than the One Before describes the generation of numbers from unity.

Arithmetic is the study of the behaviour of numbers and just as every person is different and

special so it is with numbers.

Every number is special and when we get to know numbers they are like friends.

[Some discussion about numbers and where they appear could be introduced here.]

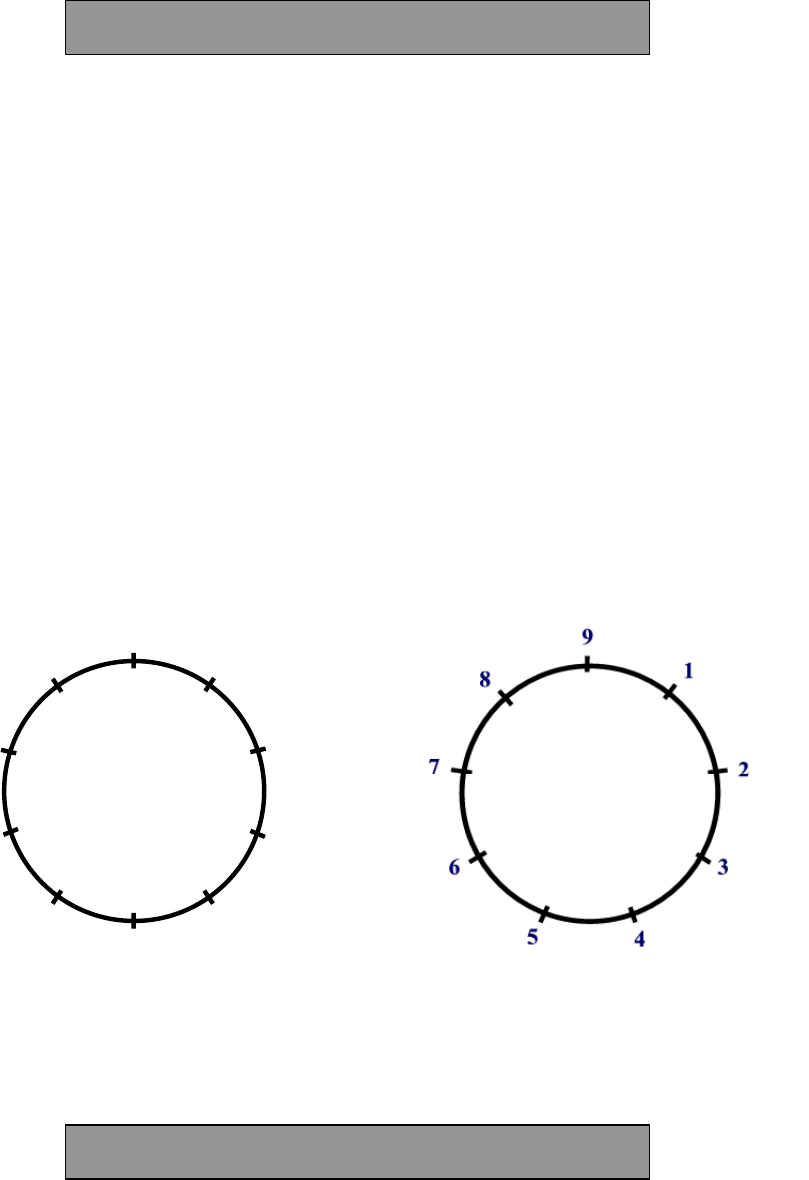
Sometimes it is useful to have the first ten numbers

around a circle like this:

We use nine figures, and zero.

For numbers beyond 9 we put two or more

of these together to make 10, 11, 12 and so on.

Continuing around the circle we can put 11

where we have 1, but further out on the 1-branch.

And number 12 goes next to 2 and so on.

This circle can be used for adding on numbers, and for taking away, just as we use a number

line. Notice that the numbers on any branch all end with the same figure and that multiples of

ten all appear on the top branch.

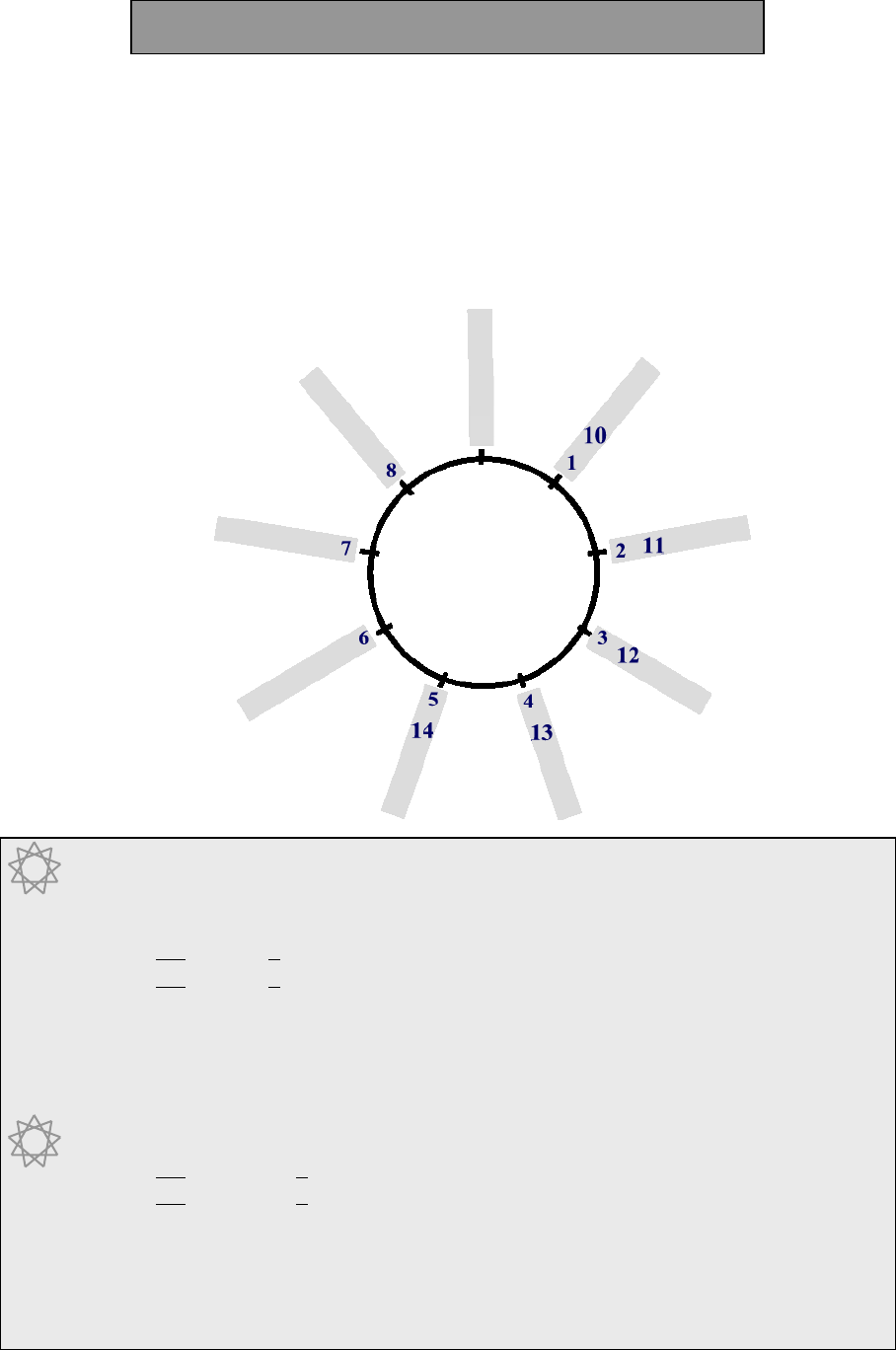
1.2 THE TEN POINT CIRCLE

1

2

3

4

5

6

7

8

9

10

1

2

3

4

5

6

7

8

9 10 11

12

13

14

15

16

17

18

19

20 21

VEDIC MATHEMATICS MANUAL 1

4

For example, 24 + 26 is easy because the 4 and 6 make ten.

So 24 + 26 = 50.

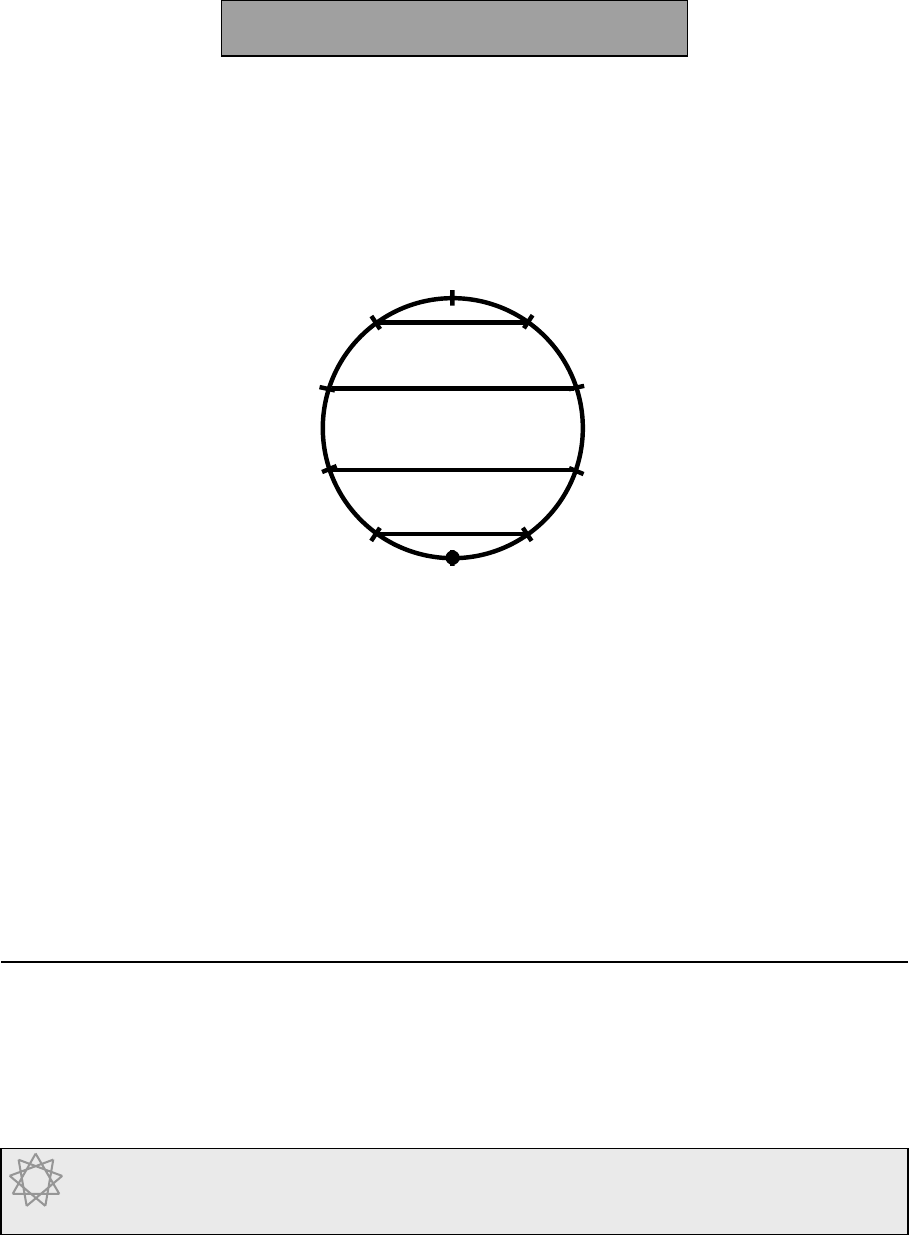
It is important to know the five pairs of numbers that add up to 10:

1 + 9 = 10, 2 + 8 = 10, 3 + 7 = 10, 4 + 6 = 10, 5 + 5 = 10.

These pairs are shown on the 10-point circle above.

The Sutra By the Completion or Non-Completion describes the ability we all have to see and

use wholeness.

 Practice A Complete the following additions:

a 6 + 4 b 4 + 16 c 5 + 25 d 13 + 7 e 22 + 8

f 38 + 2 g 54 + 6 h 47 + 3 i 61 + 9 j 85 + 5

a 10 b 20 c 30 d 20 e 30

f 40 g 60 h 50 i 70 j 90

Completing tens can be done in another way.

1.3 MULTIPLES OF TEN

1

2

3

4

5

6

7

8

9

10

1

“Little boys come dancing forward with joy and professors

ask, ‘well, how can the answer be written down withou

t

any intermediate steps of working at all?’”.

From “Vedic Metaphysics”, Page 168.

1: COMPLETING THE WHOLE

5

38 + 5 = ? You know that 38 is close to 40 and is 2 below it.

So take 2 of the 5 to make up to 40 and you have 3 more to add on,

which gives 43.

38 40 43

| | | | | | | |

 Practice B Add the following:

a 37 + 23 b 42 + 28 c 54 + 16 d 49 + 21

e 45 + 35 f 72 + 18 g 38 + 22 h 35 + 35

a 60 b 70 c 70 d 70

e 80 f 90 g 60 h 70

The Vedic Sutra By the Deficiency relates to the natural ability to see how much something

differs from wholeness.

 Practice C In the following exercise fill in the missing numbers.

a 37 is close to and is below.

b 49 is close to and is below. c 68 is close to and is below.

a 40, 3 b 50, 1 c 70, 2

DEFICIENCY AND COMPLETION TOGETHER

This makes adding easier because we can complete a whole.

1.4 DEFICIENCY FROM TEN

You can see that 39 is close to 40 and is 1 short of 40,

and that 58 is close to 60 and is 2 short of 60.

2

3

VEDIC MATHEMATICS MANUAL 1

6

We can imagine a number line, or draw one out or use the 10-point circle to add numbers like

this.

 Practice D

a 49 + 5 b 58 + 3 c 37 + 6 d 28 + 6

e 79 + 6 f 38 + 7 g 57 + 7 h 69 + 4

a 54 b 61 c 43 d 34

e 85 f 45 g 64 h 73

You can write the extra step if you like but try to do the whole thing in your head if possible.

 Practice E Try these:

a 37 + 47 b 55 + 28 c 47 + 25 d 29 + 36

e 56 + 25 f 38 + 26 g 29 + 44 h 35 + 49

a 84 b 83 c 72 d 65

e 81 f 64 g 73 h 84

1.5 MENTAL ADDITION

When an addition sum has a carry, like 56 + 26 you can add them in your head, like

this:

In 56 + 26 you get 7 tens or 70. 5 6

Then in the units you have 6 + 6 = 12. And 70 + 12 = 82. + 2 6

So 56 + 26 = 82. 8 2

1

You could also write this as 56 + 26 = 712 = 82, writing the 12 as 12 to show that the

1 in the 12 has to be carried to the left.

Similarly, 48 + 45 = 813 = 93.

4

5

“The Sutras are easy to understand, easy to appl

y

and easy to remember; and the whole work can be

truthfully summarised in one word “mental”.

From “Vedic Mathematics”, Page xvi.

1: COMPLETING THE WHOLE

7

COMPLETING THE WHOLE

In the puzzle below you have to find three numbers that add up to 10.

There are eight answers to this puzzle and one of these is given to you:

1 + 2 + 7 = 10.

But you cannot have 2 + 1 + 7 = 10 as another answer: the numbers must be different.

And you cannot use nought, but you can use a number more than once.

 Practice F See how many you can find.

1 + 2 + 7 = 10

+ + = 10

2+2+6

1+1+8 2+3+5

1+3+6 2+4+4

1+4+5 3+3+4

Where several numbers are being added it is a good idea to look for whole multiples of 10

(i.e. 10, 20, 30 etc.).

 Practice G Try these:

a 3 + 2 + 8 b 9 + 8 + 1 c 7 + 2 + 4 + 3

d 4 + 5 + 5 + 7 e 8 + 9 + 2 f 7 + 6 + 2 + 4

For example if you need to find 6 + 7 + 4 you would see that the 6 and 4 make a 10.

And you add the 7 on last to get 6 + 7 + 4 = 17.

Also in adding 3 + 6 + 2 + 5 you can see that the 3, 2 and 5 make a 10 so you ad

d

these first and add the 6 on last to get 3 + 6 + 2 + 5 = 16.

6

7

VEDIC MATHEMATICS MANUAL 1

8

g 8 + 8 + 3 + 2 h 7 + 6 + 3 + 4 i 4 + 7 + 4 + 2

j 6 + 9 + 2 + 2 k 7 + 5 + 1 + 2 l 3 + 5 + 4 + 3

a 13 b 18 c 16

d 21 e 19 f 19

g 21 h 20 i 17

j 19 k 15 l 15

You can complete multiples of ten for bigger numbers also.

You can link the numbers that make a multiple of ten as shown below:

 Practice H Use this method of completing the whole to add the following numbers.

a 29 + 7 +1 + 5 b 16 + 3 + 6 + 17 c 8 + 51 + 12 + 3

d 37 + 7 + 21 + 13 e 13 + 16 + 17 + 24 f 12 + 26 + 34 + 8

g 33 + 25 + 22 + 15 h 18 + 13 + 14 + 23 i 3 + 9 + 5 + 7 + 1

j 27 + 15 + 23 k 43 + 8 + 19 + 11 l 32 + 15 + 8 + 4

m 24 + 7 + 8 + 6 + 13 n 6 + 33 + 24 + 17 o 23 + 48 + 27

a 42 b 42 c 74

d 78 e 70 f 80

g 95 h 68 i 25

j 65 k 81 l 59

m 58 n 80 o 98

For example given 19 + 8 + 1 you can see that 19 + 1 makes a whole 20 so you add

these first and then the 8.

So 19 + 8 + 1 = 28.

Suppose you want 33 + 28 + 4 + 32.

You notice that the 28 and 32 make a multiple of ten, so you add these first to get 60.

Then adding 33 gives 93, and the 4 makes 97.

So 33 + 28 + 4 + 32 = 97.

9

8

33 + 28 + 4 + 32 = 97

1: COMPLETING THE WHOLE

9

COLUMNS OF FIGURES

Another way in which completing tens can be used is in adding columns of figures.

 Practice I Try these:

a 4 4 b 3 5 c 4 8 d 6 3 2 7 e 5 4 9

2 2 7 6 3 8 5 8 4 1 8 2

6 5 4 5 + 6 2 7 4 3 + 3 1 7

8 6 + 7 1 + 2 4 1

7 2 6

3 2 1 +

a 217 b 156 c 219 d 7654 e 2336

For example if you had to find: 2 7

3 5

6 3

8 2 +

you look in the units column and see a 7 and 3 there, which makes 10, so that there is

a total of 17 altogether in this column.

You put this down, carrying the 1 to the left as shown:

2 7

3 5

6 3

8 2 +

7

1

Then you add the tens column, looking again for tens.

You see 2 + 8 = 10 and so the total is 19.

Adding the carried 1 you get 20 which you put down:

2 7

3 5

6 3

8 2 +

2 0 7

1

10

VEDIC MATHEMATICS MANUAL 1

10

 Practice J Try these:

a 4 7 b 3 5 c 4 8 d 3 3 2 7 e 2 4 2

2 3 2 8 3 9 2 5 7 7 1 8 8

3 6 5 7 8 8 5 8 5 1 1 5

3 6 + 3 2 + 7 1 + 3 8 3 + 2 4 3

7 9 6

3 2 1

+

a 142 b 152 c 246 d 6872 e 1905

Now suppose you have: 8 2 4

6 5 6

8 5

3 8 +

You immediately see a 10 (4+6) in the first column. And there is also a 13 (5+8).

So 13 and 10 give 23 and so you put 3 and carry 2:

8 2 4

6 5 6

8 5

3 8 +

3

2

In the next column you see a 10 (2+8) and also 8 (5+3).

This gives 18 and with the carried 2 we get 20.

So put 0 and carry 2:

8 2 4

6 5 6

8 5

3 8

+

1 6 0 3

2 2

Finally we have 14 in the left column and the carried 2 makes 16, which you put

down.

11

1: COMPLETING THE WHOLE

11

Numbers like 9, 19, 18, 38, which are just under multiples of ten are particularly easy to add

and subtract (take away).

This illustrates the formula By Addition and By Subtraction.

 Practice K Try some:

a 55 + 9 b 64 + 9 c 45 + 9 d 73 + 9

e 82 + 9 f 26 + 9 g 67 + 9 h 38 + 9

a 64 b 73 c 54 d 82

e 91 f 35 g 76 h 47

 Practice L

a 44 + 19 b 55 + 29 c 36 + 49 d 73 + 19

e 47 + 39 f 26 + 59 g 17 + 69 h 28 + 29

a 63 b 84 c 85 d 92

e 86 f 85 g 86 h 57

In a similar way you could add 18 to a number by adding 20 and taking 2 away.

Or you could add 38 to a number by adding 40 and taking 2 away.

Or add 37 by adding 40 and taking 3 away.

1.6 BY ADDITION AND BY SUBTRACTION

Suppose you have to find 33 + 9.

As 9 is 1 below 10 you can do this by adding 10 and taking 1 away: 33+10–1.

Adding 10 to 33 gives 43, and taking 1 away leaves 42.

So 33 + 9 = 42.

Similarly if you are adding 19, you can add 20 and take 1 away.

So 66 + 19 = 85.

Because you can add 20 to 66 to get 86 and take 1 off to get 85.

And to find 54 + 39 you could add 40 to 54 and take 1 off to get 93.

So 54 + 39 = 93.

12

13

14

VEDIC MATHEMATICS MANUAL 1

12

 Practice M Try these:

a 44 + 18 b 44 + 27 c 55 + 28 d 35 + 37

e 62 + 29 f 36 + 37 g 19 + 19 h 28 + 29

a 62 b 71 c 83 d 72

e 91 f 73 g 38 h 57

The sums below are like the ones above except that the number which is just below a multiple

of ten is the first number in the sum.

 Practice N Try a few of these:

a 39 + 44 b 33 + 38 c 48 + 35 d 27 + 34

e 33 + 28 f 9 + 73 g 18 + 19 h 26 + 27

a 83 b 71 c 83 d 61

e 61 f 82 g 37 h 53

SUBTRACTING NUMBERS NEAR A BASE

A similar method can be used for subtracting numbers which are just below a base.

So, for example, 33 + 48 = 81 as you would add 50 to 33 to get 83 and then take 2

away, because 48 is 2 below 50.

For example you might have 29 + 55.

Here you could add 30 to 55 and take 1 off to get 29 + 55 = 84.

For example given 55 – 19 you notice that 19 is 1 below 20.

So take 20 from 55 (to get 35) and add 1 back on.

So 55 – 19 = 36.

And 61 – 38 = 23 because you take 40 from 61 (to get 21) and add 2 back on.

15

16

17

18

1: COMPLETING THE WHOLE

13

 Practice O Try these

a 44 – 19 b 66 – 29 c 88 – 49 d 55 – 9

e 52 – 28 f 72 – 48 g 66 – 38 h 81 – 58

i 83 – 36 j 90 – 66 k 55 – 27 l 60 – 57

a 25 b 37 c 39 d 46

e 24 f 24 g 28 h 23

i 47 j 24 k 28 l 3

“And we were agreeably astonished and intensel

y

g

ratified to find that exceedingly tough mathematica

l

problems (which the mathematically most advance

d

present day Western scientific world had spent huge

lots of time, energy and money on and which even no

w

it solves with the utmost difficulty and after vast labou

r

and involving large numbers of difficult, tedious an

d

cumbersome “steps” of working) can be easily an

d

readily solved with the help of these ultra-easy Vedic

Sutras (or mathematical aphorisms) contained in the

Parishishta (the Appendix-portion) of the

ATHARVAVEDA in a few simple steps and by methods

which can be conscientiously described as mere

“mental arithmetic”.

From “Vedic Mathematics”, Page xv.

SUMMARY

2.1 Doubling – multiplying by 2, 4, 8.

2.2 Halving – dividing by 2, 4, 8.

2.3 Extending your Tables – by using doubling and halving.

2.4 Multiplying by 5, 50, 25

2.6 Dividing by 5, 50, 25

Doubling and halving are very easy to do and can be used to quickly do many simple

calculations.

Adding two of the same number is called doubling.

It comes under the Proportionately formula of Vedic Mathematics.

 Practice A Double the following numbers. Just write down the answer.

a 24 b 41 c 14 d 45 e 15 f 25

g 36 h 27 i 18 j 29 k 34 l 48

a 48 b 82 c 28 d 90 e 30 f 50

g 72 h 54 i 36 j 58 k 68 l 96

LESSON 2

DOUBLING AND HALVING

For example to double 34 you can find 34 + 34, which is 68.

It is the same as multiplying 34 by 2.

34 + 34 = 2 × 34 or 34 × 2.

So double 42 is 84.

Double 35 is 70.

And double 26 is 52, because 26 + 26 = 52.

1

2

2.1 DOUBLING

2: DOUBLING AND HALVING

15

In the following exercise just write down the answers to the sums.

 Practice B Double the following numbers:

a 58 b 61 c 73 d 65 e 66

f 88 g 76 h 91 i 380

a 116 b 122 c 146 d 130 e 132

f 176 g 152 h 182 i 760

 Practice C Double these:

a 362 b 453 c 612 d 319 e 707

f 610 g 472 h 626 i 1234 j 663

a 724 b 906 c 1224 d 638 e 1414

f 1220 g 944 h 1252 i 2468 j 1326

To double 68 we just think of doubling 60 and 8 and then adding.

Double 60 is 120,

double 8 is 16.

And adding 120 and 16 gives 136.

To double 680 we double 68 and put ‘0’ on the end: 1360.

To double 273 we double 270 and 3.

So you get 540 + 6 = 546.

To double 636 you can double 600 and 36 to get 1200 and 72.

So the answer is 1272.

3

4

5

6

VEDIC MATHEMATICS MANUAL 1

16

So for 35 × 4 you double 35 to get 70,

and then double again to get 140.

Then 35 × 4 = 140.

For 26 × 8 you double three times.

Doubling 26 gives 52, doubling 52 gives 104, doubling 104 gives 208.

So 26 × 8 = 208.

For 7½ × 8 you double 7½ three times.

You get 15, 30, 60, so 7½ × 8 = 60.

For 2¾ × 8 you double 2¾ three times.

You get 5½, 11, 22, so 2¾ × 8 = 22.

MULTIPLYING BY 4, 8

You can multiply by 4 by doubling a number twice.

And to multiply by 8, double the number three times.

 Practice D Try these:

a 53 × 4 b 28 × 4 c 33 × 4 d 61 × 4

e 18 × 4 f 81 × 4 g 16 × 4 h 16 × 8

i 22 × 8 j 45 × 8

a 212 b 112 c 132 d 244

e 72 f 324 g 64 h 128

i 176 j 360

Doubling halves and quarters is also easy.

 Practice E Multiply the following:

a 8½ × 4 b 11½ × 8 c 19½ × 4 d 2¼ × 4

e 5½ × 8 f 9½ × 4 g 30½ × 4 h 3¼ × 4

a 34 b 92 c 78 d 9

e 44 f 38 g 122 h 13

7

8

9

10

2: DOUBLING AND HALVING

17

Halving is the opposite of doubling.

 Practice F Find half of the following numbers:

a 10 b 6 c 40 d 14 e 50 f 90

a 5 b 3 c 20 d 7 e 25 f 45

 Practice G Try some, halve these numbers:

a 36 b 28 c 52 d 18 e 34

f 86 g 56 h 32 i 62 j 98

a 18 b 14 c 26 d 9 e 17

f 43 g 28 h 16 i 31 j 49

So half of 8 is 4.

Half of 60 is 30.

Half of 30 is 15, because two 15’s make 30 (or by halving 20 and 10).

Also half of 46 is 23 because you can halve the 4 and the 6 to get 2 and 3.

Half of 54 is 27 because 54 is 50 and 4.

And halving 50, 4 you get 25, 2,

which make 27.

Similarly half of 78 = half of 70 + half of 8 = 35 + 4 = 39.

2.2 HALVING

11

12

14

13

VEDIC MATHEMATICS MANUAL 1

18

To halve 178 you halve 100, 70 and 8 and add the results.

Half of 100 is 50,

half of 70 is 35

and half of 8 is 4.

So half of 178 is 50 + 35 + 4 = 89.

Divide 72 by 4.

You halve 72 twice: half of 72 is 36, half of 36 is 18.

So 72 ÷ 4 = 18.

Divide 104 by 8.

Here you halve three times:

Half of 104 is 52, half of 52 is 26, half of 26 is 13.

So 104 ÷ 8 = 13.

SPLITTING NUMBERS

You can halve longer numbers easily by splitting them up.

 Practice H Halve the following numbers. Try to do them in your head.

a 164 b 820 c 216 d 152 e 94 f 326

g 234 h 416 i 380 j 256 k 456 l 57

a 82 b 410 c 108 d 76 e 47 f 163

g 117 h 208 i 190 j 128 k 228 l 28½

DIVIDING BY 4, 8

16

15

17

Halving numbers is something which can also be repeated.

So if for example you halved a number and then halved again

you would be dividing the number by 4.

2: DOUBLING AND HALVING

19

Suppose that you want to find 18 × 3.

You may think that since you know 9 × 3 = 27,

then 18 × 3 must be double this, which is 54.

Similarly if you don't know 8 × 7

but you do know that 4 × 7 = 28,

you can just double 28.

So 8 × 7 = 56.

Find 6 × 14.

Since you know that 6 × 7 = 42, it follows that 6 × 14 = 84.

 Practice I Use halving to do the following divisions.

Divide by 4: a 56 b 68 c 84 d 180 e 244

Divide by 8: f 120 g 440 h 248 i 216 j 44

a 14 b 17 c 21 d 45 e 61

f 15 g 55 h 31 i 27 j 5½

The following questions assume you know your tables up to 10 × 10, but if you don't know all

these you should still be able to find your way to the answer.

 Practice J Find the following:

a 16 × 7 b 18 × 6 c 14 × 7 d 12 × 9

e 4 × 14 f 6 × 16 g 7 × 18 h 9 × 14

a 112 b 108 c 98 d 108

e 56 f 96 g 126 h 126

2.3 EXTENDING YOUR TABLES

18

19

20

VEDIC MATHEMATICS MANUAL 1

20

Find 44 × 5.

We find half of 440, which is 220. So 44 × 5 = 220.

Find 87 × 5.

Half of 870 is 435. So 87 × 5 = 435.

Similarly 4.6 × 5 = half of 46 = 23.

Find 14 × 18.

Halving 14 and 18 gives 7 and 9, and since 7 × 9 = 63 you double this twice.

That means you double and double again.

You get 126 and 252, so 14 × 18 = 252.

 Practice K Find the following:

a 16 × 18 b 14 × 16 c 12 × 18 d 16 × 12

a 288 b 224 c 216 d 192

The numbers 2 and 5 are closely related because 2 × 5 = 10 and 10 is a base number.

 Practice L Multiply the following:

a 68 × 5 b 42 × 5 c 36 × 5 d 426 × 5

e 8.6 × 5 f 5.4 × 5 g 4.68 × 5 h 0.66 × 5

We can multiply by 5 by multiplying by 10 and halving the result.

21

2.4 MULTIPLYING BY 5, 50, 25

23

24

22

2: DOUBLING AND HALVING

21

85 ÷ 5 = 17.

So 85 is doubled to 170, and dividing by 10 gives 17.

Find 27 × 50.

We multiply 27 by 100, and halve the result. Half of 2700 is 1350.

So 27 × 50 = 1350.

Similarly 5.2 × 50 = half of 520 = 260.

Find 82 × 25.

25 is half of half of 100, so to multiply a number by 25 we multiply it by 100 and

halve twice.

So we find half of half of 8200, which is 2050. 82 × 25 = 2050.

Similarly 6.8 × 25 = half of half of 680 = 170.

a 340 b 210 c 180 d 2130

e 43 f 27 g 23.4 h 3.3

 Practice M Multiply the following:

a 46 × 50 b 864 × 50 c 72 × 25 d 85 × 25

e 86.8 × 50 f 4.2 × 50 g 34.56 × 50 h 2.8 × 25

a 2300 b 43200 c 1800 d 2125

e 4340 f 210 g 1728 h 70

DIVIDING BY 5

For dividing by 5 we can double and then divide by 10.

25

26

27

28

2.5 DIVIDING BY 5, 50, 25

29

VEDIC MATHEMATICS MANUAL 1

22

Find 750 ÷ 50.

Doubling 750 gives 1500, and dividing this by 100 gives 15.

So 750 ÷ 50 = 15.

Again the alternative formula The Ultimate and Twice the Penultimate tells us to

double the 7 and add on the one extra 50, giving 15 again.

54.32 ÷ 50 = 1.0864.

Doubling 54.32 gives 108.64, and dividing by 100 gives 1.0864.

665 ÷ 5 = 133 since 665 doubled is 1330.

73 ÷ 5 = 14.6.

Similarly here double 73 is 146, and dividing by 10 gives 14.6.

An alternative method with a different Sutra may be used here (The Ultimate and Twice the

Penultimate). Since there are two fives in every ten, in the sum 85 ÷ 5 you may decide there

are 16 5's in the 80 and therefore 17 5's in 85. In other words you would double the 8 and add

1 on.

 Practice N Divide by 5:

a 65 b 135 c 375 d 470 e 505

f 4005 g 1235 h 7070 i 885 j 49

k 52 l 22.2

a 13 b 27 c 75 d 94 e 101

f 801 g 247 h 1414 i 177 j 9.8

k 10.4 l 4.44

DIVIDING BY 50, 25

Since 50 is half of 100 dividing by 50 involves doubling and dividing by 100.

31

30

33

32

2: DOUBLING AND HALVING

23

Find 425 ÷ 25.

Doubling 425 gives 850, and doubling this gives 1700.

Dividing by 100 then gives us 17. So 425 ÷ 25 = 17.

 Practice O Divide by 50:

a 650 b 1250 c 3300 d 8.8 e 44 f 77

Divide by 25:

g 225 h 550 i 44 j 137 k 6

a 13 b 25 c 66 d 0.176 e 0.88 f 1.54

g 9 h 22 i 1.76 j 5.48 k 0.24

Another application of doubling and halving is shown in Section 4.3

25 is a quarter of 100 so to divide by 25 we can double twice and divide by 100.

34

“The Sutras are very short; but, once one

understands them and the modus operand

i

inculcated therein for their practica

l

application, the whole thing becomes a sort o

f

children’s play and ceases to be a ‘problem’.”

From “Vedic Mathematics”, Page 13.

SUMMARY

3.1 Adding Digits – obtaining digit sums.

3.2 The Nine Point Circle – representing numbers around a circle.

3.3 Casting out Nines – to simplify finding digit sums.

3.4 Digit Sum Puzzles

3.5 The Digit Sum Check – using digit sums to check addition and

multiplication sums.

3.6 The Vedic square – characteristics of the nine basic digits.

3.7 Patterns from the Vedic Square – using the Vedic Square to design patterns.

3.8 Number Nine

The word digit means a single figure number: the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0.

Sum means add.

So 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 are 1-digit numbers.

And numbers 10, 11, 12 . . . . up to 99, are 2-digit numbers.

Digit sums can be very useful: for checking calculations (see Sections 3.5, 8.1), in divisibility

testing, in finding square roots; and there is an algebraic form too (Section 11.5).

LESSON 3

DIGIT SUMS

To find the digit sum of 17, for example, you just add the 1 and 7.

1 + 7 = 8, so the digit sum of 17 is 8.

And the digit sum of 123 is 6 because 1+2+3=6.

3.1 ADDING DIGITS

1

2

The digit sum of a number is found by adding the digits in the number.

3: DIGIT SUMS

25

 Practice A Find the digit sum of the following numbers:

NUMBER DIGIT SUM

13 4

241 7

171 9

242 8

303 6

1213 7

900 9

Sometimes two steps are needed to find a digit sum.

 Practice B Find the digit sum of the following numbers:

NUMBER DIGIT SUM

83 2

614 2

345 3

5555 2

78 6

2379 3

521832 3

999 9

This means that any number of any size can be reduced to a single digit: just add all the digits,

and if you get a 2-figure number, add again.

So for the digit sum of 19 you add 1 + 9 = 10.

But since 10 is a 2-digit number you add again: 1+0 = 1.

So for the digit sum of 19 you can write:

19 J 10 J 1

Similarly for 39 you get 39 J 12 J 3.

So the digit sum of 39 is 3.

3

4

The digit sum is found by adding the digits in a number,

and adding again if necessary.

VEDIC MATHEMATICS MANUAL 1

26

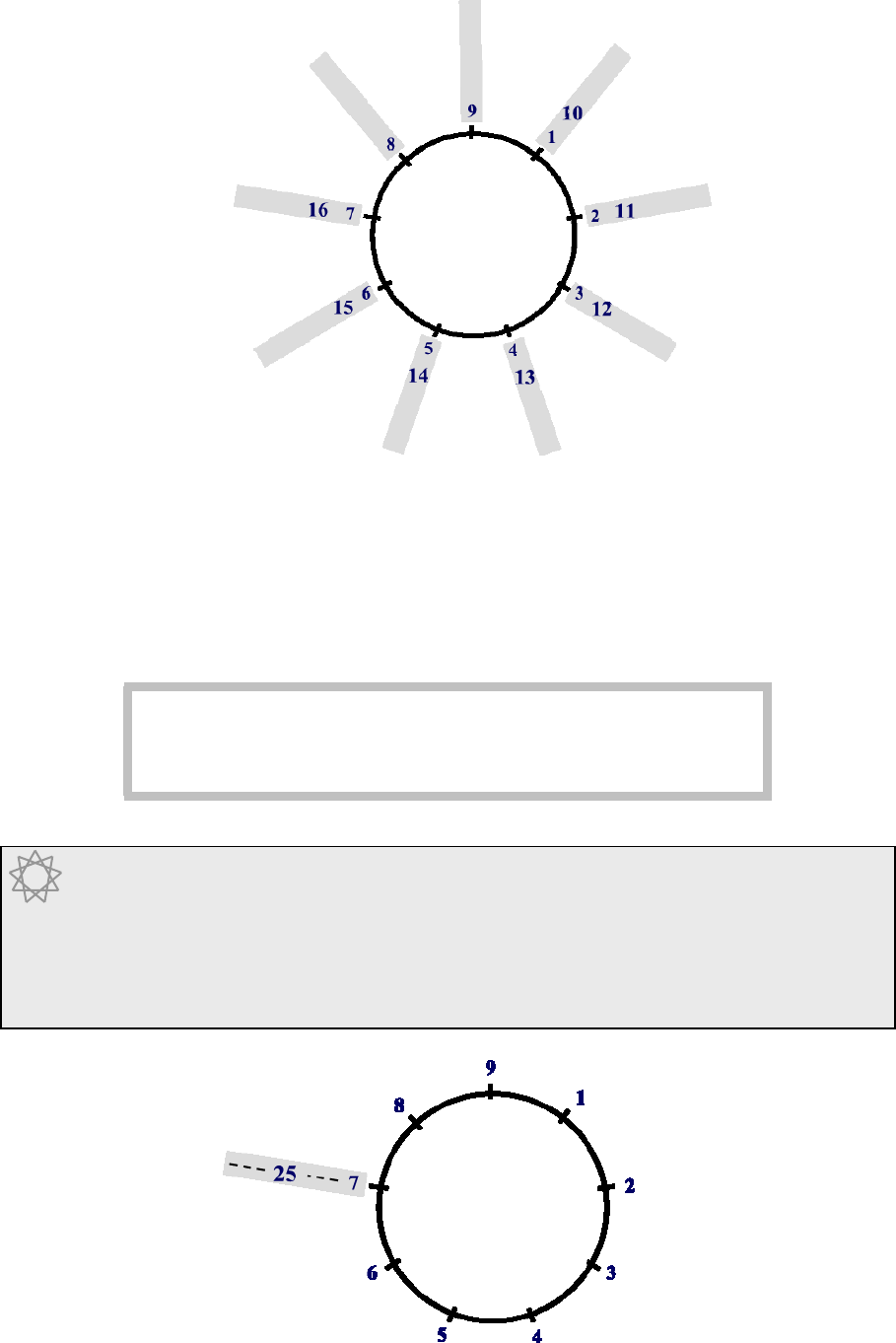
The sequence of whole numbers starts at 1 and increases by 1 each time:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 . . . . .

We are very familiar with the cycle of tens in our number system: 10, 20, 30 etc. and we have

seen this illustrated neatly in the circle of ten points.

But if we take the digit sums of the counting numbers we get:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 . . . . .

1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3 . . . . .

and here we see another cycle contained within the cycle of ten: a cycle of nine.

We therefore also need to have a circle of nine points, and this has many uses, as we will see.

10-point circle 9-point circle

The 9-point circle is a circle whose edge is divided into 9 equal parts and as with the ten-point

circle you can continue numbering round the circle as shown below.

3.2 THE NINE POINT CIRCLE

1

2

3

4

5

6

7

8

9

10

3.3 CASTING OUT NINES

3: DIGIT SUMS

27

Notice here that on any branch the digit sum of every number is the same. For example on the

1-branch we get 1, 10, 19, 28 etc. all of whose digit sums are 1.

This shows that adding 9 to a number does not affect its digit sum.

And in fact it follows that adding any number of 9’s, or subtracting any number of 9’s will not

affect the digit sum of a number.

To find the digit sum of 3949 you can cast out the nines and just add up the 3 an

d

4.

So the digit sum is 7.

Or using the longer method you add all the digits: 3+9+4+9 J 25 J 7 again.

5

3949

Adding 9 to a number does not affect its digit sum:

so 4, 40, 49, 94, 949 all have a digit sum of 4 for example.

VEDIC MATHEMATICS MANUAL 1

28

 Practice C Find the digit sums of the numbers below. Use casting out 9’s.

NUMBER DIGIT SUM

39 3

93 3

993 3

9993 3

9329 5

941992 7

79896 3

There is another way of casting out the nines from a number when you are finding its digit

sum:

Practice D Use casting out 9’s to find the digit sums of the numbers below.

Casting out of 9’s and digits totalling 9 comes under the Sutra When the Samuccaya is the

Same it is Zero. So in 465, as 4 and 5 total nine, they are cast out and the digit sum is 6: when

the total is the same (as 9) it is zero (can be cast out). Cancelling a common factor in a

fraction is another example.

NUMBER DIGIT SUM

2346 6

16271 8

9653 5

36247 4

215841 3

7152 6

9821736 9 or 0

NUMBER DIGIT SUM

465 6

274 4

3335 5

6193 1

2532 3

819 9 or 0

723 3

To find the digit sum of 24701 you see that you have 2 and 7 which add up to 9 an

d

can therefore be cast out.

This leaves only 4 and 1 which add up to 5.

So the digit sum of 24701 is 5.

Similarly with 21035 you see that 1, 3 and 5 add up to 9 and so can be cast out.

This leaves only 2 and so this is the answer.

The digit sum of 21035 is 2.

6

7

Any group of figures in a number that add up to 9 can be "cast out".

3: DIGIT SUMS

29

Some simple problems can be given here involving digit sums.

 Practice E In all of the following puzzles the answer is a 2-figure number.

Some have more than one answer.

You are given the digit sum of the answer and another fact.

DIGIT

SUM OTHER FACT NUMBER OF

ANSWERS ANSWER(S)

5 difference between the figures is 3 2 14 or 41

6 the figures are the same 1 33

6 first figure is double the second 1 42

7 difference between the figures is 3 2 25, 52

7 one figure is a 4 2 34, 43

6 both figures are odd 3 15, 51, 33

5 the figures are consecutive* 2 23, 32

9 the figures are consecutive* 2 45, 54

3 one figure is double the other 2 12, 21

8 the answer is below 20 1 17

1 number is less than 40 5 10, 19, 28, 37

1 the first figure is a 2 1 28

* Consecutive means one after the other. E.g. 6 and 7 are consecutive (or 7 and 6).

The digit sum of a 2-figure number is 8 and the figures are the same, what is the

number?

This is clearly 44.

The digit sum of a 2-figure number is 9 and the first figure is twice the second, what

is it?

This must be 63.

Give three 2-digit numbers that have a digit sum of 3.

12, 21, 30 . . .

10

9

8

3.4 DIGIT SUM PUZZLES

VEDIC MATHEMATICS MANUAL 1

30

MORE DIGIT SUM PUZZLES

Harder digit sum problems can be given.

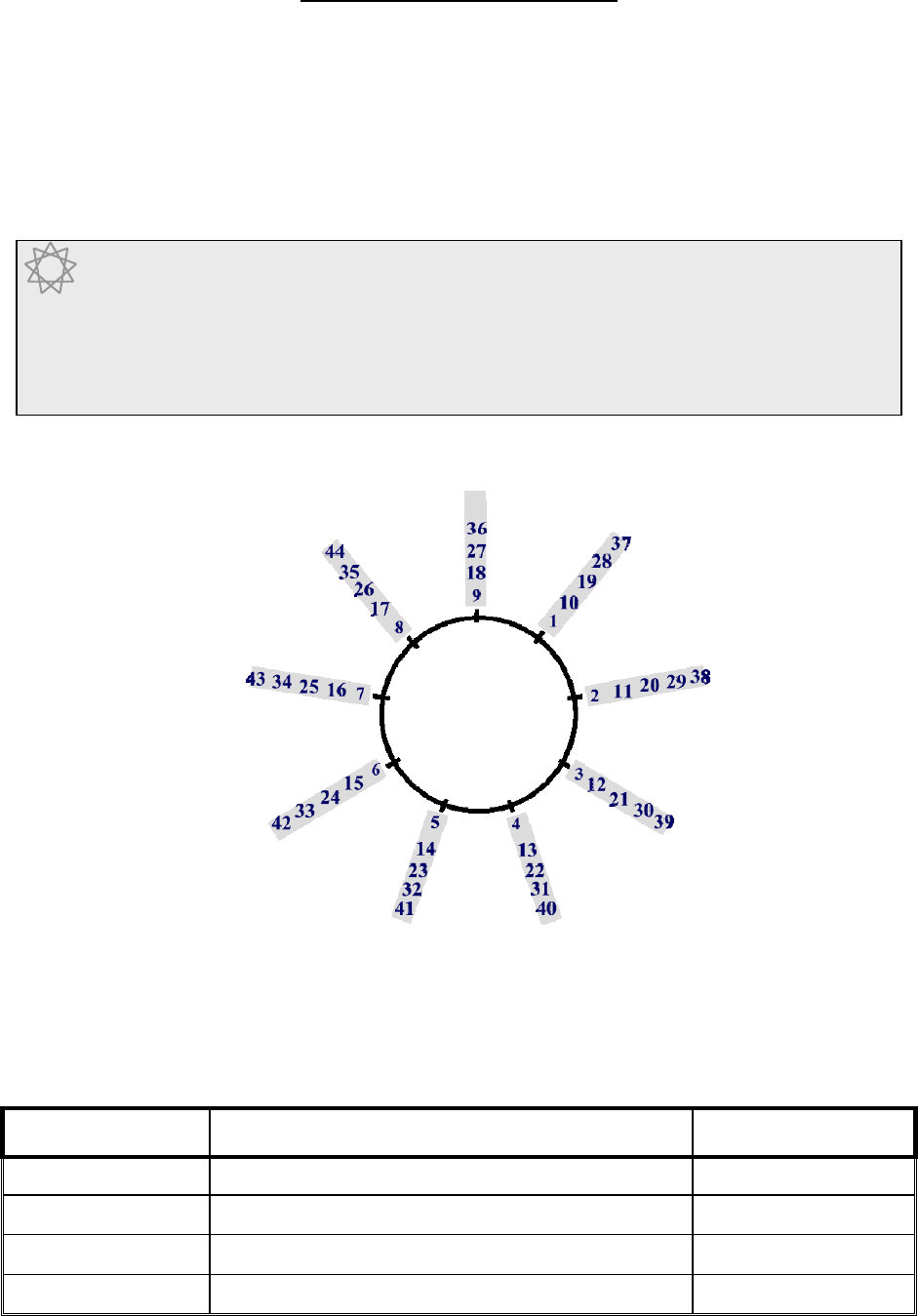
Below is the 9-point circle again but numbered up to 44.

Note that the numbers on each branch have the same digit sum. For example all the numbers

on the 3-branch have a digit sum of 3.

 Practice F In the puzzles below you will need to choose the right branch and then

select the right answer from the numbers on that branch.

All answers are 2-figure numbers.

DIGIT SUM OTHER FACT ANSWER

5 number is between 20 and 30 23

8 answer ends in 5 35

7 first figure is 2 25

2 figures differ by 7 29, 92

A 2-figure number has a digit sum of 5 and the figures are the same. What is the

number?

5 is an odd number but looking at the 9-point circle we see that 14, which is also o

n

the 5-branch can be split into 7+7. So the number must be 77.

11

3: DIGIT SUMS

31

1 answer is in the 7 × table 28

3 first figure is 3 times the second 93

4 number is in the 5 × table 40

6 figures are the same 33

8 last figure is 3 times the first 26

5 number is in the 8 × table 32

9 ends in 7 27

3 both figures are odd 57, 75, 39, 93

You can use digit sums to check that answers are right.

So there are four steps: 1. Do the sum

2. Write down the digit sums of the numbers being added

3. Add the digit sums

4. Check the two answers are the same in digit sums

Find 32 + 12 and check the answer using digit sums.

32 5

12 + 3 +

44 8

You get 44 for the answer to the sum.

Then the digit sum of 32 is 5 (3+2=5) and the digit sum of 12 is 3.

The sum (the total) of the digit sums is 5+3=8. If the sum has been done correctly,

the digit sum of the answer should also be 8.

44J8; so according to this check the answer is probably correct.

Add 365 and 208 and check the answer.

365 5 1. We get 573 for the answer.

208 + 1 + 2. We find the digit sums of 365, 208 are 5, 1.

573 6 3. Adding 5 and 1 gives 6.

1 4. 573=6 in digit sums, which confirms the answer.

12

3.5 THE DIGIT SUM CHECK

13

VEDIC MATHEMATICS MANUAL 1

32

 Practice G Add the following and check your answers using the digit sums:

a 66 b 57 c 94 d 304 e 787

77 + 29 + 58 + 271 + 176 +

__ __ __ ___ ___

f 389 g 5131 h 456 i 5555

55 + 676 + 209 + 7777 +

___ ____ ___ ____

a 143 b 86 c 152 d 575 e 963

3+5=8 3+2=5 4+4=8 7+1=8 4+5=9

f 444 g 5807 h 665 i 13332

2+1=3 1+1=2 6+2=8 2+1=3

Here is another example of a digit sum check.

 Practice H Add the following and check your answers using the digit sums:

a 35 b 56 c 35 d 52 e 456 f 188

47 + 27 + 59 + 24 + 333 + 277 +

__ __ __ __ ___ ___

g 78 h 66 i 555 j 823 k 3760

87 + 48 + 77 + 37 + 481 +

____

a 82 b 83 c 94 d 76 e 789 f 465

8+2=1 2+9=2 8+5=4 7+6=4 6+9=6 8+7=6

g 165 h 114 i 632 j 860 k 4241

6+6=3 3+3=6 6+5=2 4+1=5 7+4=2

The Vedic formula The Product of the Sum is the Sum of the Products applies for all the digit

sum checks. For addition it would be The Total of the Digit Sums is the Digit Sum of the

Total. The formula has many other applications (see Reference 3), for example in finding

areas of composite shapes (The Area of the Whole is the Sum of the Areas).

Add 77 and 124 and check.

77 5 Here, when we find 5+7 we get 12,

124 + 7 + but 12 = 3 in digit sums.

201 3 So this confirms the answer.

14

3: DIGIT SUMS

33

Sum: 3 8 Check: 2

3 × 3 ×

1 1 4 6

2

6 2 check: 8

4 × 4 ×

2 4 8 5 (since 8×4=32 and 3+2=5)

The check here confirms the answer, since the digit sum of 248 is the same as the

digit sum of 8×4.

3 8 3 9 Check: 5

6 × 6 ×

2 3 0 3 4 3

5 2 5

For the check you get the digit sum of 3839, which is 5 and find that 5 × 6 J 3.

The digit sum of 23034 is 3, so the answer is confirmed.

CAUTION!

Check the following sum: 279 The check is: 9

121 + 4 +

490 4

which confirms the answer.

However if you check the addition of the original sum you will find that it is incorrect!

This shows that the digit sum method does not always find an error. It usually works but not

always.

We will be meeting other checking devices later on.

MULTIPLICATION CHECK

Multiplying numbers, for example 38 × 3, is a straightforward process. You set the sum out as

shown below, and multiply each figure in 38 by 3, starting at the right:

The digit sum check has also been carried out above. The digit sums of the numbers being

multiplied are 2 and 3, and when these are multiplied you get 6. Since the digit sum of the

answer, 114, is also 6 this shows you that the answer is probably correct.

15

16

17

VEDIC MATHEMATICS MANUAL 1

34

 Practice I Multiply the following numbers and check each one using the digit sums:

a 88 × 8 b 32 × 3 c 73 × 4 d 717 × 6

e 234 × 5 f 533 × 2 g 3115 × 3 h 142857×7

a 704 (2) b 96 (6) c 292 (4) d 4302 (9)

e 1170 (9) f 1066 (4) g 9345 (3) h 999999 (9)

The multiplication table below has many interesting patterns and properties.

1 2 3 4 5 6 7 8 9

2 4 6 8 10 12 14 16 18

3 6 9 12 15 18 21 24 27

4 8 12 16 20 24 28 32 36

5 10 15 20 25 30 35 40 45

6 12 18 24 30 36 42 48 54

7 14 21 28 35 42 49 56 63

8 16 24 32 40 48 56 64 72

9 18 27 36 45 54 63 72 81

We make the Vedic Square by replacing every number in the table above by its digit sum as

shown below.

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

3.6 THE VEDIC SQUARE

3: DIGIT SUMS

35

To draw the pattern for the number One, for example, we colour in every square tha

t

has a “1” in it.

Alternatively, we can put a dot in the center of each square with a “1” in it and joi

n

the dots to make a pleasing pattern.

Each of the numbers 1 to 9 has its own pattern in the Vedic Square.

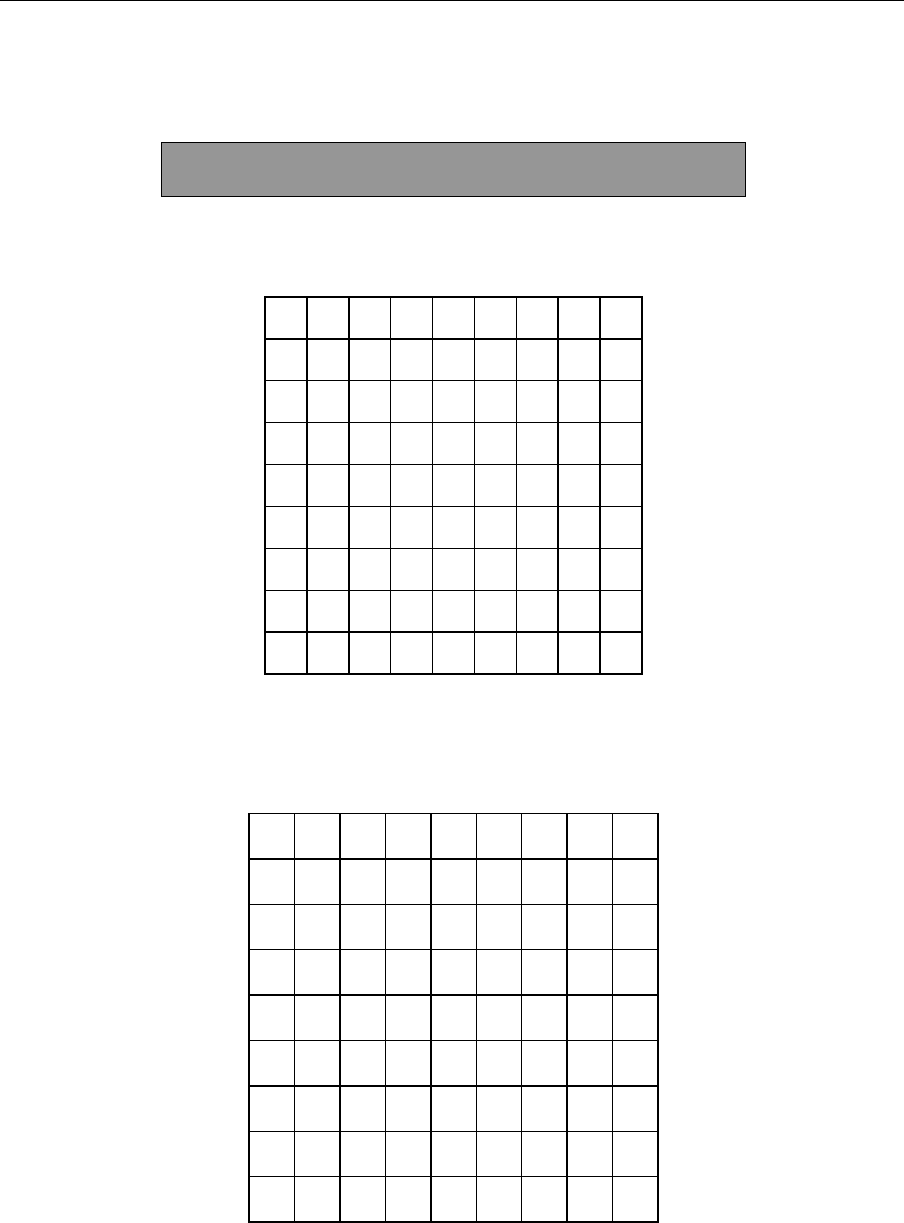
 Practice J Draw the patterns for the nine numbers using the Squares below.

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

1 23456789

2 46813579

3 69369369

4 83726159

5 16273849

6 39639639

7 53186429

8 76543219

9 99999999

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

1 23456789

2 46813579

3 69369369

4 83726159

5 16273849

6 39639639

7 53186429

8 76543219

9 99999999

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

1 23456789

2 46813579

3 69369369

4 83726159

5 16273849

6 39639639

7 53186429

8 76543219

9 99999999

1 2 3 4 5 6 7 8 9

2 4 6 8 1 3 5 7 9

3 6 9 3 6 9 3 6 9

4 8 3 7 2 6 1 5 9

5 1 6 2 7 3 8 4 9

6 3 9 6 3 9 6 3 9

7 5 3 1 8 6 4 2 9

8 7 6 5 4 3 2 1 9

9 9 9 9 9 9 9 9 9

18

VEDIC MATHEMATICS MANUAL 1

36

Suppose we choose line D (4 8 3 7 2 6 1 5 9) and start at the beginning.

We also choose a rotation of, say, 90° anticlockwise.

Take a sheet of graph paper and mark a point near the bottom left corner (you will

need 2cm to the left of this).

We always start by moving to the right and the numbers in the row we have chose

n

tell us how many centimetres to move. (It is advisable to use a pencil for this at first)

So now we can draw the design: first we draw a line 4cm to the right,

then turn 90° anticlockwise (to the left) and draw a line 8cm up.

then turn 90° anticlockwise and draw a line 3cm long,

then turn 90° anticlockwise and draw a line 7cm long,

and so on.

When you come to the end of the row of numbers you start again at the beginning o

f

that row. Eventually you will return to your starting point and the design is complete.

The Vedic Square is also useful in the design of patterns. Below is the Square again with the

nine rows labeled A to I.

A 1 2 3 4 5 6 7 8 9

B 2 4 6 8 1 3 5 7 9

C 3 6 9 3 6 9 3 6 9

D 4 8 3 7 2 6 1 5 9

E 5 1 6 2 7 3 8 4 9

F 6 3 9 6 3 9 6 3 9

G 7 5 3 1 8 6 4 2 9

H 8 7 6 5 4 3 2 1 9

I 9 9 9 9 9 9 9 9 9

To design a pattern we choose a line of the Square, a starting point in that line and an angle of

rotation.

 Practice K

a Draw the pattern described above.

b Try another design using row D again (starting at the beginning) but now the rotation angle

can be 60° and so triangular spotty paper can be used instead of graph paper:

3.7 PATTERNS FROM THE VEDIC SQUARE

19

3: DIGIT SUMS

37

(With the long side of your sheet at the bottom mark a dot near the middle of the bottom

line.

We start moving to the right again 4cm.

Then we turn 60° to the left and draw a line 8cm long.

Then we turn 60° to the left and draw a line 3cm long.

And so on, the same as previously but with a turn of 60° instead of 90°.)

c On another sheet of triangular spotty paper mark a point in the middle, and two rows down

from the top of the page. Choose row E this time (starting at the beginning) and a rotation

of 120° anticlockwise.

Draw the pattern for this.

(You can also use the columns and diagonals in the Vedic Square as well as the rows, or a

combination of them)

The diagram that appears at the beginning of each chapter of this book is formed by using the

Vedic Square in this way.

In our number system the number nine is the largest digit.

The number nine also has many other remarkable properties which make it extremely useful.

You have already seen that it can be used in finding digit sums, and that the digit sum of a

number is unchanged if 9 is added to it or subtracted from it.

Now look at the 9-times table: 9 × 1 = 9

9 × 2 = 1 8

9 × 3 = 2 7

9 × 4 = 3 6

9 × 5 = 4 5

9 × 6 = 5 4

9 × 7 = 6 3

9 × 8 = 7 2

9 × 9 = 8 1

9 × 10 = 9 0

9 × 11 = 9 9

9 × 12 =10 8

If you look at the answers you will see that in every case the digit sum is 9.

You may also see that if you read the answers as two columns the left column goes up (1, 2, 3,

. . .) and the right column goes down (9, 8, 7, . . .).

This makes it easy to get the answers in the 9 times table.

3.8 NUMBER NINE

VEDIC MATHEMATICS MANUAL 1

38

It is also possible to use your fingers to multiply by nine.

Suppose the fingers of your hands are numbered as shown below:

To multiply, say, 4 by 9, simply fold down the 4th finger.

You will find 3 fingers to the left of the folded finger and 6 fingers to the right.

So 4 × 9 = 36.

And so on.

See also Russian Peasant Multiplication on Page 69.

1

2 3 45 7 8 9

6 10

Given the addition sum 2 3

4 5

+

there is no difficulty in finding the answer.

From left to right the columns add up to 6 and 8.

So the answer is 68.

But in the sum 4 5

3 8 +

the totals we get are 7 and 13, and 13 is a 2-figure number.

The answer is not 713: the 1 in the 13 must be carried over and added to the 7.

This gives 83 as the answer.

SUMMARY

4.1 Addition: Left to Right

4.2 Multiplication: Left to Right

4.3 Doubling and Halving – converting harder products to easier ones.

4.4 Subtraction: Left to Right

4.5 Checking Subtraction Sums – using digit sums.

4.6 More Subtractions – subtracting longer numbers, left to right.

It is common to do calculations starting at the right and working towards the left.

This is however not always the best way.

Calculating from left to right is often easier, quicker and more useful.

The reason for this is that numbers are written and spoken from left to right.

Also in calculations we often only want the first one, two or three figures of an answer, and

starting on the right we would have to do the whole sum and so do a lot of useless work.

This also introduces flexibility into our work, which is a theme of the Vedic system.

In this lesson all the calculations will be done mentally: we write down only the answer.

This is easy enough to do mentally, we add the first column and increase this by 1 if there is a

carry coming over from the second column. Then we tag the last figure of the second column

onto this.

LESSON 4

LEFT TO RIGHT

4.1 ADDITION: LEFT TO RIGHT

1

2

VEDIC MATHEMATICS MANUAL 1

40

6 6 5 5 8 4 5 6

2 8 + 3 5 + 5 8 + 9 6 +

9 4 9 0 1 4 2 1 5 2

8, 1

4 = 94 8,1

0 = 90 13, 1

2 = 142 1 4, 1

2 = 152

187 + 446 = 633. 1 8 7

4 4 6 +

Here the three column totals are 5, 12 and 13 so two carries are needed.

The 1 in the 12 will be carried over to the 5 making it a 6.

So when the 5 and the 12 are combined we get 62.

The 1 in the 13 is then carried over and added onto the 2 in 62, making it 63.

So combining 62 and 13 gives the answer, 633.

It is important to get the idea of doing this mentally from left to right:

First we think of 5, the first total.

Then we have 5, 1

2 which we mentally combine into 62.

Hold this 62 in the mind, and with the third total we have 62,1

3

which becomes 633.

We use the curved lines to show which figures are to be combined.

 Practice A Add the following mentally from left to right:

a 5 6 b 8 8 c 4 5 d 5 4

6 7 + 3 3 + 6 7 + 6 4 +

____

e 3 9 f 2 7 g 7 7 h 6 3

4 9 + 5 6 + 8 8 + 7 4 +

____

a 123 b 121 c 112 d 118

e 88 f 83 g 165 h 137

3

4

In every case the tens figure in the right-hand column total

is carried over to the left-hand column total.

4: LEFT TO RIGHT

41

7 7 7

4 5 6 +

______

The first two columns give 1 

1,1 2 which becomes 122.

Then with the third column we have 12 

1,2 3 which is 1233.

5 5 5 5

3 1 3

6 2 4 +

________

Starting at the left we have 

1,5 4 = 64.

Then 64,8 = 648 (there is no carry here as 8 is a single figure).

Finally 64 

1,8 2 = 6492.

 Practice B Add the following sums mentally from left to right:

a 3 6 3 b 8 1 9 c 7 7 7 d 7 3 7

4 5 6 + 9 1 8 + 4 4 4 + 1 3 9 +

______

e 3 4 5 f 1 3 6 9 g 9 6 3 1 h 4 4 4 4

9 3 7 + 3 8 8 3 + 8 7 0 9 + 4 8 3 8

5 5 5 +

a 819 b 1737 c 1221 d 876

e 1282 f 5252 g 18340 h 9837

In all these sums the numbers are held in the mind (On the Flag) and built up digit by digit

until the answer is complete.

Mental mathematics obviously relies more on the memory than conventional methods where

every step is written down. Young children have very good memories and mental

mathematics helps to strengthen the memory further. (This means that Vedic Mathematics is

good for adults too, whose memory may not be so good.) This also gives confidence and

teaches self-reliance, showing that we do not need pencil and paper or calculator for every

sum but can find an answer without any external help.

5

6

VEDIC MATHEMATICS MANUAL 1

42

Suppose we have the sum: 2 3 7

2 ×

______

We multiply each of the figures in 237 by 2 starting at the left.

The answers we get are 4, 6, 14.

Since the 14 has two figures the 1 must be carried leftwards to the 6.

So 4, 

1,6 4 = 474.

Again we build up the answer mentally from the left: first 4, then 4,6=46,

then 4, 

1,6 4 = 474.

236 × 7 = 1652. 2 3 6

7 ×

For 73 × 7 we get 4 

2,9 1 = 511. (because 49+2 = 51)

 Practice C Multiply the following from left to right:

a

3

72

×

b

6

67

×

c

6

62

×

d

7

27

×

e

9

87

×

f

3

38

×

g

4

246

×

h

3

652

×

i

3

147

×

j

9

322

×

k

7

9501

×

l

4

1368

×

m

8

2345

×

n

7

7904

×

a 81 b 456 c 156 d 504 e 702 f 249

g 2568 h 768 i 2223 j 2007

k 7413 l 34524 m 43456 n 28679

Left to right multiplication is continued in Lesson 11.

4.2 MULTIPLICATION: LEFT TO RIGHT

7

8

9

First we have 14,

then 1 

2,4 1 = 161,

then 16 

4,1 2 = 1652.

4: LEFT TO RIGHT

43

Find 35 × 22.

We can use doubling and halving in this sum to get a much easier sum.

We double 35 and halve 22 and this gives us 70 × 11 which has the same answer as

35 × 22.

So 35 × 22 = 70 × 11 = 770.

Find 35 × 64.

Doubling and halving gives us 70 × 32.

So we can use On the Flag to find 32 × 7 and put a 0 on the end.

So 35 × 64 = 70 × 32 = 2240.

We can use doubling and halving together sometimes.

 Practice D Multiply the following:

a 15 × 18 b 15 × 24 c 46 × 15

d 82 × 35 e 66 × 15 f 124 × 45

g 15 × 54 h 55 × 16 i 75 × 18

j 446 × 15 k 132 × 35 l 85 × 18

m 16 × 4 1

2 n 24 × 3 1

2 o £4.50 × 32

a 270 b 360 c 690

d 2870 e 990 f 5580

g 810 h 880 i 1350

j 6690 k 4620 l 1530

m 72 n 84 o £144

4.3 DOUBLING AND HALVING

10

11

“People who have practical knowledge of the application

of the Sutras need not go in or the theory side of it at all.

The actual work can be done. Tremendous time is saved. I

t

is a saving not merely of time and energy and money, bu

t

more than all, I feel, it is saving the child from tears tha

t

very often accompany the study of mathematics.”.

From “Vedic Metaphysics”, Page 170.

VEDIC MATHEMATICS MANUAL 1

44

In this section we show a very easy method of subtracting numbers from left to right that you

have probably not seen before.

So in this method you start at the left, subtract, and write this down if the subtraction in the

next column can be done.

If it cannot be done you put down one less and carry 1, and then subtract in the second

column.

 Practice E Try some of these:

a 6 2 b 7 5 c 5 1 d 6 7

– 4 7 – 2 8 – 1 5 – 3 8

e 4 6 f 6 5 g 9 0 h 8 2

– 2 5 – 3 7 – 6 2 – 3 8

a 15 b 47 c 36 d 29

e 21 f 28 g 28 h 44

Find 63 – 37.

You look in the left-hand column and subtract. 6 3

You get 3. But before writing it down – 3 7

you look in the next column.

Seeing that you cannot take 7 from 3 6 1 3

you therefore put down 2 rather than 3 – 3 7

and put the other one as shown: 2

Then the final step is just 13 – 7 = 6: 6 1 3

– 3 7

2 6

So 63 – 37 = 26.

4.4 SUBTRACTION: LEFT TO RIGHT

12

4: LEFT TO RIGHT

45

Recall the 9-point circle and that 9’s in a number can be cast out when finding digit sums.

This means that in digit sums 9 and 0 are the same.

You will see them together in the circle below.

You will also remember that it is sometimes useful to use the numbers on the second ring,

which are 9 more than those in the inside ring.

Alternatively we can count backwards around the circle: . . 3, 2, 1, 0.

Find 69 – 23 and check the answer.

6 9 6 The answer is 46.

– 2 3 – 5 The digit sums of 69 and 23 are 6 and 5.

4 6 1 Then 6 – 5 = 1, which is also the digit sum of

46, so the answer is confirmed.

Note that you subtract the digit sums, because this is a subtraction sum.

7 4 2

– 5 8 – 4

1 6 7

Here we have 2 – 4 in the digit sum check so we simply add 9 to the upper figure

(the 2) and continue: 11 – 4 = 7, which is also the digit sum of 16, so the answer is

confirmed. 

4.5 CHECKING SUBTRACTION SUMS

9,0

15

18

17

16

14

13

VEDIC MATHEMATICS MANUAL 1

46

Find 35567 – 11828.

You set the sum out as normal: 3 5 5 6 7

Then starting on the left you subtract in each column. – 1 1 8 2 8

3 – 1 = 2, but before you put 2 down you check that in 2

the next column the top number is larger.

In this case 5 is larger than 1 so you put 2 down.

In the next column you have 5 – 1 = 4, but looking in the third

column you see the top number is not larger than the bottom 3 515 6 7

(5 is less than 8) so instead of putting 4 down you put 3 and the – 1 1 8 2 8

other 1 is placed On the Flag, as shown so that the 5 becomes 15. 2 3

So now you have 15 – 8 = 7. Checking in the next column

you can put this down because 6 is greater than 2. 3 515 617

In the fourth column you have 6 – 2 = 4, but looking at – 1 1 8 2 8

the next column (7 is smaller than 8) you put down only 2 3 7 3_

3 and put the other one On the Flag with the 7 as shown.

Finally 17 – 8 = 9: 3 515 617

– 1 1 8 2 8

2 3 7 3 9

 Practice F Check your answers to Practice E by using the digit sum check.

a 8-2=6 b 3-1=2 c 6-6=9 d 4-2=2

e 1-7=3 f 2-1=1 g 9-8=1 h 1-2=8

This subtraction method can be extended to the subtraction of numbers of any size.

5 6 2

– 2 9 – 2

2 7 0

In this example, the digit sum of both 56 and 29 is 2 and 2 – 2 = 0.

The digit sum of 27 is 9, but we have already seen that 9 and 0 are the same as digi

t

sums, so the answer is confirmed.

4.6 MORE SUBTRACTIONS

16

15

4: LEFT TO RIGHT

47

 Practice G Subtract the following from left to right (check your answer):

a 4 4 4 b 6 3 c 8 1 3 d 6 9 5

– 1 8 3 – 2 8 – 3 4 5 – 3 6 8

e 5 1 f 3 4 5 6 g 7 1 1 7 h 8 0 0 8

– 3 8 – 2 8 1 – 1 7 7 1 – 3 8 3 9

i 6 3 6 3 j 5 1 0 1 5 k 1 4 2 8 5 l 9 6 3 0 3 6 9

– 3 3 8 8 – 2 7 9 8 6 – 7 1 4 8 – 3 6 9 0 9 6 3

a 261 b 35 c 468 d 327

e 13 f 3175 g 5346 h 4169

i 2975 j 23029 k 7137 l 5939406

ADVANTAGES OF LEFT TO RIGHT CALCULATIONS

There are many advantages to left to right calculation as we pronounce and write numbers

from left to right. Also, sometimes we only need the first two or three significant figures and

would waste a lot of time and effort if we found all the figures of a long sum by starting at the

right. Division is always done from the left, so all calculations can be done left to right, which

means we can combine operations and, for example, find the square root of the sum of two

squares in one line (see Manual 2). For finding square roots, trig functions and so on there is

no right-hand figure to start from anyway, so there is no option but to start at the left (see

Manual 3).

You subtract in each column starting on the left, but before you put an

answer down you look in the next column.

If the top is greater than the bottom you put the figure down.

If not, you reduce the figure by 1, put that down and give the

other 1 to the smaller number at the top of the next column.

If the figures are the same you look at the next column to decide

whether to reduce or not.

If you apply All From 9 and the Last From 10 to 876

8 7 6

1 2 4

you get 124,

because you take 8 and 7 from 9 and the 6 from 10.

Similarly 3883, 64, 98, 6, 10905,

become 6117, 36, 02, 4, 89095.

SUMMARY

5.1 Applying the Formula

5.2 Subtraction – of numbers from a base.

5.3 Money – an application of subtracting numbers from a base.

All From 9 and the Last From 10 is a useful formula, as we will see.

 Practice A Apply All from 9 and the Last from 10 to the following:

a 444 b 675 c 2468 d 18276

e 8998 f 9888 g 1020304 h 7

a 556 b 325 c 7532 d 81724

e 1002 f 112 g 8979696 h 3

LESSON 5

ALL FROM 9 AND THE LAST FROM 10

5.1 APPLYING THE FORMULA

1

2

5: ALL FROM 9 AND THE LAST FROM 10

49

1000 – 864 = 136 Just apply All From 9 and the Last From 10 to 864.

8 from 9 is 1, 6 from 9 is 3, 4 from 10 is 6.

1000 – 307 = 693,

10000 – 6523 = 3477,

100 – 76 = 24,

1000 – 580 = 420. Remember: apply the formula just to 58 here.

Applying the formula to 470 or any number that ends in 0 we need to be a bit

careful.

Ignore the 0 and take 7 as the last figure: apply the formula to 47 and simply pu

t

the 0 on afterwards. So you get 530.

Similarly with 28160 you get 71840 (just apply the formula to 2816),

with 4073100 you get 5926900 (just apply the formula to 40731).

 Practice B Apply the formula to these numbers:

a 3570 b 920 c 1234560 d 3300

a 6430 b 80 c 8765440 d 6700

If you look carefully at the pairs of numbers in Example 2 you may notice that in every case

the total of the two numbers is a base number: 10, 100, 1000 etc.

This gives us an easy way to subtract from base numbers like 10, 100, 1000 . . .

In every case here the number is being subtracted from its next highest base number.

3

4

5.2 SUBTRACTION

5

The formula All From 9 and the Last From 10

subtracts numbers from the next highest base number.

VEDIC MATHEMATICS MANUAL 1

50

Suppose you had 1000 – 43.

This has three zeros, but 43 is only a 2-figure number.

You can solve this by writing 1000 – 043 = 957.

You put the extra zero in front of 43, and then apply the formula to 043.

10000 – 58.

Here we need to add two zeros: 10000 – 0058 = 9942.

 Practice C Subtract the following:

a 1000 – 481 b 1000 – 309 c 1000 – 892 d 1000 – 976

e 100 – 78 f 100 – 33 g 10000 – 8877 h 10000 – 9876

i 1000 – 808 j 1000 – 710 k 10000 – 6300

a 519 b 691 c 108 d 24

e 22 f 67 g 1123 h 124

i 192 j 290 k 3700

ADDING ZEROS

In all of the above sums you may have noticed that the number of zeros in the first number is

the same as the number of figures in the number being subtracted.

For example 1000–481 has three zeros and 481 has three figures.

In the following exercise you will need to insert zeros, but you can do that mentally.

 Practice D Subtract the following:

a 1000 – 86 b 1000 – 93 c 1000 – 35 d 10000 – 678

e 10000 – 353 f 10000 – 177 g 10000 – 62 h 10000 – 85

i 1000 – 8 j 10000 – 3

6

7

5: ALL FROM 9 AND THE LAST FROM 10

51

Find 8000 – 4222.

Considering the thousands, the 8 will be reduced by 5 (one more than 4)

because you are taking over 4 thousand away.

All from 9. . . is then applied to the 222 to give 778.

So 8000 – 4222 = 3778.

Now let’s look at 600 – 77.

You have 600 instead of 100.

In fact the 77 will come off one of those six hundreds, so that 500 will be left.

So 600 – 77 = 523

The 6 is reduced by one to 5, and the All from 9 . . . formula is applied to 77 to give

23.

5000 – 123 = 4877. The 5 is reduced by one to 4,

and the formula converts 123 to 877.

a 914 b 907 c 965 d 9322

e 9647 f 9823 g 9938 h 9915

i 992 j 9997

ONE LESS

 Practice E Try these:

a 600 – 88 b 400 – 83 c 900 – 73 d 6000 – 762

e 2000 – 979 f 50000 – 4334 g 70000 – 8012

a 512 b 317 c 827 d 5238

e 1021 f 45666 g 61988

ONE MORE

Now let’s look at another variation.

8

9

10

VEDIC MATHEMATICS MANUAL 1

52

Find 6000 – 32.

You will see here that you have a 2-figure number to subtract from 6000 which has

three zeros.

The sum can be written 6000 – 032.

Then 6000 – 032 = 5968.

The 6 is reduced to 5, and the formula converts 032 to 968.

30000 – 63 = 30000 – 0063 = 29937.

The 3 becomes 2, and 0063 becomes 9937.

When you have a sum like 8000 – 4222 where both numbers have the same number of

figures:

 Practice F Subtract the following:

a 8000 – 3504 b 5000 – 1234 c 300 – 132

d 2000 – 1444 e 700 – 232 f 60,000 – 23,331

a 4496 b 3766 c 168

d 556 e 468 f 36,669

ONE LESS AGAIN

 Practice G Subtract the following:

a 5000 – 74 b 8000 – 58 c 6000 – 94 d 4000 – 19

e 80000 – 345 f 30000 – 276 g 50000 – 44 h 700 – 8

i 30000 – 54 j 20000 – 222 k 30000 – 670 l 70000 – 99

a 4926 b 7942 c 5906 d 3981

e 79655 f 29724 g 49956 h 692

i 29946 j 19778 k 29330 l 69901

11

12

reduce the first figure of the first number by one more than the first figure of the

second number to get the first figure of the answer.

And apply the formula to the remaining figures.

5: ALL FROM 9 AND THE LAST FROM 10

53

Suppose you buy a computer game for £7.53 and you pay with a £10 note.

How much change would you expect to get?

You just apply All From 9 and the Last From 10 to 753 to get £2.47.

What change would you expect from a £20 note when paying £3.46?

The change you expect to get is £16.54 because £3.46 from £10 is £6.54 and there is

£10 to add to this.

The type of subtraction we have been doing is very useful for checking change.

 Practice H Do the following money subtractions in a similar way.

a £10 – £2.34 b £10 – £6.51 c £10 – £5.82 d £10 – £9.07

e £20 – £7.44 f £20 – £12.78 g £20 – £3.18 h £20 – £8.40

a £7.66 b £3.49 c £4.18 d £0.93

e £12.56 f £7.22 g £16.82 h £11.60

This subtraction method leads to a general subtraction process (see Lesson 9).

The final exercise is a mixture of all the types we have met:

 Practice I Subtract:

a 100 – 34 b 1000 – 474 c 5000 – 542 d 800 – 72

e 1000 – 33 f 5000 – 84 g 700 – 58 h 9000 – 186

i 10000 – 4321 j 200 – 94 k 10000 – 358 l 400 – 81

m 7000 – 88 n 900 – 17 o 30000 – 63 p 90000 – 899

a 66 b 526 c 4458 d 728

e 967 f 4916 g 642 h 8814

i 5679 j 106 k 9642 l 319

m 6912 n 883 o 29937 p 89101

5.3 MONEY

13

14

Suppose you are given the addition sum: 2 3 4 5

6 7 3 8 +

With 4-figure numbers it looks rather hard.

But if you split the sum into two parts, each part can be done easily and mentally

(see Sections 1.5, 1.6, 4.1):

On the right we have 45 + 38 which (mentally) is 83.

So you put this down.

And on the left you have 23 + 67 which is 90. So 2345 + 6738 = 9083.

SUMMARY

6.1 Addition

6.2 Subtraction

6.3 Multiplication

6.4 Division

This is a very useful device for splitting a difficult sum into two or more easy ones and comes

under the formula By Alternate Elimination and Retention.

For quick mental sums number splitting can considerably reduce the work involved in a

calculation.

 Practice A Add the following (try some of them mentally):

a 3 4 5 6 b 1 8 1 9 c 6 4 4 6 d 8 3 2 1

4 7 1 7 1 7 1 6 2 8 3 8 1 8 2 3

_______

a 81/73 b 35/35 c 92/84 d 101/44

LESSON 6

NUMBER SPLITTING

2 3 4 5

6 7 3 8 +

9 0 8 3

6.1 ADDITION

1

–

splitting difficult sums into

easy ones, all done from left

to right.

}

6: NUMBER SPLITTING

55

Consider the subtraction sum: 5 4 5 4

– 1 7 2 6

_______

You can split this up 5 4 5 4

into two easy sums: – 1 7 2 6

3 7 2 8

First 54 – 26, which is 28,

then 54 – 17, which is 37.

Find 481 + 363.

This example is done in two in ways.

Which is easier?

4 8 1

3 6 3

8 4 4

+

1

4 8 1

3 6 3

8 4 4

+

 Practice A continued Add the following (try some of them mentally):

e 7 6 7 f 3 8 3 g 4 4 4 h 8 8 8

6 1 6 3 8 4 2 4 6 7 0 7

i 5 5 1 j 4 5 5 4 k 1 2 3 4 l 5 2 3 4

6 6 2 3 6 3 6 4 9 4 4 9 3 9 3

e 13/83 f 76/7 g 6/90 h 15/95

i 121/3 j 81/90 k 61/78 l 14/62/7

You can also use Number Splitting in subtraction sums.

6.2 SUBTRACTION

2

3

You may have to think where to put the line,

but it is usually best to put it so that there are no carries over the line.

VEDIC MATHEMATICS MANUAL 1

56

352 × 2

You can split this sum like this: 35 / 2 × 2 = 704. (35 and 2 are easy to double.)

Similarly 827 × 2 becomes 8 / 27 × 2 = 1654,

604 × 7 becomes 6 / 04 × 7 = 4228,

121745 × 2 becomes 12 / 17 / 45 × 2 = 243490,

3131 × 5 becomes 3 / 13 / 1 × 5 = 15655.

 Practice B Subtract the following. Split each sum into two easy ones.

a 3 2 4 3 b 4 4 4 4 c 7 0 7 0 d 3 7 2 1

1 3 1 9 1 8 2 8 1 5 2 6 1 9 0 9

_______

e 6 8 8 9 f 8 5 2 g 7 7 7 h 6 6 6 6

1 9 3 6 1 3 9 5 8 5 2 9 3 8

_______

a 19/24 b 26/16 c 55/44 d 18/12

e 49/53 f 7/13 g 19/2 h 37/28

This same splitting technique can be applied in multiplication and division as well.

You can split the number any way you like, but it is best to:

 Practice C Multiply the following:

a 432 × 3 b 453 × 2 c 626 × 2 d 433 × 3 e 308 × 6

f 814 × 4 g 515 × 5 h 919 × 3 i 1416 × 4 j 2728 × 2

k 3193 × 3 l 131415 × 3

6.3 MULTIPLICATION

4

5

split the number so that the parts can be multiplied easily, without a carry.

6: NUMBER SPLITTING

57

The division sum 2)4 3 2 can be split into: 2)4 / 32 = 2/16 = 216.

because 4 and 32 are both easy to halve.

Similarly 2)3 4 5 6 becomes 2)34 / 56 = 17/28 = 1728.

And in 3)1266 we notice that 12 and 66 can be divided separately by 3, so:

3)12/66 = 4/22 = 422

6)6 1 2 becomes 6)6 / 12 = 1/02 = 102.

note the 0 here because the 12 takes up two places)

7)2 8 4 9 becomes 7)28 / 49 = 4/07 = 407.

a 12/96 b 90/6 c 12/52 d 12/99 e 18/48

f 32/56 g 25/75 h 27/57 i 56/64 j 54/56

k 9/57/9 l 39/42/45

Division sums can also often be simplified by this method.

 Practice D Divide the following mentally:

a 2)6 5 6 b 2)7 2 6 c 3)1 8 9 9 d 6)1 2 6 6

e 4)2 0 4 8 f 4)2 8 4 4 g 3)2 1 3 9 h 2)2 6 3 6

a 3/28 b 36/3 c 6/33 d 2/11

e 5/12 f 7/11 g 7/13 h 13/18

Sometimes we need to be a bit careful and put extra zeros.

6.4 DIVISION

6

7

8

9

10

VEDIC MATHEMATICS MANUAL 1

58

3) 2 4 4 5 3 becomes 3)24 / 45 / 3 = 8/15/1 = 8151.

 Practice D continued

i 4)2 8 1 6 j 4)8 1 2 k 6)4 8 1 8 l 3)1 2 6 6

m 5)2 0 4 5 n 2)3 8 1 4 o 7)21014

i 704 j 203 k 803 l 422

m 409 n 1907 o 3002

And sometimes we split into three sections.

 Practice D continued

p 3)9 1 8 2 7 q 2)3 8 7 2 5 2 r 8)4 0 1 6 8 s 5)1 0 3 5 4 5

t 3)1 5 0 1 5 u 13)3 9 1 3 5 2

p 30609 q 193626 r 5021 s 20709

t 5005 u 30104

11

“But, according to the Vedic system, the

multiplication tables are not reall

y

required above 5×5.”

From “Vedic Mathematics”, Page 13.

SUMMARY

7.1 Times Tables – avoiding multiplication tables above 5 × 5.

7.2 Numbers just Over Ten – multiplying numbers close to and over ten.

7.3 Multiplication Table Patterns – patterns of tables on the 9-point circle.

7.4 Numbers Close to 100 – multiplying numbers near 100.

7.5 Larger Numbers – multiplying larger numbers.

7.6 Proportionately – a further extension of the method.

7.7 Multiplying Numbers near Different Bases

7.8 Squaring Numbers near a Base

7.9 A summary – of all multiplication devices so far.

It is useful to know multiplication tables by heart. If not here is a neat and easy method to use.

LESSON 7

BASE MULTIPLICATION

7.1 TIMES TABLES

If you want 7 × 8 you know that 7 is 3 below 10

and 8 is 2 below 10.

So next to 7 put –3 and 7 – 3

next to 8 put –2, like this: × 8 – 2

Then cross-subtract to get the first figure of the answer: 7 – 2 = 5:

7 – 3

× 8 – 2

5

Or, if you prefer you can subtract the other way: 7 – 3

× 8 – 2

5 8 – 3 = 5 as well.

Finally, just multiply vertically, 3 × 2, to get 6 for the second part of the answer.

7 – 3

× 8 – 2

5 6 So 7 × 8 = 56.

1

VEDIC MATHEMATICS MANUAL 1

60

So to sum up: 1) put the differences of the numbers from 10: 3 and 2 above,

2) cross-subtract: 7–2 = 5 or 8–3 = 5 and put this down,

3) multiply vertically: 3×2 = 6 and put it down.

This comes under the Vertically and Crosswise Sutra.

Sometimes there can be a carry figure, so let’s look at this next.

 Practice A This method is very easy. Try the ones below.

a 7 b 8 c 9 d 7 e 8

× 9 × 8 × 6 × 7 × 9

f 8 g 9 h 6 i 7 j 6

× 6 × 9 × 6 × 5 × 5

a 63 b 64 c 54 d 49 e 72

f 48 g 81 h 36 i 35 j 30

So in the Vedic system multiplication tables above 9×9 are not essential.

See the note on Russian Peasant Multiplication on Page 69.

To find 6 × 7 we note 6 is 4 below 10 and 7 is 3 below 10.

So we have: 6 – 4

× 7 – 3

Then cross-subtract: 6 – 3 = 3 and put this down:

6 – 4

× 7 – 3

3

Then just multiply 4 × 3 to get 12 for the second part of the answer.

But here, as 12 is a 2-figure number you need to carry the 1 over to the 3:

6 – 4

× 7 – 3

3 2 = 42 So 6 × 7 = 42.

1

2

7: BASE MULTIPLICATION

61

For 12 × 13 you notice the numbers are close to 10 and that 12 is 2 over ten, and 13

is 3 over ten.

So set the sum out as before except that because the numbers are over ten you put

a

plus instead of a minus:

12 + 2

× 13 + 3

Then you cross-add 12 + 2

to get the first part of the answer: × 13 + 3

12 + 3 = 15 (or 13 + 2 = 15). 15

And as before you multiply vertically 12 + 2

to get the last figure: 2 × 3 = 6 × 13 + 3

15 6

So 12 × 13 = 156.

The method used in the last section can also be used for numbers just over 10 rather than

numbers just under 10.

Suppose you want to multiply 12 and 13, which are both close to 10.

 Practice B This is the same as before except that we cross-add. Try some.

There is a carry in the sums in the second row.

a 13 b 12 c 11 d 13 e 11

× 11 × 12 × 15 × 13 × 11

f 13 g 12 h 14 i 16 j 13

× 14 × 16 × 14 × 16 × 18

a 143 b 144 c 165 d 169 e 121

f 182 g 192 h 196 i 256 j 234

7.2 NUMBERS JUST OVER TEN

3

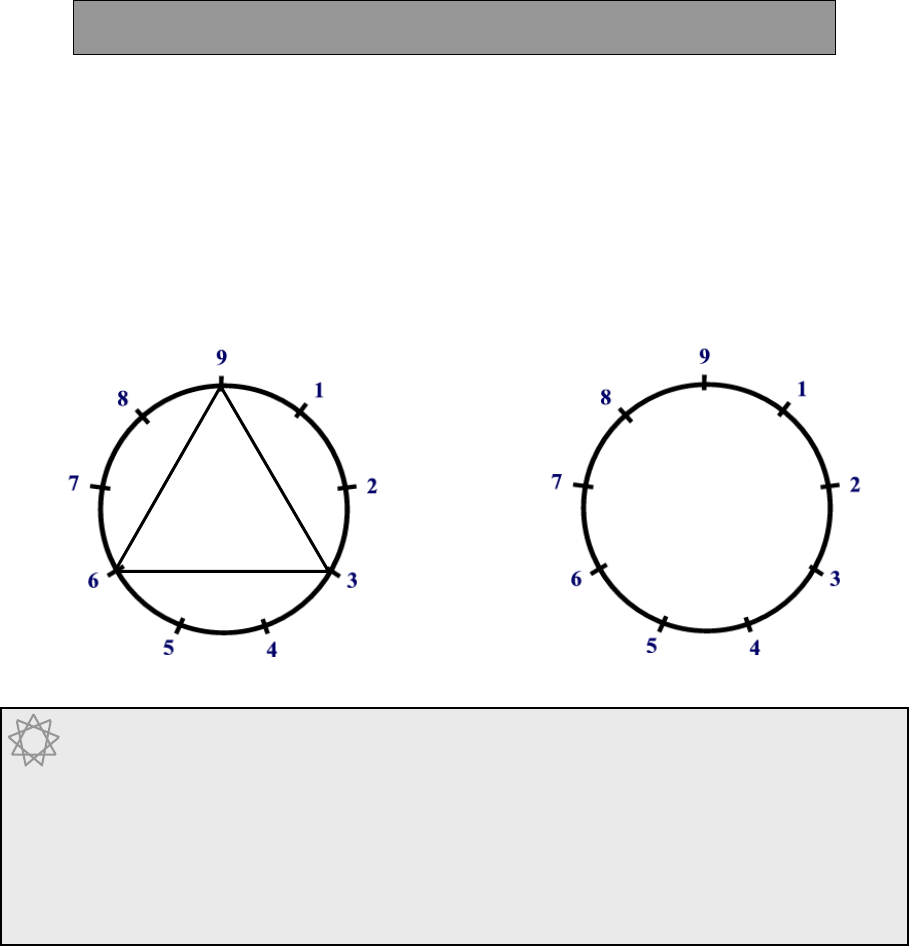
VEDIC MATHEMATICS MANUAL 1

62

In the 3-times table the answers are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 . . .

If you find the digit sums of these numbers you get 3, 6, 9, 3, 6, 9, 3, 6, 9 . . .

The same pattern 3, 6, 9 repeats over and over again.

You can show this pattern on the 9-point circle.

3 TIMES TABLE 6 TIMES TABLE

So this is the pattern for the 3-times table and it is shown above.

 Practice C

a Draw the pattern for the 6-times table on the right-hand circle above.

b Draw the patterns for the 4 and 5, 1 and 8, 2 and 7 and the 9 times tables on the circles

below.

7.3 MULTIPLICATION TABLE PATTERNS

Start at 3 and draw a line to the next number, 6

(go over the line in a colour).

Then from 6 draw a line to the next number, 9.

Then from 9 draw a line to the next number 3.

From then on the pattern goes over itself because 3, 6, 9, 3, 6, 9 . . . keeps

repeating.

4

7: BASE MULTIPLICATION

63

4 TIMES TABLE 5 TIMES TABLE

1 TIMES TABLE 8 TIMES TABLE

2 TIMES TABLE 7 TIMES TABLE

VEDIC MATHEMATICS MANUAL 1

64

9 TIMES TABLE

RECURRING DECIMALS

This 9-point circle has many uses including representing recurring decimal cycles (see

Manual 2 or The Cosmic Calculator, Books 2, 3).

For example: 1

7= 0.142857

..

which means the cycle of figures 142857 repeats itself indefinitely.

We draw this pattern by starting at 1 and drawing a line to 4 and so on until we have six lines

and the pattern starts to repeat itself. This converts the arithmetic pattern to a geometrical

pattern.

In fact any sequence can be represented on the circle: square numbers, triangular numbers,

prime numbers, the fibonacci sequence etc.

7: BASE MULTIPLICATION

65

The simple method for multiplying numbers like 7× 8 shown in Section 7.1 can be extended

to easily multiply bigger numbers.

Usually a sum like 88 × 98 is considered especially difficult because of the large figures, 8

and 9.

But since the numbers 88 and 98 are close to the base of 100 it is in fact very easy to find the

product.

88 × 98 = 8624.

We set the sum out as shown below:

88 is 12 below 100, so we put –12 next to it,

98 is 2 below 100 so we put –2 next to it.

The answer 8624 is in two parts: 86 and 24.

88 – 12

98 – 2

86 / 24

cross-subtract multiply vertically: 12 × 2 = 24

that is 88 – 2 = 86 or 98 – 12 = 86

(whichever you like),

We call the 12 and 2 deficiencies as the numbers 88 and 98 are deficient from the

unity of 100 by 12 and 2.

For 93 × 96 we get deficiencies of 7 and 4, so 93 - 07

96 - 04

89 / 28

93 – 4 = 89 or 96 – 7 = 89,

and 7 × 4 = 28.

For 98 × 97: 98 – 02

97 – 3

95 / 06

Note the zero inserted here: the numbers being multiplied are near to 100, so two

digits are required on the right, as in the other examples.

7.4 NUMBERS CLOSE TO 100

5

6

7

VEDIC MATHEMATICS MANUAL 1

66

For 89 × 89: 89 – 11

89 – 11

1

78 / 21 = 7921

Here the numbers are each 11 below 100, and 11 × 11 = 121, a 3-figure number.

The hundreds digit of this is therefore carried over to the left.

 Practice D Multiply the following:

a 94 × 94 b 97 × 89 c 87 × 99 d 87 × 98 e 87 × 95

f 95 × 95 g 79 × 96 h 98 × 96 i 92 × 99 j 99 × 99

a 88/36 b 86/33 c 86/13 d 85/26 e 82/65

f 90/25 g 75/84 h 94/08 i 91/08 j 9801

It may happen that there is a carry figure.

 Practice D continued

k 88 × 88 l 97 × 56 m 44× 98 n 97 × 63

k 7744 l 5432 m 4312 n 6111

Explanation (based on Example 5 above).

(1) 88 × 98 = 88 × 100 – 88 × 2

= 8800 – (100 × 2 – 12 × 2)

= 8800 – 200 + 12 × 2

= 8600 + 24 = 8624

(2) Alternatively consider the following geometrical explanation.

88×98 is the area of a rectangle 88 units by 98 units so we begin with a square of side 100:

8

In fact once we have got the deficiencies we apply the Vertically and Crosswise method:

we cross-subtract to get the left-hand part of the answer and

we multiply vertically in the right-hand column to get the right-hand part of the answer.

7: BASE MULTIPLICATION

67

98 2

AB

C

D

88

12

100

You can see the required area shaded in the diagram.

You can also see the deficiencies from 100: 12 and 2.

Now the area ABCD must be 8800 because the base is 100 and the height is 88.

8800 200

From this we subtract the strip on the right side, the area of which is 200:

so 8800 – 200 = 8600.

This leaves the required area but we have also subtracted the area of the small rectangle

shown shaded above on the right. This must therefore be added back on and since its area is

12×2=24 we add 24 to 8600 to get 8624.

You can probably see that this procedure will work for any product when the numbers are

close to 100 and just below it.

(3) An algebraic proof would be: (x – a)(x – b) = x(x – a – b) + ab,

where x is the base (in this example 100) and a and b are the deficiencies of the numbers from

the base (in this case 12 and 2).

The numbers being multiplied are thus (x – a) and (x – b); (x – a – b) is one number minus the

other deficiency; and the x outside the bracket on the RHS has the effect of moving the

quantity (x – a – b) to the left as many places as there are zeros in the base.

MENTALLY

Look again at the first example in this section:

88 – 12

98 – 2

86 / 24

The most efficient way to do these sums is to take one number and subtract the other

number’s deficiency from it: 88–2=86, or 98–12=86.

Then multiply the deficiencies together: 12×2=24.

We mentally adjust the first part of the answer if there is a carry figure.

VEDIC MATHEMATICS MANUAL 1

68

103 × 104 = 10712. 103 + 03

104 + 4

107 / 12

The method is similar to the previous one.

103 is 3 over 100, so put +3 next to it.

And 104 is 4 over 100 so put +4 next to it.

Then 103 + 4 = 107 or 104 + 3 = 107,

and 4 × 3 = 12.

So now we cross-add, and multiply vertically.

This is so easy it is really just mental arithmetic.

 Practice E Multiply these numbers mentally, just write down the answer:

a 87 b 79 c 98 d 94

97 98 93 95

e 96 f 88 g 89 h 93

96 96 98 96

i 93 j 97 k 96 l 95

99 97 67 75

m 8 9

? ?

8 2 7 7 find the missing numbers

a 84/39 b 77/42 c 91/14 d 89/30

e 92/16 f 84/48 g 87/22 h 89/28

i 92/07 j 94/09 k 64/32 l 71/25

m 93

NUMBERS OVER 100

Multiplying numbers that are over 100 is even easier than multiplying numbers just under

100.

Suppose we want 103 × 104.

9

7: BASE MULTIPLICATION

69

 Practice F Multiply mentally:

a 107 × 104 b 107 × 108 c 133 × 103 d 102 × 104

e 123 × 102 f 171 × 101 g 103 × 111 h 125 × 105

i 103 × 103 j 111 × 111 k 162 × 102 l 113 × 105

m 1 0 3

? ? ?

1 0 8 1 5 find the missing numbers

a 11128 b 11556 c 13699 d 10608

e 12546 f 17271 g 11433 h 13125

i 10609 j 12321 k 16524 l 11865

m 105

MENTAL MATHS

The Vedic techniques are so easy that the system of Vedic Mathematics is really a system of

mental mathematics. This has a number of further advantages as pupils seem to make faster

progress and enjoy mathematics more when they are permitted to do the calculation in their

head. After all, the objects of mathematics are mental ones, and writing down requires a

combination of mental and physical actions, so that the child’s attention is alternating between

the mental and physical realms. This alternation is an important ability to develop but working

only with mental objects also has many advantages.

Mental mathematics leads to greater creativity and the pupils understand the objects of

mathematics and their relationships better. They begin to experiment (especially if they are

encouraged to do so) and become more flexible. Memory and confidence are also improved

through mental mathematics.

RUSSIAN PEASANT MULTIPLICATION

This is using the fingers for multiplication of numbers between 5 and 9 by numbers between 5

and 9, and it is very similar to the Vedic method shown here.

The fingers are numbered as shown with the thumbs counting as 5 and the little fingers as 9.

The palms are upward. To multiply, say, 8 by 7, put together the ‘8 finger’ on the left hand

and the ‘7’ finger on the right hand. Then count the fingers above the touching fingers: there

are 5, and multiply the number of other fingers on the left hand by the number of other fingers

on the right hand: 2 × 3 = 6.

So 8 × 7 = 56.

5

6 7 89 8 7 6

9 5

VEDIC MATHEMATICS MANUAL 1

70

Find 568 × 998.

In this sum the numbers are close to 1000, and the deficiencies are 432 and 2.

The deficiency for 568 is found by applying the Sutra: All from 9 and the Last from

10.

568 – 432

998 – 2 The method here is just the same, but we allow 3 figures

566 / 864 on the right as the base is now 1000.

The differences of the numbers from 1000 are 432 and 2.

Then cross-subtracting:568 – 2 = 566,

And vertically: 432 × 2 = 864.

So 568 × 998 = 566864.

Find 68777 × 99997.

Even large numbers like this are easily and mentally multiplied by the same method.

68777 – 31223

99997 – 3

68774 / 93669

Now, what about numbers close to other bases like 1000 10,000 etc?

 Practice G

Multiply the following mentally:

a 667 × 998 b 768 × 997 c 989 × 998 d 885 × 997

e 883 × 998 f 467 × 998 g 891 × 989 h 8888 × 9996

i 6999 × 9997 j 90909 × 99994 k 78989 × 99997 l 9876 × 9998

a 665/666 b 765/696 c 987/022 d 882/345

e 881/234 f 466/066 g 881/199 h 8884/4448

i 6996/9003 j 90903/54546 k 78986/63033 l 9874/0248

The number of spaces needed on the right is the number of 0's in the base number.

7.5 LARGER NUMBERS

10

11

7: BASE MULTIPLICATION

71

1234 × 1003 = 1237702. (1234+3=1237, 234×3=702)

10021 × 10002 = 100230042. (10021+2=10023, 0021×2=0042)

With a base of 10,000 here we need 4 figures on the right.

Find 309 × 104.

You may notice here that 309 is 3 × 103.

This means we can find 103 × 104 (which have an easy method for) and multiply the

answer by 3.

103 × 104 = 10712.

And 10712 × 3 = 32136.

You can use number splitting to find 10712 × 3: 1/07/12 × 3 = 3/21/36.

NUMBERS ABOVE THE BASE

Suppose now that the numbers are above the base.

 Practice H

a 1222 × 1003 b 1051 × 1007 c 1123 × 1002

d 1007 × 1006 e 15111 × 10003

a 1225/666 b 1058/357 c 1125/246

d 1013/042 e 15115/5333

Proportionately just means that you can get an answer by doubling (or trebling etc.) another

answer.

We have been doing this quite a lot already.

7.6 PROPORTIONATELY

12

13

14

VEDIC MATHEMATICS MANUAL 1

72

Find 47 × 98.

Here you should double 47 to 94 because both the numbers are then close to 100.

So you find 94 × 98 and halve the answer.

94 × 98 = 9212

And half of 9212 is 4606.

Again use number splitting: to halve 9212 (think of 92/12).

Find 192 × 44.

Here you can halve 192 and double 44.

This converts the sum to 96 × 88 and there is no doubling or halving to be done to

the answer because the halving and doubling cancel each other out.

So 192 × 44 = 96 × 88 = 8448.

Find 192 × 92.

Here we see that if you halve 192 you get 96.

So: find 96 × 92 and double the result.

96 × 92 = 8832, by the easy Vertical and Crosswise method,

and so 192 × 92 = 17664, (by doubling 8832).

 Practice I

a 212 × 103 b 106 × 208 c 182 × 98 d 93 × 186

a 21836 b 22048 c 17836 d 17298

 Practice I continued

e 93 × 46 f 56 × 104 g 306 × 118 h 51 × 104

i 206 × 54 j 44 × 99 k 48 × 184 l 228 × 212

e 4278 f 5824 g 36108 h 5304

i 11124 j 4356 k 8832 l 48336

15

16

17

7: BASE MULTIPLICATION

73

213 × 203 = 43239. 213 + 13

203 + 3

2 × 216 / 39 = 43239

We see here that the numbers are not near any of the bases used before: 10, 100,

1000 etc.. But they are close to 200, with differences of 13 and 3 as shown above.

The usual procedure gives us 216/39 (213+3=216, 13×3=39).

Now since our base is 200 which is 100×2 we multiply only the left-hand part o

f

the answer by 2 to get 43239.

29 × 28 = 812.

The base is 30 (3×10), 29 – 1

and the deficiencies are –1 and –2. 28 – 2

Cross-subtracting gives 27, 3 × 27 / 2 = 812

then multiplying vertically on the right we get 2,

and finally 3×27 = 81.

So these are just like the previous sums but with an extra multiplication

(of the left-hand side only) at the end.

Find 33 × 34.

In this example there is a carry figure: 33 + 3

34 +

4

1

337/2

×

= 111 /12 = 1122

Note that since the right-hand side does not get multiplied by 3 we multiply the left-

hand side by 3 before carrying the 1 over to the left.

ANOTHER APPLICATION OF PROPORTIONATELY

Another way of using the Proportionately formula further extends the range of application of

this multiplication method.

 Practice J Multiply mentally:

a 41 × 42 b 204 × 207 c 321 × 303 d 203 × 208

e 902 × 909 f 48 × 47 g 188 × 196 h 199 × 198

i 189 × 194 j 207 × 211 k 312 × 307 l 5003 × 5108

m 63 × 61 n 23 × 24 o 79 × 77

18

20

19

VEDIC MATHEMATICS MANUAL 1

74

9998 × 94 = 9398/12

Here the numbers are close to different bases: 10,000 and 100,

and the deficiencies are –2 and –6.

We write, or imagine, the sum set out as shown: 9998 –02

94 –

6

9398 / 12

It is important to line the numbers up as shown because the 6 is not subtracted from

the 8, as usual, but from the 9 above the 4 in 94. That is, the second column from the

left here.

So 9998 becomes 9398.

Then multiply the deficiencies together: 2×6 = 12.

N

ote that the number of figures in the righ

t

-hand part of the answer corresponds to the

base of the lower number (94 is near 100, therefore there are 2 figures on the right).

a 172/2 b 422/28 c 972/63 d 422/24

e 8199/18 f 225/6 g 368/48 h 394/02

i 366/66 j 436/77 k 957/84 l 25555/324

m 3843 n 552 o 6083

Sometimes we need to multiply numbers that are each near a different base.

In the example below one number is close to 10,000 and the other is close to 100.

You can see why this method works by looking at the sum 9998 × 9400, which is 100 times

the sum done above:

9998 – 0002

9400 – 600

9398 / 1200

Now we can see that since 9998 × 9400 = 93981200,

then 9998 × 94 = 939812.

This also shows why the 6 is subtracted in the second column from the left.

7.7 MULTIPLYING NUMBERS NEAR DIFFERENT BASES

21

7: BASE MULTIPLICATION

75

962 = 92/16.

96 is 4 below 100, so we reduce 96 by 4, which gives us the first part of the answer,

92.

The last part is just 42 =16, as the formula says.

10007 × 1003 = 10037021.

Lining the numbers up: 10007 + 007

1003 + 3

10037 / 021

we see that we need three figures on the right and that the surplus, 3, is added in the

4th column, giving 10037.

 Practice K Find:

a 97 × 993 b 92 × 989 c 9988 × 98 d 9996 × 988

a 963/21 b 909/88 c 9788/24 d 9876/048

In the next example the numbers are close to different bases, but they are over the base rather

than under.

 Practice L Find:

a 103 × 1015 b 106 × 1012 c 10034 × 102 d 1122 × 104

a 1045/45 b 1072/72 c 10234/68 d 1166/88

This is especially easy and is for squaring numbers which are near a base.

You will recall that squaring means that a number is multiplied by itself (like 96 × 96).

This method is described by the sub-formula Reduce (or increase) by the Deficiency and also

set up the square.

7.8 SQUARING NUMBERS NEAR A BASE

22

23

VEDIC MATHEMATICS MANUAL 1

76

3042 = 3×308/16 = 92416.

This is similar but because our base is 300 the left-hand part of the answer is

multiplied by 3.

10062 = 1012/036.

Here 1006 is increased by 6 to 1012, and 62 = 36: but with a base of 1000 we need 3

figures on the right, so we put 036.

 Practice M Square the following:

a 94 b 103 c 108 d 1012

e 98 f 88 g 91 h 10006

i 988 j 997 k 9999 l 9989

m 111 n 13 o 987

a 8836 b 10609 c 11664 d 1024144

e 9604 f 7744 g 8281 h 100120036

i 976144 j 994009 k 99980001 l 99780121

m 12321 n 169 o 974169

 Practice N Square the following:

a 206 b 212 c 302 d 601

e 21 f 72 g 4012 h 511

a 424/36 b 449/44 c 912/04 d 3612/01

e 44/1 f 518/4 g 16096/144 h 2611/21

There are many special multiplication methods in the Vedic system: see Lesson 10. And the

general method (Lesson 11) is always there if no special method comes to mind.

24

25

7: BASE MULTIPLICATION

77

Here we can summarise the various methods of multiplication and squaring encountered so

far.

1. Multiplying by 4, 8 etc. we can just double twice, 3 times etc. E.g. 37×4.

2. We can use doubling to extend the multiplication tables. E.g. 14×8.

3. We can multiply from left to right using On the Flag. E.g. 456×3.

4. We can use All from 9 and the Last from 10 for multiplying numbers near a base.

E.g. 98×88, 103×104, 203×204.

5. And we can also multiply numbers near different bases. E.g. 998×97.

6. The same Sutra can be used for squaring numbers near a base. E.g. 97², 1006², 203².

 Practice O The following exercise contains a mixture of all the different types of

multiplication we have seen so far:

a 654 × 3 b 86 × 98 c 97 × 92

d 73 × 4 e 7 × 22 f 16 × 24

g 798 × 997 h 8899 × 9993 i 106²

j 996² k 103 × 109 l 123 × 104

m 203 × 209 n 188 × 197 o 87 × 97

p 32 × 33 q 2004 × 2017 r 9997 × 98

s 1023 × 102

a 1962 b 8428 c 8924

d 292 e 154 f 384

g 795606 h 88927707 i 11236

j 992016 k 11227 l 12792

m 42427 n 37036 o 8439

p 1056 q 4042068 r 979706

s 104346

7.9 A SUMMARY

“all that the student has to do is to look for certain

characteristics, spot them out, identify the particular type

and apply the formula which is applicable thereto.”

From “Vedic Mathematics”, Page 106.

LESSON 8 LESSON 8

CHECKING AND DIVISIBILITY

SUMMARY SUMMARY

8.1 Digit Sum Check for Division – checking division sums. 8.1 Digit Sum Check for Division – checking division sums.

8.2 The First by the First and the Last by the Last – more checking 8.2 The First by the First and the Last by the Last – more checking

devices. devices.

8.3 Divisibility by 4 8.3 Divisibility by 4

8.4 Divisibility by 11 8.4 Divisibility by 11

8.1 DIGIT SUM CHECK FOR DIVISION

Find 3456 ÷ 7.

7)34

652

6

4 9 3 remainder 5

The division is done in the usual way: 34÷7 = 4 rem 6, placed as shown,

65÷7 = 9 rem 2, placed as shown,

26÷7 = 3 rem 5, as shown.

So 3456 ÷ 7 = 493 rem 5.

1

If the above division is correct then 493×7 + 5 = 3456. If the above division is correct then 493×7 + 5 = 3456.

(Just as 7 ÷ 3 = 2 remainder 1 is correct because 2 × 3 + 1 = 7.) (Just as 7 ÷ 3 = 2 remainder 1 is correct because 2 × 3 + 1 = 7.)

We can check that 493×7 + 5 = 3456 is correct by changing each number to its digit sum: We can check that 493×7 + 5 = 3456 is correct by changing each number to its digit sum:

493 has a digit sum of 7, 3456 has a digit sum of 9. 493 has a digit sum of 7, 3456 has a digit sum of 9.

So 493 × 7 + 5 = 3456 So 493 × 7 + 5 = 3456

becomes 7 × 7 + 5 J 9 becomes 7 × 7 + 5 J 9

and this is true in digit sums because 7×7=49J4, and 4+5 J 9. and this is true in digit sums because 7×7=49J4, and 4+5 J 9.

(An alternative to the above line would be: 7×7 + 5 = 54, 54J9.) (An alternative to the above line would be: 7×7 + 5 = 54, 54J9.)

8: CHECKING AND DIVISIBILITY 79

Find 70809 ÷ 6.

6)71048000

9

1 1 8 0 1 rem 3 this is the answer and for the

check you show that 11801× 6 + 3 = 70809 is true in digit sums.

This becomes 2×6 + 3 J 6 in digit sums and it is correct

since 2×6=3 in digit sums and 3 + 3 = 6.

 Practice A Divide the following and check using the digit sums:

a 3)4 6 8 1 b 4)9 1 3 c 5)7 0 3 2

d 6)3 2 1 e 7)2 2 2 f 8)9 0 8 0

g 9)1 0 0 1 h 2)3 4 5 6 7

32 × 41 is approximately 1000.

By multiplying the first figure of each number together you find that 32 × 41 is

approximately 30 × 40, which is 1200.

So you expect the answer to be about 1000, rounding off to the nearest thousand.

a 1560 r1 (3×3+1J1) b 228 r1 (3×4+1J4) c 1406 r2 (2×5+2J3)

d 53 r3 (8×6+3J6) e 31 r5 (4×7+5J6) f 1135 r0 (1×8+0J8)

g 111 r2 (3×9+2J2) h 17283 r1 (3×2+1J7)

8.2 THE FIRST BY THE FIRST AND THE LAST BY THE LAST

THE FIRST BY THE FIRST

The First by the First and the Last by the Last is useful for giving approximate answers to

sums. Sometimes you may only want to find the first figure of an answer and the number of

noughts following it, rather than work out the whole sum. Then you can use this method.

2

3

VEDIC MATHEMATICS MANUAL 1

80

Find the approximate value of 641 × 82.

You want the first figure of the answer and the number of 0's that come after it.

Since 600 × 80 = 48,000 and you know the answer will be more than this you ca

n

say the answer is about 50,000 (to the nearest 10,000).

4

Find the approximate value of 39 × 63.

39 is close to 40 so that the first by the first gives 40 × 60 = 2400.

So you can say 2000.

Find an approximate value for 383 × 88.

400 × 90 = 36,000 and the answer must be below this because both 400 and 90 are

above the original numbers, so you can say 383 × 88

≈

30,000.

5

6

Note the symbol for approximately equal to. ≈

So you see that The First by the First gives us the first figure of the answer; and the number

of figures in the answer is also evident.

You may not always be certain of the first figure (as in the last example) but you will never be

more than one out.

 Practice B Approximate the following:

a 723 × 81 b 67 × 82 c 4133 × 572

d 38 × 49 e 6109 × 377 f 3333 × 4444

g 1812 × 1066

a 60,000 b 5000 or 6000 c 2,000,000

d 2000 e 2,000,000 f 10,000,000

g 2,000,000

The Sutra (in fact it is a sub-Sutra) The First by the First and the Last by the Last is used in

many ways. For example in measuring or drawing a line with a ruler (or an angle with a

protractor) we line the first point of the line with the first mark on the ruler and note the

position of the last point on the ruler.

See also Section 10.4. This Sutra is also useful in recurring decimals, divisibility and

factorizing quadratics, cubics etc. (see Reference 3).

8: CHECKING AND DIVISIBILITY 81

THE LAST BY THE LAST

The last figure of a calculation can be seen by looking at the last figures in the sum.

72 × 83 ends in 6.

by multiplying the last figure of each number together you get the last figure of the

answer:

2 × 3 = 6.

7

383 × 887 ends in 1.

since 3 × 7 = 21, which ends with a 1.

23 × 48 × 63 ends in a 2.

Because 3×8 ends in a 4 and 4×3=12 ends in a 2.

8

9

 Practice C What is the last figure in the following sums?

a 456 × 567 b 76543 × 97 c 67 × 78 × 89

d 789 + 987 e 346 × 564 f 5328 + 9845

a 2 b 7 c 4

d 6 e 4 f 3

8.3 DIVISIBILITY BY 4

The formula The Ultimate and Twice the Penultimate can be used to test whether a number

can be divided exactly by four.

The ultimate means the last figure,

and the penultimate is the figure before the last one.

VEDIC MATHEMATICS MANUAL 1

82

So in the number 12376 the formula tells you to add up the 6 and twice the 7.

This gives you 20, and since 4 goes into 20 it will also go exactly into 12376.

In the number 5554 the formula gives us 4 plus twice 5, which is 14.

But 4 will not divide exactly into 14 so 5554 is not divisible by 4.

Is 7282231 divisible by 11?

We add all the digits in the odd positions and all the digits in the even positions an

d

subtract the smaller result from the larger result.

If we end up with 0 or 11 or any multiple of 11 then the number is divisible by 11.

7 2 8 2 2 3 1 in the odd positions: 7 + 8 + 2 + 1 = 18

in the even positions: 2 + 2 + 3 = 7

Since here 18 – 7 = 11 the number 7282231 is divisible by 11.

10

So when using The Ultimate and Twice the Penultimate

you add the last figure to twice the one before it,

and if 4 divides into the result then the number is divisible by 4.

Otherwise it is not divisible by 4.

11

 Practice D For each of the numbers below, write down the totals this formula gives you

and then write down whether 4 divides into the number or not.

a 246 b 656 c 92

d 5573 e 7624 f 345678

a 14, no b 16, yes c 20, yes

d 17, no e 8, yes f 22, no

8.4 DIVISIBILITY BY 11

Testing for divisibility by 11 is particularly easy and comes under the formula By Addition

and by Subtraction.

12

8: CHECKING AND DIVISIBILITY 83

 Practice E Test the following numbers for divisibility by 11:

a 5192 b 3476 c 1358016

d 85547 e 570317 f 1030607

a Yes b Yes c Yes

d Yes e Yes f No

REMAINDER AFTER DIVISION BY 11

You have just seen, in the last exercise, that we find if a number is divisible by 11 by adding

alternate figures and subtracting.

E.g. for 727 we get 14–2=12.

Since 12 is not a multiple of 11 the number is not divisible by 11.

But this 12 is the remainder after division by 11.

Actually as 12 is 1 more than 11 we can say that the smallest remainder is 1.

Note that we do the figures in the odd positions minus the figures in the even positions.

To get the remainder for 38042 we find (3+0+2) – (8+4) = –7.

You can add 11 to this –7 to get 4 as the smallest remainder (either –7 or 4 will do

here).

13

 Practice F Find the remainder from 11 for each of the following numbers:

a 71263 b 45678 c 203527 d 67

e 349 f 3817 g 1827 h 8351

i 481 j 34143 k 523281 l 909192

a 5 b 6 c 5 d 1

e 8 f 0 g 1 h –9 or 2

i –3 or 8 j –1 or 10 k 0 l –2 or 9

VEDIC MATHEMATICS MANUAL 1

84

ANOTHER DIGIT SUM CHECK

You are already familiar with the digit sum check which helps to show if a calculation is

correct.

For example, 2434 × 32 = 77888 is confirmed by the digit sums because adding the digits

gives 4 × 5 J 2, which is correct in digit sums.

This works because adding the digits in a number gives the remainder of the number after

division by 9.

A similar method works by using the remainders of numbers after division by 11 rather than

9.

Suppose we want another check for the sum: 2434 × 32 = 77888.

We find the remainders for each of the 3 numbers as in the exercise above.

Replacing the numbers by their remainders we get: 3 × 10 J 8 and this is correct i

n

this arithmetic as 30 clearly has a remainder of 8 after division by 11.

14

 Practice G Which of the following sums are correct according to the alternative digit

sum check?

a 213312 × 45 = 9599040 b 234 × 234 = 54756 c 3741 × 45 = 186345

d 86 × 68 = 5848 e 876 × 333 = 290808 f 1011 × 1101 = 1113111

a 0×1=0: correct b 3×3=9: correct c 1×1=5: incorrect

d –2×2=7: correct e 7×3=1: incorrect f –1×1= –1: correct

LESSON 9

BAR NUMBERS

SUMMARY

9.1 Removing Bar Numbers – converting numbers containing a negative digit to positive

form.

9.2 Subtraction – a general subtraction method.

9.3 Creating Bar Numbers – removing digits over 5 from a number.

9.4 Using Bar Numbers – some applications of bar numbers.

9.1 REMOVING BAR NUMBERS

The number 19 is very close to 20.

And it can therefore be conveniently written in a different way: as 21

21 means 20 – 1, the minus is put on top of the 1.

Similarly 31 means 30 – 1 or 29.

And 42 means 38.

This is like telling the time when we say 'ten to seven' or instead of 6:50.

We pronounce 42 as "four, bar two" because the 2 has a bar on top.

72 = 68,

1

861 = 859, because 61 = 59 (the 8 is unchanged),

1272 = 1268, because 72 = 68,

630 = 570, because we have 600 – 30 (or because 63 = 57).

 Practice A Convert the following numbers:

a 61 b 82 c 33 d 57 e 462

f 9991 g 12 h 111 i 123 j 340

a 59 b 78 c 27 d 43 e 458

f 9989 g 8 h 109 i 117 j 260

VEDIC MATHEMATICS MANUAL 1

86

Any digit in a number may have a bar on it.

731 = 73/1 = 671,

5242 = 524/2 = 5162,

3215 = 32 /15 = 2815 since 32 = 28,

551/ 32=13 = 4928 since 521 = 49 and 32 = 28,

331 / 32 / 33=1 = 292827. 3233

How would you remove the bar number in 513 ?

The best way is to split the number into two parts: 51/3.

Since 51 = 49, the answer is 493.

2

If a number has a bar number in it split the number after the bar.

3

 Practice B Remove the bar numbers:

a 614 b 423 c 525 d 317

e 4523 f 33323 g 5132 h 6372

i 211 j 4131 k 11153 l 131

a 594 b 383 c 485 d 297

e 4483 f 33283 g 4932 h 5867

i 191 j 4071 k 7149 l 71

Next suppose the bar spans more than one digit in a number.

9: BAR NUMBERS 87

ALL FROM 9 AND THE LAST FROM 10

So far we have only had a bar on a single figure.

But we could have two or more bar numbers together.

Remove the bar numbers in 533 .

4

The 5 means 500, and 33 means 33 is to be subtracted.

So 533 means 500 – 33, and we have met sums like this in Lesson 5.

500 – 33 = 467 because the 33 comes off one of the hundreds, so the 5 is reduced to

4.

And applying All from 9 and the Last from 10 to 33 gives 67.

Similarly 714 = 686 the 7 reduces to 6 and the Sutra converts 14 to 86,

2621 = 2579 26 reduces to 25,

702 = 698 the Sutra converts 02 to 98,

503 = 497 50 is reduced to 49 (alternatively, write 503 as 503: see previous

example),

420 = 420 = 380.

423 1 = 3771.

Here we can split the number after the bar: 423/1.

423 changes to 377, and we just put the 1 on the end: 4231 = 3771.

Similarly 512 4 = 512 /4 = 4884,

31133 = 311/33 = 28933,

5123 = 4877,

331 / 431=14 = 29369. 31

5

6

7

 Practice C Remove the bar numbers:

a 612 b 733 c 511 d 904 e 7241 f 33322

g 6214 h 53122 i 3322 44 j 7333 k 5104 l 44112

VEDIC MATHEMATICS MANUAL 1

88

m 74031 n 71031 o 63322 p 31102 q 3 1411 r 321 22

a 588 b 667 c 489 d 896 e 7159 f 33278

g 5794 h 46922 i 327844 j 6667 k 4896 l 43888

m 73969 n 68971 o 56678 p 29098 q 28939 r 28078

ADVANTAGES OF BAR NUMBERS

Bar numbers are an ingenious device which we will be using in later work. Their main

advantages are:

1. They give us flexibility: we use the vinculum when it suits us.

2. Large numbers, like 6, 7, 8, 9 can be avoided.

3. Figures tend to cancel each other, or can be made to cancel.

4. 0 and 1 occur twice as frequently as they otherwise would.

9.2 SUBTRACTION

These bar numbers give us an alternative way of subtracting numbers.

Pupils sometimes subtract in each column in a subtraction sum regardless of whether the top

is greater than the bottom or not.

This method can however be used to give the correct answer.

4 4 4

2 8 6 –

Subtracting in each column we get 4–2 = 2, 4–8 = –4, 4–6 = –2.

Since these negative answers can be written with a bar on top we can write:

4 4 4

2 8 6 –

242 and 242 is easily converted into 158.

Similarly 6 7 6 7

1 9 0 8 –

5261 = 4859

8

9

9: BAR NUMBERS 89

 Practice D Subtract using bar numbers:  Practice D Subtract using bar numbers:

a 5 4 3 b 5 6 7 c 8 0 4 d 7 3 7 e 6 4 1 3

1 6 8

a 5 4 3 b 5 6 7 c 8 0 4 d 7 3 7 e 6 4 1 3

1 6 8 – 2 7 9 – 3 8 8 – 5 5 8 – 1 8 7 8 –

f 8 0 2 4 g 6 5 4 3 h 7 1 0 3 i 4 5 4 5 j 3 2 0 4

5 3 3 9 – 2 8 8 1 – 3 9 9 1 – 1 7 9 1 – 2 0 8 1 –

______

a 375 b 288 c 416 d 179 e 4535

f 2685 g 3662 h 3112 i 2754 j 1123

9.3 CREATING BAR NUMBERS

We may also need to put numbers into bar form.

79 = 81 because 79 is 1 less than 80,

10

239 = 241 because 39 = 41,

7689 = 7691 because 89 = 91.

508 = 512 08 becomes 12

 Practice E Put the following into bar form:

a 49 b 58 c 77 d 88

e 69 f 36 g 17 h 359

i 848 j 7719 k 328 l 33339

m 609 n 708

a 51 b 62 c 83 d 92

e 71 f 44 g 23 h 361

i 852 j 7721 k 332 l 33341

m 611 n 712

VEDIC MATHEMATICS MANUAL 1

90

One of the main advantages of bar numbers is that we can remove high digits in a number.

For example writing 19 as 21 means we do not have to deal with the large 9.

Remove the large digits from 287.

Here the 8 and the 7 are large (we say that 6, 7, 8, 9 are large digits).

So we write 287 as 313 the 2 at the beginning is increased to 3, and the Sutra Al

l

from 9 and the Last from 10 is applied to 87 to give 13.

You will agree that 287 is 13 below 300, which is what 313 says.

Similarly 479 = 52 ,

1

3888 = 4112 ,

292 = 312,

4884 = 512 4,

77 =

12 (you can think of 77 as 077),

3

and so on.

11

12

 Practice F Remove the large digits from the following:

a 38 b 388 c 298 d 378

e 3991 f 3822 g 4944 h 390

i 299 j 98 k 87 l 888

m 996 n 2939 o 1849 p 7

a 42 b 412 c 302 d 422

e 4011 f 4222 g 5144 h 410

i 301 or 301 j 102 k 113 l 1112

m 1004 n 3141 o 2251 or 2151 p 13

“And, in some very important and striking cases, sums requiring 30, 50, 100 o

r

even more numerous and cumbrous “steps” of working (according to the curren

t

Western methods) can be answered in a single and simple step of work by the Vedic

method! And little children (of only 10 or 12 years of age) merely look at the sums

written on the blackboard (on the platform) and immediately shout out and dictate

the answers from the body of the convocation hall (or other venue o

f

demonstration). And this is because, as a matter of fact, each digit automaticall

y

yields its predecessor and its successor! and the children have merely to go on

tossing off (or reeling off) the digits one after another (forwards or backwards) b

y

mere mental arithmetic (without needing pen or pencil, paper or slate etc)!”

From “Vedic Mathematics”, Page xvii.

9: BAR NUMBERS 91

9.4 USING BAR NUMBERS

Finally here are a few examples showing where bar numbers might be used.

29 + 48 = 77.

Writing 29 as

31, or 48 as 52: 29 31

52 + 48 +

77 77

623 – 188 = 435. 623

13

212 –

435

5032 + 7489 – 2883 = 10 = 9638. We just add up the first digits of the first and

second numbers and subtract the first digit of

the third number. Similarly with the second,

third and fourth digits.

438

29 × 3 = 31 × 3 = 93 = 87.

87 ÷ 3 = 93 ÷ 3 = 31 = 29.

41 ÷ 7 = 6 remainder 1.

14

15

16

17

18

These bar numbers can be very useful in more advanced work (see Manuals 2 and 3).

LESSON 10

SPECIAL MULTIPLICATION

SUMMARY

Find 52 × 11.

To multiply a 2-figure number, like 52, by 11 you write down the number being

multiplied, and put the total of the figures between the two figures: 572.

So 52 × 11 = 572, between the 5 and 2 we put 7, which is 5+2.

10.1 Multiplication by 11

10.2 By One More than the One Before – a special type of

multiplication.

10.3 Multiplication by Nines

10.4 The First by the First and the Last by the Last – a special type of multiplication.

10.5 Using the Average – of numbers to find their product.

10.6 Special Numbers – spotting factors of certain special numbers in a multiplication sum.

If there is an easy way to do a particular sum, rather than using the general method, we call it

a special method. For example to multiply a number by 10 we do not use ‘long

multiplication’. In the Vedic system there are many special methods, which adds to the fun:

the general method is always there but there is often a quick way if you can spot it.

The special methods play a large part in encouraging mental mathematics. Everyone likes a

short cut, whether it is a quick way to get from one place to another or an easy way of doing a

particular calculation. Life is full of special methods: to tackle all similar situations in the

same way is not the way most people like to function. Every mathematical calculation invites

its own unique method of solution and we should encourage children to look at the special

properties of each problem in order to understand it best and decide on the best way forward.

This is surely the intelligent way to do mathematics.

10.1 MULTIPLICATION BY 11

The 11 times table is easy to remember, and multiplying longer numbers by 11 is also easy.

If you want, say, 52×11 you want eleven 52's.

This means you want ten 52's and one 52 or 520 + 52: 5 2 0

5 2 +

5 7 2 note how the 2 and the 5

get added in the middle column.

1

10: SPECIAL MULTIPLICATION 93

 Practice A Multiply the following by 11:

a 23 × 11 b 61 × 11 c 44 × 11 d 50 × 11

a 253 b 671 c 484 d 550

And so we can often quickly tell if a number can be divided exactly by 11.

Is 473 divisible by 11?

You can see that the middle number is the sum (total) of the outer numbers:

4 + 3 = 7.

So the number is divisible by 11.

2

In the example above you also know how many times 11 divides into 473.

It must be 43 because 43 × 11 = 473.

Just look at the outer numbers 4 and 3.

 Practice B Fill in the table below.

Number Tick if Divisible No. of Times it Divides

242

594

187

791

693

Answers: 22, 54, 17, -, 63

“And as regards the time required by the students fo

r

mastering the whole course of Vedic Mathematics as

applied to all its branches, we need merely state from

our actual experience that 8 months (or 12 months) a

t

an average rate of 2 or 3 hours per day should suffice

f

or completing the whole course of mathematical studies

on these Vedic lines instead of 15 or 20 years require

d

according to the existing systems of Indian and also o

f

foreign universities.”

From “Vedic Mathematics”, Page xvii.

VEDIC MATHEMATICS MANUAL 1

94

CARRIES

Going back to multiplication by 11, there can sometimes be a carry, as the next example

shows.

Find 58 × 11.

The 5 and 8 here add up to 13 so the 1 has to be carried to the left:

58 × 11 = 5138 = 638.

Find 47 × 11.

3

The 4 and 7 here add up to 11 so again you carry 1 to the left:

47 × 11 = 4117 = 517.

Find 234 × 11.

To multiply this 3-figure number by 11 you put the first and last figures of 234 as the

first and last figures of the answer:

2 3 4

2 ? ? 4

4

 Practice C Try these:

a 68 × 11 b 79 × 11 c 47 × 11

d 86 × 11 e 55 × 11 f 93 × 11

a 748 b 869 c 517

d 946 e 605 f 1023

LONGER NUMBERS

This method can be easily extended to longer numbers.

5

10: SPECIAL MULTIPLICATION 95

Then for the second figure you add the first two figures of 234,

And for the third figure you add the last two figures of 234:

2 3 4

2 5 7 4

So 234 × 11 = 2574.

 Practice D Multiply the following by 11:

a 423 × 11 b 636 × 11 c 534 × 11

d 516 × 11 e 706 × 11 f 260 × 11

g 444 × 11 h 135 × 11 i 531 × 11

a 4653 b 6996 c 5874

d 5676 e 7766 f 2860

g 4884 h 1485 i 5841

When you add the first or last two figures you could get a 2-figure number, so that there is a

carry figure.

Find 777 × 11.

The method above gives: 714147 = 8547. We simply carry the 1’s over, as before.

6

 Practice E Multiply by 11:

a 384 × 11 b 629 × 11 c 888 × 11

d 555 × 11 e 393 × 11 f 939 × 11

a 4224 b 6919 c 9768

d 6105 e 4323 f 10329

This can be extended to numbers of any size and also to multiplying by 111, 1111 etc.

This multiplication is useful in percentages work since if we want to increase a number by

10% we multiply it by 1.1, similarly with other percentage changes (see Manual 2 or The

Cosmic Calculator, Book 2).

VEDIC MATHEMATICS MANUAL 1

96

10.2 BY ONE MORE THAN THE ONE BEFORE

This special type of multiplication is for multiplying numbers whose first figures are the same

and whose last figures add up to 10, 100 etc.

For example, 52 × 58, where both numbers start with 5 and 2 + 8 = 10.

Suppose we want to find 43 × 47 in which both numbers begin with 4 and the las

t

figures (3 and 7) add up to 10.

Multiply 4 by the number One More: 4 × 5 = 20.

Then simply multiply the last figures together: 3 × 7 = 21.

So 43 × 47 = 2021 where 20 = 4×5, 21 = 3×7.

Similarly 62 × 68 = 4216 where 42 = 6×7, 16 = 2×8.

7

8

Find 204 × 206.

9

Here both numbers start with 20, and 4 + 6 = 10, so the method applies.

204 × 206 = 42024 (420 = 20×21, 24 = 4×6).

 Practice F Multiply the following:

a 73 × 77 b 58 × 52 c 81 × 89 d 104 × 106

e 42 × 48 f 34 × 36 g 93 × 97 h 27 × 23

i 297 × 293 j 303 × 307

a 5621 b 3016 c 7209 d 11024

e 2016 f 1224 g 9021 h 621

i 87021 j 93021

93 × 39 may not look like it comes under this particular type of sum,

10 but remembering the Proportionately formula we notice that 93 = 3×31,

and 31 × 39 does come under this type:

31 × 39 = 1209 (we put 09 as we need double figures here)

so 93 × 39 = 3627 (multiply 1209 by 3)

10: SPECIAL MULTIPLICATION 97

The thing to notice in the last example is that the 39 needs a 31 for the method to work here:

and then we spot that 93 is 3×31.

Finally, consider 397 × 303.

Only the 3 at the beginning of each number is the same, but the rest of the numbers

(97 and 03) add up to 100.

So again the method applies, but this time we must expect to have four figures on the

right-hand side:

397 × 303 = 120291 where 12 = 3×4, 0291 = 97×3.

 Practice G Multiply the following:

a 64 × 38 b 88 × 46 c 33 × 74 d 66 × 28

e 36 × 78 f 46 × 54 g 298 × 202 h 391 × 309

i 795 × 705 j 401 × 499

a 2432 b 4048 c 2442 d 1848

e 2808 f 2484 g 60196 h 120819

i 560475 j 200099

763 × 999 = 762/237.

The number being multiplied by 9's is first reduced by 1: 763–1 = 762. This is the

first part of the answer.

Then

All From 9 and the Last From 10 is applied to 763 to get 237, which is the

second part of the answer.

1867 × 99999 = 1866/98133.

Here, as 1867 has 4 figures, and 99999 has 5 figures, we suppose 1867 to be 01867.

This is reduced by 1 to give 1866 for the first part of the answer.

Then applying

All From 9. . . to 01867 gives 98133 for the last part of the answer.

The Vedic formula By One Less Than the One Before, which is the converse of the formula

By One More than the One Before comes in here in combination with All From 9 and the Last

From 10.

11

10.3 MULTIPLICATION BY NINES

12

13

VEDIC MATHEMATICS MANUAL 1

98

 Practice H Find the following:

a 89 × 99 b 82 × 99 c 19 × 99 d 45 × 99

e 778 × 999 f 7654 × 9999 g 79 × 999 h 124 × 9999

i 8989 × 99999 j 47 × 99999

a 8811 b 8118 c 1881 d 4455

e 777222 f 76532346 g 78921 h 1239876

i 898891011 j 4699953

27 × 87 = 23/49.

The conditions are satisfied here as 2 + 8 = 10

and both numbers end in 7.

So

we multiply the first figure of each number together and add the

last figure: 2 × 8 = 16, 16 + 7 = 23 which is the first part of the answer.

Multiplying the last figures together: 7×7 = 49: which is the last part of the

answer.

69 × 49 = 3381.

in which

33 = 6×4 + 9, and 81 = 9×9.

10.4 THE FIRST BY THE FIRST AND THE LAST BY THE LAST

Products like 43 × 47 are easy to find because the first figures are the same and the last figures

sum to 10.

Similarly products like 27 × 87 are also easy to find because the last figures are the same

and the first figures add up to 10.

This comes under the Vedic formula The First by the First and the Last by the Last.

14

15

 Practice I Multiply the following by this method:

a 38 × 78 b 26 × 86 c 91 × 11 d 59 × 59

10: SPECIAL MULTIPLICATION 99

e 63 × 43 f 24 × 84 g 88 × 28 h 29 × 89

i 97 × 17 j 64 × 44

The following can also be done like this if you use the Proportionately formula as well:

k 31 × 42 l 46 × 83 m 93 × 71 n 88 × 32

a 2964 b 2236 c 1001 d 3481

e 2709 f 2016 g 2464 h 2581

i 1649 j 2816

k 1302 l 3818 m 6603 n 2816

10.5 USING THE AVERAGE

Here we look at a neat and easy way of multiplying numbers by using their average.

This comes under the formula Specific General.

So 26 × 34 = 302 – 42 = 900 – 16 = 884.

And 58 × 62 = 602 – 22 = 3600 – 4 = 3596.

Similarly 94 × 106 = 1002 – 62 = 10,000 – 36 = 9964.

And 37 × 33 = 352 – 22 = 1225 – 4 = 1221. See Section 12.1 for squaring numbers

that end in 5.

Suppose we want to know 29 × 31.

Since the average of 29 and 31 is 30, we might think that 29 × 31 is 30 × 30, or close

to it.

In fact 29 × 31 = 899

and this is just 1 below 900.

Now consider 28 × 32. Again 30 is their average. 28 × 32 = 896 and this is 4 below

900.

For 27 × 33 whose average is also 30: 27 × 33 = 891, which is 9 below 900.

16

17

18

In fact the rule is:

square the average and

subtract the square of the difference of either number from the average.

19

VEDIC MATHEMATICS MANUAL 1

100

This method is available for the product of any two numbers. Even if the average is not a

very attractive number this method is still often better than multiplying the numbers. For

example, for 67 × 69 it is easier to find 682 – 1 than to multiply 67 by 69.

 Practice J Find:

a 49 × 51 b 27 × 33 c 57 × 63 d 64 × 66

e 85 × 65 f 55 × 95 g 33 × 47 h 91 × 99

i 44 × 48 j 43 × 47 k 74 × 86 l 98 × 102

m 62 × 38 n 48 × 72 o 73 × 93 p 196 × 204

a 2499 b 891 c 3591 d 4224

e 5525 f 5225 g 1551 h 9009

i 2112 j 2021 k 6364 l 9996

m 2356 n 3456 o 6789 p 39984

PROOF

A geometrical explanation for 27 × 33 is shown below.

30 3

27

3

The shaded rectangle is 27 by 33 and its area is 27 ×33.

The superimposed shape is a 30 by 30 square.

This shows that the square whose area is 302 is larger than the required rectangle by 32 units,

as the top rectangle is 30 × 3 and the right-hand rectangle is 27 × 3, a difference of 3 ×3.

Here is an algebraic proof.

(a + b)(a – b) = a2 – b2, where a is the average and b the difference of each number from the

average. So (a + b) is the higher number and (a – b) is the lower number.

10: SPECIAL MULTIPLICATION 101

10.6 SPECIAL NUMBERS

REPEATING NUMBERS

Some multiplications are particularly easy.

23 × 101 = 2323.

To multiply 23 by 101 we need 23 hundreds and 23 ones, which gives 2323.

Similarly 69 × 101 = 6969.

And 473 × 1001 = 473473.

Here we have a 3-figure number multiplied by 1001 which makes the 3-figure

number repeat itself.

47 × 1001 = 47047.

Here, because we want to multiply by 1001, we can think of 47 as 047.

So we get 047047, or just 47047.

123 × 101 = 123123 = 12423.

Here we have 12300 + 123 so the 1 has to be carried over.

28 × 10101 = 282828.

20

The effect of multiplying any 2-figure by 101 is simply to make it repeat itself.

21

22

23

24

 Practice K Find:

a 46 × 101 b 246 × 1001 c 321 × 1001

d 439 × 1001 e 3456 × 10001 f 53 × 10101

VEDIC MATHEMATICS MANUAL 1

102

g 74 × 1001 h 73 × 101 i 29 × 1010101 g 74 × 1001 h 73 × 101 i 29 × 1010101

j 277 × 101 k 521 × 101 l 616 × 101 j 277 × 101 k 521 × 101 l 616 × 101

a 4646 b 246246 c 321321

d 439439 e 34563456 f 535353

g 74074 h 7373 i 29292929

j 27977 k 52621 l 62216

This type of multiplication comes under the Sutra By Mere Observation.

Multiplications by 101 etc. are useful in percentages work as we multiply a number by 1.01 to

increase it by 1% (see Manual 2 or The Cosmic Calculator, Book 2)

PROPORTIONATELY

43 × 201 = 8643.

Here we bring in the Proportionately formula: because we want to multiply by 201

rather than 101 we must put twice 43 (which is 86) then 43.

31 × 10203 = 316293 we have 31×1, 31×2, 31×3.

25

26

 Practice L Find:

a 54 × 201 b 32 × 102 c 333 × 1003 d 41 × 10201 e 33 × 30201

f 17 × 20102 g 13 × 105 h 234 × 2001 i 234 × 1003 j 43 × 203

a 10854 b 3264 c 333999 d 418241 e 996633

f 341734 g 1365 h 468234 i 234702 j 8729

DISGUISES

Now it is possible for a sum to be of the above type without it being obvious: it may be

disguised.

If we know the factors of some of these special numbers (like 1001, 203 etc.) we can make

some sums very easy.

Suppose for example you know that 3 × 67 = 201.

10: SPECIAL MULTIPLICATION 103

93 × 67 = 6231.

Since 3 × 67 = 201,

therefore 93 × 67 = 31 × (3 × 67)

= 31 × 201

= 6231.

In other words, we recognise that one of the special numbers (201 in this case) is contained in

the sum (as 3 × 67).

Now suppose we know that 3 × 37 = 111.

24 × 37 = 888.

27

We know that 3 × 37 = 111, which is a number very easy to multiply.

So 24 × 37 = 8 × (3 × 37)

= 8 × 111

= 888.

38 × 63 = 2394.

Since 38 × 63 = 2 × 19 × 3 × 21 = 6 × (19 × 21) = 6 × 401 = 2406 = 2394.

28

Also 19×21 = 399 = 401.

29

If we know the factors of these special numbers we can make good use of them when they

come up in a sum, and they arise quite frequently.

Below is a list of a few of these numbers with their factors:

67 × 3 = 201 17 × 6 = 102 11 × 9 = 101

43 × 7 = 301 13 × 8 = 104 19 × 21 = 401

7 × 11 × 13 = 1001 29 × 7 = 203 23 × 13 = 301

3 × 37 = 111 31 × 13 = 403 27 × 37 = 1001

VEDIC MATHEMATICS MANUAL 1

104

62 × 39 = 2418.

We see 31 × 13 contained in this sum: 62 × 39 = 2×31 × 3×13

= 2×3 × 31×13

= 6 × 403

=

2418.

30

 Practice M Use the special numbers to find:

a 29 × 28 b 35 × 43 c 67 × 93 d 86 × 63

e 77 × 43 f 26 × 77 g 34 × 72 h 57 × 21

i 58 × 63 j 26 × 23 k 134 × 36 l 56 × 29

m 93 × 65 n 54 × 74 o 39 × 64 p 51 × 42

a 812 b 1505 c 6231 d 5418

e 3311 f 2002 g 2448 h 1197

i 3654 j 598 k 4824 l 1624

m 6045 n 3996 o 2496 p 2142

“These and many more interesting features there are in

the Vedic decimal system, which can turn mathematics

f

or the children from its present excruciatingly painfu

l

character to the exhilaratingly pleasant and even funn

y

and delightful character it really bears .”

From “Vedic Mathematics”, Page 239.

LESSON 11

GENERAL MULTIPLICATION

SUMMARY

11.1 Revision

11.2 Two-Figure Numbers

– multiplying 2-figure numbers in one line, from left to right.

11.3 Moving Multiplier

– multiplying long numbers by a 2-figure number.

11.4 Extension

– multiplying 3-figure numbers.

Find 74 × 8.

We multiply each of the figures in 74 by 8 starting at the left:

7 × 8 = 56 and 4 × 8 = 32.

These are combined by carrying the 3 in 32 over to the 6 in 56: 5 = 592. 23,6



The inner figures are merged together. So 74 × 8 = 592.

Find 827 × 3.

The three products are 24, 6, 21.

The first two products are combined: 24,6 = 246 no carry here as 6 is a single

figure, then 246 is combined with the 21: = 2481. So 827 × 3 = 2481. 12,624 

11.5 Multiplying Binomials

– using the same pattern.

11.6 Multiplying 3-Figure Numbers – extension of previous pattern.

11.7 Written Calculations

– from left to right.

11.1 REVISION

We have seen various methods of multiplication but they were all for special cases, where

some special condition was satisfied, like both numbers being close to 100 for example.

We come now to the general multiplication technique, by which any two numbers can be

multiplied together in one line, by mere mental arithmetic.

First let us briefly revise how we multiply by a single figure number (as in Section 4.2).

You may wish to begin this lesson with written calculations rather than mental: if so go to

Section 11.7, but you will need the methods described in Sections 11.2, 11.3, 11.6.

1

2

VEDIC MATHEMATICS MANUAL 1

106

Find 21 × 23.

Think of the numbers set out one below the other: 2 1

2 3 ×

4 8 3

There are 3 steps 2 1

A. Multiply vertically in the left-hand

column: 2 × 2 = 4, 2 3 ×

so 4 is the first figure of the answer. 4

B. Multiply crosswise and add: 2 1

2 × 3 = 6, ×

1 × 2 = 2, 6 + 2 = 8, 2 3 ×

so 8 is the middle figure of the answer. 4 8

C. Multiply vertically in the right-hand 2 1

column: 1 × 3 = 3,

3 is the last figure of the answer. 2 3 ×

4 8 3

Find 77 × 4.

The products are 28, 28.

And 2 = 308 (the 28 is increased by 2 to 30). So 77 × 4 = 308. 82,8



3

 Practice A Multiply the following mentally:

a 73 × 3 b 63 × 7 c 424 × 4 d 777 × 3

e 654 × 3 f 717 × 8 g 876 × 7

a 219 b 441 c 1 696 d 2 331

e 1 962 f 5 736 g 6 132

11.2 TWO-FIGURE NUMBERS

The Vertically and Crosswise formula gives us the pattern for multiplying any numbers.

For 2-figure numbers it works like this.

4

11: GENERAL MULTIPLICATION 107

Find 23 × 41.

2 3

4 1 ×

9 4 3

The 3 steps give us: 2 × 4 = 8,

2 × 1 + 3 × 4 = 14,

3 × 1 = 3.

The 14 here involves a carry figure, so in building up the answer mentally from the

left we merge these numbers as before.

The mental steps are: 8

= 94 (the 1 is carried over to the left)

94,3 = 943

41,8



So 23 × 41 = 943.

Find 14 × 21.

1 4

2 1 ×

2 9 4

A: vertically on the left: 1 × 2 = 2,

B: crosswise: 1 × 1 = 1, 4 × 2 = 8 and 1 + 8 = 9,

C: vertically on the right: 4 × 1 = 4.

5

This is of course very easy and straightforward and is just mental arithmetic. We should now

practice this vertical and crosswise pattern to establish the method.

 Practice B Multiply mentally:

a 2 2 b 2 1 c 2 1 d 2 2 e 6 1 f 3 2 g 3 1 h 1 3

3 1× 3 1 × 2 2 × 1 3 × 3 1 × 2 1 × 3 1 × 1 3 ×

a 682 b 651 c 462 d 286

e 1 891 f 672 g 961 h 169

CARRIES

The previous examples involved no carry figures, so let us consider this next.

6

VEDIC MATHEMATICS MANUAL 1

108

Find 23 × 34.

2 3

3 4 ×

7 8 2 The steps are: 6

6 = 77 71,



7 = 782 21,7

Find 33 × 44.

3 3

4 4 ×

1 4 5 2 The steps are: 12

1= 144 42,2



14 = 1452 21,4

7

8

You can now multiply any two 2-figure numbers together in one line.

 Practice C Multiply the following mentally:

a 2 1 b 2 3 c 2 4 d 2 2 e 2 2 f 3 1

4 7 4 3 2 9 2 8 5 3 3 6

g 2 2 h 3 1 i 4 4 j 3 3 k 3 3 l 3 4

5 6 7 2 5 3 8 4 6 9 4 2

m 3 3 n 2 2 o 3 4 p 5 1 q 3 5 r 5 5

3 4 5 2 6 6 5 4 6 7 5 9

s 5 4 t 5 5 u 4 4 v 4 5 w 4 8 x 3 4

6 4 6 3 8 1 8 1 7 2 1 9

a 987 b 989 c 696 d 616 e 1 166 f 1 116

g 1 232 h 2 232 i 2 332 j 2 772 k 2 277 l 1 428

m 1 122 n 1 144 o 2 244 p 2 754 q 2 345 r 3 245

s 3 456 t 3 465 u 3 564 v 3 645 w 3 456 x 646

You may have found in this exercise that you prefer to start with the crosswise

multiplications, and put the left and right vertical multiplications on afterwards.

11: GENERAL MULTIPLICATION 109

EXPLANATION

It is easy to understand how this method works.

hundreds tens units

The vertical product on the right multiplies units by units and

so gives the number of units in the answer. The crosswise

operation multiplies tens by units and units by tens and so

gives the number of tens in the answer. And the vertical

product on the left multiplies tens by tens and gives the

number of hundreds in the answer.

So this easy multiplication method, which is quite general, is also easy to understand. It can

be done from left to right or right to left (see Section 11.7) it applies to algebraic expressions

just as well (see Section 11.5) and it can be reversed to give a simple division method (see

Section 16.4).

EXPLANATION OF EARLIER SPECIAL METHOD

We can now explain the special method of multiplication under By One More than the One

Before from Section 10.2 for multiplying numbers like 72 × 78 in which the first figures are

the same and the last figures add up to 10. 7 2

7 8

Using the present sutra for 72 × 78:

We see that the cross-product is eight 7’s and two 7’s, that is ten 7’s, or 70. The zero here

ensures that the 2-digit product 2 × 8 = 16 can go straight into the last two places, and this

will always happen when the conditions for this type of product are met. The 7 in 70 means an

extra 7 in the left-hand product: so there are eight 7’s altogether.

As the method of squaring numbers that end in 5 is a special case of the above (see Section

12.1), this can also be explained this way.

In multiplying a long number by a single figure, for example 4321 × 2, we multiply each of

the figures in the long number by the single figure. We may think of the 2 moving along the

row, multiplying each figure vertically by 2 as it goes.

11.3 MOVING MULTIPLIER

71

5616

VEDIC MATHEMATICS MANUAL 1

110

Find 4321 × 32.

4 3 2 1 Similarly here we put 32 first of all at the extreme left.

3 2 Then vertically on the left, 4 × 3 = 12.

And crosswise, 4×2 +3×3 = 17.

4 3 2 1 Then move the 32 along and multiply crosswise:

3 2 3×2 + 2×3 = 12.

4 3 2 1 Moving the 32 once again:

3 2 multiply crosswise, 2×2 + 1×3 = 7.

Finally the vertical product on the right is 1×2 = 2.

These 5 results (in bold), 12,17,12,7,2 are combined mentally, as they are obtained,

in the usual way:

1 = 137 71,2



= 1382

21,713 

1382,7,2 = 138272

So we multiply crosswise in every position, but we multiply vertically also at the very

beginning and at the very end.

9

Find 31013 × 21.

Here the 21 takes the positions:

3 1 0 1 3 3 1 0 1 3 3 1 0 1 3 3 1 0 1 3

2 1 2 1 2 1 2 1

The six mental steps give: 6,5,1,2,7,3

so the answer is 651273.

10

 Practice D Multiply using the moving multiplier method:

a 3 2 1 b 3 2 1 c 4 2 1 d 3 2 1

2 1 2 3 2 2 4 1

e 1 2 1 2 f 1 3 3 1 g 1 3 1 3 h 1 1 2 2 1

2 1 2 2 3 1 2 2

_______

a 6 741 b 7 383 c 9 262 d 13 161

e 25 452 f 29 282 g 40 703 h 246 862

11: GENERAL MULTIPLICATION 111

11.4 EXTENSION

Find 123 × 132.

1 2 3 The Vertically and Crosswise formula can be

1 3 2 × extended to deal with this, but in fact the

1 6 2 3 6 previous vertical/crosswise/vertical pattern

can be used on this sum also.

We can split the numbers up into 12/3 and 13/2, treating the 12 and 13 as if they

were single figures:

12 3 Vertically 12 × 13 = 156,

13 2 crosswise 12 × 2 + 3 × 13 = 63,

162 3 6 vertically 3 × 2 = 6.

Combining these mentally we get: 156

= 1623

36,615 

1623,6 = 16236.

304 × 412 = 125248.

Here we may decide to split the numbers after the first figure: 3/04 × 4/12.

3 04 When we split the numbers in this way the

4 12 answer appears two digits at a time.

12 52 48

The 3 steps of the pattern are: 3×4 = 12,

3×12 + 4×4 = 52,

4×12 = 48.

These give the 3 pairs of figures in the answer.

 Practice E Multiply, treating the numbers as 2-figure numbers:  Practice E Multiply, treating the numbers as 2-figure numbers:

a 1 1 2 b 1 2 3 c 1 2 3

2 0 3

a 1 1 2 b 1 2 3 c 1 2 3

2 0 3 1 3 1 1 2 2

d 1 1 2 e 4 2 1

1 2 3 2 2

a 22 736 b 16 113 c 15 006

d 13 776 e 9 262

12

11

VEDIC MATHEMATICS MANUAL 1

112

 Practice F Multiply using pairs of digits:

a 2 1 1 b 3 0 7 c 2 0 3 d 2 1 1

3 0 4 4 0 7 4 3 2 3 1 1

____

e 5 0 4 f 5 0 1 g 7 1 2 h 7 0 3

5 0 4 5 0 1 1 1 2 2 1 1

____

a 64 144 b 124 949 c 87 696 d 65 621

e 254 016 f 251 001 g 79 744 h 148 333

11.5 MULTIPLYING BINOMIALS

In the Vedic system we do not have one method for multiplying numbers and another for

multiplying algebraic expressions. The same Vertically and Crosswise pattern can be used for

both cases.

Multiply: (x + 3)(x + 4).

We have to multiply x+3 by x+4.

This means that the x and the 3 in x+3 must both multiply the x and the 4 in x+4.

The best way to do this is to use the Vertically and Crosswise method.

Put one binomial under the other: x + 3

Multiply vertically on the left: x×x = x2. x + 4

Cross-multiply and add: 4×x + 3×x = 7x. x2 + 7x + 12

Multiply vertically on the right: 3×4 = 12.

13

It is just like multiplying two 2-figure numbers together.

Multiply from left to right or right to left: whichever you like.

 Practice G Multiply:

a (x + 5)(x + 6) b (x + 2)(x + 9) c (x + 10)(x + 1) d (x + 20)(x + 20)

e (x + 1)(x + 1) f (x + 22)(x + 28) g (y + 52)(y + 4) h (x + 4)2

a x²+11x+30 b x²+11x+18 c x²+11x+10 d x²+40x+400

e x²+2x+1 f x²+50x+616 g y²+56y+208 h x²+8x+16

11: GENERAL MULTIPLICATION 113

Multiply (2x + 5)(3x + 2).

2x + 5 Vertically on the left: 2x×3x = 6x2.

3x + 2 Crosswise: 4x+15x = 19x.

6x2 + 19x + 10 Vertically on the right: 5×2 = 10.

14

Multiply (x + 3y)(5x + 7y).

x + 3y On the left: x×5x = 5x2.

5x + 7y Crosswise: 7xy + 15xy = 22xy.

5x2 + 22xy + 21y2 On the right: 3y×7y = 21y2.

Multiply (2x – 3)(3x + 4).

This is very similar. 2x – 3

2x × 3x = 6x2. 3x + 4

Crosswise: 8x – 9x = –1x or –x. 6x2 – x – 12

And –3×4 = –12.

Find (x – 3)(x – 6).

Vertically: x × x = x². x – 3

Crosswise: –6x –3x = –9x. x – 6

Vertically: –3 × –6 = +18. x² – 9x + 18

15

 Practice H Multiply the following:  Practice H Multiply the following:

a (2x + 5)(x + 4) b (x + 8)(3x + 11) c (2x + 1)(2x + 20) d (2x + 3)(3x + 7) a (2x + 5)(x + 4) b (x + 8)(3x + 11) c (2x + 1)(2x + 20) d (2x + 3)(3x + 7)

e (4x + 3)(x + 6) f (3x + 17)(3x + 4) g (6x + 1)(5x + 1) h (2x + 5)(4x + 5) e (4x + 3)(x + 6) f (3x + 17)(3x + 4) g (6x + 1)(5x + 1) h (2x + 5)(4x + 5)

i (3x + 3)(4x + 5) j (2x + 3y)(2x + 5y) k (5x + 2y)(2x + 5y) l (4x + 3y)(7x + y) i (3x + 3)(4x + 5) j (2x + 3y)(2x + 5y) k (5x + 2y)(2x + 5y) l (4x + 3y)(7x + y)

a 2x²+13x+20 b 3x²+35x+88 c 4x²+42x+20 d 6x²+23x+21

e 4x²+27x+18 f 9x²+63x+68 g 30x²+11x+1 h 8x²+30x+25

i 12x²+27x+15 j 4x²+16xy+15y² k 10x²+29xy+10y² l 28x²+25xy+3y²

So, unlike the current system, we use the same method for algebraic products as for arithmetic

ones.

Next we need to use the methods for combining negative numbers.

16

17

VEDIC MATHEMATICS MANUAL 1

114

 Practice I Multiply:  Practice I Multiply:

a (x + 3)(x – 5) b (x + 7)(x – 2) c (x – 4)(x + 5) d (x – 5)(x – 4)

e (x – 3)(x – 3) f (2x – 3)(x + 4) g (2x – 3)(3x + 6) h (3x – 1)(x + 7) e (x – 3)(x – 3) f (2x – 3)(x + 4) g (2x – 3)(3x + 6) h (3x – 1)(x + 7)

a x²–2x–15 b x²+5x–14 c x²+x–20 d x²–9x+20

e x²–6x+9 f 2x²+5x–12 g 6x²+3x–18 h 3x²+20x–7

THE DIGIT SUM CHECK

The algebraic form of the digit sum check can be used.

If, for example, we wanted to check Example 14 above: (2x + 5)(3x + 2) = 6x2 + 19x + 10

we check that the product of the sum of the coefficients in the brackets on the left-hand side

equals the sum of the coefficients on the right-hand side.

That is (2 + 5)(3 + 2) = 6 + 19 + 10.

Since both sides come to 35 this confirms the answer.

11.6 MULTIPLYING 3-FIGURE NUMBERS

Find 504 × 321.

5 0 4

3 2 1

1 6 1 7 8 4

The extended pattern for multiplying 3-figure numbers is as follows.

5 0 4

|

A Vertically on the left, 5×3 = 15. 3 2 1

1 5

B Then crosswise on the left, 5 0 4

5×2 + 0×3 = 10. ×

Combining the 15 and 10 as before: 3 2 1

= 160. 01,51 1 6 0

C Next we take 3 products and add them up,

5×1 + 0×2 + 4×3 = 17. And 16 = 1617. 5 0 4 71,0



(actually we are gathering up the hundreds 3 2 1

by multiplying hundreds by units, tens by 1 6 1 7

tens and units by hundreds)

18

11: GENERAL MULTIPLICATION 115

D Next we multiply crosswise 5 0 4

on the right, ×

0×1 + 4×2 = 8: 1617,8 = 16178. 3 2 1

1 6 1 7 8

E Finally, vertically on the right, 5 0 4

4×1 = 4: 16178,4 = 161784. |

3 2 1

1 6 1 7 8 4

Note the symmetry in the 5 steps:

first there is 1 product, then 2, then 3, then 2, then 1.

We may summarise these steps as shown below: We may summarise these steps as shown below:

A B C D E A B C D E

Find 321 × 321.

3 2 1

3 2 1 × The 5 results are 9,12,10,4,1.

103041 The mental steps are 9

= 102

21,9



= 1030

01,210 

1030,4,1 = 103041

Find 123 × 45.

This can be done with the moving multiplier method or by the smaller vertical and

crosswise pattern, treating 12 in 123 as a single digit.

Alternatively, we can put 045 for 45 and use the extended vertical and crosswise

pattern:

1 2 3

0 4 5 For the 5 steps we get 0,4,13,22,15.

5535 Mentally we think 4; 53; 552; 5535.

19

Sometimes we have a choice about how we multiply. Sometimes we have a choice about how we multiply.

20

“We thus follow a process of ascent and descent (going forward with the digits

on the upper row and coming rearward with the digits on the lower row).”

From “Vedic Mathematics”, Page 42.

VEDIC MATHEMATICS MANUAL 1

116

 Practice J Multiply (there are no carries in the first few sums):  Practice J Multiply (there are no carries in the first few sums):

a 1 2 1 b 1 3 1 c 1 2 1 d 3 1 3 a 1 2 1 b 1 3 1 c 1 2 1 d 3 1 3

1 3 1 1 3 1 2 1 2 2 2 2 1 2 1

e 2 1 2 f 1 2 3 g 2 1 2 h 2 2 2

3 1 3 3 2 1 4 1 4 3 3 3

i 2 4 6 j 1 0 5 k 1 0 6 l 5 1 5

3 3 3 5 0 7 2 2 2 5 5 5

m 4 4 4 n 3 2 1 o 1 2 3 p 1 2 4

7 7 7 3 2 1 2 7 1 3 5 6

a 15 851 b 27 772 c 26 862 d 37 873

e 66 356 f 39 483 g 87 768 h 73 926

i 81 918 j 53 235 k 23 532 l 285 825

m 344 988 n 103 041 o 33 333 p 44 144

11.7 WRITTEN CALCULATIONS

It is also useful to be able to write out our multiplications.

In the Vedic system we can do this from left to right or from right to left.

Here we use the right to left method, but the formula is the same: Vertically and Crosswise.

Find 42 × 31.

The sum is set out as before:

A. We multiply vertically on the right: 2×1 = 2,

and put this down as the right-hand figure of the answer. 4 2

3 1

B. Then we multiply crosswise and add to get 4+6 = 10. 1 3 0 2

So we put down 0 and carry 1 to the left. 1

C. Finally we multiply vertically on the left: 4×3 = 12,

12 + the carried 1 makes 13, which we put down.

21

11: GENERAL MULTIPLICATION 117

Find 86 × 23.

A. The method is as above: vertically on the right, 6×3 = 18,

put down 8 carry 1.

B. Crosswise, 24 + 12 = 36, 36 + carried 1 = 37, 8 6

put down 7 carry 3.

2 3

C. Vertically on the left, 8×2 = 16, 16 + carried 3 = 19, 1 9 7 8

put down 19.

3 1

22

Find 4321 × 24.

Here we can use the moving multiplier method.

A. First, vertically on the right, 1×4 = 4, put it down.

B. Crosswise, 8+2 = 10, put down 0, carry 1.

C. Next we cross-multiply the 32 with the 24, 4 3 2 1

this gives 12+4 = 16, 16 + carried 1 gives 17, 2 4

put down 7 carry 1. 1 0 3 7 0 4

D. Then cross-multiply the 43 with the 24, 2 1 1

this gives 16+6 = 22, 22 + carried 1 gives 23,

put down 3 carry 2.

E. Vertically on the left, 4×2 = 8, 8 + carried 2 gives 10,

put down 10.

Find 234 × 234.

2 3 4

5 4 7 5 6

1 2 2 1

We simply do the same operations as shown in Section 11.6 but start at the right

side:

4×4 = 16, put down 6 and carry 1 to the left.

3×4 + 4×3 = 24, 24 + carried 1 = 25, put down 5 and carry 2.

And so on.

23

24

 Practice K Multiply the following from right to left:  Practice K Multiply the following from right to left:

a 31 × 41 b 23 × 22 c 61 × 42 a 31 × 41 b 23 × 22 c 61 × 42

d 52 × 53 e 54 × 45 f 78 × 33

g 17 × 71 h 88 × 88 i 231 × 32 g 17 × 71 h 88 × 88 i 231 × 32

j 416 × 41 k 182 × 23 l 473 × 37 j 416 × 41 k 182 × 23 l 473 × 37

m 5432 × 32 n 6014 × 24 o 3333 × 22

p 444 × 333 q 543 × 345 r 707 × 333

VEDIC MATHEMATICS MANUAL 1

118

a 1 271 b 506 c 2 562

d 2756 e 2 430 f 2 574

g 1 207 h 7 744 i 7 392

j 17 056 k 4 186 l 17 501

m 173 824 n 144 336 o 73 326

p 147852 q 187335 r 235431

SETTING THE SUMS OUT

In Example 24 each of the five steps had a center of symmetry. 2 3 4

2 3 4 ×

5 4 7 5 6

. . . . .

The five dots on the right show these five centers and as we move

from left to right or right to left through the sum it is as if there is a dot

moving through the sum.

In the calculation shown here the units figure of the result of each of the five steps is placed

under the dot for that step.

Other ways of setting the sums and answers out are possible and may be preferred.

“On seeing this kind of work actually bein

g

performed by the little children, the doctors,

professors and other “big-

g

uns” of mathematics

are wonder struck and exclaim: “

I

s this

mathematics or magic?” And we invariabl

y

answer and say: “It is both. It is magic until you

understand it; and it is mathematics thereafter”;

and then we proceed to substantiate and prove the

correctness of this reply of ours!”

From “Vedic Mathematics”, Page xvii.

LESSON 12 LESSON 12

SQUARING

SUMMARY SUMMARY

In the case of 752, we simply multiply the 7 (the number before the 5) by the nex

t

number up, 8. This gives us 56 as the first part of the answer, and the last part is

simply 25 (52).

So 752 = 56/25 where 56=7×8, 25=52.

Similarly 652 = 4225 42=6×7, 25=52.

And 252 = 625 where 6=2×3.

Also since 4½= 4.5, the same method applies to squaring numbers ending in ½.

So 4½2 = 20¼, where 20 = 4×5 and ¼ = ½2.

The method can be applied to numbers of any size:

305 = 93025 where 930 = 30×31.

2

12.1 Squaring Numbers that end in 5 12.1 Squaring Numbers that end in 5

12.2 Squaring Numbers Near 50 12.2 Squaring Numbers Near 50

12.3 General Squaring

– from left to right. 12.3 General Squaring – from left to right.

12.4 Number Splitting

– to simplify squaring calculations. 12.4 Number Splitting – to simplify squaring calculations.

12.5 Algebraic Squaring 12.5 Algebraic Squaring

12.6 Digit Sums of squares – properties of square numbers. 12.6 Digit Sums of squares – properties of square numbers.

12.7 Square Roots of Perfect Squares – where the answer is a 2-figure number. 12.7 Square Roots of Perfect Squares – where the answer is a 2-figure number.

12.8 3 and 4-Figure Numbers – squaring bigger numbers. 12.8 3 and 4-Figure Numbers – squaring bigger numbers.

12.1 SQUARING NUMBERS THAT END IN 5

Squaring is multiplication in which a number is multiplied by itself: Squaring is multiplication in which a number is multiplied by itself:

so 75 × 75 is called "75 squared" and is written 752. so 75 × 75 is called "75 squared" and is written 752.

The formula By One More Than the One Before provides a beautifully simple way of squaring

numbers that end in 5.

The formula By One More Than the One Before provides a beautifully simple way of squaring

numbers that end in 5.

1

2

3

4

5

VEDIC MATHEMATICS MANUAL 1

120

Even for large numbers like, say, 635, it is still easier to multiply 63 by 64 and put 25 on the

end than to multiply 635 by 635.

Even for large numbers like, say, 635, it is still easier to multiply 63 by 64 and put 25 on the

end than to multiply 635 by 635.

Algebraic Proof: (ax + 5)2 = a(a + 1)x2 + 25, where x = 10. See also end of section 11.2. Algebraic Proof: (ax + 5)2 = a(a + 1)x2 + 25, where x = 10. See also end of section 11.2.

 Practice A Square the following numbers:  Practice A Square the following numbers:

a 55 b 15 c 8½ d 95

e 105 f 195 g 155 h 245

i 35 j 20½ k 8005 l 350 i 35 j 20½ k 8005 l 350

What number, when squared, gives: What number, when squared, gives:

m 2025 n 30¼ o 902500

a 3025 b 225 c 72¼ d 9025

e 11025 f 38025 g 24025 h 60025

i 1225 j 420¼ k 64080025 l 122500

m 45 n 5½ o 950

Here is another special squaring method.

53² = 2809.

The answer is in two parts: 28 and 09.

28 is simply the last figure, 3, increased by 25.

And 09 is just 32.

Similarly

52² = 2704 (2 = 2 + 25, 04 = 22).

6

12.2 SQUARING NUMBERS NEAR 50

7

Algebraic Proof: (50 + a)2 = 100(25 + a) + a2.

12: SQUARING 121

 Practice B Find:

a 54² b 56² c 57² d 58² e 61²

f 62² g 51²

a 2916 b 3136 c 3249 d 3364 e 3721

f 3844 g 2601

47² = 2209.

Similarly, for numbers below 50 we take the deficiency from 50 (3 here) from 50, to

get 47 in this case, and put the square of the deficiency, 9.

8

In the proof above ‘a’ would take negative values for numbers below 50.

 Practice C Square the following numbers by this method:

a 46 b 44 c 42 d 39 e 43

f 49 g 41 h 37

a 2116 b 1936 c 1764 d 1521 e 1849

f 2401 g 1681 h 1369

12.3 GENERAL SQUARING

The Vertically and Crosswise formula simplifies nicely when the numbers being multiplied

are the same, and gives us a very easy method for squaring numbers.

THE DUPLEX

We will use the term Duplex, D, as follows:

for 1 figure D is its square, e.g. D(4) = 42 = 16;

for 2 figures D is twice their product, e.g. D(43) = 2×4×3 = 24.

VEDIC MATHEMATICS MANUAL 1

122

 Practice D Find the Duplex of the following numbers:  Practice D Find the Duplex of the following numbers:

a 5 b 23 c 55 d 2

e 14 f 77 g 26 h 90 e 14 f 77 g 26 h 90

a 25 b 12 c 50 d 4

e 8 f 98 g 24 h 0

The square of any number is just the total of its Duplexes,

combined in the way we have been using for mental multiplication.

432 = 1849.

Working from left to right there are three duplexes in 43: D(4), D(43) and D(3).

D(4) = 16, D(43) = 24, D(3) = 9,

combining these three results in the usual way we get 16

16 = 184 ,24



184,9 =

1849.

642 = 4096.

D(6) = 36, D(64) = 48, D(4) = 16,

So mentally we get 36

= 408 84,63 

= 4096. 61,840 

9

10

Algebraic proof: (10a + b)2 = 100(a2) + 10(2ab) + b2. This method can also be explained by

multiplying a number by itself using the general multiplication method.

 Practice E Square the following:

a 31 b 14 c 41 d 26

e 23 f 32 g 21 h 66

i 81 j 91 k 56 l 63

m 77 n 33

12: SQUARING 123

a 961 b 196 c 1681 d 676

e 529 f 1024 g 441 h 4356

i 6561 j 8281 k 3136 l 3969

m 5929 n 1089

Duplexes and squares of longer numbers are covered in Section 12.8

12.4 NUMBER SPLITTING

You may recall that we could sometimes group two figures as one when we were multiplying

two 2-figure numbers together (see Section 11.4). This also applies to squaring.

1232 = 15129.

Here we may think of 123 as 12/3, as if it were a 2-figure number:

D(12) = 122 = 144,

D(12/3) = 2 × 12 × 3 = 72,

D(3) = 32 = 9.

Combining these: 14 = 1512, and 1512,9 = 15129. 27,4



 Practice F Square the following, grouping the first pair of figures together:

a 121 b 104 c 203 d 113

e 116 f 108 g 111

a 14 641 b 10 816 c 41 209 d 12 769 e 13 456 f 11 664 g 12321

The other way of splitting the numbers, shown in Section 11.4 can also be used here.

3122 = 97344.

Here we can split the number into 3/12 but we must work with pairs of digits:

D(3) = 9, D(3/12) = 72, D(12) = 144.

Combining: 9,72 = 972 we can put both figures of 72 after the 9,

97 = 97344. 441,2



11

12

VEDIC MATHEMATICS MANUAL 1

124

 Practice G Square the following, grouping the last 2 figures together:  Practice G Square the following, grouping the last 2 figures together:

a 211 b 412 c 304 d 902

e 407 f 222 g 711 e 407 f 222 g 711

a 44 521 b 169 744 c 92 416 d 813 604

e 165 649 f 49 284 g 505 521

12.5 ALGEBRAIC SQUARING

Exactly the same method we have been using for squaring numbers can be used for squaring

algebraic expressions.

Find (x + 5)2.

This is just like squaring numbers: we find the duplexes of x, x+5 and 5.

D(x) = x2, D(x+5) = 2×x×5 = 10x, D(5) = 52 = 25.

So (x + 5)2 = x2 + 10x + 25.

Find (2x + 3)2

13

.

There are three Duplexes: D(2x) = 4x2, D(2x+3) = 2×2x×3 = 12x, D(3) = 9.

So (2x + 3)2 = 4x2 + 12x + 9.

Find (x – 3y)2.

Similarly: D(x) = x2, D(x–3y) = 2×x×–3y = –6xy, D(–3y) = 9y2.

So (x – 3y)2 = x2 – 6xy + 9y2.

14

15

 Practice H Square the following:

a (3x + 4) b (5y + 2) c (2x – 1) d (x + 7)

e (x – 5) f (x + 2y) g (3x + 5y) h (2a + b)

i (2x – 3y) j (x + y) k (x – y) l (x – 8y)

12: SQUARING 125

a 9x²+24x+16 b 25y²+20y+4 c 4x²–4x+1 d x²+14x+49

e x²–10x+25 f x²+4xy+4y² g 9x²+30xy+25y² h 4a²+4ab+b²

i 4x²–12xy+9y² j x²+2xy+y² k x²–2xy+y² l x²–16xy+64y²

12.6 DIGIT SUMS OF SQUARES

Investigations of square numbers can make interesting and useful lessons, leading for example

to the following results.

Square numbers only have digit sums of 1, 4, 7, 9

and they only end in 1, 4, 5, 6, 9, 0.

This means that square numbers cannot have certain digit sums and they cannot end with

certain figures.

In the exercise below some numbers cannot be square numbers according to the above results.

 Practice I Which are not square numbers (judging by the above results)?

a 4539 b 5776 c 6889 d 5271

e 104976 f 65436 g 27478 h 75379

a, d, f, g

If a number has a valid digit sum and a valid last figure that does not mean that it is a square

number. The last number in the exercise, 75379, is not a square number even though it has an

allowed digit sum of 4 and an allowed last figure of 9.

12.7 SQUARE ROOTS OF PERFECT SQUARES

Find 6889

.

16

First note that there are two groups of figures, 68’89, so we expect a 2-figure answer.

Next we use The First by the First and the Last by the Last. Looking at the 68 at the

b

eginning we can see that since 68 is greater than 64 (8²) and less than 81 (9²) the

first figure must be 8.

Or looking at it another way 6889 is between 6400 and 8100

2

6400 = 80

6889 = 8?2

2

8100 = 90

so 6889 must be between 80 and 90. I.e. it must be eighty something.

Now we look at the last figure of 6889, which is 9.

Any number ending with 3 will end with 9 when it is squared so the number we are

looking for could be 83.

But any number ending in 7 will also end in 9 when it is squared so the numbe

r

could also be 87.

So is the answer 83 or 87?

There are two easy ways of deciding. One is to use the digit sums.

If 872 = 6889 then converting to digit sums we get 62 J 4, which is not correct.

But 832 = 6889 becomes 22 J 4, so the answer must be 83.

The other method is to recall that since 852 = 7225 and 6889 is below this

must be below 85. So it must be 83.

6889

To find the square root of a perfect 4-digit square number

we find the first figure by looking at the first figures

and we find two possible last figures by looking at the last figure.

We then decide which is correct either by considering the digit sums

or by considering the square of their mean.

12: SQUARING 127

Find 5776 .

17

The 57 at the beginning is between 49 and 64, so the first figure must be 7.

The 6 at the end tells us the square root ends in 4 or 6.

So the answer is 74 or 76.

742 = 5776 becomes 22 J 7 which is not true in terms of digit sums, so 74 is not the

answer.

762 = 5776 becomes 42 J 7, which is true, so 76 is the answer.

Alternatively to choose between 74 and 76 we note that 752= 5625 and 5776 is

greater than this so the square root must be greater than 75. So it must be 76.

In the following exercise try to find the answers mentally if you can, writing down only the

answers.

In the following exercise try to find the answers mentally if you can, writing down only the

answers.

 Practice J Find the square root of:  Practice J Find the square root of:

a 2116 b 5329 c 1444 d 6724 a 2116 b 5329 c 1444 d 6724

e 3481 f 4489 g 8836 h 361

i 784 j 3721 k 2209 l 4225 i 784 j 3721 k 2209 l 4225

m 9604 n 5929 m 9604 n 5929

a 46 b 73 c 38 d 82

e 59 f 67 g 94 h 19

i 28 j 61 k 47 l 65

m 98 n 77

As you will have seen, square numbers ending in 5 must have a square root ending in 5, there

is only one possibility for the last figure.

VEDIC MATHEMATICS MANUAL 1

128

12.8 3 AND 4-FIGURE NUMBERS

This follows on from Section 12.3. This follows on from Section 12.3.

As shown before, the duplex of a 1-digit number is its square: e.g. D(4) = 42 = 16. As shown before, the duplex of a 1-digit number is its square: e.g. D(4) = 4

And the duplex of a 2-digit number is twice the product of the digits: e.g. D(35) = 2×3×5 =

30.

And the duplex of a 2-digit number is twice the product of the digits: e.g. D(35) = 2×3×5 =

30.

2 = 16.

We can also find the duplex of 3-digit numbers or bigger. We can also find the duplex of 3-digit numbers or bigger.

For 3 digits D is twice the product of the outer pair + the square of the middle digit,

e.g. D(137) = 2×1×7 + 32 = 23;

For 3 digits D is twice the product of the outer pair + the square of the middle digit,

e.g. D(137) = 2×1×7 + 32 = 23;

for 4 digits D is twice the product of the outer pair + twice the product of the inner pair,

e.g. D(1034) = 2×1×4 + 2×0×3 = 8;

for 4 digits D is twice the product of the outer pair + twice the product of the inner pair,

e.g. D(1034) = 2×1×4 + 2×0×3 = 8;

D(10345) = 2×1×5 + 2×0×4 + 32 = 19; D(10345) = 2×1×5 + 2×0×4 + 32 = 19;

and so on. and so on.

 Practice K Find the duplex of the following numbers:  Practice K Find the duplex of the following numbers:

a 3 b 34 c 47 d 1 e 88 a 3 b 34 c 47 d 1 e 88

f 234 g 282 h 111 i 304 j 270 f 234 g 282 h 111 i 304 j 270

k 1234 l 3032 m 7130 n 20121 o 32104

a 9 b 24 c 56 d 1 e 128

f 25 g 72 h 3 i 24 j 49

k 20 l 12 m 6 n 5 o 25

As with 2-figure numbers the square of a number is just the total of its duplexes.

3412 = 116281.

Here we have a 3-figure number:

D(3) = 9, D(34) = 24, D(341) = 22, D(41) = 8, D(1) = 1.

Mentally: = 114 9,24

∪

11 = 1162 4,22

∪

1162,8,1 =

116281.

18

12: SQUARING 129

43322 = 18766224.

D(4) = 16, D(43) = 24, D(433) = 33, D(4332) = 34,

D(332) = 21, D(32) = 12, D(2) = 4.

Mentally: 16 = 184 ,24

∪

18 = 1873 4,33

∪

187 = 18764 3,34

∪

1876 = 187661 4,21

∪

18766 = 1876622 1,12

∪

1876622,4 =

18766224.

19

 Practice L Square the following numbers:  Practice L Square the following numbers:

a 212 b 131 c 204 d 513 a 212 b 131 c 204 d 513

e 263 f 264 g 313 h 217 e 263 f 264 g 313 h 217

i 3103 j 2132 k 1414 l 4144

a 44 944 b 17 161 c 41 616 d 263 169

e 69 169 f 69 696 g 97 969 h 47 089

i 9 628 609 j 4 545 424 k 1 999 396 l 17 172 736

“whatever is consistent with right reasoning should be

accepted, even though it comes from a boy or even from

a parrot; and whatever is inconsistent therewith ought to

be rejected, although emanating from an old man o

r

even from the great sage Shree Shuka himself”.

quoted in “Vedic Mathematics”, Page 1d.

LESSON 13

EQUATIONS

SUMMARY

13.1 One-step Equations

13.2 Two-Step Equations – mental, one-line solutions.

13.3 Three-Step Equations

Equations like x + 39 = 70, x – 7 = 8, 3x = 15 and x7

3

=

are easily solved using the Vedic

formula: Transpose and Apply.

Transpose means "reverse" and in solving equations Transpose and Apply means :

}

13.1 ONE-STEP EQUATIONS

where a number is added to the x-term: subtract, on the other side

where a number is subtracted: add,

where the x-term is multiplied: divide,

where the x-term is divided: multiply.

 Practice A Solve the following equations, check each answer to make sure it is right:

a x + 3 = 10 b x – 3 = 10 c 20 + x = 100 d x – 19 = 44

e x + 88 = 100 f x – 3½ = 4½ g x + 123 = 1000 h x + 1.3 = 5

i 5x = 35 j 2x = 26 k 3x = 960 l 2x = 76

m 40x = 120 n 2½x = 10 o x

7 = 7 p x

4 = 5

a 7 b 13 c 80 d 63

e 12 f 8 g 877 h 3.7

i 7 j 13 k 320 l 38

m 3 n 4 o 49 p 20

This is, of course, just a matter of mental arithmetic, and can be taught as such.

13: EQUATIONS 131

13.2 TWO-STEP EQUATIONS

Sometimes two or more applications of the Transpose and Apply formula are needed, as the

following examples show.

Solve 2x + 3 = 13.

We take 3 from both sides of the equation: this gives 2x = 10.

Then you can see that x = 5 is the answer.

To check: 2×5 + 3 = 13 so it is correct.

There are two applications of Transpose and Apply here:

First the +3 indicates that we subtract 3 from 13 (to get 10),

then the 2x indicates that we divide 10 by 2.

1

Solve 5x – 4 = 36.

Using the Sutra we add 4 to 36 to get 40,

then 40÷5 = 8, so x = 8.

Check: 5×8 – 4 = 36.

Solve x

7 + 3 = 5.

Here we take 3 from 5 to get 2,

then multiply 2 by 7, so x = 14.

Solve 2x

3= 4.

Multiply 3 by 4 to get 12,

then 12÷2=6, so x = 6.

2

Writing the sum out in steps like this is fine, 5x – 4 = 36

5x = 40

x = 8

but students should also be able to put the answer straight down.

3

4

VEDIC MATHEMATICS MANUAL 1

132

Solve 3x

5+ 4 = 10.

First 10 – 4 = 6, then 6×5 = 30, then 30÷3 = 10 so x = 10.

Solve 3x + 2

4= 8.

First 8×4 = 32, then 32–2 = 30, then 30÷3 = 10 so x = 10.

Solve −x3

4

= 5.

5

Because all the left side is divided by 4 we begin by multiplying 5 by 4,

then we add 3 to the result giving x = 23.

 Practice B Solve the following equations mentally. Check your answers.  Practice B Solve the following equations mentally. Check your answers.

a 3x + 7 = 19 b 2x + 11 = 21 c 4x – 5 = 7 d 3x – 8 = 10

e e x

3 + 4 = 6 f x

2 – 8 = 2 g 2x

3 = 8 h x4

7

+= 5

i x21

10

−= 1 j 2x + 1 = 3.8

a 4 b 5 c 3 d 6

e 6 f 20 g 12 h 31

i 31 j 1.4

13.3 THREE-STEP EQUATIONS

Sometimes we need to take three steps to solve an equation. But it still just a matter of mental

arithmetic.

6

7

13: EQUATIONS 133

Solve 2(3x + 4) = 38.

The bracket here indicates that 3x + 4 is being multiplied by the number outside the

bracket, which is 2.

So we begin by dividing 38 by 2.

First 38 ÷ 2 = 19, then 19 – 4 = 15, then 15 ÷ 3 = 5 so x = 5.

Alternatively, here, we can multiply the bracket out first:

If 2(3x + 4) = 38 then 6x + 8 = 38

and so 38 – 8 = 30 and 30 ÷ 6 = 5.

8

 Practice C Solve the following mentally:

a 2x

3+ 4 = 8 b 3x

5– 4 = 5 c 7x

2– 10 = 11 d 3x

8+17 = 20

e 2x 1

3

+= 4 f 2x 3

5

−= 3 g 5x 2

3

+

= 9 h 6x 1

7

−= 5

i 3(5x – 2) = 54 j 8(x + 3) = 64 k 3(7x – 3) = 33 l 2( 4x + 3) = 102

a 6 b 15 c 6 d 8

e 5.5 f 9 g 5 h 6

i 4 j 5 k 2 l 12

“The underlying principle behind all of them is Paravartya

Yojayet which means: ‘Transpose and adjust’. The

applications, however, are numerous and splendidly useful.”

From “Vedic Mathematics”, Page 103.

LESSON 14

FRACTIONS

SUMMARY

Find 2

3+1

7

We multiply crosswise and add the get the numerator:

2×7 + 1×3 = 17,

then multiply the denominators to get the denominator:

3×7 = 21.

So

2

3+1

7=17

21

Find 74

5+ 2 1

3.

74

5+ 2 1

3= 917

15 = 10 2

15 . Here we can add the whole parts and the fractions

separately: for the whole ones 7+2 = 9 and for the fractions: 4×3 + 1×5 = 17, the

numerator, and 5×3 = 15, the denominator.

14.1 Vertically and Crosswise – addition and subtraction of fractions.

14.2 A Simplification

14.3 Comparing Fractions

14.4 Unification of Operations: +, –, ×, ÷ of fractions are all simply related.

Addition and subtraction of fractions are usually found to be very difficult as the method is

complicated and hard to remember. But the Vertically and Crosswise formula gives the

answer immediately.

14.1 VERTICALLY AND CROSSWISE

1

21

37

The reason why this works is that in order to add the fractions we must get the denominators

to be equal, and we do this by multiplying top and bottom of 2

3 by 7 (to get a denominator of

21) and the top and bottom of 1

7 by 3 (to get the same denominator of 21). So each numerator

gets multiplied by the other denominator, and this is exactly what we did.

21

37

2

14: FRACTIONS 135

For subtractions we use the same pattern.

Find a 6

7–1

4 b 5 4

5– 1 3

4 c 4 1

3– 1 2

5.

3

a Subtraction is the same except we cross-multiply and subtract rather than add.

Be sure to start at the top left.

17

28

6

7–1

4

64- 17

74

×

= =

4

5

3

4

1

20

44- 35

54

××

×

b 5 – 1 = 4 = 4 Similarly here but deal with the whole parts

first.

1

15

1

3

2

5

14

15

c 4 – 1 = 315 = 3

- 23

35

××

×

= 2 Here we get a negative numerator, but it is

easily dealt with by taking

1

15 from one of

the whole ones.

Alternatively, to avoid the minus number here, put both fractions into top-heavy

form and subtract. This will mean dealing with larger numbers however.

 Practice A Combine the following , cancelling down your answer or leaving as mixed

numbers where necessary:

a 2

5+1

4 b 3

8+2

5 c 1

2+2

5 d 11

3+ 2 1

4

e 33

4+2 1

3 f 3

5–2

7 g 8

9–1

2 h 3

4–1

20

i 53

5– 2 1

2 j 10 2

3– 1 4

5 k 5

12 +7

18

a 13

20 b 31

40 c 9

10 d 3 7

12

e 6 1

12 f 11

35 g 7

18 h 7

10

i 3 1

10 j 8 13

15 k 29

36

Algebraic proof: a

b+c

d = ad + cb

bd .

Exactly the same pattern can be used for algebraic fractions as is used for numerical fractions.

VEDIC MATHEMATICS MANUAL 1

136

# We may note here that fractions are often written horizontally, for example 2

3 is written

2/3. This is more consistent with the ratio notation (2:3) and place value. If fractions are

written in this way then crosswise and horizontally (see Example 1) becomes crosswise

and vertically.

So for 21

37

+:

2 / 3

1 / 7 +

17 / 21

14.2 A SIMPLIFICATION

In the last question of the last exercise you did (and in question h) the numbers were rather

large and some cancelling had to be done at the end. Where the denominators of two fractions

are not relatively prime the working can be simplified as shown in the next example.

The denominators in 5

12 + 7

18 are not relatively prime: there is a common factor of 6.

We divide both denominators by this common factor and put these numbers below

the denominators:

4

(3)

7

18 29

36

(2)

5

12

+ = 53 72

12 3

×

+×

× =

So we put 2 and 3 below 12 and 18.

Then when cross-multiplying we use the 2 and 3 rather than the 12 and 18.

For the denominator of the answer we cross-multiply in the denominators:

either 12×3 or 18×2, both give 36.

Subtraction of fractions with denominators which are not relatively prime is done in just the

same way, except we subtract in the numerator as before.

 Practice B Use this simplification to add or subtract the following:

a 1

3+4

9 b 3

8+1

6 c 3

5+3

10 d 5

6–3

4

e 5

6+3

4 f 5

18 –1

27 g 33

4– 1 1

8 h 7

36 –11

60

14: FRACTIONS 137

a 7

9 b 13

24 c 9

10 d 1

12

e 1 7

12 f 13

54 g 25

8 h 1

90

14.3 COMPARING FRACTIONS

Sometimes we need to know whether one fraction is greater or smaller than another, or we

may have to put fractions in order of size.

Put the fractions 4

5, 2

3, 5

6 in ascending order.

5

Looking at the first two fractions we cross-multiply and subtract as if we wanted to

subtract the fractions.

If we find the subtraction is possible without going into negative numbers then the

first fraction must be greater: since 4×3 is greater than 2×5,

4

5must be greater tha

n

2

3.

2

3

5

6

5

6

2

3

Doing this with and we find that 2×6 is less than 5×3, so is greater than .

4

5

6

5

6

If we now cross-multiply with we find that is greater.

2

3

4

5

6

, , .

So in ascending order the fractions are:

 Practice C Put the following fractions in ascending order:

a 1

3, 2

5 b 3

4, 8

11 c 2

3, 7

12 , 3

4 d 5

6, 5

8, 6

7

a 12

35

, b 83

11 4

, c 3

72

12 3 4

,, d 556

867

,,

VEDIC MATHEMATICS MANUAL 1

138

14.4 UNIFICATION OF OPERATIONS

Multiplying and dividing fractions is also very easy.

Find a 1

2×3

4 b 3

4÷2

5

6

a 1

2×3

4=13

24

×

=3

8 We simply multiply the numerators to get the numerator of

the answer, and multiply the denominators to get the

denominator of the answer.

b 3

4÷2

5=35

24

×

=15

8= 1 7

8

We simply cross-multiply and put the first product

over the second product.

The four operations, addition, subtraction, multiplication and division are now seen to have a

much more unified relation.

We can summarise these as follows:

Addition Subtraction Multiplication Division

4

5 1

3 4

5 1

3 4

5 1

3 4

5 1

3

LESSON 15

SPECIAL DIVISION

SUMMARY SUMMARY

Find 23 ÷ 9.

9) 2 3

2 r 5

The first figure of 23 is the answer: 2.

And adding the figures of 23 gives the remainder: 2 + 3 = 5.

So 23 ÷ 9 = 2 remainder 5.

15.1 Division by 9 15.1 Division by 9

15.2 Division by 8 etc. 15.2 Division by 8 etc.

15.3 Division by 99, 98 etc. 15.3 Division by 99, 98 etc.

15.4 Divisor Below a Base Number 15.4 Divisor Below a Base Number

15.5 Divisor Above a Base Number 15.5 Divisor Above a Base Number

15.1 DIVISION BY 9

As you have seen before, the number 9 is special and there is a very easy way to divide by 9. As you have seen before, the number 9 is special and there is a very easy way to divide by 9.

1

It is easy to see why this works because every 10 contains a 9 with 1 left over. It is easy to see why this works because every 10 contains a 9 with 1 left over.

So 2 tens contains 2 nines with 2 left over. So 2 tens contains 2 nines with 2 left over.

The answer is the same as the remainder, 2. The answer is the same as the remainder, 2.

And that is why we add 2 to 3 to get the remainder. And that is why we add 2 to 3 to get the remainder.

 Practice A Divide by 9:  Practice A Divide by 9:

a 9)5 1a 9)5 1 b 9)3 4 c 9)17 d 9)4 4

e 9)6 0 f 9)7 1 g 9)2 6 h 9)4 6

a 5 r6 b 3 r7 c 1 r8 d 4 r8

e 6 r6 f 7 r8 g 2 r8 h 4 r10 = 5 r1

VEDIC MATHEMATICS MANUAL 1

140

It can happen that there is another nine in the remainder, as occurred in the last question of the

last exercise and as the next example shows.

Find 66 ÷ 9.

9)6 6

6 r 12 = 7 r 3

We get 6 remainder 12 and there is another nine in the remainder of 12.

So we add the one extra nine to the 6, which becomes 7.

And the remainder is reduced to 3 (take 9 from 12).

Find 58 ÷ 9. 9)5 8

5 r 13 = 6 r 4

2

3

Remember you are trying to find the number of nines in 66 and the first answer you get is 6

remainder 12. So there are 6 nines with 12 remaining. Since there is another nine in the 12

you therefore have 7 nines altogether and 3 remaining.

You can also get the final remainder, 3, by adding the digits in 12.

 Practice B Divide the following by 9:

a 9)57 b 9)77 c 9)58 d 9)49

e 9)64 f 9)88 g 9)96

a 6 r3 b 8 r5 c 6 r4 d 5 r4

e 7 r1 f 9 r7 g 10 r6

The unique property of number nine, that it is one unit below ten leads to many of the very

easy Vedic methods, as in Sections 15.2, 15.3, 15.4 following. See also the methods of

converting fractions to their recurring decimal form in Manual 2 (or References 1 and 3), as

well as corresponding algebraic applications.

15: SPECIAL DIVISION 141

LONGER NUMBERS

This can be easily extended to longer numbers.

2301 ÷ 9 = 255 remainder 6.

4

The sum can be set out like this: 9) 2 3 0 1

The 2 at the beginning of 2301 is brought 9) 2 3 0 1

straight down into the answer:

2

This 2 is then added to the 3 in 2301, and 5 is put down: 9) 2 3 0 1

2 5

This 5 is then added to the 0 in 2301, and 5 is put down: 9) 2 3 0 1

2 5 5

This 5 is then added to 1 to give the remainder, 6: 9) 2 3 0 1

2 5 5 r6

The first figure of the number being divided is the first figure of the answer,

and each figure in the answer is added to the next figure in the dividend

to give the next figure of the answer.

The last number we write down is the remainder.

 Practice C Divide the following:

a 9)2 1 2 3 b 9)3 1 2 c 9)1 1 2 0 2

d 9)4 3 1 e 9)5 0 3 0 f 9)7 0 7

g 9)2 0 3 0 1 0 h 9)1 6 4 i 9)3 1 0 3 2

a 235 r8 b 34 r6 c 1244 r6

d 47 r8 e 558 r8 f 78 r5

g 22556 r6 h 18 r2 i 3448 r0

VEDIC MATHEMATICS MANUAL 1

142

CARRIESCARRIES

In the method of division by 9 which you have used it can happen that a 2-figure number

appears in the answer.

Find 3172 ÷ 9.

9) 3 1 7 2

11r1334 = 352 remainder 4

Here you find you get an 11 and a 13:

the first 1 in the 11 must be carried over to the 4, giving 351,

and there is also another 1 in the remainder so we get 352 remainder 4.

 Practice D Divide the following:

a 9)6 1 5 3 b 9)3 2 8 2 c 9)5 5 5

d 9)8 2 5 2 e 9)6 6 1 f 9)4 7 4 1

Find 3172 ÷ 9.

We can avoid the build-up of large numbers like 11 and 13.

In the last example we may notice, before we put the 4 down, that the next step will

give a 2-figure number and so we put 5 down instead:

9)

3 1 7 2

3 5 2 r 4

Then add 5 to 7 to get 12, but as the 1 has already been carried over we only put the

2 down. Finally, 2+2 = 4.

g 9)1 2 3 4 5 h 9)4 7 4 7 i 9)2 0 0 8 2

a 683 rem 6 b 364 rem 6 c 61 rem 6

d 916 rem 8 e 73 rem 4 f 526 rem 7

g 1371 r6 h 527 r4 i 2231 r3

A SHORT CUT

We can avoid the double figures that crop up in some of these sums.

Let us do Example 5 above again.

5

6

15: SPECIAL DIVISION 143

Find 777 ÷ 9.

9)

7 7 7

8 6 r 3

If we put 7 for the first figure we get 14 at the next step, so we put 8.

8+7 = 15 and the 1 has already been carried over.

Now, if we put the 5 down we see a 2-figure number coming in the next step, so we

put 6 down.

6+7 = 13 and the 1 has been carried over, so just put down the 3.

 Practice E Divide the following by 9:

a 6153 b 3272 c 555 d 8252

e 661 f 4741 g 5747 h 2938

i 12345 j 75057 k 443322 l 1918161

a 683 rem 6 b 363 rem 5 c 61 rem 6 d 916 rem 8

e 73 rem 4 f 526 rem 7 g 638 rem 5 h 326 rem 4

i 1371 rem 6 j 8339 rem 6 k 49258 l 213129

Suppose we want to divide 31 by 8.

8

) 3 1

3 r 7

We bring the first 3 down into the answer.

Then instead of adding this to the 1 as we do when dividing by 9,

we add double 3 to the 1 to get 7 for the remainder.

We double the 3 because 8 is 2 below 10.

This easy way to divide by 9 can be extended for 8, 7 etc.

7

15.2 DIVISION BY 8 ETC.

8

VEDIC MATHEMATICS MANUAL 1

144

 Practice F Try some of these:  Practice F Try some of these:

a 8

) 2 2a 8) 2 2 b 8) 1 5 c 8) 2 5 d 8) 5 1

a 2 r6 b 1 r7 c 3 r1 d 6 r3

Similarly for 211 divided by 8:

8

) 2 1 1

2 5 r 11 = 26 r3

We bring down the first 2,

add double this to the 1 in the next column and put down 5,

then add double the 5 to the 1 in the last column and put down 11 as the remainder.

Since this remainder contains another 8 we convert our answer to 26 rem 3.

 Practice G Try the following.

a 8) 1 1 1 b 8) 1 5 1 c 8) 1 0 0 d 8) 2 1 4 e 8) 1 1 2 1

Now, in dividing by 7 which is 3 below 10 we must treble the last answer figure a

t

each step.

7

) 1 1 and 7) 1 2 3

1 r 4 1 5 r18 = 17 r4

a 13 r7 b 18 r7 c 12 r4 d 26 r6 e 140 r1

9

10

 Practice H Try these:

a 7) 1 3 b 7) 3 1 c 7) 2 3 d 7) 4 0

e 7) 1 0 3 f 7) 1 1 1 g 7) 1 0 0

a 1 r6 b 4 r3 c 3 r2 d 5 r5

e 14 r5 f 15 r6 g 14 r2

15: SPECIAL DIVISION 145

15.3 DIVISION BY 99, 98 ETC.

Suppose we want to divide the number 121314 by 99.

This is very similar to division by 9, but because 99 has two 9's we can get the

answer two digits at a time.

Think of the number split into pairs: 12/13/14 where the last pair is part of the

remainder.

Then put down the 12 as the first part of the answer: 99) 12 / 13 / 14

12

Then add the 12 to the 13 and put down 25 as the next part: 99) 12 / 13 / 14

12 / 25

Finally add the 25 to the last pair and put down 39 as the

remainder: 99

) 12 / 13 / 14

12 / 25 / 39

So the answer is 1225 remainder 39.

121314 ÷ 98 = 1237 remainder 88.

.

This is the same as before, but because 98 is 2 below 100 we double the last part o

f

the answer before adding it to the next part of the sum.

So we begin as before by bringing 12 down into the answer: 98 ) 12 / 13 / 14

12

Then we double 12 and add this to 13 to get 37: 98 ) 12 / 13 / 14

12 / 37

Finally double 37 and add it to 14: 98 ) 12 / 13 / 14

12 / 37 / 88 = 1237 remainder 88

 Practice I Divide by 99:

a 121416 b 213141 c 332211 d 282828 e 363432

f 11221122 (this has 4 pairs, but the method is the same) g 3456 (this has 2 pairs)

a 1226 r42 b 2152 r93 c 3355 r66 d 2856 r84 e (3670 r102) 3671 r3

f 113344 r66 g 34 r90

Dividing by 98 is similar.

12

11

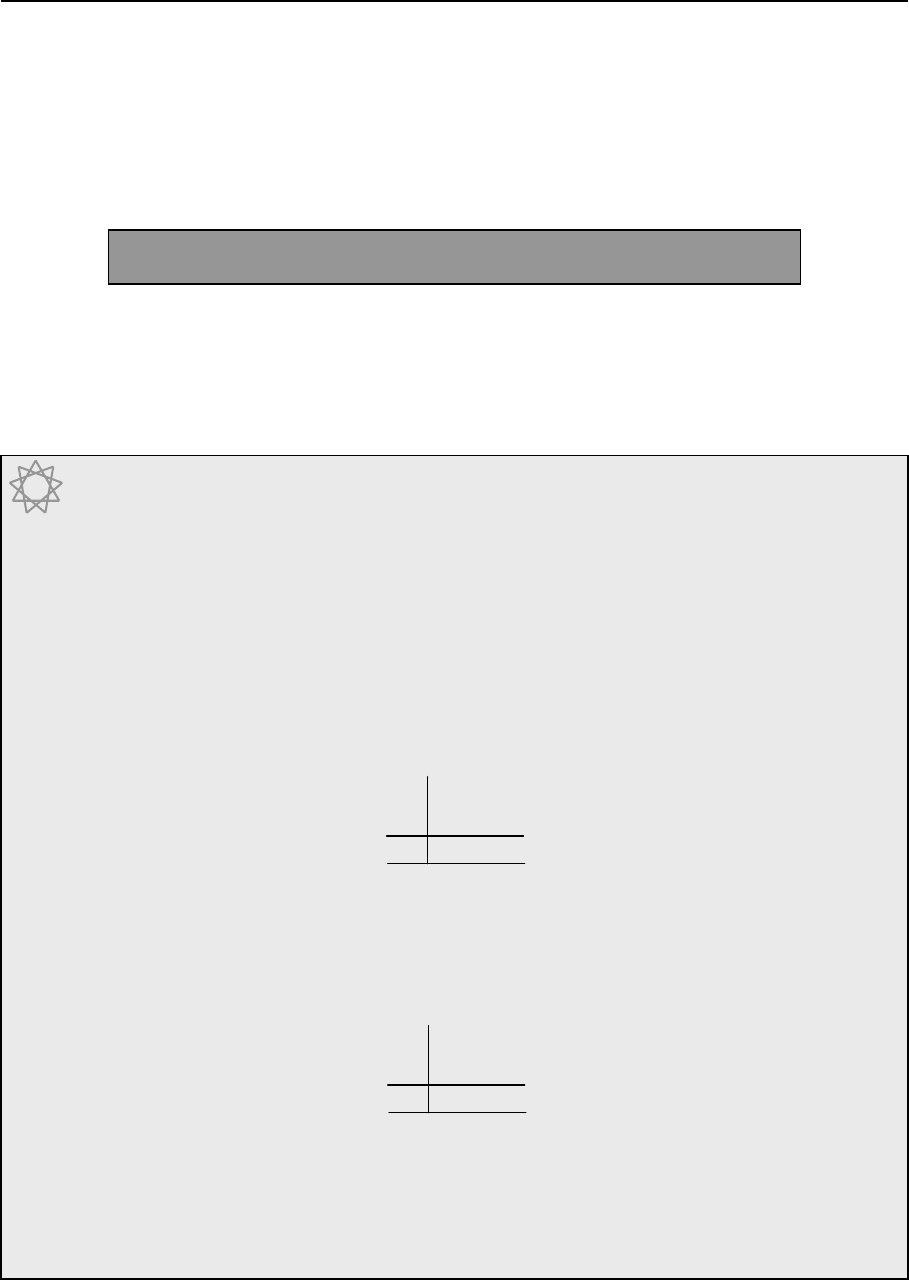
VEDIC MATHEMATICS MANUAL 1

146

 Practice J Divide by 98:

a 112203 b 102010 c 131313 d 200202 e 2131

a 1144 r91 b 1040 r90 c 1339 r91 d 2042 r86 e 21 r 73

In a similar way we can divide by numbers like 97 and 999.

15.4 DIVISOR BELOW A BASE NUMBE

R

Dividing by 9 is easy, as you have seen.

It is similarly easy to divide by numbers near other base numbers: 100, 1000 etc.

Suppose we want to divide 235 by 88 (which is close to 100).

We need to know how many times 88 can be taken from 235 and what the remainder

is.

Since every 100 must contain an 88 there are clearly two 88's in 235.

And the remainder will be two 12's (because 88 is 12 short of 100) plus the 35 in

235.

So the answer is 2 remainder 59 (24+35=59).

A neat way of doing the division is as follows.

8 8 ) 2 3 5

We separate the two figures on the right because 88 is close to 100 (which has 2

zeros).

Then since 88 is 12 below 100 we put 12 below 88, as shown below.

8 8 ) 2 3 5

1 2 2 4

2 5 9

We bring down the initial 2 into the answer.

This 2 then multiplies the flagged 12 and the 24 is placed under the 35 as shown.

We then simply add up the last 2 columns.

13

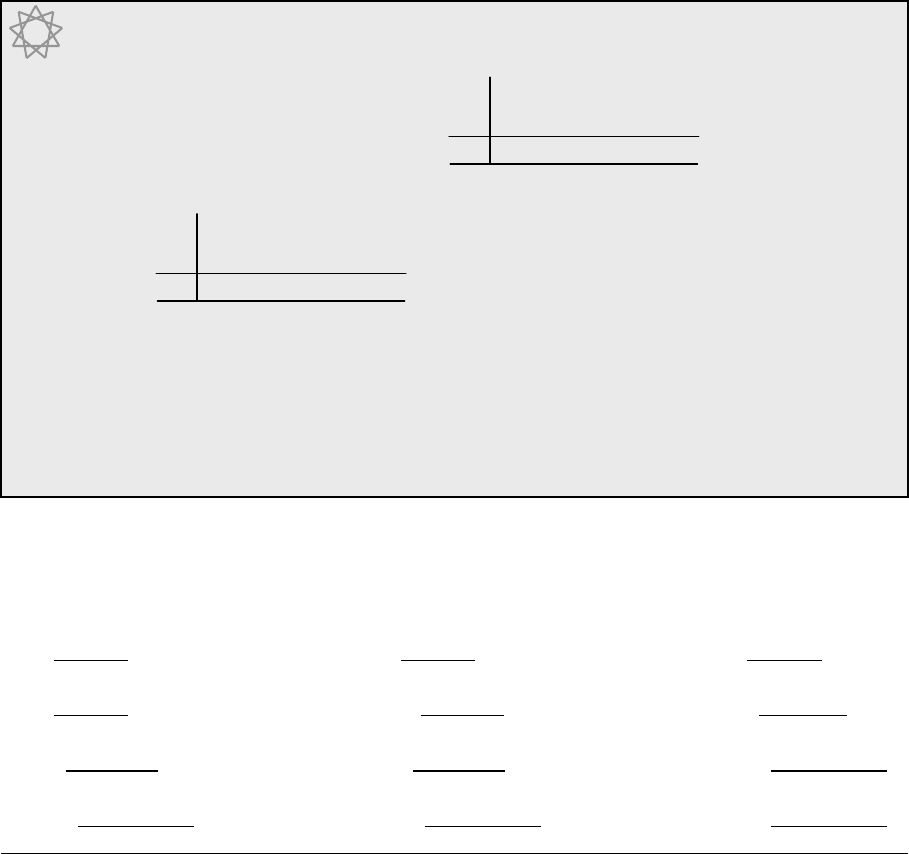
15: SPECIAL DIVISION 147

Note that the deficiency of 88 from 100 is given by the formula All from 9 and the Last from

10.

Note also that the position of the vertical line is always determined by the number of

noughts in the base number: if the base number has 4 noughts then the vertical line goes 4

digits from the right, and so on.

This is easily understood since when we bring the initial 2 down into the answer we are

expecting to find two 88’s in 235. And as there is one 88 in every hundred and 12 left over, in

two hundreds there will be two 88’s and two 12’s remainder, which must be added to the 35

to give 59 as the full remainder.

Divide 31313 by 7887.

We set the sum out as before: 7 8 8 7 ) 3 1 3 1 3

7 8 8 7 ) 3 1 3 1 3

2 1 1 3 6 3 3 9

3 7 6 5 2

Applying All From 9 and the Last From 10 to 7887 gives 2113.

Bring the 3, (the first figure of 31313) down into the answer.

We now multiply this by the flagged 2113 and put 6339 in the middle row.

Then adding up the last four columns gives the remainder of 7652.

14

 Practice K Divide the following (do as many mentally as you can):

a 88)1 2 1 b 76)2 1 1 c 83)1 3 2

d 98)3 3 3 e 887)1 2 2 3 f 867)1 5 1 3

g 779)2 2 2 2 h 765)3 0 0 1 i 8907)1 3 1 0 3

j 7999)1 2 3 2 1 k 7789)2 1 0 1 2 l 8888)4 4 3 4 4

a 1/33 b 2/59 c 1/49

d 3/39 e 1/336 f 1/646

g 2/664 h 3/706 i 1/4196

j 1/4322 k 2/5434 l 4/8792

VEDIC MATHEMATICS MANUAL 1

148

TWO-FIGURE ANSWERS

Here we consider the case where the answer consists of more than one digit.

1108 ÷ 79 = 13 remainder 81 = 14 remainder 2.

We set the sum out marking off two figures on the right and leave two rows as there

are to be two answer figures:

7 9 ) 1 1 0 8

2 1 2 1

6 3

1 3 8 1

Bring the first 1 down into the answer.

Multiply the flagged 21 by this 1 and put the answer (2 1) as shown in the second

row.

Adding in the second column we get 3 which we put down and then multiply the 21

by this 3 to get 63, which we place as shown in the third row.

Add up the last two columns, but since the remainder, 81, is greater than the divisor,

79, there is another 79 contained in 81 so there are 14 79's in 1108 with 2 remaining.

Find 1121123 ÷ 8989.

8 9 8 9 ) 1 1 2 1 1 2 3

1 0 1 1 1 0 1 1

2 0 2 2

4 0 4 4

1 2 4 6 4 8 7

The initial 1 comes down into the answer and multiplies the flagged 1011.

This is placed as shown in the second row.

Adding in the second column we put 2 down in the answer and then multiply the

1011 by it. Put 2022 in the third row.

Adding in the third column we get 4 which we put down and also multiply by 1011.

So we put 4044 in the fourth row and then add up the last four columns to get the

remainder.

15

16

15: SPECIAL DIVISION 149

Once the vertical line has been drawn in you can see the number of lines of

working needed: this is the number of figures to the left of this line (3 figures

and therefore 3 lines of working in Example 16 above).

 Practice L Divide the following:

a 8 9)1 0 2 1 b 8 8) 1 1 2 2 c 7 9)1 0 0 1

d 8 8)2 1 1 1 e 9 7) 1 1 1 1 f 8 8 8) 1 0 0 1 1

g 8 8 7)1 1 2 4 3 h 8 9 9)2 1 2 1 2 i 9 8 8)3 0 1 2 5

j 8 8 9 9)2 0 1 0 2 0

a 11/42 b 12/66 c 12/53

d 23/87 e 11/44 f 11/243

g 12/599 h 23/535 i 30/485

j 22/5242

A SIMPLIFICATION

In these examples (and in the ones in the next section) the lines of working can be dispensed

with by using the Vertically and Crosswise formula. We use the vertical and crosswise

products in the flag and answer digits.

In Example 15 we have 21 flagged and the first answer figure is 1: 2 1

1 -

The first vertical product here gives 2×1=2 which is to be added in the second column of 1108

to give 3 as the second answer figure: 2 1

1 3

So now we take the cross-product 2×3 + 1×1 = 7 and add this to the 0 in 1108 to give 7 as the

first remainder figure.

Finally the vertical product on the right in 2 1

1 3

gives 1×3=3 to be added to the last figure of 1108 which makes 11 and gives the full

remainder of 711 = 81.

Similarly longer sums like Example 16 can also be dealt with in this way.

VEDIC MATHEMATICS MANUAL 1

150

1489 ÷ 123 = 12 remainder 13.

Here we see that 123 is close to the base of 100 so we mark 2 figures off on the

right.

In fact the method is just as before except that we write the flagged numbers as ba

r

numbers:

1 2 3 ) 1 4 8 9

2 3 2 3

4 6

1 2 1 3 Bring the initial 1 down into the answer.

Multiply this 1 by the flagged 23 and write

down 2, 3.

Add in the second column and put down 2.

Multiply this 2 by the

23 and put 4, 6.

Then add up the last two columns.

A very similar method, but under the formula Transpose and Apply allows us to divide

numbers which are close to but above a base number.

15.5 DIVISOR ABOVE A BASE NUMBER

17

The Sutra in use is Transpose and Apply, as stated above, because we are actually subtracting

from the digits 4, 8 and 9.

 Practice M Divide the following:

a 1 2 3)1 3 7 7 b 1 3 1)1 4 8 1 c 1 2 1)2 5 6

d 1 3 2)1 3 6 6 e 1 2 1 2)1 3 5 4 5 f 1 6 1)1 7 8 1

g 1 0 0 3)3 2 1 9 8 7 h 1 1 1)7 9 9 9 9

a 11/24 b 11/40 c 2/14

d 10/46 e 11/213 f 11/10

g 321/24 h 720/79

Two other variations, where negative numbers come into the answer or remainder are worth

noting next.

15: SPECIAL DIVISION 151

10121 ÷ 113 = 89 remainder 64.

1 1 3 ) 1 0 1 2 1

1 3 1 3

1 3

1 1 1 6 4

When we come to the second column we find we have to bring 1 down into the

answer, multiplying this by the flagged 13 means we add 13 in the third row (two

minuses make a plus).

The answer 111 we finally arrive at is the same as 100 – 11 which is 89.

Find 2211 ÷ 112.

1 1 2 ) 2 2 1 1

1 2 2 4

0 0

2 0 3 1 = 20 rem 29 or 19 rem 83

20 remainder –29 means that 2211 is 29 short of 20 112's.

This means there are only 19 112's in 2211, so we add 112 to –29 to get 19

remainder 83.

18

19

 Practice N Divide the following:

a 1 1 2)1 2 3 4 b 1 2 1)3 9 9 3 c 1 0 3)4 3 2

d 1 0 1 2)2 1 3 1 2 e 1 2 2)3 3 3 3 f 1 2 3)2 5 8 4

g 1 1 3)1 3 6 9 6 h 1 2 1 2)1 3 7 9 8 7 i 1 1 1)7 9 9 9 9

j 1 2 1)2 6 5 2 k 1 2 3 1)3 3 0 3 3

a 11/02 b 33/00 c 4/20

d 21/060 e 27/39 f 21/01

g 121/23 h 113/1031 i 720/79

j 21/111 k 26/1027

“We go on, at last, to the long-promised Vedic process of STRAIGHT (AT SIGHT) DIVISIO

N

which is a simple and easy application of the URDHVA-TIRYAK Sutra which is capable o

f

immediate application to all cases and which we have repeatedly been describing as the

‘CROWNING GEM of all’ for the very simple reason that over and above the universality o

f

its application, it is the most supreme and superlative manifestation of the Vedic ideal of the

at-sight mental-one-line method of mathematical computation.”

From “Vedic Mathematics”, Page 240.

LESSON 16

THE CROWNING GEM

SUMMARY

Suppose we want to divide 209 by 52.

We need to know how many 52's there are in 209.

Looking at the first figures we see that since 5 goes into 20 four times we can expec

t

four 52's in 209.

We now take four 52's from 209 to see what is left.

Taking four 50's from 209 leaves 9 and we need to take four 2's away as well.

This leaves a remainder of 1.

We set the sum out like this:

2 2 0 9

5

0

4 1

The divisor, 52, is written with the 2 raised up, On the Flag, and a vertical line is

drawn one figure from the right-hand end to separate the answer, 4, from the

remainder, 1.

The steps are:

A. 5 into 20 goes 4 remainder 0, as shown.

B. Answer digit 4 multiplied by the flagged 2 gives 8, and this 8 taken from 09

leaves the remainder of 1, as shown.

16.1 Single Figure on the Flag – one-line division by 2-figure numbers.

16.2 Short Division Digression – choosing the remainder you want.

16.3 Longer Numbers – dividing numbers of any size.

16.4 Negative Flag Digits – using bar numbers to simplify the work.

16.5 Decimalising the Remainder

16.1 SINGLE FIGURE ON THE FLAG

The general division method, also called straight division, allows us to divide numbers of any

size by numbers of any size, in one line. Sri Bharati Krsna Tirthaji, the man who rediscovered

the Vedic system, called this ”the crowning gem of Vedic Mathematics”.

It comes under the Vertically and Crosswise Sutra.

1

16: THE CROWNING GEM 153

Divide 321 by 63.

We set the sum out as before:

3 3 2 1

6

2

5 6 = 5 remainder 6

Then 6 into 32 goes 5 remainder 2, as shown, and answer, 5, times the flagged 3

gives 15 which we take from the 21 to leave the remainder of 6.

2

What we are doing here is subtracting five 60's from 321, which leaves 21 and then

subtracting five 3's from the 21. That means we have subtracted five 63's and 6 is left.

What we are doing here is subtracting five 60's from 321, which leaves 21 and then

subtracting five 3's from the 21. That means we have subtracted five 63's and 6 is left.

In the following exercise set the sums out as shown above. In the following exercise set the sums out as shown above.

 Practice A Divide the following:  Practice A Divide the following:

a 103 ÷ 43 b 234 ÷ 54 c 74 ÷ 23 d 504 ÷ 72 a 103 ÷ 43 b 234 ÷ 54 c 74 ÷ 23 d 504 ÷ 72

e 444 ÷ 63 f 543 ÷ 82 g 567 ÷ 93 e 444 ÷ 63 f 543 ÷ 82 g 567 ÷ 93

a 2r17 b 4r18 c 3r5 d 7r0

e 7r3 f 6r51 g 6r9

16.2 SHORT DIVISION DIGRESSION

Suppose we want to divide 3 into 10.

The answer is clearly 3 remainder 1: 3) 1 0

3 rem 1

But other answers are possible: 3) 1 0 or 3) 1 0 or even 3) 1 0

2 rem 4 1 rem 7 4r em2

Since all of these are correct we can select the one which is best for a particular sum.

VEDIC MATHEMATICS MANUAL 1

154

 Practice B Copy each of the following sums and replace the question mark with the  Practice B Copy each of the following sums and replace the question mark with the

correct number: correct number:

a 5) 2 1a 5) 2 1 b 7) 5 1 c 4) 3 0 d 3) 2 2

3 rem ? 6 rem ? 6 rem ? ? rem 4

e 5) 4 2 f 6) 3 9 g 5) 2 4 h 7) 2 6

6 rem ? 4 rem ? 5 rem ? 4 rem ?

a 6 b 9 c 6 d 6

e 12 f 15 g 1 h 2

Find 503 ÷ 72.

If we proceed as before:

2 5 0 3

7

1

7

We find we have to take 14 from 13, which means the answer is 7 rem 1.

If a negative number is not acceptable however we can say that dividing 7 into 50 in

the sum above is not 7 rem 1, but 6 rem 8:

2 5 0 3

7

8

6 71

Then we find we can take 12 from 83 to get the positive remainder 71.

3

This reducing of the answer figure by 1 or 2 is sometimes necessary if negative numbers are

to be avoided. But it worth noting that when the answer figure is reduced by 1 the remainder

is increased by the first figure of the divisor. So in the answer above the 7 rem 1 is replaced

by 6 rem 8: the remainder is increased by 7, the first figure of 72.

Continuing the above example with the first method we would get:

2 5 0 3

7 1

7 1 = 6 rem 71.

16: THE CROWNING GEM 155

The 7 we get in the answer represents seven 72’s, so we take one of these (leaving 6 of them)

and add it to the negative remainder to get 72 +

The 7 we get in the answer represents seven 72’s, so we take one of these (leaving 6 of them)

and add it to the negative remainder to get 72 + 1 = 71 for the remainder.

 Practice C Divide the following:

a 97 ÷ 28 b 184 ÷ 47 c 210 ÷ 53 d 373 ÷ 63 e 353 ÷ 52

f 333 ÷ 44 g 267 ÷ 37 h 357 ÷ 59 i 353 ÷ 59

a 3r13 b 3r43 c 3r51 d 5r58 e 6r41

f 7r25 g 7r8 h 6r3 i 5r58

16.3 LONGER NUMBERS

17496 ÷ 72 = 243 remainder 0.

The procedure is just the same as before and goes in cycles.

We set the sum out in the usual way: 2 1 7 4 9 6

7

Then we divide 7 into 17 and put down 2 remainder 3, as shown:

2 1 7 4 9 6

7 3

2

Note the diagonal of numbers: 2, 3, 4.

Next we multiply the answer figure 2 1 7 4 9 6

by the flag figure: 2×2=4, take this 7

3 2

from the 34 to get 30, and then divide by 7 2 4

again, to get 4 remainder 2, as shown.

Then we repeat: multiply the last answer 2 1 7 4 9 6

figure by the flag to get 8, take this from 7

3 2 0

29 to get 21, then 7 into 21 goes 3 remainder 0, 2 4 3 0

as shown.

Finally we again multiply the last answer figure by the flag to get 6 and take this

from the 6 to get a remainder of 0.

4

VEDIC MATHEMATICS MANUAL 1

156

It is important to note that we proceed in cycles as shown in the diagrams above.

Each cycle is completed as each diagonal goes down.

50607 ÷ 123 = 411 rem 54.

Although the divisor has three digits here dividing by 12 is not a problem and so

we can use the same procedure:

Each cycle consists of :

A. multiplying the last answer figure by the flag,

B. taking this from the number indicated by the top two figures of the diagonal,

C. dividing the result by the first figure of the divisor and putting down the

answer and remainder.

That is: (divide), multiply, subtract, divide;

multiply, subtract, divide; . . .

×

–

÷

5

3 5 0 6 0 7

12 2 2 5

4 1 1 54

 Practice D Divide the following (the remainder is zero for the first four sums, so you

will know if it is correct):

a 19902 ÷ 62 b 44749 ÷ 73 c 1936 ÷ 88 d 4032 ÷ 72

e 4154 ÷ 92 f 23824 ÷ 51 g 92054 ÷ 63 h 142857 ÷ 61

i 12233 ÷ 53 j 9018 ÷ 71 k 8910 ÷ 72 l 23658 ÷ 112

m 40000000 ÷ 61 n 14018 ÷ 64 o 4712 ÷ 45 p 22222 ÷ 76

q 651258 ÷ 82 r 301291 ÷ 56 s 511717 ÷ 73 t 360293 ÷ 46

16: THE CROWNING GEM 157

a 321 b 613 c 22 d 56

e 45r14 f 467r7 g 1461r11 h 2341r56

i 230r43 j 127r1 k 123r54 l 211r26

m 655737r43 n 219r2 o 104r32 p 292r30

q 7942r14 r 5380r11 s 7009r60 t 7832r21

16.4 NEGATIVE FLAG DIGITS

97 ÷ 28 = 3 remainder 13.

If we proceed as usual we get: 8 9 7

2 3

3 13

We have to reduce the answer digit from 4 to 3 so that the remainder is big enough.

These reductions occur more frequently when the flag number is large (8 here).

This can be avoided however by rewriting 28 as 32:

2 9 7

3 0

3 13

3 into 9 goes 3 remainder 0.

We then multiply the 2 by 3 to get 6 and this is to be subtracted from 7.

But subtracting a negative number means adding it, so we get 7–6=13 for the

remainder.

When the flag number is large we often need to reduce more frequently. It is possible to avoid

these reductions however by using negative flag digits.

6

This is much easier and it means that:

whenever we use a bar number on the flag we add the product

at each step instead of subtracting it.

VEDIC MATHEMATICS MANUAL 1

158

 Practice E Divide the following, giving answer and remainder:

a 373 ÷ 58 b 357 ÷ 48 c 300 ÷ 59 d 321 ÷ 47

e 505 ÷ 78 f 543 ÷ 68

a 6r25 b 7r21 c 5r5 d 6r39

e 6r37 f 7r67

MULTIPLICATION REVERSED

Straight division can also be demonstrated by reversing the vertically and crosswise

multiplication method.

Given 4032÷72 for example: p q

7 2

4 0 3 2

We need the values of p and q so that the number pq multiplied by 72 gives 4032.

We see p must be 5 because p multiplied by 7 must account for the 40 in 4032 (or most of it).

And since 5×7=35 there is a remainder of 5.

So now we have: 5 q

7 2

53240

We are left with 532 to be accounted for by the crosswise multiplication and the vertical

product on the right. Considering the crosswise part we see we have 5×2=10 and we can take

this off the 53 in 532 to leave 43: to be produced by the other part of the crosswise product,

7×q. This tells us that q must be 6 and there is a remainder of 1 from the 53:

5 6

7 2

51

4032

The 12 now in the right-hand place is then fully accounted for by the vertical product on the

right, so there is no remainder.

All divisions can be done in this way, as a reversal of the multiplication process, and the on

the flag method in this chapter can be derived from it.

16: THE CROWNING GEM 159

16.5 DECIMALISING THE REMAINDER

We can continue the division when the remainder is reached and give the answer to as many

decimal places as required.

Find 40342 ÷ 73 to 5 decimal places.

7

3 4 0 3 4 2 .0 0 0 0 0 0

7 5 3 5 4 1 1 3 6 2

5 5 2. 6 3 0 1 3 7

To give an answer correct to 5 decimal places we should find 6 figures after the poin

t

in case we need to round up. So we put a decimal point and six zeros after 40342.

The decimal point in the answer goes where the vertical line went before, one figure

to the left of the last figure of the dividend.

We proceed as usual: multiply by the flag, subtract, divide by 7 for each cycle.

So the answer is 552.63014 to 5 decimal places.

Find 23.1 ÷ 83 to 3 decimal places.

8

The answer is clearly less than 1 because 23 is less than 83.

3 2 3. 1 0 0 0

8 7 9 5 2

0 . 2 7 8 3

As before the decimal point goes one figure to the left in the answer, which is 0.278.

 Practice F Find to 2 decimal places:

a 108 ÷ 31 b 4050 ÷ 73 c 9876 ÷ 94 d 25.52 ÷ 38

e 78 ÷ 49 f 6.7 ÷ 88 g 19 ÷ 62 h 62 ÷ 19

a 3.48 b 55.48 c 105.06 d 0.67

e 1.59 f 0.08 g 0.31 h 3.26

This straight division method is developed further in Manual 2 (or see References 1, 3, 5).

VEDIC MATHEMATICS MANUAL 1

160

VEDIC MATHEMATICS SUTRAS

Ek;i/ken pUveRn By One More than the One Before

1

ini%l' nvtXcrm' dxt" All from 9 and the Last from 10

Ek P 

adhikena urvena

2

¨?vRityRG>y;m' Vertically and Crosswise

pr;vTyR yojyet( Transpose and Apply

xUNy' s;MysmuCcyee If the Samuccaya is the Same it is Zero

a;nurUPye xUNy' aNyt( If One is in Ratio the Other is Zero

s'kln Vyvkln;>y;' By Addition and by Subtraction

pUr,;pUr,;>y;' By the Completion or Non-Completion

Puranapuranabhyam



clnkln;>y;m( Differential Calculus

y;vdUn' By the Deficiency

VyiP$smiP$" Specific and General

xeW;<y@en crme, The Remainders by the Last Digit

sop;NTydymNTy' The Ultimate and Twice the Penultimate

EkNyUnen pUveRn By One Less than the One Before

gui,tsmuCcy: The Product of the Sum

gu,ksmuCcy: All the Multipliers

4

5

6

7

8

9

10

11

12

13

14

15

16

3

Sunyam Samyasamuccaya



N

ikhilam N Das



avatascaramam atah



Urdhva Tiryagbhyam



Paravartya Yojayet

(Anurupya) Sunyamanyat

Sankalana Vyavakalanabhyam



Calana Kalanabhyam

Yavadunam

Vyastisamastih



 

S Cesanyankena aramena







Sopantyadvayamantyam

Ekanunena Purvena



Gunitsamuccayah



Gunakasamuccayah



SUTRAS AND SUB-SUTRAS 161

SUB-SUTRAS

a;nurUPye, Proportionately

1 A

ixPyte xeWs'D" The Remainder Remains Constant

nurupyena



a;/m;/en;NTymNTyen The First by the First and the Last by the Last

kevlw: s¢k' gu<y;t( For 7 the Multiplicand is 143

veP$nm( By Osculation

y;vdUn' t;vdun' Lessen by the Deficiency

y;vdUn' t;vdUnIkTy Whatever the Deficiency lessen by that amount

vg| c yojyet( and set up the Square of the Deficiency

aNTyyodRxkeSip Last Totalling 10

aNTyyorev Only the Last Terms

smuCcygui,t" The Sum of the Products

lopnSq;pn;>y;' By Alternate Elimination and Retention

ivlokn' By Mere Observation

gui,tsmCcuy" smuCcygui,t" The Product of the Sum is the

Sum of the Products

?vj;@ On the Flag

2 esamjnah





S Sisyate



3 Adyamadyenantyamantyena

4

5

6

7

8

9

10

11

12

13

14

Vestanam





Kevalaih Saptakam Gunyat



Samuccayagunitah



Antyayoreva

Antyayordasake'pi

Yavadunam Tavadunam



Yavadunam Tavadunikrtya Varganca Yojayet





Lopanasthapanabhyam

Vilokanam

Dhvajanka



amuccayagunitah



Gun S

 

itsamuccayah

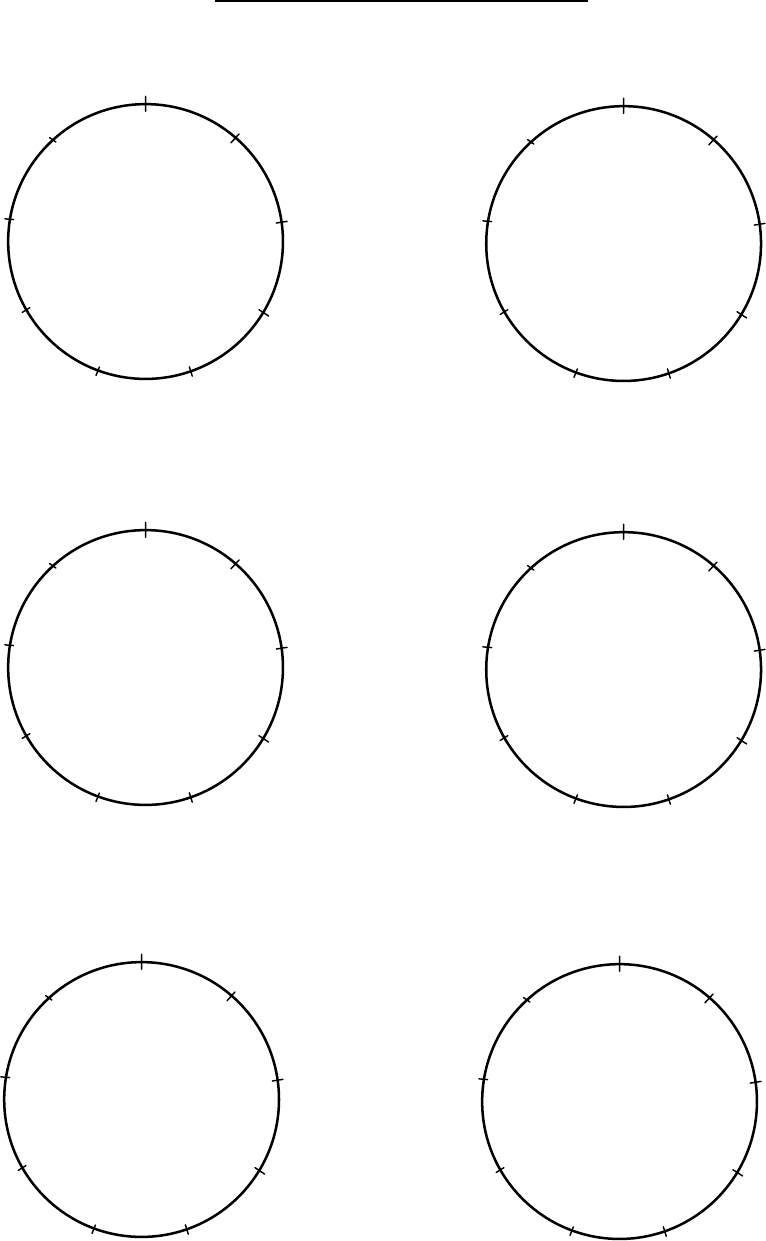
VEDIC MATHEMATICS MANUAL 1

162

9-POINT CIRCLES

1

9,0

2

3

6

8

7

5 4

1

9,0

2

3

6

8

7

54

1

9,0

2

3

6

8

7

5 4

1

9,0

2

3

6

8

7

54

1

9,0

2

3

6

8

7

5 4

1

9,0

2

3

6

8

7

54

REFERENCES

163

REFERENCES

1. Sri Bharati Krsna Tirthaji, “Vedic Mathematics”, published by Motilal Banarsidass, 1965.

ISBN 81-208-0163-6.

2. “Celebrating Perfection in Education”, Maharishi University Press 1997.

ISBN 81-7523-013-4.

3. Williams K. R. “Discover Vedic Mathematics”. Vedic Mathematics Research Group,

1984. ISBN 1-869932-01-3.

4. Williams K. R. and M. Gaskell “The Cosmic Calculator”. Motilal Banarsidass, 2002.

ISBN 81-208-1871-7.

5. Nicholas A. P., K. Williams, J. Pickles. Vertically and Crosswise. Inspiration Books, 1984.

ISBN 1-902517-03-2.

6. Sri Bharati Krsna Tirthaji, “Vedic Metaphysics”, published by Motilal Banarsidass, 1978.

ISBN 0-89581-472-2.

VEDIC MATHEMATICS MANUAL 1

164

INDEX OF THE VEDIC FORMULAE

SUTRAS

By One More than the One Before 3, 97, 109, 118

All from 9 and the Last from 10 48-, 70, 77, 87, 90, 97, 147, 149

Vertically and Crosswise 60, 66, 72, 106-, 121, 135-, 152-

Transpose and Apply 130-, 150

When the Samuccaya is the Same it is Zero 28

If One is in Ratio the Other is Zero

By Addition and by Subtraction 11, 82

By the Completion or Non-Completion 4

Differential Calculus

By the Deficiency 5, 75

Specific and General 99

The Remainders by the Last Digit

The Ultimate and Twice the Penultimate 22, 81, 82

By One Less than the One Before 51, 52, 97

The Product of the Sum 32

All the Multipliers

INDEX OF THE SUTRAS 165

INDEX OF THE VEDIC FORMULAE

SUB-SUTRAS

Proportionately 14, 71, 73, 96, 99, 102

The Remainder Remains Constant

The First by the First and the Last by the Last 79-, 98, 126

For 7 the Multiplicand is

By Osculation

Lessen by the Deficiency

Whatever the Deficiency lessen by that amount and set up the Square of the

Deficiency 75

Last Totalling Ten 98

Only the Last Terms

The Sum of the Products

By Alternate Elimination and Retention 54

By Mere Observation 102

The Product of the Sum is the Sum of the Products 32

On the Flag 41, 46, 77

VEDIC MATHEMATICS MANUAL 1

166

INDEX

Addition 4-, 54

left to right 40

of digits 24

Algebraic products 112

Algebraic squaring 124

Bar numbers 85-

advantages 88

Base multiplication 59-

Base numbers 49

Casting out nines 26

Checking calculations 79-

Completion 4-

Crowning gem 152

Deficiency 5, 65

Digit 24

Digit sum 24-

check 31, 78, 84, 114

of squares 125

puzzles 29-

Divisibility 81-

Division

by 5 etc. 21

by eight etc. 143

by 99 etc. 145

by nine 139

checking 78

by numbers just over a base 150

by numbers just under a base 146

general 152-

number splitting 57

Doubling and halving 14-, 43

Duplex 121, 128

Equations 130-

Extending tables 19

Fractions 134-

comparing 137

Halving 17

Left to right calculations

addition 40

advantages 47

subtraction 44

multiplication 42

Moving multiplier 109

Multiplication

binomials 112

by 4 etc. 16

by 5 etc. 20

by eleven 92

by nines 94

by all from 9... 59

by first by first… 98

by observation 101

by one more.. 96

by using the average 99

by vertically and crosswise 59-, 105-

checking 33

general 105-

left to right 42

moving multiplier 109

near a base 59-

near different bases 74

near a temporary base 71-

number splitting 56

reversing 158

right to left 116

squaring 119-

tables 19, 59-

Mental addition 6

Mental arithmetic 41, 69

Money 53

Moving multiplier 109

Multiples 4

Nine point circle 26

Number splitting

addition 54

division 18, 57

multiplication 56

squaring 123

subtraction 55

Percentages 102

Recurring decimals 64

Repeating numbers 101

Russian Peasant Multiplication 69

Special division 139-

Special multiplication 92-

Special numbers 101

Square roots of perfect squares 126

Squaring 119-

algebraic 124

general method 121

numbers near a base 75

numbers near 50 120

numbers ending with five 119

Straight division 105

Subtraction 12, 55

by all from 9... 49-, 88

checking 45

from a base 49

left to right 44

Ten point circle 3

Vedic Square 34-

OTHER VEDIC MATHEMATICS BOOKS

Teacher’s Manual – Intermediate

This is similar to the elementary book but covers a greater range (aimed at teachers of grades 5 to 10) including

divisibility, square roots, applications of triples, further equations, combined operations etc. ISBN 978-1-

902517-17-9

Teacher’s Manual – Advanced

This includes: calculus, series, logs and exponentials, trigonometry (including solving trig equations, proving

identities), solution of equations (special types, quadratics, cubics, transcendental), complex numbers, coordinate

geometry, transformation geometry, Simple Harmonic Motion, projectile motion, forces, work moments, etc.

ISBN 978-1-902517-18-6

The Cosmic Computer - Abridged Edition

This is a shortened version of the full course described next. It contains some of the most striking Vedic

methods. It is beautifully illustrated with full colour cover and is perfect bound (paperback). A good introduction

to Vedic Mathematics. Authors: Kenneth Williams and Mark Gaskell. 216 pages. Almost A4 in size. 1997. ISBN

978-0-9531782-0-9

The Cosmic Computer Course

This covers Key Stage 3 (age 11-14 years) of the National Curriculum for England and Wales. It consists of

three textbooks, a Teacher's Guide and an Answer Book. Much of the material in Book 1 is suitable for children

as young as eight and this is developed from here to topics such as Pythagoras' Theorem and Quadratic

Equations in Book 3. The Teacher's Guide contains a Summary of each Book, a Unified Field Chart (showing

the whole subject of mathematics and how each of the parts are related), hundreds of Mental Tests (these revise

previous work, introduce new ideas and are carefully correlated with the rest of the course), Extension Sheets

(about 16 per book) for fast pupils or for extra classwork, Revision Tests, Games, Worksheets etc.

Discover Vedic Mathematics

This has sixteen chapters each of which focuses on one of the Vedic Sutras or sub-Sutras and shows many

applications of each. It goes into some detail, showing variations and giving explanations and proofs.. Also

contains solutions to GCSE and 'A' level examination questions. Author: K. Williams, 216 pages. 1984.

Triples

This book shows applications of Pythagorean Triples (like 3,4,5). A simple, elegant system for combining these

triples gives unexpected and powerful general methods for solving a wide range of mathematical problems, with

far less effort than conventional methods use. The easy text fully explains this method which has applications in

trigonometry (you do not need any of those complicated formulae), coordinate geometry (2 and 3 dimensions)

transformations (2 and 3 dimensions), simple harmonic motion, astronomy etc. etc. Author: K. Williams, 176

pages, paperback.

Vertically and Crosswise

This is an advanced book of sixteen chapters on one Sutra ranging from elementary multiplication etc. to the

solution of non-linear partial differential equations. It deals with (i) calculation of common functions and their

series expansions, and (ii) the solution of equations, starting with simultaneous equations and moving on to

algebraic, transcendental and differential equations. Authors: A. P. Nicholas, K. Williams, J. Pickles, 200 pages,

paperback, 1999.

The Natural Calculator

This book focuses on mental mathematics and has a detailed introduction outlining its merits. There are nine

chapters, mainly on multiplication but including addition, subtraction and division. Author: K. Williams, 100

pages, paperback. ISBN 978-1-902517-15-5

For further details and other books please visit http://www.vedicmaths.org

Manual 1

Navigation menu

Versions of this User Manual:

Views

Navigation