Manual 1 Gvv Python 2d
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 4
1
JEE Problems in Linear
Algebra: 2D
G V V Sharma∗
Contents
1 Line 1
2 Medians of a Triangle 2
3 Altitudes of a Triangle 3
4 Angle Bisectors of a Triangle 4
Abstract—This manual introduces matrix computations
using python and the properties of a triangle.
1 Line
1.1 Let
A= −2
−2!,B= 1
3!,C= 4
−1!.(1)
Draw ∆ABC.
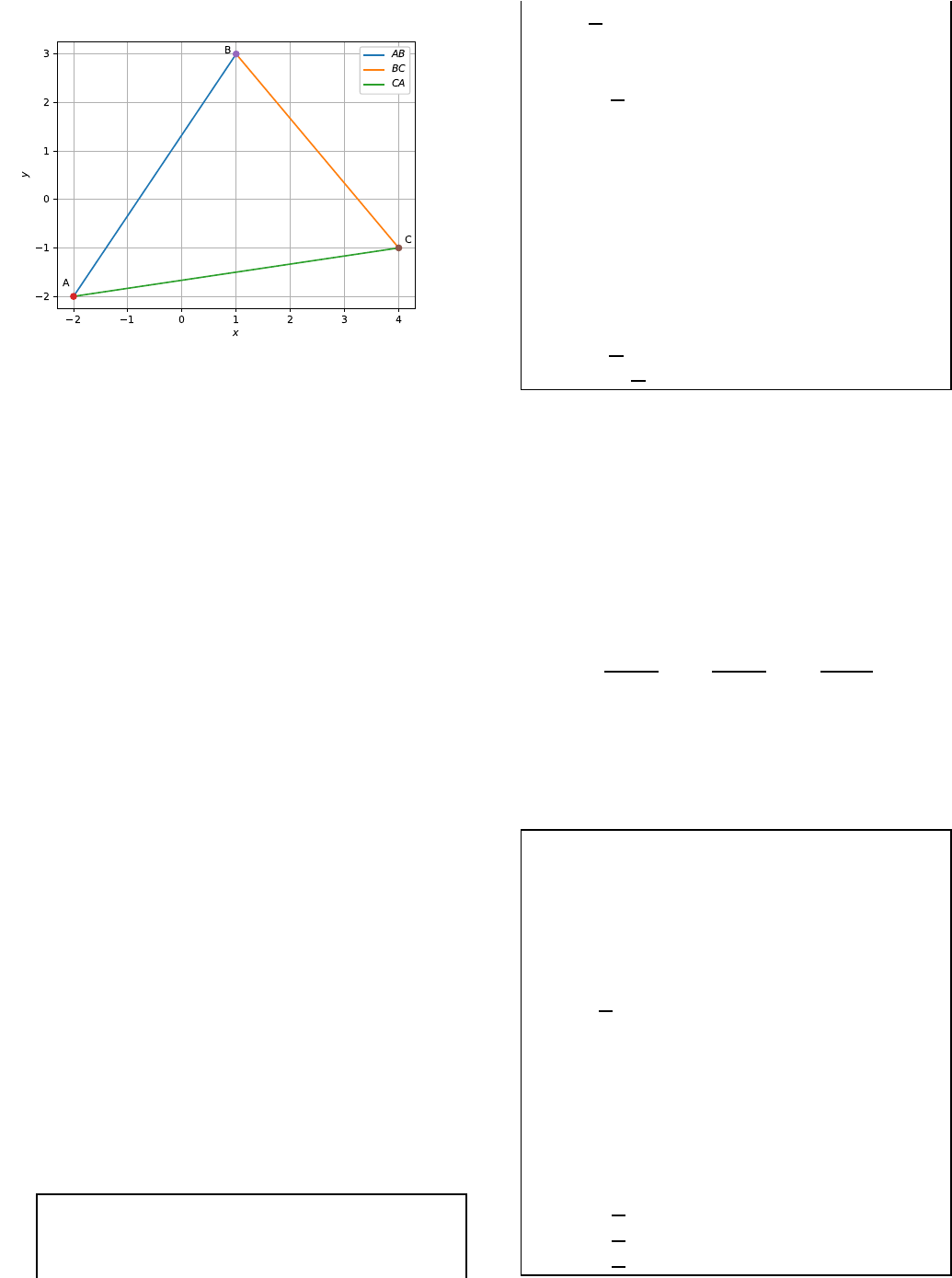
Solution: The following code yields the de-
sired plot in Fig. 1.1
#Code by GVV Sharma
#January 28, 2019
#released under GNU GPL
import numpy as np
import matplotlib.pyplot as plt
#if using termux
import subprocess
import shlex
#end if
A=np.array([−2,−2])
B=np.array([1,3])
C=np.array([4,−1])
len =10
*The author is with the Department of Electrical Engineering,
Indian Institute of Technology, Hyderabad 502285 India e-mail:
gadepall@iith.ac.in. All content in this manual is released under GNU
GPL. Free and open source.
lam 1 =np.linspace(0,1,len)
x AB =np.zeros((2,len))
x BC =np.zeros((2,len))
x CA =np.zeros((2,len))
for i in range(len):
temp1 =A+lam 1[i]∗(B−A)
x AB[:,i]=temp1.T
temp2 =B+lam 1[i]∗(C−B)
x BC[:,i]=temp2.T
temp3 =C+lam 1[i]∗(A−C)
x CA[:,i]=temp3.T
#print(x AB[0,:],x AB[1,:])
plt.plot(x AB[0,:],x AB[1,:],label=’$AB$’)
plt.plot(x BC[0,:],x BC[1,:],label=’$BC$’)
plt.plot(x CA[0,:],x CA[1,:],label=’$CA$’)
plt.plot(A[0], A[1], ’o’)
plt.text(A[0] ∗(1 +0.1), A[1] ∗(1 −0.1) , ’
A’)
plt.plot(B[0], B[1], ’o’)
plt.text(B[0] ∗(1 −0.2), B[1] ∗(1) , ’B’)
plt.plot(C[0], C[1], ’o’)
plt.text(C[0] ∗(1 +0.03), C[1] ∗(1 −0.1) ,
’C’)
plt.xlabel(’$x$’)
plt.ylabel(’$y$’)
plt.legend(loc=’best’)
plt.grid() # minor
#if using termux
plt.savefig(’../figs/triangle.pdf’)
plt.savefig(’../figs/triangle.eps’)
subprocess.run(shlex.split(”termux−open ../
figs/triangle.pdf”))
#else
#plt.show()
2
Fig. 1.1
1.2 Find the equation of AB.
Solution: The desired equation is obtained as
AB :x=A+λ1(B−A)(2)
=− 2
2!+λ1 3
5!(3)
Alternatively, the desired equation is
5−3(x−A)=0 (4)
=⇒5−3x=−5−3 2
2!=−4 (5)
1.3 Find the direction vector and the normal vector
for AB
Solution: Let
TAB =A B= −2 1
−2 3!(6)
The direction vector of AB is
m=B−A=TAB −1
1!= 3
5!(7)
The normal vector nis defined as
nTm=0 (8)
=⇒n= 0 1
−1 0!m= 5
−3!(9)
1.4 Write a python code for computing the direc-
tion and normal vectors.
import numpy as np
def dir vec(AB):
return np.matmul(AB,dvec)
def norm vec(AB):
return np.matmul(omat,np.matmul(AB,dvec
))
A=np.array([−2,−2])
B=np.array([1,3])
dvec =np.array([−1,1])
omat =np.array([[0,1],[−1,0]])
AB =np.vstack((A,B)).T
print (dir vec(AB))
print (norm vec(AB))
1.5 Find the equations of BC and CA
2 Medians of a Triangle
2.1 Find the coordinates of D,Eand Fof the
mid points of AB,BC and CA respectively for
∆ABC.
Solution: The coordinates of the mid points
are given by
D=B+C
2,E=C+A
2,F=A+B
2(10)
The following code computes the values result-
ing in
D= 2.5
1!,E= 1
−1.5!,F= −0.5
0.5!,(11)
#This program calculates the mid point
between
#any two coordinates
import numpy as np
import matplotlib.pyplot as plt
def mid pt(B,C):
D=(B+C)/2
return D
A=np. matrix(’−2;−2’)
B=np. matrix(’1;3’)
C=np. matrix(’4;−1’)
print(mid pt(B,C))
print(mid pt(C,A))
print(mid pt(A,B))
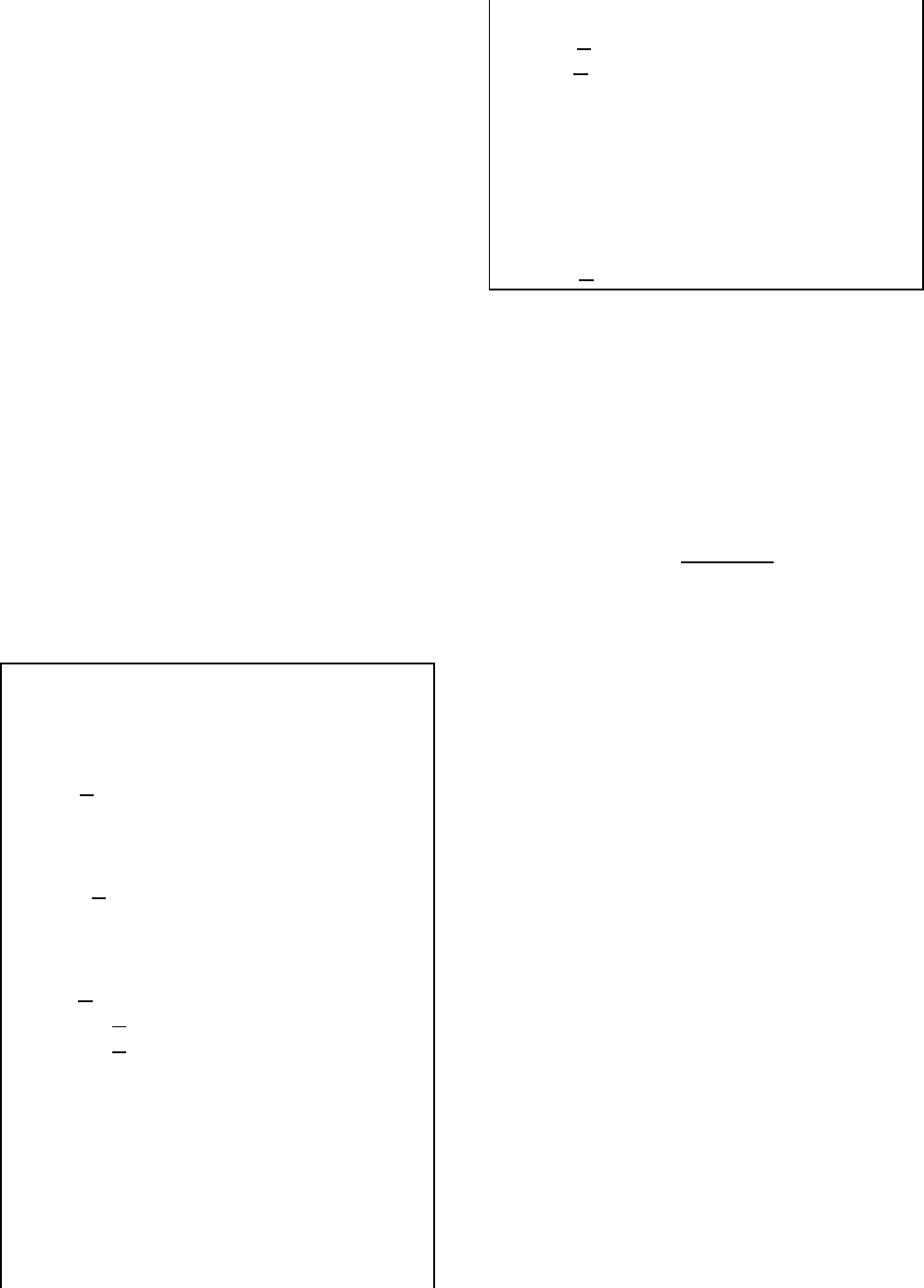
3
2.2 Find the equations of AD,BE and CF. These
lines are the medians of ∆ABC
Solution: Use the code in Problem 1.4.
2.3 Find the point of intersection of AD and CF.
Solution: Let the respective equations be
nT
1x=p1and (12)
nT
2x=p2(13)
This can be written as the matrix equation
nT
1
nT
2!x=p(14)
=⇒NTx=p(15)
where
N=n1n2,(16)
The point of intersection is then obtained as
x=NT−1p(17)
=N−Tp(18)
The following code yields the point of inter-
section
G= 1
0!(19)
#This program calculates the
#intersection of AD and CF
import numpy as np
def mid pt(B,C):
D=(B+C)/2
return D
def norm vec(AB):
return np.matmul(omat,np.matmul(AB,dvec
))
def line intersect(AD,CF):
n1=norm vec(AD)
n2=norm vec(CF)
N=np.vstack((n1,n2))
p=np.zeros(2)
p[0] =np.matmul(n1,AD[:,0])
p[1] =np.matmul(n2,CF[:,0])
return np.matmul(np.linalg.inv(N),p)
A=np.array([−2,−2])
B=np.array([1,3])
C=np.array([4,−1])
D=mid pt(B,C)
F=mid pt(A,B)
AD =np.vstack((A,D)).T
CF =np.vstack((C,F)).T
dvec =np.array([−1,1])
omat =np.array([[0,1],[−1,0]])
print(line intersect(AD,CF))
2.4 Using the code in Problem 2.3, verify that G
is the point of intersection of BE,CF as well
as AD,BE.Gis known as the centroid of
∆ABC.
2.5 Graphically show that the medians of ∆ABC
meet at the centroid.
2.6 Verify that
G=A+B+C
3(20)
3 Altitudes of a Triangle
3.1 In ∆ABC, Let Pbe a point on BC such that
AP ⊥BC. Then AP is defined to be an altitude
of ∆ABC.
3.2 Find the equation of AP.
3.3 Find the equations of the altitudes BQ and CR.
3.4 Find the point of intersection of AP and BQ.
Solution: Using the code in Problem 2.3, the
desired point of intersection is
H= 1.407
0.56 !(21)
Interestingly, BQ and CR also intersect at the
same point. Thus, the altitudes of a triangle
meet at a single point known as the orthocentre
3.5 Find P,Q,R.
Solution: P is the intersection of AP and BC.
Thus, the code in Problem 2.3 can be used to
find P. The desired coordinates are
P= 2.32
1.24!,Q= 1.73
−1.38!,R= 0.03
1.38!(22)
3.6 Draw AP,BQ and CR and verify that they meet
at H.
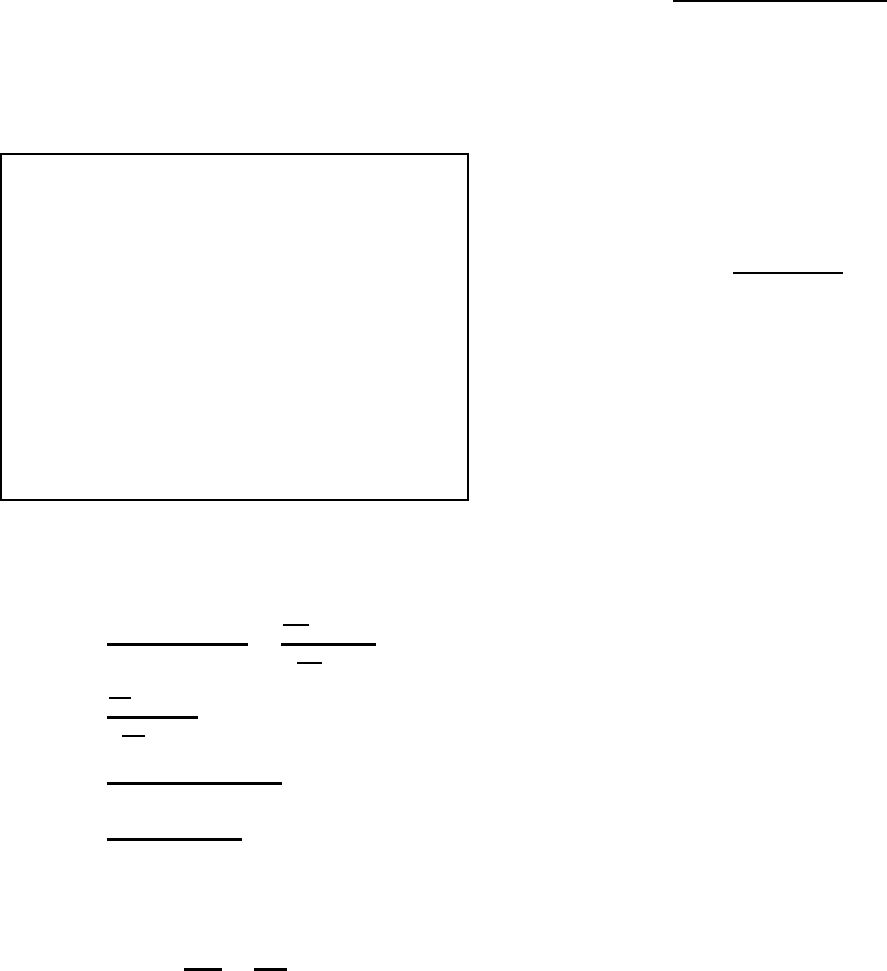
4
4 Angle Bisectors of a Triangle
4.1 In ∆ABC, let Ube a point on BC such that
∠BAU =∠CAU. Then AU is known as the
angle bisector.
4.2 Find the length of AB,BC and CA
Solution: The length of CA is given by
CA =kC−Ak(23)
The following code calculates the respective
values as
AB =5.83,BC =5,CA =6.08 (24)
#This program calculates the distance
between
#two points
import numpy as np
import matplotlib.pyplot as plt
A=np.array([−2,−2])
B=np.array([1,3])
C=np.array([4,−1])
print (np.linalg.norm(A−B))
4.3 If AU,BV and CW are the angle bisectors, find
the coordinates of U,Vand W.
Solution: Using the section formula,
W=AW.B+WB.A
AW +WB =
AW
WB .B+A
AW
WB +1(25)
=
CA
BC .B+A
CA
BC +1(26)
=CA ×B+BC ×A
BC +CA (27)
=a×A+b×B
a+b(28)
where a=BC,b=CA, since the angle bisector
has the property that
AW
WB =CA
AB (29)
4.4 Write a program to find U,V,W.
4.5 Find the intersection of AU and BV.
Solution: Using the code in Problem 2.3, the
desired point of intersection is
I= 1.15
0.14!(30)
It is easy to verify that even BV and CW meet
at the same point. Iis known as the incentre
of ∆ABC.
4.6 Draw AU,BV and CW and verify that they
meet at a point I.
4.7 Verify that
I=BC.A+CA.B+AB.C
AB +BC +CA (31)
4.8 Let the perpendicular from Ito AB be IX. If
the equation of AB is
nT(x−A)=0 (32)
show that
IX =nT(I−A)
knk(33)
Verify through a Python script.
4.9 If IY ⊥BC and IZ ⊥CA, verify that
IX =IY =IZ =r(34)
ris known as the inradius of ∆ABC.
4.10 Draw the incircle of △ABC
4.11 Draw the circumcircle of △ABC