Math SL Guide

User Manual:

Open the PDF directly: View PDF .
Page Count: 64

Introduction
Syllabus
Assessment
Appendices
- Glossary of command terms
- Notation list

Mathematics SL guide

First examinations 2014

Diploma Programme

Mathematics SL guide

First examinations 2014

Diploma Programme

Mathematics SL guide

International Baccalaureate, Baccalauréat International and Bachillerato Internacional are

registered trademarks of the International Baccalaureate Organization.

Printed in the United Kingdom by Antony Rowe Ltd, Chippenham, Wiltshire 5033

Published March 2012

Published on behalf of the International Baccalaureate Organization, a not-for-profit

educational foundation of 15 Route des Morillons, 1218 Le Grand-Saconnex, Geneva,

Switzerland by the

International Baccalaureate Organization (UK) Ltd

Peterson House, Malthouse Avenue, Cardiff Gate

Cardiff, Wales CF23 8GL

United Kingdom

Phone: +44 29 2054 7777

Fax: +44 29 2054 7778

Website: www.ibo.org

The International Baccalaureate Organization (known as the IB) offers three high-quality

and challenging educational programmes for a worldwide community of schools, aiming

to create a better, more peaceful world. This publication is one of a range of materials

produced to support these programmes.

The IB may use a variety of sources in its work and checks information to verify accuracy

and authenticity, particularly when using community-based knowledge sources such as

Wikipedia. The IB respects the principles of intellectual property and makes strenuous

efforts to identify and obtain permission before publication from rights holders of all

in this publication and will be pleased to correct any errors or omissions at the earliest

opportunity.

system, or transmitted, in any form or by any means, without the prior written permission

of the IB, or as expressly permitted by law or by the IB’s own rules and policy. See

http://www.ibo.org/copyright.

IB merchandise and publications can be purchased through the IB store at

http://store.ibo.org. General ordering queries should be directed to the Sales and Marketing

Department in Cardiff.

Phone: +44 29 2054 7746

Fax: +44 29 2054 7779

Email: sales@ibo.org

IB mission statement

The International Baccalaureate aims to develop inquiring, knowledgeable and caring young people who help to

create a better and more peaceful world through intercultural understanding and respect.

To this end the organization works with schools, governments and international organizations to develop challenging

programmes of international education and rigorous assessment.

These programmes encourage students across the world to become active, compassionate and lifelong learners who

understand that other people, with their differences, can also be right.

IB learner profile

The aim of all IB programmes is to develop internationally minded people who, recognizing their common humanity

and shared guardianship of the planet, help to create a better and more peaceful world.

IB learners strive to be:

Inquirers They develop their natural curiosity. They acquire the skills necessary to conduct inquiry

and research and show independence in learning. They actively enjoy learning and this love

of learning will be sustained throughout their lives.

Knowledgeable They explore concepts, ideas and issues that have local and global significance. In so doing,

they acquire in-depth knowledge and develop understanding across a broad and balanced

range of disciplines.

Thinkers They exercise initiative in applying thinking skills critically and creatively to recognize

and approach complex problems, and make reasoned, ethical decisions.

Communicators They understand and express ideas and information confidently and creatively in more

than one language and in a variety of modes of communication. They work effectively and

willingly in collaboration with others.

Principled They act with integrity and honesty, with a strong sense of fairness, justice and respect for

the dignity of the individual, groups and communities. They take responsibility for their

own actions and the consequences that accompany them.

Open-minded They understand and appreciate their own cultures and personal histories, and are open

to the perspectives, values and traditions of other individuals and communities. They are

accustomed to seeking and evaluating a range of points of view, and are willing to grow

from the experience.

Caring They show empathy, compassion and respect towards the needs and feelings of others.

They have a personal commitment to service, and act to make a positive difference to the

lives of others and to the environment.

Risk-takers They approach unfamiliar situations and uncertainty with courage and forethought, and

have the independence of spirit to explore new roles, ideas and strategies. They are brave

and articulate in defending their beliefs.

Balanced They understand the importance of intellectual, physical and emotional balance to achieve

personal well-being for themselves and others.

Reflective They give thoughtful consideration to their own learning and experience. They are able to

assess and understand their strengths and limitations in order to support their learning and

personal development.

Mathematics SL guide

Contents

Introduction 1

Purpose of this document 1

The Diploma Programme 2

Nature of the subject 4

Aims 8

Assessment objectives 9

Syllabus 10

Syllabus outline 10

Approaches to the teaching and learning of mathematics SL 11

Prior learning topics 15

Syllabus content 17

Assessment 37

Assessment in the Diploma Programme 37

Assessment outline 39

External assessment 40

Internal assessment 43

Appendices 50

Glossary of command terms 50

Notation list 52

Mathematics SL guide 1

Purpose of this document

Introduction

This publication is intended to guide the planning, teaching and assessment of the subject in schools. Subject

teachers are the primary audience, although it is expected that teachers will use the guide to inform students

and parents about the subject.

This guide can be found on the subject page of the online curriculum centre (OCC) at http://occ.ibo.org, a

password-protected IB website designed to support IB teachers. It can also be purchased from the IB store at

http://store.ibo.org.

Additional resources

Additional publications such as teacher support materials, subject reports, internal assessment guidance

and grade descriptors can also be found on the OCC. Specimen and past examination papers as well as

markschemes can be purchased from the IB store.

Teachers are encouraged to check the OCC for additional resources created or used by other teachers. Teachers

can provide details of useful resources, for example: websites, books, videos, journals or teaching ideas.

First examinations 2014

2Mathematics SL guide

Introduction

The Diploma Programme

The Diploma Programme is a rigorous pre-university course of study designed for students in the 16 to 19

age range. It is a broad-based two-year course that aims to encourage students to be knowledgeable and

inquiring, but also caring and compassionate. There is a strong emphasis on encouraging students to develop

intercultural understanding, open-mindedness, and the attitudes necessary for them to respect and evaluate a

range of points of view.

The Diploma Programme hexagon

The course is presented as six academic areas enclosing a central core (see figure 1). It encourages the concurrent

study of a broad range of academic areas. Students study: two modern languages (or a modern language and

a classical language); a humanities or social science subject; an experimental science; mathematics; one of

the creative arts. It is this comprehensive range of subjects that makes the Diploma Programme a demanding

course of study designed to prepare students effectively for university entrance. In each of the academic areas

students have flexibility in making their choices, which means they can choose subjects that particularly

interest them and that they may wish to study further at university.

Studies in language

and literature

Individuals

and societies

Mathematics

The arts

Experimental

sciences

Language

acquisition Group 2

Group 4

Group 6

Group 5

Group 1

Group 3

Figure 1

Diploma Programme model

Mathematics SL guide 3

The Diploma Programme

Choosing the right combination

Students are required to choose one subject from each of the six academic areas, although they can choose a

second subject from groups 1 to 5 instead of a group 6 subject. Normally, three subjects (and not more than

four) are taken at higher level (HL), and the others are taken at standard level (SL). The IB recommends 240

teaching hours for HL subjects and 150 hours for SL. Subjects at HL are studied in greater depth and breadth

than at SL.

At both levels, many skills are developed, especially those of critical thinking and analysis. At the end of

the course, students’ abilities are measured by means of external assessment. Many subjects contain some

element of coursework assessed by teachers. The courses are available for examinations in English, French and

Spanish, with the exception of groups 1 and 2 courses where examinations are in the language of study.

The core of the hexagon

All Diploma Programme students participate in the three course requirements that make up the core of the

hexagon. Reflection on all these activities is a principle that lies at the heart of the thinking behind the Diploma

Programme.

The theory of knowledge course encourages students to think about the nature of knowledge, to reflect on

the process of learning in all the subjects they study as part of their Diploma Programme course, and to make

connections across the academic areas. The extended essay, a substantial piece of writing of up to 4,000 words,

enables students to investigate a topic of special interest that they have chosen themselves. It also encourages

them to develop the skills of independent research that will be expected at university. Creativity, action, service

involves students in experiential learning through a range of artistic, sporting, physical and service activities.

The IB mission statement and the IB learner profile

The Diploma Programme aims to develop in students the knowledge, skills and attitudes they will need to

fulfill the aims of the IB, as expressed in the organization’s mission statement and the learner profile. Teaching

and learning in the Diploma Programme represent the reality in daily practice of the organization’s educational

philosophy.

4Mathematics SL guide

Nature of the subject

Introduction

The nature of mathematics can be summarized in a number of ways: for example, it can be seen as a well-

defined body of knowledge, as an abstract system of ideas, or as a useful tool. For many people it is probably

a combination of these, but there is no doubt that mathematical knowledge provides an important key to

understanding the world in which we live. Mathematics can enter our lives in a number of ways: we buy

produce in the market, consult a timetable, read a newspaper, time a process or estimate a length. Mathematics,

for most of us, also extends into our chosen profession: visual artists need to learn about perspective; musicians

need to appreciate the mathematical relationships within and between different rhythms; economists need

to recognize trends in financial dealings; and engineers need to take account of stress patterns in physical

materials. Scientists view mathematics as a language that is central to our understanding of events that occur

in the natural world. Some people enjoy the challenges offered by the logical methods of mathematics and

the adventure in reason that mathematical proof has to offer. Others appreciate mathematics as an aesthetic

experience or even as a cornerstone of philosophy. This prevalence of mathematics in our lives, with all its

interdisciplinary connections, provides a clear and sufficient rationale for making the study of this subject

compulsory for students studying the full diploma.

Summary of courses available

Because individual students have different needs, interests and abilities, there are four different courses in

mathematics. These courses are designed for different types of students: those who wish to study mathematics

in depth, either as a subject in its own right or to pursue their interests in areas related to mathematics; those

who wish to gain a degree of understanding and competence to understand better their approach to other

subjects; and those who may not as yet be aware how mathematics may be relevant to their studies and in their

daily lives. Each course is designed to meet the needs of a particular group of students. Therefore, great care

should be taken to select the course that is most appropriate for an individual student.

In making this selection, individual students should be advised to take account of the following factors:

• their own abilities in mathematics and the type of mathematics in which they can be successful

• their own interest in mathematics and those particular areas of the subject that may hold the most interest

for them

• their other choices of subjects within the framework of the Diploma Programme

• their academic plans, in particular the subjects they wish to study in future

• their choice of career.

Teachers are expected to assist with the selection process and to offer advice to students.

Mathematical studies SL

This course is available only at standard level, and is equivalent in status to mathematics SL, but addresses

different needs. It has an emphasis on applications of mathematics, and the largest section is on statistical

techniques. It is designed for students with varied mathematical backgrounds and abilities. It offers students

Mathematics SL guide 5

Nature of the subject

opportunities to learn important concepts and techniques and to gain an understanding of a wide variety

of mathematical topics. It prepares students to be able to solve problems in a variety of settings, to develop

more sophisticated mathematical reasoning and to enhance their critical thinking. The individual project is an

extended piece of work based on personal research involving the collection, analysis and evaluation of data.

Students taking this course are well prepared for a career in social sciences, humanities, languages or arts.

These students may need to utilize the statistics and logical reasoning that they have learned as part of the

mathematical studies SL course in their future studies.

Mathematics SL

This course caters for students who already possess knowledge of basic mathematical concepts, and who are

equipped with the skills needed to apply simple mathematical techniques correctly. The majority of these

students will expect to need a sound mathematical background as they prepare for future studies in subjects

such as chemistry, economics, psychology and business administration.

Mathematics HL

This course caters for students with a good background in mathematics who are competent in a range of

analytical and technical skills. The majority of these students will be expecting to include mathematics as

a major component of their university studies, either as a subject in its own right or within courses such as

physics, engineering and technology. Others may take this subject because they have a strong interest in

mathematics and enjoy meeting its challenges and engaging with its problems.

Further mathematics HL

This course is available only at higher level. It caters for students with a very strong background in mathematics

who have attained a high degree of competence in a range of analytical and technical skills, and who display

considerable interest in the subject. Most of these students will expect to study mathematics at university, either

as a subject in its own right or as a major component of a related subject. The course is designed specifically

to allow students to learn about a variety of branches of mathematics in depth and also to appreciate practical

applications. It is expected that students taking this course will also be taking mathematics HL.

Note: Mathematics HL is an ideal course for students expecting to include mathematics as a major component

of their university studies, either as a subject in its own right or within courses such as physics, engineering

or technology. It should not be regarded as necessary for such students to study further mathematics HL.

Rather, further mathematics HL is an optional course for students with a particular aptitude and interest in

mathematics, enabling them to study some wider and deeper aspects of mathematics, but is by no means a

necessary qualification to study for a degree in mathematics.

Mathematics SL—course details

The course focuses on introducing important mathematical concepts through the development of mathematical

techniques. The intention is to introduce students to these concepts in a comprehensible and coherent way,

rather than insisting on the mathematical rigour required for mathematics HL. Students should, wherever

possible, apply the mathematical knowledge they have acquired to solve realistic problems set in an appropriate

context.

The internally assessed component, the exploration, offers students the opportunity for developing

independence in their mathematical learning. Students are encouraged to take a considered approach to

various mathematical activities and to explore different mathematical ideas. The exploration also allows

students to work without the time constraints of a written examination and to develop the skills they need for

communicating mathematical ideas.

Mathematics SL guide6

Nature of the subject

This course does not have the depth found in the mathematics HL courses. Students wishing to study subjects

with a high degree of mathematical content should therefore opt for a mathematics HL course rather than a

mathematics SL course.

Prior learning

Mathematics is a linear subject, and it is expected that most students embarking on a Diploma Programme

(DP) mathematics course will have studied mathematics for at least 10 years. There will be a great variety

of topics studied, and differing approaches to teaching and learning. Thus students will have a wide variety

of skills and knowledge when they start the mathematics SL course. Most will have some background in

arithmetic, algebra, geometry, trigonometry, probability and statistics. Some will be familiar with an inquiry

approach, and may have had an opportunity to complete an extended piece of work in mathematics.

At the beginning of the syllabus section there is a list of topics that are considered to be prior learning for the

mathematics SL course. It is recognized that this may contain topics that are unfamiliar to some students, but it

is anticipated that there may be other topics in the syllabus itself that these students have already encountered.

Teachers should plan their teaching to incorporate topics mentioned that are unfamiliar to their students.

Links to the Middle Years Programme

The prior learning topics for the DP courses have been written in conjunction with the Middle Years

Programme (MYP) mathematics guide. The approaches to teaching and learning for DP mathematics build

on the approaches used in the MYP. These include investigations, exploration and a variety of different

assessment tools.

A continuum document called Mathematics: The MYP–DP continuum (November 2010) is available on the

DP mathematics home pages of the OCC. This extensive publication focuses on the alignment of mathematics

across the MYP and the DP. It was developed in response to feedback provided by IB World Schools, which

expressed the need to articulate the transition of mathematics from the MYP to the DP. The publication also

highlights the similarities and differences between MYP and DP mathematics, and is a valuable resource for

teachers.

Mathematics and theory of knowledge

The Theory of knowledge guide (March 2006) identifies four ways of knowing, and it could be claimed that

these all have some role in the acquisition of mathematical knowledge. While perhaps initially inspired by data

from sense perception, mathematics is dominated by reason, and some mathematicians argue that their subject

is a language, that it is, in some sense, universal. However, there is also no doubt that mathematicians perceive

beauty in mathematics, and that emotion can be a strong driver in the search for mathematical knowledge.

As an area of knowledge, mathematics seems to supply a certainty perhaps missing in other disciplines. This

may be related to the “purity” of the subject that makes it sometimes seem divorced from reality. However,

mathematics has also provided important knowledge about the world, and the use of mathematics in science

and technology has been one of the driving forces for scientific advances.

Despite all its undoubted power for understanding and change, mathematics is in the end a puzzling

phenomenon. A fundamental question for all knowers is whether mathematical knowledge really exists

independently of our thinking about it. Is it there “waiting to be discovered” or is it a human creation?

Mathematics SL guide 7

Nature of the subject

Students’ attention should be drawn to questions relating theory of knowledge (TOK) and mathematics, and

they should be encouraged to raise such questions themselves, in mathematics and TOK classes. This includes

questioning all the claims made above. Examples of issues relating to TOK are given in the “Links” column of

the syllabus. Teachers could also discuss questions such as those raised in the “Areas of knowledge” section of

the TOK guide.

Mathematics and the international dimension

Mathematics is in a sense an international language, and, apart from slightly differing notation, mathematicians

from around the world can communicate within their field. Mathematics transcends politics, religion and

nationality, yet throughout history great civilizations owe their success in part to their mathematicians being

able to create and maintain complex social and architectural structures.

Despite recent advances in the development of information and communication technologies, the global

exchange of mathematical information and ideas is not a new phenomenon and has been essential to the

progress of mathematics. Indeed, many of the foundations of modern mathematics were laid many centuries

ago by Arabic, Greek, Indian and Chinese civilizations, among others. Teachers could use timeline websites

to show the contributions of different civilizations to mathematics, but not just for their mathematical content.

Illustrating the characters and personalities of the mathematicians concerned and the historical context in

which they worked brings home the human and cultural dimension of mathematics.

The importance of science and technology in the everyday world is clear, but the vital role of mathematics

is not so well recognized. It is the language of science, and underpins most developments in science and

technology. A good example of this is the digital revolution, which is transforming the world, as it is all based

on the binary number system in mathematics.

Many international bodies now exist to promote mathematics. Students are encouraged to access the extensive

websites of international mathematical organizations to enhance their appreciation of the international

dimension and to engage in the global issues surrounding the subject.

Examples of global issues relating to international-mindedness (Int) are given in the “Links” column of the

syllabus.

8Mathematics SL guide

Aims

Introduction

Group 5 aims

The aims of all mathematics courses in group 5 are to enable students to:

1. enjoy mathematics, and develop an appreciation of the elegance and power of mathematics

2. develop an understanding of the principles and nature of mathematics

3. communicate clearly and confidently in a variety of contexts

4. develop logical, critical and creative thinking, and patience and persistence in problem-solving

5. employ and refine their powers of abstraction and generalization

6. apply and transfer skills to alternative situations, to other areas of knowledge and to future developments

7. appreciate how developments in technology and mathematics have influenced each other

8. appreciate the moral, social and ethical implications arising from the work of mathematicians and the

applications of mathematics

9. appreciate the international dimension in mathematics through an awareness of the universality of

mathematics and its multicultural and historical perspectives

10. appreciate the contribution of mathematics to other disciplines, and as a particular “area of knowledge”

in the TOK course.

Mathematics SL guide 9

Assessment objectives

Introduction

Problem-solving is central to learning mathematics and involves the acquisition of mathematical skills and

concepts in a wide range of situations, including non-routine, open-ended and real-world problems. Having

followed a DP mathematics SL course, students will be expected to demonstrate the following.

1. Knowledge and understanding: recall, select and use their knowledge of mathematical facts, concepts

and techniques in a variety of familiar and unfamiliar contexts.

2. Problem-solving: recall, select and use their knowledge of mathematical skills, results and models in

both real and abstract contexts to solve problems.

3. Communication and interpretation: transform common realistic contexts into mathematics; comment

on the context; sketch or draw mathematical diagrams, graphs or constructions both on paper and using

technology; record methods, solutions and conclusions using standardized notation.

4. Technology: use technology, accurately, appropriately and efficiently both to explore new ideas and to

solve problems.

5. Reasoning: construct mathematical arguments through use of precise statements, logical deduction and

inference, and by the manipulation of mathematical expressions.

6. Inquiry approaches: investigate unfamiliar situations, both abstract and real-world, involving organizing

and analysing information, making conjectures, drawing conclusions and testing their validity.

10 Mathematics SL guide

Syllabus outline

Syllabus

Syllabus component

Teaching hours

All topics are compulsory. Students must study all the sub-topics in each of the topics

in the syllabus as listed in this guide. Students are also required to be familiar with the

topics listed as prior learning.

Topic 1

Algebra

Topic 2

Functions and equations

Topic 3

Circular functions and trigonometry

Topic 4

Vectors

Topic 5

Statistics and probability

Topic 6

Calculus

Mathematical exploration

Internal assessment in mathematics SL is an individual exploration. This is a piece of

written work that involves investigating an area of mathematics.

Total teaching hours 150

Mathematics SL guide 11

Approaches to the teaching and learning

ofmathematicsSL

Syllabus

Throughout the DP mathematics SL course, students should be encouraged to develop their understanding

of the methodology and practice of the discipline of mathematics. The processes of mathematical inquiry,

mathematical modelling and applications and the use of technology should be introduced appropriately.

These processes should be used throughout the course, and not treated in isolation.

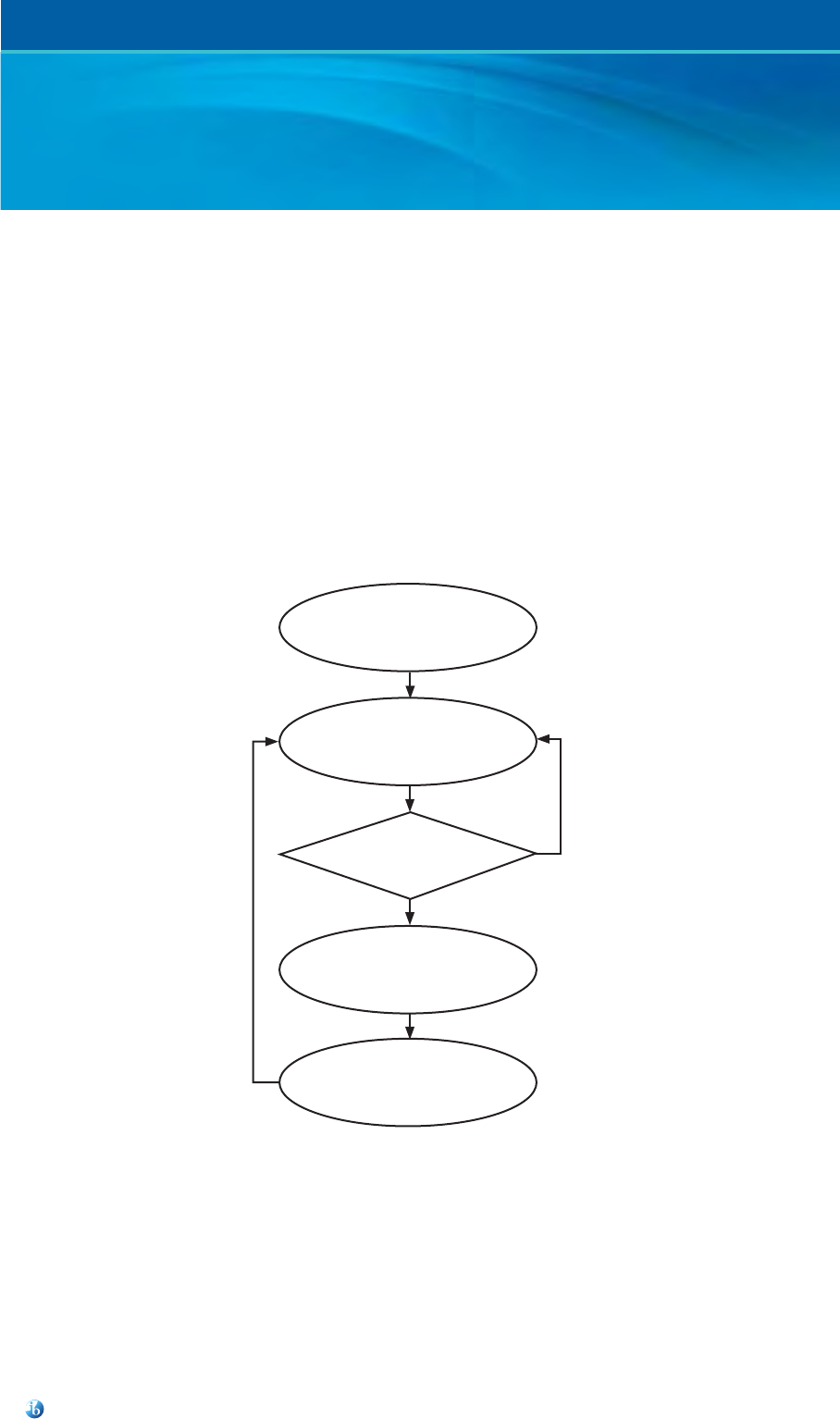
Mathematical inquiry

The IB learner profile encourages learning by experimentation, questioning and discovery. In the IB

classroom, students should generally learn mathematics by being active participants in learning activities

rather than recipients of instruction. Teachers should therefore provide students with opportunities to learn

through mathematical inquiry. This approach is illustrated in figure 2.

Explore the context

Make a conjecture

Extend

Justify

Reject

Test the conjecture

Figure 2

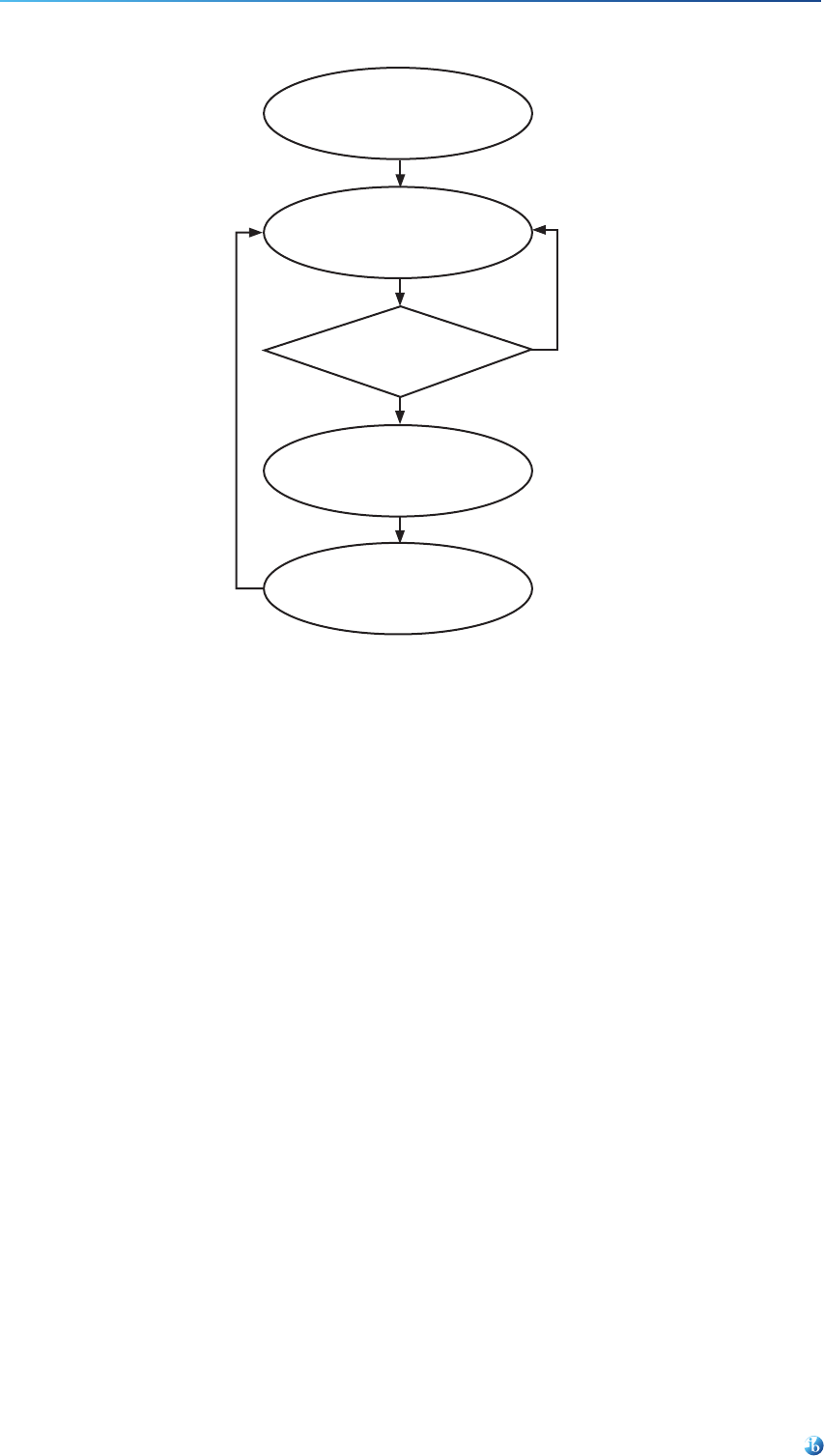
Mathematical modelling and applications

Students should be able to use mathematics to solve problems in the real world. Engaging students in the

mathematical modelling process provides such opportunities. Students should develop, apply and critically

analyse models. This approach is illustrated in figure 3.

Mathematics SL guide12

Approaches to the teaching and learning ofmathematicsSL

Pose a real-world problem

Develop a model

Extend

Reflect on and apply the model

Reject

Test the model

Figure 3

Technology

Technology is a powerful tool in the teaching and learning of mathematics. Technology can be used to enhance

visualization and support student understanding of mathematical concepts. It can assist in the collection,

recording, organization and analysis of data. Technology can increase the scope of the problem situations that

are accessible to students. The use of technology increases the feasibility of students working with interesting

problem contexts where students reflect, reason, solve problems and make decisions.

As teachers tie together the unifying themes of mathematical inquiry, mathematical modelling and

applications and the use of technology, they should begin by providing substantial guidance, and then

gradually encourage students to become more independent as inquirers and thinkers. IB students should learn

to become strong communicators through the language of mathematics. Teachers should create a safe learning

environment in which students are comfortable as risk-takers.

Teachers are encouraged to relate the mathematics being studied to other subjects and to the real world,

especially topics that have particular relevance or are of interest to their students. Everyday problems and

questions should be drawn into the lessons to motivate students and keep the material relevant; suggestions

are provided in the “Links” column of the syllabus. The mathematical exploration offers an opportunity

to investigate the usefulness, relevance and occurrence of mathematics in the real world and will add an

extra dimension to the course. The emphasis is on communication by means of mathematical forms (for

example, formulae, diagrams, graphs and so on) with accompanying commentary. Modelling, investigation,

reflection, personal engagement and mathematical communication should therefore feature prominently in the

DP mathematics classroom.

Mathematics SL guide 13

Approaches to the teaching and learning ofmathematicsSL

For further information on “Approaches to teaching a DP course”, please refer to the publication The Diploma

Programme: From principles into practice (April 2009). To support teachers, a variety of resources can be

found on the OCC and details of workshops for professional development are available on the public website.

Format of the syllabus

• Content: this column lists, under each topic, the sub-topics to be covered.

• Further guidance: this column contains more detailed information on specific sub-topics listed in the

content column. This clarifies the content for examinations.

• Links: this column provides useful links to the aims of the mathematics SL course, with suggestions for

discussion, real-life examples and ideas for further investigation. These suggestions are only a guide

for introducing and illustrating the sub-topic and are not exhaustive. Links are labelled as follows.

Appl real-life examples and links to other DP subjects

Aim 8 moral, social and ethical implications of the sub-topic

Int international-mindedness

TOK suggestions for discussion

Note that any syllabus references to other subject guides given in the “Links” column are correct for the

current (2012) published versions of the guides.

Notes on the syllabus

• Formulae are only included in this document where there may be some ambiguity. All formulae required

for the course are in the mathematics SL formula booklet.

• The term “technology” is used for any form of calculator or computer that may be available. However,

there will be restrictions on which technology may be used in examinations, which will be noted in

relevant documents.

• The terms “analysis” and “analytic approach” are generally used when referring to an approach that does

not use technology.

Course of study

The content of all six topics in the syllabus must be taught, although not necessarily in the order in which they

appear in this guide. Teachers are expected to construct a course of study that addresses the needs of their

students and includes, where necessary, the topics noted in prior learning.

Integration of the mathematical exploration

Work leading to the completion of the exploration should be integrated into the course of study. Details of how

to do this are given in the section on internal assessment and in the teacher support material.

Mathematics SL guide14

Approaches to the teaching and learning ofmathematicsSL

Time allocation

The recommended teaching time for standard level courses is 150 hours. For mathematics SL, it is expected that

10 hours will be spent on work for the exploration. The time allocations given in this guide are approximate,

and are intended to suggest how the remaining 140 hours allowed for the teaching of the syllabus might

be allocated. However, the exact time spent on each topic depends on a number of factors, including the

background knowledge and level of preparedness of each student. Teachers should therefore adjust these

timings to correspond to the needs of their students.

Use of calculators

Students are expected to have access to a graphic display calculator (GDC) at all times during the course.

The minimum requirements are reviewed as technology advances, and updated information will be provided

to schools. It is expected that teachers and schools monitor calculator use with reference to the calculator

policy. Regulations covering the types of calculators allowed in examinations are provided in the Handbook of

procedures for the Diploma Programme. Further information and advice is provided in the Mathematics HL/

SL: Graphic display calculators teacher support material (May 2005) and on the OCC.

Mathematics SL formula booklet

Each student is required to have access to a clean copy of this booklet during the examination. It is

recommended that teachers ensure students are familiar with the contents of this document from the beginning

of the course. It is the responsibility of the school to download a copy from IBIS or the OCC, check that there

are no printing errors, and ensure that there are sufficient copies available for all students.

Teacher support materials

A variety of teacher support materials will accompany this guide. These materials will include guidance for

teachers on the introduction, planning and marking of the exploration, and specimen examination papers and

markschemes.

Command terms and notation list

Teachers and students need to be familiar with the IB notation and the command terms, as these will be used

without explanation in the examination papers. The “Glossary of command terms” and “Notation list” appear

as appendices in this guide.

Mathematics SL guide 15

Syllabus

Prior learning topics

As noted in the previous section on prior learning, it is expected that all students have extensive previous

mathematical experiences, but these will vary. It is expected that mathematics SL students will be familiar with the

following topics before they take the examinations, because questions assume knowledge of them. Teachers must

therefore ensure that any topics listed here that are unknown to their students at the start of the course are included at

an early stage. They should also take into account the existing mathematical knowledge of their students to design an

appropriate course of study for mathematics SL. This table lists the knowledge, together with the syllabus content, that

is essential to successful completion of the mathematics SL course.

Students must be familiar with SI (Système International) units of length, mass and time, and their derived units.

Topic Content

Number

Routine use of addition, subtraction, multiplication and division, using integers, decimals and

fractions, including order of operations.

Simple positive exponents.

Simplification of expressions involving roots (surds or radicals).

Prime numbers and factors, including greatest common divisors and least common multiples.

Simple applications of ratio, percentage and proportion, linked to similarity.

Definition and elementary treatment of absolute value (modulus),

Rounding, decimal approximations and significant figures, including appreciation of errors.

Expression of numbers in standard form (scientific notation), that is,

1 10a≤<

k∈

Sets and numbers

Concept and notation of sets, elements, universal (reference) set, empty (null) set,

complement, subset, equality of sets, disjoint sets.

Operations on sets: union and intersection.

Commutative, associative and distributive properties.

Venn diagrams.

Number systems: natural numbers; integers, ; rationals, , and irrationals; real numbers, .

Intervals on the real number line using set notation and using inequalities. Expressing the

solution set of a linear inequality on the number line and in set notation.

Mappings of the elements of one set to another. Illustration by means of sets of ordered pairs,

tables, diagrams and graphs.

Algebra

Manipulation of simple algebraic expressions involving factorization and expansion,

including quadratic expressions.

Rearrangement, evaluation and combination of simple formulae. Examples from other subject

areas, particularly the sciences, should be included.

The linear function and its graph, gradient and y-intercept.

Addition and subtraction of algebraic fractions.

The properties of order relations:

,,,<≤>≥

Solution of equations and inequalities in one variable, including cases with rational coefficients.

Solution of simultaneous equations in two variables.

Mathematics SL guide16

Prior learning topics

Topic Content

Trigonometry

Angle measurement in degrees. Compass directions and three figure bearings.

Right-angle trigonometry. Simple applications for solving triangles.

Pythagoras’ theorem and its converse.

Geometry

Simple geometric transformations: translation, reflection, rotation, enlargement. Congruence

and similarity, including the concept of scale factor of an enlargement.

The circle, its centre and radius, area and circumference. The terms “arc”, “sector”, “chord”,

“tangent” and “segment”.

Perimeter and area of plane figures. Properties of triangles and quadrilaterals, including

parallelograms, rhombuses, rectangles, squares, kites and trapeziums (trapezoids); compound

shapes.

Volumes of prisms, pyramids, spheres, cylinders and cones.

Coordinate

geometry Elementary geometry of the plane, including the concepts of dimension for point, line, plane

and space. The equation of a line in the form

y mx c= +

Parallel and perpendicular lines, including

and

1mm = −

Geometry of simple plane figures.

The Cartesian plane: ordered pairs

(,)xy

, origin, axes.

Mid-point of a line segment and distance between two points in the Cartesian plane and in

three dimensions.

Statistics and

probability

Descriptive statistics: collection of raw data; display of data in pictorial and diagrammatic

forms, including pie charts, pictograms, stem and leaf diagrams, bar graphs and line graphs.

Obtaining simple statistics from discrete and continuous data, including mean, median, mode,

quartiles, range, interquartile range.

Calculating probabilities of simple events.

Mathematics SL guide 17

Syllabus

Syllabus content

Mathematics SL guide 1

Topic 1—Algebra 9 hours

The aim of this topic is to introduce students to some basic algebraic concepts and applications.

Content Further guidance Links

1.1

Arithmetic sequences and series; sum of finite

arithmetic series; geometric sequences and series;

sum of finite and infinite geometric series.

Sigma notation.

Technology may be used to generate and

display sequences in several ways.

Link to 2.6, exponential functions.

Int: The chess legend (Sissa ibn Dahir).

Int: Aryabhatta is sometimes considered the

“father of algebra”. Compare with

al-Khawarizmi.

TOK: How did Gauss add up integers from

1 to 100? Discuss the idea of mathematical

intuition as the basis for formal proof.

TOK: Debate over the validity of the notion of

“infinity”: finitists such as L. Kronecker

consider that “a mathematical object does not

exist unless it can be constructed from natural

numbers in a finite number of steps”.

TOK: What is Zeno’s dichotomy paradox?

How far can mathematical facts be from

intuition?

Applications.

Examples include compound interest and

population growth.

Mathematics SL guide18

Syllabus content

Mathematics SL guide 2

Content Further guidance Links

1.2

Elementary treatment of exponents and

logarithms. Examples:

16 8

;

3log 8

;

log32 5log2=

;

3 12

(2 ) 2

−

Appl: Chemistry 18.1 (Calculation of pH ).

TOK: Are logarithms an invention or

discovery? (This topic is an opportunity for

teachers to generate reflection on “the nature of

mathematics”.)

Laws of exponents; laws of logarithms.

Change of base.

Examples:

ln 7

log

ln 4

log

log log

125 3

125 25 2







Link to 2.6, logarithmic functions.

1.3

The binomial theorem:

expansion of ( ),

ab n

+∈

.

Counting principles may be used in the

development of the theorem.

Aim 8: Pascal’s triangle. Attributing the origin

of a mathematical discovery to the wrong

mathematician.

Int: The so-called “Pascal’s triangle” was

known in China much earlier than Pascal.

Calculation of binomial coefficients using

Pascal’s triangle and













should be found using both the formula

and technology.

Example: finding







from inputting

y CX=

and then reading coefficients from

the table.

Link to 5.8, binomial distribution.

Not required:

formal treatment of permutations and formula

for

Mathematics SL guide 19

Syllabus content

Mathematics SL guide 3

Topic 2—Functions and equations 24 hours

The aims of this topic are to explore the notion of a function as a unifying theme in mathematics, and to apply functional methods to a variety of

mathematical situations. It is expected that extensive use will be made of technology in both the development and the application of this topic, rather than

elaborate analytical techniques. On examination papers, questions may be set requiring the graphing of functions that do not explicitly appear on the

syllabus, and students may need to choose the appropriate viewing window. For those functions explicitly mentioned, questions may also be set on

composition of these functions with the linear function

y ax b= +

Content Further guidance Links

2.1

Concept of function

: ()f x fx

Domain, range; image (value).

Example: for

−

, domain is

2x≤

range is

0y≥

A graph is helpful in visualizing the range.

Int: The development of functions, Rene

Descartes (France), Gottfried Wilhelm Leibniz

(Germany) and Leonhard Euler (Switzerland).

Composite functions.

( )

() (())f g x fgx=

TOK: Is zero the same as “nothing”?

TOK: Is mathematics a formal language?

Identity function. Inverse function 1

f−.

( )( ) ( )( )f f x f fx x

−−

= =



On examination papers, students will only be

asked to find the inverse of a one-to-one function.

Not required:

domain restriction.

2.2

The graph of a function; its equation

()y fx=

Appl: Chemistry 11.3.1 (sketching and

interpreting graphs); geographic skills.

TOK: How accurate is a visual representation

of a mathematical concept? (Limits of graphs

in delivering information about functions and

phenomena in general, relevance of modes of

representation.)

Function graphing skills.

Investigation of key features of graphs, such as

maximum and minimum values, intercepts,

horizontal and vertical asymptotes, symmetry,

and consideration of domain and range.

Note the difference in the command terms

“draw” and “sketch”.

Use of technology to graph a variety of

functions, including ones not specifically

mentioned.

An analytic approach is also expected for

simple functions, including all those listed

under topic 2.

The graph of

()yfx

−

as the reflection in

the line

yx=

of the graph of

()y fx=

Link to 6.3, local maximum and minimum

points.

Mathematics SL guide20

Syllabus content

Mathematics SL guide 4

Content Further guidance Links

2.3

Transformations of graphs.

Technology should be used to investigate these

transformations.

Appl: Economics 1.1 (shifting of supply and

demand curves).

Translations:

()y fx b= +

;

()y fx a= −

Reflections (in both axes):

()y fx= −

;

()yfx= −

Vertical stretch with scale factor p:

()y pf x=

Stretch in the x-direction with scale factor

( )

y f qx=

Translation by the vector





−



denotes

horizontal shift of 3 units to the right, and

vertical shift of 2 down.

Composite transformations.

Example:

used to obtain

yx= +

a stretch of scale factor 3 in the y-direction

followed by a translation of







2.4

The quadratic function

x ax bx c

++

: its

graph, y-intercept

(0, )c

. Axis of symmetry.

The form

( )( )x ax p x q−−

,

x-intercepts

( , 0)p

and

( , 0)q

The form

()x ax h k

−+



, vertex

(, )hk

Candidates are expected to be able to change

from one form to another.

Links to 2.3, transformations; 2.7, quadratic

equations.

Appl: Chemistry 17.2 (equilibrium law).

Appl: Physics 2.1 (kinematics).

Appl: Physics 4.2 (simple harmonic motion).

Appl: Physics 9.1 (HL only) (projectile

motion).

Mathematics SL guide 21

Syllabus content

Mathematics SL guide 5

Content Further guidance Links

2.5

The reciprocal function



0x≠

: its

graph and self-inverse nature.

The rational function

ax b

cx d



and its

graph.

Examples:

( ) ,

32 3

hx x

= ≠

−;

25 2

= ≠

−

Vertical and horizontal asymptotes.

Diagrams should include all asymptotes and

intercepts.

2.6 Exponential functions and their graphs:

xa

0a>

x

Int: The Babylonian method of multiplication:

222

()

ab a b

ab + −−

=. Sulba Sutras in ancient

India and the Bakhshali Manuscript contained

an algebraic formula for solving quadratic

equations.

Logarithmic functions and their graphs:

log



0x>

lnxx

0x>

Relationships between these functions:

x xa

;

log

; log

0x>

Links to 1.1, geometric sequences; 1.2, laws of

exponents and logarithms; 2.1, inverse

functions; 2.2, graphs of inverses; and 6.1,

limits.

Mathematics SL guide22

Syllabus content

Mathematics SL guide 6

Content Further guidance Links

2.7 Solving equations, both graphically and

analytically.

Use of technology to solve a variety of

equations, including those where there is no

appropriate analytic approach.

Solutions may be referred to as roots of

equations or zeros of functions.

Links to 2.2, function graphing skills; and 2.3–

2.6, equations involving specific functions.

Examples:

5 60

e sin ,

+ −=

Solving

0ax bx c

+ +=

0a≠

The quadratic formula.

The discriminant

4b ac∆= −

and the nature

of the roots, that is, two distinct real roots, two

equal real roots, no real roots.

Example: Find k given that the equation

32 0kx x k

+ +=

has two equal real roots.

Solving exponential equations.

Examples:

2 10

x−







Link to 1.2, exponents and logarithms.

2.8 Applications of graphing skills and solving

equations that relate to real-life situations. Link to 1.1, geometric series. Appl: Compound interest, growth and decay;

projectile motion; braking distance; electrical

circuits.

Appl: Physics 7.2.7–7.2.9, 13.2.5, 13.2.6,

13.2.8 (radioactive decay and half-life)

Mathematics SL guide 23

Syllabus content

Mathematics SL guide 7

Topic 3—Circular functions and trigonometry 16 hours

The aims of this topic are to explore the circular functions and to solve problems using trigonometry. On examination papers, radian measure should be

assumed unless otherwise indicated.

Content Further guidance Links

3.1

The circle: radian measure of angles; length of

an arc; area of a sector.

Radian measure may be expressed as exact

multiples of

, or decimals.

Int: Seki Takakazu calculating

to ten

decimal places.

Int: Hipparchus, Menelaus and Ptolemy.

Int: Why are there 360 degrees in a complete

turn? Links to Babylonian mathematics.

TOK: Which is a better measure of angle:

radian or degree? What are the “best” criteria

by which to decide?

TOK: Euclid’s axioms as the building blocks

of Euclidean geometry. Link to non-Euclidean

geometry.

3.2

Definition of

cos

and

sin

in terms of the

unit circle.

Aim 8: Who really invented “Pythagoras’

theorem”?

Int: The first work to refer explicitly to the

sine as a function of an angle is the

Aryabhatiya of Aryabhata (ca. 510).

TOK: Trigonometry was developed by

successive civilizations and cultures. How is

mathematical knowledge considered from a

sociocultural perspective?

Definition of

tan

sin

cos

The equation of a straight line through the

origin is

tanyx

Exact values of trigonometric ratios of

π πππ

0,,,,

6 432

and their multiples.

Examples:

π 3 3π 1 3

sin , cos , tan210

32 4 3

= = − °=

Mathematics SL guide24

Syllabus content

Mathematics SL guide 8

Content Further guidance Links

3.3

The Pythagorean identity

cos sin 1

θθ

Double angle identities for sine and cosine.

Simple geometrical diagrams and/or

technology may be used to illustrate the double

angle formulae (and other trigonometric

identities).

Relationship between trigonometric ratios.

Examples:

Given

sin

, finding possible values of

tan

without finding

Given

cos

, and x is acute, find

sin2x

without finding x.

3.4

The circular functions

sin x

cos x

and

tan x

their domains and ranges; amplitude, their

periodic nature; and their graphs.

Appl: Physics 4.2 (simple harmonic motion).

Composite functions of the form

( )

( ) sin ( )fx a bx c d= ++

Examples:

( ) tan 4

fx x π



= −





( )

( ) 2cos 3( 4) 1fx x= −+

Transformations.

Example:

sinyx=

used to obtain

3sin 2yx=

by a stretch of scale factor 3 in the y-direction

and a stretch of scale factor

in the

x-direction.

Link to 2.3, transformation of graphs.

Applications.

Examples include height of tide, motion of a

Ferris wheel.

Mathematics SL guide 25

Syllabus content

Mathematics SL guide 9

Content Further guidance Links

3.5

Solving trigonometric equations in a finite

interval, both graphically and analytically.

Examples

2sin 1x=

02πx≤≤

2sin2 3cosxx=

0 180x

≤≤ ,

( )

2tan 3( 4) 1x

−=

π 3πx−≤ ≤

Equations leading to quadratic equations in

sin , cos or tanxx x

Not required:

the general solution of trigonometric equations.

Examples:

2sin 5cos 1 0xx

+ +=

for

04x≤ <π

2sin cos2xx=

ππx−≤ ≤

3.6

Solution of triangles.

Pythagoras’ theorem is a special case of the

cosine rule.

Aim 8: Attributing the origin of a

mathematical discovery to the wrong

mathematician.

Int: Cosine rule: Al-Kashi and Pythagoras.

The cosine rule.

The sine rule, including the ambiguous case.

Area of a triangle,

1sin

2ab C

Link with 4.2, scalar product, noting that:

222

2=− ⇒ = + −⋅c a b c a b ab

Applications.

Examples include navigation, problems in two

and three dimensions, including angles of

elevation and depression.

TOK: Non-Euclidean geometry: angle sum on

a globe greater than 180°.

Mathematics SL guide26

Syllabus content

Mathematics SL guide 10

Topic 4—Vectors 16 hours

The aim of this topic is to provide an elementary introduction to vectors, including both algebraic and geometric approaches. The use of dynamic geometry

software is extremely helpful to visualize situations in three dimensions.

Content Further guidance Links

4.1

Vectors as displacements in the plane and in

three dimensions.

Link to three-dimensional geometry, x, y and z-

axes.

Appl: Physics 1.3.2 (vector sums and

differences) Physics 2.2.2, 2.2.3 (vector

resultants).

TOK: How do we relate a theory to the

author? Who developed vector analysis:

JW Gibbs or O Heaviside?

Components of a vector; column

representation;

2 12 3

v vv v





= =++





v i jk

Components are with respect to the unit

vectors i, j and k (standard basis).

Algebraic and geometric approaches to the

following:

Applications to simple geometric figures are

essential.

• the sum and difference of two vectors; the

zero vector, the vector

−v

; The difference of

and

()− = +−vwv w

. Vector sums and differences

can be represented by the diagonals of a

parallelogram.

• multiplication by a scalar,

; parallel

vectors;

Multiplication by a scalar can be illustrated by

enlargement.

• magnitude of a vector,

;

• unit vectors; base vectors; i, j and k;

• position vectors

→=a

;

•

AB OB OA

→ →→

=−=−ba

Distance between points A and B is the

magnitude of

→

Mathematics SL guide 27

Syllabus content

Mathematics SL guide 11

Content Further guidance Links

4.2

The scalar product of two vectors.

The scalar product is also known as the “dot

product”.

Link to 3.6, cosine rule.

Perpendicular vectors; parallel vectors.

For non-zero vectors,

0⋅=vw

is equivalent to

the vectors being perpendicular.

For parallel vectors,

k=wv

, ⋅=vw vw.

The angle between two vectors.

4.3

Vector equation of a line in two and three

dimensions:

t= +rab

Relevance of

(position) and

(direction).

Interpretation of

as time and

as velocity,

with b representing speed.

Aim 8: Vector theory is used for tracking

displacement of objects, including for peaceful

and harmful purposes.

TOK: Are algebra and geometry two separate

domains of knowledge? (Vector algebra is a

good opportunity to discuss how geometrical

properties are described and generalized by

algebraic methods.)

The angle between two lines.

4.4

Distinguishing between coincident and parallel

lines.

Finding the point of intersection of two lines.

Determining whether two lines intersect.

Mathematics SL guide28

Syllabus content

Mathematics SL guide 12

Topic 5—Statistics and probability 35 hours

The aim of this topic is to introduce basic concepts. It is expected that most of the calculations required will be done using technology, but explanations of

calculations by hand may enhance understanding. The emphasis is on understanding and interpreting the results obtained, in context. Statistical tables will no

longer be allowed in examinations. While many of the calculations required in examinations are estimates, it is likely that the command terms “write down”,

“find” and “calculate” will be used.

Content Further guidance Links

5.1

Concepts of population, sample, random

sample, discrete and continuous data.

Presentation of data: frequency distributions

(tables); frequency histograms with equal class

intervals;

Continuous and discrete data.

Appl: Psychology: descriptive statistics,

random sample (various places in the guide).

Aim 8: Misleading statistics.

Int: The St Petersburg paradox, Chebychev,

Pavlovsky.

box-and-whisker plots; outliers.

Outlier is defined as more than

1.5 IQR×

from

the nearest quartile.

Technology may be used to produce

histograms and box-and-whisker plots.

Grouped data: use of mid-interval values for

calculations; interval width; upper and lower

interval boundaries; modal class.

Not required:

frequency density histograms.

Mathematics SL guide 29

Syllabus content

Mathematics SL guide 13

Content Further guidance Links

5.2

Statistical measures and their interpretations.

Central tendency: mean, median, mode.

Quartiles, percentiles.

On examination papers, data will be treated as

the population.

Calculation of mean using formula and

technology. Students should use mid-interval

values to estimate the mean of grouped data.

Appl: Psychology: descriptive statistics

(various places in the guide).

Appl: Statistical calculations to show patterns

and changes; geographic skills; statistical

graphs.

Appl: Biology 1.1.2 (calculating mean and

standard deviation ); Biology 1.1.4 (comparing

means and spreads between two or more

samples).

Int: Discussion of the different formulae for

variance.

TOK: Do different measures of central

tendency express different properties of the

data? Are these measures invented or

discovered? Could mathematics make

alternative, equally true, formulae? What does

this tell us about mathematical truths?

TOK: How easy is it to lie with statistics?

Dispersion: range, interquartile range,

variance, standard deviation.

Effect of constant changes to the original data.

Calculation of standard deviation/variance

using only technology.

Link to 2.3, transformations.

Examples:

If 5 is subtracted from all the data items, then

the mean is decreased by 5, but the standard

deviation is unchanged.

If all the data items are doubled, the median is

doubled, but the variance is increased by a

factor of 4.

Applications.

5.3

Cumulative frequency; cumulative frequency

graphs; use to find median, quartiles,

percentiles.

Values of the median and quartiles produced

by technology may be different from those

obtained from a cumulative frequency graph.

Mathematics SL guide30

Syllabus content

Mathematics SL guide 14

Content Further guidance Links

5.4

Linear correlation of bivariate data.

Independent variable x, dependent variable y.

Appl: Chemistry 11.3.3 (curves of best fit).

Appl: Geography (geographic skills).

Measures of correlation; geographic skills.

Appl: Biology 1.1.6 (correlation does not

imply causation).

TOK: Can we predict the value of x from y,

using this equation?

TOK: Can all data be modelled by a (known)

mathematical function? Consider the reliability

and validity of mathematical models in

describing real-life phenomena.

Pearson’s product–moment correlation

coefficient r.

Technology should be used to calculate r.

However, hand calculations of r may enhance

understanding.

Positive, zero, negative; strong, weak, no

correlation.

Scatter diagrams; lines of best fit.

The line of best fit passes through the mean

point.

Equation of the regression line of y on x.

Use of the equation for prediction purposes.

Mathematical and contextual interpretation.

Not required:

the coefficient of determination R2.

Technology should be used find the equation.

Interpolation, extrapolation.

5.5

Concepts of trial, outcome, equally likely

outcomes, sample space (U) and event.

The sample space can be represented

diagrammatically in many ways.

TOK: To what extent does mathematics offer

models of real life? Is there always a function

to model data behaviour?

The probability of an event A is

()

P( )

()

AnU

The complementary events A and

A′

(not A).

Use of Venn diagrams, tree diagrams and

tables of outcomes.

Experiments using coins, dice, cards and so on,

can enhance understanding of the distinction

between (experimental) relative frequency and

(theoretical) probability.

Simulations may be used to enhance this topic.

Links to 5.1, frequency; 5.3, cumulative

frequency.

Mathematics SL guide 31

Syllabus content

Mathematics SL guide 15

Content Further guidance Links

5.6

Combined events,

P( )AB∪

Mutually exclusive events:

P( ) 0AB∩=

Conditional probability; the definition

( )

P( )

P| P( )

AB B

∩

Independent events; the definition

( ) ( )

P| P()P|

AB A AB

′

= = .

Probabilities with and without replacement.

The non-exclusivity of “or”.

Problems are often best solved with the aid of a

Venn diagram or tree diagram, without explicit

use of formulae.

Aim 8: The gambling issue: use of probability

in casinos. Could or should mathematics help

increase incomes in gambling?

TOK: Is mathematics useful to measure risks?

TOK: Can gambling be considered as an

application of mathematics? (This is a good

opportunity to generate a debate on the nature,

role and ethics of mathematics regarding its

applications.)

5.7

Concept of discrete random variables and their

probability distributions.

Simple examples only, such as:

P( ) (4 )

Xx x= = +

for

{ }

1, 2, 3x∈

;

567

P( ) , ,

18 18 18

Xx= =

Expected value (mean),

E( )X

for discrete data.

Applications.

E( ) 0X=

indicates a fair game where X

represents the gain of one of the players.

Examples include games of chance.

Mathematics SL guide32

Syllabus content

Mathematics SL guide 16

Content Further guidance Links

5.8

Binomial distribution.

Mean and variance of the binomial

distribution.

Not required:

formal proof of mean and variance.

Link to 1.3, binomial theorem.

Conditions under which random variables have

this distribution.

Technology is usually the best way of

calculating binomial probabilities.

5.9

Normal distributions and curves.

Standardization of normal variables (z-values,

z-scores).

Properties of the normal distribution.

Probabilities and values of the variable must be

found using technology.

Link to 2.3, transformations.

The standardized value (

) gives the number

of standard deviations from the mean.

Appl: Biology 1.1.3 (links to normal

distribution).

Appl: Psychology: descriptive statistics

(various places in the guide).

Mathematics SL guide 33

Syllabus content

Mathematics SL guide 17

Topic 6—Calculus 40 hours

The aim of this topic is to introduce students to the basic concepts and techniques of differential and integral calculus and their applications.

Content Further guidance Links

6.1

Informal ideas of limit and convergence.

Example: 0.3, 0.33, 0.333, ... converges to

Technology should be used to explore ideas of

limits, numerically and graphically.

Appl: Economics 1.5 (marginal cost, marginal

revenue, marginal profit).

Appl: Chemistry 11.3.4 (interpreting the

gradient of a curve).

Aim 8: The debate over whether Newton or

Leibnitz discovered certain calculus concepts.

TOK: What value does the knowledge of

limits have? Is infinitesimal behaviour

applicable to real life?

TOK: Opportunities for discussing hypothesis

formation and testing, and then the formal

proof can be tackled by comparing certain

cases, through an investigative approach.

Limit notation.

Example:

lim 1

→∞

−







Links to 1.1, infinite geometric series; 2.5–2.7,

rational and exponential functions, and

asymptotes.

Definition of derivative from first principles as

( ) ()

( ) lim

fx h fx

fx h

→

+−



′=





Use of this definition for derivatives of simple

polynomial functions only.

Technology could be used to illustrate other

derivatives.

Link to 1.3, binomial theorem.

Use of both forms of notation,

and

( )

′

for the first derivative.

Derivative interpreted as gradient function and

as rate of change.

Identifying intervals on which functions are

increasing or decreasing.

Tangents and normals, and their equations.

Not required:

analytic methods of calculating limits.

Use of both analytic approaches and

technology.

Technology can be used to explore graphs and

their derivatives.

Mathematics SL guide34

Syllabus content

Mathematics SL guide 18

Content Further guidance Links

6.2

Derivative of

()

xn∈

sin x

cos x

tan x

ex and

ln x

Differentiation of a sum and a real multiple of

these functions.

The chain rule for composite functions.

The product and quotient rules.

Link to 2.1, composition of functions.

Technology may be used to investigate the chain

rule.

The second derivative.

Use of both forms of notation,

and

()fx

′′

Extension to higher derivatives.

and

( )

()

Mathematics SL guide 35

Syllabus content

Mathematics SL guide 19

Content Further guidance Links

6.3

Local maximum and minimum points.

Testing for maximum or minimum.

Using change of sign of the first derivative and

using sign of the second derivative.

Use of the terms “concave-up” for

() 0fx

′′

and “concave-down” for

() 0fx

′′

Appl: profit, area, volume.

Points of inflexion with zero and non-zero

gradients. At a point of inflexion ,

() 0fx

′′

and changes

sign (concavity change).

() 0fx

′′ =

is not a sufficient condition for a

point of inflexion: for example,

(0,0)

Graphical behaviour of functions,

including the relationship between the

graphs of

f′

and

f′′

Optimization.

Both “global” (for large x) and “local”

behaviour.

Technology can display the graph of a

derivative without explicitly finding an

expression for the derivative.

Use of the first or second derivative test to

justify maximum and/or minimum values.

Applications.

Not required:

points of inflexion where

()fx

′′

is not defined:

for example,

(0,0)

Examples include profit, area, volume.

Link to 2.2, graphing functions.

Mathematics SL guide36

Syllabus content

Mathematics SL guide 20

Content

Further guidance

Links

6.4

Indefinite integration as anti-differentiation.

Indefinite integral of

()

xn∈

sin x

cos x

and

1d lnx xC

= +

∫

0x>

The composites of any of these with the linear

function

ax b+

Example:

( ) cos(2 3) ( ) sin(2 3)

f x x fx x C

′= + ⇒ = ++.

Integration by inspection, or substitution of the

form

(()) '()d

fgx g x x

∫.

Examples:

( )

2 1 d, sin d, d

sin

cos

xx x x x x x

∫ ∫∫

6.5

Anti-differentiation with a boundary condition

to determine the constant term.

Example:

= +

and

10y=

when

0x=

, then

110

yx x

=++

Int: Successful calculation of the volume of

the pyramidal frustum by ancient Egyptians

(Egyptian Moscow papyrus).

Use of infinitesimals by Greek geometers.

Definite integrals, both analytically and using

technology.

( )d ( ) ( )

g x x gb ga

′= −

∫

The value of some definite integrals can only

be found using technology.

Accurate calculation of the volume of a

cylinder by Chinese mathematician Liu Hui

Areas under curves (between the curve and the

x-axis).

Areas between curves.

Volumes of revolution about the x-axis.

Students are expected to first write a correct

expression before calculating the area.

Technology may be used to enhance

understanding of area and volume.

Int: Ibn Al Haytham: first mathematician to

calculate the integral of a function, in order to

find the volume of a paraboloid.

6.6

Kinematic problems involving displacement s,

velocity v and acceleration a.

; 2

= = .

Appl: Physics 2.1 (kinematics).

Total distance travelled.

Total distance travelled 2

=∫.

Mathematics SL guide 37

Assessment in the Diploma Programme

Assessment

General

Assessment is an integral part of teaching and learning. The most important aims of assessment in the Diploma

Programme are that it should support curricular goals and encourage appropriate student learning. Both

external and internal assessment are used in the Diploma Programme. IB examiners mark work produced

for external assessment, while work produced for internal assessment is marked by teachers and externally

moderated by the IB.

There are two types of assessment identified by the IB.

• Formative assessment informs both teaching and learning. It is concerned with providing accurate and

helpful feedback to students and teachers on the kind of learning taking place and the nature of students’

strengths and weaknesses in order to help develop students’ understanding and capabilities. Formative

assessment can also help to improve teaching quality, as it can provide information to monitor progress

towards meeting the course aims and objectives.

• Summative assessment gives an overview of previous learning and is concerned with measuring student

achievement.

The Diploma Programme primarily focuses on summative assessment designed to record student achievement

at or towards the end of the course of study. However, many of the assessment instruments can also be

used formatively during the course of teaching and learning, and teachers are encouraged to do this. A

comprehensive assessment plan is viewed as being integral with teaching, learning and course organization.

For further information, see the IB Programme standards and practices document.

The approach to assessment used by the IB is criterion-related, not norm-referenced. This approach to

assessment judges students’ work by their performance in relation to identified levels of attainment, and not in

relation to the work of other students. For further information on assessment within the Diploma Programme,

please refer to the publication Diploma Programme assessment: Principles and practice.

To support teachers in the planning, delivery and assessment of the Diploma Programme courses, a variety

of resources can be found on the OCC or purchased from the IB store (http://store.ibo.org). Teacher support

materials, subject reports, internal assessment guidance, grade descriptors, as well as resources from other

teachers, can be found on the OCC. Specimen and past examination papers as well as markschemes can be

purchased from the IB store.

Methods of assessment

The IB uses several methods to assess work produced by students.

Assessment criteria

Assessment criteria are used when the assessment task is open-ended. Each criterion concentrates on a

particular skill that students are expected to demonstrate. An assessment objective describes what students

should be able to do, and assessment criteria describe how well they should be able to do it. Using assessment

criteria allows discrimination between different answers and encourages a variety of responses. Each criterion

Mathematics SL guide38

Assessment in the Diploma Programme

comprises a set of hierarchically ordered level descriptors. Each level descriptor is worth one or more marks.

Each criterion is applied independently using a best-fit model. The maximum marks for each criterion may

differ according to the criterion’s importance. The marks awarded for each criterion are added together to give

the total mark for the piece of work.

Markbands

Markbands are a comprehensive statement of expected performance against which responses are judged. They

represent a single holistic criterion divided into level descriptors. Each level descriptor corresponds to a range

of marks to differentiate student performance. A best-fit approach is used to ascertain which particular mark to

use from the possible range for each level descriptor.

Markschemes

This generic term is used to describe analytic markschemes that are prepared for specific examination papers.

Analytic markschemes are prepared for those examination questions that expect a particular kind of response

and/or a given final answer from the students. They give detailed instructions to examiners on how to break

down the total mark for each question for different parts of the response. A markscheme may include the

content expected in the responses to questions or may be a series of marking notes giving guidance on how to

apply criteria.

Mathematics SL guide 39

Assessment

Assessment outline

First examinations 2014

Assessment component Weighting

External assessment (3 hours)

Paper 1 (1 hour 30 minutes)

No calculator allowed. (90 marks)

Section A

Compulsory short-response questions based on the whole syllabus.

Section B

Compulsory extended-response questions based on the whole syllabus.

80%

40%

Paper 2 (1 hour 30 minutes)

Graphic display calculator required. (90 marks)

Section A

Compulsory short-response questions based on the whole syllabus.

Section B

Compulsory extended-response questions based on the whole syllabus.

40%

Internal assessment

This component is internally assessed by the teacher and externally moderated by the IB at

the end of the course.

Mathematical exploration

Internal assessment in mathematics SL is an individual exploration. This is a piece of

written work that involves investigating an area of mathematics. (20 marks)

20%

40 Mathematics SL guide

Assessment

External assessment

General

Markschemes are used to assess students in both papers. The markschemes are specific to each examination.

External assessment details

Paper 1 and paper 2

These papers are externally set and externally marked. Together, they contribute 80% of the final mark for

the course. These papers are designed to allow students to demonstrate what they know and what they can do.

Calculators

Paper 1

Students are not permitted access to any calculator. Questions will mainly involve analytic approaches to

solutions, rather than requiring the use of a GDC. The paper is not intended to require complicated calculations,

with the potential for careless errors. However, questions will include some arithmetical manipulations when

they are essential to the development of the question.

Paper 2

Students must have access to a GDC at all times. However, not all questions will necessarily require the use of

the GDC. Regulations covering the types of GDC allowed are provided in the Handbook of procedures for the

Diploma Programme.

Mathematics SL formula booklet

Each student must have access to a clean copy of the formula booklet during the examination. It is the

responsibility of the school to download a copy from IBIS or the OCC and to ensure that there are sufficient

copies available for all students.

Awarding of marks

Marks may be awarded for method, accuracy, answers and reasoning, including interpretation.

In paper 1 and paper 2, full marks are not necessarily awarded for a correct answer with no working.

Answers must be supported by working and/or explanations (in the form of, for example, diagrams, graphs

or calculations). Where an answer is incorrect, some marks may be given for correct method, provided this is

shown by written working. All students should therefore be advised to show their working.

Mathematics SL guide 41

External assessment

Paper 1

Duration: 1 hour 30 minutes

Weighting: 40%

• This paper consists of section A, short-response questions, and section B, extended-response questions.

• Students are not permitted access to any calculator on this paper.

Syllabus coverage

• Knowledge of all topics is required for this paper. However, not all topics are necessarily assessed in

every examination session.

Mark allocation

• This paper is worth 90 marks, representing 40% of the final mark.

• Questions of varying levels of difficulty and length are set. Therefore, individual questions may not

necessarily each be worth the same number of marks. The exact number of marks allocated to each

question is indicated at the start of the question.

Section A

This section consists of compulsory short-response questions based on the whole syllabus. It is worth

approximately 45 marks.

The intention of this section is to test students’ knowledge and understanding across the breadth of the syllabus.

However, it should not be assumed that the separate topics are given equal emphasis.

Question type

• A small number of steps is needed to solve each question.

• Questions may be presented in the form of words, symbols, diagrams or tables, or combinations of these.

Section B

This section consists of a small number of compulsory extended-response questions based on the whole

syllabus. It is worth approximately 45 marks. Individual questions may require knowledge of more than

one topic.

The intention of this section is to test students’ knowledge and understanding of the syllabus in depth. The

range of syllabus topics tested in this section may be narrower than that tested in section A.

Question type

• Questions require extended responses involving sustained reasoning.

• Individual questions will develop a single theme.

• Questions may be presented in the form of words, symbols, diagrams or tables, or combinations of these.

• Normally, each question reflects an incline of difficulty, from relatively easy tasks at the start of a

question to relatively difficult tasks at the end of a question. The emphasis is on problem-solving.

Paper 2

Duration: 1 hour 30 minutes

Weighting: 40%

This paper consists of section A, short-response questions, and section B, extended-response questions. A

GDC is required for this paper, but not every question will necessarily require its use.

Mathematics SL guide42

External assessment

Syllabus coverage

• Knowledge of all topics is required for this paper. However, not all topics are necessarily assessed in

every examination session.

Mark allocation

• This paper is worth 90 marks, representing 40% of the final mark.

• Questions of varying levels of difficulty and length are set. Therefore, individual questions may not

necessarily each be worth the same number of marks. The exact number of marks allocated to each

question is indicated at the start of the question.

Section A

This section consists of compulsory short-response questions based on the whole syllabus. It is worth

approximately 45 marks.

The intention of this section is to test students’ knowledge and understanding across the breadth of the syllabus.

However, it should not be assumed that the separate topics are given equal emphasis.

Question type

• A small number of steps is needed to solve each question.

• Questions may be presented in the form of words, symbols, diagrams or tables, or combinations of these.

Section B

This section consists of a small number of compulsory extended-response questions based on the whole

syllabus. It is worth approximately 45 marks. Individual questions may require knowledge of more than one

topic.

The intention of this section is to test students’ knowledge and understanding of the syllabus in depth. The

range of syllabus topics tested in this section may be narrower than that tested in section A.

Question type

• Questions require extended responses involving sustained reasoning.

• Individual questions will develop a single theme.

• Questions may be presented in the form of words, symbols, diagrams or tables, or combinations of these.

• Normally, each question reflects an incline of difficulty, from relatively easy tasks at the start of a

question to relatively difficult tasks at the end of a question. The emphasis is on problem-solving.

Mathematics SL guide 43

Assessment

Internal assessment

Purpose of internal assessment

Internal assessment is an integral part of the course and is compulsory for all students. It enables students to

demonstrate the application of their skills and knowledge, and to pursue their personal interests, without the

time limitations and other constraints that are associated with written examinations. The internal assessment

should, as far as possible, be woven into normal classroom teaching and not be a separate activity conducted

after a course has been taught.

Internal assessment in mathematics SL is an individual exploration. This is a piece of written work that

involves investigating an area of mathematics. It is marked according to five assessment criteria.

Guidance and authenticity

The exploration submitted for internal assessment must be the student’s own work. However, it is not the

intention that students should decide upon a title or topic and be left to work on the exploration without any

further support from the teacher. The teacher should play an important role during both the planning stage and

the period when the student is working on the exploration. It is the responsibility of the teacher to ensure that

students are familiar with:

• the requirements of the type of work to be internally assessed

• the IB academic honesty policy available on the OCC

• the assessment criteria—students must understand that the work submitted for assessment must address

these criteria effectively.

Teachers and students must discuss the exploration. Students should be encouraged to initiate discussions

with the teacher to obtain advice and information, and students must not be penalized for seeking guidance.

However, if a student could not have completed the exploration without substantial support from the teacher,

this should be recorded on the appropriate form from the Handbook of procedures for the Diploma Programme.

It is the responsibility of teachers to ensure that all students understand the basic meaning and significance

of concepts that relate to academic honesty, especially authenticity and intellectual property. Teachers must

ensure that all student work for assessment is prepared according to the requirements and must explain clearly

to students that the exploration must be entirely their own.

As part of the learning process, teachers can give advice to students on a first draft of the exploration. This

advice should be in terms of the way the work could be improved, but this first draft must not be heavily

annotated or edited by the teacher. The next version handed to the teacher after the first draft must be the final

one.

All work submitted to the IB for moderation or assessment must be authenticated by a teacher, and must not

include any known instances of suspected or confirmed malpractice. Each student must sign the coversheet for

internal assessment to confirm that the work is his or her authentic work and constitutes the final version of

that work. Once a student has officially submitted the final version of the work to a teacher (or the coordinator)

for internal assessment, together with the signed coversheet, it cannot be retracted.

Mathematics SL guide44

Internal assessment

Authenticity may be checked by discussion with the student on the content of the work, and scrutiny of one or

more of the following:

• the student’s initial proposal

• the first draft of the written work

• the references cited

• the style of writing compared with work known to be that of the student.

The requirement for teachers and students to sign the coversheet for internal assessment applies to the work of

all students, not just the sample work that will be submitted to an examiner for the purpose of moderation. If the

teacher and student sign a coversheet, but there is a comment to the effect that the work may not be authentic,

the student will not be eligible for a mark in that component and no grade will be awarded. For further details

refer to the IB publication Academic honesty and the relevant articles in the General regulations: Diploma

Programme.

The same piece of work cannot be submitted to meet the requirements of both the internal assessment and the

extended essay.

Group work

Group work should not be used for explorations. Each exploration is an individual piece of work.

It should be made clear to students that all work connected with the exploration, including the writing of

the exploration, should be their own. It is therefore helpful if teachers try to encourage in students a sense

of responsibility for their own learning so that they accept a degree of ownership and take pride in their

own work.

Time allocation

Internal assessment is an integral part of the mathematics SL course, contributing 20% to the final assessment

in the course. This weighting should be reflected in the time that is allocated to teaching the knowledge, skills

and understanding required to undertake the work as well as the total time allocated to carry out the work.

It is expected that a total of approximately 10 teaching hours should be allocated to the work. This should

include:

• time for the teacher to explain to students the requirements of the exploration

• class time for students to work on the exploration

• time for consultation between the teacher and each student

• time to review and monitor progress, and to check authenticity.

Using assessment criteria for internal assessment

For internal assessment, a number of assessment criteria have been identified. Each assessment criterion has

level descriptors describing specific levels of achievement together with an appropriate range of marks. The

level descriptors concentrate on positive achievement, although for the lower levels failure to achieve may be

included in the description.

Mathematics SL guide 45

Internal assessment

Teachers must judge the internally assessed work against the criteria using the level descriptors.

• The aim is to find, for each criterion, the descriptor that conveys most accurately the level attained by

the student.

• When assessing a student’s work, teachers should read the level descriptors for each criterion, starting

with level 0, until they reach a descriptor that describes a level of achievement that has not been reached.

The level of achievement gained by the student is therefore the preceding one, and it is this that should

be recorded.

• Only whole numbers should be recorded; partial marks, that is fractions and decimals, are not acceptable.

• Teachers should not think in terms of a pass or fail boundary, but should concentrate on identifying the

appropriate descriptor for each assessment criterion.

• The highest level descriptors do not imply faultless performance but should be achievable by a student.

Teachers should not hesitate to use the extremes if they are appropriate descriptions of the work being

assessed.

• A student who attains a high level of achievement in relation to one criterion will not necessarily attain

high levels of achievement in relation to the other criteria. Similarly, a student who attains a low level

of achievement for one criterion will not necessarily attain low achievement levels for the other criteria.

Teachers should not assume that the overall assessment of the students will produce any particular

distribution of marks.

• It is expected that the assessment criteria be made available to students.

Internal assessment details

Mathematical exploration

Duration: 10 teaching hours

Weighting: 20%

Introduction

The internally assessed component in this course is a mathematical exploration. This is a short report written

by the student based on a topic chosen by him or her, and it should focus on the mathematics of that particular

area. The emphasis is on mathematical communication (including formulae, diagrams, graphs and so on), with

accompanying commentary, good mathematical writing and thoughtful reflection. A student should develop

his or her own focus, with the teacher providing feedback via, for example, discussion and interview. This will

allow the students to develop area(s) of interest to them without a time constraint as in an examination, and

allow all students to experience a feeling of success.

The final report should be approximately 6 to 12 pages long. It can be either word processed or handwritten.

Students should be able to explain all stages of their work in such a way that demonstrates clear understanding.

While there is no requirement that students present their work in class, it should be written in such a way that

their peers would be able to follow it fairly easily. The report should include a detailed bibliography, and sources

need to be referenced in line with the IB academic honesty policy. Direct quotes must be acknowledged.

The purpose of the exploration

The aims of the mathematics SL course are carried through into the objectives that are formally assessed as

part of the course, through either written examination papers, or the exploration, or both. In addition to testing

the objectives of the course, the exploration is intended to provide students with opportunities to increase their

understanding of mathematical concepts and processes, and to develop a wider appreciation of mathematics.

These are noted in the aims of the course, in particular, aims 6–9 (applications, technology, moral, social

Mathematics SL guide46

Internal assessment

and ethical implications, and the international dimension). It is intended that, by doing the exploration,

students benefit from the mathematical activities undertaken and find them both stimulating and rewarding. It

will enable students to acquire the attributes of the IB learner profile.

The specific purposes of the exploration are to:

• develop students’ personal insight into the nature of mathematics and to develop their ability to ask their

own questions about mathematics

• provide opportunities for students to complete a piece of mathematical work over an extended period of

time

• enable students to experience the satisfaction of applying mathematical processes independently

• provide students with the opportunity to experience for themselves the beauty, power and usefulness of

mathematics

• encourage students, where appropriate, to discover, use and appreciate the power of technology as a

mathematical tool

• enable students to develop the qualities of patience and persistence, and to reflect on the significance of

their work

• provide opportunities for students to show, with confidence, how they have developed mathematically.

Management of the exploration

Work for the exploration should be incorporated into the course so that students are given the opportunity to

learn the skills needed. Time in class can therefore be used for general discussion of areas of study, as well as

familiarizing students with the criteria.

Further details on the development of the exploration are included in the teacher support material.

Requirements and recommendations

Students can choose from a wide variety of activities, for example, modelling, investigations and applications

of mathematics. To assist teachers and students in the choice of a topic, a list of stimuli is available in the

teacher support material. However, students are not restricted to this list.

The exploration should not normally exceed 12 pages, including diagrams and graphs, but excluding the

bibliography. However, it is the quality of the mathematical writing that is important, not the length.

The teacher is expected to give appropriate guidance at all stages of the exploration by, for example, directing

students into more productive routes of inquiry, making suggestions for suitable sources of information, and

providing advice on the content and clarity of the exploration in the writing-up stage.

Teachers are responsible for indicating to students the existence of errors but should not explicitly correct these

errors. It must be emphasized that students are expected to consult the teacher throughout the process.

All students should be familiar with the requirements of the exploration and the criteria by which it is assessed.

Students need to start planning their explorations as early as possible in the course. Deadlines should be firmly

established. There should be a date for submission of the exploration topic and a brief outline description, a

date for the submission of the first draft and, of course, a date for completion.

In developing their explorations, students should aim to make use of mathematics learned as part of the course.

The mathematics used should be commensurate with the level of the course, that is, it should be similar to that

suggested by the syllabus. It is not expected that students produce work that is outside the mathematics SL

syllabus—however, this is not penalized.

Mathematics SL guide 47

Internal assessment

Internal assessment criteria

The exploration is internally assessed by the teacher and externally moderated by the IB using assessment

criteria that relate to the objectives for mathematics SL.

Each exploration is assessed against the following five criteria. The final mark for each exploration is the sum

of the scores for each criterion. The maximum possible final mark is 20.

Students will not receive a grade for mathematics SL if they have not submitted an exploration.

Criterion A Communication

Criterion B Mathematical presentation

Criterion C Personal engagement

Criterion D Reflection

Criterion E Use of mathematics

Criterion A: Communication

This criterion assesses the organization and coherence of the exploration. A well-organized exploration

includes an introduction, has a rationale (which includes explaining why this topic was chosen), describes the

aim of the exploration and has a conclusion. A coherent exploration is logically developed and easy to follow.

Graphs, tables and diagrams should accompany the work in the appropriate place and not be attached as

appendices to the document.

Achievement level Descriptor

0 The exploration does not reach the standard described by the descriptors

below.

1 The exploration has some coherence.

2 The exploration has some coherence and shows some organization.

3 The exploration is coherent and well organized.

4 The exploration is coherent, well organized, concise and complete.

Criterion B: Mathematical presentation

This criterion assesses to what extent the student is able to:

• use appropriate mathematical language (notation, symbols, terminology)

• define key terms, where required

• use multiple forms of mathematical representation, such as formulae, diagrams, tables, charts, graphs

and models, where appropriate.

Students are expected to use mathematical language when communicating mathematical ideas, reasoning and

findings.

Mathematics SL guide48

Internal assessment

Students are encouraged to choose and use appropriate ICT tools such as graphic display calculators,

screenshots, graphing, spreadsheets, databases, drawing and word-processing software, as appropriate, to

enhance mathematical communication.

Achievement level Descriptor

0 The exploration does not reach the standard described by the descriptors

below.

1 There is some appropriate mathematical presentation.

2 The mathematical presentation is mostly appropriate.

3 The mathematical presentation is appropriate throughout.

Criterion C: Personal engagement

This criterion assesses the extent to which the student engages with the exploration and makes it their own.

Personal engagement may be recognized in different attributes and skills. These include thinking independently

and/or creatively, addressing personal interest and presenting mathematical ideas in their own way.

Achievement level Descriptor

0 The exploration does not reach the standard described by the descriptors

below.

1 There is evidence of limited or superficial personal engagement.

2 There is evidence of some personal engagement.

3 There is evidence of significant personal engagement.

4 There is abundant evidence of outstanding personal engagement.

Criterion D: Reflection

This criterion assesses how the student reviews, analyses and evaluates the exploration. Although reflection

may be seen in the conclusion to the exploration, it may also be found throughout the exploration.

Achievement level Descriptor

0 The exploration does not reach the standard described by the descriptors

below.

1 There is evidence of limited or superficial reflection.

2 There is evidence of meaningful reflection.

3 There is substantial evidence of critical reflection.

Mathematics SL guide 49

Internal assessment

Criterion E: Use of mathematics

This criterion assesses to what extent students use mathematics in the exploration.

Students are expected to produce work that is commensurate with the level of the course. The mathematics

explored should either be part of the syllabus, or at a similar level or beyond. It should not be completely

based on mathematics listed in the prior learning. If the level of mathematics is not commensurate with the

level of the course, a maximum of two marks can be awarded for this criterion.

The mathematics can be regarded as correct even if there are occasional minor errors as long as they do not

detract from the flow of the mathematics or lead to an unreasonable outcome.

Achievement level Descriptor

0 The exploration does not reach the standard described by the descriptors

below.

1 Some relevant mathematics is used.

2 Some relevant mathematics is used. Limited understanding is demonstrated.

3 Relevant mathematics commensurate with the level of the course is used.

Limited understanding is demonstrated.

4 Relevant mathematics commensurate with the level of the course is used.

The mathematics explored is partially correct. Some knowledge and

understanding are demonstrated.

5 Relevant mathematics commensurate with the level of the course is used. The

mathematics explored is mostly correct. Good knowledge and understanding

are demonstrated.

6 Relevant mathematics commensurate with the level of the course is used. The

mathematics explored is correct. Thorough knowledge and understanding are

demonstrated.

50 Mathematics SL guide

Glossary of command terms

Appendices

Command terms with definitions

Students should be familiar with the following key terms and phrases used in examination questions, which

are to be understood as described below. Although these terms will be used in examination questions, other

terms may be used to direct students to present an argument in a specific way.

Calculate Obtain a numerical answer showing the relevant stages in the working.

Comment Give a judgment based on a given statement or result of a calculation.

Compare Give an account of the similarities between two (or more) items or situations,

referring to both (all) of them throughout.

Compare and

contrast

Give an account of the similarities and differences between two (or more) items or

situations, referring to both (all) of them throughout.

Construct Display information in a diagrammatic or logical form.

Contrast Give an account of the differences between two (or more) items or situations,

referring to both (all) of them throughout.

Deduce Reach a conclusion from the information given.

Demonstrate Make clear by reasoning or evidence, illustrating with examples or practical

application.

Describe Give a detailed account.

Determine Obtain the only possible answer.

Differentiate Obtain the derivative of a function.

Distinguish Make clear the differences between two or more concepts or items.

Draw Represent by means of a labelled, accurate diagram or graph, using a pencil. A

ruler (straight edge) should be used for straight lines. Diagrams should be drawn

to scale. Graphs should have points correctly plotted (if appropriate) and joined in

a straight line or smooth curve.

Estimate Obtain an approximate value.

Explain Give a detailed account, including reasons or causes.

Find Obtain an answer, showing relevant stages in the working.

Hence Use the preceding work to obtain the required result.

Hence or otherwise It is suggested that the preceding work is used, but other methods could also

receive credit.

Identify Provide an answer from a number of possibilities.

Mathematics SL guide 51

Glossary of command terms

Integrate Obtain the integral of a function.

Interpret Use knowledge and understanding to recognize trends and draw conclusions from

given information.

Investigate Observe, study, or make a detailed and systematic examination, in order to

establish facts and reach new conclusions.

Justify Give valid reasons or evidence to support an answer or conclusion.

Label Add labels to a diagram.

List Give a sequence of brief answers with no explanation.

Plot Mark the position of points on a diagram.

Predict Give an expected result.

Show Give the steps in a calculation or derivation.

Show that Obtain the required result (possibly using information given) without the formality

of proof. “Show that” questions do not generally require the use of a calculator.

Sketch Represent by means of a diagram or graph (labelled as appropriate). The sketch

should give a general idea of the required shape or relationship, and should include

relevant features.

Solve Obtain the answer(s) using algebraic and/or numerical and/or graphical methods.

State Give a specific name, value or other brief answer without explanation or

calculation.

Suggest Propose a solution, hypothesis or other possible answer.

Verify Provide evidence that validates the result.

Write down Obtain the answer(s), usually by extracting information. Little or no calculation is

required. Working does not need to be shown.

52 Mathematics SL guide

Appendices

Notation list

Of the various notations in use, the IB has chosen to adopt a system of notation based on the

recommendations of the International Organization for Standardization (ISO). This notation is used in

the examination papers for this course without explanation. If forms of notation other than those listed

in this guide are used on a particular examination paper, they are defined within the question in which

they appear.

Because students are required to recognize, though not necessarily use, IB notation in examinations, it

is recommended that teachers introduce students to this notation at the earliest opportunity. Students

are not allowed access to information about this notation in the examinations.

Students must always use correct mathematical notation, not calculator notation.



the set of positive integers and zero,

{0,1, 2, 3,...}



the set of integers,

{0, 1, 2, 3,...}±± ±



the set of positive integers,

{1, 2, 3, ...}



the set of rational numbers

 the set of positive rational numbers,

{ | , 0}xx x∈>





the set of real numbers



the set of positive real numbers,

{ | , 0}xx x∈>



{ , ,...}xx

the set with elements

, ,...xx

()nA

the number of elements in the finite set A

{|}x

the set of all x such that

∈

is an element of

∉

is not an element of

∅

the empty (null) set

the universal set

∪

Union

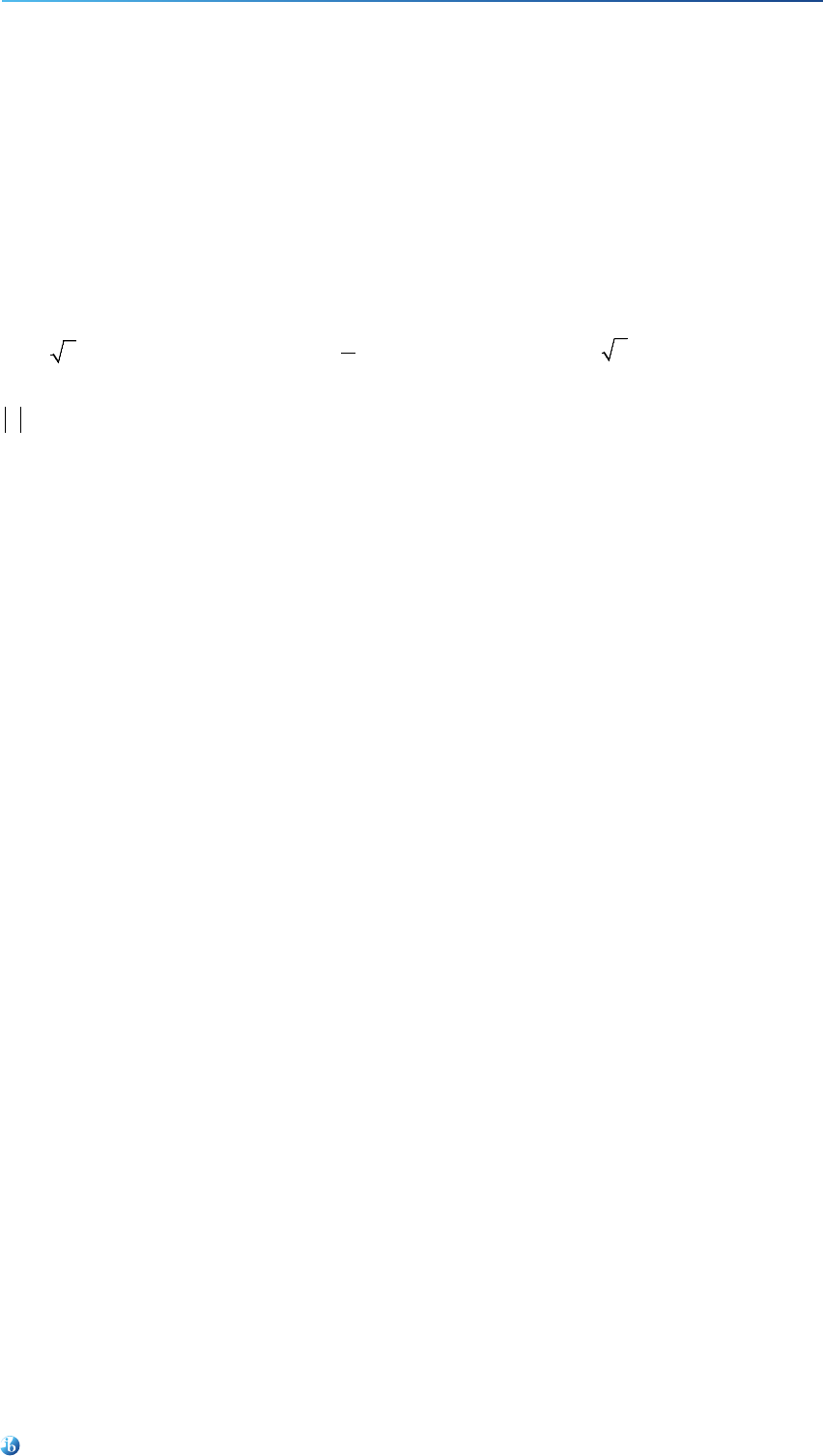
Mathematics SL guide 53

Notation list

∩

Intersection

⊂

is a proper subset of

⊆

is a subset of

A′

the complement of the set

|ab

divides

1/n

, na

to the power of

, nth root of

(if

0a≥

then

na≥

)

modulus or absolute value of

, that is

for 0,

x xx

≥∈



− <∈





≈

is approximately equal to

is greater than

≥

is greater than or equal to

is less than

≤

is less than or equal to

is not greater than

is not less than

the nth term of a sequence or series

the common difference of an arithmetic sequence

the common ratio of a geometric sequence

the sum of the first n terms of a sequence,

... n

uu u+ ++

S∞

the sum to infinity of a sequence,

...uu

∑

...

uu u+ ++







the rth binomial coefficient, r = 0, 1, 2, …, in the expansion of

()

ab+

:fA B→

is a function under which each element of set A has an image in set B

:fx y



is a function under which

is mapped to

Mathematics SL guide54

Notation list

()fx

the image of

under the function

f− the inverse function of the function



the composite function of

and

lim ( )

→

the limit of

()fx

tends to

the derivative of

with respect to

()fx

′

the derivative of

()fx

with respect to

the second derivative of

with respect to

()fx″

the second derivative of

()fx

with respect to

the nth derivative of

with respect to

()

the nth derivative of

()fx

with respect to

∫

the indefinite integral of

with respect to

∫

the definite integral of

with respect to

between the limits

xa=

and

xb=

ex exponential function (base e) of

log

logarithm to the base

ln x

the natural logarithm of

log x

sin, cos, tan the circular functions

A( , )xy

the point

in the plane with Cartesian coordinates

and

[AB]

the line segment with end points

and

AB the length of

[AB]

(AB)

the line containing points

and

the angle at

CAB

the angle between

[CA]

and

[AB]

Mathematics SL guide 55

Notation list

ABC∆

the triangle whose vertices are

and

the vector

→

the vector represented in magnitude and direction by the directed line segment

from

the position vector OA

→

i, j, k unit vectors in the directions of the Cartesian coordinate axes

the magnitude of

| AB|

→

the magnitude of

→

⋅vw

the scalar product of

and

P( )A

probability of event

P( )A′

probability of the event “not

”

P( | )AB

probability of the event

given the event

, ,...xx

Observations

, ,...

frequencies with which the observations

, ,...

occur







number of ways of selecting

items from

items

B( , )np

binomial distribution with parameters

and

N( , )

µσ

normal distribution with mean

and variance 2

~ B( , )X np

the random variable

has a binomial distribution with parameters

and

~N( , )X

µσ

the random variable

has a normal distribution with mean

and

variance 2

population mean

population variance

population standard deviation

mean of a set of data,

123

, , ,...xxx

Mathematics SL guide56

Notation list

z standardized normal random variable,

−

cumulative distribution function of the standardized normal variable with

distribution

N(0, 1)

r Pearson’s product–moment correlation coefficient

Math SL Guide

Navigation menu

Versions of this User Manual:

Views

Navigation