Multiwell User Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 236 [warning: Documents this large are best viewed by clicking the View PDF Link!]

i
February 13, 2017
MultiWell Program Suite
User Manual
(MultiWell-2017)
John R. Barker, T. Lam Nguyen, John F. Stanton,
Chiara Aieta, Michele Ceotto, Fabio Gabas, T. J. Dhilip Kumar,
Collin G. L. Li, Lawrence L. Lohr, Andrea Maranzana,
Nicholas F. Ortiz, Jack M. Preses, John M. Simmie,
Jason A. Sonk, and Philip J. Stimac
University of Michigan
Ann Arbor, MI 48109-2143
Contact:
jrbarker@umich.edu
(734) 763-6239
MultiWell Web site:
clasp-research.engin.umich.edu/multiwell
(Copyright 2017, John R. Barker)
ii
CONTENTS
0. Preliminaries 1
About the Authors 1
MultiWell Literature Citations 2
Help! Comments! Bug Reports! 3
Acknowledgements 3
1. Getting Started 5
1.1 Software Tools in the MultiWell Suite 5
1.2 How the Tools Work Together 9
1.3 Examples and Models 13
1.4 Installing and Executing the Codes 16
References 20
2. MultiWell Master Equation Code 22
2.1 Brief Description 22
2.2 Terminology 22
2.3 Default Array Dimensions 24
2.4 Notes on FORTRAN source code and compilation 24
2.5 MultiWell Input Files and Program Execution 25
2.6 MultiWell Output Files 26
2.7 MultiWell Input Data File (FileName.dat) 28
2.8 Collision Models 36
2.9 Format of External Data Files 39
2.10 Fatal Input Errors 42
References 43
3. Separable Molecular Degrees of Freedom 44
3.1 Types of Degrees of Freedom 44
3.2 Format for Input Files 48
References 51
4. DenSum: Separable Sums and Densities of States 52
4.1 Data File Format 52
4.2 DenSum in Batch Mode 54
References 56
iii
5. MomInert: Moments of Inertia 57
5.1 Data File Format 57
5.2 Computational Approach 59
References 59
6. thermo: Thermodynamics 60
6.1 Introduction 60
6.2 MultiWell Thermodynamics Database 69
References 69
7. gauss2multi: A Tool for Creating Data Files 70
References 72
8. bdens, paradensum, and sctst: non-Separable Vibrations 74
8.1 Program bdens 75
8.2 Program paradensum 81
8.3 Program sctst 86
References 91
9. lamm: Effective Mass for Internal Rotation 92
9.1 Introduction 92
9.2 Compiling and Running lamm 92
9.3 Notes and Limits 93
9.4 Data File Format 93
9.5 Example Data File 94
9.6 Example Output: 94
9.7 gauss2lamm: A script for generating lamm.dat 95
References 97
10. ktools: J-Resolved Variational Transition State Theory 100
10.1 Introduction 100
10.2 Theory 101
10.3 ktools Input File 108
10.4 Running ktools 111
10.5 ktools Output Files 111
10.6 ktools Examples 112
References 119
11. TS: J-Resolved Steady-State Master Equation Solver 120
Appendix A. Theoretical Basis 121
A.1. Introduction 121
A.2. The Active Energy Master Equation 121
iv
A.3. Stochastic Method 136
A.4. Processes 139
A.5. Initial Conditions 165
A.6. Input 168
A.7. Output 169
A.8. Concluding Remarks 170
References 172
Appendix B. Technical Notes 174
B.1 Conversion Factors (Rotational Data) 174
B.2 Anharmonic Vibrations 174
B.3 Vibrational Degeneracies 178
B.4 External molecular rotations 178
B.5 Symmetry numbers, internal rotation, and optical isomers 181
B.6 A Handy List of Lennard-Jones Parameters 187
B.7 Elements and Isotopes in MomInert and Thermo 189
B.8 Eigenstates for large amplitude motions 190
B.9 Semi-Classical Transition State Theory (SCTST) 195
B.10 Legacy and Current Versions of k0 and k∞ in MultiWell 202
Appendix C. How to … 206
C.1 How to set up the double arrays in MultiWell 206
C.2 How to test the double-array parameters in MultiWell 207
C.3 How estimate Lennard-Jones and energy transfer parameters 207
C.4 How to obtain rate constants from MultiWell simulations 208
C.5 How to tell if the simulated time is long enough 219
C.6 How to deal with Barrierless Reactions 222
C.7 Some Questions and Answers 223
Index 227
1
0. Preliminaries
About the Authors
JOHN BARKER wrote or contributed to most of the codes. The original set of codes was based
on his 1983 paper and subsequent developments.1-6
LAM NGUYEN installed a method for using quantum eigenvalues for hindered internal
rotations, wrote a code for computing the effective mass of large amplitude motions, and
helped in developing codes for non-separable vibrations,6 and semi-classical transition state
theory (SCTST).7 In addition, he and John Stanton are responsible for the code TS.
JOHN STANTON was a key participant in implementing semi-classical transition state theory 7
and vibrational anharmonicities in his quantum chemistry code CFOUR.8 He and Lam
Nguyen also are responsible for the code TS.
CHIARA AIETA, FABIO GABAS, and MICHELE CEOTTO (Università degli Studi di Milano)
developed paradensum, a parallelized code for computing sums and densities of states for
fully coupled vibrational models.9
DHILIP KUMAR wrote several scripts for automatically using output files from electronic
structure programs to build input/output files.
COLLIN LI wrote much of the code for program bdens.
LARRY LOHR contributed to the development of hindered rotor subroutines.
ANDREA MARANZANA (University of Turin) contributed codes for automatically generating
input files for the MultiWell Suite from output files produced in quantum chemical
calculations.
NICK ORTIZ (as an undergraduate student) wrote most of the code for MOMINERT.
JACK PRESES (Brookhaven Nat'l Lab.) added several helpful features.
JOHN SIMMIE (Galway, Ireland) is helping to maintain and extend the MultiWell
Thermodynamics Database.
JASON SONK wrote most of the code for ktools and has contributed to other codes as well.
PHIL STIMAC implemented 1-dimensional quantum tunneling via an unsymmetrical Eckart
barrier in the multiwell master equation code.
2
MultiWell Literature Citations
Please cite the following papers to acknowledge results obtained using this version of the
MultiWell Program Suite:
For citing the MultiWell Program Suite
In the following, <version> refers to the version number (e.g. 2017.1) and <year> refers to
the year of publication (e.g. 2017):
(a) J. R. Barker, T. L. Nguyen, J. F. Stanton, C. Aieta, M. Ceotto, F. Gabas, T. J. D. Kumar,
C. G. L. Li, L. L. Lohr, A. Maranzana, N. F. Ortiz, J. M. Preses, J. M. Simmie, J. A. Sonk,
and P. J. Stimac; MultiWell-<version> Software Suite; J. R. Barker, University of
Michigan, Ann Arbor, Michigan, USA, <year>; http://clasp-
research.engin.umich.edu/multiwell/.
(b) John R. Barker, Int. J. Chem. Kinetics, 33, 232-45 (2001).
(c) John R. Barker, Int. J. Chem. Kinetics, 41, 748-763 (2009).
References for program bdens
References (a) through (c), above, plus …
(d) M. Basire, P. Parneix, and F. Calvo, J. Chem. Phys. 129, 081101 (2008).
(e) F. Wang and D. P. Landau, Phys. Rev. Letters 86, 2050 (2001).
(f) Thanh Lam Nguyen and John R. Barker, J. Phys. Chem. A., 114, 3718–3730 (2010).
References for program paradensum
References (a) through (f), above, plus …
(g) C. Aieta, F. Gabas, and M. Ceotto, J. Phys. Chem. A, DOI: 10.1021/acs.jpca.5b12364 (2016).
References for program sctst
References (a) through (c), above, plus …
(h) W. H. Miller, J. Chem. Phys. 62, 1899 (1975).
(i) W. H. Miller, Faraday Discuss. Chem. Soc. 62, 40 (1977).
(j) W. H. Miller, R. Hernandez, N. C. Handy, D. Jayatilaka, and A. Willets, Chem. Phys. Letters
172, 62 (1990).
(k) R. Hernandez and W. H. Miller, Chem. Phys. Lett. 214 (2), 129 (1993).
(l) T. L. Nguyen, J. F. Stanton, and J. R. Barker, Chem. Phys. Letters 499, 9 (2010).
(m) T. L. Nguyen, J. F. Stanton, and J. R. Barker, J. Phys. Chem. A 115, 5118 (2011).
References for program TS
Reference (a), above, plus …
(n) "TS is a chemical kinetic program that solves a two-dimensional master-equation for gas-
phase reactions in parallel using the Steady-State approach. It is developed, implemented,
and maintained by T. L. Nguyen and J. F. Stanton, version 01-03-2017."
(o) T. L. Nguyen and J. F. Stanton, A Steady-State Approximation to the Two-Dimensional
Master Equation for Chemical Kinetics Calculations, J. Phys. Chem. A 119, 7627-7636
(2015).

3
(p) T. L. Nguyen, H. Lee, D. A. Matthews, M. C. McCarthy and J. F. Stanton, Stabilization
of the Simplest Criegee Intermediate from the Reaction between Ozone and Ethylene: A
High-Level Quantum Chemical and Kinetic Analysis of Ozonolysis, J. Phys. Chem. A
119, 5524-5533 (2015).
Help! Comments! Bug Reports!
Please send pleas for help, comments, and bug reports to the "Multiwell and Chemical
Kinetics" question and answer forum: all users are invited to join the forum, where questions
can be asked and answered, and future upgrades will be announced. This forum is set up as a
Google Group, which you can join at https://groups.google.com/. If for any reason it is difficult
for you to use Google, please contact John R. Barker (jrbarker@umich.edu) and he will answer
your question or pass it along to the appropriate person.
Acknowledgements
Thanks go to the following people for particularly helpful suggestions, discussions, de-
bugging, or other assistance:
Amity Andersen
Keith Kuwata
A. Bencsura
George Lendvay
Hans-Heinrich Carstensen
Robert G. ('Glen') MacDonald
Gabriel R. Da Silva
David M. Matheu
Theodore S. Dibble
Nigel W. Moriarty
David Edwards
William F. Schneider
Benj FitzPatrick
Colleen Shovelin
Michael Frenklach
Robert M. Shroll
David M. Golden
Gregory P. Smith
Erin Greenwald
Al Wagner
John Herbon
Ralph E. Weston, Jr.
Keith D. King
Some sections of the computer codes were developed as part of research funded by NSF
(Atmospheric Chemistry Division), NASA (Upper Atmosphere Research Program), and NASA
(Planetary Atmospheres).
Disclaimer: This material is based in part upon work supported by the National Science
Foundation. Any opinions, findings, and conclusions or recommendations expressed in this
material are those of the author(s) and do not necessarily reflect the views of the National
Science Foundation.

4
References
1. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
2. J. Shi and J. R. Barker, Incubation in Cyclohexene Decomposition at High Temperatures,
Int. J. Chem. Kinet. 22, 187-206 (1990).
3. J. R. Barker, Radiative Recombination in the Electronic Ground State, J. Phys. Chem. 96,
7361-7 (1992).
4. J. R. Barker and K. D. King, Vibrational Energy Transfer in Shock-Heated Norbornene,
J. Chem. Phys. 103, 4953-4966 (1995).
5. J. R. Barker, Energy Transfer in Master Equation Simulations: A New Approach, Int. J.
Chem. Kinet. 41, 748-763 (2009).
6. T. L. Nguyen and J. R. Barker, Sums and Densities of Fully-Coupled Anharmonic
Vibrational States: A Comparison of Three Practical Methods, J. Phys. Chem. A 114,
3718–3730 (2010).
7. T. L. Nguyen, J. F. Stanton and J. R. Barker, A Practical Implementation of Semi-
Classical Transition State Theory for Polyatomics, Chem. Phys. Letters 499, 9-15 (2010).
8. J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, A. A. Auer, R. J. Bartlett, U.
Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, M.
Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J.
Lauderdale, F. Lipparini, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R.
Price, E. Prochnow, C. Puzzarini, F. S. K. Ruud, W. Schwalbach, C. Simmons, S.
Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts, J. Almlöf, P. R. Taylor, T.
Helgaker, H. J. A. Jensen, P. Jørgensen, J. Olsen, A. V. Mitin and C. v. Wüllen.;
CFOUR, a quantum chemical program package, 2016; http://www.cfour.de.
9. C. Aieta, F. Gabas and M. Ceotto, An Efficient Computational Approach for the
Calculation of the Vibrational Density of States, J. Phys. Chem. A., DOI:
10.1021/acs.jpca.5b12364 (2016).
5
1. Getting Started
1.1 Software Tools in the MultiWell Suite
multiwell (master equation code)
Calculates time-dependent concentrations, yields, vibrational distributions, and rate
constants as functions of temperature and pressure for unimolecular reaction systems that consist
of multiple stable species, multiple reaction channels interconnecting them, and multiple
dissociation channels from each stable species. Reactions can be reversible or irreversible. Can
include tunneling and/or the effects of slow intramolecular vibrational energy redistribution
(IVR).1, 2 NOTE: k(E)'s can be calculated by other programs and read in (see Input file
description below).
Is the multiwell master equation right for your problem?
Like any other tool, this code has strengths and weaknesses. Therefore, it is more suitable
for some problems than for others. The code is based on Gillespie's stochastic simulation
algorithm (SSA),3-5 which uses Monte Carlo sampling ("stochastic trials"). This enables a very
flexible approach to simulations, but the precision of a simulation depends on the number of
stochastic trials (more trials, more precise results), as does the dynamic range, which is limited
by the number of trials. Moreover, stochastic simulations are accompanied by stochastic
sampling "noise", which is tolerable for most applications, but perhaps not for all. In multiwell,
collisions are treated very accurately and computer execution times are roughly proportional to
the number of collisions in a simulated time period. Thus, simulations can become very tedious
and time-consuming if high precision is needed in simulations that require very long simulated
time periods.
Multiwell is an extremely useful tool for simulating experiments, since no assumptions
are made beyond assuming the validity of statistical rate theory (e.g. RRKM theory). In some
cases, even the statistical assumption is not necessary, since a model1, 2, 6-8 for intramolecular
vibrational relaxation (IVR) has also been implemented.9 Multiwell is particularly useful for
simulating rapidly evolving systems that are simultaneously undergoing vibrational relaxation
and chemical reaction (e.g. photoactivation, shock excitation, chemical activation). It is not as
suitable for slowly reacting systems that are gradually approaching equilibrium or at steady state.
Note that experiments can be simulated accurately even under conditions when
phenomenological rate constants are not well-defined.
On of the principal uses in recent years of master equations has been the prediction of
reaction rate constants as functions of temperature and pressure, especially in multi-well, multi-
channel unimolecular reaction systems. For any experiment from which rate constants can be
obtained, the corresponding rate constants can be extracted from an appropriate master equation
simulation of the experiment. The data from the simulation can be analyzed by using least
squares fitting and other techniques, just as is done in analyzing experiments.10-16 This approach
is useful and accurate for relatively simple reaction systems, but not convenient for more
complicated ones. The most convenient method for extracting rate constants for the reversible
isomerization reactions in linked multi-well systems is currently the Bartis-Widom approach,17
which has been implemented in several eigenvalue codes.18-20 Because the Bartis-Widom method
relies on linear algebra techniques, it is not available for stochastic simulations, which are
6
accompanied by stochastic sampling noise. However, least squares analysis of stochastic
simulations can be used to obtain similar results.15 When the details of complicated linked
isomerization reactions are not needed, both the eigenvalue and the stochastic methods produce
satisfactory results, but if the details of the linked isomerizations are important, then the Bartis-
Widom approach is more convenient.
The stochastic method is particularly suited to systems that require high energy
resolution, such as photo-activation and chemical activation at moderate and low temperatures,
because execution time is only weakly dependent on the energy resolution, while the eigenvalue
methods are much slower when the energy grain size is reduced.16
Some information on how to extract rate constants from MultiWell master equation
simulations is provided in Sec. C.4.
In summary, the MultiWell master equation code is well suited to addressing many, but
not all, demanding problems. Users should consider the various options that are available.
Multiwell is intended to be relatively easy to use and hands-on trial runs using multiwell are a
good way to assess its utility when it is not clear which method to choose. If you would like to
discuss the various options, or have questions that are not addressed in this Manual, please
contact John Barker (jrbarker@umich.edu).
densum
Performs exact counts for sums and densities of states via the Stein-Rabinovitch
extension21 of the Beyer-Swinehart algorithm.22 This code is the best choice for separable
degrees of freedom; for coupled degrees of freedom, use bdens or paradensum. The
following types of separable modes are accepted:
a) vibrations (harmonic and anharmonic; quantized)
b) free rotations (classical or quantized)
c) hindered rotations, symmetrical and unsymmetrical (quantized eigenvalues)
d) particle in a box (quantized)
e) translation (classical)
thermo
Calculates entropy, heat capacity, and H(T)-H(0) for individual species, based on
vibrational frequencies, moments of inertia, internal rotation barriers, and electronic state
properties. It includes all of the types of modes listed for densum. It calculates equilibrium
constants, which are useful for obtaining recombination rate constants from the corresponding
unimolecular decomposition rate constants. When provided with parameters for reactants and the
transition state, it uses canonical transition state theory (CTST) to calculate rate constants
(including tunneling corrections based on the 1-D unsymmetrical Eckart barrier). By using input
files generated by Programs bdens, paradensum, or sctst (see below), thermo can
include the effects of fully coupled anharmonic vibrations and/or compute thermal rate constants
using the fully-coupled anharmonic semi-classical transition state theory (SCTST) formulated by
W. H. Miller and coworkers.
The text file named multiwell-thermo-database has been formatted for use by
program THERMO. Data for more than 100 chemical species are included in the file. See Section
6.2 of this User Manual for more information about the database.
7
mominert
Calculates principal moments of inertia for chemical species and approximate reduced
moments of inertia for internal rotors. Requires the Cartesian coordinates for the atoms in the
molecule, as obtained from many software packages in common use (e.g., HyperChem,
Chem3D, MOPAC, GAUSSIAN, C-FOUR, etc.).
gauss2multi
Reads output files from the Gaussian electronic structure program and generates data files
for the other four programs in the MultiWell Suite. (Parameters not calculated using Gaussian
must be added by hand.)
lamm
Uses Cartesian coordinates along a path (obtained from electronic structure calculations)
to compute the effective mass for hindered internal rotations. For this purpose, lamm is more
accurate than mominert. A script, gauss2lamm, is provided to read Gaussian output files and
construct most of the data file needed for lamm.
bdens
This code is available for computing sums and densities of states for non-separable
anharmonic vibrations, based on the perturbation theory expansion. It is appropriate for use with
species that contain up to perhaps 20 coupled vibrations. For larger molecules, paradensum is
a better choice. bdens computes exact counts at low energies and uses the Wang-Landau
algorithm to computed approximate counts at high energies. bdens is the best choice for highest
accuracy, but execution is very slow for very large molecules at high energies, and
paradensum is a better choice if errors of a few percent are tolerable. bdens, like densum,
produces output files that can be used directly as input files for multiwell. In addition, it
produces a file containing partition functions for the fully coupled anharmonic vibrations; these
partition functions can then be used by thermo to compute rate constants and thermodynamic
data.
paradensum
This parallelized code replaces the serial code adensum, which is no longer being
maintained (last release was multiwell-2014.1b). paradensum computes sums and densities of
states for fully coupled vibrational models that can include >150 degrees of freedom.
paradensum, like densum, produces output files that can be used directly as input files for
multiwell. In addition, it produces a file containing partition functions for the fully coupled
anharmonic vibrations; these partition functions can then be used by thermo to compute rate
constants and thermodynamic data.
sctst
This code is for using Semi-Classical Transition State Theory (SCTST), which was
formulated by W. H. Miller and coworkers23-26 to compute cumulative reaction probabilities
(CRPs), which are analogous to the sums of states for the transition state. This enables
computation for microcanonical rate constants (k(E)s), which are needed for master equation
8
simulations (using multiwell). Miller's theory is founded on second order vibrational
perturbation theory (VPT2). An additional feature of the code is the implementation of J. F.
Stanton's additional correction term, which is based on fourth-order perturbation vibrational
theory (VPT4). The code also computes the partition function corresponding to the CRP at a set
of temperatures from 50 K to 3400 K and generates a data file that can be used by program
thermo to conveniently compute thermal rate constants using SCTST.
ktools
This code implements two varieties of Variational Transition State Theory (VTST):
Canonical (i.e. thermal) and J-resolved Microcanonical (i.e. for fixed internal energies and
angular momentum). From molecular vibration frequencies, moments of inertia, and potential
energy provided at points along a reaction path to compute variationally optimized sums of states
and J-resolved microcanonical rate constants (i.e. k(E,J)) for the reaction. These quantities can be
used in 2-dimensional (i.e. depending on both E and J) master equations. By summing over J, it
also gives microcanonical VTST rate constants (i.e. k(E) that can be used in 1-D (i.e. depending
on E, alone) master equations. An important feature otf the code is that it automatically identifies
cases where two or more bottlenecks occur along the same reaction path and then uses W. H.
Miller's unified statistical theory27 to compute the over-all effective rae constant.
TS
This code features a J-resolved steady-state master equation code that is solved by
eigenvalue methods on large parallel computers. It utilizes the frozen-J approximation.
9
1.2 How the Tools Work Together
In this section, we describe the input and output of codes in the MultiWell Program Suite
and indicate how some codes generate output files that are used as input by other codes. In the
following table, <species> denotes the name of a chemical species (i.e. a Well or a Transition
State).
Table 1. Software Tools Input/Output Information
Tool
Input Quantities
Output
thermo
(Chap. 6)
Separable D.O.F. (Chap. 3)
Vibrations
Rotations
Hindered rotors
etc.
Electronic energies
Symmetries
Heat Capacity
Entropy
Enthalpy function
Equilibrium Const.
Canonical (Thermal) Rate
Constants
Input Files
Description
Generated by…
thermo.dat
<species>.qvib
<species>.crp
data file (required)
Partition functions
Partition functions
Cumulative React. Probability
User
bdens
paradensum
sctst
Output Files
Description
used by program…
thermo.out
thermo.partfxns
thermo.details
General output
Partition functions
Details
(none)
Tool
Input Quantities
Output
densum
(Chap. 4)
Separable D.O.F. (Chap. 3)
Vibrations
Rotations
Hindered rotors
etc.
G(E), sum of states
ρ(E), density of states
Input Files
Description
Generated by…
densum.dat
data file (required)
User
Output Files
Description
used by program…
densum.out
<species>.dens
General output
G(E) and ρ(E)
User
multiwell

10
Tool
Input Quantities
Output
multiwell
(Chap. 2)
Master equation
simulations.
Cartesian coordinates
Fractional concentrations vs.
time.
Branching fractions, internal
energies, etc.
Input Files
Description
Generated by…
multiwell.dat
<species name>.dens
<TS name>.crp
(other optional
input files)
data file (required)
Sums and densities of states
Cumulative Reaction
probabilities
k(E), initial energy distributions,
etc.
User
densum, ktools,
paradensum,
bdens
sctst
User
Output Files
Description
used by program…
multiwell.out
multiwell.sum
multiwell.array
multiwell.rates
multiwell.flux
multiwell.dist
General output
Output summary
Input and meta data
Reaction flux coefficients
Reactive fluxes
Energy distributions
Tool
Input Quantities
Output
mominert
(Chap. 5)
Cartesian coordinates
External moments of inertia and
rotational constants
Reduced moment of inertia and
rotational constants for
internal rotors
Input Files
Description
Generated by…
mominert.dat
data file (required)
User
Output Files
Description
used by program…
mominert.out
General output
input data used by many
of the other codes
Tool
Input Quantities
Output
lamm
(Chap. 9)
Cartesian coordinates as a
function of dihedral angle for
an internal rotation.
Reduced moment of inertia and
rotational constant as a
function of dihedral angle
Input Files
Description
Generated by…
lamm.dat
data file (required)
User
Output Files
Description
used by program…
lamm.out
General output
thermo
densum
bdens
paradensum
sctst
ktools

11
Tool
Input Quantities
Output
ktools
(Chap. 10)
J-Resolved
VTST code
For a Transition State
Separable D.O.F. (Chap. 3)
Vibrations
Rotations
Hindered rotors
etc.
Electronic energies
Symmetries
Canonical k(T) and J-resolved
microcanonical k(E,J) VTST
rate constants; also J-resolved
sums G(E,J) and densities ρ(E,J)
of states; also J-summed
quantities.
Input Files
Description
Generated by…
ktools.dat
data file (required)
User
Output Files
Description
used by …
Tool
Input Quantities
Output
bdens
(Chap. 8)
Fully coupled
vibrational
models for
small species.
Coupled vibrations (Chap. 8)
Harmonic frequencies
Anharmonicities (Xij)
Separable D.O.F. (Chap. 3)
Vibrations
Rotations
Hindered rotors
etc.
G(E), sum of states
ρ(E), density of states
partition functions
Input Files
Description
Generated by…
bdens.dat
data file (required)
User
Output Files
Description
used by program…
bdens.out
<species>.dens
<species>.qvib
General output
G(E) and ρ(E)s
Partition functions
User
multiwell
thermo
Tool
Input Quantities
Output
paradensum
(Chap. 8)
Fully coupled
vibrational
models for
large species.
Coupled vibrations (Chap. 8)
Harmonic frequencies
Anharmonicities (Xij)
Separable D.O.F. (Chap. 3)
Vibrations
Rotations
Hindered rotors, etc.
G(E), sum of states
ρ(E), density of states
partition functions
Input Files
Description
Generated by…
paradensum.dat
data file (required)
User
Output Files
Description
used by …
paradensum.out
<species>.dens
<species>.qvib
General output
G(E) and ρ(E)
Partition functions
User
multiwell
thermo
12
Tool
Input Quantities
Output
sctst
(Chap. 8)
For a Transition State
Coupled vibrations (Chap. 8)
Harmonic frequencies
Anharmonicities (Xij)
Separable D.O.F. (Chap. 3)
Vibrations
Rotations
Hindered rotors, etc.
CRP(E), cumulative reaction
probability
CRP partition function
Input Files
Description
Generated by…
sctst.dat
data file (required)
User
Output Files
Description
used by …
sctst.out
<species>.crp
<species>.qcrp
General output
CRP
CRP Partition function
User
multiwell
thermo
Preparing Input Data Files
All of the input files are text files and can be easily prepared using a text editor (a word
processor can be used, but tends to be cumbersome, since the input files do not require
formatting). Data from quantum chemistry programs can be copied and pasted into the input
files. If GAUSSIAN was used to generate molecular data, then the program gauss2multi can
be used to automatically extract data from the GAUSSIAN log files and generate major portions
of the input files, but manual entry of much information is still required.
However, we recommend that new users start by preparing the data files manually, so
that they can become familiar with the input files and the input data that cannot be obtained
from quantum chemistry programs. After learning more about the input files, experienced users
will find that gauss2multi can save them some work.
Hindered internal rotations are very important in determining thermodynamics
quantities and molecular energy state densities. The data for hindered internal rotations can be
prepared for input by first using programs mominert (for simple symmetric internal rotors) and
lamm (for any hindered internal rotor. From these data, the MultiWell codes compute the
eigenvalues of the appropriate Schrödinger equation.
Equilibrium Constants and Canonical (Thermal) Rate Constants
Equilibrium constants thermal rate constants are calculated by thermo, which normally
employs partition functions for the set of separable degrees of freedom recognized by the
MultiWell Program Suite (see Chapter 3). Rate constants for reactions with intrinsic energy
barriers are computed by thermo using tunneling corrections for the unsymmetrical Eckart
barrier.
In applications that require very accurate results for reactants and products, harmonic
frequencies and all of the Xij anharmonicity coefficients for fully coupled anharmonic vibrations
models must be computed. For these applications, programs bdens (typically ≤5 atoms) and
paradensum (typically >5 atoms) are used to compute the partition functions for the set of
13
coupled vibrations; these two programs generate output files that can be read as input to
thermo.
For tight transition states (i.e. with intrinsic energy barriers) with fully-coupled vibrations
(including the reaction coordinate), program sctst calculates the cumulative reaction
probability (CRP) and appropriate partition functions, which are placed in an output file that can
be read as input to thermo.
For loose transition states (i.e. with little or no intrinsic energy barriers), program
ktools is appropriate. This code utilizes separable degrees of freedom and information at
points along the reaction path. It automatically identifies situations with multiple transition states
along the reaction path and computes the net rate constant.
RRKM Master Equation Calculations
These calcualtions are performed using multiwell, the master equation code.
multiwell has a standard input file for many of the required parameters, but it also requires
densities of states for Wells and sums of states for Transition States. For standard calculations
that adopt separable degrees of freedom, the densities of states for the Wells are computed using
densum. For tight Transition States, densum is appropriate, but for loose Transition States,
ktools is the proper choice.
For applications that use fully coupled vibrations, bdens and paradensum can be used
to calculate the densities of states for the Wells and sctst can be used for the Transition States;
these programs generate output files that can be read by multiwell.
1.3 Examples and Models
Examples
Several examples are provided for each of the codes: multiwell, densum,
mominert, thermo, gauss2multi, ktools, bdens, and paradensum. The
densum examples include a set of cases discussed in the literature: useful for testing the
accuracy of densum. The multiwell examples include various reaction Models.
The input files found in the Examples can be used as templates to construct new input
files. Example input files can also be found in the "test" directories, which are located in each
source (src) directory (see section 1.4 for the directory structure).
The MultiWell Software Suite directory is organized as follows:
/multiwell-<version> Main MultiWell Directory
/bin binary executables
/doc version history, license, etc.
/scripts admin scripts for running tests and examples
/src
/bdens source code for bdens /test test files for densum]
/test test files
/gauss2multi source code for gauss2multi /test [test files for densum]
/test test files
14
/densum source code for densum /test [test files for densum]
/test test files
/mominert source code for mominert /test [test files for mominert]
/test test files
/multiwell source code for multiwell
/test test files
/sctst source code for sctst
/test test files
/thermo source code for thermo
/test test files
etc.
Each "test" directory associated with the source code (see above) contains an example
data file and output. In each test directory, files with the suffix ".test" are example output
files used in the testing.
15
In addition to the test directories, we provide a directory of examples. In each example,
files with the suffix ".test" are example output files generated from the data files in the
example. The data files can be used as templates when constructing new models. The
examples directory is organized as follows:
/examples
/bdens-examples
/anthracene
/CH4
/H2O2
/densum-examples
/mominert-examples
/multiwell-examples [Example multiwell Models]
/ multiwell-chemact
/multiwell-sctst
/multiwell-thermal
/multiwell-recombination
/multiwell-shock
/multiwell-tunneling
/thermo-examples
/gauss2multi-examples
etc.
Recommended Directory Structure for Models
Because there are multiple input and output files associated with any reaction model, we
have found that it is most convenient to organize them in the following way. Each model should
have its own individual directory named for the specific model. By not cluttering the
multiwell-<version> directory with input and output files for models, it is easy to install
updates without disturbing the files associated with models.
Recommended Model directory structure:
/model [name of model; e.g. "c2h6", "clo+clo", etc.]
multiwell.dat [MultiWell input data file]
multiwell.out [MultiWell output file]
multiwell.sum [MultiWell output file]
multiwell.rate [MultiWell output file]
multiwell.flux [MultiWell output file]
multiwell.array [MultiWell output file]
readme.model [read-me file for description, literature citation, etc.]
/DensData [REQUIRED for sums an densities of states used by MultiWell]
/multidata [for stored multiwell data files]
/vibs [densum data files (suggested file suffix: “.vibs”)]
/thermodata [thermo data files (suggested file suffix: “.therm”)]
/momidata [mominert data files (suggested file suffix: “.mom”)]

16
/results [stored output]
1.4 Installing and Executing the Codes
Linux/Unix (and Mac OS X) Versions
Installation of GNU Fortran
In this version, binary executables must be compiled. A previously-installed FORTRAN
compiler (e.g. GNU Fortran: https://gcc.gnu.org/fortran/) is needed to compile the source code
for most of the computer programs. For parallel codes like paradensum, OpenMPI must also
be previously-installed. (https://www.open-mpi.org/) For laptop and desktop computers, the
installations are straightforward and can be carried out by users with moderate levels of
expertise, but for installations on parallel computer clusters, it might be best for most users to
consult with their local experts.
How to build OpenMPI on laptop/desktop computers
Download from the official OpenMPI website (https://www.open-mpi.org/software/ompi/v2.0/)
the preferred compressed folder (e.g. openmpi-2.0.1.tar.gz). Then open up a terminal, move to
the directory in which you saved the compressed folder, and type the following instructions (lot
of output is produced, be patient!):
1) sudo -i
3) gunzip -c openmpi-2.0.1.tar.gz | tar xf -
4) cd openmpi-2.0.1
5) ./configure –prefix=/usr/local
6) make all install
7) exit
For more information on how to build OpenMPI and troubleshooting we refer the user to the
FAQ section of OpenMPI website (https://www.open-mpi.org/faq/?category=building)
https://gcc.gnu.org/fortran/
https://www.open-mpi.org/faq/?category=building - easy-build
https://en.wikipedia.org/wiki/Synaptic_(software
Compiling (executing "make") and Testing
A Makefile script located in the main MultiWell directory sequentially calls makefiles in
each source directory. To execute the Makefile and compile the binary executables, type the
command “make” (omit the quotation marks and use all lower case characters) followed by a
carriage return: <return>. After compiling, the binary executables are stored in directory bin.
To test that the compiled codes are operating correctly, run the script runtest_all by
going to the scripts directory and typing the command “./runtest_all”. This script will

17
run the newly compiled codes and allow you to compare the output files to “test” outputs stored
in the test directories associated with the source code. The new outputs will differ from the test
outputs with regard to date and computation time. If compiled with FORTRAN compilers other
than GNU Fortran, there may be minor numerical differences. If significant differences appear,
then it is possible that the compiled codes are not working properly.
It is highly recommended that users do not place user data files, etc., in directory
/multiwell-<version> (see Section 1.3) Instead, users should create individual directories
for user models (see Section 1.5) and execute MultiWell from within those directories. This
approach makes it very easy to replace the entire directory /multiwell-<version> with a
newer version. Programs in the MultiWell Suite are executed as described in Section 2.5.
Running Programs (except for paradensum) on Linux
Change directories until the present working directory (PWD) is the directory for a
model, i.e. the directory where the input data file resides. This Model directory (see Section 1.3)
may also contain required sub-directories, such as DensData, which is required by the
multiwell master equation code.
To run a program named "codename", type the following in the PWD:
<PATH>/multiwell-<version>/bin/codename <RETURN>
where <PATH> designates the PATH to the MultiWell directory: /multiwell-<version>.
If directory /multiwell-<version> resides in the user's home directory, type:
~/multiwell-<version>/bin/multiwell <RETURN>
For example:
~/multiwell-2017/bin/thermo
Running paradensum on Linux
paradensum is a parallel code. To compile and run the code on LINUX it is necessary
to have a previously installed version of the free Open-MPI compiler as described in the
installation Appendix Above. https://www.open-mpi.org/
If the Open-MPI compiler has been previously installed, paradensum is compiled
along with all of the other codes (the proper commands already reside in the Makefile that is
included in the src directory).
The executable (binary) program resides in (or should be placed in) the directory
multiwell-<version>/bin, where <version> is the version number. To execute the
compiled program, enter the directory that contains the input data file "paradensum.dat" and
then type:
mpirun -np <nwind> paradensum

18
where <nwind> is the number of windows. See Section 8.2 for definitions and more details.
Windows Versions
In the Windows version, binary executables (application, or .EXE files) have already
been compiled and are found in the sub-directory "multiwell-<version>/bin".
Running Programs (except paradensum) on Windows
To run any of the programs in the MultiWell Suite, except for parallel codes like
paradensum (for paradensum, see below), the steps are as follows:
1. Prepare a data file (for instructions, see the User Manual and the Examples directory) and
place it in a directory devoted to your Model (see Section 1.3). This "Model" directory may also
contain required sub-directories, such as DensData, which is required by the multiwell
master equation code.
2. Change directories until the present working directory (PWD) is the directory for a model, i.e.
the directory where the input data file resides. For densum calculations, for example, the data
file (densum.dat) may reside in the directory Model/vibs.
3. Create an alias of the executable of interest (e.g. densum.exe) and place the alias in the
Model directory (folder) as the data file. For densum calculations, for example, if the data file
densum.dat resides in the directory Model/vibs, the alias should also be placed in
directory Model/vibs.
4. Double-click the alias. The output files (e.g. densum.out, etc.) will be written to the same
directory.
Expert Users
Expert Users can set the PATH in Windows and run all of the programs, except for
paradensum, in a DOS window.
From the Model directory where the input data file resides, type:
<PATH>/multiwell-<version>/bin/densum.exe <RETURN>
For example:
~/multiwell-2017/bin/densum.exe
Running paradensum on Windows
Installation

19
1. The paradensum version for Windows can be downloaded as a precompiled executable file
paradensum.exe.
2. paradensum is a parallel code. To properly run the code it is necessary to have a
previously installed version of Microsoft MPI implementation. To download the Microsoft
MPI, the reader is referred to the website:
https://www.microsoft.com/en-us/download/details.aspx?id=54607
Download both msmpisdk.msi and MSMpiSetup.exe and execute them.
Execution
1. Put the paradensum.exe executable and parameters.dat input data file in the Model
directory.
2. Open the Windows Command Prompt and change directory to the folder that contains
paradensum.exe. To run the code with the selected number of windows <nwind>, type:
mpiexec -n <nwind> paradensum.exe
3. All of the output files are automatically generated in the same folder.
20
References
1. D. M. Leitner, B. Levine, J. Quenneville, T. J. Martinez and P. G. Wolynes, Quantum
energy flow and trans-stilbene photoisomerization: an example of a non-RRKM reaction,
J. Phys. Chem. A 107, 10706-10716 (2003).
2. D. M. Leitner and P. G. Wolynes, Quantum energy flow during molecular isomerization,
Chem. Phys. Lett. 280, 411-418 (1997).
3. D. T. Gillespie, A general method for numerically simulating the stochastic time
evolution of coupled chemical reactions, J. Comp. Phys. 22, 403-34 (1976).
4. D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys.
Chem. 81, 2340-61 (1977).
5. D. T. Gillespie, A rigorous derivation of the chemical master equation, Physica A:
Statistical and Theoretical Physics (Amsterdam) 188, 404-25 (1992).
6. D. M. Leitner, "Heat Transport in Molecules and Chemical Kinetics: The Role of
Quantum Energy Flow and Localization," in Geometric Structures of Phase Space in
Multi-Dimensional Chaos: Applications to Chemical Reaction Dynamics in Complex
Systems, Adv. Chem. Phys., vol. 130 (Part B), eds. M. Toda, T. Komatsuzaki, T.
Konishi, S. A. Rice and R. S. Berry (Wiley, 2005), pp. Wiley.
7. D. M. Leitner and P. G. Wolynes, Many-dimensional quantum energy flow at low
energy, Phys. Rev. Lett. 76, 216-219 (1996).
8. M. Gruebele and P. G. Wolynes, Vibrational energy flow and chemical reactions, Acc.
Chem. Res. 37, 261-267 (2004).
9. J. R. Barker, P. J. Stimac, K. D. King and D. M. Leitner, CF3CH3 → HF + CF2CH2: A
non-RRKM Reaction?, J. Phys. Chem. A 110, 2944-2954 (2006).
10. E. S. Lewis and M. D. Johnson, The Reactions of p-Phenylene-bis-diazonium Ion with
Water, J. Am. Chem. Soc. 82, 5399–5407 (1960).
11. J. Andraos, A Streamlined Approach to Solving Simple and Complex Kinetic Systems
Analytically, J. Chem. Educ. 76, 1578-1583 (1999).
12. A. E. Mucientes and M. A. d. l. Peña, Kinetic Analysis of Parallel-Consecutive First-
Order Reactions with a Reversible Step: Concentration–Time Integrals Method, J. Chem.
Educ. 86, 390-392 (2009).
13. M. Frenklach, A. Packard and R. Feeley, "Optimization of Reaction Models with
Solution Mapping," in Modeling of Chemical Reactions, ed. R. W. Carr (Elsevier,
Amsterdam, 2007), pp. Elsevier.
14. S. Boyd and L. Vandenberghe, Convex Optimization. (Cambridge University Press,
Cambridge, UK, 2004).
15. J. A. Miller, S. J. Klippenstein, S. H. Robertson, M. J. Pilling, R. Shannon, J. Zádor, A.
W. Jasper, C. F. Goldsmith and M. P. Burke, Comment on “When Rate Constants Are
Not Enough”, J. Phys. Chem. A 120, 306−312 (2016).
16. J. R. Barker, M. Frenklach and D. M. Golden, Reply to “Comment on ‘When Rate
Constants Are Not Enough’”, J. Phys. Chem. A 120, 313−317 (2016).
17. J. T. Bartis and B. Widom, Stochastic models of the interconversion of three or more
chemical species, J. Chem. Phys. 60, 3474-3482 (1974).
21
18. J. A. Miller and S. J. Klippenstein, Master Equation Methods in Gas Phase Chemical
Kinetics, J. Phys. Chem. A 110, 10528-10544 (2006).
19. D. R. Glowacki, C. H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, MESMER:
An Open-Source Master Equation Solver for Multi-Energy Well Reactions, J. Phys.
Chem. A 116, 9545-9560 (2012).
20. M. V. Duong, H. T. Nguyen, N. Truong, T. N. M. Le and L. K. Huynh, Multi-Species
Multi-Channel (MSMC): An Ab Initio-based Parallel Thermodynamic and Kinetic Code
for Complex Chemical Systems, Int. J. Chem. Kinet. 47, 564-575 (2015).
21. S. E. Stein and B. S. Rabinovitch, Accurate evaluation of internal energy level sums and
densities including anharmonic oscillators and hindered rotors, J. Chem. Phys. 58, 2438-
45 (1973).
22. T. Beyer and D. F. Swinehart, Number of multiply-restricted partitions, Comm. Assoc.
Comput. Machines 16, 379 (1973).
23. W. H. Miller, Semiclassical limit of quantum mechanical transition state theory for
nonseparable systems, J. Chem. Phys. 62, 1899-1906 (1975).
24. W. H. Miller, Semi-Classical Theory for Non-separable Systems: Construction of "Good"
Action-Angle Variables for Reaction Rate Constants, Faraday Discuss. Chem. Soc. 62,
40-46 (1977).
25. W. H. Miller, R. Hernandez, N. C. Handy, D. Jayatilaka and A. Willets, Ab initio
calculation of anharmonic constants for a transition state, with application to
semiclassical transition state tunneling probabilities, Chem. Phys. Letters 172, 62-68
(1990).
26. R. Hernandez and W. H. Miller, Semiclassical transition state theory, Chem. Phys. Lett.
214, 129-136 (1993).
27. W. H. Miller, Unified statistical model for "complex" and "direct" reaction mechanisms,
J. Chem. Phys. 65, 2216-2223 (1976).

22
2. MultiWell Master Equation Code
Codes, examples, and this manual are available from the MultiWell Program Suite web site:
clasp-research.engin.umich.edu/multiwell
2.1 Brief Description
MultiWell calculates time-dependent concentrations, yields, vibrational distributions, and
rate constants as functions of temperature and pressure for unimolecular reaction systems which
consist of multiple stable species, multiple reaction channels interconnecting them, and multiple
dissociation channels from each stable species. The stochastic method is used to solve the
resulting Master Equation. Users may supply unimolecular reaction rates, sums of states and
densities of states, or optionally use Forst's Inverse Laplace Transform method1-3 to calculate
k(E). For weak collisions, users can select from among many collision models, or provide user-
defined functions.
The code is intended to be relatively easy to use. It is designed so that very complicated
and very simple unimolecular reaction systems can be handled via the data file. Restructuring of
the code and recompiling are NOT necessary to handle even the most complex systems.
MultiWell is most suitable for time-dependent non-equilibrium systems. The real time
needed for a calculation depends mostly upon the number of collisions during a simulated time
period and on the number of stochastic trials needed to achieve the desired precision. For slow
reaction rates and precise yields of minor reaction products, the code will require a long run time,
but it will produce results. For long calculation runs, we often just let it run overnight.
MultiWell is based on the Gillespie Exact Stochastic algorithm,4-6 as modified and
implemented in our laboratory.7-10 It has been described in considerable detail in a recent
publication.11 An example calculation has also been published.12
In the example,12 chemical activation and shock wave simulations were carried out for a
system consisting of six isomers and 49 energy-dependent unimolecular reactions. The isomers
were interconnected by reversible isomerization reactions, and each isomer could also
decompose, resulting in 14 sets of products. Many of the capabilities of MultiWell are illustrated
in that paper.12
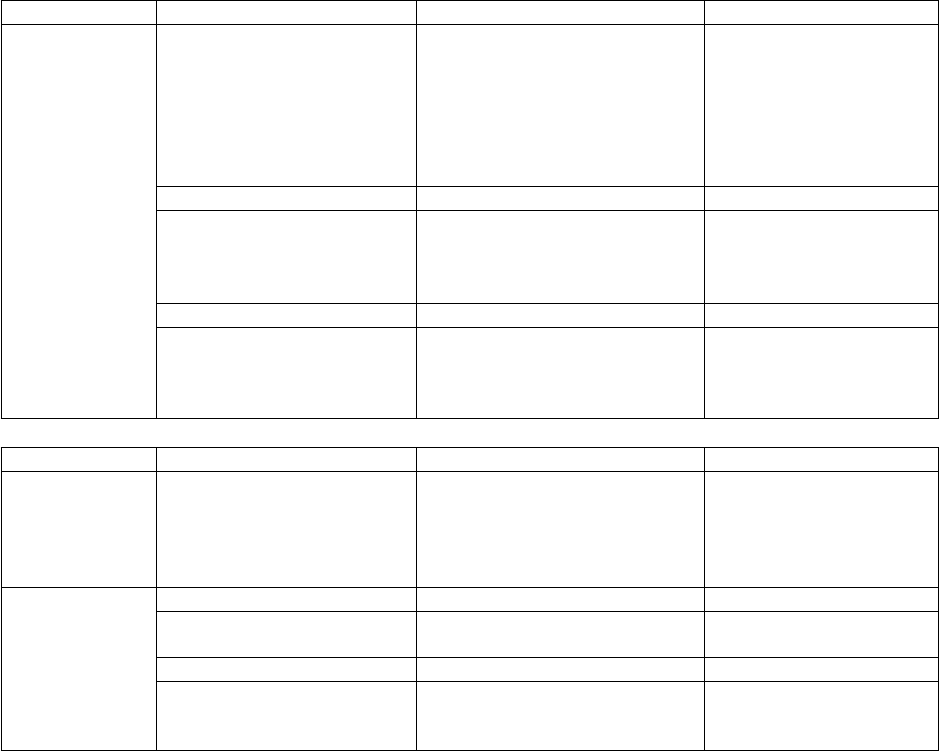
2.2 Terminology
The following sketch shows the potential energy as a function of reaction coordinate for a
typical unimolecular system with multiple wells.
Wells are chemical species corresponding to local minima on the potential energy surface
(PES). They must have at least one bound vibrational state (i.e., at least the zero point,
v=0 state). This definition is precise, sufficient, and economical; we do not find it useful
to attach any other conditions.
Transition states for reaction are defined in the usual way. They may be fixed (i.e.
associated with a local maximum on the PES), or variational.
Product sets are the fragmentation products corresponding to irreversible reaction via a
given transition state. In this user Manual, Product Sets and Reactant Sets are
synonymous, since they refer to the same reaction channel.
23
In MultiWell, each Well, each Transition State, and each Product Set is given a name and
is designated by an index number, as described below. The names and index numbers are
arbitrary, but they provide unique identification.
Collisional activation and deactivation can take place within each well and therefore
energy transfer parameters are designated for each. In most cases, energy transfer parameters are
poorly known, if known at all, and thus it is usually convenient to assign the same energy
transfer parameters to all of the wells.
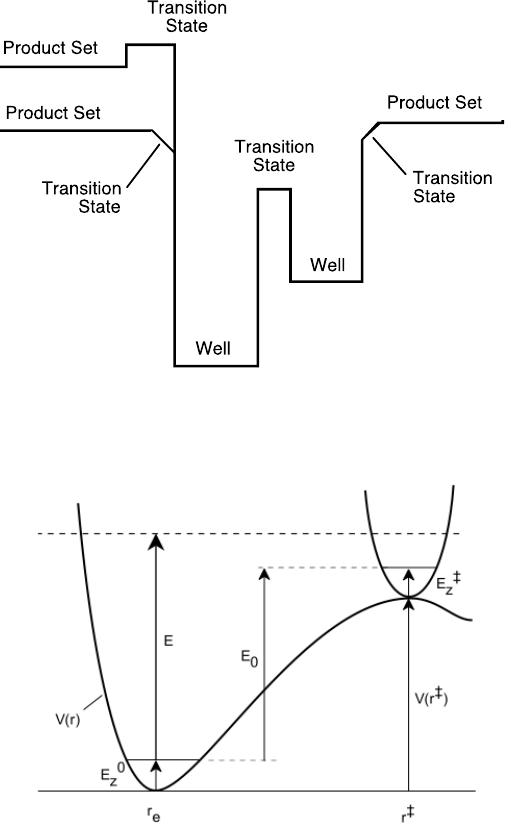
The energy scheme assumed by MultiWell is shown schematically by the following
diagram:
Figure 0. Energy schematic. The active energy E is measured from
the zero point energy of the reactant well. The critical energy E0 is
the zero point energy difference between the transition state and
the reactant well.
24
2.3 Default Array Dimensions
Array dimensions can be changed by revising the include files: Declare1.inc and
Declare2.inc. After changing the include files, the multiwell master equation code must be
completely re-compiled (To re-compile on the LINUX platform, change directories to multiwell-
<version>; type "make clean <return>" and then type "make <return>"; the entire multiwell
package will be re-compiled.) Currently, the array dimensions are set for use with up to the
following defaults. (See the Appendix Above on "Terminology".)
Up to 50 Wells.
Up to 25 Reaction channels per well for a total of up to 100 Reactions.
Up to 50 Product Sets.
Double Arrays with user-selected sizes up to 14000 elements.
100 time steps.
1000 energy bins x 100 time steps for reporting vibrational distributions.
2.4 Notes on FORTRAN source code and compilation
There are many explanatory comments embedded in the source code.
The source code is written for the GNU FORTRAN compiler for LINUX; a makefile is
distributed with the code. The code can also be compiled with almost any other
FORTRAN compiler.
A few sections of the source code are platform-dependent (e.g., OPEN statements, date &
time calls, and file & path names). These can be found in the following source code
segments:
MultiWell.f [main program]
DateTime.f
DensArray.f
Estart.f
RateArray.f
The following compiler options are required, or recommended:
-static storage (REQUIRED).
- case-sensitive (RECOMMENDED).
- variables and constants initialized to zero (RECOMMENDED).
- double precision transcendentals (RECOMMENDED).
- promote REAL and COMPLEX to double precision (RECOMMENDED).
- basic optimizations (RECOMMENDED).
25
2.5 MultiWell Input Files and Program Execution
The default input data filename is multiwell.dat (all lower case). Starting with version
2008.1, it is possible to change the input data file name and run multiple sessions in the same
directory at the same time, each with a user-selected FileName.
To run MultiWell using the default data filename (multiwell.dat):
LINUX/UNIX: in the directory where the input data file and the auxiliary directory
DensData reside, type:
<PATH>/multiwell-<version>/bin/multiwell <RETURN>
where <PATH> designates the PATH to /multiwell-<version>. If directory
/multiwell-<version> resides in the user home directory, type:
~/multiwell-<version>/bin/multiwell <RETURN>
WINDOWS in a DOS window: in the directory where the input data file and the auxiliary
directory DensData reside, type:
<PATH>/multiwell-<version>/bin/multiwell <RETURN>
For example:
~/multiwell-2013/bin/multiwell
To run MultiWell using a user-defined filename (FileName.dat):
Follow the same procedures described above, but type:
<PATH>/multiwell-<version>/bin/multiwell <FileName> <RETURN>
For example:
~/multiwell-2017/bin/multiwell final.dat
All of the resulting output files will take names with the same prefix:
final.out
final.sum
final.rate
final.dist
final.flux
final.array
26
2.6 MultiWell Output Files
Output files with an identical FileName (including the default: 'multiwell') are erased
and written-over for every calculation (for optionally naming of files at run time, see Section
2.5). To be saved, they must be re-named. Use a word processor/editor capable of wide-open (no
truncation of lines) output, because the output can be hundreds of characters in width, depending
on the number of species and products. In Linux, Xemacs, Emacs, Nedit and other editors are
available for this purpose. For Macintosh OS X, "Tex-Edit Plus" (share-ware available at
http://www.nearside.com/trans-tex/) and "TextWrangler" (free-ware available at
http://www.barebones.com/) are very convenient word processors for text files, although full-
featured word processors can be used as well.
FileName.out
Time-dependent output of concentrations and average energies. Also includes summaries
of input parameters. The time-dependent quantities are the instantaneous values at the time
indicated: they are not averaged over the time interval. Hence, the averages are only over the
number of trials.
FileName.sum
Summary output file intended for convenient calculations of fall-off curves and other
pressure-dependent quantities. This file gives all of the header material in the full output file, but
instead of the time-dependent results, only the final results of each simulation are given in the
form of a summary table.
FileName.rate
Time-dependent output of average reaction flux coefficients, which vary with time in
non-steady-state systems. (When the energy distributions are independent of time and for the
reactions are irreversible, the flux coefficients can be identified with rate constants.) Many trials
are needed to accumulate good statistics. To improve statistics, the binned results correspond to
the number of visits to the bin (which can be many times larger than the number of trials) and are
averaged over the time-bin.
FileName.dist
Time-dependent vibrational distributions in Wells (not initial or final products). Only the
non-zero array elements are listed. Many trials are needed to accumulate good statistics. Note
that the distributions are normalized according to the number of stochastic trials. Therefore, the
sum of the array elements for a chemical species (Well) at a given time is equal to the fractional
population of that species at that time. Thus the distributions report not only the relative
populations as functions of energy and time, but also the growth and decay of species
concentrations.
FileName.array
Tabulations of all energy-dependent input data. Includes tables of densities of states,
specific rate constants, collision probabilities and normalization factors, and initial energy
distributions.
27
FileName.flux
Tabulates the reactive flux via each of the unimolecular channels. The reactive flux is
useful for identifying quasi-equilibrium situations and for tracing chemical pathways.
28
2.7 MultiWell Input Data File (FileName.dat)
(See Section 2.5 for optional naming of data files at run time.)
The datafile uses free input format.
NOTES ON FREE INPUT FORMAT: Fields separated by delimiters.
- Standard delimiters on most platforms: commas and spaces.
- Additional delimiters acceptable on some platforms: tabs.
- CHARACTER constants enclosed in apostrophes (') are accepted on most platforms. Some
platforms will accept CHARACTER constants without their being enclosed in
apostrophes, but then they cannot contain any of the delimiter characters.
MULTIWELL MAJOR INPUT OPTIONS
1. Densities of states are read from an external file created by DenSum, or other code.
2. Specific Rate constants: k(E)
a) RRKM theory via sums of states read from an external file (created by DenSum, or other
code).
b) k(E) values read from external file.
c) Reversible and/or irreversible reactions.
3. Initial energy distributions:
a) thermal (with an optional energy offset), calculated internally.
b) chemical activation, calculated internally.
c) delta function
d) distribution can be read from an external file.
4. Separate initial vibrational temperature and translational temperature.
5. Can incorporate the effects of slow intramolecular vibrational energy redistribution (IVR).
6. Can include tunneling via an unsymmetrical Eckart barrier.

29
MULTIWELL INPUT DATA FILE FORMAT
Note: Starting with version 2.0, the data file format is no longer compatible
with previous versions.
APPENDIX A: PHYSICAL PARAMETERS
Line 1
TITLE (up to 100 characters)
Line 2
Egrain1, imax1, Isize , Emax2, IDUM
Egrain1 energy grain size of first segment in "double arrays", see Note (units: cm-1)
imax1 size of first segment of double array; selected so that sums or densities of states is
a smooth function of energy (less than ~1% relative fluctuations). Note that
imax1 must be less than Isize.
Isize user-selected size of double array. The Default array size starting in version 2.08
is set for a maximum of 14000 elements in the INCLUDE file "declare1.inc".
(The array size is defined by Imax=14000 in declare1.inc.) This large maximum
array size allows users to select any value of Isize ≤ 14000 elements without
having to recompile the code. If array sizes greater than 14000 elements are
needed, the Imax can be changed in the Linux/Unix version by deleting old object
files (by typing ‘make clean’ in /multiwell/src/multiwell) and then recompiling
(by typing ‘make’).
Emax2 maximum energy of 2nd segment of double arrays (units: cm-1)
IDUM random number seed (integer); EXAMPLE: "2113989025"
***** NOTE: "Double arrays" have two sections: segment 1 consists of imax1 equally
spaced (Egrain1) data ranging from E=0; segment 2 consists of equally spaced values from
E=0 to Emax2; the size of the second segment is (Isize - imax1); the energy grain of the
second segment is Emax2/(Isize - imax1 - 1).
(Appendix A, continued...)
30
Line 3
Punits, Eunits, Rotatunits
[It is required that the three keywords be entered in this exact order!]
Punits one of the following pressure units keywords:
'BAR', 'ATM', or 'MCC'[for molecules/cc] (Note that 'TOR' is no longer
accepted.)
Eunits one of the following energy units keywords:
'CM-1', 'KCAL', or 'KJOU' for cm-1, kcal/mole or kJ/mole
Rotatunits one of the following keywords for rotational information:
'AMUA', 'GMCM', 'CM-1', 'MHZ', 'GHZ'(for moments of inertia in units of
amu.Å2 or g.cm2, and rotational constants in units of cm-1. MHz, or GHz)
(some combinations of upper/lower case are also accepted)
Line 4
Temp , Tvib
Temp translational temperature (units: Kelvin)
Tvib initial vibrational temperature (units: Kelvin)
For shock-tube simulations, Temp is set equal to the shock (translational)
temperature and Tvib is set equal to the vibrational temperature prior to the
shock (usually room temperature).
Line 5
Np number of pressures
Line 6
PP(1), PP(2), ..., PP(Np)
List of Np pressures

31
APPENDIX B: PARAMETERS FOR WELLS AND FOR PRODUCT SETS
Line 7
NWells , NProds
NWells number of "wells" (includes irreversible product sets)
NProds number of entrance/exit channels; each channel has a product set associated with
it.
Line 8
IMol , MolName , HMol , MolMom , Molsym , Molele , Molopt
(REPEAT NWells times: once for each well.)
IMol index number for well (1 ... NWells)
MolName name of well (≤10 characters)
HMol enthalpy of formation at 0 K (units defined by keyword)
MolMom rotational parameter for 2-dimensional external rotation (moment of inertia or
rotational constant; units defined by keyword on Line 3)
Molsym external symmetry number for well (see Appendix B.5 for a discussion)
Molele electronic partition function for well (REAL number); depends on temperature;
can be obtained from THERMO output.
Molopt number of chiral stereoisomers (or "optical isomers") for well (see Appendix B.5
for a discussion)
See Appendix B.4 for a discussion of proper input for External Molecular Rotations.
Line 9
IMol , MolName , Hmol
(REPEAT NProds times: once for each entrance/exit channel, i.e. for each product set.)
IMol index for channel (NWells+1...NWells+NProds)
MolName name of Product set (max 10 characters)
Hmol enthalpy of formation at 0 K (units defined by keyword on Line 3) [ignored unless
tunneling is used]
***** NOTE: the numbering of entrance/exit channels starts with NWells+1.
Line 10
SigM, EpsM, AmuM, Amu
32
SigM Lennard-Jones (Å) for collider
EpsM Lennard-Jones /kB (Kelvins) for collider
AmuM Molecular weight (g/mole) of collider
Amu Molecular weight (g/mole) of reactant
Optional Line 10a
OLDET To change the default treatment of collisional energy transfer from Barker's "New
Approach" (see Ref. 13) to the traditional approach, insert the keyword OLDET
(all upper case) on a new line. The "New Approach" (the default) attenuates the
inelastic collision frequency (and hence the rate of inelastic energy transfer) at
low energies, where the densities of states are very sparse. The traditional method
was based on the convenient assumption that the inelastic collision frequency is
independent of internal energy. This feature facilitates intercomparisons between
multiwell and other master equation codes.
Line 11
Mol, Sig, Eps, ITYPE, DC(1), DC(2), ... , DC(8)
(REPEAT Lines 11 and 12 NWells times: once for each well.)
Mol index number of Well
Sig Lennard-Jones (Å) for this well
Eps Lennard-Jones /kB (Kelvins) for this well
ITYPE selects model type in Subroutine PDOWN (see below for description of collision
models). Model types and explanations are given below.
DC(8) eight (8) coefficients for energy transfer model
Line 12
LJQM keyword for type of collision rate constant:
'LJ' for Lennard-Jones collision rate constant. This rate constant is computed
using the empirical expression of Neufeld et al. for the collision integral.14
'QM' for quantum mechanical total collision rate constant15
(REPEAT Lines 11 and 12 NWells times: once for each well.)

33
SECTION C: PARAMETERS FOR TRANSITION STATES AND REACTIONS
Line 13
NForward number of forward unimolecular (not recombination) reactions to be input.
Line 14
Mol, ito, TS, RR, j, k, l, AA, EE, KEYWORD, KEYWORD, KEYWORD, KEYWORD, KEYWORD
(REPEAT NForward times: once for each forward reaction.)
Mol index of reactant well
ito index of entrance/exit channel or well
TS Name of transition state (up to 10 characters)
RR 2-D external rotational parameter (moment of inertia or rotational constant; units
defined by keyword on Line 3) ; See Appendix B.4 for a discussion of proper
input for External Molecular Rotations.
jexternal symmetry number for TS (see Appendix B.5 for a discussion)
Qel electronic partition function for TS (REAL number)
lnumber of optical isomers for TS (see Appendix B.5 for a discussion)
AA A-factor for reaction (units: s-1); only used for ILT method, but ALWAYS read in
EE reaction critical energy (E0), relative to ZPE of reactant (Mol) (See Appendix B.9
for the appropriate E0 when using SCTST)
KEYWORDS ALWAYS SPECIFY FIVE KEYWORDS, IN ANY ORDER. Select one from
each of the Five Groups below. See Section 2.10 (FATAL INPUT ERRORS)
for a list of incompatible choices.
Group 1
'NOREV' for neglecting the reverse reaction
'REV' for calculating reverse reaction rate (automatically treated as NOREV for
dissociation reactions).
Group 2
'FAST' for neglecting limitations due to IVR
'SLOW' for including IVR limitations; line 14b contains parameters (see below).
Group 3
'NOTUN' for neglecting tunneling
'TUN' for including tunneling via unsymmetrical Eckart barrier; line 14a contains
parameters (see below). This option cannot be selected if SCTST was used
to generate the cumulative reaction probability (~sum of states).

34
Group 4
'NOCENT' for no centrifugal correction
'CENT1' for quasi-diatomic centrifugal correction with 1 adiabatic external rotation
(for special cases)
'CENT2'(This is the usual choice) for quasi-diatomic centrifugal correction with 2
adiabatic external rotations
'CENTX' for legacy centrifugal correction with 2 adiabatic external rotations (not
recommended)
[Note: the calculated k∞ is numerically the same for all options in Group 4.]
Group 5
'ILT' Inverse Laplace transform method for k(E).
'SUM' External file containing sums of states (i.e. generated by densum, or bdens)
'CRP' External file containing cumulative reaction probability (i.e. generated by
program sctst)
'RKE' External file containing k(E): <TS filename>'.rke' (e.g. 'TS-1.rke').
NOTE: k(E)'s can be calculated by other programs and read in as an external
file.
Line 14: Supplementary Lines
The following supplementary lines provide additional information corresponding to some of the
Keywords in Line 14. The supplementary line immediately follows the line invoking the
Keyword. (On the rare occasion when more than one supplementary line is required, they must
be entered in the order given here.)
Supplementary Line 14a
'TUN', vimag(Mol,i)
This line appears only if KEYWORD 'TUN' was used in Line 14. It gives the imaginary
frequency (cm-1) for the specified reaction. It can only be used when 'NOCENT' is invoked.
Cannot be used simultaneously with 'ILT' or 'RKE'.
Supplementary Line 14b
'SLOW', vivr(Mol,i), vave(Mol,i), kcivr(Mol,i), tivr(Mol,i), civr(Mol,i,1),
civr(Mol,i,2), civr(Mol,i,3)
This line appears only if KEYWORD 'SLOW' was used in Line 14. It gives parameters for the
IVR transmission coefficient for this reaction:
Transmission Coefficient kIVR E
kIVR
cM
kIVR E
kIVR
cM
ivr

35
where IVR is the characteristic reaction frequency (as in RRK unimolecular reaction rate theory).
At energies above the IVR threshold energy (i.e. E ≥ EIVR0), the IVR rate constant kIVR(E) is:
kIVR EE0r
civr Mol,i,1
civr Mol,i,2
EE0r
civr Mol,i,3
EE0r
2
where E (expressed in cm-1) is the energy relative to the reactant zero point energy and E0r is the
reaction critical energy (which may include the centrifugal correction).
vivr(Mol,i) Characteristic frequency (cm-1) for the reaction; IVR/s-1 = vivr*2.9979×1010.
vave(Mol,i) Average frequency (cm-1) of the reactant; used to define an upper limit to kIVR,
the IVR rate constant: kIVR ≤ 2*vave*2.9979×1010.
kcivr Bimolecular rate constant kcIVR [cm3 molecule-1 sec-1] for collision-induced
IVR. In the absence of other information, kcIVR may be estimated as
approximately equal to the quantum mechanical total collision frequency
bimolecular rate constant, as obtained from the MultiWell output (see Line
#12, above).
tivr(Mol,i) IVR threshold energy (cm-1), measured from the reaction critical energy (i.e.
E0IVR-E0r).
civr(Mol,i,..) Three (3) coefficients for second order polynomial fit of kivr (s-1) as a function
of E-E0r (cm-1; energy measured from the reaction critical energy).
SECTION D: CALCULATION SPECIFICATIONS
Line 15
Ntrials, Tspec, Tread, KEYTEMP, Molinit, IR, Einit
Ntrials number of trials
Tspec a KEYWORD that specifies meaning of Tread (CHARACTER*4)
'TIME' indicates Tread = max time simulated (Tlim)
'COLL' indicates Tread = max time simulated is calculated from the specified
maximum number of collisions experienced by initial well number (Molinit).
Tread maximum simulated time or maximum number of collisions (see Tspec, above).
KEYTEMP a KEYWORD that specifies the type of initial energy distribution
'DELTA': Monoenergetic at energy Einit
'THERMAL': Thermal (Tvib) with energy offset Einit
'CHEMACT': Chemical activation (Tvib) from "product" #IR
'EXTERNAL': Read cumulative energy distribution from external file
"multiwell.pstart" placed in directory " DensData "
Molinit index of initial well

36
IR index number of the "product set" which reacts to produce Molinit via
chemical activation; neglected if 'CHEMACT'is not specified.
Einit initial energy (relative to ZPE of Molinit); neglected if 'CHEMACT' is
specified; same units as Eunits.
Line 16
BLANK LINE TO INSURE THAT THE LAST LINE IS FOLLOWED BY A CARRIAGE
RETURN (needed for all READ statements). THE CARRIAGE RETURN IS EASILY
OVERLOOKED!
2.8 Collision Models
(see Line 11 in multiwell data file described above)
This selection of collision models includes most of the empirical models discussed in the
literature. Function subroutine "Pdown.f" can be revised to include additional models.
For general guidance in selecting models and parameters, see Barker et al.16
For the EXPONENTIAL MODEL, use ITYPE=1 with coefficient C(4) set equal to zero so that
the second exponential term is equal to zero; Model Types 12 or 13 can also be used.
ITYPE
1 Biexponential Model
2 Density-weighted Biexponential Model
3 Off-set Gaussian with constant offset and E-dependent width
4 Biexponential Model with energy-dependent fraction
5 Generalized Gaussian with energy-dependent exponent
6 Generalized Gaussian plus Exponential term
7 Weibull Model
8 Lorentzian Step-Ladder Model
9 Exponential+Elastic Model
10 Klaus Luther's empirical function
11 Radiationless transition empirical function
12 Exponential Model with alpha(E)=linear + exponential
13 Exponential Model with alpha(E) switching function
14 Boltzmann-weighted exponential
37
FUNCTION AND COEFFICIENT DESCRIPTIONS:
ITYPE = 1 for Biexponential Model
Pdown = (1-C(4))*EXP(-(E-EE)/Alpha1) + C(4)*EXP(-(E-EE)/Alpha2)
Alpha1 = [C(1) + E*C(2) + E*E*C(3)]*(T/300)**C(8)
Alpha2 = [C(5) + E*C(6) + E*E*C(7)]*(T/300)**C(8)
ITYPE = 2 for Density-of-States-weighted Biexponential Model
Pdown = (E)*((1-C(4))*EXP(-(E-EE)/Alpha1) + C(4)*EXP(-(E-EE)/Alpha2))
Alpha1 = [C(1) + E*C(2) + E*E*C(3)]*(T/300)**C(8)
Alpha2 = [C(5) + E*C(6) + E*E*C(7)]*(T/300)**C(8)
ITYPE = 3 for Off-set Gaussian with constant offset and E-dependent width
Pdown = EXP(-(0.5*(E-EE-C(4))/Alpha1)**2)
C(4) = constant off-set, Alpha1 is the std. dev.
Alpha1 = [C(1) + E*C(2) + E*E*C(3)]*(T/300)**C(8)
ITYPE = 5 for Generalized Gaussian with energy-dependent exponent
Pdown = EXP(-[(E-EE)/Alpha]**Exponent)
Alpha = C(1) + [E*C(2) + E*E*C(3)]
exponent = C(5) + [E*C(6) + E*E*C(7)]
ITYPE = 6 for Generalized Gaussian plus Exponential term
Pdown =(1-C(6))*EXP(-[(E-EE)/Alpha1]**Exponent) + C(6)*EXP(-(E-EE)/Alpha2)
Alpha1 = C(1) + [E*C(2) + E*E*C(3)]
Alpha2 = C(7) + E*C(8)
Exponent = C(4) + E*C(5)
ITYPE = 7 for Exponential Model with Switching function
Pdown = EXP(-(E-EE)/Alp)
Alpha1 = C(1) + E*C(2)
Alpha2 = C(3) + E*C(4)
Alp = Alpha1 + 0.5*(Alpha2 - Alpha1)*(1. - TANH((C(5) - E)/C(6) ) )
38
ITYPE = 8 for Lorentzian Step-Ladder Model
Pdown = 1 / [(E-EE-Alpha)^2 + Width^2]
Alpha = C(1) + [E*C(2) + E*E*C(3)]
Width = C(5) + [E*C(6) + E*E*C(7)]
ITYPE = 9 for Exponential+Elastic Model
Pdown = [F/(F+C(4))]*EXP(-(E-EE)/Alpha) + elastic
Alpha = [C(1) + E*C(2) + E*E*C(3)]*(T/300)**C(8)
F = [C(5) + (E/C(6))**C(7)]*(T/300)**C(8); when E=EE
ITYPE = 10 for Klaus Luther's empirical function
Pdown = EXP [-[(E-EE)/Alpha]^Beta]
Alpha = C(1) + E*C(2)
Beta = C(3)
ITYPE = 11 for radiationless transition empirical Function
Pdown = EXP [-(E-EE)/Alpha]'
Alpha = C(1)*[1-exp[-(E/C(2))^C(3)] + C(4)]
ITYPE = 12 for Exponential Model with alpha(E)= Linear+exponential
Pdown = EXP(-(E-EE)/Alpha1)
Alpha1 = C(1) + E*C(2) + C(3)*exp(-E/C(4))
ITYPE = 13 for Exponential Model with Alpha(E) Switching function
Pdown = EXP(-(E-EE)/Alp)
Alp = Alpha1 + 0.5*(Alpha2 - Alpha1)*(1. - TANH((C(5) - E)/C(6) ) )
Alpha1 = C(1) + E*C(2)
Alpha2 = C(3) + E*C(4)
ITYPE = 14 for Boltzmann-Weighted Exponential
(motivated by recent trajectory calculations17)
Pdown = B(T;EE,E)*EXP( -(E-EE)/Alp )

39
B(T;EE,E) = SQRT(rho(EE)*exp(-(EE-E)/RT))
where rho(EE) = density of states
Alp = C(1)
2.9 Format of External Data Files
Location: EXTERNAL DATA FILES MUST BE STORED IN FOLDER
(DIRECTORY) "DensData", which is in the folder (directory) from which the MultiWell
application is executed.
Densities, Sums and k(E)'s
Creation: Typically, the external files for densities of states and sums of states are
generated using the program DenSum, which calculates sums and densities via exact counts. A
similar format is used for specific rate constants, as described here.
FILE NAMES
For sums and densities of states: CHARACTER*10 + '.dens'
Example: 'Ethyl-Cl .dens'
For specific rate constants [k(E)'s]: CHARACTER*10 + '.rke'
Example: 'HCl+C2H4.rke'
FILE FORMAT
Note: Starting with version 2008.1, " ____.dens" files, which contain sums and densities
of states, may have a block of comment lines preceding Line 1 (below). The first and last
comment lines in the block must have exactly the following 46 characters:
**************INPUT DATA SUMMARY**************
Line 1
Name of species or transition state [CHARACTER*10]: up to 10 characters (skipped when read
by MultiWell, and therefore can be left blank)
Line 2
Title/Comment line [CHARACTER*100]: up to 100 characters (skipped when read by
MultiWell, and therefore can be left blank)
Line 3
Egrain1 , imax1 , Emax2 , Isize , Viblo
[REAL, INTEGER, REAL, INTEGER, REAL]

40
Note that this ordering of parameters is not the same as in multiwell.dat. If Egrain1, imax1,
& Emax2 do not match those for the MultiWell run (see line #2 of the MultiWell data file), then
execution terminates with a message. In density and sums of states files, Viblo is the lowest
vibrational frequency for a given species; it is used in the collision step routines. In rate constant
input files, A real number must be input for Viblo, but it is ignored by MultiWell.
Line 4
Column label (skipped when read by MultiWell, and therefore can be left blank)
For sums of states, this line might read:
" No. (cm-1) Density Sum"
For a rate constant input file, this line might read:
" No. Energy Dummy RateConst"
Line 5
(Repeated Isize times)
j, A, B, C
[INTEGER,REAL,REAL,REAL]
FOR FILES CONTAINING SUMS & DENSITIES
j = array element index (a total of Isize elements)
A = energy [starting with E = 0.0] (units: cm-1)
B = density of states (units: states/cm-1)
C = sum of states (dimensionless)
FOR FILES CONTAINING SPECIFIC RATE CONSTANTS [k(E)'s]
j = array element index (a total of Isize elements)
A = energy [starting with E = 0.0] (units: cm-1)
B = dummy real number (ignored by MultiWell)
C = k(E) (units: s-1)
Line 6
BLANK LINE TO INSURE THAT THE LAST LINE IS FOLLOWED BY A CARRIAGE
RETURN (needed for all READ statements). THE CARRIAGE RETURN IS EASILY
OVERLOOKED.
41
Initial Energy Distribution Function
File name: "multiwell.pstart"
Location: EXTERNAL DATA FILES MUST BE STORED IN FOLDER (DIRECTORY)
"DensData", which is in the folder (directory) from which the MultiWell application is executed.
Line 1
Jsize, Hstart, Edel
Jsize user-selected array length (≤14000 elements). Jsize must be chosen to be large
enough (for a given Hstart) so that the entire initial energy distribution is
represented.
Hstart energy grain (express in cm-1) for initial energy distribution: "Pstart". Hstart
should be ≥Egrain1 used to generate sums and densities of states.
Edel energy origin of array, relative to zero point energy of initial excited well (express
in cm-1)
Line 2
(REPEAT Jsize times)
DUMMY, Pstart
DUMMY Must be input, but ignored by MultiWell (may be equal to E, for example)
Pstart NORMALIZED cumulative initial energy distribution function. Thus,
Pstart(i) ranges monotonically from Pstart(1)=0 (approximately), up to
Pstart(Jsize) = 1.0.
(Note that other columns may be present in the data file, but they will be ignored.)
Line 3
BLANK TO INSURE THAT THE LAST LINE IS FOLLOWED BY A CARRIAGE RETURN
(needed for all READ statements). THE CARRIAGE RETURN IS EASILY OVERLOOKED.
42
2.10 Fatal Input Errors
A FATAL INPUT ERROR is reported and execution is stopped if any of the following
parameters for a well or transition state does not match the corresponding value from Line 2 of
multiwell.dat:
Egrain1, imax1, Isize , Emax2
Incompatible Keywords or other Options, resulting in a Fatal Error:
ILT and CENT1, CENT2, or CENTX
ILT and TUN
RKE and TUN
CRP and TUN
CENT and TUN
CENT1, CENT2, or CENTX with TSmom(Mol,nchann) ≤ 0
(moment of inertia or rotational constant of the transition state)
43
References
1. W. Forst, Theory of Unimolecular Reactions. (Academic Press, New York, 1973).
2. W. Forst, Unimolecular rate theory test in thermal reactions, J. Phys. Chem. 76, 342-348
(1972).
3. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
4. D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys.
Chem. 81, 2340-61 (1977).
5. D. T. Gillespie, A general method for numerically simulating the stochastic time
evolution of coupled chemical reactions, J. Comp. Phys. 22, 403-34 (1976).
6. D. T. Gillespie, Monte Carlo simulation of random walks with residence time dependent
transition probability rates, J. Comp. Phys. 28, 395-407 (1978).
7. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
8. J. Shi and J. R. Barker, Incubation in Cyclohexene Decomposition at High Temperatures,
Int. J. Chem. Kinet. 22, 187-206 (1990).
9. J. R. Barker, Radiative Recombination in the Electronic Ground State, J. Phys. Chem. 96,
7361-7 (1992).
10. J. R. Barker and K. D. King, Vibrational Energy Transfer in Shock-Heated Norbornene,
J. Chem. Phys. 103, 4953-4966 (1995).
11. J. R. Barker, Multiple-well, multiple-path unimolecular reaction systems. I. MultiWell
computer program suite, Int. J. Chem. Kinet. 33, 232-245 (2001).
12. J. R. Barker and N. F. Ortiz, Multiple-Well, multiple-path unimolecular reaction systems.
II. 2-methylhexyl free radicals, Int. J. Chem. Kinet. 33, 246–261 (2001).
13. J. R. Barker, Energy Transfer in Master Equation Simulations: A New Approach, Int. J.
Chem. Kinet. 41, 748-763 (2009).
14. P. D. Neufeld, A. R. Janzen and R. A. Aziz, Empirical Equations to Calculate 16 of the
Transport Collision Integrals Ω(l, s)* for the Lennard‐Jones (12–6) Potential, J. Chem.
Phys. 57, 1100 (1972).
15. J. L. Durant and F. Kaufman, Calculation and use of total collision rates in thermal
systems, Chem. Phys. Lett. 142, 246-51 (1987).
16. J. R. Barker, L. M. Yoder and K. D. King, Feature Article: Vibrational Energy Transfer
Modeling of Non-Equilibrium Polyatomic Reaction Systems, J. Phys. Chem. A 105, 796-
809 (2001).
17. J. R. Barker and R. E. Weston, Jr., Collisional Energy Transfer Probability Densities
P(E,J;E',J') for Monatomics Colliding with Large Molecules, J. Phys. Chem. A 114,
10619–10633 (2010).
44
3. Separable Molecular Degrees of Freedom
In this chapter, the various types of separable molecular degrees of freedom recognized
by the codes in the MultiWell Program Suite are defined (Section 3.1) and the formats for the
input data are described (Section 3.2). These types of molecular degrees of freedom are used by
the following codes, which are described in the designated chapters:
densum (Chapter 4)
thermo (Chapter 6)
bdens (Chapter 8)
sctst (Chapter 8)
paradensum (Chapter 8)
ktools (Chapter 10)
3.1 Types of Degrees of Freedom
(An)Harmonic Vibration (vib)
The energy of an anharmonic oscillator is
E
ev1
2
exev1
2
2
ZPE
where ωe is the harmonic frequency and the zero point energy (v = 0) is
ZPE
e
1
2
exe
1
2
2
.
For a Morse oscillator, the anharmonicity is
exe
e
2
4De
where De is the Morse oscillator well depth (from the bottom of the potential well). Note the
sign convention for anharmonicity used here is not the usual convention.
By an "Observed frequency" (key word "obs") for a vibrational mode, we mean the
fundamental frequency, which is the 0-1 transition frequency for the specific mode when all
other vibrational quantum numbers equal zero. When ωexe≠0 for a separable mode, the
fundamental frequency ωf is related to the harmonic frequency according to the following
expression:
e
f2
exe
45
For an "observed" frequency, Densum and Thermo compute ωe from this expression and use
it to calculate the vibrational energy levels.
Classical Rotation (rot)
DenSum uses the method of Astholz et al.1 For expressions, see Appendix 5 of Robinson and
Holbrook,2 or Section 4.5 of Holbrook et al.3 Also see Appendix (Theoretical Basis),
Appendix A.2.2 Note that starting with version 2.04, classical rotations are treated purely
classically; previously, a semi-classical approximation was imposed (which amounted to
requiring that the sum of states is equal to unity at E = 0). See Appendix B.4 for a
discussion of proper input for External Molecular Rotations.
Quantized Rotation (qro)
When J = 0, E = 0 and degeneracy (g) is unity. When J >0, the degeneracy (g) and the
energy depend on the dimensionality (d) of the rotor4:
d = 1 g = 2 E = BJ2 J = 0,1,2,3,...
d = 2 g = (2J + 1) E = BJ(J+1) J = 0,1,2,3,...
d = 3 g = (2J + 1)(2J + 1) E = BJ(J+1) J = 0,1,2,3,...
Prior to version 2.04, the sum of states at E=0 was set equal to unity, regardless of
rotational symmetry number (σ). The current version gives the sum of states equal to 1/σ at
E=0.
See Appendix B.4 for a discussion of proper input for External Molecular Rotations.
Symmetric Top (top):
For a symmetric top, two of the external rotational constants are equal to each other and
one is unique: A ≠ B = C (prolate top), or A = B ≠ C (oblate top). To account for both prolate and
oblate symmetric tops, it is convenient to denote B1 for the unique 1D rotational constant and B2
for the 2D rotational constant that is twinned. Using these definitions, the rotational energy of the
symmetric top is given by
Etop B2J J 1
B1B2
K2
where J is the quantum number of total angular momentum (the "J-rotor") and K is the quantum
number for the projection of the total angular momentum vector J on the molecular symmetry
axis. Quantum number J can take integer values starting with J=0 and K is restricted to the range
–J ≤ K ≤ +J; in addition, the rotational energy of the top must be Etop ≥ 0. The densities of states
are evaluated by direct calculation using the above equation and including the restrictions on Etop
and K.
The input for the symmetric top consists of B2, B1, and the rotational symmetry number.
Users optionally may (a) set the external symmetry number to unity while specifying the
rotational symmetry number when invoking the top degree of freedom, or (b) specify the

46
external symmetry number and set the rotational symmetry number to unity; either approach is
acceptable, but the symmetry number should not be different from unity in both entries.
See Appendix B.4 for a discussion of proper input for External Molecular Rotations.
K-rotor Rotation (kro)
This degree of freedom type should NOT be selected for normal calculations using
MultiWell. It is provided in DenSum only for special purposes. See Appendix B.4 for a
discussion of proper input for External Molecular Rotations.
Particle in a Box (box)
1-D box of length L with particle of mass m:
Eh2n2
8mL2h2
8mL2
for n = 1,2,3,...
where E is the energy in excess of the "zero" point energy (ZPE), which is identified with n=1.
The codes in the MultiWell Program Suite can handle boxes of ≥1 dimensions as long as
they are "hyper-cubical", with Lx = Ly = ...= L. For an Ndim dimensional hyper-cubical box, the
eigenenergies (relative to the ZPE) and the ZPE are given by:
for ni = 1,2,3,....
Eh2
8mL2ni
21
i1
Ndim
ZPE h2Ndim
8mL2
The "frequency parameter" that is needed by the MultiWell codes is h2/(8mL2).
1-D Hindered Rotation, Symmetrical (hra, hrb, hrc)
These types are intended for use with symmetrical internal rotors, i.e. those with
symmetrical mass distribution and potential energy that can be described with acceptable
accuracy using a single sine or cosine term as a function of dihedral angle χ (e.g. the CH3–CH3
torsion). Relationships among parameters for a symmetrical hindered rotor:
B/cm116.85763
Ir/amu Å2
V1
B
n
2
where, n is the symmetry number, B is the rotational constant, Ir is the reduced moment of
inertia, V is the barrier to internal rotation, and
is the small amplitude harmonic frequency

47
(cm–1) evaluated at the minimum energy (e.g. the harmonic torsion frequency from a quantum
chemistry calculation). Because of the relationship connecting n, V,
, and Ir, only three
parameters are independent. Given the parameter n, there are three ways of choosing two
independent parameters from the set V,
, Ir. For convenience, these three combinations are
implemented as types hra, hrb and hrc.
1-D Hindered Rotation, General (hrd)
This type is general, and is particularly useful for unsymmetrical rotors, i.e. those that
lack a symmetrical mass distribution and/or have potential energy that can only be described
accurately by using multiple sine or cosine terms (e.g. the CHF2-CH2Cl torsion). For this type,
one must provide the torsional potential energy and reduced moment of inertia (or rotational
constant) as functions of the dihedral angle χ (radians).
For convenience, three forms of the torsional potential energy are accepted (all
coefficients in units of cm-1):
Type Vhrd1
V
Vn
21cos n
V
V
n1
N
Type Vhrd2
V
V0Vncos n
V
V
n1
N
Type Vhrd3
V
V0Vn
ccos n
V
V
n1
N
Vn
ssin n
V
V
n1
N
where χ is the dihedral angle (radians), σv is the symmetry number for the potential energy, φV is
a phase angle for the potential (radians).
Also for convenience, either the rotational constant or the moment of inertia, which are
functions of the dihedral angle, can be entered (all coefficients in units of cm-1). It is VERY
IMPORTANT that the angles are defined in the same way both for the potential and for the
mass factor.
Type Bhrd1 (all coefficients in units of cm-1)
B
B0Bncos n
B
B
n1
N
Type Ihrd1 (all coefficients in units of amu.Å2)
I
I0Incos n
I
I
n1
N
48
where χ is the dihedral angle (radians), σB and σI are symmetry numbers and φB and φI are phase
angles. Repeat: It is VERY IMPORTANT that the same phase angle be used both for the
potential and for the mass factor: φV = φB or φI.
If the reduced moment of inertia or rotational constant is assumed to be independent of
dihedral angle, just the one B0 or I0 term is needed.
Translation (trn)
DenSum uses an adaptation of the method of Astholz et al.,1 but applies it to relative
translations (standard state corresponding to 1 molecule/cc). According to this method, the
number of translational states (G(E)) in a single energy grain (
E) is given by
G E
F E3/2 E
E
3/2
where F is a constant that depends on µ, the reduced mass (gram atomic mass units). When
classical rotors are convolved with the 3-D translation, the following expression is used:
G E
FrEr3
/2 E
E
r3
/2
where Fr depends on µ, the number of rotor degrees of freedom (r), and the moments of
inertia. For more details, see the Appendix (Theoretical Basis). Note that G(0) = 0, since the
nominal energy corresponds to the top energy in each bin.
3.2 Format for Input Files
The following format is used for lines describing the separable molecular degrees of
freedom. The sme format is used in all of the codes listed above. Not all of the codes
recognize all of the formats. For example, THERMO does not recognize the type trns
(translation), since it automatically calculates the translational partition function without it
being specified as a degree of freedom.
Each of the separable degrees of freedom is specified on a line of the input file. The line is
formatted and the parameters have the definitions as described below.
MODE(I), IDOF(I), AAA(I), BBB(I), CCC(I)
MODE index number for degree of freedom
IDOF KEY WORD for type of degree of freedom
'vib' (vibration)
AAA = vibration frequency (cm-1) [see VHAR, line 3]
BBB = vibration anharmonicity (cm-1)
CCC = vibration degeneracy
'box' (particle-in-a-box vibration)
49
AAA = vibration frequency parameter (cm-1)
BBB = (not used; but a dummy placeholder value must be included)
CCC = vibration degeneracy
'rot' (classical rotation)
AAA = rotation moment of inertia [units specified by Vrot, Line 3]
BBB = rotation symmetry number
CCC = rotation dimension
'qro' (quantized rotation)
AAA = rotation moment of inertia [units specified by Vrot, Line 3]
BBB = rotation symmetry number
CCC = rotation dimension
'top' (symmetric top)
AAA = B2 (twinned) rotational constant [units specified by Vrot, Line 3]
BBB = B1 (unique) rotational constant [units specified by Vrot, Line 3]
CCC = rotational symmetry number
'kro' (K-rotor (1-dimensional); quantized rotation)
AAA = rotation moment of inertia [units specified by Vrot, Line 3]
BBB = rotation symmetry number
CCC = J (quantum number for total angular momentum)
'hra' (1-D symmetrical hindered rotor)
AAA = vibration frequency (cm-1)
BBB = reduced moment of inertia [units specified by Vrot, Line 3]
CCC = symmetry of Potential Energy (number of minima per 2)
[For an unsymmetrical hindered rotor, type 'hrd' is preferred. However, for a
symmetrical potential energy and unsymmetrical mass distribution, the
present type can be used for approximate results by giving the potential
energy symmetry number CCC as a negative value (i.e. -CCC) and a new line
inserted containing NSIG = symmetry number for the mass distribution]
'hrb' (1-D symmetrical hindered rotor)
AAA = vibration frequency (cm-1)
BBB = barrier (cm-1)
CCC = symmetry of Pot. Energy (number of minima per 2))
[For an unsymmetrical hindered rotor, type 'hrd' is preferred. However, for a
symmetrical potential energy and unsymmetrical mass distribution, the
present type can be used for approximate results by giving the potential
energy symmetry number CCC as a negative value (i.e. -CCC) and a new line
inserted containing NSIG = symmetry number for the mass distribution]
'hrc' (1-D symmetrical hindered rotor)
AAA = reduced moment of inertia [units specified by Vrot, Line 3]
BBB = barrier (cm-1)
CCC = symmetry of Pot. Energy (number of minima per 2))
[For an unsymmetrical hindered rotor, type 'hrd' is preferred. However, for a
symmetrical potential energy and unsymmetrical mass distribution, the
50
present type can be used for approximate results by giving the potential
energy symmetry number CCC as a negative value (i.e. -CCC) and a new line
inserted containing NSIG = symmetry number for the mass distribution]
'hrd' (1-D General hindered rotor)
Note: care must be taken to treat optical isomers and unsymmetrical
hindered internal rotors in a mutually consistent fashion (see Appendix
B.5).
AAA = total number of coefficients for potential energy function (including V0
term, if present).
BBB = total number of coefficients for rotational constant or moment of
inertia function (including I0 or B0).
CCC = symmetry number of internal hindered rotor (symmetry number of a
symmetric rotor; unity for an non-symmetric rotor)
INSERT 2 ADDITIONAL LINES:
LINE1: VTYPE, SYMMV, PHASEV, COEFF1, COEFF2, ...(in order)
VTYPE = "Vhrd1", "Vhrd2", or "Vhrd3"
SYMMV = symmetry number for the potential
PHASEV = phase angle (radians) for potential
COEFF1 = coefficients (including V0) for potential, in proper order, on
the same line (units of cm-1)
LINE2: MTYPE, SYMMM, PHASEV, COEFF1, COEFF2, ...(in order)
MTYPE = "Bhrd1" for rotational constant or "Ihrd1" for moment of
inertia
SYMMM = symmetry number for Bhrd1 or Ihrd1
PHASEM = phase angle (radians) for Bhrd1 or Ihrd1
COEFF1 = coefficients (including B0 or I0) for Bhrd1 (units of cm-1) or
Ihrd1 (amu•Å2 units), in proper order, on the same line
'trn' (3-dimensional relative translation)
AAA = mass of A (amu)
BBB = mass of B (amu)
CCC = ignored, but convenient to set it equal to "3"
51
References
1. D. C. Astholz, J. Troe and W. Wieters, Unimolecular processes in vibrationally highly
excited cycloheptatrienes. I. Thermal isomerization in shock waves, J. Chem. Phys. 70,
5107-16 (1979).
2. P. J. Robinson and K. A. Holbrook, Unimolecular Reactions. (Wiley-Interscience,
London; New York, 1972).
3. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
4. J. L. McHale, Molecular Spectroscopy. (Prentice Hall, Upper Saddle River, 1999).

52
4. DenSum: Separable Sums and Densities of States
This computer code carries out exact counts for sums and densities of states for separable
degrees of freedom via the Stein-Rabinovitch1 extension of the Beyer-Swinehart algorithm.2
Optionally, the Whitten-Rabinovitch approximation3, 4 can be used.
Default array dimensions are easily changed in file src/densum/declare.inc
150 degrees of freedom (enough for a 50 atom molecule)
50000 energy grains (enough for 100000 cm-1 energy maximum, with 2 cm-1
grains)
Output Files
densum.out File containing complete output.
densum.lev Energy levels of quantized degrees of freedom.
<FNAME>.dens File formatted for input into MultiWell.
Example data and output files are given in the examples directory:
multiwell/examples/densum-examples.
4.1 Data File Format
Note: Starting with version 2009.0, the data file format is no longer
compatible with previous versions.
Line 1
TITLE (CHARACTER*180): up to 180 characters
Line 2
FNAME
FNAME (CHARACTER*10): name of file to be created with ".dens" appended (up to 10
characters). Example: "hexadiene" produces file named "hexadiene.dens".
Line 3
N, IWR, VHAR,VROT
Nno. of DoF's, IWR (flag)
IWR 0: Uses exact state counts (energy grain = Egrain1)
1: Uses Whitten-Rabinovitch state densities
VHAR KEYWORD for vibrations
'HAR': for vibrational frequencies input as harmonic frequencies.
'OBS': for vibrational frequencies input as 0-1 fundamental frequencies.

53
VROT KEYWORD for molecular internal and external rotations, except for hindered rotors
of type hrd (see special instructions below for type hrd)
'AMUA': for moments of inertia input with units of amu Å2.
'GMCM': for moments of inertia input with units of g cm2.
'CM-1': for rotational constant input with units of cm-1.
'MHZ': for rotational constant input with MHz.
'GHZ': for rotational constant input with GHz.
(some combinations of upper/lower case are also accepted)
Notes: (a) All of the rotational information in a DenSum data file must be given in the form
specified by VROT; (b) VHAR and VROT can be stated in either order on Line 3.
Line 4
Egrain1, Imax1, Isize, Emax2
Egrain1 energy grain in units of cm-1
Imax1 number of array elements in first segment of double array*
Isize total size of double array (number of elements)
Emax2 maximum energy (cm-1) for calculation
* Starting with MultiWell Version 2.08, densum.out provides information about the
number of elements (Imax1) needed to achieve fluctuations of less than 5% in the density of
states. If Egrain1 and Imax1 are chosen so that fluctuations in the density of states is greater than
5%, a warning is printed to the screen with a suggestion as to what Imax1 should be increased to.
Note that a user can choose to disregard this warning and proceed to run MultiWell.
Line 5..N+3
MODE(I), IDOF(I), AAA(I), BBB(I), CCC(I)
MODE index number for degree of freedom
IDOF KEY WORD for type of degree of freedom
See Chapter 3 and for descriptions of the types of molecular degrees of freedom recognized by
DENSUM.
Line N+4
BLANK LINE TO INSURE THAT THE LAST LINE IS FOLLOWED BY A CARRIAGE
RETURN (needed for all READ statements). THE CARRIAGE RETURN IS EASILY
OVERLOOKED.
54
4.2 DenSum in Batch Mode
In order to run densum with the 'batch' option, one must first prepare a file:
densum.batch. This file lists the names of the DenSum data files (".vibs files") to be
processed and the energy grain and double array boundaries. The batch file format is given
below.
To use this option, the DenSum data files must all reside in one directory (e.g. directory
/vibs) and each must be named "<name>.vibs", where <name> does not contain any blank
spaces. When listed in densum.batch, each file name must be listed on a separate line,
including the extension ".vibs".
densum.batch Batch File Format
Line 1 Egrain1, Imax1, Isize, Emax2
Line 2 <name1>.vibs
Line 3 <name2>.vibs
Line 4 <name3>.vibs
.... etc.
<end of file>
-------------------------------------
Sample densum.batch for three .vibs files
10. , 400 , 500 , 50000.
B1.vibs
B2.vibs
CH3CO.vibs
------------------------------------
55
Execution
a) On linux:
From within the directory in which densum.batch and the .vibs data files
reside,
type '<PATH>densum -batch' in a terminal shell, where PATH is the full
path to the densum executable.
or
type 'densum -batch' in a terminal shell, if the PATH variable has been set to
include the /bin directory that holds the densum executable.
or
type './densum -batch' in a terminal shell, if a copy of the densum
executable resides in the same directory with densum.batch and the .vibs files.
b) On windows
There are two possibilities:
1) type "densum -batch" in a DOS shell
or
2) double-click on "densum-batch.bat". Note that densum.exe and
densum-batch.bat must be in the same directory as densum.batch and the
.vibs files.
56
References
1. S. E. Stein and B. S. Rabinovitch, Accurate evaluation of internal energy level sums and
densities including anharmonic oscillators and hindered rotors, J. Chem. Phys. 58, 2438-
45 (1973).
2. T. Beyer and D. F. Swinehart, Number of multiply-restricted partitions, Comm. Assoc.
Comput. Machines 16, 379 (1973).
3. G. Z. Whitten and B. S. Rabinovitch, Accurate and Facile Approximation for Vibrational
Energy‐Level Sums, J. Chem. Phys. 38, 2466 (1963).
4. G. Z. Whitten and B. S. Rabinovitch, Approximation for Rotation—Vibration Energy
Level Sums, J. Chem. Phys. 41, 1883 (1964).

57
5. MomInert: Moments of Inertia
This code was written mostly by Nicholas F. Ortiz under the direction of John R. Barker.
From Cartesian coordinates, it calculates the principal moments of inertia and approximate
reduced moment of inertia for an internal rotation.
Example data and output files can be down-loaded from the MultiWell web site:
http://aoss.engin.umich.edu/multiwell/.
Note that computer program lamm, described in Chapter 8 is designed to assist in
computing moments of inertia as a function of dihedral angle. Thus lamm is more appropriate
than MomInert for flexible internal rotations.
5.1 Data File Format
Note: Starting with version 2.0, the data file format is no longer compatible
with previous versions.
To run Mominert using the default filename (mominert.dat):
LINUX/UNIX: in the directory where the input data file resides, type:
<PATH>/multiwell-<version>/bin/mominert <RETURN>
where <PATH> designates the PATH to /multiwell-<version>. If directory
/multiwell-<version> resides in the user home directory, type:
~/multiwell-<version>/bin/mominert <RETURN>
WINDOWS in a DOS window: in the directory where the input data file resides, type:
<PATH>/multiwell-<version>/bin/mominert <RETURN>
For example:
~/multiwell-2013/bin/mominert
To run Mominert using a user-defined filename (FileName.dat):
Follow the same procedures described above, but type:
<PATH>/multiwell-<version>/bin/mominert <FileName> <RETURN>
For example:
~/multiwell-2013/bin/mominert final.dat
58
The resulting output file will take the same prefix: final.out.
Line 1
TITLE A line, up to 100 characters, describing the data. This title is reproduced in the
output file.
Line 2
UNITS Keyword designating units of coordinate values.
ANGS Angstrom units.
BOHR Atomic (Bohr) units (1 Bohr ≈ 0.529 Å)
Line 3
NATOMS Total number of atoms in the molecule (up to 100 atoms).
Line 4
(Repeat for every atom type [see Appendix B.7])
ATYPE, IA, X, Y, Z
ATYPE case sensitive atomic symbol, e.g. "C", "H", "Br79" (see Sec. 9.7)
IA Index number of the atom (1 to NATOMS).
X,Y,Z Cartesian coordinates (Å or Bohr; see Line 2) of the atom.
To assign an arbitrary mass to an atom:
1. Designate "XX" for ATYPE (instead of e.g. "H" or "C") in Line 3.
2. On the line following the atom type designation, insert a line giving the mass to be
assigned to this particular atom.
This must be done each time a special mass is to be assigned. It is not necessary for the mass
to always be the same. In other words, atom type "XX" may be designated multiple times in
the same molecule, and a different mass may be specified each time.
Line 5
IAI, IAJ
Atom indices for the two atoms defining the axis of internal rotation. If the atom indices are set
equal to zero, then internal rotor is not calculated and Line 6 and Line 7 can be omitted.
Line 6
59
NR
Number of atoms in one of the two rotating moieties.
Line 7
List of the atom indices that comprise the rotating moiety containing NR atoms.
Line 8
For additional internal rotors, REPEAT lines 5-7. TO TERMINATE, enter two zeros: "0 , 0".
Line 9
BLANK LINE TO INSURE THAT THE LAST LINE IS FOLLOWED BY A CARRIAGE
RETURN (needed for all READ statements). THE CARRIAGE RETURN IS EASILY
OVERLOOKED.
5.2 Computational Approach
This code uses the two axis-defining atoms and one other atom to define two
perpendicular planes which intersect at the rotation axis. The distance from all atoms in the
molecule to each plane is calculated. The Pythagorean Theorem is then used to define the
distance of each atom to the axis. The mass is defined for each atom type, and then the mass and
distance are used to calculate the moment of inertia for the internal rotations in amu Å2.
The center-of-mass is then defined. This is used to calculate all external products and
moments of inertia. These values are put into the proper matrix, and eigenvalues are found. The
eigenvalues are the principle moments of inertia.
For the reduced moment of inertia for internal rotation, MomInert uses the
approximation that the reduced moment is calculated for the axis that contains the twisting bond.
This approximation is reasonably accurate (errors of less than 5-10%) for many species.1
References
1. A. L. L. East and L. Radom, Ab initio statistical thermodynamical models for the
computation of third-law entropies, J. Chem. Phys. 106, 6655-73 (1997).
60
6. thermo: Thermodynamics
6.1 Introduction
thermo calculates equilibrium constants, thermodynamic parameters, and
canonical transition state theory rate constants (including Eckart tunneling through an
unsymmetrical barrier) via standard statistical mechanics formulae. It can also compute
canonical rate constants using W. H. Miller's Semiclassical Transition State Theory (SCTST)
when used in conjunction with programs sctst and bdens, or paradensum.
Example data and output files are given in the examples directory
Note that the data file for Thermo (thermo.dat) is intentionally very similar in
format to the data file for DenSum (densum.dat). Thus major parts of the data files can be
copied and pasted.
6.1.1 Thermodynamic Output
When given a collection of molecular properties, thermo uses statistical mechanics
formulae to calculate the corresponding thermodynamics parameters. Thermo can also calculate
canonical transition state theory rate constants. The input and output are intended to be easily
understood, but some items are explained below.
Three output files are generated by THERMO. "thermo.out" is the general output file,
which contains all of the information needed by most users. The following two output files are
useful, but of less general interest. "thermo.details" displays contributions from every
degree of freedom to the heat capacity, entropy, and enthalpy function for each chemical species
at 298.15 K and groupings of degrees of freedom at each temperature. "thermo.partfxns"
displays the partition functions for grouped degrees of freedom for each chemical species at each
temperature. (The grouped degrees of freedom include electronic, translational, vibrational, free
rotational, and hindered rotational.)
Standard State: the standard state must be selected. The conventional standard state for most
data tabulations is 1 bar, ideal gas. For analysis involving reaction rate constants, it is usually
appropriate to choose the standard state of 1 molecule cm-3. The units and numerical values of
entropies, equilibrium constants and other thermodynamic quantities are determined by the
selection of the standard state.
Standard States recognized by THERMO:
1 bar, ideal gas (keyword BAR)
1 atm, ideal gas (keyword ATM)
1 molecule cm-3, ideal gas (keyword MCC)
Molar Enthalpy: The enthalpy for formation at 0 K is required input. THERMO output echoes
the input and also reports the enthalpy of formation at 298.15 K and the standard free energy of
formation (DelG(298)).
61
For convenience, THERMO recognizes several energy units, which can be selected by the user:
kJ/mol (keyword KJOU)
kcal/mol (keyword KCAL)
cm-1 (wavenumbers) (keyword CM-1)
Equilibrium constant: Kequil is reported for each temperature. In addition, it is reported as a
function of temperature: Kequil = A(T)*exp(B(T)/T). The parameters A(T) and B(T),
which are obtained by finite differences, are functions of temperature. The accuracy of these
parameters is less than the accuracy of Kequil itself. Note that the numerical value of the
equilibrium constant depends on the standard state.
Canonical Transition State Theory Rate Constant: "RATE k(T)" is reported for each
temperature. In addition, it is reported as the Arrhenius function of temperature: k(T) =
A(T)*exp(B(T)/T). The parameters A(T) and B(T), which are obtained by finite
differences, are functions of temperature. The accuracy of these parameters is less than the
accuracy of k(T) itself. Note that the user must select the standard state of 1 molecule cm-3 (i.e.
"MCC") when calculating rate constants.
Molar Entropy: the numerical value for the entropy depends on the standard state that is
selected, as well as on the energy units selected.
Molar Heat Capacity: Cp depends on energy units selected.
Enthalpy Function: [H(T)-H(0)] depends on the energy units selected.
Accuracy:
All accuracies depend on the accuracy of the input data. For a given set of input data, the
accuracies achieved by THERMO are relative to a benchmark based on the same input data. The
benchmarks most commonly used are taken from the NIST-JANAF Thermochemical Tables.1
Note that when rotations are treated classically, the entropy, heat capacity, free energy, and
equilibrium constant are less accurate at low temperatures.
• molecular weights are accurate to 0.002 g mol-1, or better.
• enthalpies and Gibbs free energy for individual species generally agree with the JANAF tables
to within 0.05 kJ mol-1, or better.
• entropies computed for individual species are generally accurate to 0.1 J K-1 mol-1 or better.
• electronic partition function is accurate to 0.1% or better.
• enthalpy, entropy, heat capacity, and Gibbs free energy differences for reaction (DelS(rxn),
DelH(rxn), DelCp(rxn) and DelG(rxn), respectively) are generally more accurate than
the corresponding quantities for the individual species, due to cancellation of errors.
62
6.1.2 Types of Degrees of Freedom
The following types used by THERMO are described in Chapter 3:
Harmonic or Anharmonic Vibration (vib)
Classical Rotation (rot)
Quantized Rotation (qro)
Symmetric Top (top):
Particle in a Box (box)
1-D Hindered Rotation, Symmetrical (hra, hrb, hrc)
1-D Hindered Rotation, General (hrd)
The following types are unique to THERMO:
Hindered Gorin Model (gor) and Fitting (fit)
Thermo includes the capability to automatically find the hindrance parameters for the
Hindered Gorin transition state.2-9 One can choose one or both of the following types (IDOF)
of degrees of freedom.
1) IDOF = gor selected for one vibrational stretching mode. For a selected potential
energy function, Thermo finds the center of mass distance rmax corresponding to maximum of
Veffective at temperature T, where the rotational energy in the 2-D pseudo-diatomic rotation is
assumed to be RT. From the value of rmax, Thermo computes the 2-D moment of inertia.
2) IDOF = fit selected for two (linear molecule) or three (non-linear) rotational
dimensions. Thermo finds the hindrance parameters γ (gamma) and η (eta) that produce a
good fit at each temperature to experimental rate constants (one for each temperature) that
are entered.
1
1/2
If both IDOF = gor and IDOF = fit are selected, Thermo finds the maximum of
Veffective and uses it to find the hindrance parameters (gamma and eta) that produce a good
fit to experimental rate constants (one for each of the Nt temperatures) that are entered.
The selectable potential energy functions are:
MORSE (Morse Oscillator)
VMorse r
De1exp
Morse rre
2De
Morse 2
e
2De
63
VARSHNI (Varshni Oscillator10)
VVarshni (r)De1re
r
exp
Varshni r2re
2
2
De
Varshni 1
2re
2
2De
1
re
1
2re
Morse 1
re
sMORSE ("Stiff Morse" Oscillator)
This is a Morse oscillator, but replaces
Morse
with
Stiff
Morse 1csrre
2
; cs is
an empirical parameter and must be ≥0.
The input is assumed to correspond to the following generic recombination reaction:
ABC‡
In the thermo input, A and B are labeled as reactants ("reac") and C‡ is labeled as a
transition state ("ctst"). For a barrier-less recombination reaction, the enthalpy of
formation at 0 K (DelH) for C‡ must be set equal to the sum of the enthalpies of formation
for the two reactants. All of the internal and rotational degrees of freedom for A and B are
entered as usual. The internal degrees of freedom for C‡ consist of the combined degrees of
freedom (internal and external) of A and B, plus the external rotations for C‡. Thus the
number of degrees of freedom (including degeneracies and multiple dimensions) of C‡ is
nCnAnBnC
rots
where nA and nB are the total number of degrees of freedom for A and B, and nCrots is the
number of external rotations of C‡.
In order to find the center of mass distance rmax corresponding to maximum of
Veffective at temperature T, the external 2-D rotation for C‡ is labeled "gor" (see below). This
signals that this particular entry is a dummy and will be adjusted in the process of finding the
maximum Veffective. The potential energy function is specified later in the data file (see
below).
In order to adjust the "hindrance" to fit specified rate constants, some of the rotations
in C‡ that were originally associated with A and B must be multiplied by γ (see above). These
are labeled "fit" (see below). These rotations do not include internal rotation about the new
bond in C‡, but only the rotations about internal axes perpendicular to the new bond. Later in
the data file, the (experimental) rate constants to be fitted are entered... one for each
temperature.
Fully Coupled Anharmonic Vibrations (qvb)
64
This type specifies that program Thermo must read a supplementary data file named
<name>.qvb, which must be generated by program bdens (Section 8.1), or paradensum
(Section 8.2). This supplementary file must be present in the same directory as data file
thermo.dat. See Section 8.1 for more details. By using this supplementary data file, Thermo
can utilize full intermode vibrational anharmonic coupling when computing thermodynamic
data. This coupling is most important at high temperatures. This option is used when computing
thermal rate constants with semi-classical transition state theory (SCTST; see Sections 8.3 and
B.9 for more details).
Thermal Rate Constants from SCTST (crp)
This type specifies that program Thermo reads a supplementary data file named
<name>.qcrp, which must be generated previously by program sctst (Section 7.4). File
<name>.qcrp must be present in the same directory as data file thermo.dat. See Sections
8.3 and B.9 for more details. By using this supplementary data file, Thermo can utilize the
semi-classical transition state theory (SCTST) of W. H. Miller and coworkers. SCTST accounts
for fully coupled degrees of freedom, including the reaction coordinate. As a result, the theory
incorporates multidimensional quantum tunneling along the curved reaction path, which is
very important at low temperatures. To prevent applying a second tunneling correction, the
imaginary frequency, vimag, (entered on Line 5, see below) must be given a value of
vimag = 0.0 (actually <20 cm-1), or execution of THERMO will be terminated.
Note that in order to obtain the best possible accuracy at both low and high temperatures,
a fully coupled vibrational model for a unimolecular reactant is usually used in addition to the
crp degree of freedom when computing SCTST rate constants. The fully coupled vibrational
model is specified with degree of freedom type "qvb" (see above) and it requires a
supplementary data file from program bdens, or paradensum (see Chapter 8).

65
6.1.3 Data File Format
Note: Starting with version 2009.0, the data file format is no longer
compatible with previous versions.
To run Thermo using the default filename (thermo.dat):
LINUX/UNIX: in the directory where the input data file resides, type:
<PATH>/multiwell-<version>/bin/thermo <RETURN>
where <PATH> designates the PATH to /multiwell-<version>. If directory
/multiwell-<version> resides in the user home directory, type:
~/multiwell-<version>/bin/thermo <RETURN>
WINDOWS in a DOS window: in the directory where the input data file resides, type:
<PATH>/multiwell-<version>/bin/thermo <RETURN>
For example:
~/multiwell-2013/bin/thermo
To run Thermo using a user-defined filename (FileName.dat):
Follow the same procedures described above, but type:
<PATH>/multiwell-<version>/bin/thermo <FileName> <RETURN>
For example:
~/multiwell-2013/bin/thermo final.dat
The resulting output file will take the same prefix: final.out.
Line 1
EKEY , SSKEY
EKEY Key Word for Energy units: "KCAL" or "KJOU" (upper case characters). Note that
"CM-1" is a reserved keyword to be fully implemented later.
SSKEY Key Word for Standard State: "BAR", "ATM", or "MCC" (molecule/cc)
Line 2

66
Nt number of temperatures
Line 3
T1, T2, T3,... List of Nt temperatures
Line 4
Ns number of chemical species
Line 5 for reactants, products, or "none"; see below for transition states
REPROD, MOLNAME, DelH
REPROD key word:
"reac" = reactant
"prod" = product
"none" = not included in equilibrium constant
MOLNAME Name of chemical species (up to 20 characters)
DelH enthalpy of formation at 0 K
Line 5' for transition states
REPROD, MOLNAME, DelH, vimag, VVR
REPROD = "ctst"
For transition states, only. This choice calculates the canonical transition state
theory rate constant based on reactant and transition state parameters. It assumes
the reaction consists of reactants (each labeled "reac") proceeding to the
transition state (labeled "ctst"). Note that for bimolecular and termolecular
reactions, the standard state should be set to "MCC" for concentration units.
For 1-D quantum mechanical tunneling via an unsymmetrical Eckart energy
barrier, enter vimag >0 and VVR >0. Eckart tunneling is neglected when vimag
<20 cm-1 and/or VVR = 0.0.
For use with SCTST rate constants, vimag = 0.0 and/or VVR must be set
equal to 0.0 in order to prevent including tunneling twice (i.e. once via the SCTST
rate constants and again via 1-D Eckart tunneling) vimag = 0.0 and/or VVR =
0.0
MOLNAME Name of transition state (up to 10 characters)
DelH enthalpy of formation at 0 K. (Note: when using the SCTST (see section 8.3),
DelH is the enthalpy of formation of the transition state at 0 K.)

67
vimag magnitude of imaginary frequency (units of cm-1). When using "crp" files from
program sctst (see section 8.3), vimag must set to 0.0 cm-1.
VVR Height of barrier for the reverse reaction (energy units specified in Line 1). When
using crp files from program sctst (see section 8.3), VVR must be set to 0.0,
but must be entered. Eckart tunneling is neglected when VVR = 0.0.
Line 6
FORMULA Empirical chemical formula written in the usual way with atomic symbols. These
symbols include "D" for deuterium and "T" for tritium. Special atomic symbols
used for other isotopic species (e.g. "Cl35") are summarized in Section 10.7.
Whenever an atomic symbol includes numeric characters (e.g. "Cl35"), it must
be enclosed in square brackets, e.g. "[Cl35]". Examples of empirical formulas:
C2H6O, CH3CH2OH, (CH3)2OH, (CH3)2(N)O2H,
CH[Br79]2(CH3)3, CH3OD, C([C13]H3)4.
Line 7
Up to 20 comment lines. The first non-blank character on each line must be "!" (omit the
quotation marks).
Line 8
Sym, Sopt, Nele
Sym external symmetry number (INTEGER)
Sopt number of optical isomers (INTEGER)
Nele number of electronic energy levels (INTEGER)
Line 9
Elev, gele (Repeat line for Nele electronic states)
Elev electronic level energies (REAL).
NOTE: lowest level should be at energy Elev = 0.0.
gele electronic level degeneracies (INTEGER)
Line 10
N , VHAR , VROT number of vibrations and rotations to be read in
VHAR KEYWORD for vibrations
'HAR': for vibrational frequencies input as harmonic frequencies.
'OBS': for vibrational frequencies input as 0-1 fundamental frequencies.
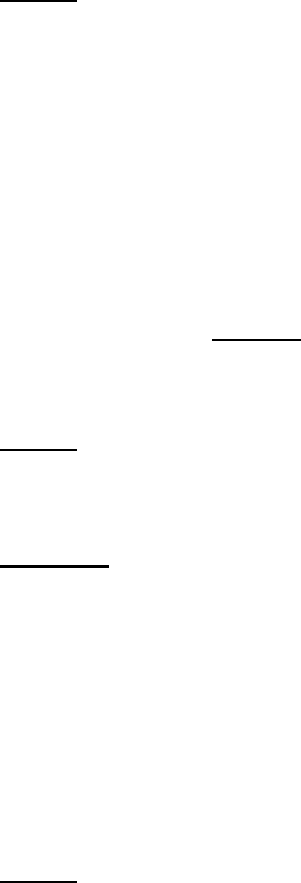
68
VROT KEYWORD for molecular internal and external rotations, except for hindered rotors
of type hrd (see special instructions below for type hrd)
'AMUA': for moments of inertia input with units of amu Å2.
'GMCM': for moments of inertia input with units of g cm2.
'CM-1': for rotational constant input with units of cm-1.
'MHZ': for rotational constant input with MHz.
'GHZ': for rotational constant input with GHz.
(some combinations of upper/lower case are also accepted)
Note: All of the rotational information for a given molecular species must be given in the form
specified by VROT for that species.
Line 11
(repeat N times for the N molecular degrees of freedom)
MODE(I), IDOF(I), AAA(I), BBB(I), CCC(I)
MODE index number for degree of freedom
IDOF KEY WORD for type of degree of freedom
See Section 6.1.2 and Chapter 3 for descriptions of the types of molecular degrees of freedom
recognized by THERMO.
RETURN TO LINE #5 and REPEAT FOR THE NEXT CHEMICAL SPECIES
AFTER ALL CHEMICAL SPECIES HAVE BEEN ENTERED, RESUME HERE:
Line 12 (when 'fit' is used)
kexp(1), kexp(2), .... list of Nt experimental recombination rate constants
(units of cm3 molecule-1 s-1): one for each of the Nt temperatures.
Line 13-17 (required if 'gor' is used)
Line 13 readpot Keyword 'MORSE', 'VARSHNI', or 'sMORSE' (Stiff-Morse).
This is the type of bonding potential energy function.
Line 14 freq Harmonic frequency (cm-1) of the normal mode associated with the
forming bond.
Line 15 De Dissociation Energy De (units of Eunit) of the forming bond.
Line 16 re EQUILIBRIUM center-of-mass distance (Å) between the of the two
fragments that are forming the new bond.
Line 17 c Stiff-Morse parameter (needed only for 'sMORSE' type of potential).
Line 18 (BLANK LINE)
69
6.2 MultiWell Thermodynamics Database
A database of molecular constants (for use by program thermo) is provided on the
MultiWell website. The chemical species in this database are of interest to us in our research. We
add entries from time to time, depending on current research interests.
The following are some excellent sources of molecular constants and enthalpies, which
can be used with program thermo to generate thermodynamics data:
NIST WebBook [http://webbook.nist.gov/chemistry/]
Active Thermochemical Tables [http://atct.anl.gov/]
NIST Computational Chemistry Comparison and Benchmark Database (NIST Standard
Reference Database Number 101 Release 18, October 2016, Editor: Russell D. Johnson
III) [http://cccbdb.nist.gov/]
NIST-JANAF Thermochemical Tables.1
References
1. M. W. Chase, Jr., NIST-JANAF Thermochemical Tables. Fourth Edition, J. Phys. Chem.
Ref. Data Monograph No. 9, 1-1951 (1998).
2. D. M. Golden, The reaction Cl+NO2 -> ClONO and ClNO2, J. Phys. Chem. A 111,
6772-6780 (2007).
3. D. M. Golden, Evaluating data for atmospheric models, an example: IO+NO2=IONO2, J.
Phys. Chem. A 110, 2940-2943 (2006).
4. D. M. Golden, Evaluating data for atmospheric models, an example:
CH3O2+NO2=CH3O2NO2, Int. J. Chem. Kinet. 37, 625-632 (2005).
5. D. M. Golden, J. R. Barker and L. L. Lohr, Master Equation Models for the Pressure- and
Temperature-Dependent Reactions HO + NO2 -> HONO2 and HO + NO2 -> HOONO, J.
Phys. Chem. A 107, 11057-11071 (2003).
6. D. M. Golden, Reaction ClO+ClO--> Products: Modeling and Paremeterization for Use
in Atmospheric Models, Int. J. Chem. Kinet. 35, 206-211 (2003).
7. D. M. Golden and G. P. Smith, Reaction of OH + NO2 + M: A new view, J. Phys. Chem.
A 104, 3991-7 (2000).
8. R. Patrick and D. M. Golden, Int. J. Chem. Kinet. 15, 1189-1227 (1983).
9. G. P. Smith and D. M. Golden, Application of RRKM Theory to Reactions
OH+NO2+N2⇌ HONO2+N2 (1) and ClO+NO2+N2 ⇌ ClONO2+N2 (2) - Modified Gorin
Model Transition-State, Int. J. Chem. Kinet. 10, 489 (1978).
10. Y. P. Varshni, Comparative Study of Potential Energy Functions for Diatomic Molecules,
Rev. Mod. Phys. 29, 664-682 (1957).
70
7. gauss2multi: A Tool for Creating Data Files
In many cases, one wants to create data files from calculated properties of molecules and
transition states. The program gauss2multi is a tool designed to assist in this process. The
source code is located in the multiwell/src directory and the executable is located in the
multiwell/bin directory. The tool reads vibrational frequencies, coordinates, and energies
from the standard .log or .out output files produced by GAUSSIAN 981 and GAUSSIAN
03.2
This tool does not create complete data files: it inserts only the data produced by quantum
chemistry codes. It inserts some additional information as placeholders: the user must review the
files created by gauss2multi and insert missing data and replace the placeholder data.
We recommend that new users create input files manually, so that they will
become familiar with the required input data. Experienced users will gain
more benefit when using gauss2multi.
In order to convert GAUSSIAN output files into multiwell input files you need:
GAUSSIAN output files with frequency calculation (file extension: .log or .out)
gauss2multi.cfg configuration file, which must reside in the same directory as the
gaussian output files. An example is found in the examples directory
The following files will be created for each GAUSSIAN file that is read:
FILE NAME DESCRIPTION (see MultiWell User Manual)
name.coords | mominert input file
name.coords.out | mominert output file
name.vibs | densum input file
name.dens | densum output file
name.therm| | thermo input file
name.therm.out | thermo output file
multiwell.dat | rough drat fof multiwell input file
("name" refers to the GAUSSIAN file name, which cannot exceed 10 characters in length)
gauss2multi.cfg Configuration File
You can create and edit the configuration file by yourself or use the step-by-step script to
create it.
The gauss2multi.cfg configuration file contains the following items (an example file is
given below):
Line:
1. Energy units: KCAL , KJOU, or CM-1 (use upper case characters)
71
2. number of temperatures
3. list of temperatures separated by one or more blank spaces
4. Pressure units: TOR, BAR, ATM, or MCC (use upper case characters). [Note: the TOR
pressure unit is not one of the allowed standard states, which are required for setting
up data file thermo.dat; therefore, BAR is used as default in creating
thermo.dat.]
5. number of pressures
6. list of pressures separated by one or more blank spaces
7. Egrain, imax1, Isize, Emax2
8. index number (ascending order), name of gaussian output file (.log or .out), type
of structure: WELL, PROD, or TS (use upper case characters)
9. Repeat Line-8 for additional species.
TO RUN gauss2multi
There are two modes of operation:
(a) To set up files for an entire multi-species model.
In this case, the energies (i.e. ∆Hf0(0 K)) for all of the species will be calculated with respect
to the energy of the first well (index number = 1) listed in gauss2multi.cfg.
In the same directory as the GAUSSIAN files, type 'gauss2multi'
or
(b) To generate data files for a single species.
In the same directory as the GAUSSIAN files, type 'gauss2multi <GAUSSIAN
_Name_File>'
IMPORTANT:
The conversion to MultiWell data files cannot be completely automated:
Many of these files will require manual changes! Be careful!
EXAMPLE CONFIGURATION FILE (gauss2multi.cfg)
KCAL
3
298.15 398 498
TOR
5
0.1 1.0 10. 100. 1000.
10. 400 900 50000.
1 A.log WELL
2 B.log WELL

72
3 TS-A-B.log TS
4 C.log PROD
References
1. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
V. G. Zakrzewski, J. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M.
Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M.
Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A.
Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K.
Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov,
G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T.
Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B.
Johnson, W. Chen, M. W. Wong, J. L. Andres, C. González, M. Head-Gordon, E. S.
Replogle and J. A. Pople; Gaussian 98, Revision A.7, Pittsburgh, 1998;
http://www.gaussian.com.
2. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar,
J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H.
Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T.
Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J.
B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev,
A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A.
Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C.
Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V.
Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A.
Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham,
C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M.
W. Wong, C. Gonzalez and J. A. Pople; Gaussian 03, Revision C.02; Gaussian, Inc.,
Wallingford CT, 2004; http://www.gaussian.com
73
74
8. bdens, paradensum, and sctst: non-Separable Vibrations
Program bdens computes sums and densities of states for non-separable vibrations. In
addition to fully-coupled non-separable vibrations, the code can also include separable degrees
of freedom, such as free rotations and hindered internal rotations. The code combines two
fundamentally different algorithms:
a) Brute force direct counting (via a recursive algorithm), which is suitable for both small
and large molecules at energies low enough so that the total sum of states is not too large. For
some small molecules, direct brute force counting can be carried out even at energies above the
dissociation energy.
b) The Wang-Landau algorithm, which his most suitable for large molecules at high
energies.1-3
Direct counting produces exact sums and densities of states, but it is very slow when the
total sum of states is large. The Wang-Landau algorithm is computationally quite efficient, but
suffers from stochastic fluctuations unless a very large number of stochastic samples is used. In
addition, its sampling is impeded when the density of states is very sparse. In program bdens,
the two algorithms are combined in one "smart" code that produces exact (directly counted)
results at low energies, where the density of states is sparse, and rapidly computed results of
sufficient accuracy at high energies, where the densities and sums of states are very large.
Program paradensum is a parallelized, improved version replacing adensum, which
is no longer supported (its last release was in multiwell-2014.1b). paradensum computes sums
and densities of states for fully-coupled vibrational models. It utilizes the Wang-Landau
algorithm with a flatness criterion and is suitable for fully-coupled vibrational models that
consist of from 3 to >100 degrees of freedom.
The third program, sctst, is for computing rate constants by using semi-classical
transition state theory (SCTST) of W. H. Miller and coworkers, as described below.
Anharmonic vibrations
For a brief introduction to non-separable anharmonic vibrations and definitions of
technical terms, see Technical Note #2 (Appendix B.2 of this User Manual). Note that "exact"
refers to exact at the level of second order vibrational perturbation theory (VPT2).
NOTE. In VPT2, the zero point energy includes contributions from the harmonic
frequencies, the anharmonicities, and an additional term denoted G0 (see Eq. 9 in Appendix
B.9).4, 5 This term, which cancels-out in spectroscopy applications but must be included for
thermochemistry and kinetics, is computed by electronic structure programs that employ VPT2
(e.g. GAUSSIAN and CFOUR), but it is not computed by MultiWell. For ab initio kinetics
calculations involving small molecules the term may be significant, but it is very small for
molecules with small rotational constants. For high accuracy ab initio kinetics calculations (e.g.
6, G0 can be included manually by modifying the reaction critical energy (E0).
Acceptable Vibrational States
The vibrational energy Ev in principle can be computed when all acceptable values of v
are known. Acceptable values of v correspond to bound vibrational states. Therefore, the
problem reduces to finding all acceptable values of v up to a given total internal energy. For a
75
separable harmonic oscillator, all quantum numbers from v=0 to v=∞ are acceptable. A Morse
oscillator, however, can dissociate and thus has a finite number of acceptable vibrational states
ranging from v=0 to v=vmax. For a coupled set of anharmonic vibrations, the maximum quantum
number allowed for the kth vibration, vD,k, depends on the quantum numbers assigned for all
other vibrations; the dissociation energy of the kth vibration corresponds to the energy at which
Ev reaches a maximum as
k is increased, i.e. (∂Ev/∂vk) = 0 at vk = vD,k.3, 6, 7 For a state to be
"bound" with respect to the kth degree of freedom, the derivative must be greater than zero for the
trial value of quantum number vk: (∂E
/∂vk)>0. In the codes bdens, paradensum, and sctst,
this criterion must be satisfied for a quantum number to be deemed "acceptable". In addition,
quantum numbers in sctst must also satisfy the condition that the amplitude of the effective
imaginary frequency (which is affected by coupling to all of the other vibrations) must be greater
than zero.
G0 Term in the ZPE from VPT2
In second order vibrational perturbation theory (VPT2), the zero point energy includes
contributions from the harmonic frequencies, the anharmonicities, and an additional term
denoted G0 (see Eq. 9 in Appendix B.9).4, 5 This term, which cancels-out in spectroscopy
applications but must be included for thermochemistry and kinetics, is computed by electronic
structure programs that employ VPT2 (e.g. GUSSIAN and CFOUR), but it is not computed by
MultiWell. For ab initio kinetics calculations involving small molecules the term may be
significant, but it is very small for molecules with small rotational constants. For high accuracy
ab initio kinetics calculations (e.g. 6, G0 can be included manually by modifying the reaction
critical energy.
8.1 Program bdens
Program bdens replaces previous programs adensum, doloops, and ansum, which
were last released in version 2014.1b. For definitions of the terms used in the following, see
Technical Note #2 (Appendix B.2 of this User Manual).
Program bdens computes sums and densities of acceptable bound and quasi-bound
states as a function of vibrational energy Ev up to a high energy (measured from the zero point
energy). The state energies are binned in energy grains specified by user (typically 10 cm-1).
Total sums and densities of states can then be computed by convoluting the results for the fully
coupled vibrational model with separable degrees of freedom, such as rotations, hindered rotors,
etc. (using the combined Beyer-Swinhart8 and Stein-Rabinovitch9 algorithms (the BSSR
algorithm)).
Program bdens combines two algorithms: direct count and the Wang-Landau algorithm.
The resulting sums and densities of states are exact at low energies (where direct counting is
used) and of very high accuracy at high energies (where the Wang-Landau) method is used. For
larger species, the combination gives both faster execution times and better accuracy at low
energies.
76
Direct count Algorithm
The direct count (DC) algorithm is a recursive version of a set of nested do-loops.
Because it is recursive, it (ideally) can be used for any number of coupled vibrational modes;
practically speaking, the default array size limits the number of vibrations to 150, which is large
enough for most applications.
Wang-Landau Algorithm
Wang and Landau1, 10 pioneered an efficient random walk algorithm in energy space to
compute densities of states for use in classical statistical models. Their approach is based on the
idea that a density-weighted Monte Carlo sampling of the energy states of the system will
produce a flat histogram of samples in equally-spaced energy bins if the density of states
function is exact, in the limit of an infinite number of trials. The algorithm is initiated with a trial
density of states in every energy bin and the density-weighted Monte Carlo sampling begins. A
histogram records every visit to an energy bin. The algorithm is designed to modify the relative
density of states G(Ei) on every visit to an energy bin (at energy Ei) in such a way so that G(Ei)
approaches exact proportionality with the true density of states after a large number of samples.1,
10 The algorithm can be halted by monitoring the "flatness" of the histogram, or by limiting the
number of Monte Carlo samples. Basire et al.2 adapted the Wang-Landau algorithm for
computing quantum densities of states for fully coupled anharmonic systems using the
perturbation theory expansion for vibrational energy. It is a powerful method. For a full
description of the algorithm and notation, see the paper by Basire et al. 2 As one of their
demonstrations, they computed the density of states for naphthalene, based on the fully-coupled
X matrix reported by Cané et al.11
We have modified the Basire et al. version2 of the Wang-Landau algorithm in several
minor ways to meet the needs for the density of states in chemical kinetics and master equation
applications. In our approach, we compute statistics for the histogram based only on energy bins
that contain states. We do not use the "flatness" criterion for halting the algorithm, but instead
use the number of Monte Carlo trials per energy bin, since that is the principal factor that
controls the relative error (see below). We also apply the tests described above to ensure that
selected states are bound or quasi-bound.
We have automated the algorithm by choosing the probability of accepting a move
(parameter p; see Basire et al. for notation) according to N, the number of DOF. As discussed by
Basire et al., if p is too large, the Monte Carlo selection can sample the entire energy range
rapidly, but there may be many wasted samples that fall out of range. On the other hand if p is
too small, the entire energy range may not be sampled efficiently, and more trials will be needed.
In this work, we adopt p =MIN(1/N, 0.25). This protocol is consistent with the values for p used
by Basire et al.2 As discussed in a later section, our results show little sensitivity to the selection
of p.
An important new modification we have made to the Basire et al. version2 of the Wang-
landau algorithm is to introduce automatic normalization of the density of states. Recall that the
Wang-Landau algorithm produces results that are proportional to the exact density of states. The
un-normalized G(Ei) may be sufficient for many applications, but the absolute density of states
ρ(Ei) is needed for calculating rate constants from statistical rate theories, for example. In our
approach, the size of the energy bins (i.e. the energy grain size ∆E) is chosen small enough so
that only one state, the lowest energy state (i.e. the zero point energy state), falls in the lowest

77
energy bin. Since we know that only one state resides in the lowest energy bin, the density of
states in lowest energy bin must be (∆E)-1, we then obtain the absolute density of states:
Ei
G Ei
G Ei0
1
E
For vibrational states, it is easy to choose ∆E small enough so that only the zero point energy
state falls within the lowest energy bin.
In the bdens code, this normalization method has been improved by taking advantage of
the exact state count obtained from the Direct Count algorithm. The DC algorithm is used to
calculate exact densities of states in an energy range that overlaps the energy range in which the
WL algorithm is used. The overlapped energy range is approximately from Eswitch to
1.1*Eswitch. Over that overlapped energy range, the ratio of the exact density of states divided
by the relative density of states is evaluated in each occupied energy grain and the average is
identified with the scale factor that normalizes the WL relative densities. Since this scale factor
depends on not just one, but on multiple energy grains, it is not as susceptible to stochastic noise
as our original normalization method.
Note that our modified version3 of the Wang-Landau algorithm1, 10 draws heavily on that
of Basire et al., 2 which should also be cited.
Switching from Direct Count to Wang-Landau
At energy Eswitch, the bdens code switches execution from the direct count (DC)
algorithm to the Wang-Landau (WL) algorithm (see next section). Eswitch can be optionally
declared manually (by choosing keyword "MAN " and giving the energy Eswitch (cm–1 units))
or automatically (keyword "AUTO"). By carrying out tests, we have determined how the
execution time using each algorithm depends on the sum of states as a function of energy. At low
energies, DC is faster than the WL, while the reverse is true at high energies. When Eswitch is
determined automatically, it is selected in order to minimize total execution time. In other words,
the "AUTO" option results nearly optimum over-all execution times.
Running bdens
The executable (binary) program resides in the directory
multiwell<version>/bin, where <version> is the version number (e.g. "2010.0")
To execute the compiled program, enter the directory that contains the bdens data file
("bdens.dat") and then type ~/multiwell<version>/bin/ bdens. Directory
multiwell<version> is assumed to reside in your Home directory. The output file
bdens.out is automatically placed in the directory that contains bdens.dat. A second
output file <name>.dens, which is designed to be an input file for the MultiWell master
equation code, is also generated, where <name> is the name of the chemical species (specified
in bdens.dat).
bdens has been designed to run using a "checkpoint file", which is generated after the
density of states of the fully coupled vibrations have been calculated, which is the most time-
consuming section. The following section convolutes the separable degrees of freedom, if any
are specified. The separable degrees of freedom may include free or hindered rotors, harmonic
78
vibrations, etc. In particular, the K-rotor and possibly other external rotational degrees of
freedom may be specified. If desired, the densities of states may be recalculated using various
combinations of separable degrees of freedom, but retaining the same set of fully coupled
vibrations. Repetitive calculations like these can be restarted using the checkpoint file, which
saves considerable computer time.
Three output files are generated by bdens: bdens.out, <name>.dens, and
<name>.qvb. The first file (bdens.out) is a standard output file, which summarizes all input
and output. The second file (<name>.dens), which takes a chemical species name as part of
the file name, gives sums and densities of states, formatted as double arrays; it can be used as
input for the MultiWell master equation code. By using this input file, master equation
calculations can be carried out with densities of states computed by including the fully-coupled
vibrations. The third file (<name>.qvb) is formatted as a supplementary input file for program
Thermo; it tabulates the partition function and other thermodynamic properties of the coupled
vibrational modes at a set of fixed temperatures from 50 K to >3000 K. Thermo can utilize
these partition functions to compute and thermodynamics data and canonical rate constants. See
Section 6.3 of this User Manual for a description of how the <name>.qvb file is used by
Thermo.
bdens.dat Data File Format
For definitions of terms, see Technical Note #9. (Appendix B.2 of this User Manual)
Line 1: Name (species name; ≤10 characters)
Line 2: Title 1 (≤100 characters)
Line 3: Title 2 (≤100 characters)
Line 4: ns (number of vibrational modes), NY (number of Y matrix elements), NZ (number of Z
matrix elements), WW (a keyword to designate frequencies as ωe or ω0)
WW = We for ω
WW = Wf for fundamental vibrations (0-1 transitions)
WW = W0 for ω0 [note: 0 is a zero]
(The distinction between ω and ω0 is explained by eqs. (II,267) through (II,269) of Herzberg 12.
The computer code carries out the conversion between them.)
Lines 5+ (5 to 4+ns): wa(i) [i = 1 , ns] vibrational frequencies (cm-1)
Line 6 (5+ns): KEYWORD for reading the X anharmonicity matrix:
= lower (for reading lower half of matrix, plus the diagonal)
= upper (for reading upper half of matrix, plus the diagonal)
79
Lines 7+ (6+ns to 5+2ns): xa(k,j) anharmonicities (cm-1) in upper or lower halves (plus the
diagonal) of the ns×ns anharmonicity matrix.
Line 8: Nsep , Vrot
Nsep = number of separable modes to be convoluted with the ns non-separable modes)
Vrot = KEYWORD for specifying units for internal and external rotations, except for
hindered rotors of type hrd (see special instructions in the chapter on DenSum for type
hrd)
'AMUA': for moments of inertia input with units of amu Å2.
'GMCM': for moments of inertia input with units of g cm2.
'CM-1': for rotational constant input with units of cm-1.
'MHZ': for rotational constant input with MHz.
'GHZ': for rotational constant input with GHz.
(some combinations of upper/lower case are also accepted)
Line 9: input data for the separable modes (classical or quantum free rotors, hindered rotors of
several types, and Morse oscillators). The various types are defined and appropriate input
format are described in Chapter 3.
Line 10: Egrain1, imax1, Isize, Emax2, KEYWORD1, KEYWORD2, Eswitch
Egrain1 = energy grain (cm-1)
imax1 = number of array elements in lower part of the Double Array (see MultiWell
User Manual)
Isize = total number elements in the Double Array.
Emax2 = upper energy limit
KEYWORD1 = controls number of stochastic trials:
Fair: low statistical accuracy (102 trials per energy grain)
Good: good statistical accuracy (103 trials per energy grain).
Better: better statistical accuracy (104 trials per energy grain)
Best: best statistical accuracy (105 trials per energy grain)
Extra: best statistical accuracy (106 trials per energy grain, but no more than
2109 total trials for all energy grains)
KEYWORD2 = controls how Eswitch is chosen
AUTO: an optimum Eswitch is chosen automatically by bdens.
MAN: Eswitch is defined manually by the User
Eswitch = defined by the User (units: cm-1) (a place-holder value must be present even
when KEYWORD2 = AUTO.
Line 11: chekpoint
If chekpoint = "chekstart" (Note the spelling!), then the new calculation starts
by reading the pre-existing checkpoint file. Otherwise, the full calculation is carried out.
Line 10 must be identical to the data file used to create the pre-existing checkpoint file.
80
Notes
1. Energies are relative to the zero point energy.
2. Be careful when using Gaussian! The Gaussian log file has two sections related to
vibrations. The first section is for the usual vibrational analysis to obtain harmonic
frequencies. These frequencies are listed from lowest to highest. The second section is for
anharmonicities. In the second section, the harmonic frequencies are listed again (along
with the fundamental frequencies), but the ordering may not be the same as in the first
section. The input for the codes distributed in MultiWell will accept the frequencies in
any order, but the ordering of the harmonic frequencies must be consistent with the
ordering used for the anharmonicities. For consistency, the Gaussian user must be sure to
use the ordering of the harmonic frequencies as listed in association with the
anharmonicities in the Gaussian log file.
81
8.2 Program paradensum
paradensum:13 parallel and improved version of adensum (adensum was last released in
multiwell-2014.1b)
Program Authors:
paradensum:C. Aieta, F. Gabas, and M. Ceotto
adensum: T. L. Nguyen and J. R. Barker
Contact: Michele Ceotto: michele.ceotto@unimi.it
(For definitions, see Technical Note #2. (Appendix B.2 of this User Manual))
Wang and Landau1, 10 pioneered an efficient random walk algorithm in energy space to
compute densities of states for use in classical statistical models. Their approach is based on the
idea that a density-weighted Monte Carlo sampling of the energy states of the system will
produce a flat histogram of samples in equally-spaced energy bins if the density of states
function is exact, in the limit of an infinite number of trials. The algorithm is initiated with a trial
density of states in every energy bin and the density-weighted Monte Carlo sampling begins. A
histogram records every visit to an energy bin. The algorithm is designed to modify the relative
density of states G(Ei) on every visit to an energy bin (at energy Ei) in such a way so that G(Ei)
approaches exact proportionality with the true density of states after a large number of samples.1,
10 The algorithm can be halted by monitoring the "flatness" of the histogram, or by limiting the
number of Monte Carlo samples. Basire et al.2 adapted the Wang-Landau algorithm for
computing quantum densities of states for fully coupled anharmonic systems using the
perturbation theory expansion for vibrational energy. It is a powerful method. For a full
description of the algorithm and notation, see the paper by Basire et al. 2 As one of their
demonstrations, they computed the density of states for naphthalene, based on the fully-coupled
X matrix reported by Cané et al.11
We have modified the Basire et al. version2 of the Wang-Landau algorithm in several
minor ways to meet the needs for the density of states in chemical kinetics and master equation
applications.3 In our approach, we compute statistics for the histogram based only on energy bins
that contain states. In paradensum we use the “flatness” criterion for halting the algorithm
(this is in contrast to adensum, which used specified numbers of stochastic trials). We also
apply the tests described elsewhere7 to ensure that selected states are bound or quasi-bound.
We have automated the algorithm by choosing the probability of accepting a move
(parameter p; see Basire et al. for notation) according to N, the number of coupled DOF.3 As
discussed by Basire et al., if p is too large, the Monte Carlo selection can sample the entire
energy range rapidly, but there may be many wasted samples that fall out of range. On the other
hand if p is too small, the entire energy range may not be sampled efficiently, and more trials
will be needed. In this work, we adopt p =MIN(1/N, 0.25). This protocol is consistent with the
values for p used by Basire et al.2 Our results show little sensitivity to the selection of p.
The most important new modification we have made to the Basire et al. version2 of the
Wang-landau algorithm is to introduce automatic normalization of the density of states.3, 13
Recall that the Wang-Landau algorithm produces results that are proportional to the exact
density of states. The un-normalized G(Ei) may be sufficient for many applications, but the
absolute density of states ρ(Ei) is needed for calculating partition functions and rate constants

82
from statistical rate theories, for example. In our approach, the size of the energy bins (i.e. the
energy grain size ∆E) is chosen small enough so that only one state, the lowest energy state (i.e.
the zero point energy state), falls in the lowest energy bin. Since we know that only one state
resides in the lowest energy bin, the density of states in lowest energy bin must be ρ(0) = 1/∆E,
we then obtain the absolute density of states:
For vibrational states, it is easy to choose ∆E small enough so that only the zero point
energy state falls within the lowest energy bin. For master equation and chemical kinetics
applications, the typical energy grain is ∆E≤10 cm-1 and vibrational frequencies are typically
much larger. If rotations were to be included with the vibrations, normalization can still be
achieved easily by using one of the other methods described above to count the number of
rotational states in the lowest energy grain and normalizing accordingly.
Our modified version of the Wang-Landau algorithm1, 10 draws heavily on that of Basire
et al., 2 and is summarized elsewhere.3, 13 Also see Section 8.1 of this User Manual for a
description of program bdens, which also uses the Wang-Landau algorithm.
paradensum is a parallel code that can exploit not only single but also multiple core
architectures. In this way the computation of the density of states is significantly accelerated
when considering high dimensionality systems. The parallelization strategy is to divide the
energy range into energy “windows” and set the calculations of G(Ei) for each window on a
single processor. This strategy is dictated by the observation that less random sampling events
and reduced computational effort is needed for Monte Carlo to converge in a restricted energy
range.
The number of processors is given by the windowing choice and, by default, all windows
have the same width. This setting can be changed modifying the appropriate keyword in the
input file. If the computational time spent by each window to reach the flatness criterion is
unbalanced, the code prints a warning in the Windows_info.txt output file. Then, the user can
decide to halve the width of the first two or the last two windows.
Since the Wang-Landau density of states is notoriously biased at the edges of small
energy windows, we always keep a percentage of overlap between neighbor windows. This is
also necessary for the normalization of the G(Ei) obtained in each window to give the complete
function on the whole energy domain.13 The code supports the possibility to run serially multiple
walkers in each energy window. This feature improves the statistics of sampling in each window
but does not have any impact on the speedup. To run the code the user has to supply the number
of processors that is equal to the number of windows and a percentage of overlap between them
as input parameters. When the number of processors (windows) is set to unity, then paradensum
will run in serial mode (i.e. it can run on a single cpu or core). The set up of the input file for
these parameters is described below. For a full description of the paradensum
implementation, see the paper by Aieta et al.13
Running paradensum
paradensum is a parallel code. To compile and run the code, it is necessary to have
previously installed supplementary software. Details are given in Section 1.4).
paradensum has been designed to run using a "checkpoint file", which is generated
after the density of states of the fully coupled vibrations have been calculated, which is the most
time-consuming section. The next section in the code convolutes the separable degrees of
83
freedom, if any are specified. The separable degrees of freedom may optionally include free or
hindered rotors, harmonic vibrations, etc. In particular, the K-rotor and possibly other external
rotational degrees of freedom may be specified. If desired, the densities of states may be
recalculated using various combinations of separable degrees of freedom, but retaining the same
set of fully coupled vibrations, available from the checkpoint file. Repetitive calculations like
these can be restarted using the checkpoint file, which saves considerable computer time. Note
that when using checkpoint file, it is not necessary to run the code in parallel mode.
The input data file paradensum.dat includes molecular parameters for computing the
densities of states, as well as parallel execution parameters. Directory multiwell-
<version> is assumed to reside in your Home directory. Execution of paradensum is
carried out within the directory that contains the input data file paradensum.dat. All of the
output files are automatically placed in the directory that contains paradensum.dat.
Four output files are generated by paradensum: paradensum.out,
<name>.dens, <name>.qvb., and Windows_info.txt. The file paradensum.out is
a standard output file, which summarizes all input and output. The file <name>.dens, which
takes a chemical species name as part of the file name, gives sums and densities of states,
formatted as double arrays; it can be used as input for the MultiWell master equation code. By
using this input file, master equation calculations can be carried out with densities of states
computed by including the fully-coupled vibrations. The file <name>.qvb is formatted as a
supplementary input file for program Thermo; it tabulates the partition function and other
thermodynamic properties of the coupled vibrational modes at a set of fixed temperatures from 1
K to >3000 K. Thermo can utilize these partition functions to compute thermodynamics data
(from statistical mechanics formulae) and canonical rate constants (from statistical rate theory).
See Section 6.1.2 of this User Manual for a description of how the <name>.qvb file is used by
Thermo. The file Windows_info.txt contains details about windows division, i.e. the total
number of energy grains, the number of energy grains in each window after the overlap has been
added, and the low and high energy boundaries of each window.
Users may also select a supplementary writing option, which generates a file called
Rank<N>.txt for each parallel process (here, <N> is an integer number that identifies the
process). These files report all details about the Wang-Landau algorithm executed by each
parallel process. Users may freely enable or disable writing the Rank<N>.txt files, which are
intended as a user check on parallel execution.
84
Format for paradensum.dat Input File
(For definitions of terms, see Technical Note #9. (Appendix B.2 of this User Manual))
Line 1: Name (species name; ≤10 characters)
Line 2: Title 1 (≤100 characters)
Line 3: Title 2 (≤100 characters)
Line 4: ns (number of vibrational modes), NY (number of Y matrix elements), NZ (number of Z
matrix elements), WW (a keyword to designate frequencies as ωe or ω0)
WW = We for ω
WW = Wf for fundamental vibrations (0-1 transitions)
WW = W0 for ω0 [note: 0 is a zero]
(The distinction between ω and ω0 is explained by eqs. (II,267) through (II,269) of
Herzberg 12. The computer code carries out the conversion between them.)
Lines 5+ (5 to 4+ns): wa(i) [i = 1 , ns] vibrational frequencies (cm-1)
Line 6 (5+ns): KEYWORD for reading the X anharmonicity matrix:
= lower (for reading lower half of matrix, plus the diagonal)
= upper (for reading upper half of matrix, plus the diagonal)
Lines 7+ (6+ns to 5+2ns): xa(k,j) anharmonicities (cm-1) in upper or lower halves (plus the
diagonal) of the ns×ns anharmonicity matrix.
Line 8: Nsep , Vrot
Nsep = number of separable modes to be convoluted with the ns non-separable modes)
Vrot = KEYWORD for specifying units for internal and external rotations, except for
hindered rotors of type hrd (see special instructions in the chapter on DenSum for type
hrd)
'AMUA': for moments of inertia input with units of amu Å2.
'GMCM': for moments of inertia input with units of g cm2.
'CM-1': for rotational constant input with units of cm-1.
'MHZ': for rotational constant input with MHz.
'GHZ': for rotational constant input with GHz.
(some combinations of upper/lower case are also accepted)
Line 9: input data for the separable modes (classical or quantum free rotors, hindered rotors of
several types, and Morse oscillators). The various types are defined and appropriate input
format are described in Chapter 3.
85
Line 10: Egrain1, imax1, Isize, Emax2
Egrain1 = energy grain (cm-1)
imax1 = number of array elements in lower part of the Double Array (see MultiWell
User Manual)
Isize = total number elements in the Double Array.
Emax2 = upper energy limit
Line 11: chekpoint
If chekpoint = "chekstart" (Note the spelling!), then the new calculation starts
by reading the pre-existing checkpoint file. Otherwise, the full calculation if is carried
out. Line 10 must be identical to the data file used to create the pre-existing checkpoint
file.
Line 12: (Blank line)
Line 13: nwalkers = number of independent random walks in each window; integer.
Line 14: perc_wind_overlap = percentage of overlap between neighboring windows; real.
Line 15: flatness = flatness criterion for halting the Wang-Landau algorithm: a real number
between 0 and 1. The closer to unity, the more accurate is the density of states.
Line 16: writing (writing out Rank<N>.txt files)
= 1 (Writing enabled.)
= 0 (Writing disabled.)
Line 17: seed_modifier = an integer number which is added to the default random number
generator seed in order to get a new random number chain. For usual applications of the
code it is set to 0.
Line 18: windbal_key = this keyword sets the windows width.
= ”const” (default) windows width is equal for all windows.
= ”low” the first two windows are smaller than the others.
= ”high” the last two windows are smaller than the others.
Notes
1. Energies are relative to the zero point energy.
2. Be careful when using Gaussian! The Gaussian log file has two sections related to
vibrations. The first section is for the usual vibrational analysis to obtain harmonic
frequencies. These frequencies are listed from lowest to highest. The second section is for
anharmonicities. In the second section, the harmonic frequencies are listed again (along
with the fundamental frequencies), but the ordering may not be the same as in the first
section. The input for the codes distributed in MultiWell will accept the frequencies in
86
any order, but the ordering of the harmonic frequencies must be consistent with the
ordering used for the anharmonicities. For consistency, the Gaussian user must be sure to
use the ordering of the harmonic frequencies as listed in association with the
anharmonicities in the Gaussian log file.
3. See Sections 1.3 and 1.4 for special instructions for executing paradensum.
8.3 Program sctst
This program is a new implementation6 of the semi-classical transition state theory
(SCTST) formulated by W. H. Miller and coworkers.14-17 Our implementation is based on the
Wang and Landau algorithm1 and the density of states algorithm of Basire et al.,2 as refined by
Nguyen and Barker.3 The literature references should be consulted for further details about the
theory, its usefulness, and applications. The literature should be cited as described at the Preface
of this User Manual.
The SCTST is a powerful method, since it can be used for computing both thermal (i.e.
canonical k(T)) and microcanonical (i.e. k(E)) rate constants, which are essential for master
equation calculations. Unlike ordinary transition state theory, the SCTST is fully non-separable:
all of the degrees of freedom may be coupled and it is not necessary to assume that the reaction
coordinate is separable from the others. It also accounts naturally for zero point energy and for
quantum mechanical tunneling along the curved reaction path in hyperdimensional space. In test
cases, it is highly accurate.18
The input is similar to that for program bdens (Section 8.1), but it also includes the
imaginary frequency and the anharmonicity coefficients associated with the reaction coordinate.
The imaginary frequency and the off-diagonal anharmonicity coefficients associated with the
reaction coordinate are pure imaginary numbers; the diagonal anharmonicity for the reaction
coordinate is a pure real number. These facts affect how the parameters are specified in the input
data file sctst.dat. In addition, SCTST as formulated by Miller and coworkers is based on
second order vibrational perturbation theory (VPT2).19 Recently, Stanton investigated SCTST
based on VPT4 (fourth order perturbation theory) and arrived as a simple correction that is
appropriate for symmetrical Eckart barriers.20 To the extent that the actual energy barrier
resembles an Eckart barrier, this VPT4 correction improves the performance of SCTST/VPT2.
Stanton suggested two slightly different versions of this correction, but the difference between
then is small. In program sctst, either of the two corrections (or neither) can be selected by
selecting the appropriate key word.
The output files are analogous to the output files from programs bdens and densum.
The general output file sctst.out summarizes the input and gives "sums" and "densities" of
states for the full energy range specified. These "sums" and "densities" actually correspond to the
cumulative reaction probability14-17 (CRP) and the corresponding energy derivative, which are
equal to the sums and densities in the absence of quantum tunneling. The second output files
takes the name of the transition state with ".dens" added: <name>.dens, just as in programs
densum and bdens. These files are formatted for use by the MultiWell master equation code.
An output file is also generated that gives the thermal partition function (excluding the
translations) for the transition state at a set of 100 fixed temperatures (25 K to 3383 K). This file,
named <name>.qcrp, is used by program Thermo to calculate canonical rate constants (see
Section 6.3 of this User Manual for a description of how the file is used by Thermo).
87
Running sctst
The executable (binary) program resides in the directory
multiwell<version>/bin, where <version> is the version number (e.g. "2014.1b")
To execute the compiled program, enter the directory that contains the sctst data file
("sctst.dat") and then type ~/multiwell-<version>/bin/sctst. Directory
multiwell<version> is assumed to reside in your Home directory. The output file
sctst.out is automatically placed in the directory that contains sctst.dat. A second
output file <name>.dens, which is designed to be an input file for the MultiWell master
equation code, is also generated, where <name> is the name of the transition state specified in
sctst.dat.
Like sctst has been designed to run using a "checkpoint file", which is generated after
the density of states of the fully coupled vibrations have been calculated, which is the most time-
consuming part of the calculation. The next part of the calculation convolutes the separable
degrees of freedom, if any are specified. The separable degrees of freedom may include free or
hindered rotors, harmonic vibrations, etc. In particular, the 1-D external rotation (the K-rotor)
and possibly also the 2-D external rotational degrees of freedom may be specified, depending on
the application. If desired, the densities of states may be recalculated using various combinations
of separable degrees of freedom, but retaining the same set of fully coupled vibrations.
Repetitive calculations like these can be restarted using the checkpoint file, which saves
considerable computer time.
Another reason for running repetitive calculations by starting with the checkpoint file is
because whenever the reaction threshold energy is changed, the SCTST requires that the density
of states of the transition state and the cumulative reaction probability be recalculated.6 Adjusting
reaction barriers to fit experimental data may require multiple repetitive calculations, and
restarting by using the checkpoint file will reduce the computer time by an order of magnitude or
more.
In summary, four output files are generated by sctst: sctst.out, <name>.crp,
<name>.chk, and <name>.qcrp. The first file (sctst.out) is a standard output file,
which summarizes all input and output. The second file (<name>.chk), which takes a chemical
species name as part of the file name, is the checkpoint file, which is an important time-saving
measure for subsequent runs using the same vibrational parameters, as described in the preceding
paragraph. The third file (<name>.crp), tabulates the cumulative reaction probability (CRP)
and its energy derivative (analogous to sums and densities of states), formatted as double arrays;
it is formatted for use as input for the MultiWell master equation code. By using this input file,
master equation calculations can be carried out with microcanonical rate constants (i.e. k(E))
computed by including the fully-coupled vibrations. The fourth file (<name>.qcrp) is
formatted as a supplementary input file for program Thermo; it tabulates the partition function
for the CRP and other thermodynamic properties of the coupled vibrational modes at a set of
fixed temperatures from 50 K to >3000 K. Thermo can utilize these partition functions to
compute thermal rate constants using the SCTST. See Section 6.3 of this User Manual for a
description.
88
Data File Format
(For definitions of terms, see Technical Note B.9 and Nguyen et al.6 )
Line 1: Name (transition state name; ≤10 characters)
Line 2: Title 1 (≤100 characters)
Line 3: Title 2 (≤100 characters)
Line 4: ns (number of orthogonal vibrational modes, not including the reaction coordinate), NY
(number of Y matrix elements), NZ (number of Z matrix elements), WW (a keyword to designate
frequencies as ωe or ω0)
WW = We for ω
WW = Wf for fundamental vibrations (0-1 transitions)
WW = W0 for ω0 [note: 0 is a zero]
(The distinction between ω and ω0 is explained by eqs. (II,267) through (II,269) of Herzberg 12.
The computer code carries out the conversion between them.)
Lines 5: wa(i) [i = 1 , ns] vibrational frequencies (cm-1) of the orthogonal vibrations (i.e. not
including the reaction coordinate)
Line 6: KEYWORD for reading the X anharmonicity matrix (not including the reaction
coordinate). The keyword must start at the beginning of the line (i.e. it cannot be
preceded by blank characters):
= lower (for reading lower half of matrix, plus the diagonal)
= upper (for reading upper half of matrix, plus the diagonal)
Lines 7: xa(k,j) anharmonicities (cm-1) in upper or lower halves (plus the diagonal) of the
ns×ns anharmonicity matrix.
Line 8: Nsep , Vrot
Nsep = number of active separable modes (as in Line 5 of Densum) to be convoluted
with the ns non-separable modes entered above)
Vrot = KEYWORD for specifying units for internal and external rotations, except for
hindered rotors of type hrd (see special instructions in the chapter on DenSum for type
hrd)
Vrot Keywords:
'AMUA': for moments of inertia input with units of amu Å2.
'GMCM': for moments of inertia input with units of g cm2.
'CM-1': for rotational constant input with units of cm-1.
'MHZ': for rotational constant input with MHz.
'GHZ': for rotational constant input with GHz.
(some combinations of upper/lower case are also accepted)
89
Line 9: input data for the separable modes (classical or quantum free rotors, hindered rotors of
several types, and Morse oscillators). The various types are defined and appropriate input
format are described in Chapter 3.
Line 10: Egrain1, imax1, Isize, Emax2, KEYWORD1
Egrain1 = energy grain (cm-1)
imax1 = number of array elements in lower part of the Double Array (see MultiWell
User Manual)
Isize = total number elements in the Double Array.
Emax2 = upper energy limit
KEYWORD1 = controls number of stochastic trials:
Fair: low statistical accuracy (102 trials per energy grain)
Good: good statistical accuracy (103 trials per energy grain).
Better: better statistical accuracy (104 trials per energy grain)
Best: best statistical accuracy (105 trials per energy grain)
Extra: best statistical accuracy (106 trials per energy grain, but no more than
2109 total trials for all energy grains)
Line 11: KEYWORD "checkpoint"
If chekpoint = "chekstart" (Note the spelling!), then the new calculation starts
by reading the pre-existing checkpoint file. Otherwise, the full calculation is carried out.
All data up to and including Line 11 must be identical to the data file used to create the
pre-existing checkpoint file in the first place.
Line 12: KEYWORD3
KEYWORD3 = controls number of samples for the semi-classical calculation (typically the
same as KEYWORD1). The samples are used to compute average quantities employed by
the theory.
Fair: low accuracy (102 samples per energy grain)
Good: good accuracy (103 samples per energy grain).
Better: better accuracy (104 samples per energy grain)
Best: best accuracy (105 samples per energy grain)
Extra: best accuracy (106 samples per energy grain, but no more than 2109 total
samples for all energy grains)
Line 13: KEYWORD "VPTx"
New Feature in 2017; this line must be added to older files that are run using 2017
version, or newer.
VPTx = controls corrections to the basic SCTST/VP2.
VPT2: no correction.
VPT4A: Recommended. VPT4 correction (Eq. 42 in the paper by Stanton.20)
VPT4B: VPT4 correction (Eq. 37 in the paper by Stanton.20)
Line 14: Vf , Vr , Eunits
90
Barrier heights (including zero point energy corrections) in forward (Vf) and reverse
(Vr) directions, and their energy units (Eunits: kcal, kjou, or cm-1)
Line 15: vimag, Xff
Imaginary frequency and the diagonal anharmonicity coefficient for the reaction
coordinate (units of cm-1)
Line 16: Xkf
Off-diagonal anharmonicity coefficients (units of cm-1) multiplied by i = (-1)1/2: ns of
them, in order. Since the Xk,F coefficients are pure imaginary, they can be written
Xk,Fi
Xk,F
, where
Xk,F
is a real number. The quantities to be input are
iXk,Fii
Xk,F
Xk,F
, which is in the same format as GAUSSIAN output. In
contrast, CFOUR output gives Xk,F expressed as
Xk,F
followed by the symbol "i", i.e. "
Xk,F
i". These conventions are equivalent, but it is easy to make a sign error. Be
careful!
Notes
1. Energies are relative to the zero point energy.
2. In second order vibrational perturbation theory (VPT2), the zero point energy (ZPE) includes
contributions from the harmonic frequencies, the anharmonicities, but it does NOT include the
harmonic imaginary frequency or any of the anharmonicity coefficients involving the imaginary
frequency. The ZPE also includes an additional term denoted G0 (see Eq. 9 in Appendix B.9),4, 5
which cancels-out in spectroscopy applications but must be included for every species in high-
accuracy thermochemistry and kinetics calculations. The value of G0 must be computed by
electronic structure programs employing VPT2 (e.g. GAUSSIAN and CFOUR), and is not
computed by MultiWell itself. For ab initio kinetics calculations involving chemical species and
transition states with large rotational constants, G0 may be significant, but it is very small for
molecules with small rotational constants. For high accuracy ab initio kinetics calculations (e.g.
Ref. 6, G0 can be included manually by modifying the reaction critical energy (which already
includes zero point energy corrections).
3. Be careful when using Gaussian! The Gaussian log file has two sections related to vibrations.
The first section is for the usual vibrational analysis to obtain harmonic frequencies. These
frequencies are listed from lowest to highest. The second section is for anharmonicities. In the
second section, the harmonic frequencies are listed again (along with the fundamental
frequencies), but the ordering may not be the same as in the first section. The input for the codes
distributed in MultiWell will accept the frequencies in any order, but the ordering of the
harmonic frequencies must be consistent with the ordering used for the anharmonicities. For
consistency, the Gaussian user must be sure to use the ordering of the harmonic frequencies as
listed in association with the anharmonicities in the Gaussian log file.
91
References
92
9. lamm: Effective Mass for Internal Rotation
lamm: Large Amplitude Motion Mass
Program Author: Thanh Lam Nguyen
Contact: LNGUYEN@cm.utexas.edu
9.1 Introduction
This program is a tool for obtaining the effective mass (as a function of angle or distance)
for large amplitude motions, such as internal rotation. The output is used as part of the input data
file needed for computing sums and densities of states (using program DenSum) and partition
functions (program Thermo).
Program lamm uses the ro-vibrational G matrix-based algorithm described in the papers
of Harthcock et al.21, 22 and others to compute the effective reduced mass for one-dimensional
torsions and other large amplitude motions, which are assumed to be separable from the other
molecular degrees of freedom.
Molecular geometries can be computed at discrete values of χ by using any of the many
available quantum chemistry codes, such as Gaussian,23 Molpro,24 CFour,25 etc. Program lamm
is intended to help users compute the torsion rotational constant Bhr(χ) and the potential energy
V(χ), based on the output from the quantum chemistry program.
For hindered internal rotation, lamm employs Cartesian coordinates obtained from
quantum chemical calculations carried out as a function of the dihedral angle χ (0≤χ2). The
output of lamm consists of the torsion rotational constant function Bhr(χ) (or the corresponding
moment of inertia function I(χ)) tabulated as a function of χ. The potential energy can also be
obtained from the quantum chemistry calculations and expressed as a function of χ. These
functions must then be fitted by the user to any one of the several truncated Fourier series that
are recognized by DenSum and Thermo (see the MultiWell User Manual). The Fourier
coefficients are used by programs DenSum and Thermo to solve the Schrödinger equation for
the energy eigenstates (see Appendix B.8), which are needed to compute densities of states and
partition functions, respectively.
A script is provided to assist users in extracting the required information from Gaussian
output files (see Section 9.7).
9.2 Compiling and Running lamm
The source directory for lamm resides in the MultiWell src directory. The program is
compiled on Linux by entering the MultiWell directory and typing “make” (omit the quotation
marks), followed by a carriage return. The executable file is stored in the MultiWell bin
directory. The default compiler is gfortran. The compiler can be changed by revising lines in
file src/lamm/Makefile. To remove old object files and executables, enter directory
src/lamm and type “make clean”, followed by a carriage return.
To execute the compiled program, enter the directory that contains the lamm data file
(“lamm.dat”) and then type ~/multiwell-<version>/bin/lamm, where <version>
refers to the multiwell version number (e.g. "2010.0"). This command executes the binary

93
executable file. The output file (“lamm.out”) is automatically placed in the directory that
contains lamm.dat.
9.3 Notes and Limits
For the current version of the lamm program, Cartesian coordinates of optimized
geometries must be obtained by constrained optimizations. When using Gaussian, the keyword
“NOSYM” and/or OPT=”Z-Matrix”, or the equivalent must be specified.
The lamm program does not automatically identify the molecular symmetry; it always
assumes that the molecule has no symmetry (C1 symmetry). Therefore the effective reduced
moment of inertia will be computed only for the number of optimized geometries that are input.
Since the derivatives of the nuclear positions with respect to the torsional coordinate are
computed by central finite differences, a fairly small torsional angle step-size must be used in
order to achieve numerical accuracy. In our experience, a step-size of ≤10° is a good choice for
most purposes.
In addition to torsional motions, the lamm program can be used for computing the
effective mass for other separable large-amplitude vibrational motions. Specific implementations
will be added in the future.
Users may be interested in program I_Eckart, which was coded in MATLAB by Wong,
Thom and Field 26. We would like to thank Dr. Wong and Prof. Field for useful discussions and
for providing a copy of their program, which we used for benchmarks.
9.4 Data File Format
Line 1: Name of molecule (≤ 100 characters)
Line 2: Title (≤ 100 characters)
Line 3: Natom (number of atoms in molecule)
Line 4: Amin (lower limit of torsion angle in degrees), M (number of optimized geometries),
DELA (step-size of torsion angle in degrees).
Line 5+ (lines 5 to 4 + N): list of atomic masses (in amu)
Line 6+ (lines 5 + N to 4 + N + N*M): list of Cartesian coordinates (in Angstroms) for M
optimized geometries as a function of the torsion dihedral angle.
Line 7 (lines 5 + N + N*M): comment line (≤100 characters)
Line 8+ (lines 6 + N + N*M to 5 + N + N*M + M): list of torsional angle (in degrees) and
relative energies (in cm-1).
94
9.5 Example Data File
H2O2
Calculated at 6-311G** level of theory
4 ! Number of atoms in the molecule
0, 36, 10 ! Minimum angle, No. of optimized geometries and Step-size
(in degrees)
1. ! list of atomic mass (in amu)
16.
16.
1.
0.000000 0.000000 0.000000 !list of X, Y, Z cartesian coordinate
0.000000 0.000000 0.966404
1.412522 0.000000 1.340839
1.891238 0.000000 0.501335
0.000000 0.000000 0.000000
0.000000 0.000000 0.966493
1.412776 0.000000 1.339296
1.886024 0.162275 0.512367
And so on ....
9.6 Example Output:
H2O2
Calculated at 6-311G** level of theory
WARNING: The zero of the relative energy is arbitrary minimum
INDEX ANG(DEG) ANG(RAD) E(cm-1) I(amu.A**2) B(cm-1)
10.0 0.000000 2980.5 0.387 43.6
2 10.0 0.174533 2913.6 0.390 43.3
3 20.0 0.349066 2720.4 0.393 42.9
4 30.0 0.523599 2421.2 0.396 42.5
5 40.0 0.698132 2047.2 0.400 42.2
6 50.0 0.872665 1635.9 0.403 41.9
7 60.0 1.047198 1224.6 0.405 41.6
8 70.0 1.221730 846.6 0.407 41.4
9 80.0 1.396263 527.1 0.410 41.2
10 90.0 1.570796 282.2 0.412 40.9
11 100.0 1.745329 116.9 0.415 40.6
12 110.0 1.919862 27.0 0.418 40.4
13 120.0 2.0943950.0 0.420 40.2
14 130.0 2.268928 19.3 0.421 40.0
15 140.0 2.443461 65.6 0.423 39.9
16 150.0 2.617994 122.1 0.423 39.8
17 160.0 2.792527 173.9 0.423 39.8
18 170.0 2.967060 209.5 0.423 39.8
19 180.0 3.141593 222.3 0.424 39.8
20 190.0 3.316126 209.5 0.423 39.8
21 200.0 3.490659 173.9 0.423 39.8
22 210.0 3.665191 122.1 0.423 39.8
23 220.0 3.839724 65.6 0.423 39.9
95
24 230.0 4.014257 19.3 0.421 40.0
25 240.0 4.1887900.0 0.420 40.2
26 250.0 4.363323 27.0 0.418 40.4
27 260.0 4.537856 116.9 0.415 40.6
28 270.0 4.712389 282.2 0.412 40.9
29 280.0 4.886922 527.1 0.410 41.2
30 290.0 5.061455 846.6 0.407 41.4
31 300.0 5.235988 1224.6 0.405 41.6
32 310.0 5.410521 1635.9 0.403 41.9
33 320.0 5.585054 2047.2 0.400 42.2
34 330.0 5.759587 2421.2 0.396 42.5
35 340.0 5.934119 2720.4 0.393 42.9
36 350.0 6.108652 2913.6 0.390 43.3
37 360.0 6.283185 2980.5 0.387 43.6
9.7 gauss2lamm: A script for generating lamm.dat
The shell script gauss2lamm.sh is designed to create data files for program lamm
(see Chapter 8), which computes effective mass for large amplitude motions, such as hindered
internal rotation. The script is located in directory multiwell-<version>/bin, where
<version> refers to the version number (e.g. "2010.0"). This script reads the input
orientations or Z-matrix of optimized geometries and corresponding energies as a function of the
appropriate coordinate (i.e. the torsion dihedral angle) from "____.log" or "____.out"
output files produced by GAUSSIAN-0327 or GAUSSIAN-0923 software.
To execute the script, enter the directory that contains the Gaussian output file and then
type ~/multiwell-<version>/bin/gauss2lamm.sh. This command goes to the
directory multiwell-<version>/bin (which is assumed to reside in your Home directory)
and executes the script file gauss2lamm.sh, which stored there.
The script generates lamm.dat in the Gaussian output file directory.
The script prompts the user to input the Gaussian output file name, number of atoms in
the molecule and minimum angle, no. of points and stepsize (in degrees) used in the calculation.
First it verifies whether the user has used the keyword “NOSYM and/or Z-Matrix” in Gaussian
output. If the keyword is found the script writes lamm.dat containing geometry and energy
(in cm-1) information. The energy is tabulated as a function of angle (in degrees). The zero of
relative energy is arbitrary minimum. If the keyword is not found in the Gaussian output, the
script prompts the user to redo the Gaussian calculation using the keyword “NOSYM and/or Z-
Matrix”.
It is important to note that the lamm.dat file created automatically from Gaussian
output needs manual changes. Line 5+ (lines 5 to 4+N) in the lamm.dat created using the
script is atomic number, where N is number of atoms in the molecule. This has to be replaced
with corresponding atomic masses (amu units) for subsequent use by program lamm.
An example Gaussian output file lamm.log is available in the examples directory and
procedure to execute gauss2lamm is shown below.
$ ./../bin/gauss2lamm.sh
Enter Gaussian Output Filename
96
lamm.log
Keyword NOSYM found in the output
Enter total number of atoms in the molecule
5
Enter MIN angle, No. of Points and Stepsize in degrees used
in the calculation
0 36 10
Proceeding to collect data from lamm.log
Lowest energy in the surface scan: -740.457504043 hartrees
97
References
1. F. Wang and D. P. Landau, Efficient, Multiple-Range Random Walk Algorithm to
Calculate the Density of States, Phys. Rev. Letters 86, 2050-2053 (2001).
2. M. Basire, P. Parneix and F. Calvo, Quantum anharmonic densities of states using the
Wang-Landau method, J. Chem. Phys. 129, 081101 (2008).
3. T. L. Nguyen and J. R. Barker, Sums and Densities of Fully-Coupled Anharmonic
Vibrational States: A Comparison of Three Practical Methods, J. Phys. Chem. A 114,
3718–3730 (2010).
4. I. M. Mills, "Vibration-Rotation Structure in Asymmetric- and Symmetric-Top
Molecules," in Molecular Spectroscopy: Modern Research, eds. K. N. Rao and C. W.
Mathews (Academic Press, New York, 1972), pp. Academic Press.
5. D. G. Truhlar and A. D. Isaacson, Simple perturbation theory estimates of equilibrium
constants from force fields, J. Chem. Phys. 94, 357-359 (1990).
6. T. L. Nguyen, J. F. Stanton and J. R. Barker, A Practical Implementation of Semi-
Classical Transition State Theory for Polyatomics, Chem. Phys. Letters 499, 9-15 (2010).
7. J. R. Barker, Sums of Quantum States for Non–Separable Degrees of Freedom:
Multidimensional Monte Carlo Integration, J. Phys. Chem. 91, 3849-54 (1987).
8. T. Beyer and D. F. Swinehart, Number of multiply-restricted partitions, Comm. Assoc.
Comput. Machines 16, 379 (1973).
9. S. E. Stein and B. S. Rabinovitch, Accurate evaluation of internal energy level sums and
densities including anharmonic oscillators and hindered rotors, J. Chem. Phys. 58, 2438-
45 (1973).
10. F. Wang and D. P. Landau, Determining the density of states for classical statistical
models: A random walk algorithm to produce a fat histogram, Phys. Rev. E 64, 056101-1
(2001).
11. E. Cané, A. Miani and A. Trombetti, Anharmonic Force Fields of Naphthalene-h8 and
Naphthalene-d8, J. Phys. Chem. A. 111, 8218-8222 (2007).
12. G. Herzberg, Molecular Spectra and Molecular Structure. II. Infrared and Raman
Spectra. (Van Nostrand Reinhold Co., Cincinnati, 1945).
13. C. Aieta, F. Gabas and M. Ceotto, An Efficient Computational Approach for the
Calculation of the Vibrational Density of States, J. Phys. Chem. A., DOI:
10.1021/acs.jpca.5b12364 (2016).
14. W. H. Miller, Semiclassical limit of quantum mechanical transition state theory for
nonseparable systems, J. Chem. Phys. 62, 1899-1906 (1975).
15. W. H. Miller, Semi-Classical Theory for Non-separable Systems: Construction of "Good"
Action-Angle Variables for Reaction Rate Constants, Faraday Discuss. Chem. Soc. 62,
40-46 (1977).
16. J. H. Miller, The kinetics of polynuclear aromatic hydrocarbon agglomeration in flames,
Proc. Combust. Inst. 23, (1990).
17. R. Hernandez and W. H. Miller, Semiclassical transition state theory, Chem. Phys. Lett.
214, 129-136 (1993).

98
18. T. L. Nguyen, J. R. Barker and J. F. Stanton, "Atmospheric Reaction Rate Constants and
Kinetic Isotope Effects Computed Using the HEAT Protocol and Semi-Classical
Transition State Theory," in Advances in Atmospheric Chemistry, eds. J. R. Barker, A. L.
Steiner and T. J. Wallington (World Scientific, Singapore, 2017), pp. World Scientific.
19. I. M. Mills, Modern Spectroscopy; Modern Research. (Academic Press, New York, NY,
1972).
20. J. F. Stanton, Semiclassical Transition-State Theory Based on Fourth-Order Vibrational
Perturbation Theory: The Symmetrical Eckart Barrier, J. Phys. Chem. Lett. 7, 2708-2713
(2016).
21. M. A. Harthcock and J. Laane, Calculation of kinetic energy terms for the vibrational
Hamiltonian: Application to large-amplitude vibrations using one-, two-, and three-
dimensional models, J. Mol. Spectros. 91, 300-324 (1982).
22. M. A. Harthcock and J. Laane, Calculation of two-dimensional vibrational potential
energy surfaces utilizing prediagonalized basis sets and Van Vleck perturbation methods,
J. Phys. Chem. 89, 4231–4240 (1985).
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li,
H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M.
Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao,
H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J.
Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K.
Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.
M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R.
Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W.
Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J.
Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J.
Cioslowski and D. J. Fox; Gaussian 09, Revision A.1; Gaussian, Inc., Wallingford CT,
2009.
24. H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G.
Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J.
Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. W. Meyer,
M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R.
Tarroni and T. Thorsteinsson; MOLPRO version 2006.1 (a package of ab initio
programs); see http://www.molpro.net., 2006; http://www.molpro.net.
25. J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, w. c. f. A. A. Auer, R. J. Bartlett, U.
Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, M. Heckert, O.
Heun, C. Huber, T.-C. Jagan, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A.
Matthews, T. Metzroth, D. P. O'Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann,
S. Stopkowicz, J. Vázquez, F. Wang and J. D. Watts; and the integral packages
MOLECULE (J. Almlöf and P.R. Taylor); PROPS (P.R. Taylor); ABACUS (T. Helgaker,
H.J. Aa. Jensen, P. Jørgensen, and J. Olsen); and ECP routines by A. V. Mitin and C.
van Wüllen. CFOUR, a quantum chemical program package (http://www.cfour.de/),
2009; <Error! Hyperlink reference not valid..
26. B. M. Wong, R. L. Thom and R. W. Field, Accurate Inertias for Large-Amplitude
Motions: Improvements on Prevailing Approximations, J. Phys. Chem. A. 110, 7406-
7413 (2006).

99
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar,
J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H.
Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T.
Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J.
B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev,
A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A.
Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C.
Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V.
Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A.
Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham,
C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M.
W. Wong, C. Gonzalez and J. A. Pople; Gaussian 03, Revision C.02; Gaussian, Inc.,
Wallingford CT, 2004; http://www.gaussian.com
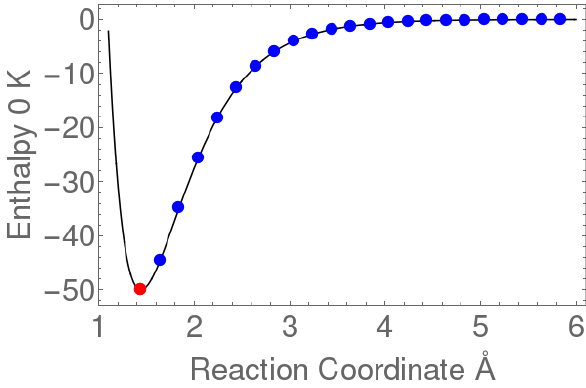
100
10. ktools: J-Resolved Variational Transition State Theory
This Chapter was written mostly by Jason A. Sonk.
For assistance: Users should submit questions to the "Multiwell and Chemical Kinetics"
question and answer forum, which is described in Chapter 0 of this User Manual.
10.1 Introduction
ktools calculates canonical and angular momentum-resolved (i.e. J-resolved)
microcanonical variational transition state theory rate constants from an input supplying
reactant and trial transition state parameters from a collection of points along a reaction
coordinate representing a unimolecular dissociation, such as shown in Fig. 1.
Figure 1. Points along a unimolecular dissociation reaction path.
The point in red corresponds to the reactant structure while the
points in blue are "trial transition states". Units of energy and zero
of energy can be designated by the user
Alternatively, if the user supplies parameters only for the reactant(s) and for a single tight
transition state (Fig. 2), ktools will calculate rate constants using both canonical and J-
resolved microcanonical transition state theories. If the user supplies the parameters only for a
single species then ktools will calculate the 2D sum of states, G(E,J), and 2D density of
states, ρ(E,J) for that species.
When a user intends to use the output from ktools for 1D applications (i.e. for input to
an energy-dependent master equation, like multiwell, which is not J-resolved), ktools will
sum the J-resolved quantities over J to obtain the total 1D sum of states, G(E), 1D density of
states, ρ(E), and 1D microcanonical rate constant, k(E), saved as double-arrays.
101
Figure 2. Points used in calculating canonical and microcanonical
rate constants for a tight transition state. The point in red
corresponds to the reactant structure while the point in blue is the
transition state. Units of energy and zero of energy can be
designated by the user.
10.2 Theory
10.2.1 Canonical Variational Transition State Theory (CVTST)
Rate constants in canonical variational transition state theory are calculated via RRKM
theory.1-4
k(T)kBT
h
‡
m
m‡
Q‡
Qexp E0
kBT
(1)
Here
Q
and
Q‡
are the total molecular partition functions of the reactant and transition state
respectively;
and
‡
are the external symmetry numbers, and m and m‡ are the number of
optical isomers (chiral stereoisomers) of the reactant and transition state, respectively;
kB
is the
Boltzmann constant,
h
is Planck’s constant,
E0
is the reaction critical energy, and
T
is a
temperature of interest. Each of the partition functions is a product of the partition functions for
the individual degrees of freedom of each species. The current code is designed to handle both
unimolecular and bimolecular reactions; therefore ktools uses the translational, vibrational,
rotational, hindered rotor and electronic degrees of freedom when calculating the molecular
partition function. The total molecular partition function calculated is then.
Qqtrans qvib qrot qhindered qelec
(2)
Reactions can be viewed as a reactive flux on a hyperdimensional potential energy
surface and the rate of reaction can be identified with the reactive flux through a dividing surface
placed between reactant(s) and product(s). The key assumption in transition state theory is that a
dividing surface (the transition state) can be found where the flux passing through the transition
102
state never returns (i.e. never re-crosses) to the reactant side.5 This idealization is never actually
achieved, but the amount of re-crossing can be minimized by placing the dividing surface where
the flux (in both directions) is a minimum. This optimal location for the transition state yields the
variationally optimal rate constant, which, for a canonical system, is proportional to Q‡ (see Eq.
1).
In order to find the optimal dividing surface, the reactive flux must first be evaluated at
many "trial" locations. In a canonical system, the reaction flux at a trial location is proportional
to Qtrial‡, the partition function at the trial dividing surface, and the corresponding trial canonical
rate constant, ktrial(T). The minimum trial canonical rate constant is optimal and corresponds to
the canonical variational transition state theory (CVTST) rate constant.
Figure 3. Points along a unimolecular dissociation reaction
coordinate (bottom) and the corresponding trial canonical rate
constants (top). The position of the minimum trial rate constant
corresponds to the variational canonical transition state, which is
the optional choice for a given temperature.
For a simple reaction that contains only a single bottleneck, the trial rate constants pass through a
single minimum, as shown in Figure 3. In many cases, however, the trial rate constants exhibit
more than one minimum, as shown in
Figure 4 for the reaction HO + OClO.6 These cases can arise when there is a dramatic change
along the reaction path in a) the potential energy, b) the vibrational frequencies, or c) the
rotational constants.
Figure 3 shows plots of the potential energy, the zero-point energy, and each of the 1D- and 2D-
rotor rotational constants (upper-left, upper-right, lower-left, lower-right respectively) for the
system used to generate
Figure 4. The system does not exhibit a dramatic change in potential energy, however
near 3.0 in the reaction coordinate the potential flattens out slightly and there is a change in both
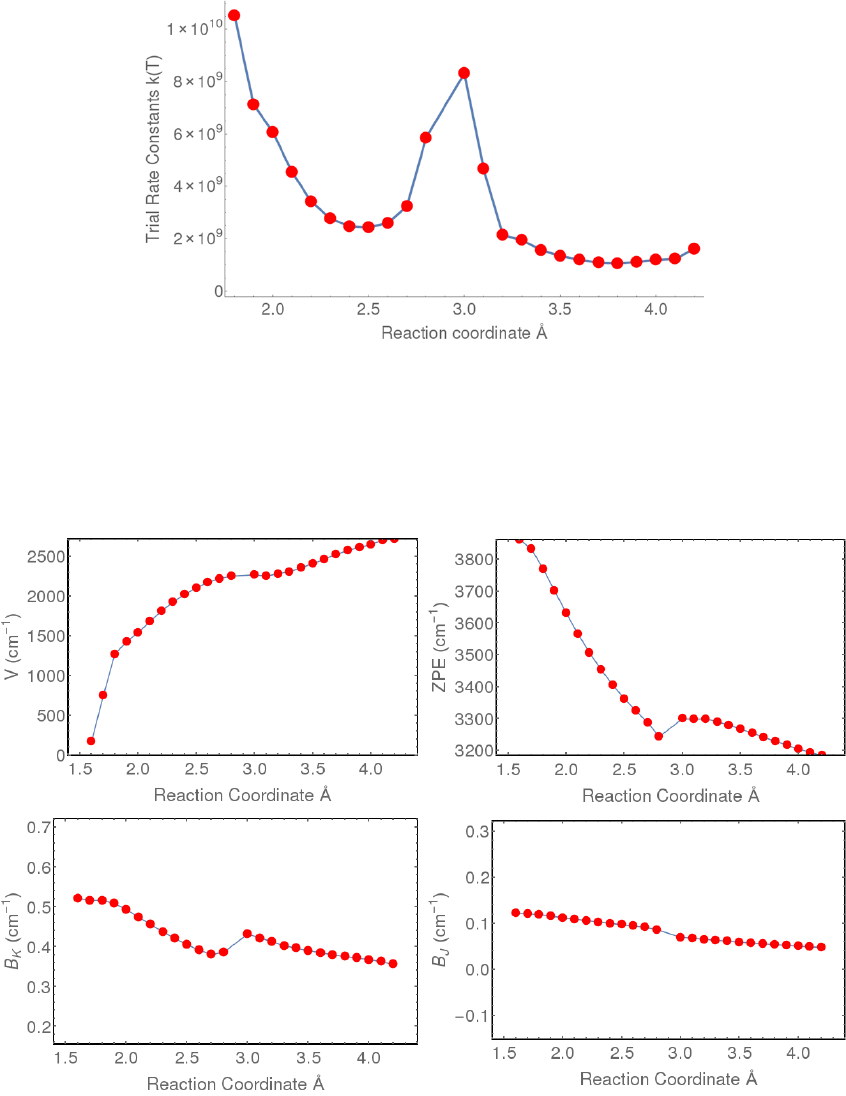
103
the ZPE and K-rotor, indicating that there is a significant change in geometry (and possibly
symmetry) in the system along this reaction coordinate.
Figure 4. Points along a unimolecular dissociation reaction
coordinate and the corresponding trial canonical rate
constants for HO+OClO.6 This system exhibits multiple
minima in k(T), one on either side of the maximum near
3.0.
Figure 3. Points along a unimolecular dissociation reaction coordinate (HO--OClO)
and the corresponding potential energy (top left), zero point energy (top right), and

104
rotational constants BK (bottom left) and BJ (bottom right) all in units of cm-1.6 Note
the change in ZPE and K-rotor rotational constant near the 3.0 reaction coordinate.
ktools automatically searches for multiple minima in the trial rate constant computed
at points along the reaction path by comparing the magnitudes of neighboring minima and
maxima. This search is not trivial, because there are several sources of numerical "noise" in the
calculations. Numerical noise can arise from incomplete convergence when optimizing
geometries and when carrying out the SCF calculations. During bond-fission reactions,
multireference contributions can erode the accuracy of quantum chemistry calculations that use
single-determinant wave functions, resulting in fluctuations. Although the errors and fluctuations
may not be very large, they contribute to the numerical noise, which interferes with searching for
the minimum trial rate constant.
To distinguish valid minima in the trial rate constants from false minima produced by
numerical noise, ktools utilizes the following algorithm. Consider two minima separated by a
maximum. If the maximum is not at least twice as large as the difference between the two
minima, the smaller of the two is kept as the local minima and the other is considered noise (i.e.
insignificant). The search then continues to the next pair of minima and repeats the test to see if
they satisfy the search condition. If they do then the minima are deemed “significant”, i.e. not
noise, and are used to find a "unified rate constant", which is the net result of two or more
significant minima, according the the theory developed by W. H. Miller.7 For a series of N
significant minima the unified canonical variational rate constant is given by Eq. 3:8
kunified T
1
kiT
i1
N
1
(3)
This unified rate constant thus accounts for two or more bottlenecks and can be described as a
"multiple-transition state model".
Miller's unified statistical theory is actually formulated in terms of microcanonical rate
constants and thus Eq. 3 is only an approximation. In the next section, the microcanonical VTST
implemented in ktools is described.
10.2.2 J-Resolved Microcanonical VTST (mVTST)
This level of VTST is based on sums and densities of states that depend on both total
energy (E) and angular momentum (quantum number J). The two-dimensional (2D) J-resolved
microcanonical reaction rate constant is given by1-4:
k E,J
1
h
G‡EE0,J,J
E,J
(4)
where
G‡(EE0,J)
is the sum of states of the transition state and
(E,J)
is the density of
states of the reactant for a given E,J. ktools calculates microcanonical rates by parametrically
setting J and calculating the density of states for the reactant and the sum of states for all the trial
transition states as functions of total energy E. Trial rate constants, ktrial(E,J), are computed at
points along the reaction path, just as in the CVTST calculations described above. The J-resolved
variational microcanonical variational TST (2DVTST) rate constant k(E,J) must meet two
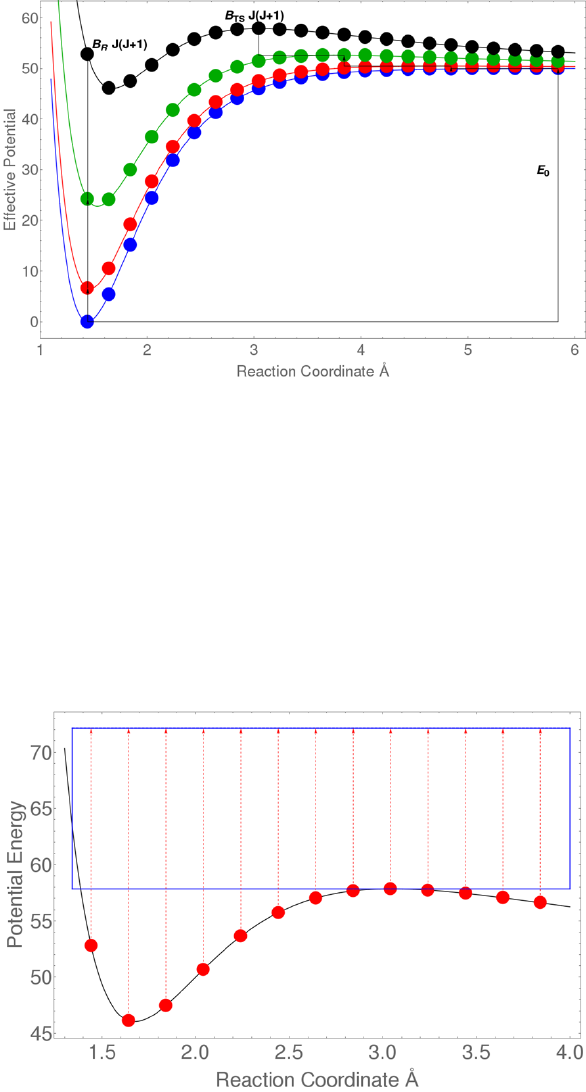
105
criteria: (a) The total energy must be greater than the centrifugal barrier and (b) k(E,J) is
identified with the minimum ktrial(E,J) at each E,J.
Figure 6. Unimolecular dissociation effective potential energy as a
function of increasing J quantum number, (Blue) J=0, (Red) J=5,
(Green) J=10, (Black) J=15. The arrows follow the reactant (left)
and centrifugal maximum (right most). E0 is the reaction critical
energy.
For a given J the effective potential is calculated at each trial location along the reaction
path, and the maximum in the effective potential is taken as the centrifugal maximum. Sums and
densities of states are calculated at each trial location at energies from the centrifugal maximum
to a user-selected maximum energy.
Figure 7. Effective potential for J=15. Blue box represents a
window of 20,000 cm-1. Red dotted lines represent the vector of
sums/densities-of-states calculated for each structure. Blue line is
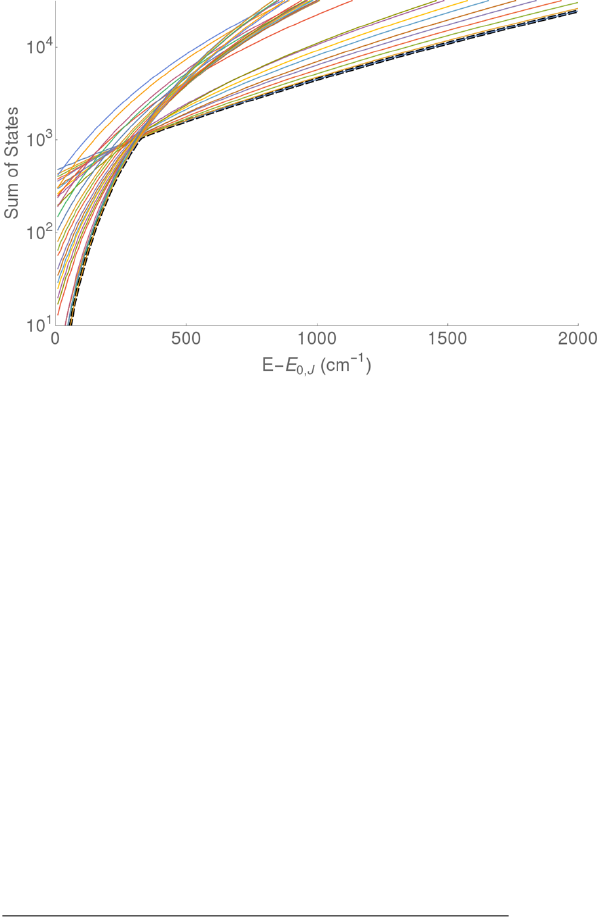
106
5000 cm-1 above the centrifugal maximum. The minimum sum of
states is evaluated at the same energy level above the centrifugal
maximum (i.e. along the blue dotted line for each energy grain).
Figure 8. Sum of states as a function of energy for trial transition
state structures along the HO--OClO reaction path for J = 15. Each
line follows the growth of the sum of states for a particular
structure on a reaction path as energy increases. The minimum
sum of states at each E is denoted with the dashed black line,
which is identified with the variationally minimized sum of states.
For each J and each energy grain (E) above the centrifugal maximum, the minimum sum
of states along the reaction path (i.e. across all trial transition state structures) is identified as the
variationally minimized sum of states at E,J. Each solid line in Figure 8 is the sum of states as a
function of energy (J = 15) measured from the centrifugal maximum for a trial transition state
structure along the reaction path. The dotted black line is the minimum sum-of-states at each
energy.
The 2DVTST rate constants, k(E,J), can be averaged over E and J at a given temperature
to obtain a canonical (thermal) rate constant,
k,
uni (T)
, which is also identified with the high
pressure limit rate constant in a unimolecular (or recombination) reaction.
k,
uni T
G‡x,J
exp xVTS BTS J J 1
/kBT
dx
x0
J0
Jmax
h
x,J
exp xV0BRJ J 1
/kBT
dx
x0
J0
Jmax
(5)
where VTS and V0 are the potential energies (including the vibrational zero point energy (VZPE)
corrections) of the variational transition state and the reactant, respectively. The VZPE
correction for the transition state includes only the vibrations orthogonal to the reaction
coordinate, while that for the reactant includes all of the vibrations. In Eq. 5, the integrals are
over energy, x, and the summations are over the quantum number, J, for total angular

107
momentum. In the numerator of Eq. 5, the argument contains
BTS J J 1
, the rotational energy
respectively of the transition state; the denominator contains
BRJ J 1
, the rotational energy of
the reactant the reactant.
ktools also reports J-summed densities of states for the reactant, sums of states for the
transition state, and microcanonical rate constants. Starting from the 2D microcanonical
quantities, the J-summed9, 10 microcanonical quantitiesare given by
E
E,J
J0
Jmax
(6)
Gi
‡E
Gi
‡E,J
J0
Jmax
(7)
Using these quantities and the "E-Model" of Miller et al.,11, 12 one obtains the 1D microcanonical
rate constants:
(8)
kiE
1
h
Gi
‡EE0,J0
E
where E0,J=0 is the critical energy for reaction. For the reactant and for fixed transition states, the
1D quantities are the same as would be obtained using program densum to calculate the total
sums and densities of states (using all degrees of freedom) with the "top" rotational degree of
freedom type (see Chap. 3). For both fixed and variational transitin states, these quantities can be
used in 1D master equation calculations that adopt the Smith and Gilbert method for reducing a
2D master equation to 1D. They are appropriate for use in a 1D master equation treatment that
makes no centrifugal corrections and treats all degrees of freedom as active.9, 10, 12, 13

108
10.3 ktools Input File
The input file for a ktools calculation is similar to the input file used by program
thermo, but with several minor additions/changes. The character-based keywords do not
depend on case. The code is based on the assumption that the molecular system of interest can
be described with sufficient accuracy as a symmetric top (the quasi-symmetric top
approximation; see Appendix B.4 of this User Manual). For that reason, the parameters for the
external rotations must be specified as a “J-rotor” and “K-rotor” (corresponding respectively to
the B2 and B1 rotational constants discussed in Appendix B.4).
Line 1 Title
Title: 180 Character limit title to be used in output files.
Line 2 Ekey, Sskey
Ekey: keyword for energy units, valid options:
kcal, kJ, cm-1
Sskey: keyword for standard state, not currently used (assumed to be MCC)
Line 3 WhatDo, Backup
WhatDo: Flag that controls which rate constants are calculated. Canonical rate
constants are inexpensive to calculate compared to the microcanonical, this
allows the user to do quick preliminary calculations to get a feel of how the data
is behaving. Valid options: canon, micro
Backup: When set to “backup” a copy of the input file will be saved as a time-
stampedname.bck. The time stamp code will be written out to outputfiles so the
two can be matched up. Valid options: backup, none
Line 4 Emax, Egrain
Emax: Max energy to calculate sums and densities of states, in units of cm-1
Egrain:energy grain used in microcanonical TST, in units of cm-1; corresponds to Egrain1
in a double array.
Line 5 Jmax, Jgrain
Jmax: Max J value to calculate sums and densities of state.
Jgrain: step size in J used in microcanonical TST, currently step size of 1 is
recommended.
Line 6 Imax1, Isize, Emax2
These parameters describe the double arrays (generated by J-summing) for use in the
multiwell master equation code (note that Egrain1 is specified on Line 4).
Imax1: Number of array elements in lower part of double array.
Isize: Total number of elements in double array.
Emax2: Maximum energy of double array.

109
Line 7 Nt
Nt: number of temperatures to be read in
Line 8 T1, T2, T3 … Tnt
T1, T2,…,Tnt: list of Nt temperatures in kelvin
Line 9 RCNT, NTTS, PCNT
RCNT: number of reactant molecules to read in (reactant count). Max=2
NTTS: number of trial transition states to read in
PCNT: number of products to read in
Default Max of RCNT+NTTS+PCNT is set to 100
Structure blocks: repeated RCNT+NTTS+PCNT times
This structure of the data block for each species is slightly different than the structure
used in program thermo!
Line 10.1 Reprod, molname, delh, dist
reprod: species identification. Options: ctst, reac, prod
molname: name of species. Used for naming relevant output files
delh: enthalpy of formation at 0 K.
dist: corresponding distance along reaction path, defined by the user but typically a
bond distance. This allows the canonical variational transition state theory
code to report the variationally optimal transition state.
Line 10.2 Formula
formula: empirical formula; used only for recombination reactions
Line 10.3 Comment line A
1st comment: 150-character limit
Line 10.4 Comment line B
2nd comment: 150-character limit
Line 10.5 Comment line C
3rd comment: 150-character limit
Line 10.6 Sym, Sopt, Nele
Sym: external symmetry number
Sopt: number of optical isomers
Nele: number of electronic energy levels
Line 10.7 Elev, gele (Repeated Nele times)
Elev: electronic energy level (lowest should be designated as Elev=0.0)
Gele: electronic energy level degeneracies
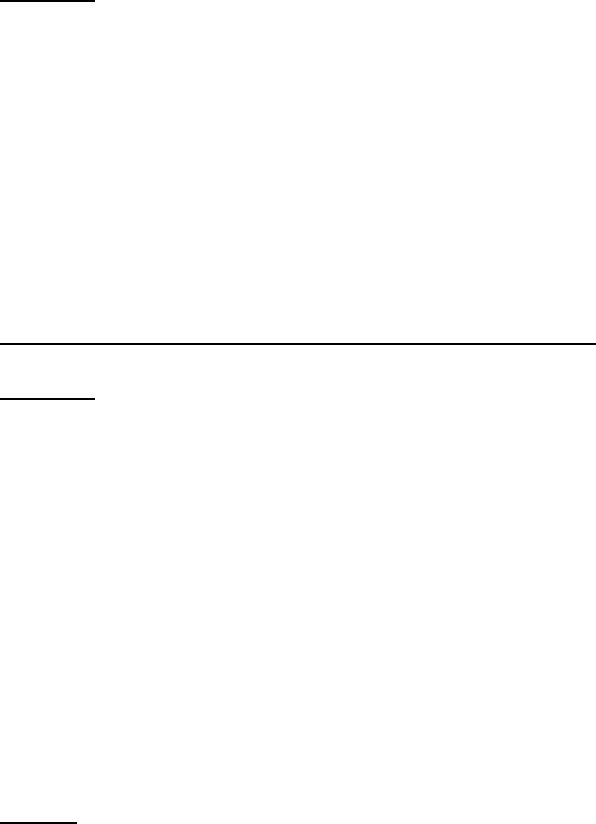
110
Line 10.8 N, Vhar, Vrot
N: number of degrees of freedom to read in
Vhar: keyword for vibrations. Options:
har
Vrot: keyword for molecular internal (hra, hrb, hrc) and external rotations (kro,
jro). Options:
amua for moments of inertia in units of amu Å2
gmcm for moments of inertia in units of g cm2
cm-1 for rotational constants in wavenumbers
mhz for rotational constants in MHz
ghz for rotational constants in GHz
Repeat Line 10.9 N times, once for each degree of freedom
Line 10.9 Mode(i), Idof(i), AAA(i), BBB(i), CCC(i)
mode: index number for degree of freedom
idof: keyword for type of degree of freedom. The separable degrees of freedom
(except for the J-rotor and K-rotor) that are recognized by ktools are defined
and the data input formats are described in Chapter 3 of this User Manual. The J-
rotor and K-rotor parameters used by ktools are described here:
kro: K-rotor 1-dimensional external rotation
AAA = rotational moment of inertia/constant in units of Vrot
BBB = rotational symmetry number
CCC = rotation dimension (should always be set to 1)
jro: J-rotor 2-dimensional external rotation
AAA = rotational moment of inertia/constant in units of Vrot
BBB = rotational symmetry number
CCC = rotation dimension (usually should be set to 2)
Line 11 (Blank Line)
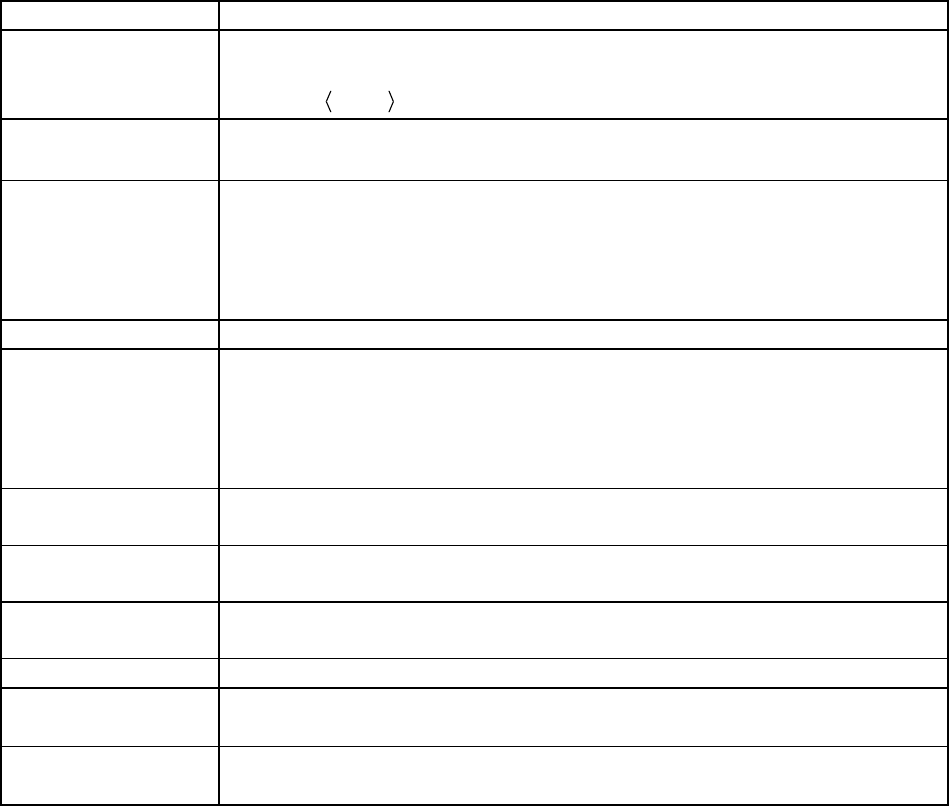
111
10.4 Running ktools
By default the program looks for the input file named “ktools.dat” and ktools can
be executed from the command line by simply typing “ktools”, followed by a carriage return
Optionally, the user can use custom names for input files. ktools is then executed by typing
“ktools filename.dat”. Where filename.dat is the filename as defined by the user.
The program expects a 3-letter extension to be used in the naming of the input file name.
10.5 ktools Output Files
ktools creates a number of output files. Below is a description of their contents.
File Name
Description
*.log
Contains information on data being generated at each step of the code
execution. Final output is the thermally averaged microcanonical rate
constant,
k(E,J)T
.
*-efile.txt
Lists
H(0K)
, ZPE,
Eelectronic
,k-rotor and j-rotor rotational constants for the
reactant and each TS all in units of cm-1.
*.canonical
Contains canonical rate constant data. Lists all trial rate constants as a
function of temperature, followed by local minimum rate constants and
final rate constants as a function of temperature. If more than one rate is
determined to be “significant” then all rates contributing to the unified
rate are listed as well
*.veff
Lists effective potential for all J from 0 to Jmax
*.2dens
*.2sums
*.u2sums
*.kej
*.ukej
Lists the rotational energies and associated 2D density of states, sum of
states, unified sum of states, microcanonical rates, unified
microcanonical rates. Sums and rates using a unified transition state7 are
designated by a “u” prefix.
*-j-000.gmat
*-j-jmax.gmat
Lists effective potential followed by the sum of states for all trial TS for
J=0 and J=Jmax
*-r.dens
*-ts.dens
J-summed9, 10 sum- and densities-of-states for the reactant, transition
state, and unified transition state. For use in 1D Multiwell calculations.
*-nmins.txt
List of all found local minima in the sums-of-state for all energies and J
values
*.bck
Backup inputfile
*-r.dens
File generated by J-summing, intended for use by the multiwell
master eqauation code: 1D density of states of the reactant.
*-ts.dens
File generated by J-summing, intended for use by the multiwell
master eqauation code: 1D sum of states of the transition state.
(* : represents a species name)

112
10.6 ktools Examples
(Example input and output files can be found in the examples/ktools directory.)
Example Input
microrun X+OH ! 1 Title
KCAL MCC ! 2 Ekey, Sskey
both backup ! 3 Whatdo, backup
30000 10.0 ! 4 Emax Egrain
70000 1 ! 5 Jmax Jgrain
3 ! 6 Nt number of temperatures
100. 500. 1000. ! 7 Nt temperatures
1 1 1 ! 8 RCNT: # of reactants , NTTS: # of trial TS, PCNT: # of products
! RCNT+NTTS+PCNT # of Structures
! RCNT #1
reac 'X-OH-PRE' 0.000 0.0 ! 9.1 reprod, molname, delh, dist
CX3O2 ! 9.2 formula
1. formaldehyde + oh reaction ! 9.3 comment line A
2. (blank comment line) ! 9.4 comment line B
3. (blank comment line) ! 9.5 comment line C
1 1 1 ! 9.6 sys, sopt, nele
0.0 2 ! 9.7 elev, gele (repeated nele times)
15 HAR ghz ! 9.8 N, Vhar, Vrot
1 vib 52.35 0 1 ! 9.9 mode, idof, AAA, BBB, CCC
2 vib 161.26 0 1 ! (repeated N times. 1 for each DOF)
3 vib 195.37 0 1
4 vib 450.63 0 1
5 vib 582.98 0 1
6 vib 1271.09 0 1
7 vib 1317.15 0 1
8 hrd 5 5 1
Vhrd2 1 33.4945 66.1601 90.72679 44.53344 1.72326 0.28367
Ihrd1 1 3.50661 0.78172 0.01627 -0.00487 -0.00111 0.00304
9 vib 1583.82 0 1
10 vib 1889.35 0 1
11 vib 3031.11 0 1
12 vib 3112.55 0 1
13 vib 3717.63 0 1
14 kro 50.63523 1 1
15 jro 4.535349039 1 2 ! Nth DOF of RCNT #1.
! NTTS #1
ctst 'TS-250' 0.88924 2.5 ! 9.1 reprod, molname, delh, dist
CH3O2 ! 9.2 formula
1. VTST ! 9.3 comment line A
2. (blank comment line) ! 9.4 comment line B
3. (blank comment line) ! 9.5 comment line C
1 1 1 ! 9.6 sys, sopt, nele
0.0 2 ! 9.7 elev, gele (repeated nele times)
14 HAR ghz ! 9.8 N, Vhar, Vrot
1 vib 33.55 0 1 ! 9.9 mode, idof, AAA, BBB, CCC
2 vib 87.6 0 1 ! (repeated N times. 1 for each DOF)
3 vib 250.22 0 1
4 vib 334.82 0 1
5 vib 1265.15 0 1
6 vib 1313.51 0 1
7 vib 1586.22 0 1
8 hrd 5 5 1
Vhrd2 1 33.49326 63.79801 90.66085 38.05053 1.04218 0.15534
Ihrd1 1 3.47908 0.78116 0.01656 -0.00431 -0.00106 0.00225
9 vib 1899.27 0 1
10 vib 3016.85 0 1
11 vib 3090.77 0 1
12 vib 3836.64 0 1
13 kro 74.85529 1 1
14 jro 3.008627473 1 2 ! Nth DOF of NTTS #1
! Blank Line

113
Example Logfile
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
John R. Barker
Ktools-2015 University of Michigan
Ann Arbor, MI 48109-2143
Jan 2015 jrbarker@umich.edu
(734) 763 6239
http://aoss.engin.umich.edu/multiwell/
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
variational tst: ch2o+oh-micro run started. ! Time stamp on initial run
mar. 2nd 2015 10:50:41:495 am
# of r # of ts ndof r 1 ndof for ts ! Summary of (r)eactants,
1 31 14 13 ! (t)ransition (s)tates, and
! the number of degrees of
! freedom for each to be read in
reactant # 1 14 0.00 0.00 ! Structure Type, #, # of DOF
# dof freq anh degen ! ΔH and reaction coordinate values
------------------------------------
1 vib 52.3500 0.0000 1 ! Reprint of degrees of freedom
2 vib 161.2600 0.0000 1
…
13 kro 50.6352 1.0000 1
14 jro 4.5353 1.0000 2 ! End of structure 1
! Repeated RCNT+NTTS times
…
! End of RCNT+NTTS structures
end of read_inp.f ! Exit subroutine and time stamp
mar. 2nd 2015 10:50:41:499 am
start bsort ! Bsort converts the rotational
mar. 2nd 2015 10:50:41:499 am ! constants
converting j-rotational constant into cm-1 ! Converting data for the 2D
! external "J-rotor"
# dof# ghz cm-1 cm-1 ! Structure number, # of dofs in
----------------------------------------------- ! that structure, rotational
1 14 4.5353 0.1513 0.1513 ! info given by the user,
2 13 3.0086 0.1004 0.1004 ! converted value, stored value
…
converting k-rotational constant into cm-1 ! Converting data for the 1D
# dof# ghz cm-1 cm-1 ! external "K-rotor"
-----------------------------------------------
1 13 50.6352 1.6890 1.6890
2 12 74.8553 2.4969 2.4969
…
(a-b) rotational constant ! Rotational energy of a symmetric
! top is Erot = BJ(J+1)+(A-B)K**2
# a b a-b check ! Structure number, K-rotor (A),
! J-rotor (B), a-b, stored a-b
-----------------------------------------------
1 1.6890 0.1513 1.5377 1.5377
2 2.4969 0.1004 2.3965 2.3965
…
end bsort ! Exit subroutine and time stamp
mar. 2nd 2015 10:50:41:500 am
114
start of hsort ! Enter subroutine and time stamp
mar. 2nd 2015 10:50:41:500 am
converting pe from kcal to cm-1 ! Hsort converts the enthalpy units
! into cm-1 & sets the 0 of energy.
# kcal cm-1 rescale cm-1
------------------------------------------------
1 0.00 0.00 0.00
2 0.89 311.02 311.02
…
exit hsort ! Exit subroutine and time stamp
mar. 2nd 2015 10:50:41:500 am
start zpe_calc ! Enter subroutine and time stamp
# of structures: 32
reporting v, zpe, and electronic (cm-1) ! zpe_calc calculates zero point
! energy and reports enthalpy at
! 0K, zpe, and electronic energy
# v zpe electronic
---------------------------------------------
1 0.0000 8682.6450 0.0000
2 311.0162 8357.3000 636.3612
…
end of zpe_calc ! Exit subroutine and time stamp
mar. 2nd 2015 10:50:41:501 am
start canonrates ! Enter subroutine and time stamp
mar. 2nd 2015 10:50:41:501 am ! canonrates calculates canonical
! partition functions and canonical
! rates for each structure for each
! temperature.
! listed are the vibrational, rotational, hindered rotation, electronic, and total
! partition functions followed by the canonical rate for going from structure #1 to the
! current structure
structure # t(k) qvib qrot qhin qele qtot k(t)
----------------------------------------------------------------------------------------
1 100.00 2.233E+00 5.478E+03 1.000E+00 2.000E+00 2.447E+04 2.083E+12
…
canonical rate constant data can be found in: Ktools.canonical ! name of canonical output
end canonrates ! Exit subroutine and time stamp
mar. 2nd 2015 12:03:23:742 pm
start find_jmax ! Enter subroutine and time stamp
mar. 2nd 2015 12:03:23:742 pm ! find_jmax runs through several
! tests to find a maximum j value
! for the system.
kb*Tmax Jmax ! List of kb*Tmax multiples and
1 161. ! the corresponding Jmax
2 227. ! E=n*kb*Tmax~=Bmin*J**2 =>
3 278. ! J=Sqrt(n*kb*Tmax/Bmin)
4 321.
5 359.
6 394.
7 425.
8 454.
9 482.
10 508.
User requested J value is higher than totally repulsive J value
115
looking for jmax
10kbt method: 508. ! 10kb*T Value of Jmax
pt1 > pt 2 method 79. ! Value of J where E(pt1)> E(pt2)
pt1 > everything: 102. ! Value of J where E(pt1)>E(pts2-N)
tot.repul.method: 791. ! Value of J where Veff is entirely repulsive
setting maxj to: 102. ! Jmax set by the program
end of find_jmax ! Exit subroutine and time stamp
mar. 2nd 2015 12:03:23:742 pm
! Start looping over every J value to Jmax and calculate all Sums and Densities of States
for j: 0 vmax@ 1245.12 6.0 ! Jvalue, Veff max, and Veffmax location
centrifugal max@ 523036243.49 29908648.83 ! Extrapolated centrifugal max and R
energy difference 523034998.36542666 ! ΔE=Centrifugal Max - Veffmax
start veff
j: 0 ! Current J value
!#, enthlapy, rotational constant, j*(j+1), veff, emax-veff
i delh b j*(j+1) veff epsilon
1 0.000000E+00 1.512830E-01 0 0.000000E+00 3.124513E+04
2 3.110162E+02 1.003570E-01 0 3.110162E+02 3.093411E+04
…
veff max is at point # 32 1245.12 ! Veff max struct. number and energy value
end veff
mar. 2nd 2015 12:03:23:764 pm ! Repeat MaxJ times
for j: 1 vmax@ 1245.18 6.0 ! Jvalue, Veff max, and Veffmax location
…
end veff ! Exit subroutine and time stamp
mar. 2nd 2015 12:05:16:702 pm
convergence for reactant ! Integration of reactant
! Temp #, Temp, J used, Energy grains used, Current Norm, Next term, Max Term
# Temps J E Norm Term Maxterm
------------------------------------------------------------------------
1 100.00 72 200 9.004825E+03 3.199051E-02 3.769884E+02
2 500.00 103 1383 4.041294E+06 3.932402E+03 7.633520E+04
3 1000.00 103 3127 2.282009E+08 1.206322E+06 3.364758E+06
convergence for transition state ! Integration of TS
# Temps J E Norm Term Maxterm
------------------------------------------------------------------------
1 100.00 103 440 1.261268E+18 6.185970E+13 2.473813E+16
2 500.00 103 2662 9.669243E+20 1.494753E+18 1.682981E+19
3 1000.00 103 3002 2.711101E+22 1.516654E+20 3.983837E+20
convergence for unified transition state ! Integration of unified TS (if present)
# Temps J E Norm Term Maxterm
------------------------------------------------------------------------
1 100.00 103 440 7.284531E+17 4.966310E+13 1.327708E+16
2 500.00 103 2662 8.431412E+20 1.447493E+18 1.450470E+19
3 1000.00 103 3002 2.653338E+22 1.508069E+20 3.898675E+20
thermally averaged microcanonical partition functions
temp q(r) q(ts) q(uts) ! temperature, Qreactant, QTS, Qunified TS
---------------------------------------------------
100.00 9.00482E+03 6.05313E+05 3.49602E+05
500.00 4.04129E+06 9.28101E+07 8.09288E+07
1000.00 2.28201E+08 1.30112E+09 1.27340E+09
thermal averaged microcanonical rate constants
# temp <kv(e)>t <ukv(e)>t ! T, T. Ave. k(e), unified T ave. k(e)
-----------------------------------------------
1 100.00 2.32334E+06 1.34186E+06
2 500.00 6.65010E+12 5.79877E+12
3 1000.00 1.98064E+13 1.93844E+13
116
mar. 6th 2015 10:10:51:889 am ! Time stamp
elapsed time: 3.16 minutes. ! Run time

117
Example Efile
Efile contains summary information about the system suitable for plotting.
It lists the structure number, the distance, enthalpies at 0K, zero point energies, electronic
energies, k-rotor rotational constants and the j-rotor rotational constants. All energies reported
are in units of cm-1 .
struct#
distance(a)
dh(cm-1)
zpe(cm-1)
delect(cm-1)
k-rot(cm-1)
j-rot(cm-1)
1
0.0
0.0000
8682.645
0.0000
1.6890
0.1513
2
2.5
311.0162
8357.300
636.3612
2.4969
0.1004
3
2.6
400.3227
8331.595
751.3727
2.5490
0.0954
4
2.7
485.2817
8308.340
859.5867
2.6261
0.0907
5
2.8
564.4243
8287.650
959.4193
2.7420
0.0861
Example Canonical File
The *.canonical file lists all canonical rate constants for each temperature. The user can use these
values to plot the rate constant as a function of reaction coordinate.
Single minimum found
canonical rates for all temperatures and ts
r 100.00 500.00 1000.00
2.50 4.97660E+010 1.07022E+013 2.55589E+013
…
3.00 4.27324E+008 1.48108E+013 7.05745E+013
3.10 2.12009E+008 1.61207E+013 8.53028E+013
3.20 1.20912E+008 1.81371E+013 1.05068E+014
3.30 6.53084E+007 1.77684E+013 1.11445E+014
3.50 4.19373E+007 3.23287E+013 2.32646E+014
3.60 5.12595E+007 6.10474E+013 4.65332E+014
3.70 3.30816E+007 5.79128E+013 4.64405E+014
3.80 2.03015E+007 5.01871E+013 4.21175E+014
…
4.60 4.07335E+006 6.26450E+013 6.69339E+014
4.70 3.71415E+006 6.64867E+013 7.24783E+014
4.80 3.51374E+006 7.23704E+013 8.03692E+014
4.90 3.51914E+006 7.89177E+013 8.86627E+014
5.00 3.12963E+006 8.48905E+013 9.77537E+014
5.50 2.85286E+006 1.29030E+014 1.58947E+015
5.60 2.93227E+006 1.40983E+014 1.75106E+015
5.70 3.02479E+006 1.54509E+014 1.93469E+015
reporting all local minima ! List all local minima & position for each
! temperature along the reaction coordinate
# temp # min r(min) min k(t)
-----------------------------------------------------------------------------------------
1 100.00 3 3.50 4.80 5.50 4.193E+07 3.514E+06 2.853E+06
2 500.00 4 2.50 3.30 3.90 4.10 1.070E+13 1.777E+13 4.790E+13 4.7447E+13
3 1000.00 2 2.50 3.90 2.556E+13 4.188E+14
unified canonical rates and contributing minima ! List minima which are not “noise” and
! list min k(t).
# temp # min r(min) min k(t)
-----------------------------------------------
1 100.00 1 5.50 2.8529E+06
2 500.00 1 2.50 1.0702E+13
3 1000.00 1 2.50 2.5559E+13

118
Multiple minima found
canonical rates for all temperatures and ts
r 180.00 242.00 253.00 293.00 298.00
1.60 7.40485E+011 1.33249E+012 1.44307E+012 1.85159E+012 1.90305E+012
…
2.30 3.06708E+006 2.71097E+008 4.82410E+008 2.77278E+009 3.34400E+009
2.40 1.89269E+006 2.13060E+008 3.91209E+008 2.47375E+009 3.01410E+009
2.50 1.36220E+006 1.88313E+008 3.55112E+008 2.43536E+009 2.99328E+009
2.60 1.11650E+006 1.83896E+008 3.54750E+008 2.60695E+009 3.22802E+009
2.70 1.12259E+006 2.12999E+008 4.18510E+008 3.25234E+009 4.05140E+009
…
3.60 1.97966E+005 5.92058E+007 1.23097E+008 1.13248E+009 1.43610E+009
3.70 1.44968E+005 4.98038E+007 1.05406E+008 1.02333E+009 1.30516E+009
3.80 1.17920E+005 4.55527E+007 9.78714E+007 9.94479E+008 1.27455E+009
3.90 1.06807E+005 4.54229E+007 9.88071E+007 1.04232E+009 1.34123E+009
4.00 9.93543E+004 4.65172E+007 1.02445E+008 1.12185E+009 1.44934E+009
4.10 8.46946E+004 4.49036E+007 1.00474E+008 1.15432E+009 1.49893E+009
4.20 1.03423E+005 5.73970E+007 1.29193E+008 1.51130E+009 1.96629E+009
reporting all local minima ! List all local minima & position for each
! temperature along the reaction coordinate
# temp # min r(min) min k(t)
-----------------------------------------------------------------------------
1 180.00 2 2.60 4.10 1.1165E+06 8.4695E+04
2 242.00 3 2.60 3.90 4.10 1.8390E+08 4.5423E+07 4.4904E+07
3 253.00 3 2.60 3.80 4.10 3.5475E+08 9.7871E+07 1.0047E+08
4 293.00 2 2.50 3.80 2.4354E+09 9.9448E+08
5 298.00 2 2.50 3.80 2.9933E+09 1.2746E+09
unified canonical rates and contributing minima ! List minima which are not “noise” and
! list min k(t) and unified k(t)
# temp uk(t) # min r(min) min k(t)
--------------------------------------------------------------
1 180.00 7.8723E+04 2 2.60 4.10 1.1165E+06 8.4695E+04
2 242.00 3.6091E+07 2 2.60 4.10 1.8390E+08 4.4904E+07
3 253.00 7.6708E+07 2 2.60 3.80 3.5475E+08 9.7871E+07
4 293.00 7.0613E+08 2 2.50 3.80 2.4354E+09 9.9448E+08
5 298.00 8.9392E+08 2 2.50 3.80 2.9933E+09 1.2746E+09
Example Veff file
*.veff lists the effective potential for each value of J. Points along the potential read from left to
right and J increases along each new line.
Pt. #1
Pt. #2
Pt. #3
Pt. #4
Pt. #5
J=0
0.00E+00
3.11E+02
4.00E+02
4.85E+02
5.64E+02
J=1
3.03E-01
3.11E+02
4.01E+02
4.85E+02
5.65E+02
J=2
9.08E-01
3.12E+02
4.01E+02
4.86E+02
5.65E+02

119
Example 2dens/2sums file
Ktools generates a *.2dens file for the 2D density of states for the reactant, a *.2sums for the 2D
sum of states for the transition state, and a *.kej for the 2D microcanonical rate constants. If
multiple minima are found among the sum of states arrays then Ktools also generates *.u2sums
and * .ukej files where the “u” designates the contents represent a unified statistical model7 has
been used. The general structure for all of these files is the same.
66.9755
! lowest vibrational frequency
0
1
2
3
! J values
Erot-TS
4.92E+02
4.92E+02
4.92E+02
4.92E+02
! Veff of R/TS
0.0
1.00E+00
3.00E+00
5.00E+00
7.00E+00
! Bin energy and data
10.0
1.00E+00
3.00E+00
5.00E+00
7.00E+00
20.0
3.00E+00
9.00E+00
1.50E+01
2.10E+01
120
References
1. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions.
(Blackwell Scientific, Oxford, 1990).
2. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
3. T. Baer and W. L. Hase, Unimolecular Reaction Dynamics. Theory and Experiments.
(Oxford University Press, New York, 1996).
4. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
5. D. G. Truhlar and B. C. Garrett, Variational Transition State Theory, Annual Review of
Physical Chemistry 35, 159-189 (1984).
6. L. Yang, J. A. Sonk and J. R. Barker, HO + OClO Reaction System: Featuring a
Barrierless Entrance Channel with Two Transition States, J. Phys. Chem. A 119, 5723–
5731 (2015).
7. W. H. Miller, Unified statistical model for ’’complex’’ and ’’direct’’ reaction
mechanisms, The Journal of Chemical Physics 65, 2216-2223 (1976).
8. W. H. Miller, Unified statistical model for "complex" and "direct" reaction mechanisms,
J. Chem. Phys. 65, 2216-2223 (1976).
9. S. C. Smith and R. G. Gilbert, Angular momentum conservation in multichannel
unimolecular reactions, Int. J. Chem. Kinet. 20, 979-990 (1988).
10. S. J. Klippenstein and L. B. Harding, A direct transition state theory based study of
methyl radical recombination kinetics, J. Phys. Chem. A 103, 9388-9398 (1999).
11. J. A. Miller, S. J. Klippenstein and C. Raffy, Solution of some one- and two-dimensional
master equation models for thermal dissociation: The dissociation of methane in the low
pressure limit, J. Phys. Chem. A 106, 4904-13 (2002).
12. J. A. Miller and S. J. Klippenstein, Master Equation Methods in Gas Phase Chemical
Kinetics, J. Phys. Chem. A 110, 10528-10544 (2006).
13. S. C. Smith and R. G. Gilbert, Angular momentum conservation in unimolecular and
recombination reactions, Int. J. Chem. Kinet. 20, 307-329 (1988).

121
11. TS: J-Resolved Steady-State Master Equation Solver
This computer code was developed by Lam Nguyen and John Stanton.
The code features a J-resolved steady-state master equation code that is solved by
eigenvalue methods on large parallel computers. It utilizes the frozen-J approximation. The TS
code and TS User Manual can be downloaded from the MultiWell web site. The code (available
only in a LIMUX version) is to be compiled separately from the rest of the MultiWell Program
Suite.
Literature citation:
"TS is a chemical kinetic program that solves a two-dimensional master-equation for gas-phase
reactions in parallel using the Steady-State approach. It is developed, implemented, and
maintained by T. L. Nguyen and J. F. Stanton, version 01-03-2017."
For assistance:
Users should submit questions to the "Multiwell and Chemical Kinetics" question and
answer forum: all users are invited to join the forum, where questions can be asked and
answered, and future upgrades will be announced. This forum is set up as a Google Group,
which you can join at https://groups.google.com/. If for any reason, a user finds it difficult to use
Google, please contact either Lam Nguyen or John Stanton:
thanhlamnguyen08@gmail.com
jfstanton@gmail.com
122
Appendix A. Theoretical Basis
Much of this Appendix is based on an expanded and corrected version of the paper
originally published in the International Journal of Chemical Kinetics: J.R. Barker, Multiple-
well, multiple-reaction-path unimolecular reaction systems. I. MultiWell computer program
suite. Int. J. Chem. Kinetics, 33, 232-45 (2001).
A.1. Introduction
Here, the theoretical basis for MultiWell is summarized. Inevitably, various
approximations and assumptions must be adopted due to computational limitations and to the
absence of physico-chemical knowledge. The numerical approximations are described so that
program users can better assess MultiWell's limitations and strengths. The principal assumptions
made in formulating the master equation are reviewed.
In the next section, the master equation is described formally. In subsequent sections, the
stochastic methodology is described along with a brief discussion of some of the merits and
limitations of the hybrid master equation approach relative to other methods. Methods for
computing microcanonical unimolecular reaction rates and energy transfer step sizes are
described, followed by a description of various initial conditions that can be selected as options.
Finally, the calculation input and output are outlined.
A.2. The Active Energy Master Equation
The current version of MultiWell is based on the one-dimensional master equation, in
which the active (randomizable) internal energy is modeled, but it is planned that future
extensions will explicitly include angular momentum (the two-dimensional master equation1-9).
The master equation provides the fundamental theoretical basis for modeling systems in which
both energy transfer and chemical reaction can occur.10-14 It is comprised of a set of coupled
integro-differential equations that describe the rates of production and loss of chemical species at
specified energies.
A.2.1 Internal Energy and Active Degrees of Freedom
Unless slow intramolecular vibrational energy redistribution (IVR) is specified, the
internal energy E is always assumed to be fully randomized among the active degrees of
freedom. The internal energy for a particular species (stable molecule or transition state) includes
the energy (measured from the zero point energy; see Figure 0) that resides in the internal modes
(vibrations, torsions, and internal rotations) and an active external rotation. Nonlinear polyatomic
species have three external rotational degrees of freedom characterized by moments of inertia IA,
IB, and IC. The usual pragmatic approach11, 12 is to assume the molecule can be approximated as a
symmetric top with two of the moments of inertia equal to one another (IB = IC), producing a
degenerate two-dimensional external rotation. The third external rotor is associated with the
symmetric top figure axis and is sometimes termed the K-rotor. The K-rotor is assumed to
exchange energy freely with the other internal degrees of freedom, while the degenerate two-
dimensional external rotation is assumed to be inactive.11-15 See Appendix B.4 of this Manual for
more discussion. (More sophisticated treatments of rotations can be utilized in the present
version of MultiWell by calculating specific rate constants (k(E)) externally and then providing
them in data files read by MultiWell.)
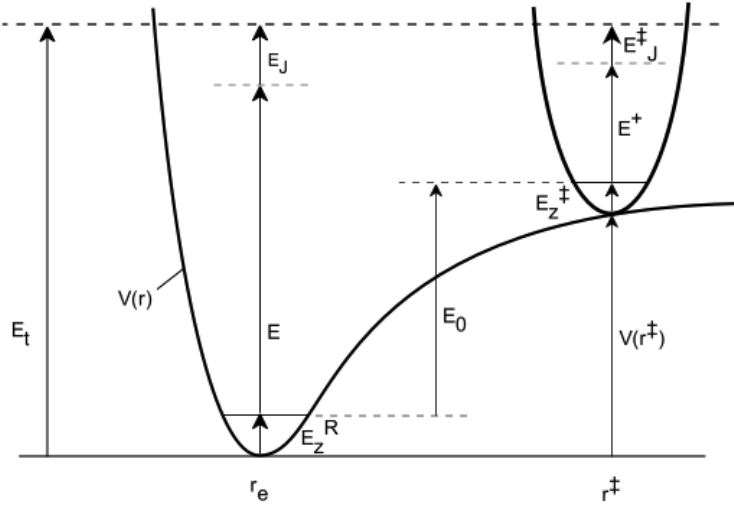
123
Figure 0. Energy schematic. The active energy E is measured from
the zero point energy of the reactant well. The critical energy E0 is
the zero point energy difference between the transition state and
the reactant well.
A.2.2 Sums and Densities of States
The MultiWell suite of computer codes includes DenSum, which utilizes the Stein-
Rabinovitch16 version of the Beyer-Swinehart algorithm17 for exact counts of states for species
comprised of separable degrees of freedom. The present version of DenSum can accommodate
harmonic oscillators, Morse oscillators, and free rotors. The K-rotor is included with the internal
degrees of freedom when calculating the sums and densities of states. There are two options for
the treatment of rotations. The usual option is to use the convolution method developed by
Astholz et al.,18 which is computationally efficient and accurate for rotors with small rotational
constants. The second method is to use exact counts of rotational states. The second method is
preferred if the rotational constant is larger than ~1 cm-1. DenSum produces an output file that is
subsequently used as an input file by MultiWell. The inactive two-dimensional external
rotation is specified in the general MultiWell data file.
Hindered Internal Rotations
In the MultiWell Program Suite, torsional modes are assumed to be separable from other
motions (i.e. translations, vibrations, external rotations and other internal rotations) and are
treated as one-dimensional quantum hindered internal rotations. The Schrödinger equation for
such 1-D torsional motions is solved as described in the Technical Notes (see Appendix B).
The 1-D torsion coordinate is defined as χ, the torsional dihedral angle (0≤χ2). Users
must supply the potential energy V(χ) and the torsion rotational constant function Bhr(χ) (or the
corresponding moment of inertia function I(χ)). Potential energies V(χ) and molecular

124
geometries can be computed at discrete values of χ by using any of the many available quantum
chemistry codes, such as Gaussian,19 Molpro,20 or CFour.21 The results for V(χ) can be fitted to a
suitable truncated Fourier series. Program lamm, a module in the MultiWell Program Suite, is
intended to help users compute Bhr(χ), based on the output from quantum chemistry programs
(see Chapter 8 of this manual).
A.2.3 Master Equation for the Vibrational Quasi-Continuum
Because of the difficulties encountered in solving the 2-D master equation, it is usually
reduced to 1-D by making simplifying assumptions, and then solving numerically by one of the
standard methods.10, 22-25 However, Marcus showed that the microcanonical RRKM specific rate
constant depends on the active energy E, i.e. the energy not constrained by conservation of
angular momentum. Thus angular momentum has an effect that must be taken into account for
accurate results. The first approach to this problem also originated with Marcus,26 who invoked
the concept of adiabatic rotation to make "centrifugal corrections". Marcus' approach has been
reviewed by Waage and Rabinovitch27 and is found in standard monographs.12, 13, 28 In this
approach, the RRKM specific rate constant k(Et,J), which is written as depending on total energy
Et and the angular momentum quantum number J is reduced to an approximate k(E) (at a given
temperature), where E is the active energy of the reactant: all explicit reference to angular
momentum quantum number J has been removed from the 2DME, which has thus been reduced
to a 1DME. This approach is outlined in the following.
At high vibrational energies, a quasicontinuum of vibrational states exists and
intramolecular vibrational redistribution (IVR) is rapid. Experiments show that IVR is slow at
low energy, exhibits multiple time scales, and becomes rapid at energies where the vibrational
state density is of the order of 102–103 states/cm-1.29 At these state densities, some vibrational
states overlap significantly within their natural widths as governed by infrared spontaneous
emission rates. At state densities greater than ~107 states/cm-1, most states are overlapped within
their natural widths. The onset of "rapid" IVR is a convenient marker for the onset of the
vibrational quasicontinuum. However, this criterion leaves some uncertainty because IVR
exhibits multiple time constants and thus some modes remain isolated even at higher vibrational
state densities.29
A shorter version of the following derivation of centrifugal corrections has been reported
elsewhere.30
In the vibrational quasicontinuum, individual quantum states cannot be resolved and the
master equation can be written as a function of either of two equivalent sets of independent
variables: Et,J or E,J. In terms of active energy E and angular momentum quantum number J, it
takes the following form 12, 13, 22, 24:
dN(
E,
J,t)
dt
F
E,
J,t
R
E,
J;E,J
N E,J;t
dE
0
J
R E,J;
E,
J
N
E,
J,t
dE
0
J
ki
E,
J
N
E,
J,t
i1
channels
(2.3-1)
where the primed E' and J' refer to the current state and the unprimed quantities refer to a
different state of the excited species, which is undergoing reaction. In Eq. 2.3-1, N(E',J',t)dE' is
the concentration of a chemical species with active energy in the range E' to E'+dE'; R(E,J;E',J')
is the (pseudo-first-order) rate coefficient for collisional energy transfer from initial energy E' to

125
energy E and quantum number J' to J; F'(E',J',t)dE' is a source term (e.g. thermal, chemical, or
photo activation, or isomerization); and ki(E',J') is the unimolecular reaction rate constant for
molecules at energy E' and rotational quantum number J' reacting via the ith reaction channel.
To reduce the 2DME to a 1DME, we first assume that the rotational population
distribution describing the adiabatic rotations is always Boltzmann:
P
eJ
QJ
1gJexp EJ/kBT
(2.3-2a)
where gJ = 2J+1 for a 2-D symmetric top (which is typically assumed; see Appendix B.4 of this
Manual) and other forms for 1-D and spherical tops; the rotational energy EJ and the rotational
partition function QJ for the adiabatic rotor(s) are given by Eq. 2.3-2b and 2.3-2c, respectively:
EJBJ J 1
(2.3-2b)
QJgJexp EJ/kBT
J
(2.3-2c)
The constant B is the rotational constant. By using these expressions, the concentrations can be
written as
N E,J,t
N E,t
P
eJ
(2.3-3)
In the same spirit, we assume the source function produces the same rotational distribution:
F
E,
J,t
F
E,t
P
eJ'
(2.3-4)
Although recent trajectory calculations show that the assumption is probably not
accurate,31) we follow Smith and Gilbert3 and Miller et al.23 in adopting the pragmatic
assumption that the collision rates in Eq. 1 can be written in a separable form:
R E,J;
E,
J
R E,
E
P
eJ
(2.3-5)
where R(E,E') has no dependence on angular momentum and can be expressed as the product of
the total vibrationally inelastic collision frequency () multiplied by the "collision step-size
distribution", P(E,E'), which expresses the probability that a molecule initially in the energy
range from E' to E'+dE' will undergo an inelastic transition to the energy range E to E+dE:
R(E,
E)dE R(E,
E)dE
0
R(E,
E)dE
R(E,
E)dE
0
, (2.3-6a)
P(E,
E)dE
(2.3-6b)
The first factor on the right hand side of Equation (2.3-6a), the integral over the rates of
all inelastic transitions from initial energy E' can be identified with the frequency of inelastic
collisions,
, which may depend on the initial active energy E'. Usually, the collision frequency
is calculated from the expression
= kc[M], where kc is the bimolecular rate constant for
inelastic collisions and [M] is bath gas concentration. The second factor (in curly brackets) on the
right hand side of Equation (2.3-6a) is P(E,E')dE. It is important to emphasize that the
126
factorization of R(E,E') in Equation (2.3-6) is merely for convenience and that kc and P(E,E')
never occur independently of one another. Furthermore, P(E,E') is only a proper probability
density function when
is exactly equal to the inelastic collision rate constant. With this
assumption, P(E,E') is normalized:
P(E,
E)dE
0
1
(2.3-7)
Note that collision step-size distributions for activating and deactivating collisions are
connected via detailed balance:
P(E,
E)
P(
E,E)
(E)
(
E)exp E
E
kBTtrans
, (2.3-8)
where
(E) is the density of states at active energy E, Ttrans is the translational temperature, and
kB is the Boltzmann constant. The relationships among P(E,E'), kc, and the normalization integral
are further discussed below.
Using these definitions, we obtain
R E,J;
E,
J
P E,
E
P
eJ
(2.3-9)
Smith and Gilbert showed that the master equation can be solved approximately when using this
separable form. In MultiWell, this separable form is adopted pragmatically in order to obtain a
semi-analytical solution to the master equation. (Miller and coworkers have further generalized
the function postulated by Smith and Gilbert,3 and the details may be found in their papers.23, 24)
After combining Eq. 2.3-1-9, we obtain
dN(
E,t)
dt P
e
J
F
E,t
P
e
J
P
eJ
P
e
J
P
E;E
N E;t
dE
0
J
N
E,t
P
e
J
P
eJ
P E;
E
dE
0
J
N
E,t
P
e
J
ki
E,
J
i1
channels
(2.3-10)
In this expression, the sums over J are equal to unity because Pe(J) is normalized. Every term
contains the factor Pe(J'). By summing every term in Eq. 2.3-6 over J' and noting that the sum
equals unity in each term except the last, we obtain
dN(
E,t)
dt F
E,t
P
E;E
N E,t
P E;
E
N
E,t
dE
0
N
E,t
ki
E
J
i1
channels
(2.3-11a)
where <ki(E')>J is the RRKM specific rate constant, averaged over the rotational energy
distribution:
ki
E
JP
e
J
ki
E,
J
J0
Jmax
(2.3-11b)
127
The upper limit of the summation (J'max) in Eq. 2.3-11b corresponds to the largest angular
momentum quantum number for which the well still exists. Eq. 2.3-11 summarizes the general
form of the 1-D master equation treated by MultiWell.
The averaging of ki(E',J') over the rotational energy distribution may be carried out as
follows, using the variables defined in Fig. 2.3-1. The RRKM specific rate constant for a specific
J' can be written26
k
E,
J
L‡
h
G‡E,
J
E,
J
(2.3-12)
where L‡ is the reaction path degeneracy, h is Planck's constant, G‡(E+,J') is the sum of states of
the transition state as a function of the active energy E+ in the transition state, and ρ(E',J') is the
density of "vibrational" states of the reactant when the rotational quantum number is J'. The
various energies are related as follows (see Fig. 2.3-1):
EEJEE0E
J
(2.3-13a)
or
EEE0 EJ
(2.3-13b)
where EJ and EJ+ are the energies of the adiabatic rotations in the reactant and in the transition
state, respectively, and ∆EJ = EJ+-EJ. The rotational energies are given by Eq. 2.3-2b and by the
analogous equation:
EJ
BJ J 1
(2.3-14)
Using these relationships, ki(E',J') can be written
k
E,
J
L‡
h
G‡
EE0 EJ
E,
J
(2.3-15)
From Eqs. 2.3-2b and 2.3-14 it is apparent that EJ = (B/B+)EJ+, and ∆EJ can be written as a
function of EJ+ alone: ∆EJ = (1−B/B+)EJ+.
For reactions involving bond fission, the rotational constant B+ for a rigid rotor transition
state is smaller than that for the reactant and ∆EJ < 0. As the angular momentum quantum
number J' increases, the quantity (E0 - ∆EJ) approaches zero. In other words, the reactant well
and the effective critical energy for reaction both vanish when J' is large enough: J'max is the
largest value of J' for which the well still exists. For J' > J'max, k(E',J') is not defined. When B+ ≤
B for rigid rotors, J'max = ∞.
The rate constant must now be averaged over the rotational population distribution:
k
E,
J
JQJ
1k
E,
J
gJ
J0
Jmax
exp EJ/kBT
(2.3-16a)
From the definition of ∆EJ, this expression can also be written
k
E,
J
JQJ
1k
E,
J
gJ
J0
Jmax
exp EJ
EJ
/kBT
(2.3-16b)
128
Equations 2.3-16a and 2.3-12b are suitable for directly averaging over the rotational
quantum number. Care must be taken however, because the rate constant is only defined at
energies E' ≥ (E0+∆EJ). Because ∆EJ ≤ 0, the reaction threshold may be significantly lower in
energy than E0, the critical energy for J = 0.
The ad hoc approximate functions postulated by Smith and Gilbert3 and by Miller and
coworkers23, 24 are almost certainly not accurate.31 Thus we feel that elaborate treatments cannot
be justified and have instead adopted the following pragmatic approach.
The active degrees of freedom may include one or more external rotations, which, to a
good approximation, may be treated as separable (see Appendix B.4). Typically, for a prolate
symmetric top, the K-rotor is regarded as active. For a rigid rotor, the K quantum number is a
"good" quantum number and is restricted to the range from −J to +J. However, a highly excited
molecule is hardly rigid and K is not conserved, although it may exhibit a "propensity" to be
conserved for some period of time. As a result, it is commonly assumed that the K-rotor of a
non-rigid top can exchange energy freely with the internal degrees of freedom: i.e. the K-rotor is
usually assumed to be an active degree of freedom.
It is common practice to allow K to vary freely, except for conservation of energy, and
treat the K-rotor as just one more separable degree of freedom when computing densities of
states.11, 12, 14, 28 In fact, treating the K-rotor in this way may be more accurate than restricting K
to the range from −J to +J.32 (This separable-rotors approximation33 is discussed in Appendix
B.4.) However, there always exist 2J'+1 states with the same value of J', even for a completely
asymmetric top. Thus neglecting the restriction on K has the effect of increasing the density and
sum of states slightly, but this error is insignificant except for molecules with small rotational
constants at very low temperatures.
Here, it is pragmatically assumed that the K-rotor is active and the K quantum number
has no restrictions other than conservation of energy. As a result, the approximate density of
states of the reactant molecule has no explicit dependence on the J quantum number: ρ(E',J') is
replaced by ρ(E') in Eq. 2.3-16 and the average specific rate constant can be written
k
E,
J
JL‡G‡
EE0 EJ
J
h
E
(2.3-17a)
where the averaged sum of states is given by
G‡
EE0 EJ
J1
QJ
G‡
EE0 EJ
gJexp EJ/kBT
J0
Jmax
(2.3-17b)
where J'max is the largest value of J' for which k(E',J') is defined.
Another pragmatic approximation is useful. Marcus showed that by substituting an
average value <∆EJ> = (1−B/B+)<EJ+> in place of ∆EJ in Eq. 2.3-13, a useful approximate
expression is obtained,26 which does not retain any explicit dependence on the rotational state J':
ka
E
L‡
h
G‡
EE0 EJ
E
(2.3-18)
where the subscript "a" was used by Marcus to denote the approximate form. For present
purposes, it is convenient to use the same approximation in the exponential factor in Eq. 2.3-16b,
giving
129
k
E
Jka
E
exp EJ/kBT
QJ
1gJ
J
exp EJ
/kBT
(2.3-19)
The remaining sum over J' in Eq. 2.3-19 can be recognized as QJ+, the rotational partition
function for the transition state. Marcus found <EJ+> = lkBT/2 (where l is the number of
adiabatic rotors), the average rotational energy in the transition state, by weighting the average
according to the reactive flux26, 34 (also see the discussion in Robinson and Holbrook14 and in
Holbrook et al.28). Using this value of <∆EJ> ≈ (1−B/B+)lkBT/2 = (1− I+/I) lkBT/2, where I and
I+ are the moments of inertia for the adiabatic rotor in the reactant and the transition state,
respectively.26 The final result can be written as
k
E
Jka
E
QJ
QJ
exp EJ/kBT
(2.3-20a)
or
k
E
Jka
E
B
B
l/2
exp l
21B
B
(2.3-20b)
or
k
E
Jka
E
I
I
l/2
exp l
21I
I
(2.3-20c)
where the ratio of the (classical) rotational partition functions has been replaced by the ratio of
the rotational constants or moments of inertia, and l is the number of adiabatic rotors. Usually it
is assumed that l = 2.
These simplified forms perform well in master equation simulations, although the energy
transfer parameters may differ to some extent from other treatments. These possible differences
are generally not considered further, because no current master equation treatment of energy
transfer is known to be correct and because energy transfer parameters and collision step-size
distributions generally are not known from other sources, but are simply used as empirical fitting
parameters.
High Pressure and Low Pressure Limits: k∞ and k0
Prior to the release of Multiwell-2011.1, we became aware of a problem with the
implementation of the centrifugal factors in MultiWell. David Golden pointed out that at very
high temperatures, where it is possible to simulate both a recombination reaction and its reverse
dissociation, the two rate constants were inconsistent with each other. This discrepancy was
traced to the centrifugal corrections. This problem has been corrected, and a discussion of the
current and prior versions of k0 and k∞ can be found in Appendix B.10 of this User Manual.
The high pressure rate constant is the average rate constant at pressures high enough so
that differences of the actual population distribution from the thermal Boltzmann distribution are
negligible. The thermal Boltzmann energy distribution for reactant A is
BA(
E,T)QA
1
A
E
exp
E/kBT
(2.3-21a)
where the partition function QA is

130
QA
A
E
exp
E/kBT
d
E
0
(2.3-21b)
The average rate constant is therefore
k(T)1
QA
ka
E
J
A
E
exp
E/kBT
d
E
0
(2.3-22a)
or
k(T)1
QA
QJ
QJ
ka
E
A
E
exp
E EJ
/kBT
d
E
0
(2.3-22b)
By transforming the variable of integration from E' to E+ (i.e. by replacing ∆EJ in Eq. 2.3-7b
with the average value, <∆EJ> and obtaining E+ = E'−E0−<∆EJ>) and changing the limits of
integration, the resulting expression for k∞ is the same as canonical TST (Eq. 4.30 of Robinson
and Holbrook,14 and Eq. 3.30 in Holbrook et al.28 at the high pressure limit).
Comparison with Other Models
Equation 3.30 in Holbrook et al.28 and Eq. 4.30 in Robinson and Holbrook14 are based on
the strong collision assumption, in which every collision results in producing a canonical active
energy distribution. In this section, the strong-collision rate constant is derived using the
rotationally averaged <k(E')>J. For convenience, concentration is written as the product of a
normalized energy distribution, y(E',t), and a time-dependent total concentration, N(t):
N
E,t
N t
y
E,t
(2.3-23)
where N(t) decays with time and the energy distribution y(E',t) is normalized at all times. With
this substitution, the LHS of Eq. 2.3-5 becomes
dN
E,t
dt y
E,t
dN t
dt N t
dy
dt
(2.3-18)
In the absence of chemical reaction and input flux, and given enough time, the population
distribution relaxes to steady state and dy/dt = 0. Furthermore, the unimolecular rate constant (for
channel i) is defined at steady state: kuni,i = −N-1dN/dt. Thus, after simplification the steady-state
master equation can be written
y
E
kuni,iF
E,t
N t
R
E;E
y E
dE
0
y
E
dE R E;
E
dE
0
ki
E
J
i1
channels
(2.3-21)
When F(E',t) = 0, Eq. 2.3-21 can be solved for the steady-state population distribution y(E'):

131
y
E
R
E;E
y E
dE
0
R E;
E
dE
0
ki
E
J
i1
channels
kuni,i
(2.3-22)
To obtain kuni,i with the strong-collider approximation, we use the following identity:
R E;
E
kc[M]
E
exp E/kBT
Q2T
(2.3-23)
where the rate of energy transfer is expressed as the product of a collision rate constant kc and
collider bath concentration [M], multiplying a thermal canonical energy distribution, which is
normalized by the partition function. Note that according to the strong-collider assumption, the
energy transfer rate has no dependence on the energy prior to collision. With this substitution,
the integrals in eq. 2.3-22 can be evaluated readily:
R
E;E
y E
dE
0
kc[M]
E
exp
E/kBT
Q2T
y E
dE
0
(2.3-24a)
kc[M]
E
exp
E/kBT
Q2T
(2.3-24b)
R E;
E
dE
0
kc[M]
Q2T
E
exp E/kBT
dE
0
kc[M]
(2.3-25)
Thus eq. 2.3-22 becomes
y
E
kc[M]
kc[M]ki
E
J
i1
channels
kuni,i
E
exp
E/kBT
Q2T
(2.3-26)
Except at extremely low internal energies, the magnitude of kuni is much smaller than the
rotationally averaged <k(E')>J and hence can be neglected in the denominator. The reaction rate
at active energy E' is given by the product of y(E') and <k(E')>J. After integrating over all
internal energies greater than E0' = E0 + <∆EJ>, the reaction critical energy, we obtain the strong-
collider unimolecular rate constant for channel i:
kuni,ikc[M]ki
E
J
kc[M]ki
E
J
i1
channels
E
exp
E/kBT
Q2T
d
E
E0 EJ
(2.3-27)
Low pressure limit:
132
klow,ikc[M]
Q2T
E
exp
E/kBT
d
E
E0 EJ
(2.3-28)
High pressure limit:
k,i1
Q2T
ki
E
J
E
exp
E/kBT
d
E
E0 EJ
(2.3-29)
A.2.4 Multiple Species (Wells) and Multiple Reaction Channels
Here we consider chemical species that can be identified with local minima (wells) on the
potential energy hypersurface. These species are distinct from transition states, which are located
at saddle points. In MultiWell, each well is assigned an arbitrary index for identification and
reactions are conveniently labeled with two indices: one to designate the reactant and the other to
designate the product. For simplicity in notation, one or more of these indices are omitted in
some of the following discussion.
A master equation such as Equation (2.3-1) can be written for each well and the equations
are coupled via the chemical reaction terms. Each reaction channel is associated either with
another well, or with fragmentation products. Each isomerization is reversible and the transition
state is the same for the corresponding forward and reverse reactions. In principle, the existence
of isomers leads to splitting of vibrational levels, as in the inversion doubling of ammonia, but if
tunneling is negligible, the wells can be considered independently.35 Thus each well has its own
vibrational assignment, molecular structure, and corresponding density of states.
Two technical problems arise when using an energy grained master equation11-14, 28 to
simulate multiple-well systems. First, the number of coupled differential equations can grow
prohibitively as the energy grain size (∆Egrain) is reduced, making the numerical solution very
difficult or impossible. Second, because each well has its own zero of energy and reaction
threshold (critical) energies, it is difficult to match the energy grain boundaries. The reaction
threshold energies for forward and reverse reactions are tied to one another. For accurate
numerical results it is necessary to match the energy grains of the coupled wells. The matching
of energy grains at one reaction threshold may lead to mis-matches at other thresholds and to
artificially shifted energies of the wells, relative to one another. These energy shifts produce
anomalous results for large grain sizes. This problem can be neglected if the energy grains are
very small, but small energy grains lead to very large sets of coupled equations. In all cases, the
calculations should be repeated with successively smaller energy grains until the results are
independent of ∆Egrain: convergence must be achieved.
When a continuum master equation is used, energy mis-matching and anomalous shifts
never create problems. However, the sparse density of states regime at low energies within wells
and for transition states near reaction thresholds is not well represented by a continuum model.
This difficulty is minimized in MultiWell by using a hybrid master equation approach.
A.2.5 Hybrid Master Equation Formulation
Effectively, the hybrid master equation formulation uses a continuum master equation in
the quasicontinuum at high vibrational energies, and an energy-grained master equation at low
energies, where the state density is distinctly discontinuous. This is accomplished by using
133
Equation (2.3-1) for the continuum master equation throughout the entire energy range but
discretizing the state density, population, and transition rates at low energy. At high energy,
Multiwell employs interpolation to determine the density of states and specific rate constants
(k(E)). Values of (E) and k(E) are stored in ordered arrays at specific values of E and
intermediate values are determined by interpolation. At low energies, ordered arrays of (E) and
k(E) are stored at smaller energy spacing (∆Egrain) and interpolation is not used: the array entries
nearest in energy are utilized directly. The two ordered arrays used for each energy-dependent
quantity ((E), k(E), etc.) are combined in "double arrays" which are discussed in the next
section. At all energies, numerical integration is carried out with the trapezoidal rule, which
introduces an energy grain in the low energy regime (where state densities are sparse), but gives
good continuum results at high energy (where the state densities are smooth).
If a stochastic trial (see below) calls for a transition from the continuum space to an
energy in the discrete space, the energy is aligned with the discrete energy grain. At low energy,
many energy grains do not contain states ((E) = 0) and transitions are not allowed to those
states in MultiWell. As a result, population only resides in energy grains that contain states and
collisional transitions low on the energy ladder can only take place with relatively large energy
changes, due to the sparse density of states.
A.2.6 Energy Grain in the Hybrid Master Equation
Through the use of double arrays, high energy resolution is achieved in densities and
sums of states at low energy and near reaction thresholds. By default, the double arrays have 500
elements (the dimensions can be changed, if desired). The low energy portion of the array is
specified according to ∆Egrain and the number of array elements assigned to the low energy
portion of the double array. The high energy portion is specified only according to the maximum
energy. Thus the number of array elements used in the high energy portion and the energy grain
in the high energy portion both depend on how many array elements remain after assigning the
low energy portion. The same specifications are used for all double arrays, including arrays for
densities of states ((E)), sums of states (G‡(E-E0)), specific rate constants (k(E-E0)), etc. The
discretization of these quantities is the natural result of exact count algorithms.
An example of a double array for the density of states (E) is shown in Figure 1 for
benzene (vibrations36 + K-rotor). In this example, the density of states was calculated using an
energy grain of ∆Egrain = 10 cm-1 and exact counts up to an energy of 85000 cm-1, although only
energies up to 10000 cm-1 are shown in the figure. In this example, the low energy regime was
defined as the first 250 elements of a double array and thus covered the range from 0 to 2490
cm-1. The remaining 250 elements of the double array overlap the low energy portion and cover
the range all the way from 0 to 85000 cm-1 (the high energy regime) with an energy grain of
341.4 cm-1. In Figure 1, (E) calculated with ∆Egrain = 10 cm-1 is shown as the thin solid line and
the double array elements are shown as the solid dots. The upper energy boundary for low
energy range was chosen to fall within the vibrational quasicontinuum, as evidenced by (E) ≥
100 states/cm-1 and by the relative smoothness of the plot of (E). When (E) is sufficiently
smooth, relatively little error is introduced by interpolating between the double array points.
In principle, convergence tests should be carried out for each simulation. Tests for
convergence as ∆Egrain is reduced reflect several simultaneous effects: the (E) grain size is
varied for every well, the G‡(E-E0) grain size is varied for every reaction, and the energy range
covered by the low energy portion of every double array is varied. Because several attributes are
affected by ∆Egrain, the variation of results with grain size cannot be interpreted precisely without
134
extensive tests. However, as long as the energy range covered by the low energy portion of the
double arrays is sufficient, smaller grain sizes will produce more accurate results and the results
are seen to converge at small ∆Egrain, as illustrated in Figure 4 of Reference 37.
Typical convergence tests37 show that 250 bins with ∆Egrain = 10 cm-1 are usually suitable
for the low energy portion of the double arrays. The upper energy bound for the high energy
portion is typically 85000 cm-1 to 100000 cm-1, depending on the temperature range and
activation method being simulated. The small grain at every reaction threshold gives accurate
results for the unimolecular reaction rates. The small grain at low energy within each well gives
a good representation of the sparse density of states regime in every well. To achieve comparable
numerical results by the matrix solution13 of an energy-grained master equation for just a single
well would require finding the eigenvalues of a matrix with 85008500 elements...a difficult
task. The hybrid master equation approach has a distinct advantage in this regard.
Figure 1. Density of states for benzene (including vibrations and one active
external rotation). Solid line: density of states from exact count (∆Egrain = 10
cm-1); solid dots: elements of double array (see text for details).
References
1. A. P. Penner and W. Forst, Transfer of vibrational-rotational energy in thermal reactions:
application to polyatomics, Chem. Phys. 13, 51-64 (1976).
2. S. C. Smith and R. G. Gilbert, Angular momentum conservation in multichannel
unimolecular reactions, Int. J. Chem. Kinet. 20, 979-990 (1988).
3. S. C. Smith and R. G. Gilbert, Angular momentum conservation in unimolecular and
recombination reactions, Int. J. Chem. Kinet. 20, 307-329 (1988).
135
4. J. Troe, Theory of thermal unimolecular reactions at low pressures. I. Solution of the
Master Equation, J. Chem. Phys. 66, 4745-57 (1977).
5. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in
FORTRAN. The Art of Scientific Computing. (Cambridge University Press, Cambridge,
1992).
6. S. C. Smith, M. J. McEwan and R. G. Gilbert, The pressure dependence of ion-molecule
association rate coefficients, J. Chem. Phys. 90, 1630-1640 (1989).
7. S. J. Jeffrey, K. E. Gates and S. C. Smith, Full iterative solution of the two-dimensional
master equation for thermal unimolecular reactions, J. Phys. Chem. 100, 7090-6 (1996).
8. S. H. Robertson, A. I. Shushin and D. M. Wardlaw, Reduction of the two dimensional
master equation to a Smolouchowsky type differential equation with application to CH4 –
> CH3 + H, J. Chem. Phys. 98, 8673-9 (1993).
9. P. K. Venkatesh, A. M. Dean, M. H. Cohen and R. W. Carr, Master equation analysis of
intermolecular energy transfer in multiple-well, multiple-channel unimolecular reactions.
I. Basic Theory, J. Chem. Phys. 107, 8904-16 (1997).
10. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
11. W. Forst, Theory of Unimolecular Reactions. (Academic Press, New York, 1973).
12. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
13. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions.
(Blackwell Scientific, Oxford, 1990).
14. P. J. Robinson and K. A. Holbrook, Unimolecular Reactions. (Wiley-Interscience,
London; New York, 1972).
15. T. Baer and W. L. Hase, Unimolecular Reaction Dynamics. Theory and Experiments.
(Oxford University Press, New York, 1996).
16. S. E. Stein and B. S. Rabinovitch, Accurate evaluation of internal energy level sums and
densities including anharmonic oscillators and hindered rotors, J. Chem. Phys. 58, 2438-
45 (1973).
17. T. Beyer and D. F. Swinehart, Number of multiply-restricted partitions, Comm. Assoc.
Comput. Machines 16, 379 (1973).
18. D. C. Astholz, J. Troe and W. Wieters, Unimolecular processes in vibrationally highly
excited cycloheptatrienes. I. Thermal isomerization in shock waves, J. Chem. Phys. 70,
5107-16 (1979).
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li,
H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M.
Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao,
H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J.
Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K.
Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.
M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R.
Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W.
Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J.
Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J.

136
Cioslowski and D. J. Fox; Gaussian 09, Revision A.1; Gaussian, Inc., Wallingford CT,
2009.
20. H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G.
Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J.
Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. W. Meyer,
M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R.
Tarroni and T. Thorsteinsson; MOLPRO version 2006.1 (a package of ab initio
programs); see http://www.molpro.net., 2006; http://www.molpro.net.
21. J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, w. c. f. A. A. Auer, R. J. Bartlett, U.
Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, M. Heckert, O.
Heun, C. Huber, T.-C. Jagan, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A.
Matthews, T. Metzroth, D. P. O'Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann,
S. Stopkowicz, J. Vázquez, F. Wang and J. D. Watts; and the integral packages
MOLECULE (J. Almlöf and P.R. Taylor); PROPS (P.R. Taylor); ABACUS (T. Helgaker,
H.J. Aa. Jensen, P. Jørgensen, and J. Olsen); and ECP routines by A. V. Mitin and C.
van Wüllen. CFOUR, a quantum chemical program package (http://www.cfour.de/),
2009; <Error! Hyperlink reference not valid..
22. M. J. Pilling and S. H. Robertson, Master equation models for chemical reactions of
importance in combustion, Ann. Rev. Phys. Chem. 54, 245-275 (2003).
23. J. A. Miller, S. J. Klippenstein and C. Raffy, Solution of some one- and two-dimensional
master equation models for thermal dissociation: The dissociation of methane in the low
pressure limit, J. Phys. Chem. A 106, 4904-13 (2002).
24. J. A. Miller and S. J. Klippenstein, Master Equation Methods in Gas Phase Chemical
Kinetics, J. Phys. Chem. A 110, 10528-10544 (2006).
25. J. R. Barker, Multiple-well, multiple-path unimolecular reaction systems. I. MultiWell
computer program suite, Int. J. Chem. Kinet. 33, 232-245 (2001).
26. R. A. Marcus, Dissociation and isomerization of vibrationally excited species. III, J.
Chem. Phys. 43, 2658-61 (1965).
27. E. V. Waage and B. S. Rabinovitch, Centrifugal effects in reaction rate theory, Chem.
Rev. 70, 377-87 (1970).
28. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
29. D. S. Perry, "Time scales and mechanisms of intramolecular energy redistribution," in
Highly Excited States: Relaxation, Reaction, and Structure, eds. A. Mullin and G. C.
Schatz (American Chemical Society, Washington DC, 1997), pp. American Chemical
Society.
30. R. E. Weston, Jr., T. L. Nguyen, J. F. Stanton and J. R. Barker, HO + CO Reaction Rates
and H/D Kinetic Isotope Effects: Master Equation Models with ab Initio SCTST Rate
Constants, J. Phys. Chem. A 117, 821-835 (2013).
31. J. R. Barker and R. E. Weston, Jr., Collisional Energy Transfer Probability Densities
P(E,J;E',J') for Monatomics Colliding with Large Molecules, J. Phys. Chem. A 114,
10619–10633 (2010).
32. E. E. Aubanel, D. M. Wardlaw, L. Zhu and W. L. Hase, Role of angular momentum in
statistical unimolecular rate theory, Int. Rev. Phys. Chem. 10, 249-86 (1991).
137
33. J. H. Current and B. S. Rabinovitch, Decomposition of Chemically Activated Ethyl-d3
Radicals. Primary Intramolecular Kinetic Isotope Effect in a Nonequilibrium System, J.
Chem. Phys. 38, 783-795 (1963).
34. R. A. Marcus, Erratum: Dissociation and Isomerization of Vibrationally Excited Species
[J. Chem. Phys. 43,2658 (1965)], J. Chem. Phys. 52, 1018 (1970).
35. E. B. Wilson, Jr., J. C. Decius and P. C. Cross, Molecular Vibrations. The Theory of
Infrared and Raman Vibrational Spectra. (McGraw-Hill Book Company, Inc., New
York, 1955).
36. L. Goodman, A. G. Ozkabak and S. N. Thakur, A benchmark vibrational potential
surface: ground state benzene, J. Phys. Chem. 95, 9044 (1991).
37. J. R. Barker and N. F. Ortiz, Multiple-Well, multiple-path unimolecular reaction systems.
II. 2-methylhexyl free radicals, Int. J. Chem. Kinet. 33, 246–261 (2001).
A.3. Stochastic Method
A.3.1 Gillespie's (Exact) Stochastic Simulation Algorithm
Gillespie showed that a stochastic method gives the exact solution to a set of ordinary
differential equations in the limit of an infinite number of stochastic trials.1, 2 The algorithm has
been described in the context of chemical kinetics.3-5 If a Markovian system is in a given state
and can make transitions to other states via a set of transition rate coefficients, then for a given
step in a stochastic simulation, Gillespie's algorithm gives a prescription for a) finding the
duration of the time step and b) selecting the transition from among the choices. This algorithm
is repeated step-by-step as long as desired and as long as transitions are possible.
Gillespie's method can be applied to both linear and non-linear systems.3 Equation (2.3-1)
is linear in y(E,t), which leads to a particularly convenient result which is described below. If
Equation (1) contained non-linear terms to describe energy pooling, for example, the terms
would contain factors such as the product y(E,t)y(E',t). To solve this system numerically
requires using an energy-grained master equation with a swarm of stochastic trials and storing an
evolving vector of populations as a function of energy. Here, the number of stochastic trials can
be identified with a number of pseudo molecules that initially are placed in a set of energy
grains. At each time step, a pseudo molecule is moved from one energy grain to another as
described by Gillespie and the swarm of pseudo molecules maps out the evolving energy
distribution. This approach has been used by Veerecken et al.6, 7 to simulate unimolecular and
recombination reactions and it can in principle be extended to non-linear systems. The
difficulties in this approach are associated with the energy-grained master equation (see above)
and with the requirement for storage of the entire vector of y(E,t) at every time step. Given the
current availability of inexpensive computer memory, the latter is not a serious limitation for
single-well reaction systems. When several wells are involved, the bookkeeping is cumbersome.
Moreover, the memory requirements of this technique can become prohibitive in the future if the
one-dimensional master equation is to be extended to two dimensions by explicitly including
angular momentum. MultiWell is designed so that the future extension to two-dimensions will be
feasible.
For linear master equations, a different strategy5 is possible using Gillespie's algorithm.
Instead of using a swarm of stochastic molecules and storage of y(E,t) at every step, stochastic

138
trials are run one at a time and snapshots of E and other variables are stored at convenient time
intervals. The vector y(E,t) does not need to be stored. A "snapshot" simply records the energy
and other properties of a single stochastic molecule as it progresses through a stochastic trial.
The snapshot has no effect on the physics of the trial. Since the system is linear, the averaged
result of an ensemble of stochastic trials gives the same result as a swarm of stochastic
molecules. By retaining only the averaged results of the snapshots, the memory storage
requirements are greatly reduced.
For a linear master equation, the loss terms can be expressed as first order in y(E,t) with
first order rate coefficients Aj for k paths. These rate coefficients can be identified with the
unimolecular rate constants and the collision frequency in Equation (2.3-1). According to
Gillespie's algorithm, the duration of the next time step is chosen by using the uniform random
deviate (i.e. random number) r1 :
ln(r
1)
AT
(3.1-1a)
where
ATAj
j1
k
(3.1-1b)
The transition is selected from among the k paths by using a second random number r2:
Aj
j1
n1
r2ATAj
jn
k
(3.1-2)
Here, the transition takes place via path n at time t+.
According to Gillespie's algorithm, the time intervals between stochastic steps are chosen
randomly by Equation (3.1-1a). Thus the progress of the stochastic simulation is monitored via
snapshots, as mentioned above. If collisional activation or deactivation is the result of a
transition, then the next stochastic step is calculated using rate coefficients appropriate to the
new energy. If isomerization to another well is the result of a transition, then the next stochastic
step is calculated using the first order rate coefficients appropriate to the new well, based on E
measured from the zero point energy of the new well. The snapshots from many stochastic trials
are averaged. The results include the time-dependent average fractional populations of the
isomers, the average internal energy of each isomer, and fractional yields of the fragmentation
products, etc.
The computer time required for any given stochastic simulation depends on Ntrials, the
simulated time duration, and on the properties of the system that affect AT in Equation (3.1-1b).
For example, one of the Aj terms is the collision frequency, which is proportional to pressure. If
the collision frequency is the dominant term in Equation (3.1-1b), then the average stochastic
time-step is inversely proportional to pressure and the number of time steps (and the
corresponding computer execution time) for the given simulated time duration is proportional to
pressure. Of course, collision frequency is not always the dominant term in Equation (3.1-1b),
but the same qualitative considerations can help in estimating required computer time.
Note that the effectiveness of Equation (3.1-2) is limited by the properties of the random
number generator. The characteristics of various random number generators are discussed
elsewhere,8-10 where many potential pitfalls are described. It is important to use random number

139
generators that have been thoroughly tested. Even assuming the random number generator
produces a sequence that has no serial correlations, the number of random numbers in a sequence
is limited and this imposes a limitation on the relative magnitudes of the Am terms that can be
selected according to Equation (3.1-2). For a 32-bit computer, a typical random number sequence
contains 231-1 ≈ 2.1109 equally-spaced numbers. Thus if the ratio of minimum to maximum
values of the rate constants is less than ~0.510-9, then the path with the smaller rate can never
be selected. Thus the random number generator places a rigorous upper bound on the dynamic
range of rates that can be selected. A more serious limitation, however, is that an extraordinarily
large number of stochastic trials is required in order to sample rare events with useful precision,
as discussed in the next section.
A.3.2 Stochastic Uncertainties
The precision of the results obtained using stochastic methods depends on the number of
stochastic trials. In the systems simulated by MultiWell, several species coexist and their relative
populations sum to unity:
1f1f2... fi
i1
species
(3.2-1)
The standard deviation in the instantaneous relative population of the ith species is the square root
of the variance calculated according to the multinomial distribution11:
i1
Ntrials
fi1fi
(3.2-2)
where fi is the fractional population of the ith species and Ntrials is the number of stochastic trials.
Note that the standard deviation is reduced as the number of trials increases. Also note that the
product fi(1-fi) appears in Equation (3.2-2). Thus, the standard deviation is the same when, for
example, fi=0.01 and when fi=0.99. These standard deviations are calculated and reported by
MultiWell in its general output.
A large number of stochastic trials is needed when rare events must be simulated with
high precision. Suppose that fi = 0.01 and the desired precision corresponds to a relative
statistical error of 1% (i.e. i/fi = 0.01). From Equation (8), one finds the required number of
stochastic trials: Ntrials ≈ 106. For a relative error of 10%, only about 104 trials are needed. Thus,
the required number of stochastic trials places a practical limit on the precision attainable for
minor pathways.

140
References
1. D. T. Gillespie, A general method for numerically simulating the stochastic time
evolution of coupled chemical reactions, J. Comp. Phys. 22, 403-34 (1976).
2. D. T. Gillespie, Monte Carlo simulation of random walks with residence time dependent
transition probability rates, J. Comp. Phys. 28, 395-407 (1978).
3. D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys.
Chem. 81, 2340-61 (1977).
4. D. T. Gillespie, A rigorous derivation of the chemical master equation, Physica A:
Statistical and Theoretical Physics (Amsterdam) 188, 404-25 (1992).
5. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
6. P. K. Venkatesh, A. M. Dean, M. H. Cohen and R. W. Carr, Master equation analysis of
intermolecular energy transfer in multiple-well, multiple-channel unimolecular reactions.
I. Basic Theory, J. Chem. Phys. 107, 8904-16 (1997).
7. L. Vereecken, G. Huyberechts and J. Peeters, Stochastic simulation of chemically
activated unimolecular reactions, J. Chem. Phys. 106, 6564-6573 (1997).
8. D. E. Knuth, Seminumerical Algorithms. (Addison-Wesley, Reading, MA, 1981).
9. W. H. Press and S. A. Teukolsky, [Random number generators], ComPh 6, 522-4 (1992).
10. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in
FORTRAN. The Art of Scientific Computing. (Cambridge University Press, Cambridge,
1992).
11. C. P. Tsokos, Probability Distributions: An Introduction to Probability Theory with
Applications. (Wadsworth Publishing Company Inc., Belmont CA, 1972).
A.4. Processes
A.4.1 Unimolecular Reactions
The energy-dependent specific unimolecular rate constant k(E) is given by the RRKM
statistical theory1-5:
k(E)m‡
m
ext
ext
‡
ge
‡
ge
1
h
G‡(EE0)
(E)
(4.1-1)
where m‡ and m are the number of optical isomers,3 ext‡ and ext are the external rotation
symmetry numbers, and ge‡ and ge are the electronic state degeneracies of the transition state and
reactant, respectively; h is Planck's constant, G‡(E-E0) is the sum of states of the transition state,
E0 is the reaction threshold energy, and (E) is the density of states of the reactant molecule. The
internal energy E is measured relative to the zero point energy of the reactant molecule and the
reaction threshold energy (critical energy) is the difference between the zero point energies of
141
reactant and transition state. Equation (4.1-1) was written by assuming that the rotational
external symmetry numbers were not used in calculating the sums and densities of states.3 It is,
however, assumed that internal rotor symmetry numbers are used explicitly in the sum and
density calculations and hence do not appear in Equation (4.1-1). Note that the quantity set off in
square brackets is the reaction path degeneracy.3
At low energies, where densities of states may be very sparse, (E) may be very small or
zero in a given energy grain (lower energy portion of the double array). In MultiWell, this is
treated as if there are no reactant states in the energy grain: k(E) is set equal to zero in that grain.
During evolution of the population distribution, population never resides in energy grains that do
not contain reactant states.
Tight Transition States
For a tight transition state, G‡(E-E0) can be calculated from a vibrational-rotational
assignment and the reaction threshold energy can be corrected approximately for angular
momentum effects by using a pseudo-diatomic model.2, 3, 6 All polyatomics are treated by
DenSum and MultiWell as SYMMETRIC TOPS with moments of inertia IA, IB = IC and
corresponding rotational constants A = ħ2/2IA and B ==ħ2/2IB. The rotational energy of a
symmetric top is given by
ErJ,K
J J 1
B(AB)K2
where quantum numbers J and K refer to the two-dimensional 2-D adiabatic rotor (i.e. the one
that conserves angular momentum J) and to one-dimensional rotation about the top axis
(projection of J on the top axis), respectively (see Appendix B.4). For a given value of J,
quantum number K can take values from -J to +J, inclusive; all such states are doubly degenerate
except for K=0, which is singly degenerate. In the present version of DenSum, the K-rotor is
normally designated as a simple 1-D rotation (either quantized or classical). The moment of
inertia for the K-rotor IK is given by
IKIA
1IB
1
1
In many applications, IK ≈ IA.
Because the K-rotor is normally designated as a simple rotation in MultiWell simulations,
the range of K is normally not restricted to ±J. When IA < IB (prolate top), then IK > 0. When IA >
IB (oblate top), then IK < 0. If the K quantum number is not constrained to K ≤ |J|, then Er(J,K)
can be <0. The unrestricted range of K is not serious a approximation for prolate tops, since the
rotational energy is >0 for all values of J and K. For oblate tops, however, Er(J,K) can be <0
when K >> J. Thus the approximate treatment of the K-rotor may fail seriously for oblate tops.
The kro degree of freedom type (see DenSum) employs the correct treatment for a user-specified
value of J.
Thus the three external rotations of a non-linear molecule consist of a 1-dimensional rotor
(the 1-D "K-rotor") and a 2-dimensional top (the 2-D adiabatic rotor). The K-ROTOR
properties are listed in densum.dat and included in density and sums of states calculations.
Pragmatically, IB is usually not equal to IC, since most chemical species are not true symmetric
tops. For almost symmetric tops (where IB ≈ IC), one can use either of two reasonable
approximations for I2D (see Appendix B.4):

142
I2DIBIC
1/2
[Ref. 2, 6] or
I2DIB
1IC
1
1
[Ref. 7]
The 2-D ADIABATIC ROTOR moment of inertia is listed in multiwell.dat on Line 8
(for wells) or Line 14 (for transition states). The moment of inertia IK of the K-rotor is given by
IKIA
1I2D
1
1
This is sometimes approximated as IK ≈ IA. The K-rotor is normally listed as a 1-D rotation in the
DenSum data file.
When k(E) is calculated according to RRKM Theory, centrifugal corrections
(recommended Keyword 'CENT2') are applied by averaging k(E,J) over a thermal distribution
of J. Here, k(E,J) is given by Eq. 4.1-1, but with the density of states in the denominator written
as in Section 4.10.1 in Robinson and Holbrook5 (or Section 3.10 of Holbrook et al.4). Essentially,
k(E,J) can be written
k(E,J)m‡
m
ext
ext
‡
ge
‡
ge
1
h
G‡(E)
(EE0∆ErJ
)
(4.1-2a)
where E+ is the active energy that is assumed to randomize rapidly and ∆Erot(J) is the difference
in the adiabatic rotational energy between transition state and reactant molecule:
∆Erot J
B‡Be
J J 1
(4.1-2b)
Here, B‡ and Be are the rotational constants (for the adiabatic 2-D rotations) of the transition state
and the equilibrium reactant molecule, respectively. Since Be is usually significantly larger than
B‡, ∆Erot(J) is usually negative. The rotational averaging is carried out as usual:
k E
1
Q2D
k E,J
2J1
exp BeJJ1
kBT
J0
(4.1-2c)
This model amounts to assigning a fixed transition state, since B‡ does not change with
rotational state (or inter-fragment distance), and thus is a relatively poor approximation for loose
transition states. The limitations of this approach are overcome to a large extent if a semi-
empirical approach like the Hindered Gorin Model (see below) is applied, where B‡ is assumed
to vary with temperature.
Loose Transition States
For loose transition states, more elaborate techniques are needed for calculating k(E)
accurately. Such techniques include Variational Transition State Theory,3, 8 Adiabatic Channel
Model,9 and Flexible Transition State Theory.10 Computer codes have been published for some
of these theories.11, 12 These methods can be used in the current version of MultiWell by
calculating k(E) externally and supplying the k(E) values an appropriately formatted external
data file. MultiWell will accept double arrays (from external files) that specify GTS(E-E0) (which
can be calculated conveniently using codes like DenSum, part of the MultiWell suite), or that
specify k(E-E0). Since a double array is used, the effective energy grain can be very small near
the reaction threshold, where high energy resolution is important.
The choice of approach depends on several factors, including personal preferences,
computational costs, required accuracy, and whether experimental data are available. MultiWell

143
can in principle be used for any method that one wishes to use, but the most sophisticated
methods require considerable work outside the MultiWell package; the simpler methods can be
implemented with built-in options. Even when computer resources are not a limitation, the
limitations of current electronic structure theories are significant, possibly leading one to choose
one of the simpler methods.
In the following, we list several methods, starting with the simplest, and describe
strengths and weaknesses. These methods require either some experimental data, or an empirical
estimation method (e.g. thermochemical kinetics13), or perhaps both. They are based on fitting
canonical (thermal) rate constants and then using the appropriate parameters in microcanonical
master equation simulations.
Inverse Laplace Transform Method
With this method, experimental Arrhenius parameters must be known or estimated for the
high-pressure limit of the thermal decomposition reaction. If the Arrhenius parameters are
known for the recombination reaction, the equilibrium constant Keq can be used to determine the
corresponding parameters for the unimolecular decomposition reaction. Since rate constants for
recombination reactions are usually only weakly dependent on temperature, the activation energy
for the recombination may be assumed to equal zero. In most cases, it is a good approximation to
assume that E∞, the Arrhenius activation energy at the high pressure limit, is equal to the critical
energy for reaction (E0). MultiWell input for ILT calls for only two parameters: E0 and the
corresponding Arrhenius A-factor.
A selectable option in MultiWell is to calculate k(E) using the Inverse Laplace Transform
method described by Forst:2, 6, 14
k(E)m‡
m
ext
ext
‡
ge
‡
ge
A
(EE)
(E)
(4.1-3)
where A∞ and E∞ are the Arrhenius parameters for the corresponding high pressure limiting
thermal rate constant. Note that the reaction path degeneracy (the quantity in square brackets)
can be absorbed into A∞ if desired. For added accuracy near the reaction threshold, E∞ may be
replaced in Equation (4.1-3) by E0, the threshold energy. This substitution may improve the
threshold behavior, but it introduces a small error in the calculated high pressure limit activation
energy.
Required info:
Experimental (or estimated) Arrhenius parameters
Reaction enthalpy and Keq are needed to obtain the rate constant for the reverse
reaction.
Strengths:
Quickest and easiest method (a built-in option in MultiWell)
Does not require TST parameters for the transition state.
Drawbacks:
Over wide temperature ranges, the thermal rate constants may not obey the strict
Arrhenius form. Errors from this source, however, are usually relatively small.
144
This method for computing k(E) is not as accurate as transition state theory (i.e.
RRKM theory).
The ILT does not allow the use of centrifugal correction factors, which are needed to
account for conservation of angular momentum. Neglect of angular momentum can
affect the magnitude and temperature-dependence of the energy transfer parameters
needed to describe pressure fall-off.
Hindered Gorin Model
When the rate constant is known from experiments, it is often convenient to use a
"restricted" or "hindered" Gorin Model with a "hindrance parameter" selected to reproduce a
known rate constant for a recombination reaction.3, 13, 15 The same transition state is appropriate
for the corresponding unimolecular decomposition reaction. The basic idea is that the TST
internal degrees of freedom consist of vibrations (the unperturbed vibrational frequencies of the
reactants) plus internal rotations (the relative rotations of the two reactants with rotational
constants modified by an empirical multiplicative constant) plus external rotations (two adiabatic
rotations and the K-rotor). The empirical factor is adjusted in order to fit the experimental
canonical recombination rate constant.
According to the Gorin model,16 the two molecular fragments rotate independently of one
another while separated at the distance corresponding to the centrifugal maximum (rmax) of the
effective potential of the bond being broken. In the present work, the rotations of both fragments
and the over-all transition state are treated approximately as symmetric tops (see Appendix B.4).
The over-all transition state has a 2-D external adiabatic rotation with moment of inertia given by
I2D‡ = µr2max, where µ is the reduced mass of the two fragments, and a 1-D external rotation (the
"K-rotor") with moment of inertia Ik. The K-rotor is not adiabatic and is assumed, according to
the usual approximation,3 to mix energy freely with the active vibrations. The internal rotations
of fragments A and B are characterized by 2-D rotations with moments of inertia Ia and Ib,
respectively, and an internal rotation with reduced moment of inertia Ir. The moments of inertia
Ir and Ik are obtained by combining the K-rotors of the individual fragments, as described by
Gilbert and Smith.3
In the restricted, or Hindered Gorin Model,3, 13, 15 it is assumed that the two fragments
interfere sterically with each another and thus cannot rotate freely. The effect is to reduce the
available phase space and hence reduce the sum of states. Operationally, a "hindrance" parameter
is defined,15 which can vary from zero (free rotation) to unity (completely hindered. The 2-D
moments of inertia Ia and Ib are multiplied by the factor (1-
)1/2 to obtain the effective 2-D
moments of inertia used for calculating the sum of states. Examples of the Hindered Gorin
Model used with MultiWell can be found elsewhere.17, 18
THERMO (in the MultiWell Program Suite) has built-in capability for using the Hindered
Gorin Model for fitting thermal recombination rate constants.
Required info:
Experimental (or estimated) recombination rate constant
Reaction enthalpy and Keq are needed to obtain the rate constant for the reverse
reaction.
Vibrational frequencies and rotational constants of the recombination reactants.
145
An assumed function for V(r) along the reaction coordinate (usually a Morse or
Varshni potential) described by the center-of-mass distance between the two
reactants.
Strengths:
Relatively easy method.
Generates TST parameters that fit the experimental canonical recombination rate
constant at a given temperature.
TST (i.e. RRKM) is a proven method; centrifugal corrections are employed.
Drawbacks:
Experimental or estimated rate constants are required at every temperature.
Fitting of the rate constants must be carried out at each temperature.
TST parameters are different at each temperature.
Separable harmonic oscillator and rigid rotor approximations may not be sufficiently
accurate. Using separable hindered internal rotations is significantly more accurate,
but more expensive.
Semi-empirical Canonical Variational Transition State Theory
We are currently using Semi-empirical Canonical Variational Transition State Theory
(VTST) for applications where electronic structure methods are not reliable, but can still supply
useful information. The basic idea is to use methods like Density Functional Theory (DFT; e.g.
B3LYP) and large basis sets to carry out constrained optimizations at fixed distances along a
reaction path in order to obtain the rotational constants and the vibrational frequencies
orthogonal to the path, but then use empirical expressions for V(r), the potential energy along the
path. For example, we have used V(r) = −Cr−n, where C is a constant and n = 6.
The vibrational frequencies, rotational constants, and V(r) vary with position along the
path. At each of the fixed points along the path, one can use those quantities as input to THERMO
(in the MultiWell Program Suite) for computing a trial rate constant for the thermal reaction. The
minimum trial rate constant corresponds to the VTST rate constant. The minimum rate constant
is best obtained by interpolation between the fixed points, but for points separated by 0.1 Å or
less it is almost as good to use the lowest trial rate constant, without interpolation. We find that
by varying the constant C, it is possible to fit the experimental recombination rate constant at a
given temperature (e.g. 298 K). According to our limited experience with this method, the value
of the constant C fitted at a single temperature is in reasonable agreement with the temperature
dependence of the recombination reaction, when known.
For a master equation simulation at temperature T, one uses the transition state
parameters (vibrational frequencies, rotational constants, and V(r)) corresponding to the
variational transition state at T.
Required info:
Experimental (or estimated) recombination rate constant
Reaction enthalpy and Keq are needed to obtain the rate constant for the reverse
reaction.
Constrained geometry optimizations at fixed distances along the reaction path; and
corresponding vibrational frequencies and rotational constants.

146
An assumed function for V(r) along the reaction coordinate (e.g. V(r) = −C/r−n with
n=6).
Strengths:
Uses theoretically calculated geometries and vibrational frequencies (which are more
trustworthy than total energies).
Generates TST parameters that fit the experimental canonical recombination rate
constant at a given temperature.
Temperature dependence of the rate constant can be estimated from fitting to the rate
constant at a single temperature.
TST (i.e. RRKM) is a proven method; centrifugal corrections are employed.
Drawbacks:
Experimental or estimated rate constants are required at every temperature.
Even for "economical" methods, the constrained optimizations and vibrational
analysis can be expensive.
For best accuracy, fitting of the rate constants must be carried out at each
temperature. (However, fitting at a single temperature provides at least a rough
estimate of the temperature dependence and may be adequate.)
TST parameters are different at each temperature.
Separable harmonic oscillator and rigid rotor approximations may not be sufficiently
accurate. Using separable hindered internal rotations is significantly more accurate,
but more expensive.
High and Low Pressure Limits
Regardless of the method for calculating k(E), the unimolecular rate constant at the high
pressure limit k∞(Ttrans) is calculated in MultiWell by using (E) and k(E). The strong-collider
rate constant at the low pressure limit is proportional to bath gas concentration: k0SC(Ttrans)[M].
The proportionality constant k0SC(Ttrans) is calculated by using (E) and kc, the bimolecular rate
constant for collisions (see Appendix A.4.3):
k(Ttrans )1
Q(Ttrans )k(E)
(E)exp(E/kBTtrans )dE
E0
(4.1-4a)
k0
SC (Ttrans )kcoll
Q(Ttrans )
(E)exp(E/kBTtrans )dE
E0
(4.1-4b)
In these expressions, Q(Ttrans) is the partition function of the reactant internal degrees of freedom
(the degrees of freedom used to calculate
(E) and k(E)) at translational temperature Ttrans:
Q(Ttrans )
(E)exp(E/kBTtrans )dE
0
(4.1-5)

147
The numerical integrations are carried out using the trapezoidal rule, because (E)
fluctuates wildly at low energies. Test show that the numerical integration produces values for
k∞(Ttrans) that are accurate within a fraction of 1% for usual values of ∆Egrain .19 The activation
energy is obtained by calculating k∞(Ttrans) at two closely-spaced temperatures:
E Rln k(T2) / k(T1)
T2
1T1
1
(4.1-6)
From the activation energy and the rate constant at one temperature, the A-factor (A∞) can be
calculated. Values for k∞(Ttrans), E∞, and A∞ calculated in this way are reported (for each
reaction) in the general output file. Note that the numerical values for the high pressure rate
constant k∞(Ttrans) (also, E∞ and A∞) should be the same, regardless of whether centrifugal
corrections are used or not (Keywords 'CENT2' or 'NOCENT'), but k0SC(Ttrans) depends on the
particular choice. The value for k∞(Ttrans) is formally identical to that given by canonical
transition state theory.
Effects of Slow IVR
RRKM theory is based on the premise that energy is completely randomized on a time
scale that is fast compared to chemical reaction. For most experiments, this condition appears to
be met, but some examples of "intrinsic non-RRKM" behavior are known. For these reactions,
the sow transfer of internal energy to the reaction coordinate from the other degrees of freedom
limits the rate constant, which falls below the RRKM statistical limit. Several theories for the
effects of slow IVR have been proposed,4, 20-24 but perhaps the most successful of these is the
local random matrix model of Wolynes and coworkers.25-29
According to most of the IVR models,24, 26 the effects of slow IVR can be accounted for
with an IVR transmission coefficient:
IVR U,M
kIVR
qU
kIVR
cM
kIVR
qU
kIVR
cM
ivr
(4.1-7)
where U is the total vibrational energy and kqIVR(U) is the collision-free IVR rate constant, which
must be calculated by one of the theories mentioned above. In particular, the Wolynes-Leitner26
has been used with MultiWell.30, 31 For convenience in MultiWell, the total vibrational energy is
measured from the reaction critical energy (U = E - E0r), and kqIVR(U) is expressed as a
polynomial:
kIVR
qU
CIVR,1 CIVR,2UCIVR,3U2
(4.1-8)
Parameter
ivr is a characteristic frequency for IVR (identified by Leitner and Wolynes26
as the imaginary frequency for an isomerization reaction) and parameter kcIVR is the bimolecular
collision rate constant (expressed in units of cm3 s-1) for collision-induced IVR. A threshold for
IVR must also be specified: tIVR, which in MultiWell is measured from the reaction critical
energy. It can be used in cases where there is a sudden on-set of kIVR(U) at the threshold,
followed by a quadratic increase with energy. The specific unimolecular rate constant as
modified by IVR is finally given by the product of the transmission coefficient
ivr(E,[M]) and
148
the specific rate constant kRRKM(E) calculated using RRKM theory, where E is the total
vibrational energy measured from the zero point energy of the reactant, as usual:
k E,M
IVR E,M
kRRKM E
(4.1-9)
The resulting specific (energy dependent) unimolecular rate constant depends on pressure, as
indicated.
Using the Leitner-Wolynes model for IVR, simulations of data for trans-stilbene
isomerization are in very good agreement with a large body of experimental data.26, 31 They
indicate that collision-induced IVR occurs with a rate constant (kcIVR) similar in magnitude to the
total collision rate constant kq calculated using the method developed by Durant and Kaufman32
(see the next section).
Tunneling: Unsymmetrical Eckart Barrier
[NOTE: for a far more sophisticated treatment of tunneling, see Semi-Classical Transition
State Theory (SCTST) in Chapter 7 and Appendix B.9.]
(This section on Eckart Tunneling contributed by Philip J. Stimac.)
Quantum mechanical tunneling corrections to the microcanonical rate constants k(E)
have been implemented in MultiWell using a one dimensional unsymmetrical Eckart barrier.33
The modification of k(E) within MultiWell is accomplished by evaluating the sum of states of
the transition state according to Eq. 9 of the paper by Miller34:
N(E)P(E1)N'(EE1)dE1
Vo
EVo
(4.1-10)
where
Vo
is the classical barrier height (in the direction of the forward reaction);
E1
is the energy
in the reaction coordinate, relative to the top of the energy barrier;
E
is the total energy;
N'(EE1)
is the density of states at energy
(EE1)
;
P(E1)
is the tunneling probability:
P(E1)sinh(a)sinh(b)
sinh2((ab) / 2)cosh2(c)
(4.1-11a)
a4
h
i
E1Vo
(Vo
0.5 V1
0.5 )
(4.1-11b)
b4
h
i
E1V1
(Vo
0.5 V1
0.5 )
(4.1-11c)
c2
VoV1
(h
i)21
16
. (4.1-11d)
In these equations,
i and V1
are the imaginary frequency (related to the curvature of the saddle
point on the potential energy surface at the transition state) and the classical barrier height
149
relative to the products, respectively. The tunneling corrections to the sum of states of the
transition state were applied using Eqs. (4.1-10) and (4.1-11) after transforming the integral in
Eq. (4.1-10) to the expression
N(E)P(EVoE†)N'(E†)dE†
0
E
. (4.1-12)
E†
is the energy in the vibrational modes orthogonal to the reaction coordinate and the quantity
(EVoE†)
is the energy in the reaction coordinate. The primary difference between Equation
(4.1-12) and Equation (4.1-10) is that the zero of energy is chosen to be at the minimum of the
reactant in Equation (4.1-12), whereas the zero of energy is chosen to be at the transition state in
Equation (4.1-10). Numerical tests showed that Equation (4.1-12) reproduces Fig. 2 of Miller.34
Equation (4.1-12) is evaluated in the subroutine Eckart within MultiWell. The integral is
only evaluated at the grain energies. Evaluation of Equation (4.1-12) begins with all the energy
in the reaction coordinate. This means that the tunneling probability is at a maximum while the
density of states of the transition state is at a minimum. The integration continues until the
tunneling probability
P(EVoE†)
become less than some cutoff value ‘tunthresh’, which is
specified in the include file declare1.inc. The default value in declare1.inc is tunthresh=1.0E-12.
The k(E) calculated using the modified sums of states of the transition state reflect the
tunneling effects. These tunneling corrected k(E) are also used to calculate the high-pressure rate
constant
k
, and are used to initialize the chemical activation distribution if both the CHEMACT
and TUN keywords are selected. Please note that the TUN keyword cannot be used with the ILT
or RKE keywords.
150
References
1. W. Forst, Unimolecular rate theory test in thermal reactions, J. Phys. Chem. 76, 342-348
(1972).
2. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
3. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions.
(Blackwell Scientific, Oxford, 1990).
4. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
5. P. J. Robinson and K. A. Holbrook, Unimolecular Reactions. (Wiley-Interscience,
London; New York, 1972).
6. W. Forst, Theory of Unimolecular Reactions. (Academic Press, New York, 1973).
7. C. H. Townes and A. L. Schlalow, Microwave Spectroscopy. (McGraw-Hill, New York,
1955).
8. T. Baer and W. L. Hase, Unimolecular Reaction Dynamics. Theory and Experiments.
(Oxford University Press, New York, 1996).
9. M. Quack and J. Troe, Specific rate constants of unimolecular processes. II. Adiabatic
channel model, Ber. Bunsen-Ges. Phys. Chem. 78, 240-52 (1974).
10. D. W. Wardlaw and R. A. Marcus, RRKM reaction rate theory for transition states of any
looseness, J. Chem. Phys. 110, 230-4 (1984).
11. Y.-Y. Chuang, J. C. Corchado, P. L. Fast, J. Villà, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K.
A. Nguyen, C. F. Jackels, M. Z. Gu, I. Rossi, E. L. Coitiño, S. Clayton, V. S. Melissas, R.
Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar; POLYRATE-version 8.1;
University of Minnesota,, Minneapolis, MN, 1999.
12. S. J. Klippenstein, A. F. Wagner, S. H. Robertson, R. Dunbar and D. M. Wardlaw;
VariFlex Software; Argonne National Laboratory, 1999.
13. S. W. Benson, Thermochemical Kinetics. (Wiley, New York, 1976).
14. W. Forst, Temperature-dependent A factor in thermal unimolecular reactions, J. Phys.
Chem. 83, 100-8 (1983).
15. G. P. Smith and D. M. Golden, Application of RRKM Theory to Reactions
OH+NO2+N2⇌ HONO2+N2 (1) and ClO+NO2+N2 ⇌ ClONO2+N2 (2) - Modified Gorin
Model Transition-State, Int. J. Chem. Kinet. 10, 489 (1978).
16. E. Gorin, Photolysis of acetaldehyde in the presence of iodine, Acta Physicochim., URSS
9, 681 (1938).
17. J. R. Barker, L. L. Lohr, R. M. Shroll and S. Reading, Modeling the Organic Nitrate
Yields in the Reaction of Alkyl Peroxy Radicals with Nitric Oxide. II. Reaction
Simulations, J. Phys. Chem. A. 107, 7434-44 (2003).
18. D. M. Golden, J. R. Barker and L. L. Lohr, Master Equation Models for the Pressure- and
Temperature-Dependent Reactions HO + NO2 -> HONO2 and HO + NO2 -> HOONO, J.
Phys. Chem. A 107, 11057-11071 (2003).
19. J. R. Barker and N. F. Ortiz, Multiple-Well, multiple-path unimolecular reaction systems.
II. 2-methylhexyl free radicals, Int. J. Chem. Kinet. 33, 246–261 (2001).
20. I. Oref and B. S. Rabinovitch, Do Highly Excited Polyatomic Molecules Behave
Ergodically?, Acc. Chem. Res. 12, 166-75 (1979).
151
21. K. Bolton and S. Nordholm, Beats in internal vibrational energy redistribution in trans-
stilbene - A study of the quantum and classical correspondence, Chem. Phys. 207, 63-76
(1996).
22. K. Bolton and S. Nordholm, Classical trajectory study of collision induced intramolecular
energy transfer in trans-stilbene, Chem. Phys. 206, 103-128 (1996).
23. K. Bolton and S. Nordholm, A classical molecular dynamics study of the intramolecular
energy transfer of model trans-stilbene, Chem. Phys. 203, 101-126 (1996).
24. S. Nordholm and A. Back, On the role of nonergodicity and slow IVR in unimolecular
reaction rate theory - A review and a view, Phys. Chem. Chem. Phys. 3, 2289-2295
(2001).
25. M. Gruebele and P. G. Wolynes, Vibrational energy flow and chemical reactions, Acc.
Chem. Res. 37, 261-267 (2004).
26. D. M. Leitner, B. Levine, J. Quenneville, T. J. Martinez and P. G. Wolynes, Quantum
energy flow and trans-stilbene photoisomerization: an example of a non-RRKM reaction,
J. Phys. Chem. A 107, 10706-10716 (2003).
27. D. M. Leitner and P. G. Wolynes, Quantum energy flow during molecular isomerization,
Chem. Phys. Lett. 280, 411-418 (1997).
28. D. M. Leitner and P. G. Wolynes, Models of intramolecular energy redistribution
spanning deterministic and statistical approaches: Comparison with experiment -
Comment, ACH Models Chem. 134, 658-659 (1997).
29. D. M. Leitner and P. G. Wolynes, Many-dimensional quantum energy flow at low
energy, Phys. Rev. Lett. 76, 216-219 (1996).
30. J. R. Barker, N. F. Ortiz, J. M. Preses, L. L. Lohr, A. Maranzana and P. J. Stimac;
MultiWell-1.5.1 Software (Development version), Ann Arbor, Michigan, USA, 2005.
31. R. E. Weston, Jr. and J. R. Barker, On modeling the pressure-dependent
photoisomerization of trans-stilbene by including slow intramolecular vibrational
redistribution, J. Phys. Chem. A. 110, 7888-7897 (2006).
32. J. L. Durant and F. Kaufman, Calculation and use of total collision rates in thermal
systems, Chem. Phys. Lett. 142, 246-51 (1987).
33. C. Eckart, The Penetration of a Potential Barrier by Electrons, Phys. Rev. 35, 1303-9
(1930).
34. W. H. Miller, Tunneling Corrections to Unimolecular Rate Constants, with Application
to Formaldehyde, J. Am. Chem. Soc. 101, 6810-6814 (1979).

152
A.4.2 Pseudo-First-Order Bimolecular Reactions
In many practical systems, unimolecular and recombination reactions may be in
competition with bimolecular reactions involving the same vibrationally excited species.1 For
example, a vibrationally excited species (A*) produced by an exothermic reaction may both
undergo isomerization and react in a bimolecular reaction with another species (B), prior to
collisional deactivation. If B is present in great excess, the pseudo-first-order approximation is
applicable and one can define a pseudo-first order rate coefficient: kI = kbim[B], where kbim is the
bimolecular rate coefficient and [B] is the concentration of the reaction partner B, which is
present in great excess.
Prior to incorporation of this feature, Moriarity and Frenklach2 used MultiWell for
assessing several complicated reaction paths that may lead to aromatic ring formation in
combustion systems. They found that certain vibrationally excited intermediates persist for
relatively long periods and therefore bimolecular reactions between energized adducts and
gaseous partners may need to be included in future calculations.
The procedure for implementation of a pseudo-first-order competitive reaction in
MultiWell depends on whether it is assumed that kbim is independent of the energy distribution of
A*. In that case, kI can be calculated using the canonical bimolecular rate constant: kI = kbim[B].
This value for kI is then used to construct an external rate constant data file (with file name suffix
".rke"), which MultiWell will treat just like an ordinary unimolecular reaction. Centrifugal
corrections should not be employed for this reaction and the reaction should be treated as non-
reversible.
If it is assumed that the bimolecular rate constant depends on the vibrational energy
distribution of species A*, then an energy dependent expression for kbim(E) must be used. In
principle, this energy-dependent rate constant can be calculated from classical trajectories,
quantum scattering, or other dynamical theories. However, since MultiWell is for the most part
based on statistical theory, it is also appropriate to use microcanonical transition state theory.3, 4
Theory
The discussion in this section was adapted from our recent paper on reactions of acetyl radical
with O2.5 (Recently, Green and Robertson confirmed this approach and extended it more
generally.6)
Bimolecular reactions can be treated by using the bimolecular pseudo-first-order
microcanonical approach. The microcanonical bimolecular rate constant is given by
kbim (E)mAB
A
B
mAmB
AB
ge(AB)
ge(A)ge(B)
1
h
GAB
(EE0)
AB (E)
(4.2-1)
AB E
AEx
Bx
dx
0
E
(4.2-2)
where E+ is the total rovibrational energy, ρAB(E+) is density of states of the A+B supermolecule,
i.e. ρAB(E+) is the convolved density of states of the two reactants A and B, including all degrees

153
of freedom except for the three coordinates of the supermolecule center of mass. The factor
G‡AB(E+-E0) is the sum of states of the transition state. The other symbols (m, ge, and σ) have the
same meaning as in Eq. 4.1-1. Here, however, the 2D-rotors are assumed to be active and hence
are included with the K-rotor in calculating ρAB(E+) and G‡AB(E+-E0). The canonical bimolecular
rate constant can be calculated by averaging over the canonical energy distribution of the A+B
supermolecule:
kbim T
kbim (E)
AB (E)eE
RT dE
E0
Qtot (T)
(4.2-3)
where Qtot(T) is the total partition function of the supermolecule at temperature T:
Qtot T
AB (E)eE
RT dE
0
(4.2-4)
We assume that reaction occurs when two conditions are met: E+ is greater than the
reaction threshold energy and the translational energy is greater than zero. For present purposes,
we assume that the degrees of freedom of the supermolecule are partitioned into two groups. The
degrees of freedom (DOF) in Group 1 are associated with the vibrations and K-rotor of excited
species A* (i.e. the active DOF of species A) and all of the remaining DOF are collected in
Group 2. We also assume that the energy distribution of the Group 2 models is thermal, while the
energy of the Group 1 DOF is held fixed (adiabatic). Thus the total energy can be expressed as
E+ = E1 + E2. Note that other groupings can be postulated, depending on the system to be
simulated, and centrifugal corrections may be included in future work.
From the partitioning of the DOF, a semi-microcanonical bimolecular rate constant that
depends on E1 and T is obtained by averaging over the canonical E2 energy distribution:
kbim (E1,T)2
kbim (E1E2)
2(E2)
Elow
exp E2
kT
dE2
Q2(T)
(4.2-5)
where Elow is the lower limit to the integral (the larger of 0 or (E0 - E1)), ρ2(E2) is the density of
states for the Group 2 DOF of the supermolecule and Q2(T) is the corresponding partition
function:
Q2(T)
2(E2) exp E2
kT
0
dE2
(4.2-6)
The canonical bimolecular rate constant can be obtained from <kbim(Ev,T)>2 by averaging over
E1:
kbim T
kbim (E1,T)2
1(E1) exp E1
kT
dE1
0
Q1(T)
(4.2-7)
where ρ1(E1) and Q1(T) are the density of states and the corresponding partition function,
respectively, of the Group 1 DOF:
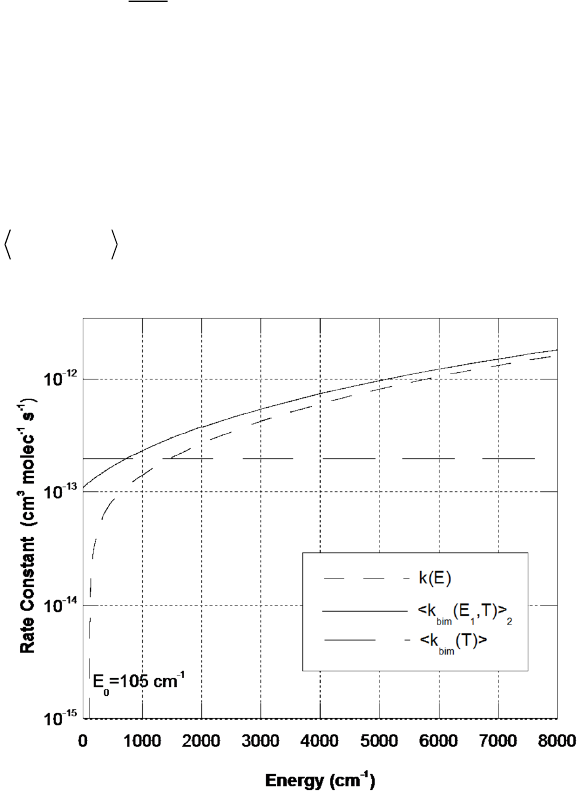
154
Q1(T)
1(E1) exp E1
kT
dE1
0
(4.2-8)
Numerical integrations of Eq. 4.2-3 and of 4.2-7, carried out by the trapezoidal rule, give
results at 300 K for the A2 + O2 reaction that agree to within ~1% when the energy grain is ≤5
cm-1.5
The semi-microcanonical pseudo-first order rate constant (units of s-1), which depends
only on the active energy of reactant A*, is obtained by multiplying <kbim(E1,T)>2 by [B], the
concentration of the reactant that is present in great excess:
kI(E,T)kbim (E1,T)2[B]
(4.2-9)
The rate constants <kbim(E1,T)>2, kbim(E1+E2), and <kbim(T)> are compared in Figure 4.2.5
FIGURE 4.2: A comparison of k(E), <kbim(E1,T)>2, and <kbim(T)> at T=298 K
for the reaction A2' + O2 → B1 [see reference 5 for details].
In order to treat competition between unimolecular and bimolecular pathways, kI(E,T) is
calculated and stored in an external data file, which is used as input to the MultiWell master
equation computer program. Group 1 consists of the active DOF in species A. Thus kI(E,T) can
be used directly in the master equation simulations as if it were an ordinary microcanonical rate
constant for a unimolecular reaction. Care must be taken, however, to treat it as an irreversible
reaction in MultiWell, since the detailed balance relations7 have been coded only for
unimolecular reactions. To include the reverse reaction would require using a theory for
partitioning energy between unimolecular reaction products8, 9 in order to obtain the energy
distribution in A (i.e. dissociation of the reaction product to regenerate A + B). Since such a
treatment has not been implemented in MultiWell, one should treat the bimolecular reaction as
irreversible. Treating such bimolecular reactions as irreversible may be a good approximation at
ambient temperature, but a poor approximation at combustion temperatures.
In master equation simulations, unimolecular reaction, bimolecular reaction, and
collisional deactivation of A* take place concurrently. Furthermore, the concentration of species
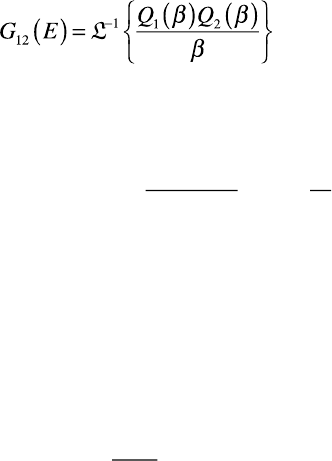
155
B determines both the rate of collisional deactivation and the rate of the pseudo-first-order
bimolecular reaction. Consequently, the importance of the microcanonical method is expected to
be significant only at low pressures. After A* is thermalized by collisions, the microcanonical
treatment coincides with the canonical approach.
DenSum Calculation
Using DenSum, it is easy to calculate the sum and density of states for the bimolecular
reaction. For the transition state, all vibrations, torsions, and external rotations should be
included in calculating the sum of states. The same is true in calculating the combined density of
states of A+B. In addition, the 3-dimensional relative translation between A and B must also be
included. Once again, centrifugal corrections should not be employed for this reaction and the
reaction should be treated as non-reversible in MultiWell.
DenSum first uses the analytic convolution of classical translational states with the
classical rotor states. The analytic expression for convolved classical trans-rot states is obtained
as follows. First, note that the classical partition function is the Laplace transform of the classical
density of states:10, 11 Q(β) = L[ρ(E)], where β is the Laplace transform parameter and can be
identified as β = (kBT)-1. The corresponding sum of states is G(E) = L-1[Q(β)/β], where the right
hand side is the inverse Laplace transform. Now consider a microcanonical system with total
energy E partitioned into two parts, the total sum of states is given by the convolution integral:11
G12 E
G1x
2Ex
dx
0
E
(4.2-10)
where G1(x) is the sum of states for the first group of degrees of freedom, which contain energy
x, and ρ2(E-x) is the density of states for the second group, which contain the remaining energy.
This convolution can also be expressed as an inverse Laplace transform:11
(4.2-11)
where Qi(β) is the partition function of the ith group of modes. For p independent classical
rotations, the partition function can be written11, 12
Qrot T
8
2IikBT
h2
di/2
di
2
i1
p
arkBT
r/2
(4.2-12a)
rdi
i1
p
(4.2-12b)
where di is the dimensionality of the ith rotation, Ii is its moment of inertia, and the other symbols
take their usual definitions.
For 3-D relative translation, the partition function can be written11
Qtrans T
2
µ
h2
3/2
V kBT
3/2 atkBT
3/2
(4.2-13)
where µ is the reduced mass and V is the volume. Therefore the total sum of states for combined
translation and rotation is obtained using Equation (4.2-11):
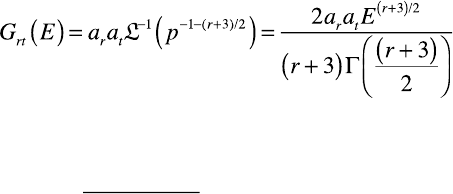
156
(4.2-14)
When no rotations are present, the sum of states is just the sum of translational states:4, 11
GtE
4
2
E
3/2
3h3V
(4.2-15)
These expressions are used by DenSum to calculate the number of states in each energy
bin when initializing the sums of states array, according to the Astholz et al.13 modification of the
Stein-Rabinovitch state-counting method.14
157
References
1. M. Olzmann, On the role of bimolecular reactions in chemical activation systems, Phys.
Chem. Chem. Phys. 4, 3614–3618 (2002).
2. N. W. Moriarity and M. Frenklach, Ab Inito Study of Naphthalene Formation by
Addition of Vinylacetylene to Phenyl, Proc. Combust. Inst. 28, 2563-2568 (2000).
3. R. A. Marcus, Chemical-Reaction Cross Sections, Quasiequilibrium, and Generalized
Activated Complexes, J. Chem. Phys. 45, 2138 (1966).
4. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics.
(Prentice-Hall, 1998).
5. A. Maranzana, J. R. Barker and G. Tonachini, Master Equation Simulations of
Competing Unimolecular and Bimolecular Reactions: Application to OH Production in
the Reaction of Acetyl Radical with O2, Phys. Chem. Chem. Phys. 9, 4129 - 4141 (2007).
6. N. J. B. Green and S. H. Robertson, General master equation formulation of a reversible
dissociation/association reaction, Chem. Phys. Letters 605, 44-46 (2014).
7. J. R. Barker, Multiple-well, multiple-path unimolecular reaction systems. I. MultiWell
computer program suite, Int. J. Chem. Kinet. 33, 232-245 (2001).
8. T. Baer and W. L. Hase, Unimolecular Reaction Dynamics. Theory and Experiments.
(Oxford University Press, New York, 1996).
9. C. Wittig, I. Nadler, H. Reisler, M. Noble, J. Catanzarite and G. Radhakrishnan, Nascent
product excitations in unimolecular reactions: The separate statistical ensembles method,
J. Chem. Phys. 83, 5581-5588 (1985).
10. W. Forst, Theory of Unimolecular Reactions. (Academic Press, New York, 1973).
11. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
12. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
13. D. C. Astholz, J. Troe and W. Wieters, Unimolecular processes in vibrationally highly
excited cycloheptatrienes. I. Thermal isomerization in shock waves, J. Chem. Phys. 70,
5107-16 (1979).
14. S. E. Stein and B. S. Rabinovitch, Accurate evaluation of internal energy level sums and
densities including anharmonic oscillators and hindered rotors, J. Chem. Phys. 58, 2438-
45 (1973).
158
A.4.3 Collisions
Frequency of Inelastic Collisions
It is conventionally assumed that the inelastic collision frequency is the same as that
experienced by molecules subject to a Lennard-Jones intermolecular potential. For the Lennard-
Jones potential, kc takes the following form:1
kc
2v2,2
*
(4.3-1)
where <v> is the average speed at the translational temperature, is the Lennard-Jones diameter,
and (2,2)* is the collision integral,2 which depends on the Lennard-Jones parameters. Since only
the product kcP(E,E') appears in the master equation, if kc is underestimated, then normalization
of the step-size distribution is not appropriate. If, on the other hand, kc is overestimated, then
P(E,E') must include elastic collisions.3 The inclusion of elastic collisions in the master equation
causes no problems in principle, except to reduce the efficiency of certain numerical solutions.
However, the fundamental question remains: is the frequency of inelastic collisions the same as
the Lennard-Jones collision frequency?
Lawrance and Knight4 used single vibrational level fluorescence and found that the
observed total cross sections for inelastic collisions are in quantitative agreement with the
Lennard-Jones collision frequency for a moderately high density of vibrational states. Classical
trajectory calculations support this assumption,5, 6 but the argument is somewhat circular in this
case since the assumed potential energy functions are often constructed from pair-wise Lennard-
Jones potentials. Recently, Xue et al.7 used quantum beat spectroscopy to investigate a single
vibrational level of SO2 at high vibrational energy, and found cross sections substantially greater
than predicted by the Lennard-Jones interaction potential. However, in the sparse density of
states regime at low vibrational energies it is well known that the inelastic collision cross section
is small8 and thus the total inelastic collision rate constant is probably smaller than kLJ.
A rigorous upper limit to kc is provided by the total collision rate constant kq, which is
based on the total quantum cross section. Because of concern about the proper choice of kc and
normalization of the step size distribution (see below), MultiWell provides an option for utilizing
the total collision rate constant, which can be estimated from Lennard-Jones parameters by using
the method of Durant and Kaufman.9
In a new development,10 it is now assumed in MultiWell that the rate constant for
inelastic collisions depends on the internal energy, reflecting the reduced rate constant for
inelastic collisions, which is expected at lower energies where the density of states is sparse. This
new development is described in the following section. (This new approach optionally can be
over-ridden by a keyword in the multiwell input file.)
Normalization
The rate coefficient R(x,y) is conventionally written as the product of the total
vibrationally inelastic collision frequency kc(y)[M] multiplied by the "collision step-size
distribution", P(x,y), which expresses the probability density that a molecule initially with initial
energy y will undergo an inelastic transition to the energy range x to x+dx:
159
R x,y
dx R x,y
dx
0
R x,y
dx R x,y
dx
0
, (4.3-2a)
kcy
P x,y
dx
(4.3-2b)
The first factor on the right hand side of Equation (4.3-2a), the integral over the rates of
all inelastic transitions from initial energy y, is the frequency of inelastic collisions, kc(y)[M] and
the second factor (in curly brackets) is P(x,y)dx. Note that P(x,y) is normalized:
P(x,y)dx 1
0
(4.3-3)
It is important to emphasize that the factorization of R(x,y) in Equation (4.3-2) is merely
for convenience and that kc(y)[M] and P(x,y) never occur independently of one another.
Furthermore, P(x,y) only has an unambiguous physical interpretation when kc(y)[M] is exactly
equal to the total inelastic collision rate constant. Since the exact inelastic collision frequency is
not known, the inevitable errors in kc(y) are compensated in part by errors in P(x,y), when
experimental data are fitted to this prescription. Thus it is important to use kc(y) and P(x,y) in a
matched pair whenever possible.11-13
By considering detailed balance at equilibrium in the absence of reactions, the
relationship between R(x,y) and R(y,x) can be found. Detailed balance requires that in every
increment of energy, the rates of forward and reverse processes must balance. The Detailed
Balance relationship between the probability densities for up- and down-collisions is given by
P x,y
P y,x
kcx
kcy
x
y
exp xy
/kBT
(4.3-4)
The total probability density for an energy changing collision is normalized (see Eq. 4.3-
3) and can be written as the sum of two integrals corresponding to down- and up-collisions:
1P x,y
dx
0
y
P x,y
dx
y
(4.3-5)
In order to construct a normalized collision step size distribution (the probability density), it is
common practice to specify a (dimensionless) non-normalized function f(x,y), which is assumed
to be proportional to P(x,y):
P x,y
f x,y
N y
(4.3-6)
where N(y) is a normalization constant. With this definition, the normalization equation becomes
1f x,y
N y
dx
0
y
f x,y
N y
dx
y
(4.3-7)
After rearranging this expression, we obtain a formal expression for the normalization constant
N(y), expressed as a sum of integrals:

160
N y
f x,y
dx
0
y
f x,y
dx
y
(4.3-8a)
Ndy
Nuy
(4.3-8b)
where subscripts d and u denote down-steps (x<y) and up-steps (x>y), respectively.
For convenience, the un-normalized function f(x,y) is usually specified for down-steps,
but one could choose to specify a function for up-steps instead. We will follow convention and
specify the function for down-steps, f(x,y) = fd(x,y) with x<y. Thus Nd(y) is easily evaluated:
Ndy
fdx,y
dx
0
y
(4.3-9)
and Nu(y) can be expressed in terms of fd(x,y) by the detailed balance relationship:
Nuy
fdy,x
N y
N x
kcx
kcy
x
y
exp xy
/kBT
dx
y
(4.3-10)
If we had assumed that f(x,y) was specified for up-steps, an analogous procedure would be
followed.
Since N(x) appears in the integral expression for Nu(y), the solution of Eq. 4.3-10 is not
completely straightforward. Normalization constant N(y) can be found by using trial values for
N(x) and employing an iterative solution14 of Eq. 4.3-10, or by rearranging the equation as
follows:
N y
fdx,y
dx
0
y
1fdy,x
N x
kcx
kcy
x
y
exp xy
/kBT
dx
y
(4.3-11)
Eq. 4.3-11 can be solved with the finite difference algorithm described by Gilbert and
coworkers 12, 15. Both of these approaches to finding N(y) are based on specifying fd(x,y) and
requiring that N(y) first be estimated at very high energies, well above the energies of interest,
where Nd(y) and Nu(y) tend to become independent of energy (at least when the average energy
transferred per collision is independent of energy).
As discussed in the previous section, kc(y) is expected to depend on the initial energy, y,
but it is common practice to assume that the inelastic collision rate constants are independent of
internal energy 13-16. This constant is conventionally identified with kLJ, the bimolecular rate
constant for collisions between particles governed by a Lennard-Jones intermolecular
potential.12, 13, 16 An accurate empirical expression for the collision integral has been reported by
Neufeld et al.17, which has been cited by, for example, Gilbert and Smith.12
Experience has shown that the assumption the kc is independent of energy leads to
problems with normalization.10 Iterative normalization14 converges reasonably rapidly at high
energies, but problems emerge at low energies, where the density of states is sparse and has large
relative fluctuations. The problems are most severe when an energy grain that contains just a few
states is bracketed on both sides by energy grains containing much higher densities of states. For
these cases, the normalization factors for some of the energy grains tend to diverge, instead of

161
converging during the iterative calculation. Because of this problem, it was necessary to limit the
number of iterations to e.g. 2-5, so that normalization at high energy converges sufficiently,
while normalization at low energy does not diverge too much. This strategy, although not
completely satisfactory, is reasonably effective in producing steady-state energy distributions
that simulate the equilibrium Boltzmann distribution.
Related problems arise at low energies when using the finite difference algorithm of
Gilbert and coworkers.12, 15 The Gilbert algorithm is quite general, but in practice the pragmatic
assumption is made that the collision frequency is independent of excitation energy. These
problems result in normalization constants that are negative and therefore un-physical in some
energy grains.
Starting with MultiWell v.2009.0, we have incorporated a new treatment of collisions that
solves the problems outlined above.10
In principle it should be possible to express kc(y) as a function of N(y), but the specific
functional dependence is not known. In the absence of specific knowledge about kc(y), we make
the simplest possible assumption: that kc(y) is directly proportional to N(y).10 With this
assumption, the following ratio, which appears in Eq. 4.3-10, equals unity
N y
N x
kcx
kcy
1
(4.3-12)
The assumption that kc(y) is directly proportional to N(y) requires that the collision frequency for
a molecule with excitation energy y be calculated using kc(y) = C•N(y) (see Eq. 4.3-12), where
the proportionality constant C must be established by some other means. Since the Lennard-
Jones rate constant kLJ conventionally has been used for calculating the low pressure limit of
unimolecular and recombination reactions, we have adopted the following form for the total
energy-dependent rate constant for the inelastic collision frequency:
N y
N x
kcx
kcy
1
(4.3-13)
where Eref is a reference energy.
In reaction studies, the rate of energy transfer is most important at energies near the
reaction critical energy. Thus we identify Eref with the critical energy of the lowest reaction
threshold energy (when multiple reaction channels are involved) that is higher in energy than the
energy boundary (parameter Emax1) between the lower and upper portions of the double array in
MultiWell. If no reaction threshold energies are below Emax1, we arbitrarily specify Eref as
equal to Emax1. At Emax1, N(y) is a relatively smooth function and the density of states is
typically >10-100 states/cm-1. Except at low energies, the numerical results obtained using this
new approach are nearly the same as those obtained using the old conventional approach.10
For convenience in the Monte Carlo selection of step sizes, both the normalization factor
N(E') and the probability of an activating collision P(E,E') =[Na(E')/N(E')] are stored in double
arrays for each well. At low state densities, P(E,E') exhibits random fluctuations and some
energy grains may contain no states, while the function is quite smooth at high energies. Since it
is desirable to be able to use arbitrary functions for the collision step size distribution, it is not
feasible to employ analytic expressions for the integrals in the normalization equation, which
would allow much shorter computer execution times. In fact, several approximate analytical
expressions were tested, but none was sufficiently accurate in the sparse density of states regime.
For this reason, normalization is carried out numerically using the open-ended trapezoidal rule,

162
which is a particularly robust algorithm.18 For low energies, the energy step size is set equal to
that used in the lower energy portion of the double arrays (∆Egrain). At higher energies, the
energy step size is set equal to a fraction (typically 0.2) of the magnitude of a characteristic
energy transfer step:
Edd(ln fd(E,
E))
dE
1
, for E' > E, (4.3-14a)
Ead(ln fa(
E,E))
dE
1
, for E' < E, (4.3-14b)
where fa(E,E') and fd(E,E') were defined above. For the exponential model,
Ed is equal to
(E),
which varies with internal energy. In general, both the characteristic energy length and the
integration step size vary with energy.
Collision Step-Size Distribution
Many step-size distribution models have been used in energy transfer studies and there is
still considerable uncertainty about the appropriate collision model and functional form of
P(E,E').1, 19, 20 Note that Pd(E,E') for de-activating collisions is expressed in terms of an un-
normalized function fd(E,E') and normalization factor N(E):
P
d(E,
E)1
N(
E)fd(E,
E)
for E' > E, (4.3-15)
To offer a wide selection, MultiWell includes a number of different optional functional
forms for fd(E,E'), including biexponential, Gaussian, Weibull distribution, etc. The best
information currently available suggests that a generalized exponential function is most
appropriate for deactivation steps:21
fd(E,
E)exp
EE
(
E)
, for E' > E, (4.3-15)
where
(E) is a linear function of vibrational energy, and
is a parameter that ranges from ~0.5
to ~1.5. The corresponding expression for activation collisions is obtained from detailed balance.
When the parameter
is less than unity, the wings of the step-size distribution have enhanced
relative probabilities that qualitatively resemble the bi-exponential distribution. When
=1,
Equation (4.3-15) gives the venerable exponential model.
Monte Carlo Selection of Step-Size
Two random numbers are used for selecting the collision step size. The first random
number selects activating, or deactivating collisions by comparison to the up-transition
probability Pup(E):
P
up (E)Na(E) / N(E)
up-transition probability (4.3-16)
0r3P
up (E)
, activating (4.3-16a)

163
P
up (E)r31
, de-activating (4.3-16b)
To select the step-size, the second random number is used with the cumulative
distribution for P(E,E') to find the final energy E, given initial energy E':14
r41
Na(
E)fa(x,
E)dx
E
E
, activating (4.3-17a)
r41
Nd(
E)fd(x,
E)dx
E
E
, de-activating (4.3-17b)
The integrals are evaluated by the trapezoidal rule, just as described in the preceding
section, until the equalities in Equation (4.3-17) are satisfied. In the high energy regime, this is
accomplished by integrating step-by-step until an integration step gives a value for the right hand
side of Equation (4.3-17) that is larger than r4. Linear interpolation is then used to find the value
of final energy E that satisfies the equality. In the low energy regime, the integration is carried
out step-by-step to find the energy step which gives the best agreement between the LHS and
right hand side of Equation (4.3-17). Note that the normalization integrals in the low energy
regime are stored in the lower energy portion of the double arrays. In the high energy regime, the
normalization integrals are found by interpolation of values stored the high energy portion of the
double arrays.
Occasionally, the normalization integrals are overestimated due to imperfect interpolation
and thus the equalities in Equation (4.3-17) cannot be satisfied. In such a case, the integral is
evaluated step-by-step until the additional partial sum is less than a selected relative error
(typically 10-6). This procedure yields an explicitly calculated value for the normalization
integral. The interpolated normalization integral is then replaced with this new value and the
energy step selection process is repeated. This procedure is somewhat cumbersome and
computationally intensive, but it was found to produce more accurate thermal distribution
functions.
References
1. D. C. Tardy and B. S. Rabinovitch, Intermolecular vibrational energy transfer in thermal
unimolecular systems, Chem. Rev. 77, 369-408 (1977).
2. J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids.
(Wiley, New York, 1964).
3. G. Lendvay and G. C. Schatz, Choice of gas kinetic rate coefficients in the vibrational
relaxation of highly excited polyatomic molecules, J. Phys. Chem. 96, 3752-6 (1992).
4. W. D. Lawrance and A. E. W. Knight, Collisional deactivation of a selected energy level
in S0 p-difluorobenzene embedded in a dense vibrational field: Absolute rate constants
for a variety of collision partners, J. Chem. Phys. 79, 6030-42 (1983).
5. A. J. Stace and J. N. Murrell, A classical trajectory study of collisional energy transfer in
thermal unimolecular reactions, J. Chem. Phys. 68, 3028-39 (1978).
164
6. L. M. Yoder and J. R. Barker, Quasiclassical Trajectory Simulations of Pyrazine-Argon
and Methylpyrazine-Argon van der Waals Cluster Predissociation and Collisional Energy
Transfer, J. Phys. Chem. A 104, 10184-10193 (2000).
7. B. Xue, J. Han and H.-L. Dai, Collision Relaxation Cross Section for Highly
Vibrationally Excited Molecules, Phys. Rev. Lett. 84, 2606-9 (2000).
8. J. T. Yardley, Introduction to Molecular Energy Transfer. (Academic Press, New York,
1980).
9. J. L. Durant and F. Kaufman, Calculation and use of total collision rates in thermal
systems, Chem. Phys. Lett. 142, 246-51 (1987).
10. J. R. Barker, Energy Transfer in Master Equation Simulations: A New Approach, Int. J.
Chem. Kinet. 41, 748-763 (2009).
11. W. Forst, Theory of Unimolecular Reactions. (Academic Press, New York, 1973).
12. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions.
(Blackwell Scientific, Oxford, 1990).
13. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
14. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
15. R. G. Gilbert and K. D. King, Gas/Gas and Gas/Wall Average Energy Transfer from
Very Low-Pressure Pyrolysis, Chem. Phys. 49, 367-375 (1980).
16. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
17. P. D. Neufeld, A. R. Janzen and R. A. Aziz, Empirical Equations to Calculate 16 of the
Transport Collision Integrals Ω(l, s)* for the Lennard‐Jones (12–6) Potential, J. Chem.
Phys. 57, 1100 (1972).
18. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in
FORTRAN. The Art of Scientific Computing. (Cambridge University Press, Cambridge,
1992).
19. J. R. Barker, L. M. Yoder and K. D. King, Feature Article: Vibrational Energy Transfer
Modeling of Non-Equilibrium Polyatomic Reaction Systems, J. Phys. Chem. A 105, 796-
809 (2001).
20. I. Oref and D. C. Tardy, Energy transfer in highly excited large polyatomic molecules,
Chem. Rev. 90, 1407-1445 (1990).
21. U. Hold, T. Lenzer, K. Luther, K. Reihs and A. C. Symonds, Collisional energy transfer
probabilities of highly excited molecules from kinetically controlled selective ionization
(KCSI). I. The KCSI technique: Experimental approach for the determination of P(E,E)
in the quasicontinuous energy range, J. Chem. Phys. 112, 4076-4089 (2000).
165
A.4.4 Other Processes
Additional processes can be incorporated into MultiWell calculations by using the
capability of reading rate constants from external data files.
Several processes have been neglected in the present version of MultiWell. For example,
spontaneous infrared emission1 by the vibrationally excited species, which is particularly
important at low pressure,2 has not been included. Similarly, stimulated emission, which is
important in laser-induced chemical reactions,3, 4 has also been neglected. Future versions of
MultiWell may include these processes, especially if the kinetics community expresses an
interest in them.
References
1. J. F. Durana and J. D. McDonald, J. Chem. Phys. 64, 2518 (1977).
2. J. R. Barker, Radiative Recombination in the Electronic Ground State, J. Phys. Chem. 96,
7361-7 (1992).
3. J. R. Barker, Infrared Multi-Photon Decomposition - a Comparison of Approximate
Models and Exact-Solutions of the Energy-Grained Master Equation, J. Chem. Phys. 72,
3686-3694 (1980).
4. D. M. Golden, M. J. Rossi, A. C. Baldwin and J. R. Barker, Infrared multiphoton
decomposition: photochemistry and photophysics, Acc. Chem. Res. 14, 56-62 (1981).
166
A.5. Initial Conditions
At the start of each stochastic trial, initial conditions must be specified. MultiWell selects
the initial energy via Monte Carlo selection techniques that are based on the cumulative
distribution function corresponding to a selected physical process. It is assumed that the reactant
is at infinite dilution in a heat bath and thus there are no temperature changes due to reaction
exothermicity or energy transfer. For most laboratory experiments, this is an acceptable
approximation.
A.5.1 Monte Carlo Selection of Initial Energies
Monte Carlo selection of the initial internal energy is carried out by equating random
number r5 to the cumulative distribution function Y0(E) corresponding to a given initial energy
density distribution y0(E'):
r5Y0(E)y0(
E)
0
E
d
E
(5.1-1)
where E' is the integration variable. In MultiWell, Y0(E) is found by rectangular rule in the lower
portion of the double array and by trapezoidal integration in the upper portion; the values are
stored as a function of initial energy in a linear array. Jsize (which user-selected) array elements
are used to cover the relevant energy range. For a thermal distribution (see below), the relevant
energy range is assumed to be ~20kBT. The Monte Carlo selection is carried out by interpolating
in the stored array to find the value of E at which Y0(E) = r5. Interpolation in this fashion is much
more computationally efficient than calculating the integral in Equation (5.1-1) for each
stochastic trial.
A.5.2 Optional Initial Energy Density Distributions
The initial energy density distributions that are included as options in MultiWell are
described here. In addition to these choices, there is also a provision for providing a user-defined
double array of Y0(E) values and for a delta function (which does not require Monte Carlo
selection). Examples of user-defined functions include prior distributions1-3 and energy
distributions that are the result of bond fission.4
Thermal Activation
In an ordinary thermal unimolecular reaction system that takes place at infinite dilution,
the translational and vibrational temperatures are equal and do not change during reaction
(Ttrans=Tvib). For shock wave simulations, it is assumed that Ttrans changed instantaneously when
the shock occurred and therefore is elevated at t=0, but Tvib remains at the temperature that
described the thermal system prior to the shock. Subsequent vibrational energy transfer collisions
cause the internal energy to increase. The only difference between shock tube and isothermal
simulations is that in the former, the two temperatures are unequal. In both cases, the initial
internal energy distribution function is a Boltzmann distribution characterized by Tvib. The
probability of the initial energy E falling in the range between E and E+dE is given by the
probability density function
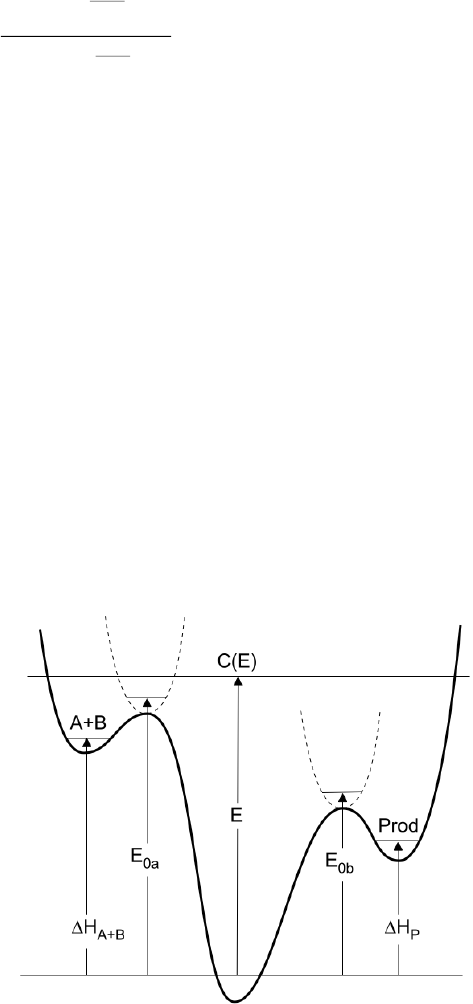
167
y0
(therm)(E)dE
(E)eE
kBTvib dE
(
E)eE
kBTvib d
E
0
(5.2-1)
Single Photon Photo-Activation
The energy distribution produced by absorption of a single photon is assumed to be
described by the thermal population at the ambient vibrational temperature added to the energy
of the photon (h
). Hence, the probability density function for photo-activation is given by
Equation (5.2-1) and the selected thermal energy is then increased by h
.
Chemical Activation and Recombination Reactions
Chemical activation is the process by which a single vibrationally excited species C(E) is
produced from the bimolecular reaction of two precursor species (A and B):
A + B C(E) (5.2-2)
where E is the vibrational energy. The excited molecule C(E) can then react by passing back out
of the entrance channel, or proceeding forward through the product channel, as shown in Fig.
5.1. The energy distribution of C(E) before it has a chance to react or be collisionally stabilized
is the known as the chemical activation distribution function. It is appropriate for any
recombination reaction that takes place under thermal conditions.
Figure 5.1. Energy diagram for chemical activation.
The chemical activation distribution function is obtained from the reverse reaction by
using detailed balance.5-9 The reverse reaction is the unimolecular decomposition reaction with
rate constant ka(E) that produces the product set A+B. The index a specifies the particular
unimolecular reaction channel C(E) → A + B. The resulting probability density function is a
thermal distribution weighted by ka(E). The probability density function and corresponding
Monte Carlo selection expression are as follows:
168
y0
(ca,i)(E)dE ka(E)
(E)eE
kBTvib dE
ka(
E)
(
E)e
E
kBTvib d
E
E0a
, for E ≥ E0a (5.2-3)
r5y0
(ca,i)(E)
E0a
E
dE
(5.2-4)
where the lower limits of the above equations are equal to E0a, the unimolecular reaction
threshold energy. The density of states ρ(E) is for the molecule C. The trapezoidal rule is used in
the selection procedure, as described above for thermal activation.
A recombination reaction produces a recombination product, which is a chemically
activated species. The chemically activated recombination product C(E) can react via the reverse
of Reaction (5.2-2), and possibly by other unimolecular pathways, in competition with
collisional energy transfer. Several quantities may be of interest, including branching ratios, net
rates of reaction to produce specific final products, etc. In all cases, the first step is to simulate
the reactions of the chemically activated recombination product C(E) under the desired
conditions of temperature and pressure. The results of the simulation can be used in various ways
to find the quantities of interest.10
The total rate constant for the recombination reaction at the high pressure limit is
obtained from detailed balance by using the equilibrium constant K(Ttrans) at translational
temperature Ttrans:
krec,kuni,/K(Ttrans )
(5.2-5)
where krec,∞ and kuni,∞ are the high pressure limiting recombination and unimolecular
decomposition rate constants, respectively; the latter of these is calculated and reported in the
MultiWell standard output. The equilibrium constant K(Ttrans) is calculated using the program
Thermo (part of the MultiWell computer program suite), which employs standard statistical
mechanics formulas11, 12 for the partition functions of the reactants A and B.
To calculate the over-all rate constant for producing the ith product, the relative
population (fraction) fi of that species at the end of the simulation is multiplied by krec,∞:
kfikrec,fikuni,/K(Ttrans )
(4.2-6)
This procedure is appropriate whether or not there is an intrinsic energy barrier for the
recombination reaction.
169
References
1. P. Urbain, B. Leyh, F. Remacle and A. J. Lorquet, Unimolecular reaction dynamics from
kinetic energy release distributions. III. A comparative study of the halogenobenzene
cations, J. Chem. Phys. 110, 2911 (1999).
2. P. K. Venkatesh, A. M. Dean, M. H. Cohen and R. W. Carr, Master equation analysis of
intermolecular energy transfer in multiple-well, multiple-channel unimolecular reactions.
I. Basic Theory, J. Chem. Phys. 107, 8904-16 (1997).
3. L. Vereecken, G. Huyberechts and J. Peeters, Stochastic simulation of chemically
activated unimolecular reactions, J. Chem. Phys. 106, 6564-6573 (1997).
4. W. Tsang, V. Bedanov and M. R. Zachariah, Master equation analysis of thermal
activation reactions: Energy-transfer constraints on falloff behavior in the decomposition
of reactive intermediates with low thresholds, J. Phys. Chem. 100, 4011-4018 (1996).
5. W. Forst, Theory of Unimolecular Reactions. (Academic Press, New York, 1973).
6. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
7. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions.
(Blackwell Scientific, Oxford, 1990).
8. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
9. P. J. Robinson and K. A. Holbrook, Unimolecular Reactions. (Wiley-Interscience,
London; New York, 1972).
10. J. R. Barker and N. F. Ortiz, Multiple-Well, multiple-path unimolecular reaction systems.
II. 2-methylhexyl free radicals, Int. J. Chem. Kinet. 33, 246–261 (2001).
11. N. Davidson, Statistical Mechanics. (McGraw-Hill Book Company, Inc., New York,
1962).
12. J. E. Mayer and M. G. Mayer, Statistical Mechanics. (John Wiley & Sons, Inc., New
York, 1940).
A.6. Input
A.6.1 Major Options
A.6.2 Densities of States:
(E)
Densities of states for the wells are provided in an external file (in the form of a double
array). DenSum is provided as a tool to calculate sums and densities of states according to the
Whitten-Rabinovitch approximation,1, 2 or according to the Stein-Rabinovitch method3 of exact
counts. Molecular assignments for use in the current version of DenSum can be expressed in any
combination of separable harmonic oscillators, Morse oscillators, and free rotors. For non-
separable degrees of freedom, other approaches will be needed (see references 4-6, for example).
The moments of inertia needed for calculating rotational constants are evaluated with the
170
program MomInert. This code requires Cartesian coordinates for the molecular structure. Such
structures can be calculated with good accuracy by using quantum chemistry programs.
A.6.3 Specific Unimolecular Rate Constants: k(E)
Specific rate constants are needed for each reaction. There are three ways to provide rate
constants: a) they may be calculated internally via the Inverse Laplace Transform (ILT) method,
b) the sums of states can be provided in an external file, and c) the k(E) values can be provided in
an external file. Data provided in an external file is in the form of a double array with energy
origin at the reaction threshold energy. The double array allows high energy resolution near the
reaction threshold where it is most important. For most purposes, it is most efficient to use
DenSum, which calculates sums of states (G‡(E-E0)) and generates an external file suitable for
input into MultiWell. However, Densum is only suitable for fixed transition states with separable
degrees of freedom and therefore other methods must be used to calculate G‡(E-E0) or k(E-E0)
for non-separable and flexible transition states. If the reaction is a reversible isomerization
reaction, MultiWell uses the same external data file to calculate k(E-E0) for both forward and
reverse reactions. By using the same external file for both forward and reverse reactions, the
reversible isomerization rates are internally self-consistent.
A.6.4 Properties of Wells and Transition States
Energies (e.g. ∆Hf° at 0 K) are required for all wells and transition states, in order to
establish the relative energies of isomers and reaction thresholds. Moments of inertia are needed
for the inactive degenerate two-dimensional external rotation. Energy transfer parameters are
needed for each well and MultiWell does not require that they be the same for all wells. One
would expect the energy transfer parameters for a cyclic species to differ from those of a linear
isomer. However, to the best of my knowledge the energy transfer parameters are not known for
more than one isomer in any system. Until additional information becomes available, it is
pragmatic to assume that all isomers have the same energy transfer parameters.
A.7. Output
MultiWell generates several output files that summarize the input data and the calculation
results.
A.7.1 multiwell.out
This general output file summarizes the input parameters, thermochemistry, high pressure
limit rate constants for each reaction, time-dependent average fractional populations (with
standard deviations from Equation (11)), and average vibrational energies. The time-dependent
quantities are the instantaneous (snapshot) values averaged over Ntrials stochastic trials: they are
not averaged over the time interval, as was done in previous master equation codes from this
laboratory.7-9
A.7.2 multiwell.rate
This file stores the time-dependent output of average unimolecular "rate constants" or
flux coefficients10-12 (which vary with time in non-steady-state systems) for every reaction
pathway:

171
rj(t)1
Ntrials
kj(Ei(t))
i1
Ntrials
(7.2-1)
where j designates the reaction channel. Many trials are needed to accumulate good statistics. To
improve statistics, the binned results correspond to the number of visits to the bin (which can be
many times larger than Ntrials) and thus are averaged over the time-duration of the bin. Note that
that this averaging method differs from the snapshot method described above, where the number
of snapshots is equal to Ntrials. In a steady-state thermal system with irreversible reactions, <r> is
independent of time and equal to the average unimolecular rate constant kuni(T), which obtains
when the energy distribution is in a steady state. In non-steady-state systems, <r(t)> varies with
time and relaxes to a constant value as the system itself undergoes relaxation. As relaxation takes
place, some reactions achieve steady-state, which is apparent as <r(t)> approaches a constant
value. Thus, this output file is useful for several purposes, including monitoring relaxation and
the approach to steady state.
A.7.3 multiwell.flux
This file stores the average time-dependent "reactive flux" through reaction channel j:
Fj(t) freact t
rj(t)
(7.1-2)
where freact(t) is the time-dependent average fraction of the reactant species and <rj(t)> is the
average flux coefficient described above by Eq. 7.2-1. When two reactions come into pseudo-
equilibrium with one another, their reactive fluxes are equal to each other. Thus, this output file
is useful for several purposes, including monitoring the evolution toward equilibrium and
diagnosing pseudo-equilibrium conditions.
A.7.4 multiwell.dist
This file stores time-dependent vibrational distributions within each well. Only the non-
zero array elements are tabulated. Many trials are needed to accumulate good statistics and thus
the binned results correspond to the number of visits to the bin (which can be many times larger
than Ntrials) and are averaged over the time-bin. To limit the size of this file, each (default) time
bin is set at ten times that of the time-bins used for the other time-dependent output.
A.7.5 multiwell.array
This file tabulates all energy-dependent input data, including densities of states, specific
rate constants for every reaction, collision up-transition probabilities and normalization factors,
and initial energy distributions.
A.8. Concluding Remarks
MultiWell calculates time-dependent concentrations, yields, vibrational distributions, and
rate constants as functions of temperature and pressure for unimolecular reaction systems that
consist of multiple stable species and multiple reaction channels interconnecting them. Users
may supply unimolecular reaction rates, sums of states and densities of states, or optionally use
the Inverse Laplace Transform method. For weak collision effects, users can select different
collision models for down-steps including exponential, biexponential, generalized exponential,
etc., and user-defined functions.
172
The code is intended to be relatively easy to use. It is designed so that even the most
complicated unimolecular reaction systems can be handled via the data file without restructuring
or recompiling the code.
MultiWell is most suitable for time-dependent non-equilibrium systems. The real time
needed for a calculation depends mostly upon the number of collisions during a simulated time
period and on the number of stochastic trials needed to achieve the desired precision. For slow
reaction rates and precise yields of minor reaction products, the code will require considerable
computer time, but it will produce results. For long calculation runs, we often just let the
simulation run overnight or over a weekend.
173
References
1. G. Z. Whitten and B. S. Rabinovitch, Accurate and Facile Approximation for Vibrational
Energy‐Level Sums, J. Chem. Phys. 38, 2466 (1963).
2. G. Z. Whitten and B. S. Rabinovitch, Approximation for Rotation—Vibration Energy
Level Sums, J. Chem. Phys. 41, 1883 (1964).
3. S. E. Stein and B. S. Rabinovitch, Accurate evaluation of internal energy level sums and
densities including anharmonic oscillators and hindered rotors, J. Chem. Phys. 58, 2438-
45 (1973).
4. J. R. Barker, Sums of Quantum States for Non–Separable Degrees of Freedom:
Multidimensional Monte Carlo Integration, J. Phys. Chem. 91, 3849-54 (1987).
5. B. M. Toselli and J. R. Barker, Symmetry Specific Densities of Rovibrational Energy
Levels for Nonseparable Systems, J. Phys. Chem. 93, 6578-81 (1989).
6. B. M. Toselli and J. R. Barker, Ro-vibrational State Densities Based on Spectroscopic
Data for Non-separable Systems, Chem. Phys. Lett. 159, 499-504 (1989).
7. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
8. J. R. Barker and K. D. King, Vibrational Energy Transfer in Shock-Heated Norbornene,
J. Chem. Phys. 103, 4953-4966 (1995).
9. J. Shi and J. R. Barker, Incubation in Cyclohexene Decomposition at High Temperatures,
Int. J. Chem. Kinet. 22, 187-206 (1990).
10. J. A. Miller and S. J. Klippenstein, Master Equation Methods in Gas Phase Chemical
Kinetics, J. Phys. Chem. A 110, 10528-10544 (2006).
11. B. Widom, Molecular Transitions and Chemical Reaction Rates, Science 148, 1555-1560
(1965).
12. B. D. Aguda and H. Pritchard, Reversible and irreversible formulation of unimolecular
reactions, J. Chem. Phys. 96, 5908-5914 (1992).
174

175
Appendix B. Technical Notes
B.1 Conversion Factors (Rotational Data)
Moment of Inertia (I):
I(amu Å2) = I(g cm2) / 1.66054
I(amu*Å2) = 16.85763 / B(cm-1)
I(amu*Å2) = 5.05385 / B(MHz)
I(amu*Å2) = 5.05382 / B(GHz)
Rotational Constant
B(cm-1) = B(Hz) / 2.997931010
B(cm-1) = B(MHz) / 2.997934
B(cm-1) = B(GHz) / 2.997931
B.2 Anharmonic Vibrations
Separable Anharmonic Vibrations
As described by Herzberg,1 ω (= ν/c, where ν is the harmonic frequency and c is the
speed of light) is used in the following expression for the vibrational energy, where s is the
number of separable oscillators, the vibrational energy Ev is expressed in units of cm-1 (relative
to the zero point energy Ez), and the other symbols have their usual meanings:
Evib
ivi1
2
i1
s
Xii
i1
s
vi1
2
2
(1)
where the zero point energy is given by
Ez1
2
i
i1
s
1
4Xii
i1
s
(2)
In DenSum and Thermo, vibrational anharmonicities can be entered directly for each
independent vibration. The energy of each oscillator is computed as
Evib = WE*(v+1/2) + ANH*(v+1/2)*(v+1/2), v=0,1,2,3,...
where parameter WE and ANH are the harmonic frequency and anharmonicity, respectively
(both expressed in cm-1 units). For a Morse oscillator, ANH < 0 for this convention. DenSum and
Thermo assume separable degrees of freedom, where inter-mode couplings are neglected. Thus
they can only consider the diagonal elements of the Xij anharmonicity coefficient matrix. Thus
parameter ANH is identified with the diagonal Xii element.

176
Because Densum and Thermo are limited to separable modes, various choices can be
made, depending on the information that is available. Sometimes the Xij anharmonicity
coefficients are available from experiments. They can also be computed as standard options by
electronic structure codes, although they are expensive to calculate. They are computed from a
perturbation theory treatment based on higher derivatives of the potential energy surface at the
equilibrium geometry. Thus they are closely related to the computed harmonic frequencies,
which are based on the 2nd derivatives of the same potential energy surface.
Possible Choices (in decreasing order of preference)
1. For densities and sums of states, treat the vibrations as non-separable. Use program
bdens instead of DenSum. See the next section.
2. If the fundamental (i.e. "observed") frequency and the full (or diagonal) Xij matrix are
known, one should use the fundamental frequency as "OBS" and the Xii diagonal term as
ANH.
3. If the harmonic frequency and the full Xij matrix are known, then one should first
compute the fundamental frequency and then use Choice #1.
4. If the harmonic frequency and the diagonal terms of the Xij matrix are known, then one
should use the harmonic frequency as "HAR" and the Xii diagonal term as ANH.
5. If the fundamental (i.e. "observed") frequency is known and the Xij matrix is not, then
one should use the fundamental frequency as "OBS" and ANH=0.0.
6. If the harmonic frequency is known and the Xij matrix is not, then one should use the
harmonic frequency as "HAR" and ANH=0.0.
7. If nothing is known, then one must use estimation methods.2
Non-Separable Anharmonic Vibrations
For asymmetric top molecules, the vibrational energy level relative to the zero point
energy is given by the following perturbation theory expansion for the vibrational energy:30,31,43
Ev Ez
i
i12
i1
N
Xij
i12
ji
N
i1
N
j12
Yijk
i12
j12
kj
N
ji
N
i1
N
k12
Zijkl
i12
lk
N
kj
N
ji
N
i1
N
j12
k12
l12
...
(3)

177
where
i is the harmonic oscillator frequency, Xij, Yijk, and Zijkl are the anharmonicity constants,
i is the vibrational quantum number, N is the number of vibrational modes, and Ez is the zero-
point vibrational energy, which is obtained by setting all
i = 0:
Ez1
2
i
i1
N
1
4Xij
ji
N
i1
N
1
8Yijk
kj
N
ji
N
i1
N
1
16 Zijkl
lk
N
kj
N
ji
N
i1
N
...
(4)
The array of harmonic frequencies () and the matrices composed of the anharmonicity
constants (X, Y, Z) can be either obtained from experiment or computed directly from first
principles, e.g. by quantum chemistry software packages equipped with VPT2. Note that the zero
point energy computed using VPT2 includes an additional small term, G0, which must be
included for high accuracy work. This term does not affect spectroscopic transitions, but it
should be included for kinetics and thermochemistry calculations.3, 4
When all quantized vibrational energy levels are known, sums and densities of states can
be counted exactly. From Eq. 3, all E can in principle be computed when all allowed values of
are known. Therefore, the problem reduces to finding all allowed values of
i up to a given total
internal energy. For a separable harmonic oscillator, all quantum numbers from
=0 to
=∞ are
allowed. A Morse oscillator, however, can dissociate and has only a finite number of vibrational
states ranging from
=0 to
=
max. The allowed quantum numbers therefore range from
=0 to
=
max. For a coupled set of anharmonic vibrations, the maximum quantum number allowed for
the kth vibration, vD,k, depends on the quantum numbers assigned for all other vibrations. When
the state energies are described by a perturbation theory expansion containing only X (i.e. Y and
Z = 0),
D,k can be found analytically27:
D,k
kXkj
j1
2
ji
2Xkk
1
2
(5)
It must be remembered that
D,k depends on all of the other quantum numbers. When Xkk<0, then
D,k is the quantum number for the highest bound level of the kth vibration and the corresponding
dissociation energy (relative to the zero point energy) of this vibrational mode is Dk:
Dk
kXjk
j1
2
jk
2
4Xkk
1
2
k1
4Xjk
jk
(6)
This dissociation energy corresponds to the energy at which E
reaches a maximum as
k is
increased, i.e. (∂Eυ/∂
k) = 0 at
k =
D,k.
While computing the sums of states from E
=0 to a maximum value E
=Etot, the range of
allowed quantum numbers is further restricted. Suppose one proceeds by first starting with all
quantum numbers set to zero and then assigning quantum numbers one at a time. After assigning
k-1 quantum numbers and before assigning the kth,
k=0 and the remaining unassigned energy Eu
is given by
EuEtot Ev,k1
(7)

178
where E
,k-1 is the vibrational energy E
computed using the k-1 quantum numbers already
assigned. The range of possible quantum numbers for the kth oscillator is therefore
k=0 to
max,k,
where
max,k depends on the amount of unassigned energy:
max,k
D,k
for Eu ≥ Dk (8a)
max,k
D,k11EuDk
for Eu ≤ Dk (8b)
When the Y and/or Z higher-order anharmonicities are included in Eq. 3, analytical
solution for
D,k is not obtainable and iterative calculations are necessary. In the present work,
max,k is computed iteratively by increasing trial values of
k by unit steps from 0 and monitoring
E
(
k) while all other quantum numbers (
i, i≠k) are held constant. The iterative procedure stops
as soon as E
(
k) becomes smaller than E
(
k-1). This decrease corresponds to passing the
maximum where (∂E
/∂
k) = 0. For a state to be "bound" with respect to the kth degree of
freedom, the derivative must be greater than zero for the trial value of
k: (∂E
/∂
k)>0. This
process is repeated by increasing
k until the (∂E
/∂
k)<0 for a trial value of
k. The assignment
of
D,k is then based on the sign of the first derivative (∂E
/∂
k) at
k-1 (see Figure 1), which
enables one to ensure that the state with
D,k is lower in energy than the classical maximum E
.
When (∂E
/∂
k) is >0 at
k-1, then
D,k =
k-1; otherwise,
D,k is set equal to
k-2.
At energies above the dissociation limit, quasi-bound states exist, where the quantum
number for every mode does not exceed the dissociation limit for that particular mode. Of
course, if the energy is redistributed, dissociation can take place. For computing RRKM rate
constants, quasi-bound states must be counted. Quasi-bound states are identified when the partial
derivatives (∂E
/∂
i)>0 for all i. Therefore, after all quantum numbers 5 have been assigned, the
partial derivatives [∂E
/∂
i]i=1,N are computed and the assigned [
i]i=1,N is accepted if all elements
are positive; otherwise the state is rejected.
References
1. G. Herzberg, Molecular Spectra and Molecular Structure. II. Infrared and Raman
Spectra. (Van Nostrand Reinhold Co., Cincinnati, 1945).
2. S. W. Benson, Thermochemical Kinetics. (Wiley, New York, 1976).
3. D. G. Truhlar and A. D. Isaacson, Simple perturbation theory estimates of equilibrium
constants from force fields, J. Chem. Phys. 94, 357-359 (1990).
4. M. J. Cohen, N. C. Handy, R. Hernandez and W. H. Miller, Cumulative reaction
probabilities for H + H2 = H2 + H from a knowledge of the anharmonic force field,
Chem. Phys. Lett. 192, 407-416 (1992).
5. T. C. Allison, B. Ramachandran, J. Senekowitsch, D. G. Truhlar and R. E. Wyatt,
Variational transition state theory calculations of thermal rate coefficients for the O(P-
3)+HCl reaction, Theochem-Journal of Molecular Structure 454, 307-314 (1998).
179
B.3 Vibrational Degeneracies
In DenSum and Thermo, vibrational degeneracies are treated as accidental. Identical
results are obtained if each vibrational degree of freedom with degeneracy NG is entered in the
data file NG times as a non-degenerate vibration.
For Harmonic oscillators, the state energies for accidental degeneracies are exactly the
same as for true degeneracies that arise, for example, from symmetry considerations. For
anharmonic vibrations, the state energies are no longer quite the same for accidental and for true
degeneracies, but the differences are small and can be neglected for most kinetics purposes.
[G. Herzberg, "Infrared and Raman Spectra", D. van Nostrand Co., Inc., 1945, p. 210 ff]
B.4 External molecular rotations
All non-linear polyatomics have principal moments of inertia IA, IB, IC and corresponding
rotational constants A = ħ2/2IA, etc. When two of the rotational constants are equal to each other,
the molecule is termed a symmetric top. Otherwise, it is an asymmetric top.
Symmetric Tops
In Eq. (1a) for the rotational energy of a symmetric top (e.g. a prolate top with rotational
constants A ≠ B = C):
ErJ,K
BJ J 1
(AB)K2
(1a)
where quantum number J is for the total angular momentum and the quantum number K is for
the projection of the total angular momentum on the symmetry axis of rotation. The first term in
Eq. 1a is identified with a two-dimensional (2D) rotor that is often loosely assumed to be most
responsible for conservation of angular momentum: a 2D adiabatic rotation referred to as the "J-
rotor". In the same spirit, the second term in Eq. 1a is loosely identified with a 1D rotation
about the top axis: the "K-rotor". For a rigid symmetric top molecule, the K quantum number is
constrained to take integer values from -J to +J. Thus each energy level with |K|≠0 is doubly
degenerate and those with K=0 are singly degenerate. Because the rotational constants may also
be related as A = B ≠ C (e.g. an oblate top), it is convenient to identify the unique rotational
constant as B1 and the twinned rotational constant at B2:
ErJ,K
B2J J 1
(B1B2)K2
(1b)
Note that it is also required that Er(J,K) must be ≥0 (this becomes an issue for oblate symmetric
tops, as discussed below).
Separable Rotors Approximation for Symmetric Tops
In a symmetric top, the J-rotor and the K-rotor are coupled, due to the constraint on the K
quantum number: –J ≤ K ≤ +J. It is often more convenient to ignore the constraint and treat the
two rotors as separable. In fact, centrifugal corrections (an option in MultiWell) require that the
rotors are treated as separable, without the constraint on K. Treating the two external rotors as a
separable 2D rotor with rotational constant B2 and a separable 1D rotor (the K-rotor) with

180
rotational constant B1 allows one to treat the K-rotor as "active" by including it with the
vibrations and internal rotations when computing the sums and densities of states (see the
following sub-section). However, there always exist 2J+1 rotational states with the same value of
J, even for a completely asymmetric top. Thus neglecting the restriction on K has the effect of
increasing the density and sum of states. Fortunately, this error is insignificant except for
molecules with small rotational constants at very low temperatures.
Current and Rabinovitch examined the separable-rotors approximation and showed that it
is reasonably accurate, especially when the following definitions are adopted: B2 = (BC)1/2, B1 =
A, and the rotational energy is given by:1, 2
ErJ,K
B2J J 1
B1K2
(3)
without any constraint on the value of K, except for energy conservation. The accuracy obtained
using this approximation is illustrated in Table 9.4. In the second column are canonical rate
constants for OH + CO → trans-HOCO computed using SCTST (Semi-classical Transition State
Theory; see Appendix B.9 of this Manual), including the proper constraint on the K quantum
number.3 In the third and fourth columns, the external rotors of the transition state were treated
with the separable rotors approximation and two choices for B1. It is clear that the separable
rotors approximation is quite accurate, especially for the choices B2 = (BC)1/2 and B2 = A.
Table 10.4. Bimolecular rate constants a for OH + CO → trans-HOCO computed using
three different treatments of the external rotors b
Properly Constrained
Separable Rotors Approximation
T(K)
-J ≤ K ≤ +J
BK = A
BK = A – B2D
200
4.517
4.496
4.642
300
8.201
8.191
8.453
500
17.25
17.29
17.84
1000
50.95
51.28
52.91
2000
146.0
147.6
152.3
a Units of 10-13 cm3 molecule-1 s-1.
b Rotational constants A, B, and C (cm-1): 3.6640, 0.2264, 0.2132; B2D = 0.2197 cm-1.
Asymmetric Tops
The rotational states of asymmetric tops cannot be calculated from a simple algebraic
formula, but partition functions and densities of states can be obtained conveniently to very good
accuracy by averaging the two rotational constants that are most similar to each other and
treating the asymmetric top as approximately symmetric. This is called the quasi-symmetric top
approximation. For this purpose, the effective rotational constant B2 for the J-Rotor is set equal
to the geometric mean of the two rotational constants that are most similar. For example, when B
≈ C and neither one is equal to A, the constant B2 = (BC)1/2. This is the same choice utilized in
the separable rotors approximation, which is quite accurate (see preceding paragraphs).
The difference between these two approximations is that in the quasi-symmetric top
approximation the K quantum number is restricted to the range -J ≤ K ≤ +J and the rotational
energy is constrained to non-negaive energies (Er(J,K) ≤ 0), while in the separable rotors
approximation the first of these constaints is abandoned. Both of these approximations are very
accurate for thermodynamics applications under most conditions. However, the separable rotors
181
approximation is utilized for making the centrifugal corrections to rate constants as described by
Marcus.4 This type of centrifugal correction is a user-selected option in the MULTIWELL master
equation code, as described elsewhere in this User Manual.
Note that treating the rotations in an asymmetric top as three separable 1D rotors is
NEVER correct, because the three external rotations are not independent of each other: they are
constrained by the total angular momentum. Thus treating the three rotors as independent 1D
rotations always leads to incorrect results. One should always use either the separable rotors
approximation or the quasi-symmetric top approximation for practical calcualtions.
Active Energy and the K-rotor
In a free molecule, only the total angular momentum is conserved. Thus the J quantum
number is assumed to be adiabatic (conserved), but the K quantum number can vary within its
constraints, as do the vibrational quantum numbers, subject to conservation of energy in the
"active" degrees of freedom. The "active energy" is the energy associated with the vibrational
quantum numbers and K, collectively. Thus it is said that the energy in the active degrees of
freedom randomizes, or the K-rotor energy "mixes" with the vibrational energy.
For a prolate symmetric top (e.g. a cigar shape), A>B and therefore B1 >0. For prolate
symmetric tops, the rigorous constraint -J≤K≤+J is often relaxed in the interest of more
convenient computation of densities of states. This popular approximation is reasonably accurate
except at the lowest total energies and is simple to implement because the rotational energy
Er(J,K) ≥0 for all values of J and K.
For an oblate symmetric top (e.g. disk-shaped), A<B and hence (A-B)<0; this can give
Er(J,K) <0 when the unconstrained K >> J. Thus the approximate treatment of the K-rotor may
fail seriously for oblate tops, since the term (A-B)K2 in Eq. 1b is <0. The Separable Rotors
Approximation avoids this issue, since the term B1K2 term in Eq. 3 is always >0.
To utilize the Separable Rotors Approximation in DenSum, Thermo, bdens, and
sctst, the K-rotor is declared as a simple 1D free rotation (type "rot" or "qro") and included with
the vibrational degrees of freedom when computing the density of states as a function of active
energy. Centrifugal corrections based on the B2J(J+1) term in Eq. 3 are applied separately in the
MultiWell master equation code: the 2D ADIABATIC ROTOR moment of inertia is listed in
data file multiwell.dat on Line 8 (for wells) or Line 14 (for transition states).
(The kro degree of freedom type employs the correct constraints on K for a single user-
specified value of J. Because it considers only a single value of J, it is not used for general
applications.)
If all degrees of freedom including the external rotations are assumed to be active (i.e.
"mixed" with the vibrations), no centrifugal corrects are to be applied in the multiwell master
equation code (use the NOCENT key word) and the "top" type of degree of freedom for
symmetrical tops can be utilized in densum, bdens, and sctst when calculating sums and densities
of states.
References

182
1. J. H. Current and B. S. Rabinovitch, Decomposition of Chemically Activated Ethyl-d3
Radicals. Primary Intramolecular Kinetic Isotope Effect in a Nonequilibrium System, J.
Chem. Phys. 38, 783-795 (1963).
2. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions. (Wiley,
Chichester, 1996).
3. T. L. Nguyen, B. Xue, R. E. Weston, Jr., J. R. Barker and J. F. Stanton, Reaction of HO
with CO: Tunneling is Indeed Important J. Phys. Chem. Letters 3, 1549–1553 (2012).
4. R. A. Marcus, Dissociation and isomerization of vibrationally excited species. III, J.
Chem. Phys. 43, 2658-61 (1965).
B.5 Symmetry numbers, internal rotation, and optical isomers
External Symmetry Numbers
For use in DenSum, MultiWell, and Thermo, we recommend the following convention
for symmetry numbers (described by Gilbert and Smith1): The EXTERNAL SYMMETRY
NUMBER should not contain any contribution from internal rotors and the external symmetry
numbers are not used in the calculation of sums and densities of states. INTERNAL ROTOR
SYMMETRIES are explicitly included in the data lines for the specific internal rotors (DenSum
and Thermo data files).
According to this convention, the EXTERNAL SYMMETRY NUMBER for Ethane is
3x2=6. The symmetry numbers for the external K-rotor and adiabatic 2-D-rotor are set equal to
unity in both DenSum and Thermo. (Of course the codes are flexible enough so that other self-
consistent conventions may be used instead.)
Hindered Internal Rotation
Internal rotors are characterized by both the symmetry of the potential energy (i.e. the
foldedness, or number of minima (and maxima) per 2 rotation), and the symmetry of the mass
distribution (or substituents) around the rotor. A potential energy surface computed using the
Born-Oppenheimer approximation is independent of the masses of the nuclei. The potential
energy surface for ethane internal rotation, for example, is 3-fold symmetric, but isotopic
substitution can give either unsymmetrical or symmetrical mass distributions. If both the PES
and the mass distribution have identical symmetries, then that is also the symmetry number of
the internal rotor. It is also the number of "indistinguishable minima"; the symmetry number
compensates for over-counting the number of indistinguishable minima when computing the
partition function:2
qhr 1
hr
exp Ei
kBT
i1
where σhr is the symmetry number for the hindered rotor and Ei is the ith energy eigenvalue.
MultiWell has provision in Thermo and DenSum for both symmetrical and
unsymmetrical hindered internal rotations. For user convenience, the parameters for
symmetrical hindered internal rotations may be entered in any one of three ways, designated
183
by degree of freedom types "hra", "hrb", and "hrc". These types assume that the reduced
internal moment of inertia is constant (independent of dihedral angle) and the potential energy of
the internal rotation is given by a simple cosine function:
V(
)U
21cos
hr
where U is the height of the hindrance barrier, and χ is the dihedral angle (for more complex
symmetrical potentials, use type "hrd", which is discussed below). If U = 0, then the internal
rotation should be modeled using a 1-D free rotor (types "rot" or "qro") with the symmetry
number for the internal rotation.
Types "hra", "hrb", and "hrc" offer three convenient methods for entering the
identical information. The information is identical because the harmonic frequency, hindrance
barrier height, and the reduced moment of inertia for a symmetrical 1-D hindered internal
rotation are related by the single equation:
t
hr
2
U
2Ir
1/2
where νt is the harmonic torsion frequency, U is the height of the hindrance barrier, and Ir is the
reduced moment of inertia. With any two of these quantities, the third is defined. Note that this
equation is only valid for σhr>1.
Unsymmetrical hindered internal rotations (σhr=1) are entered in Thermo and DenSum
by designating degree of freedom type "hrd", which is a general treatment, but especially useful
for unsymmetrical hindered internal rotations. Unsymmetrical rotation can be used to describe
internal rotation with just one well, or with two or more distinguishable wells. It can also be used
for symmetrical potentials with more complicated potential energy functions. To calculate the
internal rotor eigenvalues requires the potential energy function and the reduced moment of
inertia (or rotational constant) as a function of dihedral angle. For an example, see the data for
ClOOCl in the thermodynamics data base (directory multiwell/thermo-database/).
For convenience, three forms of the torsional potential energy are accepted by DenSum
and Thermo (all coefficients in units of cm-1) for using the General hindered internal rotation
treatment:
Type Vhrd1
V
Vn
21cos n
V
V
n1
N
Type Vhrd2
V
V0Vncos n
V
V
n1
N
Type Vhrd3
V
V0Vn
ccos n
V
V
n1
N
Vn
ssin n
V
V
n1
N
where χ is the dihedral angle (radians). The parameters σv (symmetry number for the potential
energy: SYMMV) and φV (phase angle for the potential: PHASEV (radians)) are merely for
convenience in curve-fitting.
184
Also for convenience, either the rotational constant or the moment of inertia, which are
functions of the dihedral angle, can be entered (all coefficients in units of cm-1).
Type Bhrd1 (all coefficients in units of cm-1)
B
B0Bncos n
B
B
n1
N
Type Ihrd1 (all coefficients in units of amu.Å2)
I
I0Incos n
I
I
n1
N
where χ is the dihedral angle (radians), σB and σI are symmetry numbers (SYMMM) and φB and φI
are phase angles (PHASEM). It is VERY IMPORTANT that the angles are defined in the same
way both for the potential and for the mass factor.
"hrd" Also Used for Symmetrical Internal Rotors. This degree of freedom type can also be
used for symmetrical hindered internal rotations. The rotor symmetry number (NG) must be
given, as well as coefficients for V(χ), which must have the same symmetry as the rotor
symmetry number (the parameter SYMMV may equal unity or a convenient multiple of NG; it is
only required that V(χ) have the correct symmetry). For an example, see the data for HONO2 in
the thermodynamics data base (directory multiwell/thermo-database/).
Optical Isomers
The classic example of an "optical isomer" (chiral stereoisomer) is methane substituted
with four unique atoms or isotopes. There is no internal rotation in this classic example, but
internal rotation can also produce optical isomers. For example, hydrogen peroxide has right-
handed and left-handed forms, which are identical in all respects except for their handedness.
The "gauche" structures of hydrocarbons may also be optical isomers. Consider the case of
ethane substituted with one deuterium on each carbon: CH2D-CH2D. This molecule has three
unique staggered conformers characterized by the D-C-C-D dihedral angle χ: right-handed
gauche with χ = +60°, left-handed gauche with χ = -60°, and a conformer with Cs symmetry at χ
= 180°. Usually (and maybe always), an internal rotation that connects optical isomers involves
an unsymmetrical rotor and therefore care must be taken to treat the optical isomers and
unsymmetrical hindered internal rotation in a mutually consistent fashion.
Consider, for example, hydrogen peroxide (H2O2), which has an internal rotation around
the O-O bond and two non-planar equilibrium structures,3 as shown below.
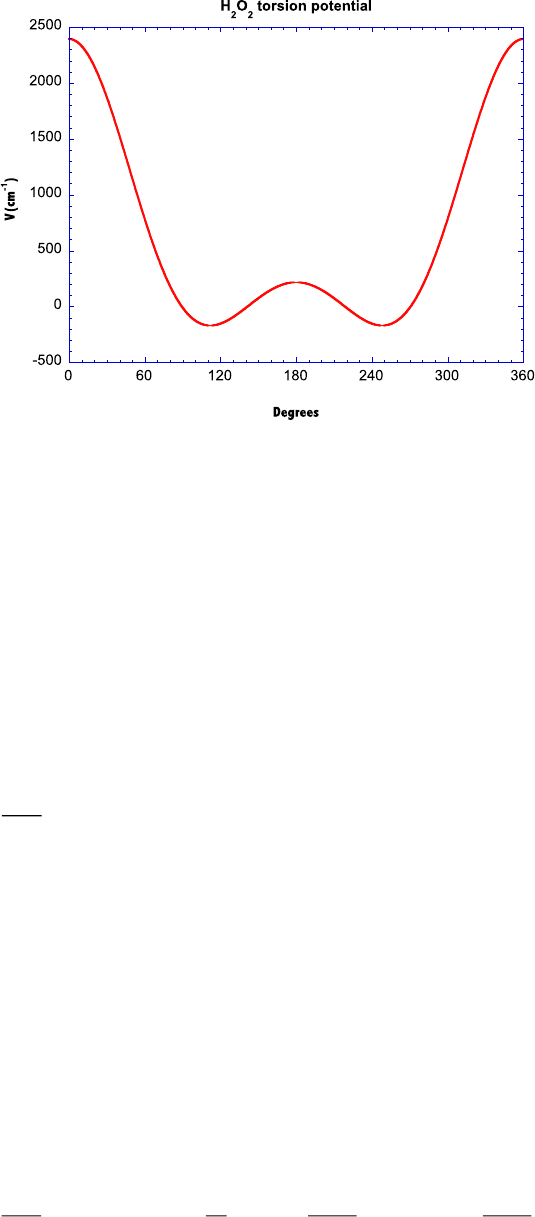
185
This V(χ) has symmetry number σv = 1. Over one full rotation, it has two wells of equal depth,
but the two maxima are of unequal height. Furthermore, the two wells are distinguishable
because their geometries cannot be superimposed by simple rigid external rotations: they are
optical isomers. Essentially, this is a double-well potential.
There are several ways of modeling this double-well potential. The simplest, but least
accurate way is to treat this double-well potential is to describe one well as a single harmonic
oscillator with harmonic frequency evaluated at the minimum and then multiply the sum of
states, density of states, or partition function by ×2, since there are twice as many states in a
double-well potential. In other words, the number of optical isomers (parameter m) is equal to
the number of wells and the exact partition function for this 1-D unsymmetrical hindered internal
rotation is being approximated as follows:
qhr exp Ei
kBT
i1
mqHO
and
hr E
m
HO E
where the harmonic oscillator partition function qHO (and density of states ρHO(E)) is calculated
using the harmonic frequency evaluated at the bottom of the well. Clearly, this approximation is
only acceptable when the lowest torsion barrier is >>kBT.
A second approximate method for treating these optical isomers is to treat the hindered
internal rotation as symmetric with σhr = m and an assumed hindrance barrier height or reduced
moment of moment of inertia Ir. Reasonable estimates for Ir at the equilibrium structure can be
obtained,4, 5 but this approximation cannot provide accurate results over the entire range of
temperatures, since it is not possible to approximate both barriers (and the angle-dependent
reduced moment of inertia) simultaneously. According to this method, the exact partition
function is approximated as follows:
qhr exp Ei
kBT
i1
mqshr m1
mexp Es,i
kBT
i1
exp Es,i
kBT
i1
186
hr E
m
shr E
where the "shr" subscript designates the symmetric hindered rotor, Ei are the exact
eigenfunctions for the unsymmetrical internal rotation, and Es,i are the eigenfunctions for the
symmetric rotor. Although not accurate over the entire temperature range, this approximation
performs slightly better than the harmonic oscillator approach at low to intermediate
temperatures.
In both of the above approximations, m (the number of optical isomers) is used as a
multiplier and must be entered in the MultiWell and Thermo input files.
The most accurate approach is to calculate the eigenvalues for the double-well potential
and use them directly in calculating the partition function for the hindered internal rotor. This is
done by specifying the "hrd" type of degree of freedom, entering the coefficients for the angle-
dependent potential energy function and angle-dependent reduced moment of inertia5 (or
rotational constant). For this calculation, m must be set equal to m = 1, since the resulting
partition function (and density of states) already has the requisite number of levels and should
not be multiplied by an additional factor. For example, see the data for HOOH in the
thermodynamics data base (directory multiwell/thermo-database/).
Of course, not all optical isomers are associated with hindered internal rotation. Those
optical isomers that are not associated with a hindered rotation should still be included in m and
entered in the data files.
Note that the external symmetry number is not affected by the hindered rotor treatment
and is the same for any treatment of internal rotation, including a harmonic oscillator
approximation. When CH2D-CH2D, HOOH, or any other unsymmetrical internal rotations are
treated using the "hrd" degree of freedom type (general hindered internal rotation), then usuers
should set the internal rotor symmetry to NG=1 and the number of optical isomers to m=1, but
the external molecular symmetry number should simply describe the over-all molecular
symmetry, which is not affected by the internal rotor treatment. Determining the external
symmetry number is usually easiest for the global minimum energy conformation.
Examples
σV: Potential
Symmetry
σM: Mass
Symmetry
σhr: Rotor
Symmetry
m: Optical
Isomers
External
Symmetry
CH3-CD3
3
3
3
1
3
CH3-CD2H
3
3
3
1
1
CH3-CDH2
3
3
3
1
1
CH3-CH3
3
3
3
1
6
CH2D-CH2D
3
1
1
2
2
CH2D-CD2H
3
1
1
2
1
CD3-CD3
3
3
3
1
6
HOOH
1
1
1
2
2
CHFClBr
—
—
—
2
1
187
References
1. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions.
(Blackwell Scientific, Oxford, 1990).
2. B. A. Ellingson, V. A. Lynch, S. L. Mielke and D. G. Truhlar, Statistical thermodynamics
of bond torsional modes: Tests of separable, almost-separable, and improved Pitzer-
Gwinn approximations, J. Chem. Phys. 125, (2006).
3. O. V. Dorofeeva, V. S. Iorish, V. P. Novikov and D. B. Neuman, NIST-JANAF
Thermochemical Tables. II Three Molecules Related to Atmospheric Chemistry: HNO3,
H2SO4, H2O2, J. Phys. Chem. Ref. Data 32, 879-901 (2003).
4. A. L. L. East and L. Radom, Ab initio statistical thermodynamical models for the
computation of third-law entropies, J. Chem. Phys. 106, 6655-73 (1997).
5. B. M. Wong, R. L. Thom and R. W. Field, Accurate Inertias for Large-Amplitude
Motions: Improvements on Prevailing Approximations, J. Phys. Chem. A. 110, 7406-
7413 (2006).

188
B.6 A Handy List of Lennard-Jones Parameters
Combining rules for Lennard-Jones parameters for A + B collisions:
AB 1
2(
A
B)
/kB
AB
/kB
A
/kB
B
1/2
Species
/ Å
/kB /K
Ref
Species
/ Å
/kB /K
Ref
He
2.5238
9.8725
1
C3F8
5.75
228
2
Ne
2.6016
75.748
1
c-C4F8
5.93
252
2
Ar
3.3237
143.78
1
C4F10
6.30
247
2
Kr
3.5160
207.44
1
C5F12
6.81
261
2
Xe
3.903
262.68
1
C6F14
7.17
265
2
H2
2.7828
63.997
1
C7F16
7.78
265
2
D2
2.73
69
2
C8F18
7.91
268
2
CO
3.70
105
2
CF3Br
4.92
249
2
N2
3.7047
84.942
1
CF3Cl
4.79
217
2
NO
3.49
117
2
CF2CCl2
5.08
276
2
O2
3.3920
121.74
1
CHClF2
4.30
331
2
CO2
3.94
201
2
CHCl2F
4.57
405
2
N2O
3.78
249
2
CHCl3
5.18
378
2
NO2
4.68
146
3
CHF3
4.04
268
2
"
3.46
357
4
CH2Cl2
4.54
458
2
H2O
2.71
506
2
CH3Br
4.31
416
2
N2O5
4.93
380
5
CH3Cl
4.07
373
2
NH3
2.90
558
6
1,1-C2H4Cl2
4.85
469
2
CH4
3.79
153
2
1,2-C2H4Cl2
4.78
503
2
C2H2
4.13
224
2
i-C3H7Cl
4.81
435
2
C2H4
4.23
217
2
t-C4H8Cl
5.23
455
2
C2H6
4.39
234
2
CS2
4.58
415
7
C3H6
4.78
271
2
SO2
4.11
336
3
c-C3H6
4.63
299
2
SF6
5.20
212
2
C3H8
4.94
275
2
C4H4N2 (Pyrazine)
5.35
307
8
1-C4H8
5.28
302
2
C2H4O (ethene oxide)
4.08
421
2
cis-2-C4H8
5.27
312
2
SiH4
4.08
208
9, 10
n-C4H10
5.40
307
2
SiH3
3.94
170
10
i-C4H10
5.39
298
2
SiH2
3.80
133
10
n-C5H12
5.85
327
2
SiH
3.66
95.8
10
neo-C5H12
5.76
312
2
Si
2.91
3036
9 10
C6H6
5.46
401
2
Si2H6
4.83
301
10
n-C6H14
6.25
343
2
Si2H5
4.72
306.9
10
c-C6H12
5.78
394
2
H3SiSiH
4.60
312.6
10
C7H8
5.92
410
2
H2SiSiH2
4.60
312.6
10
C7H16
6.65
351
2
Si2H3
4.49
318
10
C8H18
7.02
359
2
Si2H2
4.36
323.8
10
C9H20
7.34
362
2
Si2
3.28
3036
9, 10
C10H22
7.72
363
2
Si3H8
5.56
331
10
C11H24
8.02
362
2
Si3
3.55
3036
10
CF4
4.40
166
2
C2F6
5.19
201
2
189
References
1. A. B. Weaver and A. A. Alexeenko, J. Phys. Chem. Ref. Data 44, 023103 (2015).
2. H. Hippler, J. Troe and H. J. Wendelken, Collisional deactivation of vibrationally highly
excited polyatomic molecules II. Direct observations for excited toluene, J. Chem. Phys.
78, 6709-6717 (1983).
3. J. Troe, Theory of thermal unimolecular reactions at low pressures. II. Strong collision
rate constants. Applications, J. Chem. Phys. 66, 4758-4775 (1977).
4. R. Patrick and D. M. Golden, Int. J. Chem. Kinet. 15, 1189-1227 (1983).
5. M. W. Makko and J. Troe, Int. J. Chem. Kinet. 14, 399-416 (1982).
6. J. R. Barker and B. M. Toselli, Infrared Emission Studies of the Vibrational Deactivation
of Benzene Derivatives, Int. Rev. Phys. Chem. 12, 305-38 (1993).
7. F. M. Mourits and F. H. A. Rummens, A critical evaluation of Lennard-Jones and
Stockmayer potential parameters and of some correlation methods, Can. J. Chem. 55,
3007 (1977).
8. T. J. Bevilacqua and R. B. Weisman, Collisional vibrational relaxation of a triplet state:
Energy dependent energy loss from T1 pyrazine, J. Chem. Phys. 98, 6316 (1993).
9. R. A. Svehla, "NASA-TR 132," (NASA, 1962).
10. M. E. Coltrin, R. J. Kee and J. A. Miller, Electrochem. Soc. 133, 1206-1213 (1986).
190
B.7 Elements and Isotopes in MomInert and Thermo
The following atomic symbols (atom types) are recognized. Note that isotopic species
have the atomic mass associated with the name, except for Deuterium (D) and Tritium (T),
which are given their common symbols. Most atomic masses were taken from the "Table of the
relative atomic masses of the elements, 1981" [Pure Appl. Chem. 55, 1101 (1983)], which is
cited by JANAF/NIST.1 Isotopic masses were taken from N. E. Holden, "Table of the Isotopes
(Revised 1998)".2
Species
Atomic Mass
Species
Atomic Mass
H
1.00794
P
30.97376
H1
1.007825
S
32.06
D
2.014102
S32
31.9720707
T
3.016049
S33
32.97145876
He
4.00260
S34
33.9678668
Li
6.941
Cl
35.453
Li6
6.0151228
Cl35
34.96885271
Li7
7.0160046
Cl37
36.9659
Be
9.012182
Ar
39.948
B
10.81
K
39.0983
B10
10.0129
V
50.9415
B11
11.0093
Zn
65.38
C
12.011
Zn64
63.929
C12
12.0
Zn66
65.926
C13
13.003355
Zn68
67.925
C14
14.003242
Se
78.96
C16
16.0147
Se78
77.917
N
14.00674
Se80
79.917
N14
14.003074
Br
79.904
N15
15.00010897
Br79
78.918338
O
15.9994
Br81
80.916291
O16
15.994915
Kr
83.80
O17
16.9991315
Rb
85.4678
O18
17.999160
Sn
118.69
F
18.998403
I
126.9045
Ne
20.179
Te
127.60
Na
22.98977
Xe
131.29
Mg
24.305
Hg
200.59
Mg24
23.985
U
238.0289
Mg25
24.985
U235
235.04393
Mg26
25.983
U238
238.050788
Si
28.0855
Si29
28.98
Si30
29.97

191
B.8 Eigenstates for large amplitude motions
Energy eigenstates for large amplitude motions are needed for computing densities of
states and partition functions. In the MultiWell Program Suite, the eigenstates are computed by
solving the Schrödinger equation, as described here.
Theory
The Schrödinger equation for one-dimensional large-amplitude vibration separable from
all other motions in the molecule is written as follows3-6
2
2
q
1
Ieff
qV(q)
(q)E
(q)
(1)
where q is the vibrational coordinate, ħ is Planck’s constant, E and
are energy eigenvalue and
eigenvector, respectively. V(q) is the vibrational potential energy function, and Ieff is the effective
mass, which is in general a function of coordinate q, but which, depending on V(q), is sometimes
constant. Ieff can be derived from the ro-vibrational G matrix, which is defined as:3, 4, 7-9
GI X
XTY
1
(2)
where the I matrix is the 33 moment of inertia tensor, the Y matrix (NvibNvib) is the pure
vibration contribution, and the X matrix (3Nvib) corresponds to the vibration-rotation interaction
(Coriolis) terms. Here, Nvib is the number of vibration modes, which equals unity for a 1-D
separable degree of freedom. All elements of I, X, and Y can be computed from the molecular
structure as:
Ikk m
r
r
r
k
2
1
Natom
; k = x, y, or z (3a)
Ikk 'm
r
kr
k'
1
Natom
; k k’ (3b)
Xij m
r
r
qj
1
Natom
i
(4)
(5)
where the index runs on the number of atoms (Natom) in the molecule.
For one-dimensional large-amplitude vibrations, the ro-vibrational G matrix is expressed
as:
192
G
Ixx Ixy Ixz X11
Iyx Iyy Iyz X12
Izx Izy Izz X13
X11 X12 X13 Y11
1
(6)
By inverting the right hand side of eq. (6), one obtains:
G
g11 g12 g13 g14
g21 g22 g23 g24
g31 g32 g33 g34
g41 g42 g43 g44
(7)
Finally, Ieff is obtained as: Ieff = g44-1.
Note that in this work, central finite differences are used to compute the derivatives in
Eqs. (4) and (5). Thus the steps between adjacent positions (e.g. dihedral angles) must be small
enough so that the derivatives are sufficiently accurate. Acceptable step-sizes must be found by
trial and error.
Hindered internal rotations
For hindered internal rotations, the large-amplitude motions are torsional changes in
dihedral angles. The Schrödinger equation (1) for a 1-D torsion can be rewritten as follows6:
2
2
1
Ieff (
)
V(
)
(
)E
(
)
. (8a)
By defining the rotational constant
Bhr 2
2Ieff
, we obtain:
Bhr
V
E
(8b)
where χ is the torsional (dihedral) angle (0≤χ2), V(χ) is the torsional potential energy function,
and Ieff is the effective reduced moment of inertia. Both Ieff and Bhr are in general functions of
dihedral angle, but are constants for a rigid rotor. When Bhr is assumed to be a constant, which is
realistic only for symmetrical rotors, equation (8b) simplifies:
Bhr
2
2V
E
(9)
Solutions of equation (9) are not given here, but are well known.6, 10, 11
193
For the purpose of calculating densities of states and computing partition functions in the
MultiWell Suite, Eq. (8b) is diagonalized to obtain energy eigenvalues, whether or not Bhr is
assumed to be constant. The solutions are obtained by using the method described by Meyer.6
The Hamiltonian matrix of Eq. (8b) is given by:
H DBhrDVDTBhrDV
(10)
where D is the matrix of the first-order derivative (∂/∂χ) operator of the internal rotation angle,
DT is the transpose of D (i.e. DT(i,j) = D(j,i)), V(i,i) is the diagonal matrix of the potential energy
operator, and Bhr(i,i) is the diagonal matrix element of the rotational constant; the indices are for
equally spaced torsion angle grid points. For 2N +1 grid points, the elements of D are:
D i,i
0
(11a)
D(i,j) 1
ij2sin ij
/ 2N1
1
for i ≠ j(11b)
To construct the symmetric matrix H, one requires both V(χ) and Bhr(χ). Several common
representations of V(χ) and B(χ) (or the corresponding moment of inertia function I(χ)) can be
understood by MultiWell, as explained elsewhere in this manual. The matrix H is diagonalized in
order to obtain a vector of energy eigenvalues, which are convoluted with states from the other
degrees of freedom to compute ro-vibrational densities of states or partition functions.
Users must supply the functions V(χ) and Bhr(χ) (or moment of inertia function I(χ)).
Potential energies V(χ) and molecular geometries can be computed at discrete values of χ by
obtained by using any of the many available quantum chemistry codes, such as Gaussian,12 C-
Four,13, and Molpro.14. The results for V(χ) can be fitted to a suitable truncated Fourier series,
and one may use codes like the I_Eckart program15 (written for use with MatLab) or LAMM
program given in the MultiWell Suite to compute Bhr(χ) or Ihr(χ).
194
References
1. M. W. Chase, Jr., NIST-JANAF Thermochemical Tables. Fourth Edition, J. Phys. Chem.
Ref. Data Monograph No. 9, 1-1951 (1998).
2. D. R. Lide, CRC Handbook of Chemistry and Physics. (CRC Press, Boca Raton, 2000).
3. M. A. Harthcock and J. Laane, Calculation of kinetic energy terms for the vibrational
Hamiltonian: Application to large-amplitude vibrations using one-, two-, and three-
dimensional models, J. Mol. Spectros. 91, 300-324 (1982).
4. M. A. Harthcock and J. Laane, Calculation of two-dimensional vibrational potential
energy surfaces utilizing prediagonalized basis sets and Van Vleck perturbation methods,
J. Phys. Chem. 89, 4231–4240 (1985).
5. A. Meyer, J. Schroeder and J. Troe, Photoisomerization of trans-stilbene in moderately
compressed gases: Pressure-dependent effective barriers, J. Phys. Chem. A 103, 10528-
10539 (1999).
6. R. Meyer, Trigonometric Interpolation Method for One-Dimensional Quantum-
Mechanical Problems, J. Chem. Phys. 52, 2053-2059 (1970).
7. R. Meyer and H. H. Günthard, General Internal Motion of Molecules, Classical and
Quantum-Mechanical Hamiltonian, J. Chem. Phys. 49, 1510-1520 (1968).
8. H. M. Pickett, Vibration—Rotation Interactions and the Choice of Rotating Axes for
Polyatomic Molecules, J. Chem. Phys. 56, 1715-1723 (1972).
9. B. Podolsky, Quantum-Mechanically Correct Form of Hamiltonian Function for
Conservative Systems, Phys. Rev. E 32, 812-816 (1928).
10. C. C. Marston and G. G. Balint-Kurti, J. Chem. Phys. 91, 3571-3576 (1989).
11. D. T. Colbert and W. H. Miller, J. Chem. Phys. 96, 1982-1991 (1992).
12. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li,
H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M.
Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao,
H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J.
Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K.
Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.
M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R.
Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W.
Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J.
Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J.
Cioslowski and D. J. Fox; Gaussian 09, Revision A.1; Gaussian, Inc., Wallingford CT,
2009.
13. J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, w. c. f. A. A. Auer, R. J. Bartlett, U.
Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, M. Heckert, O.
Heun, C. Huber, T.-C. Jagan, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A.
Matthews, T. Metzroth, D. P. O'Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann,
S. Stopkowicz, J. Vázquez, F. Wang and J. D. Watts; and the integral packages
MOLECULE (J. Almlöf and P.R. Taylor); PROPS (P.R. Taylor); ABACUS (T. Helgaker,

195
H.J. Aa. Jensen, P. Jørgensen, and J. Olsen); and ECP routines by A. V. Mitin and C.
van Wüllen. CFOUR, a quantum chemical program package (http://www.cfour.de/),
2009; <Error! Hyperlink reference not valid..
14. H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G.
Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J.
Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. W. Meyer,
M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R.
Tarroni and T. Thorsteinsson; MOLPRO version 2006.1 (a package of ab initio
programs); see http://www.molpro.net., 2006; http://www.molpro.net.
15. B. M. Wong, R. L. Thom and R. W. Field, Accurate Inertias for Large-Amplitude
Motions: Improvements on Prevailing Approximations, J. Phys. Chem. A. 110, 7406-
7413 (2006).

196
B.9 Semi-Classical Transition State Theory (SCTST)
Much of this section was adapted from Ref. 1.
Program sctst uses a new algorithm1 developed for computing rate constants with
semi-classical transition state theory (SCTST), which was formulated by Miller and coworkers.2-
5 SCTST incorporates non-separable coupling among all degrees of freedom and multi-
dimensional quantum mechanical tunneling along the curved reaction path. The algorithm, which
is practical for reactants containing dozens of atoms, predicts both microcanonical and canonical
rate constants. In addition, the quantum chemistry code CFOUR has been extended to efficiently
compute fully coupled vibrational anharmonicities for transition states at the CCSD(T) level of
theory.
Semi-classical transition state theory (SCTST), has been described by W. H. Miller and
coworkers.2-5 In combination with second-order vibrational perturbation theory (VPT2),6 the
SCTST accounts explicitly for non-separable coupling among all degrees of freedom (including
the reaction coordinate) in the transition state region and multidimensional semi-classical
tunneling.4, 5 Miller, Handy and coworkers have shown that the SCTST thermal rate constants
are in close agreement with those of full quantum dynamic calculations and experiments.4, 7, 8
However, the SCTST method has been limited to small reaction systems having only 3-4 atoms
because of the large number of quantum states that must be computed for larger systems.4, 7, 8
The new computer code sctst makes it practical to apply the theory to polyatomic
reactions. The new algorithm is based on an extension of methods for computing sums and
densities of states for fully-coupled anharmonic vibrations, which were described recently.9 In
addition, an extension of the CFOUR electronic structure code 10 is described for computing the
anharmonicity constants of transition states at the CCSD(T) level of theory. This new extension
has enabled rate constant predictions based on a high level of theory.1
Theory
According to the SCTST of W. H. Miller and coworkers,4 the microcanonical and
canonical rate constants are written:
k(E)1
h
G‡(E)
(E)
(1)
k(T)1
h
G‡(E)exp(E/kBT)dE
Qre (T)
(2a)
where h is Planck’s constant, kB is Boltzmann’s constant, T is the temperature,
(E) is the density
of states of the reactant, Qre is the total partition function of the reactant(s), and G‡(E) is the
cumulative reaction probability (CRP).2. The center of mass translations are rigorously separable.
At temperatures that are not too high, it is a good approximation to treat the overall rotations as
separable from the vibrations (including internal rotations), so that Eq. (2a) can be written:
k(T)1
h
Qt
‡Qr
‡
QtQr
Gv
‡(Ev)exp(Ev/kBT)dEv
Qv(T)
(2b)

197
in which vibrational energy Ev is the variable of integration and the vibrational CRP is given by:
Gv
‡(Ev)... P
n(Ev)
nF10
nF20
n20
n10
(3)
In Eq. 3, F-1 is the total number of vibrational degrees of freedom orthogonal to the reaction
path. The semi-classical tunneling probability Pn is given by4
P
n(E)1
1exp[2
(n,E)]
(4)
where
(n,E)
E
F
2
114xFF E/F
2
(5)
EE VoGo
knk1
2
k1
F1
xij ni1
2
nj1
2
ji
F1
i1
F1
(6a)
F
FxkF nk1
2
k1
F1
with
F i
F
and
xkF ixkF
(7)
In these expressions,
k is the harmonic vibrational frequency,
F is the imaginary frequency of
the reaction barrier, xij are the anharmonicity constants that describe coupling among the
orthogonal degrees of freedom, xkF are the (pure imaginary) coupling terms between the reaction
coordinate and the orthogonal degrees of freedom, and xFF is the real-valued anharmonicity
constant for the reaction path, and Vo is the classical barrier height. [Note that the definition of
∆E used here and in a review article11 has the opposite sign from the definition given in the
original papers; this also affects the Eq. 5.] Note that ΩF is the amplitude of the effective
imaginary frequency, which is affected by coupling to all of the other vibrations (Eq. 7) and must
always satisfy ΩF > 0 for acceptable states; unacceptable states are discarded. The term G0 is a
constant, which is irrelevant in spectroscopic measurements (where only energy differences are
important), but which must be included for thermochemistry and kinetics.7, 12
For convenience, the reaction barrier height is often expressed as the difference between
the zero point energy of the transition state and that of the reactant(s) (i.e. the vibrationally
adiabatic ground-state potential energy difference VaG‡), giving the following expressions:
k(T)1
h
Qt
‡Qr
‡
QtQr
Gv
‡(Ev)exp(Ev/kBT)dEv
Qv(T)
(2c)
E Va
G‡EEv
‡
(6b)
Ev
‡
knk1
2
k1
F1
xij ni1
2
nj1
2
ji
F1
i1
F1
1
2
k1
4
k1
F1
xij
ji
F1
i1
F1
(8)
and Go is incorporated into the zero-point vibrational energy of the orthogonal modes:

198
Ezpe G01
2
k
k1
F1
1
4xij
ji
F1
i1
F1
(9)
There are three known scenarios where SCTST/VPT2 is not sufficient.11, 13 Two of these
scenarios start to be come important only at extremely high and extremely low energies and
temperatures. The third scenario becomes significant only at very high energies. None of these
scenarios significantly affects rate constants at the temperatures that are important for most
atmospheric and combustion applications.
Because the VPT2 approach is used, the SCTST/VPT2 model is subject to failures. In Eq.
(5), SCTST/VPT2 will fail catastrophically when the term becomes negative, or
1‒4𝑥𝐹𝐹∆𝐸/Ω2
𝐹]
. In such a case, the quadratic equation that governs the barrier penetration integral
Ω2
𝐹< 4𝑥𝐹𝐹Δ𝐸
has no physically meaningful solutions. Two possible scenarios lead to this failure: (i) First,
when (as is usually the case in calculations on real systems), it can happen when
E is
𝑥𝐹𝐹 < 0
less than and becomes negative (E < < 0). This case, which corresponds to
Ω2
𝐹/4𝑥𝐹𝐹 Ω2
𝐹/4𝑥𝐹𝐹
E values being “too negative”, occurs in the deep-tunneling regime below the TS, and
Wagner13 has given an extensive analysis of the problem, along with a suggested solution. When
this occurs in our implementation, Pn(E) is set to zero; (ii) Second, when (which is very
𝑥𝐹𝐹 > 0
uncommon), leading to E > > 0. This case, which corresponds to
E values being
Ω2
𝐹/4𝑥𝐹𝐹
“too positive”, can be seen in the high-energy regime above the TS. Our practical workaround to
this case is to set Pn(E) to unity.
The SCTST/VPT2 approach can also experience a third type of failure. When the energy
is high enough, the quantum numbers of the orthogonal degrees of freedom may be quite large.
If, in addition, the off-diagonal anharmonicities (i.e., the xkF terms) that couple the reaction
coordinate to the orthogonal modes are negative, ΩF may be reduced to zero, or even to negative
values (see Eq. 7). Since ΩF is the effective magnitude of the imaginary frequency, a reduced
value of ΩF suggests that the barrier thickness has increased and the probability of tunneling has
therefore decreased. When ΩF = 0, the barrier is essentially infinite and there is no tunneling. The
"negative omega" scenario (for ΩF ≤ 0) is considered to be unphysical: SCTST/VPT2 breaks
down because there is no effective maximum. Possibly a higher order of vibrational perturbation
theory can remedy this failure in future, but for present purposes a practical workaround is
needed for the "negative omega" scenario. Our practical approach is to regard the barrier is
infinitely thick if ΩF ≤ 0 and we thus assume in that case that the system behaves classically: the
tunneling probability Pn = 0 when ∆E ≤ 0, and Pn = 1 when ∆E > 0.
In the next section, the new algorithm for computing the CRP is presented. For canonical
(thermal) systems, Hernandez and Miller have described an efficient method for computing the
rate constants directly from SCTST without the necessity for computing the CRP.5 A small
modification of the new algorithm presented below can be used for this purpose, but will not be
described here because we are primarily interested in computing k(E), the microcanonical rate
constant, which requires the use of the CRP. However, with the CRP in hand, thermal rate
constants can easily be obtained by averaging k(E) over the thermal energy distribution function.
With minor extensions, the methods described here are also appropriate for computing k(E,J), the
microcanonical rate constant for a specified total angular momentum quantum number J.
199
New Algorithm
In Eqs. (1) and (2c), the CRP is obtained by summing over all states of the transition
state. When the state energies can be estimated from harmonic frequencies and anharmonicity
constants, the summations in Eq. 3 can be evaluated exactly. In this "exact count" method, a
realization of the vector [nk] of the vibrational quantum numbers is first determined for every
quantum state of the transition state and the CRP is obtained via nested DO-loops using Eqs. (3)-
(8). Such calculations are quite fast for systems with 3-4 atoms, but they become impossibly
slow for systems containing more atoms. The same obstacle is encountered when computing
densities of states for coupled vibrational states.9
Recently, three practical methods for computing vibrational sums and densities of states
were compared.9 These included the brute force direct method, an "efficient" Monte Carlo
method,14 and an extended version of the algorithm published by Basire et al.,15 which is based
on the Wang-Landau algorithm.16 The extended algorithm is particularly useful for large
molecular systems. As explained elsewhere,9 all three of the algorithms are based on a
perturbation theory expansion of the state energies expressed as functions of the vibrational
quantum numbers. (These algorithms are implemented in programs paradensum and bdens.)
A logical extension of these algorithms allows computation of the CRP.
According to SCTST, only
F in Eq. (7) and Ev‡ in Eq. (8) depend on the vector [nk] of
vibrational quantum numbers; all of the other quantities are constants. In the implementation of
the Wang-Landau algorithm,9 the energy axis is divided into many small grains (i.e. energy bins,
e.g. with δE=10 cm-1). The algorithm is a random walk procedure in which each step is accepted
or rejected, based on certain criteria. For each step that is accepted, a vector of quantum numbers
has been generated, which is accepted as long as each quantum number is not greater than the
highest bound state in each degree of freedom. This condition is evaluated by computing partial
derivatives of the state energy with respect to the quantum numbers, as described by Nguyen and
Barker 9. Acceptable states include the metastable states, which have total energies above the
dissociation energy (or reaction energy barrier), but do not have enough energy localized in the
reaction coordinate to react. These are the vibrational states of the transition state.
The density of states algorithm is carried out iteratively. During each iteration, each
energy bin that contains a vibrational state is sampled a large number of times. The relative
density of states estimate is up-dated on the fly and, after a series of iterations, it converges to the
exact relative density of states. After the relative density of states is normalized, the algorithm
terminates (see Ref. 9 for a detailed description). The CRP can be calculated by using the
vibrational density of states ρv‡(E) (which may have been computed previously) 9 and by
carrying out a single iterative cycle with the same stepping algorithm used for the density of
states calculation. On every accepted step into an energy bin,
F and Ev‡ are computed using the
vector of quantum numbers [nk]. From these quantities, average values and the corresponding
average probability are obtained by using Eqs. 4-7 for the ith energy bin at energy Ei: <
F>i =
Fi/Hi, < Ev‡>i = Ev‡i/Hi, and average probability <P(Ei)>, where Hi is the number of samples in
the ith bin. The averages become essentially independent of the number of samples for a
sufficiently large number (typically 104/bin). The algorithm accumulates samples in all of the
energy bins where acceptable states exist. If no acceptable states exist in a bin, then <P(Ei)>=0 in
that bin. Finally, the CRP is obtained by using the average probability multiplied by the number
of states in each energy bin (i.e. ρ(Ei)δE):

200
Gv
‡(Ev)
E
Ei
P Ei
i1
Ev/
E
(10)
Implementations
In the published bdens computer program for computing sums and densities of states,17
the number of samples in each energy bin is conveniently selected by specifying a key word:
FAIR, GOOD, BETTER, BEST, or EXTRA specifies 102, 103, 104, 105, or 106, samples per bin,
respectively. These key words are also used for specifying the number of samples used to
compute the average quantities defined above for the SCTST.
The accuracy of this new random walk algorithm was tested by comparing results
obtained using the new algorithm with those obtained from the exact count method (i.e. the
nested DO-loops method) for the OH + H2 reaction. For this reaction, the agreement between the
two approaches is excellent, as shown in Figure 1, when ≥104 samples/bin are used for
computing the averages. The differences between the "exact" CRP (obtained using explicit
nested DO-loops) and the ones based on the new algorithm are less than 5% even at the highest
energy (50000 cm–1), resulting in differences of <0.5% between the vibrational partition
functions at 2500 K for the transition state.
Program sctst (Section 8.3) generates a supplementary data filed named
<name>.qcrp, which is required when using program Thermo to compute thermal rate
constants using the SCTST. This data file contains the partition function corresponding to the
CRP.
Qv
‡T
v
‡(Ev)exp(Ev/kBT)dEv
0
kBT
1Gv
‡(Ev)exp(Ev/kBT)dEv
0
(11)
where ρ‡v(Ev) is the derivative of G‡v(Ev) with respect to Ev. The integral on the right hand side of
Eq. 11 is needed for Eq. 2c. The expression for Q‡v(T) is more convenient for use with program
Thermo.
VPT2/CCSD(T) for Transition States
All of the harmonic vibrational frequencies and xij anharmonicity coefficients can be
obtained for stable species from first principles by using second order vibrational perturbation
theory (VPT2), which has been implemented for stable molecules in quantum chemical software
packages such as GAUSSIAN 18 and CFOUR 10. The anharmonicity coefficients are obtained
from the full cubic force field together with the semi-diagonal quartic force field, which can be
computed by finite differences from the analytic first and second derivatives 10, 19. For highly
accurate methods such as CCSD(T), analytic second derivatives are only available in CFOUR 10.
For this work, VPT2 computation of the anharmonicities was implemented for transition states at
the CCSD(T) level of theory in CFOUR. Whenever Fermi resonances are detected,
deperturbation was applied using a criterion of 100 cm-1 for the frequency difference. The
combination of the new algorithm for the SCTST and implementation of VPT2 for transition
states constitutes an effective tool for computing the CRP and/or thermal rate constants from first
principles with high accuracy.
201
Reaction Critical Energy
In the absence of quantum mechanical tunneling, the critical energy E0 for a unimolecular
reaction (or a bimolecular reaction according to microcanonical TST) is the difference between
the enthalpies at 0 K of the transition state and the reactant(s):
E0 = ∆fHTS(0) - ∆fHreac(0) (12)
This definition of the reaction critical energy is not appropriate when quantum
mechanical tunneling occurs, because tunneling takes place at lower energies. Tunneling occurs
whenever the energy is below the top of the barrier (i.e. E < E0, where E0 is defined as above) but
above that of the zero point energy of the product. Thus when tunneling is included the
appropriate value to be utilized for "E0" depends on whether the reaction is endothermic or
exothermic (including zero point energy corrections), regardless of the reaction barrier height.
In the MultiWell master equation code, the critical energy is defined as in Eq. 12 even
when tunneling through an Eckart barrier is invoked (keyword 'tun' on Line 14 in the
multiwell.dat data file), because the reactant and product enthalpies are employed
automatically to account for tunneling below the top of the barrier. When using an external file
containing the CRP generated by Program sctst, this step is NOT automated and the user must
enter the value for critical energy obtained from the following:
Endothermic reactions: E0 = ∆fHprod(0) - ∆fHreac(0) (13a)
Exothermic reactions: E0 = 0 (13b)
(Note: the keyword 'tun' only applies to tunneling through an Eckart barrier and must NOT be
employed when using the CRP, since tunneling is already included in the CRP.)

202
References
1. T. L. Nguyen, J. F. Stanton and J. R. Barker, A Practical Implementation of Semi-
Classical Transition State Theory for Polyatomics, Chem. Phys. Letters 499, 9-15 (2010).
2. W. H. Miller, Semiclassical limit of quantum mechanical transition state theory for
nonseparable systems, J. Chem. Phys. 62, 1899-1906 (1975).
3. W. H. Miller, Semi-Classical Theory for Non-separable Systems: Construction of "Good"
Action-Angle Variables for Reaction Rate Constants, Faraday Discuss. Chem. Soc. 62,
40-46 (1977).
4. W. H. Miller, R. Hernandez, N. C. Handy, D. Jayatilaka and A. Willets, Ab initio
calculation of anharmonic constants for a transition state, with application to
semiclassical transition state tunneling probabilities, Chem. Phys. Letters 172, 62-68
(1990).
5. R. Hernandez and W. H. Miller, Semiclassical transition state theory, Chem. Phys. Lett.
214, 129-136 (1993).
6. I. M. Mills, "Vibration-Rotation Structure in Asymmetric- and Symmetric-Top
Molecules," in Molecular Spectroscopy: Modern Research, eds. K. N. Rao and C. W.
Mathews (Academic Press, New York, 1972), pp. Academic Press.
7. M. J. Cohen, N. C. Handy, R. Hernandez and W. H. Miller, Cumulative reaction
probabilities for H + H2 = H2 + H from a knowledge of the anharmonic force field,
Chem. Phys. Lett. 192, 407-416 (1992).
8. M. J. Cohen, A. Willetts and N. C. Handy, Cumulative reaction probabilities for OH +
H2 = H2O + H and ClH + Cl = Cl + HCl from a knowledge of the anharmonic force
field, J. Chem. Phys. 99, 5885-5897 (1993).
9. T. L. Nguyen and J. R. Barker, Sums and Densities of Fully-Coupled Anharmonic
Vibrational States: A Comparison of Three Practical Methods, J. Phys. Chem. A 114,
3718–3730 (2010).
10. J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, w. c. f. A. A. Auer, R. J. Bartlett, U.
Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, M. Heckert, O.
Heun, C. Huber, T.-C. Jagan, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A.
Matthews, T. Metzroth, D. P. O'Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann,
S. Stopkowicz, J. Vázquez, F. Wang and J. D. Watts; and the integral packages
MOLECULE (J. Almlöf and P.R. Taylor); PROPS (P.R. Taylor); ABACUS (T. Helgaker,
H.J. Aa. Jensen, P. Jørgensen, and J. Olsen); and ECP routines by A. V. Mitin and C.
van Wüllen. CFOUR, a quantum chemical program package (http://www.cfour.de/),
2009; <Error! Hyperlink reference not valid..
11. T. L. Nguyen, J. R. Barker and J. F. Stanton, "Atmospheric Reaction Rate Constants and
Kinetic Isotope Effects Computed Using the HEAT Protocol and Semi-Classical
Transition State Theory," in Advances in Atmospheric Chemistry, eds. J. R. Barker, A. L.
Steiner and T. J. Wallington (World Scientific, Singapore, 2017), pp. World Scientific.
12. D. G. Truhlar and A. D. Isaacson, Simple perturbation theory estimates of equilibrium
constants from force fields, J. Chem. Phys. 94, 357-359 (1990).
13. A. F. Wagner, Improved Multidimensional Semiclassical Tunneling Theory, J. Phys.
Chem. A 117, 13089−13100 (2013).
203
14. J. R. Barker, Sums of Quantum States for Non–Separable Degrees of Freedom:
Multidimensional Monte Carlo Integration, J. Phys. Chem. 91, 3849-54 (1987).
15. M. Basire, P. Parneix and F. Calvo, Quantum anharmonic densities of states using the
Wang-Landau method, J. Chem. Phys. 129, 081101 (2008).
16. F. Wang and D. P. Landau, Efficient, Multiple-Range Random Walk Algorithm to
Calculate the Density of States, Phys. Rev. Letters 86, 2050-2053 (2001).
17. J. R. Barker, N. F. Ortiz, J. M. Preses, L. L. Lohr, A. Maranzana, P. J. Stimac, T. L.
Nguyen and T. J. D. Kumar; MultiWell-2010.1 Software, Ann Arbor, Michigan, USA,
2010; http://aoss.engin.umich.edu/multiwell/.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman,
G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li,
H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M.
Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao,
H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J.
Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K.
Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.
M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R.
Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W.
Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J.
Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J.
Cioslowski and D. J. Fox; Gaussian 09, Revision A.1; Gaussian, Inc., Wallingford CT,
2009.
19. V. Barone, Anharmonic vibrational properties by a fully automated second-order
perturbative approach, J. Chem. Phys. 122, 014108 (2005).
B.10 Legacy and Current Versions of k0 and k∞ in MultiWell
Early in 2011 it was discovered that the centrifugal corrections had not been implemented
correctly. This affected the "informational" values if k0 and k∞ tabulated in the MultiWell output
files. This section summarizes the actual implementations. See Appendix Section 2.3 of this User
Manual for a summary of the theory.
Legacy Basis
Legacy expressions for kuni, k∞ and k0 were based on Robinson & Holbrook Eq. 4.30.1 In the
following, ω = k2[M] (in the notation of Robinson & Holbrook).
kuni Q1
Q1
1
Q2
exp E0/kT
EE0 EJ
kaEE0 EJ
eE/kT dE
kaEE0 EJ
0
where
kaEE0 EJ
L‡
h
G E
EE0 EJ
204
EJ1I
I
kT
G(E+) is the sum of states starting from the ZPE of the TS; L‡ is the reaction path degeneracy.
The limits:
kQ1
Q1
1
Q2
exp E0/kT
EE0 EJ
kaEE0 EJ
eE/kT dE
0
k0Q1
Q1
1
Q2
exp E0/kT
kLJ
EE0 EJ
eE/kT dE
0
As actually implemented in the Codes:
Multiwell-2011
CENT
kI
I
1
Q2
exp E0/kT
EE0 EJ
kaEE0 EJ
eE/kT dE
0
k0I
I
1
Q2
exp E0/kT
kLJ
EE0 EJ
eE/kT dE
0
NOCENT
kI
I
1
Q2
exp E0/kT
EE0
kaEE0
eE/kT dE
0
k0I
I
1
Q2
exp E0/kT
kLJ
EE0
eE/kT dE
0
For this case, E' = E0 + E+. Therefore:
kI
I
1
Q2
E
k
E
e
E/kT d
E
E0
k0I
I
1
Q2
kLJ
E
e
E/kT d
E
E0
205
Multiwell-2011.1 and later versions
'NOCENT' for no centrifugal correction
'CENT1' for quasi-diatomic centrifugal correction with 1 adiabatic external rotation
(for special cases)
'CENT2'(This is the usual choice for most reactins) for quasi-diatomic centrifugal
correction with 2 adiabatic external rotations
'CENTX' for legacy centrifugal correction with 2 adiabatic external rotations (not
recommended)
[Note: the calculated k∞ is numerically the same for all options.]
NOCENT
(These expressions differ from v.2011 by elimination of the factor I+/I.)
k1
Q2
E
k
E
e
E/kT d
E
E0
k01
Q2
kLJ
E
e
E/kT d
E
E0
CENT1, CENT2, and CENT3
Note: variable of integration; may be E+ or E'.
ka
E
I
Iexp EJ/kT
ka
E
k1
Q2
E
ka
E
e
E/kT d
E
E0 EJ
k01
Q2
kLJ
E
e
E/kT d
E
E0 EJ
CENTX
Here, x = E+.
kI
I
1
Q2
xE0 EJ
kaxE0 EJ
exE0
/kT dx
0
k0I
I
1
Q2
kLJ
xE0 EJ
exE0
/kT dx
0
206
References
1. P. J. Robinson and K. A. Holbrook, Unimolecular Reactions. (Wiley-Interscience,
London; New York, 1972).
207
Appendix C. How to …
This section outlines how to carry out various tasks needed by many users. It is under
development and more sections will be added in future releases of this User Manual.
C.1 How to set up the double arrays in MultiWell
The double arrays consist of two arrays in one. The lower energy portion ranges in
energy from E = 0 up to Emax1; the upper energy portion ranges in energy from E = 0 up to
Emax2. The total size of the double array is Isize and the number of "energy grains" (i.e.
energy bins) in the lower and upper parts of the double array are Imax1 and Imax2,
respectively, and the respective energy grain sizes are Egrain1 and Egrain2. The
relationships among these quantities are as follows:
Emax1 = (Imax1-1)*Egrain1
Emax2 = (Imax2-1)*Egrain2
Isize = Imax1 + Imax2
To set up double arrays, users must specify Egrain1, Imax1, Emax2, and Isize; the
remaining parameters are determined by the program from the relationships given above. The
following guidelines are useful for deciding on the values for the parameters.
Egrain1
Should be small enough so that further reductions in its size do not significantly affect the
numerical results (i.e. it should achieve numerical convergence).
Should be ~10% of kBT, or less (for good accuracy in computing k∞).
Should not be too small, since that adds a computational burden.
Typical choices: 5 or 10 cm-1 (usually 10 cm-1).
Imax1
Should be large enough so that the density of states in adjacent energy grains near
Emax1 differ by less than 5%. DenSum will give a warning if the grain-to-grain
fluctuations are too large.
Typically, Imax should be large enough so that Emax1 is greater than the highest
vibrational wavenumber (typically greater than ~3000 cm-1).
Typical choice: 400 (for Egrain1 = 10 cm-1).
Emax2
Should be high enough so that none of the stochastic trials attempt to reach a higher
energy. If that occurs, MultiWell execution will halt and a Fatal Error will be reported.
Typical choices: 50000 cm-1 for T ≤300 K; 85000 cm-1 for T≤3000 K.
Isize
Should be chosen large enough so that Egrain2 ≤ kBT/2 (for good convergence on the
numerical computation of k∞).
Typical choices: 1000 for simulations at 300 K, 1500 for very high temperatures.
208
C.2 How to test the double-array parameters in MultiWell
In principle, it is wise to test your choices of parameters to determine whether the
calculations are reaching numerical convergence. In other words, one should determine whether
the choices of Egrain1 and Egrain2 are small enough and that Emax1 and Emax2 are high
enough.
The tests are carried out on a small subset of representative simulations with pressures
and temperatures at the middle and at the extremes of their ranges, for a total of nine simulations.
For narrow pressure ranges and temperature ranges, only one representative set of conditions
may be necessary. Thus the amount of testing depends on the system and on experience with
similar simulations.
Numerical convergence has been achieved when the grain sizes are small enough and the
maximum energies are high enough so that further grain size reductions and/or further maximum
energy increases do not result in significant differences in the calculations.
The most important measure of convergence is to ascertain whether the fractional yields
computed for the same simulated time duration are independent of the grain size.
Two additional key quantities affected by grain size and maximum energy are kinf and
kosc (i.e. the high pressure limit k∞ and the low pressure limit k0), which are printed by
MultiWell for information purposes in the table summarizing transition state and reaction
properties (preceding the table summarizing the stochastic simulations). These rate constants are
not actually used by MultiWell in the simulations, but they are useful to users. The value for
k∞ should agree within a few percent with the corresponding canonical rate constant calculated
by Thermo with the same input parameters.
C.3 How estimate Lennard-Jones and energy transfer parameters
It is very difficult to compute proper energy transfer parameters. Instead, they are usually
obtained by fitting experimental rate constant data. There are two parts to the problem: obtaining
Lennard-Jones (LJ) parameters and estimating energy transfer parameter α for the exponential-
down model, which is recommended for most purposes.
The LJ parameters can be estimated by using the critical properties of the compound,
which may in turn be estimated using various empirical correlations. However, it is almost
always sufficiently accurate to estimate the parameters, based on analogy. A table of LJ
parameters can be found in Appendix B.6 of this User Manual.
Experience shows that parameter α in the exponential model (i.e. a single component of
the bi-exponential model) usually is in the range from 100 cm-1 to 1000 cm-1; 250 cm-1 is a good
first guess.
Experimental rate constant data can be fitted by varying the value of parameter α until a
good fit has been achieved. It is efficient to start by computing results for several values of α that
cover the whole range expected (typically 100, 250, 500, and 1000 cm-1). For most molecular
species, the "true" value is probably somewhere in this range. By examining a plot of the data
superimposed on a plot of this family of simulations, it will be possible to get a better estimate of
the fitted value. The plot will also demonstrate the sensitivity of the simulations to the assumed
value.
209
C.4 How to obtain rate constants from MultiWell simulations
Master equation simulations are accurate at all time-scales over which statistical rate
theory is valid, but "rate constants" are valid only after an initial energy relaxation has been
completed. When simulating experiments (in which intermediates might never be thermalized), it
is not necessary to define rate constants. In that case, the master equation results are employed
directly. However, master equations are also used to compute rate constants for predictions and
for comparisons with experimental values.
MultiWell does not calculate conventional reaction rate constants directly; the output
must be analyzed further. The data from the simulation can be analyzed by using least squares
fitting and other techniques, just as is done in analyzing experiments.1-7 In the following, several
pragmatic approaches are described.
Single-well Unimolecular Reactions
Single-well reaction systems may have multiple channels and all of the reaction channels
are irreversible unimolecular reactions in multiwell simulations. To find kuni in the pressure fall-
off regime, you need to carry out simulations at the temperature and pressure of interest. Then,
you can find kuni in one of two ways (outlined below), both of which depend on the population
distribution reaching STEADY STATE. The population distribution will approach steady-state
after an initial transient period if the reaction rates are slower than the energy relaxation rates. As
the population distributions approach steady state, the average vibrational energy of the system
(Evib in output file multiwell.out) and the reaction flux coefficients (in output file
multiwell.rates) will asymptotically approach constant values. Due to the stochastic simulation
noise that accompanies stochastic simulations, these values will usually display fluctuations.
Here are the two methods for finding unimolecular rate constants:
a) Reaction Flux Coefficients: the output file 'multiwell.rate' gives reaction flux
coefficients for all the reactions, based on the instantaneous population distributions and on k(E)
for each reaction. When the population distribution in the well is AT STEADY STATE, the flux
coefficient for each irreversible channel is equal to kuni for that channel; the total kuni is equal to
the sum of the channel-specific rate constants. To use this feature, however, requires many,
many stochastic trials in a single simulation in order to reduce the stochastic sampling noise.
This technique should not be used for multi-well reaction systems, because the reactions are
reversible and the unimolecular rate constants therefore depend algebraically on more than one
reaction flux coefficient.
b) Curve fitting: the decay of population in a SINGLE-WELL reaction is exponential
with total rate constant kuni, which may obtained from a semi-log plot: natural logarithm of
population ("fraction") vs. time; the slope of the plot is equal to -kuni. For multi-channel
reactions, the branching ratios of the individual channels can be obtained from the relative rates
of producing products or relative product yields ("fractions"), evaluated for the period over
which the population is in steady-state.
It is important to note that if the analysis requires time periods longer than needed for
more than a few thousand collisions, the simulations become very time-consuming. MultiWell is
not designed for computing slow, steady-state unimolecular reactions. The factors affecting
computation time are discussed in the following sub-section.

210
Execution Speed for Unimolecular Reactions
The time needed to perform a stochastic simulation and obtain a unimolecular rate
constant depends on several factors, including clock speed of the computer, the level of statistical
error that can be tolerated, the physical conditions being simulated (e.g., pressure and
temperature), and the complexity of multiple-well, multiple-channel reaction systems. Reactions
with slow rate constants cannot be simulated as readily as those with fast ones, because some of
these factors are limited by computer characteristics, numeric of random number generators,
computer codes, and human time constraints. Obviously, there are several possible trade-offs
among these factors.
To illustrate how these factors can affect the difficulty of extracting a rate constant, we
will consider a very simple single-well, single-channel problem. We want to find the slowest
reaction rate that can be simulated in a practical calculation using one computer processing unit
(i.e., a cpu, or core). (Note that simulations of chemical activation are much more efficient; see
later in this chapter.)
For slow reactions, the initial energy relaxation can be neglected. The stochastic
simulation produces a time-history of y vs. t, where y is the time-dependent relative
concentration of the reactant (relative to its initial concentration) and t is duration of simulated
time. Thus at t = 0, y = 1. The first order rate constant, k, can be obtained from a least-squares fit
of ln(y) vs. t, but for slow reactions we will consider the following approximation, which is
appropriate for kt << 1:
yexp kt
1kt
(1)
This approximate form is useful for 1 ≥ y ≳ 0.5.
To obtain the rate constant, the simulated time duration, t, must be long enough so that y
is significantly larger than the stochastic sampling noise. Because of stochastic sampling noise
(see Sec. A.3.2 in this User Manual), the standard deviation of the relative concentration is given
by8
yy1y
Nt
1/2
(2)
where Nt is the number of stochastic trials. When y ≈ 1, this expression reduces to
y1y
Nt
1/2
kt
Nt
1/2
(3)
From propagation of errors, the corresponding standard deviation of k is given by
kt1
y
(4)
It is convenient to define the relative stochastic error Rk in the rate constant:
Rk
k
k
y
kt 1
ktNt
1/2
(5)
211
It is clear from these expressions that the relative error is large when the simulated time duration
is too short and/or when the number of stochastic trials is too small. In principle, the number of
stochastic trials can be increased, but a practical limit of ~2×107 stochastic trials is imposed by
the random number generator that is currently in use (each stochastic trial requires at least 3
random numbers (if no collisions are involved) and at least 5 random numbers when collisions
are dominant).
In collisional systems (except at very low pressures), the cpu time is often proportional to
the total number of collisions that must be simulated. The total number of collisions, Z, depends
on the collision frequency (ω), the simulated time duration (t), and the number of stochastic trials
(Nt):
Z
tNt
(6)
From Eqs. 1, 5, and 6, we find that Z depends only on the dimensionless ratio of the collision
frequency divided by the unimolecular rate constant, and the reciprocal of the relative error,
squared:
Z1
Rk
2
k
(7)
Because computation time is approximately proportional to Z, Eq. 7 can be used to
estimate the amount of cpu time needed to obtain a unimolecular rate constant with a specified
"target" relative error Rk. In recent tests using a desktop iMac computer (2.7 GHz), MultiWell
simulated ~5×109 collisions in one hour of cpu time. Also, at 1 bar and room temperature, ω is of
the order of ~10+10 s-1. This value is useful for estimates at other temperatures, because ω is only
weakly dependent on temperature and on the identity of colliders.
Because of limitations associated with the random number generator utilized in
MultiWell, Nt can be no greater than ~2×10+7, as mentioned above. There are also limits to how
long users are willing to wait while a simulation is being performed. The figure provides an
order-of-magnitude estimate of the cpu time needed to achieve a given "target" relative error as a
function of the ω/k ratio.
10-5
10-3
10-1
101
103
105
107
1001021041061081010
10%
5%
1%
cpu time (s)
/ k
Targeted Relative
Stochastic Error
1 hour
1 day
1 week
1 month
1 minute
1 year
Computer execution time as a function of collision frequency,
rate constant, and targeted level of stochastic error.
212
From the figure, it is clear that "slow reactions" (i.e., slow compared to collision
frequency) require long simulation times in order to achieve small relative stochastic errors.
Obviously, very long simulations can be performed. In our research, we sometimes run
simulations that require ~24 hrs of wall-clock time, but rarely longer than that. Stochastic
simulations are best suited to cases where the pressure (and thus the collision frequency ω) is
small and the rate constant is large. At very low pressures, the cpu times reach a small but finite
lower limit (due to computational overhead) that is not described by Eq. 7.
Multiple-Well Unimolecular Reactions
A least squares analysis of the simulation results is useful and accurate for reaction
systems that include reversible isomerization reactions. Such systems may also include
irreversible reactions (e.g. fragmentation reactions). For very complicated reaction systems that
include reversible isomerization reactions, the most convenient method for extracting rate
constants is currently the Bartis-Widom approach,9 which has been implemented in several
eigenvalue codes.10-12 Because the Bartis-Widom method relies on linear algebra techniques, it is
not available for stochastic simulations, which are accompanied by stochastic sampling noise.
However, for systems that are not too complicated, least squares analysis of stochastic
simulations can be used to obtain similar results.6
The basic approach is to carry out simulations at various temperatures and pressures. Just
as when analyzing experimental data, the time-dependent output (fractions vs. time) can be fitted
by using a postulated mechanism with unknown rate constants (the fitting parameters). For a
postulated mechanism similar to the "phenomenological rate constants" described by Bartis-
Widom, the postulated mechanism should neglect energy transfer processes and include only
chemical transformations. For phenomena involving vibrational relaxation (e.g. incubation times
following a shock wave), the chemical mechanism can be augmented by including vibrationally
excited species and their activation/deactivation steps. The analysis will require a computer code
that can carry out a least squares analysis using an embedded numerical integration of the
coupled rate equations as a function of time (e.g. the Kintecus package by James Ianni:
www.kintecus.com). For simple cases, analytical expressions for concentration vs. time can be
fitted using standard least-squares packages.
Recombination and Chemical Activation Rate Constants
General Discussion of Chemical Activation
As explained elsewhere,8, 13 the stochastic simulations of chemical activation are carried
out for a large ensemble of chemical activation events, taken one at a time, in order determine
the probabilities of all possible outcomes of the chemical activation process. Chemical activation
(which includes recombination reactions) is the result of a bimolecular association reaction that
produces an internally excited species; in the following, we refer to this as a "capture event". The
excited species produced in the capture event subsequently may re-dissociate back along the
entrance channel, react further via other reaction channels, or be stabilized by collisions (and by
other means14). The average chemical activation rate constant for producing products other than
the initial reactants is a bimolecular rate constant:
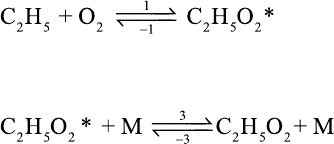
213
kiT,M
kcap,jT
fiT,M
(1)
where kcap,j(T) is the bimolecular rate constant for the initial capture event which takes place via
the jth reaction channel and fi(T,[M]) is the probability of reacting via the ith (≠j) reaction channel,
and [M] is the concentration of a collider gas. Because of back-reaction via entrance reaction
channel j, the net reaction rate constant for the recombination reaction is given by:
kjT,M
kcap,jT
1fiT,M
(2)
Since collisional stabilization depends on pressure [M] and the sum of the probabilities is equal
to unity, the bimolecular rate constants for all of these processes depend on pressure.
In the bulk, the capture events that lead to chemical activation occur randomly, whilst
obeying a second order rate law. The random initiation of these events is not convenient for
stochastic simulations, which could be carried out far more conveniently if all of the reactive
events were initiated at the same instant. Fortunately, since each capture event is completely
independent of the others, it does not matter at what time it is initiated. Thus a stochastic
algorithm exploiting this property can be used for computing the probabilities.8, 13
Using the ideas described in the previous paragraph, a time-dependent stochastic
simulation is carried out by assuming that all of the capture events producing nascent excited
species occur at t = 0 and the nascent species has an initial internal energy E (or E,J) selected
from the chemical activation distribution, which is the appropriate energy probability density
function for this process.
From statistical rate theory, the chemical activation distribution depends on temperature
and on k(E), the microcanonical rate constant describing the re-dissociation of the nascent
complex.15 The thermal average of k(E) is equal to the high pressure limit of the canonical
unimolecular rate constant for re-dissociation, kuni,∞(T) which, in turn is related via the
equilibrium constant Krec(T) to the canonical bimolecular rate constant for the association
(recombination) reaction at the high pressure limit. Since the capture rate constant can be
identified with the rate constant for the association reaction at the high pressure limit, we obtain
kcap,jT
krec,,jT
Krec,jkuni,,jT
(3)
By carrying out this algorithm for many capture events and keeping tallies of the outcomes, one
can determine the average probabilities for use in the equations given above. The statistical
uncertainties in the probabilities decrease as the number of simulations increases.
Figures 1 and 2 show results from a set of simulations of the reaction C2H5 + O2, carried
out as described above.16
(R1)
C2H5O2* 2
HO2+ C2H4
(R2)
(R3)
In these reactions, the asterisk (*) denotes vibrational excitation and M is an inert bath gas.
Figure 1 shows the fraction of the C2H5O2 initially formed that still survives at later times. At t =
0, none of the excited C2H5O2* formed in the association reaction has reacted and its energy is
distributed in the chemical activation distribution. Very quickly, the excited C2H5O2* begins to
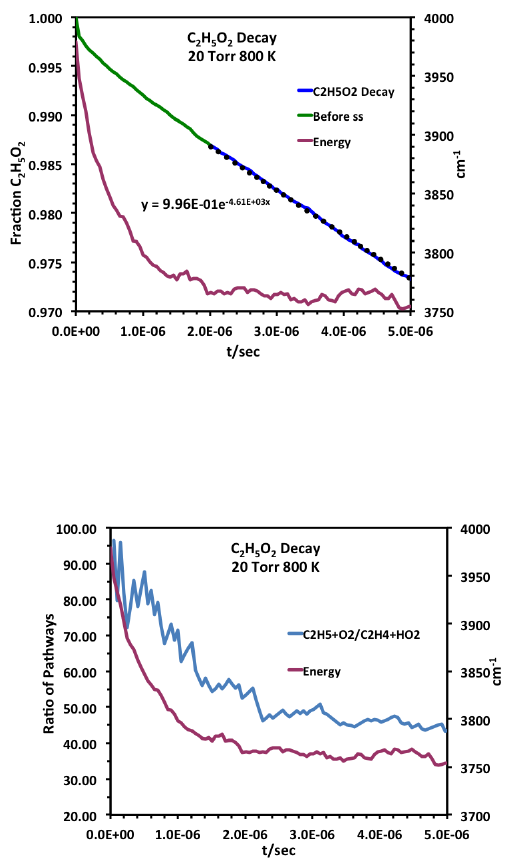
214
react by re-dissociating (Reaction -1) or by reacting via Reaction 2. The excited C2H5O2* also
undergoes non-reactive energy transfer collisions, which alter the energy distribution, resulting
in changes in the average vibrational energy (Evib) of the surviving C2H5O2. The chemical
consequences of the chemical activation process are manifest over an extended period of time.
During the first few nanoseconds, the most highly excited C2H5O2 molecules react away at rates
controlled by the sum of the k(E)s for the two reaction channels. The total rate of loos of C2H5O2
during this period is much greater than would be predicted by the sum of the corresponding high
pressure limits for the two channels, because the latter canonical rate constants are averages of
the sum of the k(E)s over a thermal distribution, while the former are averages of the sum of the
k(E)s over an energized non- thermal distribution.
Figure 1: Surviving C2H5O2 and its average vibrational energy (red line). The
green and blue lines show the fraction of C2H5O2 during the initial relaxation and
afterwards, respectively. The broken line shows the least squares fit of the
thermalized portion.16
Figure 2: Product channel branching ratio and Evib as functions of time for the
same calculation illustrated in Figure 1.16

215
After the first few nanoseconds, the most highly excited C2H5O2* molecules have already
reacted away and surviving molecules react away more slowly. During the period up to ~2 µs,
the C2H5O2 decay is almost, but not quite, first order, suggesting that the chemical activation
event has concluded. A more sensitive diagnostic, Evib for the surviving C2H5O2 molecules,
shows that the energy distribution is still evolving and the chemical activation process is still
underway up to ~2 µs. Figure 2 shows that the branching ratio between the two dissociation
pathways changes by about a factor of two during this period. This change is due to the changes
in the energy distribution function that are taking place during this initial energy relaxation
period.
From simulations such as these, it is convenient to define the bimolecular chemical
activation rate constants in terms of the probabilities evaluated at the end of the initial relaxation
period. Subsequent reaction of the thermalized species takes place at a rate controlled by the
thermal reaction. Thus a single simulation can be used to obtain both the chemical activation rate
constant and the thermal rate constant.
When the time scales of energy relaxation and the subsequent reactions of the
thermalized intermediate in a single channel reaction (e.g. C2H5O2) are widely separated, it is
easy to identify the end of the initial relaxation as the time when Evib and the reaction flux
coefficients become constant.16 For multi-channel reactions, the end of the initial relaxation is
less distinct even under favorable circumstances, since isomerization reactions can affect both
Evib and the reaction flux coefficients.6, 7 Under most conditions, the initial relaxation seldom
requires more than a few hundred collisions (when using typical Lennard-Jones and energy
transfer parameters).
At the High Pressure Limit
The best way to compute the infinite pressure limit rate constants for recombination and
unimolecular reaction is to use THERMO, which has the capability to compute canonical
transition state theory rate constants (CTST), which uses the standard separable approximation
(and can include quantum tunneling through an unsymmetrical Eckart barrier), and semi-
classical transition state theory (SCTST), which includes full inter-mode coupling and
multidimensional quantum tunneling. You will need to supply vibration/rotational constants and
relative energies for the reactant(s) and transition state.
Note that krec(T,[M]) and kuni(T,[M]), the recombination and unimolecular rate constants at
concentration [M] (which is proportional to pressure) and temperature T, are related according to
equilibrium constant:
A + B ⇌ C
Keq krec T,M
kuni T,M
This relation ship applies at all values of [M].
In the Pressure Fall-Off
To compute fall-off rate constants as a function of pressure, two or three steps are
required. The choice of procedure must account for the fact that both forward and reverse
216
reactions are taking place simultaneously, along with collisional activation and deactivation. In
most cases, the time constant for collisional activation/deactivation (typically corresponding to
50 to 1000 collisions) is much shorter than the characteristic time constant for unimolecular
reaction, and a rate constant can be defined formally, but in some cases the reaction rates cannot
be disentangled from the collisional thermalization process. Multiwell can simulate the whole
range of behaviors. The following describes strategies for the normal case when rate constants
can be defined.
In MultiWell, the chemical identity of each chemical species (MOL) is independent of its
internal energy. Thus, molecules are assumed to have unique chemical identities even when they
have energies in excess of reaction barriers and while they are undergoing activation and
deactivation.
Recombination and unimolecular dissociation reactions are closely related:
A + B ⇌ C
Where the forward reaction is recombination and the reverse is unimolecular decomposition. The
relationship between the rate constants and the equilibrium constant, which can be calculated by
THERMO, will be used later
Keq krec /kuni
In the case of a simple recombination reaction (which is one variety of a chemical
activation reaction) one can use MULTIWELL to simulate the reaction over a time interval,
typically a few hundred or a few thousand collisions. As written, the reaction has one Well ("C")
and one set of terminal products ("A+B") corresponding to a single reaction channel. It is
important to note that if the unimolecular decay requires more than a few thousand collisions, the
simulations become very time-consuming. MultiWell is not designed for computing slow,
steady-state unimolecular reactions.
Steps in the procedure:
1) Using vibrational and rotational constants for "C" and for the transition state (TS), compute
sums and densities of states using DENSUM and place the "____.dens" files in directory
DensData for use by MULTIWELL.
2) Use MULTIWELL in one of two ways, Method A or Method B, depending on the
reaction system and conditions. Both methods rely on separation of time scales: the steady-state
reaction must be considerably slower than collisional thermalization and associated relaxation of
the non-steady-state energy distribution. If one runs a longer simulation, one will often find that
product C hasn't really become constant, but is decaying with a slower time constant. If this
decay is slow enough, it can be neglected when assessing the much faster chemical activation
process.
The reliance on separation of time scales is typically a good method as long as the time
scales for the recombination and unimolecular decomposition differ by an order of magnitude or
more. When that condition is not satisfied, as is often true at high temperatures, a better course of
action is to determine the steady-state kuni(T,[M]) by Method B and use the relationship between
the rate constants and the equilibrium constant to obtain krec(T,[M]). But if the time scales are too
similar, and a steady-state energy distribution is not established, a rate constant cannot be defined
217
and it will not be possible to separate the reaction rate from the effects of collisional
thermalization.
Method A: When the unimolecular decomposition reaction rate is much slower than collisional
"thermalizaton", initiate the simulations using the chemical activation energy distribution (key
word CHEMACT) for Well "C". Run the simulations for a simulated time duration tmax
corresponding to a number of collisions sufficient for thermalizing all of the surviving
population of excited "C" (typically 50 to 1000 collisions). Over the course of time, the
population of C is affected simultaneously by both collisional deactivation and bond fission back
to the initial reactants. Thus the energy of C decreases monotonically until it reaches steady state.
At the same time, the yield of C (its "fraction") asymptotically decreases toward a constant value.
When the energy of C is low enough, the subsequent very slow steady-state unimolecular bond
fission can be neglected. MULTIWELL will report f(C, tmax), the fraction of initial "C" that
survives to the end of the simulation (conveniently reported in output file multiwell.sum).
If tmax is large enough and bond fission is slow, the numerical value of f(C, tmax) will remain
constant even if tmax is increased. The recombination and unimolecular reaction rate constants at
that pressure and temperature are given by:
krec T,M
krec,T
f C,tmax
When the reaction is just one of several in a multi-channel reaction system, it is necessary
to use the following method.
Method B: At high T, when kuni(T,[M]) is fast (i.e. when the time scale for reaction is shorter
than the time corresponding to roughly 104 collisions), it is more effective to simulate the
unimolecular decomposition reaction. This is accomplished by initiating the reaction of "C" with
the thermal energy distribution (key word THERMAL). Multiwell will report f(C,t) the fraction of
C that survives to time t in output file multiwell.out. The fraction f(C,t) is proportional to
the concentration of species "C" as a function of time. Initially, f(C,t) decays very rapidly as the
initial population distribution evolves and converges to the steady-state distribution, which is
called the "fall-off" distribution for a simple unimolecular reaction. Once the steady-state
distribution has been established, f(C,t) decays exponentially and a plot of ln[f(C,t)] v.s t will
give a straight line with slope = −kuni(T,[M]).
Thus this method requires plotting the results vs. time and extracting the rate constant. This is
easily done using spreadsheets, or data plotting applications.
For chemical activation reactions, the procedures are similar to those for recombination
reactions.
A + B ⇌ C → D
In a chemical activation reaction, the excited intermediate C initially has enough energy to react
and produce product D. The yield ("fraction") of D depends on the competition between
collisional deactivation and unimolecular reactions involving the intermediate C. The effective
chemical activation rate constant describing the production of D is obtained from the yield of D ,
which is reported by MULTIWELL as the fraction f(D,t) at the end of the simulation:
218
kABDT,M
krec,(T)f(D,)
where krec,∞(T) is the high pressure limit for A + B recombination.
With all of these methods, one must bear in mind that the presence of competing
reactions (e.g. reverse reaction and other reaction channels) may strongly influence the steady-
state energy distribution, which ultimately controls the reaction rates and derived rate constants.
The separation of time scales is often, but not always, sufficient to simplify the analysis. But
sometimes it is only possible to determine individual rate constants by analyzing the simulation
output just like analyzing experimental kinetics data.
Sometimes, steady state is never established and rate constants cannot be rigorously
defined. Even under non-steady-state conditions, however, the Multiwell simulations can be used
to accurately model the time-dependent fractions and the final product yields.
219
References
1. E. S. Lewis and M. D. Johnson, The Reactions of p-Phenylene-bis-diazonium Ion with
Water, J. Am. Chem. Soc. 82, 5399–5407 (1960).
2. J. Andraos, A Streamlined Approach to Solving Simple and Complex Kinetic Systems
Analytically, J. Chem. Educ. 76, 1578-1583 (1999).
3. A. E. Mucientes and M. A. d. l. Peña, Kinetic Analysis of Parallel-Consecutive First-
Order Reactions with a Reversible Step: Concentration–Time Integrals Method, J. Chem.
Educ. 86, 390-392 (2009).
4. M. Frenklach, A. Packard and R. Feeley, "Optimization of Reaction Models with
Solution Mapping," in Modeling of Chemical Reactions, ed. R. W. Carr (Elsevier,
Amsterdam, 2007), pp. Elsevier.
5. S. Boyd and L. Vandenberghe, Convex Optimization. (Cambridge University Press,
Cambridge, UK, 2004).
6. J. A. Miller, S. J. Klippenstein, S. H. Robertson, M. J. Pilling, R. Shannon, J. Zádor, A.
W. Jasper, C. F. Goldsmith and M. P. Burke, Comment on “When Rate Constants Are
Not Enough”, J. Phys. Chem. A 120, 306−312 (2016).
7. J. R. Barker, M. Frenklach and D. M. Golden, Reply to “Comment on ‘When Rate
Constants Are Not Enough’”, J. Phys. Chem. A 120, 313−317 (2016).
8. J. R. Barker, Multiple-well, multiple-path unimolecular reaction systems. I. MultiWell
computer program suite, Int. J. Chem. Kinet. 33, 232-245 (2001).
9. J. T. Bartis and B. Widom, Stochastic models of the interconversion of three or more
chemical species, J. Chem. Phys. 60, 3474-3482 (1974).
10. J. A. Miller and S. J. Klippenstein, Master Equation Methods in Gas Phase Chemical
Kinetics, J. Phys. Chem. A 110, 10528-10544 (2006).
11. D. R. Glowacki, C. H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, MESMER:
An Open-Source Master Equation Solver for Multi-Energy Well Reactions, J. Phys.
Chem. A 116, 9545-9560 (2012).
12. M. V. Duong, H. T. Nguyen, N. Truong, T. N. M. Le and L. K. Huynh, Multi-Species
Multi-Channel (MSMC): An Ab Initio-based Parallel Thermodynamic and Kinetic Code
for Complex Chemical Systems, Int. J. Chem. Kinet. 47, 564-575 (2015).
13. J. R. Barker, Monte-Carlo Calculations on Unimolecular Reactions, Energy-Transfer, and
IR-Multiphoton Decomposition, Chem. Phys. 77, 301-318 (1983).
14. J. R. Barker, Radiative Recombination in the Electronic Ground State, J. Phys. Chem. 96,
7361-7 (1992).
15. W. Forst, Unimolecular Reactions. A Concise Introduction. (Cambridge University Press,
Cambridge, 2003).
16. J. R. Barker, M. Frenklach and D. M. Golden, When Rate Constants Are Not Enough, J.
Phys. Chem. A 119, 7451−7461 (2015).
220
C.5 How to tell if the simulated time is long enough
Experiments
When simulating actual experiments, the simulated time should match the experiment
times. Bear in mind, however, that Multiwell is not intended for simulating slow steady state
reactions. Because it simulates every individual collision, it is most suitable for simulated times
corresponding to a few thousand collisions, or less. This is quite sufficient for many kinds of
experiments with short timescales.
For longer simulations, it is better to use Multiwell to determine individual rate constants
and then use those rate constants in an elementary reaction mechanism, which can be solved
using a suitable stiff differential equation code. One such code is KINTECUS, which was
designed for chemical kinetics and is free of charge for users at academic institutions (available
from www.kintecus.com).
Unimolecular Reactions
In general, the initial energy distribution assumed in the simulation must relax to the
steady-state distribution. The relaxation time, which depends on the initial energy distribution, is
minimized when the assumed initial energy distribution is most similar to the steady-state
distribution. For example, if the pressure is high enough so that the reaction is near the high
pressure limit, the relaxation time will be minimal if the initial energy distribution is assumed to
be thermal (THERMAL). Generally, the initial transient (when the initial distribution is relaxing to
the steady-state distribution) is quite manageable when using an initial energy distribution with
average energy close to the reaction critical energy. The final steady state distribution does not
depend on the particular choice of the initial distribution, whether it is a delta function (DELTA),
thermal distribution (THERMAL), or chemical activation distribution (CHEMACT).
The simulation must be run for a simulated time that is sufficient for steady state to be
achieved and for the rate constant to be determined. If the rate constant is to be determined by
plotting ln(fraction) vs. time (see Section C.4), then plot initially will be non-linear during the
transient period when steady state is being established, and subsequently will become linear with
slope equal to the desired rate constant. The simulation must be long enough to enable
determination of the slope of the straight line portion.
Chemical Activation or Recombination Reactions
When simulating chemical activation or recombination reactions, one should run the
simulations long enough to satisfy two criteria:
a) The average energy of a product molecule (C) is well below any of its reaction
thresholds (also remember that the distribution of internal energy extends well above the
average)
b) The yield of C becomes independent of time (when time-scale separation is sufficient).
It is best to carry out some preliminary calculations (using a smaller number of trials) to
determine the time duration (or number of collisions) that will be needed for the excited species
221
to be deactivated sufficiently. At low temperatures, this may require only a few dozen collisions,
but at high temperatures it may require several hundred.
222
223
C.6 How to deal with Barrierless Reactions
Treating barrier-less reactions with "loose transition states" is more complicated than
reactions that have intrinsic energy barriers. There are several choices of methods. Generally,
there is a trade-off between ease of use and predictive accuracy. If the method is not being used
to predict rate constants, but is instead being used to fit experimental rate constants, then the
simpler methods are usually sufficient. For all of the methods, vibrational and rotational
constants are usually obtained from quantum chemistry calculations.
In order, starting with the best (and most difficult) method:
1. Microcanonical variational transition state theory (mVTST): In the MultiWell Software Suite,
this method has been implemented in program ktools, which computes canonical (thermal)
VTST rate constants (cVTST rate constants) as well as microcanonical sums and densities of
states, which are appropritate for master equation simulations.
2. Canonical transition state theory (CTST), which uses molecular constants to compute partition
functions: CTST is implemented in thermo, which can be used with molecular constants along
a reaction path to find the canonical variational transition state and a corresponding cVTST rate
constant. The molecular data required for this calculation are exactly the same as those used by
ktools, but the ktools calculations are preferred, because they are significantly more
accurate.
3. Hindered Gorin model: see Index of this User Manual.
4. Inverse Laplace transform method: a built-in option in MULTIWELL (key word ILT). This
method is often investigated first, because it is the easiest and least expensive, but alos the least
accurate.
Methods #1 to #4 can be employed relatively easily in Multiwell. Method #1 is preferred.
Typically, #3 and #4 are used empirically by fitting a known (or estimated) thermal rate constant
at a given temperature.
Several applications of methods #2, #3, and #4 are described in recent articles.1-4
References
1. D. M. Golden and J. R. Barker, Pressure- and Temperature-Dependent Combustion
Reactions, Combust. Flame 158, 602–617 (2011).
2. M. A. Ali and J. R. Barker, Comparison of Three Isoelectronic Multiple-Well Reaction
Systems: OH + CH2O, OH + CH2CH2, and OH + CH2NH, J. Phys. Chem. A 119,
7578−7592 (2015).
3. L. Yang, J. A. Sonk and J. R. Barker, HO + OClO Reaction System: Featuring a
Barrierless Entrance Channel with Two Transition States, J. Phys. Chem. A 119, 5723–
5731 (2015).
4. M. A. Ali, J. A. Sonk and J. R. Barker, Predicted Chemical Activation Rate Constants for
HO2 + CH2NH: The Dominant Role of a Hydrogen-Bonded Pre-reactive Complex, J.
Phys. Chem. A 120, 7060−7070 (2016).
224
C.7 Some Questions and Answers
(Most of the answers were written by JRB; Some questions and answers are rather old!)
1. QUESTION: Every molecule has a 2 dimensional external inactive rotor and an external
active rotor (the K-rotor). I can see where the external inactive rotor goes but I'm not sure
about the external active rotor.
ANSWER: The parameters "MolMom" on line #8 and "RR" on line #15 of the data file
are moments of inertia for the 2-dimensional external (inactive) rotors for the reactant and the
transitions state, respectively. The external active rotor is included with the other degrees of
freedom in the density and sum of states calculation. Therefore it is included in the data file for
SumDen. For example, O3 (ozone) has 3 vibrations and 3 rotations. The SumDen data file should
include 4 degrees of freedom: 3 vibrations + 1 rotor (the active external rotation, which I usually
label the "K-rotor"). The moment of inertia for the remaining 2-D external (inactive) rotor
appears on line #15.
2. QUESTION: If there is an internal active rotor, do I remove the vibration associated
with it from the Densum input?
ANSWER: An internal degree of freedom is either a rotor, or a vibration...not both. Thus,
if you have a vibrational assignment (from Gaussian, say), you may wish to replace a low
frequency vibrational mode with a free rotor mode. Then you remove the vibration and insert the
rotor in its place, so that the number of internal degrees of freedom is preserved.
3. QUESTION: In all your examples you use an energy spacing of 10 cm-1 and when I use 1
cm-1 the code freezes. Do you recommend using 1 cm-1 and if so should I increase the size of
the array, which is currently 14000?
ANSWER: We usually recommend 10 cm-1, because we have found that for most
systems it gives excellent numerical convergence at room temperature and above, and because
few thermochemical values are known to better accuracy. In previous work, 25 cm-1 spacing also
worked very well. If you want to use a smaller grain size, then the arrays should be increased in
size. In principle, one should always test to make sure that the grain size is small enough so that
it does not affect the results significantly.
4. QUESTION: In using DenSum, when should one use quantum state counting for rotors
("qro") and when should one use classical state densities ("rot")?
ANSWER: As a rough rule of thumb, if the rotational constant is greater than B = 1 cm-1,
use "qro"; if it is less than 0.1 cm-1, use "rot"; in between, you can try it both ways and then
decide if the difference will affect your calculations. If you use "qro" for a case where the
rotational constant is extremely small, there may be computational problems... this limit has not
been tested thoroughly … and it would be better to use "rot".
225
5. QUESTION: What will happen if the density of states function is not a smooth,
continuous function at energies corresponding to the upper half of the double array?
ANSWER: Subroutine COLSTEP assumes that the density of states is smooth in the
upper portion of the double array. In general, you should plot the density of states vs. E to
confirm that the energy dividing the two portions of the double array is high enough so that the
density of states does not fluctuate more than, say, 5%. If the fluctuations are larger, they will
cause problems in selecting the step sizes, resulting in anomalously large probabilities of large
activating steps.
6. QUESTION: Why does my compiler have trouble reading the example data files that
contain names (CHARACTER CONSTANTS)?
ANSWER: If your compiler does not accept the CHARACTER CONSTANTS in the
example data files, enclose the CHARACTER CONSTANTS in apostrophes (') and try again.
"Free format" (list directed input) is used by the MultiWell suite. Different compilers may
choose to use different delimiters to separate the input fields in free format. Most compilers use
commas and spaces, but some also will recognize tabs, returns, linefeeds, and other characters.
Most compilers will recognize CHARACTER CONSTANTS (e.g. file names and chemical
species names) when they are contained in apostrophes (e.g. 'xyz'). Other compilers will also
accept quotes (e.g. "xyz"), or text without any special enclosing delimiters (e.g. xyz).
7. QUESTION: How can the 2-D hindered rotations in loose transition states be handled
using DenSum?
ANSWER: There are at least three different ways 2D-hindered rotors for loose transition
states can be handled by DenSum. The first is by using the restricted Gorin prescription of Smith
and Golden1 (see Benson's discussion2 of the Hindered Gorin Model), which is based on a
modified version of the Gorin Model.3 The second is to replace the restricted rotor formulation
with one based on particle-in-a-box. The third is to use two 1-D hindered rotors (implemented in
DenSum) instead of one 2-D hindered rotor (2-D hindered rotors are not implemented in
DenSum).
Smith and Golden1 use a "hindrance parameter" to modify the moment of inertia of a 2-D
free rotor: the Hindered Gorin Model. They find the value of the hindrance empirically by
varying it until they achieve a fit with experimental rate constant data. In my opinion, a potential
drawback of the Smith and Golden approach is that the rotor model has no zero point energy, and
restricting the range of rotational motion results in a model that is more like a particle-in-a-box,
which has a finite zero point energy. It is for this reason that I added the particle-in-a-box degree
of freedom type to DenSum. The zero point energy is important because of the role it plays in
isotopic reactions. To use particle-in-a-box energy levels (instead of free rotor levels), one can
empirically vary the "frequency" parameter until agreement with experiment is achieved, just as
done by Smith and Golden.
The third alternative is to use two 1-D hindered rotors for each 2-D internal rotation.
Here, the moment of inertia can be used directly in DenSum and the hindrance potential is then
varied until agreement with the rate constant data is achieved. I've done a few brief tests of this
226
approach and it seems to work well. The use of an actual hindered rotor is attractive to me,
because it seems more physically realistic (one of these days we'll investigate this using quantum
chemical calculations). The drawback is that state degeneracies may not be calculated correctly.
I don't know if there is a significant difference among rate constants calculated using the
methods described above. Each of the methods is probably quite adequate in fitting almost any
experimental data (a detailed comparison of the methods would be quite interesting). However,
making predictions for temperatures where no experimental data are available requires
formulation of an ad hoc model for hindrance as a function of temperature. Jordan, Smith, and
Gilbert4 have formulated such a model (based on free rotors) and have tested it for a few cases; it
is possible that their method could be used with Densum. The Marcus and Wardlaw approach5, 6
is more predictive, but only if an accurate multi-dimensional potential energy surface is
available. Miller and Klippenstein7 have used VariFlex software,8 which implements an extended
version of the Marcus-Wardlaw approach.
8. QUESTION: Why is the output "noisy" and what is the meaning of the columns labeled
"+/-error"?
ANSWER: Multiwell works by carrying out stochastic trials, each of which is a random
walk governed by the physics of the reaction system. In each trial, one or more wells may be
"visited' during the random walk and the random walker will be found in a well or reaction
product at the end of the trial. Multiwell carries out stochastic trials one at a time and sums up
the results. But it is convenient to discussed the summed result as if a whole "swarm" of random
walkers was released at the same time... an equivalent procedure. During a set f trials, each of the
time steps records a "snapshot" of the number of walkers in each well or product set at the instant
of the time step. The fractions are based on these snapshots.
For a set of, say, N=100 stochastic trials, there are 100 random walkers. If only one
random walker out of the whole set is in a well at the time of a snapshot, then the corresponding
fraction is 0.01. If 37 are in the well, then the fraction is 0.37. The smallest possible non-zero
fraction (greater than zero) is equal to 1/N. Furthermore, for a finite number of stochastic trials, a
statistical error is associated with each fraction. The estimated statistical error (specifically, 1
standard deviation) is reported by multiwell in the columns labeled "+/-Error". As the number of
stochastic trials is increased, the smallest non-zero fraction decreases and the statistical error
decreases. Thus changing the number of trials will produce small changes in the fractions...
changes that should be consistent with the actual statistical fluctuations. (The theory behind the
estimated statistical errors is presented in Appendix A.3.2 of the User Manual.)
When carrying out longer trials, the last "snapshot" occurs at a later time and the fraction
recorded by the final snapshot (reported in output file multiwell.sum) may vary with time. Even
if equilibrium has been achieved and no further time variation is expected, the stochastic "noise"
(i.e. statistical errors) associated with the finite number of stochastic trials may be observed, but
it should be consistent with the estimated statistical errors.
It is not possible to completely eliminate the stochastic noise for a finite number of trials.
You should decide what level of noise is tolerable... i.e. what statistical precision is needed... and
set the number of trials accordingly. A very large number (millions) of stochastic trials may be
needed to obtain high precision results for a reaction product that is produced with a very small
fractional yield. The required computer time is proportional both to the number of trials and to
227
the length of simulated time (see Appendix A.3.2). As a result, certain simulations are simply not
feasible, or they may be feasible if creative alternative approaches are devised.
References
1. G. P. Smith and D. M. Golden, Application of RRKM Theory to Reactions
OH+NO2+N2⇌ HONO2+N2 (1) and ClO+NO2+N2 ⇌ ClONO2+N2 (2) - Modified Gorin
Model Transition-State, Int. J. Chem. Kinet. 10, 489 (1978).
2. S. W. Benson, Thermochemical Kinetics. (Wiley, New York, 1976).
3. E. Gorin, Photolysis of acetaldehyde in the presence of iodine, Acta Physicochim., URSS
9, 681 (1938).
4. M. J. T. Jordan, S. C. Smith and R. G. Gilbert, Variational transition state theory: a
simple model for dissociation and recombination reactions of small species, J. Phys.
Chem. 95, 8685-8694 (1991).
5. D. M. Wardlaw and R. A. Marcus, Unimolecular Reaction-Rate Theory for Transition-
States of Any Looseness. 3. Application to Methyl Radical Recombination, J. Phys.
Chem. 90, 5383-5393 (1986).
6. D. W. Wardlaw and R. A. Marcus, RRKM reaction rate theory for transition states of any
looseness, J. Chem. Phys. 110, 230-4 (1984).
7. J. A. Miller and S. J. Klippenstein, Theoretical Considerations in the NH2+ NO Reaction,
J. Phys. Chem. A 104, 2061-2069 (2000).
8. S. J. Klippenstein, A. F. Wagner, S. H. Robertson, R. Dunbar and D. M. Wardlaw;
VariFlex Software; Argonne National Laboratory, 1999.
228
Index
<name>.dens, 87
<name>.qcrp, 87
2 dimensional rotor, 223
2-D adiabatic rotor, 140
2-D hindered rotations, 224
2-dimensional external rotation, 31
3-D relative translation, 154
Accuracy
Thermo, 61
active energy, 23, 180
active rotor, 223
adensum, 75
Adiabatic Channel Model, 141
adiabatic rotor, 178
A-factor, 33
angular momentum, 140
ANH, 174
Anharmonic oscillator, 44
anharmonicity coefficients, 86, 175
anharmonicity constants, 176
ansum, 75
asymmetric top, 179
atom type, 58
atom types, 189
atomic mass, 189
ATYPE, 58
average vibrational energy, 213
averaged results, 137
barrier-less reactions, 222
batch option, 54
bdens, 11, 12, 44, 75
program, 60
bdens, 199
BEST, 199
BETTER, 199
Beyer-Swinehart algorithm, 52
Biexponential Model, 36
bimolecular, 151
bimolecular rate constant, 151
BJ, 45
BK, 45
canonical bimolecular rate constant, 152
canonical rate constant
trial, 102
canonical transition state theory, 6, 61, 146, 222
capture rate constant, 212
CENT1, 34, 204
CENT2, 34, 146, 204
centrifugal corrections, 123, 146, 180
CENTX, 34, 204
CFOUR, 195, 199
checkpoint file, 87
CHEMACT, 35, 36
Chemical activation, 35, 166, 211
chiral stereoisomer, 183
COLL, 35
collision frequency, 124, 157, 160
collision integral, 32, 157, 159
collision models, 32, 36
collision step-size distribution, 124, 157
collision-induced IVR, 35, 146
competition between unimolecular and bimolecular
reactions, 153
compiler options, 24
computation time, 210
computer time, 137, 225
convergence tests, 133
Conversion Factors, 174
convolution, 154
cpu time, 211
critical energy, 23, 33, 139, 199
CRP, 86, 198
CTST, 222
cumulative reaction probabilities, 7
cumulative reaction probability, 34, 86
cVTST, 222
data files, 70
defaults, 24
definitions, 22
degeneracies, 178
degrees of freedom, 63
DELTA, 35
DensData, 35
DensData, 39
densities of states, 39, 132
Density Functional Theory, 144
density of states, 224
densum, 9, 44, 122, 223
densum.batch, 54
Batch file format, 54
densum.lev, 52
densum.out, 52
detailed balance, 125, 158
directory
DensData, 25, 35
dissociation energy, 176
dividing surface, 102
DO-loops, 199
doloops, 75
Double array, 29, 108, 132
double-well potential, 184
Eckart barrier, 6, 33, 66, 147
229
Egrain1, 29, 42, 53
Einit, 35
Elements, 189
Emax2, 29, 42, 53
energy grain, 132
energy relaxation, 208
Energy schematic, 23, 122
energy transfer, 32
energy transfer parameter, 207
energy units, 30
energy units for THERMO, 61
enthalpy for formation, 60
Enthalpy function
[H(T)-H(0)], 61
enthalpy of formation, 31
entropy, 61
equilibrium constant, 60, 61
Eunits, 30
exact counts, 122
Example multiwell Models, 15
Exponential model, 36
exponential-down model, 207
EXTERNAL, 35
external file, 34
external symmetry number, 46
EXTRA, 199
FAIR, 199
fall-off, 216
FAST, 33
FileName, 25, 26, 28
user-defined, 25, 57, 65
fit, 62
Fitting Experimental Rate Constants, 62
Flexible Transition State Theory, 141
flux coefficient, 26, 169, 170
fundamental frequency, 44
gauche structures, 183
gauss2multi, 12, 70
GAUSSIAN, 199
Gaussian 03, 70
Gaussian 98, 70
getting started, 5
Gillespie Exact Stochastic algorithm, 22
Gillespie's Exact Stochastic Method, 136
GOOD, 199
gor, 62
Gorin model, 143, 224
grain size, 223
HAR, 52, 53, 67, 68, 79, 88
harmonic frequency, 44, 174
Harmonic oscillator, 44
Heat Capacity, 61
high pressure limit, 145
high pressure rate constant, 146
Hindered Gorin Model, 62, 141, 143, 222, 224
Hindered internal rotation, 92, 122, 181
General, 47, 50, 182
Optical isomers, 183
symmetrical, 46
Unsymmetrical, 182
hindered rotor
symmetrical, 49
hindrance parameter, 62, 224
HMol, 31
hybrid master equation, 131
hydrogen peroxide, 183
IDUM, 29
ILT, 34
imaginary frequency, 34, 86, 147
imax1, 29, 42, 53
IMol, 31
inelastic collision frequency, 158, 160
inelastic collisions, 158
initial conditions, 165
initial energy relaxation, 208
initial relaxation, 214
initial well, 35
INPUT ERRORS, 42
internal rotation, 122
optical isomers, 183
unsymmetrical, 182
internal rotor symmetry, 181
internal rotors, 46, 181
Inverse Laplace Transform (ILT) Method, 142
Inverse Laplace transform method, 222
Isize, 29, 42, 53
isomerization, 131
IVR, 123, 146
IVR threshold energy, 35
IVR transmission coefficient, 34, 146
J-summed, 11
densities of states, 107
sums of states, 107
J-summing, 107, 108, 111
K quantum number restrictions, 45
k(E), 169
KEYWORD, 33, 35
Klaus Luther's empirical function, 38
K-rotor, 49, 121, 122, 140, 178, 223
ktools, 11, 44, 100, 222
ktools.dat, 111
lamm, 12, 92, 123
Laplace transform, 154
large amplitude motions, 92
Lennard-Jones parameters, 32, 157, 207
Table, 187
linear master equation, 137
loose transition state, 141, 222
loose transition states, 224
low pressure limit, 145
230
master equation, 121
J-resolved, 8, 120
steady-state, 8, 120
maximum number of collisions, 35
microcanonical, 151
microcanonical bimolecular rate constant, 151
microcanonical rate constant, 86
microcanonical transition state theory, 151
Miller, W. H., 195
Miller, W. H., 86, 195
molecular constants
sources, 69
Molele, 31
Molinit, 35
MolMom, 31
MolName, 31
Molopt, 31
Molsym, 31
moment of inertia, 31, 174
moments of inertia, 57
mominert, 10, 12
MORSE, 62
Morse oscillator, 44, 62, 174
Morse oscillator anharmonicity, 44
Morse Potential, 144
multinomial distribution, 138
multiple-transition state model, 104
multiple-well systems, 131
MultiWell, 13, 22
Data files, external, 39, 41
Examples, 143, 165
Input File, 5, 168
Input file format, 29, 52
Output files, 52, 169
Symmetry Examples, 185
MultiWell input options, 28
multiwell.array, 26, 170
multiwell.dist, 26, 170
multiwell.flux, 27, 170
multiwell.out, 26, 169
multiwell.rate, 26, 169
multiwell.sum, 26
mVTST, 222
NOCENT, 34, 146, 204
noise, 209
non-RRKM, 146
non-separable degrees of freedom, 86
non-separable vibrations, 175
NOREV, 33
normalization, 158, 159
normalization problems, 159
normalization, finite difference algorithm, 160
NOTUN, 33
Np, 30
NProds, 31
number of trials, 35
numerical convergence, 207, 223
NWells, 31
oblate symmetric top, 180
oblate top, 140
obs, 44, 52, 67
Observed frequency, 44
OLDET, 32
optical isomer, 183
optical isomers, 31, 33
Hindered internal rotation, 183
output files, 26
paradensum, 7, 11, 12, 44, 81, 82
program, 60
Particle in a Box, 46
particle-in-a-box, 48, 224
partition function, 86, 154
perturbation theory expansion, 175
Photo-Activation, 166
precision, 138
pressure units, 30
Product set, 31
Product sets, 31
Product sets, defined, 22
Program Execution, 25
prolate symmetric top, 180
prolate top, 140
pseudo-diatomic model, 140
pseudo-first-order, 151
Punits, 30
qro, 223
Quantum mechanical tunneling, 147, 199
quasi-bound states, 177
quasicontinuum, 123
quasi-symmetric top approximation, 179
Questions and Answers, 223
radiationless transitions, 38
random number generator, 137
random walkers, 225
rate constant
canonical, 195
chemical activation, 217
microcanonical, 195
unimolecular, 215
Reactant Sets, 22
reaction flux coefficient, 26, 169
reaction flux coefficients, 214
reactive flux, 128, 170
recombination, 211
recombination reaction, 63
Recombination Reactions, 166
re-crossing, 102
reduced moment of inertia, 57, 93
relative translation, 48
restricted Gorin model, 143
231
REV, 33
RKE, 34
rot, 223
Rotation, 45, 49, 121
quantized, 49
rotational, 30
Rotational Constant, 174
rotational constants, 30
rotational degrees of freedom, 63
Rotatunits, 30
RRKM theory, 139
Schrödinger equation, 92
sctst
program, 60
sctst, 12, 13, 44, 60, 64, 86, 87, 179, 195, 198, 199
SCTST, limitations, 197
sctst.out, 86, 87
selection of step sizes, 160
semi-classical transition state theory, 64, 86, 195
Semi-Classical Transition State Theory (SCTST), 7
Semi-empirical Canonical Variational Transition
State Theory, 144
semi-microcanonical bimolecular rate constant, 152
semi-microcanonical pseudo-first order rate constant,
153
separable rotors approximation, 179, 180
separable-rotors approximation, 127, 179
separation of time scales, 215
shock-tube simulations, 30
simulated time, 219
SLOW, 33, 34
Slow IVR, 146
sMORSE, 63
source code, 24
specific rate constants, 39, 132
standard state, 60
statistical errors, 225
statistical fluctuations, 225
steady-state distribution, 216
step-size distribution, 161
Stiff Morse Oscillator, 63
Stochastic Method, 136
stochastic noise, 225
stochastic sampling noise, 209
stochastic trials, 225
SUM, 34
sums and densities of states, 198
sums of states, 39, 132
symmetric top, 45, 49, 178
separable rotors approximation, 178
symmetric tops
almost symmetric, 140, 179
symmetry
internal rotation, 181
potential energy, 181
symmetry number, 31, 33
hindered internal rotation, 50
symmetry numbers, 140
Symmetry Numbers, external, 181
symmetry numbers, internal rotors, 181
Temp, 30
terminology, 22
THERMAL, 35
Thermal Activation, 165
thermo
program, 60
thermo, 9, 12, 44, 144
thermodynamics database, 69
threshold energy, 139
tight transition state, 140
TIME, 35
time step, 137
top, 49
torsion, 122
torsion rotational constant function, 122
torsions, 92
total collision rate constant, 32
total collision frequency, 35
total collision rate constant, 147, 157
transition state, 66
loose, 141
tight, 140
Transition state parameter entry, 33
transition state theory, 60, 86, 195
Transition states, 22, 131
Translation, 48, 50
translational states, 155
translational temperature, 30
trial transition states, 100
trn, 50
TS computer code, 120
TUN, 33, 34, 200
tunneling, 33, 66, 86, 147, 195
tunneling corrections, 6
tunneling probability, 147
Tvib, 30
Uncertainties, 138
unified rate constant, 104
Unimolecular Reactions, 139
unsymmetrical hindered internal rotation, 47
utilities, 70
utilities for creating data files, 70
variational transition state theory, 141, 222
canonical, 100, 101
J-resolved, 100, 104
microcanonical, 100, 104
VariFlex software, 225
VARSHNI, 63
Varshni Oscillator, 63
Viblo, 39
232
vibration, 48
vibrational
anharmonicity, 174
vibrational anharmonicity, 64, 195
vibrational energy, 174
perturbation theory expansion, 175
vibrational perturbation theory, 199
vibrational temperature, 30
vibrations
non-separable, 175
separable, 174
vimag(Mol,i), 34
VPT2, 89, 199
VPT4 correction, 89
VPT4A, 89
VPT4B, 89
VPTx, 89
Wang-Landau algorithm, 86
Wells, 31, 131
Wells, defined, 22
Whitten-Rabinovitch approximation, 52
Xij anharmonicity coefficient matrix, 174