NISTUncertainty Machine User Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 46
- NIST Uncertainty Machine for the Impatient
- Purpose
- Gauss's Formula vs. Monte Carlo Method
- Usage
- Results
- Transparency for Validation & Verification
- Example — Thermal Expansion Coefficient
- Example — End-Gauge Calibration
- Example — Dynamic Viscosity
- Example — Resistance
- Example — Stefan-Boltzmann Constant
- Example — Voltage Reflection Coefficient
- Example — Age of Allende Meteorite

VERSION 1.4 NIST UNCERTAINTY MACHINE
NIST Uncertainty Machine — User’s Manual
Thomas Lafarge Antonio Possolo
Statistical Engineering Division
Information Technology Laboratory
National Institute of Standards and Technology
Gaithersburg, Maryland, USA
October 23, 2018
1NIST Uncertainty Machine for the Impatient
• Using a Web browser, visit https://uncertainty.nist.gov/.
• Choose the number of input quantities from the drop-down menu, and
change their names if desired.
• Select a probability distribution for each of the input quantities, and enter
values for its parameters (in the absence of cogent reason to do otherwise,
assign Gaussian distributions to the input quantities, with means equal to
estimates of their values, and standard deviations equal to their standard
uncertainties);
• If there are correlations between the input quantities, then activate Correlations,
enter the values of the non-zero correlations, and select a copula to apply
them with (cf. Figure 6on Page 26).
• Specify the size of the Monte Carlo sample to be drawn from the proba-
bility distribution of the output quantity (no larger than 5 000 000).
• Enter one or more valid R expressions (one per line) into the box la-
beled Value of output quantity (R expression) such that the last
line evaluates to f(x1, . . . , xn), the right-hand side of the measurement
equation. (Refer to (U-8) on Page 11 for the case when the output quan-
tity is a vector.)
• Click the button labeled Run the computation.
LAFARGE &POSSOLO PAGE 1OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
2 Purpose
The NIST Uncertainty Machine (https://uncertainty.nist.gov/) is a Web-
based software application to evaluate the measurement uncertainty associ-
ated with an output quantity defined by a measurement model of the form
y=f(x1, . . . , xn).
The function fmust be specified fully and explicitly, either as a formula or as
an algorithm that, given vectors of values of the inputs, all of the same length,
produces a vector of values of the output, also of the same length as the inputs
— this is the sense in which we say, throughout this manual, that fmust be
“vectorized.”
The input quantities are modeled as random variables whose joint probability
distribution also has to be fully specified. In many applications, fis real-valued
(but vectorized as just mentioned). Section 12, beginning on Page 27, shows
how the NIST Uncertainty Machine may also be used to produce the elements
needed for a Monte Carlo evaluation of uncertainty for a multivariate measur-
and: that is, when, given a single set of scalar inputs x1, . . . , xn,yis a vector
(whose length may be different from n). The example presented in section 12
(Voltage Reflection Coefficient) illustrates this case.
Lafarge and Possolo [2015]describe an early version of the NIST Uncertainty
Machine and an important innovation implemented in it: the computation of
the uncertainty budget based entirely on the results of the Monte Carlo method.
Both Bell [1999]and Hall and White [2018]provide succinct, very accessible
introductions to the concepts and basic techniques for the evaluation of mea-
surement uncertainty. Possolo [2015]and Possolo and Iyer [2017]provide more
extensive introductions that include many illustrative examples drawn from the
practice of measurement science.
The NIST Uncertainty Machine evaluates measurement uncertainty by appli-
cation of two different methods:
• The method introduced by Gauss [1823]and popularized by Kline and
McClintock [1953], particularly among the engineering and physics com-
munities — this method is described succinctly by Taylor and Kuyatt [1994],
and more detailedly in the Guide to the Evaluation of Uncertainty in Mea-
surement (GUM) [Joint Committee for Guides in Metrology,2008a];
• The Monte Carlo method described by Morgan and Henrion [1992]in
the context of measurement science, which is specified in Supplements 1
(GUM-S1) and 2 (GUM-S2) to the GUM [Joint Committee for Guides in
LAFARGE &POSSOLO PAGE 2OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
Metrology,2008b,2011]—Possolo et al. [2009]dispel some common
misunderstandings about the application of the techniques described in
the GUM-S1.
3 Gauss’s Formula vs. Monte Carlo Method
The method described in the GUM produces an approximation to the standard
measurement uncertainty u(y)of the output quantity, starting from:
(a) Estimates x1,..., xnof the input quantities, which must be specified by the
user;
(b) Standard measurement uncertainties u(x1), . . . , u(xn)associated with the
input quantities, which also must be specified by the user;
(c) Correlations {ri j}between every pair of different input quantities, which
the NIST Uncertainty Machine assumes all to be zero unless the user ex-
plicitly specifies other values for them;
(d) Values of the partial derivatives of fevaluated at x1,..., xn, which the user
need not concern herself with, because the NIST Uncertainty Machine
does all the necessary calculations.
When the probability distribution of the output quantity is approximately Gaus-
sian, then the interval y±2u(y)may be interpreted as a coverage interval for
the measurand with approximately 95 % coverage probability.
By a felicitous coincidence this also holds for some markedly non-Gaussian prob-
ability distributions, including many instances of the Student’s t, lognormal,
gamma, and Weibull distributions [Freedman et al.,2007].
However, and in general, the probabilistic meaning of other intervals, for ex-
ample y±u(y)or y±3u(y), typically will be markedly dependent on the prob-
ability distribution assigned to y. For example, if this distribution is Gaussian,
then y±u(y)has coverage probability 68 %, but 76 % when the distribution is
Laplace (or double exponential).
The GUM also considers the case where the distribution of the output quantity
yis approximately Student’s twith a number of degrees of freedom that is a
function of the numbers of degrees of freedom that the {u(xj)}are based on,
computed using the Welch-Satterthwaite formula [Satterthwaite,1946,Welch,
1947].
LAFARGE &POSSOLO PAGE 3OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
In general, neither the Gaussian nor the Student’s tdistributions need model
the dispersion of values of the output quantity accurately, even when all the
input quantities are adequately modeled as Gaussian random variables.
The GUM suggests that the Central Limit Theorem (CLT) from Probability The-
ory [DeGroot and Schervish,2011]lends support to the Gaussian approxima-
tion for the distribution of the output quantity. However, without a detailed
examination of the measurement function f, and of the probability distribution
of the input quantities (examinations that the GUM does not explain how to
do), it is impossible to guarantee the adequacy of the Gaussian or Student’s t
approximations.
NOTE. The CLT states that, under specified conditions, a sum of indepen-
dent random variables has a probability distribution that is approximately
Gaussian [Billingsley,1979, Theorem 27.2]. The CLT is a limit theorem,
in the sense that it concerns an infinite sequence of sums, and provides
no indication about how close to Gaussian the distribution of a sum with
a finite number of summands will be. Other results in probability theory
provide such indications, but they involve more than just the means and
variances that are required to apply Gauss’s formula [Friedrich,1989].
NOTE. The reason why the CLT may be relevant is the following: if the
function fis sufficiently smooth in a neighborhood of the point (in n-
dimensional Euclidean space) (ξ1, . . . , ξn), whose coordinates are the true
values of the input quantities, then f(x1, . . . , xn)≈f(ξ1, . . . , ξn)+ ˙
f1(x1, . . . , xn)(x1−
ξ1) + ··· +˙
fn(x1, . . . , xn)(xn−ξn), where the {˙
fi}denote the first-order
partial derivatives of f. The right-hand side is a sum of random variables
when the {xi}are modeled as random variables.
Application of the Monte Carlo method produces an arbitrarily large sample
from the probability distribution of the output quantity, and it requires that
the joint probability distribution of the random variables modeling the input
quantities be specified fully.
This sample alone suffices: (i) to compute the standard uncertainty associated
with the output quantity; (ii) to compute and to interpret coverage intervals
probabilistically; and (iii) to estimate the proportions of the squared uncertainty
u2(y)that are attributable to the sources of uncertainty corresponding to the the
different input quantities (the so-called uncertainty budget), using the technique
described by Lafarge and Possolo [2015].
EXAMPLE. Suppose that the measurement model is y=ab/c, and that a,
b, and care modeled as independent random variables such that:
•ais Gaussian with mean 32 and standard deviation 0.5;
LAFARGE &POSSOLO PAGE 4OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
•bhas a uniform (or, rectangular) distribution with mean 0.9 and
standard deviation 0.025;
•chas a symmetrical triangular distribution with mean 1 and stan-
dard deviation 0.3.
Figure 1on Page 6shows the graphical user interface of the NIST Uncertainty
Machine filled in to reflect these modeling choices, and the results that are
returned and displayed by the browser. To load the specifications for this
example into the NIST Uncertainty Machine, click here.
The method described in the GUM produces y=32.2 and u(y) = 12.5.
According to the conventional interpretation, the interval y±2u(y) =
(18, 67.1)may be a coverage interval with approximately 95 % coverage
probability. (The results of the Monte Carlo method can be used to show
that the effective coverage of this interval is 95.5 %.)
Since the NIST Uncertainty Machine requires that the probability distribu-
tion of the input quantities be specified, in the absence of cogent reason to do
otherwise, the user may assign Gaussian (or, normal) distributions to them:
• If the input quantities are uncorrelated, then this amounts to assigning
a Gaussian distribution to each one of them, with mean and standard
deviation equal to the corresponding estimate and standard uncertainty;
• If the input quantities are correlated, then besides assigning Gaussian dis-
tributions to them as in the previous case, then the user will also need
to select the option marked Correlation in the interface of the NIST
Uncertainty Machine, and then specify the values of the correlations,
and select a Gaussian copula (if indeed a multivariate Gaussian distribu-
tion is desired) to enforce the correlations [Possolo,2010].
In many cases there is cogent reason to assign non-Gaussian distributions to at
least some of the input quantities.
For example, if the quantity takes values between known lower and upper limits,
then a (shifted and re-scaled) beta distribution with suitably chosen parameters
may be an appropriate model: the uniform (or, rectangular) distribution is a
special case of the beta distribution.
For another example, suppose that f(x1, . . . , xn)involves a ratio, as in the ex-
ample above, where y=ab/c. Then cshould not be assigned a normal distri-
bution because the corresponding probability density is positive at 0, and ywill
have infinite variance. If the true value of cis known to be positive, and b
cis its
estimate, and u(c)/b
cis less than 5 %, say, then cmay be assigned a lognormal
LAFARGE &POSSOLO PAGE 5OF 46
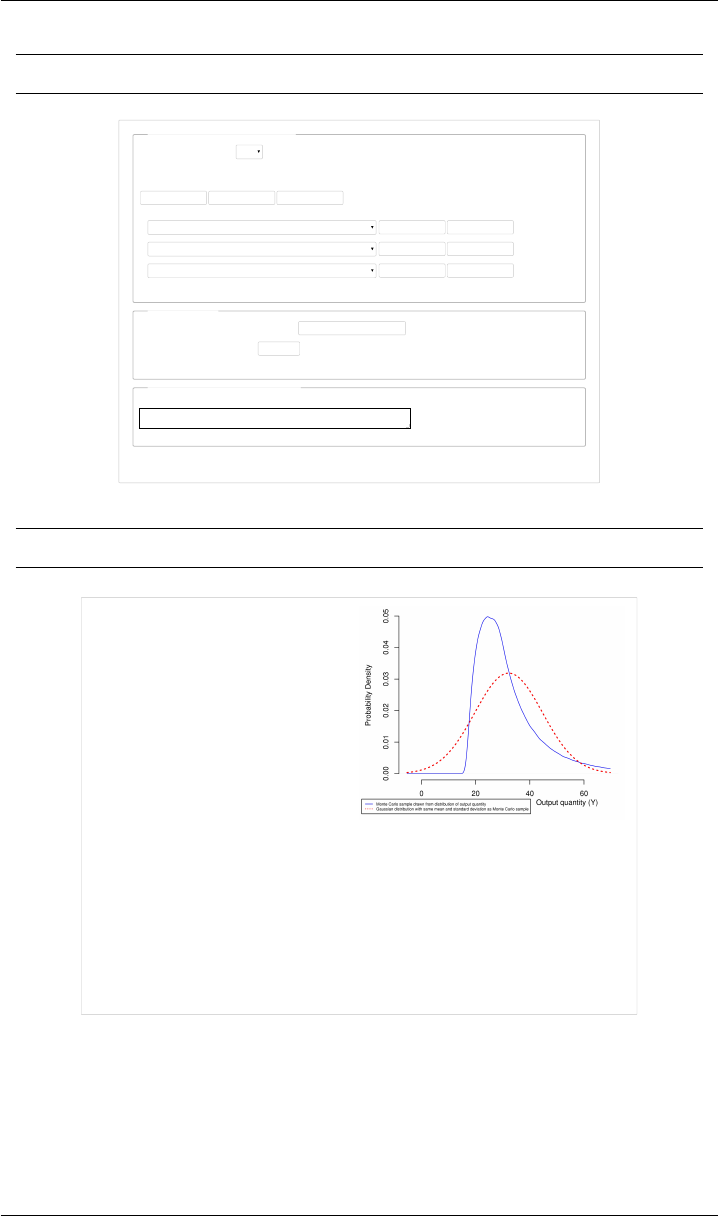
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
3
Names of input quantities:
a
b
c
a
Gaussian (Mean, StdDev)
32
0.5
b
Uniform (Mean, StdDev)
0.9
0.025
c
Triangular -- Symmetric (Mean, StdDev)
1
0.3
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
5
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
a*b/c
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 32.2
sd = 13
median = 28.8
mad = 8.9
Coverage intervals
99% ( 17.1, 85) k = 2.7
95% ( 18.2, 67) k = 2
90% ( 19.1, 57.9) k = 1.6
68% ( 21.8, 42.4) k = 0.82
ANOVA (% Contributions)
w/out Residual w/ Residual
a 0.22 0.18
b 0.62 0.52
c 99.16 81.89
Residual NA 17.42
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 28.8
u(y) = 8.7
SensitivityCoeffs Percent.u2
a 0.9 0.27
b 32.0 0.85
c -29.0 99.00
Correlations NA 0.00
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 1: ABC. Entries in the Web page correspond to the example discussed in §3.
In each numerical result, only the digits that the NIST Uncertainty Machine deems
to be significant are printed. Estimate of the probability density of the output quantity
(solid blue line), and probability density (dotted red line) of a Gaussian distribution
with the same mean and standard deviation as the output quantity. In this case, the
Gaussian approximation is very inaccurate.
LAFARGE &POSSOLO PAGE 6OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
distribution with mean b
cand standard deviation u(c), and this distribution will
be just about indistinguishable from the Gaussian distribution with the same
mean and standard deviation.
The NIST Uncertainty Machine offers a rich menu of distributions that may
be selected and assigned to the input quantities to characterize the uncertainty
associated with them. Possolo and Elster [2014]provide detailed guidance for
how to assign probability distributions to input quantities, and illustrate this
guidance with examples. The NIST Uncertainty Machine also offers the pos-
sibility of importing a file with a sample of values drawn from the distribution
one wishes to assign to an input quantity, regardless of what this distribution
may be, and without having to specify it.
4 Usage
The NIST Uncertainty Machine runs on a NIST Web server, accessible via a
Web browser at https://uncertainty.nist.gov/. The computational engine
of the NIST Uncertainty Machine is written in the R language for statistical
computing and graphics [R Core Team,2015].
NOTE. Some commercial products, and free software, are identified in
this manual in order to specify the means whereby the NIST Uncertainty
Machine may be employed. Such identification is not intended to imply
recommendation or endorsement by the National Institute of Standards
and Technology, nor is it intended to imply that the products or software
identified are necessarily the only or best available for the purpose.
Seed. The box following Random number generator seed contains an inte-
ger no larger than 100 that serves as the seed for the random number generator.
With the same seed, and with the same other inputs, the NIST Uncertainty
Machine should always produce exactly the same results. In general, the user
does not need to choose a value for the seed: a value is placed in the box auto-
matically when the Web page of the NIST Uncertainty Machine is visited.
Reset. Pressing the Reset button. will clear all the entries in the input page.
(U-1) If the user wishes to use a previously saved configuration file with in-
puts for the NIST Uncertainty Machine, then use the rectangle out-
lined with a dashed line in the input page, Drop configuration file
LAFARGE &POSSOLO PAGE 7OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
here or click to upload: either drag the file onto it, or click inside
this rectangle and then look for and select the file where the input pa-
rameters will have been saved previously. (U-12) explains how to save
a configuration file that may be used subsequently to re-run the same
computation.
(U-2) Choose the number of input quantities from the drop-down menu cor-
responding to the entry Number of input quantities. In response to
this, the Web page will update itself and show as many boxes as there
are input quantities, and assign default names to them (which may be
changed as explained next).
(U-3) Enter the names of the input quantities into the boxes following Names
of input quantities. The same names will automatically become the
labels of the rows of boxes that appear immediately below and that are
used to specify probability distributions for the input quantities.
(U-4) Assign a probability distribution to each of the input quantities using
the drop-down menus in front of them. A few commonly used distri-
butions will be readily available. Clicking on More choices will reveal
others. Once a choice is made, one or more additional input boxes will
appear, where values of parameters must be entered fully to specify the
probability distribution that was selected. If the choice is Sample values
(between 30 and 100000), then a rectangle outlined with a dashed line
will appear in the same row, saying Drop sample file here or click
to upload.
Table 2on Page 13 lists the distributions implemented currently, and
their parametrizations. Note that some distributions can be parametrized
in any one of several different ways: in such cases, only one of the
parametrizations needs to be specified. For example, specifying a rect-
angular distribution whose left and right end-points are 0.37 and 0.41 is
equivalent to specifying a rectangular distribution whose mean is (0.34+
0.42)/2=0.38 and whose standard deviation is (0.42 −0.34)/p12 =
0.023.
The NIST Uncertainty Machine does not accept standard deviations
that are set to 0 — however, this is detected only at run time (after
the user will have pressed the button labeled Run the computation).
Declaring the standard deviation to be 0 would be equivalent to speci-
fying the value of a constant, which can be done either by entering this
value as a numerical constant in the expression that defines the output
LAFARGE &POSSOLO PAGE 8OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
quantity (cf. the example in Section 11 that begins on Page 25), or by
selecting Constant as distribution type and entering the value of the con-
stant in the corresponding box.
(U-5) As already mentioned above, the NIST Uncertainty Machine allows
the user to provide a sample drawn from the probability distribution of an
input quantity instead of selecting a particular distribution from among
those that the NIST Uncertainty Machine offers.
To provide such sample, select Sample values (between 30 and 100000)
from the drop-down menu with the list of distributions, and then use the
rectangle outlined with a dashed line that will have appeared in the in-
put page, in front of the box corresponding to the input quantity, Drop
sample file here or click to upload: either drag the file onto it,
or click it and then look for and select the file containing the sample
values.
The data file is then parsed and all the numbers present in it will be
loaded. The numerical values may be arranged in the file in any way
that is convenient for the user — one or several per line —, but must be
separated from one another by any (not necessarily the same throughout
the file) non-numeric character or string of non-numeric characters. The
numbers may be written either in decimal or scientific notation, and in
this case using eor Eto denote the appropriate power of ten. For exam-
ple, 1983.76 may also be written either as 1.98376e3 or as 1.98376E3.
Once the file has been parsed the number of values loaded will be shown
to ensure that it matches the user’s expectation. The total number of
sample values provided in this way, summed across all input quantities
for which samples are provided, cannot exceed 2 400 000 approximately.
In case this limit is reached, an error message appears once the compu-
tation starts.
The NIST Uncertainty Machine operates essentially in the same way
regardless of whether parametric distributions are specified, or samples
from otherwise unspecified distributions are provided. The main differ-
ence is that, for the latter, the NIST Uncertainty Machine resamples
the values in the sample that was provided repeatedly, uniformly at ran-
dom with replacement (that is, all values in the sample provided are
equally likely to be drawn, and all are available for drawing when a draw
is made). §13 illustrates this feature, and provides additional informa-
tion about it.
LAFARGE &POSSOLO PAGE 9OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
(U-6) Enter the size of the Monte Carlo sample to be drawn from the proba-
bility distribution of the output quantity, into the box labeled Number of
realizations of the output quantity: the default value, 1 ×106, is
the minimum recommended sample size (currently the NIST Uncertainty
Machine is able to generate samples of size from 1 ×105to 5 ×106).
(U-7) Enter a valid R expression into the box labeled Value of output quantity
(R expression) that represents f(x1, . . . , xn), the right-hand side of
the measurement equation that defines the value of the output quan-
tity. This expression should involve only the input quantities, functions
and numerical constants that R knows how to evaluate, listed on ta-
ble 1. (Remember that R is case sensitive.) Refer to the current version
of An Introduction to R, freely available at https://cran.r-project.
org/manuals.html, or to one of the tutorials listed in https://cran.
r-project.org/other-docs.html.
+- * ^ %% %/%
/abs sign sqrt ceiling floor
trunc cummax cummin cumprod cumsum exp
expm1 log log10 log2 log1p cos
cosh sin sinh tan tanh acos
acosh asin asinh atan atanh cospi
sinpi tanpi gamma lgamma digamma trigamma
== < > =pi complex
Re Im Mod Arg {(
c function $ mapply matrix %*%
uniroot t solve
Table 1: Supported functions. List of functions and operators currently
supported by the NIST Uncertainty Machine.
Alternatively, the definition may comprise several R expressions, but with
only one expression per line within this box (pressing Enter on the key-
board, with the cursor in this box, creates a new line), and the last expres-
sion must evaluate the output quantity (without assigning this value to
any variable), or one component of the output quantity when the output
quantity is a vector (cf. (U-8)).
EXAMPLE. If the measurement model is A= (L1−L0)/L0(T1−
T0), then the R expression that should be entered into this box is
(L1-L0)/(L0*(T1-T0)). Alternatively, the box may comprise these
three lines:
LAFARGE &POSSOLO PAGE 10 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
N = L1-L0
D = L0*(T1-T0)
N/D
The NIST Uncertainty Machine requires that the measurement func-
tion fbe vectorized: that is, if each of its arguments is a vector of length
K, then the value of f, specified in the last line of the box, must be a
vector of length Ksuch that the kth element of this vector is the value
of fat the kth values of all the input quantities. This may not happen
automatically for some intricate measurement equations that involve op-
timizations, root-finding, or solutions of differential equations, among
others. In the example described in §13, vectorization is achieved sim-
ply by invoking the R function mapply, which applies the same function
to sets of corresponding values of its arguments.
NOTE. The NIST Uncertainty Machine may report Impossible to
evaluate the output expression. This may be caused by the use of an
R function that the NIST Uncertainty Machine does not recognize
yet. When such message is encountered, please send an eMail mes-
sage to both thomas.lafarge@nist.gov and antonio.possolo@nist.gov,
showing the inputs that induced such response.
(U-8) If the output quantity is a vector with pcomponents, press the “+” button
p−1 times to create a total of poutput fields. Enter an R expression into
each one of them similarly to how the specification of the value of the
output quantity was described in (U-7).
(U-9) If symmetrical coverage intervals are desired, then select the option marked
Symmetrical coverage intervals. These intervals take a little longer
to compute than those computed by default (which may be asymmetri-
cal), and are of the form b
y±ku(y)where b
y, the estimate of the output
quantity, is the average of the Monte Carlo sample, and the coverage fac-
tor k depends on the specified coverage probability.
NOTE. The default coverage interval with coverage probability 0 <
γ < 1 is (y∗
(1−γ)/2,y∗
(1+γ)/2), whose endpoints are the 50(1−γ)th
and 50(1+γ)th percentiles of the Monte Carlo sample drawn from
the probability distribution of the output quantity. These need not
be equidistant from the average (or from the median) of the sam-
ple. The corresponding coverage factor is computed as k= ( y∗
(1+γ)/2
−y∗
(1−γ)/2)/(2u(y)), and it is not particularly meaningful when the
interval is not symmetrical (that is, when it is not centered on the
estimate of the output quantity).
LAFARGE &POSSOLO PAGE 11 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
Even for symmetrical intervals (those that are centered on the aver-
age of the Monte Carlo sample drawn from the probability distribu-
tion of the output quantity), the coverage factor kis computed only
after the coverage interval has been derived from this sample, hence
differently from how it is computed in the GUM.
(U-10) If there are non-null correlations between input quantities that need to
be taken into account, then select the option marked Correlations, and
enter the values of non-zero correlations into the appropriate boxes in the
upper triangle of the correlation matrix that the browser will display.
NOTE. Not all combinations of values of the correlations that may be
entered produce a valid correlation matrix, which must be symmet-
rical, have all entries between −1 and +1, and have only positive
eigenvalues. The NIST Uncertainty Machine issues an error mes-
sage (Illegal correlation matrix) if these conditions are not all
met.
(U-11) If Correlations has been selected, then besides having specified cor-
relations in (U-10), also select a copula (currently, either Gaussian or
Student’s t) to manufacture a joint probability distribution for the input
quantities. This is needed because there are infinitely many multivariate
distributions with the same means, standard deviations, and correlations
[Nelsen,2006]. If the copula chosen is (multivariate) Student’s t, then
another box will appear nearby to receive the desired number of degrees
of freedom.
NOTE. The resulting joint distribution reproduces the correlation
structure that has been specified, and has the distributions specified
for the input quantities as margins. Possolo [2010]explains and
illustrates the role that copulas play in uncertainty analysis.
(U-12) Click the button labeled Run the computation. In response to this, the
browser will open a new tab where numerical and graphical results will
be displayed, which are described in §5.
The NIST Uncertainty Machine estimates the number of significant dig-
its in the results, and reports only these. To increase the number of sig-
nificant digits, another run will have to be done with a larger size for
the Monte Carlo specified in Number of realizations of the output
quantity, as explained in (U-6).
LAFARGE &POSSOLO PAGE 12 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
One of the outputs produced by the NIST Uncertainty Machine is a
plot showing two probability densities described in §5and illustrated in
Figure 1on Page 6.
Below this plot there are five clickable links: if the last one, which reads
Download Configuration File, is clicked, a plain text file named config.um
is downloaded to the local machine that specifies the inputs that were
used. This file may be renamed at will, and reused in a future run of the
NIST Uncertainty Machine, as explained in (U-1).
5 Results
The NIST Uncertainty Machine produces output on a Web page, and offers
the possibility of downloading its output in the form of four files.
• Numerical output appears to the left, and it is divided into two sections.
The top section lists results from the application of the Monte Carlo method.
The bottom section lists results from the application of the method de-
scribed in the GUM.
The results for the Monte Carlo method include a table with summary
statistics for the sample that was drawn from the probability distribution
of the output quantity: average, standard deviation, median, MAD.
The average is the common estimate of the true value of the output quan-
tity, and the standard deviation is the common evaluation of u(y). How-
ever, the median may be a reasonable, and in some cases a preferable
alternative to the average as estimate of that true value. Similarly, MAD
may be a reasonable, and in some cases a preferable alternative to the
standard deviation as evaluation of u(y). When reporting measurement
results, it is the user’s responsibility to state how the estimate of the true
value of the output quantity was obtained, and how the associated stan-
dard uncertainty was evaluated.
NOTE. “MAD” denotes the median absolute deviation from the me-
dian, multiplied by a factor (1.4826) that makes the result compara-
ble to the standard deviation when applied to samples from Gaussian
distributions.
NOTE. Neither the MAD, nor the MAD divided by the square root of the
sample size, are the standard deviation of the sampling distribution
of the median. For a sample of large size ndrawn from a continuous
LAFARGE &POSSOLO PAGE 13 OF 46

NAME PARAMETERS CONSTRAINTS
Bernoulli Prob. of success 0<Prob. of success <1
Beta Mean,StdDev 0<Mean <1, 0 <StdDev <½
Shape1,Shape2 Shape1 >0, Shape2 >0
Beta – Shifted & Rescaled Mean,StdDev,Left,Right 0<Mean <1, 0 <StdDev <½, Left <Right
Shape1,Shape2,Left,Right Shape1 >0, Shape2 >0, Left <Right
Chi-Squared DF DF >0
Constant Value —
Exponential Mean Mean >0
Gamma Mean,StdDev Mean >0, StdDev >0
Shape,Scale Shape >0, Scale >0
Gaussian Mean,StdDev StdDev >0
Gaussian – Truncated Mean,StdDev,Left,Right StdDev >0, Left <Right
Lognormal Mean,StdDev Mean >0, StdDev >0
Rectangular Mean,StdDev StdDev >0
Left,Right Left <Right
Student’s t Mean,StdDev,DF StdDev >0, DF >2
Center,Scale,DF Scale >0, DF >0
Triangular – Symmetric Mean,StdDev StdDev >0
Left,Right Left <Right
Triangular – Asymmetric Left,Right,Mode Left ¶Mode ¶Right;Left 6=Right
Uniform Mean,StdDev StdDev >0
Left,Right Left <Right
Weibull Mean,StdDev Mean >0, StdDev >0
Shape,Scale Shape >0, Scale >0
Table 2: Distributions. Several distributions are available with alternative parametrizations: for these, it suffices to select
and specify one of them. DF stands for number of degrees of freedom. Left and Right denote the left and right endpoints
of the interval to which a distribution assigns probability 1. The mode of a distribution is where its probability density
reaches its maximum. The rectangular distribution is the same as the uniform distribution. A quantity xhas a shifted and
rescaled beta distribution when (x−Left)/(Right −Left)has a conventional beta distribution. For the truncated Gaussian
distribution, Mean and StdDev denote the mean and standard deviation without truncation: the actual mean and standard
deviation depend also on the truncation points, and it is the actual mean and standard deviation that the GUM and Monte
Carlo methods use in their calculations. A Student’s tdistribution will have infinite standard deviation unless DF >2, and
its mean will be undefined unless DF >1. The values assigned to the parameters must satisfy the constraints listed.

VERSION 1.4 NIST UNCERTAINTY MACHINE
distribution with probability density g, this standard deviation is ap-
proximately equal to 1/(2g(M)pn), where Mdenotes the true value
of the median.
Also listed are coverage intervals with coverage probabilities 99 %, 95 %,
90 %, and 68 %. The interval with 68 % coverage probability is often
called a “1-sigma interval”, and the interval with 95 % coverage probabil-
ity is often called a “2-sigma interval”: however, these designations are
appropriate only when the distribution of the output quantity is approx-
imately Gaussian. Next to each interval is listed the value of the corre-
sponding coverage factor k (cf. GUM 3.3.7, and GUM 6.2). The values of
kare equal to one half the length of the interval divided by the standard
uncertainty.
If option mentioned in (U-9) above is selected prior to starting the compu-
tations then these intervals will be centered on the mean of the sample of
values of the output quantity. Otherwise their endpoints will be computed
as explained in (U-9).
The section pertaining to the Monte Carlo method concludes with a table
of analysis of variance (ANOVA) that lists, for each input quantity, the
proportion of u2(y)that the source of uncertainty corresponding to the
input quantity is responsible for, computed under the assumption that the
output quantity is a linear function of the input quantities [Lafarge and
Possolo,2015].
The line labeled “Residual” lists the proportion of u2(y)that is left unac-
counted for when that assumption of linearity does not hold. Therefore,
it provides a single-number summary of the accuracy of the approxima-
tion to u(y)given by Gauss’s formula, which is Equation (13) in the GUM
(Page 21).
The ANOVA table has two columns: the column labeled “w/out Residual”
lists the proportions recomputed out of a total that excludes the portion
deemed “residual”. These should be numerically close to the entries in
the similar table that appears at the bottom of the section of results from
the application of the method described in the GUM.
The results obtained according to the GUM are listed under Gauss’s
Formula (GUM’s Linear Approximation). These include an estimate
of the true value of the output quantity and an evaluation of the associ-
ated standard uncertainty. The former is computed according to Equa-
tion (1) in the GUM, and the latter according to Equation (13), where the
LAFARGE &POSSOLO PAGE 15 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
values of the partial derivatives are computed using numerical differen-
tiation as implemented in R function grad defined in package numDeriv
[Gilbert and Varadhan,2016].
Finally, a table shows the sensitivity coefficients as defined in the GUM
5.1.3: the values of the first-order partial derivatives of the measurement
function fevaluated at the estimates of the input quantities.
The same table also shows the percentage contributions that the different
input quantities make to the squared standard uncertainty of the output
quantity. If the input quantities are uncorrelated, then these contributions
add up to 100 % approximately. If they are correlated, then the contribu-
tions may add up to more or less than 100 %, depending on the absolute
values and signs of the correlations: in this case, the line labeled Corre-
lations will indicate the percentage of u2(y)that is attributable to those
correlations (this percentage is positive if u2(y)is larger than it would
have been in the absence of correlations).
• The plot included in the output Web page depicts an estimate of the prob-
ability density of the output quantity (smooth, continuous version of a
histogram, drawn in a solid blue line) computed as described by Silver-
man [1986]and as implemented in R function density. The plot also
shows (depicted as a red dashed line) the probability density of the Gaus-
sian distribution with the same mean and standard deviation as the Monte
Carlo sample of values of the output quantity.
• Below this plot there are five clickable links that, once clicked, download
a file to the local machine.
–Download binary R data file with Monte Carlo values
of output quantity: a binary file with suffix Rd is downloaded
that contains (in variable y) the Monte Carlo sample of values drawn
from the probability distribution of the output quantity — it can be
loaded into R using the function load.
NOTE. When the output quantity is a vector with p¾2 compo-
nents, as contemplated in (U-8), the NIST Uncertainty Machine
will first display download links relevant to all the outputs, fol-
lowed by psections, labeled Output 1,Output 2, . . . , each struc-
tured as described above. The links just mentioned, will down-
load the values sampled for all poutputs. When this file with
results is loaded into R, a list named yList is made available,
with pelements named y1,y2, ....
LAFARGE &POSSOLO PAGE 16 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
–Download a text file with Monte Carlo values of output
quantity: a plain text file is downloaded that contains the Monte
Carlo sample of values drawn from the probability distribution of the
output quantity; since preparing this file involves converting the bi-
nary file mentioned above into a plain text version, some noticeable
time may elapse before the download actually begins.
NOTE. When the output quantity is a vector with p¾2 compo-
nents, as contemplated in (U-8),the NIST Uncertainty Machine
will first display download links relevant to all the outputs, fol-
lowed by psections, labeled Output 1,Output 2, . . . , each struc-
tured as described above. The links just mentioned will down-
load the values sampled for all poutputs, arranged into a plain
text file with as many rows as the sample size of the Monte Carlo
sample, and with pvalues per line, separated from each other by
blank spaces.
–Download text file with numerical results shown on this
page: a plain text file with the same results and layout of the nu-
merical results shown on the output Web page.
–Download JPEG file with plot shown on this page: a JPEG file
with the same plot that is displayed on the Web page, showing two
probability densities.
–Download Configuration File: a plain text file with extension
.um that specifies the inputs that were used and that may be reused
as explained in (U-1).
6 Transparency for Validation & Verification
Given a configuration file produced by the NIST Uncertainty Machine, which
has been saved to the user’s local machine as explained in (U-12) on Page 12,
and passing the file name as an argument to FullScriptNUM.R, should produce
the same results as when the same configuration file is loaded into the NIST
Uncertainty Machine and run there, provided R has been installed in the local
machine.
Suppose the configuration file is called NUMConfigExample.um. (The default
extension for configuration files produced by the NIST Uncertainty Machine
is .um, but the file name may be any alphanumeric string that is a legal file
name under the applicable operating system — embedded blank spaces are
discouraged — and does not even have to have an extension.
LAFARGE &POSSOLO PAGE 17 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
The following command, executed in a terminal window (under Linux or Ma-
cOS), or at the Windows command prompt, will replicate the results that the
specified configuration file would produce if loaded into the NIST Uncertainty
Machine and run there. (In Windows other than version 10, click Start, type
cmd in the box Search programs and files, and press Enter on the keyboard.
In Windows 10 choose Command Prompt from the menu that appears after press-
ing WIN+X or right-clicking on the Start button.) Note that $denotes the
terminal prompt, hence is not part of the command:
$ Rscript FullScriptNUM.R NUMConfigExample.um
The script, which is available on the About page of https://uncertainty.
nist.gov/, will generate 3 files in the current directory or folder, with the same
prefix as the configuration file. In the case of the example above, the output files
would be:
•NUMConfigExample-results.txt: a plain text file with the same results
and layout of the numerical results shown on the NIST Uncertainty
Machine’s output Web page;
•NUMConfigExample-density.jpg: a JPEG file with the same plot that is
displayed on the NIST Uncertainty Machine’s output Web page, show-
ing the graphs of two probability densities;
•NUMConfigExample-values.Rd: a binary R data file with the replicates
of the input quantities, and with the corresponding values of the output
quantity, corresponding to the Monte Carlo method of the GUM-S1. In
R, the command load(“NUMConfigExample-values.Rd”) will create as
many vectors as there are input quantities, with their names as specified
in the configuration file, and a vector named ywith the values of the
output quantity.
The script will install any necessary R packages that may not have been previ-
ously installed in the local version of the R system. The script first writes its
version number onto the terminal window, which should be matched to the
version of the NIST Uncertainty Machine displayed at the top of the page of
the web application, for example: NIST Validation & Verification Script
Version 1.4
LAFARGE &POSSOLO PAGE 18 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
7 Example — Thermal Expansion Coefficient
To measure the coefficient of linear thermal expansion of a cylindrical copper
bar, the length L0=1.4999 m of the bar was measured with the bar at tem-
perature T0=288.15 K, and then again at temperature T1=373.10 K, yielding
L1=1.5021 m. The measurement model is A= (L1−L0)/L0(T1−T0).
For the purpose of this illustration we will assume that the input quantities are
like (scaled and shifted) Student’s trandom variables with 3 degrees of free-
dom, with means equal to the measured values given, and standard deviations
u(L0) = 0.0001 m, u(L1) = 0.0002 m, u(T0) = 0.02 K, and u(T1) = 0.05 K.
This modeling assumption is appropriate when the estimates of the input quan-
tities are averages of 4 determinations made under conditions of repeatability,
which may be regarded as samples from Gaussian distributions, and the associ-
ated uncertainties result from Type A evaluations, and are what the GUM calls
“experimental standard deviation of the mean”, computed according to Equa-
tion (5) in the GUM.
To load the specifications for this example into the NIST Uncertainty Machine,
click here. The GUM’s approach yields α=1.727 ×10−5K−1and u(α) =
2×10−6K−1, and the Monte Carlo method reproduces these results. Figure 2
on Page 20 reflects these facts, and lists the results.
8 Example — End-Gauge Calibration
In Example H.1 of the GUM (which is reconsidered by Guthrie et al. [2009]),
the measurement model is l=lS+d−lS[(δα)θ+αS(δθ )], where δα and δθ
each denotes a single input quantity, not a product of two input quantities.
The estimates and standard measurement uncertainties of the input quantities
are listed in Table 3. For the Monte Carlo method, we model the input quantities
as independent Gaussian random variables with means and standard deviations
equal to these estimates and standard measurement uncertainties. To load the
specifications for this example into the NIST Uncertainty Machine, click here.
The GUM’s approach yields l=50 000 838 nm and u(l) = 32 nm, while the
Monte Carlo method reproduces the value for lbut evaluates u(l) = 34 nm.
Refer to Figure 3on Page21.
The GUM (Page 84) gives (50 000 745 nm, 50 000 931 nm)as an approximate
99 % coverage interval for l, and the results of the Monte Carlo method confirm
this coverage probability. If the user chooses a coverage interval that is proba-
LAFARGE &POSSOLO PAGE 19 OF 46
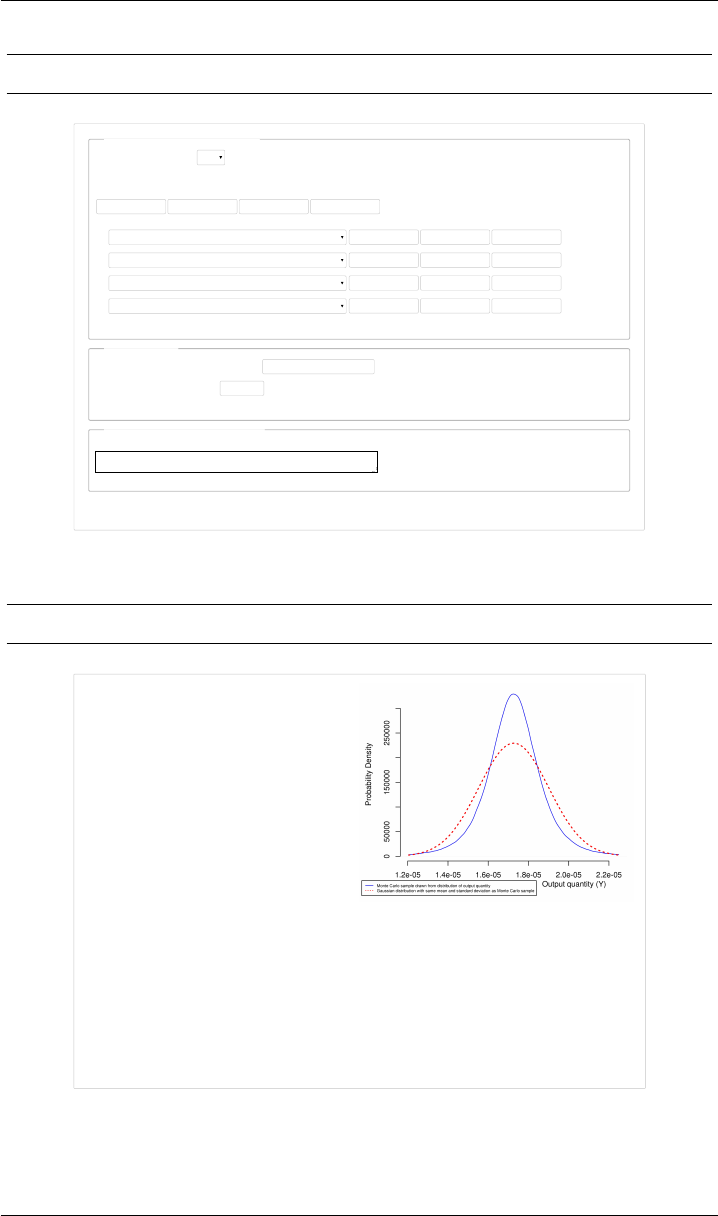
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
4
Names of input quantities:
L0
T0
L1
T1
L0
Student t (Mean, StdDev, No. of degrees of freedom)
1.4999
0.0001
3
T0
Student t (Mean, StdDev, No. of degrees of freedom)
288.15
0.02
3
L1
Student t (Mean, StdDev, No. of degrees of freedom)
1.5021
0.0002
3
T1
Student t (Mean, StdDev, No. of degrees of freedom)
373.10
0.05
3
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
5
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
(L1-L0) / (L0*(T1-T0))
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 1.727e-05
sd = 1.7e-06
median = 1.727e-05
mad = 1.2e-06
Coverage intervals
99% ( 1.2e-05, 2.3e-05) k = 3.2
95% ( 1.4e-05, 2.05e-05) k = 1.9
90% (1.48e-05, 1.97e-05) k = 1.4
68% ( 1.6e-05, 1.86e-05) k = 0.75
ANOVA (% Contributions)
w/out Residual w/ Residual
L0 20.48 20.48
T0 0.00 0.00
L1 79.52 79.52
T1 0.00 0.00
Residual NA 0.00
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 1.727e-05
u(y) = 1.8e-06
SensitivityCoeffs Percent.u2
L0 -7.9e-03 2.0e+01
T0 2.0e-07 5.4e-04
L1 7.8e-03 8.0e+01
T1 -2.0e-07 3.4e-03
Correlations NA 0.0e+00
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 2: Thermal Expansion Coefficient. Input and output Web pages for
the example discussed in §7.
LAFARGE &POSSOLO PAGE 20 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
QUANTITY x u(x)
lS50 000 623 nm 25 nm
d215 nm 9.7 nm
δα 0◦C−10.58 ×10−6◦C−1
θ−0.1 ◦C 0.41 ◦C
αS11.5 ×10−6◦C−11.2 ×10−6◦C−1
δθ 0◦C 0.029 ◦C
Table 3: End-Gauge Calibration. Estimates and standard measurement
uncertainties for the input quantities in the measurement model of Exam-
ple H.1 in the GUM.
bilistically symmetric (meaning that it leaves 0.5 % of the Monte Carlo sample
uncovered on both sides), then the Monte Carlo method produces (50 000 749 nm,
50 000 927 nm)as 99 % coverage interval, which happens not be quite centered
at the estimate of y.
9 Example — Dynamic Viscosity
The dynamic viscosity µMof a solution of sodium hydroxide in water at 20 ◦C, is
measured using a boron silica glass ball of mass density ρB=2217 kg/m3, with
measurement equation µM=µC[(ρB−ρM)/(ρB−ρC)](tM/tC), where µC=
4.63 mPa s, ρC=810 kg/m3, and tC=36.6 s denote the viscosity, mass den-
sity, and ball travel time for the calibration liquid, and ρM=1180 kg/m3and
tM=61 s denote the mass density and ball travel time for the sodium hydroxide
solution.
To load the specifications for this example into the NIST Uncertainty Machine,
click here.
If the input quantities are modeled as independent Gaussian random variables
with means equal to their assigned values, and standard deviations equal to
their associated standard uncertainties u(µC) = 0.01µC,u(ρB) = u(ρC) = u(ρM)
=0.5 kg/m3,u(tC) = 0.15tC, and u(tM) = 0.10tM, then the Monte Carlo
method of the GUM-S1 as implemented in the NIST Uncertainty Machine
produces: b
µM=5.8 mPa s, u(µM) = 1.12 mPa s, and [4.05 mPa s, 8.4 mPa s]
as an approximate 95 % coverage interval for µM. This interval is asymmetric
relative to the estimate b
µM.
If, instead, the estimates of the input quantities were substituted into the mea-
surement equation, the resulting estimate of µMwould have been 5.69 mPa s.
LAFARGE &POSSOLO PAGE 21 OF 46
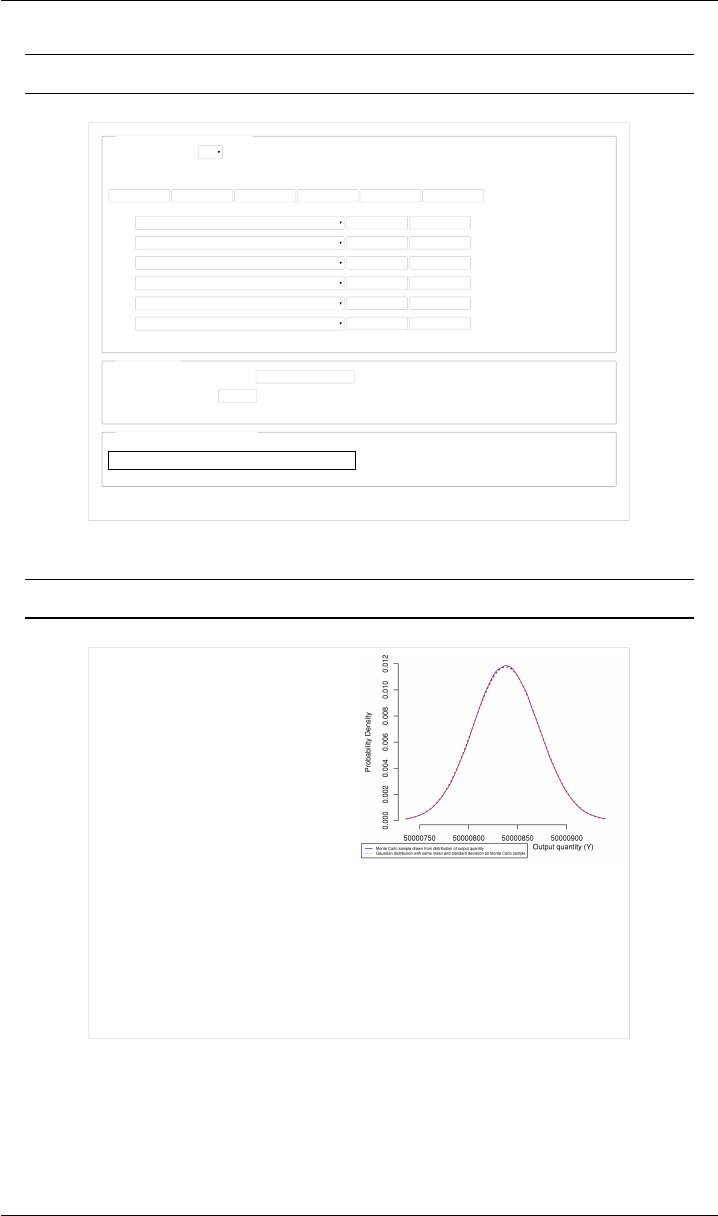
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
6
Names of input quantities:
lS
d
dalpha
theta
alphaS
dtheta
lS
Gaussian (Mean, StdDev)
50000623
25
d
Gaussian (Mean, StdDev)
215
9.7
dalpha
Gaussian (Mean, StdDev)
0
0.58e-6
theta
Gaussian (Mean, StdDev)
-0.1
0.41
alphaS
Gaussian (Mean, StdDev)
11.5e-6
1.2e-6
dtheta
Gaussian (Mean, StdDev)
0
0.029
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
5
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
lS + d - lS*(dalpha*theta + alphaS*dtheta)
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 50000837.9
sd = 33.9
median = 50000837.9
mad = 34
Coverage intervals
99% (5.00007e+07, 5.00009e+07) k = 2.6
95% (5.00008e+07, 5.00009e+07) k = 2
90% (5.00008e+07, 5.00009e+07) k = 1.7
68% (5.00008e+07, 5.00009e+07) k = 1
ANOVA (% Contributions)
w/out Residual w/ Residual
lS 62.36 54.52
d 9.23 8.07
dalpha 0.85 0.75
theta 0.00 0.00
alphaS 0.00 0.00
dtheta 27.55 24.09
Residual NA 12.57
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 50000838
u(y) = 31.7
SensitivityCoeffs Percent.u2
lS 1 62.00
d 1 9.40
dalpha 5000000 0.84
theta 0 0.00
alphaS 0 0.00
dtheta -580 28.00
Correlations NA 0.00
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 3: End-Gauge Calibration. Input and output Web pages for the exam-
ple discussed in §8. Note that the value of αS, 11.5 ×10−6◦C−1, was entered
as 11.5e-6.
LAFARGE &POSSOLO PAGE 22 OF 46
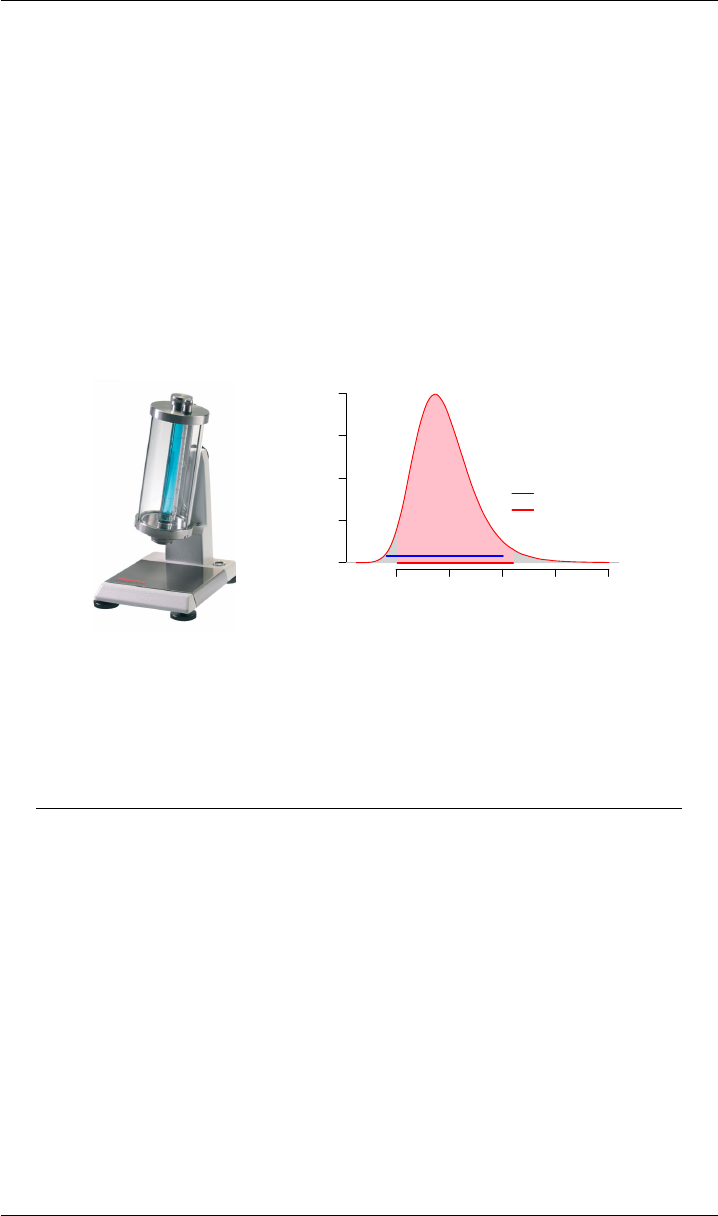
VERSION 1.4 NIST UNCERTAINTY MACHINE
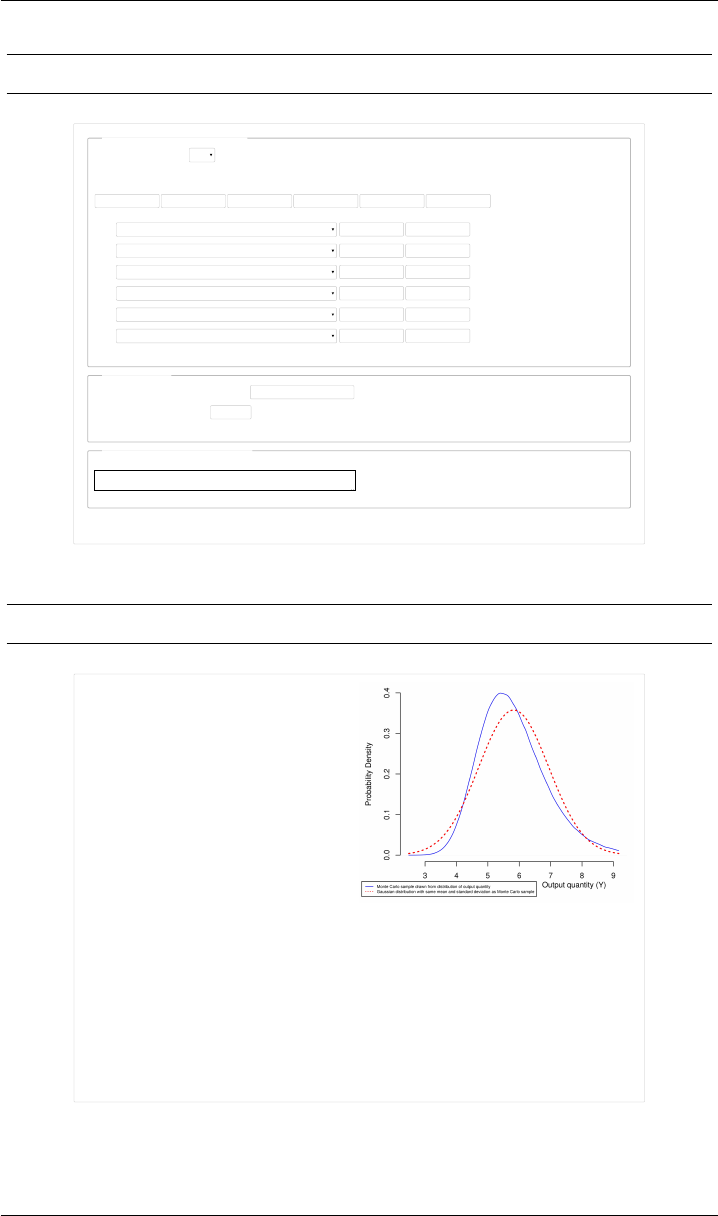
And if Gauss’s formula is used to evaluate u(µM), the result is 1.11 mPa s.
Interestingly, the evaluation of u(µM)is close to the evaluation produced by the
Monte Carlo method, but the estimates of the measurand produced by one and
by the other differ: the reason is the skewness (or, asymmetry) of the distribu-
tion of the measurand, apparent in Figure 4on Page 23.
This figure also shows that the coverage interval given above differs from the
interval corresponding to the prescription in clause 6.2.1 of the GUM (estimate
of the output quantity plus or minus twice the standard measurement uncer-
tainty evaluated using the approximate propagation of error formula). Figure 5
on Page 24 shows the corresponding input and output Web pages of the NIST
Uncertainty Machine.
4 6 8 10 12
0.0 0.1 0.2 0.3 0.4
µ / mPa s
Prob. density
●
●
●
●
GUM
GUM−S1
Figure 4: HAAKE™ falling ball viscometer from Thermo Fisher Scientific, Inc.,
(left panel), and probability density (right panel) corresponding to a Monte
Carlo sample of size 1 ×106, also showing 95 % coverage intervals for the
value of the dynamic viscosity of the liquid, one corresponding to the prescrip-
tion in clause 6.2.1 of the GUM, the other whose endpoints are the 2.5th and
97.5th percentiles of the Monte Carlo sample.
10 Example — Resistance
In Example H.2 of the GUM, the measurement model for the resistance of an
element of an electrical circuit is R= (V/I)cos(φ). The estimates and standard
uncertainties of the input quantities, and the correlations between them, are
listed in Table 4on Page 23.
For the Monte Carlo method, we model the input quantities as correlated Gaus-
sian random variables with means and standard deviations equal to the esti-
LAFARGE &POSSOLO PAGE 23 OF 46
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
6
Names of input quantities:
muC
rhoB
rhoM
rhoC
tM
tC
muC
Gaussian (Mean, StdDev)
4.63
0.0463
rhoB
Gaussian (Mean, StdDev)
2217
0.5
rhoM
Gaussian (Mean, StdDev)
1180
0.5
rhoC
Gaussian (Mean, StdDev)
810
0.5
tM
Gaussian (Mean, StdDev)
61
6.1
tC
Gaussian (Mean, StdDev)
36.6
5.49
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
5
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
muC * ((rhoB-rhoM)/(rhoB-rhoC)) * (tM/tC)
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 5.82
sd = 1.1
median = 5.69
mad = 1
Coverage intervals
99% ( 3.65, 9.7) k = 2.7
95% ( 4.05, 8.4) k = 1.9
90% ( 4.27, 7.84) k = 1.6
68% ( 4.77, 6.86) k = 0.94
ANOVA (% Contributions)
w/out Residual w/ Residual
muC 0.28 0.26
rhoB 0.00 0.00
rhoM 0.00 0.00
rhoC 0.00 0.00
tM 28.54 27.22
tC 71.18 67.88
Residual NA 4.64
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 5.69
u(y) = 1
SensitivityCoeffs Percent.u2
muC 1.2000 3.1e-01
rhoB 0.0014 4.9e-05
rhoM -0.0055 7.1e-04
rhoC 0.0040 3.9e-04
tM 0.0930 3.1e+01
tC -0.1600 6.9e+01
Correlations NA 0.0e+00
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 5: Viscosity. Input and output Web pages for the example discussed
in §9.
LAFARGE &POSSOLO PAGE 24 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
mates and standard uncertainties listed in Table 4, and with correlations identi-
cal to those given in the same table. We also adopt a Gaussian copula to manu-
facture a joint probability distribution consistent with the assumptions already
stated.
To load the specifications for this example into the NIST Uncertainty Machine,
click here.
QUANTITY x u(x)
V4.9990 V 0.0032 V
I19.6610 ×10−3A 0.0095 ×10−3A
φ1.044 46 rad 0.000 75 rad
r(V,I) = −0.36 r(V,φ) = 0.86 r(I,φ) = −0.65
Table 4: Resistance. Estimates and standard measurement uncertainties
for the input quantities in the measurement model of Example H.2 in the
GUM, and correlations between them, all as listed in Table H.2 of the GUM.
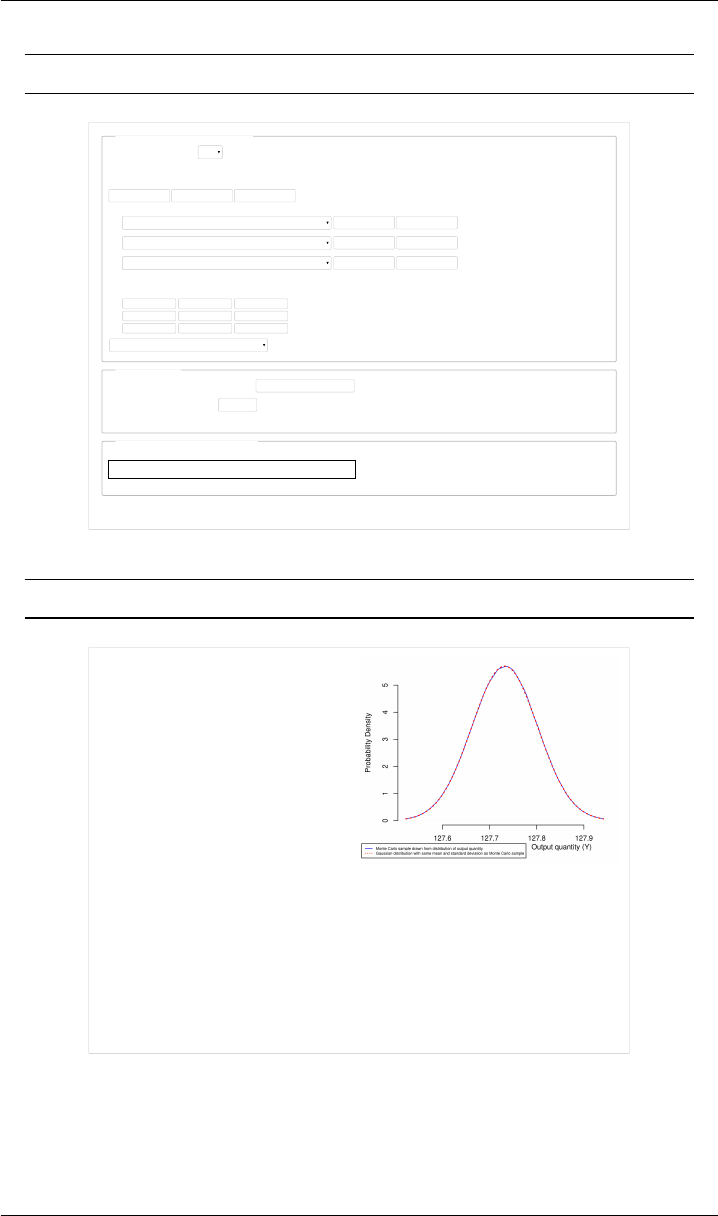
The GUM’s approach and the Monte Carlo method produce the same values
of the output quantity R=127.732 Ωand of the standard uncertainty u(R) =
0.07 Ω. The Monte Carlo method yields (127.595 Ω, 127.869 Ω)as approximate
95 % coverage interval for the resistance without invoking any additional as-
sumptions about R. Figure 6on Page 26 reflects these facts, and lists the results.
11 Example — Stefan-Boltzmann Constant
The functional relation used to define the Stefan-Boltzmann constant σinvolves
the Planck constant h, the molar gas constant R, Rydberg’s constant R∞, the
relative atomic mass of the electron Ar(e), the molar mass constant Mu, the
speed of light in vacuum c, and the fine-structure constant α:
σ=32π5hR4R4
∞
15Ar(e)4M4
uc6α8. (1)
Note that the Greek letter that is conventionally used to denote the Stefan-
Boltzmann constant is the same that is also commonly used to denote the stan-
dard deviation of a probability distribution. In this example, all instances of “σ”
refer to the Stefan-Boltzmann constant.
Table 5lists the 2010 CODATA [Mohr et al.,2012]recommended values of the
quantities that determine the value of the Stefan-Boltzmann constant, and the
LAFARGE &POSSOLO PAGE 25 OF 46
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
3
Names of input quantities:
V
I
phi
V
Gaussian (Mean, StdDev)
4.9990
0.0032
I
Gaussian (Mean, StdDev)
19.6610e-3
0.0095e-3
phi
Gaussian (Mean, StdDev)
1.04446
0.00075
Correlations
V I phi
V
1
-0.36
0.86
I
1
-0.65
phi
1
Gaussian Copula
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
5
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
(V/I)*cos(phi)
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 127.732
sd = 0.0699
median = 127.732
mad = 0.07
Coverage intervals
99% ( 127.55, 127.91) k = 2.6
95% ( 127.59, 127.87) k = 2
90% ( 127.62, 127.85) k = 1.6
68% ( 127.662, 127.802) k = 1
ANOVA (% Contributions)
w/out Residual w/ Residual
V 29.31 29.31
I 0.13 0.13
phi 70.56 70.56
Residual NA 0.00
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 127.732
u(y) = 0.07
SensitivityCoeffs Percent.u2
V 26 140
I -6500 78
phi -220 560
Correlations NA -670
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 6: Resistance. Input and output Web pages for the example discussed in §10.
Note that, in this case, the NIST Uncertainty Machine reconfigured its graphical user
interface automatically to accommodate the correlations that had to be specified.
LAFARGE &POSSOLO PAGE 26 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
measurement uncertainties associated with them. To load the specifications for
this example into the NIST Uncertainty Machine, click here.
VALUE STD.MEAS.UNC.UNIT
h6.626 069 57 ×10−34 0.000 000 29 ×10−34 J s
R8.314 462 1 0.000 007 5 J mol−1K−1
R∞10 973 731.568 539 0.000 055 m−1
Ar(e)5.485 799 094 6 ×10−40.000 000 002 2 ×10−4u
Mu1×10−30 kg/mol
c299 792 458 0 m/s
α7.297 352 569 8 ×10−30.000 000 002 4 ×10−31
Table 5: Stefan-Boltzmann. 2010 CODATA recommended values and
standard measurement uncertainties for the quantities used to define the
value of the Stefan-Boltzmann constant. Once the international system of
units (SI) will have been redefined (expected in 2018), the value of hwill
be fixed and the associated standard uncertainty will become 0 J s [Newell
et al.,2018].
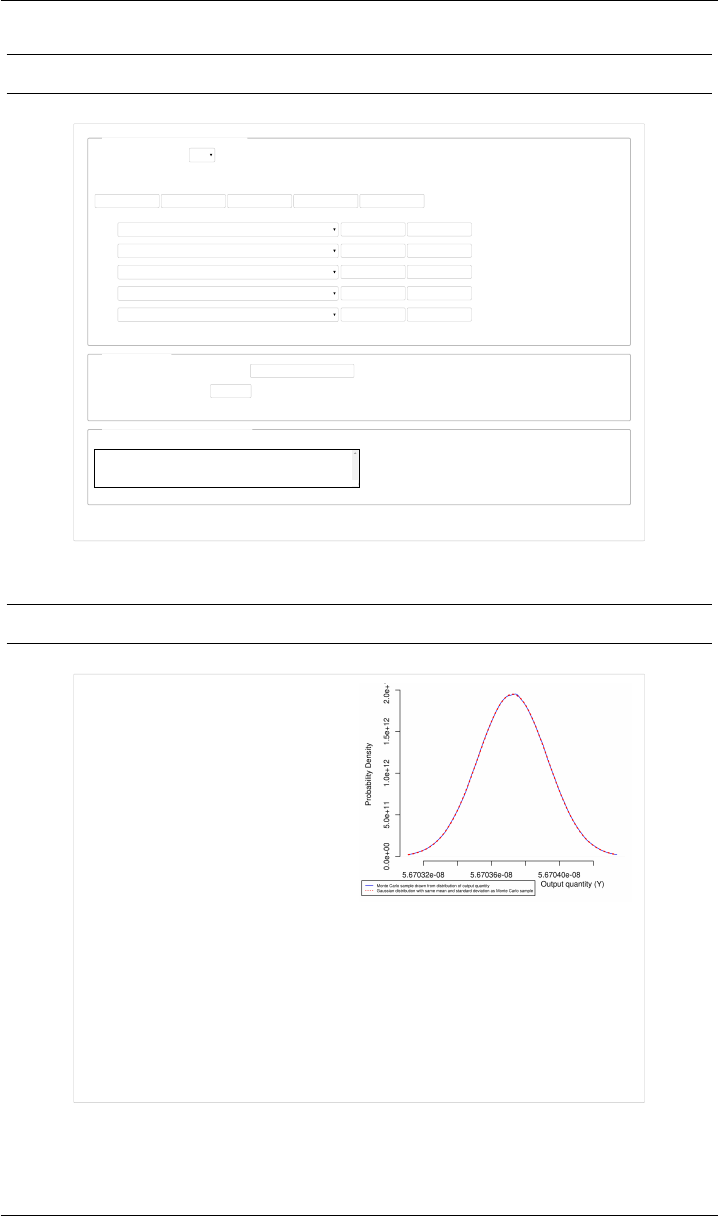
According to the GUM, the estimate of the measurand equals the value of the
measurement function evaluated at the estimates of the input quantities, as
σ=5.670 37 ×10−8W m−2K−4. Both the GUM’s approximation and the Monte
Carlo method produce the same evaluation of u(σ) = 2×10−13 W m−2K−4.
These evaluations disregard the correlations between the input quantities that
result from the adjustment process used by CODATA. However, once these cor-
relations are taken into account via Equation (13) in the GUM, the same value
still obtains for u(σ)to within the single significant digit reported above.
Without making additional assumptions, it is impossible to interpret an expres-
sion like σ±u(σ)probabilistically. The assumptions made to apply the Monte
Carlo method of the GUM-S1 deliver not only an evaluation of uncertainty, but
also enable its probabilistic interpretation.
If the measurement uncertainties associated with h,R,R∞,Ar(e), and αare
expressed by modeling these quantities as independent Gaussian random vari-
ables with means and standard deviations set equal to the values and stan-
dard measurement uncertainties listed in Table 5, then the distribution that the
Monte Carlo method of the GUM-S1 assigns to the measurand happens to be
approximately Gaussian as gauged by the Anderson-Darling test of Gaussian
shape [Anderson and Darling,1952].
Figure 7on Page 28 reflects these facts and shows the results, which imply that
the interval from 5.670 332 ×10−8W m−2K−4to 5.670 412 6 ×10−8W m−2K−4
LAFARGE &POSSOLO PAGE 27 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
is a coverage interval for σwith approximate 95 % coverage probability.
Two of the inputs, Muand c, have zero standard uncertainty. Since the NIST
Uncertainty Machine requires standard deviations to be strictly positive, the
user may either assign very small values to them, or they may be removed from
the list of input quantities and their values entered as constants in the expression
that defines the output quantity, as shown in the upper panel of Figure 7on
Page 28.
12 Example — Voltage Reflection Coefficient
Tsui et al. [2012]consider the voltage reflection coefficient Γ=S22 −S12S23/S13
of a microwave power splitter, defined as a function of elements of the corre-
sponding 3-port scattering matrix (S-parameters). Table 6reproduces the mea-
surement results for the S-parameters listed in Tsui et al. [2012, Table 5]. Since
the S-parameters (input quantities) are complex-valued, so is Γ(output quan-
tity). Therefore, in this example the measurement model is a measurement
equation with a vector-valued output quantity, (ℜ(Γ),ℑ(Γ)), whose components
are the real and imaginary parts of Γ.
Mod(S)u(Mod(S)) Arg(S)u(Arg(S))
S22 0.24776 0.00337 4.88683 0.01392
S12 0.49935 0.00340 4.78595 0.00835
S23 0.24971 0.00170 4.85989 0.00842
S13 0.49952 0.00340 4.79054 0.00835
Table 6: S-parameters expressed in polar form, and associated standard un-
certainties, with Arg(S)and u(Arg(S)) expressed in radian.
The NIST Uncertainty Machine can handle vectorial output quantities. Addi-
tional output fields are added by clicking the “+” button as explained in (U-8)
on Page 11. The NIST Uncertainty Machine produces the raw materials that
are necessary to characterize the uncertainty of a multivariate output by appli-
cation of the Monte Carlo method, but it does not provide a full characterization
of the uncertainty surrounding the multivariate output.
If y=f(x1, . . . , xn)is the measurement model for a p-dimensional output quan-
tity y= ( y1, . . . , yp), then the model may be re-written as a system of psimul-
LAFARGE &POSSOLO PAGE 28 OF 46
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
5
Names of input quantities:
h
R
Rinf
e
alpha
h
Gaussian (Mean, StdDev)
R
Gaussian (Mean, StdDev)
8.3144621
0.0000075
Rinf
Gaussian (Mean, StdDev)
0.000055
e
Gaussian (Mean, StdDev)
alpha
Gaussian (Mean, StdDev)
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
5
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
6.62606957e-34
0.00000029e-34
10973731.56853
5.4857990946e-
0.0000000022e-
7.2973525698e-
0.0000000024e-
N = 32 * (pi^5) * h * (R^4) * (Rinf^4)
D = 15 * (e^4) * ((1e-3)^4) * (299792458^6) * (alpha^8)
N / D
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 5.6703725e-08
sd = 2.05e-13
median = 5.6703725e-08
mad = 2e-13
Coverage intervals
99% (5.67032e-08, 5.67043e-08) k = 2.6
95% (5.67033e-08, 5.67041e-08) k = 2
90% (5.67034e-08, 5.67041e-08) k = 1.6
68% (5.67035e-08, 5.67039e-08) k = 1
ANOVA (% Contributions)
w/out Residual w/ Residual
R 100 99.99
Residual NA 0.01
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 5.6703725e-08
u(y) = 2.05e-13
SensitivityCoeffs Percent.u2
h 8.6e+25 1.5e-02
R 2.7e-08 1.0e+02
Rinf 2.1e-14 3.1e-09
e -4.1e-04 2.0e-05
alpha -6.2e-05 5.3e-05
Correlations NA 0.0e+00
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 7: Stefan-Boltzmann Constant. Input and output Web pages for the
example discussed in §11.
LAFARGE &POSSOLO PAGE 29 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
taneous measurement equations y1=f1(x1, . . . , xn), ..., yp=fp(x1, . . . , xn),
where f= ( f1, . . . , fp). The recommended procedure then is this:
(i) Run the NIST Uncertainty Machine with each output in its own field,
and save the file containing the samples drawn from the probability dis-
tributions of the pcomponents y1,..., ypof the vectorial output quantity;
(ii) Read this file into some suitable statistical analysis computing environ-
ment, for example R, and complete the uncertainty analysis for the output
quantity in this environment.
The S-parameters are assumed to be independent, complex-valued random vari-
ables. The modulus and argument of each S-parameter are modeled as inde-
pendent Gaussian random variables with mean and standard deviation equal
to the value and standard uncertainty listed in Exhibit 6. (Note that the results
would be different if the same modeling assumptions were made for the real
and imaginary parts of the S-parameters instead.)
The real and imaginary parts of Γare functions of the same eight input quan-
tities, which are the moduli and arguments of the four S-parameters, hence
in this case p=2 and the components of the bivariate output quantity are:
ℜ(Γ) = f1(M22,A22,M12,A12,M23,A23,M13,A13), and ℑ(Γ) = f2(M22,A22,
M12,A12,M23,A23,M13,A13). Figure 8on Page 30 shows the corresponding
input Web page of the NIST Uncertainty Machine, including the definition of
the functions f1and f2.
To load the specifications for this example into the NIST Uncertainty Machine,
click here.
It is also possible to incorporate correlations between the S-parameters, as well
as correlations between the modulus and argument of any of the S-parameters,
by specifying a suitable correlation matrix and applying it via one of the copulas
[Possolo,2010]that is available in the NIST Uncertainty Machine. Neither
was done in this case.
Once the Monte Carlo samples of the two components of the output quantity,
ℜ(Γ)and ℑ(Γ), will have been downloaded and saved, they may be imported
into any statistical computing application to characterize the uncertainty asso-
ciated with Γ, for example as depicted in Figure 9on Page 32, and as illustrated
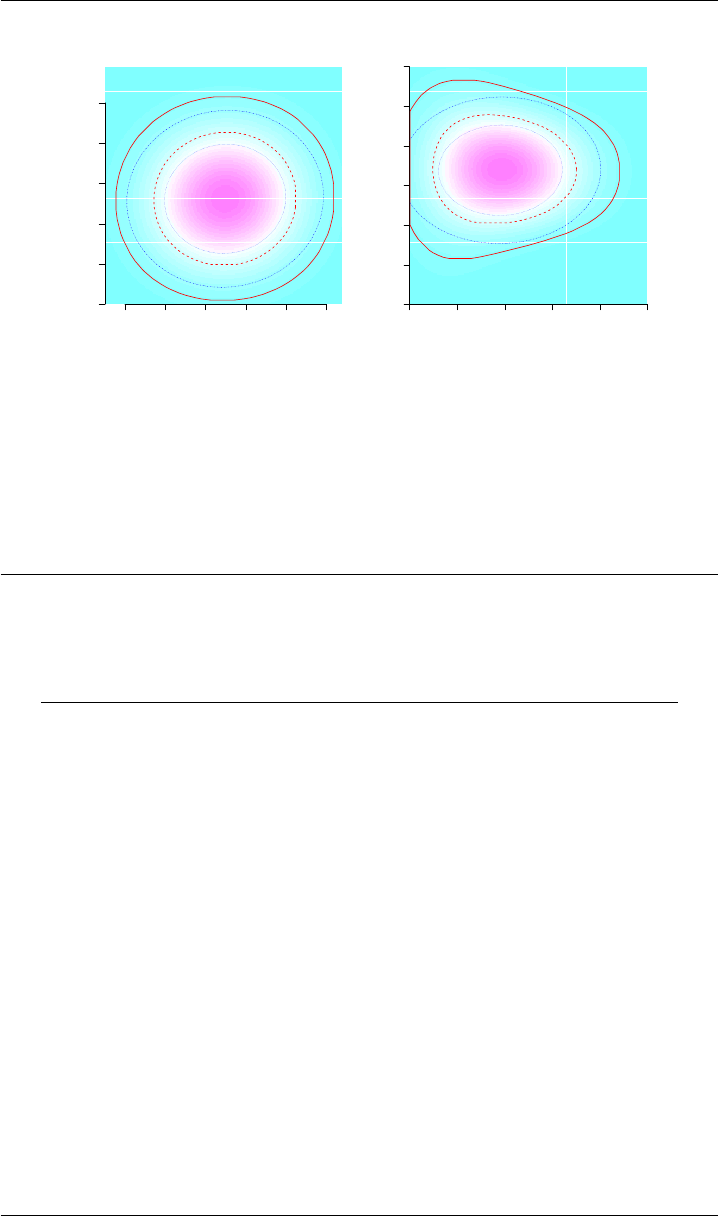
in Listing 1. The estimate of ℜ(Γ)is 0.0074 and u(ℜ(Γ)) = 0.0050. The esti-
mate of ℑ(Γ)is 0.0031 and u(ℜ(Γ)) = 0.0045. The correlation between ℜ(Γ)
and ℑ(Γ)is 0.0311.
LAFARGE &POSSOLO PAGE 30 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
1. Select Inputs & Choose Distributions
Number of input quantities:
8
Names of input quantities:
S22.Mod
S22.Arg
S12.Mod
S12.Arg
S23.Mod
S23.Arg
S13.Mod
S13.Arg
S22.Mod
Gaussian (Mean, StdDev)
0.24776
0.00337
S22.Arg
Gaussian (Mean, StdDev)
4.88683
0.01392
S12.Mod
Gaussian (Mean, StdDev)
0.49935
0.00340
S12.Arg
Gaussian (Mean, StdDev)
4.78595
0.00835
S23.Mod
Gaussian (Mean, StdDev)
0.24971
0.00170
S23.Arg
Gaussian (Mean, StdDev)
4.85989
0.00842
S13.Mod
Gaussian (Mean, StdDev)
0.49952
0.00340
S13.Arg
Gaussian (Mean, StdDev)
4.79054
0.00835
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
37
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
S22 = complex(modulus=S22.Mod, argument=S22.Arg)
S12 = complex(modulus=S12.Mod, argument=S12.Arg)
S23 = complex(modulus=S23.Mod, argument=S23.Arg)
S13 = complex(modulus=S13.Mod, argument=S13.Arg)
Gamma = S22 - S12*S23/S13
Re(Gamma)
S22 = complex(modulus=S22.Mod, argument=S22.Arg)
S12 = complex(modulus=S12.Mod, argument=S12.Arg)
S23 = complex(modulus=S23.Mod, argument=S23.Arg)
S13 = complex(modulus=S13.Mod, argument=S13.Arg)
Gamma = S22 - S12*S23/S13
Im(Gamma)
Figure 8: Voltage Reflection Coefficient. Input Web page of the NIST
Uncertainty Machine used for the real and imaginary parts of the complex-
valued output quantity Γdiscussed in §12.
LAFARGE &POSSOLO PAGE 31 OF 46
VERSION 1.4 NIST UNCERTAINTY MACHINE
Re(Γ)
Im(Γ)
−0.005 0.000 0.005 0.010 0.015 0.020
−0.010 −0.005 0.000 0.005 0.010 0.015
Mod(Γ)
Arg(Γ)
0.000 0.005 0.010 0.015 0.020 0.025
−3 −2 −1 0 1 2 3
Figure 9: The left panel shows an estimate of the probability density of the joint
distribution of the real and imaginary parts of Γ, and the right panel shows its
counterpart for the modulus and argument of Γ. The solid (red) curves out-
line 95 % coverage regions, and the dashed (red) curves outline 68 % cover-
age regions. Their (blue) counterparts, dotted and dash-dotted, are based on
the (obviously erroneous) assumption that the joint bivariate distributions are
Gaussian.
Listing 1: R code used to characterize the uncertainty associated with Γ
## Read values of output quantities produced in the two runs
## of the NIST Uncertainty Machine, assuming that R’s
## current working directory is the same that contains
## the files with the values of the output quantities
Gamma.Re = scan("NUM-Gamma-Real-Results-Values.txt")
Gamma.Im = scan("NUM-Gamma-Imaginary-Results-Values.txt")
Gamma.Mod = Mod(complex(real=Gamma.Re, imaginary=Gamma.Im))
Gamma.Arg = Arg(complex(real=Gamma.Re, imaginary=Gamma.Im))
c(mean(Gamma.Re), sd(Gamma.Re))
c(mean(Gamma.Im), sd(Gamma.Im))
cor(Gamma.Re, Gamma.Im)
require(ash)
require(car)
par(mfrow=c(1,2), mar=c(4.5, 4.5, 1.5, 1.5))
## Estimate the probability density of the bivariate
LAFARGE &POSSOLO PAGE 32 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
## joint distribution of the real and imaginary parts
## of the complex-valued measurand Gamma
ab = cbind(Gamma.Re, Gamma.Im)
abx = matrix(c(-0.0075, -0.0100, 0.0220, 0.0195), 2, 2)
nbin = c(200, 200)
bins = bin2(ab, abx, nbin)
m = c(60,60)
f = ash2(bins,m)
image(f$x, f$y, f$z, col=cm.colors(24), axes=FALSE,
xlab=expression(plain(Re)(Gamma)),
ylab=expression(plain(Im)(Gamma)))
axis(1, lwd=0.5); axis(2, lwd=0.5)
## Normalize bivariate probability density estimate
## that has been computed over each cell of a
## 200x200 grid, and determine the order of the cells
## according to decreasing values of their corresponding
## probabilities
w = (f$z[-length(f$z)]*diff(f$x)*diff(f$y)) /
sum(f$z[-length(f$z)]*diff(f$x)*diff(f$y))
iw = order(w, decreasing=TRUE)
## Determine the boundary of the smallest subset
## of the cells whose total probability is 0.95
iw95 = which.min(abs(cumsum(w[iw])-0.95))
xx = matrix(rep(f$x, 200), ncol=200)
yy = matrix(rep(f$y, 200), ncol=200, byrow=TRUE)
xx = xx[iw][1:iw95]
yy = yy[iw][1:iw95]
ixy = chull(xx, yy)
lines(c(xx[ixy], xx[ixy][1]),
c(yy[ixy], yy[ixy][1]), col="Red")
## Determine the boundary of the smallest subset
## of the cells whose total probability is 0.68
iw68 = which.min(abs(cumsum(w[iw])-0.68))
xx = matrix(rep(f$x, 200), ncol=200)
yy = matrix(rep(f$y, 200), ncol=200, byrow=TRUE)
xx = xx[iw][1:iw68]
yy = yy[iw][1:iw68]
ixy = chull(xx, yy)
lines(c(xx[ixy], xx[ixy][1]),
c(yy[ixy], yy[ixy][1]), col="Red", lty=2)
## Determine the ellipses that contain 95% or 68% of
## the replicates of Gamma, assuming that the bivariate
## distributions are Gaussian
dataEllipse(Gamma.Re, Gamma.Im, levels=0.68,
add=TRUE, plot.points=FALSE, center.cex=0,
col="Blue", lty=3, lwd=0.5)
dataEllipse(Gamma.Re, Gamma.Im, levels=0.95,
LAFARGE &POSSOLO PAGE 33 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
add=TRUE, plot.points=FALSE, center.cex=0,
col="Blue", lty=4, lwd=0.5)
## Estimate the probability density of the bivariate
## joint distribution of the modulus and argument of
## the complex-valued measurand Gamma
ab = cbind(Gamma.Mod, Gamma.Arg)
abx = matrix(c(0, -3, 0.025, 3), 2, 2)
nbin = c(200, 200)
bins = bin2(ab, abx, nbin)
m = c(60,60)
f = ash2(bins,m)
image(f$x, f$y, f$z, col=cm.colors(24), axes=FALSE,
xlab=expression(plain(Mod)(Gamma)),
ylab=expression(plain(Arg)(Gamma)))
axis(1, lwd=0.5); axis(2, lwd=0.5)
## Normalize bivariate probability density estimate
## that has been computed over each cell of a
## 200x200 grid, and determine the order of the cells
## according to decreasing values of their corresponding
## probabilities
w = (f$z[-length(f$z)]*diff(f$x)*diff(f$y)) /
sum(f$z[-length(f$z)]*diff(f$x)*diff(f$y))
iw = order(w, decreasing=TRUE)
## Determine the boundary of the smallest subset
## of the cells whose total probability is 0.95
iw95 = which.min(abs(cumsum(w[iw])-0.95))
xx = matrix(rep(f$x, 200), ncol=200)
yy = matrix(rep(f$y, 200), ncol=200, byrow=TRUE)
xx = xx[iw][1:iw95]
yy = yy[iw][1:iw95]
ixy = chull(xx, yy)
lines(c(xx[ixy], xx[ixy][1]),
c(yy[ixy], yy[ixy][1]), col="Red")
## Determine the boundary of the smallest subset
## of the cells whose total probability is 0.68
iw68 = which.min(abs(cumsum(w[iw])-0.68))
xx = matrix(rep(f$x, 200), ncol=200)
yy = matrix(rep(f$y, 200), ncol=200, byrow=TRUE)
xx = xx[iw][1:iw68]
yy = yy[iw][1:iw68]
ixy = chull(xx, yy)
lines(c(xx[ixy], xx[ixy][1]),
c(yy[ixy], yy[ixy][1]), col="Red", lty=2)
## Determine the ellipses that contain 95% or 68% of
## the replicates of Gamma, assuming that the bivariate
## distributions are Gaussian
LAFARGE &POSSOLO PAGE 34 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
dataEllipse(Gamma.Mod, Gamma.Arg, levels=0.68,
add=TRUE, plot.points=FALSE, center.cex=0,
col="Blue", lty=3, lwd=0.5)
dataEllipse(Gamma.Mod, Gamma.Arg, levels=0.95,
add=TRUE, plot.points=FALSE, center.cex=0,
col="Blue", lty=4, lwd=0.5)
13 Example — Age of Allende Meteorite
A blinding blue-white fireball, possibly a meteor, turned night into day
across Mexico and the southwestern United States early today, then
apparently dropped to earth — Washington Post, February 9, 1969.
Table 7lists isotopic ratios and associated uncertainties for several samples
drawn from two chondrules of the Allende meteorite [Clarke et al.,1971], to
measure their absolute age using a geochronometer based on isotopic ratios of
radiogenic lead.
The original data, from Table S4 of Connelly et al. [2012], comprise values
of R(204Pb/206Pb),R(207Pb/206Pb), and relative expanded uncertainties (with
coverage factor k=2) expressed as percentages. The isotopic ratios listed in
Table 7were derived from these as R(206Pb/204Pb) = 1/R(204Pb/206Pb)and
R(207Pb/204Pb) = R(207Pb/206Pb)R(206Pb/204Pb).
The standard uncertainties listed in Table 7were derived from the expanded
uncertainties in [Connelly et al.,2012, Table S4], by application of the Monte
Carlo method, modeling the isotopic ratios as Gaussian random variables, and
taking into account the correlation between R(204Pb/206Pb)and R(207Pb/206Pb)
also listed in the aforementioned Table S4. The standard uncertainties listed are
the median absolute deviations from the median, rescaled as per the default
definition of R function mad.
Since 206Pb and 207Pb both are radiogenic, being the end-products of the decay
of 235U and 238U, respectively, and 204Pb is primordial, the isotopic ratios in
Table 7may be used as a geochronometer [White,2015], under the following
assumptions:
(a) The isotopic ratio R(238U/235U)of the parent material is known;
(b) All atoms of 206Pb and 207Pb derive entirely from uranium originally in the
parent material, and none have been lost;
LAFARGE &POSSOLO PAGE 35 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
206Pb/204Pb 207Pb/204Pb
SAMPLE R u(R)R u(R)
C20-L4 22.012 0.018 18.223 0.014
C20-L5 33.078 0.043 25.145 0.028
C20-L7 55.066 0.220 38.880 0.140
C20-L8 91.684 0.348 61.765 0.219
C20-L9 217.155 5.695 140.222 3.572
C20-LR 172.028 9.454 112.025 5.969
C30-L2 23.265 0.021 18.996 0.015
C30-L5 31.195 0.056 23.958 0.036
C30-L7 59.726 0.083 41.801 0.050
C30-L8 77.310 0.054 52.799 0.033
C30-L9 97.437 0.156 65.392 0.096
C30-LR 232.829 12.658 150.096 7.929
Table 7: Allende Meteorite. Isotopic ratios and associated uncertainties
derived from measurements made and reported by Connelly et al. [2012].
“R” denotes either R(206Pb/204Pb)or R(207Pb/204Pb), which refer to ratios
of numbers of atoms of the isotopes of lead indicated. The samples listed,
from chondrules C20 and C30, are those that Connelly et al. [2012]se-
lected for their age determinations.
(c) No atoms of 204Pb have been added or removed from the chondrules since
their formation.
The absolute age Ais the root of the equation
exp(Aλ235)−1
exp(Aλ238)−1=βR(238U/235U), (2)
where λ235 and λ238 denote the decay constants of 235U and 238U, and βdenotes
the slope of the line (isochron) shown in Figure 10 [Schoene,2014].
To compute estimates of the absolute age we use Equation (2) with λ235 =
log 2/T½(235U),λ238 =log 2/T½(238U), and R(238U/235U) = 137.786 [Connelly
et al.,2012, Table 1]. This last value is noticeably different from the value,
137.818, usually accepted for terrestrial materials [Hiess et al.,2012]. The
half-lives are T½(235U) = 704 Ma [Bé et al.,2010]and T½(238U) = 4468.3 Ma
[Villa et al.,2016].
The isochron has slope β=0.6253, computed by (Gaussian maximum likeli-
hood) errors-in-variables regression that takes the uncertainty in both isotopic
ratios into account, with associated standard uncertainty u(β) = 0.0028 (which
expresses contributions only from sources (c) and (d) listed below).
LAFARGE &POSSOLO PAGE 36 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
50 100 150 200 250 300 350
50 100 150 200
R(206Pb 204Pb)
R(207Pb 204Pb)
R(206Pb 204Pb) ± 10 u(R(206Pb 204Pb))
R(207Pb 204Pb) ± 10 u(R(207Pb 204Pb))
EIV
●
●
●
●
●
●
●
●
●
●
●
●
Figure 10: Allende Isochron. Measurement results (estimates and standard
uncertainties) for lead isotope ratios used to define an isochron for chondrules
C20 and C30 from the Allende meteorite. The isochron was fitted to these
measurement results using errors-in-variables regression, by the method of
maximum likelihood, assuming that the data are outcomes of independent
Gaussian random variables with known standard deviations. The standard
uncertainties are magnified 10-fold only to facilitate comparing them visually.
LAFARGE &POSSOLO PAGE 37 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
The evaluation of uncertainty associated with age estimates needs to recognize
contributions from the following sources:
(a) The uncertainties associated with the half-lives of the relevant uranium iso-
topes: u(T½(235U)) = 1 Ma [Bé et al.,2010]and u(T½(238U)) = 4.8 Ma
[Villa et al.,2016];
(b) The uncertainty associated with the isotopic ratio of the same uranium iso-
topes: u(R(238U/235U)) = 0.013 [Connelly et al.,2012, Table 1];
(c) The measurement uncertainties associated with the measured lead isotope
ratios {u(R(206Pb/204Pb))}and {u(R(207Pb/204Pb))};
(d) The sampling uncertainty associated with the selection of the n=12 sam-
ples that were used to define the isochron.
The measurement equation is A=f(B,R,T235,T238), where the inputs are mod-
eled as random variables: Bdenoting the slope of the isochron; Rdenoting the
value of the isotopic ratio R(238U/235U);T235 denoting the half-life of 235U; and
T238 denoting the half-life of 238U.
To evaluate the uncertainty associated with A, either by application of Gauss’s
formula or of the Monte Carlo method, three obstacles must be overcome: (i)
computing values of the function f, which involves solving Equation (2) using
numerical methods; (ii) computing the values of the partial derivatives of f
that are needed in Gauss’s formula, which requires numerical differentiation;
and (iii) representing the probability distribution of Bin a form that the NIST
Uncertainty Machine can process.
While (i) would be burdensome and (ii) would be practically insurmountable
without recourse to suitably specialized software, for the NIST Uncertainty
Machine neither is challenging. Indeed, once fis determined by specifying R
commands in the appropriate box in the input page, the NIST Uncertainty
Machine will have no difficulty addressing (i) or (ii).
Bposes a difficulty of a different kind because the corresponding probability
distribution is represented by a sample drawn using a previous application of the
Monte Carlo method outside of the NIST Uncertainty Machine environment,
and none of the parametric distributions available in the NIST Uncertainty
Machine fit it adequately.
Therefore, one needs to use the sample itself, which the NIST Uncertainty
Machine also allows, as already mentioned in (U-5) on Page 8. In fact, the NIST
Uncertainty Machine can read a file with the values of such sample, and then
LAFARGE &POSSOLO PAGE 38 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
use it alongside the parametric distributions specified for the other inputs, both
when it applies Gauss’s formula, and the Monte Carlo method.
For Gauss’s formula, the NIST Uncertainty Machine simply uses the average
and the standard deviation of the sample of values of Bthat is provided. For
the Monte Carlo method, it resamples this sample repeatedly, with replacement,
thus treating it as if it were an infinite population. (Therefore, when such a
sample is provided as input, it need not be of the same size as the number
of replicates of the output quantity that are requested. However, the sample
should still be of sufficiently large size to provide an accurate representation of
the underlying distribution.)
To load the specifications for this example into the NIST Uncertainty Machine,
click here.
The probability distribution of Bexpresses the contributions from the uncer-
tainties associated with the isotopic ratios, and with the selection of the twelve
samples of the two chondrules that were used, from among those that were
measured (uncertainty sources (c) and (d) mentioned above). These contribu-
tions were evaluated by application of two variants of the statistical bootstrap
in tandem: the parametric version for (c), and the non-parametric version for
(d)[Efron and Tibshirani,1993]. Figure 11 shows the graph of an estimate of
the probability density of Bthat was derived from the input sample.
Figure 12 shows a screenshot of the input page of the NIST Uncertainty Machine
with the characterization of the input variables: Bis not assigned any paramet-
ric distribution, and only a sample of size 2023 is provided that was drawn from
its otherwise unspecified distribution; the other three are modeled as Gaussian
random variables with specified means and standard deviations. The input page
also includes the definition of the measurement equation, whose R code may
more easily be examined in Listing 2.
LAFARGE &POSSOLO PAGE 39 OF 46
VERSION 1.4 NIST UNCERTAINTY MACHINE
0.615 0.620 0.625 0.630 0.635
0 100 200 300
βEIV
Probability Density
Figure 11: Slope of Allende Meteorite Isochron. Kernel estimate [Silver-
man,1986]of the probability density of the slope of the isochron depicted in
Figure 10, based on a sample of 2023 values, expressing contributions from
the uncertainties associated with the isotopic ratios, and with the selection of
the twelve samples of the two chondrules that were used, from among those
that were measured.
Listing 2: R code used to evaluate the measurement function that computes
the age of chondrules in the Allende meteorite.
lambda235 = log(2)/T235
lambda238 = log(2)/T238
ageEquation = function (x, beta, lambdaU238, lambdaU235, RU238U235) {
(exp(x*lambdaU235)-1)/(exp(x*lambdaU238)-1) - RU238U235*beta }
lowerAge = 4e9
upperAge = 5e9
f = function(lambda238,lambda235,R,B) {
uniroot(ageEquation, lower=lowerAge, upper=upperAge,
beta=B, lambdaU238=lambda238, lambdaU235=lambda235,
RU238U235=R)$root }
mapply(f,lambda238,lambda235,R,B)
The measurement function fin A=f(B,R,T235,T238), which is defined in List-
ing 2, differs in several essential ways from the measurement functions in other
examples in this manual:
(1) It involves another function, ageEquation, that is used to define Equa-
tion (2) above, whose root is the value of f;
LAFARGE &POSSOLO PAGE 40 OF 46
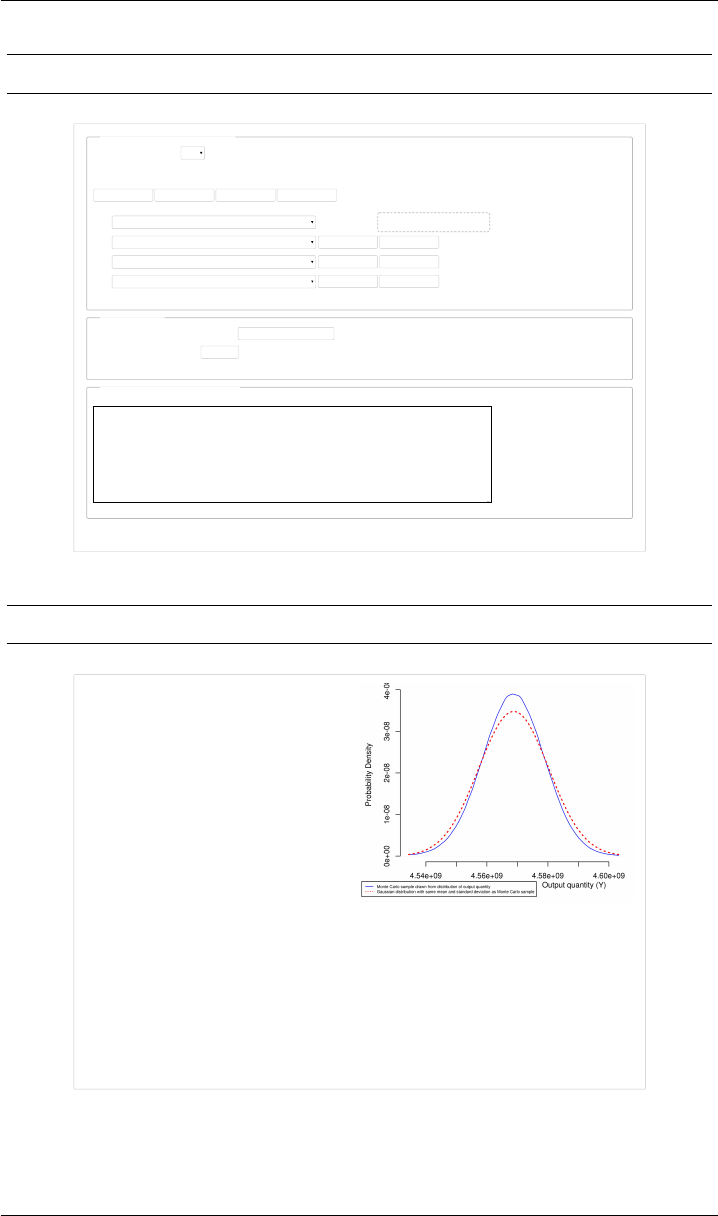
VERSION 1.4 NIST UNCERTAINTY MACHINE
INPUT
1. Select Inputs & Choose Distributions
Number of input quantities:
4
Names of input quantities:
B
R
T235
T238
B
Sample values (between 30 and 100000)
2023 Samples
loaded
Drop sample file here or click to
upload
R
Gaussian (Mean, StdDev)
137.786
0.013
T235
Gaussian (Mean, StdDev)
704e6
1e6
T238
Gaussian (Mean, StdDev)
4.4683e9
4.8e6
Correlations
2. Choose Options
Number of realizations of the output quantity:
1000000
Random number generator seed:
54
Symmetrical coverage intervals
3. Write the Definition of Output Quantity
Definition of output quantity (R expression):
- +
Run the computation
lambda235 = log(2)/T235
lambda238 = log(2)/T238
ageEquation = function (x, beta, lambdaU238, lambdaU235, RU238U235) {
(exp(x*lambdaU235)-1)/(exp(x*lambdaU238)-1) - RU238U235*beta}
lowerAge = 4e9
upperAge = 5e9
f = function(lambda238,lambda235,R,B){uniroot(ageEquation, lower=lowerAge, upper=upperAge,
beta=B,lambdaU238=lambda238,lambdaU235=lambda235,RU238U235=R)$root}
mapply(f,lambda238,lambda235,R,B)
OUTPUT
===== RESULTS ==============================
Monte Carlo Method
Summary statistics for sample of size 1000000
ave = 4568800000
sd = 1.1e+07
median = 4568700000
mad = 1e+07
Symmetrical coverage intervals
99% (4.5398e+09, 4.5978e+09) k = 2.5
95% (4.5478e+09, 4.5898e+09) k = 1.8
90% (4.5517e+09, 4.5859e+09) k = 1.5
68% (4.5586e+09, 4.579e+09) k = 0.89
ANOVA (% Contributions)
w/out Residual w/ Residual
B 29.80 29.80
R 0.01 0.01
T235 66.61 66.59
T238 3.58 3.57
Residual NA 0.02
--------------------------------------------
Gauss's Formula (GUM's Linear Approximation)
y = 4568800000
u(y) = 1.2e+07
SensitivityCoeffs Percent.u2
B 2.3e+09 31.000
R 1.1e+07 0.014
T235 9.4e+00 65.000
T238 -4.5e-01 3.500
Correlations NA 0.000
============================================
Download binary R data file with Monte Carlo values of output quantity
Download a text file with Monte Carlo values of output quantity
Download text file with numerical results shown on this page
Download JPEG file with plot shown on this page
Download configuration file
Figure 12: Allende Meteorite. Input and output Web pages for the example
discussed in §13.
LAFARGE &POSSOLO PAGE 41 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
(2) It uses a numerical method to find this root, which is implemented in R
function uniroot;
(3) A programming device (invoking mapply) is required to ensure that fis
vectorized: that is, if each of its arguments is a vector of length K, then
the value of fis a vector of length Kwhose kth element is the root of the
ageEquation that correspond to the kth set of values of the inputs.
The NIST Uncertainty Machine always requires that the measurement func-
tion fbe vectorized, in the sense just described. However, in all the other ex-
amples this is accomplished automatically owing to the evaluation rules of the R
language (which govern the interpretation of the code entered in the box where
the value of fis specified, in the input Web page of the NIST Uncertainty
Machine). Not in this case, owing to the presence of the root finder uniroot,
which does not accommodate vectorization.
Figure 12 shows two areas of the output page: the portion that summarizes the
results of the GUM calculations, including application of Gauss’s formula, and
the portion with the results of the Monte Carlo method, including the plot of
the estimate of the probability density of the output quantity (which is the age
of the chondrules).
It is worth noting, in the portion of the output produced by the Monte Carlo
method, that the percentage of the variance of the output quantity attributable
to non-linearity of the measurement function (0.02 %) is very small, even though
the function clearly is non-linear. This is attributable to the fact that, its overall
non-linearity notwithstanding, fstill is approximately linear within a neigh-
borhood of the estimates of the input quantities of size comparable to their
associated uncertainties.
The corresponding age estimate is 4569 Ma with associated standard uncer-
tainty 12 Ma according to Gauss’s formula, and 11 Ma according to the Monte
Carlo method. (Connelly et al. [2012]report 4566 Ma for C20 and 4567 Ma for
C30, with much smaller uncertainties.)
These chondrules are truly ancient, frozen remnants of the protoplanetary disk
that would evolve to become the solar system. However, Scott [2007]points
out that “the Allende chondrite is not a pristine chondrite, as was once believed.
It was severely altered by fluid-assisted metamorphism in its parent asteroid.”
Therefore, an uncertainty even larger than our calculations suggest should sur-
round the age of these chondrules.
LAFARGE &POSSOLO PAGE 42 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
Acknowledgments
The authors are grateful to their colleagues Will Guthrie, Alan Heckert, Narain
Krishnamurthy, Adam Pintar, Jolene Splett, and Jack Wang, for the many sug-
gestions that they offered for improvement of the NIST Uncertainty Machine
and of this user’s manual.
Alan Heckert, Steven Conn, Shawn Winhoven, Walter Rowe, Dale Little, and
Del Brockett, greatly facilitated the deployment of this Web-based application
for use on the World Wide Web.
The authors will be very grateful to users of the software, and to readers of this
manual, for information about errors and other deficiencies, and for suggestions
for improvement, which may be sent via eMail to thomas.lafarge@nist.gov
and to antonio.possolo@nist.gov.
References
T. W. Anderson and D. A. Darling. Asymptotic theory of certain “goodness-of-fit” criteria
based on stochastic processes. Annals of Mathematical Statistics, 23:193–212, 1952.
M.-M. Bé, V. Chisté, C. Dulieu, X. Mougeot, E. Browne, V. Chechev, N. Kuzmenco, F. Kon-
dev, A. Luca, M. Galán, A. L. Nichols, A. Arinc, and X. Huang. Table of Radionuclides,
volume 5 – A =22 to 244 of Monographie BIPM-5. Bureau International des Poids
et Mesures, Sèvres, France, 2010. ISBN 978-92-822-2234-8.
S. Bell. A Beginner’s Guide to Uncertainty of Measurement. Number 11 (Issue
2) in Measurement Good Practice Guide. National Physical Laboratory, Tedding-
ton, Middlesex, United Kingdom, 1999. URL www.npl.co.uk/publications/
guides/a-beginners-guide-to-uncertainty-of-measurement. Amendments
March 2001.
P. Billingsley. Probability and Measure. John Wiley & Sons, New York, NY, 1979.
R. S. Clarke, Jr., E. Jarosewich, B. Mason, J. Nelen, M. Gomez, and J. R. Hyde. Al-
lende, Mexico, Meteorite Shower. Number 5 in Smithsonian Contributions to the
Earth Sciences. Smithsonian Institution, Washington, DC, February 1971. doi:
10.5479/si.00810274.5.1.
J. N. Connelly, M. Bizzarro, A. N. Krot, A. Nordlund, D. Wielandt, and M. A. Ivanova.
The absolute chronology and thermal processing of solids in the solar protoplanetary
disk. Science, 338:651–655, November 2012. doi: 10.1126/science.1226919.
M. H. DeGroot and M. J. Schervish. Probability and Statistics. Addison-Wesley, 4th
edition, 2011.
LAFARGE &POSSOLO PAGE 43 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
B. Efron and R. J. Tibshirani. An Introduction to the Bootstrap. Chapman & Hall, London,
UK, 1993.
D. Freedman, R. Pisani, and R. Purves. Statistics. W. W. Norton & Company, New York,
NY, fourth edition, 2007.
K. O. Friedrich. A Berry-Esseen bound for functions of independent random variables.
The Annals of Statistics, 17(1):170–183, 1989.
C. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. In Werke,
Band IV, Wahrscheinlichkeitsrechnung und Geometrie. Könighlichen Gesellschaft der
Wissenschaften, Göttingen, 1823. gdz.sub.uni-goettingen.de/.
P. Gilbert and R. Varadhan. numDeriv: Accurate Numerical Derivatives, 2016. URL
CRAN.R-project.org/package=numDeriv. R package version 2016.8-1.
W. F. Guthrie, H.-k. Liu, A. L. Rukhin, B. Toman, J. C.M. Wang, and N.-f. Zhang. Three
statistical paradigms for the assessment and interpretation of measurement uncer-
tainty. In F. Pavese and A. B. Forbes, editors, Data Modeling for Metrology and Testing
in Measurement Science, Modeling and Simulation in Science, Engineering and Tech-
nology, pages 1–45. Birkhäuser Boston, 2009. doi: 10.1007/978-0-8176-4804-6_3.
B. D. Hall and D. R. White. An Introduction to Measurement Uncertainty. Measure-
ment Standards Laboratory of New Zealand, Lower Hutt, New Zealand, 2018. Also
available from www.lulu.com.
J. Hiess, D. J. Condon, N. McLean, and S. R. Noble. 238U/235U systematics in terrestrial
uranium-bearing minerals. Science, 335(6076):1610–1614, 2012. doi: 10.1126/
science.1215507.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Guide to
the expression of uncertainty in measurement. International Bureau of Weights and
Measures (BIPM), Sèvres, France, 2008a. URL www.bipm.org/en/publications/
guides/gum.html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM
100:2008, GUM 1995 with minor corrections.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Supple-
ment 1 to the “Guide to the expression of uncertainty in measurement” — Propagation
of distributions using a Monte Carlo method. International Bureau of Weights and
Measures (BIPM), Sèvres, France, 2008b. URL www.bipm.org/en/publications/
guides/gum.html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM
101:2008.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Supple-
ment 2 to the “Guide to the expression of uncertainty in measurement” — Extension
to any number of output quantities. International Bureau of Weights and Measures
(BIPM), Sèvres, France, 2011. URL www.bipm.org/en/publications/guides/gum.
html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 102:2011.
LAFARGE &POSSOLO PAGE 44 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
S. J. Kline and F. A. McClintock. Describing uncertainties in single-sample experiments.
Mechanical Engineering, 75(1):3–8, 1953.
T. Lafarge and A. Possolo. The NIST Uncertainty Machine. NCSLI Measure Journal of
Measurement Science, 10(3):20–27, September 2015.
P. J. Mohr, B. N. Taylor, and D. B. Newell. CODATA recommended values of the fun-
damental physical constants: 2010. Reviews of Modern Physics, 84(4):1527–1605,
October-December 2012. doi: 10.1063/1.4724320.
M. G. Morgan and M. Henrion. Uncertainty — A Guide to Dealing with Uncertainty in
Quantitative Risk and Policy Analysis. Cambridge University Press, New York, NY, first
paperback edition, 1992. 10th printing, 2007.
R. B. Nelsen. An Introduction to Copulas. Springer, New York, NY, 2nd edition, 2006.
Corrected 2nd. printing, 2007.
D. B. Newell, F. Cabiati, J. Fischer, K. Fujii, S. G. Karshenboim, H. S. Margolis, E. de Mi-
randés, P. J. Mohr, F. Nez, and K. Pachucki. The CODATA 2017 values of h,e,k,
and NAfor the revision of the SI. Metrologia, 55(1):L13–L16, January 2018. doi:
10.1088/1681-7575/aa950a.
A. Possolo. Copulas for uncertainty analysis. Metrologia, 47:262–271, 2010. doi:
10.1088/0026-1394/47/3/017.
A. Possolo. Simple Guide for Evaluating and Expressing the Uncertainty of NIST Mea-
surement Results. National Institute of Standards and Technology, Gaithersburg,
MD, 2015. URL http://dx.doi.org/10.6028/NIST.TN.1900. NIST Technical Note
1900.
A. Possolo and C. Elster. Evaluating the uncertainty of input quantities in measurement
models. Metrologia, 51(3):339–353, June 2014. doi: 10.1088/0026-1394/51/3/
339.
A. Possolo and H. K. Iyer. Concepts and tools for the evaluation of measurement un-
certainty. Review of Scientific Instruments, 88(1):011301, 2017. doi: 10.1063/1.
4974274.
A. Possolo, B. Toman, and T. Estler. Contribution to a conversation about the Supple-
ment 1 to the GUM. Metrologia, 46:L1–L7, 2009.
R Core Team. R: A Language and Environment for Statistical Computing. R Foundation
for Statistical Computing, Vienna, Austria, 2015. URL www.R-project.org/.
F. E. Satterthwaite. An approximate distribution of estimates of variance components.
Biometrics Bulletin, 2(6):110–114, December 1946.
LAFARGE &POSSOLO PAGE 45 OF 46

VERSION 1.4 NIST UNCERTAINTY MACHINE
B. Schoene. U-Th-Pb Geochronology. In H. D. Holland and K. K. Turekian, editors,
Treatise on Geochemistry, volume 4 (The Crust), chapter 10, pages 341–378. Elsevier,
Amsterdam, second edition, 2014. doi: 10.1016/B978-0-08-095975-7.00310-7.
E. R. D. Scott. Chondrites and the protoplanetary disk. Annual Review of Earth and Plan-
etary Sciences, 35:577–620, 2007. doi: 10.1146/annurev.earth.35.031306.140100.
B. W. Silverman. Density Estimation. Chapman and Hall, London, 1986.
B. N. Taylor and C. E. Kuyatt. Guidelines for Evaluating and Expressing the Uncertainty
of NIST Measurement Results. NIST Technical Note 1297. National Institute of Stan-
dards and Technology, Gaithersburg, MD, 1994. URL physics.nist.gov/Pubs/
guidelines/TN1297/tn1297s.pdf.
C. M. Tsui, A. Y. K. Yang, and H. W. Li. Software tools for evaluation of measurement
models for complex-valued quantities in accordance with Supplement 2 to the GUM.
NCSLI Measure Journal of Measurement Science, 7(3):48–55, September 2012.
I. M. Villa, M. L. Bonardi, P. De Bièvre, N. E. Holden, and P. R. Renne. IUPAC-IUGS
status report on the half-lives of 238U, 235U and 234U. Geochimica et Cosmochimica
Acta, 172:387–392, 2016. doi: 10.1016/j.gca.2015.10.011.
B. L. Welch. The generalization of ‘Student’s’ problem when several different population
variances are involved. Biometrika, 34:28–35, January 1947.
W. M. White. Isotope Geochemistry. John Wiley & Sons, New York, NY, 2015.
LAFARGE &POSSOLO PAGE 46 OF 46