NetworkX Reference Ntworkx Python Guide
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 739 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Introduction
- Graph types
- Algorithms
- Approximations and Heuristics
- Assortativity
- Bipartite
- Boundary
- Bridges
- Centrality
- Chains
- Chordal
- Clique
- Clustering
- Coloring
- Communicability
- Communities
- Components
- Connectivity
- Cores
- Covering
- Cycles
- Cuts
- Directed Acyclic Graphs
- Dispersion
- Distance Measures
- Distance-Regular Graphs
- Dominance
- Dominating Sets
- Efficiency
- Eulerian
- Flows
- Graphical degree sequence
- Hierarchy
- Hybrid
- Isolates
- Isomorphism
- Link Analysis
- Link Prediction
- Lowest Common Ancestor
- Matching
- Minors
- Maximal independent set
- Node Classification
- Operators
- Planarity
- Reciprocity
- Rich Club
- Shortest Paths
- Similarity Measures
- Simple Paths
- Similarity Measures
- s metric
- Sparsifiers
- Structural holes
- Swap
- Tournament
- Traversal
- Tree
- Triads
- Vitality
- Voronoi cells
- Wiener index
- Functions
- Graph generators
- Linear algebra
- Converting to and from other data formats
- Relabeling nodes
- Reading and writing graphs
- Drawing
- Randomness
- Exceptions
- Utilities
- Glossary
- Tutorial
- Bibliography
- Python Module Index
- Index

NetworkX Reference
Release 2.3rc1.dev20181203210840
Aric Hagberg, Dan Schult, Pieter Swart
Dec 03, 2018

CONTENTS
1 Introduction 1
1.1 NetworkX Basics ............................................. 1
1.2 Graphs .................................................. 2
1.3 Graph Creation .............................................. 2
1.4 Graph Reporting ............................................. 3
1.5 Algorithms ................................................ 4
1.6 Drawing ................................................. 4
1.7 Data Structure .............................................. 5
2 Graph types 7
2.1 Which graph class should I use? ..................................... 7
2.2 Basic graph types ............................................. 7
2.3 Graph Views ............................................... 126
3 Algorithms 129
3.1 Approximations and Heuristics ..................................... 129
3.2 Assortativity ............................................... 140
3.3 Bipartite ................................................. 150
3.4 Boundary ................................................. 178
3.5 Bridges .................................................. 180
3.6 Centrality ................................................. 182
3.7 Chains .................................................. 210
3.8 Chordal .................................................. 211
3.9 Clique .................................................. 213
3.10 Clustering ................................................ 217
3.11 Coloring ................................................. 222
3.12 Communicability ............................................. 226
3.13 Communities ............................................... 227
3.14 Components ............................................... 238
3.15 Connectivity ............................................... 251
3.16 Cores ................................................... 282
3.17 Covering ................................................. 285
3.18 Cycles .................................................. 286
3.19 Cuts .................................................... 290
3.20 Directed Acyclic Graphs ......................................... 294
3.21 Dispersion ................................................ 301
3.22 Distance Measures ............................................ 302
3.23 Distance-Regular Graphs ......................................... 305
3.24 Dominance ................................................ 307
3.25 Dominating Sets ............................................. 308
i

3.26 Efficiency ................................................. 310
3.27 Eulerian .................................................. 311
3.28 Flows ................................................... 313
3.29 Graphical degree sequence ........................................ 340
3.30 Hierarchy ................................................. 344
3.31 Hybrid .................................................. 344
3.32 Isolates .................................................. 346
3.33 Isomorphism ............................................... 347
3.34 Link Analysis ............................................... 361
3.35 Link Prediction .............................................. 367
3.36 Lowest Common Ancestor ........................................ 373
3.37 Matching ................................................. 375
3.38 Minors .................................................. 377
3.39 Maximal independent set ......................................... 383
3.40 Node Classification ............................................ 384
3.41 Operators ................................................. 386
3.42 Planarity ................................................. 395
3.43 Reciprocity ................................................ 399
3.44 Rich Club ................................................. 400
3.45 Shortest Paths .............................................. 401
3.46 Similarity Measures ........................................... 437
3.47 Simple Paths ............................................... 444
3.48 Similarity Measures ........................................... 448
3.49 s metric .................................................. 451
3.50 Sparsifiers ................................................ 452
3.51 Structural holes .............................................. 452
3.52 Swap ................................................... 455
3.53 Tournament ................................................ 457
3.54 Traversal ................................................. 460
3.55 Tree .................................................... 472
3.56 Triads ................................................... 486
3.57 Vitality .................................................. 487
3.58 Voronoi cells ............................................... 488
3.59 Wiener index ............................................... 489
4 Functions 491
4.1 Graph ................................................... 491
4.2 Nodes ................................................... 497
4.3 Edges ................................................... 499
4.4 Self loops ................................................. 500
4.5 Attributes ................................................. 501
4.6 Freezing graph structure ......................................... 506
5 Graph generators 509
5.1 Atlas ................................................... 509
5.2 Classic .................................................. 510
5.3 Expanders ................................................ 518
5.4 Lattice .................................................. 519
5.5 Small ................................................... 522
5.6 Random Graphs ............................................. 526
5.7 Duplication Divergence ......................................... 537
5.8 Degree Sequence ............................................. 539
5.9 Random Clustered ............................................ 545
5.10 Directed ................................................. 546
ii

5.11 Geometric ................................................ 550
5.12 Line Graph ................................................ 557
5.13 Ego Graph ................................................ 559
5.14 Stochastic ................................................. 560
5.15 Intersection ................................................ 560
5.16 Social Networks ............................................. 562
5.17 Community ................................................ 563
5.18 Spectral .................................................. 570
5.19 Trees ................................................... 571
5.20 Non Isomorphic Trees .......................................... 573
5.21 Triads ................................................... 573
5.22 Joint Degree Sequence .......................................... 574
5.23 Mycielski ................................................. 575
6 Linear algebra 579
6.1 Graph Matrix ............................................... 579
6.2 Laplacian Matrix ............................................. 580
6.3 Spectrum ................................................. 583
6.4 Algebraic Connectivity .......................................... 584
6.5 Attribute Matrices ............................................ 587
6.6 Modularity Matrices ........................................... 591
7 Converting to and from other data formats 595
7.1 To NetworkX Graph ........................................... 595
7.2 Dictionaries ................................................ 596
7.3 Lists ................................................... 597
7.4 Numpy .................................................. 598
7.5 Scipy ................................................... 605
7.6 Pandas .................................................. 607
8 Relabeling nodes 613
8.1 Relabeling ................................................ 613
9 Reading and writing graphs 617
9.1 Adjacency List .............................................. 617
9.2 Multiline Adjacency List ......................................... 620
9.3 Edge List ................................................. 624
9.4 GEXF ................................................... 630
9.5 GML ................................................... 633
9.6 Pickle ................................................... 638
9.7 GraphML ................................................. 639
9.8 JSON ................................................... 643
9.9 LEDA ................................................... 648
9.10 YAML .................................................. 649
9.11 SparseGraph6 .............................................. 651
9.12 Pajek ................................................... 657
9.13 GIS Shapefile ............................................... 659
10 Drawing 661
10.1 Matplotlib ................................................ 661
10.2 Graphviz AGraph (dot) .......................................... 670
10.3 Graphviz with pydot ........................................... 672
10.4 Graph Layout ............................................... 675
11 Randomness 681
iii

12 Exceptions 683
12.1 Exceptions ................................................ 683
13 Utilities 685
13.1 Helper Functions ............................................. 685
13.2 Data Structures and Algorithms ..................................... 687
13.3 Random Sequence Generators ...................................... 687
13.4 Decorators ................................................ 689
13.5 Cuthill-Mckee Ordering ......................................... 692
13.6 Context Managers ............................................ 694
14 Glossary 695
A Tutorial 697
A.1 Creating a graph ............................................. 697
A.2 Nodes ................................................... 697
A.3 Edges ................................................... 698
A.4 What to use as nodes and edges ..................................... 699
A.5 Accessing edges and neighbors ..................................... 699
A.6 Adding attributes to graphs, nodes, and edges .............................. 700
A.7 Directed graphs .............................................. 701
A.8 Multigraphs ................................................ 702
A.9 Graph generators and graph operations ................................. 702
A.10 Analyzing graphs ............................................. 703
A.11 Drawing graphs ............................................. 703
Bibliography 707
Python Module Index 709
Index 713
iv

CHAPTER
ONE
INTRODUCTION
The structure of NetworkX can be seen by the organization of its source code. The package provides classes for graph
objects, generators to create standard graphs, IO routines for reading in existing datasets, algorithms to analyze the
resulting networks and some basic drawing tools.
Most of the NetworkX API is provided by functions which take a graph object as an argument. Methods of the graph
object are limited to basic manipulation and reporting. This provides modularity of code and documentation. It also
makes it easier for newcomers to learn about the package in stages. The source code for each module is meant to be
easy to read and reading this Python code is actually a good way to learn more about network algorithms, but we have
put a lot of effort into making the documentation sufficient and friendly. If you have suggestions or questions please
contact us by joining the NetworkX Google group.
Classes are named using CamelCase (capital letters at the start of each word). functions, methods and variable
names are lower_case_underscore (lowercase with an underscore representing a space between words).
1.1 NetworkX Basics
After starting Python, import the networkx module with (the recommended way)
>>> import networkx as nx
To save repetition, in the documentation we assume that NetworkX has been imported this way.
If importing networkx fails, it means that Python cannot find the installed module. Check your installation and your
PYTHONPATH.
The following basic graph types are provided as Python classes:
Graph This class implements an undirected graph. It ignores multiple edges between two nodes. It does allow
self-loop edges between a node and itself.
DiGraph Directed graphs, that is, graphs with directed edges. Provides operations common to directed graphs, (a
subclass of Graph).
MultiGraph A flexible graph class that allows multiple undirected edges between pairs of nodes. The additional
flexibility leads to some degradation in performance, though usually not significant.
MultiDiGraph A directed version of a MultiGraph.
Empty graph-like objects are created with
>>> G=nx.Graph()
>>> G=nx.DiGraph()
>>> G=nx.MultiGraph()
>>> G=nx.MultiDiGraph()
1

NetworkX Reference, Release 2.3rc1.dev20181203210840
All graph classes allow any hashable object as a node. Hashable objects include strings, tuples, integers, and more.
Arbitrary edge attributes such as weights and labels can be associated with an edge.
The graph internal data structures are based on an adjacency list representation and implemented using Python dictio-
nary datastructures. The graph adjacency structure is implemented as a Python dictionary of dictionaries; the outer
dictionary is keyed by nodes to values that are themselves dictionaries keyed by neighboring node to the edge at-
tributes associated with that edge. This “dict-of-dicts” structure allows fast addition, deletion, and lookup of nodes
and neighbors in large graphs. The underlying datastructure is accessed directly by methods (the programming in-
terface “API”) in the class definitions. All functions, on the other hand, manipulate graph-like objects solely via
those API methods and not by acting directly on the datastructure. This design allows for possible replacement of the
‘dicts-of-dicts’-based datastructure with an alternative datastructure that implements the same methods.
1.2 Graphs
The first choice to be made when using NetworkX is what type of graph object to use. A graph (network) is a collection
of nodes together with a collection of edges that are pairs of nodes. Attributes are often associated with nodes and/or
edges. NetworkX graph objects come in different flavors depending on two main properties of the network:
• Directed: Are the edges directed? Does the order of the edge pairs (𝑢, 𝑣)matter? A directed graph is specified
by the “Di” prefix in the class name, e.g. DiGraph(). We make this distinction because many classical graph
properties are defined differently for directed graphs.
• Multi-edges: Are multiple edges allowed between each pair of nodes? As you might imagine, multiple edges
requires a different data structure, though clever users could design edge data attributes to support this function-
ality. We provide a standard data structure and interface for this type of graph using the prefix “Multi”, e.g.,
MultiGraph().
The basic graph classes are named: Graph,DiGraph,MultiGraph, and MultiDiGraph
1.2.1 Nodes and Edges
The next choice you have to make when specifying a graph is what kinds of nodes and edges to use.
If the topology of the network is all you care about then using integers or strings as the nodes makes sense and you
need not worry about edge data. If you have a data structure already in place to describe nodes you can simply use
that structure as your nodes provided it is hashable. If it is not hashable you can use a unique identifier to represent
the node and assign the data as a node attribute.
Edges often have data associated with them. Arbitrary data can be associated with edges as an edge attribute. If the
data is numeric and the intent is to represent a weighted graph then use the ‘weight’ keyword for the attribute. Some
of the graph algorithms, such as Dijkstra’s shortest path algorithm, use this attribute name by default to get the weight
for each edge.
Attributes can be assigned to an edge by using keyword/value pairs when adding edges. You can use any keyword to
name your attribute and can then query the edge data using that attribute keyword.
Once you’ve decided how to encode the nodes and edges, and whether you have an undirected/directed graph with or
without multiedges you are ready to build your network.
1.3 Graph Creation
NetworkX graph objects can be created in one of three ways:
• Graph generators—standard algorithms to create network topologies.
2 Chapter 1. Introduction

NetworkX Reference, Release 2.3rc1.dev20181203210840
• Importing data from pre-existing (usually file) sources.
• Adding edges and nodes explicitly.
Explicit addition and removal of nodes/edges is the easiest to describe. Each graph object supplies methods to manip-
ulate the graph. For example,
>>> import networkx as nx
>>> G=nx.Graph()
>>> G.add_edge(1,2)# default edge data=1
>>> G.add_edge(2,3, weight=0.9)# specify edge data
Edge attributes can be anything:
>>> import math
>>> G.add_edge('y','x', function=math.cos)
>>> G.add_node(math.cos) # any hashable can be a node
You can add many edges at one time:
>>> elist =[(1,2), (2,3), (1,4), (4,2)]
>>> G.add_edges_from(elist)
>>> elist =[('a','b',5.0), ('b','c',3.0), ('a','c',1.0), ('c','d',7.3)]
>>> G.add_weighted_edges_from(elist)
See the Tutorial for more examples.
Some basic graph operations such as union and intersection are described in the operators module documentation.
Graph generators such as binomial_graph() and erdos_renyi_graph() are provided in the graph genera-
tors subpackage.
For importing network data from formats such as GML, GraphML, edge list text files see the reading and writing
graphs subpackage.
1.4 Graph Reporting
Class views provide basic reporting of nodes, neighbors, edges and degree. These views provide iteration over the
properties as well as membership queries and data attribute lookup. The views refer to the graph data structure so
changes to the graph are reflected in the views. This is analogous to dictionary views in Python 3. If you want to
change the graph while iterating you will need to use e.g. for e in list(G.edges):. The views provide
set-like operations, e.g. union and intersection, as well as dict-like lookup and iteration of the data attributes us-
ing G.edges[u, v]['color'] and for e, datadict in G.edges.items():. Methods G.edges.
items() and G.edges.values() are familiar from python dicts. In addition G.edges.data() provides
specific attribute iteration e.g. for e, e_color in G.edges.data('color'):.
The basic graph relationship of an edge can be obtained in two ways. One can look for neighbors of a node or one can
look for edges. We jokingly refer to people who focus on nodes/neighbors as node-centric and people who focus on
edges as edge-centric. The designers of NetworkX tend to be node-centric and view edges as a relationship between
nodes. You can see this by our choice of lookup notation like G[u] providing neighbors (adjacency) while edge
lookup is G.edges[u, v]. Most data structures for sparse graphs are essentially adjacency lists and so fit this
perspective. In the end, of course, it doesn’t really matter which way you examine the graph. G.edges removes
duplicate representations of undirected edges while neighbor reporting across all nodes will naturally report both
directions.
Any properties that are more complicated than edges, neighbors and degree are provided by functions. For exam-
ple nx.triangles(G, n) gives the number of triangles which include node n as a vertex. These functions are
1.4. Graph Reporting 3

NetworkX Reference, Release 2.3rc1.dev20181203210840
grouped in the code and documentation under the term algorithms.
1.5 Algorithms
A number of graph algorithms are provided with NetworkX. These include shortest path, and breadth first search (see
traversal), clustering and isomorphism algorithms and others. There are many that we have not developed yet too. If
you implement a graph algorithm that might be useful for others please let us know through the NetworkX Google
group or the Github Developer Zone.
As an example here is code to use Dijkstra’s algorithm to find the shortest weighted path:
>>> G=nx.Graph()
>>> e=[('a','b',0.3), ('b','c',0.9), ('a','c',0.5), ('c','d',1.2)]
>>> G.add_weighted_edges_from(e)
>>> print(nx.dijkstra_path(G, 'a','d'))
['a', 'c', 'd']
1.6 Drawing
While NetworkX is not designed as a network drawing tool, we provide a simple interface to drawing packages
and some simple layout algorithms. We interface to the excellent Graphviz layout tools like dot and neato with the
(suggested) pygraphviz package or the pydot interface. Drawing can be done using external programs or the Matplotlib
Python package. Interactive GUI interfaces are possible, though not provided. The drawing tools are provided in the
module drawing.
The basic drawing functions essentially place the nodes on a scatterplot using the positions you provide via a dictionary
or the positions are computed with a layout function. The edges are lines between those dots.
>>> import matplotlib.pyplot as plt
>>> G=nx.cubical_graph()
>>> plt.subplot(121)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw(G) # default spring_layout
>>> plt.subplot(122)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw(G, pos=nx.circular_layout(G), nodecolor='r', edge_color='b')
4 Chapter 1. Introduction
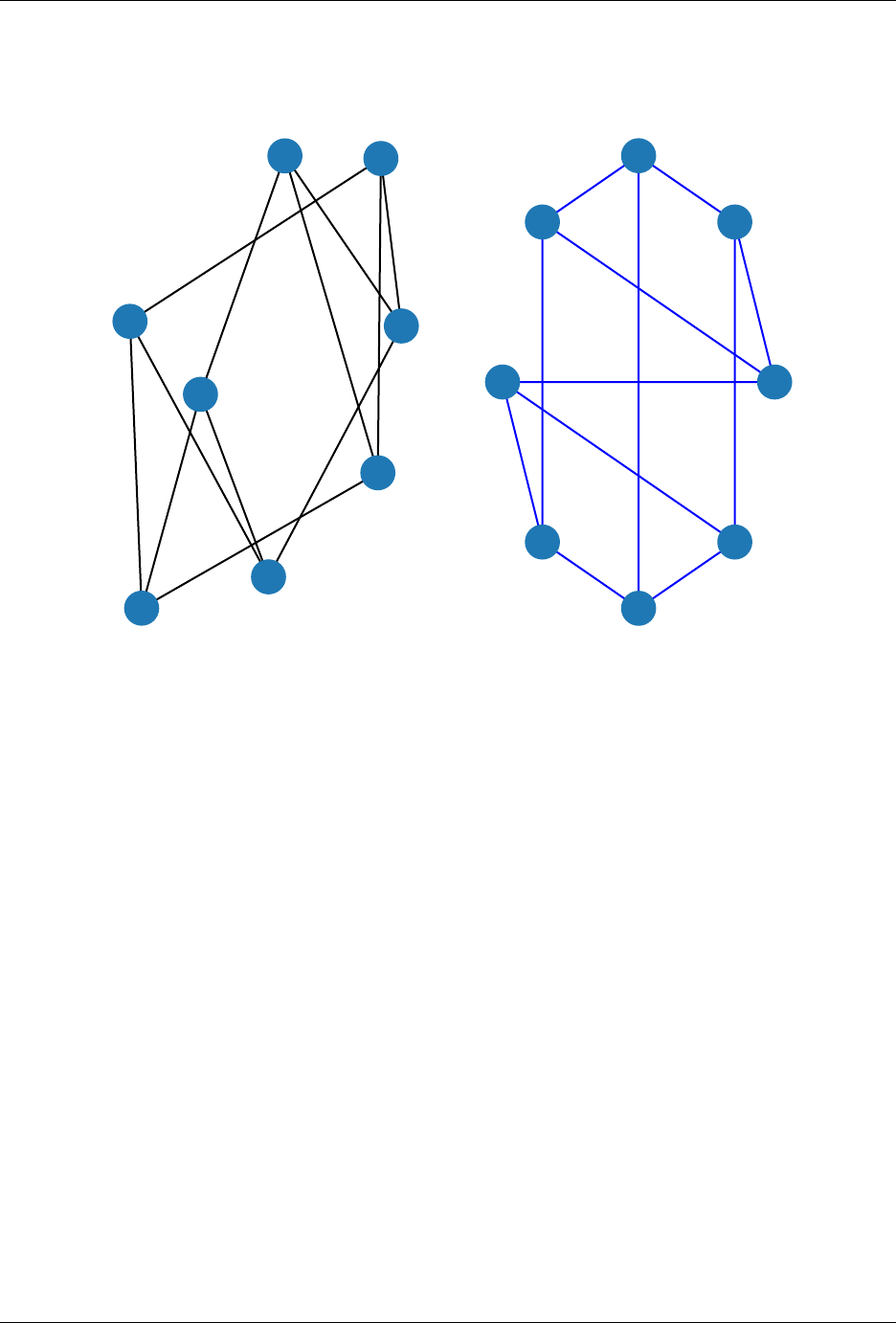
NetworkX Reference, Release 2.3rc1.dev20181203210840
See the examples for more ideas.
1.7 Data Structure
NetworkX uses a “dictionary of dictionaries of dictionaries” as the basic network data structure. This allows fast
lookup with reasonable storage for large sparse networks. The keys are nodes so G[u] returns an adjacency dictionary
keyed by neighbor to the edge attribute dictionary. A view of the adjacency data structure is provided by the dict-like
object G.adj as e.g. for node, nbrsdict in G.adj.items():. The expression G[u][v] returns the
edge attribute dictionary itself. A dictionary of lists would have also been possible, but not allow fast edge detection
nor convenient storage of edge data.
Advantages of dict-of-dicts-of-dicts data structure:
• Find edges and remove edges with two dictionary look-ups.
• Prefer to “lists” because of fast lookup with sparse storage.
• Prefer to “sets” since data can be attached to edge.
•G[u][v] returns the edge attribute dictionary.
•n in G tests if node nis in graph G.
•for n in G: iterates through the graph.
•for nbr in G[n]: iterates through neighbors.
1.7. Data Structure 5

NetworkX Reference, Release 2.3rc1.dev20181203210840
As an example, here is a representation of an undirected graph with the edges (𝐴, 𝐵)and (𝐵, 𝐶).
>>> G=nx.Graph()
>>> G.add_edge('A','B')
>>> G.add_edge('B','C')
>>> print(G.adj)
{'A': {'B': {}}, 'B': {'A': {}, 'C': {}}, 'C': {'B': {}}}
The data structure gets morphed slightly for each base graph class. For DiGraph two dict-of-dicts-of-dicts structures
are provided, one for successors (G.succ) and one for predecessors (G.pred). For MultiGraph/MultiDiGraph
we use a dict-of-dicts-of-dicts-of-dicts1where the third dictionary is keyed by an edge key identifier to the fourth
dictionary which contains the edge attributes for that edge between the two nodes.
Graphs provide two interfaces to the edge data attributes: adjacency and edges. So G[u][v]['width'] is the same
as G.edges[u, v]['width'].
>>> G=nx.Graph()
>>> G.add_edge(1,2, color='red', weight=0.84, size=300)
>>> print(G[1][2]['size'])
300
>>> print(G.edges[1,2]['color'])
red
• ;
• ;
• .
1“It’s dictionaries all the way down.”
6 Chapter 1. Introduction
CHAPTER
TWO
GRAPH TYPES
NetworkX provides data structures and methods for storing graphs.
All NetworkX graph classes allow (hashable) Python objects as nodes and any Python object can be assigned as an
edge attribute.
The choice of graph class depends on the structure of the graph you want to represent.
2.1 Which graph class should I use?
Graph Type NetworkX Class
Undirected Simple Graph
Directed Simple DiGraph
With Self-loops Graph, DiGraph
With Parallel edges MultiGraph, MultiDiGraph
2.2 Basic graph types
2.2.1 Graph—Undirected graphs with self loops
Overview
class Graph(incoming_graph_data=None,**attr)
Base class for undirected graphs.
A Graph stores nodes and edges with optional data, or attributes.
Graphs hold undirected edges. Self loops are allowed but multiple (parallel) edges are not.
Nodes can be arbitrary (hashable) Python objects with optional key/value attributes. By convention None is not
used as a node.
Edges are represented as links between nodes with optional key/value attributes.
Parameters
•incoming_graph_data (input graph (optional, default: None)) – Data to initialize graph. If
None (default) an empty graph is created. The data can be any format that is supported by
the to_networkx_graph() function, currently including edge list, dict of dicts, dict of lists,
NetworkX graph, NumPy matrix or 2d ndarray, SciPy sparse matrix, or PyGraphviz graph.
7

NetworkX Reference, Release 2.3rc1.dev20181203210840
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
DiGraph,MultiGraph,MultiDiGraph,OrderedGraph
Examples
Create an empty graph structure (a “null graph”) with no nodes and no edges.
>>> G=nx.Graph()
G can be grown in several ways.
Nodes:
Add one node at a time:
>>> G.add_node(1)
Add the nodes from any container (a list, dict, set or even the lines from a file or the nodes from another graph).
>>> G.add_nodes_from([2,3])
>>> G.add_nodes_from(range(100,110))
>>> H=nx.path_graph(10)
>>> G.add_nodes_from(H)
In addition to strings and integers any hashable Python object (except None) can represent a node, e.g. a
customized node object, or even another Graph.
>>> G.add_node(H)
Edges:
G can also be grown by adding edges.
Add one edge,
>>> G.add_edge(1,2)
a list of edges,
>>> G.add_edges_from([(1,2), (1,3)])
or a collection of edges,
>>> G.add_edges_from(H.edges)
If some edges connect nodes not yet in the graph, the nodes are added automatically. There are no errors when
adding nodes or edges that already exist.
Attributes:
Each graph, node, and edge can hold key/value attribute pairs in an associated attribute dictionary (the keys
must be hashable). By default these are empty, but can be added or changed using add_edge, add_node or direct
manipulation of the attribute dictionaries named graph, node and edge respectively.
8 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.Graph(day="Friday")
>>> G.graph
{'day': 'Friday'}
Add node attributes using add_node(), add_nodes_from() or G.nodes
>>> G.add_node(1, time='5pm')
>>> G.add_nodes_from([3], time='2pm')
>>> G.nodes[1]
{'time': '5pm'}
>>> G.nodes[1]['room']=714 # node must exist already to use G.nodes
>>> del G.nodes[1]['room']# remove attribute
>>> list(G.nodes(data=True))
[(1, {'time': '5pm'}), (3, {'time': '2pm'})]
Add edge attributes using add_edge(), add_edges_from(), subscript notation, or G.edges.
>>> G.add_edge(1,2, weight=4.7 )
>>> G.add_edges_from([(3,4), (4,5)], color='red')
>>> G.add_edges_from([(1,2, {'color':'blue'}), (2,3, {'weight':8})])
>>> G[1][2]['weight']=4.7
>>> G.edges[1,2]['weight']=4
Warning: we protect the graph data structure by making G.edges a read-only dict-like structure. However, you
can assign to attributes in e.g. G.edges[1, 2]. Thus, use 2 sets of brackets to add/change data attributes:
G.edges[1, 2]['weight'] = 4 (For multigraphs: MG.edges[u, v, key][name] = value).
Shortcuts:
Many common graph features allow python syntax to speed reporting.
>>> 1in G# check if node in graph
True
>>> [n for nin Gif n<3]# iterate through nodes
[1, 2]
>>> len(G) # number of nodes in graph
5
Often the best way to traverse all edges of a graph is via the neighbors. The neighbors are reported as an
adjacency-dict G.adj or G.adjacency()
>>> for n, nbrsdict in G.adjacency():
... for nbr, eattr in nbrsdict.items():
... if 'weight' in eattr:
... # Do something useful with the edges
... pass
But the edges() method is often more convenient:
>>> for u, v, weight in G.edges.data('weight'):
... if weight is not None:
... # Do something useful with the edges
... pass
Reporting:
Simple graph information is obtained using object-attributes and methods. Reporting typically provides
views instead of containers to reduce memory usage. The views update as the graph is updated simi-
larly to dict-views. The objects nodes, `edges and adj provide access to data attributes via lookup
2.2. Basic graph types 9

NetworkX Reference, Release 2.3rc1.dev20181203210840
(e.g. nodes[n], `edges[u, v],adj[u][v]) and iteration (e.g. nodes.items(),nodes.
data('color'),nodes.data('color', default='blue') and similarly for edges) Views exist
for nodes,edges,neighbors()/adj and degree.
For details on these and other miscellaneous methods, see below.
Subclasses (Advanced):
The Graph class uses a dict-of-dict-of-dict data structure. The outer dict (node_dict) holds adjacency information
keyed by node. The next dict (adjlist_dict) represents the adjacency information and holds edge data keyed by
neighbor. The inner dict (edge_attr_dict) represents the edge data and holds edge attribute values keyed by
attribute names.
Each of these three dicts can be replaced in a subclass by a user defined dict-like object. In general, the
dict-like features should be maintained but extra features can be added. To replace one of the dicts create
a new graph class by changing the class(!) variable holding the factory for that dict-like structure. The vari-
able names are node_dict_factory, node_attr_dict_factory, adjlist_inner_dict_factory, adjlist_outer_dict_factory,
edge_attr_dict_factory and graph_attr_dict_factory.
node_dict_factory [function, (default: dict)] Factory function to be used to create the dict containing node
attributes, keyed by node id. It should require no arguments and return a dict-like object
node_attr_dict_factory: function, (default: dict) Factory function to be used to create the node attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object
adjlist_outer_dict_factory [function, (default: dict)] Factory function to be used to create the outer-most dict
in the data structure that holds adjacency info keyed by node. It should require no arguments and return a
dict-like object.
adjlist_inner_dict_factory [function, (default: dict)] Factory function to be used to create the adjacency list
dict which holds edge data keyed by neighbor. It should require no arguments and return a dict-like object
edge_attr_dict_factory [function, (default: dict)] Factory function to be used to create the edge attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object.
graph_attr_dict_factory [function, (default: dict)] Factory function to be used to create the graph attribute
dict which holds attribute values keyed by attribute name. It should require no arguments and return a
dict-like object.
Typically, if your extension doesn’t impact the data structure all methods will inherit without issue except:
to_directed/to_undirected. By default these methods create a DiGraph/Graph class and you probably
want them to create your extension of a DiGraph/Graph. To facilitate this we define two class variables that you
can set in your subclass.
to_directed_class [callable, (default: DiGraph or MultiDiGraph)] Class to create a new graph structure in the
to_directed method. If None, a NetworkX class (DiGraph or MultiDiGraph) is used.
to_undirected_class [callable, (default: Graph or MultiGraph)] Class to create a new graph structure in the
to_undirected method. If None, a NetworkX class (Graph or MultiGraph) is used.
Examples
Create a low memory graph class that effectively disallows edge attributes by using a single attribute dict for all
edges. This reduces the memory used, but you lose edge attributes.
>>> class ThinGraph(nx.Graph):
... all_edge_dict ={'weight':1}
(continues on next page)
10 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
... def single_edge_dict(self):
... return self.all_edge_dict
... edge_attr_dict_factory =single_edge_dict
>>> G=ThinGraph()
>>> G.add_edge(2,1)
>>> G[2][1]
{'weight': 1}
>>> G.add_edge(2,2)
>>> G[2][1]is G[2][2]
True
Please see ordered for more examples of creating graph subclasses by overwriting the base class dict with
a dictionary-like object.
Methods
Adding and removing nodes and edges
Graph.__init__([incoming_graph_data]) Initialize a graph with edges, name, or graph attributes.
Graph.add_node(node_for_adding, **attr) Add a single node node_for_adding and update
node attributes.
Graph.add_nodes_from(nodes_for_adding,
**attr)
Add multiple nodes.
Graph.remove_node(n) Remove node n.
Graph.remove_nodes_from(nodes) Remove multiple nodes.
Graph.add_edge(u_of_edge, v_of_edge, **attr) Add an edge between u and v.
Graph.add_edges_from(ebunch_to_add, **attr) Add all the edges in ebunch_to_add.
Graph.add_weighted_edges_from(ebunch_to_add)Add weighted edges in ebunch_to_add with speci-
fied weight attr
Graph.remove_edge(u, v) Remove the edge between u and v.
Graph.remove_edges_from(ebunch) Remove all edges specified in ebunch.
Graph.update([edges, nodes]) Update the graph using nodes/edges/graphs as input.
Graph.clear() Remove all nodes and edges from the graph.
networkx.Graph.__init__
Graph.__init__(incoming_graph_data=None,**attr)
Initialize a graph with edges, name, or graph attributes.
Parameters
•incoming_graph_data (input graph (optional, default: None)) – Data to initialize graph. If
None (default) an empty graph is created. The data can be an edge list, or any NetworkX
graph object. If the corresponding optional Python packages are installed the data can also
be a NumPy matrix or 2d ndarray, a SciPy sparse matrix, or a PyGraphviz graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
convert()
2.2. Basic graph types 11

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G=nx.Graph(name='my graph')
>>> e=[(1,2), (2,3), (3,4)] # list of edges
>>> G=nx.Graph(e)
Arbitrary graph attribute pairs (key=value) may be assigned
>>> G=nx.Graph(e, day="Friday")
>>> G.graph
{'day': 'Friday'}
networkx.Graph.add_node
Graph.add_node(node_for_adding,**attr)
Add a single node node_for_adding and update node attributes.
Parameters
•node_for_adding (node) – A node can be any hashable Python object except None.
•attr (keyword arguments, optional) – Set or change node attributes using key=value.
See also:
add_nodes_from()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_node(1)
>>> G.add_node('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_node(K3)
>>> G.number_of_nodes()
3
Use keywords set/change node attributes:
>>> G.add_node(1, size=10)
>>> G.add_node(3, weight=0.4, UTM=('13S',382871,3972649))
Notes
A hashable object is one that can be used as a key in a Python dictionary. This includes strings, numbers, tuples
of strings and numbers, etc.
On many platforms hashable items also include mutables such as NetworkX Graphs, though one should be
careful that the hash doesn’t change on mutables.
12 Chapter 2. Graph types
NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.Graph.add_nodes_from
Graph.add_nodes_from(nodes_for_adding,**attr)
Add multiple nodes.
Parameters
•nodes_for_adding (iterable container) – A container of nodes (list, dict, set, etc.). OR A
container of (node, attribute dict) tuples. Node attributes are updated using the attribute dict.
•attr (keyword arguments, optional (default= no attributes)) – Update attributes for all nodes
in nodes. Node attributes specified in nodes as a tuple take precedence over attributes spec-
ified via keyword arguments.
See also:
add_node()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_nodes_from('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_nodes_from(K3)
>>> sorted(G.nodes(), key=str)
[0, 1, 2, 'H', 'e', 'l', 'o']
Use keywords to update specific node attributes for every node.
>>> G.add_nodes_from([1,2], size=10)
>>> G.add_nodes_from([3,4], weight=0.4)
Use (node, attrdict) tuples to update attributes for specific nodes.
>>> G.add_nodes_from([(1,dict(size=11)), (2, {'color':'blue'})])
>>> G.nodes[1]['size']
11
>>> H=nx.Graph()
>>> H.add_nodes_from(G.nodes(data=True))
>>> H.nodes[1]['size']
11
networkx.Graph.remove_node
Graph.remove_node(n)
Remove node n.
Removes the node n and all adjacent edges. Attempting to remove a non-existent node will raise an exception.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
remove_nodes_from()
2.2. Basic graph types 13

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> list(G.edges)
[(0, 1), (1, 2)]
>>> G.remove_node(1)
>>> list(G.edges)
[]
networkx.Graph.remove_nodes_from
Graph.remove_nodes_from(nodes)
Remove multiple nodes.
Parameters nodes (iterable container) – A container of nodes (list, dict, set, etc.). If a node in the
container is not in the graph it is silently ignored.
See also:
remove_node()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e=list(G.nodes)
>>> e
[0, 1, 2]
>>> G.remove_nodes_from(e)
>>> list(G.nodes)
[]
networkx.Graph.add_edge
Graph.add_edge(u_of_edge,v_of_edge,**attr)
Add an edge between u and v.
The nodes u and v will be automatically added if they are not already in the graph.
Edge attributes can be specified with keywords or by directly accessing the edge’s attribute dictionary. See
examples below.
Parameters
•u, v (nodes) – Nodes can be, for example, strings or numbers. Nodes must be hashable (and
not None) Python objects.
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
See also:
add_edges_from() add a collection of edges
14 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Adding an edge that already exists updates the edge data.
Many NetworkX algorithms designed for weighted graphs use an edge attribute (by default weight) to hold a
numerical value.
Examples
The following all add the edge e=(1, 2) to graph G:
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e=(1,2)
>>> G.add_edge(1,2)# explicit two-node form
>>> G.add_edge(*e) # single edge as tuple of two nodes
>>> G.add_edges_from([(1,2)]) # add edges from iterable container
Associate data to edges using keywords:
>>> G.add_edge(1,2, weight=3)
>>> G.add_edge(1,3, weight=7, capacity=15, length=342.7)
For non-string attribute keys, use subscript notation.
>>> G.add_edge(1,2)
>>> G[1][2].update({0:5})
>>> G.edges[1,2].update({0:5})
networkx.Graph.add_edges_from
Graph.add_edges_from(ebunch_to_add,**attr)
Add all the edges in ebunch_to_add.
Parameters
•ebunch_to_add (container of edges) – Each edge given in the container will be added to
the graph. The edges must be given as as 2-tuples (u, v) or 3-tuples (u, v, d) where d is a
dictionary containing edge data.
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
See also:
add_edge() add a single edge
add_weighted_edges_from() convenient way to add weighted edges
Notes
Adding the same edge twice has no effect but any edge data will be updated when each duplicate edge is added.
Edge attributes specified in an ebunch take precedence over attributes specified via keyword arguments.
2.2. Basic graph types 15

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edges_from([(0,1), (1,2)]) # using a list of edge tuples
>>> e=zip(range(0,3), range(1,4))
>>> G.add_edges_from(e) # Add the path graph 0-1-2-3
Associate data to edges
>>> G.add_edges_from([(1,2), (2,3)], weight=3)
>>> G.add_edges_from([(3,4), (1,4)], label='WN2898')
networkx.Graph.add_weighted_edges_from
Graph.add_weighted_edges_from(ebunch_to_add,weight=’weight’,**attr)
Add weighted edges in ebunch_to_add with specified weight attr
Parameters
•ebunch_to_add (container of edges) – Each edge given in the list or container will be added
to the graph. The edges must be given as 3-tuples (u, v, w) where w is a number.
•weight (string, optional (default= ‘weight’)) – The attribute name for the edge weights to
be added.
•attr (keyword arguments, optional (default= no attributes)) – Edge attributes to add/update
for all edges.
See also:
add_edge() add a single edge
add_edges_from() add multiple edges
Notes
Adding the same edge twice for Graph/DiGraph simply updates the edge data. For MultiGraph/MultiDiGraph,
duplicate edges are stored.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_weighted_edges_from([(0,1,3.0), (1,2,7.5)])
networkx.Graph.remove_edge
Graph.remove_edge(u,v)
Remove the edge between u and v.
Parameters u, v (nodes) – Remove the edge between nodes u and v.
Raises NetworkXError – If there is not an edge between u and v.
See also:
16 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
remove_edges_from() remove a collection of edges
Examples
>>> G=nx.path_graph(4)# or DiGraph, etc
>>> G.remove_edge(0,1)
>>> e=(1,2)
>>> G.remove_edge(*e) # unpacks e from an edge tuple
>>> e=(2,3, {'weight':7}) # an edge with attribute data
>>> G.remove_edge(*e[:2]) # select first part of edge tuple
networkx.Graph.remove_edges_from
Graph.remove_edges_from(ebunch)
Remove all edges specified in ebunch.
Parameters ebunch (list or container of edge tuples) – Each edge given in the list or container will
be removed from the graph. The edges can be:
• 2-tuples (u, v) edge between u and v.
• 3-tuples (u, v, k) where k is ignored.
See also:
remove_edge() remove a single edge
Notes
Will fail silently if an edge in ebunch is not in the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> ebunch=[(1,2), (2,3)]
>>> G.remove_edges_from(ebunch)
networkx.Graph.update
Graph.update(edges=None,nodes=None)
Update the graph using nodes/edges/graphs as input.
Like dict.update, this method takes a graph as input, adding the graph’s noes and edges to this graph. It can also
take two inputs: edges and nodes. Finally it can take either edges or nodes. To specify only nodes the keyword
nodes must be used.
The collections of edges and nodes are treated similarly to the add_edges_from/add_nodes_from methods.
When iterated, they should yield 2-tuples (u, v) or 3-tuples (u, v, datadict).
Parameters
2.2. Basic graph types 17
NetworkX Reference, Release 2.3rc1.dev20181203210840
•edges (Graph object, collection of edges, or None) – The first parameter can be a graph or
some edges. If it has attributes nodes and edges, then it is taken to be a Graph-like object
and those attributes are used as collections of nodes and edges to be added to the graph. If
the first parameter does not have those attributes, it is treated as a collection of edges and
added to the graph. If the first argument is None, no edges are added.
•nodes (collection of nodes, or None) – The second parameter is treated as a collection of
nodes to be added to the graph unless it is None. If edges is None and nodes is
None an exception is raised. If the first parameter is a Graph, then nodes is ignored.
Examples
>>> G=nx.path_graph(5)
>>> G.update(nx.complete_graph(range(4,10)))
>>> from itertools import combinations
>>> edges =((u, v, {'power': u *v})
... for u, v in combinations(range(10,20), 2)
... if u*v<225)
>>> nodes =[1000]# for singleton, use a container
>>> G.update(edges, nodes)
Notes
It you want to update the graph using an adjacency structure it is straightforward to obtain the edges/nodes from
adjacency. The following examples provide common cases, your adjacency may be slightly different and require
tweaks of these examples.
>>> # dict-of-set/list/tuple
>>> adj ={1: {2,3}, 2: {1,3}, 3: {1,2}}
>>> e=[(u, v) for u, nbrs in adj.items() for vin nbrs]
>>> G.update(edges=e, nodes=adj)
>>> DG =nx.DiGraph()
>>> # dict-of-dict-of-attribute
>>> adj ={1: {2:1.3,3:0.7}, 2: {1:1.4}, 3: {1:0.7}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # dict-of-dict-of-dict
>>> adj ={1: {2: {'weight':1.3}, 3: {'color':0.7,'weight':1.2}}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # predecessor adjacency (dict-of-set)
>>> pred ={1: {2,3}, 2: {3}, 3: {3}}
>>> e=[(v, u) for u, nbrs in pred.items() for vin nbrs]
>>> # MultiGraph dict-of-dict-of-dict-of-attribute
>>> MDG =nx.MultiDiGraph()
>>> adj ={1: {2: {0: {'weight':1.3}, 1: {'weight':1.2}}},
... 3: {2: {0: {'weight':0.7}}}}
(continues on next page)
18 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> e=[(u, v, ekey, d) for u, nbrs in adj.items()
... for v, keydict in nbrs.items()
... for ekey, d in keydict.items()]
>>> MDG.update(edges=e)
See also:
add_edges_from() add multiple edges to a graph
add_nodes_from() add multiple nodes to a graph
networkx.Graph.clear
Graph.clear()
Remove all nodes and edges from the graph.
This also removes the name, and all graph, node, and edge attributes.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.clear()
>>> list(G.nodes)
[]
>>> list(G.edges)
[]
Reporting nodes edges and neighbors
Graph.nodes A NodeView of the Graph as G.nodes or G.nodes().
Graph.__iter__() Iterate over the nodes.
Graph.has_node(n) Return True if the graph contains the node n.
Graph.__contains__(n) Return True if n is a node, False otherwise.
Graph.edges An EdgeView of the Graph as G.edges or G.edges().
Graph.has_edge(u, v) Return True if the edge (u, v) is in the graph.
Graph.get_edge_data(u, v[, default]) Return the attribute dictionary associated with edge (u,
v).
Graph.neighbors(n) Return an iterator over all neighbors of node n.
Graph.adj Graph adjacency object holding the neighbors of each
node.
Graph.__getitem__(n) Return a dict of neighbors of node n.
Graph.adjacency() Return an iterator over (node, adjacency dict) tuples for
all nodes.
Graph.nbunch_iter([nbunch]) Return an iterator over nodes contained in nbunch that
are also in the graph.
2.2. Basic graph types 19

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.Graph.nodes
Graph.nodes
A NodeView of the Graph as G.nodes or G.nodes().
Can be used as G.nodes for data lookup and for set-like operations. Can also be used as G.
nodes(data='color', default=None) to return a NodeDataView which reports specific node data
but no set operations. It presents a dict-like interface as well with G.nodes.items() iterating over (node,
nodedata) 2-tuples and G.nodes[3]['foo'] providing the value of the foo attribute for node 3. In
addition, a view G.nodes.data('foo') provides a dict-like interface to the foo attribute of each node.
G.nodes.data('foo', default=1) provides a default for nodes that do not have attribute foo.
Parameters
•data (string or bool, optional (default=False)) – The node attribute returned in 2-tuple (n,
ddict[data]). If True, return entire node attribute dict as (n, ddict). If False, return just the
nodes n.
•default (value, optional (default=None)) – Value used for nodes that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns
Allows set-like operations over the nodes as well as node attribute dict lookup and calling to
get a NodeDataView. A NodeDataView iterates over (n, data) and has no set operations. A
NodeView iterates over nand includes set operations.
When called, if data is False, an iterator over nodes. Otherwise an iterator of 2-tuples (node,
attribute value) where the attribute is specified in data. If data is True then the attribute becomes
the entire data dictionary.
Return type NodeView
Notes
If your node data is not needed, it is simpler and equivalent to use the expression for n in G, or list(G).
Examples
There are two simple ways of getting a list of all nodes in the graph:
>>> G=nx.path_graph(3)
>>> list(G.nodes)
[0, 1, 2]
>>> list(G)
[0, 1, 2]
To get the node data along with the nodes:
>>> G.add_node(1, time='5pm')
>>> G.nodes[0]['foo']='bar'
>>> list(G.nodes(data=True))
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes.data())
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
20 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> list(G.nodes(data='foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes.data('foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes(data='time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes.data('time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes(data='time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
>>> list(G.nodes.data('time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
If some of your nodes have an attribute and the rest are assumed to have a default attribute value you can create
a dictionary from node/attribute pairs using the default keyword argument to guarantee the value is never
None:
>>> G=nx.Graph()
>>> G.add_node(0)
>>> G.add_node(1, weight=2)
>>> G.add_node(2, weight=3)
>>> dict(G.nodes(data='weight', default=1))
{0: 1, 1: 2, 2: 3}
networkx.Graph.__iter__
Graph.__iter__()
Iterate over the nodes. Use: ‘for n in G’.
Returns niter – An iterator over all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for nin G]
[0, 1, 2, 3]
>>> list(G)
[0, 1, 2, 3]
networkx.Graph.has_node
Graph.has_node(n)
Return True if the graph contains the node n.
Identical to n in G
Parameters n (node)
2.2. Basic graph types 21

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_node(0)
True
It is more readable and simpler to use
>>> 0in G
True
networkx.Graph.__contains__
Graph.__contains__(n)
Return True if n is a node, False otherwise. Use: ‘n in G’.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> 1in G
True
networkx.Graph.edges
Graph.edges
An EdgeView of the Graph as G.edges or G.edges().
edges(self, nbunch=None, data=False, default=None)
The EdgeView provides set-like operations on the edge-tuples as well as edge attribute lookup. When called,
it also provides an EdgeDataView object which allows control of access to edge attributes (but does not pro-
vide set-like operations). Hence, G.edges[u, v]['color'] provides the value of the color attribute for
edge (u, v) while for (u, v, c) in G.edges.data('color', default='red'): iterates
through all the edges yielding the color attribute with default 'red' if no color attribute exists.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edges – A view of edge attributes, usually it iterates over (u, v) or (u, v, d) tuples of edges,
but can also be used for attribute lookup as edges[u, v]['foo'].
Return type EdgeView
22 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Nodes in nbunch that are not in the graph will be (quietly) ignored. For directed graphs this returns the out-edges.
Examples
>>> G=nx.path_graph(3)# or MultiGraph, etc
>>> G.add_edge(2,3, weight=5)
>>> [e for ein G.edges]
[(0, 1), (1, 2), (2, 3)]
>>> G.edges.data() # default data is {} (empty dict)
EdgeDataView([(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})])
>>> G.edges.data('weight', default=1)
EdgeDataView([(0, 1, 1), (1, 2, 1), (2, 3, 5)])
>>> G.edges([0,3]) # only edges incident to these nodes
EdgeDataView([(0, 1), (3, 2)])
>>> G.edges(0)# only edges incident to a single node (use G.adj[0]?)
EdgeDataView([(0, 1)])
networkx.Graph.has_edge
Graph.has_edge(u,v)
Return True if the edge (u, v) is in the graph.
This is the same as v in G[u] without KeyError exceptions.
Parameters u, v (nodes) – Nodes can be, for example, strings or numbers. Nodes must be hashable
(and not None) Python objects.
Returns edge_ind – True if edge is in the graph, False otherwise.
Return type bool
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_edge(0,1)# using two nodes
True
>>> e=(0,1)
>>> G.has_edge(*e) # e is a 2-tuple (u, v)
True
>>> e=(0,1, {'weight':7})
>>> G.has_edge(*e[:2]) # e is a 3-tuple (u, v, data_dictionary)
True
The following syntax are equivalent:
>>> G.has_edge(0,1)
True
>>> 1in G[0]# though this gives KeyError if 0 not in G
True
2.2. Basic graph types 23

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.Graph.get_edge_data
Graph.get_edge_data(u,v,default=None)
Return the attribute dictionary associated with edge (u, v).
This is identical to G[u][v] except the default is returned instead of an exception is the edge doesn’t exist.
Parameters
•u, v (nodes)
•default (any Python object (default=None)) – Value to return if the edge (u, v) is not found.
Returns edge_dict – The edge attribute dictionary.
Return type dictionary
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0][1]
{}
Warning: Assigning to G[u][v] is not permitted. But it is safe to assign attributes G[u][v]['foo']
>>> G[0][1]['weight']=7
>>> G[0][1]['weight']
7
>>> G[1][0]['weight']
7
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.get_edge_data(0,1)# default edge data is {}
{}
>>> e=(0,1)
>>> G.get_edge_data(*e) # tuple form
{}
>>> G.get_edge_data('a','b', default=0)# edge not in graph, return 0
0
networkx.Graph.neighbors
Graph.neighbors(n)
Return an iterator over all neighbors of node n.
This is identical to iter(G[n])
Parameters n (node) – A node in the graph
Returns neighbors – An iterator over all neighbors of node n
Return type iterator
Raises NetworkXError – If the node n is not in the graph.
24 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for nin G.neighbors(0)]
[1]
Notes
It is usually more convenient (and faster) to access the adjacency dictionary as G[n]:
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge('a','b', weight=7)
>>> G['a']
AtlasView({'b': {'weight': 7}})
>>> G=nx.path_graph(4)
>>> [n for nin G[0]]
[1]
networkx.Graph.adj
Graph.adj
Graph adjacency object holding the neighbors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is keyed
by neighbor to the edge-data-dict. So G.adj[3][2]['color'] = 'blue' sets the color of the edge (3,
2) to "blue".
Iterating over G.adj behaves like a dict. Useful idioms include for nbr, datadict in G.adj[n].
items():.
The neighbor information is also provided by subscripting the graph. So for nbr, foovalue in
G[node].data('foo', default=1): works.
For directed graphs, G.adj holds outgoing (successor) info.
networkx.Graph.__getitem__
Graph.__getitem__(n)
Return a dict of neighbors of node n. Use: ‘G[n]’.
Parameters n (node) – A node in the graph.
Returns adj_dict – The adjacency dictionary for nodes connected to n.
Return type dictionary
Notes
G[n] is the same as G.adj[n] and similar to G.neighbors(n) (which is an iterator over G.adj[n])
2.2. Basic graph types 25

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0]
AtlasView({1: {}})
networkx.Graph.adjacency
Graph.adjacency()
Return an iterator over (node, adjacency dict) tuples for all nodes.
For directed graphs, only outgoing neighbors/adjacencies are included.
Returns adj_iter – An iterator over (node, adjacency dictionary) for all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [(n, nbrdict) for n, nbrdict in G.adjacency()]
[(0, {1: {}}), (1, {0: {}, 2: {}}), (2, {1: {}, 3: {}}), (3, {2: {}})]
networkx.Graph.nbunch_iter
Graph.nbunch_iter(nbunch=None)
Return an iterator over nodes contained in nbunch that are also in the graph.
The nodes in nbunch are checked for membership in the graph and if not are silently ignored.
Parameters nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
Returns niter – An iterator over nodes in nbunch that are also in the graph. If nbunch is None,
iterate over all nodes in the graph.
Return type iterator
Raises NetworkXError – If nbunch is not a node or or sequence of nodes. If a node in nbunch is
not hashable.
See also:
Graph.__iter__()
Notes
When nbunch is an iterator, the returned iterator yields values directly from nbunch, becoming exhausted when
nbunch is exhausted.
To test whether nbunch is a single node, one can use “if nbunch in self:”, even after processing with this routine.
If nbunch is not a node or a (possibly empty) sequence/iterator or None, a NetworkXError is raised. Also, if
any object in nbunch is not hashable, a NetworkXError is raised.
26 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Counting nodes edges and neighbors
Graph.order() Return the number of nodes in the graph.
Graph.number_of_nodes() Return the number of nodes in the graph.
Graph.__len__() Return the number of nodes.
Graph.degree A DegreeView for the Graph as G.degree or G.degree().
Graph.size([weight]) Return the number of edges or total of all edge weights.
Graph.number_of_edges([u, v]) Return the number of edges between two nodes.
networkx.Graph.order
Graph.order()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
number_of_nodes(),__len__()
networkx.Graph.number_of_nodes
Graph.number_of_nodes()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
order(),__len__()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
3
networkx.Graph.__len__
Graph.__len__()
Return the number of nodes. Use: ‘len(G)’.
Returns nnodes – The number of nodes in the graph.
Return type int
2.2. Basic graph types 27

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
4
networkx.Graph.degree
Graph.degree
A DegreeView for the Graph as G.degree or G.degree().
The node degree is the number of edges adjacent to the node. The weighted node degree is the sum of the edge
weights for edges incident to that node.
This object provides an iterator for (node, degree) as well as lookup for the degree for a single node.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The name of an edge attribute that holds
the numerical value used as a weight. If None, then each edge has weight 1. The degree is
the sum of the edge weights adjacent to the node.
Returns
•If a single node is requested
•deg (int) – Degree of the node
•OR if multiple nodes are requested
•nd_view (A DegreeView object capable of iterating (node, degree) pairs)
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.degree[0]# node 0 has degree 1
1
>>> list(G.degree([0,1,2]))
[(0, 1), (1, 2), (2, 2)]
networkx.Graph.size
Graph.size(weight=None)
Return the number of edges or total of all edge weights.
Parameters weight (string or None, optional (default=None)) – The edge attribute that holds the
numerical value used as a weight. If None, then each edge has weight 1.
Returns
size – The number of edges or (if weight keyword is provided) the total weight sum.
If weight is None, returns an int. Otherwise a float (or more general numeric if the weights are
more general).
28 Chapter 2. Graph types
NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type numeric
See also:
number_of_edges()
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.size()
3
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge('a','b', weight=2)
>>> G.add_edge('b','c', weight=4)
>>> G.size()
2
>>> G.size(weight='weight')
6.0
networkx.Graph.number_of_edges
Graph.number_of_edges(u=None,v=None)
Return the number of edges between two nodes.
Parameters u, v (nodes, optional (default=all edges)) – If u and v are specified, return the number
of edges between u and v. Otherwise return the total number of all edges.
Returns nedges – The number of edges in the graph. If nodes uand vare specified return the
number of edges between those nodes. If the graph is directed, this only returns the number of
edges from uto v.
Return type int
See also:
size()
Examples
For undirected graphs, this method counts the total number of edges in the graph:
>>> G=nx.path_graph(4)
>>> G.number_of_edges()
3
If you specify two nodes, this counts the total number of edges joining the two nodes:
>>> G.number_of_edges(0,1)
1
For directed graphs, this method can count the total number of directed edges from uto v:
2.2. Basic graph types 29

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.DiGraph()
>>> G.add_edge(0,1)
>>> G.add_edge(1,0)
>>> G.number_of_edges(0,1)
1
Making copies and subgraphs
Graph.copy([as_view]) Return a copy of the graph.
Graph.to_undirected([as_view]) Return an undirected copy of the graph.
Graph.to_directed([as_view]) Return a directed representation of the graph.
Graph.subgraph(nodes) Return a SubGraph view of the subgraph induced on
nodes.
Graph.edge_subgraph(edges) Returns the subgraph induced by the specified edges.
networkx.Graph.copy
Graph.copy(as_view=False)
Return a copy of the graph.
The copy method by default returns an independent shallow copy of the graph and attributes. That is, if an
attribute is a container, that container is shared by the original an the copy. Use Python’s copy.deepcopy for
new containers.
If as_view is True then a view is returned instead of a copy.
Notes
All copies reproduce the graph structure, but data attributes may be handled in different ways. There are four
types of copies of a graph that people might want.
Deepcopy – A “deepcopy” copies the graph structure as well as all data attributes and any objects they might
contain. The entire graph object is new so that changes in the copy do not affect the original object. (see Python’s
copy.deepcopy)
Data Reference (Shallow) – For a shallow copy the graph structure is copied but the edge, node and graph at-
tribute dicts are references to those in the original graph. This saves time and memory but could cause confusion
if you change an attribute in one graph and it changes the attribute in the other. NetworkX does not provide this
level of shallow copy.
Independent Shallow – This copy creates new independent attribute dicts and then does a shallow copy of the
attributes. That is, any attributes that are containers are shared between the new graph and the original. This is
exactly what dict.copy() provides. You can obtain this style copy using:
>>> G=nx.path_graph(5)
>>> H=G.copy()
>>> H=G.copy(as_view=False)
>>> H=nx.Graph(G)
>>> H=G.__class__(G)
Fresh Data – For fresh data, the graph structure is copied while new empty data attribute dicts are created. The
resulting graph is independent of the original and it has no edge, node or graph attributes. Fresh copies are not
enabled. Instead use:
30 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> H=G.__class__()
>>> H.add_nodes_from(G)
>>> H.add_edges_from(G.edges)
View – Inspired by dict-views, graph-views act like read-only versions of the original graph, providing a copy
of the original structure without requiring any memory for copying the information.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Parameters as_view (bool, optional (default=False)) – If True, the returned graph-view provides a
read-only view of the original graph without actually copying any data.
Returns G – A copy of the graph.
Return type Graph
See also:
to_directed() return a directed copy of the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.copy()
networkx.Graph.to_undirected
Graph.to_undirected(as_view=False)
Return an undirected copy of the graph.
Parameters as_view (bool (optional, default=False)) – If True return a view of the original undi-
rected graph.
Returns G – A deepcopy of the graph.
Return type Graph/MultiGraph
See also:
Graph(),copy(),add_edge(),add_edges_from()
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar G = nx.DiGraph(D) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed DiGraph to use dict-like objects in the data structure, those changes do not
transfer to the Graph created by this method.
2.2. Basic graph types 31

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(2)# or MultiGraph, etc
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
>>> G2 =H.to_undirected()
>>> list(G2.edges)
[(0, 1)]
networkx.Graph.to_directed
Graph.to_directed(as_view=False)
Return a directed representation of the graph.
Returns G – A directed graph with the same name, same nodes, and with each edge (u, v, data)
replaced by two directed edges (u, v, data) and (v, u, data).
Return type DiGraph
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar D=DiGraph(G) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed Graph to use dict-like objects in the data structure, those changes do not
transfer to the DiGraph created by this method.
Examples
>>> G=nx.Graph() # or MultiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
If already directed, return a (deep) copy
>>> G=nx.DiGraph() # or MultiDiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1)]
networkx.Graph.subgraph
Graph.subgraph(nodes)
Return a SubGraph view of the subgraph induced on nodes.
32 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
The induced subgraph of the graph contains the nodes in nodes and the edges between those nodes.
Parameters nodes (list, iterable) – A container of nodes which will be iterated through once.
Returns G – A subgraph view of the graph. The graph structure cannot be changed but node/edge
attributes can and are shared with the original graph.
Return type SubGraph View
Notes
The graph, edge and node attributes are shared with the original graph. Changes to the graph structure is ruled
out by the view, but changes to attributes are reflected in the original graph.
To create a subgraph with its own copy of the edge/node attributes use: G.subgraph(nodes).copy()
For an inplace reduction of a graph to a subgraph you can remove nodes: G.remove_nodes_from([n for n in G
if n not in set(nodes)])
Subgraph views are sometimes NOT what you want. In most cases where you want to do more than simply look
at the induced edges, it makes more sense to just create the subgraph as its own graph with code like:
# Create a subgraph SG based on a (possibly multigraph) G
SG =G.__class__()
SG.add_nodes_from((n, G.nodes[n]) for nin largest_wcc)
if SG.is_multigraph:
SG.add_edges_from((n, nbr, key, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, keydict in nbrs.items() if nbr in largest_wcc
for key, d in keydict.items())
else:
SG.add_edges_from((n, nbr, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, d in nbrs.items() if nbr in largest_wcc)
SG.graph.update(G.graph)
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.subgraph([0,1,2])
>>> list(H.edges)
[(0, 1), (1, 2)]
networkx.Graph.edge_subgraph
Graph.edge_subgraph(edges)
Returns the subgraph induced by the specified edges.
The induced subgraph contains each edge in edges and each node incident to any one of those edges.
Parameters edges (iterable) – An iterable of edges in this graph.
Returns G – An edge-induced subgraph of this graph with the same edge attributes.
Return type Graph
2.2. Basic graph types 33

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The graph, edge, and node attributes in the returned subgraph view are references to the corresponding attributes
in the original graph. The view is read-only.
To create a full graph version of the subgraph with its own copy of the edge or node attributes, use:
>>> G.edge_subgraph(edges).copy()
Examples
>>> G=nx.path_graph(5)
>>> H=G.edge_subgraph([(0,1), (3,4)])
>>> list(H.nodes)
[0, 1, 3, 4]
>>> list(H.edges)
[(0, 1), (3, 4)]
2.2.2 DiGraph—Directed graphs with self loops
Overview
class DiGraph(incoming_graph_data=None,**attr)
Base class for directed graphs.
A DiGraph stores nodes and edges with optional data, or attributes.
DiGraphs hold directed edges. Self loops are allowed but multiple (parallel) edges are not.
Nodes can be arbitrary (hashable) Python objects with optional key/value attributes. By convention None is not
used as a node.
Edges are represented as links between nodes with optional key/value attributes.
Parameters
•incoming_graph_data (input graph (optional, default: None)) – Data to initialize graph. If
None (default) an empty graph is created. The data can be any format that is supported by
the to_networkx_graph() function, currently including edge list, dict of dicts, dict of lists,
NetworkX graph, NumPy matrix or 2d ndarray, SciPy sparse matrix, or PyGraphviz graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
Graph,MultiGraph,MultiDiGraph,OrderedDiGraph
Examples
Create an empty graph structure (a “null graph”) with no nodes and no edges.
>>> G=nx.DiGraph()
34 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
G can be grown in several ways.
Nodes:
Add one node at a time:
>>> G.add_node(1)
Add the nodes from any container (a list, dict, set or even the lines from a file or the nodes from another graph).
>>> G.add_nodes_from([2,3])
>>> G.add_nodes_from(range(100,110))
>>> H=nx.path_graph(10)
>>> G.add_nodes_from(H)
In addition to strings and integers any hashable Python object (except None) can represent a node, e.g. a
customized node object, or even another Graph.
>>> G.add_node(H)
Edges:
G can also be grown by adding edges.
Add one edge,
>>> G.add_edge(1,2)
a list of edges,
>>> G.add_edges_from([(1,2), (1,3)])
or a collection of edges,
>>> G.add_edges_from(H.edges)
If some edges connect nodes not yet in the graph, the nodes are added automatically. There are no errors when
adding nodes or edges that already exist.
Attributes:
Each graph, node, and edge can hold key/value attribute pairs in an associated attribute dictionary (the keys
must be hashable). By default these are empty, but can be added or changed using add_edge, add_node or direct
manipulation of the attribute dictionaries named graph, node and edge respectively.
>>> G=nx.DiGraph(day="Friday")
>>> G.graph
{'day': 'Friday'}
Add node attributes using add_node(), add_nodes_from() or G.nodes
>>> G.add_node(1, time='5pm')
>>> G.add_nodes_from([3], time='2pm')
>>> G.nodes[1]
{'time': '5pm'}
>>> G.nodes[1]['room']=714
>>> del G.nodes[1]['room']# remove attribute
>>> list(G.nodes(data=True))
[(1, {'time': '5pm'}), (3, {'time': '2pm'})]
2.2. Basic graph types 35

NetworkX Reference, Release 2.3rc1.dev20181203210840
Add edge attributes using add_edge(), add_edges_from(), subscript notation, or G.edges.
>>> G.add_edge(1,2, weight=4.7 )
>>> G.add_edges_from([(3,4), (4,5)], color='red')
>>> G.add_edges_from([(1,2, {'color':'blue'}), (2,3, {'weight':8})])
>>> G[1][2]['weight']=4.7
>>> G.edges[1,2]['weight']=4
Warning: we protect the graph data structure by making G.edges[1, 2] a read-only dict-like structure.
However, you can assign to attributes in e.g. G.edges[1, 2]. Thus, use 2 sets of brackets to add/change data
attributes: G.edges[1, 2]['weight'] = 4 (For multigraphs: MG.edges[u, v, key][name] =
value).
Shortcuts:
Many common graph features allow python syntax to speed reporting.
>>> 1in G# check if node in graph
True
>>> [n for nin Gif n<3]# iterate through nodes
[1, 2]
>>> len(G) # number of nodes in graph
5
Often the best way to traverse all edges of a graph is via the neighbors. The neighbors are reported as an
adjacency-dict G.adj or G.adjacency()
>>> for n, nbrsdict in G.adjacency():
... for nbr, eattr in nbrsdict.items():
... if 'weight' in eattr:
... # Do something useful with the edges
... pass
But the edges reporting object is often more convenient:
>>> for u, v, weight in G.edges(data='weight'):
... if weight is not None:
... # Do something useful with the edges
... pass
Reporting:
Simple graph information is obtained using object-attributes and methods. Reporting usually provides
views instead of containers to reduce memory usage. The views update as the graph is updated simi-
larly to dict-views. The objects nodes, `edges and adj provide access to data attributes via lookup
(e.g. nodes[n], `edges[u, v],adj[u][v]) and iteration (e.g. nodes.items(),nodes.
data('color'),nodes.data('color', default='blue') and similarly for edges) Views exist
for nodes,edges,neighbors()/adj and degree.
For details on these and other miscellaneous methods, see below.
Subclasses (Advanced):
The Graph class uses a dict-of-dict-of-dict data structure. The outer dict (node_dict) holds adjacency information
keyed by node. The next dict (adjlist_dict) represents the adjacency information and holds edge data keyed by
neighbor. The inner dict (edge_attr_dict) represents the edge data and holds edge attribute values keyed by
attribute names.
Each of these three dicts can be replaced in a subclass by a user defined dict-like object. In general, the
dict-like features should be maintained but extra features can be added. To replace one of the dicts create
36 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
a new graph class by changing the class(!) variable holding the factory for that dict-like structure. The vari-
able names are node_dict_factory, node_attr_dict_factory, adjlist_inner_dict_factory, adjlist_outer_dict_factory,
edge_attr_dict_factory and graph_attr_dict_factory.
node_dict_factory [function, (default: dict)] Factory function to be used to create the dict containing node
attributes, keyed by node id. It should require no arguments and return a dict-like object
node_attr_dict_factory: function, (default: dict) Factory function to be used to create the node attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object
adjlist_outer_dict_factory [function, (default: dict)] Factory function to be used to create the outer-most dict
in the data structure that holds adjacency info keyed by node. It should require no arguments and return a
dict-like object.
adjlist_inner_dict_factory [function, optional (default: dict)] Factory function to be used to create the adja-
cency list dict which holds edge data keyed by neighbor. It should require no arguments and return a
dict-like object
edge_attr_dict_factory [function, optional (default: dict)] Factory function to be used to create the edge at-
tribute dict which holds attribute values keyed by attribute name. It should require no arguments and return
a dict-like object.
graph_attr_dict_factory [function, (default: dict)] Factory function to be used to create the graph attribute
dict which holds attribute values keyed by attribute name. It should require no arguments and return a
dict-like object.
Typically, if your extension doesn’t impact the data structure all methods will inherited without issue except:
to_directed/to_undirected. By default these methods create a DiGraph/Graph class and you probably
want them to create your extension of a DiGraph/Graph. To facilitate this we define two class variables that you
can set in your subclass.
to_directed_class [callable, (default: DiGraph or MultiDiGraph)] Class to create a new graph structure in the
to_directed method. If None, a NetworkX class (DiGraph or MultiDiGraph) is used.
to_undirected_class [callable, (default: Graph or MultiGraph)] Class to create a new graph structure in the
to_undirected method. If None, a NetworkX class (Graph or MultiGraph) is used.
Examples
Create a low memory graph class that effectively disallows edge attributes by using a single attribute dict for all
edges. This reduces the memory used, but you lose edge attributes.
>>> class ThinGraph(nx.Graph):
... all_edge_dict ={'weight':1}
... def single_edge_dict(self):
... return self.all_edge_dict
... edge_attr_dict_factory =single_edge_dict
>>> G=ThinGraph()
>>> G.add_edge(2,1)
>>> G[2][1]
{'weight': 1}
>>> G.add_edge(2,2)
>>> G[2][1]is G[2][2]
True
Please see ordered for more examples of creating graph subclasses by overwriting the base class dict with
a dictionary-like object.
2.2. Basic graph types 37

NetworkX Reference, Release 2.3rc1.dev20181203210840
Methods
Adding and removing nodes and edges
DiGraph.__init__([incoming_graph_data]) Initialize a graph with edges, name, or graph attributes.
DiGraph.add_node(node_for_adding, **attr) Add a single node node_for_adding and update
node attributes.
DiGraph.add_nodes_from(nodes_for_adding,
**attr)
Add multiple nodes.
DiGraph.remove_node(n) Remove node n.
DiGraph.remove_nodes_from(nodes) Remove multiple nodes.
DiGraph.add_edge(u_of_edge, v_of_edge, **attr) Add an edge between u and v.
DiGraph.add_edges_from(ebunch_to_add,
**attr)
Add all the edges in ebunch_to_add.
DiGraph.add_weighted_edges_from(ebunch_to_add)Add weighted edges in ebunch_to_add with speci-
fied weight attr
DiGraph.remove_edge(u, v) Remove the edge between u and v.
DiGraph.remove_edges_from(ebunch) Remove all edges specified in ebunch.
DiGraph.update([edges, nodes]) Update the graph using nodes/edges/graphs as input.
DiGraph.clear() Remove all nodes and edges from the graph.
networkx.DiGraph.__init__
DiGraph.__init__(incoming_graph_data=None,**attr)
Initialize a graph with edges, name, or graph attributes.
Parameters
•incoming_graph_data (input graph (optional, default: None)) – Data to initialize graph. If
None (default) an empty graph is created. The data can be an edge list, or any NetworkX
graph object. If the corresponding optional Python packages are installed the data can also
be a NumPy matrix or 2d ndarray, a SciPy sparse matrix, or a PyGraphviz graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
convert()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G=nx.Graph(name='my graph')
>>> e=[(1,2), (2,3), (3,4)] # list of edges
>>> G=nx.Graph(e)
Arbitrary graph attribute pairs (key=value) may be assigned
>>> G=nx.Graph(e, day="Friday")
>>> G.graph
{'day': 'Friday'}
38 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.DiGraph.add_node
DiGraph.add_node(node_for_adding,**attr)
Add a single node node_for_adding and update node attributes.
Parameters
•node_for_adding (node) – A node can be any hashable Python object except None.
•attr (keyword arguments, optional) – Set or change node attributes using key=value.
See also:
add_nodes_from()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_node(1)
>>> G.add_node('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_node(K3)
>>> G.number_of_nodes()
3
Use keywords set/change node attributes:
>>> G.add_node(1, size=10)
>>> G.add_node(3, weight=0.4, UTM=('13S',382871,3972649))
Notes
A hashable object is one that can be used as a key in a Python dictionary. This includes strings, numbers, tuples
of strings and numbers, etc.
On many platforms hashable items also include mutables such as NetworkX Graphs, though one should be
careful that the hash doesn’t change on mutables.
networkx.DiGraph.add_nodes_from
DiGraph.add_nodes_from(nodes_for_adding,**attr)
Add multiple nodes.
Parameters
•nodes_for_adding (iterable container) – A container of nodes (list, dict, set, etc.). OR A
container of (node, attribute dict) tuples. Node attributes are updated using the attribute dict.
•attr (keyword arguments, optional (default= no attributes)) – Update attributes for all nodes
in nodes. Node attributes specified in nodes as a tuple take precedence over attributes spec-
ified via keyword arguments.
See also:
add_node()
2.2. Basic graph types 39

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_nodes_from('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_nodes_from(K3)
>>> sorted(G.nodes(), key=str)
[0, 1, 2, 'H', 'e', 'l', 'o']
Use keywords to update specific node attributes for every node.
>>> G.add_nodes_from([1,2], size=10)
>>> G.add_nodes_from([3,4], weight=0.4)
Use (node, attrdict) tuples to update attributes for specific nodes.
>>> G.add_nodes_from([(1,dict(size=11)), (2, {'color':'blue'})])
>>> G.nodes[1]['size']
11
>>> H=nx.Graph()
>>> H.add_nodes_from(G.nodes(data=True))
>>> H.nodes[1]['size']
11
networkx.DiGraph.remove_node
DiGraph.remove_node(n)
Remove node n.
Removes the node n and all adjacent edges. Attempting to remove a non-existent node will raise an exception.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
remove_nodes_from()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> list(G.edges)
[(0, 1), (1, 2)]
>>> G.remove_node(1)
>>> list(G.edges)
[]
networkx.DiGraph.remove_nodes_from
DiGraph.remove_nodes_from(nodes)
Remove multiple nodes.
Parameters nodes (iterable container) – A container of nodes (list, dict, set, etc.). If a node in the
container is not in the graph it is silently ignored.
40 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
remove_node()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e=list(G.nodes)
>>> e
[0, 1, 2]
>>> G.remove_nodes_from(e)
>>> list(G.nodes)
[]
networkx.DiGraph.add_edge
DiGraph.add_edge(u_of_edge,v_of_edge,**attr)
Add an edge between u and v.
The nodes u and v will be automatically added if they are not already in the graph.
Edge attributes can be specified with keywords or by directly accessing the edge’s attribute dictionary. See
examples below.
Parameters
•u, v (nodes) – Nodes can be, for example, strings or numbers. Nodes must be hashable (and
not None) Python objects.
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
See also:
add_edges_from() add a collection of edges
Notes
Adding an edge that already exists updates the edge data.
Many NetworkX algorithms designed for weighted graphs use an edge attribute (by default weight) to hold a
numerical value.
Examples
The following all add the edge e=(1, 2) to graph G:
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e=(1,2)
>>> G.add_edge(1,2)# explicit two-node form
>>> G.add_edge(*e) # single edge as tuple of two nodes
>>> G.add_edges_from( [(1,2)] ) # add edges from iterable container
Associate data to edges using keywords:
2.2. Basic graph types 41

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G.add_edge(1,2, weight=3)
>>> G.add_edge(1,3, weight=7, capacity=15, length=342.7)
For non-string attribute keys, use subscript notation.
>>> G.add_edge(1,2)
>>> G[1][2].update({0:5})
>>> G.edges[1,2].update({0:5})
networkx.DiGraph.add_edges_from
DiGraph.add_edges_from(ebunch_to_add,**attr)
Add all the edges in ebunch_to_add.
Parameters
•ebunch_to_add (container of edges) – Each edge given in the container will be added to the
graph. The edges must be given as 2-tuples (u, v) or 3-tuples (u, v, d) where d is a dictionary
containing edge data.
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
See also:
add_edge() add a single edge
add_weighted_edges_from() convenient way to add weighted edges
Notes
Adding the same edge twice has no effect but any edge data will be updated when each duplicate edge is added.
Edge attributes specified in an ebunch take precedence over attributes specified via keyword arguments.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edges_from([(0,1), (1,2)]) # using a list of edge tuples
>>> e=zip(range(0,3), range(1,4))
>>> G.add_edges_from(e) # Add the path graph 0-1-2-3
Associate data to edges
>>> G.add_edges_from([(1,2), (2,3)], weight=3)
>>> G.add_edges_from([(3,4), (1,4)], label='WN2898')
networkx.DiGraph.add_weighted_edges_from
DiGraph.add_weighted_edges_from(ebunch_to_add,weight=’weight’,**attr)
Add weighted edges in ebunch_to_add with specified weight attr
Parameters
42 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
•ebunch_to_add (container of edges) – Each edge given in the list or container will be added
to the graph. The edges must be given as 3-tuples (u, v, w) where w is a number.
•weight (string, optional (default= ‘weight’)) – The attribute name for the edge weights to
be added.
•attr (keyword arguments, optional (default= no attributes)) – Edge attributes to add/update
for all edges.
See also:
add_edge() add a single edge
add_edges_from() add multiple edges
Notes
Adding the same edge twice for Graph/DiGraph simply updates the edge data. For MultiGraph/MultiDiGraph,
duplicate edges are stored.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_weighted_edges_from([(0,1,3.0), (1,2,7.5)])
networkx.DiGraph.remove_edge
DiGraph.remove_edge(u,v)
Remove the edge between u and v.
Parameters u, v (nodes) – Remove the edge between nodes u and v.
Raises NetworkXError – If there is not an edge between u and v.
See also:
remove_edges_from() remove a collection of edges
Examples
>>> G=nx.Graph() # or DiGraph, etc
>>> nx.add_path(G, [0,1,2,3])
>>> G.remove_edge(0,1)
>>> e=(1,2)
>>> G.remove_edge(*e) # unpacks e from an edge tuple
>>> e=(2,3, {'weight':7}) # an edge with attribute data
>>> G.remove_edge(*e[:2]) # select first part of edge tuple
networkx.DiGraph.remove_edges_from
DiGraph.remove_edges_from(ebunch)
Remove all edges specified in ebunch.
2.2. Basic graph types 43

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters ebunch (list or container of edge tuples) – Each edge given in the list or container will
be removed from the graph. The edges can be:
• 2-tuples (u, v) edge between u and v.
• 3-tuples (u, v, k) where k is ignored.
See also:
remove_edge() remove a single edge
Notes
Will fail silently if an edge in ebunch is not in the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> ebunch =[(1,2), (2,3)]
>>> G.remove_edges_from(ebunch)
networkx.DiGraph.update
DiGraph.update(edges=None,nodes=None)
Update the graph using nodes/edges/graphs as input.
Like dict.update, this method takes a graph as input, adding the graph’s noes and edges to this graph. It can also
take two inputs: edges and nodes. Finally it can take either edges or nodes. To specify only nodes the keyword
nodes must be used.
The collections of edges and nodes are treated similarly to the add_edges_from/add_nodes_from methods.
When iterated, they should yield 2-tuples (u, v) or 3-tuples (u, v, datadict).
Parameters
•edges (Graph object, collection of edges, or None) – The first parameter can be a graph or
some edges. If it has attributes nodes and edges, then it is taken to be a Graph-like object
and those attributes are used as collections of nodes and edges to be added to the graph. If
the first parameter does not have those attributes, it is treated as a collection of edges and
added to the graph. If the first argument is None, no edges are added.
•nodes (collection of nodes, or None) – The second parameter is treated as a collection of
nodes to be added to the graph unless it is None. If edges is None and nodes is
None an exception is raised. If the first parameter is a Graph, then nodes is ignored.
Examples
>>> G=nx.path_graph(5)
>>> G.update(nx.complete_graph(range(4,10)))
>>> from itertools import combinations
>>> edges =((u, v, {'power': u *v})
... for u, v in combinations(range(10,20), 2)
... if u*v<225)
(continues on next page)
44 Chapter 2. Graph types
NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> nodes =[1000]# for singleton, use a container
>>> G.update(edges, nodes)
Notes
It you want to update the graph using an adjacency structure it is straightforward to obtain the edges/nodes from
adjacency. The following examples provide common cases, your adjacency may be slightly different and require
tweaks of these examples.
>>> # dict-of-set/list/tuple
>>> adj ={1: {2,3}, 2: {1,3}, 3: {1,2}}
>>> e=[(u, v) for u, nbrs in adj.items() for vin nbrs]
>>> G.update(edges=e, nodes=adj)
>>> DG =nx.DiGraph()
>>> # dict-of-dict-of-attribute
>>> adj ={1: {2:1.3,3:0.7}, 2: {1:1.4}, 3: {1:0.7}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # dict-of-dict-of-dict
>>> adj ={1: {2: {'weight':1.3}, 3: {'color':0.7,'weight':1.2}}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # predecessor adjacency (dict-of-set)
>>> pred ={1: {2,3}, 2: {3}, 3: {3}}
>>> e=[(v, u) for u, nbrs in pred.items() for vin nbrs]
>>> # MultiGraph dict-of-dict-of-dict-of-attribute
>>> MDG =nx.MultiDiGraph()
>>> adj ={1: {2: {0: {'weight':1.3}, 1: {'weight':1.2}}},
... 3: {2: {0: {'weight':0.7}}}}
>>> e=[(u, v, ekey, d) for u, nbrs in adj.items()
... for v, keydict in nbrs.items()
... for ekey, d in keydict.items()]
>>> MDG.update(edges=e)
See also:
add_edges_from() add multiple edges to a graph
add_nodes_from() add multiple nodes to a graph
networkx.DiGraph.clear
DiGraph.clear()
Remove all nodes and edges from the graph.
This also removes the name, and all graph, node, and edge attributes.
2.2. Basic graph types 45
NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.clear()
>>> list(G.nodes)
[]
>>> list(G.edges)
[]
Reporting nodes edges and neighbors
DiGraph.nodes A NodeView of the Graph as G.nodes or G.nodes().
DiGraph.__iter__() Iterate over the nodes.
DiGraph.has_node(n) Return True if the graph contains the node n.
DiGraph.__contains__(n) Return True if n is a node, False otherwise.
DiGraph.edges An OutEdgeView of the DiGraph as G.edges or
G.edges().
DiGraph.out_edges An OutEdgeView of the DiGraph as G.edges or
G.edges().
DiGraph.in_edges An InEdgeView of the Graph as G.in_edges or
G.in_edges().
DiGraph.has_edge(u, v) Return True if the edge (u, v) is in the graph.
DiGraph.get_edge_data(u, v[, default]) Return the attribute dictionary associated with edge (u,
v).
DiGraph.neighbors(n) Return an iterator over successor nodes of n.
DiGraph.adj Graph adjacency object holding the neighbors of each
node.
DiGraph.__getitem__(n) Return a dict of neighbors of node n.
DiGraph.successors(n) Return an iterator over successor nodes of n.
DiGraph.succ Graph adjacency object holding the successors of each
node.
DiGraph.predecessors(n) Return an iterator over predecessor nodes of n.
DiGraph.pred Graph adjacency object holding the predecessors of
each node.
DiGraph.adjacency() Return an iterator over (node, adjacency dict) tuples for
all nodes.
DiGraph.nbunch_iter([nbunch]) Return an iterator over nodes contained in nbunch that
are also in the graph.
networkx.DiGraph.nodes
DiGraph.nodes
A NodeView of the Graph as G.nodes or G.nodes().
Can be used as G.nodes for data lookup and for set-like operations. Can also be used as G.
nodes(data='color', default=None) to return a NodeDataView which reports specific node data
but no set operations. It presents a dict-like interface as well with G.nodes.items() iterating over (node,
nodedata) 2-tuples and G.nodes[3]['foo'] providing the value of the foo attribute for node 3. In
addition, a view G.nodes.data('foo') provides a dict-like interface to the foo attribute of each node.
G.nodes.data('foo', default=1) provides a default for nodes that do not have attribute foo.
Parameters
46 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
•data (string or bool, optional (default=False)) – The node attribute returned in 2-tuple (n,
ddict[data]). If True, return entire node attribute dict as (n, ddict). If False, return just the
nodes n.
•default (value, optional (default=None)) – Value used for nodes that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns
Allows set-like operations over the nodes as well as node attribute dict lookup and calling to
get a NodeDataView. A NodeDataView iterates over (n, data) and has no set operations. A
NodeView iterates over nand includes set operations.
When called, if data is False, an iterator over nodes. Otherwise an iterator of 2-tuples (node,
attribute value) where the attribute is specified in data. If data is True then the attribute becomes
the entire data dictionary.
Return type NodeView
Notes
If your node data is not needed, it is simpler and equivalent to use the expression for n in G, or list(G).
Examples
There are two simple ways of getting a list of all nodes in the graph:
>>> G=nx.path_graph(3)
>>> list(G.nodes)
[0, 1, 2]
>>> list(G)
[0, 1, 2]
To get the node data along with the nodes:
>>> G.add_node(1, time='5pm')
>>> G.nodes[0]['foo']='bar'
>>> list(G.nodes(data=True))
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes.data())
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes(data='foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes.data('foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes(data='time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes.data('time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes(data='time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
>>> list(G.nodes.data('time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
2.2. Basic graph types 47

NetworkX Reference, Release 2.3rc1.dev20181203210840
If some of your nodes have an attribute and the rest are assumed to have a default attribute value you can create
a dictionary from node/attribute pairs using the default keyword argument to guarantee the value is never
None:
>>> G=nx.Graph()
>>> G.add_node(0)
>>> G.add_node(1, weight=2)
>>> G.add_node(2, weight=3)
>>> dict(G.nodes(data='weight', default=1))
{0: 1, 1: 2, 2: 3}
networkx.DiGraph.__iter__
DiGraph.__iter__()
Iterate over the nodes. Use: ‘for n in G’.
Returns niter – An iterator over all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for nin G]
[0, 1, 2, 3]
>>> list(G)
[0, 1, 2, 3]
networkx.DiGraph.has_node
DiGraph.has_node(n)
Return True if the graph contains the node n.
Identical to n in G
Parameters n (node)
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_node(0)
True
It is more readable and simpler to use
>>> 0in G
True
networkx.DiGraph.__contains__
DiGraph.__contains__(n)
Return True if n is a node, False otherwise. Use: ‘n in G’.
48 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> 1in G
True
networkx.DiGraph.edges
DiGraph.edges
An OutEdgeView of the DiGraph as G.edges or G.edges().
edges(self, nbunch=None, data=False, default=None)
The OutEdgeView provides set-like operations on the edge-tuples as well as edge attribute lookup. When called,
it also provides an EdgeDataView object which allows control of access to edge attributes (but does not pro-
vide set-like operations). Hence, G.edges[u, v]['color'] provides the value of the color attribute for
edge (u, v) while for (u, v, c) in G.edges.data('color', default='red'): iterates
through all the edges yielding the color attribute with default 'red' if no color attribute exists.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edges – A view of edge attributes, usually it iterates over (u, v) or (u, v, d) tuples of edges,
but can also be used for attribute lookup as edges[u, v]['foo'].
Return type OutEdgeView
See also:
in_edges,out_edges
Notes
Nodes in nbunch that are not in the graph will be (quietly) ignored. For directed graphs this returns the out-edges.
Examples
>>> G=nx.DiGraph() # or MultiDiGraph, etc
>>> nx.add_path(G, [0,1,2])
>>> G.add_edge(2,3, weight=5)
>>> [e for ein G.edges]
[(0, 1), (1, 2), (2, 3)]
>>> G.edges.data() # default data is {} (empty dict)
OutEdgeDataView([(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})])
>>> G.edges.data('weight', default=1)
OutEdgeDataView([(0, 1, 1), (1, 2, 1), (2, 3, 5)])
>>> G.edges([0,2]) # only edges incident to these nodes
(continues on next page)
2.2. Basic graph types 49

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
OutEdgeDataView([(0, 1), (2, 3)])
>>> G.edges(0)# only edges incident to a single node (use G.adj[0]?)
OutEdgeDataView([(0, 1)])
networkx.DiGraph.out_edges
DiGraph.out_edges
An OutEdgeView of the DiGraph as G.edges or G.edges().
edges(self, nbunch=None, data=False, default=None)
The OutEdgeView provides set-like operations on the edge-tuples as well as edge attribute lookup. When called,
it also provides an EdgeDataView object which allows control of access to edge attributes (but does not pro-
vide set-like operations). Hence, G.edges[u, v]['color'] provides the value of the color attribute for
edge (u, v) while for (u, v, c) in G.edges.data('color', default='red'): iterates
through all the edges yielding the color attribute with default 'red' if no color attribute exists.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edges – A view of edge attributes, usually it iterates over (u, v) or (u, v, d) tuples of edges,
but can also be used for attribute lookup as edges[u, v]['foo'].
Return type OutEdgeView
See also:
in_edges,out_edges
Notes
Nodes in nbunch that are not in the graph will be (quietly) ignored. For directed graphs this returns the out-edges.
Examples
>>> G=nx.DiGraph() # or MultiDiGraph, etc
>>> nx.add_path(G, [0,1,2])
>>> G.add_edge(2,3, weight=5)
>>> [e for ein G.edges]
[(0, 1), (1, 2), (2, 3)]
>>> G.edges.data() # default data is {} (empty dict)
OutEdgeDataView([(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})])
>>> G.edges.data('weight', default=1)
OutEdgeDataView([(0, 1, 1), (1, 2, 1), (2, 3, 5)])
>>> G.edges([0,2]) # only edges incident to these nodes
OutEdgeDataView([(0, 1), (2, 3)])
(continues on next page)
50 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.edges(0)# only edges incident to a single node (use G.adj[0]?)
OutEdgeDataView([(0, 1)])
networkx.DiGraph.in_edges
DiGraph.in_edges
An InEdgeView of the Graph as G.in_edges or G.in_edges().
in_edges(self, nbunch=None, data=False, default=None):
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns in_edges – A view of edge attributes, usually it iterates over (u, v) or (u, v, d) tuples of
edges, but can also be used for attribute lookup as edges[u, v]['foo'].
Return type InEdgeView
See also:
edges
networkx.DiGraph.has_edge
DiGraph.has_edge(u,v)
Return True if the edge (u, v) is in the graph.
This is the same as v in G[u] without KeyError exceptions.
Parameters u, v (nodes) – Nodes can be, for example, strings or numbers. Nodes must be hashable
(and not None) Python objects.
Returns edge_ind – True if edge is in the graph, False otherwise.
Return type bool
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_edge(0,1)# using two nodes
True
>>> e=(0,1)
>>> G.has_edge(*e) # e is a 2-tuple (u, v)
True
>>> e=(0,1, {'weight':7})
>>> G.has_edge(*e[:2]) # e is a 3-tuple (u, v, data_dictionary)
True
2.2. Basic graph types 51
NetworkX Reference, Release 2.3rc1.dev20181203210840
The following syntax are equivalent:
>>> G.has_edge(0,1)
True
>>> 1in G[0]# though this gives KeyError if 0 not in G
True
networkx.DiGraph.get_edge_data
DiGraph.get_edge_data(u,v,default=None)
Return the attribute dictionary associated with edge (u, v).
This is identical to G[u][v] except the default is returned instead of an exception is the edge doesn’t exist.
Parameters
•u, v (nodes)
•default (any Python object (default=None)) – Value to return if the edge (u, v) is not found.
Returns edge_dict – The edge attribute dictionary.
Return type dictionary
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0][1]
{}
Warning: Assigning to G[u][v] is not permitted. But it is safe to assign attributes G[u][v]['foo']
>>> G[0][1]['weight']=7
>>> G[0][1]['weight']
7
>>> G[1][0]['weight']
7
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.get_edge_data(0,1)# default edge data is {}
{}
>>> e=(0,1)
>>> G.get_edge_data(*e) # tuple form
{}
>>> G.get_edge_data('a','b', default=0)# edge not in graph, return 0
0
networkx.DiGraph.neighbors
DiGraph.neighbors(n)
Return an iterator over successor nodes of n.
A successor of n is a node m such that there exists a directed edge from n to m.
Parameters n (node) – A node in the graph
52 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises NetworkXError – If n is not in the graph.
See also:
predecessors()
Notes
neighbors() and successors() are the same.
networkx.DiGraph.adj
DiGraph.adj
Graph adjacency object holding the neighbors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is keyed
by neighbor to the edge-data-dict. So G.adj[3][2]['color'] = 'blue' sets the color of the edge (3,
2) to "blue".
Iterating over G.adj behaves like a dict. Useful idioms include for nbr, datadict in G.adj[n].
items():.
The neighbor information is also provided by subscripting the graph. So for nbr, foovalue in
G[node].data('foo', default=1): works.
For directed graphs, G.adj holds outgoing (successor) info.
networkx.DiGraph.__getitem__
DiGraph.__getitem__(n)
Return a dict of neighbors of node n. Use: ‘G[n]’.
Parameters n (node) – A node in the graph.
Returns adj_dict – The adjacency dictionary for nodes connected to n.
Return type dictionary
Notes
G[n] is the same as G.adj[n] and similar to G.neighbors(n) (which is an iterator over G.adj[n])
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0]
AtlasView({1: {}})
networkx.DiGraph.successors
DiGraph.successors(n)
Return an iterator over successor nodes of n.
A successor of n is a node m such that there exists a directed edge from n to m.
2.2. Basic graph types 53

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
predecessors()
Notes
neighbors() and successors() are the same.
networkx.DiGraph.succ
DiGraph.succ
Graph adjacency object holding the successors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is
keyed by neighbor to the edge-data-dict. So G.succ[3][2]['color'] = 'blue' sets the color of the
edge (3, 2) to "blue".
Iterating over G.succ behaves like a dict. Useful idioms include for nbr, datadict in G.succ[n].
items():. A data-view not provided by dicts also exists: for nbr, foovalue in G.succ[node].
data('foo'): and a default can be set via a default argument to the data method.
The neighbor information is also provided by subscripting the graph. So for nbr, foovalue in
G[node].data('foo', default=1): works.
For directed graphs, G.adj is identical to G.succ.
networkx.DiGraph.predecessors
DiGraph.predecessors(n)
Return an iterator over predecessor nodes of n.
A predecessor of n is a node m such that there exists a directed edge from m to n.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
successors()
networkx.DiGraph.pred
DiGraph.pred
Graph adjacency object holding the predecessors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is
keyed by neighbor to the edge-data-dict. So G.pred[2][3]['color'] = 'blue' sets the color of the
edge (3, 2) to "blue".
Iterating over G.pred behaves like a dict. Useful idioms include for nbr, datadict in G.pred[n].
items():. A data-view not provided by dicts also exists: for nbr, foovalue in G.pred[node].
data('foo'): A default can be set via a default argument to the data method.
54 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.DiGraph.adjacency
DiGraph.adjacency()
Return an iterator over (node, adjacency dict) tuples for all nodes.
For directed graphs, only outgoing neighbors/adjacencies are included.
Returns adj_iter – An iterator over (node, adjacency dictionary) for all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [(n, nbrdict) for n, nbrdict in G.adjacency()]
[(0, {1: {}}), (1, {0: {}, 2: {}}), (2, {1: {}, 3: {}}), (3, {2: {}})]
networkx.DiGraph.nbunch_iter
DiGraph.nbunch_iter(nbunch=None)
Return an iterator over nodes contained in nbunch that are also in the graph.
The nodes in nbunch are checked for membership in the graph and if not are silently ignored.
Parameters nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
Returns niter – An iterator over nodes in nbunch that are also in the graph. If nbunch is None,
iterate over all nodes in the graph.
Return type iterator
Raises NetworkXError – If nbunch is not a node or or sequence of nodes. If a node in nbunch is
not hashable.
See also:
Graph.__iter__()
Notes
When nbunch is an iterator, the returned iterator yields values directly from nbunch, becoming exhausted when
nbunch is exhausted.
To test whether nbunch is a single node, one can use “if nbunch in self:”, even after processing with this routine.
If nbunch is not a node or a (possibly empty) sequence/iterator or None, a NetworkXError is raised. Also, if
any object in nbunch is not hashable, a NetworkXError is raised.
Counting nodes edges and neighbors
DiGraph.order() Return the number of nodes in the graph.
DiGraph.number_of_nodes() Return the number of nodes in the graph.
DiGraph.__len__() Return the number of nodes.
Continued on next page
2.2. Basic graph types 55

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 7 – continued from previous page
DiGraph.degree A DegreeView for the Graph as G.degree or G.degree().
DiGraph.in_degree An InDegreeView for (node, in_degree) or in_degree
for single node.
DiGraph.out_degree An OutDegreeView for (node, out_degree)
DiGraph.size([weight]) Return the number of edges or total of all edge weights.
DiGraph.number_of_edges([u, v]) Return the number of edges between two nodes.
networkx.DiGraph.order
DiGraph.order()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
number_of_nodes(),__len__()
networkx.DiGraph.number_of_nodes
DiGraph.number_of_nodes()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
order(),__len__()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
3
networkx.DiGraph.__len__
DiGraph.__len__()
Return the number of nodes. Use: ‘len(G)’.
Returns nnodes – The number of nodes in the graph.
Return type int
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
4
56 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.DiGraph.degree
DiGraph.degree
A DegreeView for the Graph as G.degree or G.degree().
The node degree is the number of edges adjacent to the node. The weighted node degree is the sum of the edge
weights for edges incident to that node.
This object provides an iterator for (node, degree) as well as lookup for the degree for a single node.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The name of an edge attribute that holds
the numerical value used as a weight. If None, then each edge has weight 1. The degree is
the sum of the edge weights adjacent to the node.
Returns
•If a single node is requested
•deg (int) – Degree of the node
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, degree).
See also:
in_degree,out_degree
Examples
>>> G=nx.DiGraph() # or MultiDiGraph
>>> nx.add_path(G, [0,1,2,3])
>>> G.degree(0)# node 0 with degree 1
1
>>> list(G.degree([0,1,2]))
[(0, 1), (1, 2), (2, 2)]
networkx.DiGraph.in_degree
DiGraph.in_degree
An InDegreeView for (node, in_degree) or in_degree for single node.
The node in_degree is the number of edges pointing to the node. The weighted node degree is the sum of the
edge weights for edges incident to that node.
This object provides an iteration over (node, in_degree) as well as lookup for the degree for a single node.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The name of an edge attribute that holds
the numerical value used as a weight. If None, then each edge has weight 1. The degree is
the sum of the edge weights adjacent to the node.
2.2. Basic graph types 57

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns
•If a single node is requested
•deg (int) – In-degree of the node
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, in-degree).
See also:
degree,out_degree
Examples
>>> G=nx.DiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.in_degree(0)# node 0 with degree 0
0
>>> list(G.in_degree([0,1,2]))
[(0, 0), (1, 1), (2, 1)]
networkx.DiGraph.out_degree
DiGraph.out_degree
An OutDegreeView for (node, out_degree)
The node out_degree is the number of edges pointing out of the node. The weighted node degree is the sum of
the edge weights for edges incident to that node.
This object provides an iterator over (node, out_degree) as well as lookup for the degree for a single node.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The name of an edge attribute that holds
the numerical value used as a weight. If None, then each edge has weight 1. The degree is
the sum of the edge weights adjacent to the node.
Returns
•If a single node is requested
•deg (int) – Out-degree of the node
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, out-degree).
See also:
degree,in_degree
Examples
58 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.DiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.out_degree(0)# node 0 with degree 1
1
>>> list(G.out_degree([0,1,2]))
[(0, 1), (1, 1), (2, 1)]
networkx.DiGraph.size
DiGraph.size(weight=None)
Return the number of edges or total of all edge weights.
Parameters weight (string or None, optional (default=None)) – The edge attribute that holds the
numerical value used as a weight. If None, then each edge has weight 1.
Returns
size – The number of edges or (if weight keyword is provided) the total weight sum.
If weight is None, returns an int. Otherwise a float (or more general numeric if the weights are
more general).
Return type numeric
See also:
number_of_edges()
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.size()
3
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge('a','b', weight=2)
>>> G.add_edge('b','c', weight=4)
>>> G.size()
2
>>> G.size(weight='weight')
6.0
networkx.DiGraph.number_of_edges
DiGraph.number_of_edges(u=None,v=None)
Return the number of edges between two nodes.
Parameters u, v (nodes, optional (default=all edges)) – If u and v are specified, return the number
of edges between u and v. Otherwise return the total number of all edges.
Returns nedges – The number of edges in the graph. If nodes uand vare specified return the
number of edges between those nodes. If the graph is directed, this only returns the number of
edges from uto v.
Return type int
2.2. Basic graph types 59

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
size()
Examples
For undirected graphs, this method counts the total number of edges in the graph:
>>> G=nx.path_graph(4)
>>> G.number_of_edges()
3
If you specify two nodes, this counts the total number of edges joining the two nodes:
>>> G.number_of_edges(0,1)
1
For directed graphs, this method can count the total number of directed edges from uto v:
>>> G=nx.DiGraph()
>>> G.add_edge(0,1)
>>> G.add_edge(1,0)
>>> G.number_of_edges(0,1)
1
Making copies and subgraphs
DiGraph.copy([as_view]) Return a copy of the graph.
DiGraph.to_undirected([reciprocal, as_view]) Return an undirected representation of the digraph.
DiGraph.to_directed([as_view]) Return a directed representation of the graph.
DiGraph.subgraph(nodes) Return a SubGraph view of the subgraph induced on
nodes.
DiGraph.edge_subgraph(edges) Returns the subgraph induced by the specified edges.
DiGraph.reverse([copy]) Return the reverse of the graph.
networkx.DiGraph.copy
DiGraph.copy(as_view=False)
Return a copy of the graph.
The copy method by default returns an independent shallow copy of the graph and attributes. That is, if an
attribute is a container, that container is shared by the original an the copy. Use Python’s copy.deepcopy for
new containers.
If as_view is True then a view is returned instead of a copy.
Notes
All copies reproduce the graph structure, but data attributes may be handled in different ways. There are four
types of copies of a graph that people might want.
Deepcopy – A “deepcopy” copies the graph structure as well as all data attributes and any objects they might
contain. The entire graph object is new so that changes in the copy do not affect the original object. (see Python’s
60 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
copy.deepcopy)
Data Reference (Shallow) – For a shallow copy the graph structure is copied but the edge, node and graph at-
tribute dicts are references to those in the original graph. This saves time and memory but could cause confusion
if you change an attribute in one graph and it changes the attribute in the other. NetworkX does not provide this
level of shallow copy.
Independent Shallow – This copy creates new independent attribute dicts and then does a shallow copy of the
attributes. That is, any attributes that are containers are shared between the new graph and the original. This is
exactly what dict.copy() provides. You can obtain this style copy using:
>>> G=nx.path_graph(5)
>>> H=G.copy()
>>> H=G.copy(as_view=False)
>>> H=nx.Graph(G)
>>> H=G.__class__(G)
Fresh Data – For fresh data, the graph structure is copied while new empty data attribute dicts are created. The
resulting graph is independent of the original and it has no edge, node or graph attributes. Fresh copies are not
enabled. Instead use:
>>> H=G.__class__()
>>> H.add_nodes_from(G)
>>> H.add_edges_from(G.edges)
View – Inspired by dict-views, graph-views act like read-only versions of the original graph, providing a copy
of the original structure without requiring any memory for copying the information.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Parameters as_view (bool, optional (default=False)) – If True, the returned graph-view provides a
read-only view of the original graph without actually copying any data.
Returns G – A copy of the graph.
Return type Graph
See also:
to_directed() return a directed copy of the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.copy()
networkx.DiGraph.to_undirected
DiGraph.to_undirected(reciprocal=False,as_view=False)
Return an undirected representation of the digraph.
Parameters
•reciprocal (bool (optional)) – If True only keep edges that appear in both directions in the
original digraph.
2.2. Basic graph types 61

NetworkX Reference, Release 2.3rc1.dev20181203210840
•as_view (bool (optional, default=False)) – If True return an undirected view of the original
directed graph.
Returns G – An undirected graph with the same name and nodes and with edge (u, v, data) if either
(u, v, data) or (v, u, data) is in the digraph. If both edges exist in digraph and their edge data is
different, only one edge is created with an arbitrary choice of which edge data to use. You must
check and correct for this manually if desired.
Return type Graph
See also:
Graph(),copy(),add_edge(),add_edges_from()
Notes
If edges in both directions (u, v) and (v, u) exist in the graph, attributes for the new undirected edge will be a
combination of the attributes of the directed edges. The edge data is updated in the (arbitrary) order that the
edges are encountered. For more customized control of the edge attributes use add_edge().
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar G=DiGraph(D) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed DiGraph to use dict-like objects in the data structure, those changes do not
transfer to the Graph created by this method.
Examples
>>> G=nx.path_graph(2)# or MultiGraph, etc
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
>>> G2 =H.to_undirected()
>>> list(G2.edges)
[(0, 1)]
networkx.DiGraph.to_directed
DiGraph.to_directed(as_view=False)
Return a directed representation of the graph.
Returns G – A directed graph with the same name, same nodes, and with each edge (u, v, data)
replaced by two directed edges (u, v, data) and (v, u, data).
Return type DiGraph
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
62 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
This is in contrast to the similar D=DiGraph(G) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed Graph to use dict-like objects in the data structure, those changes do not
transfer to the DiGraph created by this method.
Examples
>>> G=nx.Graph() # or MultiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
If already directed, return a (deep) copy
>>> G=nx.DiGraph() # or MultiDiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1)]
networkx.DiGraph.subgraph
DiGraph.subgraph(nodes)
Return a SubGraph view of the subgraph induced on nodes.
The induced subgraph of the graph contains the nodes in nodes and the edges between those nodes.
Parameters nodes (list, iterable) – A container of nodes which will be iterated through once.
Returns G – A subgraph view of the graph. The graph structure cannot be changed but node/edge
attributes can and are shared with the original graph.
Return type SubGraph View
Notes
The graph, edge and node attributes are shared with the original graph. Changes to the graph structure is ruled
out by the view, but changes to attributes are reflected in the original graph.
To create a subgraph with its own copy of the edge/node attributes use: G.subgraph(nodes).copy()
For an inplace reduction of a graph to a subgraph you can remove nodes: G.remove_nodes_from([n for n in G
if n not in set(nodes)])
Subgraph views are sometimes NOT what you want. In most cases where you want to do more than simply look
at the induced edges, it makes more sense to just create the subgraph as its own graph with code like:
# Create a subgraph SG based on a (possibly multigraph) G
SG =G.__class__()
SG.add_nodes_from((n, G.nodes[n]) for nin largest_wcc)
if SG.is_multigraph:
SG.add_edges_from((n, nbr, key, d)
(continues on next page)
2.2. Basic graph types 63

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, keydict in nbrs.items() if nbr in largest_wcc
for key, d in keydict.items())
else:
SG.add_edges_from((n, nbr, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, d in nbrs.items() if nbr in largest_wcc)
SG.graph.update(G.graph)
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.subgraph([0,1,2])
>>> list(H.edges)
[(0, 1), (1, 2)]
networkx.DiGraph.edge_subgraph
DiGraph.edge_subgraph(edges)
Returns the subgraph induced by the specified edges.
The induced subgraph contains each edge in edges and each node incident to any one of those edges.
Parameters edges (iterable) – An iterable of edges in this graph.
Returns G – An edge-induced subgraph of this graph with the same edge attributes.
Return type Graph
Notes
The graph, edge, and node attributes in the returned subgraph view are references to the corresponding attributes
in the original graph. The view is read-only.
To create a full graph version of the subgraph with its own copy of the edge or node attributes, use:
>>> G.edge_subgraph(edges).copy()
Examples
>>> G=nx.path_graph(5)
>>> H=G.edge_subgraph([(0,1), (3,4)])
>>> list(H.nodes)
[0, 1, 3, 4]
>>> list(H.edges)
[(0, 1), (3, 4)]
networkx.DiGraph.reverse
DiGraph.reverse(copy=True)
Return the reverse of the graph.
64 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
The reverse is a graph with the same nodes and edges but with the directions of the edges reversed.
Parameters copy (bool optional (default=True)) – If True, return a new DiGraph holding the re-
versed edges. If False, the reverse graph is created using a view of the original graph.
2.2.3 MultiGraph—Undirected graphs with self loops and parallel edges
Overview
class MultiGraph(incoming_graph_data=None,**attr)
An undirected graph class that can store multiedges.
Multiedges are multiple edges between two nodes. Each edge can hold optional data or attributes.
A MultiGraph holds undirected edges. Self loops are allowed.
Nodes can be arbitrary (hashable) Python objects with optional key/value attributes. By convention None is not
used as a node.
Edges are represented as links between nodes with optional key/value attributes.
Parameters
•incoming_graph_data (input graph (optional, default: None)) – Data to initialize graph. If
None (default) an empty graph is created. The data can be any format that is supported by
the to_networkx_graph() function, currently including edge list, dict of dicts, dict of lists,
NetworkX graph, NumPy matrix or 2d ndarray, SciPy sparse matrix, or PyGraphviz graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
Graph,DiGraph,MultiDiGraph,OrderedMultiGraph
Examples
Create an empty graph structure (a “null graph”) with no nodes and no edges.
>>> G=nx.MultiGraph()
G can be grown in several ways.
Nodes:
Add one node at a time:
>>> G.add_node(1)
Add the nodes from any container (a list, dict, set or even the lines from a file or the nodes from another graph).
>>> G.add_nodes_from([2,3])
>>> G.add_nodes_from(range(100,110))
>>> H=nx.path_graph(10)
>>> G.add_nodes_from(H)
In addition to strings and integers any hashable Python object (except None) can represent a node, e.g. a
customized node object, or even another Graph.
2.2. Basic graph types 65

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G.add_node(H)
Edges:
G can also be grown by adding edges.
Add one edge,
>>> key =G.add_edge(1,2)
a list of edges,
>>> keys =G.add_edges_from([(1,2), (1,3)])
or a collection of edges,
>>> keys =G.add_edges_from(H.edges)
If some edges connect nodes not yet in the graph, the nodes are added automatically. If an edge already exists,
an additional edge is created and stored using a key to identify the edge. By default the key is the lowest unused
integer.
>>> keys =G.add_edges_from([(4,5,{'route':28}), (4,5,{'route':37})])
>>> G[4]
AdjacencyView({3: {0: {}}, 5: {0: {}, 1: {'route': 28}, 2: {'route': 37}}})
Attributes:
Each graph, node, and edge can hold key/value attribute pairs in an associated attribute dictionary (the keys
must be hashable). By default these are empty, but can be added or changed using add_edge, add_node or direct
manipulation of the attribute dictionaries named graph, node and edge respectively.
>>> G=nx.MultiGraph(day="Friday")
>>> G.graph
{'day': 'Friday'}
Add node attributes using add_node(), add_nodes_from() or G.nodes
>>> G.add_node(1, time='5pm')
>>> G.add_nodes_from([3], time='2pm')
>>> G.nodes[1]
{'time': '5pm'}
>>> G.nodes[1]['room']=714
>>> del G.nodes[1]['room']# remove attribute
>>> list(G.nodes(data=True))
[(1, {'time': '5pm'}), (3, {'time': '2pm'})]
Add edge attributes using add_edge(), add_edges_from(), subscript notation, or G.edges.
>>> key =G.add_edge(1,2, weight=4.7 )
>>> keys =G.add_edges_from([(3,4), (4,5)], color='red')
>>> keys =G.add_edges_from([(1,2,{'color':'blue'}), (2,3,{'weight':8})])
>>> G[1][2][0]['weight']=4.7
>>> G.edges[1,2,0]['weight']=4
Warning: we protect the graph data structure by making G.edges[1, 2] a read-only dict-like structure.
However, you can assign to attributes in e.g. G.edges[1, 2]. Thus, use 2 sets of brackets to add/change data
66 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
attributes: G.edges[1, 2]['weight'] = 4 (For multigraphs: MG.edges[u, v, key][name] =
value).
Shortcuts:
Many common graph features allow python syntax to speed reporting.
>>> 1in G# check if node in graph
True
>>> [n for nin Gif n<3]# iterate through nodes
[1, 2]
>>> len(G) # number of nodes in graph
5
>>> G[1]# adjacency dict-like view keyed by neighbor to edge attributes
AdjacencyView({2: {0: {'weight': 4}, 1: {'color': 'blue'}}})
Often the best way to traverse all edges of a graph is via the neighbors. The neighbors are reported as an
adjacency-dict G.adj or G.adjacency().
>>> for n, nbrsdict in G.adjacency():
... for nbr, keydict in nbrsdict.items():
... for key, eattr in keydict.items():
... if 'weight' in eattr:
... # Do something useful with the edges
... pass
But the edges() method is often more convenient:
>>> for u, v, keys, weight in G.edges(data='weight', keys=True):
... if weight is not None:
... # Do something useful with the edges
... pass
Reporting:
Simple graph information is obtained using methods and object-attributes. Reporting usually provides
views instead of containers to reduce memory usage. The views update as the graph is updated simi-
larly to dict-views. The objects nodes, `edges and adj provide access to data attributes via lookup
(e.g. nodes[n], `edges[u, v],adj[u][v]) and iteration (e.g. nodes.items(),nodes.
data('color'),nodes.data('color', default='blue') and similarly for edges) Views exist
for nodes,edges,neighbors()/adj and degree.
For details on these and other miscellaneous methods, see below.
Subclasses (Advanced):
The MultiGraph class uses a dict-of-dict-of-dict-of-dict data structure. The outer dict (node_dict) holds adja-
cency information keyed by node. The next dict (adjlist_dict) represents the adjacency information and holds
edge_key dicts keyed by neighbor. The edge_key dict holds each edge_attr dict keyed by edge key. The inner
dict (edge_attr_dict) represents the edge data and holds edge attribute values keyed by attribute names.
Each of these four dicts in the dict-of-dict-of-dict-of-dict structure can be replaced by a user defined dict-like
object. In general, the dict-like features should be maintained but extra features can be added. To replace
one of the dicts create a new graph class by changing the class(!) variable holding the factory for that dict-
like structure. The variable names are node_dict_factory, node_attr_dict_factory, adjlist_inner_dict_factory,
adjlist_outer_dict_factory, edge_key_dict_factory, edge_attr_dict_factory and graph_attr_dict_factory.
node_dict_factory [function, (default: dict)] Factory function to be used to create the dict containing node
attributes, keyed by node id. It should require no arguments and return a dict-like object
2.2. Basic graph types 67

NetworkX Reference, Release 2.3rc1.dev20181203210840
node_attr_dict_factory: function, (default: dict) Factory function to be used to create the node attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object
adjlist_outer_dict_factory [function, (default: dict)] Factory function to be used to create the outer-most dict
in the data structure that holds adjacency info keyed by node. It should require no arguments and return a
dict-like object.
adjlist_inner_dict_factory [function, (default: dict)] Factory function to be used to create the adjacency list
dict which holds multiedge key dicts keyed by neighbor. It should require no arguments and return a
dict-like object.
edge_key_dict_factory [function, (default: dict)] Factory function to be used to create the edge key dict which
holds edge data keyed by edge key. It should require no arguments and return a dict-like object.
edge_attr_dict_factory [function, (default: dict)] Factory function to be used to create the edge attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object.
graph_attr_dict_factory [function, (default: dict)] Factory function to be used to create the graph attribute
dict which holds attribute values keyed by attribute name. It should require no arguments and return a
dict-like object.
Typically, if your extension doesn’t impact the data structure all methods will inherited without issue except:
to_directed/to_undirected. By default these methods create a DiGraph/Graph class and you probably
want them to create your extension of a DiGraph/Graph. To facilitate this we define two class variables that you
can set in your subclass.
to_directed_class [callable, (default: DiGraph or MultiDiGraph)] Class to create a new graph structure in the
to_directed method. If None, a NetworkX class (DiGraph or MultiDiGraph) is used.
to_undirected_class [callable, (default: Graph or MultiGraph)] Class to create a new graph structure in the
to_undirected method. If None, a NetworkX class (Graph or MultiGraph) is used.
Examples
Please see ordered for examples of creating graph subclasses by overwriting the base class dict with a
dictionary-like object.
Methods
Adding and removing nodes and edges
MultiGraph.__init__([incoming_graph_data]) Initialize a graph with edges, name, or graph attributes.
MultiGraph.add_node(node_for_adding, **attr) Add a single node node_for_adding and update
node attributes.
MultiGraph.add_nodes_from(nodes_for_adding,
...)
Add multiple nodes.
MultiGraph.remove_node(n) Remove node n.
MultiGraph.remove_nodes_from(nodes) Remove multiple nodes.
MultiGraph.add_edge(u_for_edge, v_for_edge) Add an edge between u and v.
MultiGraph.add_edges_from(ebunch_to_add,
**attr)
Add all the edges in ebunch_to_add.
Continued on next page
68 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 9 – continued from previous page
MultiGraph.add_weighted_edges_from(ebunch_to_add)Add weighted edges in ebunch_to_add with speci-
fied weight attr
MultiGraph.new_edge_key(u, v) Return an unused key for edges between nodes uand v.
MultiGraph.remove_edge(u, v[, key]) Remove an edge between u and v.
MultiGraph.remove_edges_from(ebunch) Remove all edges specified in ebunch.
MultiGraph.update([edges, nodes]) Update the graph using nodes/edges/graphs as input.
MultiGraph.clear() Remove all nodes and edges from the graph.
networkx.MultiGraph.__init__
MultiGraph.__init__(incoming_graph_data=None,**attr)
Initialize a graph with edges, name, or graph attributes.
Parameters
•incoming_graph_data (input graph) – Data to initialize graph. If incom-
ing_graph_data=None (default) an empty graph is created. The data can be an edge list,
or any NetworkX graph object. If the corresponding optional Python packages are installed
the data can also be a NumPy matrix or 2d ndarray, a SciPy sparse matrix, or a PyGraphviz
graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
convert()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G=nx.Graph(name='my graph')
>>> e=[(1,2), (2,3), (3,4)] # list of edges
>>> G=nx.Graph(e)
Arbitrary graph attribute pairs (key=value) may be assigned
>>> G=nx.Graph(e, day="Friday")
>>> G.graph
{'day': 'Friday'}
networkx.MultiGraph.add_node
MultiGraph.add_node(node_for_adding,**attr)
Add a single node node_for_adding and update node attributes.
Parameters
•node_for_adding (node) – A node can be any hashable Python object except None.
•attr (keyword arguments, optional) – Set or change node attributes using key=value.
See also:
add_nodes_from()
2.2. Basic graph types 69

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_node(1)
>>> G.add_node('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_node(K3)
>>> G.number_of_nodes()
3
Use keywords set/change node attributes:
>>> G.add_node(1, size=10)
>>> G.add_node(3, weight=0.4, UTM=('13S',382871,3972649))
Notes
A hashable object is one that can be used as a key in a Python dictionary. This includes strings, numbers, tuples
of strings and numbers, etc.
On many platforms hashable items also include mutables such as NetworkX Graphs, though one should be
careful that the hash doesn’t change on mutables.
networkx.MultiGraph.add_nodes_from
MultiGraph.add_nodes_from(nodes_for_adding,**attr)
Add multiple nodes.
Parameters
•nodes_for_adding (iterable container) – A container of nodes (list, dict, set, etc.). OR A
container of (node, attribute dict) tuples. Node attributes are updated using the attribute dict.
•attr (keyword arguments, optional (default= no attributes)) – Update attributes for all nodes
in nodes. Node attributes specified in nodes as a tuple take precedence over attributes spec-
ified via keyword arguments.
See also:
add_node()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_nodes_from('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_nodes_from(K3)
>>> sorted(G.nodes(), key=str)
[0, 1, 2, 'H', 'e', 'l', 'o']
Use keywords to update specific node attributes for every node.
>>> G.add_nodes_from([1,2], size=10)
>>> G.add_nodes_from([3,4], weight=0.4)
70 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Use (node, attrdict) tuples to update attributes for specific nodes.
>>> G.add_nodes_from([(1,dict(size=11)), (2, {'color':'blue'})])
>>> G.nodes[1]['size']
11
>>> H=nx.Graph()
>>> H.add_nodes_from(G.nodes(data=True))
>>> H.nodes[1]['size']
11
networkx.MultiGraph.remove_node
MultiGraph.remove_node(n)
Remove node n.
Removes the node n and all adjacent edges. Attempting to remove a non-existent node will raise an exception.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
remove_nodes_from()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> list(G.edges)
[(0, 1), (1, 2)]
>>> G.remove_node(1)
>>> list(G.edges)
[]
networkx.MultiGraph.remove_nodes_from
MultiGraph.remove_nodes_from(nodes)
Remove multiple nodes.
Parameters nodes (iterable container) – A container of nodes (list, dict, set, etc.). If a node in the
container is not in the graph it is silently ignored.
See also:
remove_node()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e=list(G.nodes)
>>> e
[0, 1, 2]
>>> G.remove_nodes_from(e)
>>> list(G.nodes)
[]
2.2. Basic graph types 71

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiGraph.add_edge
MultiGraph.add_edge(u_for_edge,v_for_edge,key=None,**attr)
Add an edge between u and v.
The nodes u and v will be automatically added if they are not already in the graph.
Edge attributes can be specified with keywords or by directly accessing the edge’s attribute dictionary. See
examples below.
Parameters
•u_for_edge, v_for_edge (nodes) – Nodes can be, for example, strings or numbers. Nodes
must be hashable (and not None) Python objects.
•key (hashable identifier, optional (default=lowest unused integer)) – Used to distinguish
multiedges between a pair of nodes.
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
Returns
Return type The edge key assigned to the edge.
See also:
add_edges_from() add a collection of edges
Notes
To replace/update edge data, use the optional key argument to identify a unique edge. Otherwise a new edge
will be created.
NetworkX algorithms designed for weighted graphs cannot use multigraphs directly because it is not clear
how to handle multiedge weights. Convert to Graph using edge attribute ‘weight’ to enable weighted graph
algorithms.
Default keys are generated using the method new_edge_key(). This method can be overridden by subclass-
ing the base class and providing a custom new_edge_key() method.
Examples
The following all add the edge e=(1, 2) to graph G:
>>> G=nx.MultiGraph()
>>> e=(1,2)
>>> ekey =G.add_edge(1,2)# explicit two-node form
>>> G.add_edge(*e) # single edge as tuple of two nodes
1
>>> G.add_edges_from( [(1,2)] ) # add edges from iterable container
[2]
Associate data to edges using keywords:
>>> ekey =G.add_edge(1,2, weight=3)
>>> ekey =G.add_edge(1,2, key=0, weight=4)# update data for key=0
>>> ekey =G.add_edge(1,3, weight=7, capacity=15, length=342.7)
72 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
For non-string attribute keys, use subscript notation.
>>> ekey =G.add_edge(1,2)
>>> G[1][2][0].update({0:5})
>>> G.edges[1,2,0].update({0:5})
networkx.MultiGraph.add_edges_from
MultiGraph.add_edges_from(ebunch_to_add,**attr)
Add all the edges in ebunch_to_add.
Parameters
•ebunch_to_add (container of edges) – Each edge given in the container will be added to
the graph. The edges can be:
–2-tuples (u, v) or
–3-tuples (u, v, d) for an edge data dict d, or
–3-tuples (u, v, k) for not iterable key k, or
–4-tuples (u, v, k, d) for an edge with data and key k
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
Returns
Return type A list of edge keys assigned to the edges in ebunch.
See also:
add_edge() add a single edge
add_weighted_edges_from() convenient way to add weighted edges
Notes
Adding the same edge twice has no effect but any edge data will be updated when each duplicate edge is added.
Edge attributes specified in an ebunch take precedence over attributes specified via keyword arguments.
Default keys are generated using the method new_edge_key(). This method can be overridden by subclass-
ing the base class and providing a custom new_edge_key() method.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edges_from([(0,1), (1,2)]) # using a list of edge tuples
>>> e=zip(range(0,3), range(1,4))
>>> G.add_edges_from(e) # Add the path graph 0-1-2-3
Associate data to edges
>>> G.add_edges_from([(1,2), (2,3)], weight=3)
>>> G.add_edges_from([(3,4), (1,4)], label='WN2898')
2.2. Basic graph types 73

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiGraph.add_weighted_edges_from
MultiGraph.add_weighted_edges_from(ebunch_to_add,weight=’weight’,**attr)
Add weighted edges in ebunch_to_add with specified weight attr
Parameters
•ebunch_to_add (container of edges) – Each edge given in the list or container will be added
to the graph. The edges must be given as 3-tuples (u, v, w) where w is a number.
•weight (string, optional (default= ‘weight’)) – The attribute name for the edge weights to
be added.
•attr (keyword arguments, optional (default= no attributes)) – Edge attributes to add/update
for all edges.
See also:
add_edge() add a single edge
add_edges_from() add multiple edges
Notes
Adding the same edge twice for Graph/DiGraph simply updates the edge data. For MultiGraph/MultiDiGraph,
duplicate edges are stored.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_weighted_edges_from([(0,1,3.0), (1,2,7.5)])
networkx.MultiGraph.new_edge_key
MultiGraph.new_edge_key(u,v)
Return an unused key for edges between nodes uand v.
The nodes uand vdo not need to be already in the graph.
Notes
In the standard MultiGraph class the new key is the number of existing edges between uand v(increased
if necessary to ensure unused). The first edge will have key 0, then 1, etc. If an edge is removed further
new_edge_keys may not be in this order.
Parameters u, v (nodes)
Returns key
Return type int
74 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiGraph.remove_edge
MultiGraph.remove_edge(u,v,key=None)
Remove an edge between u and v.
Parameters
•u, v (nodes) – Remove an edge between nodes u and v.
•key (hashable identifier, optional (default=None)) – Used to distinguish multiple edges be-
tween a pair of nodes. If None remove a single (arbitrary) edge between u and v.
Raises NetworkXError – If there is not an edge between u and v, or if there is no edge with the
specified key.
See also:
remove_edges_from() remove a collection of edges
Examples
>>> G=nx.MultiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.remove_edge(0,1)
>>> e=(1,2)
>>> G.remove_edge(*e) # unpacks e from an edge tuple
For multiple edges
>>> G=nx.MultiGraph() # or MultiDiGraph, etc
>>> G.add_edges_from([(1,2), (1,2), (1,2)]) # key_list returned
[0, 1, 2]
>>> G.remove_edge(1,2)# remove a single (arbitrary) edge
For edges with keys
>>> G=nx.MultiGraph() # or MultiDiGraph, etc
>>> G.add_edge(1,2, key='first')
'first'
>>> G.add_edge(1,2, key='second')
'second'
>>> G.remove_edge(1,2, key='second')
networkx.MultiGraph.remove_edges_from
MultiGraph.remove_edges_from(ebunch)
Remove all edges specified in ebunch.
Parameters ebunch (list or container of edge tuples) – Each edge given in the list or container will
be removed from the graph. The edges can be:
• 2-tuples (u, v) All edges between u and v are removed.
• 3-tuples (u, v, key) The edge identified by key is removed.
• 4-tuples (u, v, key, data) where data is ignored.
See also:
2.2. Basic graph types 75

NetworkX Reference, Release 2.3rc1.dev20181203210840
remove_edge() remove a single edge
Notes
Will fail silently if an edge in ebunch is not in the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> ebunch=[(1,2), (2,3)]
>>> G.remove_edges_from(ebunch)
Removing multiple copies of edges
>>> G=nx.MultiGraph()
>>> keys =G.add_edges_from([(1,2), (1,2), (1,2)])
>>> G.remove_edges_from([(1,2), (1,2)])
>>> list(G.edges())
[(1, 2)]
>>> G.remove_edges_from([(1,2), (1,2)]) # silently ignore extra copy
>>> list(G.edges) # now empty graph
[]
networkx.MultiGraph.update
MultiGraph.update(edges=None,nodes=None)
Update the graph using nodes/edges/graphs as input.
Like dict.update, this method takes a graph as input, adding the graph’s noes and edges to this graph. It can also
take two inputs: edges and nodes. Finally it can take either edges or nodes. To specify only nodes the keyword
nodes must be used.
The collections of edges and nodes are treated similarly to the add_edges_from/add_nodes_from methods.
When iterated, they should yield 2-tuples (u, v) or 3-tuples (u, v, datadict).
Parameters
•edges (Graph object, collection of edges, or None) – The first parameter can be a graph or
some edges. If it has attributes nodes and edges, then it is taken to be a Graph-like object
and those attributes are used as collections of nodes and edges to be added to the graph. If
the first parameter does not have those attributes, it is treated as a collection of edges and
added to the graph. If the first argument is None, no edges are added.
•nodes (collection of nodes, or None) – The second parameter is treated as a collection of
nodes to be added to the graph unless it is None. If edges is None and nodes is
None an exception is raised. If the first parameter is a Graph, then nodes is ignored.
Examples
>>> G=nx.path_graph(5)
>>> G.update(nx.complete_graph(range(4,10)))
>>> from itertools import combinations
>>> edges =((u, v, {'power': u *v})
(continues on next page)
76 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
... for u, v in combinations(range(10,20), 2)
... if u*v<225)
>>> nodes =[1000]# for singleton, use a container
>>> G.update(edges, nodes)
Notes
It you want to update the graph using an adjacency structure it is straightforward to obtain the edges/nodes from
adjacency. The following examples provide common cases, your adjacency may be slightly different and require
tweaks of these examples.
>>> # dict-of-set/list/tuple
>>> adj ={1: {2,3}, 2: {1,3}, 3: {1,2}}
>>> e=[(u, v) for u, nbrs in adj.items() for vin nbrs]
>>> G.update(edges=e, nodes=adj)
>>> DG =nx.DiGraph()
>>> # dict-of-dict-of-attribute
>>> adj ={1: {2:1.3,3:0.7}, 2: {1:1.4}, 3: {1:0.7}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # dict-of-dict-of-dict
>>> adj ={1: {2: {'weight':1.3}, 3: {'color':0.7,'weight':1.2}}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # predecessor adjacency (dict-of-set)
>>> pred ={1: {2,3}, 2: {3}, 3: {3}}
>>> e=[(v, u) for u, nbrs in pred.items() for vin nbrs]
>>> # MultiGraph dict-of-dict-of-dict-of-attribute
>>> MDG =nx.MultiDiGraph()
>>> adj ={1: {2: {0: {'weight':1.3}, 1: {'weight':1.2}}},
... 3: {2: {0: {'weight':0.7}}}}
>>> e=[(u, v, ekey, d) for u, nbrs in adj.items()
... for v, keydict in nbrs.items()
... for ekey, d in keydict.items()]
>>> MDG.update(edges=e)
See also:
add_edges_from() add multiple edges to a graph
add_nodes_from() add multiple nodes to a graph
networkx.MultiGraph.clear
MultiGraph.clear()
Remove all nodes and edges from the graph.
2.2. Basic graph types 77

NetworkX Reference, Release 2.3rc1.dev20181203210840
This also removes the name, and all graph, node, and edge attributes.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.clear()
>>> list(G.nodes)
[]
>>> list(G.edges)
[]
Reporting nodes edges and neighbors
MultiGraph.nodes A NodeView of the Graph as G.nodes or G.nodes().
MultiGraph.__iter__() Iterate over the nodes.
MultiGraph.has_node(n) Return True if the graph contains the node n.
MultiGraph.__contains__(n) Return True if n is a node, False otherwise.
MultiGraph.edges Return an iterator over the edges.
MultiGraph.has_edge(u, v[, key]) Return True if the graph has an edge between nodes u
and v.
MultiGraph.get_edge_data(u, v[, key, default]) Return the attribute dictionary associated with edge (u,
v).
MultiGraph.neighbors(n) Return an iterator over all neighbors of node n.
MultiGraph.adj Graph adjacency object holding the neighbors of each
node.
MultiGraph.__getitem__(n) Return a dict of neighbors of node n.
MultiGraph.adjacency() Return an iterator over (node, adjacency dict) tuples for
all nodes.
MultiGraph.nbunch_iter([nbunch]) Return an iterator over nodes contained in nbunch that
are also in the graph.
networkx.MultiGraph.nodes
MultiGraph.nodes
A NodeView of the Graph as G.nodes or G.nodes().
Can be used as G.nodes for data lookup and for set-like operations. Can also be used as G.
nodes(data='color', default=None) to return a NodeDataView which reports specific node data
but no set operations. It presents a dict-like interface as well with G.nodes.items() iterating over (node,
nodedata) 2-tuples and G.nodes[3]['foo'] providing the value of the foo attribute for node 3. In
addition, a view G.nodes.data('foo') provides a dict-like interface to the foo attribute of each node.
G.nodes.data('foo', default=1) provides a default for nodes that do not have attribute foo.
Parameters
•data (string or bool, optional (default=False)) – The node attribute returned in 2-tuple (n,
ddict[data]). If True, return entire node attribute dict as (n, ddict). If False, return just the
nodes n.
•default (value, optional (default=None)) – Value used for nodes that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns
78 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Allows set-like operations over the nodes as well as node attribute dict lookup and calling to
get a NodeDataView. A NodeDataView iterates over (n, data) and has no set operations. A
NodeView iterates over nand includes set operations.
When called, if data is False, an iterator over nodes. Otherwise an iterator of 2-tuples (node,
attribute value) where the attribute is specified in data. If data is True then the attribute becomes
the entire data dictionary.
Return type NodeView
Notes
If your node data is not needed, it is simpler and equivalent to use the expression for n in G, or list(G).
Examples
There are two simple ways of getting a list of all nodes in the graph:
>>> G=nx.path_graph(3)
>>> list(G.nodes)
[0, 1, 2]
>>> list(G)
[0, 1, 2]
To get the node data along with the nodes:
>>> G.add_node(1, time='5pm')
>>> G.nodes[0]['foo']='bar'
>>> list(G.nodes(data=True))
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes.data())
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes(data='foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes.data('foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes(data='time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes.data('time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes(data='time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
>>> list(G.nodes.data('time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
If some of your nodes have an attribute and the rest are assumed to have a default attribute value you can create
a dictionary from node/attribute pairs using the default keyword argument to guarantee the value is never
None:
>>> G=nx.Graph()
>>> G.add_node(0)
>>> G.add_node(1, weight=2)
(continues on next page)
2.2. Basic graph types 79

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.add_node(2, weight=3)
>>> dict(G.nodes(data='weight', default=1))
{0: 1, 1: 2, 2: 3}
networkx.MultiGraph.__iter__
MultiGraph.__iter__()
Iterate over the nodes. Use: ‘for n in G’.
Returns niter – An iterator over all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for nin G]
[0, 1, 2, 3]
>>> list(G)
[0, 1, 2, 3]
networkx.MultiGraph.has_node
MultiGraph.has_node(n)
Return True if the graph contains the node n.
Identical to n in G
Parameters n (node)
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_node(0)
True
It is more readable and simpler to use
>>> 0in G
True
networkx.MultiGraph.__contains__
MultiGraph.__contains__(n)
Return True if n is a node, False otherwise. Use: ‘n in G’.
80 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> 1in G
True
networkx.MultiGraph.edges
MultiGraph.edges
Return an iterator over the edges.
edges(self, nbunch=None, data=False, keys=False, default=None)
The EdgeView provides set-like operations on the edge-tuples as well as edge attribute lookup. When called,
it also provides an EdgeDataView object which allows control of access to edge attributes (but does not pro-
vide set-like operations). Hence, G.edges[u, v]['color'] provides the value of the color attribute for
edge (u, v) while for (u, v, c) in G.edges(data='color', default='red'): iterates
through all the edges yielding the color attribute.
Edges are returned as tuples with optional data and keys in the order (node, neighbor, key, data).
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•keys (bool, optional (default=False)) – If True, return edge keys with each edge.
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edges – A view of edge attributes, usually it iterates over (u, v) (u, v, k) or (u, v, k, d) tuples
of edges, but can also be used for attribute lookup as edges[u, v, k]['foo'].
Return type MultiEdgeView
Notes
Nodes in nbunch that are not in the graph will be (quietly) ignored. For directed graphs this returns the out-edges.
Examples
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> nx.add_path(G, [0,1,2])
>>> key =G.add_edge(2,3, weight=5)
>>> [e for ein G.edges()]
[(0, 1), (1, 2), (2, 3)]
>>> G.edges.data() # default data is {} (empty dict)
MultiEdgeDataView([(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})])
>>> G.edges.data('weight', default=1)
MultiEdgeDataView([(0, 1, 1), (1, 2, 1), (2, 3, 5)])
>>> G.edges(keys=True)# default keys are integers
(continues on next page)
2.2. Basic graph types 81

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
MultiEdgeView([(0, 1, 0), (1, 2, 0), (2, 3, 0)])
>>> G.edges.data(keys=True)
MultiEdgeDataView([(0, 1, 0, {}), (1, 2, 0, {}), (2, 3, 0, {'weight': 5})])
>>> G.edges.data('weight', default=1, keys=True)
MultiEdgeDataView([(0, 1, 0, 1), (1, 2, 0, 1), (2, 3, 0, 5)])
>>> G.edges([0,3])
MultiEdgeDataView([(0, 1), (3, 2)])
>>> G.edges(0)
MultiEdgeDataView([(0, 1)])
networkx.MultiGraph.has_edge
MultiGraph.has_edge(u,v,key=None)
Return True if the graph has an edge between nodes u and v.
This is the same as v in G[u] or key in G[u][v] without KeyError exceptions.
Parameters
•u, v (nodes) – Nodes can be, for example, strings or numbers.
•key (hashable identifier, optional (default=None)) – If specified return True only if the edge
with key is found.
Returns edge_ind – True if edge is in the graph, False otherwise.
Return type bool
Examples
Can be called either using two nodes u, v, an edge tuple (u, v), or an edge tuple (u, v, key).
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> nx.add_path(G, [0,1,2,3])
>>> G.has_edge(0,1)# using two nodes
True
>>> e=(0,1)
>>> G.has_edge(*e) # e is a 2-tuple (u, v)
True
>>> G.add_edge(0,1, key='a')
'a'
>>> G.has_edge(0,1, key='a')# specify key
True
>>> e=(0,1,'a')
>>> G.has_edge(*e) # e is a 3-tuple (u, v, 'a')
True
The following syntax are equivalent:
>>> G.has_edge(0,1)
True
>>> 1in G[0]# though this gives :exc:`KeyError` if 0 not in G
True
82 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiGraph.get_edge_data
MultiGraph.get_edge_data(u,v,key=None,default=None)
Return the attribute dictionary associated with edge (u, v).
This is identical to G[u][v][key] except the default is returned instead of an exception is the edge doesn’t
exist.
Parameters
•u, v (nodes)
•default (any Python object (default=None)) – Value to return if the edge (u, v) is not found.
•key (hashable identifier, optional (default=None)) – Return data only for the edge with
specified key.
Returns edge_dict – The edge attribute dictionary.
Return type dictionary
Examples
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> key =G.add_edge(0,1, key='a', weight=7)
>>> G[0][1]['a']# key='a'
{'weight': 7}
>>> G.edges[0,1,'a']# key='a'
{'weight': 7}
Warning: we protect the graph data structure by making G.edges and G[1][2] read-only dict-like structures.
However, you can assign values to attributes in e.g. G.edges[1, 2, 'a'] or G[1][2]['a'] using an
additional bracket as shown next. You need to specify all edge info to assign to the edge data associated with an
edge.
>>> G[0][1]['a']['weight']=10
>>> G.edges[0,1,'a']['weight']=10
>>> G[0][1]['a']['weight']
10
>>> G.edges[1,0,'a']['weight']
10
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> nx.add_path(G, [0,1,2,3])
>>> G.get_edge_data(0,1)
{0: {}}
>>> e=(0,1)
>>> G.get_edge_data(*e) # tuple form
{0: {}}
>>> G.get_edge_data('a','b', default=0)# edge not in graph, return 0
0
networkx.MultiGraph.neighbors
MultiGraph.neighbors(n)
Return an iterator over all neighbors of node n.
2.2. Basic graph types 83

NetworkX Reference, Release 2.3rc1.dev20181203210840
This is identical to iter(G[n])
Parameters n (node) – A node in the graph
Returns neighbors – An iterator over all neighbors of node n
Return type iterator
Raises NetworkXError – If the node n is not in the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for nin G.neighbors(0)]
[1]
Notes
It is usually more convenient (and faster) to access the adjacency dictionary as G[n]:
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge('a','b', weight=7)
>>> G['a']
AtlasView({'b': {'weight': 7}})
>>> G=nx.path_graph(4)
>>> [n for nin G[0]]
[1]
networkx.MultiGraph.adj
MultiGraph.adj
Graph adjacency object holding the neighbors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is keyed
by neighbor to the edgekey-data-dict. So G.adj[3][2][0]['color'] = 'blue' sets the color of the
edge (3, 2, 0) to "blue".
Iterating over G.adj behaves like a dict. Useful idioms include for nbr, nbrdict in G.adj[n].
items():.
The neighbor information is also provided by subscripting the graph. So for nbr, foovalue in
G[node].data('foo', default=1): works.
For directed graphs, G.adj holds outgoing (successor) info.
networkx.MultiGraph.__getitem__
MultiGraph.__getitem__(n)
Return a dict of neighbors of node n. Use: ‘G[n]’.
Parameters n (node) – A node in the graph.
Returns adj_dict – The adjacency dictionary for nodes connected to n.
Return type dictionary
84 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
G[n] is the same as G.adj[n] and similar to G.neighbors(n) (which is an iterator over G.adj[n])
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0]
AtlasView({1: {}})
networkx.MultiGraph.adjacency
MultiGraph.adjacency()
Return an iterator over (node, adjacency dict) tuples for all nodes.
For directed graphs, only outgoing neighbors/adjacencies are included.
Returns adj_iter – An iterator over (node, adjacency dictionary) for all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [(n, nbrdict) for n, nbrdict in G.adjacency()]
[(0, {1: {}}), (1, {0: {}, 2: {}}), (2, {1: {}, 3: {}}), (3, {2: {}})]
networkx.MultiGraph.nbunch_iter
MultiGraph.nbunch_iter(nbunch=None)
Return an iterator over nodes contained in nbunch that are also in the graph.
The nodes in nbunch are checked for membership in the graph and if not are silently ignored.
Parameters nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
Returns niter – An iterator over nodes in nbunch that are also in the graph. If nbunch is None,
iterate over all nodes in the graph.
Return type iterator
Raises NetworkXError – If nbunch is not a node or or sequence of nodes. If a node in nbunch is
not hashable.
See also:
Graph.__iter__()
Notes
When nbunch is an iterator, the returned iterator yields values directly from nbunch, becoming exhausted when
nbunch is exhausted.
2.2. Basic graph types 85

NetworkX Reference, Release 2.3rc1.dev20181203210840
To test whether nbunch is a single node, one can use “if nbunch in self:”, even after processing with this routine.
If nbunch is not a node or a (possibly empty) sequence/iterator or None, a NetworkXError is raised. Also, if
any object in nbunch is not hashable, a NetworkXError is raised.
Counting nodes edges and neighbors
MultiGraph.order() Return the number of nodes in the graph.
MultiGraph.number_of_nodes() Return the number of nodes in the graph.
MultiGraph.__len__() Return the number of nodes.
MultiGraph.degree A DegreeView for the Graph as G.degree or G.degree().
MultiGraph.size([weight]) Return the number of edges or total of all edge weights.
MultiGraph.number_of_edges([u, v]) Return the number of edges between two nodes.
networkx.MultiGraph.order
MultiGraph.order()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
number_of_nodes(),__len__()
networkx.MultiGraph.number_of_nodes
MultiGraph.number_of_nodes()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
order(),__len__()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
3
networkx.MultiGraph.__len__
MultiGraph.__len__()
Return the number of nodes. Use: ‘len(G)’.
Returns nnodes – The number of nodes in the graph.
Return type int
86 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
4
networkx.MultiGraph.degree
MultiGraph.degree
A DegreeView for the Graph as G.degree or G.degree().
The node degree is the number of edges adjacent to the node. The weighted node degree is the sum of the edge
weights for edges incident to that node.
This object provides an iterator for (node, degree) as well as lookup for the degree for a single node.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The name of an edge attribute that holds
the numerical value used as a weight. If None, then each edge has weight 1. The degree is
the sum of the edge weights adjacent to the node.
Returns
•If a single node is requested
•deg (int) – Degree of the node, if a single node is passed as argument.
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, degree).
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> nx.add_path(G, [0,1,2,3])
>>> G.degree(0)# node 0 with degree 1
1
>>> list(G.degree([0,1]))
[(0, 1), (1, 2)]
networkx.MultiGraph.size
MultiGraph.size(weight=None)
Return the number of edges or total of all edge weights.
Parameters weight (string or None, optional (default=None)) – The edge attribute that holds the
numerical value used as a weight. If None, then each edge has weight 1.
Returns
size – The number of edges or (if weight keyword is provided) the total weight sum.
If weight is None, returns an int. Otherwise a float (or more general numeric if the weights are
more general).
2.2. Basic graph types 87

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type numeric
See also:
number_of_edges()
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.size()
3
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge('a','b', weight=2)
>>> G.add_edge('b','c', weight=4)
>>> G.size()
2
>>> G.size(weight='weight')
6.0
networkx.MultiGraph.number_of_edges
MultiGraph.number_of_edges(u=None,v=None)
Return the number of edges between two nodes.
Parameters u, v (nodes, optional (Gefault=all edges)) – If u and v are specified, return the number
of edges between u and v. Otherwise return the total number of all edges.
Returns nedges – The number of edges in the graph. If nodes uand vare specified return the
number of edges between those nodes. If the graph is directed, this only returns the number of
edges from uto v.
Return type int
See also:
size()
Examples
For undirected multigraphs, this method counts the total number of edges in the graph:
>>> G=nx.MultiGraph()
>>> G.add_edges_from([(0,1), (0,1), (1,2)])
[0, 1, 0]
>>> G.number_of_edges()
3
If you specify two nodes, this counts the total number of edges joining the two nodes:
>>> G.number_of_edges(0,1)
2
For directed multigraphs, this method can count the total number of directed edges from uto v:
88 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.MultiDiGraph()
>>> G.add_edges_from([(0,1), (0,1), (1,0)])
[0, 1, 0]
>>> G.number_of_edges(0,1)
2
>>> G.number_of_edges(1,0)
1
Making copies and subgraphs
MultiGraph.copy([as_view]) Return a copy of the graph.
MultiGraph.to_undirected([as_view]) Return an undirected copy of the graph.
MultiGraph.to_directed([as_view]) Return a directed representation of the graph.
MultiGraph.subgraph(nodes) Return a SubGraph view of the subgraph induced on
nodes.
MultiGraph.edge_subgraph(edges) Returns the subgraph induced by the specified edges.
networkx.MultiGraph.copy
MultiGraph.copy(as_view=False)
Return a copy of the graph.
The copy method by default returns an independent shallow copy of the graph and attributes. That is, if an
attribute is a container, that container is shared by the original an the copy. Use Python’s copy.deepcopy for
new containers.
If as_view is True then a view is returned instead of a copy.
Notes
All copies reproduce the graph structure, but data attributes may be handled in different ways. There are four
types of copies of a graph that people might want.
Deepcopy – A “deepcopy” copies the graph structure as well as all data attributes and any objects they might
contain. The entire graph object is new so that changes in the copy do not affect the original object. (see Python’s
copy.deepcopy)
Data Reference (Shallow) – For a shallow copy the graph structure is copied but the edge, node and graph at-
tribute dicts are references to those in the original graph. This saves time and memory but could cause confusion
if you change an attribute in one graph and it changes the attribute in the other. NetworkX does not provide this
level of shallow copy.
Independent Shallow – This copy creates new independent attribute dicts and then does a shallow copy of the
attributes. That is, any attributes that are containers are shared between the new graph and the original. This is
exactly what dict.copy() provides. You can obtain this style copy using:
>>> G=nx.path_graph(5)
>>> H=G.copy()
>>> H=G.copy(as_view=False)
>>> H=nx.Graph(G)
>>> H=G.__class__(G)
2.2. Basic graph types 89
NetworkX Reference, Release 2.3rc1.dev20181203210840
Fresh Data – For fresh data, the graph structure is copied while new empty data attribute dicts are created. The
resulting graph is independent of the original and it has no edge, node or graph attributes. Fresh copies are not
enabled. Instead use:
>>> H=G.__class__()
>>> H.add_nodes_from(G)
>>> H.add_edges_from(G.edges)
View – Inspired by dict-views, graph-views act like read-only versions of the original graph, providing a copy
of the original structure without requiring any memory for copying the information.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Parameters as_view (bool, optional (default=False)) – If True, the returned graph-view provides a
read-only view of the original graph without actually copying any data.
Returns G – A copy of the graph.
Return type Graph
See also:
to_directed() return a directed copy of the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.copy()
networkx.MultiGraph.to_undirected
MultiGraph.to_undirected(as_view=False)
Return an undirected copy of the graph.
Returns G – A deepcopy of the graph.
Return type Graph/MultiGraph
See also:
copy(),add_edge(),add_edges_from()
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar G = nx.MultiGraph(D) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed MultiiGraph to use dict-like objects in the data structure, those changes do not
transfer to the MultiGraph created by this method.
90 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(2)# or MultiGraph, etc
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
>>> G2 =H.to_undirected()
>>> list(G2.edges)
[(0, 1)]
networkx.MultiGraph.to_directed
MultiGraph.to_directed(as_view=False)
Return a directed representation of the graph.
Returns G – A directed graph with the same name, same nodes, and with each edge (u, v, data)
replaced by two directed edges (u, v, data) and (v, u, data).
Return type MultiDiGraph
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar D=DiGraph(G) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed MultiGraph to use dict-like objects in the data structure, those changes do not
transfer to the MultiDiGraph created by this method.
Examples
>>> G=nx.Graph() # or MultiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
If already directed, return a (deep) copy
>>> G=nx.DiGraph() # or MultiDiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1)]
networkx.MultiGraph.subgraph
MultiGraph.subgraph(nodes)
Return a SubGraph view of the subgraph induced on nodes.
2.2. Basic graph types 91

NetworkX Reference, Release 2.3rc1.dev20181203210840
The induced subgraph of the graph contains the nodes in nodes and the edges between those nodes.
Parameters nodes (list, iterable) – A container of nodes which will be iterated through once.
Returns G – A subgraph view of the graph. The graph structure cannot be changed but node/edge
attributes can and are shared with the original graph.
Return type SubGraph View
Notes
The graph, edge and node attributes are shared with the original graph. Changes to the graph structure is ruled
out by the view, but changes to attributes are reflected in the original graph.
To create a subgraph with its own copy of the edge/node attributes use: G.subgraph(nodes).copy()
For an inplace reduction of a graph to a subgraph you can remove nodes: G.remove_nodes_from([n for n in G
if n not in set(nodes)])
Subgraph views are sometimes NOT what you want. In most cases where you want to do more than simply look
at the induced edges, it makes more sense to just create the subgraph as its own graph with code like:
# Create a subgraph SG based on a (possibly multigraph) G
SG =G.__class__()
SG.add_nodes_from((n, G.nodes[n]) for nin largest_wcc)
if SG.is_multigraph:
SG.add_edges_from((n, nbr, key, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, keydict in nbrs.items() if nbr in largest_wcc
for key, d in keydict.items())
else:
SG.add_edges_from((n, nbr, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, d in nbrs.items() if nbr in largest_wcc)
SG.graph.update(G.graph)
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.subgraph([0,1,2])
>>> list(H.edges)
[(0, 1), (1, 2)]
networkx.MultiGraph.edge_subgraph
MultiGraph.edge_subgraph(edges)
Returns the subgraph induced by the specified edges.
The induced subgraph contains each edge in edges and each node incident to any one of those edges.
Parameters edges (iterable) – An iterable of edges in this graph.
Returns G – An edge-induced subgraph of this graph with the same edge attributes.
Return type Graph
92 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The graph, edge, and node attributes in the returned subgraph view are references to the corresponding attributes
in the original graph. The view is read-only.
To create a full graph version of the subgraph with its own copy of the edge or node attributes, use:
>>> G.edge_subgraph(edges).copy()
Examples
>>> G=nx.path_graph(5)
>>> H=G.edge_subgraph([(0,1), (3,4)])
>>> list(H.nodes)
[0, 1, 3, 4]
>>> list(H.edges)
[(0, 1), (3, 4)]
2.2.4 MultiDiGraph—Directed graphs with self loops and parallel edges
Overview
class MultiDiGraph(incoming_graph_data=None,**attr)
A directed graph class that can store multiedges.
Multiedges are multiple edges between two nodes. Each edge can hold optional data or attributes.
A MultiDiGraph holds directed edges. Self loops are allowed.
Nodes can be arbitrary (hashable) Python objects with optional key/value attributes. By convention None is not
used as a node.
Edges are represented as links between nodes with optional key/value attributes.
Parameters
•incoming_graph_data (input graph (optional, default: None)) – Data to initialize graph. If
None (default) an empty graph is created. The data can be any format that is supported by
the to_networkx_graph() function, currently including edge list, dict of dicts, dict of lists,
NetworkX graph, NumPy matrix or 2d ndarray, SciPy sparse matrix, or PyGraphviz graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
Graph,DiGraph,MultiGraph,OrderedMultiDiGraph
Examples
Create an empty graph structure (a “null graph”) with no nodes and no edges.
>>> G=nx.MultiDiGraph()
2.2. Basic graph types 93

NetworkX Reference, Release 2.3rc1.dev20181203210840
G can be grown in several ways.
Nodes:
Add one node at a time:
>>> G.add_node(1)
Add the nodes from any container (a list, dict, set or even the lines from a file or the nodes from another graph).
>>> G.add_nodes_from([2,3])
>>> G.add_nodes_from(range(100,110))
>>> H=nx.path_graph(10)
>>> G.add_nodes_from(H)
In addition to strings and integers any hashable Python object (except None) can represent a node, e.g. a
customized node object, or even another Graph.
>>> G.add_node(H)
Edges:
G can also be grown by adding edges.
Add one edge,
>>> key =G.add_edge(1,2)
a list of edges,
>>> keys =G.add_edges_from([(1,2), (1,3)])
or a collection of edges,
>>> keys =G.add_edges_from(H.edges)
If some edges connect nodes not yet in the graph, the nodes are added automatically. If an edge already exists,
an additional edge is created and stored using a key to identify the edge. By default the key is the lowest unused
integer.
>>> keys =G.add_edges_from([(4,5,dict(route=282)), (4,5,dict(route=37))])
>>> G[4]
AdjacencyView({5: {0: {}, 1: {'route': 282}, 2: {'route': 37}}})
Attributes:
Each graph, node, and edge can hold key/value attribute pairs in an associated attribute dictionary (the keys
must be hashable). By default these are empty, but can be added or changed using add_edge, add_node or direct
manipulation of the attribute dictionaries named graph, node and edge respectively.
>>> G=nx.MultiDiGraph(day="Friday")
>>> G.graph
{'day': 'Friday'}
Add node attributes using add_node(), add_nodes_from() or G.nodes
>>> G.add_node(1, time='5pm')
>>> G.add_nodes_from([3], time='2pm')
>>> G.nodes[1]
(continues on next page)
94 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
{'time': '5pm'}
>>> G.nodes[1]['room']=714
>>> del G.nodes[1]['room']# remove attribute
>>> list(G.nodes(data=True))
[(1, {'time': '5pm'}), (3, {'time': '2pm'})]
Add edge attributes using add_edge(), add_edges_from(), subscript notation, or G.edges.
>>> key =G.add_edge(1,2, weight=4.7 )
>>> keys =G.add_edges_from([(3,4), (4,5)], color='red')
>>> keys =G.add_edges_from([(1,2,{'color':'blue'}), (2,3,{'weight':8})])
>>> G[1][2][0]['weight']=4.7
>>> G.edges[1,2,0]['weight']=4
Warning: we protect the graph data structure by making G.edges[1, 2] a read-only dict-like structure.
However, you can assign to attributes in e.g. G.edges[1, 2]. Thus, use 2 sets of brackets to add/change data
attributes: G.edges[1, 2]['weight'] = 4 (For multigraphs: MG.edges[u, v, key][name] =
value).
Shortcuts:
Many common graph features allow python syntax to speed reporting.
>>> 1in G# check if node in graph
True
>>> [n for nin Gif n<3]# iterate through nodes
[1, 2]
>>> len(G) # number of nodes in graph
5
>>> G[1]# adjacency dict-like view keyed by neighbor to edge attributes
AdjacencyView({2: {0: {'weight': 4}, 1: {'color': 'blue'}}})
Often the best way to traverse all edges of a graph is via the neighbors. The neighbors are available as an
adjacency-view G.adj object or via the method G.adjacency().
>>> for n, nbrsdict in G.adjacency():
... for nbr, keydict in nbrsdict.items():
... for key, eattr in keydict.items():
... if 'weight' in eattr:
... # Do something useful with the edges
... pass
But the edges() method is often more convenient:
>>> for u, v, keys, weight in G.edges(data='weight', keys=True):
... if weight is not None:
... # Do something useful with the edges
... pass
Reporting:
Simple graph information is obtained using methods and object-attributes. Reporting usually provides
views instead of containers to reduce memory usage. The views update as the graph is updated simi-
larly to dict-views. The objects nodes, `edges and adj provide access to data attributes via lookup
(e.g. nodes[n], `edges[u, v],adj[u][v]) and iteration (e.g. nodes.items(),nodes.
data('color'),nodes.data('color', default='blue') and similarly for edges) Views exist
for nodes,edges,neighbors()/adj and degree.
2.2. Basic graph types 95

NetworkX Reference, Release 2.3rc1.dev20181203210840
For details on these and other miscellaneous methods, see below.
Subclasses (Advanced):
The MultiDiGraph class uses a dict-of-dict-of-dict-of-dict structure. The outer dict (node_dict) holds adjacency
information keyed by node. The next dict (adjlist_dict) represents the adjacency information and holds edge_key
dicts keyed by neighbor. The edge_key dict holds each edge_attr dict keyed by edge key. The inner dict
(edge_attr_dict) represents the edge data and holds edge attribute values keyed by attribute names.
Each of these four dicts in the dict-of-dict-of-dict-of-dict structure can be replaced by a user defined dict-like
object. In general, the dict-like features should be maintained but extra features can be added. To replace
one of the dicts create a new graph class by changing the class(!) variable holding the factory for that dict-
like structure. The variable names are node_dict_factory, node_attr_dict_factory, adjlist_inner_dict_factory,
adjlist_outer_dict_factory, edge_key_dict_factory, edge_attr_dict_factory and graph_attr_dict_factory.
node_dict_factory [function, (default: dict)] Factory function to be used to create the dict containing node
attributes, keyed by node id. It should require no arguments and return a dict-like object
node_attr_dict_factory: function, (default: dict) Factory function to be used to create the node attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object
adjlist_outer_dict_factory [function, (default: dict)] Factory function to be used to create the outer-most dict
in the data structure that holds adjacency info keyed by node. It should require no arguments and return a
dict-like object.
adjlist_inner_dict_factory [function, (default: dict)] Factory function to be used to create the adjacency list
dict which holds multiedge key dicts keyed by neighbor. It should require no arguments and return a
dict-like object.
edge_key_dict_factory [function, (default: dict)] Factory function to be used to create the edge key dict which
holds edge data keyed by edge key. It should require no arguments and return a dict-like object.
edge_attr_dict_factory [function, (default: dict)] Factory function to be used to create the edge attribute dict
which holds attribute values keyed by attribute name. It should require no arguments and return a dict-like
object.
graph_attr_dict_factory [function, (default: dict)] Factory function to be used to create the graph attribute
dict which holds attribute values keyed by attribute name. It should require no arguments and return a
dict-like object.
Typically, if your extension doesn’t impact the data structure all methods will inherited without issue except:
to_directed/to_undirected. By default these methods create a DiGraph/Graph class and you probably
want them to create your extension of a DiGraph/Graph. To facilitate this we define two class variables that you
can set in your subclass.
to_directed_class [callable, (default: DiGraph or MultiDiGraph)] Class to create a new graph structure in the
to_directed method. If None, a NetworkX class (DiGraph or MultiDiGraph) is used.
to_undirected_class [callable, (default: Graph or MultiGraph)] Class to create a new graph structure in the
to_undirected method. If None, a NetworkX class (Graph or MultiGraph) is used.
Examples
Please see ordered for examples of creating graph subclasses by overwriting the base class dict with a
dictionary-like object.
96 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Methods
Adding and Removing Nodes and Edges
MultiDiGraph.__init__([incoming_graph_data]) Initialize a graph with edges, name, or graph attributes.
MultiDiGraph.add_node(node_for_adding,
**attr)
Add a single node node_for_adding and update
node attributes.
MultiDiGraph.add_nodes_from(. . . ) Add multiple nodes.
MultiDiGraph.remove_node(n) Remove node n.
MultiDiGraph.remove_nodes_from(nodes) Remove multiple nodes.
MultiDiGraph.add_edge(u_for_edge,
v_for_edge)
Add an edge between u and v.
MultiDiGraph.add_edges_from(ebunch_to_add,
...)
Add all the edges in ebunch_to_add.
MultiDiGraph.add_weighted_edges_from(. . . [,
...])
Add weighted edges in ebunch_to_add with speci-
fied weight attr
MultiDiGraph.new_edge_key(u, v) Return an unused key for edges between nodes uand v.
MultiDiGraph.remove_edge(u, v[, key]) Remove an edge between u and v.
MultiDiGraph.remove_edges_from(ebunch) Remove all edges specified in ebunch.
MultiDiGraph.update([edges, nodes]) Update the graph using nodes/edges/graphs as input.
MultiDiGraph.clear() Remove all nodes and edges from the graph.
networkx.MultiDiGraph.__init__
MultiDiGraph.__init__(incoming_graph_data=None,**attr)
Initialize a graph with edges, name, or graph attributes.
Parameters
•incoming_graph_data (input graph) – Data to initialize graph. If incom-
ing_graph_data=None (default) an empty graph is created. The data can be an edge list,
or any NetworkX graph object. If the corresponding optional Python packages are installed
the data can also be a NumPy matrix or 2d ndarray, a SciPy sparse matrix, or a PyGraphviz
graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to graph as
key=value pairs.
See also:
convert()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G=nx.Graph(name='my graph')
>>> e=[(1,2), (2,3), (3,4)] # list of edges
>>> G=nx.Graph(e)
Arbitrary graph attribute pairs (key=value) may be assigned
>>> G=nx.Graph(e, day="Friday")
>>> G.graph
{'day': 'Friday'}
2.2. Basic graph types 97

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiDiGraph.add_node
MultiDiGraph.add_node(node_for_adding,**attr)
Add a single node node_for_adding and update node attributes.
Parameters
•node_for_adding (node) – A node can be any hashable Python object except None.
•attr (keyword arguments, optional) – Set or change node attributes using key=value.
See also:
add_nodes_from()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_node(1)
>>> G.add_node('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_node(K3)
>>> G.number_of_nodes()
3
Use keywords set/change node attributes:
>>> G.add_node(1, size=10)
>>> G.add_node(3, weight=0.4, UTM=('13S',382871,3972649))
Notes
A hashable object is one that can be used as a key in a Python dictionary. This includes strings, numbers, tuples
of strings and numbers, etc.
On many platforms hashable items also include mutables such as NetworkX Graphs, though one should be
careful that the hash doesn’t change on mutables.
networkx.MultiDiGraph.add_nodes_from
MultiDiGraph.add_nodes_from(nodes_for_adding,**attr)
Add multiple nodes.
Parameters
•nodes_for_adding (iterable container) – A container of nodes (list, dict, set, etc.). OR A
container of (node, attribute dict) tuples. Node attributes are updated using the attribute dict.
•attr (keyword arguments, optional (default= no attributes)) – Update attributes for all nodes
in nodes. Node attributes specified in nodes as a tuple take precedence over attributes spec-
ified via keyword arguments.
See also:
add_node()
98 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_nodes_from('Hello')
>>> K3 =nx.Graph([(0,1), (1,2), (2,0)])
>>> G.add_nodes_from(K3)
>>> sorted(G.nodes(), key=str)
[0, 1, 2, 'H', 'e', 'l', 'o']
Use keywords to update specific node attributes for every node.
>>> G.add_nodes_from([1,2], size=10)
>>> G.add_nodes_from([3,4], weight=0.4)
Use (node, attrdict) tuples to update attributes for specific nodes.
>>> G.add_nodes_from([(1,dict(size=11)), (2, {'color':'blue'})])
>>> G.nodes[1]['size']
11
>>> H=nx.Graph()
>>> H.add_nodes_from(G.nodes(data=True))
>>> H.nodes[1]['size']
11
networkx.MultiDiGraph.remove_node
MultiDiGraph.remove_node(n)
Remove node n.
Removes the node n and all adjacent edges. Attempting to remove a non-existent node will raise an exception.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
remove_nodes_from()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> list(G.edges)
[(0, 1), (1, 2)]
>>> G.remove_node(1)
>>> list(G.edges)
[]
networkx.MultiDiGraph.remove_nodes_from
MultiDiGraph.remove_nodes_from(nodes)
Remove multiple nodes.
Parameters nodes (iterable container) – A container of nodes (list, dict, set, etc.). If a node in the
container is not in the graph it is silently ignored.
2.2. Basic graph types 99

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
remove_node()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> e=list(G.nodes)
>>> e
[0, 1, 2]
>>> G.remove_nodes_from(e)
>>> list(G.nodes)
[]
networkx.MultiDiGraph.add_edge
MultiDiGraph.add_edge(u_for_edge,v_for_edge,key=None,**attr)
Add an edge between u and v.
The nodes u and v will be automatically added if they are not already in the graph.
Edge attributes can be specified with keywords or by directly accessing the edge’s attribute dictionary. See
examples below.
Parameters
•u_for_edge, v_for_edge (nodes) – Nodes can be, for example, strings or numbers. Nodes
must be hashable (and not None) Python objects.
•key (hashable identifier, optional (default=lowest unused integer)) – Used to distinguish
multiedges between a pair of nodes.
•attr_dict (dictionary, optional (default= no attributes)) – Dictionary of edge attributes.
Key/value pairs will update existing data associated with the edge.
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
Returns
Return type The edge key assigned to the edge.
See also:
add_edges_from() add a collection of edges
Notes
To replace/update edge data, use the optional key argument to identify a unique edge. Otherwise a new edge
will be created.
NetworkX algorithms designed for weighted graphs cannot use multigraphs directly because it is not clear
how to handle multiedge weights. Convert to Graph using edge attribute ‘weight’ to enable weighted graph
algorithms.
Default keys are generated using the method new_edge_key(). This method can be overridden by subclass-
ing the base class and providing a custom new_edge_key() method.
100 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
The following all add the edge e=(1, 2) to graph G:
>>> G=nx.MultiDiGraph()
>>> e=(1,2)
>>> key =G.add_edge(1,2)# explicit two-node form
>>> G.add_edge(*e) # single edge as tuple of two nodes
1
>>> G.add_edges_from( [(1,2)] ) # add edges from iterable container
[2]
Associate data to edges using keywords:
>>> key =G.add_edge(1,2, weight=3)
>>> key =G.add_edge(1,2, key=0, weight=4)# update data for key=0
>>> key =G.add_edge(1,3, weight=7, capacity=15, length=342.7)
For non-string attribute keys, use subscript notation.
>>> ekey =G.add_edge(1,2)
>>> G[1][2][0].update({0:5})
>>> G.edges[1,2,0].update({0:5})
networkx.MultiDiGraph.add_edges_from
MultiDiGraph.add_edges_from(ebunch_to_add,**attr)
Add all the edges in ebunch_to_add.
Parameters
•ebunch_to_add (container of edges) – Each edge given in the container will be added to
the graph. The edges can be:
–2-tuples (u, v) or
–3-tuples (u, v, d) for an edge data dict d, or
–3-tuples (u, v, k) for not iterable key k, or
–4-tuples (u, v, k, d) for an edge with data and key k
•attr (keyword arguments, optional) – Edge data (or labels or objects) can be assigned using
keyword arguments.
Returns
Return type A list of edge keys assigned to the edges in ebunch.
See also:
add_edge() add a single edge
add_weighted_edges_from() convenient way to add weighted edges
Notes
Adding the same edge twice has no effect but any edge data will be updated when each duplicate edge is added.
2.2. Basic graph types 101

NetworkX Reference, Release 2.3rc1.dev20181203210840
Edge attributes specified in an ebunch take precedence over attributes specified via keyword arguments.
Default keys are generated using the method new_edge_key(). This method can be overridden by subclass-
ing the base class and providing a custom new_edge_key() method.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edges_from([(0,1), (1,2)]) # using a list of edge tuples
>>> e=zip(range(0,3), range(1,4))
>>> G.add_edges_from(e) # Add the path graph 0-1-2-3
Associate data to edges
>>> G.add_edges_from([(1,2), (2,3)], weight=3)
>>> G.add_edges_from([(3,4), (1,4)], label='WN2898')
networkx.MultiDiGraph.add_weighted_edges_from
MultiDiGraph.add_weighted_edges_from(ebunch_to_add,weight=’weight’,**attr)
Add weighted edges in ebunch_to_add with specified weight attr
Parameters
•ebunch_to_add (container of edges) – Each edge given in the list or container will be added
to the graph. The edges must be given as 3-tuples (u, v, w) where w is a number.
•weight (string, optional (default= ‘weight’)) – The attribute name for the edge weights to
be added.
•attr (keyword arguments, optional (default= no attributes)) – Edge attributes to add/update
for all edges.
See also:
add_edge() add a single edge
add_edges_from() add multiple edges
Notes
Adding the same edge twice for Graph/DiGraph simply updates the edge data. For MultiGraph/MultiDiGraph,
duplicate edges are stored.
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_weighted_edges_from([(0,1,3.0), (1,2,7.5)])
102 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiDiGraph.new_edge_key
MultiDiGraph.new_edge_key(u,v)
Return an unused key for edges between nodes uand v.
The nodes uand vdo not need to be already in the graph.
Notes
In the standard MultiGraph class the new key is the number of existing edges between uand v(increased
if necessary to ensure unused). The first edge will have key 0, then 1, etc. If an edge is removed further
new_edge_keys may not be in this order.
Parameters u, v (nodes)
Returns key
Return type int
networkx.MultiDiGraph.remove_edge
MultiDiGraph.remove_edge(u,v,key=None)
Remove an edge between u and v.
Parameters
•u, v (nodes) – Remove an edge between nodes u and v.
•key (hashable identifier, optional (default=None)) – Used to distinguish multiple edges be-
tween a pair of nodes. If None remove a single (arbitrary) edge between u and v.
Raises NetworkXError – If there is not an edge between u and v, or if there is no edge with the
specified key.
See also:
remove_edges_from() remove a collection of edges
Examples
>>> G=nx.MultiDiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.remove_edge(0,1)
>>> e=(1,2)
>>> G.remove_edge(*e) # unpacks e from an edge tuple
For multiple edges
>>> G=nx.MultiDiGraph()
>>> G.add_edges_from([(1,2), (1,2), (1,2)]) # key_list returned
[0, 1, 2]
>>> G.remove_edge(1,2)# remove a single (arbitrary) edge
For edges with keys
2.2. Basic graph types 103

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.MultiDiGraph()
>>> G.add_edge(1,2, key='first')
'first'
>>> G.add_edge(1,2, key='second')
'second'
>>> G.remove_edge(1,2, key='second')
networkx.MultiDiGraph.remove_edges_from
MultiDiGraph.remove_edges_from(ebunch)
Remove all edges specified in ebunch.
Parameters ebunch (list or container of edge tuples) – Each edge given in the list or container will
be removed from the graph. The edges can be:
• 2-tuples (u, v) All edges between u and v are removed.
• 3-tuples (u, v, key) The edge identified by key is removed.
• 4-tuples (u, v, key, data) where data is ignored.
See also:
remove_edge() remove a single edge
Notes
Will fail silently if an edge in ebunch is not in the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> ebunch=[(1,2), (2,3)]
>>> G.remove_edges_from(ebunch)
Removing multiple copies of edges
>>> G=nx.MultiGraph()
>>> keys =G.add_edges_from([(1,2), (1,2), (1,2)])
>>> G.remove_edges_from([(1,2), (1,2)])
>>> list(G.edges())
[(1, 2)]
>>> G.remove_edges_from([(1,2), (1,2)]) # silently ignore extra copy
>>> list(G.edges) # now empty graph
[]
networkx.MultiDiGraph.update
MultiDiGraph.update(edges=None,nodes=None)
Update the graph using nodes/edges/graphs as input.
Like dict.update, this method takes a graph as input, adding the graph’s noes and edges to this graph. It can also
take two inputs: edges and nodes. Finally it can take either edges or nodes. To specify only nodes the keyword
nodes must be used.
104 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
The collections of edges and nodes are treated similarly to the add_edges_from/add_nodes_from methods.
When iterated, they should yield 2-tuples (u, v) or 3-tuples (u, v, datadict).
Parameters
•edges (Graph object, collection of edges, or None) – The first parameter can be a graph or
some edges. If it has attributes nodes and edges, then it is taken to be a Graph-like object
and those attributes are used as collections of nodes and edges to be added to the graph. If
the first parameter does not have those attributes, it is treated as a collection of edges and
added to the graph. If the first argument is None, no edges are added.
•nodes (collection of nodes, or None) – The second parameter is treated as a collection of
nodes to be added to the graph unless it is None. If edges is None and nodes is
None an exception is raised. If the first parameter is a Graph, then nodes is ignored.
Examples
>>> G=nx.path_graph(5)
>>> G.update(nx.complete_graph(range(4,10)))
>>> from itertools import combinations
>>> edges =((u, v, {'power': u *v})
... for u, v in combinations(range(10,20), 2)
... if u*v<225)
>>> nodes =[1000]# for singleton, use a container
>>> G.update(edges, nodes)
Notes
It you want to update the graph using an adjacency structure it is straightforward to obtain the edges/nodes from
adjacency. The following examples provide common cases, your adjacency may be slightly different and require
tweaks of these examples.
>>> # dict-of-set/list/tuple
>>> adj ={1: {2,3}, 2: {1,3}, 3: {1,2}}
>>> e=[(u, v) for u, nbrs in adj.items() for vin nbrs]
>>> G.update(edges=e, nodes=adj)
>>> DG =nx.DiGraph()
>>> # dict-of-dict-of-attribute
>>> adj ={1: {2:1.3,3:0.7}, 2: {1:1.4}, 3: {1:0.7}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # dict-of-dict-of-dict
>>> adj ={1: {2: {'weight':1.3}, 3: {'color':0.7,'weight':1.2}}}
>>> e=[(u, v, {'weight': d}) for u, nbrs in adj.items()
... for v, d in nbrs.items()]
>>> DG.update(edges=e, nodes=adj)
>>> # predecessor adjacency (dict-of-set)
>>> pred ={1: {2,3}, 2: {3}, 3: {3}}
>>> e=[(v, u) for u, nbrs in pred.items() for vin nbrs]
2.2. Basic graph types 105

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> # MultiGraph dict-of-dict-of-dict-of-attribute
>>> MDG =nx.MultiDiGraph()
>>> adj ={1: {2: {0: {'weight':1.3}, 1: {'weight':1.2}}},
... 3: {2: {0: {'weight':0.7}}}}
>>> e=[(u, v, ekey, d) for u, nbrs in adj.items()
... for v, keydict in nbrs.items()
... for ekey, d in keydict.items()]
>>> MDG.update(edges=e)
See also:
add_edges_from() add multiple edges to a graph
add_nodes_from() add multiple nodes to a graph
networkx.MultiDiGraph.clear
MultiDiGraph.clear()
Remove all nodes and edges from the graph.
This also removes the name, and all graph, node, and edge attributes.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.clear()
>>> list(G.nodes)
[]
>>> list(G.edges)
[]
Reporting nodes edges and neighbors
MultiDiGraph.nodes A NodeView of the Graph as G.nodes or G.nodes().
MultiDiGraph.__iter__() Iterate over the nodes.
MultiDiGraph.has_node(n) Return True if the graph contains the node n.
MultiDiGraph.__contains__(n) Return True if n is a node, False otherwise.
MultiDiGraph.edges An OutMultiEdgeView of the Graph as G.edges or
G.edges().
MultiDiGraph.out_edges An OutMultiEdgeView of the Graph as G.edges or
G.edges().
MultiDiGraph.in_edges An InMultiEdgeView of the Graph as G.in_edges or
G.in_edges().
MultiDiGraph.has_edge(u, v[, key]) Return True if the graph has an edge between nodes u
and v.
MultiDiGraph.get_edge_data(u, v[, key, de-
fault])
Return the attribute dictionary associated with edge (u,
v).
MultiDiGraph.neighbors(n) Return an iterator over successor nodes of n.
MultiDiGraph.adj Graph adjacency object holding the neighbors of each
node.
Continued on next page
106 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 14 – continued from previous page
MultiDiGraph.__getitem__(n) Return a dict of neighbors of node n.
MultiDiGraph.successors(n) Return an iterator over successor nodes of n.
MultiDiGraph.succ Graph adjacency object holding the successors of each
node.
MultiDiGraph.predecessors(n) Return an iterator over predecessor nodes of n.
MultiDiGraph.succ Graph adjacency object holding the successors of each
node.
MultiDiGraph.adjacency() Return an iterator over (node, adjacency dict) tuples for
all nodes.
MultiDiGraph.nbunch_iter([nbunch]) Return an iterator over nodes contained in nbunch that
are also in the graph.
networkx.MultiDiGraph.nodes
MultiDiGraph.nodes
A NodeView of the Graph as G.nodes or G.nodes().
Can be used as G.nodes for data lookup and for set-like operations. Can also be used as G.
nodes(data='color', default=None) to return a NodeDataView which reports specific node data
but no set operations. It presents a dict-like interface as well with G.nodes.items() iterating over (node,
nodedata) 2-tuples and G.nodes[3]['foo'] providing the value of the foo attribute for node 3. In
addition, a view G.nodes.data('foo') provides a dict-like interface to the foo attribute of each node.
G.nodes.data('foo', default=1) provides a default for nodes that do not have attribute foo.
Parameters
•data (string or bool, optional (default=False)) – The node attribute returned in 2-tuple (n,
ddict[data]). If True, return entire node attribute dict as (n, ddict). If False, return just the
nodes n.
•default (value, optional (default=None)) – Value used for nodes that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns
Allows set-like operations over the nodes as well as node attribute dict lookup and calling to
get a NodeDataView. A NodeDataView iterates over (n, data) and has no set operations. A
NodeView iterates over nand includes set operations.
When called, if data is False, an iterator over nodes. Otherwise an iterator of 2-tuples (node,
attribute value) where the attribute is specified in data. If data is True then the attribute becomes
the entire data dictionary.
Return type NodeView
Notes
If your node data is not needed, it is simpler and equivalent to use the expression for n in G, or list(G).
Examples
There are two simple ways of getting a list of all nodes in the graph:
2.2. Basic graph types 107
NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(3)
>>> list(G.nodes)
[0, 1, 2]
>>> list(G)
[0, 1, 2]
To get the node data along with the nodes:
>>> G.add_node(1, time='5pm')
>>> G.nodes[0]['foo']='bar'
>>> list(G.nodes(data=True))
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes.data())
[(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes(data='foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes.data('foo'))
[(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes(data='time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes.data('time'))
[(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes(data='time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
>>> list(G.nodes.data('time', default='Not Available'))
[(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
If some of your nodes have an attribute and the rest are assumed to have a default attribute value you can create
a dictionary from node/attribute pairs using the default keyword argument to guarantee the value is never
None:
>>> G=nx.Graph()
>>> G.add_node(0)
>>> G.add_node(1, weight=2)
>>> G.add_node(2, weight=3)
>>> dict(G.nodes(data='weight', default=1))
{0: 1, 1: 2, 2: 3}
networkx.MultiDiGraph.__iter__
MultiDiGraph.__iter__()
Iterate over the nodes. Use: ‘for n in G’.
Returns niter – An iterator over all nodes in the graph.
Return type iterator
Examples
108 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [n for nin G]
[0, 1, 2, 3]
>>> list(G)
[0, 1, 2, 3]
networkx.MultiDiGraph.has_node
MultiDiGraph.has_node(n)
Return True if the graph contains the node n.
Identical to n in G
Parameters n (node)
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.has_node(0)
True
It is more readable and simpler to use
>>> 0in G
True
networkx.MultiDiGraph.__contains__
MultiDiGraph.__contains__(n)
Return True if n is a node, False otherwise. Use: ‘n in G’.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> 1in G
True
networkx.MultiDiGraph.edges
MultiDiGraph.edges
An OutMultiEdgeView of the Graph as G.edges or G.edges().
edges(self, nbunch=None, data=False, keys=False, default=None)
The OutMultiEdgeView provides set-like operations on the edge-tuples as well as edge attribute lookup. When
called, it also provides an EdgeDataView object which allows control of access to edge attributes (but does not
provide set-like operations). Hence, G.edges[u, v]['color'] provides the value of the color attribute
for edge (u, v) while for (u, v, c) in G.edges(data='color', default='red'): iter-
ates through all the edges yielding the color attribute with default 'red' if no color attribute exists.
Edges are returned as tuples with optional data and keys in the order (node, neighbor, key, data).
2.2. Basic graph types 109

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•keys (bool, optional (default=False)) – If True, return edge keys with each edge.
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edges – A view of edge attributes, usually it iterates over (u, v) (u, v, k) or (u, v, k, d) tuples
of edges, but can also be used for attribute lookup as edges[u, v, k]['foo'].
Return type EdgeView
Notes
Nodes in nbunch that are not in the graph will be (quietly) ignored. For directed graphs this returns the out-edges.
Examples
>>> G=nx.MultiDiGraph()
>>> nx.add_path(G, [0,1,2])
>>> key =G.add_edge(2,3, weight=5)
>>> [e for ein G.edges()]
[(0, 1), (1, 2), (2, 3)]
>>> list(G.edges(data=True)) # default data is {} (empty dict)
[(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})]
>>> list(G.edges(data='weight', default=1))
[(0, 1, 1), (1, 2, 1), (2, 3, 5)]
>>> list(G.edges(keys=True)) # default keys are integers
[(0, 1, 0), (1, 2, 0), (2, 3, 0)]
>>> list(G.edges(data=True, keys=True))
[(0, 1, 0, {}), (1, 2, 0, {}), (2, 3, 0, {'weight': 5})]
>>> list(G.edges(data='weight', default=1, keys=True))
[(0, 1, 0, 1), (1, 2, 0, 1), (2, 3, 0, 5)]
>>> list(G.edges([0,2]))
[(0, 1), (2, 3)]
>>> list(G.edges(0))
[(0, 1)]
See also:
in_edges,out_edges
networkx.MultiDiGraph.out_edges
MultiDiGraph.out_edges
An OutMultiEdgeView of the Graph as G.edges or G.edges().
edges(self, nbunch=None, data=False, keys=False, default=None)
110 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
The OutMultiEdgeView provides set-like operations on the edge-tuples as well as edge attribute lookup. When
called, it also provides an EdgeDataView object which allows control of access to edge attributes (but does not
provide set-like operations). Hence, G.edges[u, v]['color'] provides the value of the color attribute
for edge (u, v) while for (u, v, c) in G.edges(data='color', default='red'): iter-
ates through all the edges yielding the color attribute with default 'red' if no color attribute exists.
Edges are returned as tuples with optional data and keys in the order (node, neighbor, key, data).
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•keys (bool, optional (default=False)) – If True, return edge keys with each edge.
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edges – A view of edge attributes, usually it iterates over (u, v) (u, v, k) or (u, v, k, d) tuples
of edges, but can also be used for attribute lookup as edges[u, v, k]['foo'].
Return type EdgeView
Notes
Nodes in nbunch that are not in the graph will be (quietly) ignored. For directed graphs this returns the out-edges.
Examples
>>> G=nx.MultiDiGraph()
>>> nx.add_path(G, [0,1,2])
>>> key =G.add_edge(2,3, weight=5)
>>> [e for ein G.edges()]
[(0, 1), (1, 2), (2, 3)]
>>> list(G.edges(data=True)) # default data is {} (empty dict)
[(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})]
>>> list(G.edges(data='weight', default=1))
[(0, 1, 1), (1, 2, 1), (2, 3, 5)]
>>> list(G.edges(keys=True)) # default keys are integers
[(0, 1, 0), (1, 2, 0), (2, 3, 0)]
>>> list(G.edges(data=True, keys=True))
[(0, 1, 0, {}), (1, 2, 0, {}), (2, 3, 0, {'weight': 5})]
>>> list(G.edges(data='weight', default=1, keys=True))
[(0, 1, 0, 1), (1, 2, 0, 1), (2, 3, 0, 5)]
>>> list(G.edges([0,2]))
[(0, 1), (2, 3)]
>>> list(G.edges(0))
[(0, 1)]
See also:
in_edges,out_edges
2.2. Basic graph types 111

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiDiGraph.in_edges
MultiDiGraph.in_edges
An InMultiEdgeView of the Graph as G.in_edges or G.in_edges().
in_edges(self, nbunch=None, data=False, keys=False, default=None)
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•data (string or bool, optional (default=False)) – The edge attribute returned in 3-tuple (u, v,
ddict[data]). If True, return edge attribute dict in 3-tuple (u, v, ddict). If False, return 2-tuple
(u, v).
•keys (bool, optional (default=False)) – If True, return edge keys with each edge.
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns in_edges – A view of edge attributes, usually it iterates over (u, v) or (u, v, k) or (u, v, k, d)
tuples of edges, but can also be used for attribute lookup as edges[u, v, k]['foo'].
Return type InMultiEdgeView
See also:
edges
networkx.MultiDiGraph.has_edge
MultiDiGraph.has_edge(u,v,key=None)
Return True if the graph has an edge between nodes u and v.
This is the same as v in G[u] or key in G[u][v] without KeyError exceptions.
Parameters
•u, v (nodes) – Nodes can be, for example, strings or numbers.
•key (hashable identifier, optional (default=None)) – If specified return True only if the edge
with key is found.
Returns edge_ind – True if edge is in the graph, False otherwise.
Return type bool
Examples
Can be called either using two nodes u, v, an edge tuple (u, v), or an edge tuple (u, v, key).
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> nx.add_path(G, [0,1,2,3])
>>> G.has_edge(0,1)# using two nodes
True
>>> e=(0,1)
>>> G.has_edge(*e) # e is a 2-tuple (u, v)
True
>>> G.add_edge(0,1, key='a')
(continues on next page)
112 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
'a'
>>> G.has_edge(0,1, key='a')# specify key
True
>>> e=(0,1,'a')
>>> G.has_edge(*e) # e is a 3-tuple (u, v, 'a')
True
The following syntax are equivalent:
>>> G.has_edge(0,1)
True
>>> 1in G[0]# though this gives :exc:`KeyError` if 0 not in G
True
networkx.MultiDiGraph.get_edge_data
MultiDiGraph.get_edge_data(u,v,key=None,default=None)
Return the attribute dictionary associated with edge (u, v).
This is identical to G[u][v][key] except the default is returned instead of an exception is the edge doesn’t
exist.
Parameters
•u, v (nodes)
•default (any Python object (default=None)) – Value to return if the edge (u, v) is not found.
•key (hashable identifier, optional (default=None)) – Return data only for the edge with
specified key.
Returns edge_dict – The edge attribute dictionary.
Return type dictionary
Examples
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> key =G.add_edge(0,1, key='a', weight=7)
>>> G[0][1]['a']# key='a'
{'weight': 7}
>>> G.edges[0,1,'a']# key='a'
{'weight': 7}
Warning: we protect the graph data structure by making G.edges and G[1][2] read-only dict-like structures.
However, you can assign values to attributes in e.g. G.edges[1, 2, 'a'] or G[1][2]['a'] using an
additional bracket as shown next. You need to specify all edge info to assign to the edge data associated with an
edge.
>>> G[0][1]['a']['weight']=10
>>> G.edges[0,1,'a']['weight']=10
>>> G[0][1]['a']['weight']
10
>>> G.edges[1,0,'a']['weight']
10
2.2. Basic graph types 113

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.MultiGraph() # or MultiDiGraph
>>> nx.add_path(G, [0,1,2,3])
>>> G.get_edge_data(0,1)
{0: {}}
>>> e=(0,1)
>>> G.get_edge_data(*e) # tuple form
{0: {}}
>>> G.get_edge_data('a','b', default=0)# edge not in graph, return 0
0
networkx.MultiDiGraph.neighbors
MultiDiGraph.neighbors(n)
Return an iterator over successor nodes of n.
A successor of n is a node m such that there exists a directed edge from n to m.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
predecessors()
Notes
neighbors() and successors() are the same.
networkx.MultiDiGraph.adj
MultiDiGraph.adj
Graph adjacency object holding the neighbors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is keyed
by neighbor to the edgekey-dict. So G.adj[3][2][0]['color'] = 'blue' sets the color of the edge
(3, 2, 0) to "blue".
Iterating over G.adj behaves like a dict. Useful idioms include for nbr, datadict in G.adj[n].
items():.
The neighbor information is also provided by subscripting the graph. So for nbr, foovalue in
G[node].data('foo', default=1): works.
For directed graphs, G.adj holds outgoing (successor) info.
networkx.MultiDiGraph.__getitem__
MultiDiGraph.__getitem__(n)
Return a dict of neighbors of node n. Use: ‘G[n]’.
Parameters n (node) – A node in the graph.
Returns adj_dict – The adjacency dictionary for nodes connected to n.
Return type dictionary
114 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
G[n] is the same as G.adj[n] and similar to G.neighbors(n) (which is an iterator over G.adj[n])
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G[0]
AtlasView({1: {}})
networkx.MultiDiGraph.successors
MultiDiGraph.successors(n)
Return an iterator over successor nodes of n.
A successor of n is a node m such that there exists a directed edge from n to m.
Parameters n (node) – A node in the graph
Raises NetworkXError – If n is not in the graph.
See also:
predecessors()
Notes
neighbors() and successors() are the same.
networkx.MultiDiGraph.succ
MultiDiGraph.succ
Graph adjacency object holding the successors of each node.
This object is a read-only dict-like structure with node keys and neighbor-dict values. The neighbor-dict is keyed
by neighbor to the edgekey-dict. So G.adj[3][2][0]['color'] = 'blue' sets the color of the edge
(3, 2, 0) to "blue".
Iterating over G.adj behaves like a dict. Useful idioms include for nbr, datadict in G.adj[n].
items():.
The neighbor information is also provided by subscripting the graph. So for nbr, foovalue in
G[node].data('foo', default=1): works.
For directed graphs, G.succ is identical to G.adj.
networkx.MultiDiGraph.predecessors
MultiDiGraph.predecessors(n)
Return an iterator over predecessor nodes of n.
A predecessor of n is a node m such that there exists a directed edge from m to n.
Parameters n (node) – A node in the graph
2.2. Basic graph types 115

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises NetworkXError – If n is not in the graph.
See also:
successors()
networkx.MultiDiGraph.adjacency
MultiDiGraph.adjacency()
Return an iterator over (node, adjacency dict) tuples for all nodes.
For directed graphs, only outgoing neighbors/adjacencies are included.
Returns adj_iter – An iterator over (node, adjacency dictionary) for all nodes in the graph.
Return type iterator
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> [(n, nbrdict) for n, nbrdict in G.adjacency()]
[(0, {1: {}}), (1, {0: {}, 2: {}}), (2, {1: {}, 3: {}}), (3, {2: {}})]
networkx.MultiDiGraph.nbunch_iter
MultiDiGraph.nbunch_iter(nbunch=None)
Return an iterator over nodes contained in nbunch that are also in the graph.
The nodes in nbunch are checked for membership in the graph and if not are silently ignored.
Parameters nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
Returns niter – An iterator over nodes in nbunch that are also in the graph. If nbunch is None,
iterate over all nodes in the graph.
Return type iterator
Raises NetworkXError – If nbunch is not a node or or sequence of nodes. If a node in nbunch is
not hashable.
See also:
Graph.__iter__()
Notes
When nbunch is an iterator, the returned iterator yields values directly from nbunch, becoming exhausted when
nbunch is exhausted.
To test whether nbunch is a single node, one can use “if nbunch in self:”, even after processing with this routine.
If nbunch is not a node or a (possibly empty) sequence/iterator or None, a NetworkXError is raised. Also, if
any object in nbunch is not hashable, a NetworkXError is raised.
116 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Counting nodes edges and neighbors
MultiDiGraph.order() Return the number of nodes in the graph.
MultiDiGraph.number_of_nodes() Return the number of nodes in the graph.
MultiDiGraph.__len__() Return the number of nodes.
MultiDiGraph.degree A DegreeView for the Graph as G.degree or G.degree().
MultiDiGraph.in_degree A DegreeView for (node, in_degree) or in_degree for
single node.
MultiDiGraph.out_degree Return an iterator for (node, out-degree) or out-degree
for single node.
MultiDiGraph.size([weight]) Return the number of edges or total of all edge weights.
MultiDiGraph.number_of_edges([u, v]) Return the number of edges between two nodes.
networkx.MultiDiGraph.order
MultiDiGraph.order()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
number_of_nodes(),__len__()
networkx.MultiDiGraph.number_of_nodes
MultiDiGraph.number_of_nodes()
Return the number of nodes in the graph.
Returns nnodes – The number of nodes in the graph.
Return type int
See also:
order(),__len__()
Examples
>>> G=nx.path_graph(3)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
3
networkx.MultiDiGraph.__len__
MultiDiGraph.__len__()
Return the number of nodes. Use: ‘len(G)’.
Returns nnodes – The number of nodes in the graph.
Return type int
2.2. Basic graph types 117

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> len(G)
4
networkx.MultiDiGraph.degree
MultiDiGraph.degree
A DegreeView for the Graph as G.degree or G.degree().
The node degree is the number of edges adjacent to the node. The weighted node degree is the sum of the edge
weights for edges incident to that node.
This object provides an iterator for (node, degree) as well as lookup for the degree for a single node.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The name of an edge attribute that holds
the numerical value used as a weight. If None, then each edge has weight 1. The degree is
the sum of the edge weights adjacent to the node.
Returns
•If a single nodes is requested
•deg (int) – Degree of the node
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, degree).
See also:
out_degree,in_degree
Examples
>>> G=nx.MultiDiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.degree(0)# node 0 with degree 1
1
>>> list(G.degree([0,1,2]))
[(0, 1), (1, 2), (2, 2)]
networkx.MultiDiGraph.in_degree
MultiDiGraph.in_degree
A DegreeView for (node, in_degree) or in_degree for single node.
The node in-degree is the number of edges pointing in to the node. The weighted node degree is the sum of the
edge weights for edges incident to that node.
This object provides an iterator for (node, degree) as well as lookup for the degree for a single node.
118 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights adjacent to the node.
Returns
•If a single node is requested
•deg (int) – Degree of the node
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, in-degree).
See also:
degree,out_degree
Examples
>>> G=nx.MultiDiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.in_degree(0)# node 0 with degree 0
0
>>> list(G.in_degree([0,1,2]))
[(0, 0), (1, 1), (2, 1)]
networkx.MultiDiGraph.out_degree
MultiDiGraph.out_degree
Return an iterator for (node, out-degree) or out-degree for single node.
out_degree(self, nbunch=None, weight=None)
The node out-degree is the number of edges pointing out of the node. This function returns the out-degree for a
single node or an iterator for a bunch of nodes or if nothing is passed as argument.
Parameters
•nbunch (single node, container, or all nodes (default= all nodes)) – The view will only
report edges incident to these nodes.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights.
Returns
•If a single node is requested
•deg (int) – Degree of the node
•OR if multiple nodes are requested
•nd_iter (iterator) – The iterator returns two-tuples of (node, out-degree).
2.2. Basic graph types 119

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
degree,in_degree
Examples
>>> G=nx.MultiDiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> G.out_degree(0)# node 0 with degree 1
1
>>> list(G.out_degree([0,1,2]))
[(0, 1), (1, 1), (2, 1)]
networkx.MultiDiGraph.size
MultiDiGraph.size(weight=None)
Return the number of edges or total of all edge weights.
Parameters weight (string or None, optional (default=None)) – The edge attribute that holds the
numerical value used as a weight. If None, then each edge has weight 1.
Returns
size – The number of edges or (if weight keyword is provided) the total weight sum.
If weight is None, returns an int. Otherwise a float (or more general numeric if the weights are
more general).
Return type numeric
See also:
number_of_edges()
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.size()
3
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge('a','b', weight=2)
>>> G.add_edge('b','c', weight=4)
>>> G.size()
2
>>> G.size(weight='weight')
6.0
networkx.MultiDiGraph.number_of_edges
MultiDiGraph.number_of_edges(u=None,v=None)
Return the number of edges between two nodes.
Parameters u, v (nodes, optional (Gefault=all edges)) – If u and v are specified, return the number
of edges between u and v. Otherwise return the total number of all edges.
120 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns nedges – The number of edges in the graph. If nodes uand vare specified return the
number of edges between those nodes. If the graph is directed, this only returns the number of
edges from uto v.
Return type int
See also:
size()
Examples
For undirected multigraphs, this method counts the total number of edges in the graph:
>>> G=nx.MultiGraph()
>>> G.add_edges_from([(0,1), (0,1), (1,2)])
[0, 1, 0]
>>> G.number_of_edges()
3
If you specify two nodes, this counts the total number of edges joining the two nodes:
>>> G.number_of_edges(0,1)
2
For directed multigraphs, this method can count the total number of directed edges from uto v:
>>> G=nx.MultiDiGraph()
>>> G.add_edges_from([(0,1), (0,1), (1,0)])
[0, 1, 0]
>>> G.number_of_edges(0,1)
2
>>> G.number_of_edges(1,0)
1
Making copies and subgraphs
MultiDiGraph.copy([as_view]) Return a copy of the graph.
MultiDiGraph.to_undirected([reciprocal,
as_view])
Return an undirected representation of the digraph.
MultiDiGraph.to_directed([as_view]) Return a directed representation of the graph.
MultiDiGraph.subgraph(nodes) Return a SubGraph view of the subgraph induced on
nodes.
MultiDiGraph.edge_subgraph(edges) Returns the subgraph induced by the specified edges.
MultiDiGraph.reverse([copy]) Return the reverse of the graph.
networkx.MultiDiGraph.copy
MultiDiGraph.copy(as_view=False)
Return a copy of the graph.
The copy method by default returns an independent shallow copy of the graph and attributes. That is, if an
attribute is a container, that container is shared by the original an the copy. Use Python’s copy.deepcopy for
new containers.
2.2. Basic graph types 121
NetworkX Reference, Release 2.3rc1.dev20181203210840
If as_view is True then a view is returned instead of a copy.
Notes
All copies reproduce the graph structure, but data attributes may be handled in different ways. There are four
types of copies of a graph that people might want.
Deepcopy – A “deepcopy” copies the graph structure as well as all data attributes and any objects they might
contain. The entire graph object is new so that changes in the copy do not affect the original object. (see Python’s
copy.deepcopy)
Data Reference (Shallow) – For a shallow copy the graph structure is copied but the edge, node and graph at-
tribute dicts are references to those in the original graph. This saves time and memory but could cause confusion
if you change an attribute in one graph and it changes the attribute in the other. NetworkX does not provide this
level of shallow copy.
Independent Shallow – This copy creates new independent attribute dicts and then does a shallow copy of the
attributes. That is, any attributes that are containers are shared between the new graph and the original. This is
exactly what dict.copy() provides. You can obtain this style copy using:
>>> G=nx.path_graph(5)
>>> H=G.copy()
>>> H=G.copy(as_view=False)
>>> H=nx.Graph(G)
>>> H=G.__class__(G)
Fresh Data – For fresh data, the graph structure is copied while new empty data attribute dicts are created. The
resulting graph is independent of the original and it has no edge, node or graph attributes. Fresh copies are not
enabled. Instead use:
>>> H=G.__class__()
>>> H.add_nodes_from(G)
>>> H.add_edges_from(G.edges)
View – Inspired by dict-views, graph-views act like read-only versions of the original graph, providing a copy
of the original structure without requiring any memory for copying the information.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Parameters as_view (bool, optional (default=False)) – If True, the returned graph-view provides a
read-only view of the original graph without actually copying any data.
Returns G – A copy of the graph.
Return type Graph
See also:
to_directed() return a directed copy of the graph.
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.copy()
122 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiDiGraph.to_undirected
MultiDiGraph.to_undirected(reciprocal=False,as_view=False)
Return an undirected representation of the digraph.
Parameters
•reciprocal (bool (optional)) – If True only keep edges that appear in both directions in the
original digraph.
•as_view (bool (optional, default=False)) – If True return an undirected view of the original
directed graph.
Returns G – An undirected graph with the same name and nodes and with edge (u, v, data) if either
(u, v, data) or (v, u, data) is in the digraph. If both edges exist in digraph and their edge data is
different, only one edge is created with an arbitrary choice of which edge data to use. You must
check and correct for this manually if desired.
Return type MultiGraph
See also:
MultiGraph(),copy(),add_edge(),add_edges_from()
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar D=MultiiGraph(G) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed MultiDiGraph to use dict-like objects in the data structure, those changes do
not transfer to the MultiGraph created by this method.
Examples
>>> G=nx.path_graph(2)# or MultiGraph, etc
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
>>> G2 =H.to_undirected()
>>> list(G2.edges)
[(0, 1)]
networkx.MultiDiGraph.to_directed
MultiDiGraph.to_directed(as_view=False)
Return a directed representation of the graph.
Returns G – A directed graph with the same name, same nodes, and with each edge (u, v, data)
replaced by two directed edges (u, v, data) and (v, u, data).
Return type MultiDiGraph
2.2. Basic graph types 123

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This returns a “deepcopy” of the edge, node, and graph attributes which attempts to completely copy all of the
data and references.
This is in contrast to the similar D=DiGraph(G) which returns a shallow copy of the data.
See the Python copy module for more information on shallow and deep copies, https://docs.python.org/2/library/
copy.html.
Warning: If you have subclassed MultiGraph to use dict-like objects in the data structure, those changes do not
transfer to the MultiDiGraph created by this method.
Examples
>>> G=nx.Graph() # or MultiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1), (1, 0)]
If already directed, return a (deep) copy
>>> G=nx.DiGraph() # or MultiDiGraph, etc
>>> G.add_edge(0,1)
>>> H=G.to_directed()
>>> list(H.edges)
[(0, 1)]
networkx.MultiDiGraph.subgraph
MultiDiGraph.subgraph(nodes)
Return a SubGraph view of the subgraph induced on nodes.
The induced subgraph of the graph contains the nodes in nodes and the edges between those nodes.
Parameters nodes (list, iterable) – A container of nodes which will be iterated through once.
Returns G – A subgraph view of the graph. The graph structure cannot be changed but node/edge
attributes can and are shared with the original graph.
Return type SubGraph View
Notes
The graph, edge and node attributes are shared with the original graph. Changes to the graph structure is ruled
out by the view, but changes to attributes are reflected in the original graph.
To create a subgraph with its own copy of the edge/node attributes use: G.subgraph(nodes).copy()
For an inplace reduction of a graph to a subgraph you can remove nodes: G.remove_nodes_from([n for n in G
if n not in set(nodes)])
Subgraph views are sometimes NOT what you want. In most cases where you want to do more than simply look
at the induced edges, it makes more sense to just create the subgraph as its own graph with code like:
124 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
# Create a subgraph SG based on a (possibly multigraph) G
SG =G.__class__()
SG.add_nodes_from((n, G.nodes[n]) for nin largest_wcc)
if SG.is_multigraph:
SG.add_edges_from((n, nbr, key, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, keydict in nbrs.items() if nbr in largest_wcc
for key, d in keydict.items())
else:
SG.add_edges_from((n, nbr, d)
for n, nbrs in G.adj.items() if nin largest_wcc
for nbr, d in nbrs.items() if nbr in largest_wcc)
SG.graph.update(G.graph)
Examples
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.subgraph([0,1,2])
>>> list(H.edges)
[(0, 1), (1, 2)]
networkx.MultiDiGraph.edge_subgraph
MultiDiGraph.edge_subgraph(edges)
Returns the subgraph induced by the specified edges.
The induced subgraph contains each edge in edges and each node incident to any one of those edges.
Parameters edges (iterable) – An iterable of edges in this graph.
Returns G – An edge-induced subgraph of this graph with the same edge attributes.
Return type Graph
Notes
The graph, edge, and node attributes in the returned subgraph view are references to the corresponding attributes
in the original graph. The view is read-only.
To create a full graph version of the subgraph with its own copy of the edge or node attributes, use:
>>> G.edge_subgraph(edges).copy()
Examples
>>> G=nx.path_graph(5)
>>> H=G.edge_subgraph([(0,1), (3,4)])
>>> list(H.nodes)
[0, 1, 3, 4]
>>> list(H.edges)
[(0, 1), (3, 4)]
2.2. Basic graph types 125

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.MultiDiGraph.reverse
MultiDiGraph.reverse(copy=True)
Return the reverse of the graph.
The reverse is a graph with the same nodes and edges but with the directions of the edges reversed.
Parameters copy (bool optional (default=True)) – If True, return a new DiGraph holding the re-
versed edges. If False, the reverse graph is created using a view of the original graph.
2.2.5 Ordered Graphs—Consistently ordered graphs
Consistently ordered variants of the default base classes. Note that if you are using Python 3.6+, you shouldn’t need
these classes because the dicts in Python 3.6+ are ordered. Note also that there are many differing expectations for the
word “ordered” and that these classes may not provide the order you expect. The intent here is to give a consistent
order not a particular order.
The Ordered (Di/Multi/MultiDi) Graphs give a consistent order for reporting of nodes and edges. The order of node
reporting agrees with node adding, but for edges, the order is not necessarily the order that the edges were added.
In general, you should use the default (i.e., unordered) graph classes. However, there are times (e.g., when testing)
when you may need the order preserved.
Special care is required when using subgraphs of the Ordered classes. The order of nodes in the subclass is not
necessarily the same order as the original class. In general it is probably better to avoid using subgraphs and replace
with code similar to:
# instead of SG = G.subgraph(ordered_nodes) SG=nx.OrderedGraph()
SG.add_nodes_from(ordered_nodes) SG.add_edges_from((u, v) for (u, v) in G.edges() if u in SG
if v in SG)
class OrderedGraph(incoming_graph_data=None,**attr)
Consistently ordered variant of Graph.
class OrderedDiGraph(incoming_graph_data=None,**attr)
Consistently ordered variant of DiGraph.
class OrderedMultiGraph(incoming_graph_data=None,**attr)
Consistently ordered variant of MultiGraph.
class OrderedMultiDiGraph(incoming_graph_data=None,**attr)
Consistently ordered variant of MultiDiGraph.
Note: NetworkX uses dicts to store the nodes and neighbors in a graph. So the reporting of nodes and edges for
the base graph classes will not necessarily be consistent across versions and platforms. If you need the order of nodes
and edges to be consistent (e.g., when writing automated tests), please see OrderedGraph,OrderedDiGraph,
OrderedMultiGraph, or OrderedMultiDiGraph, which behave like the base graph classes but give a consis-
tent order for reporting of nodes and edges.
2.3 Graph Views
View of Graphs as SubGraph, Reverse, Directed, Undirected.
126 Chapter 2. Graph types

NetworkX Reference, Release 2.3rc1.dev20181203210840
In some algorithms it is convenient to temporarily morph a graph to exclude some nodes or edges. It should be better
to do that via a view than to remove and then re-add. In other algorithms it is convenient to temporarily morph a graph
to reverse directed edges, or treat a directed graph as undirected, etc. This module provides those graph views.
The resulting views are essentially read-only graphs that report data from the orignal graph object. We provide an
attribute G._graph which points to the underlying graph object.
Note: Since graphviews look like graphs, one can end up with view-of-view-of-view chains. Be careful with chains
because they become very slow with about 15 nested views. For the common simple case of node induced subgraphs
created from the graph class, we short-cut the chain by returning a subgraph of the original graph directly rather than
a subgraph of a subgraph. We are careful not to disrupt any edge filter in the middle subgraph. In general, determining
how to short-cut the chain is tricky and much harder with restricted_views than with induced subgraphs. Often it is
easiest to use .copy() to avoid chains.
generic_graph_view(G[, create_using])
subgraph_view(G[, filter_node, filter_edge])
reverse_view(G)
2.3.1 networkx.classes.graphviews.generic_graph_view
generic_graph_view(G,create_using=None)
2.3.2 networkx.classes.graphviews.subgraph_view
subgraph_view(G,filter_node=<function no_filter>,filter_edge=<function no_filter>)
2.3.3 networkx.classes.graphviews.reverse_view
reverse_view(G)
2.3. Graph Views 127

NetworkX Reference, Release 2.3rc1.dev20181203210840
128 Chapter 2. Graph types
CHAPTER
THREE
ALGORITHMS
3.1 Approximations and Heuristics
Approximations of graph properties and Heuristic functions for optimization problems.
Warning: The approximation submodule is not imported in the top-level networkx.
These functions can be imported with from networkx.algorithms import
approximation.
3.1.1 Connectivity
Fast approximation for node connectivity
all_pairs_node_connectivity(G[, nbunch,
cutoff])
Compute node connectivity between all pairs of nodes.
local_node_connectivity(G, source, target[,
...])
Compute node connectivity between source and target.
node_connectivity(G[, s, t]) Returns an approximation for node connectivity for a
graph or digraph G.
networkx.algorithms.approximation.connectivity.all_pairs_node_connectivity
all_pairs_node_connectivity(G,nbunch=None,cutoff=None)
Compute node connectivity between all pairs of nodes.
Pairwise or local node connectivity between two distinct and nonadjacent nodes is the minimum number of
nodes that must be removed (minimum separating cutset) to disconnect them. By Menger’s theorem, this is
equal to the number of node independent paths (paths that share no nodes other than source and target). Which
is what we compute in this function.
This algorithm is a fast approximation that gives an strict lower bound on the actual number of node independent
paths between two nodes1. It works for both directed and undirected graphs.
Parameters
•G(NetworkX graph)
1White, Douglas R., and Mark Newman. 2001 A Fast Algorithm for Node-Independent Paths. Santa Fe Institute Working Paper #01-07-035
http://eclectic.ss.uci.edu/~drwhite/working.pdf
129

NetworkX Reference, Release 2.3rc1.dev20181203210840
•nbunch (container) – Container of nodes. If provided node connectivity will be computed
only over pairs of nodes in nbunch.
•cutoff (integer) – Maximum node connectivity to consider. If None, the minimum degree
of source or target is used as a cutoff in each pair of nodes. Default value None.
Returns K – Dictionary, keyed by source and target, of pairwise node connectivity
Return type dictionary
See also:
local_node_connectivity(),all_pairs_node_connectivity()
References
networkx.algorithms.approximation.connectivity.local_node_connectivity
local_node_connectivity(G,source,target,cutoff=None)
Compute node connectivity between source and target.
Pairwise or local node connectivity between two distinct and nonadjacent nodes is the minimum number of
nodes that must be removed (minimum separating cutset) to disconnect them. By Menger’s theorem, this is
equal to the number of node independent paths (paths that share no nodes other than source and target). Which
is what we compute in this function.
This algorithm is a fast approximation that gives an strict lower bound on the actual number of node independent
paths between two nodes1. It works for both directed and undirected graphs.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for node connectivity
•target (node) – Ending node for node connectivity
•cutoff (integer) – Maximum node connectivity to consider. If None, the minimum degree
of source or target is used as a cutoff. Default value None.
Returns k – pairwise node connectivity
Return type integer
Examples
>>> # Platonic octahedral graph has node connectivity 4
>>> # for each non adjacent node pair
>>> from networkx.algorithms import approximation as approx
>>> G=nx.octahedral_graph()
>>> approx.local_node_connectivity(G, 0,5)
4
1White, Douglas R., and Mark Newman. 2001 A Fast Algorithm for Node-Independent Paths. Santa Fe Institute Working Paper #01-07-035
http://eclectic.ss.uci.edu/~drwhite/working.pdf
130 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This algorithm1finds node independents paths between two nodes by computing their shortest path using BFS,
marking the nodes of the path found as ‘used’ and then searching other shortest paths excluding the nodes
marked as used until no more paths exist. It is not exact because a shortest path could use nodes that, if the path
were longer, may belong to two different node independent paths. Thus it only guarantees an strict lower bound
on node connectivity.
Note that the authors propose a further refinement, losing accuracy and gaining speed, which is not implemented
yet.
See also:
all_pairs_node_connectivity(),node_connectivity()
References
networkx.algorithms.approximation.connectivity.node_connectivity
node_connectivity(G,s=None,t=None)
Returns an approximation for node connectivity for a graph or digraph G.
Node connectivity is equal to the minimum number of nodes that must be removed to disconnect G or render it
trivial. By Menger’s theorem, this is equal to the number of node independent paths (paths that share no nodes
other than source and target).
If source and target nodes are provided, this function returns the local node connectivity: the minimum number
of nodes that must be removed to break all paths from source to target in G.
This algorithm is based on a fast approximation that gives an strict lower bound on the actual number of node
independent paths between two nodes1. It works for both directed and undirected graphs.
Parameters
•G(NetworkX graph) – Undirected graph
•s(node) – Source node. Optional. Default value: None.
•t(node) – Target node. Optional. Default value: None.
Returns K – Node connectivity of G, or local node connectivity if source and target are provided.
Return type integer
Examples
>>> # Platonic octahedral graph is 4-node-connected
>>> from networkx.algorithms import approximation as approx
>>> G=nx.octahedral_graph()
>>> approx.node_connectivity(G)
4
1White, Douglas R., and Mark Newman. 2001 A Fast Algorithm for Node-Independent Paths. Santa Fe Institute Working Paper #01-07-035
http://eclectic.ss.uci.edu/~drwhite/working.pdf
3.1. Approximations and Heuristics 131

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This algorithm1finds node independents paths between two nodes by computing their shortest path using BFS,
marking the nodes of the path found as ‘used’ and then searching other shortest paths excluding the nodes
marked as used until no more paths exist. It is not exact because a shortest path could use nodes that, if the path
were longer, may belong to two different node independent paths. Thus it only guarantees an strict lower bound
on node connectivity.
See also:
all_pairs_node_connectivity(),local_node_connectivity()
References
3.1.2 K-components
Fast approximation for k-component structure
k_components(G[, min_density]) Returns the approximate k-component structure of a
graph G.
networkx.algorithms.approximation.kcomponents.k_components
k_components(G,min_density=0.95)
Returns the approximate k-component structure of a graph G.
Ak-component is a maximal subgraph of a graph G that has, at least, node connectivity k: we need to remove at
least knodes to break it into more components. k-components have an inherent hierarchical structure because
they are nested in terms of connectivity: a connected graph can contain several 2-components, each of which
can contain one or more 3-components, and so forth.
This implementation is based on the fast heuristics to approximate the k-component structure of a graph1.
Which, in turn, it is based on a fast approximation algorithm for finding good lower bounds of the number of
node independent paths between two nodes2.
Parameters
•G(NetworkX graph) – Undirected graph
•min_density (Float) – Density relaxation threshold. Default value 0.95
Returns k_components – Dictionary with connectivity level kas key and a list of sets of nodes that
form a k-component of level kas values.
Return type dict
Examples
>>> # Petersen graph has 10 nodes and it is triconnected, thus all
>>> # nodes are in a single component on all three connectivity levels
>>> from networkx.algorithms import approximation as apxa
(continues on next page)
1Torrents, J. and F. Ferraro (2015) Structural Cohesion: Visualization and Heuristics for Fast Computation. https://arxiv.org/pdf/1503.04476v1
2White, Douglas R., and Mark Newman (2001) A Fast Algorithm for Node-Independent Paths. Santa Fe Institute Working Paper #01-07-035
http://eclectic.ss.uci.edu/~drwhite/working.pdf
132 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G=nx.petersen_graph()
>>> k_components =apxa.k_components(G)
Notes
The logic of the approximation algorithm for computing the k-component structure1is based on repeatedly
applying simple and fast algorithms for k-cores and biconnected components in order to narrow down the
number of pairs of nodes over which we have to compute White and Newman’s approximation algorithm for
finding node independent paths2. More formally, this algorithm is based on Whitney’s theorem, which states
an inclusion relation among node connectivity, edge connectivity, and minimum degree for any graph G. This
theorem implies that every k-component is nested inside a k-edge-component, which in turn, is contained in a
k-core. Thus, this algorithm computes node independent paths among pairs of nodes in each biconnected part
of each k-core, and repeats this procedure for each kfrom 3 to the maximal core number of a node in the input
graph.
Because, in practice, many nodes of the core of level kinside a bicomponent actually are part of a component
of level k, the auxiliary graph needed for the algorithm is likely to be very dense. Thus, we use a complement
graph data structure (see AntiGraph) to save memory. AntiGraph only stores information of the edges that
are not present in the actual auxiliary graph. When applying algorithms to this complement graph data structure,
it behaves as if it were the dense version.
See also:
k_components()
References
3.1.3 Clique
Functions for computing large cliques.
max_clique(G) Find the Maximum Clique
clique_removal(G) Repeatedly remove cliques from the graph.
large_clique_size(G) Find the size of a large clique in a graph.
networkx.algorithms.approximation.clique.max_clique
max_clique(G)
Find the Maximum Clique
Finds the 𝑂(|𝑉|/(𝑙𝑜𝑔|𝑉|)2)apx of maximum clique/independent set in the worst case.
Parameters G (NetworkX graph) – Undirected graph
Returns clique – The apx-maximum clique of the graph
Return type set
Notes
A clique in an undirected graph G = (V, E) is a subset of the vertex set C subseteq V such that for every two
vertices in C there exists an edge connecting the two. This is equivalent to saying that the subgraph induced by
3.1. Approximations and Heuristics 133

NetworkX Reference, Release 2.3rc1.dev20181203210840
C is complete (in some cases, the term clique may also refer to the subgraph).
A maximum clique is a clique of the largest possible size in a given graph. The clique number omega(G) of
a graph G is the number of vertices in a maximum clique in G. The intersection number of G is the smallest
number of cliques that together cover all edges of G.
https://en.wikipedia.org/wiki/Maximum_clique
References
networkx.algorithms.approximation.clique.clique_removal
clique_removal(G)
Repeatedly remove cliques from the graph.
Results in a 𝑂(|𝑉|/(log |𝑉|)2)approximation of maximum clique and independent set. Returns the largest
independent set found, along with found maximal cliques.
Parameters G (NetworkX graph) – Undirected graph
Returns max_ind_cliques – 2-tuple of Maximal Independent Set and list of maximal cliques (sets).
Return type (set, list) tuple
References
networkx.algorithms.approximation.clique.large_clique_size
large_clique_size(G)
Find the size of a large clique in a graph.
Aclique is a subset of nodes in which each pair of nodes is adjacent. This function is a heuristic for finding the
size of a large clique in the graph.
Parameters G (NetworkX graph)
Returns The size of a large clique in the graph.
Return type int
Notes
This implementation is from1. Its worst case time complexity is 𝑂(𝑛𝑑2), where nis the number of nodes in the
graph and dis the maximum degree.
This function is a heuristic, which means it may work well in practice, but there is no rigorous mathematical
guarantee on the ratio between the returned number and the actual largest clique size in the graph.
References
See also:
networkx.algorithms.approximation.clique.max_clique() A function that returns an ap-
proximate maximum clique with a guarantee on the approximation ratio.
1Pattabiraman, Bharath, et al. “Fast Algorithms for the Maximum Clique Problem on Massive Graphs with Applications to Overlapping
Community Detection.” Internet Mathematics 11.4-5 (2015): 421–448. <https://doi.org/10.1080/15427951.2014.986778>
134 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.clique Functions for finding the exact maximum clique in a graph.
3.1.4 Clustering
average_clustering(G[, trials, seed]) Estimates the average clustering coefficient of G.
networkx.algorithms.approximation.clustering_coefficient.average_clustering
average_clustering(G,trials=1000,seed=None)
Estimates the average clustering coefficient of G.
The local clustering of each node in Gis the fraction of triangles that actually exist over all possible triangles in
its neighborhood. The average clustering coefficient of a graph Gis the mean of local clusterings.
This function finds an approximate average clustering coefficient for G by repeating ntimes (defined in
trials) the following experiment: choose a node at random, choose two of its neighbors at random, and
check if they are connected. The approximate coefficient is the fraction of triangles found over the number of
trials1.
Parameters
•G(NetworkX graph)
•trials (integer) – Number of trials to perform (default 1000).
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns c – Approximated average clustering coefficient.
Return type float
References
3.1.5 Dominating Set
Functions for finding node and edge dominating sets.
Adominating set for an undirected graph Gwith vertex set Vand edge set Eis a subset Dof Vsuch that every vertex
not in Dis adjacent to at least one member of D. An edge dominating set is a subset Fof Esuch that every edge not
in Fis incident to an endpoint of at least one edge in F.
min_weighted_dominating_set(G[, weight]) Returns a dominating set that approximates the mini-
mum weight node dominating set.
min_edge_dominating_set(G) Return minimum cardinality edge dominating set.
networkx.algorithms.approximation.dominating_set.min_weighted_dominating_set
min_weighted_dominating_set(G,weight=None)
Returns a dominating set that approximates the minimum weight node dominating set.
Parameters
1Schank, Thomas, and Dorothea Wagner. Approximating clustering coefficient and transitivity. Universität Karlsruhe, Fakultät für Informatik,
2004. http://www.emis.ams.org/journals/JGAA/accepted/2005/SchankWagner2005.9.2.pdf
3.1. Approximations and Heuristics 135

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(NetworkX graph) – Undirected graph.
•weight (string) – The node attribute storing the weight of an node. If provided, the node
attribute with this key must be a number for each node. If not provided, each node is assumed
to have weight one.
Returns min_weight_dominating_set – A set of nodes, the sum of whose weights is no more than
(log w(V)) w(V^*), where w(V) denotes the sum of the weights of each node in the graph
and w(V^*)denotes the sum of the weights of each node in the minimum weight dominating
set.
Return type set
Notes
This algorithm computes an approximate minimum weighted dominating set for the graph G. The returned
solution has weight (log w(V)) w(V^*), where w(V) denotes the sum of the weights of each node in the
graph and w(V^*)denotes the sum of the weights of each node in the minimum weight dominating set for the
graph.
This implementation of the algorithm runs in 𝑂(𝑚)time, where 𝑚is the number of edges in the graph.
References
networkx.algorithms.approximation.dominating_set.min_edge_dominating_set
min_edge_dominating_set(G)
Return minimum cardinality edge dominating set.
Parameters G (NetworkX graph) – Undirected graph
Returns min_edge_dominating_set – Returns a set of dominating edges whose size is no more
than 2 * OPT.
Return type set
Notes
The algorithm computes an approximate solution to the edge dominating set problem. The result is no more
than 2 * OPT in terms of size of the set. Runtime of the algorithm is 𝑂(|𝐸|).
3.1.6 Independent Set
Independent Set
Independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices
such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at
most one endpoint in I. The size of an independent set is the number of vertices it contains.
A maximum independent set is a largest independent set for a given graph G and its size is denoted 𝛼(G). The problem
of finding such a set is called the maximum independent set problem and is an NP-hard optimization problem. As
such, it is unlikely that there exists an efficient algorithm for finding a maximum independent set of a graph.
Wikipedia: Independent set
Independent set algorithm is based on the following paper:
136 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
𝑂(|𝑉|/(𝑙𝑜𝑔|𝑉|)2)apx of maximum clique/independent set.
Boppana, R., & Halldórsson, M. M. (1992). Approximating maximum independent sets by excluding subgraphs. BIT
Numerical Mathematics, 32(2), 180–196. Springer. doi:10.1007/BF01994876
maximum_independent_set(G) Return an approximate maximum independent set.
networkx.algorithms.approximation.independent_set.maximum_independent_set
maximum_independent_set(G)
Return an approximate maximum independent set.
Parameters G (NetworkX graph) – Undirected graph
Returns iset – The apx-maximum independent set
Return type Set
Notes
Finds the 𝑂(|𝑉|/(𝑙𝑜𝑔|𝑉|)2)apx of independent set in the worst case.
References
3.1.7 Matching
Graph Matching
Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a
common vertex.
Wikipedia: Matching
min_maximal_matching(G) Returns the minimum maximal matching of G.
networkx.algorithms.approximation.matching.min_maximal_matching
min_maximal_matching(G)
Returns the minimum maximal matching of G. That is, out of all maximal matchings of the graph G, the smallest
is returned.
Parameters G (NetworkX graph) – Undirected graph
Returns min_maximal_matching – Returns a set of edges such that no two edges share a common
endpoint and every edge not in the set shares some common endpoint in the set. Cardinality will
be 2*OPT in the worst case.
Return type set
Notes
The algorithm computes an approximate solution fo the minimum maximal cardinality matching problem. The
solution is no more than 2 * OPT in size. Runtime is 𝑂(|𝐸|).
3.1. Approximations and Heuristics 137
NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.1.8 Ramsey
Ramsey numbers.
ramsey_R2(G) Approximately computes the Ramsey number R(2;s,
t) for graph.
networkx.algorithms.approximation.ramsey.ramsey_R2
ramsey_R2(G)
Approximately computes the Ramsey number R(2;s,t) for graph.
Parameters G (NetworkX graph) – Undirected graph
Returns max_pair – Maximum clique, Maximum independent set.
Return type (set,set) tuple
3.1.9 Steiner Tree
metric_closure(G[, weight]) Return the metric closure of a graph.
steiner_tree(G, terminal_nodes[, weight]) Return an approximation to the minimum Steiner tree of
a graph.
networkx.algorithms.approximation.steinertree.metric_closure
metric_closure(G,weight=’weight’)
Return the metric closure of a graph.
The metric closure of a graph Gis the complete graph in which each edge is weighted by the shortest path
distance between the nodes in G.
Parameters G (NetworkX graph)
Returns Metric closure of the graph G.
Return type NetworkX graph
networkx.algorithms.approximation.steinertree.steiner_tree
steiner_tree(G,terminal_nodes,weight=’weight’)
Return an approximation to the minimum Steiner tree of a graph.
Parameters
•G(NetworkX graph)
•terminal_nodes (list) – A list of terminal nodes for which minimum steiner tree is to be
found.
Returns Approximation to the minimum steiner tree of Ginduced by terminal_nodes .
Return type NetworkX graph
138 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Steiner tree can be approximated by computing the minimum spanning tree of the subgraph of the metric closure
of the graph induced by the terminal nodes, where the metric closure of Gis the complete graph in which each
edge is weighted by the shortest path distance between the nodes in G. This algorithm produces a tree whose
weight is within a (2 - (2 / t)) factor of the weight of the optimal Steiner tree where tis number of terminal
nodes.
3.1.10 Treewidth
Functions for computing treewidth decomposition.
Treewidth of an undirected graph is a number associated with the graph. It can be defined as the size of the largest
vertex set (bag) in a tree decomposition of the graph minus one.
Wikipedia: Treewidth
The notions of treewidth and tree decomposition have gained their attractiveness partly because many graph and
network problems that are intractable (e.g., NP-hard) on arbitrary graphs become efficiently solvable (e.g., with a
linear time algorithm) when the treewidth of the input graphs is bounded by a constant12.
There are two different functions for computing a tree decomposition: treewidth_min_degree() and
treewidth_min_fill_in().
treewidth_min_degree(G) Returns a treewidth decomposition using the Minimum
Degree heuristic.
treewidth_min_fill_in(G) Returns a treewidth decomposition using the Minimum
Fill-in heuristic.
networkx.algorithms.approximation.treewidth.treewidth_min_degree
treewidth_min_degree(G)
Returns a treewidth decomposition using the Minimum Degree heuristic.
The heuristic chooses the nodes according to their degree, i.e., first the node with the lowest degree is chosen,
then the graph is updated and the corresponding node is removed. Next, a new node with the lowest degree is
chosen, and so on.
Parameters G (NetworkX graph)
Returns Treewidth decomposition – 2-tuple with treewidth and the corresponding decomposed
tree.
Return type (int,Graph) tuple
networkx.algorithms.approximation.treewidth.treewidth_min_fill_in
treewidth_min_fill_in(G)
Returns a treewidth decomposition using the Minimum Fill-in heuristic.
The heuristic chooses a node from the graph, where the number of edges added turning the neighbourhood of
the chosen node into clique is as small as possible.
1Hans L. Bodlaender and Arie M. C. A. Koster. 2010. “Treewidth computations I.Upper bounds”. Inf. Comput. 208, 3 (March 2010),259-275.
http://dx.doi.org/10.1016/j.ic.2009.03.008
2Hand L. Bodlaender. “Discovering Treewidth”. Institute of Information and Computing Sciences, Utrecht University. Technical Report
UU-CS-2005-018. http://www.cs.uu.nl
3.1. Approximations and Heuristics 139

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters G (NetworkX graph)
Returns Treewidth decomposition – 2-tuple with treewidth and the corresponding decomposed
tree.
Return type (int,Graph) tuple
3.1.11 Vertex Cover
Functions for computing an approximate minimum weight vertex cover.
Avertex cover is a subset of nodes such that each edge in the graph is incident to at least one node in the subset.
min_weighted_vertex_cover(G[, weight]) Returns an approximate minimum weighted vertex
cover.
networkx.algorithms.approximation.vertex_cover.min_weighted_vertex_cover
min_weighted_vertex_cover(G,weight=None)
Returns an approximate minimum weighted vertex cover.
The set of nodes returned by this function is guaranteed to be a vertex cover, and the total weight of the set is
guaranteed to be at most twice the total weight of the minimum weight vertex cover. In other words,
𝑤(𝑆)≤2*𝑤(𝑆*),
where 𝑆is the vertex cover returned by this function, 𝑆*is the vertex cover of minimum weight out of all vertex
covers of the graph, and 𝑤is the function that computes the sum of the weights of each node in that given set.
Parameters
•G(NetworkX graph)
•weight (string, optional (default = None)) – If None, every node has weight 1. If a string,
use this node attribute as the node weight. A node without this attribute is assumed to have
weight 1.
Returns min_weighted_cover – Returns a set of nodes whose weight sum is no more than twice
the weight sum of the minimum weight vertex cover.
Return type set
Notes
For a directed graph, a vertex cover has the same definition: a set of nodes such that each edge in the graph is
incident to at least one node in the set. Whether the node is the head or tail of the directed edge is ignored.
This is the local-ratio algorithm for computing an approximate vertex cover. The algorithm greedily reduces
the costs over edges, iteratively building a cover. The worst-case runtime of this implementation is 𝑂(𝑚log 𝑛),
where 𝑛is the number of nodes and 𝑚the number of edges in the graph.
References
3.2 Assortativity
140 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.2.1 Assortativity
degree_assortativity_coefficient(G[, x,
y, . . . ])
Compute degree assortativity of graph.
attribute_assortativity_coefficient(G,
attribute)
Compute assortativity for node attributes.
numeric_assortativity_coefficient(G,
attribute)
Compute assortativity for numerical node attributes.
degree_pearson_correlation_coefficient(G[,
...])
Compute degree assortativity of graph.
networkx.algorithms.assortativity.degree_assortativity_coefficient
degree_assortativity_coefficient(G,x=’out’,y=’in’,weight=None,nodes=None)
Compute degree assortativity of graph.
Assortativity measures the similarity of connections in the graph with respect to the node degree.
Parameters
•G(NetworkX graph)
•x(string (‘in’,’out’)) – The degree type for source node (directed graphs only).
•y(string (‘in’,’out’)) – The degree type for target node (directed graphs only).
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights adjacent to the node.
•nodes (list or iterable (optional)) – Compute degree assortativity only for nodes in container.
The default is all nodes.
Returns r – Assortativity of graph by degree.
Return type float
Examples
>>> G=nx.path_graph(4)
>>> r=nx.degree_assortativity_coefficient(G)
>>> print("%3.1f"%r)
-0.5
See also:
attribute_assortativity_coefficient(),numeric_assortativity_coefficient(),
neighbor_connectivity(),degree_mixing_dict(),degree_mixing_matrix()
Notes
This computes Eq. (21) in Ref.1, where e is the joint probability distribution (mixing matrix) of the degrees. If
G is directed than the matrix e is the joint probability of the user-specified degree type for the source and target.
1M. E. J. Newman, Mixing patterns in networks, Physical Review E, 67 026126, 2003
3.2. Assortativity 141
NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.algorithms.assortativity.attribute_assortativity_coefficient
attribute_assortativity_coefficient(G,attribute,nodes=None)
Compute assortativity for node attributes.
Assortativity measures the similarity of connections in the graph with respect to the given attribute.
Parameters
•G(NetworkX graph)
•attribute (string) – Node attribute key
•nodes (list or iterable (optional)) – Compute attribute assortativity for nodes in container.
The default is all nodes.
Returns r – Assortativity of graph for given attribute
Return type float
Examples
>>> G=nx.Graph()
>>> G.add_nodes_from([0,1],color='red')
>>> G.add_nodes_from([2,3],color='blue')
>>> G.add_edges_from([(0,1),(2,3)])
>>> print(nx.attribute_assortativity_coefficient(G,'color'))
1.0
Notes
This computes Eq. (2) in Ref.1, trace(M)-sum(M))/(1-sum(M), where M is the joint probability distribution
(mixing matrix) of the specified attribute.
References
networkx.algorithms.assortativity.numeric_assortativity_coefficient
numeric_assortativity_coefficient(G,attribute,nodes=None)
Compute assortativity for numerical node attributes.
Assortativity measures the similarity of connections in the graph with respect to the given numeric attribute.
The numeric attribute must be an integer.
Parameters
•G(NetworkX graph)
•attribute (string) – Node attribute key. The corresponding attribute value must be an integer.
•nodes (list or iterable (optional)) – Compute numeric assortativity only for attributes of
nodes in container. The default is all nodes.
Returns r – Assortativity of graph for given attribute
1M. E. J. Newman, Mixing patterns in networks, Physical Review E, 67 026126, 2003
142 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type float
Examples
>>> G=nx.Graph()
>>> G.add_nodes_from([0,1],size=2)
>>> G.add_nodes_from([2,3],size=3)
>>> G.add_edges_from([(0,1),(2,3)])
>>> print(nx.numeric_assortativity_coefficient(G,'size'))
1.0
Notes
This computes Eq. (21) in Ref.1, for the mixing matrix of of the specified attribute.
References
networkx.algorithms.assortativity.degree_pearson_correlation_coefficient
degree_pearson_correlation_coefficient(G,x=’out’,y=’in’,weight=None,nodes=None)
Compute degree assortativity of graph.
Assortativity measures the similarity of connections in the graph with respect to the node degree.
This is the same as degree_assortativity_coefficient but uses the potentially faster scipy.stats.pearsonr function.
Parameters
•G(NetworkX graph)
•x(string (‘in’,’out’)) – The degree type for source node (directed graphs only).
•y(string (‘in’,’out’)) – The degree type for target node (directed graphs only).
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights adjacent to the node.
•nodes (list or iterable (optional)) – Compute pearson correlation of degrees only for speci-
fied nodes. The default is all nodes.
Returns r – Assortativity of graph by degree.
Return type float
Examples
>>> G=nx.path_graph(4)
>>> r=nx.degree_pearson_correlation_coefficient(G)
>>> print("%3.1f"%r)
-0.5
1M. E. J. Newman, Mixing patterns in networks Physical Review E, 67 026126, 2003
3.2. Assortativity 143

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This calls scipy.stats.pearsonr.
References
3.2.2 Average neighbor degree
average_neighbor_degree(G[, source, target,
...])
Returns the average degree of the neighborhood of each
node.
networkx.algorithms.assortativity.average_neighbor_degree
average_neighbor_degree(G,source=’out’,target=’out’,nodes=None,weight=None)
Returns the average degree of the neighborhood of each node.
The average neighborhood degree of a node iis
𝑘𝑛𝑛,𝑖 =1
|𝑁(𝑖)|
𝑗∈𝑁(𝑖)
𝑘𝑗
where N(i) are the neighbors of node iand k_j is the degree of node jwhich belongs to N(i). For weighted
graphs, an analogous measure can be defined1,
𝑘𝑤
𝑛𝑛,𝑖 =1
𝑠𝑖
𝑗∈𝑁(𝑖)
𝑤𝑖𝑗 𝑘𝑗
where s_i is the weighted degree of node i,w_{ij} is the weight of the edge that links iand jand N(i)
are the neighbors of node i.
Parameters
•G(NetworkX graph)
•source (string (“in”|”out”)) – Directed graphs only. Use “in”- or “out”-degree for source
node.
•target (string (“in”|”out”)) – Directed graphs only. Use “in”- or “out”-degree for target
node.
•nodes (list or iterable, optional) – Compute neighbor degree for specified nodes. The default
is all nodes in the graph.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1.
Returns d – A dictionary keyed by node with average neighbors degree value.
Return type dict
Examples
1A. Barrat, M. Barthélemy, R. Pastor-Satorras, and A. Vespignani, “The architecture of complex weighted networks”. PNAS 101 (11):
3747–3752 (2004).
144 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(4)
>>> G.edges[0,1]['weight']=5
>>> G.edges[2,3]['weight']=3
>>> nx.average_neighbor_degree(G)
{0: 2.0, 1: 1.5, 2: 1.5, 3: 2.0}
>>> nx.average_neighbor_degree(G, weight='weight')
{0: 2.0, 1: 1.1666666666666667, 2: 1.25, 3: 2.0}
>>> G=nx.DiGraph()
>>> nx.add_path(G, [0,1,2,3])
>>> nx.average_neighbor_degree(G, source='in', target='in')
{0: 1.0, 1: 1.0, 2: 1.0, 3: 0.0}
>>> nx.average_neighbor_degree(G, source='out', target='out')
{0: 1.0, 1: 1.0, 2: 0.0, 3: 0.0}
Notes
For directed graphs you can also specify in-degree or out-degree by passing keyword arguments.
See also:
average_degree_connectivity()
References
3.2.3 Average degree connectivity
average_degree_connectivity(G[, source,
...])
Compute the average degree connectivity of graph.
k_nearest_neighbors(G[, source, target, . . . ]) Compute the average degree connectivity of graph.
networkx.algorithms.assortativity.average_degree_connectivity
average_degree_connectivity(G,source=’in+out’,target=’in+out’,nodes=None,weight=None)
Compute the average degree connectivity of graph.
The average degree connectivity is the average nearest neighbor degree of nodes with degree k. For weighted
graphs, an analogous measure can be computed using the weighted average neighbors degree defined in1, for a
node i, as
𝑘𝑤
𝑛𝑛,𝑖 =1
𝑠𝑖
𝑗∈𝑁(𝑖)
𝑤𝑖𝑗 𝑘𝑗
where s_i is the weighted degree of node i,w_{ij} is the weight of the edge that links iand j, and N(i)
are the neighbors of node i.
Parameters
•G(NetworkX graph)
1A. Barrat, M. Barthélemy, R. Pastor-Satorras, and A. Vespignani, “The architecture of complex weighted networks”. PNAS 101 (11):
3747–3752 (2004).
3.2. Assortativity 145

NetworkX Reference, Release 2.3rc1.dev20181203210840
•source (“in”|”out”|”in+out” (default:”in+out”)) – Directed graphs only. Use “in”- or
“out”-degree for source node.
•target (“in”|”out”|”in+out” (default:”in+out”) – Directed graphs only. Use “in”- or
“out”-degree for target node.
•nodes (list or iterable (optional)) – Compute neighbor connectivity for these nodes. The
default is all nodes.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1.
Returns d – A dictionary keyed by degree k with the value of average connectivity.
Return type dict
Raises ValueError – If either source or target are not one of ‘in’, ‘out’, or ‘in+out’.
Examples
>>> G=nx.path_graph(4)
>>> G.edges[1,2]['weight']=3
>>> nx.k_nearest_neighbors(G)
{1: 2.0, 2: 1.5}
>>> nx.k_nearest_neighbors(G, weight='weight')
{1: 2.0, 2: 1.75}
See also:
neighbors_average_degree()
Notes
This algorithm is sometimes called “k nearest neighbors” and is also available as k_nearest_neighbors.
References
networkx.algorithms.assortativity.k_nearest_neighbors
k_nearest_neighbors(G,source=’in+out’,target=’in+out’,nodes=None,weight=None)
Compute the average degree connectivity of graph.
The average degree connectivity is the average nearest neighbor degree of nodes with degree k. For weighted
graphs, an analogous measure can be computed using the weighted average neighbors degree defined in1, for a
node i, as
𝑘𝑤
𝑛𝑛,𝑖 =1
𝑠𝑖
𝑗∈𝑁(𝑖)
𝑤𝑖𝑗 𝑘𝑗
where s_i is the weighted degree of node i,w_{ij} is the weight of the edge that links iand j, and N(i)
are the neighbors of node i.
Parameters
•G(NetworkX graph)
1A. Barrat, M. Barthélemy, R. Pastor-Satorras, and A. Vespignani, “The architecture of complex weighted networks”. PNAS 101 (11):
3747–3752 (2004).
146 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•source (“in”|”out”|”in+out” (default:”in+out”)) – Directed graphs only. Use “in”- or
“out”-degree for source node.
•target (“in”|”out”|”in+out” (default:”in+out”) – Directed graphs only. Use “in”- or
“out”-degree for target node.
•nodes (list or iterable (optional)) – Compute neighbor connectivity for these nodes. The
default is all nodes.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1.
Returns d – A dictionary keyed by degree k with the value of average connectivity.
Return type dict
Raises ValueError – If either source or target are not one of ‘in’, ‘out’, or ‘in+out’.
Examples
>>> G=nx.path_graph(4)
>>> G.edges[1,2]['weight']=3
>>> nx.k_nearest_neighbors(G)
{1: 2.0, 2: 1.5}
>>> nx.k_nearest_neighbors(G, weight='weight')
{1: 2.0, 2: 1.75}
See also:
neighbors_average_degree()
Notes
This algorithm is sometimes called “k nearest neighbors” and is also available as k_nearest_neighbors.
References
3.2.4 Mixing
attribute_mixing_matrix(G, attribute[, . . . ]) Return mixing matrix for attribute.
degree_mixing_matrix(G[, x, y, weight, . . . ]) Return mixing matrix for attribute.
numeric_mixing_matrix(G, attribute[, nodes,
...])
Return numeric mixing matrix for attribute.
attribute_mixing_dict(G, attribute[, nodes,
...])
Return dictionary representation of mixing matrix for
attribute.
degree_mixing_dict(G[, x, y, weight, nodes,
...])
Return dictionary representation of mixing matrix for
degree.
mixing_dict(xy[, normalized]) Return a dictionary representation of mixing matrix.
networkx.algorithms.assortativity.attribute_mixing_matrix
attribute_mixing_matrix(G,attribute,nodes=None,mapping=None,normalized=True)
Return mixing matrix for attribute.
Parameters
3.2. Assortativity 147

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(graph) – NetworkX graph object.
•attribute (string) – Node attribute key.
•nodes (list or iterable (optional)) – Use only nodes in container to build the matrix. The
default is all nodes.
•mapping (dictionary, optional) – Mapping from node attribute to integer index in matrix. If
not specified, an arbitrary ordering will be used.
•normalized (bool (default=True)) – Return counts if False or probabilities if True.
Returns m – Counts or joint probability of occurrence of attribute pairs.
Return type numpy array
networkx.algorithms.assortativity.degree_mixing_matrix
degree_mixing_matrix(G,x=’out’,y=’in’,weight=None,nodes=None,normalized=True)
Return mixing matrix for attribute.
Parameters
•G(graph) – NetworkX graph object.
•x(string (‘in’,’out’)) – The degree type for source node (directed graphs only).
•y(string (‘in’,’out’)) – The degree type for target node (directed graphs only).
•nodes (list or iterable (optional)) – Build the matrix using only nodes in container. The
default is all nodes.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights adjacent to the node.
•normalized (bool (default=True)) – Return counts if False or probabilities if True.
Returns m – Counts, or joint probability, of occurrence of node degree.
Return type numpy array
networkx.algorithms.assortativity.numeric_mixing_matrix
numeric_mixing_matrix(G,attribute,nodes=None,normalized=True)
Return numeric mixing matrix for attribute.
The attribute must be an integer.
Parameters
•G(graph) – NetworkX graph object.
•attribute (string) – Node attribute key. The corresponding attribute must be an integer.
•nodes (list or iterable (optional)) – Build the matrix only with nodes in container. The
default is all nodes.
•normalized (bool (default=True)) – Return counts if False or probabilities if True.
Returns m – Counts, or joint, probability of occurrence of node attribute pairs.
Return type numpy array
148 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.assortativity.attribute_mixing_dict
attribute_mixing_dict(G,attribute,nodes=None,normalized=False)
Return dictionary representation of mixing matrix for attribute.
Parameters
•G(graph) – NetworkX graph object.
•attribute (string) – Node attribute key.
•nodes (list or iterable (optional)) – Unse nodes in container to build the dict. The default is
all nodes.
•normalized (bool (default=False)) – Return counts if False or probabilities if True.
Examples
>>> G=nx.Graph()
>>> G.add_nodes_from([0,1],color='red')
>>> G.add_nodes_from([2,3],color='blue')
>>> G.add_edge(1,3)
>>> d=nx.attribute_mixing_dict(G,'color')
>>> print(d['red']['blue'])
1
>>> print(d['blue']['red']) # d symmetric for undirected graphs
1
Returns d – Counts or joint probability of occurrence of attribute pairs.
Return type dictionary
networkx.algorithms.assortativity.degree_mixing_dict
degree_mixing_dict(G,x=’out’,y=’in’,weight=None,nodes=None,normalized=False)
Return dictionary representation of mixing matrix for degree.
Parameters
•G(graph) – NetworkX graph object.
•x(string (‘in’,’out’)) – The degree type for source node (directed graphs only).
•y(string (‘in’,’out’)) – The degree type for target node (directed graphs only).
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights adjacent to the node.
•normalized (bool (default=False)) – Return counts if False or probabilities if True.
Returns d – Counts or joint probability of occurrence of degree pairs.
Return type dictionary
3.2. Assortativity 149

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.assortativity.mixing_dict
mixing_dict(xy,normalized=False)
Return a dictionary representation of mixing matrix.
Parameters
•xy (list or container of two-tuples) – Pairs of (x,y) items.
•attribute (string) – Node attribute key
•normalized (bool (default=False)) – Return counts if False or probabilities if True.
Returns d – Counts or Joint probability of occurrence of values in xy.
Return type dictionary
3.3 Bipartite
This module provides functions and operations for bipartite graphs. Bipartite graphs B = (U, V, E) have two
node sets U,V and edges in Ethat only connect nodes from opposite sets. It is common in the literature to use an
spatial analogy referring to the two node sets as top and bottom nodes.
The bipartite algorithms are not imported into the networkx namespace at the top level so the easiest way to use them
is with:
>>> import networkx as nx
>>> from networkx.algorithms import bipartite
NetworkX does not have a custom bipartite graph class but the Graph() or DiGraph() classes can be used to represent
bipartite graphs. However, you have to keep track of which set each node belongs to, and make sure that there is no
edge between nodes of the same set. The convention used in NetworkX is to use a node attribute named bipartite
with values 0 or 1 to identify the sets each node belongs to. This convention is not enforced in the source code of
bipartite functions, it’s only a recommendation.
For example:
>>> B=nx.Graph()
>>> # Add nodes with the node attribute "bipartite"
>>> B.add_nodes_from([1,2,3,4], bipartite=0)
>>> B.add_nodes_from(['a','b','c'], bipartite=1)
>>> # Add edges only between nodes of opposite node sets
>>> B.add_edges_from([(1,'a'), (1,'b'), (2,'b'), (2,'c'), (3,'c'), (4,'a')])
Many algorithms of the bipartite module of NetworkX require, as an argument, a container with all the nodes that
belong to one set, in addition to the bipartite graph B. The functions in the bipartite package do not check that the node
set is actually correct nor that the input graph is actually bipartite. If Bis connected, you can find the two node sets
using a two-coloring algorithm:
>>> nx.is_connected(B)
True
>>> bottom_nodes, top_nodes =bipartite.sets(B)
However, if the input graph is not connected, there are more than one possible colorations. This is the reason why we
require the user to pass a container with all nodes of one bipartite node set as an argument to most bipartite functions.
In the face of ambiguity, we refuse the temptation to guess and raise an AmbiguousSolution Exception if the
input graph for bipartite.sets is disconnected.
150 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Using the bipartite node attribute, you can easily get the two node sets:
>>> top_nodes ={n for n, d in B.nodes(data=True)if d['bipartite']==0}
>>> bottom_nodes =set(B) -top_nodes
So you can easily use the bipartite algorithms that require, as an argument, a container with all nodes that belong to
one node set:
>>> print(round(bipartite.density(B, bottom_nodes), 2))
0.5
>>> G=bipartite.projected_graph(B, top_nodes)
All bipartite graph generators in NetworkX build bipartite graphs with the bipartite node attribute. Thus, you can
use the same approach:
>>> RB =bipartite.random_graph(5,7,0.2)
>>> RB_top ={n for n, d in RB.nodes(data=True)if d['bipartite']==0}
>>> RB_bottom =set(RB) -RB_top
>>> list(RB_top)
[0, 1, 2, 3, 4]
>>> list(RB_bottom)
[5, 6, 7, 8, 9, 10, 11]
For other bipartite graph generators see Generators.
3.3.1 Basic functions
Bipartite Graph Algorithms
is_bipartite(G) Returns True if graph G is bipartite, False if not.
is_bipartite_node_set(G, nodes) Returns True if nodes and G/nodes are a bipartition of
G.
sets(G[, top_nodes]) Returns bipartite node sets of graph G.
color(G) Returns a two-coloring of the graph.
density(B, nodes) Return density of bipartite graph B.
degrees(B, nodes[, weight]) Return the degrees of the two node sets in the bipartite
graph B.
networkx.algorithms.bipartite.basic.is_bipartite
is_bipartite(G)
Returns True if graph G is bipartite, False if not.
Parameters G (NetworkX graph)
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)
>>> print(bipartite.is_bipartite(G))
True
See also:
3.3. Bipartite 151

NetworkX Reference, Release 2.3rc1.dev20181203210840
color(),is_bipartite_node_set()
networkx.algorithms.bipartite.basic.is_bipartite_node_set
is_bipartite_node_set(G,nodes)
Returns True if nodes and G/nodes are a bipartition of G.
Parameters
•G(NetworkX graph)
•nodes (list or container) – Check if nodes are a one of a bipartite set.
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)
>>> X=set([1,3])
>>> bipartite.is_bipartite_node_set(G,X)
True
Notes
For connected graphs the bipartite sets are unique. This function handles disconnected graphs.
networkx.algorithms.bipartite.basic.sets
sets(G,top_nodes=None)
Returns bipartite node sets of graph G.
Raises an exception if the graph is not bipartite or if the input graph is disconnected and thus more than one valid
solution exists. See bipartite documentation for further details on how bipartite graphs are handled in
NetworkX.
Parameters
•G(NetworkX graph)
•top_nodes (container) – Container with all nodes in one bipartite node set. If not supplied
it will be computed. But if more than one solution exists an exception will be raised.
Returns (X,Y) – One set of nodes for each part of the bipartite graph.
Return type two-tuple of sets
Raises
•AmbiguousSolution : Exception – Raised if the input bipartite graph is disconnected and no
container with all nodes in one bipartite set is provided. When determining the nodes in
each bipartite set more than one valid solution is possible if the input graph is disconnected.
•NetworkXError: Exception – Raised if the input graph is not bipartite.
152 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)
>>> X,Y=bipartite.sets(G)
>>> list(X)
[0, 2]
>>> list(Y)
[1, 3]
See also:
color()
networkx.algorithms.bipartite.basic.color
color(G)
Returns a two-coloring of the graph.
Raises an exception if the graph is not bipartite.
Parameters G (NetworkX graph)
Returns color – A dictionary keyed by node with a 1 or 0 as data for each node color.
Return type dictionary
Raises exc:NetworkXError if the graph is not two-colorable.
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)
>>> c=bipartite.color(G)
>>> print(c)
{0: 1, 1: 0, 2: 1, 3: 0}
You can use this to set a node attribute indicating the biparite set:
>>> nx.set_node_attributes(G, c, 'bipartite')
>>> print(G.nodes[0]['bipartite'])
1
>>> print(G.nodes[1]['bipartite'])
0
networkx.algorithms.bipartite.basic.density
density(B,nodes)
Return density of bipartite graph B.
Parameters
•G(NetworkX graph)
•nodes (list or container) – Nodes in one node set of the bipartite graph.
Returns d – The bipartite density
3.3. Bipartite 153

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type float
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.complete_bipartite_graph(3,2)
>>> X=set([0,1,2])
>>> bipartite.density(G,X)
1.0
>>> Y=set([3,4])
>>> bipartite.density(G,Y)
1.0
Notes
The container of nodes passed as argument must contain all nodes in one of the two bipartite node sets to avoid
ambiguity in the case of disconnected graphs. See bipartite documentation for further details on how
bipartite graphs are handled in NetworkX.
See also:
color()
networkx.algorithms.bipartite.basic.degrees
degrees(B,nodes,weight=None)
Return the degrees of the two node sets in the bipartite graph B.
Parameters
•G(NetworkX graph)
•nodes (list or container) – Nodes in one node set of the bipartite graph.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1. The degree is the sum of
the edge weights adjacent to the node.
Returns (degX,degY) – The degrees of the two bipartite sets as dictionaries keyed by node.
Return type tuple of dictionaries
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.complete_bipartite_graph(3,2)
>>> Y=set([3,4])
>>> degX,degY=bipartite.degrees(G,Y)
>>> dict(degX)
{0: 2, 1: 2, 2: 2}
154 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The container of nodes passed as argument must contain all nodes in one of the two bipartite node sets to avoid
ambiguity in the case of disconnected graphs. See bipartite documentation for further details on how
bipartite graphs are handled in NetworkX.
See also:
color(),density()
3.3.2 Matching
Provides functions for computing a maximum cardinality matching in a bipartite graph.
If you don’t care about the particular implementation of the maximum matching algorithm, simply use the
maximum_matching(). If you do care, you can import one of the named maximum matching algorithms directly.
For example, to find a maximum matching in the complete bipartite graph with two vertices on the left and three
vertices on the right:
>>> import networkx as nx
>>> G=nx.complete_bipartite_graph(2,3)
>>> left, right =nx.bipartite.sets(G)
>>> list(left)
[0, 1]
>>> list(right)
[2, 3, 4]
>>> nx.bipartite.maximum_matching(G)
{0: 2, 1: 3, 2: 0, 3: 1}
The dictionary returned by maximum_matching() includes a mapping for vertices in both the left and right vertex
sets.
eppstein_matching(G[, top_nodes]) Returns the maximum cardinality matching of the bipar-
tite graph G.
hopcroft_karp_matching(G[, top_nodes]) Returns the maximum cardinality matching of the bipar-
tite graph G.
to_vertex_cover(G, matching[, top_nodes]) Returns the minimum vertex cover corresponding to the
given maximum matching of the bipartite graph G.
networkx.algorithms.bipartite.matching.eppstein_matching
eppstein_matching(G,top_nodes=None)
Returns the maximum cardinality matching of the bipartite graph G.
Parameters
•G(NetworkX graph) – Undirected bipartite graph
•top_nodes (container) – Container with all nodes in one bipartite node set. If not supplied
it will be computed. But if more than one solution exists an exception will be raised.
Returns matches – The matching is returned as a dictionary, matching, such that matching[v]
== w if node vis matched to node w. Unmatched nodes do not occur as a key in mate.
Return type dictionary
3.3. Bipartite 155

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises AmbiguousSolution : Exception – Raised if the input bipartite graph is disconnected and no
container with all nodes in one bipartite set is provided. When determining the nodes in each
bipartite set more than one valid solution is possible if the input graph is disconnected.
Notes
This function is implemented with David Eppstein’s version of the algorithm Hopcroft–Karp algorithm (see
hopcroft_karp_matching()), which originally appeared in the Python Algorithms and Data Structures
library (PADS).
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
hopcroft_karp_matching()
networkx.algorithms.bipartite.matching.hopcroft_karp_matching
hopcroft_karp_matching(G,top_nodes=None)
Returns the maximum cardinality matching of the bipartite graph G.
Parameters
•G(NetworkX graph) – Undirected bipartite graph
•top_nodes (container) – Container with all nodes in one bipartite node set. If not supplied
it will be computed. But if more than one solution exists an exception will be raised.
Returns matches – The matching is returned as a dictionary, matches, such that matches[v]
== w if node vis matched to node w. Unmatched nodes do not occur as a key in mate.
Return type dictionary
Raises AmbiguousSolution : Exception – Raised if the input bipartite graph is disconnected and no
container with all nodes in one bipartite set is provided. When determining the nodes in each
bipartite set more than one valid solution is possible if the input graph is disconnected.
Notes
This function is implemented with the Hopcroft–Karp matching algorithm for bipartite graphs.
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
eppstein_matching()
References
networkx.algorithms.bipartite.matching.to_vertex_cover
to_vertex_cover(G,matching,top_nodes=None)
Returns the minimum vertex cover corresponding to the given maximum matching of the bipartite graph G.
Parameters
•G(NetworkX graph) – Undirected bipartite graph
156 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•matching (dictionary) – A dictionary whose keys are vertices in Gand whose values are the
distinct neighbors comprising the maximum matching for G, as returned by, for example,
maximum_matching(). The dictionary must represent the maximum matching.
•top_nodes (container) – Container with all nodes in one bipartite node set. If not supplied
it will be computed. But if more than one solution exists an exception will be raised.
Returns vertex_cover – The minimum vertex cover in G.
Return type set
Raises AmbiguousSolution : Exception – Raised if the input bipartite graph is disconnected and no
container with all nodes in one bipartite set is provided. When determining the nodes in each
bipartite set more than one valid solution is possible if the input graph is disconnected.
Notes
This function is implemented using the procedure guaranteed by Konig’s theorem, which proves an equivalence
between a maximum matching and a minimum vertex cover in bipartite graphs.
Since a minimum vertex cover is the complement of a maximum independent set for any graph, one can compute
the maximum independent set of a bipartite graph this way:
>>> import networkx as nx
>>> G=nx.complete_bipartite_graph(2,3)
>>> matching =nx.bipartite.maximum_matching(G)
>>> vertex_cover =nx.bipartite.to_vertex_cover(G, matching)
>>> independent_set =set(G) -vertex_cover
>>> print(list(independent_set))
[2, 3, 4]
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
3.3.3 Matrix
Biadjacency matrices
biadjacency_matrix(G, row_order[, . . . ]) Return the biadjacency matrix of the bipartite graph G.
from_biadjacency_matrix(A[, create_using,
...])
Creates a new bipartite graph from a biadjacency matrix
given as a SciPy sparse matrix.
networkx.algorithms.bipartite.matrix.biadjacency_matrix
biadjacency_matrix(G,row_order,column_order=None,dtype=None,weight=’weight’,format=’csr’)
Return the biadjacency matrix of the bipartite graph G.
Let G = (U, V, E) be a bipartite graph with node sets U = u_{1},...,u_{r} and V = v_{1},..
.,v_{s}. The biadjacency matrix1is the rxsmatrix Bin which b_{i,j} = 1 if, and only if, (u_i,
v_j) in E. If the parameter weight is not None and matches the name of an edge attribute, its value is
used instead of 1.
Parameters
•G(graph) – A NetworkX graph
1https://en.wikipedia.org/wiki/Adjacency_matrix#Adjacency_matrix_of_a_bipartite_graph
3.3. Bipartite 157

NetworkX Reference, Release 2.3rc1.dev20181203210840
•row_order (list of nodes) – The rows of the matrix are ordered according to the list of nodes.
•column_order (list, optional) – The columns of the matrix are ordered according to the list
of nodes. If column_order is None, then the ordering of columns is arbitrary.
•dtype (NumPy data-type, optional) – A valid NumPy dtype used to initialize the array. If
None, then the NumPy default is used.
•weight (string or None, optional (default=’weight’)) – The edge data key used to provide
each value in the matrix. If None, then each edge has weight 1.
•format (str in {‘bsr’, ‘csr’, ‘csc’, ‘coo’, ‘lil’, ‘dia’, ‘dok’}) – The type of the matrix to be
returned (default ‘csr’). For some algorithms different implementations of sparse matrices
can perform better. See2for details.
Returns M – Biadjacency matrix representation of the bipartite graph G.
Return type SciPy sparse matrix
Notes
No attempt is made to check that the input graph is bipartite.
For directed bipartite graphs only successors are considered as neighbors. To obtain an adjacency matrix with
ones (or weight values) for both predecessors and successors you have to generate two biadjacency matrices
where the rows of one of them are the columns of the other, and then add one to the transpose of the other.
See also:
adjacency_matrix(),from_biadjacency_matrix()
References
networkx.algorithms.bipartite.matrix.from_biadjacency_matrix
from_biadjacency_matrix(A,create_using=None,edge_attribute=’weight’)
Creates a new bipartite graph from a biadjacency matrix given as a SciPy sparse matrix.
Parameters
•A(scipy sparse matrix) – A biadjacency matrix representation of a graph
•create_using (NetworkX graph) – Use specified graph for result. The default is Graph()
•edge_attribute (string) – Name of edge attribute to store matrix numeric value. The data
will have the same type as the matrix entry (int, float, (real,imag)).
Notes
The nodes are labeled with the attribute bipartite set to an integer 0 or 1 representing membership in part 0
or part 1 of the bipartite graph.
If create_using is an instance of networkx.MultiGraph or networkx.MultiDiGraph and the
entries of Aare of type int, then this function returns a multigraph (of the same type as create_using)
with parallel edges. In this case, edge_attribute will be ignored.
See also:
biadjacency_matrix(),from_numpy_matrix()
2Scipy Dev. References, “Sparse Matrices”, https://docs.scipy.org/doc/scipy/reference/sparse.html
158 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
[1] https://en.wikipedia.org/wiki/Adjacency_matrix#Adjacency_matrix_of_a_bipartite_graph
3.3.4 Projections
One-mode (unipartite) projections of bipartite graphs.
projected_graph(B, nodes[, multigraph]) Returns the projection of B onto one of its node sets.
weighted_projected_graph(B, nodes[, ratio]) Returns a weighted projection of B onto one of its node
sets.
collaboration_weighted_projected_graph(B,
nodes)
Newman’s weighted projection of B onto one of its node
sets.
overlap_weighted_projected_graph(B,
nodes[, . . . ])
Overlap weighted projection of B onto one of its node
sets.
generic_weighted_projected_graph(B,
nodes[, . . . ])
Weighted projection of B with a user-specified weight
function.
networkx.algorithms.bipartite.projection.projected_graph
projected_graph(B,nodes,multigraph=False)
Returns the projection of B onto one of its node sets.
Returns the graph G that is the projection of the bipartite graph B onto the specified nodes. They retain their
attributes and are connected in G if they have a common neighbor in B.
Parameters
•B(NetworkX graph) – The input graph should be bipartite.
•nodes (list or iterable) – Nodes to project onto (the “bottom” nodes).
•multigraph (bool (default=False)) – If True return a multigraph where the multiple edges
represent multiple shared neighbors. They edge key in the multigraph is assigned to the
label of the neighbor.
Returns Graph – A graph that is the projection onto the given nodes.
Return type NetworkX graph or multigraph
Examples
>>> from networkx.algorithms import bipartite
>>> B=nx.path_graph(4)
>>> G=bipartite.projected_graph(B, [1,3])
>>> list(G)
[1, 3]
>>> list(G.edges())
[(1, 3)]
If nodes a, and bare connected through both nodes 1 and 2 then building a multigraph results in two edges in
the projection onto [a,b]:
3.3. Bipartite 159

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> B=nx.Graph()
>>> B.add_edges_from([('a',1), ('b',1), ('a',2), ('b',2)])
>>> G=bipartite.projected_graph(B, ['a','b'], multigraph=True)
>>> print([sorted((u, v)) for u, v in G.edges()])
[['a', 'b'], ['a', 'b']]
Notes
No attempt is made to verify that the input graph B is bipartite. Returns a simple graph that is the projection of
the bipartite graph B onto the set of nodes given in list nodes. If multigraph=True then a multigraph is returned
with an edge for every shared neighbor.
Directed graphs are allowed as input. The output will also then be a directed graph with edges if there is a
directed path between the nodes.
The graph and node properties are (shallow) copied to the projected graph.
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
is_bipartite(),is_bipartite_node_set(),sets(),weighted_projected_graph(),
collaboration_weighted_projected_graph(),overlap_weighted_projected_graph(),
generic_weighted_projected_graph()
networkx.algorithms.bipartite.projection.weighted_projected_graph
weighted_projected_graph(B,nodes,ratio=False)
Returns a weighted projection of B onto one of its node sets.
The weighted projected graph is the projection of the bipartite network B onto the specified nodes with weights
representing the number of shared neighbors or the ratio between actual shared neighbors and possible shared
neighbors if ratio is True1. The nodes retain their attributes and are connected in the resulting graph if
they have an edge to a common node in the original graph.
Parameters
•B(NetworkX graph) – The input graph should be bipartite.
•nodes (list or iterable) – Nodes to project onto (the “bottom” nodes).
•ratio (Bool (default=False)) – If True, edge weight is the ratio between actual shared neigh-
bors and maximum possible shared neighbors (i.e., the size of the other node set). If False,
edges weight is the number of shared neighbors.
Returns Graph – A graph that is the projection onto the given nodes.
Return type NetworkX graph
Examples
1Borgatti, S.P. and Halgin, D. In press. “Analyzing Affiliation Networks”. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social
Network Analysis. Sage Publications.
160 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx.algorithms import bipartite
>>> B=nx.path_graph(4)
>>> G=bipartite.weighted_projected_graph(B, [1,3])
>>> list(G)
[1, 3]
>>> list(G.edges(data=True))
[(1, 3, {'weight': 1})]
>>> G=bipartite.weighted_projected_graph(B, [1,3], ratio=True)
>>> list(G.edges(data=True))
[(1, 3, {'weight': 0.5})]
Notes
No attempt is made to verify that the input graph B is bipartite. The graph and node properties are (shallow)
copied to the projected graph.
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
is_bipartite(),is_bipartite_node_set(),sets(),collaboration_weighted_projected_graph(),
overlap_weighted_projected_graph(),generic_weighted_projected_graph(),
projected_graph()
References
networkx.algorithms.bipartite.projection.collaboration_weighted_projected_graph
collaboration_weighted_projected_graph(B,nodes)
Newman’s weighted projection of B onto one of its node sets.
The collaboration weighted projection is the projection of the bipartite network B onto the specified nodes with
weights assigned using Newman’s collaboration model1:
𝑤𝑢,𝑣 =
𝑘
𝛿𝑘
𝑢𝛿𝑘
𝑣
𝑑𝑘−1
where uand vare nodes from the bottom bipartite node set, and kis a node of the top node set. The value d_k
is the degree of node kin the bipartite network and delta_{u}^{k} is 1 if node uis linked to node kin the
original bipartite graph or 0 otherwise.
The nodes retain their attributes and are connected in the resulting graph if have an edge to a common node in
the original bipartite graph.
Parameters
•B(NetworkX graph) – The input graph should be bipartite.
•nodes (list or iterable) – Nodes to project onto (the “bottom” nodes).
Returns Graph – A graph that is the projection onto the given nodes.
Return type NetworkX graph
1Scientific collaboration networks: II. Shortest paths, weighted networks, and centrality, M. E. J. Newman, Phys. Rev. E 64, 016132 (2001).
3.3. Bipartite 161

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> from networkx.algorithms import bipartite
>>> B=nx.path_graph(5)
>>> B.add_edge(1,5)
>>> G=bipartite.collaboration_weighted_projected_graph(B, [0,2,4,5])
>>> list(G)
[0, 2, 4, 5]
>>> for edge in G.edges(data=True): print(edge)
...
(0, 2, {'weight': 0.5})
(0, 5, {'weight': 0.5})
(2, 4, {'weight': 1.0})
(2, 5, {'weight': 0.5})
Notes
No attempt is made to verify that the input graph B is bipartite. The graph and node properties are (shallow)
copied to the projected graph.
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
is_bipartite(),is_bipartite_node_set(),sets(),weighted_projected_graph(),
overlap_weighted_projected_graph(),generic_weighted_projected_graph(),
projected_graph()
References
networkx.algorithms.bipartite.projection.overlap_weighted_projected_graph
overlap_weighted_projected_graph(B,nodes,jaccard=True)
Overlap weighted projection of B onto one of its node sets.
The overlap weighted projection is the projection of the bipartite network B onto the specified nodes with
weights representing the Jaccard index between the neighborhoods of the two nodes in the original bipartite
network1:
𝑤𝑣,𝑢 =|𝑁(𝑢)∩𝑁(𝑣)|
|𝑁(𝑢)∪𝑁(𝑣)|
or if the parameter ‘jaccard’ is False, the fraction of common neighbors by minimum of both nodes degree in
the original bipartite graph1:
𝑤𝑣,𝑢 =|𝑁(𝑢)∩𝑁(𝑣)|
𝑚𝑖𝑛(|𝑁(𝑢)|,|𝑁(𝑣)|)
The nodes retain their attributes and are connected in the resulting graph if have an edge to a common node in
the original bipartite graph.
Parameters
•B(NetworkX graph) – The input graph should be bipartite.
1Borgatti, S.P. and Halgin, D. In press. Analyzing Affiliation Networks. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social
Network Analysis. Sage Publications.
162 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•nodes (list or iterable) – Nodes to project onto (the “bottom” nodes).
•jaccard (Bool (default=True))
Returns Graph – A graph that is the projection onto the given nodes.
Return type NetworkX graph
Examples
>>> from networkx.algorithms import bipartite
>>> B=nx.path_graph(5)
>>> nodes =[0,2,4]
>>> G=bipartite.overlap_weighted_projected_graph(B, nodes)
>>> list(G)
[0, 2, 4]
>>> list(G.edges(data=True))
[(0, 2, {'weight': 0.5}), (2, 4, {'weight': 0.5})]
>>> G=bipartite.overlap_weighted_projected_graph(B, nodes, jaccard=False)
>>> list(G.edges(data=True))
[(0, 2, {'weight': 1.0}), (2, 4, {'weight': 1.0})]
Notes
No attempt is made to verify that the input graph B is bipartite. The graph and node properties are (shallow)
copied to the projected graph.
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
is_bipartite(),is_bipartite_node_set(),sets(),weighted_projected_graph(),
collaboration_weighted_projected_graph(),generic_weighted_projected_graph(),
projected_graph()
References
networkx.algorithms.bipartite.projection.generic_weighted_projected_graph
generic_weighted_projected_graph(B,nodes,weight_function=None)
Weighted projection of B with a user-specified weight function.
The bipartite network B is projected on to the specified nodes with weights computed by a user-specified func-
tion. This function must accept as a parameter the neighborhood sets of two nodes and return an integer or a
float.
The nodes retain their attributes and are connected in the resulting graph if they have an edge to a common node
in the original graph.
Parameters
•B(NetworkX graph) – The input graph should be bipartite.
•nodes (list or iterable) – Nodes to project onto (the “bottom” nodes).
•weight_function (function) – This function must accept as parameters the same input graph
that this function, and two nodes; and return an integer or a float. The default function
computes the number of shared neighbors.
3.3. Bipartite 163

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns Graph – A graph that is the projection onto the given nodes.
Return type NetworkX graph
Examples
>>> from networkx.algorithms import bipartite
>>> # Define some custom weight functions
>>> def jaccard(G, u, v):
... unbrs =set(G[u])
... vnbrs =set(G[v])
... return float(len(unbrs &vnbrs)) /len(unbrs |vnbrs)
...
>>> def my_weight(G, u, v, weight='weight'):
... w=0
... for nbr in set(G[u]) &set(G[v]):
... w+= G[u][nbr].get(weight, 1)+G[v][nbr].get(weight, 1)
... return w
...
>>> # A complete bipartite graph with 4 nodes and 4 edges
>>> B=nx.complete_bipartite_graph(2,2)
>>> # Add some arbitrary weight to the edges
>>> for i,(u,v) in enumerate(B.edges()):
... B.edges[u, v]['weight']=i+1
...
>>> for edge in B.edges(data=True):
... print(edge)
...
(0, 2, {'weight': 1})
(0, 3, {'weight': 2})
(1, 2, {'weight': 3})
(1, 3, {'weight': 4})
>>> # By default, the weight is the number of shared neighbors
>>> G=bipartite.generic_weighted_projected_graph(B, [0,1])
>>> print(list(G.edges(data=True)))
[(0, 1, {'weight': 2})]
>>> # To specify a custom weight function use the weight_function parameter
>>> G=bipartite.generic_weighted_projected_graph(B, [0,1], weight_
˓→function=jaccard)
>>> print(list(G.edges(data=True)))
[(0, 1, {'weight': 1.0})]
>>> G=bipartite.generic_weighted_projected_graph(B, [0,1], weight_function=my_
˓→weight)
>>> print(list(G.edges(data=True)))
[(0, 1, {'weight': 10})]
Notes
No attempt is made to verify that the input graph B is bipartite. The graph and node properties are (shallow)
copied to the projected graph.
See bipartite documentation for further details on how bipartite graphs are handled in NetworkX.
See also:
is_bipartite(),is_bipartite_node_set(),sets(),weighted_projected_graph(),
collaboration_weighted_projected_graph(),overlap_weighted_projected_graph(),
164 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
projected_graph()
3.3.5 Spectral
Spectral bipartivity measure.
spectral_bipartivity(G[, nodes, weight]) Returns the spectral bipartivity.
networkx.algorithms.bipartite.spectral.spectral_bipartivity
spectral_bipartivity(G,nodes=None,weight=’weight’)
Returns the spectral bipartivity.
Parameters
•G(NetworkX graph)
•nodes (list or container optional(default is all nodes)) – Nodes to return value of spectral
bipartivity contribution.
•weight (string or None optional (default = ‘weight’)) – Edge data key to use for edge
weights. If None, weights set to 1.
Returns sb – A single number if the keyword nodes is not specified, or a dictionary keyed by node
with the spectral bipartivity contribution of that node as the value.
Return type float or dict
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)
>>> bipartite.spectral_bipartivity(G)
1.0
Notes
This implementation uses Numpy (dense) matrices which are not efficient for storing large sparse graphs.
See also:
color()
References
3.3.6 Clustering
clustering(G[, nodes, mode]) Compute a bipartite clustering coefficient for nodes.
average_clustering(G[, nodes, mode]) Compute the average bipartite clustering coefficient.
latapy_clustering(G[, nodes, mode]) Compute a bipartite clustering coefficient for nodes.
robins_alexander_clustering(G) Compute the bipartite clustering of G.
3.3. Bipartite 165

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.bipartite.cluster.clustering
clustering(G,nodes=None,mode=’dot’)
Compute a bipartite clustering coefficient for nodes.
The bipartie clustering coefficient is a measure of local density of connections defined as1:
𝑐𝑢=𝑣∈𝑁(𝑁(𝑢)) 𝑐𝑢𝑣
|𝑁(𝑁(𝑢))|
where N(N(u)) are the second order neighbors of uin Gexcluding u, and c_{uv} is the pairwise clustering
coefficient between nodes uand v.
The mode selects the function for c_{uv} which can be:
dot:
𝑐𝑢𝑣 =|𝑁(𝑢)∩𝑁(𝑣)|
|𝑁(𝑢)∪𝑁(𝑣)|
min:
𝑐𝑢𝑣 =|𝑁(𝑢)∩𝑁(𝑣)|
𝑚𝑖𝑛(|𝑁(𝑢)|,|𝑁(𝑣)|)
max:
𝑐𝑢𝑣 =|𝑁(𝑢)∩𝑁(𝑣)|
𝑚𝑎𝑥(|𝑁(𝑢)|,|𝑁(𝑣)|)
Parameters
•G(graph) – A bipartite graph
•nodes (list or iterable (optional)) – Compute bipartite clustering for these nodes. The default
is all nodes in G.
•mode (string) – The pariwise bipartite clustering method to be used in the computation. It
must be “dot”, “max”, or “min”.
Returns clustering – A dictionary keyed by node with the clustering coefficient value.
Return type dictionary
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)# path graphs are bipartite
>>> c=bipartite.clustering(G)
>>> c[0]
0.5
>>> c=bipartite.clustering(G,mode='min')
>>> c[0]
1.0
See also:
robins_alexander_clustering(),square_clustering(),average_clustering()
1Latapy, Matthieu, Clémence Magnien, and Nathalie Del Vecchio (2008). Basic notions for the analysis of large two-mode networks. Social
Networks 30(1), 31–48.
166 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.algorithms.bipartite.cluster.average_clustering
average_clustering(G,nodes=None,mode=’dot’)
Compute the average bipartite clustering coefficient.
A clustering coefficient for the whole graph is the average,
𝐶=1
𝑛
𝑣∈𝐺
𝑐𝑣,
where nis the number of nodes in G.
Similar measures for the two bipartite sets can be defined1
𝐶𝑋=1
|𝑋|
𝑣∈𝑋
𝑐𝑣,
where Xis a bipartite set of G.
Parameters
•G(graph) – a bipartite graph
•nodes (list or iterable, optional) – A container of nodes to use in computing the average.
The nodes should be either the entire graph (the default) or one of the bipartite sets.
•mode (string) – The pariwise bipartite clustering method. It must be “dot”, “max”, or “min”
Returns clustering – The average bipartite clustering for the given set of nodes or the entire graph
if no nodes are specified.
Return type float
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.star_graph(3)# star graphs are bipartite
>>> bipartite.average_clustering(G)
0.75
>>> X,Y=bipartite.sets(G)
>>> bipartite.average_clustering(G,X)
0.0
>>> bipartite.average_clustering(G,Y)
1.0
See also:
clustering()
Notes
The container of nodes passed to this function must contain all of the nodes in one of the bipartite sets
(“top” or “bottom”) in order to compute the correct average bipartite clustering coefficients. See bipartite
documentation for further details on how bipartite graphs are handled in NetworkX.
1Latapy, Matthieu, Clémence Magnien, and Nathalie Del Vecchio (2008). Basic notions for the analysis of large two-mode networks. Social
Networks 30(1), 31–48.
3.3. Bipartite 167

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.algorithms.bipartite.cluster.latapy_clustering
latapy_clustering(G,nodes=None,mode=’dot’)
Compute a bipartite clustering coefficient for nodes.
The bipartie clustering coefficient is a measure of local density of connections defined as1:
𝑐𝑢=𝑣∈𝑁(𝑁(𝑢)) 𝑐𝑢𝑣
|𝑁(𝑁(𝑢))|
where N(N(u)) are the second order neighbors of uin Gexcluding u, and c_{uv} is the pairwise clustering
coefficient between nodes uand v.
The mode selects the function for c_{uv} which can be:
dot:
𝑐𝑢𝑣 =|𝑁(𝑢)∩𝑁(𝑣)|
|𝑁(𝑢)∪𝑁(𝑣)|
min:
𝑐𝑢𝑣 =|𝑁(𝑢)∩𝑁(𝑣)|
𝑚𝑖𝑛(|𝑁(𝑢)|,|𝑁(𝑣)|)
max:
𝑐𝑢𝑣 =|𝑁(𝑢)∩𝑁(𝑣)|
𝑚𝑎𝑥(|𝑁(𝑢)|,|𝑁(𝑣)|)
Parameters
•G(graph) – A bipartite graph
•nodes (list or iterable (optional)) – Compute bipartite clustering for these nodes. The default
is all nodes in G.
•mode (string) – The pariwise bipartite clustering method to be used in the computation. It
must be “dot”, “max”, or “min”.
Returns clustering – A dictionary keyed by node with the clustering coefficient value.
Return type dictionary
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4)# path graphs are bipartite
>>> c=bipartite.clustering(G)
>>> c[0]
0.5
>>> c=bipartite.clustering(G,mode='min')
>>> c[0]
1.0
See also:
robins_alexander_clustering(),square_clustering(),average_clustering()
1Latapy, Matthieu, Clémence Magnien, and Nathalie Del Vecchio (2008). Basic notions for the analysis of large two-mode networks. Social
Networks 30(1), 31–48.
168 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.algorithms.bipartite.cluster.robins_alexander_clustering
robins_alexander_clustering(G)
Compute the bipartite clustering of G.
Robins and Alexander1defined bipartite clustering coefficient as four times the number of four cycles C_4
divided by the number of three paths L_3 in a bipartite graph:
𝐶𝐶4=4*𝐶4
𝐿3
Parameters G (graph) – a bipartite graph
Returns clustering – The Robins and Alexander bipartite clustering for the input graph.
Return type float
Examples
>>> from networkx.algorithms import bipartite
>>> G=nx.davis_southern_women_graph()
>>> print(round(bipartite.robins_alexander_clustering(G), 3))
0.468
See also:
latapy_clustering(),square_clustering()
References
3.3.7 Redundancy
Node redundancy for bipartite graphs.
node_redundancy(G[, nodes]) Computes the node redundancy coefficients for the
nodes in the bipartite graph G.
networkx.algorithms.bipartite.redundancy.node_redundancy
node_redundancy(G,nodes=None)
Computes the node redundancy coefficients for the nodes in the bipartite graph G.
The redundancy coefficient of a node vis the fraction of pairs of neighbors of vthat are both linked to other
nodes. In a one-mode projection these nodes would be linked together even if vwere not there.
More formally, for any vertex v, the redundancy coefficient of ‘v‘ is defined by
𝑟𝑐(𝑣) = |{{𝑢, 𝑤} ⊆ 𝑁(𝑣),∃𝑣′̸=𝑣, (𝑣′, 𝑢)∈𝐸and (𝑣′, 𝑤)∈𝐸}|
|𝑁(𝑣)|(|𝑁(𝑣)|−1)
2
,
where N(v) is the set of neighbors of vin G.
1Robins, G. and M. Alexander (2004). Small worlds among interlocking directors: Network structure and distance in bipartite graphs. Compu-
tational & Mathematical Organization Theory 10(1), 69–94.
3.3. Bipartite 169

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(graph) – A bipartite graph
•nodes (list or iterable (optional)) – Compute redundancy for these nodes. The default is all
nodes in G.
Returns redundancy – A dictionary keyed by node with the node redundancy value.
Return type dictionary
Examples
Compute the redundancy coefficient of each node in a graph:
>>> import networkx as nx
>>> from networkx.algorithms import bipartite
>>> G=nx.cycle_graph(4)
>>> rc =bipartite.node_redundancy(G)
>>> rc[0]
1.0
Compute the average redundancy for the graph:
>>> import networkx as nx
>>> from networkx.algorithms import bipartite
>>> G=nx.cycle_graph(4)
>>> rc =bipartite.node_redundancy(G)
>>> sum(rc.values()) /len(G)
1.0
Compute the average redundancy for a set of nodes:
>>> import networkx as nx
>>> from networkx.algorithms import bipartite
>>> G=nx.cycle_graph(4)
>>> rc =bipartite.node_redundancy(G)
>>> nodes =[0,2]
>>> sum(rc[n] for nin nodes) /len(nodes)
1.0
Raises NetworkXError – If any of the nodes in the graph (or in nodes, if specified) has (out-
)degree less than two (which would result in division by zero, according to the definition of the
redundancy coefficient).
References
3.3.8 Centrality
closeness_centrality(G, nodes[, normalized]) Compute the closeness centrality for nodes in a bipartite
network.
degree_centrality(G, nodes) Compute the degree centrality for nodes in a bipartite
network.
Continued on next page
170 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 24 – continued from previous page
betweenness_centrality(G, nodes) Compute betweenness centrality for nodes in a bipartite
network.
networkx.algorithms.bipartite.centrality.closeness_centrality
closeness_centrality(G,nodes,normalized=True)
Compute the closeness centrality for nodes in a bipartite network.
The closeness of a node is the distance to all other nodes in the graph or in the case that the graph is not connected
to all other nodes in the connected component containing that node.
Parameters
•G(graph) – A bipartite network
•nodes (list or container) – Container with all nodes in one bipartite node set.
•normalized (bool, optional) – If True (default) normalize by connected component size.
Returns closeness – Dictionary keyed by node with bipartite closeness centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),degree_centrality(),sets(),is_bipartite()
Notes
The nodes input parameter must contain all nodes in one bipartite node set, but the dictionary returned contains
all nodes from both node sets. See bipartite documentation for further details on how bipartite graphs
are handled in NetworkX.
Closeness centrality is normalized by the minimum distance possible. In the bipartite case the minimum distance
for a node in one bipartite node set is 1 from all nodes in the other node set and 2 from all other nodes in its own
set1. Thus the closeness centrality for node vin the two bipartite sets Uwith nnodes and Vwith mnodes is
𝑐𝑣=𝑚+ 2(𝑛−1)
𝑑,for𝑣∈𝑈,
𝑐𝑣=𝑛+ 2(𝑚−1)
𝑑,for𝑣∈𝑉,
where dis the sum of the distances from vto all other nodes.
Higher values of closeness indicate higher centrality.
As in the unipartite case, setting normalized=True causes the values to normalized further to n-1 / size(G)-1
where n is the number of nodes in the connected part of graph containing the node. If the graph is not completely
connected, this algorithm computes the closeness centrality for each connected part separately.
References
networkx.algorithms.bipartite.centrality.degree_centrality
degree_centrality(G,nodes)
Compute the degree centrality for nodes in a bipartite network.
1Borgatti, S.P. and Halgin, D. In press. “Analyzing Affiliation Networks”. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social
Network Analysis. Sage Publications. http://www.steveborgatti.com/research/publications/bhaffiliations.pdf
3.3. Bipartite 171

NetworkX Reference, Release 2.3rc1.dev20181203210840
The degree centrality for a node vis the fraction of nodes connected to it.
Parameters
•G(graph) – A bipartite network
•nodes (list or container) – Container with all nodes in one bipartite node set.
Returns centrality – Dictionary keyed by node with bipartite degree centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),closeness_centrality(),sets(),is_bipartite()
Notes
The nodes input parameter must contain all nodes in one bipartite node set, but the dictionary returned con-
tains all nodes from both bipartite node sets. See bipartite documentation for further details on how
bipartite graphs are handled in NetworkX.
For unipartite networks, the degree centrality values are normalized by dividing by the maximum possible degree
(which is n-1 where nis the number of nodes in G).
In the bipartite case, the maximum possible degree of a node in a bipartite node set is the number of nodes in the
opposite node set1. The degree centrality for a node vin the bipartite sets Uwith nnodes and Vwith mnodes is
𝑑𝑣=𝑑𝑒𝑔(𝑣)
𝑚,for𝑣∈𝑈,
𝑑𝑣=𝑑𝑒𝑔(𝑣)
𝑛,for𝑣∈𝑉,
where deg(v) is the degree of node v.
References
networkx.algorithms.bipartite.centrality.betweenness_centrality
betweenness_centrality(G,nodes)
Compute betweenness centrality for nodes in a bipartite network.
Betweenness centrality of a node vis the sum of the fraction of all-pairs shortest paths that pass through v.
Values of betweenness are normalized by the maximum possible value which for bipartite graphs is limited by
the relative size of the two node sets1.
Let nbe the number of nodes in the node set Uand mbe the number of nodes in the node set V, then nodes in U
are normalized by dividing by
1
2[𝑚2(𝑠+ 1)2+𝑚(𝑠+ 1)(2𝑡−𝑠−1) −𝑡(2𝑠−𝑡+ 3)],
where
𝑠= (𝑛−1) ÷𝑚, 𝑡 = (𝑛−1) mod 𝑚,
1Borgatti, S.P. and Halgin, D. In press. “Analyzing Affiliation Networks”. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social
Network Analysis. Sage Publications. http://www.steveborgatti.com/research/publications/bhaffiliations.pdf
1Borgatti, S.P. and Halgin, D. In press. “Analyzing Affiliation Networks”. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social
Network Analysis. Sage Publications. http://www.steveborgatti.com/research/publications/bhaffiliations.pdf
172 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
and nodes in Vare normalized by dividing by
1
2[𝑛2(𝑝+ 1)2+𝑛(𝑝+ 1)(2𝑟−𝑝−1) −𝑟(2𝑝−𝑟+ 3)],
where,
𝑝= (𝑚−1) ÷𝑛, 𝑟 = (𝑚−1) mod 𝑛.
Parameters
•G(graph) – A bipartite graph
•nodes (list or container) – Container with all nodes in one bipartite node set.
Returns betweenness – Dictionary keyed by node with bipartite betweenness centrality as the value.
Return type dictionary
See also:
degree_centrality(),closeness_centrality(),sets(),is_bipartite()
Notes
The nodes input parameter must contain all nodes in one bipartite node set, but the dictionary returned contains
all nodes from both node sets. See bipartite documentation for further details on how bipartite graphs
are handled in NetworkX.
References
3.3.9 Generators
Generators and functions for bipartite graphs.
complete_bipartite_graph(n1, n2[, cre-
ate_using])
Return the complete bipartite graph K_{n_1,n_2}.
configuration_model(aseq, bseq[, . . . ]) Return a random bipartite graph from two given degree
sequences.
havel_hakimi_graph(aseq, bseq[, create_using]) Return a bipartite graph from two given degree se-
quences using a Havel-Hakimi style construction.
reverse_havel_hakimi_graph(aseq, bseq[,
...])
Return a bipartite graph from two given degree se-
quences using a Havel-Hakimi style construction.
alternating_havel_hakimi_graph(aseq,
bseq[, . . . ])
Return a bipartite graph from two given degree se-
quences using an alternating Havel-Hakimi style con-
struction.
preferential_attachment_graph(aseq, p[,
...])
Create a bipartite graph with a preferential attachment
model from a given single degree sequence.
random_graph(n, m, p[, seed, directed]) Return a bipartite random graph.
gnmk_random_graph(n, m, k[, seed, directed]) Return a random bipartite graph G_{n,m,k}.
3.3. Bipartite 173

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.bipartite.generators.complete_bipartite_graph
complete_bipartite_graph(n1,n2,create_using=None)
Return the complete bipartite graph K_{n_1,n_2}.
Composed of two partitions with n_1 nodes in the first and n_2 nodes in the second. Each node in the first is
connected to each node in the second.
Parameters
•n1 (integer) – Number of nodes for node set A.
•n2 (integer) – Number of nodes for node set B.
•create_using (NetworkX graph instance, optional) – Return graph of this type.
Notes
Node labels are the integers 0 to n_1 + n_2 - 1.
The nodes are assigned the attribute ‘bipartite’ with the value 0 or 1 to indicate which bipartite set the node
belongs to.
networkx.algorithms.bipartite.generators.configuration_model
configuration_model(aseq,bseq,create_using=None,seed=None)
Return a random bipartite graph from two given degree sequences.
Parameters
•aseq (list) – Degree sequence for node set A.
•bseq (list) – Degree sequence for node set B.
•create_using (NetworkX graph instance, optional) – Return graph of this type.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•Nodes from the set A are connected to nodes in the set B by
•choosing randomly from the possible free stubs, one in A and
•one in B.
Notes
The sum of the two sequences must be equal: sum(aseq)=sum(bseq) If no graph type is specified use MultiGraph
with parallel edges. If you want a graph with no parallel edges use create_using=Graph() but then the resulting
degree sequences might not be exact.
The nodes are assigned the attribute ‘bipartite’ with the value 0 or 1 to indicate which bipartite set the node
belongs to.
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
174 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.bipartite.generators.havel_hakimi_graph
havel_hakimi_graph(aseq,bseq,create_using=None)
Return a bipartite graph from two given degree sequences using a Havel-Hakimi style construction.
Nodes from the set A are connected to nodes in the set B by connecting the highest degree nodes in set A to the
highest degree nodes in set B until all stubs are connected.
Parameters
•aseq (list) – Degree sequence for node set A.
•bseq (list) – Degree sequence for node set B.
•create_using (NetworkX graph instance, optional) – Return graph of this type.
Notes
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
The sum of the two sequences must be equal: sum(aseq)=sum(bseq) If no graph type is specified use MultiGraph
with parallel edges. If you want a graph with no parallel edges use create_using=Graph() but then the resulting
degree sequences might not be exact.
The nodes are assigned the attribute ‘bipartite’ with the value 0 or 1 to indicate which bipartite set the node
belongs to.
networkx.algorithms.bipartite.generators.reverse_havel_hakimi_graph
reverse_havel_hakimi_graph(aseq,bseq,create_using=None)
Return a bipartite graph from two given degree sequences using a Havel-Hakimi style construction.
Nodes from set A are connected to nodes in the set B by connecting the highest degree nodes in set A to the
lowest degree nodes in set B until all stubs are connected.
Parameters
•aseq (list) – Degree sequence for node set A.
•bseq (list) – Degree sequence for node set B.
•create_using (NetworkX graph instance, optional) – Return graph of this type.
Notes
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
The sum of the two sequences must be equal: sum(aseq)=sum(bseq) If no graph type is specified use MultiGraph
with parallel edges. If you want a graph with no parallel edges use create_using=Graph() but then the resulting
degree sequences might not be exact.
The nodes are assigned the attribute ‘bipartite’ with the value 0 or 1 to indicate which bipartite set the node
belongs to.
3.3. Bipartite 175

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.bipartite.generators.alternating_havel_hakimi_graph
alternating_havel_hakimi_graph(aseq,bseq,create_using=None)
Return a bipartite graph from two given degree sequences using an alternating Havel-Hakimi style construction.
Nodes from the set A are connected to nodes in the set B by connecting the highest degree nodes in set A to
alternatively the highest and the lowest degree nodes in set B until all stubs are connected.
Parameters
•aseq (list) – Degree sequence for node set A.
•bseq (list) – Degree sequence for node set B.
•create_using (NetworkX graph instance, optional) – Return graph of this type.
Notes
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
The sum of the two sequences must be equal: sum(aseq)=sum(bseq) If no graph type is specified use MultiGraph
with parallel edges. If you want a graph with no parallel edges use create_using=Graph() but then the resulting
degree sequences might not be exact.
The nodes are assigned the attribute ‘bipartite’ with the value 0 or 1 to indicate which bipartite set the node
belongs to.
networkx.algorithms.bipartite.generators.preferential_attachment_graph
preferential_attachment_graph(aseq,p,create_using=None,seed=None)
Create a bipartite graph with a preferential attachment model from a given single degree sequence.
Parameters
•aseq (list) – Degree sequence for node set A.
•p(float) – Probability that a new bottom node is added.
•create_using (NetworkX graph instance, optional) – Return graph of this type.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
References
Notes
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
networkx.algorithms.bipartite.generators.random_graph
random_graph(n,m,p,seed=None,directed=False)
Return a bipartite random graph.
This is a bipartite version of the binomial (Erd˝
os-Rényi) graph.
176 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•n(int) – The number of nodes in the first bipartite set.
•m(int) – The number of nodes in the second bipartite set.
•p(float) – Probability for edge creation.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True return a directed graph
Notes
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
The bipartite random graph algorithm chooses each of the n*m (undirected) or 2*nm (directed) possible edges
with probability p.
This algorithm is 𝑂(𝑛+𝑚)where 𝑚is the expected number of edges.
The nodes are assigned the attribute ‘bipartite’ with the value 0 or 1 to indicate which bipartite set the node
belongs to.
See also:
gnp_random_graph(),configuration_model()
References
networkx.algorithms.bipartite.generators.gnmk_random_graph
gnmk_random_graph(n,m,k,seed=None,directed=False)
Return a random bipartite graph G_{n,m,k}.
Produces a bipartite graph chosen randomly out of the set of all graphs with n top nodes, m bottom nodes, and
k edges.
Parameters
•n(int) – The number of nodes in the first bipartite set.
•m(int) – The number of nodes in the second bipartite set.
•k(int) – The number of edges
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True return a directed graph
Examples
from nx.algorithms import bipartite G = bipartite.gnmk_random_graph(10,20,50)
See also:
gnm_random_graph()
3.3. Bipartite 177

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This function is not imported in the main namespace. To use it you have to explicitly import the bipartite
package.
If k > m * n then a complete bipartite graph is returned.
This graph is a bipartite version of the G_{nm} random graph model.
3.3.10 Covering
Functions related to graph covers.
min_edge_cover(G[, matching_algorithm]) Returns a set of edges which constitutes the minimum
edge cover of the graph.
networkx.algorithms.bipartite.covering.min_edge_cover
min_edge_cover(G,matching_algorithm=None)
Returns a set of edges which constitutes the minimum edge cover of the graph.
The smallest edge cover can be found in polynomial time by finding a maximum matching and extending it
greedily so that all nodes are covered.
Parameters
•G(NetworkX graph) – An undirected bipartite graph.
•matching_algorithm (function) – A function that returns a maximum cardinality matching
in a given bipartite graph. The function must take one input, the graph G, and return a dic-
tionary mapping each node to its mate. If not specified, hopcroft_karp_matching()
will be used. Other possibilities include eppstein_matching(),
Returns A set of the edges in a minimum edge cover of the graph, given as pairs of nodes. It contains
both the edges (u, v) and (v, u) for given nodes uand vamong the edges of minimum
edge cover.
Return type set
Notes
An edge cover of a graph is a set of edges such that every node of the graph is incident to at least one edge of
the set. A minimum edge cover is an edge covering of smallest cardinality.
Due to its implementation, the worst-case running time of this algorithm is bounded by the worst-case running
time of the function matching_algorithm.
3.4 Boundary
Routines to find the boundary of a set of nodes.
An edge boundary is a set of edges, each of which has exactly one endpoint in a given set of nodes (or, in the case of
directed graphs, the set of edges whose source node is in the set).
A node boundary of a set Sof nodes is the set of (out-)neighbors of nodes in Sthat are outside S.
178 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
edge_boundary(G, nbunch1[, nbunch2, data, . . . ]) Returns the edge boundary of nbunch1.
node_boundary(G, nbunch1[, nbunch2]) Returns the node boundary of nbunch1.
3.4.1 networkx.algorithms.boundary.edge_boundary
edge_boundary(G,nbunch1,nbunch2=None,data=False,keys=False,default=None)
Returns the edge boundary of nbunch1.
The edge boundary of a set Swith respect to a set Tis the set of edges (u,v) such that uis in Sand vis in T. If
Tis not specified, it is assumed to be the set of all nodes not in S.
Parameters
•G(NetworkX graph)
•nbunch1 (iterable) – Iterable of nodes in the graph representing the set of nodes whose edge
boundary will be returned. (This is the set Sfrom the definition above.)
•nbunch2 (iterable) – Iterable of nodes representing the target (or “exterior”) set of nodes.
(This is the set Tfrom the definition above.) If not specified, this is assumed to be the set of
all nodes in Gnot in nbunch1.
•keys (bool) – This parameter has the same meaning as in MultiGraph.edges().
•data (bool or object) – This parameter has the same meaning as in MultiGraph.
edges().
•default (object) – This parameter has the same meaning as in MultiGraph.edges().
Returns An iterator over the edges in the boundary of nbunch1 with respect to nbunch2. If
keys,data, or default are specified and Gis a multigraph, then edges are returned with
keys and/or data, as in MultiGraph.edges().
Return type iterator
Notes
Any element of nbunch that is not in the graph Gwill be ignored.
nbunch1 and nbunch2 are usually meant to be disjoint, but in the interest of speed and generality, that is not
required here.
3.4.2 networkx.algorithms.boundary.node_boundary
node_boundary(G,nbunch1,nbunch2=None)
Returns the node boundary of nbunch1.
The node boundary of a set Swith respect to a set Tis the set of nodes vin Tsuch that for some uin S, there is
an edge joining uto v. If Tis not specified, it is assumed to be the set of all nodes not in S.
Parameters
•G(NetworkX graph)
•nbunch1 (iterable) – Iterable of nodes in the graph representing the set of nodes whose node
boundary will be returned. (This is the set Sfrom the definition above.)
3.4. Boundary 179
NetworkX Reference, Release 2.3rc1.dev20181203210840
•nbunch2 (iterable) – Iterable of nodes representing the target (or “exterior”) set of nodes.
(This is the set Tfrom the definition above.) If not specified, this is assumed to be the set of
all nodes in Gnot in nbunch1.
Returns The node boundary of nbunch1 with respect to nbunch2.
Return type set
Notes
Any element of nbunch that is not in the graph Gwill be ignored.
nbunch1 and nbunch2 are usually meant to be disjoint, but in the interest of speed and generality, that is not
required here.
3.5 Bridges
Bridge-finding algorithms.
bridges(G[, root]) Generate all bridges in a graph.
has_bridges(G[, root]) Decide whether a graph has any bridges.
local_bridges(G[, with_span, weight]) Iterate over local bridges of Goptionally computing the
span
3.5.1 networkx.algorithms.bridges.bridges
bridges(G,root=None)
Generate all bridges in a graph.
Abridge in a graph is an edge whose removal causes the number of connected components of the graph to
increase. Equivalently, a bridge is an edge that does not belong to any cycle.
Parameters
•G(undirected graph)
•root (node (optional)) – A node in the graph G. If specified, only the bridges in the connected
component containing this node will be returned.
Yields e (edge) – An edge in the graph whose removal disconnects the graph (or causes the number
of connected components to increase).
Raises NodeNotFound – If root is not in the graph G.
Examples
The barbell graph with parameter zero has a single bridge:
>>> G=nx.barbell_graph(10,0)
>>> list(nx.bridges(G))
[(9, 10)]
180 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This is an implementation of the algorithm described in _[1]. An edge is a bridge if and only if it is not contained
in any chain. Chains are found using the networkx.chain_decomposition() function.
Ignoring polylogarithmic factors, the worst-case time complexity is the same as the networkx.
chain_decomposition() function, 𝑂(𝑚+𝑛), where 𝑛is the number of nodes in the graph and 𝑚is
the number of edges.
References
3.5.2 networkx.algorithms.bridges.has_bridges
has_bridges(G,root=None)
Decide whether a graph has any bridges.
Abridge in a graph is an edge whose removal causes the number of connected components of the graph to
increase.
Parameters
•G(undirected graph)
•root (node (optional)) – A node in the graph G. If specified, only the bridges in the connected
component containing this node will be considered.
Returns Whether the graph (or the connected component containing root) has any bridges.
Return type bool
Raises NodeNotFound – If root is not in the graph G.
Examples
The barbell graph with parameter zero has a single bridge:
>>> G=nx.barbell_graph(10,0)
>>> nx.has_bridges(G)
True
On the other hand, the cycle graph has no bridges:
>>> G=nx.cycle_graph(5)
>>> nx.has_bridges(G)
False
Notes
This implementation uses the networkx.bridges() function, so it shares its worst-case time complexity,
𝑂(𝑚+𝑛), ignoring polylogarithmic factors, where 𝑛is the number of nodes in the graph and 𝑚is the number
of edges.
3.5. Bridges 181

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.5.3 networkx.algorithms.bridges.local_bridges
local_bridges(G,with_span=True,weight=None)
Iterate over local bridges of Goptionally computing the span
Alocal bridge is an edge whose endpoints have no common neighbors. That is, the edge is not part of a triangle
in the graph.
The span of a local bridge is the shortest path length between the endpoints if the local bridge is removed.
Parameters
•G(undirected graph)
•with_span (bool) – If True, yield a 3-tuple (u, v, span)
•weight (function, string or None (default: None)) – If function, used to compute edge
weights for the span. If string, the edge data attribute used in calculating span. If None,
all edges have weight 1.
Yields e (edge) – The local bridges as an edge 2-tuple of nodes (u, v) or as a 3-tuple (u, v,
span) when with_span is True.
Examples
A cycle graph has every edge a local bridge with span N-1.
>>> G=nx.cycle_graph(9)
>>> (0,8,8)in set(nx.local_bridges(G))
True
3.6 Centrality
3.6.1 Degree
degree_centrality(G) Compute the degree centrality for nodes.
in_degree_centrality(G) Compute the in-degree centrality for nodes.
out_degree_centrality(G) Compute the out-degree centrality for nodes.
networkx.algorithms.centrality.degree_centrality
degree_centrality(G)
Compute the degree centrality for nodes.
The degree centrality for a node v is the fraction of nodes it is connected to.
Parameters G (graph) – A networkx graph
Returns nodes – Dictionary of nodes with degree centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),load_centrality(),eigenvector_centrality()
182 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The degree centrality values are normalized by dividing by the maximum possible degree in a simple graph n-1
where n is the number of nodes in G.
For multigraphs or graphs with self loops the maximum degree might be higher than n-1 and values of degree
centrality greater than 1 are possible.
networkx.algorithms.centrality.in_degree_centrality
in_degree_centrality(G)
Compute the in-degree centrality for nodes.
The in-degree centrality for a node v is the fraction of nodes its incoming edges are connected to.
Parameters G (graph) – A NetworkX graph
Returns nodes – Dictionary of nodes with in-degree centrality as values.
Return type dictionary
Raises NetworkXNotImplemented: – If G is undirected.
See also:
degree_centrality(),out_degree_centrality()
Notes
The degree centrality values are normalized by dividing by the maximum possible degree in a simple graph n-1
where n is the number of nodes in G.
For multigraphs or graphs with self loops the maximum degree might be higher than n-1 and values of degree
centrality greater than 1 are possible.
networkx.algorithms.centrality.out_degree_centrality
out_degree_centrality(G)
Compute the out-degree centrality for nodes.
The out-degree centrality for a node v is the fraction of nodes its outgoing edges are connected to.
Parameters G (graph) – A NetworkX graph
Returns nodes – Dictionary of nodes with out-degree centrality as values.
Return type dictionary
Raises NetworkXNotImplemented: – If G is undirected.
See also:
degree_centrality(),in_degree_centrality()
3.6. Centrality 183

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The degree centrality values are normalized by dividing by the maximum possible degree in a simple graph n-1
where n is the number of nodes in G.
For multigraphs or graphs with self loops the maximum degree might be higher than n-1 and values of degree
centrality greater than 1 are possible.
3.6.2 Eigenvector
eigenvector_centrality(G[, max_iter, tol,
...])
Compute the eigenvector centrality for the graph G.
eigenvector_centrality_numpy(G[, weight,
...])
Compute the eigenvector centrality for the graph G.
katz_centrality(G[, alpha, beta, max_iter, . . . ]) Compute the Katz centrality for the nodes of the graph
G.
katz_centrality_numpy(G[, alpha, beta, . . . ]) Compute the Katz centrality for the graph G.
networkx.algorithms.centrality.eigenvector_centrality
eigenvector_centrality(G,max_iter=100,tol=1e-06,nstart=None,weight=None)
Compute the eigenvector centrality for the graph G.
Eigenvector centrality computes the centrality for a node based on the centrality of its neighbors. The eigenvec-
tor centrality for node 𝑖is the 𝑖-th element of the vector 𝑥defined by the equation
𝐴𝑥 =𝜆𝑥
where 𝐴is the adjacency matrix of the graph Gwith eigenvalue 𝜆. By virtue of the Perron–Frobenius theorem,
there is a unique solution 𝑥, all of whose entries are positive, if 𝜆is the largest eigenvalue of the adjacency
matrix 𝐴(2).
Parameters
•G(graph) – A networkx graph
•max_iter (integer, optional (default=100)) – Maximum number of iterations in power
method.
•tol (float, optional (default=1.0e-6)) – Error tolerance used to check convergence in power
method iteration.
•nstart (dictionary, optional (default=None)) – Starting value of eigenvector iteration for
each node.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
Returns nodes – Dictionary of nodes with eigenvector centrality as the value.
Return type dictionary
2Mark E. J. Newman. Networks: An Introduction. Oxford University Press, USA, 2010, pp. 169.
184 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> centrality =nx.eigenvector_centrality(G)
>>> sorted((v, '{:0.2f}'.format(c)) for v, c in centrality.items())
[(0, '0.37'), (1, '0.60'), (2, '0.60'), (3, '0.37')]
Raises
•NetworkXPointlessConcept – If the graph Gis the null graph.
•NetworkXError – If each value in nstart is zero.
•PowerIterationFailedConvergence – If the algorithm fails to converge to the
specified tolerance within the specified number of iterations of the power iteration method.
See also:
eigenvector_centrality_numpy(),pagerank(),hits()
Notes
The measure was introduced by1and is discussed in2.
The power iteration method is used to compute the eigenvector and convergence is not guaranteed. Our method
stops after max_iter iterations or when the change in the computed vector between two iterations is smaller
than an error tolerance of G.number_of_nodes() *tol. This implementation uses (𝐴+𝐼) rather than
the adjacency matrix 𝐴because it shifts the spectrum to enable discerning the correct eigenvector even for
networks with multiple dominant eigenvalues.
For directed graphs this is “left” eigenvector centrality which corresponds to the in-edges in the graph. For
out-edges eigenvector centrality first reverse the graph with G.reverse().
References
networkx.algorithms.centrality.eigenvector_centrality_numpy
eigenvector_centrality_numpy(G,weight=None,max_iter=50,tol=0)
Compute the eigenvector centrality for the graph G.
Eigenvector centrality computes the centrality for a node based on the centrality of its neighbors. The eigenvec-
tor centrality for node 𝑖is
𝐴𝑥 =𝜆𝑥
where 𝐴is the adjacency matrix of the graph G with eigenvalue 𝜆. By virtue of the Perron–Frobenius theorem,
there is a unique and positive solution if 𝜆is the largest eigenvalue associated with the eigenvector of the
adjacency matrix 𝐴(2).
Parameters
•G(graph) – A networkx graph
1Phillip Bonacich. “Power and Centrality: A Family of Measures.” American Journal of Sociology 92(5):1170–1182, 1986 <http://www.
leonidzhukov.net/hse/2014/socialnetworks/papers/Bonacich-Centrality.pdf>
2Mark E. J. Newman: Networks: An Introduction. Oxford University Press, USA, 2010, pp. 169.
3.6. Centrality 185

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (None or string, optional (default=None)) – The name of the edge attribute used as
weight. If None, all edge weights are considered equal.
•max_iter (integer, optional (default=100)) – Maximum number of iterations in power
method.
•tol (float, optional (default=1.0e-6)) – Relative accuracy for eigenvalues (stopping crite-
rion). The default value of 0 implies machine precision.
Returns nodes – Dictionary of nodes with eigenvector centrality as the value.
Return type dictionary
Examples
>>> G=nx.path_graph(4)
>>> centrality =nx.eigenvector_centrality_numpy(G)
>>> print(['{} {:0.2f}'.format(node, centrality[node]) for node in centrality])
['0 0.37', '1 0.60', '2 0.60', '3 0.37']
See also:
eigenvector_centrality(),pagerank(),hits()
Notes
The measure was introduced by1.
This algorithm uses the SciPy sparse eigenvalue solver (ARPACK) to find the largest eigenvalue/eigenvector
pair.
For directed graphs this is “left” eigenvector centrality which corresponds to the in-edges in the graph. For
out-edges eigenvector centrality first reverse the graph with G.reverse().
Raises NetworkXPointlessConcept – If the graph Gis the null graph.
References
networkx.algorithms.centrality.katz_centrality
katz_centrality(G,alpha=0.1,beta=1.0,max_iter=1000,tol=1e-06,nstart=None,normalized=True,
weight=None)
Compute the Katz centrality for the nodes of the graph G.
Katz centrality computes the centrality for a node based on the centrality of its neighbors. It is a generalization
of the eigenvector centrality. The Katz centrality for node 𝑖is
𝑥𝑖=𝛼
𝑗
𝐴𝑖𝑗 𝑥𝑗+𝛽,
where 𝐴is the adjacency matrix of graph G with eigenvalues 𝜆.
The parameter 𝛽controls the initial centrality and
𝛼 < 1
𝜆max
.
1Phillip Bonacich: Power and Centrality: A Family of Measures. American Journal of Sociology 92(5):1170–1182, 1986 http://www.
leonidzhukov.net/hse/2014/socialnetworks/papers/Bonacich-Centrality.pdf
186 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Katz centrality computes the relative influence of a node within a network by measuring the number of the
immediate neighbors (first degree nodes) and also all other nodes in the network that connect to the node under
consideration through these immediate neighbors.
Extra weight can be provided to immediate neighbors through the parameter 𝛽. Connections made with distant
neighbors are, however, penalized by an attenuation factor 𝛼which should be strictly less than the inverse largest
eigenvalue of the adjacency matrix in order for the Katz centrality to be computed correctly. More information
is provided in1.
Parameters
•G(graph) – A NetworkX graph.
•alpha (float) – Attenuation factor
•beta (scalar or dictionary, optional (default=1.0)) – Weight attributed to the immediate
neighborhood. If not a scalar, the dictionary must have an value for every node.
•max_iter (integer, optional (default=1000)) – Maximum number of iterations in power
method.
•tol (float, optional (default=1.0e-6)) – Error tolerance used to check convergence in power
method iteration.
•nstart (dictionary, optional) – Starting value of Katz iteration for each node.
•normalized (bool, optional (default=True)) – If True normalize the resulting values.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
Returns nodes – Dictionary of nodes with Katz centrality as the value.
Return type dictionary
Raises
•NetworkXError – If the parameter beta is not a scalar but lacks a value for at least one
node
•PowerIterationFailedConvergence – If the algorithm fails to converge to the
specified tolerance within the specified number of iterations of the power iteration method.
Examples
>>> import math
>>> G=nx.path_graph(4)
>>> phi =(1+math.sqrt(5)) /2.0 # largest eigenvalue of adj matrix
>>> centrality =nx.katz_centrality(G, 1/phi -0.01)
>>> for n, c in sorted(centrality.items()):
... print("%d %0.2f"%(n, c))
0 0.37
1 0.60
2 0.60
3 0.37
See also:
katz_centrality_numpy(),eigenvector_centrality(),eigenvector_centrality_numpy(),
pagerank(),hits()
1Mark E. J. Newman: Networks: An Introduction. Oxford University Press, USA, 2010, p. 720.
3.6. Centrality 187

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Katz centrality was introduced by2.
This algorithm it uses the power method to find the eigenvector corresponding to the largest eigenvalue of the
adjacency matrix of G. The parameter alpha should be strictly less than the inverse of largest eigenvalue of the
adjacency matrix for the algorithm to converge. You can use max(nx.adjacency_spectrum(G)) to get
𝜆max the largest eigenvalue of the adjacency matrix. The iteration will stop after max_iter iterations or an
error tolerance of number_of_nodes(G) *tol has been reached.
When 𝛼= 1/𝜆max and 𝛽= 0, Katz centrality is the same as eigenvector centrality.
For directed graphs this finds “left” eigenvectors which corresponds to the in-edges in the graph. For out-edges
Katz centrality first reverse the graph with G.reverse().
References
networkx.algorithms.centrality.katz_centrality_numpy
katz_centrality_numpy(G,alpha=0.1,beta=1.0,normalized=True,weight=None)
Compute the Katz centrality for the graph G.
Katz centrality computes the centrality for a node based on the centrality of its neighbors. It is a generalization
of the eigenvector centrality. The Katz centrality for node 𝑖is
𝑥𝑖=𝛼
𝑗
𝐴𝑖𝑗 𝑥𝑗+𝛽,
where 𝐴is the adjacency matrix of graph G with eigenvalues 𝜆.
The parameter 𝛽controls the initial centrality and
𝛼 < 1
𝜆max
.
Katz centrality computes the relative influence of a node within a network by measuring the number of the
immediate neighbors (first degree nodes) and also all other nodes in the network that connect to the node under
consideration through these immediate neighbors.
Extra weight can be provided to immediate neighbors through the parameter 𝛽. Connections made with distant
neighbors are, however, penalized by an attenuation factor 𝛼which should be strictly less than the inverse largest
eigenvalue of the adjacency matrix in order for the Katz centrality to be computed correctly. More information
is provided in1.
Parameters
•G(graph) – A NetworkX graph
•alpha (float) – Attenuation factor
•beta (scalar or dictionary, optional (default=1.0)) – Weight attributed to the immediate
neighborhood. If not a scalar the dictionary must have an value for every node.
•normalized (bool) – If True normalize the resulting values.
•weight (None or string, optional) – If None, all edge weights are considered equal. Other-
wise holds the name of the edge attribute used as weight.
2Leo Katz: A New Status Index Derived from Sociometric Index. Psychometrika 18(1):39–43, 1953 http://phya.snu.ac.kr/~dkim/
PRL87278701.pdf
1Mark E. J. Newman: Networks: An Introduction. Oxford University Press, USA, 2010, p. 720.
188 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns nodes – Dictionary of nodes with Katz centrality as the value.
Return type dictionary
Raises NetworkXError – If the parameter beta is not a scalar but lacks a value for at least one
node
Examples
>>> import math
>>> G=nx.path_graph(4)
>>> phi =(1+math.sqrt(5)) /2.0 # largest eigenvalue of adj matrix
>>> centrality =nx.katz_centrality_numpy(G, 1/phi)
>>> for n, c in sorted(centrality.items()):
... print("%d %0.2f"%(n, c))
0 0.37
1 0.60
2 0.60
3 0.37
See also:
katz_centrality(),eigenvector_centrality_numpy(),eigenvector_centrality(),
pagerank(),hits()
Notes
Katz centrality was introduced by2.
This algorithm uses a direct linear solver to solve the above equation. The parameter alpha should be strictly
less than the inverse of largest eigenvalue of the adjacency matrix for there to be a solution. You can use
max(nx.adjacency_spectrum(G)) to get 𝜆max the largest eigenvalue of the adjacency matrix.
When 𝛼= 1/𝜆max and 𝛽= 0, Katz centrality is the same as eigenvector centrality.
For directed graphs this finds “left” eigenvectors which corresponds to the in-edges in the graph. For out-edges
Katz centrality first reverse the graph with G.reverse().
References
3.6.3 Closeness
closeness_centrality(G[, u, distance, . . . ]) Compute closeness centrality for nodes.
networkx.algorithms.centrality.closeness_centrality
closeness_centrality(G,u=None,distance=None,wf_improved=True,reverse=False)
Compute closeness centrality for nodes.
Closeness centrality1of a node uis the reciprocal of the average shortest path distance to uover all n-1
2Leo Katz: A New Status Index Derived from Sociometric Index. Psychometrika 18(1):39–43, 1953 http://phya.snu.ac.kr/~dkim/
PRL87278701.pdf
1Linton C. Freeman: Centrality in networks: I. Conceptual clarification. Social Networks 1:215-239, 1979. http://leonidzhukov.ru/hse/2013/
socialnetworks/papers/freeman79-centrality.pdf
3.6. Centrality 189

NetworkX Reference, Release 2.3rc1.dev20181203210840
reachable nodes.
𝐶(𝑢) = 𝑛−1
𝑛−1
𝑣=1 𝑑(𝑣, 𝑢),
where d(v, u) is the shortest-path distance between vand u, and nis the number of nodes that can reach u.
Notice that higher values of closeness indicate higher centrality.
Wasserman and Faust propose an improved formula for graphs with more than one connected component. The
result is “a ratio of the fraction of actors in the group who are reachable, to the average distance” from the
reachable actors2. You might think this scale factor is inverted but it is not. As is, nodes from small components
receive a smaller closeness value. Letting Ndenote the number of nodes in the graph,
𝐶𝑊 𝐹 (𝑢) = 𝑛−1
𝑁−1
𝑛−1
𝑛−1
𝑣=1 𝑑(𝑣, 𝑢),
Parameters
•G(graph) – A NetworkX graph
•u(node, optional) – Return only the value for node u
•distance (edge attribute key, optional (default=None)) – Use the specified edge attribute as
the edge distance in shortest path calculations
•wf_improved (bool, optional (default=True)) – If True, scale by the fraction of nodes reach-
able. This gives the Wasserman and Faust improved formula. For single component graphs
it is the same as the original formula.
•reverse (bool, optional (default=False)) – If True and G is a digraph, reverse the edges of
G, using successors instead of predecessors.
Returns nodes – Dictionary of nodes with closeness centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),load_centrality(),eigenvector_centrality(),
degree_centrality()
Notes
The closeness centrality is normalized to (n-1)/(|G|-1) where nis the number of nodes in the connected
part of graph containing the node. If the graph is not completely connected, this algorithm computes the close-
ness centrality for each connected part separately scaled by that parts size.
If the ‘distance’ keyword is set to an edge attribute key then the shortest-path length will be computed using
Dijkstra’s algorithm with that edge attribute as the edge weight.
References
3.6.4 Current Flow Closeness
2pg. 201 of Wasserman, S. and Faust, K., Social Network Analysis: Methods and Applications, 1994, Cambridge University Press.
190 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
current_flow_closeness_centrality(G[,
...])
Compute current-flow closeness centrality for nodes.
information_centrality(G[, weight, dtype,
...])
Compute current-flow closeness centrality for nodes.
networkx.algorithms.centrality.current_flow_closeness_centrality
current_flow_closeness_centrality(G,weight=None,dtype=<class ’float’>,solver=’lu’)
Compute current-flow closeness centrality for nodes.
Current-flow closeness centrality is variant of closeness centrality based on effective resistance between nodes
in a network. This metric is also known as information centrality.
Parameters
•G(graph) – A NetworkX graph.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
•dtype (data type (default=float)) – Default data type for internal matrices. Set to np.float32
for lower memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
Returns nodes – Dictionary of nodes with current flow closeness centrality as the value.
Return type dictionary
See also:
closeness_centrality()
Notes
The algorithm is from Brandes1.
See also2for the original definition of information centrality.
References
networkx.algorithms.centrality.information_centrality
information_centrality(G,weight=None,dtype=<class ’float’>,solver=’lu’)
Compute current-flow closeness centrality for nodes.
Current-flow closeness centrality is variant of closeness centrality based on effective resistance between nodes
in a network. This metric is also known as information centrality.
Parameters
•G(graph) – A NetworkX graph.
1Ulrik Brandes and Daniel Fleischer, Centrality Measures Based on Current Flow. Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
2Karen Stephenson and Marvin Zelen: Rethinking centrality: Methods and examples. Social Networks 11(1):1-37, 1989. https://doi.org/10.
1016/0378-8733(89)90016-6
3.6. Centrality 191

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
•dtype (data type (default=float)) – Default data type for internal matrices. Set to np.float32
for lower memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
Returns nodes – Dictionary of nodes with current flow closeness centrality as the value.
Return type dictionary
See also:
closeness_centrality()
Notes
The algorithm is from Brandes1.
See also2for the original definition of information centrality.
References
3.6.5 (Shortest Path) Betweenness
betweenness_centrality(G[, k, normalized,
...])
Compute the shortest-path betweenness centrality for
nodes.
edge_betweenness_centrality(G[, k, . . . ]) Compute betweenness centrality for edges.
betweenness_centrality_subset(G, sources,
...)
Compute betweenness centrality for a subset of nodes.
edge_betweenness_centrality_subset(G,
...[, ...])
Compute betweenness centrality for edges for a subset
of nodes.
networkx.algorithms.centrality.betweenness_centrality
betweenness_centrality(G,k=None,normalized=True,weight=None,endpoints=False,seed=None)
Compute the shortest-path betweenness centrality for nodes.
Betweenness centrality of a node 𝑣is the sum of the fraction of all-pairs shortest paths that pass through 𝑣
𝑐𝐵(𝑣) =
𝑠,𝑡∈𝑉
𝜎(𝑠, 𝑡|𝑣)
𝜎(𝑠, 𝑡)
where 𝑉is the set of nodes, 𝜎(𝑠, 𝑡)is the number of shortest (𝑠, 𝑡)-paths, and 𝜎(𝑠, 𝑡|𝑣)is the number of those
paths passing through some node 𝑣other than 𝑠, 𝑡. If 𝑠=𝑡,𝜎(𝑠, 𝑡) = 1, and if 𝑣∈𝑠, 𝑡,𝜎(𝑠, 𝑡|𝑣)=02.
Parameters
•G(graph) – A NetworkX graph.
1Ulrik Brandes and Daniel Fleischer, Centrality Measures Based on Current Flow. Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
2Karen Stephenson and Marvin Zelen: Rethinking centrality: Methods and examples. Social Networks 11(1):1-37, 1989. https://doi.org/10.
1016/0378-8733(89)90016-6
2Ulrik Brandes: On Variants of Shortest-Path Betweenness Centrality and their Generic Computation. Social Networks 30(2):136-145, 2008.
http://www.inf.uni-konstanz.de/algo/publications/b-vspbc-08.pdf
192 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•k(int, optional (default=None)) – If k is not None use k node samples to estimate between-
ness. The value of k <= n where n is the number of nodes in the graph. Higher values give
better approximation.
•normalized (bool, optional) – If True the betweenness values are normalized by 2/
((n-1)(n-2)) for graphs, and 1/((n-1)(n-2)) for directed graphs where nis the
number of nodes in G.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
•endpoints (bool, optional) – If True include the endpoints in the shortest path counts.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness. Note that this is only used if k is not None.
Returns nodes – Dictionary of nodes with betweenness centrality as the value.
Return type dictionary
See also:
edge_betweenness_centrality(),load_centrality()
Notes
The algorithm is from Ulrik Brandes1. See4for the original first published version and2for details on algorithms
for variations and related metrics.
For approximate betweenness calculations set k=#samples to use k nodes (“pivots”) to estimate the betweenness
values. For an estimate of the number of pivots needed see3.
For weighted graphs the edge weights must be greater than zero. Zero edge weights can produce an infinite
number of equal length paths between pairs of nodes.
References
networkx.algorithms.centrality.edge_betweenness_centrality
edge_betweenness_centrality(G,k=None,normalized=True,weight=None,seed=None)
Compute betweenness centrality for edges.
Betweenness centrality of an edge 𝑒is the sum of the fraction of all-pairs shortest paths that pass through 𝑒
𝑐𝐵(𝑒) =
𝑠,𝑡∈𝑉
𝜎(𝑠, 𝑡|𝑒)
𝜎(𝑠, 𝑡)
where 𝑉is the set of nodes, 𝜎(𝑠, 𝑡)is the number of shortest (𝑠, 𝑡)-paths, and 𝜎(𝑠, 𝑡|𝑒)is the number of those
paths passing through edge 𝑒2.
Parameters
•G(graph) – A NetworkX graph.
1Ulrik Brandes: A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology 25(2):163-177, 2001. http://www.inf.
uni-konstanz.de/algo/publications/b-fabc-01.pdf
4Linton C. Freeman: A set of measures of centrality based on betweenness. Sociometry 40: 35–41, 1977 http://moreno.ss.uci.edu/23.pdf
3Ulrik Brandes and Christian Pich: Centrality Estimation in Large Networks. International Journal of Bifurcation and Chaos 17(7):2303-2318,
2007. http://www.inf.uni-konstanz.de/algo/publications/bp-celn-06.pdf
2Ulrik Brandes: On Variants of Shortest-Path Betweenness Centrality and their Generic Computation. Social Networks 30(2):136-145, 2008.
http://www.inf.uni-konstanz.de/algo/publications/b-vspbc-08.pdf
3.6. Centrality 193

NetworkX Reference, Release 2.3rc1.dev20181203210840
•k(int, optional (default=None)) – If k is not None use k node samples to estimate between-
ness. The value of k <= n where n is the number of nodes in the graph. Higher values give
better approximation.
•normalized (bool, optional) – If True the betweenness values are normalized by 2/(𝑛(𝑛−
1)) for graphs, and 1/(𝑛(𝑛−1)) for directed graphs where 𝑛is the number of nodes in G.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness. Note that this is only used if k is not None.
Returns edges – Dictionary of edges with betweenness centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),edge_load()
Notes
The algorithm is from Ulrik Brandes1.
For weighted graphs the edge weights must be greater than zero. Zero edge weights can produce an infinite
number of equal length paths between pairs of nodes.
References
networkx.algorithms.centrality.betweenness_centrality_subset
betweenness_centrality_subset(G,sources,targets,normalized=False,weight=None)
Compute betweenness centrality for a subset of nodes.
𝑐𝐵(𝑣) =
𝑠∈𝑆,𝑡∈𝑇
𝜎(𝑠, 𝑡|𝑣)
𝜎(𝑠, 𝑡)
where 𝑆is the set of sources, 𝑇is the set of targets, 𝜎(𝑠, 𝑡)is the number of shortest (𝑠, 𝑡)-paths, and 𝜎(𝑠, 𝑡|𝑣)
is the number of those paths passing through some node 𝑣other than 𝑠, 𝑡. If 𝑠=𝑡,𝜎(𝑠, 𝑡)=1, and if 𝑣∈𝑠, 𝑡,
𝜎(𝑠, 𝑡|𝑣) = 02.
Parameters
•G(graph) – A NetworkX graph.
•sources (list of nodes) – Nodes to use as sources for shortest paths in betweenness
•targets (list of nodes) – Nodes to use as targets for shortest paths in betweenness
•normalized (bool, optional) – If True the betweenness values are normalized by 2/((𝑛−
1)(𝑛−2)) for graphs, and 1/((𝑛−1)(𝑛−2)) for directed graphs where 𝑛is the number of
nodes in G.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
1A Faster Algorithm for Betweenness Centrality. Ulrik Brandes, Journal of Mathematical Sociology 25(2):163-177, 2001. http://www.inf.
uni-konstanz.de/algo/publications/b-fabc-01.pdf
2Ulrik Brandes: On Variants of Shortest-Path Betweenness Centrality and their Generic Computation. Social Networks 30(2):136-145, 2008.
http://www.inf.uni-konstanz.de/algo/publications/b-vspbc-08.pdf
194 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns nodes – Dictionary of nodes with betweenness centrality as the value.
Return type dictionary
See also:
edge_betweenness_centrality(),load_centrality()
Notes
The basic algorithm is from1.
For weighted graphs the edge weights must be greater than zero. Zero edge weights can produce an infinite
number of equal length paths between pairs of nodes.
The normalization might seem a little strange but it is the same as in between-
ness_centrality() and is designed to make betweenness_centrality(G) be the same as between-
ness_centrality_subset(G,sources=G.nodes(),targets=G.nodes()).
References
networkx.algorithms.centrality.edge_betweenness_centrality_subset
edge_betweenness_centrality_subset(G,sources,targets,normalized=False,weight=None)
Compute betweenness centrality for edges for a subset of nodes.
𝑐𝐵(𝑣) =
𝑠∈𝑆,𝑡∈𝑇
𝜎(𝑠, 𝑡|𝑒)
𝜎(𝑠, 𝑡)
where 𝑆is the set of sources, 𝑇is the set of targets, 𝜎(𝑠, 𝑡)is the number of shortest (𝑠, 𝑡)-paths, and 𝜎(𝑠, 𝑡|𝑒)
is the number of those paths passing through edge 𝑒2.
Parameters
•G(graph) – A networkx graph.
•sources (list of nodes) – Nodes to use as sources for shortest paths in betweenness
•targets (list of nodes) – Nodes to use as targets for shortest paths in betweenness
•normalized (bool, optional) – If True the betweenness values are normalized by 2/
(n(n-1)) for graphs, and 1/(n(n-1)) for directed graphs where nis the number of
nodes in G.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
Returns edges – Dictionary of edges with Betweenness centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),edge_load()
1Ulrik Brandes, A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology 25(2):163-177, 2001. http://www.inf.
uni-konstanz.de/algo/publications/b-fabc-01.pdf
2Ulrik Brandes: On Variants of Shortest-Path Betweenness Centrality and their Generic Computation. Social Networks 30(2):136-145, 2008.
http://www.inf.uni-konstanz.de/algo/publications/b-vspbc-08.pdf
3.6. Centrality 195

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The basic algorithm is from1.
For weighted graphs the edge weights must be greater than zero. Zero edge weights can produce an infinite
number of equal length paths between pairs of nodes.
The normalization might seem a little strange but it is the same as in
edge_betweenness_centrality() and is designed to make edge_betweenness_centrality(G) be the same as
edge_betweenness_centrality_subset(G,sources=G.nodes(),targets=G.nodes()).
References
3.6.6 Current Flow Betweenness
current_flow_betweenness_centrality(G[,
...])
Compute current-flow betweenness centrality for nodes.
edge_current_flow_betweenness_centrality(G)Compute current-flow betweenness centrality for edges.
approximate_current_flow_betweenness_centrality(G)Compute the approximate current-flow betweenness
centrality for nodes.
current_flow_betweenness_centrality_subset(G,
...)
Compute current-flow betweenness centrality for sub-
sets of nodes.
edge_current_flow_betweenness_centrality_subset(G,
...)
Compute current-flow betweenness centrality for edges
using subsets of nodes.
networkx.algorithms.centrality.current_flow_betweenness_centrality
current_flow_betweenness_centrality(G,normalized=True,weight=None,dtype=<class
’float’>,solver=’full’)
Compute current-flow betweenness centrality for nodes.
Current-flow betweenness centrality uses an electrical current model for information spreading in contrast to
betweenness centrality which uses shortest paths.
Current-flow betweenness centrality is also known as random-walk betweenness centrality2.
Parameters
•G(graph) – A NetworkX graph
•normalized (bool, optional (default=True)) – If True the betweenness values are normalized
by 2/[(n-1)(n-2)] where n is the number of nodes in G.
•weight (string or None, optional (default=None)) – Key for edge data used as the edge
weight. If None, then use 1 as each edge weight.
•dtype (data type (float)) – Default data type for internal matrices. Set to np.float32 for lower
memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
Returns nodes – Dictionary of nodes with betweenness centrality as the value.
Return type dictionary
1Ulrik Brandes, A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology 25(2):163-177, 2001. http://www.inf.
uni-konstanz.de/algo/publications/b-fabc-01.pdf
2A measure of betweenness centrality based on random walks, M. E. J. Newman, Social Networks 27, 39-54 (2005).
196 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
approximate_current_flow_betweenness_centrality(),betweenness_centrality(),
edge_betweenness_centrality(),edge_current_flow_betweenness_centrality()
Notes
Current-flow betweenness can be computed in 𝑂(𝐼(𝑛−1) + 𝑚𝑛 log 𝑛)time1, where 𝐼(𝑛−1) is the time
needed to compute the inverse Laplacian. For a full matrix this is 𝑂(𝑛3)but using sparse methods you can
achieve 𝑂(𝑛𝑚√𝑘)where 𝑘is the Laplacian matrix condition number.
The space required is 𝑂(𝑛𝑤)where 𝑤is the width of the sparse Laplacian matrix. Worse case is 𝑤=𝑛for
𝑂(𝑛2).
If the edges have a ‘weight’ attribute they will be used as weights in this algorithm. Unspecified weights are set
to 1.
References
networkx.algorithms.centrality.edge_current_flow_betweenness_centrality
edge_current_flow_betweenness_centrality(G,normalized=True,weight=None,
dtype=<class ’float’>,solver=’full’)
Compute current-flow betweenness centrality for edges.
Current-flow betweenness centrality uses an electrical current model for information spreading in contrast to
betweenness centrality which uses shortest paths.
Current-flow betweenness centrality is also known as random-walk betweenness centrality2.
Parameters
•G(graph) – A NetworkX graph
•normalized (bool, optional (default=True)) – If True the betweenness values are normalized
by 2/[(n-1)(n-2)] where n is the number of nodes in G.
•weight (string or None, optional (default=None)) – Key for edge data used as the edge
weight. If None, then use 1 as each edge weight.
•dtype (data type (default=float)) – Default data type for internal matrices. Set to np.float32
for lower memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
Returns nodes – Dictionary of edge tuples with betweenness centrality as the value.
Return type dictionary
Raises NetworkXError – The algorithm does not support DiGraphs. If the input graph is an
instance of DiGraph class, NetworkXError is raised.
See also:
betweenness_centrality(),edge_betweenness_centrality(),
current_flow_betweenness_centrality()
1Centrality Measures Based on Current Flow. Ulrik Brandes and Daniel Fleischer, Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
2A measure of betweenness centrality based on random walks, M. E. J. Newman, Social Networks 27, 39-54 (2005).
3.6. Centrality 197

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Current-flow betweenness can be computed in 𝑂(𝐼(𝑛−1) + 𝑚𝑛 log 𝑛)time1, where 𝐼(𝑛−1) is the time
needed to compute the inverse Laplacian. For a full matrix this is 𝑂(𝑛3)but using sparse methods you can
achieve 𝑂(𝑛𝑚√𝑘)where 𝑘is the Laplacian matrix condition number.
The space required is 𝑂(𝑛𝑤)where 𝑤is the width of the sparse Laplacian matrix. Worse case is 𝑤=𝑛for
𝑂(𝑛2).
If the edges have a ‘weight’ attribute they will be used as weights in this algorithm. Unspecified weights are set
to 1.
References
networkx.algorithms.centrality.approximate_current_flow_betweenness_centrality
approximate_current_flow_betweenness_centrality(G,normalized=True,weight=None,
dtype=<class ’float’>,solver=’full’,
epsilon=0.5,kmax=10000,
seed=None)
Compute the approximate current-flow betweenness centrality for nodes.
Approximates the current-flow betweenness centrality within absolute error of epsilon with high probability1.
Parameters
•G(graph) – A NetworkX graph
•normalized (bool, optional (default=True)) – If True the betweenness values are normalized
by 2/[(n-1)(n-2)] where n is the number of nodes in G.
•weight (string or None, optional (default=None)) – Key for edge data used as the edge
weight. If None, then use 1 as each edge weight.
•dtype (data type (float)) – Default data type for internal matrices. Set to np.float32 for lower
memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
•epsilon (float) – Absolute error tolerance.
•kmax (int) – Maximum number of sample node pairs to use for approximation.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns nodes – Dictionary of nodes with betweenness centrality as the value.
Return type dictionary
See also:
current_flow_betweenness_centrality()
1Centrality Measures Based on Current Flow. Ulrik Brandes and Daniel Fleischer, Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
1Ulrik Brandes and Daniel Fleischer: Centrality Measures Based on Current Flow. Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
198 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The running time is 𝑂((1/𝜖2)𝑚√𝑘log 𝑛)and the space required is 𝑂(𝑚)for 𝑛nodes and 𝑚edges.
If the edges have a ‘weight’ attribute they will be used as weights in this algorithm. Unspecified weights are set
to 1.
References
networkx.algorithms.centrality.current_flow_betweenness_centrality_subset
current_flow_betweenness_centrality_subset(G,sources,targets,normalized=True,
weight=None,dtype=<class ’float’>,
solver=’lu’)
Compute current-flow betweenness centrality for subsets of nodes.
Current-flow betweenness centrality uses an electrical current model for information spreading in contrast to
betweenness centrality which uses shortest paths.
Current-flow betweenness centrality is also known as random-walk betweenness centrality2.
Parameters
•G(graph) – A NetworkX graph
•sources (list of nodes) – Nodes to use as sources for current
•targets (list of nodes) – Nodes to use as sinks for current
•normalized (bool, optional (default=True)) – If True the betweenness values are normalized
by b=b/(n-1)(n-2) where n is the number of nodes in G.
•weight (string or None, optional (default=None)) – Key for edge data used as the edge
weight. If None, then use 1 as each edge weight.
•dtype (data type (float)) – Default data type for internal matrices. Set to np.float32 for lower
memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
Returns nodes – Dictionary of nodes with betweenness centrality as the value.
Return type dictionary
See also:
approximate_current_flow_betweenness_centrality(),betweenness_centrality(),
edge_betweenness_centrality(),edge_current_flow_betweenness_centrality()
Notes
Current-flow betweenness can be computed in 𝑂(𝐼(𝑛−1) + 𝑚𝑛 log 𝑛)time1, where 𝐼(𝑛−1) is the time
needed to compute the inverse Laplacian. For a full matrix this is 𝑂(𝑛3)but using sparse methods you can
achieve 𝑂(𝑛𝑚√𝑘)where 𝑘is the Laplacian matrix condition number.
2A measure of betweenness centrality based on random walks, M. E. J. Newman, Social Networks 27, 39-54 (2005).
1Centrality Measures Based on Current Flow. Ulrik Brandes and Daniel Fleischer, Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
3.6. Centrality 199

NetworkX Reference, Release 2.3rc1.dev20181203210840
The space required is 𝑂(𝑛𝑤)where 𝑤is the width of the sparse Laplacian matrix. Worse case is 𝑤=𝑛for
𝑂(𝑛2).
If the edges have a ‘weight’ attribute they will be used as weights in this algorithm. Unspecified weights are set
to 1.
References
networkx.algorithms.centrality.edge_current_flow_betweenness_centrality_subset
edge_current_flow_betweenness_centrality_subset(G,sources,targets,normalized=True,
weight=None,dtype=<class ’float’>,
solver=’lu’)
Compute current-flow betweenness centrality for edges using subsets of nodes.
Current-flow betweenness centrality uses an electrical current model for information spreading in contrast to
betweenness centrality which uses shortest paths.
Current-flow betweenness centrality is also known as random-walk betweenness centrality2.
Parameters
•G(graph) – A NetworkX graph
•sources (list of nodes) – Nodes to use as sources for current
•targets (list of nodes) – Nodes to use as sinks for current
•normalized (bool, optional (default=True)) – If True the betweenness values are normalized
by b=b/(n-1)(n-2) where n is the number of nodes in G.
•weight (string or None, optional (default=None)) – Key for edge data used as the edge
weight. If None, then use 1 as each edge weight.
•dtype (data type (float)) – Default data type for internal matrices. Set to np.float32 for lower
memory consumption.
•solver (string (default=’lu’)) – Type of linear solver to use for computing the flow matrix.
Options are “full” (uses most memory), “lu” (recommended), and “cg” (uses least memory).
Returns nodes – Dictionary of edge tuples with betweenness centrality as the value.
Return type dict
See also:
betweenness_centrality(),edge_betweenness_centrality(),
current_flow_betweenness_centrality()
Notes
Current-flow betweenness can be computed in 𝑂(𝐼(𝑛−1) + 𝑚𝑛 log 𝑛)time1, where 𝐼(𝑛−1) is the time
needed to compute the inverse Laplacian. For a full matrix this is 𝑂(𝑛3)but using sparse methods you can
achieve 𝑂(𝑛𝑚√𝑘)where 𝑘is the Laplacian matrix condition number.
The space required is 𝑂(𝑛𝑤)where 𝑤is the width of the sparse Laplacian matrix. Worse case is 𝑤=𝑛for
𝑂(𝑛2).
2A measure of betweenness centrality based on random walks, M. E. J. Newman, Social Networks 27, 39-54 (2005).
1Centrality Measures Based on Current Flow. Ulrik Brandes and Daniel Fleischer, Proc. 22nd Symp. Theoretical Aspects of Computer Science
(STACS ‘05). LNCS 3404, pp. 533-544. Springer-Verlag, 2005. http://algo.uni-konstanz.de/publications/bf-cmbcf-05.pdf
200 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
If the edges have a ‘weight’ attribute they will be used as weights in this algorithm. Unspecified weights are set
to 1.
References
3.6.7 Communicability Betweenness
communicability_betweenness_centrality(G[,
...])
Return subgraph communicability for all pairs of nodes
in G.
networkx.algorithms.centrality.communicability_betweenness_centrality
communicability_betweenness_centrality(G,normalized=True)
Return subgraph communicability for all pairs of nodes in G.
Communicability betweenness measure makes use of the number of walks connecting every pair of nodes as the
basis of a betweenness centrality measure.
Parameters G (graph)
Returns nodes – Dictionary of nodes with communicability betweenness as the value.
Return type dictionary
Raises NetworkXError – If the graph is not undirected and simple.
Notes
Let G=(V,E) be a simple undirected graph with nnodes and medges, and Adenote the adjacency matrix of G.
Let G(r)=(V,E(r)) be the graph resulting from removing all edges connected to node rbut not the node
itself.
The adjacency matrix for G(r) is A+E(r), where E(r) has nonzeros only in row and column r.
The subraph betweenness of a node ris1
𝜔𝑟=1
𝐶
𝑝
𝑞
𝐺𝑝𝑟𝑞
𝐺𝑝𝑞
, 𝑝 ̸=𝑞, 𝑞 ̸=𝑟,
where G_{prq}=(e^{A}_{pq} - (e^{A+E(r)})_{pq} is the number of walks involving node r,
G_{pq}=(e^{A})_{pq} is the number of closed walks starting at node pand ending at node q, and
C=(n-1)^{2}-(n-1) is a normalization factor equal to the number of terms in the sum.
The resulting omega_{r} takes values between zero and one. The lower bound cannot be attained for a
connected graph, and the upper bound is attained in the star graph.
References
Examples
1Ernesto Estrada, Desmond J. Higham, Naomichi Hatano, “Communicability Betweenness in Complex Networks” Physica A 388 (2009) 764-
774. https://arxiv.org/abs/0905.4102
3.6. Centrality 201

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)])
>>> cbc =nx.communicability_betweenness_centrality(G)
3.6.8 Load
load_centrality(G[, v, cutoff, normalized, . . . ]) Compute load centrality for nodes.
edge_load_centrality(G[, cutoff]) Compute edge load.
networkx.algorithms.centrality.load_centrality
load_centrality(G,v=None,cutoff=None,normalized=True,weight=None)
Compute load centrality for nodes.
The load centrality of a node is the fraction of all shortest paths that pass through that node.
Parameters
•G(graph) – A networkx graph.
•normalized (bool, optional (default=True)) – If True the betweenness values are normalized
by b=b/(n-1)(n-2) where n is the number of nodes in G.
•weight (None or string, optional (default=None)) – If None, edge weights are ignored.
Otherwise holds the name of the edge attribute used as weight.
•cutoff (bool, optional (default=None)) – If specified, only consider paths of length <= cut-
off.
Returns nodes – Dictionary of nodes with centrality as the value.
Return type dictionary
See also:
betweenness_centrality()
Notes
Load centrality is slightly different than betweenness. It was originally introduced by2. For this load algorithm
see1.
References
networkx.algorithms.centrality.edge_load_centrality
edge_load_centrality(G,cutoff=False)
Compute edge load.
WARNING: This concept of edge load has not been analysed or discussed outside of NetworkX that we know
of. It is based loosely on load_centrality in the sense that it counts the number of shortest paths which cross
each edge. This function is for demonstration and testing purposes.
2Kwang-Il Goh, Byungnam Kahng and Doochul Kim Universal behavior of Load Distribution in Scale-Free Networks. Physical Review Letters
87(27):1–4, 2001. http://phya.snu.ac.kr/~dkim/PRL87278701.pdf
1Mark E. J. Newman: Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Physical Review E 64, 016132,
2001. http://journals.aps.org/pre/abstract/10.1103/PhysRevE.64.016132
202 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(graph) – A networkx graph
•cutoff (bool, optional (default=False)) – If specified, only consider paths of length <= cut-
off.
Returns
•A dict keyed by edge 2-tuple to the number of shortest paths
•which use that edge. Where more than one path is shortest
•the count is divided equally among paths.
3.6.9 Subgraph
subgraph_centrality(G) Return subgraph centrality for each node in G.
subgraph_centrality_exp(G) Return the subgraph centrality for each node of G.
estrada_index(G) Return the Estrada index of a the graph G.
networkx.algorithms.centrality.subgraph_centrality
subgraph_centrality(G)
Return subgraph centrality for each node in G.
Subgraph centrality of a node nis the sum of weighted closed walks of all lengths starting and ending at node
n. The weights decrease with path length. Each closed walk is associated with a connected subgraph (1).
Parameters G (graph)
Returns nodes – Dictionary of nodes with subgraph centrality as the value.
Return type dictionary
Raises NetworkXError – If the graph is not undirected and simple.
See also:
subgraph_centrality_exp() Alternative algorithm of the subgraph centrality for each node of G.
Notes
This version of the algorithm computes eigenvalues and eigenvectors of the adjacency matrix.
Subgraph centrality of a node uin G can be found using a spectral decomposition of the adjacency matrix1,
𝑆𝐶(𝑢) =
𝑁
𝑗=1
(𝑣𝑢
𝑗)2𝑒𝜆𝑗,
where v_j is an eigenvector of the adjacency matrix Aof G corresponding corresponding to the eigenvalue
lambda_j.
1Ernesto Estrada, Juan A. Rodriguez-Velazquez, “Subgraph centrality in complex networks”, Physical Review E 71, 056103 (2005). https:
//arxiv.org/abs/cond-mat/0504730
3.6. Centrality 203

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
(Example from1) >>> G = nx.Graph([(1,2),(1,5),(1,8),(2,3),(2,8),(3,4),(3,6),(4,5),(4,7),(5,6),(6,7),(7,8)]) >>> sc
= nx.subgraph_centrality(G) >>> print([‘%s %0.2f’%(node,sc[node]) for node in sorted(sc)]) [‘1 3.90’, ‘2 3.90’,
‘3 3.64’, ‘4 3.71’, ‘5 3.64’, ‘6 3.71’, ‘7 3.64’, ‘8 3.90’]
References
networkx.algorithms.centrality.subgraph_centrality_exp
subgraph_centrality_exp(G)
Return the subgraph centrality for each node of G.
Subgraph centrality of a node nis the sum of weighted closed walks of all lengths starting and ending at node
n. The weights decrease with path length. Each closed walk is associated with a connected subgraph (1).
Parameters G (graph)
Returns nodes – Dictionary of nodes with subgraph centrality as the value.
Return type dictionary
Raises NetworkXError – If the graph is not undirected and simple.
See also:
subgraph_centrality() Alternative algorithm of the subgraph centrality for each node of G.
Notes
This version of the algorithm exponentiates the adjacency matrix.
The subgraph centrality of a node uin G can be found using the matrix exponential of the adjacency matrix of
G1,
𝑆𝐶(𝑢) = (𝑒𝐴)𝑢𝑢.
References
Examples
(Example from1) >>> G = nx.Graph([(1,2),(1,5),(1,8),(2,3),(2,8),(3,4),(3,6),(4,5),(4,7),(5,6),(6,7),(7,8)]) >>> sc
= nx.subgraph_centrality_exp(G) >>> print([‘%s %0.2f’%(node,sc[node]) for node in sorted(sc)]) [‘1 3.90’, ‘2
3.90’, ‘3 3.64’, ‘4 3.71’, ‘5 3.64’, ‘6 3.71’, ‘7 3.64’, ‘8 3.90’]
networkx.algorithms.centrality.estrada_index
estrada_index(G)
Return the Estrada index of a the graph G.
The Estrada Index is a topological index of folding or 3D “compactness” (1).
1Ernesto Estrada, Juan A. Rodriguez-Velazquez, “Subgraph centrality in complex networks”, Physical Review E 71, 056103 (2005). https:
//arxiv.org/abs/cond-mat/0504730
1E. Estrada, “Characterization of 3D molecular structure”, Chem. Phys. Lett. 319, 713 (2000). https://doi.org/10.1016/S0009-2614(00)00158-5
204 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters G (graph)
Returns estrada index
Return type float
Raises NetworkXError – If the graph is not undirected and simple.
Notes
Let G=(V,E) be a simple undirected graph with nnodes and let
lambda_{1}leqlambda_{2}leqcdotslambda_{n} be a non-increasing ordering of the eigen-
values of its adjacency matrix A. The Estrada index is (1,2)
𝐸𝐸(𝐺) =
𝑛
𝑗=1
𝑒𝜆𝑗.
References
Examples
>>> G=nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)])
>>> ei=nx.estrada_index(G)
3.6.10 Harmonic Centrality
harmonic_centrality(G[, nbunch, distance]) Compute harmonic centrality for nodes.
networkx.algorithms.centrality.harmonic_centrality
harmonic_centrality(G,nbunch=None,distance=None)
Compute harmonic centrality for nodes.
Harmonic centrality1of a node uis the sum of the reciprocal of the shortest path distances from all other nodes
to u
𝐶(𝑢) =
𝑣̸=𝑢
1
𝑑(𝑣, 𝑢)
where d(v, u) is the shortest-path distance between vand u.
Notice that higher values indicate higher centrality.
Parameters
•G(graph) – A NetworkX graph
•nbunch (container) – Container of nodes. If provided harmonic centrality will be computed
only over the nodes in nbunch.
2José Antonio de la Peñaa, Ivan Gutman, Juan Rada, “Estimating the Estrada index”, Linear Algebra and its Applications. 427, 1 (2007).
https://doi.org/10.1016/j.laa.2007.06.020
1Boldi, Paolo, and Sebastiano Vigna. “Axioms for centrality.” Internet Mathematics 10.3-4 (2014): 222-262.
3.6. Centrality 205
NetworkX Reference, Release 2.3rc1.dev20181203210840
•distance (edge attribute key, optional (default=None)) – Use the specified edge attribute as
the edge distance in shortest path calculations. If None, then each edge will have distance
equal to 1.
Returns nodes – Dictionary of nodes with harmonic centrality as the value.
Return type dictionary
See also:
betweenness_centrality(),load_centrality(),eigenvector_centrality(),
degree_centrality(),closeness_centrality()
Notes
If the ‘distance’ keyword is set to an edge attribute key then the shortest-path length will be computed using
Dijkstra’s algorithm with that edge attribute as the edge weight.
References
3.6.11 Reaching
local_reaching_centrality(G, v[, paths,
...])
Returns the local reaching centrality of a node in a di-
rected graph.
global_reaching_centrality(G[, weight,
...])
Returns the global reaching centrality of a directed
graph.
networkx.algorithms.centrality.local_reaching_centrality
local_reaching_centrality(G,v,paths=None,weight=None,normalized=True)
Returns the local reaching centrality of a node in a directed graph.
The local reaching centrality of a node in a directed graph is the proportion of other nodes reachable from that
node1.
Parameters
•G(DiGraph) – A NetworkX DiGraph.
•v(node) – A node in the directed graph G.
•paths (dictionary (default=None)) – If this is not None it must be a dictionary rep-
resentation of single-source shortest paths, as computed by, for example, networkx.
shortest_path() with source node v. Use this keyword argument if you intend to
invoke this function many times but don’t want the paths to be recomputed each time.
•weight (None or string, optional (default=None)) – Attribute to use for edge weights. If
None, each edge weight is assumed to be one. A higher weight implies a stronger connec-
tion between nodes and a shorter path length.
•normalized (bool, optional (default=True)) – Whether to normalize the edge weights by
the total sum of edge weights.
Returns h – The local reaching centrality of the node vin the graph G.
1Mones, Enys, Lilla Vicsek, and Tamás Vicsek. “Hierarchy Measure for Complex Networks.” PLoS ONE 7.3 (2012): e33799. https://doi.org/
10.1371/journal.pone.0033799
206 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type float
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edges_from([(1,2), (1,3)])
>>> nx.local_reaching_centrality(G, 3)
0.0
>>> G.add_edge(3,2)
>>> nx.local_reaching_centrality(G, 3)
0.5
See also:
global_reaching_centrality()
References
networkx.algorithms.centrality.global_reaching_centrality
global_reaching_centrality(G,weight=None,normalized=True)
Returns the global reaching centrality of a directed graph.
The global reaching centrality of a weighted directed graph is the average over all nodes of the difference
between the local reaching centrality of the node and the greatest local reaching centrality of any node in the
graph1. For more information on the local reaching centrality, see local_reaching_centrality().
Informally, the local reaching centrality is the proportion of the graph that is reachable from the neighbors of
the node.
Parameters
•G(DiGraph) – A networkx DiGraph.
•weight (None or string, optional (default=None)) – Attribute to use for edge weights. If
None, each edge weight is assumed to be one. A higher weight implies a stronger connec-
tion between nodes and a shorter path length.
•normalized (bool, optional (default=True)) – Whether to normalize the edge weights by
the total sum of edge weights.
Returns h – The global reaching centrality of the graph.
Return type float
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edge(1,2)
>>> G.add_edge(1,3)
>>> nx.global_reaching_centrality(G)
1.0
(continues on next page)
1Mones, Enys, Lilla Vicsek, and Tamás Vicsek. “Hierarchy Measure for Complex Networks.” PLoS ONE 7.3 (2012): e33799. https://doi.org/
10.1371/journal.pone.0033799
3.6. Centrality 207

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.add_edge(3,2)
>>> nx.global_reaching_centrality(G)
0.75
See also:
local_reaching_centrality()
References
3.6.12 Percolation
percolation_centrality(G[, attribute, . . . ]) Compute the percolation centrality for nodes.
networkx.algorithms.centrality.percolation_centrality
percolation_centrality(G,attribute=’percolation’,states=None,weight=None)
Compute the percolation centrality for nodes.
Percolation centrality of a node 𝑣, at a given time, is defined as the proportion of ‘percolated paths’ that go
through that node.
This measure quantifies relative impact of nodes based on their topological connectivity, as well as their perco-
lation states.
Percolation states of nodes are used to depict network percolation scenarios (such as during infection transmis-
sion in a social network of individuals, spreading of computer viruses on computer networks, or transmission
of disease over a network of towns) over time. In this measure usually the percolation state is expressed as a
decimal between 0.0 and 1.0.
When all nodes are in the same percolated state this measure is equivalent to betweenness centrality.
Parameters
•G(graph) – A NetworkX graph.
•attribute (None or string, optional (default=’percolation’)) – Name of the node attribute to
use for percolation state, used if states is None.
•states (None or dict, optional (default=None)) – Specify percolation states for the nodes,
nodes as keys states as values.
•weight (None or string, optional (default=None)) – If None, all edge weights are considered
equal. Otherwise holds the name of the edge attribute used as weight.
Returns nodes – Dictionary of nodes with percolation centrality as the value.
Return type dictionary
See also:
betweenness_centrality()
208 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The algorithm is from Mahendra Piraveenan, Mikhail Prokopenko, and Liaquat Hossain1Pair dependecies are
calculated and accumulated using2
For weighted graphs the edge weights must be greater than zero. Zero edge weights can produce an infinite
number of equal length paths between pairs of nodes.
References
3.6.13 Second Order Centrality
second_order_centrality(G) Compute the second order centrality for nodes of G.
networkx.algorithms.centrality.second_order_centrality
second_order_centrality(G)
Compute the second order centrality for nodes of G.
The second order centrality of a given node is the standard deviation of the return times to that node of a
perpetual random walk on G:
Parameters G (graph) – A NetworkX connected and undirected graph.
Returns nodes – Dictionary keyed by node with second order centrality as the value.
Return type dictionary
Examples
>>> G=nx.star_graph(10)
>>> soc =nx.second_order_centrality(G)
>>> print(sorted(soc.items(), key=lambda x:x[1])[0][0]) # pick first id
0
Raises NetworkXException – If the graph G is empty, non connected or has negative weights.
See also:
betweenness_centrality()
Notes
Lower values of second order centrality indicate higher centrality.
The algorithm is from Kermarrec, Le Merrer, Sericola and Trédan1.
1Mahendra Piraveenan, Mikhail Prokopenko, Liaquat Hossain Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during
Percolation in Networks http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0053095
2Ulrik Brandes: A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology 25(2):163-177, 2001. http://www.inf.
uni-konstanz.de/algo/publications/b-fabc-01.pdf
1Anne-Marie Kermarrec, Erwan Le Merrer, Bruno Sericola, Gilles Trédan “Second order centrality: Distributed assessment of nodes criticity
in complex networks”, Elsevier Computer Communications 34(5):619-628, 2011.
3.6. Centrality 209

NetworkX Reference, Release 2.3rc1.dev20181203210840
This code implements the analytical version of the algorithm, i.e., there is no simulation of a random walk
process involved. The random walk is here unbiased (corresponding to eq 6 of the paper1), thus the centrality
values are the standard deviations for random walk return times on the transformed input graph G (equal in-
degree at each nodes by adding self-loops).
Complexity of this implementation, made to run locally on a single machine, is O(n^3), with n the size of G,
which makes it viable only for small graphs.
References
3.7 Chains
Functions for finding chains in a graph.
chain_decomposition(G[, root]) Return the chain decomposition of a graph.
3.7.1 networkx.algorithms.chains.chain_decomposition
chain_decomposition(G,root=None)
Return the chain decomposition of a graph.
The chain decomposition of a graph with respect a depth-first search tree is a set of cycles or paths derived from
the set of fundamental cycles of the tree in the following manner. Consider each fundamental cycle with respect
to the given tree, represented as a list of edges beginning with the nontree edge oriented away from the root of
the tree. For each fundamental cycle, if it overlaps with any previous fundamental cycle, just take the initial
non-overlapping segment, which is a path instead of a cycle. Each cycle or path is called a chain. For more
information, see1.
Parameters
•G(undirected graph)
•root (node (optional)) – A node in the graph G. If specified, only the chain decomposition
for the connected component containing this node will be returned. This node indicates the
root of the depth-first search tree.
Yields chain (list) – A list of edges representing a chain. There is no guarantee on the orientation
of the edges in each chain (for example, if a chain includes the edge joining nodes 1 and 2, the
chain may include either (1, 2) or (2, 1)).
Raises NodeNotFound – If root is not in the graph G.
Notes
The worst-case running time of this implementation is linear in the number of nodes and number of edges1.
1Jens M. Schmidt (2013). “A simple test on 2-vertex- and 2-edge-connectivity.” Information Processing Letters, 113, 241–244. Elsevier.
<https://doi.org/10.1016/j.ipl.2013.01.016>
210 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.8 Chordal
Algorithms for chordal graphs.
A graph is chordal if every cycle of length at least 4 has a chord (an edge joining two nodes not adjacent in the cycle).
https://en.wikipedia.org/wiki/Chordal_graph
is_chordal(G) Checks whether G is a chordal graph.
chordal_graph_cliques(G) Returns the set of maximal cliques of a chordal graph.
chordal_graph_treewidth(G) Returns the treewidth of the chordal graph G.
find_induced_nodes(G, s, t[, treewidth_bound]) Returns the set of induced nodes in the path from s to t.
3.8.1 networkx.algorithms.chordal.is_chordal
is_chordal(G)
Checks whether G is a chordal graph.
A graph is chordal if every cycle of length at least 4 has a chord (an edge joining two nodes not adjacent in the
cycle).
Parameters G (graph) – A NetworkX graph.
Returns chordal – True if G is a chordal graph and False otherwise.
Return type bool
Raises NetworkXError – The algorithm does not support DiGraph, MultiGraph and MultiDi-
Graph. If the input graph is an instance of one of these classes, a NetworkXError is raised.
Examples
>>> import networkx as nx
>>> e=[(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)]
>>> G=nx.Graph(e)
>>> nx.is_chordal(G)
True
Notes
The routine tries to go through every node following maximum cardinality search. It returns False when it finds
that the separator for any node is not a clique. Based on the algorithms in1.
References
3.8.2 networkx.algorithms.chordal.chordal_graph_cliques
chordal_graph_cliques(G)
Returns the set of maximal cliques of a chordal graph.
1R. E. Tarjan and M. Yannakakis, Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively
reduce acyclic hypergraphs, SIAM J. Comput., 13 (1984), pp. 566–579.
3.8. Chordal 211

NetworkX Reference, Release 2.3rc1.dev20181203210840
The algorithm breaks the graph in connected components and performs a maximum cardinality search in each
component to get the cliques.
Parameters G (graph) – A NetworkX graph
Returns cliques
Return type A set containing the maximal cliques in G.
Raises NetworkXError – The algorithm does not support DiGraph, MultiGraph and MultiDi-
Graph. If the input graph is an instance of one of these classes, a NetworkXError is raised.
The algorithm can only be applied to chordal graphs. If the input graph is found to be non-
chordal, a NetworkXError is raised.
Examples
>>> import networkx as nx
>>> e=[(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),(7,8)]
>>> G=nx.Graph(e)
>>> G.add_node(9)
>>> setlist =nx.chordal_graph_cliques(G)
3.8.3 networkx.algorithms.chordal.chordal_graph_treewidth
chordal_graph_treewidth(G)
Returns the treewidth of the chordal graph G.
Parameters G (graph) – A NetworkX graph
Returns treewidth – The size of the largest clique in the graph minus one.
Return type int
Raises NetworkXError – The algorithm does not support DiGraph, MultiGraph and MultiDi-
Graph. If the input graph is an instance of one of these classes, a NetworkXError is raised.
The algorithm can only be applied to chordal graphs. If the input graph is found to be non-
chordal, a NetworkXError is raised.
Examples
>>> import networkx as nx
>>> e=[(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),(7,8)]
>>> G=nx.Graph(e)
>>> G.add_node(9)
>>> nx.chordal_graph_treewidth(G)
3
References
3.8.4 networkx.algorithms.chordal.find_induced_nodes
find_induced_nodes(G,s,t,treewidth_bound=9223372036854775807)
Returns the set of induced nodes in the path from s to t.
Parameters
212 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(graph) – A chordal NetworkX graph
•s(node) – Source node to look for induced nodes
•t(node) – Destination node to look for induced nodes
•treewith_bound (float) – Maximum treewidth acceptable for the graph H. The search for
induced nodes will end as soon as the treewidth_bound is exceeded.
Returns I – The set of induced nodes in the path from s to t in G
Return type Set of nodes
Raises NetworkXError – The algorithm does not support DiGraph, MultiGraph and MultiDi-
Graph. If the input graph is an instance of one of these classes, a NetworkXError is raised.
The algorithm can only be applied to chordal graphs. If the input graph is found to be non-
chordal, a NetworkXError is raised.
Examples
>>> import networkx as nx
>>> G=nx.Graph()
>>> G=nx.generators.classic.path_graph(10)
>>> I=nx.find_induced_nodes(G,1,9,2)
>>> list(I)
[1, 2, 3, 4, 5, 6, 7, 8, 9]
Notes
G must be a chordal graph and (s,t) an edge that is not in G.
If a treewidth_bound is provided, the search for induced nodes will end as soon as the treewidth_bound is
exceeded.
The algorithm is inspired by Algorithm 4 in1. A formal definition of induced node can also be found on that
reference.
References
3.9 Clique
Functions for finding and manipulating cliques.
Finding the largest clique in a graph is NP-complete problem, so most of these algorithms have an exponential running
time; for more information, see the Wikipedia article on the clique problem1.
enumerate_all_cliques(G) Returns all cliques in an undirected graph.
find_cliques(G) Returns all maximal cliques in an undirected graph.
make_max_clique_graph(G[, create_using]) Returns the maximal clique graph of the given graph.
make_clique_bipartite(G[, fpos, . . . ]) Returns the bipartite clique graph corresponding to G.
graph_clique_number(G[, cliques]) Returns the clique number of the graph.
Continued on next page
1Learning Bounded Treewidth Bayesian Networks. Gal Elidan, Stephen Gould; JMLR, 9(Dec):2699–2731, 2008. http://jmlr.csail.mit.edu/
papers/volume9/elidan08a/elidan08a.pdf
1clique problem:: https://en.wikipedia.org/wiki/Clique_problem
3.9. Clique 213

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 44 – continued from previous page
graph_number_of_cliques(G[, cliques]) Returns the number of maximal cliques in the graph.
node_clique_number(G[, nodes, cliques]) Returns the size of the largest maximal clique contain-
ing each given node.
number_of_cliques(G[, nodes, cliques]) Returns the number of maximal cliques for each node.
cliques_containing_node(G[, nodes, cliques]) Returns a list of cliques containing the given node.
3.9.1 networkx.algorithms.clique.enumerate_all_cliques
enumerate_all_cliques(G)
Returns all cliques in an undirected graph.
This function returns an iterator over cliques, each of which is a list of nodes. The iteration is ordered by
cardinality of the cliques: first all cliques of size one, then all cliques of size two, etc.
Parameters G (NetworkX graph) – An undirected graph.
Returns An iterator over cliques, each of which is a list of nodes in G. The cliques are ordered
according to size.
Return type iterator
Notes
To obtain a list of all cliques, use list(enumerate_all_cliques(G)). However, be aware that in the
worst-case, the length of this list can be exponential in the number of nodes in the graph (for example, when
the graph is the complete graph). This function avoids storing all cliques in memory by only keeping current
candidate node lists in memory during its search.
The implementation is adapted from the algorithm by Zhang, et al. (2005)1to output all cliques discovered.
This algorithm ignores self-loops and parallel edges, since cliques are not conventionally defined with such
edges.
References
3.9.2 networkx.algorithms.clique.find_cliques
find_cliques(G)
Returns all maximal cliques in an undirected graph.
For each node v, a maximal clique for v is a largest complete subgraph containing v. The largest maximal clique
is sometimes called the maximum clique.
This function returns an iterator over cliques, each of which is a list of nodes. It is an iterative implementation,
so should not suffer from recursion depth issues.
Parameters G (NetworkX graph) – An undirected graph.
Returns An iterator over maximal cliques, each of which is a list of nodes in G. The order of cliques
is arbitrary.
Return type iterator
1Yun Zhang, Abu-Khzam, F.N., Baldwin, N.E., Chesler, E.J., Langston, M.A., Samatova, N.F., “Genome-Scale Computational Approaches to
Memory-Intensive Applications in Systems Biology”. Supercomputing, 2005. Proceedings of the ACM/IEEE SC 2005 Conference, pp. 12, 12–18
Nov. 2005. <https://doi.org/10.1109/SC.2005.29>.
214 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
find_cliques_recursive() A recursive version of the same algorithm.
Notes
To obtain a list of all maximal cliques, use list(find_cliques(G)). However, be aware that in the worst-
case, the length of this list can be exponential in the number of nodes in the graph (for example, when the graph
is the complete graph). This function avoids storing all cliques in memory by only keeping current candidate
node lists in memory during its search.
This implementation is based on the algorithm published by Bron and Kerbosch (1973)1, as adapted by Tomita,
Tanaka and Takahashi (2006)2and discussed in Cazals and Karande (2008)3. It essentially unrolls the re-
cursion used in the references to avoid issues of recursion stack depth (for a recursive implementation, see
find_cliques_recursive()).
This algorithm ignores self-loops and parallel edges, since cliques are not conventionally defined with such
edges.
References
3.9.3 networkx.algorithms.clique.make_max_clique_graph
make_max_clique_graph(G,create_using=None)
Returns the maximal clique graph of the given graph.
The nodes of the maximal clique graph of Gare the cliques of Gand an edge joins two cliques if the cliques are
not disjoint.
Parameters
•G(NetworkX graph)
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns A graph whose nodes are the cliques of Gand whose edges join two cliques if they are not
disjoint.
Return type NetworkX graph
Notes
This function behaves like the following code:
import networkx as nx
G=nx.make_clique_bipartite(G)
cliques =[v for vin G.nodes() if G.nodes[v]['bipartite']== 0]
G=nx.bipartite.project(G, cliques)
G=nx.relabel_nodes(G, {-v:v-1for vin G})
1Bron, C. and Kerbosch, J. “Algorithm 457: finding all cliques of an undirected graph”. Communications of the ACM 16, 9 (Sep. 1973),
575–577. <http://portal.acm.org/citation.cfm?doid=362342.362367>
2Etsuji Tomita, Akira Tanaka, Haruhisa Takahashi, “The worst-case time complexity for generating all maximal cliques and computational
experiments”, Theoretical Computer Science, Volume 363, Issue 1, Computing and Combinatorics, 10th Annual International Conference on
Computing and Combinatorics (COCOON 2004), 25 October 2006, Pages 28–42 <https://doi.org/10.1016/j.tcs.2006.06.015>
3F. Cazals, C. Karande, “A note on the problem of reporting maximal cliques”, Theoretical Computer Science, Volume 407, Issues 1–3, 6
November 2008, Pages 564–568, <https://doi.org/10.1016/j.tcs.2008.05.010>
3.9. Clique 215

NetworkX Reference, Release 2.3rc1.dev20181203210840
It should be faster, though, since it skips all the intermediate steps.
3.9.4 networkx.algorithms.clique.make_clique_bipartite
make_clique_bipartite(G,fpos=None,create_using=None,name=None)
Returns the bipartite clique graph corresponding to G.
In the returned bipartite graph, the “bottom” nodes are the nodes of Gand the “top” nodes represent the maximal
cliques of G. There is an edge from node vto clique Cin the returned graph if and only if vis an element of C.
Parameters
•G(NetworkX graph) – An undirected graph.
•fpos (bool) – If True or not None, the returned graph will have an additional attribute, pos,
a dictionary mapping node to position in the Euclidean plane.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns
A bipartite graph whose “bottom” set is the nodes of the graph G, whose “top” set is the cliques
of G, and whose edges join nodes of Gto the cliques that contain them.
The nodes of the graph Ghave the node attribute ‘bipartite’ set to 1 and the nodes representing
cliques have the node attribute ‘bipartite’ set to 0, as is the convention for bipartite graphs in
NetworkX.
Return type NetworkX graph
3.9.5 networkx.algorithms.clique.graph_clique_number
graph_clique_number(G,cliques=None)
Returns the clique number of the graph.
The clique number of a graph is the size of the largest clique in the graph.
Parameters
•G(NetworkX graph) – An undirected graph.
•cliques (list) – A list of cliques, each of which is itself a list of nodes. If not specified, the
list of all cliques will be computed, as by find_cliques().
Returns The size of the largest clique in G.
Return type int
Notes
You should provide cliques if you have already computed the list of maximal cliques, in order to avoid an
exponential time search for maximal cliques.
216 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.9.6 networkx.algorithms.clique.graph_number_of_cliques
graph_number_of_cliques(G,cliques=None)
Returns the number of maximal cliques in the graph.
Parameters
•G(NetworkX graph) – An undirected graph.
•cliques (list) – A list of cliques, each of which is itself a list of nodes. If not specified, the
list of all cliques will be computed, as by find_cliques().
Returns The number of maximal cliques in G.
Return type int
Notes
You should provide cliques if you have already computed the list of maximal cliques, in order to avoid an
exponential time search for maximal cliques.
3.9.7 networkx.algorithms.clique.node_clique_number
node_clique_number(G,nodes=None,cliques=None)
Returns the size of the largest maximal clique containing each given node.
Returns a single or list depending on input nodes. Optional list of cliques can be input if already computed.
3.9.8 networkx.algorithms.clique.number_of_cliques
number_of_cliques(G,nodes=None,cliques=None)
Returns the number of maximal cliques for each node.
Returns a single or list depending on input nodes. Optional list of cliques can be input if already computed.
3.9.9 networkx.algorithms.clique.cliques_containing_node
cliques_containing_node(G,nodes=None,cliques=None)
Returns a list of cliques containing the given node.
Returns a single list or list of lists depending on input nodes. Optional list of cliques can be input if already
computed.
3.10 Clustering
Algorithms to characterize the number of triangles in a graph.
triangles(G[, nodes]) Compute the number of triangles.
transitivity(G) Compute graph transitivity, the fraction of all possible
triangles present in G.
clustering(G[, nodes, weight]) Compute the clustering coefficient for nodes.
Continued on next page
3.10. Clustering 217

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 45 – continued from previous page
average_clustering(G[, nodes, weight, . . . ]) Compute the average clustering coefficient for the graph
G.
square_clustering(G[, nodes]) Compute the squares clustering coefficient for nodes.
generalized_degree(G[, nodes]) Compute the generalized degree for nodes.
3.10.1 networkx.algorithms.cluster.triangles
triangles(G,nodes=None)
Compute the number of triangles.
Finds the number of triangles that include a node as one vertex.
Parameters
•G(graph) – A networkx graph
•nodes (container of nodes, optional (default= all nodes in G)) – Compute triangles for nodes
in this container.
Returns out – Number of triangles keyed by node label.
Return type dictionary
Examples
>>> G=nx.complete_graph(5)
>>> print(nx.triangles(G,0))
6
>>> print(nx.triangles(G))
{0: 6, 1: 6, 2: 6, 3: 6, 4: 6}
>>> print(list(nx.triangles(G,(0,1)).values()))
[6, 6]
Notes
When computing triangles for the entire graph each triangle is counted three times, once at each node. Self
loops are ignored.
3.10.2 networkx.algorithms.cluster.transitivity
transitivity(G)
Compute graph transitivity, the fraction of all possible triangles present in G.
Possible triangles are identified by the number of “triads” (two edges with a shared vertex).
The transitivity is
𝑇= 3#𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒𝑠
#𝑡𝑟𝑖𝑎𝑑𝑠 .
Parameters G (graph)
Returns out – Transitivity
Return type float
218 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.complete_graph(5)
>>> print(nx.transitivity(G))
1.0
3.10.3 networkx.algorithms.cluster.clustering
clustering(G,nodes=None,weight=None)
Compute the clustering coefficient for nodes.
For unweighted graphs, the clustering of a node 𝑢is the fraction of possible triangles through that node that
exist,
𝑐𝑢=2𝑇(𝑢)
𝑑𝑒𝑔(𝑢)(𝑑𝑒𝑔(𝑢)−1) ,
where 𝑇(𝑢)is the number of triangles through node 𝑢and 𝑑𝑒𝑔(𝑢)is the degree of 𝑢.
For weighted graphs, there are several ways to define clustering1. the one used here is defined as the geometric
average of the subgraph edge weights2,
𝑐𝑢=1
𝑑𝑒𝑔(𝑢)(𝑑𝑒𝑔(𝑢)−1))
𝑣𝑤
( ˆ𝑤𝑢𝑣 ˆ𝑤𝑢𝑤 ˆ𝑤𝑣𝑤)1/3.
The edge weights ˆ𝑤𝑢𝑣 are normalized by the maximum weight in the network ˆ𝑤𝑢𝑣 =𝑤𝑢𝑣/max(𝑤).
The value of 𝑐𝑢is assigned to 0 if 𝑑𝑒𝑔(𝑢)<2.
For directed graphs, the clustering is similarly defined as the fraction of all possible directed triangles or geo-
metric average of the subgraph edge weights for unweighted and weighted directed graph respectively3.
𝑐𝑢=1
𝑑𝑒𝑔𝑡𝑜𝑡(𝑢)(𝑑𝑒𝑔𝑡𝑜𝑡(𝑢)−1) −2𝑑𝑒𝑔↔(𝑢)𝑇(𝑢),
where 𝑇(𝑢)is the number of directed triangles through node 𝑢,𝑑𝑒𝑔𝑡𝑜𝑡(𝑢)is the sum of in degree and out degree
of 𝑢and 𝑑𝑒𝑔↔(𝑢)is the reciprocal degree of 𝑢.
Parameters
•G(graph)
•nodes (container of nodes, optional (default=all nodes in G)) – Compute clustering for
nodes in this container.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1.
Returns out – Clustering coefficient at specified nodes
Return type float, or dictionary
1Generalizations of the clustering coefficient to weighted complex networks by J. Saramäki, M. Kivelä, J.-P. Onnela, K. Kaski, and J. Kertész,
Physical Review E, 75 027105 (2007). http://jponnela.com/web_documents/a9.pdf
2Intensity and coherence of motifs in weighted complex networks by J. P. Onnela, J. Saramäki, J. Kertész, and K. Kaski, Physical Review E,
71(6), 065103 (2005).
3Clustering in complex directed networks by G. Fagiolo, Physical Review E, 76(2), 026107 (2007).
3.10. Clustering 219

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.complete_graph(5)
>>> print(nx.clustering(G,0))
1.0
>>> print(nx.clustering(G))
{0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0, 4: 1.0}
Notes
Self loops are ignored.
References
3.10.4 networkx.algorithms.cluster.average_clustering
average_clustering(G,nodes=None,weight=None,count_zeros=True)
Compute the average clustering coefficient for the graph G.
The clustering coefficient for the graph is the average,
𝐶=1
𝑛
𝑣∈𝐺
𝑐𝑣,
where 𝑛is the number of nodes in G.
Parameters
•G(graph)
•nodes (container of nodes, optional (default=all nodes in G)) – Compute average clustering
for nodes in this container.
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used as a weight. If None, then each edge has weight 1.
•count_zeros (bool) – If False include only the nodes with nonzero clustering in the average.
Returns avg – Average clustering
Return type float
Examples
>>> G=nx.complete_graph(5)
>>> print(nx.average_clustering(G))
1.0
Notes
This is a space saving routine; it might be faster to use the clustering function to get a list and then take the
average.
Self loops are ignored.
220 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.10.5 networkx.algorithms.cluster.square_clustering
square_clustering(G,nodes=None)
Compute the squares clustering coefficient for nodes.
For each node return the fraction of possible squares that exist at the node1
𝐶4(𝑣) = 𝑘𝑣
𝑢=1 𝑘𝑣
𝑤=𝑢+1 𝑞𝑣(𝑢, 𝑤)
𝑘𝑣
𝑢=1 𝑘𝑣
𝑤=𝑢+1[𝑎𝑣(𝑢, 𝑤) + 𝑞𝑣(𝑢, 𝑤)] ,
where 𝑞𝑣(𝑢, 𝑤)are the number of common neighbors of 𝑢and 𝑤other than 𝑣(ie squares), and 𝑎𝑣(𝑢, 𝑤) =
(𝑘𝑢−(1 + 𝑞𝑣(𝑢, 𝑤) + 𝜃𝑢𝑣))(𝑘𝑤−(1 + 𝑞𝑣(𝑢, 𝑤) + 𝜃𝑢𝑤)), where 𝜃𝑢𝑤 = 1 if 𝑢and 𝑤are connected and 0
otherwise.
Parameters
•G(graph)
•nodes (container of nodes, optional (default=all nodes in G)) – Compute clustering for
nodes in this container.
Returns c4 – A dictionary keyed by node with the square clustering coefficient value.
Return type dictionary
Examples
>>> G=nx.complete_graph(5)
>>> print(nx.square_clustering(G,0))
1.0
>>> print(nx.square_clustering(G))
{0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0, 4: 1.0}
Notes
While 𝐶3(𝑣)(triangle clustering) gives the probability that two neighbors of node v are connected with each
other, 𝐶4(𝑣)is the probability that two neighbors of node v share a common neighbor different from v. This
algorithm can be applied to both bipartite and unipartite networks.
References
3.10.6 networkx.algorithms.cluster.generalized_degree
generalized_degree(G,nodes=None)
Compute the generalized degree for nodes.
For each node, the generalized degree shows how many edges of given triangle multiplicity the node is connected
to. The triangle multiplicity of an edge is the number of triangles an edge participates in. The generalized degree
of node 𝑖can be written as a vector k𝑖= (𝑘(0)
𝑖, . . . , 𝑘(𝑁−2)
𝑖)where 𝑘(𝑗)
𝑖is the number of edges attached to node
𝑖that participate in 𝑗triangles.
1Pedro G. Lind, Marta C. González, and Hans J. Herrmann. 2005 Cycles and clustering in bipartite networks. Physical Review E (72) 056127.
3.10. Clustering 221

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(graph)
•nodes (container of nodes, optional (default=all nodes in G)) – Compute the generalized
degree for nodes in this container.
Returns out – Generalized degree of specified nodes. The Counter is keyed by edge triangle multi-
plicity.
Return type Counter, or dictionary of Counters
Examples
>>> G=nx.complete_graph(5)
>>> print(nx.generalized_degree(G,0))
Counter({3: 4})
>>> print(nx.generalized_degree(G))
{0: Counter({3: 4}), 1: Counter({3: 4}), 2: Counter({3: 4}), 3: Counter({3: 4}),
˓→4: Counter({3: 4})}
To recover the number of triangles attached to a node:
>>> k1 =nx.generalized_degree(G,0)
>>> sum([k*vfor k,v in k1.items()])/2== nx.triangles(G,0)
True
Notes
In a network of N nodes, the highest triangle multiplicty an edge can have is N-2.
The return value does not include a zero entry if no edges of a particular triangle multiplicity are present.
The number of triangles node 𝑖is attached to can be recovered from the generalized degree k𝑖=
(𝑘(0)
𝑖, . . . , 𝑘(𝑁−2)
𝑖)by (𝑘(1)
𝑖+ 2𝑘(2)
𝑖+. . . + (𝑁−2)𝑘(𝑁−2)
𝑖)/2.
References
3.11 Coloring
greedy_color(G[, strategy, interchange]) Color a graph using various strategies of greedy graph
coloring.
3.11.1 networkx.algorithms.coloring.greedy_color
greedy_color(G,strategy=’largest_first’,interchange=False)
Color a graph using various strategies of greedy graph coloring.
Attempts to color a graph using as few colors as possible, where no neighbours of a node can have same color
as the node itself. The given strategy determines the order in which nodes are colored.
The strategies are described in1, and smallest-last is based on2.
1Adrian Kosowski, and Krzysztof Manuszewski, Classical Coloring of Graphs, Graph Colorings, 2-19, 2004. ISBN 0-8218-3458-4.
2David W. Matula, and Leland L. Beck, “Smallest-last ordering and clustering and graph coloring algorithms.” J. ACM 30, 3 (July 1983),
222 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•strategy (string or function(G, colors)) – A function (or a string representing a function) that
provides the coloring strategy, by returning nodes in the ordering they should be colored. G
is the graph, and colors is a dictionary of the currently assigned colors, keyed by nodes.
The function must return an iterable over all the nodes in G.
If the strategy function is an iterator generator (that is, a function with yield statements),
keep in mind that the colors dictionary will be updated after each yield, since this
function chooses colors greedily.
If strategy is a string, it must be one of the following, each of which represents one of
the built-in strategy functions.
–'largest_first'
–'random_sequential'
–'smallest_last'
–'independent_set'
–'connected_sequential_bfs'
–'connected_sequential_dfs'
–'connected_sequential' (alias for the previous strategy)
–'strategy_saturation_largest_first'
–'DSATUR' (alias for the previous strategy)
•interchange (bool) – Will use the color interchange algorithm described by3if set to True.
Note that strategy_saturation_largest_first and
strategy_independent_set do not work with interchange. Furthermore, if
you use interchange with your own strategy function, you cannot rely on the values in the
colors argument.
Returns
•A dictionary with keys representing nodes and values representing
•corresponding coloring.
Examples
>>> G=nx.cycle_graph(4)
>>> d=nx.coloring.greedy_color(G, strategy='largest_first')
>>> din [{0:0,1:1,2:0,3:1}, {0:1,1:0,2:1,3:0}]
True
Raises NetworkXPointlessConcept – If strategy is
strategy_saturation_largest_first or strategy_independent_set
and interchange is True.
417–427. <https://doi.org/10.1145/2402.322385>
3Maciej M. Sysło, Marsingh Deo, Janusz S. Kowalik, Discrete Optimization Algorithms with Pascal Programs, 415-424, 1983. ISBN 0-486-
45353-7.
3.11. Coloring 223

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
Some node ordering strategies are provided for use with greedy_color().
strategy_connected_sequential(G, colors[,
...])
Returns an iterable over nodes in Gin the order given by
a breadth-first or depth-first traversal.
strategy_connected_sequential_dfs(G,
colors)
Returns an iterable over nodes in Gin the order given by
a depth-first traversal.
strategy_connected_sequential_bfs(G,
colors)
Returns an iterable over nodes in Gin the order given by
a breadth-first traversal.
strategy_independent_set(G, colors) Uses a greedy independent set removal strategy to de-
termine the colors.
strategy_largest_first(G, colors) Returns a list of the nodes of Gin decreasing order by
degree.
strategy_random_sequential(G, colors[,
seed])
Returns a random permutation of the nodes of Gas a
list.
strategy_saturation_largest_first(G,
colors)
Iterates over all the nodes of Gin “saturation order”
(also known as “DSATUR”).
strategy_smallest_last(G, colors) Returns a deque of the nodes of G, “smallest” last.
3.11.2 networkx.algorithms.coloring.strategy_connected_sequential
strategy_connected_sequential(G,colors,traversal=’bfs’)
Returns an iterable over nodes in Gin the order given by a breadth-first or depth-first traversal.
traversal must be one of the strings 'dfs' or 'bfs', representing depth-first traversal or breadth-first
traversal, respectively.
The generated sequence has the property that for each node except the first, at least one neighbor appeared
earlier in the sequence.
Gis a NetworkX graph. colors is ignored.
3.11.3 networkx.algorithms.coloring.strategy_connected_sequential_dfs
strategy_connected_sequential_dfs(G,colors)
Returns an iterable over nodes in Gin the order given by a depth-first traversal.
The generated sequence has the property that for each node except the first, at least one neighbor appeared
earlier in the sequence.
Gis a NetworkX graph. colors is ignored.
3.11.4 networkx.algorithms.coloring.strategy_connected_sequential_bfs
strategy_connected_sequential_bfs(G,colors)
Returns an iterable over nodes in Gin the order given by a breadth-first traversal.
The generated sequence has the property that for each node except the first, at least one neighbor appeared
earlier in the sequence.
Gis a NetworkX graph. colors is ignored.
224 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.11.5 networkx.algorithms.coloring.strategy_independent_set
strategy_independent_set(G,colors)
Uses a greedy independent set removal strategy to determine the colors.
This function updates colors in-place and return None, unlike the other strategy functions in this module.
This algorithm repeatedly finds and removes a maximal independent set, assigning each node in the set an
unused color.
Gis a NetworkX graph.
This strategy is related to strategy_smallest_last(): in that strategy, an independent set of size one is
chosen at each step instead of a maximal independent set.
3.11.6 networkx.algorithms.coloring.strategy_largest_first
strategy_largest_first(G,colors)
Returns a list of the nodes of Gin decreasing order by degree.
Gis a NetworkX graph. colors is ignored.
3.11.7 networkx.algorithms.coloring.strategy_random_sequential
strategy_random_sequential(G,colors,seed=None)
Returns a random permutation of the nodes of Gas a list.
Gis a NetworkX graph. colors is ignored.
seed [integer, random_state, or None (default)] Indicator of random number generation state. See Randomness.
3.11.8 networkx.algorithms.coloring.strategy_saturation_largest_first
strategy_saturation_largest_first(G,colors)
Iterates over all the nodes of Gin “saturation order” (also known as “DSATUR”).
Gis a NetworkX graph. colors is a dictionary mapping nodes of Gto colors, for those nodes that have already
been colored.
3.11.9 networkx.algorithms.coloring.strategy_smallest_last
strategy_smallest_last(G,colors)
Returns a deque of the nodes of G, “smallest” last.
Specifically, the degrees of each node are tracked in a bucket queue. From this, the node of minimum degree is
repeatedly popped from the graph, updating its neighbors’ degrees.
Gis a NetworkX graph. colors is ignored.
This implementation of the strategy runs in 𝑂(𝑛+𝑚)time (ignoring polylogarithmic factors), where 𝑛is the
number of nodes and 𝑚is the number of edges.
This strategy is related to strategy_independent_set(): if we interpret each node removed as an
independent set of size one, then this strategy chooses an independent set of size one instead of a maximal
independent set.
3.11. Coloring 225

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.12 Communicability
Communicability.
communicability(G) Return communicability between all pairs of nodes in
G.
communicability_exp(G) Return communicability between all pairs of nodes in
G.
3.12.1 networkx.algorithms.communicability_alg.communicability
communicability(G)
Return communicability between all pairs of nodes in G.
The communicability between pairs of nodes in G is the sum of closed walks of different lengths starting at node
u and ending at node v.
Parameters G (graph)
Returns comm – Dictionary of dictionaries keyed by nodes with communicability as the value.
Return type dictionary of dictionaries
Raises NetworkXError – If the graph is not undirected and simple.
See also:
communicability_exp() Communicability between all pairs of nodes in G using spectral decomposition.
communicability_betweenness_centrality() Communicability betweeness centrality for each
node in G.
Notes
This algorithm uses a spectral decomposition of the adjacency matrix. Let G=(V,E) be a simple undirected
graph. Using the connection between the powers of the adjacency matrix and the number of walks in the graph,
the communicability between nodes uand vbased on the graph spectrum is1
𝐶(𝑢, 𝑣) =
𝑛
𝑗=1
𝜑𝑗(𝑢)𝜑𝑗(𝑣)𝑒𝜆𝑗,
where phi_{j}(u) is the urm{th} element of the jrm{th} orthonormal eigenvector of the adjacency
matrix associated with the eigenvalue lambda_{j}.
References
Examples
>>> G=nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)])
>>> c=nx.communicability(G)
1Ernesto Estrada, Naomichi Hatano, “Communicability in complex networks”, Phys. Rev. E 77, 036111 (2008). https://arxiv.org/abs/0707.0756
226 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.12.2 networkx.algorithms.communicability_alg.communicability_exp
communicability_exp(G)
Return communicability between all pairs of nodes in G.
Communicability between pair of node (u,v) of node in G is the sum of closed walks of different lengths starting
at node u and ending at node v.
Parameters G (graph)
Returns comm – Dictionary of dictionaries keyed by nodes with communicability as the value.
Return type dictionary of dictionaries
Raises NetworkXError – If the graph is not undirected and simple.
See also:
communicability() Communicability between pairs of nodes in G.
communicability_betweenness_centrality() Communicability betweeness centrality for each
node in G.
Notes
This algorithm uses matrix exponentiation of the adjacency matrix.
Let G=(V,E) be a simple undirected graph. Using the connection between the powers of the adjacency matrix
and the number of walks in the graph, the communicability between nodes u and v is1,
𝐶(𝑢, 𝑣) = (𝑒𝐴)𝑢𝑣,
where Ais the adjacency matrix of G.
References
Examples
>>> G=nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)])
>>> c=nx.communicability_exp(G)
3.13 Communities
Functions for computing and measuring community structure.
The functions in this class are not imported into the top-level networkx namespace. You can access these functions
by importing the networkx.algorithms.community module, then accessing the functions as attributes of
community. For example:
>>> import networkx as nx
>>> from networkx.algorithms import community
>>> G=nx.barbell_graph(5,1)
>>> communities_generator =community.girvan_newman(G)
(continues on next page)
1Ernesto Estrada, Naomichi Hatano, “Communicability in complex networks”, Phys. Rev. E 77, 036111 (2008). https://arxiv.org/abs/0707.0756
3.13. Communities 227

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> top_level_communities =next(communities_generator)
>>> next_level_communities =next(communities_generator)
>>> sorted(map(sorted, next_level_communities))
[[0, 1, 2, 3, 4], [5], [6, 7, 8, 9, 10]]
3.13.1 Bipartitions
Functions for computing the Kernighan–Lin bipartition algorithm.
kernighan_lin_bisection(G[, partition, . . . ]) Partition a graph into two blocks using the
Kernighan–Lin algorithm.
networkx.algorithms.community.kernighan_lin.kernighan_lin_bisection
kernighan_lin_bisection(G,partition=None,max_iter=10,weight=’weight’,seed=None)
Partition a graph into two blocks using the Kernighan–Lin algorithm.
This algorithm paritions a network into two sets by iteratively swapping pairs of nodes to reduce the edge cut
between the two sets.
Parameters
•G(graph)
•partition (tuple) – Pair of iterables containing an initial partition. If not specified, a random
balanced partition is used.
•max_iter (int) – Maximum number of times to attempt swaps to find an improvemement
before giving up.
•weight (key) – Edge data key to use as weight. If None, the weights are all set to one.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness. Only used if partition is None
Returns partition – A pair of sets of nodes representing the bipartition.
Return type tuple
Raises NetworkXError – If partition is not a valid partition of the nodes of the graph.
References
3.13.2 Generators
Functions for generating graphs with community structure.
LFR_benchmark_graph(n, tau1, tau2, mu[, . . . ]) Returns the LFR benchmark graph for testing
community-finding algorithms.
228 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.community.community_generators.LFR_benchmark_graph
LFR_benchmark_graph(n,tau1,tau2,mu,average_degree=None,min_degree=None,max_degree=None,
min_community=None,max_community=None,tol=1e-07,max_iters=500,
seed=None)
Returns the LFR benchmark graph for testing community-finding algorithms.
This algorithm proceeds as follows:
1) Find a degree sequence with a power law distribution, and minimum value min_degree, which has
approximate average degree average_degree. This is accomplished by either
a) specifying min_degree and not average_degree,
b) specifying average_degree and not min_degree, in which case a suitable minimum degree
will be found.
max_degree can also be specified, otherwise it will be set to n. Each node uwill have mu
mathrm{deg}(u) edges joining it to nodes in communities other than its own and (1 - mu)
mathrm{deg}(u) edges joining it to nodes in its own community.
2) Generate community sizes according to a power law distribution with exponent tau2. If
min_community and max_community are not specified they will be selected to be min_degree
and max_degree, respectively. Community sizes are generated until the sum of their sizes equals n.
3) Each node will be randomly assigned a community with the condition that the community is large enough
for the node’s intra-community degree, (1 - mu) mathrm{deg}(u) as described in step 2. If a
community grows too large, a random node will be selected for reassignment to a new community, until
all nodes have been assigned a community.
4) Each node uthen adds (1 - mu) mathrm{deg}(u) intra-community edges and mu
mathrm{deg}(u) inter-community edges.
Parameters
•n(int) – Number of nodes in the created graph.
•tau1 (float) – Power law exponent for the degree distribution of the created graph. This
value must be strictly greater than one.
•tau2 (float) – Power law exponent for the community size distribution in the created graph.
This value must be strictly greater than one.
•mu (float) – Fraction of intra-community edges incident to each node. This value must be
in the interval [0, 1].
•average_degree (float) – Desired average degree of nodes in the created graph. This value
must be in the interval [0, n]. Exactly one of this and min_degree must be specified,
otherwise a NetworkXError is raised.
•min_degree (int) – Minimum degree of nodes in the created graph. This value must be in
the interval [0, n]. Exactly one of this and average_degree must be specified, otherwise
aNetworkXError is raised.
•max_degree (int) – Maximum degree of nodes in the created graph. If not specified, this is
set to n, the total number of nodes in the graph.
•min_community (int) – Minimum size of communities in the graph. If not specified, this is
set to min_degree.
•max_community (int) – Maximum size of communities in the graph. If not specified, this
is set to n, the total number of nodes in the graph.
3.13. Communities 229

NetworkX Reference, Release 2.3rc1.dev20181203210840
•tol (float) – Tolerance when comparing floats, specifically when comparing average degree
values.
•max_iters (int) – Maximum number of iterations to try to create the community sizes, de-
gree distribution, and community affiliations.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns
G– The LFR benchmark graph generated according to the specified parameters.
Each node in the graph has a node attribute 'community' that stores the community (that is,
the set of nodes) that includes it.
Return type NetworkX graph
Raises
•NetworkXError – If any of the parameters do not meet their upper and lower bounds:
–tau1 and tau2 must be strictly greater than 1.
–mu must be in [0, 1].
–max_degree must be in {1, . . . , n}.
–min_community and max_community must be in {0, . . . , n}.
If not exactly one of average_degree and min_degree is specified.
If min_degree is not specified and a suitable min_degree cannot be found.
•ExceededMaxIterations – If a valid degree sequence cannot be created within
max_iters number of iterations.
If a valid set of community sizes cannot be created within max_iters number of iterations.
If a valid community assignment cannot be created within 10 *n*max_iters num-
ber of iterations.
Examples
Basic usage:
>>> from networkx.algorithms.community import LFR_benchmark_graph
>>> n=250
>>> tau1 =3
>>> tau2 =1.5
>>> mu =0.1
>>> G=LFR_benchmark_graph(n, tau1, tau2, mu, average_degree=5,
... min_community=20, seed=10)
Continuing the example above, you can get the communities from the node attributes of the graph:
>>> communities ={frozenset(G.nodes[v]['community']) for vin G}
Notes
This algorithm differs slightly from the original way it was presented in [1].
230 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
1) Rather than connecting the graph via a configuration model then rewiring to match the intra-community
and inter-community degrees, we do this wiring explicitly at the end, which should be equivalent.
2) The code posted on the author’s website [2] calculates the random power law distributed variables and their
average using continuous approximations, whereas we use the discrete distributions here as both degree
and community size are discrete.
Though the authors describe the algorithm as quite robust, testing during development indicates that a somewhat
narrower parameter set is likely to successfully produce a graph. Some suggestions have been provided in the
event of exceptions.
References
3.13.3 K-Clique
k_clique_communities(G, k[, cliques]) Find k-clique communities in graph using the percola-
tion method.
networkx.algorithms.community.kclique.k_clique_communities
k_clique_communities(G,k,cliques=None)
Find k-clique communities in graph using the percolation method.
A k-clique community is the union of all cliques of size k that can be reached through adjacent (sharing k-1
nodes) k-cliques.
Parameters
•G(NetworkX graph)
•k(int) – Size of smallest clique
•cliques (list or generator) – Precomputed cliques (use networkx.find_cliques(G))
Returns
Return type Yields sets of nodes, one for each k-clique community.
Examples
>>> from networkx.algorithms.community import k_clique_communities
>>> G=nx.complete_graph(5)
>>> K5 =nx.convert_node_labels_to_integers(G,first_label=2)
>>> G.add_edges_from(K5.edges())
>>> c=list(k_clique_communities(G, 4))
>>> list(c[0])
[0, 1, 2, 3, 4, 5, 6]
>>> list(k_clique_communities(G, 6))
[]
References
3.13.4 Modularity-based communities
Functions for detecting communities based on modularity.
3.13. Communities 231

NetworkX Reference, Release 2.3rc1.dev20181203210840
greedy_modularity_communities(G[,
weight])
Find communities in graph using Clauset-Newman-
Moore greedy modularity maximization.
networkx.algorithms.community.modularity_max.greedy_modularity_communities
greedy_modularity_communities(G,weight=None)
Find communities in graph using Clauset-Newman-Moore greedy modularity maximization. This method cur-
rently supports the Graph class and does not consider edge weights.
Greedy modularity maximization begins with each node in its own community and joins the pair of communities
that most increases modularity until no such pair exists.
Parameters G (NetworkX graph)
Returns
Return type Yields sets of nodes, one for each community.
Examples
>>> from networkx.algorithms.community import greedy_modularity_communities
>>> G=nx.karate_club_graph()
>>> c=list(greedy_modularity_communities(G))
>>> sorted(c[0])
[8, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]
References
3.13.5 Label propagation
Label propagation community detection algorithms.
asyn_lpa_communities(G[, weight, seed]) Returns communities in Gas detected by asynchronous
label propagation.
label_propagation_communities(G) Generates community sets determined by label propa-
gation
networkx.algorithms.community.label_propagation.asyn_lpa_communities
asyn_lpa_communities(G,weight=None,seed=None)
Returns communities in Gas detected by asynchronous label propagation.
The asynchronous label propagation algorithm is described in1. The algorithm is probabilistic and the found
communities may vary on different executions.
The algorithm proceeds as follows. After initializing each node with a unique label, the algorithm repeatedly sets
the label of a node to be the label that appears most frequently among that nodes neighbors. The algorithm halts
when each node has the label that appears most frequently among its neighbors. The algorithm is asynchronous
because each node is updated without waiting for updates on the remaining nodes.
1Raghavan, Usha Nandini, Réka Albert, and Soundar Kumara. “Near linear time algorithm to detect community structures in large-scale
networks.” Physical Review E 76.3 (2007): 036106.
232 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
This generalized version of the algorithm in1accepts edge weights.
Parameters
•G(Graph)
•weight (string) – The edge attribute representing the weight of an edge. If None, each
edge is assumed to have weight one. In this algorithm, the weight of an edge is used in
determining the frequency with which a label appears among the neighbors of a node: a
higher weight means the label appears more often.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns communities – Iterable of communities given as sets of nodes.
Return type iterable
Notes
Edge weight attributes must be numerical.
References
networkx.algorithms.community.label_propagation.label_propagation_communities
label_propagation_communities(G)
Generates community sets determined by label propagation
Finds communities in Gusing a semi-synchronous label propagation method[1]_. This method combines the
advantages of both the synchronous and asynchronous models. Not implemented for directed graphs.
Parameters G (graph) – An undirected NetworkX graph.
Yields communities (generator) – Yields sets of the nodes in each community.
Raises NetworkXNotImplemented – If the graph is directed
References
3.13.6 Fluid Communities
Asynchronous Fluid Communities algorithm for community detection.
asyn_fluidc(G, k[, max_iter, seed]) Returns communities in Gas detected by Fluid Commu-
nities algorithm.
networkx.algorithms.community.asyn_fluid.asyn_fluidc
asyn_fluidc(G,k,max_iter=100,seed=None)
Returns communities in Gas detected by Fluid Communities algorithm.
The asynchronous fluid communities algorithm is described in1. The algorithm is based on the simple idea of
1Parés F., Garcia-Gasulla D. et al. “Fluid Communities: A Competitive and Highly Scalable Community Detection Algorithm”. [https:
//arxiv.org/pdf/1703.09307.pdf].
3.13. Communities 233

NetworkX Reference, Release 2.3rc1.dev20181203210840
fluids interacting in an environment, expanding and pushing each other. It’s initialization is random, so found
communities may vary on different executions.
The algorithm proceeds as follows. First each of the initial k communities is initialized in a random vertex in the
graph. Then the algorithm iterates over all vertices in a random order, updating the community of each vertex
based on its own community and the communities of its neighbours. This process is performed several times
until convergence. At all times, each community has a total density of 1, which is equally distributed among
the vertices it contains. If a vertex changes of community, vertex densities of affected communities are adjusted
immediately. When a complete iteration over all vertices is done, such that no vertex changes the community it
belongs to, the algorithm has converged and returns.
This is the original version of the algorithm described in1. Unfortunately, it does not support weighted graphs
yet.
Parameters
•G(Graph)
•k(integer) – The number of communities to be found.
•max_iter (integer) – The number of maximum iterations allowed. By default 15.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns communities – Iterable of communities given as sets of nodes.
Return type iterable
Notes
k variable is not an optional argument.
References
3.13.7 Measuring partitions
Functions for measuring the quality of a partition (into communities).
coverage(G, partition) Returns the coverage of a partition.
performance(G, partition) Returns the performance of a partition.
networkx.algorithms.community.quality.coverage
coverage(G,partition)
Returns the coverage of a partition.
The coverage of a partition is the ratio of the number of intra-community edges to the total number of edges in
the graph.
Parameters
•G(NetworkX graph)
•partition (sequence) – Partition of the nodes of G, represented as a sequence of sets of
nodes. Each block of the partition represents a community.
Returns The coverage of the partition, as defined above.
234 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type float
Raises NetworkXError – If partition is not a valid partition of the nodes of G.
Notes
If Gis a multigraph, the multiplicity of edges is counted.
References
networkx.algorithms.community.quality.performance
performance(G,partition)
Returns the performance of a partition.
The performance of a partition is the ratio of the number of intra-community edges plus inter-community non-
edges with the total number of potential edges.
Parameters
•G(NetworkX graph) – A simple graph (directed or undirected).
•partition (sequence) – Partition of the nodes of G, represented as a sequence of sets of
nodes. Each block of the partition represents a community.
Returns The performance of the partition, as defined above.
Return type float
Raises NetworkXError – If partition is not a valid partition of the nodes of G.
References
3.13.8 Partitions via centrality measures
Functions for computing communities based on centrality notions.
girvan_newman(G[, most_valuable_edge]) Finds communities in a graph using the Gir-
van–Newman method.
networkx.algorithms.community.centrality.girvan_newman
girvan_newman(G,most_valuable_edge=None)
Finds communities in a graph using the Girvan–Newman method.
Parameters
•G(NetworkX graph)
•most_valuable_edge (function) – Function that takes a graph as input and outputs an edge.
The edge returned by this function will be recomputed and removed at each iteration of the
algorithm.
If not specified, the edge with the highest networkx.
edge_betweenness_centrality() will be used.
3.13. Communities 235

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns Iterator over tuples of sets of nodes in G. Each set of node is a community, each tuple is a
sequence of communities at a particular level of the algorithm.
Return type iterator
Examples
To get the first pair of communities:
>>> G=nx.path_graph(10)
>>> comp =girvan_newman(G)
>>> tuple(sorted(c) for cin next(comp))
([0, 1, 2, 3, 4], [5, 6, 7, 8, 9])
To get only the first ktuples of communities, use itertools.islice():
>>> import itertools
>>> G=nx.path_graph(8)
>>> k=2
>>> comp =girvan_newman(G)
>>> for communities in itertools.islice(comp, k):
... print(tuple(sorted(c) for cin communities))
...
([0, 1, 2, 3], [4, 5, 6, 7])
([0, 1], [2, 3], [4, 5, 6, 7])
To stop getting tuples of communities once the number of communities is greater than k, use itertools.
takewhile():
>>> import itertools
>>> G=nx.path_graph(8)
>>> k=4
>>> comp =girvan_newman(G)
>>> limited =itertools.takewhile(lambda c: len(c) <= k, comp)
>>> for communities in limited:
... print(tuple(sorted(c) for cin communities))
...
([0, 1, 2, 3], [4, 5, 6, 7])
([0, 1], [2, 3], [4, 5, 6, 7])
([0, 1], [2, 3], [4, 5], [6, 7])
To just choose an edge to remove based on the weight:
>>> from operator import itemgetter
>>> G=nx.path_graph(10)
>>> edges =G.edges()
>>> nx.set_edge_attributes(G, {(u, v): v for u, v in edges}, 'weight')
>>> def heaviest(G):
... u,v,w=max(G.edges(data='weight'), key=itemgetter(2))
... return (u, v)
...
>>> comp =girvan_newman(G, most_valuable_edge=heaviest)
>>> tuple(sorted(c) for cin next(comp))
([0, 1, 2, 3, 4, 5, 6, 7, 8], [9])
To utilize edge weights when choosing an edge with, for example, the highest betweenness centrality:
236 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx import edge_betweenness_centrality as betweenness
>>> def most_central_edge(G):
... centrality =betweenness(G, weight='weight')
... return max(centrality, key=centrality.get)
...
>>> G=nx.path_graph(10)
>>> comp =girvan_newman(G, most_valuable_edge=most_central_edge)
>>> tuple(sorted(c) for cin next(comp))
([0, 1, 2, 3, 4], [5, 6, 7, 8, 9])
To specify a different ranking algorithm for edges, use the most_valuable_edge keyword argument:
>>> from networkx import edge_betweenness_centrality
>>> from random import random
>>> def most_central_edge(G):
... centrality =edge_betweenness_centrality(G)
... max_cent =max(centrality.values())
... # Scale the centrality values so they are between 0 and 1,
... # and add some random noise.
... centrality ={e: c /max_cent for e, c in centrality.items()}
... # Add some random noise.
... centrality ={e: c +random() for e, c in centrality.items()}
... return max(centrality, key=centrality.get)
...
>>> G=nx.path_graph(10)
>>> comp =girvan_newman(G, most_valuable_edge=most_central_edge)
Notes
The Girvan–Newman algorithm detects communities by progressively removing edges from the original graph.
The algorithm removes the “most valuable” edge, traditionally the edge with the highest betweenness centrality,
at each step. As the graph breaks down into pieces, the tightly knit community structure is exposed and the
result can be depicted as a dendrogram.
3.13.9 Validating partitions
Helper functions for community-finding algorithms.
is_partition(G, communities) Return True if and only if communities is a partition
of the nodes of G.
networkx.algorithms.community.community_utils.is_partition
is_partition(G,communities)
Return True if and only if communities is a partition of the nodes of G.
A partition of a universe set is a family of pairwise disjoint sets whose union is the entire universe set.
Gis a NetworkX graph.
communities is an iterable of sets of nodes of G. This iterable will be consumed multiple times during the
execution of this function.
3.13. Communities 237

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.14 Components
3.14.1 Connectivity
is_connected(G) Return True if the graph is connected, False otherwise.
number_connected_components(G) Return the number of connected components.
connected_components(G) Generate connected components.
connected_component_subgraphs(G[, copy]) DEPRECATED: Use (G.subgraph(c) for c
in connected_components(G))
node_connected_component(G, n) Return the set of nodes in the component of graph con-
taining node n.
networkx.algorithms.components.is_connected
is_connected(G)
Return True if the graph is connected, False otherwise.
Parameters G (NetworkX Graph) – An undirected graph.
Returns connected – True if the graph is connected, false otherwise.
Return type bool
Raises NetworkXNotImplemented: – If G is directed.
Examples
>>> G=nx.path_graph(4)
>>> print(nx.is_connected(G))
True
See also:
is_strongly_connected(),is_weakly_connected(),is_semiconnected(),
is_biconnected(),connected_components()
Notes
For undirected graphs only.
networkx.algorithms.components.number_connected_components
number_connected_components(G)
Return the number of connected components.
Parameters G (NetworkX graph) – An undirected graph.
Returns n – Number of connected components
Return type integer
See also:
connected_components(),number_weakly_connected_components(),
number_strongly_connected_components()
238 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
For undirected graphs only.
networkx.algorithms.components.connected_components
connected_components(G)
Generate connected components.
Parameters G (NetworkX graph) – An undirected graph
Returns comp – A generator of sets of nodes, one for each component of G.
Return type generator of sets
Raises NetworkXNotImplemented: – If G is directed.
Examples
Generate a sorted list of connected components, largest first.
>>> G=nx.path_graph(4)
>>> nx.add_path(G, [10,11,12])
>>> [len(c) for cin sorted(nx.connected_components(G), key=len, reverse=True)]
[4, 3]
If you only want the largest connected component, it’s more efficient to use max instead of sort.
>>> largest_cc =max(nx.connected_components(G), key=len)
See also:
strongly_connected_components(),weakly_connected_components()
Notes
For undirected graphs only.
networkx.algorithms.components.connected_component_subgraphs
connected_component_subgraphs(G,copy=True)
DEPRECATED: Use (G.subgraph(c) for c in connected_components(G))
Or (G.subgraph(c).copy() for c in connected_components(G))
networkx.algorithms.components.node_connected_component
node_connected_component(G,n)
Return the set of nodes in the component of graph containing node n.
Parameters
•G(NetworkX Graph) – An undirected graph.
•n(node label) – A node in G
3.14. Components 239

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns comp – A set of nodes in the component of G containing node n.
Return type set
Raises NetworkXNotImplemented: – If G is directed.
See also:
connected_components()
Notes
For undirected graphs only.
3.14.2 Strong connectivity
is_strongly_connected(G) Test directed graph for strong connectivity.
number_strongly_connected_components(G) Return number of strongly connected components in
graph.
strongly_connected_components(G) Generate nodes in strongly connected components of
graph.
strongly_connected_component_subgraphs(G[,
copy])
DEPRECATED: Use (G.subgraph(c) for c
in strongly_connected_components(G))
strongly_connected_components_recursive(G)Generate nodes in strongly connected components of
graph.
kosaraju_strongly_connected_components(G[,
...])
Generate nodes in strongly connected components of
graph.
condensation(G[, scc]) Returns the condensation of G.
networkx.algorithms.components.is_strongly_connected
is_strongly_connected(G)
Test directed graph for strong connectivity.
A directed graph is strongly connected if and only if every vertex in the graph is reachable from every other
vertex.
Parameters G (NetworkX Graph) – A directed graph.
Returns connected – True if the graph is strongly connected, False otherwise.
Return type bool
Raises NetworkXNotImplemented: – If G is undirected.
See also:
is_weakly_connected(),is_semiconnected(),is_connected(),is_biconnected(),
strongly_connected_components()
Notes
For directed graphs only.
240 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.components.number_strongly_connected_components
number_strongly_connected_components(G)
Return number of strongly connected components in graph.
Parameters G (NetworkX graph) – A directed graph.
Returns n – Number of strongly connected components
Return type integer
Raises NetworkXNotImplemented: – If G is undirected.
See also:
strongly_connected_components(),number_connected_components(),
number_weakly_connected_components()
Notes
For directed graphs only.
networkx.algorithms.components.strongly_connected_components
strongly_connected_components(G)
Generate nodes in strongly connected components of graph.
Parameters G (NetworkX Graph) – A directed graph.
Returns comp – A generator of sets of nodes, one for each strongly connected component of G.
Return type generator of sets
Raises NetworkXNotImplemented : – If G is undirected.
Examples
Generate a sorted list of strongly connected components, largest first.
>>> G=nx.cycle_graph(4, create_using=nx.DiGraph())
>>> nx.add_cycle(G, [10,11,12])
>>> [len(c) for cin sorted(nx.strongly_connected_components(G),
... key=len, reverse=True)]
[4, 3]
If you only want the largest component, it’s more efficient to use max instead of sort.
>>> largest =max(nx.strongly_connected_components(G), key=len)
See also:
connected_components(),weakly_connected_components(),
kosaraju_strongly_connected_components()
Notes
Uses Tarjan’s algorithm[1]_ with Nuutila’s modifications[2]_. Nonrecursive version of algorithm.
3.14. Components 241

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.algorithms.components.strongly_connected_component_subgraphs
strongly_connected_component_subgraphs(G,copy=True)
DEPRECATED: Use (G.subgraph(c) for c in strongly_connected_components(G))
Or (G.subgraph(c).copy() for c in strongly_connected_components(G))
networkx.algorithms.components.strongly_connected_components_recursive
strongly_connected_components_recursive(G)
Generate nodes in strongly connected components of graph.
Recursive version of algorithm.
Parameters G (NetworkX Graph) – A directed graph.
Returns comp – A generator of sets of nodes, one for each strongly connected component of G.
Return type generator of sets
Raises NetworkXNotImplemented : – If G is undirected.
Examples
Generate a sorted list of strongly connected components, largest first.
>>> G=nx.cycle_graph(4, create_using=nx.DiGraph())
>>> nx.add_cycle(G, [10,11,12])
>>> [len(c) for cin sorted(nx.strongly_connected_components_recursive(G),
... key=len, reverse=True)]
[4, 3]
If you only want the largest component, it’s more efficient to use max instead of sort.
>>> largest =max(nx.strongly_connected_components_recursive(G), key=len)
See also:
connected_components()
Notes
Uses Tarjan’s algorithm[1]_ with Nuutila’s modifications[2]_.
References
networkx.algorithms.components.kosaraju_strongly_connected_components
kosaraju_strongly_connected_components(G,source=None)
Generate nodes in strongly connected components of graph.
Parameters G (NetworkX Graph) – A directed graph.
Returns comp – A genrator of sets of nodes, one for each strongly connected component of G.
242 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type generator of sets
Raises NetworkXNotImplemented: – If G is undirected.
Examples
Generate a sorted list of strongly connected components, largest first.
>>> G=nx.cycle_graph(4, create_using=nx.DiGraph())
>>> nx.add_cycle(G, [10,11,12])
>>> [len(c) for cin sorted(nx.kosaraju_strongly_connected_components(G),
... key=len, reverse=True)]
[4, 3]
If you only want the largest component, it’s more efficient to use max instead of sort.
>>> largest =max(nx.kosaraju_strongly_connected_components(G), key=len)
See also:
strongly_connected_components()
Notes
Uses Kosaraju’s algorithm.
networkx.algorithms.components.condensation
condensation(G,scc=None)
Returns the condensation of G.
The condensation of G is the graph with each of the strongly connected components contracted into a single
node.
Parameters
•G(NetworkX DiGraph) – A directed graph.
•scc (list or generator (optional, default=None)) – Strongly connected components. If pro-
vided, the elements in scc must partition the nodes in G. If not provided, it will be calculated
as scc=nx.strongly_connected_components(G).
Returns C – The condensation graph C of G. The node labels are integers corresponding to the index
of the component in the list of strongly connected components of G. C has a graph attribute
named ‘mapping’ with a dictionary mapping the original nodes to the nodes in C to which they
belong. Each node in C also has a node attribute ‘members’ with the set of original nodes in G
that form the SCC that the node in C represents.
Return type NetworkX DiGraph
Raises NetworkXNotImplemented: – If G is undirected.
Notes
After contracting all strongly connected components to a single node, the resulting graph is a directed acyclic
graph.
3.14. Components 243

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.14.3 Weak connectivity
is_weakly_connected(G) Test directed graph for weak connectivity.
number_weakly_connected_components(G) Return the number of weakly connected components in
G.
weakly_connected_components(G) Generate weakly connected components of G.
weakly_connected_component_subgraphs(G[,
copy])
DEPRECATED: Use (G.subgraph(c) for c
in weakly_connected_components(G))
networkx.algorithms.components.is_weakly_connected
is_weakly_connected(G)
Test directed graph for weak connectivity.
A directed graph is weakly connected if and only if the graph is connected when the direction of the edge
between nodes is ignored.
Note that if a graph is strongly connected (i.e. the graph is connected even when we account for directionality),
it is by definition weakly connected as well.
Parameters G (NetworkX Graph) – A directed graph.
Returns connected – True if the graph is weakly connected, False otherwise.
Return type bool
Raises NetworkXNotImplemented: – If G is undirected.
See also:
is_strongly_connected(),is_semiconnected(),is_connected(),is_biconnected(),
weakly_connected_components()
Notes
For directed graphs only.
networkx.algorithms.components.number_weakly_connected_components
number_weakly_connected_components(G)
Return the number of weakly connected components in G.
Parameters G (NetworkX graph) – A directed graph.
Returns n – Number of weakly connected components
Return type integer
Raises NetworkXNotImplemented: – If G is undirected.
See also:
weakly_connected_components(),number_connected_components(),
number_strongly_connected_components()
Notes
For directed graphs only.
244 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.components.weakly_connected_components
weakly_connected_components(G)
Generate weakly connected components of G.
Parameters G (NetworkX graph) – A directed graph
Returns comp – A generator of sets of nodes, one for each weakly connected component of G.
Return type generator of sets
Raises NetworkXNotImplemented: – If G is undirected.
Examples
Generate a sorted list of weakly connected components, largest first.
>>> G=nx.path_graph(4, create_using=nx.DiGraph())
>>> nx.add_path(G, [10,11,12])
>>> [len(c) for cin sorted(nx.weakly_connected_components(G),
... key=len, reverse=True)]
[4, 3]
If you only want the largest component, it’s more efficient to use max instead of sort:
>>> largest_cc =max(nx.weakly_connected_components(G), key=len)
See also:
connected_components(),strongly_connected_components()
Notes
For directed graphs only.
networkx.algorithms.components.weakly_connected_component_subgraphs
weakly_connected_component_subgraphs(G,copy=True)
DEPRECATED: Use (G.subgraph(c) for c in weakly_connected_components(G))
Or (G.subgraph(c).copy() for c in weakly_connected_components(G))
3.14.4 Attracting components
is_attracting_component(G) Returns True if Gconsists of a single attracting compo-
nent.
number_attracting_components(G) Returns the number of attracting components in G.
attracting_components(G) Generates the attracting components in G.
attracting_component_subgraphs(G[,
copy])
DEPRECATED: Use (G.subgraph(c) for c
in attracting_components(G))
3.14. Components 245

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.components.is_attracting_component
is_attracting_component(G)
Returns True if Gconsists of a single attracting component.
Parameters G (DiGraph, MultiDiGraph) – The graph to be analyzed.
Returns attracting – True if Ghas a single attracting component. Otherwise, False.
Return type bool
Raises NetworkXNotImplemented : – If the input graph is undirected.
See also:
attracting_components(),number_attracting_components()
networkx.algorithms.components.number_attracting_components
number_attracting_components(G)
Returns the number of attracting components in G.
Parameters G (DiGraph, MultiDiGraph) – The graph to be analyzed.
Returns n – The number of attracting components in G.
Return type int
Raises NetworkXNotImplemented : – If the input graph is undirected.
See also:
attracting_components(),is_attracting_component()
networkx.algorithms.components.attracting_components
attracting_components(G)
Generates the attracting components in G.
An attracting component in a directed graph Gis a strongly connected component with the property that a
random walker on the graph will never leave the component, once it enters the component.
The nodes in attracting components can also be thought of as recurrent nodes. If a random walker enters the
attractor containing the node, then the node will be visited infinitely often.
Parameters G (DiGraph, MultiDiGraph) – The graph to be analyzed.
Returns attractors – A generator of sets of nodes, one for each attracting component of G.
Return type generator of sets
Raises NetworkXNotImplemented : – If the input graph is undirected.
See also:
number_attracting_components(),is_attracting_component()
246 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.components.attracting_component_subgraphs
attracting_component_subgraphs(G,copy=True)
DEPRECATED: Use (G.subgraph(c) for c in attracting_components(G))
Or (G.subgraph(c).copy() for c in attracting_components(G))
3.14.5 Biconnected components
is_biconnected(G) Return True if the graph is biconnected, False otherwise.
biconnected_components(G) Return a generator of sets of nodes, one set for each
biconnected component of the graph
biconnected_component_edges(G) Return a generator of lists of edges, one list for each
biconnected component of the input graph.
biconnected_component_subgraphs(G[,
copy])
DEPRECATED: Use (G.subgraph(c) for c
in biconnected_components(G))
articulation_points(G) Yield the articulation points, or cut vertices, of a graph.
networkx.algorithms.components.is_biconnected
is_biconnected(G)
Return True if the graph is biconnected, False otherwise.
A graph is biconnected if, and only if, it cannot be disconnected by removing only one node (and all edges
incident on that node). If removing a node increases the number of disconnected components in the graph, that
node is called an articulation point, or cut vertex. A biconnected graph has no articulation points.
Parameters G (NetworkX Graph) – An undirected graph.
Returns biconnected – True if the graph is biconnected, False otherwise.
Return type bool
Raises NetworkXNotImplemented : – If the input graph is not undirected.
Examples
>>> G=nx.path_graph(4)
>>> print(nx.is_biconnected(G))
False
>>> G.add_edge(0,3)
>>> print(nx.is_biconnected(G))
True
See also:
biconnected_components(),articulation_points(),biconnected_component_edges(),
is_strongly_connected(),is_weakly_connected(),is_connected(),
is_semiconnected()
Notes
The algorithm to find articulation points and biconnected components is implemented using a non-recursive
depth-first-search (DFS) that keeps track of the highest level that back edges reach in the DFS tree. A node n
3.14. Components 247

NetworkX Reference, Release 2.3rc1.dev20181203210840
is an articulation point if, and only if, there exists a subtree rooted at nsuch that there is no back edge from
any successor of nthat links to a predecessor of nin the DFS tree. By keeping track of all the edges traversed
by the DFS we can obtain the biconnected components because all edges of a bicomponent will be traversed
consecutively between articulation points.
References
networkx.algorithms.components.biconnected_components
biconnected_components(G)
Return a generator of sets of nodes, one set for each biconnected component of the graph
Biconnected components are maximal subgraphs such that the removal of a node (and all edges incident on that
node) will not disconnect the subgraph. Note that nodes may be part of more than one biconnected component.
Those nodes are articulation points, or cut vertices. The removal of articulation points will increase the number
of connected components of the graph.
Notice that by convention a dyad is considered a biconnected component.
Parameters G (NetworkX Graph) – An undirected graph.
Returns nodes – Generator of sets of nodes, one set for each biconnected component.
Return type generator
Raises NetworkXNotImplemented : – If the input graph is not undirected.
See also:
k_components() this function is a special case where k=2
bridge_components() similar to this function, but is defined using 2-edge-connectivity instead of 2-node-
connectivity.
Examples
>>> G=nx.lollipop_graph(5,1)
>>> print(nx.is_biconnected(G))
False
>>> bicomponents =list(nx.biconnected_components(G))
>>> len(bicomponents)
2
>>> G.add_edge(0,5)
>>> print(nx.is_biconnected(G))
True
>>> bicomponents =list(nx.biconnected_components(G))
>>> len(bicomponents)
1
You can generate a sorted list of biconnected components, largest first, using sort.
>>> G.remove_edge(0,5)
>>> [len(c) for cin sorted(nx.biconnected_components(G), key=len, reverse=True)]
[5, 2]
If you only want the largest connected component, it’s more efficient to use max instead of sort.
248 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> Gc =max(nx.biconnected_components(G), key=len)
See also:
is_biconnected(),articulation_points(),biconnected_component_edges()
Notes
The algorithm to find articulation points and biconnected components is implemented using a non-recursive
depth-first-search (DFS) that keeps track of the highest level that back edges reach in the DFS tree. A node n
is an articulation point if, and only if, there exists a subtree rooted at nsuch that there is no back edge from
any successor of nthat links to a predecessor of nin the DFS tree. By keeping track of all the edges traversed
by the DFS we can obtain the biconnected components because all edges of a bicomponent will be traversed
consecutively between articulation points.
References
networkx.algorithms.components.biconnected_component_edges
biconnected_component_edges(G)
Return a generator of lists of edges, one list for each biconnected component of the input graph.
Biconnected components are maximal subgraphs such that the removal of a node (and all edges incident on that
node) will not disconnect the subgraph. Note that nodes may be part of more than one biconnected compo-
nent. Those nodes are articulation points, or cut vertices. However, each edge belongs to one, and only one,
biconnected component.
Notice that by convention a dyad is considered a biconnected component.
Parameters G (NetworkX Graph) – An undirected graph.
Returns edges – Generator of lists of edges, one list for each bicomponent.
Return type generator of lists
Raises NetworkXNotImplemented : – If the input graph is not undirected.
Examples
>>> G=nx.barbell_graph(4,2)
>>> print(nx.is_biconnected(G))
False
>>> bicomponents_edges =list(nx.biconnected_component_edges(G))
>>> len(bicomponents_edges)
5
>>> G.add_edge(2,8)
>>> print(nx.is_biconnected(G))
True
>>> bicomponents_edges =list(nx.biconnected_component_edges(G))
>>> len(bicomponents_edges)
1
See also:
is_biconnected(),biconnected_components(),articulation_points()
3.14. Components 249

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The algorithm to find articulation points and biconnected components is implemented using a non-recursive
depth-first-search (DFS) that keeps track of the highest level that back edges reach in the DFS tree. A node n
is an articulation point if, and only if, there exists a subtree rooted at nsuch that there is no back edge from
any successor of nthat links to a predecessor of nin the DFS tree. By keeping track of all the edges traversed
by the DFS we can obtain the biconnected components because all edges of a bicomponent will be traversed
consecutively between articulation points.
References
networkx.algorithms.components.biconnected_component_subgraphs
biconnected_component_subgraphs(G,copy=True)
DEPRECATED: Use (G.subgraph(c) for c in biconnected_components(G))
Or (G.subgraph(c).copy() for c in biconnected_components(G))
networkx.algorithms.components.articulation_points
articulation_points(G)
Yield the articulation points, or cut vertices, of a graph.
An articulation point or cut vertex is any node whose removal (along with all its incident edges) increases the
number of connected components of a graph. An undirected connected graph without articulation points is
biconnected. Articulation points belong to more than one biconnected component of a graph.
Notice that by convention a dyad is considered a biconnected component.
Parameters G (NetworkX Graph) – An undirected graph.
Yields node – An articulation point in the graph.
Raises NetworkXNotImplemented : – If the input graph is not undirected.
Examples
>>> G=nx.barbell_graph(4,2)
>>> print(nx.is_biconnected(G))
False
>>> len(list(nx.articulation_points(G)))
4
>>> G.add_edge(2,8)
>>> print(nx.is_biconnected(G))
True
>>> len(list(nx.articulation_points(G)))
0
See also:
is_biconnected(),biconnected_components(),biconnected_component_edges()
250 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The algorithm to find articulation points and biconnected components is implemented using a non-recursive
depth-first-search (DFS) that keeps track of the highest level that back edges reach in the DFS tree. A node n
is an articulation point if, and only if, there exists a subtree rooted at nsuch that there is no back edge from
any successor of nthat links to a predecessor of nin the DFS tree. By keeping track of all the edges traversed
by the DFS we can obtain the biconnected components because all edges of a bicomponent will be traversed
consecutively between articulation points.
References
3.14.6 Semiconnectedness
is_semiconnected(G) Return True if the graph is semiconnected, False other-
wise.
networkx.algorithms.components.is_semiconnected
is_semiconnected(G)
Return True if the graph is semiconnected, False otherwise.
A graph is semiconnected if, and only if, for any pair of nodes, either one is reachable from the other, or they
are mutually reachable.
Parameters G (NetworkX graph) – A directed graph.
Returns semiconnected – True if the graph is semiconnected, False otherwise.
Return type bool
Raises
•NetworkXNotImplemented : – If the input graph is undirected.
•NetworkXPointlessConcept : – If the graph is empty.
Examples
>>> G=nx.path_graph(4,create_using=nx.DiGraph())
>>> print(nx.is_semiconnected(G))
True
>>> G=nx.DiGraph([(1,2), (3,2)])
>>> print(nx.is_semiconnected(G))
False
See also:
is_strongly_connected(),is_weakly_connected(),is_connected(),
is_biconnected()
3.15 Connectivity
Connectivity and cut algorithms
3.15. Connectivity 251

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.15.1 Edge-augmentation
Algorithms for finding k-edge-augmentations
A k-edge-augmentation is a set of edges, that once added to a graph, ensures that the graph is k-edge-connected; i.e.
the graph cannot be disconnected unless k or more edges are removed. Typically, the goal is to find the augmentation
with minimum weight. In general, it is not guaranteed that a k-edge-augmentation exists.
See also:
edge_kcomponents algorithms for finding k-edge-connected components
connectivity algorithms for determening edge connectivity.
k_edge_augmentation(G, k[, avail, weight, . . . ]) Finds set of edges to k-edge-connect G.
is_k_edge_connected(G, k) Tests to see if a graph is k-edge-connected.
is_locally_k_edge_connected(G, s, t, k) Tests to see if an edge in a graph is locally k-edge-
connected.
networkx.algorithms.connectivity.edge_augmentation.k_edge_augmentation
k_edge_augmentation(G,k,avail=None,weight=None,partial=False)
Finds set of edges to k-edge-connect G.
Adding edges from the augmentation to G make it impossible to disconnect G unless k or more edges are
removed. This function uses the most efficient function available (depending on the value of k and if the problem
is weighted or unweighted) to search for a minimum weight subset of available edges that k-edge-connects G. In
general, finding a k-edge-augmentation is NP-hard, so solutions are not garuenteed to be minimal. Furthermore,
a k-edge-augmentation may not exist.
Parameters
•G(NetworkX graph) – An undirected graph.
•k(integer) – Desired edge connectivity
•avail (dict or a set of 2 or 3 tuples) – The available edges that can be used in the augmenta-
tion.
If unspecified, then all edges in the complement of G are available. Otherwise, each item is
an available edge (with an optional weight).
In the unweighted case, each item is an edge (u, v).
In the weighted case, each item is a 3-tuple (u, v, d) or a dict with items (u, v):
d. The third item, d, can be a dictionary or a real number. If dis a dictionary d[weight]
correspondings to the weight.
•weight (string) – key to use to find weights if avail is a set of 3-tuples where the third
item in each tuple is a dictionary.
•partial (boolean) – If partial is True and no feasible k-edge-augmentation exists, then all a
partial k-edge-augmentation is generated. Adding the edges in a partial augmentation to G,
minimizes the number of k-edge-connected components and maximizes the edge connectiv-
ity between those components. For details, see partial_k_edge_augmentation().
Yields edge (tuple) – Edges that, once added to G, would cause G to become k-edge-connected.
If partial is False, an error is raised if this is not possible. Otherwise, generated edges form a
partial augmentation, which k-edge-connects any part of G where it is possible, and maximally
connects the remaining parts.
252 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises
• NetworkXUnfeasible: – If partial is False and no k-edge-augmentation exists.
• NetworkXNotImplemented: – If the input graph is directed or a multigraph.
• ValueError: – If k is less than 1
Notes
When k=1 this returns an optimal solution.
When k=2 and avail is None, this returns an optimal solution. Otherwise when k=2, this returns a 2-
approximation of the optimal solution.
For k>3, this problem is NP-hard and this uses a randomized algorithm that produces a feasible solution,
but provides no guarantees on the solution weight.
Example
>>> # Unweighted cases
>>> G=nx.path_graph((1,2,3,4))
>>> G.add_node(5)
>>> sorted(nx.k_edge_augmentation(G, k=1))
[(1, 5)]
>>> sorted(nx.k_edge_augmentation(G, k=2))
[(1, 5), (5, 4)]
>>> sorted(nx.k_edge_augmentation(G, k=3))
[(1, 4), (1, 5), (2, 5), (3, 5), (4, 5)]
>>> complement =list(nx.k_edge_augmentation(G, k=5, partial=True))
>>> G.add_edges_from(complement)
>>> nx.edge_connectivity(G)
4
Example
>>> # Weighted cases
>>> G=nx.path_graph((1,2,3,4))
>>> G.add_node(5)
>>> # avail can be a tuple with a dict
>>> avail =[(1,5, {'weight':11}), (2,5, {'weight':10})]
>>> sorted(nx.k_edge_augmentation(G, k=1, avail=avail, weight='weight'))
[(2, 5)]
>>> # or avail can be a 3-tuple with a real number
>>> avail =[(1,5,11), (2,5,10), (4,3,1), (4,5,51)]
>>> sorted(nx.k_edge_augmentation(G, k=2, avail=avail))
[(1, 5), (2, 5), (4, 5)]
>>> # or avail can be a dict
>>> avail ={(1,5): 11, (2,5): 10, (4,3): 1, (4,5): 51}
>>> sorted(nx.k_edge_augmentation(G, k=2, avail=avail))
[(1, 5), (2, 5), (4, 5)]
>>> # If augmentation is infeasible, then a partial solution can be found
>>> avail ={(1,5): 11}
>>> sorted(nx.k_edge_augmentation(G, k=2, avail=avail, partial=True))
[(1, 5)]
3.15. Connectivity 253

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.connectivity.edge_augmentation.is_k_edge_connected
is_k_edge_connected(G,k)
Tests to see if a graph is k-edge-connected.
Is it impossible to disconnect the graph by removing fewer than k edges? If so, then G is k-edge-connected.
Parameters
•G(NetworkX graph) – An undirected graph.
•k(integer) – edge connectivity to test for
Returns True if G is k-edge-connected.
Return type boolean
See also:
is_locally_k_edge_connected()
Example
>>> G=nx.barbell_graph(10,0)
>>> nx.is_k_edge_connected(G, k=1)
True
>>> nx.is_k_edge_connected(G, k=2)
False
networkx.algorithms.connectivity.edge_augmentation.is_locally_k_edge_connected
is_locally_k_edge_connected(G,s,t,k)
Tests to see if an edge in a graph is locally k-edge-connected.
Is it impossible to disconnect s and t by removing fewer than k edges? If so, then s and t are locally k-edge-
connected in G.
Parameters
•G(NetworkX graph) – An undirected graph.
•s(node) – Source node
•t(node) – Target node
•k(integer) – local edge connectivity for nodes s and t
Returns True if s and t are locally k-edge-connected in G.
Return type boolean
See also:
is_k_edge_connected()
Example
254 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx.algorithms.connectivity import is_locally_k_edge_connected
>>> G=nx.barbell_graph(10,0)
>>> is_locally_k_edge_connected(G, 5,15, k=1)
True
>>> is_locally_k_edge_connected(G, 5,15, k=2)
False
>>> is_locally_k_edge_connected(G, 1,5, k=2)
True
3.15.2 K-edge-components
Algorithms for finding k-edge-connected components and subgraphs.
A k-edge-connected component (k-edge-cc) is a maximal set of nodes in G, such that all pairs of node have an edge-
connectivity of at least k.
A k-edge-connected subgraph (k-edge-subgraph) is a maximal set of nodes in G, such that the subgraph of G defined
by the nodes has an edge-connectivity at least k.
k_edge_components(G, k) Generates nodes in each maximal k-edge-connected
component in G.
k_edge_subgraphs(G, k) Generates nodes in each maximal k-edge-connected
subgraph in G.
bridge_components(G) Finds all bridge-connected components G.
EdgeComponentAuxGraph A simple algorithm to find all k-edge-connected com-
ponents in a graph.
networkx.algorithms.connectivity.edge_kcomponents.k_edge_components
k_edge_components(G,k)
Generates nodes in each maximal k-edge-connected component in G.
Parameters
•G(NetworkX graph)
•k(Integer) – Desired edge connectivity
Returns k_edge_components – will have k-edge-connectivity in the graph G.
Return type a generator of k-edge-ccs. Each set of returned nodes
See also:
local_edge_connectivity()
k_edge_subgraphs() similar to this function, but the subgraph defined by the nodes must also have k-
edge-connectivity.
k_components() similar to this function, but uses node-connectivity instead of edge-connectivity
Raises
• NetworkXNotImplemented: – If the input graph is a multigraph.
• ValueError: – If k is less than 1
3.15. Connectivity 255

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Attempts to use the most efficient implementation available based on k. If k=1, this is simply simply connected
components for directed graphs and connected components for undirected graphs. If k=2 on an efficient bridge
connected component algorithm from _[1] is run based on the chain decomposition. Otherwise, the algorithm
from _[2] is used.
Example
>>> import itertools as it
>>> from networkx.utils import pairwise
>>> paths =[
... (1,2,4,3,1,4),
... (5,6,7,8,5,7,8,6),
... ]
>>> G=nx.Graph()
>>> G.add_nodes_from(it.chain(*paths))
>>> G.add_edges_from(it.chain(*[pairwise(path) for path in paths]))
>>> # note this returns {1, 4} unlike k_edge_subgraphs
>>> sorted(map(sorted, nx.k_edge_components(G, k=3)))
[[1, 4], [2], [3], [5, 6, 7, 8]]
References
networkx.algorithms.connectivity.edge_kcomponents.k_edge_subgraphs
k_edge_subgraphs(G,k)
Generates nodes in each maximal k-edge-connected subgraph in G.
Parameters
•G(NetworkX graph)
•k(Integer) – Desired edge connectivity
Returns k_edge_subgraphs – Each k-edge-subgraph is a maximal set of nodes that defines a sub-
graph of G that is k-edge-connected.
Return type a generator of k-edge-subgraphs
See also:
edge_connectivity()
k_edge_components() similar to this function, but nodes only need to have k-edge-connctivity within the
graph G and the subgraphs might not be k-edge-connected.
Raises
• NetworkXNotImplemented: – If the input graph is a multigraph.
• ValueError: – If k is less than 1
Notes
Attempts to use the most efficient implementation available based on k. If k=1, or k=2 and the graph is undi-
rected, then this simply calls k_edge_components. Otherwise the algorithm from _[1] is used.
256 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Example
>>> import itertools as it
>>> from networkx.utils import pairwise
>>> paths =[
... (1,2,4,3,1,4),
... (5,6,7,8,5,7,8,6),
... ]
>>> G=nx.Graph()
>>> G.add_nodes_from(it.chain(*paths))
>>> G.add_edges_from(it.chain(*[pairwise(path) for path in paths]))
>>> # note this does not return {1, 4} unlike k_edge_components
>>> sorted(map(sorted, nx.k_edge_subgraphs(G, k=3)))
[[1], [2], [3], [4], [5, 6, 7, 8]]
References
networkx.algorithms.connectivity.edge_kcomponents.bridge_components
bridge_components(G)
Finds all bridge-connected components G.
Parameters G (NetworkX undirected graph)
Returns bridge_components
Return type a generator of 2-edge-connected components
See also:
k_edge_subgraphs() this function is a special case for an undirected graph where k=2.
biconnected_components() similar to this function, but is defined using 2-node-connectivity instead of
2-edge-connectivity.
Raises NetworkXNotImplemented: – If the input graph is directed or a multigraph.
Notes
Bridge-connected components are also known as 2-edge-connected components.
Example
>>> # The barbell graph with parameter zero has a single bridge
>>> G=nx.barbell_graph(5,0)
>>> from networkx.algorithms.connectivity.edge_kcomponents import bridge_
˓→components
>>> sorted(map(sorted, bridge_components(G)))
[[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
3.15. Connectivity 257

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.connectivity.edge_kcomponents.EdgeComponentAuxGraph
class EdgeComponentAuxGraph
A simple algorithm to find all k-edge-connected components in a graph.
Constructing the AuxillaryGraph (which may take some time) allows for the k-edge-ccs to be found in linear
time for arbitrary k.
Notes
This implementation is based on1. The idea is to construct an auxiliary graph from which the k-edge-ccs can be
extracted in linear time. The auxiliary graph is constructed in 𝑂(|𝑉| · 𝐹)operations, where F is the complexity
of max flow. Querying the components takes an additional 𝑂(|𝑉|)operations. This algorithm can be slow for
large graphs, but it handles an arbitrary k and works for both directed and undirected inputs.
The undirected case for k=1 is exactly connected components. The undirected case for k=2 is exactly bridge
connected components. The directed case for k=1 is exactly strongly connected components.
References
Example
>>> import itertools as it
>>> from networkx.utils import pairwise
>>> from networkx.algorithms.connectivity import EdgeComponentAuxGraph
>>> # Build an interesting graph with multiple levels of k-edge-ccs
>>> paths =[
... (1,2,3,4,1,3,4,2), # a 3-edge-cc (a 4 clique)
... (5,6,7,5), # a 2-edge-cc (a 3 clique)
... (1,5), # combine first two ccs into a 1-edge-cc
... (0,), # add an additional disconnected 1-edge-cc
... ]
>>> G=nx.Graph()
>>> G.add_nodes_from(it.chain(*paths))
>>> G.add_edges_from(it.chain(*[pairwise(path) for path in paths]))
>>> # Constructing the AuxGraph takes about O(n ** 4)
>>> aux_graph =EdgeComponentAuxGraph.construct(G)
>>> # Once constructed, querying takes O(n)
>>> sorted(map(sorted, aux_graph.k_edge_components(k=1)))
[[0], [1, 2, 3, 4, 5, 6, 7]]
>>> sorted(map(sorted, aux_graph.k_edge_components(k=2)))
[[0], [1, 2, 3, 4], [5, 6, 7]]
>>> sorted(map(sorted, aux_graph.k_edge_components(k=3)))
[[0], [1, 2, 3, 4], [5], [6], [7]]
>>> sorted(map(sorted, aux_graph.k_edge_components(k=4)))
[[0], [1], [2], [3], [4], [5], [6], [7]]
Example
1Wang, Tianhao, et al. (2015) A simple algorithm for finding all k-edge-connected components. http://journals.plos.org/plosone/article?id=10.
1371/journal.pone.0136264
258 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> # The auxiliary graph is primarilly used for k-edge-ccs but it
>>> # can also speed up the queries of k-edge-subgraphs by refining the
>>> # search space.
>>> import itertools as it
>>> from networkx.utils import pairwise
>>> from networkx.algorithms.connectivity import EdgeComponentAuxGraph
>>> paths =[
... (1,2,4,3,1,4),
... ]
>>> G=nx.Graph()
>>> G.add_nodes_from(it.chain(*paths))
>>> G.add_edges_from(it.chain(*[pairwise(path) for path in paths]))
>>> aux_graph =EdgeComponentAuxGraph.construct(G)
>>> sorted(map(sorted, aux_graph.k_edge_subgraphs(k=3)))
[[1], [2], [3], [4]]
>>> sorted(map(sorted, aux_graph.k_edge_components(k=3)))
[[1, 4], [2], [3]]
__init__()
Initialize self. See help(type(self)) for accurate signature.
Methods
construct(G) Builds an auxiliary graph encoding edge-
connectivity between nodes.
k_edge_components(k) Queries the auxiliary graph for k-edge-connected
components.
k_edge_subgraphs(k) Queries the auxiliary graph for k-edge-connected
subgraphs.
3.15.3 K-node-components
Moody and White algorithm for k-components
k_components(G[, flow_func]) Returns the k-component structure of a graph G.
networkx.algorithms.connectivity.kcomponents.k_components
k_components(G,flow_func=None)
Returns the k-component structure of a graph G.
Ak-component is a maximal subgraph of a graph G that has, at least, node connectivity k: we need to remove at
least knodes to break it into more components. k-components have an inherent hierarchical structure because
they are nested in terms of connectivity: a connected graph can contain several 2-components, each of which
can contain one or more 3-components, and so forth.
Parameters
•G(NetworkX graph)
•flow_func (function) – Function to perform the underlying flow computations. Default value
edmonds_karp(). This function performs better in sparse graphs with right tailed degree
distributions. shortest_augmenting_path() will perform better in denser graphs.
3.15. Connectivity 259

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns k_components – Dictionary with all connectivity levels kin the input Graph as keys and a
list of sets of nodes that form a k-component of level kas values.
Return type dict
Raises NetworkXNotImplemented: – If the input graph is directed.
Examples
>>> # Petersen graph has 10 nodes and it is triconnected, thus all
>>> # nodes are in a single component on all three connectivity levels
>>> G=nx.petersen_graph()
>>> k_components =nx.k_components(G)
Notes
Moody and White1(appendix A) provide an algorithm for identifying k-components in a graph, which is
based on Kanevsky’s algorithm2for finding all minimum-size node cut-sets of a graph (implemented in
all_node_cuts() function):
1. Compute node connectivity, k, of the input graph G.
2. Identify all k-cutsets at the current level of connectivity using Kanevsky’s algorithm.
3. Generate new graph components based on the removal of these cutsets. Nodes in a cutset belong to both
sides of the induced cut.
4. If the graph is neither complete nor trivial, return to 1; else end.
This implementation also uses some heuristics (see3for details) to speed up the computation.
See also:
node_connectivity(),all_node_cuts()
biconnected_components() special case of this function when k=2
k_edge_components() similar to this function, but uses edge-connectivity instead of node-connectivity
References
3.15.4 K-node-cutsets
Kanevsky all minimum node k cutsets algorithm.
all_node_cuts(G[, k, flow_func]) Returns all minimum k cutsets of an undirected graph
G.
1Moody, J. and D. White (2003). Social cohesion and embeddedness: A hierarchical conception of social groups. American Sociological
Review 68(1), 103–28. http://www2.asanet.org/journals/ASRFeb03MoodyWhite.pdf
2Kanevsky, A. (1993). Finding all minimum-size separating vertex sets in a graph. Networks 23(6), 533–541. http://onlinelibrary.wiley.com/
doi/10.1002/net.3230230604/abstract
3Torrents, J. and F. Ferraro (2015). Structural Cohesion: Visualization and Heuristics for Fast Computation. https://arxiv.org/pdf/1503.04476v1
260 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.connectivity.kcutsets.all_node_cuts
all_node_cuts(G,k=None,flow_func=None)
Returns all minimum k cutsets of an undirected graph G.
This implementation is based on Kanevsky’s algorithm1for finding all minimum-size node cut-sets of an undi-
rected graph G; ie the set (or sets) of nodes of cardinality equal to the node connectivity of G. Thus if removed,
would break G into two or more connected components.
Parameters
•G(NetworkX graph) – Undirected graph
•k(Integer) – Node connectivity of the input graph. If k is None, then it is computed. Default
value: None.
•flow_func (function) – Function to perform the underlying flow computations. Default value
edmonds_karp. This function performs better in sparse graphs with right tailed degree dis-
tributions. shortest_augmenting_path will perform better in denser graphs.
Returns cuts – Each node cutset has cardinality equal to the node connectivity of the input graph.
Return type a generator of node cutsets
Examples
>>> # A two-dimensional grid graph has 4 cutsets of cardinality 2
>>> G=nx.grid_2d_graph(5,5)
>>> cutsets =list(nx.all_node_cuts(G))
>>> len(cutsets)
4
>>> all(2== len(cutset) for cutset in cutsets)
True
>>> nx.node_connectivity(G)
2
Notes
This implementation is based on the sequential algorithm for finding all minimum-size separating vertex sets in
a graph1. The main idea is to compute minimum cuts using local maximum flow computations among a set of
nodes of highest degree and all other non-adjacent nodes in the Graph. Once we find a minimum cut, we add an
edge between the high degree node and the target node of the local maximum flow computation to make sure
that we will not find that minimum cut again.
See also:
node_connectivity(),edmonds_karp(),shortest_augmenting_path()
References
3.15.5 Flow-based disjoint paths
Flow based node and edge disjoint paths.
1Kanevsky, A. (1993). Finding all minimum-size separating vertex sets in a graph. Networks 23(6), 533–541. http://onlinelibrary.wiley.com/
doi/10.1002/net.3230230604/abstract
3.15. Connectivity 261

NetworkX Reference, Release 2.3rc1.dev20181203210840
edge_disjoint_paths(G, s, t[, flow_func, . . . ]) Returns the edges disjoint paths between source and tar-
get.
node_disjoint_paths(G, s, t[, flow_func, . . . ]) Computes node disjoint paths between source and tar-
get.
networkx.algorithms.connectivity.disjoint_paths.edge_disjoint_paths
edge_disjoint_paths(G,s,t,flow_func=None,cutoff=None,auxiliary=None,residual=None)
Returns the edges disjoint paths between source and target.
Edge disjoint paths are paths that do not share any edge. The number of edge disjoint paths between source and
target is equal to their edge connectivity.
Parameters
•G(NetworkX graph)
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. The choice of the default function may change from version
to version and should not be relied on. Default value: None.
•cutoff (int) – Maximum number of paths to yield. Some of the maximum flow algorithms,
such as edmonds_karp() (the default) and shortest_augmenting_path() sup-
port the cutoff parameter, and will terminate when the flow value reaches or exceeds the
cutoff. Other algorithms will ignore this parameter. Default value: None.
•auxiliary (NetworkX DiGraph) – Auxiliary digraph to compute flow based edge connectiv-
ity. It has to have a graph attribute called mapping with a dictionary mapping node names
in G and in the auxiliary digraph. If provided it will be reused instead of recreated. Default
value: None.
•residual (NetworkX DiGraph) – Residual network to compute maximum flow. If provided
it will be reused instead of recreated. Default value: None.
Returns paths – A generator of edge independent paths.
Return type generator
Raises
•NetworkXNoPath : exception – If there is no path between source and target.
•NetworkXError : exception – If source or target are not in the graph G.
See also:
node_disjoint_paths(),edge_connectivity(),maximum_flow(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
262 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
We use in this example the platonic icosahedral graph, which has node edge connectivity 5, thus there are 5 edge
disjoint paths between any pair of nodes.
>>> G=nx.icosahedral_graph()
>>> len(list(nx.edge_disjoint_paths(G, 0,6)))
5
If you need to compute edge disjoint paths on several pairs of nodes in the same graph, it is recommended that
you reuse the data structures that NetworkX uses in the computation: the auxiliary digraph for edge connectivity,
and the residual network for the underlying maximum flow computation.
Example of how to compute edge disjoint paths among all pairs of nodes of the platonic icosahedral graph
reusing the data structures.
>>> import itertools
>>> # You also have to explicitly import the function for
>>> # building the auxiliary digraph from the connectivity package
>>> from networkx.algorithms.connectivity import (
... build_auxiliary_edge_connectivity)
>>> H=build_auxiliary_edge_connectivity(G)
>>> # And the function for building the residual network from the
>>> # flow package
>>> from networkx.algorithms.flow import build_residual_network
>>> # Note that the auxiliary digraph has an edge attribute named capacity
>>> R=build_residual_network(H, 'capacity')
>>> result ={n: {} for nin G}
>>> # Reuse the auxiliary digraph and the residual network by passing them
>>> # as arguments
>>> for u, v in itertools.combinations(G, 2):
... k=len(list(nx.edge_disjoint_paths(G, u, v, auxiliary=H, residual=R)))
... result[u][v] =k
>>> all(result[u][v] == 5for u, v in itertools.combinations(G, 2))
True
You can also use alternative flow algorithms for computing edge disjoint paths. For instance, in dense
networks the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp() which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> len(list(nx.edge_disjoint_paths(G, 0,6, flow_func=shortest_augmenting_path)))
5
Notes
This is a flow based implementation of edge disjoint paths. We compute the maximum flow between source and
target on an auxiliary directed network. The saturated edges in the residual network after running the maximum
flow algorithm correspond to edge disjoint paths between source and target in the original network. This function
handles both directed and undirected graphs, and can use all flow algorithms from NetworkX flow package.
3.15. Connectivity 263

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.connectivity.disjoint_paths.node_disjoint_paths
node_disjoint_paths(G,s,t,flow_func=None,cutoff=None,auxiliary=None,residual=None)
Computes node disjoint paths between source and target.
Node dijoint paths are paths that only share their first and last nodes. The number of node independent paths
between two nodes is equal to their local node connectivity.
Parameters
•G(NetworkX graph)
•s(node) – Source node.
•t(node) – Target node.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
•cutoff (int) – Maximum number of paths to yield. Some of the maximum flow algorithms,
such as edmonds_karp() (the default) and shortest_augmenting_path() sup-
port the cutoff parameter, and will terminate when the flow value reaches or exceeds the
cutoff. Other algorithms will ignore this parameter. Default value: None.
•auxiliary (NetworkX DiGraph) – Auxiliary digraph to compute flow based node connectiv-
ity. It has to have a graph attribute called mapping with a dictionary mapping node names
in G and in the auxiliary digraph. If provided it will be reused instead of recreated. Default
value: None.
•residual (NetworkX DiGraph) – Residual network to compute maximum flow. If provided
it will be reused instead of recreated. Default value: None.
Returns paths – Generator of node disjoint paths.
Return type generator
Raises
•NetworkXNoPath : exception – If there is no path between source and target.
•NetworkXError : exception – If source or target are not in the graph G.
Examples
We use in this example the platonic icosahedral graph, which has node node connectivity 5, thus there are 5
node disjoint paths between any pair of non neighbor nodes.
>>> G=nx.icosahedral_graph()
>>> len(list(nx.node_disjoint_paths(G, 0,6)))
5
If you need to compute node disjoint paths between several pairs of nodes in the same graph, it is recommended
that you reuse the data structures that NetworkX uses in the computation: the auxiliary digraph for node con-
nectivity and node cuts, and the residual network for the underlying maximum flow computation.
Example of how to compute node disjoint paths reusing the data structures:
264 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> # You also have to explicitly import the function for
>>> # building the auxiliary digraph from the connectivity package
>>> from networkx.algorithms.connectivity import (
... build_auxiliary_node_connectivity)
>>> H=build_auxiliary_node_connectivity(G)
>>> # And the function for building the residual network from the
>>> # flow package
>>> from networkx.algorithms.flow import build_residual_network
>>> # Note that the auxiliary digraph has an edge attribute named capacity
>>> R=build_residual_network(H, 'capacity')
>>> # Reuse the auxiliary digraph and the residual network by passing them
>>> # as arguments
>>> len(list(nx.node_disjoint_paths(G, 0,6, auxiliary=H, residual=R)))
5
You can also use alternative flow algorithms for computing node disjoint paths. For instance, in dense
networks the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp() which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> len(list(nx.node_disjoint_paths(G, 0,6, flow_func=shortest_augmenting_path)))
5
Notes
This is a flow based implementation of node disjoint paths. We compute the maximum flow between source
and target on an auxiliary directed network. The saturated edges in the residual network after running the
maximum flow algorithm correspond to node disjoint paths between source and target in the original network.
This function handles both directed and undirected graphs, and can use all flow algorithms from NetworkX flow
package.
See also:
edge_disjoint_paths(),node_connectivity(),maximum_flow(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
3.15.6 Flow-based Connectivity
Flow based connectivity algorithms
average_node_connectivity(G[, flow_func]) Returns the average connectivity of a graph G.
all_pairs_node_connectivity(G[, nbunch,
...])
Compute node connectivity between all pairs of nodes
of G.
edge_connectivity(G[, s, t, flow_func, cutoff]) Returns the edge connectivity of the graph or digraph G.
local_edge_connectivity(G, s, t[, . . . ]) Returns local edge connectivity for nodes s and t in G.
local_node_connectivity(G, s, t[, . . . ]) Computes local node connectivity for nodes s and t.
node_connectivity(G[, s, t, flow_func]) Returns node connectivity for a graph or digraph G.
3.15. Connectivity 265

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.connectivity.connectivity.average_node_connectivity
average_node_connectivity(G,flow_func=None)
Returns the average connectivity of a graph G.
The average connectivity bar{kappa} of a graph G is the average of local node connectivity over all pairs of
nodes of G1.
¯𝜅(𝐺) = 𝑢,𝑣 𝜅𝐺(𝑢, 𝑣)
𝑛
2
Parameters
•G(NetworkX graph) – Undirected graph
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See local_node_connectivity() for details. The
choice of the default function may change from version to version and should not be relied
on. Default value: None.
Returns K – Average node connectivity
Return type float
See also:
local_node_connectivity(),node_connectivity(),edge_connectivity(),
maximum_flow(),edmonds_karp(),preflow_push(),shortest_augmenting_path()
References
networkx.algorithms.connectivity.connectivity.all_pairs_node_connectivity
all_pairs_node_connectivity(G,nbunch=None,flow_func=None)
Compute node connectivity between all pairs of nodes of G.
Parameters
•G(NetworkX graph) – Undirected graph
•nbunch (container) – Container of nodes. If provided node connectivity will be computed
only over pairs of nodes in nbunch.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
Returns all_pairs – A dictionary with node connectivity between all pairs of nodes in G, or in
nbunch if provided.
Return type dict
1Beineke, L., O. Oellermann, and R. Pippert (2002). The average connectivity of a graph. Discrete mathematics 252(1-3), 31-45. http:
//www.sciencedirect.com/science/article/pii/S0012365X01001807
266 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
local_node_connectivity(),edge_connectivity(),local_edge_connectivity(),
maximum_flow(),edmonds_karp(),preflow_push(),shortest_augmenting_path()
networkx.algorithms.connectivity.connectivity.edge_connectivity
edge_connectivity(G,s=None,t=None,flow_func=None,cutoff=None)
Returns the edge connectivity of the graph or digraph G.
The edge connectivity is equal to the minimum number of edges that must be removed to disconnect G or render
it trivial. If source and target nodes are provided, this function returns the local edge connectivity: the minimum
number of edges that must be removed to break all paths from source to target in G.
Parameters
•G(NetworkX graph) – Undirected or directed graph
•s(node) – Source node. Optional. Default value: None.
•t(node) – Target node. Optional. Default value: None.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
•cutoff (integer, float) – If specified, the maximum flow algorithm will terminate when the
flow value reaches or exceeds the cutoff. This is only for the algorithms that support the
cutoff parameter: edmonds_karp() and shortest_augmenting_path(). Other
algorithms will ignore this parameter. Default value: None.
Returns K – Edge connectivity for G, or local edge connectivity if source and target were provided
Return type integer
Examples
>>> # Platonic icosahedral graph is 5-edge-connected
>>> G=nx.icosahedral_graph()
>>> nx.edge_connectivity(G)
5
You can use alternative flow algorithms for the underlying maximum flow computation. In dense net-
works the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp(), which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> nx.edge_connectivity(G, flow_func=shortest_augmenting_path)
5
If you specify a pair of nodes (source and target) as parameters, this function returns the value of local edge
connectivity.
3.15. Connectivity 267

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> nx.edge_connectivity(G, 3,7)
5
If you need to perform several local computations among different pairs of nodes on the same graph,
it is recommended that you reuse the data structures used in the maximum flow computations. See
local_edge_connectivity() for details.
Notes
This is a flow based implementation of global edge connectivity. For undirected graphs the algorithm works by
finding a ‘small’ dominating set of nodes of G (see algorithm 7 in1) and computing local maximum flow (see
local_edge_connectivity()) between an arbitrary node in the dominating set and the rest of nodes in
it. This is an implementation of algorithm 6 in1. For directed graphs, the algorithm does n calls to the maximum
flow function. This is an implementation of algorithm 8 in1.
See also:
local_edge_connectivity(),local_node_connectivity(),node_connectivity(),
maximum_flow(),edmonds_karp(),preflow_push(),shortest_augmenting_path(),
k_edge_components(),k_edge_subgraphs()
References
networkx.algorithms.connectivity.connectivity.local_edge_connectivity
local_edge_connectivity(G,s,t,flow_func=None,auxiliary=None,residual=None,cutoff=None)
Returns local edge connectivity for nodes s and t in G.
Local edge connectivity for two nodes s and t is the minimum number of edges that must be removed to discon-
nect them.
This is a flow based implementation of edge connectivity. We compute the maximum flow on an auxiliary
digraph build from the original network (see below for details). This is equal to the local edge connectivity
because the value of a maximum s-t-flow is equal to the capacity of a minimum s-t-cut (Ford and Fulkerson
theorem)1.
Parameters
•G(NetworkX graph) – Undirected or directed graph
•s(node) – Source node
•t(node) – Target node
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
•auxiliary (NetworkX DiGraph) – Auxiliary digraph for computing flow based edge connec-
tivity. If provided it will be reused instead of recreated. Default value: None.
1Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
1Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
268 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•residual (NetworkX DiGraph) – Residual network to compute maximum flow. If provided
it will be reused instead of recreated. Default value: None.
•cutoff (integer, float) – If specified, the maximum flow algorithm will terminate when the
flow value reaches or exceeds the cutoff. This is only for the algorithms that support the
cutoff parameter: edmonds_karp() and shortest_augmenting_path(). Other
algorithms will ignore this parameter. Default value: None.
Returns K – local edge connectivity for nodes s and t.
Return type integer
Examples
This function is not imported in the base NetworkX namespace, so you have to explicitly import it from the
connectivity package:
>>> from networkx.algorithms.connectivity import local_edge_connectivity
We use in this example the platonic icosahedral graph, which has edge connectivity 5.
>>> G=nx.icosahedral_graph()
>>> local_edge_connectivity(G, 0,6)
5
If you need to compute local connectivity on several pairs of nodes in the same graph, it is recommended that
you reuse the data structures that NetworkX uses in the computation: the auxiliary digraph for edge connectivity,
and the residual network for the underlying maximum flow computation.
Example of how to compute local edge connectivity among all pairs of nodes of the platonic icosahedral graph
reusing the data structures.
>>> import itertools
>>> # You also have to explicitly import the function for
>>> # building the auxiliary digraph from the connectivity package
>>> from networkx.algorithms.connectivity import (
... build_auxiliary_edge_connectivity)
>>> H=build_auxiliary_edge_connectivity(G)
>>> # And the function for building the residual network from the
>>> # flow package
>>> from networkx.algorithms.flow import build_residual_network
>>> # Note that the auxiliary digraph has an edge attribute named capacity
>>> R=build_residual_network(H, 'capacity')
>>> result =dict.fromkeys(G, dict())
>>> # Reuse the auxiliary digraph and the residual network by passing them
>>> # as parameters
>>> for u, v in itertools.combinations(G, 2):
... k=local_edge_connectivity(G, u, v, auxiliary=H, residual=R)
... result[u][v] =k
>>> all(result[u][v] == 5for u, v in itertools.combinations(G, 2))
True
You can also use alternative flow algorithms for computing edge connectivity. For instance, in dense
networks the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp() which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
3.15. Connectivity 269

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> local_edge_connectivity(G, 0,6, flow_func=shortest_augmenting_path)
5
Notes
This is a flow based implementation of edge connectivity. We compute the maximum flow using, by default, the
edmonds_karp() algorithm on an auxiliary digraph build from the original input graph:
If the input graph is undirected, we replace each edge (u,‘v‘) with two reciprocal arcs (u,v) and (v,u) and
then we set the attribute ‘capacity’ for each arc to 1. If the input graph is directed we simply add the ‘capacity’
attribute. This is an implementation of algorithm 1 in1.
The maximum flow in the auxiliary network is equal to the local edge connectivity because the value of a
maximum s-t-flow is equal to the capacity of a minimum s-t-cut (Ford and Fulkerson theorem).
See also:
edge_connectivity(),local_node_connectivity(),node_connectivity(),
maximum_flow(),edmonds_karp(),preflow_push(),shortest_augmenting_path()
References
networkx.algorithms.connectivity.connectivity.local_node_connectivity
local_node_connectivity(G,s,t,flow_func=None,auxiliary=None,residual=None,cutoff=None)
Computes local node connectivity for nodes s and t.
Local node connectivity for two non adjacent nodes s and t is the minimum number of nodes that must be
removed (along with their incident edges) to disconnect them.
This is a flow based implementation of node connectivity. We compute the maximum flow on an auxiliary
digraph build from the original input graph (see below for details).
Parameters
•G(NetworkX graph) – Undirected graph
•s(node) – Source node
•t(node) – Target node
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
•auxiliary (NetworkX DiGraph) – Auxiliary digraph to compute flow based node connectiv-
ity. It has to have a graph attribute called mapping with a dictionary mapping node names
in G and in the auxiliary digraph. If provided it will be reused instead of recreated. Default
value: None.
•residual (NetworkX DiGraph) – Residual network to compute maximum flow. If provided
it will be reused instead of recreated. Default value: None.
270 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•cutoff (integer, float) – If specified, the maximum flow algorithm will terminate when the
flow value reaches or exceeds the cutoff. This is only for the algorithms that support the
cutoff parameter: edmonds_karp() and shortest_augmenting_path(). Other
algorithms will ignore this parameter. Default value: None.
Returns K – local node connectivity for nodes s and t
Return type integer
Examples
This function is not imported in the base NetworkX namespace, so you have to explicitly import it from the
connectivity package:
>>> from networkx.algorithms.connectivity import local_node_connectivity
We use in this example the platonic icosahedral graph, which has node connectivity 5.
>>> G=nx.icosahedral_graph()
>>> local_node_connectivity(G, 0,6)
5
If you need to compute local connectivity on several pairs of nodes in the same graph, it is recommended that
you reuse the data structures that NetworkX uses in the computation: the auxiliary digraph for node connectivity,
and the residual network for the underlying maximum flow computation.
Example of how to compute local node connectivity among all pairs of nodes of the platonic icosahedral graph
reusing the data structures.
>>> import itertools
>>> # You also have to explicitly import the function for
>>> # building the auxiliary digraph from the connectivity package
>>> from networkx.algorithms.connectivity import (
... build_auxiliary_node_connectivity)
...
>>> H=build_auxiliary_node_connectivity(G)
>>> # And the function for building the residual network from the
>>> # flow package
>>> from networkx.algorithms.flow import build_residual_network
>>> # Note that the auxiliary digraph has an edge attribute named capacity
>>> R=build_residual_network(H, 'capacity')
>>> result =dict.fromkeys(G, dict())
>>> # Reuse the auxiliary digraph and the residual network by passing them
>>> # as parameters
>>> for u, v in itertools.combinations(G, 2):
... k=local_node_connectivity(G, u, v, auxiliary=H, residual=R)
... result[u][v] =k
...
>>> all(result[u][v] == 5for u, v in itertools.combinations(G, 2))
True
You can also use alternative flow algorithms for computing node connectivity. For instance, in dense
networks the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp() which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
3.15. Connectivity 271

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> local_node_connectivity(G, 0,6, flow_func=shortest_augmenting_path)
5
Notes
This is a flow based implementation of node connectivity. We compute the maximum flow using, by default,
the edmonds_karp() algorithm (see: maximum_flow()) on an auxiliary digraph build from the original
input graph:
For an undirected graph G having nnodes and medges we derive a directed graph H with 2n nodes and 2m+n
arcs by replacing each original node vwith two nodes v_A,v_B linked by an (internal) arc in H. Then for each
edge (u,v) in G we add two arcs (u_B,v_A) and (v_B,u_A) in H. Finally we set the attribute capacity = 1 for
each arc in H1.
For a directed graph G having nnodes and marcs we derive a directed graph H with 2n nodes and m+n arcs by
replacing each original node vwith two nodes v_A,v_B linked by an (internal) arc (v_A,v_B) in H. Then for
each arc (u,v) in G we add one arc (u_B,v_A) in H. Finally we set the attribute capacity = 1 for each arc in H.
This is equal to the local node connectivity because the value of a maximum s-t-flow is equal to the capacity of
a minimum s-t-cut.
See also:
local_edge_connectivity(),node_connectivity(),minimum_node_cut(),
maximum_flow(),edmonds_karp(),preflow_push(),shortest_augmenting_path()
References
networkx.algorithms.connectivity.connectivity.node_connectivity
node_connectivity(G,s=None,t=None,flow_func=None)
Returns node connectivity for a graph or digraph G.
Node connectivity is equal to the minimum number of nodes that must be removed to disconnect G or render it
trivial. If source and target nodes are provided, this function returns the local node connectivity: the minimum
number of nodes that must be removed to break all paths from source to target in G.
Parameters
•G(NetworkX graph) – Undirected graph
•s(node) – Source node. Optional. Default value: None.
•t(node) – Target node. Optional. Default value: None.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
Returns K – Node connectivity of G, or local node connectivity if source and target are provided.
1Kammer, Frank and Hanjo Taubig. Graph Connectivity. in Brandes and Erlebach, ‘Network Analysis: Methodological Foundations’,
Lecture Notes in Computer Science, Volume 3418, Springer-Verlag, 2005. http://www.informatik.uni-augsburg.de/thi/personen/kammer/Graph_
Connectivity.pdf
272 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type integer
Examples
>>> # Platonic icosahedral graph is 5-node-connected
>>> G=nx.icosahedral_graph()
>>> nx.node_connectivity(G)
5
You can use alternative flow algorithms for the underlying maximum flow computation. In dense net-
works the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp(), which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> nx.node_connectivity(G, flow_func=shortest_augmenting_path)
5
If you specify a pair of nodes (source and target) as parameters, this function returns the value of local node
connectivity.
>>> nx.node_connectivity(G, 3,7)
5
If you need to perform several local computations among different pairs of nodes on the same graph,
it is recommended that you reuse the data structures used in the maximum flow computations. See
local_node_connectivity() for details.
Notes
This is a flow based implementation of node connectivity. The algorithm works by solving 𝑂((𝑛−𝛿−1+ 𝛿(𝛿−
1)/2)) maximum flow problems on an auxiliary digraph. Where 𝛿is the minimum degree of G. For details about
the auxiliary digraph and the computation of local node connectivity see local_node_connectivity().
This implementation is based on algorithm 11 in1.
See also:
local_node_connectivity(),edge_connectivity(),maximum_flow(),
edmonds_karp(),preflow_push(),shortest_augmenting_path()
References
3.15.7 Flow-based Minimum Cuts
Flow based cut algorithms
minimum_edge_cut(G[, s, t, flow_func]) Returns a set of edges of minimum cardinality that dis-
connects G.
minimum_node_cut(G[, s, t, flow_func]) Returns a set of nodes of minimum cardinality that dis-
connects G.
minimum_st_edge_cut(G, s, t[, flow_func, . . . ]) Returns the edges of the cut-set of a minimum (s, t)-cut.
Continued on next page
1Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
3.15. Connectivity 273

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 71 – continued from previous page
minimum_st_node_cut(G, s, t[, flow_func, . . . ]) Returns a set of nodes of minimum cardinality that dis-
connect source from target in G.
networkx.algorithms.connectivity.cuts.minimum_edge_cut
minimum_edge_cut(G,s=None,t=None,flow_func=None)
Returns a set of edges of minimum cardinality that disconnects G.
If source and target nodes are provided, this function returns the set of edges of minimum cardinality that, if
removed, would break all paths among source and target in G. If not, it returns a set of edges of minimum
cardinality that disconnects G.
Parameters
•G(NetworkX graph)
•s(node) – Source node. Optional. Default value: None.
•t(node) – Target node. Optional. Default value: None.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
Returns cutset – Set of edges that, if removed, would disconnect G. If source and target nodes are
provided, the set contains the edges that if removed, would destroy all paths between source and
target.
Return type set
Examples
>>> # Platonic icosahedral graph has edge connectivity 5
>>> G=nx.icosahedral_graph()
>>> len(nx.minimum_edge_cut(G))
5
You can use alternative flow algorithms for the underlying maximum flow computation. In dense net-
works the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp(), which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> len(nx.minimum_edge_cut(G, flow_func=shortest_augmenting_path))
5
If you specify a pair of nodes (source and target) as parameters, this function returns the value of local edge
connectivity.
>>> nx.edge_connectivity(G, 3,7)
5
274 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
If you need to perform several local computations among different pairs of nodes on the same graph,
it is recommended that you reuse the data structures used in the maximum flow computations. See
local_edge_connectivity() for details.
Notes
This is a flow based implementation of minimum edge cut. For undirected graphs the algorithm works by
finding a ‘small’ dominating set of nodes of G (see algorithm 7 in1) and computing the maximum flow between
an arbitrary node in the dominating set and the rest of nodes in it. This is an implementation of algorithm 6
in1. For directed graphs, the algorithm does n calls to the max flow function. The function raises an error if the
directed graph is not weakly connected and returns an empty set if it is weakly connected. It is an implementation
of algorithm 8 in1.
See also:
minimum_st_edge_cut(),minimum_node_cut(),stoer_wagner(),
node_connectivity(),edge_connectivity(),maximum_flow(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
References
networkx.algorithms.connectivity.cuts.minimum_node_cut
minimum_node_cut(G,s=None,t=None,flow_func=None)
Returns a set of nodes of minimum cardinality that disconnects G.
If source and target nodes are provided, this function returns the set of nodes of minimum cardinality that, if
removed, would destroy all paths among source and target in G. If not, it returns a set of nodes of minimum
cardinality that disconnects G.
Parameters
•G(NetworkX graph)
•s(node) – Source node. Optional. Default value: None.
•t(node) – Target node. Optional. Default value: None.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
Returns cutset – Set of nodes that, if removed, would disconnect G. If source and target nodes are
provided, the set contains the nodes that if removed, would destroy all paths between source and
target.
Return type set
Examples
1Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
3.15. Connectivity 275

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> # Platonic icosahedral graph has node connectivity 5
>>> G=nx.icosahedral_graph()
>>> node_cut =nx.minimum_node_cut(G)
>>> len(node_cut)
5
You can use alternative flow algorithms for the underlying maximum flow computation. In dense net-
works the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp(), which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> node_cut == nx.minimum_node_cut(G, flow_func=shortest_augmenting_path)
True
If you specify a pair of nodes (source and target) as parameters, this function returns a local st node cut.
>>> len(nx.minimum_node_cut(G, 3,7))
5
If you need to perform several local st cuts among different pairs of nodes on the same graph, it is recommended
that you reuse the data structures used in the maximum flow computations. See minimum_st_node_cut()
for details.
Notes
This is a flow based implementation of minimum node cut. The algorithm is based in solving a number of
maximum flow computations to determine the capacity of the minimum cut on an auxiliary directed network that
corresponds to the minimum node cut of G. It handles both directed and undirected graphs. This implementation
is based on algorithm 11 in1.
See also:
minimum_st_node_cut(),minimum_cut(),minimum_edge_cut(),stoer_wagner(),
node_connectivity(),edge_connectivity(),maximum_flow(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
References
networkx.algorithms.connectivity.cuts.minimum_st_edge_cut
minimum_st_edge_cut(G,s,t,flow_func=None,auxiliary=None,residual=None)
Returns the edges of the cut-set of a minimum (s, t)-cut.
This function returns the set of edges of minimum cardinality that, if removed, would destroy all paths among
source and target in G. Edge weights are not considered. See minimum_cut() for computing minimum cuts
considering edge weights.
Parameters
•G(NetworkX graph)
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
1Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
276 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•auxiliary (NetworkX DiGraph) – Auxiliary digraph to compute flow based node connectiv-
ity. It has to have a graph attribute called mapping with a dictionary mapping node names
in G and in the auxiliary digraph. If provided it will be reused instead of recreated. Default
value: None.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See node_connectivity() for details. The choice of
the default function may change from version to version and should not be relied on. Default
value: None.
•residual (NetworkX DiGraph) – Residual network to compute maximum flow. If provided
it will be reused instead of recreated. Default value: None.
Returns cutset – Set of edges that, if removed from the graph, will disconnect it.
Return type set
See also:
minimum_cut(),minimum_node_cut(),minimum_edge_cut(),stoer_wagner(),
node_connectivity(),edge_connectivity(),maximum_flow(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
Examples
This function is not imported in the base NetworkX namespace, so you have to explicitly import it from the
connectivity package:
>>> from networkx.algorithms.connectivity import minimum_st_edge_cut
We use in this example the platonic icosahedral graph, which has edge connectivity 5.
>>> G=nx.icosahedral_graph()
>>> len(minimum_st_edge_cut(G, 0,6))
5
If you need to compute local edge cuts on several pairs of nodes in the same graph, it is recommended that you
reuse the data structures that NetworkX uses in the computation: the auxiliary digraph for edge connectivity,
and the residual network for the underlying maximum flow computation.
Example of how to compute local edge cuts among all pairs of nodes of the platonic icosahedral graph reusing
the data structures.
>>> import itertools
>>> # You also have to explicitly import the function for
>>> # building the auxiliary digraph from the connectivity package
>>> from networkx.algorithms.connectivity import (
... build_auxiliary_edge_connectivity)
>>> H=build_auxiliary_edge_connectivity(G)
>>> # And the function for building the residual network from the
>>> # flow package
>>> from networkx.algorithms.flow import build_residual_network
>>> # Note that the auxiliary digraph has an edge attribute named capacity
>>> R=build_residual_network(H, 'capacity')
>>> result =dict.fromkeys(G, dict())
(continues on next page)
3.15. Connectivity 277

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> # Reuse the auxiliary digraph and the residual network by passing them
>>> # as parameters
>>> for u, v in itertools.combinations(G, 2):
... k=len(minimum_st_edge_cut(G, u, v, auxiliary=H, residual=R))
... result[u][v] =k
>>> all(result[u][v] == 5for u, v in itertools.combinations(G, 2))
True
You can also use alternative flow algorithms for computing edge cuts. For instance, in dense networks the algo-
rithm shortest_augmenting_path() will usually perform better than the default edmonds_karp()
which is faster for sparse networks with highly skewed degree distributions. Alternative flow functions have to
be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> len(minimum_st_edge_cut(G, 0,6, flow_func=shortest_augmenting_path))
5
networkx.algorithms.connectivity.cuts.minimum_st_node_cut
minimum_st_node_cut(G,s,t,flow_func=None,auxiliary=None,residual=None)
Returns a set of nodes of minimum cardinality that disconnect source from target in G.
This function returns the set of nodes of minimum cardinality that, if removed, would destroy all paths among
source and target in G.
Parameters
•G(NetworkX graph)
•s(node) – Source node.
•t(node) – Target node.
•flow_func (function) – A function for computing the maximum flow among a pair of
nodes. The function has to accept at least three parameters: a Digraph, a source node,
and a target node. And return a residual network that follows NetworkX conventions (see
maximum_flow() for details). If flow_func is None, the default maximum flow function
(edmonds_karp()) is used. See below for details. The choice of the default function
may change from version to version and should not be relied on. Default value: None.
•auxiliary (NetworkX DiGraph) – Auxiliary digraph to compute flow based node connectiv-
ity. It has to have a graph attribute called mapping with a dictionary mapping node names
in G and in the auxiliary digraph. If provided it will be reused instead of recreated. Default
value: None.
•residual (NetworkX DiGraph) – Residual network to compute maximum flow. If provided
it will be reused instead of recreated. Default value: None.
Returns cutset – Set of nodes that, if removed, would destroy all paths between source and target
in G.
Return type set
Examples
This function is not imported in the base NetworkX namespace, so you have to explicitly import it from the
connectivity package:
278 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx.algorithms.connectivity import minimum_st_node_cut
We use in this example the platonic icosahedral graph, which has node connectivity 5.
>>> G=nx.icosahedral_graph()
>>> len(minimum_st_node_cut(G, 0,6))
5
If you need to compute local st cuts between several pairs of nodes in the same graph, it is recommended that
you reuse the data structures that NetworkX uses in the computation: the auxiliary digraph for node connectivity
and node cuts, and the residual network for the underlying maximum flow computation.
Example of how to compute local st node cuts reusing the data structures:
>>> # You also have to explicitly import the function for
>>> # building the auxiliary digraph from the connectivity package
>>> from networkx.algorithms.connectivity import (
... build_auxiliary_node_connectivity)
>>> H=build_auxiliary_node_connectivity(G)
>>> # And the function for building the residual network from the
>>> # flow package
>>> from networkx.algorithms.flow import build_residual_network
>>> # Note that the auxiliary digraph has an edge attribute named capacity
>>> R=build_residual_network(H, 'capacity')
>>> # Reuse the auxiliary digraph and the residual network by passing them
>>> # as parameters
>>> len(minimum_st_node_cut(G, 0,6, auxiliary=H, residual=R))
5
You can also use alternative flow algorithms for computing minimum st node cuts. For instance, in dense
networks the algorithm shortest_augmenting_path() will usually perform better than the default
edmonds_karp() which is faster for sparse networks with highly skewed degree distributions. Alternative
flow functions have to be explicitly imported from the flow package.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> len(minimum_st_node_cut(G, 0,6, flow_func=shortest_augmenting_path))
5
Notes
This is a flow based implementation of minimum node cut. The algorithm is based in solving a number of
maximum flow computations to determine the capacity of the minimum cut on an auxiliary directed network that
corresponds to the minimum node cut of G. It handles both directed and undirected graphs. This implementation
is based on algorithm 11 in1.
See also:
minimum_node_cut(),minimum_edge_cut(),stoer_wagner(),node_connectivity(),
edge_connectivity(),maximum_flow(),edmonds_karp(),preflow_push(),
shortest_augmenting_path()
1Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
3.15. Connectivity 279

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.15.8 Stoer-Wagner minimum cut
Stoer-Wagner minimum cut algorithm.
stoer_wagner(G[, weight, heap]) Returns the weighted minimum edge cut using the
Stoer-Wagner algorithm.
networkx.algorithms.connectivity.stoerwagner.stoer_wagner
stoer_wagner(G,weight=’weight’,heap=<class ’networkx.utils.heaps.BinaryHeap’>)
Returns the weighted minimum edge cut using the Stoer-Wagner algorithm.
Determine the minimum edge cut of a connected graph using the Stoer-Wagner algorithm. In weighted cases,
all weights must be nonnegative.
The running time of the algorithm depends on the type of heaps used:
Type of heap Running time
Binary heap 𝑂(𝑛(𝑚+𝑛) log 𝑛)
Fibonacci heap 𝑂(𝑛𝑚 +𝑛2log 𝑛)
Pairing heap 𝑂(22√log log 𝑛𝑛𝑚 +𝑛2log 𝑛)
Parameters
•G(NetworkX graph) – Edges of the graph are expected to have an attribute named by the
weight parameter below. If this attribute is not present, the edge is considered to have unit
weight.
•weight (string) – Name of the weight attribute of the edges. If the attribute is not present,
unit weight is assumed. Default value: ‘weight’.
•heap (class) – Type of heap to be used in the algorithm. It should be a subclass of MinHeap
or implement a compatible interface.
If a stock heap implementation is to be used, BinaryHeap is recommended over
PairingHeap for Python implementations without optimized attribute accesses (e.g.,
CPython) despite a slower asymptotic running time. For Python implementations with opti-
mized attribute accesses (e.g., PyPy), PairingHeap provides better performance. Default
value: BinaryHeap.
Returns
•cut_value (integer or float) – The sum of weights of edges in a minimum cut.
•partition (pair of node lists) – A partitioning of the nodes that defines a minimum cut.
Raises
•NetworkXNotImplemented – If the graph is directed or a multigraph.
•NetworkXError – If the graph has less than two nodes, is not connected or has a negative-
weighted edge.
280 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph()
>>> G.add_edge('x','a', weight=3)
>>> G.add_edge('x','b', weight=1)
>>> G.add_edge('a','c', weight=3)
>>> G.add_edge('b','c', weight=5)
>>> G.add_edge('b','d', weight=4)
>>> G.add_edge('d','e', weight=2)
>>> G.add_edge('c','y', weight=2)
>>> G.add_edge('e','y', weight=3)
>>> cut_value, partition =nx.stoer_wagner(G)
>>> cut_value
4
3.15.9 Utils for flow-based connectivity
Utilities for connectivity package
build_auxiliary_edge_connectivity(G) Auxiliary digraph for computing flow based edge con-
nectivity
build_auxiliary_node_connectivity(G) Creates a directed graph D from an undirected graph G
to compute flow based node connectivity.
networkx.algorithms.connectivity.utils.build_auxiliary_edge_connectivity
build_auxiliary_edge_connectivity(G)
Auxiliary digraph for computing flow based edge connectivity
If the input graph is undirected, we replace each edge (u,‘v‘) with two reciprocal arcs (u,v) and (v,u) and
then we set the attribute ‘capacity’ for each arc to 1. If the input graph is directed we simply add the ‘capacity’
attribute. Part of algorithm 1 in1.
References
networkx.algorithms.connectivity.utils.build_auxiliary_node_connectivity
build_auxiliary_node_connectivity(G)
Creates a directed graph D from an undirected graph G to compute flow based node connectivity.
For an undirected graph G having nnodes and medges we derive a directed graph D with 2n nodes and 2m+n
arcs by replacing each original node vwith two nodes vA,vB linked by an (internal) arc in D. Then for each
edge (u,v) in G we add two arcs (uB,vA) and (vB,uA) in D. Finally we set the attribute capacity = 1 for each
arc in D1.
For a directed graph having nnodes and marcs we derive a directed graph D with 2n nodes and m+n arcs by
replacing each original node vwith two nodes vA,vB linked by an (internal) arc (vA,vB) in D. Then for each
arc (u,v) in G we add one arc (uB,vA) in D. Finally we set the attribute capacity = 1 for each arc in D.
1Abdol-Hossein Esfahanian. Connectivity Algorithms. (this is a chapter, look for the reference of the book). http://www.cse.msu.edu/~cse835/
Papers/Graph_connectivity_revised.pdf
1Kammer, Frank and Hanjo Taubig. Graph Connectivity. in Brandes and Erlebach, ‘Network Analysis: Methodological Foundations’,
Lecture Notes in Computer Science, Volume 3418, Springer-Verlag, 2005. http://www.informatik.uni-augsburg.de/thi/personen/kammer/Graph_
Connectivity.pdf
3.15. Connectivity 281

NetworkX Reference, Release 2.3rc1.dev20181203210840
A dictionary with a mapping between nodes in the original graph and the auxiliary digraph is stored as a graph
attribute: H.graph[‘mapping’].
References
3.16 Cores
Find the k-cores of a graph.
The k-core is found by recursively pruning nodes with degrees less than k.
See the following references for details:
An O(m) Algorithm for Cores Decomposition of Networks Vladimir Batagelj and Matjaz Zaversnik, 2003. https:
//arxiv.org/abs/cs.DS/0310049
Generalized Cores Vladimir Batagelj and Matjaz Zaversnik, 2002. https://arxiv.org/pdf/cs/0202039
For directed graphs a more general notion is that of D-cores which looks at (k, l) restrictions on (in, out) degree. The
(k, k) D-core is the k-core.
D-cores: Measuring Collaboration of Directed Graphs Based on Degeneracy Christos Giatsidis, Dimitrios M. Thilikos,
Michalis Vazirgiannis, ICDM 2011. http://www.graphdegeneracy.org/dcores_ICDM_2011.pdf
core_number(G) Return the core number for each vertex.
k_core(G[, k, core_number]) Return the k-core of G.
k_shell(G[, k, core_number]) Return the k-shell of G.
k_crust(G[, k, core_number]) Return the k-crust of G.
k_corona(G, k[, core_number]) Return the k-corona of G.
3.16.1 networkx.algorithms.core.core_number
core_number(G)
Return the core number for each vertex.
A k-core is a maximal subgraph that contains nodes of degree k or more.
The core number of a node is the largest value k of a k-core containing that node.
Parameters G (NetworkX graph) – A graph or directed graph
Returns core_number – A dictionary keyed by node to the core number.
Return type dictionary
Raises NetworkXError – The k-core is not implemented for graphs with self loops or parallel
edges.
Notes
Not implemented for graphs with parallel edges or self loops.
For directed graphs the node degree is defined to be the in-degree + out-degree.
282 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.16.2 networkx.algorithms.core.k_core
k_core(G,k=None,core_number=None)
Return the k-core of G.
A k-core is a maximal subgraph that contains nodes of degree k or more.
Parameters
•G(NetworkX graph) – A graph or directed graph
•k(int, optional) – The order of the core. If not specified return the main core.
•core_number (dictionary, optional) – Precomputed core numbers for the graph G.
Returns G – The k-core subgraph
Return type NetworkX graph
Raises NetworkXError – The k-core is not defined for graphs with self loops or parallel edges.
Notes
The main core is the core with the largest degree.
Not implemented for graphs with parallel edges or self loops.
For directed graphs the node degree is defined to be the in-degree + out-degree.
Graph, node, and edge attributes are copied to the subgraph.
See also:
core_number()
References
3.16.3 networkx.algorithms.core.k_shell
k_shell(G,k=None,core_number=None)
Return the k-shell of G.
The k-shell is the subgraph induced by nodes with core number k. That is, nodes in the k-core that are not in the
(k+1)-core.
Parameters
•G(NetworkX graph) – A graph or directed graph.
•k(int, optional) – The order of the shell. If not specified return the outer shell.
•core_number (dictionary, optional) – Precomputed core numbers for the graph G.
Returns G – The k-shell subgraph
Return type NetworkX graph
Raises NetworkXError – The k-shell is not implemented for graphs with self loops or parallel
edges.
3.16. Cores 283
NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This is similar to k_corona but in that case only neighbors in the k-core are considered.
Not implemented for graphs with parallel edges or self loops.
For directed graphs the node degree is defined to be the in-degree + out-degree.
Graph, node, and edge attributes are copied to the subgraph.
See also:
core_number(),k_corona()
References
3.16.4 networkx.algorithms.core.k_crust
k_crust(G,k=None,core_number=None)
Return the k-crust of G.
The k-crust is the graph G with the k-core removed.
Parameters
•G(NetworkX graph) – A graph or directed graph.
•k(int, optional) – The order of the shell. If not specified return the main crust.
•core_number (dictionary, optional) – Precomputed core numbers for the graph G.
Returns G – The k-crust subgraph
Return type NetworkX graph
Raises NetworkXError – The k-crust is not implemented for graphs with self loops or parallel
edges.
Notes
This definition of k-crust is different than the definition in1. The k-crust in1is equivalent to the k+1 crust of this
algorithm.
Not implemented for graphs with parallel edges or self loops.
For directed graphs the node degree is defined to be the in-degree + out-degree.
Graph, node, and edge attributes are copied to the subgraph.
See also:
core_number()
1A model of Internet topology using k-shell decomposition Shai Carmi, Shlomo Havlin, Scott Kirkpatrick, Yuval Shavitt, and Eran Shir, PNAS
July 3, 2007 vol. 104 no. 27 11150-11154 http://www.pnas.org/content/104/27/11150.full
284 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.16.5 networkx.algorithms.core.k_corona
k_corona(G,k,core_number=None)
Return the k-corona of G.
The k-corona is the subgraph of nodes in the k-core which have exactly k neighbours in the k-core.
Parameters
•G(NetworkX graph) – A graph or directed graph
•k(int) – The order of the corona.
•core_number (dictionary, optional) – Precomputed core numbers for the graph G.
Returns G – The k-corona subgraph
Return type NetworkX graph
Raises NetworkXError – The k-cornoa is not defined for graphs with self loops or parallel edges.
Notes
Not implemented for graphs with parallel edges or self loops.
For directed graphs the node degree is defined to be the in-degree + out-degree.
Graph, node, and edge attributes are copied to the subgraph.
See also:
core_number()
References
3.17 Covering
Functions related to graph covers.
min_edge_cover(G[, matching_algorithm]) Returns a set of edges which constitutes the minimum
edge cover of the graph.
is_edge_cover(G, cover) Decides whether a set of edges is a valid edge cover of
the graph.
3.17.1 networkx.algorithms.covering.min_edge_cover
min_edge_cover(G,matching_algorithm=None)
Returns a set of edges which constitutes the minimum edge cover of the graph.
A smallest edge cover can be found in polynomial time by finding a maximum matching and extending it
greedily so that all nodes are covered.
Parameters
•G(NetworkX graph) – An undirected bipartite graph.
3.17. Covering 285

NetworkX Reference, Release 2.3rc1.dev20181203210840
•matching_algorithm (function) – A function that returns a maximum cardinality matching
in a given bipartite graph. The function must take one input, the graph G, and return a dic-
tionary mapping each node to its mate. If not specified, hopcroft_karp_matching()
will be used. Other possibilities include eppstein_matching(), or matching algo-
rithms in the networkx.algorithms.matching module.
Returns min_cover – It contains all the edges of minimum edge cover in form of tuples. It contains
both the edges (u, v) and (v, u) for given nodes uand vamong the edges of minimum
edge cover.
Return type set
Notes
An edge cover of a graph is a set of edges such that every node of the graph is incident to at least one edge of
the set. The minimum edge cover is an edge covering of smallest cardinality.
Due to its implementation, the worst-case running time of this algorithm is bounded by the worst-case running
time of the function matching_algorithm.
Minimum edge cover for bipartite graph can also be found using the function present in networkx.
algorithms.bipartite.covering
3.17.2 networkx.algorithms.covering.is_edge_cover
is_edge_cover(G,cover)
Decides whether a set of edges is a valid edge cover of the graph.
Given a set of edges, whether it is an edge covering can be decided if we just check whether all nodes of the
graph has an edge from the set, incident on it.
Parameters
•G(NetworkX graph) – An undirected bipartite graph.
•cover (set) – Set of edges to be checked.
Returns Whether the set of edges is a valid edge cover of the graph.
Return type bool
Notes
An edge cover of a graph is a set of edges such that every node of the graph is incident to at least one edge of
the set.
3.18 Cycles
3.18.1 Cycle finding algorithms
cycle_basis(G[, root]) Returns a list of cycles which form a basis for cycles of
G.
Continued on next page
286 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 76 – continued from previous page
simple_cycles(G) Find simple cycles (elementary circuits) of a directed
graph.
find_cycle(G[, source, orientation]) Returns a cycle found via depth-first traversal.
minimum_cycle_basis(G[, weight]) Returns a minimum weight cycle basis for G
3.18.2 networkx.algorithms.cycles.cycle_basis
cycle_basis(G,root=None)
Returns a list of cycles which form a basis for cycles of G.
A basis for cycles of a network is a minimal collection of cycles such that any cycle in the network can be written
as a sum of cycles in the basis. Here summation of cycles is defined as “exclusive or” of the edges. Cycle bases
are useful, e.g. when deriving equations for electric circuits using Kirchhoff’s Laws.
Parameters
•G(NetworkX Graph)
•root (node, optional) – Specify starting node for basis.
Returns
•A list of cycle lists. Each cycle list is a list of nodes
•which forms a cycle (loop) in G.
Examples
>>> G=nx.Graph()
>>> nx.add_cycle(G, [0,1,2,3])
>>> nx.add_cycle(G, [0,3,4,5])
>>> print(nx.cycle_basis(G, 0))
[[3, 4, 5, 0], [1, 2, 3, 0]]
Notes
This is adapted from algorithm CACM 4911.
References
See also:
simple_cycles()
3.18.3 networkx.algorithms.cycles.simple_cycles
simple_cycles(G)
Find simple cycles (elementary circuits) of a directed graph.
Asimple cycle, or elementary circuit, is a closed path where no node appears twice. Two elemen-
tary circuits are distinct if they are not cyclic permutations of each other.
1Paton, K. An algorithm for finding a fundamental set of cycles of a graph. Comm. ACM 12, 9 (Sept 1969), 514-518.
3.18. Cycles 287
NetworkX Reference, Release 2.3rc1.dev20181203210840
This is a nonrecursive, iterator/generator version of Johnson’s algorithm1. There may be better algorithms for
some cases23.
Parameters G (NetworkX DiGraph) – A directed graph
Returns cycle_generator – A generator that produces elementary cycles of the graph. Each cycle
is represented by a list of nodes along the cycle.
Return type generator
Examples
>>> edges =[(0,0), (0,1), (0,2), (1,2), (2,0), (2,1), (2,2)]
>>> G=nx.DiGraph(edges)
>>> len(list(nx.simple_cycles(G)))
5
To filter the cycles so that they don’t include certain nodes or edges, copy your graph and eliminate those nodes
or edges before calling
>>> copyG =G.copy()
>>> copyG.remove_nodes_from([1])
>>> copyG.remove_edges_from([(0,1)])
>>> len(list(nx.simple_cycles(copyG)))
3
Notes
The implementation follows pp. 79-80 in1.
The time complexity is 𝑂((𝑛+𝑒)(𝑐+ 1)) for 𝑛nodes, 𝑒edges and 𝑐elementary circuits.
References
See also:
cycle_basis()
3.18.4 networkx.algorithms.cycles.find_cycle
find_cycle(G,source=None,orientation=None)
Returns a cycle found via depth-first traversal.
The cycle is a list of edges indicating the cyclic path. Orientation of directed edges is controlled by
orientation.
Parameters
•G(graph) – A directed/undirected graph/multigraph.
1Finding all the elementary circuits of a directed graph. D. B. Johnson, SIAM Journal on Computing 4, no. 1, 77-84, 1975. https://doi.org/10.
1137/0204007
2Enumerating the cycles of a digraph: a new preprocessing strategy. G. Loizou and P. Thanish, Information Sciences, v. 27, 163-182, 1982.
3A search strategy for the elementary cycles of a directed graph. J.L. Szwarcfiter and P.E. Lauer, BIT NUMERICAL MATHEMATICS, v. 16,
no. 2, 192-204, 1976.
288 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•source (node, list of nodes) – The node from which the traversal begins. If None, then a
source is chosen arbitrarily and repeatedly until all edges from each node in the graph are
searched.
•orientation (None | ‘original’ | ‘reverse’ | ‘ignore’ (default: None)) – For directed graphs
and directed multigraphs, edge traversals need not respect the original orientation of the
edges. When set to ‘reverse’ every edge is traversed in the reverse direction. When set to
‘ignore’, every edge is treated as undirected. When set to ‘original’, every edge is treated as
directed. In all three cases, the yielded edge tuples add a last entry to indicate the direction
in which that edge was traversed. If orientation is None, the yielded edge has no direction
indicated. The direction is respected, but not reported.
Returns edges – A list of directed edges indicating the path taken for the loop. If no cycle is found,
then an exception is raised. For graphs, an edge is of the form (u, v) where uand vare the
tail and head of the edge as determined by the traversal. For multigraphs, an edge is of the form
(u, v, key), where key is the key of the edge. When the graph is directed, then uand v
are always in the order of the actual directed edge. If orientation is not None then the edge tuple
is extended to include the direction of traversal (‘forward’ or ‘reverse’) on that edge.
Return type directed edges
Raises NetworkXNoCycle – If no cycle was found.
Examples
In this example, we construct a DAG and find, in the first call, that there are no directed cycles, and so an
exception is raised. In the second call, we ignore edge orientations and find that there is an undirected cycle.
Note that the second call finds a directed cycle while effectively traversing an undirected graph, and so, we
found an “undirected cycle”. This means that this DAG structure does not form a directed tree (which is also
known as a polytree).
>>> import networkx as nx
>>> G=nx.DiGraph([(0,1), (0,2), (1,2)])
>>> try:
... nx.find_cycle(G, orientation='original')
... except:
... pass
...
>>> list(nx.find_cycle(G, orientation='ignore'))
[(0, 1, 'forward'), (1, 2, 'forward'), (0, 2, 'reverse')]
3.18.5 networkx.algorithms.cycles.minimum_cycle_basis
minimum_cycle_basis(G,weight=None)
Returns a minimum weight cycle basis for G
Minimum weight means a cycle basis for which the total weight (length for unweighted graphs) of all the cycles
is minimum.
Parameters
•G(NetworkX Graph)
•weight (string) – name of the edge attribute to use for edge weights
Returns
•A list of cycle lists. Each cycle list is a list of nodes
3.18. Cycles 289

NetworkX Reference, Release 2.3rc1.dev20181203210840
•which forms a cycle (loop) in G. Note that the nodes are not
•necessarily returned in a order by which they appear in the cycle
Examples
>>> G=nx.Graph()
>>> G.add_cycle([0,1,2,3])
>>> G.add_cycle([0,3,4,5])
>>> print(nx.minimum_cycle_basis(G))
[[0, 1, 2, 3], [0, 3, 4, 5]]
References
[1] Kavitha, Telikepalli, et al. “An O(m^2n) Algorithm for Minimum Cycle Basis of Graphs.” http://link.
springer.com/article/10.1007/s00453-007-9064-z [2] de Pina, J. 1995. Applications of shortest path methods.
Ph.D. thesis, University of Amsterdam, Netherlands
See also:
simple_cycles(),cycle_basis()
3.19 Cuts
Functions for finding and evaluating cuts in a graph.
boundary_expansion(G, S) Returns the boundary expansion of the set S.
conductance(G, S[, T, weight]) Returns the conductance of two sets of nodes.
cut_size(G, S[, T, weight]) Returns the size of the cut between two sets of nodes.
edge_expansion(G, S[, T, weight]) Returns the edge expansion between two node sets.
mixing_expansion(G, S[, T, weight]) Returns the mixing expansion between two node sets.
node_expansion(G, S) Returns the node expansion of the set S.
normalized_cut_size(G, S[, T, weight]) Returns the normalized size of the cut between two sets
of nodes.
volume(G, S[, weight]) Returns the volume of a set of nodes.
3.19.1 networkx.algorithms.cuts.boundary_expansion
boundary_expansion(G,S)
Returns the boundary expansion of the set S.
The boundary expansion is the quotient of the size of the edge boundary and the cardinality of S. [1]
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
Returns The boundary expansion of the set S.
Return type number
See also:
290 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
edge_expansion(),mixing_expansion(),node_expansion()
References
3.19.2 networkx.algorithms.cuts.conductance
conductance(G,S,T=None,weight=None)
Returns the conductance of two sets of nodes.
The conductance is the quotient of the cut size and the smaller of the volumes of the two sets. [1]
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
•T(sequence) – A sequence of nodes in G.
•weight (object) – Edge attribute key to use as weight. If not specified, edges have weight
one.
Returns The conductance between the two sets Sand T.
Return type number
See also:
cut_size(),edge_expansion(),normalized_cut_size(),volume()
References
3.19.3 networkx.algorithms.cuts.cut_size
cut_size(G,S,T=None,weight=None)
Returns the size of the cut between two sets of nodes.
Acut is a partition of the nodes of a graph into two sets. The cut size is the sum of the weights of the edges
“between” the two sets of nodes.
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
•T(sequence) – A sequence of nodes in G. If not specified, this is taken to be the set comple-
ment of S.
•weight (object) – Edge attribute key to use as weight. If not specified, edges have weight
one.
Returns Total weight of all edges from nodes in set Sto nodes in set T(and, in the case of directed
graphs, all edges from nodes in Tto nodes in S).
Return type number
3.19. Cuts 291

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
In the graph with two cliques joined by a single edges, the natural bipartition of the graph into two blocks, one
for each clique, yields a cut of weight one:
>>> G=nx.barbell_graph(3,0)
>>> S={0,1,2}
>>> T={3,4,5}
>>> nx.cut_size(G, S, T)
1
Each parallel edge in a multigraph is counted when determining the cut size:
>>> G=nx.MultiGraph(['ab','ab'])
>>> S={'a'}
>>> T={'b'}
>>> nx.cut_size(G, S, T)
2
Notes
In a multigraph, the cut size is the total weight of edges including multiplicity.
3.19.4 networkx.algorithms.cuts.edge_expansion
edge_expansion(G,S,T=None,weight=None)
Returns the edge expansion between two node sets.
The edge expansion is the quotient of the cut size and the smaller of the cardinalities of the two sets. [1]
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
•T(sequence) – A sequence of nodes in G.
•weight (object) – Edge attribute key to use as weight. If not specified, edges have weight
one.
Returns The edge expansion between the two sets Sand T.
Return type number
See also:
boundary_expansion(),mixing_expansion(),node_expansion()
References
3.19.5 networkx.algorithms.cuts.mixing_expansion
mixing_expansion(G,S,T=None,weight=None)
Returns the mixing expansion between two node sets.
The mixing expansion is the quotient of the cut size and twice the number of edges in the graph. [1]
292 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
•T(sequence) – A sequence of nodes in G.
•weight (object) – Edge attribute key to use as weight. If not specified, edges have weight
one.
Returns The mixing expansion between the two sets Sand T.
Return type number
See also:
boundary_expansion(),edge_expansion(),node_expansion()
References
3.19.6 networkx.algorithms.cuts.node_expansion
node_expansion(G,S)
Returns the node expansion of the set S.
The node expansion is the quotient of the size of the node boundary of Sand the cardinality of S. [1]
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
Returns The node expansion of the set S.
Return type number
See also:
boundary_expansion(),edge_expansion(),mixing_expansion()
References
3.19.7 networkx.algorithms.cuts.normalized_cut_size
normalized_cut_size(G,S,T=None,weight=None)
Returns the normalized size of the cut between two sets of nodes.
The normalized cut size is the cut size times the sum of the reciprocal sizes of the volumes of the two sets. [1]
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
•T(sequence) – A sequence of nodes in G.
•weight (object) – Edge attribute key to use as weight. If not specified, edges have weight
one.
Returns The normalized cut size between the two sets Sand T.
3.19. Cuts 293

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type number
Notes
In a multigraph, the cut size is the total weight of edges including multiplicity.
See also:
conductance(),cut_size(),edge_expansion(),volume()
References
3.19.8 networkx.algorithms.cuts.volume
volume(G,S,weight=None)
Returns the volume of a set of nodes.
The volume of a set Sis the sum of the (out-)degrees of nodes in S(taking into account parallel edges in
multigraphs). [1]
Parameters
•G(NetworkX graph)
•S(sequence) – A sequence of nodes in G.
•weight (object) – Edge attribute key to use as weight. If not specified, edges have weight
one.
Returns The volume of the set of nodes represented by Sin the graph G.
Return type number
See also:
conductance(),cut_size(),edge_expansion(),edge_boundary(),
normalized_cut_size()
References
3.20 Directed Acyclic Graphs
Algorithms for directed acyclic graphs (DAGs).
Note that most of these functions are only guaranteed to work for DAGs. In general, these functions do not check for
acyclic-ness, so it is up to the user to check for that.
ancestors(G, source) Return all nodes having a path to source in G.
descendants(G, source) Return all nodes reachable from source in G.
topological_sort(G) Return a generator of nodes in topologically sorted or-
der.
all_topological_sorts(G) Returns a generator of _all_ topological sorts of the di-
rected graph G.
lexicographical_topological_sort(G[,
key])
Return a generator of nodes in lexicographically topo-
logically sorted order.
Continued on next page
294 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 78 – continued from previous page
is_directed_acyclic_graph(G) Return True if the graph Gis a directed acyclic graph
(DAG) or False if not.
is_aperiodic(G) Return True if Gis aperiodic.
transitive_closure(G) Returns transitive closure of a directed graph
transitive_reduction(G) Returns transitive reduction of a directed graph
antichains(G) Generates antichains from a directed acyclic graph
(DAG).
dag_longest_path(G[, weight, default_weight]) Returns the longest path in a directed acyclic graph
(DAG).
dag_longest_path_length(G[, weight, . . . ]) Returns the longest path length in a DAG
dag_to_branching(G) Returns a branching representing all (overlapping) paths
from root nodes to leaf nodes in the given directed
acyclic graph.
3.20.1 networkx.algorithms.dag.ancestors
ancestors(G,source)
Return all nodes having a path to source in G.
Parameters
•G(NetworkX DiGraph) – A directed acyclic graph (DAG)
•source (node in G)
Returns The ancestors of source in G
Return type set()
3.20.2 networkx.algorithms.dag.descendants
descendants(G,source)
Return all nodes reachable from source in G.
Parameters
•G(NetworkX DiGraph) – A directed acyclic graph (DAG)
•source (node in G)
Returns The descendants of source in G
Return type set()
3.20.3 networkx.algorithms.dag.topological_sort
topological_sort(G)
Return a generator of nodes in topologically sorted order.
A topological sort is a nonunique permutation of the nodes such that an edge from u to v implies that u appears
before v in the topological sort order.
Parameters G (NetworkX digraph) – A directed acyclic graph (DAG)
Returns An iterable of node names in topological sorted order.
Return type iterable
3.20. Directed Acyclic Graphs 295

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises
•NetworkXError – Topological sort is defined for directed graphs only. If the graph Gis
undirected, a NetworkXError is raised.
•NetworkXUnfeasible – If Gis not a directed acyclic graph (DAG) no topological sort
exists and a NetworkXUnfeasible exception is raised. This can also be raised if Gis
changed while the returned iterator is being processed
•RuntimeError – If Gis changed while the returned iterator is being processed.
Examples
To get the reverse order of the topological sort:
>>> DG =nx.DiGraph([(1,2), (2,3)])
>>> list(reversed(list(nx.topological_sort(DG))))
[3, 2, 1]
If your DiGraph naturally has the edges representing tasks/inputs and nodes representing people/processes that
initiate tasks, then topological_sort is not quite what you need. You will have to change the tasks to nodes with
dependence reflected by edges. The result is a kind of topological sort of the edges. This can be done with
networkx.line_graph() as follows:
>>> list(nx.topological_sort(nx.line_graph(DG)))
[(1, 2), (2, 3)]
Notes
This algorithm is based on a description and proof in “Introduction to Algorithms: A Creative Approach”1.
See also:
is_directed_acyclic_graph(),lexicographical_topological_sort()
References
3.20.4 networkx.algorithms.dag.all_topological_sorts
all_topological_sorts(G)
Returns a generator of _all_ topological sorts of the directed graph G.
A topological sort is a nonunique permutation of the nodes such that an edge from u to v implies that u appears
before v in the topological sort order.
Parameters G (NetworkX DiGraph) – A directed graph
Returns All topological sorts of the digraph G
Return type generator
Raises
•NetworkXNotImplemented – If Gis not directed
•NetworkXUnfeasible – If Gis not acyclic
1Manber, U. (1989). Introduction to Algorithms - A Creative Approach. Addison-Wesley.
296 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
To enumerate all topological sorts of directed graph:
>>> DG =nx.DiGraph([(1,2), (2,3), (2,4)])
>>> list(nx.all_topological_sorts(DG))
[[1, 2, 4, 3], [1, 2, 3, 4]]
Notes
Implements an iterative version of the algorithm given in [1].
References
3.20.5 networkx.algorithms.dag.lexicographical_topological_sort
lexicographical_topological_sort(G,key=None)
Return a generator of nodes in lexicographically topologically sorted order.
A topological sort is a nonunique permutation of the nodes such that an edge from u to v implies that u appears
before v in the topological sort order.
Parameters
•G(NetworkX digraph) – A directed acyclic graph (DAG)
•key (function, optional) – This function maps nodes to keys with which to resolve ambigui-
ties in the sort order. Defaults to the identity function.
Returns An iterable of node names in lexicographical topological sort order.
Return type iterable
Raises
•NetworkXError – Topological sort is defined for directed graphs only. If the graph Gis
undirected, a NetworkXError is raised.
•NetworkXUnfeasible – If Gis not a directed acyclic graph (DAG) no topological sort
exists and a NetworkXUnfeasible exception is raised. This can also be raised if Gis
changed while the returned iterator is being processed
•RuntimeError – If Gis changed while the returned iterator is being processed.
Notes
This algorithm is based on a description and proof in “Introduction to Algorithms: A Creative Approach”1.
See also:
topological_sort()
1Manber, U. (1989). Introduction to Algorithms - A Creative Approach. Addison-Wesley.
3.20. Directed Acyclic Graphs 297

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.20.6 networkx.algorithms.dag.is_directed_acyclic_graph
is_directed_acyclic_graph(G)
Return True if the graph Gis a directed acyclic graph (DAG) or False if not.
Parameters G (NetworkX graph)
Returns True if Gis a DAG, False otherwise
Return type bool
3.20.7 networkx.algorithms.dag.is_aperiodic
is_aperiodic(G)
Return True if Gis aperiodic.
A directed graph is aperiodic if there is no integer k > 1 that divides the length of every cycle in the graph.
Parameters G (NetworkX DiGraph) – A directed graph
Returns True if the graph is aperiodic False otherwise
Return type bool
Raises NetworkXError – If Gis not directed
Notes
This uses the method outlined in1, which runs in 𝑂(𝑚)time given 𝑚edges in G. Note that a graph is not
aperiodic if it is acyclic as every integer trivial divides length 0 cycles.
References
3.20.8 networkx.algorithms.dag.transitive_closure
transitive_closure(G)
Returns transitive closure of a directed graph
The transitive closure of G = (V,E) is a graph G+ = (V,E+) such that for all v,w in V there is an edge (v,w) in E+
if and only if there is a non-null path from v to w in G.
Parameters G (NetworkX DiGraph) – A directed graph
Returns The transitive closure of G
Return type NetworkX DiGraph
Raises NetworkXNotImplemented – If Gis not directed
1Jarvis, J. P.; Shier, D. R. (1996), “Graph-theoretic analysis of finite Markov chains,” in Shier, D. R.; Wallenius, K. T., Applied Mathematical
Modeling: A Multidisciplinary Approach, CRC Press.
298 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.20.9 networkx.algorithms.dag.transitive_reduction
transitive_reduction(G)
Returns transitive reduction of a directed graph
The transitive reduction of G = (V,E) is a graph G- = (V,E-) such that for all v,w in V there is an edge (v,w) in
E- if and only if (v,w) is in E and there is no path from v to w in G with length greater than 1.
Parameters G (NetworkX DiGraph) – A directed acyclic graph (DAG)
Returns The transitive reduction of G
Return type NetworkX DiGraph
Raises NetworkXError – If Gis not a directed acyclic graph (DAG) transitive reduction is not
uniquely defined and a NetworkXError exception is raised.
References
https://en.wikipedia.org/wiki/Transitive_reduction
3.20.10 networkx.algorithms.dag.antichains
antichains(G)
Generates antichains from a directed acyclic graph (DAG).
An antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable.
Parameters G (NetworkX DiGraph) – A directed acyclic graph (DAG)
Returns
Return type generator object
Raises
•NetworkXNotImplemented – If Gis not directed
•NetworkXUnfeasible – If Gcontains a cycle
Notes
This function was originally developed by Peter Jipsen and Franco Saliola for the SAGE project. It’s included
in NetworkX with permission from the authors. Original SAGE code at:
https://github.com/sagemath/sage/blob/master/src/sage/combinat/posets/hasse_diagram.py
References
3.20.11 networkx.algorithms.dag.dag_longest_path
dag_longest_path(G,weight=’weight’,default_weight=1)
Returns the longest path in a directed acyclic graph (DAG).
If Ghas edges with weight attribute the edge data are used as weight values.
3.20. Directed Acyclic Graphs 299

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX DiGraph) – A directed acyclic graph (DAG)
•weight (str, optional) – Edge data key to use for weight
•default_weight (int, optional) – The weight of edges that do not have a weight attribute
Returns Longest path
Return type list
Raises NetworkXNotImplemented – If Gis not directed
See also:
dag_longest_path_length()
3.20.12 networkx.algorithms.dag.dag_longest_path_length
dag_longest_path_length(G,weight=’weight’,default_weight=1)
Returns the longest path length in a DAG
Parameters
•G(NetworkX DiGraph) – A directed acyclic graph (DAG)
•weight (string, optional) – Edge data key to use for weight
•default_weight (int, optional) – The weight of edges that do not have a weight attribute
Returns Longest path length
Return type int
Raises NetworkXNotImplemented – If Gis not directed
See also:
dag_longest_path()
3.20.13 networkx.algorithms.dag.dag_to_branching
dag_to_branching(G)
Returns a branching representing all (overlapping) paths from root nodes to leaf nodes in the given directed
acyclic graph.
As described in networkx.algorithms.tree.recognition, a branching is a directed forest in which
each node has at most one parent. In other words, a branching is a disjoint union of arborescences. For this
function, each node of in-degree zero in Gbecomes a root of one of the arborescences, and there will be one leaf
node for each distinct path from that root to a leaf node in G.
Each node vin Gwith kparents becomes kdistinct nodes in the returned branching, one for each parent, and
the sub-DAG rooted at vis duplicated for each copy. The algorithm then recurses on the children of each copy
of v.
Parameters G (NetworkX graph) – A directed acyclic graph.
Returns
The branching in which there is a bijection between root-to-leaf paths in G(in which multiple
paths may share the same leaf) and root-to-leaf paths in the branching (in which there is a unique
path from a root to a leaf).
300 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Each node has an attribute ‘source’ whose value is the original node to which this node corre-
sponds. No other graph, node, or edge attributes are copied into this new graph.
Return type DiGraph
Raises
•NetworkXNotImplemented – If Gis not directed, or if Gis a multigraph.
•HasACycle – If Gis not acyclic.
Examples
To examine which nodes in the returned branching were produced by which original node in the directed acyclic
graph, we can collect the mapping from source node to new nodes into a dictionary. For example, consider the
directed diamond graph:
>>> from collections import defaultdict
>>> from operator import itemgetter
>>>
>>> G=nx.DiGraph(nx.utils.pairwise('abd'))
>>> G.add_edges_from(nx.utils.pairwise('acd'))
>>> B=nx.dag_to_branching(G)
>>>
>>> sources =defaultdict(set)
>>> for v, source in B.nodes(data='source'):
... sources[source].add(v)
>>> len(sources['a'])
1
>>> len(sources['d'])
2
To copy node attributes from the original graph to the new graph, you can use a dictionary like the one con-
structed in the above example:
>>> for source, nodes in sources.items():
... for vin nodes:
... B.node[v].update(G.node[source])
Notes
This function is not idempotent in the sense that the node labels in the returned branching may be uniquely
generated each time the function is invoked. In fact, the node labels may not be integers; in order to relabel
the nodes to be more readable, you can use the networkx.convert_node_labels_to_integers()
function.
The current implementation of this function uses networkx.prefix_tree(), so it is subject to the limita-
tions of that function.
3.21 Dispersion
3.21.1 Dispersion
3.21. Dispersion 301

NetworkX Reference, Release 2.3rc1.dev20181203210840
dispersion(G[, u, v, normalized, alpha, b, c]) Calculate dispersion between uand vin G.
networkx.algorithms.centrality.dispersion
dispersion(G,u=None,v=None,normalized=True,alpha=1.0,b=0.0,c=0.0)
Calculate dispersion between uand vin G.
A link between two actors (uand v) has a high dispersion when their mutual ties (sand t) are not well connected
with each other.
Parameters
•G(graph) – A NetworkX graph.
•u(node, optional) – The source for the dispersion score (e.g. ego node of the network).
•v(node, optional) – The target of the dispersion score if specified.
•normalized (bool) – If True (default) normalize by the embededness of the nodes (u and v).
Returns nodes – If u (v) is specified, returns a dictionary of nodes with dispersion score for all
“target” (“source”) nodes. If neither u nor v is specified, returns a dictionary of dictionaries for
all nodes ‘u’ in the graph with a dispersion score for each node ‘v’.
Return type dictionary
Notes
This implementation follows Lars Backstrom and Jon Kleinberg1. Typical usage would be to run dispersion on
the ego network 𝐺𝑢if 𝑢were specified. Running dispersion() with neither 𝑢nor 𝑣specified can take some
time to complete.
References
3.22 Distance Measures
Graph diameter, radius, eccentricity and other properties.
center(G[, e, usebounds]) Return the center of the graph G.
diameter(G[, e, usebounds]) Return the diameter of the graph G.
eccentricity(G[, v, sp]) Return the eccentricity of nodes in G.
extrema_bounding(G[, compute]) Compute requested extreme distance metric of undi-
rected graph G
periphery(G[, e, usebounds]) Return the periphery of the graph G.
radius(G[, e, usebounds]) Return the radius of the graph G.
3.22.1 networkx.algorithms.distance_measures.center
center(G,e=None,usebounds=False)
Return the center of the graph G.
1Romantic Partnerships and the Dispersion of Social Ties: A Network Analysis of Relationship Status on Facebook. Lars Backstrom, Jon
Kleinberg. https://arxiv.org/pdf/1310.6753v1.pdf
302 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
The center is the set of nodes with eccentricity equal to radius.
Parameters
•G(NetworkX graph) – A graph
•e(eccentricity dictionary, optional) – A precomputed dictionary of eccentricities.
Returns c – List of nodes in center
Return type list
3.22.2 networkx.algorithms.distance_measures.diameter
diameter(G,e=None,usebounds=False)
Return the diameter of the graph G.
The diameter is the maximum eccentricity.
Parameters
•G(NetworkX graph) – A graph
•e(eccentricity dictionary, optional) – A precomputed dictionary of eccentricities.
Returns d – Diameter of graph
Return type integer
See also:
eccentricity()
3.22.3 networkx.algorithms.distance_measures.eccentricity
eccentricity(G,v=None,sp=None)
Return the eccentricity of nodes in G.
The eccentricity of a node v is the maximum distance from v to all other nodes in G.
Parameters
•G(NetworkX graph) – A graph
•v(node, optional) – Return value of specified node
•sp (dict of dicts, optional) – All pairs shortest path lengths as a dictionary of dictionaries
Returns ecc – A dictionary of eccentricity values keyed by node.
Return type dictionary
3.22.4 networkx.algorithms.distance_measures.extrema_bounding
extrema_bounding(G,compute=’diameter’)
Compute requested extreme distance metric of undirected graph G
Computation is based on smart lower and upper bounds, and in practice linear in the number of nodes, rather
than quadratic (except for some border cases such as complete graphs or circle shaped graphs).
Parameters
•G(NetworkX graph) – An undirected graph
3.22. Distance Measures 303

NetworkX Reference, Release 2.3rc1.dev20181203210840
•compute (string denoting the requesting metric) – “diameter” for the maximal eccentricity
value, “radius” for the minimal eccentricity value, “periphery” for the set of nodes with
eccentricity equal to the diameter “center” for the set of nodes with eccentricity equal to the
radius
Returns value – int for “diameter” and “radius” or list of nodes for “center” and “periphery”
Return type value of the requested metric
Raises NetworkXError – If the graph consists of multiple components
Notes
This algorithm was proposed in the following papers:
F.W. Takes and W.A. Kosters, Determining the Diameter of Small World Networks, in Proceedings of the 20th
ACM International Conference on Information and Knowledge Management (CIKM 2011), pp. 1191-1196,
2011. doi: https://doi.org/10.1145/2063576.2063748
F.W. Takes and W.A. Kosters, Computing the Eccentricity Distribution of Large Graphs, Algorithms 6(1): 100-
118, 2013. doi: https://doi.org/10.3390/a6010100
M. Borassi, P. Crescenzi, M. Habib, W.A. Kosters, A. Marino and F.W. Takes, Fast Graph Diameter and Radius
BFS-Based Computation in (Weakly Connected) Real-World Graphs, Theoretical Computer Science 586: 59-
80, 2015. doi: https://doi.org/10.1016/j.tcs.2015.02.033
3.22.5 networkx.algorithms.distance_measures.periphery
periphery(G,e=None,usebounds=False)
Return the periphery of the graph G.
The periphery is the set of nodes with eccentricity equal to the diameter.
Parameters
•G(NetworkX graph) – A graph
•e(eccentricity dictionary, optional) – A precomputed dictionary of eccentricities.
Returns p – List of nodes in periphery
Return type list
3.22.6 networkx.algorithms.distance_measures.radius
radius(G,e=None,usebounds=False)
Return the radius of the graph G.
The radius is the minimum eccentricity.
Parameters
•G(NetworkX graph) – A graph
•e(eccentricity dictionary, optional) – A precomputed dictionary of eccentricities.
Returns r – Radius of graph
Return type integer
304 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.23 Distance-Regular Graphs
3.23.1 Distance-regular graphs
is_distance_regular(G) Returns True if the graph is distance regular, False oth-
erwise.
is_strongly_regular(G) Returns True if and only if the given graph is strongly
regular.
intersection_array(G) Returns the intersection array of a distance-regular
graph.
global_parameters(b, c) Return global parameters for a given intersection array.
3.23.2 networkx.algorithms.distance_regular.is_distance_regular
is_distance_regular(G)
Returns True if the graph is distance regular, False otherwise.
A connected graph G is distance-regular if for any nodes x,y and any integers i,j=0,1,. . . ,d (where d is the graph
diameter), the number of vertices at distance i from x and distance j from y depends only on i,j and the graph
distance between x and y, independently of the choice of x and y.
Parameters G (Networkx graph (undirected))
Returns True if the graph is Distance Regular, False otherwise
Return type bool
Examples
>>> G=nx.hypercube_graph(6)
>>> nx.is_distance_regular(G)
True
See also:
intersection_array(),global_parameters()
Notes
For undirected and simple graphs only
References
3.23.3 networkx.algorithms.distance_regular.is_strongly_regular
is_strongly_regular(G)
Returns True if and only if the given graph is strongly regular.
An undirected graph is strongly regular if
• it is regular,
• each pair of adjacent vertices has the same number of neighbors in common,
3.23. Distance-Regular Graphs 305
NetworkX Reference, Release 2.3rc1.dev20181203210840
• each pair of nonadjacent vertices has the same number of neighbors in common.
Each strongly regular graph is a distance-regular graph. Conversely, if a distance-regular graph has di-
ameter two, then it is a strongly regular graph. For more information on distance-regular graphs, see
is_distance_regular().
Parameters G (NetworkX graph) – An undirected graph.
Returns Whether Gis strongly regular.
Return type bool
Examples
The cycle graph on five vertices is strongly regular. It is two-regular, each pair of adjacent vertices has no shared
neighbors, and each pair of nonadjacent vertices has one shared neighbor:
>>> import networkx as nx
>>> G=nx.cycle_graph(5)
>>> nx.is_strongly_regular(G)
True
3.23.4 networkx.algorithms.distance_regular.intersection_array
intersection_array(G)
Returns the intersection array of a distance-regular graph.
Given a distance-regular graph G with integers b_i, c_i,i = 0,. . . .,d such that for any 2 vertices x,y in G at a
distance i=d(x,y), there are exactly c_i neighbors of y at a distance of i-1 from x and b_i neighbors of y at a
distance of i+1 from x.
A distance regular graph’s intersection array is given by, [b_0,b_1,. . . ..b_{d-1};c_1,c_2,. . . ..c_d]
Parameters G (Networkx graph (undirected))
Returns b,c
Return type tuple of lists
Examples
>>> G=nx.icosahedral_graph()
>>> nx.intersection_array(G)
([5, 2, 1], [1, 2, 5])
References
See also:
global_parameters()
306 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.23.5 networkx.algorithms.distance_regular.global_parameters
global_parameters(b,c)
Return global parameters for a given intersection array.
Given a distance-regular graph G with integers b_i, c_i,i = 0,. . . .,d such that for any 2 vertices x,y in G at a
distance i=d(x,y), there are exactly c_i neighbors of y at a distance of i-1 from x and b_i neighbors of y at a
distance of i+1 from x.
Thus, a distance regular graph has the global parameters, [[c_0,a_0,b_0],[c_1,a_1,b_1],. . . . . . ,[c_d,a_d,b_d]] for
the intersection array [b_0,b_1,. . . ..b_{d-1};c_1,c_2,. . . ..c_d] where a_i+b_i+c_i=k , k= degree of every vertex.
Parameters
•b(list)
•c(list)
Returns An iterable over three tuples.
Return type iterable
Examples
>>> G=nx.dodecahedral_graph()
>>> b,c=nx.intersection_array(G)
>>> list(nx.global_parameters(b, c))
[(0, 0, 3), (1, 0, 2), (1, 1, 1), (1, 1, 1), (2, 0, 1), (3, 0, 0)]
References
See also:
intersection_array()
3.24 Dominance
Dominance algorithms.
immediate_dominators(G, start) Returns the immediate dominators of all nodes of a di-
rected graph.
dominance_frontiers(G, start) Returns the dominance frontiers of all nodes of a di-
rected graph.
3.24.1 networkx.algorithms.dominance.immediate_dominators
immediate_dominators(G,start)
Returns the immediate dominators of all nodes of a directed graph.
Parameters
•G(a DiGraph or MultiDiGraph) – The graph where dominance is to be computed.
•start (node) – The start node of dominance computation.
3.24. Dominance 307

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns idom – A dict containing the immediate dominators of each node reachable from start.
Return type dict keyed by nodes
Raises
•NetworkXNotImplemented – If Gis undirected.
•NetworkXError – If start is not in G.
Notes
Except for start, the immediate dominators are the parents of their corresponding nodes in the dominator tree.
Examples
>>> G=nx.DiGraph([(1,2), (1,3), (2,5), (3,4), (4,5)])
>>> sorted(nx.immediate_dominators(G, 1).items())
[(1, 1), (2, 1), (3, 1), (4, 3), (5, 1)]
References
3.24.2 networkx.algorithms.dominance.dominance_frontiers
dominance_frontiers(G,start)
Returns the dominance frontiers of all nodes of a directed graph.
Parameters
•G(a DiGraph or MultiDiGraph) – The graph where dominance is to be computed.
•start (node) – The start node of dominance computation.
Returns df – A dict containing the dominance frontiers of each node reachable from start as lists.
Return type dict keyed by nodes
Raises
•NetworkXNotImplemented – If Gis undirected.
•NetworkXError – If start is not in G.
Examples
>>> G=nx.DiGraph([(1,2), (1,3), (2,5), (3,4), (4,5)])
>>> sorted((u, sorted(df)) for u, df in nx.dominance_frontiers(G, 1).items())
[(1, []), (2, [5]), (3, [5]), (4, [5]), (5, [])]
References
3.25 Dominating Sets
Functions for computing dominating sets in a graph.
308 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
dominating_set(G[, start_with]) Finds a dominating set for the graph G.
is_dominating_set(G, nbunch) Checks if nbunch is a dominating set for G.
3.25.1 networkx.algorithms.dominating.dominating_set
dominating_set(G,start_with=None)
Finds a dominating set for the graph G.
Adominating set for a graph with node set Vis a subset Dof Vsuch that every node not in Dis adjacent to at
least one member of D1.
Parameters
•G(NetworkX graph)
•start_with (node (default=None)) – Node to use as a starting point for the algorithm.
Returns D – A dominating set for G.
Return type set
Notes
This function is an implementation of algorithm 7 in2which finds some dominating set, not necessarily the
smallest one.
See also:
is_dominating_set()
References
3.25.2 networkx.algorithms.dominating.is_dominating_set
is_dominating_set(G,nbunch)
Checks if nbunch is a dominating set for G.
Adominating set for a graph with node set Vis a subset Dof Vsuch that every node not in Dis adjacent to at
least one member of D1.
Parameters
•G(NetworkX graph)
•nbunch (iterable) – An iterable of nodes in the graph G.
See also:
dominating_set()
1https://en.wikipedia.org/wiki/Dominating_set
2Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf
1https://en.wikipedia.org/wiki/Dominating_set
3.25. Dominating Sets 309

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.26 Efficiency
Provides functions for computing the efficiency of nodes and graphs.
efficiency(G, u, v) Returns the efficiency of a pair of nodes in a graph.
local_efficiency(G) Returns the average local efficiency of the graph.
global_efficiency(G) Returns the average global efficiency of the graph.
3.26.1 networkx.algorithms.efficiency.efficiency
efficiency(G,u,v)
Returns the efficiency of a pair of nodes in a graph.
The efficiency of a pair of nodes is the multiplicative inverse of the shortest path distance between the nodes1.
Returns 0 if no path between nodes.
Parameters
•G(networkx.Graph) – An undirected graph for which to compute the average local
efficiency.
•u, v (node) – Nodes in the graph G.
Returns Multiplicative inverse of the shortest path distance between the nodes.
Return type float
Notes
Edge weights are ignored when computing the shortest path distances.
See also:
local_efficiency(),global_efficiency()
References
3.26.2 networkx.algorithms.efficiency.local_efficiency
local_efficiency(G)
Returns the average local efficiency of the graph.
The efficiency of a pair of nodes in a graph is the multiplicative inverse of the shortest path distance between the
nodes. The local efficiency of a node in the graph is the average global efficiency of the subgraph induced by
the neighbors of the node. The average local efficiency is the average of the local efficiencies of each node1.
Parameters G (networkx.Graph) – An undirected graph for which to compute the average local
efficiency.
1Latora, Vito, and Massimo Marchiori. “Efficient behavior of small-world networks.” Physical Review Letters 87.19 (2001): 198701. <https:
//doi.org/10.1103/PhysRevLett.87.198701>
1Latora, Vito, and Massimo Marchiori. “Efficient behavior of small-world networks.” Physical Review Letters 87.19 (2001): 198701. <https:
//doi.org/10.1103/PhysRevLett.87.198701>
310 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns The average local efficiency of the graph.
Return type float
Notes
Edge weights are ignored when computing the shortest path distances.
See also:
global_efficiency()
References
3.26.3 networkx.algorithms.efficiency.global_efficiency
global_efficiency(G)
Returns the average global efficiency of the graph.
The efficiency of a pair of nodes in a graph is the multiplicative inverse of the shortest path distance between the
nodes. The average global efficiency of a graph is the average efficiency of all pairs of nodes1.
Parameters G (networkx.Graph) – An undirected graph for which to compute the average
global efficiency.
Returns The average global efficiency of the graph.
Return type float
Notes
Edge weights are ignored when computing the shortest path distances.
See also:
local_efficiency()
References
3.27 Eulerian
Eulerian circuits and graphs.
is_eulerian(G) Returns True if and only if Gis Eulerian.
eulerian_circuit(G[, source, keys]) Returns an iterator over the edges of an Eulerian circuit
in G.
eulerize(G) Transforms a graph into an Eulerian graph
1Latora, Vito, and Massimo Marchiori. “Efficient behavior of small-world networks.” Physical Review Letters 87.19 (2001): 198701. <https:
//doi.org/10.1103/PhysRevLett.87.198701>
3.27. Eulerian 311

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.27.1 networkx.algorithms.euler.is_eulerian
is_eulerian(G)
Returns True if and only if Gis Eulerian.
A graph is Eulerian if it has an Eulerian circuit. An Eulerian circuit is a closed walk that includes each edge of
a graph exactly once.
Parameters G (NetworkX graph) – A graph, either directed or undirected.
Examples
>>> nx.is_eulerian(nx.DiGraph({0: [3], 1: [2], 2: [3], 3: [0,1]}))
True
>>> nx.is_eulerian(nx.complete_graph(5))
True
>>> nx.is_eulerian(nx.petersen_graph())
False
Notes
If the graph is not connected (or not strongly connected, for directed graphs), this function returns False.
3.27.2 networkx.algorithms.euler.eulerian_circuit
eulerian_circuit(G,source=None,keys=False)
Returns an iterator over the edges of an Eulerian circuit in G.
An Eulerian circuit is a closed walk that includes each edge of a graph exactly once.
Parameters
•G(NetworkX graph) – A graph, either directed or undirected.
•source (node, optional) – Starting node for circuit.
•keys (bool) – If False, edges generated by this function will be of the form (u, v). Oth-
erwise, edges will be of the form (u, v, k). This option is ignored unless Gis a multi-
graph.
Returns edges – An iterator over edges in the Eulerian circuit.
Return type iterator
Raises NetworkXError – If the graph is not Eulerian.
See also:
is_eulerian()
Notes
This is a linear time implementation of an algorithm adapted from1.
For general information about Euler tours, see2.
1J. Edmonds, E. L. Johnson. Matching, Euler tours and the Chinese postman. Mathematical programming, Volume 5, Issue 1 (1973), 111-114.
2https://en.wikipedia.org/wiki/Eulerian_path
312 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
Examples
To get an Eulerian circuit in an undirected graph:
>>> G=nx.complete_graph(3)
>>> list(nx.eulerian_circuit(G))
[(0, 2), (2, 1), (1, 0)]
>>> list(nx.eulerian_circuit(G, source=1))
[(1, 2), (2, 0), (0, 1)]
To get the sequence of vertices in an Eulerian circuit:
>>> [u for u, v in nx.eulerian_circuit(G)]
[0, 2, 1]
3.27.3 networkx.algorithms.euler.eulerize
eulerize(G)
Transforms a graph into an Eulerian graph
Parameters G (NetworkX graph) – An undirected graph
Returns G
Return type NetworkX multigraph
Raises NetworkXError – If the graph is not connected.
See also:
is_eulerian(),eulerian_circuit()
References
Examples
>>> G=nx.complete_graph(10)
>>> H=nx.eulerize(G)
>>> nx.is_eulerian(H)
True
3.28 Flows
3.28.1 Maximum Flow
maximum_flow(flowG, _s, _t[, capacity, . . . ]) Find a maximum single-commodity flow.
maximum_flow_value(flowG, _s, _t[, . . . ]) Find the value of maximum single-commodity flow.
minimum_cut(flowG, _s, _t[, capacity, flow_func]) Compute the value and the node partition of a minimum
(s, t)-cut.
minimum_cut_value(flowG, _s, _t[, capacity, . . . ]) Compute the value of a minimum (s, t)-cut.
3.28. Flows 313

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.flow.maximum_flow
maximum_flow(flowG,_s,_t,capacity=’capacity’,flow_func=None,**kwargs)
Find a maximum single-commodity flow.
Parameters
•flowG (NetworkX graph) – Edges of the graph are expected to have an attribute called ‘ca-
pacity’. If this attribute is not present, the edge is considered to have infinite capacity.
•_s (node) – Source node for the flow.
•_t (node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•flow_func (function) – A function for computing the maximum flow among a pair of nodes
in a capacitated graph. The function has to accept at least three parameters: a Graph or
Digraph, a source node, and a target node. And return a residual network that follows Net-
workX conventions (see Notes). If flow_func is None, the default maximum flow function
(preflow_push()) is used. See below for alternative algorithms. The choice of the
default function may change from version to version and should not be relied on. Default
value: None.
•kwargs (Any other keyword parameter is passed to the function that) – computes the maxi-
mum flow.
Returns
•flow_value (integer, float) – Value of the maximum flow, i.e., net outflow from the source.
•flow_dict (dict) – A dictionary containing the value of the flow that went through each edge.
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow_value(),minimum_cut(),minimum_cut_value(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
Notes
The function used in the flow_func parameter has to return a residual network that follows NetworkX conven-
tions:
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
314 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. Reacha-
bility to tusing only edges (u, v) such that R[u][v]['flow'] < R[u][v]['capacity'] induces
a minimum s-tcut.
Specific algorithms may store extra data in R.
The function should supports an optional boolean parameter value_only. When True, it can optionally terminate
the algorithm as soon as the maximum flow value and the minimum cut can be determined.
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
maximum_flow returns both the value of the maximum flow and a dictionary with all flows.
>>> flow_value, flow_dict =nx.maximum_flow(G, 'x','y')
>>> flow_value
3.0
>>> print(flow_dict['x']['b'])
1.0
You can also use alternative algorithms for computing the maximum flow by using the flow_func parameter.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> flow_value == nx.maximum_flow(G, 'x','y',
... flow_func=shortest_augmenting_path)[0]
True
networkx.algorithms.flow.maximum_flow_value
maximum_flow_value(flowG,_s,_t,capacity=’capacity’,flow_func=None,**kwargs)
Find the value of maximum single-commodity flow.
Parameters
•flowG (NetworkX graph) – Edges of the graph are expected to have an attribute called ‘ca-
pacity’. If this attribute is not present, the edge is considered to have infinite capacity.
•_s (node) – Source node for the flow.
•_t (node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•flow_func (function) – A function for computing the maximum flow among a pair of nodes
in a capacitated graph. The function has to accept at least three parameters: a Graph or
3.28. Flows 315

NetworkX Reference, Release 2.3rc1.dev20181203210840
Digraph, a source node, and a target node. And return a residual network that follows Net-
workX conventions (see Notes). If flow_func is None, the default maximum flow function
(preflow_push()) is used. See below for alternative algorithms. The choice of the
default function may change from version to version and should not be relied on. Default
value: None.
•kwargs (Any other keyword parameter is passed to the function that) – computes the maxi-
mum flow.
Returns flow_value – Value of the maximum flow, i.e., net outflow from the source.
Return type integer, float
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow(),minimum_cut(),minimum_cut_value(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
Notes
The function used in the flow_func parameter has to return a residual network that follows NetworkX conven-
tions:
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. Reacha-
bility to tusing only edges (u, v) such that R[u][v]['flow'] < R[u][v]['capacity'] induces
a minimum s-tcut.
Specific algorithms may store extra data in R.
The function should supports an optional boolean parameter value_only. When True, it can optionally terminate
the algorithm as soon as the maximum flow value and the minimum cut can be determined.
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
(continues on next page)
316 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
maximum_flow_value computes only the value of the maximum flow:
>>> flow_value =nx.maximum_flow_value(G, 'x','y')
>>> flow_value
3.0
You can also use alternative algorithms for computing the maximum flow by using the flow_func parameter.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> flow_value == nx.maximum_flow_value(G, 'x','y',
... flow_func=shortest_augmenting_path)
True
networkx.algorithms.flow.minimum_cut
minimum_cut(flowG,_s,_t,capacity=’capacity’,flow_func=None,**kwargs)
Compute the value and the node partition of a minimum (s, t)-cut.
Use the max-flow min-cut theorem, i.e., the capacity of a minimum capacity cut is equal to the flow value of a
maximum flow.
Parameters
•flowG (NetworkX graph) – Edges of the graph are expected to have an attribute called ‘ca-
pacity’. If this attribute is not present, the edge is considered to have infinite capacity.
•_s (node) – Source node for the flow.
•_t (node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•flow_func (function) – A function for computing the maximum flow among a pair of nodes
in a capacitated graph. The function has to accept at least three parameters: a Graph or
Digraph, a source node, and a target node. And return a residual network that follows Net-
workX conventions (see Notes). If flow_func is None, the default maximum flow function
(preflow_push()) is used. See below for alternative algorithms. The choice of the
default function may change from version to version and should not be relied on. Default
value: None.
•kwargs (Any other keyword parameter is passed to the function that) – computes the maxi-
mum flow.
Returns
•cut_value (integer, float) – Value of the minimum cut.
•partition (pair of node sets) – A partitioning of the nodes that defines a minimum cut.
Raises NetworkXUnbounded – If the graph has a path of infinite capacity, all cuts have infinite
capacity and the function raises a NetworkXError.
3.28. Flows 317

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
maximum_flow(),maximum_flow_value(),minimum_cut_value(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
Notes
The function used in the flow_func parameter has to return a residual network that follows NetworkX conven-
tions:
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. Reacha-
bility to tusing only edges (u, v) such that R[u][v]['flow'] < R[u][v]['capacity'] induces
a minimum s-tcut.
Specific algorithms may store extra data in R.
The function should supports an optional boolean parameter value_only. When True, it can optionally terminate
the algorithm as soon as the maximum flow value and the minimum cut can be determined.
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity =3.0)
>>> G.add_edge('x','b', capacity =1.0)
>>> G.add_edge('a','c', capacity =3.0)
>>> G.add_edge('b','c', capacity =5.0)
>>> G.add_edge('b','d', capacity =4.0)
>>> G.add_edge('d','e', capacity =2.0)
>>> G.add_edge('c','y', capacity =2.0)
>>> G.add_edge('e','y', capacity =3.0)
minimum_cut computes both the value of the minimum cut and the node partition:
>>> cut_value, partition =nx.minimum_cut(G, 'x','y')
>>> reachable, non_reachable =partition
‘partition’ here is a tuple with the two sets of nodes that define the minimum cut. You can compute the cut set
of edges that induce the minimum cut as follows:
>>> cutset =set()
>>> for u, nbrs in ((n, G[n]) for nin reachable):
... cutset.update((u, v) for vin nbrs if vin non_reachable)
>>> print(sorted(cutset))
[('c', 'y'), ('x', 'b')]
>>> cut_value == sum(G.edges[u, v]['capacity']for (u, v) in cutset)
True
318 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
You can also use alternative algorithms for computing the minimum cut by using the flow_func parameter.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> cut_value == nx.minimum_cut(G, 'x','y',
... flow_func=shortest_augmenting_path)[0]
True
networkx.algorithms.flow.minimum_cut_value
minimum_cut_value(flowG,_s,_t,capacity=’capacity’,flow_func=None,**kwargs)
Compute the value of a minimum (s, t)-cut.
Use the max-flow min-cut theorem, i.e., the capacity of a minimum capacity cut is equal to the flow value of a
maximum flow.
Parameters
•flowG (NetworkX graph) – Edges of the graph are expected to have an attribute called ‘ca-
pacity’. If this attribute is not present, the edge is considered to have infinite capacity.
•_s (node) – Source node for the flow.
•_t (node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•flow_func (function) – A function for computing the maximum flow among a pair of nodes
in a capacitated graph. The function has to accept at least three parameters: a Graph or
Digraph, a source node, and a target node. And return a residual network that follows Net-
workX conventions (see Notes). If flow_func is None, the default maximum flow function
(preflow_push()) is used. See below for alternative algorithms. The choice of the
default function may change from version to version and should not be relied on. Default
value: None.
•kwargs (Any other keyword parameter is passed to the function that) – computes the maxi-
mum flow.
Returns cut_value – Value of the minimum cut.
Return type integer, float
Raises NetworkXUnbounded – If the graph has a path of infinite capacity, all cuts have infinite
capacity and the function raises a NetworkXError.
See also:
maximum_flow(),maximum_flow_value(),minimum_cut(),edmonds_karp(),
preflow_push(),shortest_augmenting_path()
Notes
The function used in the flow_func parameter has to return a residual network that follows NetworkX conven-
tions:
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
3.28. Flows 319
NetworkX Reference, Release 2.3rc1.dev20181203210840
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. Reacha-
bility to tusing only edges (u, v) such that R[u][v]['flow'] < R[u][v]['capacity'] induces
a minimum s-tcut.
Specific algorithms may store extra data in R.
The function should supports an optional boolean parameter value_only. When True, it can optionally terminate
the algorithm as soon as the maximum flow value and the minimum cut can be determined.
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity =3.0)
>>> G.add_edge('x','b', capacity =1.0)
>>> G.add_edge('a','c', capacity =3.0)
>>> G.add_edge('b','c', capacity =5.0)
>>> G.add_edge('b','d', capacity =4.0)
>>> G.add_edge('d','e', capacity =2.0)
>>> G.add_edge('c','y', capacity =2.0)
>>> G.add_edge('e','y', capacity =3.0)
minimum_cut_value computes only the value of the minimum cut:
>>> cut_value =nx.minimum_cut_value(G, 'x','y')
>>> cut_value
3.0
You can also use alternative algorithms for computing the minimum cut by using the flow_func parameter.
>>> from networkx.algorithms.flow import shortest_augmenting_path
>>> cut_value == nx.minimum_cut_value(G, 'x','y',
... flow_func=shortest_augmenting_path)
True
3.28.2 Edmonds-Karp
edmonds_karp(G, s, t[, capacity, residual, . . . ]) Find a maximum single-commodity flow using the
Edmonds-Karp algorithm.
networkx.algorithms.flow.edmonds_karp
edmonds_karp(G,s,t,capacity=’capacity’,residual=None,value_only=False,cutoff=None)
Find a maximum single-commodity flow using the Edmonds-Karp algorithm.
This function returns the residual network resulting after computing the maximum flow. See below for details
about the conventions NetworkX uses for defining residual networks.
This algorithm has a running time of 𝑂(𝑛𝑚2)for 𝑛nodes and 𝑚edges.
320 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph) – Edges of the graph are expected to have an attribute called ‘capacity’.
If this attribute is not present, the edge is considered to have infinite capacity.
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•residual (NetworkX graph) – Residual network on which the algorithm is to be executed. If
None, a new residual network is created. Default value: None.
•value_only (bool) – If True compute only the value of the maximum flow. This parameter
will be ignored by this algorithm because it is not applicable.
•cutoff (integer, float) – If specified, the algorithm will terminate when the flow value reaches
or exceeds the cutoff. In this case, it may be unable to immediately determine a minimum
cut. Default value: None.
Returns R – Residual network after computing the maximum flow.
Return type NetworkX DiGraph
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow(),minimum_cut(),preflow_push(),shortest_augmenting_path()
Notes
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. If
cutoff is not specified, reachability to tusing only edges (u, v) such that R[u][v]['flow'] <
R[u][v]['capacity'] induces a minimum s-tcut.
Examples
>>> import networkx as nx
>>> from networkx.algorithms.flow import edmonds_karp
3.28. Flows 321

NetworkX Reference, Release 2.3rc1.dev20181203210840
The functions that implement flow algorithms and output a residual network, such as this one, are not imported
to the base NetworkX namespace, so you have to explicitly import them from the flow package.
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
>>> R=edmonds_karp(G, 'x','y')
>>> flow_value =nx.maximum_flow_value(G, 'x','y')
>>> flow_value
3.0
>>> flow_value == R.graph['flow_value']
True
3.28.3 Shortest Augmenting Path
shortest_augmenting_path(G, s, t[, . . . ]) Find a maximum single-commodity flow using the
shortest augmenting path algorithm.
networkx.algorithms.flow.shortest_augmenting_path
shortest_augmenting_path(G,s,t,capacity=’capacity’,residual=None,value_only=False,
two_phase=False,cutoff=None)
Find a maximum single-commodity flow using the shortest augmenting path algorithm.
This function returns the residual network resulting after computing the maximum flow. See below for details
about the conventions NetworkX uses for defining residual networks.
This algorithm has a running time of 𝑂(𝑛2𝑚)for 𝑛nodes and 𝑚edges.
Parameters
•G(NetworkX graph) – Edges of the graph are expected to have an attribute called ‘capacity’.
If this attribute is not present, the edge is considered to have infinite capacity.
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•residual (NetworkX graph) – Residual network on which the algorithm is to be executed. If
None, a new residual network is created. Default value: None.
•value_only (bool) – If True compute only the value of the maximum flow. This parameter
will be ignored by this algorithm because it is not applicable.
•two_phase (bool) – If True, a two-phase variant is used. The two-phase variant improves
the running time on unit-capacity networks from 𝑂(𝑛𝑚)to 𝑂(min(𝑛2/3, 𝑚1/2)𝑚). Default
value: False.
322 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•cutoff (integer, float) – If specified, the algorithm will terminate when the flow value reaches
or exceeds the cutoff. In this case, it may be unable to immediately determine a minimum
cut. Default value: None.
Returns R – Residual network after computing the maximum flow.
Return type NetworkX DiGraph
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow(),minimum_cut(),edmonds_karp(),preflow_push()
Notes
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. If
cutoff is not specified, reachability to tusing only edges (u, v) such that R[u][v]['flow'] <
R[u][v]['capacity'] induces a minimum s-tcut.
Examples
>>> import networkx as nx
>>> from networkx.algorithms.flow import shortest_augmenting_path
The functions that implement flow algorithms and output a residual network, such as this one, are not imported
to the base NetworkX namespace, so you have to explicitly import them from the flow package.
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
>>> R=shortest_augmenting_path(G, 'x','y')
>>> flow_value =nx.maximum_flow_value(G, 'x','y')
>>> flow_value
3.0
(continues on next page)
3.28. Flows 323

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> flow_value == R.graph['flow_value']
True
3.28.4 Preflow-Push
preflow_push(G, s, t[, capacity, residual, . . . ]) Find a maximum single-commodity flow using the
highest-label preflow-push algorithm.
networkx.algorithms.flow.preflow_push
preflow_push(G,s,t,capacity=’capacity’,residual=None,global_relabel_freq=1,value_only=False)
Find a maximum single-commodity flow using the highest-label preflow-push algorithm.
This function returns the residual network resulting after computing the maximum flow. See below for details
about the conventions NetworkX uses for defining residual networks.
This algorithm has a running time of 𝑂(𝑛2√𝑚)for 𝑛nodes and 𝑚edges.
Parameters
•G(NetworkX graph) – Edges of the graph are expected to have an attribute called ‘capacity’.
If this attribute is not present, the edge is considered to have infinite capacity.
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•residual (NetworkX graph) – Residual network on which the algorithm is to be executed. If
None, a new residual network is created. Default value: None.
•global_relabel_freq (integer, float) – Relative frequency of applying the global relabeling
heuristic to speed up the algorithm. If it is None, the heuristic is disabled. Default value: 1.
•value_only (bool) – If False, compute a maximum flow; otherwise, compute a maximum
preflow which is enough for computing the maximum flow value. Default value: False.
Returns R – Residual network after computing the maximum flow.
Return type NetworkX DiGraph
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow(),minimum_cut(),edmonds_karp(),shortest_augmenting_path()
324 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G. For each node uin R,R.nodes[u]['excess'] represents the difference between flow into uand flow
out of u.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. Reacha-
bility to tusing only edges (u, v) such that R[u][v]['flow'] < R[u][v]['capacity'] induces
a minimum s-tcut.
Examples
>>> import networkx as nx
>>> from networkx.algorithms.flow import preflow_push
The functions that implement flow algorithms and output a residual network, such as this one, are not imported
to the base NetworkX namespace, so you have to explicitly import them from the flow package.
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
>>> R=preflow_push(G, 'x','y')
>>> flow_value =nx.maximum_flow_value(G, 'x','y')
>>> flow_value == R.graph['flow_value']
True
>>> # preflow_push also stores the maximum flow value
>>> # in the excess attribute of the sink node t
>>> flow_value == R.nodes['y']['excess']
True
>>> # For some problems, you might only want to compute a
>>> # maximum preflow.
>>> R=preflow_push(G, 'x','y', value_only=True)
>>> flow_value == R.graph['flow_value']
True
>>> flow_value == R.nodes['y']['excess']
True
3.28.5 Dinitz
3.28. Flows 325

NetworkX Reference, Release 2.3rc1.dev20181203210840
dinitz(G, s, t[, capacity, residual, . . . ]) Find a maximum single-commodity flow using Dinitz’
algorithm.
networkx.algorithms.flow.dinitz
dinitz(G,s,t,capacity=’capacity’,residual=None,value_only=False,cutoff=None)
Find a maximum single-commodity flow using Dinitz’ algorithm.
This function returns the residual network resulting after computing the maximum flow. See below for details
about the conventions NetworkX uses for defining residual networks.
This algorithm has a running time of 𝑂(𝑛2𝑚)for 𝑛nodes and 𝑚edges1.
Parameters
•G(NetworkX graph) – Edges of the graph are expected to have an attribute called ‘capacity’.
If this attribute is not present, the edge is considered to have infinite capacity.
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•residual (NetworkX graph) – Residual network on which the algorithm is to be executed. If
None, a new residual network is created. Default value: None.
•value_only (bool) – If True compute only the value of the maximum flow. This parameter
will be ignored by this algorithm because it is not applicable.
•cutoff (integer, float) – If specified, the algorithm will terminate when the flow value reaches
or exceeds the cutoff. In this case, it may be unable to immediately determine a minimum
cut. Default value: None.
Returns R – Residual network after computing the maximum flow.
Return type NetworkX DiGraph
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow(),minimum_cut(),preflow_push(),shortest_augmenting_path()
Notes
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
1Dinitz’ Algorithm: The Original Version and Even’s Version. 2006. Yefim Dinitz. In Theoretical Computer Science. Lecture Notes in
Computer Science. Volume 3895. pp 218-240. http://www.cs.bgu.ac.il/~dinitz/Papers/Dinitz_alg.pdf
326 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. If
cutoff is not specified, reachability to tusing only edges (u, v) such that R[u][v]['flow'] <
R[u][v]['capacity'] induces a minimum s-tcut.
Examples
>>> import networkx as nx
>>> from networkx.algorithms.flow import dinitz
The functions that implement flow algorithms and output a residual network, such as this one, are not imported
to the base NetworkX namespace, so you have to explicitly import them from the flow package.
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
>>> R=dinitz(G, 'x','y')
>>> flow_value =nx.maximum_flow_value(G, 'x','y')
>>> flow_value
3.0
>>> flow_value == R.graph['flow_value']
True
References
3.28.6 Boykov-Kolmogorov
boykov_kolmogorov(G, s, t[, capacity, . . . ]) Find a maximum single-commodity flow using Boykov-
Kolmogorov algorithm.
networkx.algorithms.flow.boykov_kolmogorov
boykov_kolmogorov(G,s,t,capacity=’capacity’,residual=None,value_only=False,cutoff=None)
Find a maximum single-commodity flow using Boykov-Kolmogorov algorithm.
This function returns the residual network resulting after computing the maximum flow. See below for details
about the conventions NetworkX uses for defining residual networks.
This algorithm has worse case complexity 𝑂(𝑛2𝑚|𝐶|)for 𝑛nodes, 𝑚edges, and |𝐶|the cost of the minimum
cut1. This implementation uses the marking heuristic defined in2which improves its running time in many
1Boykov, Y., & Kolmogorov, V. (2004). An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision.
Pattern Analysis and Machine Intelligence, IEEE Transactions on, 26(9), 1124-1137. http://www.csd.uwo.ca/~yuri/Papers/pami04.pdf
2Vladimir Kolmogorov. Graph-based Algorithms for Multi-camera Reconstruction Problem. PhD thesis, Cornell University, CS Department,
3.28. Flows 327

NetworkX Reference, Release 2.3rc1.dev20181203210840
practical problems.
Parameters
•G(NetworkX graph) – Edges of the graph are expected to have an attribute called ‘capacity’.
If this attribute is not present, the edge is considered to have infinite capacity.
•s(node) – Source node for the flow.
•t(node) – Sink node for the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•residual (NetworkX graph) – Residual network on which the algorithm is to be executed. If
None, a new residual network is created. Default value: None.
•value_only (bool) – If True compute only the value of the maximum flow. This parameter
will be ignored by this algorithm because it is not applicable.
•cutoff (integer, float) – If specified, the algorithm will terminate when the flow value reaches
or exceeds the cutoff. In this case, it may be unable to immediately determine a minimum
cut. Default value: None.
Returns R – Residual network after computing the maximum flow.
Return type NetworkX DiGraph
Raises
•NetworkXError – The algorithm does not support MultiGraph and MultiDiGraph. If the
input graph is an instance of one of these two classes, a NetworkXError is raised.
•NetworkXUnbounded – If the graph has a path of infinite capacity, the value of a feasible
flow on the graph is unbounded above and the function raises a NetworkXUnbounded.
See also:
maximum_flow(),minimum_cut(),preflow_push(),shortest_augmenting_path()
Notes
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. If
cutoff is not specified, reachability to tusing only edges (u, v) such that R[u][v]['flow'] <
R[u][v]['capacity'] induces a minimum s-tcut.
2003. pp. 109-114. https://pub.ist.ac.at/~vnk/papers/thesis.pdf
328 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> import networkx as nx
>>> from networkx.algorithms.flow import boykov_kolmogorov
The functions that implement flow algorithms and output a residual network, such as this one, are not imported
to the base NetworkX namespace, so you have to explicitly import them from the flow package.
>>> G=nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
>>> R=boykov_kolmogorov(G, 'x','y')
>>> flow_value =nx.maximum_flow_value(G, 'x','y')
>>> flow_value
3.0
>>> flow_value == R.graph['flow_value']
True
A nice feature of the Boykov-Kolmogorov algorithm is that a partition of the nodes that defines a minimum cut
can be easily computed based on the search trees used during the algorithm. These trees are stored in the graph
attribute trees of the residual network.
>>> source_tree, target_tree =R.graph['trees']
>>> partition =(set(source_tree), set(G) -set(source_tree))
Or equivalently:
>>> partition =(set(G) -set(target_tree), set(target_tree))
References
3.28.7 Gomory-Hu Tree
gomory_hu_tree(G[, capacity, flow_func]) Returns the Gomory-Hu tree of an undirected graph G.
networkx.algorithms.flow.gomory_hu_tree
gomory_hu_tree(G,capacity=’capacity’,flow_func=None)
Returns the Gomory-Hu tree of an undirected graph G.
A Gomory-Hu tree of an undirected graph with capacities is a weighted tree that represents the minimum s-t
cuts for all s-t pairs in the graph.
It only requires n-1 minimum cut computations instead of the obvious n(n-1)/2. The tree represents all
s-t cuts as the minimum cut value among any pair of nodes is the minimum edge weight in the shortest path
between the two nodes in the Gomory-Hu tree.
The Gomory-Hu tree also has the property that removing the edge with the minimum weight in the shortest path
between any two nodes leaves two connected components that form a partition of the nodes in G that defines the
3.28. Flows 329

NetworkX Reference, Release 2.3rc1.dev20181203210840
minimum s-t cut.
See Examples section below for details.
Parameters
•G(NetworkX graph) – Undirected graph
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•flow_func (function) – Function to perform the underlying flow computations. Default value
edmonds_karp(). This function performs better in sparse graphs with right tailed degree
distributions. shortest_augmenting_path() will perform better in denser graphs.
Returns Tree – A NetworkX graph representing the Gomory-Hu tree of the input graph.
Return type NetworkX graph
Raises
•NetworkXNotImplemented : Exception – Raised if the input graph is directed.
•NetworkXError: Exception – Raised if the input graph is an empty Graph.
Examples
>>> G=nx.karate_club_graph()
>>> nx.set_edge_attributes(G, 1,'capacity')
>>> T=nx.gomory_hu_tree(G)
>>> # The value of the minimum cut between any pair
... # of nodes in G is the minimum edge weight in the
... # shortest path between the two nodes in the
... # Gomory-Hu tree.
... def minimum_edge_weight_in_shortest_path(T, u, v):
... path =nx.shortest_path(T, u, v, weight='weight')
... return min((T[u][v]['weight'], (u,v)) for (u, v) in zip(path, path[1:]))
>>> u,v=0,33
>>> cut_value, edge =minimum_edge_weight_in_shortest_path(T, u, v)
>>> cut_value
10
>>> nx.minimum_cut_value(G, u, v)
10
>>> # The Comory-Hu tree also has the property that removing the
... # edge with the minimum weight in the shortest path between
... # any two nodes leaves two connected components that form
... # a partition of the nodes in G that defines the minimum s-t
... # cut.
... cut_value, edge =minimum_edge_weight_in_shortest_path(T, u, v)
>>> T.remove_edge(*edge)
>>> U,V=list(nx.connected_components(T))
>>> # Thus U and V form a partition that defines a minimum cut
... # between u and v in G. You can compute the edge cut set,
... # that is, the set of edges that if removed from G will
... # disconnect u from v in G, with this information:
... cutset =set()
>>> for x, nbrs in ((n, G[n]) for nin U):
... cutset.update((x, y) for yin nbrs if yin V)
>>> # Because we have set the capacities of all edges to 1
(continues on next page)
330 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
... # the cutset contains ten edges
... len(cutset)
10
>>> # You can use any maximum flow algorithm for the underlying
... # flow computations using the argument flow_func
... from networkx.algorithms import flow
>>> T=nx.gomory_hu_tree(G, flow_func=flow.boykov_kolmogorov)
>>> cut_value, edge =minimum_edge_weight_in_shortest_path(T, u, v)
>>> cut_value
10
>>> nx.minimum_cut_value(G, u, v, flow_func=flow.boykov_kolmogorov)
10
Notes
This implementation is based on Gusfield approach1to compute Comory-Hu trees, which does not require node
contractions and has the same computational complexity than the original method.
See also:
minimum_cut(),maximum_flow()
References
3.28.8 Utils
build_residual_network(G, capacity) Build a residual network and initialize a zero flow.
networkx.algorithms.flow.build_residual_network
build_residual_network(G,capacity)
Build a residual network and initialize a zero flow.
The residual network Rfrom an input graph Ghas the same nodes as G.Ris a DiGraph that contains a pair of
edges (u, v) and (v, u) iff (u, v) is not a self-loop, and at least one of (u, v) and (v, u) exists in
G.
For each edge (u, v) in R,R[u][v]['capacity'] is equal to the capacity of (u, v) in Gif it exists in
Gor zero otherwise. If the capacity is infinite, R[u][v]['capacity'] will have a high arbitrary finite value
that does not affect the solution of the problem. This value is stored in R.graph['inf']. For each edge (u,
v) in R,R[u][v]['flow'] represents the flow function of (u, v) and satisfies R[u][v]['flow']
== -R[v][u]['flow'].
The flow value, defined as the total flow into t, the sink, is stored in R.graph['flow_value']. If
cutoff is not specified, reachability to tusing only edges (u, v) such that R[u][v]['flow'] <
R[u][v]['capacity'] induces a minimum s-tcut.
3.28.9 Network Simplex
1Gusfield D: Very simple methods for all pairs network flow analysis. SIAM J Comput 19(1):143-155, 1990.
3.28. Flows 331

NetworkX Reference, Release 2.3rc1.dev20181203210840
network_simplex(G[, demand, capacity, weight]) Find a minimum cost flow satisfying all demands in di-
graph G.
min_cost_flow_cost(G[, demand, capacity,
weight])
Find the cost of a minimum cost flow satisfying all de-
mands in digraph G.
min_cost_flow(G[, demand, capacity, weight]) Return a minimum cost flow satisfying all demands in
digraph G.
cost_of_flow(G, flowDict[, weight]) Compute the cost of the flow given by flowDict on graph
G.
max_flow_min_cost(G, s, t[, capacity, weight]) Return a maximum (s, t)-flow of minimum cost.
networkx.algorithms.flow.network_simplex
network_simplex(G,demand=’demand’,capacity=’capacity’,weight=’weight’)
Find a minimum cost flow satisfying all demands in digraph G.
This is a primal network simplex algorithm that uses the leaving arc rule to prevent cycling.
G is a digraph with edge costs and capacities and in which nodes have demand, i.e., they want to send or receive
some amount of flow. A negative demand means that the node wants to send flow, a positive demand means
that the node want to receive flow. A flow on the digraph G satisfies all demand if the net flow into each node is
equal to the demand of that node.
Parameters
•G(NetworkX graph) – DiGraph on which a minimum cost flow satisfying all demands is to
be found.
•demand (string) – Nodes of the graph G are expected to have an attribute demand that indi-
cates how much flow a node wants to send (negative demand) or receive (positive demand).
Note that the sum of the demands should be 0 otherwise the problem in not feasible. If this
attribute is not present, a node is considered to have 0 demand. Default value: ‘demand’.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•weight (string) – Edges of the graph G are expected to have an attribute weight that indicates
the cost incurred by sending one unit of flow on that edge. If not present, the weight is
considered to be 0. Default value: ‘weight’.
Returns
•flowCost (integer, float) – Cost of a minimum cost flow satisfying all demands.
•flowDict (dictionary) – Dictionary of dictionaries keyed by nodes such that flowDict[u][v]
is the flow edge (u, v).
Raises
•NetworkXError – This exception is raised if the input graph is not directed, not con-
nected or is a multigraph.
•NetworkXUnfeasible – This exception is raised in the following situations:
–The sum of the demands is not zero. Then, there is no flow satisfying all demands.
–There is no flow satisfying all demand.
•NetworkXUnbounded – This exception is raised if the digraph G has a cycle of negative
cost and infinite capacity. Then, the cost of a flow satisfying all demands is unbounded
below.
332 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This algorithm is not guaranteed to work if edge weights or demands are floating point numbers (overflows and
roundoff errors can cause problems). As a workaround you can use integer numbers by multiplying the relevant
edge attributes by a convenient constant factor (eg 100).
See also:
cost_of_flow(),max_flow_min_cost(),min_cost_flow(),min_cost_flow_cost()
Examples
A simple example of a min cost flow problem.
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_node('a', demand=-5)
>>> G.add_node('d', demand=5)
>>> G.add_edge('a','b', weight=3, capacity=4)
>>> G.add_edge('a','c', weight=6, capacity=10)
>>> G.add_edge('b','d', weight=1, capacity=9)
>>> G.add_edge('c','d', weight=2, capacity=5)
>>> flowCost, flowDict =nx.network_simplex(G)
>>> flowCost
24
>>> flowDict # doctest: +SKIP
{'a': {'c': 1, 'b': 4}, 'c': {'d': 1}, 'b': {'d': 4}, 'd': {}}
The mincost flow algorithm can also be used to solve shortest path problems. To find the shortest path between
two nodes u and v, give all edges an infinite capacity, give node u a demand of -1 and node v a demand a 1. Then
run the network simplex. The value of a min cost flow will be the distance between u and v and edges carrying
positive flow will indicate the path.
>>> G=nx.DiGraph()
>>> G.add_weighted_edges_from([('s','u' ,10), ('s' ,'x' ,5),
... ('u','v' ,1), ('u' ,'x' ,2),
... ('v','y' ,1), ('x' ,'u' ,3),
... ('x','v' ,5), ('x' ,'y' ,2),
... ('y','s' ,7), ('y' ,'v' ,6)])
>>> G.add_node('s', demand = -1)
>>> G.add_node('v', demand =1)
>>> flowCost, flowDict =nx.network_simplex(G)
>>> flowCost == nx.shortest_path_length(G, 's','v', weight='weight')
True
>>> sorted([(u, v) for uin flowDict for vin flowDict[u] if flowDict[u][v] >0])
[('s', 'x'), ('u', 'v'), ('x', 'u')]
>>> nx.shortest_path(G, 's','v', weight ='weight')
['s', 'x', 'u', 'v']
It is possible to change the name of the attributes used for the algorithm.
>>> G=nx.DiGraph()
>>> G.add_node('p', spam=-4)
>>> G.add_node('q', spam=2)
>>> G.add_node('a', spam=-2)
>>> G.add_node('d', spam=-1)
>>> G.add_node('t', spam=2)
(continues on next page)
3.28. Flows 333

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.add_node('w', spam=3)
>>> G.add_edge('p','q', cost=7, vacancies=5)
>>> G.add_edge('p','a', cost=1, vacancies=4)
>>> G.add_edge('q','d', cost=2, vacancies=3)
>>> G.add_edge('t','q', cost=1, vacancies=2)
>>> G.add_edge('a','t', cost=2, vacancies=4)
>>> G.add_edge('d','w', cost=3, vacancies=4)
>>> G.add_edge('t','w', cost=4, vacancies=1)
>>> flowCost, flowDict =nx.network_simplex(G, demand='spam',
... capacity='vacancies',
... weight='cost')
>>> flowCost
37
>>> flowDict # doctest: +SKIP
{'a': {'t': 4}, 'd': {'w': 2}, 'q': {'d': 1}, 'p': {'q': 2, 'a': 2}, 't': {'q': 1,
˓→'w': 1}, 'w': {}}
References
networkx.algorithms.flow.min_cost_flow_cost
min_cost_flow_cost(G,demand=’demand’,capacity=’capacity’,weight=’weight’)
Find the cost of a minimum cost flow satisfying all demands in digraph G.
G is a digraph with edge costs and capacities and in which nodes have demand, i.e., they want to send or receive
some amount of flow. A negative demand means that the node wants to send flow, a positive demand means
that the node want to receive flow. A flow on the digraph G satisfies all demand if the net flow into each node is
equal to the demand of that node.
Parameters
•G(NetworkX graph) – DiGraph on which a minimum cost flow satisfying all demands is to
be found.
•demand (string) – Nodes of the graph G are expected to have an attribute demand that indi-
cates how much flow a node wants to send (negative demand) or receive (positive demand).
Note that the sum of the demands should be 0 otherwise the problem in not feasible. If this
attribute is not present, a node is considered to have 0 demand. Default value: ‘demand’.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•weight (string) – Edges of the graph G are expected to have an attribute weight that indicates
the cost incurred by sending one unit of flow on that edge. If not present, the weight is
considered to be 0. Default value: ‘weight’.
Returns flowCost – Cost of a minimum cost flow satisfying all demands.
Return type integer, float
Raises
•NetworkXError – This exception is raised if the input graph is not directed or not con-
nected.
•NetworkXUnfeasible – This exception is raised in the following situations:
–The sum of the demands is not zero. Then, there is no flow satisfying all demands.
334 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
–There is no flow satisfying all demand.
•NetworkXUnbounded – This exception is raised if the digraph G has a cycle of negative
cost and infinite capacity. Then, the cost of a flow satisfying all demands is unbounded
below.
See also:
cost_of_flow(),max_flow_min_cost(),min_cost_flow(),network_simplex()
Notes
This algorithm is not guaranteed to work if edge weights or demands are floating point numbers (overflows and
roundoff errors can cause problems). As a workaround you can use integer numbers by multiplying the relevant
edge attributes by a convenient constant factor (eg 100).
Examples
A simple example of a min cost flow problem.
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_node('a', demand = -5)
>>> G.add_node('d', demand =5)
>>> G.add_edge('a','b', weight =3, capacity =4)
>>> G.add_edge('a','c', weight =6, capacity =10)
>>> G.add_edge('b','d', weight =1, capacity =9)
>>> G.add_edge('c','d', weight =2, capacity =5)
>>> flowCost =nx.min_cost_flow_cost(G)
>>> flowCost
24
networkx.algorithms.flow.min_cost_flow
min_cost_flow(G,demand=’demand’,capacity=’capacity’,weight=’weight’)
Return a minimum cost flow satisfying all demands in digraph G.
G is a digraph with edge costs and capacities and in which nodes have demand, i.e., they want to send or receive
some amount of flow. A negative demand means that the node wants to send flow, a positive demand means
that the node want to receive flow. A flow on the digraph G satisfies all demand if the net flow into each node is
equal to the demand of that node.
Parameters
•G(NetworkX graph) – DiGraph on which a minimum cost flow satisfying all demands is to
be found.
•demand (string) – Nodes of the graph G are expected to have an attribute demand that indi-
cates how much flow a node wants to send (negative demand) or receive (positive demand).
Note that the sum of the demands should be 0 otherwise the problem in not feasible. If this
attribute is not present, a node is considered to have 0 demand. Default value: ‘demand’.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
3.28. Flows 335

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (string) – Edges of the graph G are expected to have an attribute weight that indicates
the cost incurred by sending one unit of flow on that edge. If not present, the weight is
considered to be 0. Default value: ‘weight’.
Returns flowDict – Dictionary of dictionaries keyed by nodes such that flowDict[u][v] is the flow
edge (u, v).
Return type dictionary
Raises
•NetworkXError – This exception is raised if the input graph is not directed or not con-
nected.
•NetworkXUnfeasible – This exception is raised in the following situations:
–The sum of the demands is not zero. Then, there is no flow satisfying all demands.
–There is no flow satisfying all demand.
•NetworkXUnbounded – This exception is raised if the digraph G has a cycle of negative
cost and infinite capacity. Then, the cost of a flow satisfying all demands is unbounded
below.
See also:
cost_of_flow(),max_flow_min_cost(),min_cost_flow_cost(),network_simplex()
Notes
This algorithm is not guaranteed to work if edge weights or demands are floating point numbers (overflows and
roundoff errors can cause problems). As a workaround you can use integer numbers by multiplying the relevant
edge attributes by a convenient constant factor (eg 100).
Examples
A simple example of a min cost flow problem.
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_node('a', demand = -5)
>>> G.add_node('d', demand =5)
>>> G.add_edge('a','b', weight =3, capacity =4)
>>> G.add_edge('a','c', weight =6, capacity =10)
>>> G.add_edge('b','d', weight =1, capacity =9)
>>> G.add_edge('c','d', weight =2, capacity =5)
>>> flowDict =nx.min_cost_flow(G)
networkx.algorithms.flow.cost_of_flow
cost_of_flow(G,flowDict,weight=’weight’)
Compute the cost of the flow given by flowDict on graph G.
Note that this function does not check for the validity of the flow flowDict. This function will fail if the graph G
and the flow don’t have the same edge set.
Parameters
336 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(NetworkX graph) – DiGraph on which a minimum cost flow satisfying all demands is to
be found.
•weight (string) – Edges of the graph G are expected to have an attribute weight that indicates
the cost incurred by sending one unit of flow on that edge. If not present, the weight is
considered to be 0. Default value: ‘weight’.
•flowDict (dictionary) – Dictionary of dictionaries keyed by nodes such that flowDict[u][v]
is the flow edge (u, v).
Returns cost – The total cost of the flow. This is given by the sum over all edges of the product of
the edge’s flow and the edge’s weight.
Return type Integer, float
See also:
max_flow_min_cost(),min_cost_flow(),min_cost_flow_cost(),network_simplex()
Notes
This algorithm is not guaranteed to work if edge weights or demands are floating point numbers (overflows and
roundoff errors can cause problems). As a workaround you can use integer numbers by multiplying the relevant
edge attributes by a convenient constant factor (eg 100).
networkx.algorithms.flow.max_flow_min_cost
max_flow_min_cost(G,s,t,capacity=’capacity’,weight=’weight’)
Return a maximum (s, t)-flow of minimum cost.
G is a digraph with edge costs and capacities. There is a source node s and a sink node t. This function finds a
maximum flow from s to t whose total cost is minimized.
Parameters
•G(NetworkX graph) – DiGraph on which a minimum cost flow satisfying all demands is to
be found.
•s(node label) – Source of the flow.
•t(node label) – Destination of the flow.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•weight (string) – Edges of the graph G are expected to have an attribute weight that indicates
the cost incurred by sending one unit of flow on that edge. If not present, the weight is
considered to be 0. Default value: ‘weight’.
Returns flowDict – Dictionary of dictionaries keyed by nodes such that flowDict[u][v] is the flow
edge (u, v).
Return type dictionary
Raises
•NetworkXError – This exception is raised if the input graph is not directed or not con-
nected.
3.28. Flows 337

NetworkX Reference, Release 2.3rc1.dev20181203210840
•NetworkXUnbounded – This exception is raised if there is an infinite capacity path from
s to t in G. In this case there is no maximum flow. This exception is also raised if the digraph
G has a cycle of negative cost and infinite capacity. Then, the cost of a flow is unbounded
below.
See also:
cost_of_flow(),min_cost_flow(),min_cost_flow_cost(),network_simplex()
Notes
This algorithm is not guaranteed to work if edge weights or demands are floating point numbers (overflows and
roundoff errors can cause problems). As a workaround you can use integer numbers by multiplying the relevant
edge attributes by a convenient constant factor (eg 100).
Examples
>>> G=nx.DiGraph()
>>> G.add_edges_from([(1,2, {'capacity':12,'weight':4}),
... (1,3, {'capacity':20,'weight':6}),
... (2,3, {'capacity':6,'weight':-3}),
... (2,6, {'capacity':14,'weight':1}),
... (3,4, {'weight':9}),
... (3,5, {'capacity':10,'weight':5}),
... (4,2, {'capacity':19,'weight':13}),
... (4,5, {'capacity':4,'weight':0}),
... (5,7, {'capacity':28,'weight':2}),
... (6,5, {'capacity':11,'weight':1}),
... (6,7, {'weight':8}),
... (7,4, {'capacity':6,'weight':6})])
>>> mincostFlow =nx.max_flow_min_cost(G, 1,7)
>>> mincost =nx.cost_of_flow(G, mincostFlow)
>>> mincost
373
>>> from networkx.algorithms.flow import maximum_flow
>>> maxFlow =maximum_flow(G, 1,7)[1]
>>> nx.cost_of_flow(G, maxFlow) >= mincost
True
>>> mincostFlowValue =(sum((mincostFlow[u][7]for uin G.predecessors(7)))
... -sum((mincostFlow[7][v] for vin G.successors(7))))
>>> mincostFlowValue == nx.maximum_flow_value(G, 1,7)
True
3.28.10 Capacity Scaling Minimum Cost Flow
capacity_scaling(G[, demand, capacity, . . . ]) Find a minimum cost flow satisfying all demands in di-
graph G.
networkx.algorithms.flow.capacity_scaling
capacity_scaling(G,demand=’demand’,capacity=’capacity’,weight=’weight’,heap=<class ’net-
workx.utils.heaps.BinaryHeap’>)
Find a minimum cost flow satisfying all demands in digraph G.
338 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
This is a capacity scaling successive shortest augmenting path algorithm.
G is a digraph with edge costs and capacities and in which nodes have demand, i.e., they want to send or receive
some amount of flow. A negative demand means that the node wants to send flow, a positive demand means
that the node want to receive flow. A flow on the digraph G satisfies all demand if the net flow into each node is
equal to the demand of that node.
Parameters
•G(NetworkX graph) – DiGraph or MultiDiGraph on which a minimum cost flow satisfying
all demands is to be found.
•demand (string) – Nodes of the graph G are expected to have an attribute demand that indi-
cates how much flow a node wants to send (negative demand) or receive (positive demand).
Note that the sum of the demands should be 0 otherwise the problem in not feasible. If this
attribute is not present, a node is considered to have 0 demand. Default value: ‘demand’.
•capacity (string) – Edges of the graph G are expected to have an attribute capacity that
indicates how much flow the edge can support. If this attribute is not present, the edge is
considered to have infinite capacity. Default value: ‘capacity’.
•weight (string) – Edges of the graph G are expected to have an attribute weight that indicates
the cost incurred by sending one unit of flow on that edge. If not present, the weight is
considered to be 0. Default value: ‘weight’.
•heap (class) – Type of heap to be used in the algorithm. It should be a subclass of MinHeap
or implement a compatible interface.
If a stock heap implementation is to be used, BinaryHeap is recommended over
PairingHeap for Python implementations without optimized attribute accesses (e.g.,
CPython) despite a slower asymptotic running time. For Python implementations with opti-
mized attribute accesses (e.g., PyPy), PairingHeap provides better performance. Default
value: BinaryHeap.
Returns
•flowCost (integer) – Cost of a minimum cost flow satisfying all demands.
•flowDict (dictionary) – If G is a digraph, a dict-of-dicts keyed by nodes such that flow-
Dict[u][v] is the flow on edge (u, v). If G is a MultiDiGraph, a dict-of-dicts-of-dicts keyed
by nodes so that flowDict[u][v][key] is the flow on edge (u, v, key).
Raises
•NetworkXError – This exception is raised if the input graph is not directed, not con-
nected.
•NetworkXUnfeasible – This exception is raised in the following situations:
–The sum of the demands is not zero. Then, there is no flow satisfying all demands.
–There is no flow satisfying all demand.
•NetworkXUnbounded – This exception is raised if the digraph G has a cycle of negative
cost and infinite capacity. Then, the cost of a flow satisfying all demands is unbounded
below.
Notes
This algorithm does not work if edge weights are floating-point numbers.
See also:
3.28. Flows 339

NetworkX Reference, Release 2.3rc1.dev20181203210840
network_simplex()
Examples
A simple example of a min cost flow problem.
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_node('a', demand = -5)
>>> G.add_node('d', demand =5)
>>> G.add_edge('a','b', weight =3, capacity =4)
>>> G.add_edge('a','c', weight =6, capacity =10)
>>> G.add_edge('b','d', weight =1, capacity =9)
>>> G.add_edge('c','d', weight =2, capacity =5)
>>> flowCost, flowDict =nx.capacity_scaling(G)
>>> flowCost
24
>>> flowDict # doctest: +SKIP
{'a': {'c': 1, 'b': 4}, 'c': {'d': 1}, 'b': {'d': 4}, 'd': {}}
It is possible to change the name of the attributes used for the algorithm.
>>> G=nx.DiGraph()
>>> G.add_node('p', spam = -4)
>>> G.add_node('q', spam =2)
>>> G.add_node('a', spam = -2)
>>> G.add_node('d', spam = -1)
>>> G.add_node('t', spam =2)
>>> G.add_node('w', spam =3)
>>> G.add_edge('p','q', cost =7, vacancies =5)
>>> G.add_edge('p','a', cost =1, vacancies =4)
>>> G.add_edge('q','d', cost =2, vacancies =3)
>>> G.add_edge('t','q', cost =1, vacancies =2)
>>> G.add_edge('a','t', cost =2, vacancies =4)
>>> G.add_edge('d','w', cost =3, vacancies =4)
>>> G.add_edge('t','w', cost =4, vacancies =1)
>>> flowCost, flowDict =nx.capacity_scaling(G, demand ='spam',
... capacity ='vacancies',
... weight ='cost')
>>> flowCost
37
>>> flowDict # doctest: +SKIP
{'a': {'t': 4}, 'd': {'w': 2}, 'q': {'d': 1}, 'p': {'q': 2, 'a': 2}, 't': {'q': 1,
˓→'w': 1}, 'w': {}}
3.29 Graphical degree sequence
Test sequences for graphiness.
is_graphical(sequence[, method]) Returns True if sequence is a valid degree sequence.
is_digraphical(in_sequence, out_sequence) Returns True if some directed graph can realize the in-
and out-degree sequences.
Continued on next page
340 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 96 – continued from previous page
is_multigraphical(sequence) Returns True if some multigraph can realize the se-
quence.
is_pseudographical(sequence) Returns True if some pseudograph can realize the se-
quence.
is_valid_degree_sequence_havel_hakimi(. . . )Returns True if deg_sequence can be realized by a sim-
ple graph.
is_valid_degree_sequence_erdos_gallai(. . . )Returns True if deg_sequence can be realized by a sim-
ple graph.
3.29.1 networkx.algorithms.graphical.is_graphical
is_graphical(sequence,method=’eg’)
Returns True if sequence is a valid degree sequence.
A degree sequence is valid if some graph can realize it.
Parameters
•sequence (list or iterable container) – A sequence of integer node degrees
•method (“eg” | “hh”) – The method used to validate the degree sequence. “eg” corresponds
to the Erd˝
os-Gallai algorithm, and “hh” to the Havel-Hakimi algorithm.
Returns valid – True if the sequence is a valid degree sequence and False if not.
Return type bool
Examples
>>> G=nx.path_graph(4)
>>> sequence =(d for n, d in G.degree())
>>> nx.is_graphical(sequence)
True
References
Erd˝
os-Gallai [?], [?]
Havel-Hakimi [?], [?], [?]
3.29.2 networkx.algorithms.graphical.is_digraphical
is_digraphical(in_sequence,out_sequence)
Returns True if some directed graph can realize the in- and out-degree sequences.
Parameters
•in_sequence (list or iterable container) – A sequence of integer node in-degrees
•out_sequence (list or iterable container) – A sequence of integer node out-degrees
Returns valid – True if in and out-sequences are digraphic False if not.
Return type bool
3.29. Graphical degree sequence 341

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This algorithm is from Kleitman and Wang1. The worst case runtime is 𝑂(𝑠×log 𝑛)where 𝑠and 𝑛are the sum
and length of the sequences respectively.
References
3.29.3 networkx.algorithms.graphical.is_multigraphical
is_multigraphical(sequence)
Returns True if some multigraph can realize the sequence.
Parameters sequence (list) – A list of integers
Returns valid – True if deg_sequence is a multigraphic degree sequence and False if not.
Return type bool
Notes
The worst-case run time is 𝑂(𝑛)where 𝑛is the length of the sequence.
References
3.29.4 networkx.algorithms.graphical.is_pseudographical
is_pseudographical(sequence)
Returns True if some pseudograph can realize the sequence.
Every nonnegative integer sequence with an even sum is pseudographical (see1).
Parameters sequence (list or iterable container) – A sequence of integer node degrees
Returns valid – True if the sequence is a pseudographic degree sequence and False if not.
Return type bool
Notes
The worst-case run time is 𝑂(𝑛)where n is the length of the sequence.
References
3.29.5 networkx.algorithms.graphical.is_valid_degree_sequence_havel_hakimi
is_valid_degree_sequence_havel_hakimi(deg_sequence)
Returns True if deg_sequence can be realized by a simple graph.
The validation proceeds using the Havel-Hakimi theorem. Worst-case run time is 𝑂(𝑠)where 𝑠is the sum of
the sequence.
1D.J. Kleitman and D.L. Wang Algorithms for Constructing Graphs and Digraphs with Given Valences and Factors, Discrete Mathematics,
6(1), pp. 79-88 (1973)
1F. Boesch and F. Harary. “Line removal algorithms for graphs and their degree lists”, IEEE Trans. Circuits and Systems, CAS-23(12), pp.
778-782 (1976).
342 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters deg_sequence (list) – A list of integers where each element specifies the degree of a
node in a graph.
Returns valid – True if deg_sequence is graphical and False if not.
Return type bool
Notes
The ZZ condition says that for the sequence d if
|𝑑|>=(max(𝑑) + min(𝑑) + 1)2
4*min(𝑑)
then d is graphical. This was shown in Theorem 6 in1.
References
[?], [?], [?]
3.29.6 networkx.algorithms.graphical.is_valid_degree_sequence_erdos_gallai
is_valid_degree_sequence_erdos_gallai(deg_sequence)
Returns True if deg_sequence can be realized by a simple graph.
The validation is done using the Erd˝
os-Gallai theorem [?].
Parameters deg_sequence (list) – A list of integers
Returns valid – True if deg_sequence is graphical and False if not.
Return type bool
Notes
This implementation uses an equivalent form of the Erd˝
os-Gallai criterion. Worst-case run time is 𝑂(𝑛)where
𝑛is the length of the sequence.
Specifically, a sequence d is graphical if and only if the sum of the sequence is even and for all strong indices k
in the sequence,
𝑘
𝑖=1
𝑑𝑖≤𝑘(𝑘−1) +
𝑛
𝑗=𝑘+1
min(𝑑𝑖, 𝑘) = 𝑘(𝑛−1) −(𝑘
𝑘−1
𝑗=0
𝑛𝑗−
𝑘−1
𝑗=0
𝑗𝑛𝑗)
A strong index k is any index where d_k >= k and the value n_j is the number of occurrences of j in d. The
maximal strong index is called the Durfee index.
This particular rearrangement comes from the proof of Theorem 3 in2.
The ZZ condition says that for the sequence d if
|𝑑|>=(max(𝑑) + min(𝑑) + 1)2
4*min(𝑑)
1I.E. Zverovich and V.E. Zverovich. “Contributions to the theory of graphic sequences”, Discrete Mathematics, 105, pp. 292-303 (1992).
2I.E. Zverovich and V.E. Zverovich. “Contributions to the theory of graphic sequences”, Discrete Mathematics, 105, pp. 292-303 (1992).
3.29. Graphical degree sequence 343

NetworkX Reference, Release 2.3rc1.dev20181203210840
then d is graphical. This was shown in Theorem 6 in2.
References
[?], [?]
3.30 Hierarchy
Flow Hierarchy.
flow_hierarchy(G[, weight]) Returns the flow hierarchy of a directed network.
3.30.1 networkx.algorithms.hierarchy.flow_hierarchy
flow_hierarchy(G,weight=None)
Returns the flow hierarchy of a directed network.
Flow hierarchy is defined as the fraction of edges not participating in cycles in a directed graph1.
Parameters
•G(DiGraph or MultiDiGraph) – A directed graph
•weight (key,optional (default=None)) – Attribute to use for node weights. If None the
weight defaults to 1.
Returns h – Flow hierarchy value
Return type float
Notes
The algorithm described in1computes the flow hierarchy through exponentiation of the adjacency matrix. This
function implements an alternative approach that finds strongly connected components. An edge is in a cycle if
and only if it is in a strongly connected component, which can be found in 𝑂(𝑚)time using Tarjan’s algorithm.
References
3.31 Hybrid
Provides functions for finding and testing for locally (k, l)-connected graphs.
kl_connected_subgraph(G, k, l[, low_memory,
...])
Returns the maximum locally (k, l)-connected sub-
graph of G.
is_kl_connected(G, k, l[, low_memory]) Returns True if and only if Gis locally (k, l)-
connected.
1Luo, J.; Magee, C.L. (2011), Detecting evolving patterns of self-organizing networks by flow hierarchy measurement, Complexity, Volume 16
Issue 6 53-61. DOI: 10.1002/cplx.20368 http://web.mit.edu/~cmagee/www/documents/28-DetectingEvolvingPatterns_FlowHierarchy.pdf
344 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.31.1 networkx.algorithms.hybrid.kl_connected_subgraph
kl_connected_subgraph(G,k,l,low_memory=False,same_as_graph=False)
Returns the maximum locally (k, l)-connected subgraph of G.
A graph is locally (k, l)-connected if for each edge (u, v) in the graph there are at least ledge-disjoint
paths of length at most kjoining uto v.
Parameters
•G(NetworkX graph) – The graph in which to find a maximum locally (k, l)-connected
subgraph.
•k(integer) – The maximum length of paths to consider. A higher number means a looser
connectivity requirement.
•l(integer) – The number of edge-disjoint paths. A higher number means a stricter connec-
tivity requirement.
•low_memory (bool) – If this is True, this function uses an algorithm that uses slightly more
time but less memory.
•same_as_graph (bool) – If True then return a tuple of the form (H, is_same), where
His the maximum locally (k, l)-connected subgraph and is_same is a Boolean repre-
senting whether Gis locally (k, l)-connected (and hence, whether His simply a copy of
the input graph G).
Returns If same_as_graph is True, then this function returns a two-tuple as described above.
Otherwise, it returns only the maximum locally (k, l)-connected subgraph.
Return type NetworkX graph or two-tuple
See also:
is_kl_connected()
References
3.31.2 networkx.algorithms.hybrid.is_kl_connected
is_kl_connected(G,k,l,low_memory=False)
Returns True if and only if Gis locally (k, l)-connected.
A graph is locally (k, l)-connected if for each edge (u, v) in the graph there are at least ledge-disjoint
paths of length at most kjoining uto v.
Parameters
•G(NetworkX graph) – The graph to test for local (k, l)-connectedness.
•k(integer) – The maximum length of paths to consider. A higher number means a looser
connectivity requirement.
•l(integer) – The number of edge-disjoint paths. A higher number means a stricter connec-
tivity requirement.
•low_memory (bool) – If this is True, this function uses an algorithm that uses slightly more
time but less memory.
Returns Whether the graph is locally (k, l)-connected subgraph.
Return type bool
3.31. Hybrid 345

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
kl_connected_subgraph()
References
3.32 Isolates
Functions for identifying isolate (degree zero) nodes.
is_isolate(G, n) Determines whether a node is an isolate.
isolates(G) Iterator over isolates in the graph.
number_of_isolates(G) Returns the number of isolates in the graph.
3.32.1 networkx.algorithms.isolate.is_isolate
is_isolate(G,n)
Determines whether a node is an isolate.
An isolate is a node with no neighbors (that is, with degree zero). For directed graphs, this means no in-neighbors
and no out-neighbors.
Parameters
•G(NetworkX graph)
•n(node) – A node in G.
Returns is_isolate – True if and only if nhas no neighbors.
Return type bool
Examples
>>> G=nx.Graph()
>>> G.add_edge(1,2)
>>> G.add_node(3)
>>> nx.is_isolate(G,2)
False
>>> nx.is_isolate(G,3)
True
3.32.2 networkx.algorithms.isolate.isolates
isolates(G)
Iterator over isolates in the graph.
An isolate is a node with no neighbors (that is, with degree zero). For directed graphs, this means no in-neighbors
and no out-neighbors.
Parameters G (NetworkX graph)
Returns An iterator over the isolates of G.
Return type iterator
346 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
To get a list of all isolates of a graph, use the list constructor:
>>> G=nx.Graph()
>>> G.add_edge(1,2)
>>> G.add_node(3)
>>> list(nx.isolates(G))
[3]
To remove all isolates in the graph, first create a list of the isolates, then use Graph.
remove_nodes_from():
>>> G.remove_nodes_from(list(nx.isolates(G)))
>>> list(G)
[1, 2]
For digraphs, isolates have zero in-degree and zero out_degre:
>>> G=nx.DiGraph([(0,1), (1,2)])
>>> G.add_node(3)
>>> list(nx.isolates(G))
[3]
3.32.3 networkx.algorithms.isolate.number_of_isolates
number_of_isolates(G)
Returns the number of isolates in the graph.
An isolate is a node with no neighbors (that is, with degree zero). For directed graphs, this means no in-neighbors
and no out-neighbors.
Parameters G (NetworkX graph)
Returns The number of degree zero nodes in the graph G.
Return type int
3.33 Isomorphism
is_isomorphic(G1, G2[, node_match,
edge_match])
Returns True if the graphs G1 and G2 are isomorphic
and False otherwise.
could_be_isomorphic(G1, G2) Returns False if graphs are definitely not isomorphic.
fast_could_be_isomorphic(G1, G2) Returns False if graphs are definitely not isomorphic.
faster_could_be_isomorphic(G1, G2) Returns False if graphs are definitely not isomorphic.
3.33.1 networkx.algorithms.isomorphism.is_isomorphic
is_isomorphic(G1,G2,node_match=None,edge_match=None)
Returns True if the graphs G1 and G2 are isomorphic and False otherwise.
Parameters
•G1, G2 (graphs) – The two graphs G1 and G2 must be the same type.
3.33. Isomorphism 347

NetworkX Reference, Release 2.3rc1.dev20181203210840
•node_match (callable) – A function that returns True if node n1 in G1 and n2 in G2 should
be considered equal during the isomorphism test. If node_match is not specified then node
attributes are not considered.
The function will be called like
node_match(G1.nodes[n1], G2.nodes[n2]).
That is, the function will receive the node attribute dictionaries for n1 and n2 as inputs.
•edge_match (callable) – A function that returns True if the edge attribute dictionary for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during the
isomorphism test. If edge_match is not specified then edge attributes are not considered.
The function will be called like
edge_match(G1[u1][v1], G2[u2][v2]).
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation.
Notes
Uses the vf2 algorithm1.
Examples
>>> import networkx.algorithms.isomorphism as iso
For digraphs G1 and G2, using ‘weight’ edge attribute (default: 1)
>>> G1 =nx.DiGraph()
>>> G2 =nx.DiGraph()
>>> nx.add_path(G1, [1,2,3,4], weight=1)
>>> nx.add_path(G2, [10,20,30,40], weight=2)
>>> em =iso.numerical_edge_match('weight',1)
>>> nx.is_isomorphic(G1, G2) # no weights considered
True
>>> nx.is_isomorphic(G1, G2, edge_match=em) # match weights
False
For multidigraphs G1 and G2, using ‘fill’ node attribute (default: ‘’)
>>> G1 =nx.MultiDiGraph()
>>> G2 =nx.MultiDiGraph()
>>> G1.add_nodes_from([1,2,3], fill='red')
>>> G2.add_nodes_from([10,20,30,40], fill='red')
>>> nx.add_path(G1, [1,2,3,4], weight=3, linewidth=2.5)
>>> nx.add_path(G2, [10,20,30,40], weight=3)
>>> nm =iso.categorical_node_match('fill','red')
>>> nx.is_isomorphic(G1, G2, node_match=nm)
True
For multidigraphs G1 and G2, using ‘weight’ edge attribute (default: 7)
1L. P. Cordella, P. Foggia, C. Sansone, M. Vento, “An Improved Algorithm for Matching Large Graphs”, 3rd IAPR-TC15 Workshop on Graph-
based Representations in Pattern Recognition, Cuen, pp. 149-159, 2001. http://amalfi.dis.unina.it/graph/db/papers/vf-algorithm.pdf
348 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G1.add_edge(1,2, weight=7)
1
>>> G2.add_edge(10,20)
1
>>> em =iso.numerical_multiedge_match('weight',7, rtol=1e-6)
>>> nx.is_isomorphic(G1, G2, edge_match=em)
True
For multigraphs G1 and G2, using ‘weight’ and ‘linewidth’ edge attributes with default values 7 and 2.5. Also
using ‘fill’ node attribute with default value ‘red’.
>>> em =iso.numerical_multiedge_match(['weight','linewidth'], [7,2.5])
>>> nm =iso.categorical_node_match('fill','red')
>>> nx.is_isomorphic(G1, G2, edge_match=em, node_match=nm)
True
See also:
numerical_node_match(),numerical_edge_match(),numerical_multiedge_match(),
categorical_node_match(),categorical_edge_match(),categorical_multiedge_match()
References
3.33.2 networkx.algorithms.isomorphism.could_be_isomorphic
could_be_isomorphic(G1,G2)
Returns False if graphs are definitely not isomorphic. True does NOT guarantee isomorphism.
Parameters G1, G2 (graphs) – The two graphs G1 and G2 must be the same type.
Notes
Checks for matching degree, triangle, and number of cliques sequences.
3.33.3 networkx.algorithms.isomorphism.fast_could_be_isomorphic
fast_could_be_isomorphic(G1,G2)
Returns False if graphs are definitely not isomorphic.
True does NOT guarantee isomorphism.
Parameters G1, G2 (graphs) – The two graphs G1 and G2 must be the same type.
Notes
Checks for matching degree and triangle sequences.
3.33.4 networkx.algorithms.isomorphism.faster_could_be_isomorphic
faster_could_be_isomorphic(G1,G2)
Returns False if graphs are definitely not isomorphic.
True does NOT guarantee isomorphism.
3.33. Isomorphism 349

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters G1, G2 (graphs) – The two graphs G1 and G2 must be the same type.
Notes
Checks for matching degree sequences.
3.33.5 Advanced Interface to VF2 Algorithm
VF2 Algorithm
VF2 Algorithm
An implementation of VF2 algorithm for graph ismorphism testing.
The simplest interface to use this module is to call networkx.is_isomorphic().
Introduction
The GraphMatcher and DiGraphMatcher are responsible for matching graphs or directed graphs in a predetermined
manner. This usually means a check for an isomorphism, though other checks are also possible. For example, a
subgraph of one graph can be checked for isomorphism to a second graph.
Matching is done via syntactic feasibility. It is also possible to check for semantic feasibility. Feasibility, then, is
defined as the logical AND of the two functions.
To include a semantic check, the (Di)GraphMatcher class should be subclassed, and the semantic_feasibility() function
should be redefined. By default, the semantic feasibility function always returns True. The effect of this is that
semantics are not considered in the matching of G1 and G2.
Examples
Suppose G1 and G2 are isomorphic graphs. Verification is as follows:
>>> from networkx.algorithms import isomorphism
>>> G1 =nx.path_graph(4)
>>> G2 =nx.path_graph(4)
>>> GM =isomorphism.GraphMatcher(G1,G2)
>>> GM.is_isomorphic()
True
GM.mapping stores the isomorphism mapping from G1 to G2.
>>> GM.mapping
{0: 0, 1: 1, 2: 2, 3: 3}
Suppose G1 and G2 are isomorphic directed graphs graphs. Verification is as follows:
>>> G1 =nx.path_graph(4, create_using=nx.DiGraph())
>>> G2 =nx.path_graph(4, create_using=nx.DiGraph())
>>> DiGM =isomorphism.DiGraphMatcher(G1,G2)
>>> DiGM.is_isomorphic()
True
350 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
DiGM.mapping stores the isomorphism mapping from G1 to G2.
>>> DiGM.mapping
{0: 0, 1: 1, 2: 2, 3: 3}
Subgraph Isomorphism
Graph theory literature can be ambiguious about the meaning of the above statement, and we seek to clarify it now.
In the VF2 literature, a mapping M is said to be a graph-subgraph isomorphism iff M is an isomorphism between G2
and a subgraph of G1. Thus, to say that G1 and G2 are graph-subgraph isomorphic is to say that a subgraph of G1 is
isomorphic to G2.
Other literature uses the phrase ‘subgraph isomorphic’ as in ‘G1 does not have a subgraph isomorphic to G2’. Another
use is as an in adverb for isomorphic. Thus, to say that G1 and G2 are subgraph isomorphic is to say that a subgraph
of G1 is isomorphic to G2.
Finally, the term ‘subgraph’ can have multiple meanings. In this context, ‘subgraph’ always means a ‘node-induced
subgraph’. Edge-induced subgraph isomorphisms are not directly supported, but one should be able to perform the
check by making use of nx.line_graph(). For subgraphs which are not induced, the term ‘monomorphism’ is preferred
over ‘isomorphism’. Currently, it is not possible to check for monomorphisms.
Let G=(N,E) be a graph with a set of nodes N and set of edges E.
If G’=(N’,E’) is a subgraph, then: N’ is a subset of N E’ is a subset of E
If G’=(N’,E’) is a node-induced subgraph, then: N’ is a subset of N E’ is the subset of edges in E relating nodes in
N’
If G’=(N’,E’) is an edge-induced subgraph, then: N’ is the subset of nodes in N related by edges in E’ E’ is a subset
of E
References
[1] Luigi P. Cordella, Pasquale Foggia, Carlo Sansone, Mario Vento, “A (Sub)Graph Isomorphism Algorithm for
Matching Large Graphs”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, no. 10, pp.
1367-1372, Oct., 2004. http://ieeexplore.ieee.org/iel5/34/29305/01323804.pdf
[2] L. P. Cordella, P. Foggia, C. Sansone, M. Vento, “An Improved Algorithm for Matching Large Graphs”, 3rd
IAPR-TC15 Workshop on Graph-based Representations in Pattern Recognition, Cuen, pp. 149-159, 2001.
http://amalfi.dis.unina.it/graph/db/papers/vf-algorithm.pdf
See also:
syntactic_feasibliity,semantic_feasibility
Notes
The implementation handles both directed and undirected graphs as well as multigraphs.
In general, the subgraph isomorphism problem is NP-complete whereas the graph isomorphism problem is most likely
not NP-complete (although no polynomial-time algorithm is known to exist).
Graph Matcher
3.33. Isomorphism 351

NetworkX Reference, Release 2.3rc1.dev20181203210840
GraphMatcher.__init__(G1, G2[, node_match,
...])
Initialize graph matcher.
GraphMatcher.initialize() Reinitializes the state of the algorithm.
GraphMatcher.is_isomorphic() Returns True if G1 and G2 are isomorphic graphs.
GraphMatcher.subgraph_is_isomorphic() Returns True if a subgraph of G1 is isomorphic to G2.
GraphMatcher.isomorphisms_iter() Generator over isomorphisms between G1 and G2.
GraphMatcher.subgraph_isomorphisms_iter()Generator over isomorphisms between a subgraph of G1
and G2.
GraphMatcher.candidate_pairs_iter() Iterator over candidate pairs of nodes in G1 and G2.
GraphMatcher.match() Extends the isomorphism mapping.
GraphMatcher.semantic_feasibility(G1_node,
...)
Returns True if mapping G1_node to G2_node is se-
mantically feasible.
GraphMatcher.syntactic_feasibility(G1_node,
...)
Returns True if adding (G1_node, G2_node) is syntac-
tically feasible.
networkx.algorithms.isomorphism.GraphMatcher.__init__
GraphMatcher.__init__(G1,G2,node_match=None,edge_match=None)
Initialize graph matcher.
Parameters
•G1, G2 (graph) – The graphs to be tested.
•node_match (callable) – A function that returns True iff node n1 in G1 and n2 in G2 should
be considered equal during the isomorphism test. The function will be called like:
node_match(G1.nodes[n1], G2.nodes[n2])
That is, the function will receive the node attribute dictionaries of the nodes under consider-
ation. If None, then no attributes are considered when testing for an isomorphism.
•edge_match (callable) – A function that returns True iff the edge attribute dictionary for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during the
isomorphism test. The function will be called like:
edge_match(G1[u1][v1], G2[u2][v2])
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation. If None, then no attributes are considered when testing for an isomorphism.
networkx.algorithms.isomorphism.GraphMatcher.initialize
GraphMatcher.initialize()
Reinitializes the state of the algorithm.
This method should be redefined if using something other than GMState. If only subclassing GraphMatcher, a
redefinition is not necessary.
networkx.algorithms.isomorphism.GraphMatcher.is_isomorphic
GraphMatcher.is_isomorphic()
Returns True if G1 and G2 are isomorphic graphs.
352 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.isomorphism.GraphMatcher.subgraph_is_isomorphic
GraphMatcher.subgraph_is_isomorphic()
Returns True if a subgraph of G1 is isomorphic to G2.
networkx.algorithms.isomorphism.GraphMatcher.isomorphisms_iter
GraphMatcher.isomorphisms_iter()
Generator over isomorphisms between G1 and G2.
networkx.algorithms.isomorphism.GraphMatcher.subgraph_isomorphisms_iter
GraphMatcher.subgraph_isomorphisms_iter()
Generator over isomorphisms between a subgraph of G1 and G2.
networkx.algorithms.isomorphism.GraphMatcher.candidate_pairs_iter
GraphMatcher.candidate_pairs_iter()
Iterator over candidate pairs of nodes in G1 and G2.
networkx.algorithms.isomorphism.GraphMatcher.match
GraphMatcher.match()
Extends the isomorphism mapping.
This function is called recursively to determine if a complete isomorphism can be found between G1 and G2. It
cleans up the class variables after each recursive call. If an isomorphism is found, we yield the mapping.
networkx.algorithms.isomorphism.GraphMatcher.semantic_feasibility
GraphMatcher.semantic_feasibility(G1_node,G2_node)
Returns True if mapping G1_node to G2_node is semantically feasible.
networkx.algorithms.isomorphism.GraphMatcher.syntactic_feasibility
GraphMatcher.syntactic_feasibility(G1_node,G2_node)
Returns True if adding (G1_node, G2_node) is syntactically feasible.
This function returns True if it is adding the candidate pair to the current partial isomorphism mapping is
allowable. The addition is allowable if the inclusion of the candidate pair does not make it impossible for an
isomorphism to be found.
DiGraph Matcher
DiGraphMatcher.__init__(G1, G2[, . . . ]) Initialize graph matcher.
DiGraphMatcher.initialize() Reinitializes the state of the algorithm.
Continued on next page
3.33. Isomorphism 353

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 102 – continued from previous page
DiGraphMatcher.is_isomorphic() Returns True if G1 and G2 are isomorphic graphs.
DiGraphMatcher.subgraph_is_isomorphic() Returns True if a subgraph of G1 is isomorphic to G2.
DiGraphMatcher.isomorphisms_iter() Generator over isomorphisms between G1 and G2.
DiGraphMatcher.subgraph_isomorphisms_iter()Generator over isomorphisms between a subgraph of G1
and G2.
DiGraphMatcher.candidate_pairs_iter() Iterator over candidate pairs of nodes in G1 and G2.
DiGraphMatcher.match() Extends the isomorphism mapping.
DiGraphMatcher.semantic_feasibility(G1_node,
...)
Returns True if mapping G1_node to G2_node is se-
mantically feasible.
DiGraphMatcher.syntactic_feasibility(. . . )Returns True if adding (G1_node, G2_node) is syntac-
tically feasible.
networkx.algorithms.isomorphism.DiGraphMatcher.__init__
DiGraphMatcher.__init__(G1,G2,node_match=None,edge_match=None)
Initialize graph matcher.
Parameters
•G1, G2 (graph) – The graphs to be tested.
•node_match (callable) – A function that returns True iff node n1 in G1 and n2 in G2 should
be considered equal during the isomorphism test. The function will be called like:
node_match(G1.nodes[n1], G2.nodes[n2])
That is, the function will receive the node attribute dictionaries of the nodes under consider-
ation. If None, then no attributes are considered when testing for an isomorphism.
•edge_match (callable) – A function that returns True iff the edge attribute dictionary for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during the
isomorphism test. The function will be called like:
edge_match(G1[u1][v1], G2[u2][v2])
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation. If None, then no attributes are considered when testing for an isomorphism.
networkx.algorithms.isomorphism.DiGraphMatcher.initialize
DiGraphMatcher.initialize()
Reinitializes the state of the algorithm.
This method should be redefined if using something other than DiGMState. If only subclassing GraphMatcher,
a redefinition is not necessary.
networkx.algorithms.isomorphism.DiGraphMatcher.is_isomorphic
DiGraphMatcher.is_isomorphic()
Returns True if G1 and G2 are isomorphic graphs.
354 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.isomorphism.DiGraphMatcher.subgraph_is_isomorphic
DiGraphMatcher.subgraph_is_isomorphic()
Returns True if a subgraph of G1 is isomorphic to G2.
networkx.algorithms.isomorphism.DiGraphMatcher.isomorphisms_iter
DiGraphMatcher.isomorphisms_iter()
Generator over isomorphisms between G1 and G2.
networkx.algorithms.isomorphism.DiGraphMatcher.subgraph_isomorphisms_iter
DiGraphMatcher.subgraph_isomorphisms_iter()
Generator over isomorphisms between a subgraph of G1 and G2.
networkx.algorithms.isomorphism.DiGraphMatcher.candidate_pairs_iter
DiGraphMatcher.candidate_pairs_iter()
Iterator over candidate pairs of nodes in G1 and G2.
networkx.algorithms.isomorphism.DiGraphMatcher.match
DiGraphMatcher.match()
Extends the isomorphism mapping.
This function is called recursively to determine if a complete isomorphism can be found between G1 and G2. It
cleans up the class variables after each recursive call. If an isomorphism is found, we yield the mapping.
networkx.algorithms.isomorphism.DiGraphMatcher.semantic_feasibility
DiGraphMatcher.semantic_feasibility(G1_node,G2_node)
Returns True if mapping G1_node to G2_node is semantically feasible.
networkx.algorithms.isomorphism.DiGraphMatcher.syntactic_feasibility
DiGraphMatcher.syntactic_feasibility(G1_node,G2_node)
Returns True if adding (G1_node, G2_node) is syntactically feasible.
This function returns True if it is adding the candidate pair to the current partial isomorphism mapping is
allowable. The addition is allowable if the inclusion of the candidate pair does not make it impossible for an
isomorphism to be found.
Match helpers
3.33. Isomorphism 355

NetworkX Reference, Release 2.3rc1.dev20181203210840
categorical_node_match(attr, default) Returns a comparison function for a categorical node
attribute.
categorical_edge_match(attr, default) Returns a comparison function for a categorical edge at-
tribute.
categorical_multiedge_match(attr, default) Returns a comparison function for a categorical edge at-
tribute.
numerical_node_match(attr, default[, rtol, atol]) Returns a comparison function for a numerical node at-
tribute.
numerical_edge_match(attr, default[, rtol, atol]) Returns a comparison function for a numerical edge at-
tribute.
numerical_multiedge_match(attr, default[,
...])
Returns a comparison function for a numerical edge at-
tribute.
generic_node_match(attr, default, op) Returns a comparison function for a generic attribute.
generic_edge_match(attr, default, op) Returns a comparison function for a generic attribute.
generic_multiedge_match(attr, default, op) Returns a comparison function for a generic attribute.
networkx.algorithms.isomorphism.categorical_node_match
categorical_node_match(attr,default)
Returns a comparison function for a categorical node attribute.
The value(s) of the attr(s) must be hashable and comparable via the == operator since they are placed into a
set([]) object. If the sets from G1 and G2 are the same, then the constructed function returns True.
Parameters
•attr (string | list) – The categorical node attribute to compare, or a list of categorical node
attributes to compare.
•default (value | list) – The default value for the categorical node attribute, or a list of default
values for the categorical node attributes.
Returns match – The customized, categorical node_match function.
Return type function
Examples
>>> import networkx.algorithms.isomorphism as iso
>>> nm =iso.categorical_node_match('size',1)
>>> nm =iso.categorical_node_match(['color','size'], ['red',2])
networkx.algorithms.isomorphism.categorical_edge_match
categorical_edge_match(attr,default)
Returns a comparison function for a categorical edge attribute.
The value(s) of the attr(s) must be hashable and comparable via the == operator since they are placed into a
set([]) object. If the sets from G1 and G2 are the same, then the constructed function returns True.
Parameters
•attr (string | list) – The categorical edge attribute to compare, or a list of categorical edge
attributes to compare.
356 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•default (value | list) – The default value for the categorical edge attribute, or a list of default
values for the categorical edge attributes.
Returns match – The customized, categorical edge_match function.
Return type function
Examples
>>> import networkx.algorithms.isomorphism as iso
>>> nm =iso.categorical_edge_match('size',1)
>>> nm =iso.categorical_edge_match(['color','size'], ['red',2])
networkx.algorithms.isomorphism.categorical_multiedge_match
categorical_multiedge_match(attr,default)
Returns a comparison function for a categorical edge attribute.
The value(s) of the attr(s) must be hashable and comparable via the == operator since they are placed into a
set([]) object. If the sets from G1 and G2 are the same, then the constructed function returns True.
Parameters
•attr (string | list) – The categorical edge attribute to compare, or a list of categorical edge
attributes to compare.
•default (value | list) – The default value for the categorical edge attribute, or a list of default
values for the categorical edge attributes.
Returns match – The customized, categorical edge_match function.
Return type function
Examples
>>> import networkx.algorithms.isomorphism as iso
>>> nm =iso.categorical_multiedge_match('size',1)
>>> nm =iso.categorical_multiedge_match(['color','size'], ['red',2])
networkx.algorithms.isomorphism.numerical_node_match
numerical_node_match(attr,default,rtol=1e-05,atol=1e-08)
Returns a comparison function for a numerical node attribute.
The value(s) of the attr(s) must be numerical and sortable. If the sorted list of values from G1 and G2 are the
same within some tolerance, then the constructed function returns True.
Parameters
•attr (string | list) – The numerical node attribute to compare, or a list of numerical node
attributes to compare.
•default (value | list) – The default value for the numerical node attribute, or a list of default
values for the numerical node attributes.
•rtol (float) – The relative error tolerance.
3.33. Isomorphism 357

NetworkX Reference, Release 2.3rc1.dev20181203210840
•atol (float) – The absolute error tolerance.
Returns match – The customized, numerical node_match function.
Return type function
Examples
>>> import networkx.algorithms.isomorphism as iso
>>> nm =iso.numerical_node_match('weight',1.0)
>>> nm =iso.numerical_node_match(['weight','linewidth'], [.25,.5])
networkx.algorithms.isomorphism.numerical_edge_match
numerical_edge_match(attr,default,rtol=1e-05,atol=1e-08)
Returns a comparison function for a numerical edge attribute.
The value(s) of the attr(s) must be numerical and sortable. If the sorted list of values from G1 and G2 are the
same within some tolerance, then the constructed function returns True.
Parameters
•attr (string | list) – The numerical edge attribute to compare, or a list of numerical edge
attributes to compare.
•default (value | list) – The default value for the numerical edge attribute, or a list of default
values for the numerical edge attributes.
•rtol (float) – The relative error tolerance.
•atol (float) – The absolute error tolerance.
Returns match – The customized, numerical edge_match function.
Return type function
Examples
>>> import networkx.algorithms.isomorphism as iso
>>> nm =iso.numerical_edge_match('weight',1.0)
>>> nm =iso.numerical_edge_match(['weight','linewidth'], [.25,.5])
networkx.algorithms.isomorphism.numerical_multiedge_match
numerical_multiedge_match(attr,default,rtol=1e-05,atol=1e-08)
Returns a comparison function for a numerical edge attribute.
The value(s) of the attr(s) must be numerical and sortable. If the sorted list of values from G1 and G2 are the
same within some tolerance, then the constructed function returns True.
Parameters
•attr (string | list) – The numerical edge attribute to compare, or a list of numerical edge
attributes to compare.
•default (value | list) – The default value for the numerical edge attribute, or a list of default
values for the numerical edge attributes.
358 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•rtol (float) – The relative error tolerance.
•atol (float) – The absolute error tolerance.
Returns match – The customized, numerical edge_match function.
Return type function
Examples
>>> import networkx.algorithms.isomorphism as iso
>>> nm =iso.numerical_multiedge_match('weight',1.0)
>>> nm =iso.numerical_multiedge_match(['weight','linewidth'], [.25,.5])
networkx.algorithms.isomorphism.generic_node_match
generic_node_match(attr,default,op)
Returns a comparison function for a generic attribute.
The value(s) of the attr(s) are compared using the specified operators. If all the attributes are equal, then the
constructed function returns True.
Parameters
•attr (string | list) – The node attribute to compare, or a list of node attributes to compare.
•default (value | list) – The default value for the node attribute, or a list of default values for
the node attributes.
•op (callable | list) – The operator to use when comparing attribute values, or a list of opera-
tors to use when comparing values for each attribute.
Returns match – The customized, generic node_match function.
Return type function
Examples
>>> from operator import eq
>>> from networkx.algorithms.isomorphism.matchhelpers import close
>>> from networkx.algorithms.isomorphism import generic_node_match
>>> nm =generic_node_match('weight',1.0, close)
>>> nm =generic_node_match('color','red', eq)
>>> nm =generic_node_match(['weight','color'], [1.0,'red'], [close, eq])
networkx.algorithms.isomorphism.generic_edge_match
generic_edge_match(attr,default,op)
Returns a comparison function for a generic attribute.
The value(s) of the attr(s) are compared using the specified operators. If all the attributes are equal, then the
constructed function returns True.
Parameters
•attr (string | list) – The edge attribute to compare, or a list of edge attributes to compare.
3.33. Isomorphism 359

NetworkX Reference, Release 2.3rc1.dev20181203210840
•default (value | list) – The default value for the edge attribute, or a list of default values for
the edge attributes.
•op (callable | list) – The operator to use when comparing attribute values, or a list of opera-
tors to use when comparing values for each attribute.
Returns match – The customized, generic edge_match function.
Return type function
Examples
>>> from operator import eq
>>> from networkx.algorithms.isomorphism.matchhelpers import close
>>> from networkx.algorithms.isomorphism import generic_edge_match
>>> nm =generic_edge_match('weight',1.0, close)
>>> nm =generic_edge_match('color','red', eq)
>>> nm =generic_edge_match(['weight','color'], [1.0,'red'], [close, eq])
networkx.algorithms.isomorphism.generic_multiedge_match
generic_multiedge_match(attr,default,op)
Returns a comparison function for a generic attribute.
The value(s) of the attr(s) are compared using the specified operators. If all the attributes are equal, then the
constructed function returns True. Potentially, the constructed edge_match function can be slow since it must
verify that no isomorphism exists between the multiedges before it returns False.
Parameters
•attr (string | list) – The edge attribute to compare, or a list of node attributes to compare.
•default (value | list) – The default value for the edge attribute, or a list of default values for
the dgeattributes.
•op (callable | list) – The operator to use when comparing attribute values, or a list of opera-
tors to use when comparing values for each attribute.
Returns match – The customized, generic edge_match function.
Return type function
Examples
>>> from operator import eq
>>> from networkx.algorithms.isomorphism.matchhelpers import close
>>> from networkx.algorithms.isomorphism import generic_node_match
>>> nm =generic_node_match('weight',1.0, close)
>>> nm =generic_node_match('color','red', eq)
>>> nm =generic_node_match(['weight','color'],
... [1.0,'red'],
... [close, eq])
...
360 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.34 Link Analysis
3.34.1 PageRank
PageRank analysis of graph structure.
pagerank(G[, alpha, personalization, . . . ]) Return the PageRank of the nodes in the graph.
pagerank_numpy(G[, alpha, personalization, . . . ]) Return the PageRank of the nodes in the graph.
pagerank_scipy(G[, alpha, personalization, . . . ]) Return the PageRank of the nodes in the graph.
google_matrix(G[, alpha, personalization, . . . ]) Return the Google matrix of the graph.
networkx.algorithms.link_analysis.pagerank_alg.pagerank
pagerank(G,alpha=0.85,personalization=None,max_iter=100,tol=1e-06,nstart=None,weight=’weight’,
dangling=None)
Return the PageRank of the nodes in the graph.
PageRank computes a ranking of the nodes in the graph G based on the structure of the incoming links. It was
originally designed as an algorithm to rank web pages.
Parameters
•G(graph) – A NetworkX graph. Undirected graphs will be converted to a directed graph
with two directed edges for each undirected edge.
•alpha (float, optional) – Damping parameter for PageRank, default=0.85.
•personalization (dict, optional) – The “personalization vector” consisting of a dictionary
with a key some subset of graph nodes and personalization value each of those. At least one
personalization value must be non-zero. If not specfiied, a nodes personalization value will
be zero. By default, a uniform distribution is used.
•max_iter (integer, optional) – Maximum number of iterations in power method eigenvalue
solver.
•tol (float, optional) – Error tolerance used to check convergence in power method solver.
•nstart (dictionary, optional) – Starting value of PageRank iteration for each node.
•weight (key, optional) – Edge data key to use as weight. If None weights are set to 1.
•dangling (dict, optional) – The outedges to be assigned to any “dangling” nodes, i.e., nodes
without any outedges. The dict key is the node the outedge points to and the dict value
is the weight of that outedge. By default, dangling nodes are given outedges according to
the personalization vector (uniform if not specified). This must be selected to result in an
irreducible transition matrix (see notes under google_matrix). It may be common to have
the dangling dict to be the same as the personalization dict.
Returns pagerank – Dictionary of nodes with PageRank as value
Return type dictionary
Examples
>>> G=nx.DiGraph(nx.path_graph(4))
>>> pr =nx.pagerank(G, alpha=0.9)
3.34. Link Analysis 361

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The eigenvector calculation is done by the power iteration method and has no guarantee of convergence. The
iteration will stop after an error tolerance of len(G) *tol has been reached. If the number of iterations
exceed max_iter, a networkx.exception.PowerIterationFailedConvergence exception is
raised.
The PageRank algorithm was designed for directed graphs but this algorithm does not check if the input graph
is directed and will execute on undirected graphs by converting each edge in the directed graph to two edges.
See also:
pagerank_numpy(),pagerank_scipy(),google_matrix()
Raises PowerIterationFailedConvergence – If the algorithm fails to converge to the
specified tolerance within the specified number of iterations of the power iteration method.
References
networkx.algorithms.link_analysis.pagerank_alg.pagerank_numpy
pagerank_numpy(G,alpha=0.85,personalization=None,weight=’weight’,dangling=None)
Return the PageRank of the nodes in the graph.
PageRank computes a ranking of the nodes in the graph G based on the structure of the incoming links. It was
originally designed as an algorithm to rank web pages.
Parameters
•G(graph) – A NetworkX graph. Undirected graphs will be converted to a directed graph
with two directed edges for each undirected edge.
•alpha (float, optional) – Damping parameter for PageRank, default=0.85.
•personalization (dict, optional) – The “personalization vector” consisting of a dictionary
with a key some subset of graph nodes and personalization value each of those. At least one
personalization value must be non-zero. If not specfiied, a nodes personalization value will
be zero. By default, a uniform distribution is used.
•weight (key, optional) – Edge data key to use as weight. If None weights are set to 1.
•dangling (dict, optional) – The outedges to be assigned to any “dangling” nodes, i.e., nodes
without any outedges. The dict key is the node the outedge points to and the dict value
is the weight of that outedge. By default, dangling nodes are given outedges according to
the personalization vector (uniform if not specified) This must be selected to result in an
irreducible transition matrix (see notes under google_matrix). It may be common to have
the dangling dict to be the same as the personalization dict.
Returns pagerank – Dictionary of nodes with PageRank as value.
Return type dictionary
Examples
>>> G=nx.DiGraph(nx.path_graph(4))
>>> pr =nx.pagerank_numpy(G, alpha=0.9)
362 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The eigenvector calculation uses NumPy’s interface to the LAPACK eigenvalue solvers. This will be the fastest
and most accurate for small graphs.
This implementation works with Multi(Di)Graphs. For multigraphs the weight between two nodes is set to be
the sum of all edge weights between those nodes.
See also:
pagerank(),pagerank_scipy(),google_matrix()
References
networkx.algorithms.link_analysis.pagerank_alg.pagerank_scipy
pagerank_scipy(G,alpha=0.85,personalization=None,max_iter=100,tol=1e-06,weight=’weight’,dan-
gling=None)
Return the PageRank of the nodes in the graph.
PageRank computes a ranking of the nodes in the graph G based on the structure of the incoming links. It was
originally designed as an algorithm to rank web pages.
Parameters
•G(graph) – A NetworkX graph. Undirected graphs will be converted to a directed graph
with two directed edges for each undirected edge.
•alpha (float, optional) – Damping parameter for PageRank, default=0.85.
•personalization (dict, optional) – The “personalization vector” consisting of a dictionary
with a key some subset of graph nodes and personalization value each of those. At least one
personalization value must be non-zero. If not specfiied, a nodes personalization value will
be zero. By default, a uniform distribution is used.
•max_iter (integer, optional) – Maximum number of iterations in power method eigenvalue
solver.
•tol (float, optional) – Error tolerance used to check convergence in power method solver.
•weight (key, optional) – Edge data key to use as weight. If None weights are set to 1.
•dangling (dict, optional) – The outedges to be assigned to any “dangling” nodes, i.e., nodes
without any outedges. The dict key is the node the outedge points to and the dict value
is the weight of that outedge. By default, dangling nodes are given outedges according to
the personalization vector (uniform if not specified) This must be selected to result in an
irreducible transition matrix (see notes under google_matrix). It may be common to have
the dangling dict to be the same as the personalization dict.
Returns pagerank – Dictionary of nodes with PageRank as value
Return type dictionary
Examples
>>> G=nx.DiGraph(nx.path_graph(4))
>>> pr =nx.pagerank_scipy(G, alpha=0.9)
3.34. Link Analysis 363

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The eigenvector calculation uses power iteration with a SciPy sparse matrix representation.
This implementation works with Multi(Di)Graphs. For multigraphs the weight between two nodes is set to be
the sum of all edge weights between those nodes.
See also:
pagerank(),pagerank_numpy(),google_matrix()
Raises PowerIterationFailedConvergence – If the algorithm fails to converge to the
specified tolerance within the specified number of iterations of the power iteration method.
References
networkx.algorithms.link_analysis.pagerank_alg.google_matrix
google_matrix(G,alpha=0.85,personalization=None,nodelist=None,weight=’weight’,dan-
gling=None)
Return the Google matrix of the graph.
Parameters
•G(graph) – A NetworkX graph. Undirected graphs will be converted to a directed graph
with two directed edges for each undirected edge.
•alpha (float) – The damping factor.
•personalization (dict, optional) – The “personalization vector” consisting of a dictionary
with a key some subset of graph nodes and personalization value each of those. At least one
personalization value must be non-zero. If not specfiied, a nodes personalization value will
be zero. By default, a uniform distribution is used.
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (key, optional) – Edge data key to use as weight. If None weights are set to 1.
•dangling (dict, optional) – The outedges to be assigned to any “dangling” nodes, i.e., nodes
without any outedges. The dict key is the node the outedge points to and the dict value
is the weight of that outedge. By default, dangling nodes are given outedges according to
the personalization vector (uniform if not specified) This must be selected to result in an
irreducible transition matrix (see notes below). It may be common to have the dangling dict
to be the same as the personalization dict.
Returns A – Google matrix of the graph
Return type NumPy matrix
Notes
The matrix returned represents the transition matrix that describes the Markov chain used in PageRank. For
PageRank to converge to a unique solution (i.e., a unique stationary distribution in a Markov chain), the transition
matrix must be irreducible. In other words, it must be that there exists a path between every pair of nodes in the
graph, or else there is the potential of “rank sinks.”
This implementation works with Multi(Di)Graphs. For multigraphs the weight between two nodes is set to be
the sum of all edge weights between those nodes.
364 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
pagerank(),pagerank_numpy(),pagerank_scipy()
3.34.2 Hits
Hubs and authorities analysis of graph structure.
hits(G[, max_iter, tol, nstart, normalized]) Return HITS hubs and authorities values for nodes.
hits_numpy(G[, normalized]) Return HITS hubs and authorities values for nodes.
hits_scipy(G[, max_iter, tol, normalized]) Return HITS hubs and authorities values for nodes.
hub_matrix(G[, nodelist]) Return the HITS hub matrix.
authority_matrix(G[, nodelist]) Return the HITS authority matrix.
networkx.algorithms.link_analysis.hits_alg.hits
hits(G,max_iter=100,tol=1e-08,nstart=None,normalized=True)
Return HITS hubs and authorities values for nodes.
The HITS algorithm computes two numbers for a node. Authorities estimates the node value based on the
incoming links. Hubs estimates the node value based on outgoing links.
Parameters
•G(graph) – A NetworkX graph
•max_iter (integer, optional) – Maximum number of iterations in power method.
•tol (float, optional) – Error tolerance used to check convergence in power method iteration.
•nstart (dictionary, optional) – Starting value of each node for power method iteration.
•normalized (bool (default=True)) – Normalize results by the sum of all of the values.
Returns (hubs,authorities) – Two dictionaries keyed by node containing the hub and authority
values.
Return type two-tuple of dictionaries
Raises PowerIterationFailedConvergence – If the algorithm fails to converge to the
specified tolerance within the specified number of iterations of the power iteration method.
Examples
>>> G=nx.path_graph(4)
>>> h,a=nx.hits(G)
Notes
The eigenvector calculation is done by the power iteration method and has no guarantee of convergence. The
iteration will stop after max_iter iterations or an error tolerance of number_of_nodes(G)*tol has been reached.
The HITS algorithm was designed for directed graphs but this algorithm does not check if the input graph is
directed and will execute on undirected graphs.
3.34. Link Analysis 365

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.algorithms.link_analysis.hits_alg.hits_numpy
hits_numpy(G,normalized=True)
Return HITS hubs and authorities values for nodes.
The HITS algorithm computes two numbers for a node. Authorities estimates the node value based on the
incoming links. Hubs estimates the node value based on outgoing links.
Parameters
•G(graph) – A NetworkX graph
•normalized (bool (default=True)) – Normalize results by the sum of all of the values.
Returns (hubs,authorities) – Two dictionaries keyed by node containing the hub and authority
values.
Return type two-tuple of dictionaries
Examples
>>> G=nx.path_graph(4)
>>> h,a=nx.hits(G)
Notes
The eigenvector calculation uses NumPy’s interface to LAPACK.
The HITS algorithm was designed for directed graphs but this algorithm does not check if the input graph is
directed and will execute on undirected graphs.
References
networkx.algorithms.link_analysis.hits_alg.hits_scipy
hits_scipy(G,max_iter=100,tol=1e-06,normalized=True)
Return HITS hubs and authorities values for nodes.
The HITS algorithm computes two numbers for a node. Authorities estimates the node value based on the
incoming links. Hubs estimates the node value based on outgoing links.
Parameters
•G(graph) – A NetworkX graph
•max_iter (integer, optional) – Maximum number of iterations in power method.
•tol (float, optional) – Error tolerance used to check convergence in power method iteration.
•nstart (dictionary, optional) – Starting value of each node for power method iteration.
•normalized (bool (default=True)) – Normalize results by the sum of all of the values.
Returns (hubs,authorities) – Two dictionaries keyed by node containing the hub and authority
values.
Return type two-tuple of dictionaries
366 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> h,a=nx.hits(G)
Notes
This implementation uses SciPy sparse matrices.
The eigenvector calculation is done by the power iteration method and has no guarantee of convergence. The
iteration will stop after max_iter iterations or an error tolerance of number_of_nodes(G)*tol has been reached.
The HITS algorithm was designed for directed graphs but this algorithm does not check if the input graph is
directed and will execute on undirected graphs.
Raises PowerIterationFailedConvergence – If the algorithm fails to converge to the
specified tolerance within the specified number of iterations of the power iteration method.
References
networkx.algorithms.link_analysis.hits_alg.hub_matrix
hub_matrix(G,nodelist=None)
Return the HITS hub matrix.
networkx.algorithms.link_analysis.hits_alg.authority_matrix
authority_matrix(G,nodelist=None)
Return the HITS authority matrix.
3.35 Link Prediction
Link prediction algorithms.
resource_allocation_index(G[, ebunch]) Compute the resource allocation index of all node pairs
in ebunch.
jaccard_coefficient(G[, ebunch]) Compute the Jaccard coefficient of all node pairs in
ebunch.
adamic_adar_index(G[, ebunch]) Compute the Adamic-Adar index of all node pairs in
ebunch.
preferential_attachment(G[, ebunch]) Compute the preferential attachment score of all node
pairs in ebunch.
cn_soundarajan_hopcroft(G[, ebunch, com-
munity])
Count the number of common neighbors of all node
pairs in ebunch
ra_index_soundarajan_hopcroft(G[,
ebunch, . . . ])
Compute the resource allocation index of all node pairs
in ebunch using community information.
within_inter_cluster(G[, ebunch, delta, . . . ]) Compute the ratio of within- and inter-cluster common
neighbors of all node pairs in ebunch.
3.35. Link Prediction 367

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.35.1 networkx.algorithms.link_prediction.resource_allocation_index
resource_allocation_index(G,ebunch=None)
Compute the resource allocation index of all node pairs in ebunch.
Resource allocation index of uand vis defined as
𝑤∈Γ(𝑢)∩Γ(𝑣)
1
|Γ(𝑤)|
where Γ(𝑢)denotes the set of neighbors of 𝑢.
Parameters
•G(graph) – A NetworkX undirected graph.
•ebunch (iterable of node pairs, optional (default = None)) – Resource allocation index will
be computed for each pair of nodes given in the iterable. The pairs must be given as 2-tuples
(u, v) where u and v are nodes in the graph. If ebunch is None then all non-existent edges in
the graph will be used. Default value: None.
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their resource allocation index.
Return type iterator
Examples
>>> import networkx as nx
>>> G=nx.complete_graph(5)
>>> preds =nx.resource_allocation_index(G, [(0,1), (2,3)])
>>> for u, v, p in preds:
... '(%d,%d) -> %.8f'%(u, v, p)
...
'(0, 1) -> 0.75000000'
'(2, 3) -> 0.75000000'
References
3.35.2 networkx.algorithms.link_prediction.jaccard_coefficient
jaccard_coefficient(G,ebunch=None)
Compute the Jaccard coefficient of all node pairs in ebunch.
Jaccard coefficient of nodes uand vis defined as
|Γ(𝑢)∩Γ(𝑣)|
|Γ(𝑢)∪Γ(𝑣)|
where Γ(𝑢)denotes the set of neighbors of 𝑢.
Parameters
•G(graph) – A NetworkX undirected graph.
•ebunch (iterable of node pairs, optional (default = None)) – Jaccard coefficient will be
computed for each pair of nodes given in the iterable. The pairs must be given as 2-tuples
(u, v) where u and v are nodes in the graph. If ebunch is None then all non-existent edges in
the graph will be used. Default value: None.
368 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their Jaccard coefficient.
Return type iterator
Examples
>>> import networkx as nx
>>> G=nx.complete_graph(5)
>>> preds =nx.jaccard_coefficient(G, [(0,1), (2,3)])
>>> for u, v, p in preds:
... '(%d,%d) -> %.8f'%(u, v, p)
...
'(0, 1) -> 0.60000000'
'(2, 3) -> 0.60000000'
References
3.35.3 networkx.algorithms.link_prediction.adamic_adar_index
adamic_adar_index(G,ebunch=None)
Compute the Adamic-Adar index of all node pairs in ebunch.
Adamic-Adar index of uand vis defined as
𝑤∈Γ(𝑢)∩Γ(𝑣)
1
log |Γ(𝑤)|
where Γ(𝑢)denotes the set of neighbors of 𝑢.
Parameters
•G(graph) – NetworkX undirected graph.
•ebunch (iterable of node pairs, optional (default = None)) – Adamic-Adar index will be
computed for each pair of nodes given in the iterable. The pairs must be given as 2-tuples
(u, v) where u and v are nodes in the graph. If ebunch is None then all non-existent edges in
the graph will be used. Default value: None.
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their Adamic-Adar index.
Return type iterator
Examples
>>> import networkx as nx
>>> G=nx.complete_graph(5)
>>> preds =nx.adamic_adar_index(G, [(0,1), (2,3)])
>>> for u, v, p in preds:
... '(%d,%d) -> %.8f'%(u, v, p)
...
'(0, 1) -> 2.16404256'
'(2, 3) -> 2.16404256'
3.35. Link Prediction 369

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.35.4 networkx.algorithms.link_prediction.preferential_attachment
preferential_attachment(G,ebunch=None)
Compute the preferential attachment score of all node pairs in ebunch.
Preferential attachment score of uand vis defined as
|Γ(𝑢)||Γ(𝑣)|
where Γ(𝑢)denotes the set of neighbors of 𝑢.
Parameters
•G(graph) – NetworkX undirected graph.
•ebunch (iterable of node pairs, optional (default = None)) – Preferential attachment score
will be computed for each pair of nodes given in the iterable. The pairs must be given as
2-tuples (u, v) where u and v are nodes in the graph. If ebunch is None then all non-existent
edges in the graph will be used. Default value: None.
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their preferential attachment score.
Return type iterator
Examples
>>> import networkx as nx
>>> G=nx.complete_graph(5)
>>> preds =nx.preferential_attachment(G, [(0,1), (2,3)])
>>> for u, v, p in preds:
... '(%d,%d) -> %d'%(u, v, p)
...
'(0, 1) -> 16'
'(2, 3) -> 16'
References
3.35.5 networkx.algorithms.link_prediction.cn_soundarajan_hopcroft
cn_soundarajan_hopcroft(G,ebunch=None,community=’community’)
Count the number of common neighbors of all node pairs in ebunch using community information.
For two nodes 𝑢and 𝑣, this function computes the number of common neighbors and bonus one for each
common neighbor belonging to the same community as 𝑢and 𝑣. Mathematically,
|Γ(𝑢)∩Γ(𝑣)|+
𝑤∈Γ(𝑢)∩Γ(𝑣)
𝑓(𝑤)
where 𝑓(𝑤)equals 1 if 𝑤belongs to the same community as 𝑢and 𝑣or 0 otherwise and Γ(𝑢)denotes the set of
neighbors of 𝑢.
Parameters
•G(graph) – A NetworkX undirected graph.
370 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•ebunch (iterable of node pairs, optional (default = None)) – The score will be computed
for each pair of nodes given in the iterable. The pairs must be given as 2-tuples (u, v) where
u and v are nodes in the graph. If ebunch is None then all non-existent edges in the graph
will be used. Default value: None.
•community (string, optional (default = ‘community’)) – Nodes attribute name containing
the community information. G[u][community] identifies which community u belongs to.
Each node belongs to at most one community. Default value: ‘community’.
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their score.
Return type iterator
Examples
>>> import networkx as nx
>>> G=nx.path_graph(3)
>>> G.nodes[0]['community']=0
>>> G.nodes[1]['community']=0
>>> G.nodes[2]['community']=0
>>> preds =nx.cn_soundarajan_hopcroft(G, [(0,2)])
>>> for u, v, p in preds:
... '(%d,%d) -> %d'%(u, v, p)
'(0, 2) -> 2'
References
3.35.6 networkx.algorithms.link_prediction.ra_index_soundarajan_hopcroft
ra_index_soundarajan_hopcroft(G,ebunch=None,community=’community’)
Compute the resource allocation index of all node pairs in ebunch using community information.
For two nodes 𝑢and 𝑣, this function computes the resource allocation index considering only common neighbors
belonging to the same community as 𝑢and 𝑣. Mathematically,
𝑤∈Γ(𝑢)∩Γ(𝑣)
𝑓(𝑤)
|Γ(𝑤)|
where 𝑓(𝑤)equals 1 if 𝑤belongs to the same community as 𝑢and 𝑣or 0 otherwise and Γ(𝑢)denotes the set of
neighbors of 𝑢.
Parameters
•G(graph) – A NetworkX undirected graph.
•ebunch (iterable of node pairs, optional (default = None)) – The score will be computed
for each pair of nodes given in the iterable. The pairs must be given as 2-tuples (u, v) where
u and v are nodes in the graph. If ebunch is None then all non-existent edges in the graph
will be used. Default value: None.
•community (string, optional (default = ‘community’)) – Nodes attribute name containing
the community information. G[u][community] identifies which community u belongs to.
Each node belongs to at most one community. Default value: ‘community’.
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their score.
3.35. Link Prediction 371

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type iterator
Examples
>>> import networkx as nx
>>> G=nx.Graph()
>>> G.add_edges_from([(0,1), (0,2), (1,3), (2,3)])
>>> G.nodes[0]['community']=0
>>> G.nodes[1]['community']=0
>>> G.nodes[2]['community']=1
>>> G.nodes[3]['community']=0
>>> preds =nx.ra_index_soundarajan_hopcroft(G, [(0,3)])
>>> for u, v, p in preds:
... '(%d,%d) -> %.8f'%(u, v, p)
'(0, 3) -> 0.50000000'
References
3.35.7 networkx.algorithms.link_prediction.within_inter_cluster
within_inter_cluster(G,ebunch=None,delta=0.001,community=’community’)
Compute the ratio of within- and inter-cluster common neighbors of all node pairs in ebunch.
For two nodes uand v, if a common neighbor wbelongs to the same community as them, wis considered as
within-cluster common neighbor of uand v. Otherwise, it is considered as inter-cluster common neighbor of
uand v. The ratio between the size of the set of within- and inter-cluster common neighbors is defined as the
WIC measure.1
Parameters
•G(graph) – A NetworkX undirected graph.
•ebunch (iterable of node pairs, optional (default = None)) – The WIC measure will be
computed for each pair of nodes given in the iterable. The pairs must be given as 2-tuples
(u, v) where u and v are nodes in the graph. If ebunch is None then all non-existent edges in
the graph will be used. Default value: None.
•delta (float, optional (default = 0.001)) – Value to prevent division by zero in case there
is no inter-cluster common neighbor between two nodes. See1for details. Default value:
0.001.
•community (string, optional (default = ‘community’)) – Nodes attribute name containing
the community information. G[u][community] identifies which community u belongs to.
Each node belongs to at most one community. Default value: ‘community’.
Returns piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is
their WIC measure.
Return type iterator
1Jorge Carlos Valverde-Rebaza and Alneu de Andrade Lopes. Link prediction in complex networks based on cluster information. In Proceedings
of the 21st Brazilian conference on Advances in Artificial Intelligence (SBIA‘12) https://doi.org/10.1007/978-3-642-34459-6_10
372 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> import networkx as nx
>>> G=nx.Graph()
>>> G.add_edges_from([(0,1), (0,2), (0,3), (1,4), (2,4), (3,4)])
>>> G.nodes[0]['community']=0
>>> G.nodes[1]['community']=1
>>> G.nodes[2]['community']=0
>>> G.nodes[3]['community']=0
>>> G.nodes[4]['community']=0
>>> preds =nx.within_inter_cluster(G, [(0,4)])
>>> for u, v, p in preds:
... '(%d,%d) -> %.8f'%(u, v, p)
...
'(0, 4) -> 1.99800200'
>>> preds =nx.within_inter_cluster(G, [(0,4)], delta=0.5)
>>> for u, v, p in preds:
... '(%d,%d) -> %.8f'%(u, v, p)
...
'(0, 4) -> 1.33333333'
References
3.36 Lowest Common Ancestor
Algorithms for finding the lowest common ancestor of trees and DAGs.
all_pairs_lowest_common_ancestor(G[,
pairs])
Compute the lowest common ancestor for pairs of
nodes.
tree_all_pairs_lowest_common_ancestor(G[,
...])
Yield the lowest common ancestor for sets of pairs in a
tree.
lowest_common_ancestor(G, node1, node2[,
...])
Compute the lowest common ancestor of the given pair
of nodes.
3.36.1 networkx.algorithms.lowest_common_ancestors.all_pairs_lowest_common_ancestor
all_pairs_lowest_common_ancestor(G,pairs=None)
Compute the lowest common ancestor for pairs of nodes.
Parameters
•G(NetworkX directed graph)
•pairs (iterable of pairs of nodes, optional (default: all pairs)) – The pairs of nodes of
interest. If None, will find the LCA of all pairs of nodes.
Returns
•An iterator over ((node1, node2), lca) where (node1, node2) are
•the pairs specified and lca is a lowest common ancestor of the pair.
•Note that for the default of all pairs in G, we consider
•unordered pairs, e.g. you will not get both (b, a) and (a, b).
3.36. Lowest Common Ancestor 373

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Only defined on non-null directed acyclic graphs.
Uses the 𝑂(𝑛3)ancestor-list algorithm from: M. A. Bender, M. Farach-Colton, G. Pemmasani, S. Skiena, P.
Sumazin. “Lowest common ancestors in trees and directed acyclic graphs.” Journal of Algorithms, 57(2): 75-94,
2005.
See also:
tree_all_pairs_lowest_common_ancestor(),lowest_common_ancestor()
3.36.2 networkx.algorithms.lowest_common_ancestors.tree_all_pairs_lowest_common_ancestor
tree_all_pairs_lowest_common_ancestor(G,root=None,pairs=None)
Yield the lowest common ancestor for sets of pairs in a tree.
Parameters
•G(NetworkX directed graph (must be a tree))
•root (node, optional (default: None)) – The root of the subtree to operate on. If None,
assume the entire graph has exactly one source and use that.
•pairs (iterable or iterator of pairs of nodes, optional (default: None)) – The pairs of interest.
If None, Defaults to all pairs of nodes under root that have a lowest common ancestor.
Returns lcas – in pairs and lca is their lowest common ancestor.
Return type generator of tuples ((u, v), lca) where uand vare nodes
Notes
Only defined on non-null trees represented with directed edges from parents to children. Uses Tarjan’s off-line
lowest-common-ancestors algorithm. Runs in time 𝑂(4 ×(𝑉+𝐸+𝑃)) time, where 4 is the largest value of
the inverse Ackermann function likely to ever come up in actual use, and 𝑃is the number of pairs requested (or
𝑉2if all are needed).
Tarjan, R. E. (1979), “Applications of path compression on balanced trees”, Journal of the ACM 26 (4): 690-715,
doi:10.1145/322154.322161.
See also:
all_pairs_lowest_common_ancestor(),lowest_common_ancestor()
3.36.3 networkx.algorithms.lowest_common_ancestors.lowest_common_ancestor
lowest_common_ancestor(G,node1,node2,default=None)
Compute the lowest common ancestor of the given pair of nodes.
Parameters
•G(NetworkX directed graph)
•node1, node2 (nodes in the graph.)
•default (object) – Returned if no common ancestor between node1 and node2
Returns
374 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•The lowest common ancestor of node1 and node2,
•or default if they have no common ancestors.
Notes
Only defined on non-null directed acyclic graphs. Takes n log(n) time in the size of the graph. See
all_pairs_lowest_common_ancestor when you have more than one pair of nodes of interest.
See also:
tree_all_pairs_lowest_common_ancestor(),all_pairs_lowest_common_ancestor()
3.37 Matching
Functions for computing and verifying matchings in a graph.
is_matching(G, matching) Decides whether the given set or dictionary represents a
valid matching in G.
is_maximal_matching(G, matching) Decides whether the given set or dictionary represents a
valid maximal matching in G.
is_perfect_matching(G, matching) Decides whether the given set represents a valid perfect
matching in G.
maximal_matching(G) Find a maximal matching in the graph.
max_weight_matching(G[, maxcardinality,
weight])
Compute a maximum-weighted matching of G.
3.37.1 networkx.algorithms.matching.is_matching
is_matching(G,matching)
Decides whether the given set or dictionary represents a valid matching in G.
Amatching in a graph is a set of edges in which no two distinct edges share a common endpoint.
Parameters
•G(NetworkX graph)
•matching (dict or set) – A dictionary or set representing a matching. If a dictionary, it
must have matching[u] == v and matching[v] == u for each edge (u, v) in
the matching. If a set, it must have elements of the form (u, v), where (u, v) is an
edge in the matching.
Returns Whether the given set or dictionary represents a valid matching in the graph.
Return type bool
3.37.2 networkx.algorithms.matching.is_maximal_matching
is_maximal_matching(G,matching)
Decides whether the given set or dictionary represents a valid maximal matching in G.
Amaximal matching in a graph is a matching in which adding any edge would cause the set to no longer be a
valid matching.
3.37. Matching 375

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•matching (dict or set) – A dictionary or set representing a matching. If a dictionary, it
must have matching[u] == v and matching[v] == u for each edge (u, v) in
the matching. If a set, it must have elements of the form (u, v), where (u, v) is an
edge in the matching.
Returns Whether the given set or dictionary represents a valid maximal matching in the graph.
Return type bool
3.37.3 networkx.algorithms.matching.is_perfect_matching
is_perfect_matching(G,matching)
Decides whether the given set represents a valid perfect matching in G.
Aperfect matching in a graph is a matching in which exactly one edge is incident upon each vertex.
Parameters
•G(NetworkX graph)
•matching (dict or set) – A dictionary or set representing a matching. If a dictionary, it
must have matching[u] == v and matching[v] == u for each edge (u, v) in
the matching. If a set, it must have elements of the form (u, v), where (u, v) is an
edge in the matching.
Returns Whether the given set or dictionary represents a valid perfect matching in the graph.
Return type bool
3.37.4 networkx.algorithms.matching.maximal_matching
maximal_matching(G)
Find a maximal matching in the graph.
A matching is a subset of edges in which no node occurs more than once. A maximal matching cannot add more
edges and still be a matching.
Parameters G (NetworkX graph) – Undirected graph
Returns matching – A maximal matching of the graph.
Return type set
Notes
The algorithm greedily selects a maximal matching M of the graph G (i.e. no superset of M exists). It runs in
𝑂(|𝐸|)time.
3.37.5 networkx.algorithms.matching.max_weight_matching
max_weight_matching(G,maxcardinality=False,weight=’weight’)
Compute a maximum-weighted matching of G.
376 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
A matching is a subset of edges in which no node occurs more than once. The weight of a matching is the sum
of the weights of its edges. A maximal matching cannot add more edges and still be a matching. The cardinality
of a matching is the number of matched edges.
Parameters
•G(NetworkX graph) – Undirected graph
•maxcardinality (bool, optional (default=False)) – If maxcardinality is True, compute the
maximum-cardinality matching with maximum weight among all maximum-cardinality
matchings.
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight. If key not found, uses 1 as weight.
Returns matching – A maximal matching of the graph.
Return type set
Notes
If G has edges with weight attributes the edge data are used as weight values else the weights are assumed to be
1.
This function takes time O(number_of_nodes ** 3).
If all edge weights are integers, the algorithm uses only integer computations. If floating point weights are used,
the algorithm could return a slightly suboptimal matching due to numeric precision errors.
This method is based on the “blossom” method for finding augmenting paths and the “primal-dual” method for
finding a matching of maximum weight, both methods invented by Jack Edmonds1.
Bipartite graphs can also be matched using the functions present in networkx.algorithms.bipartite.
matching.
References
3.38 Minors
Provides functions for computing minors of a graph.
contracted_edge(G, edge[, self_loops]) Returns the graph that results from contracting the spec-
ified edge.
contracted_nodes(G, u, v[, self_loops]) Returns the graph that results from contracting uand v.
identified_nodes(G, u, v[, self_loops]) Returns the graph that results from contracting uand v.
quotient_graph(G, partition[, . . . ]) Returns the quotient graph of Gunder the specified
equivalence relation on nodes.
3.38.1 networkx.algorithms.minors.contracted_edge
contracted_edge(G,edge,self_loops=True)
Returns the graph that results from contracting the specified edge.
Edge contraction identifies the two endpoints of the edge as a single node incident to any edge that was incident
1“Efficient Algorithms for Finding Maximum Matching in Graphs”, Zvi Galil, ACM Computing Surveys, 1986.
3.38. Minors 377
NetworkX Reference, Release 2.3rc1.dev20181203210840
to the original two nodes. A graph that results from edge contraction is called a minor of the original graph.
Parameters
•G(NetworkX graph) – The graph whose edge will be contracted.
•edge (tuple) – Must be a pair of nodes in G.
•self_loops (Boolean) – If this is True, any edges (including edge) joining the endpoints of
edge in Gbecome self-loops on the new node in the returned graph.
Returns A new graph object of the same type as G(leaving Gunmodified) with endpoints of edge
identified in a single node. The right node of edge will be merged into the left one, so only the
left one will appear in the returned graph.
Return type Networkx graph
Raises ValueError – If edge is not an edge in G.
Examples
Attempting to contract two nonadjacent nodes yields an error:
>>> import networkx as nx
>>> G=nx.cycle_graph(4)
>>> nx.contracted_edge(G, (1,3))
Traceback (most recent call last):
...
ValueError: Edge (1, 3) does not exist in graph G; cannot contract it
Contracting two adjacent nodes in the cycle graph on nnodes yields the cycle graph on n-1nodes:
>>> import networkx as nx
>>> C5 =nx.cycle_graph(5)
>>> C4 =nx.cycle_graph(4)
>>> M=nx.contracted_edge(C5, (0,1), self_loops=False)
>>> nx.is_isomorphic(M, C4)
True
See also:
contracted_nodes(),quotient_graph()
3.38.2 networkx.algorithms.minors.contracted_nodes
contracted_nodes(G,u,v,self_loops=True)
Returns the graph that results from contracting uand v.
Node contraction identifies the two nodes as a single node incident to any edge that was incident to the original
two nodes.
Parameters
•G(NetworkX graph) – The graph whose nodes will be contracted.
•u, v (nodes) – Must be nodes in G.
•self_loops (Boolean) – If this is True, any edges joining uand vin Gbecome self-loops on
the new node in the returned graph.
378 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns A new graph object of the same type as G(leaving Gunmodified) with uand videntified
in a single node. The right node vwill be merged into the node u, so only uwill appear in the
returned graph.
Return type Networkx graph
Notes
For multigraphs, the edge keys for the realigned edges may not be the same as the edge keys for the old edges.
This is natural because edge keys are unique only within each pair of nodes.
Examples
Contracting two nonadjacent nodes of the cycle graph on four nodes C_4 yields the path graph (ignoring parallel
edges):
>>> G=nx.cycle_graph(4)
>>> M=nx.contracted_nodes(G, 1,3)
>>> P3 =nx.path_graph(3)
>>> nx.is_isomorphic(M, P3)
True
>>> G=nx.MultiGraph(P3)
>>> M=nx.contracted_nodes(G, 0,2)
>>> M.edges
MultiEdgeView([(0, 1, 0), (0, 1, 1)])
>>> G=nx.Graph([(1,2), (2,2)])
>>> H=nx.contracted_nodes(G, 1,2, self_loops=False)
>>> list(H.nodes())
[1]
>>> list(H.edges())
[(1, 1)]
See also:
contracted_edge(),quotient_graph()
Notes
This function is also available as identified_nodes.
3.38.3 networkx.algorithms.minors.identified_nodes
identified_nodes(G,u,v,self_loops=True)
Returns the graph that results from contracting uand v.
Node contraction identifies the two nodes as a single node incident to any edge that was incident to the original
two nodes.
Parameters
•G(NetworkX graph) – The graph whose nodes will be contracted.
•u, v (nodes) – Must be nodes in G.
3.38. Minors 379

NetworkX Reference, Release 2.3rc1.dev20181203210840
•self_loops (Boolean) – If this is True, any edges joining uand vin Gbecome self-loops on
the new node in the returned graph.
Returns A new graph object of the same type as G(leaving Gunmodified) with uand videntified
in a single node. The right node vwill be merged into the node u, so only uwill appear in the
returned graph.
Return type Networkx graph
Notes
For multigraphs, the edge keys for the realigned edges may not be the same as the edge keys for the old edges.
This is natural because edge keys are unique only within each pair of nodes.
Examples
Contracting two nonadjacent nodes of the cycle graph on four nodes C_4 yields the path graph (ignoring parallel
edges):
>>> G=nx.cycle_graph(4)
>>> M=nx.contracted_nodes(G, 1,3)
>>> P3 =nx.path_graph(3)
>>> nx.is_isomorphic(M, P3)
True
>>> G=nx.MultiGraph(P3)
>>> M=nx.contracted_nodes(G, 0,2)
>>> M.edges
MultiEdgeView([(0, 1, 0), (0, 1, 1)])
>>> G=nx.Graph([(1,2), (2,2)])
>>> H=nx.contracted_nodes(G, 1,2, self_loops=False)
>>> list(H.nodes())
[1]
>>> list(H.edges())
[(1, 1)]
See also:
contracted_edge(),quotient_graph()
Notes
This function is also available as identified_nodes.
3.38.4 networkx.algorithms.minors.quotient_graph
quotient_graph(G,partition,edge_relation=None,node_data=None,edge_data=None,relabel=False,
create_using=None)
Returns the quotient graph of Gunder the specified equivalence relation on nodes.
Parameters
•G(NetworkX graph) – The graph for which to return the quotient graph with the specified
node relation.
380 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•partition (function or list of sets) – If a function, this function must represent an equivalence
relation on the nodes of G. It must take two arguments uand vand return True exactly when
uand vare in the same equivalence class. The equivalence classes form the nodes in the
returned graph.
If a list of sets, the list must form a valid partition of the nodes of the graph. That is, each
node must be in exactly one block of the partition.
•edge_relation (Boolean function with two arguments) – This function must represent an
edge relation on the blocks of Gin the partition induced by node_relation. It must take
two arguments, Band C, each one a set of nodes, and return True exactly when there should
be an edge joining block Bto block Cin the returned graph.
If edge_relation is not specified, it is assumed to be the following relation. Block Bis
related to block Cif and only if some node in Bis adjacent to some node in C, according to
the edge set of G.
•edge_data (function) – This function takes two arguments, Band C, each one a set of nodes,
and must return a dictionary representing the edge data attributes to set on the edge joining
Band C, should there be an edge joining Band Cin the quotient graph (if no such edge
occurs in the quotient graph as determined by edge_relation, then the output of this
function is ignored).
If the quotient graph would be a multigraph, this function is not applied, since the edge data
from each edge in the graph Gappears in the edges of the quotient graph.
•node_data (function) – This function takes one argument, B, a set of nodes in G, and must
return a dictionary representing the node data attributes to set on the node representing Bin
the quotient graph. If None, the following node attributes will be set:
–‘graph’, the subgraph of the graph Gthat this block represents,
–‘nnodes’, the number of nodes in this block,
–‘nedges’, the number of edges within this block,
–‘density’, the density of the subgraph of Gthat this block represents.
•relabel (bool) – If True, relabel the nodes of the quotient graph to be nonnegative integers.
Otherwise, the nodes are identified with frozenset instances representing the blocks
given in partition.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns The quotient graph of Gunder the equivalence relation specified by partition. If the
partition were given as a list of set instances and relabel is False, each node will be a
frozenset corresponding to the same set.
Return type NetworkX graph
Raises NetworkXException – If the given partition is not a valid partition of the nodes of G.
Examples
The quotient graph of the complete bipartite graph under the “same neighbors” equivalence relation is K_2.
Under this relation, two nodes are equivalent if they are not adjacent but have the same neighbor set:
3.38. Minors 381

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> import networkx as nx
>>> G=nx.complete_bipartite_graph(2,3)
>>> same_neighbors =lambda u, v: (u not in G[v] and vnot in G[u]
... and G[u] == G[v])
>>> Q=nx.quotient_graph(G, same_neighbors)
>>> K2 =nx.complete_graph(2)
>>> nx.is_isomorphic(Q, K2)
True
The quotient graph of a directed graph under the “same strongly connected component” equivalence relation
is the condensation of the graph (see condensation()). This example comes from the Wikipedia article
‘Strongly connected component‘_:
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> edges =['ab','be','bf','bc','cg','cd','dc','dh','ea',
... 'ef','fg','gf','hd','hf']
>>> G.add_edges_from(tuple(x) for xin edges)
>>> components =list(nx.strongly_connected_components(G))
>>> sorted(sorted(component) for component in components)
[['a', 'b', 'e'], ['c', 'd', 'h'], ['f', 'g']]
>>>
>>> C=nx.condensation(G, components)
>>> component_of =C.graph['mapping']
>>> same_component =lambda u, v: component_of[u] == component_of[v]
>>> Q=nx.quotient_graph(G, same_component)
>>> nx.is_isomorphic(C, Q)
True
Node identification can be represented as the quotient of a graph under the equivalence relation that places the
two nodes in one block and each other node in its own singleton block:
>>> import networkx as nx
>>> K24 =nx.complete_bipartite_graph(2,4)
>>> K34 =nx.complete_bipartite_graph(3,4)
>>> C=nx.contracted_nodes(K34, 1,2)
>>> nodes ={1,2}
>>> is_contracted =lambda u, v: u in nodes and vin nodes
>>> Q=nx.quotient_graph(K34, is_contracted)
>>> nx.is_isomorphic(Q, C)
True
>>> nx.is_isomorphic(Q, K24)
True
The blockmodeling technique described in1can be implemented as a quotient graph:
>>> G=nx.path_graph(6)
>>> partition =[{0,1}, {2,3}, {4,5}]
>>> M=nx.quotient_graph(G, partition, relabel=True)
>>> list(M.edges())
[(0, 1), (1, 2)]
1Patrick Doreian, Vladimir Batagelj, and Anuska Ferligoj. Generalized Blockmodeling. Cambridge University Press, 2004.
382 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.39 Maximal independent set
Algorithm to find a maximal (not maximum) independent set.
maximal_independent_set(G[, nodes, seed]) Return a random maximal independent set guaranteed
to contain a given set of nodes.
3.39.1 networkx.algorithms.mis.maximal_independent_set
maximal_independent_set(G,nodes=None,seed=None)
Return a random maximal independent set guaranteed to contain a given set of nodes.
An independent set is a set of nodes such that the subgraph of G induced by these nodes contains no edges. A
maximal independent set is an independent set such that it is not possible to add a new node and still get an
independent set.
Parameters
•G(NetworkX graph)
•nodes (list or iterable) – Nodes that must be part of the independent set. This set of nodes
must be independent.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns indep_nodes – List of nodes that are part of a maximal independent set.
Return type list
Raises
•NetworkXUnfeasible – If the nodes in the provided list are not part of the graph or do
not form an independent set, an exception is raised.
•NetworkXNotImplemented – If Gis directed.
Examples
>>> G=nx.path_graph(5)
>>> nx.maximal_independent_set(G) # doctest: +SKIP
[4, 0, 2]
>>> nx.maximal_independent_set(G, [1]) # doctest: +SKIP
[1, 3]
Notes
This algorithm does not solve the maximum independent set problem.
3.39. Maximal independent set 383

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.40 Node Classification
This module provides the functions for node classification problem.
The functions in this module are not imported into the top level networkx namespace. You can access these functions
by importing the networkx.algorithms.node_classification modules, then accessing the functions as
attributes of node_classification. For example:
>>> import networkx as nx
>>> from networkx.algorithms import node_classification
>>> G=nx.path_graph(4)
>>> G.edges()
EdgeView([(0, 1), (1, 2), (2, 3)])
>>> G.node[0]['label']='A'
>>> G.node[3]['label']='B'
>>> node_classification.harmonic_function(G) # doctest: +SKIP
['A', 'A', 'B', 'B']
3.40.1 Harmonic Function
Function for computing Harmonic function algorithm by Zhu et al.
References
Zhu, X., Ghahramani, Z., & Lafferty, J. (2003, August). Semi-supervised learning using gaussian fields and harmonic
functions. In ICML (Vol. 3, pp. 912-919).
harmonic_function(G[, max_iter, label_name]) Node classification by Harmonic function
networkx.algorithms.node_classification.hmn.harmonic_function
harmonic_function(G,max_iter=30,label_name=’label’)
Node classification by Harmonic function
Parameters
•G(NetworkX Graph)
•max_iter (int) – maximum number of iterations allowed
•label_name (string) – name of target labels to predict
Raises NetworkXError if no nodes on Ghas label_name.
Returns predicted – Array of predicted labels
Return type array, shape = [n_samples]
Examples
>>> from networkx.algorithms import node_classification
>>> G=nx.path_graph(4)
>>> G.node[0]['label']='A'
(continues on next page)
384 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.node[3]['label']='B'
>>> G.nodes(data=True)
NodeDataView({0: {'label': 'A'}, 1: {}, 2: {}, 3: {'label': 'B'}})
>>> G.edges()
EdgeView([(0, 1), (1, 2), (2, 3)])
>>> predicted =node_classification.harmonic_function(G)
>>> predicted
['A', 'A', 'B', 'B']
References
Zhu, X., Ghahramani, Z., & Lafferty, J. (2003, August). Semi-supervised learning using gaussian fields and
harmonic functions. In ICML (Vol. 3, pp. 912-919).
3.40.2 Local and Global Consistency
Function for computing Local and global consistency algorithm by Zhou et al.
References
Zhou, D., Bousquet, O., Lal, T. N., Weston, J., & Schölkopf, B. (2004). Learning with local and global consistency.
Advances in neural information processing systems, 16(16), 321-328.
local_and_global_consistency(G[, alpha,
...])
Node classification by Local and Global Consistency
networkx.algorithms.node_classification.lgc.local_and_global_consistency
local_and_global_consistency(G,alpha=0.99,max_iter=30,label_name=’label’)
Node classification by Local and Global Consistency
Parameters
•G(NetworkX Graph)
•alpha (float) – Clamping factor
•max_iter (int) – Maximum number of iterations allowed
•label_name (string) – Name of target labels to predict
Raises NetworkXError if no nodes on Ghas label_name.
Returns predicted – Array of predicted labels
Return type array, shape = [n_samples]
Examples
>>> from networkx.algorithms import node_classification
>>> G=nx.path_graph(4)
>>> G.node[0]['label']='A'
(continues on next page)
3.40. Node Classification 385
NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G.node[3]['label']='B'
>>> G.nodes(data=True)
NodeDataView({0: {'label': 'A'}, 1: {}, 2: {}, 3: {'label': 'B'}})
>>> G.edges()
EdgeView([(0, 1), (1, 2), (2, 3)])
>>> predicted =node_classification.local_and_global_consistency(G)
>>> predicted
['A', 'A', 'B', 'B']
References
Zhou, D., Bousquet, O., Lal, T. N., Weston, J., & Schölkopf, B. (2004). Learning with local and global consis-
tency. Advances in neural information processing systems, 16(16), 321-328.
3.41 Operators
Unary operations on graphs
complement(G) Return the graph complement of G.
reverse(G[, copy]) Return the reverse directed graph of G.
3.41.1 networkx.algorithms.operators.unary.complement
complement(G)
Return the graph complement of G.
Parameters G (graph) – A NetworkX graph
Returns GC
Return type A new graph.
Notes
Note that complement() does not create self-loops and also does not produce parallel edges for MultiGraphs.
Graph, node, and edge data are not propagated to the new graph.
3.41.2 networkx.algorithms.operators.unary.reverse
reverse(G,copy=True)
Return the reverse directed graph of G.
Parameters
•G(directed graph) – A NetworkX directed graph
•copy (bool) – If True, then a new graph is returned. If False, then the graph is reversed in
place.
Returns H – The reversed G.
386 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type directed graph
Operations on graphs including union, intersection, difference.
compose(G, H) Return a new graph of G composed with H.
union(G, H[, rename, name]) Return the union of graphs G and H.
disjoint_union(G, H) Return the disjoint union of graphs G and H.
intersection(G, H) Return a new graph that contains only the edges that
exist in both G and H.
difference(G, H) Return a new graph that contains the edges that exist in
G but not in H.
symmetric_difference(G, H) Return new graph with edges that exist in either G or H
but not both.
3.41.3 networkx.algorithms.operators.binary.compose
compose(G,H)
Return a new graph of G composed with H.
Composition is the simple union of the node sets and edge sets. The node sets of G and H do not need to be
disjoint.
Parameters G, H (graph) – A NetworkX graph
Returns C
Return type A new graph with the same type as G
Notes
It is recommended that G and H be either both directed or both undirected. Attributes from H take precedent
over attributes from G.
For MultiGraphs, the edges are identified by incident nodes AND edge-key. This can cause surprises (i.e., edge
(1, 2) may or may not be the same in two graphs) if you use MultiGraph without keeping track of edge keys.
3.41.4 networkx.algorithms.operators.binary.union
union(G,H,rename=(None,None),name=None)
Return the union of graphs G and H.
Graphs G and H must be disjoint, otherwise an exception is raised.
Parameters
•G,H (graph) – A NetworkX graph
•rename (bool , default=(None, None)) – Node names of G and H can be changed by spec-
ifying the tuple rename=(‘G-‘,’H-‘) (for example). Node “u” in G is then renamed “G-u”
and “v” in H is renamed “H-v”.
•name (string) – Specify the name for the union graph
Returns U
Return type A union graph with the same type as G.
3.41. Operators 387

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
To force a disjoint union with node relabeling, use disjoint_union(G,H) or convert_node_labels_to integers().
Graph, edge, and node attributes are propagated from G and H to the union graph. If a graph attribute is present
in both G and H the value from H is used.
See also:
disjoint_union()
3.41.5 networkx.algorithms.operators.binary.disjoint_union
disjoint_union(G,H)
Return the disjoint union of graphs G and H.
This algorithm forces distinct integer node labels.
Parameters G,H (graph) – A NetworkX graph
Returns U
Return type A union graph with the same type as G.
Notes
A new graph is created, of the same class as G. It is recommended that G and H be either both directed or both
undirected.
The nodes of G are relabeled 0 to len(G)-1, and the nodes of H are relabeled len(G) to len(G)+len(H)-1.
Graph, edge, and node attributes are propagated from G and H to the union graph. If a graph attribute is present
in both G and H the value from H is used.
3.41.6 networkx.algorithms.operators.binary.intersection
intersection(G,H)
Return a new graph that contains only the edges that exist in both G and H.
The node sets of H and G must be the same.
Parameters G,H (graph) – A NetworkX graph. G and H must have the same node sets.
Returns GH
Return type A new graph with the same type as G.
Notes
Attributes from the graph, nodes, and edges are not copied to the new graph. If you want a new graph of the
intersection of G and H with the attributes (including edge data) from G use remove_nodes_from() as follows
>>> G=nx.path_graph(3)
>>> H=nx.path_graph(5)
>>> R=G.copy()
>>> R.remove_nodes_from(n for nin Gif nnot in H)
388 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.41.7 networkx.algorithms.operators.binary.difference
difference(G,H)
Return a new graph that contains the edges that exist in G but not in H.
The node sets of H and G must be the same.
Parameters G,H (graph) – A NetworkX graph. G and H must have the same node sets.
Returns D
Return type A new graph with the same type as G.
Notes
Attributes from the graph, nodes, and edges are not copied to the new graph. If you want a new graph of
the difference of G and H with with the attributes (including edge data) from G use remove_nodes_from() as
follows:
>>> G=nx.path_graph(3)
>>> H=nx.path_graph(5)
>>> R=G.copy()
>>> R.remove_nodes_from(n for nin Gif nin H)
3.41.8 networkx.algorithms.operators.binary.symmetric_difference
symmetric_difference(G,H)
Return new graph with edges that exist in either G or H but not both.
The node sets of H and G must be the same.
Parameters G,H (graph) – A NetworkX graph. G and H must have the same node sets.
Returns D
Return type A new graph with the same type as G.
Notes
Attributes from the graph, nodes, and edges are not copied to the new graph.
Operations on many graphs.
compose_all(graphs) Return the composition of all graphs.
union_all(graphs[, rename]) Return the union of all graphs.
disjoint_union_all(graphs) Return the disjoint union of all graphs.
intersection_all(graphs) Return a new graph that contains only the edges that
exist in all graphs.
3.41.9 networkx.algorithms.operators.all.compose_all
compose_all(graphs)
Return the composition of all graphs.
Composition is the simple union of the node sets and edge sets. The node sets of the supplied graphs need not
3.41. Operators 389

NetworkX Reference, Release 2.3rc1.dev20181203210840
be disjoint.
Parameters graphs (list) – List of NetworkX graphs
Returns C
Return type A graph with the same type as the first graph in list
Raises ValueError – If graphs is an empty list.
Notes
It is recommended that the supplied graphs be either all directed or all undirected.
Graph, edge, and node attributes are propagated to the union graph. If a graph attribute is present in multiple
graphs, then the value from the last graph in the list with that attribute is used.
3.41.10 networkx.algorithms.operators.all.union_all
union_all(graphs,rename=(None,))
Return the union of all graphs.
The graphs must be disjoint, otherwise an exception is raised.
Parameters
•graphs (list of graphs) – List of NetworkX graphs
•rename (bool , default=(None, None)) – Node names of G and H can be changed by spec-
ifying the tuple rename=(‘G-‘,’H-‘) (for example). Node “u” in G is then renamed “G-u”
and “v” in H is renamed “H-v”.
Returns U
Return type a graph with the same type as the first graph in list
Raises ValueError – If graphs is an empty list.
Notes
To force a disjoint union with node relabeling, use disjoint_union_all(G,H) or convert_node_labels_to integers().
Graph, edge, and node attributes are propagated to the union graph. If a graph attribute is present in multiple
graphs, then the value from the last graph in the list with that attribute is used.
See also:
union(),disjoint_union_all()
3.41.11 networkx.algorithms.operators.all.disjoint_union_all
disjoint_union_all(graphs)
Return the disjoint union of all graphs.
This operation forces distinct integer node labels starting with 0 for the first graph in the list and numbering
consecutively.
Parameters graphs (list) – List of NetworkX graphs
Returns U
390 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type A graph with the same type as the first graph in list
Raises ValueError – If graphs is an empty list.
Notes
It is recommended that the graphs be either all directed or all undirected.
Graph, edge, and node attributes are propagated to the union graph. If a graph attribute is present in multiple
graphs, then the value from the last graph in the list with that attribute is used.
3.41.12 networkx.algorithms.operators.all.intersection_all
intersection_all(graphs)
Return a new graph that contains only the edges that exist in all graphs.
All supplied graphs must have the same node set.
Parameters graphs (list) – List of NetworkX graphs
Returns R
Return type A new graph with the same type as the first graph in list
Raises ValueError – If graphs is an empty list.
Notes
Attributes from the graph, nodes, and edges are not copied to the new graph.
Graph products.
cartesian_product(G, H) Return the Cartesian product of G and H.
lexicographic_product(G, H) Return the lexicographic product of G and H.
rooted_product(G, H, root) Return the rooted product of graphs G and H rooted at
root in H.
strong_product(G, H) Return the strong product of G and H.
tensor_product(G, H) Return the tensor product of G and H.
power(G, k) Returns the specified power of a graph.
3.41.13 networkx.algorithms.operators.product.cartesian_product
cartesian_product(G,H)
Return the Cartesian product of G and H.
The Cartesian product 𝑃of the graphs 𝐺and 𝐻has a node set that is the Cartesian product of the node sets,
𝑉(𝑃) = 𝑉(𝐺)×𝑉(𝐻).𝑃has an edge ((𝑢, 𝑣),(𝑥, 𝑦)) if and only if either 𝑢is equal to 𝑥and both 𝑣and 𝑦are
adjacent in 𝐻or if 𝑣is equal to 𝑦and both 𝑢and 𝑥are adjacent in 𝐺.
Parameters G, H (graphs) – Networkx graphs.
Returns P – The Cartesian product of G and H. P will be a multi-graph if either G or H is a multi-
graph. Will be a directed if G and H are directed, and undirected if G and H are undirected.
Return type NetworkX graph
Raises NetworkXError – If G and H are not both directed or both undirected.
3.41. Operators 391

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Node attributes in P are two-tuple of the G and H node attributes. Missing attributes are assigned None.
Examples
>>> G=nx.Graph()
>>> H=nx.Graph()
>>> G.add_node(0, a1=True)
>>> H.add_node('a', a2='Spam')
>>> P=nx.cartesian_product(G, H)
>>> list(P)
[(0, 'a')]
Edge attributes and edge keys (for multigraphs) are also copied to the new product graph
3.41.14 networkx.algorithms.operators.product.lexicographic_product
lexicographic_product(G,H)
Return the lexicographic product of G and H.
The lexicographical product 𝑃of the graphs 𝐺and 𝐻has a node set that is the Cartesian product of the node
sets, 𝑉(𝑃) = 𝑉(𝐺)×𝑉(𝐻).𝑃has an edge ((𝑢, 𝑣),(𝑥, 𝑦)) if and only if (𝑢, 𝑣)is an edge in 𝐺or 𝑢== 𝑣and
(𝑥, 𝑦)is an edge in 𝐻.
Parameters G, H (graphs) – Networkx graphs.
Returns P – The Cartesian product of G and H. P will be a multi-graph if either G or H is a multi-
graph. Will be a directed if G and H are directed, and undirected if G and H are undirected.
Return type NetworkX graph
Raises NetworkXError – If G and H are not both directed or both undirected.
Notes
Node attributes in P are two-tuple of the G and H node attributes. Missing attributes are assigned None.
Examples
>>> G=nx.Graph()
>>> H=nx.Graph()
>>> G.add_node(0, a1=True)
>>> H.add_node('a', a2='Spam')
>>> P=nx.lexicographic_product(G, H)
>>> list(P)
[(0, 'a')]
Edge attributes and edge keys (for multigraphs) are also copied to the new product graph
392 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.41.15 networkx.algorithms.operators.product.rooted_product
rooted_product(G,H,root)
Return the rooted product of graphs G and H rooted at root in H.
A new graph is constructed representing the rooted product of the inputted graphs, G and H, with a root in H. A
rooted product duplicates H for each nodes in G with the root of H corresponding to the node in G. Nodes are
renamed as the direct product of G and H. The result is a subgraph of the cartesian product.
Parameters
•G,H (graph) – A NetworkX graph
•root (node) – A node in H
Returns R
Return type The rooted product of G and H with a specified root in H
Notes
The nodes of R are the Cartesian Product of the nodes of G and H. The nodes of G and H are not relabeled.
3.41.16 networkx.algorithms.operators.product.strong_product
strong_product(G,H)
Return the strong product of G and H.
The strong product 𝑃of the graphs 𝐺and 𝐻has a node set that is the Cartesian product of the node sets,
𝑉(𝑃) = 𝑉(𝐺)×𝑉(𝐻).𝑃has an edge ((𝑢, 𝑣),(𝑥, 𝑦)) if and only if 𝑢== 𝑣and (𝑥, 𝑦)is an edge in 𝐻, or
𝑥== 𝑦and (𝑢, 𝑣)is an edge in 𝐺, or (𝑢, 𝑣)is an edge in 𝐺and (𝑥, 𝑦)is an edge in 𝐻.
Parameters G, H (graphs) – Networkx graphs.
Returns P – The Cartesian product of G and H. P will be a multi-graph if either G or H is a multi-
graph. Will be a directed if G and H are directed, and undirected if G and H are undirected.
Return type NetworkX graph
Raises NetworkXError – If G and H are not both directed or both undirected.
Notes
Node attributes in P are two-tuple of the G and H node attributes. Missing attributes are assigned None.
Examples
>>> G=nx.Graph()
>>> H=nx.Graph()
>>> G.add_node(0, a1=True)
>>> H.add_node('a', a2='Spam')
>>> P=nx.strong_product(G, H)
>>> list(P)
[(0, 'a')]
Edge attributes and edge keys (for multigraphs) are also copied to the new product graph
3.41. Operators 393

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.41.17 networkx.algorithms.operators.product.tensor_product
tensor_product(G,H)
Return the tensor product of G and H.
The tensor product 𝑃of the graphs 𝐺and 𝐻has a node set that is the tensor product of the node sets, 𝑉(𝑃) =
𝑉(𝐺)×𝑉(𝐻).𝑃has an edge ((𝑢, 𝑣),(𝑥, 𝑦)) if and only if (𝑢, 𝑥)is an edge in 𝐺and (𝑣, 𝑦)is an edge in 𝐻.
Tensor product is sometimes also referred to as the categorical product, direct product, cardinal product or
conjunction.
Parameters G, H (graphs) – Networkx graphs.
Returns P – The tensor product of G and H. P will be a multi-graph if either G or H is a multi-graph,
will be a directed if G and H are directed, and undirected if G and H are undirected.
Return type NetworkX graph
Raises NetworkXError – If G and H are not both directed or both undirected.
Notes
Node attributes in P are two-tuple of the G and H node attributes. Missing attributes are assigned None.
Examples
>>> G=nx.Graph()
>>> H=nx.Graph()
>>> G.add_node(0, a1=True)
>>> H.add_node('a', a2='Spam')
>>> P=nx.tensor_product(G, H)
>>> list(P)
[(0, 'a')]
Edge attributes and edge keys (for multigraphs) are also copied to the new product graph
3.41.18 networkx.algorithms.operators.product.power
power(G,k)
Returns the specified power of a graph.
The 𝑘, denoted 𝐺𝑘, is a graph on the same set of nodes in which two distinct nodes 𝑢and 𝑣are adjacent in 𝐺𝑘
if and only if the shortest path distance between 𝑢and 𝑣in 𝐺is at most 𝑘.
Parameters
•G(graph) – A NetworkX simple graph object.
•k(positive integer) – The power to which to raise the graph G.
Returns Gto the power k.
Return type NetworkX simple graph
Raises
•ValueError – If the exponent kis not positive.
•NetworkXNotImplemented – If Gis not a simple graph.
394 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
The number of edges will never decrease when taking successive powers:
>>> G=nx.path_graph(4)
>>> list(nx.power(G, 2).edges)
[(0, 1), (0, 2), (1, 2), (1, 3), (2, 3)]
>>> list(nx.power(G, 3).edges)
[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]
The k`th power of a cycle graph on *n*nodes is the complete graph on *n*
nodes, if `k is at least n // 2:
>>> G=nx.cycle_graph(5)
>>> H=nx.complete_graph(5)
>>> nx.is_isomorphic(nx.power(G, 2), H)
True
>>> G=nx.cycle_graph(8)
>>> H=nx.complete_graph(8)
>>> nx.is_isomorphic(nx.power(G, 4), H)
True
References
Notes
This definition of “power graph” comes from Exercise 3.1.6 of Graph Theory by Bondy and Murty1.
3.42 Planarity
check_planarity(G[, counterexample]) Check if a graph is planar and return a counterexample
or an embedding.
3.42.1 networkx.algorithms.planarity.check_planarity
check_planarity(G,counterexample=False)
Check if a graph is planar and return a counterexample or an embedding.
A graph is planar iff it can be drawn in a plane without any edge intersections.
Parameters
•G(NetworkX graph)
•counterexample (bool) – A Kuratowski subgraph (to proof non planarity) is only returned
if set to true.
Returns (is_planar, certificate) – is_planar is true if the graph is planar. If the graph is planar
certificate is a PlanarEmbedding otherwise it is a Kuratowski subgraph.
Return type (bool, NetworkX graph) tuple
1
J. A. Bondy, U. S. R. Murty, Graph Theory. Springer, 2008.
3.42. Planarity 395

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
A (combinatorial) embedding consists of cyclic orderings of the incident edges at each vertex. Given such
an embedding there are multiple approaches discussed in literature to drawing the graph (subject to various
constraints, e.g. integer coordinates), see e.g. [2].
The planarity check algorithm and extraction of the combinatorial embedding is based on the Left-Right Pla-
narity Test [1].
A counterexample is only generated if the corresponding parameter is set, because the complexity of the coun-
terexample generation is higher.
References
class PlanarEmbedding(incoming_graph_data=None,**attr)
Represents a planar graph with its planar embedding.
The planar embedding is given by a combinatorial embedding.
Neighbor ordering:
In comparison to a usual graph structure, the embedding also stores the order of all neighbors for every vertex.
The order of the neighbors can be given in clockwise (cw) direction or counterclockwise (ccw) direction. This
order is stored as edge attributes in the underlying directed graph. For the edge (u, v) the edge attribute ‘cw’ is
set to the neighbor of u that follows immediately after v in clockwise direction.
In order for a PlanarEmbedding to be valid it must fulfill multiple conditions. It is possible to check if these
conditions are fulfilled with the method check_structure(). The conditions are:
• Edges must go in both directions (because the edge attributes differ)
• Every edge must have a ‘cw’ and ‘ccw’ attribute which corresponds to a correct planar embedding.
• A node with non zero degree must have a node attribute ‘first_nbr’.
As long as a PlanarEmbedding is invalid only the following methods should be called:
•add_half_edge_ccw()
•add_half_edge_cw()
•connect_components()
•add_half_edge_first()
Even though the graph is a subclass of nx.DiGraph, it can still be used for algorithms that require undirected
graphs, because the method is_directed() is overridden. This is possible, because a valid PlanarGraph
must have edges in both directions.
Half edges:
In methods like add_half_edge_ccw the term “half-edge” is used, which is a term that is used in doubly
connected edge lists. It is used to emphasize that the edge is only in one direction and there exists another
half-edge in the opposite direction. While conventional edges always have two faces (including outer face) next
to them, it is possible to assign each half-edge exactly one face. For a half-edge (u, v) that is orientated such that
u is below v then the face that belongs to (u, v) is to the right of this half-edge.
Examples
Create an embedding of a star graph (compare nx.star_graph(3)):
396 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.PlanarEmbedding()
>>> G.add_half_edge_cw(0,1,None)
>>> G.add_half_edge_cw(0,2,1)
>>> G.add_half_edge_cw(0,3,2)
>>> G.add_half_edge_cw(1,0,None)
>>> G.add_half_edge_cw(2,0,None)
>>> G.add_half_edge_cw(3,0,None)
Alternatively the same embedding can also be defined in counterclockwise orientation. The following results in
exactly the same PlanarEmbedding:
>>> G=nx.PlanarEmbedding()
>>> G.add_half_edge_ccw(0,1,None)
>>> G.add_half_edge_ccw(0,3,1)
>>> G.add_half_edge_ccw(0,2,3)
>>> G.add_half_edge_ccw(1,0,None)
>>> G.add_half_edge_ccw(2,0,None)
>>> G.add_half_edge_ccw(3,0,None)
After creating a graph, it is possible to validate that the PlanarEmbedding object is correct:
>>> G.check_structure()
add_half_edge_ccw(start_node,end_node,reference_neighbor)
Adds a half-edge from start_node to end_node.
The half-edge is added counter clockwise next to the existing half-edge (start_node, reference_neighbor).
Parameters
•start_node (node) – Start node of inserted edge.
•end_node (node) – End node of inserted edge.
•reference_neighbor (node) – End node of reference edge.
Raises nx.NetworkXException – If the reference_neighbor does not exist.
See also:
add_half_edge_cw(),connect_components(),add_half_edge_first()
add_half_edge_cw(start_node,end_node,reference_neighbor)
Adds a half-edge from start_node to end_node.
The half-edge is added clockwise next to the existing half-edge (start_node, reference_neighbor).
Parameters
•start_node (node) – Start node of inserted edge.
•end_node (node) – End node of inserted edge.
•reference_neighbor (node) – End node of reference edge.
Raises nx.NetworkXException – If the reference_neighbor does not exist.
See also:
add_half_edge_ccw(),connect_components(),add_half_edge_first()
add_half_edge_first(start_node,end_node)
The added half-edge is inserted at the first position in the order.
3.42. Planarity 397

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•start_node (node)
•end_node (node)
See also:
add_half_edge_ccw(),add_half_edge_cw(),connect_components()
check_structure()
Runs without exceptions if this object is valid.
Checks that the following properties are fulfilled:
• Edges go in both directions (because the edge attributes differ).
• Every edge has a ‘cw’ and ‘ccw’ attribute which corresponds to a correct planar embedding.
• A node with a degree larger than 0 has a node attribute ‘first_nbr’.
Running this method verifies that the underlying Graph must be planar.
Raises nx.NetworkXException – This exception is raised with a short explanation if the
PlanarEmbedding is invalid.
connect_components(v,w)
Adds half-edges for (v, w) and (w, v) at some position.
This method should only be called if v and w are in different components, or it might break the embed-
ding. This especially means that if connect_components(v, w) is called it is not allowed to call
connect_components(w, v) afterwards. The neighbor orientations in both directions are all set
correctly after the first call.
Parameters
•v(node)
•w(node)
See also:
add_half_edge_ccw(),add_half_edge_cw(),add_half_edge_first()
get_data()
Converts the adjacency structure into a better readable structure.
Returns embedding – A dict mapping all nodes to a list of neighbors sorted in clockwise order.
Return type dict
is_directed()
A valid PlanarEmbedding is undirected.
All reverse edges are contained, i.e. for every existing half-edge (v, w) the half-edge in the opposite
direction (w, v) is also contained.
neighbors_cw_order(v)
Generator for the neighbors of v in clockwise order.
Parameters v (node)
Yields node
next_face_half_edge(v,w)
Returns the following half-edge left of a face.
Parameters
398 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•v(node)
•w(node)
Returns half-edge
Return type tuple
traverse_face(v,w,mark_half_edges=None)
Returns nodes on the face that belong to the half-edge (v, w).
The face that is traversed lies to the right of the half-edge (in an orientation where v is below w).
Optionally it is possible to pass a set to which all encountered half edges are added. Before calling this
method, this set must not include any half-edges that belong to the face.
Parameters
•v(node) – Start node of half-edge.
•w(node) – End node of half-edge.
•mark_half_edges (set, optional) – Set to which all encountered half-edges are added.
Returns face – A list of nodes that lie on this face.
Return type list
3.43 Reciprocity
Algorithms to calculate reciprocity in a directed graph.
reciprocity(G[, nodes]) Compute the reciprocity in a directed graph.
overall_reciprocity(G) Compute the reciprocity for the whole graph.
3.43.1 networkx.algorithms.reciprocity.reciprocity
reciprocity(G,nodes=None)
Compute the reciprocity in a directed graph.
The reciprocity of a directed graph is defined as the ratio of the number of edges pointing in both directions to
the total number of edges in the graph. Formally, 𝑟=|(𝑢, 𝑣)∈𝐺|(𝑣, 𝑢)∈𝐺|/|(𝑢, 𝑣)∈𝐺|.
The reciprocity of a single node u is defined similarly, it is the ratio of the number of edges in both directions to
the total number of edges attached to node u.
Parameters
•G(graph) – A networkx directed graph
•nodes (container of nodes, optional (default=whole graph)) – Compute reciprocity for
nodes in this container.
Returns out – Reciprocity keyed by node label.
Return type dictionary
3.43. Reciprocity 399

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The reciprocity is not defined for isolated nodes. In such cases this function will return None.
3.43.2 networkx.algorithms.reciprocity.overall_reciprocity
overall_reciprocity(G)
Compute the reciprocity for the whole graph.
See the doc of reciprocity for the definition.
Parameters G (graph) – A networkx graph
3.44 Rich Club
Functions for computing rich-club coefficients.
rich_club_coefficient(G[, normalized, Q,
seed])
Returns the rich-club coefficient of the graph G.
3.44.1 networkx.algorithms.richclub.rich_club_coefficient
rich_club_coefficient(G,normalized=True,Q=100,seed=None)
Returns the rich-club coefficient of the graph G.
For each degree k, the rich-club coefficient is the ratio of the number of actual to the number of potential edges
for nodes with degree greater than k:
𝜑(𝑘) = 2𝐸𝑘
𝑁𝑘(𝑁𝑘−1)
where N_k is the number of nodes with degree larger than k, and E_k is the number of edges among those
nodes.
Parameters
•G(NetworkX graph) – Undirected graph with neither parallel edges nor self-loops.
•normalized (bool (optional)) – Normalize using randomized network as in1
•Q(float (optional, default=100)) – If normalized is True, perform Q*mdouble-edge
swaps, where mis the number of edges in G, to use as a null-model for normalization.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns rc – A dictionary, keyed by degree, with rich-club coefficient values.
Return type dictionary
1Julian J. McAuley, Luciano da Fontoura Costa, and Tibério S. Caetano, “The rich-club phenomenon across complex network hierarchies”,
Applied Physics Letters Vol 91 Issue 8, August 2007. https://arxiv.org/abs/physics/0701290
400 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.Graph([(0,1), (0,2), (1,2), (1,3), (1,4), (4,5)])
>>> rc =nx.rich_club_coefficient(G, normalized=False)
>>> rc[0]# doctest: +SKIP
0.4
Notes
The rich club definition and algorithm are found in1. This algorithm ignores any edge weights and is not defined
for directed graphs or graphs with parallel edges or self loops.
Estimates for appropriate values of Qare found in2.
References
3.45 Shortest Paths
Compute the shortest paths and path lengths between nodes in the graph.
These algorithms work with undirected and directed graphs.
shortest_path(G[, source, target, weight, . . . ]) Compute shortest paths in the graph.
all_shortest_paths(G, source, target[, . . . ]) Compute all shortest paths in the graph.
shortest_path_length(G[, source, target, . . . ]) Compute shortest path lengths in the graph.
average_shortest_path_length(G[, weight,
method])
Return the average shortest path length.
has_path(G, source, target) Return True if Ghas a path from source to target.
3.45.1 networkx.algorithms.shortest_paths.generic.shortest_path
shortest_path(G,source=None,target=None,weight=None,method=’dijkstra’)
Compute shortest paths in the graph.
Parameters
•G(NetworkX graph)
•source (node, optional) – Starting node for path. If not specified, compute shortest paths for
each possible starting node.
•target (node, optional) – Ending node for path. If not specified, compute shortest paths to
all possible nodes.
•weight (None or string, optional (default = None)) – If None, every edge has
weight/distance/cost 1. If a string, use this edge attribute as the edge weight. Any edge
attribute not present defaults to 1.
•method (string, optional (default = ‘dijkstra’)) – The algorithm to use to compute the
path. Supported options: ‘dijkstra’, ‘bellman-ford’. Other inputs produce a ValueError.
If weight is None, unweighted graph methods are used, and this suggestion is ignored.
2R. Milo, N. Kashtan, S. Itzkovitz, M. E. J. Newman, U. Alon, “Uniform generation of random graphs with arbitrary degree sequences”, 2006.
https://arxiv.org/abs/cond-mat/0312028
3.45. Shortest Paths 401
NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns
path – All returned paths include both the source and target in the path.
If the source and target are both specified, return a single list of nodes in a shortest path from the
source to the target.
If only the source is specified, return a dictionary keyed by targets with a list of nodes in a
shortest path from the source to one of the targets.
If only the target is specified, return a dictionary keyed by sources with a list of nodes in a
shortest path from one of the sources to the target.
If neither the source nor target are specified return a dictionary of dictionaries with
path[source][target]=[list of nodes in path].
Return type list or dictionary
Raises
•NodeNotFound – If source is not in G.
•ValueError – If method is not among the supported options.
Examples
>>> G=nx.path_graph(5)
>>> print(nx.shortest_path(G, source=0, target=4))
[0, 1, 2, 3, 4]
>>> p=nx.shortest_path(G, source=0)# target not specified
>>> p[4]
[0, 1, 2, 3, 4]
>>> p=nx.shortest_path(G, target=4)# source not specified
>>> p[0]
[0, 1, 2, 3, 4]
>>> p=nx.shortest_path(G) # source, target not specified
>>> p[0][4]
[0, 1, 2, 3, 4]
Notes
There may be more than one shortest path between a source and target. This returns only one of them.
See also:
all_pairs_shortest_path(),all_pairs_dijkstra_path(),
all_pairs_bellman_ford_path(),single_source_shortest_path(),
single_source_dijkstra_path(),single_source_bellman_ford_path()
3.45.2 networkx.algorithms.shortest_paths.generic.all_shortest_paths
all_shortest_paths(G,source,target,weight=None,method=’dijkstra’)
Compute all shortest paths in the graph.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path.
402 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•target (node) – Ending node for path.
•weight (None or string, optional (default = None)) – If None, every edge has
weight/distance/cost 1. If a string, use this edge attribute as the edge weight. Any edge
attribute not present defaults to 1.
•method (string, optional (default = ‘dijkstra’)) – The algorithm to use to compute the path
lengths. Supported options: ‘dijkstra’, ‘bellman-ford’. Other inputs produce a ValueError.
If weight is None, unweighted graph methods are used, and this suggestion is ignored.
Returns paths – A generator of all paths between source and target.
Return type generator of lists
Raises
•ValueError – If method is not among the supported options.
•NetworkXNoPath – If target cannot be reached from source.
Examples
>>> G=nx.Graph()
>>> nx.add_path(G, [0,1,2])
>>> nx.add_path(G, [0,10,2])
>>> print([p for pin nx.all_shortest_paths(G, source=0, target=2)])
[[0, 1, 2], [0, 10, 2]]
Notes
There may be many shortest paths between the source and target.
See also:
shortest_path(),single_source_shortest_path(),all_pairs_shortest_path()
3.45.3 networkx.algorithms.shortest_paths.generic.shortest_path_length
shortest_path_length(G,source=None,target=None,weight=None,method=’dijkstra’)
Compute shortest path lengths in the graph.
Parameters
•G(NetworkX graph)
•source (node, optional) – Starting node for path. If not specified, compute shortest path
lengths using all nodes as source nodes.
•target (node, optional) – Ending node for path. If not specified, compute shortest path
lengths using all nodes as target nodes.
•weight (None or string, optional (default = None)) – If None, every edge has
weight/distance/cost 1. If a string, use this edge attribute as the edge weight. Any edge
attribute not present defaults to 1.
•method (string, optional (default = ‘dijkstra’)) – The algorithm to use to compute the path
length. Supported options: ‘dijkstra’, ‘bellman-ford’. Other inputs produce a ValueError. If
weight is None, unweighted graph methods are used, and this suggestion is ignored.
3.45. Shortest Paths 403
NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns
length – If the source and target are both specified, return the length of the shortest path from
the source to the target.
If only the source is specified, return a dict keyed by target to the shortest path length from the
source to that target.
If only the target is specified, return a dict keyed by source to the shortest path length from that
source to the target.
If neither the source nor target are specified, return an iterator over (source, dictionary) where
dictionary is keyed by target to shortest path length from source to that target.
Return type int or iterator
Raises
•NodeNotFound – If source is not in G.
•NetworkXNoPath – If no path exists between source and target.
•ValueError – If method is not among the supported options.
Examples
>>> G=nx.path_graph(5)
>>> nx.shortest_path_length(G, source=0, target=4)
4
>>> p=nx.shortest_path_length(G, source=0)# target not specified
>>> p[4]
4
>>> p=nx.shortest_path_length(G, target=4)# source not specified
>>> p[0]
4
>>> p=dict(nx.shortest_path_length(G)) # source,target not specified
>>> p[0][4]
4
Notes
The length of the path is always 1 less than the number of nodes involved in the path since the length measures
the number of edges followed.
For digraphs this returns the shortest directed path length. To find path lengths in the reverse direction use
G.reverse(copy=False) first to flip the edge orientation.
See also:
all_pairs_shortest_path_length(),all_pairs_dijkstra_path_length(),
all_pairs_bellman_ford_path_length(),single_source_shortest_path_length(),
single_source_dijkstra_path_length(),single_source_bellman_ford_path_length()
3.45.4 networkx.algorithms.shortest_paths.generic.average_shortest_path_length
average_shortest_path_length(G,weight=None,method=’dijkstra’)
Return the average shortest path length.
404 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
The average shortest path length is
𝑎=
𝑠,𝑡∈𝑉
𝑑(𝑠, 𝑡)
𝑛(𝑛−1)
where Vis the set of nodes in G,d(s, t) is the shortest path from sto t, and nis the number of nodes in G.
Parameters
•G(NetworkX graph)
•weight (None or string, optional (default = None)) – If None, every edge has
weight/distance/cost 1. If a string, use this edge attribute as the edge weight. Any edge
attribute not present defaults to 1.
•method (string, optional (default = ‘dijkstra’)) – The algorithm to use to compute the path
lengths. Supported options: ‘dijkstra’, ‘bellman-ford’. Other inputs produce a ValueError.
If weight is None, unweighted graph methods are used, and this suggestion is ignored.
Raises
•NetworkXPointlessConcept – If Gis the null graph (that is, the graph on zero nodes).
•NetworkXError – If Gis not connected (or not weakly connected, in the case of a directed
graph).
•ValueError – If method is not among the supported options.
Examples
>>> G=nx.path_graph(5)
>>> nx.average_shortest_path_length(G)
2.0
For disconnected graphs, you can compute the average shortest path length for each component
>>> G=nx.Graph([(1,2), (3,4)])
>>> for Cin nx.connected_component_subgraphs(G):
... print(nx.average_shortest_path_length(C))
1.0
1.0
3.45.5 networkx.algorithms.shortest_paths.generic.has_path
has_path(G,source,target)
Return True if Ghas a path from source to target.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path
•target (node) – Ending node for path
3.45. Shortest Paths 405

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.45.6 Advanced Interface
Shortest path algorithms for unweighted graphs.
single_source_shortest_path(G, source[,
cutoff])
Compute shortest path between source and all other
nodes reachable from source.
single_source_shortest_path_length(G,
source)
Compute the shortest path lengths from source to all
reachable nodes.
single_target_shortest_path(G, target[,
cutoff])
Compute shortest path to target from all nodes that reach
target.
single_target_shortest_path_length(G,
target)
Compute the shortest path lengths to target from all
reachable nodes.
bidirectional_shortest_path(G, source, tar-
get)
Return a list of nodes in a shortest path between source
and target.
all_pairs_shortest_path(G[, cutoff]) Compute shortest paths between all nodes.
all_pairs_shortest_path_length(G[, cut-
off])
Computes the shortest path lengths between all nodes in
G.
predecessor(G, source[, target, cutoff, . . . ]) Returns dict of predecessors for the path from source to
all nodes in G
networkx.algorithms.shortest_paths.unweighted.single_source_shortest_path
single_source_shortest_path(G,source,cutoff=None)
Compute shortest path between source and all other nodes reachable from source.
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•cutoff (integer, optional) – Depth to stop the search. Only paths of length <= cutoff are
returned.
Returns lengths – Dictionary, keyed by target, of shortest paths.
Return type dictionary
Examples
>>> G=nx.path_graph(5)
>>> path =nx.single_source_shortest_path(G, 0)
>>> path[4]
[0, 1, 2, 3, 4]
Notes
The shortest path is not necessarily unique. So there can be multiple paths between the source and each target
node, all of which have the same ‘shortest’ length. For each target node, this function returns only one of those
paths.
See also:
shortest_path()
406 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.unweighted.single_source_shortest_path_length
single_source_shortest_path_length(G,source,cutoff=None)
Compute the shortest path lengths from source to all reachable nodes.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path
•cutoff (integer, optional) – Depth to stop the search. Only paths of length <= cutoff are
returned.
Returns lengths – Dict keyed by node to shortest path length to source.
Return type dict
Examples
>>> G=nx.path_graph(5)
>>> length =nx.single_source_shortest_path_length(G, 0)
>>> length[4]
4
>>> for node in length:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 3
4: 4
See also:
shortest_path_length()
networkx.algorithms.shortest_paths.unweighted.single_target_shortest_path
single_target_shortest_path(G,target,cutoff=None)
Compute shortest path to target from all nodes that reach target.
Parameters
•G(NetworkX graph)
•target (node label) – Target node for path
•cutoff (integer, optional) – Depth to stop the search. Only paths of length <= cutoff are
returned.
Returns lengths – Dictionary, keyed by target, of shortest paths.
Return type dictionary
Examples
3.45. Shortest Paths 407

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(5, create_using=nx.DiGraph())
>>> path =nx.single_target_shortest_path(G, 4)
>>> path[0]
[0, 1, 2, 3, 4]
Notes
The shortest path is not necessarily unique. So there can be multiple paths between the source and each target
node, all of which have the same ‘shortest’ length. For each target node, this function returns only one of those
paths.
See also:
shortest_path(),single_source_shortest_path()
networkx.algorithms.shortest_paths.unweighted.single_target_shortest_path_length
single_target_shortest_path_length(G,target,cutoff=None)
Compute the shortest path lengths to target from all reachable nodes.
Parameters
•G(NetworkX graph)
•target (node) – Target node for path
•cutoff (integer, optional) – Depth to stop the search. Only paths of length <= cutoff are
returned.
Returns lengths – (source, shortest path length) iterator
Return type iterator
Examples
>>> G=nx.path_graph(5, create_using=nx.DiGraph())
>>> length =dict(nx.single_target_shortest_path_length(G, 4))
>>> length[0]
4
>>> for node in range(5):
... print('{}:{}'.format(node, length[node]))
0: 4
1: 3
2: 2
3: 1
4: 0
See also:
single_source_shortest_path_length(),shortest_path_length()
networkx.algorithms.shortest_paths.unweighted.bidirectional_shortest_path
bidirectional_shortest_path(G,source,target)
Return a list of nodes in a shortest path between source and target.
408 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•source (node label) – starting node for path
•target (node label) – ending node for path
Returns path – List of nodes in a path from source to target.
Return type list
Raises NetworkXNoPath – If no path exists between source and target.
See also:
shortest_path()
Notes
This algorithm is used by shortest_path(G, source, target).
networkx.algorithms.shortest_paths.unweighted.all_pairs_shortest_path
all_pairs_shortest_path(G,cutoff=None)
Compute shortest paths between all nodes.
Parameters
•G(NetworkX graph)
•cutoff (integer, optional) – Depth at which to stop the search. Only paths of length at most
cutoff are returned.
Returns lengths – Dictionary, keyed by source and target, of shortest paths.
Return type dictionary
Examples
>>> G=nx.path_graph(5)
>>> path =dict(nx.all_pairs_shortest_path(G))
>>> print(path[0][4])
[0, 1, 2, 3, 4]
See also:
floyd_warshall()
networkx.algorithms.shortest_paths.unweighted.all_pairs_shortest_path_length
all_pairs_shortest_path_length(G,cutoff=None)
Computes the shortest path lengths between all nodes in G.
Parameters
•G(NetworkX graph)
•cutoff (integer, optional) – Depth at which to stop the search. Only paths of length at most
cutoff are returned.
3.45. Shortest Paths 409

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns lengths – (source, dictionary) iterator with dictionary keyed by target and shortest path
length as the key value.
Return type iterator
Notes
The iterator returned only has reachable node pairs.
Examples
>>> G=nx.path_graph(5)
>>> length =dict(nx.all_pairs_shortest_path_length(G))
>>> for node in [0,1,2,3,4]:
... print('1 - {}:{}'.format(node, length[1][node]))
1-0:1
1-1:0
1-2:1
1-3:2
1-4:3
>>> length[3][2]
1
>>> length[2][2]
0
networkx.algorithms.shortest_paths.unweighted.predecessor
predecessor(G,source,target=None,cutoff=None,return_seen=None)
Returns dict of predecessors for the path from source to all nodes in G
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•target (node label, optional) – Ending node for path. If provided only predecessors between
source and target are returned
•cutoff (integer, optional) – Depth to stop the search. Only paths of length <= cutoff are
returned.
Returns pred – Dictionary, keyed by node, of predecessors in the shortest path.
Return type dictionary
Examples
>>> G=nx.path_graph(4)
>>> list(G)
[0, 1, 2, 3]
>>> nx.predecessor(G, 0)
{0: [], 1: [0], 2: [1], 3: [2]}
410 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Shortest path algorithms for weighed graphs.
dijkstra_predecessor_and_distance(G,
source)
Compute weighted shortest path length and predeces-
sors.
dijkstra_path(G, source, target[, weight]) Returns the shortest weighted path from source to target
in G.
dijkstra_path_length(G, source, target[,
weight])
Returns the shortest weighted path length in G from
source to target.
single_source_dijkstra(G, source[, target,
...])
Find shortest weighted paths and lengths from a source
node.
single_source_dijkstra_path(G, source[,
...])
Find shortest weighted paths in G from a source node.
single_source_dijkstra_path_length(G,
source)
Find shortest weighted path lengths in G from a source
node.
multi_source_dijkstra(G, sources[, target,
...])
Find shortest weighted paths and lengths from a given
set of source nodes.
multi_source_dijkstra_path(G, sources[,
...])
Find shortest weighted paths in G from a given set of
source nodes.
multi_source_dijkstra_path_length(G,
sources)
Find shortest weighted path lengths in G from a given
set of source nodes.
all_pairs_dijkstra(G[, cutoff, weight]) Find shortest weighted paths and lengths between all
nodes.
all_pairs_dijkstra_path(G[, cutoff, weight]) Compute shortest paths between all nodes in a weighted
graph.
all_pairs_dijkstra_path_length(G[, cut-
off, . . . ])
Compute shortest path lengths between all nodes in a
weighted graph.
bidirectional_dijkstra(G, source, target[,
...])
Dijkstra’s algorithm for shortest paths using bidirec-
tional search.
bellman_ford_path(G, source, target[, weight]) Returns the shortest path from source to target in a
weighted graph G.
bellman_ford_path_length(G, source, target) Returns the shortest path length from source to target in
a weighted graph.
single_source_bellman_ford(G, source[,
...])
Compute shortest paths and lengths in a weighted graph
G.
single_source_bellman_ford_path(G,
source[, . . . ])
Compute shortest path between source and all other
reachable nodes for a weighted graph.
single_source_bellman_ford_path_length(G,
source)
Compute the shortest path length between source and all
other reachable nodes for a weighted graph.
all_pairs_bellman_ford_path(G[, weight]) Compute shortest paths between all nodes in a weighted
graph.
all_pairs_bellman_ford_path_length(G[,
weight])
Compute shortest path lengths between all nodes in a
weighted graph.
bellman_ford_predecessor_and_distance(G,
source)
Compute shortest path lengths and predecessors on
shortest paths in weighted graphs.
negative_edge_cycle(G[, weight]) Return True if there exists a negative edge cycle any-
where in G.
goldberg_radzik(G, source[, weight]) Compute shortest path lengths and predecessors on
shortest paths in weighted graphs.
johnson(G[, weight]) Uses Johnson’s Algorithm to compute shortest paths.
3.45. Shortest Paths 411

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.weighted.dijkstra_predecessor_and_distance
dijkstra_predecessor_and_distance(G,source,cutoff=None,weight=’weight’)
Compute weighted shortest path length and predecessors.
Uses Dijkstra’s Method to obtain the shortest weighted paths and return dictionaries of predecessors for each
node and distance for each node from the source.
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns pred, distance – Returns two dictionaries representing a list of predecessors of a node and
the distance to each node. Warning: If target is specified, the dicts are incomplete as they only
contain information for the nodes along a path to target.
Return type dictionaries
Raises NodeNotFound – If source is not in G.
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The list of predecessors contains more than one element only when there are more than one shortest paths to the
key node.
Examples
>>> import networkx as nx
>>> G=nx.path_graph(5, create_using =nx.DiGraph())
>>> pred, dist =nx.dijkstra_predecessor_and_distance(G, 0)
>>> sorted(pred.items())
[(0, []), (1, [0]), (2, [1]), (3, [2]), (4, [3])]
>>> sorted(dist.items())
[(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)]
>>> pred, dist =nx.dijkstra_predecessor_and_distance(G, 0,1)
>>> sorted(pred.items())
[(0, []), (1, [0])]
>>> sorted(dist.items())
[(0, 0), (1, 1)]
412 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.weighted.dijkstra_path
dijkstra_path(G,source,target,weight=’weight’)
Returns the shortest weighted path from source to target in G.
Uses Dijkstra’s Method to compute the shortest weighted path between two nodes in a graph.
Parameters
•G(NetworkX graph)
•source (node) – Starting node
•target (node) – Ending node
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns path – List of nodes in a shortest path.
Return type list
Raises
•NodeNotFound – If source is not in G.
•NetworkXNoPath – If no path exists between source and target.
Examples
>>> G=nx.path_graph(5)
>>> print(nx.dijkstra_path(G,0,4))
[0, 1, 2, 3, 4]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
The weight function can be used to include node weights.
>>> def func(u, v, d):
... node_u_wt =G.nodes[u].get('node_weight',1)
... node_v_wt =G.nodes[v].get('node_weight',1)
... edge_wt =d.get('weight',1)
... return node_u_wt/2+node_v_wt/2+edge_wt
In this example we take the average of start and end node weights of an edge and add it to the weight of the
edge.
See also:
bidirectional_dijkstra(),bellman_ford_path()
3.45. Shortest Paths 413

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.weighted.dijkstra_path_length
dijkstra_path_length(G,source,target,weight=’weight’)
Returns the shortest weighted path length in G from source to target.
Uses Dijkstra’s Method to compute the shortest weighted path length between two nodes in a graph.
Parameters
•G(NetworkX graph)
•source (node label) – starting node for path
•target (node label) – ending node for path
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns length – Shortest path length.
Return type number
Raises
•NodeNotFound – If source is not in G.
•NetworkXNoPath – If no path exists between source and target.
Examples
>>> G=nx.path_graph(5)
>>> print(nx.dijkstra_path_length(G,0,4))
4
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
See also:
bidirectional_dijkstra(),bellman_ford_path_length()
networkx.algorithms.shortest_paths.weighted.single_source_dijkstra
single_source_dijkstra(G,source,target=None,cutoff=None,weight=’weight’)
Find shortest weighted paths and lengths from a source node.
Compute the shortest path length between source and all other reachable nodes for a weighted graph.
Uses Dijkstra’s algorithm to compute shortest paths and lengths between a source and all other reachable nodes
in a weighted graph.
414 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•target (node label, optional) – Ending node for path
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns distance, path – If target is None, paths and lengths to all nodes are computed. The return
value is a tuple of two dictionaries keyed by target nodes. The first dictionary stores distance to
each target node. The second stores the path to each target node. If target is not None, returns
a tuple (distance, path), where distance is the distance from source to target and path is a list
representing the path from source to target.
Return type pair of dictionaries, or numeric and list.
Raises NodeNotFound – If source is not in G.
Examples
>>> G=nx.path_graph(5)
>>> length, path =nx.single_source_dijkstra(G, 0)
>>> print(length[4])
4
>>> for node in [0,1,2,3,4]:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 3
4: 4
>>> path[4]
[0, 1, 2, 3, 4]
>>> length, path =nx.single_source_dijkstra(G, 0,1)
>>> length
1
>>> path
[0, 1]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
3.45. Shortest Paths 415

NetworkX Reference, Release 2.3rc1.dev20181203210840
Based on the Python cookbook recipe (119466) at http://aspn.activestate.com/ASPN/Cookbook/Python/Recipe/
119466
This algorithm is not guaranteed to work if edge weights are negative or are floating point numbers (overflows
and roundoff errors can cause problems).
See also:
single_source_dijkstra_path(),single_source_dijkstra_path_length(),
single_source_bellman_ford()
networkx.algorithms.shortest_paths.weighted.single_source_dijkstra_path
single_source_dijkstra_path(G,source,cutoff=None,weight=’weight’)
Find shortest weighted paths in G from a source node.
Compute shortest path between source and all other reachable nodes for a weighted graph.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path.
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns paths – Dictionary of shortest path lengths keyed by target.
Return type dictionary
Raises NodeNotFound – If source is not in G.
Examples
>>> G=nx.path_graph(5)
>>> path=nx.single_source_dijkstra_path(G,0)
>>> path[4]
[0, 1, 2, 3, 4]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
See also:
single_source_dijkstra(),single_source_bellman_ford()
416 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.weighted.single_source_dijkstra_path_length
single_source_dijkstra_path_length(G,source,cutoff=None,weight=’weight’)
Find shortest weighted path lengths in G from a source node.
Compute the shortest path length between source and all other reachable nodes for a weighted graph.
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns length – Dict keyed by node to shortest path length from source.
Return type dict
Raises NodeNotFound – If source is not in G.
Examples
>>> G=nx.path_graph(5)
>>> length =nx.single_source_dijkstra_path_length(G, 0)
>>> length[4]
4
>>> for node in [0,1,2,3,4]:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 3
4: 4
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
See also:
single_source_dijkstra(),single_source_bellman_ford_path_length()
3.45. Shortest Paths 417

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.weighted.multi_source_dijkstra
multi_source_dijkstra(G,sources,target=None,cutoff=None,weight=’weight’)
Find shortest weighted paths and lengths from a given set of source nodes.
Uses Dijkstra’s algorithm to compute the shortest paths and lengths between one of the source nodes and the
given target, or all other reachable nodes if not specified, for a weighted graph.
Parameters
•G(NetworkX graph)
•sources (non-empty set of nodes) – Starting nodes for paths. If this is just a set containing a
single node, then all paths computed by this function will start from that node. If there are
two or more nodes in the set, the computed paths may begin from any one of the start nodes.
•target (node label, optional) – Ending node for path
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns distance, path – If target is None, returns a tuple of two dictionaries keyed by node. The
first dictionary stores distance from one of the source nodes. The second stores the path from
one of the sources to that node. If target is not None, returns a tuple of (distance, path) where
distance is the distance from source to target and path is a list representing the path from source
to target.
Return type pair of dictionaries, or numeric and list
Examples
>>> G=nx.path_graph(5)
>>> length, path =nx.multi_source_dijkstra(G, {0,4})
>>> for node in [0,1,2,3,4]:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 1
4: 0
>>> path[1]
[0, 1]
>>> path[3]
[4, 3]
>>> length, path =nx.multi_source_dijkstra(G, {0,4}, 1)
>>> length
1
>>> path
[0, 1]
418 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
Based on the Python cookbook recipe (119466) at http://aspn.activestate.com/ASPN/Cookbook/Python/Recipe/
119466
This algorithm is not guaranteed to work if edge weights are negative or are floating point numbers (overflows
and roundoff errors can cause problems).
Raises
•ValueError – If sources is empty.
•NodeNotFound – If any of sources is not in G.
See also:
multi_source_dijkstra_path(),multi_source_dijkstra_path_length()
networkx.algorithms.shortest_paths.weighted.multi_source_dijkstra_path
multi_source_dijkstra_path(G,sources,cutoff=None,weight=’weight’)
Find shortest weighted paths in G from a given set of source nodes.
Compute shortest path between any of the source nodes and all other reachable nodes for a weighted graph.
Parameters
•G(NetworkX graph)
•sources (non-empty set of nodes) – Starting nodes for paths. If this is just a set containing a
single node, then all paths computed by this function will start from that node. If there are
two or more nodes in the set, the computed paths may begin from any one of the start nodes.
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns paths – Dictionary of shortest paths keyed by target.
Return type dictionary
Examples
>>> G=nx.path_graph(5)
>>> path =nx.multi_source_dijkstra_path(G, {0,4})
>>> path[1]
[0, 1]
(continues on next page)
3.45. Shortest Paths 419

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> path[3]
[4, 3]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
Raises
•ValueError – If sources is empty.
•NodeNotFound – If any of sources is not in G.
See also:
multi_source_dijkstra(),multi_source_bellman_ford()
networkx.algorithms.shortest_paths.weighted.multi_source_dijkstra_path_length
multi_source_dijkstra_path_length(G,sources,cutoff=None,weight=’weight’)
Find shortest weighted path lengths in G from a given set of source nodes.
Compute the shortest path length between any of the source nodes and all other reachable nodes for a weighted
graph.
Parameters
•G(NetworkX graph)
•sources (non-empty set of nodes) – Starting nodes for paths. If this is just a set containing a
single node, then all paths computed by this function will start from that node. If there are
two or more nodes in the set, the computed paths may begin from any one of the start nodes.
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns length – Dict keyed by node to shortest path length to nearest source.
Return type dict
Examples
420 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(5)
>>> length =nx.multi_source_dijkstra_path_length(G, {0,4})
>>> for node in [0,1,2,3,4]:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 1
4: 0
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The weight function can be used to hide edges by returning None. So weight = lambda u, v, d: 1
if d['color']=="red" else None will find the shortest red path.
Raises
•ValueError – If sources is empty.
•NodeNotFound – If any of sources is not in G.
See also:
multi_source_dijkstra()
networkx.algorithms.shortest_paths.weighted.all_pairs_dijkstra
all_pairs_dijkstra(G,cutoff=None,weight=’weight’)
Find shortest weighted paths and lengths between all nodes.
Parameters
•G(NetworkX graph)
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be
G.edge[u][v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Yields (node, (distance, path)) ((node obj, (dict, dict))) – Each source node has two associated
dicts. The first holds distance keyed by target and the second holds paths keyed by target.
(See single_source_dijkstra for the source/target node terminology.) If desired you can apply
dict() to this function to create a dict keyed by source node to the two dicts.
Examples
3.45. Shortest Paths 421

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(5)
>>> len_path =dict(nx.all_pairs_dijkstra(G))
>>> print(len_path[3][0][1])
2
>>> for node in [0,1,2,3,4]:
... print('3 - {}:{}'.format(node, len_path[3][0][node]))
3-0:3
3-1:2
3-2:1
3-3:0
3-4:1
>>> len_path[3][1][1]
[3, 2, 1]
>>> for n, (dist, path) in nx.all_pairs_dijkstra(G):
... print(path[1])
[0, 1]
[1]
[2, 1]
[3, 2, 1]
[4, 3, 2, 1]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The yielded dicts only have keys for reachable nodes.
networkx.algorithms.shortest_paths.weighted.all_pairs_dijkstra_path
all_pairs_dijkstra_path(G,cutoff=None,weight=’weight’)
Compute shortest paths between all nodes in a weighted graph.
Parameters
•G(NetworkX graph)
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns distance – Dictionary, keyed by source and target, of shortest paths.
Return type dictionary
Examples
422 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(5)
>>> path =dict(nx.all_pairs_dijkstra_path(G))
>>> print(path[0][4])
[0, 1, 2, 3, 4]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
floyd_warshall(),all_pairs_bellman_ford_path()
networkx.algorithms.shortest_paths.weighted.all_pairs_dijkstra_path_length
all_pairs_dijkstra_path_length(G,cutoff=None,weight=’weight’)
Compute shortest path lengths between all nodes in a weighted graph.
Parameters
•G(NetworkX graph)
•cutoff (integer or float, optional) – Depth to stop the search. Only return paths with length
<= cutoff.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns distance – (source, dictionary) iterator with dictionary keyed by target and shortest path
length as the key value.
Return type iterator
Examples
>>> G=nx.path_graph(5)
>>> length =dict(nx.all_pairs_dijkstra_path_length(G))
>>> for node in [0,1,2,3,4]:
... print('1 - {}:{}'.format(node, length[1][node]))
1-0:1
1-1:0
1-2:1
1-3:2
1-4:3
>>> length[3][2]
1
>>> length[2][2]
0
3.45. Shortest Paths 423

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The dictionary returned only has keys for reachable node pairs.
networkx.algorithms.shortest_paths.weighted.bidirectional_dijkstra
bidirectional_dijkstra(G,source,target,weight=’weight’)
Dijkstra’s algorithm for shortest paths using bidirectional search.
Parameters
•G(NetworkX graph)
•source (node) – Starting node.
•target (node) – Ending node.
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns length, path – length is the distance from source to target. path is a list of nodes on a path
from source to target.
Return type number and list
Raises
•NodeNotFound – If either source or target is not in G.
•NetworkXNoPath – If no path exists between source and target.
Examples
>>> G=nx.path_graph(5)
>>> length, path =nx.bidirectional_dijkstra(G, 0,4)
>>> print(length)
4
>>> print(path)
[0, 1, 2, 3, 4]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
In practice bidirectional Dijkstra is much more than twice as fast as ordinary Dijkstra.
Ordinary Dijkstra expands nodes in a sphere-like manner from the source. The radius of this sphere will even-
tually be the length of the shortest path. Bidirectional Dijkstra will expand nodes from both the source and
the target, making two spheres of half this radius. Volume of the first sphere is pi*r*rwhile the others are
2*pi*r/2*r/2, making up half the volume.
424 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
This algorithm is not guaranteed to work if edge weights are negative or are floating point numbers (overflows
and roundoff errors can cause problems).
See also:
shortest_path(),shortest_path_length()
networkx.algorithms.shortest_paths.weighted.bellman_ford_path
bellman_ford_path(G,source,target,weight=’weight’)
Returns the shortest path from source to target in a weighted graph G.
Parameters
•G(NetworkX graph)
•source (node) – Starting node
•target (node) – Ending node
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight
Returns path – List of nodes in a shortest path.
Return type list
Raises
•NodeNotFound – If source is not in G.
•NetworkXNoPath – If no path exists between source and target.
Examples
>>> G=nx.path_graph(5)
>>> print(nx.bellman_ford_path(G, 0,4))
[0, 1, 2, 3, 4]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
dijkstra_path(),bellman_ford_path_length()
networkx.algorithms.shortest_paths.weighted.bellman_ford_path_length
bellman_ford_path_length(G,source,target,weight=’weight’)
Returns the shortest path length from source to target in a weighted graph.
Parameters
•G(NetworkX graph)
•source (node label) – starting node for path
•target (node label) – ending node for path
3.45. Shortest Paths 425

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight
Returns length – Shortest path length.
Return type number
Raises
•NodeNotFound – If source is not in G.
•NetworkXNoPath – If no path exists between source and target.
Examples
>>> G=nx.path_graph(5)
>>> print(nx.bellman_ford_path_length(G,0,4))
4
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
dijkstra_path_length(),bellman_ford_path()
networkx.algorithms.shortest_paths.weighted.single_source_bellman_ford
single_source_bellman_ford(G,source,target=None,weight=’weight’)
Compute shortest paths and lengths in a weighted graph G.
Uses Bellman-Ford algorithm for shortest paths.
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•target (node label, optional) – Ending node for path
Returns distance, path – If target is None, returns a tuple of two dictionaries keyed by node. The
first dictionary stores distance from one of the source nodes. The second stores the path from
one of the sources to that node. If target is not None, returns a tuple of (distance, path) where
distance is the distance from source to target and path is a list representing the path from source
to target.
Return type pair of dictionaries, or numeric and list
Raises NodeNotFound – If source is not in G.
Examples
426 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(5)
>>> length, path =nx.single_source_bellman_ford(G, 0)
>>> print(length[4])
4
>>> for node in [0,1,2,3,4]:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 3
4: 4
>>> path[4]
[0, 1, 2, 3, 4]
>>> length, path =nx.single_source_bellman_ford(G, 0,1)
>>> length
1
>>> path
[0, 1]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
single_source_dijkstra(),single_source_bellman_ford_path(),
single_source_bellman_ford_path_length()
networkx.algorithms.shortest_paths.weighted.single_source_bellman_ford_path
single_source_bellman_ford_path(G,source,weight=’weight’)
Compute shortest path between source and all other reachable nodes for a weighted graph.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path.
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight
Returns paths – Dictionary of shortest path lengths keyed by target.
Return type dictionary
Raises NodeNotFound – If source is not in G.
Examples
>>> G=nx.path_graph(5)
>>> path=nx.single_source_bellman_ford_path(G,0)
>>> path[4]
[0, 1, 2, 3, 4]
3.45. Shortest Paths 427

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
single_source_dijkstra(),single_source_bellman_ford()
networkx.algorithms.shortest_paths.weighted.single_source_bellman_ford_path_length
single_source_bellman_ford_path_length(G,source,weight=’weight’)
Compute the shortest path length between source and all other reachable nodes for a weighted graph.
Parameters
•G(NetworkX graph)
•source (node label) – Starting node for path
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight.
Returns length – (target, shortest path length) iterator
Return type iterator
Raises NodeNotFound – If source is not in G.
Examples
>>> G=nx.path_graph(5)
>>> length =dict(nx.single_source_bellman_ford_path_length(G, 0))
>>> length[4]
4
>>> for node in [0,1,2,3,4]:
... print('{}:{}'.format(node, length[node]))
0: 0
1: 1
2: 2
3: 3
4: 4
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
single_source_dijkstra(),single_source_bellman_ford()
networkx.algorithms.shortest_paths.weighted.all_pairs_bellman_ford_path
all_pairs_bellman_ford_path(G,weight=’weight’)
Compute shortest paths between all nodes in a weighted graph.
Parameters
•G(NetworkX graph)
428 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight
Returns distance – Dictionary, keyed by source and target, of shortest paths.
Return type dictionary
Examples
>>> G=nx.path_graph(5)
>>> path =dict(nx.all_pairs_bellman_ford_path(G))
>>> print(path[0][4])
[0, 1, 2, 3, 4]
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
See also:
floyd_warshall(),all_pairs_dijkstra_path()
networkx.algorithms.shortest_paths.weighted.all_pairs_bellman_ford_path_length
all_pairs_bellman_ford_path_length(G,weight=’weight’)
Compute shortest path lengths between all nodes in a weighted graph.
Parameters
•G(NetworkX graph)
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight
Returns distance – (source, dictionary) iterator with dictionary keyed by target and shortest path
length as the key value.
Return type iterator
Examples
>>> G=nx.path_graph(5)
>>> length =dict(nx.all_pairs_bellman_ford_path_length(G))
>>> for node in [0,1,2,3,4]:
... print('1 - {}:{}'.format(node, length[1][node]))
1-0:1
1-1:0
1-2:1
1-3:2
1-4:3
>>> length[3][2]
1
>>> length[2][2]
0
3.45. Shortest Paths 429

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The dictionary returned only has keys for reachable node pairs.
networkx.algorithms.shortest_paths.weighted.bellman_ford_predecessor_and_distance
bellman_ford_predecessor_and_distance(G,source,target=None,weight=’weight’)
Compute shortest path lengths and predecessors on shortest paths in weighted graphs.
The algorithm has a running time of 𝑂(𝑚𝑛)where 𝑛is the number of nodes and 𝑚is the number of edges. It
is slower than Dijkstra but can handle negative edge weights.
Parameters
•G(NetworkX graph) – The algorithm works for all types of graphs, including directed
graphs and multigraphs.
•source (node label) – Starting node for path
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns pred, dist – Returns two dictionaries keyed by node to predecessor in the path and to the
distance from the source respectively.
Return type dictionaries
Raises
•NodeNotFound – If source is not in G.
•NetworkXUnbounded – If the (di)graph contains a negative cost (di)cycle, the algorithm
raises an exception to indicate the presence of the negative cost (di)cycle. Note: any negative
weight edge in an undirected graph is a negative cost cycle.
Examples
>>> import networkx as nx
>>> G=nx.path_graph(5, create_using =nx.DiGraph())
>>> pred, dist =nx.bellman_ford_predecessor_and_distance(G, 0)
>>> sorted(pred.items())
[(0, []), (1, [0]), (2, [1]), (3, [2]), (4, [3])]
>>> sorted(dist.items())
[(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)]
>>> pred, dist =nx.bellman_ford_predecessor_and_distance(G, 0,1)
>>> sorted(pred.items())
[(0, []), (1, [0]), (2, [1]), (3, [2]), (4, [3])]
>>> sorted(dist.items())
[(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)]
430 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from nose.tools import assert_raises
>>> G=nx.cycle_graph(5, create_using =nx.DiGraph())
>>> G[1][2]['weight']= -7
>>> assert_raises(nx.NetworkXUnbounded, nx.bellman_ford_
˓→predecessor_and_distance, G, 0)
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The dictionaries returned only have keys for nodes reachable from the source.
In the case where the (di)graph is not connected, if a component not containing the source contains a negative
cost (di)cycle, it will not be detected.
In NetworkX v2.1 and prior, the source node had predecessor [None]. In NetworkX v2.2 this changed to the
source node having predecessor []
networkx.algorithms.shortest_paths.weighted.negative_edge_cycle
negative_edge_cycle(G,weight=’weight’)
Return True if there exists a negative edge cycle anywhere in G.
Parameters
•G(NetworkX graph)
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns negative_cycle – True if a negative edge cycle exists, otherwise False.
Return type bool
Examples
>>> import networkx as nx
>>> G=nx.cycle_graph(5, create_using =nx.DiGraph())
>>> print(nx.negative_edge_cycle(G))
False
>>> G[1][2]['weight']= -7
>>> print(nx.negative_edge_cycle(G))
True
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
3.45. Shortest Paths 431

NetworkX Reference, Release 2.3rc1.dev20181203210840
This algorithm uses bellman_ford_predecessor_and_distance() but finds negative cycles on any component by
first adding a new node connected to every node, and starting bellman_ford_predecessor_and_distance on that
node. It then removes that extra node.
networkx.algorithms.shortest_paths.weighted.goldberg_radzik
goldberg_radzik(G,source,weight=’weight’)
Compute shortest path lengths and predecessors on shortest paths in weighted graphs.
The algorithm has a running time of 𝑂(𝑚𝑛)where 𝑛is the number of nodes and 𝑚is the number of edges. It
is slower than Dijkstra but can handle negative edge weights.
Parameters
•G(NetworkX graph) – The algorithm works for all types of graphs, including directed
graphs and multigraphs.
•source (node label) – Starting node for path
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns pred, dist – Returns two dictionaries keyed by node to predecessor in the path and to the
distance from the source respectively.
Return type dictionaries
Raises
•NodeNotFound – If source is not in G.
•NetworkXUnbounded – If the (di)graph contains a negative cost (di)cycle, the algorithm
raises an exception to indicate the presence of the negative cost (di)cycle. Note: any negative
weight edge in an undirected graph is a negative cost cycle.
Examples
>>> import networkx as nx
>>> G=nx.path_graph(5, create_using =nx.DiGraph())
>>> pred, dist =nx.goldberg_radzik(G, 0)
>>> sorted(pred.items())
[(0, None), (1, 0), (2, 1), (3, 2), (4, 3)]
>>> sorted(dist.items())
[(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)]
>>> from nose.tools import assert_raises
>>> G=nx.cycle_graph(5, create_using =nx.DiGraph())
>>> G[1][2]['weight']= -7
>>> assert_raises(nx.NetworkXUnbounded, nx.goldberg_radzik, G, 0)
432 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Edge weight attributes must be numerical. Distances are calculated as sums of weighted edges traversed.
The dictionaries returned only have keys for nodes reachable from the source.
In the case where the (di)graph is not connected, if a component not containing the source contains a negative
cost (di)cycle, it will not be detected.
networkx.algorithms.shortest_paths.weighted.johnson
johnson(G,weight=’weight’)
Uses Johnson’s Algorithm to compute shortest paths.
Johnson’s Algorithm finds a shortest path between each pair of nodes in a weighted graph even if negative
weights are present.
Parameters
•G(NetworkX graph)
•weight (string or function) – If this is a string, then edge weights will be accessed via
the edge attribute with this key (that is, the weight of the edge joining uto vwill be G.
edges[u, v][weight]). If no such edge attribute exists, the weight of the edge is
assumed to be one.
If this is a function, the weight of an edge is the value returned by the function. The func-
tion must accept exactly three positional arguments: the two endpoints of an edge and the
dictionary of edge attributes for that edge. The function must return a number.
Returns distance – Dictionary, keyed by source and target, of shortest paths.
Return type dictionary
Raises NetworkXError – If given graph is not weighted.
Examples
>>> import networkx as nx
>>> graph =nx.DiGraph()
>>> graph.add_weighted_edges_from([('0','3',3), ('0','1',-5),
... ('0','2',2), ('1','2',4), ('2','3',1)])
>>> paths =nx.johnson(graph, weight='weight')
>>> paths['0']['2']
['0', '1', '2']
Notes
Johnson’s algorithm is suitable even for graphs with negative weights. It works by using the Bellman–Ford
algorithm to compute a transformation of the input graph that removes all negative weights, allowing Dijkstra’s
algorithm to be used on the transformed graph.
The time complexity of this algorithm is 𝑂(𝑛2log 𝑛+𝑛𝑚), where 𝑛is the number of nodes and 𝑚the number
of edges in the graph. For dense graphs, this may be faster than the Floyd–Warshall algorithm.
See also:
3.45. Shortest Paths 433

NetworkX Reference, Release 2.3rc1.dev20181203210840
floyd_warshall_predecessor_and_distance(),floyd_warshall_numpy(),
all_pairs_shortest_path(),all_pairs_shortest_path_length(),
all_pairs_dijkstra_path(),bellman_ford_predecessor_and_distance(),
all_pairs_bellman_ford_path(),all_pairs_bellman_ford_path_length()
3.45.7 Dense Graphs
Floyd-Warshall algorithm for shortest paths.
floyd_warshall(G[, weight]) Find all-pairs shortest path lengths using Floyd’s algo-
rithm.
floyd_warshall_predecessor_and_distance(G[,
...])
Find all-pairs shortest path lengths using Floyd’s algo-
rithm.
floyd_warshall_numpy(G[, nodelist, weight]) Find all-pairs shortest path lengths using Floyd’s algo-
rithm.
reconstruct_path(source, target, predecessors) Reconstruct a path from source to target us-
ing the predecessors dict as returned by
floyd_warshall_predecessor_and_distance
networkx.algorithms.shortest_paths.dense.floyd_warshall
floyd_warshall(G,weight=’weight’)
Find all-pairs shortest path lengths using Floyd’s algorithm.
Parameters
•G(NetworkX graph)
•weight (string, optional (default= ‘weight’)) – Edge data key corresponding to the edge
weight.
Returns distance – A dictionary, keyed by source and target, of shortest paths distances between
nodes.
Return type dict
Notes
Floyd’s algorithm is appropriate for finding shortest paths in dense graphs or graphs with negative weights when
Dijkstra’s algorithm fails. This algorithm can still fail if there are negative cycles. It has running time 𝑂(𝑛3)
with running space of 𝑂(𝑛2).
See also:
floyd_warshall_predecessor_and_distance(),floyd_warshall_numpy(),
all_pairs_shortest_path(),all_pairs_shortest_path_length()
networkx.algorithms.shortest_paths.dense.floyd_warshall_predecessor_and_distance
floyd_warshall_predecessor_and_distance(G,weight=’weight’)
Find all-pairs shortest path lengths using Floyd’s algorithm.
Parameters
•G(NetworkX graph)
434 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (string, optional (default= ‘weight’)) – Edge data key corresponding to the edge
weight.
Returns predecessor,distance – Dictionaries, keyed by source and target, of predecessors and dis-
tances in the shortest path.
Return type dictionaries
Examples
>>> G=nx.DiGraph()
>>> G.add_weighted_edges_from([('s','u',10), ('s','x',5),
... ('u','v',1), ('u','x',2), ('v','y',1), ('x','u',3),
... ('x','v',5), ('x','y',2), ('y','s',7), ('y','v',6)])
>>> predecessors, _ =nx.floyd_warshall_predecessor_and_distance(G)
>>> print(nx.reconstruct_path('s','v', predecessors))
['s', 'x', 'u', 'v']
Notes
Floyd’s algorithm is appropriate for finding shortest paths in dense graphs or graphs with negative weights when
Dijkstra’s algorithm fails. This algorithm can still fail if there are negative cycles. It has running time 𝑂(𝑛3)
with running space of 𝑂(𝑛2).
See also:
floyd_warshall(),floyd_warshall_numpy(),all_pairs_shortest_path(),
all_pairs_shortest_path_length()
networkx.algorithms.shortest_paths.dense.floyd_warshall_numpy
floyd_warshall_numpy(G,nodelist=None,weight=’weight’)
Find all-pairs shortest path lengths using Floyd’s algorithm.
Parameters
•G(NetworkX graph)
•nodelist (list, optional) – The rows and columns are ordered by the nodes in nodelist. If
nodelist is None then the ordering is produced by G.nodes().
•weight (string, optional (default= ‘weight’)) – Edge data key corresponding to the edge
weight.
Returns distance – A matrix of shortest path distances between nodes. If there is no path between
to nodes the corresponding matrix entry will be Inf.
Return type NumPy matrix
Notes
Floyd’s algorithm is appropriate for finding shortest paths in dense graphs or graphs with negative weights when
Dijkstra’s algorithm fails. This algorithm can still fail if there are negative cycles. It has running time 𝑂(𝑛3)
with running space of 𝑂(𝑛2).
3.45. Shortest Paths 435

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.shortest_paths.dense.reconstruct_path
reconstruct_path(source,target,predecessors)
Reconstruct a path from source to target using the predecessors dict as returned by
floyd_warshall_predecessor_and_distance
Parameters
•source (node) – Starting node for path
•target (node) – Ending node for path
•predecessors (dictionary) – Dictionary, keyed by source and target, of predecessors in the
shortest path, as returned by floyd_warshall_predecessor_and_distance
Returns
path – A list of nodes containing the shortest path from source to target
If source and target are the same, an empty list is returned
Return type list
Notes
This function is meant to give more applicability to the floyd_warshall_predecessor_and_distance function
See also:
floyd_warshall_predecessor_and_distance()
3.45.8 A* Algorithm
Shortest paths and path lengths using the A* (“A star”) algorithm.
astar_path(G, source, target[, heuristic, . . . ]) Return a list of nodes in a shortest path between source
and target using the A* (“A-star”) algorithm.
astar_path_length(G, source, target[, . . . ]) Return the length of the shortest path between source
and target using the A* (“A-star”) algorithm.
networkx.algorithms.shortest_paths.astar.astar_path
astar_path(G,source,target,heuristic=None,weight=’weight’)
Return a list of nodes in a shortest path between source and target using the A* (“A-star”) algorithm.
There may be more than one shortest path. This returns only one.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path
•target (node) – Ending node for path
•heuristic (function) – A function to evaluate the estimate of the distance from the a node to
the target. The function takes two nodes arguments and must return a number.
436 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•weight (string, optional (default=’weight’)) – Edge data key corresponding to the edge
weight.
Raises NetworkXNoPath – If no path exists between source and target.
Examples
>>> G=nx.path_graph(5)
>>> print(nx.astar_path(G, 0,4))
[0, 1, 2, 3, 4]
>>> G=nx.grid_graph(dim=[3,3]) # nodes are two-tuples (x,y)
>>> nx.set_edge_attributes(G, {e: e[1][0]*2for ein G.edges()}, 'cost')
>>> def dist(a, b):
... (x1, y1) =a
... (x2, y2) =b
... return ((x1 -x2) ** 2+(y1 -y2) ** 2)** 0.5
>>> print(nx.astar_path(G, (0,0), (2,2), heuristic=dist, weight='cost'))
[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2)]
See also:
shortest_path(),dijkstra_path()
networkx.algorithms.shortest_paths.astar.astar_path_length
astar_path_length(G,source,target,heuristic=None,weight=’weight’)
Return the length of the shortest path between source and target using the A* (“A-star”) algorithm.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path
•target (node) – Ending node for path
•heuristic (function) – A function to evaluate the estimate of the distance from the a node to
the target. The function takes two nodes arguments and must return a number.
Raises NetworkXNoPath – If no path exists between source and target.
See also:
astar_path()
3.46 Similarity Measures
Functions measuring similarity using graph edit distance.
The graph edit distance is the number of edge/node changes needed to make two graphs isomorphic.
The default algorithm/implementation is sub-optimal for some graphs. The problem of finding the exact Graph Edit
Distance (GED) is NP-hard so it is often slow. If the simple interface graph_edit_distance takes too long for
your graph, try optimize_graph_edit_distance and/or optimize_edit_paths.
At the same time, I encourage capable people to investigate alternative GED algorithms, in order to improve the
choices available.
3.46. Similarity Measures 437

NetworkX Reference, Release 2.3rc1.dev20181203210840
graph_edit_distance(G1, G2[, node_match,
...])
Returns GED (graph edit distance) between graphs G1
and G2.
optimal_edit_paths(G1, G2[, node_match, . . . ]) Returns all minimum-cost edit paths transforming G1 to
G2.
optimize_graph_edit_distance(G1, G2[,
...])
Returns consecutive approximations of GED (graph edit
distance) between graphs G1 and G2.
optimize_edit_paths(G1, G2[, node_match,
...])
GED (graph edit distance) calculation: advanced inter-
face.
3.46.1 networkx.algorithms.similarity.graph_edit_distance
graph_edit_distance(G1,G2,node_match=None,edge_match=None,node_subst_cost=None,
node_del_cost=None,node_ins_cost=None,edge_subst_cost=None,
edge_del_cost=None,edge_ins_cost=None,upper_bound=None)
Returns GED (graph edit distance) between graphs G1 and G2.
Graph edit distance is a graph similarity measure analogous to Levenshtein distance for strings. It is defined
as minimum cost of edit path (sequence of node and edge edit operations) transforming graph G1 to graph
isomorphic to G2.
Parameters
•G1, G2 (graphs) – The two graphs G1 and G2 must be of the same type.
•node_match (callable) – A function that returns True if node n1 in G1 and n2 in G2 should
be considered equal during matching.
The function will be called like
node_match(G1.nodes[n1], G2.nodes[n2]).
That is, the function will receive the node attribute dictionaries for n1 and n2 as inputs.
Ignored if node_subst_cost is specified. If neither node_match nor node_subst_cost are
specified then node attributes are not considered.
•edge_match (callable) – A function that returns True if the edge attribute dictionaries for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during
matching.
The function will be called like
edge_match(G1[u1][v1], G2[u2][v2]).
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation.
Ignored if edge_subst_cost is specified. If neither edge_match nor edge_subst_cost are spec-
ified then edge attributes are not considered.
•node_subst_cost, node_del_cost, node_ins_cost (callable) – Functions that return the
costs of node substitution, node deletion, and node insertion, respectively.
The functions will be called like
node_subst_cost(G1.nodes[n1], G2.nodes[n2]), node_del_cost(G1.nodes[n1]),
node_ins_cost(G2.nodes[n2]).
That is, the functions will receive the node attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
438 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Function node_subst_cost overrides node_match if specified. If neither node_match nor
node_subst_cost are specified then default node substitution cost of 0 is used (node attributes
are not considered during matching).
If node_del_cost is not specified then default node deletion cost of 1 is used. If
node_ins_cost is not specified then default node insertion cost of 1 is used.
•edge_subst_cost, edge_del_cost, edge_ins_cost (callable) – Functions that return the costs
of edge substitution, edge deletion, and edge insertion, respectively.
The functions will be called like
edge_subst_cost(G1[u1][v1], G2[u2][v2]), edge_del_cost(G1[u1][v1]),
edge_ins_cost(G2[u2][v2]).
That is, the functions will receive the edge attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function edge_subst_cost overrides edge_match if specified. If neither edge_match nor
edge_subst_cost are specified then default edge substitution cost of 0 is used (edge attributes
are not considered during matching).
If edge_del_cost is not specified then default edge deletion cost of 1 is used. If edge_ins_cost
is not specified then default edge insertion cost of 1 is used.
•upper_bound (numeric) – Maximum edit distance to consider. Return None if no edit
distance under or equal to upper_bound exists.
Examples
>>> G1 =nx.cycle_graph(6)
>>> G2 =nx.wheel_graph(7)
>>> nx.graph_edit_distance(G1, G2)
7.0
See also:
optimal_edit_paths(),optimize_graph_edit_distance(),is_isomorphic()
References
3.46.2 networkx.algorithms.similarity.optimal_edit_paths
optimal_edit_paths(G1,G2,node_match=None,edge_match=None,node_subst_cost=None,
node_del_cost=None,node_ins_cost=None,edge_subst_cost=None,
edge_del_cost=None,edge_ins_cost=None,upper_bound=None)
Returns all minimum-cost edit paths transforming G1 to G2.
Graph edit path is a sequence of node and edge edit operations transforming graph G1 to graph isomorphic to
G2. Edit operations include substitutions, deletions, and insertions.
Parameters
•G1, G2 (graphs) – The two graphs G1 and G2 must be of the same type.
•node_match (callable) – A function that returns True if node n1 in G1 and n2 in G2 should
be considered equal during matching.
The function will be called like
3.46. Similarity Measures 439

NetworkX Reference, Release 2.3rc1.dev20181203210840
node_match(G1.nodes[n1], G2.nodes[n2]).
That is, the function will receive the node attribute dictionaries for n1 and n2 as inputs.
Ignored if node_subst_cost is specified. If neither node_match nor node_subst_cost are
specified then node attributes are not considered.
•edge_match (callable) – A function that returns True if the edge attribute dictionaries for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during
matching.
The function will be called like
edge_match(G1[u1][v1], G2[u2][v2]).
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation.
Ignored if edge_subst_cost is specified. If neither edge_match nor edge_subst_cost are spec-
ified then edge attributes are not considered.
•node_subst_cost, node_del_cost, node_ins_cost (callable) – Functions that return the
costs of node substitution, node deletion, and node insertion, respectively.
The functions will be called like
node_subst_cost(G1.nodes[n1], G2.nodes[n2]), node_del_cost(G1.nodes[n1]),
node_ins_cost(G2.nodes[n2]).
That is, the functions will receive the node attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function node_subst_cost overrides node_match if specified. If neither node_match nor
node_subst_cost are specified then default node substitution cost of 0 is used (node attributes
are not considered during matching).
If node_del_cost is not specified then default node deletion cost of 1 is used. If
node_ins_cost is not specified then default node insertion cost of 1 is used.
•edge_subst_cost, edge_del_cost, edge_ins_cost (callable) – Functions that return the costs
of edge substitution, edge deletion, and edge insertion, respectively.
The functions will be called like
edge_subst_cost(G1[u1][v1], G2[u2][v2]), edge_del_cost(G1[u1][v1]),
edge_ins_cost(G2[u2][v2]).
That is, the functions will receive the edge attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function edge_subst_cost overrides edge_match if specified. If neither edge_match nor
edge_subst_cost are specified then default edge substitution cost of 0 is used (edge attributes
are not considered during matching).
If edge_del_cost is not specified then default edge deletion cost of 1 is used. If edge_ins_cost
is not specified then default edge insertion cost of 1 is used.
•upper_bound (numeric) – Maximum edit distance to consider.
Returns
•edit_paths (list of tuples (node_edit_path, edge_edit_path)) – node_edit_path : list of tuples
(u, v) edge_edit_path : list of tuples ((u1, v1), (u2, v2))
•cost (numeric) – Optimal edit path cost (graph edit distance).
440 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G1 =nx.cycle_graph(6)
>>> G2 =nx.wheel_graph(7)
>>> paths, cost =nx.optimal_edit_paths(G1, G2)
>>> len(paths)
84
>>> cost
7.0
See also:
graph_edit_distance(),optimize_edit_paths()
References
3.46.3 networkx.algorithms.similarity.optimize_graph_edit_distance
optimize_graph_edit_distance(G1,G2,node_match=None,edge_match=None,
node_subst_cost=None,node_del_cost=None,
node_ins_cost=None,edge_subst_cost=None,
edge_del_cost=None,edge_ins_cost=None,upper_bound=None)
Returns consecutive approximations of GED (graph edit distance) between graphs G1 and G2.
Graph edit distance is a graph similarity measure analogous to Levenshtein distance for strings. It is defined
as minimum cost of edit path (sequence of node and edge edit operations) transforming graph G1 to graph
isomorphic to G2.
Parameters
•G1, G2 (graphs) – The two graphs G1 and G2 must be of the same type.
•node_match (callable) – A function that returns True if node n1 in G1 and n2 in G2 should
be considered equal during matching.
The function will be called like
node_match(G1.nodes[n1], G2.nodes[n2]).
That is, the function will receive the node attribute dictionaries for n1 and n2 as inputs.
Ignored if node_subst_cost is specified. If neither node_match nor node_subst_cost are
specified then node attributes are not considered.
•edge_match (callable) – A function that returns True if the edge attribute dictionaries for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during
matching.
The function will be called like
edge_match(G1[u1][v1], G2[u2][v2]).
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation.
Ignored if edge_subst_cost is specified. If neither edge_match nor edge_subst_cost are spec-
ified then edge attributes are not considered.
•node_subst_cost, node_del_cost, node_ins_cost (callable) – Functions that return the
costs of node substitution, node deletion, and node insertion, respectively.
3.46. Similarity Measures 441

NetworkX Reference, Release 2.3rc1.dev20181203210840
The functions will be called like
node_subst_cost(G1.nodes[n1], G2.nodes[n2]), node_del_cost(G1.nodes[n1]),
node_ins_cost(G2.nodes[n2]).
That is, the functions will receive the node attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function node_subst_cost overrides node_match if specified. If neither node_match nor
node_subst_cost are specified then default node substitution cost of 0 is used (node attributes
are not considered during matching).
If node_del_cost is not specified then default node deletion cost of 1 is used. If
node_ins_cost is not specified then default node insertion cost of 1 is used.
•edge_subst_cost, edge_del_cost, edge_ins_cost (callable) – Functions that return the costs
of edge substitution, edge deletion, and edge insertion, respectively.
The functions will be called like
edge_subst_cost(G1[u1][v1], G2[u2][v2]), edge_del_cost(G1[u1][v1]),
edge_ins_cost(G2[u2][v2]).
That is, the functions will receive the edge attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function edge_subst_cost overrides edge_match if specified. If neither edge_match nor
edge_subst_cost are specified then default edge substitution cost of 0 is used (edge attributes
are not considered during matching).
If edge_del_cost is not specified then default edge deletion cost of 1 is used. If edge_ins_cost
is not specified then default edge insertion cost of 1 is used.
•upper_bound (numeric) – Maximum edit distance to consider.
Returns
Return type Generator of consecutive approximations of graph edit distance.
Examples
>>> G1 =nx.cycle_graph(6)
>>> G2 =nx.wheel_graph(7)
>>> for vin nx.optimize_graph_edit_distance(G1, G2):
... minv =v
>>> minv
7.0
See also:
graph_edit_distance(),optimize_edit_paths()
442 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.46.4 networkx.algorithms.similarity.optimize_edit_paths
optimize_edit_paths(G1,G2,node_match=None,edge_match=None,node_subst_cost=None,
node_del_cost=None,node_ins_cost=None,edge_subst_cost=None,
edge_del_cost=None,edge_ins_cost=None,upper_bound=None,
strictly_decreasing=True)
GED (graph edit distance) calculation: advanced interface.
Graph edit path is a sequence of node and edge edit operations transforming graph G1 to graph isomorphic to
G2. Edit operations include substitutions, deletions, and insertions.
Graph edit distance is defined as minimum cost of edit path.
Parameters
•G1, G2 (graphs) – The two graphs G1 and G2 must be of the same type.
•node_match (callable) – A function that returns True if node n1 in G1 and n2 in G2 should
be considered equal during matching.
The function will be called like
node_match(G1.nodes[n1], G2.nodes[n2]).
That is, the function will receive the node attribute dictionaries for n1 and n2 as inputs.
Ignored if node_subst_cost is specified. If neither node_match nor node_subst_cost are
specified then node attributes are not considered.
•edge_match (callable) – A function that returns True if the edge attribute dictionaries for
the pair of nodes (u1, v1) in G1 and (u2, v2) in G2 should be considered equal during
matching.
The function will be called like
edge_match(G1[u1][v1], G2[u2][v2]).
That is, the function will receive the edge attribute dictionaries of the edges under consider-
ation.
Ignored if edge_subst_cost is specified. If neither edge_match nor edge_subst_cost are spec-
ified then edge attributes are not considered.
•node_subst_cost, node_del_cost, node_ins_cost (callable) – Functions that return the
costs of node substitution, node deletion, and node insertion, respectively.
The functions will be called like
node_subst_cost(G1.nodes[n1], G2.nodes[n2]), node_del_cost(G1.nodes[n1]),
node_ins_cost(G2.nodes[n2]).
That is, the functions will receive the node attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function node_subst_cost overrides node_match if specified. If neither node_match nor
node_subst_cost are specified then default node substitution cost of 0 is used (node attributes
are not considered during matching).
If node_del_cost is not specified then default node deletion cost of 1 is used. If
node_ins_cost is not specified then default node insertion cost of 1 is used.
3.46. Similarity Measures 443

NetworkX Reference, Release 2.3rc1.dev20181203210840
•edge_subst_cost, edge_del_cost, edge_ins_cost (callable) – Functions that return the costs
of edge substitution, edge deletion, and edge insertion, respectively.
The functions will be called like
edge_subst_cost(G1[u1][v1], G2[u2][v2]), edge_del_cost(G1[u1][v1]),
edge_ins_cost(G2[u2][v2]).
That is, the functions will receive the edge attribute dictionaries as inputs. The functions are
expected to return positive numeric values.
Function edge_subst_cost overrides edge_match if specified. If neither edge_match nor
edge_subst_cost are specified then default edge substitution cost of 0 is used (edge attributes
are not considered during matching).
If edge_del_cost is not specified then default edge deletion cost of 1 is used. If edge_ins_cost
is not specified then default edge insertion cost of 1 is used.
•upper_bound (numeric) – Maximum edit distance to consider.
•strictly_decreasing (bool) – If True, return consecutive approximations of strictly decreas-
ing cost. Otherwise, return all edit paths of cost less than or equal to the previous minimum
cost.
Returns node_edit_path : list of tuples (u, v) edge_edit_path : list of tuples ((u1, v1), (u2, v2)) cost
: numeric
Return type Generator of tuples (node_edit_path, edge_edit_path, cost)
See also:
graph_edit_distance(),optimize_graph_edit_distance(),optimal_edit_paths()
References
3.47 Simple Paths
all_simple_paths(G, source, target[, cutoff]) Generate all simple paths in the graph G from source to
target.
is_simple_path(G, nodes) Returns True if and only if the given nodes form a sim-
ple path in G.
shortest_simple_paths(G, source, target[, . . . ]) Generate all simple paths in the graph G from source to
target,
3.47.1 networkx.algorithms.simple_paths.all_simple_paths
all_simple_paths(G,source,target,cutoff=None)
Generate all simple paths in the graph G from source to target.
A simple path is a path with no repeated nodes.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path
•target (nodes) – Single node or iterable of nodes at which to end path
444 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
•cutoff (integer, optional) – Depth to stop the search. Only paths of length <= cutoff are
returned.
Returns path_generator – A generator that produces lists of simple paths. If there are no paths
between the source and target within the given cutoff the generator produces no output.
Return type generator
Examples
This iterator generates lists of nodes:
>>> G=nx.complete_graph(4)
>>> for path in nx.all_simple_paths(G, source=0, target=3):
... print(path)
...
[0, 1, 2, 3]
[0, 1, 3]
[0, 2, 1, 3]
[0, 2, 3]
[0, 3]
You can generate only those paths that are shorter than a certain length by using the cutoff keyword argument:
>>> paths =nx.all_simple_paths(G, source=0, target=3, cutoff=2)
>>> print(list(paths))
[[0, 1, 3], [0, 2, 3], [0, 3]]
To get each path as the corresponding list of edges, you can use the networkx.utils.pairwise() helper
function:
>>> paths =nx.all_simple_paths(G, source=0, target=3)
>>> for path in map(nx.utils.pairwise, paths):
... print(list(path))
[(0, 1), (1, 2), (2, 3)]
[(0, 1), (1, 3)]
[(0, 2), (2, 1), (1, 3)]
[(0, 2), (2, 3)]
[(0, 3)]
Pass an iterable of nodes as target to generate all paths ending in any of several nodes:
>>> G=nx.complete_graph(4)
>>> for path in nx.all_simple_paths(G, source=0, target=[3,2]):
... print(path)
...
[0, 1, 2]
[0, 1, 3]
[0, 2]
[0, 3]
Iterate over each path from the root nodes to the leaf nodes in a directed acyclic graph using a functional
programming approach:
>>> from itertools import chain
>>> from itertools import product
>>> from itertools import starmap
(continues on next page)
3.47. Simple Paths 445

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> from functools import partial
>>>
>>> chaini =chain.from_iterable
>>>
>>> G=nx.DiGraph([(0,1), (1,2), (0,3), (3,2)])
>>> roots =(v for v, d in G.in_degree() if d== 0)
>>> leaves =(v for v, d in G.out_degree() if d== 0)
>>> all_paths =partial(nx.all_simple_paths, G)
>>> list(chaini(starmap(all_paths, product(roots, leaves))))
[[0, 1, 2], [0, 3, 2]]
The same list computed using an iterative approach:
>>> G=nx.DiGraph([(0,1), (1,2), (0,3), (3,2)])
>>> roots =(v for v, d in G.in_degree() if d== 0)
>>> leaves =(v for v, d in G.out_degree() if d== 0)
>>> all_paths =[]
>>> for root in roots:
... for leaf in leaves:
... paths =nx.all_simple_paths(G, root, leaf)
... all_paths.extend(paths)
>>> all_paths
[[0, 1, 2], [0, 3, 2]]
Iterate over each path from the root nodes to the leaf nodes in a directed acyclic graph passing all leaves together
to avoid unnecessary compute:
>>> G=nx.DiGraph([(0,1), (2,1), (1,3), (1,4)])
>>> roots =(v for v, d in G.in_degree() if d== 0)
>>> leaves =[v for v, d in G.out_degree() if d== 0]
>>> all_paths =[]
>>> for root in roots:
... paths =nx.all_simple_paths(G, root, leaves)
... all_paths.extend(paths)
>>> all_paths
[[0, 1, 3], [0, 1, 4], [2, 1, 3], [2, 1, 4]]
Notes
This algorithm uses a modified depth-first search to generate the paths1. A single path can be found in 𝑂(𝑉+𝐸)
time but the number of simple paths in a graph can be very large, e.g. 𝑂(𝑛!) in the complete graph of order 𝑛.
References
See also:
all_shortest_paths(),shortest_path()
3.47.2 networkx.algorithms.simple_paths.is_simple_path
is_simple_path(G,nodes)
Returns True if and only if the given nodes form a simple path in G.
1R. Sedgewick, “Algorithms in C, Part 5: Graph Algorithms”, Addison Wesley Professional, 3rd ed., 2001.
446 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Asimple path in a graph is a nonempty sequence of nodes in which no node appears more than once in the
sequence, and each adjacent pair of nodes in the sequence is adjacent in the graph.
Parameters nodes (list) – A list of one or more nodes in the graph G.
Returns Whether the given list of nodes represents a simple path in G.
Return type bool
Notes
A list of zero nodes is not a path and a list of one node is a path. Here’s an explanation why.
This function operates on node paths. One could also consider edge paths. There is a bijection between node
paths and edge paths.
The length of a path is the number of edges in the path, so a list of nodes of length ncorresponds to a path of
length n- 1. Thus the smallest edge path would be a list of zero edges, the empty path. This corresponds to a
list of one node.
To convert between a node path and an edge path, you can use code like the following:
>>> from networkx.utils import pairwise
>>> nodes =[0,1,2,3]
>>> edges =list(pairwise(nodes))
>>> edges
[(0, 1), (1, 2), (2, 3)]
>>> nodes =[edges[0][0]] +[v for u, v in edges]
>>> nodes
[0, 1, 2, 3]
Examples
>>> G=nx.cycle_graph(4)
>>> nx.is_simple_path(G, [2,3,0])
True
>>> nx.is_simple_path(G, [0,2])
False
3.47.3 networkx.algorithms.simple_paths.shortest_simple_paths
shortest_simple_paths(G,source,target,weight=None)
Generate all simple paths in the graph G from source to target, starting from shortest ones.
A simple path is a path with no repeated nodes.
If a weighted shortest path search is to be used, no negative weights are allowed.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for path
•target (node) – Ending node for path
•weight (string) – Name of the edge attribute to be used as a weight. If None all edges are
considered to have unit weight. Default value None.
3.47. Simple Paths 447

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns path_generator – A generator that produces lists of simple paths, in order from shortest to
longest.
Return type generator
Raises
•NetworkXNoPath – If no path exists between source and target.
•NetworkXError – If source or target nodes are not in the input graph.
•NetworkXNotImplemented – If the input graph is a Multi[Di]Graph.
Examples
>>> G=nx.cycle_graph(7)
>>> paths =list(nx.shortest_simple_paths(G, 0,3))
>>> print(paths)
[[0, 1, 2, 3], [0, 6, 5, 4, 3]]
You can use this function to efficiently compute the k shortest/best paths between two nodes.
>>> from itertools import islice
>>> def k_shortest_paths(G, source, target, k, weight=None):
... return list(islice(nx.shortest_simple_paths(G, source, target,
˓→weight=weight), k))
>>> for path in k_shortest_paths(G, 0,3,2):
... print(path)
[0, 1, 2, 3]
[0, 6, 5, 4, 3]
Notes
This procedure is based on algorithm by Jin Y. Yen1. Finding the first 𝐾paths requires 𝑂(𝐾𝑁3)operations.
See also:
all_shortest_paths(),shortest_path(),all_simple_paths()
References
3.48 Similarity Measures
Functions for estimating the small-world-ness of graphs.
A small world network is characterized by a small average shortest path length, and a large clustering coefficient.
Small-worldness is commonly measured with the coefficient sigma or omega.
Both coefficients compare the average clustering coefficient and shortest path length of a given graph against the same
quantities for an equivalent random or lattice graph.
For more information, see the Wikipedia article on small-world network1.
1Jin Y. Yen, “Finding the K Shortest Loopless Paths in a Network”, Management Science, Vol. 17, No. 11, Theory Series (Jul., 1971), pp.
712-716.
1Small-world network:: https://en.wikipedia.org/wiki/Small-world_network
448 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
random_reference(G[, niter, connectivity, seed]) Compute a random graph by swapping edges of a given
graph.
lattice_reference(G[, niter, D, . . . ]) Latticize the given graph by swapping edges.
sigma(G[, niter, nrand, seed]) Return the small-world coefficient (sigma) of the given
graph.
omega(G[, niter, nrand, seed]) Return the small-world coefficient (omega) of a graph
3.48.1 networkx.algorithms.smallworld.random_reference
random_reference(G,niter=1,connectivity=True,seed=None)
Compute a random graph by swapping edges of a given graph.
Parameters
•G(graph) – An undirected graph with 4 or more nodes.
•niter (integer (optional, default=1)) – An edge is rewired approximately niter times.
•connectivity (boolean (optional, default=True)) – When True, ensure connectivity for the
randomized graph.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – The randomized graph.
Return type graph
Notes
The implementation is adapted from the algorithm by Maslov and Sneppen (2002)1.
References
3.48.2 networkx.algorithms.smallworld.lattice_reference
lattice_reference(G,niter=1,D=None,connectivity=True,seed=None)
Latticize the given graph by swapping edges.
Parameters
•G(graph) – An undirected graph with 4 or more nodes.
•niter (integer (optional, default=1)) – An edge is rewired approximatively niter times.
•D(numpy.array (optional, default=None)) – Distance to the diagonal matrix.
•connectivity (boolean (optional, default=True)) – Ensure connectivity for the latticized
graph when set to True.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – The latticized graph.
Return type graph
1Maslov, Sergei, and Kim Sneppen. “Specificity and stability in topology of protein networks.” Science 296.5569 (2002): 910-913.
3.48. Similarity Measures 449

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The implementation is adapted from the algorithm by Sporns et al.1. which is inspired from the original work
by Maslov and Sneppen(2002)2.
References
3.48.3 networkx.algorithms.smallworld.sigma
sigma(G,niter=100,nrand=10,seed=None)
Return the small-world coefficient (sigma) of the given graph.
The small-world coefficient is defined as: sigma = C/Cr / L/Lr where C and L are respectively the average
clustering coefficient and average shortest path length of G. Cr and Lr are respectively the average clustering
coefficient and average shortest path length of an equivalent random graph.
A graph is commonly classified as small-world if sigma>1.
Parameters
•G(NetworkX graph) – An undirected graph.
•niter (integer (optional, default=100)) – Approximate number of rewiring per edge to com-
pute the equivalent random graph.
•nrand (integer (optional, default=10)) – Number of random graphs generated to compute
the average clustering coefficient (Cr) and average shortest path length (Lr).
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns sigma – The small-world coefficient of G.
Return type float
Notes
The implementation is adapted from Humphries et al.12.
References
3.48.4 networkx.algorithms.smallworld.omega
omega(G,niter=100,nrand=10,seed=None)
Return the small-world coefficient (omega) of a graph
The small-world coefficient of a graph G is:
omega = Lr/L - C/Cl
1Sporns, Olaf, and Jonathan D. Zwi. “The small world of the cerebral cortex.” Neuroinformatics 2.2 (2004): 145-162.
2Maslov, Sergei, and Kim Sneppen. “Specificity and stability in topology of protein networks.” Science 296.5569 (2002): 910-913.
1The brainstem reticular formation is a small-world, not scale-free, network M. D. Humphries, K. Gurney and T. J. Prescott, Proc. Roy. Soc. B
2006 273, 503-511, doi:10.1098/rspb.2005.3354.
2Humphries and Gurney (2008). “Network ‘Small-World-Ness’: A Quantitative Method for Determining Canonical Network Equivalence”.
PLoS One. 3 (4). PMID 18446219. doi:10.1371/journal.pone.0002051.
450 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
where C and L are respectively the average clustering coefficient and average shortest path length of G. Lr is
the average shortest path length of an equivalent random graph and Cl is the average clustering coefficient of an
equivalent lattice graph.
The small-world coefficient (omega) ranges between -1 and 1. Values close to 0 means the G features small-
world characteristics. Values close to -1 means G has a lattice shape whereas values close to 1 means G is a
random graph.
Parameters
•G(NetworkX graph) – An undirected graph.
•niter (integer (optional, default=100)) – Approximate number of rewiring per edge to com-
pute the equivalent random graph.
•nrand (integer (optional, default=10)) – Number of random graphs generated to compute
the average clustering coefficient (Cr) and average shortest path length (Lr).
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns omega – The small-work coefficient (omega)
Return type float
Notes
The implementation is adapted from the algorithm by Telesford et al.1.
References
3.49 s metric
s_metric(G[, normalized]) Return the s-metric of graph.
3.49.1 networkx.algorithms.smetric.s_metric
s_metric(G,normalized=True)
Return the s-metric of graph.
The s-metric is defined as the sum of the products deg(u)*deg(v) for every edge (u,v) in G. If norm is provided
construct the s-max graph and compute it’s s_metric, and return the normalized s value
Parameters
•G(graph) – The graph used to compute the s-metric.
•normalized (bool (optional)) – Normalize the value.
Returns s – The s-metric of the graph.
Return type float
1Telesford, Joyce, Hayasaka, Burdette, and Laurienti (2011). “The Ubiquity of Small-World Networks”. Brain Connectivity. 1 (0038): 367-75.
PMC 3604768. PMID 22432451. doi:10.1089/brain.2011.0038.
3.49. s metric 451

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.50 Sparsifiers
Functions for computing sparsifiers of graphs.
spanner(G, stretch[, weight, seed]) Returns a spanner of the given graph with the given
stretch.
3.50.1 networkx.algorithms.sparsifiers.spanner
spanner(G,stretch,weight=None,seed=None)
Returns a spanner of the given graph with the given stretch.
A spanner of a graph G = (V, E) with stretch t is a subgraph H = (V, E_S) such that E_S is a subset of E and the
distance between any pair of nodes in H is at most t times the distance between the nodes in G.
Parameters
•G(NetworkX graph) – An undirected simple graph.
•stretch (float) – The stretch of the spanner.
•weight (object) – The edge attribute to use as distance.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns A spanner of the given graph with the given stretch.
Return type NetworkX graph
Raises ValueError – If a stretch less than 1 is given.
Notes
This function implements the spanner algorithm by Baswana and Sen, see [1].
This algorithm is a randomized las vegas algorithm: The expected running time is O(km) where k = (stretch +
1) // 2 and m is the number of edges in G. The returned graph is always a spanner of the given graph with the
specified stretch. For weighted graphs the number of edges in the spanner is O(k * n^(1 + 1 / k)) where k is
defined as above and n is the number of nodes in G. For unweighted graphs the number of edges is O(n^(1 + 1 /
k) + kn).
References
[1] S. Baswana, S. Sen. A Simple and Linear Time Randomized Algorithm for Computing Sparse Spanners in
Weighted Graphs. Random Struct. Algorithms 30(4): 532-563 (2007).
3.51 Structural holes
Functions for computing measures of structural holes.
452 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
constraint(G[, nodes, weight]) Returns the constraint on all nodes in the graph G.
effective_size(G[, nodes, weight]) Returns the effective size of all nodes in the graph G.
local_constraint(G, u, v[, weight]) Returns the local constraint on the node uwith respect
to the node vin the graph G.
3.51.1 networkx.algorithms.structuralholes.constraint
constraint(G,nodes=None,weight=None)
Returns the constraint on all nodes in the graph G.
The constraint is a measure of the extent to which a node vis invested in those nodes that are themselves invested
in the neighbors of v. Formally, the constraint on v, denoted c(v), is defined by
𝑐(𝑣) =
𝑤∈𝑁(𝑣)∖{𝑣}
ℓ(𝑣, 𝑤)
where N(v) is the subset of the neighbors of vthat are either predecessors or successors of vand
ell(v, w) is the local constraint on vwith respect to w1. For the definition of local constraint, see
local_constraint().
Parameters
•G(NetworkX graph) – The graph containing v. This can be either directed or undirected.
•nodes (container, optional) – Container of nodes in the graph Gto compute the constraint.
If None, the constraint of every node is computed.
•weight (None or string, optional) – If None, all edge weights are considered equal. Other-
wise holds the name of the edge attribute used as weight.
Returns Dictionary with nodes as keys and the constraint on the node as values.
Return type dict
See also:
local_constraint()
References
3.51.2 networkx.algorithms.structuralholes.effective_size
effective_size(G,nodes=None,weight=None)
Returns the effective size of all nodes in the graph G.
The effective size of a node’s ego network is based on the concept of redundancy. A person’s ego network
has redundancy to the extent that her contacts are connected to each other as well. The nonredundant part of a
person’s relationships it’s the effective size of her ego network1. Formally, the effective size of a node 𝑢, denoted
𝑒(𝑢), is defined by
𝑒(𝑢) =
𝑣∈𝑁(𝑢)∖{𝑢}
⎛
⎝1−
𝑤∈𝑁(𝑣)
𝑝𝑢𝑤𝑚𝑣𝑤⎞
⎠
1Burt, Ronald S. “Structural holes and good ideas”. American Journal of Sociology (110): 349–399.
1Burt, Ronald S. Structural Holes: The Social Structure of Competition. Cambridge: Harvard University Press, 1995.
3.51. Structural holes 453

NetworkX Reference, Release 2.3rc1.dev20181203210840
where 𝑁(𝑢)is the set of neighbors of 𝑢and 𝑝𝑢𝑤 is the normalized mutual weight of the (directed or undirected)
edges joining 𝑢and 𝑣, for each vertex 𝑢and 𝑣1. And 𝑚𝑣𝑤 is the mutual weight of 𝑣and 𝑤divided by 𝑣highest
mutual weight with any of its neighbors. The mutual weight of 𝑢and 𝑣is the sum of the weights of edges joining
them (edge weights are assumed to be one if the graph is unweighted).
For the case of unweighted and undirected graphs, Borgatti proposed a simplified formula to compute effective
size2
𝑒(𝑢) = 𝑛−2𝑡
𝑛
where tis the number of ties in the ego network (not including ties to ego) and nis the number of nodes
(excluding ego).
Parameters
•G(NetworkX graph) – The graph containing v. Directed graphs are treated like undirected
graphs when computing neighbors of v.
•nodes (container, optional) – Container of nodes in the graph Gto compute the effective
size. If None, the effective size of every node is computed.
•weight (None or string, optional) – If None, all edge weights are considered equal. Other-
wise holds the name of the edge attribute used as weight.
Returns Dictionary with nodes as keys and the constraint on the node as values.
Return type dict
Notes
Burt also defined the related concept of efficiency of a node’s ego network, which is its effective size divided by
the degree of that node1. So you can easily compute efficiency:
>>> G=nx.DiGraph()
>>> G.add_edges_from([(0,1), (0,2), (1,0), (2,1)])
>>> esize =nx.effective_size(G)
>>> efficiency ={n: v /G.degree(n) for n, v in esize.items()}
See also:
constraint()
References
3.51.3 networkx.algorithms.structuralholes.local_constraint
local_constraint(G,u,v,weight=None)
Returns the local constraint on the node uwith respect to the node vin the graph G.
Formally, the local constraint on u with respect to v, denoted ℓ(𝑣), is defined by
ℓ(𝑢, 𝑣) = ⎛
⎝𝑝𝑢𝑣 +
𝑤∈𝑁(𝑣)
𝑝𝑢𝑤𝑝𝑤𝑣⎞
⎠
2
,
2Borgatti, S. “Structural Holes: Unpacking Burt’s Redundancy Measures” CONNECTIONS 20(1):35-38. http://www.analytictech.com/
connections/v20(1)/holes.htm
454 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
where 𝑁(𝑣)is the set of neighbors of 𝑣and 𝑝𝑢𝑣 is the normalized mutual weight of the (directed or undirected)
edges joining 𝑢and 𝑣, for each vertex 𝑢and 𝑣1. The mutual weight of 𝑢and 𝑣is the sum of the weights of edges
joining them (edge weights are assumed to be one if the graph is unweighted).
Parameters
•G(NetworkX graph) – The graph containing uand v. This can be either directed or undi-
rected.
•u(node) – A node in the graph G.
•v(node) – A node in the graph G.
•weight (None or string, optional) – If None, all edge weights are considered equal. Other-
wise holds the name of the edge attribute used as weight.
Returns The constraint of the node vin the graph G.
Return type float
See also:
constraint()
References
3.52 Swap
Swap edges in a graph.
double_edge_swap(G[, nswap, max_tries, seed]) Swap two edges in the graph while keeping the node
degrees fixed.
connected_double_edge_swap(G[, nswap,
...])
Attempts the specified number of double-edge swaps in
the graph G.
3.52.1 networkx.algorithms.swap.double_edge_swap
double_edge_swap(G,nswap=1,max_tries=100,seed=None)
Swap two edges in the graph while keeping the node degrees fixed.
A double-edge swap removes two randomly chosen edges u-v and x-y and creates the new edges u-x and v-y:
u--v u v
becomes | |
x--y x y
If either the edge u-x or v-y already exist no swap is performed and another attempt is made to find a suitable
edge pair.
Parameters
•G(graph) – An undirected graph
•nswap (integer (optional, default=1)) – Number of double-edge swaps to perform
•max_tries (integer (optional)) – Maximum number of attempts to swap edges
1Burt, Ronald S. “Structural holes and good ideas”. American Journal of Sociology (110): 349–399.
3.52. Swap 455

NetworkX Reference, Release 2.3rc1.dev20181203210840
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – The graph after double edge swaps.
Return type graph
Notes
Does not enforce any connectivity constraints.
The graph G is modified in place.
3.52.2 networkx.algorithms.swap.connected_double_edge_swap
connected_double_edge_swap(G,nswap=1,_window_threshold=3,seed=None)
Attempts the specified number of double-edge swaps in the graph G.
A double-edge swap removes two randomly chosen edges (u, v) and (x, y) and creates the new edges
(u, x) and (v, y):
u--v u v
becomes | |
x--y x y
If either (u, x) or (v, y) already exist, then no swap is performed so the actual number of swapped edges
is always at most nswap.
Parameters
•G(graph) – An undirected graph
•nswap (integer (optional, default=1)) – Number of double-edge swaps to perform
•_window_threshold (integer) – The window size below which connectedness of the graph
will be checked after each swap.
The “window” in this function is a dynamically updated integer that represents the number of
swap attempts to make before checking if the graph remains connected. It is an optimization
used to decrease the running time of the algorithm in exchange for increased complexity of
implementation.
If the window size is below this threshold, then the algorithm checks after each swap if the
graph remains connected by checking if there is a path joining the two nodes whose edge
was just removed. If the window size is above this threshold, then the algorithm performs
do all the swaps in the window and only then check if the graph is still connected.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns The number of successful swaps
Return type int
Raises NetworkXError – If the input graph is not connected, or if the graph has fewer than four
nodes.
456 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The initial graph Gmust be connected, and the resulting graph is connected. The graph Gis modified in place.
References
3.53 Tournament
Functions concerning tournament graphs.
Atournament graph is a complete oriented graph. In other words, it is a directed graph in which there is exactly one
directed edge joining each pair of distinct nodes. For each function in this module that accepts a graph as input, you
must provide a tournament graph. The responsibility is on the caller to ensure that the graph is a tournament graph.
To access the functions in this module, you must access them through the networkx.algorithms.tournament
module:
>>> import networkx as nx
>>> from networkx.algorithms import tournament
>>> G=nx.DiGraph([(0,1), (1,2), (2,0)])
>>> tournament.is_tournament(G)
True
hamiltonian_path(G) Returns a Hamiltonian path in the given tournament
graph.
is_reachable(G, s, t) Decides whether there is a path from sto tin the tour-
nament.
is_strongly_connected(G) Decides whether the given tournament is strongly con-
nected.
is_tournament(G) Returns True if and only if Gis a tournament.
random_tournament(n[, seed]) Returns a random tournament graph on nnodes.
score_sequence(G) Returns the score sequence for the given tournament
graph.
3.53.1 networkx.algorithms.tournament.hamiltonian_path
hamiltonian_path(G)
Returns a Hamiltonian path in the given tournament graph.
Each tournament has a Hamiltonian path. If furthermore, the tournament is strongly connected, then the returned
Hamiltonian path is a Hamiltonian cycle (by joining the endpoints of the path).
Parameters G (NetworkX graph) – A directed graph representing a tournament.
Returns Whether the given graph is a tournament graph.
Return type bool
Notes
This is a recursive implementation with an asymptotic running time of 𝑂(𝑛2), ignoring multiplicative polylog-
arithmic factors, where 𝑛is the number of nodes in the graph.
3.53. Tournament 457

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.53.2 networkx.algorithms.tournament.is_reachable
is_reachable(G,s,t)
Decides whether there is a path from sto tin the tournament.
This function is more theoretically efficient than the reachability checks than the shortest path algorithms in
networkx.algorithms.shortest_paths.
The given graph must be a tournament, otherwise this function’s behavior is undefined.
Parameters
•G(NetworkX graph) – A directed graph representing a tournament.
•s(node) – A node in the graph.
•t(node) – A node in the graph.
Returns Whether there is a path from sto tin G.
Return type bool
Notes
Although this function is more theoretically efficient than the generic shortest path functions, a speedup requires
the use of parallelism. Though it may in the future, the current implementation does not use parallelism, thus
you may not see much of a speedup.
This algorithm comes from [1].
References
3.53.3 networkx.algorithms.tournament.is_strongly_connected
is_strongly_connected(G)
Decides whether the given tournament is strongly connected.
This function is more theoretically efficient than the is_strongly_connected() function.
The given graph must be a tournament, otherwise this function’s behavior is undefined.
Parameters G (NetworkX graph) – A directed graph representing a tournament.
Returns Whether the tournament is strongly connected.
Return type bool
Notes
Although this function is more theoretically efficient than the generic strong connectivity function, a speedup
requires the use of parallelism. Though it may in the future, the current implementation does not use parallelism,
thus you may not see much of a speedup.
This algorithm comes from [1].
458 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.53.4 networkx.algorithms.tournament.is_tournament
is_tournament(G)
Returns True if and only if Gis a tournament.
A tournament is a directed graph, with neither self-loops nor multi-edges, in which there is exactly one directed
edge joining each pair of distinct nodes.
Parameters G (NetworkX graph) – A directed graph representing a tournament.
Returns Whether the given graph is a tournament graph.
Return type bool
Notes
Some definitions require a self-loop on each node, but that is not the convention used here.
3.53.5 networkx.algorithms.tournament.random_tournament
random_tournament(n,seed=None)
Returns a random tournament graph on nnodes.
Parameters
•n(int) – The number of nodes in the returned graph.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns Whether the given graph is a tournament graph.
Return type bool
Notes
This algorithm adds, for each pair of distinct nodes, an edge with uniformly random orientation. In other words,
binom{n}{2} flips of an unbiased coin decide the orientations of the edges in the graph.
3.53.6 networkx.algorithms.tournament.score_sequence
score_sequence(G)
Returns the score sequence for the given tournament graph.
The score sequence is the sorted list of the out-degrees of the nodes of the graph.
Parameters G (NetworkX graph) – A directed graph representing a tournament.
Returns A sorted list of the out-degrees of the nodes of G.
Return type list
3.53. Tournament 459

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.54 Traversal
3.54.1 Depth First Search
Basic algorithms for depth-first searching the nodes of a graph.
dfs_edges(G[, source, depth_limit]) Iterate over edges in a depth-first-search (DFS).
dfs_tree(G[, source, depth_limit]) Return oriented tree constructed from a depth-first-
search from source.
dfs_predecessors(G[, source, depth_limit]) Return dictionary of predecessors in depth-first-search
from source.
dfs_successors(G[, source, depth_limit]) Return dictionary of successors in depth-first-search
from source.
dfs_preorder_nodes(G[, source, depth_limit]) Generate nodes in a depth-first-search pre-ordering
starting at source.
dfs_postorder_nodes(G[, source, depth_limit]) Generate nodes in a depth-first-search post-ordering
starting at source.
dfs_labeled_edges(G[, source, depth_limit]) Iterate over edges in a depth-first-search (DFS) labeled
by type.
networkx.algorithms.traversal.depth_first_search.dfs_edges
dfs_edges(G,source=None,depth_limit=None)
Iterate over edges in a depth-first-search (DFS).
Perform a depth-first-search over the nodes of G and yield the edges in order. This may not generate all edges
in G (see edge_dfs).
Parameters
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search and return edges in the
component reachable from source.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns edges – A generator of edges in the depth-first-search.
Return type generator
Examples
>>> G=nx.path_graph(5)
>>> list(nx.dfs_edges(G, source=0))
[(0, 1), (1, 2), (2, 3), (3, 4)]
>>> list(nx.dfs_edges(G, source=0, depth_limit=2))
[(0, 1), (1, 2)]
Notes
If a source is not specified then a source is chosen arbitrarily and repeatedly until all components in the graph
are searched.
460 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
The implementation of this function is adapted from David Eppstein’s depth-first search function in PADS, with
modifications to allow depth limits based on the Wikipedia article “Depth-limited search”.
See also:
dfs_preorder_nodes(),dfs_postorder_nodes(),dfs_labeled_edges(),edge_dfs()
networkx.algorithms.traversal.depth_first_search.dfs_tree
dfs_tree(G,source=None,depth_limit=None)
Return oriented tree constructed from a depth-first-search from source.
Parameters
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns T – An oriented tree
Return type NetworkX DiGraph
Examples
>>> G=nx.path_graph(5)
>>> T=nx.dfs_tree(G, source=0, depth_limit=2)
>>> list(T.edges())
[(0, 1), (1, 2)]
>>> T=nx.dfs_tree(G, source=0)
>>> list(T.edges())
[(0, 1), (1, 2), (2, 3), (3, 4)]
networkx.algorithms.traversal.depth_first_search.dfs_predecessors
dfs_predecessors(G,source=None,depth_limit=None)
Return dictionary of predecessors in depth-first-search from source.
Parameters
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search and return edges in the
component reachable from source.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns pred – A dictionary with nodes as keys and predecessor nodes as values.
Return type dict
Examples
3.54. Traversal 461

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(4)
>>> nx.dfs_predecessors(G, source=0)
{1: 0, 2: 1, 3: 2}
>>> nx.dfs_predecessors(G, source=0, depth_limit=2)
{1: 0, 2: 1}
Notes
If a source is not specified then a source is chosen arbitrarily and repeatedly until all components in the graph
are searched.
The implementation of this function is adapted from David Eppstein’s depth-first search function in PADS, with
modifications to allow depth limits based on the Wikipedia article “Depth-limited search”.
networkx.algorithms.traversal.depth_first_search.dfs_successors
dfs_successors(G,source=None,depth_limit=None)
Return dictionary of successors in depth-first-search from source.
Parameters
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search and return edges in the
component reachable from source.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns succ – A dictionary with nodes as keys and list of successor nodes as values.
Return type dict
Examples
>>> G=nx.path_graph(5)
>>> nx.dfs_successors(G, source=0)
{0: [1], 1: [2], 2: [3], 3: [4]}
>>> nx.dfs_successors(G, source=0, depth_limit=2)
{0: [1], 1: [2]}
Notes
If a source is not specified then a source is chosen arbitrarily and repeatedly until all components in the graph
are searched.
The implementation of this function is adapted from David Eppstein’s depth-first search function in PADS, with
modifications to allow depth limits based on the Wikipedia article “Depth-limited search”.
networkx.algorithms.traversal.depth_first_search.dfs_preorder_nodes
dfs_preorder_nodes(G,source=None,depth_limit=None)
Generate nodes in a depth-first-search pre-ordering starting at source.
Parameters
462 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search and return edges in the
component reachable from source.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns nodes – A generator of nodes in a depth-first-search pre-ordering.
Return type generator
Examples
>>> G=nx.path_graph(5)
>>> list(nx.dfs_preorder_nodes(G, source=0))
[0, 1, 2, 3, 4]
>>> list(nx.dfs_preorder_nodes(G, source=0, depth_limit=2))
[0, 1, 2]
Notes
If a source is not specified then a source is chosen arbitrarily and repeatedly until all components in the graph
are searched.
The implementation of this function is adapted from David Eppstein’s depth-first search function in PADS, with
modifications to allow depth limits based on the Wikipedia article “Depth-limited search”.
See also:
dfs_edges(),dfs_postorder_nodes(),dfs_labeled_edges()
networkx.algorithms.traversal.depth_first_search.dfs_postorder_nodes
dfs_postorder_nodes(G,source=None,depth_limit=None)
Generate nodes in a depth-first-search post-ordering starting at source.
Parameters
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search and return edges in the
component reachable from source.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns nodes – A generator of nodes in a depth-first-search post-ordering.
Return type generator
Examples
>>> G=nx.path_graph(5)
>>> list(nx.dfs_postorder_nodes(G, source=0))
[4, 3, 2, 1, 0]
>>> list(nx.dfs_postorder_nodes(G, source=0, depth_limit=2))
[1, 0]
3.54. Traversal 463

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
If a source is not specified then a source is chosen arbitrarily and repeatedly until all components in the graph
are searched.
The implementation of this function is adapted from David Eppstein’s depth-first search function in PADS, with
modifications to allow depth limits based on the Wikipedia article “Depth-limited search”.
See also:
dfs_edges(),dfs_preorder_nodes(),dfs_labeled_edges()
networkx.algorithms.traversal.depth_first_search.dfs_labeled_edges
dfs_labeled_edges(G,source=None,depth_limit=None)
Iterate over edges in a depth-first-search (DFS) labeled by type.
Parameters
•G(NetworkX graph)
•source (node, optional) – Specify starting node for depth-first search and return edges in the
component reachable from source.
•depth_limit (int, optional (default=len(G))) – Specify the maximum search depth.
Returns edges – A generator of triples of the form (u,v,d), where (u,v) is the edge being explored
in the depth-first search and dis one of the strings ‘forward’, ‘nontree’, or ‘reverse’. A ‘forward’
edge is one in which uhas been visited but vhas not. A ‘nontree’ edge is one in which both u
and vhave been visited but the edge is not in the DFS tree. A ‘reverse’ edge is on in which both
uand vhave been visited and the edge is in the DFS tree.
Return type generator
Examples
The labels reveal the complete transcript of the depth-first search algorithm in more detail than, for example,
dfs_edges():
>>> from pprint import pprint
>>>
>>> G=nx.DiGraph([(0,1), (1,2), (2,1)])
>>> pprint(list(nx.dfs_labeled_edges(G, source=0)))
[(0, 0, 'forward'),
(0, 1, 'forward'),
(1, 2, 'forward'),
(2, 1, 'nontree'),
(1, 2, 'reverse'),
(0, 1, 'reverse'),
(0, 0, 'reverse')]
Notes
If a source is not specified then a source is chosen arbitrarily and repeatedly until all components in the graph
are searched.
464 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
The implementation of this function is adapted from David Eppstein’s depth-first search function in PADS, with
modifications to allow depth limits based on the Wikipedia article “Depth-limited search”.
See also:
dfs_edges(),dfs_preorder_nodes(),dfs_postorder_nodes()
3.54.2 Breadth First Search
Basic algorithms for breadth-first searching the nodes of a graph.
bfs_edges(G, source[, reverse, depth_limit]) Iterate over edges in a breadth-first-search starting at
source.
bfs_tree(G, source[, reverse, depth_limit]) Return an oriented tree constructed from of a breadth-
first-search starting at source.
bfs_predecessors(G, source[, depth_limit]) Returns an iterator of predecessors in breadth-first-
search from source.
bfs_successors(G, source[, depth_limit]) Returns an iterator of successors in breadth-first-search
from source.
networkx.algorithms.traversal.breadth_first_search.bfs_edges
bfs_edges(G,source,reverse=False,depth_limit=None)
Iterate over edges in a breadth-first-search starting at source.
Parameters
•G(NetworkX graph)
•source (node) – Specify starting node for breadth-first search and return edges in the com-
ponent reachable from source.
•reverse (bool, optional) – If True traverse a directed graph in the reverse direction
•depth_limit (int, optional(default=len(G))) – Specify the maximum search depth
Returns edges – A generator of edges in the breadth-first-search.
Return type generator
Examples
To get the edges in a breadth-first search:
>>> G=nx.path_graph(3)
>>> list(nx.bfs_edges(G, 0))
[(0, 1), (1, 2)]
>>> list(nx.bfs_edges(G, source=0, depth_limit=1))
[(0, 1)]
To get the nodes in a breadth-first search order:
>>> G=nx.path_graph(3)
>>> root =2
>>> edges =nx.bfs_edges(G, root)
>>> nodes =[root] +[v for u, v in edges]
(continues on next page)
3.54. Traversal 465

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> nodes
[2, 1, 0]
Notes
Based on http://www.ics.uci.edu/~eppstein/PADS/BFS.py. by D. Eppstein, July 2004. The modifications to
allow depth limits based on the Wikipedia article “Depth-limited-search”.
networkx.algorithms.traversal.breadth_first_search.bfs_tree
bfs_tree(G,source,reverse=False,depth_limit=None)
Return an oriented tree constructed from of a breadth-first-search starting at source.
Parameters
•G(NetworkX graph)
•source (node) – Specify starting node for breadth-first search and return edges in the com-
ponent reachable from source.
•reverse (bool, optional) – If True traverse a directed graph in the reverse direction
•depth_limit (int, optional(default=len(G))) – Specify the maximum search depth
Returns T – An oriented tree
Return type NetworkX DiGraph
Examples
>>> G=nx.path_graph(3)
>>> print(list(nx.bfs_tree(G,1).edges()))
[(1, 0), (1, 2)]
>>> H=nx.Graph()
>>> nx.add_path(H, [0,1,2,3,4,5,6])
>>> nx.add_path(H, [2,7,8,9,10])
>>> print(sorted(list(nx.bfs_tree(H, source=3, depth_limit=3).edges())))
[(1, 0), (2, 1), (2, 7), (3, 2), (3, 4), (4, 5), (5, 6), (7, 8)]
Notes
Based on http://www.ics.uci.edu/~eppstein/PADS/BFS.py by D. Eppstein, July 2004. The modifications to allow
depth limits based on the Wikipedia article “Depth-limited-search”.
networkx.algorithms.traversal.breadth_first_search.bfs_predecessors
bfs_predecessors(G,source,depth_limit=None)
Returns an iterator of predecessors in breadth-first-search from source.
Parameters
•G(NetworkX graph)
466 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•source (node) – Specify starting node for breadth-first search and return edges in the com-
ponent reachable from source.
•depth_limit (int, optional(default=len(G))) – Specify the maximum search depth
Returns pred – (node, predecessors) iterator where predecessors is the list of predecessors of the
node.
Return type iterator
Examples
>>> G=nx.path_graph(3)
>>> print(dict(nx.bfs_predecessors(G, 0)))
{1: 0, 2: 1}
>>> H=nx.Graph()
>>> H.add_edges_from([(0,1), (0,2), (1,3), (1,4), (2,5), (2,6)])
>>> print(dict(nx.bfs_predecessors(H, 0)))
{1: 0, 2: 0, 3: 1, 4: 1, 5: 2, 6: 2}
>>> M=nx.Graph()
>>> nx.add_path(M, [0,1,2,3,4,5,6])
>>> nx.add_path(M, [2,7,8,9,10])
>>> print(sorted(nx.bfs_predecessors(M, source=1, depth_limit=3)))
[(0, 1), (2, 1), (3, 2), (4, 3), (7, 2), (8, 7)]
Notes
Based on http://www.ics.uci.edu/~eppstein/PADS/BFS.py by D. Eppstein, July 2004. The modifications to allow
depth limits based on the Wikipedia article “Depth-limited-search”.
networkx.algorithms.traversal.breadth_first_search.bfs_successors
bfs_successors(G,source,depth_limit=None)
Returns an iterator of successors in breadth-first-search from source.
Parameters
•G(NetworkX graph)
•source (node) – Specify starting node for breadth-first search and return edges in the com-
ponent reachable from source.
•depth_limit (int, optional(default=len(G))) – Specify the maximum search depth
Returns succ – (node, successors) iterator where successors is the list of successors of the node.
Return type iterator
Examples
>>> G=nx.path_graph(3)
>>> print(dict(nx.bfs_successors(G,0)))
{0: [1], 1: [2]}
>>> H=nx.Graph()
>>> H.add_edges_from([(0,1), (0,2), (1,3), (1,4), (2,5), (2,6)])
(continues on next page)
3.54. Traversal 467

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> print(dict(nx.bfs_successors(H, 0)))
{0: [1, 2], 1: [3, 4], 2: [5, 6]}
>>> G=nx.Graph()
>>> nx.add_path(G, [0,1,2,3,4,5,6])
>>> nx.add_path(G, [2,7,8,9,10])
>>> print(dict(nx.bfs_successors(G, source=1, depth_limit=3)))
{1: [0, 2], 2: [3, 7], 3: [4], 7: [8]}
Notes
Based on http://www.ics.uci.edu/~eppstein/PADS/BFS.py by D. Eppstein, July 2004.The modifications to allow
depth limits based on the Wikipedia article “Depth-limited-search”.
3.54.3 Beam search
Basic algorithms for breadth-first searching the nodes of a graph.
bfs_beam_edges(G, source, value[, width]) Iterates over edges in a beam search.
networkx.algorithms.traversal.beamsearch.bfs_beam_edges
bfs_beam_edges(G,source,value,width=None)
Iterates over edges in a beam search.
The beam search is a generalized breadth-first search in which only the “best” wneighbors of the current node
are enqueued, where wis the beam width and “best” is an application-specific heuristic. In general, a beam
search with a small beam width might not visit each node in the graph.
Parameters
•G(NetworkX graph)
•source (node) – Starting node for the breadth-first search; this function iterates over only
those edges in the component reachable from this node.
•value (function) – A function that takes a node of the graph as input and returns a real
number indicating how “good” it is. A higher value means it is more likely to be visited
sooner during the search. When visiting a new node, only the width neighbors with the
highest value are enqueued (in decreasing order of value).
•width (int (default = None)) – The beam width for the search. This is the number of neigh-
bors (ordered by value) to enqueue when visiting each new node.
Yields edge – Edges in the beam search starting from source, given as a pair of nodes.
Examples
To give nodes with, for example, a higher centrality precedence during the search, set the value function to
return the centrality value of the node:
>>> G=nx.karate_club_graph()
>>> centrality =nx.eigenvector_centrality(G)
(continues on next page)
468 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> source =0
>>> width =5
>>> for u, v in nx.bfs_beam_edges(G, source, centrality.get, width):
... print((u, v))
3.54.4 Depth First Search on Edges
Depth First Search on Edges
Algorithms for a depth-first traversal of edges in a graph.
edge_dfs(G[, source, orientation]) A directed, depth-first-search of edges in G, beginning
at source.
networkx.algorithms.traversal.edgedfs.edge_dfs
edge_dfs(G,source=None,orientation=None)
A directed, depth-first-search of edges in G, beginning at source.
Yield the edges of G in a depth-first-search order continuing until all edges are generated.
Parameters
•G(graph) – A directed/undirected graph/multigraph.
•source (node, list of nodes) – The node from which the traversal begins. If None, then a
source is chosen arbitrarily and repeatedly until all edges from each node in the graph are
searched.
•orientation (None | ‘original’ | ‘reverse’ | ‘ignore’ (default: None)) – For directed graphs
and directed multigraphs, edge traversals need not respect the original orientation of the
edges. When set to ‘reverse’ every edge is traversed in the reverse direction. When set to
‘ignore’, every edge is treated as undirected. When set to ‘original’, every edge is treated as
directed. In all three cases, the yielded edge tuples add a last entry to indicate the direction
in which that edge was traversed. If orientation is None, the yielded edge has no direction
indicated. The direction is respected, but not reported.
Yields edge (directed edge) – A directed edge indicating the path taken by the depth-first traversal.
For graphs, edge is of the form (u, v) where uand vare the tail and head of the edge as
determined by the traversal. For multigraphs, edge is of the form (u, v, key), where key
is the key of the edge. When the graph is directed, then uand vare always in the order of the
actual directed edge. If orientation is not None then the edge tuple is extended to include the
direction of traversal (‘forward’ or ‘reverse’) on that edge.
Examples
>>> import networkx as nx
>>> nodes =[0,1,2,3]
>>> edges =[(0,1), (1,0), (1,0), (2,1), (3,1)]
>>> list(nx.edge_dfs(nx.Graph(edges), nodes))
[(0, 1), (1, 2), (1, 3)]
3.54. Traversal 469

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> list(nx.edge_dfs(nx.DiGraph(edges), nodes))
[(0, 1), (1, 0), (2, 1), (3, 1)]
>>> list(nx.edge_dfs(nx.MultiGraph(edges), nodes))
[(0, 1, 0), (1, 0, 1), (0, 1, 2), (1, 2, 0), (1, 3, 0)]
>>> list(nx.edge_dfs(nx.MultiDiGraph(edges), nodes))
[(0, 1, 0), (1, 0, 0), (1, 0, 1), (2, 1, 0), (3, 1, 0)]
>>> list(nx.edge_dfs(nx.DiGraph(edges), nodes, orientation='ignore'))
[(0, 1, 'forward'), (1, 0, 'forward'), (2, 1, 'reverse'), (3, 1, 'reverse')]
>>> list(nx.edge_dfs(nx.MultiDiGraph(edges), nodes, orientation='ignore'))
[(0, 1, 0, 'forward'), (1, 0, 0, 'forward'), (1, 0, 1, 'reverse'), (2, 1, 0,
˓→'reverse'), (3, 1, 0, 'reverse')]
Notes
The goal of this function is to visit edges. It differs from the more familiar depth-first traversal of nodes, as
provided by networkx.algorithms.traversal.depth_first_search.dfs_edges(), in that
it does not stop once every node has been visited. In a directed graph with edges [(0, 1), (1, 2), (2, 1)], the edge
(2, 1) would not be visited if not for the functionality provided by this function.
See also:
dfs_edges()
3.54.5 Depth First Search on Edges
Breadth First Search on Edges
Algorithms for a depth-first traversal of edges in a graph.
edge_bfs(G[, source, orientation]) A directed, breadth-first-search of edges in G, beginning
at source.
networkx.algorithms.traversal.edgebfs.edge_bfs
edge_bfs(G,source=None,orientation=None)
A directed, breadth-first-search of edges in G, beginning at source.
Yield the edges of G in a breadth-first-search order continuing until all edges are generated.
Parameters
•G(graph) – A directed/undirected graph/multigraph.
•source (node, list of nodes) – The node from which the traversal begins. If None, then a
source is chosen arbitrarily and repeatedly until all edges from each node in the graph are
searched.
•orientation (None | ‘original’ | ‘reverse’ | ‘ignore’ (default: None)) – For directed graphs
and directed multigraphs, edge traversals need not respect the original orientation of the
470 Chapter 3. Algorithms
NetworkX Reference, Release 2.3rc1.dev20181203210840
edges. When set to ‘reverse’ every edge is traversed in the reverse direction. When set to
‘ignore’, every edge is treated as undirected. When set to ‘original’, every edge is treated as
directed. In all three cases, the yielded edge tuples add a last entry to indicate the direction
in which that edge was traversed. If orientation is None, the yielded edge has no direction
indicated. The direction is respected, but not reported.
Yields edge (directed edge) – A directed edge indicating the path taken by the breadth-first-search.
For graphs, edge is of the form (u, v) where uand vare the tail and head of the edge as
determined by the traversal. For multigraphs, edge is of the form (u, v, key), where key
is the key of the edge. When the graph is directed, then uand vare always in the order of the
actual directed edge. If orientation is not None then the edge tuple is extended to include the
direction of traversal (‘forward’ or ‘reverse’) on that edge.
Examples
>>> import networkx as nx
>>> nodes =[0,1,2,3]
>>> edges =[(0,1), (1,0), (1,0), (2,0), (2,1), (3,1)]
>>> list(nx.edge_bfs(nx.Graph(edges), nodes))
[(0, 1), (0, 2), (1, 2), (1, 3)]
>>> list(nx.edge_bfs(nx.DiGraph(edges), nodes))
[(0, 1), (1, 0), (2, 0), (2, 1), (3, 1)]
>>> list(nx.edge_bfs(nx.MultiGraph(edges), nodes))
[(0, 1, 0), (0, 1, 1), (0, 1, 2), (0, 2, 0), (1, 2, 0), (1, 3, 0)]
>>> list(nx.edge_bfs(nx.MultiDiGraph(edges), nodes))
[(0, 1, 0), (1, 0, 0), (1, 0, 1), (2, 0, 0), (2, 1, 0), (3, 1, 0)]
>>> list(nx.edge_bfs(nx.DiGraph(edges), nodes, orientation='ignore'))
[(0, 1, 'forward'), (1, 0, 'reverse'), (2, 0, 'reverse'), (2, 1, 'reverse'), (3,
˓→1, 'reverse')]
>>> list(nx.edge_bfs(nx.MultiDiGraph(edges), nodes, orientation='ignore'))
[(0, 1, 0, 'forward'), (1, 0, 0, 'reverse'), (1, 0, 1, 'reverse'), (2, 0, 0,
˓→'reverse'), (2, 1, 0, 'reverse'), (3, 1, 0, 'reverse')]
Notes
The goal of this function is to visit edges. It differs from the more familiar breadth-first-search of nodes,
as provided by networkx.algorithms.traversal.breadth_first_search.bfs_edges(), in
that it does not stop once every node has been visited. In a directed graph with edges [(0, 1), (1, 2), (2, 1)], the
edge (2, 1) would not be visited if not for the functionality provided by this function.
See also:
bfs_edges(),bfs_tree(),edge_dfs()
3.54. Traversal 471

NetworkX Reference, Release 2.3rc1.dev20181203210840
3.55 Tree
3.55.1 Recognition
Recognition Tests
Aforest is an acyclic, undirected graph, and a tree is a connected forest. Depending on the subfield, there are various
conventions for generalizing these definitions to directed graphs.
In one convention, directed variants of forest and tree are defined in an identical manner, except that the direction of
the edges is ignored. In effect, each directed edge is treated as a single undirected edge. Then, additional restrictions
are imposed to define branchings and arborescences.
In another convention, directed variants of forest and tree correspond to the previous convention’s branchings and
arborescences, respectively. Then two new terms, polyforest and polytree, are defined to correspond to the other
convention’s forest and tree.
Summarizing:
+-----------------------------+
|Convention A |Convention B |
+=============================+
|forest |polyforest |
|tree |polytree |
|branching |forest |
|arborescence |tree |
+-----------------------------+
Each convention has its reasons. The first convention emphasizes definitional similarity in that directed forests and
trees are only concerned with acyclicity and do not have an in-degree constraint, just as their undirected counterparts do
not. The second convention emphasizes functional similarity in the sense that the directed analog of a spanning tree is
a spanning arborescence. That is, take any spanning tree and choose one node as the root. Then every edge is assigned
a direction such there is a directed path from the root to every other node. The result is a spanning arborescence.
NetworkX follows convention “A”. Explicitly, these are:
undirected forest An undirected graph with no undirected cycles.
undirected tree A connected, undirected forest.
directed forest A directed graph with no undirected cycles. Equivalently, the underlying graph structure (which
ignores edge orientations) is an undirected forest. In convention B, this is known as a polyforest.
directed tree A weakly connected, directed forest. Equivalently, the underlying graph structure (which ignores edge
orientations) is an undirected tree. In convention B, this is known as a polytree.
branching A directed forest with each node having, at most, one parent. So the maximum in-degree is equal to 1. In
convention B, this is known as a forest.
arborescence A directed tree with each node having, at most, one parent. So the maximum in-degree is equal to 1.
In convention B, this is known as a tree.
For trees and arborescences, the adjective “spanning” may be added to designate that the graph, when considered as
a forest/branching, consists of a single tree/arborescence that includes all nodes in the graph. It is true, by definition,
that every tree/arborescence is spanning with respect to the nodes that define the tree/arborescence and so, it might
seem redundant to introduce the notion of “spanning”. However, the nodes may represent a subset of nodes from a
larger graph, and it is in this context that the term “spanning” becomes a useful notion.
472 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
is_tree(G) Returns True if Gis a tree.
is_forest(G) Returns True if Gis a forest.
is_arborescence(G) Returns True if Gis an arborescence.
is_branching(G) Returns True if Gis a branching.
networkx.algorithms.tree.recognition.is_tree
is_tree(G)
Returns True if Gis a tree.
A tree is a connected graph with no undirected cycles.
For directed graphs, Gis a tree if the underlying graph is a tree. The underlying graph is obtained by treating
each directed edge as a single undirected edge in a multigraph.
Parameters G (graph) – The graph to test.
Returns b – A boolean that is True if Gis a tree.
Return type bool
Notes
In another convention, a directed tree is known as a polytree and then tree corresponds to an arborescence.
See also:
is_arborescence()
networkx.algorithms.tree.recognition.is_forest
is_forest(G)
Returns True if Gis a forest.
A forest is a graph with no undirected cycles.
For directed graphs, Gis a forest if the underlying graph is a forest. The underlying graph is obtained by treating
each directed edge as a single undirected edge in a multigraph.
Parameters G (graph) – The graph to test.
Returns b – A boolean that is True if Gis a forest.
Return type bool
Notes
In another convention, a directed forest is known as a polyforest and then forest corresponds to a branching.
See also:
is_branching()
3.55. Tree 473

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.tree.recognition.is_arborescence
is_arborescence(G)
Returns True if Gis an arborescence.
An arborescence is a directed tree with maximum in-degree equal to 1.
Parameters G (graph) – The graph to test.
Returns b – A boolean that is True if Gis an arborescence.
Return type bool
Notes
In another convention, an arborescence is known as a tree.
See also:
is_tree()
networkx.algorithms.tree.recognition.is_branching
is_branching(G)
Returns True if Gis a branching.
A branching is a directed forest with maximum in-degree equal to 1.
Parameters G (directed graph) – The directed graph to test.
Returns b – A boolean that is True if Gis a branching.
Return type bool
Notes
In another convention, a branching is also known as a forest.
See also:
is_forest()
3.55.2 Branchings and Spanning Arborescences
Algorithms for finding optimum branchings and spanning arborescences.
This implementation is based on:
J. Edmonds, Optimum branchings, J. Res. Natl. Bur. Standards 71B (1967), 233–240. URL: http:
//archive.org/details/jresv71Bn4p233
branching_weight(G[, attr, default]) Returns the total weight of a branching.
greedy_branching(G[, attr, default, kind, seed]) Returns a branching obtained through a greedy algo-
rithm.
maximum_branching(G[, attr, default, . . . ]) Returns a maximum branching from G.
minimum_branching(G[, attr, default, . . . ]) Returns a minimum branching from G.
Continued on next page
474 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 139 – continued from previous page
maximum_spanning_arborescence(G[, attr,
...])
Returns a maximum spanning arborescence from G.
minimum_spanning_arborescence(G[, attr,
...])
Returns a minimum spanning arborescence from G.
Edmonds(G[, seed]) Edmonds algorithm for finding optimal branchings and
spanning arborescences.
networkx.algorithms.tree.branchings.branching_weight
branching_weight(G,attr=’weight’,default=1)
Returns the total weight of a branching.
networkx.algorithms.tree.branchings.greedy_branching
greedy_branching(G,attr=’weight’,default=1,kind=’max’,seed=None)
Returns a branching obtained through a greedy algorithm.
This algorithm is wrong, and cannot give a proper optimal branching. However, we include it for pedagogical
reasons, as it can be helpful to see what its outputs are.
The output is a branching, and possibly, a spanning arborescence. However, it is not guaranteed to be optimal
in either case.
Parameters
•G(DiGraph) – The directed graph to scan.
•attr (str) – The attribute to use as weights. If None, then each edge will be treated equally
with a weight of 1.
•default (float) – When attr is not None, then if an edge does not have that attribute,
default specifies what value it should take.
•kind (str) – The type of optimum to search for: ‘min’ or ‘max’ greedy branching.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns B – The greedily obtained branching.
Return type directed graph
networkx.algorithms.tree.branchings.maximum_branching
maximum_branching(G,attr=’weight’,default=1,preserve_attrs=False)
Returns a maximum branching from G.
Parameters
•G((multi)digraph-like) – The graph to be searched.
•attr (str) – The edge attribute used to in determining optimality.
•default (float) – The value of the edge attribute used if an edge does not have the attribute
attr.
•preserve_attrs (bool) – If True, preserve the other attributes of the original graph (that are
not passed to attr)
3.55. Tree 475

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns B – A maximum branching.
Return type (multi)digraph-like
networkx.algorithms.tree.branchings.minimum_branching
minimum_branching(G,attr=’weight’,default=1,preserve_attrs=False)
Returns a minimum branching from G.
Parameters
•G((multi)digraph-like) – The graph to be searched.
•attr (str) – The edge attribute used to in determining optimality.
•default (float) – The value of the edge attribute used if an edge does not have the attribute
attr.
•preserve_attrs (bool) – If True, preserve the other attributes of the original graph (that are
not passed to attr)
Returns B – A minimum branching.
Return type (multi)digraph-like
networkx.algorithms.tree.branchings.maximum_spanning_arborescence
maximum_spanning_arborescence(G,attr=’weight’,default=1,preserve_attrs=False)
Returns a maximum spanning arborescence from G.
Parameters
•G((multi)digraph-like) – The graph to be searched.
•attr (str) – The edge attribute used to in determining optimality.
•default (float) – The value of the edge attribute used if an edge does not have the attribute
attr.
•preserve_attrs (bool) – If True, preserve the other attributes of the original graph (that are
not passed to attr)
Returns B – A maximum spanning arborescence.
Return type (multi)digraph-like
Raises NetworkXException – If the graph does not contain a maximum spanning arborescence.
networkx.algorithms.tree.branchings.minimum_spanning_arborescence
minimum_spanning_arborescence(G,attr=’weight’,default=1,preserve_attrs=False)
Returns a minimum spanning arborescence from G.
Parameters
•G((multi)digraph-like) – The graph to be searched.
•attr (str) – The edge attribute used to in determining optimality.
•default (float) – The value of the edge attribute used if an edge does not have the attribute
attr.
476 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
•preserve_attrs (bool) – If True, preserve the other attributes of the original graph (that are
not passed to attr)
Returns B – A minimum spanning arborescence.
Return type (multi)digraph-like
Raises NetworkXException – If the graph does not contain a minimum spanning arborescence.
networkx.algorithms.tree.branchings.Edmonds
class Edmonds(G,seed=None)
Edmonds algorithm for finding optimal branchings and spanning arborescences.
__init__(G,seed=None)
Initialize self. See help(type(self)) for accurate signature.
Methods
__init__(G[, seed]) Initialize self.
find_optimum([attr, default, kind, style, . . . ]) Returns a branching from G.
3.55.3 Encoding and decoding
Functions for encoding and decoding trees.
Since a tree is a highly restricted form of graph, it can be represented concisely in several ways. This module includes
functions for encoding and decoding trees in the form of nested tuples and Prüfer sequences. The former requires a
rooted tree, whereas the latter can be applied to unrooted trees. Furthermore, there is a bijection from Prüfer sequences
to labeled trees.
from_nested_tuple(sequence[, . . . ]) Returns the rooted tree corresponding to the given
nested tuple.
to_nested_tuple(T, root[, canonical_form]) Returns a nested tuple representation of the given tree.
from_prufer_sequence(sequence) Returns the tree corresponding to the given Prüfer se-
quence.
to_prufer_sequence(T) Returns the Prüfer sequence of the given tree.
networkx.algorithms.tree.coding.from_nested_tuple
from_nested_tuple(sequence,sensible_relabeling=False)
Returns the rooted tree corresponding to the given nested tuple.
The nested tuple representation of a tree is defined recursively. The tree with one node and no edges is rep-
resented by the empty tuple, (). A tree with ksubtrees is represented by a tuple of length kin which each
element is the nested tuple representation of a subtree.
Parameters
•sequence (tuple) – A nested tuple representing a rooted tree.
•sensible_relabeling (bool) – Whether to relabel the nodes of the tree so that nodes are
labeled in increasing order according to their breadth-first search order from the root node.
3.55. Tree 477

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns The tree corresponding to the given nested tuple, whose root node is node 0. If
sensible_labeling is True, nodes will be labeled in breadth-first search order starting
from the root node.
Return type NetworkX graph
Notes
This function is not the inverse of to_nested_tuple(); the only guarantee is that the rooted trees are
isomorphic.
See also:
to_nested_tuple(),from_prufer_sequence()
Examples
Sensible relabeling ensures that the nodes are labeled from the root starting at 0:
>>> balanced =(((), ()), ((), ()))
>>> T=nx.from_nested_tuple(balanced, sensible_relabeling=True)
>>> edges =[(0,1), (0,2), (1,3), (1,4), (2,5), (2,6)]
>>> all((u, v) in T.edges() or (v, u) in T.edges() for (u, v) in edges)
True
networkx.algorithms.tree.coding.to_nested_tuple
to_nested_tuple(T,root,canonical_form=False)
Returns a nested tuple representation of the given tree.
The nested tuple representation of a tree is defined recursively. The tree with one node and no edges is rep-
resented by the empty tuple, (). A tree with ksubtrees is represented by a tuple of length kin which each
element is the nested tuple representation of a subtree.
Parameters
•T(NetworkX graph) – An undirected graph object representing a tree.
•root (node) – The node in Tto interpret as the root of the tree.
•canonical_form (bool) – If True, each tuple is sorted so that the function returns a canon-
ical form for rooted trees. This means “lighter” subtrees will appear as nested tuples before
“heavier” subtrees. In this way, each isomorphic rooted tree has the same nested tuple rep-
resentation.
Returns A nested tuple representation of the tree.
Return type tuple
Notes
This function is not the inverse of from_nested_tuple(); the only guarantee is that the rooted trees are
isomorphic.
See also:
from_nested_tuple(),to_prufer_sequence()
478 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
The tree need not be a balanced binary tree:
>>> T=nx.Graph()
>>> T.add_edges_from([(0,1), (0,2), (0,3)])
>>> T.add_edges_from([(1,4), (1,5)])
>>> T.add_edges_from([(3,6), (3,7)])
>>> root =0
>>> nx.to_nested_tuple(T, root)
(((), ()), (), ((), ()))
Continuing the above example, if canonical_form is True, the nested tuples will be sorted:
>>> nx.to_nested_tuple(T, root, canonical_form=True)
((), ((), ()), ((), ()))
Even the path graph can be interpreted as a tree:
>>> T=nx.path_graph(4)
>>> root =0
>>> nx.to_nested_tuple(T, root)
((((),),),)
networkx.algorithms.tree.coding.from_prufer_sequence
from_prufer_sequence(sequence)
Returns the tree corresponding to the given Prüfer sequence.
APrüfer sequence is a list of n- 2 numbers between 0 and n- 1, inclusive. The tree corresponding to a given
Prüfer sequence can be recovered by repeatedly joining a node in the sequence with a node with the smallest
potential degree according to the sequence.
Parameters sequence (list) – A Prüfer sequence, which is a list of n- 2 integers between zero and
n- 1, inclusive.
Returns The tree corresponding to the given Prüfer sequence.
Return type NetworkX graph
Notes
There is a bijection from labeled trees to Prüfer sequences. This function is the inverse of the
from_prufer_sequence() function.
Sometimes Prüfer sequences use nodes labeled from 1 to ninstead of from 0 to n- 1. This function requires
nodes to be labeled in the latter form. You can use networkx.relabel_nodes() to relabel the nodes of
your tree to the appropriate format.
This implementation is from1and has a running time of 𝑂(𝑛log 𝑛).
1Wang, Xiaodong, Lei Wang, and Yingjie Wu. “An optimal algorithm for Prufer codes.” Journal of Software Engineering and Applications
2.02 (2009): 111. <https://doi.org/10.4236/jsea.2009.22016>
3.55. Tree 479

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
See also:
from_nested_tuple(),to_prufer_sequence()
Examples
There is a bijection between Prüfer sequences and labeled trees, so this function is the inverse of the
to_prufer_sequence() function:
>>> edges =[(0,3), (1,3), (2,3), (3,4), (4,5)]
>>> tree =nx.Graph(edges)
>>> sequence =nx.to_prufer_sequence(tree)
>>> sequence
[3, 3, 3, 4]
>>> tree2 =nx.from_prufer_sequence(sequence)
>>> list(tree2.edges()) == edges
True
networkx.algorithms.tree.coding.to_prufer_sequence
to_prufer_sequence(T)
Returns the Prüfer sequence of the given tree.
APrüfer sequence is a list of n- 2 numbers between 0 and n- 1, inclusive. The tree corresponding to a given
Prüfer sequence can be recovered by repeatedly joining a node in the sequence with a node with the smallest
potential degree according to the sequence.
Parameters T (NetworkX graph) – An undirected graph object representing a tree.
Returns The Prüfer sequence of the given tree.
Return type list
Raises
•NetworkXPointlessConcept – If the number of nodes in Tis less than two.
•NotATree – If Tis not a tree.
•KeyError – If the set of nodes in Tis not {0, . . . , n- 1}.
Notes
There is a bijection from labeled trees to Prüfer sequences. This function is the inverse of the
from_prufer_sequence() function.
Sometimes Prüfer sequences use nodes labeled from 1 to ninstead of from 0 to n- 1. This function requires
nodes to be labeled in the latter form. You can use relabel_nodes() to relabel the nodes of your tree to the
appropriate format.
This implementation is from1and has a running time of 𝑂(𝑛log 𝑛).
See also:
to_nested_tuple(),from_prufer_sequence()
1Wang, Xiaodong, Lei Wang, and Yingjie Wu. “An optimal algorithm for Prufer codes.” Journal of Software Engineering and Applications
2.02 (2009): 111. <https://doi.org/10.4236/jsea.2009.22016>
480 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
Examples
There is a bijection between Prüfer sequences and labeled trees, so this function is the inverse of the
from_prufer_sequence() function:
>>> edges =[(0,3), (1,3), (2,3), (3,4), (4,5)]
>>> tree =nx.Graph(edges)
>>> sequence =nx.to_prufer_sequence(tree)
>>> sequence
[3, 3, 3, 4]
>>> tree2 =nx.from_prufer_sequence(sequence)
>>> list(tree2.edges()) == edges
True
3.55.4 Operations
Operations on trees.
join(rooted_trees[, label_attribute]) Returns a new rooted tree with a root node joined with
the roots of each of the given rooted trees.
networkx.algorithms.tree.operations.join
join(rooted_trees,label_attribute=None)
Returns a new rooted tree with a root node joined with the roots of each of the given rooted trees.
Parameters
•rooted_trees (list) – A list of pairs in which each left element is a NetworkX graph object
representing a tree and each right element is the root node of that tree. The nodes of these
trees will be relabeled to integers.
•label_attribute (str) – If provided, the old node labels will be stored in the new tree under
this node attribute. If not provided, the node attribute '_old' will store the original label
of the node in the rooted trees given in the input.
Returns The rooted tree whose subtrees are the given rooted trees. The new root node is la-
beled 0. Each non-root node has an attribute, as described under the keyword argument
label_attribute, that indicates the label of the original node in the input tree.
Return type NetworkX graph
Notes
Graph, edge, and node attributes are propagated from the given rooted trees to the created tree. If there are
any overlapping graph attributes, those from later trees will overwrite those from earlier trees in the tuple of
positional arguments.
Examples
Join two full balanced binary trees of height hto get a full balanced binary tree of depth h+ 1:
3.55. Tree 481

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> h=4
>>> left =nx.balanced_tree(2, h)
>>> right =nx.balanced_tree(2, h)
>>> joined_tree =nx.join([(left, 0), (right, 0)])
>>> nx.is_isomorphic(joined_tree, nx.balanced_tree(2,h+1))
True
3.55.5 Spanning Trees
Algorithms for calculating min/max spanning trees/forests.
minimum_spanning_tree(G[, weight, . . . ]) Returns a minimum spanning tree or forest on an undi-
rected graph G.
maximum_spanning_tree(G[, weight, . . . ]) Returns a maximum spanning tree or forest on an undi-
rected graph G.
minimum_spanning_edges(G[, algorithm, . . . ]) Generate edges in a minimum spanning forest of an
undirected weighted graph.
maximum_spanning_edges(G[, algorithm, . . . ]) Generate edges in a maximum spanning forest of an
undirected weighted graph.
networkx.algorithms.tree.mst.minimum_spanning_tree
minimum_spanning_tree(G,weight=’weight’,algorithm=’kruskal’,ignore_nan=False)
Returns a minimum spanning tree or forest on an undirected graph G.
Parameters
•G(undirected graph) – An undirected graph. If Gis connected, then the algorithm finds a
spanning tree. Otherwise, a spanning forest is found.
•weight (str) – Data key to use for edge weights.
•algorithm (string) – The algorithm to use when finding a minimum spanning tree. Valid
choices are ‘kruskal’, ‘prim’, or ‘boruvka’. The default is ‘kruskal’.
•ignore_nan (bool (default: False)) – If a NaN is found as an edge weight normally an
exception is raised. If ignore_nan is True then that edge is ignored instead.
Returns G – A minimum spanning tree or forest.
Return type NetworkX Graph
Examples
>>> G=nx.cycle_graph(4)
>>> G.add_edge(0,3, weight=2)
>>> T=nx.minimum_spanning_tree(G)
>>> sorted(T.edges(data=True))
[(0, 1, {}), (1, 2, {}), (2, 3, {})]
Notes
For Bor˚uvka’s algorithm, each edge must have a weight attribute, and each edge weight must be distinct.
482 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
For the other algorithms, if the graph edges do not have a weight attribute a default weight of 1 will be used.
There may be more than one tree with the same minimum or maximum weight. See networkx.tree.
recognition for more detailed definitions.
Isolated nodes with self-loops are in the tree as edgeless isolated nodes.
networkx.algorithms.tree.mst.maximum_spanning_tree
maximum_spanning_tree(G,weight=’weight’,algorithm=’kruskal’,ignore_nan=False)
Returns a maximum spanning tree or forest on an undirected graph G.
Parameters
•G(undirected graph) – An undirected graph. If Gis connected, then the algorithm finds a
spanning tree. Otherwise, a spanning forest is found.
•weight (str) – Data key to use for edge weights.
•algorithm (string) – The algorithm to use when finding a maximum spanning tree. Valid
choices are ‘kruskal’, ‘prim’, or ‘boruvka’. The default is ‘kruskal’.
•ignore_nan (bool (default: False)) – If a NaN is found as an edge weight normally an
exception is raised. If ignore_nan is True then that edge is ignored instead.
Returns G – A maximum spanning tree or forest.
Return type NetworkX Graph
Examples
>>> G=nx.cycle_graph(4)
>>> G.add_edge(0,3, weight=2)
>>> T=nx.maximum_spanning_tree(G)
>>> sorted(T.edges(data=True))
[(0, 1, {}), (0, 3, {'weight': 2}), (1, 2, {})]
Notes
For Bor˚uvka’s algorithm, each edge must have a weight attribute, and each edge weight must be distinct.
For the other algorithms, if the graph edges do not have a weight attribute a default weight of 1 will be used.
There may be more than one tree with the same minimum or maximum weight. See networkx.tree.
recognition for more detailed definitions.
Isolated nodes with self-loops are in the tree as edgeless isolated nodes.
networkx.algorithms.tree.mst.minimum_spanning_edges
minimum_spanning_edges(G,algorithm=’kruskal’,weight=’weight’,keys=True,data=True,ig-
nore_nan=False)
Generate edges in a minimum spanning forest of an undirected weighted graph.
A minimum spanning tree is a subgraph of the graph (a tree) with the minimum sum of edge weights. A spanning
forest is a union of the spanning trees for each connected component of the graph.
Parameters
3.55. Tree 483
NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(undirected Graph) – An undirected graph. If Gis connected, then the algorithm finds a
spanning tree. Otherwise, a spanning forest is found.
•algorithm (string) – The algorithm to use when finding a minimum spanning tree. Valid
choices are ‘kruskal’, ‘prim’, or ‘boruvka’. The default is ‘kruskal’.
•weight (string) – Edge data key to use for weight (default ‘weight’).
•keys (bool) – Whether to yield edge key in multigraphs in addition to the edge. If Gis not a
multigraph, this is ignored.
•data (bool, optional) – If True yield the edge data along with the edge.
•ignore_nan (bool (default: False)) – If a NaN is found as an edge weight normally an
exception is raised. If ignore_nan is True then that edge is ignored instead.
Returns
edges – An iterator over edges in a maximum spanning tree of G. Edges connecting nodes uand
vare represented as tuples: (u, v, k, d) or (u, v, k) or (u, v, d) or (u, v)
If Gis a multigraph, keys indicates whether the edge key kwill be reported in the third position
in the edge tuple. data indicates whether the edge datadict dwill appear at the end of the edge
tuple.
If Gis not a multigraph, the tuples are (u, v, d) if data is True or (u, v) if data is
False.
Return type iterator
Examples
>>> from networkx.algorithms import tree
Find minimum spanning edges by Kruskal’s algorithm
>>> G=nx.cycle_graph(4)
>>> G.add_edge(0,3, weight=2)
>>> mst =tree.minimum_spanning_edges(G, algorithm='kruskal', data=False)
>>> edgelist =list(mst)
>>> sorted(edgelist)
[(0, 1), (1, 2), (2, 3)]
Find minimum spanning edges by Prim’s algorithm
>>> G=nx.cycle_graph(4)
>>> G.add_edge(0,3, weight=2)
>>> mst =tree.minimum_spanning_edges(G, algorithm='prim', data=False)
>>> edgelist =list(mst)
>>> sorted(edgelist)
[(0, 1), (1, 2), (2, 3)]
Notes
For Bor˚uvka’s algorithm, each edge must have a weight attribute, and each edge weight must be distinct.
For the other algorithms, if the graph edges do not have a weight attribute a default weight of 1 will be used.
Modified code from David Eppstein, April 2006 http://www.ics.uci.edu/~eppstein/PADS/
484 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.tree.mst.maximum_spanning_edges
maximum_spanning_edges(G,algorithm=’kruskal’,weight=’weight’,keys=True,data=True,ig-
nore_nan=False)
Generate edges in a maximum spanning forest of an undirected weighted graph.
A maximum spanning tree is a subgraph of the graph (a tree) with the maximum possible sum of edge weights.
A spanning forest is a union of the spanning trees for each connected component of the graph.
Parameters
•G(undirected Graph) – An undirected graph. If Gis connected, then the algorithm finds a
spanning tree. Otherwise, a spanning forest is found.
•algorithm (string) – The algorithm to use when finding a maximum spanning tree. Valid
choices are ‘kruskal’, ‘prim’, or ‘boruvka’. The default is ‘kruskal’.
•weight (string) – Edge data key to use for weight (default ‘weight’).
•keys (bool) – Whether to yield edge key in multigraphs in addition to the edge. If Gis not a
multigraph, this is ignored.
•data (bool, optional) – If True yield the edge data along with the edge.
•ignore_nan (bool (default: False)) – If a NaN is found as an edge weight normally an
exception is raised. If ignore_nan is True then that edge is ignored instead.
Returns
edges – An iterator over edges in a maximum spanning tree of G. Edges connecting nodes uand
vare represented as tuples: (u, v, k, d) or (u, v, k) or (u, v, d) or (u, v)
If Gis a multigraph, keys indicates whether the edge key kwill be reported in the third position
in the edge tuple. data indicates whether the edge datadict dwill appear at the end of the edge
tuple.
If Gis not a multigraph, the tuples are (u, v, d) if data is True or (u, v) if data is
False.
Return type iterator
Examples
>>> from networkx.algorithms import tree
Find maximum spanning edges by Kruskal’s algorithm
>>> G=nx.cycle_graph(4)
>>> G.add_edge(0,3, weight=2)
>>> mst =tree.maximum_spanning_edges(G, algorithm='kruskal', data=False)
>>> edgelist =list(mst)
>>> sorted(edgelist)
[(0, 1), (0, 3), (1, 2)]
Find maximum spanning edges by Prim’s algorithm
>>> G=nx.cycle_graph(4)
>>> G.add_edge(0,3, weight=2)# assign weight 2 to edge 0-3
>>> mst =tree.maximum_spanning_edges(G, algorithm='prim', data=False)
>>> edgelist =list(mst)
(continues on next page)
3.55. Tree 485

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> sorted(edgelist)
[(0, 1), (0, 3), (3, 2)]
Notes
For Bor˚uvka’s algorithm, each edge must have a weight attribute, and each edge weight must be distinct.
For the other algorithms, if the graph edges do not have a weight attribute a default weight of 1 will be used.
Modified code from David Eppstein, April 2006 http://www.ics.uci.edu/~eppstein/PADS/
3.55.6 Exceptions
Functions for encoding and decoding trees.
Since a tree is a highly restricted form of graph, it can be represented concisely in several ways. This module includes
functions for encoding and decoding trees in the form of nested tuples and Prüfer sequences. The former requires a
rooted tree, whereas the latter can be applied to unrooted trees. Furthermore, there is a bijection from Prüfer sequences
to labeled trees.
NotATree Raised when a function expects a tree (that is, a con-
nected undirected graph with no cycles) but gets a non-
tree graph as input instead.
networkx.algorithms.tree.coding.NotATree
exception NotATree
Raised when a function expects a tree (that is, a connected undirected graph with no cycles) but gets a non-tree
graph as input instead.
3.56 Triads
Functions for analyzing triads of a graph.
triadic_census(G) Determines the triadic census of a directed graph.
3.56.1 networkx.algorithms.triads.triadic_census
triadic_census(G)
Determines the triadic census of a directed graph.
The triadic census is a count of how many of the 16 possible types of triads are present in a directed graph.
Parameters G (digraph) – A NetworkX DiGraph
Returns census – Dictionary with triad names as keys and number of occurrences as values.
Return type dict
486 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This algorithm has complexity 𝑂(𝑚)where 𝑚is the number of edges in the graph.
See also:
triad_graph()
References
3.57 Vitality
Vitality measures.
closeness_vitality(G[, node, weight, . . . ]) Returns the closeness vitality for nodes in the graph.
3.57.1 networkx.algorithms.vitality.closeness_vitality
closeness_vitality(G,node=None,weight=None,wiener_index=None)
Returns the closeness vitality for nodes in the graph.
The closeness vitality of a node, defined in Section 3.6.2 of [1], is the change in the sum of distances between
all node pairs when excluding that node.
Parameters
•G(NetworkX graph) – A strongly-connected graph.
•weight (string) – The name of the edge attribute used as weight. This is passed directly to
the wiener_index() function.
•node (object) – If specified, only the closeness vitality for this node will be returned. Oth-
erwise, a dictionary mapping each node to its closeness vitality will be returned.
Other Parameters wiener_index (number) – If you have already computed the Wiener index of the
graph G, you can provide that value here. Otherwise, it will be computed for you.
Returns
If node is None, this function returns a dictionary with nodes as keys and closeness vitality as
the value. Otherwise, it returns only the closeness vitality for the specified node.
The closeness vitality of a node may be negative infinity if removing that node would disconnect
the graph.
Return type dictionary or float
Examples
>>> G=nx.cycle_graph(3)
>>> nx.closeness_vitality(G)
{0: 2.0, 1: 2.0, 2: 2.0}
See also:
closeness_centrality()
3.57. Vitality 487

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.58 Voronoi cells
Functions for computing the Voronoi cells of a graph.
voronoi_cells(G, center_nodes[, weight]) Returns the Voronoi cells centered at center_nodes
with respect to the shortest-path distance metric.
3.58.1 networkx.algorithms.voronoi.voronoi_cells
voronoi_cells(G,center_nodes,weight=’weight’)
Returns the Voronoi cells centered at center_nodes with respect to the shortest-path distance metric.
If Cis a set of nodes in the graph and cis an element of C, the Voronoi cell centered at a node cis the set of all
nodes vthat are closer to cthan to any other center node in Cwith respect to the shortest-path distance metric.1
For directed graphs, this will compute the “outward” Voronoi cells, as defined in1, in which distance is measured
from the center nodes to the target node. For the “inward” Voronoi cells, use the DiGraph.reverse()
method to reverse the orientation of the edges before invoking this function on the directed graph.
Parameters
•G(NetworkX graph)
•center_nodes (set) – A nonempty set of nodes in the graph Gthat represent the center of the
Voronoi cells.
•weight (string or function) – The edge attribute (or an arbitrary function) representing
the weight of an edge. This keyword argument is as described in the documentation for
multi_source_dijkstra_path(), for example.
Returns A mapping from center node to set of all nodes in the graph closer to that center node than
to any other center node. The keys of the dictionary are the element of center_nodes, and
the values of the dictionary form a partition of the nodes of G.
Return type dictionary
Examples
To get only the partition of the graph induced by the Voronoi cells, take the collection of all values in the returned
dictionary:
>>> G=nx.path_graph(6)
>>> center_nodes ={0,3}
>>> cells =nx.voronoi_cells(G, center_nodes)
>>> partition =set(map(frozenset, cells.values()))
>>> sorted(map(sorted, partition))
[[0, 1], [2, 3, 4, 5]]
Raises ValueError – If center_nodes is empty.
1Erwig, Martin. (2000), “The graph Voronoi diagram with applications.” Networks, 36: 156–163. <dx.doi.org/10.1002/1097-
0037(200010)36:3<156::AID-NET2>3.0.CO;2-L>
488 Chapter 3. Algorithms

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
3.59 Wiener index
Functions related to the Wiener index of a graph.
wiener_index(G[, weight]) Returns the Wiener index of the given graph.
3.59.1 networkx.algorithms.wiener.wiener_index
wiener_index(G,weight=None)
Returns the Wiener index of the given graph.
The Wiener index of a graph is the sum of the shortest-path distances between each pair of reachable nodes. For
pairs of nodes in undirected graphs, only one orientation of the pair is counted.
Parameters
•G(NetworkX graph)
•weight (object) – The edge attribute to use as distance when computing shortest-path dis-
tances. This is passed directly to the networkx.shortest_path_length() func-
tion.
Returns The Wiener index of the graph G.
Return type float
Raises NetworkXError – If the graph Gis not connected.
Notes
If a pair of nodes is not reachable, the distance is assumed to be infinity. This means that for graphs that are not
strongly-connected, this function returns inf.
The Wiener index is not usually defined for directed graphs, however this function uses the natural generalization
of the Wiener index to directed graphs.
Examples
The Wiener index of the (unweighted) complete graph on nnodes equals the number of pairs of the nnodes,
since each pair of nodes is at distance one:
>>> import networkx as nx
>>> n=10
>>> G=nx.complete_graph(n)
>>> nx.wiener_index(G) == n*(n -1)/2
True
Graphs that are not strongly-connected have infinite Wiener index:
>>> G=nx.empty_graph(2)
>>> nx.wiener_index(G)
inf
3.59. Wiener index 489

NetworkX Reference, Release 2.3rc1.dev20181203210840
490 Chapter 3. Algorithms

CHAPTER
FOUR
FUNCTIONS
Functional interface to graph methods and assorted utilities.
4.1 Graph
degree(G[, nbunch, weight]) Return a degree view of single node or of nbunch of
nodes.
degree_histogram(G) Return a list of the frequency of each degree value.
density(G) Return the density of a graph.
info(G[, n]) Print short summary of information for the graph G or
the node n.
create_empty_copy(G[, with_data]) Return a copy of the graph G with all of the edges re-
moved.
is_directed(G) Return True if graph is directed.
to_directed(graph) Return a directed view of the graph graph.
to_undirected(graph) Return an undirected view of the graph graph.
is_empty(G) Returns True if Ghas no edges.
add_star(G_to_add_to, nodes_for_star, **attr) Add a star to Graph G_to_add_to.
add_path(G_to_add_to, nodes_for_path, **attr) Add a path to the Graph G_to_add_to.
add_cycle(G_to_add_to, nodes_for_cycle, **attr) Add a cycle to the Graph G_to_add_to.
subgraph(G, nbunch) Return the subgraph induced on nodes in nbunch.
induced_subgraph(G, nbunch) Return a SubGraph view of Gshowing only nodes in
nbunch.
restricted_view(G, nodes, edges) Returns a view of Gwith hidden nodes and edges.
reverse_view(digraph) Provide a reverse view of the digraph with edges re-
versed.
edge_subgraph(G, edges) Returns a view of the subgraph induced by the specified
edges.
4.1.1 networkx.classes.function.degree
degree(G,nbunch=None,weight=None)
Return a degree view of single node or of nbunch of nodes. If nbunch is omitted, then return degrees of all
nodes.
491

NetworkX Reference, Release 2.3rc1.dev20181203210840
4.1.2 networkx.classes.function.degree_histogram
degree_histogram(G)
Return a list of the frequency of each degree value.
Parameters G (Networkx graph) – A graph
Returns hist – A list of frequencies of degrees. The degree values are the index in the list.
Return type list
Notes
Note: the bins are width one, hence len(list) can be large (Order(number_of_edges))
4.1.3 networkx.classes.function.density
density(G)
Return the density of a graph.
The density for undirected graphs is
𝑑=2𝑚
𝑛(𝑛−1),
and for directed graphs is
𝑑=𝑚
𝑛(𝑛−1),
where nis the number of nodes and mis the number of edges in G.
Notes
The density is 0 for a graph without edges and 1 for a complete graph. The density of multigraphs can be higher
than 1.
Self loops are counted in the total number of edges so graphs with self loops can have density higher than 1.
4.1.4 networkx.classes.function.info
info(G,n=None)
Print short summary of information for the graph G or the node n.
Parameters
•G(Networkx graph) – A graph
•n(node (any hashable)) – A node in the graph G
4.1.5 networkx.classes.function.create_empty_copy
create_empty_copy(G,with_data=True)
Return a copy of the graph G with all of the edges removed.
Parameters
492 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(graph) – A NetworkX graph
•with_data (bool (default=True)) – Propagate Graph and Nodes data to the new graph.
See also:
empty_graph()
4.1.6 networkx.classes.function.is_directed
is_directed(G)
Return True if graph is directed.
4.1.7 networkx.classes.function.to_directed
to_directed(graph)
Return a directed view of the graph graph.
Identical to graph.to_directed(as_view=True) Note that graph.to_directed defaults to as_view=False while
this function always provides a view.
4.1.8 networkx.classes.function.to_undirected
to_undirected(graph)
Return an undirected view of the graph graph.
Identical to graph.to_undirected(as_view=True) Note that graph.to_undirected defaults to as_view=False
while this function always provides a view.
4.1.9 networkx.classes.function.is_empty
is_empty(G)
Returns True if Ghas no edges.
Parameters G (graph) – A NetworkX graph.
Returns True if Ghas no edges, and False otherwise.
Return type bool
Notes
An empty graph can have nodes but not edges. The empty graph with zero nodes is known as the null graph.
This is an 𝑂(𝑛)operation where n is the number of nodes in the graph.
4.1.10 networkx.classes.function.add_star
add_star(G_to_add_to,nodes_for_star,**attr)
Add a star to Graph G_to_add_to.
The first node in nodes_for_star is the middle of the star. It is connected to all other nodes.
Parameters
4.1. Graph 493
NetworkX Reference, Release 2.3rc1.dev20181203210840
•G_to_add_to (graph) – A NetworkX graph
•nodes_for_star (iterable container) – A container of nodes.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to every edge
in star.
See also:
add_path(),add_cycle()
Examples
>>> G=nx.Graph()
>>> nx.add_star(G, [0,1,2,3])
>>> nx.add_star(G, [10,11,12], weight=2)
4.1.11 networkx.classes.function.add_path
add_path(G_to_add_to,nodes_for_path,**attr)
Add a path to the Graph G_to_add_to.
Parameters
•G_to_add_to (graph) – A NetworkX graph
•nodes_for_path (iterable container) – A container of nodes. A path will be constructed
from the nodes (in order) and added to the graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to every edge
in path.
See also:
add_star(),add_cycle()
Examples
>>> G=nx.Graph()
>>> nx.add_path(G, [0,1,2,3])
>>> nx.add_path(G, [10,11,12], weight=7)
4.1.12 networkx.classes.function.add_cycle
add_cycle(G_to_add_to,nodes_for_cycle,**attr)
Add a cycle to the Graph G_to_add_to.
Parameters
•G_to_add_to (graph) – A NetworkX graph
•nodes_for_cycle (iterable container) – A container of nodes. A cycle will be constructed
from the nodes (in order) and added to the graph.
•attr (keyword arguments, optional (default= no attributes)) – Attributes to add to every edge
in cycle.
494 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
add_path(),add_star()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> nx.add_cycle(G, [0,1,2,3])
>>> nx.add_cycle(G, [10,11,12], weight=7)
4.1.13 networkx.classes.function.subgraph
subgraph(G,nbunch)
Return the subgraph induced on nodes in nbunch.
Parameters
•G(graph) – A NetworkX graph
•nbunch (list, iterable) – A container of nodes that will be iterated through once (thus it
should be an iterator or be iterable). Each element of the container should be a valid node
type: any hashable type except None. If nbunch is None, return all edges data in the graph.
Nodes in nbunch that are not in the graph will be (quietly) ignored.
Notes
subgraph(G) calls G.subgraph()
4.1.14 networkx.classes.function.induced_subgraph
induced_subgraph(G,nbunch)
Return a SubGraph view of Gshowing only nodes in nbunch.
The induced subgraph of a graph on a set of nodes N is the graph with nodes N and edges from G which have
both ends in N.
Parameters
•G(NetworkX Graph)
•nbunch (node, container of nodes or None (for all nodes))
Returns subgraph – A read-only view of the subgraph in Ginduced by the nodes. Changes to the
graph Gwill be reflected in the view.
Return type SubGraph View
Notes
To create a mutable subgraph with its own copies of nodes edges and attributes use subgraph.copy() or
Graph(subgraph)
For an inplace reduction of a graph to a subgraph you can remove nodes: G.remove_nodes_from(n in
G if n not in set(nbunch))
4.1. Graph 495

NetworkX Reference, Release 2.3rc1.dev20181203210840
If you are going to compute subgraphs of your subgraphs you could end up with a chain of views that can be
very slow once the chain has about 15 views in it. If they are all induced subgraphs, you can short-cut the chain
by making them all subgraphs of the original graph. The graph class method G.subgraph does this when G
is a subgraph. In contrast, this function allows you to choose to build chains or not, as you wish. The returned
subgraph is a view on G.
Examples
>>> import networkx as nx
>>> G=nx.path_graph(4)# or DiGraph, MultiGraph, MultiDiGraph, etc
>>> H=G.subgraph([0,1,2])
>>> list(H.edges)
[(0, 1), (1, 2)]
4.1.15 networkx.classes.function.restricted_view
restricted_view(G,nodes,edges)
Returns a view of Gwith hidden nodes and edges.
The resulting subgraph filters out node nodes and edges edges. Filtered out nodes also filter out any of their
edges.
Parameters
•G(NetworkX Graph)
•nodes (iterable) – An iterable of nodes. Nodes not present in Gare ignored.
•edges (iterable) – An iterable of edges. Edges not present in Gare ignored.
Returns subgraph – A read-only restricted view of Gfiltering out nodes and edges. Changes to G
are reflected in the view.
Return type SubGraph View
Notes
To create a mutable subgraph with its own copies of nodes edges and attributes use subgraph.copy() or
Graph(subgraph)
If you create a subgraph of a subgraph recursively you may end up with a chain of subgraph views. Such
chains can get quite slow for lengths near 15. To avoid long chains, try to make your subgraph based on the
original graph. We do not rule out chains programmatically so that odd cases like an edge_subgraph of a
restricted_view can be created.
Examples
>>> import networkx as nx
>>> G=nx.path_graph(5)
>>> H=nx.restricted_view(G, [0], [(1,2), (3,4)])
>>> list(H.nodes)
[1, 2, 3, 4]
>>> list(H.edges)
[(2, 3)]
496 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
4.1.16 networkx.classes.function.reverse_view
reverse_view(digraph)
Provide a reverse view of the digraph with edges reversed.
Identical to digraph.reverse(copy=False)
4.1.17 networkx.classes.function.edge_subgraph
edge_subgraph(G,edges)
Returns a view of the subgraph induced by the specified edges.
The induced subgraph contains each edge in edges and each node incident to any of those edges.
Parameters
•G(NetworkX Graph)
•edges (iterable) – An iterable of edges. Edges not present in Gare ignored.
Returns subgraph – A read-only edge-induced subgraph of G. Changes to Gare reflected in the
view.
Return type SubGraph View
Notes
To create a mutable subgraph with its own copies of nodes edges and attributes use subgraph.copy() or
Graph(subgraph)
If you create a subgraph of a subgraph recursively you can end up with a chain of subgraphs that becomes very
slow with about 15 nested subgraph views. Luckily the edge_subgraph filter nests nicely so you can use the
original graph as G in this function to avoid chains. We do not rule out chains programmatically so that odd
cases like an edge_subgraph of a restricted_view can be created.
Examples
>>> import networkx as nx
>>> G=nx.path_graph(5)
>>> H=G.edge_subgraph([(0,1), (3,4)])
>>> list(H.nodes)
[0, 1, 3, 4]
>>> list(H.edges)
[(0, 1), (3, 4)]
4.2 Nodes
nodes(G) Return an iterator over the graph nodes.
number_of_nodes(G) Return the number of nodes in the graph.
neighbors(G, n) Return a list of nodes connected to node n.
all_neighbors(graph, node) Returns all of the neighbors of a node in the graph.
non_neighbors(graph, node) Returns the non-neighbors of the node in the graph.
Continued on next page
4.2. Nodes 497

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 2 – continued from previous page
common_neighbors(G, u, v) Return the common neighbors of two nodes in a graph.
4.2.1 networkx.classes.function.nodes
nodes(G)
Return an iterator over the graph nodes.
4.2.2 networkx.classes.function.number_of_nodes
number_of_nodes(G)
Return the number of nodes in the graph.
4.2.3 networkx.classes.function.neighbors
neighbors(G,n)
Return a list of nodes connected to node n.
4.2.4 networkx.classes.function.all_neighbors
all_neighbors(graph,node)
Returns all of the neighbors of a node in the graph.
If the graph is directed returns predecessors as well as successors.
Parameters
•graph (NetworkX graph) – Graph to find neighbors.
•node (node) – The node whose neighbors will be returned.
Returns neighbors – Iterator of neighbors
Return type iterator
4.2.5 networkx.classes.function.non_neighbors
non_neighbors(graph,node)
Returns the non-neighbors of the node in the graph.
Parameters
•graph (NetworkX graph) – Graph to find neighbors.
•node (node) – The node whose neighbors will be returned.
Returns non_neighbors – Iterator of nodes in the graph that are not neighbors of the node.
Return type iterator
498 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
4.2.6 networkx.classes.function.common_neighbors
common_neighbors(G,u,v)
Return the common neighbors of two nodes in a graph.
Parameters
•G(graph) – A NetworkX undirected graph.
•u, v (nodes) – Nodes in the graph.
Returns cnbors – Iterator of common neighbors of u and v in the graph.
Return type iterator
Raises NetworkXError – If u or v is not a node in the graph.
Examples
>>> G=nx.complete_graph(5)
>>> sorted(nx.common_neighbors(G, 0,1))
[2, 3, 4]
4.3 Edges
edges(G[, nbunch]) Return an edge view of edges incident to nodes in
nbunch.
number_of_edges(G) Return the number of edges in the graph.
density(G) Return the density of a graph.
non_edges(graph) Returns the non-existent edges in the graph.
4.3.1 networkx.classes.function.edges
edges(G,nbunch=None)
Return an edge view of edges incident to nodes in nbunch.
Return all edges if nbunch is unspecified or nbunch=None.
For digraphs, edges=out_edges
4.3.2 networkx.classes.function.number_of_edges
number_of_edges(G)
Return the number of edges in the graph.
4.3.3 networkx.classes.function.non_edges
non_edges(graph)
Returns the non-existent edges in the graph.
Parameters graph (NetworkX graph.) – Graph to find non-existent edges.
Returns non_edges – Iterator of edges that are not in the graph.
4.3. Edges 499

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type iterator
4.4 Self loops
selfloop_edges(G[, data, keys, default]) Returns an iterator over selfloop edges.
number_of_selfloops(G) Return the number of selfloop edges.
nodes_with_selfloops(G) Returns an iterator over nodes with self loops.
4.4.1 networkx.classes.function.selfloop_edges
selfloop_edges(G,data=False,keys=False,default=None)
Returns an iterator over selfloop edges.
A selfloop edge has the same node at both ends.
Parameters
•data (string or bool, optional (default=False)) – Return selfloop edges as two tuples (u,
v) (data=False) or three-tuples (u, v, datadict) (data=True) or three-tuples (u, v, datavalue)
(data=’attrname’)
•keys (bool, optional (default=False)) – If True, return edge keys with each edge.
•default (value, optional (default=None)) – Value used for edges that don’t have the re-
quested attribute. Only relevant if data is not True or False.
Returns edgeiter – An iterator over all selfloop edges.
Return type iterator over edge tuples
See also:
nodes_with_selfloops(),number_of_selfloops()
Examples
>>> G=nx.MultiGraph() # or Graph, DiGraph, MultiDiGraph, etc
>>> ekey =G.add_edge(1,1)
>>> ekey =G.add_edge(1,2)
>>> list(nx.selfloop_edges(G))
[(1, 1)]
>>> list(nx.selfloop_edges(G, data=True))
[(1, 1, {})]
>>> list(nx.selfloop_edges(G, keys=True))
[(1, 1, 0)]
>>> list(nx.selfloop_edges(G, keys=True, data=True))
[(1, 1, 0, {})]
4.4.2 networkx.classes.function.number_of_selfloops
number_of_selfloops(G)
Return the number of selfloop edges.
A selfloop edge has the same node at both ends.
500 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns nloops – The number of selfloops.
Return type int
See also:
nodes_with_selfloops(),selfloop_edges()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge(1,1)
>>> G.add_edge(1,2)
>>> nx.number_of_selfloops(G)
1
4.4.3 networkx.classes.function.nodes_with_selfloops
nodes_with_selfloops(G)
Returns an iterator over nodes with self loops.
A node with a self loop has an edge with both ends adjacent to that node.
Returns nodelist – A iterator over nodes with self loops.
Return type iterator
See also:
selfloop_edges(),number_of_selfloops()
Examples
>>> G=nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc
>>> G.add_edge(1,1)
>>> G.add_edge(1,2)
>>> list(nx.nodes_with_selfloops(G))
[1]
4.5 Attributes
is_weighted(G[, edge, weight]) Returns True if Ghas weighted edges.
is_negatively_weighted(G[, edge, weight]) Returns True if Ghas negatively weighted edges.
set_node_attributes(G, values[, name]) Sets node attributes from a given value or dictionary of
values.
get_node_attributes(G, name) Get node attributes from graph
set_edge_attributes(G, values[, name]) Sets edge attributes from a given value or dictionary of
values.
get_edge_attributes(G, name) Get edge attributes from graph
4.5. Attributes 501

NetworkX Reference, Release 2.3rc1.dev20181203210840
4.5.1 networkx.classes.function.is_weighted
is_weighted(G,edge=None,weight=’weight’)
Returns True if Ghas weighted edges.
Parameters
•G(graph) – A NetworkX graph.
•edge (tuple, optional) – A 2-tuple specifying the only edge in Gthat will be tested. If None,
then every edge in Gis tested.
•weight (string, optional) – The attribute name used to query for edge weights.
Returns A boolean signifying if G, or the specified edge, is weighted.
Return type bool
Raises NetworkXError – If the specified edge does not exist.
Examples
>>> G=nx.path_graph(4)
>>> nx.is_weighted(G)
False
>>> nx.is_weighted(G, (2,3))
False
>>> G=nx.DiGraph()
>>> G.add_edge(1,2, weight=1)
>>> nx.is_weighted(G)
True
4.5.2 networkx.classes.function.is_negatively_weighted
is_negatively_weighted(G,edge=None,weight=’weight’)
Returns True if Ghas negatively weighted edges.
Parameters
•G(graph) – A NetworkX graph.
•edge (tuple, optional) – A 2-tuple specifying the only edge in Gthat will be tested. If None,
then every edge in Gis tested.
•weight (string, optional) – The attribute name used to query for edge weights.
Returns A boolean signifying if G, or the specified edge, is negatively weighted.
Return type bool
Raises NetworkXError – If the specified edge does not exist.
Examples
502 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.Graph()
>>> G.add_edges_from([(1,3), (2,4), (2,6)])
>>> G.add_edge(1,2, weight=4)
>>> nx.is_negatively_weighted(G, (1,2))
False
>>> G[2][4]['weight']= -2
>>> nx.is_negatively_weighted(G)
True
>>> G=nx.DiGraph()
>>> edges =[('0','3',3), ('0','1',-5), ('1','0',-2)]
>>> G.add_weighted_edges_from(edges)
>>> nx.is_negatively_weighted(G)
True
4.5.3 networkx.classes.function.set_node_attributes
set_node_attributes(G,values,name=None)
Sets node attributes from a given value or dictionary of values.
Warning: The call order of arguments values and name switched between v1.x & v2.x.
Parameters
•G(NetworkX Graph)
•values (scalar value, dict-like) – What the node attribute should be set to. If values is not
a dictionary, then it is treated as a single attribute value that is then applied to every node in
G. This means that if you provide a mutable object, like a list, updates to that object will be
reflected in the node attribute for every node. The attribute name will be name.
If values is a dict or a dict of dict, it should be keyed by node to either an attribute value
or a dict of attribute key/value pairs used to update the node’s attributes.
•name (string (optional, default=None)) – Name of the node attribute to set if values is a
scalar.
Examples
After computing some property of the nodes of a graph, you may want to assign a node attribute to store the
value of that property for each node:
>>> G=nx.path_graph(3)
>>> bb =nx.betweenness_centrality(G)
>>> isinstance(bb, dict)
True
>>> nx.set_node_attributes(G, bb, 'betweenness')
>>> G.nodes[1]['betweenness']
1.0
If you provide a list as the second argument, updates to the list will be reflected in the node attribute for each
node:
4.5. Attributes 503

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.path_graph(3)
>>> labels =[]
>>> nx.set_node_attributes(G, labels, 'labels')
>>> labels.append('foo')
>>> G.nodes[0]['labels']
['foo']
>>> G.nodes[1]['labels']
['foo']
>>> G.nodes[2]['labels']
['foo']
If you provide a dictionary of dictionaries as the second argument, the outer dictionary is assumed to be keyed
by node to an inner dictionary of node attributes for that node:
>>> G=nx.path_graph(3)
>>> attrs ={0: {'attr1':20,'attr2':'nothing'}, 1: {'attr2':3}}
>>> nx.set_node_attributes(G, attrs)
>>> G.nodes[0]['attr1']
20
>>> G.nodes[0]['attr2']
'nothing'
>>> G.nodes[1]['attr2']
3
>>> G.nodes[2]
{}
4.5.4 networkx.classes.function.get_node_attributes
get_node_attributes(G,name)
Get node attributes from graph
Parameters
•G(NetworkX Graph)
•name (string) – Attribute name
Returns
Return type Dictionary of attributes keyed by node.
Examples
>>> G=nx.Graph()
>>> G.add_nodes_from([1,2,3], color='red')
>>> color =nx.get_node_attributes(G, 'color')
>>> color[1]
'red'
4.5.5 networkx.classes.function.set_edge_attributes
set_edge_attributes(G,values,name=None)
Sets edge attributes from a given value or dictionary of values.
504 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
Warning: The call order of arguments values and name switched between v1.x & v2.x.
Parameters
•G(NetworkX Graph)
•values (scalar value, dict-like) – What the edge attribute should be set to. If values is not
a dictionary, then it is treated as a single attribute value that is then applied to every edge in
G. This means that if you provide a mutable object, like a list, updates to that object will be
reflected in the edge attribute for each edge. The attribute name will be name.
If values is a dict or a dict of dict, it should be keyed by edge tuple to either an attribute
value or a dict of attribute key/value pairs used to update the edge’s attributes. For multi-
graphs, the edge tuples must be of the form (u, v, key), where uand vare nodes and
key is the edge key. For non-multigraphs, the keys must be tuples of the form (u, v).
•name (string (optional, default=None)) – Name of the edge attribute to set if values is a
scalar.
Examples
After computing some property of the edges of a graph, you may want to assign a edge attribute to store the
value of that property for each edge:
>>> G=nx.path_graph(3)
>>> bb =nx.edge_betweenness_centrality(G, normalized=False)
>>> nx.set_edge_attributes(G, bb, 'betweenness')
>>> G.edges[1,2]['betweenness']
2.0
If you provide a list as the second argument, updates to the list will be reflected in the edge attribute for each
edge:
>>> labels =[]
>>> nx.set_edge_attributes(G, labels, 'labels')
>>> labels.append('foo')
>>> G.edges[0,1]['labels']
['foo']
>>> G.edges[1,2]['labels']
['foo']
If you provide a dictionary of dictionaries as the second argument, the entire dictionary will be used to update
edge attributes:
>>> G=nx.path_graph(3)
>>> attrs ={(0,1): {'attr1':20,'attr2':'nothing'},
... (1,2): {'attr2':3}}
>>> nx.set_edge_attributes(G, attrs)
>>> G[0][1]['attr1']
20
>>> G[0][1]['attr2']
'nothing'
>>> G[1][2]['attr2']
3
4.5. Attributes 505

NetworkX Reference, Release 2.3rc1.dev20181203210840
4.5.6 networkx.classes.function.get_edge_attributes
get_edge_attributes(G,name)
Get edge attributes from graph
Parameters
•G(NetworkX Graph)
•name (string) – Attribute name
Returns
•Dictionary of attributes keyed by edge. For (di)graphs, the keys are
•2-tuples of the form ((u, v). For multi(di)graphs, the keys are 3-tuples of )
•the form ((u, v, key).)
Examples
>>> G=nx.Graph()
>>> nx.add_path(G, [1,2,3], color='red')
>>> color =nx.get_edge_attributes(G, 'color')
>>> color[(1,2)]
'red'
4.6 Freezing graph structure
freeze(G) Modify graph to prevent further change by adding or
removing nodes or edges.
is_frozen(G) Return True if graph is frozen.
4.6.1 networkx.classes.function.freeze
freeze(G)
Modify graph to prevent further change by adding or removing nodes or edges.
Node and edge data can still be modified.
Parameters G (graph) – A NetworkX graph
Examples
>>> G=nx.path_graph(4)
>>> G=nx.freeze(G)
>>> try:
... G.add_edge(4,5)
... except nx.NetworkXError as e:
... print(str(e))
Frozen graph can't be modified
506 Chapter 4. Functions

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
To “unfreeze” a graph you must make a copy by creating a new graph object:
>>> graph =nx.path_graph(4)
>>> frozen_graph =nx.freeze(graph)
>>> unfrozen_graph =nx.Graph(frozen_graph)
>>> nx.is_frozen(unfrozen_graph)
False
See also:
is_frozen()
4.6.2 networkx.classes.function.is_frozen
is_frozen(G)
Return True if graph is frozen.
Parameters G (graph) – A NetworkX graph
See also:
freeze()
4.6. Freezing graph structure 507

NetworkX Reference, Release 2.3rc1.dev20181203210840
508 Chapter 4. Functions

CHAPTER
FIVE
GRAPH GENERATORS
5.1 Atlas
Generators for the small graph atlas.
graph_atlas(i) Returns graph number ifrom the Graph Atlas.
graph_atlas_g() Return the list of all graphs with up to seven nodes
named in the Graph Atlas.
5.1.1 networkx.generators.atlas.graph_atlas
graph_atlas(i)
Returns graph number ifrom the Graph Atlas.
For more information, see graph_atlas_g().
Parameters i (int) – The index of the graph from the atlas to get. The graph at index 0 is assumed
to be the null graph.
Returns A list of Graph objects, the one at index icorresponding to the graph iin the Graph Atlas.
Return type list
See also:
graph_atlas_g()
Notes
The time required by this function increases linearly with the argument i, since it reads a large file sequentially
in order to generate the graph1.
References
5.1.2 networkx.generators.atlas.graph_atlas_g
graph_atlas_g()
Return the list of all graphs with up to seven nodes named in the Graph Atlas.
The graphs are listed in increasing order by
1Ronald C. Read and Robin J. Wilson, An Atlas of Graphs. Oxford University Press, 1998.
509

NetworkX Reference, Release 2.3rc1.dev20181203210840
1. number of nodes,
2. number of edges,
3. degree sequence (for example 111223 < 112222),
4. number of automorphisms,
in that order, with three exceptions as described in the Notes section below. This causes the list to correspond
with the index of the graphs in the Graph Atlas [atlas], with the first graph, G[0], being the null graph.
Returns A list of Graph objects, the one at index icorresponding to the graph iin the Graph Atlas.
Return type list
See also:
graph_atlas()
Notes
This function may be expensive in both time and space, since it reads a large file sequentially in order to populate
the list.
Although the NetworkX atlas functions match the order of graphs given in the “Atlas of Graphs” book, there
are (at least) three errors in the ordering described in the book. The following three pairs of nodes violate the
lexicographically nondecreasing sorted degree sequence rule:
• graphs 55 and 56 with degree sequences 001111 and 000112,
• graphs 1007 and 1008 with degree sequences 3333444 and 3333336,
• graphs 1012 and 1213 with degree sequences 1244555 and 1244456.
References
5.2 Classic
Generators for some classic graphs.
The typical graph generator is called as follows:
>>> G=nx.complete_graph(100)
returning the complete graph on n nodes labeled 0, .., 99 as a simple graph. Except for empty_graph, all the generators
in this module return a Graph class (i.e. a simple, undirected graph).
balanced_tree(r, h[, create_using]) Return the perfectly balanced r-ary tree of height h.
barbell_graph(m1, m2[, create_using]) Return the Barbell Graph: two complete graphs con-
nected by a path.
complete_graph(n[, create_using]) Return the complete graph K_n with n nodes.
complete_multipartite_graph(*subset_sizes) Returns the complete multipartite graph with the speci-
fied subset sizes.
circular_ladder_graph(n[, create_using]) Return the circular ladder graph 𝐶𝐿𝑛of length n.
circulant_graph(n, offsets[, create_using]) Generates the circulant graph 𝐶𝑖𝑛(𝑥1, 𝑥2, ..., 𝑥𝑚)with
𝑛vertices.
Continued on next page
510 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 2 – continued from previous page
cycle_graph(n[, create_using]) Return the cycle graph 𝐶𝑛of cyclically connected
nodes.
dorogovtsev_goltsev_mendes_graph(n[,
...])
Return the hierarchically constructed Dorogovtsev-
Goltsev-Mendes graph.
empty_graph([n, create_using, default]) Return the empty graph with n nodes and zero edges.
full_rary_tree(r, n[, create_using]) Creates a full r-ary tree of n vertices.
ladder_graph(n[, create_using]) Return the Ladder graph of length n.
lollipop_graph(m, n[, create_using]) Return the Lollipop Graph; K_m connected to P_n.
null_graph([create_using]) Return the Null graph with no nodes or edges.
path_graph(n[, create_using]) Return the Path graph P_n of linearly connected nodes.
star_graph(n[, create_using]) Return the star graph
trivial_graph([create_using]) Return the Trivial graph with one node (with label 0)
and no edges.
turan_graph(n, r) Return the Turan Graph
wheel_graph(n[, create_using]) Return the wheel graph
5.2.1 networkx.generators.classic.balanced_tree
balanced_tree(r,h,create_using=None)
Return the perfectly balanced r-ary tree of height h.
Parameters
•r(int) – Branching factor of the tree; each node will have rchildren.
•h(int) – Height of the tree.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns G – A balanced r-ary tree of height h.
Return type NetworkX graph
Notes
This is the rooted tree where all leaves are at distance hfrom the root. The root has degree rand all other
internal nodes have degree r+1.
Node labels are integers, starting from zero.
A balanced tree is also known as a complete r-ary tree.
5.2.2 networkx.generators.classic.barbell_graph
barbell_graph(m1,m2,create_using=None)
Return the Barbell Graph: two complete graphs connected by a path.
For 𝑚1>1and 𝑚2>= 0.
Two identical complete graphs 𝐾𝑚1form the left and right bells, and are connected by a path 𝑃𝑚2.
The 2*m1+m2 nodes are numbered 0, ..., m1-1 for the left barbell, m1, ..., m1+m2-1 for the
path, and m1+m2, ..., 2*m1+m2-1 for the right barbell.
5.2. Classic 511

NetworkX Reference, Release 2.3rc1.dev20181203210840
The 3 subgraphs are joined via the edges (m1-1, m1) and (m1+m2-1, m1+m2). If m2=0, this is merely
two complete graphs joined together.
This graph is an extremal example in David Aldous and Jim Fill’s e-text on Random Walks on Graphs.
5.2.3 networkx.generators.classic.complete_graph
complete_graph(n,create_using=None)
Return the complete graph K_n with n nodes.
Parameters
•n(int or iterable container of nodes) – If n is an integer, nodes are from range(n). If n is a
container of nodes, those nodes appear in the graph.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Examples
>>> G=nx.complete_graph(9)
>>> len(G)
9
>>> G.size()
36
>>> G=nx.complete_graph(range(11,14))
>>> list(G.nodes())
[11, 12, 13]
>>> G=nx.complete_graph(4, nx.DiGraph())
>>> G.is_directed()
True
5.2.4 networkx.generators.classic.complete_multipartite_graph
complete_multipartite_graph(*subset_sizes)
Returns the complete multipartite graph with the specified subset sizes.
Parameters subset_sizes (tuple of integers or tuple of node iterables) – The arguments can either
all be integer number of nodes or they can all be iterables of nodes. If integers, they represent
the number of vertices in each subset of the multipartite graph. If iterables, each is used to create
the nodes for that subset. The length of subset_sizes is the number of subsets.
Returns
G– Returns the complete multipartite graph with the specified subsets.
For each node, the node attribute ‘subset’ is an integer indicating which subset contains the node.
Return type NetworkX Graph
Examples
Creating a complete tripartite graph, with subsets of one, two, and three vertices, respectively.
512 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> import networkx as nx
>>> G=nx.complete_multipartite_graph(1,2,3)
>>> [G.nodes[u]['subset']for uin G]
[0, 1, 1, 2, 2, 2]
>>> list(G.edges(0))
[(0, 1), (0, 2), (0, 3), (0, 4), (0, 5)]
>>> list(G.edges(2))
[(2, 0), (2, 3), (2, 4), (2, 5)]
>>> list(G.edges(4))
[(4, 0), (4, 1), (4, 2)]
>>> G=nx.complete_multipartite_graph('a','bc','def')
>>> [G.nodes[u]['subset']for uin sorted(G)]
[0, 1, 1, 2, 2, 2]
Notes
This function generalizes several other graph generator functions.
• If no subset sizes are given, this returns the null graph.
• If a single subset size nis given, this returns the empty graph on nnodes.
• If two subset sizes mand nare given, this returns the complete bipartite graph on m+nnodes.
• If subset sizes 1and nare given, this returns the star graph on n+1nodes.
See also:
complete_bipartite_graph()
5.2.5 networkx.generators.classic.circular_ladder_graph
circular_ladder_graph(n,create_using=None)
Return the circular ladder graph 𝐶𝐿𝑛of length n.
𝐶𝐿𝑛consists of two concentric n-cycles in which each of the n pairs of concentric nodes are joined by an edge.
Node labels are the integers 0 to n-1
5.2.6 networkx.generators.classic.circulant_graph
circulant_graph(n,offsets,create_using=None)
Generates the circulant graph 𝐶𝑖𝑛(𝑥1, 𝑥2, ..., 𝑥𝑚)with 𝑛vertices.
Returns
•The graph :math:‘Ci_n(x_1, . . . , x_m)‘ consisting of :math:‘n‘ vertices :math:‘0, . . . , n-1‘
such
•that the vertex with label :math:‘i‘ is connected to the vertices labelled :math:‘(i + x)‘
•and :math:‘(i - x)‘, for all :math:‘x‘ in :math:‘x_1‘ up to :math:‘x_m‘, with the indices taken
modulo :math:‘n‘.
Parameters
•n(integer) – The number of vertices the generated graph is to contain.
5.2. Classic 513

NetworkX Reference, Release 2.3rc1.dev20181203210840
•offsets (list of integers) – A list of vertex offsets, 𝑥1up to 𝑥𝑚, as described above.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Examples
Many well-known graph families are subfamilies of the circulant graphs; for example, to generate the cycle
graph on n points, we connect every vertex to every other at offset plus or minus one. For n = 10,
>>> import networkx
>>> G=networkx.generators.classic.circulant_graph(10, [1])
>>> edges =[
... (0,9), (0,1), (1,2), (2,3), (3,4),
... (4,5), (5,6), (6,7), (7,8), (8,9)]
...
>>> sorted(edges) == sorted(G.edges())
True
Similarly, we can generate the complete graph on 5 points with the set of offsets [1, 2]:
>>> G=networkx.generators.classic.circulant_graph(5, [1,2])
>>> edges =[
... (0,1), (0,2), (0,3), (0,4), (1,2),
... (1,3), (1,4), (2,3), (2,4), (3,4)]
...
>>> sorted(edges) == sorted(G.edges())
True
5.2.7 networkx.generators.classic.cycle_graph
cycle_graph(n,create_using=None)
Return the cycle graph 𝐶𝑛of cyclically connected nodes.
𝐶𝑛is a path with its two end-nodes connected.
Parameters
•n(int or iterable container of nodes) – If n is an integer, nodes are from range(n). If n is
a container of nodes, those nodes appear in the graph.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Notes
If create_using is directed, the direction is in increasing order.
5.2.8 networkx.generators.classic.dorogovtsev_goltsev_mendes_graph
dorogovtsev_goltsev_mendes_graph(n,create_using=None)
Return the hierarchically constructed Dorogovtsev-Goltsev-Mendes graph.
n is the generation. See: arXiv:/cond-mat/0112143 by Dorogovtsev, Goltsev and Mendes.
514 Chapter 5. Graph generators
NetworkX Reference, Release 2.3rc1.dev20181203210840
5.2.9 networkx.generators.classic.empty_graph
empty_graph(n=0,create_using=None,default=<class ’networkx.classes.graph.Graph’>)
Return the empty graph with n nodes and zero edges.
Parameters
•n(int or iterable container of nodes (default = 0)) – If n is an integer, nodes are from
range(n). If n is a container of nodes, those nodes appear in the graph.
•create_using (Graph Instance, Constructor or None) – Indicator of type of graph to return.
If a Graph-type instance, then clear and use it. If None, use the default constructor. If a
constructor, call it to create an empty graph.
•default (Graph constructor (optional, default = nx.Graph)) – The constructor to use if cre-
ate_using is None. If None, then nx.Graph is used. This is used when passing an unknown
create_using value through your home-grown function to empty_graph and you
want a default constructor other than nx.Graph.
Examples
>>> G=nx.empty_graph(10)
>>> G.number_of_nodes()
10
>>> G.number_of_edges()
0
>>> G=nx.empty_graph("ABC")
>>> G.number_of_nodes()
3
>>> sorted(G)
['A', 'B', 'C']
Notes
The variable create_using should be a Graph Constructor or a “graph”-like object. Constructors, e.g. nx.
Graph or nx.MultiGraph will be used to create the returned graph. “graph”-like objects will be cleared
(nodes and edges will be removed) and refitted as an empty “graph” with nodes specified in n. This capability is
useful for specifying the class-nature of the resulting empty “graph” (i.e. Graph, DiGraph, MyWeirdGraphClass,
etc.).
The variable create_using has three main uses: Firstly, the variable create_using can be used to create an empty
digraph, multigraph, etc. For example,
>>> n=10
>>> G=nx.empty_graph(n, create_using=nx.DiGraph)
will create an empty digraph on n nodes.
Secondly, one can pass an existing graph (digraph, multigraph, etc.) via create_using. For example, if G is an
existing graph (resp. digraph, multigraph, etc.), then empty_graph(n, create_using=G) will empty G (i.e. delete
all nodes and edges using G.clear()) and then add n nodes and zero edges, and return the modified graph.
Thirdly, when constructing your home-grown graph creation function you can use empty_graph to construct the
graph by passing a user defined create_using to empty_graph. In this case, if you want the default constructor
to be other than nx.Graph, specify default.
5.2. Classic 515

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> def mygraph(n, create_using=None):
... G=nx.empty_graph(n, create_using, nx.MultiGraph)
... G.add_edges_from([(0,1), (0,1)])
... return G
>>> G=mygraph(3)
>>> G.is_multigraph()
True
>>> G=mygraph(3, nx.Graph)
>>> G.is_multigraph()
False
See also create_empty_copy(G).
5.2.10 networkx.generators.classic.full_rary_tree
full_rary_tree(r,n,create_using=None)
Creates a full r-ary tree of n vertices.
Sometimes called a k-ary, n-ary, or m-ary tree. “. . . all non-leaf vertices have exactly r children and all levels
are full except for some rightmost position of the bottom level (if a leaf at the bottom level is missing, then so
are all of the leaves to its right.”1
Parameters
•r(int) – branching factor of the tree
•n(int) – Number of nodes in the tree
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns G – An r-ary tree with n nodes
Return type networkx Graph
References
5.2.11 networkx.generators.classic.ladder_graph
ladder_graph(n,create_using=None)
Return the Ladder graph of length n.
This is two paths of n nodes, with each pair connected by a single edge.
Node labels are the integers 0 to 2*n - 1.
5.2.12 networkx.generators.classic.lollipop_graph
lollipop_graph(m,n,create_using=None)
Return the Lollipop Graph; K_m connected to P_n.
This is the Barbell Graph without the right barbell.
Parameters
1An introduction to data structures and algorithms, James Andrew Storer, Birkhauser Boston 2001, (page 225).
516 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•m, n (int or iterable container of nodes (default = 0)) – If an integer, nodes are from
range(m) and range(m,m+n). If a container, the entries are the coordinate of the node.
The nodes for m appear in the complete graph 𝐾𝑚and the nodes for n appear in the path
𝑃𝑛
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Notes
The 2 subgraphs are joined via an edge (m-1, m). If n=0, this is merely a complete graph.
(This graph is an extremal example in David Aldous and Jim Fill’s etext on Random Walks on Graphs.)
5.2.13 networkx.generators.classic.null_graph
null_graph(create_using=None)
Return the Null graph with no nodes or edges.
See empty_graph for the use of create_using.
5.2.14 networkx.generators.classic.path_graph
path_graph(n,create_using=None)
Return the Path graph P_n of linearly connected nodes.
Parameters
•n(int or iterable) – If an integer, node labels are 0 to n with center 0. If an iterable of nodes,
the center is the first.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
5.2.15 networkx.generators.classic.star_graph
star_graph(n,create_using=None)
Return the star graph
The star graph consists of one center node connected to n outer nodes.
Parameters
•n(int or iterable) – If an integer, node labels are 0 to n with center 0. If an iterable of nodes,
the center is the first.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Notes
The graph has n+1 nodes for integer n. So star_graph(3) is the same as star_graph(range(4)).
5.2. Classic 517

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.2.16 networkx.generators.classic.trivial_graph
trivial_graph(create_using=None)
Return the Trivial graph with one node (with label 0) and no edges.
5.2.17 networkx.generators.classic.turan_graph
turan_graph(n,r)
Return the Turan Graph
The Turan Graph is a complete multipartite graph on 𝑛vertices with 𝑟disjoint subsets. It is the graph with the
edges for any graph with 𝑛vertices and 𝑟disjoint subsets.
Given 𝑛and 𝑟, we generate a complete multipartite graph with 𝑟−(𝑛mod 𝑟)partitions of size 𝑛/𝑟, rounded
down, and 𝑛mod 𝑟partitions of size 𝑛/𝑟 + 1, rounded down.
Parameters
•n(int) – The number of vertices.
•r(int) – The number of partitions. Must be less than or equal to n.
Notes
Must satisfy 1<=𝑟 <=𝑛. The graph has (𝑟−1)(𝑛2)/(2𝑟)edges, rounded down.
5.2.18 networkx.generators.classic.wheel_graph
wheel_graph(n,create_using=None)
Return the wheel graph
The wheel graph consists of a hub node connected to a cycle of (n-1) nodes.
Parameters
•n(int or iterable) – If an integer, node labels are 0 to n with center 0. If an iterable of nodes,
the center is the first.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•Node labels are the integers 0 to n - 1.
5.3 Expanders
Provides explicit constructions of expander graphs.
margulis_gabber_galil_graph(n[, cre-
ate_using])
Return the Margulis-Gabber-Galil undirected Multi-
Graph on n^2 nodes.
chordal_cycle_graph(p[, create_using]) Return the chordal cycle graph on pnodes.
518 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.3.1 networkx.generators.expanders.margulis_gabber_galil_graph
margulis_gabber_galil_graph(n,create_using=None)
Return the Margulis-Gabber-Galil undirected MultiGraph on n^2 nodes.
The undirected MultiGraph is regular with degree 8. Nodes are integer pairs. The second-largest eigenvalue of
the adjacency matrix of the graph is at most 5 sqrt{2}, regardless of n.
Parameters
•n(int) – Determines the number of nodes in the graph: n^2.
•create_using (NetworkX graph constructor, optional (default MultiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns G – The constructed undirected multigraph.
Return type graph
Raises NetworkXError – If the graph is directed or not a multigraph.
5.3.2 networkx.generators.expanders.chordal_cycle_graph
chordal_cycle_graph(p,create_using=None)
Return the chordal cycle graph on pnodes.
The returned graph is a cycle graph on pnodes with chords joining each vertex xto its inverse modulo p. This
graph is a (mildly explicit) 3-regular expander1.
pmust be a prime number.
Parameters
•p(a prime number) – The number of vertices in the graph. This also indicates where the
chordal edges in the cycle will be created.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns G – The constructed undirected multigraph.
Return type graph
Raises NetworkXError – If create_using indicates directed or not a multigraph.
References
5.4 Lattice
Functions for generating grid graphs and lattices
The grid_2d_graph(),triangular_lattice_graph(), and hexagonal_lattice_graph() func-
tions correspond to the three regular tilings of the plane, the square, triangular, and hexagonal tilings, respectively.
grid_graph() and hypercube_graph() are similar for arbitrary dimensions. Useful relevant discussion can
be found about Triangular Tiling, and Square, Hex and Triangle Grids
1Theorem 4.4.2 in A. Lubotzky. “Discrete groups, expanding graphs and invariant measures”, volume 125 of Progress in Mathematics.
Birkhäuser Verlag, Basel, 1994.
5.4. Lattice 519

NetworkX Reference, Release 2.3rc1.dev20181203210840
grid_2d_graph(m, n[, periodic, create_using]) Returns the two-dimensional grid graph.
grid_graph(dim[, periodic]) Returns the n-dimensional grid graph.
hexagonal_lattice_graph(m, n[, periodic,
...])
Returns an mby nhexagonal lattice graph.
hypercube_graph(n) Returns the n-dimensional hypercube graph.
triangular_lattice_graph(m, n[, periodic,
...])
Returns the 𝑚by 𝑛triangular lattice graph.
5.4.1 networkx.generators.lattice.grid_2d_graph
grid_2d_graph(m,n,periodic=False,create_using=None)
Returns the two-dimensional grid graph.
The grid graph has each node connected to its four nearest neighbors.
Parameters
•m, n (int or iterable container of nodes) – If an integer, nodes are from range(n). If a
container, elements become the coordinate of the nodes.
•periodic (bool (default: False)) – If this is True the nodes on the grid boundaries are joined
to the corresponding nodes on the opposite grid boundaries.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns The (possibly periodic) grid graph of the specified dimensions.
Return type NetworkX graph
5.4.2 networkx.generators.lattice.grid_graph
grid_graph(dim,periodic=False)
Returns the n-dimensional grid graph.
The dimension nis the length of the list dim and the size in each dimension is the value of the corresponding
list element.
Parameters
•dim (list or tuple of numbers or iterables of nodes) – ‘dim’ is a tuple or list with, for each
dimension, either a number that is the size of that dimension or an iterable of nodes for that
dimension. The dimension of the grid_graph is the length of dim.
•periodic (bool) – If periodic is True the nodes on the grid boundaries are joined to
the corresponding nodes on the opposite grid boundaries.
Returns The (possibly periodic) grid graph of the specified dimensions.
Return type NetworkX graph
Examples
To produce a 2 by 3 by 4 grid graph, a graph on 24 nodes:
520 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx import grid_graph
>>> G=grid_graph(dim=[2,3,4])
>>> len(G)
24
>>> G=grid_graph(dim=[range(7,9), range(3,6)])
>>> len(G)
6
5.4.3 networkx.generators.lattice.hexagonal_lattice_graph
hexagonal_lattice_graph(m,n,periodic=False,with_positions=True,create_using=None)
Returns an mby nhexagonal lattice graph.
The hexagonal lattice graph is a graph whose nodes and edges are the hexagonal tiling of the plane.
The returned graph will have mrows and ncolumns of hexagons. Odd numbered columns are shifted up relative
to even numbered columns.
Positions of nodes are computed by default or with_positions is True. Node positions creating the
standard embedding in the plane with sidelength 1 and are stored in the node attribute ‘pos’. pos = nx.
get_node_attributes(G, 'pos') creates a dict ready for drawing.
Parameters
•m(int) – The number of rows of hexagons in the lattice.
•n(int) – The number of columns of hexagons in the lattice.
•periodic (bool) – Whether to make a periodic grid by joining the boundary vertices. For
this to work nmust be odd and both n>1and m>1. The periodic connections create
another row and column of hexagons so these graphs have fewer nodes as boundary nodes
are identified.
•with_positions (bool (default: True)) – Store the coordinates of each node in the graph node
attribute ‘pos’. The coordinates provide a lattice with vertical columns of hexagons offset
to interleave and cover the plane. Periodic positions shift the nodes vertically in a nonlinear
way so the edges don’t overlap so much.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated. If graph is directed, edges will
point up or right.
Returns The mby nhexagonal lattice graph.
Return type NetworkX graph
5.4.4 networkx.generators.lattice.hypercube_graph
hypercube_graph(n)
Returns the n-dimensional hypercube graph.
The nodes are the integers between 0 and 2** n-1, inclusive.
For more information on the hypercube graph, see the Wikipedia article Hypercube graph.
Parameters n (int) – The dimension of the hypercube. The number of nodes in the graph will be 2
** n.
Returns The hypercube graph of dimension n.
5.4. Lattice 521

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type NetworkX graph
5.4.5 networkx.generators.lattice.triangular_lattice_graph
triangular_lattice_graph(m,n,periodic=False,with_positions=True,create_using=None)
Returns the 𝑚by 𝑛triangular lattice graph.
The triangular lattice graph is a two-dimensional grid graph in which each square unit has a diagonal edge (each
grid unit has a chord).
The returned graph has 𝑚rows and 𝑛columns of triangles. Rows and columns include both triangles pointing
up and down. Rows form a strip of constant height. Columns form a series of diamond shapes, staggered with
the columns on either side. Another way to state the size is that the nodes form a grid of m+1 rows and (n +
1) // 2 columns. The odd row nodes are shifted horizontally relative to the even rows.
Directed graph types have edges pointed up or right.
Positions of nodes are computed by default or with_positions is True. The position of each node
(embedded in a euclidean plane) is stored in the graph using equilateral triangles with sidelength 1. The height
between rows of nodes is thus (3)/2. Nodes lie in the first quadrant with the node (0,0) at the origin.
Parameters
•m(int) – The number of rows in the lattice.
•n(int) – The number of columns in the lattice.
•periodic (bool (default: False)) – If True, join the boundary vertices of the grid using pe-
riodic boundary conditions. The join between boundaries is the final row and column of
triangles. This means there is one row and one column fewer nodes for the periodic lattice.
Periodic lattices require m >= 3,n >= 5 and are allowed but misaligned if mor nare odd
•with_positions (bool (default: True)) – Store the coordinates of each node in the graph
node attribute ‘pos’. The coordinates provide a lattice with equilateral triangles. Periodic
positions shift the nodes vertically in a nonlinear way so the edges don’t overlap so much.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns The mby ntriangular lattice graph.
Return type NetworkX graph
5.5 Small
Various small and named graphs, together with some compact generators.
make_small_graph(graph_description[, . . . ]) Return the small graph described by graph_description.
LCF_graph(n, shift_list, repeats[, create_using]) Return the cubic graph specified in LCF notation.
bull_graph([create_using]) Return the Bull graph.
chvatal_graph([create_using]) Return the Chvátal graph.
cubical_graph([create_using]) Return the 3-regular Platonic Cubical graph.
desargues_graph([create_using]) Return the Desargues graph.
diamond_graph([create_using]) Return the Diamond graph.
dodecahedral_graph([create_using]) Return the Platonic Dodecahedral graph.
frucht_graph([create_using]) Return the Frucht Graph.
Continued on next page
522 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 5 – continued from previous page
heawood_graph([create_using]) Return the Heawood graph, a (3,6) cage.
hoffman_singleton_graph() Return the Hoffman-Singleton Graph.
house_graph([create_using]) Return the House graph (square with triangle on top).
house_x_graph([create_using]) Return the House graph with a cross inside the house
square.
icosahedral_graph([create_using]) Return the Platonic Icosahedral graph.
krackhardt_kite_graph([create_using]) Return the Krackhardt Kite Social Network.
moebius_kantor_graph([create_using]) Return the Moebius-Kantor graph.
octahedral_graph([create_using]) Return the Platonic Octahedral graph.
pappus_graph() Return the Pappus graph.
petersen_graph([create_using]) Return the Petersen graph.
sedgewick_maze_graph([create_using]) Return a small maze with a cycle.
tetrahedral_graph([create_using]) Return the 3-regular Platonic Tetrahedral graph.
truncated_cube_graph([create_using]) Return the skeleton of the truncated cube.
truncated_tetrahedron_graph([create_using]) Return the skeleton of the truncated Platonic tetrahe-
dron.
tutte_graph([create_using]) Return the Tutte graph.
5.5.1 networkx.generators.small.make_small_graph
make_small_graph(graph_description,create_using=None)
Return the small graph described by graph_description.
graph_description is a list of the form [ltype,name,n,xlist]
Here ltype is one of “adjacencylist” or “edgelist”, name is the name of the graph and n the number of nodes.
This constructs a graph of n nodes with integer labels 0,..,n-1.
If ltype=”adjacencylist” then xlist is an adjacency list with exactly n entries, in with the j’th entry (which can be
empty) specifies the nodes connected to vertex j. e.g. the “square” graph C_4 can be obtained by
>>> G=nx.make_small_graph(["adjacencylist","C_4",4,[[2,4],[1,3],[2,4],[1,3]]])
or, since we do not need to add edges twice,
>>> G=nx.make_small_graph(["adjacencylist","C_4",4,[[2,4],[3],[4],[]]])
If ltype=”edgelist” then xlist is an edge list written as [[v1,w2],[v2,w2],. . . ,[vk,wk]], where vj and wj integers
in the range 1,..,n e.g. the “square” graph C_4 can be obtained by
>>> G=nx.make_small_graph(["edgelist","C_4",4,[[1,2],[3,4],[2,3],[4,1]]])
Use the create_using argument to choose the graph class/type.
5.5.2 networkx.generators.small.LCF_graph
LCF_graph(n,shift_list,repeats,create_using=None)
Return the cubic graph specified in LCF notation.
LCF notation (LCF=Lederberg-Coxeter-Fruchte) is a compressed notation used in the generation of various
cubic Hamiltonian graphs of high symmetry. See, for example, dodecahedral_graph, desargues_graph, hea-
wood_graph and pappus_graph below.
5.5. Small 523

NetworkX Reference, Release 2.3rc1.dev20181203210840
n (number of nodes) The starting graph is the n-cycle with nodes 0,. . . ,n-1. (The null graph is returned if n <
0.)
shift_list = [s1,s2,..,sk], a list of integer shifts mod n,
repeats integer specifying the number of times that shifts in shift_list are successively applied to each v_current
in the n-cycle to generate an edge between v_current and v_current+shift mod n.
For v1 cycling through the n-cycle a total of k*repeats with shift cycling through shiftlist repeats times connect
v1 with v1+shift mod n
The utility graph 𝐾3,3
>>> G=nx.LCF_graph(6, [3,-3], 3)
The Heawood graph
>>> G=nx.LCF_graph(14, [5,-5], 7)
See http://mathworld.wolfram.com/LCFNotation.html for a description and references.
5.5.3 networkx.generators.small.bull_graph
bull_graph(create_using=None)
Return the Bull graph.
5.5.4 networkx.generators.small.chvatal_graph
chvatal_graph(create_using=None)
Return the Chvátal graph.
5.5.5 networkx.generators.small.cubical_graph
cubical_graph(create_using=None)
Return the 3-regular Platonic Cubical graph.
5.5.6 networkx.generators.small.desargues_graph
desargues_graph(create_using=None)
Return the Desargues graph.
5.5.7 networkx.generators.small.diamond_graph
diamond_graph(create_using=None)
Return the Diamond graph.
5.5.8 networkx.generators.small.dodecahedral_graph
dodecahedral_graph(create_using=None)
Return the Platonic Dodecahedral graph.
524 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.5.9 networkx.generators.small.frucht_graph
frucht_graph(create_using=None)
Return the Frucht Graph.
The Frucht Graph is the smallest cubical graph whose automorphism group consists only of the identity element.
5.5.10 networkx.generators.small.heawood_graph
heawood_graph(create_using=None)
Return the Heawood graph, a (3,6) cage.
5.5.11 networkx.generators.small.hoffman_singleton_graph
hoffman_singleton_graph()
Return the Hoffman-Singleton Graph.
5.5.12 networkx.generators.small.house_graph
house_graph(create_using=None)
Return the House graph (square with triangle on top).
5.5.13 networkx.generators.small.house_x_graph
house_x_graph(create_using=None)
Return the House graph with a cross inside the house square.
5.5.14 networkx.generators.small.icosahedral_graph
icosahedral_graph(create_using=None)
Return the Platonic Icosahedral graph.
5.5.15 networkx.generators.small.krackhardt_kite_graph
krackhardt_kite_graph(create_using=None)
Return the Krackhardt Kite Social Network.
A 10 actor social network introduced by David Krackhardt to illustrate: degree, betweenness, centrality, close-
ness, etc. The traditional labeling is: Andre=1, Beverley=2, Carol=3, Diane=4, Ed=5, Fernando=6, Garth=7,
Heather=8, Ike=9, Jane=10.
5.5.16 networkx.generators.small.moebius_kantor_graph
moebius_kantor_graph(create_using=None)
Return the Moebius-Kantor graph.
5.5. Small 525

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.5.17 networkx.generators.small.octahedral_graph
octahedral_graph(create_using=None)
Return the Platonic Octahedral graph.
5.5.18 networkx.generators.small.pappus_graph
pappus_graph()
Return the Pappus graph.
5.5.19 networkx.generators.small.petersen_graph
petersen_graph(create_using=None)
Return the Petersen graph.
5.5.20 networkx.generators.small.sedgewick_maze_graph
sedgewick_maze_graph(create_using=None)
Return a small maze with a cycle.
This is the maze used in Sedgewick,3rd Edition, Part 5, Graph Algorithms, Chapter 18, e.g. Figure 18.2 and
following. Nodes are numbered 0,..,7
5.5.21 networkx.generators.small.tetrahedral_graph
tetrahedral_graph(create_using=None)
Return the 3-regular Platonic Tetrahedral graph.
5.5.22 networkx.generators.small.truncated_cube_graph
truncated_cube_graph(create_using=None)
Return the skeleton of the truncated cube.
5.5.23 networkx.generators.small.truncated_tetrahedron_graph
truncated_tetrahedron_graph(create_using=None)
Return the skeleton of the truncated Platonic tetrahedron.
5.5.24 networkx.generators.small.tutte_graph
tutte_graph(create_using=None)
Return the Tutte graph.
5.6 Random Graphs
Generators for random graphs.
526 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
fast_gnp_random_graph(n, p[, seed, directed]) Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-
Rényi graph or a binomial graph.
gnp_random_graph(n, p[, seed, directed]) Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-
Rényi graph or a binomial graph.
dense_gnm_random_graph(n, m[, seed]) Returns a 𝐺𝑛,𝑚 random graph.
gnm_random_graph(n, m[, seed, directed]) Returns a 𝐺𝑛,𝑚 random graph.
erdos_renyi_graph(n, p[, seed, directed]) Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-
Rényi graph or a binomial graph.
binomial_graph(n, p[, seed, directed]) Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-
Rényi graph or a binomial graph.
newman_watts_strogatz_graph(n, k, p[, seed]) Return a Newman–Watts–Strogatz small-world graph.
watts_strogatz_graph(n, k, p[, seed]) Return a Watts–Strogatz small-world graph.
connected_watts_strogatz_graph(n, k, p[,
...])
Returns a connected Watts–Strogatz small-world graph.
random_regular_graph(d, n[, seed]) Returns a random 𝑑-regular graph on 𝑛nodes.
barabasi_albert_graph(n, m[, seed]) Returns a random graph according to the
Barabási–Albert preferential attachment model.
dual_barabasi_albert_graph(n, m1, m2, p[,
seed])
Returns a random graph according to the dual
Barabási–Albert preferential attachment model.
extended_barabasi_albert_graph(n, m, p,
q[, . . . ])
Returns an extended Barabási–Albert model graph.
powerlaw_cluster_graph(n, m, p[, seed]) Holme and Kim algorithm for growing graphs with
powerlaw degree distribution and approximate average
clustering.
random_kernel_graph(n, kernel_integral[, . . . ]) Return an random graph based on the specified kernel.
random_lobster(n, p1, p2[, seed]) Returns a random lobster graph.
random_shell_graph(constructor[, seed]) Returns a random shell graph for the constructor given.
random_powerlaw_tree(n[, gamma, seed, tries]) Returns a tree with a power law degree distribution.
random_powerlaw_tree_sequence(n[, gamma,
...])
Returns a degree sequence for a tree with a power law
distribution.
random_kernel_graph(n, kernel_integral[, . . . ]) Return an random graph based on the specified kernel.
5.6.1 networkx.generators.random_graphs.fast_gnp_random_graph
fast_gnp_random_graph(n,p,seed=None,directed=False)
Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-Rényi graph or a binomial graph.
Parameters
•n(int) – The number of nodes.
•p(float) – Probability for edge creation.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True, this function returns a directed graph.
Notes
The 𝐺𝑛,𝑝 graph algorithm chooses each of the [𝑛(𝑛−1)]/2(undirected) or 𝑛(𝑛−1) (directed) possible edges
with probability 𝑝.
5.6. Random Graphs 527

NetworkX Reference, Release 2.3rc1.dev20181203210840
This algorithm1runs in 𝑂(𝑛+𝑚)time, where mis the expected number of edges, which equals 𝑝𝑛(𝑛−1)/2.
This should be faster than gnp_random_graph() when 𝑝is small and the expected number of edges is small
(that is, the graph is sparse).
See also:
gnp_random_graph()
References
5.6.2 networkx.generators.random_graphs.gnp_random_graph
gnp_random_graph(n,p,seed=None,directed=False)
Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-Rényi graph or a binomial graph.
The 𝐺𝑛,𝑝 model chooses each of the possible edges with probability 𝑝.
The functions binomial_graph() and erdos_renyi_graph() are aliases of this function.
Parameters
•n(int) – The number of nodes.
•p(float) – Probability for edge creation.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True, this function returns a directed graph.
See also:
fast_gnp_random_graph()
Notes
This algorithm2runs in 𝑂(𝑛2)time. For sparse graphs (that is, for small values of 𝑝),
fast_gnp_random_graph() is a faster algorithm.
References
5.6.3 networkx.generators.random_graphs.dense_gnm_random_graph
dense_gnm_random_graph(n,m,seed=None)
Returns a 𝐺𝑛,𝑚 random graph.
In the 𝐺𝑛,𝑚 model, a graph is chosen uniformly at random from the set of all graphs with 𝑛nodes and 𝑚edges.
This algorithm should be faster than gnm_random_graph() for dense graphs.
Parameters
•n(int) – The number of nodes.
•m(int) – The number of edges.
1Vladimir Batagelj and Ulrik Brandes, “Efficient generation of large random networks”, Phys. Rev. E, 71, 036113, 2005.
2
E. N. Gilbert, Random Graphs, Ann. Math. Stat., 30, 1141 (1959).
528 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
See also:
gnm_random_graph()
Notes
Algorithm by Keith M. Briggs Mar 31, 2006. Inspired by Knuth’s Algorithm S (Selection sampling technique),
in section 3.4.2 of1.
References
5.6.4 networkx.generators.random_graphs.gnm_random_graph
gnm_random_graph(n,m,seed=None,directed=False)
Returns a 𝐺𝑛,𝑚 random graph.
In the 𝐺𝑛,𝑚 model, a graph is chosen uniformly at random from the set of all graphs with 𝑛nodes and 𝑚edges.
This algorithm should be faster than dense_gnm_random_graph() for sparse graphs.
Parameters
•n(int) – The number of nodes.
•m(int) – The number of edges.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True return a directed graph
See also:
dense_gnm_random_graph()
5.6.5 networkx.generators.random_graphs.erdos_renyi_graph
erdos_renyi_graph(n,p,seed=None,directed=False)
Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-Rényi graph or a binomial graph.
The 𝐺𝑛,𝑝 model chooses each of the possible edges with probability 𝑝.
The functions binomial_graph() and erdos_renyi_graph() are aliases of this function.
Parameters
•n(int) – The number of nodes.
•p(float) – Probability for edge creation.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True, this function returns a directed graph.
1Donald E. Knuth, The Art of Computer Programming, Volume 2/Seminumerical algorithms, Third Edition, Addison-Wesley, 1997.
5.6. Random Graphs 529

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
fast_gnp_random_graph()
Notes
This algorithm2runs in 𝑂(𝑛2)time. For sparse graphs (that is, for small values of 𝑝),
fast_gnp_random_graph() is a faster algorithm.
References
5.6.6 networkx.generators.random_graphs.binomial_graph
binomial_graph(n,p,seed=None,directed=False)
Returns a 𝐺𝑛,𝑝 random graph, also known as an Erd˝
os-Rényi graph or a binomial graph.
The 𝐺𝑛,𝑝 model chooses each of the possible edges with probability 𝑝.
The functions binomial_graph() and erdos_renyi_graph() are aliases of this function.
Parameters
•n(int) – The number of nodes.
•p(float) – Probability for edge creation.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool, optional (default=False)) – If True, this function returns a directed graph.
See also:
fast_gnp_random_graph()
Notes
This algorithm2runs in 𝑂(𝑛2)time. For sparse graphs (that is, for small values of 𝑝),
fast_gnp_random_graph() is a faster algorithm.
References
5.6.7 networkx.generators.random_graphs.newman_watts_strogatz_graph
newman_watts_strogatz_graph(n,k,p,seed=None)
Return a Newman–Watts–Strogatz small-world graph.
Parameters
•n(int) – The number of nodes.
•k(int) – Each node is joined with its knearest neighbors in a ring topology.
2
E. N. Gilbert, Random Graphs, Ann. Math. Stat., 30, 1141 (1959).
2
E. N. Gilbert, Random Graphs, Ann. Math. Stat., 30, 1141 (1959).
530 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•p(float) – The probability of adding a new edge for each edge.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Notes
First create a ring over 𝑛nodes1. Then each node in the ring is connected with its 𝑘nearest neighbors (or 𝑘−1
neighbors if 𝑘is odd). Then shortcuts are created by adding new edges as follows: for each edge (𝑢, 𝑣)in the
underlying “𝑛-ring with 𝑘nearest neighbors” with probability 𝑝add a new edge (𝑢, 𝑤)with randomly-chosen
existing node 𝑤. In contrast with watts_strogatz_graph(), no edges are removed.
See also:
watts_strogatz_graph()
References
5.6.8 networkx.generators.random_graphs.watts_strogatz_graph
watts_strogatz_graph(n,k,p,seed=None)
Return a Watts–Strogatz small-world graph.
Parameters
•n(int) – The number of nodes
•k(int) – Each node is joined with its knearest neighbors in a ring topology.
•p(float) – The probability of rewiring each edge
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
See also:
newman_watts_strogatz_graph(),connected_watts_strogatz_graph()
Notes
First create a ring over 𝑛nodes1. Then each node in the ring is joined to its 𝑘nearest neighbors (or 𝑘−1
neighbors if 𝑘is odd). Then shortcuts are created by replacing some edges as follows: for each edge (𝑢, 𝑣)
in the underlying “𝑛-ring with 𝑘nearest neighbors” with probability 𝑝replace it with a new edge (𝑢, 𝑤)with
uniformly random choice of existing node 𝑤.
In contrast with newman_watts_strogatz_graph(), the random rewiring does not in-
crease the number of edges. The rewired graph is not guaranteed to be connected as in
connected_watts_strogatz_graph().
1M. E. J. Newman and D. J. Watts, Renormalization group analysis of the small-world network model, Physics Letters A, 263, 341, 1999.
https://doi.org/10.1016/S0375-9601(99)00757-4
1Duncan J. Watts and Steven H. Strogatz, Collective dynamics of small-world networks, Nature, 393, pp. 440–442, 1998.
5.6. Random Graphs 531

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
5.6.9 networkx.generators.random_graphs.connected_watts_strogatz_graph
connected_watts_strogatz_graph(n,k,p,tries=100,seed=None)
Returns a connected Watts–Strogatz small-world graph.
Attempts to generate a connected graph by repeated generation of Watts–Strogatz small-world graphs. An
exception is raised if the maximum number of tries is exceeded.
Parameters
•n(int) – The number of nodes
•k(int) – Each node is joined with its knearest neighbors in a ring topology.
•p(float) – The probability of rewiring each edge
•tries (int) – Number of attempts to generate a connected graph.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Notes
First create a ring over 𝑛nodes1. Then each node in the ring is joined to its 𝑘nearest neighbors (or 𝑘−1
neighbors if 𝑘is odd). Then shortcuts are created by replacing some edges as follows: for each edge (𝑢, 𝑣)
in the underlying “𝑛-ring with 𝑘nearest neighbors” with probability 𝑝replace it with a new edge (𝑢, 𝑤)with
uniformly random choice of existing node 𝑤. The entire process is repeated until a connected graph results.
See also:
newman_watts_strogatz_graph(),watts_strogatz_graph()
References
5.6.10 networkx.generators.random_graphs.random_regular_graph
random_regular_graph(d,n,seed=None)
Returns a random 𝑑-regular graph on 𝑛nodes.
The resulting graph has no self-loops or parallel edges.
Parameters
•d(int) – The degree of each node.
•n(integer) – The number of nodes. The value of 𝑛×𝑑must be even.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
1Duncan J. Watts and Steven H. Strogatz, Collective dynamics of small-world networks, Nature, 393, pp. 440–442, 1998.
532 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The nodes are numbered from 0to 𝑛−1.
Kim and Vu’s paper2shows that this algorithm samples in an asymptotically uniform way from the space of
random graphs when 𝑑=𝑂(𝑛1/3−𝜖).
Raises NetworkXError – If 𝑛×𝑑is odd or 𝑑is greater than or equal to 𝑛.
References
5.6.11 networkx.generators.random_graphs.barabasi_albert_graph
barabasi_albert_graph(n,m,seed=None)
Returns a random graph according to the Barabási–Albert preferential attachment model.
A graph of 𝑛nodes is grown by attaching new nodes each with 𝑚edges that are preferentially attached to
existing nodes with high degree.
Parameters
•n(int) – Number of nodes
•m(int) – Number of edges to attach from a new node to existing nodes
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G
Return type Graph
Raises NetworkXError – If mdoes not satisfy 1<=m<n.
References
5.6.12 networkx.generators.random_graphs.dual_barabasi_albert_graph
dual_barabasi_albert_graph(n,m1,m2,p,seed=None)
Returns a random graph according to the dual Barabási–Albert preferential attachment model.
A graph of 𝑛nodes is grown by attaching new nodes each with either 𝑚1edges (with probability 𝑝) or 𝑚2edges
(with probability 1−𝑝) that are preferentially attached to existing nodes with high degree.
Parameters
•n(int) – Number of nodes
•m1 (int) – Number of edges to attach from a new node to existing nodes with probability 𝑝
•m2 (int) – Number of edges to attach from a new node to existing nodes with probability
1−𝑝
•p(float) – The probability of attaching 𝑚1edges (as opposed to 𝑚2edges)
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G
2Jeong Han Kim and Van H. Vu, Generating random regular graphs, Proceedings of the thirty-fifth ACM symposium on Theory of computing,
San Diego, CA, USA, pp 213–222, 2003. http://portal.acm.org/citation.cfm?id=780542.780576
5.6. Random Graphs 533

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type Graph
Raises NetworkXError – If m1 and m2 do not satisfy 1 <= m1,m2 < n or pdoes not satisfy
0<=p<=1.
References
5.6.13 networkx.generators.random_graphs.extended_barabasi_albert_graph
extended_barabasi_albert_graph(n,m,p,q,seed=None)
Returns an extended Barabási–Albert model graph.
An extended Barabási–Albert model graph is a random graph constructed using preferential attachment. The
extended model allows new edges, rewired edges or new nodes. Based on the probabilities 𝑝and 𝑞with 𝑝+𝑞 < 1,
the growing behavior of the graph is determined as:
1) With 𝑝probability, 𝑚new edges are added to the graph, starting from randomly chosen existing nodes and
attached preferentially at the other end.
2) With 𝑞probability, 𝑚existing edges are rewired by randomly choosing an edge and rewiring one end to a
preferentially chosen node.
3) With (1 −𝑝−𝑞)probability, 𝑚new nodes are added to the graph with edges attached preferentially.
When 𝑝=𝑞= 0, the model behaves just like the Barabási–Alber mo
Parameters
•n(int) – Number of nodes
•m(int) – Number of edges with which a new node attaches to existing nodes
•p(float) – Probability value for adding an edge between existing nodes. p + q < 1
•q(float) – Probability value of rewiring of existing edges. p + q < 1
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G
Return type Graph
Raises NetworkXError – If mdoes not satisfy 1<=m<nor 1>=p+q
References
5.6.14 networkx.generators.random_graphs.powerlaw_cluster_graph
powerlaw_cluster_graph(n,m,p,seed=None)
Holme and Kim algorithm for growing graphs with powerlaw degree distribution and approximate average
clustering.
Parameters
•n(int) – the number of nodes
•m(int) – the number of random edges to add for each new node
•p(float,) – Probability of adding a triangle after adding a random edge
534 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Notes
The average clustering has a hard time getting above a certain cutoff that depends on m. This cutoff is often
quite low. The transitivity (fraction of triangles to possible triangles) seems to decrease with network size.
It is essentially the Barabási–Albert (BA) growth model with an extra step that each random edge is followed
by a chance of making an edge to one of its neighbors too (and thus a triangle).
This algorithm improves on BA in the sense that it enables a higher average clustering to be attained if desired.
It seems possible to have a disconnected graph with this algorithm since the initial mnodes may not be all linked
to a new node on the first iteration like the BA model.
Raises NetworkXError – If mdoes not satisfy 1<=m<=nor pdoes not satisfy 0 <= p
<= 1.
References
5.6.15 networkx.generators.random_graphs.random_kernel_graph
random_kernel_graph(n,kernel_integral,kernel_root=None,seed=None)
Return an random graph based on the specified kernel.
The algorithm chooses each of the [𝑛(𝑛−1)]/2possible edges with probability specified by a kernel 𝜅(𝑥, 𝑦)1.
The kernel 𝜅(𝑥, 𝑦)must be a symmetric (in 𝑥, 𝑦), non-negative, bounded function.
Parameters
•n(int) – The number of nodes
•kernal_integral (function) – Function that returns the definite integral of the kernel 𝜅(𝑥, 𝑦),
𝐹(𝑦, 𝑎, 𝑏) := 𝑏
𝑎𝜅(𝑥, 𝑦)𝑑𝑥
•kernel_root (function (optional)) – Function that returns the root 𝑏of the equation
𝐹(𝑦, 𝑎, 𝑏) = 𝑟. If None, the root is found using scipy.optimize.brentq() (this
requires SciPy).
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Notes
The kernel is specified through its definite integral which must be provided as one of the arguments. If the
integral and root of the kernel integral can be found in 𝑂(1) time then this algorithm runs in time 𝑂(𝑛+𝑚)
where m is the expected number of edges2.
The nodes are set to integers from 0to 𝑛−1.
1Bollobás, Béla, Janson, S. and Riordan, O. “The phase transition in inhomogeneous random graphs”, Random Structures Algorithms, 31,
3–122, 2007.
2Hagberg A, Lemons N (2015), “Fast Generation of Sparse Random Kernel Graphs”. PLoS ONE 10(9): e0135177, 2015.
doi:10.1371/journal.pone.0135177
5.6. Random Graphs 535

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
Generate an Erd˝
os–Rényi random graph 𝐺(𝑛, 𝑐/𝑛), with kernel 𝜅(𝑥, 𝑦) = 𝑐where 𝑐is the mean expected
degree.
>>> def integral(u, w, z):
... return c*(z -w)
>>> def root(u, w, r):
... return r/c+w
>>> c=1
>>> graph =nx.random_kernel_graph(1000, integral, root)
See also:
gnp_random_graph(),expected_degree_graph()
References
5.6.16 networkx.generators.random_graphs.random_lobster
random_lobster(n,p1,p2,seed=None)
Returns a random lobster graph.
A lobster is a tree that reduces to a caterpillar when pruning all leaf nodes. A caterpillar is a tree that reduces to
a path graph when pruning all leaf nodes; setting p2 to zero produces a caterpillar.
Parameters
•n(int) – The expected number of nodes in the backbone
•p1 (float) – Probability of adding an edge to the backbone
•p2 (float) – Probability of adding an edge one level beyond backbone
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
5.6.17 networkx.generators.random_graphs.random_shell_graph
random_shell_graph(constructor,seed=None)
Returns a random shell graph for the constructor given.
Parameters
•constructor (list of three-tuples) – Represents the parameters for a shell, starting at the
center shell. Each element of the list must be of the form (n, m, d), where nis the
number of nodes in the shell, mis the number of edges in the shell, and dis the ratio of
inter-shell (next) edges to intra-shell edges. If dis zero, there will be no intra-shell edges,
and if dis one there will be all possible intra-shell edges.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Examples
>>> constructor =[(10,20,0.8), (20,40,0.8)]
>>> G=nx.random_shell_graph(constructor)
536 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.6.18 networkx.generators.random_graphs.random_powerlaw_tree
random_powerlaw_tree(n,gamma=3,seed=None,tries=100)
Returns a tree with a power law degree distribution.
Parameters
•n(int) – The number of nodes.
•gamma (float) – Exponent of the power law.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•tries (int) – Number of attempts to adjust the sequence to make it a tree.
Raises NetworkXError – If no valid sequence is found within the maximum number of attempts.
Notes
A trial power law degree sequence is chosen and then elements are swapped with new elements from a powerlaw
distribution until the sequence makes a tree (by checking, for example, that the number of edges is one smaller
than the number of nodes).
5.6.19 networkx.generators.random_graphs.random_powerlaw_tree_sequence
random_powerlaw_tree_sequence(n,gamma=3,seed=None,tries=100)
Returns a degree sequence for a tree with a power law distribution.
Parameters
•n(int,) – The number of nodes.
•gamma (float) – Exponent of the power law.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•tries (int) – Number of attempts to adjust the sequence to make it a tree.
Raises NetworkXError – If no valid sequence is found within the maximum number of attempts.
Notes
A trial power law degree sequence is chosen and then elements are swapped with new elements from a power
law distribution until the sequence makes a tree (by checking, for example, that the number of edges is one
smaller than the number of nodes).
5.7 Duplication Divergence
Functions for generating graphs based on the “duplication” method.
These graph generators start with a small initial graph then duplicate nodes and (partially) duplicate their edges. These
functions are generally inspired by biological networks.
5.7. Duplication Divergence 537

NetworkX Reference, Release 2.3rc1.dev20181203210840
duplication_divergence_graph(n, p[, seed]) Returns an undirected graph using the duplication-
divergence model.
partial_duplication_graph(N, n, p, q[, seed]) Return a random graph using the partial duplication
model.
5.7.1 networkx.generators.duplication.duplication_divergence_graph
duplication_divergence_graph(n,p,seed=None)
Returns an undirected graph using the duplication-divergence model.
A graph of nnodes is created by duplicating the initial nodes and retaining edges incident to the original nodes
with a retention probability p.
Parameters
•n(int) – The desired number of nodes in the graph.
•p(float) – The probability for retaining the edge of the replicated node.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G
Return type Graph
Raises NetworkXError – If pis not a valid probability. If nis less than 2.
Notes
This algorithm appears in [1].
This implementation disallows the possibility of generating disconnected graphs.
References
5.7.2 networkx.generators.duplication.partial_duplication_graph
partial_duplication_graph(N,n,p,q,seed=None)
Return a random graph using the partial duplication model.
Parameters
•N(int) – The total number of nodes in the final graph.
•n(int) – The number of nodes in the initial clique.
•p(float) – The probability of joining each neighbor of a node to the duplicate node. Must
be a number in the between zero and one, inclusive.
•q(float) – The probability of joining the source node to the duplicate node. Must be a
number in the between zero and one, inclusive.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
538 Chapter 5. Graph generators
NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
A graph of nodes is grown by creating a fully connected graph of size n. The following procedure is then
repeated until a total of Nnodes have been reached.
1. A random node, u, is picked and a new node, v, is created.
2. For each neighbor of uan edge from the neighbor to vis created with probability p.
3. An edge from uto vis created with probability q.
This algorithm appears in [1].
This implementation allows the possibility of generating disconnected graphs.
References
5.8 Degree Sequence
Generate graphs with a given degree sequence or expected degree sequence.
configuration_model(deg_sequence[, . . . ]) Return a random graph with the given degree sequence.
directed_configuration_model(. . . [, . . . ]) Return a directed_random graph with the given degree
sequences.
expected_degree_graph(w[, seed, selfloops]) Return a random graph with given expected degrees.
havel_hakimi_graph(deg_sequence[, cre-
ate_using])
Return a simple graph with given degree sequence con-
structed using the Havel-Hakimi algorithm.
directed_havel_hakimi_graph(in_deg_sequence,
...)
Return a directed graph with the given degree se-
quences.
degree_sequence_tree(deg_sequence[, . . . ]) Make a tree for the given degree sequence.
random_degree_sequence_graph(sequence[,
...])
Return a simple random graph with the given degree se-
quence.
5.8.1 networkx.generators.degree_seq.configuration_model
configuration_model(deg_sequence,create_using=None,seed=None)
Return a random graph with the given degree sequence.
The configuration model generates a random pseudograph (graph with parallel edges and self loops) by ran-
domly assigning edges to match the given degree sequence.
Parameters
•deg_sequence (list of nonnegative integers) – Each list entry corresponds to the degree of a
node.
•create_using (NetworkX graph constructor, optional (default MultiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – A graph with the specified degree sequence. Nodes are labeled starting at 0 with an
index corresponding to the position in deg_sequence.
Return type MultiGraph
5.8. Degree Sequence 539

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises NetworkXError – If the degree sequence does not have an even sum.
See also:
is_graphical()
Notes
As described by Newman1.
A non-graphical degree sequence (not realizable by some simple graph) is allowed since this function returns
graphs with self loops and parallel edges. An exception is raised if the degree sequence does not have an even
sum.
This configuration model construction process can lead to duplicate edges and loops. You can remove the
self-loops and parallel edges (see below) which will likely result in a graph that doesn’t have the exact degree
sequence specified.
The density of self-loops and parallel edges tends to decrease as the number of nodes increases. However,
typically the number of self-loops will approach a Poisson distribution with a nonzero mean, and similarly for
the number of parallel edges. Consider a node with kstubs. The probability of being joined to another stub of
the same node is basically (k-1) / N, where kis the degree and Nis the number of nodes. So the probability of
a self-loop scales like c/Nfor some constant c. As Ngrows, this means we expect cself-loops. Similarly for
parallel edges.
References
Examples
You can create a degree sequence following a particular distribution by using the one of the distribution functions
in random_sequence (or one of your own). For example, to create an undirected multigraph on one hundred
nodes with degree sequence chosen from the power law distribution:
>>> sequence =nx.random_powerlaw_tree_sequence(100, tries=5000)
>>> G=nx.configuration_model(sequence)
>>> len(G)
100
>>> actual_degrees =[d for v, d in G.degree()]
>>> actual_degrees == sequence
True
The returned graph is a multigraph, which may have parallel edges. To remove any parallel edges from the
returned graph:
>>> G=nx.Graph(G)
Similarly, to remove self-loops:
>>> G.remove_edges_from(nx.selfloop_edges(G))
1M.E.J. Newman, “The structure and function of complex networks”, SIAM REVIEW 45-2, pp 167-256, 2003.
540 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.8.2 networkx.generators.degree_seq.directed_configuration_model
directed_configuration_model(in_degree_sequence,out_degree_sequence,create_using=None,
seed=None)
Return a directed_random graph with the given degree sequences.
The configuration model generates a random directed pseudograph (graph with parallel edges and self loops) by
randomly assigning edges to match the given degree sequences.
Parameters
•in_degree_sequence (list of nonnegative integers) – Each list entry corresponds to the in-
degree of a node.
•out_degree_sequence (list of nonnegative integers) – Each list entry corresponds to the
out-degree of a node.
•create_using (NetworkX graph constructor, optional (default MultiDiGraph)) – Graph type
to create. If graph instance, then cleared before populated.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – A graph with the specified degree sequences. Nodes are labeled starting at 0 with an
index corresponding to the position in deg_sequence.
Return type MultiDiGraph
Raises NetworkXError – If the degree sequences do not have the same sum.
See also:
configuration_model()
Notes
Algorithm as described by Newman1.
A non-graphical degree sequence (not realizable by some simple graph) is allowed since this function returns
graphs with self loops and parallel edges. An exception is raised if the degree sequences does not have the same
sum.
This configuration model construction process can lead to duplicate edges and loops. You can remove the
self-loops and parallel edges (see below) which will likely result in a graph that doesn’t have the exact degree
sequence specified. This “finite-size effect” decreases as the size of the graph increases.
References
Examples
One can modify the in- and out-degree sequences from an existing directed graph in order to create a new
directed graph. For example, here we modify the directed path graph:
>>> D=nx.DiGraph([(0,1), (1,2), (2,3)])
>>> din =list(d for n, d in D.in_degree())
>>> dout =list(d for n, d in D.out_degree())
>>> din.append(1)
(continues on next page)
1Newman, M. E. J. and Strogatz, S. H. and Watts, D. J. Random graphs with arbitrary degree distributions and their applications Phys. Rev. E,
64, 026118 (2001)
5.8. Degree Sequence 541

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> dout[0]=2
>>> # We now expect an edge from node 0 to a new node, node 3.
... D=nx.directed_configuration_model(din, dout)
The returned graph is a directed multigraph, which may have parallel edges. To remove any parallel edges from
the returned graph:
>>> D=nx.DiGraph(D)
Similarly, to remove self-loops:
>>> D.remove_edges_from(nx.selfloop_edges(D))
5.8.3 networkx.generators.degree_seq.expected_degree_graph
expected_degree_graph(w,seed=None,selfloops=True)
Return a random graph with given expected degrees.
Given a sequence of expected degrees 𝑊= (𝑤0, 𝑤1, . . . , 𝑤𝑛−1)of length 𝑛this algorithm assigns an edge
between node 𝑢and node 𝑣with probability
𝑝𝑢𝑣 =𝑤𝑢𝑤𝑣
𝑘𝑤𝑘
.
Parameters
•w(list) – The list of expected degrees.
•selfloops (bool (default=True)) – Set to False to remove the possibility of self-loop edges.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns
Return type Graph
Examples
>>> z=[10 for iin range(100)]
>>> G=nx.expected_degree_graph(z)
Notes
The nodes have integer labels corresponding to index of expected degrees input sequence.
The complexity of this algorithm is 𝒪(𝑛+𝑚)where 𝑛is the number of nodes and 𝑚is the expected number
of edges.
The model in1includes the possibility of self-loop edges. Set selfloops=False to produce a graph without self
loops.
1Fan Chung and L. Lu, Connected components in random graphs with given expected degree sequences, Ann. Combinatorics, 6, pp. 125-145,
2002.
542 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
For finite graphs this model doesn’t produce exactly the given expected degree sequence. Instead the expected
degrees are as follows.
For the case without self loops (selfloops=False),
𝐸[𝑑𝑒𝑔(𝑢)] =
𝑣̸=𝑢
𝑝𝑢𝑣 =𝑤𝑢1−𝑤𝑢
𝑘𝑤𝑘.
NetworkX uses the standard convention that a self-loop edge counts 2 in the degree of a node, so with self loops
(selfloops=True),
𝐸[𝑑𝑒𝑔(𝑢)] =
𝑣̸=𝑢
𝑝𝑢𝑣 + 2𝑝𝑢𝑢 =𝑤𝑢1 + 𝑤𝑢
𝑘𝑤𝑘.
References
5.8.4 networkx.generators.degree_seq.havel_hakimi_graph
havel_hakimi_graph(deg_sequence,create_using=None)
Return a simple graph with given degree sequence constructed using the Havel-Hakimi algorithm.
Parameters
•deg_sequence (list of integers) – Each integer corresponds to the degree of a node (need not
be sorted).
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated. Directed graphs are not allowed.
Raises NetworkXException – For a non-graphical degree sequence (i.e. one not realizable by
some simple graph).
Notes
The Havel-Hakimi algorithm constructs a simple graph by successively connecting the node of highest degree
to other nodes of highest degree, resorting remaining nodes by degree, and repeating the process. The resulting
graph has a high degree-associativity. Nodes are labeled 1,.., len(deg_sequence), corresponding to their position
in deg_sequence.
The basic algorithm is from Hakimi1and was generalized by Kleitman and Wang2.
References
5.8.5 networkx.generators.degree_seq.directed_havel_hakimi_graph
directed_havel_hakimi_graph(in_deg_sequence,out_deg_sequence,create_using=None)
Return a directed graph with the given degree sequences.
Parameters
•in_deg_sequence (list of integers) – Each list entry corresponds to the in-degree of a node.
1Hakimi S., On Realizability of a Set of Integers as Degrees of the Vertices of a Linear Graph. I, Journal of SIAM, 10(3), pp. 496-506 (1962)
2Kleitman D.J. and Wang D.L. Algorithms for Constructing Graphs and Digraphs with Given Valences and Factors Discrete Mathematics, 6(1),
pp. 79-88 (1973)
5.8. Degree Sequence 543

NetworkX Reference, Release 2.3rc1.dev20181203210840
•out_deg_sequence (list of integers) – Each list entry corresponds to the out-degree of a
node.
•create_using (NetworkX graph constructor, optional (default DiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns G – A graph with the specified degree sequences. Nodes are labeled starting at 0 with an
index corresponding to the position in deg_sequence
Return type DiGraph
Raises NetworkXError – If the degree sequences are not digraphical.
See also:
configuration_model()
Notes
Algorithm as described by Kleitman and Wang1.
References
5.8.6 networkx.generators.degree_seq.degree_sequence_tree
degree_sequence_tree(deg_sequence,create_using=None)
Make a tree for the given degree sequence.
A tree has #nodes-#edges=1 so the degree sequence must have len(deg_sequence)-sum(deg_sequence)/2=1
5.8.7 networkx.generators.degree_seq.random_degree_sequence_graph
random_degree_sequence_graph(sequence,seed=None,tries=10)
Return a simple random graph with the given degree sequence.
If the maximum degree 𝑑𝑚in the sequence is 𝑂(𝑚1/4)then the algorithm produces almost uniform random
graphs in 𝑂(𝑚𝑑𝑚)time where 𝑚is the number of edges.
Parameters
•sequence (list of integers) – Sequence of degrees
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•tries (int, optional) – Maximum number of tries to create a graph
Returns G – A graph with the specified degree sequence. Nodes are labeled starting at 0 with an
index corresponding to the position in the sequence.
Return type Graph
Raises
•NetworkXUnfeasible – If the degree sequence is not graphical.
•NetworkXError – If a graph is not produced in specified number of tries
1D.J. Kleitman and D.L. Wang Algorithms for Constructing Graphs and Digraphs with Given Valences and Factors Discrete Mathematics, 6(1),
pp. 79-88 (1973)
544 Chapter 5. Graph generators
NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
is_graphical(),configuration_model()
Notes
The generator algorithm1is not guaranteed to produce a graph.
References
Examples
>>> sequence =[1,2,2,3]
>>> G=nx.random_degree_sequence_graph(sequence)
>>> sorted(d for n, d in G.degree())
[1, 2, 2, 3]
5.9 Random Clustered
Generate graphs with given degree and triangle sequence.
random_clustered_graph(joint_degree_sequence) Generate a random graph with the given joint indepen-
dent edge degree and triangle degree sequence.
5.9.1 networkx.generators.random_clustered.random_clustered_graph
random_clustered_graph(joint_degree_sequence,create_using=None,seed=None)
Generate a random graph with the given joint independent edge degree and triangle degree sequence.
This uses a configuration model-like approach to generate a random graph (with parallel edges and self-loops)
by randomly assigning edges to match the given joint degree sequence.
The joint degree sequence is a list of pairs of integers of the form [(𝑑1,𝑖, 𝑑1,𝑡),...,(𝑑𝑛,𝑖, 𝑑𝑛,𝑡)]. According to
this list, vertex 𝑢is a member of 𝑑𝑢,𝑡 triangles and has 𝑑𝑢,𝑖 other edges. The number 𝑑𝑢,𝑡 is the triangle degree
of 𝑢and the number 𝑑𝑢,𝑖 is the independent edge degree.
Parameters
•joint_degree_sequence (list of integer pairs) – Each list entry corresponds to the indepen-
dent edge degree and triangle degree of a node.
•create_using (NetworkX graph constructor, optional (default MultiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – A graph with the specified degree sequence. Nodes are labeled starting at 0 with an
index corresponding to the position in deg_sequence.
Return type MultiGraph
1Moshen Bayati, Jeong Han Kim, and Amin Saberi, A sequential algorithm for generating random graphs. Algorithmica, Volume 58, Number
4, 860-910, DOI: 10.1007/s00453-009-9340-1
5.9. Random Clustered 545
NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises NetworkXError – If the independent edge degree sequence sum is not even or the triangle
degree sequence sum is not divisible by 3.
Notes
As described by Miller1(see also Newman2for an equivalent description).
A non-graphical degree sequence (not realizable by some simple graph) is allowed since this function returns
graphs with self loops and parallel edges. An exception is raised if the independent degree sequence does not
have an even sum or the triangle degree sequence sum is not divisible by 3.
This configuration model-like construction process can lead to duplicate edges and loops. You can remove the
self-loops and parallel edges (see below) which will likely result in a graph that doesn’t have the exact degree
sequence specified. This “finite-size effect” decreases as the size of the graph increases.
References
Examples
>>> deg =[(1,0), (1,0), (1,0), (2,0), (1,0), (2,1), (0,1), (0,1)]
>>> G=nx.random_clustered_graph(deg)
To remove parallel edges:
>>> G=nx.Graph(G)
To remove self loops:
>>> G.remove_edges_from(nx.selfloop_edges(G))
5.10 Directed
Generators for some directed graphs, including growing network (GN) graphs and scale-free graphs.
gn_graph(n[, kernel, create_using, seed]) Return the growing network (GN) digraph with nnodes.
gnr_graph(n, p[, create_using, seed]) Return the growing network with redirection (GNR) di-
graph with nnodes and redirection probability p.
gnc_graph(n[, create_using, seed]) Return the growing network with copying (GNC) di-
graph with nnodes.
random_k_out_graph(n, k, alpha[, . . . ]) Returns a random k-out graph with preferential attach-
ment.
scale_free_graph(n[, alpha, beta, gamma, . . . ]) Returns a scale-free directed graph.
5.10.1 networkx.generators.directed.gn_graph
gn_graph(n,kernel=None,create_using=None,seed=None)
Return the growing network (GN) digraph with nnodes.
1Joel C. Miller. “Percolation and epidemics in random clustered networks”. In: Physical review. E, Statistical, nonlinear, and soft matter
physics 80 (2 Part 1 August 2009).
2M. E. J. Newman. “Random Graphs with Clustering”. In: Physical Review Letters 103 (5 July 2009)
546 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
The GN graph is built by adding nodes one at a time with a link to one previously added node. The target node
for the link is chosen with probability based on degree. The default attachment kernel is a linear function of the
degree of a node.
The graph is always a (directed) tree.
Parameters
•n(int) – The number of nodes for the generated graph.
•kernel (function) – The attachment kernel.
•create_using (NetworkX graph constructor, optional (default DiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Examples
To create the undirected GN graph, use the to_directed() method:
>>> D=nx.gn_graph(10)# the GN graph
>>> G=D.to_undirected() # the undirected version
To specify an attachment kernel, use the kernel keyword argument:
>>> D=nx.gn_graph(10, kernel=lambda x: x ** 1.5)# A_k = k^1.5
References
5.10.2 networkx.generators.directed.gnr_graph
gnr_graph(n,p,create_using=None,seed=None)
Return the growing network with redirection (GNR) digraph with nnodes and redirection probability p.
The GNR graph is built by adding nodes one at a time with a link to one previously added node. The previous
target node is chosen uniformly at random. With probabiliy pthe link is instead “redirected” to the successor
node of the target.
The graph is always a (directed) tree.
Parameters
•n(int) – The number of nodes for the generated graph.
•p(float) – The redirection probability.
•create_using (NetworkX graph constructor, optional (default DiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Examples
To create the undirected GNR graph, use the to_directed() method:
5.10. Directed 547

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> D=nx.gnr_graph(10,0.5)# the GNR graph
>>> G=D.to_undirected() # the undirected version
References
5.10.3 networkx.generators.directed.gnc_graph
gnc_graph(n,create_using=None,seed=None)
Return the growing network with copying (GNC) digraph with nnodes.
The GNC graph is built by adding nodes one at a time with a link to one previously added node (chosen
uniformly at random) and to all of that node’s successors.
Parameters
•n(int) – The number of nodes for the generated graph.
•create_using (NetworkX graph constructor, optional (default DiGraph)) – Graph type to
create. If graph instance, then cleared before populated.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
References
5.10.4 networkx.generators.directed.random_k_out_graph
random_k_out_graph(n,k,alpha,self_loops=True,seed=None)
Returns a random k-out graph with preferential attachment.
A random k-out graph with preferential attachment is a multidigraph generated by the following algorithm.
1. Begin with an empty digraph, and initially set each node to have weight alpha.
2. Choose a node uwith out-degree less than kuniformly at random.
3. Choose a node vfrom with probability proportional to its weight.
4. Add a directed edge from uto v, and increase the weight of vby one.
5. If each node has out-degree k, halt, otherwise repeat from step 2.
For more information on this model of random graph, see [1].
Parameters
•n(int) – The number of nodes in the returned graph.
•k(int) – The out-degree of each node in the returned graph.
•alpha (float) – A positive float representing the initial weight of each vertex. A higher
number means that in step 3 above, nodes will be chosen more like a true uniformly random
sample, and a lower number means that nodes are more likely to be chosen as their in-degree
increases. If this parameter is not positive, a ValueError is raised.
•self_loops (bool) – If True, self-loops are allowed when generating the graph.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns Ak-out-regular multidigraph generated according to the above algorithm.
548 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type MultiDiGraph
Raises ValueError – If alpha is not positive.
Notes
The returned multidigraph may not be strongly connected, or even weakly connected.
References
[1]: Peterson, Nicholas R., and Boris Pittel. “Distance between two random k-out digraphs, with and without
preferential attachment.” arXiv preprint arXiv:1311.5961 (2013). <https://arxiv.org/abs/1311.5961>
5.10.5 networkx.generators.directed.scale_free_graph
scale_free_graph(n,alpha=0.41,beta=0.54,gamma=0.05,delta_in=0.2,delta_out=0,cre-
ate_using=None,seed=None)
Returns a scale-free directed graph.
Parameters
•n(integer) – Number of nodes in graph
•alpha (float) – Probability for adding a new node connected to an existing node chosen
randomly according to the in-degree distribution.
•beta (float) – Probability for adding an edge between two existing nodes. One existing node
is chosen randomly according the in-degree distribution and the other chosen randomly
according to the out-degree distribution.
•gamma (float) – Probability for adding a new node connected to an existing node chosen
randomly according to the out-degree distribution.
•delta_in (float) – Bias for choosing nodes from in-degree distribution.
•delta_out (float) – Bias for choosing nodes from out-degree distribution.
•create_using (NetworkX graph constructor, optional) – The default is a MultiDiGraph 3-
cycle. If a graph instance, use it without clearing first. If a graph constructor, call it to
construct an empty graph.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Examples
Create a scale-free graph on one hundred nodes:
>>> G=nx.scale_free_graph(100)
Notes
The sum of alpha,beta, and gamma must be 1.
5.10. Directed 549

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
5.11 Geometric
Generators for geometric graphs.
random_geometric_graph(n, radius[, dim, . . . ]) Returns a random geometric graph in the unit cube of
dimensions dim.
soft_random_geometric_graph(n, radius[,
...])
Returns a soft random geometric graph in the unit cube.
geographical_threshold_graph(n, theta[,
...])
Returns a geographical threshold graph.
waxman_graph(n[, beta, alpha, L, domain, . . . ]) Return a Waxman random graph.
navigable_small_world_graph(n[, p, q, r,
...])
Return a navigable small-world graph.
thresholded_random_geometric_graph(n,
...[, ...])
Returns a thresholded random geometric graph in the
unit cube.
5.11.1 networkx.generators.geometric.random_geometric_graph
random_geometric_graph(n,radius,dim=2,pos=None,p=2,seed=None)
Returns a random geometric graph in the unit cube of dimensions dim.
The random geometric graph model places nnodes uniformly at random in the unit cube. Two nodes are joined
by an edge if the distance between the nodes is at most radius.
Edges are determined using a KDTree when SciPy is available. This reduces the time complexity from 𝑂(𝑛2)
to 𝑂(𝑛).
Parameters
•n(int or iterable) – Number of nodes or iterable of nodes
•radius (float) – Distance threshold value
•dim (int, optional) – Dimension of graph
•pos (dict, optional) – A dictionary keyed by node with node positions as values.
•p(float, optional) – Which Minkowski distance metric to use. phas to meet the condition
1 <= p <= infinity.
If this argument is not specified, the 𝐿2metric (the Euclidean distance metric), p = 2 is used.
This should not be confused with the pof an Erd˝
os-Rényi random graph, which represents
probability.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns A random geometric graph, undirected and without self-loops. Each node has a node at-
tribute 'pos' that stores the position of that node in Euclidean space as provided by the pos
keyword argument or, if pos was not provided, as generated by this function.
Return type Graph
550 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
Create a random geometric graph on twenty nodes where nodes are joined by an edge if their distance is at most
0.1:
>>> G=nx.random_geometric_graph(20,0.1)
Notes
This uses a k-d tree to build the graph.
The pos keyword argument can be used to specify node positions so you can create an arbitrary distribution
and domain for positions.
For example, to use a 2D Gaussian distribution of node positions with mean (0, 0) and standard deviation 2:
>>> import random
>>> n=20
>>> pos ={i: (random.gauss(0,2), random.gauss(0,2)) for iin range(n)}
>>> G=nx.random_geometric_graph(n, 0.2, pos=pos)
References
5.11.2 networkx.generators.geometric.soft_random_geometric_graph
soft_random_geometric_graph(n,radius,dim=2,pos=None,p=2,p_dist=None,seed=None)
Returns a soft random geometric graph in the unit cube.
The soft random geometric graph [1] model places nnodes uniformly at random in the unit cube in dimension
dim. Two nodes of distance, dist, computed by the p-Minkowski distance metric are joined by an edge with
probability p_dist if the computed distance metric value of the nodes is at most radius, otherwise they are
not joined.
Edges within radius of each other are determined using a KDTree when SciPy is available. This reduces the
time complexity from 𝑂(𝑛2)to 𝑂(𝑛).
Parameters
•n(int or iterable) – Number of nodes or iterable of nodes
•radius (float) – Distance threshold value
•dim (int, optional) – Dimension of graph
•pos (dict, optional) – A dictionary keyed by node with node positions as values.
•p(float, optional) – Which Minkowski distance metric to use. phas to meet the condition
1 <= p <= infinity.
If this argument is not specified, the 𝐿2metric (the Euclidean distance metric), p = 2 is used.
This should not be confused with the pof an Erd˝
os-Rényi random graph, which represents
probability.
•p_dist (function, optional) – A probability density function computing the probability of
connecting two nodes that are of distance, dist, computed by the Minkowski distance met-
ric. The probability density function, p_dist, must be any function that takes the metric
value as input and outputs a single probability value between 0-1. The scipy.stats package
has many probability distribution functions implemented and tools for custom probability
5.11. Geometric 551

NetworkX Reference, Release 2.3rc1.dev20181203210840
distribution definitions [2], and passing the .pdf method of scipy.stats distributions can be
used here. If the probability function, p_dist, is not supplied, the default function is an
exponential distribution with rate parameter 𝜆= 1.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns A soft random geometric graph, undirected and without self-loops. Each node has a node
attribute 'pos' that stores the position of that node in Euclidean space as provided by the pos
keyword argument or, if pos was not provided, as generated by this function.
Return type Graph
Examples
Default Graph:
G = nx.soft_random_geometric_graph(50, 0.2)
Custom Graph:
Create a soft random geometric graph on 100 uniformly distributed nodes where nodes are joined by an edge
with probability computed from an exponential distribution with rate parameter 𝜆= 1 if their Euclidean distance
is at most 0.2.
Notes
This uses a k-d tree to build the graph.
The pos keyword argument can be used to specify node positions so you can create an arbitrary distribution
and domain for positions.
For example, to use a 2D Gaussian distribution of node positions with mean (0, 0) and standard deviation 2
The scipy.stats package can be used to define the probability distribution with the .pdf method used as p_dist.
>>> import random
>>> import math
>>> n=100
>>> pos ={i: (random.gauss(0,2), random.gauss(0,2)) for iin range(n)}
>>> p_dist =lambda dist : math.exp(-dist)
>>> G=nx.soft_random_geometric_graph(n, 0.2, pos=pos, p_dist=p_dist)
References
5.11.3 networkx.generators.geometric.geographical_threshold_graph
geographical_threshold_graph(n,theta,dim=2,pos=None,weight=None,metric=None,
p_dist=None,seed=None)
Returns a geographical threshold graph.
The geographical threshold graph model places 𝑛nodes uniformly at random in a rectangular domain. Each
node 𝑢is assigned a weight 𝑤𝑢. Two nodes 𝑢and 𝑣are joined by an edge if
(𝑤𝑢+𝑤𝑣)ℎ(𝑟)≥𝜃
where ris the distance between uand v, h(r) is a probability of connection as a function of r, and 𝜃as the
threshold parameter. h(r) corresponds to the p_dist parameter.
552 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•n(int or iterable) – Number of nodes or iterable of nodes
•theta (float) – Threshold value
•dim (int, optional) – Dimension of graph
•pos (dict) – Node positions as a dictionary of tuples keyed by node.
•weight (dict) – Node weights as a dictionary of numbers keyed by node.
•metric (function) – A metric on vectors of numbers (represented as lists or tuples). This
must be a function that accepts two lists (or tuples) as input and yields a number as output.
The function must also satisfy the four requirements of a metric. Specifically, if 𝑑is the
function and 𝑥,𝑦, and 𝑧are vectors in the graph, then 𝑑must satisfy
1. 𝑑(𝑥, 𝑦)≥0,
2. 𝑑(𝑥, 𝑦)=0if and only if 𝑥=𝑦,
3. 𝑑(𝑥, 𝑦) = 𝑑(𝑦, 𝑥),
4. 𝑑(𝑥, 𝑧)≤𝑑(𝑥, 𝑦) + 𝑑(𝑦, 𝑧).
If this argument is not specified, the Euclidean distance metric is used.
•p_dist (function, optional) – A probability density function computing the probability of
connecting two nodes that are of distance, r, computed by metric. The probability density
function, p_dist, must be any function that takes the metric value as input and outputs a
single probability value between 0-1. The scipy.stats package has many probability distri-
bution functions implemented and tools for custom probability distribution definitions [2],
and passing the .pdf method of scipy.stats distributions can be used here. If the probability
function, p_dist, is not supplied, the default exponential function :math: r^{-2} is used.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns
A random geographic threshold graph, undirected and without self-loops.
Each node has a node attribute pos that stores the position of that node in Euclidean space
as provided by the pos keyword argument or, if pos was not provided, as generated by this
function. Similarly, each node has a node attribute weight that stores the weight of that node
as provided or as generated.
Return type Graph
Examples
Specify an alternate distance metric using the metric keyword argument. For example, to use the taxicab
metric instead of the default Euclidean metric:
>>> dist =lambda x, y: sum(abs(a -b) for a, b in zip(x, y))
>>> G=nx.geographical_threshold_graph(10,0.1, metric=dist)
Notes
If weights are not specified they are assigned to nodes by drawing randomly from the exponential distribution
with rate parameter 𝜆= 1. To specify weights from a different distribution, use the weight keyword argument:
5.11. Geometric 553

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> import random
>>> n=20
>>> w={i: random.expovariate(5.0)for iin range(n)}
>>> G=nx.geographical_threshold_graph(20,50, weight=w)
If node positions are not specified they are randomly assigned from the uniform distribution.
Starting in NetworkX 2.1 the parameter alpha is deprecated and replaced with the customizable p_dist
function parameter, which defaults to r^-2 if p_dist is not supplied. To reproduce networks of earlier Net-
workX versions, a custom function needs to be defined and passed as the p_dist parameter. For example,
if the parameter alpha = 2 was used in NetworkX 2.0, the custom function def custom_dist(r): r**-2 can be
passed in versions >=2.1 as the parameter p_dist = custom_dist to produce an equivalent network. Note the
change in sign from +2 to -2 in this parameter change.
References
5.11.4 networkx.generators.geometric.waxman_graph
waxman_graph(n,beta=0.4,alpha=0.1,L=None,domain=(0,0,1,1),metric=None,seed=None)
Return a Waxman random graph.
The Waxman random graph model places nnodes uniformly at random in a rectangular domain. Each pair of
nodes at distance dis joined by an edge with probability
𝑝=𝛽exp(−𝑑/𝛼𝐿).
This function implements both Waxman models, using the Lkeyword argument.
• Waxman-1: if Lis not specified, it is set to be the maximum distance between any pair of nodes.
• Waxman-2: if Lis specified, the distance between a pair of nodes is chosen uniformly at random from the
interval [0, L].
Parameters
•n(int or iterable) – Number of nodes or iterable of nodes
•beta (float) – Model parameter
•alpha (float) – Model parameter
•L(float, optional) – Maximum distance between nodes. If not specified, the actual distance
is calculated.
•domain (four-tuple of numbers, optional) – Domain size, given as a tuple of the form
(x_min, y_min, x_max, y_max).
•metric (function) – A metric on vectors of numbers (represented as lists or tuples). This
must be a function that accepts two lists (or tuples) as input and yields a number as output.
The function must also satisfy the four requirements of a metric. Specifically, if 𝑑is the
function and 𝑥,𝑦, and 𝑧are vectors in the graph, then 𝑑must satisfy
1. 𝑑(𝑥, 𝑦)≥0,
2. 𝑑(𝑥, 𝑦)=0if and only if 𝑥=𝑦,
3. 𝑑(𝑥, 𝑦) = 𝑑(𝑦, 𝑥),
4. 𝑑(𝑥, 𝑧)≤𝑑(𝑥, 𝑦) + 𝑑(𝑦, 𝑧).
If this argument is not specified, the Euclidean distance metric is used.
554 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns A random Waxman graph, undirected and without self-loops. Each node has a node at-
tribute 'pos' that stores the position of that node in Euclidean space as generated by this
function.
Return type Graph
Examples
Specify an alternate distance metric using the metric keyword argument. For example, to use the “taxicab
metric” instead of the default Euclidean metric:
>>> dist =lambda x, y: sum(abs(a -b) for a, b in zip(x, y))
>>> G=nx.waxman_graph(10,0.5,0.1, metric=dist)
Notes
Starting in NetworkX 2.0 the parameters alpha and beta align with their usual roles in the probability distribution.
In earlier versions their positions in the expression were reversed. Their position in the calling sequence reversed
as well to minimize backward incompatibility.
References
5.11.5 networkx.generators.geometric.navigable_small_world_graph
navigable_small_world_graph(n,p=1,q=1,r=2,dim=2,seed=None)
Return a navigable small-world graph.
A navigable small-world graph is a directed grid with additional long-range connections that are chosen ran-
domly.
[. . . ] we begin with a set of nodes [. . . ] that are identified with the set of lattice points in an 𝑛×𝑛
square, {(𝑖, 𝑗) : 𝑖∈ {1,2, . . . , 𝑛}, 𝑗 ∈ {1,2, . . . , 𝑛}}, and we define the lattice distance between
two nodes (𝑖, 𝑗)and (𝑘, 𝑙)to be the number of “lattice steps” separating them: 𝑑((𝑖, 𝑗),(𝑘, 𝑙)) =
|𝑘−𝑖|+|𝑙−𝑗|.
For a universal constant 𝑝 >= 1, the node 𝑢has a directed edge to every other node within lattice
distance 𝑝—these are its local contacts. For universal constants 𝑞 >= 0 and 𝑟 >= 0 we also
construct directed edges from 𝑢to 𝑞other nodes (the long-range contacts) using independent random
trials; the 𝑖has endpoint 𝑣with probability proportional to [𝑑(𝑢, 𝑣)]−𝑟.
—1
Parameters
•n(int) – The length of one side of the lattice; the number of nodes in the graph is therefore
𝑛2.
•p(int) – The diameter of short range connections. Each node is joined with every other node
within this lattice distance.
•q(int) – The number of long-range connections for each node.
1J. Kleinberg. The small-world phenomenon: An algorithmic perspective. Proc. 32nd ACM Symposium on Theory of Computing, 2000.
5.11. Geometric 555

NetworkX Reference, Release 2.3rc1.dev20181203210840
•r(float) – Exponent for decaying probability of connections. The probability of connecting
to a node at lattice distance 𝑑is 1/𝑑𝑟.
•dim (int) – Dimension of grid
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
References
5.11.6 networkx.generators.geometric.thresholded_random_geometric_graph
thresholded_random_geometric_graph(n,radius,theta,dim=2,pos=None,weight=None,p=2,
seed=None)
Returns a thresholded random geometric graph in the unit cube.
The thresholded random geometric graph [1] model places nnodes uniformly at random in the unit cube of
dimensions dim. Each node uis assigned a weight 𝑤𝑢. Two nodes uand vare joined by an edge if they are
within the maximum connection distance, radius computed by the p-Minkowski distance and the summation
of weights 𝑤𝑢+𝑤𝑣is greater than or equal to the threshold parameter theta.
Edges within radius of each other are determined using a KDTree when SciPy is available. This reduces the
time complexity from 𝑂(𝑛2)to 𝑂(𝑛).
Parameters
•n(int or iterable) – Number of nodes or iterable of nodes
•radius (float) – Distance threshold value
•theta (float) – Threshold value
•dim (int, optional) – Dimension of graph
•pos (dict, optional) – A dictionary keyed by node with node positions as values.
•weight (dict, optional) – Node weights as a dictionary of numbers keyed by node.
•p(float, optional) – Which Minkowski distance metric to use. phas to meet the condition
1 <= p <= infinity.
If this argument is not specified, the 𝐿2metric (the Euclidean distance metric), p = 2 is used.
This should not be confused with the pof an Erd˝
os-Rényi random graph, which represents
probability.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns
A thresholded random geographic graph, undirected and without self-loops.
Each node has a node attribute 'pos' that stores the position of that node in Euclidean space
as provided by the pos keyword argument or, if pos was not provided, as generated by this
function. Similarly, each node has a nodethre attribute 'weight' that stores the weight of that
node as provided or as generated.
Return type Graph
556 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
Default Graph:
G = nx.thresholded_random_geometric_graph(50, 0.2, 0.1)
Custom Graph:
Create a thresholded random geometric graph on 50 uniformly distributed nodes where nodes are joined by
an edge if their sum weights drawn from a exponential distribution with rate = 5 are >= theta = 0.1 and their
Euclidean distance is at most 0.2.
Notes
This uses a k-d tree to build the graph.
The pos keyword argument can be used to specify node positions so you can create an arbitrary distribution
and domain for positions.
For example, to use a 2D Gaussian distribution of node positions with mean (0, 0) and standard deviation 2
If weights are not specified they are assigned to nodes by drawing randomly from the exponential distribution
with rate parameter 𝜆= 1. To specify weights from a different distribution, use the weight keyword argument:
::
>>> import random
>>> import math
>>> n=50
>>> pos ={i: (random.gauss(0,2), random.gauss(0,2)) for iin range(n)}
>>> w={i: random.expovariate(5.0)for iin range(n)}
>>> G=nx.thresholded_random_geometric_graph(n, 0.2,0.1,2, pos, w)
References
5.12 Line Graph
Functions for generating line graphs.
line_graph(G[, create_using]) Returns the line graph of the graph or digraph G.
inverse_line_graph(G) Returns the inverse line graph of graph G.
5.12.1 networkx.generators.line.line_graph
line_graph(G,create_using=None)
Returns the line graph of the graph or digraph G.
The line graph of a graph Ghas a node for each edge in Gand an edge joining those nodes if the two edges in
Gshare a common node. For directed graphs, nodes are adjacent exactly when the edges they represent form a
directed path of length two.
The nodes of the line graph are 2-tuples of nodes in the original graph (or 3-tuples for multigraphs, with the key
of the edge as the third element).
5.12. Line Graph 557

NetworkX Reference, Release 2.3rc1.dev20181203210840
For information about self-loops and more discussion, see the Notes section below.
Parameters
•G(graph) – A NetworkX Graph, DiGraph, MultiGraph, or MultiDigraph.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Returns L – The line graph of G.
Return type graph
Examples
>>> import networkx as nx
>>> G=nx.star_graph(3)
>>> L=nx.line_graph(G)
>>> print(sorted(map(sorted, L.edges()))) # makes a 3-clique, K3
[[(0, 1), (0, 2)], [(0, 1), (0, 3)], [(0, 2), (0, 3)]]
Notes
Graph, node, and edge data are not propagated to the new graph. For undirected graphs, the nodes in G must be
sortable, otherwise the constructed line graph may not be correct.
Self-loops in undirected graphs
For an undirected graph Gwithout multiple edges, each edge can be written as a set {u, v}. Its line graph
Lhas the edges of Gas its nodes. If xand yare two nodes in L, then {x, y} is an edge in Lif and only
if the intersection of xand yis nonempty. Thus, the set of all edges is determined by the set of all pairwise
intersections of edges in G.
Trivially, every edge in G would have a nonzero intersection with itself, and so every node in Lshould have
a self-loop. This is not so interesting, and the original context of line graphs was with simple graphs, which
had no self-loops or multiple edges. The line graph was also meant to be a simple graph and thus, self-loops in
Lare not part of the standard definition of a line graph. In a pairwise intersection matrix, this is analogous to
excluding the diagonal entries from the line graph definition.
Self-loops and multiple edges in Gadd nodes to Lin a natural way, and do not require any fundamental changes
to the definition. It might be argued that the self-loops we excluded before should now be included. However,
the self-loops are still “trivial” in some sense and thus, are usually excluded.
Self-loops in directed graphs
For a directed graph Gwithout multiple edges, each edge can be written as a tuple (u, v). Its line graph Lhas
the edges of Gas its nodes. If xand yare two nodes in L, then (x, y) is an edge in Lif and only if the tail of
xmatches the head of y, for example, if x = (a, b) and y = (b, c) for some vertices a,b, and cin G.
Due to the directed nature of the edges, it is no longer the case that every edge in Gshould have a self-loop in
L. Now, the only time self-loops arise is if a node in Gitself has a self-loop. So such self-loops are no longer
“trivial” but instead, represent essential features of the topology of G. For this reason, the historical development
of line digraphs is such that self-loops are included. When the graph Ghas multiple edges, once again only
superficial changes are required to the definition.
558 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
• Harary, Frank, and Norman, Robert Z., “Some properties of line digraphs”, Rend. Circ. Mat. Palermo, II.
Ser. 9 (1960), 161–168.
• Hemminger, R. L.; Beineke, L. W. (1978), “Line graphs and line digraphs”, in Beineke, L. W.; Wilson, R.
J., Selected Topics in Graph Theory, Academic Press Inc., pp. 271–305.
5.12.2 networkx.generators.line.inverse_line_graph
inverse_line_graph(G)
Returns the inverse line graph of graph G.
If H is a graph, and G is the line graph of H, such that H = L(G). Then H is the inverse line graph of G.
Not all graphs are line graphs and these do not have an inverse line graph. In these cases this generator returns
a NetworkXError.
Parameters G (graph) – A NetworkX Graph
Returns H – The inverse line graph of G.
Return type graph
Raises
•NetworkXNotImplemented – If G is directed or a multigraph
•NetworkXError – If G is not a line graph
Notes
This is an implementation of the Roussopoulos algorithm.
References
• Roussopolous, N, “A max {m, n} algorithm for determining the graph H from its line graph G”, Informa-
tion Processing Letters 2, (1973), 108–112.
5.13 Ego Graph
Ego graph.
ego_graph(G, n[, radius, center, . . . ]) Returns induced subgraph of neighbors centered at node
n within a given radius.
5.13.1 networkx.generators.ego.ego_graph
ego_graph(G,n,radius=1,center=True,undirected=False,distance=None)
Returns induced subgraph of neighbors centered at node n within a given radius.
Parameters
•G(graph) – A NetworkX Graph or DiGraph
5.13. Ego Graph 559

NetworkX Reference, Release 2.3rc1.dev20181203210840
•n(node) – A single node
•radius (number, optional) – Include all neighbors of distance<=radius from n.
•center (bool, optional) – If False, do not include center node in graph
•undirected (bool, optional) – If True use both in- and out-neighbors of directed graphs.
•distance (key, optional) – Use specified edge data key as distance. For example, setting
distance=’weight’ will use the edge weight to measure the distance from the node n.
Notes
For directed graphs D this produces the “out” neighborhood or successors. If you want the neighborhood of
predecessors first reverse the graph with D.reverse(). If you want both directions use the keyword argument
undirected=True.
Node, edge, and graph attributes are copied to the returned subgraph.
5.14 Stochastic
Functions for generating stochastic graphs from a given weighted directed graph.
stochastic_graph(G[, copy, weight]) Returns a right-stochastic representation of directed
graph G.
5.14.1 networkx.generators.stochastic.stochastic_graph
stochastic_graph(G,copy=True,weight=’weight’)
Returns a right-stochastic representation of directed graph G.
A right-stochastic graph is a weighted digraph in which for each node, the sum of the weights of all the out-edges
of that node is 1. If the graph is already weighted (for example, via a ‘weight’ edge attribute), the reweighting
takes that into account.
Parameters
•G(directed graph)–ADiGraph or MultiDiGraph.
•copy (boolean, optional) – If this is True, then this function returns a new graph with the
stochastic reweighting. Otherwise, the original graph is modified in-place (and also re-
turned, for convenience).
•weight (edge attribute key (optional, default=’weight’)) – Edge attribute key used for read-
ing the existing weight and setting the new weight. If no attribute with this key is found for
an edge, then the edge weight is assumed to be 1. If an edge has a weight, it must be a a
positive number.
5.15 Intersection
Generators for random intersection graphs.
560 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
uniform_random_intersection_graph(n, m,
p[, . . . ])
Return a uniform random intersection graph.
k_random_intersection_graph(n, m, k[,
seed])
Return a intersection graph with randomly chosen at-
tribute sets for each node that are of equal size (k).
general_random_intersection_graph(n, m,
p[, . . . ])
Return a random intersection graph with independent
probabilities for connections between node and attribute
sets.
5.15.1 networkx.generators.intersection.uniform_random_intersection_graph
uniform_random_intersection_graph(n,m,p,seed=None)
Return a uniform random intersection graph.
Parameters
•n(int) – The number of nodes in the first bipartite set (nodes)
•m(int) – The number of nodes in the second bipartite set (attributes)
•p(float) – Probability of connecting nodes between bipartite sets
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
See also:
gnp_random_graph()
References
5.15.2 networkx.generators.intersection.k_random_intersection_graph
k_random_intersection_graph(n,m,k,seed=None)
Return a intersection graph with randomly chosen attribute sets for each node that are of equal size (k).
Parameters
•n(int) – The number of nodes in the first bipartite set (nodes)
•m(int) – The number of nodes in the second bipartite set (attributes)
•k(float) – Size of attribute set to assign to each node.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
See also:
gnp_random_graph(),uniform_random_intersection_graph()
References
5.15.3 networkx.generators.intersection.general_random_intersection_graph
general_random_intersection_graph(n,m,p,seed=None)
Return a random intersection graph with independent probabilities for connections between node and attribute
sets.
5.15. Intersection 561

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•n(int) – The number of nodes in the first bipartite set (nodes)
•m(int) – The number of nodes in the second bipartite set (attributes)
•p(list of floats of length m) – Probabilities for connecting nodes to each attribute
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
See also:
gnp_random_graph(),uniform_random_intersection_graph()
References
5.16 Social Networks
Famous social networks.
karate_club_graph() Return Zachary’s Karate Club graph.
davis_southern_women_graph() Return Davis Southern women social network.
florentine_families_graph() Return Florentine families graph.
5.16.1 networkx.generators.social.karate_club_graph
karate_club_graph()
Return Zachary’s Karate Club graph.
Each node in the returned graph has a node attribute ‘club’ that indicates the name of the club to which the
member represented by that node belongs, either ‘Mr. Hi’ or ‘Officer’.
Examples
To get the name of the club to which a node belongs:
>>> import networkx as nx
>>> G=nx.karate_club_graph()
>>> G.nodes[5]['club']
'Mr. Hi'
>>> G.nodes[9]['club']
'Officer'
References
5.16.2 networkx.generators.social.davis_southern_women_graph
davis_southern_women_graph()
Return Davis Southern women social network.
This is a bipartite graph.
562 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
5.16.3 networkx.generators.social.florentine_families_graph
florentine_families_graph()
Return Florentine families graph.
References
5.17 Community
Generators for classes of graphs used in studying social networks.
caveman_graph(l, k) Returns a caveman graph of lcliques of size k.
connected_caveman_graph(l, k) Returns a connected caveman graph of lcliques of size
k.
relaxed_caveman_graph(l, k, p[, seed]) Return a relaxed caveman graph.
random_partition_graph(sizes, p_in, p_out[,
...])
Return the random partition graph with a partition of
sizes.
planted_partition_graph(l, k, p_in, p_out[,
...])
Return the planted l-partition graph.
gaussian_random_partition_graph(n, s, v,
...)
Generate a Gaussian random partition graph.
ring_of_cliques(num_cliques, clique_size) Defines a “ring of cliques” graph.
stochastic_block_model(sizes, p[, nodelist,
...])
Return a stochastic block model graph.
windmill_graph(n, k) Generate a windmill graph.
5.17.1 networkx.generators.community.caveman_graph
caveman_graph(l,k)
Returns a caveman graph of lcliques of size k.
Parameters
•l(int) – Number of cliques
•k(int) – Size of cliques
Returns G – caveman graph
Return type NetworkX Graph
Notes
This returns an undirected graph, it can be converted to a directed graph using nx.to_directed(), or a
multigraph using nx.MultiGraph(nx.caveman_graph(l, k)). Only the undirected version is de-
scribed in1and it is unclear which of the directed generalizations is most useful.
1Watts, D. J. ‘Networks, Dynamics, and the Small-World Phenomenon.’ Amer. J. Soc. 105, 493-527, 1999.
5.17. Community 563
NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.caveman_graph(3,3)
See also:
connected_caveman_graph()
References
5.17.2 networkx.generators.community.connected_caveman_graph
connected_caveman_graph(l,k)
Returns a connected caveman graph of lcliques of size k.
The connected caveman graph is formed by creating ncliques of size k, then a single edge in each clique is
rewired to a node in an adjacent clique.
Parameters
•l(int) – number of cliques
•k(int) – size of cliques
Returns G – connected caveman graph
Return type NetworkX Graph
Notes
This returns an undirected graph, it can be converted to a directed graph using nx.to_directed(), or a
multigraph using nx.MultiGraph(nx.caveman_graph(l, k)). Only the undirected version is de-
scribed in1and it is unclear which of the directed generalizations is most useful.
Examples
>>> G=nx.connected_caveman_graph(3,3)
References
5.17.3 networkx.generators.community.relaxed_caveman_graph
relaxed_caveman_graph(l,k,p,seed=None)
Return a relaxed caveman graph.
A relaxed caveman graph starts with lcliques of size k. Edges are then randomly rewired with probability pto
link different cliques.
Parameters
•l(int) – Number of groups
•k(int) – Size of cliques
1Watts, D. J. ‘Networks, Dynamics, and the Small-World Phenomenon.’ Amer. J. Soc. 105, 493-527, 1999.
564 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•p(float) – Probabilty of rewiring each edge.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – Relaxed Caveman Graph
Return type NetworkX Graph
Raises NetworkXError: – If p is not in [0,1]
Examples
>>> G=nx.relaxed_caveman_graph(2,3,0.1, seed=42)
References
5.17.4 networkx.generators.community.random_partition_graph
random_partition_graph(sizes,p_in,p_out,seed=None,directed=False)
Return the random partition graph with a partition of sizes.
A partition graph is a graph of communities with sizes defined by s in sizes. Nodes in the same group are
connected with probability p_in and nodes of different groups are connected with probability p_out.
Parameters
•sizes (list of ints) – Sizes of groups
•p_in (float) – probability of edges with in groups
•p_out (float) – probability of edges between groups
•directed (boolean optional, default=False) – Whether to create a directed graph
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – random partition graph of size sum(gs)
Return type NetworkX Graph or DiGraph
Raises NetworkXError – If p_in or p_out is not in [0,1]
Examples
>>> G=nx.random_partition_graph([10,10,10],.25,.01)
>>> len(G)
30
>>> partition =G.graph['partition']
>>> len(partition)
3
5.17. Community 565

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This is a generalization of the planted-l-partition described in1. It allows for the creation of groups of any size.
The partition is store as a graph attribute ‘partition’.
References
5.17.5 networkx.generators.community.planted_partition_graph
planted_partition_graph(l,k,p_in,p_out,seed=None,directed=False)
Return the planted l-partition graph.
This model partitions a graph with n=l*k vertices in l groups with k vertices each. Vertices of the same group
are linked with a probability p_in, and vertices of different groups are linked with probability p_out.
Parameters
•l(int) – Number of groups
•k(int) – Number of vertices in each group
•p_in (float) – probability of connecting vertices within a group
•p_out (float) – probability of connected vertices between groups
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (bool,optional (default=False)) – If True return a directed graph
Returns G – planted l-partition graph
Return type NetworkX Graph or DiGraph
Raises NetworkXError: – If p_in,p_out are not in [0,1] or
Examples
>>> G=nx.planted_partition_graph(4,3,0.5,0.1, seed=42)
See also:
random_partition_model()
References
5.17.6 networkx.generators.community.gaussian_random_partition_graph
gaussian_random_partition_graph(n,s,v,p_in,p_out,directed=False,seed=None)
Generate a Gaussian random partition graph.
A Gaussian random partition graph is created by creating k partitions each with a size drawn from a normal
distribution with mean s and variance s/v. Nodes are connected within clusters with probability p_in and between
clusters with probability p_out[1]
Parameters
1Santo Fortunato ‘Community Detection in Graphs’ Physical Reports Volume 486, Issue 3-5 p. 75-174. https://arxiv.org/abs/0906.0612
566 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
•n(int) – Number of nodes in the graph
•s(float) – Mean cluster size
•v(float) – Shape parameter. The variance of cluster size distribution is s/v.
•p_in (float) – Probabilty of intra cluster connection.
•p_out (float) – Probability of inter cluster connection.
•directed (boolean, optional default=False) – Whether to create a directed graph or not
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – gaussian random partition graph
Return type NetworkX Graph or DiGraph
Raises NetworkXError – If s is > n If p_in or p_out is not in [0,1]
Notes
Note the number of partitions is dependent on s,v and n, and that the last partition may be considerably smaller,
as it is sized to simply fill out the nodes [1]
See also:
random_partition_graph()
Examples
>>> G=nx.gaussian_random_partition_graph(100,10,10,.25,.1)
>>> len(G)
100
References
5.17.7 networkx.generators.community.ring_of_cliques
ring_of_cliques(num_cliques,clique_size)
Defines a “ring of cliques” graph.
A ring of cliques graph is consisting of cliques, connected through single links. Each clique is a complete graph.
Parameters
•num_cliques (int) – Number of cliques
•clique_size (int) – Size of cliques
Returns G – ring of cliques graph
Return type NetworkX Graph
Raises NetworkXError – If the number of cliques is lower than 2 or if the size of cliques is
smaller than 2.
5.17. Community 567

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.ring_of_cliques(8,4)
See also:
connected_caveman_graph()
Notes
The connected_caveman_graph graph removes a link from each clique to connect it with the next clique.
Instead, the ring_of_cliques graph simply adds the link without removing any link from the cliques.
5.17.8 networkx.generators.community.stochastic_block_model
stochastic_block_model(sizes,p,nodelist=None,seed=None,directed=False,selfloops=False,
sparse=True)
Return a stochastic block model graph.
This model partitions the nodes in blocks of arbitrary sizes, and places edges between pairs of nodes indepen-
dently, with a probability that depends on the blocks.
Parameters
•sizes (list of ints) – Sizes of blocks
•p(list of list of floats) – Element (r,s) gives the density of edges going from the nodes of
group r to nodes of group s. p must match the number of groups (len(sizes) == len(p)), and
it must be symmetric if the graph is undirected.
•nodelist (list, optional) – The block tags are assigned according to the node identifiers in
nodelist. If nodelist is None, then the ordering is the range [0,sum(sizes)-1].
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
•directed (boolean optional, default=False) – Whether to create a directed graph or not.
•selfloops (boolean optional, default=False) – Whether to include self-loops or not.
•sparse (boolean optional, default=True) – Use the sparse heuristic to speed up the generator.
Returns g – Stochastic block model graph of size sum(sizes)
Return type NetworkX Graph or DiGraph
Raises NetworkXError – If probabilities are not in [0,1]. If the probability matrix is not square
(directed case). If the probability matrix is not symmetric (undirected case). If the sizes list does
not match nodelist or the probability matrix. If nodelist contains duplicate.
Examples
>>> sizes =[75,75,300]
>>> probs =[[0.25,0.05,0.02],
... [0.05,0.35,0.07],
... [0.02,0.07,0.40]]
>>> g=nx.stochastic_block_model(sizes, probs, seed=0)
(continues on next page)
568 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> len(g)
450
>>> H=nx.quotient_graph(g, g.graph['partition'], relabel=True)
>>> for vin H.nodes(data=True):
... print(round(v[1]['density'], 3))
...
0.245
0.348
0.405
>>> for vin H.edges(data=True):
... print(round(1.0 *v[2]['weight']/(sizes[v[0]] *sizes[v[1]]), 3))
...
0.051
0.022
0.07
See also:
random_partition_graph(),planted_partition_graph(),gaussian_random_partition_graph(),
gnp_random_graph()
References
5.17.9 networkx.generators.community.windmill_graph
windmill_graph(n,k)
Generate a windmill graph. A windmill graph is a graph of ncliques each of size kthat are all joined at one
node. It can be thought of as taking a disjoint union of ncliques of size k, selecting one point from each, and
contracting all of the selected points. Alternatively, one could generate ncliques of size k-1 and one node that
is connected to all other nodes in the graph.
Parameters
•n(int) – Number of cliques
•k(int) – Size of cliques
Returns G – windmill graph with n cliques of size k
Return type NetworkX Graph
Raises NetworkXError – If the number of cliques is less than two If the size of the cliques are
less than two
Examples
>>> G=nx.windmill_graph(4,5)
Notes
The node labeled 0will be the node connected to all other nodes. Note that windmill graphs are usually denoted
Wd(k,n), so the parameters are in the opposite order as the parameters of this method.
5.17. Community 569

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.18 Spectral
Generates graphs with a given eigenvector structure
spectral_graph_forge(G, alpha[, . . . ]) Return a random simple graph with spectrum resem-
bling that of G
5.18.1 networkx.generators.spectral_graph_forge.spectral_graph_forge
spectral_graph_forge(G,alpha,transformation=’identity’,seed=None)
Return a random simple graph with spectrum resembling that of G
This algorithm, called Spectral Graph Forge (SGF), computes the eigenvectors of a given graph adjacency ma-
trix, filters them and builds a random graph with a similar eigenstructure. SGF has been proved to be particularly
useful for synthesizing realistic social networks and it can also be used to anonymize graph sensitive data.
Parameters
•G(Graph)
•alpha (float) – Ratio representing the percentage of eigenvectors of G to consider, values in
[0,1].
•transformation (string, optional) – Represents the intended matrix linear transformation,
possible values are ‘identity’ and ‘modularity’
•seed (integer, random_state, or None (default)) – Indicator of numpy random number gen-
eration state. See Randomness.
Returns H – A graph with a similar eigenvector structure of the input one.
Return type Graph
Raises NetworkXError – If transformation has a value different from ‘identity’ or ‘modularity’
Notes
Spectral Graph Forge (SGF) generates a random simple graph resembling the global properties of the given
one. It leverages the low-rank approximation of the associated adjacency matrix driven by the alpha precision
parameter. SGF preserves the number of nodes of the input graph and their ordering. This way, nodes of output
graphs resemble the properties of the input one and attributes can be directly mapped.
It considers the graph adjacency matrices which can optionally be transformed to other symmetric real matrices
(currently transformation options include identity and modularity). The modularity transformation, in the sense
of Newman’s modularity matrix allows the focusing on community structure related properties of the graph.
SGF applies a low-rank approximation whose fixed rank is computed from the ratio alpha of the input graph
adjacency matrix dimension. This step performs a filtering on the input eigenvectors similar to the low pass
filtering common in telecommunications.
The filtered values (after truncation) are used as input to a Bernoulli sampling for constructing a random adja-
cency matrix.
570 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
Examples
>>> import networkx as nx
>>> G=nx.karate_club_graph()
>>> H=nx.spectral_graph_forge(G, 0.3)
>>>
5.19 Trees
Functions for generating trees.
random_tree(n[, seed]) Returns a uniformly random tree on nnodes.
prefix_tree(paths) Creates a directed prefix tree from the given list of iter-
ables.
5.19.1 networkx.generators.trees.random_tree
random_tree(n,seed=None)
Returns a uniformly random tree on nnodes.
Parameters
•n(int) – A positive integer representing the number of nodes in the tree.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns A tree, given as an undirected graph, whose nodes are numbers in the set {0, . . . , n- 1}.
Return type NetworkX graph
Raises NetworkXPointlessConcept – If nis zero (because the null graph is not a tree).
Notes
The current implementation of this function generates a uniformly random Prüfer sequence then converts that
to a tree via the from_prufer_sequence() function. Since there is a bijection between Prüfer sequences
of length n- 2 and trees on nnodes, the tree is chosen uniformly at random from the set of all trees on nnodes.
5.19.2 networkx.generators.trees.prefix_tree
prefix_tree(paths)
Creates a directed prefix tree from the given list of iterables.
Parameters paths (iterable of lists) – An iterable over “paths”, which are themselves lists of nodes.
Common prefixes among these paths are converted into common initial segments in the gener-
ated tree.
Most commonly, this may be an iterable over lists of integers, or an iterable over Python strings.
Returns
5.19. Trees 571

NetworkX Reference, Release 2.3rc1.dev20181203210840
•T(DiGraph) – A directed graph representing an arborescence consisting of the prefix tree
generated by paths. Nodes are directed “downward”, from parent to child. A special
“synthetic” root node is added to be the parent of the first node in each path. A special
“synthetic” leaf node, the “nil” node, is added to be the child of all nodes representing
the last element in a path. (The addition of this nil node technically makes this not an
arborescence but a directed acyclic graph; removing the nil node makes it an arborescence.)
Each node has an attribute ‘source’ whose value is the original element of the path to which
this node corresponds. The ‘source’ of the root node is None, and the ‘source’ of the nil
node is NIL.
The root node is the only node of in-degree zero in the graph, and the nil node is the only
node of out-degree zero. For convenience, the nil node can be accessed via the NIL attribute;
for example:
>>> from networkx.generators.trees import NIL
>>> paths =['ab','abs','ad']
>>> T, root =nx.prefix_tree(paths)
>>> T.predecessors(NIL)
•root (string) – The randomly generated uuid of the root node.
Notes
The prefix tree is also known as a trie.
Examples
Create a prefix tree from a list of strings with some common prefixes:
>>> strings =['ab','abs','ad']
>>> T, root =nx.prefix_tree(strings)
Continuing the above example, to recover the original paths that generated the prefix tree, traverse up the tree
from the NIL node to the root:
>>> from networkx.generators.trees import NIL
>>>
>>> strings =['ab','abs','ad']
>>> T, root =nx.prefix_tree(strings)
>>> recovered =[]
>>> for vin T.predecessors(NIL):
... s=''
... while v!= root:
... # Prepend the character `v` to the accumulator `s`.
... s=str(T.node[v]['source']) +s
... # Each non-nil, non-root node has exactly one parent.
... v=next(T.predecessors(v))
... recovered.append(s)
>>> sorted(recovered)
['ab', 'abs', 'ad']
572 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
5.20 Non Isomorphic Trees
Implementation of the Wright, Richmond, Odlyzko and McKay (WROM) algorithm for the enumeration of all non-
isomorphic free trees of a given order. Rooted trees are represented by level sequences, i.e., lists in which the i-th
element specifies the distance of vertex i to the root.
nonisomorphic_trees(order[, create]) Returns a list of nonisomporphic trees
number_of_nonisomorphic_trees(order) Returns the number of nonisomorphic trees
5.20.1 networkx.generators.nonisomorphic_trees.nonisomorphic_trees
nonisomorphic_trees(order,create=’graph’)
Returns a list of nonisomporphic trees
Parameters
•order (int) – order of the desired tree(s)
•create (graph or matrix (default=”Graph)) – If graph is selected a list of trees will be
returned, if matrix is selected a list of adjancency matrix will be returned
Returns
•G(List of NetworkX Graphs)
•M(List of Adjacency matrices)
References
5.20.2 networkx.generators.nonisomorphic_trees.number_of_nonisomorphic_trees
number_of_nonisomorphic_trees(order)
Returns the number of nonisomorphic trees
Parameters order (int) – order of the desired tree(s)
Returns length
Return type Number of nonisomorphic graphs for the given order
References
5.21 Triads
Functions that generate the triad graphs, that is, the possible digraphs on three nodes.
triad_graph(triad_name) Returns the triad graph with the given name.
5.21.1 networkx.generators.triads.triad_graph
triad_graph(triad_name)
Returns the triad graph with the given name.
5.21. Triads 573

NetworkX Reference, Release 2.3rc1.dev20181203210840
Each string in the following tuple is a valid triad name:
('003','012','102','021D','021U','021C','111D','111U',
'030T','030C','201','120D','120U','120C','210','300')
Each triad name corresponds to one of the possible valid digraph on three nodes.
Parameters triad_name (string) – The name of a triad, as described above.
Returns The digraph on three nodes with the given name. The nodes of the graph are the single-
character strings ‘a’, ‘b’, and ‘c’.
Return type DiGraph
Raises ValueError – If triad_name is not the name of a triad.
See also:
triadic_census()
5.22 Joint Degree Sequence
Generate graphs with a given joint degree
is_valid_joint_degree(joint_degrees) Checks whether the given joint degree dictionary is re-
alizable as a simple graph.
joint_degree_graph(joint_degrees[, seed]) Generates a random simple graph with the given joint
degree dictionary.
5.22.1 networkx.generators.joint_degree_seq.is_valid_joint_degree
is_valid_joint_degree(joint_degrees)
Checks whether the given joint degree dictionary is realizable as a simple graph.
Ajoint degree dictionary is a dictionary of dictionaries, in which entry joint_degrees[k][l] is an integer
representing the number of edges joining nodes of degree kwith nodes of degree l. Such a dictionary is realizable
as a simple graph if and only if the following conditions are satisfied.
• each entry must be an integer,
• the total number of nodes of degree k, computed by sum(joint_degrees[k].values()) / k,
must be an integer,
•the total number of edges joining nodes of degree kwith nodes of degree lcannot exceed the total
number of possible edges,
• each diagonal entry joint_degrees[k][k] must be even (this is a convention assumed by the
joint_degree_graph() function).
Parameters joint_degrees (dictionary of dictionary of integers) – A joint degree dictionary in which
entry joint_degrees[k][l] is the number of edges joining nodes of degree kwith nodes
of degree l.
Returns Whether the given joint degree dictionary is realizable as a simple graph.
Return type bool
574 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
5.22.2 networkx.generators.joint_degree_seq.joint_degree_graph
joint_degree_graph(joint_degrees,seed=None)
Generates a random simple graph with the given joint degree dictionary.
Parameters
•joint_degrees (dictionary of dictionary of integers) – A joint degree dictionary in which
entry joint_degrees[k][l] is the number of edges joining nodes of degree kwith
nodes of degree l.
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns G – A graph with the specified joint degree dictionary.
Return type Graph
Raises NetworkXError – If joint_degrees dictionary is not realizable.
Notes
In each iteration of the “while loop” the algorithm picks two disconnected nodes vand w, of degree kand l
correspondingly, for which joint_degrees[k][l] has not reached its target yet. It then adds edge (v,w)
and increases the number of edges in graph G by one.
The intelligence of the algorithm lies in the fact that it is always possible to add an edge between such discon-
nected nodes vand w, even if one or both nodes do not have free stubs. That is made possible by executing a
“neighbor switch”, an edge rewiring move that releases a free stub while keeping the joint degree of G the same.
The algorithm continues for E (number of edges) iterations of the “while loop”, at the which point all entries of
the given joint_degrees[k][l] have reached their target values and the construction is complete.
References
Examples
>>> import networkx as nx
>>> joint_degrees ={1: {4:1},
... 2: {2:2,3:2,4:2},
... 3: {2:2,4:1},
... 4: {1:1,2:2,3:1}}
>>> G=nx.joint_degree_graph(joint_degrees)
>>>
5.23 Mycielski
Functions related to the Mycielski Operation and the Mycielskian family of graphs.
mycielskian(G[, iterations]) Returns the Mycielskian of a simple, undirected graph
G
Continued on next page
5.23. Mycielski 575

NetworkX Reference, Release 2.3rc1.dev20181203210840
Table 23 – continued from previous page
mycielski_graph(n) Generator for the n_th Mycielski Graph.
5.23.1 networkx.generators.mycielski.mycielskian
mycielskian(G,iterations=1)
Returns the Mycielskian of a simple, undirected graph G
The Mycielskian of graph preserves a graph’s triangle free property while increasing the chromatic number by
1.
The Mycielski Operation on a graph, 𝐺= (𝑉, 𝐸), constructs a new graph with 2|𝑉|+ 1 nodes and 3|𝐸|+|𝑉|
edges.
The construction is as follows:
Let 𝑉= 0, ..., 𝑛 −1. Construct another vertex set 𝑈=𝑛, ..., 2𝑛and a vertex, w. Construct a new graph, M,
with vertices 𝑈𝑉𝑤. For edges, (𝑢, 𝑣)∈𝐸add edges (𝑢, 𝑣),(𝑢, 𝑣 +𝑛), and (𝑢+𝑛, 𝑣)to M. Finally, for
all vertices 𝑢∈𝑈, add edge (𝑢, 𝑤)to M.
The Mycielski Operation can be done multiple times by repeating the above process iteratively.
More information can be found at https://en.wikipedia.org/wiki/Mycielskian
Parameters
•G(graph) – A simple, undirected NetworkX graph
•iterations (int) – The number of iterations of the Mycielski operation to perform on G.
Defaults to 1. Must be a non-negative integer.
Returns M – The Mycielskian of G after the specified number of iterations.
Return type graph
Notes
Graph, node, and edge data are not necessarily propagated to the new graph.
5.23.2 networkx.generators.mycielski.mycielski_graph
mycielski_graph(n)
Generator for the n_th Mycielski Graph.
The Mycielski family of graphs is an infinite set of graphs. 𝑀1is the singleton graph, 𝑀2is two vertices with
an edge, and, for 𝑖 > 2,𝑀𝑖is the Mycielskian of 𝑀𝑖−1.
More information can be found at http://mathworld.wolfram.com/MycielskiGraph.html
Parameters n (int) – The desired Mycielski Graph.
Returns M – The n_th Mycielski Graph
Return type graph
576 Chapter 5. Graph generators

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The first graph in the Mycielski sequence is the singleton graph. The Mycielskian of this graph is not the 𝑃2
graph, but rather the 𝑃2graph with an extra, isolated vertex. The second Mycielski graph is the 𝑃2graph, so the
first two are hard coded. The remaining graphs are generated using the Mycielski operation.
5.23. Mycielski 577

NetworkX Reference, Release 2.3rc1.dev20181203210840
578 Chapter 5. Graph generators

CHAPTER
SIX
LINEAR ALGEBRA
6.1 Graph Matrix
Adjacency matrix and incidence matrix of graphs.
adjacency_matrix(G[, nodelist, weight]) Return adjacency matrix of G.
incidence_matrix(G[, nodelist, edgelist, . . . ]) Return incidence matrix of G.
6.1.1 networkx.linalg.graphmatrix.adjacency_matrix
adjacency_matrix(G,nodelist=None,weight=’weight’)
Return adjacency matrix of G.
Parameters
•G(graph) – A NetworkX graph
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (string or None, optional (default=’weight’)) – The edge data key used to provide
each value in the matrix. If None, then each edge has weight 1.
Returns A – Adjacency matrix representation of G.
Return type SciPy sparse matrix
Notes
For directed graphs, entry i,j corresponds to an edge from i to j.
If you want a pure Python adjacency matrix representation try networkx.convert.to_dict_of_dicts which will
return a dictionary-of-dictionaries format that can be addressed as a sparse matrix.
For MultiGraph/MultiDiGraph with parallel edges the weights are summed. See to_numpy_matrix for other
options.
The convention used for self-loop edges in graphs is to assign the diagonal matrix entry value to the edge weight
attribute (or the number 1 if the edge has no weight attribute). If the alternate convention of doubling the edge
weight is desired the resulting Scipy sparse matrix can be modified as follows:
579

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> import scipy as sp
>>> G=nx.Graph([(1,1)])
>>> A=nx.adjacency_matrix(G)
>>> print(A.todense())
[[1]]
>>> A.setdiag(A.diagonal()*2)
>>> print(A.todense())
[[2]]
See also:
to_numpy_matrix(),to_scipy_sparse_matrix(),to_dict_of_dicts()
6.1.2 networkx.linalg.graphmatrix.incidence_matrix
incidence_matrix(G,nodelist=None,edgelist=None,oriented=False,weight=None)
Return incidence matrix of G.
The incidence matrix assigns each row to a node and each column to an edge. For a standard incidence matrix a
1 appears wherever a row’s node is incident on the column’s edge. For an oriented incidence matrix each edge
is assigned an orientation (arbitrarily for undirected and aligning to direction for directed). A -1 appears for the
tail of an edge and 1 for the head of the edge. The elements are zero otherwise.
Parameters
•G(graph) – A NetworkX graph
•nodelist (list, optional (default= all nodes in G)) – The rows are ordered according to the
nodes in nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•edgelist (list, optional (default= all edges in G)) – The columns are ordered according to
the edges in edgelist. If edgelist is None, then the ordering is produced by G.edges().
•oriented (bool, optional (default=False)) – If True, matrix elements are +1 or -1 for the
head or tail node respectively of each edge. If False, +1 occurs at both nodes.
•weight (string or None, optional (default=None)) – The edge data key used to provide each
value in the matrix. If None, then each edge has weight 1. Edge weights, if used, should be
positive so that the orientation can provide the sign.
Returns A – The incidence matrix of G.
Return type SciPy sparse matrix
Notes
For MultiGraph/MultiDiGraph, the edges in edgelist should be (u,v,key) 3-tuples.
“Networks are the best discrete model for so many problems in applied mathematics”1.
References
6.2 Laplacian Matrix
Laplacian matrix of graphs.
1Gil Strang, Network applications: A = incidence matrix, http://academicearth.org/lectures/network-applications-incidence-matrix
580 Chapter 6. Linear algebra

NetworkX Reference, Release 2.3rc1.dev20181203210840
laplacian_matrix(G[, nodelist, weight]) Return the Laplacian matrix of G.
normalized_laplacian_matrix(G[, nodelist,
...])
Return the normalized Laplacian matrix of G.
directed_laplacian_matrix(G[, nodelist,
...])
Return the directed Laplacian matrix of G.
6.2.1 networkx.linalg.laplacianmatrix.laplacian_matrix
laplacian_matrix(G,nodelist=None,weight=’weight’)
Return the Laplacian matrix of G.
The graph Laplacian is the matrix L = D - A, where A is the adjacency matrix and D is the diagonal matrix of
node degrees.
Parameters
•G(graph) – A NetworkX graph
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (string or None, optional (default=’weight’)) – The edge data key used to compute
each value in the matrix. If None, then each edge has weight 1.
Returns L – The Laplacian matrix of G.
Return type SciPy sparse matrix
Notes
For MultiGraph/MultiDiGraph, the edges weights are summed.
See also:
to_numpy_matrix(),normalized_laplacian_matrix()
6.2.2 networkx.linalg.laplacianmatrix.normalized_laplacian_matrix
normalized_laplacian_matrix(G,nodelist=None,weight=’weight’)
Return the normalized Laplacian matrix of G.
The normalized graph Laplacian is the matrix
𝑁=𝐷−1/2𝐿𝐷−1/2
where Lis the graph Laplacian and Dis the diagonal matrix of node degrees.
Parameters
•G(graph) – A NetworkX graph
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (string or None, optional (default=’weight’)) – The edge data key used to compute
each value in the matrix. If None, then each edge has weight 1.
Returns N – The normalized Laplacian matrix of G.
6.2. Laplacian Matrix 581

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type NumPy matrix
Notes
For MultiGraph/MultiDiGraph, the edges weights are summed. See to_numpy_matrix for other options.
If the Graph contains selfloops, D is defined as diag(sum(A,1)), where A is the adjacency matrix2.
See also:
laplacian_matrix()
References
6.2.3 networkx.linalg.laplacianmatrix.directed_laplacian_matrix
directed_laplacian_matrix(G,nodelist=None,weight=’weight’,walk_type=None,alpha=0.95)
Return the directed Laplacian matrix of G.
The graph directed Laplacian is the matrix
𝐿=𝐼−(Φ1/2𝑃Φ−1/2+ Φ−1/2𝑃𝑇Φ1/2)/2
where Iis the identity matrix, Pis the transition matrix of the graph, and Phi a matrix with the Perron vector
of Pin the diagonal and zeros elsewhere.
Depending on the value of walk_type, Pcan be the transition matrix induced by a random walk, a lazy random
walk, or a random walk with teleportation (PageRank).
Parameters
•G(DiGraph) – A NetworkX graph
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (string or None, optional (default=’weight’)) – The edge data key used to compute
each value in the matrix. If None, then each edge has weight 1.
•walk_type (string or None, optional (default=None)) – If None, Pis selected depending on
the properties of the graph. Otherwise is one of ‘random’, ‘lazy’, or ‘pagerank’
•alpha (real) – (1 - alpha) is the teleportation probability used with pagerank
Returns L – Normalized Laplacian of G.
Return type NumPy array
Raises
•NetworkXError – If NumPy cannot be imported
•NetworkXNotImplemented – If G is not a DiGraph
2Steve Butler, Interlacing For Weighted Graphs Using The Normalized Laplacian, Electronic Journal of Linear Algebra, Volume 16, pp. 90-98,
March 2007.
582 Chapter 6. Linear algebra
NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Only implemented for DiGraphs
See also:
laplacian_matrix()
References
6.3 Spectrum
Eigenvalue spectrum of graphs.
laplacian_spectrum(G[, weight]) Return eigenvalues of the Laplacian of G
adjacency_spectrum(G[, weight]) Return eigenvalues of the adjacency matrix of G.
modularity_spectrum(G) Return eigenvalues of the modularity matrix of G.
6.3.1 networkx.linalg.spectrum.laplacian_spectrum
laplacian_spectrum(G,weight=’weight’)
Return eigenvalues of the Laplacian of G
Parameters
•G(graph) – A NetworkX graph
•weight (string or None, optional (default=’weight’)) – The edge data key used to compute
each value in the matrix. If None, then each edge has weight 1.
Returns evals – Eigenvalues
Return type NumPy array
Notes
For MultiGraph/MultiDiGraph, the edges weights are summed. See to_numpy_matrix for other options.
See also:
laplacian_matrix()
6.3.2 networkx.linalg.spectrum.adjacency_spectrum
adjacency_spectrum(G,weight=’weight’)
Return eigenvalues of the adjacency matrix of G.
Parameters
•G(graph) – A NetworkX graph
•weight (string or None, optional (default=’weight’)) – The edge data key used to compute
each value in the matrix. If None, then each edge has weight 1.
Returns evals – Eigenvalues
6.3. Spectrum 583

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type NumPy array
Notes
For MultiGraph/MultiDiGraph, the edges weights are summed. See to_numpy_matrix for other options.
See also:
adjacency_matrix()
6.3.3 networkx.linalg.spectrum.modularity_spectrum
modularity_spectrum(G)
Return eigenvalues of the modularity matrix of G.
Parameters G (Graph) – A NetworkX Graph or DiGraph
Returns evals – Eigenvalues
Return type NumPy array
See also:
modularity_matrix()
References
6.4 Algebraic Connectivity
Algebraic connectivity and Fiedler vectors of undirected graphs.
algebraic_connectivity(G[, weight, . . . ]) Return the algebraic connectivity of an undirected
graph.
fiedler_vector(G[, weight, normalized, tol, . . . ]) Return the Fiedler vector of a connected undirected
graph.
spectral_ordering(G[, weight, normalized, . . . ]) Compute the spectral_ordering of a graph.
6.4.1 networkx.linalg.algebraicconnectivity.algebraic_connectivity
algebraic_connectivity(G,weight=’weight’,normalized=False,tol=1e-08,method=’tracemin_pcg’,
seed=None)
Return the algebraic connectivity of an undirected graph.
The algebraic connectivity of a connected undirected graph is the second smallest eigenvalue of its Laplacian
matrix.
Parameters
•G(NetworkX graph) – An undirected graph.
•weight (object, optional (default: None)) – The data key used to determine the weight of
each edge. If None, then each edge has unit weight.
•normalized (bool, optional (default: False)) – Whether the normalized Laplacian matrix is
used.
584 Chapter 6. Linear algebra

NetworkX Reference, Release 2.3rc1.dev20181203210840
•tol (float, optional (default: 1e-8)) – Tolerance of relative residual in eigenvalue computa-
tion.
•method (string, optional (default: ‘tracemin_pcg’)) – Method of eigenvalue computation. It
must be one of the tracemin options shown below (TraceMIN), ‘lanczos’ (Lanczos iteration)
or ‘lobpcg’ (LOBPCG).
The TraceMIN algorithm uses a linear system solver. The following values allow specifying
the solver to be used.
Value Solver
‘tracemin_pcg’ Preconditioned conjugate gradient method
‘tracemin_chol’ Cholesky factorization
‘tracemin_lu’ LU factorization
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns algebraic_connectivity – Algebraic connectivity.
Return type float
Raises
•NetworkXNotImplemented – If G is directed.
•NetworkXError – If G has less than two nodes.
Notes
Edge weights are interpreted by their absolute values. For MultiGraph’s, weights of parallel edges are summed.
Zero-weighted edges are ignored.
To use Cholesky factorization in the TraceMIN algorithm, the scikits.sparse package must be installed.
See also:
laplacian_matrix()
6.4.2 networkx.linalg.algebraicconnectivity.fiedler_vector
fiedler_vector(G,weight=’weight’,normalized=False,tol=1e-08,method=’tracemin_pcg’,
seed=None)
Return the Fiedler vector of a connected undirected graph.
The Fiedler vector of a connected undirected graph is the eigenvector corresponding to the second smallest
eigenvalue of the Laplacian matrix of of the graph.
Parameters
•G(NetworkX graph) – An undirected graph.
•weight (object, optional (default: None)) – The data key used to determine the weight of
each edge. If None, then each edge has unit weight.
•normalized (bool, optional (default: False)) – Whether the normalized Laplacian matrix is
used.
•tol (float, optional (default: 1e-8)) – Tolerance of relative residual in eigenvalue computa-
tion.
6.4. Algebraic Connectivity 585

NetworkX Reference, Release 2.3rc1.dev20181203210840
•method (string, optional (default: ‘tracemin_pcg’)) – Method of eigenvalue computation. It
must be one of the tracemin options shown below (TraceMIN), ‘lanczos’ (Lanczos iteration)
or ‘lobpcg’ (LOBPCG).
The TraceMIN algorithm uses a linear system solver. The following values allow specifying
the solver to be used.
Value Solver
‘tracemin_pcg’ Preconditioned conjugate gradient method
‘tracemin_chol’ Cholesky factorization
‘tracemin_lu’ LU factorization
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns fiedler_vector – Fiedler vector.
Return type NumPy array of floats.
Raises
•NetworkXNotImplemented – If G is directed.
•NetworkXError – If G has less than two nodes or is not connected.
Notes
Edge weights are interpreted by their absolute values. For MultiGraph’s, weights of parallel edges are summed.
Zero-weighted edges are ignored.
To use Cholesky factorization in the TraceMIN algorithm, the scikits.sparse package must be installed.
See also:
laplacian_matrix()
6.4.3 networkx.linalg.algebraicconnectivity.spectral_ordering
spectral_ordering(G,weight=’weight’,normalized=False,tol=1e-08,method=’tracemin_pcg’,
seed=None)
Compute the spectral_ordering of a graph.
The spectral ordering of a graph is an ordering of its nodes where nodes in the same weakly connected compo-
nents appear contiguous and ordered by their corresponding elements in the Fiedler vector of the component.
Parameters
•G(NetworkX graph) – A graph.
•weight (object, optional (default: None)) – The data key used to determine the weight of
each edge. If None, then each edge has unit weight.
•normalized (bool, optional (default: False)) – Whether the normalized Laplacian matrix is
used.
•tol (float, optional (default: 1e-8)) – Tolerance of relative residual in eigenvalue computa-
tion.
586 Chapter 6. Linear algebra

NetworkX Reference, Release 2.3rc1.dev20181203210840
•method (string, optional (default: ‘tracemin_pcg’)) – Method of eigenvalue computation. It
must be one of the tracemin options shown below (TraceMIN), ‘lanczos’ (Lanczos iteration)
or ‘lobpcg’ (LOBPCG).
The TraceMIN algorithm uses a linear system solver. The following values allow specifying
the solver to be used.
Value Solver
‘tracemin_pcg’ Preconditioned conjugate gradient method
‘tracemin_chol’ Cholesky factorization
‘tracemin_lu’ LU factorization
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns spectral_ordering – Spectral ordering of nodes.
Return type NumPy array of floats.
Raises NetworkXError – If G is empty.
Notes
Edge weights are interpreted by their absolute values. For MultiGraph’s, weights of parallel edges are summed.
Zero-weighted edges are ignored.
To use Cholesky factorization in the TraceMIN algorithm, the scikits.sparse package must be installed.
See also:
laplacian_matrix()
6.5 Attribute Matrices
Functions for constructing matrix-like objects from graph attributes.
attr_matrix(G[, edge_attr, node_attr, . . . ]) Returns a NumPy matrix using attributes from G.
attr_sparse_matrix(G[, edge_attr, . . . ]) Returns a SciPy sparse matrix using attributes from G.
6.5.1 networkx.linalg.attrmatrix.attr_matrix
attr_matrix(G,edge_attr=None,node_attr=None,normalized=False,rc_order=None,dtype=None,or-
der=None)
Returns a NumPy matrix using attributes from G.
If only Gis passed in, then the adjacency matrix is constructed.
Let A be a discrete set of values for the node attribute node_attr. Then the elements of A represent the rows
and columns of the constructed matrix. Now, iterate through every edge e=(u,v) in Gand consider the value
of the edge attribute edge_attr. If ua and va are the values of the node attribute node_attr for u and v,
respectively, then the value of the edge attribute is added to the matrix element at (ua, va).
Parameters
•G(graph) – The NetworkX graph used to construct the NumPy matrix.
6.5. Attribute Matrices 587

NetworkX Reference, Release 2.3rc1.dev20181203210840
•edge_attr (str, optional) – Each element of the matrix represents a running total of the
specified edge attribute for edges whose node attributes correspond to the rows/cols of the
matirx. The attribute must be present for all edges in the graph. If no attribute is specified,
then we just count the number of edges whose node attributes correspond to the matrix
element.
•node_attr (str, optional) – Each row and column in the matrix represents a particular value
of the node attribute. The attribute must be present for all nodes in the graph. Note, the
values of this attribute should be reliably hashable. So, float values are not recommended.
If no attribute is specified, then the rows and columns will be the nodes of the graph.
•normalized (bool, optional) – If True, then each row is normalized by the summation of its
values.
•rc_order (list, optional) – A list of the node attribute values. This list specifies the ordering
of rows and columns of the array. If no ordering is provided, then the ordering will be
random (and also, a return value).
Other Parameters
•dtype (NumPy data-type, optional) – A valid NumPy dtype used to initialize the array.
Keep in mind certain dtypes can yield unexpected results if the array is to be normalized.
The parameter is passed to numpy.zeros(). If unspecified, the NumPy default is used.
•order ({‘C’, ‘F’}, optional) – Whether to store multidimensional data in C- or Fortran-
contiguous (row- or column-wise) order in memory. This parameter is passed to
numpy.zeros(). If unspecified, the NumPy default is used.
Returns
•M(NumPy matrix) – The attribute matrix.
•ordering (list) – If rc_order was specified, then only the matrix is returned. However, if
rc_order was None, then the ordering used to construct the matrix is returned as well.
Examples
Construct an adjacency matrix:
>>> import numpy as np
>>> try:
... np.set_printoptions(legacy="1.13")
... except TypeError:
... pass
>>> G=nx.Graph()
>>> G.add_edge(0,1, thickness=1, weight=3)
>>> G.add_edge(0,2, thickness=2)
>>> G.add_edge(1,2, thickness=3)
>>> nx.attr_matrix(G, rc_order=[0,1,2])
matrix([[ 0., 1., 1.],
[ 1., 0., 1.],
[ 1., 1., 0.]])
Alternatively, we can obtain the matrix describing edge thickness.
>>> nx.attr_matrix(G, edge_attr='thickness', rc_order=[0,1,2])
matrix([[ 0., 1., 2.],
[ 1., 0., 3.],
[ 2., 3., 0.]])
588 Chapter 6. Linear algebra

NetworkX Reference, Release 2.3rc1.dev20181203210840
We can also color the nodes and ask for the probability distribution over all edges (u,v) describing:
Pr(v has color Y | u has color X)
>>> G.nodes[0]['color']='red'
>>> G.nodes[1]['color']='red'
>>> G.nodes[2]['color']='blue'
>>> rc =['red','blue']
>>> nx.attr_matrix(G, node_attr='color', normalized=True, rc_order=rc)
matrix([[ 0.33333333, 0.66666667],
[ 1. , 0. ]])
For example, the above tells us that for all edges (u,v):
Pr( v is red | u is red) = 1/3 Pr( v is blue | u is red) = 2/3
Pr( v is red | u is blue) = 1 Pr( v is blue | u is blue) = 0
Finally, we can obtain the total weights listed by the node colors.
>>> nx.attr_matrix(G, edge_attr='weight', node_attr='color', rc_order=rc)
matrix([[ 3., 2.],
[ 2., 0.]])
Thus, the total weight over all edges (u,v) with u and v having colors:
(red, red) is 3 # the sole contribution is from edge (0,1) (red, blue) is 2 # contributions from edges
(0,2) and (1,2) (blue, red) is 2 # same as (red, blue) since graph is undirected (blue, blue) is 0 # there
are no edges with blue endpoints
6.5.2 networkx.linalg.attrmatrix.attr_sparse_matrix
attr_sparse_matrix(G,edge_attr=None,node_attr=None,normalized=False,rc_order=None,
dtype=None)
Returns a SciPy sparse matrix using attributes from G.
If only Gis passed in, then the adjacency matrix is constructed.
Let A be a discrete set of values for the node attribute node_attr. Then the elements of A represent the rows
and columns of the constructed matrix. Now, iterate through every edge e=(u,v) in Gand consider the value
of the edge attribute edge_attr. If ua and va are the values of the node attribute node_attr for u and v,
respectively, then the value of the edge attribute is added to the matrix element at (ua, va).
Parameters
•G(graph) – The NetworkX graph used to construct the NumPy matrix.
•edge_attr (str, optional) – Each element of the matrix represents a running total of the
specified edge attribute for edges whose node attributes correspond to the rows/cols of the
matirx. The attribute must be present for all edges in the graph. If no attribute is specified,
then we just count the number of edges whose node attributes correspond to the matrix
element.
•node_attr (str, optional) – Each row and column in the matrix represents a particular value
of the node attribute. The attribute must be present for all nodes in the graph. Note, the
values of this attribute should be reliably hashable. So, float values are not recommended.
If no attribute is specified, then the rows and columns will be the nodes of the graph.
•normalized (bool, optional) – If True, then each row is normalized by the summation of its
values.
6.5. Attribute Matrices 589

NetworkX Reference, Release 2.3rc1.dev20181203210840
•rc_order (list, optional) – A list of the node attribute values. This list specifies the ordering
of rows and columns of the array. If no ordering is provided, then the ordering will be
random (and also, a return value).
Other Parameters dtype (NumPy data-type, optional) – A valid NumPy dtype used to initialize the
array. Keep in mind certain dtypes can yield unexpected results if the array is to be normalized.
The parameter is passed to numpy.zeros(). If unspecified, the NumPy default is used.
Returns
•M(SciPy sparse matrix) – The attribute matrix.
•ordering (list) – If rc_order was specified, then only the matrix is returned. However, if
rc_order was None, then the ordering used to construct the matrix is returned as well.
Examples
Construct an adjacency matrix:
>>> import numpy as np
>>> try:
... np.set_printoptions(legacy="1.13")
... except TypeError:
... pass
>>> G=nx.Graph()
>>> G.add_edge(0,1,thickness=1,weight=3)
>>> G.add_edge(0,2,thickness=2)
>>> G.add_edge(1,2,thickness=3)
>>> M=nx.attr_sparse_matrix(G, rc_order=[0,1,2])
>>> M.todense()
matrix([[ 0., 1., 1.],
[ 1., 0., 1.],
[ 1., 1., 0.]])
Alternatively, we can obtain the matrix describing edge thickness.
>>> M=nx.attr_sparse_matrix(G, edge_attr='thickness', rc_order=[0,1,2])
>>> M.todense()
matrix([[ 0., 1., 2.],
[ 1., 0., 3.],
[ 2., 3., 0.]])
We can also color the nodes and ask for the probability distribution over all edges (u,v) describing:
Pr(v has color Y | u has color X)
>>> G.nodes[0]['color']='red'
>>> G.nodes[1]['color']='red'
>>> G.nodes[2]['color']='blue'
>>> rc =['red','blue']
>>> M=nx.attr_sparse_matrix(G, node_attr='color',
˓→normalized=True, rc_order=rc)
>>> M.todense()
matrix([[ 0.33333333, 0.66666667],
[ 1. , 0. ]])
For example, the above tells us that for all edges (u,v):
Pr( v is red | u is red) = 1/3 Pr( v is blue | u is red) = 2/3
590 Chapter 6. Linear algebra

NetworkX Reference, Release 2.3rc1.dev20181203210840
Pr( v is red | u is blue) = 1 Pr( v is blue | u is blue) = 0
Finally, we can obtain the total weights listed by the node colors.
>>> M=nx.attr_sparse_matrix(G, edge_attr='weight',
˓→node_attr='color', rc_order=rc)
>>> M.todense()
matrix([[ 3., 2.],
[ 2., 0.]])
Thus, the total weight over all edges (u,v) with u and v having colors:
(red, red) is 3 # the sole contribution is from edge (0,1) (red, blue) is 2 # contributions from edges
(0,2) and (1,2) (blue, red) is 2 # same as (red, blue) since graph is undirected (blue, blue) is 0 # there
are no edges with blue endpoints
6.6 Modularity Matrices
Modularity matrix of graphs.
modularity_matrix(G[, nodelist, weight]) Return the modularity matrix of G.
directed_modularity_matrix(G[, nodelist,
weight])
Return the directed modularity matrix of G.
6.6.1 networkx.linalg.modularitymatrix.modularity_matrix
modularity_matrix(G,nodelist=None,weight=None)
Return the modularity matrix of G.
The modularity matrix is the matrix B = A - <A>, where A is the adjacency matrix and <A> is the average
adjacency matrix, assuming that the graph is described by the configuration model.
More specifically, the element B_ij of B is defined as
𝐴𝑖𝑗 −𝑘𝑖𝑘𝑗𝑚
2
where k_i is the degree of node i, and were m is the number of edges in the graph. When weight is set to a name
of an attribute edge, Aij, k_i, k_j and m are computed using its value.
Parameters
•G(Graph) – A NetworkX graph
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used for the edge weight. If None then all edge weights are 1.
Returns B – The modularity matrix of G.
Return type Numpy matrix
6.6. Modularity Matrices 591

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> import networkx as nx
>>> k=[3,2,2,1,0]
>>> G=nx.havel_hakimi_graph(k)
>>> B=nx.modularity_matrix(G)
See also:
to_numpy_matrix(),adjacency_matrix(),laplacian_matrix(),
directed_modularity_matrix()
References
6.6.2 networkx.linalg.modularitymatrix.directed_modularity_matrix
directed_modularity_matrix(G,nodelist=None,weight=None)
Return the directed modularity matrix of G.
The modularity matrix is the matrix B = A - <A>, where A is the adjacency matrix and <A> is the expected
adjacency matrix, assuming that the graph is described by the configuration model.
More specifically, the element B_ij of B is defined as
𝐵𝑖𝑗 =𝐴𝑖𝑗 −𝑘𝑜𝑢𝑡
𝑖𝑘𝑖𝑛
𝑗/𝑚
where 𝑘𝑖𝑛
𝑖is the in degree of node i, and 𝑘𝑜𝑢𝑡
𝑗is the out degree of node j, with m the number of edges in the
graph. When weight is set to a name of an attribute edge, Aij, k_i, k_j and m are computed using its value.
Parameters
•G(DiGraph) – A NetworkX DiGraph
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•weight (string or None, optional (default=None)) – The edge attribute that holds the numer-
ical value used for the edge weight. If None then all edge weights are 1.
Returns B – The modularity matrix of G.
Return type Numpy matrix
Examples
>>> import networkx as nx
>>> G=nx.DiGraph()
>>> G.add_edges_from(((1,2), (1,3), (3,1), (3,2), (3,5), (4,5), (4,6),
... (5,4), (5,6), (6,4)))
>>> B=nx.directed_modularity_matrix(G)
Notes
NetworkX defines the element A_ij of the adjacency matrix as 1 if there is a link going from node i to node j.
Leicht and Newman use the opposite definition. This explains the different expression for B_ij.
See also:
592 Chapter 6. Linear algebra

NetworkX Reference, Release 2.3rc1.dev20181203210840
594 Chapter 6. Linear algebra
CHAPTER
SEVEN
CONVERTING TO AND FROM OTHER DATA FORMATS
7.1 To NetworkX Graph
Functions to convert NetworkX graphs to and from other formats.
The preferred way of converting data to a NetworkX graph is through the graph constructor. The constructor calls the
to_networkx_graph() function which attempts to guess the input type and convert it automatically.
Examples
Create a graph with a single edge from a dictionary of dictionaries
>>> d={0: {1:1}} # dict-of-dicts single edge (0,1)
>>> G=nx.Graph(d)
See also:
nx_agraph,nx_pydot
to_networkx_graph(data[, create_using, . . . ]) Make a NetworkX graph from a known data structure.
7.1.1 networkx.convert.to_networkx_graph
to_networkx_graph(data,create_using=None,multigraph_input=False)
Make a NetworkX graph from a known data structure.
The preferred way to call this is automatically from the class constructor
>>> d={0: {1: {'weight':1}}} # dict-of-dicts single edge (0,1)
>>> G=nx.Graph(d)
instead of the equivalent
>>> G=nx.from_dict_of_dicts(d)
Parameters
•data (object to be converted) –
Current known types are: any NetworkX graph dict-of-dicts dict-of-lists list of edges
Pandas DataFrame (row per edge) numpy matrix numpy ndarray scipy sparse matrix py-
graphviz agraph
595

NetworkX Reference, Release 2.3rc1.dev20181203210840
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•multigraph_input (bool (default False)) – If True and data is a dict_of_dicts, try to create
a multigraph assuming dict_of_dict_of_lists. If data and create_using are both multigraphs
then create a multigraph from a multigraph.
7.2 Dictionaries
to_dict_of_dicts(G[, nodelist, edge_data]) Return adjacency representation of graph as a dictionary
of dictionaries.
from_dict_of_dicts(d[, create_using, . . . ]) Return a graph from a dictionary of dictionaries.
7.2.1 networkx.convert.to_dict_of_dicts
to_dict_of_dicts(G,nodelist=None,edge_data=None)
Return adjacency representation of graph as a dictionary of dictionaries.
Parameters
•G(graph) – A NetworkX graph
•nodelist (list) – Use only nodes specified in nodelist
•edge_data (list, optional) – If provided, the value of the dictionary will be set to edge_data
for all edges. This is useful to make an adjacency matrix type representation with 1 as
the edge data. If edgedata is None, the edgedata in G is used to fill the values. If G is a
multigraph, the edgedata is a dict for each pair (u,v).
7.2.2 networkx.convert.from_dict_of_dicts
from_dict_of_dicts(d,create_using=None,multigraph_input=False)
Return a graph from a dictionary of dictionaries.
Parameters
•d(dictionary of dictionaries) – A dictionary of dictionaries adjacency representation.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•multigraph_input (bool (default False)) – When True, the values of the inner dict are as-
sumed to be containers of edge data for multiple edges. Otherwise this routine assumes the
edge data are singletons.
Examples
>>> dod ={0: {1: {'weight':1}}} # single edge (0,1)
>>> G=nx.from_dict_of_dicts(dod)
or
>>> G=nx.Graph(dod) # use Graph constructor
596 Chapter 7. Converting to and from other data formats

NetworkX Reference, Release 2.3rc1.dev20181203210840
7.3 Lists
to_dict_of_lists(G[, nodelist]) Return adjacency representation of graph as a dictionary
of lists.
from_dict_of_lists(d[, create_using]) Return a graph from a dictionary of lists.
to_edgelist(G[, nodelist]) Return a list of edges in the graph.
from_edgelist(edgelist[, create_using]) Return a graph from a list of edges.
7.3.1 networkx.convert.to_dict_of_lists
to_dict_of_lists(G,nodelist=None)
Return adjacency representation of graph as a dictionary of lists.
Parameters
•G(graph) – A NetworkX graph
•nodelist (list) – Use only nodes specified in nodelist
Notes
Completely ignores edge data for MultiGraph and MultiDiGraph.
7.3.2 networkx.convert.from_dict_of_lists
from_dict_of_lists(d,create_using=None)
Return a graph from a dictionary of lists.
Parameters
•d(dictionary of lists) – A dictionary of lists adjacency representation.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Examples
>>> dol ={0: [1]} # single edge (0,1)
>>> G=nx.from_dict_of_lists(dol)
or
>>> G=nx.Graph(dol) # use Graph constructor
7.3.3 networkx.convert.to_edgelist
to_edgelist(G,nodelist=None)
Return a list of edges in the graph.
Parameters
•G(graph) – A NetworkX graph
7.3. Lists 597

NetworkX Reference, Release 2.3rc1.dev20181203210840
•nodelist (list) – Use only nodes specified in nodelist
7.3.4 networkx.convert.from_edgelist
from_edgelist(edgelist,create_using=None)
Return a graph from a list of edges.
Parameters
•edgelist (list or iterator) – Edge tuples
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Examples
>>> edgelist =[(0,1)] # single edge (0,1)
>>> G=nx.from_edgelist(edgelist)
or
>>> G=nx.Graph(edgelist) # use Graph constructor
7.4 Numpy
Functions to convert NetworkX graphs to and from numpy/scipy matrices.
The preferred way of converting data to a NetworkX graph is through the graph constructor. The constructor calls the
to_networkx_graph() function which attempts to guess the input type and convert it automatically.
Examples
Create a 10 node random graph from a numpy matrix
>>> import numpy as np
>>> a=np.random.randint(0,2, size=(10,10))
>>> D=nx.DiGraph(a)
or equivalently
>>> D=nx.to_networkx_graph(a, create_using=nx.DiGraph)
See also:
nx_agraph,nx_pydot
to_numpy_matrix(G[, nodelist, dtype, order, . . . ]) Return the graph adjacency matrix as a NumPy matrix.
to_numpy_array(G[, nodelist, dtype, order, . . . ]) Return the graph adjacency matrix as a NumPy array.
to_numpy_recarray(G[, nodelist, dtype, order]) Return the graph adjacency matrix as a NumPy recarray.
from_numpy_matrix(A[, parallel_edges, . . . ]) Return a graph from numpy matrix.
from_numpy_array(A[, parallel_edges, . . . ]) Return a graph from NumPy array.
598 Chapter 7. Converting to and from other data formats

NetworkX Reference, Release 2.3rc1.dev20181203210840
7.4.1 networkx.convert_matrix.to_numpy_matrix
to_numpy_matrix(G,nodelist=None,dtype=None,order=None,multigraph_weight=<built-in function
sum>,weight=’weight’,nonedge=0.0)
Return the graph adjacency matrix as a NumPy matrix.
Parameters
•G(graph) – The NetworkX graph used to construct the NumPy matrix.
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•dtype (NumPy data type, optional) – A valid single NumPy data type used to initialize the
array. This must be a simple type such as int or numpy.float64 and not a compound data
type (see to_numpy_recarray) If None, then the NumPy default is used.
•order ({‘C’, ‘F’}, optional) – Whether to store multidimensional data in C- or Fortran-
contiguous (row- or column-wise) order in memory. If None, then the NumPy default is
used.
•multigraph_weight ({sum, min, max}, optional) – An operator that determines how weights
in multigraphs are handled. The default is to sum the weights of the multiple edges.
•weight (string or None optional (default = ‘weight’)) – The edge attribute that holds the
numerical value used for the edge weight. If an edge does not have that attribute, then the
value 1 is used instead.
•nonedge (float (default = 0.0)) – The matrix values corresponding to nonedges are typically
set to zero. However, this could be undesirable if there are matrix values corresponding to
actual edges that also have the value zero. If so, one might prefer nonedges to have some
other value, such as nan.
Returns M – Graph adjacency matrix
Return type NumPy matrix
See also:
to_numpy_recarray(),from_numpy_matrix()
Notes
The matrix entries are assigned to the weight edge attribute. When an edge does not have a weight attribute, the
value of the entry is set to the number 1. For multiple (parallel) edges, the values of the entries are determined
by the multigraph_weight parameter. The default is to sum the weight attributes for each of the parallel
edges.
When nodelist does not contain every node in G, the matrix is built from the subgraph of Gthat is induced
by the nodes in nodelist.
The convention used for self-loop edges in graphs is to assign the diagonal matrix entry value to the weight
attribute of the edge (or the number 1 if the edge has no weight attribute). If the alternate convention of doubling
the edge weight is desired the resulting Numpy matrix can be modified as follows:
>>> import numpy as np
>>> try:
... np.set_printoptions(legacy="1.13")
... except TypeError:
... pass
(continues on next page)
7.4. Numpy 599

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> G=nx.Graph([(1,1)])
>>> A=nx.to_numpy_matrix(G)
>>> A
matrix([[ 1.]])
>>> A.A[np.diag_indices_from(A)] *=2
>>> A
matrix([[ 2.]])
Examples
>>> G=nx.MultiDiGraph()
>>> G.add_edge(0,1, weight=2)
0
>>> G.add_edge(1,0)
0
>>> G.add_edge(2,2, weight=3)
0
>>> G.add_edge(2,2)
1
>>> nx.to_numpy_matrix(G, nodelist=[0,1,2])
matrix([[ 0., 2., 0.],
[ 1., 0., 0.],
[ 0., 0., 4.]])
7.4.2 networkx.convert_matrix.to_numpy_array
to_numpy_array(G,nodelist=None,dtype=None,order=None,multigraph_weight=<built-in function
sum>,weight=’weight’,nonedge=0.0)
Return the graph adjacency matrix as a NumPy array.
Parameters
•G(graph) – The NetworkX graph used to construct the NumPy array.
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•dtype (NumPy data type, optional) – A valid single NumPy data type used to initialize the
array. This must be a simple type such as int or numpy.float64 and not a compound data
type (see to_numpy_recarray) If None, then the NumPy default is used.
•order ({‘C’, ‘F’}, optional) – Whether to store multidimensional data in C- or Fortran-
contiguous (row- or column-wise) order in memory. If None, then the NumPy default is
used.
•multigraph_weight ({sum, min, max}, optional) – An operator that determines how weights
in multigraphs are handled. The default is to sum the weights of the multiple edges.
•weight (string or None optional (default = ‘weight’)) – The edge attribute that holds the
numerical value used for the edge weight. If an edge does not have that attribute, then the
value 1 is used instead.
•nonedge (float (default = 0.0)) – The array values corresponding to nonedges are typically
set to zero. However, this could be undesirable if there are array values corresponding to
actual edges that also have the value zero. If so, one might prefer nonedges to have some
other value, such as nan.
600 Chapter 7. Converting to and from other data formats

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns A – Graph adjacency matrix
Return type NumPy ndarray
See also:
from_numpy_array()
Notes
Entries in the adjacency matrix are assigned to the weight edge attribute. When an edge does not have a weight
attribute, the value of the entry is set to the number 1. For multiple (parallel) edges, the values of the entries are
determined by the multigraph_weight parameter. The default is to sum the weight attributes for each of
the parallel edges.
When nodelist does not contain every node in G, the adjacency matrix is built from the subgraph of Gthat is
induced by the nodes in nodelist.
The convention used for self-loop edges in graphs is to assign the diagonal array entry value to the weight
attribute of the edge (or the number 1 if the edge has no weight attribute). If the alternate convention of doubling
the edge weight is desired the resulting NumPy array can be modified as follows:
>>> import numpy as np
>>> try:
... np.set_printoptions(legacy="1.13")
... except TypeError:
... pass
>>> G=nx.Graph([(1,1)])
>>> A=nx.to_numpy_array(G)
>>> A
array([[ 1.]])
>>> A[np.diag_indices_from(A)] *=2
>>> A
array([[ 2.]])
Examples
>>> G=nx.MultiDiGraph()
>>> G.add_edge(0,1, weight=2)
0
>>> G.add_edge(1,0)
0
>>> G.add_edge(2,2, weight=3)
0
>>> G.add_edge(2,2)
1
>>> nx.to_numpy_array(G, nodelist=[0,1,2])
array([[ 0., 2., 0.],
[ 1., 0., 0.],
[ 0., 0., 4.]])
7.4.3 networkx.convert_matrix.to_numpy_recarray
to_numpy_recarray(G,nodelist=None,dtype=None,order=None)
Return the graph adjacency matrix as a NumPy recarray.
7.4. Numpy 601

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(graph) – The NetworkX graph used to construct the NumPy matrix.
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•dtype (NumPy data-type, optional) – A valid NumPy named dtype used to initialize the
NumPy recarray. The data type names are assumed to be keys in the graph edge attribute
dictionary.
•order ({‘C’, ‘F’}, optional) – Whether to store multidimensional data in C- or Fortran-
contiguous (row- or column-wise) order in memory. If None, then the NumPy default is
used.
Returns M – The graph with specified edge data as a Numpy recarray
Return type NumPy recarray
Notes
When nodelist does not contain every node in G, the matrix is built from the subgraph of Gthat is induced
by the nodes in nodelist.
Examples
>>> G=nx.Graph()
>>> G.add_edge(1,2, weight=7.0, cost=5)
>>> A=nx.to_numpy_recarray(G, dtype=[('weight',float), ('cost',int)])
>>> print(A.weight)
[[ 0. 7.]
[ 7. 0.]]
>>> print(A.cost)
[[0 5]
[5 0]]
7.4.4 networkx.convert_matrix.from_numpy_matrix
from_numpy_matrix(A,parallel_edges=False,create_using=None)
Return a graph from numpy matrix.
The numpy matrix is interpreted as an adjacency matrix for the graph.
Parameters
•A(numpy matrix) – An adjacency matrix representation of a graph
•parallel_edges (Boolean) – If True, create_using is a multigraph, and Ais an integer
matrix, then entry (i, j) in the matrix is interpreted as the number of parallel edges joining
vertices iand jin the graph. If False, then the entries in the adjacency matrix are interpreted
as the weight of a single edge joining the vertices.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
602 Chapter 7. Converting to and from other data formats
NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
If create_using is networkx.MultiGraph or networkx.MultiDiGraph,parallel_edges
is True, and the entries of Aare of type int, then this function returns a multigraph (constructed from
create_using) with parallel edges.
If create_using indicates an undirected multigraph, then only the edges indicated by the upper triangle of
the matrix Awill be added to the graph.
If the numpy matrix has a single data type for each matrix entry it will be converted to an appropriate Python
data type.
If the numpy matrix has a user-specified compound data type the names of the data fields will be used as attribute
keys in the resulting NetworkX graph.
See also:
to_numpy_matrix(),to_numpy_recarray()
Examples
Simple integer weights on edges:
>>> import numpy as np
>>> A=np.matrix([[1,1], [2,1]])
>>> G=nx.from_numpy_matrix(A)
If create_using indicates a multigraph and the matrix has only integer entries and parallel_edges is
False, then the entries will be treated as weights for edges joining the nodes (without creating parallel edges):
>>> A=np.matrix([[1,1], [1,2]])
>>> G=nx.from_numpy_matrix(A, create_using=nx.MultiGraph)
>>> G[1][1]
AtlasView({0: {'weight': 2}})
If create_using indicates a multigraph and the matrix has only integer entries and parallel_edges is
True, then the entries will be treated as the number of parallel edges joining those two vertices:
>>> A=np.matrix([[1,1], [1,2]])
>>> temp =nx.MultiGraph()
>>> G=nx.from_numpy_matrix(A, parallel_edges=True, create_using=temp)
>>> G[1][1]
AtlasView({0: {'weight': 1}, 1: {'weight': 1}})
User defined compound data type on edges:
>>> dt =[('weight',float), ('cost',int)]
>>> A=np.matrix([[(1.0,2)]], dtype=dt)
>>> G=nx.from_numpy_matrix(A)
>>> list(G.edges())
[(0, 0)]
>>> G[0][0]['cost']
2
>>> G[0][0]['weight']
1.0
7.4. Numpy 603

NetworkX Reference, Release 2.3rc1.dev20181203210840
7.4.5 networkx.convert_matrix.from_numpy_array
from_numpy_array(A,parallel_edges=False,create_using=None)
Return a graph from NumPy array.
The NumPy array is interpreted as an adjacency matrix for the graph.
Parameters
•A(NumPy ndarray) – An adjacency matrix representation of a graph
•parallel_edges (Boolean) – If this is True, create_using is a multigraph, and Ais an
integer array, then entry (i, j) in the array is interpreted as the number of parallel edges
joining vertices iand jin the graph. If it is False, then the entries in the array are interpreted
as the weight of a single edge joining the vertices.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Notes
If create_using is networkx.MultiGraph or networkx.MultiDiGraph,parallel_edges
is True, and the entries of Aare of type int, then this function returns a multigraph (of the same type as
create_using) with parallel edges.
If create_using indicates an undirected multigraph, then only the edges indicated by the upper triangle of
the array Awill be added to the graph.
If the NumPy array has a single data type for each array entry it will be converted to an appropriate Python data
type.
If the NumPy array has a user-specified compound data type the names of the data fields will be used as attribute
keys in the resulting NetworkX graph.
See also:
to_numpy_array()
Examples
Simple integer weights on edges:
>>> import numpy as np
>>> A=np.array([[1,1], [2,1]])
>>> G=nx.from_numpy_array(A)
>>> G.edges(data=True)
EdgeDataView([(0, 0, {'weight': 1}), (0, 1, {'weight': 2}), (1, 1, {'weight': 1}
˓→)])
If create_using indicates a multigraph and the array has only integer entries and parallel_edges is
False, then the entries will be treated as weights for edges joining the nodes (without creating parallel edges):
>>> A=np.array([[1,1], [1,2]])
>>> G=nx.from_numpy_array(A, create_using=nx.MultiGraph)
>>> G[1][1]
AtlasView({0: {'weight': 2}})
If create_using indicates a multigraph and the array has only integer entries and parallel_edges is
True, then the entries will be treated as the number of parallel edges joining those two vertices:
604 Chapter 7. Converting to and from other data formats
NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> A=np.array([[1,1], [1,2]])
>>> temp =nx.MultiGraph()
>>> G=nx.from_numpy_array(A, parallel_edges=True, create_using=temp)
>>> G[1][1]
AtlasView({0: {'weight': 1}, 1: {'weight': 1}})
User defined compound data type on edges:
>>> dt =[('weight',float), ('cost',int)]
>>> A=np.array([[(1.0,2)]], dtype=dt)
>>> G=nx.from_numpy_array(A)
>>> G.edges()
EdgeView([(0, 0)])
>>> G[0][0]['cost']
2
>>> G[0][0]['weight']
1.0
7.5 Scipy
to_scipy_sparse_matrix(G[, nodelist, dtype,
...])
Return the graph adjacency matrix as a SciPy sparse ma-
trix.
from_scipy_sparse_matrix(A[, . . . ]) Creates a new graph from an adjacency matrix given as
a SciPy sparse matrix.
7.5.1 networkx.convert_matrix.to_scipy_sparse_matrix
to_scipy_sparse_matrix(G,nodelist=None,dtype=None,weight=’weight’,format=’csr’)
Return the graph adjacency matrix as a SciPy sparse matrix.
Parameters
•G(graph) – The NetworkX graph used to construct the NumPy matrix.
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•dtype (NumPy data-type, optional) – A valid NumPy dtype used to initialize the array. If
None, then the NumPy default is used.
•weight (string or None optional (default=’weight’)) – The edge attribute that holds the
numerical value used for the edge weight. If None then all edge weights are 1.
•format (str in {‘bsr’, ‘csr’, ‘csc’, ‘coo’, ‘lil’, ‘dia’, ‘dok’}) – The type of the matrix to be
returned (default ‘csr’). For some algorithms different implementations of sparse matrices
can perform better. See1for details.
Returns M – Graph adjacency matrix.
Return type SciPy sparse matrix
1Scipy Dev. References, “Sparse Matrices”, https://docs.scipy.org/doc/scipy/reference/sparse.html
7.5. Scipy 605

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
The matrix entries are populated using the edge attribute held in parameter weight. When an edge does not have
that attribute, the value of the entry is 1.
For multiple edges the matrix values are the sums of the edge weights.
When nodelist does not contain every node in G, the matrix is built from the subgraph of Gthat is induced
by the nodes in nodelist.
Uses coo_matrix format. To convert to other formats specify the format= keyword.
The convention used for self-loop edges in graphs is to assign the diagonal matrix entry value to the weight
attribute of the edge (or the number 1 if the edge has no weight attribute). If the alternate convention of doubling
the edge weight is desired the resulting Scipy sparse matrix can be modified as follows:
>>> import scipy as sp
>>> G=nx.Graph([(1,1)])
>>> A=nx.to_scipy_sparse_matrix(G)
>>> print(A.todense())
[[1]]
>>> A.setdiag(A.diagonal() *2)
>>> print(A.todense())
[[2]]
Examples
>>> G=nx.MultiDiGraph()
>>> G.add_edge(0,1, weight=2)
0
>>> G.add_edge(1,0)
0
>>> G.add_edge(2,2, weight=3)
0
>>> G.add_edge(2,2)
1
>>> S=nx.to_scipy_sparse_matrix(G, nodelist=[0,1,2])
>>> print(S.todense())
[[0 2 0]
[1 0 0]
[0 0 4]]
References
7.5.2 networkx.convert_matrix.from_scipy_sparse_matrix
from_scipy_sparse_matrix(A,parallel_edges=False,create_using=None,edge_attribute=’weight’)
Creates a new graph from an adjacency matrix given as a SciPy sparse matrix.
Parameters
•A(scipy sparse matrix) – An adjacency matrix representation of a graph
•parallel_edges (Boolean) – If this is True, create_using is a multigraph, and Ais an
integer matrix, then entry (i, j) in the matrix is interpreted as the number of parallel edges
joining vertices iand jin the graph. If it is False, then the entries in the matrix are interpreted
as the weight of a single edge joining the vertices.
606 Chapter 7. Converting to and from other data formats
NetworkX Reference, Release 2.3rc1.dev20181203210840
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•edge_attribute (string) – Name of edge attribute to store matrix numeric value. The data
will have the same type as the matrix entry (int, float, (real,imag)).
Notes
If create_using is networkx.MultiGraph or networkx.MultiDiGraph,parallel_edges
is True, and the entries of Aare of type int, then this function returns a multigraph (constructed from
create_using) with parallel edges. In this case, edge_attribute will be ignored.
If create_using indicates an undirected multigraph, then only the edges indicated by the upper triangle of
the matrix Awill be added to the graph.
Examples
>>> import scipy as sp
>>> A=sp.sparse.eye(2,2,1)
>>> G=nx.from_scipy_sparse_matrix(A)
If create_using indicates a multigraph and the matrix has only integer entries and parallel_edges is
False, then the entries will be treated as weights for edges joining the nodes (without creating parallel edges):
>>> A=sp.sparse.csr_matrix([[1,1], [1,2]])
>>> G=nx.from_scipy_sparse_matrix(A, create_using=nx.MultiGraph)
>>> G[1][1]
AtlasView({0: {'weight': 2}})
If create_using indicates a multigraph and the matrix has only integer entries and parallel_edges is
True, then the entries will be treated as the number of parallel edges joining those two vertices:
>>> A=sp.sparse.csr_matrix([[1,1], [1,2]])
>>> G=nx.from_scipy_sparse_matrix(A, parallel_edges=True,
... create_using=nx.MultiGraph)
>>> G[1][1]
AtlasView({0: {'weight': 1}, 1: {'weight': 1}})
7.6 Pandas
to_pandas_adjacency(G[, nodelist, dtype, . . . ]) Return the graph adjacency matrix as a Pandas
DataFrame.
from_pandas_adjacency(df[, create_using]) Return a graph from Pandas DataFrame.
to_pandas_edgelist(G[, source, target, . . . ]) Return the graph edge list as a Pandas DataFrame.
from_pandas_edgelist(df[, source, target, . . . ]) Return a graph from Pandas DataFrame containing an
edge list.
7.6. Pandas 607

NetworkX Reference, Release 2.3rc1.dev20181203210840
7.6.1 networkx.convert_matrix.to_pandas_adjacency
to_pandas_adjacency(G,nodelist=None,dtype=None,order=None,multigraph_weight=<built-in
function sum>,weight=’weight’,nonedge=0.0)
Return the graph adjacency matrix as a Pandas DataFrame.
Parameters
•G(graph) – The NetworkX graph used to construct the Pandas DataFrame.
•nodelist (list, optional) – The rows and columns are ordered according to the nodes in
nodelist. If nodelist is None, then the ordering is produced by G.nodes().
•multigraph_weight ({sum, min, max}, optional) – An operator that determines how weights
in multigraphs are handled. The default is to sum the weights of the multiple edges.
•weight (string or None, optional) – The edge attribute that holds the numerical value used
for the edge weight. If an edge does not have that attribute, then the value 1 is used instead.
•nonedge (float, optional) – The matrix values corresponding to nonedges are typically set to
zero. However, this could be undesirable if there are matrix values corresponding to actual
edges that also have the value zero. If so, one might prefer nonedges to have some other
value, such as nan.
Returns df – Graph adjacency matrix
Return type Pandas DataFrame
Notes
The DataFrame entries are assigned to the weight edge attribute. When an edge does not have a weight attribute,
the value of the entry is set to the number 1. For multiple (parallel) edges, the values of the entries are determined
by the ‘multigraph_weight’ parameter. The default is to sum the weight attributes for each of the parallel edges.
When nodelist does not contain every node in G, the matrix is built from the subgraph of Gthat is induced
by the nodes in nodelist.
The convention used for self-loop edges in graphs is to assign the diagonal matrix entry value to the weight
attribute of the edge (or the number 1 if the edge has no weight attribute). If the alternate convention of doubling
the edge weight is desired the resulting Pandas DataFrame can be modified as follows:
>>> import pandas as pd
>>> pd.options.display.max_columns =20
>>> import numpy as np
>>> G=nx.Graph([(1,1)])
>>> df =nx.to_pandas_adjacency(G, dtype=int)
>>> df
1
1 1
>>> df.values[np.diag_indices_from(df)] *=2
>>> df
1
1 2
Examples
608 Chapter 7. Converting to and from other data formats

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.MultiDiGraph()
>>> G.add_edge(0,1, weight=2)
0
>>> G.add_edge(1,0)
0
>>> G.add_edge(2,2, weight=3)
0
>>> G.add_edge(2,2)
1
>>> nx.to_pandas_adjacency(G, nodelist=[0,1,2], dtype=int)
012
0020
1100
2004
7.6.2 networkx.convert_matrix.from_pandas_adjacency
from_pandas_adjacency(df,create_using=None)
Return a graph from Pandas DataFrame.
The Pandas DataFrame is interpreted as an adjacency matrix for the graph.
Parameters
•df (Pandas DataFrame) – An adjacency matrix representation of a graph
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Notes
If the numpy matrix has a single data type for each matrix entry it will be converted to an appropriate Python
data type.
If the numpy matrix has a user-specified compound data type the names of the data fields will be used as attribute
keys in the resulting NetworkX graph.
See also:
to_pandas_adjacency()
Examples
Simple integer weights on edges:
>>> import pandas as pd
>>> pd.options.display.max_columns =20
>>> df =pd.DataFrame([[1,1], [2,1]])
>>> df
0 1
011
121
>>> G=nx.from_pandas_adjacency(df)
>>> G.name ='Graph from pandas adjacency matrix'
>>> print(nx.info(G))
Name: Graph from pandas adjacency matrix
(continues on next page)
7.6. Pandas 609

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
Type: Graph
Number of nodes: 2
Number of edges: 3
Average degree: 3.0000
7.6.3 networkx.convert_matrix.to_pandas_edgelist
to_pandas_edgelist(G,source=’source’,target=’target’,nodelist=None,dtype=None,order=None)
Return the graph edge list as a Pandas DataFrame.
Parameters
•G(graph) – The NetworkX graph used to construct the Pandas DataFrame.
•source (str or int, optional) – A valid column name (string or integer) for the source nodes
(for the directed case).
•target (str or int, optional) – A valid column name (string or integer) for the target nodes
(for the directed case).
•nodelist (list, optional) – Use only nodes specified in nodelist
Returns df – Graph edge list
Return type Pandas DataFrame
Examples
>>> G=nx.Graph([('A','B', {'cost':1,'weight':7}),
... ('C','E', {'cost':9,'weight':10})])
>>> df =nx.to_pandas_edgelist(G, nodelist=['A','C'])
>>> df[['source','target','cost','weight']]
source target cost weight
0 A B 1 7
1 C E 9 10
7.6.4 networkx.convert_matrix.from_pandas_edgelist
from_pandas_edgelist(df,source=’source’,target=’target’,edge_attr=None,create_using=None)
Return a graph from Pandas DataFrame containing an edge list.
The Pandas DataFrame should contain at least two columns of node names and zero or more columns of edge
attributes. Each row will be processed as one edge instance.
Note: This function iterates over DataFrame.values, which is not guaranteed to retain the data type across
columns in the row. This is only a problem if your row is entirely numeric and a mix of ints and floats. In that
case, all values will be returned as floats. See the DataFrame.iterrows documentation for an example.
Parameters
•df (Pandas DataFrame) – An edge list representation of a graph
•source (str or int) – A valid column name (string or integer) for the source nodes (for the
directed case).
610 Chapter 7. Converting to and from other data formats

NetworkX Reference, Release 2.3rc1.dev20181203210840
•target (str or int) – A valid column name (string or integer) for the target nodes (for the
directed case).
•edge_attr (str or int, iterable, True) – A valid column name (str or integer) or list of column
names that will be used to retrieve items from the row and add them to the graph as edge
attributes. If True, all of the remaining columns will be added.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
See also:
to_pandas_edgelist()
Examples
Simple integer weights on edges:
>>> import pandas as pd
>>> pd.options.display.max_columns =20
>>> import numpy as np
>>> rng =np.random.RandomState(seed=5)
>>> ints =rng.randint(1,11, size=(3,2))
>>> a=['A','B','C']
>>> b=['D','A','E']
>>> df =pd.DataFrame(ints, columns=['weight','cost'])
>>> df[0]=a
>>> df['b']=b
>>> df[['weight','cost',0,'b']]
weight cost 0 b
0 4 7 A D
1 7 1 B A
2 10 9 C E
>>> G=nx.from_pandas_edgelist(df, 0,'b', ['weight','cost'])
>>> G['E']['C']['weight']
10
>>> G['E']['C']['cost']
9
>>> edges =pd.DataFrame({'source': [0,1,2],
... 'target': [2,2,3],
... 'weight': [3,4,5],
... 'color': ['red','blue','blue']})
>>> G=nx.from_pandas_edgelist(edges, edge_attr=True)
>>> G[0][2]['color']
'red'
7.6. Pandas 611

NetworkX Reference, Release 2.3rc1.dev20181203210840
612 Chapter 7. Converting to and from other data formats

CHAPTER
EIGHT
RELABELING NODES
8.1 Relabeling
convert_node_labels_to_integers(G[,
...])
Return a copy of the graph G with the nodes relabeled
using consecutive integers.
relabel_nodes(G, mapping[, copy]) Relabel the nodes of the graph G.
8.1.1 networkx.relabel.convert_node_labels_to_integers
convert_node_labels_to_integers(G,first_label=0,ordering=’default’,label_attribute=None)
Return a copy of the graph G with the nodes relabeled using consecutive integers.
Parameters
•G(graph) – A NetworkX graph
•first_label (int, optional (default=0)) – An integer specifying the starting offset in number-
ing nodes. The new integer labels are numbered first_label, . . . , n-1+first_label.
•ordering (string) – “default” : inherit node ordering from G.nodes() “sorted” : inherit node
ordering from sorted(G.nodes()) “increasing degree” : nodes are sorted by increasing degree
“decreasing degree” : nodes are sorted by decreasing degree
•label_attribute (string, optional (default=None)) – Name of node attribute to store old
label. If None no attribute is created.
Notes
Node and edge attribute data are copied to the new (relabeled) graph.
There is no guarantee that the relabeling of nodes to integers will give the same two integers for two (even
identical graphs). Use the ordering argument to try to preserve the order.
See also:
relabel_nodes()
8.1.2 networkx.relabel.relabel_nodes
relabel_nodes(G,mapping,copy=True)
Relabel the nodes of the graph G.
Parameters
613

NetworkX Reference, Release 2.3rc1.dev20181203210840
•G(graph) – A NetworkX graph
•mapping (dictionary) – A dictionary with the old labels as keys and new labels as values.
A partial mapping is allowed.
•copy (bool (optional, default=True)) – If True return a copy, or if False relabel the nodes in
place.
Examples
To create a new graph with nodes relabeled according to a given dictionary:
>>> G=nx.path_graph(3)
>>> sorted(G)
[0, 1, 2]
>>> mapping ={0:'a',1:'b',2:'c'}
>>> H=nx.relabel_nodes(G, mapping)
>>> sorted(H)
['a', 'b', 'c']
Nodes can be relabeled with any hashable object, including numbers and strings:
>>> import string
>>> G=nx.path_graph(26)# nodes are integers 0 through 25
>>> sorted(G)[:3]
[0, 1, 2]
>>> mapping =dict(zip(G, string.ascii_lowercase))
>>> G=nx.relabel_nodes(G, mapping) # nodes are characters a through z
>>> sorted(G)[:3]
['a', 'b', 'c']
>>> mapping =dict(zip(G, range(1,27)))
>>> G=nx.relabel_nodes(G, mapping) # nodes are integers 1 through 26
>>> sorted(G)[:3]
[1, 2, 3]
To perform a partial in-place relabeling, provide a dictionary mapping only a subset of the nodes, and set the
copy keyword argument to False:
>>> G=nx.path_graph(3)# nodes 0-1-2
>>> mapping ={0:'a',1:'b'}# 0->'a' and 1->'b'
>>> G=nx.relabel_nodes(G, mapping, copy=False)
>>> sorted(G, key=str)
[2, 'a', 'b']
A mapping can also be given as a function:
>>> G=nx.path_graph(3)
>>> H=nx.relabel_nodes(G, lambda x: x ** 2)
>>> list(H)
[0, 1, 4]
Notes
Only the nodes specified in the mapping will be relabeled.
The keyword setting copy=False modifies the graph in place. Relabel_nodes avoids naming collisions by build-
ing a directed graph from mapping which specifies the order of relabelings. Naming collisions, such as a->b,
614 Chapter 8. Relabeling nodes

NetworkX Reference, Release 2.3rc1.dev20181203210840
b->c, are ordered such that “b” gets renamed to “c” before “a” gets renamed “b”. In cases of circular mappings
(e.g. a->b, b->a), modifying the graph is not possible in-place and an exception is raised. In that case, use
copy=True.
See also:
convert_node_labels_to_integers()
8.1. Relabeling 615

NetworkX Reference, Release 2.3rc1.dev20181203210840
616 Chapter 8. Relabeling nodes

CHAPTER
NINE
READING AND WRITING GRAPHS
9.1 Adjacency List
9.1.1 Adjacency List
Read and write NetworkX graphs as adjacency lists.
Adjacency list format is useful for graphs without data associated with nodes or edges and for nodes that can be
meaningfully represented as strings.
Format
The adjacency list format consists of lines with node labels. The first label in a line is the source node. Further labels
in the line are considered target nodes and are added to the graph along with an edge between the source node and
target node.
The graph with edges a-b, a-c, d-e can be represented as the following adjacency list (anything following the # in a
line is a comment):
abc# source target target
d e
read_adjlist(path[, comments, delimiter, . . . ]) Read graph in adjacency list format from path.
write_adjlist(G, path[, comments, . . . ]) Write graph G in single-line adjacency-list format to
path.
parse_adjlist(lines[, comments, delimiter, . . . ]) Parse lines of a graph adjacency list representation.
generate_adjlist(G[, delimiter]) Generate a single line of the graph G in adjacency list
format.
9.1.2 networkx.readwrite.adjlist.read_adjlist
read_adjlist(path,comments=’#’,delimiter=None,create_using=None,nodetype=None,encoding=’utf-
8’)
Read graph in adjacency list format from path.
Parameters
•path (string or file) – Filename or file handle to read. Filenames ending in .gz or .bz2 will
be uncompressed.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
617

NetworkX Reference, Release 2.3rc1.dev20181203210840
create. If graph instance, then cleared before populated.
•nodetype (Python type, optional) – Convert nodes to this type.
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels. The default is whitespace.
Returns G – The graph corresponding to the lines in adjacency list format.
Return type NetworkX graph
Examples
>>> G=nx.path_graph(4)
>>> nx.write_adjlist(G, "test.adjlist")
>>> G=nx.read_adjlist("test.adjlist")
The path can be a filehandle or a string with the name of the file. If a filehandle is provided, it has to be opened
in ‘rb’ mode.
>>> fh=open("test.adjlist",'rb')
>>> G=nx.read_adjlist(fh)
Filenames ending in .gz or .bz2 will be compressed.
>>> nx.write_adjlist(G,"test.adjlist.gz")
>>> G=nx.read_adjlist("test.adjlist.gz")
The optional nodetype is a function to convert node strings to nodetype.
For example
>>> G=nx.read_adjlist("test.adjlist", nodetype=int)
will attempt to convert all nodes to integer type.
Since nodes must be hashable, the function nodetype must return hashable types (e.g. int, float, str, frozenset -
or tuples of those, etc.)
The optional create_using parameter indicates the type of NetworkX graph created. The default is nx.Graph,
an undirected graph. To read the data as a directed graph use
>>> G=nx.read_adjlist("test.adjlist", create_using=nx.DiGraph)
Notes
This format does not store graph or node data.
See also:
write_adjlist()
9.1.3 networkx.readwrite.adjlist.write_adjlist
write_adjlist(G,path,comments=’#’,delimiter=’ ’,encoding=’utf-8’)
Write graph G in single-line adjacency-list format to path.
618 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•path (string or file) – Filename or file handle for data output. Filenames ending in .gz or
.bz2 will be compressed.
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels
•encoding (string, optional) – Text encoding.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_adjlist(G,"test.adjlist")
The path can be a filehandle or a string with the name of the file. If a filehandle is provided, it has to be opened
in ‘wb’ mode.
>>> fh=open("test.adjlist",'wb')
>>> nx.write_adjlist(G, fh)
Notes
This format does not store graph, node, or edge data.
See also:
read_adjlist(),generate_adjlist()
9.1.4 networkx.readwrite.adjlist.parse_adjlist
parse_adjlist(lines,comments=’#’,delimiter=None,create_using=None,nodetype=None)
Parse lines of a graph adjacency list representation.
Parameters
•lines (list or iterator of strings) – Input data in adjlist format
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•nodetype (Python type, optional) – Convert nodes to this type.
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels. The default is whitespace.
Returns G – The graph corresponding to the lines in adjacency list format.
Return type NetworkX graph
Examples
9.1. Adjacency List 619

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> lines =['1 2 5',
... '2 3 4',
... '3 5',
... '4',
... '5']
>>> G=nx.parse_adjlist(lines, nodetype=int)
>>> nodes =[1,2,3,4,5]
>>> all(node in Gfor node in nodes)
True
>>> edges =[(1,2), (1,5), (2,3), (2,4), (3,5)]
>>> all((u, v) in G.edges() or (v, u) in G.edges() for (u, v) in edges)
True
See also:
read_adjlist()
9.1.5 networkx.readwrite.adjlist.generate_adjlist
generate_adjlist(G,delimiter=’ ’)
Generate a single line of the graph G in adjacency list format.
Parameters
•G(NetworkX graph)
•delimiter (string, optional) – Separator for node labels
Returns lines – Lines of data in adjlist format.
Return type string
Examples
>>> G=nx.lollipop_graph(4,3)
>>> for line in nx.generate_adjlist(G):
... print(line)
0123
123
2 3
3 4
4 5
5 6
6
See also:
write_adjlist(),read_adjlist()
9.2 Multiline Adjacency List
9.2.1 Multi-line Adjacency List
Read and write NetworkX graphs as multi-line adjacency lists.
620 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
The multi-line adjacency list format is useful for graphs with nodes that can be meaningfully represented as strings.
With this format simple edge data can be stored but node or graph data is not.
Format
The first label in a line is the source node label followed by the node degree d. The next d lines are target node labels
and optional edge data. That pattern repeats for all nodes in the graph.
The graph with edges a-b, a-c, d-e can be represented as the following adjacency list (anything following the # in a
line is a comment):
# example.multiline-adjlist
a2
b
c
d1
e
read_multiline_adjlist(path[, comments,
...])
Read graph in multi-line adjacency list format from
path.
write_multiline_adjlist(G, path[, . . . ]) Write the graph G in multiline adjacency list format to
path
parse_multiline_adjlist(lines[, comments,
...])
Parse lines of a multiline adjacency list representation
of a graph.
generate_multiline_adjlist(G[, delimiter]) Generate a single line of the graph G in multiline adja-
cency list format.
9.2.2 networkx.readwrite.multiline_adjlist.read_multiline_adjlist
read_multiline_adjlist(path,comments=’#’,delimiter=None,create_using=None,nodetype=None,
edgetype=None,encoding=’utf-8’)
Read graph in multi-line adjacency list format from path.
Parameters
•path (string or file) – Filename or file handle to read. Filenames ending in .gz or .bz2 will
be uncompressed.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•nodetype (Python type, optional) – Convert nodes to this type.
•edgetype (Python type, optional) – Convert edge data to this type.
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels. The default is whitespace.
Returns G
Return type NetworkX graph
9.2. Multiline Adjacency List 621

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> nx.write_multiline_adjlist(G,"test.adjlist")
>>> G=nx.read_multiline_adjlist("test.adjlist")
The path can be a file or a string with the name of the file. If a file s provided, it has to be opened in ‘rb’ mode.
>>> fh=open("test.adjlist",'rb')
>>> G=nx.read_multiline_adjlist(fh)
Filenames ending in .gz or .bz2 will be compressed.
>>> nx.write_multiline_adjlist(G,"test.adjlist.gz")
>>> G=nx.read_multiline_adjlist("test.adjlist.gz")
The optional nodetype is a function to convert node strings to nodetype.
For example
>>> G=nx.read_multiline_adjlist("test.adjlist", nodetype=int)
will attempt to convert all nodes to integer type.
The optional edgetype is a function to convert edge data strings to edgetype.
>>> G=nx.read_multiline_adjlist("test.adjlist")
The optional create_using parameter is a NetworkX graph container. The default is Graph(), an undirected
graph. To read the data as a directed graph use
>>> G=nx.read_multiline_adjlist("test.adjlist", create_using=nx.DiGraph)
Notes
This format does not store graph, node, or edge data.
See also:
write_multiline_adjlist()
9.2.3 networkx.readwrite.multiline_adjlist.write_multiline_adjlist
write_multiline_adjlist(G,path,delimiter=’ ’,comments=’#’,encoding=’utf-8’)
Write the graph G in multiline adjacency list format to path
Parameters
•G(NetworkX graph)
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels
•encoding (string, optional) – Text encoding.
622 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> nx.write_multiline_adjlist(G,"test.adjlist")
The path can be a file handle or a string with the name of the file. If a file handle is provided, it has to be opened
in ‘wb’ mode.
>>> fh=open("test.adjlist",'wb')
>>> nx.write_multiline_adjlist(G,fh)
Filenames ending in .gz or .bz2 will be compressed.
>>> nx.write_multiline_adjlist(G,"test.adjlist.gz")
See also:
read_multiline_adjlist()
9.2.4 networkx.readwrite.multiline_adjlist.parse_multiline_adjlist
parse_multiline_adjlist(lines,comments=’#’,delimiter=None,create_using=None,node-
type=None,edgetype=None)
Parse lines of a multiline adjacency list representation of a graph.
Parameters
•lines (list or iterator of strings) – Input data in multiline adjlist format
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•nodetype (Python type, optional) – Convert nodes to this type.
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels. The default is whitespace.
Returns G – The graph corresponding to the lines in multiline adjacency list format.
Return type NetworkX graph
Examples
>>> lines =['1 2',
... "2 {'weight':3, 'name': 'Frodo'}",
... "3 {}",
... "2 1",
... "5 {'weight':6, 'name': 'Saruman'}"]
>>> G=nx.parse_multiline_adjlist(iter(lines), nodetype=int)
>>> list(G)
[1, 2, 3, 5]
9.2.5 networkx.readwrite.multiline_adjlist.generate_multiline_adjlist
generate_multiline_adjlist(G,delimiter=’ ’)
Generate a single line of the graph G in multiline adjacency list format.
9.2. Multiline Adjacency List 623

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(NetworkX graph)
•delimiter (string, optional) – Separator for node labels
Returns lines – Lines of data in multiline adjlist format.
Return type string
Examples
>>> G=nx.lollipop_graph(4,3)
>>> for line in nx.generate_multiline_adjlist(G):
... print(line)
0 3
1 {}
2 {}
3 {}
1 2
2 {}
3 {}
2 1
3 {}
3 1
4 {}
4 1
5 {}
5 1
6 {}
6 0
See also:
write_multiline_adjlist(),read_multiline_adjlist()
9.3 Edge List
9.3.1 Edge Lists
Read and write NetworkX graphs as edge lists.
The multi-line adjacency list format is useful for graphs with nodes that can be meaningfully represented as strings.
With the edgelist format simple edge data can be stored but node or graph data is not. There is no way of representing
isolated nodes unless the node has a self-loop edge.
Format
You can read or write three formats of edge lists with these functions.
Node pairs with no data:
1 2
Python dictionary as data:
624 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
12{'weight':7,'color':'green'}
Arbitrary data:
127green
read_edgelist(path[, comments, delimiter, . . . ]) Read a graph from a list of edges.
write_edgelist(G, path[, comments, . . . ]) Write graph as a list of edges.
read_weighted_edgelist(path[, comments,
...])
Read a graph as list of edges with numeric weights.
write_weighted_edgelist(G, path[, comments,
...])
Write graph G as a list of edges with numeric weights.
generate_edgelist(G[, delimiter, data]) Generate a single line of the graph G in edge list format.
parse_edgelist(lines[, comments, delimiter, . . . ]) Parse lines of an edge list representation of a graph.
9.3.2 networkx.readwrite.edgelist.read_edgelist
read_edgelist(path,comments=’#’,delimiter=None,create_using=None,nodetype=None,data=True,
edgetype=None,encoding=’utf-8’)
Read a graph from a list of edges.
Parameters
•path (file or string) – File or filename to read. If a file is provided, it must be opened in ‘rb’
mode. Filenames ending in .gz or .bz2 will be uncompressed.
•comments (string, optional) – The character used to indicate the start of a comment.
•delimiter (string, optional) – The string used to separate values. The default is whitespace.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•nodetype (int, float, str, Python type, optional) – Convert node data from strings to specified
type
•data (bool or list of (label,type) tuples) – Tuples specifying dictionary key names and types
for edge data
•edgetype (int, float, str, Python type, optional OBSOLETE) – Convert edge data from strings
to specified type and use as ‘weight’
•encoding (string, optional) – Specify which encoding to use when reading file.
Returns G – A networkx Graph or other type specified with create_using
Return type graph
Examples
>>> nx.write_edgelist(nx.path_graph(4), "test.edgelist")
>>> G=nx.read_edgelist("test.edgelist")
>>> fh=open("test.edgelist",'rb')
>>> G=nx.read_edgelist(fh)
>>> fh.close()
9.3. Edge List 625

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.read_edgelist("test.edgelist", nodetype=int)
>>> G=nx.read_edgelist("test.edgelist",create_using=nx.DiGraph)
Edgelist with data in a list:
>>> textline ='1 2 3'
>>> fh =open('test.edgelist','w')
>>> d=fh.write(textline)
>>> fh.close()
>>> G=nx.read_edgelist('test.edgelist', nodetype=int, data=(('weight',float),))
>>> list(G)
[1, 2]
>>> list(G.edges(data=True))
[(1, 2, {'weight': 3.0})]
See parse_edgelist() for more examples of formatting.
See also:
parse_edgelist()
Notes
Since nodes must be hashable, the function nodetype must return hashable types (e.g. int, float, str, frozenset -
or tuples of those, etc.)
9.3.3 networkx.readwrite.edgelist.write_edgelist
write_edgelist(G,path,comments=’#’,delimiter=’ ’,data=True,encoding=’utf-8’)
Write graph as a list of edges.
Parameters
•G(graph) – A NetworkX graph
•path (file or string) – File or filename to write. If a file is provided, it must be opened in
‘wb’ mode. Filenames ending in .gz or .bz2 will be compressed.
•comments (string, optional) – The character used to indicate the start of a comment
•delimiter (string, optional) – The string used to separate values. The default is whitespace.
•data (bool or list, optional) – If False write no edge data. If True write a string representation
of the edge data dictionary.. If a list (or other iterable) is provided, write the keys specified
in the list.
•encoding (string, optional) – Specify which encoding to use when writing file.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_edgelist(G, "test.edgelist")
>>> G=nx.path_graph(4)
>>> fh=open("test.edgelist",'wb')
>>> nx.write_edgelist(G, fh)
>>> nx.write_edgelist(G, "test.edgelist.gz")
>>> nx.write_edgelist(G, "test.edgelist.gz", data=False)
626 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.Graph()
>>> G.add_edge(1,2,weight=7,color='red')
>>> nx.write_edgelist(G,'test.edgelist',data=False)
>>> nx.write_edgelist(G,'test.edgelist',data=['color'])
>>> nx.write_edgelist(G,'test.edgelist',data=['color','weight'])
See also:
write_edgelist(),write_weighted_edgelist()
9.3.4 networkx.readwrite.edgelist.read_weighted_edgelist
read_weighted_edgelist(path,comments=’#’,delimiter=None,create_using=None,nodetype=None,
encoding=’utf-8’)
Read a graph as list of edges with numeric weights.
Parameters
•path (file or string) – File or filename to read. If a file is provided, it must be opened in ‘rb’
mode. Filenames ending in .gz or .bz2 will be uncompressed.
•comments (string, optional) – The character used to indicate the start of a comment.
•delimiter (string, optional) – The string used to separate values. The default is whitespace.
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•nodetype (int, float, str, Python type, optional) – Convert node data from strings to specified
type
•encoding (string, optional) – Specify which encoding to use when reading file.
Returns G – A networkx Graph or other type specified with create_using
Return type graph
Notes
Since nodes must be hashable, the function nodetype must return hashable types (e.g. int, float, str, frozenset -
or tuples of those, etc.)
Example edgelist file format.
With numeric edge data:
# read with
# >>> G=nx.read_weighted_edgelist(fh)
# source target data
ab1
ac3.14159
de42
9.3.5 networkx.readwrite.edgelist.write_weighted_edgelist
write_weighted_edgelist(G,path,comments=’#’,delimiter=’ ’,encoding=’utf-8’)
Write graph G as a list of edges with numeric weights.
9.3. Edge List 627

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(graph) – A NetworkX graph
•path (file or string) – File or filename to write. If a file is provided, it must be opened in
‘wb’ mode. Filenames ending in .gz or .bz2 will be compressed.
•comments (string, optional) – The character used to indicate the start of a comment
•delimiter (string, optional) – The string used to separate values. The default is whitespace.
•encoding (string, optional) – Specify which encoding to use when writing file.
Examples
>>> G=nx.Graph()
>>> G.add_edge(1,2,weight=7)
>>> nx.write_weighted_edgelist(G, 'test.weighted.edgelist')
See also:
read_edgelist(),write_edgelist(),write_weighted_edgelist()
9.3.6 networkx.readwrite.edgelist.generate_edgelist
generate_edgelist(G,delimiter=’ ’,data=True)
Generate a single line of the graph G in edge list format.
Parameters
•G(NetworkX graph)
•delimiter (string, optional) – Separator for node labels
•data (bool or list of keys) – If False generate no edge data. If True use a dictionary repre-
sentation of edge data. If a list of keys use a list of data values corresponding to the keys.
Returns lines – Lines of data in adjlist format.
Return type string
Examples
>>> G=nx.lollipop_graph(4,3)
>>> G[1][2]['weight']=3
>>> G[3][4]['capacity']=12
>>> for line in nx.generate_edgelist(G, data=False):
... print(line)
0 1
0 2
0 3
1 2
1 3
2 3
3 4
4 5
5 6
628 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> for line in nx.generate_edgelist(G):
... print(line)
0 1 {}
0 2 {}
0 3 {}
1 2 {'weight': 3}
1 3 {}
2 3 {}
3 4 {'capacity': 12}
4 5 {}
5 6 {}
>>> for line in nx.generate_edgelist(G,data=['weight']):
... print(line)
0 1
0 2
0 3
123
1 3
2 3
3 4
4 5
5 6
See also:
write_adjlist(),read_adjlist()
9.3.7 networkx.readwrite.edgelist.parse_edgelist
parse_edgelist(lines,comments=’#’,delimiter=None,create_using=None,nodetype=None,
data=True)
Parse lines of an edge list representation of a graph.
Parameters
•lines (list or iterator of strings) – Input data in edgelist format
•comments (string, optional) – Marker for comment lines
•delimiter (string, optional) – Separator for node labels
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
•nodetype (Python type, optional) – Convert nodes to this type.
•data (bool or list of (label,type) tuples) – If False generate no edge data or if True use a
dictionary representation of edge data or a list tuples specifying dictionary key names and
types for edge data.
Returns G – The graph corresponding to lines
Return type NetworkX Graph
Examples
Edgelist with no data:
9.3. Edge List 629

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> lines =["1 2",
... "2 3",
... "3 4"]
>>> G=nx.parse_edgelist(lines, nodetype =int)
>>> list(G)
[1, 2, 3, 4]
>>> list(G.edges())
[(1, 2), (2, 3), (3, 4)]
Edgelist with data in Python dictionary representation:
>>> lines =["1 2 {'weight':3}",
... "2 3 {'weight':27}",
... "3 4 {'weight':3.0}"]
>>> G=nx.parse_edgelist(lines, nodetype =int)
>>> list(G)
[1, 2, 3, 4]
>>> list(G.edges(data=True))
[(1, 2, {'weight': 3}), (2, 3, {'weight': 27}), (3, 4, {'weight': 3.0})]
Edgelist with data in a list:
>>> lines =["1 2 3",
... "2 3 27",
... "3 4 3.0"]
>>> G=nx.parse_edgelist(lines, nodetype =int, data=(('weight',float),))
>>> list(G)
[1, 2, 3, 4]
>>> list(G.edges(data=True))
[(1, 2, {'weight': 3.0}), (2, 3, {'weight': 27.0}), (3, 4, {'weight': 3.0})]
See also:
read_weighted_edgelist()
9.4 GEXF
Read and write graphs in GEXF format.
GEXF (Graph Exchange XML Format) is a language for describing complex network structures, their associated data
and dynamics.
This implementation does not support mixed graphs (directed and undirected edges together).
9.4.1 Format
GEXF is an XML format. See https://gephi.org/gexf/format/schema.html for the specification and https://gephi.org/
gexf/format/basic.html for examples.
read_gexf(path[, node_type, relabel, version]) Read graph in GEXF format from path.
write_gexf(G, path[, encoding, prettyprint, . . . ]) Write G in GEXF format to path.
generate_gexf(G[, encoding, prettyprint, . . . ]) Generate lines of GEXF format representation of G.
relabel_gexf_graph(G) Relabel graph using “label” node keyword for node la-
bel.
630 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
9.4.2 networkx.readwrite.gexf.read_gexf
read_gexf(path,node_type=None,relabel=False,version=’1.2draft’)
Read graph in GEXF format from path.
“GEXF (Graph Exchange XML Format) is a language for describing complex networks structures, their associ-
ated data and dynamics”1.
Parameters
•path (file or string) – File or file name to write. File names ending in .gz or .bz2 will be
compressed.
•node_type (Python type (default: None)) – Convert node ids to this type if not None.
•relabel (bool (default: False)) – If True relabel the nodes to use the GEXF node “label”
attribute instead of the node “id” attribute as the NetworkX node label.
•version (string (default: 1.2draft)) – Version of GEFX File Format (see https://gephi.org/
gexf/format/schema.html). Supported values: “1.1draft”, “1.2draft”
Returns graph – If no parallel edges are found a Graph or DiGraph is returned. Otherwise a Multi-
Graph or MultiDiGraph is returned.
Return type NetworkX graph
Notes
This implementation does not support mixed graphs (directed and undirected edges together).
References
9.4.3 networkx.readwrite.gexf.write_gexf
write_gexf(G,path,encoding=’utf-8’,prettyprint=True,version=’1.2draft’)
Write G in GEXF format to path.
“GEXF (Graph Exchange XML Format) is a language for describing complex networks structures, their associ-
ated data and dynamics”1.
Node attributes are checked according to the version of the GEXF schemas used for parameters which are not
user defined, e.g. visualization ‘viz’2. See example for usage.
Parameters
•G(graph) – A NetworkX graph
•path (file or string) – File or file name to write. File names ending in .gz or .bz2 will be
compressed.
•encoding (string (optional, default: ‘utf-8’)) – Encoding for text data.
•prettyprint (bool (optional, default: True)) – If True use line breaks and indenting in output
XML.
1GEXF File Format, https://gephi.org/gexf/format/
1GEXF File Format, https://gephi.org/gexf/format/
2GEXF viz schema 1.1, https://gephi.org/gexf/1.1draft/viz
9.4. GEXF 631

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> nx.write_gexf(G, "test.gexf")
# visualization data >>> G.nodes[0][‘viz’] = {‘size’: 54} >>> G.nodes[0][‘viz’][‘position’] = {‘x’ : 0, ‘y’ : 1}
>>> G.nodes[0][‘viz’][‘color’] = {‘r’ : 0, ‘g’ : 0, ‘b’ : 256}
Notes
This implementation does not support mixed graphs (directed and undirected edges together).
The node id attribute is set to be the string of the node label. If you want to specify an id use set it as node data,
e.g. node[‘a’][‘id’]=1 to set the id of node ‘a’ to 1.
References
9.4.4 networkx.readwrite.gexf.generate_gexf
generate_gexf(G,encoding=’utf-8’,prettyprint=True,version=’1.2draft’)
Generate lines of GEXF format representation of G.
“GEXF (Graph Exchange XML Format) is a language for describing complex networks structures, their associ-
ated data and dynamics”1.
Parameters
•G(graph) – A NetworkX graph
•encoding (string (optional, default: ‘utf-8’)) – Encoding for text data.
•prettyprint (bool (optional, default: True)) – If True use line breaks and indenting in output
XML.
•version (string (default: 1.2draft)) – Version of GEFX File Format (see https://gephi.org/
gexf/format/schema.html). Supported values: “1.1draft”, “1.2draft”
Examples
>>> G=nx.path_graph(4)
>>> linefeed =chr(10)# linefeed=
>>> s=linefeed.join(nx.generate_gexf(G)) # doctest: +SKIP
>>> for line in nx.generate_gexf(G): # doctest: +SKIP
... print line
Notes
This implementation does not support mixed graphs (directed and undirected edges together).
The node id attribute is set to be the string of the node label. If you want to specify an id use set it as node data,
e.g. node[‘a’][‘id’]=1 to set the id of node ‘a’ to 1.
1GEXF File Format, https://gephi.org/gexf/format/
632 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
9.4.5 networkx.readwrite.gexf.relabel_gexf_graph
relabel_gexf_graph(G)
Relabel graph using “label” node keyword for node label.
Parameters G (graph) – A NetworkX graph read from GEXF data
Returns H – A NetworkX graph with relabed nodes
Return type graph
Raises NetworkXError – If node labels are missing or not unique while relabel=True.
Notes
This function relabels the nodes in a NetworkX graph with the “label” attribute. It also handles relabeling the
specific GEXF node attributes “parents”, and “pid”.
9.5 GML
Read graphs in GML format.
“GML, the G>raph Modelling Language, is our proposal for a portable file format for graphs. GML’s key features are
portability, simple syntax, extensibility and flexibility. A GML file consists of a hierarchical key-value lists. Graphs
can be annotated with arbitrary data structures. The idea for a common file format was born at the GD‘95; this proposal
is the outcome of many discussions. GML is the standard file format in the Graphlet graph editor system. It has been
overtaken and adapted by several other systems for drawing graphs.”
GML files are stored using a 7-bit ASCII encoding with any extended ASCII characters (iso8859-1) appearing as
HTML character entities. You will need to give some thought into how the exported data should interact with different
languages and even different Python versions. Re-importing from gml is also a concern.
Without specifying a stringizer/destringizer, the code is capable of handling
int/float/str/dict/list data as required by the GML specification. For other data types, you need to
explicitly supply a stringizer/destringizer.
For better interoperability of data generated by Python 2 and Python 3, we’ve provided literal_stringizer
and literal_destringizer.
For additional documentation on the GML file format, please see the GML website.
Several example graphs in GML format may be found on Mark Newman’s Network data page.
read_gml(path[, label, destringizer]) Read graph in GML format from path.
write_gml(G, path[, stringizer]) Write a graph Gin GML format to the file or file handle
path.
parse_gml(lines[, label, destringizer]) Parse GML graph from a string or iterable.
generate_gml(G[, stringizer]) Generate a single entry of the graph Gin GML format.
literal_destringizer(rep) Convert a Python literal to the value it represents.
literal_stringizer(value) Convert a value to a Python literal in GML represen-
tation.
9.5. GML 633

NetworkX Reference, Release 2.3rc1.dev20181203210840
9.5.1 networkx.readwrite.gml.read_gml
read_gml(path,label=’label’,destringizer=None)
Read graph in GML format from path.
Parameters
•path (filename or filehandle) – The filename or filehandle to read from.
•label (string, optional) – If not None, the parsed nodes will be renamed according to node
attributes indicated by label. Default value: ‘label’.
•destringizer (callable, optional)–Adestringizer that recovers values stored as strings
in GML. If it cannot convert a string to a value, a ValueError is raised. Default value :
None.
Returns G – The parsed graph.
Return type NetworkX graph
Raises NetworkXError – If the input cannot be parsed.
See also:
write_gml(),parse_gml(),literal_destringizer()
Notes
GML files are stored using a 7-bit ASCII encoding with any extended ASCII characters (iso8859-1) appearing
as HTML character entities. Without specifying a stringizer/destringizer, the code is capable of
handling int/float/str/dict/list data as required by the GML specification. For other data types, you
need to explicitly supply a stringizer/destringizer.
For additional documentation on the GML file format, please see the GML website.
See the module docstring networkx.readwrite.gml for more details.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_gml(G, 'test.gml')
>>> H=nx.read_gml('test.gml')
9.5.2 networkx.readwrite.gml.write_gml
write_gml(G,path,stringizer=None)
Write a graph Gin GML format to the file or file handle path.
Parameters
•G(NetworkX graph) – The graph to be converted to GML.
•path (filename or filehandle) – The filename or filehandle to write. Files whose names end
with .gz or .bz2 will be compressed.
•stringizer (callable, optional) – A stringizer which converts non-int/non-float/non-dict
values into strings. If it cannot convert a value into a string, it should raise a ValueError
to indicate that. Default value: None.
634 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
Raises NetworkXError – If stringizer cannot convert a value into a string, or the value to
convert is not a string while stringizer is None.
See also:
read_gml(),generate_gml(),literal_stringizer()
Notes
Graph attributes named ‘directed’, ‘multigraph’, ‘node’ or ‘edge’, node attributes named ‘id’ or ‘label’, edge
attributes named ‘source’ or ‘target’ (or ‘key’ if Gis a multigraph) are ignored because these attribute names are
used to encode the graph structure.
GML files are stored using a 7-bit ASCII encoding with any extended ASCII characters (iso8859-1) appearing
as HTML character entities. Without specifying a stringizer/destringizer, the code is capable of
handling int/float/str/dict/list data as required by the GML specification. For other data types, you
need to explicitly supply a stringizer/destringizer.
Note that while we allow non-standard GML to be read from a file, we make sure to write GML format. In
particular, underscores are not allowed in attribute names. For additional documentation on the GML file format,
please see the GML website.
See the module docstring networkx.readwrite.gml for more details.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_gml(G, "test.gml")
Filenames ending in .gz or .bz2 will be compressed.
>>> nx.write_gml(G, "test.gml.gz")
9.5.3 networkx.readwrite.gml.parse_gml
parse_gml(lines,label=’label’,destringizer=None)
Parse GML graph from a string or iterable.
Parameters
•lines (string or iterable of strings) – Data in GML format.
•label (string, optional) – If not None, the parsed nodes will be renamed according to node
attributes indicated by label. Default value: ‘label’.
•destringizer (callable, optional)–Adestringizer that recovers values stored as strings
in GML. If it cannot convert a string to a value, a ValueError is raised. Default value :
None.
Returns G – The parsed graph.
Return type NetworkX graph
Raises NetworkXError – If the input cannot be parsed.
See also:
write_gml(),read_gml(),literal_destringizer()
9.5. GML 635

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This stores nested GML attributes as dictionaries in the NetworkX graph, node, and edge attribute structures.
GML files are stored using a 7-bit ASCII encoding with any extended ASCII characters (iso8859-1) appearing
as HTML character entities. Without specifying a stringizer/destringizer, the code is capable of
handling int/float/str/dict/list data as required by the GML specification. For other data types, you
need to explicitly supply a stringizer/destringizer.
For additional documentation on the GML file format, please see the GML website.
See the module docstring networkx.readwrite.gml for more details.
9.5.4 networkx.readwrite.gml.generate_gml
generate_gml(G,stringizer=None)
Generate a single entry of the graph Gin GML format.
Parameters
•G(NetworkX graph) – The graph to be converted to GML.
•stringizer (callable, optional) – A stringizer which converts non-int/non-float/non-dict
values into strings. If it cannot convert a value into a string, it should raise a ValueError
to indicate that. Default value: None.
Returns lines – Lines of GML data. Newlines are not appended.
Return type generator of strings
Raises NetworkXError – If stringizer cannot convert a value into a string, or the value to
convert is not a string while stringizer is None.
See also:
literal_stringizer()
Notes
Graph attributes named ‘directed’, ‘multigraph’, ‘node’ or ‘edge’, node attributes named ‘id’ or ‘label’, edge
attributes named ‘source’ or ‘target’ (or ‘key’ if Gis a multigraph) are ignored because these attribute names are
used to encode the graph structure.
GML files are stored using a 7-bit ASCII encoding with any extended ASCII characters (iso8859-1) appearing
as HTML character entities. Without specifying a stringizer/destringizer, the code is capable of
handling int/float/str/dict/list data as required by the GML specification. For other data types, you
need to explicitly supply a stringizer/destringizer.
For additional documentation on the GML file format, please see the GML website.
See the module docstring networkx.readwrite.gml for more details.
Examples
>>> G=nx.Graph()
>>> G.add_node("1")
>>> print("\n".join(nx.generate_gml(G)))
graph [
(continues on next page)
636 Chapter 9. Reading and writing graphs
NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
node [
id 0
label "1"
]
]
>>> G=nx.OrderedMultiGraph([("a","b"), ("a","b")])
>>> print("\n".join(nx.generate_gml(G)))
graph [
multigraph 1
node [
id 0
label "a"
]
node [
id 1
label "b"
]
edge [
source 0
target 1
key 0
]
edge [
source 0
target 1
key 1
]
]
9.5.5 networkx.readwrite.gml.literal_destringizer
literal_destringizer(rep)
Convert a Python literal to the value it represents.
Parameters rep (string) – A Python literal.
Returns value – The value of the Python literal.
Return type object
Raises ValueError – If rep is not a Python literal.
9.5.6 networkx.readwrite.gml.literal_stringizer
literal_stringizer(value)
Convert a value to a Python literal in GML representation.
Parameters value (object) – The value to be converted to GML representation.
Returns rep – A double-quoted Python literal representing value. Unprintable characters are re-
placed by XML character references.
Return type string
Raises ValueError – If value cannot be converted to GML.
9.5. GML 637

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
literal_stringizer is largely the same as repr in terms of functionality but attempts prefix unicode
and bytes literals with uand bto provide better interoperability of data generated by Python 2 and Python 3.
The original value can be recovered using the networkx.readwrite.gml.
literal_destringizer() function.
9.6 Pickle
9.6.1 Pickled Graphs
Read and write NetworkX graphs as Python pickles.
“The pickle module implements a fundamental, but powerful algorithm for serializing and de-serializing a Python
object structure. “Pickling” is the process whereby a Python object hierarchy is converted into a byte stream, and
“unpickling” is the inverse operation, whereby a byte stream is converted back into an object hierarchy.”
Note that NetworkX graphs can contain any hashable Python object as node (not just integers and strings). For arbitrary
data types it may be difficult to represent the data as text. In that case using Python pickles to store the graph data can
be used.
Format
See https://docs.python.org/2/library/pickle.html
read_gpickle(path) Read graph object in Python pickle format.
write_gpickle(G, path[, protocol]) Write graph in Python pickle format.
9.6.2 networkx.readwrite.gpickle.read_gpickle
read_gpickle(path)
Read graph object in Python pickle format.
Pickles are a serialized byte stream of a Python object1. This format will preserve Python objects used as nodes
or edges.
Parameters path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
uncompressed.
Returns G – A NetworkX graph
Return type graph
Examples
>>> G=nx.path_graph(4)
>>> nx.write_gpickle(G, "test.gpickle")
>>> G=nx.read_gpickle("test.gpickle")
1https://docs.python.org/2/library/pickle.html
638 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
9.6.3 networkx.readwrite.gpickle.write_gpickle
write_gpickle(G,path,protocol=4)
Write graph in Python pickle format.
Pickles are a serialized byte stream of a Python object1. This format will preserve Python objects used as nodes
or edges.
Parameters
•G(graph) – A NetworkX graph
•path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
compressed.
•protocol (integer) – Pickling protocol to use. Default value: pickle.
HIGHEST_PROTOCOL.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_gpickle(G, "test.gpickle")
References
9.7 GraphML
9.7.1 GraphML
Read and write graphs in GraphML format.
This implementation does not support mixed graphs (directed and unidirected edges together), hyperedges, nested
graphs, or ports.
“GraphML is a comprehensive and easy-to-use file format for graphs. It consists of a language core to describe the
structural properties of a graph and a flexible extension mechanism to add application-specific data. Its main features
include support of
• directed, undirected, and mixed graphs,
• hypergraphs,
• hierarchical graphs,
• graphical representations,
• references to external data,
• application-specific attribute data, and
• light-weight parsers.
1https://docs.python.org/2/library/pickle.html
9.7. GraphML 639

NetworkX Reference, Release 2.3rc1.dev20181203210840
Unlike many other file formats for graphs, GraphML does not use a custom syntax. Instead, it is based on XML and
hence ideally suited as a common denominator for all kinds of services generating, archiving, or processing graphs.”
http://graphml.graphdrawing.org/
Format
GraphML is an XML format. See http://graphml.graphdrawing.org/specification.html for the specification and http:
//graphml.graphdrawing.org/primer/graphml-primer.html for examples.
read_graphml(path[, node_type, edge_key_type]) Read graph in GraphML format from path.
write_graphml(G, path[, encoding, . . . ]) Write G in GraphML XML format to path
generate_graphml(G[, encoding, prettyprint]) Generate GraphML lines for G
parse_graphml(graphml_string[, node_type]) Read graph in GraphML format from string.
9.7.2 networkx.readwrite.graphml.read_graphml
read_graphml(path,node_type=<class ’str’>,edge_key_type=<class ’int’>)
Read graph in GraphML format from path.
Parameters
•path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
compressed.
•node_type (Python type (default: str)) – Convert node ids to this type
•edge_key_type (Python type (default: int)) – Convert graphml edge ids to this type as key
of multi-edges
Returns graph – If no parallel edges are found a Graph or DiGraph is returned. Otherwise a Multi-
Graph or MultiDiGraph is returned.
Return type NetworkX graph
Notes
Default node and edge attributes are not propagated to each node and edge. They can be obtained from G.
graph and applied to node and edge attributes if desired using something like this:
>>> default_color =G.graph['node_default']['color']# doctest: +SKIP
>>> for node, data in G.nodes(data=True): # doctest: +SKIP
... if 'color' not in data:
... data['color']=default_color
>>> default_color =G.graph['edge_default']['color']# doctest: +SKIP
>>> for u, v, data in G.edges(data=True): # doctest: +SKIP
... if 'color' not in data:
... data['color']=default_color
This implementation does not support mixed graphs (directed and unidirected edges together), hypergraphs,
nested graphs, or ports.
For multigraphs the GraphML edge “id” will be used as the edge key. If not specified then they “key” attribute
will be used. If there is no “key” attribute a default NetworkX multigraph edge key will be provided.
Files with the yEd “yfiles” extension will can be read but the graphics information is discarded.
640 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
yEd compressed files (“file.graphmlz” extension) can be read by renaming the file to “file.graphml.gz”.
9.7.3 networkx.readwrite.graphml.write_graphml
write_graphml(G,path,encoding=’utf-8’,prettyprint=True,infer_numeric_types=False)
Write G in GraphML XML format to path
This function uses the LXML framework and should be faster than the version using the xml library.
Parameters
•G(graph) – A networkx graph
•path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
compressed.
•encoding (string (optional)) – Encoding for text data.
•prettyprint (bool (optional)) – If True use line breaks and indenting in output XML.
•infer_numeric_types (boolean) – Determine if numeric types should be generalized. For
example, if edges have both int and float ‘weight’ attributes, we infer in GraphML that both
are floats.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_graphml_lxml(G, "fourpath.graphml")# doctest: +SKIP
Notes
This implementation does not support mixed graphs (directed and unidirected edges together) hyperedges,
nested graphs, or ports.
9.7.4 networkx.readwrite.graphml.generate_graphml
generate_graphml(G,encoding=’utf-8’,prettyprint=True)
Generate GraphML lines for G
Parameters
•G(graph) – A networkx graph
•encoding (string (optional)) – Encoding for text data.
•prettyprint (bool (optional)) – If True use line breaks and indenting in output XML.
Examples
>>> G=nx.path_graph(4)
>>> linefeed =chr(10)# linefeed =
>>> s=linefeed.join(nx.generate_graphml(G)) # doctest: +SKIP
>>> for line in nx.generate_graphml(G): # doctest: +SKIP
... print(line)
9.7. GraphML 641

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
This implementation does not support mixed graphs (directed and unidirected edges together) hyperedges,
nested graphs, or ports.
9.7.5 networkx.readwrite.graphml.parse_graphml
parse_graphml(graphml_string,node_type=<class ’str’>)
Read graph in GraphML format from string.
Parameters
•graphml_string (string) – String containing graphml information (e.g., contents of a
graphml file).
•node_type (Python type (default: str)) – Convert node ids to this type
Returns graph – If no parallel edges are found a Graph or DiGraph is returned. Otherwise a Multi-
Graph or MultiDiGraph is returned.
Return type NetworkX graph
Examples
>>> G=nx.path_graph(4)
>>> linefeed =chr(10)# linefeed =
>>> s=linefeed.join(nx.generate_graphml(G))
>>> H=nx.parse_graphml(s)
Notes
Default node and edge attributes are not propagated to each node and edge. They can be obtained from G.
graph and applied to node and edge attributes if desired using something like this:
>>> default_color =G.graph['node_default']['color']# doctest: +SKIP
>>> for node, data in G.nodes(data=True): # doctest: +SKIP
... if 'color' not in data:
... data['color']=default_color
>>> default_color =G.graph['edge_default']['color']# doctest: +SKIP
>>> for u, v, data in G.edges(data=True): # doctest: +SKIP
... if 'color' not in data:
... data['color']=default_color
This implementation does not support mixed graphs (directed and unidirected edges together), hypergraphs,
nested graphs, or ports.
For multigraphs the GraphML edge “id” will be used as the edge key. If not specified then they “key” attribute
will be used. If there is no “key” attribute a default NetworkX multigraph edge key will be provided.
642 Chapter 9. Reading and writing graphs
NetworkX Reference, Release 2.3rc1.dev20181203210840
9.8 JSON
9.8.1 JSON data
Generate and parse JSON serializable data for NetworkX graphs.
These formats are suitable for use with the d3.js examples https://d3js.org/
The three formats that you can generate with NetworkX are:
• node-link like in the d3.js example https://bl.ocks.org/mbostock/4062045
• tree like in the d3.js example https://bl.ocks.org/mbostock/4063550
• adjacency like in the d3.js example https://bost.ocks.org/mike/miserables/
node_link_data(G[, attrs]) Return data in node-link format that is suitable for JSON
serialization and use in Javascript documents.
node_link_graph(data[, directed, . . . ]) Return graph from node-link data format.
adjacency_data(G[, attrs]) Return data in adjacency format that is suitable for
JSON serialization and use in Javascript documents.
adjacency_graph(data[, directed, . . . ]) Return graph from adjacency data format.
cytoscape_data(G[, attrs]) Return data in Cytoscape JSON format (cyjs).
cytoscape_graph(data[, attrs])
tree_data(G, root[, attrs]) Return data in tree format that is suitable for JSON se-
rialization and use in Javascript documents.
tree_graph(data[, attrs]) Return graph from tree data format.
jit_data(G[, indent]) Return data in JIT JSON format.
jit_graph(data[, create_using]) Read a graph from JIT JSON.
9.8.2 networkx.readwrite.json_graph.node_link_data
node_link_data(G,attrs=None)
Return data in node-link format that is suitable for JSON serialization and use in Javascript documents.
Parameters
•G(NetworkX graph)
•attrs (dict) – A dictionary that contains five keys ‘source’, ‘target’, ‘name’, ‘key’ and ‘link’.
The corresponding values provide the attribute names for storing NetworkX-internal graph
data. The values should be unique. Default value:
dict(source='source', target='target', name='id',
key='key', link='links')
If some user-defined graph data use these attribute names as data keys, they may be silently
dropped.
Returns data – A dictionary with node-link formatted data.
Return type dict
Raises NetworkXError – If values in attrs are not unique.
9.8. JSON 643

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> from networkx.readwrite import json_graph
>>> G=nx.Graph([('A','B')])
>>> data1 =json_graph.node_link_data(G)
>>> H=nx.gn_graph(2)
>>> data2 =json_graph.node_link_data(H, {'link':'edges','source':'from',
˓→'target':'to'})
To serialize with json
>>> import json
>>> s1 =json.dumps(data1)
>>> s2 =json.dumps(data2, default={'link':'edges','source':'from','target':
˓→'to'})
Notes
Graph, node, and link attributes are stored in this format. Note that attribute keys will be converted to strings in
order to comply with JSON.
Attribute ‘key’ is only used for multigraphs.
See also:
node_link_graph(),adjacency_data(),tree_data()
9.8.3 networkx.readwrite.json_graph.node_link_graph
node_link_graph(data,directed=False,multigraph=True,attrs=None)
Return graph from node-link data format.
Parameters
•data (dict) – node-link formatted graph data
•directed (bool) – If True, and direction not specified in data, return a directed graph.
•multigraph (bool) – If True, and multigraph not specified in data, return a multigraph.
•attrs (dict) – A dictionary that contains five keys ‘source’, ‘target’, ‘name’, ‘key’ and ‘link’.
The corresponding values provide the attribute names for storing NetworkX-internal graph
data. Default value:
dict(source=’source’, target=’target’, name=’id’, key=’key’, link=’links’)
Returns G – A NetworkX graph object
Return type NetworkX graph
Examples
>>> from networkx.readwrite import json_graph
>>> G=nx.Graph([('A','B')])
>>> data =json_graph.node_link_data(G)
>>> H=json_graph.node_link_graph(data)
644 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
Attribute ‘key’ is only used for multigraphs.
See also:
node_link_data(),adjacency_data(),tree_data()
9.8.4 networkx.readwrite.json_graph.adjacency_data
adjacency_data(G,attrs={’id’: ’id’,’key’: ’key’})
Return data in adjacency format that is suitable for JSON serialization and use in Javascript documents.
Parameters
•G(NetworkX graph)
•attrs (dict) – A dictionary that contains two keys ‘id’ and ‘key’. The corresponding values
provide the attribute names for storing NetworkX-internal graph data. The values should be
unique. Default value: dict(id='id', key='key').
If some user-defined graph data use these attribute names as data keys, they may be silently
dropped.
Returns data – A dictionary with adjacency formatted data.
Return type dict
Raises NetworkXError – If values in attrs are not unique.
Examples
>>> from networkx.readwrite import json_graph
>>> G=nx.Graph([(1,2)])
>>> data =json_graph.adjacency_data(G)
To serialize with json
>>> import json
>>> s=json.dumps(data)
Notes
Graph, node, and link attributes will be written when using this format but attribute keys must be strings if you
want to serialize the resulting data with JSON.
The default value of attrs will be changed in a future release of NetworkX.
See also:
adjacency_graph(),node_link_data(),tree_data()
9.8.5 networkx.readwrite.json_graph.adjacency_graph
adjacency_graph(data,directed=False,multigraph=True,attrs={’id’: ’id’,’key’: ’key’})
Return graph from adjacency data format.
9.8. JSON 645

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters data (dict) – Adjacency list formatted graph data
Returns
•G(NetworkX graph) – A NetworkX graph object
•directed (bool) – If True, and direction not specified in data, return a directed graph.
•multigraph (bool) – If True, and multigraph not specified in data, return a multigraph.
•attrs (dict) – A dictionary that contains two keys ‘id’ and ‘key’. The corresponding values
provide the attribute names for storing NetworkX-internal graph data. The values should be
unique. Default value: dict(id='id', key='key').
Examples
>>> from networkx.readwrite import json_graph
>>> G=nx.Graph([(1,2)])
>>> data =json_graph.adjacency_data(G)
>>> H=json_graph.adjacency_graph(data)
Notes
The default value of attrs will be changed in a future release of NetworkX.
See also:
adjacency_graph(),node_link_data(),tree_data()
9.8.6 networkx.readwrite.json_graph.cytoscape_data
cytoscape_data(G,attrs=None)
Return data in Cytoscape JSON format (cyjs).
Parameters G (NetworkX Graph)
Returns data – A dictionary with cyjs formatted data.
Return type dict
Raises NetworkXError – If values in attrs are not unique.
9.8.7 networkx.readwrite.json_graph.cytoscape_graph
cytoscape_graph(data,attrs=None)
9.8.8 networkx.readwrite.json_graph.tree_data
tree_data(G,root,attrs={’children’: ’children’,’id’: ’id’})
Return data in tree format that is suitable for JSON serialization and use in Javascript documents.
Parameters
•G(NetworkX graph) – G must be an oriented tree
•root (node) – The root of the tree
646 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
•attrs (dict) – A dictionary that contains two keys ‘id’ and ‘children’. The corresponding
values provide the attribute names for storing NetworkX-internal graph data. The values
should be unique. Default value: dict(id='id', children='children').
If some user-defined graph data use these attribute names as data keys, they may be silently
dropped.
Returns data – A dictionary with node-link formatted data.
Return type dict
Raises NetworkXError – If values in attrs are not unique.
Examples
>>> from networkx.readwrite import json_graph
>>> G=nx.DiGraph([(1,2)])
>>> data =json_graph.tree_data(G,root=1)
To serialize with json
>>> import json
>>> s=json.dumps(data)
Notes
Node attributes are stored in this format but keys for attributes must be strings if you want to serialize with
JSON.
Graph and edge attributes are not stored.
The default value of attrs will be changed in a future release of NetworkX.
See also:
tree_graph(),node_link_data(),node_link_data()
9.8.9 networkx.readwrite.json_graph.tree_graph
tree_graph(data,attrs={’children’: ’children’,’id’: ’id’})
Return graph from tree data format.
Parameters data (dict) – Tree formatted graph data
Returns
•G(NetworkX DiGraph)
•attrs (dict) – A dictionary that contains two keys ‘id’ and ‘children’. The corresponding
values provide the attribute names for storing NetworkX-internal graph data. The values
should be unique. Default value: dict(id='id', children='children').
Examples
9.8. JSON 647

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> from networkx.readwrite import json_graph
>>> G=nx.DiGraph([(1,2)])
>>> data =json_graph.tree_data(G,root=1)
>>> H=json_graph.tree_graph(data)
Notes
The default value of attrs will be changed in a future release of NetworkX.
See also:
tree_graph(),node_link_data(),adjacency_data()
9.8.10 networkx.readwrite.json_graph.jit_data
jit_data(G,indent=None)
Return data in JIT JSON format.
Parameters
•G(NetworkX Graph)
•indent (optional, default=None) – If indent is a non-negative integer, then JSON array el-
ements and object members will be pretty-printed with that indent level. An indent level
of 0, or negative, will only insert newlines. None (the default) selects the most compact
representation.
Returns data
Return type JIT JSON string
9.8.11 networkx.readwrite.json_graph.jit_graph
jit_graph(data,create_using=None)
Read a graph from JIT JSON.
Parameters
•data (JSON Graph Object)
•create_using (Networkx Graph, optional (default: Graph())) – Return graph of this type.
The provided instance will be cleared.
Returns G
Return type NetworkX Graph built from create_using if provided.
9.9 LEDA
Read graphs in LEDA format.
LEDA is a C++ class library for efficient data types and algorithms.
648 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
9.9.1 Format
See http://www.algorithmic-solutions.info/leda_guide/graphs/leda_native_graph_fileformat.html
read_leda(path[, encoding]) Read graph in LEDA format from path.
parse_leda(lines) Read graph in LEDA format from string or iterable.
9.9.2 networkx.readwrite.leda.read_leda
read_leda(path,encoding=’UTF-8’)
Read graph in LEDA format from path.
Parameters path (file or string) – File or filename to read. Filenames ending in .gz or .bz2 will be
uncompressed.
Returns G
Return type NetworkX graph
Examples
G=nx.read_leda(‘file.leda’)
References
9.9.3 networkx.readwrite.leda.parse_leda
parse_leda(lines)
Read graph in LEDA format from string or iterable.
Parameters lines (string or iterable) – Data in LEDA format.
Returns G
Return type NetworkX graph
Examples
G=nx.parse_leda(string)
References
9.10 YAML
9.10.1 YAML
Read and write NetworkX graphs in YAML format.
“YAML is a data serialization format designed for human readability and interaction with scripting languages.” See
http://www.yaml.org for documentation.
9.10. YAML 649

NetworkX Reference, Release 2.3rc1.dev20181203210840
Format
http://pyyaml.org/wiki/PyYAML
read_yaml(path) Read graph in YAML format from path.
write_yaml(G_to_be_yaml, . . . ) Write graph G in YAML format to path.
9.10.2 networkx.readwrite.nx_yaml.read_yaml
read_yaml(path)
Read graph in YAML format from path.
YAML is a data serialization format designed for human readability and interaction with scripting languages1.
Parameters path (file or string) – File or filename to read. Filenames ending in .gz or .bz2 will be
uncompressed.
Returns G
Return type NetworkX graph
Examples
>>> G=nx.path_graph(4)
>>> nx.write_yaml(G,'test.yaml')
>>> G=nx.read_yaml('test.yaml')
References
9.10.3 networkx.readwrite.nx_yaml.write_yaml
write_yaml(G_to_be_yaml,path_for_yaml_output,**kwds)
Write graph G in YAML format to path.
YAML is a data serialization format designed for human readability and interaction with scripting languages1.
Parameters
•G(graph) – A NetworkX graph
•path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
compressed.
Notes
To use encoding on the output file include e.g. encoding='utf-8' in the keyword arguments.
1http://www.yaml.org
1http://www.yaml.org
650 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> nx.write_yaml(G,'test.yaml')
References
9.11 SparseGraph6
Functions for reading and writing graphs in the graph6 or sparse6 file formats.
According to the author of these formats,
graph6 and sparse6 are formats for storing undirected graphs in a compact manner, using only printable
ASCII characters. Files in these formats have text type and contain one line per graph.
graph6 is suitable for small graphs, or large dense graphs. sparse6 is more space-efficient for large sparse
graphs.
—graph6 and sparse6 homepage
9.11.1 Graph6
Functions for reading and writing graphs in the graph6 format.
The graph6 file format is suitable for small graphs or large dense graphs. For large sparse graphs, use the sparse6
format.
For more information, see the graph6 homepage.
from_graph6_bytes(string) Read a simple undirected graph in graph6 format from
string.
read_graph6(path) Read simple undirected graphs in graph6 format from
path.
to_graph6_bytes(G[, nodes, header]) Convert a simple undirected graph to bytes in graph6
format.
write_graph6(G, path[, nodes, header]) Write a simple undirected graph to a path in graph6 for-
mat.
networkx.readwrite.graph6.from_graph6_bytes
from_graph6_bytes(string)
Read a simple undirected graph in graph6 format from string.
Parameters string (string) – Data in graph6 format, without a trailing newline.
Returns G
Return type Graph
Raises
•NetworkXError – If the string is unable to be parsed in graph6 format
9.11. SparseGraph6 651

NetworkX Reference, Release 2.3rc1.dev20181203210840
•ValueError – If any character cin the input string does not satisfy 63 <= ord(c) <
127.
Examples
>>> G=nx.from_graph6_bytes(b'A_')
>>> sorted(G.edges())
[(0, 1)]
See also:
read_graph6(),write_graph6()
References
networkx.readwrite.graph6.read_graph6
read_graph6(path)
Read simple undirected graphs in graph6 format from path.
Parameters path (file or string) – File or filename to write.
Returns G – If the file contains multiple lines then a list of graphs is returned
Return type Graph or list of Graphs
Raises NetworkXError – If the string is unable to be parsed in graph6 format
Examples
You can read a graph6 file by giving the path to the file:
>>> import tempfile
>>> with tempfile.NamedTemporaryFile() as f:
... _=f.write(b'>>graph6<<A_\n')
... _=f.seek(0)
... G=nx.read_graph6(f.name)
>>> list(G.edges())
[(0, 1)]
You can also read a graph6 file by giving an open file-like object:
>>> import tempfile
>>> with tempfile.NamedTemporaryFile() as f:
... _=f.write(b'>>graph6<<A_\n')
... _=f.seek(0)
... G=nx.read_graph6(f)
>>> list(G.edges())
[(0, 1)]
See also:
from_graph6_bytes(),write_graph6()
652 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
References
networkx.readwrite.graph6.to_graph6_bytes
to_graph6_bytes(G,nodes=None,header=True)
Convert a simple undirected graph to bytes in graph6 format.
Parameters
•G(Graph (undirected))
•nodes (list or iterable) – Nodes are labeled 0. . . n-1 in the order provided. If None the
ordering given by G.nodes() is used.
•header (bool) – If True add ‘>>graph6<<’ bytes to head of data.
Raises
•NetworkXNotImplemented – If the graph is directed or is a multigraph.
•ValueError – If the graph has at least 2** 36 nodes; the graph6 format is only defined
for graphs of order less than 2** 36.
Examples
>>> nx.to_graph6_bytes(nx.path_graph(2)) # doctest: +SKIP
b'>>graph6<<A_\n'
See also:
from_graph6_bytes(),read_graph6(),write_graph6_bytes()
Notes
The returned bytes end with a newline character.
The format does not support edge or node labels, parallel edges or self loops. If self loops are present they are
silently ignored.
References
networkx.readwrite.graph6.write_graph6
write_graph6(G,path,nodes=None,header=True)
Write a simple undirected graph to a path in graph6 format.
Parameters
•G(Graph (undirected))
•path (str) – The path naming the file to which to write the graph.
•nodes (list or iterable) – Nodes are labeled 0. . . n-1 in the order provided. If None the
ordering given by G.nodes() is used.
•header (bool) – If True add ‘>>graph6<<’ string to head of data
Raises
•NetworkXNotImplemented – If the graph is directed or is a multigraph.
9.11. SparseGraph6 653

NetworkX Reference, Release 2.3rc1.dev20181203210840
•ValueError – If the graph has at least 2** 36 nodes; the graph6 format is only defined
for graphs of order less than 2** 36.
Examples
You can write a graph6 file by giving the path to a file:
>>> import tempfile
>>> with tempfile.NamedTemporaryFile() as f:
... nx.write_graph6(nx.path_graph(2), f.name)
... _=f.seek(0)
... print(f.read())
b'>>graph6<<A_\n'
See also:
from_graph6_bytes(),read_graph6()
Notes
The function writes a newline character after writing the encoding of the graph.
The format does not support edge or node labels, parallel edges or self loops. If self loops are present they are
silently ignored.
References
9.11.2 Sparse6
Functions for reading and writing graphs in the sparse6 format.
The sparse6 file format is a space-efficient format for large sparse graphs. For small graphs or large dense graphs, use
the graph6 file format.
For more information, see the sparse6 homepage.
from_sparse6_bytes(string) Read an undirected graph in sparse6 format from string.
read_sparse6(path) Read an undirected graph in sparse6 format from path.
to_sparse6_bytes(G[, nodes, header]) Convert an undirected graph to bytes in sparse6 format.
write_sparse6(G, path[, nodes, header]) Write graph G to given path in sparse6 format.
networkx.readwrite.sparse6.from_sparse6_bytes
from_sparse6_bytes(string)
Read an undirected graph in sparse6 format from string.
Parameters string (string) – Data in sparse6 format
Returns G
Return type Graph
Raises NetworkXError – If the string is unable to be parsed in sparse6 format
654 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.from_sparse6_bytes(b':A_')
>>> sorted(G.edges())
[(0, 1), (0, 1), (0, 1)]
See also:
read_sparse6(),write_sparse6()
References
networkx.readwrite.sparse6.read_sparse6
read_sparse6(path)
Read an undirected graph in sparse6 format from path.
Parameters path (file or string) – File or filename to write.
Returns G – If the file contains multiple lines then a list of graphs is returned
Return type Graph/Multigraph or list of Graphs/MultiGraphs
Raises NetworkXError – If the string is unable to be parsed in sparse6 format
Examples
You can read a sparse6 file by giving the path to the file:
>>> import tempfile
>>> with tempfile.NamedTemporaryFile() as f:
... _=f.write(b'>>sparse6<<:An\n')
... _=f.seek(0)
... G=nx.read_sparse6(f.name)
>>> list(G.edges())
[(0, 1)]
You can also read a sparse6 file by giving an open file-like object:
>>> import tempfile
>>> with tempfile.NamedTemporaryFile() as f:
... _=f.write(b'>>sparse6<<:An\n')
... _=f.seek(0)
... G=nx.read_sparse6(f)
>>> list(G.edges())
[(0, 1)]
See also:
read_sparse6(),from_sparse6_bytes()
References
networkx.readwrite.sparse6.to_sparse6_bytes
to_sparse6_bytes(G,nodes=None,header=True)
Convert an undirected graph to bytes in sparse6 format.
9.11. SparseGraph6 655

NetworkX Reference, Release 2.3rc1.dev20181203210840
Parameters
•G(Graph (undirected))
•nodes (list or iterable) – Nodes are labeled 0. . . n-1 in the order provided. If None the
ordering given by G.nodes() is used.
•header (bool) – If True add ‘>>sparse6<<’ bytes to head of data.
Raises
•NetworkXNotImplemented – If the graph is directed.
•ValueError – If the graph has at least 2** 36 nodes; the sparse6 format is only de-
fined for graphs of order less than 2** 36.
Examples
>>> nx.to_sparse6_bytes(nx.path_graph(2)) # doctest: +SKIP
b'>>sparse6<<:An\n'
See also:
to_sparse6_bytes(),read_sparse6(),write_sparse6_bytes()
Notes
The returned bytes end with a newline character.
The format does not support edge or node labels.
References
networkx.readwrite.sparse6.write_sparse6
write_sparse6(G,path,nodes=None,header=True)
Write graph G to given path in sparse6 format.
Parameters
•G(Graph (undirected))
•path (file or string) – File or filename to write
•nodes (list or iterable) – Nodes are labeled 0. . . n-1 in the order provided. If None the
ordering given by G.nodes() is used.
•header (bool) – If True add ‘>>sparse6<<’ string to head of data
Raises NetworkXError – If the graph is directed
Examples
You can write a sparse6 file by giving the path to the file:
656 Chapter 9. Reading and writing graphs

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> import tempfile
>>> with tempfile.NamedTemporaryFile() as f:
... nx.write_sparse6(nx.path_graph(2), f.name)
... print(f.read())
b'>>sparse6<<:An\n'
You can also write a sparse6 file by giving an open file-like object:
>>> with tempfile.NamedTemporaryFile() as f:
... nx.write_sparse6(nx.path_graph(2), f)
... _=f.seek(0)
... print(f.read())
b'>>sparse6<<:An\n'
See also:
read_sparse6(),from_sparse6_bytes()
Notes
The format does not support edge or node labels.
References
9.12 Pajek
9.12.1 Pajek
Read graphs in Pajek format.
This implementation handles directed and undirected graphs including those with self loops and parallel edges.
Format
See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/draweps.htm for format information.
read_pajek(path[, encoding]) Read graph in Pajek format from path.
write_pajek(G, path[, encoding]) Write graph in Pajek format to path.
parse_pajek(lines) Parse Pajek format graph from string or iterable.
generate_pajek(G) Generate lines in Pajek graph format.
9.12.2 networkx.readwrite.pajek.read_pajek
read_pajek(path,encoding=’UTF-8’)
Read graph in Pajek format from path.
Parameters path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
uncompressed.
Returns G
Return type NetworkX MultiGraph or MultiDiGraph.
9.12. Pajek 657

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> nx.write_pajek(G, "test.net")
>>> G=nx.read_pajek("test.net")
To create a Graph instead of a MultiGraph use
>>> G1=nx.Graph(G)
References
See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/draweps.htm for format information.
9.12.3 networkx.readwrite.pajek.write_pajek
write_pajek(G,path,encoding=’UTF-8’)
Write graph in Pajek format to path.
Parameters
•G(graph) – A Networkx graph
•path (file or string) – File or filename to write. Filenames ending in .gz or .bz2 will be
compressed.
Examples
>>> G=nx.path_graph(4)
>>> nx.write_pajek(G, "test.net")
Warning: Optional node attributes and edge attributes must be non-empty strings. Otherwise it will not be
written into the file. You will need to convert those attributes to strings if you want to keep them.
References
See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/draweps.htm for format information.
9.12.4 networkx.readwrite.pajek.parse_pajek
parse_pajek(lines)
Parse Pajek format graph from string or iterable.
Parameters lines (string or iterable) – Data in Pajek format.
Returns G
Return type NetworkX graph
See also:
read_pajek()
658 Chapter 9. Reading and writing graphs
NetworkX Reference, Release 2.3rc1.dev20181203210840
9.12.5 networkx.readwrite.pajek.generate_pajek
generate_pajek(G)
Generate lines in Pajek graph format.
Parameters G (graph) – A Networkx graph
References
See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/draweps.htm for format information.
9.13 GIS Shapefile
9.13.1 Shapefile
Generates a networkx.DiGraph from point and line shapefiles.
“The Esri Shapefile or simply a shapefile is a popular geospatial vector data format for geographic information systems
software. It is developed and regulated by Esri as a (mostly) open specification for data interoperability among Esri
and other software products.” See https://en.wikipedia.org/wiki/Shapefile for additional information.
read_shp(path[, simplify, geom_attrs, strict]) Generates a networkx.DiGraph from shapefiles.
write_shp(G, outdir) Writes a networkx.DiGraph to two shapefiles, edges and
nodes.
9.13.2 networkx.readwrite.nx_shp.read_shp
read_shp(path,simplify=True,geom_attrs=True,strict=True)
Generates a networkx.DiGraph from shapefiles. Point geometries are translated into nodes, lines into edges.
Coordinate tuples are used as keys. Attributes are preserved, line geometries are simplified into start and end
coordinates. Accepts a single shapefile or directory of many shapefiles.
“The Esri Shapefile or simply a shapefile is a popular geospatial vector data format for geographic information
systems software1.”
Parameters
•path (file or string) – File, directory, or filename to read.
•simplify (bool) – If True, simplify line geometries to start and end coordinates. If False, and
line feature geometry has multiple segments, the non-geometric attributes for that feature
will be repeated for each edge comprising that feature.
•geom_attrs (bool) – If True, include the Wkb, Wkt and Json geometry attributes with each
edge.
NOTE: if these attributes are available, write_shp will use them to write the geometry. If
nodes store the underlying coordinates for the edge geometry as well (as they do when they
are read via this method) and they change, your geomety will be out of sync.
•strict (bool) – If True, raise NetworkXError when feature geometry is missing or Geom-
etryType is not supported. If False, silently ignore missing or unsupported geometry in
features.
1https://en.wikipedia.org/wiki/Shapefile
9.13. GIS Shapefile 659

NetworkX Reference, Release 2.3rc1.dev20181203210840
Returns G
Return type NetworkX graph
Raises
•ImportError – If ogr module is not available.
•RuntimeError – If file cannot be open or read.
•NetworkXError – If strict=True and feature is missing geometry or GeometryType is not
supported.
Examples
>>> G=nx.read_shp('test.shp')# doctest: +SKIP
References
9.13.3 networkx.readwrite.nx_shp.write_shp
write_shp(G,outdir)
Writes a networkx.DiGraph to two shapefiles, edges and nodes. Nodes and edges are expected to have a Well
Known Binary (Wkb) or Well Known Text (Wkt) key in order to generate geometries. Also acceptable are nodes
with a numeric tuple key (x,y).
“The Esri Shapefile or simply a shapefile is a popular geospatial vector data format for geographic information
systems software1.”
Parameters outdir (directory path) – Output directory for the two shapefiles.
Returns
Return type None
Examples
nx.write_shp(digraph, ‘/shapefiles’) # doctest +SKIP
References
1https://en.wikipedia.org/wiki/Shapefile
660 Chapter 9. Reading and writing graphs

CHAPTER
TEN
DRAWING
NetworkX provides basic functionality for visualizing graphs, but its main goal is to enable graph analysis rather than
perform graph visualization. In the future, graph visualization functionality may be removed from NetworkX or only
available as an add-on package.
Proper graph visualization is hard, and we highly recommend that people visualize their graphs with tools dedicated to
that task. Notable examples of dedicated and fully-featured graph visualization tools are Cytoscape,Gephi,Graphviz
and, for LaTeX typesetting, PGF/TikZ. To use these and other such tools, you should export your NetworkX graph into
a format that can be read by those tools. For example, Cytoscape can read the GraphML format, and so, networkx.
write_graphml(G) might be an appropriate choice.
10.1 Matplotlib
10.1.1 Matplotlib
Draw networks with matplotlib.
See also:
matplotlib http://matplotlib.org/
pygraphviz http://pygraphviz.github.io/
draw(G[, pos, ax]) Draw the graph G with Matplotlib.
draw_networkx(G[, pos, arrows, with_labels]) Draw the graph G using Matplotlib.
draw_networkx_nodes(G, pos[, nodelist, . . . ]) Draw the nodes of the graph G.
draw_networkx_edges(G, pos[, edgelist, . . . ]) Draw the edges of the graph G.
draw_networkx_labels(G, pos[, labels, . . . ]) Draw node labels on the graph G.
draw_networkx_edge_labels(G, pos[, . . . ]) Draw edge labels.
draw_circular(G, **kwargs) Draw the graph G with a circular layout.
draw_kamada_kawai(G, **kwargs) Draw the graph G with a Kamada-Kawai force-directed
layout.
draw_random(G, **kwargs) Draw the graph G with a random layout.
draw_spectral(G, **kwargs) Draw the graph G with a spectral layout.
draw_spring(G, **kwargs) Draw the graph G with a spring layout.
draw_shell(G, **kwargs) Draw networkx graph with shell layout.
661
NetworkX Reference, Release 2.3rc1.dev20181203210840
10.1.2 networkx.drawing.nx_pylab.draw
draw(G,pos=None,ax=None,**kwds)
Draw the graph G with Matplotlib.
Draw the graph as a simple representation with no node labels or edge labels and using the full Matplotlib figure
area and no axis labels by default. See draw_networkx() for more full-featured drawing that allows title, axis
labels etc.
Parameters
•G(graph) – A networkx graph
•pos (dictionary, optional) – A dictionary with nodes as keys and positions as values. If
not specified a spring layout positioning will be computed. See networkx.drawing.
layout for functions that compute node positions.
•ax (Matplotlib Axes object, optional) – Draw the graph in specified Matplotlib axes.
•kwds (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords.
Examples
>>> G=nx.dodecahedral_graph()
>>> nx.draw(G)
>>> nx.draw(G, pos=nx.spring_layout(G)) # use spring layout
See also:
draw_networkx(),draw_networkx_nodes(),draw_networkx_edges(),
draw_networkx_labels(),draw_networkx_edge_labels()
Notes
This function has the same name as pylab.draw and pyplot.draw so beware when using
>>> from networkx import *
since you might overwrite the pylab.draw function.
With pyplot use
>>> import matplotlib.pyplot as plt
>>> import networkx as nx
>>> G=nx.dodecahedral_graph()
>>> nx.draw(G) # networkx draw()
>>> plt.draw() # pyplot draw()
Also see the NetworkX drawing examples at https://networkx.github.io/documentation/latest/auto_examples/
index.html
10.1.3 networkx.drawing.nx_pylab.draw_networkx
draw_networkx(G,pos=None,arrows=True,with_labels=True,**kwds)
Draw the graph G using Matplotlib.
662 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
Draw the graph with Matplotlib with options for node positions, labeling, titles, and many other drawing fea-
tures. See draw() for simple drawing without labels or axes.
Parameters
•G(graph) – A networkx graph
•pos (dictionary, optional) – A dictionary with nodes as keys and positions as values. If
not specified a spring layout positioning will be computed. See networkx.drawing.
layout for functions that compute node positions.
•arrows (bool, optional (default=True)) – For directed graphs, if True draw arrowheads.
Note: Arrows will be the same color as edges.
•arrowstyle (str, optional (default=’-|>’)) – For directed graphs, choose the style of the
arrowsheads. See :py:class: matplotlib.patches.ArrowStyle for more options.
•arrowsize (int, optional (default=10)) – For directed graphs, choose the size of the
arrow head head’s length and width. See :py:class: matplotlib.patches.
FancyArrowPatch for attribute mutation_scale for more info.
•with_labels (bool, optional (default=True)) – Set to True to draw labels on the nodes.
•ax (Matplotlib Axes object, optional) – Draw the graph in the specified Matplotlib axes.
•nodelist (list, optional (default G.nodes())) – Draw only specified nodes
•edgelist (list, optional (default=G.edges())) – Draw only specified edges
•node_size (scalar or array, optional (default=300)) – Size of nodes. If an array is specified
it must be the same length as nodelist.
•node_color (color string, or array of floats, (default=’#1f78b4’)) – Node color. Can be
a single color format string, or a sequence of colors with the same length as nodelist. If
numeric values are specified they will be mapped to colors using the cmap and vmin,vmax
parameters. See matplotlib.scatter for more details.
•node_shape (string, optional (default=’o’)) – The shape of the node. Specification is as
matplotlib.scatter marker, one of ‘so^>v<dph8’.
•alpha (float, optional (default=1.0)) – The node and edge transparency
•cmap (Matplotlib colormap, optional (default=None)) – Colormap for mapping intensities
of nodes
•vmin,vmax (float, optional (default=None)) – Minimum and maximum for node colormap
scaling
•linewidths ([None | scalar | sequence]) – Line width of symbol border (default =1.0)
•width (float, optional (default=1.0)) – Line width of edges
•edge_color (color string, or array of floats (default=’r’)) – Edge color. Can be a single color
format string, or a sequence of colors with the same length as edgelist. If numeric values are
specified they will be mapped to colors using the edge_cmap and edge_vmin,edge_vmax
parameters.
•edge_cmap (Matplotlib colormap, optional (default=None)) – Colormap for mapping in-
tensities of edges
•edge_vmin,edge_vmax (floats, optional (default=None)) – Minimum and maximum for
edge colormap scaling
•style (string, optional (default=’solid’)) – Edge line style (solid|dashed|dotted,dashdot)
10.1. Matplotlib 663

NetworkX Reference, Release 2.3rc1.dev20181203210840
•labels (dictionary, optional (default=None)) – Node labels in a dictionary keyed by node of
text labels
•font_size (int, optional (default=12)) – Font size for text labels
•font_color (string, optional (default=’k’ black)) – Font color string
•font_weight (string, optional (default=’normal’)) – Font weight
•font_family (string, optional (default=’sans-serif ’)) – Font family
•label (string, optional) – Label for graph legend
Notes
For directed graphs, arrows are drawn at the head end. Arrows can be turned off with keyword arrows=False.
Examples
>>> G=nx.dodecahedral_graph()
>>> nx.draw(G)
>>> nx.draw(G, pos=nx.spring_layout(G)) # use spring layout
>>> import matplotlib.pyplot as plt
>>> limits =plt.axis('off')# turn of axis
Also see the NetworkX drawing examples at https://networkx.github.io/documentation/latest/auto_examples/
index.html
See also:
draw(),draw_networkx_nodes(),draw_networkx_edges(),draw_networkx_labels(),
draw_networkx_edge_labels()
10.1.4 networkx.drawing.nx_pylab.draw_networkx_nodes
draw_networkx_nodes(G,pos,nodelist=None,node_size=300,node_color=’#1f78b4’,node_shape=’o’,
alpha=1.0,cmap=None,vmin=None,vmax=None,ax=None,linewidths=None,
edgecolors=None,label=None,**kwds)
Draw the nodes of the graph G.
This draws only the nodes of the graph G.
Parameters
•G(graph) – A networkx graph
•pos (dictionary) – A dictionary with nodes as keys and positions as values. Positions should
be sequences of length 2.
•ax (Matplotlib Axes object, optional) – Draw the graph in the specified Matplotlib axes.
•nodelist (list, optional) – Draw only specified nodes (default G.nodes())
•node_size (scalar or array) – Size of nodes (default=300). If an array is specified it must
be the same length as nodelist.
664 Chapter 10. Drawing
NetworkX Reference, Release 2.3rc1.dev20181203210840
•node_color (color string, or array of floats) – Node color. Can be a single color format
string (default=’#1f78b4’), or a sequence of colors with the same length as nodelist. If
numeric values are specified they will be mapped to colors using the cmap and vmin,vmax
parameters. See matplotlib.scatter for more details.
•node_shape (string) – The shape of the node. Specification is as matplotlib.scatter marker,
one of ‘so^>v<dph8’ (default=’o’).
•alpha (float or array of floats) – The node transparency. This can be a single alpha value
(default=1.0), in which case it will be applied to all the nodes of color. Otherwise, if it is
an array, the elements of alpha will be applied to the colors in order (cycling through alpha
multiple times if necessary).
•cmap (Matplotlib colormap) – Colormap for mapping intensities of nodes (default=None)
•vmin,vmax (floats) – Minimum and maximum for node colormap scaling (default=None)
•linewidths ([None | scalar | sequence]) – Line width of symbol border (default =1.0)
•edgecolors ([None | scalar | sequence]) – Colors of node borders (default = node_color)
•label ([None| string]) – Label for legend
Returns PathCollection of the nodes.
Return type matplotlib.collections.PathCollection
Examples
>>> G=nx.dodecahedral_graph()
>>> nodes =nx.draw_networkx_nodes(G, pos=nx.spring_layout(G))
Also see the NetworkX drawing examples at https://networkx.github.io/documentation/latest/auto_examples/
index.html
See also:
draw(),draw_networkx(),draw_networkx_edges(),draw_networkx_labels(),
draw_networkx_edge_labels()
10.1.5 networkx.drawing.nx_pylab.draw_networkx_edges
draw_networkx_edges(G,pos,edgelist=None,width=1.0,edge_color=’k’,style=’solid’,alpha=1.0,
arrowstyle=’-|>’,arrowsize=10,edge_cmap=None,edge_vmin=None,
edge_vmax=None,ax=None,arrows=True,label=None,node_size=300,
nodelist=None,node_shape=’o’,**kwds)
Draw the edges of the graph G.
This draws only the edges of the graph G.
Parameters
•G(graph) – A networkx graph
•pos (dictionary) – A dictionary with nodes as keys and positions as values. Positions should
be sequences of length 2.
•edgelist (collection of edge tuples) – Draw only specified edges(default=G.edges())
•width (float, or array of floats) – Line width of edges (default=1.0)
10.1. Matplotlib 665

NetworkX Reference, Release 2.3rc1.dev20181203210840
•edge_color (color string, or array of floats) – Edge color. Can be a single color format string
(default=’r’), or a sequence of colors with the same length as edgelist. If numeric values are
specified they will be mapped to colors using the edge_cmap and edge_vmin,edge_vmax
parameters.
•style (string) – Edge line style (default=’solid’) (solid|dashed|dotted,dashdot)
•alpha (float) – The edge transparency (default=1.0)
•edge_ cmap (Matplotlib colormap) – Colormap for mapping intensities of edges (de-
fault=None)
•edge_vmin,edge_vmax (floats) – Minimum and maximum for edge colormap scaling (de-
fault=None)
•ax (Matplotlib Axes object, optional) – Draw the graph in the specified Matplotlib axes.
•arrows (bool, optional (default=True)) – For directed graphs, if True draw arrowheads.
Note: Arrows will be the same color as edges.
•arrowstyle (str, optional (default=’-|>’)) – For directed graphs, choose the style of the
arrow heads. See :py:class: matplotlib.patches.ArrowStyle for more options.
•arrowsize (int, optional (default=10)) – For directed graphs, choose the size of the
arrow head head’s length and width. See :py:class: matplotlib.patches.
FancyArrowPatch for attribute mutation_scale for more info.
•label ([None| string]) – Label for legend
Returns
•matplotlib.collection.LineCollection –LineCollection of the edges
•list of matplotlib.patches.FancyArrowPatch –FancyArrowPatch instances of the di-
rected edges
•Depending whether the drawing includes arrows or not.
Notes
For directed graphs, arrows are drawn at the head end. Arrows can be turned off with keyword arrows=False.
Be sure to include node_size as a keyword argument; arrows are drawn considering the size of nodes.
Examples
>>> G=nx.dodecahedral_graph()
>>> edges =nx.draw_networkx_edges(G, pos=nx.spring_layout(G))
>>> G=nx.DiGraph()
>>> G.add_edges_from([(1,2), (1,3), (2,3)])
>>> arcs =nx.draw_networkx_edges(G, pos=nx.spring_layout(G))
>>> alphas =[0.3,0.4,0.5]
>>> for i, arc in enumerate(arcs): # change alpha values of arcs
... arc.set_alpha(alphas[i])
Also see the NetworkX drawing examples at https://networkx.github.io/documentation/latest/auto_examples/
index.html
See also:
666 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
draw(),draw_networkx(),draw_networkx_nodes(),draw_networkx_labels(),
draw_networkx_edge_labels()
10.1.6 networkx.drawing.nx_pylab.draw_networkx_labels
draw_networkx_labels(G,pos,labels=None,font_size=12,font_color=’k’,font_family=’sans-serif’,
font_weight=’normal’,alpha=1.0,bbox=None,ax=None,**kwds)
Draw node labels on the graph G.
Parameters
•G(graph) – A networkx graph
•pos (dictionary) – A dictionary with nodes as keys and positions as values. Positions should
be sequences of length 2.
•labels (dictionary, optional (default=None)) – Node labels in a dictionary keyed by node of
text labels Node-keys in labels should appear as keys in pos. If needed use: {n:lab for
n,lab in labels.items() if n in pos}
•font_size (int) – Font size for text labels (default=12)
•font_color (string) – Font color string (default=’k’ black)
•font_family (string) – Font family (default=’sans-serif’)
•font_weight (string) – Font weight (default=’normal’)
•alpha (float) – The text transparency (default=1.0)
•ax (Matplotlib Axes object, optional) – Draw the graph in the specified Matplotlib axes.
Returns dict of labels keyed on the nodes
Return type dict
Examples
>>> G=nx.dodecahedral_graph()
>>> labels =nx.draw_networkx_labels(G, pos=nx.spring_layout(G))
Also see the NetworkX drawing examples at https://networkx.github.io/documentation/latest/auto_examples/
index.html
See also:
draw(),draw_networkx(),draw_networkx_nodes(),draw_networkx_edges(),
draw_networkx_edge_labels()
10.1.7 networkx.drawing.nx_pylab.draw_networkx_edge_labels
draw_networkx_edge_labels(G,pos,edge_labels=None,label_pos=0.5,font_size=10,
font_color=’k’,font_family=’sans-serif’,font_weight=’normal’,
alpha=1.0,bbox=None,ax=None,rotate=True,**kwds)
Draw edge labels.
Parameters
•G(graph) – A networkx graph
10.1. Matplotlib 667

NetworkX Reference, Release 2.3rc1.dev20181203210840
•pos (dictionary) – A dictionary with nodes as keys and positions as values. Positions should
be sequences of length 2.
•ax (Matplotlib Axes object, optional) – Draw the graph in the specified Matplotlib axes.
•alpha (float) – The text transparency (default=1.0)
•edge_labels (dictionary) – Edge labels in a dictionary keyed by edge two-tuple of text labels
(default=None). Only labels for the keys in the dictionary are drawn.
•label_pos (float) – Position of edge label along edge (0=head, 0.5=center, 1=tail)
•font_size (int) – Font size for text labels (default=12)
•font_color (string) – Font color string (default=’k’ black)
•font_weight (string) – Font weight (default=’normal’)
•font_family (string) – Font family (default=’sans-serif’)
•bbox (Matplotlib bbox) – Specify text box shape and colors.
•clip_on (bool) – Turn on clipping at axis boundaries (default=True)
Returns dict of labels keyed on the edges
Return type dict
Examples
>>> G=nx.dodecahedral_graph()
>>> edge_labels =nx.draw_networkx_edge_labels(G, pos=nx.spring_layout(G))
Also see the NetworkX drawing examples at https://networkx.github.io/documentation/latest/auto_examples/
index.html
See also:
draw(),draw_networkx(),draw_networkx_nodes(),draw_networkx_edges(),
draw_networkx_labels()
10.1.8 networkx.drawing.nx_pylab.draw_circular
draw_circular(G,**kwargs)
Draw the graph G with a circular layout.
Parameters
•G(graph) – A networkx graph
•kwargs (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords, with the exception of the pos parameter which is not used by this function.
10.1.9 networkx.drawing.nx_pylab.draw_kamada_kawai
draw_kamada_kawai(G,**kwargs)
Draw the graph G with a Kamada-Kawai force-directed layout.
Parameters
•G(graph) – A networkx graph
668 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
•kwargs (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords, with the exception of the pos parameter which is not used by this function.
10.1.10 networkx.drawing.nx_pylab.draw_random
draw_random(G,**kwargs)
Draw the graph G with a random layout.
Parameters
•G(graph) – A networkx graph
•kwargs (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords, with the exception of the pos parameter which is not used by this function.
10.1.11 networkx.drawing.nx_pylab.draw_spectral
draw_spectral(G,**kwargs)
Draw the graph G with a spectral layout.
Parameters
•G(graph) – A networkx graph
•kwargs (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords, with the exception of the pos parameter which is not used by this function.
10.1.12 networkx.drawing.nx_pylab.draw_spring
draw_spring(G,**kwargs)
Draw the graph G with a spring layout.
Parameters
•G(graph) – A networkx graph
•kwargs (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords, with the exception of the pos parameter which is not used by this function.
10.1.13 networkx.drawing.nx_pylab.draw_shell
draw_shell(G,**kwargs)
Draw networkx graph with shell layout.
Parameters
•G(graph) – A networkx graph
•kwargs (optional keywords) – See networkx.draw_networkx() for a description of optional
keywords, with the exception of the pos parameter which is not used by this function.
10.1. Matplotlib 669

NetworkX Reference, Release 2.3rc1.dev20181203210840
10.2 Graphviz AGraph (dot)
10.2.1 Graphviz AGraph
Interface to pygraphviz AGraph class.
Examples
>>> G=nx.complete_graph(5)
>>> A=nx.nx_agraph.to_agraph(G)
>>> H=nx.nx_agraph.from_agraph(A)
See also:
Pygraphviz http://pygraphviz.github.io/
from_agraph(A[, create_using]) Return a NetworkX Graph or DiGraph from a Py-
Graphviz graph.
to_agraph(N) Return a pygraphviz graph from a NetworkX graph N.
write_dot(G, path) Write NetworkX graph G to Graphviz dot format on
path.
read_dot(path) Return a NetworkX graph from a dot file on path.
graphviz_layout(G[, prog, root, args]) Create node positions for G using Graphviz.
pygraphviz_layout(G[, prog, root, args]) Create node positions for G using Graphviz.
10.2.2 networkx.drawing.nx_agraph.from_agraph
from_agraph(A,create_using=None)
Return a NetworkX Graph or DiGraph from a PyGraphviz graph.
Parameters
•A(PyGraphviz AGraph) – A graph created with PyGraphviz
•create_using (NetworkX graph constructor, optional (default=nx.Graph)) – Graph type to
create. If graph instance, then cleared before populated.
Examples
>>> K5 =nx.complete_graph(5)
>>> A=nx.nx_agraph.to_agraph(K5)
>>> G=nx.nx_agraph.from_agraph(A)
Notes
The Graph G will have a dictionary G.graph_attr containing the default graphviz attributes for graphs, nodes
and edges.
Default node attributes will be in the dictionary G.node_attr which is keyed by node.
Edge attributes will be returned as edge data in G. With edge_attr=False the edge data will be the Graphviz edge
weight attribute or the value 1 if no edge weight attribute is found.
670 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
10.2.3 networkx.drawing.nx_agraph.to_agraph
to_agraph(N)
Return a pygraphviz graph from a NetworkX graph N.
Parameters N (NetworkX graph) – A graph created with NetworkX
Examples
>>> K5 =nx.complete_graph(5)
>>> A=nx.nx_agraph.to_agraph(K5)
Notes
If N has an dict N.graph_attr an attempt will be made first to copy properties attached to the graph (see
from_agraph) and then updated with the calling arguments if any.
10.2.4 networkx.drawing.nx_agraph.write_dot
write_dot(G,path)
Write NetworkX graph G to Graphviz dot format on path.
Parameters
•G(graph) – A networkx graph
•path (filename) – Filename or file handle to write
10.2.5 networkx.drawing.nx_agraph.read_dot
read_dot(path)
Return a NetworkX graph from a dot file on path.
Parameters path (file or string) – File name or file handle to read.
10.2.6 networkx.drawing.nx_agraph.graphviz_layout
graphviz_layout(G,prog=’neato’,root=None,args=”)
Create node positions for G using Graphviz.
Parameters
•G(NetworkX graph) – A graph created with NetworkX
•prog (string) – Name of Graphviz layout program
•root (string, optional) – Root node for twopi layout
•args (string, optional) – Extra arguments to Graphviz layout program
•Returns (dictionary) – Dictionary of x, y, positions keyed by node.
10.2. Graphviz AGraph (dot) 671

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.petersen_graph()
>>> pos =nx.nx_agraph.graphviz_layout(G)
>>> pos =nx.nx_agraph.graphviz_layout(G, prog='dot')
Notes
This is a wrapper for pygraphviz_layout.
10.2.7 networkx.drawing.nx_agraph.pygraphviz_layout
pygraphviz_layout(G,prog=’neato’,root=None,args=”)
Create node positions for G using Graphviz.
Parameters
•G(NetworkX graph) – A graph created with NetworkX
•prog (string) – Name of Graphviz layout program
•root (string, optional) – Root node for twopi layout
•args (string, optional) – Extra arguments to Graphviz layout program
•Returns (dictionary) – Dictionary of x, y, positions keyed by node.
Examples
>>> G=nx.petersen_graph()
>>> pos =nx.nx_agraph.graphviz_layout(G)
>>> pos =nx.nx_agraph.graphviz_layout(G, prog='dot')
Notes
If you use complex node objects, they may have the same string representation and GraphViz could treat them
as the same node. The layout may assign both nodes a single location. See Issue #1568 If this occurs in your
case, consider relabeling the nodes just for the layout computation using something similar to:
H = nx.convert_node_labels_to_integers(G, label_attribute=’node_label’) H_layout =
nx.nx_agraph.pygraphviz_layout(G, prog=’dot’) G_layout = {H.nodes[n][‘node_label’]: p for
n, p in H_layout.items()}
10.3 Graphviz with pydot
10.3.1 Pydot
Import and export NetworkX graphs in Graphviz dot format using pydot.
Either this module or nx_agraph can be used to interface with graphviz.
See also:
672 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
pydot https://github.com/erocarrera/pydot
Graphviz http://www.research.att.com/sw/tools/graphviz/
DOT
from_pydot(P) Return a NetworkX graph from a Pydot graph.
to_pydot(N) Return a pydot graph from a NetworkX graph N.
write_dot(G, path) Write NetworkX graph G to Graphviz dot format on
path.
read_dot(path) Return a NetworkX MultiGraph or
MultiDiGraph from the dot file with the passed
path.
graphviz_layout(G[, prog, root]) Create node positions using Pydot and Graphviz.
pydot_layout(G[, prog, root]) Create node positions using pydot and Graphviz.
10.3.2 networkx.drawing.nx_pydot.from_pydot
from_pydot(P)
Return a NetworkX graph from a Pydot graph.
Parameters P (Pydot graph) – A graph created with Pydot
Returns G – A MultiGraph or MultiDiGraph.
Return type NetworkX multigraph
Examples
>>> K5 =nx.complete_graph(5)
>>> A=nx.nx_pydot.to_pydot(K5)
>>> G=nx.nx_pydot.from_pydot(A) # return MultiGraph
# make a Graph instead of MultiGraph >>> G = nx.Graph(nx.nx_pydot.from_pydot(A))
10.3.3 networkx.drawing.nx_pydot.to_pydot
to_pydot(N)
Return a pydot graph from a NetworkX graph N.
Parameters N (NetworkX graph) – A graph created with NetworkX
Examples
>>> K5 =nx.complete_graph(5)
>>> P=nx.nx_pydot.to_pydot(K5)
10.3. Graphviz with pydot 673

NetworkX Reference, Release 2.3rc1.dev20181203210840
Notes
10.3.4 networkx.drawing.nx_pydot.write_dot
write_dot(G,path)
Write NetworkX graph G to Graphviz dot format on path.
Path can be a string or a file handle.
10.3.5 networkx.drawing.nx_pydot.read_dot
read_dot(path)
Return a NetworkX MultiGraph or MultiDiGraph from the dot file with the passed path.
If this file contains multiple graphs, only the first such graph is returned. All graphs _except_ the first are silently
ignored.
Parameters path (str or file) – Filename or file handle.
Returns G – A MultiGraph or MultiDiGraph.
Return type MultiGraph or MultiDiGraph
Notes
Use G = nx.Graph(read_dot(path)) to return a Graph instead of a MultiGraph.
10.3.6 networkx.drawing.nx_pydot.graphviz_layout
graphviz_layout(G,prog=’neato’,root=None,**kwds)
Create node positions using Pydot and Graphviz.
Returns a dictionary of positions keyed by node.
Examples
>>> G=nx.complete_graph(4)
>>> pos =nx.nx_pydot.graphviz_layout(G)
>>> pos =nx.nx_pydot.graphviz_layout(G, prog='dot')
Notes
This is a wrapper for pydot_layout.
10.3.7 networkx.drawing.nx_pydot.pydot_layout
pydot_layout(G,prog=’neato’,root=None,**kwds)
Create node positions using pydot and Graphviz.
Parameters
•G(Graph) – NetworkX graph to be laid out.
674 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
•prog (optional[str]) – Basename of the GraphViz command with which to layout this graph.
Defaults to neato: default GraphViz command for undirected graphs.
Returns Dictionary of positions keyed by node.
Return type dict
Examples
>>> G=nx.complete_graph(4)
>>> pos =nx.nx_pydot.pydot_layout(G)
>>> pos =nx.nx_pydot.pydot_layout(G, prog='dot')
Notes
If you use complex node objects, they may have the same string representation and GraphViz could treat them
as the same node. The layout may assign both nodes a single location. See Issue #1568 If this occurs in your
case, consider relabeling the nodes just for the layout computation using something similar to:
H = nx.convert_node_labels_to_integers(G, label_attribute=’node_label’) H_layout =
nx.nx_pydot.pydot_layout(G, prog=’dot’) G_layout = {H.nodes[n][‘node_label’]: p for n, p in
H_layout.items()}
10.4 Graph Layout
10.4.1 Layout
Node positioning algorithms for graph drawing.
For random_layout() the possible resulting shape is a square of side [0, scale] (default: [0, 1]) Changing center
shifts the layout by that amount.
For the other layout routines, the extent is [center - scale, center + scale] (default: [-1, 1]).
Warning: Most layout routines have only been tested in 2-dimensions.
bipartite_layout(G, nodes[, align, scale, . . . ]) Position nodes in two straight lines.
circular_layout(G[, scale, center, dim]) Position nodes on a circle.
kamada_kawai_layout(G[, dist, pos, weight, . . . ]) Position nodes using Kamada-Kawai path-length cost-
function.
random_layout(G[, center, dim, seed]) Position nodes uniformly at random in the unit square.
rescale_layout(pos[, scale]) Return scaled position array to (-scale, scale) in all axes.
shell_layout(G[, nlist, scale, center, dim]) Position nodes in concentric circles.
spring_layout(G[, k, pos, fixed, . . . ]) Position nodes using Fruchterman-Reingold force-
directed algorithm.
spectral_layout(G[, weight, scale, center, dim]) Position nodes using the eigenvectors of the graph
Laplacian.
10.4. Graph Layout 675

NetworkX Reference, Release 2.3rc1.dev20181203210840
10.4.2 networkx.drawing.layout.bipartite_layout
bipartite_layout(G,nodes,align=’vertical’,scale=1,center=None,as-
pect_ratio=1.3333333333333333)
Position nodes in two straight lines.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
•nodes (list or container) – Nodes in one node set of the bipartite graph. This set will be
placed on left or top.
•align (string (default=’vertical’)) – The alignment of nodes. Vertical or horizontal.
•scale (number (default: 1)) – Scale factor for positions.
•center (array-like or None) – Coordinate pair around which to center the layout.
•aspect_ratio (number (default=4/3):) – The ratio of the width to the height of the layout.
Returns pos – A dictionary of positions keyed by node.
Return type dict
Examples
>>> G=nx.bipartite.gnmk_random_graph(3,5,10, seed=123)
>>> top =nx.bipartite.sets(G)[0]
>>> pos =nx.bipartite_layout(G, top)
Notes
This algorithm currently only works in two dimensions and does not try to minimize edge crossings.
10.4.3 networkx.drawing.layout.circular_layout
circular_layout(G,scale=1,center=None,dim=2)
Position nodes on a circle.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
•scale (number (default: 1)) – Scale factor for positions.
•center (array-like or None) – Coordinate pair around which to center the layout.
•dim (int) – Dimension of layout. If dim>2, the remaining dimensions are set to zero in the
returned positions. If dim<2, a ValueError is raised.
Returns pos – A dictionary of positions keyed by node
Return type dict
Raises ValueError – If dim < 2
676 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> pos =nx.circular_layout(G)
Notes
This algorithm currently only works in two dimensions and does not try to minimize edge crossings.
10.4.4 networkx.drawing.layout.kamada_kawai_layout
kamada_kawai_layout(G,dist=None,pos=None,weight=’weight’,scale=1,center=None,dim=2)
Position nodes using Kamada-Kawai path-length cost-function.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
•dist (float (default=None)) – A two-level dictionary of optimal distances between nodes,
indexed by source and destination node. If None, the distance is computed using short-
est_path_length().
•pos (dict or None optional (default=None)) – Initial positions for nodes as a dictionary with
node as keys and values as a coordinate list or tuple. If None, then use circular_layout() for
dim >= 2 and a linear layout for dim == 1.
•weight (string or None optional (default=’weight’)) – The edge attribute that holds the
numerical value used for the edge weight. If None, then all edge weights are 1.
•scale (number (default: 1)) – Scale factor for positions.
•center (array-like or None) – Coordinate pair around which to center the layout.
•dim (int) – Dimension of layout.
Returns pos – A dictionary of positions keyed by node
Return type dict
Examples
>>> G=nx.path_graph(4)
>>> pos =nx.kamada_kawai_layout(G)
10.4.5 networkx.drawing.layout.random_layout
random_layout(G,center=None,dim=2,seed=None)
Position nodes uniformly at random in the unit square.
For every node, a position is generated by choosing each of dim coordinates uniformly at random on the interval
[0.0, 1.0).
NumPy (http://scipy.org) is required for this function.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
10.4. Graph Layout 677

NetworkX Reference, Release 2.3rc1.dev20181203210840
•center (array-like or None) – Coordinate pair around which to center the layout.
•dim (int) – Dimension of layout.
•seed (int, RandomState instance or None optional (default=None)) – Set the random state
for deterministic node layouts. If int, seed is the seed used by the random number gen-
erator, if numpy.random.RandomState instance, seed is the random number generator, if
None, the random number generator is the RandomState instance used by numpy.random.
Returns pos – A dictionary of positions keyed by node
Return type dict
Examples
>>> G=nx.lollipop_graph(4,3)
>>> pos =nx.random_layout(G)
10.4.6 networkx.drawing.layout.rescale_layout
rescale_layout(pos,scale=1)
Return scaled position array to (-scale, scale) in all axes.
The function acts on NumPy arrays which hold position information. Each position is one row of the array. The
dimension of the space equals the number of columns. Each coordinate in one column.
To rescale, the mean (center) is subtracted from each axis separately. Then all values are scaled so that the
largest magnitude value from all axes equals scale (thus, the aspect ratio is preserved). The resulting NumPy
Array is returned (order of rows unchanged).
Parameters
•pos (numpy array) – positions to be scaled. Each row is a position.
•scale (number (default: 1)) – The size of the resulting extent in all directions.
Returns pos – scaled positions. Each row is a position.
Return type numpy array
10.4.7 networkx.drawing.layout.shell_layout
shell_layout(G,nlist=None,scale=1,center=None,dim=2)
Position nodes in concentric circles.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
•nlist (list of lists) – List of node lists for each shell.
•scale (number (default: 1)) – Scale factor for positions.
•center (array-like or None) – Coordinate pair around which to center the layout.
•dim (int) – Dimension of layout, currently only dim=2 is supported. Other dimension values
result in a ValueError.
Returns pos – A dictionary of positions keyed by node
678 Chapter 10. Drawing

NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type dict
Raises ValueError – If dim != 2
Examples
>>> G=nx.path_graph(4)
>>> shells =[[0], [1,2,3]]
>>> pos =nx.shell_layout(G, shells)
Notes
This algorithm currently only works in two dimensions and does not try to minimize edge crossings.
10.4.8 networkx.drawing.layout.spring_layout
spring_layout(G,k=None,pos=None,fixed=None,iterations=50,threshold=0.0001,weight=’weight’,
scale=1,center=None,dim=2,seed=None)
Position nodes using Fruchterman-Reingold force-directed algorithm.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
•k(float (default=None)) – Optimal distance between nodes. If None the distance is set to
1/sqrt(n) where n is the number of nodes. Increase this value to move nodes farther apart.
•pos (dict or None optional (default=None)) – Initial positions for nodes as a dictionary
with node as keys and values as a coordinate list or tuple. If None, then use random initial
positions.
•fixed (list or None optional (default=None)) – Nodes to keep fixed at initial position.
•iterations (int optional (default=50)) – Maximum number of iterations taken
•threshold (float optional (default = 1e-4)) – Threshold for relative error in node position
changes. The iteration stops if the error is below this threshold.
•weight (string or None optional (default=’weight’)) – The edge attribute that holds the
numerical value used for the edge weight. If None, then all edge weights are 1.
•scale (number (default: 1)) – Scale factor for positions. Not used unless fixed is None.
•center (array-like or None) – Coordinate pair around which to center the layout. Not used
unless fixed is None.
•dim (int) – Dimension of layout.
•seed (int, RandomState instance or None optional (default=None)) – Set the random state
for deterministic node layouts. If int, seed is the seed used by the random number gen-
erator, if numpy.random.RandomState instance, seed is the random number generator, if
None, the random number generator is the RandomState instance used by numpy.random.
Returns pos – A dictionary of positions keyed by node
Return type dict
10.4. Graph Layout 679

NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
>>> G=nx.path_graph(4)
>>> pos =nx.spring_layout(G)
# The same using longer but equivalent function name >>> pos = nx.fruchterman_reingold_layout(G)
10.4.9 networkx.drawing.layout.spectral_layout
spectral_layout(G,weight=’weight’,scale=1,center=None,dim=2)
Position nodes using the eigenvectors of the graph Laplacian.
Parameters
•G(NetworkX graph or list of nodes) – A position will be assigned to every node in G.
•weight (string or None optional (default=’weight’)) – The edge attribute that holds the
numerical value used for the edge weight. If None, then all edge weights are 1.
•scale (number (default: 1)) – Scale factor for positions.
•center (array-like or None) – Coordinate pair around which to center the layout.
•dim (int) – Dimension of layout.
Returns pos – A dictionary of positions keyed by node
Return type dict
Examples
>>> G=nx.path_graph(4)
>>> pos =nx.spectral_layout(G)
Notes
Directed graphs will be considered as undirected graphs when positioning the nodes.
For larger graphs (>500 nodes) this will use the SciPy sparse eigenvalue solver (ARPACK).
680 Chapter 10. Drawing

CHAPTER
ELEVEN
RANDOMNESS
Random Number Generators (RNGs) are often used when generating, drawing and computing properties or manipu-
lating networks. NetworkX provides functions which use one of two standard RNGs: NumPy’s package numpy.
random or Python’s built-in package random. They each provide the same algorithm for generating numbers
(Mersenne Twister). Their interfaces are similar (dangerously similar) and yet distinct. They each provide a global
default instance of their generator that is shared by all programs in a single session. For the most part you can use
the RNGs as NetworkX has them set up and you’ll get reasonable pseudorandom results (results that are statistically
random, but created in a deterministic manner).
Sometimes you want more control over how the numbers are generated. In particular, you need to set the seed of the
generator to make your results reproducible – either for scientific publication or for debugging. Both RNG packages
have easy functions to set the seed to any integer, thus determining the subsequent generated values. Since this package
(and many others) use both RNGs you may need to set the seed of both RNGs. Even if we strictly only used one of
the RNGs, you may find yourself using another package that uses the other. Setting the state of the two global RNGs
is as simple setting the seed of each RNG to an arbitrary integer:
>>> import random
>>> random.seed(246)# or any integer
>>> import numpy
>>> numpy.random.seed(4812)
Many users will be satisfied with this level of control.
For people who want even more control, we include an optional argument to functions that use an RNG. This argument
is called seed, but determines more than the seed of the RNG. It tells the function which RNG package to use, and
whether to use a global or local RNG.
>>> from networkx import path_graph, random_layout
>>> G=path_graph(9)
>>> pos =random_layout(G, seed=None)# use (either) global default RNG
>>> pos =random_layout(G, seed=42)# local RNG just for this call
>>> pos =random_layout(G, seed=numpy.random) # use numpy global RNG
>>> random_state =numpy.random.RandomState(42)
>>> pos =random_layout(G, seed=random_state) # use/reuse your own RNG
Each NetworkX function that uses an RNG was written with one RNG package in mind. It either uses random
or numpy.random by default. But some users want to only use a single RNG for all their code. This seed
argument provides a mechanism so that any function can use a numpy.random RNG even if the function is written
for random. It works as follows.
The default behavior (when seed=None) is to use the global RNG for the function’s preferred package. If seed is set
to an integer value, a local RNG is created with the indicated seed value and is used for the duration of that function
(including any calls to other functions) and then discarded. Alternatively, you can specify seed=numpy.random
to ensure that the global numpy RNG is used whether the function expects it or not. Finally, you can provide a numpy
681

NetworkX Reference, Release 2.3rc1.dev20181203210840
RNG to be used by the function. The RNG is then available to use in other functions or even other package like
sklearn. In this way you can use a single RNG for all random numbers in your project.
While it is possible to assign seed arandom-style RNG for NetworkX functions written for the random package
API, the numpy RNG interface has too many nice features for us to ensure a random-style RNG will work in all
functions. In practice, you can do most things using only random RNGs (useful if numpy is not available). But your
experience will be richer if numpy is available.
To summarize, you can easily ignore the seed argument and use the global RNGs. You can specify to use only the
numpy global RNG with seed=numpy.random. You can use a local RNG by providing an integer seed value. And
you can provide your own numpy RNG, reusing it for all functions. It is easier to use numpy RNGs if you want a
single RNG for your computations.
682 Chapter 11. Randomness

CHAPTER
TWELVE
EXCEPTIONS
12.1 Exceptions
Base exceptions and errors for NetworkX.
class NetworkXException
Base class for exceptions in NetworkX.
class NetworkXError
Exception for a serious error in NetworkX
class NetworkXPointlessConcept
Raised when a null graph is provided as input to an algorithm that cannot use it.
The null graph is sometimes considered a pointless concept1, thus the name of the exception.
References
class NetworkXAlgorithmError
Exception for unexpected termination of algorithms.
class NetworkXUnfeasible
Exception raised by algorithms trying to solve a problem instance that has no feasible solution.
class NetworkXNoPath
Exception for algorithms that should return a path when running on graphs where such a path does not exist.
class NetworkXNoCycle
Exception for algorithms that should return a cycle when running on graphs where such a cycle does not exist.
class NodeNotFound
Exception raised if requested node is not present in the graph
class HasACycle
Raised if a graph has a cycle when an algorithm expects that it will have no cycles.
class NetworkXUnbounded
Exception raised by algorithms trying to solve a maximization or a minimization problem instance that is un-
bounded.
class NetworkXNotImplemented
Exception raised by algorithms not implemented for a type of graph.
1Harary, F. and Read, R. “Is the Null Graph a Pointless Concept?” In Graphs and Combinatorics Conference, George Washington University.
New York: Springer-Verlag, 1973.
683

NetworkX Reference, Release 2.3rc1.dev20181203210840
class AmbiguousSolution
Raised if more than one valid solution exists for an intermediary step of an algorithm.
In the face of ambiguity, refuse the temptation to guess. This may occur, for example, when trying to determine
the bipartite node sets in a disconnected bipartite graph when computing bipartite matchings.
class ExceededMaxIterations
Raised if a loop iterates too many times without breaking.
This may occur, for example, in an algorithm that computes progressively better approximations to a value but
exceeds an iteration bound specified by the user.
class PowerIterationFailedConvergence(num_iterations,*args,**kw)
Raised when the power iteration method fails to converge within a specified iteration limit.
num_iterations is the number of iterations that have been completed when this exception was raised.
684 Chapter 12. Exceptions

CHAPTER
THIRTEEN
UTILITIES
13.1 Helper Functions
Miscellaneous Helpers for NetworkX.
These are not imported into the base networkx namespace but can be accessed, for example, as
>>> import networkx
>>> networkx.utils.is_string_like('spam')
True
is_string_like(obj) Check if obj is string.
flatten(obj[, result]) Return flattened version of (possibly nested) iterable ob-
ject.
iterable(obj) Return True if obj is iterable with a well-defined len().
is_list_of_ints(intlist) Return True if list is a list of ints.
make_str(x) Return the string representation of t.
generate_unique_node() Generate a unique node label.
default_opener(filename) Opens filename using system’s default program.
pairwise(iterable[, cyclic]) s -> (s0, s1), (s1, s2), (s2, s3), . . .
groups(many_to_one) Converts a many-to-one mapping into a one-to-many
mapping.
create_random_state([random_state]) Returns a numpy.random.RandomState instance de-
pending on input.
13.1.1 networkx.utils.misc.is_string_like
is_string_like(obj)
Check if obj is string.
13.1.2 networkx.utils.misc.flatten
flatten(obj,result=None)
Return flattened version of (possibly nested) iterable object.
685

NetworkX Reference, Release 2.3rc1.dev20181203210840
13.1.3 networkx.utils.misc.iterable
iterable(obj)
Return True if obj is iterable with a well-defined len().
13.1.4 networkx.utils.misc.is_list_of_ints
is_list_of_ints(intlist)
Return True if list is a list of ints.
13.1.5 networkx.utils.misc.make_str
make_str(x)
Return the string representation of t.
13.1.6 networkx.utils.misc.generate_unique_node
generate_unique_node()
Generate a unique node label.
13.1.7 networkx.utils.misc.default_opener
default_opener(filename)
Opens filename using system’s default program.
Parameters filename (str) – The path of the file to be opened.
13.1.8 networkx.utils.misc.pairwise
pairwise(iterable,cyclic=False)
s -> (s0, s1), (s1, s2), (s2, s3), . . .
13.1.9 networkx.utils.misc.groups
groups(many_to_one)
Converts a many-to-one mapping into a one-to-many mapping.
many_to_one must be a dictionary whose keys and values are all hashable.
The return value is a dictionary mapping values from many_to_one to sets of keys from many_to_one that
have that value.
For example:
>>> from networkx.utils import groups
>>> many_to_one ={'a':1,'b':1,'c':2,'d':3,'e':3}
>>> groups(many_to_one)
{1: {'a', 'b'}, 2: {'c'}, 3: {'d', 'e'}}
686 Chapter 13. Utilities

NetworkX Reference, Release 2.3rc1.dev20181203210840
13.1.10 networkx.utils.misc.create_random_state
create_random_state(random_state=None)
Returns a numpy.random.RandomState instance depending on input.
Parameters random_state (int or RandomState instance or None optional (default=None)) – If int,
return a numpy.random.RandomState instance set with seed=int. if numpy.random.RandomState
instance, return it. if None or numpy.random, return the global random number generator used
by numpy.random.
13.2 Data Structures and Algorithms
Union-find data structure.
UnionFind.union(*objects) Find the sets containing the objects and merge them all.
13.2.1 networkx.utils.union_find.UnionFind.union
UnionFind.union(*objects)
Find the sets containing the objects and merge them all.
13.3 Random Sequence Generators
Utilities for generating random numbers, random sequences, and random selections.
powerlaw_sequence(n[, exponent, seed]) Return sample sequence of length n from a power law
distribution.
cumulative_distribution(distribution) Return normalized cumulative distribution from discrete
distribution.
discrete_sequence(n[, distribution, . . . ]) Return sample sequence of length n from a given dis-
crete distribution or discrete cumulative distribution.
zipf_rv(alpha[, xmin, seed]) Return a random value chosen from the Zipf distribu-
tion.
random_weighted_sample(mapping, k[, seed]) Return k items without replacement from a weighted
sample.
weighted_choice(mapping[, seed]) Return a single element from a weighted sample.
13.3.1 networkx.utils.random_sequence.powerlaw_sequence
powerlaw_sequence(n,exponent=2.0,seed=None)
Return sample sequence of length n from a power law distribution.
13.3.2 networkx.utils.random_sequence.cumulative_distribution
cumulative_distribution(distribution)
Return normalized cumulative distribution from discrete distribution.
13.3. Random Sequence Generators 687

NetworkX Reference, Release 2.3rc1.dev20181203210840
13.3.3 networkx.utils.random_sequence.discrete_sequence
discrete_sequence(n,distribution=None,cdistribution=None,seed=None)
Return sample sequence of length n from a given discrete distribution or discrete cumulative distribution.
One of the following must be specified.
distribution = histogram of values, will be normalized
cdistribution = normalized discrete cumulative distribution
13.3.4 networkx.utils.random_sequence.zipf_rv
zipf_rv(alpha,xmin=1,seed=None)
Return a random value chosen from the Zipf distribution.
The return value is an integer drawn from the probability distribution
𝑝(𝑥) = 𝑥−𝛼
𝜁(𝛼, 𝑥min),
where 𝜁(𝛼, 𝑥min)is the Hurwitz zeta function.
Parameters
•alpha (float) – Exponent value of the distribution
•xmin (int) – Minimum value
•seed (integer, random_state, or None (default)) – Indicator of random number generation
state. See Randomness.
Returns x – Random value from Zipf distribution
Return type int
Raises ValueError: – If xmin < 1 or If alpha <= 1
Notes
The rejection algorithm generates random values for a the power-law distribution in uniformly bounded expected
time dependent on parameters. See1for details on its operation.
Examples
>>> nx.zipf_rv(alpha=2, xmin=3, seed=42)# doctest: +SKIP
References
13.3.5 networkx.utils.random_sequence.random_weighted_sample
random_weighted_sample(mapping,k,seed=None)
Return k items without replacement from a weighted sample.
The input is a dictionary of items with weights as values.
1Luc Devroye, Non-Uniform Random Variate Generation, Springer-Verlag, New York, 1986.
688 Chapter 13. Utilities

NetworkX Reference, Release 2.3rc1.dev20181203210840
13.3.6 networkx.utils.random_sequence.weighted_choice
weighted_choice(mapping,seed=None)
Return a single element from a weighted sample.
The input is a dictionary of items with weights as values.
13.4 Decorators
open_file(path_arg[, mode]) Decorator to ensure clean opening and closing of files.
not_implemented_for(*graph_types) Decorator to mark algorithms as not implemented
nodes_or_number(which_args) Decorator to allow number of nodes or container of
nodes.
preserve_random_state(func) Decorator to preserve the numpy.random state during a
function.
random_state(random_state_index) Decorator to generate a numpy.random.RandomState
instance.
13.4.1 networkx.utils.decorators.open_file
open_file(path_arg,mode=’r’)
Decorator to ensure clean opening and closing of files.
Parameters
•path_arg (int) – Location of the path argument in args. Even if the argument is a named
positional argument (with a default value), you must specify its index as a positional argu-
ment.
•mode (str) – String for opening mode.
Returns _open_file – Function which cleanly executes the io.
Return type function
Examples
Decorate functions like this:
@open_file(0,'r')
def read_function(pathname):
pass
@open_file(1,'w')
def write_function(G,pathname):
pass
@open_file(1,'w')
def write_function(G, pathname='graph.dot')
pass
@open_file('path','w+')
def another_function(arg, **kwargs):
(continues on next page)
13.4. Decorators 689

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
path =kwargs['path']
pass
13.4.2 networkx.utils.decorators.not_implemented_for
not_implemented_for(*graph_types)
Decorator to mark algorithms as not implemented
Parameters graph_types (container of strings) – Entries must be one of ‘directed’,’undirected’,
‘multigraph’, ‘graph’.
Returns _require – The decorated function.
Return type function
Raises
•NetworkXNotImplemented
• If any of the packages cannot be imported
Notes
Multiple types are joined logically with “and”. For “or” use multiple @not_implemented_for() lines.
Examples
Decorate functions like this:
@not_implemnted_for('directed')
def sp_function(G):
pass
@not_implemnted_for('directed','multigraph')
def sp_np_function(G):
pass
13.4.3 networkx.utils.decorators.nodes_or_number
nodes_or_number(which_args)
Decorator to allow number of nodes or container of nodes.
Parameters which_args (int or sequence of ints) – Location of the node arguments in args. Even if
the argument is a named positional argument (with a default value), you must specify its index
as a positional argument. If more than one node argument is allowed, can be a list of locations.
Returns _nodes_or_numbers – Function which replaces int args with ranges.
Return type function
690 Chapter 13. Utilities
NetworkX Reference, Release 2.3rc1.dev20181203210840
Examples
Decorate functions like this:
@nodes_or_number(0)
def empty_graph(nodes):
pass
@nodes_or_number([0,1])
def grid_2d_graph(m1, m2, periodic=False):
pass
@nodes_or_number(1)
def full_rary_tree(r, n)
# r is a number. n can be a number of a list of nodes
pass
13.4.4 networkx.utils.decorators.preserve_random_state
preserve_random_state(func)
Decorator to preserve the numpy.random state during a function.
Parameters func (function) – function around which to preserve the random state.
Returns wrapper – Function which wraps the input function by saving the state before calling the
function and restoring the function afterward.
Return type function
Examples
Decorate functions like this:
@preserve_random_state
def do_random_stuff(x, y):
return x+y*numpy.random.random()
Notes
If numpy.random is not importable, the state is not saved or restored.
13.4.5 networkx.utils.decorators.random_state
random_state(random_state_index)
Decorator to generate a numpy.random.RandomState instance.
Argument position random_state_index is processed by create_random_state. The result is a
numpy.random.RandomState instance.
Parameters random_state_index (int) – Location of the random_state argument in args that is to
be used to generate the numpy.random.RandomState instance. Even if the argument is a named
positional argument (with a default value), you must specify its index as a positional argument.
Returns _random_state – Function whose random_state keyword argument is a RandomState in-
stance.
13.4. Decorators 691
NetworkX Reference, Release 2.3rc1.dev20181203210840
Return type function
Examples
Decorate functions like this:
@np_random_state(0)
def random_float(random_state=None):
return random_state.rand()
@np_random_state(1)
def random_array(dims, random_state=1):
return random_state.rand(*dims)
See also:
py_random_state()
13.5 Cuthill-Mckee Ordering
Cuthill-McKee ordering of graph nodes to produce sparse matrices
cuthill_mckee_ordering(G[, heuristic]) Generate an ordering (permutation) of the graph nodes
to make a sparse matrix.
reverse_cuthill_mckee_ordering(G[,
heuristic])
Generate an ordering (permutation) of the graph nodes
to make a sparse matrix.
13.5.1 networkx.utils.rcm.cuthill_mckee_ordering
cuthill_mckee_ordering(G,heuristic=None)
Generate an ordering (permutation) of the graph nodes to make a sparse matrix.
Uses the Cuthill-McKee heuristic (based on breadth-first search)1.
Parameters
•G(graph) – A NetworkX graph
•heuristic (function, optional) – Function to choose starting node for RCM algorithm. If
None a node from a pseudo-peripheral pair is used. A user-defined function can be supplied
that takes a graph object and returns a single node.
Returns nodes – Generator of nodes in Cuthill-McKee ordering.
Return type generator
Examples
>>> from networkx.utils import cuthill_mckee_ordering
>>> G=nx.path_graph(4)
(continues on next page)
1E. Cuthill and J. McKee. Reducing the bandwidth of sparse symmetric matrices, In Proc. 24th Nat. Conf. ACM, pages 157-172, 1969.
http://doi.acm.org/10.1145/800195.805928
692 Chapter 13. Utilities

NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> rcm =list(cuthill_mckee_ordering(G))
>>> A=nx.adjacency_matrix(G, nodelist=rcm) # doctest: +SKIP
Smallest degree node as heuristic function:
>>> def smallest_degree(G):
... return min(G, key=G.degree)
>>> rcm =list(cuthill_mckee_ordering(G, heuristic=smallest_degree))
See also:
reverse_cuthill_mckee_ordering()
Notes
The optimal solution the the bandwidth reduction is NP-complete2.
References
13.5.2 networkx.utils.rcm.reverse_cuthill_mckee_ordering
reverse_cuthill_mckee_ordering(G,heuristic=None)
Generate an ordering (permutation) of the graph nodes to make a sparse matrix.
Uses the reverse Cuthill-McKee heuristic (based on breadth-first search)1.
Parameters
•G(graph) – A NetworkX graph
•heuristic (function, optional) – Function to choose starting node for RCM algorithm. If
None a node from a pseudo-peripheral pair is used. A user-defined function can be supplied
that takes a graph object and returns a single node.
Returns nodes – Generator of nodes in reverse Cuthill-McKee ordering.
Return type generator
Examples
>>> from networkx.utils import reverse_cuthill_mckee_ordering
>>> G=nx.path_graph(4)
>>> rcm =list(reverse_cuthill_mckee_ordering(G))
>>> A=nx.adjacency_matrix(G, nodelist=rcm) # doctest: +SKIP
Smallest degree node as heuristic function:
>>> def smallest_degree(G):
... return min(G, key=G.degree)
>>> rcm =list(reverse_cuthill_mckee_ordering(G, heuristic=smallest_degree))
2Steven S. Skiena. 1997. The Algorithm Design Manual. Springer-Verlag New York, Inc., New York, NY, USA.
1E. Cuthill and J. McKee. Reducing the bandwidth of sparse symmetric matrices, In Proc. 24th Nat. Conf. ACM, pages 157-72, 1969.
http://doi.acm.org/10.1145/800195.805928
13.5. Cuthill-Mckee Ordering 693

NetworkX Reference, Release 2.3rc1.dev20181203210840
See also:
cuthill_mckee_ordering()
Notes
The optimal solution the the bandwidth reduction is NP-complete2.
References
13.6 Context Managers
reversed(G) A context manager for temporarily reversing a directed
graph in place.
13.6.1 networkx.utils.contextmanagers.reversed
reversed(G)
A context manager for temporarily reversing a directed graph in place.
This is a no-op for undirected graphs.
Parameters G (graph) – A NetworkX graph.
2Steven S. Skiena. 1997. The Algorithm Design Manual. Springer-Verlag New York, Inc., New York, NY, USA.
694 Chapter 13. Utilities

CHAPTER
FOURTEEN
GLOSSARY
dictionary A Python dictionary maps keys to values. Also known as “hashes”, or “associative arrays” in other pro-
gramming languages. See https://docs.python.org/2/tutorial/datastructures.html#dictionaries
edge Edges are either two-tuples of nodes (u, v) or three tuples of nodes with an edge attribute dictionary (u,
v, dict).
ebunch An iteratable container of edge tuples like a list, iterator, or file.
edge attribute Edges can have arbitrary Python objects assigned as attributes by using keyword/value pairs when
adding an edge assigning to the G.edges[u][v] attribute dictionary for the specified edge u-v.
hashable An object is hashable if it has a hash value which never changes during its lifetime (it needs a __hash__()
method), and can be compared to other objects (it needs an __eq__() or __cmp__() method). Hashable
objects which compare equal must have the same hash value.
Hashability makes an object usable as a dictionary key and a set member, because these data structures use the
hash value internally.
All of Python’s immutable built-in objects are hashable, while no mutable containers (such as lists or dictionar-
ies) are. Objects which are instances of user-defined classes are hashable by default; they all compare unequal,
and their hash value is their id().
Definition from https://docs.python.org/2/glossary.html
nbunch An nbunch is a single node, container of nodes or None (representing all nodes). It can be a list, set, graph,
etc.. To filter an nbunch so that only nodes actually in Gappear, use G.nbunch_iter(nbunch).
node A node can be any hashable Python object except None.
node attribute Nodes can have arbitrary Python objects assigned as attributes by using keyword/value pairs when
adding a node or assigning to the G.nodes[n] attribute dictionary for the specified node n.
695

NetworkX Reference, Release 2.3rc1.dev20181203210840
696 Chapter 14. Glossary

APPENDIX
A
TUTORIAL
This guide can help you start working with NetworkX.
A.1 Creating a graph
Create an empty graph with no nodes and no edges.
>>> import networkx as nx
>>> G=nx.Graph()
By definition, a Graph is a collection of nodes (vertices) along with identified pairs of nodes (called edges, links,
etc). In NetworkX, nodes can be any hashable object e.g., a text string, an image, an XML object, another Graph, a
customized node object, etc.
Note: Python’s None object should not be used as a node as it determines whether optional function arguments have
been assigned in many functions.
A.2 Nodes
The graph Gcan be grown in several ways. NetworkX includes many graph generator functions and facilities to read
and write graphs in many formats. To get started though we’ll look at simple manipulations. You can add one node at
a time,
>>> G.add_node(1)
add a list of nodes,
>>> G.add_nodes_from([2,3])
or add any iterable container of nodes. You can also add nodes along with node attributes if your container yields
2-tuples (node, node_attribute_dict). Node attributes are discussed further below.
>>> H=nx.path_graph(10)
>>> G.add_nodes_from(H)
Note that Gnow contains the nodes of Has nodes of G. In contrast, you could use the graph Has a node in G.
>>> G.add_node(H)
697

NetworkX Reference, Release 2.3rc1.dev20181203210840
The graph Gnow contains Has a node. This flexibility is very powerful as it allows graphs of graphs, graphs of files,
graphs of functions and much more. It is worth thinking about how to structure your application so that the nodes are
useful entities. Of course you can always use a unique identifier in Gand have a separate dictionary keyed by identifier
to the node information if you prefer.
Note: You should not change the node object if the hash depends on its contents.
A.3 Edges
Gcan also be grown by adding one edge at a time,
>>> G.add_edge(1,2)
>>> e=(2,3)
>>> G.add_edge(*e) # unpack edge tuple*
by adding a list of edges,
>>> G.add_edges_from([(1,2), (1,3)])
or by adding any ebunch of edges. An ebunch is any iterable container of edge-tuples. An edge-tuple can be a
2-tuple of nodes or a 3-tuple with 2 nodes followed by an edge attribute dictionary, e.g., (2, 3, {'weight':
3.1415}). Edge attributes are discussed further below
>>> G.add_edges_from(H.edges)
There are no complaints when adding existing nodes or edges. For example, after removing all nodes and edges,
>>> G.clear()
we add new nodes/edges and NetworkX quietly ignores any that are already present.
>>> G.add_edges_from([(1,2), (1,3)])
>>> G.add_node(1)
>>> G.add_edge(1,2)
>>> G.add_node("spam")# adds node "spam"
>>> G.add_nodes_from("spam")# adds 4 nodes: 's', 'p', 'a', 'm'
>>> G.add_edge(3,'m')
At this stage the graph Gconsists of 8 nodes and 3 edges, as can be seen by:
>>> G.number_of_nodes()
8
>>> G.number_of_edges()
3
We can examine the nodes and edges. Four basic graph properties facilitate reporting: G.nodes,G.edges,G.adj
and G.degree. These are set-like views of the nodes, edges, neighbors (adjacencies), and degrees of nodes in a
graph. They offer a continually updated read-only view into the graph structure. They are also dict-like in that you
can look up node and edge data attributes via the views and iterate with data attributes using methods .items(),
.data('span'). If you want a specific container type instead of a view, you can specify one. Here we use lists,
though sets, dicts, tuples and other containers may be better in other contexts.
698 Appendix A. Tutorial

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> list(G.nodes)
[1, 2, 3, 'spam', 's', 'p', 'a', 'm']
>>> list(G.edges)
[(1, 2), (1, 3), (3, 'm')]
>>> list(G.adj[1]) # or list(G.neighbors(1))
[2, 3]
>>> G.degree[1]# the number of edges incident to 1
2
One can specify to report the edges and degree from a subset of all nodes using an nbunch. An nbunch is any of: None
(meaning all nodes), a node, or an iterable container of nodes that is not itself a node in the graph.
>>> G.edges([2,'m'])
EdgeDataView([(2, 1), ('m', 3)])
>>> G.degree([2,3])
DegreeView({2: 1, 3: 2})
One can remove nodes and edges from the graph in a similar fashion to adding. Use meth-
ods Graph.remove_node(),Graph.remove_nodes_from(),Graph.remove_edge() and Graph.
remove_edges_from(), e.g.
>>> G.remove_node(2)
>>> G.remove_nodes_from("spam")
>>> list(G.nodes)
[1, 3, 'spam']
>>> G.remove_edge(1,3)
When creating a graph structure by instantiating one of the graph classes you can specify data in several formats.
>>> G.add_edge(1,2)
>>> H=nx.DiGraph(G) # create a DiGraph using the connections from G
>>> list(H.edges())
[(1, 2), (2, 1)]
>>> edgelist =[(0,1), (1,2), (2,3)]
>>> H=nx.Graph(edgelist)
A.4 What to use as nodes and edges
You might notice that nodes and edges are not specified as NetworkX objects. This leaves you free to use meaningful
items as nodes and edges. The most common choices are numbers or strings, but a node can be any hashable object
(except None), and an edge can be associated with any object xusing G.add_edge(n1, n2, object=x).
As an example, n1 and n2 could be protein objects from the RCSB Protein Data Bank, and xcould refer to an XML
record of publications detailing experimental observations of their interaction.
We have found this power quite useful, but its abuse can lead to unexpected surprises unless one is familiar with Python.
If in doubt, consider using convert_node_labels_to_integers() to obtain a more traditional graph with
integer labels.
A.5 Accessing edges and neighbors
In addition to the views Graph.edges(), and Graph.adj(), access to edges and neighbors is possible using
subscript notation.
A.4. What to use as nodes and edges 699

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G[1]# same as G.adj[1]
AtlasView({2: {}})
>>> G[1][2]
{}
>>> G.edges[1,2]
{}
You can get/set the attributes of an edge using subscript notation if the edge already exists.
>>> G.add_edge(1,3)
>>> G[1][3]['color']="blue"
>>> G.edges[1,2]['color']="red"
Fast examination of all (node, adjacency) pairs is achieved using G.adjacency(), or G.adj.items(). Note
that for undirected graphs, adjacency iteration sees each edge twice.
>>> FG =nx.Graph()
>>> FG.add_weighted_edges_from([(1,2,0.125), (1,3,0.75), (2,4,1.2), (3,4,0.
˓→375)])
>>> for n, nbrs in FG.adj.items():
... for nbr, eattr in nbrs.items():
... wt =eattr['weight']
... if wt <0.5:print('(%d,%d,%.3f)' %(n, nbr, wt))
(1, 2, 0.125)
(2, 1, 0.125)
(3, 4, 0.375)
(4, 3, 0.375)
Convenient access to all edges is achieved with the edges property.
>>> for (u, v, wt) in FG.edges.data('weight'):
... if wt <0.5:print('(%d,%d,%.3f)' %(u, v, wt))
(1, 2, 0.125)
(3, 4, 0.375)
A.6 Adding attributes to graphs, nodes, and edges
Attributes such as weights, labels, colors, or whatever Python object you like, can be attached to graphs, nodes, or
edges.
Each graph, node, and edge can hold key/value attribute pairs in an associated attribute dictionary (the keys must be
hashable). By default these are empty, but attributes can be added or changed using add_edge,add_node or direct
manipulation of the attribute dictionaries named G.graph,G.nodes, and G.edges for a graph G.
A.6.1 Graph attributes
Assign graph attributes when creating a new graph
>>> G=nx.Graph(day="Friday")
>>> G.graph
{'day': 'Friday'}
Or you can modify attributes later
700 Appendix A. Tutorial

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G.graph['day']="Monday"
>>> G.graph
{'day': 'Monday'}
A.6.2 Node attributes
Add node attributes using add_node(),add_nodes_from(), or G.nodes
>>> G.add_node(1, time='5pm')
>>> G.add_nodes_from([3], time='2pm')
>>> G.nodes[1]
{'time': '5pm'}
>>> G.nodes[1]['room']=714
>>> G.nodes.data()
NodeDataView({1: {'time': '5pm', 'room': 714}, 3: {'time': '2pm'}})
Note that adding a node to G.nodes does not add it to the graph, use G.add_node() to add new nodes. Similarly
for edges.
A.6.3 Edge Attributes
Add/change edge attributes using add_edge(),add_edges_from(), or subscript notation.
>>> G.add_edge(1,2, weight=4.7 )
>>> G.add_edges_from([(3,4), (4,5)], color='red')
>>> G.add_edges_from([(1,2, {'color':'blue'}), (2,3, {'weight':8})])
>>> G[1][2]['weight']=4.7
>>> G.edges[3,4]['weight']=4.2
The special attribute weight should be numeric as it is used by algorithms requiring weighted edges.
A.7 Directed graphs
The DiGraph class provides additional properties specific to directed edges, e.g., DiGraph.out_edges(),
DiGraph.in_degree(),DiGraph.predecessors(),DiGraph.successors() etc. To allow algo-
rithms to work with both classes easily, the directed versions of neighbors() is equivalent to successors()
while degree reports the sum of in_degree and out_degree even though that may feel inconsistent at times.
>>> DG =nx.DiGraph()
>>> DG.add_weighted_edges_from([(1,2,0.5), (3,1,0.75)])
>>> DG.out_degree(1, weight='weight')
0.5
>>> DG.degree(1, weight='weight')
1.25
>>> list(DG.successors(1))
[2]
>>> list(DG.neighbors(1))
[2]
Some algorithms work only for directed graphs and others are not well defined for directed graphs. Indeed the tendency
to lump directed and undirected graphs together is dangerous. If you want to treat a directed graph as undirected for
some measurement you should probably convert it using Graph.to_undirected() or with
A.7. Directed graphs 701

NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> H=nx.Graph(G) # convert G to undirected graph
A.8 Multigraphs
NetworkX provides classes for graphs which allow multiple edges between any pair of nodes. The MultiGraph
and MultiDiGraph classes allow you to add the same edge twice, possibly with different edge data. This can be
powerful for some applications, but many algorithms are not well defined on such graphs. Where results are well
defined, e.g., MultiGraph.degree() we provide the function. Otherwise you should convert to a standard graph
in a way that makes the measurement well defined.
>>> MG =nx.MultiGraph()
>>> MG.add_weighted_edges_from([(1,2,0.5), (1,2,0.75), (2,3,0.5)])
>>> dict(MG.degree(weight='weight'))
{1: 1.25, 2: 1.75, 3: 0.5}
>>> GG =nx.Graph()
>>> for n, nbrs in MG.adjacency():
... for nbr, edict in nbrs.items():
... minvalue =min([d['weight']for din edict.values()])
... GG.add_edge(n, nbr, weight =minvalue)
...
>>> nx.shortest_path(GG, 1,3)
[1, 2, 3]
A.9 Graph generators and graph operations
In addition to constructing graphs node-by-node or edge-by-edge, they can also be generated by
1. Applying classic graph operations, such as:
subgraph(G, nbunch) -induced subgraph view of G on nodes in nbunch
union(G1,G2) -graph union
disjoint_union(G1,G2) -graph union assuming all nodes are different
cartesian_product(G1,G2) -return Cartesian product graph
compose(G1,G2) -combine graphs identifying nodes common to both
complement(G) -graph complement
create_empty_copy(G) -return an empty copy of the same graph class
to_undirected(G) -return an undirected representation of G
to_directed(G) -return a directed representation of G
2. Using a call to one of the classic small graphs, e.g.,
>>> petersen =nx.petersen_graph()
>>> tutte =nx.tutte_graph()
>>> maze =nx.sedgewick_maze_graph()
>>> tet =nx.tetrahedral_graph()
3. Using a (constructive) generator for a classic graph, e.g.,
>>> K_5 =nx.complete_graph(5)
>>> K_3_5 =nx.complete_bipartite_graph(3,5)
>>> barbell =nx.barbell_graph(10,10)
>>> lollipop =nx.lollipop_graph(10,20)
702 Appendix A. Tutorial

NetworkX Reference, Release 2.3rc1.dev20181203210840
4. Using a stochastic graph generator, e.g.,
>>> er =nx.erdos_renyi_graph(100,0.15)
>>> ws =nx.watts_strogatz_graph(30,3,0.1)
>>> ba =nx.barabasi_albert_graph(100,5)
>>> red =nx.random_lobster(100,0.9,0.9)
5. Reading a graph stored in a file using common graph formats, such as edge lists, adjacency lists, GML,
GraphML, pickle, LEDA and others.
>>> nx.write_gml(red, "path.to.file")
>>> mygraph =nx.read_gml("path.to.file")
For details on graph formats see Reading and writing graphs and for graph generator functions see Graph generators
A.10 Analyzing graphs
The structure of Gcan be analyzed using various graph-theoretic functions such as:
>>> G=nx.Graph()
>>> G.add_edges_from([(1,2), (1,3)])
>>> G.add_node("spam")# adds node "spam"
>>> list(nx.connected_components(G))
[{1, 2, 3}, {'spam'}]
>>> sorted(d for n, d in G.degree())
[0, 1, 1, 2]
>>> nx.clustering(G)
{1: 0, 2: 0, 3: 0, 'spam': 0}
Some functions with large output iterate over (node, value) 2-tuples. These are easily stored in a dict structure if
you desire.
>>> sp =dict(nx.all_pairs_shortest_path(G))
>>> sp[3]
{3: [3], 1: [3, 1], 2: [3, 1, 2]}
See Algorithms for details on graph algorithms supported.
A.11 Drawing graphs
NetworkX is not primarily a graph drawing package but basic drawing with Matplotlib as well as an interface to use
the open source Graphviz software package are included. These are part of the networkx.drawing module and
will be imported if possible.
First import Matplotlib’s plot interface (pylab works too)
>>> import matplotlib.pyplot as plt
You may find it useful to interactively test code using ipython -pylab, which combines the power of ipython and
matplotlib and provides a convenient interactive mode.
To test if the import of networkx.drawing was successful draw Gusing one of
A.10. Analyzing graphs 703
NetworkX Reference, Release 2.3rc1.dev20181203210840
>>> G=nx.petersen_graph()
>>> plt.subplot(121)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw(G, with_labels=True, font_weight='bold')
>>> plt.subplot(122)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw_shell(G, nlist=[range(5,10), range(5)], with_labels=True, font_weight=
˓→'bold')
when drawing to an interactive display. Note that you may need to issue a Matplotlib
>>> plt.show()
command if you are not using matplotlib in interactive mode (see Matplotlib FAQ ).
>>> options ={
... 'node_color':'black',
... 'node_size':100,
... 'width':3,
... }
>>> plt.subplot(221)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw_random(G, **options)
>>> plt.subplot(222)
<matplotlib.axes._subplots.AxesSubplot object at ...>
(continues on next page)
704 Appendix A. Tutorial
NetworkX Reference, Release 2.3rc1.dev20181203210840
(continued from previous page)
>>> nx.draw_circular(G, **options)
>>> plt.subplot(223)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw_spectral(G, **options)
>>> plt.subplot(224)
<matplotlib.axes._subplots.AxesSubplot object at ...>
>>> nx.draw_shell(G, nlist=[range(5,10), range(5)], **options)
You can find additional options via draw_networkx() and layouts via layout. You can use multiple shells with
draw_shell().
>>> G=nx.dodecahedral_graph()
>>> shells =[[2,3,4,5,6], [8,1,0,19,18,17,16,15,14,7], [9,10,11,12,
˓→13]]
>>> nx.draw_shell(G, nlist=shells, **options)
A.11. Drawing graphs 705
NetworkX Reference, Release 2.3rc1.dev20181203210840
To save drawings to a file, use, for example
>>> nx.draw(G)
>>> plt.savefig("path.png")
writes to the file path.png in the local directory. If Graphviz and PyGraphviz or pydot, are available on your system,
you can also use nx_agraph.graphviz_layout(G) or nx_pydot.graphviz_layout(G) to get the node
positions, or write the graph in dot format for further processing.
>>> from networkx.drawing.nx_pydot import write_dot
>>> pos =nx.nx_agraph.graphviz_layout(G)
>>> nx.draw(G, pos=pos)
>>> write_dot(G, 'file.dot')
See Drawing for additional details.
• ;
• ;
• .
706 Appendix A. Tutorial

BIBLIOGRAPHY
[atlas] Ronald C. Read and Robin J. Wilson, An Atlas of Graphs. Oxford University Press, 1998.
707

NetworkX Reference, Release 2.3rc1.dev20181203210840
708 Bibliography

PYTHON MODULE INDEX
a
networkx.algorithms.approximation,129
networkx.algorithms.approximation.clique,
133
networkx.algorithms.approximation.clustering_coefficient,
135
networkx.algorithms.approximation.connectivity,
129
networkx.algorithms.approximation.dominating_set,
135
networkx.algorithms.approximation.independent_set,
136
networkx.algorithms.approximation.kcomponents,
132
networkx.algorithms.approximation.matching,
137
networkx.algorithms.approximation.ramsey,
138
networkx.algorithms.approximation.steinertree,
138
networkx.algorithms.approximation.treewidth,
139
networkx.algorithms.approximation.vertex_cover,
140
networkx.algorithms.assortativity,140
networkx.algorithms.bipartite,150
networkx.algorithms.bipartite.basic,151
networkx.algorithms.bipartite.centrality,
170
networkx.algorithms.bipartite.cluster,
165
networkx.algorithms.bipartite.covering,
178
networkx.algorithms.bipartite.generators,
173
networkx.algorithms.bipartite.matching,
155
networkx.algorithms.bipartite.matrix,
157
networkx.algorithms.bipartite.projection,
159
networkx.algorithms.bipartite.redundancy,
169
networkx.algorithms.bipartite.spectral,
165
networkx.algorithms.boundary,178
networkx.algorithms.bridges,180
networkx.algorithms.centrality,301
networkx.algorithms.chains,210
networkx.algorithms.chordal,211
networkx.algorithms.clique,213
networkx.algorithms.cluster,217
networkx.algorithms.coloring,222
networkx.algorithms.communicability_alg,
226
networkx.algorithms.community,227
networkx.algorithms.community.asyn_fluid,
233
networkx.algorithms.community.centrality,
235
networkx.algorithms.community.community_generators,
228
networkx.algorithms.community.community_utils,
237
networkx.algorithms.community.kclique,
231
networkx.algorithms.community.kernighan_lin,
228
networkx.algorithms.community.label_propagation,
232
networkx.algorithms.community.modularity_max,
231
networkx.algorithms.community.quality,
234
networkx.algorithms.components,238
networkx.algorithms.connectivity,251
networkx.algorithms.connectivity.connectivity,
265
networkx.algorithms.connectivity.cuts,
273
networkx.algorithms.connectivity.disjoint_paths,
261
networkx.algorithms.connectivity.edge_augmentation,
252
709

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.connectivity.edge_kcomponents,
255
networkx.algorithms.connectivity.kcomponents,
259
networkx.algorithms.connectivity.kcutsets,
260
networkx.algorithms.connectivity.stoerwagner,
280
networkx.algorithms.connectivity.utils,
281
networkx.algorithms.core,282
networkx.algorithms.covering,285
networkx.algorithms.cuts,290
networkx.algorithms.cycles,286
networkx.algorithms.dag,294
networkx.algorithms.distance_measures,
302
networkx.algorithms.distance_regular,
305
networkx.algorithms.dominance,307
networkx.algorithms.dominating,308
networkx.algorithms.efficiency,310
networkx.algorithms.euler,311
networkx.algorithms.flow,313
networkx.algorithms.graphical,340
networkx.algorithms.hierarchy,344
networkx.algorithms.hybrid,344
networkx.algorithms.isolate,346
networkx.algorithms.isomorphism,347
networkx.algorithms.isomorphism.isomorphvf2,
350
networkx.algorithms.link_analysis.hits_alg,
365
networkx.algorithms.link_analysis.pagerank_alg,
361
networkx.algorithms.link_prediction,367
networkx.algorithms.lowest_common_ancestors,
373
networkx.algorithms.matching,375
networkx.algorithms.minors,377
networkx.algorithms.mis,383
networkx.algorithms.node_classification,
384
networkx.algorithms.node_classification.hmn,
384
networkx.algorithms.node_classification.lgc,
385
networkx.algorithms.operators.all,389
networkx.algorithms.operators.binary,
387
networkx.algorithms.operators.product,
391
networkx.algorithms.operators.unary,386
networkx.algorithms.planarity,395
networkx.algorithms.reciprocity,399
networkx.algorithms.richclub,400
networkx.algorithms.shortest_paths.astar,
436
networkx.algorithms.shortest_paths.dense,
434
networkx.algorithms.shortest_paths.generic,
401
networkx.algorithms.shortest_paths.unweighted,
406
networkx.algorithms.shortest_paths.weighted,
411
networkx.algorithms.similarity,437
networkx.algorithms.simple_paths,444
networkx.algorithms.smallworld,448
networkx.algorithms.smetric,451
networkx.algorithms.sparsifiers,452
networkx.algorithms.structuralholes,452
networkx.algorithms.swap,455
networkx.algorithms.tournament,457
networkx.algorithms.traversal.beamsearch,
468
networkx.algorithms.traversal.breadth_first_search,
465
networkx.algorithms.traversal.depth_first_search,
460
networkx.algorithms.traversal.edgebfs,
470
networkx.algorithms.traversal.edgedfs,
469
networkx.algorithms.tree.branchings,474
networkx.algorithms.tree.coding,477
networkx.algorithms.tree.mst,482
networkx.algorithms.tree.operations,481
networkx.algorithms.tree.recognition,
472
networkx.algorithms.triads,486
networkx.algorithms.vitality,487
networkx.algorithms.voronoi,488
networkx.algorithms.wiener,489
c
networkx.classes.function,491
networkx.classes.graphviews,126
networkx.classes.ordered,126
networkx.convert,595
networkx.convert_matrix,598
d
networkx.drawing.layout,675
networkx.drawing.nx_agraph,670
networkx.drawing.nx_pydot,672
networkx.drawing.nx_pylab,661
710 Python Module Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
e
networkx.exception,683
g
networkx.generators.atlas,509
networkx.generators.classic,510
networkx.generators.community,563
networkx.generators.degree_seq,539
networkx.generators.directed,546
networkx.generators.duplication,537
networkx.generators.ego,559
networkx.generators.expanders,518
networkx.generators.geometric,550
networkx.generators.intersection,560
networkx.generators.joint_degree_seq,
574
networkx.generators.lattice,519
networkx.generators.line,557
networkx.generators.mycielski,575
networkx.generators.nonisomorphic_trees,
573
networkx.generators.random_clustered,
545
networkx.generators.random_graphs,526
networkx.generators.small,522
networkx.generators.social,562
networkx.generators.spectral_graph_forge,
570
networkx.generators.stochastic,560
networkx.generators.trees,571
networkx.generators.triads,573
l
networkx.linalg.algebraicconnectivity,
584
networkx.linalg.attrmatrix,587
networkx.linalg.graphmatrix,579
networkx.linalg.laplacianmatrix,580
networkx.linalg.modularitymatrix,591
networkx.linalg.spectrum,583
r
networkx.readwrite.adjlist,617
networkx.readwrite.edgelist,624
networkx.readwrite.gexf,630
networkx.readwrite.gml,633
networkx.readwrite.gpickle,638
networkx.readwrite.graph6,651
networkx.readwrite.graphml,639
networkx.readwrite.json_graph,643
networkx.readwrite.leda,648
networkx.readwrite.multiline_adjlist,
620
networkx.readwrite.nx_shp,659
networkx.readwrite.nx_yaml,649
networkx.readwrite.pajek,657
networkx.readwrite.sparse6,654
networkx.relabel,613
u
networkx.utils,685
networkx.utils.contextmanagers,694
networkx.utils.decorators,689
networkx.utils.misc,685
networkx.utils.random_sequence,687
networkx.utils.rcm,692
networkx.utils.union_find,687
Python Module Index 711

NetworkX Reference, Release 2.3rc1.dev20181203210840
712 Python Module Index

INDEX
Symbols
__contains__() (DiGraph method), 48
__contains__() (Graph method), 22
__contains__() (MultiDiGraph method), 109
__contains__() (MultiGraph method), 80
__getitem__() (DiGraph method), 53
__getitem__() (Graph method), 25
__getitem__() (MultiDiGraph method), 114
__getitem__() (MultiGraph method), 84
__init__() (DiGraph method), 38
__init__() (DiGraphMatcher method), 354
__init__() (EdgeComponentAuxGraph method), 259
__init__() (Edmonds method), 477
__init__() (Graph method), 11
__init__() (GraphMatcher method), 352
__init__() (MultiDiGraph method), 97
__init__() (MultiGraph method), 69
__iter__() (DiGraph method), 48
__iter__() (Graph method), 21
__iter__() (MultiDiGraph method), 108
__iter__() (MultiGraph method), 80
__len__() (DiGraph method), 56
__len__() (Graph method), 27
__len__() (MultiDiGraph method), 117
__len__() (MultiGraph method), 86
A
adamic_adar_index() (in module net-
workx.algorithms.link_prediction), 369
add_cycle() (in module networkx.classes.function),
494
add_edge() (DiGraph method), 41
add_edge() (Graph method), 14
add_edge() (MultiDiGraph method), 100
add_edge() (MultiGraph method), 72
add_edges_from() (DiGraph method), 42
add_edges_from() (Graph method), 15
add_edges_from() (MultiDiGraph method), 101
add_edges_from() (MultiGraph method), 73
add_half_edge_ccw() (PlanarEmbedding
method), 397
add_half_edge_cw() (PlanarEmbedding method),
397
add_half_edge_first() (PlanarEmbedding
method), 397
add_node() (DiGraph method), 39
add_node() (Graph method), 12
add_node() (MultiDiGraph method), 98
add_node() (MultiGraph method), 69
add_nodes_from() (DiGraph method), 39
add_nodes_from() (Graph method), 13
add_nodes_from() (MultiDiGraph method), 98
add_nodes_from() (MultiGraph method), 70
add_path() (in module networkx.classes.function),
494
add_star() (in module networkx.classes.function),
493
add_weighted_edges_from() (DiGraph method),
42
add_weighted_edges_from() (Graph method),
16
add_weighted_edges_from() (MultiDiGraph
method), 102
add_weighted_edges_from() (MultiGraph
method), 74
adj (DiGraph attribute), 53
adj (Graph attribute), 25
adj (MultiDiGraph attribute), 114
adj (MultiGraph attribute), 84
adjacency() (DiGraph method), 55
adjacency() (Graph method), 26
adjacency() (MultiDiGraph method), 116
adjacency() (MultiGraph method), 85
adjacency_data() (in module net-
workx.readwrite.json_graph), 645
adjacency_graph() (in module net-
workx.readwrite.json_graph), 645
adjacency_matrix() (in module net-
workx.linalg.graphmatrix), 579
adjacency_spectrum() (in module net-
workx.linalg.spectrum), 583
algebraic_connectivity() (in module net-
workx.linalg.algebraicconnectivity), 584
713

NetworkX Reference, Release 2.3rc1.dev20181203210840
all_neighbors() (in module net-
workx.classes.function), 498
all_node_cuts() (in module net-
workx.algorithms.connectivity.kcutsets),
261
all_pairs_bellman_ford_path() (in module
networkx.algorithms.shortest_paths.weighted),
428
all_pairs_bellman_ford_path_length()
(in module net-
workx.algorithms.shortest_paths.weighted),
429
all_pairs_dijkstra() (in module net-
workx.algorithms.shortest_paths.weighted),
421
all_pairs_dijkstra_path() (in module net-
workx.algorithms.shortest_paths.weighted),
422
all_pairs_dijkstra_path_length()
(in module net-
workx.algorithms.shortest_paths.weighted),
423
all_pairs_lowest_common_ancestor()
(in module net-
workx.algorithms.lowest_common_ancestors),
373
all_pairs_node_connectivity()
(in module net-
workx.algorithms.approximation.connectivity),
129
all_pairs_node_connectivity() (in module
networkx.algorithms.connectivity.connectivity),
266
all_pairs_shortest_path() (in module net-
workx.algorithms.shortest_paths.unweighted),
409
all_pairs_shortest_path_length()
(in module net-
workx.algorithms.shortest_paths.unweighted),
409
all_shortest_paths() (in module net-
workx.algorithms.shortest_paths.generic),
402
all_simple_paths() (in module net-
workx.algorithms.simple_paths), 444
all_topological_sorts() (in module net-
workx.algorithms.dag), 296
alternating_havel_hakimi_graph() (in mod-
ule networkx.algorithms.bipartite.generators),
176
AmbiguousSolution (class in networkx), 683
ancestors() (in module networkx.algorithms.dag),
295
antichains() (in module networkx.algorithms.dag),
299
approximate_current_flow_betweenness_centrality()
(in module networkx.algorithms.centrality),
198
articulation_points() (in module net-
workx.algorithms.components), 250
astar_path() (in module net-
workx.algorithms.shortest_paths.astar),
436
astar_path_length() (in module net-
workx.algorithms.shortest_paths.astar),
437
asyn_fluidc() (in module net-
workx.algorithms.community.asyn_fluid),
233
asyn_lpa_communities() (in module net-
workx.algorithms.community.label_propagation),
232
attr_matrix() (in module net-
workx.linalg.attrmatrix), 587
attr_sparse_matrix() (in module net-
workx.linalg.attrmatrix), 589
attracting_component_subgraphs() (in mod-
ule networkx.algorithms.components), 247
attracting_components() (in module net-
workx.algorithms.components), 246
attribute_assortativity_coefficient()
(in module networkx.algorithms.assortativity),
142
attribute_mixing_dict() (in module net-
workx.algorithms.assortativity), 149
attribute_mixing_matrix() (in module net-
workx.algorithms.assortativity), 147
authority_matrix() (in module net-
workx.algorithms.link_analysis.hits_alg),
367
average_clustering() (in module net-
workx.algorithms.approximation.clustering_coefficient),
135
average_clustering() (in module net-
workx.algorithms.bipartite.cluster), 167
average_clustering() (in module net-
workx.algorithms.cluster), 220
average_degree_connectivity() (in module
networkx.algorithms.assortativity), 145
average_neighbor_degree() (in module net-
workx.algorithms.assortativity), 144
average_node_connectivity() (in module
networkx.algorithms.connectivity.connectivity),
266
average_shortest_path_length() (in module
networkx.algorithms.shortest_paths.generic),
404
714 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
B
balanced_tree() (in module net-
workx.generators.classic), 511
barabasi_albert_graph() (in module net-
workx.generators.random_graphs), 533
barbell_graph() (in module net-
workx.generators.classic), 511
bellman_ford_path() (in module net-
workx.algorithms.shortest_paths.weighted),
425
bellman_ford_path_length() (in module net-
workx.algorithms.shortest_paths.weighted),
425
bellman_ford_predecessor_and_distance()
(in module net-
workx.algorithms.shortest_paths.weighted),
430
betweenness_centrality() (in module net-
workx.algorithms.bipartite.centrality), 172
betweenness_centrality() (in module net-
workx.algorithms.centrality), 192
betweenness_centrality_subset() (in mod-
ule networkx.algorithms.centrality), 194
bfs_beam_edges() (in module net-
workx.algorithms.traversal.beamsearch),
468
bfs_edges() (in module net-
workx.algorithms.traversal.breadth_first_search),
465
bfs_predecessors() (in module net-
workx.algorithms.traversal.breadth_first_search),
466
bfs_successors() (in module net-
workx.algorithms.traversal.breadth_first_search),
467
bfs_tree() (in module net-
workx.algorithms.traversal.breadth_first_search),
466
biadjacency_matrix() (in module net-
workx.algorithms.bipartite.matrix), 157
biconnected_component_edges() (in module
networkx.algorithms.components), 249
biconnected_component_subgraphs() (in
module networkx.algorithms.components), 250
biconnected_components() (in module net-
workx.algorithms.components), 248
bidirectional_dijkstra() (in module net-
workx.algorithms.shortest_paths.weighted),
424
bidirectional_shortest_path()
(in module net-
workx.algorithms.shortest_paths.unweighted),
408
binomial_graph() (in module net-
workx.generators.random_graphs), 530
bipartite_layout() (in module net-
workx.drawing.layout), 676
boundary_expansion() (in module net-
workx.algorithms.cuts), 290
boykov_kolmogorov() (in module net-
workx.algorithms.flow), 327
branching_weight() (in module net-
workx.algorithms.tree.branchings), 475
bridge_components() (in module net-
workx.algorithms.connectivity.edge_kcomponents),
257
bridges() (in module networkx.algorithms.bridges),
180
build_auxiliary_edge_connectivity() (in
module networkx.algorithms.connectivity.utils),
281
build_auxiliary_node_connectivity() (in
module networkx.algorithms.connectivity.utils),
281
build_residual_network() (in module net-
workx.algorithms.flow), 331
bull_graph() (in module net-
workx.generators.small), 524
C
candidate_pairs_iter() (DiGraphMatcher
method), 355
candidate_pairs_iter() (GraphMatcher
method), 353
capacity_scaling() (in module net-
workx.algorithms.flow), 338
cartesian_product() (in module net-
workx.algorithms.operators.product), 391
categorical_edge_match() (in module net-
workx.algorithms.isomorphism), 356
categorical_multiedge_match() (in module
networkx.algorithms.isomorphism), 357
categorical_node_match() (in module net-
workx.algorithms.isomorphism), 356
caveman_graph() (in module net-
workx.generators.community), 563
center() (in module net-
workx.algorithms.distance_measures), 302
chain_decomposition() (in module net-
workx.algorithms.chains), 210
check_planarity() (in module net-
workx.algorithms.planarity), 395
check_structure() (PlanarEmbedding method),
398
chordal_cycle_graph() (in module net-
workx.generators.expanders), 519
chordal_graph_cliques() (in module net-
workx.algorithms.chordal), 211
Index 715

NetworkX Reference, Release 2.3rc1.dev20181203210840
chordal_graph_treewidth() (in module net-
workx.algorithms.chordal), 212
chvatal_graph() (in module net-
workx.generators.small), 524
circulant_graph() (in module net-
workx.generators.classic), 513
circular_ladder_graph() (in module net-
workx.generators.classic), 513
circular_layout() (in module net-
workx.drawing.layout), 676
clear() (DiGraph method), 45
clear() (Graph method), 19
clear() (MultiDiGraph method), 106
clear() (MultiGraph method), 77
clique_removal() (in module net-
workx.algorithms.approximation.clique),
134
cliques_containing_node() (in module net-
workx.algorithms.clique), 217
closeness_centrality() (in module net-
workx.algorithms.bipartite.centrality), 171
closeness_centrality() (in module net-
workx.algorithms.centrality), 189
closeness_vitality() (in module net-
workx.algorithms.vitality), 487
clustering() (in module net-
workx.algorithms.bipartite.cluster), 166
clustering() (in module net-
workx.algorithms.cluster), 219
cn_soundarajan_hopcroft() (in module net-
workx.algorithms.link_prediction), 370
collaboration_weighted_projected_graph()
(in module net-
workx.algorithms.bipartite.projection), 161
color() (in module net-
workx.algorithms.bipartite.basic), 153
common_neighbors() (in module net-
workx.classes.function), 499
communicability() (in module net-
workx.algorithms.communicability_alg),
226
communicability_betweenness_centrality()
(in module networkx.algorithms.centrality),
201
communicability_exp() (in module net-
workx.algorithms.communicability_alg),
227
complement() (in module net-
workx.algorithms.operators.unary), 386
complete_bipartite_graph() (in module net-
workx.algorithms.bipartite.generators), 174
complete_graph() (in module net-
workx.generators.classic), 512
complete_multipartite_graph() (in module
networkx.generators.classic), 512
compose() (in module net-
workx.algorithms.operators.binary), 387
compose_all() (in module net-
workx.algorithms.operators.all), 389
condensation() (in module net-
workx.algorithms.components), 243
conductance() (in module net-
workx.algorithms.cuts), 291
configuration_model() (in module net-
workx.algorithms.bipartite.generators), 174
configuration_model() (in module net-
workx.generators.degree_seq), 539
connect_components() (PlanarEmbedding
method), 398
connected_caveman_graph() (in module net-
workx.generators.community), 564
connected_component_subgraphs() (in mod-
ule networkx.algorithms.components), 239
connected_components() (in module net-
workx.algorithms.components), 239
connected_double_edge_swap() (in module net-
workx.algorithms.swap), 456
connected_watts_strogatz_graph() (in mod-
ule networkx.generators.random_graphs), 532
constraint() (in module net-
workx.algorithms.structuralholes), 453
contracted_edge() (in module net-
workx.algorithms.minors), 377
contracted_nodes() (in module net-
workx.algorithms.minors), 378
convert_node_labels_to_integers() (in
module networkx.relabel), 613
copy() (DiGraph method), 60
copy() (Graph method), 30
copy() (MultiDiGraph method), 121
copy() (MultiGraph method), 89
core_number() (in module net-
workx.algorithms.core), 282
cost_of_flow() (in module net-
workx.algorithms.flow), 336
could_be_isomorphic() (in module net-
workx.algorithms.isomorphism), 349
coverage() (in module net-
workx.algorithms.community.quality), 234
create_empty_copy() (in module net-
workx.classes.function), 492
create_random_state() (in module net-
workx.utils.misc), 687
cubical_graph() (in module net-
workx.generators.small), 524
cumulative_distribution() (in module net-
workx.utils.random_sequence), 687
current_flow_betweenness_centrality()
716 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
(in module networkx.algorithms.centrality),
196
current_flow_betweenness_centrality_subset()
(in module networkx.algorithms.centrality),
199
current_flow_closeness_centrality() (in
module networkx.algorithms.centrality), 191
cut_size() (in module networkx.algorithms.cuts),
291
cuthill_mckee_ordering() (in module net-
workx.utils.rcm), 692
cycle_basis() (in module net-
workx.algorithms.cycles), 287
cycle_graph() (in module net-
workx.generators.classic), 514
cytoscape_data() (in module net-
workx.readwrite.json_graph), 646
cytoscape_graph() (in module net-
workx.readwrite.json_graph), 646
D
dag_longest_path() (in module net-
workx.algorithms.dag), 299
dag_longest_path_length() (in module net-
workx.algorithms.dag), 300
dag_to_branching() (in module net-
workx.algorithms.dag), 300
davis_southern_women_graph() (in module net-
workx.generators.social), 562
default_opener() (in module networkx.utils.misc),
686
degree (DiGraph attribute), 57
degree (Graph attribute), 28
degree (MultiDiGraph attribute), 118
degree (MultiGraph attribute), 87
degree() (in module networkx.classes.function), 491
degree_assortativity_coefficient() (in
module networkx.algorithms.assortativity), 141
degree_centrality() (in module net-
workx.algorithms.bipartite.centrality), 171
degree_centrality() (in module net-
workx.algorithms.centrality), 182
degree_histogram() (in module net-
workx.classes.function), 492
degree_mixing_dict() (in module net-
workx.algorithms.assortativity), 149
degree_mixing_matrix() (in module net-
workx.algorithms.assortativity), 148
degree_pearson_correlation_coefficient()
(in module networkx.algorithms.assortativity),
143
degree_sequence_tree() (in module net-
workx.generators.degree_seq), 544
degrees() (in module net-
workx.algorithms.bipartite.basic), 154
dense_gnm_random_graph() (in module net-
workx.generators.random_graphs), 528
density() (in module net-
workx.algorithms.bipartite.basic), 153
density() (in module networkx.classes.function), 492
desargues_graph() (in module net-
workx.generators.small), 524
descendants() (in module net-
workx.algorithms.dag), 295
dfs_edges() (in module net-
workx.algorithms.traversal.depth_first_search),
460
dfs_labeled_edges() (in module net-
workx.algorithms.traversal.depth_first_search),
464
dfs_postorder_nodes() (in module net-
workx.algorithms.traversal.depth_first_search),
463
dfs_predecessors() (in module net-
workx.algorithms.traversal.depth_first_search),
461
dfs_preorder_nodes() (in module net-
workx.algorithms.traversal.depth_first_search),
462
dfs_successors() (in module net-
workx.algorithms.traversal.depth_first_search),
462
dfs_tree() (in module net-
workx.algorithms.traversal.depth_first_search),
461
diameter() (in module net-
workx.algorithms.distance_measures), 303
diamond_graph() (in module net-
workx.generators.small), 524
dictionary,695
difference() (in module net-
workx.algorithms.operators.binary), 389
DiGraph (class in networkx), 34
dijkstra_path() (in module net-
workx.algorithms.shortest_paths.weighted),
413
dijkstra_path_length() (in module net-
workx.algorithms.shortest_paths.weighted),
414
dijkstra_predecessor_and_distance()
(in module net-
workx.algorithms.shortest_paths.weighted),
412
dinitz() (in module networkx.algorithms.flow), 326
directed_configuration_model() (in module
networkx.generators.degree_seq), 541
directed_havel_hakimi_graph() (in module
Index 717

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.generators.degree_seq), 543
directed_laplacian_matrix() (in module net-
workx.linalg.laplacianmatrix), 582
directed_modularity_matrix() (in module net-
workx.linalg.modularitymatrix), 592
discrete_sequence() (in module net-
workx.utils.random_sequence), 688
disjoint_union() (in module net-
workx.algorithms.operators.binary), 388
disjoint_union_all() (in module net-
workx.algorithms.operators.all), 390
dispersion() (in module net-
workx.algorithms.centrality), 302
dodecahedral_graph() (in module net-
workx.generators.small), 524
dominance_frontiers() (in module net-
workx.algorithms.dominance), 308
dominating_set() (in module net-
workx.algorithms.dominating), 309
dorogovtsev_goltsev_mendes_graph() (in
module networkx.generators.classic), 514
double_edge_swap() (in module net-
workx.algorithms.swap), 455
draw() (in module networkx.drawing.nx_pylab), 662
draw_circular() (in module net-
workx.drawing.nx_pylab), 668
draw_kamada_kawai() (in module net-
workx.drawing.nx_pylab), 668
draw_networkx() (in module net-
workx.drawing.nx_pylab), 662
draw_networkx_edge_labels() (in module net-
workx.drawing.nx_pylab), 667
draw_networkx_edges() (in module net-
workx.drawing.nx_pylab), 665
draw_networkx_labels() (in module net-
workx.drawing.nx_pylab), 667
draw_networkx_nodes() (in module net-
workx.drawing.nx_pylab), 664
draw_random() (in module net-
workx.drawing.nx_pylab), 669
draw_shell() (in module net-
workx.drawing.nx_pylab), 669
draw_spectral() (in module net-
workx.drawing.nx_pylab), 669
draw_spring() (in module net-
workx.drawing.nx_pylab), 669
dual_barabasi_albert_graph() (in module net-
workx.generators.random_graphs), 533
duplication_divergence_graph() (in module
networkx.generators.duplication), 538
E
ebunch,695
eccentricity() (in module net-
workx.algorithms.distance_measures), 303
edge,695
edge attribute,695
edge_betweenness_centrality() (in module
networkx.algorithms.centrality), 193
edge_betweenness_centrality_subset() (in
module networkx.algorithms.centrality), 195
edge_bfs() (in module net-
workx.algorithms.traversal.edgebfs), 470
edge_boundary() (in module net-
workx.algorithms.boundary), 179
edge_connectivity() (in module net-
workx.algorithms.connectivity.connectivity),
267
edge_current_flow_betweenness_centrality()
(in module networkx.algorithms.centrality),
197
edge_current_flow_betweenness_centrality_subset()
(in module networkx.algorithms.centrality),
200
edge_dfs() (in module net-
workx.algorithms.traversal.edgedfs), 469
edge_disjoint_paths() (in module net-
workx.algorithms.connectivity.disjoint_paths),
262
edge_expansion() (in module net-
workx.algorithms.cuts), 292
edge_load_centrality() (in module net-
workx.algorithms.centrality), 202
edge_subgraph() (DiGraph method), 64
edge_subgraph() (Graph method), 33
edge_subgraph() (in module net-
workx.classes.function), 497
edge_subgraph() (MultiDiGraph method), 125
edge_subgraph() (MultiGraph method), 92
EdgeComponentAuxGraph (class in net-
workx.algorithms.connectivity.edge_kcomponents),
258
edges (DiGraph attribute), 49
edges (Graph attribute), 22
edges (MultiDiGraph attribute), 109
edges (MultiGraph attribute), 81
edges() (in module networkx.classes.function), 499
Edmonds (class in net-
workx.algorithms.tree.branchings), 477
edmonds_karp() (in module net-
workx.algorithms.flow), 320
effective_size() (in module net-
workx.algorithms.structuralholes), 453
efficiency() (in module net-
workx.algorithms.efficiency), 310
ego_graph() (in module networkx.generators.ego),
559
718 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
eigenvector_centrality() (in module net-
workx.algorithms.centrality), 184
eigenvector_centrality_numpy() (in module
networkx.algorithms.centrality), 185
empty_graph() (in module net-
workx.generators.classic), 515
enumerate_all_cliques() (in module net-
workx.algorithms.clique), 214
eppstein_matching() (in module net-
workx.algorithms.bipartite.matching), 155
erdos_renyi_graph() (in module net-
workx.generators.random_graphs), 529
estrada_index() (in module net-
workx.algorithms.centrality), 204
eulerian_circuit() (in module net-
workx.algorithms.euler), 312
eulerize() (in module networkx.algorithms.euler),
313
ExceededMaxIterations (class in networkx), 684
expected_degree_graph() (in module net-
workx.generators.degree_seq), 542
extended_barabasi_albert_graph() (in mod-
ule networkx.generators.random_graphs), 534
extrema_bounding() (in module net-
workx.algorithms.distance_measures), 303
F
fast_could_be_isomorphic() (in module net-
workx.algorithms.isomorphism), 349
fast_gnp_random_graph() (in module net-
workx.generators.random_graphs), 527
faster_could_be_isomorphic() (in module net-
workx.algorithms.isomorphism), 349
fiedler_vector() (in module net-
workx.linalg.algebraicconnectivity), 585
find_cliques() (in module net-
workx.algorithms.clique), 214
find_cycle() (in module net-
workx.algorithms.cycles), 288
find_induced_nodes() (in module net-
workx.algorithms.chordal), 212
flatten() (in module networkx.utils.misc), 685
florentine_families_graph() (in module net-
workx.generators.social), 563
flow_hierarchy() (in module net-
workx.algorithms.hierarchy), 344
floyd_warshall() (in module net-
workx.algorithms.shortest_paths.dense),
434
floyd_warshall_numpy() (in module net-
workx.algorithms.shortest_paths.dense), 435
floyd_warshall_predecessor_and_distance()
(in module net-
workx.algorithms.shortest_paths.dense),
434
freeze() (in module networkx.classes.function), 506
from_agraph() (in module net-
workx.drawing.nx_agraph), 670
from_biadjacency_matrix() (in module net-
workx.algorithms.bipartite.matrix), 158
from_dict_of_dicts() (in module net-
workx.convert), 596
from_dict_of_lists() (in module net-
workx.convert), 597
from_edgelist() (in module networkx.convert), 598
from_graph6_bytes() (in module net-
workx.readwrite.graph6), 651
from_nested_tuple() (in module net-
workx.algorithms.tree.coding), 477
from_numpy_array() (in module net-
workx.convert_matrix), 604
from_numpy_matrix() (in module net-
workx.convert_matrix), 602
from_pandas_adjacency() (in module net-
workx.convert_matrix), 609
from_pandas_edgelist() (in module net-
workx.convert_matrix), 610
from_prufer_sequence() (in module net-
workx.algorithms.tree.coding), 479
from_pydot() (in module net-
workx.drawing.nx_pydot), 673
from_scipy_sparse_matrix() (in module net-
workx.convert_matrix), 606
from_sparse6_bytes() (in module net-
workx.readwrite.sparse6), 654
frucht_graph() (in module net-
workx.generators.small), 525
full_rary_tree() (in module net-
workx.generators.classic), 516
G
gaussian_random_partition_graph() (in
module networkx.generators.community), 566
general_random_intersection_graph() (in
module networkx.generators.intersection), 561
generalized_degree() (in module net-
workx.algorithms.cluster), 221
generate_adjlist() (in module net-
workx.readwrite.adjlist), 620
generate_edgelist() (in module net-
workx.readwrite.edgelist), 628
generate_gexf() (in module net-
workx.readwrite.gexf ), 632
generate_gml() (in module net-
workx.readwrite.gml), 636
generate_graphml() (in module net-
workx.readwrite.graphml), 641
Index 719

NetworkX Reference, Release 2.3rc1.dev20181203210840
generate_multiline_adjlist() (in module net-
workx.readwrite.multiline_adjlist), 623
generate_pajek() (in module net-
workx.readwrite.pajek), 659
generate_unique_node() (in module net-
workx.utils.misc), 686
generic_edge_match() (in module net-
workx.algorithms.isomorphism), 359
generic_graph_view() (in module net-
workx.classes.graphviews), 127
generic_multiedge_match() (in module net-
workx.algorithms.isomorphism), 360
generic_node_match() (in module net-
workx.algorithms.isomorphism), 359
generic_weighted_projected_graph()
(in module net-
workx.algorithms.bipartite.projection), 163
geographical_threshold_graph() (in module
networkx.generators.geometric), 552
get_data() (PlanarEmbedding method), 398
get_edge_attributes() (in module net-
workx.classes.function), 506
get_edge_data() (DiGraph method), 52
get_edge_data() (Graph method), 24
get_edge_data() (MultiDiGraph method), 113
get_edge_data() (MultiGraph method), 83
get_node_attributes() (in module net-
workx.classes.function), 504
girvan_newman() (in module net-
workx.algorithms.community.centrality),
235
global_efficiency() (in module net-
workx.algorithms.efficiency), 311
global_parameters() (in module net-
workx.algorithms.distance_regular), 307
global_reaching_centrality() (in module net-
workx.algorithms.centrality), 207
gn_graph() (in module networkx.generators.directed),
546
gnc_graph() (in module net-
workx.generators.directed), 548
gnm_random_graph() (in module net-
workx.generators.random_graphs), 529
gnmk_random_graph() (in module net-
workx.algorithms.bipartite.generators), 177
gnp_random_graph() (in module net-
workx.generators.random_graphs), 528
gnr_graph() (in module net-
workx.generators.directed), 547
goldberg_radzik() (in module net-
workx.algorithms.shortest_paths.weighted),
432
gomory_hu_tree() (in module net-
workx.algorithms.flow), 329
google_matrix() (in module net-
workx.algorithms.link_analysis.pagerank_alg),
364
Graph (class in networkx), 7
graph_atlas() (in module net-
workx.generators.atlas), 509
graph_atlas_g() (in module net-
workx.generators.atlas), 509
graph_clique_number() (in module net-
workx.algorithms.clique), 216
graph_edit_distance() (in module net-
workx.algorithms.similarity), 438
graph_number_of_cliques() (in module net-
workx.algorithms.clique), 217
graphviz_layout() (in module net-
workx.drawing.nx_agraph), 671
graphviz_layout() (in module net-
workx.drawing.nx_pydot), 674
greedy_branching() (in module net-
workx.algorithms.tree.branchings), 475
greedy_color() (in module net-
workx.algorithms.coloring), 222
greedy_modularity_communities()
(in module net-
workx.algorithms.community.modularity_max),
232
grid_2d_graph() (in module net-
workx.generators.lattice), 520
grid_graph() (in module net-
workx.generators.lattice), 520
groups() (in module networkx.utils.misc), 686
H
hamiltonian_path() (in module net-
workx.algorithms.tournament), 457
harmonic_centrality() (in module net-
workx.algorithms.centrality), 205
harmonic_function() (in module net-
workx.algorithms.node_classification.hmn),
384
has_bridges() (in module net-
workx.algorithms.bridges), 181
has_edge() (DiGraph method), 51
has_edge() (Graph method), 23
has_edge() (MultiDiGraph method), 112
has_edge() (MultiGraph method), 82
has_node() (DiGraph method), 48
has_node() (Graph method), 21
has_node() (MultiDiGraph method), 109
has_node() (MultiGraph method), 80
has_path() (in module net-
workx.algorithms.shortest_paths.generic),
405
HasACycle (class in networkx), 683
720 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
hashable,695
havel_hakimi_graph() (in module net-
workx.algorithms.bipartite.generators), 175
havel_hakimi_graph() (in module net-
workx.generators.degree_seq), 543
heawood_graph() (in module net-
workx.generators.small), 525
hexagonal_lattice_graph() (in module net-
workx.generators.lattice), 521
hits() (in module net-
workx.algorithms.link_analysis.hits_alg),
365
hits_numpy() (in module net-
workx.algorithms.link_analysis.hits_alg),
366
hits_scipy() (in module net-
workx.algorithms.link_analysis.hits_alg),
366
hoffman_singleton_graph() (in module net-
workx.generators.small), 525
hopcroft_karp_matching() (in module net-
workx.algorithms.bipartite.matching), 156
house_graph() (in module net-
workx.generators.small), 525
house_x_graph() (in module net-
workx.generators.small), 525
hub_matrix() (in module net-
workx.algorithms.link_analysis.hits_alg),
367
hypercube_graph() (in module net-
workx.generators.lattice), 521
I
icosahedral_graph() (in module net-
workx.generators.small), 525
identified_nodes() (in module net-
workx.algorithms.minors), 379
immediate_dominators() (in module net-
workx.algorithms.dominance), 307
in_degree (DiGraph attribute), 57
in_degree (MultiDiGraph attribute), 118
in_degree_centrality() (in module net-
workx.algorithms.centrality), 183
in_edges (DiGraph attribute), 51
in_edges (MultiDiGraph attribute), 112
incidence_matrix() (in module net-
workx.linalg.graphmatrix), 580
induced_subgraph() (in module net-
workx.classes.function), 495
info() (in module networkx.classes.function), 492
information_centrality() (in module net-
workx.algorithms.centrality), 191
initialize() (DiGraphMatcher method), 354
initialize() (GraphMatcher method), 352
intersection() (in module net-
workx.algorithms.operators.binary), 388
intersection_all() (in module net-
workx.algorithms.operators.all), 391
intersection_array() (in module net-
workx.algorithms.distance_regular), 306
inverse_line_graph() (in module net-
workx.generators.line), 559
is_aperiodic() (in module net-
workx.algorithms.dag), 298
is_arborescence() (in module net-
workx.algorithms.tree.recognition), 474
is_attracting_component() (in module net-
workx.algorithms.components), 246
is_biconnected() (in module net-
workx.algorithms.components), 247
is_bipartite() (in module net-
workx.algorithms.bipartite.basic), 151
is_bipartite_node_set() (in module net-
workx.algorithms.bipartite.basic), 152
is_branching() (in module net-
workx.algorithms.tree.recognition), 474
is_chordal() (in module net-
workx.algorithms.chordal), 211
is_connected() (in module net-
workx.algorithms.components), 238
is_digraphical() (in module net-
workx.algorithms.graphical), 341
is_directed() (in module net-
workx.classes.function), 493
is_directed() (PlanarEmbedding method), 398
is_directed_acyclic_graph() (in module net-
workx.algorithms.dag), 298
is_distance_regular() (in module net-
workx.algorithms.distance_regular), 305
is_dominating_set() (in module net-
workx.algorithms.dominating), 309
is_edge_cover() (in module net-
workx.algorithms.covering), 286
is_empty() (in module networkx.classes.function),
493
is_eulerian() (in module net-
workx.algorithms.euler), 312
is_forest() (in module net-
workx.algorithms.tree.recognition), 473
is_frozen() (in module networkx.classes.function),
507
is_graphical() (in module net-
workx.algorithms.graphical), 341
is_isolate() (in module net-
workx.algorithms.isolate), 346
is_isomorphic() (DiGraphMatcher method), 354
is_isomorphic() (GraphMatcher method), 352
is_isomorphic() (in module net-
Index 721

NetworkX Reference, Release 2.3rc1.dev20181203210840
workx.algorithms.isomorphism), 347
is_k_edge_connected() (in module net-
workx.algorithms.connectivity.edge_augmentation),
254
is_kl_connected() (in module net-
workx.algorithms.hybrid), 345
is_list_of_ints() (in module net-
workx.utils.misc), 686
is_locally_k_edge_connected()
(in module net-
workx.algorithms.connectivity.edge_augmentation),
254
is_matching() (in module net-
workx.algorithms.matching), 375
is_maximal_matching() (in module net-
workx.algorithms.matching), 375
is_multigraphical() (in module net-
workx.algorithms.graphical), 342
is_negatively_weighted() (in module net-
workx.classes.function), 502
is_partition() (in module net-
workx.algorithms.community.community_utils),
237
is_perfect_matching() (in module net-
workx.algorithms.matching), 376
is_pseudographical() (in module net-
workx.algorithms.graphical), 342
is_reachable() (in module net-
workx.algorithms.tournament), 458
is_semiconnected() (in module net-
workx.algorithms.components), 251
is_simple_path() (in module net-
workx.algorithms.simple_paths), 446
is_string_like() (in module networkx.utils.misc),
685
is_strongly_connected() (in module net-
workx.algorithms.components), 240
is_strongly_connected() (in module net-
workx.algorithms.tournament), 458
is_strongly_regular() (in module net-
workx.algorithms.distance_regular), 305
is_tournament() (in module net-
workx.algorithms.tournament), 459
is_tree() (in module net-
workx.algorithms.tree.recognition), 473
is_valid_degree_sequence_erdos_gallai()
(in module networkx.algorithms.graphical),
343
is_valid_degree_sequence_havel_hakimi()
(in module networkx.algorithms.graphical),
342
is_valid_joint_degree() (in module net-
workx.generators.joint_degree_seq), 574
is_weakly_connected() (in module net-
workx.algorithms.components), 244
is_weighted() (in module net-
workx.classes.function), 502
isolates() (in module networkx.algorithms.isolate),
346
isomorphisms_iter() (DiGraphMatcher method),
355
isomorphisms_iter() (GraphMatcher method),
353
iterable() (in module networkx.utils.misc), 686
J
jaccard_coefficient() (in module net-
workx.algorithms.link_prediction), 368
jit_data() (in module net-
workx.readwrite.json_graph), 648
jit_graph() (in module net-
workx.readwrite.json_graph), 648
johnson() (in module net-
workx.algorithms.shortest_paths.weighted),
433
join() (in module net-
workx.algorithms.tree.operations), 481
joint_degree_graph() (in module net-
workx.generators.joint_degree_seq), 575
K
k_clique_communities() (in module net-
workx.algorithms.community.kclique), 231
k_components() (in module net-
workx.algorithms.approximation.kcomponents),
132
k_components() (in module net-
workx.algorithms.connectivity.kcomponents),
259
k_core() (in module networkx.algorithms.core), 283
k_corona() (in module networkx.algorithms.core),
285
k_crust() (in module networkx.algorithms.core), 284
k_edge_augmentation() (in module net-
workx.algorithms.connectivity.edge_augmentation),
252
k_edge_components() (in module net-
workx.algorithms.connectivity.edge_kcomponents),
255
k_edge_subgraphs() (in module net-
workx.algorithms.connectivity.edge_kcomponents),
256
k_nearest_neighbors() (in module net-
workx.algorithms.assortativity), 146
k_random_intersection_graph() (in module
networkx.generators.intersection), 561
k_shell() (in module networkx.algorithms.core), 283
722 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
kamada_kawai_layout() (in module net-
workx.drawing.layout), 677
karate_club_graph() (in module net-
workx.generators.social), 562
katz_centrality() (in module net-
workx.algorithms.centrality), 186
katz_centrality_numpy() (in module net-
workx.algorithms.centrality), 188
kernighan_lin_bisection() (in module net-
workx.algorithms.community.kernighan_lin),
228
kl_connected_subgraph() (in module net-
workx.algorithms.hybrid), 345
kosaraju_strongly_connected_components()
(in module networkx.algorithms.components),
242
krackhardt_kite_graph() (in module net-
workx.generators.small), 525
L
label_propagation_communities()
(in module net-
workx.algorithms.community.label_propagation),
233
ladder_graph() (in module net-
workx.generators.classic), 516
laplacian_matrix() (in module net-
workx.linalg.laplacianmatrix), 581
laplacian_spectrum() (in module net-
workx.linalg.spectrum), 583
large_clique_size() (in module net-
workx.algorithms.approximation.clique),
134
latapy_clustering() (in module net-
workx.algorithms.bipartite.cluster), 168
lattice_reference() (in module net-
workx.algorithms.smallworld), 449
LCF_graph() (in module networkx.generators.small),
523
lexicographic_product() (in module net-
workx.algorithms.operators.product), 392
lexicographical_topological_sort() (in
module networkx.algorithms.dag), 297
LFR_benchmark_graph() (in module net-
workx.algorithms.community.community_generators),
229
line_graph() (in module networkx.generators.line),
557
literal_destringizer() (in module net-
workx.readwrite.gml), 637
literal_stringizer() (in module net-
workx.readwrite.gml), 637
load_centrality() (in module net-
workx.algorithms.centrality), 202
local_and_global_consistency() (in module
networkx.algorithms.node_classification.lgc),
385
local_bridges() (in module net-
workx.algorithms.bridges), 182
local_constraint() (in module net-
workx.algorithms.structuralholes), 454
local_edge_connectivity() (in module net-
workx.algorithms.connectivity.connectivity),
268
local_efficiency() (in module net-
workx.algorithms.efficiency), 310
local_node_connectivity() (in module net-
workx.algorithms.approximation.connectivity),
130
local_node_connectivity() (in module net-
workx.algorithms.connectivity.connectivity),
270
local_reaching_centrality() (in module net-
workx.algorithms.centrality), 206
lollipop_graph() (in module net-
workx.generators.classic), 516
lowest_common_ancestor() (in module net-
workx.algorithms.lowest_common_ancestors),
374
M
make_clique_bipartite() (in module net-
workx.algorithms.clique), 216
make_max_clique_graph() (in module net-
workx.algorithms.clique), 215
make_small_graph() (in module net-
workx.generators.small), 523
make_str() (in module networkx.utils.misc), 686
margulis_gabber_galil_graph() (in module
networkx.generators.expanders), 519
match() (DiGraphMatcher method), 355
match() (GraphMatcher method), 353
max_clique() (in module net-
workx.algorithms.approximation.clique),
133
max_flow_min_cost() (in module net-
workx.algorithms.flow), 337
max_weight_matching() (in module net-
workx.algorithms.matching), 376
maximal_independent_set() (in module net-
workx.algorithms.mis), 383
maximal_matching() (in module net-
workx.algorithms.matching), 376
maximum_branching() (in module net-
workx.algorithms.tree.branchings), 475
maximum_flow() (in module net-
workx.algorithms.flow), 314
Index 723

NetworkX Reference, Release 2.3rc1.dev20181203210840
maximum_flow_value() (in module net-
workx.algorithms.flow), 315
maximum_independent_set() (in module net-
workx.algorithms.approximation.independent_set),
137
maximum_spanning_arborescence() (in mod-
ule networkx.algorithms.tree.branchings), 476
maximum_spanning_edges() (in module net-
workx.algorithms.tree.mst), 485
maximum_spanning_tree() (in module net-
workx.algorithms.tree.mst), 483
metric_closure() (in module net-
workx.algorithms.approximation.steinertree),
138
min_cost_flow() (in module net-
workx.algorithms.flow), 335
min_cost_flow_cost() (in module net-
workx.algorithms.flow), 334
min_edge_cover() (in module net-
workx.algorithms.bipartite.covering), 178
min_edge_cover() (in module net-
workx.algorithms.covering), 285
min_edge_dominating_set() (in module net-
workx.algorithms.approximation.dominating_set),
136
min_maximal_matching() (in module net-
workx.algorithms.approximation.matching),
137
min_weighted_dominating_set()
(in module net-
workx.algorithms.approximation.dominating_set),
135
min_weighted_vertex_cover() (in module net-
workx.algorithms.approximation.vertex_cover),
140
minimum_branching() (in module net-
workx.algorithms.tree.branchings), 476
minimum_cut() (in module net-
workx.algorithms.flow), 317
minimum_cut_value() (in module net-
workx.algorithms.flow), 319
minimum_cycle_basis() (in module net-
workx.algorithms.cycles), 289
minimum_edge_cut() (in module net-
workx.algorithms.connectivity.cuts), 274
minimum_node_cut() (in module net-
workx.algorithms.connectivity.cuts), 275
minimum_spanning_arborescence() (in mod-
ule networkx.algorithms.tree.branchings), 476
minimum_spanning_edges() (in module net-
workx.algorithms.tree.mst), 483
minimum_spanning_tree() (in module net-
workx.algorithms.tree.mst), 482
minimum_st_edge_cut() (in module net-
workx.algorithms.connectivity.cuts), 276
minimum_st_node_cut() (in module net-
workx.algorithms.connectivity.cuts), 278
mixing_dict() (in module net-
workx.algorithms.assortativity), 150
mixing_expansion() (in module net-
workx.algorithms.cuts), 292
modularity_matrix() (in module net-
workx.linalg.modularitymatrix), 591
modularity_spectrum() (in module net-
workx.linalg.spectrum), 584
moebius_kantor_graph() (in module net-
workx.generators.small), 525
multi_source_dijkstra() (in module net-
workx.algorithms.shortest_paths.weighted),
418
multi_source_dijkstra_path() (in module
networkx.algorithms.shortest_paths.weighted),
419
multi_source_dijkstra_path_length()
(in module net-
workx.algorithms.shortest_paths.weighted),
420
MultiDiGraph (class in networkx), 93
MultiGraph (class in networkx), 65
mycielski_graph() (in module net-
workx.generators.mycielski), 576
mycielskian() (in module net-
workx.generators.mycielski), 576
N
navigable_small_world_graph() (in module
networkx.generators.geometric), 555
nbunch,695
nbunch_iter() (DiGraph method), 55
nbunch_iter() (Graph method), 26
nbunch_iter() (MultiDiGraph method), 116
nbunch_iter() (MultiGraph method), 85
negative_edge_cycle() (in module net-
workx.algorithms.shortest_paths.weighted),
431
neighbors() (DiGraph method), 52
neighbors() (Graph method), 24
neighbors() (in module networkx.classes.function),
498
neighbors() (MultiDiGraph method), 114
neighbors() (MultiGraph method), 83
neighbors_cw_order() (PlanarEmbedding
method), 398
network_simplex() (in module net-
workx.algorithms.flow), 332
networkx.algorithms.approximation (mod-
ule), 129
724 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.approximation.clique
(module), 133
networkx.algorithms.approximation.clustering_coefficient
(module), 135
networkx.algorithms.approximation.connectivity
(module), 129
networkx.algorithms.approximation.dominating_set
(module), 135
networkx.algorithms.approximation.independent_set
(module), 136
networkx.algorithms.approximation.kcomponents
(module), 132
networkx.algorithms.approximation.matching
(module), 137
networkx.algorithms.approximation.ramsey
(module), 138
networkx.algorithms.approximation.steinertree
(module), 138
networkx.algorithms.approximation.treewidth
(module), 139
networkx.algorithms.approximation.vertex_cover
(module), 140
networkx.algorithms.assortativity (mod-
ule), 140
networkx.algorithms.bipartite (module),
150
networkx.algorithms.bipartite.basic
(module), 151
networkx.algorithms.bipartite.centrality
(module), 170
networkx.algorithms.bipartite.cluster
(module), 165
networkx.algorithms.bipartite.covering
(module), 178
networkx.algorithms.bipartite.generators
(module), 173
networkx.algorithms.bipartite.matching
(module), 155
networkx.algorithms.bipartite.matrix
(module), 157
networkx.algorithms.bipartite.projection
(module), 159
networkx.algorithms.bipartite.redundancy
(module), 169
networkx.algorithms.bipartite.spectral
(module), 165
networkx.algorithms.boundary (module), 178
networkx.algorithms.bridges (module), 180
networkx.algorithms.centrality (module),
182,301
networkx.algorithms.chains (module), 210
networkx.algorithms.chordal (module), 211
networkx.algorithms.clique (module), 213
networkx.algorithms.cluster (module), 217
networkx.algorithms.coloring (module), 222
networkx.algorithms.communicability_alg
(module), 226
networkx.algorithms.community (module),
227
networkx.algorithms.community.asyn_fluid
(module), 233
networkx.algorithms.community.centrality
(module), 235
networkx.algorithms.community.community_generators
(module), 228
networkx.algorithms.community.community_utils
(module), 237
networkx.algorithms.community.kclique
(module), 231
networkx.algorithms.community.kernighan_lin
(module), 228
networkx.algorithms.community.label_propagation
(module), 232
networkx.algorithms.community.modularity_max
(module), 231
networkx.algorithms.community.quality
(module), 234
networkx.algorithms.components (module),
238
networkx.algorithms.connectivity (mod-
ule), 251
networkx.algorithms.connectivity.connectivity
(module), 265
networkx.algorithms.connectivity.cuts
(module), 273
networkx.algorithms.connectivity.disjoint_paths
(module), 261
networkx.algorithms.connectivity.edge_augmentation
(module), 252
networkx.algorithms.connectivity.edge_kcomponents
(module), 255
networkx.algorithms.connectivity.kcomponents
(module), 259
networkx.algorithms.connectivity.kcutsets
(module), 260
networkx.algorithms.connectivity.stoerwagner
(module), 280
networkx.algorithms.connectivity.utils
(module), 281
networkx.algorithms.core (module), 282
networkx.algorithms.covering (module), 285
networkx.algorithms.cuts (module), 290
networkx.algorithms.cycles (module), 286
networkx.algorithms.dag (module), 294
networkx.algorithms.distance_measures
(module), 302
networkx.algorithms.distance_regular
(module), 305
Index 725

NetworkX Reference, Release 2.3rc1.dev20181203210840
networkx.algorithms.dominance (module),
307
networkx.algorithms.dominating (module),
308
networkx.algorithms.efficiency (module),
310
networkx.algorithms.euler (module), 311
networkx.algorithms.flow (module), 313
networkx.algorithms.graphical (module),
340
networkx.algorithms.hierarchy (module),
344
networkx.algorithms.hybrid (module), 344
networkx.algorithms.isolate (module), 346
networkx.algorithms.isomorphism (module),
347
networkx.algorithms.isomorphism.isomorphvf2
(module), 350
networkx.algorithms.link_analysis.hits_alg
(module), 365
networkx.algorithms.link_analysis.pagerank_alg
(module), 361
networkx.algorithms.link_prediction
(module), 367
networkx.algorithms.lowest_common_ancestors
(module), 373
networkx.algorithms.matching (module), 375
networkx.algorithms.minors (module), 377
networkx.algorithms.mis (module), 383
networkx.algorithms.node_classification
(module), 384
networkx.algorithms.node_classification.hmn
(module), 384
networkx.algorithms.node_classification.lgc
(module), 385
networkx.algorithms.operators.all (mod-
ule), 389
networkx.algorithms.operators.binary
(module), 387
networkx.algorithms.operators.product
(module), 391
networkx.algorithms.operators.unary
(module), 386
networkx.algorithms.planarity (module),
395
networkx.algorithms.reciprocity (module),
399
networkx.algorithms.richclub (module), 400
networkx.algorithms.shortest_paths.astar
(module), 436
networkx.algorithms.shortest_paths.dense
(module), 434
networkx.algorithms.shortest_paths.generic
(module), 401
networkx.algorithms.shortest_paths.unweighted
(module), 406
networkx.algorithms.shortest_paths.weighted
(module), 411
networkx.algorithms.similarity (module),
437
networkx.algorithms.simple_paths (mod-
ule), 444
networkx.algorithms.smallworld (module),
448
networkx.algorithms.smetric (module), 451
networkx.algorithms.sparsifiers (module),
452
networkx.algorithms.structuralholes
(module), 452
networkx.algorithms.swap (module), 455
networkx.algorithms.tournament (module),
457
networkx.algorithms.traversal.beamsearch
(module), 468
networkx.algorithms.traversal.breadth_first_search
(module), 465
networkx.algorithms.traversal.depth_first_search
(module), 460
networkx.algorithms.traversal.edgebfs
(module), 470
networkx.algorithms.traversal.edgedfs
(module), 469
networkx.algorithms.tree.branchings
(module), 474
networkx.algorithms.tree.coding (module),
477
networkx.algorithms.tree.mst (module), 482
networkx.algorithms.tree.operations
(module), 481
networkx.algorithms.tree.recognition
(module), 472
networkx.algorithms.triads (module), 486
networkx.algorithms.vitality (module), 487
networkx.algorithms.voronoi (module), 488
networkx.algorithms.wiener (module), 489
networkx.classes.function (module), 491
networkx.classes.graphviews (module), 126
networkx.classes.ordered (module), 126
networkx.convert (module), 595
networkx.convert_matrix (module), 598
networkx.drawing.layout (module), 675
networkx.drawing.nx_agraph (module), 670
networkx.drawing.nx_pydot (module), 672
networkx.drawing.nx_pylab (module), 661
networkx.exception (module), 683
networkx.generators.atlas (module), 509
networkx.generators.classic (module), 510
networkx.generators.community (module),
726 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
563
networkx.generators.degree_seq (module),
539
networkx.generators.directed (module), 546
networkx.generators.duplication (module),
537
networkx.generators.ego (module), 559
networkx.generators.expanders (module),
518
networkx.generators.geometric (module),
550
networkx.generators.intersection (mod-
ule), 560
networkx.generators.joint_degree_seq
(module), 574
networkx.generators.lattice (module), 519
networkx.generators.line (module), 557
networkx.generators.mycielski (module),
575
networkx.generators.nonisomorphic_trees
(module), 573
networkx.generators.random_clustered
(module), 545
networkx.generators.random_graphs (mod-
ule), 526
networkx.generators.small (module), 522
networkx.generators.social (module), 562
networkx.generators.spectral_graph_forge
(module), 570
networkx.generators.stochastic (module),
560
networkx.generators.trees (module), 571
networkx.generators.triads (module), 573
networkx.linalg.algebraicconnectivity
(module), 584
networkx.linalg.attrmatrix (module), 587
networkx.linalg.graphmatrix (module), 579
networkx.linalg.laplacianmatrix (module),
580
networkx.linalg.modularitymatrix (mod-
ule), 591
networkx.linalg.spectrum (module), 583
networkx.readwrite.adjlist (module), 617
networkx.readwrite.edgelist (module), 624
networkx.readwrite.gexf (module), 630
networkx.readwrite.gml (module), 633
networkx.readwrite.gpickle (module), 638
networkx.readwrite.graph6 (module), 651
networkx.readwrite.graphml (module), 639
networkx.readwrite.json_graph (module),
643
networkx.readwrite.leda (module), 648
networkx.readwrite.multiline_adjlist
(module), 620
networkx.readwrite.nx_shp (module), 659
networkx.readwrite.nx_yaml (module), 649
networkx.readwrite.pajek (module), 657
networkx.readwrite.sparse6 (module), 654
networkx.relabel (module), 613
networkx.utils (module), 685
networkx.utils.contextmanagers (module),
694
networkx.utils.decorators (module), 689
networkx.utils.misc (module), 685
networkx.utils.random_sequence (module),
687
networkx.utils.rcm (module), 692
networkx.utils.union_find (module), 687
NetworkXAlgorithmError (class in networkx), 683
NetworkXError (class in networkx), 683
NetworkXException (class in networkx), 683
NetworkXNoCycle (class in networkx), 683
NetworkXNoPath (class in networkx), 683
NetworkXNotImplemented (class in networkx), 683
NetworkXPointlessConcept (class in networkx),
683
NetworkXUnbounded (class in networkx), 683
NetworkXUnfeasible (class in networkx), 683
new_edge_key() (MultiDiGraph method), 103
new_edge_key() (MultiGraph method), 74
newman_watts_strogatz_graph() (in module
networkx.generators.random_graphs), 530
next_face_half_edge() (PlanarEmbedding
method), 398
node,695
node attribute,695
node_boundary() (in module net-
workx.algorithms.boundary), 179
node_clique_number() (in module net-
workx.algorithms.clique), 217
node_connected_component() (in module net-
workx.algorithms.components), 239
node_connectivity() (in module net-
workx.algorithms.approximation.connectivity),
131
node_connectivity() (in module net-
workx.algorithms.connectivity.connectivity),
272
node_disjoint_paths() (in module net-
workx.algorithms.connectivity.disjoint_paths),
264
node_expansion() (in module net-
workx.algorithms.cuts), 293
node_link_data() (in module net-
workx.readwrite.json_graph), 643
node_link_graph() (in module net-
workx.readwrite.json_graph), 644
node_redundancy() (in module net-
Index 727

NetworkX Reference, Release 2.3rc1.dev20181203210840
workx.algorithms.bipartite.redundancy),
169
NodeNotFound (class in networkx), 683
nodes (DiGraph attribute), 46
nodes (Graph attribute), 20
nodes (MultiDiGraph attribute), 107
nodes (MultiGraph attribute), 78
nodes() (in module networkx.classes.function), 498
nodes_or_number() (in module net-
workx.utils.decorators), 690
nodes_with_selfloops() (in module net-
workx.classes.function), 501
non_edges() (in module networkx.classes.function),
499
non_neighbors() (in module net-
workx.classes.function), 498
nonisomorphic_trees() (in module net-
workx.generators.nonisomorphic_trees),
573
normalized_cut_size() (in module net-
workx.algorithms.cuts), 293
normalized_laplacian_matrix() (in module
networkx.linalg.laplacianmatrix), 581
not_implemented_for() (in module net-
workx.utils.decorators), 690
NotATree,486
null_graph() (in module net-
workx.generators.classic), 517
number_attracting_components() (in module
networkx.algorithms.components), 246
number_connected_components() (in module
networkx.algorithms.components), 238
number_of_cliques() (in module net-
workx.algorithms.clique), 217
number_of_edges() (DiGraph method), 59
number_of_edges() (Graph method), 29
number_of_edges() (in module net-
workx.classes.function), 499
number_of_edges() (MultiDiGraph method), 120
number_of_edges() (MultiGraph method), 88
number_of_isolates() (in module net-
workx.algorithms.isolate), 347
number_of_nodes() (DiGraph method), 56
number_of_nodes() (Graph method), 27
number_of_nodes() (in module net-
workx.classes.function), 498
number_of_nodes() (MultiDiGraph method), 117
number_of_nodes() (MultiGraph method), 86
number_of_nonisomorphic_trees() (in mod-
ule networkx.generators.nonisomorphic_trees),
573
number_of_selfloops() (in module net-
workx.classes.function), 500
number_strongly_connected_components()
(in module networkx.algorithms.components),
241
number_weakly_connected_components() (in
module networkx.algorithms.components), 244
numeric_assortativity_coefficient() (in
module networkx.algorithms.assortativity), 142
numeric_mixing_matrix() (in module net-
workx.algorithms.assortativity), 148
numerical_edge_match() (in module net-
workx.algorithms.isomorphism), 358
numerical_multiedge_match() (in module net-
workx.algorithms.isomorphism), 358
numerical_node_match() (in module net-
workx.algorithms.isomorphism), 357
O
octahedral_graph() (in module net-
workx.generators.small), 526
omega() (in module networkx.algorithms.smallworld),
450
open_file() (in module networkx.utils.decorators),
689
optimal_edit_paths() (in module net-
workx.algorithms.similarity), 439
optimize_edit_paths() (in module net-
workx.algorithms.similarity), 443
optimize_graph_edit_distance() (in module
networkx.algorithms.similarity), 441
order() (DiGraph method), 56
order() (Graph method), 27
order() (MultiDiGraph method), 117
order() (MultiGraph method), 86
OrderedDiGraph (class in networkx), 126
OrderedGraph (class in networkx), 126
OrderedMultiDiGraph (class in networkx), 126
OrderedMultiGraph (class in networkx), 126
out_degree (DiGraph attribute), 58
out_degree (MultiDiGraph attribute), 119
out_degree_centrality() (in module net-
workx.algorithms.centrality), 183
out_edges (DiGraph attribute), 50
out_edges (MultiDiGraph attribute), 110
overall_reciprocity() (in module net-
workx.algorithms.reciprocity), 400
overlap_weighted_projected_graph()
(in module net-
workx.algorithms.bipartite.projection), 162
P
pagerank() (in module net-
workx.algorithms.link_analysis.pagerank_alg),
361
pagerank_numpy() (in module net-
workx.algorithms.link_analysis.pagerank_alg),
728 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
362
pagerank_scipy() (in module net-
workx.algorithms.link_analysis.pagerank_alg),
363
pairwise() (in module networkx.utils.misc), 686
pappus_graph() (in module net-
workx.generators.small), 526
parse_adjlist() (in module net-
workx.readwrite.adjlist), 619
parse_edgelist() (in module net-
workx.readwrite.edgelist), 629
parse_gml() (in module networkx.readwrite.gml),
635
parse_graphml() (in module net-
workx.readwrite.graphml), 642
parse_leda() (in module networkx.readwrite.leda),
649
parse_multiline_adjlist() (in module net-
workx.readwrite.multiline_adjlist), 623
parse_pajek() (in module net-
workx.readwrite.pajek), 658
partial_duplication_graph() (in module net-
workx.generators.duplication), 538
path_graph() (in module net-
workx.generators.classic), 517
percolation_centrality() (in module net-
workx.algorithms.centrality), 208
performance() (in module net-
workx.algorithms.community.quality), 235
periphery() (in module net-
workx.algorithms.distance_measures), 304
petersen_graph() (in module net-
workx.generators.small), 526
PlanarEmbedding (class in net-
workx.algorithms.planarity), 396
planted_partition_graph() (in module net-
workx.generators.community), 566
power() (in module net-
workx.algorithms.operators.product), 394
PowerIterationFailedConvergence (class in
networkx), 684
powerlaw_cluster_graph() (in module net-
workx.generators.random_graphs), 534
powerlaw_sequence() (in module net-
workx.utils.random_sequence), 687
pred (DiGraph attribute), 54
predecessor() (in module net-
workx.algorithms.shortest_paths.unweighted),
410
predecessors() (DiGraph method), 54
predecessors() (MultiDiGraph method), 115
preferential_attachment() (in module net-
workx.algorithms.link_prediction), 370
preferential_attachment_graph() (in mod-
ule networkx.algorithms.bipartite.generators),
176
prefix_tree() (in module net-
workx.generators.trees), 571
preflow_push() (in module net-
workx.algorithms.flow), 324
preserve_random_state() (in module net-
workx.utils.decorators), 691
projected_graph() (in module net-
workx.algorithms.bipartite.projection), 159
pydot_layout() (in module net-
workx.drawing.nx_pydot), 674
pygraphviz_layout() (in module net-
workx.drawing.nx_agraph), 672
Q
quotient_graph() (in module net-
workx.algorithms.minors), 380
R
ra_index_soundarajan_hopcroft() (in mod-
ule networkx.algorithms.link_prediction), 371
radius() (in module net-
workx.algorithms.distance_measures), 304
ramsey_R2() (in module net-
workx.algorithms.approximation.ramsey),
138
random_clustered_graph() (in module net-
workx.generators.random_clustered), 545
random_degree_sequence_graph() (in module
networkx.generators.degree_seq), 544
random_geometric_graph() (in module net-
workx.generators.geometric), 550
random_graph() (in module net-
workx.algorithms.bipartite.generators), 176
random_k_out_graph() (in module net-
workx.generators.directed), 548
random_kernel_graph() (in module net-
workx.generators.random_graphs), 535
random_layout() (in module net-
workx.drawing.layout), 677
random_lobster() (in module net-
workx.generators.random_graphs), 536
random_partition_graph() (in module net-
workx.generators.community), 565
random_powerlaw_tree() (in module net-
workx.generators.random_graphs), 537
random_powerlaw_tree_sequence() (in mod-
ule networkx.generators.random_graphs), 537
random_reference() (in module net-
workx.algorithms.smallworld), 449
random_regular_graph() (in module net-
workx.generators.random_graphs), 532
Index 729

NetworkX Reference, Release 2.3rc1.dev20181203210840
random_shell_graph() (in module net-
workx.generators.random_graphs), 536
random_state() (in module net-
workx.utils.decorators), 691
random_tournament() (in module net-
workx.algorithms.tournament), 459
random_tree() (in module net-
workx.generators.trees), 571
random_weighted_sample() (in module net-
workx.utils.random_sequence), 688
read_adjlist() (in module net-
workx.readwrite.adjlist), 617
read_dot() (in module networkx.drawing.nx_agraph),
671
read_dot() (in module networkx.drawing.nx_pydot),
674
read_edgelist() (in module net-
workx.readwrite.edgelist), 625
read_gexf() (in module networkx.readwrite.gexf ),
631
read_gml() (in module networkx.readwrite.gml), 634
read_gpickle() (in module net-
workx.readwrite.gpickle), 638
read_graph6() (in module net-
workx.readwrite.graph6), 652
read_graphml() (in module net-
workx.readwrite.graphml), 640
read_leda() (in module networkx.readwrite.leda),
649
read_multiline_adjlist() (in module net-
workx.readwrite.multiline_adjlist), 621
read_pajek() (in module networkx.readwrite.pajek),
657
read_shp() (in module networkx.readwrite.nx_shp),
659
read_sparse6() (in module net-
workx.readwrite.sparse6), 655
read_weighted_edgelist() (in module net-
workx.readwrite.edgelist), 627
read_yaml() (in module net-
workx.readwrite.nx_yaml), 650
reciprocity() (in module net-
workx.algorithms.reciprocity), 399
reconstruct_path() (in module net-
workx.algorithms.shortest_paths.dense),
436
relabel_gexf_graph() (in module net-
workx.readwrite.gexf ), 633
relabel_nodes() (in module networkx.relabel), 613
relaxed_caveman_graph() (in module net-
workx.generators.community), 564
remove_edge() (DiGraph method), 43
remove_edge() (Graph method), 16
remove_edge() (MultiDiGraph method), 103
remove_edge() (MultiGraph method), 75
remove_edges_from() (DiGraph method), 43
remove_edges_from() (Graph method), 17
remove_edges_from() (MultiDiGraph method),
104
remove_edges_from() (MultiGraph method), 75
remove_node() (DiGraph method), 40
remove_node() (Graph method), 13
remove_node() (MultiDiGraph method), 99
remove_node() (MultiGraph method), 71
remove_nodes_from() (DiGraph method), 40
remove_nodes_from() (Graph method), 14
remove_nodes_from() (MultiDiGraph method), 99
remove_nodes_from() (MultiGraph method), 71
rescale_layout() (in module net-
workx.drawing.layout), 678
resource_allocation_index() (in module net-
workx.algorithms.link_prediction), 368
restricted_view() (in module net-
workx.classes.function), 496
reverse() (DiGraph method), 64
reverse() (in module net-
workx.algorithms.operators.unary), 386
reverse() (MultiDiGraph method), 126
reverse_cuthill_mckee_ordering() (in mod-
ule networkx.utils.rcm), 693
reverse_havel_hakimi_graph() (in module net-
workx.algorithms.bipartite.generators), 175
reverse_view() (in module net-
workx.classes.function), 497
reverse_view() (in module net-
workx.classes.graphviews), 127
reversed() (in module net-
workx.utils.contextmanagers), 694
rich_club_coefficient() (in module net-
workx.algorithms.richclub), 400
ring_of_cliques() (in module net-
workx.generators.community), 567
robins_alexander_clustering() (in module
networkx.algorithms.bipartite.cluster), 169
rooted_product() (in module net-
workx.algorithms.operators.product), 393
S
s_metric() (in module networkx.algorithms.smetric),
451
scale_free_graph() (in module net-
workx.generators.directed), 549
score_sequence() (in module net-
workx.algorithms.tournament), 459
second_order_centrality() (in module net-
workx.algorithms.centrality), 209
sedgewick_maze_graph() (in module net-
workx.generators.small), 526
730 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
selfloop_edges() (in module net-
workx.classes.function), 500
semantic_feasibility() (DiGraphMatcher
method), 355
semantic_feasibility() (GraphMatcher
method), 353
set_edge_attributes() (in module net-
workx.classes.function), 504
set_node_attributes() (in module net-
workx.classes.function), 503
sets() (in module net-
workx.algorithms.bipartite.basic), 152
shell_layout() (in module net-
workx.drawing.layout), 678
shortest_augmenting_path() (in module net-
workx.algorithms.flow), 322
shortest_path() (in module net-
workx.algorithms.shortest_paths.generic),
401
shortest_path_length() (in module net-
workx.algorithms.shortest_paths.generic),
403
shortest_simple_paths() (in module net-
workx.algorithms.simple_paths), 447
sigma() (in module networkx.algorithms.smallworld),
450
simple_cycles() (in module net-
workx.algorithms.cycles), 287
single_source_bellman_ford() (in module
networkx.algorithms.shortest_paths.weighted),
426
single_source_bellman_ford_path()
(in module net-
workx.algorithms.shortest_paths.weighted),
427
single_source_bellman_ford_path_length()
(in module net-
workx.algorithms.shortest_paths.weighted),
428
single_source_dijkstra() (in module net-
workx.algorithms.shortest_paths.weighted),
414
single_source_dijkstra_path() (in module
networkx.algorithms.shortest_paths.weighted),
416
single_source_dijkstra_path_length()
(in module net-
workx.algorithms.shortest_paths.weighted),
417
single_source_shortest_path()
(in module net-
workx.algorithms.shortest_paths.unweighted),
406
single_source_shortest_path_length()
(in module net-
workx.algorithms.shortest_paths.unweighted),
407
single_target_shortest_path()
(in module net-
workx.algorithms.shortest_paths.unweighted),
407
single_target_shortest_path_length()
(in module net-
workx.algorithms.shortest_paths.unweighted),
408
size() (DiGraph method), 59
size() (Graph method), 28
size() (MultiDiGraph method), 120
size() (MultiGraph method), 87
soft_random_geometric_graph() (in module
networkx.generators.geometric), 551
spanner() (in module net-
workx.algorithms.sparsifiers), 452
spectral_bipartivity() (in module net-
workx.algorithms.bipartite.spectral), 165
spectral_graph_forge() (in module net-
workx.generators.spectral_graph_forge),
570
spectral_layout() (in module net-
workx.drawing.layout), 680
spectral_ordering() (in module net-
workx.linalg.algebraicconnectivity), 586
spring_layout() (in module net-
workx.drawing.layout), 679
square_clustering() (in module net-
workx.algorithms.cluster), 221
star_graph() (in module net-
workx.generators.classic), 517
steiner_tree() (in module net-
workx.algorithms.approximation.steinertree),
138
stochastic_block_model() (in module net-
workx.generators.community), 568
stochastic_graph() (in module net-
workx.generators.stochastic), 560
stoer_wagner() (in module net-
workx.algorithms.connectivity.stoerwagner),
280
strategy_connected_sequential() (in mod-
ule networkx.algorithms.coloring), 224
strategy_connected_sequential_bfs() (in
module networkx.algorithms.coloring), 224
strategy_connected_sequential_dfs() (in
module networkx.algorithms.coloring), 224
strategy_independent_set() (in module net-
workx.algorithms.coloring), 225
strategy_largest_first() (in module net-
workx.algorithms.coloring), 225
Index 731

NetworkX Reference, Release 2.3rc1.dev20181203210840
strategy_random_sequential() (in module net-
workx.algorithms.coloring), 225
strategy_saturation_largest_first() (in
module networkx.algorithms.coloring), 225
strategy_smallest_last() (in module net-
workx.algorithms.coloring), 225
strong_product() (in module net-
workx.algorithms.operators.product), 393
strongly_connected_component_subgraphs()
(in module networkx.algorithms.components),
242
strongly_connected_components() (in mod-
ule networkx.algorithms.components), 241
strongly_connected_components_recursive()
(in module networkx.algorithms.components),
242
subgraph() (DiGraph method), 63
subgraph() (Graph method), 32
subgraph() (in module networkx.classes.function),
495
subgraph() (MultiDiGraph method), 124
subgraph() (MultiGraph method), 91
subgraph_centrality() (in module net-
workx.algorithms.centrality), 203
subgraph_centrality_exp() (in module net-
workx.algorithms.centrality), 204
subgraph_is_isomorphic() (DiGraphMatcher
method), 355
subgraph_is_isomorphic() (GraphMatcher
method), 353
subgraph_isomorphisms_iter() (DiGraph-
Matcher method), 355
subgraph_isomorphisms_iter() (Graph-
Matcher method), 353
subgraph_view() (in module net-
workx.classes.graphviews), 127
succ (DiGraph attribute), 54
succ (MultiDiGraph attribute), 115
successors() (DiGraph method), 53
successors() (MultiDiGraph method), 115
symmetric_difference() (in module net-
workx.algorithms.operators.binary), 389
syntactic_feasibility() (DiGraphMatcher
method), 355
syntactic_feasibility() (GraphMatcher
method), 353
T
tensor_product() (in module net-
workx.algorithms.operators.product), 394
tetrahedral_graph() (in module net-
workx.generators.small), 526
thresholded_random_geometric_graph() (in
module networkx.generators.geometric), 556
to_agraph() (in module net-
workx.drawing.nx_agraph), 671
to_dict_of_dicts() (in module networkx.convert),
596
to_dict_of_lists() (in module networkx.convert),
597
to_directed() (DiGraph method), 62
to_directed() (Graph method), 32
to_directed() (in module net-
workx.classes.function), 493
to_directed() (MultiDiGraph method), 123
to_directed() (MultiGraph method), 91
to_edgelist() (in module networkx.convert), 597
to_graph6_bytes() (in module net-
workx.readwrite.graph6), 653
to_nested_tuple() (in module net-
workx.algorithms.tree.coding), 478
to_networkx_graph() (in module net-
workx.convert), 595
to_numpy_array() (in module net-
workx.convert_matrix), 600
to_numpy_matrix() (in module net-
workx.convert_matrix), 599
to_numpy_recarray() (in module net-
workx.convert_matrix), 601
to_pandas_adjacency() (in module net-
workx.convert_matrix), 608
to_pandas_edgelist() (in module net-
workx.convert_matrix), 610
to_prufer_sequence() (in module net-
workx.algorithms.tree.coding), 480
to_pydot() (in module networkx.drawing.nx_pydot),
673
to_scipy_sparse_matrix() (in module net-
workx.convert_matrix), 605
to_sparse6_bytes() (in module net-
workx.readwrite.sparse6), 655
to_undirected() (DiGraph method), 61
to_undirected() (Graph method), 31
to_undirected() (in module net-
workx.classes.function), 493
to_undirected() (MultiDiGraph method), 123
to_undirected() (MultiGraph method), 90
to_vertex_cover() (in module net-
workx.algorithms.bipartite.matching), 156
topological_sort() (in module net-
workx.algorithms.dag), 295
transitive_closure() (in module net-
workx.algorithms.dag), 298
transitive_reduction() (in module net-
workx.algorithms.dag), 299
transitivity() (in module net-
workx.algorithms.cluster), 218
traverse_face() (PlanarEmbedding method), 399
732 Index

NetworkX Reference, Release 2.3rc1.dev20181203210840
tree_all_pairs_lowest_common_ancestor()
(in module net-
workx.algorithms.lowest_common_ancestors),
374
tree_data() (in module net-
workx.readwrite.json_graph), 646
tree_graph() (in module net-
workx.readwrite.json_graph), 647
treewidth_min_degree() (in module net-
workx.algorithms.approximation.treewidth),
139
treewidth_min_fill_in() (in module net-
workx.algorithms.approximation.treewidth),
139
triad_graph() (in module net-
workx.generators.triads), 573
triadic_census() (in module net-
workx.algorithms.triads), 486
triangles() (in module net-
workx.algorithms.cluster), 218
triangular_lattice_graph() (in module net-
workx.generators.lattice), 522
trivial_graph() (in module net-
workx.generators.classic), 518
truncated_cube_graph() (in module net-
workx.generators.small), 526
truncated_tetrahedron_graph() (in module
networkx.generators.small), 526
turan_graph() (in module net-
workx.generators.classic), 518
tutte_graph() (in module net-
workx.generators.small), 526
U
uniform_random_intersection_graph() (in
module networkx.generators.intersection), 561
union() (in module net-
workx.algorithms.operators.binary), 387
union() (UnionFind method), 687
union_all() (in module net-
workx.algorithms.operators.all), 390
update() (DiGraph method), 44
update() (Graph method), 17
update() (MultiDiGraph method), 104
update() (MultiGraph method), 76
V
volume() (in module networkx.algorithms.cuts), 294
voronoi_cells() (in module net-
workx.algorithms.voronoi), 488
W
watts_strogatz_graph() (in module net-
workx.generators.random_graphs), 531
waxman_graph() (in module net-
workx.generators.geometric), 554
weakly_connected_component_subgraphs()
(in module networkx.algorithms.components),
245
weakly_connected_components() (in module
networkx.algorithms.components), 245
weighted_choice() (in module net-
workx.utils.random_sequence), 689
weighted_projected_graph() (in module net-
workx.algorithms.bipartite.projection), 160
wheel_graph() (in module net-
workx.generators.classic), 518
wiener_index() (in module net-
workx.algorithms.wiener), 489
windmill_graph() (in module net-
workx.generators.community), 569
within_inter_cluster() (in module net-
workx.algorithms.link_prediction), 372
write_adjlist() (in module net-
workx.readwrite.adjlist), 618
write_dot() (in module net-
workx.drawing.nx_agraph), 671
write_dot() (in module networkx.drawing.nx_pydot),
674
write_edgelist() (in module net-
workx.readwrite.edgelist), 626
write_gexf() (in module networkx.readwrite.gexf ),
631
write_gml() (in module networkx.readwrite.gml),
634
write_gpickle() (in module net-
workx.readwrite.gpickle), 639
write_graph6() (in module net-
workx.readwrite.graph6), 653
write_graphml() (in module net-
workx.readwrite.graphml), 641
write_multiline_adjlist() (in module net-
workx.readwrite.multiline_adjlist), 622
write_pajek() (in module net-
workx.readwrite.pajek), 658
write_shp() (in module networkx.readwrite.nx_shp),
660
write_sparse6() (in module net-
workx.readwrite.sparse6), 656
write_weighted_edgelist() (in module net-
workx.readwrite.edgelist), 627
write_yaml() (in module net-
workx.readwrite.nx_yaml), 650
Z
zipf_rv() (in module net-
workx.utils.random_sequence), 688
Index 733
