Num Py Beginner's Guide, 2nd Edition

User Manual:

Open the PDF directly: View PDF PDF.
Page Count: 310 [warning: Documents this large are best viewed by clicking the View PDF Link!]

www.it-ebooks.info
NumPy Beginner's Guide
Second Edition
An acon packed guide using real world examples of the
easy to use, high performance, free open source NumPy
mathemacal library
Ivan Idris
BIRMINGHAM - MUMBAI
www.it-ebooks.info
Numpy Beginner's Guide
Second Edition
Copyright © 2013 Packt Publishing
All rights reserved. No part of this book may be reproduced, stored in a retrieval system,
or transmied in any form or by any means, without the prior wrien permission of the
publisher, except in the case of brief quotaons embedded in crical arcles or reviews.
Every eort has been made in the preparaon of this book to ensure the accuracy of the
informaon presented. However, the informaon contained in this book is sold without
warranty, either express or implied. Neither the author, nor Packt Publishing, and its dealers
and distributors will be held liable for any damages caused or alleged to be caused directly
or indirectly by this book.
Packt Publishing has endeavored to provide trademark informaon about all of the
companies and products menoned in this book by the appropriate use of capitals.
However, Packt Publishing cannot guarantee the accuracy of this informaon.
First published: November 2011
Second edion: April 2013
Producon Reference: 1170413
Published by Packt Publishing Ltd.
Livery Place
35 Livery Street
Birmingham B3 2PB, UK.
ISBN 978-1-78216-608-5
www.packtpub.com
Cover Image by Suresh Mogre (suresh.mogre.99@gmail.com)
www.it-ebooks.info
Credits
Author
Ivan Idris
Reviewers
Jaidev Deshpande
Dr. Alexandre Devert
Mark Livingstone
Miklós Prisznyák
Nikolay Karelin
Acquision Editor
Usha Iyer
Lead Technical Editor
Joel Noronha
Technical Editors
Soumya Kan
Devdu Kulkarni
Project Coordinator
Abhishek Kori
Proofreader
Mario Cecere
Indexer
Hemangini Bari
Graphics
Sheetal Aute
Ronak Dhruv
Producon Coordinator
Melwyn D'sa
Cover Work
Melwyn D'sa
www.it-ebooks.info
About the Author
Ivan Idris has an MSc in Experimental Physics. His graduaon thesis had a strong emphasis
on Applied Computer Science. Aer graduang, he worked for several companies as a Java
Developer, Datawarehouse Developer, and QA Analyst. His main professional interests are
Business Intelligence, Big Data, and Cloud Compung. Ivan Idris enjoys wring clean testable
code and interesng technical arcles. Ivan Idris is the author of NumPy Beginner's Guide
& Cookbook. You can nd more informaon and a blog with a few NumPy examples at
ivanidris.net.
I would like to take this opportunity to thank the reviewers and the team
at Packt Publishing for making this book possible. Also thanks goes to
my teachers, professors, and colleagues who taught me about science
and programming. Last but not the least, I would like to acknowledge my
parents, family, and friends for their support.
www.it-ebooks.info
About the Reviewers
Jaidev Deshpande is an intern at Enthought, Inc, where he works on soware for data
analysis and visualizaon. He is an avid scienc programmer and works on many open
source packages in signal processing, data analysis, and machine learning.
Dr. Alexandre Devert is teaching data-mining and soware engineering at the University
of Science and Technology of China. Alexandre also works as a researcher, both as an
academic on opmizaon problems, and on data-mining problems for a biotechnology
startup. In all those contexts, Alexandre very happily uses Python, Numpy, and Scipy.
Mark Livingstone started his career by working for many years for three internaonal
computer companies (which no longer exist) in engineering/support/programming/training
roles, but got red of being made redundant. He then graduated from Grith University on
the Gold Coast, Australia, in 2011 with a Bachelor of Informaon Technology. He is currently
in his nal semester of his B.InfoTech (Hons) degree researching in the area of Proteomics
algorithms with all his research soware wrien in Python on a Mac, and his Supervisor and
research group one by one discovering the joys of Python.
Mark enjoys mentoring rst year students with special needs, is the Chair of the IEEE Grith
University Gold Coast Student Branch, and volunteers as a Qualied Jusce of the Peace at
the local District Courthouse, has been a Credit Union Director, and will have completed 100
blood donaons by the end of 2013.
In his copious spare me, he co-develops the S2 Salstat Stascs Package available
at http://code.google.com/p/salstat-statistics-package-2/ which is
mulplaorm and uses wxPython, NumPy, SciPy, Scikit, Matplotlib, and a number
of other Python modules.
www.it-ebooks.info
Miklós Prisznyák is a senior soware engineer with a scienc background. He graduated
as a physicist from the Eötvös Lóránd University, the largest and oldest university in Hungary.
He did his MSc thesis on Monte Carlo simulaons of non-Abelian lace quantum eld
theories in 1992. Having worked three years in the Central Research Instute for Physics
of Hungary, he joined MulRáció K. in Budapest, a company founded by physicists,
which specialized in mathemacal data analysis and forecasng economic data. His main
project was the Small Area Unemployment Stascs System which has been in ocial
use at the Hungarian Public Employment Service since then. He learned about the Python
programming language here in 2000. He set up his own consulng company in 2002 and
then he worked on various projects for insurance, pharmacy and e-commerce companies,
using Python whenever he could. He also worked in a European Union research instute
in Italy, tesng and enhanching a distributed, Python-based Zope/Plone web applicaon.
He moved to Great Britain in 2007 and rst he worked at a Scosh start-up, using Twisted
Python, then in the aerospace industry in England using, among others, the PyQt windowing
toolkit, the Enthought applicaon framework, and the NumPy and SciPy libraries. He
returned to Hungary in 2012 and he rejoined MulRáció where now he is working on a
Python extension module to OpenOce/EuroOce, using NumPy and SciPy again, which will
allow users to solve non-linear and stochasc opmizaon problems. Miklós likes to travel,
read, and he is interested in sciences, linguiscs, history, polics, the board game of go, and
in quite a few other topics. Besides he always enjoys a good cup of coee. However, nothing
beats spending me with his brilliant 10 year old son Zsombor for him.
Nikolay Karelin holds a PhD degree in opcs and used various methods of numerical
simulaons and analysis for nearly 20 years, rst in academia and then in the industry
(simulaon of ber opcs communicaon links). Aer inial learning curve with Python
and NumPy, these excellent tools became his main choice for almost all numerical analysis
and scripng, since past ve years.
I wish to thank my family for understanding and keeping paence during
long evenings when I was working on reviews for the "NumPy Beginner’s
Guide."
www.it-ebooks.info
www.PacktPub.com
Support les, eBooks, discount offers and more
You might want to visit www.PacktPub.com for support les and downloads related to
your book.
Did you know that Packt oers eBook versions of every book published, with PDF and ePub les
available? You can upgrade to the eBook version at www.PacktPub.com and as a print book
customer, you are entled to a discount on the eBook copy. Get in touch with us at service@
packtpub.com for more details.
At www.PacktPub.com, you can also read a collecon of free technical arcles, sign up for a
range of free newsleers and receive exclusive discounts and oers on Packt books and eBooks.
http://PacktLib.PacktPub.com
Do you need instant soluons to your IT quesons? PacktLib is Packt's online digital book
library. Here, you can access, read and search across Packt's enre library of books.
Why Subscribe?
Fully searchable across every book published by Packt
Copy and paste, print and bookmark content
On demand and accessible via web browser
Free Access for Packt account holders
If you have an account with Packt at www.PacktPub.com, you can use this to access
PacktLib today and view nine enrely free books. Simply use your login credenals for
immediate access.
www.it-ebooks.info
www.it-ebooks.info
To my family and friends.
www.it-ebooks.info
www.it-ebooks.info
Table of Contents
Preface 1
Chapter 1: NumPy Quick Start 9
Python 9
Time for acon – installing Python on dierent operang systems 10
Windows 10
Time for acon – installing NumPy, Matplotlib, SciPy, and IPython
on Windows 11
Linux 13
Time for acon – installing NumPy, Matplotlib, SciPy, and IPython on Linux 13
Mac OS X 14
Time for acon – installing NumPy, Matplotlib, and SciPy on Mac OS X 14
Time for acon – installing NumPy, SciPy, Matplotlib, and IPython
with MacPorts or Fink 17
Building from source 17
Arrays 17
Time for acon – adding vectors 18
IPython—an interacve shell 21
Online resources and help 25
Summary 26
Chapter 2: Beginning with NumPy Fundamentals 27
NumPy array object 28
Time for acon – creang a muldimensional array 29
Selecng elements 30
NumPy numerical types 30
Data type objects 32
Character codes 32
dtype constructors 33
dtype aributes 34
www.it-ebooks.info
Table of Contents
[ ii ]
Time for acon – creang a record data type 34
One-dimensional slicing and indexing 35
Time for acon – slicing and indexing muldimensional arrays 35
Time for acon – manipulang array shapes 38
Stacking 39
Time for acon – stacking arrays 40
Spling 43
Time for acon – spling arrays 43
Array aributes 45
Time for acon – converng arrays 48
Summary 49
Chapter 3: Get in Terms with Commonly Used Funcons 51
File I/O 51
Time for acon – reading and wring les 52
CSV les 52
Time for acon – loading from CSV les 53
Volume-weighted average price 53
Time for acon – calculang volume-weighted average price 54
The mean funcon 54
Time-weighted average price 54
Value range 55
Time for acon – nding highest and lowest values 55
Stascs 56
Time for acon – doing simple stascs 57
Stock returns 59
Time for acon – analyzing stock returns 59
Dates 61
Time for acon – dealing with dates 61
Weekly summary 65
Time for acon – summarizing data 65
Average true range 69
Time for acon – calculang the average true range 69
Simple moving average 72
Time for acon – compung the simple moving average 72
Exponenal moving average 74
Time for acon – calculang the exponenal moving average 74
Bollinger bands 76
Time for acon – enveloping with Bollinger bands 76
Linear model 80
www.it-ebooks.info
Table of Contents
[ iii ]
Time for acon – predicng price with a linear model 80
Trend lines 82
Time for acon – drawing trend lines 82
Methods of ndarray 86
Time for acon – clipping and compressing arrays 87
Factorial 87
Time for acon – calculang the factorial 88
Summary 89
Chapter 4: Convenience Funcons for Your Convenience 91
Correlaon 92
Time for acon – trading correlated pairs 92
Polynomials 96
Time for acon – ng to polynomials 96
On-balance volume 99
Time for acon – balancing volume 100
Simulaon 102
Time for acon – avoiding loops with vectorize 102
Smoothing 105
Time for acon – smoothing with the hanning funcon 105
Summary 109
Chapter 5: Working with Matrices and ufuncs 111
Matrices 111
Time for acon – creang matrices 112
Creang a matrix from other matrices 113
Time for acon – creang a matrix from other matrices 113
Universal funcons 114
Time for acon – creang universal funcon 115
Universal funcon methods 116
Time for acon – applying the ufunc methods on add 116
Arithmec funcons 118
Time for acon – dividing arrays 119
Time for acon – compung the modulo 121
Fibonacci numbers 122
Time for acon – compung Fibonacci numbers 122
Lissajous curves 123
Time for acon – drawing Lissajous curves 124
Square waves 125
Time for acon – drawing a square wave 125
Sawtooth and triangle waves 127
www.it-ebooks.info
Table of Contents
[ iv ]
Time for acon – drawing sawtooth and triangle waves 127
Bitwise and comparison funcons 129
Time for acon – twiddling bits 129
Summary 131
Chapter 6: Move Further with NumPy Modules 133
Linear algebra 133
Time for acon – inverng matrices 133
Solving linear systems 135
Time for acon – solving a linear system 136
Finding eigenvalues and eigenvectors 137
Time for acon – determining eigenvalues and eigenvectors 137
Singular value decomposion 139
Time for acon – decomposing a matrix 139
Pseudoinverse 141
Time for acon – compung the pseudo inverse of a matrix 141
Determinants 142
Time for acon – calculang the determinant of a matrix 142
Fast Fourier transform 143
Time for acon – calculang the Fourier transform 143
Shiing 145
Time for acon – shiing frequencies 145
Random numbers 147
Time for acon – gambling with the binomial 147
Hypergeometric distribuon 149
Time for acon – simulang a game show 149
Connuous distribuons 151
Time for acon – drawing a normal distribuon 151
Lognormal distribuon 153
Time for acon – drawing the lognormal distribuon 153
Summary 154
Chapter 7: Peeking into Special Rounes 155
Sorng 155
Time for acon – sorng lexically 156
Complex numbers 157
Time for acon – sorng complex numbers 157
Searching 158
Time for acon – using searchsorted 159
Array elements' extracon 160
www.it-ebooks.info
Table of Contents
[ v ]
Time for acon – extracng elements from an array 160
Financial funcons 161
Time for acon – determining future value 161
Present value 163
Time for acon – geng the present value 163
Net present value 163
Time for acon – calculang the net present value 163
Internal rate of return 164
Time for acon – determining the internal rate of return 164
Periodic payments 165
Time for acon – calculang the periodic payments 165
Number of payments 165
Time for acon – determining the number of periodic payments 165
Interest rate 166
Time for acon – guring out the rate 166
Window funcons 166
Time for acon – plong the Bartle window 167
Blackman window 167
Time for acon – smoothing stock prices with the Blackman window 168
Hamming window 170
Time for acon – plong the Hamming window 170
Kaiser window 171
Time for acon – plong the Kaiser window 171
Special mathemacal funcons 172
Time for acon – plong the modied Bessel funcon 172
sinc 173
Time for acon – plong the sinc funcon 173
Summary 175
Chapter 8: Assure Quality with Tesng 177
Assert funcons 178
Time for acon – asserng almost equal 178
Approximately equal arrays 179
Time for acon – asserng approximately equal 180
Almost equal arrays 180
Time for acon – asserng arrays almost equal 181
Equal arrays 182
Time for acon – comparing arrays 182
Ordering arrays 183
www.it-ebooks.info
Table of Contents
[ vi ]
Time for acon – checking the array order 183
Objects comparison 184
Time for acon – comparing objects 184
String comparison 184
Time for acon – comparing strings 185
Floang point comparisons 185
Time for acon – comparing with assert_array_almost_equal_nulp 186
Comparison of oats with more ULPs 187
Time for acon – comparing using maxulp of 2 187
Unit tests 187
Time for acon – wring a unit test 188
Nose tests decorators 190
Time for acon – decorang tests 191
Docstrings 193
Time for acon – execung doctests 194
Summary 195
Chapter 9: Plong with Matplotlib 197
Simple plots 198
Time for acon – plong a polynomial funcon 198
Plot format string 200
Time for acon – plong a polynomial and its derivave 200
Subplots 201
Time for acon – plong a polynomial and its derivaves 201
Finance 204
Time for acon – plong a year’s worth of stock quotes 204
Histograms 207
Time for acon – charng stock price distribuons 207
Logarithmic plots 209
Time for acon – plong stock volume 209
Scaer plots 211
Time for acon – plong price and volume returns with scaer plot 211
Fill between 213
Time for acon – shading plot regions based on a condion 213
Legend and annotaons 215
Time for acon – using legend and annotaons 215
Three dimensional plots 218
Time for acon – plong in three dimensions 219
Contour plots 220
Time for acon – drawing a lled contour plot 220
www.it-ebooks.info
Table of Contents
[ vii ]
Animaon 222
Time for acon – animang plots 222
Summary 223
Chapter 10: When NumPy is Not Enough – SciPy and Beyond 225
MATLAB and Octave 225
Time for acon – saving and loading a .mat le 226
Stascs 227
Time for acon – analyzing random values 227
Samples’ comparison and SciKits 230
Time for acon – comparing stock log returns 230
Signal processing 232
Time for acon – detecng a trend in QQQ 233
Fourier analysis 235
Time for acon – ltering a detrended signal 236
Mathemacal opmizaon 238
Time for acon – ng to a sine 239
Numerical integraon 242
Time for acon – calculang the Gaussian integral 242
Interpolaon 243
Time for acon – interpolang in one dimension 243
Image processing 245
Time for acon – manipulang Lena 245
Audio processing 247
Time for acon – replaying audio clips 247
Summary 249
Chapter 11: Playing with Pygame 251
Pygame 251
Time for acon – installing Pygame 252
Hello World 252
Time for acon – creang a simple game 252
Animaon 255
Time for acon – animang objects with NumPy and Pygame 255
Matplotlib 258
Time for acon – using Matplotlib in Pygame 258
Surface pixels 261
Time for acon – accessing surface pixel data with NumPy 262
Arcial intelligence 263
Time for acon – clustering points 264
OpenGL and Pygame 266
www.it-ebooks.info
Table of Contents
[ viii ]
Time for acon – drawing the Sierpinski gasket 267
Simulaon game with PyGame 270
Time for acon – simulang life 270
Summary 274
Pop Quiz Answers 275
Index 277
www.it-ebooks.info
Preface
Sciensts, engineers, and quantave data analysts face many challenges nowadays.
Data sciensts want to be able to do numerical analysis of large datasets with minimal
programming eort. They want to write readable, ecient, and fast code, which is as close
as possible to the mathemacal language package they are used to. A number of accepted
soluons are available in the scienc compung world.
The C, C++, and Fortran programming languages have their benets, but they are not
interacve and considered too complex by many. The common commercial alternaves are
amongst others, Matlab, Maple and Mathemaca. These products provide powerful scripng
languages, which are sll more limited than any general purpose programming language.
Other open source tools similar to Matlab exist such as R, GNU Octave, and Scilab. Obviously,
they also lack the power of a language such as Python.
Python is a popular general-purpose programming language, widely used in the scienc
community. You can access legacy C, Fortran, or R code easily from Python. It is object-oriented
and considered more high level than C or Fortran. Python allows you to write readable and
clean code with minimal fuss. However, it lacks a Matlab equivalent out of the box. That's
where NumPy comes in. This book is about NumPy and related Python libraries such as SciPy
and Matplotlib.
What is NumPy?
NumPy (from Numerical Python) is an open-source Python library for scienc compung.
NumPy let's you work with arrays and matrices in a natural way. The library contains
a long list of useful mathemacal funcons including some for linear algebra, Fourier
transformaon, and random number generaon rounes. LAPACK, a linear algebra library,
is used by the NumPy linear algebra module (that is, if you have LAPACK installed on your
system), otherwise, NumPy provides its own implementaon. LAPACK is a well-known library
originally wrien in Fortran on which Matlab relies as well. In a sense, NumPy replaces some
of the funconality of Matlab and Mathemaca, allowing rapid interacve prototyping.
www.it-ebooks.info
Preface
[ 2 ]
We will not be discussing NumPy from a developing contributor perspecve, but more from
a user's perspecve. NumPy is a very acve project and has a lot of contributors. Maybe, one
day you will be one of them!
History
NumPy is based on its predecessor Numeric. Numeric was rst released in 1995 and has
a deprecated status now. Neither Numeric nor NumPy made it into the standard Python
library for various reasons. However, you can install NumPy separately as will be explained
in Chapter 1, Numpy Quick Start.
In 2001, a number of people inspired by Numeric created SciPy—an open-source Python
scienc compung library, that provides funconality similar to that of Matlab, Maple, and
Mathemaca. Around this me, people were growing increasingly unhappy with Numeric.
Numarray was created as alternave to Numeric. Numarray was beer in some areas than
Numeric, but worked very dierently. For that reason, SciPy kept on depending on the
Numeric philosophy and the Numeric array object. As is customary with new "latest and
greatest" soware, the arrival of Numarray led to the development of an enre ecosystem
around it with a range of useful tools.
In 2005, Travis Oliphant, an early contributor to SciPy, decided to do something about this
situaon. He tried to integrate some of the Numarray features into Numeric. A complete
rewrite took place that culminated in the release of NumPy 1.0 in 2006. At this me, NumPy
has all of the features of Numeric and Numarray and more. Upgrade tools are available to
facilitate the upgrade from Numeric and Numarray. The upgrade is recommended since
Numeric and Numarray are not acvely supported any more.
Originally, the NumPy code was part of SciPy. It was later separated and is now used by SciPy
for array and matrix processing.
Why use NumPy?
NumPy code is much cleaner than "straight" Python code that tries to accomplish the same
task. There are less loops required, because operaons work directly on arrays and matrices.
The many convenience and mathemacal funcons make life easier as well. The underlying
algorithms have stood the test of me and have been designed with high performance in mind.
www.it-ebooks.info
Preface
[ 3 ]
NumPy's arrays are stored more eciently than an equivalent data structure in base Python
such as list of lists. Array IO is signicantly faster too. The performance improvement scales
with the number of elements of an array. For large arrays it really pays o to use NumPy.
Files as large as several terabytes can be memory-mapped to arrays, leading to opmal
reading and wring of data. The drawback of NumPy arrays is that they are more specialized
than plain lists. Outside of the context of numerical computaons, NumPy arrays are less
useful. The technical details of NumPy arrays will be discussed in the later chapters.
Large porons of NumPy are wrien in C. That makes NumPy faster than pure Python code.
A NumPy C API exists as well and it allows further extension of the funconality with the
help of the C language of NumPy. The C API falls outside the scope of this book. Finally,
since NumPy is open-source, you get all of the related advantages. The price is the lowest
possible—free as in "beer". You don't have to worry about licenses every me somebody
joins your team or you need an upgrade of the soware. The source code is available to
everyone. This of course is benecial to the code quality.
Limitations of NumPy
If you are a Java programmer, you might be interested in Jython, the Java implementaon
of Python. In that case, I have bad news for you. Unfortunately, Jython runs on the Java
Virtual Machine and cannot access NumPy, because NumPy's modules are mostly wrien in
C. You could say that Jython and Python are two totally dierent worlds, although, they do
implement the same specicaon. There are some workarounds for this that are discussed in
NumPy Cookbook, Ivan Idris, Packt Publishing.
What this book covers
Chapter 1, NumPy Quick Start will guide you through the steps needed to install NumPy
on your system and create a basic NumPy applicaon.
Chapter 2, Beginning with NumPy Fundamentals introduces you to NumPy arrays
and fundamentals.
Chapter 3, Get to Terms with Commonly Used Funcons will teach you about the most
commonly used NumPy funcons—the basic mathemacal and stascal funcons.
Chapter 4, Convenience Funcons for Your Convenience will teach you about funcons that
make working with NumPy easier. This includes funcons that select certain parts of your
arrays, for instance, based on a Boolean condion. You will also learn about polynomials,
and manipulang the shape of NumPy objects.
www.it-ebooks.info
Preface
[ 4 ]
Chapter 5, Working with Matrices and ufuncs covers matrices and universal funcons.
Matrices are well known in mathemacs and have their representaon in NumPy as well.
Universal funcons (ufuncs) work on arrays element-by-element or on scalars. Ufuncs expect
a set of scalars as input and produce a set of scalars as output.
Chapter 6, Move Further with Numpy Modules discusses the number of basic modules
of Universal funcons. Universal funcons can typically be mapped to mathemacal
counterparts such as add, subtract, divide, and mulply.
Chapter 7, Peeking into Special Rounes describes some of the more specialized NumPy
funcons. As NumPy users, we somemes nd ourselves having special needs. Fortunately,
NumPy provides for most of our needs.
In Chapter 8, Assure Quality with Tesng you will learn how to write NumPy unit tests.
Chapter 9, Plong with Matplotlib covers in-depth Matplotlib, a very useful Python plong
library. NumPy on its own cannot be used to create graphs and plots. But Matplotlib
integrates nicely with NumPy and has plong capabilies comparable to Matlab.
Chapter 10, When NumPy is Not Enough – SciPy and Beyond goes into more detail about
SciPy, we know that SciPy and NumPy are historically related. SciPy, as menoned in the
History secon, is a high level Python scienc compung framework built on top of NumPy.
It can be used in conjuncon with NumPy.
Chapter 11, Playing with Pygame is the dessert of this book. We will learn how to create fun
games with NumPy and Pygame. We also get a taste of arcial intelligence.
What you need for this book
To try out the code samples in this book you will need a recent build of NumPy. This means
that you will need to have one of the Python versions supported by NumPy as well. Some
code samples make use of the Matplotlib for illustraon purposes. Matplotlib is not strictly
required to follow the examples, but it is recommended that you install it too. The last
chapter is about SciPy and has one example involving Scikits.
Here is a list of soware used to develop and test the code examples:
Python 2.7
NumPy 2.0.0.dev20100915
SciPy 0.9.0.dev20100915
Matplotlib 1.1.1
Pygame 1.9.1
IPython 0.14.dev
www.it-ebooks.info
Preface
[ 5 ]
Needless to say, you don't need to have exactly this soware and these versions on your
computer. Python and NumPy is the absolute minimum you will need.
Who this book is for
This book is for you the scienst, engineer, programmer, or analyst, looking for a high quality
open source mathemacal library. Knowledge of Python is assumed. Also, some anity or at
least interest in mathemacs and stascs is required.
Conventions
In this book, you will nd a number of styles of text that disnguish between dierent kinds
of informaon. Here are some examples of these styles, and an explanaon of their meaning.
Code words in text are shown as follows: "Noce that numpysum() does not need a
for loop."
A block of code is set as follows:
def numpysum(n):
a = numpy.arange(n) ** 2
b = numpy.arange(n) ** 3
c = a + b
return c
When we wish to draw your aenon to a parcular part of a code block, the relevant lines
or items are set in bold:
reals = np.isreal(xpoints)
print "Real number?", reals
Real number? [ True True True True False False False False]
Any command-line input or output is wrien as follows:
>>>fromnumpy.testing import rundocs
>>>rundocs('docstringtest.py')
New terms and important words are shown in bold. Words that you see on the screen,
in menus or dialog boxes for example, appear in the text like this: "clicking the Next buon
moves you to the next screen".
www.it-ebooks.info
Preface
[ 6 ]
Warnings or important notes appear in a box like this.
Tips and tricks appear like this.
Reader feedback
Feedback from our readers is always welcome. Let us know what you think about this
book—what you liked or may have disliked. Reader feedback is important for us to develop
tles that you really get the most out of.
To send us general feedback, simply send an e-mail to feedback@packtpub.com, and
menon the book tle via the subject of your message.
If there is a book that you need and would like to see us publish, please send us a note in
the SUGGEST A TITLE form on www.packtpub.com or e-mail suggest@packtpub.com.
If there is a topic that you have experse in and you are interested in either wring or
contribung to a book, see our author guide on www.packtpub.com/authors.
Customer support
Now that you are the proud owner of a Packt book, we have a number of things to help you
to get the most from your purchase.
Downloading the example code
You can download the example code les for all Packt books you have purchased from your
account at http://www.PacktPub.com. If you purchased this book elsewhere, you can
visit http://www.PacktPub.com/support and register to have the les e-mailed directly
to you.
www.it-ebooks.info
Preface
[ 7 ]
Errata
Although we have taken every care to ensure the accuracy of our content, mistakes do
happen. If you nd a mistake in one of our books—maybe a mistake in the text or the
code—we would be grateful if you would report this to us. By doing so, you can save other
readers from frustraon and help us improve subsequent versions of this book. If you
nd any errata, please report them by vising http://www.packtpub.com/support,
selecng your book, clicking on the errata submission form link, and entering the details
of your errata. Once your errata are veried, your submission will be accepted and the
errata will be uploaded on our website, or added to any list of exisng errata, under the
Errata secon of that tle. Any exisng errata can be viewed by selecng your tle from
http://www.packtpub.com/support.
Piracy
Piracy of copyright material on the Internet is an ongoing problem across all media. At Packt,
we take the protecon of our copyright and licenses very seriously. If you come across any
illegal copies of our works, in any form, on the Internet, please provide us with the locaon
address or website name immediately so that we can pursue a remedy.
Please contact us at copyright@packtpub.com with a link to the suspected
pirated material.
We appreciate your help in protecng our authors, and our ability to bring you
valuable content.
Questions
You can contact us at questions@packtpub.com if you are having a problem with any
aspect of the book, and we will do our best to address it.
www.it-ebooks.info
www.it-ebooks.info
NumPy Quick Start
Let's get started. We will install NumPy and related software on different
operating systems and have a look at some simple code that uses NumPy. The
IPython interactive shell is introduced briefly. As mentioned in the Preface, SciPy
is closely related to NumPy, so you will see the SciPy name appearing here and
there. At the end of this chapter, you will find pointers on how to find additional
information online if you get stuck or are uncertain about the best way to solve
problems.
In this chapter, we shall:
Install Python, SciPy, Matplotlib, IPython, and NumPy on Windows, Linux,
and Macintosh
Write simple NumPy code
Get to know IPython
Browse online documentaon and resources
Python
NumPy is based on Python, so it is required to have Python installed. On some operang
systems, Python is already installed. However, you need to check whether the Python version
corresponds with the NumPy version you want to install. There are many implementaons of
Python, including commercial implementaons and distribuon. In this book we will focus on
the standard CPython implementaon, which is guaranteed to be compable with NumPy.
1
www.it-ebooks.info
NumPy Quick Start
[ 10 ]
Time for action – installing Python on different operating
systems
NumPy has binary installers for Windows, various Linux distribuons, and Mac OS X. There is
also a source distribuon, if you prefer that. You need to have Python 2.4.x or above installed
on your system. We will go through the various steps required to install Python on the
following operang systems:
1. Debian and Ubuntu: Python might already be installed on Debian and Ubuntu but
the development headers are usually not. On Debian and Ubuntu install python and
python-dev with the following commands:
sudo apt-get install python
sudo apt-get install python-dev
2. Windows: The Windows Python installer can be found at www.python.org/
download. On this website, we can also nd installers for Mac OS X and source
tarballs for Linux, Unix, and Mac OS X.
3. Mac: Python comes pre-installed on Mac OS X. We can also get Python through
MacPorts, Fink, or similar projects. We can install, for instance, the Python 2.7
port by running the following command:
sudo port install python27
LAPACK does not need to be present but, if it is, NumPy will detect it and use it
during the installaon phase. It is recommended to install LAPACK for serious
numerical analysis as it has useful numerical linear algebra funconality.
What just happened?
We installed Python on Debian, Ubuntu, Windows, and the Mac.
Windows
Installing NumPy on Windows is straighorward. You only need to download an installer,
and a wizard will guide you through the installaon steps.
www.it-ebooks.info
Chapter 1
[ 11 ]
Time for action – installing NumPy, Matplotlib, SciPy, and IPython
on Windows
Installing NumPy on Windows is necessary but, fortunately, a straighorward task that we
will cover in detail. It is recommended to install Matplotlib, SciPy, and IPython. However,
this is not required to enjoy this book. The acons we will take are as follows:
1. Download a NumPy installer for Windows from the SourceForge website
http://sourceforge.net/projects/numpy/files/.
Choose the appropriate version. In this example, we chose numpy-1.7.0-win32-
superpack-python2.7.exe.
www.it-ebooks.info
NumPy Quick Start
[ 12 ]
2. Open the EXE installer by double clicking on it.
3. Now, we can see a descripon of NumPy and its features as shown in the previous
screenshot. Click on the Next buon.
4. If you have Python installed, it should automacally be detected. If it is not
detected, maybe your path sengs are wrong. At the end of this chapter,
resources are listed in case you have problems installing NumPy.
www.it-ebooks.info
Chapter 1
[ 13 ]
5. In this example, Python 2.7 was found. Click on the Next buon if Python is found;
otherwise, click on the Cancel buon and install Python (NumPy cannot be installed
without Python). Click on the Next buon. This is the point of no return. Well, kind
of, but it is best to make sure that you are installing to the proper directory and so
on and so forth. Now the real installaon starts. This may take a while.
6. Install SciPy and Matplotlib with the Enthought distribuon http://www.
enthought.com/products/epd.php. It might be necessary to put the msvcp71.
dll le in your C:\Windows\system32 directory. You can get it from http://
www.dll-files.com/dllindex/dll-files.shtml?msvcp71. A Windows
IPython installer is available on the IPython website (see http://ipython.
scipy.org/Wiki/IpythonOnWindows).
What just happened?
We installed NumPy, SciPy, Matplotlib, and IPython on Windows.
Linux
Installing NumPy and related recommended soware on Linux depends on the distribuon
you have. We will discuss how you would install NumPy from the command line, although,
you could probably use graphical installers; it depends on your distribuon (distro). The
commands to install Matplotlib, SciPy, and IPython are the same – only the package names
are dierent. Installing Matplotlib, SciPy, and IPython is recommended, but oponal.
Time for action – installing NumPy, Matplotlib, SciPy, and IPython
on Linux
Most Linux distribuons have NumPy packages. We will go through the necessary steps
for some of the popular Linux distros:
1. Run the following instrucons from the command line for installing NumPy
and Red Hat:
yum install python-numpy
2. To install NumPy on Mandriva, run the following command-line instrucon:
urpmi python-numpy
3. To install NumPy on Gentoo run the following command-line instrucon:
sudo emerge numpy
www.it-ebooks.info
NumPy Quick Start
[ 14 ]
4. To install NumPy on Debian or Ubuntu, we need to type the following :
sudo apt-get install python-numpy
The following table gives an overview of the Linux distribuons and corresponding package
names for NumPy, SciPy, Matplotlib, and IPython.
Linux
distribution
NumPy SciPy Matplotlib IPython
Arch Linux python-
numpy
python-
scipy
python-
matplotlib
ipython
Debian python-
numpy
python-
scipy
python-
matplotlib
ipython
Fedora numpy python-
scipy
python-
matplotlib
ipython
Gentoo dev-python/
numpy
scipy matplotlib ipython
OpenSUSE python-
numpy,
python-
numpy-devel
python-
scipy
python-
matplotlib
ipython
Slackware numpy scipy matplotlib ipython
What just happened?
We installed NumPy, SciPy, Matplotlib, and IPython on various Linux distribuons.
Mac OS X
You can install NumPy, Matplotlib, and SciPy on the Mac with a graphical installer or from the
command line with a port manager such as MacPorts or Fink, depending on your preference.
Time for action – installing NumPy, Matplotlib, and SciPy on Mac
OS X
We will install NumPy with a GUI installer using the following steps:
1. We can get a NumPy installer from the SourceForge website http://
sourceforge.net/projects/numpy/files/. Similar les exist for Matplotlib
and SciPy. Just change numpy in the previous URL to scipy or matplotlib.
IPython didn't have a GUI installer at the me of wring. Download the appropriate
DMG le as shown in the following screenshot, usually the latest one is the best:
www.it-ebooks.info
Chapter 1
[ 15 ]
2. Open the DMG le as shown in the following screenshot (in this example,
numpy-1.7.0-py2.7-python.org-macosx10.6.dmg):
Double-click on the icon of the opened box, the one having a subscript
that ends with .mpkg. We will be presented with the welcome screen
of the installer.
www.it-ebooks.info
NumPy Quick Start
[ 16 ]
Click on the Continue button to go to the Read Me screen, where we
will be presented with a short description of NumPy as shown in the
following screenshot:
Click on the Continue button to the License the screen.
3. Read the license, click on the Connue buon and then on the Accept buon, when
prompted to accept the license. Connue through the next screens and click on the
Finish buon at the end.
What just happened?
We installed NumPy on Mac OS X with a GUI installer. The steps to install SciPy and
Matplotlib are similar and can be performed using the URLs menoned in the rst step.
www.it-ebooks.info
Chapter 1
[ 17 ]
Time for action – installing NumPy, SciPy, Matplotlib, and IPython
with MacPorts or Fink
Alternavely, we can install NumPy, SciPy, Matplotlib, and IPython through the MacPorts
route or with Fink. The following installaon steps shown install all these packages. We
only need NumPy for all the tutorials in this book, so please omit the packages you are not
interested in.
1. For installing with MacPorts, type the following command:
sudo port install py-numpy py-scipy py-matplotlib py-ipython
2. Fink also has packages for NumPy: scipy-core-py24, scipy-core-py25, and
scipy-core-py26. The SciPy packages are: scipy-py24, scipy-py25, and
scipy-py26. We can install NumPy and the other recommended packages we will
be using in this book for Python 2.6 with the following command:
fink install scipy-core-py26 scipy-py26 matplotlib-py26
What just happened?
We installed NumPy and other recommended soware on Mac OS X with MacPorts and Fink.
Building from source
We can retrieve the source code for NumPy with git as follows:
git clone git://github.com/numpy/numpy.git numpy
Install /usr/local with the following command:
python setup.py build
sudo python setup.py install --prefix=/usr/local
To build, we need a C compiler such as GCC and the Python header les in the python-dev
or python-devel package.
Arrays
Aer going through the installaon of NumPy, it's me to have a look at NumPy arrays.
NumPy arrays are more ecient than Python lists, when it comes to numerical operaons.
NumPy code requires less explicit loops than equivalent Python code.
www.it-ebooks.info
NumPy Quick Start
[ 18 ]
Time for action – adding vectors
Imagine that we want to add two vectors called a and b. Vector is used here in the
mathemacal sense meaning a one-dimensional array. We will learn in Chapter 5, Working
with Matrices and ufuncs, about specialized NumPy arrays which represent matrices. The
vector a holds the squares of integers 0 to n, for instance, if n is equal to 3, then a is equal
to 0, 1, or 4. The vector b holds the cubes of integers 0 to n, so if n is equal to 3, then the
vector b is equal to 0, 1, or 8. How would you do that using plain Python? Aer we come up
with a soluon, we will compare it with the NumPy equivalent.
1. The following funcon solves the vector addion problem using pure Python
without NumPy:
def pythonsum(n):
a = range(n)
b = range(n)
c = []
for i in range(len(a)):
a[i] = i ** 2
b[i] = i ** 3
c.append(a[i] + b[i])
return c
2. The following is a funcon that achieves the same with NumPy:
def numpysum(n):
a = numpy.arange(n) ** 2
b = numpy.arange(n) ** 3
c = a + b
return c
Noce that numpysum() does not need a for loop. Also, we used the arange funcon
from NumPy that creates a NumPy array for us with integers 0 to n. The arange funcon
was imported; that is why it is prexed with numpy.
Now comes the fun part. Remember that it is menoned in the Preface that NumPy is faster
when it comes to array operaons. How much faster is Numpy, though? The following
program will show us by measuring the elapsed me in microseconds, for the numpysum and
pythonsum funcons. It also prints the last two elements of the vector sum. Let's check that
we get the same answers by using Python and NumPy:
#!/usr/bin/env/python
import sys
www.it-ebooks.info
Chapter 1
[ 19 ]
from datetime import datetime
import numpy as np
"""
Chapter 1 of NumPy Beginners Guide.
This program demonstrates vector addition the Python way.
Run from the command line as follows
python vectorsum.py n
where n is an integer that specifies the size of the vectors.
The first vector to be added contains the squares of 0 up to n.
The second vector contains the cubes of 0 up to n.
The program prints the last 2 elements of the sum and the elapsed
time.
"""
def numpysum(n):
a = np.arange(n) ** 2
b = np.arange(n) ** 3
c = a + b
return c
def pythonsum(n):
a = range(n)
b = range(n)
c = []
for i in range(len(a)):
a[i] = i ** 2
b[i] = i ** 3
c.append(a[i] + b[i])
return c
size = int(sys.argv[1])
start = datetime.now()
c = pythonsum(size)
delta = datetime.now() - start
print "The last 2 elements of the sum", c[-2:]
print "PythonSum elapsed time in microseconds", delta.microseconds
www.it-ebooks.info
NumPy Quick Start
[ 20 ]
start = datetime.now()
c = numpysum(size)
delta = datetime.now() - start
print "The last 2 elements of the sum", c[-2:]
print "NumPySum elapsed time in microseconds", delta.microseconds
The output of the program for 1000, 2000, and 3000 vector elements is as follows:
$ python vectorsum.py 1000
The last 2 elements of the sum [995007996, 998001000]
PythonSum elapsed time in microseconds 707
The last 2 elements of the sum [995007996 998001000]
NumPySum elapsed time in microseconds 171
$ python vectorsum.py 2000
The last 2 elements of the sum [7980015996, 7992002000]
PythonSum elapsed time in microseconds 1420
The last 2 elements of the sum [7980015996 7992002000]
NumPySum elapsed time in microseconds 168
$ python vectorsum.py 4000
The last 2 elements of the sum [63920031996, 63968004000]
PythonSum elapsed time in microseconds 2829
The last 2 elements of the sum [63920031996 63968004000]
NumPySum elapsed time in microseconds 274
You can download the example code les for all Packt books you have
purchased from your account at http://www.PacktPub.com. If you
purchased this book elsewhere, you can visit http://www.PacktPub.
com/support and register to have the les e-mailed directly to you.
What just happened?
Clearly, NumPy is much faster than the equivalent normal Python code. One thing is certain;
we get the same results whether we are using NumPy or not. However, the result that is
printed diers in representaon. Noce that the result from the numpysum funcon does
not have any commas. How come? Obviously we are not dealing with a Python list but with
a NumPy array. It was menoned in the Preface that NumPy arrays are specialized data
structures for numerical data. We will learn more about NumPy arrays in the next chapter.
www.it-ebooks.info
Chapter 1
[ 21 ]
Pop quiz Functioning of the arange function
Q1. What does arange(5) do?
1. Creates a Python list of 5 elements with values 1 to 5.
2. Creates a Python list of 5 elements with values 0 to 4.
3. Creates a NumPy array with values 1 to 5.
4. Creates a NumPy array with values 0 to 4.
5. None of the above.
Have a go hero – continue the analysis
The program we used here to compare the speed of NumPy and regular Python is not very
scienc. We should at least repeat each measurement a couple of mes. It would be nice to
be able to calculate some stascs such as average mes, and so on. Also, you might want to
show plots of the measurements to friends and colleagues.
Hints to help can be found in the online documentaon and resources listed at
the end of this chapter. NumPy has, by the way, stascal funcons that can
calculate averages for you. I recommend using Matplotlib to produce plots.
Chapter 9, Plong with Matplotlib, gives a quick overview of Matplotlib.
IPython—an interactive shell
Sciensts and engineers are used to experimenng. IPython was created by sciensts with
experimentaon in mind. The interacve environment that IPython provides is viewed by
many as a direct answer to Matlab, Mathemaca, and Maple. You can nd more informaon,
including installaon instrucons, at: http://ipython.org/.
IPython is free, open source, and available for Linux, Unix, Mac OS X, and Windows.
The IPython authors only request that you cite IPython in scienc work where IPython
was used. Here is the list of basic IPython features:
Tab compleon
History mechanism
Inline eding
Ability to call external Python scripts with %run
www.it-ebooks.info
NumPy Quick Start
[ 22 ]
Access to system commands
Pylab switch
Access to Python debugger and proler
The Pylab switch imports all the Scipy, NumPy, and Matplotlib packages. Without this
switch, we would have to import every package we need, ourselves.
All we need to do is enter the following instrucon on the command line:
$ ipython --pylab
Python 2.7.2 (default, Jun 20 2012, 16:23:33)
Type "copyright", "credits" or "license" for more information.
IPython 0.14.dev -- An enhanced Interactive Python.
? -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help -> Python's own help system.
object? -> Details about 'object', use 'object??' for extra details.
Welcome to pylab, a matplotlib-based Python environment [backend:
MacOSX].
For more information, type 'help(pylab)'.
In [1]: quit()
The quit() funcon or Ctrl + D quits the IPython shell. We might want to be able to go back
to our experiments. In IPython, it is easy to save a session for later:
In [1]: %logstart
Activating auto-logging. Current session state plus future input saved.
Filename : ipython_log.py
Mode : rotate
Output logging : False
Raw input log : False
Timestamping : False
State : active
Let's say we have the vector addion program that we made in the current directory. We can
run the script as follows:
In [1]: ls
README vectorsum.py
www.it-ebooks.info
Chapter 1
[ 23 ]
In [2]: %run -i vectorsum.py 1000
As you probably remember, 1000 species the number of elements in a vector. The -d
switch of %run starts an ipdb debugger and on typing c, the script is started. n steps
through the code. Typing quit at the ipdb prompt exits the debugger.
In [2]: %run -d vectorsum.py 1000
*** Blank or comment
*** Blank or comment
Breakpoint 1 at: /Users/…/vectorsum.py:3
Type c at the ipdb> prompt to start your script.
><string>(1)<module>()
ipdb> c
> /Users/…/vectorsum.py(3)<module>()
2
1---> 3 import sys
4 from datetime import datetime
ipdb> n
>
/Users/…/vectorsum.py(4)<module>()
1 3 import sys
----> 4 from datetime import datetime
5 import numpy
ipdb> n
> /Users/…/vectorsum.py(5)<module>()
4 from datetime import datetime
----> 5 import numpy
6
ipdb> quit
We can also prole our script by passing the -p opon to %run.
In [4]: %run -p vectorsum.py 1000
1058 function calls (1054 primitive calls) in 0.002 CPU seconds
Ordered by: internal time
ncallstottimepercallcumtimepercallfilename:lineno(function)
1 0.001 0.001 0.001 0.001 vectorsum.py:28(pythonsum)
1 0.001 0.001 0.002 0.002 {execfile}
www.it-ebooks.info
NumPy Quick Start
[ 24 ]
1000 0.000 0.0000.0000.000 {method 'append' of 'list' objects}
1 0.000 0.000 0.002 0.002 vectorsum.py:3(<module>)
1 0.000 0.0000.0000.000 vectorsum.py:21(numpysum)
3 0.000 0.0000.0000.000 {range}
1 0.000 0.0000.0000.000 arrayprint.py:175(_array2string)
3/1 0.000 0.0000.0000.000 arrayprint.py:246(array2string)
2 0.000 0.0000.0000.000 {method 'reduce' of 'numpy.ufunc' objects}
4 0.000 0.0000.0000.000 {built-in method now}
2 0.000 0.0000.0000.000 arrayprint.py:486(_formatInteger)
2 0.000 0.0000.0000.000 {numpy.core.multiarray.arange}
1 0.000 0.0000.0000.000 arrayprint.py:320(_formatArray)
3/1 0.000 0.0000.0000.000 numeric.py:1390(array_str)
1 0.000 0.0000.0000.000 numeric.py:216(asarray)
2 0.000 0.0000.0000.000 arrayprint.py:312(_extendLine)
1 0.000 0.0000.0000.000 fromnumeric.py:1043(ravel)
2 0.000 0.0000.0000.000 arrayprint.py:208(<lambda>)
1 0.000 0.000 0.002 0.002<string>:1(<module>)
11 0.000 0.0000.0000.000 {len}
2 0.000 0.0000.0000.000 {isinstance}
1 0.000 0.0000.0000.000 {reduce}
1 0.000 0.0000.0000.000 {method 'ravel' of 'numpy.ndarray' objects}
4 0.000 0.0000.0000.000 {method 'rstrip' of 'str' objects}
3 0.000 0.0000.0000.000 {issubclass}
2 0.000 0.0000.0000.000 {method 'item' of 'numpy.ndarray' objects}
1 0.000 0.0000.0000.000 {max}
1 0.000 0.0000.0000.000 {method 'disable' of '_lsprof.Profiler'
objects}
This gives us a bit more insight into the workings of our program. In addion, we can now
idenfy performance bolenecks. The %hist command shows the commands history.
In [2]: a=2+2
In [3]: a
Out[3]: 4
In [4]: %hist
1: _ip.magic("hist ")
2: a=2+2
3: a
I hope you agree that IPython is a really useful tool!
www.it-ebooks.info
Chapter 1
[ 25 ]
Online resources and help
When we are in IPython's pylab mode, we can open manual pages for NumPy funcons with
the help command. It is not necessary to know the name of a funcon. We can type a few
characters and then let tab compleon do its work. Let's, for instance, browse the available
informaon for the arange funcon.
In [2]: help ar<Tab>
arange
arccosh
arcsin
arcsinh
arctan
arccos arctan2
arctanh
argmax
argmin
argsort
argwhere
around
array
array2string
array_equal
array_equiv
array_repr
array_split
array_str
arrow
In [2]: help arange
Another opon is to put a queson mark behind the funcon name:
In [3]: arange?
The main documentaon website for NumPy and SciPy is at http://docs.scipy.org/
doc/. Through this webpage, we can browse the NumPy reference at http://docs.
scipy.org/doc/numpy/reference/ and the user guide as well as several tutorials.
NumPy has a wiki with lots of documentaon at http://docs.scipy.org/numpy/
Front%20Page/.
The NumPy and SciPy forum can be found at http://ask.scipy.org/en.
The popular Stack Overow soware development forum has hundreds of quesons tagged
numpy. To view them, go to http://stackoverflow.com/questions/tagged/numpy.
If you are really stuck with a problem or you want to be kept informed of NumPy
development, you can subscribe to the NumPy discussion mailing list. The e-mail address is
numpy-discussion@scipy.org. The number of e-mails per day is not too high and there
is almost no spam to speak of. Most importantly, developers acvely involved with NumPy
also answer quesons asked on the discussion group. The complete list can be found at
http://www.scipy.org/Mailing_Lists.
www.it-ebooks.info
NumPy Quick Start
[ 26 ]
For IRC users, there is an IRC channel on irc.freenode.net. The channel is called #scipy,
but you can also ask NumPy quesons since SciPy users also have knowledge of NumPy, as
SciPy is based on NumPy. There are at least 50 members on the SciPy channel at all mes.
Summary
In this chapter, we installed NumPy and other recommended soware that we will be using
in some tutorials. We got a vector addion program working and convinced ourselves that
NumPy has superior performance. We were introduced to the IPython interacve shell. In
addion, we explored the available NumPy documentaon and online resources.
In the next chapter, we will take a look under the hood and explore some fundamental
concepts including arrays and data types.
www.it-ebooks.info
Beginning with NumPy Fundamentals
After installing NumPy and getting some code to work, it's time to cover NumPy
basics.
The topics we shall cover in this chapter are:
Data types
Array types
Type conversions
Array creaon
Indexing
Slicing
Shape manipulaon
Before we start, let me make a few remarks about the code examples in this chapter. The
code snippets in this chapter show input and output from several IPython sessions. Recall
that IPython was introduced in Chapter 1, NumPy Quick Start, as the interacve Python
shell of choice for scienc compung. The advantages of IPython are the PyLab switch that
imports many scienc compung Python packages, including NumPy, and the fact that it is
not necessary to explicitly call the print funcon to display variable values. However, the
source code delivered alongside the book is regular Python code that uses imports and
print statements.
2
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 28 ]
NumPy array object
NumPy has a mul-dimensional array object called ndarray. It consists of two parts:
The actual data
Some metadata describing the data
The majority of array operaons leave the raw data untouched. The only aspect that changes
is the metadata.
We have already learned, in the previous chapter, how to create an array using the arange
funcon. Actually, we created a one-dimensional array that contained a set of numbers.
ndarray can have more than one dimension.
The NumPy array is in general homogeneous (there is a special array type that is
heterogeneous)—the items in the array have to be of the same type. The advantage is that,
if we know that the items in the array are of the same type, it is easy to determine the
storage size required for the array.
NumPy arrays are indexed just like in Python, starng from 0. Data types are represented
by special objects. These objects will be discussed comprehensively in this chapter.
We will create an array with the arange funcon again. Here's how to get the data type
of an array:
In: a = arange(5)
In: a.dtype
Out: dtype('int64')
The data type of array a is int64 (at least on my machine), but you may get int32 as
output if you are using 32-bit Python. In both cases, we are dealing with integers (64-bit
or 32-bit). Besides the data type of an array, it is important to know its shape.
The example in Chapter 1, NumPy Quick Start, demonstrated how to create a vector
(actually, a one-dimensional NumPy array). A vector is commonly used in mathemacs but,
most of the me, we need higher-dimensional objects. Let's determine the shape of the
vector we created a few minutes ago:
In [4]: a
Out[4]: array([0, 1, 2, 3, 4])
In: a.shape
Out: (5,)
As you can see, the vector has ve elements with values ranging from 0 to 4. The shape
aribute of the array is a tuple, in this case a tuple of 1 element, which contains the length
in each dimension.
www.it-ebooks.info
Chapter 2
[ 29 ]
Time for action – creating a multidimensional array
Now that we know how to create a vector, we are ready to create a muldimensional NumPy
array. Aer we create the matrix, we would again want to display its shape.
1. Create a muldimensional array.
2. Show the array shape:
In: m = array([arange(2), arange(2)])
In: m
Out:
array([[0, 1],
[0, 1]])
In: m.shape
Out: (2, 2)
What just happened?
We created a two-by-two array with the arange funcon we have come to trust and love.
Without any warning, the array funcon appeared on the stage.
The array funcon creates an array from an object that you give to it. The object needs
to be array-like, for instance, a Python list. In the preceding example, we passed in a list of
arrays. The object is the only required argument of the array funcon. NumPy funcons
tend to have a lot of oponal arguments with predened defaults.
Pop quiz – the shape of ndarray
Q1. How is the shape of an ndarray stored?
1. It is stored in a comma-separated string.
2. It is stored in a list.
3. It is stored in a tuple.
Have a go hero – create a three-by-three matrix
It shouldn't be too hard now to create a three-by-three matrix. Give it a go and check
whether the array shape is as expected.
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 30 ]
Selecting elements
From me to me, we will want to select a parcular element of an array. We will take a look
at how to do this, but rst, let's create a two-by-two matrix again:
In: a = array([[1,2],[3,4]])
In: a
Out:
array([[1, 2],
[3, 4]])
The matrix was created this me by passing the array funcon a list of lists. We will now
select each item of the matrix one-by-one. Remember, the indices are numbered starng
from 0.
In: a[0,0]
Out: 1
In: a[0,1]
Out: 2
In: a[1,0]
Out: 3
In: a[1,1]
Out: 4
As you can see, selecng elements of the array is prey simple. For the array a, we just use
the notaon a[m,n], where m and n are the indices of the item in the array as shown in the
following diagram:
NumPy numerical types
Python has an integer type, a oat type, and a complex type, however, this is not enough for
scienc compung and, for this reason, NumPy has a lot more data types. In pracce, we
need even more types with varying precision and, therefore, dierent memory size of the
type. The majority of the NumPy numerical types end with a number. This number indicates
the number of bits associated with the type. The following table (adapted from the NumPy
user guide) gives an overview of NumPy numerical types:
www.it-ebooks.info
Chapter 2
[ 31 ]
Type Description
bool Boolean (True or False) stored as a bit
inti Platform integer (normally either int32 or int64)
int8 Byte (-128 to 127)
int16 Integer (-32768 to 32767)
int32 Integer (-2 ** 31 to 2 ** 31 -1)
int64 Integer (-2 ** 63 to 2 ** 63 -1)
uint8 Unsigned integer (0 to 255)
uint16 Unsigned integer (0 to 65535)
uint32 Unsigned integer (0 to 2 ** 32 - 1)
uint64 Unsigned integer (0 to 2 ** 64 - 1)
float16 Half precision float: sign bit, 5 bits exponent, 10 bits mantissa
float32 Single precision float: sign bit, 8 bits exponent, 23 bits mantissa
float64 or float Double precision float: sign bit, 11 bits exponent, 52 bits mantissa
complex64 Complex number, represented by two 32-bit floats (real and
imaginary components)
complex128 or
complex
Complex number, represented by two 64-bit floats (real and
imaginary components)
For each data type, there exists a corresponding conversion funcon:
In: float64(42)
Out: 42.0
In: int8(42.0)
Out: 42
In: bool(42)
Out: True
In: bool(0)
Out: False
In: bool(42.0)
Out: True
In: float(True)
Out: 1.0
In: float(False)
Out: 0.0
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 32 ]
Many funcons have a data type argument, which is oen oponal:
In: arange(7, dtype=uint16)
Out: array([0, 1, 2, 3, 4, 5, 6], dtype=uint16)
It is important to know that you are not allowed to convert a complex number into an
integer. Trying to do that triggers a TypeError:
In [1] : int(42.0+1.j)
TypeError
<ipython-input-1-5e824780381a> in <modu
-------> 1 int(42.0.+1.j)
TypeError: can’t convert complex to int
The same goes for conversion of a complex number into a oat. By the way, the j part is the
imaginary coecient of the complex number. However, you can convert a oat to a complex
number, for instance complex(1.0).
Data type objects
Data type objects are instances of the numpy.dtype class. Once again, arrays have a data
type. To be precise, every element in a NumPy array has the same data type. The data type
object can tell you the size of the data in bytes. The size in bytes is given by the itemsize
aribute of the dtype class:
In: a.dtype.itemsize
Out: 8
Character codes
Character codes are included for backward compability with Numeric. Numeric is the
predecessor of NumPy. Their use is not recommended, but the codes are provided here
because they pop up in several places. You should instead use dtype objects.
Type Character code
integer i
Unsigned integer u
Single precision float f
Double precision float d
bool b
complex D
string S
www.it-ebooks.info
Chapter 2
[ 33 ]
Type Character code
unicode U
Void V
Look at the following code to create an array of single precision oats:
In: arange(7, dtype='f')
Out: array([ 0., 1., 2., 3., 4., 5., 6.], dtype=float32)
Likewise this creates an array of complex numbers
In: arange(7, dtype='D')
Out: array([ 0.+0.j, 1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j, 5.+0.j,
6.+0.j])
dtype constructors
We have a variety of ways to create data types. Take the case of oang point data:
We can use the general Python oat:
In: dtype(float)
Out: dtype('float64')
We can specify a single precision oat with a character code:
In: dtype('f')
Out: dtype('float32')
We can use a double precision oat character code:
In: dtype('d')
Out: dtype('float64')
We can give the data type constructor a two-character code. The rst character
signies the type; the second character is a number specifying the number of
bytes in the type (the numbers 2, 4 and 8 correspond to 16, 32 and 64 bit oats):
In: dtype('f8')
Out: dtype('float64')
A lisng of all full data type names can be found in sctypeDict.keys():
In: sctypeDict.keys()
Out: [0, …
'i2',
'int0']
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 34 ]
dtype attributes
The dtype class has a number of useful aributes. For example, we can get informaon
about the character code of a data type through the aributes of dtype:
In: t = dtype('Float64')
In: t.char
Out: 'd'
The type aribute corresponds to the type of object of the array elements:
In: t.type
Out: <type 'numpy.float64'>
The str aribute of dtype gives a string representaon of the data type. It starts with a
character represenng endianness, if appropriate, then a character code, followed by a
number corresponding to the number of bytes that each array item requires. Endianness,
here, means the way bytes are ordered within a 32 or 64-bit word. In big-endian order, the
most signicant byte is stored rst; indicated by >. In lile-endian order, the least signicant
byte is stored rst; indicated by <:
In: t.str
Out: '<f8'
Time for action – creating a record data type
The record data type is a heterogeneous data type—think of it as represenng a row in a
spreadsheet or a database. To give an example of a record data type, we will create a record
for a shop inventory. The record contains the name of the item, a 40-character string, the
number of items in the store represented by a 32-bit integer and, nally, a price represented
by a 32-bit oat. The following steps show how to create a record data type:
1. Create the record:
In: t = dtype([('name', str_, 40), ('numitems', int32), ('price',
float32)])
In: t
Out: dtype([('name', '|S40'), ('numitems', '<i4'), ('price',
'<f4')])
2. View the type (we can view the type of a eld as well):
In: t['name']
Out: dtype('|S40')
www.it-ebooks.info
Chapter 2
[ 35 ]
If you don't give the array funcon a data type, it will assume that it is dealing with oang
point numbers. To create the array now, we really have to specify the data type; otherwise,
we will get a TypeError:
In: itemz = array([('Meaning of life DVD', 42, 3.14), ('Butter', 13,
2.72)], dtype=t)
In: itemz[1]
Out: ('Butter', 13, 2.7200000286102295)
What just happened?
We created a record data type, which is a heterogeneous data type. The record contained
a name as a character string, a number as an integer and a price represented by a oat.
One-dimensional slicing and indexing
Slicing of one-dimensional NumPy arrays works just like slicing of Python lists. We can select
a piece of an array from index 3 to 7 that extracts the elements 3 through 6:
In: a = arange(9)
In: a[3:7]
Out: array([3, 4, 5, 6])
We can select elements from index 0 to 7 with a step of 2:
In: a[:7:2]
Out: array([0, 2, 4, 6])
Similarly as in Python, we can use negave indices and reverse the array:
In: a[::-1]
Out: array([8, 7, 6, 5, 4, 3, 2, 1, 0])
Time for action – slicing and indexing multidimensional arrays
A ndarray supports slicing over mulple dimensions. For convenience, we refer to many
dimensions at once, with an ellipsis.
1. To illustrate, we will create an array with the arange funcon and reshape it:
In: b = arange(24).reshape(2,3,4)
In: b.shape
Out: (2, 3, 4)
In: b
Out:
array([[[ 0, 1, 2, 3],
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 36 ]
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
The array b has 24 elements with values 0 to 23 and we reshaped it to be a two-by-
three-by-four, three-dimensional array. We can visualize this as a two-story building
with 12 rooms on each oor, three rows and four columns (alternavely, you can
think of it as a spreadsheet with sheets, rows, and columns). As you have probably
guessed, the reshape funcon changes the shape of an array. You give it a tuple of
integers, corresponding to the new shape. If the dimensions are not compable with
the data, an excepon is thrown.
2. We can select a single room by using its three coordinates, namely, the oor, column,
and row. For example, the room on the rst oor, in the rst row, and in the rst
column (you can have oor 0 and room 0—it's just a maer of convenon) can be
represented by:
In: b[0,0,0]
Out: 0
3. If we don't care about the oor, but sll want the rst column and row, we replace
the rst index by a : (colon) because we just need to specify the oor number and
omit the other indices:
In: b[:,0,0]
Out: array([ 0, 12])
This selects the first floor
In: b[0]
Out:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
We could also have wrien:
In: b[0, :, :]
Out:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
An … (ellipsis) replaces mulple colons, so, the preceding code is equivalent to:
In: b[0, ...]
Out:
array([[ 0, 1, 2, 3],
www.it-ebooks.info
Chapter 2
[ 37 ]
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
Further, we get the second row on the rst oor with:
In: b[0,1]
Out: array([4, 5, 6, 7])
4. Furthermore, we can also select each second element of this selecon:
In: b[0,1,::2]
Out: array([4, 6])
5. If we want to select all the rooms on both oors that are in the second column,
regardless of the row, we will type the following code snippet:
In: b[...,1]
Out:
array([[ 1, 5, 9],
[13, 17, 21]])
Similarly, we can select all the rooms on the second row, regardless of oor
and column, by wring the following code snippet:
In: b[:,1]
Out:
array([[ 4, 5, 6, 7],
[16, 17, 18, 19]])
If we want to select rooms on the ground oor second column, then type the
following code snippet:
In: b[0,:,1]
Out: array([1, 5, 9])
6. If we want to select the rst oor, last column, then type the following code snippet:
In: b[0,:,-1]
Out: array([ 3, 7, 11])
If we want to select rooms on the ground oor, last column reversed, then type the
following code snippet:
In: b[0,::-1, -1]
Out: array([11, 7, 3])
Every second element of that slice:
In: b[0,::2,-1]
Out: array([ 3, 11])
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 38 ]
The command that reverses a one-dimensional array puts the top oor following the
ground oor:
In: b[::-1]
Out:
array([[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]])
What just happened?
We sliced a muldimensional NumPy array using several dierent methods.
Time for action – manipulating array shapes
We already learned about the reshape funcon. Another recurring task is aening
of arrays.
1. Ravel: We can accomplish this with the ravel funcon:
In: b
Out:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
In: b.ravel()
Out:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
2. Flaen: The appropriately-named funcon, flatten, does the same as ravel,
but flatten always allocates new memory whereas ravel might return a view
of the array.
In: b.flatten()
Out:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
www.it-ebooks.info
Chapter 2
[ 39 ]
3. Seng the shape with a tuple: Besides the reshape funcon, we can also set the
shape directly with a tuple, which is shown as follows:
In: b.shape = (6,4)
In: b
Out:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
As you can see, this changes the array directly. Now, we have a six-by-four array.
4. Transpose: In linear algebra, it is common to transpose matrices. We can do that
too, by using the following code:
In: b.transpose()
Out:
array([[ 0, 4, 8, 12, 16, 20],
[ 1, 5, 9, 13, 17, 21],
[ 2, 6, 10, 14, 18, 22],
[ 3, 7, 11, 15, 19, 23]])
5. Resize: The resize method works just like the reshape method, but modies the
array it operates on:
In: b.resize((2,12))
In: b
Out:
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]])
What just happened?
We manipulated the shapes of NumPy arrays using the ravel funcon, the flatten
funcon, the reshape funcon, and the resize method.
Stacking
Arrays can be stacked horizontally, depth-wise, or vercally. We can use, for that purpose,
the vstack, dstack, hstack, column_stack, row_stack, and concatenate funcons.
www.it-ebooks.info
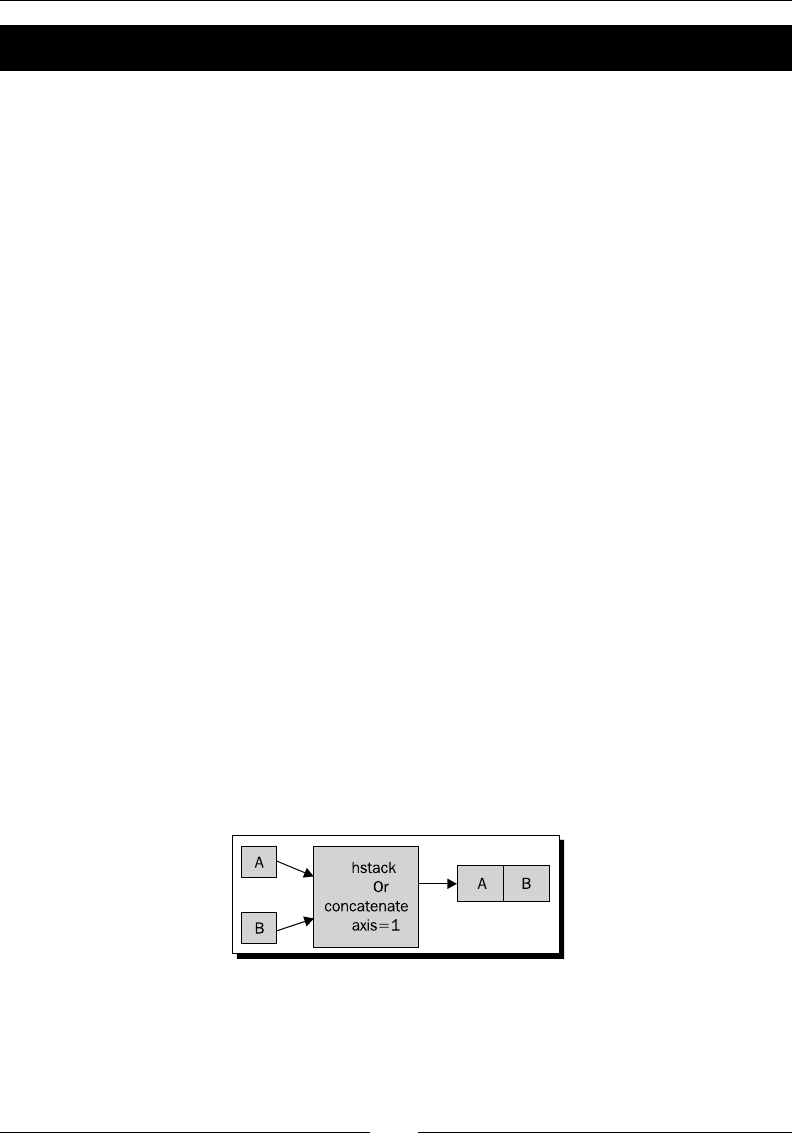
Beginning with NumPy Fundamentals
[ 40 ]
Time for action – stacking arrays
First, let's set up some arrays:
In: a = arange(9).reshape(3,3)
In: a
Out:
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
In: b = 2 * a
In: b
Out:
array([[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]])
1. Horizontal stacking: Starng with horizontal stacking, we will form a tuple
of ndarrays and give it to the hstack funcon. This is shown as follows:
In: hstack((a, b))
Out:
array([[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8, 10],
[ 6, 7, 8, 12, 14, 16]])
We can achieve the same with the concatenate funcon, which is shown
as follows:
In: concatenate((a, b), axis=1)
Out:
array([[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8, 10],
[ 6, 7, 8, 12, 14, 16]])
www.it-ebooks.info
Chapter 2
[ 41 ]
2. Vercal stacking: With vercal stacking, again, a tuple is formed. This me, it is
given to the vstack funcon. This can be seen as follows:
In: vstack((a, b))
Out:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]])
The concatenate funcon produces the same result with the axis set to 0.
This is the default value for the axis argument.
In: concatenate((a, b), axis=0)
Out:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]])
3. Depth stacking: Addionally, there is the depth-wise stacking using dstack and a
tuple, of course. This means stacking of a list of arrays along the third axis (depth).
For instance, we could stack 2D arrays of image data on top of each other.
In: dstack((a, b))
Out:
array([[[ 0, 0],
[ 1, 2],
[ 2, 4]],
[[ 3, 6],
[ 4, 8],
[ 5, 10]],
[[ 6, 12],
[ 7, 14],
[ 8, 16]]])
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 42 ]
4. Column stacking: The column_stack funcon stacks 1D arrays column-wise.
It's shown as follows:
In: oned = arange(2)
In: oned
Out: array([0, 1])
In: twice_oned = 2 * oned
In: twice_oned
Out: array([0, 2])
In: column_stack((oned, twice_oned))
Out:
array([[0, 0],
[1, 2]])
2D arrays are stacked the way hstack stacks them:
In: column_stack((a, b))
Out:
array([[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8, 10],
[ 6, 7, 8, 12, 14, 16]])
In: column_stack((a, b)) == hstack((a, b))
Out:
array([[ True, True, True, True, True, True],
[ True, True, True, True, True, True],
[ True, True, True, True, True, True]], dtype=bool)
Yes, you guessed it right! We compared two arrays with the == operator. Isn't
it beauful?
5. Row stacking: NumPy, of course, also has a funcon that does row-wise stacking.
It is called row_stack and, for 1D arrays, it just stacks the arrays in rows into
a 2D array.
In: row_stack((oned, twice_oned))
Out:
array([[0, 1],
[0, 2]])
The row_stack funcon results for 2D arrays are equal to, yes, exactly, the vstack
funcon results.
In: row_stack((a, b))
Out:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
www.it-ebooks.info
Chapter 2
[ 43 ]
[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]])
In: row_stack((a,b)) == vstack((a, b))
Out:
array([[ True, True, True],
[ True, True, True],
[ True, True, True],
[ True, True, True],
[ True, True, True],
[ True, True, True]], dtype=bool)
What just happened?
We stacked arrays horizontally, depth-wise, and vercally. We used the vstack, dstack,
hstack, column_stack, row_stack, and concatenate funcons.
Splitting
Arrays can be split vercally, horizontally, or depth wise. The funcons involved are hsplit,
vsplit, dsplit, and split. We can either split into arrays of the same shape or indicate
the posion aer which the split should occur.
Time for action – splitting arrays
1. Horizontal spling: The ensuing code splits an array along its horizontal axis into
three pieces of the same size and shape:
In: a
Out:
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
In: hsplit(a, 3)
Out:
[array([[0],
[3],
[6]]),
array([[1],
[4],
[7]]),
array([[2],
[5],
[8]])]
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 44 ]
Compare it with a call of the split funcon, with extra parameter axis=1:
In: split(a, 3, axis=1)
Out:
[array([[0],
[3],
[6]]),
array([[1],
[4],
[7]]),
array([[2],
[5],
[8]])]
2. Vercal spling: The vsplit funcon splits along the vercal axis:
In: vsplit(a, 3)
Out: [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7,
8]])]
The split funcon, with axis=0, also splits along the vercal axis:
In: split(a, 3, axis=0)
Out: [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7,
8]])]
3. Depth-wise spling: The dsplit funcon, unsurprisingly, splits depth-wise.
We will need an array of rank three rst:
In: c = arange(27).reshape(3, 3, 3)
In: c
Out:
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
In: dsplit(c, 3)
Out:
[array([[[ 0],
[ 3],
[ 6]],
[[ 9],
www.it-ebooks.info
Chapter 2
[ 45 ]
[12],
[15]],
[[18],
[21],
[24]]]),
array([[[ 1],
[ 4],
[ 7]],
[[10],
[13],
[16]],
[[19],
[22],
[25]]]),
array([[[ 2],
[ 5],
[ 8]],
[[11],
[14],
[17]],
[[20],
[23],
[26]]])]
What just happened?
We split arrays using the hsplit, vsplit, dsplit, and split funcons.
Array attributes
Besides the shape and dtype aributes, ndarray has a number of other aributes,
as shown in the following list:
The ndim aribute gives the number of dimensions:
In: b
Out:
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]])
In: b.ndim
Out: 2
www.it-ebooks.info
Beginning with NumPy Fundamentals
[ 46 ]
The size aribute contains the number of elements. This is shown a follows:
In: b.size
Out: 24
The itemsize aribute gives the number of bytes for each element in the array:
In: b.itemsize
Out: 8
If you want the total number of bytes the array requires, you can have a look at
nbytes. This is just a product of the itemsize and size aributes:
In: b.nbytes
Out: 192
In: b.size * b.itemsize
Out: 192
The T aribute has the same eect as the transpose funcon, which is shown
as follows:
In: b.resize(6,4)
In: b
Out:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
In: b.T
Out:
array([[ 0, 4, 8, 12, 16, 20],
[ 1, 5, 9, 13, 17, 21],
[ 2, 6, 10, 14, 18, 22],
[ 3, 7, 11, 15, 19, 23]])
If the array has a rank lower than two, we will just get a view of the array:
In: b.ndim
Out: 1
In: b.T
Out: array([0, 1, 2, 3, 4])
Complex numbers in NumPy are represented by j. For example, we can create an
array with complex numbers:
In: b = array([1.j + 1, 2.j + 3])
In: b
Out: array([ 1.+1.j, 3.+2.j])
www.it-ebooks.info
Chapter 2
[ 47 ]
The real aribute gives us the real part of the array, or the array itself if it only
contains real numbers:
In: b.real
Out: array([ 1., 3.])
The imag aribute contains the imaginary part of the array:
In: b.imag
Out: array([ 1., 2.])
If the array contains complex numbers, then the data type is automacally
also complex:
In: b.dtype
Out: dtype('complex128')
In: b.dtype.str
Out: '<c16'
The flat aribute returns a numpy.flatiter object. This is the only way to
acquire a flatiter—we do not have access to a flatiter constructor. The at
iterator enables us to loop through an array as if it is a at array, as shown next:
In: b = arange(4).reshape(2,2)
In: b
Out:
array([[0, 1],
[2, 3]])
In: f = b.flat
In: f
Out: <numpy.flatiter object at 0x103013e00>
In: for item in f: print item
.....:
0
1
2
3
It is possible to directly get an element with the flatiter object:
In: b.flat[2]
Out: 2
Or mulple elements:
In: b.flat[[1,3]]
Out: array([1, 3])
www.it-ebooks.info
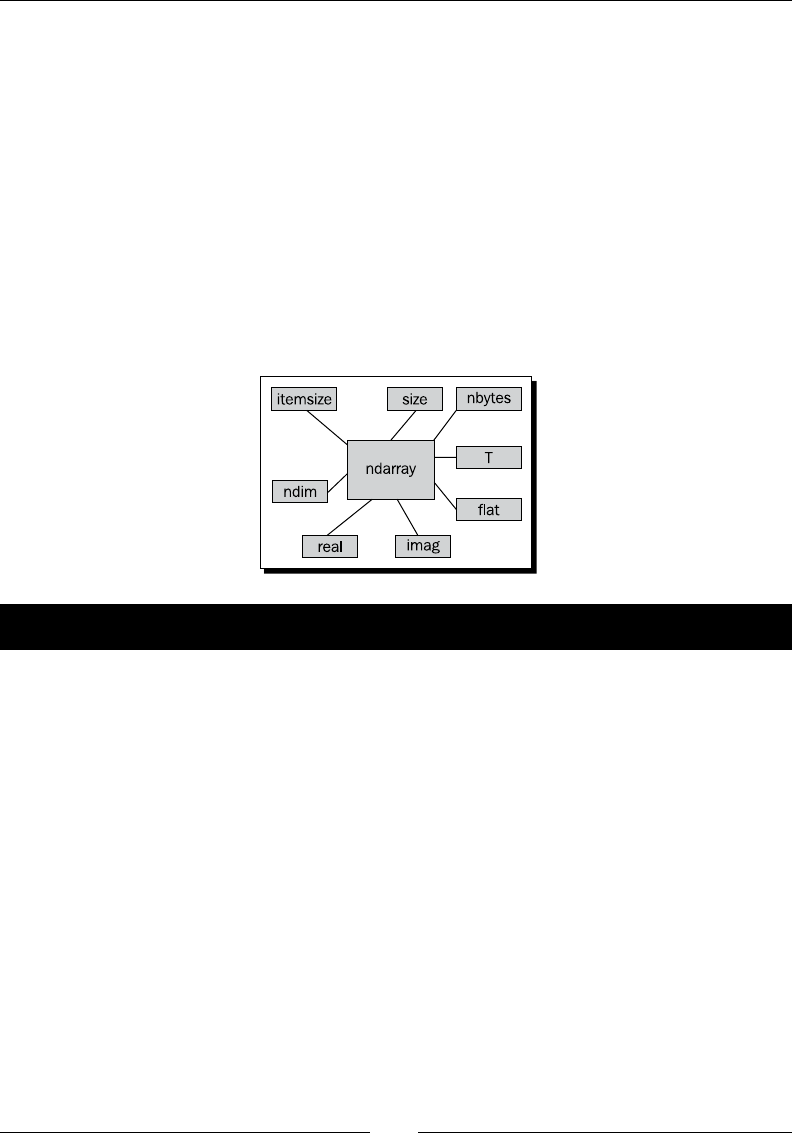
Beginning with NumPy Fundamentals
[ 48 ]
The flat aribute is seable. Seng the value of the flat aribute leads to
overwring the values of the whole array:
In: b.flat = 7
In: b
Out:
array([[7, 7],
[7, 7]])
or selected elements
In: b.flat[[1,3]] = 1
In: b
Out:
array([[7, 1],
[7, 1]])
Time for action – converting arrays
We can convert a NumPy array to a Python list with the tolist funcon:
1. Convert to a list:
In: b
Out: array([ 1.+1.j, 3.+2.j])
In: b.tolist()
Out: [(1+1j), (3+2j)]
2. The astype funcon converts the array to an array of the specied type:
In: b
Out: array([ 1.+1.j, 3.+2.j])
In: b.astype(int)
/usr/local/bin/ipython:1: ComplexWarning: Casting complex values
to real discards the imaginary part
#!/usr/bin/python
Out: array([1, 3])
www.it-ebooks.info
Chapter 2
[ 49 ]
We are losing the imaginary part when casting from complex type to int.
The astype function also accepts the name of a type as a string.
In: b.astype('complex')
Out: array([ 1.+1.j, 3.+2.j])
It won't show any warning this time, because we used the proper data type.
What just happened?
We converted NumPy arrays to a list and to arrays of dierent data types.
Summary
We learned a lot in this chapter about the NumPy fundamentals: data types and arrays.
Arrays have several aributes describing them. We learned that one of these aributes
is the data type, which in NumPy, is represented by a full-edged object.
NumPy arrays can be sliced and indexed in an ecient manner, just like Python lists.
NumPy arrays have the added ability of working with mulple dimensions.
The shape of an array can be manipulated in many ways—stacking, resizing, reshaping,
and spling. A great number of convenience funcons for shape manipulaon were
demonstrated in this chapter.
Having learned about the basics, it's me to move on to the study of commonly-used
funcons in Chapter 3, Get to Terms with Commonly Used Funcons. This includes basic
stascal and mathemacal funcons.
www.it-ebooks.info
www.it-ebooks.info
Get in Terms with Commonly
Used Functions
In this chapter, we will have a look at common NumPy functions. In particular,
we will learn how to load data from files using a historical stock prices example.
Also, we will get to see the basic NumPy mathematical and statistical functions.
We will learn how to read from and write to files. Also, we will get a taste of the
functional programming and linear algebra possibilities in NumPy.
In this chapter, we shall cover the following topics:
Funcons working on arrays
Loading arrays from les
Wring arrays to les
Simple mathemacal and stascal funcons
File I/O
First, we will learn about le I/O with NumPy. Data is usually stored in les. You will not get
far if you are not able to read from and write to les.
3
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 52 ]
Time for action – reading and writing les
As an example of le I/O, we will create an identy matrix and store its contents in a le.
Perform the following steps to do so:
1. The identy matrix is a square matrix with ones on the main diagonal and zeroes
for the rest. The identy matrix can be created with the eye funcon. The only
argument we need to give the eye funcon is the number of ones. So, for instance,
for a 2 x 2 matrix, write the following code:
i2 = np.eye(2)
print i2
The output is:
[[ 1. 0.]
[ 0. 1.]]
2. Save the data using the savetxt funcon. We obviously need to specify the name
of the le that we want to save the data in and the array containing the data itself.
np.savetxt("eye.txt", i2)
A le called eye.txt should have been created. You can check for yourself whether the
contents are as expected. The code for this example can be downloaded from the book
support website http://www.packtpub.com/support (see save.py).
import numpy as np
i2 = np.eye(2)
print i2
np.savetxt("eye.txt", i2)
What just happened?
Reading and wring les is a necessary skill for data analysis. We wrote to a le using
savetxt. We made an identy matrix with the eye funcon.
CSV les
Files in the comma-separated values (CSV) format are encountered quite frequently. Oen,
the CSV le is just a dump from a database le. Usually, each eld in the CSV le corresponds
to a database table column. As we all know, spreadsheet programs, such as Excel, can
produce CSV les as well.
www.it-ebooks.info
Chapter 3
[ 53 ]
Time for action – loading from CSV les
How do we deal with CSV les? Luckily, the loadtxt funcon can conveniently read CSV
les, split up the elds, and load the data into NumPy arrays. In the following example, we
will load historical price data for Apple (the company, not the fruit). The data is in the CSV
format. The rst column contains a symbol that idenes the stock. In our case, it is AAPL.
Second is the date in the dd-mm-yyyy format. The third column is empty. Then, in order, we
have the open, high, low, and close price. Last, but not least, is the volume of the day. This is
what a line looks like:
AAPL,28-01-2011, ,344.17,344.4,333.53,336.1,21144800
For now, we are only interested in the close price and volume. In the preceding sample, that
would be 336.1 and 21144800. Store the close price and volume in two arrays, as follows:
c,v=np.loadtxt('data.csv', delimiter=',', usecols=(6,7), unpack=True)
As you can see, data is stored in the data.csv le. We have set the delimiter to ','
(comma), since we are dealing with a comma-separated value le. The usecols parameter
is set through a tuple to get the seventh and eighth elds, which correspond to the close
price and volume. unpack is set to True, which means that data will be unpacked and
assigned to the c and v variables that will hold the close price and volume, respecvely.
What just happened?
CSV les are a special type of le that we have to deal with frequently. We read a CSV le
containing stock quotes with the loadtxt funcon. We indicated to the loadtxt funcon
that the delimiter of our le was a comma. We specied which columns we were interested
in, through the usecols argument, and set the unpack parameter to True so that the data
was unpacked for further use.
Volume-weighted average price
Volume-weighted average price (VWAP) is a very important quanty in nance. It represents
an "average" price for a nancial asset. The higher the volume, the more signicant a price
move typically is. VWAP is oen used in algorithmic trading and is calculated by using volume
values as weights.
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 54 ]
Time for action – calculating volume-weighted average price
The following are the acons that we will take:
1. Read the data into arrays.
2. Calculate VWAP.
import numpy as np
c,v=np.loadtxt('data.csv', delimiter=',', usecols=(6,7),
unpack=True)
vwap = np.average(c, weights=v)
print "VWAP =", vwap
The output is
VWAP = 350.589549353
What just happened?
That wasn't very hard, was it? We just called the average funcon and set its weights
parameter to use the v array for weights. By the way, NumPy also has a funcon to calculate
the arithmec mean.
The mean function
The mean funcon is quite friendly and not so mean. This funcon calculates the arithmec
mean of an array. Let's see it in acon:
print "mean =", np.mean(c)
mean = 351.037666667
Time-weighted average price
In nance, TWAP is another "average" price measure. Now that we are at it, let's compute
the me-weighted average price, too. It is just a variaon on a theme really. The idea is that
recent price quotes are more important, so we should give recent prices higher weights. The
easiest way is to create an array with the arange funcon of increasing values from zero to
the number of elements in the close price array. This is not necessarily the correct way. In
fact, most of the examples concerning stock price analysis in this book are only illustrave.
The following is the TWAP code:
t = np.arange(len(c))
print "twap =", np.average(c, weights=t)
It produces the following output:
twap = 352.428321839
The TWAP is even higher than the mean.
www.it-ebooks.info
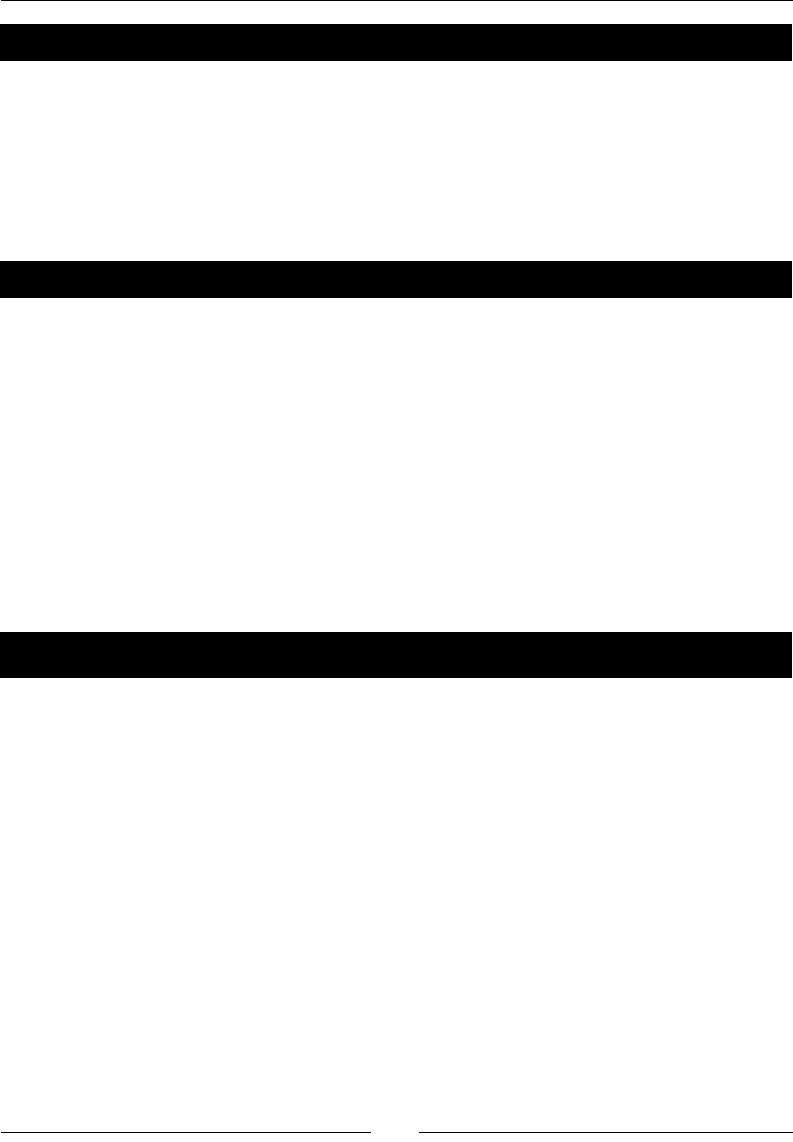
Chapter 3
[ 55 ]
Pop quiz – computing the weighted average
Q1. Which funcon returns the weighted average of an array?
1. weighted average
2. waverage
3. average
4. avg
Have a go hero – calculating other averages
Try doing the same calculaon using the open price. Calculate the mean for the volume and
the other prices.
Value range
Usually, we don't only want to know the average or arithmec mean of a set of values, which
are sort of in the middle; we also want the extremes, the full range—the highest and lowest
values. The sample data that we are using here already has those values per day—the high
and low price. However, we need to know the highest value of the high price and the lowest
price value of the low price. Aer all, how else would we know how much our Apple stocks
would gain or lose?
Time for action – nding highest and lowest values
The min and max funcons are the answer to our requirement. Perform the following steps
to nd highest and lowest values:
1. First, we will need to read our le again and store the values for the high and low
prices into arrays.
h,l=np.loadtxt('data.csv', delimiter=',', usecols=(4,5),
unpack=True)
The only thing that changed is the usecols parameter, since the high and low
prices are situated in dierent columns.
2. The following code gets the price range:
print "highest =", np.max(h)
print "lowest =", np.min(l)
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 56 ]
These are the values returned:
highest = 364.9
lowest = 333.53
Now, it's trivial to get a midpoint, so it is le as an exercise for the reader to aempt.
3. NumPy allows us to compute the spread of an array with a funcon called ptp. The
ptp funcon returns the dierence between the maximum and minimum values of
an array. In other words, it is equal to max(array) - min(array). Call the ptp funcon.
print "Spread high price", np.ptp(h)
print "Spread low price", np.ptp(l)
You will see the following:
Spread high price 24.86
Spread low price 26.97
What just happened?
We dened a range of highest to lowest values for the price. The highest value was given by
applying the max funcon to the high price array. Similarly, the lowest value was found by
calling the min funcon to the low price array. We also calculated the peak-to-peak distance
with the ptp funcon.
import numpy as np
h,l=np.loadtxt('data.csv', delimiter=',', usecols=(4,5), unpack=True)
print "highest =", np.max(h)
print "lowest =", np.min(l)
print (np.max(h) + np.min(l)) /2
print "Spread high price", np.ptp(h)
print "Spread low price", np.ptp(l)
Statistics
Stock traders are interested in the most probable close price. Common sense says that this
should be close to some kind of an average. The arithmec mean and weighted average are
ways to nd the center of a distribuon of values. However, neither are robust nor sensive
to outliers. For instance, if we had a close price value of a million dollars, this would have
inuenced the outcome of our calculaons.
www.it-ebooks.info
Chapter 3
[ 57 ]
Time for action – doing simple statistics
We can use some kind of threshold to weed out outliers, but there is a beer way. It is called
the median, and it basically picks the middle value of a sorted set of values. For example, if
we have the values of 1, 2, 3, 4, and 5, the median would be 3, since it is in the middle. The
following are the steps to calculate the median:
1. Determine the median of the close price. Create a new Python script and call it
simplestats.py. You already know how to load the data from a CSV le into an
array. So, copy that line of code and make sure that it only gets the close price. The
code should appear like the following, by now:
c=np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
2. The funcon that will do the magic for us is called median. We will call it and print
the result immediately. Add the following line of code:
print "median =", np.median(c)
The program prints the following output:
median = 352.055
3. Since it is our rst me using the median funcon, we would like to check whether
this is correct. Not because we are paranoid or anything! Obviously, we could do
it by just going through the le and nding the correct value, but that is no fun.
Instead, we will just mimic the median algorithm by sorng the close price array and
prinng the middle value of the sorted array. The msort funcon does the rst part
for us. We will call the funcon, store the sorted array, and then print it.
sorted_close = np.msort(c)
print "sorted =", sorted_close
This prints the following output:
Yup, it works! Let's now get the middle value of the sorted array:
N = len(c)
print "middle =", sorted[(N - 1)/2]
It gives us the following output:
middle = 351.99
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 58 ]
4. Hey, that's a dierent value than the one the median funcon gave us. How come?
Upon further invesgaon we nd that the median funcon return value doesn't
even appear in our le. That's even stranger! Before ling bugs with the NumPy
team, let's have a look at the documentaon. This mystery is easy to solve. It turns
out that our naive algorithm only works for arrays with odd lengths. For even-length
arrays, the median is calculated from the average of the two array values in the
middle. Therefore, type the following code:
print "average middle =", (sorted[N /2] + sorted[(N - 1) / 2]) / 2
This prints the following output:
average middle = 352.055
Success!
5. Another stascal measure that we are concerned with is variance. Variance tells
us how much a variable varies. In our case, it also tells us how risky an investment
is, since a stock price that varies too wildly is bound to get us into trouble. With
NumPy, this is just a one liner. See the following code:
print "variance =", np.var(c)
This gives us the following output:
variance = 50.1265178889
6. Not that we don't trust NumPy or anything, but let's double-check using the
denion of variance, as found in the documentaon. Mind you, this denion
might be dierent than the one in your stascs book, but that is quite common
in the eld of stascs.
The variance is defined as the mean of the square of deviations from the
mean, divided by the number of elements in the array.
Some books tell us to divide by the number of elements in the array minus one.
print "variance from definition =", np.mean((c - c.mean())**2)
The output is as follows:
variance from definition = 50.1265178889
Just as we expected!
www.it-ebooks.info
Chapter 3
[ 59 ]
What just happened?
Maybe you noced something new. We suddenly called the mean funcon on the c
array. Yes, this is legal, because the ndarray object has a mean method. This is for your
convenience. For now, just keep in mind that this is possible. The code for this example can
be found in simplestats.py.
import numpy as np
c=np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
print "median =", np.median(c)
sorted = np.msort(c)
print "sorted =", sorted
N = len(c)
print "middle =", sorted[(N - 1)/2]
print "average middle =", (sorted[N /2] + sorted[(N - 1) / 2]) / 2
print "variance =", np.var(c)
print "variance from definition =", np.mean((c - c.mean())**2)
Stock returns
In academic literature it is more common to base analysis on stock returns and log returns
of the close price. Simple returns are just the rate of change from one value to the next.
Logarithmic returns or log returns are determined by taking the log of all the prices and
calculang the dierences between them. In high school, we learned that the dierence
between the log of "a" and the log of "b" is equal to the log of "a divided by b". Log returns,
therefore, also measure rate of change. Returns are dimensionless, since, in the act of dividing,
we divide dollar by dollar (or some other currency). Anyway, investors are most likely to be
interested in the variance or standard deviaon of the returns, as this represents risk.
Time for action – analyzing stock returns
Perform the following steps to analyze stock returns:
1. First, let's calculate simple returns. NumPy has the diff funcon that returns an
array built up of the dierence between two consecuve array elements. This is sort
of like dierenaon in calculus. To get the returns, we also have to divide by the
value of the previous day. We must be careful though. The array returned by diff
is one element shorter than the close prices array. Aer careful deliberaon, we get
the following code:
returns = np.diff( arr ) / arr[ : -1]
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 60 ]
Noce that we don't use the last value in the divisor. Let's compute the standard
deviaon using the std funcon:
print "Standard deviation =", np.std(returns)
This results in the following output:
Standard deviation = 0.0129221344368
2. The log return is even easier to calculate. We use the log funcon to get the log of
the close price and then unleash the diff funcon on the result.
logreturns = np.diff( np.log(c) )
Normally, we would have to check that the input array doesn't have zeroes or
negave numbers. If it did, we would have got an error. Stock prices are, however,
always posive, so we didn't have to check.
3. Quite likely, we will be interested in days when the return is posive. In the current
setup, we can get the next best thing with the where funcon, which returns the
indices of an array that sases a condion. Just type the following code:
posretindices = np.where(returns > 0)
print "Indices with positive returns", posretindices
This gives us a number of indices for the array elements that are posive.
Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9,
10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)
4. In invesng, volality measures price variaon of a nancial security. Historical
volality is calculated from historical price data. The logarithmic returns are
interesng if you want to know the historical volality—for instance, the annualized
or monthly volality. The annualized volality is equal to the standard deviaon of
the log returns as a rao of its mean, divided by one over the square root of the
number of business days in a year, usually one assumes 252. Calculate it with the
std and mean funcons. See the following code:
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility / np.sqrt(1./252.)
print annual_volatility
5. Take note of the division within the sqrt funcon. Since, in Python, integer division
works dierently than oat division, we needed to use oats to make sure that we
get the proper results. Similarly, the monthly volality is given by:
print "Monthly volatility", annual_volatility * np.sqrt(1./12.)
www.it-ebooks.info
Chapter 3
[ 61 ]
What just happened?
We calculated the simple stock returns with the diff funcon, which calculates dierences
between sequenal elements. The log funcon computes the natural logarithms of array
elements. We used it to calculate the logarithmic returns. At the end of the tutorial we
calculated the annual and monthly volality (see returns.py).
import numpy as np
c=np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
returns = np.diff( c ) / c[ : -1]
print "Standard deviation =", np.std(returns)
logreturns = np.diff( np.log(c) )
posretindices = np.where(returns > 0)
print "Indices with positive returns", posretindices
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility / np.sqrt(1./252.)
print "Annual volatility", annual_volatility
print "Monthly volatility", annual_volatility * np.sqrt(1./12.)
Dates
Do you somemes have the Monday blues or the Friday fever? Ever wondered whether
the stock market suers from said phenomena? Well, I think this certainly warrants
extensive research.
Time for action – dealing with dates
First, we will read the close price data. Second, we will split the prices according to the day
of the week. Third, for each weekday, we will calculate the average price. Finally, we will
nd out which day of the week has the highest average and which has the lowest average.
A health warning before we commence – you might be tempted to use the result to buy
stock on one day and sell on the other. However, we don't have enough data to make this
kind of decision. Please consult a professional stascian rst!
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 62 ]
Coders hate dates because they are so complicated! NumPy is very much oriented towards
oang point operaons. For that reason, we need to take extra eort to process dates. Try
it out yourself; put the following code in a script or use the one that comes with the book:
dates, close=np.loadtxt('data.csv', delimiter=',',
usecols=(1,6), unpack=True)
Execute the script and the following error will appear:
ValueError: invalid literal for float(): 28-01-2011
Now perform the following steps to deal with dates:
1. Obviously, NumPy tried to convert the dates into oats. What we have to do is
explicitly tell NumPy how to convert the dates. The loadtxt funcon has a special
parameter for this purpose. The parameter is called converters and is a diconary
that links columns with so-called converter funcons. It is our responsibility to write
the converter funcon.
Let's write the funcon down:
# Monday 0
# Tuesday 1
# Wednesday 2
# Thursday 3
# Friday 4
# Saturday 5
# Sunday 6
def datestr2num(s):
return datetime.datetime.strptime
(s, "%d-%m-%Y").date().weekday()
We give the datestr2num funcon dates as a string, such as "28-01-2011". The
string is rst turned into a datetime object using a specied format "%d-%m-%Y".
This is, by the way, standard Python and is not related to NumPy itself. Second, the
datetime object is turned into a day. Finally the weekday method is called on the
date to return a number. As you can read in the comments, the number is between
0 and 6. 0 is for instance Monday and 6 is Sunday. The actual number, of course, is
not important for our algorithm; it is only used as idencaon.
2. Now we will hook up our date converter funcon to load the data.
dates, close=np.loadtxt('data.csv', delimiter=',', usecols=(1,6),
converters={1: datestr2num}, unpack=True)
print "Dates =", dates
www.it-ebooks.info
Chapter 3
[ 63 ]
This prints the following output:
Dates = [ 4. 0. 1. 2. 3. 4. 0. 1. 2. 3. 4. 0. 1. 2.
3. 4. 1. 2. 4. 0. 1. 2. 3. 4. 0. 1. 2. 3. 4.]
No Saturdays and Sundays, as you can see. Exchanges are closed over the weekend.
3. We will now make an array that has ve elements for each day of the week.
The values of the array will be inialized to 0.
averages = np.zeros(5)
This array will hold the averages for each weekday.
4. We already learned about the where funcon that returns indices of the array for
elements that conform to a specied condion. The take funcon can use these
indices and takes the values of the corresponding array items. We will use the
take funcon to get the close prices for each weekday. In the following loop we
go through the date values 0 to 4, beer known as Monday to Friday. We get the
indices with the where funcon for each day and store it in the indices array.
Then, we retrieve the values corresponding to the indices, using the take funcon.
Finally, we compute an average for each weekday and store it in the averages
array, as follows:
for i in range(5):
indices = np.where(dates == i)
prices = np.take(close, indices)
avg = np.mean(prices)
print "Day", i, "prices", prices, "Average", avg
averages[i] = avg
The loop prints the following output:
Day 0 prices [[ 339.32 351.88 359.18 353.21 355.36]] Average
351.79
Day 1 prices [[ 345.03 355.2 359.9 338.61 349.31 355.76]]
Average 350.635
Day 2 prices [[ 344.32 358.16 363.13 342.62 352.12 352.47]]
Average 352.136666667
Day 3 prices [[ 343.44 354.54 358.3 342.88 359.56 346.67]]
Average 350.898333333
Day 4 prices [[ 336.1 346.5 356.85 350.56 348.16 360.
351.99]] Average 350.022857143
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 64 ]
5. If you want, you can go ahead and nd out which day has the highest, and which
the lowest, average. However, it is just as easy to nd this out with the max and min
funcons, as shown next:
top = np.max(averages)
print "Highest average", top
print "Top day of the week", np.argmax(averages)
bottom = np.min(averages)
print "Lowest average", bottom
print "Bottom day of the week", np.argmin(averages)
The output is as follows:
Highest average 352.136666667
Top day of the week 2
Lowest average 350.022857143
Bottom day of the week 4
What just happened?
The argmin funcon returned the index of the lowest value in the averages array.
The index returned was 4, which corresponds to Friday. The argmax funcon returned
the index of the highest value in the averages array. The index returned was 2, which
corresponds to Wednesday (see weekdays.py).
import numpy as np
from datetime import datetime
# Monday 0
# Tuesday 1
# Wednesday 2
# Thursday 3
# Friday 4
# Saturday 5
# Sunday 6
def datestr2num(s):
return datetime.strptime(s, "%d-%m-%Y").date().weekday()
dates, close=np.loadtxt('data.csv', delimiter=',', usecols=(1,6),
converters={1: datestr2num}, unpack=True)
print "Dates =", dates
averages = np.zeros(5)
for i in range(5):
indices = np.where(dates == i)
prices = np.take(close, indices)
avg = np.mean(prices)
www.it-ebooks.info
Chapter 3
[ 65 ]
print "Day", i, "prices", prices, "Average", avg
averages[i] = avg
top = np.max(averages)
print "Highest average", top
print "Top day of the week", np.argmax(averages)
bottom = np.min(averages)
print "Lowest average", bottom
print "Bottom day of the week", np.argmin(averages
Have a go hero – looking at VWAP and TWAP
Hey, that was fun! For the sample data, it appears that Friday is the cheapest day and
Wednesday is the day when your Apple stock will be worth the most. Ignoring the fact that
we have very lile data, is there a beer method to compute the averages? Shouldn't we
involve volume data as well? Maybe it makes more sense to you to do a me-weighted
average. Give it a go! Calculate the VWAP and TWAP. You can nd some hints on how to go
about doing this at the beginning of this chapter.
Weekly summary
The data that we used in the previous Time for acon tutorials is end-of-day data.
In essence, it is summarized data compiled from trade data for a certain day. If you are
interested in the coon market and have decades of data, you might want to summarize
and compress the data even further. Let's do that. Let's summarize the data of Apple stocks
to give us weekly summaries.
Time for action – summarizing data
The data we will summarize will be for a whole business week from Monday to Friday. During
the period covered by the data, there was one holiday on February 21st, President's Day.
This happened to be a Monday and the US stock exchanges were closed on this day. As a
consequence, there is no entry for this day, in the sample. The rst day in the sample is a
Friday, which is inconvenient. Use the following instrucons to summarize data:
1. To simplify, we will just have a look at the rst three weeks in the sample—you can
later have a go at improving this.
close = close[:16]
dates = dates[:16]
We will build on the code from the Time for acon – dealing with dates tutorial.
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 66 ]
2. Commencing, we will nd the rst Monday in our sample data. Recall that Mondays
have the code 0 in Python. This is what we will put in the condion of a where
funcon. Then, we will need to extract the rst element that has index 0. The result
would be a muldimensional array. Flaen that with the ravel funcon.
# get first Monday
first_monday = np.ravel(np.where(dates == 0))[0]
print "The first Monday index is", first_monday
This will print the following output:
The first Monday index is 1
3. The next logical step is to nd the Friday before last Friday in the sample. The
logic is similar to the one for nding the rst Monday, and the code for Friday is 4.
Addionally, we are looking for the second-to-last element with index 2.
# get last Friday
last_friday = np.ravel(np.where(dates == 4))[-2]
print "The last Friday index is", last_friday
This will give us the following output:
The last Friday index is 15
Next, create an array with the indices of all the days in the three weeks:
weeks_indices = np.arange(first_monday, last_friday + 1)
print "Weeks indices initial", weeks_indices
4. Split the array in pieces of size 5 with the split funcon.
weeks_indices = np.split(weeks_indices, 5)
print "Weeks indices after split", weeks_indices
It splits the array, as follows:
Weeks indices after split [array([1, 2, 3, 4, 5]), array([ 6, 7,
8, 9, 10]), array([11, 12, 13, 14, 15])]
5. In NumPy, dimensions are called axes. Now, we will get fancy with the apply_
along_axis funcon. This funcon calls another funcon, which we will provide,
to operate on each of the elements of an array. Currently, we have an array with
three elements. Each array item corresponds to one week in our sample and
contains indices of the corresponding items. Call the apply_along_axis funcon
by supplying the name of our funcon, called summarize, that we will dene
shortly. Further specify the axis or dimension number (such as 1), the array to
operate on, and a variable number of arguments for the summarize funcon, if any.
weeksummary = np.apply_along_axis(summarize, 1, weeks_indices,
open, high, low, close)
print "Week summary", weeksummary
www.it-ebooks.info
Chapter 3
[ 67 ]
6. Write the summarize funcon. The summarize funcon returns, for each week,
a tuple that holds the open, high, low, and close prices for the week, similarly to
end-of-day data.
def summarize(a, o, h, l, c):
monday_open = o[a[0]]
week_high = np.max( np.take(h, a) )
week_low = np.min( np.take(l, a) )
friday_close = c[a[-1]]
return("APPL", monday_open, week_high, week_low, friday_close)
Noce that we used the take funcon to get the actual values from indices.
Calculang the high and low values of the week was easily done with the max and
min funcons. open for the week is the open for the rst day in the week—Monday.
Likewise, close is the close for the last day of the week—Friday.
Week summary [['APPL' '335.8' '346.7' '334.3' '346.5']
['APPL' '347.89' '360.0' '347.64' '356.85']
['APPL' '356.79' '364.9' '349.52' '350.56']]
7. Store the data in a le with the NumPy savetxt funcon.
np.savetxt("weeksummary.csv", weeksummary, delimiter=",",
fmt="%s")
As you can see, we specify a lename, the array we want to store, a delimiter
(in this case a comma), and the format we want to store oang point numbers in.
The format string starts with a percent sign. Second is an oponal ag. The - ag
means le jusfy, 0 means le pad with zeroes, + means precede with + or -.
Third is an oponal width. The width indicates the minimum number of characters.
Fourth, a dot is followed by a number linked to precision. Finally, there comes a
character specier; in our example, the character specier is a string.
Character code Description
ccharacter
d or isigned decimal integer
e or Escientific notation with e or E
fdecimal floating point
g or Guse the shorter of e, E, or f
osigned octal
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 68 ]
Character code Description
sstring of characters
uunsigned decimal integer
x or Xunsigned hexadecimal integer
View the generated le in your favorite editor or type in the following commands
in the command line:
cat weeksummary.csv
APPL,335.8,346.7,334.3,346.5
APPL,347.89,360.0,347.64,356.85
APPL,356.79,364.9,349.52,350.56
What just happened?
We did something that is not even possible in some programming languages. We dened a
funcon and passed it as an argument to the apply_along_axis funcon. Arguments for the
summarize funcon were neatly passed by apply_along_axis (see weeksummary.py).
import numpy as np
from datetime import datetime
# Monday 0
# Tuesday 1
# Wednesday 2
# Thursday 3
# Friday 4
# Saturday 5
# Sunday 6
def datestr2num(s):
return datetime.strptime(s, "%d-%m-%Y").date().weekday()
dates, open, high, low, close=np.loadtxt('data.csv', delimiter=',',
usecols=(1, 3, 4, 5, 6), converters={1: datestr2num}, unpack=True)
close = close[:16]
dates = dates[:16]
# get first Monday
first_monday = np.ravel(np.where(dates == 0))[0]
print "The first Monday index is", first_monday
# get last Friday
www.it-ebooks.info
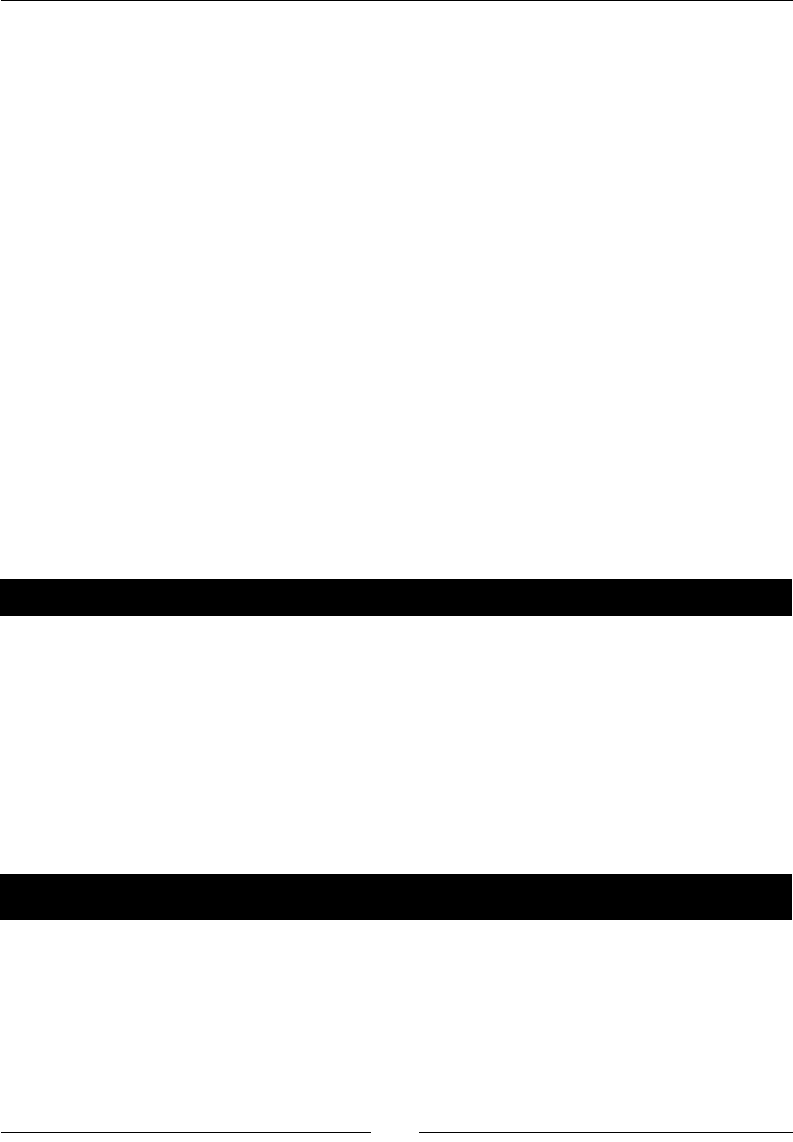
Chapter 3
[ 69 ]
last_friday = np.ravel(np.where(dates == 4))[-1]
print "The last Friday index is", last_friday
weeks_indices = np.arange(first_monday, last_friday + 1)
print "Weeks indices initial", weeks_indices
weeks_indices = np.split(weeks_indices, 3)
print "Weeks indices after split", weeks_indices
def summarize(a, o, h, l, c):
monday_open = o[a[0]]
week_high = np.max( np.take(h, a) )
week_low = np.min( np.take(l, a) )
friday_close = c[a[-1]]
return("APPL", monday_open, week_high, week_low, friday_close)
weeksummary = np.apply_along_axis(summarize, 1, weeks_indices, open,
high, low, close)
print "Week summary", weeksummary
np.savetxt("weeksummary.csv", weeksummary, delimiter=",", fmt="%s")
Have a go hero – improving the code
Change the code to deal with a holiday. Time the code to see how big the speedup due to
apply_along_axis is.
Average true range
The average true range (ATR) is a technical indicator that measures volality of stock prices.
The ATR calculaon is not important further but will serve as an example of several NumPy
funcons, including the maximum funcon.
Time for action – calculating the average true range
To calculate the average true range, perform the following steps:
1. The ATR is based on the low and high price of N days, usually the last 20 days.
N = int(sys.argv[1])
h = h[-N:]
l = l[-N:]
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 70 ]
2. We also need to know the close price of the previous day.
previousclose = c[-N -1: -1]
For each day, we calculate the following:
h – l: The daily range (the difference between high and low price)
h – previousclose: The difference between high price and
previous close
previousclose – l: The difference between the previous close and the
low price
3. The max funcon returns the maximum of an array. Based on those three values,
we calculate the so-called true range, which is the maximum of these values. We are
now interested in the element-wise maxima across arrays—meaning the maxima of
the rst elements in the arrays, the second elements in the arrays, and so on. Use
the NumPy maximum funcon instead of the max funcon for this purpose.
truerange = np.maximum(h - l, h - previousclose, previousclose -
l)
4. Create an atr array of size N and inialize its values to 0.
atr = np.zeros(N)
5. The rst value of the array is just the average of the truerange array.
atr[0] = np.mean(truerange)
Calculate the other values with the following formula:
Here, PATR is the previous day's ATR; TR is the true range.
for i in range(1, N):
atr[i] = (N - 1) * atr[i - 1] + truerange[i]
atr[i] /= N
What just happened?
We formed three arrays, one for each of the three ranges—daily range, the gap between the
high of today and the close of yesterday, and the gap between the close of yesterday and the
low of today. This tells us how much the stock price moved and, therefore, how volale it is.
The algorithm requires us to nd the maximum value for each day. The max funcon that we
used before can give us the maximum value within an array, but that is not what we want
www.it-ebooks.info
Chapter 3
[ 71 ]
here. We need the maximum value across arrays, so we want the maximum value of the rst
elements in the three arrays, the second elements, and so on. In this Time for acon tutorial,
we saw that the maximum funcon can do this. Aer that, we computed a moving average of
the true range values (see atr.py).
import numpy as np
import sys
h, l, c = np.loadtxt('data.csv', delimiter=',', usecols=(4, 5, 6),
unpack=True)
N = int(sys.argv[1])
h = h[-N:]
l = l[-N:]
print "len(h)", len(h), "len(l)", len(l)
print "Close", c
previousclose = c[-N -1: -1]
print "len(previousclose)", len(previousclose)
print "Previous close", previousclose
truerange = np.maximum(h - l, h - previousclose, previousclose - l)
print "True range", truerange
atr = np.zeros(N)
atr[0] = np.mean(truerange)
for i in range(1, N):
atr[i] = (N - 1) * atr[i - 1] + truerange[i]
atr[i] /= N
print "ATR", atr
In the following tutorials, we will learn beer ways to calculate moving averages.
Have a go hero – taking the minimum function for a spin
Besides the maximum funcon, there is a minimum funcon. You can probably guess what it
does. Make a small script or start an interacve session in IPython to prove your assumpons.
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 72 ]
Simple moving average
The simple moving average is commonly used to analyze me-series data. To calculate it,
we dene a moving window of N periods, N days in our case. We move this window along
the data and calculate the mean of the values inside the window.
Time for action – computing the simple moving average
The moving average is easy enough to compute with a few loops and the mean funcon,
but NumPy has a beer alternave—the convolve funcon. The simple moving average is,
aer all, nothing more than a convoluon with equal weights or, if you like, unweighted.
Convoluon is a mathemacal operaon on two funcons dened as the
integral of the product of the two funcons aer one of the funcons is
reversed and shied.
Use the following steps to compute the simple moving average:
1. Use the ones funcon to create an array of size N and elements inialized to 1;
then, divide the array by N to give us the weights, as follows:
N = int(sys.argv[1])
weights = np.ones(N) / N
print "Weights", weights
For N = 5, this code gives us the following output:
Weights [ 0.2 0.2 0.2 0.2 0.2]
2. Now call the convolve funcon with the following weights:
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,),
unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]]
3. From the array returned by convolve, we extracted the data in the center of size N.
The following code makes an array of me values and plots with Matplotlib that
we will be covering in a later chapter.
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,),
unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))
plot(t, c[N-1:], lw=1.0)
plot(t, sma, lw=2.0)
show()
www.it-ebooks.info
Chapter 3
[ 73 ]
In the following chart, the smooth thick line is the 5-day simple moving average
and the jagged thin line is the close price:
What just happened?
We computed the simple moving average for the close stock price. Truly, great riches are
within your reach. It turns out that the simple moving average is just a signal processing
technique—a convoluon with weights 1 / N, where N is the size of the moving average
window. We learned that the ones funcon can create an array with ones and the
convolve funcon calculates the convoluon of a data set with specied weights
(see sma.py).
import numpy as np
import sys
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
N = int(sys.argv[1])
weights = np.ones(N) / N
print "Weights", weights
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 74 ]
plot(t, c[N-1:], lw=1.0)
plot(t, sma, lw=2.0)
show()
Exponential moving average
The exponenal moving average is a popular alternave to the simple moving average.
This method uses exponenally decreasing weights. The weights for points in the past
decrease exponenally but never reach zero. We will learn about the exp and linspace
funcons while calculang the weights.
Time for action – calculating the exponential moving average
Given an array, the exp funcon calculates the exponenal of each array element. For
example, look at the following code:
x = np.arange(5)
print "Exp", np.exp(x)
It gives the following output:
Exp [ 1. 2.71828183 7.3890561 20.08553692 54.59815003]
The linspace funcon takes, as parameters, a start and a stop and oponally an array size.
It returns an array of evenly spaced numbers. The following is an example:
print "Linspace", np.linspace(-1, 0, 5)
This will give us the following output:
Linspace [-1. -0.75 -0.5 -0.25 0. ]
Let's calculate the exponenal moving average for our data:
1. Now, back to the weights—calculate them with exp and linspace.
N = int(sys.argv[1])
weights = np.exp(np.linspace(-1., 0., N))
2. Normalize the weights. The ndarray object has a sum method that we will use.
weights /= weights.sum()
print "Weights", weights
For N = 5, we get the following weights:
Weights [ 0.11405072 0.14644403 0.18803785 0.24144538
0.31002201]
www.it-ebooks.info
Chapter 3
[ 75 ]
3. Aer that, it's easy going—we just use the convolve funcon that we learned
about in the simple moving average tutorial. We will also plot the results.
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,),
unpack=True)
ema = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))
plot(t, c[N-1:], lw=1.0)
plot(t, ema, lw=2.0)
show()
That gives this nice chart where, again, the close price is the thin jagged line and the
exponenal moving average is the smooth thick line:
What just happened?
We calculated the exponenal moving average of the close price. First, we computed
exponenally decreasing weights with the exp and linspace funcons. linspace gave
us an array with evenly spaced elements, and then, we calculated the exponenal for these
numbers. We called the ndarray sum method in order to normalize the weights. Aer that,
we applied the convolve trick that we learned in the simple moving average tutorial
(see ema.py).
import numpy as np
import sys
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
x = np.arange(5)
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 76 ]
print "Exp", np.exp(x)
print "Linspace", np.linspace(-1, 0, 5)
N = int(sys.argv[1])
weights = np.exp(np.linspace(-1., 0., N))
weights /= weights.sum()
print "Weights", weights
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
ema = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))
plot(t, c[N-1:], lw=1.0)
plot(t, ema, lw=2.0)
show()
Bollinger bands
Bollinger bands are yet another technical indicator. Yes, there are thousands of them.
This one is named aer its inventor and indicates a range for the price of a nancial security.
It consists of three parts, as follows:
A simple moving average
An upper band of two standard deviaons above this moving average—the standard
deviaon is derived from the same data with which the moving average is calculated
A lower band of two standard deviaons below the moving average
Time for action – enveloping with Bollinger bands
We already know how to calculate the simple moving average. So, if you need to, please
review the Time for acon – compung the simple moving average secon in this chapter.
This example will introduce the NumPy fill funcon. The fill funcon sets the value of
an array to a scalar value. The funcon should be faster than array.flat = scalar or
you have to set the values of the array one by one in a loop. Perform the following steps to
envelope with Bollinger bands:
www.it-ebooks.info
Chapter 3
[ 77 ]
1. Starng with an array called sma that contains the moving average values, we will
loop through all the data sets corresponding to those values. Aer forming the
data set, calculate the standard deviaon. Note that it is necessary, at a certain
point, to calculate the dierence between each data point and the corresponding
average value. If we did not have NumPy, we would loop through these points and
subtract each of the values one by one from the corresponding average. However,
the NumPy fill funcon allows us to construct an array having elements set to the
same value. This enables us to save on one loop and subtract arrays in one go.
deviation = []
C = len(c)
for i in range(N - 1, C):
if i + N < C:
dev = c[i: i + N]
else:
dev = c[-N:]
averages = np.zeros(N)
averages.fill(sma[i - N - 1])
dev = dev - averages
dev = dev ** 2
dev = np.sqrt(np.mean(dev)))
deviation.append(dev)
deviation = 2 * np.array(deviation)
upperBB = sma + deviation
lowerBB = sma – deviation
2. To plot the bands, we will use the following code (don't worry about it now;
we will see how this works in Chapter 9, Plong with Matplotlib):
t = numpy.arange(N - 1, C)
plot(t, c_slice, lw=1.0)
plot(t, sma, lw=2.0)
plot(t, upperBB, lw=3.0)
plot(t, lowerBB, lw=4.0)
show()
www.it-ebooks.info
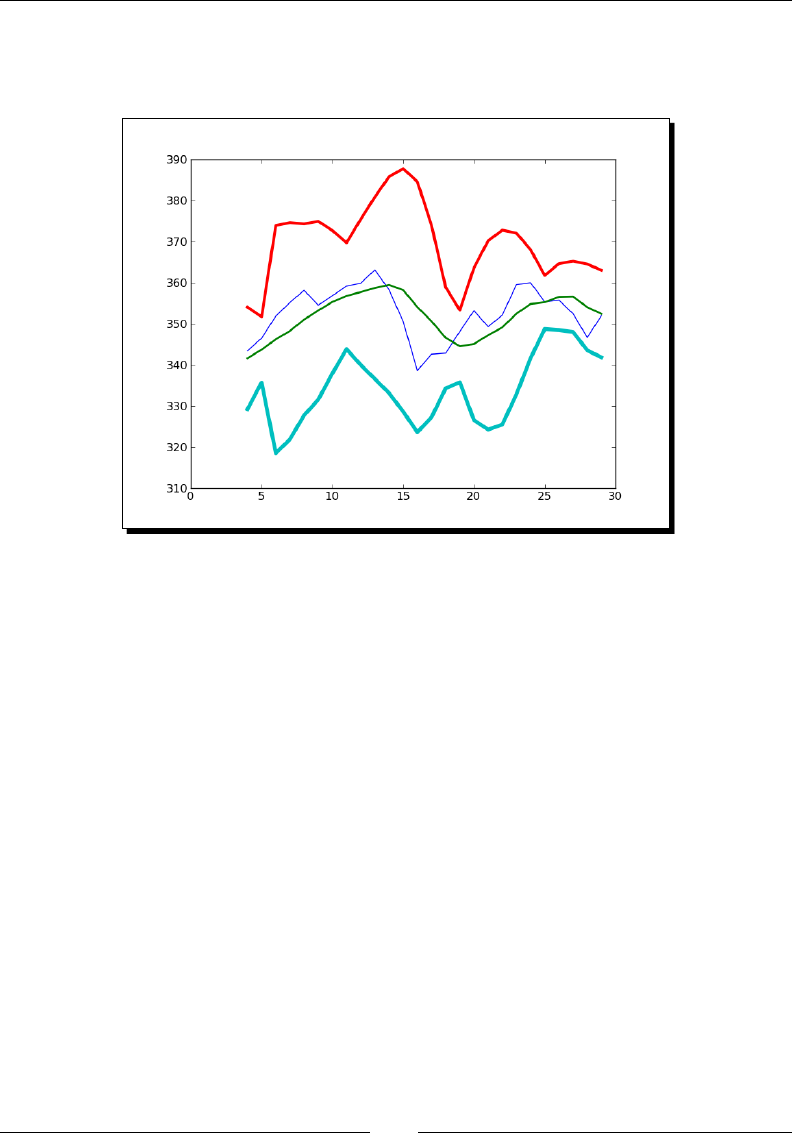
Get in Terms with Commonly Used Funcons
[ 78 ]
The following is a chart of the Bollinger bands for our data. The jagged thin line in the
middle represents the close price and the slightly thicker, smoother line crossing it is the
moving average:
What just happened?
We worked out the Bollinger bands that envelope the close price of our data.
More importantly, we got acquainted with the NumPy fill funcon. This funcon
lls an array with a scalar value. This is the only parameter of the fill funcon
(see bollingerbands.py).
import numpy as np
import sys
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
N = int(sys.argv[1])
weights = np.ones(N) / N
print "Weights", weights
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]
deviation = []
C = len(c)
www.it-ebooks.info
Chapter 3
[ 79 ]
for i in range(N - 1, C):
if i + N < C:
dev = c[i: i + N]
else:
dev = c[-N:]
averages = np.zeros(N)
averages.fill(sma[i - N - 1])
dev = dev - averages
dev = dev ** 2
dev = np.sqrt(np.mean(dev))
deviation.append(dev)
deviation = 2 * np.array(deviation)
print len(deviation), len(sma)
upperBB = sma + deviation
lowerBB = sma - deviation
c_slice = c[N-1:]
between_bands = np.where((c_slice < upperBB) & (c_slice > lowerBB))
print lowerBB[between_bands]
print c[between_bands]
print upperBB[between_bands]
between_bands = len(np.ravel(between_bands))
print "Ratio between bands", float(between_bands)/len(c_slice)
t = np.arange(N - 1, C)
plot(t, c_slice, lw=1.0)
plot(t, sma, lw=2.0)
plot(t, upperBB, lw=3.0)
plot(t, lowerBB, lw=4.0)
show()
Have a go hero – switching to exponential moving average
It is customary to choose the simple moving average to center the Bollinger band on.
The second most popular choice is the exponenal moving average, so try that as an
exercise. You can nd a suitable example in this chapter, if you need pointers.
Check that the fill funcon is faster or is as fast as array.flat = scalar, or set the
value in a loop.
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 80 ]
Linear model
Many phenomena in science have a related linear relaonship model. The NumPy linalg
package deals with linear algebra computaons. We will begin with the assumpon that a
price value can be derived from N previous prices based on a linear relaonship.
Time for action – predicting price with a linear model
Keeping an open mind, let's assume that we can express a stock price as a linear combinaon
of previous values, that is, a sum of those values mulplied by certain coecients we need
to determine. In linear algebra terms, this boils down to nding a least squares soluon.
This recipe goes as follows.
1. First, form a vector bbx containing N price values.
bbx = c[-N:]
bbx = b[::-1]
print "bbx", x
The result is as follows:
bbx [ 351.99 346.67 352.47 355.76 355.36]
2. Second, pre-inialize the matrix A to be N x N and containing zeroes.
A = np.zeros((N, N), float)
print "Zeros N by N", A
Zeros N by N [[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
3. Third, ll the matrix A with N preceding price values for each value in bbx.
for i in range(N):
A[i, ] = c[-N - 1 - i: - 1 - i]
print "A", A
Now, A looks like this:
A [[ 360. 355.36 355.76 352.47 346.67]
[ 359.56 360. 355.36 355.76 352.47]
[ 352.12 359.56 360. 355.36 355.76]
[ 349.31 352.12 359.56 360. 355.36]
[ 353.21 349.31 352.12 359.56 360. ]]
www.it-ebooks.info
Chapter 3
[ 81 ]
4. The objecve is to determine the coecients that sasfy our linear model, by
solving the least squares problem. Employ the lstsq funcon of the NumPy
linalg package to do that.
(x, residuals, rank, s) = np.linalg.lstsq(A, b)
print x, residuals, rank, s
The result is as follows:
[ 0.78111069 -1.44411737 1.63563225 -0.89905126 0.92009049]
[] 5 [ 1.77736601e+03 1.49622969e+01 8.75528492e+00
5.15099261e+00 1.75199608e+00]
The tuple returned contains the coecients xxb that we were aer, an array
comprising of residuals, the rank of matrix A, and the singular values of A.
5. Once we have the coecients of our linear model, we can predict the next price
value. Compute the dot product (with the NumPy dot funcon) of the coecients
and the last known N prices.
print numpy.dot(b, x)
The dot product is the linear combinaon of the coecients xxb and the prices x.
As a result, we get the following:
357.939161015
I looked it up; the actual close price of the next day was 353.56. So, our esmate
with N = 5 was not that far o.
What just happened?
We predicted tomorrow's stock price today. If this works in pracce, we could rere
early! See, this book was a good investment aer all! We designed a linear model for the
predicons. The nancial problem was reduced to a linear algebraic one. NumPy's linalg
package has a praccal lstsq funcon that helped us with the task at hand—esmang
the coecients of a linear model. Aer obtaining a soluon, we plugged the numbers in
the NumPy dot funcon that presented us an esmate through linear regression (see
linearmodel.py).
import numpy as np
import sys
N = int(sys.argv[1])
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 82 ]
b = c[-N:]
b = b[::-1]
print "b", b
A = np.zeros((N, N), float)
print "Zeros N by N", A
for i in range(N):
A[i, ] = c[-N - 1 - i: - 1 - i]
print "A", A
(x, residuals, rank, s) = np.linalg.lstsq(A, b)
print x, residuals, rank, s
print np.dot(b, x)
Trend lines
A trend line is a line among a number of so-called pivot points on a stock chart. As the name
suggests, the line's trend portrays the trend of the price development. In the past, traders
drew trend lines on paper; but, nowadays, we can let a computer draw it for us. In this
tutorial, we shall resort to a very simple approach that is probably not very useful in real life,
but it should clarify the principle well.
Time for action – drawing trend lines
Perform the following steps to draw trend lines:
1. First, we need to determine the pivot points. We shall pretend they are equal to the
arithmec mean of the high, low, and close price.
h, l, c = np.loadtxt('data.csv', delimiter=',', usecols=(4, 5,
6), unpack=True)
pivots = (h + l + c) / 3
print "Pivots", pivots
From the pivots, we can deduce the so-called resistance and support levels. The
support level is the lowest level at which the price rebounds. The resistance level is
the highest level at which the price bounces back. These are not natural phenomena;
mind you, they are merely esmates. Based on these esmates, it is possible to draw
www.it-ebooks.info
Chapter 3
[ 83 ]
support and resistance trend lines. We will dene the daily spread to be the dierence
between the high and low price.
2. Dene a funcon to t line to data to a line where y = at + b. The funcon
should return a and b. This is another opportunity to apply the lstsq funcon of
the NumPy linalg package. Rewrite the line equaon to y = Ax, where A = [t
1] and x = [a b]. Form A with the NumPy ones and vstack funcons.
def fit_line(t, y):
A = np.vstack([t, np.ones_like(t)])]).T
return np.linalg.lstsq(A, y)[0]
3. Assuming that support levels are one daily spread below the pivots, and that
resistance levels are one daily spread above the pivots, t the support and
resistance trend lines.
t = np.arange(len(c))
sa, sb = fit_line(t, pivots - (h - l))
ra, rb = fit_line(t, pivots + (h - l))
support = sa * t + sb
resistance = ra * t + rb
4. At this juncture, we have all the necessary informaon to draw the trend lines,
however, it is wise to check how many points fall between the support and
resistance levels. Obviously, if only a small percentage of the data is between the
trend lines, this setup is of no use to us. Make up a condion for points between
the bands and select the where funcon based on that condion.
condition = (c > support) & (c < resistance)
print "Condition", condition
between_bands = np.where(condition)
The following are the condion values:
Condition [False False True True True True True False False
True False False
False False False True False False False True True True True
False False True True True False True]
Double-check the values:
print support[between_bands]
print c[between_bands]
print resistance[between_bands]
The array returned by the where funcon has rank 2, so call the ravel funcon
before calling the len funcon.
between_bands = len(np.ravel(between_bands))
print "Number points between bands", between_bands
print "Ratio between bands", float(between_bands)/len(c)
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 84 ]
You will get the following result:
Number points between bands 15
Ratio between bands 0.5
As an extra bonus, we gained a predicve model. Extrapolate the next day resistance
and support levels.
print "Tomorrows support", sa * (t[-1] + 1) + sb
print "Tomorrows resistance", ra * (t[-1] + 1) + rb
This results in the following:
Tomorrows support 349.389157088
Tomorrows resistance 360.749340996
Another approach to gure out how many points are between the support and
resistance esmates is to use [] and intersect1d. Dene selecon criteria in the
[] operator and intersect the results with the intersect1d funcon.
a1 = c[c > support]
a2 = c[c < resistance]
print "Number of points between bands 2nd approach" ,len(np.
intersect1d(a1, a2))
Not surprisingly, we get the following:
Number of points between bands 2nd approach 15
5. Once more, we will plot the results, as follows:
plot(t, c)
plot(t, support)
plot(t, resistance)
show()
www.it-ebooks.info
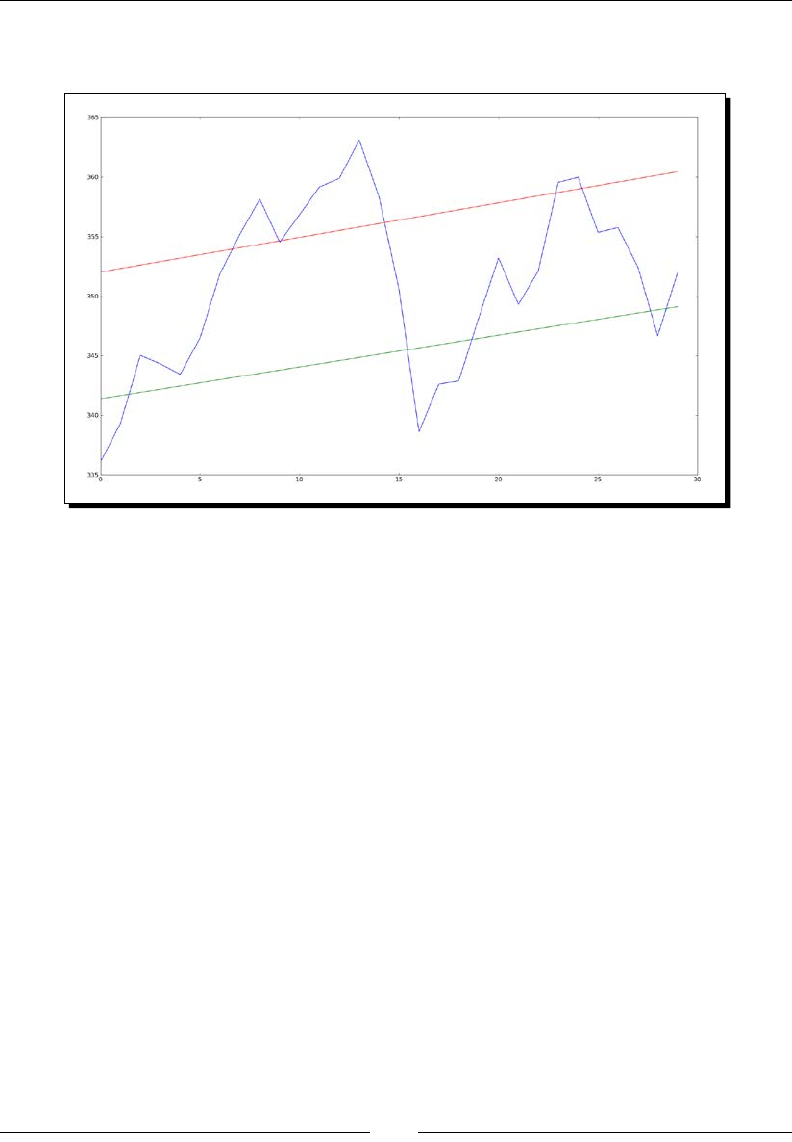
Chapter 3
[ 85 ]
We will get the following plot in which we have the price data and the
corresponding support and resistance lines:
What just happened?
We drew trend lines without having to mess around with rulers, pencils, and paper charts.
We dened a funcon that can t data to a line with the NumPy vstack, ones, and lstsq
funcons. We t the data in order to dene support and resistance trend lines. Then we
gured out how many points are within the support and resistance range. We did this using
two separate methods that produced the same result.
The rst method used the where funcon with a Boolean condion. The second method
made use of the [] operator and the intersect1d funcon. The intersect1d funcon
returns an array of common elements from two arrays (see trendline.py).
import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
def fit_line(t, y):
A = np.vstack([t, np.ones_like(t)]).T
return np.linalg.lstsq(A, y)[0]
h, l, c = np.loadtxt('data.csv', delimiter=',', usecols=(4, 5, 6),
unpack=True)
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 86 ]
pivots = (h + l + c) / 3
print "Pivots", pivots
t = np.arange(len(c))
sa, sb = fit_line(t, pivots - (h - l))
ra, rb = fit_line(t, pivots + (h - l))
support = sa * t + sb
resistance = ra * t + rb
condition = (c > support) & (c < resistance)
print "Condition", condition
between_bands = np.where(condition)
print support[between_bands]
print c[between_bands]
print resistance[between_bands]
between_bands = len(np.ravel(between_bands))
print "Number points between bands", between_bands
print "Ratio between bands", float(between_bands)/len(c)
print "Tomorrows support", sa * (t[-1] + 1) + sb
print "Tomorrows resistance", ra * (t[-1] + 1) + rb
a1 = c[c > support]
a2 = c[c < resistance]
print "Number of points between bands 2nd approach" ,len(np.
intersect1d(a1, a2))
plot(t, c)
plot(t, support)
plot(t, resistance)
show()
Methods of ndarray
The NumPy ndarray class has a lot of methods that work on the array. Most of the me,
these methods return an array. You may have noced that many of the funcons that are a
part of the NumPy library have a counterpart with the same name and funconality in the
ndarray object. This is mostly due to the historical development of NumPy.
The list of ndarray methods is prey long, so we cannot cover them all. The var, sum, std,
argmax, argmin, and mean funcons that we saw earlier are also ndarray methods.
To clip and compress arrays, look at the following secon.
www.it-ebooks.info
Chapter 3
[ 87 ]
Time for action – clipping and compressing arrays
Here are a few examples of ndarray methods. Perform the following steps to clip and
compress arrays:
1. The clip method returns a clipped array, so that all values above a maximum value
are set to the maximum and values below a minimum are set to the minimum value.
Clip an array with values 0 to 4 to 1 and 2.
a = np.arange(5)
print "a =", a
print "Clipped", a.clip(1, 2)
This gives the following output:
a = [0 1 2 3 4]
Clipped [1 1 2 2 2]
2. The ndarray compress method returns an array based on a condion. For
instance, look at the following code:
a = np.arange(4)
print a
print "Compressed", a.compress(a > 2)
This returns the following output:
[0 1 2 3]
Compressed [3]
What just happened?
We created an array with values 0 to 3 and selected the last element with the compress
funcon based on the condion a > 2.
Factorial
Many programming books have an example of calculang the factorial. We should not break
with this tradion.
www.it-ebooks.info
Get in Terms with Commonly Used Funcons
[ 88 ]
Time for action – calculating the factorial
The ndarray class has the prod method, which computes the product of the elements in an
array. Perform the following steps to calculate the factorial:
1. Calculate the factorial of eight. To do that, generate an array with values 1 to 8 and
call the prod funcon on it.
b = np.arange(1, 9)
print "b =", b
print "Factorial", b.prod()
Check the result with your pocket calculator.
b = [1 2 3 4 5 6 7 8]
Factorial 40320
This is nice, but what if we want to know all the factorials from 1 to 8?
2. No problem! Call the cumprod method, which computes the cumulave product
of an array.
print "Factorials", b.cumprod()
It's pocket calculator me again.
Factorials [ 1 2 6 24 120 720 5040 40320]
What just happened?
We used the prod and cumprod funcons to calculate factorials
(see ndarraymethods.py).
import numpy as np
a = np.arange(5)
print "a =", a
print "Clipped", a.clip(1, 2)
a = np.arange(4)
print a
print "Compressed", a.compress(a > 2)
b = np.arange(1, 9)
print "b =", b
print "Factorial", b.prod()
print "Factorials", b.cumprod()
www.it-ebooks.info
Chapter 3
[ 89 ]
Summary
This chapter informed us about a great number of common NumPy funcons. We read a le
with loadtxt and wrote to a le with savetxt. We made an identy matrix with the eye
funcon. We read a CSV le containing stock quotes with the loadtxt funcon. The NumPy
average and mean funcons allow one to calculate the weighted average and arithmec
mean of a data set.
A few common stascs funcons were also menoned – rst, the min and max funcons
that we used to determine the range of the stock prices; second, the median funcon
that gives the median of a data set; and nally, the std and var funcons that return the
standard deviaon and variance of a set of numbers.
We calculated the simple stock returns with the diff funcon that returns back the
dierences between sequenal elements. The log funcon computes the natural
logarithms of array elements.
By default, loadtxt tries to convert all data into oats. The loadtxt funcon has a special
parameter for this purpose. The parameter is called converters and is a diconary that
links columns with the so-called converter funcons.
We dened a funcon and passed it as an argument to the apply_along_axis
funcon. We implemented an algorithm with the requirement to nd the maximum
value across arrays.
We learned that the ones funcon can create an array with ones and the convolve
funcon calculates the convoluon of a data set with the specied weights.
We computed exponenally decreasing weights with the exp and linspace funcons.
linspace gave us an array with evenly spaced elements, and then we calculated the
exponenal for these numbers. We called the ndarray sum method in order to normalize
the weights.
We got acquainted with the NumPy fill funcon. This funcon lls an array with a scalar
value, the only parameter of the fill funcon.
Aer this tour through the common NumPy funcons, we will connue covering
convenience NumPy funcons such as polyfit, sign, and piecewise in the next chapter.
www.it-ebooks.info
www.it-ebooks.info
Convenience Functions for
Your Convenience
As we have noticed, NumPy has a great number of functions. Many of these
functions are there just for your convenience. Knowing these functions will
greatly increase your productivity. This includes functions that select certain
parts of your arrays (for instance, based on a Boolean condition) or manipulate
polynomials. An example of computing correlation of stock returns is provided
to give you a taste of data analysis in NumPy.
In this chapter, we shall cover the following topics:
Data selecon and extracon
Simple data analysis
Examples of correlaon of returns
Polynomials
Linear algebra funcons
In the previous chapter, we had one single data le to play around with. Things have
signicantly improved in this chapter—we now have two data les. Let's go ahead and
explore the data with NumPy.
4
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 92 ]
Correlation
Have you noced that the stock price of some companies is closely followed by another one,
usually a rival in the same sector? The theorecal explanaon is that, because these two
companies are in the same type of business, they share the same challenges, require the
same materials and resources, and compete for the same type of customers.
You could think of many possible pairs, but you would want to check whether a real
relaonship exists. One way is to have a look at the correlaon of the stock returns of
both stocks. A high correlaon implies a relaonship of some sort. It is not proof though,
especially if you don't use sucient data.
Time for action – trading correlated pairs
For this tutorial, we will use two sample data sets, containing the bare minimum of
end-of-day price data. The rst company is BHP Billiton (BHP), which is acve in the
mining of petroleum, metals, and diamonds. The second is Vale (VALE), which is also
a metals and mining company. So there is some overlap, albeit not one hundred percent.
For trading correlated pairs, follow these steps:
1. First, load the data, specically the close price of the two securies, from the CSV
les in the example code directory of this chapter and calculate the returns. If you
don't remember how to do it, there are plenty of examples in the previous chapter.
2. Covariance tells us how two variables vary together; it is nothing more than
unnormalized correlaon. Compute the covariance matrix from the returns with the
cov funcon (it's not strictly necessary to do this, but it will allow us to demonstrate
a few matrix operaons):
covariance = np.cov(bhp_returns, vale_returns)
print "Covariance", covariance
The covariance matrix is as follows:
Covariance [[ 0.00028179 0.00019766]
[ 0.00019766 0.00030123]]
3. View the values on the diagonal with the diagonal funcon:
print "Covariance diagonal", covariance.diagonal()
The diagonal values of the covariance matrix are as follows:
Covariance diagonal [ 0.00028179 0.00030123]
www.it-ebooks.info
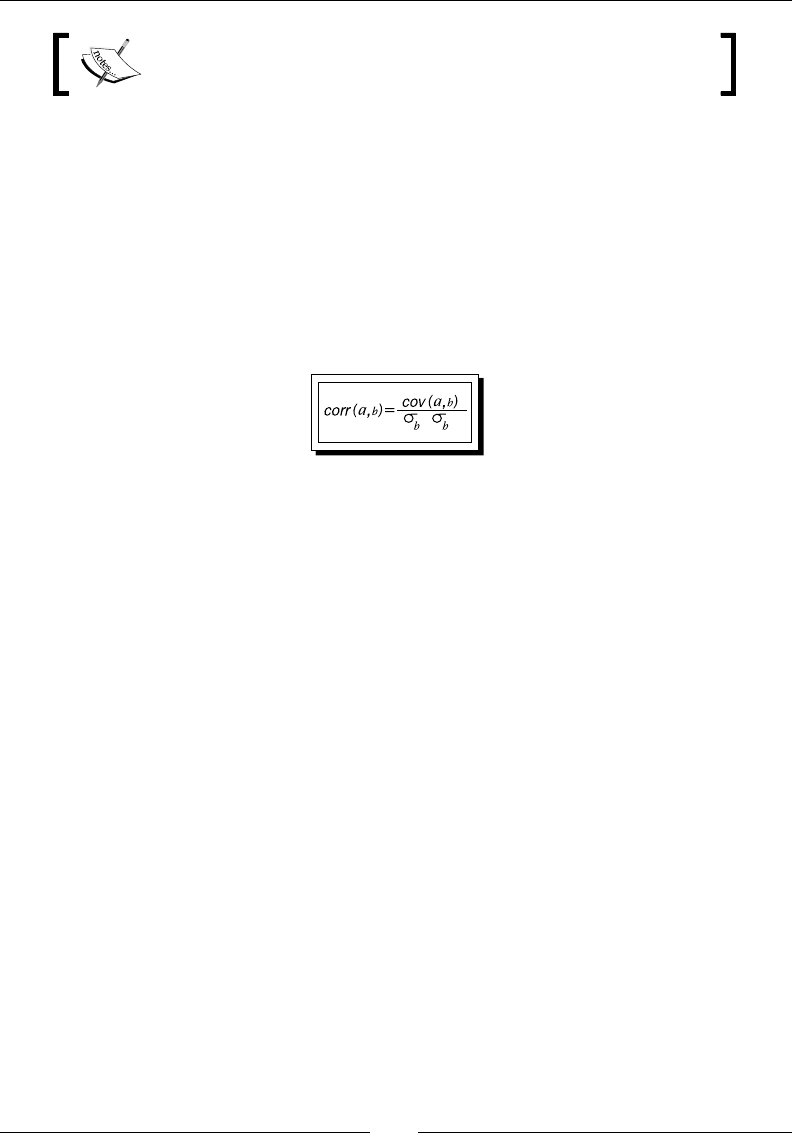
Chapter 4
[ 93 ]
Notice that the values on the diagonal are not equal to each other,
this is different from the correlation matrix.
4. Compute the trace, the sum of the diagonal values, with the trace funcon:
print "Covariance trace", covariance.trace()
The trace values of the covariance matrix are as follows:
Covariance trace 0.00058302354992
5. The correlaon of two vectors is dened as the covariance, divided by the product
of the respecve standard deviaons of the vectors. The equaon for vectors a
and b is:
Try it out:
print covariance/ (bhp_returns.std() * vale_returns.std())
The correlaon matrix is as follows:
[[ 1.00173366 0.70264666]
[ 0.70264666 1.0708476 ]]
6. We will measure the correlaon of our pair with the correlaon coecient. The
correlaon coecient takes values between -1 to 1. The correlaon of a set of
values with itself is 1 by denion. This would be the ideal value; however, we will
be also happy with a slightly lower value. Calculate the correlaon coecient
(or, more accurately, the correlaon matrix) with the corrcoef funcon:
print "Correlation coefficient", np.corrcoef(bhp_returns,
vale_returns)
The coecients are as follows:
[[ 1. 0.67841747]
[ 0.67841747 1. ]]
The values on the diagonal are just the correlaons of the BHP and VALE with
themselves and are, therefore, equal to 1. In all probability, no real calculaon takes
place. The other two values are equal to each other since correlaon is symmetrical,
meaning that the correlaon of BHP with VALE is equal to the correlaon of VALE
with BHP. It seems that the correlaon is not that strong.
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 94 ]
7. Another important point is whether the two stocks under consideraon are in sync
or not. Two stocks are considered out of sync if their dierence is two standard
deviaons from the mean of the dierences.
If they are out of sync, we could iniate a trade, hoping that they eventually will
get back in sync again. Compute the dierence between the close prices of the two
securies to check the synchronizaon:
difference = bhp - vale
Check whether the last dierence in price is out of sync; see the following code:
avg = np.mean(difference)
dev = np.std(difference)
print "Out of sync", np.abs(difference[-1] – avg) > 2 * dev
Unfortunately, we cannot trade yet:
Out of sync False
8. Plong requires Matplotlib; this will be discussed in Chapter 9, Plong with
Matplotlib. Plong can be done as follows:
t = np.arange(len(bhp_returns))
plot(t, bhp_returns, lw=1)
plot(t, vale_returns, lw=2)
show()
The resulng plot:
www.it-ebooks.info
Chapter 4
[ 95 ]
What just happened?
We analyzed the relaon of the closing stock prices of BHP and VALE. To be precise, we
calculated the correlaon of their stock returns. This was achieved with the corrcoef
funcon. Further, we saw how the covariance matrix can be computed, from which the
correlaon can be derived. As a bonus, a demonstraon was given of the diagonal and
trace funcons that can give us the diagonal values and the trace of a matrix, respecvely
(see correlation.py):
import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
bhp = np.loadtxt('BHP.csv', delimiter=',', usecols=(6,), unpack=True)
bhp_returns = np.diff(bhp) / bhp[ : -1]
vale = np.loadtxt('VALE.csv', delimiter=',', usecols=(6,),
unpack=True)
vale_returns = np.diff(vale) / vale[ : -1]
covariance = np.cov(bhp_returns, vale_returns)
print "Covariance", covariance
print "Covariance diagonal", covariance.diagonal()
print "Covariance trace", covariance.trace()
print covariance/ (bhp_returns.std() * vale_returns.std())
print "Correlation coefficient", np.corrcoef(bhp_returns, vale_
returns)
difference = bhp - vale
avg = np.mean(difference)
dev = np.std(difference)
print "Out of sync", np.abs(difference[-1] - avg) > 2 * dev
t = np.arange(len(bhp_returns))
plot(t, bhp_returns, lw=1)
plot(t, vale_returns, lw=2)
show()
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 96 ]
Pop quiz – calculating covariance
Q1. Which funcon returns the covariance of two arrays?
1. covariance
2. covar
3. cov
4. cvar
Polynomials
Do you like calculus? Me, I love it! One of the ideas in calculus is Taylor expansion, that is,
represenng a dierenable funcon as an innite series. In pracce, this means that any
dierenable, and therefore, connuous funcon can be esmated by a polynomial of a
high degree. The terms of the higher degree would then be assumed to be negligibly small.
Time for action – tting to polynomials
The NumPy polyfit funcon can t a set of data points to a polynomial even if the
underlying funcon is not connuous:
1. Connuing with the price data of BHP and VALE, let's look at the dierence of their
close prices and t it to a polynomial of the third power:
bhp=np.loadtxt('BHP.csv', delimiter=',', usecols=(6,),
unpack=True)
vale=np.loadtxt('VALE.csv', delimiter=',', usecols=(6,),
unpack=True)
t = np.arange(len(bhp))
poly = np.polyfit(t, bhp - vale, int(sys.argv[1]))
print "Polynomial fit", poly
The polynomial t (in this example, a cubic polynomial was chosen):
Polynomial fit [ 1.11655581e-03 -5.28581762e-02
5.80684638e-01 5.79791202e+01]
2. The numbers you see are the coecients of the polynomial. Extrapolate to the next
value with the polyval funcon and the polynomial object we got from the t:
print "Next value", np.polyval(poly, t[-1] + 1)
The next value we predict will be:
Next value 57.9743076081
www.it-ebooks.info
Chapter 4
[ 97 ]
3. Ideally, the dierence between the close prices of BHP and VALE should be as small
as possible. In an extreme case, it might be zero at some point. Find out when our
polynomial t reaches zero with the roots funcon:
print "Roots", np.roots(poly)
The roots of the polynomial are as follows:
Roots [ 35.48624287+30.62717062j 35.48624287-30.62717062j
-23.63210575 +0.j ]
4. Another thing we learned in calculus class was to nd extrema—these could be
potenal maxima or minima. Remember, from calculus, that these are the points
where the derivave of our funcon is zero. Dierenate the polynomial t with the
polyder funcon:
der = np.polyder(poly)
print "Derivative", der
The coecients of the derivave polynomial are as follows:
Derivative [ 0.00334967 -0.10571635 0.58068464]
The numbers you see are the coecients of the derivave polynomial.
5. Get the roots of the derivave and nd the extrema:
print "Extremas", np.roots(der)
The extrema that we get are:
Extremas [ 24.47820054 7.08205278]
Let's double check; compute the values of the t with polyval:
vals = np.polyval(poly, t)
6. Now, nd the maximum and minimum values with argmax and argmin:
vals = np.polyval(poly, t)
print np.argmax(vals)
print np.argmin(vals)
This gives us the following expected results. Ok, not quite the same results, but, if
we backtrack to step 1, we can see that t was dened with the arange funcon:
7
24
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 98 ]
7. Plot the data and the t it as follows:
plot(t, bhp - vale)
plot(t, vals)
show()
It results in this plot:
Obviously, the smooth line is the t and the jagged line is the underlying data. It's not that
good a t, so you might want to try a higher order polynomial.
What just happened?
We t data to a polynomial with the polyfit funcon. We learned about the polyval
funcon that computes the values of a polynomial, the roots funcon that returns the
roots of the polynomial, and the polyder funcon that gives back the derivave of a
polynomial (see polynomials.py):
import numpy as np
import sys
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
bhp=np.loadtxt('BHP.csv', delimiter=',', usecols=(6,),
unpack=True)
vale=np.loadtxt('VALE.csv', delimiter=',', usecols=(6,),
unpack=True)
www.it-ebooks.info
Chapter 4
[ 99 ]
t = np.arange(len(bhp))
poly = np.polyfit(t, bhp - vale, int(sys.argv[1]))
print "Polynomial fit", poly
print "Next value", np.polyval(poly, t[-1] + 1)
print "Roots", np.roots(poly)
der = np.polyder(poly)
print "Derivative", der
print "Extremas", np.roots(der)
vals = np.polyval(poly, t)
print np.argmax(vals)
print np.argmin(vals)
plot(t, bhp - vale)
plot(t, vals)
show()
Have a go hero – improving the t
There are a number of things you could do to improve the t. Try a dierent power as, in this
tutorial, a cubic polynomial was chosen. Consider smoothing the data before ng it. One
way you could smooth is with a moving average. Examples of simple and exponenal moving
average calculaons can be found in the previous chapter.
On-balance volume
Volume is a very important variable in invesng; it indicates how big a price move is. The
on-balance volume indicator is one of the simplest stock price indicators. It is based on the
close price of the current and previous days and the volume of the current day. For each day,
if the close price today is higher than the close price of yesterday then the value of the on-
balance volume is equal to the volume of today. On the other hand, if today's close price is
lower than yesterday's close price then the value of the on-balance volume indicator is the
dierence between the on-balance volume and the volume of today. If the close price did
not change then the value of the on-balance volume is zero.
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 100 ]
Time for action – balancing volume
In other words we need to mulply the sign of the close price with the volume. In this
tutorial, we will go over two approaches to this problem, one using the NumPy sign
funcon, and the other using the NumPy piecewise funcon.
1. Load the BHP data into a close and volume array:
c, v=np.loadtxt('BHP.csv', delimiter=',', usecols=(6, 7),
unpack=True)
Compute the absolute value changes. Calculate the change of the close price
with the diff funcon. The diff funcon computes the dierence between
two sequenal array elements and returns an array containing these dierences:
change = np.diff(c)
print "Change", change
The changes of the close price are shown as follows:
Change [ 1.92 -1.08 -1.26 0.63 -1.54 -0.28 0.25 -0.6 2.15
0.69 -1.33 1.16
1.59 -0.26 -1.29 -0.13 -2.12 -3.91 1.28 -0.57 -2.07 -2.07
2.5 1.18
-0.88 1.31 1.24 -0.59]
2. The NumPy sign funcon returns the signs for each element in an array. -1 is
returned for a negave number, 1 for a posive number, and 0, otherwise. Apply the
sign funcon to the change array:
signs = np.sign(change)
print "Signs", signs
The signs of the change array are as follows:
Signs [ 1. -1. -1. 1. -1. -1. 1. -1. 1. 1. -1. 1. 1. -1. -1.
-1. -1. -1.
-1. -1. -1. 1. 1. 1. -1. 1. 1. -1.]
Alternavely, we can calculate the signs with the piecewise funcon. The
piecewise funcon, as its name suggests, evaluates a funcon piece-by-piece. Call
the funcon with the appropriate return values and condions:
pieces = np.piecewise(change, [change < 0, change > 0], [-1,
1])
print "Pieces", pieces
www.it-ebooks.info
Chapter 4
[ 101 ]
The signs are shown again, as follows:
Pieces [ 1. -1. -1. 1. -1. -1. 1. -1. 1. 1. -1. 1. 1. -1.
-1. -1. -1. -1.
-1. -1. -1. 1. 1. 1. -1. 1. 1. -1.]
Check that the outcome is the same:
print "Arrays equal?", np.array_equal(signs, pieces)
And the outcome is as follows:
Arrays equal? True
3. The on-balance volume depends on the change of the previous close, so we cannot
calculate it for the rst day in our sample:
print "On balance volume", v[1:] * signs
The on-balance volume is as follows:
[ 2620800. -2461300. -3270900. 2650200. -4667300. -5359800.
7768400.
-4799100. 3448300. 4719800. -3898900. 3727700. 3379400.
-2463900.
-3590900. -3805000. -3271700. -5507800. 2996800. -3434800.
-5008300.
-7809799. 3947100. 3809700. 3098200. -3500200. 4285600.
3918800.
-3632200.]
What just happened?
We computed the on-balance volume that depends on the change of the closing price.
Using the NumPy sign and piecewise funcons, we went over two dierent methods to
determine the sign of the change (see obv.py):
import numpy as np
c, v=np.loadtxt('BHP.csv', delimiter=',', usecols=(6, 7), unpack=True)
change = np.diff(c)
print "Change", change
signs = np.sign(change)
print "Signs", signs
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 102 ]
pieces = np.piecewise(change, [change < 0, change > 0], [-1, 1])
print "Pieces", pieces
print "Arrays equal?", np.array_equal(signs, pieces)
print "On balance volume", v[1:] * signs
Simulation
Oen, you would want to try something out. Play around, experiment, but preferably
without blowing things up or geng dirty. NumPy is perfect for experimentaon. We will use
NumPy to simulate a trading day, without actually losing money. Many people like to buy on
the dip or, in other words, wait for the price of stocks to drop before buying. A variant of that
is to wait for the price to drop a small percentage, say, 0.1 percent below the opening price
of the day.
Time for action – avoiding loops with vectorize
The vectorize funcon is a yet another trick to reduce the number of loops in your
programs. We will let it calculate the prot of a single trading day:
1. First, load the data:
o, h, l, c = np.loadtxt('BHP.csv', delimiter=',', usecols=(3,
4, 5, 6), unpack=True)
2. The vectorize funcon is the NumPy equivalent of the Python map funcon.
Call the vectorize funcon, giving it as an argument the calc_profit funcon
that we sll have to write:
func = np.vectorize(calc_profit)
3. We can now apply func as if it is a funcon. Apply the func result that we got,
to the price arrays:
profits = func(o, h, l, c)
4. The calc_profit funcon is prey simple. First, we try to buy slightly below the
open price. If this is outside of the daily range, then, obviously our aempt failed and
no prot was made, or we incurred a loss, therefore, we will return 0. Otherwise, we
sell at the close price and the prot is just the dierence between the buy price and
the close price. Actually, it is more interesng to have a look at the relave prot:
def calc_profit((open, high, low, close):
#buy just below the open
buy = open * float(sys.argv[1])
# daily range
www.it-ebooks.info
Chapter 4
[ 103 ]
if low < buy < high:
return (close - buy)/buy
else:
return 0
print "Profits", profits
5. There are two days with zero prots: there was either no net gain, or a loss.
Select the days with trades and calculate averages:
real_trades = profits[profits != 0]
print "Number of trades", len(real_trades), round(100.0 *
len(real_trades)/len(c), 2), "%"
print "Average profit/loss %", round(np.mean(real_trades) *
100, 2)
The trades summary are shown as follows:
Number of trades 28 93.33 %
Average profit/loss % 0.02
6. As opmists, we are interested in winning trades with a gain greater than zero.
Select the days with winning trades and calculate averages:
winning_trades = profits[profits > 0]
print "Number of winning trades", len(winning_trades),
round(100.0
* len(winning_trades)/len(c), 2), "%"
print "Average profit %", round(np.mean(winning_trades) * 100,
2)
The winning trades are:
Number of winning trades 16 53.33 %
Average profit % 0.72
7. As pessimists, we are interested in losing trades with prot less than zero. Select the
days with losing trades and calculate averages:
losing_trades = profits[profits < 0]
print "Number of losing trades", len(losing_trades),
round(100.0 *
len(losing_trades)/len(c), 2), "%"
print "Average loss %", round(np.mean(losing_trades) * 100, 2)
The losing trades are:
Number of losing trades 12 40.0 %
Average loss % -0.92
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 104 ]
What just happened?
We vectorized a funcon, which is just another way to avoid using loops. We simulated
a trading day with a funcon, which returned the relave prot of each day's trade. We
printed a summary of the losing and winning trades (see simulation.py):
import numpy as np
import sys
o, h, l, c = np.loadtxt('BHP.csv', delimiter=',', usecols=(3, 4, 5,
6), unpack=True)
def calc_profit(open, high, low, close):
#buy just below the open
buy = open * float(sys.argv[1])
# daily range
if low < buy < high:
return (close - buy)/buy
else:
return 0
func = np.vectorize(calc_profit)
profits = func(o, h, l, c)
print "Profits", profits
real_trades = profits[profits != 0]
print "Number of trades", len(real_trades), round(100.0 * len(real_
trades)/len(c), 2), "%"
print "Average profit/loss %", round(np.mean(real_trades) * 100, 2)
winning_trades = profits[profits > 0]
print "Number of winning trades", len(winning_trades), round(100.0 *
len(winning_trades)/len(c), 2), "%"
print "Average profit %", round(np.mean(winning_trades) * 100, 2)
losing_trades = profits[profits < 0]
print "Number of losing trades", len(losing_trades), round(100.0 *
len(losing_trades)/len(c), 2), "%"
print "Average loss %", round(np.mean(losing_trades) * 100, 2)
www.it-ebooks.info
Chapter 4
[ 105 ]
Have a go hero – analyzing consecutive wins and losses
Although the average prot is posive, it is also important to know whether we had to
endure a long streak of consecuve losses. If this is the case, we might be le with lile
or no capital, and then the average prot would not maer that much.
Find out if there was such a losing streak. If you want, you can also nd out if there was a
prolonged winning streak.
Smoothing
Noisy data is dicult to deal with, so we oen need to do some smoothing. Besides
calculang moving averages, we can use one of the NumPy funcons to smooth data.
The hanning funcon is a windowing funcon formed by a weighted cosine. There are
other window funcons that will be covered in greater detail in later chapters.
Time for action – smoothing with the hanning function
We will use the hanning funcon to smooth arrays of stock returns, as shown in the
following steps:
1. Call the hanning funcon to compute weights, for a certain N length window
(in this example, N is 8):
N = int(sys.argv[1])
weights = np.hanning(N)
print "Weights", weights
The weights are as follows:
Weights [ 0. 0.1882551 0.61126047 0.95048443
0.95048443 0.61126047
0.1882551 0. ]
2. Calculate the stock returns for the BHP and VALE quotes using convolve with
normalized weights:
bhp = np.loadtxt('BHP.csv', delimiter=',', usecols=(6,),
unpack=True)
bhp_returns = np.diff(bhp) / bhp[ : -1]
smooth_bhp = np.convolve(weights/weights.sum(), bhp_returns)
[N-1:-N+1]
vale = np.loadtxt('VALE.csv', delimiter=',', usecols=(6,),
unpack=True)
vale_returns = np.diff(vale) / vale[ : -1]
smooth_vale = np.convolve(weights/weights.sum(), vale_returns)
[N-1:-N+1]
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 106 ]
3. Plong with Matplotlib:
t = np.arange(N - 1, len(bhp_returns))
plot(t, bhp_returns[N-1:], lw=1.0)
plot(t, smooth_bhp, lw=2.0)
plot(t, vale_returns[N-1:], lw=1.0)
plot(t, smooth_vale, lw=2.0)
show()
The chart would appear as follows:
The thin lines on the chart are the stock returns and the thick lines are the result
of smoothing. As you can see, the lines cross a few mes. These points might be
important, because the trend might have changed there. Or, at least, the relaon
of BHP to VALE might have changed. These turning inecon points probably occur
oen, so we might want to project into the future.
4. Fit the result of the smoothing step to polynomials:
K = int(sys.argv[1])
t = np.arange(N - 1, len(bhp_returns))
poly_bhp = np.polyfit(t, smooth_bhp, K)
poly_vale = np.polyfit(t, smooth_vale, K)
www.it-ebooks.info
Chapter 4
[ 107 ]
5. Now, we need to compute for a situaon where the polynomials we found in
the previous step are equal to each other. This boils down to subtracng the
polynomials and nding the roots of the resulng polynomial. Subtract the
polynomials using polysub:
poly_sub = np.polysub(poly_bhp, poly_vale)
xpoints = np.roots(poly_sub)
print "Intersection points", xpoints
The points are shown as follows:
Intersection points [ 27.73321597+0.j 27.51284094+0.j
24.32064343+0.j
18.86423973+0.j 12.43797190+1.73218179j 12.43797190-
1.73218179j
6.34613053+0.62519463j 6.34613053-0.62519463j]
6. The numbers we get are complex; that is not good for us, unless there is such a thing
as imaginary me. Check which numbers are real with the isreal funcon:
reals = np.isreal(xpoints)
print "Real number?", reals
The result is as follows:
Real number? [ True True True True False False False False]
Some of the numbers are real, so select them with the select funcon. The select
funcon forms an array by taking elements from a list of choices, based on a list of
condions:
xpoints = np.select([reals], [xpoints])
xpoints = xpoints.real
print "Real intersection points", xpoints
The real intersecon points are as follows:
Real intersection points [ 27.73321597 27.51284094
24.32064343 18.86423973 0. 0. 0. 0.]
7. We managed to pick up some zeroes. The trim_zeros funcon strips the
leading and trailing zeros from a one-dimensional array. Get rid of the zeroes
with trim_zeros:
print "Sans 0s", np.trim_zeros(xpoints)
The zeroes are gone, and the output is shown as follows:
Sans 0s [ 27.73321597 27.51284094 24.32064343 18.86423973]
www.it-ebooks.info
Convenience Funcons for Your Convenience
[ 108 ]
What just happened?
We applied the hanning funcon to smooth arrays containing stock returns. We subtracted
two polynomials with the polysub funcon. We checked for real numbers with the isreal
funcon and selected the real numbers with the select funcon. Finally, we stripped
zeroes from an array with the strip_zeroes funcon (see smoothing.py):
import numpy as np
import sys
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
N = int(sys.argv[1])
weights = np.hanning(N)
print "Weights", weights
bhp = np.loadtxt('BHP.csv', delimiter=',', usecols=(6,), unpack=True)
bhp_returns = np.diff(bhp) / bhp[ : -1]
smooth_bhp = np.convolve(weights/weights.sum(), bhp_returns)[N-1:
-N+1]
vale = np.loadtxt('VALE.csv', delimiter=',', usecols=(6,), un
pack=True)
vale_returns = np.diff(vale) / vale[ : -1]
smooth_vale = np.convolve(weights/weights.sum(), vale_returns)[N-1:
-N+1]
K = int(sys.argv[1])
t = np.arange(N - 1, len(bhp_returns))
poly_bhp = np.polyfit(t, smooth_bhp, K)
poly_vale = np.polyfit(t, smooth_vale, K)
poly_sub = np.polysub(poly_bhp, poly_vale)
xpoints = np.roots(poly_sub)
print "Intersection points", xpoints
reals = np.isreal(xpoints)
print "Real number?", reals
xpoints = np.select([reals], [xpoints])
xpoints = xpoints.real
print "Real intersection points", xpoints
www.it-ebooks.info
Chapter 4
[ 109 ]
print "Sans 0s", np.trim_zeros(xpoints)
plot(t, bhp_returns[N-1:], lw=1.0)
plot(t, smooth_bhp, lw=2.0)
plot(t, vale_returns[N-1:], lw=1.0)
plot(t, smooth_vale, lw=2.0)
show()
Have a go hero – smoothing variations
Experiment with the other smoothing funcons—hamming, blackman, bartlett,
and kaiser. They work more or less in the same way as hanning.
Summary
We calculated the correlaon of the stock returns of two stocks with the corrcoef funcon.
As a bonus, a demonstraon of the diagonal and trace funcons was given, which can
give us the diagonal and trace of a matrix.
We t data to a polynomial with the polyfit funcon. We learned about the polyval
funcon that computes the values of a polynomial, the roots funcon that returns the
roots of the polynomial, and the polyder funcon that gives back the derivave of
a polynomial.
Hopefully, we increased our producvity so that we can connue in the next chapter
with matrices and universal funcons (ufuncs).
www.it-ebooks.info
www.it-ebooks.info
Working with Matrices and ufuncs
This chapter covers matrices and universal functions (ufuncs). Matrices are
well known in mathematics and have their representation in NumPy as well.
Universal functions work on arrays, element-by-element, or on scalars. ufuncs
expect a set of scalars as input and produce a set of scalars as output. Universal
functions can typically be mapped to mathematical counterparts, such as
add, subtract, divide, multiply, and likewise. We will also be introduced to
trigonometric, bitwise, and comparison universal functions.
In this chapter, we shall cover the following topics:
Matrix creaon
Matrix operaons
Basic ufuncs
Trigonometric funcons
Bitwise funcons
Comparison funcons
Matrices
Matrices in NumPy are subclasses of ndarray. Matrices can be created using a special string
format. They are, just like in mathemacs, two-dimensional. Matrix mulplicaon is, as you
would expect, dierent from the normal NumPy mulplicaon. The same is true for the
power operator. We can create matrices with the mat, matrix, and bmat funcons.
5
www.it-ebooks.info
Working with Matrices and ufuncs
[ 112 ]
Time for action – creating matrices
Matrices can be created with the mat funcon. This funcon does not make a copy if the
input is already a matrix or an ndarray. Calling this funcon is equivalent to calling
matrix(data, copy=False). We will also demonstrate transposing and inverng matrices.
1. Rows are delimited by a semicolon, values by a space. Call the mat funcon with the
following string to create a matrix:
A = np.mat('1 2 3; 4 5 6; 7 8 9')
print "Creation from string", A
The matrix output should be the following matrix:
Creation from string [[1 2 3]
[4 5 6]
[7 8 9]]
2. Transpose the matrix with the T aribute, as follows:
print "transpose A", A.T
The following is the transposed matrix:
transpose A [[1 4 7]
[2 5 8]
[3 6 9]]
3. The matrix can be inverted with the I aribute, as follows:
print "Inverse A", A.I
The inverse matrix is printed as follows (be warned that this is a O(n3) operaon):
Inverse A [[ -4.50359963e+15 9.00719925e+15 -4.50359963e+15]
[ 9.00719925e+15 -1.80143985e+16 9.00719925e+15]
[ -4.50359963e+15 9.00719925e+15 -4.50359963e+15]]
4. Instead of using a string to create a matrix, let's do it with an array:
print "Creation from array", np.mat(np.arange(9).reshape(3, 3))
The newly-created array is printed as follows:
Creation from array [[0 1 2]
[3 4 5]
[6 7 8]]
www.it-ebooks.info
Chapter 5
[ 113 ]
What just happened?
We created matrices with the mat funcon. We transposed the matrices with the T aribute
and inverted them with the I aribute (see matrixcreation.py):
import numpy as np
A = np.mat('1 2 3; 4 5 6; 7 8 9')
print "Creation from string", A
print "transpose A", A.T
print "Inverse A", A.I
print "Check Inverse", A * A.I
print "Creation from array", np.mat(np.arange(9).reshape(3, 3))
Creating a matrix from other matrices
Somemes we want to create a matrix from other smaller matrices. We can do this with
the bmat funcon. The b here stands for block matrix.
Time for action – creating a matrix from other matrices
We will create a matrix from two smaller matrices, as follows:
1. First create a two-by-two identy matrix:
A = np.eye(2)
print "A", A
The identy matrix looks like this:
A [[ 1. 0.]
[ 0. 1.]]
Create another matrix like A and mulply by 2:
B = 2 * A
print "B", B
The second matrix is as follows:
B [[ 2. 0.]
[ 0. 2.]]
www.it-ebooks.info
Working with Matrices and ufuncs
[ 114 ]
2. Create the compound matrix from a string. The string uses the same format as the
mat funcon; only, you can use matrices instead of numbers.
print "Compound matrix\n", np.bmat("A B; A B")
The compound matrix is shown as follows:
Compound matrix
[[ 1. 0. 2. 0.]
[ 0. 1. 0. 2.]
[ 1. 0. 2. 0.]
[ 0. 1. 0. 2.]]
What just happened?
We created a block matrix from two smaller matrices, with the bmat funcon.
We gave the funcon a string containing the names of matrices instead of numbers
(see bmatcreation.py):
import numpy as np
A = np.eye(2)
print "A", A
B = 2 * A
print "B", B
print "Compound matrix\n", np.bmat("A B; A B")
Pop quiz – dening a matrix with a string
Q1. What is the row delimiter in a string accepted by the mat and bmat funcons?
1. Semicolon
2. Colon
3. Comma
4. Space
Universal functions
Ufuncs expect a set of scalars as input and produce a set of scalars as output. Universal
funcons can typically be mapped to mathemacal counterparts, such as, add, subtract,
divide, mulply, and likewise.
www.it-ebooks.info
Chapter 5
[ 115 ]
Time for action – creating universal function
We can create a universal funcon from a Python funcon with the NumPy frompyfunc
funcon, as follows:
1. Dene a Python funcon that answers the ulmate queson to the universe,
existence, and the rest (it's from The Hitchhiker's Guide to the Galaxy; if you
haven't read it, you can safely ignore this).
def ultimate_answer(a):
So far, nothing special; we gave the funcon the name ultimate_answer
and dened one parameter, a.
2. Create a result consisng of all zeros, that has the same shape as a, with the
zeros_like funcon:
result = np.zeros_like(a)
3. Now set the elements of the inialized array to the answer 42 and return the result.
The complete funcon should appear as shown, in the following code snippet. The
flat aribute gives us access to a at iterator that allows us to set the value of
the array:
def ultimate_answer(a):
result = np.zeros_like(a)
result.flat = 42
return result
4. Create a universal funcon with frompyfunc; specify 1 as as number of input
parameter followed by 1 as the number of output parameters:
ufunc = np.frompyfunc(ultimate_answer, 1, 1)
print "The answer", ufunc(np.arange(4))
The result for a one-dimensional array is shown as follows:
The answer [42 42 42 42]
We can do the same for a two-dimensional array by using the following code:
print "The answer", ufunc(np.arange(4).reshape(2, 2))
The output for a two dimensional array is shown as follows
The answer [[42 42]
[[42 42]
[42 42]]
www.it-ebooks.info
Working with Matrices and ufuncs
[ 116 ]
What just happened?
We dened a Python funcon. In this funcon, we inialized to zero the elements of an
array, based on the shape of an input argument, with the zeros_like funcon. Then,
with the flat aribute of ndarray, we set the array elements to the ulmate answer,
42 (see answer42.py):
import numpy as np
def ultimate_answer(a):
result = np.zeros_like(a)
result.flat = 42
return result
ufunc = np.frompyfunc(ultimate_answer, 1, 1)
print "The answer", ufunc(np.arange(4))
print "The answer", ufunc(np.arange(4).reshape(2, 2))
Universal function methods
How can funcons have methods? As we said earlier, universal funcons are not funcons
but objects represenng funcons. Universal funcons have four methods. They only make
sense for funcons such as add. That is, they have two input parameters and return one
output parameter. If the signature of an ufunc does not match this condion, this will result
in a ValueError, so call this method only for binary universal funcons. The four methods
are listed as follows:
reduce
accumulate
reduceat
outer
Time for action – applying the ufunc methods on add
Let's call the four methods on add funcon.
1. The input array is reduced by applying the universal funcon recursively along
a specied axis on consecuve elements. For the add funcon, the result of
reducing is similar to calculang the sum of an array. Call the reduce method:
a = np.arange(9)
print "Reduce", np.add.reduce(a)
www.it-ebooks.info
Chapter 5
[ 117 ]
The reduced array should be as follows:
Reduce 36
2. The accumulate method also recursively goes through the input array. But,
contrary to the reduce method, it stores the intermediate results in an array and
returns that. The result, in the case of the add funcon, is equivalent to calling the
cumsum funcon. Call the accumulate method on the add funcon:
print "Accumulate", np.add.accumulate(a)
The accumulated array:
Accumulate [ 0 1 3 6 10 15 21 28 36]
3. The reduceat method is a bit complicated to explain, so let's call it and go through
its algorithm, step-by-step. The reduceat method requires as arguments, an input
array and a list of indices:
print "Reduceat", np.add.reduceat(a, [0, 5, 2, 7])
The result is shown as follows:
Reduceat [10 5 20 15]
The rst step concerns the indices 0 and 5. This step results in a reduce operaon
of the array elements between indices 0 and 5.
print "Reduceat step I", np.add.reduce(a[0:5])
The output of step 1 is as follows:
Reduceat step I 10
The second step concerns indices 5 and 2. Since 2 is less than 5, the array element
at index 5 is returned:
print "Reduceat step II", a[5]
The second step results in the following output:
Reduceat step II 5
The third step concerns indices 2 and 7. This step results in a reduce operaon
of the array elements between indices 2 and 7:
print "Reduceat step III", np.add.reduce(a[2:7])
The result of the third step is shown as follows:
Reduceat step III 20
www.it-ebooks.info
Working with Matrices and ufuncs
[ 118 ]
The fourth step concerns index 7. This step results in a reduce operaon of the array
elements from index 7 to the end of the array:
print "Reduceat step IV", np.add.reduce(a[7:])
The fourth step result is shown as follows:
Reduceat step IV 15
4. The outer method returns an array that has a rank, which is the sum of the ranks
of its two input arrays. The method is applied to all possible pairs of the input array
elements. Call the outer method on the add funcon:
print "Outer", np.add.outer(np.arange(3), a)
The outer sum output result is as follows:
Outer [[ 0 1 2 3 4 5 6 7 8]
[ 1 2 3 4 5 6 7 8 9]
[ 2 3 4 5 6 7 8 9 10]]
What just happened?
We applied the four methods, reduce, accumulate, reduceat, and outer, of universal
funcons to the add funcon (see ufuncmethods.py):
import numpy as np
a = np.arange(9)
print "Reduce", np.add.reduce(a)
print "Accumulate", np.add.accumulate(a)
print "Reduceat", np.add.reduceat(a, [0, 5, 2, 7])
print "Reduceat step I", np.add.reduce(a[0:5])
print "Reduceat step II", a[5]
print "Reduceat step III", np.add.reduce(a[2:7])
print "Reduceat step IV", np.add.reduce(a[7:])
print "Outer", np.add.outer(np.arange(3), a)
Arithmetic functions
The common arithmec operators +, -, and * are implicitly linked to the add, subtract,
and multiply universal funcons. This means that when you use one of those operators
on a NumPy array, the corresponding universal funcon will get called. Division involves a
slightly more complex process. There are three universal funcons that have to do with array
division: divide, true_divide, and floor_division. Two operators correspond to
division: / and //.
www.it-ebooks.info
Chapter 5
[ 119 ]
Time for action – dividing arrays
Let's see the array division in acon:
1. The divide funcon does truncate integer division and normal
oang-point division:
a = np.array([2, 6, 5])
b = np.array([1, 2, 3])
print "Divide", np.divide(a, b), np.divide(b, a)
The result of the divide funcon is shown as follows:
Divide [2 3 1] [0 0 0]
As you can see, truncaon took place.
2. The true_divide funcon comes closer to the mathemacal denion of division.
Integer division returns a oang-point result and no truncaon occurs:
print "True Divide", np.true_divide(a, b), np.true_divide(b, a)
The result of the true_divide funcon is as follows:
True Divide [ 2. 3. 1.66666667] [ 0.5
0.33333333 0.6 ]
3. The floor_divide funcon always returns an integer result. It is equivalent to
calling the floor funcon aer calling the divide funcon. The floor funcon
discards the decimal part of a oang-point number and returns an integer:
print "Floor Divide", np.floor_divide(a, b), np.floor_divide(b, a)
c = 3.14 * b
print "Floor Divide 2", np.floor_divide(c, b), np.floor_divide(b,
c)
The floor_divide funcon results in:
Floor Divide [2 3 1] [0 0 0]
Floor Divide 2 [ 3. 3. 3.] [ 0. 0. 0.]
4. By default, the / operator is equivalent to calling the divide funcon:
from __future__ import division
However, if this line is found at the beginning of a Python program, the true_
divide funcon is called instead. So, this code would appear as follows:
print "/ operator", a/b, b/a
www.it-ebooks.info
Working with Matrices and ufuncs
[ 120 ]
The result is shown as follows:
/ operator [ 2. 3. 1.66666667] [ 0.5
0.33333333 0.6 ]
5. The // operator is equivalent to calling the floor_divide funcon. For example,
look at the following code snippet:
print "// operator", a//b, b//a
print "// operator 2", c//b, b//c
The // operator result is shown as follows:
// operator [2 3 1] [0 0 0]
// operator 2 [ 3. 3. 3.] [ 0. 0. 0.]
What just happened?
We found that there are three dierent NumPy division funcons. The divide funcon
truncates the integer division and normal oang-point division. The true_divide funcon
always returns a oang-point result without any truncaon. The floor_divide funcon
always returns an integer result; the result is the same that you would get by calling the
divide and floor funcons consecuvely (see dividing.py):
from __future__ import division
import numpy as np
a = np.array([2, 6, 5])
b = np.array([1, 2, 3])
print "Divide", np.divide(a, b), np.divide(b, a)
print "True Divide", np.true_divide(a, b), np.true_divide(b, a)
print "Floor Divide", np.floor_divide(a, b), np.floor_divide(b, a)
c = 3.14 * b
print "Floor Divide 2", np.floor_divide(c, b), np.floor_divide(b, c)
print "/ operator", a/b, b/a
print "// operator", a//b, b//a
print "// operator 2", c//b, b//c
Have a go hero – experimenting with __future__.division
Experiment to conrm the impact of imporng __future__.division.
www.it-ebooks.info
Chapter 5
[ 121 ]
Modulo operation
The modulo or remainder can be calculated using the NumPy mod, remainder, and fmod
funcons. Also, one can use the % operator. The main dierence among these funcons is
how they deal with negave numbers. The odd one out in this group is the fmod funcon.
Time for action – computing the modulo
Let's call the previously menoned funcons:
1. The remainder funcon returns the remainder of the two arrays, element-wise. 0
is returned if the second number is 0:
a = np.arange(-4, 4)
print "Remainder", np.remainder(a, 2)
The result of the remainder funcon is shown as follows:
Remainder [0 1 0 1 0 1 0 1]
2. The mod funcon does exactly the same as the remainder funcon:
print "Mod", np.mod(a, 2)
The result of the mod funcon is shown as follows:
Mod [0 1 0 1 0 1 0 1]
3. The % operator is just shorthand for the remainder funcon:
print "% operator", a % 2
The result of the % operator is shown as follows:
% operator [0 1 0 1 0 1 0 1]
4. The fmod funcon handles negave numbers dierently than mod, fmod, and % do.
The sign of the remainder is the sign of the dividend, and the sign of the divisor has
no inuence on the results:
print "Fmod", np.fmod(a, 2)
The fmod result is printed as follows:
Fmod [ 0 -1 0 -1 0 1 0 1]
www.it-ebooks.info
Working with Matrices and ufuncs
[ 122 ]
What just happened?
We demonstrated the NumPy mod, remainder, and fmod funcons, which compute the
modulo, or remainder (see modulo.py):
import numpy as np
a = np.arange(-4, 4)
print "Remainder", np.remainder(a, 2)
print "Mod", np.mod(a, 2)
print "% operator", a % 2
print "Fmod", np.fmod(a, 2)
Fibonacci numbers
The Fibonacci numbers are based on a recurrence relaon. It is dicult to express this
relaon directly with NumPy code. However, we can express this relaon in a matrix form
or use the golden rao formula. This will introduce the matrix and rint funcons. The
matrix funcon creates matrices and the rint funcon rounds numbers to the closest
integer, but the result is not integer.
Time for action – computing Fibonacci numbers
The Fibonacci recurrence relaon can be represented by a matrix. Calculaon of Fibonacci
numbers can be expressed as repeated matrix mulplicaon:
1. Create the Fibonacci matrix as follows:
F = np.matrix([[1, 1], [1, 0]])
print "F", F
The Fibonacci matrix appears as follows:
F [[1 1]
[1 0]]
2. Calculate the eighth Fibonacci number (ignoring 0), by subtracng 1 from 8 and
taking the power of the matrix. The Fibonacci number then appears on the diagonal:
print "8th Fibonacci", (F ** 7)[0, 0]
The Fibonacci number is:
8th Fibonacci 21
www.it-ebooks.info
Chapter 5
[ 123 ]
3. The golden rao formula, beer known as Binet's formula, allows us to calculate
Fibonacci numbers with a rounding step at the end. Calculate the rst eight
Fibonacci numbers:
n = np.arange(1, 9)
sqrt5 = np.sqrt(5)
phi = (1 + sqrt5)/2
fibonacci = np.rint((phi**n - (-1/phi)**n)/sqrt5)
print "Fibonacci", fibonacci
The Fibonacci numbers are:
Fibonacci [ 1. 1. 2. 3. 5. 8. 13. 21.]
What just happened?
We computed Fibonacci numbers in two ways. In the process, we learned about the matrix
funcon that creates matrices. We also learned about the rint funcon that rounds numbers
to the closest integer but does not change the type to integer (see fibonacci.py):
import numpy as np
F = np.matrix([[1, 1], [1, 0]])
print "F", F
print "8th Fibonacci", (F ** 7)[0, 0]
n = np.arange(1, 9)
sqrt5 = np.sqrt(5)
phi = (1 + sqrt5)/2
fibonacci = np.rint((phi**n - (-1/phi)**n)/sqrt5)
print "Fibonacci", fibonacci
Have a go hero – timing the calculations
You are probably wondering which approach is faster; so go ahead me it. Create a universal
Fibonacci funcon with frompyfunc and me it too.
Lissajous curves
All the standard trigonometric funcons, such as, sin, cos, tan and likewise are represented
by universal funcons in NumPy. Lissajous curves are a fun way of using trigonometry.
I remember producing Lissajous gures on an oscilloscope in the physics lab. Two
parametric equaons can describe the gures:
x = A sin(at + π/2)
y = B sin(bt)
www.it-ebooks.info
Working with Matrices and ufuncs
[ 124 ]
Time for action – drawing Lissajous curves
The Lissajous gures are determined by four parameters A, B, a, and b. Let's set A and B to 1
for simplicity:
1. Inialize t with the linspace funcon from -pi to pi with 201 points:
a = float(sys.argv[1])
b = float(sys.argv[2])
t = np.linspace(-np.pi, np.pi, 201)
2. Calculate x with the sin funcon and np.pi:
x = np.sin(a * t + np.pi/2)
3. Calculate y with the sin funcon:
y = np.sin(b * t)
4. Matplotlib will be covered later in Chapter 9, Plong with Matplotlib. Plot as
shown here:
plot(x, y)
show()
The result for a = 9 and b = 8:
What just happened?
We ploed the Lissajous curve with the previously menoned parametric equaons where
A=B=1, a=9, and, b=8. We used the sin and linspace funcons as well as the NumPy pi
constant (see lissajous.py):
www.it-ebooks.info
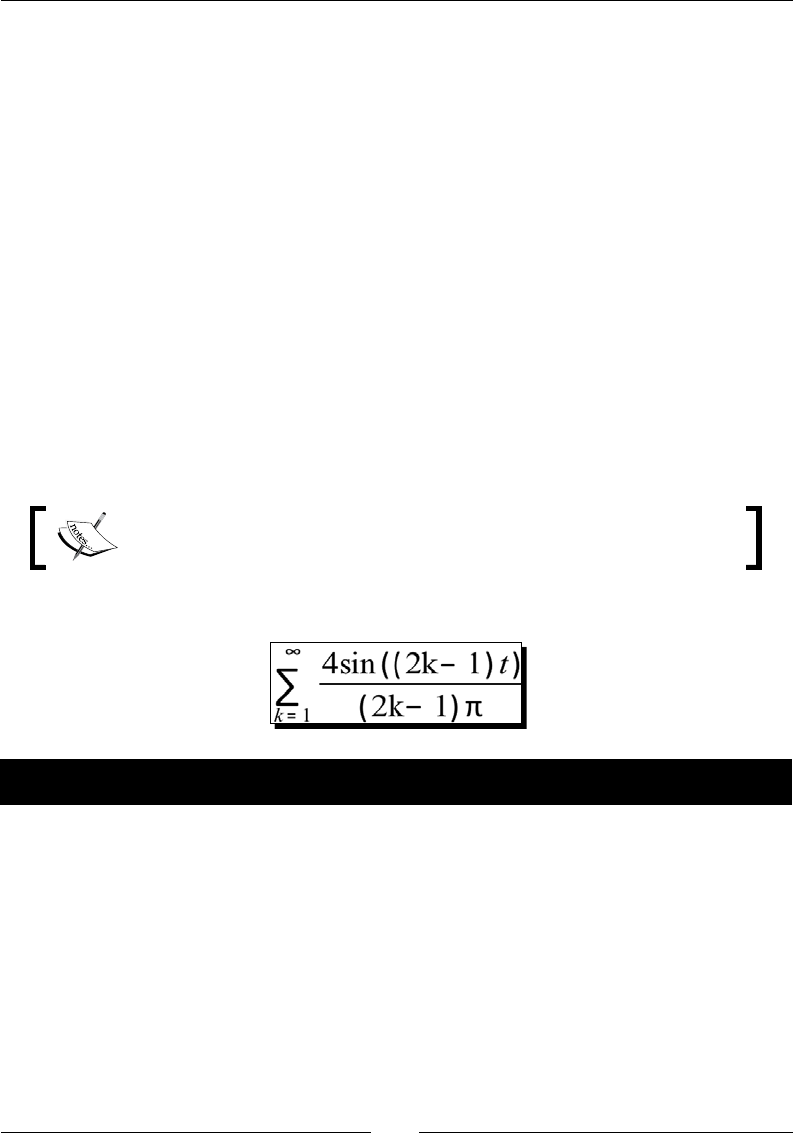
Chapter 5
[ 125 ]
import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import sys
a = float(sys.argv[1])
b = float(sys.argv[2])
t = np.linspace(-np.pi, np.pi, 201)
x = np.sin(a * t + np.pi/2)
y = np.sin(b * t)
plot(x, y)
show()
Square waves
Square waves are also one of those neat things that you can view on an oscilloscope.
They can be approximated prey well with sine waves; aer all, a square wave is a
signal that can be represented by an innite Fourier series.
A Fourier series is the sum of a series of sine and cosine terms named aer
the famous mathemacian Jean-Bapste Fourier.
The formula of this parcular series represenng the square wave is as follows:
Time for action – drawing a square wave
We will inialize t just like in the previous tutorial. We need to sum a number of terms.
The higher the number of terms, the more accurate the result; k = 99 should be sucient.
In order to draw a square wave, follow these steps:
1. We will start by inializing t and k. Set inial values for the funcon to 0:
t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, float(sys.argv[1]))
k = 2 * k - 1
f = np.zeros_like(t)
www.it-ebooks.info
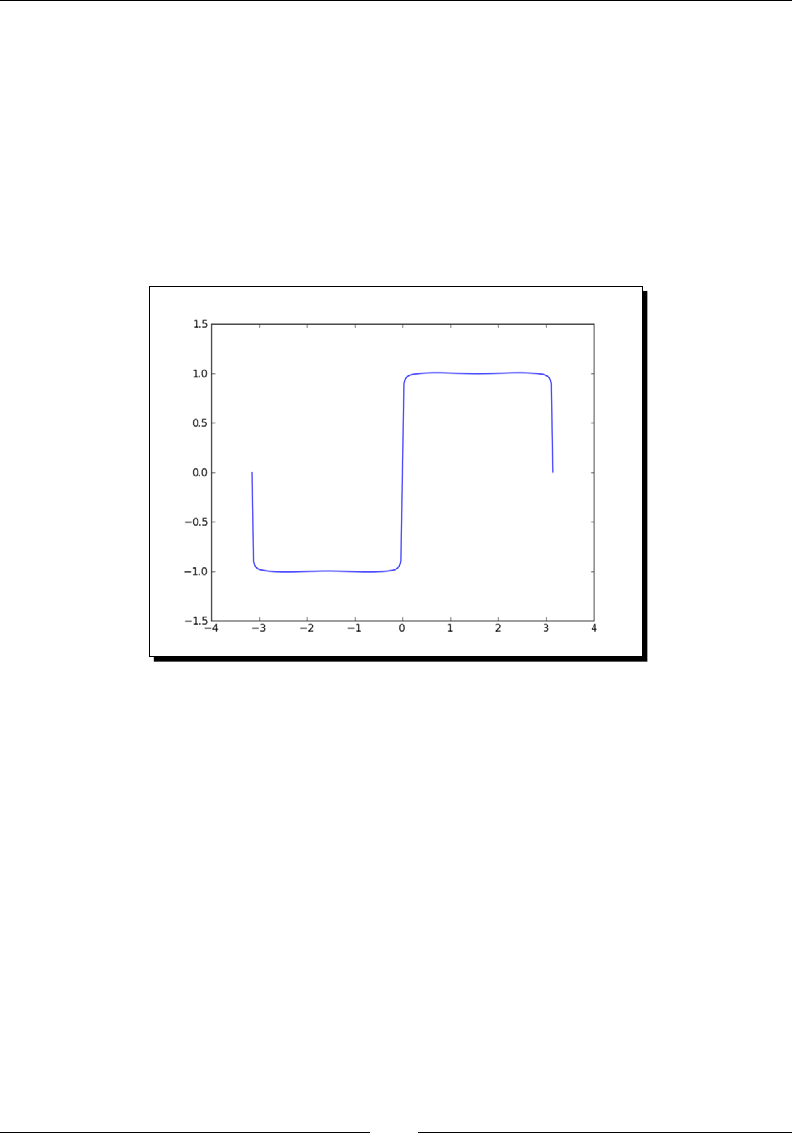
Working with Matrices and ufuncs
[ 126 ]
2. This step should be a straighorward applicaon of the sin and sum funcons:
for i in range(len(t)):
f[i] = np.sum(np.sin(k * t[i])/k)
f = (4 / np.pi) * f
3. The code to plot is almost idencal to the one in the previous tutorial:
plot(t, f)
show()
The resulng square wave generated with k = 99 is as follows:
What just happened?
We generated a square wave or, at least, a fair approximaon of it, using the sin funcon.
The input values were assembled with linspace and the k values with the arange funcon
(see squarewave.py):
import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import sys
t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, float(sys.argv[1]))
k = 2 * k - 1
f = np.zeros_like(t)
for i in range(len(t)):
www.it-ebooks.info
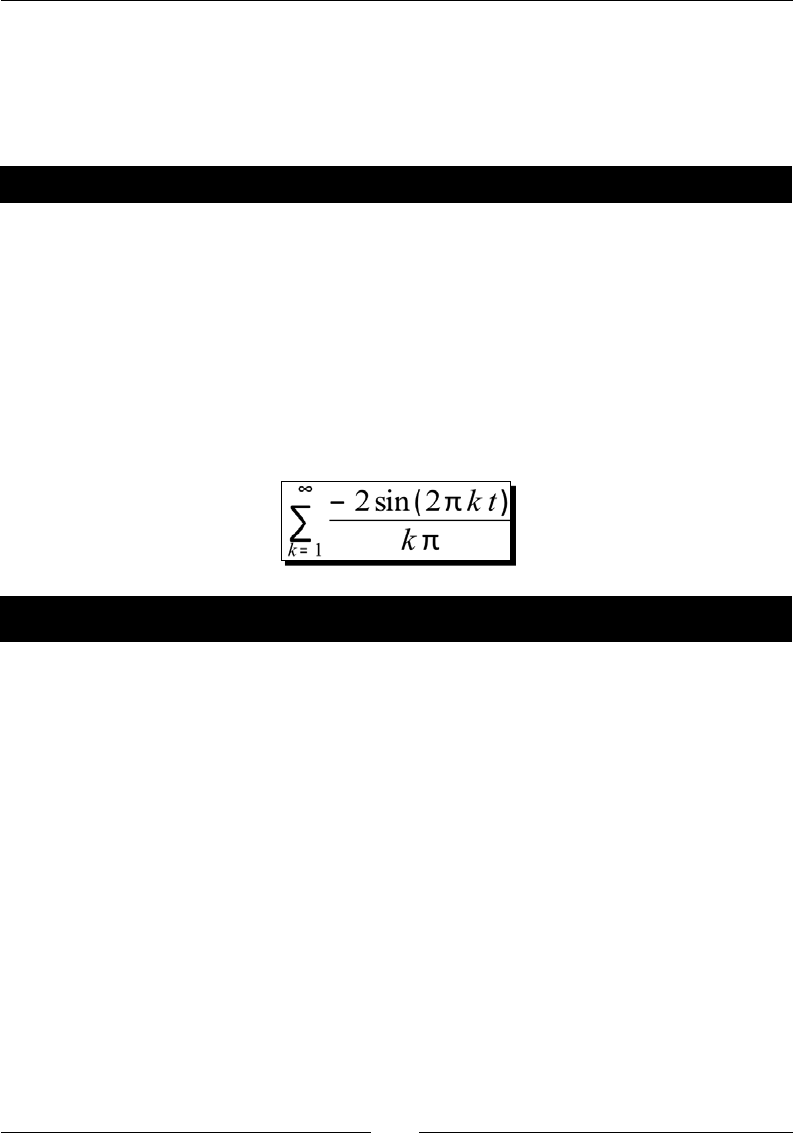
Chapter 5
[ 127 ]
f[i] = np.sum(np.sin(k * t[i])/k)
f = (4 / np.pi) * f
plot(t, f)
show()
Have a go hero – getting rid of the loop
You may have noced that there is one loop in the code. Get rid of it with NumPy funcons
and make sure the performance is also improved.
Sawtooth and triangle waves
Sawtooth and triangle waves are also a phenomenon easily viewed on an oscilloscope.
Just like with square waves, we can dene an innite Fourier series. The triangle waves
can be found by taking the absolute value of a sawtooth wave. The formula for the
representaon of a series of sawtooth waves is:
Time for action – drawing sawtooth and triangle waves
We will inialize t just like in the previous tutorial. Again, k = 99 should be sucient.
In order to draw sawtooth and triangle waves, follow these steps:
1. Set inial values for the funcon to zero:
t = np.linspace(-ny.pi, np.pi, 201)
k = np.arange(1, float(sys.argv[1]))
f = np.zeros_like(t)
2. This computaon of funcon values should again be a straighorward applicaon
for the sin and sum funcons:
for i in range(len(t)):
f[i] = np.sum(np.sin(2 * np.pi * k * t[i])/k)
f = (-2 / np.pi) * f
www.it-ebooks.info
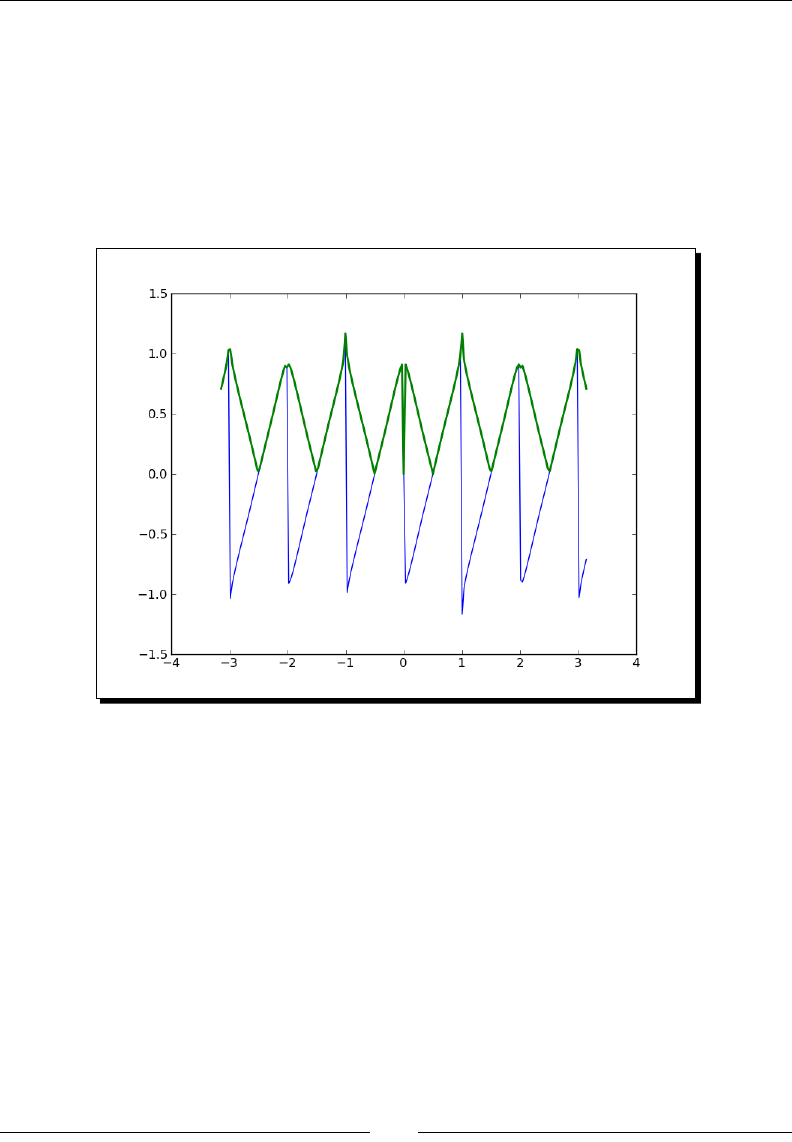
Working with Matrices and ufuncs
[ 128 ]
3. It's easy to plot the sawtooth and triangle waves, since the value of the triangle
wave should be equal to the absolute value of the sawtooth wave. Plot the waves
as shown here:
plot(t, f, lw=1.0)
plot(t, np.abs(f), lw=2.0)
show()
In the following gure, the triangle wave is the one with the thicker line:
What just happened?
We drew a sawtooth wave using the sin funcon. The input values were assembled with
linspace and the k values with the arange funcon. A triangle wave was derived from
the sawtooth wave by taking the absolute value (see sawtooth.py):
import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import sys
t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, float(sys.argv[1]))
f = np.zeros_like(t)
for i in range(len(t)):
f[i] = np.sum(np.sin(2 * np.pi * k * t[i])/k)
www.it-ebooks.info
Chapter 5
[ 129 ]
f = (-2 / np.pi) * f
plot(t, f, lw=1.0)
plot(t, np.abs(f), lw=2.0)
show()
Have a go hero – getting rid of the loop
Your challenge, should you choose to accept it, is to get rid of the loop in the program.
It should be doable with NumPy funcons and the performance should double.
Bitwise and comparison functions
Bitwise funcons operate on the bits of integers or integer arrays, since they are universal
funcons. The operators ^, &, |, <<, >>, and so on, have their NumPy counterparts. The
same goes for comparison operators, such as, <, >, ==, and likewise. These operators allow
you to do some clever tricks, which should be good for performance; however, they could
make your code quite unreadable, so use them with care.
Time for action – twiddling bits
We will go over three tricks—checking whether the signs of integers are dierent, checking
whether a number is a power of two, and calculang the modulus of a number that is a
power of two. We will show an operators-only notaon and one using the corresponding
NumPy funcons:
1. The rst trick depends on the XOR or ^ operator. The XOR operator is also called
the inequality operator; so, if the sign bit of the two operands is dierent, the XOR
operaon will lead to a negave number. ^ corresponds to the bitwise_xor
funcon. < corresponds to the less funcon.
x = np.arange(-9, 9)
y = -x
print "Sign different?", (x ^ y) < 0
print "Sign different?", np.less(np.bitwise_xor(x, y), 0)
The result is shown as follows:
Sign different? [ True True True True True True True True
True False True True
True True True True True True]
Sign different? [ True True True True True True True True
True False True True
True True True True True True]
As expected, all the signs dier, except for zero.
www.it-ebooks.info
Working with Matrices and ufuncs
[ 130 ]
2. A power of two is represented by a 1, followed by a series of trailing zeroes in binary
notaon. For instance, 10, 100, or 1000. A number one less than a power of two
would be represented by a row of ones in binary. For instance, 11, 111, or 1111
(or 3, 7, and 15, in the decimal system). Now, if we bitwise the AND operator a power
of two, and the integer that is one less than that, then we should get 0. The NumPy
counterpart of & is bitwise_and; the counterpart of == is the equal
universal funcon.
print "Power of 2?\n", x, "\n", (x & (x - 1)) == 0
print "Power of 2?\n", x, "\n", np.equal(np.bitwise_and(x,
(x - 1)), 0)
The result is shown as follows:
Power of 2?
[-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8]
[False False False False False False False False False True True
True
False True False False False True]
Power of 2?
[-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8]
[False False False False False False False False False True True
True
False True False False False True]
3. The trick of compung the modulus of four actually works when taking the modulus
of integers that are a power of two, such as, 4, 8, 16, and likewise. A bitwise le shi
leads to doubling of values. We saw in the previous step that subtracng one from a
power of two leads to a number in binary notaon that has a row of ones, such as,
11, 111, or 1111. This basically gives us a mask. Bitwise-ANDing with such a number
gives you the remainder with a power of two. The NumPy equivalent of << is the
left_shift universal funcon.
print "Modulus 4\n", x, "\n", x & ((1 << 2) - 1)
print "Modulus 4\n", x, "\n", np.bitwise_and(x,
np.left_shift(1, 2) - 1)
The result is shown as follows:
Modulus 4
[-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8]
[3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0]
Modulus 4
[-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8]
[3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0]
www.it-ebooks.info
Chapter 5
[ 131 ]
What just happened?
We covered three bit-twiddling hacks—checking whether the signs of integers are dierent,
checking whether a number is a power of two, and calculang the modulus of a number that
is a power of two. We saw the NumPy counterparts of the operators ^, &, <<, and < (see
bittwidling.py):
import numpy as np
x = np.arange(-9, 9)
y = -x
print "Sign different?", (x ^ y) < 0
print "Sign different?", np.less(np.bitwise_xor(x, y), 0)
print "Power of 2?\n", x, "\n", (x & (x - 1)) == 0
print "Power of 2?\n", x, "\n", np.equal(np.bitwise_and(x, (x - 1)),
0)
print "Modulus 4\n", x, "\n", x & ((1 << 2) - 1)
print "Modulus 4\n", x, "\n", np.bitwise_and(x, np.left_shift(1, 2) -
1)
Summary
We learned, in this chapter, about matrices and universal funcons. We covered how to
create matrices and how universal funcons work. We had a brief introducon to arithmec,
trigonometric, bitwise, and comparison universal funcons.
In the next chapter, we shall cover the NumPy modules.
www.it-ebooks.info
www.it-ebooks.info
Move Further with NumPy Modules
NumPy has a number of modules that have been inherited from its predecessor,
Numeric. Some of these packages have a SciPy counterpart, which may have
fuller functionality. This will be discussed in a later chapter. The numpy.dual
package contains functions that are defined both in NumPy and SciPy. The
packages discussed in this chapter are also part of the numpy.dual package.
In this chapter, we shall cover the following topics:
The linalg package
The fft package
Random numbers
Connuous and discrete distribuons
Linear algebra
Linear algebra is an important branch of mathemacs. The numpy.linalg package contains
linear algebra funcons. With this module, you can invert matrices, calculate eigenvalues,
solve linear equaons, and determine determinants, among other things.
Time for action – inverting matrices
The inverse of a matrix A in linear algebra is the matrix A-1, which when mulplied with the
original matrix, is equal to the identy matrix I. This can be wrien, as A* A-1 = I.
6
www.it-ebooks.info
Move Further with NumPy Modules
[ 134 ]
The inv funcon in the numpy.linalg package can do this for us. Let's invert an example
matrix. To invert matrices, perform the following steps:
1. We will create the example matrix with the mat funcon that we used in the
previous chapters.
A = np.mat("0 1 2;1 0 3;4 -3 8")
print "A\n", A
The A matrix is printed as follows:
A
[[ 0 1 2]
[ 1 0 3]
[ 4 -3 8]]
2. Now, we can see the inv funcon in acon, using which we will invert the matrix.
inverse = np.linalg.inv(A)
print "inverse of A\n", inverse
The inverse matrix is shown as follows:
inverse of A
[[-4.5 7. -1.5]
[-2. 4. -1. ]
[ 1.5 -2. 0.5]]
If the matrix is singular or not square, a LinAlgError exception is raised.
If you want, you can check the result manually. This is left as an exercise for
the reader.
3. Let's check what we get when we mulply the original matrix with the result of the
inv funcon:
print "Check\n", A * inverse
The result is the identy matrix, as expected.
Check
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
www.it-ebooks.info
Chapter 6
[ 135 ]
What just happened?
We calculated the inverse of a matrix with the inv funcon of the numpy.linalg
package. We checked, with matrix mulplicaon, whether this is indeed the inverse
matrix (see inversion.py).
import numpy as np
A = np.mat("0 1 2;1 0 3;4 -3 8")
print "A\n", A
inverse = np.linalg.inv(A)
print "inverse of A\n", inverse
print "Check\n", A * inverse
Pop quiz – creating a matrix
Q1. Which funcon can create matrices?
1. array
2. create_matrix
3. mat
4. vector
Have a go hero – inverting your own matrix
Create your own matrix and invert it. The inverse is only dened for square matrices.
The matrix must be square and inverble; otherwise, a LinAlgError excepon is raised.
Solving linear systems
A matrix transforms a vector into another vector in a linear way. This transformaon
mathemacally corresponds to a system of linear equaons. The numpy.linalg funcon,
solve, solves systems of linear equaons of the form Ax = b; here A is a matrix, b can be
1D or 2D array, and x is an unknown variable. We will see the dot funcon in acon. This
funcon returns the dot product of two oang-point arrays.
www.it-ebooks.info
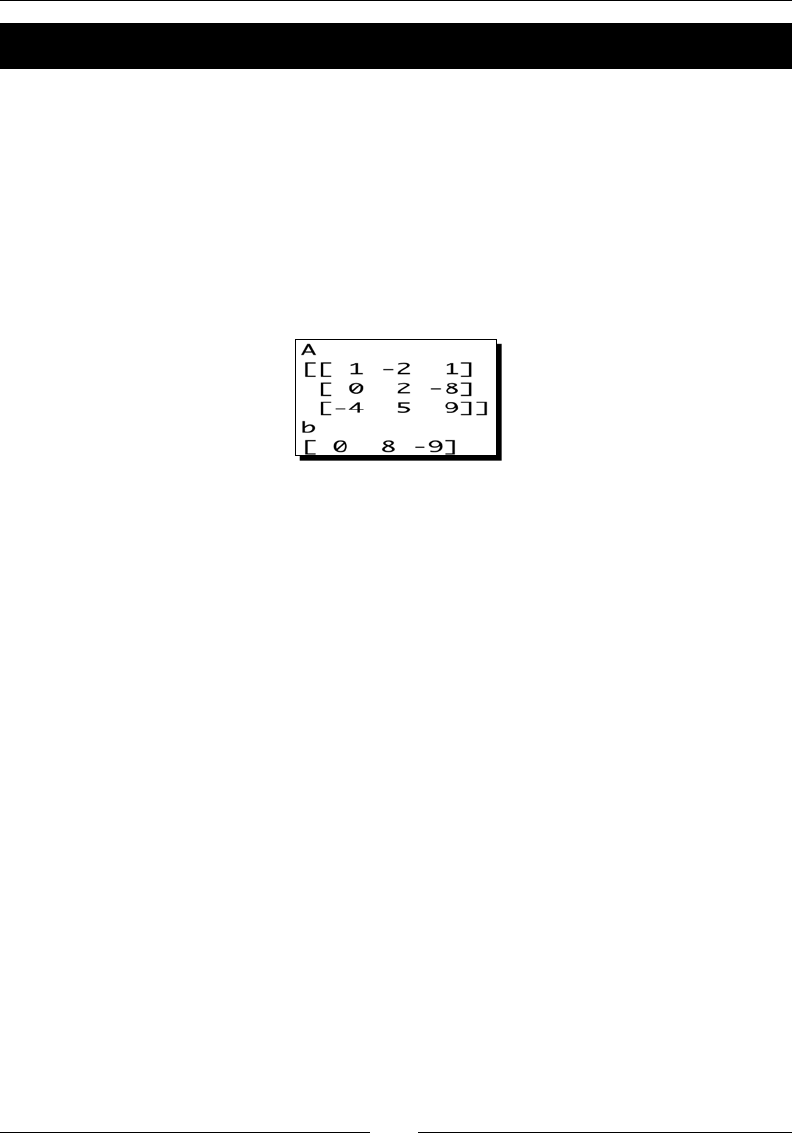
Move Further with NumPy Modules
[ 136 ]
Time for action – solving a linear system
Let's solve an example of a linear system. To solve a linear system, perform the
following steps:
1. Let's create the matrices A and b.
A = np.mat("1 -2 1;0 2 -8;-4 5 9")
print "A\n", A
b = np.array([0, 8, -9])
print "b\n", b
The matrices A and b are shown as follows:
2. Solve this linear system by calling the solve funcon.
x = np.linalg.solve(A, b)
print "Solution", x
The following is the soluon of the linear system:
Solution [ 29. 16. 3.]
3. Check whether the soluon is correct with the dot funcon.
print "Check\n", np.dot(A , x)
The result is as expected:
Check
[[ 0. 8. -9.]]
What just happened?
We solved a linear system using the solve funcon from the NumPy linalg module
and checked the soluon with the dot funcon (see solution.py).
import numpy as np
A = np.mat("1 -2 1;0 2 -8;-4 5 9")
print "A\n", A
b = np.array([0, 8, -9])
www.it-ebooks.info
Chapter 6
[ 137 ]
print "b\n", b
x = np.linalg.solve(A, b)
print "Solution", x
print "Check\n", np.dot(A , x)
Finding eigenvalues and eigenvectors
Eigenvalues are scalar soluons to the equaon Ax = ax, where A is a two-dimensional
matrix and x is a one-dimensional vector. Eigenvectors are vectors corresponding to
eigenvalues. The eigvals funcon in the numpy.linalg package calculates eigenvalues.
The eig funcon returns a tuple containing eigenvalues and eigenvectors.
Time for action – determining eigenvalues and eigenvectors
Let's calculate the eigenvalues of a matrix. Perform the following steps to do so:
1. Create a matrix as follows:
A = np.mat("3 -2;1 0")
print "A\n", A
The matrix we created looks like the following:
A
[[ 3 -2]
[ 1 0]]
2. Calculate eigenvalues by calling the eig funcon.
print "Eigenvalues", np.linalg.eigvals(A)
The eigenvalues of the matrix are as follows:
Eigenvalues [ 2. 1.]
3. Determine eigenvalues and eigenvectors with the eig funcon. This funcon
returns a tuple, where the rst element contains eigenvalues and the second
element contains corresponding Eigenvectors, arranged column-wise.
eigenvalues, eigenvectors = np.linalg.eig(A)
print "First tuple of eig", eigenvalues
print "Second tuple of eig\n", eigenvectors
www.it-ebooks.info
Move Further with NumPy Modules
[ 138 ]
The eigenvalues and eigenvectors will be shown as follows:
First tuple of eig [ 2. 1.]
Second tuple of eig
[[ 0.89442719 0.70710678]
[ 0.4472136 0.70710678]]
4. Check the result with the dot funcon by calculang the right- and le-hand sides
of the eigenvalues equaon Ax = ax.
for i in range(len(eigenvalues)):
print "Left", np.dot(A, eigenvectors[:,i])
print "Right", eigenvalues[i] * eigenvectors[:,i]
print
The output is as follows:
Left [[ 1.78885438]
[ 0.89442719]]
Right [[ 1.78885438]
[ 0.89442719]]
Left [[ 0.70710678]
[ 0.70710678]]
Right [[ 0.70710678]
[ 0.70710678]]
What just happened?
We found the eigenvalues and eigenvectors of a matrix with the eigvals and eig
funcons of the numpy.linalg module. We checked the result using the dot funcon
(see eigenvalues.py).
import numpy as np
A = np.mat("3 -2;1 0")
print "A\n", A
print "Eigenvalues", np.linalg.eigvals(A)
eigenvalues, eigenvectors = np.linalg.eig(A)
print "First tuple of eig", eigenvalues
print "Second tuple of eig\n", eigenvectors
for i in range(len(eigenvalues)):
print "Left", np.dot(A, eigenvectors[:,i])
print "Right", eigenvalues[i] * eigenvectors[:,i]
print
www.it-ebooks.info
Chapter 6
[ 139 ]
Singular value decomposition
Singular value decomposion is a type of factorizaon that decomposes a matrix into
a product of three matrices. The singular value decomposion is a generalizaon of the
previously discussed eigenvalue decomposion. The svd funcon in the numpy.linalg
package can perform this decomposion. This funcon returns three matrices – U, Sigma,
and V – such that U and V are orthogonal and Sigma contains the singular values of the
input matrix.
The asterisk denotes the Hermian conjugate or the conjugate transpose.
Time for action – decomposing a matrix
It's me to decompose a matrix with the singular value decomposion. In order to
decompose a matrix, perform the following steps:
1. First, create a matrix as follows:
A = np.mat("4 11 14;8 7 -2")
print "A\n", A
The matrix we created looks like the following:
A
[[ 4 11 14]
[ 8 7 -2]]
2. Decompose the matrix with the svd funcon.
U, Sigma, V = np.linalg.svd(A, full_matrices=False)
print "U"
print U
print "Sigma"
print Sigma
print "V"
print V
The result is a tuple containing the two orthogonal matrices U and V on the
le- and right-hand sides and the singular values of the middle matrix.
U
[[-0.9486833 -0.31622777]
[-0.31622777 0.9486833 ]]
www.it-ebooks.info
Move Further with NumPy Modules
[ 140 ]
Sigma
[ 18.97366596 9.48683298]
V
[[-0.33333333 -0.66666667 -0.66666667]
[ 0.66666667 0.33333333 -0.66666667]]
3. We do not actually have the middle matrix—we only have the diagonal values.
The other values are all 0. We can form the middle matrix with the diag funcon.
Mulply the three matrices. This is shown, as follows:
print "Product\n", U * np.diag(Sigma) * V
The product of the three matrices looks like the following:
Product
[[ 4. 11. 14.]
[ 8. 7. -2.]]
What just happened?
We decomposed a matrix and checked the result by matrix mulplicaon. We used
the svd funcon from the NumPy linalg module (see decomposition.py).
import numpy as np
A = np.mat("4 11 14;8 7 -2")
print "A\n", A
U, Sigma, V = np.linalg.svd(A, full_matrices=False)
print "U"
print U
print "Sigma"
print Sigma
print "V"
print V
print "Product\n", U * np.diag(Sigma) * V
www.it-ebooks.info
Chapter 6
[ 141 ]
Pseudoinverse
The Moore-Penrose pseudoinverse of a matrix can be computed with the pinv
funcon of the numpy.linalg module (visit http://en.wikipedia.org/wiki/
Moore%E2%80%93Penrose_pseudoinverse). The pseudoinverse is calculated using the
singular value decomposion. The inv funcon only accepts square matrices; the pinv
funcon does not have this restricon.
Time for action – computing the pseudo inverse of a matrix
Let's compute the pseudo inverse of a matrix. Perform the following steps to do so:
1. First, create a matrix as follows:
A = np.mat("4 11 14;8 7 -2")
print "A\n", A
The matrix we created looks like the following:
A
[[ 4 11 14]
[ 8 7 -2]]
2. Calculate the pseudoinverse matrix with the pinv funcon, as follows:
pseudoinv = np.linalg.pinv(A)
print "Pseudo inverse\n", pseudoinv
The following is the pseudoinverse:
Pseudo inverse
[[-0.00555556 0.07222222]
[ 0.02222222 0.04444444]
[ 0.05555556 -0.05555556]]
3. Mulply the original and pseudoinverse matrices.
print "Check", A * pseudoinv
What we get is not an identy matrix, but it comes close to it, as follows:
Check [[ 1.00000000e+00 0.00000000e+00]
[ 8.32667268e-17 1.00000000e+00]]
www.it-ebooks.info
Move Further with NumPy Modules
[ 142 ]
What just happened?
We computed the pseudoinverse of a matrix with the pinv funcon of the numpy.linalg
module. The check by matrix mulplicaon resulted in a matrix that is approximately an
identy matrix (see pseudoinversion.py).
import numpy as np
A = np.mat("4 11 14;8 7 -2")
print "A\n", A
pseudoinv = np.linalg.pinv(A)
print "Pseudo inverse\n", pseudoinv
print "Check", A * pseudoinv
Determinants
The determinant is a value associated with a square matrix. It is used throughout
mathemacs; for more details please visit http://en.wikipedia.org/wiki/
Determinant. For an n x n real value matrix the determinant corresponds to the scaling an
n-dimensional volume undergoes when transformed by the matrix. The posive sign of the
determinant means the volume preserves its orientaon ("clockwise" or "anclockwise"),
while a negave sign means reversed orientaon. The numpy.linalg module has a det
funcon that returns the determinant of a matrix.
Time for action – calculating the determinant of a matrix
To calculate the determinant of a matrix, perform the following steps:
1. Create the matrix as follows:
A = np.mat("3 4;5 6")
print "A\n", A
The matrix we created is shown as follows:
A
[[ 3. 4.]
[ 5. 6.]]
2. Compute the determinant with the det funcon.
print "Determinant", np.linalg.det(A)
The determinant is shown as follows:
Determinant -2.0
www.it-ebooks.info
Chapter 6
[ 143 ]
What just happened?
We calculated the determinant of a matrix with the det funcon from the numpy.linalg
module (see determinant.py).
import numpy as np
A = np.mat("3 4;5 6")
print "A\n", A
print "Determinant", np.linalg.det(A)
Fast Fourier transform
The fast Fourier transform (FFT) is an ecient algorithm to calculate the discrete Fourier
transform (DFT). FFT improves on more naïve algorithms and is of order O(NlogN). DFT has
applicaons in signal processing, image processing, solving paral dierenal equaons,
and more. NumPy has a module called fft that oers fast Fourier transform funconality.
A lot of the funcons in this module are paired; this means that, for many funcons, there is
a funcon that does the inverse operaon. For instance, the fft and ifft funcons form
such a pair.
Time for action – calculating the Fourier transform
First, we will create a signal to transform. In order to calculate the Fourier transform,
perform the following steps:
1. Create a cosine wave with 30 points, as follows:
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
2. Transform the cosine wave with the fft funcon.
transformed = np.fft.fft(wave)
3. Apply the inverse transform with the ifft funcon. It should approximately return
the original signal.
print np.all(np.abs(np.fft.ifft(transformed) - wave) < 10 ** -9)
The result is shown as follows:
True
www.it-ebooks.info
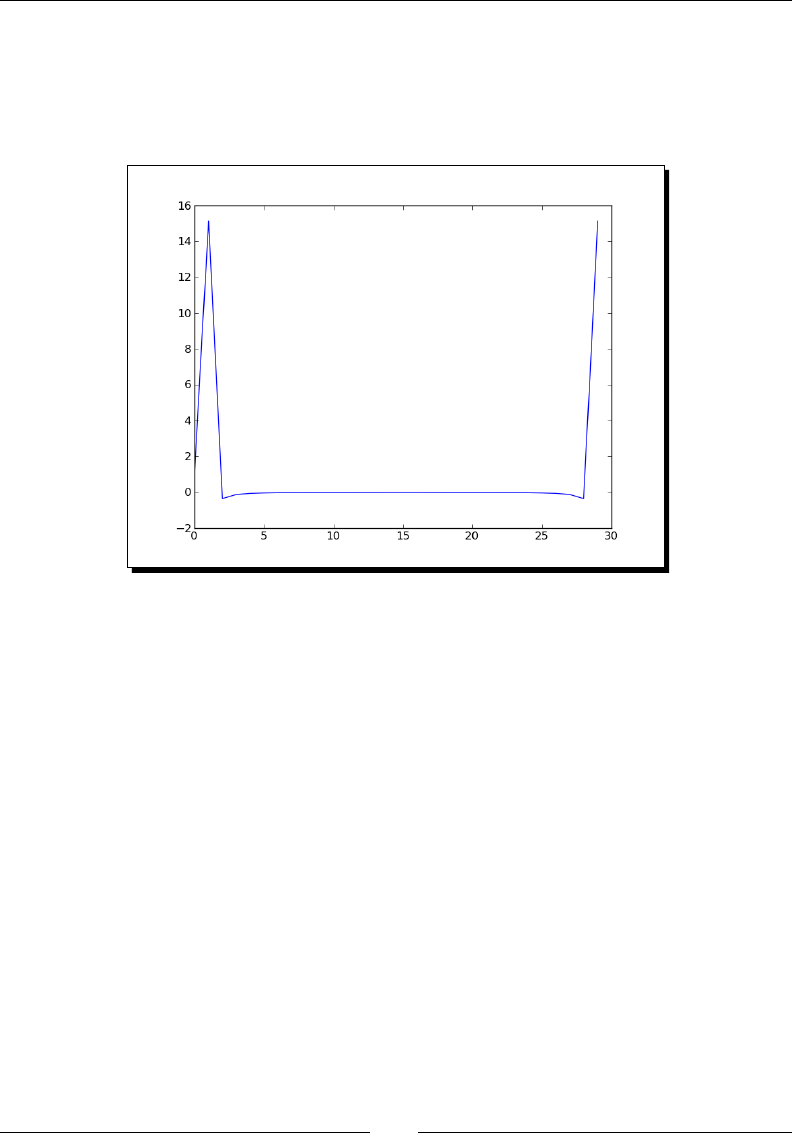
Move Further with NumPy Modules
[ 144 ]
4. Plot the transformed signal with Matplotlib.
plot(transformed)
show()
The resulng screenshot shows the fast Fourier transform:
What just happened?
We applied the fft funcon to a cosine wave. Aer applying the ifft funcon we got our
signal back (see fourier.py).
import numpy as np
from matplotlib.pyplot import plot, show
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
transformed = np.fft.fft(wave)
print np.all(np.abs(np.fft.ifft(transformed) - wave) < 10 ** -9)
plot(transformed)
show()
www.it-ebooks.info
Chapter 6
[ 145 ]
Shifting
The fftshift funcon of the numpy.linalg module shis zero-frequency components to
the center of a spectrum. The ifftshift funcon reverses this operaon.
Time for action – shifting frequencies
We will create a signal, transform it, and then shi the signal. In order to shi the
frequencies, perform the following steps:
1. Create a cosine wave with 30 points.
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
2. Transform the cosine wave with the fft funcon.
transformed = np.fft.fft(wave)
3. Shi the signal with the fftshift funcon.
shifted = np.fft.fftshift(transformed)
4. Reverse the shi with the ifftshift funcon. This should undo the shi.
print np.all((np.fft.ifftshift(shifted) - transformed) < 10 ** -9)
The result is shown as follows:
True
5. Plot the signal and transform it with Matplotlib.
plot(transformed, lw=2)
plot(shifted, lw=3)
show()
www.it-ebooks.info
Move Further with NumPy Modules
[ 146 ]
The following screenshot shows the shi in the fast Fourier transform:
What just happened?
We applied the fftshift funcon to a cosine wave. Aer applying the ifftshift
funcon, we got our signal back (see fouriershift.py).
import numpy as np
from matplotlib.pyplot import plot, show
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
transformed = np.fft.fft(wave)
shifted = np.fft.fftshift(transformed)
print np.all(np.abs(np.fft.ifftshift(shifted) - transformed) < 10 **
-9)
plot(transformed, lw=2)
plot(shifted, lw=3)
show()
www.it-ebooks.info
Chapter 6
[ 147 ]
Random numbers
Random numbers are used in Monte Carlo methods, stochasc calculus, and more. Real
random numbers are hard to generate, so in pracce we use pseudo random numbers.
Pseudo random numbers are random enough for most intents and purposes, except for
some very special cases. The funcons related to random numbers can be found in the
NumPy random module. The core random number generator is based on the Mersenne
Twister algorithm. Random numbers can be generated from discrete or connuous
distribuons. The distribuon funcons have an oponal size parameter, which tells
NumPy how many numbers to generate. You can specify either an integer or a tuple as
size. This will result in an array lled with random numbers of appropriate shape. Discrete
distribuons include the geometric, hypergeometric, and binomial distribuons.
Time for action – gambling with the binomial
The binomial distribuon models the number of successes in an integer number of
independent trials of an experiment, where the probability of success in each experiment
is a xed number.
Imagine a 17th-century gambling house where you can bet on ipping of pieces of eight.
Nine coins are ipped. If less than ve are heads, then you lose one piece of eight, otherwise
you win one. Let's simulate this, starng with 1000 coins in our possession. We will use the
binomial funcon from the random module for that purpose.
In order to understand the binomial funcon, go through the following steps:
1. Inialize an array, which represents the cash balance, to zeros. Call the binomial
funcon with a size of 10000. This represents 10,000 coin ips in our casino.
cash = np.zeros(10000)
cash[0] = 1000
outcome = np.random.binomial(9, 0.5, size=len(cash))
2. Go through the outcomes of the coin ips and update the cash array. Print
the minimum and maximum of outcome, just to make sure we don't have any
strange outliers.
for i in range(1, len(cash)):
if outcome[i] < 5:
cash[i] = cash[i - 1] - 1
elif outcome[i] < 10:
cash[i] = cash[i - 1] + 1
else:
raise AssertionError("Unexpected outcome " + outcome)
print outcome.min(), outcome.max()
www.it-ebooks.info
Move Further with NumPy Modules
[ 148 ]
As expected, the values are between 0 and 9.
0 9
3. Plot the cash array with Matplotlib.
plot(np.arange(len(cash)), cash)
show()
As you can see in the following screenshot, our cash balance performs
a random walk:
What just happened?
We did a random walk experiment using the binomial funcon from the NumPy random
module (see headortail.py).
import numpy as np
from matplotlib.pyplot import plot, show
cash = np.zeros(10000)
cash[0] = 1000
outcome = np.random.binomial(9, 0.5, size=len(cash))
for i in range(1, len(cash)):
www.it-ebooks.info
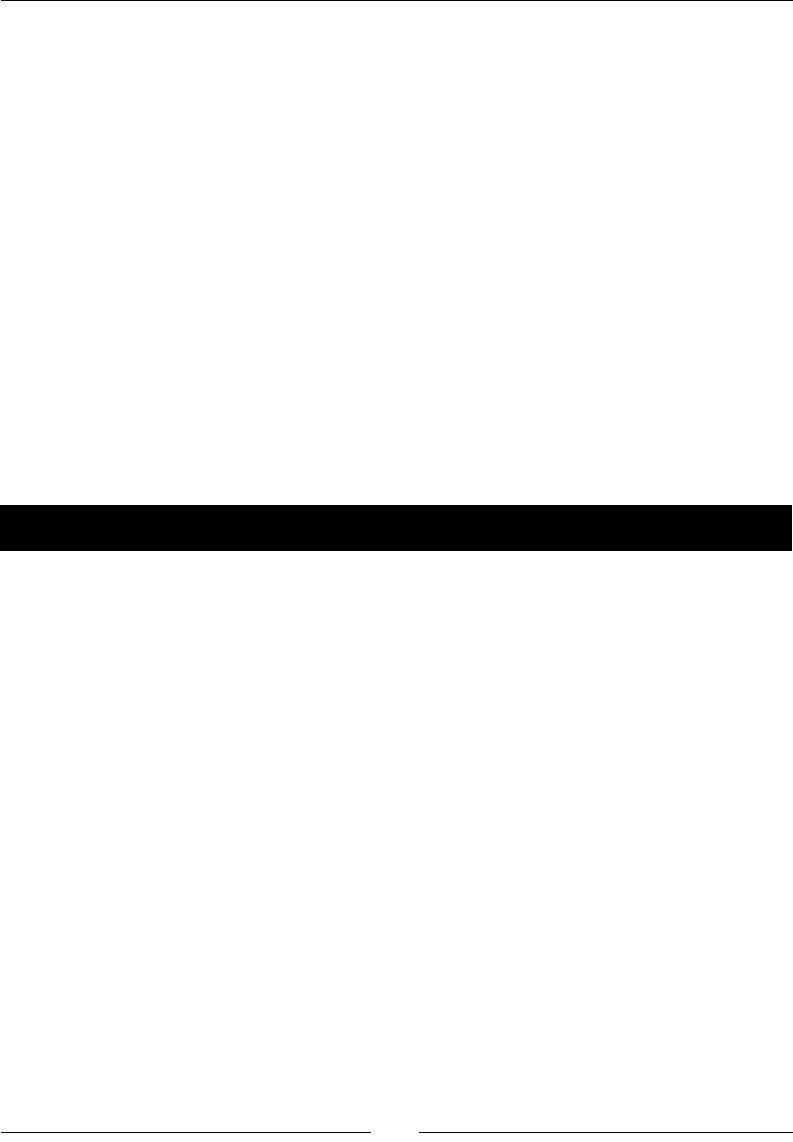
Chapter 6
[ 149 ]
if outcome[i] < 5:
cash[i] = cash[i - 1] - 1
elif outcome[i] < 10:
cash[i] = cash[i - 1] + 1
else:
raise AssertionError("Unexpected outcome " + outcome)
print outcome.min(), outcome.max()
plot(np.arange(len(cash)), cash)
show()
Hypergeometric distribution
The hypergeometric distribuon models a jar with two types of objects in it. The model
tells us how many objects of one type we can get if we take a specied number of items
out of the jar without replacing them. The NumPy random module has a hypergeometric
funcon that simulates this situaon.
Time for action – simulating a game show
Imagine a game show where every me the contestants answer a queson correctly, they
get to pull three balls from a jar and then put them back. Now there is a catch, there is
one ball in there that is bad. Every me it is pulled out, the contestants lose six points. If
however, they manage to get out three of the 25 normal balls, they get one point. So, what
is going to happen if we have 100 quesons in total? In order to get a soluon for this, go
through the following steps:
1. Inialize the outcome of the game with the hypergeometric funcon. The rst
parameter of this funcon is the number of ways to make a good selecon, the
second parameter is the number of ways to make a bad selecon, and the third
parameter is the number of items sampled.
points = np.zeros(100)
outcomes = np.random.hypergeometric(25, 1, 3, size=len(points))
2. Set the scores based on the outcomes from the previous step.
for i in range(len(points)):
if outcomes[i] == 3:
points[i] = points[i - 1] + 1
elif outcomes[i] == 2:
points[i] = points[i - 1] - 6
else:
print outcomes[i]
www.it-ebooks.info
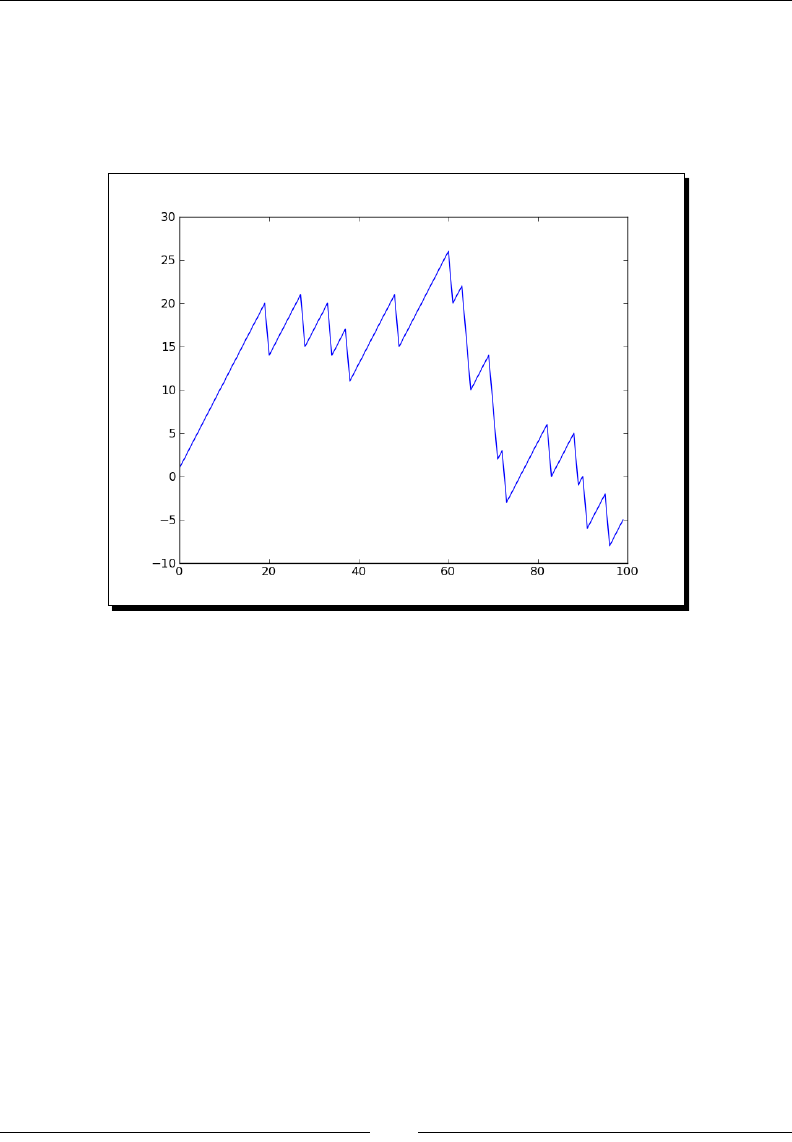
Move Further with NumPy Modules
[ 150 ]
3. Plot the points array with Matplotlib.
plot(np.arange(len(points)), points)
show()
The following screenshot shows how the scoring evolved:
What just happened?
We simulated a game show using the hypergeometric funcon from the NumPy random
module. The game scoring depends on how many good and how many bad balls are pulled
out of a jar in each session (see urn.py).
import numpy as np
from matplotlib.pyplot import plot, show
points = np.zeros(100)
outcomes = np.random.hypergeometric(25, 1, 3, size=len(points))
for i in range(len(points)):
if outcomes[i] == 3:
points[i] = points[i - 1] + 1
elif outcomes[i] == 2:
points[i] = points[i - 1] - 6
else:
print outcomes[i]
www.it-ebooks.info
Chapter 6
[ 151 ]
plot(np.arange(len(points)), points)
show()
Continuous distributions
Connuous distribuons are modeled by the probability density funcons (pdf).
The probability for a certain interval is determined by integraon of the probability
density funcon. The NumPy random module has a number of funcons that represent
connuous distribuons—beta, chisquare, exponential, f, gamma, gumbel,
laplace, lognormal, logistic, multivariate_normal, noncentral_chisquare,
noncentral_f, normal, and others.
Time for action – drawing a normal distribution
Random numbers can be generated from a normal distribuon and their distribuon may be
visualized with a histogram. To draw a normal distribuon, perform the following steps:
1. Generate random numbers for a given sample size using the normal funcon from
the random NumPy module.
N=10000
normal_values = np.random.normal(size=N)
2. Draw the histogram and theorecal pdf: Draw the histogram and theorecal pdf
with a center value of 0 and standard deviaon of 1. We will use Matplotlib for
this purpose.
dummy, bins, dummy = plt.hist(normal_values,
np.sqrt(N), normed=True, lw=1)
sigma = 1
mu = 0
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi))
* np.exp( - (bins - mu)**2 / (2 * sigma**2) ),lw=2)
plt.show()
www.it-ebooks.info
Move Further with NumPy Modules
[ 152 ]
In the following screenshot, we see the familiar bell curve:
What just happened?
We visualized the normal distribuon using the normal funcon from the random NumPy
module. We did this by drawing the bell curve and a histogram of randomly generated values
(see normaldist.py).
import numpy as np
import matplotlib.pyplot as plt
N=10000
normal_values = np.random.normal(size=N)
dummy, bins, dummy = plt.hist(normal_values, np.sqrt(N), normed=True,
lw=1)
sigma = 1
mu = 0
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins -
mu)**2 / (2 * sigma**2) ),lw=2)
plt.show()
www.it-ebooks.info
Chapter 6
[ 153 ]
Lognormal distribution
A lognormal distribuon is a distribuon of a variable whose natural logarithm is normally
distributed. The lognormal funcon of the random NumPy module models this distribuon.
Time for action – drawing the lognormal distribution
Let's visualize the lognormal distribuon and its probability density funcon with
a histogram. Perform the following steps:
1. Generate random numbers using the normal funcon from the random
NumPy module.
N=10000
lognormal_values = np.random.lognormal(size=N)
2. Draw the histogram and theorecal pdf: Draw the histogram and theorecal pdf
with a center value of 0 and standard deviaon of 1. We will use Matplotlib for
this purpose.
dummy, bins, dummy = plt.hist(lognormal_values,
np.sqrt(N), normed=True, lw=1)
sigma = 1
mu = 0
x = np.linspace(min(bins), max(bins), len(bins))
pdf = np.exp(-(numpy.log(x) - mu)**2 / (2 * sigma**2))/ (x *
sigma * np.sqrt(2 * np.pi))
plt.plot(x, pdf,lw=3)
plt.show()
The t of the histogram and theorecal pdf is excellent, as you can see in the
following screenshot:
www.it-ebooks.info
Move Further with NumPy Modules
[ 154 ]
What just happened?
We visualized the lognormal distribuon using the lognormal funcon from the random
NumPy module. We did this by drawing the curve of the theorecal probability density
funcon and a histogram of randomly generated values (see lognormaldist.py).
import numpy as np
import matplotlib.pyplot as plt
N=10000
lognormal_values = np.random.lognormal(size=N)
dummy, bins, dummy = plt.hist(lognormal_values, np.sqrt(N),
normed=True, lw=1)
sigma = 1
mu = 0
x = np.linspace(min(bins), max(bins), len(bins))
pdf = np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))/ (x * sigma *
np.sqrt(2 * np.pi))
plt.plot(x, pdf,lw=3)
plt.show()
Summary
We learned a lot in this chapter about NumPy modules. We covered linear algebra,
the fast Fourier transform, connuous and discrete distribuons, and random numbers.
In the next chapter, we shall cover specialized rounes. These are funcons that you
probably would not use oen, but are very useful when you do need them.
www.it-ebooks.info
Peeking into Special Routines
As NumPy users, we sometimes find ourselves having special needs for instance
financial calculations or signal processing. Fortunately, NumPy provides for
most of our needs. This chapter describes some of the more specialized NumPy
functions.
In this chapter we will cover the following topics:
Sorng and searching
Special funcons
Financial ulies
Window funcons
Sorting
NumPy has several data sorng rounes, as follows:
The sort funcon returns a sorted array
The lexsort funcon performs sorng with a list of keys
The argsort funcon returns the indices that would sort an array
The ndarray class has a sort method that performs place sorng
The msort funcon sorts an array along the rst axis
The sort_complex funcon sorts complex numbers by their real part
and then their imaginary part
From this list argsort and sort are available as methods on NumPy arrays as well.
7
www.it-ebooks.info
Peeking into Special Rounes
[ 156 ]
Time for action – sorting lexically
The NumPy lexsort funcon returns an array of indices of the input array elements
corresponding to lexically sorng an array. We need to give the funcon an array or tuple
of sort keys. Perform the following steps:
1. Now for something completely dierent, let's go back to Chapter 3, Get to Terms
with Commonly Used Funcons. In that chapter we used stock price data of AAPL.
This is by now prey old data. We will load the close prices and the always complex
dates. In fact, we will need a converter funcon just for the dates.
def datestr2num(s):
return datetime.datetime.strptime
(s, "%d-%m-%Y").toordinal()
dates,closes=np.loadtxt('AAPL.csv', delimiter=',',
usecols=(1, 6), converters={1:datestr2num}, unpack=True)
2. Sort the names lexically with the lexsort funcon. The data is already sorted
by date, but we will now sort it by close as well.
indices = np.lexsort((dates, closes))
print "Indices", indices
print ["%s %s" % (datetime.date.fromordinal(dates[i]),
closes[i]) for i in indices]
The code prints the following:
['2011-01-28 336.1', '2011-02-22 338.61', '2011-01-31 339.32',
'2011-02-23 342.62', '2011-02-24 342.88', '2011-02-03 343.44',
'2011-02-02 344.32', '2011-02-01 345.03', '2011-02-04 346.5',
'2011-03-10 346.67', '2011-02-25 348.16', '2011-03-01 349.31',
'2011-02-18 350.56', '2011-02-07 351.88', '2011-03-11 351.99',
'2011-03-02 352.12', '2011-03-09 352.47', '2011-02-28 353.21',
'2011-02-10 354.54', '2011-02-08 355.2', '2011-03-07 355.36',
'2011-03-08 355.76', '2011-02-11 356.85', '2011-02-09 358.16',
'2011-02-17 358.3', '2011-02-14 359.18', '2011-03-03 359.56',
'2011-02-15 359.9', '2011-03-04 360.0', '2011-02-16 363.13']
What just happened?
We sorted the close prices of AAPL lexically using the NumPy lexsort funcon.
The funcon returned the indices corresponding with sorng the array (see lex.py).
import numpy as np
import datetime
www.it-ebooks.info
Chapter 7
[ 157 ]
def datestr2num(s):
return datetime.datetime.strptime(s, "%d-%m-%Y").toordinal()
dates,closes=np.loadtxt('AAPL.csv', delimiter=',', usecols=(1, 6),
converters={1:datestr2num}, unpack=True)
indices = np.lexsort((dates, closes))
print "Indices", indices
print ["%s %s" % (datetime.date.fromordinal(int(dates[i])),
closes[i]) for i in indices]
Have a go hero – trying a different sort order
We sorted using the dates, close price sort order. Try a dierent order. Generate random
numbers using the random module we learned about in the previous chapter and sort those
using lexsort.
Complex numbers
Complex numbers are numbers that have a real and imaginary part. As you remember from
previous chapters, NumPy has special complex data types that represent complex numbers
by two oang point numbers. These numbers can be sorted using the NumPy sort_
complex funcon. This funcon sorts the real part rst and then the imaginary part.
Time for action – sorting complex numbers
We will create an array of complex numbers and sort it. Perform the following steps to do so:
1. Generate ve random numbers for the real part of the complex numbers and ve
numbers for the imaginary part. Seed the random generator to 42.
np.random.seed(42)
complex_numbers = np.random.random(5) + 1j * np.random.random(5)
print "Complex numbers\n", complex_numbers
2. Call the sort_complex funcon to sort the complex numbers we generated in the
previous step.
print "Sorted\n", np.sort_complex(complex_numbers)
The sorted numbers would be shown as follows:
Sorted
[ 0.39342751+0.34955771j 0.40597665+0.77477433j
0.41516850+0.26221878j
0.86631422+0.74612422j 0.92293095+0.81335691j]
www.it-ebooks.info
Peeking into Special Rounes
[ 158 ]
What just happened?
We generated random complex numbers and sorted them using the sort_complex
funcon (see sortcomplex.py).
import numpy as np
np.random.seed(42)
complex_numbers = np.random.random(5) + 1j * np.random.random(5)
print "Complex numbers\n", complex_numbers
print "Sorted\n", np.sort_complex(complex_numbers)
Pop quiz – generating random numbers
Q1. Which NumPy module deals with random numbers?
1. Randnum
2. random
3. randomutil
4. rand
Searching
NumPy has several funcons that can search through arrays, as follows:
The argmax funcon gives the indices of the maximum values of an array.
>>> a = np.array([2, 4, 8])
>>> np.argmax(a)
2
The nanargmax funcon does the same but ignores NaN values.
>>> b = np.array([np.nan, 2, 4])
>>> np.nanargmax(b)
2
The argmin and nanargmin funcons provide similar funconality but pertaining
to minimum values.
www.it-ebooks.info
Chapter 7
[ 159 ]
The argwhere funcon searches for non-zero values and returns the corresponding
indices grouped by element.
>>> a = np.array([2, 4, 8])
>>> np.argwhere(a <= 4)
array([[0],
[1]])
The searchsorted funcon tells you the index in an array where a specied
value could be inserted to maintain the sort order. It uses binary search, which is
a O(log n) algorithm. We will see this funcon in acon shortly.
The extract funcon retrieves values from an array based on a condion.
Time for action – using searchsorted
The searchsorted funcon allows us to get the index of a value in a sorted array, where
it could be inserted so that the array remains sorted. An example should make this clear.
Perform the following steps:
1. To demonstrate we will need an array that is sorted. Create an array with arange,
which of course is sorted.
a = np.arange(5)
2. It's me to call the searchsorted funcon.
indices = np.searchsorted(a, [-2, 7])
print "Indices", indices
The following are the indices which should maintain the sort order:
Indices [0 5]
3. Let's construct the full array with the insert funcon.
print "The full array", np.insert(a, indices, [-2, 7])
This gives us the full array:
The full array [-2 0 1 2 3 4 7]
www.it-ebooks.info
Peeking into Special Rounes
[ 160 ]
What just happened?
The searchsorted funcon gave us indices 5 and 0 for 7 and -2. With these indices,
we would make the array [-2, 0, 1, 2, 3, 4, 7]—so the array remains sorted
(see sortedsearch.py).
import numpy as np
a = np.arange(5)
indices = np.searchsorted(a, [-2, 7])
print "Indices", indices
print "The full array", np.insert(a, indices, [-2, 7])
Array elements' extraction
The NumPy extract funcon allows us to extract items from an array based on a condion.
This funcon is similar to the where funcon we encountered in Chapter 3, Get to Terms
with Commonly Used Funcons. The special nonzero funcon selects non-zero elements.
Time for action – extracting elements from an array
Let's extract the even elements from an array. Perform the following steps to do so:
1. Create the array with the arange funcon.
a = np.arange(7)
2. Create the condion that selects the even elements.
condition = (a % 2) == 0
3. Extract the even elements based on our condion with the extract funcon.
print "Even numbers", np.extract(condition, a)
This gives us the even numbers, as required:
Even numbers [0 2 4 6]
4. Select non-zero values with the nonzero funcon.
print "Non zero", np.nonzero(a)
This prints all the non-zero values of the array, as follows:
Non zero (array([1, 2, 3, 4, 5, 6]),)
www.it-ebooks.info
Chapter 7
[ 161 ]
What just happened?
We extracted the even elements from an array based on a Boolean condion with the
NumPy extract funcon (see extracted.py).
import numpy as np
a = np.arange(7)
condition = (a % 2) == 0
print "Even numbers", np.extract(condition, a)
print "Non zero", np.nonzero(a)
Financial functions
NumPy has a number of nancial funcons, as follows:
The fv funcon calculates the so-called future value. The future value gives the
value of a nancial instrument at a future date, based on certain assumpons.
The pv funcon computes the present value. The present value is the value of an
asset today.
The npv funcon returns the net present value. The net present value is dened as
the sum of all the present value cash ows.
The pmt funcon computes the payment against loan principal plus interest.
The irr funcon calculates the internal rate of return. The internal rate of return is
the eecve interested rate, which does not take into account inaon.
The mirr funcon calculates the modied internal rate of return. The modied
internal rate of return is an improved version of the internal rate of return.
The nper funcon returns the number of periodic payments.
The rate funcon calculates the rate of interest.
Time for action – determining future value
The future value gives the value of a nancial instrument at a future date, based on certain
assumpons. The future value depends on four parameters—the interest rate, the number
of periods, a periodic payment, and the present value. In this tutorial, let's take an interest
rate of three percent, quarterly payments of 10 for 5 years and present value of 1,000.
Call the fv funcon with the appropriate values to calculate the future value.
print "Future value", np.fv(0.03/4, 5 * 4, -10, -1000)
www.it-ebooks.info
Peeking into Special Rounes
[ 162 ]
The future value is as follows:
Future value 1376.09633204
This corresponds with saving for 10 years, with quarterly addional savings of 10 at an
interest rate of three percent. If we vary the number of years and if we save and keep the
other parameters constant, we will get following plot:
What just happened?
We calculated the future value using the NumPy fv funcon starng with a present value of
1,000; interest rate of three percent; and quarterly payments of 10 for 5 years. We ploed
the future value for various saving periods (see futurevalue.py).
import numpy as np
from matplotlib.pyplot import plot, show
print "Future value", np.fv(0.03/4, 5 * 4, -10, -1000)
fvals = []
for i in xrange(1, 10):
fvals.append(np.fv(.03/4, i * 4, -10, -1000))
plot(fvals, 'bo')
show()
www.it-ebooks.info
Chapter 7
[ 163 ]
Present value
The present value is the value of an asset today. The NumPy pv funcon can calculate the
present value. This funcon mirrors the fv funcon and requires the interest rate, number
of periods, and the periodic payment as well, but here we start with the future value.
Time for action – getting the present value
Let's reverse—compute the present value with numbers from the previous tutorial.
Plug in the gures from the Time for acon – determining future value tutorial to calculate
the present value.
print "Present value", np.pv(0.03/4, 5 * 4, -10, 1376.09633204)
This gives us 1,000 as expected apart from a ny numerical error. Actually, it is not an error
but a representaon issue. We are dealing here with outgoing cash ow, that is the reason
for the negave value.
Present value -999.999999999
What just happened?
We did the reverse computaon of the previous Time for acon tutorial to get the present
value from the future value. This was done with the NumPy pv funcon.
Net present value
The net present value is dened as the sum of all the present value cash ows.
The NumPy npv funcon returns the net present value of cash ows. The funcon
requires two arguments, the rate and an array represenng the cash ows.
Time for action – calculating the net present value
We will calculate the net present value for a randomly generated cash ow series. Perform
the following steps to do so:
1. Generate ve random values for the cash ow series. Insert -100 as the start value.
cashflows = np.random.randint(100, size=5)
cashflows = np.insert(cashflows, 0, -100)
print "Cashflows", cashflows
www.it-ebooks.info
Peeking into Special Rounes
[ 164 ]
The cash ows would be shown as follows:
Cashflows [-100 38 48 90 17 36]
2. Call the npv funcon to calculate the net present value from the cash ow series we
generated in the previous step. Use a rate of three percent.
print "Net present value", np.npv(0.03, cashflows)
The net present value would be shown as follows:
Net present value 107.435682443
What just happened?
We computed the net present value from a randomly generated cash ow series with the
NumPy npv funcon (see netpresentvalue.py).
import numpy as np
cashflows = np.random.randint(100, size=5)
cashflows = np.insert(cashflows, 0, -100)
print "Cashflows", cashflows
print "Net present value", np.npv(0.03, cashflows)
Internal rate of return
The internal rate of return is the eecve interest rate, which does not take into
account inaon. The NumPy irr funcon returns the internal rate of return for
a given cash ow series.
Time for action – determining the internal rate of return
Let's reuse the cash ow series from the Time for acon – calculang the net present
value tutorial.
Call the irr funcon with the cash ow series from the previous Time for acon tutorial.
print "Internal rate of return", np.irr([-100, 38, 48, 90,
17, 36])
The internal rate of return would be shown as follows:
Internal rate of return 0.373420226888
www.it-ebooks.info
Chapter 7
[ 165 ]
What just happened?
We calculated the internal rate of return from the cash ow series of the previous Time for
acon tutorial. The value was given by the NumPy irr funcon.
Periodic payments
The NumPy pmt funcon allows you to compute periodic payments for a loan based on an
interest rate and the number of periodic payments.
Time for action – calculating the periodic payments
Suppose you have a loan of 1 million with interest rate of 10 percent. You have 30 years to
pay the loan back. How much do you have to pay each month? Let's nd out.
Call the pmt funcon with the values menoned previously.
print "Payment", np.pmt(0.01/12, 12 * 30, 10000000)
The monthly payment would be shown as follows:
Payment -32163.9520447
What just happened?
We calculated the monthly payment for a loan of 1 million at an annual rate of 10 percent.
Given that we have 30 years to repay the loan, the pmt funcon tells us that we need to pay
32,163.9520447 per month.
Number of payments
The NumPy nper funcon tells us how many periodic payments are necessary to pay o a
loan. The required parameters are the interest rate of the loan, the xed amount periodic
payment, and the present value.
Time for action – determining the number of periodic payments
Consider a loan of 9,000 at a rate of 10 percent with xed monthly payments of 100.
Find out how many payments are required with the NumPy nper funcon.
print "Number of payments", np.nper(0.10/12, -100, 9000)
www.it-ebooks.info
Peeking into Special Rounes
[ 166 ]
The number of payments would be shown as follows:
Number of payments 167.047511801
What just happened?
We determined the number of payments needed to pay o a loan of 9,000 with an interest
rate of 10 percent and monthly payments of 100. The number of payments returned was 167.
Interest rate
The NumPy rate funcon calculates the interest rate given the number of periodic
payments, the payment amount or amounts, and the present value and future value.
Time for action – guring out the rate
Let's take the values from the Time for acon – determining the number of periodic
payments tutorial and reverse compute the interest rate from the other parameters.
Fill in the numbers from the previous Time for acon tutorial.
print "Interest rate", 12 * np.rate(167, -100, 9000, 0)
The interest rate is approximately 10 percent, as expected.
Interest rate 0.0999756420664
What just happened?
We used the NumPy rate funcon and the values from the previous Time for acon tutorial
to compute the interest rate of the loan. Ignoring the rounding errors we got the inial 10
percent we started with.
Window functions
Window funcons are mathemacal funcons commonly used in signal processing.
Applicaons include spectral analysis and lter design. These funcons are dened to be 0
outside a specied domain. NumPy has a number of window funcons such as bartlett,
blackman, hamming, hanning, and kaiser. An example of the hanning funcon can be
found in Chapter 4, Convenience Funcons for Your Convenience and Chapter 3, Get to Terms
with Commonly Used Funcons.
www.it-ebooks.info
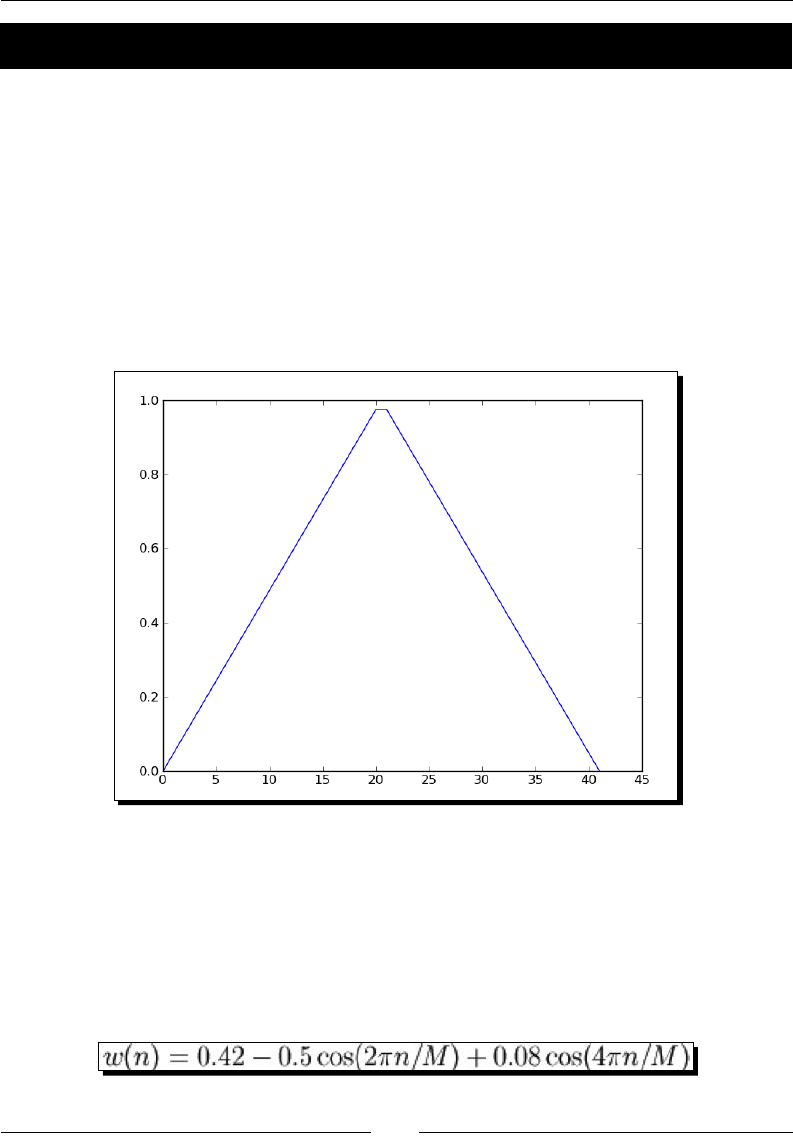
Chapter 7
[ 167 ]
Time for action – plotting the Bartlett window
The Bartle window is a triangular smoothing window. Perform the following steps to plot
the Bartle window:
1. Call the NumPy bartlett funcon to calculate the Bartle window.
window = np.bartlett(42)
2. Plot the Bartle window with Matplotlib, which is very easy.
plot(window)
show()
The following is the Bartle window, which is triangular, as expected:
What just happened?
We ploed the Bartle window with the NumPy bartlett funcon.
Blackman window
The Blackman window is formed by summing the rst three terms of cosines, as follows:
www.it-ebooks.info
Peeking into Special Rounes
[ 168 ]
The NumPy blackman funcon returns the Blackman window. The only parameter is the
number of points in the output window. If this number is 0 or less than 0, an empty array
is returned.
Time for action – smoothing stock prices with the Blackman
window
Let's smooth the close prices from the small AAPL stock prices data le. Perform the
following steps to do so:
1. Load the data into a NumPy array. Call the NumPy blackman funcon to form
a window and then use this window to smooth the price signal.
closes=np.loadtxt('AAPL.csv', delimiter=',', usecols=(6,),
converters={1:datestr2num}, unpack=True)
N = int(sys.argv[1])
window = np.blackman(N)
smoothed = np.convolve(window/window.sum(),
closes, mode='same')
2. Plot the smoothed prices with Matplotlib. We will omit the rst ve and the last
ve data points in this example. The reason for this is that there is a strong
boundary eect.
plot(smoothed[N:-N], lw=2, label="smoothed")
plot(closes[N:-N], label="closes")
legend(loc='best')
show()
The closing prices of AAPL smoothed with the Blackman window should appear,
as follows:
www.it-ebooks.info
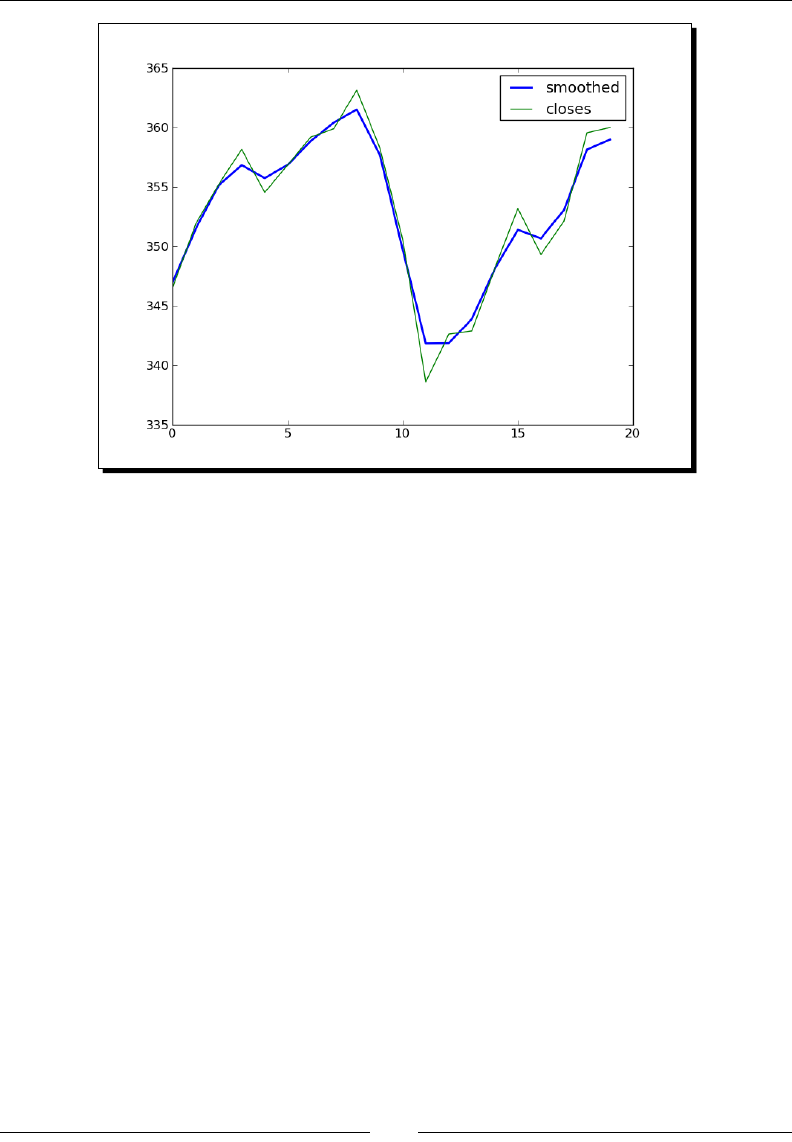
Chapter 7
[ 169 ]
What just happened?
We ploed the closing price of AAPL from our sample data le that was smoothed using
the Blackman window with the NumPy blackman funcon (see plot_blackman.py).
import numpy as np
from matplotlib.pyplot import plot, show, legend
from matplotlib.dates import datestr2num
import sys
closes=np.loadtxt('AAPL.csv', delimiter=',', usecols=(6,),
converters={1:datestr2num}, unpack=True)
N = int(sys.argv[1])
window = np.blackman(N)
smoothed = np.convolve(window/window.sum(), closes, mode='same')
plot(smoothed[N:-N], lw=2, label="smoothed")
plot(closes[N:-N], label="closes")
legend(loc='best')
show()
www.it-ebooks.info
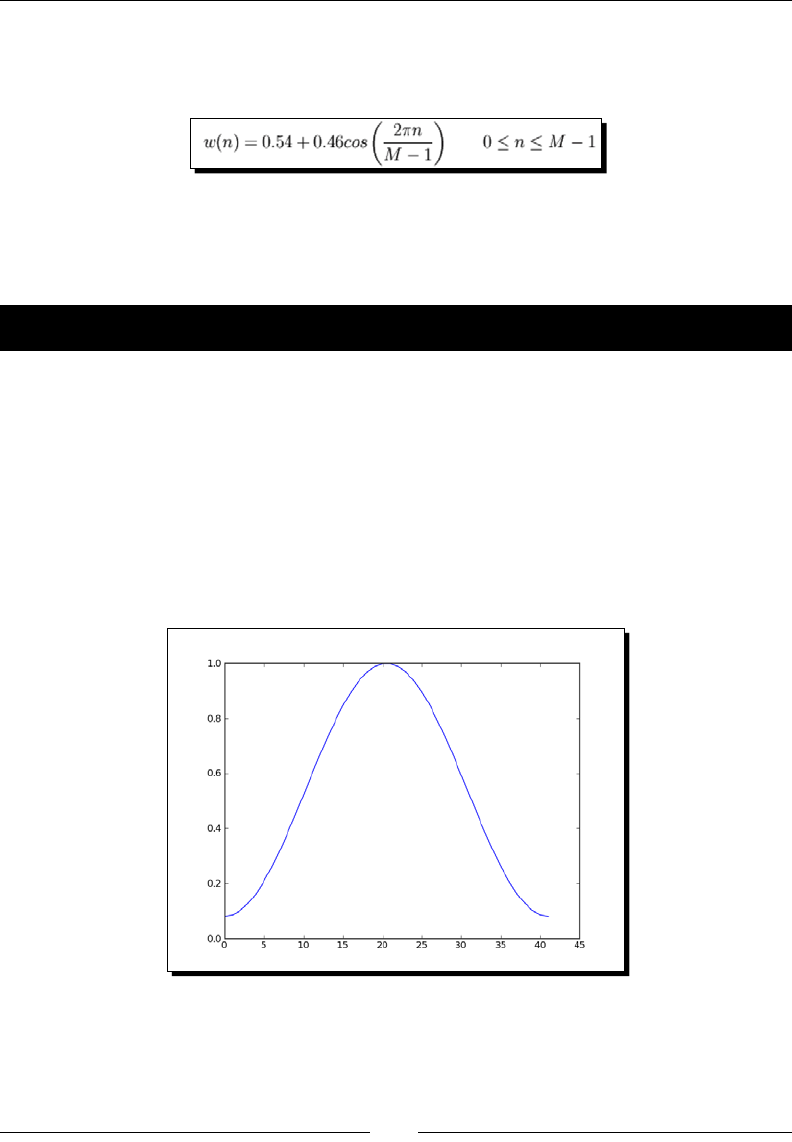
Peeking into Special Rounes
[ 170 ]
Hamming window
The Hamming window is formed by a weighted cosine. The formula is as follows:
The NumPy hamming funcon returns the Hamming window. The only parameter is the
number of points in the output window. If this number is 0 or less than 0, an empty array
is returned.
Time for action – plotting the Hamming window
Let's plot the Hamming window. Perform the following steps to do so:
1. Call the NumPy hamming funcon to calculate the Hamming window.
window = np.hamming(42)
2. Plot the window with Matplotlib.
plot(window)
show()
The Hamming window plot is shown as follows:
What just happened?
We ploed the Hamming window with the NumPy hamming funcon.
www.it-ebooks.info
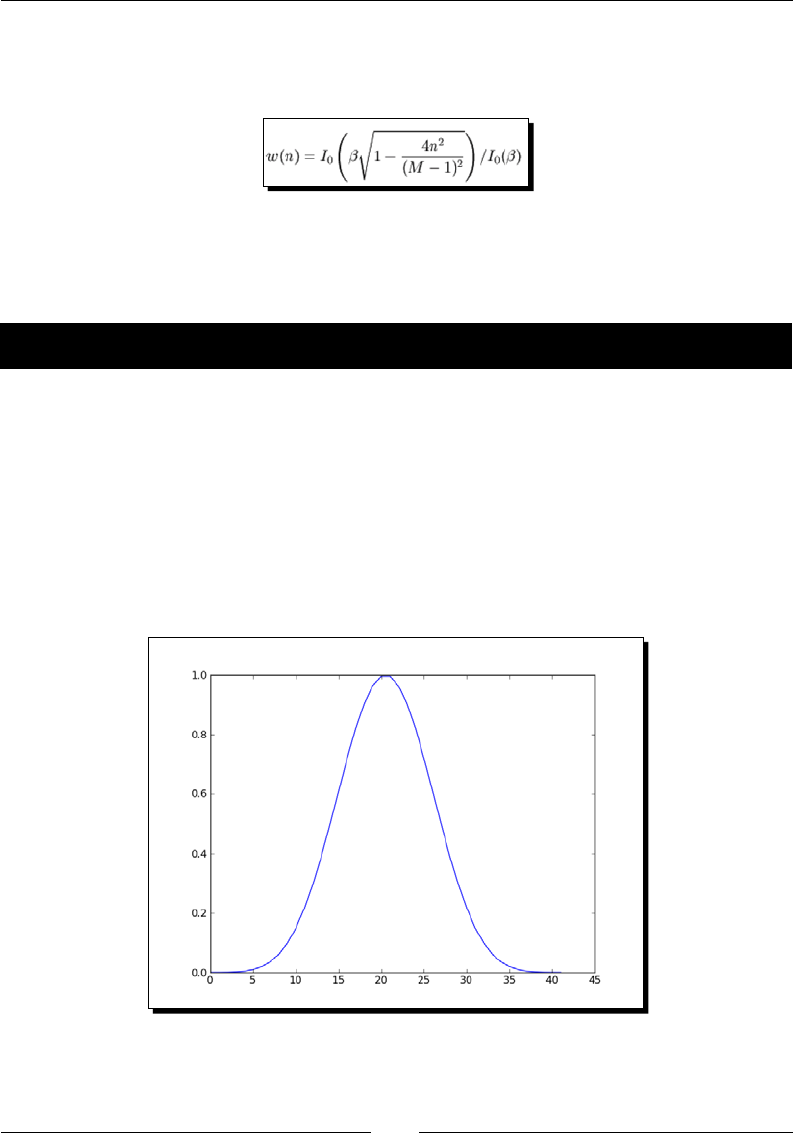
Chapter 7
[ 171 ]
Kaiser window
The Kaiser window is formed by the Bessel funcon. The formula is as follows:
Here I0 is the zero order Bessel funcon The NumPy kaiser funcon returns the Kaiser
window. The rst parameter is the number of points in the output window. If this number
is 0 or less than 0, an empty array is returned. The second parameter is the beta.
Time for action – plotting the Kaiser window
Let's plot the Kaiser window. Perform the following steps to do so:
1. Call the NumPy kaiser funcon to calculate the Kaiser window.
window = np.kaiser(42, 14)
2. Plot the window with Matplotlib.
plot(window)
show()
The Kaiser window would appear as follows:
www.it-ebooks.info
Peeking into Special Rounes
[ 172 ]
What just happened?
We ploed the Hamming window with the NumPy kaiser funcon.
Special mathematical functions
We will end this chapter with some special mathemacal funcons. Bessel funcons are
soluons of the Bessel dierenal equaons (visit http://en.wikipedia.org/wiki/
Bessel_function). The modied Bessel funcon of the rst kind 0th order is represented
in NumPy by i0. The sinc funcon is represented in NumPy by a funcon with the same
name and there is also a two-dimensional version of this funcon. sinc is a trigonometric
funcon; for more details visit http://en.wikipedia.org/wiki/Sinc_function.
Time for action – plotting the modied Bessel function
Let's see what the modied Bessel funcon of the rst kind 0th order looks like:
1. Compute evenly spaced values with the NumPy linspace funcon.
x = np.linspace(0, 4, 100)
2. Call the NumPy i0 funcon to calculate the funcon values.
vals = np.i0(x)
3. Plot the modied Bessel funcon with Matplotlib.
plot(x, vals)
show()
The modied Bessel funcon would have the following output:
www.it-ebooks.info
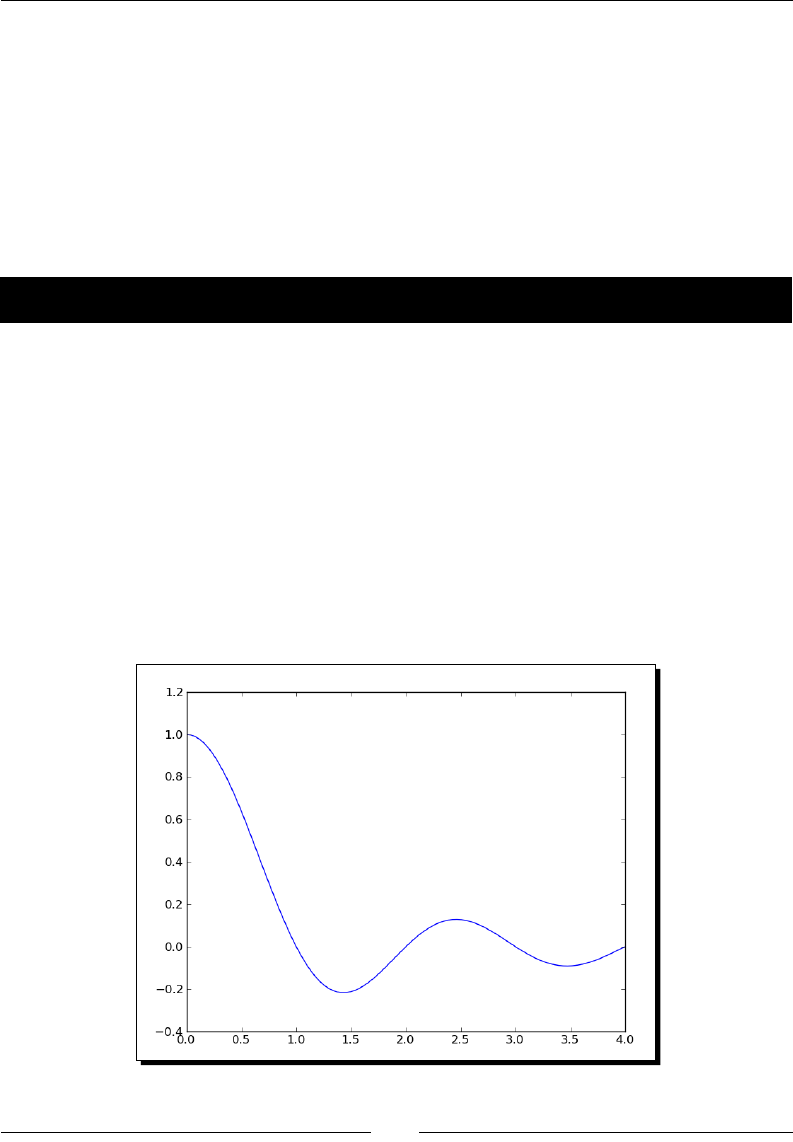
Chapter 7
[ 173 ]
What just happened?
We ploed the modied Bessel funcon of the rst kind 0th order with the
NumPy i0 funcon.
sinc
The sinc funcon is widely used in Mathemacs and signal processing. NumPy has a
funcon with the same name. A two-dimensional funcon exists as well.
Time for action – plotting the sinc function
We will plot the sinc funcon. Perform the following steps to do so:
1. Compute evenly spaced values with the NumPy linspace funcon.
x = np.linspace(0, 4, 100)
2. Call the NumPy sinc funcon to compute the funcon values.
vals = np.sinc(x)
3. Plot the sinc funcon with Matplotlib.
plot(x, vals)
show()
The sinc funcon would have the following output:
www.it-ebooks.info
Peeking into Special Rounes
[ 174 ]
The sinc2d funcon requires a two-dimensional array. We can create it with the
outer funcon resulng in the following plot:
What just happened?
We ploed the well-known sinc funcon with the NumPy sinc funcon
(see plot_sinc.py).
import numpy as np
from matplotlib.pyplot import plot, show
x = np.linspace(0, 4, 100)
vals = np.sinc(x)
plot(x, vals)
show()
We did the same for two dimensions (see sinc2d.py).
import numpy as np
from matplotlib.pyplot import imshow, show
x = np.linspace(0, 4, 100)
xx = np.outer(x, x)
vals = np.sinc(xx)
imshow(vals)
show()
www.it-ebooks.info
Chapter 7
[ 175 ]
Summary
This was a special chapter covering some of the more special NumPy topics. We covered
sorng and searching, special funcons, nancial ulies, and window funcons.
The next chapter will be about the very important subject of tesng.
www.it-ebooks.info
www.it-ebooks.info
Assure Quality with Testing
Some programmers test only in production. If you are not one of them you're
probably familiar with the concept of unit testing. Unit tests are automated
tests written by a programmer to test his or her code. These tests could, for
example, test a function or part of a function in isolation. Only a small unit of
code is tested by each test. The benefits are increased confidence in the quality
of the code, reproducible tests, and as a side effect, more clear code.
Python has good support for unit testing. Additionally, NumPy adds the numpy.
testing package to that for NumPy code unit testing.
Test driven development (TDD) is one of the most important things that happened to
soware development. TDD focuses a lot on automated unit tesng. The goal is to test
automacally as much as possible of the code. The next me the code is changed we can
run the tests and catch potenal regressions. In other words funconality already present
will sll work.
This chapter's topics include:
Unit tesng
Asserts
Floang point precision
8
www.it-ebooks.info
Assure Quality with Tesng
[ 178 ]
Assert functions
Unit tests usually use funcons, which assert something as part of the test. When
doing numerical calculaons, oen we have the fundamental issue of trying to compare
oang-point numbers that are almost equal. For integers, comparison is a trivial operaon,
but for oang-point numbers it is not because of the inexact representaon by computers.
The numpy.testing package has a number of ulity funcons that test whether a
precondion is true or not, taking into account the problem of oang-point comparisons:
Function Description
assert_almost_equal Raises an exception if two numbers are not equal up to a
specified precision
assert_approx_equal Raises an exception if two numbers are not equal up to a
certain significance
assert_array_almost_equal Raises an exception if two arrays are not equal up to a
specified precision
assert_array_equal Raises an exception if two arrays are not equal
assert_array_less Raises an exception if two arrays do not have the same
shape and the elements of the first array are strictly less
than the elements of the second array
assert_equal Raises an exception if two objects are not equal
assert_raises Fails if a specified exception is not raised by a callable
invoked with defined arguments
assert_warns Fails if a specified warning is not thrown
assert_string_equal Asserts that two strings are equal
assert_allclose Raise an assertion if two objects are not equal up to
desired tolerance
Time for action – asserting almost equal
Imagine that you have two numbers that are almost equal. Let's use the assert_almost_
equal funcon to check whether they are equal:
1. Call the funcon with low precision (up to seven decimal places):
print "Decimal 6", np.testing.assert_almost_equal(0.123456789,
0.123456780, decimal=7)
Note that no excepon is raised, as you can see in the following result:
Decimal 6 None
www.it-ebooks.info
Chapter 8
[ 179 ]
2. Call the funcon with higher precision (up to eight decimal places):
print "Decimal 7", np.testing.assert_almost_equal(0.123456789,
0.123456780, decimal=8)
The result is:
Decimal 7
Traceback (most recent call last):
…
raiseAssertionError(msg)
AssertionError:
Arrays are not almost equal
ACTUAL: 0.123456789
DESIRED: 0.12345678
What just happened?
We used the assert_almost_equal funcon from the NumPy testing package to
check whether 0.123456789 and 0.123456780 are equal for dierent decimal precision.
Pop quiz – specifying decimal precision
Q1. Which parameter of the assert_almost_equal funcon species the
decimal precision?
1. decimal
2. precision
3. tolerance
4. significant
Approximately equal arrays
The assert_approx_equal funcon raises an excepon if two numbers are not equal up
to a certain number of signicant digits. The funcon result is an excepon that is triggered
by the condion:
abs(actual - expected) >= 10**-(significant - 1)
www.it-ebooks.info
Assure Quality with Tesng
[ 180 ]
Time for action – asserting approximately equal
Let's take the numbers from the previous Time for acon tutorial and let the
assert_approx_equal funcon work on them:
1. Call the funcon with low signicance:
print "Significance 8", np.testing.assert_approx_
equal(0.123456789, 0.123456780,
significant=8)
The result is:
Significance 8 None
2. Call the funcon with high signicance:
print "Significance 9",
np.testing.assert_approx_equal
(0.123456789, 0.123456780, significant=9)
An excepon is thrown:
Significance 9
Traceback (most recent call last):
...
raiseAssertionError(msg)
AssertionError:
Items are not equal to 9 significant digits:
ACTUAL: 0.123456789
DESIRED: 0.12345678
What just happened?
We used the assert_approx_equal funcon from the numpy.testing package to
check whether 0.123456789 and 0.123456780 are equal for dierent decimal precision.
Almost equal arrays
The assert_array_almost_equal funcon raises an excepon if two arrays are not
equal up to a specied precision. The funcon checks whether the two arrays have the
same shape. Then, the values of the arrays are compared element by element with:
|expected - actual| < 0.5 10-decimal
www.it-ebooks.info
Chapter 8
[ 181 ]
Time for action – asserting arrays almost equal
Let's form arrays with the values from the previous Time for acon tutorial by adding a 0 to
each array:
1. Calling the funcon with lower precision:
print "Decimal 8", np.testing.assert_array_almost_equal([0,
0.123456789], [0, 0.123456780], decimal=8)
The result is:
Decimal 8 None
2. Calling the funcon with higher precision:
print "Decimal 9", np.testing.assert_array_almost_equal([0,
0.123456789], [0, 0.123456780], decimal=9)
An excepon is thrown:
Decimal 9
Traceback (most recent call last):
…
assert_array_compare
raiseAssertionError(msg)
AssertionError:
Arrays are not almost equal
(mismatch 50.0%)
x: array([ 0. , 0.12345679])
y: array([ 0. , 0.12345678])
What just happened?
We compared two arrays with the NumPy array_almost_equal funcon
Have a go hero – comparing array with different shapes
Use the NumPy array_almost_equal funcon to compare two arrays with
dierent shapes.
www.it-ebooks.info
Assure Quality with Tesng
[ 182 ]
Equal arrays
The assert_array_equal funcon raises an excepon if two arrays are not equal. The
shapes of the arrays have to be equal and the elements of each array must be equal. NaNs
are allowed in the arrays. Alternavely, arrays can be compared with the array_allclose
funcon. This funcon has the parameters atol (absolute tolerance) and rtol (relave
tolerance). For two arrays a and b, these parameters sasfy the equaon:
|a - b| <= (atol + rtol * |b|)
Time for action – comparing arrays
Let's compare two arrays with the funcons we just menoned. We will reuse the arrays
from the previous Time for acon tutorial and add a NaN to them:
1. Call the array_allclose funcon:
print "Pass", np.testing.assert_allclose([0, 0.123456789,
np.nan], [0, 0.123456780, np.nan], rtol=1e-7, atol=0)
The result is:
Pass None
2. Call the array_equal funcon:
print "Fail", np.testing.assert_array_equal([0, 0.123456789,
np.nan], [0, 0.123456780, np.nan])
An excepon is thrown:
Fail
Traceback (most recent call last):
…
assert_array_compare
raiseAssertionError(msg)
AssertionError:
Arrays are not equal
(mismatch 50.0%)
x: array([ 0. , 0.12345679, nan])
y: array([ 0. , 0.12345678, nan])
www.it-ebooks.info
Chapter 8
[ 183 ]
What just happened?
We compared two arrays with the array_allclose funcon and the
array_equal funcon.
Ordering arrays
The assert_array_less funcon raises an excepon if two arrays do not have the
same shape and the elements of the rst array are strictly less than the elements of the
second array.
Time for action – checking the array order
Let's check whether one array is strictly greater than another array:
1. Call the assert_array_less funcon with two strictly ordered arrays:
print "Pass", np.testing.assert_array_less([0, 0.123456789,
np.nan], [1, 0.23456780, np.nan])
The result:
Pass None
2. Call the assert_array_less funcon on failing the test:
print "Fail", np.testing.assert_array_less([0, 0.123456789,
np.nan], [0, 0.123456780, np.nan])
An excepon is thrown:
Fail
Traceback (most recent call last):
...
raiseAssertionError(msg)
AssertionError:
Arrays are not less-ordered
(mismatch 100.0%)
x: array([ 0. , 0.12345679, nan])
y: array([ 0. , 0.12345678, nan])
www.it-ebooks.info
Assure Quality with Tesng
[ 184 ]
What just happened?
We checked the ordering of two arrays with the assert_array_less funcon.
Objects comparison
The assert_equal funcon raises an excepon if two objects are not equal. The objects do
not have to be NumPy arrays, they can also be lists, tuples, or diconaries.
Time for action – comparing objects
Suppose you need to compare two tuples. We can use the assert_equal funcon to
do that:
1. Call the assert_equal funcon:
print "Equal?", np.testing.assert_equal((1, 2), (1, 3))
An excepon is thrown:
Equal?
Traceback (most recent call last):
...
raiseAssertionError(msg)
AssertionError:
Items are not equal:
item=1
ACTUAL: 2
DESIRED: 3
What just happened?
We compared two tuples with the assert_equal funcon—an excepon was raised
because the tuples were not equal to each other.
String comparison
The assert_string_equal funcon asserts that two strings are equal. If the test fails an
excepon is thrown and the dierence between the strings is shown. The case of the string
characters maers.
www.it-ebooks.info
Chapter 8
[ 185 ]
Time for action – comparing strings
Let's compare strings. Both strings are the word "NumPy":
1. Call the assert_string_equal funcon to compare a string with itself. This test,
of course, should pass:
print "Pass", np.testing.assert_string_equal("NumPy", "NumPy")
The test passes:
Pass None
2. Call the assert_string_equal funcon to compare a string with another string
with the same leers but dierent casing. This test should throw an excepon:
print "Fail", np.testing.assert_string_equal("NumPy", "Numpy")
An excepon is thrown:
Fail
Traceback (most recent call last):
…
raiseAssertionError(msg)
AssertionError: Differences in strings:
- NumPy? ^
+ Numpy? ^
What just happened?
We compared two strings with the assert_string_equal funcon. The test threw an
excepon when the casing did not match.
Floating point comparisons
The representaon of oang-point numbers in computers is not exact. This leads to issues
when comparing oang-point numbers. The assert_array_almost_equal_nulp and
assert_array_max_ulp NumPy funcons provide consistent oang-point comparisons.
ULP stands for Unit of Least Precision of oang point numbers. According to the IEEE 754
specicaon, a half ULP precision is required for elementary arithmec operaons. You can
compare this to a ruler. A metric system ruler usually has cks for millimetres, but beyond
that you can only esmate half millimetres.
www.it-ebooks.info
Assure Quality with Tesng
[ 186 ]
Machine epsilon is the largest relave rounding error in oang point arithmec. Machine
epsilon is equal to ULP relave to one. The NumPy finfo funcon allows us to determine
the machine epsilon. The Python standard library also can give you the machine epsilon
value. The value should be the same as that given by NumPy.
Time for action – comparing with assert_array_almost_equal_
nulp
Let's see the assert_array_almost_equal_nulp funcon in acon:
1. Determine the machine epsilon with the finfo funcon:
eps = np.finfo(float).eps
print "EPS", eps
The epsilon would be:
EPS 2.22044604925e-16
2. Compare two almost equal oats: Compare 1.0 with 1 + epsilon (eps) using the
assert_almost_equal_nulp funcon. Do the same for 1 + 2 * epsilon (eps):
print "1",
np.testing.assert_array_almost_equal_nulp(1.0, 1.0 + eps)
print "2",
np.testing.assert_array_almost_equal_nulp(1.0, 1.0 + 2 * eps)
The result:
1 None
2
Traceback (most recent call last):
…
assert_array_almost_equal_nulp
raiseAssertionError(msg)
AssertionError: X and Y are not equal to 1 ULP (max is 2)
What just happened?
We determined the machine epsilon with the finfo funcon. We then compared 1.0
with 1 + epsilon (eps) with the assert_almost_equal_nulp funcon. This test passed,
however, adding another epsilon resulted in an excepon.
www.it-ebooks.info
Chapter 8
[ 187 ]
Comparison of oats with more ULPs
The assert_array_max_ulp funcon allows you to specify an upper bound for the
number of ULPs you would allow. The maxulp parameter accepts an integer value for
the limit. The value of this parameter is 1 by default.
Time for action – comparing using maxulp of 2
Let's do the same comparisons as in the previous Time for acon tutorial, but specify
a maxulp of 2 when necessary:
1. Determine the machine epsilon with the finfo funcon:
eps = np.finfo(float).eps
print "EPS", eps
The epsilon would be:
EPS 2.22044604925e-16
2. Do the comparisons as done in the previous Time for acon tutorial, but use
the assert_array_max_ulp funcon with the appropriate maxulp value:
print "1", np.testing.assert_array_max_ulp(1.0, 1.0 + eps)
print "2", np.testing.assert_array_max_ulp(1.0, 1 + 2 * eps,
maxulp=2)
The output:
1 1.0
2 2.0
What just happened?
We compared the same values as the previous Time for acon tutorial, but specied a
maxulp of 2 in the second comparison. Using the assert_array_max_ulp funcon with
the appropriate maxulp value, these tests passed with a return value of the number of ULPs.
Unit tests
Unit tests are automated tests, which test a small piece of code, usually a funcon or
method. Python has the PyUnit API for unit tesng. As NumPy users we can make use
of the assert funcons we saw in acon before.
www.it-ebooks.info
Assure Quality with Tesng
[ 188 ]
Time for action – writing a unit test
We will write tests for a simple factorial funcon. The tests will check for the so called happy
path and for abnormal condions.
1. We start by wring the factorial funcon
def factorial(n):
if n == 0:
return 1
if n < 0:
raise ValueError, "Unexpected negative value"
return np.arange(1, n+1).cumprod()
The code is using the arange and cumprod funcons we have already seen to
create arrays and calculate the cumulave product, but we added a few checks for
boundary condions.
2. Now we will write the unit test. Let's write a class that will contain the unit tests.
It extends the TestCase class from the unittest module which is part of standard
Python. We test for calling the factorial funcon with:
a positive number, the happy path
boundary condition 0
negative numbers, which should result in an error
class FactorialTest(unittest.TestCase):
def test_factorial(self):
#Test for the factorial of 3 that should pass.
self.assertEqual(6, factorial(3)[-1])
np.testing.assert_equal(np.array([1, 2, 6]), factorial(3))
def test_zero(self):
#Test for the factorial of 0 that should pass.
self.assertEqual(1, factorial(0))
def test_negative(self):
#Test for the factorial of negative numbers that should fail.
# It should throw a ValueError, but we expect IndexError
self.assertRaises(IndexError, factorial(-10))
We rigged one of the tests to fail as you can see in the following output:
www.it-ebooks.info
Chapter 8
[ 189 ]
$ python unit_test.py
.E.
==================================================================
====
ERROR: test_negative (__main__.FactorialTest)
------------------------------------------------------------------
----
Traceback (most recent call last):
File "unit_test.py", line 26, in test_negative
self.assertRaises(IndexError, factorial(-10))
File "unit_test.py", line 9, in factorial
raiseValueError, "Unexpected negative value"
ValueError: Unexpected negative value
------------------------------------------------------------------
----
Ran 3 tests in 0.003s
FAILED (errors=1)
What just happened?
We made some happy path tests for factorial funcon code. We let the boundary condion
test fail on purpose (see unit_test.py):
import numpy as np
import unittest
def factorial(n):
if n == 0:
return 1
if n < 0:
raise ValueError, "Unexpected negative value"
return np.arange(1, n+1).cumprod()
class FactorialTest(unittest.TestCase):
def test_factorial(self):
www.it-ebooks.info
Assure Quality with Tesng
[ 190 ]
#Test for the factorial of 3 that should pass.
self.assertEqual(6, factorial(3)[-1])
np.testing.assert_equal(np.array([1, 2, 6]), factorial(3))
def test_zero(self):
#Test for the factorial of 0 that should pass.
self.assertEqual(1, factorial(0))
def test_negative(self):
#Test for the factorial of negative numbers that should fail.
# It should throw a ValueError, but we expect IndexError
self.assertRaises(IndexError, factorial(-10))
if __name__ == '__main__':
unittest.main()
Nose tests decorators
A nose is an organ above the mouth that is used by humans and animals to breathe and
smell. It is also a Python framework that makes (unit) tesng easier. Nose helps you organize
tests. According to the nose documentaon: "any python source le, directory, or package
that matches the testMatch regular expression (by default: (?:^|[b_.-])[Tt]est)
will be collected as a test". Nose makes extensive use of decorators. Python decorators are
annotaons that indicate something about a method or a funcon. The numpy.testing
module has a number of decorators:
Decorator Description
numpy.testing.decorators.
deprecated
Filters deprecation warnings when running
tests.
numpy.testing.decorators.
knownfailureif
Raises KnownFailureTest exception
based on a condition.
numpy.testing.decorators.
setastest
Marks a function as being a test or not being
a test.
numpy.testing.decorators.skipif Raises SkipTest exception based on a
condition.
numpy.testing.decorators.slow Labels test functions or methods as slow.
Addionally we can call the decorate_methods funcon to apply decorators on methods
of a class matching a regular expression or a string.
www.it-ebooks.info
Chapter 8
[ 191 ]
Time for action – decorating tests
We will apply the setastest decorator directly to test funcons. Then we will apply the
same decorator to a method to disable it. Also we will skip one of the tests and fail another.
First we will install nose in case you don't have it yet.
1. Install nose with setuptools
easy_install nose
Or pip:
pip install nose
2. We will apply one funcon as being a test and another as not being a test.
@setastest(False)
def test_false():
pass
@setastest(True)
def test_true():
pass
3. We can skip tests with the skipif decorator. Let's use a condion that always leads
to a test being skipped.
@skipif(True)
def test_skip():
pass
4. Add a test funcon that always passes. Then decorate it with the knownfailureif
decorator so that the test always fails.
@knownfailureif(True)
def test_alwaysfail():
pass
5. We will dene some test classes with methods that normally should be executed by
nose.
class TestClass():
def test_true2(self):
pass
class TestClass2():
def test_false2(self):
pass
www.it-ebooks.info
Assure Quality with Tesng
[ 192 ]
6. Let's disable the second test method from the previous step.
decorate_methods(TestClass2, setastest(False), 'test_false2')
7. We can run the tests with the following command:
nosetests -v decorator_setastest.py
decorator_setastest.TestClass.test_true2 ... ok
decorator_setastest.test_true ... ok
decorator_test.test_skip ... SKIP: Skipping test: test_skipTest
skipped due to test condition
decorator_test.test_alwaysfail ... ERROR
==================================================================
====
ERROR: decorator_test.test_alwaysfail
------------------------------------------------------------------
----
Traceback (most recent call last):
File "…/nose/case.py", line 197, in runTest
self.test(*self.arg)
File …/numpy/testing/decorators.py", line 213, in knownfailer
raiseKnownFailureTest(msg)
KnownFailureTest: Test skipped due to known failure
------------------------------------------------------------------
----
Ran 4 tests in 0.001s
FAILED (SKIP=1, errors=1)
What just happened?
We decorated some funcons and methods as not being tests, so that they were ignored
by nose. We skipped one test and failed another too. We did this by applying decorators
directly and with the decorate_methods funcon (see decorator_test.py):
from numpy.testing.decorators import setastest
from numpy.testing.decorators import skipif
from numpy.testing.decorators import knownfailureif
from numpy.testing import decorate_methods
www.it-ebooks.info
Chapter 8
[ 193 ]
@setastest(False)
def test_false():
pass
@setastest(True)
def test_true():
pass
@skipif(True)
def test_skip():
pass
@knownfailureif(True)
def test_alwaysfail():
pass
class TestClass():
def test_true2(self):
pass
class TestClass2():
def test_false2(self):
pass
decorate_methods(TestClass2, setastest(False), 'test_false2')
Docstrings
Docstrings are strings embedded in Python code that resemble interacve sessions.
These strings can be used to test certain assumpons, or just provide examples.
The numpy.testing module has a funcon to run these tests.
www.it-ebooks.info
Assure Quality with Tesng
[ 194 ]
Time for action – executing doctests
Let's write a simple example that is supposed to calculate the well-known factorial, but
doesn't cover all the possible boundary condions. In other words some tests will fail.
1. The docstring will look like text you would see in a Python shell (including a prompt).
We will rig one of the tests to fail, just to see what will happen.
"""
Test for the factorial of 3 that should pass.
>>> factorial(3)
6
Test for the factorial of 0 that should fail.
>>> factorial(0)
1
"""
2. We will write the following line of NumPy code to compute the factorial:
return np.arange(1, n+1).cumprod()[-1]
We want this code to fail from me to me for demonstraon purposes.
3. We can run the doctest by calling the rundocs funcon of the numpy.testing
module for instance in the Python shell.
>>>from numpy.testing import rundocs
>>>rundocs('docstringtest.py')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "…/numpy/testing/utils.py", line 998, in rundocs
raiseAssertionError("Some doctests failed:\n%s" % "\n".join(msg))
AssertionError: Some doctests failed:
******************************************************************
****
File "docstringtest.py", line 10, in docstringtest.factorial
Failed example:
factorial(0)
Exception raised:
Traceback (most recent call last):
File "…/doctest.py", line 1254, in __run
compileflags, 1) in test.globs
www.it-ebooks.info
Chapter 8
[ 195 ]
File "<doctestdocstringtest.factorial[1]>", line 1, in
<module>
factorial(0)
File "docstringtest.py", line 13, in factorial
return np.arange(1, n+1).cumprod()[-1]
IndexError: index -1 is out of bounds for axis 0 with size 0
What just happened?
We wrote a docstring test which didn't take into account 0 and negave numbers. We run
the test with the rundocs funcon from the numpy.testing module and got an index
error as a result (see docstringtest.py):
import numpy as np
def factorial(n):
"""
Test for the factorial of 3 that should pass.
>>> factorial(3)
6
Test for the factorial of 0 that should fail.
>>> factorial(0)
1
"""
return np.arange(1, n+1).cumprod()[-1]
Summary
We learned about tesng and NumPy tesng ulies in this chapter. We covered unit tesng,
docstring tests, assert funcons, and oang point precision. Most of the NumPy assert
funcons take care of the complexies of oang point numbers. We demonstrated NumPy
decorators that can be used by nose. Decorators make tesng easier and document the
developer intenon.
The topic of the next chapter is Matplotlib—the Python scienc visualizaon and graphing
open-source library.
www.it-ebooks.info
www.it-ebooks.info
Plotting with Matplotlib
Matplotlib is a very useful Python plotting library. It integrates nicely with
NumPy but is a separate open source project. You can find a gallery of beautiful
examples at http://matplotlib.sourceforge.net/gallery.html.
Matplotlib also has utility functions to download and manipulate data from
Yahoo Finance. We will see several examples of stock charts.
This chapter features extended coverage of:
Simple plots
Subplots
Histograms
Plot customizaon
Three-dimensional plots
Contour plots
Animaon
Logplots
9
www.it-ebooks.info
Plong with Matplotlib
[ 198 ]
Simple plots
The matplotlib.pyplot package contains funconality for simple plots. It is important
to remember that each subsequent funcon call changes the state of the current plot.
Eventually we will want to either save the plot in a le or display it with the show funcon.
However, if we are in IPython running on a Qt or Wx backend the gure will be updated
interacvely without waing for the show funcon. This is comparable to the way text
output is printed on the y.
Time for action – plotting a polynomial function
To illustrate how plong works, let’s display some polynomial graphs. We will use the
NumPy polynomial funcon poly1d to create a polynomial.
1. Take the standard input values as polynomial coecients. Use the NumPy poly1d
funcon to create a polynomial.
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
2. Create the x values with the NumPy linspace funcon. Use the range -10 to 10
and create 30 even spaced values.
x = np.linspace(-10, 10, 30)
3. Calculate the polynomial values using the polynomial that we created in the
rst step.
y = func(x)
4. Call the plot funcon; this does not immediately display the graph.
plt.plot(x, y)
5. Add a label to the x axis with xlabel funcon.
plt.xlabel('x’)
6. Add a label to the y axis with ylabel funcon.
plt.ylabel('y(x)’)
7. Call the show funcon to display the graph.
plt.show()
www.it-ebooks.info
Chapter 9
[ 199 ]
Here is a plot with polynomial coecients 1, 2, 3, and 4:
What just happened?
We displayed a graph of a polynomial on our screen. We added labels to the x and y axis
(see polyplot.py):
import numpy as np
import matplotlib.pyplot as plt
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
x = np.linspace(-10, 10, 30)
y = func(x)
plt.plot(x, y)
plt.xlabel('x’)
plt.ylabel('y(x)’)
plt.show()
Pop quiz – the plot function
Q1. What does the plot funcon do?
1. It displays two-dimensional plots on screen.
2. It saves an image of a two-dimensional plot in a le.
3. It does both 1 and 2.
4. It does neither 1, 2, or 3.
www.it-ebooks.info
Plong with Matplotlib
[ 200 ]
Plot format string
The plot funcon accepts an unlimited number of arguments. In the previous secon
we gave it two arrays as arguments. We could also specify the line color and style with an
oponal format string. By default, it is a solid blue line denoted as b-, but you can specify a
dierent color and style such as red dashes.
Time for action – plotting a polynomial and its derivative
Let’s plot a polynomial and its rst order derivave using the derive funcon with m as 1.
We already did the rst part in the previous Time for acon tutorial. We want to have two
dierent line styles to be able to discern what is what.
1. Create and dierenate the polynomial.
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
func1 = func.deriv(m=1)
x = np.linspace(-10, 10, 30)
y = func(x)
y1 = func1(x)
2. Plot the polynomial and its derivave in two dierent styles: red circles and green
dashes. You cannot see the colors in a print copy of this book so you will have to try
it out for yourself.
plt.plot(x, y, 'ro’, x, y1, 'g--’)
plt.xlabel('x’)
plt.ylabel('y’)
plt.show()
The graph again with polynomial coecients 1, 2, 3, and 4:
www.it-ebooks.info
Chapter 9
[ 201 ]
What just happened?
We ploed a polynomial and its derivave using two dierent line styles and one call of the
plot funcon (see polyplot2.py):
import numpy as np
import matplotlib.pyplot as plt
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
func1 = func.deriv(m=1)
x = np.linspace(-10, 10, 30)
y = func(x)
y1 = func1(x)
plt.plot(x, y, 'ro’, x, y1, 'g--’)
plt.xlabel('x’)
plt.ylabel('y’)
plt.show()
Subplots
At a certain point you will have too many lines in one plot. Sll, you would like to have
everything grouped together. We can achieve this with the subplot funcon.
Time for action – plotting a polynomial and its derivatives
Let’s plot a polynomial and its rst and second derivave. We will make three subplots
for the sake of clarity:
1. Create a polynomial and its derivaves using the following code.
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
x = np.linspace(-10, 10, 30)
y = func(x)
func1 = func.deriv(m=1)
y1 = func1(x)
func2 = func.deriv(m=2)
y2 = func2(x)
www.it-ebooks.info
Plong with Matplotlib
[ 202 ]
2. Create the rst subplot of the polynomial with the subplot funcon. The rst
parameter of this funcon is the number of rows, the second parameter is the
number of columns, and the third parameter is an index number starng with 1.
Alternavely, you can combine the three parameters into a single number such as
311. The subplots will be organized in 3 rows and 1 column. Give the subplot the
tle "Polynomial". Make a solid red line.
plt.subplot(311)
plt.plot(x, y, 'r-’)
plt.title("Polynomial")
3. Create the third subplot of the rst derivave with the subplot funcon.
Give the subplot the tle "First Derivative". Use a line of blue triangles.
plt.subplot(312)
plt.plot(x, y1, 'b^’)
plt.title("First Derivative")
4. Create the second subplot of the second derivave with the subplot funcon.
Give the subplot the tle "Second Derivative". Use a line of green circles.
plt.subplot(313)
plt.plot(x, y2, 'go’)
plt.title("Second Derivative")
plt.xlabel('x’)
plt.ylabel('y’)
plt.show()
www.it-ebooks.info
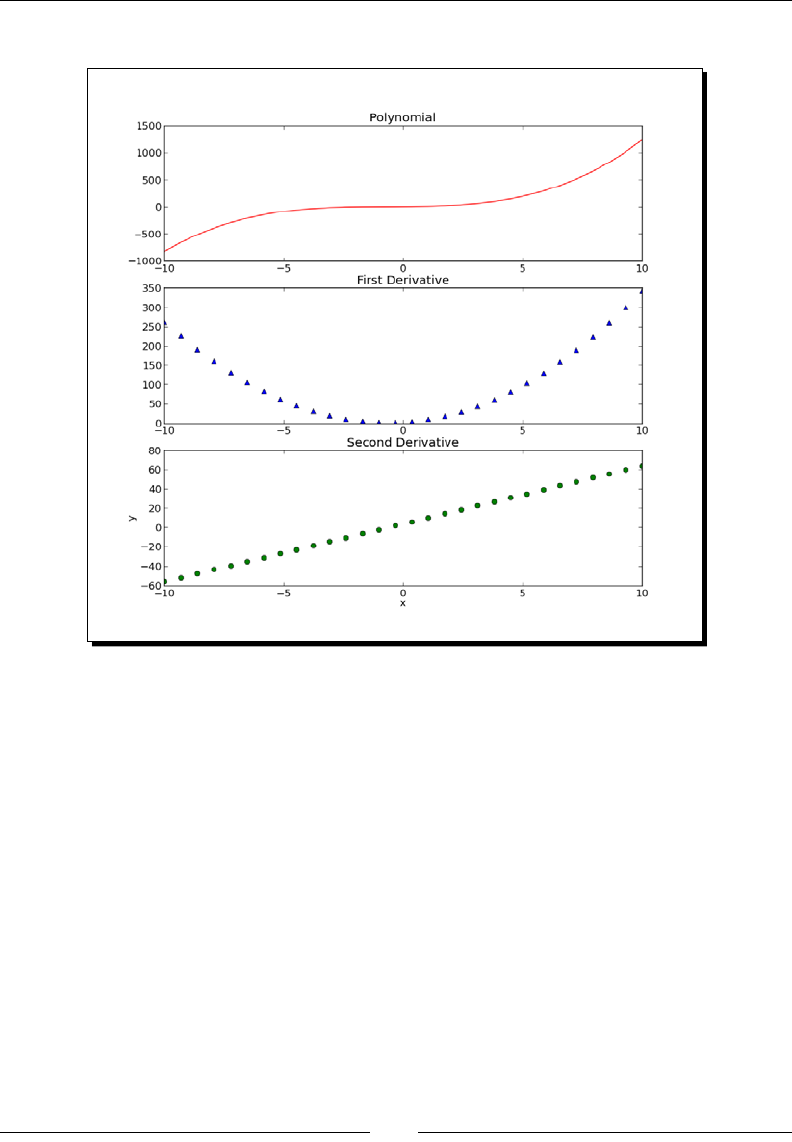
Chapter 9
[ 203 ]
The three subplots with polynomial coecients 1, 2, 3, and 4:
What just happened?
We ploed a polynomial and its rst and second derivave using three dierent line styles
and three subplots in 3 rows and 1 column (see polyplot3.py):
import numpy as np
import matplotlib.pyplot as plt
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
x = np.linspace(-10, 10, 30)
y = func(x)
func1 = func.deriv(m=1)
y1 = func1(x)
func2 = func.deriv(m=2)
y2 = func2(x)
plt.subplot(311)
plt.plot(x, y, 'r-’)
www.it-ebooks.info
Plong with Matplotlib
[ 204 ]
plt.title("Polynomial")
plt.subplot(312)
plt.plot(x, y1, 'b^’)
plt.title("First Derivative")
plt.subplot(313)
plt.plot(x, y2, 'go’)
plt.title("Second Derivative")
plt.xlabel('x’)
plt.ylabel('y’)
plt.show()
Finance
Matplotlib can help us monitor our stock investments. The matplotlib.finance
package has ulies with which we can download stock quotes from Yahoo Finance
(http://finance.yahoo.com/). The data can then be ploed as candlescks.
Time for action – plotting a year’s worth of stock quotes
We can plot a year’s worth of stock quotes data with the matplotlib.finance package.
This will require a connecon to Yahoo Finance, which will be the data source.
1. Determine the start date by subtracng 1 year from today.
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
from matplotlib.finance import quotes_historical_yahoo
from matplotlib.finance import candlestick
import sys
from datetime import date
import matplotlib.pyplot as plt
today = date.today()
start = (today.year - 1, today.month, today.day)
2. We need to create so-called locators. These objects from the matplotlib.dates
package are needed to locate months and days on the x-axis.
alldays = DayLocator()
months = MonthLocator()
www.it-ebooks.info
Chapter 9
[ 205 ]
3. Create a date formaer to format the dates on the x axis. This formaer will create a
string containing the short name of a month and the year.
month_formatter = DateFormatter("%b %Y")
4. Download the stock quote data from Yahoo nance with the following code:
quotes = quotes_historical_yahoo(symbol, start, today)
5. Create a Matplotlib figure object—this is a top-level container for plot
components.
fig = plt.figure()
6. Add a subplot to the gure.
ax = fig.add_subplot(111)
7. Set the major locator on the x axis to the months locator. This locator is responsible
for the big cks on the x axis.
ax.xaxis.set_major_locator(months)
8. Set the minor locator on the x axis to the days locator. This locator is responsible for
the small cks on the x axis.
ax.xaxis.set_minor_locator(alldays)
9. Set the major formaer on the x axis to the months formaer. This formaer is
responsible for the labels of the big cks on the x axis.
ax.xaxis.set_major_formatter(month_formatter)
10. A funcon in the matplotlib.finance package allows us to display candlescks.
Create the candlescks using the quotes data. It is possible to specify the width of
the candlescks. For now, use the default value.
candlestick(ax, quotes)
11. Format the labels on the x axis as dates. This should rotate the labels on the x axis,
so that they t beer.
fig.autofmt_xdate()
plt.show()
www.it-ebooks.info
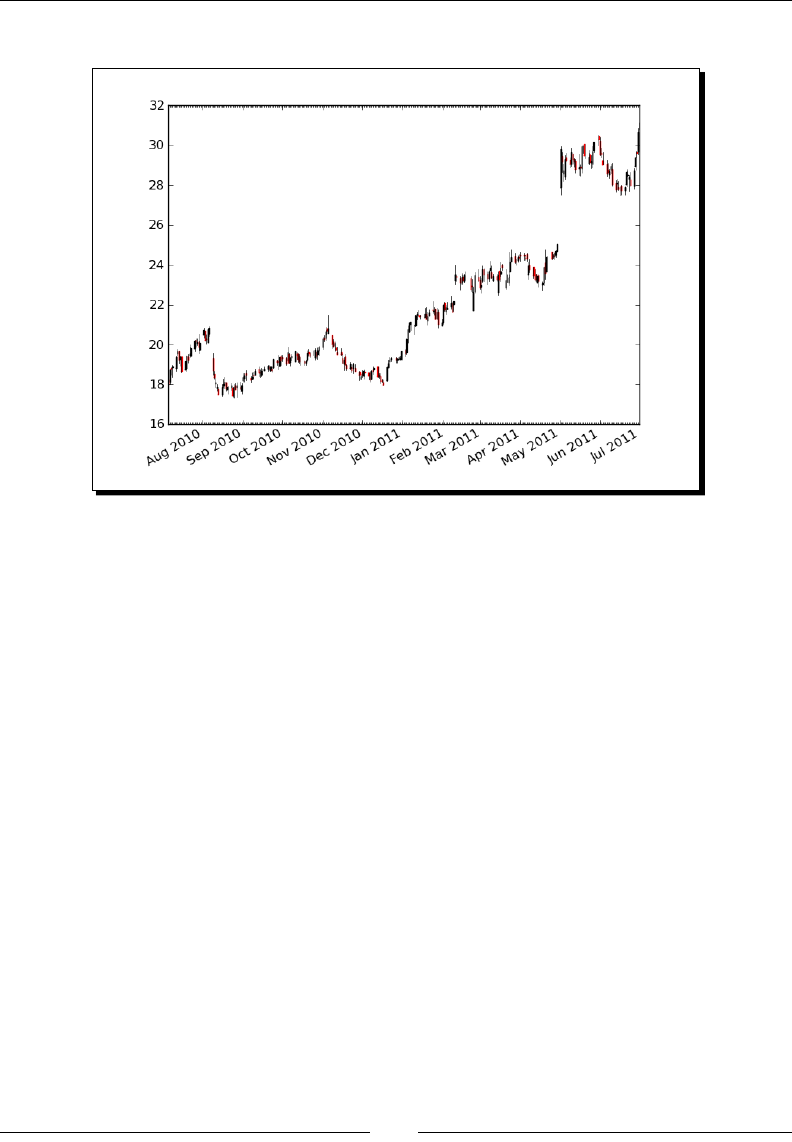
Plong with Matplotlib
[ 206 ]
The candlesck chart for DISH (Dish Network Corp.) would appear as follows:
What just happened?
We downloaded a year’s worth of data from Yahoo Finance. We charted this data using
candlescks (see candlesticks.py):
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
from matplotlib.finance import quotes_historical_yahoo
from matplotlib.finance import candlestick
import sys
from datetime import date
import matplotlib.pyplot as plt
today = date.today()
start = (today.year - 1, today.month, today.day)
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter("%b %Y")
symbol = 'DISH’
if len(sys.argv) == 2:
www.it-ebooks.info
Chapter 9
[ 207 ]
symbol = sys.argv[1]
quotes = quotes_historical_yahoo(symbol, start, today)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_formatter(month_formatter)
candlestick(ax, quotes)
fig.autofmt_xdate()
plt.show()
Histograms
Histograms visualize the distribuon of numerical data. Matplotlib has the handy hist
funcon that graphs histograms. The hist funcon has two arguments—the array
containing the data and the number of bars.
Time for action – charting stock price distributions
Let’s chart the stock price distribuon of quotes from Yahoo Finance.
1. Download the data going back 1 year.
today = date.today()
start = (today.year - 1, today.month, today.day)
quotes = quotes_historical_yahoo(symbol, start, today)
2. The quotes data in the previous step is stored in a Python list. Convert this
to a NumPy array and extract the close prices.
quotes = np.array(quotes)
close = quotes.T[4]
3. Draw the histogram with a reasonable number of bars.
plt.hist(close, np.sqrt(len(close)))
plt.show()
www.it-ebooks.info
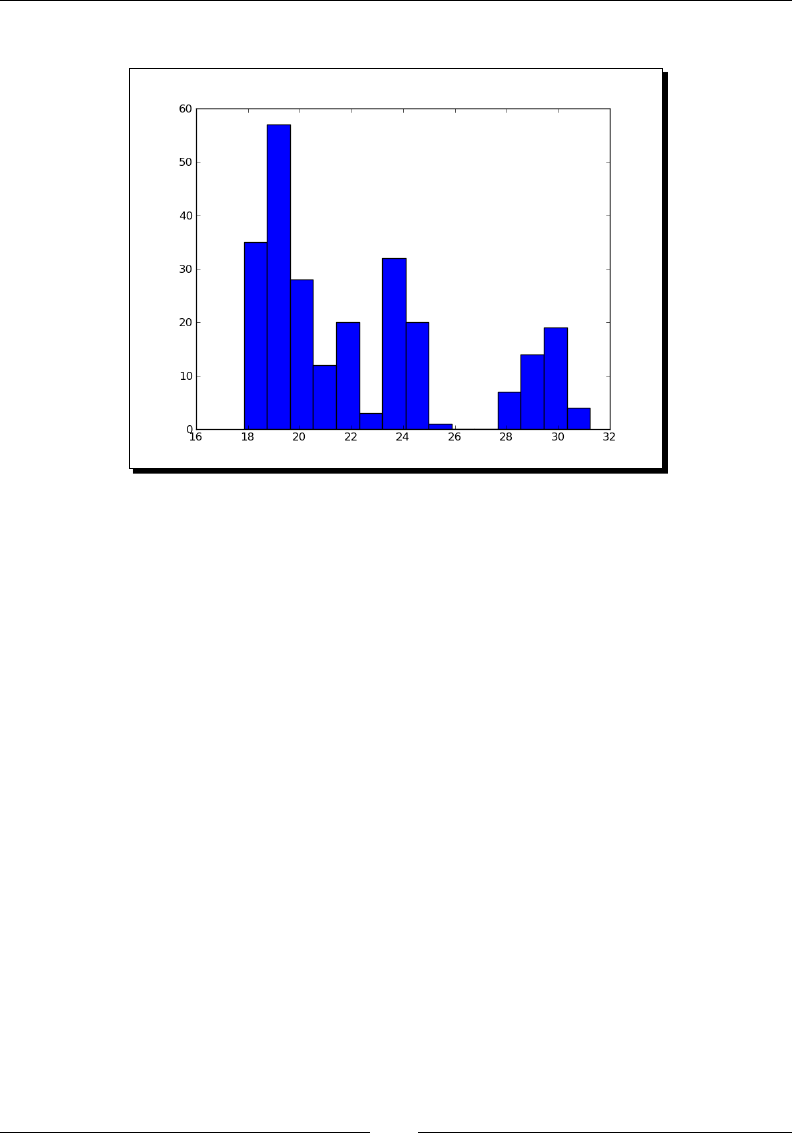
Plong with Matplotlib
[ 208 ]
The histogram for DISH would appear as follows:
What just happened?
We charted the stock price distribuon of DISH as histogram (see stockhistogram.py):
from matplotlib.finance import quotes_historical_yahoo
import sys
from datetime import date
import matplotlib.pyplot as plt
import numpy as np
today = date.today()
start = (today.year - 1, today.month, today.day)
symbol = 'DISH’
if len(sys.argv) == 2:
symbol = sys.argv[1]
quotes = quotes_historical_yahoo(symbol, start, today)
quotes = np.array(quotes)
close = quotes.T[4]
plt.hist(close, np.sqrt(len(close)))
plt.show()
www.it-ebooks.info
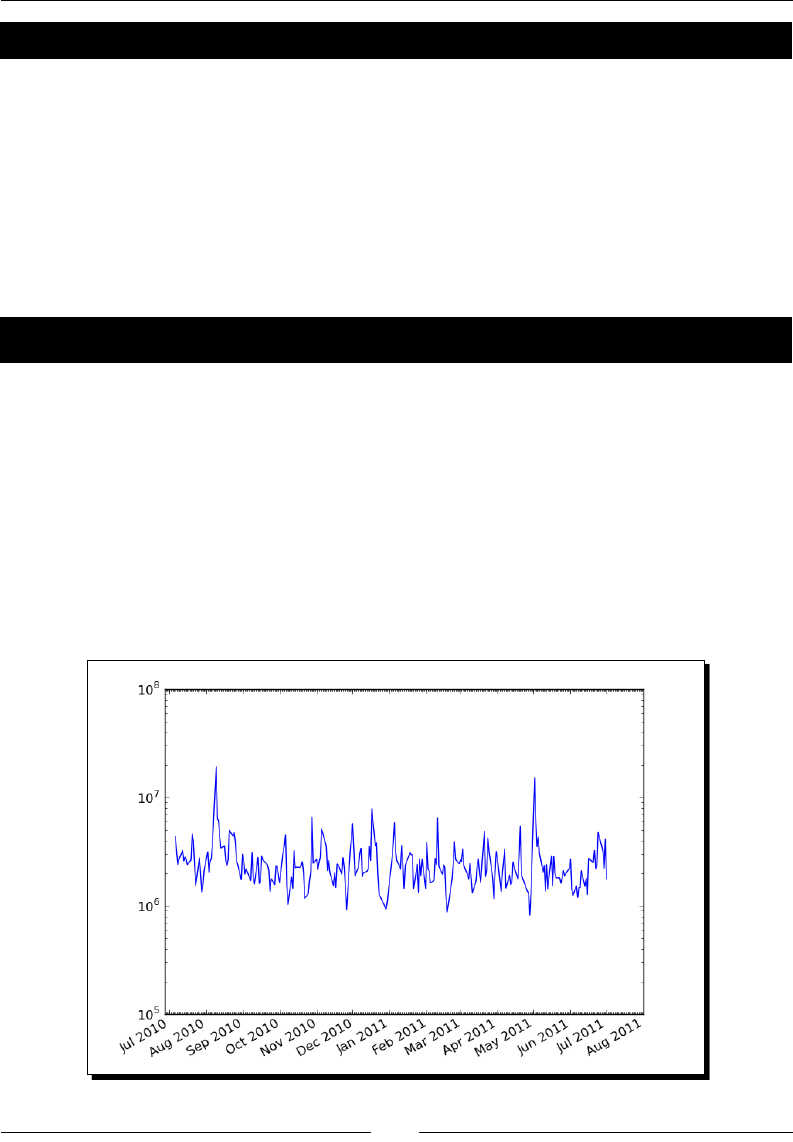
Chapter 9
[ 209 ]
Have a go hero – drawing a bell curve
Overlay a bell curve (related to Gaussian or normal distribuon) using the average price
and standard deviaon. This is, of course, only an exercise.
Logarithmic plots
Logarithmic plots are useful when the data has a wide range of values. Matplotlib has the
funcons semilogx (logarithmic x axis), semilogy (logarithmic y axis), and loglog (x and y
axis logarithmic).
Time for action – plotting stock volume
Stock volume varies a lot, so let’s plot it on a logarithmic scale. First we need to download
historical data from Yahoo Finance, extract the dates and volume, create locators and a date
formaer, create the gure, and add to it a subplot. We already went through these steps in
the previous Time for acon tutorial, so we will skip them here.
1. Plot the volume using a logarithmic scale.
plt.semilogy(dates, volume)
Now set the locators and format the x-axis as dates. Instrucons for these steps can
be found in the previous Time for acon tutorial as well. The stock volume using a
logarithmic scale for DISH would appear as follows:
www.it-ebooks.info
Plong with Matplotlib
[ 210 ]
What just happened?
We ploed stock volume using a logarithmic scale (see logy.py):
from matplotlib.finance import quotes_historical_yahoo
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
import sys
from datetime import date
import matplotlib.pyplot as plt
import numpy as np
today = date.today()
start = (today.year - 1, today.month, today.day)
symbol = 'DISH’
if len(sys.argv) == 2:
symbol = sys.argv[1]
quotes = quotes_historical_yahoo(symbol, start, today)
quotes = np.array(quotes)
dates = quotes.T[0]
volume = quotes.T[5]
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter("%b %Y")
fig = plt.figure()
ax = fig.add_subplot(111)
plt.semilogy(dates, volume)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_formatter(month_formatter)
fig.autofmt_xdate()
plt.show
www.it-ebooks.info
Chapter 9
[ 211 ]
Scatter plots
A scaer plot displays values for two numerical variables in the same data set.
The Matplotlib scatter funcon creates a scaer plot. Oponally, we can specify
the color and size of the data points in the plot as well as alpha transparency.
Time for action – plotting price and volume returns with scatter
plot
We can easily make a scaer plot of the stock price and volume returns. Again, let’s
download the necessary data from Yahoo Finance.
1. The quotes data in the previous step is stored in a Python list. Convert this to a
NumPy array and extract the close and volume values.
dates = quotes.T[4]
volume = quotes.T[5]
2. Calculate the close price and volume returns.
ret = np.diff(close)/close[:-1]
volchange = np.diff(volume)/volume[:-1]
3. Create a Matplotlib figure object
fig = pyplot.figure()
4. Add a subplot to the gure.
ax = fig.add_subplot(111)
5. Create the scatter plot with the color of the data points linked to the close return,
and the size linked to the volume change.
ax.scatter(ret, volchange, c=ret * 100,
s=volchange * 100, alpha=0.5
6. Set the title of the plot and put a grid on it.
ax.set_title('Close and volume returns’)
ax.grid(True)
pyplot.show()
www.it-ebooks.info
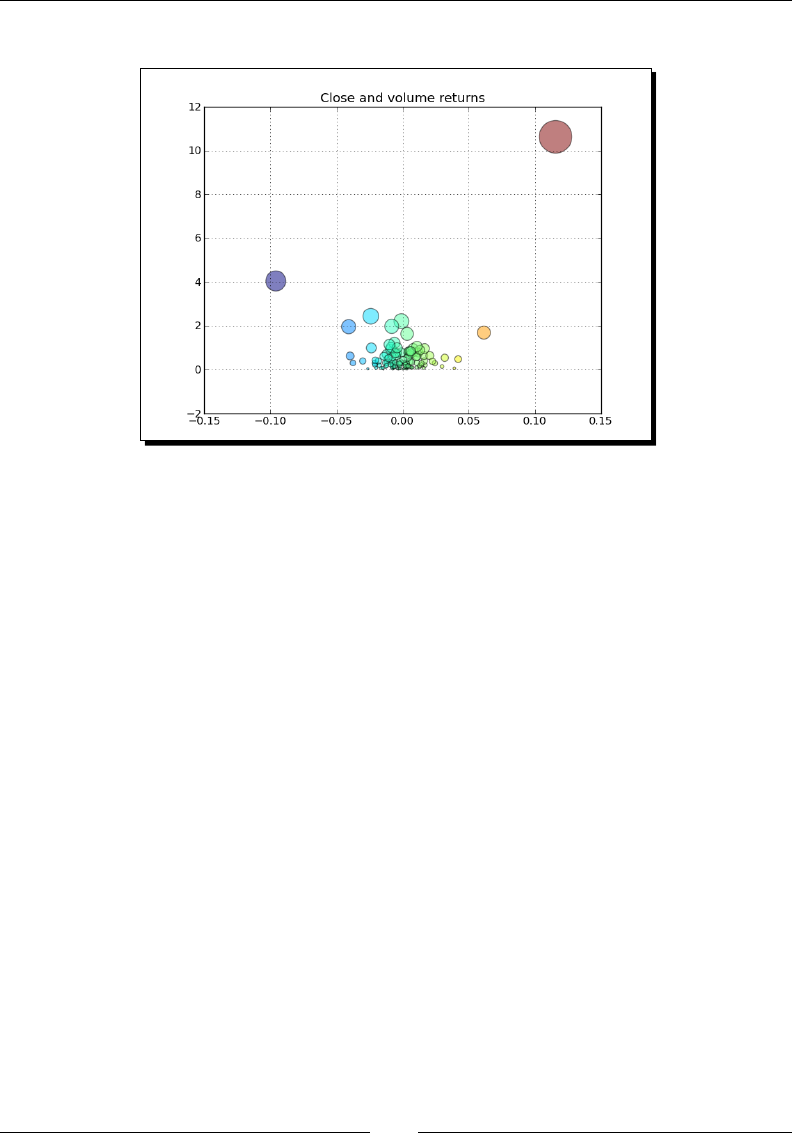
Plong with Matplotlib
[ 212 ]
The scaer plot for DISH will appear as follows:
What just happened?
We made a scaer plot of the close price and volume returns for DISH
(see scatterprice.py):
from matplotlib.finance import quotes_historical_yahoo
import sys
from datetime import date
import matplotlib.pyplot as plt
import numpy as np
today = date.today()
start = (today.year - 1, today.month, today.day)
symbol = 'DISH’
if len(sys.argv) == 2:
symbol = sys.argv[1]
quotes = quotes_historical_yahoo(symbol, start, today)
quotes = np.array(quotes)
close = quotes.T[4]
volume = quotes.T[5]
ret = np.diff(close)/close[:-1]
volchange = np.diff(volume)/volume[:-1]
www.it-ebooks.info
Chapter 9
[ 213 ]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(ret, volchange, c=ret * 100, s=volchange * 100, alpha=0.5)
ax.set_title('Close and volume returns’)
ax.grid(True)
plt.show()
Fill between
The fill_between funcon lls a region of a plot with a specied color. We can also
choose an alpha channel value. The funcon also has a where parameter so that we can
shade a region based on a condion.
Time for action – shading plot regions based on a condition
Imagine that you want to shade the region of a stock chart, where the closing price is below
average, with a dierent color than when it is above the mean. The fill_between funcon
is the best choice for the job. We will again omit the steps of downloading historical data
going back 1 year, extracng dates and close prices, and creang locators and date formaer.
1. Create a Matplotlib gure object.
fig = plt.figure()
2. Add a subplot to the gure.
ax = fig.add_subplot(111)
3. Plot the closing price.
ax.plot(dates, close)
4. Shade the regions of the plot below the closing price using dierent colors
depending whether the values are below or above the average price.
plt.fill_between(dates, close.min(), close,
where=close>close.mean(), facecolor="green", alpha=0.4)
plt.fill_between(dates, close.min(), close,
where=close<close.mean(), facecolor="red", alpha=0.4)
www.it-ebooks.info
Plong with Matplotlib
[ 214 ]
Now we can nish the plot by seng locators and formang the x-axis values
as dates. The stock price using condional shading for DISH:
What just happened?
We shaded the region of a stock chart, where the closing price is below average,
with a dierent color than when it is above the mean (see fillbetween.py):
from matplotlib.finance import quotes_historical_yahoo
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
import sys
from datetime import date
import matplotlib.pyplot as plt
import numpy as np
today = date.today()
start = (today.year - 1, today.month, today.day)
symbol = 'DISH’
if len(sys.argv) == 2:
symbol = sys.argv[1]
quotes = quotes_historical_yahoo(symbol, start, today)
www.it-ebooks.info
Chapter 9
[ 215 ]
quotes = np.array(quotes)
dates = quotes.T[0]
close = quotes.T[4]
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter("%b %Y")
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(dates, close)
plt.fill_between(dates, close.min(), close, where=close>close.mean(),
facecolor="green", alpha=0.4)
plt.fill_between(dates, close.min(), close, where=close<close.mean(),
facecolor="red", alpha=0.4)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_formatter(month_formatter)
ax.grid(True)
fig.autofmt_xdate()
plt.show()
Legend and annotations
Legends and annotaons are essenal for good plots. We can create transparent legends
with the legend funcon and let Matplotlib gure out where to place them. Also, with
the annotate funcon we can put annotaons very accurately on a plot. There are a large
number of annotaon and arrow styles.
Time for action – using legend and annotations
In Chapter 3, Geng to Terms with Commonly Used Funcons we learned how to calculate
the exponenal moving average of stock prices. We will plot the close price of a stock and
three of its exponenal moving averages. To clarify the plot, we will add a legend. Also,
we will indicate crossovers of two of the averages with annotaons. Some steps are again
omied to avoid repeon.
www.it-ebooks.info
Plong with Matplotlib
[ 216 ]
1. Calculate and plot the exponenal moving averages: Go back to Chapter 3, Geng
to Terms with Commonly Used Funcons if needed and review the exponenal
moving average algorithm. Calculate and plot the exponenal moving averages of 9,
12, and 15 periods.
emas = []
for i in range(9, 18, 3):
weights = np.exp(np.linspace(-1., 0., i))
weights /= weights.sum()
ema = np.convolve(weights, close)[i-1:-i+1]
idx = (i - 6)/3
ax.plot(dates[i-1:], ema, lw=idx, label="EMA(%s)" % (i))
data = np.column_stack((dates[i-1:], ema))
emas.append(np.rec.fromrecords(
data, names=["dates", "ema"]))
Noce that the plot funcon call needs a label for the legend. We stored the
moving averages in record arrays for the next step.
2. Let’s nd the crossover points of the rst two moving averages
first = emas[0]["ema"].flatten()
second = emas[1]["ema"].flatten()
bools = np.abs(first[-len(second):] - second)/second < 0.0001
xpoints = np.compress(bools, emas[1])
3. Now that we have the crossover points, annotate them with arrows. Make sure that
the annotaon text is slightly away from the crossover points.
for xpoint in xpoints:
ax.annotate('x’, xy=xpoint, textcoords=’offset points’,
xytext=(-50, 30),
arrowprops=dict(arrowstyle="->"))
4. Add a legend and let Matplotlib decide where to put it.
leg = ax.legend(loc=’best’, fancybox=True)
5. Make the legend transparent by seng the alpha channel value
leg.get_frame().set_alpha(0.5)
www.it-ebooks.info
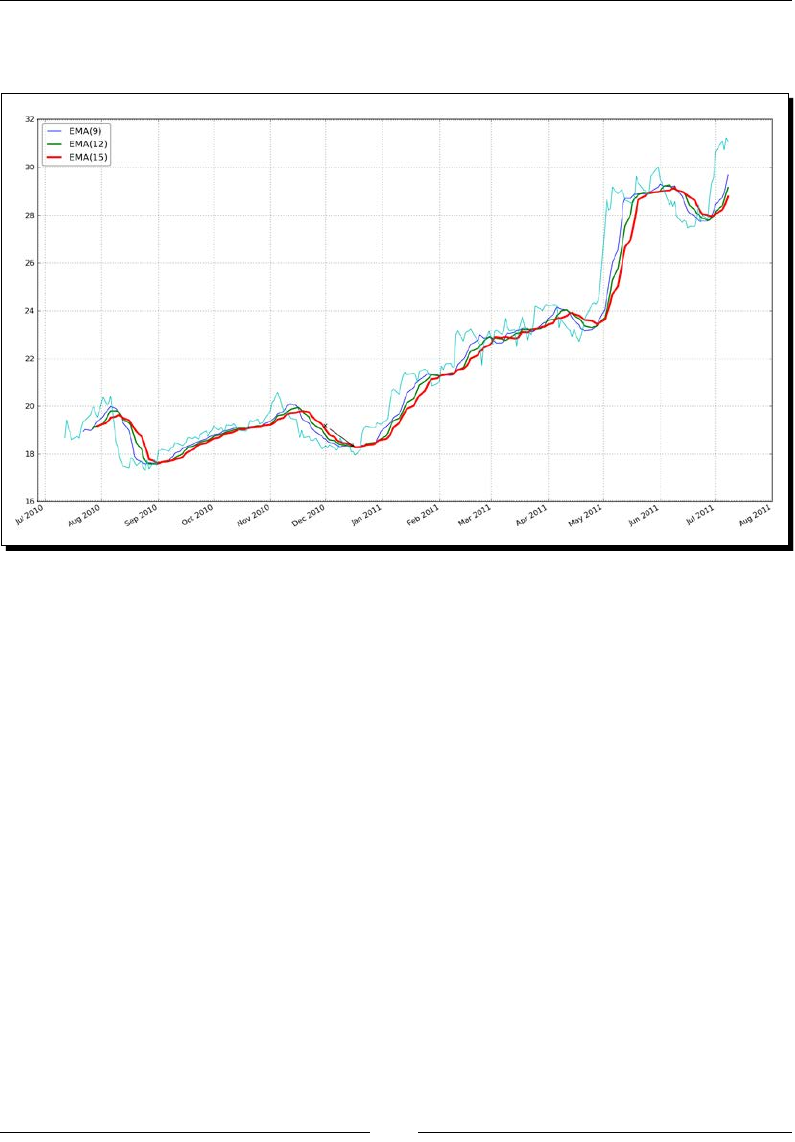
Chapter 9
[ 217 ]
The stock price and moving averages with legend and annotaons would appear
as follows:
What just happened?
We ploed the close price of a stock and three of its exponenal moving averages.
We added a legend to the plot. We annotated the crossover points of the rst two
averages with annotaons (see emalegend.py):
from matplotlib.finance import quotes_historical_yahoo
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
import sys
from datetime import date
import matplotlib.pyplot as plt
import numpy as np
today = date.today()
start = (today.year - 1, today.month, today.day)
symbol = 'DISH’
if len(sys.argv) == 2:
symbol = sys.argv[1]
www.it-ebooks.info
Plong with Matplotlib
[ 218 ]
quotes = quotes_historical_yahoo(symbol, start, today)
quotes = np.array(quotes)
dates = quotes.T[0]
close = quotes.T[4]
fig = plt.figure()
ax = fig.add_subplot(111)
emas = []
for i in range(9, 18, 3):
weights = np.exp(np.linspace(-1., 0., i))
weights /= weights.sum()
ema = np.convolve(weights, close)[i-1:-i+1]
idx = (i - 6)/3
ax.plot(dates[i-1:], ema, lw=idx, label="EMA(%s)" % (i))
data = np.column_stack((dates[i-1:], ema))
emas.append(np.rec.fromrecords(data, names=["dates", "ema"]))
first = emas[0]["ema"].flatten()
second = emas[1]["ema"].flatten()
bools = np.abs(first[-len(second):] - second)/second < 0.0001
xpoints = np.compress(bools, emas[1])
for xpoint in xpoints:
ax.annotate('x’, xy=xpoint, textcoords=’offset points’,
xytext=(-50, 30),
arrowprops=dict(arrowstyle="->"))
leg = ax.legend(loc=’best’, fancybox=True)
leg.get_frame().set_alpha(0.5)
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter("%b %Y")
ax.plot(dates, close, lw=1.0, label="Close")
ax.xaxis.set_major_locator(months)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_formatter(month_formatter)
ax.grid(True)
fig.autofmt_xdate()
plt.show()
Three dimensional plots
Three-dimensional plots are prey spectacular so we have to cover them here too.
For 3D plots, we need an Axes3D object associated with a 3d projecon.
www.it-ebooks.info
Chapter 9
[ 219 ]
Time for action – plotting in three dimensions
We will plot in three dimensions a simple three-dimensional funcon:
1. We need to use the 3d keyword to specify a three-dimensional projecon
for the plot.
ax = fig.add_subplot(111, projection=’3d’)
2. To create a square two-dimensional grid, we will use the meshgrid funcon.
This will be used to inialize the x and y values.
u = np.linspace(-1, 1, 100)
x, y = np.meshgrid(u, u)
3. We will specify the row strides, column strides, and the color map for the surface
plot. The strides determine the size of the "les" on the surface. The choice for
colormap is a maer of taste.
ax.plot_surface(x, y, z, rstride=4, cstride=4,
cmap=cm.YlGnBu_r)
The result is the following 3D plot:
www.it-ebooks.info
Plong with Matplotlib
[ 220 ]
What just happened?
We created a plot of a three dimensional funcon (see three_d.py):
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
fig = plt.figure()
ax = fig.add_subplot(111, projection=’3d’)
u = np.linspace(-1, 1, 100)
x, y = np.meshgrid(u, u)
z = x ** 2 + y ** 2
ax.plot_surface(x, y, z, rstride=4, cstride=4, cmap=cm.YlGnBu_r)
plt.show()
Contour plots
Matplotlib contour 3D plots come in two avors—lled and unlled. We can create normal
contour plots with the contour funcon. For the lled contour plots we can use the
contourf funcon.
Time for action – drawing a lled contour plot
We will draw a lled contour plot of the three-dimensional mathemacal funcon in the
previous Time for Acon. The code is also prey similar. One key dierence is that we don’t
need the 3d projecon parameter any more. To draw the lled contour plot we need this
line of code:
ax.contourf(x, y, z)
www.it-ebooks.info
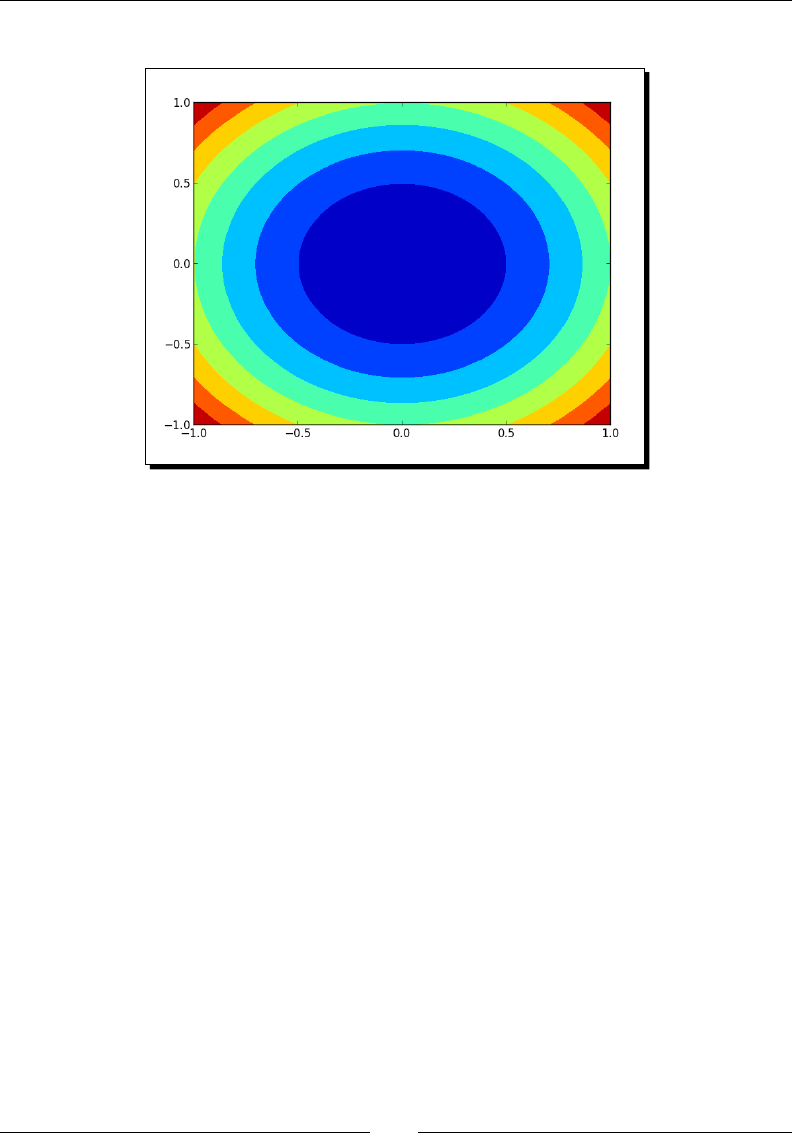
Chapter 9
[ 221 ]
This gives us the following lled contour plot.
What just happened?
We created a lled contour plot of a three-dimensional mathemacal funcon
(see contour.py):
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
fig = plt.figure()
ax = fig.add_subplot(111)
u = np.linspace(-1, 1, 100)
x, y = np.meshgrid(u, u)
z = x ** 2 + y ** 2
ax.contourf(x, y, z)
plt.show()
www.it-ebooks.info
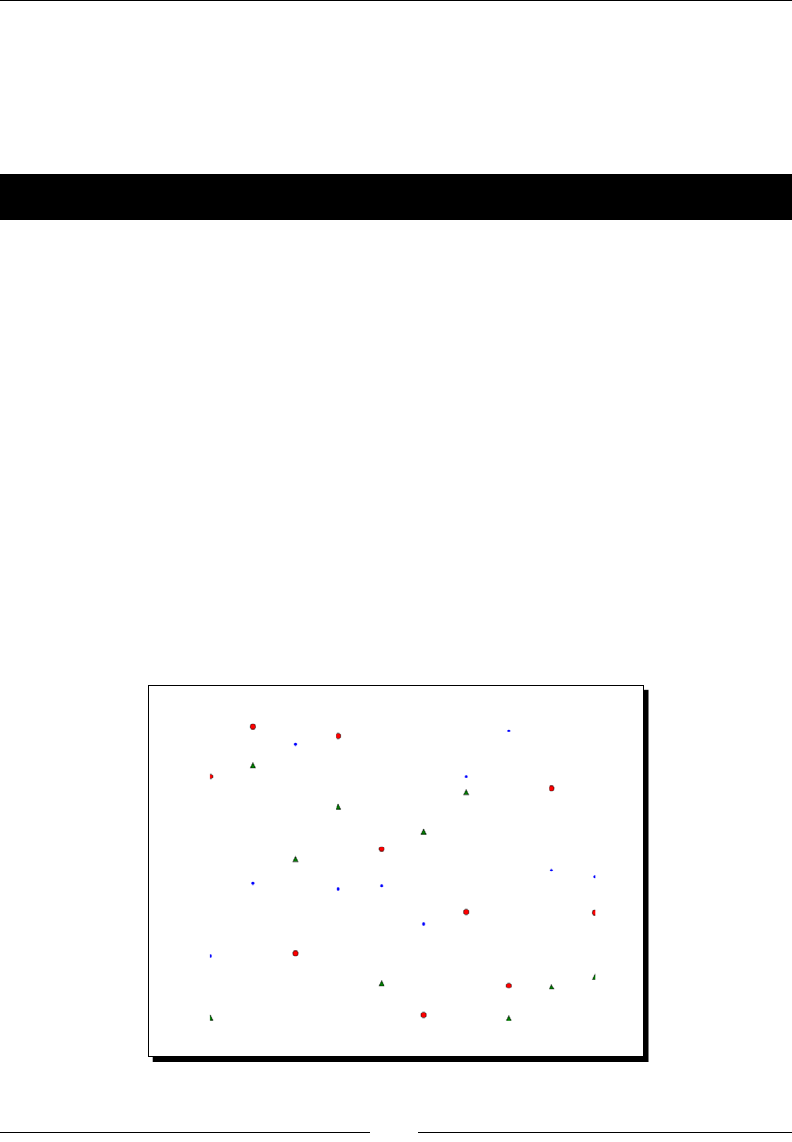
Plong with Matplotlib
[ 222 ]
Animation
Matplotlib oers fancy animaon capabilies. Matplotlib has a special animaon module.
We need to dene a callback funcon that is used to regularly update the screen. We also
need a funcon to generate data to be ploed.
Time for action – animating plots
We will plot three random datasets and display them as circles, dots, and triangles.
However, we will only update two of those datasets with random values.
1. We will plot 3 random datasets as circles, dots and triangles in dierent colors.
circles, triangles, dots = ax.plot(x, 'ro’, y, 'g^’, z, 'b.’)
2. This funcon will get called to update the screen regularly. We will update two
of the plots with new y values.
def update(data):
circles.set_ydata(data[0])
triangles.set_ydata(data[1])
return circles, triangles
3. We will generate random data with NumPy.
def generate():
while True: yield np.random.rand(2, N)
Here is a snapshot of the animaon in acon:
www.it-ebooks.info
Chapter 9
[ 223 ]
What just happened?
We created an animaon of random data points (see animation.py):
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure()
ax = fig.add_subplot(111)
N = 10
x = np.random.rand(N)
y = np.random.rand(N)
z = np.random.rand(N)
circles, triangles, dots = ax.plot(x, 'ro’, y, 'g^’, z, 'b.’)
ax.set_ylim(0, 1)
plt.axis('off’)
def update(data):
circles.set_ydata(data[0])
triangles.set_ydata(data[1])
return circles, triangles
def generate():
while True: yield np.random.rand(2, N)
anim = animation.FuncAnimation(fig, update, generate, interval=150)
plt.show()
Summary
This chapter was about Matplotlib—a Python plong library. We covered simple plots,
histograms, plot customizaon, subplots, 3D plots, contour plots, and logplots. We also saw
a few examples of displaying stock charts. Obviously, we only scratched the surface and saw
the p of the iceberg. Matplotlib is very feature rich, so we didn’t have space to cover LaTex
support, polar coordinates support, and other funconality.
The author of Matplotlib, John Hunter, passed away in August, 2012. One of the
technical reviewers of this book suggested menoning the John Hunter Memorial Fund
(hp://numfocus.org/johnhunter/). The memorial fund set up by the NumFocus Foundaon
is an opportunity for us, as fans of John Hunter’s work, to "give back" so to say. Again, for
more details, check out the previous link to the NumFocus website.
The next chapter is about SciPy—a scienc Python framework that is built on top of NumPy.
www.it-ebooks.info
www.it-ebooks.info
When NumPy is Not
Enough – SciPy and Beyond
SciPy is the world famous Python open-source scientific computing library
built on top of NumPy. It adds functionality such as numerical integration,
optimization, statistics, and special functions.
In this chapter we will cover the following topics:
File I/O
Stascs
Signal processing
Opmizaon
Interpolaon
Image and audio processing
MATLAB and Octave
MATLAB and its open source alternave Octave are popular mathemacal programs.
The scipy.io package has funcons that let you load MATLAB or Octave matrices and
arrays of numbers or strings in Python programs and vice versa. The loadmat funcon loads
a .mat le. The savemat funcon saves a diconary of names and arrays into a .mat le.
10
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 226 ]
Time for action – saving and loading a .mat le
If we start with NumPy arrays and decide to use the said arrays within a MATLAB or Octave
environment, the easiest thing to do is create a .mat le. We then can load the le within
MATLAB or Octave. Let’s go through the necessary steps:
1. Create a NumPy array and call savemat to create a .mat le. This funcon has two
parameters – a lename and a diconary containing variable names and values.
a = np.arange(7)
io.savemat(“a.mat”, {“array”: a})
2. Within a MATLAB or Octave environment, load the .mat le and check the
stored array.
octave-3.4.0:7> load a.mat
octave-3.4.0:8> a
octave-3.4.0:8> array
array =
0
1
2
3
4
5
6
What just happened?
We created a .mat le from NumPy code and loaded it within Octave. We checked the
NumPy array that was created (see scipyio.py).
import numpy as np
from scipy import io
a = np.arange(7)
io.savemat(“a.mat”, {“array”: a})
www.it-ebooks.info
Chapter 10
[ 227 ]
Pop quiz – loading .mat les
Q1. Which funcon loads .mat les?
1. Loadmatlab
2. loadmat
3. loadoct
4. frommat
Statistics
The SciPy stascs module is called scipy.stats. There is one class that implements
connuous distribuons and one class that implements discrete distribuons. Also in this
module, funcons can be found that can perform a great number of stascal tests.
Time for action – analyzing random values
We will generate random values that mimic a normal distribuon and analyze the generated
data with stascal funcons from the scipy.stats package. Perform the following steps
to do so:
1. Generate random values from a normal distribuon using the
scipy.stats package.
generated = stats.norm.rvs(size=900)
2. Fit the generated values to a normal distribuon. This basically gives us the mean
and standard deviaon of the data set.
print “Mean”, “Std”, stats.norm.fit(generated)
The mean and standard deviaon would be shown as follows:
Mean Std (0.0071293257063200707, 0.95537708218972528)
3. Skewness tells us how skewed (asymmetric) a probability distribuon is. Perform
a skewness test. This test returns two values. The second value is the p-value; the
probability that the skewness of the data set corresponds to a normal distribuon.
The pvalue instances range from 0 to 1.
print “Skewtest”, “pvalue”, stats.skewtest(generated)
The result of the skewness test would be shown as follows:
Skewtest pvalue (-0.62120640688766893, 0.5344638245033837)
So there is a 53 percent chance that we are dealing with a normal distribuon.
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 228 ]
4. Kurtosis tells us how “curved” a probability distribuon is. Perform a kurtosis
test. This test is set up in a similar way as the skewness test, but of course,
applies to kurtosis.
print “Kurtosistest”, “pvalue”,
stats.kurtosistest(generated)
The result of the kurtosis test would be shown as follows:
Kurtosistest pvalue (1.3065381019536981, 0.19136963054975586)
5. A normality test tells us how likely it is that a data set complies to the normal
distribuon. Perform a normality test. This test also returns two values,
of which the second is the p-value
print “Normaltest”, “pvalue”, stats.normaltest(generated)
The result of the normality test would be shown as follows:
Normaltest pvalue (2.09293921181506, 0.35117535059841687)
6. We can easily nd the value at a certain percenle with SciPy.
print “95 percentile”,
stats.scoreatpercentile(generated, 95)
The value at the 95th percenle would be shown as follows:
95 percentile 1.54048860252
7. Do the opposite of the previous step to nd the percenle at 1.
print “Percentile at 1”,
stats.percentileofscore(generated, 1)
The percenle at 1 would be shown as follows:
Percentile at 1 85.5555555556
8. Plot the generated values in a histogram with Matplotlib. More informaon about
Matplotlib can be found in the previous chapter.
plt.hist(generated)
plt.show()
www.it-ebooks.info
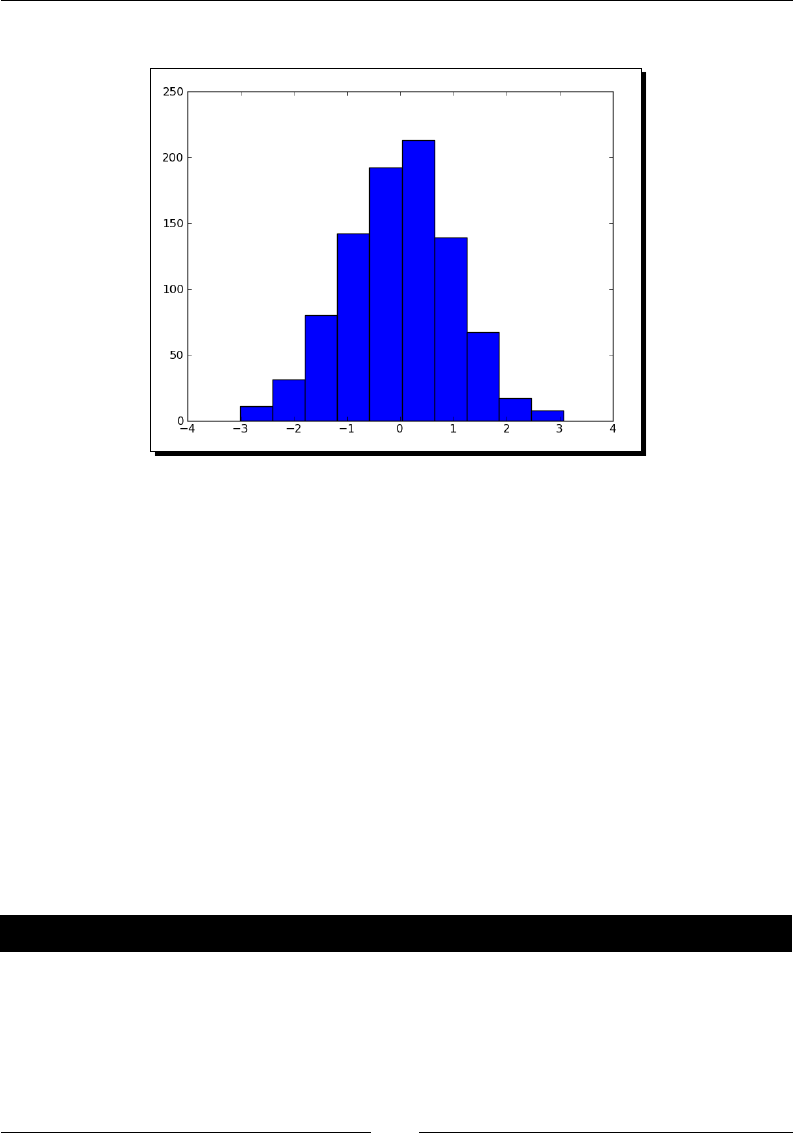
Chapter 10
[ 229 ]
The following is the histogram of the generated random values:
What just happened?
We created a data set from a normal distribuon and analyzed it with the scipy.stats
module (see statistics.py).
from scipy import stats
import matplotlib.pyplot as plt
generated = stats.norm.rvs(size=900)
print “Mean”, “Std”, stats.norm.fit(generated)
print “Skewtest”, “pvalue”, stats.skewtest(generated)
print “Kurtosistest”, “pvalue”, stats.kurtosistest(generated)
print “Normaltest”, “pvalue”, stats.normaltest(generated)
print “95 percentile”, stats.scoreatpercentile(generated, 95)
print “Percentile at 1”, stats.percentileofscore(generated, 1)
plt.hist(generated)
plt.show()
Have a go hero – improving the data generation
Judging from the histogram in the Time for acon – analyzing random values secon, there
is sll room for improvement when it comes to generang the data. Try using NumPy or
dierent parameters of the scipy.stats.norm.rvs funcon.
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 230 ]
Samples’ comparison and SciKits
Oen we will have two data samples, maybe from dierent experiments, that are somehow
related. Stascal tests exist that can compare the samples. Some of these have been
implemented in the scipy.stats module.
Another stascal test that I like is the Jarque-Bera normality test from scikits.
statsmodels.stattools. SciKits are small experimental Python soware toolkits. They
are not part of SciPy. There is also pandas, which is an oshoot of scikits.statsmodels.
A list of SciKits can be found at https://scikits.appspot.com/scikits. You can
install statsmodels using setuptools with the following command:
easy_install statsmodels
Time for action – comparing stock log returns
We will download the stock quotes for the last year of two trackers using Matplotlib. As
menoned in the previous chapter, we can retrieve quotes from Yahoo! Finance. We will
compare the log returns of the close price of DIA and SPY. Also we will perform the Jarque-
Bera test on the dierence of the log returns. Perform the following steps to do so:
1. Write a funcon that can return the close price for a specied stock.
def get_close(symbol):
today = date.today()
start = (today.year - 1, today.month, today.day)
quotes = quotes_historical_yahoo(symbol, start, today)
quotes = np.array(quotes)
return quotes.T[4]
2. Calculate the log returns for DIA and SPY. The log returns are calculated by taking the
natural logarithm of the close price and then taking the dierence of consecuve
values.
spy = np.diff(np.log(get_close(“SPY”)))
dia = np.diff(np.log(get_close(“DIA”)))
3. The means comparison test checks whether two dierent samples could have the
same mean value. Two values are returned, of which the second is a p-value from
0 to 1.
print “Means comparison”, stats.ttest_ind(spy, dia)
The result of the means comparison test would be shown as follows:
Means comparison (-0.017995865641886155, 0.98564930169871368)
www.it-ebooks.info
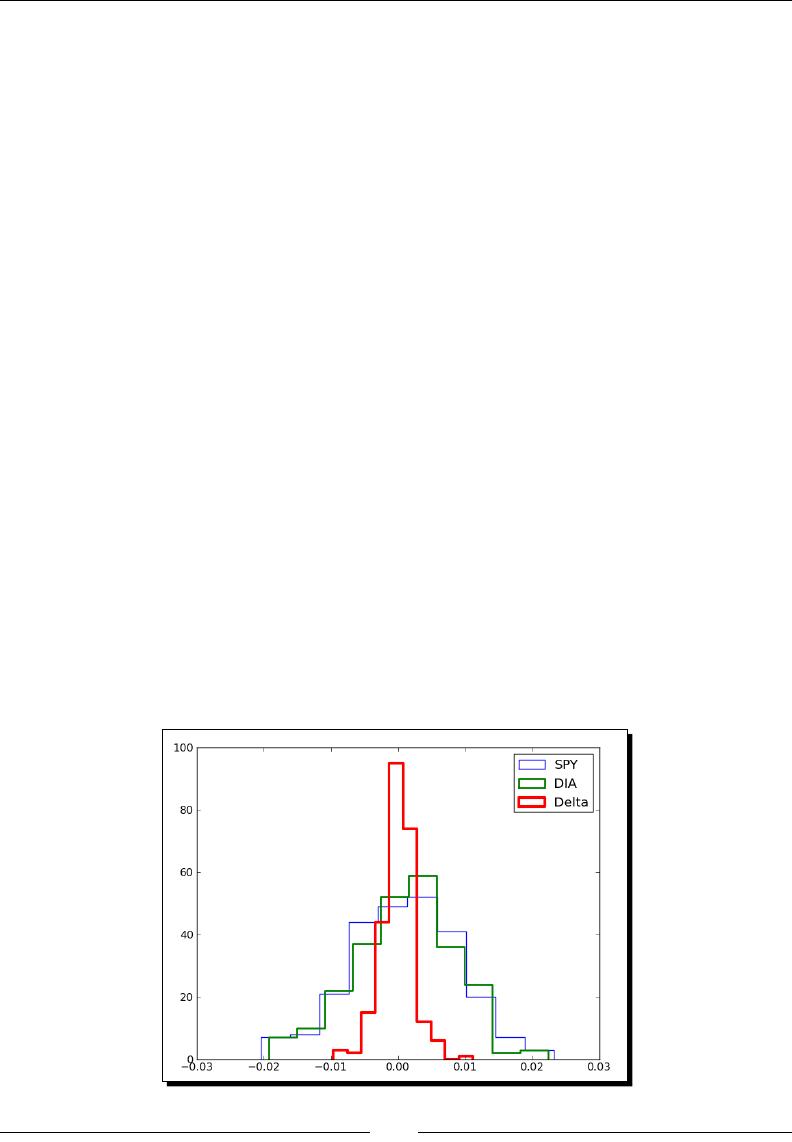
Chapter 10
[ 231 ]
So there is about a 98 percent chance that the two samples have the same mean
log return.
4. The Kolmogorov-Smirnov two samples test tells us how likely it is that two samples
are drawn from the same distribuon.
print “Kolmogorov smirnov test”, stats.ks_2samp(spy, dia)
Again, two values are returned of which the second value is the p-value.
Kolmogorov smirnov test (0.063492063492063516,
0.67615647616238039)
5. Unleash the Jarque-Bera normality test on the dierence of the log returns.
print “Jarque Bera test”,
jarque_bera(spy – dia)[1]
The p-value of the Jarque-Bera normality test would be shown as follows:
Jarque Bera test 0.596125711042
6. Plot the histograms of the log returns and the dierence thereof with Matplotlib.
plt.hist(spy, histtype=”step”, lw=1, label=”SPY”)
plt.hist(dia, histtype=”step”, lw=2, label=”DIA”)
plt.hist(spy - dia, histtype=”step”, lw=3,
label=”Delta”)
plt.legend()
plt.show()
The histograms of the log returns and dierence are shown in the
following screenshot:
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 232 ]
What just happened?
We compared samples of log returns for DIA and SPY. We also performed the Jarque-Bera
test on the dierence of the log returns (see pair.py).
from matplotlib.finance import quotes_historical_yahoo
from datetime import date
import numpy as np
from scipy import stats
from statsmodels.stats.stattools import jarque_bera
import matplotlib.pyplot as plt
def get_close(symbol):
today = date.today()
start = (today.year - 1, today.month, today.day)
quotes = quotes_historical_yahoo(symbol, start, today)
quotes = np.array(quotes)
return quotes.T[4]
spy = np.diff(np.log(get_close(“SPY”)))
dia = np.diff(np.log(get_close(“DIA”)))
print “Means comparison”, stats.ttest_ind(spy, dia)
print “Kolmogorov smirnov test”, stats.ks_2samp(spy, dia)
print “Jarque Bera test”, jarque_bera(spy - dia)[1]
plt.hist(spy, histtype=”step”, lw=1, label=”SPY”)
plt.hist(dia, histtype=”step”, lw=2, label=”DIA”)
plt.hist(spy - dia, histtype=”step”, lw=3, label=”Delta”)
plt.legend()
plt.show()
Signal processing
The scipy.signal module contains lter funcons and B-spline interpolaon algorithms.
www.it-ebooks.info
Chapter 10
[ 233 ]
Spline interpolaon uses a polynomial called a spline for interpolaon.
The interpolaon then tries to glue splines together to t the data.
B-spline is a type of spline.
A SciPy signal is dened as an array of numbers. An example of a lter is the detrend
funcon. This funcon takes a signal and does a linear t on it. This trend is then subtracted
from the original input data.
Time for action – detecting a trend in QQQ
Oen we are more interested in the trend of a data sample than in detrending it. Sll we can
get the trend back easily aer detrending. Let’s do that for 1 year of price data for QQQ:
1. Write code that gets the close price and corresponding dates for QQQ.
today = date.today()
start = (today.year - 1, today.month, today.day)
quotes = quotes_historical_yahoo(“QQQ”, start, today)
quotes = np.array(quotes)
dates = quotes.T[0]
qqq = quotes.T[4]
2. Detrend the signal.
y = signal.detrend(qqq)
3. Create month and day locators for the dates.
alldays = DayLocator()
months = MonthLocator ()
4. Create a date formaer that creates a string of month name and year.
month_formatter = DateFormatter(“%b %Y”)
5. Create a gure and subplot.
fig = plt.figure()
ax = fig.add_subplot(111)
6. Plot the data and underlying trend by subtracng the detrended signal.
plt.plot(dates, qqq, ‘o’, dates, qqq - y, ‘-’)
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 234 ]
7. Set the locators and formaer.
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(month_formatter)
8. Format the x-axis labels as dates.
fig.autofmt_xdate()
plt.show()
The following screenshot shows the QQQ prices with a trend line:
What just happened?
We ploed the closing price for QQQ with a trend line (see trend.py).
from matplotlib.finance import quotes_historical_yahoo
from datetime import date
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
today = date.today()
start = (today.year - 1, today.month, today.day)
www.it-ebooks.info
Chapter 10
[ 235 ]
quotes = quotes_historical_yahoo(“QQQ”, start, today)
quotes = np.array(quotes)
dates = quotes.T[0]
qqq = quotes.T[4]
y = signal.detrend(qqq)
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter(“%b %Y”)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(dates, qqq, ‘o’, dates, qqq - y, ‘-’)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(month_formatter)
fig.autofmt_xdate()
plt.show()
Fourier analysis
Signals in the real world oen have a periodic nature. A commonly used tool to deal with
these signals is the Fourier transform. The Fourier transform is a transformaon from the
me domain into the frequency domain, that is, the linear decomposion of a periodic signal
into sine and cosine funcons with various frequencies.
The funcons for Fourier transforms can be found in the scipy.fftpack module (NumPy
also has its own Fourier package, numpy.fft). Included in the package are fast Fourier
transforms, dierenal and pseudo-dierenal operators, as well as several helper funcons.
MATLAB users will be pleased to know that a number of funcons in the scipy.fftpack
module have the same names as their MATLAB counterparts and similar funcons as their
MATLAB equivalents.
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 236 ]
Time for action – ltering a detrended signal
We learned in how to detrend a signal in the Time for acon – detecng a trend in QQQ
secon. This detrended signal could have a cyclical component. Let’s try to visualize this.
Some of the steps are a repeon of steps in the previous Time for acon tutorial, such as
downloading the data and seng up Matplotlib objects. These steps are omied here.
1. Apply Fourier transforms, which will give us the frequency spectrum.
amps = np.abs(fftpack.fftshift(fftpack.rfft(y)))
2. Filter out the noise. Let’s say if the magnitude of a frequency component is below 10
percent of the strongest component, throw it out.
amps[amps < 0.1 * amps.max()] = 0
3. Transform the ltered signal back to the original domain and plot it together with
the detrended signal.
plt.plot(dates, y, ‘o’, label=”detrended”)
plt.plot(dates,
-fftpack.irfft(fftpack.ifftshift(amps)),
label=”filtered”)
4. Format the x-axis labels as dates and add a legend with extra large size.
fig.autofmt_xdate()
plt.legend(prop={‘size’:’x-large’})
5. Add a second subplot and plot the frequency spectrum aer ltering.
ax2 = fig.add_subplot(212)
N = len(qqq)
plt.plot(np.linspace(-N/2, N/2, N), amps,
label=”transformed”)
6. Display the legend and plot.
plt.legend(prop={‘size’:’x-large’})
plt.show()
www.it-ebooks.info
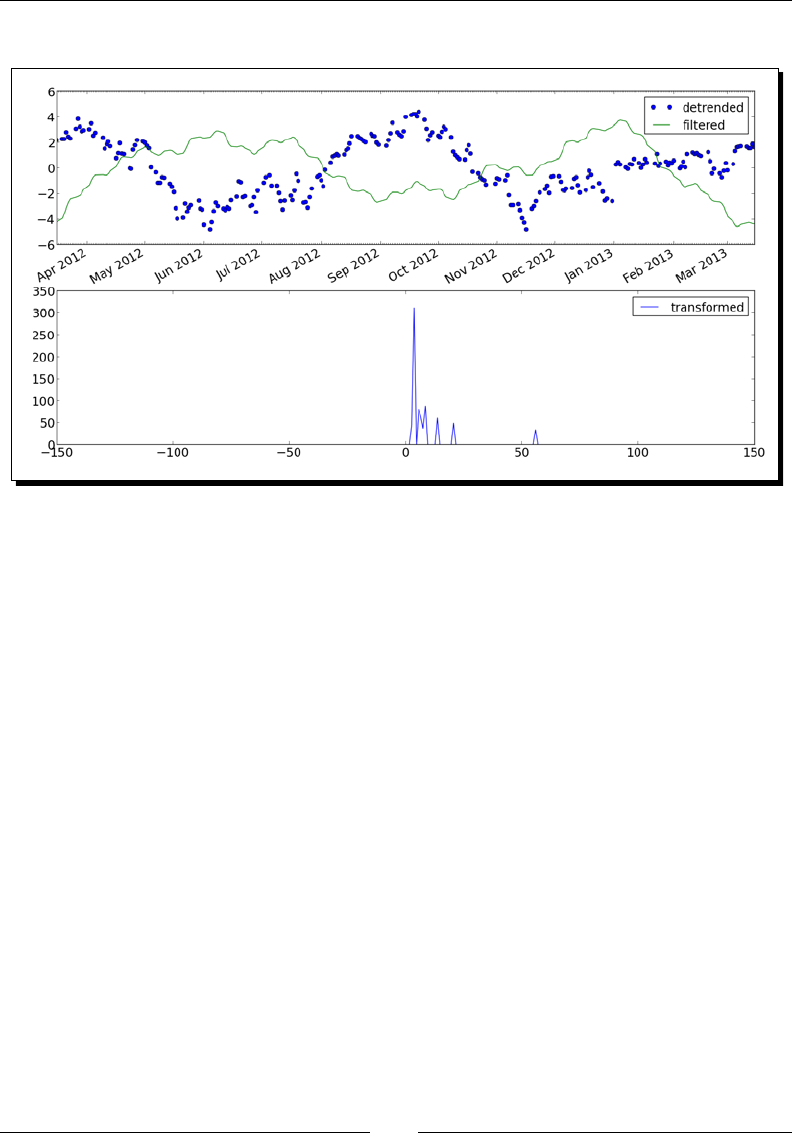
Chapter 10
[ 237 ]
The following plots are of the signal and frequency spectrum:
What just happened?
We detrended a signal and applied a simple lter on it using the scipy.fftpack module
(see frequencies.py).
from matplotlib.finance import quotes_historical_yahoo
from datetime import date
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
from scipy import fftpack
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
today = date.today()
start = (today.year - 1, today.month, today.day)
quotes = quotes_historical_yahoo(“QQQ”, start, today)
quotes = np.array(quotes)
dates = quotes.T[0]
qqq = quotes.T[4]
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 238 ]
y = signal.detrend(qqq)
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter(“%b %Y”)
fig = plt.figure()
fig.subplots_adjust(hspace=.3)
ax = fig.add_subplot(211)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(month_formatter)
# make font size bigger
ax.tick_params(axis=’both’, which=’major’, labelsize=’x-large’)
amps = np.abs(fftpack.fftshift(fftpack.rfft(y)))
amps[amps < 0.1 * amps.max()] = 0
plt.plot(dates, y, ‘o’, label=”detrended”)
plt.plot(dates, -fftpack.irfft(fftpack.ifftshift(amps)),
label=”filtered”)
fig.autofmt_xdate()
plt.legend(prop={‘size’:’x-large’})
ax2 = fig.add_subplot(212)
ax2.tick_params(axis=’both’, which=’major’, labelsize=’x-large’)
N = len(qqq)
plt.plot(np.linspace(-N/2, N/2, N), amps, label=”transformed”)
plt.legend(prop={‘size’:’x-large’})
plt.show()
Mathematical optimization
Opmizaon algorithms try to nd the opmal soluon for a problem, for instance nding
the maximum or the minimum of a funcon. The funcon can be linear or non-linear. The
soluon could also have special constraints. For example, the soluon may not be allowed to
have negave values. Several opmizaon algorithms are provided by the scipy.optimize
module. One of the algorithms is a least squares ng funcon, leastsq. When calling this
funcon, we are required to provide a residuals (error terms) funcon. This funcon is used
to minimize the sum of the squares of the residuals. It corresponds to our mathemacal
www.it-ebooks.info
Chapter 10
[ 239 ]
model for the soluon. Also, it is necessary to give the algorithm a starng point. This should
be a best guess—as close as possible to the real soluon. Otherwise, execuon will stop aer
about 800 iteraons.
Time for action – tting to a sine
In the Time for acon – ltering a detrended signal secon we created a simple lter for
detrended data. Now let’s use a more restricve lter that will leave us only with the main
frequency component. We will t a sinusoidal paern to it and plot our results. This model
has four parameters—amplitude, frequency, phase, and vercal oset. Perform the following
steps to t to a sine:
1. Dene a residuals funcon based on a sine wave model.
def residuals(p, y, x):
A,k,theta,b = p
err = y-A * np.sin(2* np.pi* k * x + theta) + b
return err
2. Transform the ltered signal back to the original domain.
filtered = -fftpack.irfft(fftpack.ifftshift(amps))
3. Guess the values of the parameters for which we are trying to esmate a
transformaon from the me domain into the frequency domain.
N = len(qqq)
f = np.linspace(-N/2, N/2, N)
p0 = [filtered.max(), f[amps.argmax()]/(2*N), 0, 0]
print “P0”, p0
The inial values would be shown as follows:
P0 [2.6679532410065212, 0.00099598469163686377, 0, 0]
4. Call the leastsq funcon.
plsq = optimize.leastsq(residuals, p0, args=(filtered,
dates))
p = plsq[0]
print “P”, p
The following are the nal parameter values:
P [ 2.67678014e+00 2.73033206e-03 -8.00007036e+03
-5.01260321e-03]
www.it-ebooks.info
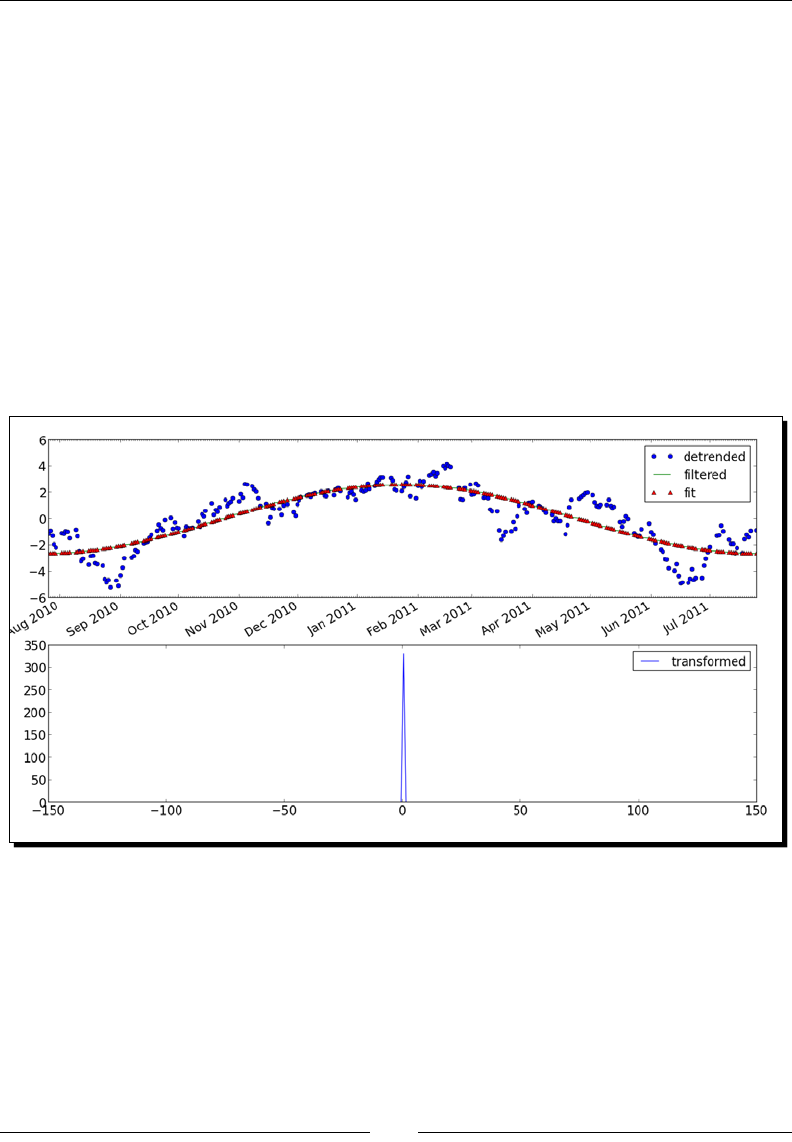
When NumPy is Not Enough – SciPy and Beyond
[ 240 ]
5. Finish the rst subplot with detrended data, ltered data, and t of the ltered data.
Use a date format for the horizontal axis and add a legend.
plt.plot(dates, y, ‘o’, label=”detrended”)
plt.plot(dates, filtered, label=”filtered”)
plt.plot(dates, p[0] * np.sin(2 * np.pi *
dates * p[1] + p[2]) + p[3], ‘^’, label=”fit”)
fig.autofmt_xdate()
plt.legend(prop={‘size’:’x-large’})
6. Add a second subplot with a legend of the main component of the
frequency spectrum.
ax2 = fig.add_subplot(212)
plt.plot(f, amps, label=”transformed”)
The following shows the resulng charts:
What just happened?
We detrended 1 year of price data for QQQ. This signal was then ltered unl only the main
component of the frequency spectrum was le over. We ed a sine to the ltered signal
using the scipy.optimize module (see optfit.py).
from matplotlib.finance import quotes_historical_yahoo
import numpy as np
import matplotlib.pyplot as plt
www.it-ebooks.info
Chapter 10
[ 241 ]
from scipy import fftpack
from scipy import signal
from matplotlib.dates import DateFormatter
from matplotlib.dates import DayLocator
from matplotlib.dates import MonthLocator
from scipy import optimize
start = (2010, 7, 25)
end = (2011, 7, 25)
quotes = quotes_historical_yahoo(“QQQ”, start, end)
quotes = np.array(quotes)
dates = quotes.T[0]
qqq = quotes.T[4]
y = signal.detrend(qqq)
alldays = DayLocator()
months = MonthLocator()
month_formatter = DateFormatter(“%b %Y”)
fig = plt.figure()
fig.subplots_adjust(hspace=.3)
ax = fig.add_subplot(211)
ax.xaxis.set_minor_locator(alldays)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(month_formatter)
ax.tick_params(axis=’both’, which=’major’, labelsize=’x-large’)
amps = np.abs(fftpack.fftshift(fftpack.rfft(y)))
amps[amps < amps.max()] = 0
def residuals(p, y, x):
A,k,theta,b = p
err = y-A * np.sin(2* np.pi* k * x + theta) + b
return err
filtered = -fftpack.irfft(fftpack.ifftshift(amps))
N = len(qqq)
f = np.linspace(-N/2, N/2, N)
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 242 ]
p0 = [filtered.max(), f[amps.argmax()]/(2*N), 0, 0]
print “P0”, p0
plsq = optimize.leastsq(residuals, p0, args=(filtered, dates))
p = plsq[0]
print “P”, p
plt.plot(dates, y, ‘o’, label=”detrended”)
plt.plot(dates, filtered, label=”filtered”)
plt.plot(dates, p[0] * np.sin(2 * np.pi * dates * p[1] + p[2]) + p[3],
‘^’, label=”fit”)
fig.autofmt_xdate()
plt.legend(prop={‘size’:’x-large’})
ax2 = fig.add_subplot(212)
ax2.tick_params(axis=’both’, which=’major’, labelsize=’x-large’)
plt.plot(f, amps, label=”transformed”)
plt.legend(prop={‘size’:’x-large’})
plt.show()
Numerical integration
SciPy has a numerical integraon package, scipy.integrate, which has no equivalent in
NumPy. The quad funcon can integrate a one-variable funcon between two points. These
points can be at innity. The funcon uses the simplest numerical integraon method, the
trapezoid rule.
Time for action – calculating the Gaussian integral
The Gaussian integral is related to the error funcon (also known as erf in mathemacs),
but has no nite limits. It evaluates to the square root of pi. Let’s calculate the integral with
the quad funcon.
Calculate the Gaussian integral with the quad funcon.
print “Gaussian integral”, np.sqrt(np.pi),
integrate.quad(lambda x: np.exp(-x**2),
-np.inf, np.inf)
The return value is the outcome and its error would be shown as follows:
Gaussian integral 1.77245385091 (1.7724538509055159, 1.4202636780944923e-
08)
www.it-ebooks.info
Chapter 10
[ 243 ]
What just happened?
We calculated the Gaussian integral with the quad funcon.
Interpolation
Interpolaon “lls in the blanks” between known data points in a data set. The scipy.
interpolate funcon interpolates a funcon based on experimental data. The interp1d
class can create a linear or cubic interpolaon funcon. By default a linear interpolaon
funcon is constructed, but if the kind parameter is set, a cubic interpolaon funcon is
created instead. The interp2d class works the same way, but in 2D.
Time for action – interpolating in one dimension
We will create data points using a sinc funcon and add some random noise to them. Aer
that, we will do a linear and cubic interpolaon, and plot the results. Perform the following
steps to do so:
1. Create the data points and add noise to them.
x = np.linspace(-18, 18, 36)
noise = 0.1 * np.random.random(len(x))
signal = np.sinc(x) + noise
2. Create a linear interpolaon funcon and apply it to an input array with ve mes
as many data points.
interpreted = interpolate.interp1d(x, signal)
x2 = np.linspace(-18, 18, 180)
y = interpreted(x2)
3. Do the same as in the previous step, but with cubic interpolaon.
cubic = interpolate.interp1d(x, signal, kind=”cubic”)
y2 = cubic(x2)
4. Plot the results with Matplotlib.
plt.plot(x, signal, ‘o’, label=”data”)
plt.plot(x2, y, ‘-’, label=”linear”)
plt.plot(x2, y2, ‘-’, lw=2, label=”cubic”)
plt.legend()
plt.show()
www.it-ebooks.info
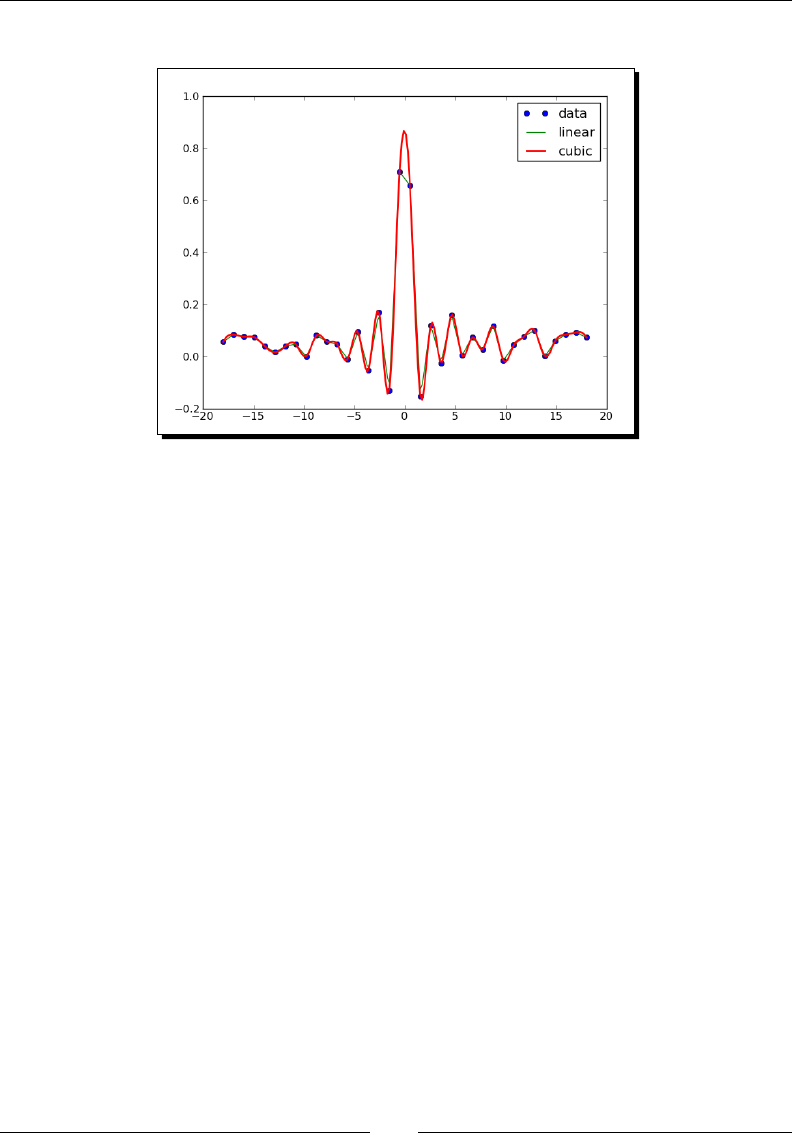
When NumPy is Not Enough – SciPy and Beyond
[ 244 ]
The following screenshot is a plot of the data, linear, and cubic interpolaon:
What just happened?
We created a data set from the sinc funcon and added noise to it. We then did linear and
cubic interpolaon using the interp1d class of the scipy.interpolate module (see
sincinterp.py).
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(-18, 18, 36)
noise = 0.1 * np.random.random(len(x))
signal = np.sinc(x) + noise
interpreted = interpolate.interp1d(x, signal)
x2 = np.linspace(-18, 18, 180)
y = interpreted(x2)
cubic = interpolate.interp1d(x, signal, kind=”cubic”)
y2 = cubic(x2)
plt.plot(x, signal, ‘o’, label=”data”)
plt.plot(x2, y, ‘-’, label=”linear”)
plt.plot(x2, y2, ‘-’, lw=2, label=”cubic”)
plt.legend()
plt.show()
www.it-ebooks.info
Chapter 10
[ 245 ]
Image processing
With SciPy, we can do image processing using the scipy.ndimage package. The module
contains various image lters and ulies.
Time for action – manipulating Lena
In the scipy.misc module, there is a ulity that loads the image of “Lena”. This is the
image of Lena Soderberg tradionally used for image processing examples. We will apply
some lters on this image and rotate it. Perform the following steps to do so:
1. Load the “Lena” image and display it in a subplot with grayscale colormap.
image = misc.lena().astype(np.float32)
plt.subplot(221)
plt.title(“Original Image”)
img = plt.imshow(image, cmap=plt.cm.gray)
Note that we are dealing with a float32 array.
2. The median lter scans the signal and replaces each item by the median of
neighboring data points. Apply a median lter to the image and display it in a
second subplot.
plt.subplot(222)
plt.title(“Median Filter”)
filtered = ndimage.median_filter(image, size=(42,42))
plt.imshow(filtered, cmap=plt.cm.gray)
3. Rotate the image and display it in the third subplot.
plt.subplot(223)
plt.title(“Rotated”)
rotated = ndimage.rotate(image, 90)
plt.imshow(rotated, cmap=plt.cm.gray)
4. The Prewi lter is based on compung the gradient of image intensity. Apply a
Prewi lter to the image and display it in the fourth subplot.
plt.subplot(224)
plt.title(“Prewitt Filter”)
filtered = ndimage.prewitt(image)
plt.imshow(filtered, cmap=plt.cm.gray)
plt.show()
www.it-ebooks.info
When NumPy is Not Enough – SciPy and Beyond
[ 246 ]
The following are the resulng images:
What just happened?
We manipulated the image of “Lena” in several ways using the scipy.ndimage module
(see images.py).
from scipy import misc
import numpy as np
import matplotlib.pyplot as plt
from scipy import ndimage
image = misc.lena().astype(np.float32)
plt.subplot(221)
plt.title(“Original Image”)
img = plt.imshow(image, cmap=plt.cm.gray)
plt.axis(“off”)
plt.subplot(222)
plt.title(“Median Filter”)
filtered = ndimage.median_filter(image, size=(42,42))
plt.imshow(filtered, cmap=plt.cm.gray)
plt.axis(“off”)
www.it-ebooks.info
Chapter 10
[ 247 ]
plt.subplot(223)
plt.title(“Rotated”)
rotated = ndimage.rotate(image, 90)
plt.imshow(rotated, cmap=plt.cm.gray)
plt.axis(“off”)
plt.subplot(224)
plt.title(“Prewitt Filter”)
filtered = ndimage.prewitt(image)
plt.imshow(filtered, cmap=plt.cm.gray)
plt.axis(“off”)
plt.show()
Audio processing
Now that we have done some image processing, you will probably be not surprised that we
can do excing things with WAV les too. Let’s download a WAV le and replay it a couple of
mes. We will skip the explanaon of the download part, which is just regular Python.
Time for action – replaying audio clips
We will download a WAV le of Ausn Powers exclaiming “Smashing, baby!”. This le can be
converted to a NumPy array with the read funcon from the scipy.io.wavfile module.
The write funcon from the same package will be used to create a new WAV le at the end
of this tutorial. We will further use the tile funcon to replay the audio clip several mes.
Perform the following steps to do so:
1. Read the le with the read funcon.
sample_rate, data = wavfile.read(WAV_FILE)
This gives us two items – sample rate and audio data. For this tutorial we are only
interested in the audio data.
2. Apply the tile funcon.
repeated = np.tile(data, int(sys.argv[1]))
3. Write a new le with the write funcon.
wavfile.write(“repeated_yababy.wav”,
sample_rate, repeated)
www.it-ebooks.info
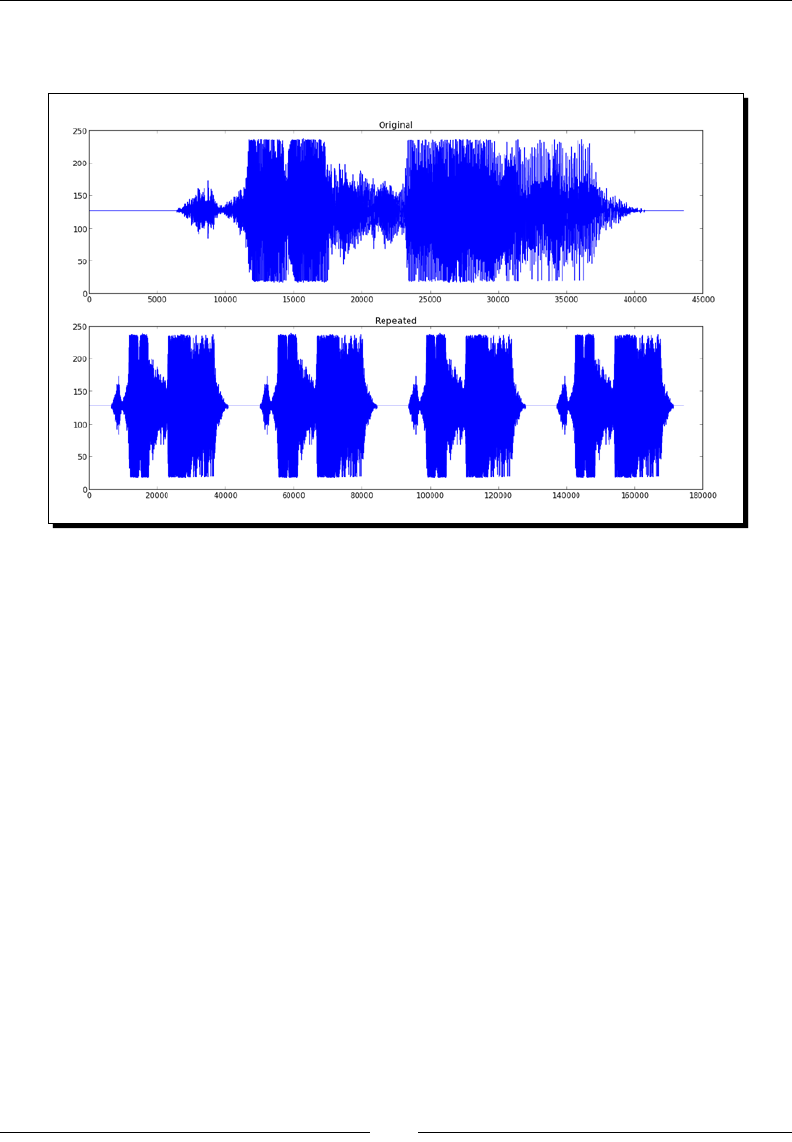
When NumPy is Not Enough – SciPy and Beyond
[ 248 ]
The original audio data and the audio clip repeated four mes are shown in the
following plot:
What just happened?
We read an audio clip, repeated it four mes and then created a new WAV le with the new
array (see repeat_audio.py).
from scipy.io import wavfile
import matplotlib.pyplot as plt
import urllib2
import numpy as np
import sys
response = urllib2.urlopen(‘http://www.thesoundarchive.com/
austinpowers/smashingbaby.wav’)
print response.info()
WAV_FILE = ‘smashingbaby.wav’
filehandle = open(WAV_FILE, ‘w’)
filehandle.write(response.read())
filehandle.close()
sample_rate, data = wavfile.read(WAV_FILE)
print “Data type”, data.dtype, “Shape”, data.shape
plt.subplot(2, 1, 1)
plt.title(“Original”)
www.it-ebooks.info
Chapter 10
[ 249 ]
plt.plot(data)
plt.subplot(2, 1, 2)
# Repeat the audio fragment
repeated = np.tile(data, int(sys.argv[1]))
# Plot the audio data
plt.title(“Repeated”)
plt.plot(repeated)
wavfile.write(“repeated_yababy.wav”,
sample_rate, repeated)
plt.show ()
Summary
In this chapter we only scratched the surface of what is possible with SciPy and SciKits. Sll,
we learned a bit about le I/O, stascs, signal processing, opmizaon, interpolaon, and
audio and image processing.
In the next chapter we will create some simple, yet fun, games with Pygame – the
open-source Python game library. During this process we will learn about NumPy
integraon with Pygame, a machine learning Scikits module and more.
www.it-ebooks.info
www.it-ebooks.info
Playing with Pygame
This chapter is for developers who want to create games with NumPy and
Pygame quickly and easily. Basic game development experience would help but
isn't necessary.
In this chapter we will cover the following topics:
Pygame basics
Matplotlib integraon
Surface pixel arrays
Arcial intelligence
Animaon
OpenGL
Pygame
Pygame is a Python framework originally wrien by Pete Shinners, which, as its name
suggests, can be used to create video games. Pygame is free, open source since 2004 and
licensed under the General Public License, which means that you are allowed to basically
make any type of game. Pygame is built on top of the Simple DirectMedia Layer (SDL). SDL
is a C framework that gives access to graphics, sound, keyboard, and other input devices on
various operang systems including Linux, Mac OS X, and Windows.
11
www.it-ebooks.info
Playing with Pygame
[ 252 ]
Time for action – installing Pygame
We will install Pygame in this tutorial. Pygame should be compable with all Python versions.
At the me of wring there were some incompability issues with Python 3, but in all
probability, these will be xed soon. Perform the following steps to install Pygame:
1. Depending on the operang system, you have the following opons with which you
install Pygame:
Debian and Ubuntu: Pygame can be found in the Debian archives
at http://packages.qa.debian.org/p/pygame.html.
Windows: From the Pygame website (http://www.pygame.org/
download.shtml) we can download the appropriate binary installer
for the Python version we are using.
Mac: Binary Pygame packages for Mac OS X 10.3 and up can be found
at http://www.pygame.org/download.shtml.
2. Pygame uses the distutils system for compiling and installing. To start installing
Pygame with the default opons, simply run the following command:
python setup.py
If you need more informaon about the available opons, type:
python setup.py help
3. In order to compile the code, you need to have a compiler for your operang
system. Seng this up is beyond the scope of this book. More informaon about
compiling Pygame on Windows can be found at http://pygame.org/wiki/
CompileWindows. More informaon about compiling Pygame on Mac OS X can be
found at http://pygame.org/wiki/MacCompile.
Hello World
We will create a simple game that we will further improve later in this chapter. As is
tradional in books about programming, we will start with a "Hello World" example.
Time for action – creating a simple game
It's important to noce the so-called main game loop where all the acon happens and
the usage of the Font module to render text. In this program we will manipulate a Pygame
Surface object that is used for drawing, and we will handle a quit event. Perform the
following steps to create a simple game:
www.it-ebooks.info
Chapter 11
[ 253 ]
1. First import the required Pygame modules. If Pygame is installed properly, we should
get no errors, otherwise please return to the installaon recipe.
import pygame, sys
from pygame.locals import *
2. We will inialize Pygame, create a display of 400 x 300 pixels, and set the window
tle to Hello World!.
pygame.init()
screen = pygame.display.set_mode((400, 300))
pygame.display.set_caption('Hello World!')
3. Games usually have a game loop, which runs forever unl for instance a quit
event occurs. In this example we will only set a label with the text Hello World at
coordinates (100, 100). The text has font size of 19 and a red color.
while True:
sysFont = pygame.font.SysFont("None", 19)
rendered = sysFont.render
('Hello World', 0, (255, 100, 100))
screen.blit(rendered, (100, 100))
for event in pygame.event.get():
if event.type == QUIT:
pygame.quit()
sys.exit()
pygame.display.update()
We get the following screenshot as an end result:
www.it-ebooks.info
Playing with Pygame
[ 254 ]
The following is the complete code for the "Hello World" example:
import pygame, sys
from pygame.locals import *
pygame.init()
screen = pygame.display.set_mode((400, 300))
pygame.display.set_caption('Hello World!')
while True:
sysFont = pygame.font.SysFont("None", 19)
rendered = sysFont.render
('Hello World', 0, (255, 100, 100))
screen.blit(rendered, (100, 100))
for event in pygame.event.get():
if event.type == QUIT:
pygame.quit()
sys.exit()
pygame.display.update()
What just happened?
It might not seem like much, but we learned a lot in this tutorial. The funcons that passed
the review are summarized in the following table:
Function Description
pygame.init() This function does initialization and needs to be
called before other Pygame functions are called.
pygame.display.set_mode((400,
300))
This creates a so-called Surface object
to draw on. We give this function a tuple
representing the dimensions of the surface.
pygame.display.set_
caption('Hello World!')
This sets the window title to a specified string
value.
pygame.font.SysFont("None", 19) This creates a system font from a comma-
separated list of fonts (in this case. none) and a
font size parameter.
sysFont.render('Hello World',
0, (255, 100, 100))
This draws text on a Surface object. The
last parameter is a tuple representing the RGB
values of a color.
www.it-ebooks.info
Chapter 11
[ 255 ]
Function Description
screen.blit(rendered, (100,
100))
This draws on a Surface object.
pygame.event.get() This gets a list of Event objects. The Event
objects represent some special occurrence in
the system, such as a user quitting the game.
pygame.quit() This cleans up resources used by Pygame. Call
this function before exiting the game.
pygame.display.update() This refreshes the surface.
Animation
Most games, even the most stac ones, have some level of animaon. From a programmer's
standpoint, animaon is nothing more than displaying an object at a dierent place at a
dierent me, thus simulang movement.
Pygame oers a Clock object, which manages how many frames are drawn per second.
This ensures that animaon is independent of how fast the user's CPU is.
Time for action – animating objects with NumPy and Pygame
We will load an image and use NumPy again to dene a clockwise path around the screen.
Perform the following steps to do so:
1. We can create a Pygame clock, as follows:
clock = pygame.time.Clock()
2. As part of the source code accompanying this book, there should be a picture of a
head. We will load this image and move it around on the screen.
img = pygame.image.load('head.jpg')
3. We will dene some arrays to hold the coordinates of the posions where we would
like to put the image during the animaon. Since the object will be moved, there are
four logical secons of the path – right, down, le, and up. Each of these secons
will have 40 equidistant steps. We will inialize all the values in these secons to 0.
steps = np.linspace(20, 360, 40).astype(int)
right = np.zeros((2, len(steps)))
down = np.zeros((2, len(steps)))
left = np.zeros((2, len(steps)))
up = np.zeros((2, len(steps)))
www.it-ebooks.info
Playing with Pygame
[ 256 ]
4. It's trivial to set the coordinates of the posions of the image. However, there is one
tricky bit to be aware of – the [::-1] notaon leads to reversing the order of the
array elements.
right[0] = steps
right[1] = 20
down[0] = 360
down[1] = steps
left[0] = steps[::-1]
left[1] = 360
up[0] = 20
up[1] = steps[::-1]
5. The path secons can be joined, but before we can do this, the arrays have to
be transposed with the T operator, because they are not aligned properly for
concatenaon.
pos = np.concatenate((right.T, down.T, left.T, up.T))
6. In the main event loop we will set the clock ck at a rate of 30 frames per second:
clock.tick(30)
The following is a screenshot of the moving head:
You should be able to watch a movie of this animaon at https://www.youtube.
com/watch?v=m2TagGiq1fs.
The code of this example uses almost everything we learned so far, but should sll
be simple enough to understand:
import pygame, sys
from pygame.locals import *
import numpy as np
www.it-ebooks.info
Chapter 11
[ 257 ]
pygame.init()
clock = pygame.time.Clock()
screen = pygame.display.set_mode((400, 400))
pygame.display.set_caption('Animating Objects')
img = pygame.image.load('head.jpg')
steps = np.linspace(20, 360, 40).astype(int)
right = np.zeros((2, len(steps)))
down = np.zeros((2, len(steps)))
left = np.zeros((2, len(steps)))
up = np.zeros((2, len(steps)))
right[0] = steps
right[1] = 20
down[0] = 360
down[1] = steps
left[0] = steps[::-1]
left[1] = 360
up[0] = 20
up[1] = steps[::-1]
pos = np.concatenate((right.T, down.T, left.T, up.T))
i = 0
while True:
# Erase screen
screen.fill((255, 255, 255))
if i >= len(pos):
i = 0
screen.blit(img, pos[i])
i += 1
for event in pygame.event.get():
if event.type == QUIT:
pygame.quit()
sys.exit()
pygame.display.update()
clock.tick(30)
www.it-ebooks.info
Playing with Pygame
[ 258 ]
What just happened?
We learned a bit about animaon in this tutorial. The most important concept we learned
about, is about the clock. The new funcons that we used are described in the following table:
Function Description
pygame.time.Clock() This creates a game clock.
clock.tick(30) This executes a "tick" of the game clock. Here 30 is
the number of frames per second.
Matplotlib
Matplotlib is an open-source library for easy plong that we learned about in Chapter 9,
Plong with Matplotlib. We can integrate Matplotlib into a Pygame game and create
various plots.
Time for action – using Matplotlib in Pygame
In this recipe we will take the posion coordinates of the previous tutorial and make a graph
from them. Perform the following steps to do so:
1. Using a noninteracve backend: In order to integrate Matplotlib with Pygame we
need to use a noninteracve backend, otherwise Matplotlib will present us with
a GUI window by default. We will import the main Matplotlib module and call the
use funcon. This funcon has to be called immediately aer imporng the main
Matplotlib module and before other Matplotlib modules are imported.
import matplotlib as mpl
mpl.use("Agg")
2. Noninteracve plots can be drawn on a Matplotlib canvas. Creang this canvas
requires imports, creang a gure and a subplot. We will specify the gure to be 3 x
3 inches large. More details can be found at the end of this secon.
import matplotlib.pyplot as plt
import matplotlib.backends.backend_agg as agg
fig = plt.figure(figsize=[3, 3])
ax = fig.add_subplot(111)
canvas = agg.FigureCanvasAgg(fig)
www.it-ebooks.info
Chapter 11
[ 259 ]
3. In noninteracve mode, plong data is a bit more complicated than in the default
mode. Since we need to plot repeatedly, it makes sense to organize the plong
code in a funcon. The plot is eventually drawn on the canvas. The canvas adds a bit
of complexity to our setup. At the end of this example you can nd a more detailed
explanaon of the funcons.
def plot(data):
ax.plot(data)
canvas.draw()
renderer = canvas.get_renderer()
raw_data = renderer.tostring_rgb()
size = canvas.get_width_height()
return pygame.image.fromstring(raw_data, size, "RGB")
The following screenshot shows the animaon in acon. You can also view a
screencast on YouTube at https://www.youtube.com/watch?v=t6qTeXxtnl4.
4. We get the following code aer the changes:
import pygame, sys
from pygame.locals import *
import numpy as np
import matplotlib as mpl
mpl.use("Agg")
www.it-ebooks.info
Playing with Pygame
[ 260 ]
import matplotlib.pyplot as plt
import matplotlib.backends.backend_agg as agg
fig = plt.figure(figsize=[3, 3])
ax = fig.add_subplot(111)
canvas = agg.FigureCanvasAgg(fig)
def plot(data):
ax.plot(data)
canvas.draw()
renderer = canvas.get_renderer()
raw_data = renderer.tostring_rgb()
size = canvas.get_width_height()
return pygame.image.fromstring(raw_data, size, "RGB")
pygame.init()
clock = pygame.time.Clock()
screen = pygame.display.set_mode((400, 400))
pygame.display.set_caption('Animating Objects')
img = pygame.image.load('head.jpg')
steps = np.linspace(20, 360, 40).astype(int)
right = np.zeros((2, len(steps)))
down = np.zeros((2, len(steps)))
left = np.zeros((2, len(steps)))
up = np.zeros((2, len(steps)))
right[0] = steps
right[1] = 20
down[0] = 360
down[1] = steps
left[0] = steps[::-1]
left[1] = 360
up[0] = 20
up[1] = steps[::-1]
pos = np.concatenate((right.T, down.T, left.T, up.T))
www.it-ebooks.info
Chapter 11
[ 261 ]
i = 0
history = np.array([])
surf = plot(history)
while True:
# Erase screen
screen.fill((255, 255, 255))
if i >= len(pos):
i = 0
surf = plot(history)
screen.blit(img, pos[i])
history = np.append(history, pos[i])
screen.blit(surf, (100, 100))
i += 1
for event in pygame.event.get():
if event.type == QUIT:
pygame.quit()
sys.exit()
pygame.display.update()
clock.tick(30)
What just happened?
The plong-related funcons are explained in the following table:
Function Description
mpl.use("Agg") This specifies the use of the noninteractive backend.
plt.figure(figsize=[3, 3]) This creates a figure of 3 x 3 inches.
agg.FigureCanvasAgg(fig) This creates a canvas in noninteractive mode.
canvas.draw() This draws on the canvas.
canvas.get_renderer() This gets a renderer for the canvas.
Surface pixels
The Pygame surfarray module handles the conversion between Pygame Surface
objects and NumPy arrays. As you may recall, NumPy can manipulate big arrays in a fast
and ecient manner.
www.it-ebooks.info
Playing with Pygame
[ 262 ]
Time for action – accessing surface pixel data with NumPy
In this tutorial we will le a small image to ll the game screen. Perform the following steps
to do so:
1. The array2d funcon copies pixels into a two-dimensional array. There is a similar
funcon for three-dimensional arrays. We will copy the pixels from the avatar image
into an array:
pixels = pygame.surfarray.array2d(img)
2. Let's create the game screen from the shape of the pixels array using the shape
aribute of the array. The screen will be seven mes larger in both direcons.
X = pixels.shape[0] * 7
Y = pixels.shape[1] * 7
screen = pygame.display.set_mode((X, Y))
3. Tiling the image is easy with the NumPy tile funcon. The data needs to be
converted to integer values, since colors are dened as integers.
new_pixels = np.tile(pixels, (7, 7)).astype(int)
4. The surfarray module has a special funcon (blit_array) to display the array
on the screen.
pygame.surfarray.blit_array(screen, new_pixels)
This produces the following screenshot:
www.it-ebooks.info
Chapter 11
[ 263 ]
The following code does the ling of the image:
import pygame, sys
from pygame.locals import *
import numpy as np
pygame.init()
img = pygame.image.load('head.jpg')
pixels = pygame.surfarray.array2d(img)
X = pixels.shape[0] * 7
Y = pixels.shape[1] * 7
screen = pygame.display.set_mode((X, Y))
pygame.display.set_caption('Surfarray Demo')
new_pixels = np.tile(pixels, (7, 7)).astype(int)
while True:
screen.fill((255, 255, 255))
pygame.surfarray.blit_array(screen, new_pixels)
for event in pygame.event.get():
if event.type == QUIT:
pygame.quit()
sys.exit()
pygame.display.update()
What just happened?
The following is a brief descripon of the new funcons and aributes we used:
Function Description
pygame.surfarray.array2d(img) This copies pixel data into a 2D array.
pygame.surfarray.blit_
array(screen, new_pixels)
This displays array values on the screen.
Articial intelligence
Oen we need to mimic intelligent behavior within a game. The scikit-learn project
aims to provide an API for machine learning. What I like the most about it is the amazing
documentaon. We can install scikit-learn with the package manager of our operang
system. This opon may or may not be available depending on the operang system, but
should be the most convenient route. Windows users can just download an installer from the
project website.
www.it-ebooks.info
Playing with Pygame
[ 264 ]
On Debian and Ubuntu the project is called python-sklearn. On MacPorts the ports are
called py26-scikits-learn and py27-scikits-learn. We can also install from source
or using easy_install. There are third-party distribuons from Python(x, y) – Enthought
and NetBSD.
We can install scikit-learn by typing in the following command at the command line:
pip install -U scikit-learn
Or you can also do it with the following command:
easy_install -U scikit-learn
This might not work because of permissions, so you may need to put sudo in front of the
commands or log in as an admin.
Time for action – clustering points
We will generate some random points and cluster them, which means that points that are
close to each other are put in the same cluster. This is only one of the many techniques
that you can apply with scikit-learn. Clustering is a type of machine learning algorithm,
which aims to group items based on similaries. Second, we will calculate a square anity
matrix. An anity matrix is a matrix containing anity values; for instance, distances
between points. Finally, we will cluster the points with the AffinityPropagation class
from scikit-learn. Perform the following steps to cluster points:
1. We will generate 30 random point posions within a square of 400 x 400 pixels:
positions = np.random.randint(0, 400, size=(30, 2))
2. We will use the Euclidean distance to the origin as anity matrix.
positions_norms = np.sum(positions ** 2, axis=1)
S = - positions_norms[:, np.newaxis] - positions_norms[np.newaxis,
:] + 2 * np.dot(positions, positions.T)
3. Give the AffinityPropagation class the result from the previous step. This class
labels the points with the appropriate cluster number.
aff_pro = sklearn.cluster.AffinityPropagation().fit(S)
labels = aff_pro.labels_
4. We will draw polygons for each cluster. The funcon involved requires a list of
points, a color (let's paint it red), and a surface.
pygame.draw.polygon(screen, (255, 0, 0), polygon_points[i])
www.it-ebooks.info
Chapter 11
[ 265 ]
The result is a bunch of polygons for each cluster, as shown in the
following screenshot:
The clustering example code is as follows:
import numpy as np
import sklearn.cluster
import pygame, sys
from pygame.locals import *
positions = np.random.randint(0, 400, size=(30, 2))
positions_norms = np.sum(positions ** 2, axis=1)
S = - positions_norms[:, np.newaxis] - positions_norms[np.newaxis,
:] + 2 * np.dot(positions, positions.T)
aff_pro = sklearn.cluster.AffinityPropagation().fit(S)
labels = aff_pro.labels_
polygon_points = []
for i in xrange(max(labels) + 1):
polygon_points.append([])
# Sorting points by cluster
for i in xrange(len(labels)):
polygon_points[labels[i]].append(positions[i])
www.it-ebooks.info
Playing with Pygame
[ 266 ]
pygame.init()
screen = pygame.display.set_mode((400, 400))
while True:
for i in xrange(len(polygon_points)):
pygame.draw.polygon(screen, (255, 0, 0), polygon_points[i])
for event in pygame.event.get():
if event.type == QUIT:
pygame.quit()
sys.exit()
pygame.display.update()
What just happened?
The most important lines in the arcial intelligence example are described in more detail in
the following table:
Function Description
sklearn.cluster.AffinityPropagation().
fit(S)
This creates an
AffinityPropagation object and
performs a fit using an affinity matrix.
pygame.draw.polygon(screen, (255, 0,
0), polygon_points[i])
This draws a polygon given a surface,
a color (red in this case), and a list of
points.
OpenGL and Pygame
OpenGL species an API for 2D and 3D computer graphics. The API consists of funcons and
constants. We will be concentrang on the Python implementaon called PyOpenGL. Install
PyOpenGL with the following command:
pip install PyOpenGL PyOpenGL_accelerate
You might need to have root access to execute this command. The following is the
corresponding easy_install command:
easy_install PyOpenGL PyOpenGL_accelerate
www.it-ebooks.info
Chapter 11
[ 267 ]
Time for action – drawing the Sierpinski gasket
For the purpose of demonstraon we will draw a Sierpinski gasket, also known as Sierpinski
triangle or Sierpinski Sieve with OpenGL. This is a fractal paern in the shape of a triangle
created by the mathemacian Waclaw Sierpinski. The triangle is obtained via a recursive and,
in principle, innite procedure. Perform the following steps to draw the Sierpinski gasket:
1. First, we will start out by inializing some of the OpenGL-related primives. This
includes seng the display mode and background color. A line-by-line explanaon is
given at the end of this secon.
def display_openGL(w, h):
pygame.display.set_mode((w,h),
pygame.OPENGL|pygame.DOUBLEBUF)
glClearColor(0.0, 0.0, 0.0, 1.0)
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)
gluOrtho2D(0, w, 0, h)
2. The algorithm requires us to display points, the more the beer. First, we set the
drawing color to red. Second, we dene the verces (I call them points myself) of a
triangle. Then we dene random indices, which are to be used to choose one of the
three triangle verces. We pick a random point somewhere in the middle – it doesn't
really maer where. Aer that we draw points halfway between the previous point
and one of the verces picked at random. Finally, we "ush" the result.
glColor3f(1.0, 0, 0)
vertices = np.array([[0, 0], [DIM/2, DIM], [DIM, 0]])
NPOINTS = 9000
indices = np.random.random_integers(0, 2, NPOINTS)
point = [175.0, 150.0]
for i in xrange(NPOINTS):
glBegin(GL_POINTS)
point = (point + vertices
[indices[i]])/2.0
glVertex2fv(point)
glEnd()
glFlush()
www.it-ebooks.info
Playing with Pygame
[ 268 ]
The Sierpinski triangle looks like the following screenshot:
The following is the full Sierpinski gasket demo code with all the imports:
import pygame
from pygame.locals import *
import numpy as np
from OpenGL.GL import *
from OpenGL.GLU import *
def display_openGL(w, h):
pygame.display.set_mode((w,h), pygame.OPENGL|pygame.DOUBLEBUF)
glClearColor(0.0, 0.0, 0.0, 1.0)
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)
gluOrtho2D(0, w, 0, h)
def main():
pygame.init()
pygame.display.set_caption('OpenGL Demo')
DIM = 400
display_openGL(DIM, DIM)
glColor3f(1.0, 0, 0)
vertices = np.array([[0, 0], [DIM/2, DIM], [DIM, 0]])
NPOINTS = 9000
indices = np.random.random_integers(0, 2, NPOINTS)
point = [175.0, 150.0]
for i in xrange(NPOINTS):
www.it-ebooks.info
Chapter 11
[ 269 ]
glBegin(GL_POINTS)
point = (point + vertices[indices[i]])/2.0
glVertex2fv(point)
glEnd()
glFlush()
pygame.display.flip()
while True:
for event in pygame.event.get():
if event.type == QUIT:
return
if __name__ == '__main__':
main()
What just happened?
As promised, the following is a line-by-line explanaon of the most important parts of
the example:
Function Description
pygame.display.set_mode((w,h),
pygame.OPENGL|pygame.DOUBLEBUF)
This sets the display mode to the required
width, height, and OpenGL display.
glClear(GL_COLOR_BUFFER_BIT|GL_
DEPTH_BUFFER_BIT)
This clears the buffers using a mask. Here
we clear the color buffer and depth buffer
bits.
gluOrtho2D(0, w, 0, h) This defines a 2D orthographic projection
matrix with the coordinates of the left,
right, top, and bottom clipping planes.
glColor3f(1.0, 0, 0) This defines the current drawing color using
three float values for RGB. In this case we
will be painting in red.
glBegin(GL_POINTS) This delimits the vertices of primitives or a
group of primitives. Here the primitives are
points.
glVertex2fv(point) This renders a point given a vertex.
glEnd() This closes a section of code started with
glBegin.
glFlush() This forces execution of GL commands.
www.it-ebooks.info
Playing with Pygame
[ 270 ]
Simulation game with PyGame
As a last example, we will simulate life with Conway's Game of Life. The original game
of life is based on a few basic rules. We start out with a random conguraon on a
two-dimensional square grid. Each cell in the grid can be either dead or alive. This
state depends on the eight neighbors of the cell. Convoluon can be used to evaluate
the basic rules of the game. We will need the SciPy package for the convoluon process.
Time for action – simulating life
The following code is an implementaon of Game of Life with some modicaons,
as follows:
Clicking once with the mouse draws a cross unl we click again
Pressing the r key resets the grid to a random state
Pressing b creates blocks based on the mouse posion
Pressing g creates gliders
The most important data structure in the code is a two-dimensional array holding the color
values of the pixels on the game screen. This array is inialized with random values and
then recalculated for each iteraon of the game loop. More informaon about the involved
funcons can be found in the next secon.
1. To evaluate the rules, we will use convoluon, as follows.
def get_pixar(arr, weights):
states = ndimage.convolve(arr, weights, mode='wrap')
bools = (states == 13) | (states == 12 ) | (states == 3)
return bools.astype(int)
2. We can draw a cross using basic indexing tricks that we learned in Chapter 2,
Beginning with NumPy Fundamentals.
def draw_cross(pixar):
(posx, posy) = pygame.mouse.get_pos()
pixar[posx, :] = 1
pixar[:, posy] = 1
3. Inialize the grid with random values:
def random_init(n):
return np.random.random_integers(0, 1, (n, n))
www.it-ebooks.info
Chapter 11
[ 271 ]
The following is the code in its enrety:
import os, pygame
from pygame.locals import *
import numpy as np
from scipy import ndimage
def get_pixar(arr, weights):
states = ndimage.convolve(arr, weights, mode='wrap')
bools = (states == 13) | (states == 12 ) | (states == 3)
return bools.astype(int)
def draw_cross(pixar):
(posx, posy) = pygame.mouse.get_pos()
pixar[posx, :] = 1
pixar[:, posy] = 1
def random_init(n):
return np.random.random_integers(0, 1, (n, n))
def draw_pattern(pixar, pattern):
print pattern
if pattern == 'glider':
coords = [(0,1), (1,2), (2,0), (2,1), (2,2)]
elif pattern == 'block':
coords = [(3,3), (3,2), (2,3), (2,2)]
elif pattern == 'exploder':
coords = [(0,1), (1,2), (2,0), (2,1), (2,2), (3,3)]
elif pattern == 'fpentomino':
coords = [(2,3),(3,2),(4,2),(3,3),(3,4)]
pos = pygame.mouse.get_pos()
xs = np.arange(0, pos[0], 10)
ys = np.arange(0, pos[1], 10)
for x in xs:
for y in ys:
for i, j in coords:
pixar[x + i, y + j] = 1
www.it-ebooks.info
Playing with Pygame
[ 272 ]
def main():
pygame.init ()
N = 400
pygame.display.set_mode((N, N))
pygame.display.set_caption("Life Demo")
screen = pygame.display.get_surface()
pixar = random_init(N)
weights = np.array([[1,1,1], [1,10,1], [1,1,1]])
cross_on = False
while True:
pixar = get_pixar(pixar, weights)
if cross_on:
draw_cross(pixar)
pygame.surfarray.blit_array(screen, pixar * 255 ** 3)
pygame.display.flip()
for event in pygame.event.get():
if event.type == QUIT:
return
if event.type == MOUSEBUTTONDOWN:
cross_on = not cross_on
if event.type == KEYDOWN:
if event.key == ord('r'):
pixar = random_init(N)
print "Random init"
if event.key == ord('g'):
draw_pattern(pixar, 'glider')
if event.key == ord('b'):
draw_pattern(pixar, 'block')
if event.key == ord('e'):
draw_pattern(pixar, 'exploder')
if event.key == ord('f'):
draw_pattern(pixar, 'fpentomino')
if __name__ == '__main__':
main()
www.it-ebooks.info
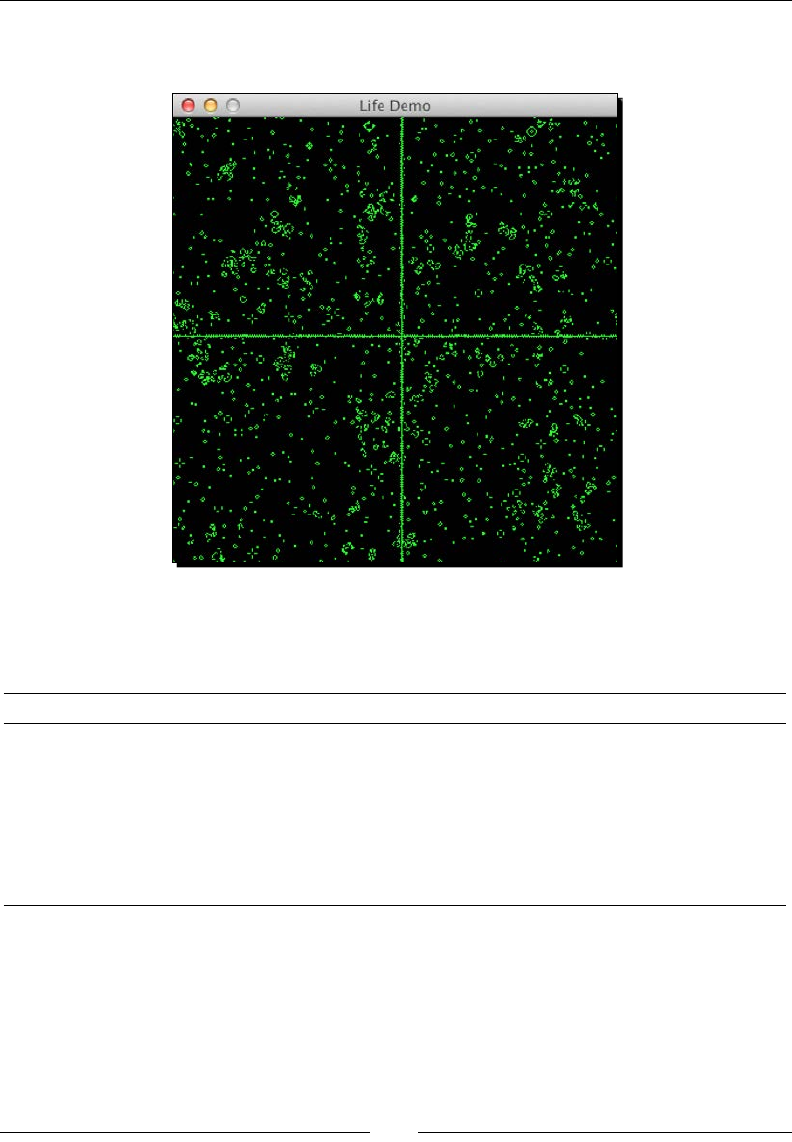
Chapter 11
[ 273 ]
You should able to view a screencast on YouTube at https://www.youtube.com/
watch?v=NNsU-yWTkXM. The following is a screenshot of the game in acon:
What just happened?
We used some NumPy and SciPy funcons that need an explanaon, as follows:
Function Description
ndimage.convolve(arr, weights,
mode='wrap')
This applies the convolve operation on the
given array, using weights in wrap mode. The
mode has to do it with the array borders.
bools.astype(int) This converts the array of Booleans to integers.
np.arange(0, pos[0], 10) This creates an array from 0 to pos[0] in steps
of 10. So if pos[0] is equal to 1000, we will get
0, 10, 20, …, 990.
www.it-ebooks.info
Playing with Pygame
[ 274 ]
Summary
You might have found the menon of Pygame in this book a bit odd. Aer reading this
chapter I hope you realized that NumPy and Pygame go well together. Games, aer all,
involve lots of computaon for which NumPy and SciPy are ideal choices. They also
require arcial intelligence capabilies as found in scikit-learn. Anyway, making
games is fun and we hope this last chapter was the equivalent of a nice dessert or coee
aer a ten-course meal. If you are sll hungry for more, please check out NumPy Cookbook,
Ivan Idris, Packt Publishing; it builds further on this book with minimum overlap.
www.it-ebooks.info
Pop Quiz Answers
Chapter 1, NumPy Quick Start
What does arrange(5) do? It creates a NumPy array with values 0 to 4.
The created NumPy array has values 0, 1, 2, 3, 4.
Chapter 2, Beginning with NumPy Fundamentals
How is the shape of an ndarray stored? It is stored in a tuple.
Chapter 3, Get into Terms with Commonly Used Functions
Which function returns the weighted average of an array? average
Chapter 4, Convenience functions for your convenience
Which function returns the covariance of two arrays? cov
Chapter 5, Working with Matrices and ufuncs
What is the row delimiter in a string accepted by the mat
and bmat functions?
Semicolon
www.it-ebooks.info
Pop Quiz Answers
[ 276 ]
Chapter 6, Move further with NumPy modules
Which function can create matrices? mat
Chapter 7, Peeking into special routines
Which NumPy module deals with random numbers? random
Chapter 8, Assure Quality with Testing
Which parameter of the assert_almost_equal
function specifies the decimal precision?
decimal
Chapter 9, Plotting with Matplotlib
What does the plot function do? It does neither 1, 2, or 3.
Chapter 10, When NumPy is not enough Scipy and beyond
Which function loads .mat files? loadmat
www.it-ebooks.info
Index
Symbols
.mat le
loading 226, 227
saving 226
% operator 121
A
accumulate method
applying, on add funcon 117
AnityPropagaon class 264
agg.FigureCanvasAgg() funcon 261
AI
about 263
points, clustering 264, 266
almost equal arrays
asserng 178
AND operator 130
annotate funcon 215
apply_along_axis funcon 66
approximately equal arrays
asserng 180
arange funcon 28, 29, 97, 160
argmax funcon 158
argmin funcon 64, 158
argsort funcon 155
argwhere funcon 159
arithmec funcons
about 118
array division 119, 120
array aributes
about 45
dtype 45
at 47
imag 47
itemsize 46
ndim 45
real 47
shape 45
size 46
T aribute 46
arrays
comparing 182
converng 48
ordering 183
arrays almost equal
asserng 181
array shapes
manipulang 38
array shapes, manipulang
aen funcon 38
ravel funcon 38
reshape funcon 39
resize method 39
transpose matrices 39
arrays, NumPy
about 17
spling 43
stacking 39
arrays spilng
about 43
depth-wise spling 44
horizontal spling 43
vercal spling 44
arrays stacking
column stacking 42
depth stacking 41
horizontal stacking 40
row stacking 42
www.it-ebooks.info
[ 278 ]
vercal stacking 41
assert_allclose funcon 178
assert_almost_equal funcon
about 178
using 178
assert_approx_equal funcon
about 178
using 179
assert_array_almost_equal funcon
about 178
using 180
assert_array_almost_equal_nulp funcon
using 186
assert_array_equal funcon
about 178
using 182
assert_array_less funcon
about 178
using 183
assert_array_max_ulp funcon
about 187
using 187
assert_equal funcon
about 178
using 184
assert funcons
about 178
assert_allclose 178
assert_almost_equal 178
assert_approx_equal 178
assert_array_almost_equal 178
assert_array_equal 178
assert_array_less 178
assert_equal 178
assert_raises 178
assert_string_equal 178
assert_warns 178
assert_raises funcon 178
assert_string_equal funcon
about 178
using 184, 185
assert_warns funcon 178
astype funcon 48
audio clips
replaying 247, 248
audio processing
about 247
audio clips, replaying 247, 248
average true range (ATR)
about 69
calculang 69-71
B
bartle funcon 109, 167
Bartle window
about 167
plong 167
binomial distribuon models 147
binomial funcon
using 147, 148
bits
twiddling 129, 130
bitwise_and funcon 130
Bitwise-ANDing 130
bitwise funcons 129
bitwise_xor funcon 129
blackman funcon 109, 168
Blackman window
about 167
plong 168, 169
Bollinger bands
about 76
enveloping with 76-78
bools.astype() funcon 273
C
calc_prot funcon 102
canvas.draw() funcon 261
canvas.get_renderer() funcon 261
character codes 32
clip method 87
clock object, Pygame
animang 255, 256
column_stack funcon 42
column stacking 42
comma-separated values. See CSV les
comparison funcons 129
complex numbers
about 157
sorng 157, 158
compress method 87
concatenate funcon 40
www.it-ebooks.info
[ 279 ]
consecuve wins and losses
analyzing 105
connuous distribuons 151
contour funcon 220
contour plots
about 220
lled contour plot, drawing 220
convoluon 72
convolve funcon 73
correlaon
about 92
correlated pairs, trading 92-95
CPython 9
CSV les
about 52
dealing with 53
loading from 53
cumprod method 88
D
data
summarizing weekly 65-68
data sorng rounes
AAPL stock prices, sorng lexically 156
argsort funcon 155
lexsort funcon 155
msort funcon 155
sort_complex funcon 155
sort funcon 155
sort method 155
data type objects 32
dates
dealing with 61-64
Debian and Ubuntu
NumPy, installing 14
Python, installing 10
decorate_methods funcon
calling 190
depth stacking 41
depth-wise spling 44
determinant, of matrix
about 142
calculang 142
detrended signal
ltering 236, 237
detrend funcon 233
di funcon 59, 100
discrete Fourier transform (DFT) 143
DISH (Dish Network Corp.) 206
divide funcon 119
docstrings
about 193
doctests, execung 194
doctests
execung 194
documentaon website, NumPy and SciPy
URL 25
dsplit funcon 44
dstack funcon 41
dtype aribute 34, 45
dtype constructors 33
E
easy_install command 266
Eigenvalues
about 137
determining 137, 138
Eigenvectors
about 137
determining 137, 138
elements
extracng, from array 160, 161
error funcon 242
exponenal moving average
calculang 74, 75
extract funcon 159, 160
F
factorial
calculang 88
fast Fourier transform (FFT)
about 143
calculang 143, 144
tshi funcon 145
Fibonacci numbers
about 122
compung 122, 123
le I/O
les, reading and wring 52
www.it-ebooks.info
[ 280 ]
ll_between funcon
about 213
using 213
nancial funcons 161
future value, determining 161
fv 161
irr 161
mirr 161
nper 161
npv 161
pmt 161
pv 161
rate 161
at aribute 47
oang-point comparisons
about 185
assert_array_almost_equal_nulp funcon,
using 185
oats
comapring, maxulp of 2 used 187
oor_divide funcon 119
fmod funcon 121
Fourier analysis
about 235
detrended signal, ltering 236, 237
frequencies
shiing 145, 146
fv funcon 161
G
Game of Life
implemenng 270, 273
Gaussian integral
calculang 242
Gentoo
NumPy, installing 13
glBegin() funcon 269
glClear() funcon 269
glColor3f() funcon 269
glEnd() funcon 269
glFlush() funcon 269
gluOrtho2D() funcon 269
glVertex2fv() funcon 269
H
hamming funcon 109, 170
Hamming window
about 170
plong 170
hanning funcon 105
Hello World example 252
hist funcon 207
histograms
about 207
stock price distribuons, charng 207, 208
horizontal spling 43
horizontal stacking 40
hstack funcon 40
hypergeometric distribuon
about 149
game show, simulang 149, 150
I
imag aribute 47
image processing
about 245
image processingLena, manipulang 245, 249
Lena image, manipulang 245, 246
installaon, Python
on Debian and Ubuntu 10
on Mac 10
on Windows 10
interest rate
calculang 166
internal rate of return
about 164
determining 164
interp1d class 243, 244
interp2d class 243
interpolaon
about 243
in one dimension 243, 244
IPython
about 21
features 21
installaon instrucons 21
installing, on Linux 13
www.it-ebooks.info
[ 281 ]
installing, on Mac OS X 14
installing, on Windows 13
installing, with MacPorts or Fink 17
online resources 25
packages, imporng 22-24
pylab mode 25
Pylab switch 22
IRC channel 26
irr funcon 161
isreal funcon 108
itemsize aribute 46
K
kaiser funcon 109, 171
Kaiser window
about 171
plong 171
L
leastsq funcon 239
le_shi universal funcon 130
legend funcon 215
legends and annotaons
about 215
using 215, 217
Lena image
manipulang 245, 246
lexsort funcon
about 155
using 156
linear algebra
about 133
matrices, inverng 133-135
linear model
price, predicng with 80, 81
linear systems
solving 135, 136
linspace funcon 124
about 74
Linux
IPython, installing 13
Matplotlib, installing 13
NumPy, installing 13
SciPy, installing 13
Lissajous curves
about 123
drawing 124
loadmat funcon 225
loadtxt funcon 53, 62
logarithmic plots
about 209
stock volume, plong 209
log funcon 60
lognormal distribuon
about 153
drawing 153
lstsq funcon 81
M
Mac
Python, installing 10
Mac OS X
IPython, installing 14
Matplotlib, installing 14
NumPy, installing 14-16
SciPy, installing 14
Mandriva
NumPy, installing 13
mathemacal opmizaon
about 238
sine, ng to ltered signal 239, 240
Matlab
Matlababout 225
MATLAB 225
Matplotlib
about 197, 258
contour plots 220
ll_between funcon 213
nance 204
histograms 207
installing, on Linux 13
installing, on Mac OS X 14
installing, on Windows 13
installing, with MacPorts or Fink 17
legend and annotaons 215
logarithmic plots 209
plot format string 200
plots, animang 222
scaer plots 211
simple plots 198
www.it-ebooks.info
[ 282 ]
subplots 201
three dimensional plots 218
using, in Pygame 258, 259
matplotlib.pyplot package 198
matrices
about 111
creang 112, 113
matrix
creang, from matrices 113, 114
matrix funcon 122
max funcon 56
mean funcon 54, 58
median funcon 58
Mersenne Twister algorithm 147
meshgrid funcon 219
min funcon 56
mirr funcon 161
mod funcon 121
modied Bessel funcon
about 172
plong 172, 173
modulo operaon
about 121
compung 121
Moore-Penrose pseudoinverse 141
mpl.use() funcon 261
msort funcon 57, 155
muldimensional arrays
indexing 36, 37
slicing 35
muldimensional NumPy array
creang 29
N
nanargmax funcon 158
nanargmin funcon 158
ndarray 28
ndarray methods
about 86
clip method 87
compress method 87
ndimage.convolve() funcon 273
ndim aribute 45
net present value
about 163
calculang 163
nonzero funcon 160
normal distribuon
drawing 151, 152
nose tests decorators
about 190
numpy.tesng.decorators.deprecated 190
numpy.tesng.decorators.knownfailureif 190
numpy.tesng.decorators.setastest 190
numpy.tesng.decorators.skipif 190
numpy.tesng.decorators.slow 190
np.arange() funcon 273
nper funcon 161
npv funcon 161
number of periodic payments
determining 165
numerical integraon
about 242
Gaussian integral, calculang 242
NumPy
about 9
approximately equal arrays, asserng 180
arithmec funcons 118
array order, checking 183
arrays 17
arrays almost equal, asserng 181
assert funcons 178
ATR calculaon 69
bitwise funcons 129
Blackman window 167
Bollinger bands 76
character codes 32
comparison funcons 129
complex numbers, sorng 157
connuous distribuons 151
correlaon 92
CSV les 52
data sorng rounes 155
data, summarizing weekly 65
data type objects 32
dates, dealing with 61
determinants, calculang 142
docstrings 193
dtype aributes 34
dtype constructors 33
Eigenvalues, nding 137
Eigenvectors, nding 137
elements, extracng from array 160
www.it-ebooks.info
[ 283 ]
elements, selecng 30
equal arrays, asserng 182
exponenal moving average, calculang 74
factorial, calculang 87
Fast Fourier transform, calculang 143
le I/O 51
oang point comparisons 185
oats, comparing with ULPs 187
frequencies, shiing 145
Hamming window 170
hypergeometric distribuon 149
installing, on Debian or Ubuntu 14
installing, on Gentoo 13
installing, on Linux 13
installing, on Mac OS X 14, 15
installing, on Mandriva 13
installing, on Windows 10-12
installing, with MacPorts or Fink 17
interest rate, calculang 166
internal rate of return, determining 164
Kaiser window 171
linear algebra 133
linear model 80
linear systems, solving 136
Lissajous curves 123
lognormal distribuon 153
matrices 111
modulo operaon 121
ndarray methods 86
net present value 163
nose tests decorators 190
number of periodic payments, determining 165
numerical types 30
objects, comparing 184
on-balance volume 99
one-dimensional slicing 35
periodic payments, calculang 165
polynomials 96
present value 163
pseudoinverse, calculang 141
random numbers 147
searching 158
simple moving average, compung 72
simulaon 102
sinc funcon 173
singular value decomposion 139
smoothing 105
source code, retrieving 17
special mathemacal funcons 172
square waves 125
stascs, performing 56
stock returns, analyzing 59
strings, comparing 185
trend line 82
unit tests 187
universal funcons 114
value range, nding 55
vectors, adding 18, 20
VWAP, calculang 53
window funcons 166
NumPy and SciPy forum
URL 25
NumPy array object
about 28
mul-dimensional array object 28
NumPy division funcons
divide funcon 119
oor_divide funcon 120
true_divide funcon 119
numpy.linalg package 133
NumPy numerical types
about 30, 32
bool 31
complex64 31
complex128 31
oat16 31
oat32 31
oat64 31
int8 31
int16 31
int32 31
int64 31
in 31
uint8 31
uint16 31
uint32 31
uint64 31
NumPy reference
URL 25
NumPy wiki documentaon
URL 25
www.it-ebooks.info
[ 284 ]
O
objects
comparing 184
Octave 225
on-balance volume
compung 99
one-dimensional slicing 35
opmizaon
about 238
sine, ng to 239, 240
outer method
applying, on add funcon 118
P
periodic payments
calculang 165
piecewise funcon 100
plot format string
about 200
polynomial and derivave, plong 200, 201
plot regions
shading, based on condion 213
plots
animang 222, 223
plt.gure() funcon 261
pmt funcon 161
polyder funcon 97
polyt funcon 96, 98
polynomial funcon
plong 198, 199
polynomials
about 96
ng to 96-98
polysub funcon 108
polyval funcon 96
present value
about 163
compung 163
probability density funcons (pdf) 151
prod funcon 88
pseudoinverse 141
pseudoinverse, of matrix
compung 141
Pseudo random numbers 147
pv funcon 161
Pygame
about 251
AI 263
animaon 255
clock object 255
for Debian and Ubuntu 252
for Mac 252
for Windows 252
game, simulang 270
Hello World example 252
installing 252
Matplotlib, using 258
surface pixel data, accessing 261
pygame.display.set_capon() funcon 254
pygame.display.set_mode() funcon 254
pygame.display.set_mode((w,h) funcon 269
pygame.display.update() funcon 255
pygame.draw.polygon(screen, (255, 0, 0), poly-
gon_points[i]) funcon 266
pygame.event.get() funcon 255
pygame.font.SysFont() funcon 254
pygame.init() funcon 254
pygame.OPENGL|pygame.DOUBLEBUF) funcon
269
pygame.quit() funcon 255
pygame.surfarray.array2d() funcon 263
pygame.surfarray.blit_array() funcon 263
Pygame surfarray module 261
pylab mode, IPython 25
PyOpenGL
about 266
installing 266
Sierpinski gasket, drawing 267, 268
Python
about 9
installing, on Debian and Ubuntu 10
installing, on Mac 10
installing, on Windows 10
Q
quad funcon 242, 243
R
random numbers 147
rate funcon 161
www.it-ebooks.info
[ 285 ]
real aribute 47
Real random numbers 147
record data type
creang 34
reduceat method
applying, on add funcon 117
reduce method
applying, on add funcon 116
remainder funcon 121
reshape funcon 38
rint funcon 122
row_stack funcon 42
row stacking 42
rundocs funcon 195
S
sample comparison
stock log returns, comparing 230, 231
savemat funcon 225
savetxt funcon 52, 67
sawtooth and triangle waves
about 127
drawing 127, 128
formula 127
scaer funcon 211
scaer plots
about 211
price and volume returns, plong 211
scikit-learn project 263
SciKits 230
scikits.statsmodels.staools 230
SciPy
about 225
audio processing 247
Fourier analysis 235
image processing 245
installing, on Linux 13
installing, on Mac OS X 14
installing, on Windows 13
installing, with MacPorts or Fink 17
interpolaon 243
mathemacal opmizaon 238
MATLAB or Octave matrices, loading 226
numerical integraon 242
SciPyscipy.stats 227
signal processing 232
stascs 227
stock log returns, comparing 230
SciPy channel 26
scipy.tpack module 235, 237
scipy.interpolate funcon 243
scipy.interpolate module 244
scipy.io package 225
scipy.io.wavle module 247
scipy.ndimage module 246
scipy.opmize module 238, 240
SciPy signal
about 233
trend, detecng in QQQ 233, 234
scipy.signal module 232
stascs module
about 227
random values, analyzing 227-229
scipy.stats
about 227
data generaon, improving 229
random values, analyzing 227-229
scipy.stats.norm.rvs funcon 229
screen.blit() funcon 255
sctypeDict.keys() 33
SDL 251
searching, through arrays
argmax funcon 158
argmin funcon 158
argwhere funcon 159
extract funcon 159
nanargmax funcon 158
nanargmin funcon 158
searchsorted funcon 159
searchsorted funcon
about 159
using 159, 160
setastest decorator
applying, to methods 191, 192
applying, to test funcons 191, 192
shape aribute 45
Sierpinski gasket
drawing 267, 268
signal processing
about 232
trend detecng, in QQQ 233
sign funcon 100
www.it-ebooks.info
[ 286 ]
Simple DirectMedia Layer. See SDL
simple game
creang 252, 253
simple moving average
about 72
compung 72, 73
simple plots
about 198
polynomial funcon, plong 198, 199
simulaon
about 102
loops, avoiding with vectorize 102, 103
sinc funcon 244
about 173
plong 173, 174
sin funcon 124
singular value decomposion
about 139
matrix, decomposing 139, 140
size aribute 46
sklearn.cluster.AnityPropagaon().t(S)
funcon 266
smoothing
hanning funcon, used 105-107
smoothing variaons 109
sort_complex funcon 155
sort funcon 155
special mathemacal funcons
about 172
Bessel funcon 172
split funcon 44, 66
sqrt funcon 60
square waves
about 125
drawing 125, 126
formula 125
represenng 125
Stack Overow soware development forum
URL 25
stascs
about 56
simple stascs, performing 57, 58
std funcon 59
stock log returns
comparing 230, 232
stock log returns, comparing
histograms plong, Matplotlib used 231
Jarque Bera test 231
Kolmogorov Smirnov test 231
log returns, calculang 230
quotes, downloading 230
stock quotes
plong 204-206
stock returns
analyzing 59, 60
stock volume
plong 209, 210
strings
comparing 185
strip_zeroes funcon 108
subplot funcon 202
subplots
about 201
polynomial and its derivaves, plong 201,
203
summarize funcon 66
surface pixel data
accessing, with NumPy 262, 263
sysFont.render() funcon 254
T
take funcon 63
T aribute 46
Test driven development (TDD) 177
three-by-three matrix
creang 29
three-dimensional plots
about 218
plong 219, 220
Time-weighted average price. See TWAP
trend
detecng, in QQQ 233, 234
trend detecng, in QQQ
date, formaer 233
diagram 234
locators, creang 233
signal, detrending 233
X axis labels 234
trend line
about 82
drawing 82- 85
www.it-ebooks.info
[ 287 ]
true_divide funcon 119
TWAP
about 54
calculang 54
U
Unit of Least Precision (ULP)
comparing 185
unit tests
about 178, 187
wring 188, 189
universal funcon methods
accumulate 116
applying, on add funcon 116, 117
out 116
reduce 116
reduceat 116
universal funcons
about 114
creang 115
methods 116
usecols parameter 53
V
ValueError 116
value range
about 55
highest value, nding 55
lowest value, nding 56
variance 58
vectorize funcon 102
vectors, NumPy
adding 18, 20
vercal spling 44
vercal stacking 41
volume
about 99
balancing 100, 101
Volume-weighted average price. See VWAP
vsplit funcon 44
vstack funcon 41
VWAP
about 53
calculang 54
W
where funcon 60
window funcons
about 166
bartle 166
Bartle window, plong 167
blackman 166
hamming 166
hanning 166
kaiser 166
Windows
IPython, installing 13
Matplotlib, installing 13
NumPy, installing 10, 11, 12
Python, installing 10
SciPy, installing 13
write funcon 247
X
XOR operator 129
Y
Yahoo Finance
URL 204
www.it-ebooks.info
www.it-ebooks.info
Thank you for buying
Numpy Beginner's Guide
About Packt Publishing
Packt, pronounced 'packed', published its rst book "Mastering phpMyAdmin for Eecve
MySQL Management" in April 2004 and subsequently connued to specialize in publishing
highly focused books on specic technologies and soluons.
Our books and publicaons share the experiences of your fellow IT professionals in adapng
and customizing today's systems, applicaons, and frameworks. Our soluon based books
give you the knowledge and power to customize the soware and technologies you're
using to get the job done. Packt books are more specic and less general than the IT books
you have seen in the past. Our unique business model allows us to bring you more focused
informaon, giving you more of what you need to know, and less of what you don't.
Packt is a modern, yet unique publishing company, which focuses on producing quality,
cung-edge books for communies of developers, administrators, and newbies alike. For
more informaon, please visit our website: www.packtpub.com.
About Packt Open Source
In 2010, Packt launched two new brands, Packt Open Source and Packt Enterprise, in order
to connue its focus on specializaon. This book is part of the Packt Open Source brand,
home to books published on soware built around Open Source licences, and oering
informaon to anybody from advanced developers to budding web designers. The Open
Source brand also runs Packt's Open Source Royalty Scheme, by which Packt gives a royalty
to each Open Source project about whose soware a book is sold.
Writing for Packt
We welcome all inquiries from people who are interested in authoring. Book proposals
should be sent to author@packtpub.com. If your book idea is sll at an early stage and you
would like to discuss it rst before wring a formal book proposal, contact us; one of our
commissioning editors will get in touch with you.
We're not just looking for published authors; if you have strong technical skills but no wring
experience, our experienced editors can help you develop a wring career, or simply get
some addional reward for your experse.
www.it-ebooks.info
Learning SciPy for Numerical and Scientic
Computing
ISBN: 978-1-78216-162-2 Paperback: 150 pages
A praccal tutorial that guarantees fast, accurate,
and easy-to-code soluons to your numerical and
scienc compung problems with the power of
SciPy and Python
1. Perform complex operaons with large
matrices, including eigenvalue problems, matrix
decomposions, or soluon to large systems of
equaons
2. Step-by-step examples to easily implement
stascal analysis and data mining that rivals in
performance any of the costly specialized soware
suites
NumPy Cookbook
ISBN: 978-1-84951-892-5 Paperback: 226 pages
Over 70 interesng recipes for learning the Python
open source mathemacal library, NumPy
1. Do high performance calculaons with clean and
ecient NumPy code
2. Analyze large sets of data with stascal funcons
3. Execute complex linear algebra and mathemacal
computaons
Please check www.PacktPub.com for information on our titles
www.it-ebooks.info
Programming ArcGIS 10.1 with Python Cookbook
ISBN: 978-1-84969-444-5 Paperback: 304 pages
Over 75 recipes to help you automate geoprocessing
tasks, create soluons, and solve problems for ArcGIS
with Python
1. Learn how to create geoprocessing scripts with
ArcPy
2. Customize and modify ArcGIS with Python
3. Create me-saving tools and scripts for ArcGIS
MATLAB Graphics and Data Visualization Cookbook
ISBN: 978-1-84969-316-5 Paperback: 284 pages
Tell data stories with compelling graphics using this
collecon of data visualizaon recipes
1. Collecon of data visualizaon recipes with
funconalized versions of common tasks for easy
integraon into your data analysis workow
2. Recipes cross-referenced with MATLAB product
pages and MATLAB Central File Exchange resources
for improved coverage
3. Includes hand created indices to nd exactly
what you need; such as applicaon driven, or
funconality driven soluons
Please check www.PacktPub.com for information on our titles
www.it-ebooks.info

Navigation menu