Open GL Programming Guide 7Edition
OpenGL%20Programming%20Guide%207th
OpenGL%20Programming%20Guide%207th
OpenGL%20Programming%20Guide%207th
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 1019 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Cover Page
- Title Page
- ISBN 978-0321552624
- Contents
- Figures
- Tables
- Examples
- About This Guide
- Acknowledgments
- 1. Introduction to OpenGL
- 2. State Management and Drawing Geometric Objects
- 3. Viewing
- 4. Color
- 5. Lighting
- 6. Blending, Antialiasing, Fog, and Polygon Offset
- 7. Display Lists
- 8. Drawing Pixels, Bitmaps, Fonts, and Images
- 9. Texture Mapping
- 10. The Framebuffer
- 11. Tessellators and Quadrics
- 12. Evaluators and NURBS
- 13. Selection and Feedback
- 14. Now That You Know
- Error Handling
- Which Version Am I Using?
- Extensions to the Standard
- Cheesy Translucency
- An Easy Fade Effect
- Object Selection Using the Back Buffer
- Cheap Image Transformation
- Displaying Layers
- Antialiased Characters
- Drawing Round Points
- Interpolating Images
- Making Decals
- Drawing Filled, Concave Polygons Using the Stencil Buffer
- Finding Interference Regions
- Shadows
- Hidden-Line Removal
- Texture Mapping Applications
- Drawing Depth-Buffered Images
- Dirichlet Domains
- Life in the Stencil Buffer
- Alternative Uses for glDrawPixels() and glCopyPixels()
- 15. The OpenGL Shading Language
- A. Basics of GLUT: The OpenGL Utility Toolkit
- B. State Variables
- The Query Commands
- OpenGL State Variables
- Current Values and Associated Data
- Vertex Array Data State (Not Included in Vertex Array Object State)
- Vertex Array Object State
- Transformation
- Coloring
- Lighting
- Rasterization
- Multisampling
- Texturing
- Pixel Operations
- Framebuffer Control
- Framebuffer Object State
- Renderbuffer Object State
- Pixels
- Evaluators
- Shader Object State
- Program Object State
- Query Object State
- Transform Feedback State
- Vertex Shader State
- Hints
- Implementation-Dependent Values
- Implementation-Dependent Pixel Depths
- Miscellaneous
- C. Homogeneous Coordinates and Transformation Matrices
- D. OpenGL and Window Systems
- Glossary
- Index
- E. Order of Operations
- F. Programming Tips
- G. OpenGL Invariance
- H. Calculating Normal Vectors
- I. Built-In OpenGL Shading Language Variables and Functions
- J. Floating-Point Formats for Textures, Framebuffers, and Renderbuffers
- K. RGTC Compressed Texture Format
- L. std140 Uniform Buffer Layout

OpenGL®
Programming Guide
Seventh Edition

The OpenGL graphics system is a software interface to graphics
hardware. (“GL” stands for “Graphics Library.”) It allows you to
create interactive programs that produce color images of moving, three-
dimensional objects. With OpenGL, you can control computer-graphics
technology to produce realistic pictures, or ones that depart from reality
in imaginative ways.
The OpenGL Series from Addison-Wesley Professional comprises
tutorial and reference books that help programmers gain a practical
understanding of OpenGL standards, along with the insight needed to
unlock OpenGL’s full potential.
Visit informit.com/opengl for a complete list of available products
OpenGL® Series

OpenGL®
Programming Guide
Seventh Edition
The Official Guide to
Learning OpenGL®, Versions 3.0 and 3.1
Dave Shreiner
The Khronos OpenGL ARB Working Group
Upper Saddle River, NJ • Boston • Indianapolis • San Francisco
New York • Toronto • Montreal • London • Munich • Paris • Madrid
Capetown • Sydney • Tokyo • Singapore • Mexico City
Many of the designations used by manufacturers and sellers to distinguish their products are
claimed as trademarks. Where those designations appear in this book, and the publisher was
aware of a trademark claim, the designations have been printed with initial capital letters or
in all capitals.
The authors and publisher have taken care in the preparation of this book, but make no
expressed or implied warranty of any kind and assume no responsibility for errors or
omissions. No liability is assumed for incidental or consequential damages in connection
with or arising out of the use of the information or programs contained herein.
The publisher offers excellent discounts on this book when ordered in quantity for bulk
purchases or special sales, which may include electronic versions and/or custom covers and
content particular to your business, training goals, marketing focus, and branding interests.
For more information, please contact:
U.S. Corporate and Government Sales
(800) 382-3419
corpsales@pearsontechgroup.com
For sales outside of the U.S., please contact:
International Sales
international@pearsoned.com
Visit us on the Web: informit.com/aw
Library of Congress Cataloging-in-Publication Data
Shreiner, Dave.
OpenGL programming guide : the official guide to learning OpenGL, versions 3.0 and 3.1
/ Dave Shreiner; the Khronos OpenGL ARB Working Group — 7th ed.
p. cm.
Includes index.
ISBN 978-0-321-55262-4 (pbk. : alk. paper)
1. Computer graphics. 2. OpenGL. I. Title.
T385.O635 2009
006.6'6—dc22
2009018793
Copyright © 2010 Pearson Education, Inc.
All rights reserved. Printed in the United States of America. This publication is protected by
copyright, and permission must be obtained from the publisher prior to any prohibited
reproduction, storage in a retrieval system, or transmission in any form or by any means,
electronic, mechanical, photocopying, recording, or likewise. For information regarding
permissions, write to:
Pearson Education, Inc.
Rights and Contracts Department
501 Boylston Street, Suite 900
Boston, MA 02116
Fax (617) 671-3447
ISBN 13: 978-0-321-55262-4
ISBN 10: 0-321-55262-8
Text printed in the United States on recycled paper at Edwards Brothers in Ann Arbor, Michigan.
First printing, July 2009
For my family—Felicity, Max, Sarah, and Scout.
—JLN
For my family—Ellyn, Ricky, and Lucy.
—TRD
To Tom Doeppner and Andy van Dam, who started me along this path.
—MW
For my family—Vicki, Bonnie, Bob, Phantom, Squiggles, Tuxedo, and Toby.
—DRS
In memory of Phil Karlton, Celeste Fowler, and Ben Cheatham.
This page intentionally left blank
vii
Contents
Figures ................................................................................................xxi
Tables ................................................................................................ xxv
Examples ..........................................................................................xxix
About This Guide ............................................................................. xxxv
What This Guide Contains............................................................... xxxv
What’s New in This Edition ..........................................................xxxviii
What You Should Know Before Reading This Guide............................xl
How to Obtain the Sample Code .........................................................xli
Errata....................................................................................................xlii
Style Conventions ...............................................................................xlii
Distinguishing Deprecated Features...................................................xliii
Acknowledgments .................................................................................xlv
1. Introduction to OpenGL............................................................................1
What Is OpenGL? ...................................................................................2
A Smidgen of OpenGL Code .................................................................. 5
OpenGL Command Syntax....................................................................7
OpenGL as a State Machine ...................................................................9
OpenGL Rendering Pipeline.................................................................10
Display Lists....................................................................................11
Evaluators .......................................................................................11
Per-Vertex Operations ....................................................................12
Primitive Assembly.........................................................................12

viii Contents
Pixel Operations............................................................................. 13
Texture Assembly........................................................................... 13
Rasterization................................................................................... 14
Fragment Operations ..................................................................... 14
OpenGL-Related Libraries .................................................................... 14
Include Files ................................................................................... 15
GLUT, the OpenGL Utility Toolkit................................................ 17
Animation ............................................................................................ 22
The Refresh That Pauses................................................................. 23
Motion = Redraw + Swap ............................................................... 24
OpenGL and Its Deprecation Mechanism ........................................... 27
OpenGL Contexts .......................................................................... 27
Accessing OpenGL Functions ........................................................ 29
2. State Management and Drawing Geometric Objects .......................... 31
A Drawing Survival Kit......................................................................... 34
Clearing the Window .................................................................... 34
Specifying a Color.......................................................................... 37
Forcing Completion of Drawing.................................................... 38
Coordinate System Survival Kit ..................................................... 40
Describing Points, Lines, and Polygons............................................... 42
What Are Points, Lines, and Polygons?......................................... 42
Specifying Vertices ......................................................................... 46
OpenGL Geometric Drawing Primitives........................................ 47
Basic State Management ...................................................................... 53
Displaying Points, Lines, and Polygons............................................... 55
Point Details................................................................................... 55
Line Details .................................................................................... 56
Polygon Details .............................................................................. 60
Normal Vectors .................................................................................... 68
Vertex Arrays ........................................................................................ 70
Step 1: Enabling Arrays .................................................................. 72
Step 2: Specifying Data for the Arrays ........................................... 73
Step 3: Dereferencing and Rendering ............................................ 77
Restarting Primitives ...................................................................... 83
Instanced Drawing......................................................................... 86
Interleaved Arrays .......................................................................... 88

Contents ix
Buffer Objects .......................................................................................91
Creating Buffer Objects ..................................................................92
Making a Buffer Object Active .......................................................93
Allocating and Initializing Buffer Objects with Data.....................93
Updating Data Values in Buffer Objects ........................................96
Copying Data Between Buffer Objects.........................................101
Cleaning Up Buffer Objects..........................................................102
Using Buffer Objects with Vertex-Array Data ..............................102
Vertex-Array Objects...........................................................................104
Attribute Groups.................................................................................110
Some Hints for Building Polygonal Models of Surfaces .....................113
An Example: Building an Icosahedron ........................................115
3. Viewing.................................................................................................. 123
Overview: The Camera Analogy.........................................................126
A Simple Example: Drawing a Cube ............................................129
General-Purpose Transformation Commands .............................134
Viewing and Modeling Transformations ...........................................137
Thinking about Transformations .................................................137
Modeling Transformations...........................................................140
Viewing Transformations.............................................................146
Projection Transformations................................................................152
Perspective Projection ..................................................................153
Orthographic Projection ..............................................................156
Viewing Volume Clipping............................................................158
Viewport Transformation ...................................................................158
Defining the Viewport .................................................................159
The Transformed Depth Coordinate............................................161
Troubleshooting Transformations......................................................162
Manipulating the Matrix Stacks .........................................................164
The Modelview Matrix Stack........................................................167
The Projection Matrix Stack.........................................................168
Additional Clipping Planes.................................................................168
Examples of Composing Several Transformations.............................172
Building a Solar System ................................................................172
Building an Articulated Robot Arm..............................................175
Reversing or Mimicking Transformations..........................................179

xContents
4. Color ...................................................................................................... 185
Color Perception ................................................................................ 186
Computer Color ................................................................................. 188
RGBA versus Color-Index Mode ........................................................ 190
RGBA Display Mode..................................................................... 191
Color-Index Display Mode........................................................... 193
Choosing between RGBA and Color-Index Mode....................... 195
Changing between Display Modes .............................................. 196
Specifying a Color and a Shading Model........................................... 196
Specifying a Color in RGBA Mode............................................... 197
Specifying a Color in Color-Index Mode..................................... 199
Specifying a Shading Model......................................................... 200
5. Lighting ................................................................................................. 203
A Hidden-Surface Removal Survival Kit............................................. 205
Real-World and OpenGL Lighting..................................................... 207
Ambient, Diffuse, Specular, and Emissive Light.......................... 208
Material Colors............................................................................. 209
RGB Values for Lights and Materials ........................................... 209
A Simple Example: Rendering a Lit Sphere........................................ 210
Creating Light Sources ....................................................................... 214
Color ............................................................................................ 216
Position and Attenuation ............................................................ 217
Spotlights ..................................................................................... 219
Multiple Lights............................................................................. 220
Controlling a Light’s Position and Direction .............................. 221
Selecting a Lighting Model ................................................................ 227
Global Ambient Light .................................................................. 228
Local or Infinite Viewpoint ......................................................... 229
Two-Sided Lighting...................................................................... 229
Secondary Specular Color ............................................................ 230
Enabling Lighting ........................................................................ 231
Defining Material Properties .............................................................. 231
Diffuse and Ambient Reflection .................................................. 233
Specular Reflection....................................................................... 234
Emission....................................................................................... 234

Contents xi
Changing Material Properties ......................................................235
Color Material Mode ....................................................................237
The Mathematics of Lighting .............................................................240
Material Emission.........................................................................241
Scaled Global Ambient Light .......................................................242
Contributions from Light Sources ...............................................242
Putting It All Together..................................................................244
Secondary Specular Color.............................................................245
Lighting in Color-Index Mode ...........................................................246
The Mathematics of Color-Index Mode Lighting ........................247
6. Blending, Antialiasing, Fog, and Polygon Offset .............................. 249
Blending..............................................................................................251
The Source and Destination Factors.............................................252
Enabling Blending ........................................................................255
Combining Pixels Using Blending Equations..............................255
Sample Uses of Blending ..............................................................258
A Blending Example .....................................................................260
Three-Dimensional Blending with the Depth Buffer...................263
Antialiasing.........................................................................................267
Antialiasing Points or Lines..........................................................269
Antialiasing Geometric Primitives with Multisampling ..............275
Antialiasing Polygons...................................................................279
Fog.......................................................................................................280
Using Fog......................................................................................281
Fog Equations ...............................................................................284
Point Parameters.................................................................................291
Polygon Offset ....................................................................................293
7. Display Lists ......................................................................................... 297
Why Use Display Lists?.......................................................................298
An Example of Using a Display List ...................................................299
Display List Design Philosophy..........................................................302
Creating and Executing a Display List ...............................................305
Naming and Creating a Display List ............................................306
What’s Stored in a Display List?...................................................307

xii Contents
Executing a Display List............................................................... 309
Hierarchical Display Lists............................................................. 310
Managing Display List Indices..................................................... 311
Executing Multiple Display Lists........................................................ 312
Managing State Variables with Display Lists ..................................... 318
Encapsulating Mode Changes...................................................... 319
8. Drawing Pixels, Bitmaps, Fonts, and Images .................................... 321
Bitmaps and Fonts.............................................................................. 323
The Current Raster Position......................................................... 325
Drawing the Bitmap..................................................................... 327
Choosing a Color for the Bitmap ................................................ 328
Fonts and Display Lists ................................................................ 329
Defining and Using a Complete Font.......................................... 331
Images ................................................................................................ 333
Reading, Writing, and Copying Pixel Data ................................. 333
Imaging Pipeline ................................................................................ 343
Pixel Packing and Unpacking ...................................................... 346
Controlling Pixel-Storage Modes ................................................. 347
Pixel-Transfer Operations ............................................................ 351
Pixel Mapping .............................................................................. 354
Magnifying, Reducing, or Flipping an Image.............................. 356
Reading and Drawing Pixel Rectangles.............................................. 359
The Pixel Rectangle Drawing Process .......................................... 359
Using Buffer Objects with Pixel Rectangle Data ................................ 362
Using Buffer Objects to Transfer Pixel Data ................................ 363
Using Buffer Objects to Retrieve Pixel Data ................................ 365
Tips for Improving Pixel Drawing Rates ............................................ 366
Imaging Subset ................................................................................... 367
Color Tables ................................................................................. 369
Convolutions ............................................................................... 374
Color Matrix................................................................................. 382
Histogram..................................................................................... 383
Minmax........................................................................................ 387

Contents xiii
9. Texture Mapping................................................................................... 389
An Overview and an Example............................................................395
Steps in Texture Mapping ............................................................395
A Sample Program ........................................................................397
Specifying the Texture........................................................................400
Texture Proxy ...............................................................................406
Replacing All or Part of a Texture Image......................................408
One-Dimensional Textures ..........................................................412
Three-Dimensional Textures ........................................................414
Texture Arrays ..............................................................................419
Compressed Texture Images.........................................................420
Using a Texture’s Borders.............................................................423
Mipmaps: Multiple Levels of Detail .............................................423
Filtering...............................................................................................434
Texture Objects...................................................................................437
Naming a Texture Object .............................................................438
Creating and Using Texture Objects ............................................438
Cleaning Up Texture Objects .......................................................441
A Working Set of Resident Textures.............................................442
Texture Functions...............................................................................444
Assigning Texture Coordinates ..........................................................448
Computing Appropriate Texture Coordinates.............................450
Repeating and Clamping Textures...............................................452
Automatic Texture-Coordinate Generation .......................................457
Creating Contours........................................................................458
Sphere Map...................................................................................463
Cube Map Textures.......................................................................465
Multitexturing ....................................................................................467
Texture Combiner Functions .............................................................472
The Interpolation Combiner Function ........................................477
Applying Secondary Color after Texturing ........................................478
Secondary Color When Lighting Is Disabled...............................478
Secondary Specular Color When Lighting Is Enabled .................479
Point Sprites........................................................................................479
The Texture Matrix Stack....................................................................481

xiv Contents
Depth Textures................................................................................... 483
Creating a Shadow Map............................................................... 483
Generating Texture Coordinates and Rendering ........................ 485
10. The Framebuffer ................................................................................... 489
Buffers and Their Uses........................................................................ 492
Color Buffers ................................................................................ 493
Clearing Buffers............................................................................ 495
Selecting Color Buffers for Writing and Reading ........................ 497
Masking Buffers............................................................................ 499
Testing and Operating on Fragments ................................................ 501
Scissor Test ................................................................................... 502
Alpha Test .................................................................................... 502
Stencil Test ................................................................................... 504
Depth Test.................................................................................... 510
Occlusion Query .......................................................................... 511
Conditional Rendering ................................................................ 514
Blending, Dithering, and Logical Operations.............................. 515
The Accumulation Buffer ................................................................... 518
Motion Blur.................................................................................. 520
Depth of Field .............................................................................. 520
Soft Shadows ................................................................................ 525
Jittering ........................................................................................ 525
Framebuffer Objects ........................................................................... 526
Renderbuffers ............................................................................... 529
Copying Pixel Rectangles............................................................. 539
11. Tessellators and Quadrics................................................................... 541
Polygon Tessellation .......................................................................... 542
Creating a Tessellation Object ..................................................... 544
Tessellation Callback Routines .................................................... 544
Tessellation Properties ................................................................. 549
Polygon Definition ...................................................................... 554
Deleting a Tessellation Object ..................................................... 557
Tessellation Performance Tips ..................................................... 557
Describing GLU Errors ................................................................. 557
Backward Compatibility .............................................................. 558

Contents xv
Quadrics: Rendering Spheres, Cylinders, and Disks...........................559
Managing Quadrics Objects .........................................................560
Controlling Quadrics Attributes...................................................561
Quadrics Primitives ......................................................................563
12. Evaluators and NURBS........................................................................ 569
Prerequisites........................................................................................571
Evaluators ...........................................................................................572
One-Dimensional Evaluators .......................................................572
Two-Dimensional Evaluators .......................................................578
Using Evaluators for Textures ......................................................584
The GLU NURBS Interface..................................................................586
A Simple NURBS Example ............................................................587
Managing a NURBS Object...........................................................591
Creating a NURBS Curve or Surface.............................................595
Trimming a NURBS Surface..........................................................601
13. Selection and Feedback ...................................................................... 605
Selection..............................................................................................606
The Basic Steps .............................................................................607
Creating the Name Stack..............................................................608
The Hit Record..............................................................................610
A Selection Example.....................................................................611
Picking ..........................................................................................614
Hints for Writing a Program That Uses Selection........................625
Feedback .............................................................................................627
The Feedback Array ......................................................................629
Using Markers in Feedback Mode ................................................630
A Feedback Example.....................................................................630
14. Now That You Know............................................................................. 635
Error Handling....................................................................................637
Which Version Am I Using?...............................................................639
Utility Library Version..................................................................641
Window System Extension Versions............................................641
Extensions to the Standard.................................................................641
Extensions to the Standard for Microsoft Windows (WGL)........643

xvi Contents
Cheesy Translucency.......................................................................... 644
An Easy Fade Effect ............................................................................ 645
Object Selection Using the Back Buffer ............................................. 646
Cheap Image Transformation ............................................................ 647
Displaying Layers ............................................................................... 649
Antialiased Characters........................................................................ 650
Drawing Round Points ....................................................................... 653
Interpolating Images .......................................................................... 653
Making Decals .................................................................................... 653
Drawing Filled, Concave Polygons Using the Stencil Buffer............. 655
Finding Interference Regions ............................................................. 656
Shadows.............................................................................................. 658
Hidden-Line Removal ........................................................................ 659
Hidden-Line Removal with Polygon Offset................................. 659
Hidden-Line Removal with the Stencil Buffer............................. 660
Texture Mapping Applications .......................................................... 661
Drawing Depth-Buffered Images........................................................ 662
Dirichlet Domains.............................................................................. 662
Life in the Stencil Buffer .................................................................... 664
Alternative Uses for glDrawPixels() and glCopyPixels() .................... 665
15. The OpenGL Shading Language......................................................... 667
The OpenGL Graphics Pipeline and Programmable Shading ........... 668
Vertex Processing ......................................................................... 670
Fragment Processing .................................................................... 671
Using GLSL Shaders............................................................................ 672
A Sample Shader .......................................................................... 672
OpenGL / GLSL Interface............................................................. 673
The OpenGL Shading Language ........................................................ 681
Creating Shaders with GLSL .............................................................. 681
The Starting Point ........................................................................ 681
Declaring Variables ...................................................................... 682
Aggregate Types ........................................................................... 684
Uniform Blocks .................................................................................. 692
Specifying Uniform Variables Blocks in Shaders ......................... 693
Accessing Uniform Blocks from Your Application...................... 695
Computational Invariance........................................................... 701

Contents xvii
Statements ....................................................................................702
Functions......................................................................................706
Using OpenGL State Values in GLSL Programs ...........................707
Accessing Texture Maps in Shaders....................................................707
Shader Preprocessor ............................................................................711
Preprocessor Directives.................................................................712
Macro Definition..........................................................................712
Preprocessor Conditionals............................................................713
Compiler Control .........................................................................713
Extension Processing in Shaders ........................................................714
Vertex Shader Specifics .......................................................................715
Transform Feedback............................................................................722
Fragment Shader Specifics ..................................................................727
Rendering to Multiple Output Buffers .........................................729
A. Basics of GLUT: The OpenGL Utility Toolkit ..................................... 731
Initializing and Creating a Window...................................................732
Handling Window and Input Events .................................................733
Loading the Color Map ......................................................................735
Initializing and Drawing Three-Dimensional Objects .......................735
Managing a Background Process ........................................................736
Running the Program .........................................................................737
B. State Variables...................................................................................... 739
The Query Commands .......................................................................740
OpenGL State Variables......................................................................743
Current Values and Associated Data ............................................744
Vertex Array Data State (Not Included in
Vertex Array Object State)............................................................746
Vertex Array Object State ............................................................746
Transformation.............................................................................753
Coloring........................................................................................755
Lighting ........................................................................................756
Rasterization .................................................................................758
Multisampling ..............................................................................760
Texturing ......................................................................................761
Pixel Operations ...........................................................................768

xviii Contents
Framebuffer Control .................................................................... 771
Framebuffer Object State ............................................................. 772
Renderbuffer Object State ............................................................ 775
Pixels ............................................................................................ 776
Evaluators..................................................................................... 783
Shader Object State ...................................................................... 784
Program Object State ................................................................... 785
Query Object State ....................................................................... 789
Transform Feedback State ............................................................ 789
Vertex Shader State ...................................................................... 791
Hints............................................................................................. 791
Implementation-Dependent Values ............................................ 792
Implementation-Dependent Pixel Depths .................................. 800
Miscellaneous .............................................................................. 800
C. Homogeneous Coordinates and Transformation Matrices .............. 803
Homogeneous Coordinates................................................................ 804
Transforming Vertices.................................................................. 804
Transforming Normals................................................................. 805
Transformation Matrices.................................................................... 805
Translation ................................................................................... 806
Scaling .......................................................................................... 806
Rotation ....................................................................................... 806
Perspective Projection.................................................................. 807
Orthographic Projection.............................................................. 808
D. OpenGL and Window Systems ........................................................... 809
Accessing New OpenGL Functions .................................................... 810
GLEW: The OpenGL Extension Wrangler................................... 811
GLX: OpenGL Extension for the X Window System......................... 812
Initialization ................................................................................ 813
Controlling Rendering................................................................. 814
GLX Prototypes............................................................................ 816
AGL: OpenGL Extensions for the Apple Macintosh.......................... 819
Initialization ................................................................................ 820
Rendering and Contexts .............................................................. 820

Contents xix
Managing an OpenGL Rendering Context..................................820
On-Screen Rendering....................................................................821
Off-Screen Rendering ...................................................................821
Full-Screen Rendering...................................................................821
Swapping Buffers ..........................................................................821
Updating the Rendering Buffers...................................................821
Using an Apple Macintosh Font ..................................................822
Error Handling..............................................................................822
AGL Prototypes.............................................................................822
WGL: OpenGL Extension for Microsoft
Windows 95/98/NT/ME/2000/XP ......................................................824
Initialization .................................................................................825
Controlling Rendering .................................................................825
WGL Prototypes ...........................................................................827
Glossary ................................................................................................ 831
Index ...................................................................................................... 857
The following appendices are available online at
http://www.opengl-redbook.com/appendices/.
E. Order of Operations
F. Programming Tips
G. OpenGL Invariance
H. Calculating Normal Vectors
I. Built-In OpenGL Shading Language Variables and Functions
J. Floating-Point Formats for Textures, Framebuffers, and Renderbuffers
K. RGTC Compressed Texture Format
L. std140 Uniform Buffer Layout
This page intentionally left blank
xxi
Figures
Figure 1-1 White Rectangle on a Black Background...............................6
Figure 1-2 Order of Operations.............................................................11
Figure 1-3 Double-Buffered Rotating Square ........................................25
Figure 2-1 Coordinate System Defined by w = 50, h = 50.....................41
Figure 2-2 Two Connected Series of Line Segments .............................43
Figure 2-3 Valid and Invalid Polygons..................................................44
Figure 2-4 Nonplanar Polygon Transformed to Nonsimple Polygon ..45
Figure 2-5 Approximating Curves.........................................................46
Figure 2-6 Drawing a Polygon or a Set of Points ..................................47
Figure 2-7 Geometric Primitive Types ..................................................49
Figure 2-8 Stippled Lines.......................................................................58
Figure 2-9 Wide Stippled Lines .............................................................58
Figure 2-10 Constructing a Polygon Stipple Pattern ..............................64
Figure 2-11 Stippled Polygons ................................................................ 65
Figure 2-12 Subdividing a Nonconvex Polygon .....................................67
Figure 2-13 Outlined Polygon Drawn Using Edge Flags.........................68
Figure 2-14 Six Sides, Eight Shared Vertices ........................................... 71
Figure 2-15 Cube with Numbered Vertices.............................................79
Figure 2-16 Modifying an Undesirable T-Intersection ......................... 114
Figure 2-17 Subdividing to Improve a Polygonal Approximation
to a Surface.........................................................................118
Figure 3-1 The Camera Analogy ......................................................... 127
Figure 3-2 Stages of Vertex Transformation .......................................128
Figure 3-3 Transformed Cube .............................................................129
Figure 3-4 Rotating First or Translating First ...................................... 138

xxii Figures
Figure 3-5 Translating an Object ........................................................ 141
Figure 3-6 Rotating an Object............................................................. 142
Figure 3-7 Scaling and Reflecting an Object....................................... 143
Figure 3-8 Modeling Transformation Example .................................. 144
Figure 3-9 Object and Viewpoint at the Origin ................................. 147
Figure 3-10 Separating the Viewpoint and the Object......................... 147
Figure 3-11 Default Camera Position ................................................... 149
Figure 3-12 Using gluLookAt().............................................................. 150
Figure 3-13 Perspective Viewing Volume Specified by glFrustum()..... 154
Figure 3-14 Perspective Viewing Volume Specified
by gluPerspective()............................................................. 155
Figure 3-15 Orthographic Viewing Volume ......................................... 157
Figure 3-16 Viewport Rectangle............................................................ 159
Figure 3-17 Mapping the Viewing Volume to the Viewport................ 160
Figure 3-18 Perspective Projection and Transformed
Depth Coordinates ............................................................ 161
Figure 3-19 Using Trigonometry to Calculate the Field of View ......... 163
Figure 3-20 Modelview and Projection Matrix Stacks.......................... 165
Figure 3-21 Pushing and Popping the Matrix Stack............................. 166
Figure 3-22 Additional Clipping Planes and the Viewing Volume...... 169
Figure 3-23 Clipped Wireframe Sphere ................................................ 170
Figure 3-24 Planet and Sun................................................................... 173
Figure 3-25 Robot Arm ......................................................................... 176
Figure 3-26 Robot Arm with Fingers .................................................... 179
Figure 4-1 The Color Cube in Black and White ................................. 189
Figure 4-2 RGB Values from the Bitplanes ......................................... 191
Figure 4-3 Dithering Black and White to Create Gray ....................... 193
Figure 4-4 A Color Map ...................................................................... 194
Figure 4-5 Using a Color Map to Paint a Picture................................ 194
Figure 5-1 A Lit and an Unlit Sphere.................................................. 204
Figure 5-2 GL_SPOT_CUTOFF Parameter ........................................... 219
Figure 6-1 Creating a Nonrectangular Raster Image .......................... 260
Figure 6-2 Aliased and Antialiased Lines ............................................ 267
Figure 6-3 Determining Coverage Values........................................... 268
Figure 6-4 Fog-Density Equations....................................................... 285

Figures xxiii
Figure 6-5 Polygons and Their Depth Slopes......................................295
Figure 7-1 Stroked Font That Defines the Characters A, E, P, R, S .....314
Figure 8-1 Bitmapped F and Its Data ..................................................324
Figure 8-2 Bitmap and Its Associated Parameters ...............................327
Figure 8-3 Simplistic Diagram of Pixel Data Flow ..............................334
Figure 8-4 Component Ordering for Some Data Types
and Pixel Formats...............................................................340
Figure 8-5 Imaging Pipeline ................................................................343
Figure 8-6 glCopyPixels() Pixel Path ...................................................344
Figure 8-7 glBitmap() Pixel Path .........................................................345
Figure 8-8 glTexImage*(), glTexSubImage*(), and
glGetTexImage() Pixel Paths ..............................................345
Figure 8-9 glCopyTexImage*() and
glCopyTexSubImage*() Pixel Paths....................................346
Figure 8-10 Byte Swap Effect on Byte, Short, and Integer Data............349
Figure 8-11 *SKIP_ROWS, *SKIP_PIXELS, and
*ROW_LENGTH Parameters...............................................350
Figure 8-12 Drawing Pixels with glDrawPixels()...................................359
Figure 8-13 Reading Pixels with glReadPixels() ....................................361
Figure 8-14 Imaging Subset Operations ................................................368
Figure 8-15 The Pixel Convolution Operation .....................................375
Figure 9-1 Texture-Mapping Process...................................................391
Figure 9-2 Texture-Mapped Squares....................................................397
Figure 9-3 Texture with Subimage Added...........................................409
Figure 9-4 *IMAGE_HEIGHT Pixel-Storage Mode...............................418
Figure 9-5 *SKIP_IMAGES Pixel-Storage Mode....................................419
Figure 9-6 Mipmaps ............................................................................424
Figure 9-7 Using a Mosaic Texture......................................................431
Figure 9-8 Texture Magnification and Minification ...........................435
Figure 9-9 Texture-Map Distortion .....................................................451
Figure 9-10 Repeating a Texture ...........................................................453
Figure 9-11 Comparing GL_REPEAT to GL_MIRRORED_REPEAT........454
Figure 9-12 Clamping a Texture ...........................................................454
Figure 9-13 Repeating and Clamping a Texture ...................................454
Figure 9-14 Multitexture Processing Pipeline .......................................467

xxiv Figures
Figure 9-15 Comparison of Antialiased Points and Textured
Point Sprites....................................................................... 480
Figure 9-16 Assignment of Texture Coordinates Based on the
Setting of GL_POINT_SPRITE_COORD_ORIGIN .............. 481
Figure 10-1 Region Occupied by a Pixel ............................................... 490
Figure 10-2 Motion-Blurred Object ...................................................... 521
Figure 10-3 Jittered Viewing Volume for Depth-of-Field Effects.......... 522
Figure 11-1 Contours That Require Tessellation .................................. 543
Figure 11-2 Winding Numbers for Sample Contours .......................... 551
Figure 11-3 How Winding Rules Define Interiors ................................ 552
Figure 12-1 Bézier Curve....................................................................... 573
Figure 12-2 Bézier Surface..................................................................... 580
Figure 12-3 Lit, Shaded Bézier Surface Drawn with a Mesh................. 583
Figure 12-4 NURBS Surface................................................................... 588
Figure 12-5 Parametric Trimming Curves ............................................ 602
Figure 12-6 Trimmed NURBS Surface................................................... 603
Figure 14-1 Antialiased Characters....................................................... 651
Figure 14-2 Concave Polygon............................................................... 655
Figure 14-3 Dirichlet Domains ............................................................. 663
Figure 14-4 Six Generations from the Game of Life ............................ 664
Figure 15-1 Overview of the OpenGL Fixed-Function Pipeline........... 668
Figure 15-2 Vertex Processing Pipeline................................................. 670
Figure 15-3 Fragment Processing Pipeline............................................ 671
Figure 15-4 Shader Creation Flowchart................................................ 674
Figure 15-5 GLSL Vertex Shader Input and Output Variables ............. 716
Figure 15-6 Fragment Shader Built-In Variables................................... 727
xxv
Tables
Table 1-1 Command Suffixes and Argument Data Types .....................8
Table 2-1 Clearing Buffers....................................................................36
Table 2-2 Geometric Primitive Names and Meanings.........................48
Table 2-3 Valid Commands between glBegin() and glEnd() ...............51
Table 2-4 Vertex Array Sizes (Values per Vertex) and Data Types....... 75
Table 2-5 Variables That Direct glInterleavedArrays().........................90
Table 2-6 Values for usage Parameter of glBufferData().......................95
Table 2-7 Values for the access Parameter of glMapBufferRange() ......99
Table 2-8 Attribute Groups ................................................................ 111
Table 2-9 Client Attribute Groups .....................................................113
Table 4-1 Converting Color Values to Floating-Point Numbers ...... 198
Table 4-2 Values for Use with glClampColor()..................................199
Table 4-3 How OpenGL Selects a Color for the ith
Flat-Shaded Polygon ..........................................................202
Table 5-1 Default Values for pname Parameter of glLight*() .............215
Table 5-2 Default Values for pname Parameter of glLightModel*()...228
Table 5-3 Default Values for pname Parameter of glMaterial*() ........232
Table 6-1 Source and Destination Blending Factors..........................254
Table 6-2 Blending Equation Mathematical Operations...................256
Table 6-3 Values for Use with glHint() ..............................................269
Table 7-1 OpenGL Functions That Cannot Be
Stored in Display Lists .......................................................308
Table 8-1 Pixel Formats for glReadPixels() or glDrawPixels()............ 335
Table 8-2 Data Types for glReadPixels() or glDrawPixels()................336
Table 8-3 Valid Pixel Formats for Packed Data Types .......................338

xxvi Tables
Table 8-4 glPixelStore() Parameters ................................................... 348
Table 8-5 glPixelTransfer*() Parameters ............................................ 352
Table 8-6 glPixelMap*() Parameter Names and Values ..................... 354
Table 8-7 When Color Table Operations Occur in the
Imaging Pipeline................................................................ 369
Table 8-8 Color Table Pixel Replacement ......................................... 370
Table 8-9 How Convolution Filters Affect RGBA
Pixel Components ............................................................. 376
Table 9-1 Mipmapping Level Parameter Controls ............................ 432
Table 9-2 Mipmapping Level-of-Detail Parameter Controls............. 433
Table 9-3 Filtering Methods for Magnification and Minification .... 435
Table 9-4 Deriving Color Values from Different Texture Formats ... 445
Table 9-5 Replace, Modulate, and Decal Texture Functions............. 446
Table 9-6 Blend and Add Texture Functions..................................... 447
Table 9-7 glTexParameter*() Parameters ........................................... 455
Table 9-8 Texture Environment Parameters If target Is
GL_TEXTURE_ENV............................................................ 473
Table 9-9 GL_COMBINE_RGB and GL_COMBINE_ALPHA
Functions ........................................................................... 474
Table 9-10 Default Values for Some Texture Environment Modes..... 478
Table 10-1 Query Parameters for Per-Pixel Buffer Storage .................. 493
Table 10-2 glAlphaFunc() Parameter Values ....................................... 503
Table 10-3 Query Values for the Stencil Test ...................................... 506
Table 10-4 Sixteen Logical Operations................................................ 518
Table 10-5 Sample Jittering Values...................................................... 525
Table 10-6 Framebuffer Attachments.................................................. 532
Table 10-7 Errors returned by glCheckFramebufferStatus()................ 539
Table 12-1 Types of Control Points for glMap1*() .............................. 576
Table 13-1 glFeedbackBuffer() type Values .......................................... 628
Table 13-2 Feedback Array Syntax....................................................... 629
Table 14-1 OpenGL Error Codes ......................................................... 638
Table 14-2 Eight Combinations of Layers........................................... 649
Table 15-1 Basic Data Types in GLSL .................................................. 682
Table 15-2 GLSL Vector and Matrix Types.......................................... 684
Table 15-3 Vector Component Accessors............................................ 686

Tables xxvii
Table 15-4 GLSL Type Modifiers......................................................... 688
Table 15-5 Additional in Keyword Qualifiers (for Fragment Shader
Inputs) ................................................................................689
Table 15-6 Layout Qualifiers for Uniform Blocks................................694
Table 15-7 GLSL Operators and Their Precedence ..............................702
Table 15-8 GLSL Flow-Control Statements..........................................705
Table 15-9 GLSL Function Parameter Access Modifiers ......................707
Table 15-10 Fragment Shader Texture Sampler Types...........................708
Table 15-11 GLSL Preprocessor Directives.............................................712
Table 15-12 GLSL Preprocessor Predefined Macros...............................713
Table 15-13 GLSL Extension Directive Modifiers..................................715
Table 15-14 Vertex Shader Attribute Global Variables..........................717
Table 15-15 Vertex Shader Special Global Variables .............................720
Table 15-16 Vertex Shader Varying Global Variables............................721
Table 15-17 Transform Feedback Primitives and Their Permitted
OpenGL Rendering Types..................................................724
Table 15-18 Fragment Shader Varying Global Variables.......................728
Table 15-19 Fragment Shader Output Global Variables........................728
Table B-1 State Variables for Current Values and Associated Data ...744
Table B-2 Vertex Array Data State Variables ......................................746
Table B-3 Vertex Array Object State Variables ...................................746
Table B-4 Vertex Buffer Object State Variables ..................................752
Table B-5 Transformation State Variables..........................................753
Table B-6 Coloring State Variables.....................................................755
Table B-7 Lighting State Variables .....................................................756
Table B-8 Rasterization State Variables ..............................................758
Table B-9 Multisampling....................................................................760
Table B-10 Texturing State Variables ...................................................761
Table B-11 Pixel Operations.................................................................768
Table B-12 Framebuffer Control State Variables..................................771
Table B-13 Framebuffer Object State Variables....................................772
Table B-14 Renderbuffer Object State Variables ..................................775
Table B-15 Pixel State Variables ...........................................................776
Table B-16 Evaluator State Variables....................................................783
Table B-17 Shader Object State Variables ............................................784

xxviii Tables
Table B-18 Program Object State Variables ......................................... 785
Table B-19 Query Object State Variables ............................................. 789
Table B-20 Transform Feedback State Variables .................................. 789
Table B-21 Vertex Shader State Variables ............................................ 791
Table B-22 Hint State Variables ........................................................... 791
Table B-23 Implementation-Dependent State Variables..................... 792
Table B-24 Implementation-Dependent Pixel-Depth
State Variables.................................................................... 800
Table B-25 Miscellaneous State Variables............................................ 800
xxix
Examples
Example 1-1 Chunk of OpenGL Code........................................................ 6
Example 1-2 Simple OpenGL Program Using GLUT: hello.c ................... 19
Example 1-3 Double-Buffered Program: double.c ....................................25
Example 1-4 Creating an OpenGL Version 3.0 Context Using GLUT .....28
Example 2-1 Reshape Callback Function..................................................41
Example 2-2 Legal Uses of glVertex*() ......................................................46
Example 2-3 Filled Polygon ......................................................................47
Example 2-4 Other Constructs between glBegin() and glEnd() ...............52
Example 2-5 Line Stipple Patterns: lines.c................................................59
Example 2-6 Polygon Stipple Patterns: polys.c.........................................65
Example 2-7 Marking Polygon Boundary Edges.......................................68
Example 2-8 Surface Normals at Vertices ................................................. 69
Example 2-9 Enabling and Loading Vertex Arrays: varray.c ....................75
Example 2-10 Using glArrayElement() to Define Colors and Vertices.......77
Example 2-11 Using glDrawElements() to Dereference Several
Array Elements.....................................................................79
Example 2-12 Compacting Several glDrawElements() Calls into One.......80
Example 2-13 Two glDrawElements() Calls That Render Two
Line Strips ............................................................................80
Example 2-14 Use of glMultiDrawElements(): mvarray.c ..........................81
Example 2-15 Using glPrimitiveRestartIndex() to Render Multiple
Triangle Strips: primrestart.c. ..............................................84
Example 2-16 Effect of glInterleavedArrays(format, stride, pointer) .........89
Example 2-17 Using Buffer Objects with Vertex Data..............................103
Example 2-18 Using Vertex-Array Objects: vao.c .....................................106

xxx Examples
Example 2-19 Drawing an Icosahedron ................................................... 115
Example 2-20 Generating Normal Vectors for a Surface.......................... 117
Example 2-21 Calculating the Normalized Cross Product of
Two Vectors ....................................................................... 117
Example 2-22 Single Subdivision ............................................................. 119
Example 2-23 Recursive Subdivision ........................................................ 120
Example 2-24 Generalized Subdivision .................................................... 121
Example 3-1 Transformed Cube: cube.c................................................. 130
Example 3-2 Using Modeling Transformations: model.c ...................... 145
Example 3-3 Calculating Field of View .................................................. 163
Example 3-4 Pushing and Popping the Matrix ...................................... 166
Example 3-5 Wireframe Sphere with Two Clipping Planes: clip.c ........ 170
Example 3-6 Planetary System: planet.c................................................. 173
Example 3-7 Robot Arm: robot.c ............................................................ 177
Example 3-8 Reversing the Geometric Processing Pipeline:
unproject.c......................................................................... 180
Example 4-1 Drawing a Smooth-Shaded Triangle: smooth.c ................ 200
Example 5-1 Drawing a Lit Sphere: light.c............................................. 210
Example 5-2 Defining Colors and Position for a Light Source .............. 215
Example 5-3 Second Light Source .......................................................... 221
Example 5-4 Stationary Light Source ..................................................... 222
Example 5-5 Independently Moving Light Source ................................ 223
Example 5-6 Moving a Light with Modeling Transformations:
movelight.c........................................................................ 224
Example 5-7 Light Source That Moves with the Viewpoint .................. 226
Example 5-8 Different Material Properties: material.c........................... 235
Example 5-9 Using glColorMaterial(): colormat.c.................................. 238
Example 6-1 Demonstrating the Blend Equation Modes:
blendeqn.c ......................................................................... 256
Example 6-2 Blending Example: alpha.c................................................ 261
Example 6-3 Three-Dimensional Blending: alpha3D.c.......................... 264
Example 6-4 Antialiased Lines: aargb.c .................................................. 270
Example 6-5 Antialiasing in Color-Index Mode: aaindex.c ................... 272
Example 6-6 Enabling Multisampling: multisamp.c.............................. 276
Example 6-7 Five Fogged Spheres in RGBA Mode: fog.c........................ 281

Examples xxxi
Example 6-8 Fog in Color-Index Mode: fogindex.c................................286
Example 6-9 Fog Coordinates: fogcoord.c ..............................................289
Example 6-10 Point Parameters: pointp.c.................................................292
Example 6-11 Polygon Offset to Eliminate Visual Artifacts: polyoff.c.....296
Example 7-1 Creating a Display List: torus.c ..........................................299
Example 7-2 Using a Display List: list.c ..................................................305
Example 7-3 Hierarchical Display List ....................................................311
Example 7-4 Defining Multiple Display Lists .........................................313
Example 7-5 Multiple Display Lists to Define a Stroked
Font: stroke.c......................................................................314
Example 7-6 Persistence of State Changes after Execution of a
Display List.........................................................................318
Example 7-7 Restoring State Variables within a Display List .................319
Example 7-8 The Display List May or May Not Affect drawLine().........319
Example 7-9 Display Lists for Mode Changes ........................................320
Example 8-1 Drawing a Bitmapped Character: drawf.c..........................324
Example 8-2 Drawing a Complete Font: font.c ......................................331
Example 8-3 Use of glDrawPixels(): image.c...........................................341
Example 8-4 Drawing, Copying, and Zooming Pixel Data: image.c ......357
Example 8-5 Drawing, Copying, and Zooming Pixel Data Stored
in a Buffer Object: pboimage.c ..........................................364
Example 8-6 Retrieving Pixel Data Using Buffer Objects .......................365
Example 8-7 Pixel Replacement Using Color Tables: colortable.c .........371
Example 8-8 Using Two-Dimensional Convolution Filters:
convolution.c .....................................................................376
Example 8-9 Exchanging Color Components Using the Color
Matrix: colormatrix.c .........................................................382
Example 8-10 Computing and Diagramming an Image’s Histogram:
histogram.c ........................................................................385
Example 8-11 Computing Minimum and Maximum Pixel Values:
minmax.c ...........................................................................388
Example 9-1 Texture-Mapped Checkerboard: checker.c ........................398
Example 9-2 Querying Texture Resources with a Texture Proxy ...........408
Example 9-3 Replacing a Texture Subimage: texsub.c............................410
Example 9-4 Three-Dimensional Texturing: texture3d.c .......................415
Example 9-5 Mipmap Textures: mipmap.c.............................................426

xxxii Examples
Example 9-6 Setting Base and Maximum Mipmap Levels ..................... 433
Example 9-7 Binding Texture Objects: texbind.c................................... 439
Example 9-8 Automatic Texture-Coordinate Generation: texgen.c ...... 459
Example 9-9 Generating Cube Map Texture Coordinates:
cubemap.c.......................................................................... 466
Example 9-10 Initializing Texture Units for Multitexturing:
multitex.c........................................................................... 469
Example 9-11 Specifying Vertices for Multitexturing .............................. 471
Example 9-12 Reverting to Texture Unit 0............................................... 472
Example 9-13 Setting the Programmable Combiner Functions .............. 474
Example 9-14 Setting the Combiner Function Sources ........................... 475
Example 9-15 Using an Alpha Value for RGB Combiner Operations...... 476
Example 9-16 Interpolation Combiner Function: combiner.c ................ 477
Example 9-17 Configuring a Point Sprite for Texture Mapping: sprite.c .... 481
Example 9-18 Rendering Scene with Viewpoint at Light Source:
shadowmap.c..................................................................... 484
Example 9-19 Calculating Texture Coordinates: shadowmap.c .............. 485
Example 9-20 Rendering Scene Comparing r Coordinate:
shadowmap.c..................................................................... 486
Example 10-1 Using the Stencil Test: stencil.c......................................... 507
Example 10-2 Rendering Geometry with Occlusion Query: occquery.c ... 512
Example 10-3 Retrieving the Results of an Occlusion Query:
occquery.c.......................................................................... 513
Example 10-4 Rendering Using Conditional Rendering: condrender.c .. 515
Example 10-5 Depth-of-Field Effect: dof.c ............................................... 522
Example 10-6 Creating an RGBA Color Renderbuffer: fbo.c ................... 532
Example 10-7 Attaching a Renderbuffer for Rendering: fbo.c ................. 533
Example 10-8 Attaching a Texture Level as a Framebuffer
Attachment: fbotexture.c .................................................. 536
Example 11-1 Registering Tessellation Callbacks: tess.c .......................... 546
Example 11-2 Vertex and Combine Callbacks: tess.c .............................. 548
Example 11-3 Polygon Definition: tess.c ................................................. 556
Example 11-4 Quadrics Objects: quadric.c............................................... 565
Example 12-1 Bézier Curve with Four Control Points: bezcurve.c .......... 573
Example 12-2 Bézier Surface: bezsurf.c..................................................... 580

Examples xxxiii
Example 12-3 Lit, Shaded Bézier Surface Using a Mesh: bezmesh.c ........582
Example 12-4 Using Evaluators for Textures: texturesurf.c......................584
Example 12-5 NURBS Surface: surface.c ...................................................588
Example 12-6 Registering NURBS Tessellation Callbacks: surfpoints.c....599
Example 12-7 The NURBS Tessellation Callbacks: surfpoints.c ...............600
Example 12-8 Trimming a NURBS Surface: trim.c....................................603
Example 13-1 Creating a Name Stack.......................................................609
Example 13-2 Selection Example: select.c ................................................611
Example 13-3 Picking Example: picksquare.c...........................................616
Example 13-4 Creating Multiple Names...................................................619
Example 13-5 Using Multiple Names .......................................................620
Example 13-6 Picking with Depth Values: pickdepth.c ...........................621
Example 13-7 Feedback Mode: feedback.c................................................631
Example 14-1 Querying and Printing an Error ........................................639
Example 14-2 Determining if an Extension Is Supported
(Prior to GLU 1.3) ..............................................................643
Example 14-3 Locating an OpenGL Extension with
wglGetProcAddress() ..........................................................644
Example 15-1 A Sample GLSL (Version 1.30) Vertex Shader....................673
Example 15-2 The Same GLSL Vertex Shader (Version 1.40) ...................673
Example 15-3 Creating and Liking GLSL shaders.....................................678
Example 15-4 Obtaining a Uniform Variable’s Index and
Assigning Values ................................................................692
Example 15-5 Declaring a Uniform Variable Block ..................................693
Example 15-6 Initializing Uniform Variables in a Named Uniform
Block: ubo.c........................................................................697
Example 15-7 Associating Texture Units with Sampler Variables............709
Example 15-8 Sampling a Texture Within a GLSL Shader .......................709
Example 15-9 Dependent Texture Reads in GLSL ....................................710
Example 15-10 Using Transform Feedback to Capture Geometric
Primitives: xfb.c .................................................................724
This page intentionally left blank

About This Guide xxxv
0.About This Guide
The OpenGL graphics system is a software interface to graphics hardware.
“GL” stands for “Graphics Library.” It allows you to create interactive
programs that produce color images of moving, three-dimensional objects.
With OpenGL, you can control computer-graphics technology to produce
realistic pictures, or ones that depart from reality in imaginative ways. This
guide explains how to program with the OpenGL graphics system to deliver
the visual effect you want.
What This Guide Contains
This guide has 15 chapters. The first five chapters present basic information
that you need to understand to be able to draw a properly colored and lit
three-dimensional object on the screen.
•Chapter1, “Introduction to OpenGL,” provides a glimpse into the
kinds of things OpenGL can do. It also presents a simple OpenGL pro-
gram and explains essential programming details you need to know for
subsequent chapters.
•Chapter2, “State Management and Drawing Geometric Objects,”
explains how to create a three-dimensional geometric description of an
object that is eventually drawn on the screen.
•Chapter3, “Viewing,” describes how such three-dimensional models
are transformed before being drawn on a two-dimensional screen. You
can control these transformations to show a particular view of a model.
•Chapter4, “Color,” describes how to specify the color and shading
method used to draw an object.

xxxvi About This Guide
•Chapter5, “Lighting,” explains how to control the lighting condi-
tions surrounding an object and how that object responds to light
(that is, how it reflects or absorbs light). Lighting is an important topic,
since objects usually don’t look three-dimensional until they’re lit.
The remaining chapters explain how to optimize or add sophisticated
features to your three-dimensional scene. You might choose not to take
advantage of many of these features until you’re more comfortable with
OpenGL. Particularly advanced topics are noted in the text where they
occur.
•Chapter6, “Blending, Antialiasing, Fog, and Polygon Offset,”
describes techniques essential to creating a realistic scene—alpha
blending (to create transparent objects), antialiasing (to eliminate
jagged edges), atmospheric effects (to simulate fog or smog), and
polygon offset (to remove visual artifacts when highlighting the
edges of filled polygons).
•Chapter7, “Display Lists,” discusses how to store a series of OpenGL
commands for execution at a later time. You’ll want to use this feature
to increase the performance of your OpenGL program.
•Chapter8, “Drawing Pixels, Bitmaps, Fonts, and Images,” discusses
how to work with sets of two-dimensional data as bitmaps or images.
One typical use for bitmaps is describing characters in fonts.
•Chapter9, “Texture Mapping,” explains how to map one-, two-, and
three-dimensional images called textures onto three-dimensional
objects. Many marvelous effects can be achieved through texture
mapping.
•Chapter10, “The Framebuffer,” describes all the possible buffers that
can exist in an OpenGL implementation and how you can control
them. You can use the buffers for such effects as hidden-surface elimi-
nation, stenciling, masking, motion blur, and depth-of-field focusing.
•Chapter11, “Tessellators and Quadrics,” shows how to use the
tessellation and quadrics routines in the GLU (OpenGL Utility Library).
•Chapter12, “Evaluators and NURBS,” gives an introduction to
advanced techniques for efficient generation of curves or surfaces.
•Chapter13, “Selection and Feedback,” explains how you can use
OpenGL’s selection mechanism to select an object on the screen.
Additionally, the chapter explains the feedback mechanism, which
allows you to collect the drawing information OpenGL produces,
rather than having it be used to draw on the screen.

About This Guide xxxvii
•Chapter14, “Now That You Know,” describes how to use OpenGL
in several clever and unexpected ways to produce interesting results.
These techniques are drawn from years of experience with both
OpenGL and the technological precursor to OpenGL, the Silicon
Graphics IRIS Graphics Library.
•Chapter15, “The OpenGL Shading Language,” discusses the changes
that occurred starting with OpenGL Version 2.0. This includes an
introduction to the OpenGL Shading Language, also commonly called
the “GLSL,” which allows you to take control of portions of OpenGL’s
processing for vertices and fragments. This functionality can greatly
enhance the image quality and computational power of OpenGL.
There are also several appendices that you will likely find useful:
• Appendix A, “Basics of GLUT: The OpenGL Utility Toolkit,” dis-
cusses the library that handles window system operations. GLUT is
portable and it makes code examples shorter and more comprehensible.
• Appendix B, “State Variables,” lists the state variables that OpenGL
maintains and describes how to obtain their values.
• Appendix C, “Homogeneous Coordinates and Transformation
Matrices,” explains some of the mathematics behind matrix
transformations.
• Appendix D, “OpenGL and Window Systems,” briefly describes the
routines available in window-system-specific libraries, which are
extended to support OpenGL rendering. Window system interfaces
to the X Window System, Apple’s Mac OS, and Microsoft Windows are
discussed here.
Finally, an extensive Glossary defines the key terms used in this guide.
In addition, the appendices listed below are available at the following Web site:
http://www.opengl-redbook.com/appendices/
• Appendix E, “Order of Operations,” gives a technical overview of the
operations OpenGL performs, briefly describing them in the order in
which they occur as an application executes.
• Appendix F, “Programming Tips,” lists some programming tips based
on the intentions of the designers of OpenGL that you might find
useful.
•AppendixG, “OpenGL Invariance,” describes when and where an
OpenGL implementation must generate the exact pixel values described
in the OpenGL specification.

xxxviii About This Guide
• Appendix H, “Calculating Normal Vectors,” tells you how to
calculate normal vectors for different types of geometric objects.
• Appendix I, “Built-In OpenGL Shading Language Variables and
Functions,” describes the built-in variables and functions available in
the OpenGL Shading Language.
• Appendix J, “Floating-Point Formats for Textures, Framebuffers,
and Renderbuffers,” documents the various floating-point and
shared-exponent pixel and texel formats.
• Appendix K, “RGTC Compressed Texture Format,” describes
the texture format for storing one- and two-component compressed
textures.
• Appendix L, “std140 Uniform Buffer Layout,” documents the
standard memory layout of uniform-variable buffers for GLSL 1.40.
What’s New in This Edition
This seventh edition of the OpenGL Programming Guide includes new and
updated material covering OpenGL Versions 3.0 and 3.1. With those
versions, OpenGL—which is celebrating its eighteenth birthday the year of
this writing—has undergone a drastic departure from its previous revisions.
Version 3.0 added a number of new features as well as a depreciation model,
which sets the way for antiquated features to be removed from the library.
Note that only new features were added to Version 3.0, making it
completely source and binary backward compatible with previous versions.
However, a number of features were marked as deprecated, indicating that
they may potentially be removed from future versions of the API.
Updates related to OpenGL Version 3.0 that are discussed in this edition
include the following items:
• New features in OpenGL:
– An update to the OpenGL Shading Language, creating version 1.30
of GLSL
– Conditional rendering
– Finer-grained access to mapping buffer objects’ memory for update
and reading
– Floating-point pixel formats for framebuffers in addition to texture
map formats (which were added in OpenGL Version 2.1)

About This Guide xxxix
– Framebuffer and renderbuffer objects
– Compact floating-point representations for reducing the memory
storage usage for small dynamic-range data
– Improved support for multisample buffer interactions when
copying data
– Non-normalized integer values in texture maps and renderbuffers
whose values retain their original representation, as compared to
OpenGL’s normal operation of mapping those values into the
range [0,1]
– One- and two-dimensional texture array support
– Additional packed-pixel formats allowing access to the new
renderbuffer support
– Separate blending and writemask control for multiple rendering
targets
– Texture compression format
– Single- and double-component internal formats for textures
– Transform feedback
– Vertex-array objects
– sRGB framebuffer format
• An in-depth discussion of the deprecation model
• Bug fixes and updated token names
And for OpenGL Version 3.1:
• Identification of features removed due to deprecation in Version 3.0
• New features:
– An update to the OpenGL Shading Language, creating version 1.40
of GLSL
– Instanced rendering
– Efficient server-side copies of data between buffers
– Rendering of multiple similar primitives within a single draw call
using a special (user-specified) token to indicate when to restart a
primitive
– Texture buffer objects

xl About This Guide
– Texture rectangles
– Uniform buffer objects
– Signed normalized texel formats
What You Should Know Before Reading This Guide
This guide assumes only that you know how to program in the C language
and that you have some background in mathematics (geometry, trigonom-
etry, linear algebra, calculus, and differential geometry). Even if you have
little or no experience with computer graphics technology, you should be
able to follow most of the discussions in this book. Of course, computer
graphics is an ever-expanding subject, so you may want to enrich your
learning experience with supplemental reading:
•Computer Graphics: Principles and Practice by James D. Foley, Andries van
Dam, Steven K. Feiner, and John F. Hughes (Addison-Wesley, 1990)—
This book is an encyclopedic treatment of the subject of computer
graphics. It includes a wealth of information but is probably best read
after you have some experience with the subject.
•3D Computer Graphics by Andrew S. Glassner (The Lyons Press, 1994)—
This book is a nontechnical, gentle introduction to computer graphics.
It focuses on the visual effects that can be achieved, rather than on the
techniques needed to achieve them.
Another great place for all sorts of general information is the official
OpenGL Web site. This Web site contains software, sample programs,
documentation, FAQs, discussion boards, and news. It is always a good
place to start any search for answers to your OpenGL questions:
http://www.opengl.org/
Additionally, full documentation of all the procedures that compose
OpenGL Versions 3.0 and 3.1 will be documented at the official OpenGL
Web site. These Web pages replace the OpenGL Reference Manual that was
published by the OpenGL Architecture Review Board and Addison-Wesley.
OpenGL is really a hardware-independent specification of a programming
interface, and you use a particular implementation of it on a particular kind
of hardware. This guide explains how to program with any OpenGL imple-
mentation. However, since implementations may vary slightly—in perfor-
mance and in providing additional, optional features, for example—you
might want to investigate whether supplementary documentation is avail-

About This Guide xli
able for the particular implementation you’re using. In addition, the pro-
vider of your particular implementation might have OpenGL-related
utilities, toolkits, programming and debugging support, widgets, sample
programs, and demos available at its Web site.
How to Obtain the Sample Code
This guide contains many sample programs to illustrate the use of particular
OpenGL programming techniques. As the audience for this guide has a wide
range of experience—from novice to seasoned veteran—with both
computer graphics and OpenGL, the examples published in these pages
usually present the simplest approach to a particular rendering situation,
demonstrated using the OpenGL Version 3.0 interface. This is done mainly
to make the presentation straightforward and obtainable to those readers
just starting with OpenGL. For those of you with extensive experience
looking for implementations using the latest features of the API, we first
thank you for your patience with those following in your footsteps, and ask
that you please visit our Web site:
http://www.opengl-redbook.com/
There, you will find the source code for all examples in this text,
implementations using the latest features, and additional discussion
describing the modifications required in moving from one version of
OpenGL to another.
All of the programs contained within this book use the OpenGL Utility
Toolkit (GLUT), originally authored by Mark Kilgard. For this edition,
we use the open-source version of the GLUT interface from the folks
developing the freeglut project. They have enhanced Mark’s original work
(which is thoroughly documented in his book, OpenGL Programming for the
X Window System (Addison-Wesley, 1996)). You can find their open-source
project page at the following address:
http://freeglut.sourceforge.net/
You can obtain code and binaries of their implementation at this site.
The section “OpenGL-Related Libraries” in Chapter 1 and Appendix A give
more information about using GLUT. Additional resources to help
accelerate your learning and programming of OpenGL and GLUT can be
found at the OpenGL Web site’s resource pages:
http://www.opengl.org/resources/

xlii About This Guide
Many implementations of OpenGL might also include the code samples as
part of the system. This source code is probably the best source for your
implementation, because it might have been optimized for your system.
Read your machine-specific OpenGL documentation to see where those
code samples can be found.
Errata
Unfortunately, it is likely this book will have errors. Additionally,
OpenGL is updated during the publication of this guide: Errors are
corrected and clarifications are made to the specification, and new
specifications are released. We keep a list of bugs and updates at our Web
site, http://www.opengl-redbook.com/, where we also offer facilities for
reporting any new bugs you might find. If you find an error, please accept
our apologies, and our thanks in advance for reporting it. We’ll get it
corrected as soon as possible.
Style Conventions
These style conventions are used in this guide:
•Bold—Command and routine names and matrices
•Italics—Variables, arguments, parameter names, spatial dimensions,
matrix components, and first occurrences of key terms
• Regular—Enumerated types and defined constants
Code examples are set off from the text in a monospace font, and command
summaries are shaded with gray boxes.
In a command summary, braces are used to identify options among data
types. In the following example, glCommand has four possible suffixes:
s, i, f, and d, which stand for the data types GLshort, GLint, GLfloat, and
GLdouble. In the function prototype for glCommand,TYPE is a wildcard
that represents the data type indicated by the suffix.
void glCommand{sifd}(TYPE x1,TYPE y1,TYPE x2,TYPE y2);

About This Guide xliii
Distinguishing Deprecated Features
As mentioned, this edition of the OpenGL Programming Guide details
Versions 3.0 and 3.1. OpenGL Version 3.0 is entirely backward compatible
with all of the versions made available to this point. However, Version 3.1
employed the deprecation model to remove a number of older features that
were less compatible with modern graphics systems. While numerous
features were removed from the “core” of OpenGL, to ease the transition
between versions, the OpenGL ARB released the GL_ARB_compatibility
extension. If your implementation supports this extension, it will be able to
use all of the removed functionality. To easily identify features that were
removed from OpenGL in Version 3.1, but are still supported by the
compatibility extension, an informational table listing the affected
functions or tokens will be shown in the margin of this book next to where
the command or feature is introduced in its gray box.
While only features from OpenGL were deprecated and removed, some of
those features affect libraries, such as the OpenGL Utility Library, commonly
called GLU. Those functions that are affected by the changes in OpenGL
Version 3.1 are also listed in a table in the margin.
Compatibility
Extension
glBegin
GL_POLYGON
This page intentionally left blank
xlv
0.Acknowledgments
The Seventh Edition
OpenGL Versions 3.0 and 3.1, which this guide covers, mark a new era in
the evolution of OpenGL. Once again, the members of the OpenGL ARB
Working Group, as part of the Khronos Group, have worked tirelessly to
provide new versions that leverage the latest developments in graphics
technology. Barthold Lichtenbelt, Bill Licea-Kane, Jeremy Sandmel, and Jon
Leech, all of whom lead the technical sub-groups of the OpenGL ARB
Working group deserve our thanks. Additionally, without the tireless efforts
of Neil Trevett, President of the Khronos Group, who has carried the torch
on open-standard media APIs.
The staff at Addison-Wesley once again worked miracles in producing this
edition. Debra Williams Cauley, Anna Popick, John Fuller, Molly Sharp,
and Jill Hobbs helped with advice and recommendations in making this
manuscript better. A thorough technical review was provided by Sean
Carmody and Bob Kuehne. Their help is greatly appreciated.
The Sixth Edition
As with the seven preceding versions of OpenGL, the guidance of the
OpenGL Architecture Review Board was paramount in its evolution and
development. Without the ARB’s guidance and devotion, OpenGL would
surely languish, and once again we express our gratitude for their efforts.
Once again, the staff of Addison-Wesley provided the support and
encouragement to have this edition come to fruition. Debra Williams
Cauley, Tyrrell Albaugh, and John Fuller once again worked miracles in
producing this manuscript. Thanks once again for an effort second to none.

xlvi Acknowledgments
The Fifth Edition
OpenGL continued its evolutionary track under the careful guidance of
the OpenGL Architecture Review Board and its working groups. The small
committees that help unify the various business and technical differences
among the ARB’s membership deserve our thanks and gratitude. They
continue to push OpenGL’s success to new levels.
As always, the ever-patient and helpful staff at Addison-Wesley were
indispensable. Once again, Mary O’Brien, perhaps OpenGL’s most devoted
non-programming (at least to our knowledge) proponent, continues to
encourage us to update the programming guide for the community. Tyrrell
Albaugh and John Fuller worked tirelessly in preparing the manuscript for
production. Thanks to you all.
The Fourth Edition
OpenGL continued its evolution and success with the aid of many individ-
uals. The OpenGL Architecture Review Board, along with its many partici-
pants, help to mold OpenGL. Their contributions were much appreciated.
Numerous example programs were written by Stace Peterson. Helpful dis-
cussions and clarifications were provided by Maryann Simmons, Patrick
Brown, Alan Commike, Brad Grantham, Bob Kuehne, Jon Leech, Benjamin
Lipchak, Marc Olano, and Vicki Shreiner.
Once again, the editorial and production staff at Addison-Wesley were
extremely helpful. Thanks to Mary O’Brien, John Fuller, and Brenda
Mulligan.
The Third Edition
The third edition of this book required the support of many individuals.
Special thanks are due to the reviewers who volunteered and trudged through
the now seven hundred pages of technical material that constitute the third
edition: Bill Armstrong, Bob Beretta, David Blythe, Dan Brokenshire,
Norman Chin, Steve Cunningham, Angus Dorbie, Laurence Feldman,
Celeste Fowler, Jeffery Galinovsky, Brad Grantham, Eric Haines, David
Ishimoto, Mark Kilgard, Dale Kirkland, Jon Leech, Seth Livingston, Chikai
Ohazama, Bimal Poddar, Mike Schmit, John Stauffer, R. Scott Thompson,
David Yu, and Hansong Zhang. Their careful diligence has greatly improved
the quality of this book.

Acknowledgments xlvii
An immeasurable debt of gratitude goes to Laura Cooper, Dany Galgani,
and Dan Young for their production support, and to Mary O’Brien,
Elizabeth Spainhour, Chanda Leary, and John Fuller of Addison-Wesley.
Additionally, Miriam Geller, Shawn Hopwood, Stacy Maller, and David
Story were instrumental in the coordination and marketing of this effort.
The First and Second Editions
Thanks to the long list of pioneers and past contributors to the success of
OpenGL and of this book.
Thanks to the chief architects of OpenGL: Mark Segal and Kurt Akeley.
Special recognition goes to the pioneers who heavily contributed to the
initial design and functionality of OpenGL: Allen Akin, David Blythe, Jim
Bushnell, Dick Coulter, John Dennis, Raymond Drewry, Fred Fisher, Celeste
Fowler, Chris Frazier, Momi Furuya, Bill Glazier, Kipp Hickman, Paul Ho,
Rick Hodgson, Simon Hui, Lesley Kalmin, Phil Karlton, On Lee, Randi Rost,
Kevin P. Smith, Murali Sundaresan, Pierre Tardif, Linas Vepstas, Chuck
Whitmer, Jim Winget, and Wei Yen.
The impetus for the second edition began with Paula Womack and Tom
McReynolds of Silicon Graphics, who recognized the need for a revision and
also contributed some of the new material. John Schimpf, OpenGL Product
Manager at Silicon Graphics, was instrumental in getting the revision off
and running.
Many thanks go to the people who contributed to the success of the
first and second editions of this book: Cindy Ahuna, Kurt Akeley, Bill
Armstrong, Otto Berkes, Andy Bigos, Drew Bliss, Patrick Brown, Brian
Cabral, Norman Chin, Bill Clifford, Jim Cobb, Dick Coulter, Kathleen
Danielson, Suzy Deffeyes, Craig Dunwoody, Fred Fisher, Chris Frazier, Ken
Garnett, Kathy Gochenour, Michael Gold, Mike Heck, Paul Ho, Deanna
Hohn, Brian Hook, Kevin Hunter, Phil Huxley, Renate Kempf, Mark Kilgard,
Dale Kirkland, David Koller, Kevin LeFebvre, Hock San Lee, Zicheng Liu,
Rob Mace, Kay Maitz, Tim Misner, Jeremy Morris, Dave Orton, Bimal
Poddar, Susan Riley, Randi Rost, Mark Segal, Igor Sinyak, Bill Sweeney, Pierre
Tardif, Andy Vesper, Henri Warren, Paula Womack, Gilman Wong, Steve
Wright, and David Yu.
The color plates received a major overhaul for this edition. The sequence of
plates based on the cover image (Plates 1 through 9) was created by Thad
Beier, Seth Katz, and Mason Woo. Plates 10 through 20, 22, and 23 are
snapshots of programs created by Mason Woo. Plate 21 was created by Paul
Haeberli. Plate 24 was created by Cyril Kardassevitch of the Institue de

xlviii Acknowledgments
Recherche en Informatique de Toulouse. Plate 25 was created by Yukari Ito
and Keisuke Kirii of Nihon SGI. Plate 26 was created by John Coggi and
David Stodden of The Aerospace Company. Plate 27 was created by Rainer
Goebel, Max Planck Institute for Brain Research. Plate 28 was created by
Stefan Brabec and Wolfgang Heidrich of the Max Planck Institute for
Computer Science. Plate 29 was created by Mikko Blomqvist, Mediaclick
OY. Plate 30 was created by Bernd Lutz of Fraunhofer IGD. Finally, Plates 31
and 32, screenshots from the Quake series of games, were created by id
Software.
For the color plates that appeared in the previous editions, we would like to
thank Gavin Bell, Barry Brouillette, Rikk Carey, Sharon Clay, Mark Daly,
Alain Dumesny, Ben Garlick, Kevin Goldsmith, Jim Helman, Dave Immel,
Paul Isaacs, Michael Jones, Carl Korobkin, Howard Look, David Mott, Craig
Phillips, John Rohlf, Linda Roy, Paul Strauss, and Doug Voorhies.
And now, each of the authors would like to take the 15 minutes that have
been allotted to them by Andy Warhol to say thank you.
From the first and second editions:
I’d like to thank my managers at Silicon Graphics—Dave Larson and Way
Ting—and the members of my group—Patricia Creek, Arthur Evans, Beth
Fryer, Jed Hartman, Ken Jones, Robert Reimann, Eve Stratton (aka Margaret-
Anne Halse), John Stearns, and Josie Wernecke—for their support during
this lengthy process. Last, but surely not least, I want to thank those whose
contributions toward this project are too deep and mysterious to elucidate:
Yvonne Leach, Kathleen Lancaster, Caroline Rose, Cindy Kleinfeld, and my
parents, Florence and Ferdinand Neider.
—JLN
In addition to my parents, Edward and Irene Davis, I’d like to thank the
people who taught me most of what I know about computers and computer
graphics—Doug Engelbart and Jim Clark.
—TRD
I’d like to thank the many past and current members of Silicon Graphics
whose accommodation and enlightenment were essential to my contribu-
tion to this book: Gerald Anderson, Wendy Chin, Bert Fornaciari, Bill Gla-
zier, Jill Huchital, Howard Look, Bill Mannel, David Marsland, Dave Orton,
Linda Roy, Keith Seto, and Dave Shreiner. Very special thanks to Karrin
Nicol, Leilani Gayles, Kevin Dankwardt, Kiyoshi Hasegawa, and Raj Singh
for their guidance throughout my career. I also bestow much gratitude to

Acknowledgments xlix
my teammates on the Stanford B ice hockey team for periods of glorious dis-
traction throughout the initial writing of this book. Finally, I’d like to thank
my family, especially my mother, Bo, and my late father, Henry.
—MW
And for the third edition:
I’d first like to acknowledge Mason, who aside from helping me with this
undertaking, has been a great friend and mentor over the years. My
knowledge of OpenGL would be nothing without the masters who have
patiently answered my questions: Kurt Akeley, Allen Akin, David Blythe,
Chris Frazier, Mark Kilgard, Mark Segal, Paula Womack, and David Yu and
my current teammates working on OpenGL: Paul Ho, George Kyriazis, Jon
Leech, Ken Nicholson, and David Yu. Additionally, I’d like to recognize
Doug Doren, Kerwin Dobbs, and Karl Sohlberg, who started me on this
odyssey so long ago, and Andrew Walton, John Harechmak, and Alan Dare,
who have provided illuminating conversations about graphics over the
years. Finally and most important, I’d like to thank Vicki, my loving wife,
my parents, Bonnie and Bob, and Squiggles and Phantom, who endlessly
encourage me in all that I do and have taught me to enjoy life to the fullest.
—DRS
And for the fourth edition:
Once again, I owe Mason a debt of thanks for helping to jump start this
project. Without him, we all might be waiting for an update. I’d also like to
extend my appreciation to Alan Chalmers, James Gain, Geoff Leach, and
their students for their enthusiasm and encouragement. I’d also like to
thank ACM/SIGGRAPH, Afrigraph, Seagraph, and SGI for the ample
opportunities to talk about OpenGL to wonderful audiences worldwide.
Brad Grantham, who’s been willing to help out with all my OpenGL
escapades, deserves special thanks. A couple of friends who deserve special
mention are Eric England and Garth Honhart. The biggest thanks goes to
those I love most: Vicki, my folks, and Squiggles, Phantom, and Toby. They
continue to make me more successful than I ever imagined.
—DRS
And for the fifth edition:
First and foremost, a tremendous thanks goes to Vicki, my wife, who
patiently waited the countless hours needed to finish this project, and to
the rest of my family: Phantom, Toby, Bonnie, and Bob. I also wish to thank
the OpenGL and SIGGRAPH communities, which continue to encourage

lAcknowledgments
me in these endeavors. And thanks to Alan Commike, Bob Kuehne, Brad
Grantham, and Tom True for their help and support in the various OpenGL
activities I coerce them into helping me with.
—DRS
And for the sixth edition:
As always, my deepest appreciation goes to Vicki and Phantom who waited
patiently while I toiled on this edition, and to my parents: Bonnie and Bob,
who still encourage and compliment my efforts (and dig the fact that I
actually wound up doing something useful in life). I’d also like to thank the
members of the OpenGL ARB Working Group (now part of the Khronos
Group) and its Ecosystem Technical Subgroup for their efforts in making
documentation and information about OpenGL all the more accessible.
A great thanks goes to the Graphics group at the University of Cape Town’s
Visual Computing Laboratory: James Gain, Patrick Marais, Gary Marsden,
Bruce Merry, Carl Hultquist, Christopher de Kadt, Ilan Angel, and Shaun
Nirenstein; and Jason Moore. Last, but certainly not least, thanks once
again to the OpenGL and SIGGRAPH communities for encouraging me to
continue this project and providing ever needed feedback. Thanks to you all.
—DRS
And for the seventh edition:
As with every edition, I am entirely endebted to Vicki and Phantom, for
their support and patience. Likewise, my parents, Bonnie and Bob, who wax
lyrical over my efforts; no son could be luckier or prouder.
A very large thanks goes to my employer, ARM, Inc., and in particular to
Jem Davies, my manager, for his patience and support when this project
interrupted my responsibilties at work. Likewise, Bruce Merry of ARM
whose attention to detail helped clarify a number of points. Additionally,
I’d like to thank my colleagues at ARM who provide endless entertainment
and discussions on graphics and media. And as with every edition, my
sincerest appreciation to the readers of this guide, and the practitioners of
OpenGL worldwide. Thanks for giving me a reason to keep writing.
—DRS

1
Chapter 1
1.Introduction to OpenGL
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Appreciate in general terms what OpenGL does
• Identify different levels of rendering complexity
• Understand the basic structure of an OpenGL program
• Recognize OpenGL command syntax
• Identify the sequence of operations of the OpenGL rendering pipeline
• Understand in general terms how to animate graphics in an OpenGL
program

2Chapter 1: Introduction to OpenGL
This chapter introduces OpenGL. It has the following major sections:
• “What Is OpenGL?” explains what OpenGL is, what it does and doesn’t
do, and how it works.
• “A Smidgen of OpenGL Code” presents a small OpenGL program and
briefly discusses it. This section also defines a few basic computer-
graphics terms.
• “OpenGL Command Syntax” explains some of the conventions and
notations used by OpenGL commands.
• “OpenGL as a State Machine” describes the use of state variables in
OpenGL and the commands for querying, enabling, and disabling
states.
• “OpenGL Rendering Pipeline” shows a typical sequence of operations
for processing geometric and image data.
• “OpenGL-Related Libraries” describes sets of OpenGL-related routines,
including a detailed introduction to GLUT (Graphics Library Utility
Toolkit), a portable toolkit.
• “Animation” explains in general terms how to create pictures on the
screen that move.
• “OpenGL and Its Deprecation Mechanism” describes which changes
deprecation brought into the latest version(s) of OpenGL, how those
changes will affect your applications, and how OpenGL will evolve in
the future in light of those changes.
What Is OpenGL?
OpenGL is a software interface to graphics hardware. This interface consists
of more than 700 distinct commands (about 670 commands as specified for
OpenGL Version 3.0 and another 50 in the OpenGL Utility Library) that
you use to specify the objects and operations needed to produce interactive
three-dimensional applications.
OpenGL is designed as a streamlined, hardware-independent interface to be
implemented on many different hardware platforms. To achieve these qual-
ities, no commands for performing windowing tasks or obtaining user input
are included in OpenGL; instead, you must work through whatever win-
dowing system controls the particular hardware you’re using. Similarly,
OpenGL doesn’t provide high-level commands for describing models of

What Is OpenGL? 3
three-dimensional objects. Such commands might allow you to specify
relatively complicated shapes such as automobiles, parts of the body, air-
planes, or molecules. With OpenGL, you must build your desired model
from a small set of geometric primitives—points, lines, and polygons.
A sophisticated library that provides these features could certainly be built
on top of OpenGL. The OpenGL Utility Library (GLU) provides many of the
modeling features, such as quadric surfaces and NURBS curves and surfaces.
GLU is a standard part of every OpenGL implementation.
Now that you know what OpenGL doesn’t do, here’s what it does do. Take a
look at the color plates—they illustrate typical uses of OpenGL. They show
the scene on the cover of this book, rendered (which is to say, drawn) by a
computer using OpenGL in successively more complicated ways. The
following list describes in general terms how these pictures were made.
• Plate 1 shows the entire scene displayed as a wireframe model—that is,
as if all the objects in the scene were made of wire. Each line of wire
corresponds to an edge of a primitive (typically a polygon). For exam-
ple, the surface of the table is constructed from triangular polygons
that are positioned like slices of pie.
Note that you can see portions of objects that would be obscured if the
objects were solid rather than wireframe. For example, you can see the
entire model of the hills outside the window even though most of this
model is normally hidden by the wall of the room. The globe appears
to be nearly solid because it’s composed of hundreds of colored blocks,
and you see the wireframe lines for all the edges of all the blocks, even
those forming the back side of the globe. The way the globe is con-
structed gives you an idea of how complex objects can be created by
assembling lower-level objects.
• Plate 2 shows a depth-cued version of the same wireframe scene. Note
that the lines farther from the eye are dimmer, just as they would be in
real life, thereby giving a visual cue of depth. OpenGL uses atmospheric
effects (collectively referred to as fog) to achieve depth cueing.
• Plate 3 shows an antialiased version of the wireframe scene. Antialias-
ing is a technique for reducing the jagged edges (also known as jaggies)
created when approximating smooth edges using pixels—short for pic-
ture elements—which are confined to a rectangular grid. Such jaggies
are usually the most visible, with near-horizontal or near-vertical lines.
• Plate 4 shows a flat-shaded,unlit version of the scene. The objects in
the scene are now shown as solid. They appear “flat” in the sense that
only one color is used to render each polygon, so they don’t appear
smoothly rounded. There are no effects from any light sources.

4Chapter 1: Introduction to OpenGL
• Plate 5 shows a lit, smooth-shaded version of the scene. Note how the
scene looks much more realistic and three-dimensional when the
objects are shaded to respond to the light sources in the room, as if
the objects were smoothly rounded.
• Plate 6 adds shadows and textures to the previous version of the scene.
Shadows aren’t an explicitly defined feature of OpenGL (there is no
“shadow command”), but you can create them yourself using the
techniques described in Chapter 9 and Chapter 14. Texture mapping
allows you to apply a two-dimensional image onto a three-dimensional
object. In this scene, the top on the table surface is the most vibrant
example of texture mapping. The wood grain on the floor and table
surface are all texture mapped, as well as the wallpaper and the toy top
(on the table).
• Plate 7 shows a motion-blurred object in the scene. The sphinx (or dog,
depending on your Rorschach tendencies) appears to be captured
moving forward, leaving a blurred trace of its path of motion.
• Plate 8 shows the scene as it was drawn for the cover of the book from
a different viewpoint. This plate illustrates that the image really is a
snapshot of models of three-dimensional objects.
• Plate 9 brings back the use of fog, which was shown in Plate 2 to simu-
late the presence of smoke particles in the air. Note how the same
effect in Plate 2 now has a more dramatic impact in Plate 9.
• Plate 10 shows the depth-of-field effect, which simulates the inability of
a camera lens to maintain all objects in a photographed scene in focus.
The camera focuses on a particular spot in the scene. Objects that are
significantly closer or farther than that spot are somewhat blurred.
The color plates give you an idea of the kinds of things you can do with the
OpenGL graphics system. The following list briefly describes the major
graphics operations that OpenGL performs to render an image on the
screen. (See “OpenGL Rendering Pipeline” on page 10 for detailed
information on this order of operations.)
1. Construct shapes from geometric primitives, thereby creating mathe-
matical descriptions of objects. (OpenGL considers points, lines, poly-
gons, images, and bitmaps to be primitives.)
2. Arrange the objects in three-dimensional space and select the desired
vantage point for viewing the composed scene.
3. Calculate the colors of all the objects. The colors might be explicitly
assigned by the application, determined from specified lighting

A Smidgen of OpenGL Code 5
conditions, obtained by pasting textures onto the objects, or some
combination of these operations. These actions may be carried out using
shaders, where you explicitly control all the color computations, or they
may be performed internally in OpenGL using its preprogrammed
algorithms (by what is commonly termed the fixed-function pipeline).
4. Convert the mathematical description of objects and their associated
color information to pixels on the screen. This process is called
rasterization.
During these stages, OpenGL might perform other operations, such as
eliminating parts of objects that are hidden by other objects. In addition,
after the scene is rasterized but before it’s drawn on the screen, you can
perform some operations on the pixel data if you want.
In some implementations (such as with the X Window System), OpenGL is
designed to work even if the computer that displays the graphics you create
isn’t the computer that runs your graphics program. This might be the case
if you work in a networked computer environment where many computers
are connected to one another by a network. In this situation, the computer
on which your program runs and issues OpenGL drawing commands is
called the client, and the computer that receives those commands and per-
forms the drawing is called the server. The format for transmitting OpenGL
commands (called the protocol) from the client to the server is always the
same, so OpenGL programs can work across a network even if the client and
server are different kinds of computers. If an OpenGL program isn’t running
across a network, then there’s only one computer, and it is both the client
and the server.
A Smidgen of OpenGL Code
Because you can do so many things with the OpenGL graphics system, an
OpenGL program can be complicated. However, the basic structure of a
useful program can be simple: its tasks are to initialize certain states that
control how OpenGL renders and to specify objects to be rendered.
Before you look at some OpenGL code, let’s go over a few terms. Rendering,
which you’ve already seen used, is the process by which a computer creates
images from models. These models, or objects, are constructed from geometric
primitives—points, lines, and polygons—that are specified by their vertices.
The final rendered image consists of pixels drawn on the screen; a pixel is
the smallest visible element the display hardware can put on the screen.

6Chapter 1: Introduction to OpenGL
Information about the pixels (for instance, what color they’re supposed to
be) is organized in memory into bitplanes. A bitplane is an area of memory
that holds one bit of information for every pixel on the screen; the bit might
indicate how red a particular pixel is supposed to be, for example. The
bitplanes are themselves organized into a framebuffer, which holds all the
information that the graphics display needs to control the color and
intensity of all the pixels on the screen.
Now look at what an OpenGL program might look like. Example 1-1
renders a white rectangle on a black background, as shown in Figure 1-1.
Example 1-1 Chunk of OpenGL Code
#include <whateverYouNeed.h>
main() {
InitializeAWindowPlease();
glClearColor(0.0, 0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glOrtho(0.0, 1.0, 0.0, 1.0, -1.0, 1.0);
glBegin(GL_POLYGON);
glVertex3f(0.25, 0.25, 0.0);
glVertex3f(0.75, 0.25, 0.0);
glVertex3f(0.75, 0.75, 0.0);
glVertex3f(0.25, 0.75, 0.0);
glEnd();
glFlush();
UpdateTheWindowAndCheckForEvents();
}
Figure 1-1 White Rectangle on a Black Background

OpenGL Command Syntax 7
The first line of the main() routine initializes a window on the screen:
The InitializeAWindowPlease() routine is meant as a placeholder for
window-system-specific routines, which are generally not OpenGL calls.
The next two lines are OpenGL commands that clear the window to black:
glClearColor() establishes what color the window will be cleared to, and
glClear() actually clears the window. Once the clearing color is set, the
window is cleared to that color whenever glClear() is called. This clearing
color can be changed with another call to glClearColor(). Similarly, the
glColor3f() command establishes what color to use for drawing objects—in
this case, the color is white. All objects drawn after this point use this color,
until it’s changed with another call to set the color.
The next OpenGL command used in the program, glOrtho(), specifies the
coordinate system OpenGL assumes as it draws the final image and how
the image is mapped to the screen. The next calls, which are bracketed by
glBegin() and glEnd(), define the object to be drawn—in this example,
a polygon with four vertices. The polygon’s “corners” are defined by the
glVertex3f() commands. As you might be able to guess from the arguments,
which are (x, y, z) coordinates, the polygon is a rectangle on the z = 0 plane.
Finally, glFlush() ensures that the drawing commands are actually executed,
rather than stored in a buffer awaiting additional OpenGL commands. The
UpdateTheWindowAndCheckForEvents() placeholder routine manages
the contents of the window and begins event processing.
Actually, this piece of OpenGL code isn’t well structured. You may be asking,
“What happens if I try to move or resize the window?” or “Do I need to
reset the coordinate system each time I draw the rectangle?”. Later in this
chapter, you will see replacements for both InitializeAWindowPlease() and
UpdateTheWindowAndCheckForEvents() that actually work but require
restructuring of the code to make it efficient.
OpenGL Command Syntax
As you might have observed from the simple program in the preceding
section, OpenGL commands use the prefix gl and initial capital letters
for each word making up the command name (recall glClearColor(), for
example). Similarly, OpenGL defined constants begin with GL_, use all
capital letters, and use underscores to separate words (for example,
GL_COLOR_BUFFER_BIT).
You might also have noticed some seemingly extraneous letters appended to
some command names (for example, the 3f in glColor3f() and glVertex3f()).

8Chapter 1: Introduction to OpenGL
It’s true that the Color part of the command name glColor3f() is enough to
define the command as one that sets the current color. However, more than
one such command has been defined so that you can use different types
of arguments. In particular, the 3 part of the suffix indicates that three
arguments are given; another version of the Color command takes four
arguments. The f part of the suffix indicates that the arguments are floating-
point numbers. Having different formats allows OpenGL to accept the
user’s data in his or her own data format.
Some OpenGL commands accept as many as eight different data types for
their arguments. The letters used as suffixes to specify these data types for
ISO C implementations of OpenGL are shown in Table 1-1, along with the
corresponding OpenGL type definitions. The particular implementation of
OpenGL that you’re using might not follow this scheme exactly; an imple-
mentation in C++ or Ada that supports function overloading, for example,
wouldn’t necessarily need to.
Thus, the two commands
glVertex2i(1, 3);
glVertex2f(1.0, 3.0);
are equivalent, except that the first specifies the vertex’s coordinates as
32-bit integers, and the second specifies them as single-precision floating-
point numbers.
Suffix Data Type Typical Corresponding
C-Language Type
OpenGL Type Definition
b 8-bit integer signed char GLbyte
s 16-bit integer short GLshort
i 32-bit integer int or long GLint, GLsizei
f 32-bit floating-point float GLfloat, GLclampf
d 64-bit floating-point double GLdouble, GLclampd
ub 8-bit unsigned integer unsigned char GLubyte, GLboolean
us 16-bit unsigned integer unsigned short GLushort
ui 32-bit unsigned integer unsigned int or
unsigned long
GLuint, GLenum,
GLbitfield
Table 1-1 Command Suffixes and Argument Data Types

OpenGL as a State Machine 9
Note: Implementations of OpenGL have leeway in selecting which C data
type to use to represent OpenGL data types. If you resolutely use the
OpenGL defined data types throughout your application, you will
avoid mismatched types when porting your code between different
implementations.
Some OpenGL commands can take a final letter v, which indicates that the
command takes a pointer to a vector (or array) of values, rather than a series
of individual arguments. Many commands have both vector and nonvector
versions, but some commands accept only individual arguments and others
require that at least some of the arguments be specified as a vector. The
following lines show how you might use a vector and a nonvector version
of the command that sets the current color:
glColor3f(1.0, 0.0, 0.0);
GLfloat color_array[] = {1.0, 0.0, 0.0};
glColor3fv(color_array);
Finally, OpenGL defines the type of GLvoid. This is most often used for
OpenGL commands that accept pointers to arrays of values.
In the rest of this guide (except in actual code examples), OpenGL com-
mands are referred to by their base names only, and an asterisk is included
to indicate that there may be more to the command name. For example,
glColor*() stands for all variations of the command you use to set the cur-
rent color. If we want to make a specific point about one version of a partic-
ular command, we include the suffix necessary to define that version. For
example, glVertex*v() refers to all the vector versions of the command you
use to specify vertices.
OpenGL as a State Machine
OpenGL is a state machine, particularly if you’re using the fixed-function
pipeline. You put it into various states (or modes) that then remain in effect
until you change them. As you’ve already seen, the current color is a state
variable. You can set the current color to white, red, or any other color, and
thereafter every object is drawn with that color until you set the current
color to something else. The current color is only one of many state vari-
ables that OpenGL maintains. Others control such things as the current
viewing and projection transformations, line and polygon stipple patterns,
polygon drawing modes, pixel-packing conventions, positions and charac-
teristics of lights, and material properties of the objects being drawn. Many

10 Chapter 1: Introduction to OpenGL
state variables refer to modes that are enabled or disabled with the com-
mand glEnable() or glDisable().
If you’re using programmable shaders, depending on which version of
OpenGL you’re using, the amount of state that is exposed to your shaders
will vary.
Each state variable or mode has a default value, and at any point you can
query the system for each variable’s current value. Typically, you use one of
the six following commands to do this: glGetBooleanv(), glGetDoublev(),
glGetFloatv(),glGetIntegerv(),glGetPointerv(), or glIsEnabled(). Which
of these commands you select depends on what data type you want the
answer to be given in. Some state variables have a more specific query com-
mand (such as glGetLight*(),glGetError(), or glGetPolygonStipple()). In
addition, you can save a collection of state variables on an attribute stack
with glPushAttrib() or glPushClientAttrib(), temporarily modify them,
and later restore the values with glPopAttrib() or glPopClientAttrib(). For
temporary state changes, you should use these commands rather than any
of the query commands, as they’re likely to be more efficient.
See Appendix B for the complete list of state variables you can query. For
each variable, the appendix also lists a suggested glGet*() command that
returns the variable’s value, the attribute class to which it belongs, and the
variable’s default value.
OpenGL Rendering Pipeline
Most implementations of OpenGL have a similar order of operations, a series
of processing stages called the OpenGL rendering pipeline. This ordering, as
shown in Figure 1-2, is not a strict rule about how OpenGL is implemented,
but it provides a reliable guide for predicting what OpenGL will do.
If you are new to three-dimensional graphics, the upcoming description
may seem like drinking water out of a fire hose. You can skim this now, but
come back to Figure 1-2 as you go through each chapter in this book.
The following diagram shows the Henry Ford assembly line approach,
which OpenGL takes to processing data. Geometric data (vertices, lines, and
polygons) follow the path through the row of boxes that includes evalua-
tors and per-vertex operations, while pixel data (pixels, images, and bit-
maps) are treated differently for part of the process. Both types of data
undergo the same final steps (rasterization and per-fragment operations)
before the final pixel data is written into the framebuffer.
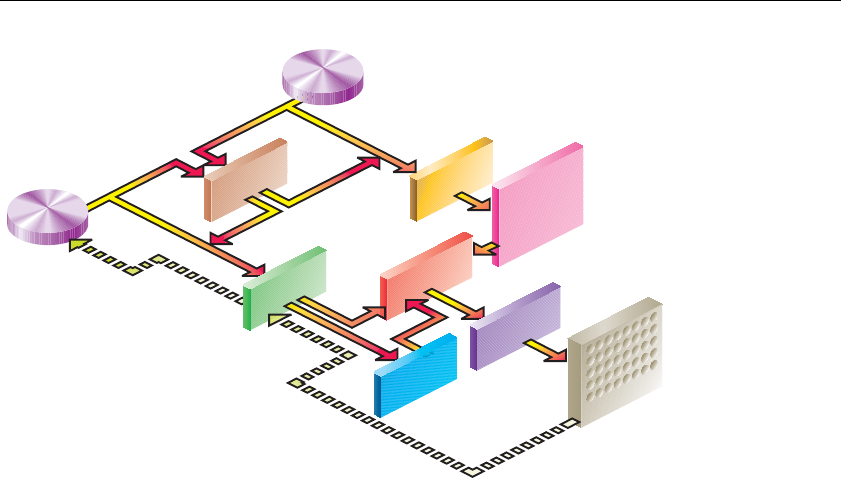
OpenGL Rendering Pipeline 11
Now you’ll see more detail about the key stages in the OpenGL rendering
pipeline.
Display Lists
All data, whether it describes geometry or pixels, can be saved in a display
list for current or later use. (The alternative to retaining data in a display list
is processing the data immediately—also known as immediate mode.) When
a display list is executed, the retained data is sent from the display list just
as if it were sent by the application in immediate mode. (See Chapter 7 for
more information about display lists.)
Evaluators
All geometric primitives are eventually described by vertices. Parametric
curves and surfaces may be initially described by control points and poly-
nomial functions called basis functions. Evaluators provide a method for
deriving the vertices used to represent the surface from the control points.
Evaluators
Per-vertex
operations
and primitive
assembly
Display list
Pixel
data
Ver tex
data
Pixel
operations
Rasterization
Per-fragment
operations
Framebuffer
Texture
assembly
Figure 1-2 Order of Operations

12 Chapter 1: Introduction to OpenGL
The method is a polynomial mapping, which can produce surface normal,
texture coordinates, colors, and spatial coordinate values from the control
points. (See Chapter 12 to learn more about evaluators.)
Per-Vertex Operations
For vertex data, next is the “per-vertex operations” stage, which converts
the vertices into primitives. Some types of vertex data (for example, spatial
coordinates) are transformed by 4 u4 floating-point matrices. Spatial coor-
dinates are projected from a position in the 3D world to a position on your
screen. (See Chapter 3 for details about the transformation matrices.)
If advanced features are enabled, this stage is even busier. If texturing is
used, texture coordinates may be generated and transformed here. If
lighting is enabled, the lighting calculations are performed using the
transformed vertex, surface normal, light source position, material
properties, and other lighting information to produce a color value.
Since OpenGL Version 2.0, you’ve had the option of using fixed-function
vertex processing, as just previously described, or completely controlling
the operation of the per-vertex operations by using vertex shaders. If you
employ shaders, all of the operations in the per-vertex operations stage are
replaced by your shader. In Version 3.1, all of the fixed-function vertex
operations are removed (unless your implementation supports the
GL_ARB_compatibility extension), and using a vertex shader is mandatory.
Primitive Assembly
Clipping, a major part of primitive assembly, is the elimination of portions
of geometry that fall outside a half-space, defined by a plane. Point clipping
simply passes or rejects vertices; line or polygon clipping can add additional
vertices depending on how the line or polygon is clipped.
In some cases, this is followed by perspective division, which makes distant
geometric objects appear smaller than closer objects. Then viewport and
depth (z-coordinate) operations are applied. If culling is enabled and the
primitive is a polygon, it then may be rejected by a culling test. Depending
on the polygon mode, a polygon may be drawn as points or lines. (See
“Polygon Details” in Chapter 2.)
The results of this stage are complete geometric primitives, which are the
transformed and clipped vertices with related color, depth, and sometimes
texture-coordinate values and guidelines for the rasterization step.

OpenGL Rendering Pipeline 13
Pixel Operations
While geometric data takes one path through the OpenGL rendering
pipeline, pixel data takes a different route. Pixels from an array in system
memory are first unpacked from one of a variety of formats into the proper
number of components. Next the data is scaled, biased, and processed by a
pixel map. The results are clamped and then either written into texture
memory or sent to the rasterization step. (See “Imaging Pipeline” in
Chapter 8.)
If pixel data is read from the framebuffer, pixel-transfer operations (scale,
bias, mapping, and clamping) are performed. Then these results are packed
into an appropriate format and returned to an array in system memory.
There are special pixel copy operations for copying data in the framebuffer
to other parts of the framebuffer or to the texture memory. A single pass is
made through the pixel-transfer operations before the data is written to the
texture memory or back to the framebuffer.
Many of the pixel operations described are part of the fixed-function pixel
pipeline and often move large amounts of data around the system. Modern
graphics implementations tend to optimize performance by trying to
localize graphics operations to the memory local to the graphics hardware
(this description is a generalization, of course, but it is how most systems
are currently implemented). OpenGL Version 3.0, which supports all of
these operations, also introduces framebuffer objects that help optimize these
data movements, in particular, these objects can eliminate some of these
transfers entirely. Framebuffer objects, combined with programmable
fragment shaders replace many of these operations (most notably, those
classified as pixel transfers) and provide significantly more flexibility.
Texture Assembly
OpenGL applications can apply texture images to geometric objects to make
the objects look more realistic, which is one of the numerous techniques
enabled by texture mapping. If several texture images are used, it’s wise to
put them into texture objects so that you can easily switch among them.
Almost all OpenGL implementations have special resources for accelerating
texture performance (which may be allocated from a shared pool of
resources in the graphics implementation). To help your OpenGL
implementation manage these memory resources efficiently, texture

14 Chapter 1: Introduction to OpenGL
objects may be prioritized to help control potential caching and locality
issues of texture maps. (See Chapter 9.)
Rasterization
Rasterization is the conversion of both geometric and pixel data into
fragments. Each fragment square corresponds to a pixel in the framebuffer.
Line and polygon stipples, line width, point size, shading model, and cov-
erage calculations to support antialiasing are taken into consideration as
vertices are connected into lines or the interior pixels are calculated for a
filled polygon. Color and depth values are generated for each fragment
square.
Fragment Operations
Before values are actually stored in the framebuffer, a series of operations are
performed that may alter or even throw out fragments. All these operations
can be enabled or disabled.
The first operation that a fragment might encounter is texturing, where a texel
(texture element) is generated from texture memory for each fragment and
applied to the fragment. Next, primary and secondary colors are combined,
and a fog calculation may be applied. If your application is employing
fragment shaders, the preceding three operations may be done in a shader.
After the final color and depth generation of the previous operations, the
scissor test, the alpha test, the stencil test, and the depth-buffer test (the
depth buffer is does hidden-surface removal) are evaluated, if enabled.
Failing an enabled test may end the continued processing of a fragment’s
square. Then, blending, dithering, logical operation, and masking by a
bitmask may be performed. (See Chapter 6 and Chapter 10.) Finally, the
thoroughly processed fragment is drawn into the appropriate buffer, where
it has finally become a pixel and achieved its final resting place.
OpenGL-Related Libraries
OpenGL provides a powerful but primitive set of rendering commands,
and all higher-level drawing must be done in terms of these commands.
Also, OpenGL programs have to use the underlying mechanisms of the

OpenGL-Related Libraries 15
windowing system. Several libraries enable you to simplify your program-
ming tasks, including the following:
• The OpenGL Utility Library (GLU) contains several routines that use
lower-level OpenGL commands to perform such tasks as setting up
matrices for specific viewing orientations and projections, performing
polygon tessellation, and rendering surfaces. This library is provided
as part of every OpenGL implementation. The more useful GLU rou-
tines are described in this guide, where they’re relevant to the topic
being discussed, such as in all of Chapter 11 and in the section “The
GLU NURBS Interface” in Chapter 12. GLU routines use the prefix glu.
• For every window system, there is a library that extends the functional-
ity of that window system to support OpenGL rendering. For machines
that use the X Window System, the OpenGL Extension to the X Win-
dow System (GLX) is provided as an adjunct to OpenGL. GLX routines
use the prefix glX. For Microsoft Windows, the WGL routines provide
the Windows to OpenGL interface. All WGL routines use the prefix
wgl. For Mac OS, three interfaces are available: AGL (with prefix agl),
CGL (cgl), and Cocoa (NSOpenGL classes).
All of these window system extension libraries are described in more
detail in Appendix D.
• The OpenGL Utility Toolkit (GLUT) is a window-system-independent
toolkit, originally written by Mark Kilgard, that hides the complexities
of differing window system APIs. In this edition, we use an open-source
implementation of GLUT named freeglut, which extends the original
functionality of GLUT. The next section describes the fundamental
routines necessary to author programs using GLUT, all of which are
prefixed with glut. In most parts of the text, we continue to use the
term GLUT, with the understanding that we are using the Freeglut
implementation.
Include Files
For all OpenGL applications, you want to include the OpenGL header files
in every file. Many OpenGL applications may use GLU, the aforementioned
OpenGL Utility Library, which requires inclusion of the glu.h header file. So
almost every OpenGL source file begins with
#include <GL/gl.h>
#include <GL/glu.h>

16 Chapter 1: Introduction to OpenGL
Note: Microsoft Windows requires that windows.h be included before either
gl.h or glu.h, because some macros used internally in the Microsoft
Windows version of gl.h and glu.h are defined in windows.h.
The OpenGL library changes all the time. The various vendors that make
graphics hardware add new features that may be too new to have been
incorporated in gl.h. In order for you to take advantage of these new
extensions to OpenGL, an additional header file is available, named glext.h.
This header contains all of the latest version and extension functions and
tokens and is available in the OpenGL Registry at the OpenGL Web site
(http://www.opengl.org/registry). The Registry also contains the speci-
fications for every OpenGL extension published. As with any header, you
could include it with the following statement:
#include “glext.h”
You probably noticed the quotes around the filename, as compared to the
normal angle brackets. Because glext.h is how graphics card vendors enable
access to new extensions, you will probably need to download versions fre-
quently from the Internet, so having a local copy to compile your program
is not a bad idea. Additionally, you may not have permission to place the
glext.h header file in a system header-file include directory (such as
/usr/include on Unix-type systems).
If you are directly accessing a window interface library to support OpenGL,
such as GLX, WGL, or CGL, you must include additional header files. For
example, if you are calling GLX, you may need to add these lines to
your code:
#include <X11/Xlib.h>
#include <GL/glx.h>
In Microsoft Windows, the WGL routines are made accessible with
#include <windows.h>
If you are using GLUT for managing your window manager tasks, you
should include
#include <freeglut.h>
Note: The original GLUT header file was named glut.h. Both glut.h and
freeglut.h guarantee that gl.h and glu.h are properly included for you,
so including all three files is redundant. Additionally, these headers
make sure that any internal operating system dependent macros are

OpenGL-Related Libraries 17
properly defined before including gl.h and glu.h. To make your GLUT
programs portable, include glut.h or freeglut.h and do not explicitly
include either gl.h or glu.h.
Most OpenGL applications also use standard C library system calls, so it is
common to include header files that are not related to graphics, such as
#include <stdlib.h>
#include <stdio.h>
We don’t include the header file declarations for our examples in this text,
so our examples are less cluttered.
Header Files for OpenGL Version 3.1
As compared to OpenGL Version 3.0, which only added new functions and
features to the sum of OpenGL’s functionality, OpenGL Version 3.1
removed functions marked as deprecated. To make that transition easier for
software authors, OpenGL Version 3.1 provides an entire new set of header
files, and recommends a location for vendor to integrate them into the
respective operating systems. You can still use the gl.h and glext.h files,
which will continue to document all OpenGL entry points, regardless of
version.
However, if you’re porting code to be used only with Version 3.1, you might
consider using the new OpenGL Version 3.1 headers:
#include <GL3/gl3.h>
#include <GL3/gl3ext.h>
They include functions and tokens for Version 3.1 (for future versions, the
features set will be restricted to that particular version). You should find that
these headers simplify the process of moving existing OpenGL code to
newer versions. Like any OpenGL headers, these files are available for
download from the OpenGL Registry (http://www.opengl.org/registry).
GLUT, the OpenGL Utility Toolkit
As you know, OpenGL contains rendering commands but is designed to be
independent of any window system or operating system. Consequently, it
contains no commands for opening windows or reading events from the
keyboard or mouse. Unfortunately, it’s impossible to write a complete
graphics program without at least opening a window, and most interesting
programs require a bit of user input or other services from the operating
system or window system. In many cases, complete programs make the

18 Chapter 1: Introduction to OpenGL
most interesting examples, so this book uses GLUT to simplify opening
windows, detecting input, and so on. If you have implementations of
OpenGL and GLUT on your system, the examples in this book should
run without change when linked with your OpenGL and GLUT libraries.
In addition, since OpenGL drawing commands are limited to those that
generate simple geometric primitives (points, lines, and polygons), GLUT
includes several routines that create more complicated three-dimensional
objects, such as a sphere, a torus, and a teapot. This way, snapshots of
program output can be interesting to look at. (Note that the OpenGL Utility
Library, GLU, also has quadrics routines that create some of the same three-
dimensional objects as GLUT, such as a sphere, cylinder, or cone.)
GLUT may not be satisfactory for full-featured OpenGL applications, but
you may find it a useful starting point for learning OpenGL. The rest of this
section briefly describes a small subset of GLUT routines so that you can
follow the programming examples in the rest of this book. (See Appendix A
for more details GLUT).
Window Management
Several routines perform tasks necessary for initializing a window:
•glutInit(int *argc, char **argv) initializes GLUT and processes any com-
mand line arguments (for X, this would be options such as -display and
-geometry). glutInit() should be called before any other GLUT routine.
•glutInitDisplayMode(unsigned int mode) specifies whether to use an
RGBA or color-index color model. You can also specify whether you
want a single- or double-buffered window. (If you’re working in color-
index mode, you’ll want to load certain colors into the color map; use
glutSetColor() to do this.) Finally, you can use this routine to indicate
that you want the window to have an associated depth, stencil,
multisampling, and/or accumulation buffer. For example, if you want
a window with double buffering, the RGBA color model, and a depth
buffer, you might call glutInitDisplayMode(GLUT_DOUBLE |
GLUT_RGBA | GLUT_DEPTH).
•glutInitWindowPosition(int x, int y) specifies the screen location for
the upper-left corner of your window.
•glutInitWindowSize(int width, int height) specifies the size, in pixels,
of your window.
•glutInitContextVersion(int majorVersion, int minorVersion) specifies
which version of OpenGL you want to use. (This is a new addition
available only when using Freeglut, and was introduced with OpenGL

OpenGL-Related Libraries 19
Version 3.0. See “OpenGL Contexts” on page 27 for more details on
OpenGL contexts and versions.)
•glutInitContextFlags(int flags) specifes the type of OpenGL context
you want to use. For normal OpenGL operation, you can omit this call
from your program. However, if you want to use a forward-compatible
OpenGL context, you will need to call this routine. (This is also a new
addition available only in Freeglut, and was introduced with OpenGL
Version 3.0. See “OpenGL Contexts” on page 27 for more details on
the types of OpenGL contexts.)
•int glutCreateWindow(char *string) creates a window with an OpenGL
context. It returns a unique identifier for the new window. Be warned:
until glutMainLoop() is called, the window is not yet displayed.
The Display Callback
glutDisplayFunc(void (*func)(void)) is the first and most important event
callback function you will see. Whenever GLUT determines that the
contents of the window need to be redisplayed, the callback function regis-
tered by glutDisplayFunc() is executed. Therefore, you should put all the
routines you need to redraw the scene in the display callback function.
If your program changes the contents of the window, sometimes you will
have to call glutPostRedisplay(), which gives glutMainLoop() a nudge to
call the registered display callback at its next opportunity.
Running the Program
The very last thing you must do is call glutMainLoop(). All windows that
have been created are now shown, and rendering to those windows is now
effective. Event processing begins, and the registered display callback is
triggered. Once this loop is entered, it is never exited!
Example 1-2 shows how you might use GLUT to create the simple program
shown in Example 1-1. Note the restructuring of the code. To maximize effi-
ciency, operations that need to be called only once (setting the background
color and coordinate system) are now in a procedure called init(). Opera-
tions to render (and possibly re-render) the scene are in the display() pro-
cedure, which is the registered GLUT display callback.
Example 1-2 Simple OpenGL Program Using GLUT: hello.c
void display(void)
{
/* clear all pixels */
glClear(GL_COLOR_BUFFER_BIT);

20 Chapter 1: Introduction to OpenGL
/* draw white polygon (rectangle) with corners at
* (0.25, 0.25, 0.0) and (0.75, 0.75, 0.0)
*/
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_POLYGON);
glVertex3f(0.25, 0.25, 0.0);
glVertex3f(0.75, 0.25, 0.0);
glVertex3f(0.75, 0.75, 0.0);
glVertex3f(0.25, 0.75, 0.0);
glEnd();
/* don’t wait!
* start processing buffered OpenGL routines
*/
glFlush();
}
void init(void)
{
/* select clearing (background) color */
glClearColor(0.0, 0.0, 0.0, 0.0);
/* initialize viewing values */
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0.0, 1.0, 0.0, 1.0, -1.0, 1.0);
}
/*
* Declare initial window size, position, and display mode
* (single buffer and RGBA). Open window with “hello”
* in its title bar. Call initialization routines.
* Register callback function to display graphics.
* Enter main loop and process events.
*/
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(250, 250);
glutInitWindowPosition(100, 100);
glutCreateWindow(“hello”);
init();
glutDisplayFunc(display);
glutMainLoop();
return 0; /* ISO C requires main to return int. */
}

OpenGL-Related Libraries 21
Handling Input Events
You can use the following routines to register callback commands that are
invoked when specified events occur:
•glutReshapeFunc(void (*func)(int w, int h)) indicates what action
should be taken when the window is resized.
•glutKeyboardFunc(void (*func)(unsigned char key, int x, int y)) and
glutMouseFunc(void (*func)(int button, int state, int x, int y)) allow you
to link a keyboard key or a mouse button with a routine that’s invoked
when the key or mouse button is pressed or released.
•glutMotionFunc(void (*func)(int x, int y)) registers a routine to call
back when the mouse is moved while a mouse button is also pressed.
Managing a Background Process
You can specify a function that’s to be executed if no other events are
pending—for example, when the event loop would otherwise be idle—with
glutIdleFunc(void (*func)(void)). This routine takes a pointer to the function
as its only argument. Pass in NULL (zero) to disable the execution of the
function.
Drawing Three-Dimensional Objects
GLUT includes several routines for drawing these three-dimensional
objects:
You can draw these objects as wireframes or as solid shaded objects with
surface normals defined. For example, the routines for a cube and a sphere
are as follows:
void glutWireCube(GLdouble size);
void glutSolidCube(GLdouble size);
void glutWireSphere(GLdouble radius, GLint slices, GLint stacks);
void glutSolidSphere(GLdouble radius, GLint slices, GLint stacks);
cone icosahedron teapot
cube octahedron tetrahedron
dodecahedron sphere torus

22 Chapter 1: Introduction to OpenGL
All these models are drawn centered at the origin of the world coordinate
system. (See Appendix A for information on the prototypes of all these
drawing routines.)
Animation
One of the most exciting things you can do on a graphics computer is draw
pictures that move. Whether you’re an engineer trying to see all sides of a
mechanical part you’re designing, a pilot learning to fly an airplane using a
simulation, or merely a computer-game aficionado, it’s clear that animation
is an important part of computer graphics.
In a movie theater, motion is achieved by taking a sequence of pictures and
projecting them at 24 frames per second on the screen. Each frame is moved
into position behind the lens, the shutter is opened, and the frame is dis-
played. The shutter is momentarily closed while the film is advanced to the
next frame, then that frame is displayed, and so on. Although you’re watch-
ing 24 different frames each second, your brain blends them all into a
smooth animation. (The old Charlie Chaplin movies were shot at 16 frames
per second and are noticeably jerky.) Computer-graphics screens typically
refresh (redraw the picture) approximately 60 to 76 times per second, and
some even run at about 120 refreshes per second. Clearly, 60 per second is
smoother than 30, and 120 is perceptively better than 60. Refresh rates
faster than 120, however, may approach a point of diminishing returns,
depending on the limits of perception.
The key reason that motion picture projection works is that each frame is
complete when it is displayed. Suppose you try to do computer animation
of your million-frame movie with a program such as this:
open_window();
for (i = 0; i < 1000000; i++) {
clear_the_window();
draw_frame(i);
wait_until_a_24th_of_a_second_is_over();
}
If you add the time it takes for your system to clear the screen and to draw
a typical frame, this program gives increasingly poor results, depending on
how close to 1/24 second it takes to clear and draw. Suppose the drawing
takes nearly a full 1/24 second. Items drawn first are visible for the full 1/24
second and present a solid image on the screen; items drawn toward the end
are instantly cleared as the program starts on the next frame. This presents

Animation 23
at best a ghostlike image, as for most of the 1/24 second your eye is viewing
the cleared background instead of the items that were unlucky enough to
be drawn last. The problem is that this program doesn’t display completely
drawn frames; instead, you watch the drawing as it happens.
Most OpenGL implementations provide double-buffering—hardware or soft-
ware that supplies two complete color buffers. One is displayed while the
other is being drawn. When the drawing of a frame is complete, the two buff-
ers are swapped, so the one that was being viewed is now used for drawing,
and vice versa. This is like a movie projector with only two frames in a loop;
while one is being projected on the screen, an artist is desperately erasing and
redrawing the frame that’s not visible. As long as the artist is quick enough,
the viewer notices no difference between this setup and one in which all the
frames are already drawn, and the projector is simply displaying them one
after the other. With double-buffering, every frame is shown only when the
drawing is complete; the viewer never sees a partially drawn frame.
A modified version that displays smoothly animated graphics using double-
buffering might look like the following:
open_window_in_double_buffer_mode();
for (i = 0; i < 1000000; i++) {
clear_the_window();
draw_frame(i);
swap_the_buffers();
}
The Refresh That Pauses
For some OpenGL implementations, in addition to simply swapping the
viewable and drawable buffers, the swap_the_buffers() routine waits until
the current screen refresh period is over so that the previous buffer is com-
pletely displayed. This routine also allows the new buffer to be completely
displayed, starting from the beginning. Assuming that your system refreshes
the display 60 times per second, this means that the fastest frame rate you
can achieve is 60 frames per second (fps), and if all your frames can be
cleared and drawn in under 1/60 second, your animation will run smoothly
at that rate.
What often happens on such a system is that the frame is too complicated
to draw in 1/60 second, so each frame is displayed more than once. If, for
example, it takes 1/45 second to draw a frame, you get 30 fps, and the
graphics are idle for 1/30 1/45 = 1/90 second per frame, or one-third of
the time.

24 Chapter 1: Introduction to OpenGL
In addition, the video refresh rate is constant, which can have some unex-
pected performance consequences. For example, with the 1/60 second per
refresh monitor and a constant frame rate, you can run at 60 fps, 30 fps,
20 fps, 15 fps, 12 fps, and so on (60/1, 60/2, 60/3, 60/4, 60/5,...). This means
that if you’re writing an application and gradually adding features (say it’s
a flight simulator, and you’re adding ground scenery), at first each feature
you add has no effect on the overall performance—you still get 60 fps.
Then, all of a sudden, you add one new feature, and the system can’t quite
draw the whole thing in 1/60 of a second, so the animation slows from
60 fps to 30 fps because it misses the first possible buffer-swapping time.
A similar thing happens when the drawing time per frame is more than
1/30 second—the animation drops from 30 to 20 fps.
If the scene’s complexity is close to any of the magic times (1/60 second,
2/60 second, 3/60 second, and so on in this example), then, because of
random variation, some frames go slightly over the time and some slightly
under. Then the frame rate is irregular, which can be visually disturbing.
In this case, if you can’t simplify the scene so that all the frames are fast
enough, it might be better to add an intentional, tiny delay to make sure
they all miss, giving a constant, slower frame rate. If your frames have
drastically different complexities, a more sophisticated approach might
be necessary.
Motion = Redraw + Swap
The structure of real animation programs does not differ very much from
this description. Usually, it is easier to redraw the entire buffer from scratch
for each frame than to figure out which parts require redrawing. This is
especially true with applications such as three-dimensional flight simula-
tors, where a tiny change in the plane’s orientation changes the position of
everything outside the window.
In most animations, the objects in a scene are simply redrawn with
different transformations—the viewpoint of the viewer moves, or a car
moves down the road a bit, or an object is rotated slightly. If significant
recomputation is required for nondrawing operations, the attainable frame
rate often slows down. Keep in mind, however, that the idle time after the
swap_the_buffers() routine can often be used for such calculations.
OpenGL doesn’t have a swap_the_buffers() command because the fea-
ture might not be available on all hardware and, in any case, it’s highly
dependent on the window system. For example, if you are using the

Animation 25
X Window System and accessing it directly, you might use the following
GLX routine:
void glXSwapBuffers(Display *dpy, Window window);
(See Appendix D for equivalent routines for other window systems.)
If you are using the GLUT library, you’ll want to call this routine:
void glutSwapBuffers(void);
Example 1-3 illustrates the use of glutSwapBuffers() in drawing a spinning
square, as shown in Figure 1-3. This example also shows how to use GLUT
to control an input device and turn on and off an idle function. In this
example, the mouse buttons toggle the spinning on and off.
Example 1-3 Double-Buffered Program: double.c
static GLfloat spin = 0.0;
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glPushMatrix();
glRotatef(spin, 0.0, 0.0, 1.0);
glColor3f(1.0, 1.0, 1.0);
glRectf(-25.0, -25.0, 25.0, 25.0);
glPopMatrix();
glutSwapBuffers();
}
Frame 0 Frame 10
Frame 20 Frame 30
Frame 40
Figure 1-3 Double-Buffered Rotating Square

26 Chapter 1: Introduction to OpenGL
void spinDisplay(void)
{
spin = spin + 2.0;
if (spin > 360.0)
spin = spin - 360.0;
glutPostRedisplay();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(-50.0, 50.0, -50.0, 50.0, -1.0, 1.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void mouse(int button, int state, int x, int y)
{
switch (button) {
case GLUT_LEFT_BUTTON:
if (state == GLUT_DOWN)
glutIdleFunc(spinDisplay);
break;
case GLUT_MIDDLE_BUTTON:
if (state == GLUT_DOWN)
glutIdleFunc(NULL);
break;
default:
break;
}
}
/*
* Request double buffer display mode.
* Register mouse input callback functions
*/
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(250, 250);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();

OpenGL and Its Deprecation Mechanism 27
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMouseFunc(mouse);
glutMainLoop();
return 0;
}
OpenGL and Its Deprecation Mechanism
Advanced
As mentioned earlier, OpenGL is continuously undergoing improvement
and refinement. New ways of doing graphics operations are developed, and
entire new fields, such as GPGPU (short for “general-purpose computing on
graphics processing units”), arise that lead to evolution in graphics
hardware capabilities. New extensions to OpenGL are suggested by vendors,
and eventually some of those extensions are incorporated as part of a new
core revision of OpenGL. Over the years, this development process has
allowed numerous redundant methods for accomplishing the same activity
to appear in the API. In many cases, while the functionality was similar, the
methods’ application performance generally was not, giving the impression
that aspects of the OpenGL API were slow and didn’t work well on modern
hardware. With OpenGL Version 3.0, the Khronos OpenGL ARB Working
Group specified a depreciation model that indicated how features could be
removed from the API. However, this change required more than just
changes to the core OpenGL API—it also affected how OpenGL contexts
were created, and the types of contexts available.
OpenGL Contexts
An OpenGL context is the data structure where OpenGL stores state
information to be used when you’re rendering images. It includes things
like textures, server-side buffer objects, function entry points, blending
states, and compiled shader objects—in short, all the things discussed in the
chapters that follow. In versions of OpenGL prior to Version 3.0, there was
a single type of OpenGL context—the full context; it contained everything
available in that implementation of OpenGL, and there was only one way
to create a context (which is window-system dependent).
With Version 3.0, a new type of context was created—the forward-compatible
context—which hides the features marked for future removal from the
Advanced

28 Chapter 1: Introduction to OpenGL
OpenGL API to help application developers modify their applications to
accommodate future versions of OpenGL.
Profiles
In addition to the various types of contexts added to Version 3.0, the concept
of profiles was introduced. A profile is subset of OpenGL functionality
specific to an application domain, such as gaming, computer-aided design
(CAD), or programs written for embedded platforms.
Currently, only a single profile is defined, which exposes the entire set of
functionality supported in the created OpenGL context. New types of
profiles may be introduced in future versions of OpenGL.
Each window system has its own set of functions for incorporating OpenGL
into its operation (e.g., WGL for Microsoft Windows), which is what really
creates the type of OpenGL context you request (also based on the profile).
As such, while the procedure is basically the same, the function calls used
are window-system specific. Fortunately, GLUT hides the details of this
operation. At some point, you may need to know the details. We defer that
conversation to Appendix D where you can find information about the
routines specific to your windowing system.
Specifying OpenGL Context Versions with GLUT
The GLUT library automatically takes care of creating an OpenGL
context when glutCreateWindow() is called. Be default, the requested
OpenGL context will be compatible with OpenGL Version 2.1. To
allocate a context for OpenGL Version 3.0 and later, you’ll need to
call glutInitContextVersion(). Likewise, if you want to use a forward-
compatible context for porting, you will also need to specify that context
attribute by calling glutInitContextFlags(). Both of these concepts are
demonstrated in Example 1-4. These functions are described in more detail
in Appendix A, “Basics of GLUT: The OpenGL Utility Toolkit.”
Example 1-4 Creating an OpenGL Version 3.0 Context Using GLUT
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGBA | GLUT_DEPTH | GLUT_DOUBLE);
glutInitWindowSize(width, height);
glutInitWindowPosition(xPos, yPos);
glutInitContextVersion(3, 0);
glutInitContextFlags(GLUT_FORWARD_COMPATIBLE);
glutCreateWindow(argv[0]);

OpenGL and Its Deprecation Mechanism 29
Accessing OpenGL Functions
Depending on the operating system on which you’re developing your
applications, you may need to do some additional work to access certain
OpenGL functions. You’ll know when this need arises because your
compiler will report that various functions are undefined (of course, every
compiler will report this error differently, but that’s crux of the matter). In
these situations, you’ll need to retrieve the function’s address (into a
function pointer). There are various ways to accomplish this:
• If your application uses the native windowing system for
opening windows and event processing, then use the appropriate
*GetProcAddress() function for the operating system your
application will be using. Examples of these functions include
wglGetProcAddress() and glXGetProcAddress().
• If you are using GLUT, then use GLUT’s function pointer retrieval
routine, glutGetProcAddress().
• Use the open-source project GLEW (short for “OpenGL Extension
Wrangler”). GLEW defines every OpenGL function, retrieving function
pointers and verifying extensions automatically for you. Go to
http://glew.sourceforge.net/ to find more details and to obtain
the code or binaries.
While we don’t explicitly show any of these options in the programs
included in the text, we use GLEW to simplify the process for us.
This page intentionally left blank

31
Chapter 2
2.State Management and Drawing
Geometric Objects
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Clear the window to an arbitrary color
• Force any pending drawing to complete
• Draw with any geometric primitive—point, line, or polygon—in two or
three dimensions
• Turn states on and off and query state variables
• Control the display of geometric primitives—for example, draw dashed
lines or outlined polygons
•Specify normal vectors at appropriate points on the surfaces of solid
objects
•Use vertex arrays and buffer objects to store and access geometric data
with fewer function calls
• Save and restore several state variables at once

32 Chapter 2: State Management and Drawing Geometric Objects
Although you can draw complex and interesting pictures using OpenGL,
they’re all constructed from a small number of primitive graphical items.
This shouldn’t be too surprising—look at what Leonardo da Vinci
accomplished with just pencils and paintbrushes.
At the highest level of abstraction, there are three basic drawing operations:
clearing the window, drawing a geometric object, and drawing a raster
object. Raster objects, which include such things as two-dimensional
images, bitmaps, and character fonts, are covered in Chapter 8. In this
chapter, you learn how to clear the screen and draw geometric objects,
including points, straight lines, and flat polygons.
You might think to yourself, “Wait a minute. I’ve seen lots of computer
graphics in movies and on television, and there are plenty of beautifully
shaded curved lines and surfaces. How are those drawn if OpenGL can draw
only straight lines and flat polygons?” Even the image on the cover of this
book includes a round table and objects on the table that have curved
surfaces. It turns out that all the curved lines and surfaces you’ve seen are
approximated by large numbers of little flat polygons or straight lines, in
much the same way that the globe on the cover is constructed from a large
set of rectangular blocks. The globe doesn’t appear to have a smooth surface
because the blocks are relatively large compared with the globe. Later in this
chapter, we show you how to construct curved lines and surfaces from lots
of small geometric primitives.
This chapter has the following major sections:
• “A Drawing Survival Kit” explains how to clear the window and force
drawing to be completed. It also gives you basic information about
controlling the colors of geometric objects and describing a coordinate
system.
• “Describing Points, Lines, and Polygons” shows you the set of primi-
tive geometric objects and how to draw them.
• “Basic State Management” describes how to turn on and off some
states (modes) and query state variables.
• “Displaying Points, Lines, and Polygons” explains what control you
have over the details of how primitives are drawn—for example, what
diameters points have, whether lines are solid or dashed, and whether
polygons are outlined or filled.
• “Normal Vectors” discusses how to specify normal vectors for
geometric objects and (briefly) what these vectors are for.

33
• “Vertex Arrays” shows you how to put large amounts of geometric data
into just a few arrays and how, with only a few function calls, to render
the geometry it describes. Reducing function calls may increase the
efficiency and performance of rendering.
• “Buffer Objects” details how to use server-side memory buffers to store
vertex array data for more efficient geometric rendering.
• “Vertex-Array Objects” expands the discussions of vertex arrays and
buffer objects by describing how to efficiently change among sets of
vertex arrays.
• “Attribute Groups” reveals how to query the current value of state variables
and how to save and restore several related state values all at once.
• “Some Hints for Building Polygonal Models of Surfaces” explores the
issues and techniques involved in constructing polygonal approxima-
tions to surfaces.
One thing to keep in mind as you read the rest of this chapter is that with
OpenGL, unless you specify otherwise, every time you issue a drawing com-
mand, the specified object is drawn. This might seem obvious, but in some
systems, you first make a list of things to draw. When your list is complete,
you tell the graphics hardware to draw the items in the list. The first style is
called immediate-mode graphics and is the default OpenGL style. In addition
to using immediate mode, you can choose to save some commands in a list
(called a display list) for later drawing. Immediate-mode graphics are typi-
cally easier to program, but display lists are often more efficient. Chapter 7
tells you how to use display lists and why you might want to use them.
Version 1.1 of OpenGL introduced vertex arrays.
In Version 1.2, scaling of surface normals (GL_RESCALE_NORMAL) was added
to OpenGL. Also, glDrawRangeElements() supplemented vertex arrays.
Version 1.3 marked the initial support for texture coordinates for multiple
texture units in the OpenGL core feature set. Previously, multitexturing had
been an optional OpenGL extension.
In Version 1.4, fog coordinates and secondary colors may be stored in vertex
arrays, and the commands glMultiDrawArrays() and glMultiDrawElements()
may be used to render primitives from vertex arrays.
In Version 1.5, vertex arrays may be stored in buffer objects that may be able
to use server memory for storing arrays and potentially accelerating their
rendering.
Chapter 2: State Management and Drawing Geometric Objects

34 Chapter 2: State Management and Drawing Geometric Objects
Version 3.0 added support for vertex array objects, allowing all of the state
related to vertex arrays to be bundled and activated with a single call. This,
in turn, makes switching between sets of vertex arrays simpler and faster.
Version 3.1 removed most of the immediate-mode routines and added the
primitive restart index, which allows you to render multiple primitives (of
the same type) with a single drawing call.
A Drawing Survival Kit
This section explains how to clear the window in preparation for drawing,
set the colors of objects that are to be drawn, and force drawing to be
completed. None of these subjects has anything to do with geometric
objects in a direct way, but any program that draws geometric objects has to
deal with these issues.
Clearing the Window
Drawing on a computer screen is different from drawing on paper in that
the paper starts out white, and all you have to do is draw the picture. On a
computer, the memory holding the picture is usually filled with the last pic-
ture you drew, so you typically need to clear it to some background color
before you start to draw the new scene. The color you use for the back-
ground depends on the application. For a word processor, you might clear
to white (the color of the paper) before you begin to draw the text. If you’re
drawing a view from a spaceship, you clear to the black of space before
beginning to draw the stars, planets, and alien spaceships. Sometimes you
might not need to clear the screen at all; for example, if the image is the
inside of a room, the entire graphics window is covered as you draw all
the walls.
At this point, you might be wondering why we keep talking about clearing
the window—why not just draw a rectangle of the appropriate color that’s
large enough to cover the entire window? First, a special command to clear
a window can be much more efficient than a general-purpose drawing com-
mand. In addition, as you’ll see in Chapter 3, OpenGL allows you to set the
coordinate system, viewing position, and viewing direction arbitrarily, so
it might be difficult to figure out an appropriate size and location for a
window-clearing rectangle. Finally, on many machines, the graphics

A Drawing Survival Kit 35
hardware consists of multiple buffers in addition to the buffer containing
colors of the pixels that are displayed. These other buffers must be cleared
from time to time, and it’s convenient to have a single command that can
clear any combination of them. (See Chapter 10 for a discussion of all the
possible buffers.)
You must also know how the colors of pixels are stored in the graphics
hardware known as bitplanes. There are two methods of storage. Either the
red, green, blue, and alpha (RGBA) values of a pixel can be directly stored in
the bitplanes, or a single index value that references a color lookup table is
stored. RGBA color-display mode is more commonly used, so most of the
examples in this book use it. (See Chapter 4 for more information about
both display modes.) You can safely ignore all references to alpha values
until Chapter 6.
As an example, these lines of code clear an RGBA mode window to black:
glClearColor(0.0, 0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
The first line sets the clearing color to black, and the next command clears
the entire window to the current clearing color. The single parameter to
glClear() indicates which buffers are to be cleared. In this case, the program
clears only the color buffer, where the image displayed on the screen is kept.
Typically, you set the clearing color once, early in your application, and
then you clear the buffers as often as necessary. OpenGL keeps track of the
current clearing color as a state variable, rather than requiring you to specify
it each time a buffer is cleared.
Chapter 4 and Chapter 10 discuss how other buffers are used. For now, all
you need to know is that clearing them is simple. For example, to clear both
the color buffer and the depth buffer, you would use the following sequence
of commands:
glClearColor(0.0, 0.0, 0.0, 0.0);
glClearDepth(1.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
In this case, the call to glClearColor() is the same as before, the glClearDepth()
command specifies the value to which every pixel of the depth buffer is to be
set, and the parameter to the glClear() command now consists of the bitwise
logical OR of all the buffers to be cleared. The following summary of glClear()
includes a table that lists the buffers that can be cleared, their names, and the
chapter in which each type of buffer is discussed.
36 Chapter 2: State Management and Drawing Geometric Objects
Before issuing a command to clear multiple buffers, you have to set the
values to which each buffer is to be cleared if you want something other
than the default RGBA color, depth value, accumulation color, and stencil
index. In addition to the glClearColor() and glClearDepth() commands
that set the current values for clearing the color and depth buffers,
glClearIndex(),glClearAccum(), and glClearStencil() specify the color
index, accumulation color, and stencil index used to clear the corresponding
buffers. (See Chapter 4 and Chapter 10 for descriptions of these buffers and
their uses.)
OpenGL allows you to specify multiple buffers because clearing is generally
a slow operation, as every pixel in the window (possibly millions) is
touched, and some graphics hardware allows sets of buffers to be cleared
simultaneously. Hardware that doesn’t support simultaneous clears
performs them sequentially. The difference between
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
void glClearColor(GLclampf red, GLclampf green, GLclampf blue,
GLclampf alpha);
Sets the current clearing color for use in clearing color buffers in RGBA
mode. (See Chapter 4 for more information on RGBA mode.) The red,
green,blue, and alpha values are clamped if necessary to the range [0, 1].
The default clearing color is (0, 0, 0, 0), which is black.
void glClear(GLbitfield mask);
Clears the specified buffers to their current clearing values. The mask
argument is a bitwise logical OR combination of the values listed in
Table 2-1.
Buffer Name Reference
Color buffer GL_COLOR_BUFFER_BIT Chapter 4
Depth buffer GL_DEPTH_BUFFER_BIT Chapter 10
Accumulation buffer GL_ACCUM_BUFFER_BIT Chapter 10
Stencil buffer GL_STENCIL_BUFFER_BIT Chapter 10
Table 2-1 Clearing Buffers
Compatibility
Extension
GL_ACCUM_
BUFFER_BIT

A Drawing Survival Kit 37
and
glClear(GL_COLOR_BUFFER_BIT);
glClear(GL_DEPTH_BUFFER_BIT);
is that although both have the same final effect, the first example might run
faster on many machines. It certainly won’t run more slowly.
Specifying a Color
With OpenGL, the description of the shape of an object being drawn is
independent of the description of its color. Whenever a particular geometric
object is drawn, it’s drawn using the currently specified coloring scheme.
The coloring scheme might be as simple as “draw everything in fire-engine
red” or as complicated as “assume the object is made out of blue plastic, that
there’s a yellow spotlight pointed in such and such a direction, and that
there’s a general low-level reddish-brown light everywhere else.” In general,
an OpenGL programmer first sets the color or coloring scheme and then
draws the objects. Until the color or coloring scheme is changed, all objects
are drawn in that color or using that coloring scheme. This method helps
OpenGL achieve higher drawing performance than would result if it didn’t
keep track of the current color.
For example, the pseudocode
set_current_color(red);
draw_object(A);
draw_object(B);
set_current_color(green);
set_current_color(blue);
draw_object(C);
draws objects A and B in red, and object C in blue. The command on the
fourth line that sets the current color to green is wasted.
Coloring, lighting, and shading are all large topics with entire chapters or
large sections devoted to them. To draw geometric primitives that can be
seen, however, you need some basic knowledge of how to set the current
color; this information is provided in the next few paragraphs. (See
Chapter 4 and Chapter 5 for details on these topics.)
To set a color, use the command glColor3f(). It takes three parameters, all
of which are floating-point numbers between 0.0 and 1.0. The parameters
are, in order, the red, green, and blue components of the color. You can think
of these three values as specifying a “mix” of colors: 0.0 means don’t use any

38 Chapter 2: State Management and Drawing Geometric Objects
of that component, and 1.0 means use all you can of that component. Thus,
the code
glColor3f(1.0, 0.0, 0.0);
makes the brightest red the system can draw, with no green or blue compo-
nents. All zeros makes black; in contrast, all ones makes white. Setting all
three components to 0.5 yields gray (halfway between black and white).
Here are eight commands and the colors they would set:
glColor3f(0.0, 0.0, 0.0); /* black */
glColor3f(1.0, 0.0, 0.0); /* red */
glColor3f(0.0, 1.0, 0.0); /* green */
glColor3f(1.0, 1.0, 0.0); /* yellow */
glColor3f(0.0, 0.0, 1.0); /* blue */
glColor3f(1.0, 0.0, 1.0); /* magenta */
glColor3f(0.0, 1.0, 1.0); /* cyan */
glColor3f(1.0, 1.0, 1.0); /* white */
You might have noticed earlier that the routine for setting the clearing
color, glClearColor(), takes four parameters, the first three of which match
the parameters for glColor3f(). The fourth parameter is the alpha value; it’s
covered in detail in “Blending” in Chapter 6. For now, set the fourth param-
eter of glClearColor() to 0.0, which is its default value.
Forcing Completion of Drawing
As you saw in “OpenGL Rendering Pipeline” in Chapter 1, most modern
graphics systems can be thought of as an assembly line. The main central
processing unit (CPU) issues a drawing command. Perhaps other hardware
does geometric transformations. Clipping is performed, followed by shad-
ing and/or texturing. Finally, the values are written into the bitplanes for
display. In high-end architectures, each of these operations is performed by
a different piece of hardware that’s been designed to perform its particular
task quickly. In such an architecture, there’s no need for the CPU to wait for
each drawing command to complete before issuing the next one. While the
CPU is sending a vertex down the pipeline, the transformation hardware
is working on transforming the last one sent, the one before that is being
clipped, and so on. In such a system, if the CPU waited for each command
to complete before issuing the next, there could be a huge performance
penalty.

A Drawing Survival Kit 39
In addition, the application might be running on more than one machine.
For example, suppose that the main program is running elsewhere (on a
machine called the client) and that you’re viewing the results of the draw-
ing on your workstation or terminal (the server), which is connected by a
network to the client. In that case, it might be horribly inefficient to send
each command over the network one at a time, as considerable overhead is
often associated with each network transmission. Usually, the client gathers
a collection of commands into a single network packet before sending it.
Unfortunately, the network code on the client typically has no way of
knowing that the graphics program is finished drawing a frame or scene. In
the worst case, it waits forever for enough additional drawing commands to
fill a packet, and you never see the completed drawing.
For this reason, OpenGL provides the command glFlush(), which forces the
client to send the network packet even though it might not be full. Where
there is no network and all commands are truly executed immediately on
the server, glFlush() might have no effect. However, if you’re writing a pro-
gram that you want to work properly both with and without a network,
include a call to glFlush() at the end of each frame or scene. Note that
glFlush() doesn’t wait for the drawing to complete—it just forces the draw-
ing to begin execution, thereby guaranteeing that all previous commands
execute in finite time even if no further rendering commands are executed.
There are other situations in which glFlush() is useful:
• Software renderers that build images in system memory and don’t
want to constantly update the screen.
• Implementations that gather sets of rendering commands to amortize
start-up costs. The aforementioned network transmission example is
one instance of this.
void glFlush(void);
Forces previously issued OpenGL commands to begin execution, thus
guaranteeing that they complete in finite time.
A few commands—for example, commands that swap buffers in double-
buffer mode—automatically flush pending commands onto the network
before they can occur.

40 Chapter 2: State Management and Drawing Geometric Objects
Coordinate System Survival Kit
Whenever you initially open a window or later move or resize that window,
the window system will send an event to notify you. If you are using GLUT,
the notification is automated; whatever routine has been registered to
glutReshapeFunc() will be called. You must register a callback function
that will
• Reestablish the rectangular region that will be the new rendering
canvas
• Define the coordinate system to which objects will be drawn
In Chapter 3, you’ll see how to define three-dimensional coordinate
systems, but right now just create a simple, basic two-dimensional
coordinate system into which you can draw a few objects. Call
glutReshapeFunc(reshape), where reshape() is the following function
shown in Example 2-1.
If glFlush() isn’t sufficient for you, try glFinish(). This command flushes
the network as glFlush() does and then waits for notification from the
graphics hardware or network indicating that the drawing is complete in
the framebuffer. You might need to use glFinish() if you want to synchro-
nize tasks—for example, to make sure that your three-dimensional render-
ing is on the screen before you use Display PostScript to draw labels on top
of the rendering. Another example would be to ensure that the drawing is
complete before it begins to accept user input. After you issue a glFinish()
command, your graphics process is blocked until it receives notification
from the graphics hardware that the drawing is complete. Keep in mind
that excessive use of glFinish() can reduce the performance of your appli-
cation, especially if you’re running over a network, because it requires
round-trip communication. If glFlush() is sufficient for your needs, use it
instead of glFinish().
void glFinish(void);
Forces all previously issued OpenGL commands to complete. This com-
mand doesn’t return until all effects from previous commands are fully
realized.
A Drawing Survival Kit 41
Example 2-1 Reshape Callback Function
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);
}
The kernel of GLUT will pass this function two arguments: the width and
height, in pixels, of the new, moved, or resized window. glViewport()
adjusts the pixel rectangle for drawing to be the entire new window. The
next three routines adjust the coordinate system for drawing so that the
lower left corner is (0, 0) and the upper right corner is (w,h) (see Figure 2-1).
To explain it another way, think about a piece of graphing paper. The w and
h values in reshape() represent how many columns and rows of squares are
on your graph paper. Then you have to put axes on the graph paper. The
gluOrtho2D() routine puts the origin, (0, 0), in the lowest, leftmost square,
and makes each square represent one unit. Now, when you render the
points, lines, and polygons in the rest of this chapter, they will appear on
this paper in easily predictable squares. (For now, keep all your objects two-
dimensional.)
(0, 0)
(50, 50)
Figure 2-1 Coordinate System Defined by w = 50, h = 50

42 Chapter 2: State Management and Drawing Geometric Objects
Describing Points, Lines, and Polygons
This section explains how to describe OpenGL geometric primitives. All
geometric primitives are eventually described in terms of their vertices—
coordinates that define the points themselves, the endpoints of line seg-
ments, or the corners of polygons. The next section discusses how these
primitives are displayed and what control you have over their display.
What Are Points, Lines, and Polygons?
You probably have a fairly good idea of what a mathematician means by the
terms point,line, and polygon. The OpenGL meanings are similar, but not
quite the same.
One difference comes from the limitations of computer-based calculations.
In any OpenGL implementation, floating-point calculations are of finite
precision, and they have round-off errors. Consequently, the coordinates of
OpenGL points, lines, and polygons suffer from the same problems.
A more important difference arises from the limitations of a raster graphics
display. On such a display, the smallest displayable unit is a pixel, and
although pixels might be less than 1/100 of an inch wide, they are still
much larger than the mathematician’s concepts of infinitely small (for
points) and infinitely thin (for lines). When OpenGL performs calculations,
it assumes that points are represented as vectors of floating-point numbers.
However, a point is typically (but not always) drawn as a single pixel, and
many different points with slightly different coordinates could be drawn by
OpenGL on the same pixel.
Points
A point is represented by a set of floating-point numbers called a vertex. All
internal calculations are done as if vertices are three-dimensional. Vertices
specified by the user as two-dimensional (that is, with only x- and y-
coordinates) are assigned a z-coordinate equal to zero by OpenGL.
Advanced
OpenGL works in the homogeneous coordinates of three-dimensional projec-
tive geometry, so for internal calculations, all vertices are represented with
four floating-point coordinates (x,y,z,w). If w is different from zero, these
coordinates correspond to the Euclidean, three-dimensional point (x/w, y/w,
z/w). You can specify the w-coordinate in OpenGL commands, but this is
Advanced

Describing Points, Lines, and Polygons 43
rarely done. If the w-coordinate isn’t specified, it is understood to be 1.0.
(See Appendix C for more information about homogeneous coordinate
systems.)
Lines
In OpenGL, the term line refers to a line segment, not the mathematician’s
version that extends to infinity in both directions. There are easy ways to
specify a connected series of line segments, or even a closed, connected
series of segments (see Figure 2-2). In all cases, though, the lines consti-
tuting the connected series are specified in terms of the vertices at their
endpoints.
Polygons
Polygons are the areas enclosed by single closed loops of line segments,
where the line segments are specified by the vertices at their endpoints.
Polygons are typically drawn with the pixels in the interior filled in, but you
can also draw them as outlines or a set of points. (See “Polygon Details” on
page 60.)
In general, polygons can be complicated, so OpenGL imposes some strong
restrictions on what constitutes a primitive polygon. First, the edges of
OpenGL polygons can’t intersect (a mathematician would call a polygon
satisfying this condition a simple polygon). Second, OpenGL polygons must
be convex, meaning that they cannot have indentations. Stated precisely, a
region is convex if, given any two points in the interior, the line segment
joining them is also in the interior. See Figure 2-3 for some examples of
valid and invalid polygons. OpenGL, however, doesn’t restrict the number
of line segments making up the boundary of a convex polygon. Note that
polygons with holes can’t be described. They are nonconvex, and they can’t
be drawn with a boundary made up of a single closed loop. Be aware that if
Figure 2-2 Two Connected Series of Line Segments
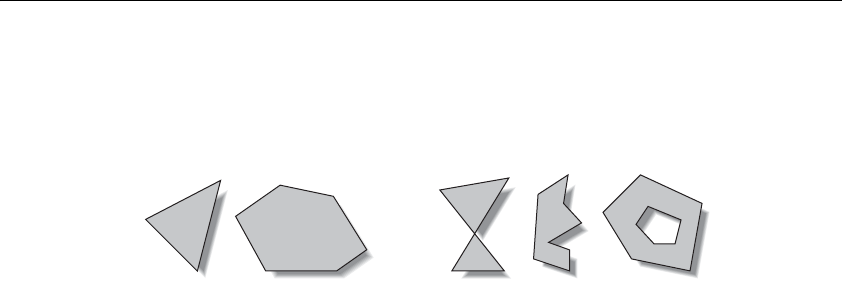
44 Chapter 2: State Management and Drawing Geometric Objects
you present OpenGL with a nonconvex filled polygon, it might not draw it
as you expect. For instance, on most systems, no more than the convex hull
of the polygon would be filled. On some systems, less than the convex hull
might be filled.
The reason for the OpenGL restrictions on valid polygon types is that it’s
simpler to provide fast polygon-rendering hardware for that restricted class
of polygons. Simple polygons can be rendered quickly. The difficult cases
are hard to detect quickly, so for maximum performance, OpenGL crosses
its fingers and assumes the polygons are simple.
Many real-world surfaces consist of nonsimple polygons, nonconvex poly-
gons, or polygons with holes. Since all such polygons can be formed from
unions of simple convex polygons, some routines to build more complex
objects are provided in the GLU library. These routines take complex
descriptions and tessellate them, or break them down into groups of the
simpler OpenGL polygons that can then be rendered. (See “Polygon Tessel-
lation” in Chapter 11 for more information about the tessellation routines.)
Since OpenGL vertices are always three-dimensional, the points forming the
boundary of a particular polygon don’t necessarily lie on the same plane in
space. (Of course, they do in many cases—if all the z-coordinates are zero, for
example, or if the polygon is a triangle.) If a polygon’s vertices don’t lie in the
same plane, then after various rotations in space, changes in the viewpoint,
and projection onto the display screen, the points might no longer form a
simple convex polygon. For example, imagine a four-point quadrilateral
where the points are slightly out of plane, and look at it almost edge-on.
You can get a nonsimple polygon that resembles a bow tie, as shown in
Figure 2-4, which isn’t guaranteed to be rendered correctly. This situation
isn’t all that unusual if you approximate curved surfaces by quadrilaterals
made of points lying on the true surface. You can always avoid the problem
by using triangles, as any three points always lie on a plane.
Valid Invalid
Figure 2-3 Valid and Invalid Polygons
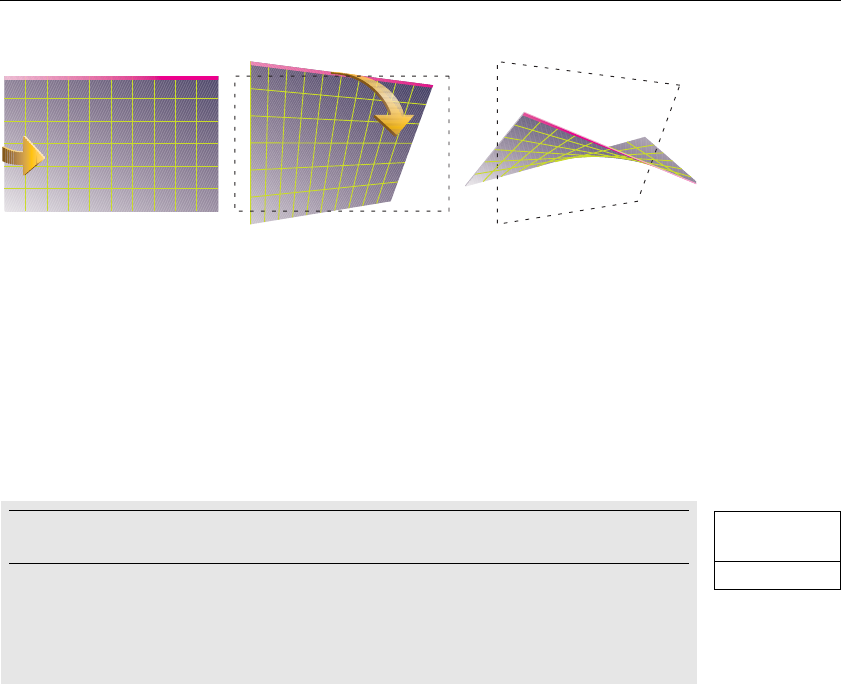
Describing Points, Lines, and Polygons 45
Rectangles
Since rectangles are so common in graphics applications, OpenGL provides
a filled-rectangle drawing primitive, glRect*(). You can draw a rectangle as
a polygon, as described in “OpenGL Geometric Drawing Primitives” on
page 47, but your particular implementation of OpenGL might have
optimized glRect*() for rectangles.
Note that although the rectangle begins with a particular orientation in
three-dimensional space (in the xy-plane and parallel to the axes), you can
change this by applying rotations or other transformations. (See Chapter 3
for information about how to do this.)
Curves and Curved Surfaces
Any smoothly curved line or surface can be approximated—to any arbitrary
degree of accuracy—by short line segments or small polygonal regions.
Thus, subdividing curved lines and surfaces sufficiently and then approxi-
mating them with straight line segments or flat polygons makes them
appear curved (see Figure 2-5). If you’re skeptical that this really works,
imagine subdividing until each line segment or polygon is so tiny that
it’s smaller than a pixel on the screen.
void glRect{sifd}(TYPE x1,TYPE y1,TYPE x2,TYPE y2);
void glRect{sifd}v(const TYPE *v1, const TYPE *v2);
Draws the rectangle defined by the corner points (x1, y1) and (x2, y2). The
rectangle lies in the plane z = 0 and has sides parallel to the x- and y-axes.
If the vector form of the function is used, the corners are given by two
pointers to arrays, each of which contains an (x, y) pair.
Figure 2-4 Nonplanar Polygon Transformed to Nonsimple Polygon
Compatibility
Extension
glRect
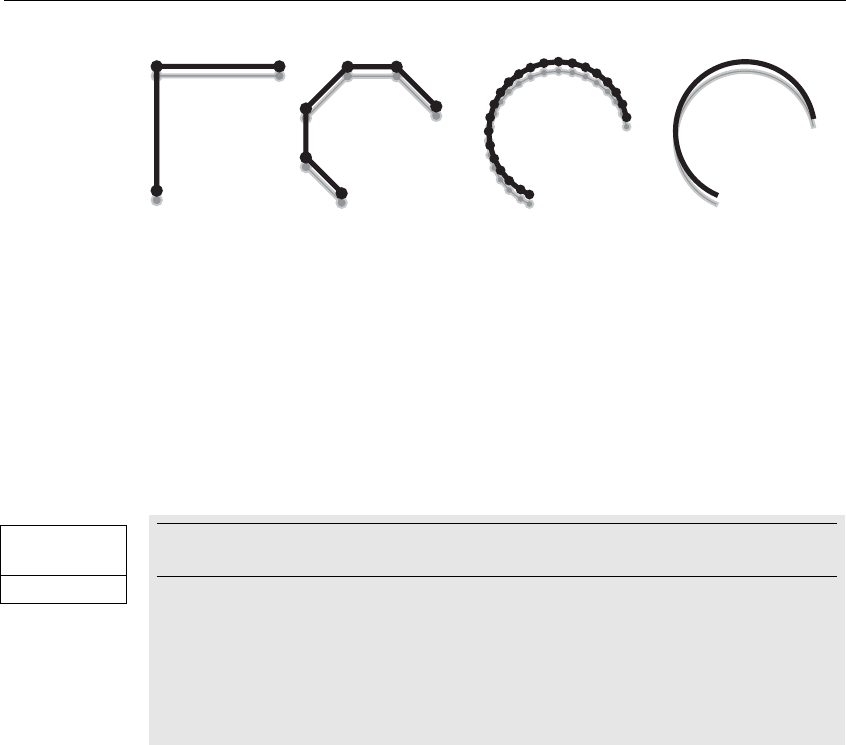
46 Chapter 2: State Management and Drawing Geometric Objects
Even though curves aren’t geometric primitives, OpenGL provides some
direct support for subdividing and drawing them. (See Chapter 12 for
information about how to draw curves and curved surfaces.)
Specifying Vertices
With OpenGL, every geometric object is ultimately described as an ordered
set of vertices. You use the glVertex*() command to specify a vertex.
Example 2-2 provides some examples of using glVertex*().
Example 2-2 Legal Uses of glVertex*()
glVertex2s(2, 3);
glVertex3d(0.0, 0.0, 3.1415926535898);
glVertex4f(2.3, 1.0, -2.2, 2.0);
GLdouble dvect[3] = {5.0, 9.0, 1992.0};
glVertex3dv(dvect);
The first example represents a vertex with three-dimensional coordi-
nates (2, 3, 0). (Remember that if it isn’t specified, the z-coordinate is
understood to be 0.) The coordinates in the second example are (0.0, 0.0,
void glVertex[234]{sifd}(TYPE coords);
void glVertex[234]{sifd}v(const TYPE* coords);
Specifies a vertex for use in describing a geometric object. You can supply
up to four coordinates (x, y, z, w) for a particular vertex or as few as two
(x, y) by selecting the appropriate version of the command. If you use a
version that doesn’t explicitly specify z or w,z is understood to be 0, and
w is understood to be 1. Calls to glVertex*() are effective only between a
glBegin() and glEnd() pair.
Figure 2-5 Approximating Curves
Compatibility
Extension
glVertex
Describing Points, Lines, and Polygons 47
3.1415926535898) (double-precision floating-point numbers). The third
example represents the vertex with three-dimensional coordinates (1.15,
0.5, 1.1) as a homogenous coordinate. (Remember that the x-, y-, and
z-coordinates are eventually divided by the w-coordinate.) In the final
example, dvect is a pointer to an array of three double-precision floating-
point numbers.
On some machines, the vector form of glVertex*() is more efficient, since
only a single parameter needs to be passed to the graphics subsystem. Spe-
cial hardware might be able to send a whole series of coordinates in a single
batch. If your machine is like this, it’s to your advantage to arrange your
data so that the vertex coordinates are packed sequentially in memory. In
this case, there may be some gain in performance by using the vertex array
operations of OpenGL. (See “Vertex Arrays” on page 70.)
OpenGL Geometric Drawing Primitives
Now that you’ve seen how to specify vertices, you still need to know how
to tell OpenGL to create a set of points, a line, or a polygon from those ver-
tices. To do this, you bracket each set of vertices between a call to glBegin()
and a call to glEnd(). The argument passed to glBegin() determines what
sort of geometric primitive is constructed from the vertices. For instance,
Example 2-3 specifies the vertices for the polygon shown in Figure 2-6.
Example 2-3 Filled Polygon
glBegin(GL_POLYGON);
glVertex2f(0.0, 0.0);
glVertex2f(0.0, 3.0);
glVertex2f(4.0, 3.0);
glVertex2f(6.0, 1.5);
glVertex2f(4.0, 0.0);
glEnd();
GL_POLYGON GL_POINTS
Figure 2-6 Drawing a Polygon or a Set of Points
48 Chapter 2: State Management and Drawing Geometric Objects
If you had used GL_POINTS instead of GL_POLYGON, the primitive would
have been simply the five points shown in Figure 2-6. Table 2-2 in the fol-
lowing function summary for glBegin() lists the 10 possible arguments and
the corresponding types of primitives.
void glBegin(GLenum mode);
Marks the beginning of a vertex-data list that describes a geometric prim-
itive. The type of primitive is indicated by mode, which can be any of the
values shown in Table 2-2.
Value Meaning
GL_POINTS Individual points
GL_LINES Pairs of vertices interpreted as individual line segments
GL_LINE_STRIP Series of connected line segments
GL_LINE_LOOP Same as above, with a segment added between last and
first vertices
GL_TRIANGLES Triples of vertices interpreted as triangles
GL_TRIANGLE_STRIP Linked strip of triangles
GL_TRIANGLE_FAN Linked fan of triangles
GL_QUADS Quadruples of vertices interpreted as four-sided polygons
GL_QUAD_STRIP Linked strip of quadrilaterals
GL_POLYGON Boundary of a simple, convex polygon
Table 2-2 Geometric Primitive Names and Meanings
void glEnd(void);
Marks the end of a vertex-data list.
Compatibility
Extension
glBegin
GL_QUADS
GL_QUAD_STRIP
GL_POLYGON
Compatibility
Extension
glEnd
Describing Points, Lines, and Polygons 49
Figure 2-7 shows examples of all the geometric primitives listed in Table 2-2,
with descriptions of the pixels that are drawn for each of the objects. Note
that in addition to points, several types of lines and polygons are defined.
Obviously, you can find many ways to draw the same primitive. The
method you choose depends on your vertex data.
GL_POINTS
GL_LINES GL_LINE_STRIP
GL_TRIANGLES GL_TRIANGLE_STRIP GL_TRIANGLE_FAN
GL_QUADS GL_POLYGON
V0
V1
V2
V3
V4
V5
V0
V0
V1
V2
V2
V1
V3
V3
V4
V5
V5
V4
V0
V3V2
V1V4
V7
V6
V5
GL_QUAD_STRIP
V1
V0
V3
V2
V5
V4
V7
V6
V6
V7
V0
V1
V2
V3
V4
V0
V1
V2
V3
V4
V0
V4V3
V2
V1
V0V4
V3
V2
V1
V5
GL_LINE_LOOP
V0
V1V2
V3
V4
V5
F
igure 2-7 Geometric Primitive Types

50 Chapter 2: State Management and Drawing Geometric Objects
As you read the following descriptions, assume that n vertices (v0, v1, v2, ... ,
vn–1) are described between a glBegin() and glEnd() pair.
GL_POINTS Draws a point at each of the n vertices.
GL_LINES Draws a series of unconnected line segments.
Segments are drawn between v0 and v1,
between v2 and v3, and so on. If n is odd, the
last segment is drawn between vn–3 and vn–2,
and vn–1 is ignored.
GL_LINE_STRIP Draws a line segment from v0 to v1, then from
v1 to v2, and so on, finally drawing the segment
from vn–2 to vn–1. Thus, a total of n – 1 line
segments are drawn. Nothing is drawn unless n
is larger than 1. There are no restrictions on the
vertices describing a line strip (or a line loop);
the lines can intersect arbitrarily.
GL_LINE_LOOP Same as GL_LINE_STRIP, except that a final line
segment is drawn from vn–1 to v0, completing
a loop.
GL_TRIANGLES Draws a series of triangles (three-sided polygons)
using vertices v0, v1, v2, then v3, v4, v5, and so
on. If n isn’t a multiple of 3, the final one or two
vertices are ignored.
GL_TRIANGLE_STRIP Draws a series of triangles (three-sided
polygons) using vertices v0, v1, v2, then v2, v1,
v3 (note the order), then v2, v3, v4, and so on.
The ordering is to ensure that the triangles are
all drawn with the same orientation so that
the strip can correctly form part of a surface.
Preserving the orientation is important for some
operations, such as culling (see “Reversing and
Culling Polygon Faces” on page 61). n must be
at least 3 for anything to be drawn.
GL_TRIANGLE_FAN Same as GL_TRIANGLE_STRIP, except that the
vertices are v0, v1, v2, then v0, v2, v3, then v0,
v3, v4, and so on (see Figure 2-7).

Describing Points, Lines, and Polygons 51
Restrictions on Using glBegin() and glEnd()
The most important information about vertices is their coordinates, which
are specified by the glVertex*() command. You can also supply additional
vertex-specific data for each vertex—a color, a normal vector, texture coor-
dinates, or any combination of these—using special commands. In addi-
tion, a few other commands are valid between a glBegin() and glEnd() pair.
Table 2-3 contains a complete list of such valid commands.
GL_QUADS Draws a series of quadrilaterals (four-sided
polygons) using vertices v0, v1, v2, v3, then v4,
v5, v6, v7, and so on. If n isn’t a multiple of 4,
the final one, two, or three vertices are ignored.
GL_QUAD_STRIP Draws a series of quadrilaterals (four-sided
polygons) beginning with v0, v1, v3, v2, then
v2, v3, v5, v4, then v4, v5, v7, v6, and so on (see
Figure 2-7). n must be at least 4 before anything
is drawn. If n is odd, the final vertex is ignored.
GL_POLYGON Draws a polygon using the points v0, ... , vn–1 as
vertices. n must be at least 3, or nothing is
drawn. In addition, the polygon specified must
not intersect itself and must be convex. If the
vertices don’t satisfy these conditions, the
results are unpredictable.
Command Purpose of Command Reference
glVertex*() set vertex coordinates Chapter 2
glColor*() set RGBA color Chapter 4
glIndex*() set color index Chapter 4
glSecondaryColor*() set secondary color for post-
texturing application
Chapter 9
glNormal*() set normal vector coordinates Chapter 2
glMaterial*() set material properties Chapter 5
glFogCoord*() set fog coordinates Chapter 6
Table 2-3 Valid Commands between glBegin() and glEnd()

52 Chapter 2: State Management and Drawing Geometric Objects
No other OpenGL commands are valid between a glBegin() and glEnd()
pair, and making most other OpenGL calls generates an error. Some vertex
array commands, such as glEnableClientState() and glVertexPointer(),
when called between glBegin() and glEnd(), have undefined behavior but
do not necessarily generate an error. (Also, routines related to OpenGL, such
as glX*() routines, have undefined behavior between glBegin() and glEnd().)
These cases should be avoided, and debugging them may be more difficult.
Note, however, that only OpenGL commands are restricted; you can
certainly include other programming-language constructs (except for calls,
such as the aforementioned glX*() routines). For instance, Example 2-4
draws an outlined circle.
Example 2-4 Other Constructs between glBegin() and glEnd()
#define PI 3.1415926535898
GLint circle_points = 100;
glBegin(GL_LINE_LOOP);
for (i = 0; i < circle_points; i++) {
angle = 2*PI*i/circle_points;
glVertex2f(cos(angle), sin(angle));
}
glEnd();
Note: This example isn’t the most efficient way to draw a circle, especially
if you intend to do it repeatedly. The graphics commands used are
typically very fast, but this code calculates an angle and calls the
sin() and cos() routines for each vertex; in addition, there’s the loop
glTexCoord*() set texture coordinates Chapter 9
glMultiTexCoord*() set texture coordinates for
multitexturing
Chapter 9
glVertexAttrib*() set generic vertex attribute Chapter 15
glEdgeFlag*() control drawing of edges Chapter 2
glArrayElement() extract vertex array data Chapter 2
glEvalCoord*(), glEvalPoint*() generate coordinates Chapter 12
glCallList(), glCallLists() execute display list(s) Chapter 7
Command Purpose of Command Reference
Table 2-3 (continued) Valid Commands between glBegin() and glEnd()

Basic State Management 53
overhead. (Another way to calculate the vertices of a circle is to use
a GLU routine; see “Quadrics: Rendering Spheres, Cylinders, and
Disks” in Chapter 11.) If you need to draw numerous circles, calculate
the coordinates of the vertices once and save them in an array and
create a display list (see Chapter 7), or use vertex arrays to render them.
Unless they are being compiled into a display list, all glVertex*() commands
should appear between a glBegin() and glEnd() combination. (If they
appear elsewhere, they don’t accomplish anything.) If they appear in a
display list, they are executed only if they appear between a glBegin() and
aglEnd(). (See Chapter 7 for more information about display lists.)
Although many commands are allowed between glBegin() and glEnd(),
vertices are generated only when a glVertex*() command is issued. At the
moment glVertex*() is called, OpenGL assigns the resulting vertex the
current color, texture coordinates, normal vector information, and so on. To
see this, look at the following code sequence. The first point is drawn in red,
and the second and third ones in blue, despite the extra color commands:
glBegin(GL_POINTS);
glColor3f(0.0, 1.0, 0.0); /* green */
glColor3f(1.0, 0.0, 0.0); /* red */
glVertex(...);
glColor3f(1.0, 1.0, 0.0); /* yellow */
glColor3f(0.0, 0.0, 1.0); /* blue */
glVertex(...);
glVertex(...);
glEnd();
You can use any combination of the 24 versions of the glVertex*()
command between glBegin() and glEnd(), although in real applications all
the calls in any particular instance tend to be of the same form. If your
vertex-data specification is consistent and repetitive (for example, glColor*,
glVertex*,glColor*,glVertex*,...), you may enhance your program’s
performance by using vertex arrays. (See “Vertex Arrays” on page 70.)
Basic State Management
In the preceding section, you saw an example of a state variable, the current
RGBA color, and how it can be associated with a primitive. OpenGL
maintains many states and state variables. An object may be rendered with
lighting, texturing, hidden surface removal, fog, and other states affecting
its appearance.

54 Chapter 2: State Management and Drawing Geometric Objects
By default, most of these states are initially inactive. These states may be
costly to activate; for example, turning on texture mapping will almost
certainly slow down the process of rendering a primitive. However, the
image will improve in quality and will look more realistic, owing to the
enhanced graphics capabilities.
To turn many of these states on and off, use these two simple commands:
You can also check whether a state is currently enabled or disabled.
The states you have just seen have two settings: on and off. However, most
OpenGL routines set values for more complicated state variables. For
example, the routine glColor3f() sets three values, which are part of the
GL_CURRENT_COLOR state. There are five querying routines used to find
out what values are set for many states:
void glEnable(GLenum capability);
void glDisable(GLenum capability);
glEnable() turns on a capability, and glDisable() turns it off. More than 60
enumerated values can be passed as parameters to glEnable() or glDisable().
Some examples are GL_BLEND (which controls blending of RGBA values),
GL_DEPTH_TEST (which controls depth comparisons and updates to the
depth buffer), GL_FOG (which controls fog), GL_LINE_STIPPLE (patterned
lines), and GL_LIGHTING (you get the idea).
GLboolean glIsEnabled(GLenum capability)
Returns GL_TRUE or GL_FALSE, depending on whether or not the queried
capability is currently activated.
void glGetBooleanv(GLenum pname, GLboolean *params);
void glGetIntegerv(GLenum pname, GLint *params);
void glGetFloatv(GLenum pname, GLfloat *params);
void glGetDoublev(GLenum pname, GLdouble *params);
void glGetPointerv(GLenum pname, GLvoid **params);

Displaying Points, Lines, and Polygons 55
These querying routines handle most, but not all, requests for obtaining
state information. (See “The Query Commands” in Appendix B for a list of
all of the available OpenGL state querying routines.)
Displaying Points, Lines, and Polygons
By default, a point is drawn as a single pixel on the screen, a line is drawn
solid and 1 pixel wide, and polygons are drawn solidly filled in. The following
paragraphs discuss the details of how to change these default display modes.
Point Details
To control the size of a rendered point, use glPointSize() and supply the
desired size in pixels as the argument.
The actual collection of pixels on the screen that are drawn for various point
widths depends on whether antialiasing is enabled. (Antialiasing is a tech-
nique for smoothing points and lines as they’re rendered; see “Antialiasing”
and “Point Parameters” in Chapter 6 for more detail.) If antialiasing is dis-
abled (the default), fractional widths are rounded to integer widths, and a
screen-aligned square region of pixels is drawn. Thus, if the width is 1.0, the
square is 1 pixel by 1 pixel; if the width is 2.0, the square is 2 pixels by 2
pixels; and so on.
Obtains Boolean, integer, floating-point, double-precision, or pointer
state variables. The pname argument is a symbolic constant indicating the
state variable to return, and params is a pointer to an array of the indicated
type in which to place the returned data. See the tables in Appendix B for
the possible values for pname. For example, to get the current RGBA color,
a table in Appendix B suggests you use glGetIntegerv(GL_CURRENT_
COLOR, params) or glGetFloatv(GL_CURRENT_COLOR, params). A type
conversion is performed, if necessary, to return the desired variable as the
requested data type.
void glPointSize(GLfloat size);
Sets the width in pixels for rendered points; size must be greater than 0.0
and by default is 1.0.
56 Chapter 2: State Management and Drawing Geometric Objects
With antialiasing or multisampling enabled, a circular group of pixels is
drawn, and the pixels on the boundaries are typically drawn at less than full
intensity to give the edge a smoother appearance. In this mode, noninteger
widths aren’t rounded.
Most OpenGL implementations support very large point sizes. You can
query the minimum and maximum sized for aliased points by using
GL_ALIASED_POINT_SIZE_RANGE with glGetFloatv(). Likewise, you
can obtain the range of supported sizes for antialiased points by passing
GL_SMOOTH_POINT_SIZE_RANGE to glGetFloatv(). The sizes of sup-
ported antialiased points are evenly spaced between the minimum and
maximum sizes for the range. Calling glGetFloatv() with the parameter
GL_SMOOTH_POINT_SIZE_GRANULARITY will return how accurately
a given antialiased point size is supported. For example, if you request
glPointSize(2.37) and the granularity returned is 0.1, then the point size
is rounded to 2.4.
Line Details
With OpenGL, you can specify lines with different widths and lines that are
stippled in various ways—dotted, dashed, drawn with alternating dots and
dashes, and so on.
Wide Lines
The actual rendering of lines is affected if either antialiasing or multisam-
pling is enabled. (See “Antialiasing Points or Lines” on page 269 and “Anti-
aliasing Geometric Primitives with Multisampling” on page 275.) Without
antialiasing, widths of 1, 2, and 3 draw lines 1, 2, and 3 pixels wide. With
antialiasing enabled, noninteger line widths are possible, and pixels on the
boundaries are typically drawn at less than full intensity. As with point
sizes, a particular OpenGL implementation might limit the width of non-
antialiased lines to its maximum antialiased line width, rounded to the
nearest integer value. You can obtain the range of supported aliased line
void glLineWidth(GLfloat width);
Sets the width, in pixels, for rendered lines; width must be greater than 0.0
and by default is 1.0.
Version 3.1 does not support values greater than 1.0, and will generate a
GL_INVALID_VALUE error if a value greater than 1.0 is specified.

Displaying Points, Lines, and Polygons 57
widths by using GL_ALIASED_LINE_WIDTH_RANGE with glGetFloatv().
To determine the supported minimum and maximum sizes of antialiased
line widths, and what granularity your implementation supports, call
glGetFloatv(), with GL_SMOOTH_LINE_WIDTH_RANGE and GL_
SMOOTH_LINE_WIDTH_GRANULARITY.
Note: Keep in mind that, by default, lines are 1 pixel wide, so they appear
wider on lower-resolution screens. For computer displays, this isn’t
typically an issue, but if you’re using OpenGL to render to a high-
resolution plotter, 1-pixel lines might be nearly invisible. To obtain
resolution-independent line widths, you need to take into account
the physical dimensions of pixels.
Advanced
With non-antialiased wide lines, the line width isn’t measured perpendicu-
lar to the line. Instead, it’s measured in the y-direction if the absolute value
of the slope is less than 1.0; otherwise, it’s measured in the x-direction. The
rendering of an antialiased line is exactly equivalent to the rendering of a
filled rectangle of the given width, centered on the exact line.
Stippled Lines
To make stippled (dotted or dashed) lines, you use the command
glLineStipple() to define the stipple pattern, and then you enable line
stippling with glEnable().
glLineStipple(1, 0x3F07);
glEnable(GL_LINE_STIPPLE);
With the preceding example and the pattern 0x3F07 (which translates
to 0011111100000111 in binary), a line would be drawn with 3 pixels on,
then 5 off, 6 on, and 2 off. (If this seems backward, remember that the
void glLineStipple(GLint factor, GLushort pattern);
Sets the current stippling pattern for lines. The pattern argument is a 16-bit
series of 0s and 1s, and it’s repeated as necessary to stipple a given line. A
1 indicates that drawing occurs, and a 0 that it does not, on a pixel-by-
pixel basis, beginning with the low-order bit of the pattern. The pattern
can be stretched out by using factor, which multiplies each subseries of
consecutive 1s and 0s. Thus, if three consecutive 1s appear in the pattern,
they’re stretched to six if factor is 2. factor is clamped to lie between 1 and
256. Line stippling must be enabled by passing GL_LINE_STIPPLE to
glEnable(); it’s disabled by passing the same argument to glDisable().
Advanced
Compatibility
Extension
glLineStipple
GL_LINE_
STIPPLE

58 Chapter 2: State Management and Drawing Geometric Objects
low-order bit is used first.) If factor had been 2, the pattern would have been
elongated: 6 pixels on, 10 off, 12 on, and 4 off. Figure 2-8 shows lines drawn
with different patterns and repeat factors. If you don’t enable line stippling,
drawing proceeds as if pattern were 0xFFFF and factor were 1. (Use
glDisable() with GL_LINE_STIPPLE to disable stippling.) Note that stippling
can be used in combination with wide lines to produce wide stippled lines.
One way to think of the stippling is that as the line is being drawn, the
pattern is shifted by 1 bit each time a pixel is drawn (or factor pixels are
drawn, if factor isn’t 1). When a series of connected line segments is drawn
between a single glBegin() and glEnd(), the pattern continues to shift as
one segment turns into the next. This way, a stippling pattern continues
across a series of connected line segments. When glEnd() is executed, the
pattern is reset, and if more lines are drawn before stippling is disabled the
stippling restarts at the beginning of the pattern. If you’re drawing lines
with GL_LINES, the pattern resets for each independent line.
Example 2-5 illustrates the results of drawing with a couple of different
stipple patterns and line widths. It also illustrates what happens if the lines
are drawn as a series of individual segments instead of a single connected
line strip. The results of running the program appear in Figure 2-9.
PATTERN
0x00FF
0x00FF
0x0C0F
0x0C0F
0xAAAA
0xAAAA
0xAAAA
0xAAAA
FACTOR
1
2
1
3
1
2
3
4
Figure 2-8 Stippled Lines
Figure 2-9 Wide Stippled Lines

Displaying Points, Lines, and Polygons 59
Example 2-5 Line Stipple Patterns: lines.c
#define drawOneLine(x1,y1,x2,y2) glBegin(GL_LINES); \
glVertex2f((x1),(y1)); glVertex2f((x2),(y2)); glEnd();
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}
void display(void)
{
int i;
glClear(GL_COLOR_BUFFER_BIT);
/* select white for all lines */
glColor3f(1.0, 1.0, 1.0);
/* in 1st row, 3 lines, each with a different stipple */
glEnable(GL_LINE_STIPPLE);
glLineStipple(1, 0x0101); /* dotted */
drawOneLine(50.0, 125.0, 150.0, 125.0);
glLineStipple(1, 0x00FF); /* dashed */
drawOneLine(150.0, 125.0, 250.0, 125.0);
glLineStipple(1, 0x1C47); /* dash/dot/dash */
drawOneLine(250.0, 125.0, 350.0, 125.0);
/* in 2nd row, 3 wide lines, each with different stipple */
glLineWidth(5.0);
glLineStipple(1, 0x0101); /* dotted */
drawOneLine(50.0, 100.0, 150.0, 100.0);
glLineStipple(1, 0x00FF); /* dashed */
drawOneLine(150.0, 100.0, 250.0, 100.0);
glLineStipple(1, 0x1C47); /* dash/dot/dash */
drawOneLine(250.0, 100.0, 350.0, 100.0);
glLineWidth(1.0);
/* in 3rd row, 6 lines, with dash/dot/dash stipple */
/* as part of a single connected line strip */
glLineStipple(1, 0x1C47); /* dash/dot/dash */
glBegin(GL_LINE_STRIP);
for (i = 0; i < 7; i++)
glVertex2f(50.0 + ((GLfloat) i * 50.0), 75.0);
glEnd();

60 Chapter 2: State Management and Drawing Geometric Objects
/* in 4th row, 6 independent lines with same stipple */
for (i = 0; i < 6; i++) {
drawOneLine(50.0 + ((GLfloat) i * 50.0), 50.0,
50.0 + ((GLfloat)(i+1) * 50.0), 50.0);
}
/* in 5th row, 1 line, with dash/dot/dash stipple */
/* and a stipple repeat factor of 5 */
glLineStipple(5, 0x1C47); /* dash/dot/dash */
drawOneLine(50.0, 25.0, 350.0, 25.0);
glDisable(GL_LINE_STIPPLE);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(400, 150);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}
Polygon Details
Polygons are typically drawn by filling in all the pixels enclosed within the
boundary, but you can also draw them as outlined polygons or simply as
points at the vertices. A filled polygon might be solidly filled or stippled with
a certain pattern. Although the exact details are omitted here, filled polygons
are drawn in such a way that if adjacent polygons share an edge or vertex,
the pixels making up the edge or vertex are drawn exactly once—they’re
Displaying Points, Lines, and Polygons 61
included in only one of the polygons. This is done so that partially
transparent polygons don’t have their edges drawn twice, which would
make those edges appear darker (or brighter, depending on what color
you’re drawing with). Note that it might result in narrow polygons having
no filled pixels in one or more rows or columns of pixels.
To antialias filled polygons, multisampling is highly recommended. For details,
see “Antialiasing Geometric Primitives with Multisampling” in Chapter 6.
Polygons as Points, Outlines, or Solids
A polygon has two sides—front and back—and might be rendered differ-
ently depending on which side is facing the viewer. This allows you to have
cutaway views of solid objects in which there is an obvious distinction
between the parts that are inside and those that are outside. By default, both
front and back faces are drawn in the same way. To change this, or to draw
only outlines or vertices, use glPolygonMode().
For example, you can have the front faces filled and the back faces outlined
with two calls to this routine:
glPolygonMode(GL_FRONT, GL_FILL);
glPolygonMode(GL_BACK, GL_LINE);
Reversing and Culling Polygon Faces
By convention, polygons whose vertices appear in counterclockwise order
on the screen are called front-facing. You can construct the surface of any
“reasonable” solid—a mathematician would call such a surface an orient-
able manifold (spheres, donuts, and teapots are orientable; Klein bottles and
Möbius strips aren’t)—from polygons of consistent orientation. In other
words, you can use all clockwise polygons or all counterclockwise polygons.
(This is essentially the mathematical definition of orientable.)
void glPolygonMode(GLenum face, GLenum mode);
Controls the drawing mode for a polygon’s front and back faces. The
parameter face can be GL_FRONT_AND_BACK, GL_FRONT, or GL_BACK;
mode can be GL_POINT, GL_LINE, or GL_FILL to indicate whether the
polygon should be drawn as points, outlined, or filled. By default, both
the front and back faces are drawn filled.
Version 3.1 only accepts GL_FRONT_AND_BACK as a value for face, and
renders polygons the same way regardless of whether they’re front- or
back-facing.
Compatibility
Extension
GL_FRONT
GL_BACK

62 Chapter 2: State Management and Drawing Geometric Objects
Suppose you’ve consistently described a model of an orientable surface but
happen to have the clockwise orientation on the outside. You can swap
what OpenGL considers the back face by using the function glFrontFace(),
supplying the desired orientation for front-facing polygons.
Note: The orientation (clockwise or counterclockwise) of the vertices is also
known as its winding.
In a completely enclosed surface constructed from opaque polygons with
a consistent orientation, none of the back-facing polygons are ever visible—
they’re always obscured by the front-facing polygons. If you are outside
this surface, you might enable culling to discard polygons that OpenGL deter-
mines are back-facing. Similarly, if you are inside the object, only back-
facing polygons are visible. To instruct OpenGL to discard front- or
back-facing polygons, use the command glCullFace() and enable culling
with glEnable().
Advanced
In more technical terms, deciding whether a face of a polygon is front-
or back-facing depends on the sign of the polygon’s area computed in
window coordinates. One way to compute this area is
void glFrontFace(GLenum mode);
Controls how front-facing polygons are determined. By default, mode is
GL_CCW, which corresponds to a counterclockwise orientation of the
ordered vertices of a projected polygon in window coordinates. If mode is
GL_CW, faces with a clockwise orientation are considered front-facing.
void glCullFace(GLenum mode);
Indicates which polygons should be discarded (culled) before they’re
converted to screen coordinates. The mode is either GL_FRONT,
GL_BACK, or GL_FRONT_AND_BACK to indicate front-facing, back-
facing, or all polygons. To take effect, culling must be enabled using
glEnable() with GL_CULL_FACE; it can be disabled with glDisable() and
the same argument.
Advanced

Displaying Points, Lines, and Polygons 63
where xiand yi are the x and y window coordinates of the ith vertex of the
n-vertex polygon and
Assuming that GL_CCW has been specified, if a> 0, the polygon corre-
sponding to that vertex is considered to be front-facing; otherwise, it’s back-
facing. If GL_CW is specified and if a< 0, then the corresponding polygon
is front-facing; otherwise, it’s back-facing.
Try This
Modify Example 2-5 by adding some filled polygons. Experiment with differ-
ent colors. Try different polygon modes. Also, enable culling to see its effect.
Stippling Polygons
By default, filled polygons are drawn with a solid pattern. They can also be
filled with a 32-bit by 32-bit window-aligned stipple pattern, which you
specify with glPolygonStipple().
In addition to defining the current polygon stippling pattern, you must
enable stippling:
glEnable(GL_POLYGON_STIPPLE);
Use glDisable() with the same argument to disable polygon stippling.
Figure 2-11 shows the results of polygons drawn unstippled and then with
two different stippling patterns. The program is shown in Example 2-6. The
reversal of white to black (from Figure 2-10 to Figure 2-11) occurs because
the program draws in white over a black background, using the pattern in
Figure 2-10 as a stencil.
void glPolygonStipple(const GLubyte *mask);
Defines the current stipple pattern for filled polygons. The argument mask
is a pointer to a 32 u
32 bitmap that’s interpreted as a mask of 0s and 1s.
Where a 1 appears, the corresponding pixel in the polygon is drawn, and
where a 0 appears, nothing is drawn. Figure 2-10 shows how a stipple
pattern is constructed from the characters in mask. Polygon stippling
is enabled and disabled by using glEnable() and glDisable() with GL_
POLYGON_STIPPLE as the argument. The interpretation of the mask data
is affected by the glPixelStore*() GL_UNPACK* modes. (See “Controlling
Pixel-Storage Modes” in Chapter 8.)
i+1 is (i+1) mod n.
Try This
Compatibility
Extension
glPolygonStipple
GL_POLYGON_
STIPPLE
64 Chapter 2: State Management and Drawing Geometric Objects
128 64 32 16 8 4 2 1
By default, for each byte the most significant bit is first.
Bit ordering can be changed by calling glPixelStore*().
128 64 32 16 8 4 2 1 128 64 32 16 8 4 2 1 128 64 32 16 8 4 2 1
128 64 32 16 8 4 2 1
Figure 2-10 Constructing a Polygon Stipple Pattern

Displaying Points, Lines, and Polygons 65
Example 2-6 Polygon Stipple Patterns: polys.c
void display(void)
{
GLubyte fly[] = {
0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00,
0x03, 0x80, 0x01, 0xC0, 0x06, 0xC0, 0x03, 0x60,
0x04, 0x60, 0x06, 0x20, 0x04, 0x30, 0x0C, 0x20,
0x04, 0x18, 0x18, 0x20, 0x04, 0x0C, 0x30, 0x20,
0x04, 0x06, 0x60, 0x20, 0x44, 0x03, 0xC0, 0x22,
0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22,
0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22,
0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22,
0x66, 0x01, 0x80, 0x66, 0x33, 0x01, 0x80, 0xCC,
0x19, 0x81, 0x81, 0x98, 0x0C, 0xC1, 0x83, 0x30,
0x07, 0xe1, 0x87, 0xe0, 0x03, 0x3f, 0xfc, 0xc0,
0x03, 0x31, 0x8c, 0xc0, 0x03, 0x33, 0xcc, 0xc0,
0x06, 0x64, 0x26, 0x60, 0x0c, 0xcc, 0x33, 0x30,
0x18, 0xcc, 0x33, 0x18, 0x10, 0xc4, 0x23, 0x08,
0x10, 0x63, 0xC6, 0x08, 0x10, 0x30, 0x0c, 0x08,
0x10, 0x18, 0x18, 0x08, 0x10, 0x00, 0x00, 0x08};
GLubyte halftone[] = {
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
Figure 2-11 Stippled Polygons

66 Chapter 2: State Management and Drawing Geometric Objects
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55,
0xAA, 0xAA, 0xAA, 0xAA, 0x55, 0x55, 0x55, 0x55};
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
/* draw one solid, unstippled rectangle, */
/* then two stippled rectangles */
glRectf(25.0, 25.0, 125.0, 125.0);
glEnable(GL_POLYGON_STIPPLE);
glPolygonStipple(fly);
glRectf(125.0, 25.0, 225.0, 125.0);
glPolygonStipple(halftone);
glRectf(225.0, 25.0, 325.0, 125.0);
glDisable(GL_POLYGON_STIPPLE);
glFlush();
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(350, 150);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);

Displaying Points, Lines, and Polygons 67
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}
You might want to use display lists to store polygon stipple patterns to
maximize efficiency. (See “Display List Design Philosophy” in Chapter 7.)
Marking Polygon Boundary Edges
Advanced
OpenGL can render only convex polygons, but many nonconvex poly-
gons arise in practice. To draw these nonconvex polygons, you typically
subdivide them into convex polygons—usually triangles, as shown in
Figure 2-12—and then draw the triangles. Unfortunately, if you decompose
a general polygon into triangles and draw the triangles, you can’t really use
glPolygonMode() to draw the polygon’s outline, as you get all the triangle
outlines inside it. To solve this problem, you can tell OpenGL whether a par-
ticular vertex precedes a boundary edge; OpenGL keeps track of this infor-
mation by passing along with each vertex a bit indicating whether that
vertex is followed by a boundary edge. Then, when a polygon is drawn in
GL_LINE mode, the nonboundary edges aren’t drawn. In Figure 2-12, the
dashed lines represent added edges.
By default, all vertices are marked as preceding a boundary edge, but
you can manually control the setting of the edge flag with the command
glEdgeFlag*(). This command is used between glBegin() and glEnd() pairs,
and it affects all the vertices specified after it until the next glEdgeFlag() call
is made. It applies only to vertices specified for polygons, triangles, and
quads, not to those specified for strips of triangles or quads.
Advanced
Figure 2-12 Subdividing a Nonconvex Polygon

68 Chapter 2: State Management and Drawing Geometric Objects
For instance, Example 2-7 draws the outline shown in Figure 2-13.
Example 2-7 Marking Polygon Boundary Edges
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
glBegin(GL_POLYGON);
glEdgeFlag(GL_TRUE);
glVertex3fv(V0);
glEdgeFlag(GL_FALSE);
glVertex3fv(V1);
glEdgeFlag(GL_TRUE);
glVertex3fv(V2);
glEnd();
Normal Vectors
Anormal vector (or normal, for short) is a vector that points in a direction
that’s perpendicular to a surface. For a flat surface, one perpendicular direc-
tion is the same for every point on the surface, but for a general curved sur-
face, the normal direction might be different at each point on the surface.
With OpenGL, you can specify a normal for each polygon or for each ver-
tex. Vertices of the same polygon might share the same normal (for a flat
surface) or have different normals (for a curved surface). You can’t assign
normals anywhere other than at the vertices.
void glEdgeFlag(GLboolean flag);
void glEdgeFlagv(const GLboolean *flag);
Indicates whether a vertex should be considered as initializing a boundary
edge of a polygon. If flag is GL_TRUE, the edge flag is set to TRUE (the
default), and any vertices created are considered to precede boundary
edges until this function is called again with flag being GL_FALSE.
Compatibility
Extension
glEdgeFlag
V0
V2
V1
Figure 2-13 Outlined Polygon Drawn Using Edge Flags

Normal Vectors 69
An object’s normal vectors define the orientation of its surface in space—in
particular, its orientation relative to light sources. These vectors are used by
OpenGL to determine how much light the object receives at its vertices.
Lighting—a large topic by itself—is the subject of Chapter 5, and you might
want to review the following information after you’ve read that chapter.
Normal vectors are discussed briefly here because you define normal vectors
for an object at the same time you define the object’s geometry.
You use glNormal*() to set the current normal to the value of the argument
passed in. Subsequent calls to glVertex*() cause the specified vertices to be
assigned the current normal. Often, each vertex has a different normal,
which necessitates a series of alternating calls, as in Example 2-8.
Example 2-8 Surface Normals at Vertices
glBegin (GL_POLYGON);
glNormal3fv(n0);
glVertex3fv(v0);
glNormal3fv(n1);
glVertex3fv(v1);
glNormal3fv(n2);
glVertex3fv(v2);
glNormal3fv(n3);
glVertex3fv(v3);
glEnd();
There’s no magic to finding the normals for an object—most likely, you
have to perform some calculations that might include taking derivatives—
but there are several techniques and tricks you can use to achieve certain
effects. Appendix H, “Calculating Normal Vectors,”1 explains how to find
normal vectors for surfaces. If you already know how to do this, if you can
count on always being supplied with normal vectors, or if you don’t want
to use the OpenGL lighting facilities, you don’t need to read this appendix.
void glNormal3{bsidf}(TYPE nx,TYPE ny,TYPE nz);
void glNormal3{bsidf}v(const TYPE *v);
Sets the current normal vector as specified by the arguments. The
nonvector version (without the v) takes three arguments, which specify
an (nx, ny, nz) vector that’s taken to be the normal. Alternatively, you can
use the vector version of this function (with the v) and supply a single
array of three elements to specify the desired normal. The b,s, and i
versions scale their parameter values linearly to the range [
1.0, 1.0].
1This appendix is available online at http://www.opengl-redbook.com/appendices/.
Compatibility
Extension
glNormal

70 Chapter 2: State Management and Drawing Geometric Objects
Note that at a given point on a surface, two vectors are perpendicular to the
surface, and they point in opposite directions. By convention, the normal
is the one that points to the outside of the surface being modeled. (If you
get inside and outside reversed in your model, just change every normal
vector from (x, y, z) to (x, y, z)).
Also, keep in mind that since normal vectors indicate direction only, their
lengths are mostly irrelevant. You can specify normals of any length, but
eventually they have to be converted to a length of 1 before lighting calcu-
lations are performed. (A vector that has a length of 1 is said to be of unit
length, or normalized.) In general, you should supply normalized normal
vectors. To make a normal vector of unit length, divide each of its x-, y-,
z-components by the length of the normal:
Normal vectors remain normalized as long as your model transformations
include only rotations and translations. (See Chapter 3 for a discussion of
transformations.) If you perform irregular transformations (such as scaling
or multiplying by a shear matrix), or if you specify nonunit-length normals,
then you should have OpenGL automatically normalize your normal vec-
tors after the transformations. To do this, call glEnable(GL_NORMALIZE).
If you supply unit-length normals, and you perform only uniform scaling
(that is, the same scaling value for x,y, and z), you can use glEnable(GL_
RESCALE_NORMAL) to scale the normals by a constant factor, derived
from the modelview transformation matrix, to return them to unit length
after transformation.
Note that automatic normalization or rescaling typically requires additional
calculations that might reduce the performance of your application. Rescal-
ing normals uniformly with GL_RESCALE_NORMAL is usually less expen-
sive than performing full-fledged normalization with GL_NORMALIZE. By
default, both automatic normalizing and rescaling operations are disabled.
Vertex Arrays
You may have noticed that OpenGL requires many function calls to render
geometric primitives. Drawing a 20-sided polygon requires at least 22 func-
tion calls: one call to glBegin(), one call for each of the vertices, and a final
call to glEnd(). In the two previous code examples, additional information
(polygon boundary edge flags or surface normals) added function calls for
x2 + y2 + z2
Compatibility
Extension
GL_NORMALIZE
GL_RESCALE_
NORMAL

Vertex Arrays 71
each vertex. This can quickly double or triple the number of function calls
required for one geometric object. For some systems, function calls have a
great deal of overhead and can hinder performance.
An additional problem is the redundant processing of vertices that are
shared between adjacent polygons. For example, the cube in Figure 2-14 has
six faces and eight shared vertices. Unfortunately, if the standard method of
describing this object is used, each vertex has to be specified three times:
once for every face that uses it. Therefore, 24 vertices are processed, even
though eight would be enough.
OpenGL has vertex array routines that allow you to specify a lot of vertex-
related data with just a few arrays and to access that data with equally few
function calls. Using vertex array routines, all 20 vertices in a 20-sided
polygon can be put into one array and called with one function. If each
vertex also has a surface normal, all 20 surface normals can be put into
another array and also called with one function.
Arranging data in vertex arrays may increase the performance of your
application. Using vertex arrays reduces the number of function calls,
which improves performance. Also, using vertex arrays may allow reuse of
already processed shared vertices.
Note: Vertex arrays became standard in Version 1.1 of OpenGL. Version 1.4
added support for storing fog coordinates and secondary colors in
vertex arrays.
There are three steps to using vertex arrays to render geometry:
1. Activate (enable) the appropriate arrays, with each storing a different
type of data: vertex coordinates, surface normals, RGBA colors,
secondary colors, color indices, fog coordinates, texture coordinates,
polygon edge flags, or vertex attributes for use in a vertex shader.
Figure 2-14 Six Sides, Eight Shared Vertices
72 Chapter 2: State Management and Drawing Geometric Objects
2. Put data into the array or arrays. The arrays are accessed by the
addresses of (that is, pointers to) their memory locations. In the
client-server model, this data is stored in the client’s address space,
unless you choose to use buffer objects (see “Buffer Objects” on
page 91), for which the arrays are stored in server memory.
3. Draw geometry with the data. OpenGL obtains the data from all
activated arrays by dereferencing the pointers. In the client-server
model, the data is transferred to the server’s address space. There are
three ways to do this:
• Accessing individual array elements (randomly hopping around)
• Creating a list of individual array elements (methodically hopping
around)
• Processing sequential array elements
The dereferencing method you choose may depend on the type of
problem you encounter. Version 1.4 added support for multiple array
access from a single function call.
Interleaved vertex array data is another common method of organization.
Instead of several different arrays, each maintaining a different type of data
(color, surface normal, coordinate, and so on), you may have the different
types of data mixed into a single array. (See “Interleaved Arrays” on page 88.)
Step 1: Enabling Arrays
The first step is to call glEnableClientState() with an enumerated parame-
ter, which activates the chosen array. In theory, you may need to call this
up to eight times to activate the eight available arrays. In practice, you’ll
probably activate up to six arrays. For example, it is unlikely that you would
activate both GL_COLOR_ARRAY and GL_INDEX_ARRAY, as your program’s
display mode supports either RGBA mode or color-index mode, but proba-
bly not both simultaneously.
void glEnableClientState(GLenum array)
Specifies the array to enable. The symbolic constants GL_VERTEX_ARRAY,
GL_COLOR_ARRAY, GL_SECONDARY_COLOR_ARRAY,
GL_INDEX_ARRAY, GL_NORMAL_ARRAY,
GL_FOG_COORD_ARRAY, GL_TEXTURE_COORD_ARRAY, and
GL_EDGE_FLAG_ARRAY are acceptable parameters.
Compatibility
Extension
glEnableClientState

Vertex Arrays 73
Note: Version 3.1 supports only vertex array data stored in buffer objects
(see “Buffer Objects” on page 91 for details).
If you use lighting, you may want to define a surface normal for every
vertex. (See “Normal Vectors” on page 68.) To use vertex arrays for that case,
you activate both the surface normal and vertex coordinate arrays:
glEnableClientState(GL_NORMAL_ARRAY);
glEnableClientState(GL_VERTEX_ARRAY);
Suppose that you want to turn off lighting at some point and just draw
the geometry using a single color. You want to call glDisable() to turn off
lighting states (see Chapter 5). Now that lighting has been deactivated, you
also want to stop changing the values of the surface normal state, which is
wasted effort. To do this, you call
glDisableClientState(GL_NORMAL_ARRAY);
You might be asking yourself why the architects of OpenGL created these
new (and long) command names, like gl*ClientState(), for example.
Why can’t you just call glEnable() and glDisable()? One reason is that
glEnable() and glDisable() can be stored in a display list, but the specifica-
tion of vertex arrays cannot, because the data remains on the client’s side.
If multitexturing is enabled, enabling and disabling client arrays affects
only the active texturing unit. See “Multitexturing” on page 467 for more
details.
Step 2: Specifying Data for the Arrays
There is a straightforward way by which a single command specifies a single
array in the client space. There are eight different routines for specifying
arrays—one routine for each kind of array. There is also a command that can
specify several client-space arrays at once, all originating from a single
interleaved array.
void glDisableClientState(GLenum array);
Specifies the array to disable. It accepts the same symbolic constants as
glEnableClientState().
Compatibility
Extension
glDisableClientState
74 Chapter 2: State Management and Drawing Geometric Objects
To access the other seven arrays, there are seven similar routines:
Note: Additional vertex attributes, used by programmable shaders, can be
stored in vertex arrays. Because of their association with shaders,
they are discussed in Chapter 15, “The OpenGL Shading Language,”
on page 720. For Version 3.1, only generic vertex arrays are
supported for storing vertex data.
The main difference among the routines is whether size and type are unique
or must be specified. For example, a surface normal always has three com-
ponents, so it is redundant to specify its size. An edge flag is always a single
Boolean, so neither size nor type needs to be mentioned. Table 2-4 displays
legal values for size and data types.
For OpenGL implementations that support multitexturing, specifying a tex-
ture coordinate array with glTexCoordPointer() only affects the currently
active texture unit. See “Multitexturing” on page 467 for more information.
void glVertexPointer(GLint size, GLenum type, GLsizei stride,
const GLvoid *pointer);
Specifies where spatial coordinate data can be accessed. pointer is the memory
address of the first coordinate of the first vertex in the array. type specifies
the data type (GL_SHORT, GL_INT, GL_FLOAT, or GL_DOUBLE) of each
coordinate in the array. size is the number of coordinates per vertex, which
must be 2, 3, or 4. stride is the byte offset between consecutive vertices. If
stride is 0, the vertices are understood to be tightly packed in the array.
void glColorPointer(GLint size, GLenum type, GLsizei stride,
const GLvoid *pointer);
void glSecondaryColorPointer(GLint size, GLenum type, GLsizei stride,
const GLvoid *pointer);
void glIndexPointer(GLenum type, GLsizei stride, const GLvoid *pointer);
void glNormalPointer(GLenum type, GLsizei stride,
const GLvoid *pointer);
void glFogCoordPointer(GLenum type, GLsizei stride,
const GLvoid *pointer);
void glTexCoordPointer(GLint size, GLenum type, GLsizei stride,
const GLvoid *pointer);
void glEdgeFlagPointer(GLsizei stride, const GLvoid *pointer);
Compatibility
Extension
glVertexPointer
Compatibility
Extension
glColorPointer
glSecondaryColor
Pointer
glIndexPointer
glNormalPointer
glFogCoordPointer
glTexCoordPointer
glEdgeFlagPointer

Vertex Arrays 75
Example 2-9 uses vertex arrays for both RGBA colors and vertex coordinates.
RGB floating-point values and their corresponding (x,y) integer coordi-
nates are loaded into the GL_COLOR_ARRAY and GL_VERTEX_ARRAY.
Example 2-9 Enabling and Loading Vertex Arrays: varray.c
static GLint vertices[] = {25, 25,
100, 325,
175, 25,
175, 325,
250, 25,
325, 325};
static GLfloat colors[] = {1.0, 0.2, 0.2,
0.2, 0.2, 1.0,
0.8, 1.0, 0.2,
0.75, 0.75, 0.75,
0.35, 0.35, 0.35,
0.5, 0.5, 0.5};
Command Sizes Values for type Argument
glVertexPointer 2, 3, 4 GL_SHORT, GL_INT, GL_FLOAT,
GL_DOUBLE
glColorPointer 3, 4 GL_BYTE, GL_UNSIGNED_BYTE,
GL_SHORT, GL_UNSIGNED_SHORT,
GL_INT, GL_UNSIGNED_INT, GL_FLOAT,
GL_DOUBLE
glSecondaryColorPointer 3 GL_BYTE, GL_UNSIGNED_BYTE,
GL_SHORT, GL_UNSIGNED_SHORT,
GL_INT, GL_UNSIGNED_INT, GL_FLOAT,
GL_DOUBLE
glIndexPointer 1 GL_UNSIGNED_BYTE, GL_SHORT, GL_INT,
GL_FLOAT, GL_DOUBLE
glNormalPointer 3 GL_BYTE, GL_SHORT, GL_INT, GL_FLOAT,
GL_DOUBLE
glFogCoordPointer 1 GL_FLOAT, GL_DOUBLE
glTexCoordPointer 1, 2, 3, 4 GL_SHORT, GL_INT, GL_FLOAT, GL_DOUBLE
glEdgeFlagPointer 1 no type argument (type of data must be
GLboolean)
Table 2-4 Vertex Array Sizes (Values per Vertex) and Data Types

76 Chapter 2: State Management and Drawing Geometric Objects
glEnableClientState(GL_COLOR_ARRAY);
glEnableClientState(GL_VERTEX_ARRAY);
glColorPointer(3, GL_FLOAT, 0, colors);
glVertexPointer(2, GL_INT, 0, vertices);
Stride
The stride parameter for the gl*Pointer() routines tells OpenGL how to
access the data you provide in your pointer arrays. Its value should be the
number of bytes between the starts of two successive pointer elements, or
zero, which is a special case. For example, suppose you stored both your
vertex’s RGB and (x,y,z) coordinates in a single array, such as the following:
static GLfloat intertwined[] =
{1.0, 0.2, 1.0, 100.0, 100.0, 0.0,
1.0, 0.2, 0.2, 0.0, 200.0, 0.0,
1.0, 1.0, 0.2, 100.0, 300.0, 0.0,
0.2, 1.0, 0.2, 200.0, 300.0, 0.0,
0.2, 1.0, 1.0, 300.0, 200.0, 0.0,
0.2, 0.2, 1.0, 200.0, 100.0, 0.0};
To reference only the color values in the intertwined array, the following
call starts from the beginning of the array (which could also be passed as
&intertwined[0]) and jumps ahead 6 * sizeof(GLfloat) bytes, which is the size
of both the color and vertex coordinate values. This jump is enough to get
to the beginning of the data for the next vertex:
glColorPointer(3, GL_FLOAT, 6*sizeof(GLfloat), &intertwined[0]);
For the vertex coordinate pointer, you need to start from further in the
array, at the fourth element of intertwined (remember that C programmers
start counting at zero):
glVertexPointer(3, GL_FLOAT, 6*sizeof(GLfloat), &intertwined[3]);
If your data is stored similar to the intertwined array above, you may find the
approach described in “Interleaved Arrays” on page 88 more convenient for
storing your data.
With a stride of zero, each type of vertex array (RGB color, color index,
vertex coordinate, and so on) must be tightly packed. The data in the array
must be homogeneous; that is, the data must be all RGB color values, all
vertex coordinates, or all some other data similar in some fashion.

Vertex Arrays 77
Step 3: Dereferencing and Rendering
Until the contents of the vertex arrays are dereferenced, the arrays remain
on the client side, and their contents are easily changed. In Step 3, contents
of the arrays are obtained, sent to the server, and then sent down the
graphics processing pipeline for rendering.
You can obtain data from a single array element (indexed location), from an
ordered list of array elements (which may be limited to a subset of the entire
vertex array data), or from a sequence of array elements.
Dereferencing a Single Array Element
glArrayElement() is usually called between glBegin() and glEnd(). (If
called outside, glArrayElement() sets the current state for all enabled
arrays, except for vertex, which has no current state.) In Example 2-10, a
triangle is drawn using the third, fourth, and sixth vertices from enabled
vertex arrays. (Again, remember that C programmers begin counting array
locations with zero.)
Example 2-10 Using glArrayElement() to Define Colors and Vertices
glEnableClientState(GL_COLOR_ARRAY);
glEnableClientState(GL_VERTEX_ARRAY);
glColorPointer(3, GL_FLOAT, 0, colors);
glVertexPointer(2, GL_INT, 0, vertices);
glBegin(GL_TRIANGLES);
glArrayElement(2);
glArrayElement(3);
glArrayElement(5);
glEnd();
void glArrayElement(GLint ith)
Obtains the data of one (the ith) vertex for all currently enabled arrays.
For the vertex coordinate array, the corresponding command would be
glVertex[size][type]v(), where size is one of [2, 3, 4], and type is one of
[s,i,f,d] for GLshort, GLint, GLfloat, and GLdouble, respectively. Both size
and type were defined by glVertexPointer(). For other enabled arrays,
glArrayElement() calls glEdgeFlagv(),glTexCoord[size][type]v(),
glColor[size][type]v(),glSecondaryColor3[type]v(),glIndex[type]v(),
glNormal3[type]v(), and glFogCoord[type]v(). If the vertex coordinate
array is enabled, the glVertex*v() routine is executed last, after the
execution (if enabled) of up to seven corresponding array values.
Compatibility
Extension
glArrayElement

78 Chapter 2: State Management and Drawing Geometric Objects
When executed, the latter five lines of code have the same effect as
glBegin(GL_TRIANGLES);
glColor3fv(colors + (2 * 3));
glVertex2iv(vertices + (2 * 2));
glColor3fv(colors + (3 * 3));
glVertex2iv(vertices + (3 * 2));
glColor3fv(colors + (5 * 3));
glVertex2iv(vertices + (5 * 2));
glEnd();
Since glArrayElement() is only a single function call per vertex, it may
reduce the number of function calls, which increases overall performance.
Be warned that if the contents of the array are changed between glBegin()
and glEnd(), there is no guarantee that you will receive original data or
changed data for your requested element. To be safe, don’t change the
contents of any array element that might be accessed until the primitive
is completed.
Dereferencing a List of Array Elements
glArrayElement() is good for randomly “hopping around” your data
arrays. Similar routines, glDrawElements(),glMultiDrawElements(), and
glDrawRangeElements(), are good for hopping around your data arrays in
a more orderly manner.
The effect of glDrawElements() is almost the same as this command
sequence:
glBegin(mode);
for (i = 0; i < count; i++)
glArrayElement(indices[i]);
glEnd();
void glDrawElements(GLenum mode, GLsizei count, GLenum type,
const GLvoid *indices);
Defines a sequence of geometric primitives using count number of ele-
ments, whose indices are stored in the array indices.type must be one of
GL_UNSIGNED_BYTE, GL_UNSIGNED_SHORT, or GL_UNSIGNED_INT,
indicating the data type of the indices array. mode specifies what kind of
primitives are constructed and is one of the same values that is accepted
by glBegin(); for example, GL_POLYGON, GL_LINE_LOOP, GL_LINES,
GL_POINTS, and so on.

glDrawElements() additionally checks to make sure mode,count, and type
are valid. Also, unlike the preceding sequence, executing glDrawElements()
leaves several states indeterminate. After execution of glDrawElements(),
current RGB color, secondary color, color index, normal coordinates, fog
coordinates, texture coordinates, and edge flag are indeterminate if the
corresponding array has been enabled.
With glDrawElements(), the vertices for each face of the cube can be placed in
an array of indices. Example 2-11 shows two ways to use glDrawElements()
to render the cube. Figure 2-15 shows the numbering of the vertices used in
Example 2-11.
Vertex Arrays 79
Example 2-11 Using glDrawElements() to Dereference Several Array Elements
static GLubyte frontIndices[] = {4, 5, 6, 7};
static GLubyte rightIndices[] = {1, 2, 6, 5};
static GLubyte bottomIndices[] = {0, 1, 5, 4};
static GLubyte backIndices[] = {0, 3, 2, 1};
static GLubyte leftIndices[] = {0, 4, 7, 3};
static GLubyte topIndices[] = {2, 3, 7, 6};
glDrawElements(GL_QUADS, 4, GL_UNSIGNED_BYTE, frontIndices);
glDrawElements(GL_QUADS, 4, GL_UNSIGNED_BYTE, rightIndices);
glDrawElements(GL_QUADS, 4, GL_UNSIGNED_BYTE, bottomIndices);
glDrawElements(GL_QUADS, 4, GL_UNSIGNED_BYTE, backIndices);
glDrawElements(GL_QUADS, 4, GL_UNSIGNED_BYTE, leftIndices);
glDrawElements(GL_QUADS, 4, GL_UNSIGNED_BYTE, topIndices);
Note: It is an error to encapsulate glDrawElements() between a
glBegin()/glEnd() pair.
With several primitive types (such as GL_QUADS, GL_TRIANGLES, and GL_
LINES), you may be able to compact several lists of indices together into a
single array. Since the GL_QUADS primitive interprets each group of four
Figure 2-15 Cube with Numbered Vertices

vertices as a single polygon, you may compact all the indices used in
Example 2-11 into a single array, as shown in Example 2-12:
Example 2-12 Compacting Several glDrawElements() Calls into One
static GLubyte allIndices[] = {4, 5, 6, 7, 1, 2, 6, 5,
0, 1, 5, 4, 0, 3, 2, 1,
0, 4, 7, 3, 2, 3, 7, 6};
glDrawElements(GL_QUADS, 24, GL_UNSIGNED_BYTE, allIndices);
For other primitive types, compacting indices from several arrays into
a single array renders a different result. In Example 2-13, two calls to
glDrawElements() with the primitive GL_LINE_STRIP render two line
strips. You cannot simply combine these two arrays and use a single call to
glDrawElements() without concatenating the lines into a single strip that
would connect vertices #6 and #7. (Note that vertex #1 is being used in both
line strips just to show that this is legal.)
Example 2-13 Two glDrawElements() Calls That Render Two Line Strips
static GLubyte oneIndices[] = {0, 1, 2, 3, 4, 5, 6};
static GLubyte twoIndices[] = {7, 1, 8, 9, 10, 11};
glDrawElements(GL_LINE_STRIP, 7, GL_UNSIGNED_BYTE, oneIndices);
glDrawElements(GL_LINE_STRIP, 6, GL_UNSIGNED_BYTE, twoIndices);
The routine glMultiDrawElements() was introduced in OpenGL Version
1.4 to enable combining the effects of several glDrawElements() calls into
a single call.
void glMultiDrawElements(GLenum mode, GLsizei *count,
GLenum type, const GLvoid **indices,
GLsizei primcount);
Calls a sequence of primcount (a number of) glDrawElements() com-
mands. indices is an array of pointers to lists of array elements. count is
an array of how many vertices are found in each respective array element
list. mode (primitive type) and type (data type) are the same as they are in
glDrawElements().
80 Chapter 2: State Management and Drawing Geometric Objects
The effect of glMultiDrawElements() is the same as
for (i = 0; i < primcount; i++) {
if (count[i] > 0)
glDrawElements(mode, count[i], type, indices[i]);
}

Vertex Arrays 81
The calls to glDrawElements() in Example 2-13 can be combined into a
single call of glMultiDrawElements(), as shown in Example 2-14:
Example 2-14 Use of glMultiDrawElements(): mvarray.c
static GLubyte oneIndices[] = {0, 1, 2, 3, 4, 5, 6};
static GLubyte twoIndices[] = {7, 1, 8, 9, 10, 11};
static GLsizei count[] = {7, 6};
static GLvoid * indices[2] = {oneIndices, twoIndices};
glMultiDrawElements(GL_LINE_STRIP, count, GL_UNSIGNED_BYTE,
indices, 2);
Like glDrawElements() or glMultiDrawElements(),glDrawRangeElements()
is also good for hopping around data arrays and rendering their contents.
glDrawRangeElements() also introduces the added restriction of a range
of legal values for its indices, which may increase program performance.
For optimal performance, some OpenGL implementations may be able to
prefetch (obtain prior to rendering) a limited amount of vertex array data.
glDrawRangeElements() allows you to specify the range of vertices to be
prefetched.
It is a mistake for vertices in the array indices to reference outside the range
[start, end]. However, OpenGL implementations are not required to find or
report this mistake. Therefore, illegal index values may or may not generate
an OpenGL error condition, and it is entirely up to the implementation to
decide what to do.
You can use glGetIntegerv() with GL_MAX_ELEMENTS_VERTICES and
GL_MAX_ELEMENTS_INDICES to find out, respectively, the recommended
maximum number of vertices to be prefetched and the maximum number
void glDrawRangeElements(GLenum mode, GLuint start,
GLuint end, GLsizei count,
GLenum type, const GLvoid *indices);
Creates a sequence of geometric primitives that is similar to, but more
restricted than, the sequence created by glDrawElements(). Several
parameters of glDrawRangeElements() are the same as counterparts in
glDrawElements(), including mode (kind of primitives), count (number
of elements), type (data type), and indices (array locations of vertex data).
glDrawRangeElements() introduces two new parameters: start and end,
which specify a range of acceptable values for indices. To be valid, values
in the array indices must lie between start and end, inclusive.

82 Chapter 2: State Management and Drawing Geometric Objects
of indices (indicating the number of vertices to be rendered) to be refer-
enced. If end – start + 1 is greater than the recommended maximum of
prefetched vertices, or if count is greater than the recommended maximum
of indices, glDrawRangeElements() should still render correctly, but per-
formance may be reduced.
Not all vertices in the range [start, end] have to be referenced. However,
on some implementations, if you specify a sparsely used range, you may
unnecessarily process many vertices that go unused.
With glArrayElement(),glDrawElements(),glMultiDrawElements(), and
glDrawRangeElements(), it is possible that your OpenGL implementation
caches recently processed (meaning transformed, lit) vertices, allowing your
application to “reuse” them by not sending them down the transformation
pipeline additional times. Take the aforementioned cube, for example,
which has six faces (polygons) but only eight vertices. Each vertex is used
by exactly three faces. Without gl*Elements(), rendering all six faces would
require processing 24 vertices, even though 16 vertices are redundant. Your
implementation of OpenGL may be able to minimize redundancy and
process as few as eight vertices. (Reuse of vertices may be limited to all
vertices within a single glDrawElements() or glDrawRangeElements() call,
a single index array for glMultiDrawElements(), or, for glArrayElement(),
within one glBegin()/glEnd() pair.)
Dereferencing a Sequence of Array Elements
While glArrayElement(),glDrawElements(), and glDrawRangeElements()
“hop around” your data arrays, glDrawArrays() plows straight through them.
The effect of glDrawArrays() is almost the same as this command sequence:
glBegin (mode);
for (i = 0; i < count; i++)
glArrayElement(first + i);
glEnd();
void glDrawArrays(GLenum mode, GLint first, GLsizei count);
Constructs a sequence of geometric primitives using array elements
starting at first and ending at first + count – 1 of each enabled array. mode
specifies what kinds of primitives are constructed and is one of the same
values accepted by glBegin(); for example, GL_POLYGON, GL_LINE_
LOOP, GL_LINES, GL_POINTS, and so on.

Vertex Arrays 83
As is the case with glDrawElements(),glDrawArrays() also performs error
checking on its parameter values and leaves the current RGB color, secondary
color, color index, normal coordinates, fog coordinates, texture coordinates,
and edge flag with indeterminate values if the corresponding array has been
enabled.
Try This
Change the icosahedron drawing routine in Example 2-19 on page 115 to
use vertex arrays.
Similar to glMultiDrawElements(), the routine glMultiDrawArrays() was
introduced in OpenGL Version 1.4 to combine several glDrawArrays() calls
into a single call.
The effect of glMultiDrawArrays() is the same as
for (i = 0; i < primcount; i++) {
if (count[i] > 0)
glDrawArrays(mode, first[i], count[i]);
}
Restarting Primitives
As you start working with larger sets of vertex data, you are likely to find
that you need to make numerous calls to the OpenGL drawing routines,
usually rendering the same type of primitive (such as GL_TRIANGLE_STRIP,
for example) that you used in the previous drawing call. Of course, you can
use the glMultiDraw*() routines, but they require the overhead of
maintaining the arrays for the starting index and length of each primitive.
OpenGL Version 3.1 added the ability to restart primitives within the same
drawing call by specifying a special value, the primitive restart index, which
void glMultiDrawArrays(GLenum mode, GLint *first, GLsizei *count
GLsizei primcount);
Calls a sequence of primcount (a number of) glDrawArrays() commands.
mode specifies the primitive type with the same values as accepted by
glBegin().first and count contain lists of array locations indicating where
to process each list of array elements. Therefore, for the ith list of array
elements, a geometric primitive is constructed starting at first[i] and
ending at first[i] + count[i] – 1.
Try This

84 Chapter 2: State Management and Drawing Geometric Objects
is specially processed by OpenGL. When the primitive restart index is
encountered in a draw call, a new rendering primitive of the same type is
started with the vertex following the index. The primitive restart index is
specified by the glPrimitiveRestartIndex() routine.
Primitive restarting is controlled by calling glEnable() or glDisable() and
specifying GL_PRIMITIVE_RESTART, as demonstrated in Example 2-15.
Example 2-15 Using glPrimitiveRestartIndex() to Render Multiple Triangle Strips:
primrestart.c.
#define BUFFER_OFFSET(offset) ((GLvoid *) NULL + offset)
#define XStart -0.8
#define XEnd 0.8
#define YStart -0.8
#define YEnd 0.8
#define NumXPoints 11
#define NumYPoints 11
#define NumPoints (NumXPoints * NumYPoints)
#define NumPointsPerStrip (2*NumXPoints)
#define NumStrips (NumYPoints-1)
#define RestartIndex 0xffff
void
init()
{
GLuint vbo, ebo;
GLfloat *vertices;
GLushort *indices;
/* Set up vertex data */
glGenBuffers(1, &vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, 2*NumPoints*sizeof(GLfloat),
NULL, GL_STATIC_DRAW);
void glPrimitiveRestartIndex(GLuint index);
Specifies the vertex array element index used to indicate that a new
primitive should be started during rendering. When processing of vertex
array element indices encounters a value that matches index, no vertex
data is processed, the current graphics primitive is terminated, and a new
one of the identical type is started.

Vertex Arrays 85
vertices = glMapBuffer(GL_ARRAY_BUFFER, GL_WRITE_ONLY);
if (vertices == NULL) {
fprintf(stderr, "Unable to map vertex buffer\n");
exit(EXIT_FAILURE);
}
else {
int i, j;
GLfloat dx = (XEnd - XStart) / (NumXPoints - 1);
GLfloat dy = (YEnd - YStart) / (NumYPoints - 1);
GLfloat *tmp = vertices;
int n = 0;
for (j = 0; j < NumYPoints; ++j) {
GLfloat y = YStart + j*dy;
for (i = 0; i < NumXPoints; ++i) {
GLfloat x = XStart + i*dx;
*tmp++ = x;
*tmp++ = y;
}
}
glUnmapBuffer(GL_ARRAY_BUFFER);
glVertexPointer(2, GL_FLOAT, 0, BUFFER_OFFSET(0));
glEnableClientState(GL_VERTEX_ARRAY);
}
/* Set up index data */
glGenBuffers(1, &ebo);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, ebo);
/* We allocate an extra restart index because it simplifies
** the element-array loop logic */
glBufferData( GL_ELEMENT_ARRAY_BUFFER,
NumStrips*(NumPointsPerStrip+1)*sizeof(GLushort),
NULL, GL_STATIC_DRAW );
indices = glMapBuffer(GL_ELEMENT_ARRAY_BUFFER,
GL_WRITE_ONLY);
if (indices == NULL) {
fprintf(stderr, "Unable to map index buffer\n");
exit(EXIT_FAILURE);
}
else {
int i, j;
GLushort *index = indices;

86 Chapter 2: State Management and Drawing Geometric Objects
for (j = 0; j < NumStrips; ++j) {
GLushort bottomRow = j*NumYPoints;
GLushort topRow = bottomRow + NumYPoints;
for (i = 0; i < NumXPoints; ++i) {
*index++ = topRow + i;
*index++ = bottomRow + i;
}
*index++ = RestartIndex;
}
glUnmapBuffer(GL_ELEMENT_ARRAY_BUFFER);
}
glPrimitiveRestartIndex(RestartIndex);
glEnable(GL_PRIMITIVE_RESTART);
}
void
display()
{
int i, start;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(1, 1, 1);
glDrawElements(GL_TRIANGLE_STRIP,
NumStrips*(NumPointsPerStrip + 1),
GL_UNSIGNED_SHORT, BUFFER_OFFSET(0));
glutSwapBuffers();
}
Instanced Drawing
Advanced
OpenGL Version 3.1 (specifically, GLSL version 1.40) added support for
instanced drawing, which provides an additional value—gl_InstanceID,
called the instance ID, and accessible only in a vertex shader—that is
monotonically incremented for each group of primitives specified.
Advanced

Vertex Arrays 87
glDrawArraysInstanced() operates similarly to glMultiDrawArrays(),
except that the starting index and vertex count (as specified by first and
count, respectively) are the same for each call to glDrawArrays().
glDrawArraysInstanced() has the same effect as this call sequence (except
that your application cannot manually update gl_InstanceID):
for (i = 0; i < primcount; i++) {
gl_InstanceID = i;
glDrawArrays(mode, first, count);
}
gl_InstanceID = 0;
Likewise, glDrawElementsInstanced() performs the same operation, but
allows random-access to the data in the vertex array:
The implementation of glDrawElementsInstanced() is shown here:
for (i = 0; i < primcount; i++) {
gl_InstanceID = i;
glDrawElements(mode, count, type, indicies);
}
gl_InstanceID = 0;
void glDrawArraysInstanced(GLenum mode, GLint first, GLsizei count,
GLsizei primcount);
Effectively calls glDrawArrays() primcount times, setting the GLSL vertex
shader value gl_InstanceID before each call. mode specifies the primitive
type. first and count specify the range of array elements that are passed to
glDrawArrays().
void glDrawElementsInstanced(GLenum mode, GLsizei count,
GLenum type, const void *indicies,
GLsizei primcount);
Effectively calls glDrawElements() primcount times, setting the GLSL
vertex shader value gl_InstanceID before each call. mode specifies the
primitive type. type indicates the data type of the array indices and must
be one of the following: GL_UNSIGNED_BYTE, GL_UNSIGNED_SHORT,
or GL_UNSIGNED_INT. indicies and count specify the range of array
elements that are passed to glDrawElements().

88 Chapter 2: State Management and Drawing Geometric Objects
Interleaved Arrays
Advanced
Earlier in this chapter (see “Stride” on page 76), the special case of inter-
leaved arrays was examined. In that section, the array intertwined, which
interleaves RGB color and 3D vertex coordinates, was accessed by calls to
glColorPointer() and glVertexPointer(). Careful use of stride helped prop-
erly specify the arrays:
static GLfloat intertwined[] =
{1.0, 0.2, 1.0, 100.0, 100.0, 0.0,
1.0, 0.2, 0.2, 0.0, 200.0, 0.0,
1.0, 1.0, 0.2, 100.0, 300.0, 0.0,
0.2, 1.0, 0.2, 200.0, 300.0, 0.0,
0.2, 1.0, 1.0, 300.0, 200.0, 0.0,
0.2, 0.2, 1.0, 200.0, 100.0, 0.0};
There is also a behemoth routine, glInterleavedArrays(), that can specify
several vertex arrays at once. glInterleavedArrays() also enables and dis-
ables the appropriate arrays (so it combines “Step 1: Enabling Arrays” on
page 72 and “Step 2: Specifying Data for the Arrays” on page 73). The array
intertwined exactly fits one of the 14 data-interleaving configurations sup-
ported by glInterleavedArrays(). Therefore, to specify the contents of the
array intertwined into the RGB color and vertex arrays and enable both
arrays, call
glInterleavedArrays(GL_C3F_V3F, 0, intertwined);
This call to glInterleavedArrays() enables GL_COLOR_ARRAY and
GL_VERTEX_ARRAY. It disables GL_SECONDARY_COLOR_ARRAY,
GL_INDEX_ARRAY, GL_NORMAL_ARRAY, GL_FOG_COORD_ARRAY,
GL_TEXTURE_COORD_ARRAY, and GL_EDGE_FLAG_ARRAY.
This call also has the same effect as calling glColorPointer() and
glVertexPointer() to specify the values for six vertices in each array. Now
you are ready for Step 3: calling glArrayElement(),glDrawElements(),
glDrawRangeElements(),orglDrawArrays() to dereference array
elements.
Note that glInterleavedArrays() does not support edge flags.
The mechanics of glInterleavedArrays() are intricate and require reference
to Example 2-16 and Table 2-5. In that example and table, you’ll see et, ec,
and en, which are the Boolean values for the enabled or disabled texture
coordinate, color, and normal arrays; and you’ll see st, sc, and sv, which are
the sizes (numbers of components) for the texture coordinate, color, and
Advanced

Vertex Arrays 89
vertex arrays. tc is the data type for RGBA color, which is the only array that
can have nonfloating-point interleaved values. pc, pn, and pv are the calcu-
lated strides for jumping into individual color, normal, and vertex values;
and s is the stride (if one is not specified by the user) to jump from one array
element to the next.
The effect of glInterleavedArrays() is the same as calling the command
sequence in Example 2-16 with many values defined in Table 2-5. All
pointer arithmetic is performed in units of sizeof(GLubyte).
Example 2-16 Effect of glInterleavedArrays(format, stride, pointer)
int str;
/* set et, ec, en, st, sc, sv, tc, pc, pn, pv, and s
* as a function of Table 2-5 and the value of format
*/
str = stride;
if (str == 0)
str = s;
glDisableClientState(GL_EDGE_FLAG_ARRAY);
glDisableClientState(GL_INDEX_ARRAY);
glDisableClientState(GL_SECONDARY_COLOR_ARRAY);
glDisableClientState(GL_FOG_COORD_ARRAY);
if (et) {
glEnableClientState(GL_TEXTURE_COORD_ARRAY);
glTexCoordPointer(st, GL_FLOAT, str, pointer);
}
else
void glInterleavedArrays(GLenum format,
GLsizei stride, const GLvoid *pointer)
Initializes all eight arrays, disabling arrays that are not specified in format,
and enabling the arrays that are specified. format is one of 14 symbolic
constants, which represent 14 data configurations; Table 2-5 displays
format values. stride specifies the byte offset between consecutive vertices.
If stride is 0, the vertices are understood to be tightly packed in the array.
pointer is the memory address of the first coordinate of the first vertex in
the array.
If multitexturing is enabled, glInterleavedArrays() affects only the active
texture unit. See “Multitexturing” on page 467 for details.
Compatibility
Extension
glInterleavedArrays
90 Chapter 2: State Management and Drawing Geometric Objects
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
if (ec) {
glEnableClientState(GL_COLOR_ARRAY);
glColorPointer(sc, tc, str, pointer+pc);
}
else
glDisableClientState(GL_COLOR_ARRAY);
if (en) {
glEnableClientState(GL_NORMAL_ARRAY);
glNormalPointer(GL_FLOAT, str, pointer+pn);
}
else
glDisableClientState(GL_NORMAL_ARRAY);
glEnableClientState(GL_VERTEX_ARRAY);
glVertexPointer(sv, GL_FLOAT, str, pointer+pv);
In Table 2-5, T and F are True and False. f is sizeof(GLfloat). c is 4 times
sizeof(GLubyte), rounded up to the nearest multiple of f.
Start by learning the simpler formats, GL_V2F, GL_V3F, and GL_C3F_V3F. If
you use any of the formats with C4UB, you may have to use a struct data
Format etecenstscsvtcpcpnpvs
GL_V2F F F F 2 0 2f
GL_V3F F F F 3 0 3f
GL_C4UB_V2F F T F 4 2 GL_UNSIGNED_BYTE 0 c c+2f
GL_C4UB_V3F F T F 4 3 GL_UNSIGNED_BYTE 0 c c+3f
GL_C3F_V3F F T F 3 3 GL_FLOAT 0 3f 6f
GL_N3F_V3F F F T 3 0 3f 6f
GL_C4F_N3F_V3F F T T 4 3 GL_FLOAT 0 4f 7f 10f
GL_T2F_V3F T F F 2 3 2f 5f
GL_T4F_V4F T F F 4 4 4f 8f
GL_T2F_C4UB_V3F T T F 2 4 3 GL_UNSIGNED_BYTE 2f c+2f c+5f
GL_T2F_C3F_V3F T T F 2 3 3 GL_FLOAT 2f 5f 8f
GL_T2F_N3F_V3F T F T 2 3 2f 5f 8f
GL_T2F_C4F_N3F_V3F T T T 2 4 3 GL_FLOAT 2f 6f 9f 12f
GL_T4F_C4F_N3F_V4F T T T 4 4 4 GL_FLOAT 4f 8f 11f 15f
Table 2-5 Variables That Direct glInterleavedArrays()

Buffer Objects 91
type or do some delicate type casting and pointer math to pack four
unsigned bytes into a single 32-bit word.
For some OpenGL implementations, use of interleaved arrays may increase
application performance. With an interleaved array, the exact layout of
your data is known. You know your data is tightly packed and may be
accessed in one chunk. If interleaved arrays are not used, the stride and size
information has to be examined to detect whether data is tightly packed.
Note: glInterleavedArrays() only enables and disables vertex arrays
and specifies values for the vertex-array data. It does not render any-
thing. You must still complete “Step 3: Dereferencing and Render-
ing” on page 77 and call glArrayElement(),glDrawElements(),
glDrawRangeElements(), or glDrawArrays() to dereference
the pointers and render graphics.
Buffer Objects
Advanced
There are many operations in OpenGL where you send a large block of data
to OpenGL, such as passing vertex array data for processing. Transferring
that data may be as simple as copying from your system’s memory down
to your graphics card. However, because OpenGL was designed as a client-
server model, any time that OpenGL needs data, it will have to be transferred
from the client’s memory. If that data doesn’t change, or if the client and
server reside on different computers (distributed rendering), that data
transfer may be slow, or redundant.
Buffer objects were added to OpenGL Version 1.5 to allow an application to
explicitly specify which data it would like to be stored in the graphics server.
Many different types of buffer objects are used in the current versions of
OpenGL:
• Vertex data in arrays can be stored in server-side buffer objects starting
with OpenGL Version 1.5. They are described in “Using Buffer Objects
with Vertex-Array Data” on page 102 of this chapter.
• Support for storing pixel data, such as texture maps or blocks of pixels,
in buffer objects was added into OpenGL Version 2.1 It is described in
“Using Buffer Objects with Pixel Rectangle Data” in Chapter 8.
Advanced

92 Chapter 2: State Management and Drawing Geometric Objects
• Version 3.1 added uniform buffer objects for storing blocks of uniform-
variable data for use with shaders.
You will find many other features in OpenGL that use the term “objects,”
but not all apply to storing blocks of data. For example, texture objects
(introduced in OpenGL Version 1.1) merely encapsulate various state
settings associated with texture maps (See “Texture Objects” on page 437).
Likewise, vertex-array objects, added in Version 3.0, encapsulate the state
parameters associated with using vertex arrays. These types of objects allow
you to alter numerous state settings with many fewer function calls. For
maximum performance, you should try to use them whenever possible,
once you’re comfortable with their operation.
Note: An object is referred to by its name, which is an unsigned integer
identifier. Starting with Version 3.1, all names must be generated by
OpenGL using one of the glGen*() routines; user-defined names are
no longer accepted.
Creating Buffer Objects
In OpenGL Version 3.0, any nonzero unsigned integer may used as a buffer
object identifier. You may either arbitrarily select representative values or let
OpenGL allocate and manage those identifiers for you. Why the difference?
By having OpenGL allocate identifiers, you are guaranteed to avoid an
already used buffer object identifier. This helps to eliminate the risk of
modifying data unintentionally. In fact, OpenGL Version 3.1 requires that
all object identifiers be generated, disallowing user-defined names.
To have OpenGL allocate buffer objects identifiers, call glGenBuffers().
void glGenBuffers(GLsizei n, GLuint *buffers);
Returns n currently unused names for buffer objects in the array buffers.
The names returned in buffers do not have to be a contiguous set of
integers.
The names returned are marked as used for the purposes of allocating
additional buffer objects, but only acquire a valid state once they have
been bound.
Zero is a reserved buffer object name and is never returned as a buffer
object by glGenBuffers().

Buffer Objects 93
You can also determine whether an identifier is a currently used buffer
object identifier by calling glIsBuffer().
Making a Buffer Object Active
To make a buffer object active, it needs to be bound. Binding selects which
buffer object future operations will affect, either for initializing data or
using that buffer for rendering. That is, if you have more than one buffer
object in your application, you’ll likely call glBindBuffer() multiple times:
once to initialize the object and its data, and then subsequent times either
to select that object for use in rendering or to update its data.
To disable use of buffer objects, call glBindBuffer() with zero as the buffer
identifier. This switches OpenGL to the default mode of not using buffer
objects.
Allocating and Initializing Buffer Objects with Data
Once you’ve bound a buffer object, you need to reserve space for storing
your data. This is done by calling glBufferData().
GLboolean glIsBuffer(GLuint buffer);
Returns GL_TRUE if buffer is the name of a buffer object that has been
bound, but has not been subsequently deleted. Returns GL_FALSE if buffer
is zero or if buffer is a nonzero value that is not the name of a buffer object.
void glBindBuffer(GLenum target, GLuint buffer);
Specifies the current active buffer object. target must be set to one of
GL_ARRAY_BUFFER, GL_ELEMENT_ARRAY_BUFFER, GL_PIXEL_PACK_
BUFFER, GL_PIXEL_UNPACK_BUFFER, GL_COPY_READ_BUFFER,
GL_COPY_WRITE_BUFFER, GL_TRANSFORM_FEEDBACK_BUFFER, or
GL_UNIFORM_BUFFER. buffer specifies the buffer object to be bound to.
glBindBuffer() does three things: 1. When using buffer of an unsigned
integer other than zero for the first time, a new buffer object is created and
assigned that name. 2. When binding to a previously created buffer
object, that buffer object becomes the active buffer object. 3. When
binding to a buffer value of zero, OpenGL stops using buffer objects.

94 Chapter 2: State Management and Drawing Geometric Objects
glBufferData() first allocates memory in the OpenGL server for storing your
data. If you request too much memory, a GL_OUT_OF_MEMORY error will
be set. Once the storage has been reserved, and if the data parameter is not
NULL, size units of storage (usually bytes) are copied from the client’s
memory into the buffer object. However, if you need to dynamically load
the data at some point after the buffer is created, pass NULL in for the data
pointer. This will reserve the appropriate storage for your data, but leave it
uninitialized.
void glBufferData(GLenum target, GLsizeiptr size, const GLvoid *data,
GLenum usage);
Allocates size storage units (usually bytes) of OpenGL server memory for
storing vertex array data or indices. Any previous data associated with the
currently bound object will be deleted.
target may be either GL_ARRAY_BUFFER for vertex data; GL_ELEMENT_
ARRAY_BUFFER for index data; GL_PIXEL_UNPACK_BUFFER for pixel
data being passed into OpenGL; GL_PIXEL_PACK_BUFFER for pixel data
being retrieved from OpenGL; GL_COPY_READ_BUFFER and GL_COPY_
WRITE_BUFFER for data copied between buffers; GL_TEXTURE_BUFFER
for texture data stored as a texture buffer; GL_TRANSFORM_FEEDBACK_
BUFFER for results from executing a transform feedback shader; or
GL_UNIFORM_BUFFER for uniform variable values.
size is the amount of storage required for storing the respective data. This
value is generally number of elements in the data multiplied by their
respective storage size.
data is either a pointer to a client memory that is used to initialize the
buffer object or NULL. If a valid pointer is passed, size units of storage are
copied from the client to the server. If NULL is passed, size units of storage
are reserved for use, but are left uninitialized.
usage provides a hint as to how the data will be read and written after
allocation. Valid values are GL_STREAM_DRAW, GL_STREAM_READ, GL_
STREAM_COPY, GL_STATIC_DRAW, GL_STATIC_READ, GL_STATIC_COPY,
GL_DYNAMIC_DRAW, GL_DYNAMIC_READ, GL_DYNAMIC_COPY.
glBufferData() will generate a GL_OUT_OF_MEMORY error if the
requested size exceeds what the server is able to allocate. It will generate a
GL_INVALID_VALUE error if usage is not one of the permitted values.

Buffer Objects 95
The final parameter to glBufferData(),usage, is a performance hint to
OpenGL. Based upon the value you specify for usage, OpenGL may be able
to optimize the data for better performance, or it can choose to ignore the
hint. There are three operations that can be done to buffer object data:
1. Drawing—the client specifies data that is used for rendering.
2. Reading—data values are read from an OpenGL buffer (such as the
framebuffer) and used in the application in various computations not
immediately related to rendering.
3. Copying—data values are read from an OpenGL buffer and then used
as data for rendering.
Additionally, depending upon how often you intend to update the data,
there are various operational hints for describing how often the data will be
read or used in rendering:
• Stream mode—you specify the data once, and use it only a few times in
drawing or other operations.
• Static mode—you specify the data once, but use the values often.
• Dynamic mode—you may update the data often and use the data
values in the buffer object many times as well.
Possible values for usage are described in Table 2-6.
Parameter Meaning
GL_STREAM_DRAW Data is specified once and used at most a few times
as the source of drawing and image specification
commands.
GL_STREAM_READ Data is copied once from an OpenGL buffer and is
used at most a few times by the application as data
values.
GL_STREAM_COPY Data is copied once from an OpenGL buffer and is
used at most a few times as the source for drawing or
image specification commands.
GL_STATIC_DRAW Data is specified once and used many times as the
source of drawing or image specification commands.
GL_STATIC_READ Data is copied once from an OpenGL buffer and is
used many times by the application as data values.
Table 2-6 Values for usage Parameter of glBufferData()

96 Chapter 2: State Management and Drawing Geometric Objects
Updating Data Values in Buffer Objects
There are two methods for updating data stored in a buffer object. The first
method assumes that you have data of the same type prepared in a buffer
in your application. glBufferSubData() will replace some subset of the data
in the bound buffer object with the data you provide.
The second method allows you more control over which data values are
updated in the buffer. glMapBuffer() and glMapBufferRange() return a
pointer to the buffer object memory, into which you can write new values
GL_STATIC_COPY Data is copied once from an OpenGL buffer and is
used many times as the source for drawing or image
specification commands.
GL_DYNAMIC_DRAW Data is specified many times and used many times
as the source of drawing and image specification
commands.
GL_DYNAMIC_READ Data is copied many times from an OpenGL buffer and
is used many times by the application as data values.
GL_DYNAMIC_COPY Data is copied many times from an OpenGL buffer and
is used many times as the source for drawing or image
specification commands.
void glBufferSubData(GLenum target, GLintptr offset, GLsizeiptr size,
const GLvoid *data);
Update size bytes starting at offset (also measured in bytes) in the currently
bound buffer object associated with target using the data pointed to by
data. target must be one of GL_ARRAY_BUFFER, GL_ELEMENT_ARRAY_
BUFFER, GL_PIXEL_UNPACK_BUFFER, GL_PIXEL_PACK_BUFFER,
GL_COPY_READ_BUFFER, GL_COPY_WRITE_BUFFER, GL_TRANSFORM_
FEEDBACK_BUFFER, or GL_UNIFORM_BUFFER.
glBufferSubData() will generate a GL_INVALID_VALUE error if size is less
than zero or if size + offset is greater than the original size specified when
the buffer object was created.
Parameter Meaning
Table 2-6 (continued) Values for usage Parameter of glBufferData()

Buffer Objects 97
(or simply read the data, depending on your choice of memory access
permissions), just as if you were assigning values to an array. When you’ve
completed updating the values in the buffer, you call glUnmapBuffer() to
signify that you’ve completed updating the data.
glMapBuffer() provides access to the entire set of data contained in the
buffer object. This approach is useful if you need to modify much of the
data in buffer, but may be inefficient if you have a large buffer and need to
update only a small portion of the values.
When you’ve completed accessing the storage, you can unmap the buffer
by calling glUnmapBuffer().
As a simple example of how you might selectively update elements of your
data, we’ll use glMapBuffer() to obtain a pointer to the data in a buffer
object containing three-dimensional positional coordinates, and then
update only the z-coordinates.
GLvoid *glMapBuffer(GLenum target, GLenum access);
Returns a pointer to the data storage for the currently bound buffer
object associated with target, which must be one of GL_ARRAY_BUFFER,
GL_ELEMENT_ARRAY_BUFFER, GL_PIXEL_PACK_BUFFER, GL_PIXEL_
UNPACK_BUFFER, GL_COPY_READ_BUFFER, GL_COPY_WRITE_
BUFFER, GL_TRANSFORM_FEEDBACK_BUFFER, or GL_UNIFORM_
BUFFER. access must be either GL_READ_ONLY, GL_WRITE_ONLY, or
GL_READ_WRITE, indicating the operations that a client may do on the data.
glMapBuffer() will return NULL either if the buffer cannot be mapped
(setting the OpenGL error state to GL_OUT_OF_MEMORY) or if the buffer
was already mapped previously (where the OpenGL error state will be set
to GL_INVALID_OPERATION).
GLboolean glUnmapBuffer(GLenum target);
Indicates that updates to the currently bound buffer object are complete,
and the buffer may be released. target must be one of GL_ARRAY_BUFFER,
GL_ELEMENT_ARRAY_BUFFER, GL_PIXEL_PACK_BUFFER, GL_PIXEL_
UNPACK_BUFFER, GL_COPY_READ_BUFFER, GL_COPY_WRITE_
BUFFER, GL_TRANSFORM_FEEDBACK_BUFFER, or GL_UNIFORM_
BUFFER.

98 Chapter 2: State Management and Drawing Geometric Objects
GLfloat* data;
data = (GLfloat*) glMapBuffer(GL_ARRAY_BUFFER, GL_READ_WRITE);
if (data != (GLfloat*) NULL) {
for( i = 0; i < 8; ++i )
data[3*i+2] *= 2.0; /* Modify Z values */
glUnmapBuffer(GL_ARRAY_BUFFER);
} else {
/* Handle not being able to update data */
}
If you need to update only a relatively small number of values in the buffer
(as compared to its total size), or small contiguous ranges of values in a very
large buffer object, it may be more efficient to use glMapBufferRange(). It
allows you to map only the range of data values you need.
GLvoid *glMapBufferRange(GLenum target, GLintptr offset,
GLsizeiptr length, GLbitfield access);
Returns a pointer into the data storage for the currently bound buffer object
associated with target, which must be one of GL_ARRAY_BUFFER,
GL_ELEMENT_ARRAY_BUFFER, GL_PIXEL_PACK_BUFFER, GL_PIXEL_
UNPACK_BUFFER, GL_COPY_READ_BUFFER, GL_COPY_WRITE_BUFFER,
GL_TRANSFORM_FEEDBACK_BUFFER, or GL_UNIFORM_BUFFER. offset
and length specify the range to be mapped. access is a bitmask composed of
GL_MAP_READ_BIT, GL_MAP_WRITE_BIT, which indicate the operations
that a client may do on the data, and optionally GL_MAP_INVALIDATE_
RANGE_BIT, GL_MAP_INVALIDATE_BUFFER_BIT, GL_MAP_FLUSH_
EXPLICIT_BIT, or GL_MAP_UNSYNCHRONIZED_BIT, which provide hints
on how OpenGL should manage the data in the buffer.
glMapBufferRange() will return NULL if an error occurs. GL_INVALID_
VALUE is generated if offset or length are negative, or offset+length is greater
than the buffer size. GL_OUT_OF_MEMORY error is generated if adequate
memory cannot be obtained to map the buffer. GL_INVALID_OPERATION
is generated if any of the following occur: The buffer is already mapped;
access does not have either GL_MAP_READ_BIT or GL_MAP_WRITE_BIT
set; access has GL_MAP_READ_BIT set and any of GL_MAP_INVALIDATE_
RANGE_BIT, GL_MAP_INVALIDATE_BUFFER_BIT, or GL_MAP_
UNSYNCHRONIZED_BIT is also set; or both GL_MAP_WRITE_BIT and
GL_MAP_FLUSH_EXPLICIT_BIT are set in access.

Buffer Objects 99
Using glMapBufferRange(), you can specify optional hints by setting
additional bits within access. These flags describe how the OpenGL server
needs to preserve data that was originally in the buffer before you mapped
it. The hints are meant to aid the OpenGL implementation in determining
which data values it needs to retain, or for how long, to keep any internal
copies of the data correct and consistent.
Parameter Meaning
GL_MAP_INVALIDATE_RANGE_BIT Specify that the previous values in the
mapped range may be discarded, but
preserve the other values within the
buffer. Data within this range are
undefined unless explicitly written. No
OpenGL error is generated if later OpenGL
calls access undefined data, and the results
of such calls are undefined (but may cause
application or system errors). This flag
may not be used in conjunction with the
GL_READ_BIT.
GL_MAP_INVALIDATE_BUFFER_BIT Specify that the previous values of the
entire buffer may be discarded, and all
values with the buffer are undefined
unless explicitly written. No OpenGL
error is generated if later OpenGL calls
access undefined data, and the results of
such calls are undefined (but may cause
application or system errors). This flag
may not be used in conjunction with the
GL_READ_BIT.
GL_MAP_FLUSH_EXPLICIT_BIT Indicate that discrete ranges of the
mapped region may be updated, that the
application will signal when
modifications to a range should be
considered completed by calling
glFlushMappedBufferRange(). No
OpenGL error is generated if a range of the
mapped buffer is updated but not flushed,
however, the values are undefined until
flushed.
Using this option will require any modified
ranges to be explicitly flushed to the
OpenGL server—glUnmapBuffer() will
not automatically flush the buffer’s data.
Table 2-7 Values for the access Parameter of glMapBufferRange()

100 Chapter 2: State Management and Drawing Geometric Objects
As described in Table 2-7, specifying GL_MAP_FLUSH_EXPLICIT_BIT in the
access flags when mapping a buffer region with glMapBufferRange()
requires ranges modified within the mapped buffer to be indicated to the
OpenGL by a call to glFlushMappedBufferRange().
GL_MAP_UNSYNCHRONIZED_BIT Specify that OpenGL should not attempt
to synchronize pending operations on a
buffer (e.g., updating data with a call to
glBufferData(), or the application is
trying to use the data in the buffer for
rendering) until the call to
glMapBufferRange() has completed.
No OpenGL errors are generated for the
pending operations that access or modify
the mapped region, but the results of
those operations is undefined.
GLvoid glFlushMappedBufferRange(GLenum target, GLintptr offset,
GLsizeiptr length);
Signal that values within a mapped buffer range have been modified,
which may cause the OpenGL server to update cached copies of the buffer
object. target must be one of the following: GL_ARRAY_BUFFER,
GL_ELEMENT_ARRAY_BUFFER, GL_PIXEL_PACK_BUFFER, GL_PIXEL_
UNPACK_BUFFER, GL_COPY_READ_BUFFER, GL_COPY_WRITE_
BUFFER, GL_TRANSFORM_FEEDBACK_BUFFER, or GL_UNIFORM_
BUFFER. offset and length specify the range of the mapped buffer region,
relative to the beginning of the mapped range of the buffer.
A GL_INVALID_VALUE error is generated if offset or length is negative or if
offset+length is greater than the size of the mapped region. A GL_INVALID_
OPERATION error is generated if there is no buffer bound to target (i.e.,
zero was specified as the buffer to be bound in a call to glBindBuffer() for
target), or if the buffer bound to target is not mapped, or if it is mapped
without having set the GL_MAP_FLUSH_EXPLICIT_BIT.
Parameter Meaning
Table 2-7 (continued) Values for the access Parameter of glMapBufferRange()

Buffer Objects 101
Copying Data Between Buffer Objects
On some occasions, you may need to copy data from one buffer object to
another. In versions of OpenGL prior to Version 3.1, this would be a two-
step process:
1. Copy the data from the buffer object into memory in your application.
You would do this either by mapping the buffer and copying it into a
local memory buffer, or by calling glGetBufferSubData() to copy the
data from the server.
2. Update the data in another buffer object by binding to the new object
and then sending the new data using glBufferData() (or
glBufferSubData() if you’re replacing only a subset). Alternatively, you
could map the buffer, and then copy the data from a local memory
buffer into the mapped buffer.
In OpenGL Version 3.1, the glCopyBufferSubData() command copies data
without forcing it to make a temporary stop in your application’s memory.
void glCopyBufferSubData(GLenum readbuffer, GLenum writebuffer,
GLintptr readoffset, GLintptr writeoffset,
GLsizeiptr size);
Copy data from the buffer object associated with readbuffer to the buffer
object bound to writebuffer.readbuffer and writebuffer must be one of GL_
ARRAY_BUFFER, GL_COPY_READ_BUFFER, GL_COPY_WRITE_BUFFER,
GL_ELEMENT_ARRAY_BUFFER, GL_PIXEL_PACK_BUFFER, GL_PIXEL_
UNPACK_BUFFER, GL_TEXTURE_BUFFER, GL_TRANSFORM_
FEEDBACK_BUFFER, or GL_UNIFORM_BUFFER.
readoffset and size specify the amount of data copied into the destination
buffer object, replacing the same size of data starting at writeoffset.
Numerous situations will cause a GL_INVALID_VALUE error to be
generated: readoffset,writeoffset, or size being negative; readoffset + size
exceeding the extent of the buffer object bound to readbuffer;writeoffset +
size exceeding the extent of the buffer object bound to writebuffer; or if
readbuffer and writebuffer are bound to the same object, and the regions
specified by readoffset and size overlap the region defined by writeoffset
and size.
A GL_INVALID_OPERATION error is generated if either readbuffer or
writebuffer is bound to zero, or either buffer is currently mapped.

102 Chapter 2: State Management and Drawing Geometric Objects
Cleaning Up Buffer Objects
When you’re finished with a buffer object, you can release its resources and
make its identifier available by calling glDeleteBuffers(). Any bindings to
currently bound objects that are deleted are reset to zero.
Using Buffer Objects with Vertex-Array Data
To store your vertex-array data in buffer objects, you will need to add a few
steps to your application.
1. (Optional) Generate buffer object identifiers.
2. Bind a buffer object, specifying that it will be used for either storing
vertex data or indices.
3. Request storage for your data, and optionally initialize those data
elements.
4. Specify offsets relative to the start of the buffer object to initialize the
vertex-array functions, such as glVertexPointer().
5. Bind the appropriate buffer object to be utilized in rendering.
6. Render using an appropriate vertex-array rendering function, such as
glDrawArrays() or glDrawElements().
If you need to initialize multiple buffer objects, you will repeat steps 2
through 4 for each buffer object.
Both “formats” of vertex-array data are available for use in buffer objects. As
described in “Step 2: Specifying Data for the Arrays,” vertex, color, lighting
normal, or any other type of associated vertex data can be stored in a buffer
void glDeleteBuffers(GLsizei n, const GLuint *buffers);
Deletes n buffer objects, named by elements in the array buffers. The freed
buffer objects may now be reused (for example, by glGenBuffers()).
If a buffer object is deleted while bound, all bindings to that object are
reset to the default buffer object, as if glBindBuffer() had been called with
zero as the specified buffer object. Attempts to delete nonexistent buffer
objects or the buffer object named zero are ignored without generating
an error.

Buffer Objects 103
object. Additionally, interleaved vertex array data, as described in “Inter-
leaved Arrays,” can also be stored in a buffer object. In either case, you
would create a single buffer object to hold all of the data to be used as vertex
arrays.
As compared to specifying a memory address in the client’s memory where
OpenGL should access the vertex-array data, you specify the offset in
machine units (usually bytes) to the data in the buffer. To help illustrate
computing the offset, and to frustrate the purists in the audience, we’ll use
the following macro to simplify expressing the offset:
#define BUFFER_OFFSET(bytes) ((GLubyte*) NULL + (bytes))
For example, if you had floating-point color and position data for each
vertex, perhaps represented as the following array
GLfloat vertexData[][6] = {
{ R0, G0, B0, X0, Y0, Z0 },
{ R1, G1, B1, X1, Y1, Z1 },
...
{ Rn, Gn, Bn, Xn, Yn, Zn }
};
that were used to initialize the buffer object, you could specify the data as
two separate vertex array calls, one for colors and one for vertices:
glColorPointer(3, GL_FLOAT, 6*sizeof(GLfloat),BUFFER_OFFSET(0));
glVertexPointer(3, GL_FLOAT, 6*sizeof(GLfloat),
BUFFER_OFFSET(3*sizeof(GLfloat));
glEnableClientState(GL_COLOR_ARRAY);
glEnableClientState(GL_VERTEX_ARRAY);
Conversely, since the data in vertexData matches a format for an interleaved
vertex array, you could use glInterleavedArrays() for specifying the vertex-
array data:
glInterleavedArrays(GL_C3F_V3F, 0, BUFFER_OFFSET(0));
Putting this all together, Example 2-17 demonstrates how buffer objects of
vertex data might be used. The example creates two buffer objects, one
containing vertex data and the other containing index data.
Example 2-17 Using Buffer Objects with Vertex Data
#define VERTICES 0
#define INDICES 1
#define NUM_BUFFERS 2

104 Chapter 2: State Management and Drawing Geometric Objects
GLuint buffers[NUM_BUFFERS];
GLfloat vertices[][3] = {
{ -1.0, -1.0, -1.0 },
{ 1.0, -1.0, -1.0 },
{ 1.0, 1.0, -1.0 },
{ -1.0, 1.0, -1.0 },
{ -1.0, -1.0, 1.0 },
{ 1.0, -1.0, 1.0 },
{ 1.0, 1.0, 1.0 },
{ -1.0, 1.0, 1.0 }
};
GLubyte indices[][4] = {
{ 0, 1, 2, 3 },
{ 4, 7, 6, 5 },
{ 0, 4, 5, 1 },
{ 3, 2, 6, 7 },
{ 0, 3, 7, 4 },
{ 1, 5, 6, 2 }
};
glGenBuffers(NUM_BUFFERS, buffers);
glBindBuffer(GL_ARRAY_BUFFER, buffers[VERTICES]);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices,
GL_STATIC_DRAW);
glVertexPointer(3, GL_FLOAT, 0, BUFFER_OFFSET(0));
glEnableClientState(GL_VERTEX_ARRAY);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, buffers[INDICES]);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices
GL_STATIC_DRAW);
glDrawElements(GL_QUADS, 24, GL_UNSIGNED_BYTE,
BUFFER_OFFSET(0));
Vertex-Array Objects
As your programs grow larger and use more models, you will probably
find that you switch between multiple sets of vertex arrays each frame.
Depending on how many vertex attributes you’re using for each vertex, the
number of calls—such as to glVertexPointer()—may start to become large.

Vertex-Array Objects 105
Vertex-array objects bundle collections of calls for setting the vertex array’s
state. After being initialized, you can quickly change between different sets
of vertex arrays with a single call.
To create a vertex-array object, first call glGenVertexArrays(), which will
create the requested number of uninitialized objects:
After creating your vertex-array objects, you’ll need to initialize the new
objects, and associate the set of vertex-array data that you want to enable
with the individual allocated objects. You do this with the
glBindVertexArray() routine. Once you initialize all of your vertex-array
objects, you can use glBindVertexArray() to switch between the different
sets of vertex arrays that you’ve set up.
Example 2-18 demonstrates switching between two sets of vertex arrays
using vertex-arrays objects.
void glGenVertexArrays(GLsizei n, GLuint *arrays);
Returns n currently unused names for use as vertex-array objects in the
array arrays. The names returned are marked as used for the purposes of
allocating additional buffer objects, and initialized with values
representing the default state of the collection of uninitialized vertex
arrays.
GLvoid gBindVertexArray(GLuint array);
glBindVertexArray() does three things. When using the value array that
is other than zero and was returned from glGenVertexArrays(), a new
vertex-array object is created and assigned that name. When binding to a
previously created vertex-array object, that vertex array object becomes
active, which additionally affects the vertex array state stored in the
object. When binding to an array value of zero, OpenGL stops using
vertex-array objects and returns to the default state for vertex arrays.
A GL_INVALID_OPERATION error is generated if array is not a value
previously returned from glGenVertexArrays(), or if it is a value that has
been released by glDeleteVertexArrays(), or if any of the gl*Pointer()
routines are called to specify a vertex array that is not associated with a
buffer object while a non-zero vertex-array object is bound (i.e., using a
client-side vertex array storage).

106 Chapter 2: State Management and Drawing Geometric Objects
Example 2-18 Using Vertex-Array Objects: vao.c
#define BUFFER_OFFSET(offset) ((GLvoid*) NULL + offset)
#define NumberOf(array) (sizeof(array)/sizeof(array[0]))
typedef struct {
GLfloat x, y, z;
} vec3;
typedef struct {
vec3 xlate; /* Translation */
GLfloat angle;
vec3 axis;
} XForm;
enum { Cube, Cone, NumVAOs };
GLuint VAO[NumVAOs];
GLenum PrimType[NumVAOs];
GLsizei NumElements[NumVAOs];
XForm Xform[NumVAOs] = {
{ { -2.0, 0.0, 0.0 }, 0.0, { 0.0, 1.0, 0.0 } },
{ { 0.0, 0.0, 2.0 }, 0.0, { 1.0, 0.0, 0.0 } }
};
GLfloat Angle = 0.0;
void
init()
{
enum { Vertices, Colors, Elements, NumVBOs };
GLuint buffers[NumVBOs];
glGenVertexArrays(NumVAOs, VAO);
{
GLfloat cubeVerts[][3] = {
{ -1.0, -1.0, -1.0 },
{ -1.0, -1.0, 1.0 },
{ -1.0, 1.0, -1.0 },
{ -1.0, 1.0, 1.0 },
{ 1.0, -1.0, -1.0 },
{ 1.0, -1.0, 1.0 },
{ 1.0, 1.0, -1.0 },
{ 1.0, 1.0, 1.0 },
};

Vertex-Array Objects 107
GLfloat cubeColors[][3] = {
{ 0.0, 0.0, 0.0 },
{ 0.0, 0.0, 1.0 },
{ 0.0, 1.0, 0.0 },
{ 0.0, 1.0, 1.0 },
{ 1.0, 0.0, 0.0 },
{ 1.0, 0.0, 1.0 },
{ 1.0, 1.0, 0.0 },
{ 1.0, 1.0, 1.0 },
};
GLubyte cubeIndices[] = {
0, 1, 3, 2,
4, 6, 7, 5,
2, 3, 7, 6,
0, 4, 5, 1,
0, 2, 6, 4,
1, 5, 7, 3
};
glBindVertexArray(VAO[Cube]);
glGenBuffers(NumVBOs, buffers);
glBindBuffer(GL_ARRAY_BUFFER, buffers[Vertices]);
glBufferData(GL_ARRAY_BUFFER, sizeof(cubeVerts),
cubeVerts, GL_STATIC_DRAW);
glVertexPointer(3, GL_FLOAT, 0, BUFFER_OFFSET(0));
glEnableClientState(GL_VERTEX_ARRAY);
glBindBuffer(GL_ARRAY_BUFFER, buffers[Colors]);
glBufferData(GL_ARRAY_BUFFER, sizeof(cubeColors),
cubeColors, GL_STATIC_DRAW);
glColorPointer(3, GL_FLOAT, 0, BUFFER_OFFSET(0));
glEnableClientState(GL_COLOR_ARRAY);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER,
buffers[Elements]);
glBufferData(GL_ELEMENT_ARRAY_BUFFER,
sizeof(cubeIndices), cubeIndices, GL_STATIC_DRAW);
PrimType[Cube] = GL_QUADS;
NumElements[Cube] = NumberOf(cubeIndices);
}
{
int i, idx;
float dTheta;

108 Chapter 2: State Management and Drawing Geometric Objects
#define NumConePoints 36
/* We add one more vertex for the cone's apex */
GLfloat coneVerts[NumConePoints+1][3] = {
{0.0, 0.0, 1.0}
};
GLfloat coneColors[NumConePoints+1][3] = {
{1.0, 1.0, 1.0}
};
GLubyte coneIndices[NumConePoints+1];
dTheta = 2*M_PI / (NumConePoints - 1);
idx = 1;
for (i = 0; i < NumConePoints; ++i, ++idx) {
float theta = i*dTheta;
coneVerts[idx][0] = cos(theta);
coneVerts[idx][1] = sin(theta);
coneVerts[idx][2] = 0.0;
coneColors[idx][0] = cos(theta);
coneColors[idx][1] = sin(theta);
coneColors[idx][2] = 0.0;
coneIndices[idx] = idx;
}
glBindVertexArray(VAO[Cone]);
glGenBuffers(NumVBOs, buffers);
glBindBuffer(GL_ARRAY_BUFFER, buffers[Vertices]);
glBufferData(GL_ARRAY_BUFFER, sizeof(coneVerts),
coneVerts, GL_STATIC_DRAW);
glVertexPointer(3, GL_FLOAT, 0, BUFFER_OFFSET(0));
glEnableClientState(GL_VERTEX_ARRAY);
glBindBuffer(GL_ARRAY_BUFFER, buffers[Colors]);
glBufferData(GL_ARRAY_BUFFER, sizeof(coneColors),
coneColors, GL_STATIC_DRAW);
glColorPointer(3, GL_FLOAT, 0, BUFFER_OFFSET(0));
glEnableClientState(GL_COLOR_ARRAY);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER,
buffers[Elements]);
glBufferData(GL_ELEMENT_ARRAY_BUFFER,
sizeof(coneIndices), coneIndices, GL_STATIC_DRAW);
PrimType[Cone] = GL_TRIANGLE_FAN;
NumElements[Cone] = NumberOf(coneIndices);
}
glEnable(GL_DEPTH_TEST);
}

Vertex-Array Objects 109
void
display()
{
int i;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glRotatef(Angle, 0.0, 1.0, 0.0);
for (i = 0; i < NumVAOs; ++i) {
glPushMatrix();
glTranslatef(Xform[i].xlate.x, Xform[i].xlate.y,
Xform[i].xlate.z);
glRotatef(Xform[i].angle, Xform[i].axis.x,
Xform[i].axis.y, Xform[i].axis.z);
glBindVertexArray(VAO[i]);
glDrawElements(PrimType[i], NumElements[i],
GL_UNSIGNED_BYTE, BUFFER_OFFSET(0));
glPopMatrix();
}
glPopMatrix();
glutSwapBuffers();
}
To delete vertex-array objects and release their names for reuse, call
glDeleteVertexArrays(). If you’re using buffer objects for storing data, they
are not deleted when the vertex-array object referencing them is deleted.
They continue to exist (until you delete them). The only change that occurs
is if the buffer objects were currently bound when you deleted the vertex-
array object, they become unbound.
void glDeleteVertexArrays(GLsizei n, GLuint *arrays);
Deletes the n vertex-arrays objects specified in arrays, enabling the names
for reuse as vertex arrays later. If a bound vertex array is deleted, the
bindings for that vertex array become zero (as if you had called
glBindBuffer() with a value of zero), and the default vertex array becomes
the current one. Unused names in arrays are released, but no changes to
the current vertex array state are made.

110 Chapter 2: State Management and Drawing Geometric Objects
Finally, if you need to determine whether a particular value might represent
an allocated (but not necessarily initialized) vertex-array object, you can
check by calling glIsVertexArray().
Attribute Groups
In “Basic State Management” you saw how to set or query an individual
state or state variable. You can also save and restore the values of a
collection of related state variables with a single command.
OpenGL groups related state variables into an attribute group. For example,
the GL_LINE_BIT attribute consists of five state variables: the line width,
the GL_LINE_STIPPLE enable status, the line stipple pattern, the line
stipple repeat counter, and the GL_LINE_SMOOTH enable status. (See
“Antialiasing” in Chapter 6.) With the commands glPushAttrib() and
glPopAttrib(), you can save and restore all five state variables at once.
Some state variables are in more than one attribute group. For example,
the state variable GL_CULL_FACE is part of both the polygon and the
enable attribute groups.
In OpenGL Version 1.1, there are now two different attribute stacks. In addi-
tion to the original attribute stack (which saves the values of server state
variables), there is also a client attribute stack, accessible by the commands
glPushClientAttrib() and glPopClientAttrib().
In general, it’s faster to use these commands than to get, save, and restore
the values yourself. Some values might be maintained in the hardware, and
getting them might be expensive. Also, if you’re operating on a remote
client, all the attribute data has to be transferred across the network connec-
tion and back as it is obtained, saved, and restored. However, your OpenGL
implementation keeps the attribute stack on the server, avoiding unneces-
sary network delays.
GLboolean glIsVertexArray(GLuint array);
Returns GL_TRUE if array is the name of a vertex-array object that was
previously generated with glGenVertexArrays(), but has not been
subsequently deleted. Returns GL_FALSE if array is zero or a nonzero value
that is not the name of a vertex-array object.

Attribute Groups 111
There are about 20 different attribute groups, which can be saved and
restored by glPushAttrib() and glPopAttrib(). There are two client attribute
groups, which can be saved and restored by glPushClientAttrib() and
glPopClientAttrib(). For both server and client, the attributes are stored on
a stack, which has a depth of at least 16 saved attribute groups. (The actual
stack depths for your implementation can be obtained using GL_MAX_
ATTRIB_STACK_DEPTH and GL_MAX_CLIENT_ATTRIB_STACK_DEPTH
with glGetIntegerv().) Pushing a full stack or popping an empty one gener-
ates an error.
(See the tables in Appendix B to find out exactly which attributes are saved
for particular mask values—that is, which attributes are in a particular
attribute group.)
The special mask GL_ALL_ATTRIB_BITS is used to save and restore all the
state variables in all the attribute groups.
void glPushAttrib(GLbitfield mask);
void glPopAttrib(void);
glPushAttrib() saves all the attributes indicated by bits in mask by
pushing them onto the attribute stack. glPopAttrib() restores the values
of those state variables that were saved with the last glPushAttrib().
Table 2-8 lists the possible mask bits that can be logically ORed together
to save any combination of attributes. Each bit corresponds to a collection
of individual state variables. For example, GL_LIGHTING_BIT refers to all
the state variables related to lighting, which include the current material
color; the ambient, diffuse, specular, and emitted light; a list of the lights
that are enabled; and the directions of the spotlights. When glPopAttrib()
is called, all these variables are restored.
Mask Bit Attribute Group
GL_ACCUM_BUFFER_BIT accum-buffer
GL_ALL_ATTRIB_BITS —
GL_COLOR_BUFFER_BIT color-buffer
GL_CURRENT_BIT current
GL_DEPTH_BUFFER_BIT depth-buffer
Table 2-8 Attribute Groups
Compatibility
Extension
glPushAttrib
glPopAttrib
GL_ACCUM_
BUFFER_BIT
GL_ALL_ATTRIB_
BITS
GL_COLOR_
BUFFER_BIT
GL_CURRENT_BIT
GL_DEPTH_
BUFFER_BIT
GL_ENABLE_BIT
GL_EVAL_BIT
GL_FOG_BIT
GL_HINT_BIT
GL_LIGHTING_BIT
GL_LINE_BIT
GL_LIST_BIT
GL_
MULTISAMPLE_BIT
GL_PIXEL_MODE_
BIT
GL_POINT_BIT
GL_POLYGON_BIT
GL_POLYGON_
STIPPLE_BIT
GL_SCISSOR_BIT
GL_STENCIL_
BUFFER_BIT
GL_TEXTURE_BIT
GL_TRANSFORM_
BIT
GL_VIEWPORT_BIT

112 Chapter 2: State Management and Drawing Geometric Objects
GL_ENABLE_BIT enable
GL_EVAL_BIT eval
GL_FOG_BIT fog
GL_HINT_BIT hint
GL_LIGHTING_BIT lighting
GL_LINE_BIT line
GL_LIST_BIT list
GL_MULTISAMPLE_BIT multisample
GL_PIXEL_MODE_BIT pixel
GL_POINT_BIT point
GL_POLYGON_BIT polygon
GL_POLYGON_STIPPLE_BIT polygon-stipple
GL_SCISSOR_BIT scissor
GL_STENCIL_BUFFER_BIT stencil-buffer
GL_TEXTURE_BIT texture
GL_TRANSFORM_BIT transform
GL_VIEWPORT_BIT viewport
void glPushClientAttrib(GLbitfield mask);
void glPopClientAttrib(void);
glPushClientAttrib() saves all the attributes indicated by bits in mask
by pushing them onto the client attribute stack. glPopClientAttrib()
restores the values of those state variables that were saved with the last
glPushClientAttrib(). Table 2-9 lists the possible mask bits that can be
logically ORed together to save any combination of client attributes.
Two client attribute groups, feedback and select, cannot be saved or
restored with the stack mechanism.
Mask Bit Attribute Group
Table 2-8 (continued) Attribute Groups
Compatibility
Extension
glPushClientAttrib
glPopClientAttrib
GL_CLIENT_
PIXEL_STORE_
BIT
GL_CLIENT_
VERTEX_ARRAY_
BIT
GL_CLIENT_ALL_
ATTRIB_BITS

Some Hints for Building Polygonal Models of Surfaces 113
Some Hints for Building Polygonal Models
of Surfaces
Following are some techniques that you can use as you build polygonal
approximations of surfaces. You might want to review this section after
you’ve read Chapter 5 on lighting and Chapter 7 on display lists. The light-
ing conditions affect how models look once they’re drawn, and some of the
following techniques are much more efficient when used in conjunction
with display lists. As you read these techniques, keep in mind that when
lighting calculations are enabled, normal vectors must be specified to get
proper results.
Constructing polygonal approximations to surfaces is an art, and there is no
substitute for experience. This section, however, lists a few pointers that
might make it a bit easier to get started.
• Keep polygon orientations (windings) consistent. Make sure that when
viewed from the outside, all the polygons on the surface are oriented in
the same direction (all clockwise or all counterclockwise). Consistent
orientation is important for polygon culling and two-sided lighting.
Try to get this right the first time, as it’s excruciatingly painful to fix
the problem later. (If you use glScale*() to reflect geometry around
some axis of symmetry, you might change the orientation with
glFrontFace() to keep the orientations consistent.)
• When you subdivide a surface, watch out for any nontriangular
polygons. The three vertices of a triangle are guaranteed to lie on a
plane; any polygon with four or more vertices might not. Nonplanar
Mask Bit Attribute Group
GL_CLIENT_PIXEL_STORE_BIT pixel-store
GL_CLIENT_VERTEX_ARRAY_BIT vertex-array
GL_CLIENT_ALL_ATTRIB_BITS --
can’t be pushed or popped feedback
can’t be pushed or popped select
Table 2-9 Client Attribute Groups
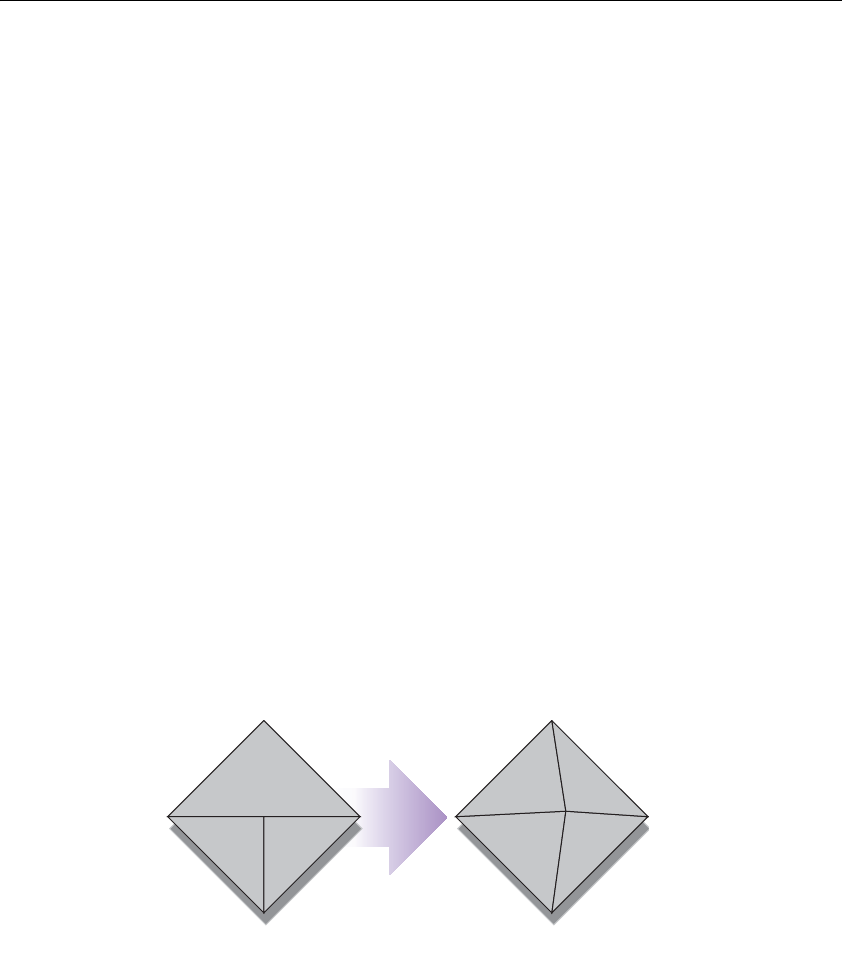
114 Chapter 2: State Management and Drawing Geometric Objects
polygons can be viewed from some orientation such that the edges
cross each other, and OpenGL might not render such polygons
correctly.
• There’s always a trade-off between the display speed and the quality of
the image. If you subdivide a surface into a small number of polygons,
it renders quickly but might have a jagged appearance; if you subdivide
it into millions of tiny polygons, it probably looks good but might take
a long time to render. Ideally, you can provide a parameter to the sub-
division routines that indicates how fine a subdivision you want, and if
the object is farther from the eye, you can use a coarser subdivision.
Also, when you subdivide, use large polygons where the surface is rela-
tively flat, and small polygons in regions of high curvature.
• For high-quality images, it’s a good idea to subdivide more on the sil-
houette edges than in the interior. If the surface is to be rotated relative
to the eye, this is tougher to do, as the silhouette edges keep moving.
Silhouette edges occur where the normal vectors are perpendicular to
the vector from the surface to the viewpoint—that is, when their vec-
tor dot product is zero. Your subdivision algorithm might choose to
subdivide more if this dot product is near zero.
• Try to avoid T-intersections in your models (see Figure 2-16). As shown,
there’s no guarantee that the line segments AB and BC lie on exactly
the same pixels as the segment AC. Sometimes they do, and sometimes
they don’t, depending on the transformations and orientation. This
can cause cracks to appear intermittently in the surface.
ABC
Undesirable OK
Figure 2-16 Modifying an Undesirable T-Intersection

Some Hints for Building Polygonal Models of Surfaces 115
• If you’re constructing a closed surface, be sure to use exactly the same
numbers for coordinates at the beginning and end of a closed loop, or
you can get gaps and cracks due to numerical round-off. Here’s an
example of bad code for a two-dimensional circle:
/* don’t use this code */
#define PI 3.14159265
#define EDGES 30
/* draw a circle */
glBegin(GL_LINE_STRIP);
for (i = 0; i <= EDGES; i++)
glVertex2f(cos((2*PI*i)/EDGES), sin((2*PI*i)/EDGES));
glEnd();
The edges meet exactly only if your machine manages to calculate
exactly the same values for the sine and cosine of 0 and of
(2*PI*EDGES/EDGES). If you trust the floating-point unit on your
machine to do this right, the authors have a bridge they’d like to sell
you} To correct the code, make sure that when i == EDGES, you use 0
for the sine and cosine, not 2*PI*EDGES/EDGES. (Or simpler still, use
GL_LINE_LOOP instead of GL_LINE_STRIP, and change the loop
termination condition to i < EDGES.)
An Example: Building an Icosahedron
To illustrate some of the considerations that arise in approximating a sur-
face, let’s look at some example code sequences. This code concerns the
vertices of a regular icosahedron (which is a Platonic solid composed of
20 faces that span 12 vertices, the face of each being an equilateral triangle).
An icosahedron can be considered a rough approximation of a sphere.
Example 2-19 defines the vertices and triangles making up an icosahedron
and then draws the icosahedron.
Example 2-19 Drawing an Icosahedron
#define X .525731112119133606
#define Z .850650808352039932
static GLfloat vdata[12][3] = {
{-X, 0.0, Z}, {X, 0.0, Z}, {-X, 0.0, -Z}, {X, 0.0, -Z},
{0.0, Z, X}, {0.0, Z, -X}, {0.0, -Z, X}, {0.0, -Z, -X},
{Z, X, 0.0}, {-Z, X, 0.0}, {Z, -X, 0.0}, {-Z, -X, 0.0}
};

116 Chapter 2: State Management and Drawing Geometric Objects
static GLuint tindices[20][3] = {
{1,4,0}, {4,9,0}, {4,5,9}, {8,5,4}, {1,8,4},
{1,10,8}, {10,3,8}, {8,3,5}, {3,2,5}, {3,7,2},
{3,10,7}, {10,6,7}, {6,11,7}, {6,0,11}, {6,1,0},
{10,1,6}, {11,0,9}, {2,11,9}, {5,2,9}, {11,2,7}
};
int i;
glBegin(GL_TRIANGLES);
for (i = 0; i < 20; i++) {
/* color information here */
glVertex3fv(&vdata[tindices[i][0]][0]);
glVertex3fv(&vdata[tindices[i][1]][0]);
glVertex3fv(&vdata[tindices[i][2]][0]);
}
glEnd();
The strange numbers X and Z are chosen so that the distance from the
origin to any of the vertices of the icosahedron is 1.0. The coordinates of
the 12 vertices are given in the array vdata[][], where the zeroth vertex is
^X, 0.0, Z}, the first is {X, 0.0, Z}, and so on. The array tindices[][] tells how
to link the vertices to make triangles. For example, the first triangle is made
from the zeroth, fourth, and first vertices. If you take the vertices for tri-
angles in the order given, all the triangles have the same orientation.
The line that mentions color information should be replaced by a com-
mand that sets the color of the ith face. If no code appears here, all faces are
drawn in the same color, and it will be impossible to discern the three-
dimensional quality of the object. An alternative to explicitly specifying
colors is to define surface normals and use lighting, as described in the next
subsection.
Note: In all the examples described in this section, unless the surface is to
be drawn only once, you should probably save the calculated vertex
and normal coordinates so that the calculations don’t need to be
repeated each time the surface is drawn. This can be done using your
own data structures or by constructing display lists (see Chapter 7).
Calculating Normal Vectors for a Surface
If a surface is to be lit, you need to supply the vector normal to the surface.
Calculating the normalized cross product of two vectors on that surface
provides their normal vector. With the flat surfaces of an icosahedron, all

Some Hints for Building Polygonal Models of Surfaces 117
three vertices defining a surface have the same normal vector. In this case,
the normal needs to be specified only once for each set of three vertices. The
code in Example 2-20 can replace the “color information here” line in
Example 2-19 for drawing the icosahedron.
Example 2-20 Generating Normal Vectors for a Surface
GLfloat d1[3], d2[3], norm[3];
for (j = 0; j < 3; j++) {
d1[j] = vdata[tindices[i][0]][j] - vdata[tindices[i][1]][j];
d2[j] = vdata[tindices[i][1]][j] - vdata[tindices[i][2]][j];
}
normcrossprod(d1, d2, norm);
glNormal3fv(norm);
The function normcrossprod() produces the normalized cross product of
two vectors, as shown in Example 2-21.
Example 2-21 Calculating the Normalized Cross Product of Two Vectors
void normalize(float v[3])
{
GLfloat d = sqrt(v[0]*v[0]+v[1]*v[1]+v[2]*v[2]);
if (d == 0.0) {
error(“zero length vector”);
return;
}
v[0] /= d;
v[1] /= d;
v[2] /= d;
}
void normcrossprod(float v1[3], float v2[3], float out[3])
{
out[0] = v1[1]*v2[2] - v1[2]*v2[1];
out[1] = v1[2]*v2[0] - v1[0]*v2[2];
out[2] = v1[0]*v2[1] - v1[1]*v2[0];
normalize(out);
}
If you’re using an icosahedron as an approximation for a shaded sphere,
you’ll want to use normal vectors that are perpendicular to the true surface
of the sphere, rather than perpendicular to the faces. For a sphere, the nor-
mal vectors are simple; each points in the same direction as the vector from

118 Chapter 2: State Management and Drawing Geometric Objects
the origin to the corresponding vertex. Since the icosahedron vertex data is
for an icosahedron of radius 1, the normal data and vertex data are identi-
cal. Here is the code that would draw an icosahedral approximation of a
smoothly shaded sphere (assuming that lighting is enabled, as described
in Chapter 5):
glBegin(GL_TRIANGLES);
for (i = 0; i < 20; i++) {
glNormal3fv(&vdata[tindices[i][0]][0]);
glVertex3fv(&vdata[tindices[i][0]][0]);
glNormal3fv(&vdata[tindices[i][1]][0]);
glVertex3fv(&vdata[tindices[i][1]][0]);
glNormal3fv(&vdata[tindices[i][2]][0]);
glVertex3fv(&vdata[tindices[i][2]][0]);
}
glEnd();
Improving the Model
A 20-sided approximation to a sphere doesn’t look good unless the image of
the sphere on the screen is quite small, but there’s an easy way to increase
the accuracy of the approximation. Imagine the icosahedron inscribed in
a sphere, and subdivide the triangles as shown in Figure 2-17. The newly
introduced vertices lie slightly inside the sphere, so push them to the sur-
face by normalizing them (dividing them by a factor to make them have
length 1). This subdivision process can be repeated for arbitrary accuracy.
The three objects shown in Figure 2-17 use 20, 80, and 320 approximating
triangles, respectively.
Figure 2-17 Subdividing to Improve a Polygonal Approximation to a Surface

Some Hints for Building Polygonal Models of Surfaces 119
Example 2-22 performs a single subdivision, creating an 80-sided spherical
approximation.
Example 2-22 Single Subdivision
void drawtriangle(float *v1, float *v2, float *v3)
{
glBegin(GL_TRIANGLES);
glNormal3fv(v1);
glVertex3fv(v1);
glNormal3fv(v2);
glVertex3fv(v2);
glNormal3fv(v3);
glVertex3fv(v3);
glEnd();
}
void subdivide(float *v1, float *v2, float *v3)
{
GLfloat v12[3], v23[3], v31[3];
GLint i;
for (i = 0; i < 3; i++) {
v12[i] = (v1[i]+v2[i])/2.0;
v23[i] = (v2[i]+v3[i])/2.0;
v31[i] = (v3[i]+v1[i])/2.0;
}
normalize(v12);
normalize(v23);
normalize(v31);
drawtriangle(v1, v12, v31);
drawtriangle(v2, v23, v12);
drawtriangle(v3, v31, v23);
drawtriangle(v12, v23, v31);
}
for (i = 0; i < 20; i++) {
subdivide(&vdata[tindices[i][0]][0],
&vdata[tindices[i][1]][0],
&vdata[tindices[i][2]][0]);
}
Example 2-23 is a slight modification of Example 2-22 that recursively
subdivides the triangles to the proper depth. If the depth value is 0, no

120 Chapter 2: State Management and Drawing Geometric Objects
subdivisions are performed, and the triangle is drawn as is. If the depth is 1,
a single subdivision is performed, and so on.
Example 2-23 Recursive Subdivision
void subdivide(float *v1, float *v2, float *v3, long depth)
{
GLfloat v12[3], v23[3], v31[3];
GLint i;
if (depth == 0) {
drawtriangle(v1, v2, v3);
return;
}
for (i = 0; i < 3; i++) {
v12[i] = (v1[i]+v2[i])/2.0;
v23[i] = (v2[i]+v3[i])/2.0;
v31[i] = (v3[i]+v1[i])/2.0;
}
normalize(v12);
normalize(v23);
normalize(v31);
subdivide(v1, v12, v31, depth-1);
subdivide(v2, v23, v12, depth-1);
subdivide(v3, v31, v23, depth-1);
subdivide(v12, v23, v31, depth-1);
}
Generalized Subdivision
A recursive subdivision technique such as the one described in Example 2-23
can be used for other types of surfaces. Typically, the recursion ends
if either a certain depth is reached or some condition on the curvature
is satisfied (highly curved parts of surfaces look better with more
subdivision).
To look at a more general solution to the problem of subdivision, consider
an arbitrary surface parameterized by two variables, u[0] and u[1]. Suppose
that two routines are provided:
void surf(GLfloat u[2], GLfloat vertex[3], GLfloat normal[3]);
float curv(GLfloat u[2]);
If u[] is passed to surf(), the corresponding three-dimensional vertex and
normal vectors (of length 1) are returned. If u[] is passed to curv(), the
curvature of the surface at that point is calculated and returned. (See an

Some Hints for Building Polygonal Models of Surfaces 121
introductory textbook on differential geometry for more information about
measuring surface curvature.)
Example 2-24 shows the recursive routine that subdivides a triangle until
either the maximum depth is reached or the maximum curvature at the
three vertices is less than some cutoff.
Example 2-24 Generalized Subdivision
void subdivide(float u1[2], float u2[2], float u3[2],
float cutoff, long depth)
{
GLfloat v1[3], v2[3], v3[3], n1[3], n2[3], n3[3];
GLfloat u12[2], u23[2], u32[2];
GLint i;
if (depth == maxdepth || (curv(u1) < cutoff &&
curv(u2) < cutoff && curv(u3) < cutoff)) {
surf(u1, v1, n1);
surf(u2, v2, n2);
surf(u3, v3, n3);
glBegin(GL_POLYGON);
glNormal3fv(n1); glVertex3fv(v1);
glNormal3fv(n2); glVertex3fv(v2);
glNormal3fv(n3); glVertex3fv(v3);
glEnd();
return;
}
for (i = 0; i < 2; i++) {
u12[i] = (u1[i] + u2[i])/2.0;
u23[i] = (u2[i] + u3[i])/2.0;
u31[i] = (u3[i] + u1[i])/2.0;
}
subdivide(u1, u12, u31, cutoff, depth+1);
subdivide(u2, u23, u12, cutoff, depth+1);
subdivide(u3, u31, u23, cutoff, depth+1);
subdivide(u12, u23, u31, cutoff, depth+1);
}
This page intentionally left blank

123
Chapter 3
3.Viewing
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
•View a geometric model in any orientation by transforming it in three-
dimensional space
• Control the location in three-dimensional space from which the model
is viewed
• Clip undesired portions of the model out of the scene that’s to be
viewed
• Manipulate the appropriate matrix stacks that control model
transformation for viewing, and project the model onto the screen
• Combine multiple transformations to mimic sophisticated systems in
motion, such as a solar system or an articulated robot arm
• Reverse or mimic the operations of the geometric processing pipeline

124 Chapter 3: Viewing
Note: For OpenGL Version 3.1, many of the techniques and functions
described in this chapter were removed through deprecation. The
concepts are still relevant, but the transformations described need to
be implemented in a vertex shader, as described in “Vertex
Processing” in Chapter 15.
Chapter 2 explained how to instruct OpenGL to draw the geometric models
you want displayed in your scene. Now you must decide how you want to
position the models in the scene, and you must choose a vantage point
from which to view the scene. You can use the default positioning and
vantage point, but most likely you want to specify them.
Look at the image on the cover of this book. The program that produced
that image contained a single geometric description of a building block.
Each block was carefully positioned in the scene: Some blocks were scattered
on the floor, some were stacked on top of each other on the table, and some
were assembled to make the globe. Also, a particular viewpoint had to be
chosen. Obviously, we wanted to look at the corner of the room containing
the globe. But how far away from the scene—and where exactly—should
the viewer be? We wanted to make sure that the final image of the scene
contained a good view out the window, that a portion of the floor was
visible, and that all the objects in the scene were not only visible but
presented in an interesting arrangement. This chapter explains how to use
OpenGL to accomplish these tasks: how to position and orient models in
three-dimensional space and how to establish the location—also in three-
dimensional space—of the viewpoint. All of these factors help determine
exactly what image appears on the screen.
You want to remember that the point of computer graphics is to create a
two-dimensional image of three-dimensional objects (it has to be two-
dimensional because it’s drawn on a flat screen), but you need to think in
three-dimensional coordinates while making many of the decisions that
determine what is drawn on the screen. A common mistake people make
when creating three-dimensional graphics is to start thinking too soon that
the final image appears on a flat, two-dimensional screen. Avoid thinking
about which pixels need to be drawn, and instead try to visualize three-
dimensional space. Create your models in some three-dimensional universe
that lies deep inside your computer, and let the computer do its job of
calculating which pixels to color.
A series of three computer operations converts an object’s three-dimensional
coordinates to pixel positions on the screen:

125
• Transformations, which are represented by matrix multiplication,
include modeling, viewing, and projection operations. Such operations
include rotation, translation, scaling, reflecting, orthographic projec-
tion, and perspective projection. Generally, you use a combination of
several transformations to draw a scene.
• Since the scene is rendered on a rectangular window, objects (or parts
of objects) that lie outside the window must be clipped. In three-
dimensional computer graphics, clipping occurs by throwing out
objects on one side of a clipping plane.
• Finally, a correspondence must be established between the transformed
coordinates and screen pixels. This is known as a viewport
transformation.
This chapter describes all of these operations, and how to control them, in
the following major sections:
• “Overview: The Camera Analogy” gives an overview of the transforma-
tion process by describing the analogy of taking a photograph with a
camera, presents a simple example program that transforms an object,
and briefly describes the basic OpenGL transformation commands.
• “Viewing and Modeling Transformations” explains in detail how to
specify and imagine the effect of viewing and modeling transforma-
tions. These transformations orient the model and the camera relative
to each other to obtain the desired final image.
• “Projection Transformations” describes how to specify the shape and
orientation of the viewing volume. The viewing volume determines how
a scene is projected onto the screen (with a perspective or orthographic
projection) and which objects or parts of objects are clipped out of the
scene.
• “Viewport Transformation” explains how to control the conversion of
three-dimensional model coordinates to screen coordinates.
• “Troubleshooting Transformations” presents some tips for discovering
why you might not be getting the desired effect from your modeling,
viewing, projection, and viewport transformations.
• “Manipulating the Matrix Stacks” discusses how to save and restore
certain transformations. This is particularly useful when you’re
drawing complicated objects that are built from simpler ones.
Chapter 3: Viewing

126 Chapter 3: Viewing
• “Additional Clipping Planes” describes how to specify additional
clipping planes beyond those defined by the viewing volume.
• “Examples of Composing Several Transformations” walks you through
a couple of more complicated uses for transformations.
• “Reversing or Mimicking Transformations” shows you how to take a
transformed point in window coordinates and reverse the transfor-
mation to obtain its original object coordinates. The transformation
itself (without reversal) can also be emulated.
In Version 1.3, new OpenGL functions were added to directly support row-
major (in OpenGL terms, transposed) matrices.
Overview: The Camera Analogy
The transformation process used to produce the desired scene for viewing is
analogous to taking a photograph with a camera. As shown in Figure 3-1,
the steps with a camera (or a computer) might be the following:
1. Set up your tripod and point the camera at the scene (viewing
transformation).
2. Arrange the scene to be photographed into the desired composition
(modeling transformation).
3. Choose a camera lens or adjust the zoom (projection transformation).
4. Determine how large you want the final photograph to be—for
example, you might want it enlarged (viewport transformation).
After these steps have been performed, the picture can be snapped or the
scene can be drawn.
Note that these steps correspond to the order in which you specify the
desired transformations in your program, not necessarily the order in which
the relevant mathematical operations are performed on an object’s vertices.
The viewing transformations must precede the modeling transformations
in your code, but you can specify the projection and viewport transforma-
tions at any point before drawing occurs. Figure 3-2 shows the order in
which these operations occur on your computer.

Overview: The Camera Analogy 127
With a computer
Viewing
Positioning the
viewing volume
in the world
Modeling
Projection
Viewport
Positioning the
models in the
world
Determining
the shape of
the viewing
volume
Tripod
Model
Lens
With a camera
Photograph
Figure 3-1 The Camera Analogy
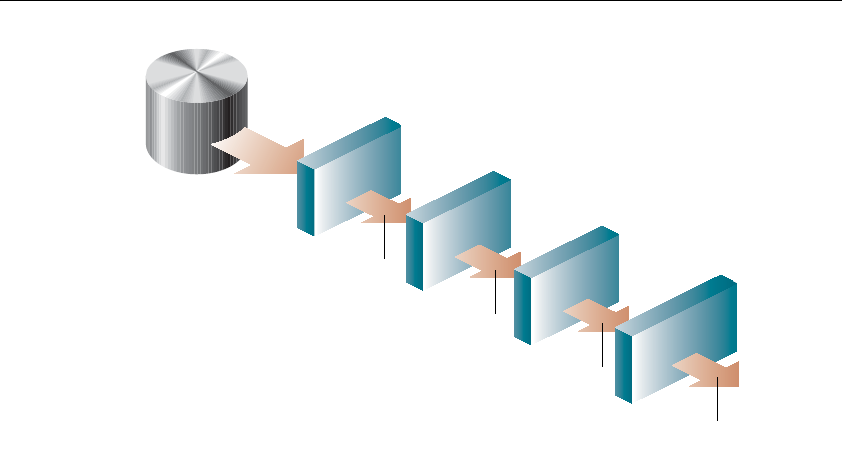
128 Chapter 3: Viewing
To specify viewing, modeling, and projection transformations, you con-
struct a 4 u4 matrix M, which is then multiplied by the coordinates of each
vertex v in the scene to accomplish the transformation:
v’ = Mv
(Remember that vertices always have four coordinates (x, y, z, w), although
in most cases w is 1, and for two-dimensional data, z is 0.) Note that view-
ing and modeling transformations are automatically applied to surface
normal vectors, in addition to vertices. (Normal vectors are used only in
eye coordinates.) This ensures that the normal vector’s relationship to the
vertex data is properly preserved.
The viewing and modeling transformations you specify are combined
to form the modelview matrix, which is applied to the incoming object
coordinates to yield eye coordinates. Next, if you’ve specified additional
clipping planes to remove certain objects from the scene or to provide
cutaway views of objects, these clipping planes are applied.
After that, OpenGL applies the projection matrix to yield clip coordinates.
This transformation defines a viewing volume; objects outside this volume
are clipped so that they’re not drawn in the final scene. After this point,
the perspective division is performed by dividing coordinate values by w, to
produce normalized device coordinates. (See for more information about the
Modelview
matrix
Projection
matrix
Perspective
division
Viewport
transformation
Vertex
Eye
coordinates
Object
coordinates
Clip
coordinates
Normalized
device
coordinates
Window
coordinates
x
y
z
w
Figure 3-2 Stages of Vertex Transformation

Overview: The Camera Analogy 129
meaning of the w-coordinate and how it affects matrix transformations.)
Finally, the transformed coordinates are converted to window coordinates by
applying the viewport transformation. You can manipulate the dimensions
of the viewport to cause the final image to be enlarged, shrunk, or stretched.
You might correctly suppose that the x- and y-coordinates are sufficient to
determine which pixels need to be drawn on the screen. However, all the
transformations are performed on the z-coordinates as well. This way, at the
end of this transformation process, the z-values correctly reflect the depth
of a given vertex (measured in distance away from the screen). One use for
this depth value is to eliminate unnecessary drawing. For example, suppose
two vertices have the same x- and y-values but different z-values. OpenGL
can use this information to determine which surfaces are obscured by other
surfaces and can then avoid drawing the hidden surfaces. (See Chapter 5
and Chapter 10 for more information about this technique, which is called
hidden-surface removal.)
As you’ve probably guessed by now, you need to know a few things about
matrix mathematics to get the most out of this chapter. If you want to brush
up on your knowledge in this area, you might consult a textbook on linear
algebra.
A Simple Example: Drawing a Cube
Example 3-1 draws a cube that’s scaled by a modeling transformation (see
Figure 3-3). The viewing transformation, gluLookAt(), positions and aims
the camera toward where the cube is drawn. A projection transformation
and a viewport transformation are also specified. The rest of this section
walks you through Example 3-1 and briefly explains the transformation
commands it uses. The succeeding sections contain a complete, detailed
discussion of all OpenGL transformation commands.
Figure 3-3 Transformed Cube

130 Chapter 3: Viewing
Example 3-1 Transformed Cube: cube.c
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glLoadIdentity(); /* clear the matrix */
/* viewing transformation */
gluLookAt(0.0, 0.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
glScalef(1.0, 2.0, 1.0); /* modeling transformation */
glutWireCube(1.0);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glFrustum(-1.0, 1.0, -1.0, 1.0, 1.5, 20.0);
glMatrixMode(GL_MODELVIEW);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}
The Viewing Transformation
Recall that the viewing transformation is analogous to positioning and
aiming a camera. In this code example, before the viewing transformation

Overview: The Camera Analogy 131
can be specified, the current matrix is set to the identity matrix with
glLoadIdentity(). This step is necessary since most of the transformation
commands multiply the current matrix by the specified matrix and then set
the result to be the current matrix. If you don’t clear the current matrix by
loading it with the identity matrix, you continue to combine previous
transformation matrices with the new one you supply. In some cases, you
do want to perform such combinations, but you also need to clear the
matrix sometimes.
In Example 3-1, after the matrix is initialized, the viewing transformation
is specified with gluLookAt(). The arguments for this command indicate
where the camera (or eye position) is placed, where it is aimed, and which
way is up. The arguments used here place the camera at (0, 0, 5), aim the
camera lens toward (0, 0, 0), and specify the up-vector as (0, 1, 0). The up-
vector defines a unique orientation for the camera.
If gluLookAt() was not called, the camera has a default position and orien-
tation. By default, the camera is situated at the origin, points down the
negative z-axis, and has an up-vector of (0, 1, 0). Therefore, in Example 3-1,
the overall effect is that gluLookAt() moves the camera five units along the
z-axis. (See “Viewing and Modeling Transformations” on page 137 for more
information about viewing transformations.)
The Modeling Transformation
You use the modeling transformation to position and orient the model. For
example, you can rotate, translate, or scale the model—or perform some
combination of these operations. In Example 3-1, glScalef() is the model-
ing transformation that is used. The arguments for this command specify
how scaling should occur along the three axes. If all the arguments are 1.0,
this command has no effect. In Example 3-1, the cube is drawn twice as
large in the y-direction. Thus, if one corner of the cube had originally been
at (3.0, 3.0, 3.0), that corner would wind up being drawn at (3.0, 6.0, 3.0).
The effect of this modeling transformation is to transform the cube so that
it isn’t a cube but a rectangular box.
Try This
Change the gluLookAt() call in Example 3-1 to the modeling transforma-
tion glTranslatef() with parameters (0.0, 0.0, –5.0). The result should look
exactly the same as when you used gluLookAt(). Why are the effects of
these two commands similar?
Note that instead of moving the camera (with a viewing transformation) so
that the cube could be viewed, you could have moved the cube away from
Try This

132 Chapter 3: Viewing
the camera (with a modeling transformation). This duality in the nature of
viewing and modeling transformations is why you need to think about the
effects of both types of transformations simultaneously. It doesn’t make
sense to try to separate the effects, but sometimes it’s easier to think about
them in one way more than in the other. This is also why modeling and
viewing transformations are combined into the modelview matrix before the
transformations are applied. (See “Viewing and Modeling Transformations”
on page 137 for more information about on how to think about modeling
and viewing transformations and how to specify them to get the results
you want.)
Also note that the modeling and viewing transformations are included
in the display() routine, along with the call that’s used to draw the cube,
glutWireCube(). In this way, display() can be used repeatedly to draw the
contents of the window if, for example, the window is moved or uncovered,
and you’ve ensured that the cube is drawn in the desired way each time, with
the appropriate transformations. The potential repeated use of display()
underscores the need to load the identity matrix before performing the view-
ing and modeling transformations, especially when other transformations
might be performed between calls to display().
The Projection Transformation
Specifying the projection transformation is like choosing a lens for a
camera. You can think of this transformation as determining what the field
of view or viewing volume is and therefore what objects are inside it and to
some extent how they look. This is equivalent to choosing among wide-
angle, normal, and telephoto lenses, for example. With a wide-angle lens,
you can include a wider scene in the final photograph than you can with a
telephoto lens, but a telephoto lens allows you to photograph objects as
though they’re closer to you than they actually are. In computer graphics,
you don’t have to pay $10,000 for a 2,000-millimeter telephoto lens; once
you’ve bought your graphics workstation, all you need to do is use a smaller
number for your field of view.
In addition to the field-of-view considerations, the projection transforma-
tion determines how objects are projected onto the screen, as the term sug-
gests. Two basic types of projections are provided for you by OpenGL, along
with several corresponding commands for describing the relevant parame-
ters in different ways. One type is the perspective projection, which matches
how you see things in daily life. Perspective makes objects that are farther
away appear smaller; for example, it makes railroad tracks appear to converge
Overview: The Camera Analogy 133
in the distance. If you’re trying to make realistic pictures, you’ll want to
choose perspective projection, which is specified with the glFrustum()
command in , “Viewing,”Example 3-1.
The other type of projection is orthographic, which maps objects directly
onto the screen without affecting their relative sizes. Orthographic
projection is used in architectural and computer-aided design applications
where the final image needs to reflect the measurements of objects, rather
than how they might look. Architects create perspective drawings to show
how particular buildings or interior spaces look when viewed from various
vantage points; the need for orthographic projection arises when blueprint
plans or elevations, which are used in the construction of buildings, are
generated. (See “Projection Transformations” on page 152 for a discussion
of ways to specify both kinds of projection transformations.)
Before glFrustum() can be called to set the projection transformation, some
preparation is needed. As shown in the reshape() routine in Example 3-1,
the command called glMatrixMode() is used first, with the argument
GL_PROJECTION. This indicates that the current matrix specifies the pro-
jection transformation and that subsequent transformation calls affect the
projection matrix. As you can see, a few lines later, glMatrixMode() is called
again, this time with GL_MODELVIEW as the argument. This indicates that
succeeding transformations now affect the modelview matrix instead of the
projection matrix. (See “Manipulating the Matrix Stacks” on page 164 for
more information about how to control the projection and modelview
matrices.)
Note that glLoadIdentity() is used to initialize the current projection
matrix so that only the specified projection transformation has an effect.
Now glFrustum() can be called, with arguments that define the parameters
of the projection transformation. In this example, both the projection
transformation and the viewport transformation are contained in the
reshape() routine, which is called when the window is first created and
whenever the window is moved or reshaped. This makes sense, because
both projecting (the width-to-height aspect ratio of the projection viewing
volume) and applying the viewport relate directly to the screen, and
specifically to the size or aspect ratio of the window on the screen.
Try This
Change the glFrustum() call in Example 3-1 to the more commonly used
Utility Library routine gluPerspective(), with parameters (60.0, 1.0, 1.5,
20.0). Then experiment with different values, especially for fovy and aspect.Try This

134 Chapter 3: Viewing
The Viewport Transformation
Together, the projection transformation and the viewport transformation
determine how a scene is mapped onto the computer screen. The projection
transformation specifies the mechanics of how the mapping should occur,
and the viewport indicates the shape of the available screen area into which
the scene is mapped. Since the viewport specifies the region the image occu-
pies on the computer screen, you can think of the viewport transformation
as defining the size and location of the final processed photograph—for
example, whether the photograph should be enlarged or shrunk.
The arguments for glViewport() describe the origin of the available screen
space within the window—(0, 0) in this example—and the width and
height of the available screen area, all measured in pixels on the screen. This
is why this command needs to be called within reshape(): If the window
changes size, the viewport needs to change accordingly. Note that the width
and height are specified using the actual width and height of the window;
often, you want to specify the viewport in this way, rather than give an
absolute size. (See “Viewport Transformation” on page 158 for more
information about how to define the viewport.)
Drawing the Scene
Once all the necessary transformations have been specified, you can draw
the scene (that is, take the photograph). As the scene is drawn, OpenGL
transforms each vertex of every object in the scene by the modeling and
viewing transformations. Each vertex is then transformed as specified by
the projection transformation and clipped if it lies outside the viewing
volume described by the projection transformation. Finally, the remaining
transformed vertices are divided by w and mapped onto the viewport.
General-Purpose Transformation Commands
This section discusses some OpenGL commands that you might find useful
as you specify desired transformations. You’ve already seen two of these com-
mands: glMatrixMode() and glLoadIdentity(). Four commands described
here—glLoadMatrix*(),glLoadTransposeMatrix*(),glMultMatrix*(), and
glMultTransposeMatrix*()—allow you to specify any transformation matrix
directly or to multiply the current matrix by that specified matrix. More
specific transformation commands—such as gluLookAt() and glScale*()—
are described in later sections.
Overview: The Camera Analogy 135
As described in the preceding section, you need to state whether you want
to modify the modelview or projection matrix before supplying a transfor-
mation command. You choose the matrix with glMatrixMode(). When you
use nested sets of OpenGL commands that might be called repeatedly,
remember to reset the matrix mode correctly. (The glMatrixMode() com-
mand can also be used to indicate the texture matrix; texturing is discussed
in detail in “The Texture Matrix Stack” in Chapter 9.)
You use the glLoadIdentity() command to clear the currently modifiable
matrix for future transformation commands, as these commands modify
the current matrix. Typically, you always call this command before specify-
ing projection or viewing transformations, but you might also call it before
specifying a modeling transformation.
If you want to specify explicitly a particular matrix to be loaded as the
current matrix, use glLoadMatrix*() or glLoadTransposeMatrix*().
Similarly, use glMultMatrix*() or glMultTransposeMatrix*() to multiply
the current matrix by the matrix passed in as an argument.
void glMatrixMode(GLenum mode);
Specifies whether the modelview, projection, or texture matrix will be
modified, using the argument GL_MODELVIEW, GL_PROJECTION, or
GL_TEXTURE for mode. Subsequent transformation commands affect the
specified matrix. Note that only one matrix can be modified at a time. By
default, the modelview matrix is the one that’s modifiable, and all three
matrices contain the identity matrix.
void glLoadIdentity(void);
Sets the currently modifiable matrix to the 4 u4 identity matrix.
void glLoadMatrix{fd}(const TYPE *m);
Sets the 16 values of the current matrix to those specified by m.
void glMultMatrix{fd}(const TYPE *m);
Multiplies the matrix specified by the 16 values pointed to by m by the
current matrix and stores the result as the current matrix.
Compatibility
Extension
glMatrixMode
GL_MODELVIEW
GL_PROJECTION
GL_TEXTURE
Compatibility
Extension
glLoadIdentity
Compatibility
Extension
glLoadMatrix
glMultMatrix

136 Chapter 3: Viewing
All matrix multiplication with OpenGL occurs as follows. Suppose the cur-
rent matrix is C, and the matrix specified with glMultMatrix*() or any of
the transformation commands is M. After multiplication, the final matrix is
always CM. Since matrix multiplication isn’t generally commutative, the
order makes a difference.
The argument for glLoadMatrix*() and glMultMatrix*() is a vector of 16
values (m1,m2, ... , m16) that specifies a matrix M stored in column-major
order as follows:
If you’re programming in C and you declare a matrix as m[4][4], then the
element m[i][j] is in the ith column and jth row of the common OpenGL
transformation matrix. This is the reverse of the standard C convention in
which m[i][j] is in row i and column j. One way to avoid confusion between
the column and the row is to declare your matrices as m[16].
Another way to avoid possible confusion is to call the OpenGL routines
glLoadTransposeMatrix*() and glMultTransposeMatrix*(), which use
row-major (the standard C convention) matrices as arguments.
You might be able to maximize efficiency by using display lists to store fre-
quently used matrices (and their inverses), rather than recomputing them.
void glLoadTransposeMatrix{fd}(const TYPE *m);
Sets the 16 values of the current matrix to those specified by m, whose
values are stored in row-major order. glLoadTransposeMatrix*(m) has
the same effect as glLoadMatrix*(mT).
void glMultTransposeMatrix{fd}(const TYPE *m);
Multiplies the matrix specified by the 16 values pointed to by m
by the current matrix and stores the result as the current matrix.
glMultTransposeMatrix*(m) has the same effect as glMultMatrix*(mT).
M =
m
1
m
5
m
9
m
13
m
2
m
6
m
10
m
14
m
3
m
7
m
11
m
15
m
4
m
8
m
12
m
16
Compatibility
Extension
glLoadTranspose
Matrix
glMultTranspose
Matrix

Viewing and Modeling Transformations 137
(See “Display List Design Philosophy” in Chapter 7.) OpenGL implementa-
tions often must compute the inverse of the modelview matrix so that nor-
mals and clipping planes can be correctly transformed to eye coordinates.
Viewing and Modeling Transformations
Viewing and modeling transformations are inextricably related in OpenGL
and are, in fact, combined into a single modelview matrix. (See “A Simple
Example: Drawing a Cube” on page 129.) One of the toughest problems
newcomers to computer graphics face is understanding the effects of com-
bined three-dimensional transformations. As you’ve already seen, there are
alternative ways to think about transformations—do you want to move the
camera in one direction or move the object in the opposite direction? Each
way of thinking about transformations has advantages and disadvantages,
but in some cases one way more naturally matches the effect of the
intended transformation. If you can find a natural approach for your partic-
ular application, it’s easier to visualize the necessary transformations and
then write the corresponding code to specify the matrix manipulations. The
first part of this section discusses how to think about transformations; later,
specific commands are presented. For now, we use only the matrix-manip-
ulation commands you’ve already seen. Finally, keep in mind that you must
call glMatrixMode() with GL_MODELVIEW as its argument prior to per-
forming modeling or viewing transformations.
Thinking about Transformations
Let’s start with a simple case of two transformations: a 45-degree counter-
clockwise rotation about the origin around the z-axis and a translation
down the x-axis. Suppose that the object you’re drawing is small compared
with the translation (so that you can see the effect of the translation) and
that it’s originally located at the origin. If you rotate the object first and
then translate it, the rotated object appears on the x-axis. If you translate it
down the x-axis first, however, and then rotate about the origin, the object
is on the line y = x, as shown in Figure 3-4. In general, the order of transfor-
mations is critical. If you do transformation A and then transformation B,
you almost always get something different than if you do them in the oppo-
site order.
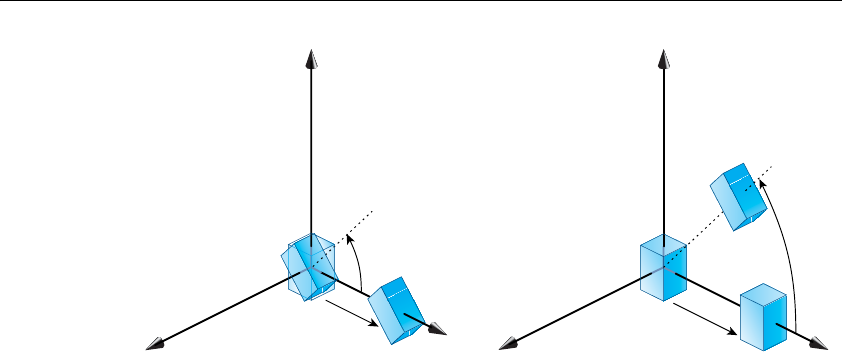
138 Chapter 3: Viewing
Now let’s talk about the order in which you specify a series of transforma-
tions. All viewing and modeling transformations are represented as 4 u4
matrices. Each successive glMultMatrix*() or transformation command
multiplies a new 4 u4 matrix M by the current modelview matrix C to yield
CM. Finally, vertices v are multiplied by the current modelview matrix. This
process means that the last transformation command called in your pro-
gram is actually the first one applied to the vertices: CMv. Thus, one way of
looking at it is to say that you have to specify the matrices in the reverse
order. Like many other things, however, once you’ve gotten used to think-
ing about this correctly, backward will seem like forward.
Consider the following code sequence, which draws a single point using
three transformations:
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glMultMatrixf(N); /* apply transformation N */
glMultMatrixf(M); /* apply transformation M */
glMultMatrixf(L); /* apply transformation L */
glBegin(GL_POINTS);
glVertex3f(v); /* draw transformed vertex v */
glEnd();
With this code, the modelview matrix successively contains I,N,NM, and
finally NML, where I represents the identity matrix. The transformed vertex
is NMLv. Thus, the vertex transformation is N(M(Lv))—that is, v is multi-
plied first by L, the resulting Lv is multiplied by M, and the resulting MLv
is multiplied by N. Notice that the transformations to vertex v effectively
y
x
1-Rotate
2-Translate
x
zz
y
2-Rotate
1-Translate
Figure 3-4 Rotating First or Translating First

Viewing and Modeling Transformations 139
occur in the opposite order than they were specified. (Actually, only a single
multiplication of a vertex by the modelview matrix occurs; in this example,
the N,M, and L matrices are already multiplied into a single matrix before
it’s applied to v.)
Grand, Fixed Coordinate System
Thus, if you like to think in terms of a grand, fixed coordinate system—in
which matrix multiplications affect the position, orientation, and scaling of
your model—you have to think of the multiplications as occurring in the
opposite order from how they appear in the code. Using the simple example
shown on the left side of Figure 3-4 (a rotation about the origin and a trans-
lation along the x-axis), if you want the object to appear on the axis after
the operations, the rotation must occur first, followed by the translation. To
do this, you’ll need to reverse the order of operations, so the code looks
something like this (where R is the rotation matrix and T is the translation
matrix):
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glMultMatrixf(T); /* translation */
glMultMatrixf(R); /* rotation */
draw_the_object();
Moving a Local Coordinate System
Another way to view matrix multiplications is to forget about a grand, fixed
coordinate system in which your model is transformed and instead imagine
that a local coordinate system is tied to the object you’re drawing. All
operations occur relative to this changing coordinate system. With this
approach, the matrix multiplications now appear in the natural order in
the code. (Regardless of which analogy you’re using, the code is the same,
but how you think about it differs.) To see this in the translation-rotation
example, begin by visualizing the object with a coordinate system tied to it.
The translation operation moves the object and its coordinate system down
the x-axis. Then, the rotation occurs about the (now-translated) origin, so
the object rotates in place in its position on the axis.
This approach is what you should use for applications such as articulated
robot arms, where there are joints at the shoulder, elbow, and wrist, and on
each of the fingers. To figure out where the tips of the fingers go relative to
the body, you’d like to start at the shoulder, go down to the wrist, and so
on, applying the appropriate rotations and translations at each joint.
Thinking about it in reverse would be far more confusing.

140 Chapter 3: Viewing
This second approach can be problematic, however, in cases where scaling
occurs, and especially so when the scaling is nonuniform (scaling different
amounts along the different axes). After uniform scaling, translations move
a vertex by a multiple of what they did before, as the coordinate system is
stretched. Nonuniform scaling mixed with rotations may make the axes of
the local coordinate system nonperpendicular.
As mentioned earlier, you normally issue viewing transformation commands
in your program before any modeling transformations. In this way, a vertex
in a model is first transformed into the desired orientation and then trans-
formed by the viewing operation. Since the matrix multiplications must be
specified in reverse order, the viewing commands need to come first. Note,
however, that you don’t need to specify either viewing or modeling trans-
formations if you’re satisfied with the default conditions. If there’s no view-
ing transformation, the “camera” is left in the default position at the origin,
pointing toward the negative z-axis; if there’s no modeling transformation,
the model isn’t moved, and it retains its specified position, orientation,
and size.
Since the commands for performing modeling transformations can be
used to perform viewing transformations, modeling transformations are
discussed first, even if viewing transformations are actually issued first. This
order for discussion also matches the way many programmers think when
planning their code. Often, they write all the code necessary to compose the
scene, which involves transformations to position and orient objects cor-
rectly relative to each other. Next, they decide where they want the view-
point to be relative to the scene they’ve composed, and then they write the
viewing transformations accordingly.
Modeling Transformations
The three OpenGL routines for modeling transformations are glTranslate*(),
glRotate*(), and glScale*(). As you might suspect, these routines transform
an object (or coordinate system, if you’re thinking of it in that way) by
moving, rotating, stretching, shrinking, or reflecting it. All three commands
are equivalent to producing an appropriate translation, rotation, or scaling
matrix, and then calling glMultMatrix*() with that matrix as the argu-
ment. However, using these three routines might be faster than using
glMultMatrix*(). OpenGL automatically computes the matrices for you.
(See if you’re interested in the details.)
Viewing and Modeling Transformations 141
In the command summaries that follow, each matrix multiplication is
described in terms of what it does to the vertices of a geometric object using
the fixed coordinate system approach, and in terms of what it does to the
local coordinate system that’s attached to an object.
Translate
Figure 3-5 shows the effect of glTranslate*().
Note that using (0.0, 0.0, 0.0) as the argument for glTranslate*() is the
identity operation—that is, it has no effect on an object or its local
coordinate system.
void glTranslate{fd}(TYPE x,TYPE y,TYPE z);
Multiplies the current matrix by a matrix that moves (translates) an object
by the given x-, y-, and z-values (or moves the local coordinate system by
the same amounts).
Compatibility
Extension
glTranslate
x
z
y
Figure 3-5 Translating an Object

142 Chapter 3: Viewing
Rotate
The effect of glRotatef(45.0, 0.0, 0.0, 1.0), which is a rotation of 45 degrees
about the z-axis, is shown in Figure 3-6.
Note that an object that lies farther from the axis of rotation is more dra-
matically rotated (has a larger orbit) than an object drawn near the axis.
Also, if the angle argument is zero, the glRotate*() command has no effect.
Scale
void glRotate{fd}(TYPE angle,TYPE x,TYPE y,TYPE z);
Multiplies the current matrix by a matrix that rotates an object (or the
local coordinate system) in a counterclockwise direction about the ray
from the origin through the point (x, y, z). The angle parameter specifies
the angle of rotation in degrees.
void glScale{fd}(TYPE x,TYPE y,TYPE z);
Multiplies the current matrix by a matrix that stretches, shrinks, or reflects
an object along the axes. Each x-,y-, and z-coordinate of every point in
the object is multiplied by the corresponding argument x,y, or z. With the
local coordinate system approach, the local coordinate axes are stretched,
shrunk, or reflected by the x-,y-, and z-factors, and the associated object
is transformed with them.
Compatibility
Extension
glRotate
y
x
z
Figure 3-6 Rotating an Object
Compatibility
Extension
glScale
Viewing and Modeling Transformations 143
Figure 3-7 shows the effect of glScalef(2.0, –0.5, 1.0).
glScale*() is the only one of the three modeling transformations that changes
the apparent size of an object: Scaling with values greater than 1.0 stretches
an object, and using values less than 1.0 shrinks it. Scaling with a 1.0 value
reflects an object across an axis. The identity values for scaling are (1.0, 1.0,
1.0). In general, you should limit your use of glScale*() to those cases where
it is necessary. Using glScale*() decreases the performance of lighting
calculations, because the normal vectors have to be renormalized after
transformation.
Note: A scale value of zero collapses all object coordinates along that axis to
zero. It’s usually not a good idea to do this, because such an operation
cannot be undone. Mathematically speaking, the matrix cannot be
inverted, and inverse matrices are required for certain lighting oper-
ations (see Chapter 5). Sometimes collapsing coordinates does make
sense; the calculation of shadows on a planar surface is one such
application (see “Shadows” in Chapter 14). In general, if a coordinate
system is to be collapsed, the projection matrix should be used, rather
than the modelview matrix.
A Modeling Transformation Code Example
Example 3-2 is a portion of a program that renders a triangle four times, as
shown in Figure 3-8. These are the four transformed triangles:
• A solid wireframe triangle is drawn with no modeling
transformation.
x
z
x
zy
y
Figure 3-7 Scaling and Reflecting an Object
144 Chapter 3: Viewing
• The same triangle is drawn again, but with a dashed line stipple, and
translated (to the left—along the negative x-axis).
• A triangle is drawn with a long dashed line stipple, with its height
(y-axis) halved and its width (x-axis) increased by 50 percent.
• A rotated triangle, made of dotted lines, is drawn.
x
z
y
x
z
y
x
z
y
x
z
y
Figure 3-8 Modeling Transformation Example

Viewing and Modeling Transformations 145
Example 3-2 Using Modeling Transformations: model.c
glLoadIdentity();
glColor3f(1.0, 1.0, 1.0);
draw_triangle(); /* solid lines */
glEnable(GL_LINE_STIPPLE); /* dashed lines */
glLineStipple(1, 0xF0F0);
glLoadIdentity();
glTranslatef(-20.0, 0.0, 0.0);
draw_triangle();
glLineStipple(1, 0xF00F); /*long dashed lines */
glLoadIdentity();
glScalef(1.5, 0.5, 1.0);
draw_triangle();
glLineStipple(1, 0x8888); /* dotted lines */
glLoadIdentity();
glRotatef(90.0, 0.0, 0.0, 1.0);
draw_triangle();
glDisable(GL_LINE_STIPPLE);
Note the use of glLoadIdentity() to isolate the effects of modeling transfor-
mations; initializing the matrix values prevents successive transformations
from having a cumulative effect. Even though using glLoadIdentity()
repeatedly has the desired effect, it may be inefficient, because you may
have to respecify viewing or modeling transformations. (See “Manipulating
the Matrix Stacks” on page 164 for a better way to isolate transformations.)
Note: Sometimes, programmers who want a continuously rotating object
attempt to achieve this by repeatedly applying a rotation matrix that
has small values. The problem with this technique is that because of
round-off errors, the product of thousands of tiny rotations gradually
drifts away from the value you really want (it might even become
something that isn’t a rotation). Instead of using this technique,
increment the angle and issue a new rotation command with the
new angle at each update step.
Nate Robins’ Transformation Tutorial
If you have downloaded Nate Robins’ suite of tutorial programs, this is an
opportune time to run the transformation tutorial. (For information on
how and where to download these programs, see “Errata” on page xlii.)
With this tutorial, you can experiment with the effects of rotation,
translation, and scaling.

146 Chapter 3: Viewing
Viewing Transformations
A viewing transformation changes the position and orientation of the
viewpoint. If you recall the camera analogy, the viewing transformation
positions the camera tripod, pointing the camera toward the model. Just
as you move the camera to some position and rotate it until it points in
the desired direction, viewing transformations are generally composed of
translations and rotations. Also remember that to achieve a certain scene
composition in the final image or photograph, you can either move the
camera or move all the objects in the opposite direction. Thus, a modeling
transformation that rotates an object counterclockwise is equivalent to
a viewing transformation that rotates the camera clockwise, for example.
Finally, keep in mind that the viewing transformation commands must be
called before any modeling transformations are performed, so that the
modeling transformations take effect on the objects first.
You can manufacture a viewing transformation in any of several ways,
as described next. You can also choose to use the default location and
orientation of the viewpoint, which is at the origin, looking down the
negative z-axis.
• Use one or more modeling transformation commands (that is,
glTranslate*() and glRotate*()). You can think of the effect of these
transformations as moving the camera position or as moving all the
objects in the world, relative to a stationary camera.
• Use the Utility Library routine gluLookAt() to define a line of sight. This
routine encapsulates a series of rotation and translation commands.
• Create your own utility routine to encapsulate rotations and transla-
tions. Some applications might require custom routines that allow you
to specify the viewing transformation in a convenient way. For example,
you might want to specify the roll, pitch, and heading rotation angles
of a plane in flight, or you might want to specify a transformation in
terms of polar coordinates for a camera that’s orbiting around an
object.
Using glTranslate*() and glRotate*()
When you use modeling transformation commands to emulate viewing
transformations, you’re trying to move the viewpoint in a desired way
while keeping the objects in the world stationary. Since the viewpoint
is initially located at the origin and since objects are often most easily
constructed there as well (see Figure 3-9), you generally have to perform

Viewing and Modeling Transformations 147
some transformation so that the objects can be viewed. Note that, as shown
in the figure, the camera initially points down the negative z-axis. (You’re
seeing the back of the camera.)
In the simplest case, you can move the viewpoint backward, away from
the objects; this has the same effect as moving the objects forward, or
away from the viewpoint. Remember that, by default, forward is down the
negative z-axis; if you rotate the viewpoint, forward has a different mean-
ing. Therefore, to put five units of distance between the viewpoint and
the objects by moving the viewpoint, as shown in Figure 3-10, use
glTranslatef(0.0, 0.0, -5.0);
x
z
y
Figure 3-9 Object and Viewpoint at the Origin
x
y
z
x
y
z
Figure 3-10 Separating the Viewpoint and the Object

148 Chapter 3: Viewing
This routine moves the objects in the scene –5 units along the z-axis. This
is also equivalent to moving the camera +5 units along the z-axis.
Now suppose you want to view the objects from the side. Should you issue
a rotate command before or after the translate command? If you’re thinking
in terms of a grand, fixed coordinate system, first imagine both the object
and the camera at the origin. You could rotate the object first and then
move it away from the camera so that the desired side is visible. You know
that with the fixed coordinate system approach, commands have to be
issued in the opposite order in which they should take effect, so you know
that you need to write the translate command in your code first and follow
it with the rotate command.
Now let’s use the local coordinate system approach. In this case, think about
moving the object and its local coordinate system away from the origin; then,
the rotate command is carried out using the now-translated coordinate sys-
tem. With this approach, commands are issued in the order in which they’re
applied, so once again the translate command comes first. Thus, the sequence
of transformation commands to produce the desired result is
glTranslatef(0.0, 0.0, -5.0);
glRotatef(90.0, 0.0, 1.0, 0.0);
If you’re having trouble keeping track of the effect of successive matrix mul-
tiplications, try using both the fixed and local coordinate system approaches
and see whether one makes more sense to you. Note that with the fixed
coordinate system, rotations always occur about the grand origin, whereas
with the local coordinate system, rotations occur about the origin of the
local system. You might also try using the gluLookAt() utility routine
described next.
Using the gluLookAt() Utility Routine
Often, programmers construct a scene around the origin or some other conve-
nient location and then want to look at it from an arbitrary point to get a good
view of it. As its name suggests, the gluLookAt() utility routine is designed for
just this purpose. It takes three sets of arguments, which specify the location
of the viewpoint, define a reference point toward which the camera is aimed,
and indicate which direction is up. Choose the viewpoint to yield the desired
view of the scene. The reference point is typically somewhere in the middle of
the scene. (If you’ve built your scene at the origin, the reference point is prob-
ably the origin.) It might be a little trickier to specify the correct up-vector.
Again, if you’ve built some real-world scene at or around the origin and if
you’ve been taking the positive y-axis to point upward, then that’s your up-
vector for gluLookAt(). However, if you’re designing a flight simulator, up is
Viewing and Modeling Transformations 149
the direction perpendicular to the plane’s wings, from the plane toward the
sky when the plane is right-side-up on the ground.
The gluLookAt() routine is particularly useful when you want to pan across
a landscape, for instance. With a viewing volume that’s symmetric in both
x and y, the (eyex, eyey, eyez) point specified is always in the center of the
image on the screen, so you can use a series of commands to move this
point slightly, thereby panning across the scene.
In the default position, the camera is at the origin, is looking down the
negative z-axis, and has the positive y-axis as straight up. This is the same
as calling
gluLookAt(0.0, 0.0, 0.0, 0.0, 0.0, -100.0, 0.0, 1.0, 0.0);
The z-value of the reference point is –100.0, but could be any negative z,
because the line of sight will remain the same. In this case, you don’t actu-
ally want to call gluLookAt(), because this is the default (see Figure 3-11),
void gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez,
GLdouble centerx, GLdouble centery, GLdouble centerz,
GLdouble upx, GLdouble upy, GLdouble upz);
Defines a viewing matrix and multiplies it to the right of the current
matrix. The desired viewpoint is specified by eyex,eyey, and eyez. The
centerx,centery, and centerz arguments specify any point along the desired
line of sight, but typically they specify some point in the center of the
scene being looked at. The upx,upy, and upz arguments indicate which
direction is up (that is, the direction from the bottom to the top of the
viewing volume).
x
y
z
Up-vector
Figure 3-11 Default Camera Position

150 Chapter 3: Viewing
and you are already there. (The lines extending from the camera represent
the viewing volume, which indicates its field of view.)
Figure 3-12 shows the effect of a typical gluLookAt() routine. The camera
position (eyex, eyey, eyez) is at (4, 2, 1). In this case, the camera is looking
right at the model, so the reference point is at (2, 4, –3). An orientation
vector of (2, 2, –1) is chosen to rotate the viewpoint to this 45-degree angle.
Therefore, to achieve this effect, call
gluLookAt(4.0, 2.0, 1.0, 2.0, 4.0, -3.0, 2.0, 2.0, -1.0);
Note that gluLookAt() is part of the Utility Library, rather than the basic
OpenGL library. This isn’t because it’s not useful, but because it encapsulates
several basic OpenGL commands—specifically, glTranslate*() and
glRotate*(). To see this, imagine a camera located at an arbitrary viewpoint
and oriented according to a line of sight, both as specified with gluLookAt()
and a scene located at the origin. To “undo” what gluLookAt() does, you
need to transform the camera so that it sits at the origin and points down
the negative z-axis, the default position. A simple translate moves the cam-
era to the origin. You can easily imagine a series of rotations about each of
the three axes of a fixed coordinate system that would orient the camera
so that it pointed toward negative z-values. Since OpenGL allows rotation
about an arbitrary axis, you can accomplish any desired rotation of the cam-
era with a single glRotate*() command.
x
y
z
Up-vector
Figure 3-12 Using gluLookAt()

Viewing and Modeling Transformations 151
Note: You can have only one active viewing transformation. You cannot try
to combine the effects of two viewing transformations, any more
than a camera can have two tripods. If you want to change the posi-
tion of the camera, make sure you call glLoadIdentity() to erase the
effects of any current viewing transformation.
Nate Robins’ Projection Tutorial
If you have Nate Robins’ suite of tutorial programs, run the projection
tutorial. With this tutorial, you can see the effects of changes to the
parameters of gluLookAt().
Advanced
To transform any arbitrary vector so that it’s coincident with another
arbitrary vector (for instance, the negative z-axis), you need to do a little
mathematics. The axis about which you want to rotate is given by the cross
product of the two normalized vectors. To find the angle of rotation, nor-
malize the initial two vectors. The cosine of the desired angle between the
vectors is equal to the dot product of the normalized vectors. The angle of
rotation around the axis given by the cross product is always between 0 and
180 degrees. (See Appendix I, “Built-In OpenGL Shading Language Vari-
ables and Functions,”1 for definitions of cross and dot products.)
Note that computing the angle between two normalized vectors by taking
the inverse cosine of their dot product is not very accurate, especially for
small angles, but it should work well enough to get you started.
Creating a Custom Utility Routine
Advanced
For some specialized applications, you might want to define your own
transformation routine. Since this is rarely done and is a fairly advanced
topic, it’s left mostly as an exercise for the reader. The following exercises
suggest two custom viewing transformations that might be useful.
Try This
• Suppose you’re writing a flight simulator and you’d like to display
the world from the point of view of the pilot of a plane. The world is
described in a coordinate system with the origin on the runway and
the plane at coordinates (x, y, z). Suppose further that the plane has
some roll,pitch, and heading (these are rotation angles of the plane
relative to its center of gravity).
1This appendix is available online at http://www.opengl-redbook.com/appendices/.
Advanced
Advanced
Try This

152 Chapter 3: Viewing
Show that the following routine could serve as the viewing
transformation:
void pilotView{GLdouble planex, GLdouble planey,
GLdouble planez, GLdouble roll,
GLdouble pitch, GLdouble heading)
{
glRotated(roll, 0.0, 0.0, 1.0);
glRotated(pitch, 0.0, 1.0, 0.0);
glRotated(heading, 1.0, 0.0, 0.0);
glTranslated(-planex, -planey, -planez);
}
• Suppose your application involves orbiting the camera around an
object that’s centered at the origin. In this case, you’d like to specify
the viewing transformation by using polar coordinates. Let the distance
variable define the radius of the orbit or how far the camera is from the
origin. (Initially, the camera is moved distance units along the positive
z-axis.) The azimuth describes the angle of rotation of the camera about
the object in the xy-plane, measured from the positive y-axis. Similarly,
elevation is the angle of rotation of the camera in the yz-plane measured
from the positive z-axis. Finally, twist represents the rotation of the
viewing volume around its line of sight.
Show that the following routine could serve as the viewing
transformation:
void polarView{GLdouble distance, GLdouble twist,
GLdouble elevation, GLdouble azimuth)
{
glTranslated(0.0, 0.0, -distance);
glRotated(-twist, 0.0, 0.0, 1.0);
glRotated(-elevation, 1.0, 0.0, 0.0);
glRotated(azimuth, 0.0, 0.0, 1.0);
}
Projection Transformations
The preceding section described how to compose the desired modelview
matrix so that the correct modeling and viewing transformations are
applied. This section explains how to define the desired projection matrix,
which is also used to transform the vertices in your scene. Before you issue
any of the transformation commands described in this section, remember
to call

Projection Transformations 153
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
so that the commands affect the projection matrix, rather than the model-
view matrix, and so that you avoid compound projection transformations.
Since each projection transformation command completely describes a par-
ticular transformation, typically you don’t want to combine a projection
transformation with another transformation.
The purpose of the projection transformation is to define a viewing volume,
which is used in two ways. The viewing volume determines how an object
is projected onto the screen (that is, by using a perspective or an orthographic
projection), and it defines which objects or portions of objects are clipped
out of the final image. You can think of the viewpoint we’ve been talking
about as existing at one end of the viewing volume. At this point, you might
want to reread “A Simple Example: Drawing a Cube” on page 129 for its
overview of all the transformations, including projection transformations.
Perspective Projection
The most unmistakable characteristic of perspective projection is fore-
shortening: The farther an object is from the camera, the smaller it appears
in the final image. This occurs because the viewing volume for a perspective
projection is a frustum of a pyramid (a truncated pyramid whose top has
been cut off by a plane parallel to its base). Objects that fall within the view-
ing volume are projected toward the apex of the pyramid, where the camera
or viewpoint is. Objects that are closer to the viewpoint appear larger
because they occupy a proportionally larger amount of the viewing volume
than those that are farther away, in the larger part of the frustum. This
method of projection is commonly used for animation, visual simulation,
and any other applications that strive for some degree of realism, because
it’s similar to how our eye (or a camera) works.
The command to define a frustum, glFrustum(), calculates a matrix that
accomplishes perspective projection and multiplies the current projection
matrix (typically the identity matrix) by it. Recall that the viewing volume
is used to clip objects that lie outside of it; the four sides of the frustum, its
top, and its base correspond to the six clipping planes of the viewing vol-
ume, as shown in Figure 3-13. Objects or parts of objects outside these
planes are clipped from the final image. Note that glFrustum() doesn’t
require you to define a symmetric viewing volume.
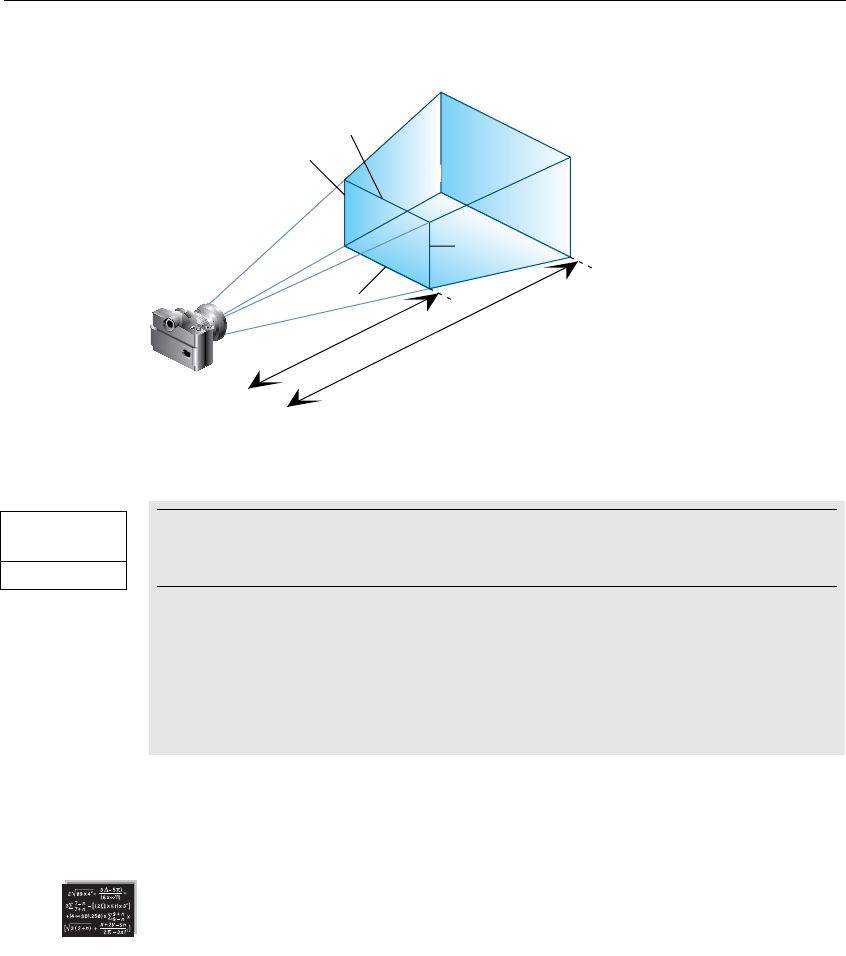
154 Chapter 3: Viewing
The frustum has a default orientation in three-dimensional space. You can
perform rotations or translations on the projection matrix to alter this
orientation, but this is tricky and nearly always avoidable.
Advanced
The frustum doesn’t have to be symmetrical, and its axis isn’t necessarily
aligned with the z-axis. For example, you can use glFrustum() to draw
a picture as if you were looking through a rectangular window of a house,
where the window was above and to the right of you. Photographers use
such a viewing volume to create false perspectives. You might use it to have
the hardware calculate images at resolutions much higher than normal, per-
haps for use on a printer. For example, if you want an image that has twice
void glFrustum(GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top,
GLdouble near, GLdouble far);
Creates a matrix for a perspective-view frustum and multiplies the current
matrix by it. The frustum’s viewing volume is defined by the parameters:
(left, bottom, –near) and (right, top, –near) specify the (x, y, z) coordinates of
the lower left and upper right corners, respectively, of the near clipping
plane; near and far give the distances from the viewpoint to the near and
far clipping planes. They should always be positive.
near
far
left
right
top
bottom
Frustum
Figure 3-13 Perspective Viewing Volume Specified by glFrustum()
Compatibility
Extension
glFrustum
Advanced
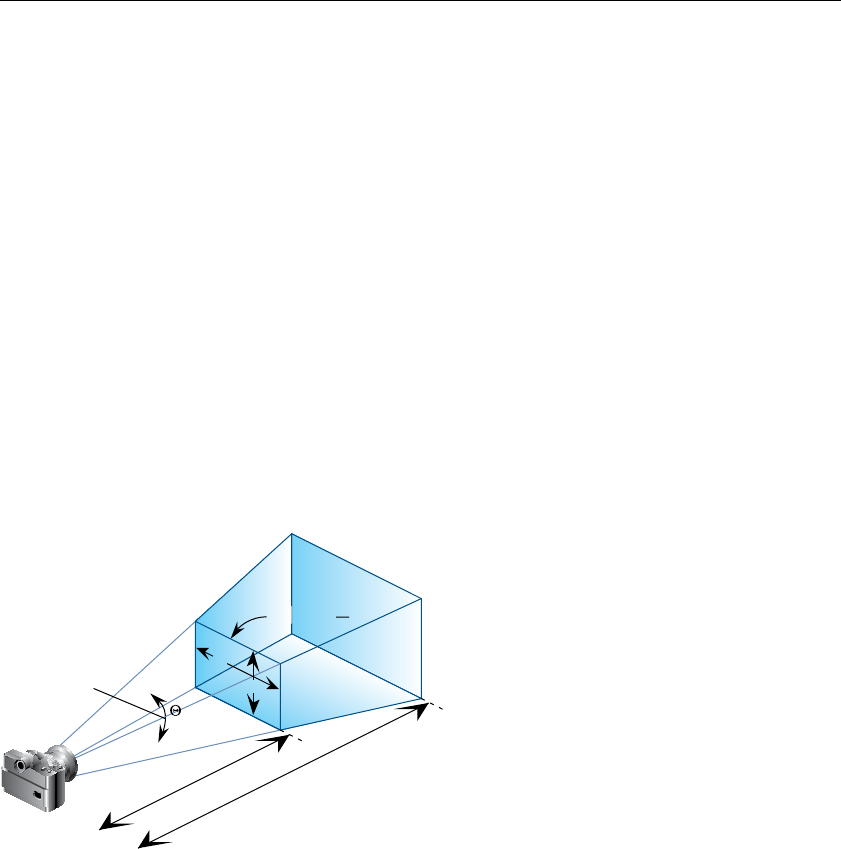
Projection Transformations 155
the resolution of your screen, draw the same picture four times, each time
using the frustum to cover the entire screen with one-quarter of the image.
After each quarter of the image is rendered, you can read the pixels back to
collect the data for the higher-resolution image. (See Chapter 8 for more
information about reading pixel data.)
Although it’s easy to understand conceptually, glFrustum() isn’t intuitive
to use. Instead, you might try the Utility Library routine gluPerspective().
This routine creates a viewing volume of the same shape as glFrustum()
does, but you specify it in a different way. Rather than specifying corners of
the near clipping plane, you specify the angle of the field of view (4 or
theta, in Figure 3-14) in the y-direction and the aspect ratio of the width to
the height (x/y). (For a square portion of the screen, the aspect ratio is 1.0.)
These two parameters are enough to determine an untruncated pyramid
along the line of sight, as shown in Figure 3-14. You also specify the dis-
tance between the viewpoint and the near and far clipping planes, thereby
truncating the pyramid. Note that gluPerspective() is limited to creating
frustums that are symmetric in both the x- and y-axes along the line of
sight, but this is usually what you want.
Just as with glFrustum(), you can apply rotations or translations to change
the default orientation of the viewing volume created by gluPerspective().
With no such transformations, the viewpoint remains at the origin, and the
line of sight points down the negative z-axis.
With gluPerspective(), you need to pick appropriate values for the field of
view, otherwise the image may look distorted. To get a perfect field of
view, figure out how far your eye normally is from the screen and how big
near
far
Aspect =
w
h
w
h
fovy
Figure 3-14 Perspective Viewing Volume Specified by gluPerspective()

156 Chapter 3: Viewing
the window is, and calculate the angle the window subtends at that size
and distance. It’s probably smaller than you would guess. Another way
to think about it is that a 94-degree field of view with a 35-millimeter
camera requires a 20-millimeter lens, which is a very wide-angle lens. (See
“Troubleshooting Transformations” on page 162 for more details on how
to calculate the desired field of view.)
The preceding paragraph suggests inches and millimeters—do these really
have anything to do with OpenGL? The answer is, in a word, no. The pro-
jection and other transformations are inherently unitless. If you want to
think of the near and far clipping planes as located at 1.0 and 20.0 meters,
inches, kilometers, or leagues, it’s up to you. The only rule is that you have
to use a consistent unit of measurement. Then the resulting image is drawn
to scale.
Orthographic Projection
With an orthographic projection, the viewing volume is a rectangular par-
allelepiped, or, more informally, a box (see Figure 3-15). Unlike perspective
projection, the size of the viewing volume doesn’t change from one end to
the other, so distance from the camera doesn’t affect how large an object
appears. This type of projection is used for applications for architectural
blueprints and computer-aided design, where it’s crucial to maintain the
actual sizes of objects and the angles between them as they’re projected.
The command glOrtho() creates an orthographic parallel viewing volume.
As with glFrustum(), you specify the corners of the near clipping plane and
the distance to the far clipping plane.
With no other transformations, the direction of projection is parallel to the
z-axis, and the viewpoint faces toward the negative z-axis.
void gluPerspective(GLdouble fovy, GLdouble aspect,
GLdouble near, GLdouble far);
Creates a matrix for a symmetric perspective-view frustum and multiplies
the current matrix by it. fovy is the angle of the field of view in the
yz-plane; its value must be in the range [0.0, 180.0]. aspect is the aspect
ratio of the frustum, its width divided by its height. near and far values are
the distances between the viewpoint and the clipping planes, along the
negative z-axis. They should always be positive.

Projection Transformations 157
For the special case of projecting a two-dimensional image onto a two-
dimensional screen, use the Utility Library routine gluOrtho2D(). This
routine is identical to the three-dimensional version, glOrtho(), except that
all the z coordinates for objects in the scene are assumed to lie between 1.0
and 1.0. If you’re drawing two-dimensional objects using the two-dimensional
vertex commands, all the z coordinates are zero; thus, no object is clipped
because of its z-value.
void glOrtho(GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top,
GLdouble near, GLdouble far);
Creates a matrix for an orthographic parallel viewing volume and multi-
plies the current matrix by it. (left, bottom, –near) and (right, top, –near) are
points on the near clipping plane that are mapped to the lower left and
upper right corners of the viewport window, respectively. (left, bottom,
–far) and (right, top, –far) are points on the far clipping plane that are
mapped to the same respective corners of the viewport. Both near and
far may be positive, negative, or even set to zero. However, near and far
should not be the same value.
left
right
far
bottom
top
near
Toward the
viewpoint
Viewing
volume
Figure 3-15 Orthographic Viewing Volume
Compatibility
Extension
glOrtho

158 Chapter 3: Viewing
Nate Robins’ Projection Tutorial
If you have Nate Robins’ suite of tutorial programs, run the projection
tutorial once again. This time, experiment with the parameters of the
gluPerspective(), glOrtho(), and glFrustum() routines.
Viewing Volume Clipping
After the vertices of the objects in the scene have been transformed by
the modelview and projection matrices, any primitives that lie outside
the viewing volume are clipped. The six clipping planes used are those
that define the sides and ends of the viewing volume. You can specify
additional clipping planes and locate them wherever you choose. (See
“Additional Clipping Planes” on page 168 for information about this
relatively advanced topic.) Keep in mind that OpenGL reconstructs the
edges of polygons that are clipped.
Viewport Transformation
Recalling the camera analogy, you know that the viewport transformation
corresponds to the stage where the size of the developed photograph is
chosen. Do you want a wallet-size or a poster-size photograph? Since this is
computer graphics, the viewport is the rectangular region of the window
where the image is drawn. Figure 3-16 shows a viewport that occupies most
of the screen. The viewport is measured in window coordinates, which
reflect the positions of pixels on the screen relative to the lower left corner
of the window. Keep in mind that all vertices have been transformed by the
modelview and projection matrices by this point, and vertices outside the
viewing volume have been clipped.
void gluOrtho2D(GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top);
Creates a matrix for projecting two-dimensional coordinates onto the
screen and multiplies the current projection matrix by it. The clipping
region is a rectangle with the lower left corner at (left, bottom) and the
upper right corner at (right, top).
Viewport Transformation 159
Defining the Viewport
The window system, not OpenGL, is responsible for opening a window on
the screen. However, by default, the viewport is set to the entire pixel rect-
angle of the window that’s opened. You use the glViewport() command to
choose a smaller drawing region; for example, you can subdivide the win-
dow to create a split-screen effect for multiple views in the same window.
The aspect ratio of a viewport should generally equal the aspect ratio of the
viewing volume. If the two ratios are different, the projected image will be
distorted when mapped to the viewport, as shown in Figure 3-17. Note that
subsequent changes in the size of the window don’t explicitly affect the
viewport. Your application should detect window resize events and modify
the viewport appropriately.
In Figure 3-17, the left figure shows a projection that maps a square image
onto a square viewport using these routines:
gluPerspective(fovy, 1.0, near, far);
glViewport(0, 0, 400, 400);
void glViewport(GLint x, GLint y, GLsizei width, GLsizei height);
Defines a pixel rectangle in the window into which the final image is
mapped. The (x, y) parameter specifies the lower left corner of the view-
port, and width and height are the size of the viewport rectangle. By
default, the initial viewport values are (0, 0, winWidth, winHeight),
where winWidth and winHeight specify the size of the window.
Figure 3-16 Viewport Rectangle

160 Chapter 3: Viewing
However, in the right figure, the window has been resized to a nonequilat-
eral rectangular viewport, but the projection is unchanged. The image
appears compressed along the x-axis:
gluPerspective(fovy, 1.0, near, far);
glViewport(0, 0, 400, 200);
To avoid the distortion, modify the aspect ratio of the projection to match
the viewport:
gluPerspective(fovy, 2.0, near, far);
glViewport(0, 0, 400, 200);
Try This
Modify an existing program so that an object is drawn twice, in different
viewports. You might draw the object with different projection and/or viewing
transformations for each viewport. To create two side-by-side viewports, you
might issue these commands, along with the appropriate modeling, viewing,
and projection transformations:
glViewport(0, 0, sizex/2, sizey);
.
.
.
glViewport(sizex/2, 0, sizex/2, sizey);
Undistorted Distorted
Figure 3-17 Mapping the Viewing Volume to the Viewport
Try This
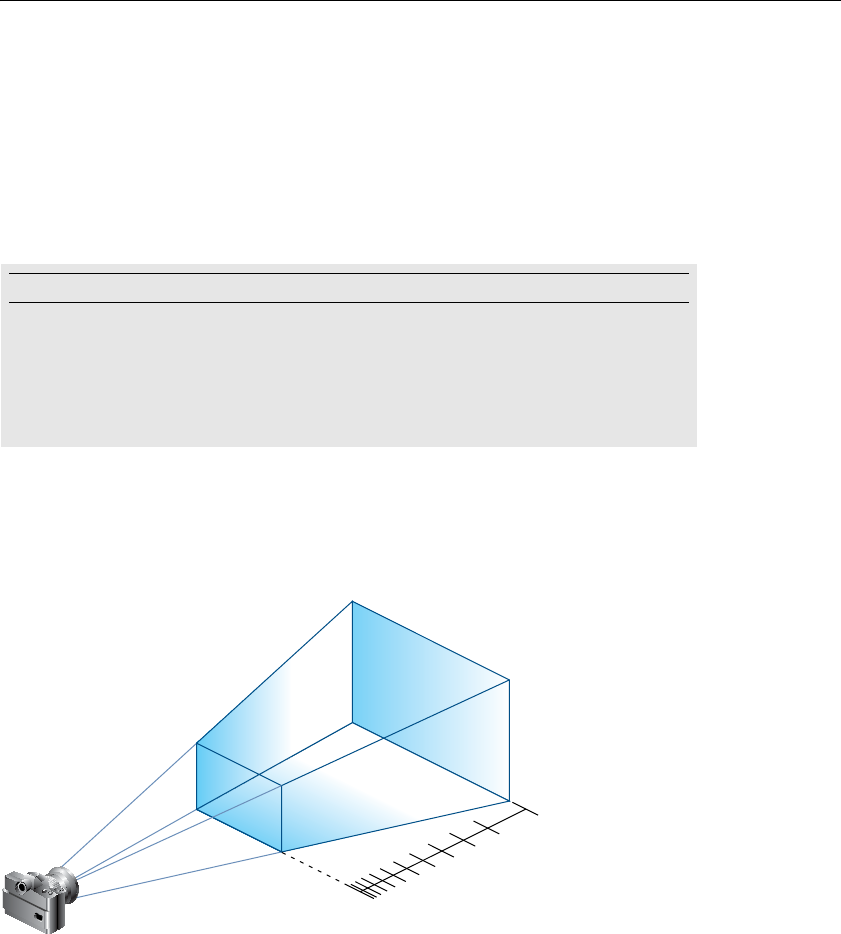
Viewport Transformation 161
The Transformed Depth Coordinate
The depth (z) coordinate is encoded during the viewport transformation
(and later stored in the depth buffer). You can scale z-values to lie within a
desired range with the glDepthRange() command. (Chapter 10 discusses
the depth buffer and the corresponding uses of the depth coordinate.)
Unlike x and y window coordinates, z window coordinates are treated by
OpenGL as though they always range from 0.0 to 1.0.
In perspective projection, the transformed depth coordinate (like the x- and
y-coordinates) is subject to perspective division by the w-coordinate. As the
transformed depth coordinate moves farther away from the near clipping
plane, its location becomes increasingly less precise. (See Figure 3-18.)
Therefore, perspective division affects the accuracy of operations that rely
on the transformed depth coordinate, especially depth-buffering, which is
used for hidden-surface removal.
void glDepthRange(GLclampd near, GLclampd far);
Defines an encoding for z-coordinates that’s performed during the
viewport transformation. The near and far values represent adjustments
to the minimum and maximum values that can be stored in the depth
buffer. By default, they’re 0.0 and 1.0, respectively, which work for most
applications. These parameters are clamped to lie within [0, 1].
Depth coordinate spacing
Figure 3-18 Perspective Projection and Transformed Depth Coordinates

162 Chapter 3: Viewing
Troubleshooting Transformations
It’s pretty easy to get a camera pointed in the right direction, but in com-
puter graphics, you have to specify position and direction with coordinates
and angles. As we can attest, it’s all too easy to achieve the well-known
black-screen effect. Although any number of things can go wrong, often
you get this effect—which results in absolutely nothing being drawn in the
window you open on the screen—from incorrectly aiming the “camera”
and taking a picture with the model behind you. A similar problem arises if
you don’t choose a field of view that’s wide enough to view your objects but
narrow enough so they appear reasonably large.
If you find yourself exerting great programming effort only to create a black
window, try these diagnostic steps:
1. Check the obvious possibilities. Make sure your system is plugged in.
Make sure you’re drawing your objects with a color that’s different from
the color with which you’re clearing the screen. Make sure that whatever
states you’re using (such as lighting, texturing, alpha blending, logical
operations, or antialiasing) are correctly turned on or off, as desired.
2. Remember that with the projection commands, the near and far coor-
dinates measure distance from the viewpoint and that (by default) you’re
looking down the negative z-axis. Thus, if the near value is 1.0 and the
far value is 3.0, objects must have z-coordinates between 1.0 and 3.0
in order to be visible. To ensure that you haven’t clipped everything
out of your scene, temporarily set the near and far clipping planes to
some absurdly inclusive values, such as 0.001 and 1000000.0. This
alters appearance for operations such as depth-buffering and fog, but
it might uncover inadvertently clipped objects.
3. Determine where the viewpoint is, in which direction you’re looking, and
where your objects are. It might help to create a real three-dimensional
space—using your hands, for instance—to figure these things out.
4. Make sure you know where you’re rotating about. You might be rotat-
ing about some arbitrary location unless you translated back to the ori-
gin first. It’s OK to rotate about any point unless you’re expecting to
rotate about the origin.
5. Check your aim. Use gluLookAt() to aim the viewing volume at your
objects, or draw your objects at or near the origin, and use glTranslate*()
as a viewing transformation to move the camera just far enough in the z-
direction so that the objects fall within the viewing volume. Once you’ve
managed to make your objects visible, try to change the viewing volume
incrementally to achieve the exact result you want, as described next.
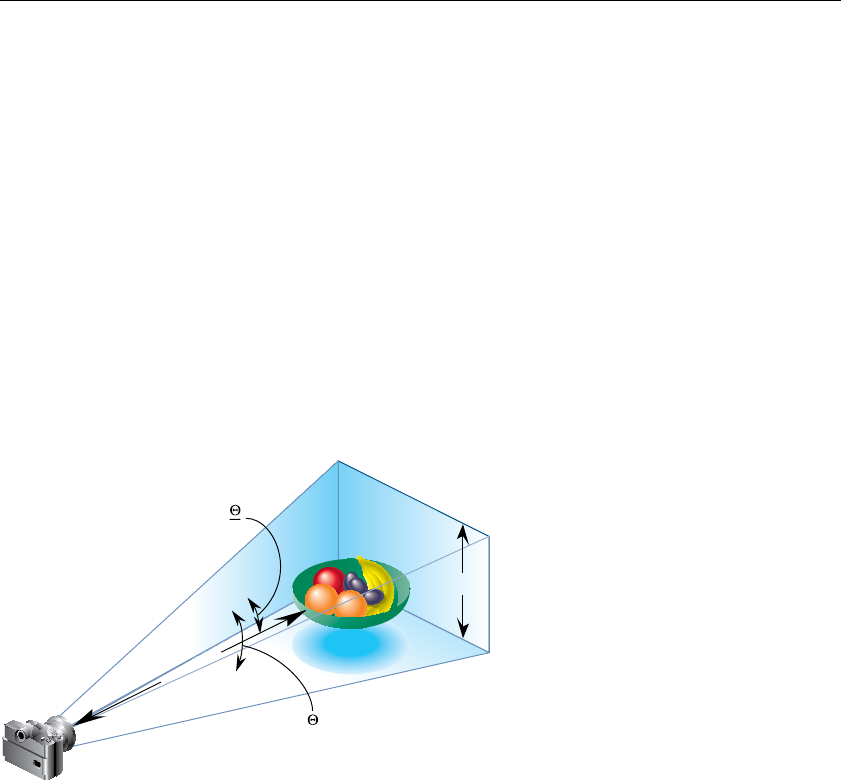
Troubleshooting Transformations 163
6. For perspective transformations, be certain the near clipping plane is
not too close to the viewer (camera), otherwise depth-buffering
accuracy may be adversely affected.
Even after you’ve aimed the camera in the correct direction and you can
see your objects, they might appear too small or too large. If you’re using
gluPerspective(), you might need to alter the angle defining the field of
view by changing the value of the first parameter for this command. You
can use trigonometry to calculate the desired field of view given the size
of the object and its distance from the viewpoint: The tangent of half the
desired angle is half the size of the object divided by the distance to the
object (see Figure 3-19). Thus, you can use an arctangent routine to com-
pute half the desired angle. Example 3-3 assumes such a routine, atan2(),
which calculates the arctangent given the length of the opposite and adja-
cent sides of a right triangle. This result then needs to be converted from
radians to degrees.
Example 3-3 Calculating Field of View
#define PI 3.1415926535
double calculateAngle(double size, double distance)
{
double radtheta, degtheta;
radtheta = 2.0 * atan2 (size/2.0, distance);
degtheta = (180.0 * radtheta) / PI;
return degtheta;
}
Distance
Size
2
Figure 3-19 Using Trigonometry to Calculate the Field of View

164 Chapter 3: Viewing
Typically, of course, you don’t know the exact size of an object, and only
the distance between the viewpoint and a single point in your scene can be
determined. To obtain a fairly good approximate value, find the bounding
box for your scene by determining the maximum and minimum x-,y-, and
z-coordinates of all the objects in your scene. Then calculate the radius of a
bounding sphere for that box, and use the center of the sphere to determine
the distance and the radius to determine the size.
For example, suppose all the coordinates in your object satisfy the equations
–1 dxd3, 5 dyd7, and –5 dzd5. The center of the bounding box is (1, 6,
0), and the radius of a bounding sphere is the distance from the center of
the box to any corner—say (3, 7, 5)—or
If the viewpoint is at (8, 9, 10), the distance between it and the center is
The tangent of the half-angle is 5.477 divided by 12.570, which equals
0.4357, so the half-angle is 23.54 degrees.
Remember that the field-of-view angle affects the optimal position for the
viewpoint, if you’re trying to achieve a realistic image. For example, if your
calculations indicate that you need a 179-degree field of view, the viewpoint
must be a fraction of an inch from the screen to achieve realism. If your
calculated field of view is too large, you might need to move the viewpoint
farther away from the object.
Manipulating the Matrix Stacks
The modelview and projection matrices you’ve been creating, loading, and
multiplying have been only the visible tips of their respective icebergs. Each
of these matrices is actually the topmost member of a stack of matrices (see
Figure 3-20).
A stack of matrices is useful for constructing hierarchical models, in which
complicated objects are constructed from simpler ones. For example, sup-
pose you’re drawing an automobile that has four wheels, each of which is
attached to the car with five bolts. You have a single routine to draw a wheel
and another to draw a bolt, since all the wheels and all the bolts look the
31–
276–
250–
2
++ 30 5.477==
81–
296–
210 0–
2
++ 158 12.570==
Manipulating the Matrix Stacks 165
same. These routines draw a wheel or a bolt in some convenient position
and orientation; for example, centered at the origin with its axis coincident
with the z-axis. When you draw the car, including the wheels and bolts, you
want to call the wheel-drawing routine four times, with different transfor-
mations in effect each time to position the wheels correctly. As you draw
each wheel, you want to draw the bolts five times, each time translated
appropriately relative to the wheel.
Suppose for a minute that all you have to do is draw the car body and the
wheels. The English description of what you want to do might be
something like this:
Draw the car body. Remember where you are, and translate to the right
front wheel. Draw the wheel and throw away the last translation so
your current position is back at the origin of the car body. Remember
where you are, and translate to the left front wheel}
Similarly, for each wheel, you want to draw the wheel, remember where you
are, and successively translate to each of the positions where bolts are
drawn, throwing away the transformations after each bolt is drawn.
Since the transformations are stored as matrices, a matrix stack provides an
ideal mechanism for doing this sort of successive remembering, translating,
and throwing away. All the matrix operations that have been described
so far (glLoadMatrix(),glLoadTransposeMatrix(),glMultMatrix(),
glMultTransposeMatrix(),glLoadIdentity(), and the commands that
create specific transformation matrices) deal with the current matrix or
the top matrix on the stack. You can control which matrix is on top with
the commands that perform stack operations: glPushMatrix(), which
copies the current matrix and adds the copy to the top of the stack, and
glPopMatrix(), which discards the top matrix on the stack, as shown in
Figure 3-21. (Remember that the current matrix is always the matrix on the
Modelview
matrix stack
(32 4 x 4 matrices)
Projection
matrix stack
(2 4 x 4 matrices)
a b c d
e f g h
i j k l
m n o p
a b c d
e f g h
i j k l
m n o p
q p o n
m l k j
i h g f
e d c b
Figure 3-20 Modelview and Projection Matrix Stacks
166 Chapter 3: Viewing
top.) In effect, glPushMatrix() means “remember where you are” and
glPopMatrix() means “go back to where you were.”
Example 3-4 draws an automobile, assuming the existence of routines that
draw the car body, a wheel, and a bolt.
Example 3-4 Pushing and Popping the Matrix
draw_wheel_and_bolts()
{
int i;
draw_wheel();
for(i=0;i<5;i++){
glPushMatrix();
glRotatef(72.0*i, 0.0, 0.0, 1.0);
glTranslatef(3.0, 0.0, 0.0);
void glPushMatrix(void);
Pushes all matrices in the current stack down one level. The current stack
is determined by glMatrixMode(). The topmost matrix is copied, so its
contents are duplicated in both the top and second-from-the-top matrix.
If too many matrices are pushed, an error is generated.
void glPopMatrix(void);
Pops the top matrix off the stack, destroying the contents of the popped
matrix. What was the second-from-the-top matrix becomes the top matrix.
The current stack is determined by glMatrixMode(). If the stack contains
a single matrix, calling glPopMatrix() generates an error.
a b c d
e f g h
i j k l
m n o p
a b c d
e f g h
i j k l
m n o p
Current
matrix
copy
Add
Figure 3-21 Pushing and Popping the Matrix Stack
Compatibility
Extension
glPushMatrix
glPopMatrix

Manipulating the Matrix Stacks 167
draw_bolt();
glPopMatrix();
}
}
draw_body_and_wheel_and_bolts()
{
draw_car_body();
glPushMatrix();
glTranslatef(40, 0, 30); /*move to first wheel position*/
draw_wheel_and_bolts();
glPopMatrix();
glPushMatrix();
glTranslatef(40, 0, -30); /*move to 2nd wheel position*/
draw_wheel_and_bolts();
glPopMatrix();
... /*draw last two wheels similarly*/
}
This code assumes that the wheel and bolt axes are coincident with the
z-axis; that the bolts are evenly spaced every 72 degrees, 3 units (maybe
inches) from the center of the wheel; and that the front wheels are 40 units
in front of and 30 units to the right and left of the car’s origin.
A stack is more efficient than an individual matrix, especially if the stack
is implemented in hardware. When you push a matrix, you don’t need to
copy the current data back to the main process, and the hardware may be
able to copy more than one element of the matrix at a time. Sometimes you
might want to keep an identity matrix at the bottom of the stack so that
you don’t need to call glLoadIdentity() repeatedly.
The Modelview Matrix Stack
As you’ve seen earlier in “Viewing and Modeling Transformations,” the mod-
elview matrix contains the cumulative product of multiplying viewing and
modeling transformation matrices. Each viewing or modeling transforma-
tion creates a new matrix that multiplies the current modelview matrix; the
result, which becomes the new current matrix, represents the composite
transformation. The modelview matrix stack contains at least 32 4 u4 matri-
ces; initially, the topmost matrix is the identity matrix. Some implementa-
tions of OpenGL may support more than 32 matrices on the stack. To find the
maximum allowable number of matrices, you can use the query command
glGetIntegerv(GL_MAX_MODELVIEW_STACK_DEPTH, GLint *params).

168 Chapter 3: Viewing
The Projection Matrix Stack
The projection matrix contains a matrix for the projection transformation,
which describes the viewing volume. Generally, you don’t want to compose
projection matrices, so you issue glLoadIdentity() before performing a
projection transformation. Also for this reason, the projection matrix
stack need be only two levels deep; some OpenGL implementations
may allow more than two 4 u4 matrices. To find the stack depth, call
glGetIntegerv(GL_MAX_PROJECTION_STACK_DEPTH, GLint *params).
One use for a second matrix in the stack would be an application that needs
to display a help window with text in it, in addition to its normal window
showing a three-dimensional scene. Since text is most easily positioned
with an orthographic projection, you could change temporarily to an
orthographic projection, display the help, and then return to your previous
projection:
glMatrixMode(GL_PROJECTION);
glPushMatrix(); /*save the current projection*/
glLoadIdentity();
glOrtho(...); /*set up for displaying help*/
display_the_help();
glPopMatrix();
Note that you’d probably also have to change the modelview matrix
appropriately.
Advanced
If you know enough mathematics, you can create custom projection
matrices that perform arbitrary projective transformations. For example,
OpenGL and its Utility Library have no built-in mechanism for two-point
perspective. If you were trying to emulate the drawings in drafting texts,
you might need such a projection matrix.
Additional Clipping Planes
In addition to the six clipping planes of the viewing volume (left, right,
bottom, top, near, and far), you can define up to six additional clipping
planes for further restriction of the viewing volume, as shown in Figure 3-22.
This is useful for removing extraneous objects in a scene—for example, if
you want to display a cutaway view of an object.
Advanced
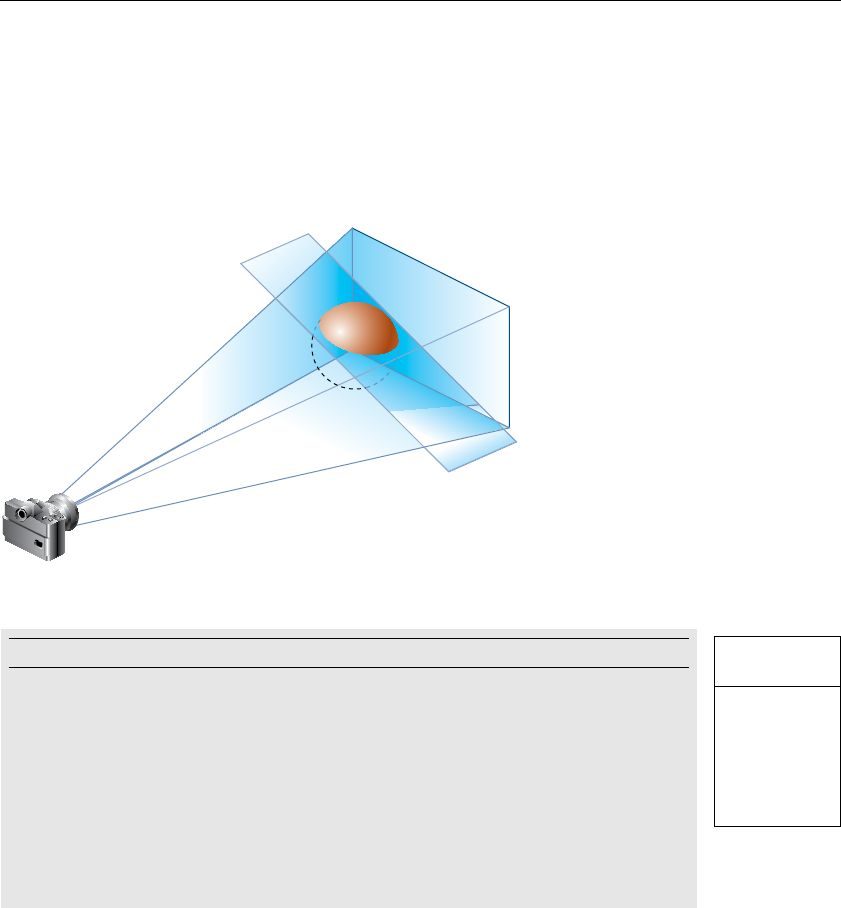
Additional Clipping Planes 169
Each plane is specified by the coefficients of its equation: Ax+ By+ Cz+ D = 0.
The clipping planes are automatically transformed appropriately by model-
ing and viewing transformations. The clipping volume becomes the inter-
section of the viewing volume and all half-spaces defined by the additional
clipping planes. Remember that polygons that get clipped automatically
have their edges reconstructed appropriately by OpenGL.
You need to enable each additional clipping plane you define:
glEnable(GL_CLIP_PLANEi);
You can disable a plane with
glDisable(GL_CLIP_PLANEi);
void glClipPlane(GLenum plane, const GLdouble *equation);
Defines a clipping plane. The equation argument points to the four coeffi-
cients of the plane equation, Ax+ By+ Cz+ D = 0. All points with eye coor-
dinates (xe,ye,ze,we) that satisfy (A B C D)M-1(xe ye ze we)Tt 0 lie in the
half-space defined by the plane, where M is the current modelview matrix
at the time glClipPlane() is called. All points not in this half-space are
clipped away. The plane argument is GL_CLIP_DISTANCEi (named GL_
CLIP_PLANEi prior to OpenGL version 3.0), where i is an integer specify-
ing which of the available clipping planes to define. i is a number between
0 and one less than the maximum number of additional clipping planes.
Figure 3-22 Additional Clipping Planes and the Viewing Volume
Compatibility
Extension
glClipPlane
GL_CLIP_
DISTANCEi
GL_CLIP_PLANEi
GL_MAX_CLIP_
PLANES

170 Chapter 3: Viewing
All implementations of OpenGL must support at least six additional
clipping planes, although some implementations may allow more. You can
use glGetIntegerv() with GL_MAX_CLIP_PLANES to determine how many
clipping planes are supported.
Note: Clipping performed as a result of glClipPlane() is done in eye
coordinates, not in clip coordinates. This difference is noticeable
if the projection matrix is singular (that is, a real projection matrix
that flattens three-dimensional coordinates to two-dimensional
ones). Clipping performed in eye coordinates continues to take
place in three dimensions even when the projection matrix is
singular.
A Clipping Plane Code Example
Example 3-5 renders a wireframe sphere with two clipping planes that slice
away three-quarters of the original sphere, as shown in Figure 3-23.
Example 3-5 Wireframe Sphere with Two Clipping Planes: clip.c
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}
void display(void)
{
Figure 3-23 Clipped Wireframe Sphere

Additional Clipping Planes 171
GLdouble eqn[4] = {0.0, 1.0, 0.0, 0.0};
GLdouble eqn2[4] = {1.0, 0.0, 0.0, 0.0};
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glPushMatrix();
glTranslatef(0.0, 0.0, -5.0);
/* clip lower half -- y < 0 */
glClipPlane(GL_CLIP_PLANE0, eqn);
glEnable(GL_CLIP_PLANE0);
/* clip left half -- x < 0 */
glClipPlane(GL_CLIP_PLANE1, eqn2);
glEnable(GL_CLIP_PLANE1);
glRotatef(90.0, 1.0, 0.0, 0.0);
glutWireSphere(1.0, 20, 16);
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, (GLfloat) w/(GLfloat) h, 1.0, 20.0);
glMatrixMode(GL_MODELVIEW);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}

Try This
• Try changing the coefficients that describe the clipping planes in
Example 3-5.
• Try calling a modeling transformation, such as glRotate*(), to affect
glClipPlane(). Make the clipping plane move independently of the
objects in the scene.
Examples of Composing Several Transformations
This section demonstrates how to combine several transformations to
achieve a particular result. The two examples discussed are a solar system,
in which objects need to rotate on their axes as well as in orbit around each
other, and a robot arm, which has several joints that effectively transform
coordinate systems as they move relative to each other.
Building a Solar System
172 Chapter 3: Viewing
The program described in this section draws a simple solar system with a
planet and a sun, both using the same sphere-drawing routine. To write
this program, you need to use glRotate*() for the revolution of the planet
around the sun and for the rotation of the planet around its own axis. You
also need glTranslate*() to move the planet out to its orbit, away from the
origin of the solar system. Remember that you can specify the desired sizes
of the two spheres by supplying the appropriate arguments for the
glutWireSphere() routine.
To draw the solar system, you first want to set up a projection and a viewing
transformation. For this example, gluPerspective() and gluLookAt() are used.
Drawing the sun is straightforward, since it should be located at the origin
of the grand, fixed coordinate system, which is where the sphere routine
places it. Thus, drawing the sun doesn’t require translation; you can use
glRotate*() to make the sun rotate about an arbitrary axis. Drawing a planet
rotating around the sun, as shown in Figure 3-24, requires several modeling
transformations. The planet needs to rotate about its own axis once a day;
and once a year, the planet completes one revolution around the sun.
To determine the order of modeling transformations, visualize what hap-
pens to the local coordinate system. An initial glRotate*() rotates the local
coordinate system that initially coincides with the grand coordinate system.
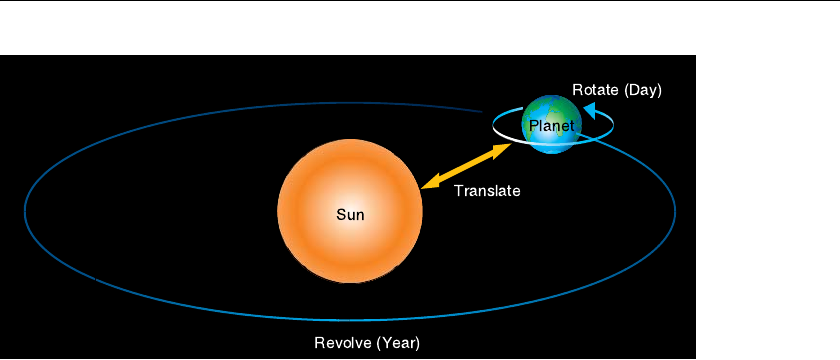
Next, glTranslate*() moves the local coordinate system to a position on the
planet’s orbit; the distance moved should equal the radius of the orbit. Thus,
the initial glRotate*() actually determines where along the orbit the planet
is (or what time of year it is).
A second glRotate*() rotates the local coordinate system around the local
axes, thus determining the time of day for the planet. Once you’ve issued
all these transformation commands, the planet can be drawn.
In summary, the following OpenGL commands draw the sun and planet;
the full program is shown in Example 3-6:
glPushMatrix();
glutWireSphere(1.0, 20, 16); /* draw sun */
glRotatef((GLfloat) year, 0.0, 1.0, 0.0);
glTranslatef(2.0, 0.0, 0.0);
glRotatef((GLfloat) day, 0.0, 1.0, 0.0);
glutWireSphere(0.2, 10, 8); /* draw smaller planet */
glPopMatrix();
Example 3-6 Planetary System: planet.c
Figure 3-24 Planet and Sun
Examples of Composing Several Transformations 173
static int year = 0, day = 0;
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}

174 Chapter 3: Viewing
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glPushMatrix();
glutWireSphere(1.0, 20, 16); /* draw sun */
glRotatef((GLfloat) year, 0.0, 1.0, 0.0);
glTranslatef(2.0, 0.0, 0.0);
glRotatef((GLfloat) day, 0.0, 1.0, 0.0);
glutWireSphere(0.2, 10, 8); /* draw smaller planet */
glPopMatrix();
glutSwapBuffers();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, (GLfloat) w/(GLfloat) h, 1.0, 20.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(0.0, 0.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘d’:
day = (day + 10) % 360;
glutPostRedisplay();
break;
case ‘D’:
day = (day - 10) % 360;
glutPostRedisplay();
break;
case ‘y’:
year = (year + 5) % 360;
glutPostRedisplay();
break;
case ‘Y’:
year = (year - 5) % 360;
glutPostRedisplay();
break;
default:

Examples of Composing Several Transformations 175
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutMainLoop();
return 0;
}
Try This
• Try adding a moon to the planet, or try several moons and additional
planets. Hint: Use glPushMatrix() and glPopMatrix() to save and restore
the position and orientation of the coordinate system at appropriate
moments. If you’re going to draw several moons around a planet, you
need to save the coordinate system prior to positioning each moon
and restore the coordinate system after each moon is drawn.
• Try tilting the planet’s axis.
Building an Articulated Robot Arm
This section discusses a program that creates an articulated robot arm with
two or more segments. The arm should be connected with pivot points at
the shoulder, elbow, or other joints. Figure 3-25 shows a single joint of such
an arm.
You can use a scaled cube as a segment of the robot arm, but first you
must call the appropriate modeling transformations to orient each
segment. Since the origin of the local coordinate system is initially at the
center of the cube, you need to move the local coordinate system to one
edge of the cube. Otherwise, the cube rotates about its center, rather than
the pivot point.
Try This
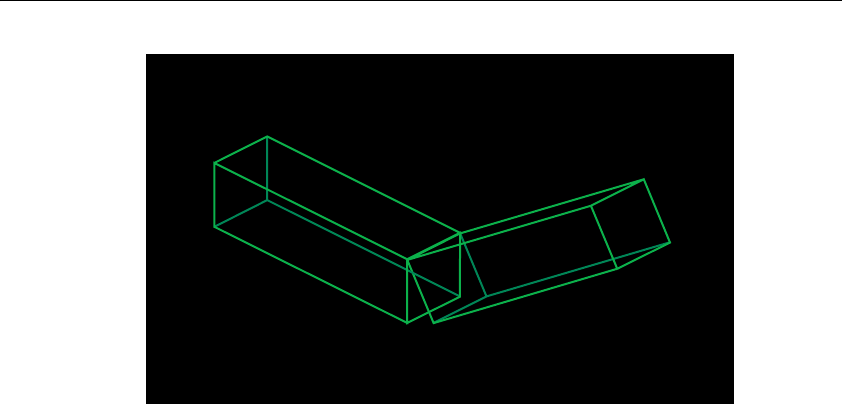
176 Chapter 3: Viewing
After you call glTranslate*() to establish the pivot point and glRotate*() to
pivot the cube, translate back to the center of the cube. Then the cube is
scaled (flattened and widened) before it is drawn. The glPushMatrix() and
glPopMatrix() commands restrict the effect of glScale*(). Here’s what your
code might look like for this first segment of the arm (the entire program is
shown in Example 3-7):
glTranslatef(-1.0, 0.0, 0.0);
glRotatef((GLfloat) shoulder, 0.0, 0.0, 1.0);
glTranslatef(1.0, 0.0, 0.0);
glPushMatrix();
glScalef(2.0, 0.4, 1.0);
glutWireCube(1.0);
glPopMatrix();
To build a second segment, you need to move the local coordinate system
to the next pivot point. Since the coordinate system has previously been
rotated, the x-axis is already oriented along the length of the rotated arm.
Therefore, translating along the x-axis moves the local coordinate system to
the next pivot point. Once it’s at that pivot point, you can use the same
code to draw the second segment as you used for the first one. This can be
continued for an indefinite number of segments (shoulder, elbow, wrist,
fingers):
Figure 3-25 Robot Arm

Examples of Composing Several Transformations 177
glTranslatef(1.0, 0.0, 0.0);
glRotatef((GLfloat) elbow, 0.0, 0.0, 1.0);
glTranslatef(1.0, 0.0, 0.0);
glPushMatrix();
glScalef(2.0, 0.4, 1.0);
glutWireCube(1.0);
glPopMatrix();
Example 3-7 Robot Arm: robot.c
static int shoulder = 0, elbow = 0;
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glPushMatrix();
glTranslatef(-1.0, 0.0, 0.0);
glRotatef((GLfloat) shoulder, 0.0, 0.0, 1.0);
glTranslatef(1.0, 0.0, 0.0);
glPushMatrix();
glScalef(2.0, 0.4, 1.0);
glutWireCube(1.0);
glPopMatrix();
glTranslatef(1.0, 0.0, 0.0);
glRotatef((GLfloat) elbow, 0.0, 0.0, 1.0);
glTranslatef(1.0, 0.0, 0.0);
glPushMatrix();
glScalef(2.0, 0.4, 1.0);
glutWireCube(1.0);
glPopMatrix();
glPopMatrix();
glutSwapBuffers();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);

178 Chapter 3: Viewing
glLoadIdentity();
gluPerspective(65.0, (GLfloat) w/(GLfloat) h, 1.0, 20.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0, 0.0, -5.0);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘s’: /* s key rotates at shoulder */
shoulder = (shoulder + 5) % 360;
glutPostRedisplay();
break;
case ‘S’:
shoulder = (shoulder - 5) % 360;
glutPostRedisplay();
break;
case ‘e’: /* e key rotates at elbow */
elbow = (elbow + 5) % 360;
glutPostRedisplay();
break;
case ‘E’:
elbow = (elbow - 5) % 360;
glutPostRedisplay();
break;
default:
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutMainLoop();
return 0;
}

Reversing or Mimicking Transformations 179
Try This
• Modify Example 3-7 to add additional segments to the robot arm.
• Modify Example 3-7 to add additional segments at the same position.
For example, give the robot arm several “fingers” at the wrist, as shown
in Figure 3-26. Hint: Use glPushMatrix() and glPopMatrix() to save
and restore the position and orientation of the coordinate system at
the wrist. If you’re going to draw fingers at the wrist, you need to save
the current matrix prior to positioning each finger, and restore the
current matrix after each finger is drawn.
Nate Robins’ Transformation Tutorial
If you have Nate Robins’ suite of tutorial programs, go back to the transfor-
mation tutorial and run it again. Use the popup menu interface to change
the order of glRotate*() and glTranslate(), and note the effect of swapping
the order of these routines.
Reversing or Mimicking Transformations
The geometric processing pipeline is very good at using viewing and projec-
tion matrices and a viewport for clipping to transform the world (or object)
coordinates of a vertex into window (or screen) coordinates. However, there
are situations in which you want to reverse that process. A common situa-
tion is when an application user utilizes the mouse to choose a location in
three dimensions. The mouse returns only a two-dimensional value, which
is the screen location of the cursor. Therefore, the application will have to
reverse the transformation process to determine where in three-dimensional
space this screen location originated.
Try This
Figure 3-26 Robot Arm with Fingers

180 Chapter 3: Viewing
The Utility Library routines gluUnProject() and gluUnProject4() perform
this reversal of the transformations. Given the three-dimensional window
coordinates for a transformed vertex and all the transformations that affected
it, gluUnProject() returns the original world coordinates of that vertex. (Use
gluUnProject4() if the depth range is other than the default [0, 1].)
There are inherent difficulties in trying to reverse the transformation
process. A two-dimensional screen location could have originated from
anywhere on an entire line in three-dimensional space. To disambiguate
the result, gluUnProject() requires that a window depth coordinate (winz)
be provided, specified in terms of glDepthRange(). (For more about depth
range, see “The Transformed Depth Coordinate” on page 161.) For the
default values of glDepthRange(),winz at 0.0 will request the world
coordinates of the transformed point at the near clipping plane, while
winz at 1.0 will request the point at the far clipping plane.
Example 3-8 demonstrates gluUnProject() by reading the mouse position
and determining the three-dimensional points at the near and far clipping
planes from which the mouse position was transformed. The computed
world coordinates are printed to standard output, but the rendered window
itself is just black.
Example 3-8 Reversing the Geometric Processing Pipeline: unproject.c
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
int gluUnProject(GLdouble winx, GLdouble winy, GLdouble winz,
const GLdouble modelMatrix[16],
const GLdouble projMatrix[16],
const GLint viewport[4],
GLdouble *objx, GLdouble *objy, GLdouble *objz);
Maps the specified window coordinates (winx, winy, winz) into object
coordinates, using transformations defined by a modelview matrix
(modelMatrix), projection matrix (projMatrix), and viewport (viewport). The
resulting object coordinates are returned in objx, objy, and objz. The func-
tion returns GL_TRUE, indicating success, or GL_FALSE, indicating failure
(such as a noninvertible matrix). This operation does not attempt to clip
the coordinates to the viewport or eliminate depth values that fall outside
of glDepthRange().

Reversing or Mimicking Transformations 181
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0, (GLfloat) w/(GLfloat) h, 1.0, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void mouse(int button, int state, int x, int y)
{
GLint viewport[4];
GLdouble mvmatrix[16], projmatrix[16];
GLint realy; /* OpenGL y coordinate position */
GLdouble wx, wy, wz; /* returned world x, y, z coords */
switch (button) {
case GLUT_LEFT_BUTTON:
if (state == GLUT_DOWN) {
glGetIntegerv(GL_VIEWPORT, viewport);
glGetDoublev(GL_MODELVIEW_MATRIX, mvmatrix);
glGetDoublev(GL_PROJECTION_MATRIX, projmatrix);
/* note viewport[3] is height of window in pixels */
realy = viewport[3] - (GLint) y - 1;
printf(“Coordinates at cursor are (%4d, %4d)\n”,
x, realy);
gluUnProject((GLdouble) x, (GLdouble) realy, 0.0,
mvmatrix, projmatrix, viewport, &wx, &wy, &wz);
printf(“World coords at z=0.0 are (%f, %f, %f)\n”,
wx, wy, wz);
gluUnProject((GLdouble) x, (GLdouble) realy, 1.0,
mvmatrix, projmatrix, viewport, &wx, &wy, &wz);
printf(“World coords at z=1.0 are (%f, %f, %f)\n”,
wx, wy, wz);
}
break;
case GLUT_RIGHT_BUTTON:
if (state == GLUT_DOWN)
exit(0);
break;
default:
break;

182 Chapter 3: Viewing
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMouseFunc(mouse);
glutMainLoop();
return 0;
}
GLU 1.3 introduces a modified version of gluUnProject().gluUnProject4()
can handle nonstandard glDepthRange() values and also w-coordinate
values other than 1.
gluProject() is another Utility Library routine, which is related to
gluUnProject(). gluProject() mimics the actions of the transformation
pipeline. Given three-dimensional world coordinates and all the transfor-
mations that affect them, gluProject() returns the transformed window
coordinates.
int gluUnProject4(GLdouble winx, GLdouble winy, GLdouble winz,
GLdouble clipw, const GLdouble modelMatrix[16],
const GLdouble projMatrix[16],
const GLint viewport[4],
GLclampd zNear, GLclampd zFar,
GLdouble *objx, GLdouble *objy,
GLdouble *objz, GLdouble *objw);
Overall, the operation is similar to gluUnProject(). Maps the specified
window coordinates (winx, winy, winz, clipw) into object coordinates,
using transformations defined by a modelview matrix (modelMatrix),
projection matrix (projMatrix), viewport (viewport), and the depth range
values zNear and zFar. The resulting object coordinates are returned in
objx, objy, objz, and objw.

Reversing or Mimicking Transformations 183
Note: The matrices passed to gluUnProject(),gluUnProject4(), and
gluProject() are in the OpenGL-standard column-major order.
You might use glGetDoublev() and glGetIntegerv() to obtain the
current GL_MODELVIEW_MATRIX, GL_PROJECTION_MATRIX,
and GL_VIEWPORT values for use with gluUnProject(),
gluUnProject4(), or gluProject().
int gluProject(GLdouble objx, GLdouble objy, GLdouble objz,
const GLdouble modelMatrix[16],
const GLdouble projMatrix[16],
const GLint viewport[4],
GLdouble *winx, GLdouble *winy, GLdouble *winz);
Maps the specified object coordinates (objx, objy, objz) into window
coordinates, using transformations defined by a modelview matrix
(modelMatrix), projection matrix (projMatrix), and viewport (viewport).
The resulting window coordinates are returned in winx, winy, and winz.
The function returns GL_TRUE, indicating success, or GL_FALSE,
indicating failure.
This page intentionally left blank

185
Chapter 4
4.Color
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Decide between using RGBA or color-index mode for your application
• Specify desired colors for drawing objects
• Use smooth shading to draw a single polygon with more than one
color
Note: In OpenGL Version 3.1, many of the techniques and functions
described in this chapter were removed through deprecation. In
particular, color-index rendering is not supported. The concepts
relating to RGBA color modes are still relevant, but need to be
implemented in vertex or fragment shaders, as described in
Chapter 15.

186 Chapter 4: Color
The goal of almost all OpenGL applications is to draw color pictures in a
window on the screen. The window is a rectangular array of pixels, each of
which contains and displays its own color. Thus, in a sense, the point of all
the calculations performed by an OpenGL implementation—calculations
that take into account OpenGL commands, state information, and values
of parameters—is to determine the final color of every pixel that’s to be
drawn in the window. This chapter explains the commands for specifying
colors and how OpenGL interprets them in the following major sections:
• “Color Perception” discusses how the eye perceives color.
• “Computer Color” describes the relationship between pixels on a
computer monitor and their colors; it also defines the two display
modes: RGBA and color index.
• “RGBA versus Color-Index Mode” explains how the two display modes
use graphics hardware and how to decide which mode to use.
• “Specifying a Color and a Shading Model” describes the OpenGL
commands you use to specify the desired color or shading model.
Color Perception
Physically, light is composed of photons—tiny particles of light, each trav-
eling along its own path, and each vibrating at its own frequency (or wave-
length or energy—any one of frequency, wavelength, or energy determines
the others). A photon is completely characterized by its position, direction,
and frequency/wavelength/energy. Photons with wavelengths ranging
from about 390 nanometers (nm) (violet) and 720 nm (red) cover the colors
of the visible spectrum, forming the colors of a rainbow (violet, indigo,
blue, green, yellow, orange, red). However, your eyes perceive lots of colors
that aren’t in the rainbow—white, black, brown, and pink, for example.
How does this happen?
What your eye actually sees is a mixture of photons of different frequencies.
Real light sources are characterized by the distribution of photon frequencies
they emit. Ideal white light consists of an equal amount of light of all
frequencies. Laser light is usually very pure, and all photons are almost
identical in frequency (and in direction and phase as well). Light from a
sodium-vapor lamp has more light in the yellow frequency. Light from most
stars in space has a distribution that depends heavily on their temperatures
(black-body radiation). The frequency distribution of light from most
sources in your immediate environment is more complicated.

Color Perception 187
The human eye perceives color when certain cells in the retina (called cone
cells, or just cones) become excited after being struck by photons. The three
different kinds of cone cells respond best to three different wavelengths of
light: One type of cone cell responds best to red light, one to green light,
and the other to blue light. (A person who is color-blind is usually missing
one or more types of cone cells.) When a given mixture of photons enters
the eye, the cone cells in the retina register different degrees of excitation
depending on their types, and if a different mixture of photons happens to
excite the three types of cone cells to the same degree, its color is indistin-
guishable from that of the first mixture.
Since each color is recorded by the eye as the levels of excitation of the cone
cells produced by the incoming photons, the eye can perceive colors that
aren’t in the spectrum produced by a prism or rainbow. For example, if you
send a mixture of red and blue photons so that both the red and blue cones
in the retina are excited, your eye sees it as magenta, which isn’t in the
spectrum. Other combinations give browns, turquoises, and mauves, none
of which appears in the color spectrum.
A computer-graphics monitor emulates visible colors by lighting pixels with
a combination of red, green, and blue light in proportions that excite the
red-, green-, and blue-sensitive cones in the retina in such a way that it
matches the excitation levels generated by the photon mix it’s trying to
emulate. If humans had more types of cone cells, some that were yellow-
sensitive for example, color monitors would probably have a yellow gun as
well, and we’d use RGBY (red, green, blue, yellow) quadruples to specify
colors. And if everyone were color-blind in the same way, this chapter
would be simpler.
To display a particular color, the monitor sends the right amounts of red,
green, and blue (RGB) light to stimulate appropriately the different types of
cone cells in your eye. A color monitor can send different proportions of
red, green, and blue to each of the pixels, and the eye sees a million or so
pinpoints of light, each with its own color.
Note: There are many other representations of color, or color models, with
acronyms such as HLS, HSV, and CMYK. If your data needs to be in
one of these color models, you need to convert to and from RGB. For
the formulas to perform these conversions, see Foley, van Dam, et al.,
Computer Graphics: Principles and Practice (Addison-Wesley, 1990).
This section considers only how the eye perceives combinations of photons
that enter it. The situation for light bouncing off materials and entering the
eye is even more complex—white light bouncing off a red ball will appear

188 Chapter 4: Color
red, and yellow light shining through blue glass appears almost black, for
example. (See “Real-World and OpenGL Lighting” in Chapter 5 for a
discussion of these effects.)
Computer Color
On a color computer screen, the hardware causes each pixel on the screen
to emit different amounts of red, green, and blue light. These are called the
R, G, and B values. They’re often packed together (sometimes with a fourth
value, called alpha, or A), and the packed value is called the RGB (or RGBA)
value. (See “Blending” in Chapter 6 for an explanation of the alpha values.)
The color information at each pixel can be stored either in RGBA mode, in
which the R, G, B, and possibly A values are kept for each pixel, or in color-
index mode, in which a single number (called the color index) is stored for
each pixel. Each color index indicates an entry in a table that defines a
particular set of R, G, and B values. Such a table is called a color map.
In color-index mode, you might want to alter the values in the color map.
Since color maps are controlled by the window system, there are no OpenGL
commands to do this. All the examples in this book initialize the color-
display mode at the time the window is opened by using routines from the
GLUT library. (See Appendix A for details.)
There is a great deal of variation among the different graphics hardware
platforms in both the size of the pixel array and the number of colors that
can be displayed at each pixel. On any graphics system, each pixel has the
same amount of memory for storing its color, and all the memory for all
the pixels is called the color buffer. The size of a buffer is usually measured
in bits, so an 8-bit buffer could store 8 bits of data (256 possible different
colors) for each pixel. The size of the possible buffers varies from machine
to machine. (See Chapter 10 for more information.)
The R, G, and B values can range from 0.0 (none) to 1.0 (full intensity). For
example, R = 0.0, G = 0.0, and B = 1.0 represents the brightest possible blue.
If R, G, and B are all 0.0, the pixel is black; if all are 1.0, the pixel is drawn
in the brightest white that can be displayed on the screen. Blending green
and blue creates shades of cyan. Blue and red combine for magenta. Red and
green create yellow. To help you create the colors you want from the R, G,
and B components, look at the color cube shown in Plate 12. The axes of
this cube represent intensities of red, blue, and green. A black-and-white
version of the cube is shown in Figure 4-1.
Computer Color 189
The commands used to specify a color for an object (in this case, a point)
can be as simple as this:
glColor3f(1.0, 0.0, 0.0); /* the current RGB color is red: */
/* full red, no green, no blue. */
glBegin(GL_POINTS);
glVertex3fv(point_array);
glEnd();
In certain modes (for example, if lighting or texturing calculations are
performed), the assigned color might go through other operations before
arriving in the framebuffer as a value representing a color for a pixel. In fact,
the color of a pixel is determined by a lengthy sequence of operations.
Early in a program’s execution, the color-display mode is set to either RGBA
mode or color-index mode. Once the color-display mode is initialized, it
can’t be changed. As the program executes, a color (either a color index or
an RGBA value) is determined on a per-vertex basis for each geometric prim-
itive. This color either is a color you’ve explicitly specified for a vertex or, if
lighting is enabled, is determined from the interaction of the transformation
Red
Green
Blue
Black
Yellow
Magenta
Cyan
White
Figure 4-1 The Color Cube in Black and White

190 Chapter 4: Color
matrices with the surface normals and other material properties. In other
words, a red ball with a blue light shining on it looks different from the
same ball with no light on it. (See Chapter 5 for details.) After the relevant
lighting calculations have been performed, the chosen shading model is
applied. As explained in “Specifying a Color and a Shading Model,” you can
choose flat or smooth shading, each of which has different effects on the
eventual color of a pixel.
Next, the primitives are rasterized, or converted to a two-dimensional image.
Rasterizing involves determining which squares of an integer grid in win-
dow coordinates are occupied by the primitive, and then assigning color
and other values to each such square. A grid square along with its associated
values of color, z (depth), and texture coordinates is called a fragment. Pixels
are elements of the framebuffer; a fragment comes from a primitive and is
combined with its corresponding pixel to yield a new pixel. Once a frag-
ment has been constructed, texturing, fog, and antialiasing are applied—if
they’re enabled—to the fragments. After that, any specified alpha blending,
dithering, and bitwise logical operations are carried out using the fragment
and the pixel already stored in the framebuffer. Finally, the fragment’s color
value (either color index or RGBA) is written into the pixel and displayed in
the window using the window’s color-display mode.
RGBA versus Color-Index Mode
In either color-index or RGBA mode, a certain amount of color data is stored
at each pixel. This amount is determined by the number of bitplanes in the
framebuffer. A bitplane contains 1 bit of data for each pixel. If there are 8
color bitplanes, there are 8 color bits per pixel, and hence 28 = 256 different
values or colors that can be stored at the pixel.
Bitplanes are often divided evenly into storage for R, G, and B components
(that is, a 24-bitplane system devotes 8 bits each to red, green, and blue),
but this isn’t always true. To find out the number of bitplanes available
on your system for red, green, blue, alpha, or color-index values, use
glGetIntegerv() with GL_RED_BITS, GL_GREEN_BITS, GL_BLUE_BITS,
GL_ALPHA_BITS, and GL_INDEX_BITS.
Note: Color intensities on most computer screens aren’t perceived as linear
by the human eye. Consider colors consisting of just a red component,
with green and blue set at zero. As the intensity varies from 0.0 (off)
to 1.0 (full on), the number of electrons striking the pixels increases,
but the question is, does 0.5 appear to be halfway between 0.0 and
1.0? To test this, write a program that draws alternate pixels in a
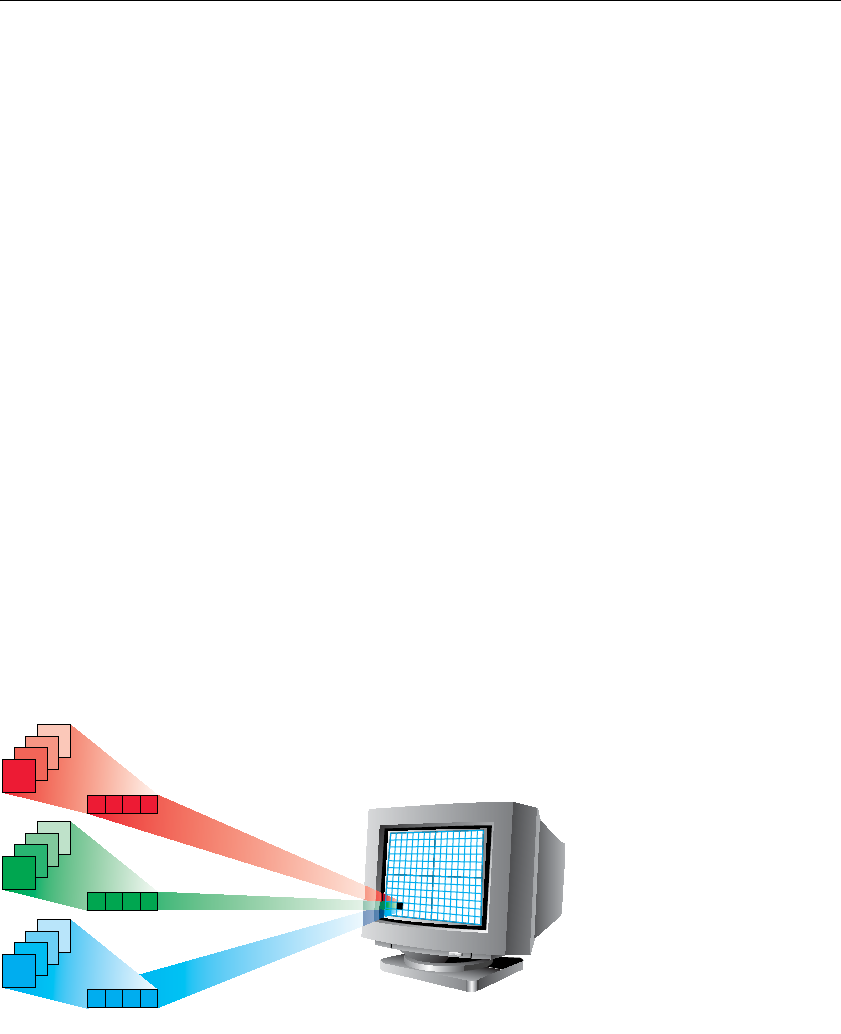
RGBA versus Color-Index Mode 191
checkerboard pattern to intensities 0.0 and 1.0, and compare it with
a region drawn solidly in color 0.5. At a reasonable distance from the
screen, the two regions should appear to have the same intensity. If
they look noticeably different, you need to use whatever correction
mechanism is provided on your particular system. For example, many
systems have a table to adjust intensities so that 0.5 appears to be
halfway between 0.0 and 1.0. The mapping generally used is an expo-
nential one, with the exponent referred to as gamma (hence the term
gamma correction). Using the same gamma for the red, green, and blue
components gives pretty good results, but three different gamma values
might give slightly better results. (For more details on this topic, see
Foley, van Dam, et al., Computer Graphics: Principles and Practice.
Addison-Wesley, 1990.)
RGBA Display Mode
In RGBA mode, the hardware sets aside a certain number of bitplanes for
each of the R, G, B, and A components (not necessarily the same number
for each component), as shown in Figure 4-2. The R, G, and B values are
typically stored as integers, rather than floating-point numbers, and they’re
scaled to the number of available bits for storage and retrieval. For example,
if a system has 8 bits available for the R component, integers between 0 and
255 can be stored; thus, 0, 1, 2, ..., 255 in the bitplanes would correspond
to R values of 0/255 = 0.0, 1/255, 2/255, ..., 255/255 = 1.0. Regardless of the
number of bitplanes, 0.0 specifies the minimum intensity, and 1.0 specifies
the maximum intensity.
Red
Green
Blue
F
igure 4-2 RGB Values from the Bitplanes

192 Chapter 4: Color
Note: The alpha value (the A in RGBA) has no direct effect on the color
displayed on the screen. It can be used for many things, including
blending and transparency, and it can have an effect on the values of
R, G, and B that are written. (See “Blending” in Chapter 6 for more
information about alpha values.)
The number of distinct colors that can be displayed at a single pixel depends
on the number of bitplanes and the capacity of the hardware to interpret
those bitplanes. The number of distinct colors can’t exceed 2n, where n is
the number of bitplanes. Thus, a machine with 24 bitplanes for RGB can
display up to 16.77 million distinct colors.
Dithering
Advanced
Some graphics hardware uses dithering to increase the number of apparent
colors. Dithering is the technique of using combinations of some colors to
create the effects of other colors. To illustrate how dithering works, suppose
your system has only 1 bit each for R, G, and B and thus can display only
eight colors: black, white, red, blue, green, yellow, cyan, and magenta. To
display a pink region, the hardware can fill the region in a checkerboard
manner, alternating red and white pixels. If your eye is far enough away
from the screen that it can’t distinguish individual pixels, the region appears
pink—the average of red and white. Redder pinks can be achieved by filling
a higher proportion of the pixels with red, whiter pinks would use more
white pixels, and so on.
With this technique, there are no pink pixels. The only way to achieve the
effect of “pinkness” is to cover a region consisting of multiple pixels—you
can’t dither a single pixel. If you specify an RGB value for an unavailable
color and fill a polygon, the hardware fills the pixels in the interior of the
polygon with a mixture of nearby colors whose average appears to your eye
to be the color you want. (Remember, though, that if you’re reading pixel
information out of the framebuffer, you get the actual red and white pixel
values, since there aren’t any pink ones. See Chapter 8 for more information
about reading pixel values.)
Figure 4-3 illustrates some simple dithering of black and white pixels to
make shades of gray. From left to right, the 4u4 patterns at the top represent
dithering patterns for 50 percent, 19 percent, and 69 percent gray. Under
each pattern, you can see repeated reduced copies of each pattern, but these
black and white squares are still bigger than most pixels. If you look at them
from across the room, you can see that they blur together and appear as
three levels of gray.
Advanced

RGBA versus Color-Index Mode 193
With about 8 bits each of R, G, and B, you can get a fairly high-quality image
without dithering. Just because your machine has 24 color bitplanes, how-
ever, doesn’t mean that dithering won’t be desirable. For example, if you are
running in double-buffer mode, the bitplanes might be divided into two
sets of 12, so there are really only 4 bits each per R, G, and B component.
Without dithering, 4-bit-per-component color can give less than satisfac-
tory results in many situations.
You enable or disable dithering by passing GL_DITHER to glEnable() or
glDisable(). Note that dithering, unlike many other features, is enabled by
default.
Color-Index Display Mode
With color-index mode, OpenGL uses a color map (or lookup table), which
is similar to using a palette to mix paints to prepare for a paint-by-number
scene. A painter’s palette provides spaces to mix paints together; similarly,
a computer’s color map provides indices where the primary red, green, and
blue values can be mixed, as shown in Figure 4-4.
Figure 4-3 Dithering Black and White to Create Gray
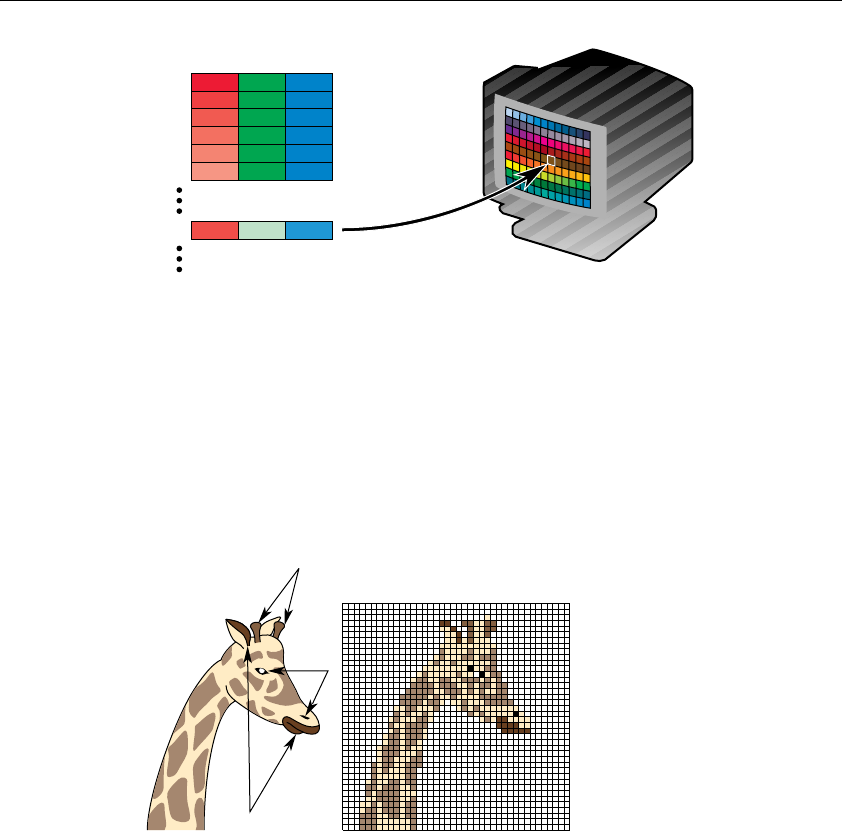
194 Chapter 4: Color
A painter filling in a paint-by-number scene chooses a color from the color
palette and fills the corresponding numbered regions with that color. A
computer stores the color index in the bitplanes for each pixel. Then those
bitplane values reference the color map, and the screen is painted with the
corresponding red, green, and blue values from the color map, as shown in
Figure 4-5.
In color-index mode, the number of simultaneously available colors is lim-
ited by the size of the color map and the number of bitplanes available. The
size of the color map is determined by the amount of hardware dedicated
to it. The size of the color map is always a power of 2, and typical sizes range
from 256 (28) to 4096 (212), where the exponent is the number of bitplanes
Index
0
1
2
3
4
5
296
Red Green Blue
Figure 4-4 A Color Map
1
2
4
3
3
3
3
Figure 4-5 Using a Color Map to Paint a Picture

RGBA versus Color-Index Mode 195
being used. If there are 2n indices in the color map and m available bit-
planes, the number of usable entries is the smaller of 2n and 2m.
With RGBA mode, each pixel’s color is independent of other pixels. How-
ever, in color-index mode, each pixel with the same index stored in its bit-
planes shares the same color-map location. If the contents of an entry in the
color map change, then all pixels of that color index change their color.
Choosing between RGBA and Color-Index Mode
You should base your decision to use RGBA or color-index mode on what
hardware is available and on what your application requires. For most
systems, more colors can be simultaneously represented with RGBA mode
than with color-index mode. Also, for several effects, such as shading,
lighting, texture mapping, and fog, RGBA provides more flexibility than
color-index mode.
You might prefer to use color-index mode in the following cases:
• If you’re porting an existing application that makes significant use of
color-index mode, it might be easier not to change to RGBA mode.
• If you have a small number of bitplanes available, RGBA mode may
produce noticeably coarse shades of colors. For example, if you have
only 8 bitplanes, in RGBA mode you may have only 3 bits for red,
3 bits for green, and 2 bits for blue. You’d have only 8 (23) shades of
red and green, and only 4 shades of blue. The gradients between color
shades are likely to be very obvious.
In this situation, if you have limited shading requirements, you can
use the color-lookup table to load more shades of colors. For example,
if you need only shades of blue, you can use color-index mode and
store up to 256 (28) shades of blue in the color-lookup table, which is
much better than the 4 shades you would have in RGBA mode. Of
course, this example would use up your entire color-lookup table, so
you would have no shades of red, green, or other combined colors.
• Color-index mode can be useful for various tricks, such as color-map
animation and drawing in layers. (See Chapter 14 for more information.)
In general, use RGBA mode wherever possible. It works with texture
mapping and works better with lighting, shading, fog, antialiasing, and
blending.

196 Chapter 4: Color
Changing between Display Modes
In the best of all possible worlds, you might want to avoid making a choice
between RGBA and color-index display mode. For example, you may want
to use color-index mode for a color-map animation effect and then, when
needed, immediately change the scene to RGBA mode for texture mapping.
Similarly, you may desire to switch between single and double buffering. For
example, you may have very few bitplanes; let’s say 8 bitplanes. In single-
buffer mode, you’ll have 256 (28) colors, but if you are using double-buffer
mode to eliminate flickering from your animated program, you may have
only 16 (24) colors. Perhaps you want to draw a moving object without
flicker and are willing to sacrifice colors for using double-buffer mode
(maybe the object is moving so fast that the viewer won’t notice the details).
But when the object comes to rest, you will want to draw it in single-buffer
mode so that you can use more colors.
Unfortunately, most window systems won’t allow an easy switch. For
example, with the X Window System, the color-display mode is an attribute
of the X Visual. An X Visual must be specified before the window is created.
Once it is specified, it cannot be changed for the life of the window. After
you create a window with a double-buffered, RGBA display mode, you’re
stuck with it.
A tricky solution to this problem is to create more than one window, each
with a different display mode. You must control the visibility of each
window (for example, mapping or unmapping an X Window, or managing
or unmanaging a Motif or Athena widget) and draw the object in the
appropriate, visible window.
Specifying a Color and a Shading Model
OpenGL maintains a current color (in RGBA mode) and a current color
index (in color-index mode). Unless you’re using a more complicated
coloring model such as lighting or texture mapping, each object is drawn
using the current color (or color index). Look at the following pseudocode
sequence:
set_color(RED);
draw_item(A);
draw_item(B);
set_color(GREEN);
set_color(BLUE);
draw_item(C);

Specifying a Color and a Shading Model 197
Items A and B are drawn in red, and item C is drawn in blue. The fourth
line, which sets the current color to green, has no effect (except to waste
a bit of time). With no lighting or texturing, when the current color is set,
all items drawn afterward are drawn in that color until the current color
is changed.
Specifying a Color in RGBA Mode
In RGBA mode, use the glColor*() command to select a current color.
For the versions of glColor*() that accept floating-point data types, the
values should typically range between 0.0 and 1.0, the minimum and
maximum values that can be stored in the framebuffer. Unsigned-integer
color components, when specified, are linearly mapped to floating-point
values such that the largest representable value maps to 1.0 (full intensity),
and zero maps to 0.0 (zero intensity). Signed-integer color components,
when specified, are linearly mapped to floating-point values such that
the most positive representable value maps to 1.0, and the most negative
representable value maps to 1.0 (see Table 4-1).
Neither floating-point nor signed-integer values are clamped to the range
[0, 1] before updating the current color or current lighting material param-
eters. After lighting calculations, resulting color values outside the range [0, 1]
are clamped to the range [0, 1] before they are interpolated or written into
void glColor3{b s i f d ub us ui}(TYPE r,TYPE g,TYPE b);
void glColor4{b s i f d ub us ui}(TYPE r,TYPE g,TYPE b,TYPE a);
void glColor3{b s i f d ub us ui}v(const TYPE *v);
void glColor4{b s i f d ub us ui}v(const TYPE *v);
Sets the current red, green, blue, and alpha values. This command can
have up to three suffixes, which differentiate variations of the parameters
accepted. The first suffix is either 3 or 4, to indicate whether you supply
an alpha value in addition to the red, green, and blue values. If you don’t
supply an alpha value, it’s automatically set to 1.0. The second suffix
indicates the data type for parameters: byte, short, integer, float, double,
unsigned byte, unsigned short, or unsigned integer. The third suffix is an
optional v, which indicates that the argument is a pointer to an array of
values of the given data type.
Compatibility
Extension
glColor

198 Chapter 4: Color
a color buffer. Even if lighting is disabled, the color components are clamped
before rasterization.
The similar routine glSecondaryColor*() is used to specify a color to be
applied after texture mapping (if lighting is disabled). For more detail, see
“Applying Secondary Color after Texturing” on page 478.
Color Clamping
OpenGL Version 3.0 introduced floating-point framebuffers, where RGBA
color components are stored as true floating-point values. Given the greater
dynamic range of floating-point values, you may want to allow color values
that fall outside the range of clamped color values originally specified by
OpenGL: 0.0 to 1.0.
The color-clamping options available in OpenGL Version 3.0 are described
in Table 4-2.
Suffix Data Type Minimum
Value
Min Value
Maps to
Maximum
Value
Max Value
Maps to
b 1-byte integer 128 1.0 127 1.0
s 2-byte integer 32,768 1.0 32,767 1.0
i 4-byte integer 2,147,483,648 1.0 2,147,483,647 1.0
ub unsigned 1-byte
integer
0 0.0 255 1.0
us unsigned 2-byte
integer
0 0.0 65,535 1.0
ui unsigned 4-byte
integer
0 0.0 4,294,967,295 1.0
Table 4-1 Converting Color Values to Floating-Point Numbers
void glClampColor(GLenum target, GLenum clamp);
Specify whether the primary and secondary color values are clamped.
target must be set to GL_CLAMP_VERTEX_COLOR, GL_CLAMP_
FRAGMENT_COLOR, or GL_CLAMP_READ_COLOR, and clamp must be
one of GL_TRUE, GL_FALSE, or GL_FIXED_ONLY.
Compatibility
Extension
GL_CLAMP_
VERTEX_COLOR
GL_CLAMP_
FRAGMENT_
COLOR
Specifying a Color and a Shading Model 199
Specifying a Color in Color-Index Mode
In color-index mode, use the glIndex*() command to select a single-valued
color index as the current color index.
In “Clearing the Window” in Chapter 2, you saw the specification of
glClearColor(). For color-index mode, there is a corresponding glClearIndex().
Note: OpenGL does not have any routines to load values into the color-
lookup table. Window systems typically already have such operations.
GLUT has the routine glutSetColor() to call the window-system-
specific commands.
Parameter Specifies
GL_TRUE Colors should be clamped to the range [0, 1]
GL_FALSE Colors are not to be clamped
GL_FIXED_ONLY Colors are only clamped if the destination
framebuffer format is fixed-point
Table 4-2 Values for use with glClampColor()
void glIndex{sifd ub}(TYPE c);
void glIndex{sifd ub}v(const TYPE *c);
Sets the current color index to c. The first suffix for this command
indicates the data type for parameters: short, integer, float, double, or
unsigned byte. The second, optional suffix is v, which indicates that the
argument is an array of values of the given data type (the array contains
only one value).
void glClearIndex(GLfloat cindex);
Sets the current clearing color in color-index mode. In a color-index mode
window, a call to glClear(GL_COLOR_BUFFER_BIT) will use cindex to clear
the buffer. The default clearing index is 0.0.
Compatibility
Extension
glIndex
Compatibility
Extension
glClearIndex

200 Chapter 4: Color
Advanced
The current index is stored as a floating-point value. Integer values are
converted directly to floating-point values, with no special mapping. Index
values outside the representable range of the color-index buffer aren’t
clamped. However, before an index is dithered (if enabled) and written to
the framebuffer, it’s converted to fixed-point format. Any bits in the integer
portion of the resulting fixed-point value that don’t correspond to bits in
the framebuffer are masked out.
Specifying a Shading Model
A line or a filled polygon primitive can be drawn with a single color (flat
shading) or with many different colors (smooth shading, also called Gouraud
shading). You specify the desired shading technique with glShadeModel().
With flat shading, the color of one particular vertex of an independent
primitive is duplicated across all the primitive’s vertices to render that prim-
itive. With smooth shading, the color at each vertex is treated individually.
For a line primitive, the colors along the line segment are interpolated
between the vertex colors. For a polygon primitive, the colors for the inte-
rior of the polygon are interpolated between the vertex colors. Example 4-1
draws a smooth-shaded triangle, as shown in Plate 11.
Example 4-1 Drawing a Smooth-Shaded Triangle: smooth.c
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_SMOOTH);
}
void triangle(void)
{
glBegin(GL_TRIANGLES);
glColor3f(1.0, 0.0, 0.0);
glVertex2f(5.0, 5.0);
glColor3f(0.0, 1.0, 0.0);
void glShadeModel(GLenum mode);
Sets the shading model. The mode parameter can be either GL_SMOOTH
(the default) or GL_FLAT.
Advanced
Compatibility
Extension
glShadeModel

Specifying a Color and a Shading Model 201
glVertex2f(25.0, 5.0);
glColor3f(0.0, 0.0, 1.0);
glVertex2f(5.0, 25.0);
glEnd();
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
triangle();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
gluOrtho2D(0.0, 30.0, 0.0, 30.0*(GLfloat) h/(GLfloat) w);
else
gluOrtho2D(0.0, 30.0*(GLfloat) w/(GLfloat) h, 0.0, 30.0);
glMatrixMode(GL_MODELVIEW);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}
With smooth shading, neighboring pixels have slightly different color
values. In RGBA mode, adjacent pixels with slightly different values look
similar, so the color changes across a polygon appear gradual. In color-index
mode, adjacent pixels may reference different locations in the color-index
table, which may not have similar colors at all. Adjacent color-index entries
may contain wildly different colors, so a smooth-shaded polygon in color-
index mode can look psychedelic.

202 Chapter 4: Color
To avoid this problem, you have to create a color ramp of smoothly changing
colors among a contiguous set of indices in the color map. Remember that
loading colors into a color map is performed through your window system,
rather than through OpenGL. If you use GLUT, you can use glutSetColor()
to load a single index in the color map with specified red, green, and blue
values. The first argument for glutSetColor() is the index, and the others are
the red, green, and blue values. To load 32 contiguous color indices (color
indices 16 to 47) with slightly differing shades of yellow, you might call
for (i = 0; i < 32; i++) {
glutSetColor(16+i, 1.0*(i/32.0), 1.0*(i/32.0), 0.0);
}
Now, if you render smooth-shaded polygons that use only the colors from
indices 16 to 47, those polygons will have gradually differing shades of
yellow.
With flat shading, the color of a single vertex defines the color of an entire
primitive. For a line segment, the color of the line is the current color
when the second (ending) vertex is specified. For a polygon, the color used
is the one that’s in effect when a particular vertex is specified, as shown in
Table 4-3. The table counts vertices and polygons starting from 1. OpenGL
follows these rules consistently, but the best way to avoid uncertainty
about how a flat-shaded primitive will be drawn is to specify only one
color for the primitive.
Type of Polygon Vertex Used to Select the Color for the
ith Polygon
single polygon 1
triangle strip i+ 2
triangle fan i+ 2
independent triangle 3i
quad strip 2i+ 2
independent quad 4i
Table 4-3 How OpenGL Selects a Color for the ith Flat-Shaded Polygon

203
Chapter 5
5.Lighting
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Understand how real-world lighting conditions are approximated by
OpenGL
• Render illuminated objects by defining light source, material, and
lighting model properties
• Define the material properties of the objects being illuminated
• Manipulate the matrix stack to control the positions of light sources
Note: In OpenGL Version 3.1, many of the techniques and functions
described in this chapter were removed through deprecation. The
concepts are still relevant, but computing colors through lighting
must be done in either a vertex or fragment shader. These topics
are briefly described in Chapter 15, and fully explained in the
companion text, The OpenGL Shading Language Guide.

204 Chapter 5: Lighting
As you saw in Chapter 4, OpenGL computes the color of each pixel in a
final, displayed scene that’s held in the framebuffer. Part of this computa-
tion depends on what lighting is used in the scene and on how objects in
the scene reflect or absorb that light. As an example of this, recall that the
ocean has a different color on a bright, sunny day than it does on a gray,
cloudy day. The presence of sunlight or clouds determines whether you see
the ocean as bright turquoise or murky gray-green. In fact, most objects
don’t even look three-dimensional until they’re lit. Figure 5-1 shows two
versions of the exact same scene (a single sphere), one with lighting and one
without.
As you can see, an unlit sphere looks no different from a two-dimensional
disk. This demonstrates how critical the interaction between objects and
light is in creating a three-dimensional scene.
With OpenGL, you can manipulate the lighting and objects in a scene to
create many different kinds of effects. This chapter begins with a primer on
hidden-surface removal. Then it explains how to control the lighting in a
scene, discusses the OpenGL conceptual model of lighting, and describes in
detail how to set the numerous illumination parameters to achieve certain
effects. Toward the end of the chapter, the mathematical computations that
determine how lighting affects color are presented.
This chapter contains the following major sections:
• “A Hidden-Surface Removal Survival Kit” describes the basics of
removing hidden surfaces from view.
• “Real-World and OpenGL Lighting” explains in general terms how
light behaves in the world and how OpenGL models this behavior.
Figure 5-1 A Lit and an Unlit Sphere

A Hidden-Surface Removal Survival Kit 205
• “A Simple Example: Rendering a Lit Sphere” introduces the OpenGL
lighting facility by presenting a short program that renders a lit sphere.
• “Creating Light Sources” explains how to define and position light
sources.
• “Selecting a Lighting Model” discusses the elements of a lighting
model and how to specify them.
• “Defining Material Properties” explains how to describe the properties
of objects so that they interact with light in a desired way.
• “The Mathematics of Lighting” presents the mathematical calculations
used by OpenGL to determine the effect of lights in a scene.
• “Lighting in Color-Index Mode” discusses the differences between
using RGBA mode and color-index mode for lighting.
Lighting calculations typically take place prior to texturing. Version 1.2
introduced a lighting mode (GL_SEPARATE_SPECULAR_COLOR) whereby
the calculation of the specular color is done separately from the emissive,
ambient, and diffuse components, and then the application of the specular
color takes place after texturing. Using a separate specular color often
enhances a highlight, making it less influenced by the color of the texture
image.
A Hidden-Surface Removal Survival Kit
With this section, you begin to draw shaded, three-dimensional objects
in earnest. With shaded polygons, it becomes very important to draw the
objects that are closer to the viewing position and to eliminate objects
obscured by others nearer to the eye.
When you draw a scene composed of three-dimensional objects, some of
them might obscure all or parts of others. Changing your viewpoint can
change the obscuring relationship. For example, if you view the scene from
the opposite direction, any object that was previously in front of another is
now behind it. To draw a realistic scene, these obscuring relationships must
be maintained. Suppose your code works like this:
while (1) {
get_viewing_point_from_mouse_position();
glClear(GL_COLOR_BUFFER_BIT);
draw_3d_object_A();
draw_3d_object_B();
}

206 Chapter 5: Lighting
For some mouse positions, object A might obscure object B. For others, the
reverse may hold. If nothing special is done, the preceding code always
draws object B second (and thus on top of object A) no matter what viewing
position is selected. In a worst-case scenario, if objects A and B intersect one
another so that part of object A obscures object B, and part of B obscures A,
changing the drawing order does not provide a solution.
The elimination of parts of solid objects that are obscured by others is called
hidden-surface removal. (Hidden-line removal, which does the same job
for objects represented as wireframe skeletons, is a bit trickier and isn’t
discussed here. See “Hidden-Line Removal” in Chapter 14 for details.) The
easiest way to achieve hidden-surface removal is to use the depth buffer
(sometimes called a z-buffer). (Also see Chapter 10.)
A depth buffer works by associating a depth, or a distance, from the view
plane (usually the near clipping plane), with each pixel on the window.
Initially, the depth values for all pixels are set to the largest possible distance
(usually the far clipping plane) using the glClear() command with GL_
DEPTH_BUFFER_BIT. Then the objects in the scene are drawn in any order.
Graphical calculations in hardware or software convert each surface that’s
drawn to a set of pixels on the window where the surface will appear if it
isn’t obscured by something else. In addition, the distance from the view
plane is computed. With depth-buffering enabled, before each pixel is drawn
a comparison is done with the depth value already stored at the pixel. If
the new pixel is closer than (in front of) what’s there, the new pixel’s color
and depth values replace those that are currently written into the pixel. If
the new pixel’s depth is greater than what’s currently there, the new pixel
is obscured, and the color and depth information for the incoming pixel is
discarded.
To use depth-buffering, you need to enable it. This has to be done only
once. Before drawing, each time you draw the scene, you need to clear
the depth buffer and then draw the objects in the scene in any order.
To convert the preceding code example so that it performs hidden-surface
removal, modify it to the following:
glutInitDisplayMode(GLUT_DEPTH | .... );
glEnable(GL_DEPTH_TEST);
...
while (1) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
get_viewing_point_from_mouse_position();
draw_3d_object_A();
draw_3d_object_B();
}

Real-World and OpenGL Lighting 207
The argument for glClear() clears both the depth and color buffers.
Depth-buffer testing can affect the performance of your application. Since
information is discarded, rather than used for drawing, hidden-surface
removal can increase your performance slightly. However, the implementa-
tion of your depth buffer probably has the greatest effect on performance.
A “software” depth buffer (implemented with processor memory) may be
much slower than one implemented with a specialized hardware depth
buffer.
Real-World and OpenGL Lighting
When you look at a physical surface, your eye’s perception of the color
depends on the distribution of photon energies that arrive and trigger your
cone cells. (See “Color Perception” in Chapter 4.) Those photons come from
a light source or combination of sources, some of which are absorbed and
some of which are reflected by the surface. In addition, different surfaces
may have very different properties—some are shiny and preferentially
reflect light in certain directions, while others scatter incoming light
equally in all directions. Most surfaces are somewhere in between.
OpenGL approximates light and lighting as if light can be broken into red,
green, and blue components. Thus, the color of a light source is character-
ized by the amounts of red, green, and blue light it emits, and the material
of a surface is characterized by the percentages of the incoming red, green,
and blue components that are reflected in various directions. The OpenGL
lighting equations are just approximations, but ones that work fairly well
and can be computed relatively quickly. If you want a more accurate (or just
different) lighting model, you have to do your own calculations in software.
Such software can be enormously complex, as a few hours of reading any
optics textbook should convince you.
In the OpenGL lighting model, the light in a scene comes from several light
sources that can be individually turned on and off. Some light comes from
a particular direction or position, and some light is generally scattered
about the scene. For example, when you turn on a lightbulb in a room, most
of the light comes from the bulb, but some light results from bouncing off
one, two, three, or more walls. This bounced light (called ambient light) is
assumed to be so scattered that there is no way to tell its original direction,
but it disappears if a particular light source is turned off.

208 Chapter 5: Lighting
Finally, there might be a general ambient light in the scene that comes from
no particular source, as if it had been scattered so many times that its orig-
inal source is impossible to determine.
In the OpenGL model, the light sources have effects only when there are
surfaces that absorb and reflect light. Each surface is assumed to be composed
of a material with various properties. A material might emit its own light
(such as headlights on an automobile), it might scatter some incoming light
in all directions, and it might reflect some portion of the incoming light in a
preferential direction (such as a mirror or other shiny surface).
The OpenGL lighting model considers the lighting to be divided into four
independent components: ambient, diffuse, specular, and emissive. All four
components are computed independently and then added together.
Ambient, Diffuse, Specular, and Emissive Light
Ambient illumination is light that’s been scattered so much by the environ-
ment that its direction is impossible to determine—it seems to come from
all directions. Backlighting in a room has a large ambient component, since
most of the light that reaches your eye has first bounced off many surfaces.
A spotlight outdoors has a tiny ambient component; most of the light trav-
els in the same direction, and since you’re outdoors, very little of the light
reaches your eye after bouncing off other objects. When ambient light
strikes a surface, it’s scattered equally in all directions.
The diffuse component is the light that comes from one direction, so it’s
brighter if it comes squarely down on a surface than if it barely glances off
the surface. Once it hits a surface, however, it’s scattered equally in all direc-
tions, so it appears equally bright, no matter where the eye is located. Any
light coming from a particular position or direction probably has a diffuse
component.
Specular light comes from a particular direction, and it tends to bounce off
the surface in a preferred direction. A well-collimated laser beam bouncing
off a high-quality mirror produces almost 100 percent specular reflection.
Shiny metal or plastic has a high specular component, and chalk or carpet
has almost none. You can think of specularity as shininess.
In addition to ambient, diffuse, and specular colors, materials may have
an emissive color, which simulates light originating from an object. In the
OpenGL lighting model, the emissive color of a surface adds intensity to the
object, but is unaffected by any light sources. Also, the emissive color does
not introduce any additional light into the overall scene.

Real-World and OpenGL Lighting 209
Although a light source delivers a single distribution of frequencies, the
ambient, diffuse, and specular components might be different. For example,
if you have a white light in a room with red walls, the scattered light tends
to be red, although the light directly striking objects is white. OpenGL
allows you to set the red, green, and blue values for each component of light
independently.
Material Colors
The OpenGL lighting model approximates a material’s color from the
percentages of the incoming red, green, and blue light it reflects. For
example, a perfectly red ball reflects all the incoming red light and absorbs
all the green and blue light that strikes it. If you view such a ball in white
light (composed of equal amounts of red, green, and blue light), all the red
is reflected, and you see a red ball. If the ball is viewed in pure red light, it
also appears to be red. If, however, the red ball is viewed in pure green light,
it appears black (all the green is absorbed and there’s no incoming red, so
no light is reflected).
Like lights, materials have different ambient, diffuse, and specular colors,
which determine the ambient, diffuse, and specular reflectances of the
material. A material’s ambient reflectance is combined with the ambient
component of each incoming light source, the diffuse reflectance with the
light’s diffuse component, and similarly for the specular reflectance and
specular component. Ambient and diffuse reflectances define the color of
the material and are typically similar if not identical. Specular reflectance is
usually white or gray, so that specular highlights end up being the color of
the light source’s specular intensity. If you think of a white light shining on
a shiny red plastic sphere, most of the sphere appears red, but the shiny
highlight is white.
RGB Values for Lights and Materials
The color components specified for lights mean something different than
for materials. For a light, the numbers correspond to a percentage of full
intensity for each color. If the R, G, and B values for a light’s color are all 1.0,
the light is the brightest possible white. If the values are 0.5, the color is still
white, but only at half intensity, so it appears gray. If R = G = 1 and B = 0
(full red and green with no blue), the light appears yellow.

210 Chapter 5: Lighting
For materials, the numbers correspond to the reflected proportions of those
colors. So if R = 1, G = 0.5, and B = 0 for a material, that material reflects all
the incoming red light, half the incoming green light, and none of the
incoming blue light. In other words, if an OpenGL light has components
(LR, LG, LB), and a material has corresponding components (MR, MG, MB),
then, ignoring all other reflectivity effects, the light that arrives at the eye
is given by (LRMR, LG MG, LBMB).
Similarly, if you have two lights that send (R1, G1, B1) and (R2, G2, B2) to
the eye, OpenGL adds the components, giving (R1 + R2, G1 + G2, B1 + B2).
If any of the sums is greater than 1 (corresponding to a color brighter than
the equipment can display), the component is clamped to 1.
A Simple Example: Rendering a Lit Sphere
These are the steps required to add lighting to your scene:
1. Define normal vectors for each vertex of every object. These normals
determine the orientation of the object relative to the light sources.
2. Create, select, and position one or more light sources.
3. Create and select a lighting model, which defines the level of global
ambient light and the effective location of the viewpoint (for the
purposes of lighting calculations).
4. Define material properties for the objects in the scene.
Example 5-1 accomplishes these tasks. It displays a sphere illuminated by a
single light source, as shown earlier in Figure 5-1.
Example 5-1 Drawing a Lit Sphere: light.c
void init(void)
{
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat mat_shininess[] = { 50.0 };
GLfloat light_position[] = { 1.0, 1.0, 1.0, 0.0 };
GLfloat white_light[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat lmodel_ambient[] = { 0.1, 0.1, 0.1, 1.0 };
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_SMOOTH);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);

A Simple Example: Rendering a Lit Sphere 211
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
glLightfv(GL_LIGHT0, GL_DIFFUSE, white_light);
glLightfv(GL_LIGHT0, GL_SPECULAR, white_light);
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, lmodel_ambient);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_DEPTH_TEST);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glutSolidSphere(1.0, 20, 16);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-1.5, 1.5, -1.5*(GLfloat)h/(GLfloat)w,
1.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0);
else
glOrtho(-1.5*(GLfloat)w/(GLfloat)h,
1.5*(GLfloat)w/(GLfloat)h, -1.5, 1.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}

212 Chapter 5: Lighting
The lighting-related calls are in the init() command; they’re discussed
briefly in the following paragraphs and in more detail later in this chapter.
One thing to note about Example 5-1 is that it uses RGBA color mode, not
color-index mode. The OpenGL lighting calculation is different for the two
modes, and in fact the lighting capabilities are more limited in color-index
mode. Thus, RGBA is the preferred mode when doing lighting, and all the
examples in this chapter use it. (See “Lighting in Color-Index Mode” on
page 246 for more information.)
Define Normal Vectors for Each Vertex of Every Object
An object’s normals determine its orientation relative to the light sources.
For each vertex, OpenGL uses the assigned normal to determine how much
light that particular vertex receives from each light source. In this example,
the normals for the sphere are defined as part of the glutSolidSphere()
routine.
For proper lighting, surface normals must be of unit length. You must
also be careful that the modelview transformation matrix does not scale
the surface normal, so that the resulting normal is no longer of unit
length. To ensure that normals are of unit length, you may need to
call glEnable() with GL_NORMALIZE or GL_RESCALE_NORMAL as a
parameter.
GL_RESCALE_NORMAL causes each component in a surface normal to be
multiplied by the same value, which is determined from the modelview
transformation matrix. Therefore, it works correctly only if the normal
was scaled uniformly and was a unit-length vector to begin with. GL_
NORMALIZE is a more thorough operation than GL_RESCALE_NORMAL.
When GL_NORMALIZE is enabled, the length of the normal vector is cal-
culated, and then each component of the normal is divided by the calcu-
lated length. This operation guarantees that the resulting normal is of
unit length, but may be more expensive than simply rescaling normals.
(See “Normal Vectors” in Chapter 2 and Appendix I, “Built-In OpenGL
Shading Language Variables and Functions,”1 for more details on how to
define normals.)
Note: Some OpenGL implementations may implement GL_RESCALE_
NORMAL by actually normalizing the normal vectors, not just
scaling them. However, you cannot determine whether your
implementation does this, nor should you usually rely on this.
1This appendix is available online at http://www.opengl-redbook.com/appendices/.

A Simple Example: Rendering a Lit Sphere 213
Create, Position, and Enable One or More Light Sources
Example 5-1 uses only one, white light source; its location is specified by
the glLightfv() call. This example specifies white as the color for light zero
(GL_LIGHT0) for calculations of diffuse and specular reflection. If you want
a differently colored light, modify glLight*().
You can also include at least eight different light sources of various colors in
your scene. (The particular implementation of OpenGL you’re using might
allow more than eight.) The default color of lights other than GL_LIGHT0
is black. You can also locate the lights wherever you desire: You can position
them near the scene, as a desk lamp would be, or infinitely far away to
simulate sunlight, for example. In addition, you can control whether a light
produces a narrow, focused beam or a wider beam. Remember that each
light source adds significantly to the calculations needed to render the
scene, so performance is affected by the number of lights in the scene. (See
“Creating Light Sources” on page 214 for more information about how to
create lights with the desired characteristics.)
After you’ve defined the characteristics of the lights you want, you have to
turn them on with the glEnable() command. You also need to call glEnable()
with GL_LIGHTING as a parameter to prepare OpenGL to perform lighting
calculations. (See “Enabling Lighting” on page 231 for more information.)
Select a Lighting Model
As you might expect, the glLightModel*() command describes the param-
eters of a lighting model. In Example 5-1, the only element of the lighting
model that’s defined explicitly is the global ambient light. The lighting
model also defines whether the viewer of the scene should be considered to
be infinitely far away or local to the scene, and whether lighting calcula-
tions should be performed differently for the front and back surfaces of
objects in the scene. Example 5-1 uses the default settings for these two
aspects of the model—a viewer infinitely far away (“infinite viewer” mode)
and one-sided lighting. Using a local viewer adds significantly to the com-
plexity of the calculations that must be performed, because OpenGL must
calculate the angle between the viewpoint and each object. With an infinite
viewer, however, the angle is ignored, and the results are slightly less realis-
tic. Further, since in this example the back surface of the sphere is never
seen (it’s the inside of the sphere), one-sided lighting is sufficient. (See
“Selecting a Lighting Model” on page 227 for a more detailed description
of the elements of an OpenGL lighting model.)

214 Chapter 5: Lighting
Define Material Properties for the Objects in the Scene
An object’s material properties determine how it reflects light and therefore
of what material it seems to be made. Because the interaction between an
object’s material surface and incident light is complex, specifying material
properties so that an object has a certain desired appearance is an art. You
can specify a material’s ambient, diffuse, and specular colors and how
shiny it is. In this example, only the last two material properties—the
specular material color and shininess—are explicitly specified (with the
glMaterialfv() calls). (See “Defining Material Properties” on page 231 for
descriptions and examples of all material-property parameters.)
Some Important Notes
As you write your own lighting program, remember that you can use the
default values for some lighting parameters, whereas others need to be
changed. Also, don’t forget to enable whatever lights you define and to
enable lighting calculations. Finally, remember that you might be able to
use display lists to maximize efficiency as you change lighting conditions.
(See “Display List Design Philosophy” in Chapter 7.)
Creating Light Sources
Light sources have several properties, such as color, position, and direction.
The following sections explain how to control these properties and what
the resulting light looks like. The command used to specify all properties of
lights is glLight*(). Its three arguments identify the light whose property is
being specified, the property, and the desired value for that property.
void glLight{if}(GLenum light, GLenum pname,TYPE param);
void glLight{if}v(GLenum light, GLenum pname, const TYPE *param);
Creates the light specified by light, which can be GL_LIGHT0, GL_LIGHT1,
... , or GL_LIGHT7. The characteristic of the light being set is defined by
pname, which specifies a named parameter (see Table 5-1). param indicates
the values to which the pname characteristic is set; it’s a pointer to a group
of values if the vector version is used or the value itself if the nonvector
version is used. The nonvector version can be used to set only single-valued
light characteristics.
Compatibility
Extension
glLight
GL_LIGHTi
GL_AMBIENT
GL_DIFFUSE
GL_SPECULAR
GL_POSITION
GL_SPOT_
DIRECTION
GL_SPOT_
EXPONENT
GL_SPOT_
CUTOFF
GL_CONSTANT_
ATTENUATION
GL_LINEAR_
ATTENUATION
GL_QUADRATIC_
ATTENUATION

Creating Light Sources 215
Note: The default values listed for GL_DIFFUSE and GL_SPECULAR in
Table 5-1 differ from GL_LIGHT0 to other lights (GL_LIGHT1, GL_
LIGHT2, etc.). For GL_LIGHT0, the default value is (1.0, 1.0, 1.0, 1.0)
for both GL_DIFFUSE and GL_SPECULAR. For other lights, the
default value is (0.0, 0.0, 0.0, 1.0) for the same light source properties.
Example 5-2 shows how to use glLight*():
Example 5-2 Defining Colors and Position for a Light Source
GLfloat light_ambient[] = { 0.0, 0.0, 0.0, 1.0 };
GLfloat light_diffuse[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat light_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat light_position[] = { 1.0, 1.0, 1.0, 0.0 };
glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diffuse);
glLightfv(GL_LIGHT0, GL_SPECULAR, light_specular);
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
Parameter Name Default Values Meaning
GL_AMBIENT (0.0, 0.0, 0.0, 1.0) ambient intensity of light
GL_DIFFUSE (1.0, 1.0, 1.0, 1.0)
or
(0.0, 0.0, 0.0, 1.0)
diffuse intensity of light
(default for light 0 is white;
for other lights, black)
GL_SPECULAR (1.0, 1.0, 1.0, 1.0)
or
(0.0, 0.0, 0.0, 1.0)
specular intensity of light
(default for light 0 is white;
for other lights, black)
GL_POSITION (0.0, 0.0, 1.0, 0.0) (x, y, z, w) position of light
GL_SPOT_DIRECTION (0.0, 0.0,1.0) (x, y, z) direction of
spotlight
GL_SPOT_EXPONENT 0.0 spotlight exponent
GL_SPOT_CUTOFF 180.0 spotlight cutoff angle
GL_CONSTANT_ATTENUATION 1.0 constant attenuation factor
GL_LINEAR_ATTENUATION 0.0 linear attenuation factor
GL_QUADRATIC_ATTENUATION 0.0 quadratic attenuation
factor
Table 5-1 Default Values for pname Parameter of glLight*()

216 Chapter 5: Lighting
As you can see, arrays are defined for the parameter values, and glLightfv()
is called repeatedly to set the various parameters. In this example, the first
three calls to glLightfv() are superfluous, since they’re being used to specify
the default values for the GL_AMBIENT, GL_DIFFUSE, and
GL_SPECULAR parameters.
Note: Remember to turn on each light with glEnable(). (See “Enabling
Lighting” for more information about how to do this.)
All the parameters for glLight*() and their possible values are explained in
the following sections. These parameters interact with those that define the
overall lighting model for a particular scene and an object’s material prop-
erties. (See “Selecting a Lighting Model” and “Defining Material Properties”
for more information about these two topics. “The Mathematics of Light-
ing” explains how all these parameters interact mathematically.)
Color
OpenGL allows you to associate three different color-related parameters—
GL_AMBIENT, GL_DIFFUSE, and GL_SPECULAR—with any particular light.
The GL_AMBIENT parameter refers to the RGBA intensity of the ambient
light that a particular light source adds to the scene. As you can see in
Table 5-1, by default there is no ambient light since GL_AMBIENT is (0.0,
0.0, 0.0, 1.0). This value was used in Example 5-1. If this program had
specified blue ambient light as
GLfloat light_ambient[] = { 0.0, 0.0, 1.0, 1.0};
glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);
the result would have been as shown on the left side of Plate 13.
The GL_DIFFUSE parameter probably most closely correlates with what you
naturally think of as “the color of a light.” It defines the RGBA color of
the diffuse light that a particular light source adds to a scene. By default,
GL_DIFFUSE is (1.0, 1.0, 1.0, 1.0) for GL_LIGHT0, which produces a bright,
white light, as shown on the left side of Plate 13. The default value for any
other light (GL_LIGHT1, ... , GL_LIGHT7) is (0.0, 0.0, 0.0, 0.0).
The GL_SPECULAR parameter affects the color of the specular highlight on
an object. Typically, a real-world object such as a glass bottle has a specular
highlight that’s the color of the light shining on it (which is often white).
Therefore, if you want to create a realistic effect, set the GL_SPECULAR
parameter to the same value as the GL_DIFFUSE parameter. By default,

Creating Light Sources 217
GL_SPECULAR is (1.0, 1.0, 1.0, 1.0) for GL_LIGHT0, and (0.0, 0.0, 0.0, 0.0)
for any other light.
Note: The alpha component of these colors is not used until blending is
enabled (see Chapter 6). Until then, the alpha value can be safely
ignored.
Position and Attenuation
As previously mentioned, you can choose between a light source that’s
treated as though it’s located infinitely far away from the scene and one
that’s nearer to the scene. The first type is referred to as a directional light
source; the effect of an infinite location is that the rays of light can be con-
sidered parallel by the time they reach an object. An example of a real-world
directional light source is the sun. The second type is called a positional light
source, since its exact position within the scene determines the effect it has
on a scene and, specifically, the direction from which the light rays come.
A desk lamp is an example of a positional light source. You can see the dif-
ference between directional and positional lights in Plate 13. The light used
in Example 5-1 is a directional one:
GLfloat light_position[] = { 1.0, 1.0, 1.0, 0.0 };
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
As shown, you supply a vector of four values (x, y, z, w) for the GL_POSITION
parameter. If the last value, w, is zero, the corresponding light source is a
directional one, and the (x, y, z) values describe its direction. This direction
is transformed by the modelview matrix. By default, GL_POSITION is (0, 0,
1, 0), which defines a directional light that points along the negative z-axis.
(Note that nothing prevents you from creating a directional light with the
direction of (0, 0, 0), but such a light won’t help you much.)
If the w–value is nonzero, the light is positional, and the (x, y, z) values
specify the location of the light in homogeneous object coordinates (see
Appendix C). This location is transformed by the modelview matrix and
stored in eye coordinates. (See “Controlling a Light’s Position and Direc-
tion” on page 221 for more information about how to control the transfor-
mation of the light’s location.) Also, by default, a positional light radiates in
all directions, but you can restrict it to producing a cone of illumination by
defining the light as a spotlight. (See “Spotlights” on page 219 for an expla-
nation of how to define a light as a spotlight.)

218 Chapter 5: Lighting
Note: Remember that the colors across the face of a smooth-shaded polygon
are determined by the colors calculated for the vertices. Because of
this, you probably want to avoid using large polygons with local
lights. If you locate the light near the middle of the polygon, the
vertices might be too far away to receive much light, and the whole
polygon will look darker than you intended. To avoid this problem,
break up the large polygon into smaller ones.
For real-world lights, the intensity of light decreases as distance from the
light increases. Since a directional light is infinitely far away, it doesn’t make
sense to attenuate its intensity over distance, so attenuation is disabled for
a directional light. However, you might want to attenuate the light from a
positional light. OpenGL attenuates a light source by multiplying the
contribution of that source by an attenuation factor:
where
d = distance between the light’s position and the vertex
kc = GL_CONSTANT_ATTENUATION
kl= GL_LINEAR_ATTENUATION
kq = GL_QUADRATIC_ATTENUATION
By default, kc is 1.0 and both kl and kq are zero, but you can give these
parameters different values:
glLightf(GL_LIGHT0, GL_CONSTANT_ATTENUATION, 2.0);
glLightf(GL_LIGHT0, GL_LINEAR_ATTENUATION, 1.0);
glLightf(GL_LIGHT0, GL_QUADRATIC_ATTENUATION, 0.5);
Note that the ambient, diffuse, and specular contributions are all attenu-
ated. Only the emission and global ambient values aren’t attenuated. Also
note that since attenuation requires an additional division (and possibly
more math) for each calculated color, using attenuated lights may slow
down application performance.
attenuation factor = 1
kc + kld + kqd2

Creating Light Sources 219
Spotlights
As previously mentioned, you can have a positional light source act as a
spotlight by restricting the shape of the light it emits to a cone. To create a
spotlight, you need to determine the spread of the cone of light you desire.
(Remember that since spotlights are positional lights, you also have to
locate them where you want them. Again, note that nothing prevents you
from creating a directional spotlight, but it won’t give you the result you
want.) To specify the angle between the axis of the cone and a ray along the
edge of the cone, use the GL_SPOT_CUTOFF parameter. The angle of the
cone at the apex is then twice this value, as shown in Figure 5-2.
Note that no light is emitted beyond the edges of the cone. By default, the
spotlight feature is disabled because the GL_SPOT_CUTOFF parameter is
180.0. This value means that light is emitted in all directions (the angle
at the cone’s apex is 360 degrees, so it isn’t a cone at all). The value for
GL_SPOT_CUTOFF
Figure 5-2 GL_SPOT_CUTOFF Parameter

220 Chapter 5: Lighting
GL_SPOT_CUTOFF is restricted to the range [0.0, 90.0] (unless it has the special
value 180.0). The following line sets the cutoff parameter to 45 degrees:
glLightf(GL_LIGHT0, GL_SPOT_CUTOFF, 45.0);
You also need to specify a spotlight’s direction, which determines the axis
of the cone of light:
GLfloat spot_direction[] = { -1.0, -1.0, 0.0 };
glLightfv(GL_LIGHT0, GL_SPOT_DIRECTION, spot_direction);
The direction is specified in object coordinates. By default, the direction
is (0.0, 0.0, 1.0), so if you don’t explicitly set the value of GL_SPOT_
DIRECTION, the light points down the negative z-axis. Also, keep in mind
that a spotlight’s direction is transformed by the modelview matrix just as
though it were a normal vector, and the result is stored in eye coordinates.
(See “Controlling a Light’s Position and Direction” for more information
about such transformations.)
In addition to the spotlight’s cutoff angle and direction, there are two ways
you can control the intensity distribution of the light within the cone. First,
you can set the attenuation factor described earlier, which is multiplied by
the light’s intensity. You can also set the GL_SPOT_EXPONENT parameter,
which by default is zero, to control how concentrated the light is. The
light’s intensity is highest in the center of the cone. It’s attenuated toward
the edges of the cone by the cosine of the angle between the direction of
the light and the direction from the light to the vertex being lit, raised to
the power of the spot exponent. Thus, higher spot exponents result in a
more focused light source. (See “The Mathematics of Lighting” for more
details on the equations used to calculate light intensity.)
Multiple Lights
As mentioned, you can have at least eight lights in your scene (possibly
more, depending on your OpenGL implementation). Since OpenGL needs
to perform calculations to determine how much light each vertex receives
from each light source, increasing the number of lights adversely affects per-
formance. The constants used to refer to the eight lights are GL_LIGHT0,
GL_LIGHT1, GL_LIGHT2, GL_LIGHT3, and so on. In the preceding discus-
sions, parameters related to GL_LIGHT0 were set. If you want an additional
light, you need to specify its parameters; also, remember that the default
values are different for these other lights than they are for GL_LIGHT0, as
explained in Table 5-1. Example 5-3 defines a white attenuated spotlight.

Creating Light Sources 221
Example 5-3 Second Light Source
GLfloat light1_ambient[] = { 0.2, 0.2, 0.2, 1.0 };
GLfloat light1_diffuse[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat light1_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat light1_position[] = { -2.0, 2.0, 1.0, 1.0 };
GLfloat spot_direction[] = { -1.0, -1.0, 0.0 };
glLightfv(GL_LIGHT1, GL_AMBIENT, light1_ambient);
glLightfv(GL_LIGHT1, GL_DIFFUSE, light1_diffuse);
glLightfv(GL_LIGHT1, GL_SPECULAR, light1_specular);
glLightfv(GL_LIGHT1, GL_POSITION, light1_position);
glLightf(GL_LIGHT1, GL_CONSTANT_ATTENUATION, 1.5);
glLightf(GL_LIGHT1, GL_LINEAR_ATTENUATION, 0.5);
glLightf(GL_LIGHT1, GL_QUADRATIC_ATTENUATION, 0.2);
glLightf(GL_LIGHT1, GL_SPOT_CUTOFF, 45.0);
glLightfv(GL_LIGHT1, GL_SPOT_DIRECTION, spot_direction);
glLightf(GL_LIGHT1, GL_SPOT_EXPONENT, 2.0);
glEnable(GL_LIGHT1);
If these lines were added to Example 5-1, the sphere would be lit with two
lights, one directional and one spotlight.
Try This
Modify Example 5-1 in the following manner:
• Change the first light to be a positional colored light, rather than a
directional white one.
• Add an additional colored spotlight. Hint: Use some of the code shown
in the preceding section.
• Measure how these two changes affect performance.
Controlling a Light’s Position and Direction
OpenGL treats the position and direction of a light source just as it treats
the position of a geometric primitive. In other words, a light source is sub-
ject to the same matrix transformations as a primitive. More specifically,
when glLight*() is called to specify the position or the direction of a light
source, the position or direction is transformed by the current modelview
matrix and stored in eye coordinates. This means you can manipulate a
light source’s position or direction by changing the contents of the modelview
Try This

222 Chapter 5: Lighting
matrix. (The projection matrix has no effect on a light’s position or direc-
tion.) This section explains how to achieve the following three different
effects by changing the point in the program at which the light position is
set, relative to modeling or viewing transformations:
• A light position that remains fixed
• A light that moves around a stationary object
• A light that moves along with the viewpoint
Keeping the Light Stationary
In the simplest example, as in Example 5-1, the light position remains fixed.
To achieve this effect, you need to set the light position after whatever
viewing and/or modeling transformation you use. Example 5-4 shows how
the relevant code from the init() and reshape() routines might look.
Example 5-4 Stationary Light Source
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-1.5, 1.5, -1.5*h/w, 1.5*h/w, -10.0, 10.0);
else
glOrtho(-1.5*w/h, 1.5*w/h, -1.5, 1.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
/* later in init() */
GLfloat light_position[] = { 1.0, 1.0, 1.0, 1.0 };
glLightfv(GL_LIGHT0, GL_POSITION, position);
As you can see, the viewport and projection matrices are established first.
Then, the identity matrix is loaded as the modelview matrix, after which
the light position is set. Since the identity matrix is used, the originally
specified light position (1.0, 1.0, 1.0) isn’t changed by being multiplied
by the modelview matrix. Then, since neither the light position nor the
modelview matrix is modified after this point, the direction of the light
remains (1.0, 1.0, 1.0).
Independently Moving the Light
Now suppose you want to rotate or translate the light position so that the
light moves relative to a stationary object. One way to do this is to set

Creating Light Sources 223
the light position after the modeling transformation, which is itself
changed specifically to modify the light position. You can begin with the
same series of calls in init() early in the program. Then you need to perform
the desired modeling transformation (on the modelview stack) and reset the
light position, probably in display(). Example 5-5 shows what display()
might be.
Example 5-5 Independently Moving Light Source
static GLdouble spin;
void display(void)
{
GLfloat light_position[] = { 0.0, 0.0, 1.5, 1.0 };
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
gluLookAt(0.0, 0.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
glPushMatrix();
glRotated(spin, 1.0, 0.0, 0.0);
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
glPopMatrix();
glutSolidTorus(0.275, 0.85, 8, 15);
glPopMatrix();
glFlush();
}
spin is a global variable and is probably controlled by an input device.
display() causes the scene to be redrawn with the light rotated spin
degrees around a stationary torus. Note the two pairs of glPushMatrix()
and glPopMatrix() calls, which are used to isolate the viewing and model-
ing transformations, all of which occur on the modelview stack. Since in
Example 5-5 the viewpoint remains constant, the current matrix is pushed
down the stack, and then the desired viewing transformation is loaded with
gluLookAt(). The matrix stack is pushed again before the modeling trans-
formation glRotated() is specified. Then the light position is set in the new,
rotated coordinate system so that the light itself appears to be rotated from
its previous position. (Remember that the light position is stored in eye
coordinates, which are obtained after transformation by the modelview
matrix.) After the rotated matrix is popped off the stack, the torus is drawn.
Example 5-6 is a program that rotates a light source around an object. When
the left mouse button is pressed, the light position rotates an additional
30 degrees. A small, unlit, wireframe cube is drawn to represent the position
of the light in the scene.

224 Chapter 5: Lighting
Example 5-6 Moving a Light with Modeling Transformations: movelight.c
static int spin = 0;
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_SMOOTH);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_DEPTH_TEST);
}
/* Here is where the light position is reset after the modeling
* transformation (glRotated) is called. This places the
* light at a new position in world coordinates. The cube
* represents the position of the light.
*/
void display(void)
{
GLfloat position[] = { 0.0, 0.0, 1.5, 1.0 };
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glTranslatef(0.0, 0.0, -5.0);
glPushMatrix();
glRotated((GLdouble) spin, 1.0, 0.0, 0.0);
glLightfv(GL_LIGHT0, GL_POSITION, position);
glTranslated(0.0, 0.0, 1.5);
glDisable(GL_LIGHTING);
glColor3f(0.0, 1.0, 1.0);
glutWireCube(0.1);
glEnable(GL_LIGHTING);
glPopMatrix();
glutSolidTorus(0.275, 0.85, 8, 15);
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();

Creating Light Sources 225
gluPerspective(40.0, (GLfloat) w/(GLfloat) h, 1.0, 20.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void mouse(int button, int state, int x, int y)
{
switch (button) {
case GLUT_LEFT_BUTTON:
if (state == GLUT_DOWN) {
spin = (spin + 30) % 360;
glutPostRedisplay();
}
break;
default:
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMouseFunc(mouse);
glutMainLoop();
return 0;
}
Moving the Light Source Together with the Viewpoint
To create a light that moves along with the viewpoint, you need to set
the light position before the viewing transformation. Then the viewing
transformation affects both the light and the viewpoint in the same way.
Remember that the light position is stored in eye coordinates, and this is
one of the few times when eye coordinates are critical. In Example 5-7, the
light position is defined in init(), which stores the light position at (0, 0, 0)
in eye coordinates. In other words, the light is shining from the lens of the
camera.

226 Chapter 5: Lighting
Example 5-7 Light Source That Moves with the Viewpoint
GLfloat light_position[] = { 0.0, 0.0, 0.0, 1.0 };
glViewport(0, 0, (GLint) w, (GLint) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(40.0, (GLfloat) w/(GLfloat) h, 1.0, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
If the viewpoint is now moved, the light will move along with it, maintain-
ing (0, 0, 0) distance, relative to the eye. In the continuation of Example 5-7,
which follows next, the global variables (ex,ey,ez) control the position of
the viewpoint, and (upx,upy,upz) control the value of the up-vector. The
display() routine that’s called from the event loop to redraw the scene
might be as follows:
static GLdouble ex, ey, ez, upx, upy, upz;
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
gluLookAt(ex, ey, ez, 0.0, 0.0, 0.0, upx, upy, upz);
glutSolidTorus(0.275, 0.85, 8, 15);
glPopMatrix();
glFlush();
}
When the lit torus is redrawn, both the light position and the viewpoint are
moved to the same location. As the values passed to gluLookAt() change
and the eye moves, the object will never appear dark, because it is always
being illuminated from the eye position. Even though you haven’t respeci-
fied the light position, the light moves because the eye coordinate system
has changed.
This method of moving the light can be represented by simulating the illu-
mination from a miner’s hat. Another example would be carrying a candle
or lantern. The light position specified by the call to glLightfv(GL_LIGHTi,
GL_POSITION, position) would be the x-, y-, and z-distances from the eye
position to the illumination source. Then, as the eye position moves, the
light will remain the same relative distance away.

Selecting a Lighting Model 227
Try This
Modify Example 5-6 in the following manner:
• Make the light translate past the object instead of rotating around it.
Hint: Use glTranslated() rather than the first glRotated() in display(),
and choose an appropriate value to use instead of spin.
• Change the attenuation so that the light decreases in intensity as it is
moved away from the object. Hint: Add calls to glLight*() to set the
desired attenuation parameters.
Nate Robins’ Lightposition Tutorial
If you have downloaded Nate Robins’ suite of tutorial programs, now run
the lightposition tutorial. (For information on how and where to download
these programs, see “Errata” on page xlii.) With this tutorial, you can
experiment with the light source position and the effect of the modelview
matrix.
Selecting a Lighting Model
The OpenGL notion of a lighting model has four components:
• The global ambient light intensity
• Whether the viewpoint position is local to the scene or should be
considered to be an infinite distance away
• Whether lighting calculations should be performed differently for both
the front and back faces of objects
• Whether the specular color should be separated from ambient and
diffuse colors and applied after the texturing operation
This section explains how to specify a lighting model. It also discusses how
to enable lighting—that is, how to tell OpenGL that you want lighting
calculations to be performed.
The command used to specify all properties of the lighting model is
glLightModel*().glLightModel*() has two arguments: the lighting model
property and the desired value for that property.
Try This
228 Chapter 5: Lighting
Global Ambient Light
As discussed earlier, each light source can contribute ambient light to a
scene. In addition, there can be other ambient light that’s not from any
particular source. To specify the RGBA intensity of such global ambient
light, use the GL_LIGHT_MODEL_AMBIENT parameter as follows:
GLfloat lmodel_ambient[] = { 0.2, 0.2, 0.2, 1.0 };
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, lmodel_ambient);
void glLightModel{if}(GLenum pname,TYPE param);
void glLightModel{if}v(GLenum pname, const TYPE *param);
Sets properties of the lighting model. The characteristic of the lighting
model being set is defined by pname, which specifies a named parameter
(see Table 5-2). param indicates the values to which the pname character-
istic is set; it’s a pointer to a group of values if the vector version is used or
the value itself if the nonvector version is used. The nonvector version can
be used to set only single-valued lighting model characteristics, not for
GL_LIGHT_MODEL_AMBIENT.
Parameter Name Default Value Meaning
GL_LIGHT_MODEL_AMBIENT (0.2, 0.2, 0.2, 1.0) ambient RGBA
intensity of the
entire scene
GL_LIGHT_MODEL_LOCAL_VIEWER 0.0 or GL_FALSE how specular
reflection angles
are computed
GL_LIGHT_MODEL_TWO_SIDE 0.0 or GL_FALSE specifies one-
sided or two-
sided lighting
GL_LIGHT_MODEL_COLOR_CONTROL GL_SINGLE_COLOR whether specular
color is calculated
separately from
ambient and
diffuse
Table 5-2 Default Values for pname Parameter of glLightModel*()
Compatibility
Extension
glLightModel
GL_LIGHT_
MODEL_AMBIENT
GL_LIGHT_
MODEL_LOCAL_
VIEWER
GL_LIGHT_
MODEL_TWO_
SIDE
GL_LIGHT_
MODEL_COLOR_
CONTROL

Selecting a Lighting Model 229
In this example, the values used for lmodel_ambient are the default values for
GL_LIGHT_MODEL_AMBIENT. Since these numbers yield a small amount
of white ambient light, even if you don’t add a specific light source to your
scene, you can still see the objects in the scene. Plate 14 shows the effects of
different amounts of global ambient light.
Local or Infinite Viewpoint
The location of the viewpoint affects the calculations for highlights pro-
duced by specular reflectance. More specifically, the intensity of the high-
light at a particular vertex depends on the normal at that vertex, the
direction from the vertex to the light source, and the direction from the
vertex to the viewpoint. Keep in mind that the viewpoint isn’t actually
being moved by calls to lighting commands (you need to change the pro-
jection transformation, as described in “Projection Transformations” in
Chapter 3); instead, different assumptions are made for the lighting calcu-
lations, as if the viewpoint were moved.
With an infinite viewpoint, the direction between it and any vertex in the
scene remains constant. A local viewpoint tends to yield more realistic
results, but since the direction has to be calculated for each vertex, overall
performance is decreased with a local viewpoint. By default, an infinite
viewpoint is assumed. Here’s how to change to a local viewpoint:
glLightModeli(GL_LIGHT_MODEL_LOCAL_VIEWER, GL_TRUE);
This call places the viewpoint at (0, 0, 0) in eye coordinates. To switch back
to an infinite viewpoint, pass in GL_FALSE as the argument.
Two-Sided Lighting
Lighting calculations are performed for all polygons, whether they’re front-
facing or back-facing. Since you usually set up lighting conditions with the
front-facing polygons in mind, however, the back-facing ones typically
aren’t correctly illuminated. In Example 5-1, where the object is a sphere,
only the front faces are ever seen, since they’re the ones on the outside of
the sphere. Therefore, in this case, it doesn’t matter what the back-facing
polygons look like. If the sphere is going to be cut away so that its inside
surface will be visible, however, you might want to have the inside surface

230 Chapter 5: Lighting
fully lit according to the lighting conditions you’ve defined; you might also
want to supply a different material description for the back faces. When you
turn on two-sided lighting with
glLightModeli(GL_LIGHT_MODEL_TWO_SIDE, GL_TRUE);
OpenGL reverses the surface normals for back-facing polygons; typically,
this means that the surface normals of visible back- and front-facing
polygons face, rather than point away from, the viewer. As a result, all
polygons are illuminated correctly. However, these additional operations
usually make two-sided lighting perform more slowly than the default one-
sided lighting.
To turn two-sided lighting off, pass in GL_FALSE as the argument in the pre-
ceding call. (See “Defining Material Properties” on page 231 for information
about how to supply material properties for both faces.) You can also con-
trol which faces OpenGL considers to be front-facing with the command
glFrontFace(). (See “Reversing and Culling Polygon Faces” on page 61 for
more information.)
Secondary Specular Color
For typical lighting calculations, the ambient, diffuse, specular, and
emissive contributions are calculated and simply added together. By
default, texture mapping is applied after lighting, so specular highlights
may appear muted, or texturing may look undesirable in other ways. To
delay application of the specular color until after texturing, call
glLightModeli(GL_LIGHT_MODEL_COLOR_CONTROL,
GL_SEPARATE_SPECULAR_COLOR);
In this mode, lighting produces two colors per vertex: a primary color,
which consists of all nonspecular lighting contributions, and a secondary
color, which is a sum of all specular lighting contributions. During texture
mapping, only the primary color is combined with the texture colors. After
texturing, the secondary color is added to the resulting combination of
primary and texture colors (see “Applying Secondary Color after Texturing”
on page 478). Objects that are lit and textured using a separate specular
color usually have more visible and prominent specular highlights.

Defining Material Properties 231
To restore the default, call
glLightModeli(GL_LIGHT_MODEL_COLOR_CONTROL, GL_SINGLE_COLOR);
Once again, the primary color includes all contributing colors: ambient,
diffuse, specular, and emissive. Lighting contributions are not added after
texturing. (If you are not performing texture mapping, there isn’t any
reason to separate the specular color from the other lighting components.)
Enabling Lighting
With OpenGL, you need to enable (or disable) lighting explicitly. If lighting
isn’t enabled, the current color is simply mapped onto the current vertex,
and no calculations concerning normals, light sources, the lighting model,
or material properties are performed. Here’s how to enable lighting:
glEnable(GL_LIGHTING);
To disable lighting, call glDisable() with GL_LIGHTING as the argument.
You also need explicitly to enable each light source that you define, after
you’ve specified the parameters for that source. Example 5-1 uses only one
light, GL_LIGHT0:
glEnable(GL_LIGHT0);
Defining Material Properties
You’ve seen how to create light sources with certain characteristics and how
to define the desired lighting model. This section describes how to define
the material properties of the objects in the scene: the ambient, diffuse, and
specular color, the shininess, and the color of any emitted light. (See “The
Mathematics of Lighting” for the equations used in the lighting and mate-
rial-property calculations.) Most of the material properties are conceptually
similar to ones you’ve already used to create light sources. The mechanism
for setting them is similar, except that the command used is called
glMaterial*().
Compatibility
Extension
GL_LIGHTING
GL_LIGHTi
232 Chapter 5: Lighting
As discussed in “Selecting a Lighting Model,” you can choose to have
lighting calculations performed differently for the front- and back-facing
polygons of objects. If the back faces might indeed be seen, you can supply
different material properties for the front and back surfaces by using the face
parameter of glMaterial*(). See Plate 14 for an example of an object drawn
with different inside and outside material properties.
To give you an idea of the possible effects you can achieve by manipulating
material properties, see Plate 16. This figure shows the same object drawn
with several different sets of material properties. The same light source and
void glMaterial{if}(GLenum face, GLenum pname,TYPE param);
void glMaterial{if}v(GLenum face, GLenum pname, const TYPE *param);
Specifies a current material property for use in lighting calculations. face
can be GL_FRONT, GL_BACK, or GL_FRONT_AND_BACK to indicate to
which faces of the object the material should be applied. The particular
material property being set is identified by pname, and the desired values
for that property are given by param, which is either a pointer to a
group of values (if the vector version is used) or the actual value (if the
nonvector version is used). The nonvector version works only for setting
GL_SHININESS. The possible values for pname are shown in Table 5-3. Note
that GL_AMBIENT_AND_DIFFUSE allows you to set both the ambient and
diffuse material colors simultaneously to the same RGBA value.
Parameter Name Default Value Meaning
GL_AMBIENT (0.2, 0.2, 0.2, 1.0) ambient color of material
GL_DIFFUSE (0.8, 0.8, 0.8, 1.0) diffuse color of material
GL_AMBIENT_AND_DIFFUSE ambient and diffuse color
of material
GL_SPECULAR (0.0, 0.0, 0.0, 1.0) specular color of material
GL_SHININESS 0.0 specular exponent
GL_EMISSION (0.0, 0.0, 0.0, 1.0) emissive color of material
GL_COLOR_INDEXES (0, 1, 1) ambient, diffuse, and
specular color indices
Table 5-3 Default Values for pname Parameter of glMaterial*()
Compatibility
Extension
glMaterial
GL_AMBIENT
GL_DIFFUSE
GL_AMBIENT_
AND_DIFFUSE
GL_SPECULAR
GL_SHININESS
GL_COLOR_
INDEXES

Defining Material Properties 233
lighting model are used for the entire figure. The sections that follow
discuss the specific properties used to draw each of these spheres.
Note that most of the material properties set with glMaterial*() are (R, G, B,
A) colors. Regardless of what alpha values are supplied for other parameters,
the alpha value at any particular vertex is the diffuse-material alpha value
(that is, the alpha value given to GL_DIFFUSE with the glMaterial*() com-
mand, as described in the next section). (See “Blending” in Chapter 6 for a
complete discussion of alpha values.) Also, none of the RGBA material prop-
erties apply in color-index mode. (See “Lighting in Color-Index Mode” on
page 246 for more information about what parameters are relevant in color-
index mode.)
Diffuse and Ambient Reflection
The GL_DIFFUSE and GL_AMBIENT parameters set with glMaterial*()
affect the colors of the diffuse and ambient light reflected by an object. Dif-
fuse reflectance plays the most important role in determining what you per-
ceive the color of an object to be. Your perception is affected by the color of
the incident diffuse light and the angle of the incident light relative to the
normal direction. (It’s most intense where the incident light falls perpendic-
ular to the surface.) The position of the viewpoint doesn’t affect diffuse
reflectance at all.
Ambient reflectance affects the overall color of the object. Because diffuse
reflectance is brightest where an object is directly illuminated, ambient
reflectance is most noticeable where an object receives no direct illumina-
tion. An object’s total ambient reflectance is affected by the global ambient
light and ambient light from individual light sources. Like diffuse reflec-
tance, ambient reflectance isn’t affected by the position of the viewpoint.
For real-world objects, diffuse and ambient reflectance are normally the
same color. For this reason, OpenGL provides you with a convenient way of
assigning the same value to both simultaneously with glMaterial*():
GLfloat mat_amb_diff[] = { 0.1, 0.5, 0.8, 1.0 };
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT_AND_DIFFUSE,
mat_amb_diff);
In this example, the RGBA color (0.1, 0.5, 0.8, 1.0)—a deep blue color—
represents the current ambient and diffuse reflectance for both the front-
and back-facing polygons.
In Plate 16, the first row of spheres has no ambient reflectance (0.0, 0.0, 0.0,
0.0), and the second row has a significant amount of it (0.7, 0.7, 0.7, 1.0).

234 Chapter 5: Lighting
Specular Reflection
Specular reflection from an object produces highlights. Unlike ambient and
diffuse reflection, the amount of specular reflection seen by a viewer does
depend on the location of the viewpoint—it is brightest along the direct
angle of reflection. To see this, imagine looking at a metallic ball outdoors
in the sunlight. As you move your head, the highlight created by the
sunlight moves with you to some extent. However, if you move your head
too much, you lose the highlight entirely.
OpenGL allows you to set the effect that the material has on reflected light
(with GL_SPECULAR) and control the size and brightness of the highlight
(with GL_SHININESS). You can assign a number in the range [0.0, 128.0]
to GL_SHININESS: the higher the value, the smaller and brighter (more
focused) the highlight. (See “The Mathematics of Lighting” on page 240
for details about how specular highlights are calculated.)
In Plate 16, the spheres in the first column have no specular reflection. In
the second column, GL_SPECULAR and GL_SHININESS are assigned values
as follows:
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat low_shininess[] = { 5.0 };
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, low_shininess);
In the third column, the GL_SHININESS parameter is increased to 100.0.
Emission
By specifying an RGBA color for GL_EMISSION, you can make an object
appear to be giving off light of that color. Since most real-world objects
(except lights) don’t emit light, you’ll probably use this feature mostly to
simulate lamps and other light sources in a scene. In Plate 16, the spheres
in the fourth column have a reddish-gray value for GL_EMISSION:
GLfloat mat_emission[] = {0.3, 0.2, 0.2, 0.0};
glMaterialfv(GL_FRONT, GL_EMISSION, mat_emission);
Notice that the spheres appear to be slightly glowing; however, they’re not
actually acting as light sources. You would need to create a light source and
position it at the same location as the sphere to create such an effect.

Defining Material Properties 235
Changing Material Properties
Example 5-1 uses the same material properties for all vertices of the only
object in the scene (the sphere). In other situations, you might want to
assign different material properties for different vertices on the same object.
More likely, you have more than one object in the scene, and each object
has different material properties. For example, the code that produced Plate
16 has to draw 12 different objects (all spheres), each with different material
properties. Example 5-8 shows a portion of the code in display().
Example 5-8 Different Material Properties: material.c
GLfloat no_mat[] = { 0.0, 0.0, 0.0, 1.0 };
GLfloat mat_ambient[] = { 0.7, 0.7, 0.7, 1.0 };
GLfloat mat_ambient_color[] = { 0.8, 0.8, 0.2, 1.0 };
GLfloat mat_diffuse[] = { 0.1, 0.5, 0.8, 1.0 };
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat no_shininess[] = { 0.0 };
GLfloat low_shininess[] = { 5.0 };
GLfloat high_shininess[] = { 100.0 };
GLfloat mat_emission[] = {0.3, 0.2, 0.2, 0.0};
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
/* draw sphere in first row, first column
* diffuse reflection only; no ambient or specular
*/
glPushMatrix();
glTranslatef(-3.75, 3.0, 0.0);
glMaterialfv(GL_FRONT, GL_AMBIENT, no_mat);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, no_mat);
glMaterialfv(GL_FRONT, GL_SHININESS, no_shininess);
glMaterialfv(GL_FRONT, GL_EMISSION, no_mat);
glutSolidSphere(1.0, 16, 16);
glPopMatrix();
/* draw sphere in first row, second column
* diffuse and specular reflection; low shininess; no ambient
*/
glPushMatrix();
glTranslatef(-1.25, 3.0, 0.0);
glMaterialfv(GL_FRONT, GL_AMBIENT, no_mat);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);

236 Chapter 5: Lighting
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, low_shininess);
glMaterialfv(GL_FRONT, GL_EMISSION, no_mat);
glutSolidSphere(1.0, 16, 16);
glPopMatrix();
/* draw sphere in first row, third column
* diffuse and specular reflection; high shininess; no ambient
*/
glPushMatrix();
glTranslatef(1.25, 3.0, 0.0);
glMaterialfv(GL_FRONT, GL_AMBIENT, no_mat);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, high_shininess);
glMaterialfv(GL_FRONT, GL_EMISSION, no_mat);
glutSolidSphere(1.0, 16, 16);
glPopMatrix();
/* draw sphere in first row, fourth column
* diffuse reflection; emission; no ambient or specular refl.
*/
glPushMatrix();
glTranslatef(3.75, 3.0, 0.0);
glMaterialfv(GL_FRONT, GL_AMBIENT, no_mat);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, no_mat);
glMaterialfv(GL_FRONT, GL_SHININESS, no_shininess);
glMaterialfv(GL_FRONT, GL_EMISSION, mat_emission);
glutSolidSphere(1.0, 16, 16);
glPopMatrix();
As you can see, glMaterialfv() is called repeatedly to set the desired material
property for each sphere. Note that it needs to be called only to change a
property that has to be respecified. The second, third, and fourth spheres
use the same ambient and diffuse properties as the first sphere, so these
properties do not need to be respecified. Since glMaterial*() has a perfor-
mance cost associated with its use, Example 5-8 could be rewritten to
minimize material-property changes.
Nate Robins’ Lightmaterial Tutorial
If you have downloaded Nate Robins’ suite of tutorial programs, now run
the lightmaterial tutorial. With this tutorial, you can experiment with the
colors of material properties, including ambient, diffuse, and specular
colors, as well as the shininess exponent.

Defining Material Properties 237
Color Material Mode
Another technique for minimizing performance costs associated with
changing material properties is to use glColorMaterial().
Note that glColorMaterial() specifies two independent values: The first
determines which face or faces are updated, and the second determines
which material property or properties of those faces are updated. OpenGL
does not maintain separate mode variables for each face.
After calling glColorMaterial(), you need to call glEnable() with GL_
COLOR_MATERIAL as the parameter. Then, you can change the current
color using glColor*() (or other material properties, using glMaterial*())
as needed as you draw:
glEnable(GL_COLOR_MATERIAL);
glColorMaterial(GL_FRONT, GL_DIFFUSE);
/* now glColor* changes diffuse reflection */
glColor3f(0.2, 0.5, 0.8);
/* draw some objects here */
glColorMaterial(GL_FRONT, GL_SPECULAR);
/* glColor* no longer changes diffuse reflection
* now glColor* changes specular reflection */
glColor3f(0.9, 0.0, 0.2);
/* draw other objects here */
glDisable(GL_COLOR_MATERIAL);
You should use glColorMaterial() whenever you need to change a single
material parameter for most vertices in your scene. If you need to change
more than one material parameter, as was the case for Plate 16, use
glMaterial*(). When you don’t need the capabilities of glColorMaterial()
anymore, be sure to disable it so that you don’t get undesired material
void glColorMaterial(GLenum face, GLenum mode);
Causes the material property (or properties) specified by mode of the
specified material face (or faces) specified by face to track the value of the
current color at all times. A change to the current color (using glColor*())
immediately updates the specified material properties. The face parameter
can be GL_FRONT, GL_BACK, or GL_FRONT_AND_BACK (the default).
The mode parameter can be GL_AMBIENT, GL_DIFFUSE, GL_SPECULAR,
GL_AMBIENT_AND_DIFFUSE (the default), or GL_EMISSION. At any
given time, only one mode is active. glColorMaterial() has no effect on
color-index lighting.
Compatibility
Extension
glColorMaterial

238 Chapter 5: Lighting
properties and don’t incur the performance cost associated with it. The
performance value in using glColorMaterial() varies, depending on your
OpenGL implementation. Some implementations may be able to optimize
the vertex routines so that they can quickly update material properties
based on the current color.
Example 5-9 shows an interactive program that uses glColorMaterial() to
change material parameters. Pressing each of the three mouse buttons
changes the color of the diffuse reflection.
Example 5-9 Using glColorMaterial(): colormat.c
GLfloat diffuseMaterial[4] = { 0.5, 0.5, 0.5, 1.0 };
void init(void)
{
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat light_position[] = { 1.0, 1.0, 1.0, 0.0 };
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_SMOOTH);
glEnable(GL_DEPTH_TEST);
glMaterialfv(GL_FRONT, GL_DIFFUSE, diffuseMaterial);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialf(GL_FRONT, GL_SHININESS, 25.0);
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glColorMaterial(GL_FRONT, GL_DIFFUSE);
glEnable(GL_COLOR_MATERIAL);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glutSolidSphere(1.0, 20, 16);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);

Defining Material Properties 239
glLoadIdentity();
if (w <= h)
glOrtho(-1.5, 1.5, -1.5*(GLfloat)h/(GLfloat)w,
1.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0);
else
glOrtho(-1.5*(GLfloat)w/(GLfloat)h,
1.5*(GLfloat)w/(GLfloat)h, -1.5, 1.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void mouse(int button, int state, int x, int y)
{
switch (button) {
case GLUT_LEFT_BUTTON:
if (state == GLUT_DOWN) { /* change red */
diffuseMaterial[0] += 0.1;
if (diffuseMaterial[0] > 1.0)
diffuseMaterial[0] = 0.0;
glColor4fv(diffuseMaterial);
glutPostRedisplay();
}
break;
case GLUT_MIDDLE_BUTTON:
if (state == GLUT_DOWN) { /* change green */
diffuseMaterial[1] += 0.1;
if (diffuseMaterial[1] > 1.0)
diffuseMaterial[1] = 0.0;
glColor4fv(diffuseMaterial);
glutPostRedisplay();
}
break;
case GLUT_RIGHT_BUTTON:
if (state == GLUT_DOWN) { /* change blue */
diffuseMaterial[2] += 0.1;
if (diffuseMaterial[2] > 1.0)
diffuseMaterial[2] = 0.0;
glColor4fv(diffuseMaterial);
glutPostRedisplay();
}
break;
default:
break;
}
}
240 Chapter 5: Lighting
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMouseFunc(mouse);
glutMainLoop();
return 0;
}
Try This
Modify Example 5-8 in the following manner:
• Change the global ambient light in the scene. Hint: Alter the value of
the GL_LIGHT_MODEL_AMBIENT parameter.
• Change the diffuse, ambient, and specular reflection parameters, the
shininess exponent, and the emission color. Hint: Use the glMaterial*()
command, but avoid making excessive calls.
• Use two-sided materials and add a user-defined clipping plane so that
you can see the inside and outside of a row or column of spheres.
(See “Additional Clipping Planes” in Chapter 3, if you need to recall
user-defined clipping planes.) Hint: Turn on two-sided lighting with
GL_LIGHT_MODEL_TWO_SIDE, set the desired material properties,
and add a clipping plane.
• Remove the glMaterialfv() call for setting the GL_DIFFUSE value, and
use the more efficient glColorMaterial() calls to achieve the same
lighting.
The Mathematics of Lighting
Advanced
This section presents the equations used by OpenGL to perform lighting cal-
culations to determine colors when in RGBA mode. (See “The Mathematics
Try This
Advanced

The Mathematics of Lighting 241
of Color-Index Mode Lighting” for corresponding calculations for color-index
mode.) You don’t need to read this section if you’re willing to experiment
to obtain the lighting conditions you want. Even after reading this section,
you’ll probably have to experiment, but you’ll have a better idea of how
the values of parameters affect a vertex’s color. Remember that if lighting
is not enabled, the color of a vertex is simply the current color; if it is
enabled, the lighting computations described here are carried out in eye
coordinates.
In the following equations, mathematical operations are performed sepa-
rately on the R, G, and B components. Thus, for example, when three
terms are shown as added together, the R values, the G values, and the
B values for each term are separately added to form the final RGB color
(R1+ R2+ R3, G1+ G2+ G3, B1+ B2 + B3). When three terms are multiplied,
the calculation is (R1R2R3, G1G2G3, B1B2B3). (Remember that the final A or
alpha component at a vertex is equal to the material’s diffuse alpha value at
that vertex.)
The color produced by lighting a vertex is computed as follows:
vertex color = the material emission at that vertex +
the global ambient light scaled by the material’s
ambient property at that vertex +
the ambient, diffuse, and specular contributions from
all the light sources, properly attenuated
After lighting calculations are performed, the color values are clamped (in
RGBA mode) to the range [0, 1].
Note that OpenGL lighting calculations don’t take into account the possi-
bility of one object blocking light from another; as a result, shadows aren’t
automatically created. (See “Shadows” in Chapter 14 for a technique used
to create shadows.) Also keep in mind that with OpenGL, illuminated
objects don’t radiate light onto other objects.
Material Emission
The material emission term is the simplest. It’s the RGB value assigned to
the GL_EMISSION parameter.

242 Chapter 5: Lighting
Scaled Global Ambient Light
The second term is computed by multiplying the global ambient light (as
defined by the GL_LIGHT_MODEL_AMBIENT parameter) by the material’s
ambient property (GL_AMBIENT value as assigned with glMaterial*()):
ambientlight model ambientmaterial
Each of the R, G, and B values for these two parameters are multiplied
separately to compute the final RGB value for this term: (R1R2, G1G2, B1B2).
Contributions from Light Sources
Each light source may contribute to a vertex’s color, and these contributions
are added together. The equation for computing each light source’s
contribution is as follows:
contribution = attenuation factor spotlight effect
(ambient term + diffuse term + specular term)
Attenuation Factor
The attenuation factor was described in “Position and Attenuation”:
where
d = distance between the light’s position and the vertex
kc = GL_CONSTANT_ATTENUATION
kl= GL_LINEAR_ATTENUATION
kq= GL_QUADRATIC_ATTENUATION
If the light is a directional one, the attenuation factor is 1.
Spotlight Effect
The spotlight effect evaluates to one of three possible values, depending on
whether or not the light is actually a spotlight and whether the vertex lies
inside or outside the cone of illumination produced by the spotlight:
attenuation factor = 1
kc + kld + kqd2

The Mathematics of Lighting 243
• 1 if the light isn’t a spotlight (GL_SPOT_CUTOFF is 180.0).
• 0 if the light is a spotlight, but the vertex lies outside the cone of
illumination produced by the spotlight.
•(max {v · d, 0})GL_SPOT_EXPONENT where:
v = (vx, vy, vz) is the unit vector that points from the spotlight
(GL_POSITION) to the vertex.
d = (dx,d
y,d
z) is the spotlight’s direction (GL_SPOT_DIRECTION),
assuming the light is a spotlight and the vertex lies inside the cone
of illumination produced by the spotlight.
The dot product of the two vectors v and d varies as the cosine of
the angle between them; hence, objects directly in line get maximum
illumination, and objects off the axis have their illumination drop as
the cosine of the angle.
To determine whether a particular vertex lies within the cone of illumina-
tion, OpenGL evaluates (max {v · d, 0}), where v and d are as defined in the
preceding discussion. If this value is less than the cosine of the spotlight’s
cutoff angle (GL_SPOT_CUTOFF), then the vertex lies outside the cone;
otherwise, it’s inside the cone.
Ambient Term
The ambient term is simply the ambient color of the light scaled by the
ambient material property:
ambientlight ambientmaterial
Diffuse Term
The diffuse term needs to take into account whether or not light falls
directly on the vertex, the diffuse color of the light, and the diffuse material
property:
(max {L · n, 0}) diffuselight diffusematerial
where
L = (Lx,Ly,Lz) is the unit vector that points from the vertex to the light
position (GL_POSITION).
n = (nx,ny,nz) is the unit normal vector at the vertex.

244 Chapter 5: Lighting
Specular Term
The specular term also depends on whether or not light falls directly on the
vertex. If L · n is less than or equal to zero, there is no specular component
at the vertex. (If it’s less than zero, the light is on the wrong side of the
surface.) If there’s a specular component, it depends on the following:
• The unit normal vector at the vertex (nx, ny, nz)
• The sum of the two unit vectors that point between (1) the vertex
and the light position (or light direction) and (2) the vertex and the
viewpoint (assuming that GL_LIGHT_MODEL_LOCAL_VIEWER is true;
if it’s not true, the vector (0, 0, 1) is used as the second vector in the
sum). This vector sum is normalized (by dividing each component by
the magnitude of the vector) to yield s = (sx,sy, sz).
• The specular exponent (GL_SHININESS)
• The specular color of the light (GL_SPECULARlight)
• The specular property of the material (GL_SPECULARmaterial)
Using these definitions, here’s how OpenGL calculates the specular term:
(max {s· n, 0})shininess specularlight specularmaterial
However, if L · n = 0, the specular term is 0.
Putting It All Together
Using the definitions of terms described in the preceding paragraphs, the
following represents the entire lighting calculation in RGBA mode:
vertex color = emissionmaterial +
ambientlight model ambientmaterial +
[ambientlight ambientmaterial +
(max { L · n , 0} ) diffuselight diffusematerial +
(max { s · n , 0} )shininess specularlight specularmaterial ] i
( )
n-1 1 * (spotlight effect)i *
i=0 kc + kld + kqd
2
i

The Mathematics of Lighting 245
Secondary Specular Color
If GL_SEPARATE_SPECULAR_COLOR is the current lighting model color
control, then a primary and secondary color are produced for each vertex,
which are computed as follows:
primary color = the material emission at that vertex +
the global ambient light scaled by the material’s
ambient property at that vertex +
the ambient and diffuse contributions from all the light
sources, properly attenuated
secondary color = the specular contributions from all the light sources,
properly attenuated
The following two equations represent the lighting calculations for the
primary and secondary colors:
primary color = emissionmaterial +
ambientlight model ambientmaterial +
[ambientlight ambientmaterial +
(max { L · n , 0} ) diffuselight diffusematerial]i
secondary color =
[(max { s · n , 0} )shininess specularlight specularmaterial ] i
During texture mapping, only the primary color is combined with the
texture colors. After the texturing operation, the secondary color is added
to the resulting combination of the primary and texture colors.
( )
n-1 1 * (spotlight effect)i *
i=0 kc + kld + kqd
2
i
( )
n-1 1 * (spotlight effect)i *
i=0 kc + kld + kqd
2
i

246 Chapter 5: Lighting
Lighting in Color-Index Mode
In color-index mode, the parameters comprising RGBA values either have
no effect or have a special interpretation. Since it’s much harder to achieve
certain effects in color-index mode, you should use RGBA whenever
possible. In fact, the only light-source, lighting-model, or material
parameters in an RGBA form that are used in color-index mode are the
light-source parameters GL_DIFFUSE and GL_SPECULAR, and the material
parameter GL_SHININESS. GL_DIFFUSE and GL_SPECULAR (dl and sl,
respectively) are used to compute color-index diffuse and specular light
intensities (dci and sci), as follows:
dci = 0.30R(dl) + 0.59G(dl) + 0.11B(dl)
sci = 0.30R(sl) + 0.59G(sl) + 0.11B(sl)
where R(x), G(x), and B(x) refer to the red, green, and blue components,
respectively, of color x. The weighting values 0.30, 0.59, and 0.11 reflect the
“perceptual” weights that red, green, and blue have for your eye—your eye
is most sensitive to green and least sensitive to blue.
To specify material colors in color-index mode, use glMaterial*() with the
special parameter GL_COLOR_INDEXES, as follows:
GLfloat mat_colormap[] = { 16.0, 47.0, 79.0 };
glMaterialfv(GL_FRONT, GL_COLOR_INDEXES, mat_colormap);
The three numbers supplied for GL_COLOR_INDEXES specify the color
indices for the ambient, diffuse, and specular material colors, respectively.
In other words, OpenGL regards the color associated with the first index
(16.0 in this example) as the pure ambient color, with the second index
(47.0) as the pure diffuse color, and with the third index (79.0) as the pure
specular color. (By default, the ambient color index is 0.0, and the diffuse
and specular color indices are both 1.0. Note that glColorMaterial() has no
effect on color-index lighting.)
As it draws a scene, OpenGL uses colors associated with indices between
these numbers to shade objects in the scene. Therefore, you must build a
color ramp between the indicated indices (in this example, between indices
16 and 47, and then between indices 47 and 79). Often, the color ramp is
built smoothly, but you might want to use other formulations to achieve
different effects. Here’s an example of a smooth color ramp that starts with
a black ambient color and goes through a magenta diffuse color to a white
specular color:

Lighting in Color-Index Mode 247
for (i = 0; i < 32; i++) {
glutSetColor(16 + i, 1.0 * (i/32.0), 0.0, 1.0 * (i/32.0));
glutSetColor(48 + i, 1.0, 1.0 * (i/32.0), 1.0);
}
The GLUT library command glutSetColor() takes four arguments. It
associates the color index indicated by the first argument with the RGB
triplet specified by the last three arguments. When i = 0, the color index 16
is assigned the RGB value (0.0, 0.0, 0.0), or black. The color ramp builds
smoothly up to the diffuse material color at index 47 (when i = 31), which
is assigned the pure magenta RGB value (1.0, 0.0, 1.0). The second loop
builds the ramp between the magenta diffuse color and the white (1.0, 1.0,
1.0) specular color (index 79). Plate 15 shows the result of using this color
ramp with a single lit sphere.
The Mathematics of Color-Index Mode Lighting
Advanced
As you might expect, since the allowable parameters are different for color-
index mode than for RGBA mode, the calculations are different as well.
Since there’s no material emission and no ambient light, the only terms of
interest from the RGBA equations are the diffuse and specular contributions
from the light sources and the shininess. Even these terms need to be
modified, however, as explained next.
Begin with the diffuse and specular terms from the RGBA equations. In the
diffuse term, instead of diffuselight diffusematerial, substitute dci as defined in
the preceding section for color-index mode. Similarly, in the specular term,
instead of specularlight specularmaterial, use sci as defined in the preceding
section. (Calculate the attenuation, the spotlight effect, and all other
components of these terms as before.) Call these modified diffuse and specular
terms d and s, respectively. Now, let s’ =min{ s, 1 }, and then compute
c = am + d(1– s’)(dm–am) + s’(sm–am)
where am,dm, and sm are the ambient, diffuse, and specular material indices
specified using GL_COLOR_INDEXES. The final color index is
c’ = min { c, sm }
After lighting calculations are performed, the color-index values are con-
verted to fixed-point (with an unspecified number of bits to the right of
the binary point). Then the integer portion is masked (bitwise ANDed) with
2n1, where n is the number of bits in a color in the color-index buffer.
Advanced
This page intentionally left blank

249
Chapter 6
6.Blending, Antialiasing, Fog, and
Polygon Offset
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Blend colors to achieve such effects as making objects appear
translucent
• Smooth jagged edges of lines and polygons with antialiasing
• Create scenes with realistic atmospheric effects
• Render rounded (antialiased) points with varying sizes, based upon
distance from the viewpoint
• Draw geometry at or near the same depth, but avoid unaesthetic
artifacts from intersecting geometry

250 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
The preceding chapters have given you the basic information you need to
create a computer-graphics scene; you’ve learned how to do the following:
• Draw geometric shapes
• Transform those geometric shapes so that they can be viewed from
whatever perspective you wish
• Specify how the geometric shapes in your scene should be colored and
shaded
• Add lights and indicate how they should affect the shapes in your scene
Now you’re ready to get a little fancier. This chapter discusses five tech-
niques that can add extra detail and polish to your scene. None of these
techniques is hard to use—in fact, it’s probably harder to explain them than
to use them. Each of these techniques is described in its own major section:
• “Blending” tells you how to specify a blending function that combines
color values from a source and a destination. The final effect is that
parts of your scene appear translucent.
• “Antialiasing” explains this relatively subtle effect that alters colors so
that the edges of points, lines, and polygons appear smooth rather
than angular and jagged. Multisampling is a powerful technique to
antialias all of the primitives in your entire scene.
• “Fog” describes how to create the illusion of depth by computing the
color values of an object based on its distance from the viewpoint.
Thus, objects that are far away appear to fade into the background, just
as they do in real life.
• “Point Parameters” discusses an efficient technique for rendering point
primitives with different sizes and color, depending upon distance
from the viewpoint. Point parameters can be useful for modeling
particle systems.
• If you’ve tried to draw a wireframe outline atop a shaded object and
used the same vertices, you’ve probably noticed some ugly visual
artifacts. “Polygon Offset” shows you how to tweak (offset) depth
values to make an outlined, shaded object look beautiful.
OpenGL Version 1.1 added the polygon offset capability.
Version 1.2 of OpenGL introduced a selectable blending equation
(glBlendEquation()), a constant blending color (glBlendColor()), and the
blending factors: GL_CONSTANT_COLOR, GL_ONE_MINUS_CONSTANT_
COLOR, GL_CONSTANT_ALPHA, and GL_ONE_MINUS_CONSTANT_ALPHA.

Blending 251
In Version 1.2 and 1.3, these features were supported only if the OpenGL
implementation supported the imaging subset. In Version 1.4, the blending
equation, constant blending color, and constant blending factors became
mandatory.
In Version 1.3, multisampling became a core feature of OpenGL.
Version 1.4 also added the following new features, which are covered in this
chapter:
• Use of GL_SRC_COLOR and GL_ONE_MINUS_SRC_COLOR as
source blending factors. (Prior to Version 1.4, GL_SRC_COLOR and
GL_ONE_MINUS_SRC_COLOR had to be destination factors.)
• Use of GL_DST_COLOR and GL_ONE_MINUS_DST_COLOR as
destination blending factors. (Prior to Version 1.4, GL_DST_COLOR
and GL_ONE_MINUS_DST_COLOR had to be source factors.)
• Explicit specification of fog coordinates
• Point parameters to control characteristics of point primitives
• Capability to blend RGB and alpha color components with
separate blending functions
Blending
What’s it all about, alpha? You’ve already seen alpha values (alpha is the A
in RGBA), but they’ve been ignored until now. Alpha values are specified
with glColor*() when using glClearColor() to specify a clearing color and
when specifying certain lighting parameters such as a material property or
light source intensity. As you learned in Chapter 4, the pixels on a monitor
screen emit red, green, and blue light, which is controlled by the red, green,
and blue color values. So how does an alpha value affect what is drawn in a
window on the screen?
When blending is enabled, the alpha value is often used to combine the
color value of the fragment being processed with that of the pixel already
stored in the framebuffer. Blending occurs after your scene has been
rasterized and converted to fragments, but just before the final pixels are
drawn in the framebuffer. Alpha values can also be used in the alpha test to
accept or reject a fragment based on its alpha value. (See Chapter 10 for
more information about this process.)

252 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
Without blending, each new fragment overwrites any existing color values
in the framebuffer, as though the fragment were opaque. With blending,
you can control how (and how much of) the existing color value should be
combined with the new fragment’s value. Thus, you can use alpha blending
to create a translucent fragment that lets some of the previously stored color
value “show through.” Color blending lies at the heart of techniques such
as transparency, digital compositing, and painting.
Note: Alpha values aren’t specified in color-index mode, so blending
operations aren’t performed in color-index mode.
The most natural way to think of blending operations is to think of the RGB
components of a fragment as representing its color, and the alpha compo-
nent as representing opacity. Transparent or translucent surfaces have lower
opacity than opaque ones and, therefore, lower alpha values. For example,
if you’re viewing an object through green glass, the color you see is partly
green from the glass and partly the color of the object. The percentage varies
depending on the transmission properties of the glass: If the glass transmits
80 percent of the light that strikes it (that is, has an opacity of 20 percent),
the color you see is a combination of 20 percent glass color and 80 percent
the color of the object behind it. You can easily imagine situations with
multiple translucent surfaces. If you look at an automobile, for instance, its
interior has one piece of glass between it and your viewpoint; some objects
behind the automobile are visible through two pieces of glass.
The Source and Destination Factors
During blending, color values of the incoming fragment (the source) are
combined with the color values of the corresponding currently stored pixel
(the destination) in a two-stage process. First you specify how to compute
source and destination factors. These factors are RGBA quadruplets that are
multiplied by each component of the R, G, B, and A values in the source and
destination, respectively. Then the corresponding components in the two
sets of RGBA quadruplets are combined. To show this mathematically, let
the source and destination blending factors be (Sr, Sg, Sb, Sa) and (Dr, Dg, Db,
Da), respectively, and let the RGBA values of the source and destination be
indicated with a subscript of s or d. Then the final, blended RGBA values are
given by
(RsSr+RdDr, GsSg+GdDg, BsSb+BdDb, AsSa+AdDa)
Each component of this quadruplet is eventually clamped to [0, 1] (unless
color clamping is disabled. See “Color Clamping” on page 198).

Blending 253
The default way to combine the source and destination fragments is to add
their values together (CsS+CdD). See “Combining Pixels Using Blending
Equations” on page 255 for information on how to select other
mathematical operations to combine fragments.
You have two different ways to choose the source and destination blending
factors. You may call glBlendFunc() and choose two blending factors: the
first factor for the source RGBA and the second for the destination RGBA.
Or, you may use glBlendFuncSeparate() and choose four blending factors,
which allows you to use one blending operation for RGB and a different one
for its corresponding alpha.
void glBlendFunc(GLenum srcfactor, GLenum destfactor);
Controls how color values in the fragment being processed (the source)
are combined with those already stored in the framebuffer (the destina-
tion). The possible values for these arguments are explained in Table 6-1.
The argument srcfactor indicates how to compute a source blending factor;
destfactor indicates how to compute a destination blending factor.
The blend factors are assumed to lie in the range [0, 1]. After the color
values in the source and destination are combined, they’re clamped to the
range [0, 1].
void glBlendFuncSeparate(GLenum srcRGB, GLenum destRGB,
GLenum srcAlpha, GLenum destAlpha);
Similar to glBlendFunc(),glBlendFuncSeparate() also controls how
source color values (fragment) are combined with destination values
(framebuffer). glBlendFuncSeparate() also accepts the same arguments
(shown in Table 6-1) as glBlendFunc(). The argument srcRGB indicates
the source blending factor for color values; destRGB is the destination
blending factor for color values. The argument srcAlpha indicates the
source blending factor for alpha values; destAlpha is the destination
blending factor for alpha values.
The blend factors are assumed to lie in the range [0, 1]. After the color
values in the source and destination are combined, they’re clamped to the
range [0, 1].

254 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
Note: In Table 6-1, the RGBA values of the source, destination, and constant
colors are indicated with the subscripts s, d, and c, respectively.
Subtraction of quadruplets means subtracting them componentwise.
GL_SRC_ALPHA_SATURATE may be used only as a source blend factor.
If you use one of the GL*CONSTANT* blending functions, you need to use
glBlendColor() to specify a constant color.
Constant RGB
Blend Factor
Alpha
Blend Factor
GL_ZERO (0, 0, 0) 0
GL_ONE (1, 1, 1) 1
GL_SRC_COLOR (Rs, Gs, Bs)A
s
GL_ONE_MINUS_SRC_COLOR (1, 1, 1)(Rs, Gs, Bs)1 As
GL_DST_COLOR (Rd, Gd, Bd)A
d
GL_ONE_MINUS_DST_COLOR (1, 1, 1)(Rd, Gd, Bd)1 Ad
GL_SRC_ALPHA (As, As, As)A
s
GL_ONE_MINUS_SRC_ALPHA (1, 1, 1)(As, As, As)1 As
GL_DST_ALPHA (Ad, Ad, Ad)A
d
GL_ONE_MINUS_DST_ALPHA (1, 1, 1)(Ad, Ad, Ad)1 Ad
GL_CONSTANT_COLOR (Rc, Gc, Bc)A
c
GL_ONE_MINUS_CONSTANT_COLOR (1, 1, 1)(Rc, Gc, Bc)1 Ac
GL_CONSTANT_ALPHA (Ac, Ac, Ac)A
c
GL_ONE_MINUS_CONSTANT_ALPHA (1, 1, 1)(Ac, Ac, Ac)1 Ac
GL_SRC_ALPHA_SATURATE (f, f, f ); f=min(A
s, 1Ad)1
Table 6-1 Source and Destination Blending Factors
void glBlendColor(GLclampf red, GLclampf green, GLclampf blue,
GLclampf alpha);
Sets the current red,green,blue, and alpha values for use as the constant
color (Rc, Gc, Bc, Ac) in blending operations.

Blending 255
Enabling Blending
No matter how you specify the blending function, you also need to enable
blending to have it take effect:
glEnable(GL_BLEND);
Use glDisable() with GL_BLEND to disable blending. Note that using the
constants GL_ONE (source) and GL_ZERO (destination) gives the same
results as when blending is disabled; these values are the default.
Advanced
OpenGL Version 2.0 introduced the ability to render into multiple buffers
simultaneously (see “Selecting Color Buffers for Writing and Reading” on
page 497 for details). In versions prior to OpenGL Version 3.0, all buffers
enabled and disabled blending simultaneously (using glEnable() and
glDisable()). As of Version 3.0, however, blending settings can be managed on
a per-buffer basis, using glEnablei() and glDisablei() (described on page 516).
Combining Pixels Using Blending Equations
With standard blending, colors in the framebuffer are combined (using
addition) with incoming fragment colors to produce the new framebuffer
color. Either glBlendEquation() or glBlendEquationSeparate() may be
used to select other mathematical operations to compute the difference,
minimum, or maximum between color fragments and framebuffer pixels.
void glBlendEquation(GLenum mode);
Specifies how framebuffer and source colors are blended together.
The allowable values for mode are GL_FUNC_ADD (the default), GL_
FUNC_SUBTRACT, GL_FUNC_REVERSE_SUBTRACT, GL_MIN, and GL_
MAX, of GL_LOGIC_OP. The possible modes are described in Table 6-2.
void glBlendEquationSeparate(GLenum modeRGB,
GLenum modeAlpha);
Specifies how framebuffer and source colors are blended together,
but allows for different blending modes for the rgb and alpha color
components. The allowable values for modeRGB and modeAlpha are
identical for the modes accepted by glBlendEquation().
Advanced

256 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
In Table 6-2, Cs and Cd represent the source and destination colors. The S
and D parameters in the table represent the source and destination blending
factors as specified with glBlendFunc() or glBlendFuncSeparate(). For
GL_LOGIC_OP, the logical operator is specified by calling glLogicOp().
(See Table 10-4, “Sixteen Logical Operations,” on page 518 for the list of
supported logical operations.)
In Example 6-1, the different blending equation modes are demonstrated.
The ‘a’, ‘s’, ‘r’, ‘m’, and ‘x’ keys are used to select which blending mode to
use. A blue square is used for the source color, and the yellow background
is used as the destination color. The blending factor for each color is set to
GL_ONE using glBlendFunc().
Example 6-1 Demonstrating the Blend Equation Modes: blendeqn.c
/* The following keys change the selected blend equation mode
*
* ‘a’ -> GL_FUNC_ADD
* ‘s’ -> GL_FUNC_SUBTRACT
* ‘r’ -> GL_FUNC_REVERSE_SUBTRACT
* ‘m’ -> GL_MIN
* ‘x’ -> GL_MAX
*/
void init(void)
{
glClearColor(1.0, 1.0, 0.0, 0.0);
glBlendFunc(GL_ONE, GL_ONE);
glEnable(GL_BLEND);
}
Blending Mode Parameter Mathematical Operation
GL_FUNC_ADD CsS + CdD
GL_FUNC_SUBTRACT CsS CdD
GL_FUNC_REVERSE_SUBTRACT CdD CsS
GL_MIN min(CsS, CdD)
GL_MAX max(CsS, CdD)
GL_LOGIC_OP CSop CD
Table 6-2 Blending Equation Mathematical Operations

Blending 257
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0, 0.0, 1.0);
glRectf(-0.5, -0.5, 0.5, 0.5);
glFlush();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘a’: case ‘A’:
/* Colors are added as: (1,1,0) + (0,0,1) = (1,1,1) which
* will produce a white square on a yellow background. */
glBlendEquation(GL_FUNC_ADD);
break;
case ‘s’: case ‘S’:
/* Colors are subtracted as: (0,0,1) - (1,1,0) = (-1,-1,1)
* which is clamped to (0, 0, 1), producing a blue square
* on a yellow background. */
glBlendEquation(GL_FUNC_SUBTRACT);
break;
case ‘r’: case ‘R’:
/* Colors are subtracted as: (1,1,0) - (0,0,1) = (1,1,-1)
* which is clamped to (1, 1, 0). This produces yellow for
* both the square and the background. */
glBlendEquation(GL_FUNC_REVERSE_SUBTRACT);
break;
case ‘m’: case ‘M’:
/* The minimum of each component is computed, as
* [min(1,0),min(1,0),min(0,1)] which equates to (0,0,0).
* This will produce a black square on the yellow
* background. */
glBlendEquation(GL_MIN);
break;
case ‘x’: case ‘X’:
/* The minimum of each component is computed, as
* [max(1, 0), max(1, 0), max(0, 1)] which equates to
* (1, 1, 1). This will produce a white square on the
* yellow background. */
glBlendEquation(GL_MAX);
break;

258 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
case 27:
exit(0);
} break;
glutPostRedisplay();
}
Sample Uses of Blending
Not all combinations of source and destination factors make sense. Most
applications use a small number of combinations. The following paragraphs
describe typical uses for particular combinations of source and destination
factors. Some of these examples use only the incoming alpha value, so they
work even when alpha values aren’t stored in the framebuffer. Note that
often there’s more than one way to achieve some of these effects.
• One way to draw a picture composed half of one image and half of
another, equally blended, is to set the source factor to GL_ONE and
the destination factor to GL_ZERO, and draw the first image. Then
set the source factor to GL_SRC_ALPHA and the destination factor
to GL_ONE_MINUS_SRC_ALPHA, and draw the second image with
alpha equal to 0.5. This pair of factors probably represents the most
commonly used blending operation. If the picture is supposed to be
blended with 0.75 of the first image and 0.25 of the second, draw the
first image as before, and draw the second with an alpha of 0.25.
• To blend three different images equally, set the destination factor to
GL_ONE and the source factor to GL_SRC_ALPHA. Draw each of the
images with alpha equal to 0.3333333. With this technique, each
image is only one-third of its original brightness, which is noticeable
where the images don’t overlap.
• Suppose you’re writing a paint program, and you want to have a brush
that gradually adds color so that each brush stroke blends in a little
more color with whatever is currently in the image (say, 10 percent
color with 90 percent image on each pass). To do this, draw the image
of the brush with alpha of 10 percent and use GL_SRC_ALPHA (source)
and GL_ONE_MINUS_SRC_ALPHA (destination). Note that you can
vary the alphas across the brush to make the brush add more of its
color in the middle and less on the edges, for an antialiased brush
shape (see “Antialiasing”). Similarly, erasers can be implemented by
setting the eraser color to the background color.

Blending 259
• The blending functions that use the source or destination colors—
GL_DST_COLOR or GL_ONE_MINUS_DST_COLOR for the source factor
and GL_SRC_COLOR or GL_ONE_MINUS_SRC_COLOR for the desti-
nation factor—effectively allow you to modulate each color compo-
nent individually. This operation is equivalent to applying a simple
filter—for example, multiplying the red component by 80 percent, the
green component by 40 percent, and the blue component by 72 per-
cent would simulate viewing the scene through a photographic filter
that blocks 20 percent of red light, 60 percent of green, and 28 percent
of blue.
• Suppose you want to draw a picture composed of three translucent
surfaces, some obscuring others, and all over a solid background.
Assume the farthest surface transmits 80 percent of the color behind it,
the next transmits 40 percent, and the closest transmits 90 percent. To
compose this picture, draw the background first with the default source
and destination factors, and then change the blending factors to GL_
SRC_ALPHA (source) and GL_ONE_MINUS_SRC_ALPHA (destination).
Next, draw the farthest surface with an alpha of 0.2, then the middle
surface with an alpha of 0.6, and finally the closest surface with an
alpha of 0.1.
• If your system has alpha planes, you can render objects one at a time
(including their alpha values), read them back, and then perform inter-
esting matting or compositing operations with the fully rendered
objects. (See “Compositing 3D Rendered Images” by Tom Duff,
SIGGRAPH 1985 Proceedings, pp. 41–44, for examples of this tech-
nique.) Note that objects used for picture composition can come from
any source—they can be rendered using OpenGL commands, rendered
using techniques such as ray-tracing or radiosity that are implemented
in another graphics library, or obtained by scanning in existing images.
• You can create the effect of a nonrectangular raster image by assigning
different alpha values to individual fragments in the image. In most
cases, you would assign an alpha of 0 to each “invisible” fragment and
an alpha of 1.0 to each opaque fragment. For example, you can draw a
polygon in the shape of a tree and apply a texture map of foliage; the
viewer can see through parts of the rectangular texture that aren’t part
of the tree if you’ve assigned them alpha values of 0. This method,
sometimes called billboarding, is much faster than creating the tree out
of three-dimensional polygons. An example of this technique is shown
in Figure 6-1, in which the tree is a single rectangular polygon that can
be rotated about the center of the trunk, as shown by the outlines, so
that it’s always facing the viewer. (See “Texture Functions” in
Chapter 9 for more information about blending textures.)

260 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
• Blending is also used for antialiasing, which is a rendering technique to
reduce the jagged appearance of primitives drawn on a raster screen.
(See “Antialiasing” for more information.)
A Blending Example
Example 6-2 draws two overlapping colored triangles, each with an alpha of
0.75. Blending is enabled and the source and destination blending factors
are set to GL_SRC_ALPHA and GL_ONE_MINUS_SRC_ALPHA, respectively.
When the program starts up, a yellow triangle is drawn on the left and then
a cyan triangle is drawn on the right so that in the center of the window,
where the triangles overlap, cyan is blended with the original yellow. You
can change which triangle is drawn first by typing ‘t’ in the window.
Figure 6-1 Creating a Nonrectangular Raster Image

Blending 261
Example 6-2 Blending Example: alpha.c
static int leftFirst = GL_TRUE;
/* Initialize alpha blending function. */
static void init(void)
{
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
glShadeModel(GL_FLAT);
glClearColor(0.0, 0.0, 0.0, 0.0);
}
static void drawLeftTriangle(void)
{
/* draw yellow triangle on LHS of screen */
glBegin(GL_TRIANGLES);
glColor4f(1.0, 1.0, 0.0, 0.75);
glVertex3f(0.1, 0.9, 0.0);
glVertex3f(0.1, 0.1, 0.0);
glVertex3f(0.7, 0.5, 0.0);
glEnd();
}
static void drawRightTriangle(void)
{
/* draw cyan triangle on RHS of screen */
glBegin(GL_TRIANGLES);
glColor4f(0.0, 1.0, 1.0, 0.75);
glVertex3f(0.9, 0.9, 0.0);
glVertex3f(0.3, 0.5, 0.0);
glVertex3f(0.9, 0.1, 0.0);
glEnd();
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
if (leftFirst) {
drawLeftTriangle();
drawRightTriangle();
}

262 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
else {
drawRightTriangle();
drawLeftTriangle();
}
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
gluOrtho2D(0.0, 1.0, 0.0, 1.0*(GLfloat)h/(GLfloat)w);
else
gluOrtho2D(0.0, 1.0*(GLfloat)w/(GLfloat)h, 0.0, 1.0);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘t’:
case ‘T’:
leftFirst = !leftFirst;
glutPostRedisplay();
break;
case 27: /* Escape key */
exit(0);
break;
default:
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(200, 200);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}

Blending 263
The order in which the triangles are drawn affects the color of the over-
lapping region. When the left triangle is drawn first, cyan fragments (the
source) are blended with yellow fragments, which are already in the frame-
buffer (the destination). When the right triangle is drawn first, yellow is
blended with cyan. Because the alpha values are all 0.75, the actual blending
factors become 0.75 for the source and 1.0 0.75 = 0.25 for the destination.
In other words, the source fragments are somewhat translucent, but they
have more effect on the final color than do the destination fragments.
Three-Dimensional Blending with the Depth Buffer
As you saw in the previous example, the order in which polygons are drawn
greatly affects the blended result. When drawing three-dimensional trans-
lucent objects, you can get different appearances depending on whether
you draw the polygons from back to front or from front to back. You also
need to consider the effect of the depth buffer when determining the cor-
rect order. (See “A Hidden-Surface Removal Survival Kit” in Chapter 5 for an
introduction to the depth buffer. Also see “Depth Test” in Chapter 10 for
more information.) The depth buffer keeps track of the distance between
the viewpoint and the portion of the object occupying a given pixel in a
window on the screen; when another candidate color arrives for that pixel,
it’s drawn only if its object is closer to the viewpoint, in which case its depth
value is stored in the depth buffer. With this method, obscured (or hidden)
portions of surfaces aren’t necessarily drawn and therefore aren’t used for
blending.
If you want to render both opaque and translucent objects in the same
scene, then you want to use the depth buffer to perform hidden-surface
removal for any objects that lie behind the opaque objects. If an opaque
object hides either a translucent object or another opaque object, you want
the depth buffer to eliminate the more distant object. If the translucent
object is closer, however, you want to blend it with the opaque object. You
can generally figure out the correct order in which to draw the polygons if
everything in the scene is stationary, but the problem can quickly become
too hard if either the viewpoint or the object is moving.
The solution is to enable depth buffering but make the depth buffer read-
only while drawing the translucent objects. First you draw all the opaque
objects, with the depth buffer in normal operation. Then you preserve these
depth values by making the depth buffer read-only. When the translucent
objects are drawn, their depth values are still compared with the values
established by the opaque objects, so they aren’t drawn if they’re behind the

264 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
opaque ones. If they’re closer to the viewpoint, however, they don’t elimi-
nate the opaque objects, since the depth-buffer values can’t change. Instead,
they’re blended with the opaque objects. To control whether the depth
buffer is writable, use glDepthMask(); if you pass GL_FALSE as the argu-
ment, the buffer becomes read-only, whereas GL_TRUE restores the normal,
writable operation.
Example 6-3 demonstrates how to use this method to draw opaque and
translucent three-dimensional objects. In the program, typing ‘a’ triggers an
animation sequence in which a translucent cube moves through an opaque
sphere. Pressing the ‘r’ key resets the objects in the scene to their initial
positions. To get the best results when transparent objects overlap, draw the
objects from back to front.
Example 6-3 Three-Dimensional Blending: alpha3D.c
#define MAXZ 8.0
#define MINZ -8.0
#define ZINC 0.4
static float solidZ = MAXZ;
static float transparentZ = MINZ;
static GLuint sphereList, cubeList;
static void init(void)
{
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 0.15 };
GLfloat mat_shininess[] = { 100.0 };
GLfloat position[] = { 0.5, 0.5, 1.0, 0.0 };
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);
glLightfv(GL_LIGHT0, GL_POSITION, position);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_DEPTH_TEST);
sphereList = glGenLists(1);
glNewList(sphereList, GL_COMPILE);
glutSolidSphere(0.4, 16, 16);
glEndList();
cubeList = glGenLists(1);
glNewList(cubeList, GL_COMPILE);
glutSolidCube(0.6);
glEndList();
}

Blending 265
void display(void)
{
GLfloat mat_solid[] = { 0.75, 0.75, 0.0, 1.0 };
GLfloat mat_zero[] = { 0.0, 0.0, 0.0, 1.0 };
GLfloat mat_transparent[] = { 0.0, 0.8, 0.8, 0.6 };
GLfloat mat_emission[] = { 0.0, 0.3, 0.3, 0.6 };
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glTranslatef(-0.15, -0.15, solidZ);
glMaterialfv(GL_FRONT, GL_EMISSION, mat_zero);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_solid);
glCallList(sphereList);
glPopMatrix();
glPushMatrix();
glTranslatef(0.15, 0.15, transparentZ);
glRotatef(15.0, 1.0, 1.0, 0.0);
glRotatef(30.0, 0.0, 1.0, 0.0);
glMaterialfv(GL_FRONT, GL_EMISSION, mat_emission);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_transparent);
glEnable(GL_BLEND);
glDepthMask(GL_FALSE);
glBlendFunc(GL_SRC_ALPHA, GL_ONE);
glCallList(cubeList);
glDepthMask(GL_TRUE);
glDisable(GL_BLEND);
glPopMatrix();
glutSwapBuffers();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLint) w, (GLint) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-1.5, 1.5, -1.5*(GLfloat)h/(GLfloat)w,
1.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0);
else
glOrtho(-1.5*(GLfloat)w/(GLfloat)h,
1.5*(GLfloat)w/(GLfloat)h, -1.5, 1.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}

266 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
void animate(void)
{
if (solidZ <= MINZ || transparentZ >= MAXZ)
glutIdleFunc(NULL);
else {
solidZ -= ZINC;
transparentZ += ZINC;
glutPostRedisplay();
}
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘a’:
case ‘A’:
solidZ = MAXZ;
transparentZ = MINZ;
glutIdleFunc(animate);
break;
case ‘r’:
case ‘R’:
solidZ = MAXZ;
transparentZ = MINZ;
glutPostRedisplay();
break;
case 27:
exit(0);
} break;
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
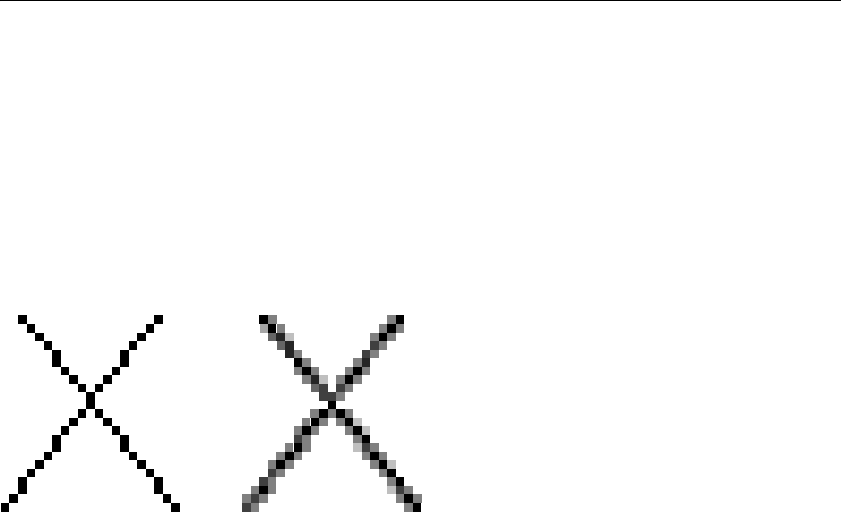
Antialiasing 267
Antialiasing
You might have noticed in some of your OpenGL pictures that lines,
especially nearly horizontal and nearly vertical ones, appear jagged. These
“jaggies” appear because the ideal line is approximated by a series of pixels
that must lie on the pixel grid. The jaggedness is called aliasing, and this
section describes antialiasing techniques for reducing it. Figure 6-2 shows
two intersecting lines, both aliased and antialiased. The pictures have been
magnified to show the effect.
Figure 6-3 shows how a diagonal line 1 pixel wide covers more of some pixel
squares than others. In fact, when performing antialiasing, OpenGL calculates
acoverage value for each fragment based on the fraction of the pixel square
on the screen that it would cover. Figure 6-3 shows these coverage values for
the line. In RGBA mode, OpenGL multiplies the fragment’s alpha value by
its coverage. You can then use the resulting alpha value to blend the frag-
ment with the corresponding pixel already in the framebuffer. In color-
index mode, OpenGL sets the least significant 4 bits of the color index based
on the fragment’s coverage (0000 for no coverage and 1111 for complete
coverage). It’s up to you to load your color map and apply it appropriately
to take advantage of this coverage information.
The details of calculating coverage values are complex, are difficult to
specify in general, and in fact may vary slightly depending on your
particular implementation of OpenGL. You can use the glHint() command
to exercise some control over the trade-off between image quality and
speed, but not all implementations will take the hint.
Figure 6-2 Aliased and Antialiased Lines

268 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
void glHint(GLenum target, GLenum hint);
Controls certain aspects of OpenGL behavior. The target parameter
indicates which behavior is to be controlled; its possible values are shown
in Table 6-3. The hint parameter can be GL_FASTEST to indicate that
the most efficient option should be chosen, GL_NICEST to indicate the
highest-quality option, or GL_DONT_CARE to indicate no preference.
The interpretation of hints is implementation-dependent; an OpenGL
implementation can ignore them entirely. (For more information about
the relevant topics, see this section for details about sampling and “Fog”
for details about fog.)
The GL_PERSPECTIVE_CORRECTION_HINT target parameter refers
to how color values and texture coordinates are interpolated across a
primitive: either linearly in screen space (a relatively simple calculation)
or in a perspective-correct manner (which requires more computation).
Often, systems perform linear color interpolation because the results,
while not technically correct, are visually acceptable; however, in most
cases, textures require perspective-correct interpolation to be visually
acceptable. Thus, an OpenGL implementation can choose to use this
parameter to control the method used for interpolation. (See Chapter 3
for a discussion of perspective projection, Chapter 4 for a discussion of
color, and Chapter 9 for a discussion of texture mapping.)
N
J K L M
F G H I
B C D E
A
A
B
C
D
E
F
G
H
I
J
K
L
M
N
.040510
.040510
.878469
.434259
.007639
.141435
.759952
.759952
.141435
.007639
.434259
.878469
.040510
.040510
Figure 6-3 Determining Coverage Values
Compatibility
Extension
GL_
PERSPECTIVE_
CORRECTION_
HINT
GL_FOG_HINT
GL_POINT_
SMOOTH_HINT
GL_GENERATE_
MIPMAP_HINT

Antialiasing 269
Antialiasing Points or Lines
One way to antialias points or lines is to turn on antialiasing with glEnable(),
passing in GL_POINT_SMOOTH or GL_LINE_SMOOTH, as appropriate. You
might also want to provide a quality hint with glHint(). (Remember that
you can set the size of a point or the width of a line. You can also stipple a
line. See “Line Details” in Chapter 2.) Then follow the procedures described
in one of the following sections, depending on whether you’re in RGBA or
color-index mode.
Another way to antialias points or lines is to use multisampling, as described
in “Antialiasing Geometric Primitives with Multisampling.”
Antialiasing in RGBA Mode
In RGBA mode, you need to enable blending. The blending factors you most
likely want to use are GL_SRC_ALPHA (source) and GL_ONE_MINUS_SRC_
ALPHA (destination). Alternatively, you can use GL_ONE for the destination
factor to make lines a little brighter where they intersect. Now you’re ready
Parameter Specifies
GL_POINT_SMOOTH_HINT, GL_LINE_
SMOOTH_HINT, GL_POLYGON_
SMOOTH_HINT
sampling quality of points, lines,
or polygons during antialiasing
operations
GL_FOG_HINT whether fog calculations are done
per pixel (GL_NICEST) or per vertex
(GL_FASTEST)
GL_PERSPECTIVE_CORRECTION_HINT quality of color and texture-
coordinate interpolation
GL_GENERATE_MIPMAP_HINT quality and performance of
automatic mipmap level generation
GL_TEXTURE_COMPRESSION_HINT quality and performance of
compressing texture images
GL_FRAGMENT_SHADER_DERIVATIVE_
HINT
derivative accuracy for fragment
processing for built-in GLSL shader
functions dFdx, dFdy, and fwidth
Table 6-3 Values for Use with glHint()

270 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
to draw whatever points or lines you want antialiased. The antialiased effect
is most noticeable if you use a fairly high alpha value. Remember that since
you’re performing blending, you might need to consider the rendering
order as described in “Three-Dimensional Blending with the Depth Buffer.”
However, in most cases, the ordering can be ignored without significant
adverse effects. Example 6-4 initializes the necessary modes for antialiasing
and then draws two intersecting diagonal lines. When you run this program,
press the ‘r’ key to rotate the lines so that you can see the effect of antialiasing
on lines of different slopes. Note that the depth buffer isn’t enabled in this
example.
Example 6-4 Antialiased Lines: aargb.c
static float rotAngle = 0.;
/* Initialize antialiasing for RGBA mode, including alpha
* blending, hint, and line width. Print out implementation-
* specific info on line width granularity and width.
*/
void init(void)
{
GLfloat values[2];
glGetFloatv(GL_LINE_WIDTH_GRANULARITY, values);
printf(“GL_LINE_WIDTH_GRANULARITY value is %3.1f\n”,
values[0]);
glGetFloatv(GL_LINE_WIDTH_RANGE, values);
printf(“GL_LINE_WIDTH_RANGE values are %3.1f %3.1f\n”,
values[0], values[1]);
glEnable(GL_LINE_SMOOTH);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
glHint(GL_LINE_SMOOTH_HINT, GL_DONT_CARE);
glLineWidth(1.5);
glClearColor(0.0, 0.0, 0.0, 0.0);
}
/* Draw 2 diagonal lines to form an X */
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0, 1.0, 0.0);
glPushMatrix();
glRotatef(-rotAngle, 0.0, 0.0, 0.1);

Antialiasing 271
glBegin(GL_LINES);
glVertex2f(-0.5, 0.5);
glVertex2f(0.5, -0.5);
glEnd();
glPopMatrix();
glColor3f(0.0, 0.0, 1.0);
glPushMatrix();
glRotatef(rotAngle, 0.0, 0.0, 0.1);
glBegin(GL_LINES);
glVertex2f(0.5, 0.5);
glVertex2f(-0.5, -0.5);
glEnd();
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLint) w, (GLint) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
gluOrtho2D(-1.0, 1.0,
-1.0*(GLfloat)h/(GLfloat)w, 1.0*(GLfloat)h/(GLfloat)w);
else
gluOrtho2D(-1.0*(GLfloat)w/(GLfloat)h,
1.0*(GLfloat)w/(GLfloat)h, -1.0, 1.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘r’:
case ‘R’:
rotAngle += 20.;
if (rotAngle >= 360.) rotAngle = 0.;
glutPostRedisplay();
break;
case 27: /* Escape Key */
exit(0);
break;
default:
break;

272 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(200, 200);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Antialiasing in Color-Index Mode
The tricky part about antialiasing in color-index mode is loading and using
the color map. Since the last 4 bits of the color index indicate the coverage
value, you need to load 16 contiguous indices with a color ramp from the
background color to the object’s color. (The ramp has to start with an index
value that’s a multiple of 16.) Then you clear the color buffer to the first of
the 16 colors in the ramp and draw your points or lines using colors in the
ramp. Example 6-5 demonstrates how to construct the color ramp to draw
antialiased lines in color-index mode. In this example, two color ramps
are created: One contains shades of green and the other shades of blue.
Example 6-5 Antialiasing in Color-Index Mode: aaindex.c
#define RAMPSIZE 16
#define RAMP1START 32
#define RAMP2START 48
static float rotAngle = 0.;
/* Initialize antialiasing for color-index mode,
* including loading a green color ramp starting
* at RAMP1START and a blue color ramp starting
* at RAMP2START. The ramps must be a multiple of 16.
*/

Antialiasing 273
void init(void)
{
int i;
for (i = 0; i < RAMPSIZE; i++) {
GLfloat shade;
shade = (GLfloat) i/(GLfloat) RAMPSIZE;
glutSetColor(RAMP1START+(GLint)i, 0., shade, 0.);
glutSetColor(RAMP2START+(GLint)i, 0., 0., shade);
}
glEnable(GL_LINE_SMOOTH);
glHint(GL_LINE_SMOOTH_HINT, GL_DONT_CARE);
glLineWidth(1.5);
glClearIndex((GLfloat) RAMP1START);
}
/* Draw 2 diagonal lines to form an X */
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glIndexi(RAMP1START);
glPushMatrix();
glRotatef(-rotAngle, 0.0, 0.0, 0.1);
glBegin(GL_LINES);
glVertex2f(-0.5, 0.5);
glVertex2f(0.5, -0.5);
glEnd();
glPopMatrix();
glIndexi(RAMP2START);
glPushMatrix();
glRotatef(rotAngle, 0.0, 0.0, 0.1);
glBegin(GL_LINES);
glVertex2f(0.5, 0.5);
glVertex2f(-0.5, -0.5);
glEnd();
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();

274 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
if (w <= h)
gluOrtho2D(-1.0, 1.0,
-1.0*(GLfloat)h/(GLfloat)w, 1.0*(GLfloat)h/(GLfloat)w);
else
gluOrtho2D(-1.0*(GLfloat)w/(GLfloat)h,
1.0*(GLfloat)w/(GLfloat)h, -1.0, 1.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘r’:
case ‘R’:
rotAngle += 20.;
if (rotAngle >= 360.) rotAngle = 0.;
glutPostRedisplay();
break;
case 27: /* Escape Key */
exit(0);
break;
default:
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_INDEX);
glutInitWindowSize(200, 200);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Since the color ramp goes from the background color to the object’s color,
the antialiased lines look correct only in the areas where they are drawn on
top of the background. When the blue line is drawn, it erases part of the
green line at the point where the lines intersect. To fix this, you would need
to redraw the area where the lines intersect using a ramp that goes from

Antialiasing 275
green (the color of the line in the framebuffer) to blue (the color of the line
being drawn). However, this requires additional calculations, and it is
usually not worth the effort since the intersection area is small. Note that
this is not a problem in RGBA mode, since the colors of objects being drawn
are blended with the color already in the framebuffer.
You may also want to enable the depth test when drawing antialiased points
and lines in color-index mode. In this example, the depth test is disabled
since both of the lines lie in the same z-plane. However, if you want to draw
a three-dimensional scene, you should enable the depth buffer so that the
resulting pixel colors correspond to the “nearest” objects.
The trick described in “Three-Dimensional Blending with the Depth Buffer”
can also be used to mix antialiased points and lines with aliased, depth-
buffered polygons. To do this, draw the polygons first, then make the depth
buffer read-only and draw the points and lines. The points and lines
intersect nicely with each other but will be obscured by nearer polygons.
Try This
Take a previous program, such as the robot arm or solar system examples
described in “Examples of Composing Several Transformations” in
Chapter 3, and draw wireframe objects with antialiasing. Try it in either
RGBA or color-index mode. Also try different line widths and point sizes to
see their effects.
Antialiasing Geometric Primitives with Multisampling
Multisampling is a technique that uses additional color, depth, and stencil
information (samples) to antialias OpenGL primitives: points, lines, poly-
gons, bitmaps, and images. Each fragment, instead of having a single color,
single depth, and single set of texture coordinates, has multiple colors,
depths, and texture coordinate sets, based upon the number of subpixel
samples. Calculations aren’t at the dead center of each pixel (as they typi-
cally are when you have one sample), but are dispersed at several sample
locations. Instead of using alpha values to represent how much a primitive
covers a pixel, antialiasing coverage values are calculated from the samples
saved in a multisample buffer.
Multisampling is especially good for antialiasing the edges of polygons,
because sorting isn’t needed. (If you are using alpha values to antialias poly-
gons, the order in which translucent objects are drawn affects the color of
the results.) Multisampling takes care of traditionally difficult cases, such as
intersecting or adjacent polygons.
Try This

276 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
Multisampling is trivial to add to an application. Just follow these three
steps:
1. Obtain a window that supports multisampling. With GLUT, you can
ask for one by calling
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB |
GLUT_MULTISAMPLE);
2. After you’ve opened a window, you will need to verify that multi-
sampling is available. For instance, GLUT may give you a window
with “almost” what you have asked for. If querying the state variable
GL_SAMPLE_BUFFERS returns a value of one and GL_SAMPLES returns
a value greater than one, then you’ll be able to use multisampling.
(GL_SAMPLES returns the number of subpixel samples. If there is only
one sample, multisampling is effectively disabled.)
GLint bufs, samples;
glGetIntegerv(GL_SAMPLE_BUFFERS, &bufs);
glGetIntegerv(GL_SAMPLES, &samples);
3. To turn on multisampling, call
glEnable(GL_MULTISAMPLE);
Example 6-6 displays two sets of primitives side-by-side so that you can see
the difference that multisampling makes. init() checks the multisampling
state variables and then two display lists are compiled: one list with a “pin-
wheel” of lines of different widths and triangles (filled polygons) and the
other with a checkerboard background. In display(), the pinwheel is drawn
both with multisampling (on the left) and without (right). You should com-
pare the aliasing of the two objects. A contrasting background sometimes
accentuates aliasing, and other times it may obscure it. You can press the ‘b’
key to redraw the scene with or without the checkerboard background.
Example 6-6 Enabling Multisampling: multisamp.c
static int bgtoggle = 1;
/*
* Print out state values related to multisampling.
* Create display list with "pinwheel" of lines and
* triangles.
*/
void init(void)
{

Antialiasing 277
GLint buf, sbuf;
int i, j;
glClearColor(0.0, 0.0, 0.0, 0.0);
glGetIntegerv(GL_SAMPLE_BUFFERS, &buf);
printf("number of sample buffers is %d\n", buf);
glGetIntegerv(GL_SAMPLES, &sbuf);
printf("number of samples is %d\n", sbuf);
glNewList(1, GL_COMPILE);
for (i = 0; i < 19; i++) {
glPushMatrix();
glRotatef(360.0*(float)i/19.0, 0.0, 0.0, 1.0);
glColor3f (1.0, 1.0, 1.0);
glLineWidth((i%3)+1.0);
glBegin(GL_LINES);
glVertex2f(0.25, 0.05);
glVertex2f(0.9, 0.2);
glEnd();
glColor3f(0.0, 1.0, 1.0);
glBegin(GL_TRIANGLES);
glVertex2f(0.25, 0.0);
glVertex2f(0.9, 0.0);
glVertex2f(0.875, 0.10);
glEnd();
glPopMatrix();
}
glEndList();
glNewList(2, GL_COMPILE);
glColor3f(1.0, 0.5, 0.0);
glBegin(GL_QUADS);
for (i = 0; i < 16; i++) {
for (j = 0; j < 16; j++) {
if (((i + j) % 2) == 0) {
glVertex2f(-2.0 + (i * 0.25), -2.0 + (j * 0.25));
glVertex2f(-2.0 + (i * 0.25), -1.75 + (j * 0.25));
glVertex2f(-1.75 + (i * 0.25), -1.75 + (j * 0.25));
glVertex2f(-1.75 + (i * 0.25), -2.0 + (j * 0.25));
}
}
}
glEnd();
glEndList();
}

278 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
/* Draw two sets of primitives so that you can
* compare the user of multisampling against its absence.
*
* This code enables antialiasing and draws one display list,
* and then it disables and draws the other display list.
*/
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
if (bgtoggle)
glCallList(2);
glEnable(GL_MULTISAMPLE);
glPushMatrix();
glTranslatef(-1.0, 0.0, 0.0);
glCallList(1);
glPopMatrix();
glDisable(GL_MULTISAMPLE);
glPushMatrix();
glTranslatef(1.0, 0.0, 0.0);
glCallList(1);
glPopMatrix();
glutSwapBuffers();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ’b’:
case ’B’:
bgtoggle = !bgtoggle;
glutPostRedisplay();
break;
case 27: /* Escape Key */
exit(0);
break;
default:
break;
}
}
With a standard implementation, you can’t fine-tune multisampling. You
can’t change the number of samples or specify (or even query) the subpixel
sample locations.

Antialiasing 279
If multisampling is enabled and there’s also a multisample buffer, then
points, lines, and polygons generate fragments that are intended for
antialiasing. For example, a large-sized point primitive is rounded, not
square, whether GL_POINT_SMOOTH has been enabled or disabled. The
states of GL_LINE_SMOOTH and GL_POLYGON_SMOOTH are similarly
ignored. Other primitive attributes, such as point size and line width, are
supported during multisampling.
Alpha and Multisampling Coverage
By default, multisampling calculates fragment coverage values that are
independent of alpha. However, if you enable one of the following special
modes, then a fragment’s alpha value is taken into consideration when
calculating the coverage. The special modes are as follows:
• GL_SAMPLE_ALPHA_TO_COVERAGE uses the alpha value of the
fragment to compute the final coverage value.
• GL_SAMPLE_ALPHA_TO_ONE sets the fragment’s alpha value to one,
the maximum alpha value, and then uses that value in the coverage
calculation.
• GL_SAMPLE_COVERAGE uses the value set with the glSampleCoverage()
routine, which is combined (ANDed) with the calculated coverage value.
Additionally, this mode can be inverted by setting the invert flag with
the glSampleCoverage() routine.
Antialiasing Polygons
Antialiasing the edges of filled polygons is similar to antialiasing points and
lines. When different polygons have overlapping edges, you need to blend
the color values appropriately. You can use the method described in this
section, or you can use the accumulation buffer to perform antialiasing for
your entire scene. Using the accumulation buffer, which is described in
void glSampleCoverage(GLclampf value, GLboolean invert);
Sets parameters to be used to interpret alpha values while computing
multisampling coverage. value is a temporary coverage value that is used
if GL_SAMPLE_COVERAGE or GL_SAMPLE_ALPHA_TO_COVERAGE has
been enabled. invert is a Boolean that indicates whether the temporary
coverage value ought to be bitwise inverted before it is used (ANDed) with
the fragment coverage.

280 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
Chapter 10, is easier from your point of view, but it’s much more
computation-intensive and therefore slower. However, as you’ll see, the
method described here is rather cumbersome.
Note: If you draw your polygons as points at the vertices or as outlines—
that is, by passing GL_POINT or GL_LINE to glPolygonMode()—
point or line antialiasing is applied, if enabled as described earlier.
The rest of this section addresses polygon antialiasing when you’re
using GL_FILL as the polygon mode.
In theory, you can antialias polygons in either RGBA or color-index mode.
However, object intersections affect polygon antialiasing more than they
affect point or line antialiasing, so rendering order and blending accuracy
become more critical. In fact, they’re so critical that if you’re antialiasing
more than one polygon, you need to order the polygons from front to back,
and then use glBlendFunc() with GL_SRC_ALPHA_SATURATE for the
source factor and GL_ONE for the destination factor. Thus, antialiasing
polygons in color-index mode normally isn’t practical.
To antialias polygons in RGBA mode, you use the alpha value to represent
coverage values of polygon edges. You need to enable polygon antialiasing
by passing GL_POLYGON_SMOOTH to glEnable(). This causes pixels on
the edges of the polygon to be assigned fractional alpha values based on
their coverage, as though they were lines being antialiased. Also, if you
desire, you can supply a value for GL_POLYGON_SMOOTH_HINT.
Now you need to blend overlapping edges appropriately. First, turn off
the depth buffer so that you have control over how overlapping pixels
are drawn. Then set the blending factors to GL_SRC_ALPHA_SATURATE
(source) and GL_ONE (destination). With this specialized blending function,
the final color is the sum of the destination color and the scaled source color;
the scale factor is the smaller of either the incoming source alpha value or
1 minus the destination alpha value. This means that for a pixel with a large
alpha value, successive incoming pixels have little effect on the final color
because 1 minus the destination alpha is almost zero. With this method, a pixel
on the edge of a polygon might be blended eventually with the colors from
another polygon that’s drawn later. Finally, you need to sort all the polygons in
your scene so that they’re ordered from front to back before drawing them.
Fog
Computer images sometimes seem unrealistically sharp and well defined.
Antialiasing makes an object appear more realistic by smoothing its edges.

Fog 281
Additionally, you can make an entire image appear more natural by adding
fog, which makes objects fade into the distance. “Fog” is a general term that
describes similar forms of atmospheric effects; it can be used to simulate
haze, mist, smoke, or pollution (see Plate 9). Fog is essential in visual-
simulation applications, where limited visibility needs to be approximated.
It’s often incorporated into flight-simulator displays.
When fog is enabled, objects that are farther from the viewpoint begin
to fade into the fog color. You can control the density of the fog, which
determines the rate at which objects fade as the distance increases, as well
as the fog’s color. You can also explicitly specify a fog coordinate per-vertex
for fog distance calculations, rather than use an automatically calculated
depth value.
Fog is available in both RGBA and color-index modes, although the
calculations are slightly different in the two modes. Since fog is applied after
matrix transformations, lighting, and texturing are performed, it affects
transformed, lit, and textured objects. Note that with large simulation
programs, fog can improve performance, since you can choose not to draw
objects that would be too fogged to be visible.
All types of geometric primitives can be fogged, including points and lines.
Using the fog effect on points and lines is also called depth-cuing (as shown
in Plate 2) and is popular in molecular modeling and other applications.
Using Fog
Using fog is easy. You enable it by passing GL_FOG to glEnable(), and you
choose the color and the equation that controls the density with glFog*().
If you want, you can supply a value for GL_FOG_HINT with glHint(),
as described in Table 6-3. Example 6-7 draws five red spheres, each at a
different distance from the viewpoint. Pressing the ‘f’ key selects among the
three different fog equations, which are described in the next section.
Example 6-7 Five Fogged Spheres in RGBA Mode: fog.c
static GLint fogMode;
static void init(void)
{
GLfloat position[] = { 0.5, 0.5, 3.0, 0.0 };
glEnable(GL_DEPTH_TEST);
glLightfv(GL_LIGHT0, GL_POSITION, position);

282 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
{
GLfloat mat[3] = {0.1745, 0.01175, 0.01175};
glMaterialfv(GL_FRONT, GL_AMBIENT, mat);
mat[0] = 0.61424; mat[1] = 0.04136; mat[2] = 0.04136;
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat);
mat[0] = 0.727811; mat[1] = 0.626959; mat[2] = 0.626959;
glMaterialfv(GL_FRONT, GL_SPECULAR, mat);
glMaterialf(GL_FRONT, GL_SHININESS, 0.6*128.0);
}
glEnable(GL_FOG);
{
GLfloat fogColor[4] = {0.5, 0.5, 0.5, 1.0};
fogMode = GL_EXP;
glFogi(GL_FOG_MODE, fogMode);
glFogfv(GL_FOG_COLOR, fogColor);
glFogf(GL_FOG_DENSITY, 0.35);
glHint(GL_FOG_HINT, GL_DONT_CARE);
glFogf(GL_FOG_START, 1.0);
glFogf(GL_FOG_END, 5.0);
}
glClearColor(0.5, 0.5, 0.5, 1.0); /* fog color */
}
static void renderSphere(GLfloat x, GLfloat y, GLfloat z)
{
glPushMatrix();
glTranslatef(x, y, z);
glutSolidSphere(0.4, 16, 16);
glPopMatrix();
}
/* display() draws 5 spheres at different z positions.
*/
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
renderSphere(-2., -0.5, -1.0);
renderSphere(-1., -0.5, -2.0);
renderSphere(0., -0.5, -3.0);
renderSphere(1., -0.5, -4.0);
renderSphere(2., -0.5, -5.0);
glFlush();
}

Fog 283
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-2.5, 2.5, -2.5*(GLfloat)h/(GLfloat)w,
2.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0);
else
glOrtho(-2.5*(GLfloat)w/(GLfloat)h,
2.5*(GLfloat)w/(GLfloat)h, -2.5, 2.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘f’:
case ‘F’:
if (fogMode == GL_EXP) {
fogMode = GL_EXP2;
printf(“Fog mode is GL_EXP2\n”);
}
else if (fogMode == GL_EXP2) {
fogMode = GL_LINEAR;
printf(“Fog mode is GL_LINEAR\n”);
}
else if (fogMode == GL_LINEAR) {
fogMode = GL_EXP;
printf(“Fog mode is GL_EXP\n”);
}
glFogi(GL_FOG_MODE, fogMode);
glutPostRedisplay();
break;
case 27:
exit(0);
break;
default:
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);

glutInitWindowSize(500, 500);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Fog Equations
Fog blends a fog color with an incoming fragment’s color using a fog blend-
ing factor. This factor, f, is computed with one of these three equations and
then clamped to the range [0, 1]:
In these three equations, z is the eye-coordinate distance between the view-
point and the fragment center. You may have added control over the z eye-
coordinate distance with per-vertex fog coordinates, which is described in
“Fog Coordinates.” The values for density, start, and end are all specified with
glFog*(). The f factor is used differently, depending on whether you’re in
RGBA mode or color-index mode, as explained in the following subsections.
f
= e −(density z) (GL_EXP)
f
= e −(density z)
2
(GL_EXP2)
f
= end − z (GL_LINEAR)
end − start
void glFog{if}(GLenum pname,TYPE param);
void glFog{if}v(GLenum pname, const TYPE *params);
Sets the parameters and function for calculating fog. If pname
MODE, then param is GL_EXP (the default), GL_EXP2, or GL_LINEAR
to select one of the three fog factors. If pname is GL_FOG_DENSITY,
GL_FOG_START, or GL_FOG_END, then param is (or points to, with the
vector version of the command) a value for density,start, or end in the
equations. (The default values are 1, 0, and 1, respectively.) In RGBA
mode, pname can be GL_FOG_COLOR, in which case params points to
four values that specify the fog’s RGBA color values. The corresponding
value for pname in color-index mode is GL_FOG_INDEX, for which param
284 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
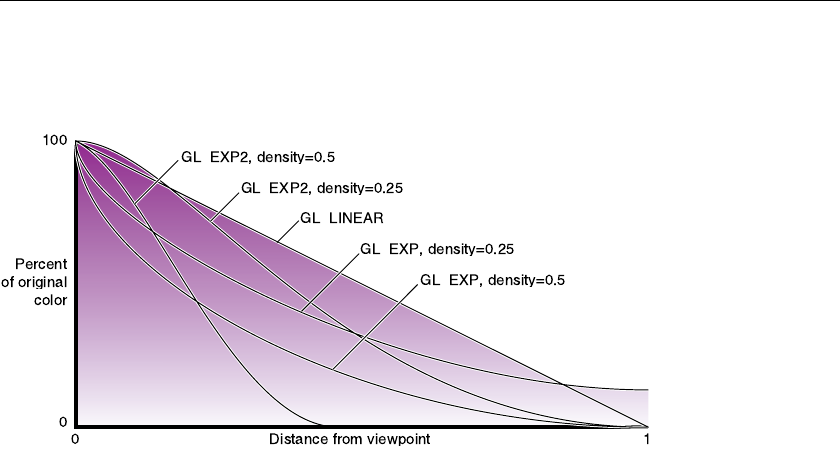
Figure 6-4 plots the fog-density equations for various values of the
parameters.
Fog in RGBA Mode
In RGBA mode, the fog factor f is used as follows to calculate the final
fogged color:
C = f Ci + (1 f ) Cf
where Ci represents the incoming fragment’s RGBA values and Cf the fog-
color values assigned with GL_FOG_COLOR.
Fog in Color-Index Mode
In color-index mode, the final fogged color index is computed as follows:
I = Ii + (1 f ) If
where Ii is the incoming fragment’s color index and If is the fog’s color index
as specified with GL_FOG_INDEX.
To use fog in color-index mode, you have to load appropriate values in a
color ramp. The first color in the ramp is the color of the object without fog,
and the last color in the ramp is the color of the completely fogged object.
You probably want to use glClearIndex() to initialize the background color
index so that it corresponds to the last color in the ramp; this way, totally
Figure 6-4 Fog-Density Equations
Fog 285

286 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
fogged objects blend into the background. Similarly, before objects are
drawn, you should call glIndex*() and pass in the index of the first color
in the ramp (the unfogged color). Finally, to apply fog to different colored
objects in the scene, you need to create several color ramps and call
glIndex*() before each object is drawn to set the current color index to
the start of each color ramp. Example 6-8 illustrates how to initialize
appropriate conditions and then apply fog in color-index mode.
Example 6-8 Fog in Color-Index Mode: fogindex.c
/* Initialize color map and fog. Set screen clear color
* to end of color ramp.
*/
#define NUMCOLORS 32
#define RAMPSTART 16
static void init(void)
{
int i;
glEnable(GL_DEPTH_TEST);
for (i = 0; i < NUMCOLORS; i++) {
GLfloat shade;
shade = (GLfloat) (NUMCOLORS-i)/(GLfloat) NUMCOLORS;
glutSetColor(RAMPSTART + i, shade, shade, shade);
}
glEnable(GL_FOG);
glFogi(GL_FOG_MODE, GL_LINEAR);
glFogi(GL_FOG_INDEX, NUMCOLORS);
glFogf(GL_FOG_START, 1.0);
glFogf(GL_FOG_END, 6.0);
glHint(GL_FOG_HINT, GL_NICEST);
glClearIndex((GLfloat) (NUMCOLORS+RAMPSTART-1));
}
static void renderSphere(GLfloat x, GLfloat y, GLfloat z)
{
glPushMatrix();
glTranslatef(x, y, z);
glutWireSphere(0.4, 16, 16);
glPopMatrix();
}

Fog 287
/* display() draws 5 spheres at different z positions.
*/
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glIndexi(RAMPSTART);
renderSphere(-2., -0.5, -1.0);
renderSphere(-1., -0.5, -2.0);
renderSphere(0., -0.5, -3.0);
renderSphere(1., -0.5, -4.0);
renderSphere(2., -0.5, -5.0);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-2.5, 2.5, -2.5*(GLfloat)h/(GLfloat)w,
2.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0);
else
glOrtho(-2.5*(GLfloat)w/(GLfloat)h,
2.5*(GLfloat)w/(GLfloat)h, -2.5, 2.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case 27:
exit(0);
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_INDEX | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutCreateWindow(argv[0]);
288 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Fog Coordinates
As discussed earlier, the fog equations use a fog coordinate, z, to calculate a
color value:
By default, z is automatically calculated as the distance from the eye to a
fragment, but you may want greater control over how fog is calculated. You
may want to simulate a fog equation other than those offered by OpenGL.
For example, you might want a flight simulation with “ground-based” fog,
so you’ll use denser fog closer to sea level.
In OpenGL Version 1.4, you can explicitly specify values for z on a per-vertex
basis by calling glFog(GL_FOG_COORD_SRC, GL_FOG_COORD). In
explicit fog coordinate mode, you may specify the fog coordinate at each
vertex with glFogCoord*().
Within a geometric primitive, the fog coordinates may be interpolated for
each fragment.
void glFogCoord{fd}(TYPE z);
void glFogCoord{fd}v(const TYPE *z);
Sets the current fog coordinate to z. If GL_FOG_COORD is the current fog
coordinate source, the current fog coordinate is used by the current fog
equation (GL_LINEAR, GL_EXP, or GL_EXP2) to calculate fog.
Values of z should be positive, representing eye-coordinate distance.
You should avoid using negative values for fog coordinates, because the
calculations may result in strange colors.
f
= e −(density z) (GL_EXP)
f
= e −(density z)
2
(GL_EXP2)
f
= end − z (GL_LINEAR)
end − start
Compatibility
Extension
glFogCoord

Fog 289
The sample program in Example 6-9 renders a triangle and allows you to
change the fog coordinate at each vertex by pressing several numerical keys.
While in explicit fog coordinate mode, moving the viewpoint forward and
backward (pressing the ‘f’ and ‘b’ keys) does not transform the fog coordi-
nates and therefore does not affect the colors of the vertices. If you stop
using explicit fog coordinates (pressing the ‘c’ key), moving the viewpoint
once again dramatically affects colors calculated for fog.
Example 6-9 Fog Coordinates: fogcoord.c
static GLfloat f1, f2, f3;
/* Initialize fog
*/
static void init(void)
{
GLfloat fogColor[4] = {0.0, 0.25, 0.25, 1.0};
f1 = 1.0f;
f2 = 5.0f;
f3 = 10.0f;
glEnable(GL_FOG);
glFogi (GL_FOG_MODE, GL_EXP);
glFogfv (GL_FOG_COLOR, fogColor);
glFogf (GL_FOG_DENSITY, 0.25);
glHint (GL_FOG_HINT, GL_DONT_CARE);
glFogi(GL_FOG_COORD_SRC, GL_FOG_COORD);
glClearColor(0.0, 0.25, 0.25, 1.0); /* fog color */
}
/* display() draws a triangle at an angle.
*/
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0f, 0.75f, 0.0f);
glBegin(GL_TRIANGLES);
glFogCoordf(f1);
glVertex3f(2.0f, -2.0f, 0.0f);
glFogCoordf(f2);
glVertex3f(-2.0f, 0.0f, -5.0f);
glFogCoordf(f3);
glVertex3f(0.0f, 2.0f, -10.0f);
glEnd();

290 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
glutSwapBuffers();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ’c’:
glFogi(GL_FOG_COORD_SRC, GL_FRAGMENT_DEPTH);
glutPostRedisplay();
break;
case ’C’:
glFogi(GL_FOG_COORD_SRC, GL_FOG_COORD);
glutPostRedisplay();
break;
case ’1’:
f1 = f1 + 0.25;
glutPostRedisplay();
break;
case ’2’:
f2 = f2 + 0.25;
glutPostRedisplay();
break;
case ’3’:
f3 = f3 + 0.25;
glutPostRedisplay();
break;
case ’8’:
if (f1 > 0.25) {
f1 = f1 - 0.25;
glutPostRedisplay();
}
break;
case ’9’:
if (f2 > 0.25) {
f2 = f2 - 0.25;
glutPostRedisplay();
}
break;
case ’0’:
if (f3 > 0.25) {
f3 = f3 - 0.25;
glutPostRedisplay();
}
break;
case ’b’:

Point Parameters 291
glMatrixMode(GL_MODELVIEW);
glTranslatef(0.0, 0.0, -0.25);
glutPostRedisplay();
break;
case ’f’:
glMatrixMode(GL_MODELVIEW);
glTranslatef(0.0, 0.0, 0.25);
glutPostRedisplay();
break;
case 27:
exit(0);
break;
default:
break;
}
}
Point Parameters
In some situations, you may want to render objects that resemble small cir-
cles or spheres, but you don’t want to use inefficient, multisided polygonal
models. For example, in a flight-simulation application, you may want to
model runway landing lights—so as an aircraft approaches a runway, the
landing lights appear larger and possibly also brighter. Or, when rendering
liquid droplets (such as rain or, for you videogamers, splattered blood), you
want to simulate the phenomena using a particle system.
The landing lights or drops of liquid may be rendered as point primitives,
but the points may need to be able to change apparent size and brightness.
Using glPointSize() and glEnable(GL_POINT_SMOOTH) to make larger,
rounded points is a step toward a solution, possibly using fog to suggest
distance. However, glPointSize() can’t be called within glBegin() and
glEnd(), so it’s hard to vary the size of different points. You would have
to recalculate the point sizes on the fly and then, for best performance,
regroup them by size.
Point parameters are an automated, elegant solution, attenuating the size of
point primitives and optionally their brightness, based upon distance to the
view point. You use glPointParameterf*() to specify the coefficients of the
attenuation equation and the alpha component of points (which controls
brightness).

292 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
The GL_POINT_DISTANCE_ATTENUATION distance calculation is similar
to the math used with the coefficients for attenuated local light sources. In
Example 6-10, pressing the ‘c’, ‘l’, or ‘q’ key switches the attenuation equa-
tion among constant, linear, and quadratic attenuation. Pressing the ‘f’ or
‘b’ key moves the viewer forward or backward, which makes the points
appear larger or smaller for the linear and quadratic attenuation modes.
Example 6-10 Point Parameters: pointp.c
static GLfloat constant[3] = {1.0, 0.0, 0.0};
static GLfloat linear[3] = {0.0, 0.12, 0.0};
static GLfloat quadratic[3] = {0.0, 0.0, 0.01};
...
void glPointParameter{if}(GLenum pname, GLfloat param);
void glPointParameter{if}v(GLenum pname, const TYPE *param);
Sets values related to rendering point primitives.
If pname is GL_POINT_DISTANCE_ATTENUATION, then param is an array
of three floating-point values (a, b, c), containing the constant, linear, and
quadratic coefficients for deriving the size and brightness of a point, based
upon eye-coordinate distance, d:
If pname is set to GL_POINT_SIZE_MIN or GL_POINT_SIZE_MAX, param is
an absolute limit (either lower or upper bound, respectively) used in the
previous equation to clamp the derived point size.
If multisampling is enabled and pname is GL_POINT_FADE_THRESHOLD_
SIZE, then param specifies a different lower limit (threshold) for the size of
a point. If derivedSize < threshold, then the factor fade is computed to
modulate the point’s alpha, thus diminishing its brightness:
If pname is GL_POINT_SPRITE_COORD_ORIGIN, and param is GL_
LOWER_LEFT, then the origin for iterated texture coordinates on point
sprites is the lower-left fragment, with the t texture coordinate increasing
vertically from bottom to top across the fragments. Alternatively, if param
is set to GL_UPPER_LEFT, the t texture coordinate decreases from top to
bottom vertically.
Compatibility
Extension
GL_POINT_SIZE_
MIN
GL_POINT_SIZE_
MAX
GL_POINT_
DISTANCE_
ATTENUATION
d
erivedSize clamp size 1
abducd
2
u++
-----------------------------------------
©¹
§·
u
©¹
¨¸
§·
=
f
ade derivedSize
threshold
-------------------------------
©¹
§·
2
=

Polygon Offset 293
void keyboard(unsigned char key, int x, int y) {
switch (key) {
case ’c’:
glPointParameterfv (GL_POINT_DISTANCE_ATTENUATION, constant);
glutPostRedisplay();
break;
case ’l’:
glPointParameterfv (GL_POINT_DISTANCE_ATTENUATION, linear);
glutPostRedisplay();
break;
case ’q’:
glPointParameterfv (GL_POINT_DISTANCE_ATTENUATION, quadratic);
glutPostRedisplay();
break;
case ’b’:
glMatrixMode (GL_MODELVIEW);
glTranslatef (0.0, 0.0, -0.5);
glutPostRedisplay();
break;
case ’f’:
glMatrixMode (GL_MODELVIEW);
glTranslatef (0.0, 0.0, 0.5);
glutPostRedisplay();
break;
...
With the chosen linear and quadratic attenuation coefficients in
Example 6-10, moving the eye very close to a point may actually increase
the derived point size, by dividing the original point size by a proper frac-
tion. To lessen or prevent this, you can increase the constant attenuation
coefficient or add a size limiting value with GL_POINT_SIZE_MAX.
With point parameters, you almost certainly want round, rather than
square, points, so you’ll have to enable point antialiasing, as described in
“Antialiasing Points or Lines” on page 269. These lines of code will do
the trick:
glEnable(GL_POINT_SMOOTH);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
Polygon Offset
If you want to highlight the edges of a solid object, you might draw the
object with polygon mode set to GL_FILL, and then draw it again, but in
294 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
a different color and with the polygon mode set to GL_LINE. However,
because lines and filled polygons are not rasterized in exactly the same way,
the depth values generated for the line and polygon edge are usually not the
same, even between the same two vertices. The highlighting lines may fade
in and out of the coincident polygons, which is sometimes called
“stitching” and is visually unpleasant.
This undesirable effect can be eliminated by using polygon offset, which
adds an appropriate offset to force coincident z-values apart, separating
a polygon edge from its highlighting line. (The stencil buffer, described
in “Stencil Test” in Chapter 10, can also be used to eliminate stitching.
However, polygon offset is almost always faster than stenciling.) Polygon
offset is also useful for applying decals to surfaces by rendering images with
hidden-line removal. In addition to lines and filled polygons, this
technique can also be used with points.
There are three different ways to turn on polygon offset, one for each type of
polygon rasterization mode: GL_FILL, GL_LINE, and GL_POINT. You enable
the polygon offset by passing the appropriate parameter to glEnable()—
either GL_POLYGON_OFFSET_FILL, GL_POLYGON_OFFSET_LINE, or
GL_POLYGON_OFFSET_POINT. You must also call glPolygonMode() to
set the current polygon rasterization method.
To achieve a nice rendering of the highlighted solid object without visual
artifacts, you can add either a positive offset to the solid object (push it away
from you) or a negative offset to the wireframe (pull it toward you). The big
question is: How much offset is enough? Unfortunately, the offset required
depends on various factors, including the depth slope of each polygon and
the width of the lines in the wireframe.
void glPolygonOffset(GLfloat factor, GLfloat units);
When enabled, the depth value of each fragment is modified by adding a
calculated offset value before the depth test is performed. The offset value
offset is calculated by
offset = mfactor + runits
where m is the maximum depth slope of the polygon (computed during
rasterization), and r is the smallest value guaranteed to produce a resolvable
difference in depth values and is an implementation-specific constant.
Both factor and units may be negative.
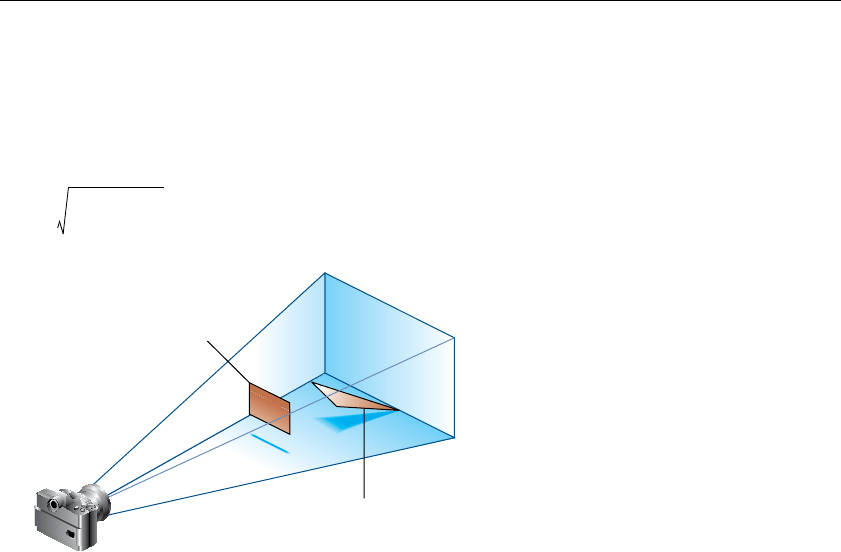
Polygon Offset 295
OpenGL calculates the depth slope (see Figure 6-5), which is the z- (depth)
value divided by the change in either x- or y-coordinates as you traverse the
polygon. The depth values are clamped to the range [0, 1], and the x- and
y-coordinates are in window coordinates. To estimate the maximum depth
slope of a polygon (m in the offset equation), use the formula
(or an implementation may use the approximation ).
For polygons that are parallel to the near and far clipping planes, the
depth slope is zero. Those polygons can use a small constant offset, which
you can specify by setting factor = 0.0 and units = 1.0 in your call to
glPolygonOffset().
For polygons that are at a great angle to the clipping planes, the depth slope
can be significantly greater than zero, and a larger offset may be needed. A
small, nonzero value for factor, such as 0.75 or 1.0, is probably enough to
generate distinct depth values and eliminate the unpleasant visual artifacts.
Example 6-11 shows a portion of code where a display list (which presum-
ably draws a solid object) is first rendered with lighting, the default polygon
mode of GL_FILL, and polygon offset with a factor value of 1.0 and a units
value of 1.0. These values ensure that the offset is enough for all polygons
in your scene, regardless of depth slope. (These values may actually be a lit-
tle more offset than the minimum needed, but too much offset is less
noticeable than too little.) Then, to highlight the edges of the first object,
the object is rendered as an unlit wireframe with the offset disabled.
mzw
xw
-----
©¹
§·
2zw
yw
-----
©¹
§·
+
2
=
Polygon with depth slope = 0
Polygon with depth slope > 0
Figure 6-5 Polygons and Their Depth Slopes
mmax
zw
xw
----- zw
yw
-----
©¹
§·
=

296 Chapter 6: Blending, Antialiasing, Fog, and Polygon Offset
Example 6-11 Polygon Offset to Eliminate Visual Artifacts: polyoff.c
glEnable(GL_LIGHT0);
glEnable(GL_LIGHTING);
glPolygonOffset(1.0, 1.0);
glEnable(GL_POLYGON_OFFSET_FILL);
glCallList(list);
glDisable(GL_POLYGON_OFFSET_FILL);
glDisable(GL_LIGHTING);
glDisable(GL_LIGHT0);
glColor3f(1.0, 1.0, 1.0);
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
glCallList(list);
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
In some situations, the simplest values for factor and units (1.0 and 1.0)
aren’t the answer. For instance, if the widths of the lines that are highlight-
ing the edges are greater than 1, then increasing the value of factor may be
necessary. Also, since depth values while using a perspective projection are
unevenly transformed into window coordinates (see “The Transformed
Depth Coordinate” in Chapter 3), less offset is needed for polygons that
are closer to the near clipping plane, and more offset is needed for polygons
that are farther away. You may need to experiment with the values you pass
to glPolygonOffset() to get the result you’re looking for.

297
Chapter 7
7.Display Lists
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Understand how display lists can be used along with commands in
immediate mode to organize your data and improve performance
• Maximize performance by knowing how and when to use display lists
Note: In OpenGL Version 3.1, all of the techniques and functions described
in this chapter were removed through deprecation.

298 Chapter 7: Display Lists
Adisplay list is a group of OpenGL commands that have been stored for later
execution. When a display list is invoked, the commands in it are executed
in the order in which they were issued. Most OpenGL commands can be
either stored in a display list or issued in immediate mode, which causes them
to be executed immediately. You can freely mix immediate-mode program-
ming and display lists within a single program. The programming examples
you’ve seen so far have used immediate mode. This chapter discusses what
display lists are and how best to use them. It has the following major
sections:
• “Why Use Display Lists?” explains when to use display lists.
• “An Example of Using a Display List” gives a brief example, showing
the basic commands for using display lists.
• “Display List Design Philosophy” explains why certain design choices
were made (such as making display lists uneditable) and what perfor-
mance optimizations you might expect to see when using display lists.
• “Creating and Executing a Display List” discusses in detail the com-
mands for creating, executing, and deleting display lists.
• “Executing Multiple Display Lists” shows how to execute several
display lists in succession, using a small character set as an example.
• “Managing State Variables with Display Lists” illustrates how to use
display lists to save and restore OpenGL commands that set state
variables.
Why Use Display Lists?
Display lists may improve performance since you can use them to store
OpenGL commands for later execution. It is often a good idea to cache com-
mands in a display list if you plan to redraw the same geometry multiple
times, or if you have a set of state changes that need to be applied multiple
times. Using display lists, you can define the geometry and/or state changes
once and execute them multiple times.
To see how you can use display lists to store geometry just once, consider
drawing a tricycle. The two wheels on the back are the same size but are
offset from each other. The front wheel is larger than the back wheels and
also in a different location. An efficient way to render the wheels on the
tricycle would be to store the geometry for one wheel in a display list and

An Example of Using a Display List 299
then execute the list three times. You would need to set the modelview
matrix appropriately each time before executing the list to calculate the
correct size and location of each wheel.
When running OpenGL programs remotely to another machine on the
network, it is especially important to cache commands in a display list.
In this case, the server is a machine other than the host. (See “What Is
OpenGL?” in Chapter 1 for a discussion of the OpenGL client-server model.)
Since display lists are part of the server state and therefore reside on the
server machine, you can reduce the cost of repeatedly transmitting that data
over a network if you store repeatedly used commands in a display list.
When running locally, you can often improve performance by storing fre-
quently used commands in a display list. Some graphics hardware may store
display lists in dedicated memory or may store the data in an optimized
form that is more compatible with the graphics hardware or software.
(See “Display List Design Philosophy” for a detailed discussion of these
optimizations.)
An Example of Using a Display List
A display list is a convenient and efficient way to name and organize a set
of OpenGL commands. For example, suppose you want to draw a torus and
view it from different angles. The most efficient way to do this would be to
store the torus in a display list. Then, whenever you want to change the
view, you would change the modelview matrix and execute the display list
to draw the torus. Example 7-1 illustrates this.
Example 7-1 Creating a Display List: torus.c
GLuint theTorus;
/* Draw a torus */
static void torus(int numc, int numt)
{
int i, j, k;
double s, t, x, y, z, twopi;
twopi = 2 * (double)M_PI;
for (i = 0; i < numc; i++) {
glBegin(GL_QUAD_STRIP);

300 Chapter 7: Display Lists
for (j = 0; j <= numt; j++) {
for (k = 1; k >= 0; k--) {
s = (i + k) % numc + 0.5;
t = j % numt;
x = (1+.1*cos(s*twopi/numc))*cos(t*twopi/numt);
y = (1+.1*cos(s*twopi/numc))*sin(t*twopi/numt);
z = .1 * sin(s * twopi / numc);
glVertex3f(x, y, z);
}
}
glEnd();
}
}
/* Create display list with Torus and initialize state */
static void init(void)
{
theTorus = glGenLists(1);
glNewList(theTorus, GL_COMPILE);
torus(8, 25);
glEndList();
glShadeModel(GL_FLAT);
glClearColor(0.0, 0.0, 0.0, 0.0);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glCallList(theTorus);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(30, (GLfloat) w/(GLfloat) h, 1.0, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(0, 0, 10, 0, 0, 0, 0, 1, 0);
}

An Example of Using a Display List 301
/* Rotate about x-axis when “x” typed; rotate about y-axis
when “y” typed; “i” returns torus to original view */
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘x’:
case ‘X’:
glRotatef(30., 1.0, 0.0, 0.0);
glutPostRedisplay();
break;
case ‘y’:
case ‘Y’:
glRotatef(30., 0.0, 1.0, 0.0);
glutPostRedisplay();
break;
case ‘i’:
case ‘I’:
glLoadIdentity();
gluLookAt(0, 0, 10, 0, 0, 0, 0, 1, 0);
glutPostRedisplay();
break;
case 27:
exit(0);
break;
}
}
int main(int argc, char **argv)
{
glutInitWindowSize(200, 200);
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Let’s start by looking at init(). It creates a display list for the torus and
initializes the OpenGL rendering state. Note that the routine for drawing a
torus (torus()) is bracketed by glNewList() and glEndList(), which defines
a display list. The argument listName for glNewList() is an integer index,
generated by glGenLists(), that uniquely identifies this display list.

302 Chapter 7: Display Lists
The user can rotate the torus about the x- or y-axis by pressing the ‘x’ or ‘y’
key when the window has focus. Whenever this happens, the callback
function keyboard() is called, which concatenates a 30-degree rotation
matrix (about the x- or y-axis) with the current modelview matrix. Then
glutPostRedisplay() is called, which will cause glutMainLoop() to call
display() and render the torus after other events have been processed.
When the ‘i’ key is pressed, keyboard() restores the initial modelview
matrix and returns the torus to its original location.
The display() function is very simple. It clears the window and then calls
glCallList() to execute the commands in the display list. If we hadn’t used
display lists, display() would have to reissue the commands to draw the
torus each time it was called.
A display list contains only OpenGL commands. In Example 7-1, only the
glBegin(),glVertex(), and glEnd() calls are stored in the display list. Their
parameters are evaluated, and the resulting values are copied into the display
list when it is created. All the trigonometry to create the torus is done only
once, which should increase rendering performance. However, the values in
the display list can’t be changed later, and once a command has been stored
in a list it is not possible to remove it. Neither can you add any new com-
mands to the list after it has been defined. You can delete the entire display
list and create a new one, but you can’t edit it.
Note: Display lists also work well with GLU commands, since those opera-
tions are ultimately broken down into low-level OpenGL commands,
which can easily be stored in display lists. Use of display lists with
GLU is particularly important for optimizing performance of GLU
tessellators (see Chapter 11) and NURBS (see Chapter 12).
Display List Design Philosophy
To optimize performance, an OpenGL display list is a cache of commands,
rather than a dynamic database. In other words, once a display list is
created, it can’t be modified. If a display list were modifiable, performance
could be reduced by the overhead required to search through the display
list and perform memory management. As portions of a modifiable
display list were changed, memory allocation and deallocation might
lead to memory fragmentation. Any modifications that the OpenGL
implementation made to the display list commands in order to make
them more efficient to render would need to be redone. Also, the display

Display List Design Philosophy 303
list might be difficult to access, cached somewhere over a network or a
system bus.
The way in which the commands in a display list are optimized may vary
from implementation to implementation. For example, a command as
simple as glRotate*() might show a significant improvement if it’s in a
display list, since the calculations to produce the rotation matrix aren’t
trivial (they can involve square roots and trigonometric functions). In the
display list, however, only the final rotation matrix needs to be stored, so a
display list rotation command can be executed as fast as the hardware can
execute glMultMatrix*(). A sophisticated OpenGL implementation might
even concatenate adjacent transformation commands into a single matrix
multiplication.
Although you’re not guaranteed that your OpenGL implementation opti-
mizes display lists for any particular uses, executing display lists is no slower
than executing the commands contained within them individually. There
is some overhead, however, involved in jumping to a display list. If a partic-
ular list is small, this overhead could exceed any execution advantage. The
most likely possibilities for optimization are listed next, with references to
the chapters in which the topics are discussed:
• Matrix operations (Chapter 3). Most matrix operations require OpenGL
to compute inverses. Both the computed matrix and its inverse might
be stored by a particular OpenGL implementation in a display list.
• Raster bitmaps and images (Chapter 8). The format in which you spec-
ify raster data isn’t likely to be one that’s ideal for the hardware. When
a display list is compiled, OpenGL might transform the data into the
representation preferred by the hardware. This can have a significant
effect on the speed of raster character drawing, since character strings
usually consist of a series of small bitmaps.
• Lights, material properties, and lighting models (Chapter 5). When
you draw a scene with complex lighting conditions, you might change
the materials for each item in the scene. Setting the materials can be
slow, since it might involve significant calculations. If you put the
material definitions in display lists, these calculations don’t have to
be done each time you switch materials, since only the results of the
calculations need to be stored; as a result, rendering lit scenes might be
faster. (See “Encapsulating Mode Changes” for more details on using
display lists to change such values as lighting conditions.)
• Polygon stipple patterns (Chapter 2).

304 Chapter 7: Display Lists
Note: To optimize texture images, you should store texture data in texture
objects instead of display lists.
Some of the commands used for specifying the properties listed here are
context-sensitive, so you need to take this into account to ensure optimum
performance. For example, when GL_COLOR_MATERIAL is enabled, some
of the material properties will track the current color (see Chapter 5). Any
glMaterial*() calls that set the same material properties are ignored.
It may improve performance to store state settings with geometry. For
example, suppose you want to apply a transformation to some geometric
objects and then draw the results. Your code may look like this:
glNewList(1, GL_COMPILE);
draw_some_geometric_objects();
glEndList();
glLoadMatrix(M);
glCallList(1);
However, if the geometric objects are to be transformed in the same way
each time, it is better to store the matrix in the display list. For example,
if you write your code as follows, some implementations may be able to
improve performance by transforming the objects when they are defined
instead of each time they are drawn:
glNewList(1, GL_COMPILE);
glLoadMatrix(M);
draw_some_geometric_objects();
glEndList();
glCallList(1);
A more likely situation occurs during rendering of images. As you will see
in Chapter 8, you can modify pixel-transfer state variables and control the
way images and bitmaps are rasterized. If the commands that set these state
variables precede the definition of the image or bitmap in the display list,
the implementation may be able to perform some of the operations ahead
of time and cache the results.
Remember that display lists have some disadvantages. Very small lists
may not perform well since there is some overhead when executing a list.
Another disadvantage is the immutability of the contents of a display list.
To optimize performance, an OpenGL display list can’t be changed, and its
contents can’t be read. If the application needs to maintain data separately
from the display list (for example, for continued data processing), then a lot
of additional memory may be required.

Creating and Executing a Display List 305
Creating and Executing a Display List
As you’ve already seen, glNewList() and glEndList() are used to begin and
end the definition of a display list, which is then invoked by supplying its
identifying index with glCallList(). In Example 7-2, a display list is created
in the init() routine. This display list contains OpenGL commands to draw
a red triangle. Then, in the display() routine, the display list is executed
10 times. In addition, a line is drawn in immediate mode. Note that the
display list allocates memory to store the commands and the values of any
necessary variables.
Example 7-2 Using a Display List: list.c
GLuint listName;
static void init(void)
{
listName = glGenLists(1);
glNewList(listName, GL_COMPILE);
glColor3f(1.0, 0.0, 0.0); /* current color red */
glBegin(GL_TRIANGLES);
glVertex2f(0.0, 0.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, 1.0);
glEnd();
glTranslatef(1.5, 0.0, 0.0); /* move position */
glEndList();
glShadeModel(GL_FLAT);
}
static void drawLine(void)
{
glBegin(GL_LINES);
glVertex2f(0.0, 0.5);
glVertex2f(15.0, 0.5);
glEnd();
}
void display(void)
{
GLuint i;
306 Chapter 7: Display Lists
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0, 1.0, 0.0); /* current color green */
for (i = 0; i < 10; i++) /* draw 10 triangles */
glCallList(listName);
drawLine(); /* Is this line green? NO! */
/* Where is the line drawn? */
glFlush();
}
The glTranslatef() routine in the display list alters the position of the next
object to be drawn. Without it, calling the display list twice would just draw
the triangle on top of itself. The drawLine() routine, which is called in
immediate mode, is also affected by the 10 glTranslatef() calls that precede
it. Therefore, if you call transformation commands within a display list,
don’t forget to take into account the effect those commands will have later
in your program.
Only one display list can be created at a time. In other words, you must
eventually follow glNewList() with glEndList() to end the creation of
a display list before starting another one. As you might expect, calling
glEndList() without having started a display list generates the error
GL_INVALID_OPERATION. (See “Error Handling” in Chapter 14 for
more information about processing errors.)
Naming and Creating a Display List
Each display list is identified by an integer index. When creating a display
list, you want to be careful that you don’t accidentally choose an index
that’s already in use, thereby overwriting an existing display list. To avoid
accidental deletions, use glGenLists() to generate one or more unused
indices.
GLuint glGenLists(GLsizei range);
Allocates range number of contiguous, previously unallocated display list
indices. The integer returned is the index that marks the beginning of a
contiguous block of empty display list indices. The returned indices are
all marked as empty and used, so subsequent calls to glGenLists() don’t
return these indices until they’re deleted. Zero is returned if the requested
number of indices isn’t available, or if range is zero.
Compatibility
Extension
glGenLists
Creating and Executing a Display List 307
In the following example, a single index is requested, and if it proves to be
available it’s used to create a new display list:
listIndex = glGenLists(1);
if (listIndex != 0) {
glNewList(listIndex,GL_COMPILE);
...
glEndList();
}
Note: Zero is not a valid display list index.
When a display list is created, it is stored with the current OpenGL context.
Thus, when the context is destroyed, the display list is also destroyed. Some
windowing systems allow multiple contexts to share display lists. In this
case, the display list is destroyed when the last context in the share group is
destroyed.
What’s Stored in a Display List?
When you’re building a display list, only the values for expressions are
stored in the list. If values in an array are subsequently changed, the display
list values don’t change. In the following code fragment, the display list
void glNewList(GLuint list, GLenum mode);
Specifies the start of a display list. OpenGL routines that are called
subsequently (until glEndList() is called to end the display list) are stored
in a display list, except for a few restricted OpenGL routines that can’t be
stored. (Those restricted routines are executed immediately, during the
creation of the display list.) list is a nonzero positive integer that uniquely
identifies the display list. The possible values for mode are GL_COMPILE
and GL_COMPILE_AND_EXECUTE. Use GL_COMPILE if you don’t want
the OpenGL commands executed as they’re placed in the display list; to
cause the commands to be both executed immediately and placed in the
display list for later use, specify GL_COMPILE_AND_EXECUTE.
void glEndList(void);
Marks the end of a display list.
Compatibility
Extension
glNewList
glEndList
GL_COMPILE
GL_COMPILE_
AND_EXECUTE

308 Chapter 7: Display Lists
contains a command to set the current RGBA color to black (0.0, 0.0, 0.0).
The subsequent change of the value of the color_vector array to red (1.0, 0.0,
0.0) has no effect on the display list because the display list contains the
values that were in effect when it was created:
GLfloat color_vector[3] = {0.0, 0.0, 0.0};
glNewList(1, GL_COMPILE);
glColor3fv(color_vector);
glEndList();
color_vector[0] = 1.0;
Not all OpenGL commands can be stored and executed from within a
display list. For example, commands that set client state and commands
that retrieve state values aren’t stored in a display list. (Many of these
commands are easily identifiable because they return values in parameters
passed by reference or return a value directly.) If these commands are called
when making a display list, they’re executed immediately.
Table 7-1 enumerates OpenGL commands that cannot be stored in a display
list. (Note also that glNewList() itself generates an error if it’s called while
already creating a display list.) Some of these commands haven’t been
described yet; you can look in the index to see where they’re discussed.
glAreTexturesResident glEdgeFlagPointer glIsShader
glAttachShader glEnableClientState glIsTexture
glBindAttribLocation glEnableVertexAttribArray glLinkProgram
glBindBuffer glFeedbackBuffer glMapBuffer
glBufferData glFinish glNormalPointer
glBufferSubData glFlush glPixelStore
glClientActiveTexture glFogCoordPointer glPopClientAttrib
glColorPointer glFogCoordPointer glPushClientAttrib
glCompileShader glGenBuffers glReadPixels
glCreateProgram glGenLists glRenderMode
glCreateShader glGenQueries glSecondaryColorPointer
glDeleteBuffers glGenTextures glSecondaryColorPointer
glDeleteLists glGet* glSelectBuffer
glDeleteProgram glIndexPointer glShaderSource
glDeleteQueries glInterleavedArrays glTexCoordPointer
glDeleteShader glIsBuffer glUnmapBuffer
glDeleteTextures glIsEnabled glValidateProgram
Table 7-1 OpenGL Functions That Cannot Be Stored in Display Lists

Creating and Executing a Display List 309
To understand more clearly why these commands can’t be stored in a
display list, remember that when you’re using OpenGL across a network,
the client may be on one machine and the server on another. After a display
list is created, it resides with the server, so the server can’t rely on the client
for any information related to the display list. If querying commands, such
as glGet*() or glIs*(), were allowed in a display list, the calling program
would be surprised at random times by data returned over the network.
Without parsing the display list as it was sent, the calling program wouldn’t
know where to put the data. Therefore, any command that returns a value
can’t be stored in a display list.
Commands that change client state, such as glPixelStore(),glSelectBuffer(),
and the commands to define vertex arrays, can’t be stored in a display list.
For example, the vertex-array specification routines (such as glVertexPointer(),
glColorPointer(), and glInterleavedArrays()) set client state pointers and
cannot be stored in a display list. glArrayElement(),glDrawArrays(), and
glDrawElements() send data to the server state to construct primitives from
elements in the enabled arrays, so these operations can be stored in a display
list. (See “Vertex Arrays” in Chapter 2.) The vertex-array data stored in this
display list is obtained by dereferencing data from the pointers, not by
storing the pointers themselves. Therefore, subsequent changes to the data
in the vertex arrays will not affect the definition of the primitive in the
display list.
In addition, any commands that use the pixel-storage modes use the modes
that are in effect when they are placed in the display list. (See “Controlling
Pixel-Storage Modes” in Chapter 8.) Other routines that rely upon client
state—such as glFlush() and glFinish()—can’t be stored in a display list
because they depend on the client state that is in effect when they are
executed.
Executing a Display List
After you’ve created a display list, you can execute it by calling glCallList().
Naturally, you can execute the same display list many times, and you can
glDetachShader glIsList glVertexAttribPointer
glDisableClientState glIsProgram glVertexPointer
glDisableVertexAttribArray glIsQuery
Table 7-1 (continued) OpenGL Functions That Cannot Be Stored in Display Lists

310 Chapter 7: Display Lists
mix calls to execute display lists with calls to perform immediate-mode
graphics, as you’ve already seen.
You can call glCallList() from anywhere within a program, as long as an
OpenGL context that can access the display list is active (that is, the context
that was active when the display list was created or a context in the same
share group). A display list can be created in one routine and executed in a
different one, since its index uniquely identifies it. Also, there is no facility
for saving the contents of a display list into a data file, nor a facility for
creating a display list from a file. In this sense, a display list is designed for
temporary use.
Hierarchical Display Lists
You can create a hierarchical display list, which is a display list that executes
another display list by calling glCallList() between a glNewList() and
glEndList() pair. A hierarchical display list is useful for an object made of
components, especially if some of those components are used more than
once. For example, this is a display list that renders a bicycle by calling other
display lists to render parts of the bicycle:
glNewList(listIndex,GL_COMPILE);
glCallList(handlebars);
glCallList(frame);
glTranslatef(1.0, 0.0, 0.0);
glCallList(wheel);
glTranslatef(3.0, 0.0, 0.0);
glCallList(wheel);
glEndList();
To avoid infinite recursion, there’s a limit on the nesting level of display
lists; the limit is at least 64, but it might be higher, depending on the
implementation. To determine the nesting limit for your implementation
of OpenGL, call
glGetIntegerv(GL_MAX_LIST_NESTING, GLint *data);
void glCallList(GLuint list);
This routine executes the display list specified by list. The commands in
the display list are executed in the order they were saved, just as if they
were issued without using a display list. If list hasn’t been defined,
nothing happens.
Compatibility
Extension
glCallList

Creating and Executing a Display List 311
OpenGL allows you to create a display list that calls another list that hasn’t
been created yet. Nothing happens when the first list calls the second,
undefined one.
You can use a hierarchical display list to approximate an editable display list
by wrapping a list around several lower-level lists. For example, to put a
polygon in a display list while allowing yourself to be able to edit its vertices
easily, you could use the code in Example 7-3.
Example 7-3 Hierarchical Display List
glNewList(1,GL_COMPILE);
glVertex3fv(v1);
glEndList();
glNewList(2,GL_COMPILE);
glVertex3fv(v2);
glEndList();
glNewList(3,GL_COMPILE);
glVertex3fv(v3);
glEndList();
glNewList(4,GL_COMPILE);
glBegin(GL_POLYGON);
glCallList(1);
glCallList(2);
glCallList(3);
glEnd();
glEndList();
To render the polygon, call display list number 4. To edit a vertex, you need
only re-create the single display list corresponding to that vertex. Since an
index number uniquely identifies a display list, creating one with the same
index as an existing one automatically deletes the old one. Keep in mind
that this technique doesn’t necessarily provide optimal memory usage or
peak performance, but it’s acceptable and useful in some cases.
Managing Display List Indices
So far, we’ve recommended the use of glGenLists() to obtain unused display
list indices. If you insist on avoiding glGenLists(), then be sure to use
glIsList() to determine whether a specific index is in use.
You can explicitly delete a specific display list or a contiguous range of lists
with glDeleteLists(). Using glDeleteLists() makes those indices available
again.
312 Chapter 7: Display Lists
Executing Multiple Display Lists
OpenGL provides an efficient mechanism for executing several display lists
in succession. This mechanism requires that you put the display list indices
in an array and call glCallLists(). An obvious use for such a mechanism
occurs when display list indices correspond to meaningful values. For
example, if you’re creating a font, each display list index might correspond
to the ASCII value of a character in that font. To have several such fonts, you
would need to establish a different initial display list index for each font.
You can specify this initial index by using glListBase() before calling
glCallLists().
The type parameter indicates the data type of the values in lists. It can be set
to GL_BYTE, GL_UNSIGNED_BYTE, GL_SHORT, GL_UNSIGNED_SHORT,
GL_INT, GL_UNSIGNED_INT, or GL_FLOAT, indicating that lists should be
GLboolean glIsList(GLuint list);
Returns GL_TRUE if list is already used for a display list, and GL_FALSE
otherwise.
void glDeleteLists(GLuint list, GLsizei range);
Deletes range display lists, starting at the index specified by list. An
attempt to delete a list that has never been created is ignored.
void glListBase(GLuint base);
Specifies the offset that’s added to the display list indices in glCallLists()
to obtain the final display list indices. The default display list base is 0. The
list base has no effect on glCallList(), which executes only one display list,
or on glNewList().
void glCallLists(GLsizei n, GLenum type, const GLvoid *lists);
Executes n display lists. The indices of the lists to be executed are
computed by adding the offset indicated by the current display list base
(specified with glListBase()) to the signed integer values in the array
pointed to by lists.
Compatibility
Extension
glIsList
Compatibility
Extension
glDeleteLists
Compatibility
Extension
glListBase
glCallLists

Executing Multiple Display Lists 313
treated as an array of bytes, unsigned bytes, shorts, unsigned shorts, inte-
gers, unsigned integers, or floats, respectively. Type can also be GL_2_BYTES,
GL_3_BYTES, or GL_4_BYTES, in which case sequences of 2, 3, or 4 bytes are
read from lists and then shifted and added together, byte by byte, to calcu-
late the display list offset. The following algorithm is used (where byte[0] is
the start of a byte sequence):
/* b = 2, 3, or 4; bytes are numbered 0, 1, 2, 3 in array */
offset = 0;
for (i = 0; i < b; i++) {
offset = offset << 8;
offset += byte[i];
}
index = offset + listbase;
For multiple-byte data, the highest-order data comes first, as bytes are taken
from the array in order.
As an example of the use of multiple display lists, look at the program frag-
ments in Example 7-4 taken from the full program in Example 7-5. This
program draws characters with a stroked font (a set of letters made from line
segments). The routine initStrokedFont() sets up the display list indices for
each letter so that they correspond with their ASCII values.
Example 7-4 Defining Multiple Display Lists
void initStrokedFont(void)
{
GLuint base;
base = glGenLists(128);
glListBase(base);
glNewList(base+’A’, GL_COMPILE);
drawLetter(Adata); glEndList();
glNewList(base+’E’, GL_COMPILE);
drawLetter(Edata); glEndList();
glNewList(base+’P’, GL_COMPILE);
drawLetter(Pdata); glEndList();
glNewList(base+’R’, GL_COMPILE);
drawLetter(Rdata); glEndList();
glNewList(base+’S’, GL_COMPILE);
drawLetter(Sdata); glEndList();
glNewList(base+’ ’, GL_COMPILE); /* space character */
glTranslatef(8.0, 0.0, 0.0);
glEndList();
}

314 Chapter 7: Display Lists
The glGenLists() command allocates 128 contiguous display list indices.
The first of the contiguous indices becomes the display list base. A display
list is made for each letter; each display list index is the sum of the base and
the ASCII value of that letter. In this example, only a few letters and the
space character are created.
After the display lists have been created, glCallLists() can be called to
execute the display lists. For example, you can pass a character string to the
subroutine printStrokedString():
void printStrokedString(GLbyte *s)
{
GLint len = strlen(s);
glCallLists(len, GL_BYTE, s);
}
The ASCII value for each letter in the string is used as the offset into the
display list indices. The current list base is added to the ASCII value of each
letter to determine the final display list index to be executed. The output
produced by Example 7-5 is shown in Figure 7-1.
Example 7-5 Multiple Display Lists to Define a Stroked Font: stroke.c
#define PT 1
#define STROKE 2
#define END 3
typedef struct charpoint {
GLfloat x, y;
int type;
} CP;
CP Adata[] = {
{ 0, 0, PT}, {0, 9, PT}, {1, 10, PT}, {4, 10, PT},
{5, 9, PT}, {5, 0, STROKE}, {0, 5, PT}, {5, 5, END}
};
Figure 7-1 Stroked Font That Defines the Characters A, E, P, R, S

Executing Multiple Display Lists 315
CP Edata[] = {
{5, 0, PT}, {0, 0, PT}, {0, 10, PT}, {5, 10, STROKE},
{0, 5, PT}, {4, 5, END}
};
CP Pdata[] = {
{0, 0, PT}, {0, 10, PT}, {4, 10, PT}, {5, 9, PT}, {5, 6, PT},
{4, 5, PT}, {0, 5, END}
};
CP Rdata[] = {
{0, 0, PT}, {0, 10, PT}, {4, 10, PT}, {5, 9, PT}, {5, 6, PT},
{4, 5, PT}, {0, 5, STROKE}, {3, 5, PT}, {5, 0, END}
};
CP Sdata[] = {
{0, 1, PT}, {1, 0, PT}, {4, 0, PT}, {5, 1, PT}, {5, 4, PT},
{4, 5, PT}, {1, 5, PT}, {0, 6, PT}, {0, 9, PT}, {1, 10, PT},
{4, 10, PT}, {5, 9, END}
};
/* drawLetter() interprets the instructions from the array
* for that letter and renders the letter with line segments.
*/
static void drawLetter(CP *l)
{
glBegin(GL_LINE_STRIP);
while (1) {
switch (l->type) {
case PT:
glVertex2fv(&l->x);
break;
case STROKE:
glVertex2fv(&l->x);
glEnd();
glBegin(GL_LINE_STRIP);
break;
case END:
glVertex2fv(&l->x);
glEnd();
glTranslatef(8.0, 0.0, 0.0);
return;
}
l++;
}
}

316 Chapter 7: Display Lists
/* Create a display list for each of 6 characters. */
static void init(void)
{
GLuint base;
glShadeModel(GL_FLAT);
base = glGenLists(128);
glListBase(base);
glNewList(base+’A’, GL_COMPILE);
drawLetter(Adata);
glEndList();
glNewList(base+’E’, GL_COMPILE);
drawLetter(Edata);
glEndList();
glNewList(base+’P’, GL_COMPILE);
drawLetter(Pdata);
glEndList();
glNewList(base+’R’, GL_COMPILE);
drawLetter(Rdata);
glEndList();
glNewList(base+’S’, GL_COMPILE);
drawLetter(Sdata);
glEndList();
glNewList(base+’ ’, GL_COMPILE);
glTranslatef(8.0, 0.0, 0.0);
glEndList();
}
char *test1 = “A SPARE SERAPE APPEARS AS”;
char *test2 = “APES PREPARE RARE PEPPERS”;
static void printStrokedString(char *s)
{
GLsizei len = strlen(s);
glCallLists(len, GL_BYTE, (GLbyte *)s);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glPushMatrix();
glScalef(2.0, 2.0, 2.0);

Executing Multiple Display Lists 317
glTranslatef(10.0, 30.0, 0.0);
printStrokedString(test1);
glPopMatrix();
glPushMatrix();
glScalef(2.0, 2.0, 2.0);
glTranslatef(10.0, 13.0, 0.0);
printStrokedString(test2);
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ’ ’:
glutPostRedisplay();
break;
case 27:
exit(0);
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(440, 120);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}

318 Chapter 7: Display Lists
Managing State Variables with Display Lists
A display list can contain calls that change the values of OpenGL state
variables. These values change as the display list is executed, just as if the
commands were called in immediate mode, and the changes persist after
execution of the display list is completed. As previously seen in Example 7-2,
and as shown in Example 7-6, which follows, the changes in the current
color and current matrix made during the execution of the display list
remain in effect after it has been called.
Example 7-6 Persistence of State Changes after Execution of a Display List
glNewList(listIndex,GL_COMPILE);
glColor3f(1.0, 0.0, 0.0);
glBegin(GL_POLYGON);
glVertex2f(0.0, 0.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, 1.0);
glEnd();
glTranslatef(1.5, 0.0, 0.0);
glEndList();
If you now call the following sequence, the line drawn after the display list
is drawn with red as the current color and translated by an additional (1.5,
0.0, 0.0):
glCallList(listIndex);
glBegin(GL_LINES);
glVertex2f(2.0,-1.0);
glVertex2f(1.0, 0.0);
glEnd();
Sometimes you want state changes to persist, but other times you want to
save the values of state variables before executing a display list and then
restore these values after the list has been executed. Remember that you
cannot use glGet*() in a display list, so you must use another way to query
and store the values of state variables.
You can use glPushAttrib() to save a group of state variables and glPopAttrib()
to restore the values when you’re ready for them. To save and restore the
current matrix, use glPushMatrix() and glPopMatrix() as described in
“Manipulating the Matrix Stacks” in Chapter 3. These push and pop
routines can be legally cached in a display list. To restore the state variables
in Example 7-6, you might use the code shown in Example 7-7.

Managing State Variables with Display Lists 319
Example 7-7 Restoring State Variables within a Display List
glNewList(listIndex,GL_COMPILE);
glPushMatrix();
glPushAttrib(GL_CURRENT_BIT);
glColor3f(1.0, 0.0, 0.0);
glBegin(GL_POLYGON);
glVertex2f(0.0, 0.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, 1.0);
glEnd();
glTranslatef(1.5, 0.0, 0.0);
glPopAttrib();
glPopMatrix();
glEndList();
If you use the display list from Example 7-7, which restores values, the code
in Example 7-8 draws a green, untranslated line. With the display list in
Example 7-6, which doesn’t save and restore values, the line is drawn red,
and its position is translated 10 times (1.5, 0.0, 0.0).
Example 7-8 The Display List May or May Not Affect drawLine()
void display(void)
{
GLint i;
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0, 1.0, 0.0); /* set current color to green */
for (i = 0; i < 10; i++)
glCallList(listIndex); /* display list called 10 times */
drawLine(); /* how and where does this line appear? */
glFlush();
}
Encapsulating Mode Changes
You can use display lists to organize and store groups of commands to
change various modes or set various parameters. When you want to switch
from one group of settings to another, using display lists might be more
efficient than making the calls directly, since the settings might be cached
in a format that matches the requirements of your graphics system.
Display lists may be more efficient than immediate mode for switching
among various lighting, lighting-model, and material-parameter settings.
You might also use display lists for stipple patterns, fog parameters, and

320 Chapter 7: Display Lists
clipping-plane equations. In general, you’ll find that executing display lists
is at least as fast as making the relevant calls directly, but remember that
some overhead is involved in jumping to a display list.
Example 7-9 shows how to use display lists to switch among three different
line stipples. First, you call glGenLists() to allocate a display list for each
stipple pattern and create a display list for each pattern. Then, you use
glCallList() to switch from one stipple pattern to another.
Example 7-9 Display Lists for Mode Changes
GLuint offset;
offset = glGenLists(3);
glNewList(offset, GL_COMPILE);
glDisable(GL_LINE_STIPPLE);
glEndList();
glNewList(offset+1, GL_COMPILE);
glEnable(GL_LINE_STIPPLE);
glLineStipple(1, 0x0F0F);
glEndList();
glNewList(offset+2, GL_COMPILE);
glEnable(GL_LINE_STIPPLE);
glLineStipple(1, 0x1111);
glEndList();
#define drawOneLine(x1,y1,x2,y2) glBegin(GL_LINES); \
glVertex2f((x1),(y1)); glVertex2f((x2),(y2)); glEnd();
glCallList(offset);
drawOneLine(50.0, 125.0, 350.0, 125.0);
glCallList(offset+1);
drawOneLine(50.0, 100.0, 350.0, 100.0);
glCallList(offset+2);
drawOneLine(50.0, 75.0, 350.0, 75.0);

321
Chapter 8
8.Drawing Pixels, Bitmaps, Fonts,
and Images
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Position and draw bitmapped data
• Read pixel data (bitmaps and images) from the framebuffer into
processor memory and from memory into the framebuffer
• Copy pixel data from one color buffer to another, or to another
location in the same buffer
• Magnify or reduce an image as it’s written to the framebuffer
• Control pixel data formatting and perform other transformations as
the data is moved to and from the framebuffer
• Perform pixel processing using the Imaging Subset
• Use buffer objects for storing pixel data
Note: Much of the functionality discussed in this chapter was deprecated in
OpenGL Version 3.0, and was removed from Version 3.1. It was
replaced with more capable functionality using framebuffer objects,
which are described in Chapter 10.

322 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
So far, most of the discussion in this guide has concerned the rendering of
geometric data—points, lines, and polygons. Two other important classes of
data can be rendered by OpenGL:
• Bitmaps, typically used for characters in fonts
• Image data, which might have been scanned in or calculated
Both bitmaps and image data take the form of rectangular arrays of pixels.
One difference between them is that a bitmap consists of a single bit of
information about each pixel, and image data typically includes several
pieces of data per pixel (the complete red, green, blue, and alpha color
components, for example). Also, bitmaps are like masks in that they’re used
to overlay another image, but image data simply overwrites or is blended
with whatever data is in the framebuffer.
This chapter describes first how to draw pixel data (bitmaps and images)
from processor memory to the framebuffer and how to read pixel data from
the framebuffer into processor memory. It also describes how to copy pixel
data from one position to another, either from one buffer to another or
within a single buffer.
Note: OpenGL does not support reading or saving pixels and images to files.
This chapter contains the following major sections:
• “Bitmaps and Fonts” describes the commands for positioning and
drawing bitmapped data. Such data may describe a font.
• “Images” presents basic information about drawing, reading, and
copying pixel data.
• “Imaging Pipeline” describes the operations that are performed on
images and bitmaps when they are read from the framebuffer and
when they are written to the framebuffer.
• “Reading and Drawing Pixel Rectangles” covers all the details about
how pixel data is stored in memory and how to transform it as it’s
moved into or out of memory.
• “Using Buffer Objects with Pixel Rectangle Data” discusses using server-
side buffer objects to store and retrieve pixel data more efficiently.
• “Tips for Improving Pixel Drawing Rates” lists tips for getting better
performance when drawing pixel rectangles.
• “Imaging Subset” presents additional pixel processing operations
found in this OpenGL extension.

Bitmaps and Fonts 323
In most cases, the necessary pixel operations are simple, so the first three
sections might be all you need to read for your application. However, pixel
manipulation can be complex—there are many ways to store pixel data in
memory, and you can apply any of several operations to pixels as they’re
moved to and from the framebuffer. These details are the subject of the
fourth section of this chapter. Most likely, you’ll want to read this section
only when you actually need to make use of the information. “Tips for
Improving Pixel Drawing Rates” provides useful tips to get the best
performance when rendering bitmaps and images.
OpenGL Version 1.2 added packed data types (such as GL_UNSIGNED_
BYTE_3_3_2 and GL_UNSIGNED_INT_10_10_10_2) and swizzled pixel
formats (such as BGR and BGRA), which match some windowing-system
formats better.
Also in Version 1.2, a set of imaging operations, including color matrix
transformations, color lookup tables, histograms, and new blending oper-
ations (glBlendEquation(), glBlendColor(), and several constant blend-
ing modes), became an ARB-approved extension named the Imaging
Subset. In Version 1.4, the blending operations of the Imaging Subset were
promoted to the core OpenGL feature set, and are no longer optional
functionality.
Version 1.4 introduced use of GL_SRC_COLOR and GL_ONE_MINUS_SRC_
COLOR as source blending functions as well as use of GL_DST_COLOR and
GL_ONE_MINUS_DST_COLOR as destination blending functions. Also
introduced in Version 1.4 was glWindowPos*() for specifying the raster
position in window coordinates.
Version 3.0 introduced numerous additional data types and pixel formats
described in this chapter. Many of these formats are more useful as texture
formats (see Chapter 9, “Texture Mapping,” for details) and as renderbuffer
formats, which are part of the new functionality of framebuffer objects
(details are discussed in “Framebuffer Objects” in Chapter 10).
Bitmaps and Fonts
A bitmap is a rectangular array of 0s and 1s that serves as a drawing mask for a
rectangular portion of the window. Suppose you’re drawing a bitmap and the
current raster color is red. Wherever there’s a 1 in the bitmap, the correspond-
ing pixel in the framebuffer is replaced by a red pixel (or combined with a red
pixel, depending on which per-fragment operations are in effect). (See “Testing
and Operating on Fragments” in Chapter 10.) If there’s a 0 in the bitmap, no

324 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
fragments are generated, and the contents of the pixel are unaffected. The
most common use of bitmaps is for drawing characters on the screen.
OpenGL provides only the lowest level of support for drawing strings of
characters and manipulating fonts. The commands glRasterPos*() (or alter-
natively glWindowPos*()) and glBitmap() position and draw a single bit-
map on the screen. In addition, through the display-list mechanism, you
can use a sequence of character codes to index into a corresponding series
of bitmaps representing those characters. (See Chapter 7 for more informa-
tion about display lists.) You’ll have to write your own routines to provide
any other support you need for manipulating bitmaps, fonts, and strings of
characters.
Consider Example 8-1, which draws the character F three times on the screen.
Figure 8-1 shows the F as a bitmap and its corresponding bitmap data.
Example 8-1 Drawing a Bitmapped Character: drawf.c
GLubyte rasters[24] = {
0xc0, 0x00, 0xc0, 0x00, 0xc0, 0x00, 0xc0, 0x00, 0xc0, 0x00,
0xff, 0x00, 0xff, 0x00, 0xc0, 0x00, 0xc0, 0x00, 0xc0, 0x00,
0xff, 0xc0, 0xff, 0xc0};
void init(void)
{
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glClearColor(0.0, 0.0, 0.0, 0.0);
}
void display(void)
0xff, 0xc0
0xff, 0xc0
0xc0, 0x00
0xc0, 0x00
0xc0, 0x00
0xff, 0x00
0xff, 0x00
0xc0, 0x00
0xc0, 0x00
0xc0, 0x00
0xc0, 0x00
0xc0, 0x00
Figure 8-1 Bitmapped F and Its Data

Bitmaps and Fonts 325
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glRasterPos2i(20, 20);
glBitmap(10, 12, 0.0, 0.0, 11.0, 0.0, rasters);
glBitmap(10, 12, 0.0, 0.0, 11.0, 0.0, rasters);
glBitmap(10, 12, 0.0, 0.0, 11.0, 0.0, rasters);
glFlush();
}
In Figure 8-1, note that the visible part of the F character is at most 10 bits
wide. Bitmap data is always stored in chunks that are multiples of 8 bits, but
the width of the actual bitmap doesn’t have to be a multiple of 8. The bits
making up a bitmap are drawn starting from the lower left corner: First, the
bottom row is drawn, then the next row above it, and so on. As you can tell
from the code, the bitmap is stored in memory in this order—the array of
rasters begins with 0xc0, 0x00, 0xc0, 0x00 for the bottom two rows of the F
and continues to 0xff, 0xc0, 0xff, 0xc0 for the top two rows.
The commands of interest in this example are glRasterPos2i() and
glBitmap(); they’re discussed in detail in the next section. For now, ignore
the call to glPixelStorei(); it describes how the bitmap data is stored in
computer memory. (See “Controlling Pixel-Storage Modes” for more
information.)
The Current Raster Position
The current raster position is the screen position where the next bitmap (or
image) is to be drawn. In the F example, the raster position was set by calling
glRasterPos*() with coordinates (20, 20), which is where the lower left
corner of the F was drawn:
glRasterPos2i(20, 20);
void glRasterPos{234}{sifd}(TYPE x, TYPE y, TYPE z, TYPE w);
void glRasterPos{234}{sifd}v(const TYPE *coords);
Sets the current raster position. The x, y, z, and w arguments specify the
coordinates of the raster position. If the vector form of the function is
used, the coords array contains the coordinates of the raster position. If
glRasterPos2*() is used, z is implicitly set to zero and w is implicitly set
to 1; similarly, with glRasterPos3*(),w is set to 1.
Compatibility
Extension
glRasterPos

326 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
The coordinates of the raster position are transformed to screen coordinates
in exactly the same way as coordinates supplied with a glVertex*() com-
mand (that is, with the modelview and perspective matrices). After transfor-
mation, either they define a valid spot in the viewport, or they’re clipped
because the coordinates were outside the viewing volume. If the trans-
formed point is clipped out, the current raster position is invalid.
Prior to Version 1.4, if you wanted to specify the raster position in window
(screen) coordinates, you had to set up the modelview and projection
matrices for simple 2D rendering, with something like the following
sequence of commands, where width and height are also the size (in pixels)
of the viewport:
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLfloat) width, 0.0, (GLfloat) height);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
In Version 1.4, glWindowPos*() was introduced as an alternative to
glRasterPos*().glWindowPos*() specifies the current raster position in
window coordinates, without the transformation of its x and y coordinates
by the modelview or projection matrices, nor clipping to the viewport.
glWindowPos*() makes it much easier to intermix 2D text and 3D graphics
at the same time without the repetitious switching of transformation state.
To obtain the current raster position (whether set by glRasterPos*() or
glWindowPos*()), you can use the query command glGetFloatv() with
GL_CURRENT_RASTER_POSITION as the first argument. The second
argument should be a pointer to an array that can hold the (x, y, z, w) values
as floating-point numbers. Call glGetBooleanv() with GL_CURRENT_
RASTER_POSITION_VALID as the first argument to determine whether
the current raster position is valid.
void glWindowPos{23}{sifd}(TYPE x, TYPE y, TYPE z);
void glWindowPos{23}{sifd}v(const TYPE *coords);
Sets the current raster position using the xand y arguments as window
coordinates without matrix transformation, clipping, lighting, or texture
coordinate generation. The z value is transformed by (and clamped to) the
current near and far values set by glDepthRange(). If the vector form of
the function is used, the coords array contains the coordinates of the raster
position. If glWindowPos2*() is used, z is implicitly set to zero.
Compatibility
Extension
glWindowPos

Bitmaps and Fonts 327
Drawing the Bitmap
Once you’ve set the desired raster position, you can use the glBitmap()
command to draw the data.
Allowing the origin of the bitmap to be placed arbitrarily makes it easy for
characters to extend below the origin (typically used for characters with
descenders, such as g, j, and y), or to extend beyond the left of the origin
void glBitmap(GLsizei width, GLsizei height,
GLfloat xbo, GLfloat ybo,
GLfloat xbi, GLfloat ybi,
const GLubyte *bitmap);
Draws the bitmap specified by bitmap, which is a pointer to the bitmap
image. The origin of the bitmap is placed at the current raster position.
If the current raster position is invalid, nothing is drawn, and the raster
position remains invalid. The width and height arguments indicate the
width and height, in pixels, of the bitmap. The width need not be a
multiple of 8, although the data is stored in unsigned characters of 8 bits
each. (In the F example, it wouldn’t matter if there were garbage bits in
the data beyond the tenth bit; since glBitmap() was called with a width
of 10, only 10 bits of the row are rendered.) Use xbo and ybo to define the
origin of the bitmap, which is positioned at the current raster position
(positive values move the origin up and to the right of the raster position;
negative values move it down and to the left); xbi and ybi indicate the x
and y increments that are added to the raster position after the bitmap is
rasterized (see Figure 8-2).
Compatibility
Extension
glBitmap
(xbo,ybo) = (0, 0)
(xbi,ybi) = (11, 0)
w = 10
h = 12
0, 0 11, 0
Figure 8-2 Bitmap and Its Associated Parameters

328 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
(used for various swash characters, which have extended flourishes, or for
characters in fonts that lean to the left).
After the bitmap is drawn, the current raster position is advanced by xbi and
ybi in the x- and y-directions, respectively. (If you just want to advance the
current raster position without drawing anything, call glBitmap() with the
bitmap parameter set to NULL and the width and height parameters set to
zero.) For standard Latin fonts, ybi is typically 0.0 and xbi is positive (since
successive characters are drawn from left to right). For Hebrew, where char-
acters go from right to left, the xbi values would typically be negative. Fonts
that draw successive characters vertically in columns would use zero for xbi
and nonzero values for ybi. In Figure 8-2, each time the F is drawn, the cur-
rent raster position advances by 11 pixels, allowing a 1-pixel space between
successive characters.
Since xbo,ybo,xbi, and ybi are floating-point values, characters need not be
an integral number of pixels apart. Actual characters are drawn on exact
pixel boundaries, but the current raster position is kept in floating point so
that each character is drawn as close as possible to where it belongs. For
example, if the code in the F example were modified such that xbi was 11.5
instead of 12, and if more characters were drawn, the space between letters
would alternate between 1 and 2 pixels, giving the best approximation to
the requested 1.5-pixel space.
Note: You can’t rotate bitmap fonts because the bitmap is always drawn
aligned to the x and y framebuffer axes. Additionally, bitmaps can’t
be zoomed.
Choosing a Color for the Bitmap
You are familiar with using glColor*() and glIndex*() to set the current
color or index for drawing geometric primitives. The same commands are
used to set different state variables, GL_CURRENT_RASTER_COLOR and
GL_CURRENT_RASTER_INDEX, for rendering bitmaps. The raster color
state variables are set from the current color when glRasterPos*() is called,
which can lead to a trap. In the following sequence of code, what is the
color of the bitmap?
glColor3f(1.0, 1.0, 1.0); /* white */
glRasterPos3fv(position);
glColor3f(1.0, 0.0, 0.0); /* red */
glBitmap(....);

Bitmaps and Fonts 329
Are you surprised to learn that the bitmap is white? The GL_CURRENT_
RASTER_COLOR is set to white when glRasterPos3fv() is called. The
second call to glColor3f() changes the value of GL_CURRENT_COLOR for
future geometric rendering, but the color used to render the bitmap is
unchanged.
To obtain the current raster color or index, you can use the query commands
glGetFloatv() or glGetIntegerv() with GL_CURRENT_RASTER_COLOR or
GL_CURRENT_RASTER_INDEX as the first argument.
Fonts and Display Lists
Display lists are discussed in general terms in Chapter 7. However, a few of
the display-list management commands have special relevance for drawing
strings of characters. As you read this section, keep in mind that the ideas
presented here apply equally well to characters that are drawn using bitmap
data and those drawn using geometric primitives (points, lines, and poly-
gons). (See “Executing Multiple Display Lists” in Chapter 7 for an example
of a geometric font.)
A font typically consists of a set of characters, where each character has an
identifying number (usually the ASCII code) and a drawing method. For a
standard ASCII character set, the capital letter A is number 65, B is 66, and
so on. The string “DAB” would be represented by the three indices 68, 65,
66. In the simplest approach, display-list number 65 draws an A, number 66
draws a B, and so on. To draw the string 68, 65, 66, just execute the corre-
sponding display lists.
You can use the command glCallLists() in just this way:
void glCallLists(GLsizei n, GLenum type, const GLvoid *lists);
The first argument, n, indicates the number of characters to be drawn, type
is usually GL_BYTE, and lists is an array of character codes.
Since many applications need to draw character strings in multiple fonts
and sizes, this simplest approach isn’t convenient. Instead, you’d like to use
65 as A no matter what font is currently active. You could force font 1 to
encode A, B, and C as 1065, 1066, 1067, and font 2 as 2065, 2066, 2067, but
then any numbers larger than 256 would no longer fit in an 8-bit byte. A
better solution is to add an offset to every entry in the string before choosing
the display list. In this case, font 1 has A, B, and C represented by 1065,

330 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
1066, and 1067, and in font 2, they might be 2065, 2066, and 2067. To draw
characters in font 1, set the offset to 1000 and draw display lists 65, 66, and
67. To draw that same string in font 2, set the offset to 2000 and draw the
same lists.
To set the offset, use the command glListBase(). For the preceding
examples, it should be called with 1000 or 2000 as the (only) argument.
Now what you need is a contiguous list of unused display-list numbers,
which you can obtain from glGenLists():
GLuint glGenLists(GLsizei range);
This function returns a block of range display-list identifiers. The returned
lists are all marked as “used” even though they’re empty, so that subsequent
calls to glGenLists() never return the same lists (unless you’ve explicitly
deleted them previously). Therefore, if you use 4 as the argument and if
glGenLists() returns 81, you can use display-list identifiers 81, 82, 83,
and 84 for your characters. If glGenLists() can’t find a block of unused
identifiers of the requested length, it returns 0. (Note that the command
glDeleteLists() makes it easy to delete all the lists associated with a font in
a single operation.)
Most American and European fonts have a small number of characters
(fewer than 256), so it’s easy to represent each character with a different
code that can be stored in a single byte. Asian fonts, among others, may
require much larger character sets, so a byte-per-character encoding is
impossible. OpenGL allows strings to be composed of 1-, 2-, 3-, or 4-byte
characters through the type parameter in glCallLists(). This parameter can
have any of the following values:
GL_BYTE GL_UNSIGNED_BYTE
GL_SHORT GL_UNSIGNED_SHORT
GL_INT GL_UNSIGNED_INT
GL_FLOAT GL_2_BYTES
GL_3_BYTES GL_4_BYTES
(See “Executing Multiple Display Lists” in Chapter 7 for more information
about these values.)

Bitmaps and Fonts 331
Defining and Using a Complete Font
The glBitmap() command and the display-list mechanism described in
the preceding section make it easy to define a raster font. In Example 8-2, the
upper-case characters of an ASCII font are defined. In this example, each
character has the same width, but this is not always the case. Once the char-
acters are defined, the program prints the message “THE QUICK BROWN
FOX JUMPS OVER A LAZY DOG.”
The code in Example 8-2 is similar to the F example, except that each
character’s bitmap is stored in its own display list. When combined with the
offset returned by glGenLists(), the display list identifier is equal to the
ASCII code for the character.
Example 8-2 Drawing a Complete Font: font.c
GLubyte space[] =
{0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00};
GLubyte letters[][13] = {
{0x00, 0x00, 0xc3, 0xc3, 0xc3, 0xc3, 0xff, 0xc3, 0xc3, 0xc3, 0x66, 0x3c, 0x18},
{0x00, 0x00, 0xfe, 0xc7, 0xc3, 0xc3, 0xc7, 0xfe, 0xc7, 0xc3, 0xc3, 0xc7, 0xfe},
{0x00, 0x00, 0x7e, 0xe7, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xe7, 0x7e},
{0x00, 0x00, 0xfc, 0xce, 0xc7, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc7, 0xce, 0xfc},
{0x00, 0x00, 0xff, 0xc0, 0xc0, 0xc0, 0xc0, 0xfc, 0xc0, 0xc0, 0xc0, 0xc0, 0xff},
{0x00, 0x00, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xfc, 0xc0, 0xc0, 0xc0, 0xff},
{0x00, 0x00, 0x7e, 0xe7, 0xc3, 0xc3, 0xcf, 0xc0, 0xc0, 0xc0, 0xc0, 0xe7, 0x7e},
{0x00, 0x00, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xff, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3},
{0x00, 0x00, 0x7e, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x7e},
{0x00, 0x00, 0x7c, 0xee, 0xc6, 0x06, 0x06, 0x06, 0x06, 0x06, 0x06, 0x06, 0x06},
{0x00, 0x00, 0xc3, 0xc6, 0xcc, 0xd8, 0xf0, 0xe0, 0xf0, 0xd8, 0xcc, 0xc6, 0xc3},
{0x00, 0x00, 0xff, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0},
{0x00, 0x00, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xdb, 0xff, 0xff, 0xe7, 0xc3},
{0x00, 0x00, 0xc7, 0xc7, 0xcf, 0xcf, 0xdf, 0xdb, 0xfb, 0xf3, 0xf3, 0xe3, 0xe3},
{0x00, 0x00, 0x7e, 0xe7, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xe7, 0x7e},
{0x00, 0x00, 0xc0, 0xc0, 0xc0, 0xc0, 0xc0, 0xfe, 0xc7, 0xc3, 0xc3, 0xc7, 0xfe},
{0x00, 0x00, 0x3f, 0x6e, 0xdf, 0xdb, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0x66, 0x3c},
{0x00, 0x00, 0xc3, 0xc6, 0xcc, 0xd8, 0xf0, 0xfe, 0xc7, 0xc3, 0xc3, 0xc7, 0xfe},
{0x00, 0x00, 0x7e, 0xe7, 0x03, 0x03, 0x07, 0x7e, 0xe0, 0xc0, 0xc0, 0xe7, 0x7e},
{0x00, 0x00, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0xff},
{0x00, 0x00, 0x7e, 0xe7, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3},
{0x00, 0x00, 0x18, 0x3c, 0x3c, 0x66, 0x66, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3},
{0x00, 0x00, 0xc3, 0xe7, 0xff, 0xff, 0xdb, 0xdb, 0xc3, 0xc3, 0xc3, 0xc3, 0xc3},
{0x00, 0x00, 0xc3, 0x66, 0x66, 0x3c, 0x3c, 0x18, 0x3c, 0x3c, 0x66, 0x66, 0xc3},
{0x00, 0x00, 0x18, 0x18, 0x18, 0x18, 0x18, 0x18, 0x3c, 0x3c, 0x66, 0x66, 0xc3},
{0x00, 0x00, 0xff, 0xc0, 0xc0, 0x60, 0x30, 0x7e, 0x0c, 0x06, 0x03, 0x03, 0xff}
};
GLuint fontOffset;
void makeRasterFont(void)
{

332 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
GLuint i, j;
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
fontOffset = glGenLists(128);
for (i = 0,j = ‘A’; i < 26; i++,j++) {
glNewList(fontOffset + j, GL_COMPILE);
glBitmap(8, 13, 0.0, 2.0, 10.0, 0.0, letters[i]);
glEndList();
}
glNewList(fontOffset + ‘ ‘, GL_COMPILE);
glBitmap(8, 13, 0.0, 2.0, 10.0, 0.0, space);
glEndList();
}
void init(void)
{
glShadeModel(GL_FLAT);
makeRasterFont();
}
void printString(char *s)
{
glPushAttrib(GL_LIST_BIT);
glListBase(fontOffset);
glCallLists(strlen(s), GL_UNSIGNED_BYTE, (GLubyte *) s);
glPopAttrib();
}
/* Everything above this line could be in a library
* that defines a font. To make it work, you’ve got
* to call makeRasterFont() before you start making
* calls to printString().
*/
void display(void)
{
GLfloat white[3] = { 1.0, 1.0, 1.0 };
glClear(GL_COLOR_BUFFER_BIT);
glColor3fv(white);
glRasterPos2i(20, 60);
printString(“THE QUICK BROWN FOX JUMPS”);
glRasterPos2i(20, 40);
printString(“OVER A LAZY DOG”);
glFlush();
}

Images 333
Images
An image—or more precisely, a pixel rectangle—is similar to a bitmap.
Instead of containing only a single bit for each pixel in a rectangular region
of the screen, however, an image can contain much more information. For
example, an image can contain a complete (R, G, B, A) color stored at each
pixel. Images can come from several sources, such as
• A photograph that’s digitized with a scanner
• An image that was first generated on the screen by a graphics program
using the graphics hardware and then read back pixel by pixel
• A software program that generated the image in memory pixel by
pixel
The images you normally think of as pictures come from the color buffers.
However, you can read or write rectangular regions of pixel data from or to
the depth buffer or the stencil buffer. (See Chapter 10 for an explanation of
these other buffers.)
In addition to simply being displayed on the screen, images can be used for
texture maps, in which case they’re essentially pasted onto polygons that
are rendered on the screen in the normal way. (See Chapter 9 for more
information about this technique.)
Reading, Writing, and Copying Pixel Data
OpenGL provides three basic commands that manipulate image data:
•glReadPixels()—Reads a rectangular array of pixels from the
framebuffer and stores the data in processor memory.
•glDrawPixels()—Writes a rectangular array of pixels from data kept in
processor memory into the framebuffer at the current raster position
specified by glRasterPos*().
•glCopyPixels()—Copies a rectangular array of pixels from one part of
the framebuffer to another. This command behaves similarly to a call
to glReadPixels() followed by a call to glDrawPixels(), but the data is
never written into processor memory.
For the aforementioned commands, the order of pixel data processing
operations is shown in Figure 8-3.

334 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Figure 8-3 presents the basic flow of pixels as they are processed. The coor-
dinates of glRasterPos*(), which specify the current raster position used by
glDrawPixels() and glCopyPixels(), are transformed by the geometric pro-
cessing pipeline. Both glDrawPixels() and glCopyPixels() are affected by
rasterization and per-fragment operations. (But when drawing or copying
a pixel rectangle, there’s almost never a reason to have fog or texture
enabled.)
However, complications arise because there are many kinds of framebuffer
data, many ways to store pixel information in computer memory, and var-
ious data conversions that can be performed during the reading, writing,
and copying operations. These possibilities translate to many different
modes of operation. If all your program does is copy images on the screen
or read them into memory temporarily so that they can be copied out later,
you can ignore most of these modes. However, if you want your program to
modify the data while it’s in memory—for example, if you have an image
stored in one format but the window requires a different format, or if you
want to save image data to a file for future restoration in another session or
on another kind of machine with significantly different graphical capabili-
ties—you have to understand the various modes.
The rest of this section describes the basic commands in detail. The follow-
ing sections discuss the details of the series of imaging operations that
Per-fragment
operations
Per-vertex
operations
and primitive
assembly
Rasterization
(fog, texture)
Framebuffer
glCopyPixels
glReadPixels
glDrawPixels
Processor
memory
glRasterPos*
Figure 8-3 Simplistic Diagram of Pixel Data Flow

Images 335
comprise the Imaging Pipeline: pixel-storage modes, pixel-transfer opera-
tions, and pixel-mapping operations.
Reading Pixel Data from Framebuffer to Processor Memory
If you are using glReadPixels() to obtain RGBA or color-index information,
you may need to clarify which buffer you are trying to access. For example,
if you have a double-buffered window, you need to specify whether you are
reading data from the front buffer or back buffer. To control the current
read source buffer, call glReadBuffer(). (See “Selecting Color Buffers for
Writing and Reading” in Chapter 10.)
void glReadPixels(GLint x, GLint y, GLsizei width, GLsizei height,
GLenum format, GLenum type, GLvoid *pixels);
Reads pixel data from the framebuffer rectangle whose lower-left corner
is at (x, y) in window coordinates and whose dimensions are width and
height, and then stores the data in the array pointed to by pixels.format
indicates the kind of pixel data elements that are read (a color-index,
depth, or stencil value or an R, G, B, or A component value, as listed
in Table 8-1), and type indicates the data type of each element (see
Table 8-2).
glReadPixels() can generate a few OpenGL errors: A GL_INVALID_
OPERATION error will be generated if format is set to GL_DEPTH, and
there is no depth buffer; or if format is GL_STENCIL, and there is no stencil
buffer; or if format is set to GL_DEPTH_STENCIL, and there are not both a
depth and a stencil buffer associated with the framebuffer, or if type is
neither GL_UNSIGNED_INT_24_8, nor GL_FLOAT_32_UNSIGNED_INT_
24_8_REV, then GL_INVALID_ENUM is set.
format Constant Pixel Format
GL_COLOR_INDEX a single color index
GL_RG or
GL_RG_INTEGER
a red color component, followed by a green color
component
GL_RGB or
GL_RGB_INTEGER
a red color component, followed by green and blue
color components
GL_RGBA or
GL_RGBA_INTEGER
a red color component, followed by green, blue,
and alpha color components
Table 8-1 Pixel Formats for glReadPixels() or glDrawPixels()

336 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
GL_BGR or
GL_BGR_INTEGER
a blue color component, followed by green and red
color components
GL_BGRA or
GL_BGRA_INTEGER
a blue color component, followed by green, red,
and alpha color components
GL_RED or
GL_RED_INTEGER
a single red color component
GL_GREEN or
GL_GREEN_INTEGER
a single green color component
GL_BLUE or
GL_BLUE_INTEGER
a single blue color component
GL_ALPHA or
GL_ALPHA_INTEGER
a single alpha color component
GL_LUMINANCE a single luminance component
GL_LUMINANCE_ALPHA a luminance component followed by an alpha color
component
GL_STENCIL_INDEX a single stencil index
GL_DEPTH_COMPONENT a single depth component
GL_DEPTH_STENCIL combined depth and stencil components
type Constant Data Type
GL_UNSIGNED_BYTE unsigned 8-bit integer
GL_BYTE signed 8-bit integer
GL_BITMAP single bits in unsigned 8-bit integers
using the same format as glBitmap()
GL_UNSIGNED_SHORT unsigned 16-bit integer
GL_SHORT signed 16-bit integer
GL_UNSIGNED_INT unsigned 32-bit integer
GL_INT signed 32-bit integer
Table 8-2 Data Types for glReadPixels() or glDrawPixels()
format Constant Pixel Format
Table 8-1 (continued) Pixel Formats for glReadPixels() or glDrawPixels()

Images 337
Note: The GL_*_REV pixel formats are particularly useful on Microsoft’s
Windows operating systems.
GL_FLOAT single-precision floating point
GL_HALF_FLOAT a 16-bit floating-point value
GL_UNSIGNED_BYTE_3_3_2 packed into unsigned 8-bit integer
GL_UNSIGNED_BYTE_2_3_3_REV packed into unsigned 8-bit integer
GL_UNSIGNED_SHORT_5_6_5 packed into unsigned 16-bit integer
GL_UNSIGNED_SHORT_5_6_5_REV packed into unsigned 16-bit integer
GL_UNSIGNED_SHORT_4_4_4_4 packed into unsigned 16-bit integer
GL_UNSIGNED_SHORT_4_4_4_4_REV packed into unsigned 16-bit integer
GL_UNSIGNED_SHORT_5_5_5_1 packed into unsigned 16-bit integer
GL_UNSIGNED_SHORT_1_5_5_5_REV packed into unsigned 16-bit integer
GL_UNSIGNED_INT_8_8_8_8 packed into unsigned 32-bit integer
GL_UNSIGNED_INT_8_8_8_8_REV packed into unsigned 32-bit integer
GL_UNSIGNED_INT_10_10_10_2 packed into unsigned 32-bit integer
GL_UNSIGNED_INT_2_10_10_10_REV packed into unsigned 32-bit integer
GL_UNSIGNED_INT_24_8 packed into unsigned 32-bit integer.
(For use exclusively with a format of
GL_DEPTH_STENCIL)
GL_UNSIGNED_INT_10F_11F_10F_
11F_REV
10- and 11-bit floating-point values
packed into unsigned 32-bit integer
GL_UNSIGNED_INT_5_9_9_9_REV three 9-bit floating-poing values sharing
their exponent 5-bit value packed into an
unsigned 32-bit integer
GL_FLOAT_32_ UNSIGNED_INT_
24_8_REV
depth and stencil values packed into two
32-bit quantities: 32-bit floating-point
depth value, and an 8-bit unsigned
stencil value. (The “middle” 24 bits are
unused.)
type Constant Data Type
Table 8-2 (continued) Data Types for glReadPixels() or glDrawPixels()

338 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Remember that, depending on the format, anywhere from one to four ele-
ments are read (or written). For example, if the format is GL_RGBA and
you’re reading into 32-bit integers (that is, if type is equal to GL_UNSIGNED_
INT or GL_INT), then every pixel read requires 16 bytes of storage (four com-
ponents u four bytes/component).
Each element of the image is stored in memory, as indicated in Table 8-2. If
the element represents a continuous value, such as a red, green, blue, or
luminance component, each value is scaled to fit into the available number
of bits. For example, assume the red component is initially specified as a
floating-point value between 0.0 and 1.0. If it needs to be packed into an
unsigned byte, only 8 bits of precision are kept, even if more bits are allo-
cated to the red component in the framebuffer. GL_UNSIGNED_SHORT and
GL_UNSIGNED_INT give 16 and 32 bits of precision, respectively. The
signed versions of GL_BYTE, GL_SHORT, and GL_INT have 7, 15, and 31
bits of precision, since the negative values are typically not used.
If the element is an index (a color index or a stencil index, for example), and
the type is not GL_FLOAT, the value is simply masked against the available
bits in the type. The signed versions—GL_BYTE, GL_SHORT, and GL_INT—
have masks with one fewer bit. For example, if a color index is to be stored
in a signed 8-bit integer, it’s first masked against 0x7f. If the type is GL_
FLOAT, the index is simply converted into a single-precision floating-point
number (for example, the index 17 is converted to the float 17.0).
For integer-based packed data types (denoted by constants that begin with
GL_UNSIGNED_BYTE_*, GL_UNSIGNED_SHORT_*, or GL_UNSIGNED_
INT_*), color components of each pixel are squeezed into a single unsigned
data type: one of byte, short integer, or standard integer. Valid formats are
limited for each type, as indicated in Table 8-3. If an invalid pixel format is
used for a packed pixel data type, a GL_INVALID_OPERATION error is
generated.
Packed type Constants Valid Pixel Formats
GL_UNSIGNED_BYTE_3_3_2 GL_RGB
GL_UNSIGNED_BYTE_2_3_3_REV GL_RGB
GL_UNSIGNED_SHORT_5_6_5 GL_RGB
GL_UNSIGNED_SHORT_5_6_5_REV GL_RGB
Table 8-3 Valid Pixel Formats for Packed Data Types

Images 339
The order of color values in bitfield locations of packed pixel data is deter-
mined by both the pixel format and whether the type constant contains
_REV. Without the _REV suffix, the color components are normally assigned
with the first color component occupying the most significant locations.
With the _REV suffix, the component packing order is reversed, with the
first color component starting with the least significant locations.
To illustrate this, Figure 8-4 shows the bitfield ordering of GL_UNSIGNED_
BYTE_3_3_2, GL_UNSIGNED_BYTE_2_3_3_REV, and four valid combina-
tions of GL_UNSIGNED_SHORT_4_4_4_4 (and _REV) data types and the
RGBA/BGRA pixel formats. The bitfield organizations for the other 14 valid
combinations of packed pixel data types and pixel formats follow similar
patterns.
The most significant bit of each color component is always packed in the
most significant bit location. Storage of a single component is not affected
by any pixel storage modes, although storage of an entire pixel may be
affected by the byte swapping mode. (For details on byte swapping, see
“Controlling Pixel-Storage Modes” on page 347.)
GL_UNSIGNED_SHORT_4_4_4_4 GL_RGBA, GL_BGRA
GL_UNSIGNED_SHORT_4_4_4_4_REV GL_RGBA, GL_BGRA
GL_UNSIGNED_SHORT_5_5_5_1 GL_RGBA, GL_BGRA
GL_UNSIGNED_SHORT_1_5_5_5_REV GL_RGBA, GL_BGRA
GL_UNSIGNED_INT_8_8_8_8 GL_RGBA, GL_BGRA
GL_UNSIGNED_INT_8_8_8_8_REV GL_RGBA, GL_BGRA
GL_UNSIGNED_INT_10_10_10_2 GL_RGBA, GL_BGRA
GL_UNSIGNED_INT_2_10_10_10_REV GL_RGBA, GL_BGRA
GL_UNSIGNED_INT_24_8 GL_DEPTH_STENCIL
GL_UNSIGNED_INT_10F_11F_11F GL_RGB
GL_UNSIGNED_INT_5_9_9_9_REV GL_RGB
GL_FLOAT_32_UNSIGNED_INT_24_8_REV GL_DEPTH_STENCIL
Packed type Constants Valid Pixel Formats
Table 8-3 (continued) Valid Pixel Formats for Packed Data Types

340 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Writing Pixel Data from Processor Memory to Framebuffer
void glDrawPixels(GLsizei width, GLsizei height, GLenum format,
GLenum type, const GLvoid *pixels);
Draws a rectangle of pixel data with dimensions width and height. The
pixel rectangle is drawn with its lower-left corner at the current raster
position. format and type have the same meaning as with glReadPixels().
(For legal values for format and type, see Tables 8-1 and 8-2.) The array
pointed to by pixels contains the pixel data to be drawn. If the current
raster position is invalid, nothing is drawn, and the raster position
remains invalid.
A GL_INVALID_OPERATION is generated if format is GL_STENCIL and
there isn’t a stencil buffer associated with the framebuffer, or likewise, if
format is GL_DEPTH_STENCIL, and there is not both a depth and stencil
buffer.
Red Green Blue
7 6 5 4 3 2 1 0
Blue Green
Red
7 6 5 4 3 2 1 0
GL_UNSIGNED_BYTE_3_3_2 with GL_RGB
Red Green Blue Alpha
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
GL_UNSIGNED_SHORT_4_4_4_4 with GL_RGBA
Blue Green Red Alpha
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
GL_UNSIGNED_SHORT_4_4_4_4 with GL_BGRA
Alpha Blue Green Red
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
GL_UNSIGNED_SHORT_4_4_4_4_REV with GL_RGBA
Alpha Red Green Blue
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
GL_UNSIGNED_SHORT_4_4_4_4_REV with GL_BGRA
GL_UNSIGNED_BYTE_2_3_3_REV with GL_RGB
Figure 8-4 Component Ordering for Some Data Types and Pixel Formats
Compatibility
Extension
glDrawPixels

Images 341
Example 8-3 is a portion of a program that uses glDrawPixels() to draw a
pixel rectangle in the lower left corner of a window. makeCheckImage()
creates a 64 u64 RGB array of a black-and-white checkerboard image.
glRasterPos2i(0, 0) positions the lower left corner of the image. For now,
ignore glPixelStorei().
Example 8-3 Use of glDrawPixels(): image.c
#define checkImageWidth 64
#define checkImageHeight 64
GLubyte checkImage[checkImageHeight][checkImageWidth][3];
void makeCheckImage(void)
{
int i, j, c;
for (i = 0; i < checkImageHeight; i++) {
for (j = 0; j < checkImageWidth; j++) {
c = (((i&0x8)==0)^((j&0x8)==0))*255;
checkImage[i][j][0] = (GLubyte) c;
checkImage[i][j][1] = (GLubyte) c;
checkImage[i][j][2] = (GLubyte) c;
}
}
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
makeCheckImage();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(0, 0);
glDrawPixels(checkImageWidth, checkImageHeight, GL_RGB,
GL_UNSIGNED_BYTE, checkImage);
glFlush();
}
When using glDrawPixels() to write RGBA or color-index information, you
may need to control the current drawing buffers with glDrawBuffer(),

342 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
which, along with glReadBuffer(), is also described in “Selecting Color
Buffers for Writing and Reading” in Chapter 10.
glDrawPixels() operates slightly differently when the format parameter is
set to GL_STENCIL or GL_DEPTH_STENCIL. In the cases where the stencil
buffer is affected, the window positions that would be written have their
stencil values updated (subject to the current front stencil mask), but
no values in the color buffer are generated or affected (i.e., no fragments
are generated; if a fragment shader is bound, it is not executed for those
positions during that drawing operation). Likewise, if a depth is also
provided, and you can write to the depth buffer (i.e., the depth mask is
GL_TRUE), then the depth values are written directly to the depth buffer,
which remains unaffected by the settings of the depth test.
Copying Pixel Data within the Framebuffer
Note that there’s no need for a format or data parameter for glCopyPixels(),
since the data is never copied into processor memory. The read source buffer
and the destination buffer of glCopyPixels() are specified by glReadBuffer()
void glCopyPixels(GLint x, GLint y, GLsizei width, GLsizei height,
GLenum buffer);
Copies pixel data from the read framebuffer rectangle whose lower left
corner is at (x, y) and whose dimensions are width and height. The data
is copied to a new position in the write framebuffer whose lower left
corner is given by the current raster position. buffer is either GL_COLOR,
GL_STENCIL, GL_DEPTH, or GL_DEPTH_STENCIL specifying the frame-
buffer that is used. glCopyPixels() behaves similarly to a glReadPixels()
followed by a glDrawPixels(), with the following translation for the buffer
to format parameter:
•If buffer is GL_DEPTH or GL_STENCIL, then GL_DEPTH_
COMPONENT or GL_STENCIL_INDEX is used, respectively. If
GL_DEPTH_STENCIL is specified for buffer and any of those buffers
are not present (e.g., there’s no stencil buffer associated with the
framebuffer), then it’s as if there were zeroes in the channel for the
data for the missing buffer.
• If GL_COLOR is specified, GL_RGBA or GL_COLOR_INDEX is used,
depending on whether the system is in RGBA or color-index mode.
Compatibility
Extension
glCopyPixels
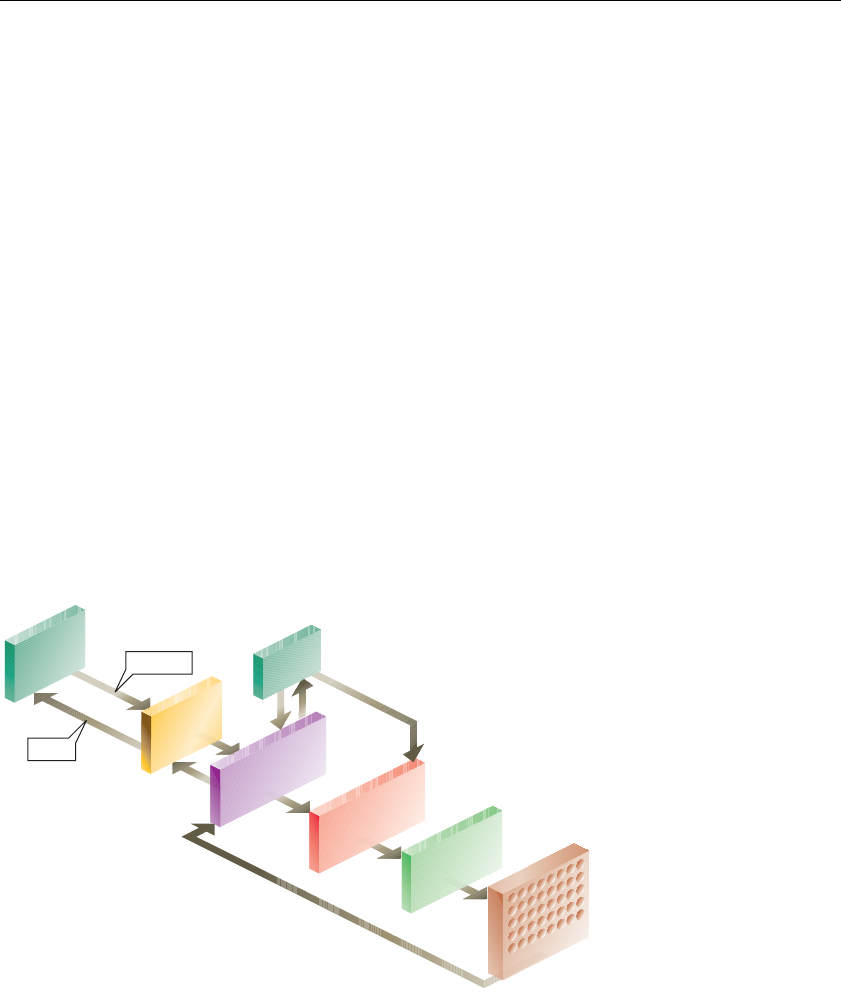
Imaging Pipeline 343
and glDrawBuffer(), respectively. Both glDrawPixels() and glCopyPixels()
are used in Example 8-4.
For all three functions, the exact conversions of the data going to or coming
from the framebuffer depend on the modes in effect at the time. See the
next section for details.
OpenGL Version 3.0 introduced a new pixel copy command called
glBlitFramebuffer(), which subsumes the functionality of glCopyPixels()
and glPixelZoom(). It is described in full detail at “Copying Pixel
Rectangles” on page 539, as it leverages some of the functionality of
framebuffer objects.
Imaging Pipeline
This section discusses the complete Imaging Pipeline: the pixel-storage
modes and pixel-transfer operations, which include how to set up an
arbitrary mapping to convert pixel data. You can also magnify or reduce
a pixel rectangle before it’s drawn by calling glPixelZoom(). The order of
these operations is shown in Figure 8-5.
Per-fragment
operations
Texture
memory
Pixel-transfer
operations
(and pixel map)
Rasterization
(including
pixel zoom)
Framebuffer
Processor
memory
Pixel
storage
modes
Unpack
Pack
Figure 8-5 Imaging Pipeline

344 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
When glDrawPixels() is called, the data is first unpacked from processor
memory according to the pixel-storage modes that are in effect, and then
the pixel-transfer operations are applied. The resulting pixels are then
rasterized. During rasterization, the pixel rectangle may be zoomed up or
down, depending on the current state. Finally, the fragment operations are
applied, and the pixels are written into the framebuffer. (See “Testing and
Operating on Fragments” in Chapter 10 for a discussion of the fragment
operations.)
When glReadPixels() is called, data is read from the framebuffer, the pixel-
transfer operations are performed, and then the resulting data is packed
into processor memory.
glCopyPixels() applies all the pixel-transfer operations during what would
be the glReadPixels() activity. The resulting data is written as it would be
by glDrawPixels(), but the transformations aren’t applied a second time.
Figure 8-6 shows how glCopyPixels() moves pixel data, starting from the
framebuffer.
From “Drawing the Bitmap” and Figure 8-7, you can see that rendering
bitmaps is simpler than rendering images. Neither the pixel-transfer
operations nor the pixel-zoom operation are applied.
Per-fragment
operations
Pixel-transfer
operations
(and pixel map)
Rasterization
(including
pixel zoom)
Framebuffer
(start)
Figure 8-6 glCopyPixels() Pixel Path

Imaging Pipeline 345
Note that the pixel-storage modes and pixel-transfer operations are
applied to textures as they are read from or written to texture memory.
Figure 8-8 shows the effect on glTexImage*(),glTexSubImage*(), and
glGetTexImage().
As shown in Figure 8-9, when pixel data is copied from the framebuffer into
texture memory (glCopyTexImage*() or glCopyTexSubImage*()), only
pixel-transfer operations are applied. (See Chapter 9 for more information
on textures.)
Per-fragment
operations
Rasterization
Framebuffer
Processor
memory
Pixel
storage
modes
Unpack
F
igure 8-7 glBitmap() Pixel Path
Texture
memory
Pixel-transfer
operations
(and pixel map)
Processor
memory
Pixel
storage
modes
Unpack
Pack
Figure 8-8 glTexImage*(), glTexSubImage*(), and glGetTexImage() Pixel Paths
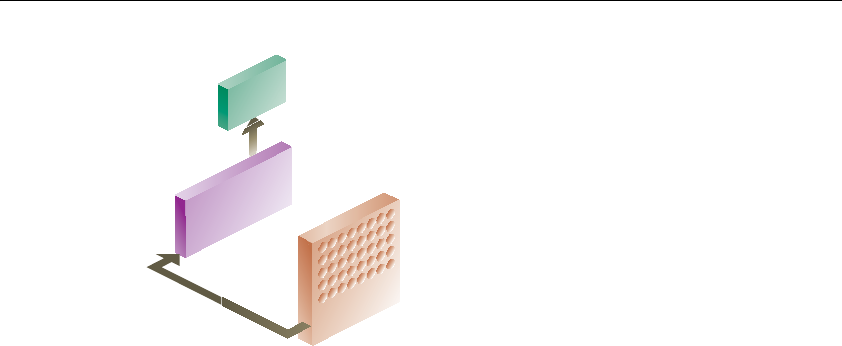
346 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Pixel Packing and Unpacking
Packing and unpacking refer to the way in which pixel data is written to and
read from processor memory.
An image stored in memory has between one and four chunks of data,
called elements. The data might consist of just the color index or the lumi-
nance (luminance is the weighted sum of the red, green, and blue values),
or it might consist of the red, green, blue, and alpha components for each
pixel. The possible arrangements of pixel data, or formats, determine the
number of elements stored for each pixel and their order.
Some elements (such as a color index or a stencil index) are integers, and
others (such as the red, green, blue, and alpha components, or the depth
component) are floating-point values, typically ranging between 0.0 and 1.0.
Floating-point components are usually stored in the framebuffer with lower
resolution than a full floating-point number would require (for example,
color components may be stored in 8 bits). The exact number of bits used to
represent the components depends on the particular hardware being used.
Thus, it’s often wasteful to store each component as a full 32-bit floating-
point number, especially since images can easily contain a million pixels.
Elements can be stored in memory as various data types, ranging from 8-bit
bytes to 32-bit integers or floating-point numbers. OpenGL explicitly defines
the conversion of each component in each format to each of the possible
data types. Keep in mind that you may lose data if you try to store a high-
resolution component in a type represented by a small number of bits.
Texture
memory
Pixel-transfer
operations
(and pixel map)
Framebuffer
(start)
Figure 8-9 glCopyTexImage*() and glCopyTexSubImage*() Pixel Paths

Imaging Pipeline 347
Controlling Pixel-Storage Modes
Image data is typically stored in processor memory in rectangular two- or
three-dimensional arrays. Often, you want to display or store a subimage that
corresponds to a subrectangle of the array. In addition, you might need to
take into account that different machines have different byte-ordering con-
ventions. Finally, some machines have hardware that is far more efficient
at moving data to and from the framebuffer if the data is aligned on 2-byte,
4-byte, or 8-byte boundaries in processor memory. For such machines, you
probably want to control the byte alignment. All the issues raised in this para-
graph are controlled as pixel-storage modes, which are discussed in the next
subsection. You specify these modes by using glPixelStore*(), which you’ve
already seen used in a couple of example programs.
All pixel-storage modes that OpenGL supports are controlled with the
glPixelStore*() command. Typically, several successive calls are made with
this command to set several parameter values.
void glPixelStore{if}(GLenum pname,TYPE param);
Sets the pixel-storage modes, which affect the operation of glDrawPixels(),
glReadPixels(),glBitmap(),glPolygonStipple(),glTexImage1D(),
glTexImage2D(),glTexImage3D(),glTexSubImage1D(),
glTexSubImage2D(),glTexSubImage3D(),glGetTexImage(), and, if
the Imaging Subset is available (see “Imaging Subset” on page 367), also
glGetColorTable(), glGetConvolutionFilter(), glGetSeparableFilter(),
glGetHistogram(), and glGetMinmax().
The possible parameter names for pname are shown in Table 8-4, along
with their data types, initial values, and valid ranges of values. The
GL_UNPACK* parameters control how data is unpacked from memory
by glDrawPixels(),glBitmap(),glPolygonStipple(),glTexImage1D(),
glTexImage2D(),glTexImage3D(), glTexSubImage1D(),
glTexSubImage2D(), and glTexSubImage3D(). The GL_PACK*
parameters control how data is packed into memory by glReadPixels()
and glGetTexImage(), and, if the Imaging Subset is available, also
glGetColorTable(), glGetConvolutionFilter(), glGetSeparableFilter(),
glGetHistogram(), and glGetMinmax().
GL_UNPACK_IMAGE_HEIGHT, GL_PACK_IMAGE_HEIGHT, GL_UNPACK_
SKIP_IMAGES, and GL_PACK_SKIP_IMAGES affect only 3D texturing
(glTexImage3D(),glTexSubImage3D(), and glGetTexImage(GL_
TEXTURE_3D,...)).

348 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Since the corresponding parameters for packing and unpacking have
the same meanings, they’re discussed together in the rest of this section
and referred to without the GL_PACK or GL_UNPACK prefix. For example,
*SWAP_BYTES refers to GL_PACK_SWAP_BYTES and GL_UNPACK_SWAP_
BYTES.
If the *SWAP_BYTES parameter is FALSE (the default), the ordering of the
bytes in memory is whatever is native for the OpenGL client; otherwise, the
bytes are reversed. The byte reversal applies to any size element, but has a
meaningful effect only for multibyte elements.
The effect of swapping bytes may differ among OpenGL implementations.
If on an implementation, GLubyte has 8 bits, GLushort has 16 bits, and
GLuint has 32 bits, then Figure 8-10 illustrates how bytes are swapped
for different data types. Note that byte swapping has no effect on single-
byte data.
Parameter Name Type Initial Value Valid Range
GL_UNPACK_SWAP_BYTES,
GL_PACK_SWAP_BYTES
GLboolean FALSE TRUE/FALSE
GL_UNPACK_LSB_FIRST,
GL_PACK_LSB_FIRST
GLboolean FALSE TRUE/FALSE
GL_UNPACK_ROW_LENGTH,
GL_PACK_ROW_LENGTH
GLint 0 any non-negative
integer
GL_UNPACK_SKIP_ROWS,
GL_PACK_SKIP_ROWS
GLint 0 any non-negative
integer
GL_UNPACK_SKIP_PIXELS,
GL_PACK_SKIP_PIXELS
GLint 0 any non-negative
integer
GL_UNPACK_ALIGNMENT,
GL_PACK_ALIGNMENT
GLint 4 1, 2, 4, 8
GL_UNPACK_IMAGE_HEIGHT,
GL_PACK_IMAGE_HEIGHT
GLint 0 any non-negative
integer
GL_UNPACK_SKIP_IMAGES,
GL_PACK_SKIP_IMAGES
GLint 0 any non-negative
integer
Table 8-4 glPixelStore() Parameters
Imaging Pipeline 349
Note: As long as your OpenGL application doesn’t share images with other
machines, you can ignore the issue of byte ordering. If your applica-
tion must render an OpenGL image that was created on a different
machine and the two machines have different byte orders, byte
ordering can be swapped using *SWAP_BYTES. However, *SWAP_
BYTES does not allow you to reorder elements (for example, to
swap red and green).
The *LSB_FIRST parameter applies only when drawing or reading 1-bit
images or bitmaps for which a single bit of data is saved or restored for each
pixel. If *LSB_FIRST is FALSE (the default), the bits are taken from the bytes
starting with the most significant bit; otherwise, they’re taken in the oppo-
site order. For example, if *LSB_FIRST is FALSE, and the byte in question is
0x31, the bits, in order, are {0, 0, 1, 1, 0, 0, 0, 1}. If *LSB_FIRST is TRUE, the
order is {1, 0, 0, 0, 1, 1, 0, 0}.
Sometimes you want to draw or read only a subrectangle of the entire
rectangle of image data stored in memory. If the rectangle in memory is
larger than the subrectangle that’s being drawn or read, you need to spec-
ify the actual length (measured in pixels) of the larger rectangle with
*ROW_LENGTH. If *ROW_LENGTH is zero (which it is by default), the
row length is understood to be the same as the width that’s specified with
glReadPixels(),glDrawPixels(), or glCopyPixels(). You also need to
specify the number of rows and pixels to skip before starting to copy the
Short (byte 0) Short (byte 1)
7 6 5 4 3 2 1 0
7 6 5 4 3 2 1 0
15 14 13 12 11 10 9 8 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
Integer (byte 0) Integer (byte 1)
31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16
Integer (byte 2) Integer (byte 3)
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
Integer (byte 0)Integer (byte 1)
31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16
Integer (byte 2)Integer (byte 3)
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
7 6 5 4 3 2 1 0
Short (byte 1) Short (byte 0)
Byte Byte
Figure 8-10 Byte Swap Effect on Byte, Short, and Integer Data

350 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
data for the subrectangle. These numbers are set using the parameters
*SKIP_ROWS and *SKIP_PIXELS, as shown in Figure 8-11. By default, both
parameters are 0, so you start at the lower left corner.
Often a particular machine’s hardware is optimized for moving pixel data
to and from memory, if the data is saved in memory with a particular byte
alignment. For example, in a machine with 32-bit words, hardware can
often retrieve data much faster if it’s initially aligned on a 32-bit boundary,
which typically has an address that is a multiple of 4. Likewise, 64-bit archi-
tectures might work better when the data is aligned to 8-byte boundaries.
On some machines, however, byte alignment makes no difference.
As an example, suppose your machine works better with pixel data aligned
to a 4-byte boundary. Images are most efficiently saved by forcing the data
for each row of the image to begin on a 4-byte boundary. If the image is
5 pixels wide and each pixel consists of 1 byte each of red, green, and blue
information, a row requires 5 u 3 = 15 bytes of data. Maximum display
efficiency can be achieved if the first row, and each successive row, begins
on a 4-byte boundary, so there is 1 byte of waste in the memory storage for
Image
Subimage
*SKIP_PIXELS
*ROW_LENGTH
*SKIP_ROWS
Figure 8-11 *SKIP_ROWS, *SKIP_PIXELS, and *ROW_LENGTH Parameters

Imaging Pipeline 351
each row. If your data is stored in this way, set the *ALIGNMENT parameter
appropriately (to 4, in this case).
If *ALIGNMENT is set to 1, the next available byte is used. If it’s 2, a byte is
skipped if necessary at the end of each row so that the first byte of the next
row has an address that’s a multiple of 2. In the case of bitmaps (or 1-bit
images), where a single bit is saved for each pixel, the same byte alignment
works, although you have to count individual bits. For example, if you’re
saving a single bit per pixel, if the row length is 75, and if the alignment is
4, then each row requires 75/8, or 9 3/8 bytes. Since 12 is the smallest mul-
tiple of 4 that is bigger than 9 3/8, 12 bytes of memory are used for each row.
If the alignment is 1, then 10 bytes are used for each row, as 9 3/8 is rounded
up to the next byte. (There is a simple use of glPixelStorei() shown in
Example 8-4.)
Note: The default value for *ALIGNMENT is 4. A common programming
mistake is assuming that image data is tightly packed and byte
aligned (which assumes that *ALIGNMENT is set to 1).
The parameters *IMAGE_HEIGHT and *SKIP_IMAGES affect only the
defining and querying of three-dimensional textures. For details on these
pixel-storage modes, see “Pixel-Storage Modes for Three-Dimensional
Textures” on page 417.
Pixel-Transfer Operations
As image data is transferred from memory into the framebuffer, or from the
framebuffer into memory, OpenGL can perform several operations on it.
For example, the ranges of components can be altered—normally, the red
component is between 0.0 and 1.0, but you might prefer to keep it in some
other range; or perhaps the data you’re using from a different graphics
system stores the red component in a different range. You can even create
maps to perform arbitrary conversions of color indices or color components
during pixel transfer. Such conversions performed during the transfer of
pixels to and from the framebuffer are called pixel-transfer operations. They’re
controlled with the glPixelTransfer*() and glPixelMap*() commands.
Be aware that although color, depth, and stencil buffers have many
similarities, they don’t behave identically, and a few of the modes have
special cases. All the mode details are covered in this section and the
sections that follow, including all the special cases.
352 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Some of the pixel-transfer function characteristics are set with
glPixelTransfer*(). The other characteristics are specified with glPixelMap*(),
which is described in the next section.
void glPixelTransfer{if}(GLenum pname,TYPE param);
Sets pixel-transfer modes that affect the operation of glDrawPixels(),
glReadPixels(),glCopyPixels(), glTexImage1D(),glTexImage2D(),
glTexImage3D(),glCopyTexImage1D(),glCopyTexImage2D(),
glTexSubImage1D(),glTexSubImage2D(),glTexSubImage3D(),
glCopyTexSubImage1D(),glCopyTexSubImage2D(),
glCopyTexSubImage3D(), and glGetTexImage(). The parameter
pname must be one of those listed in the first column of Table 8-5,
and its value, param, must be in the valid range shown.
Parameter Name Type Initial
Value
Valid Range
GL_MAP_COLOR GLboolean FALSE TRUE/FALSE
GL_MAP_STENCIL GLboolean FALSE TRUE/FALSE
GL_INDEX_SHIFT GLint 0 (f,f)
GL_INDEX_OFFSET GLint 0 (f,f)
GL_RED_SCALE GLfloat 1.0 (f,f)
GL_GREEN_SCALE GLfloat 1.0 (f,f)
GL_BLUE_SCALE GLfloat 1.0 (f,f)
GL_ALPHA_SCALE GLfloat 1.0 (f,f)
GL_DEPTH_SCALE GLfloat 1.0 (f,f)
GL_RED_BIAS GLfloat 0.0 (f,f)
GL_GREEN_BIAS GLfloat 0.0 (f,f)
GL_BLUE_BIAS GLfloat 0.0 (f,f)
GL_ALPHA_BIAS GLfloat 0.0 (f,f)
GL_DEPTH_BIAS GLfloat 0.0 (f,f)
Table 8-5 glPixelTransfer*() Parameters
Compatibility
Extension
glPixelTransfer
and any accepted
tokens

Imaging Pipeline 353
Caution: GL_POST_CONVOLUTION_* and GL_POST_COLOR_MATRIX_*
parameters are present only if the Imaging Subset is supported by
your OpenGL implementation. See “Imaging Subset” on
page 367 for more details.
If the GL_MAP_COLOR or GL_MAP_STENCIL parameter is TRUE, then
mapping is enabled. See the next subsection to learn how the mapping is
done and how to change the contents of the maps. All the other parameters
directly affect the pixel component values.
A scale and bias can be applied to the red, green, blue, alpha, and depth
components. For example, you may wish to scale red, green, and blue
GL_POST_CONVOLUTION_RED_SCALE GLfloat 1.0 (f,f)
GL_POST_CONVOLUTION_GREEN_SCALE GLfloat 1.0 (f,f)
GL_POST_CONVOLUTION_BLUE_SCALE GLfloat 1.0 (f,f)
GL_POST_CONVOLUTION_ALPHA_SCALE GLfloat 1.0 (f,f)
GL_POST_CONVOLUTION_RED_BIAS GLfloat 0.0 (f,f)
GL_POST_CONVOLUTION_GREEN_BIAS GLfloat 0.0 (f,f)
GL_POST_CONVOLUTION_BLUE_BIAS GLfloat 0.0 (f,f)
GL_POST_CONVOLUTION_ALPHA_BIAS GLfloat 0.0 (f,f)
GL_POST_COLOR_MATRIX_RED_SCALE GLfloat 1.0 (f,f)
GL_POST_COLOR_MATRIX_GREEN_SCALE GLfloat 1.0 (f,f)
GL_POST_COLOR_MATRIX_BLUE_SCALE GLfloat 1.0 (f,f)
GL_POST_COLOR_MATRIX_ALPHA_SCALE GLfloat 1.0 (f,f)
GL_POST_COLOR_MATRIX_RED_BIAS GLfloat 0.0 (f,f)
GL_POST_COLOR_MATRIX_GREEN_BIAS GLfloat 0.0 (f,f)
GL_POST_COLOR_MATRIX_BLUE_BIAS GLfloat 0.0 (f,f)
GL_POST_COLOR_MATRIX_ALPHA_BIAS GLfloat 0.0 (f,f)
Parameter Name Type Initial
Value
Valid Range
Table 8-5 (continued) glPixelTransfer*() Parameters
354 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
components that were read from the framebuffer before converting them to
a luminance format in processor memory. Luminance is computed as the
sum of the red, green, and blue components, so if you use the default value
for GL_RED_SCALE, GL_GREEN_SCALE, and GL_BLUE_SCALE, the compo-
nents all contribute equally to the final intensity or luminance value. If you
want to convert RGB to luminance, according to the NTSC standard, you
set GL_RED_SCALE to .30, GL_GREEN_SCALE to .59, and GL_BLUE_SCALE
to .11.
Indices (color and stencil) can also be transformed. In the case of indices, a
shift and an offset are applied. This is useful if you need to control which
portion of the color table is used during rendering.
Pixel Mapping
All the color components, color indices, and stencil indices can be modified
by means of a table lookup before they are placed in screen memory. The
command for controlling this mapping is glPixelMap*().
void glPixelMap{ui us f}v(GLenum map, GLint mapsize,
const TYPE *values);
Loads the pixel map indicated by map with mapsize entries, whose values
are pointed to by values. Table 8-6 lists the map names and values; the
default sizes are all 1, and the default values are all 0. Each map’s size must
be a power of 2.
Map Name Address Value
GL_PIXEL_MAP_I_TO_I color index color index
GL_PIXEL_MAP_S_TO_S stencil index stencil index
GL_PIXEL_MAP_I_TO_R color index R
GL_PIXEL_MAP_I_TO_G color index G
GL_PIXEL_MAP_I_TO_B color index B
Table 8-6 glPixelMap*() Parameter Names and Values
Compatibility
Extension
glPixelMap and
any accepted
tokens

Imaging Pipeline 355
The maximum size of the maps is machine-dependent. You can find the
sizes of the pixel maps supported on your machine with glGetIntegerv().
Use the query argument GL_MAX_PIXEL_MAP_TABLE to obtain the maxi-
mum size for all the pixel map tables, and use GL_PIXEL_MAP_*_TO_*_SIZE
to obtain the current size of the specified map. The six maps whose address
is a color index or stencil index must always be sized to an integral power
of 2. The four RGBA maps can be any size from 1 through GL_MAX_PIXEL_
MAP_TABLE.
To understand how a table works, consider a simple example. Suppose that
you want to create a 256-entry table that maps color indices to color
indices using GL_PIXEL_MAP_I_TO_I. You create a table with an entry
for each of the values between 0 and 255 and initialize the table with
glPixelMap*(). Assume you’re using the table for thresholding and want
to map indices below 101 (indices 0 to 100) to 0, and all indices 101 and
above to 255. In this case, your table consists of 101 0s and 155 255s. The
pixel map is enabled using the routine glPixelTransfer*() to set the
parameter GL_MAP_COLOR to TRUE. Once the pixel map is loaded and
enabled, incoming color indices below 101 come out as 0, and incoming
pixels from 101 to 255 are mapped to 255. If the incoming pixel is larger
than 255, it’s first masked by 255, throwing out all the bits above the
eighth, and the resulting masked value is looked up in the table. If the
incoming index is a floating-point value (say 88.14585), it’s rounded to
the nearest integer value (giving 88), and that number is looked up in the
table (giving 0).
Using pixel maps, you can also map stencil indices or convert color indices
to RGB. (See “Reading and Drawing Pixel Rectangles” for information about
the conversion of indices.)
GL_PIXEL_MAP_I_TO_A color index A
GL_PIXEL_MAP_R_TO_R R R
GL_PIXEL_MAP_G_TO_G G G
GL_PIXEL_MAP_B_TO_B B B
GL_PIXEL_MAP_A_TO_A A A
Map Name Address Value
Table 8-6 (continued) glPixelMap*() Parameter Names and Values

356 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Magnifying, Reducing, or Flipping an Image
After the pixel-storage modes and pixel-transfer operations are applied,
images and bitmaps are rasterized. Normally, each pixel in an image
is written to a single pixel on the screen. However, you can arbitrarily
magnify, reduce, or even flip (reflect) an image by using glPixelZoom().
During rasterization, each image pixel is treated as a zoomxuzoomy
rectangle, and fragments are generated for all the pixels whose centers lie
within the rectangle. More specifically, let (xrp,yrp) be the current raster
position. If a particular group of elements (indices or components) is the
nth in a row and belongs to the mth column, consider the region in window
coordinates bounded by the rectangle with corners at
(xrp + zoomx n,yrp + zoomy m) and (xrp + zoomx(n+1), yrp + zoomy(m+1))
Any fragments whose centers lie inside this rectangle (or on its bottom or
left boundaries) are produced in correspondence with this particular group
of elements.
A negative zoom can be useful for flipping an image. OpenGL describes
images from the bottom row of pixels to the top (and from left to right). If
you have a “top to bottom” image, such as a frame of video, you may want
to use glPixelZoom(1.0, 1.0) to make the image right side up for OpenGL.
Be sure that you reset the current raster position appropriately, if needed.
Example 8-4 shows the use of glPixelZoom(). A checkerboard image is
initially drawn in the lower left corner of the window. By pressing a mouse
button and moving the mouse, you can use glCopyPixels() to copy the
lower left corner of the window to the current cursor location. (If you copy
the image onto itself, it looks wacky!) The copied image is zoomed, but
initially it is zoomed by the default value of 1.0, so you won’t notice. The
‘z’ and ‘Z’ keys increase and decrease the zoom factors by 0.5. Any window
damage causes the contents of the window to be redrawn. Pressing the ‘r’
key resets the image and zoom factors.
void glPixelZoom(GLfloat zoomx, GLfloat zoomy);
Sets the magnification or reduction factors for pixel-write operations
(glDrawPixels() and glCopyPixels()) in the x- and y-dimensions. By
default, zoomx and zoomy are 1.0. If they’re both 2.0, each image pixel is
drawn to 4 screen pixels. Note that fractional magnification or reduction
factors are allowed, as are negative factors. Negative zoom factors reflect
the resulting image about the current raster position.
Compatibility
Extension
glPixelZoom

Imaging Pipeline 357
Example 8-4 Drawing, Copying, and Zooming Pixel Data: image.c
#define checkImageWidth 64
#define checkImageHeight 64
GLubyte checkImage[checkImageHeight][checkImageWidth][3];
static GLdouble zoomFactor = 1.0;
static GLint height;
void makeCheckImage(void)
{
int i, j, c;
for (i = 0; i < checkImageHeight; i++) {
for (j = 0; j < checkImageWidth; j++) {
c = (((i&0x8)==0)^((j&0x8)==0))*255;
checkImage[i][j][0] = (GLubyte) c;
checkImage[i][j][1] = (GLubyte) c;
checkImage[i][j][2] = (GLubyte) c;
}
}
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
makeCheckImage();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(0, 0);
glDrawPixels(checkImageWidth, checkImageHeight, GL_RGB,
GL_UNSIGNED_BYTE, checkImage);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
height = (GLint) h;
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);

358 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void motion(int x, int y)
{
static GLint screeny;
screeny = height - (GLint) y;
glRasterPos2i(x, screeny);
glPixelZoom(zoomFactor, zoomFactor);
glCopyPixels(0, 0, checkImageWidth, checkImageHeight,
GL_COLOR);
glPixelZoom(1.0, 1.0);
glFlush();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘r’:
case ‘R’:
zoomFactor = 1.0;
glutPostRedisplay();
printf(“zoomFactor reset to 1.0\n”);
break;
case ‘z’:
zoomFactor += 0.5;
if (zoomFactor >= 3.0)
zoomFactor = 3.0;
printf(“zoomFactor is now %4.1f\n”, zoomFactor);
break;
case ‘Z’:
zoomFactor -= 0.5;
if (zoomFactor <= 0.5)
zoomFactor = 0.5;
printf(“zoomFactor is now %4.1f\n”, zoomFactor);
break;
case 27:
exit(0);
break;
default:
break;
}
}

Reading and Drawing Pixel Rectangles 359
Reading and Drawing Pixel Rectangles
This section describes the reading and drawing processes in detail. The pixel
conversions performed when going from framebuffer to memory (reading)
are similar but not identical to the conversions performed when going in
the opposite direction (drawing), as explained in the following sections.
You may wish to skip this section the first time through, especially if you
do not plan to use the pixel-transfer operations right away.
The Pixel Rectangle Drawing Process
Figure 8-12 and the following list describe the operation of drawing pixels
into the framebuffer.
1
2
Scale
bias
3
Index
- RGBA
lookup
7Index
- index
lookup
7
RGBA
- RGBA
lookup
4
Shift
offset
6
Convert
to [0, 1]
Convert
L- RGBA
RGBA L, Z
Indices
Components
Pixel-storage
operations
Pixel-transfer
operations
5Clamp
to [0, 1]
8mask to
[0.0, 2n-1]
Unpack
Byte short
int float
Data Stream
(index or
component)
RGBA
Z
Index (stencil,
color index)
Pixel data out
Imaging
subset
(optional)
Figure 8-12 Drawing Pixels with glDrawPixels()

360 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
1. If the pixels are not indices (that is, if the format isn’t GL_COLOR_
INDEX or GL_STENCIL_INDEX), the first step is to convert the compo-
nents to floating-point format if necessary. (See Table 4-1 for the details
of the conversion.)
2. If the format is GL_LUMINANCE or GL_LUMINANCE_ALPHA,
the luminance element is converted into R, G, and B by using the
luminance value for each of the R, G, and B components. In GL_
LUMINANCE_ALPHA format, the alpha value becomes the A value.
If GL_LUMINANCE is specified, the A value is set to 1.0.
3. Each component (R, G, B, A, or depth) is multiplied by the appropriate
scale, and the appropriate bias is added. For example, the R component
is multiplied by the value corresponding to GL_RED_SCALE and added
to the value corresponding to GL_RED_BIAS.
4. If GL_MAP_COLOR is TRUE, each of the R, G, B, and A components is
clamped to the range [0.0, 1.0], multiplied by an integer 1 less than the
table size, truncated, and looked up in the table. (See “Tips for Improv-
ing Pixel Drawing Rates” for more details.)
5. Next, the R, G, B, and A components are clamped to [0.0, 1.0], if they
weren’t already, and are converted to fixed-point with as many bits to
the left of the binary point as there are in the corresponding
framebuffer component.
6. If you’re working with index values (stencil or color indices), then the
values are first converted to fixed-point (if they were initially floating-
point numbers), with some unspecified bits to the right of the binary
point. Indices that were initially fixed-point remain so, and any bits to
the right of the binary point are set to zero.
The resulting index value is then shifted right or left by the absolute
value of GL_INDEX_SHIFT bits; the value is shifted left if GL_INDEX_
SHIFT > 0, and right otherwise. Finally, GL_INDEX_OFFSET is added to
the index.
7. The next step with indices depends on whether you’re using RGBA
mode or color-index mode. In RGBA mode, a color index is converted
to RGBA using the color components specified by GL_PIXEL_MAP_
I_TO_R, GL_PIXEL_MAP_I_TO_G, GL_PIXEL_MAP_I_TO_B, and GL_
PIXEL_MAP_I_TO_A (see “Pixel Mapping” for details). Otherwise, if
GL_MAP_COLOR is GL_TRUE, a color index is looked up through the
table GL_PIXEL_MAP_I_TO_I. (If GL_MAP_COLOR is GL_FALSE, the
index is unchanged). If the image is made up of stencil indices rather

Reading and Drawing Pixel Rectangles 361
than color indices, and if GL_MAP_STENCIL is GL_TRUE, the index is
looked up in the table corresponding to GL_PIXEL_MAP_S_TO_S. If
GL_MAP_STENCIL is FALSE, the stencil index is unchanged.
8. Finally, if the indices haven’t been converted to RGBA, the indices are
then masked to the number of bits of either the color-index or stencil
buffer, whichever is appropriate.
The Pixel Rectangle Reading Process
Many of the conversions done during the pixel rectangle drawing process
are also done during the pixel rectangle reading process. The pixel reading
process is shown in Figure 8-13 and described in the following list.
1
Scale
bias
2
RGBA
- RGBA
lookup
2
Shift
offset
3
Map
to [0, 1]
RGBA
Z
L
Index
Pixel-transfer
operations
Pixel-storage
operations
2Clamp
to [0, 1]
2Convert
to L
4mask to
[0.0, 2n-1]
RGBA
Z
Index (stencil,
color index)
Pack
Byte short
int float
Data Stream
(index or
component)
Pixels from Framebuffer
Index
- index
lookup
3
5Index
- RGBA
lookup
Imaging
subset
(optional)
Figure 8-13 Reading Pixels with glReadPixels()

362 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
1. If the pixels to be read aren’t indices (that is, if the format isn’t GL_
COLOR_INDEX or GL_STENCIL_INDEX), the components are mapped to
[0.0, 1.0]—that is, in exactly the opposite way that they are when written.
2. Next, the scales and biases are applied to each component. If GL_MAP_
COLOR is GL_TRUE, they’re mapped and again clamped to [0.0, 1.0]. If
luminance is desired instead of RGB, the R, G, and B components are
added (L = R + G + B).
3. If the pixels are indices (color or stencil), they’re shifted, offset, and, if
GL_MAP_COLOR is GL_TRUE, also mapped.
4. If the storage format is either GL_COLOR_INDEX or GL_STENCIL_
INDEX, the pixel indices are masked to the number of bits of the storage
type (1, 8, 16, or 32) and packed into memory as previously described.
5. If the storage format is one of the component types (such as luminance
or RGB), the pixels are always mapped by the index-to-RGBA maps.
Then, they’re treated as though they had been RGBA pixels in the first
place (including potential conversion to luminance).
6. Finally, for both index and component data, the results are packed into
memory according to the GL_PACK* modes set with glPixelStore*().
The scaling, bias, shift, and offset values are the same as those used in
drawing pixels, so if you’re both reading and drawing pixels, be sure to reset
these components to the appropriate values before doing a read or a draw.
Similarly, the various maps must be properly reset if you intend to use maps
for both reading and drawing.
Note: It might seem that luminance is handled incorrectly in both the read-
ing and drawing operations. For example, luminance is not usually
equally dependent on the R, G, and B components as it may be
assumed from both Figure 8-12 and Figure 8-13. For example, if you
want your luminance to be calculated such that the R, G, and B com-
ponents contribute 30, 59, and 11 percent, respectively, you can set
GL_RED_SCALE to 0.30, GL_RED_BIAS to 0.0, and so on. The com-
puted L is then .30R + .59G + .11B.
Using Buffer Objects with Pixel Rectangle Data
Advanced
In the same way that storing vertex-array data in buffer objects, as described
in “Using Buffer Objects with Vertex-Array Data” in Chapter 2, can increase
Advanced

Using Buffer Objects with Pixel Rectangle Data 363
application performance, storing pixel data in buffer objects can yield
similar performance benefits.
By storing pixel rectangles in server-side buffer objects, you can eliminate
the need to transfer data from the client’s memory to the OpenGL server
each frame. You might do this if you render an image as the background,
instead of calling glClear(), for example.
Compared to vertex-array data in buffer objects, pixel buffer objects can be
both read from (just like their vertex counterparts) and written to. Writing
to a buffer object occurs when you retrieve pixel data from OpenGL, like
when you call glReadPixels() or when you retrieve a texture’s texels with
glGetTexImage().
Using Buffer Objects to Transfer Pixel Data
OpenGL functions that transfer data from the client application’s
memory to the OpenGL server, such as glDrawPixels(), glTexImage*D(),
glCompressedTexImage*D(),glPixelMap*(), and similar functions in
the Imaging Subset that take an array of pixels, can use buffer objects for
storing pixel data on the server.
To store your pixel rectangle data in buffer objects, you will need to add a
few steps to your application.
1. (Optional) Generate buffer object identifiers by calling glGenBuffers().
2. Bind a buffer object for pixel unpacking by calling glBindBuffer() with
a GL_PIXEL_UNPACK_BUFFER.
3. Request storage for your data and optionally initialize those data
elements using glBufferData(), once again specifying GL_PIXEL_
UNPACK_BUFFER as the target parameter.
4. Bind the appropriate buffer object to be used during rendering by once
again calling glBindBuffer().
5. Use the data by calling the appropriate function, such as
glDrawPixels() or glTexImage2D().
If you need to initialize multiple buffer objects, you will repeat steps 2
and 3 for each buffer object.
Example 8-5 modifies the image.c program (shown in Example 8-4) to use
pixel buffer objects.

364 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Example 8-5 Drawing, Copying, and Zooming Pixel Data Stored in a Buffer
Object: pboimage.c
#define BUFFER_OFFSET(bytes) ((GLubyte*) NULL + (bytes))
/*Create checkerboard image*/
#definecheckImageWidth 64
#definecheckImageHeight 64
GLubyte checkImage[checkImageHeight][checkImageWidth][3];
static GLdouble zoomFactor = 1.0;
static GLint height;
static GLuint pixelBuffer;
void makeCheckImage(void)
{
int i, j, c;
for (i = 0; i < checkImageHeight; i++) {
for (j = 0; j < checkImageWidth; j++) {
c = (((i&0x8)==0)^((j&0x8)==0))*255;
checkImage[i][j][0] = (GLubyte) c;
checkImage[i][j][1] = (GLubyte) c;
checkImage[i][j][2] = (GLubyte) c;
}
}
}
void init(void)
{
glewInit();
glClearColor (0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
makeCheckImage();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glGenBuffers(1, &pixelBuffer);
glBindBuffer(GL_PIXEL_UNPACK_BUFFER, pixelBuffer);
glBufferData(GL_PIXEL_UNPACK_BUFFER,
3*checkImageWidth*checkImageHeight,
checkImage, GL_STATIC_DRAW);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);

Using Buffer Objects with Pixel Rectangle Data 365
glRasterPos2i(0, 0);
glBindBuffer(GL_PIXEL_UNPACK_BUFFER, pixelBuffer);
glDrawPixels(checkImageWidth, checkImageHeight, GL_RGB,
GL_UNSIGNED_BYTE, BUFFER_OFFSET(0));
glFlush();
}
Using Buffer Objects to Retrieve Pixel Data
Pixel buffer objects can also be used as destinations for operations that read
pixels from OpenGL buffers and pass those pixels back to the application.
Functions like glReadPixels() and glGetTexImage() can be provided an
offset into a currently bound pixel buffer and update the data values in the
buffer objects with the retrieved pixels.
Initializing and using a buffer object as the destination for pixel retrieval
operations is almost identical to those steps described in “Using Buffer
Objects to Transfer Pixel Data,” except that the buffer target parameter for
all buffer object-related calls needs to be GL_PIXEL_PACK_BUFFER.
After the completion of the OpenGL function retrieving the pixels,
you can access the data values in the buffer object either by using the
glMapBuffer() function (described in “Buffer Objects” in Chapter 2) or by
glGetBufferSubData(). In some cases, glGetBufferSubData() may result
in a more efficient transfer of data than glMapBuffer().
Example 8-6 demonstrates using a pixel buffer object to store and access the
pixels rendered after retrieving the image by calling glReadPixels().
Example 8-6 Retrieving Pixel Data Using Buffer Objects
#define BUFFER_OFFSET(bytes) ((GLubyte*) NULL + (bytes))
GLuint pixelBuffer;
GLsizei imageWidth;
GLsizei imageHeight;
GLsizei numComponents = 4; /* four components for GL_RGBA */
GLsizei bufferSize;
void
init(void)
{
bufferSize = imageWidth * imageHeight * numComponents
* sizeof(GLfloat); /* machine storage size */
glGenBuffers(1, &pixelBuffer);

366 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
glBindBuffer(GL_PIXEL_PACK_BUFFER, pixelBuffer);
glBufferData(GL_PIXEL_PACK_BUFFER, bufferSize,
NULL, /* allocate but don’t initialize data */
GL_STREAM_READ);
}
void
display(void)
{
int i;
GLsizei numPixels = imageWidth * imageHeight;
/* Draw frame */
glReadPixels(0, 0, imageWidth, imageHeight, GL_RGBA,
GL_FLOAT, BUFFER_OFFSET(0));
GLfloat *pixels = glMapBuffer(GL_PIXEL_PACK_BUFFER,
GL_READ_ONLY);
for ( i = 0; i < numPixels; ++i ) {
/* insert your pixel processing here
process( &pixels[i*numComponents] );
*/
}
glUnmapBuffer(GL_PIXEL_PACK_BUFFER);
}
Tips for Improving Pixel Drawing Rates
As you can see, OpenGL has a rich set of features for reading, drawing, and
manipulating pixel data. Although these features are often very useful,
they can also decrease performance. Here are some tips for improving pixel
draw rates:
• For best performance, set all pixel-transfer parameters to their default
values, and set pixel zoom to (1.0, 1.0).
• A series of fragment operations is applied to pixels as they are drawn
into the framebuffer. (See “Testing and Operating on Fragments” in
Chapter 10.) For optimum performance, disable all necessary fragment
operations.
• While performing pixel operations, disable other costly states, such as
texture mapping or blending.

Imaging Subset 367
• If you use a pixel format and type that match those of the framebuffer,
your OpenGL implementation doesn’t need to convert the pixels
into the format that matches the framebuffer. For example, if you
are writing images to an RGB framebuffer with 8 bits per component,
call glDrawPixels() with format set to RGB and type set to GL_
UNSIGNED_BYTE.
• For many implementations, unsigned image formats are faster to use
than signed image formats.
• It is usually faster to draw a large pixel rectangle than to draw several
small ones, since the cost of transferring the pixel data can be
amortized over many pixels.
• If possible, reduce the amount of data that needs to be copied by using
small data types (for example, use GL_UNSIGNED_BYTE) and fewer
components (for example, use format GL_LUMINANCE_ALPHA).
• Pixel-transfer operations, including pixel mapping and values for scale,
bias, offset, and shift other than the defaults, may decrease
performance.
• If you need to render the same image each frame (as a background, for
example), render it as a textured quadrilateral, as compared to calling
glDrawPixels(). Having it stored as a texture requires that the data be
downloaded into OpenGL once. See Chapter 9 for a discussion of
texture mapping.
Imaging Subset
The Imaging Subset is a collection of routines that provide additional pixel
processing capabilities. With it, you can:
• Use color lookup tables to replace pixel values.
• Use convolutions to filter images.
• Use color matrix transformations to do color space conversions and
other linear transformations.
• Collect histogram statistics and minimum and maximum color
component information about images.
You should use the Imaging Subset if you need more pixel processing
capabilities than those provided by glPixelTransfer*() and glPixelMap*().

368 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
The Imaging Subset is an extension to OpenGL. If the token GL_ARB_
imaging is defined in the strings returned when querying extensions, then
the subset is present, and all the functionality that is described in the
following sections is available for you to use. If the token is not defined,
none of the functionality is present in your implementation. To see if your
implementation supports the Imaging Subset, see “Extensions to the
Standard” on page 641.
Note: Although the Imaging Subset has always been an OpenGL extension,
its functionality was deprecated in OpenGL Version 3.0, and was
removed from Version 3.1 of the OpenGL specification.
Whenever pixels are passed to or read from OpenGL, they are processed by
any of the enabled features of the subset. Routines that are affected by the
Imaging Subset include functions that
• Draw and read pixel rectangles: glReadPixels(),glDrawPixels(),
glCopyPixels().
• Define textures: glTexImage1D(), glTexImage2D(),
glCopyTexImage*D(), glTexSubImage1D(),glTexSubImage2d() and
glCopyTexSubImage*D().
Figure 8-14 illustrates the operations that the Imaging Subset performs on
pixels that are passed into or read from OpenGL. Most of the features of the
Imaging Subset may be enabled and disabled, with the exception of the
color matrix transformation, which is always enabled.
Color lookup table
Convolution
scale and bias
Post-convolution
color lookup table
Post-convolution
color lookup table
Post-color matrix
color lookup table
Color matrix
scale and bias
Histogram
Minmax
Unpacked
pixel data
in
Pixel data
out
Figure 8-14 Imaging Subset Operations

Imaging Subset 369
Color Tables
Color tables are lookup tables used to replace a pixel’s color. In applications,
color tables may be used for contrast enhancement, filtering, and image
equalization.
There are three different color lookup tables available, which operate at
different stages of the pixel pipeline. Table 8-7 shows where in the pipeline
pixels may be replaced by the respective color table.
Each color table can be enabled separately using glEnable() with the
respective parameter from Table 8-7.
Specifying Color Tables
Color tables are specified similarly to one-dimensional images. As shown in
Figure 8-14, there are three color tables available for updating pixel values.
glColorTable() is used to define each color table.
Color Table Parameter Operates on Pixels
GL_COLOR_TABLE when they enter the imaging
pipeline
GL_POST_CONVOLUTION_COLOR_TABLE after convolution
GL_POST_COLOR_MATRIX_COLOR_TABLE after the color matrix
transformation
Table 8-7 When Color Table Operations Occur in the Imaging Pipeline
void glColorTable(GLenum target, GLenum internalFormat,
GLsizei width, GLenum format, GLenum type,
const GLvoid *data);
Defines the specified color table when target is set to GL_COLOR_TABLE,
GL_POST_CONVOLUTION_COLOR_TABLE, or GL_POST_COLOR_
MATRIX_COLOR_TABLE. If target is set to GL_PROXY_COLOR_TABLE,
GL_PROXY_POST_CONVOLUTION_COLOR_TABLE, or GL_PROXY_
POST_COLOR_MATRIX_COLOR_TABLE, then glColorTable() verifies
that the specified color table fits into the available resources.

370 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
The internal format of the table determines which components of the
image’s pixels are replaced. For example, if you specify the format to be
GL_RGB, then the red, green, and blue components of each incoming
pixel are looked up in the appropriate color table and replaced. Table 8-8
describes which pixel components are replaced for a given base internal
format.
The internalFormat variable is used to determine the internal OpenGL
representation of data. It can be one of the following symbolic
constants: GL_ALPHA, GL_ALPHA4, GL_ALPHA8, GL_ALPHA12,
GL_ALPHA16, GL_LUMINANCE, GL_LUMINANCE4, GL_LUMINANCE8,
GL_LUMINANCE12, GL_LUMINANCE16, GL_LUMINANCE_ALPHA,
GL_LUMINANCE4_ALPHA4, GL_LUMINANCE6_ALPHA2, GL_
LUMINANCE8_ALPHA8, GL_LUMINANCE12_ALPHA4, GL_
LUMINANCE12_ALPHA12, GL_LUMINANCE16_ALPHA16, GL_INTENSITY,
GL_INTENSITY4, GL_INTENSITY8, GL_INTENSITY12, GL_INTENSITY16,
GL_RGB, GL_R3_G3_B2, GL_RGB4, GL_RGB5, GL_RGB8, GL_RGB10,
GL_RGB12, GL_RGB16, GL_RGBA, GL_RGBA2, GL_RGBA4, GL_RGB5_A1,
GL_RGBA8, GL_RGB10_A2, GL_RGBA12, and GL_RGBA16.
The width parameter, which must be a power of 2, indicates the number
of pixels in the color table. The format and type describe the format and
data type of the color table data. They have the same meaning as
equivalent parameters of glDrawPixels().
Base Internal Format Red
Component
Green
Component
Blue
Component
Alpha
Component
GL_ALPHA Unchanged Unchanged Unchanged At
GL_LUMINANCE LtLtLtUnchanged
GL_LUMINANCE_ALPHA LtLtLtAt
GL_INTENSITY ItItItIt
GL_RGB RtGtBtUnchanged
GL_RGBA RtGtBtAt
Table 8-8 Color Table Pixel Replacement

Imaging Subset 371
In Table 8-8, Lt represents luminance entries in the defined color table,
which affect only red, green, and blue components. It represents intensity
entries, which affect red, green, blue, and alpha identically.
After the appropriate color table has been applied to the image, the pixels
can be scaled and biased, after which their values are clamped to the range
[0, 1]. The GL_COLOR_TABLE_SCALE and GL_COLOR_TABLE_BIAS factors
are set for each color table with the glColorTableParameter*() routine.
Example 8-7 shows how an image can be inverted using color tables. The
color table is set up to replace each color component with its inverse color.
Example 8-7 Pixel Replacement Using Color Tables: colortable.c
extern GLubyte* readImage(const char*, GLsizei*, GLsizei* );
GLubyte *pixels;
GLsizei width, height;
void init(void)
{
int i;
GLubyte colorTable[256][3];
pixels = readImage(“Data/leeds.bin”, &width, &height);
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glClearColor(0, 0, 0, 0);
void glColorTableParameter{if}v(GLenum target, GLenum pname,
TYPE *param);
Sets the GL_COLOR_TABLE_SCALE and GL_COLOR_TABLE_BIAS param-
eters for each color table. The target parameter is one of GL_COLOR_
TABLE, GL_POST_CONVOLUTION_COLOR_TABLE, or GL_POST_
COLOR_MATRIX_COLOR_TABLE, and it specifies which color table’s
scale and bias values to set.
The possible values for pname are GL_COLOR_TABLE_SCALE and
GL_COLOR_TABLE_BIAS.
The value for param points to an array of four values, representing the red,
green, blue, and alpha modifiers, respectively.
372 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
/* Set up an inverting color table */
for (i = 0; i < 256; ++i) {
colorTable[i][0] = 255 - i;
colorTable[i][1] = 255 - i;
colorTable[i][2] = 255 - i;
}
glColorTable(GL_COLOR_TABLE, GL_RGB, 256, GL_RGB,
GL_UNSIGNED_BYTE, colorTable);
glEnable(GL_COLOR_TABLE);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(1, 1);
glDrawPixels(width, height, GL_RGB, GL_UNSIGNED_BYTE,
pixels);
glFlush();
}
Note: Example 8-7 introduces a new function, readImage(), which is
presented to simplify the example programs. In general, you need to
use a routine that can read the image file format that you require. The
file format that readImage() understands is listed below. The data is
listed sequentially in the file.
• Width of the image, stored as a GLsizei
• Height of the image, stored as a GLsizei
• RGB triples, stored with a GLubyte per color
component
In addition to specifying a color table explicitly from your application, you
may want to use an image created in the framebuffer as the definition for a
color table. The glCopyColorTable() routine lets you specify a single row of
pixels that are read from the framebuffer and used to define a color table.
void glCopyColorTable(GLenum target, GLenum internalFormat,
GLint x, GLint y, GLsizei width);
Creates a color table using framebuffer data to define the elements of the
color table. The pixels are read from the current GL_READ_BUFFER and
are processed exactly as if glCopyPixels() had been called but stopped
before final conversion. The glPixelTransfer*() settings are applied.
width height

Imaging Subset 373
Replacing All or Part of a Color Table
If you would like to replace a part of a color table, then color subtable
commands let you reload an arbitrary section of a color table with new
values.
Querying a Color Table’s Values
The pixel values stored in the color tables can be retrieved using the
glGetColorTable() function. Refer to “The Query Commands” on page 740
for more details.
The target parameter must be set to one of the targets of glColorTable().
The internalFormat parameter uses the same symbolic constants as the
internalFormat parameter of glColorTable(). The color array is defined by
the width pixels in the row starting at (x, y) in the framebuffer.
void glColorSubTable(GLenum target, GLsizei start, GLsizei count,
GLenum format, GLenum type,
const GLvoid *data);
Replaces color table entries start to start + count 1 with values stored
in data.
The target parameter is GL_COLOR_TABLE, GL_POST_CONVOLUTION_
COLOR_TABLE, or GL_POST_COLOR_MATRIX_COLOR_TABLE. The
format and type parameters are identical to those of glColorTable() and
describe the pixel values stored in data.
void glCopyColorSubTable(GLenum target, GLsizei start, GLint x,
GLint y, GLsizei count);
Replaces color table entries start to start + count 1 with count color pixel
values from the row in the framebuffer starting at position (x, y). The
pixels are converted into the internalFormat of the original color table.

374 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Color Table Proxies
Color table proxies provide a way to query OpenGL to see if there are
enough resources available to store your color table. If glColorTable() is
called with one of the following proxy targets:
• GL_PROXY_COLOR_TABLE
• GL_PROXY_POST_CONVOLUTION_COLOR_TABLE
• GL_PROXY_POST_COLOR_MATRIX_COLOR_TABLE
then OpenGL determines if the required color table resources are available.
If the color table does not fit, the width, format, and component resolution
values are all set to zero. To check if your color table fits, query one of the
state values mentioned above. For example:
glColorTable(GL_PROXY_COLOR_TABLE, GL_RGB, 1024, GL_RGB,
GL_UNSIGNED_BYTE, null);
glGetColorTableParameteriv(GL_PROXY_COLOR_TABLE,
GL_COLOR_TABLE_WIDTH, &width);
if (width == 0)
/* color table didn’t fit as requested */
For more details on glGetColorTableParameter*(), see “The Query Com-
mands” on page 740.
Convolutions
Convolutions are pixel filters that replace each pixel with a weighted aver-
age of its neighboring pixels and itself. Blurring and sharpening images,
finding edges, and adjusting image contrast are examples of how convolu-
tions are used.
Figure 8-15 shows how pixel P00 and related pixels are processed by the
3u3 convolution filter to produce pixel P’11.
Convolutions are arrays of pixel weights and operate only on RGBA pixels.
A filter, which is also known as a kernel, is simply a two-dimensional array
of pixel weights. Each pixel in the output image of the convolution process
is created by multiplying a set of the input image’s pixels by the pixel
weights in the convolution kernel and summing the results. For example,
in Figure 8-15, pixel P’11 is computed by summing the products of the nine
pixels from the input image and the nine pixel weights in the convolution
filter.

Imaging Subset 375
void glConvolutionFilter2D(GLenum target, GLenum internalFormat,
GLsizei width, GLsizei height,
GLenum format, GLenum type,
const GLvoid *image);
Defines a two-dimensional convolution filter where the target parameter
must be GL_CONVOLUTION_2D.
The internalFormat parameter defines which pixel components the
convolution operation is performed on, and can be one of the 38 symbolic
constants that are used for the internalFormat parameter for glColorTable().
The width and height parameters specify the size of the filter in pixels. The
maximum width and height for convolution filters may be queried with
glGetConvolutionParameter*(). Refer to “The Query Commands” on
page 740 for more details.
As with glDrawPixels(), the format and type parameters specify the format
of the pixels stored in image.
P20
P21
P22
P10
P11
P12
P00
P01
P02
C20
C21
C22
C10
C11
C12
C00
C01
C02
P'
20
P'
21
P'
22
P'
10
P'
11
P'
12
P'
00
P'
01
P'
02
i + 1, j + 1
Figure 8-15 The Pixel Convolution Operation

376 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Similar to color tables, the internal format of the convolution filter deter-
mines which components of the image are operated on. Table 8-9 describes
how the different base filter formats affect pixels. Rs, Gs, Bs, and As represent
the color components of the source pixels. Lf represents the luminance
value of a GL_LUMINANCE filter, and If corresponds to the intensity value
of a GL_INTENSITY filter. Finally, Rf, Gf, Bf, and Af represent the red, green,
blue, and alpha components of the convolution filter.
Use glEnable(GL_CONVOLUTION_2D) to enable 2D convolution
processing.
Example 8-8 demonstrates the use of several 3 u3 GL_LUMINANCE convo-
lution filters to find edges in an RGB image. The ‘h’, ‘l’, and ‘v’ keys change
among the various filters.
Example 8-8 Using Two-Dimensional Convolution Filters: convolution.c
extern GLubyte* readImage(const char*, GLsizei*, GLsizei*);
GLubyte *pixels;
GLsizei width, height;
/* Define convolution filters */
GLfloat horizontal[3][3] = {
{ 0, -1, 0 },
{ 0, 1, 0 },
{ 0, 0, 0 }
};
Base Filter Format Red Result Green Result Blue Result Alpha Result
GL_ALPHA Unchanged Unchanged Unchanged As Af
GL_LUMINANCE Rs LfGs LfBs LfUnchanged
GL_LUMINANCE_ALPHA Rs LfGs LfBs LfAs Af
GL_INTENSITY Rs IfGs IfBs IfAs If
GL_RGB Rs RfGs GfBs BfUnchanged
GL_RGBA Rs RfGs GfBs BfAs Af
Table 8-9 How Convolution Filters Affect RGBA Pixel Components

Imaging Subset 377
GLfloat vertical[3][3] = {
{ 0, 0, 0 },
{ -1, 1, 0 },
{ 0, 0, 0 }
};
GLfloat laplacian[3][3] = {
{ -0.125, -0.125, -0.125 },
{ -0.125, 1.0, -0.125 },
{ -0.125, -0.125, -0.125 }
};
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(1, 1);
glDrawPixels(width, height, GL_RGB, GL_UNSIGNED_BYTE,
pixels);
glFlush();
}
void init(void)
{
pixels = readImage(“Data/leeds.bin”, &width, &height);
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glClearColor(0.0, 0.0, 0.0, 0.0);
printf(“Using horizontal filter\n”);
glConvolutionFilter2D(GL_CONVOLUTION_2D, GL_LUMINANCE, 3, 3,
GL_LUMINANCE, GL_FLOAT, horizontal);
glEnable(GL_CONVOLUTION_2D);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘h’ :
printf(“Using horizontal filter\n”);
glConvolutionFilter2D(GL_CONVOLUTION_2D, GL_LUMINANCE,
3, 3, GL_LUMINANCE, GL_FLOAT, horizontal );
break;
case ‘v’ :
printf(“Using vertical filter\n” );

378 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
glConvolutionFilter2D( GL_CONVOLUTION_2D, GL_LUMINANCE,
3, 3, GL_LUMINANCE, GL_FLOAT, vertical );
break;
case ‘l’ :
printf(“Using laplacian filter\n”);
glConvolutionFilter2D(GL_CONVOLUTION_2D, GL_LUMINANCE,
3, 3, GL_LUMINANCE, GL_FLOAT, laplacian );
break;
case 27: /* Escape Key */
exit(0)
break;
}
glutPostRedisplay();
}
As with color tables, you may want to specify a convolution filter with pixel
values from the framebuffer. glCopyConvolutionFilter2D() copies a
rectangle of pixels from the current GL_READ_BUFFER to use as the
definition of the convolution filter. If GL_LUMINANCE or GL_INTENSITY
is specified for the internalFormat, the red component of the pixel is used to
define the convolution filter’s value.
Specifying Separable Two-Dimensional Convolution Filters
Convolution filters are separable if they can be represented by the outer
product of two one-dimensional filters.
glSeparableFilter2D() is used to specify the two one-dimensional filters
that represent the separable two-dimensional convolution filter. As with
void glCopyConvolutionFilter2D(GLenum target,
GLenum internalFormat,
GLint x, GLint y,
GLsizei width, GLsizei height);
Defines a two-dimensional convolution filter initialized with pixels
from the color framebuffer. target must be GL_CONVOLUTION_2D, and
internalFormat must be set to one of the internal formats defined for
glConvolutionFilter2D().
The pixel rectangle with lower left pixel (x,y) and size width by height is
read from the framebuffer and converted into the specified internalFormat.

Imaging Subset 379
glConvolutionFilter2D(), the internal format of the convolution filter
determines how an image’s pixels are processed.
For example, you might construct a 3 u3 convolution filter by specifying
the one-dimensional filter for both row and column for a
GL_LUMINANCE separable convolution filter. OpenGL would compute the
convolution of the source image using the two one-dimensional filters in
the same manner as if it computed a complete two-dimensional filter by
computing the following outer product:
Using separable convolution filters is computationally more efficient than
using a nonseparable two-dimensional convolution filter.
void glSeparableFilter2D(GLenum target, GLenum internalFormat,
GLsizei width, GLsizei height, GLenum format,
GLenum type, const GLvoid *row,
const GLvoid *column);
Defines a two-dimensional separable convolution filter. target must be set
to GL_SEPARABLE_2D. The internalFormat parameter uses the same values
that are used for glConvolutionFilter2D().
width specifies the number of pixels in the row array. Likewise, height
specifies the number of pixels in the column array. type and format define
the storage format for row and column in the same manner as
glConvolutionFilter2D().
Use glEnable(GL_SEPARABLE_2D) to enable convolutions using a two-
dimensional separable convolution filter. GL_CONVOLUTION_2D takes
precedence if both GL_CONVOLUTION_2D and GL_SEPARABLE_2D are
specified.
A GL_INVALID_OPERATION error is set if an unpack pixel buffer object
is bound and the combination of width, height, format, and type, plus the
specified offsets into the bound buffer object would cause a memory access
outside of the memory allocated when the buffer object was created.
[ 1/2, 1, 1/2 ]
−1/2
1
−1/2
1/4
−1/2
1/4
1/4
−1/2
1/4
−1/2
1
−1/2
−1/2 1 −1/2 =

380 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
One-Dimensional Convolution Filters
One-dimensional convolutions are identical to the two-dimensional ver-
sion except that the filter’s height parameter is assumed to be 1. However,
they affect only the specification of one-dimensional textures (see “Texture
Rectangles” on page 412 for details).
When a convolution filter is specified, it can be scaled and biased. The scale
and bias values are specified with the glConvolutionParameter*(). No
clamping of the convolution filter occurs after scaling or biasing.
void glConvolutionFilter1D(GLenum target, GLenum internalFormat,
GLsizei width, GLenum format,
GLenum type, const GLvoid *image);
Specifies a one-dimensional convolution filter. target must be set to
GL_CONVOLUTION_1D. width specifies the number of pixels in the filter.
The internalFormat,format, and type have the same meanings as they do
for the respective parameters to glConvolutionFilter2D().image points to
the one-dimensional image to be used as the convolution filter.
Use glEnable(GL_CONVOLUTION_1D) to enable one-dimensional
convolutions.
You may want to specify the convolution filter with values generated from
the framebuffer. glCopyConvolutionFilter1D() copies a row of pixels
from the current GL_READ_BUFFER, converts them into the specified
internalFormat, and uses them to define the convolution filter.
A GL_INVALID_OPERATION error is set if an unpack pixel buffer object is
bound and the combination of width, format, and type, plus the specified
offset into the bound buffer object would cause a memory access outside
of the memory allocated when the buffer object was created.
void glCopyConvolutionFilter1D(GLenum target,
GLenum internalFormat, GLint x,
GLint y, GLsizei width);
Defines a one-dimensional convolution filter with pixel values from the
framebuffer. glCopyConvolutionFilter1D() copies width pixels starting at
(x,y) and converts the pixels into the specified internalFormat.

Imaging Subset 381
Convolution Border Modes
The convolutions of pixels at the edges of an image are handled differently
from the interior pixels. Their convolutions are modified by the
convolution border mode. There are three options for computing border
convolutions:
• GL_REDUCE mode causes the resulting image to shrink in each
dimension by the size of the convolution filter. The width of the
resulting image is (width Wf), and the height of the resulting image is
(height Hf), where Wf and Hf are the width and height of the convolu-
tion filter, respectively. If this produces an image with zero or negative
width or height, no output is generated, nor are any errors.
• GL_CONSTANT_BORDER computes the convolutions of border pixels
by using a constant pixel value for pixels outside of the source image.
The constant pixel value is set using the glConvolutionParameter*()
function. The resulting image’s size matches that of the source image.
• GL_REPLICATE_BORDER computes the convolution in the same
manner as in GL_CONSTANT_BORDER mode, except the outermost
row or column of pixels is used for the pixels that lie outside of the
source image. The resulting image’s size matches that of the source
image.
void glConvolutionParameter{if}(GLenum target, GLenum pname,
TYPE param);
void glConvolutionParameter{if}v(GLenum target, GLenum pname,
const TYPE *params);
Sets parameters that control how a convolution is performed. target
must be GL_CONVOLUTION_1D, GL_CONVOLUTION_2D, or
GL_SEPARABLE_2D.
pname must be GL_CONVOLUTION_BORDER_MODE,
GL_CONVOLUTION_FILTER_SCALE, or GL_CONVOLUTION_FILTER_
BIAS. Specifying pname as GL_CONVOLUTION_BORDER_MODE defines
the convolution border mode. In this case, params must be GL_REDUCE,
GL_CONSTANT_BORDER, or GL_REPLICATE_BORDER. If pname is set to
either GL_CONVOLUTION_FILTER_SCALE or GL_CONVOLUTION_
FILTER_BIAS, then params points to an array of four color values for red,
green, blue, and alpha, respectively.

382 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Post-Convolution Operations
After the convolution operation is completed, the pixels of the resulting image
may be scaled and biased, and are clamped to the range [0, 1]. The scale and
bias values are specified by calling glPixelTransfer*(), with either GL_POST_
CONVOLUTION_*_SCALE or GL_POST_CONVOLUTION_*_BIAS, respectively.
Specifying a GL_POST_CONVOLUTION_COLOR_TABLE with glColorTable()
allows pixel components to be replaced using a color lookup table.
Color Matrix
For color space conversions and linear transformations on pixel values,
the Imaging Subset supports a 4 u4 matrix stack, selected by setting
glMatrixMode(GL_COLOR). For example, to convert from RGB color space
to CMY (cyan, magenta, yellow) color space, you might call
GLfloat rgb2cmy[16] = {
-1, 0, 0, 0,
0, -1, 0, 0,
0, 0, -1, 0,
1, 1, 1, 1
};
glMatrixMode(GL_COLOR); /* enter color matrix mode */
glLoadMatrixf(rgb2cmy);
glMatrixMode(GL_MODELVIEW); /* back to modelview mode */
Note: Recall that OpenGL matrices are stored in a column-major format. See
“General-Purpose Transformation Commands” on page 134 for more
detail about using matrices with OpenGL.
The color matrix stack has at least two matrix entries. (See “The Query
Commands” on page 740 for details on determining the depth of the color
matrix stack.) Unlike the other parts of the Imaging Subset, the color matrix
transformation is always performed and cannot be disabled.
Example 8-9 illustrates using the color matrix to exchange the red and
green color components of an image.
Example 8-9 Exchanging Color Components Using the Color Matrix:
colormatrix.c
extern GLubyte* readImage(const char*, GLsizei*, GLsizei*);
GLubyte *pixels;
GLsizei width, height;

Imaging Subset 383
void init(void)
{
/* Specify a color matrix to reorder a pixel’s components
* from RGB to GBR */
GLfloat m[16] = {
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
1.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 1.0
};
pixels = readImage(“Data/leeds.bin”, &width, &height);
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glClearColor(0.0, 0.0, 0.0, 0.0);
glMatrixMode(GL_COLOR);
glLoadMatrixf(m);
glMatrixMode(GL_MODELVIEW);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(1, 1);
glDrawPixels(width, height, GL_RGB, GL_UNSIGNED_BYTE,
pixels);
glFlush();
}
Post-Color Matrix Transformation Operations
Similar to the post-convolution operations, pixels can be scaled and biased
after the color matrix step. Calling glPixelTransfer*() with either GL_POST_
COLOR_MATRIX_*_SCALE or GL_POST_COLOR_MATRIX_*_BIAS defines the
scale and bias values for the post color matrix operation. Pixel values after
scaling and biasing are clamped to the range [0, 1].
Histogram
Using the Imaging Subset, you can collect statistics about images.
Histogramming determines the distribution of color values in an image,
which can be used to determine how to balance an image’s contrast, for
example.

384 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
glHistogram() specifies what components of the image you want to
histogram, and whether you want only to collect statistics or to continue
processing the image. To collect histogram statistics, you must call
glEnable(GL_HISTOGRAM).
Similar to the color tables described in “Color Tables” on page 369, a
proxy mechanism is available with glHistogram() to determine if there
are enough resources to store the requested histogram. If resources are not
available, the histogram’s width, format, and component resolutions
are set to zero. You can query the results of a histogram proxy using
glGetHistogramParameter(), described in “The Query Commands” on
page 740.
void glHistogram(GLenum target, GLsizei width,
GLenum internalFormat, GLboolean sink);
Defines how an image’s histogram data should be stored. The target
parameter must be set to either GL_HISTOGRAM or GL_PROXY_
HISTOGRAM. The width parameter specifies the number of entries in the
histogram table. Its value must be a power of 2.
The internalFormat parameter defines how the histogram data should be
stored. The allowable values are GL_ALPHA, GL_ALPHA4, GL_ALPHA8,
GL_ALPHA12, GL_ALPHA16, GL_LUMINANCE, GL_LUMINANCE4,
GL_LUMINANCE8, GL_LUMINANCE12, GL_LUMINANCE16, GL_
LUMINANCE_ALPHA, GL_LUMINANCE4_ALPHA4, GL_LUMINANCE6_
ALPHA2, GL_LUMINANCE8_ALPHA8, GL_LUMINANCE12_ALPHA4,
GL_LUMINANCE12_ALPHA12, GL_LUMINANCE16_ALPHA16, GL_RGB,
GL_RGB2, GL_RGB4, GL_RGB5, GL_RGB8, GL_RGB10, GL_RGB12,
GL_RGB16, GL_RGBA, GL_RGBA2, GL_RGBA4, GL_RGB5_A1, GL_RGBA8,
GL_RGB10_A2, GL_RGBA12, and GL_RGBA16. This list does not include
GL_INTENSITY* values. This differs from the list of values accepted by
glColorTable().
The sink parameter indicates whether the pixels should continue to the
minmax stage of the pipeline or be discarded.
After you’ve passed the pixels to the imaging pipeline using
glDrawPixels(), you can retrieve the results of the histogram using
glGetHistogram(). In addition to returning the histogram’s values,
glGetHistogram() can be used to reset the histogram’s internal storage.
The internal storage can also be reset using glResetHistogram(), which is
described on page 386.
Imaging Subset 385
Example 8-10 Computing and Diagramming an Image’s Histogram: histogram.c
#define HISTOGRAM_SIZE 256 /* Must be a power of 2 */
extern GLubyte* readImage(const char*, GLsizei*, GLsizei*);
GLubyte *pixels;
GLsizei width, height;
void init(void)
{
pixels = readImage(“Data/leeds.bin”, &width, &height);
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glClearColor(0.0, 0.0, 0.0, 0.0);
glHistogram(GL_HISTOGRAM, HISTOGRAM_SIZE, GL_RGB, GL_FALSE);
glEnable(GL_HISTOGRAM);
}
void display(void)
{
int i;
GLushort values[HISTOGRAM_SIZE][3];
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(1, 1);
glDrawPixels(width, height, GL_RGB, GL_UNSIGNED_BYTE,
pixels);
glGetHistogram(GL_HISTOGRAM, GL_TRUE, GL_RGB,
GL_UNSIGNED_SHORT, values);
void glGetHistogram(GLenum target, GLboolean reset, GLenum format,
GLenum type, GLvoid *values);
Returns the collected histogram statistics. target must be GL_HISTOGRAM.
reset specifies if the internal histogram tables should be cleared.
The format and type parameters specify the storage type of values, and how
the histogram data should be returned to the application. They accept the
same values at their respective parameters in glDrawPixels().
In Example 8-10, the program computes the histogram of an image and
plots resulting distributions in the window. The ‘s’ key in the example
shows the effect of the sink parameter, which controls whether the pixels
are passed to the subsequent imaging pipeline operations.

386 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
/* Plot histogram */
glBegin(GL_LINE_STRIP);
glColor3f(1.0, 0.0, 0.0);
for (i = 0; i < HISTOGRAM_SIZE; i++)
glVertex2s(i, values[i][0]);
glEnd();
glBegin(GL_LINE_STRIP);
glColor3f(0.0, 1.0, 0.0);
for (i = 0; i < HISTOGRAM_SIZE; i++)
glVertex2s(i, values[i][1]);
glEnd();
glBegin(GL_LINE_STRIP);
glColor3f(0.0, 0.0, 1.0);
for (i = 0; i < HISTOGRAM_SIZE; i++)
glVertex2s(i, values[i][2]);
glEnd();
glFlush();
}
void keyboard(unsigned char key, int x, int y)
{
static GLboolean sink = GL_FALSE;
switch (key) {
case ‘s’ :
sink = !sink;
glHistogram(GL_HISTOGRAM, HISTOGRAM_SIZE, GL_RGB,
sink);
break;
case 27: /* Escape Key */
exit(0);
break;
}
glutPostRedisplay();
}
glResetHistogram() will discard the histogram without retrieving the values.
void glResetHistogram(GLenum target);
Resets the histogram counters to zero. The target parameter must be
GL_HISTOGRAM.

Imaging Subset 387
Minmax
glMinmax() computes the minimum and maximum pixel component
values for a pixel rectangle. As with glHistogram(), you can compute the
minimum and maximum values and either render the image or discard the
pixels.
glGetMinmax() is used to retrieve the computed minimum and maximum
values. Similar to glHistogram(), the internal values for the minimum and
maximum can be reset when they are accessed.
Example 8-11 demonstrates the use of glMinmax() to compute the mini-
mum and maximum pixel values in GL_RGB format. The minmax opera-
tion must be enabled with glEnable(GL_MINMAX).
The minimum and maximum values returned in the array values from
glMinmax() command are grouped by component. For example, if you
request GL_RGB values as the format, the first three values in the values
array represent the minimum red, green, and blue values, followed by the
maximum red, green, and blue values for the processed pixels.
void glMinmax(GLenum target, GLenum internalFormat,
GLboolean sink);
Computes the minimum and maximum pixel values for an image. target
must be GL_MINMAX.
internalFormat specifies for which color components the minimum and
maximum values should be computed. glMinmax() accepts the same
values for internalFormat as glHistogram() accepts.
If GL_TRUE is specified for sink, then the pixels are discarded and not
written to the framebuffer. GL_FALSE renders the image.
void glGetMinmax(GLenum target, GLboolean reset, GLenum format,
GLenum type, GLvoid *values);
Returns the results of the minmax operation. target must be GL_MINMAX.
If the reset parameter is set to GL_TRUE, the minimum and maximum
values are reset to their initial values. The format and type parameters
describe the format of the minmax data returned in values, and use the
same values as glDrawPixels().
388 Chapter 8: Drawing Pixels, Bitmaps, Fonts, and Images
Example 8-11 Computing Minimum and Maximum Pixel Values: minmax.c
extern GLubyte* readImage(const char*, GLsizei*, GLsizei*);
GLubyte *pixels;
GLsizei width, height;
void init(void)
{
pixels = readImage(“Data/leeds.bin”, &width, &height);
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glClearColor(0.0, 0.0, 0.0, 0.0);
glMinmax(GL_MINMAX, GL_RGB, GL_FALSE);
glEnable(GL_MINMAX);
}
void display(void)
{
GLubyte values[6];
glClear(GL_COLOR_BUFFER_BIT);
glRasterPos2i(1, 1);
glDrawPixels(width, height, GL_RGB, GL_UNSIGNED_BYTE,
pixels);
glGetMinmax(GL_MINMAX, GL_TRUE, GL_RGB, GL_UNSIGNED_BYTE,
values);
glFlush();
printf(“Red : min = %d max = %d\n”, values[0], values[3]);
printf(“Green: min = %d max = %d\n”, values[1], values[4]);
printf(“Blue : min = %d max = %d\n”, values[2], values[5]);
}
Even though glGetMinmax() can reset the minmax values when they are
retrieved, you can explicitly reset the internal tables at any time by calling
glResetMinmax().
void glResetMinmax(GLenum target);
Resets the minimum and maximum values to their initial values. The
target parameter must be GL_MINMAX.

389
Chapter 9
9.Texture Mapping
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Understand what texture mapping can add to your scene
• Specify texture images in compressed and uncompressed formats
• Control how a texture image is filtered as it is applied to a fragment
• Create and manage texture images in texture objects, and control a
high-performance working set of those texture objects
• Specify how the texture and fragment colors are combined
• Supply texture coordinates describing how the texture image should be
mapped onto objects in your scene
• Generate texture coordinates automatically to produce effects such as
contour maps and environment maps
• Perform complex texture operations in a single pass with
multitexturing (sequential texture units)
• Use texture combiner functions to mathematically operate on texture,
fragment, and constant color values
• After texturing, process fragments with secondary colors
• Specify textures to be used for processing point sprites
• Transform texture coordinates using the texture matrix
• Render shadowed objects, using depth textures

390 Chapter 9: Texture Mapping
So far, every geometric primitive has been drawn as either a solid color or
smoothly shaded between the colors at its vertices—that is, they’ve been
drawn without texture mapping. If you want to draw a large brick wall
without texture mapping, for example, each brick must be drawn as a
separate polygon. Without texturing, a large flat wall—which is really a
single rectangle—might require thousands of individual bricks, and even
then the bricks may appear too smooth and regular to be realistic.
Texture mapping allows you to glue an image of a brick wall (obtained,
perhaps, by taking a photograph of a real wall) to a polygon and to draw the
entire wall as a single polygon. Texture mapping ensures that all the right
things happen as the polygon is transformed and rendered. For example,
when the wall is viewed in perspective, the bricks may appear smaller as the
wall gets farther from the viewpoint. Other uses for texture mapping
include depicting vegetation on large polygons representing the ground in
flight simulation; wallpaper patterns; and textures that make polygons look
like natural substances such as marble, wood, and cloth. The possibilities
are endless. Although it’s most natural to think of applying textures to
polygons, textures can be applied to all primitives—points, lines, polygons,
bitmaps, and images. Plates 6, 8, 18–21, and 24–32 all demonstrate the use
of textures.
Because there are so many possibilities, texture mapping is a fairly large,
complex subject, and you must make several programming choices when
using it. For starters, most people intuitively understand a two-dimensional
texture, but a texture may be one-dimensional or even three-dimensional.
You can map textures to surfaces made of a set of polygons or to curved
surfaces, and you can repeat a texture in one, two, or three directions
(depending on how many dimensions the texture is described in) to cover
the surface. In addition, you can automatically map a texture onto an object
in such a way that the texture indicates contours or other properties of the
item being viewed. Shiny objects can be textured so that they appear to be
in the center of a room or other environment, reflecting the surroundings
from their surfaces. Finally, a texture can be applied to a surface in different
ways. It can be painted on directly (like a decal placed on a surface), used to
modulate the color the surface would have been painted otherwise, or used
to blend a texture color with the surface color. If this is your first exposure
to texture mapping, you might find that the discussion in this chapter
moves fairly quickly. As an additional reference, you might look at the
chapter on texture mapping in 3D Computer Graphics by Alan Watt
(Addison-Wesley, 1999).
Textures are simply rectangular arrays of data—for example, color data,
luminance data, or color and alpha data. The individual values in a texture

391
array are often called texels. What makes texture mapping tricky is that a
rectangular texture can be mapped to nonrectangular regions, and this
must be done in a reasonable way.
Figure 9-1 illustrates the texture-mapping process. The left side of the figure
represents the entire texture, and the black outline represents a quadrilateral
shape whose corners are mapped to those spots on the texture. When the
quadrilateral is displayed on the screen, it might be distorted by applying
various transformations—rotations, translations, scaling, and projections. The
right side of the figure shows how the texture-mapped quadrilateral might
appear on your screen after these transformations. (Note that this quadrilat-
eral is concave and might not be rendered correctly by OpenGL without
prior tessellation. See Chapter 11 for more information about tessellating
polygons.)
Notice how the texture is distorted to match the distortion of the quadrilat-
eral. In this case, it’s stretched in the x-direction and compressed in the
y-direction; there’s a bit of rotation and shearing going on as well. Depend-
ing on the texture size, the quadrilateral’s distortion, and the size of the
screen image, some of the texels might be mapped to more than one frag-
ment, and some fragments might be covered by multiple texels. Since the
texture is made up of discrete texels (in this case, 256u256 of them), filter-
ing operations must be performed to map texels to fragments. For example,
if many texels correspond to a fragment, they’re averaged down to fit; if
texel boundaries fall across fragment boundaries, a weighted average of the
applicable texels is performed. Because of these calculations, texturing is
computationally expensive, which is why many specialized graphics sys-
tems include hardware support for texture mapping.
Figure 9-1 Texture-Mapping Process
Chapter 9: Texture Mapping

392 Chapter 9: Texture Mapping
An application may establish texture objects, with each texture object rep-
resenting a single texture (and possible associated mipmaps). Some imple-
mentations of OpenGL can support a special working set of texture objects
that have better performance than texture objects outside the working set.
These high-performance texture objects are said to be resident and may
have special hardware and/or software acceleration available. You may use
OpenGL to create and delete texture objects and to determine which tex-
tures constitute your working set.
This chapter covers the OpenGL’s texture-mapping facility in the following
major sections.
• “An Overview and an Example” gives a brief, broad look at the steps
required to perform texture mapping. It also presents a relatively
simple example of texture mapping.
• “Specifying the Texture” explains how to specify one-, two-, or three-
dimensional textures. It also discusses how to use a texture’s borders,
how to supply a series of related textures of different sizes, and how
to control the filtering methods used to determine how an applied
texture is mapped to screen coordinates.
• “Filtering” details how textures are either magnified or minified as they
are applied to the pixels of polygons. Minification using special mipmap
textures is also explained.
• “Texture Objects” describes how to put texture images into objects so
that you can control several textures at one time. With texture objects,
you may be able to create a working set of high-performance textures,
which are said to be resident. You may also prioritize texture objects to
increase or decrease the likelihood that a texture object is resident.
• “Texture Functions” discusses the methods used for painting a texture
onto a surface. You can choose to have the texture color values replace
those that would be used if texturing were not in effect, or you can
have the final color be a combination of the two.
• “Assigning Texture Coordinates” describes how to compute and assign
appropriate texture coordinates to the vertices of an object. It also
explains how to control the behavior of coordinates that lie outside the
default range—that is, how to repeat or clamp textures across a surface.
• “Automatic Texture-Coordinate Generation” shows how to have
OpenGL automatically generate texture coordinates so that you can
achieve such effects as contour and environment maps.

393
• “Multitexturing” details how textures may be applied in a serial pipe-
line of successive texturing operations.
• “Texture Combiner Functions” explains how you can control mathe-
matical operations (multiplication, addition, subtraction, interpolation,
and even dot products) on the RGB and alpha values of textures, con-
stant colors, and incoming fragments. Combiner functions expose
flexible, programmable fragment processing.
• “Applying Secondary Color after Texturing” shows how secondary
colors are applied to fragments after texturing.
• “Point Sprites” discusses how textures can be applied to large points to
improve their visual quality.
• “The Texture Matrix Stack” explains how to manipulate the texture
matrix stack and use the q texture coordinate.
• “Depth Textures” describes the process for using the values stored in the
depth buffer as a texture for use in determining shadowing for a scene.
Version 1.1 of OpenGL introduced several texture-mapping operations:
• Additional internal texture image formats
• Texture proxy, to query whether there are enough resources to
accommodate a given texture image
• Texture subimage, to replace all or part of an existing texture
image, rather than completely delete and create a texture to
achieve the same effect
• Specifying texture data from framebuffer memory (as well as from
system memory)
• Texture objects, including resident textures and prioritizing
Version 1.2 added:
• 3D texture images
• A new texture-coordinate wrapping mode, GL_CLAMP_TO_EDGE,
which derives texels from the edge of a texture image, not its border
• Greater control over mipmapped textures to represent different
levels of detail (LOD)
• Calculating specular highlights (from lighting) after texturing
operations
Chapter 9: Texture Mapping

394 Chapter 9: Texture Mapping
Version 1.3 granted more texture-mapping operations:
• Compressed textures
• Cube map textures
• Multitexturing, which is applying several textures to render a
single primitive
• Texture-wrapping mode, GL_CLAMP_TO_BORDER
• Texture environment modes: GL_ADD and GL_COMBINE
(including the dot product combination function)
Version 1.4 supplied these texture capabilities:
• Texture-wrapping mode, GL_MIRRORED_REPEAT
• Automatic mipmap generation with GL_GENERATE_MIPMAP
• Texture parameter GL_TEXTURE_LOD_BIAS, which alters selection
of the mipmap level of detail
• Application of a secondary color (specified by glSecondaryColor*())
after texturing
• During the texture combine environment mode, the ability to use
texture color from different texture units as sources for the texture
combine function
• Use of depth (r coordinate) as an internal texture format and
texturing modes that compare depth texels to decide upon texture
application
Version 1.5 added support for:
• Additional texture-comparison modes for use of textures for shadow
mapping
Version 2.0 modified texture capabilities by:
• Removing the power-of-two restriction on texture maps
• Iterated texture coordinates across point sprites
Version 2.1 added the following enhancements:
• Specifying textures in sRGB format, which accepts gamma-corrected
red, green, and blue texture components
• Specifying and retrieving pixel rectangle data in server-side buffer
objects. See “Using Buffer Objects with Pixel Rectangle Data” in
Chapter 8 for details on using pixel buffer objects.

An Overview and an Example 395
Version 3.0 contributed even more texturing features:
• Storing texels in floating-point, signed integer, and unsigned integer
formats without being normalized (mapped into the range [-1,1] or
[0,1] respectively)
• One- and two-dimensional texture arrays, which allow indexing into
an array of one- or two-dimensional texture maps using the next-
higher-dimension texture coordinate
• A standardized texture format, RGTC, for one- and two-component
textures
If you try to use one of these texture-mapping operations and can’t find it,
check the version number of your implementation of OpenGL to see if it
actually supports it. (See “Which Version Am I Using?” in Chapter 14.) In
some implementations, a particular feature may be available only as an
extension.
For example, in OpenGL Version 1.2, multitexturing was approved by the
Khronos OpenGL ARB Working Group, the governing body for OpenGL,
as an optional extension. An implementation of OpenGL 1.2 supporting
multitexturing would have function and constant names suffixed with
ARB, such as glActiveTextureARB(GL_TEXTURE1_ARB). In OpenGL 1.3,
multitexturing became mandatory, and the ARB suffix was removed.
An Overview and an Example
This section gives an overview of the steps necessary to perform texture
mapping. It also presents a relatively simple texture-mapping program. Of
course, you know that texture mapping can be a very involved process.
Steps in Texture Mapping
To use texture mapping, you perform the following steps:
1. Create a texture object and specify a texture for that object.
2. Indicate how the texture is to be applied to each pixel.
3. Enable texture mapping.
4. Draw the scene, supplying both texture and geometric coordinates.

396 Chapter 9: Texture Mapping
Keep in mind that texture mapping works only in RGBA mode. Texture
mapping results in color-index mode are undefined.
Create a Texture Object and Specify a Texture for That Object
A texture is usually thought of as being two-dimensional, like most images,
but it can also be one-dimensional or three-dimensional. The data describ-
ing a texture may consist of one, two, three, or four elements per texel and
may represent an (R, G, B, A) quadruple, a modulation constant, or a depth
component.
In Example 9-1, which is very simple, a single texture object is created to
maintain a single uncompressed, two-dimensional texture. This example
does not find out how much memory is available. Since only one texture is
created, there is no attempt to prioritize or otherwise manage a working set
of texture objects. Other advanced techniques, such as texture borders,
mipmaps, or cube maps, are not used in this simple example.
Indicate How the Texture Is to Be Applied to Each Pixel
You can choose any of four possible functions for computing the final
RGBA value from the fragment color and the texture image data. One
possibility is simply to use the texture color as the final color; this is the
replace mode, in which the texture is painted on top of the fragment, just
as a decal would be applied. (Example 9-1 uses replace mode.) Another
method is to use the texture to modulate, or scale, the fragment’s color; this
technique is useful for combining the effects of lighting with texturing.
Finally, a constant color can be blended with that of the fragment, based
on the texture value.
Enable Texture Mapping
You need to enable texturing before drawing your scene. Texturing is
enabled or disabled using glEnable() or glDisable(), with the symbolic
constant GL_TEXTURE_1D, GL_TEXTURE_2D, GL_TEXTURE_3D, or
GL_TEXTURE_CUBE_MAP for one-, two-, three-dimensional, or cube map
texturing, respectively. (If two or all three of the dimensional texturing
modes are enabled, the largest dimension enabled is used. If cube map
textures are enabled, it trumps all the others. For the sake of clean programs,
you should enable only the one you want to use.)

An Overview and an Example 397
Draw the Scene, Supplying Both Texture and Geometric Coordinates
You need to indicate how the texture should be aligned relative to the frag-
ments to which it’s to be applied before it’s “glued on.” That is, you need to
specify both texture coordinates and geometric coordinates as you specify
the objects in your scene. For a two-dimensional texture map, for example,
the texture coordinates range from 0.0 to 1.0 in both directions, but the
coordinates of the items being textured can be anything. To apply the brick
texture to a wall, for example, assuming the wall is square and meant to rep-
resent one copy of the texture, the code would probably assign texture coor-
dinates (0, 0), (1, 0), (1, 1), and (0, 1) to the four corners of the wall. If the
wall is large, you might want to paint several copies of the texture map on
it. If you do so, the texture map must be designed so that the bricks at the
left edge match up nicely with the bricks at the right edge, and similarly for
the bricks at the top and bottom.
You must also indicate how texture coordinates outside the range [0.0, 1.0]
should be treated. Do the textures repeat to cover the object, or are they
clamped to a boundary value?
A Sample Program
One of the problems with showing sample programs to illustrate texture
mapping is that interesting textures are large. Typically, textures are read
from an image file, since specifying a texture programmatically could take
hundreds of lines of code. In Example 9-1, the texture—which consists of
alternating white and black squares, like a checkerboard—is generated by
the program. The program applies this texture to two squares, which are
then rendered in perspective, one of them facing the viewer squarely and
the other tilting back at 45 degrees, as shown in Figure 9-2. In object
coordinates, both squares are the same size.
Figure 9-2 Texture-Mapped Squares

398 Chapter 9: Texture Mapping
Example 9-1 Texture-Mapped Checkerboard: checker.c
/* Create checkerboard texture */
#define checkImageWidth 64
#define checkImageHeight 64
static GLubyte checkImage[checkImageHeight][checkImageWidth][4];
static GLuint texName;
void makeCheckImage(void)
{
int i, j, c;
for (i = 0; i < checkImageHeight; i++) {
for (j = 0; j < checkImageWidth; j++) {
c = (((i&0x8)==0)^((j&0x8))==0)*255;
checkImage[i][j][0] = (GLubyte) c;
checkImage[i][j][1] = (GLubyte) c;
checkImage[i][j][2] = (GLubyte) c;
checkImage[i][j][3] = (GLubyte) 255;
}
}
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
glEnable(GL_DEPTH_TEST);
makeCheckImage();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glGenTextures(1, &texName);
glBindTexture(GL_TEXTURE_2D, texName);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, checkImageWidth,
checkImageHeight, 0, GL_RGBA, GL_UNSIGNED_BYTE,
checkImage);
}
void display(void)
{

An Overview and an Example 399
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnable(GL_TEXTURE_2D);
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);
glBindTexture(GL_TEXTURE_2D, texName);
glBegin(GL_QUADS);
glTexCoord2f(0.0, 0.0); glVertex3f(-2.0, -1.0, 0.0);
glTexCoord2f(0.0, 1.0); glVertex3f(-2.0, 1.0, 0.0);
glTexCoord2f(1.0, 1.0); glVertex3f(0.0, 1.0, 0.0);
glTexCoord2f(1.0, 0.0); glVertex3f(0.0, -1.0, 0.0);
glTexCoord2f(0.0, 0.0); glVertex3f(1.0, -1.0, 0.0);
glTexCoord2f(0.0, 1.0); glVertex3f(1.0, 1.0, 0.0);
glTexCoord2f(1.0, 1.0); glVertex3f(2.41421, 1.0, -1.41421);
glTexCoord2f(1.0, 0.0); glVertex3f(2.41421, -1.0, -1.41421);
glEnd();
glFlush();
glDisable(GL_TEXTURE_2D);
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, (GLfloat) w/(GLfloat) h, 1.0, 30.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0, 0.0, -3.6);
}
/* keyboard() and main() deleted to reduce printing */
The checkerboard texture is generated in the routine makeCheckImage(),
and all the texture-mapping initialization occurs in the routine init().
glGenTextures() and glBindTexture() name and create a texture object for a
texture image. (See “Texture Objects” on page 437.) The single, full-resolution
texture map is specified by glTexImage2D(), whose parameters indicate the
size, type, location, and other properties of the texture image. (See “Specifying
the Texture” below for more information about glTexImage2D().)
The four calls to glTexParameter*() specify how the texture is to be wrapped
and how the colors are to be filtered if there isn’t an exact match between
texels in the texture and pixels on the screen. (See “Filtering” on page 434
and “Repeating and Clamping Textures” on page 452.)
In display(),glEnable() turns on texturing. glTexEnv*() sets the drawing
mode to GL_REPLACE so that the textured polygons are drawn using the
400 Chapter 9: Texture Mapping
colors from the texture map (rather than taking into account the color in
which the polygons would have been drawn without the texture).
Then, two polygons are drawn. Note that texture coordinates are specified
along with vertex coordinates. The glTexCoord*() command behaves simi-
larly to the glNormal() command. glTexCoord*() sets the current texture
coordinates; any subsequent vertex command has those texture coordinates
associated with it until glTexCoord*() is called again.
Note: The checkerboard image on the tilted polygon might look wrong
when you compile and run it on your machine—for example,
it might look like two triangles with different projections of the
checkerboard image on them. If so, try setting the parameter
GL_PERSPECTIVE_CORRECTION_HINT to GL_NICEST and
running the example again. To do this, use glHint().
Specifying the Texture
The command glTexImage2D() defines a two-dimensional texture. It takes
several arguments, which are described briefly here and in more detail in
the subsections that follow. The related commands for one- and three-
dimensional textures, glTexImage1D() and glTexImage3D(), are described
in “Texture Rectangles” and “Three-Dimensional Textures,” respectively.
void glTexImage2D(GLenum target, GLint level, GLint internalFormat,
GLsizei width, GLsizei height, GLint border,
GLenum format, GLenum type, const GLvoid *texels);
Defines a two-dimensional texture, or a one-dimensional texture array.
The target parameter is set to one of the constants: GL_TEXTURE_2D,
GL_PROXY_TEXTURE_2D, GL_TEXTURE_CUBE_MAP_POSITIVE_X,
GL_TEXTURE_CUBE_MAP_NEGATIVE_X, GL_TEXTURE_CUBE_MAP_
POSITIVE_Y, GL_TEXTURE_CUBE_MAP_NEGATIVE_Y, GL_TEXTURE_
CUBE_MAP_POSITIVE_Z, GL_TEXTURE_CUBE_MAP_NEGATIVE_Z,
or GL_PROXY_TEXTURE_CUBE_MAP for defining two-dimensional
textures, (See “Cube Map Textures” for information about use of the
GL_*CUBE_MAP* constants with glTexImage2D and related functions),
and GL_TEXTURE_1D_ARRAY and GL_PROXY_TEXTURE_1D_ARRAY for
defining a one-dimensional texture array (which are only available if the
OpenGL version is 3.0 or greater. See “Texture Arrays” on page 419.), or
GL_TEXTURE_RECTANGLE and GL_PROXY_TEXTURE_RECTANGLE.

Specifying the Texture 401
You use the level parameter if you’re supplying multiple resolutions of the
texture map; with only one resolution, level should be 0. (See “Mipmaps:
Multiple Levels of Detail” for more information about using multiple
resolutions.)
The next parameter, internalFormat, indicates which components
(RGBA, depth, luminance, or intensity) are selected for the texels of an
image. There are three groups of internal formats. First, the following
symbolic constants for internalFormat specify that texel values should be
normalized (mapped into the range [0,1]) and stored in a fixed-point
representation (of the number of bits specified if there’s a numeric value
included in the token name): GL_ALPHA, GL_ALPHA4, GL_ALPHA8,
GL_ALPHA12, GL_ALPHA16, GL_COMPRESSED_ALPHA,
GL_COMPRESSED_LUMINANCE, GL_COMPRESSED_LUMINANCE_
ALPHA, GL_COMPRESSED_INTENSITY, GL_COMPRESSED_RGB,
GL_COMPRESSED_RGBA, GL_DEPTH_COMPONENT, GL_DEPTH_
COMPONENT16, GL_DEPTH_COMPONENT24, GL_DEPTH_
COMPONENT32, GL_DEPTH_STENCIL, GL_INTENSITY,
GL_INTENSITY4, GL_INTENSITY8, GL_INTENSITY12, GL_INTENSITY16,
GL_LUMINANCE, GL_LUMINANCE4, GL_LUMINANCE8,
GL_LUMINANCE12, GL_LUMINANCE16, GL_LUMINANCE_ALPHA,
GL_LUMINANCE4_ALPHA4, GL_LUMINANCE6_ALPHA2,
GL_LUMINANCE8_ALPHA8, GL_LUMINANCE12_ALPHA4,
GL_LUMINANCE12_ALPHA12, GL_LUMINANCE16_ALPHA16, GL_RED,
GL_R8, GL_R16, GL_RG, GL_RG8, GL_RG16, GL_RGB, GL_R3_G3_B2,
GL_RGB4, GL_RGB5, GL_RGB8, GL_RGB10, GL_RGB12, GL_RGB16,
GL_RGBA, GL_RGBA2, GL_RGBA4, GL_RGB5_A1, GL_RGBA8, GL_RGB10_A2,
GL_RGBA12, GL_RGBA16, GL_SRGB, GL_SRGB8, GL_SRGB_ALPHA,
GL_SRGB8_ALPHA8, GL_SLUMINANCE_ALPHA, GL_SLUMINANCE8_
ALPHA8, GL_SLUMINANCE, GL_SLUMINANCE8, GL_COMPRESSED_
SRGB, GL_COMPRESSED_SRGB_ALPHA, GL_COMPRESSED_
SLUMINANCE, or GL_COMPRESSED_SLUMINANCE_ALPHA. (See
“Texture Functions” for a discussion of how these selected components
are applied, and see “Compressed Texture Images” for a discussion of how
compressed textures are handled.)
The next sets of symbolic constants for internalFormat were added in
OpenGL version 3.0, and specify floating-point pixel formats, which are
not normalized (and stored in floating-point values of the specified
number of bits): GL_R16F, GL_R32F, GL_RG16F, GL_RG32F, GL_RGB16F,
GL_RGB32F, GL_RGBA16F, GL_RGBA32F, GL_R11F_G11F_B10F, and
GL_RGB9_E5. Another set of symbolic constants accepted represent signed-
and unsigned-integer (denoted with the additional “U” in the token)

402 Chapter 9: Texture Mapping
formats (stored in the respective integer types of the specified bitwidth):
GL_R8I, GL_R8UI, GL_R16I, GL_R16UI, GL_R32I, GL_R32UI, GL_RG8I,
GL_RG8UI, GL_RG16I, GL_RG16UI, GL_RG32I, GL_RG32UI, GL_RGB8I,
GL_RGB8UI, GL_RGB16I, GL_RGB16UI, GL_RGB32I, GL_RGB32UI,
GL_RGBA8I, GL_RGBA8UI, GL_RGBA16I, GL_RGBA16UI, GL_RGBA32I,
and GL_RGBA32UI. Additionally, textures can be stored in a compressed
form if internalFormat is one of: GL_COMPRESSED_RED, GL_COMPRESSED_
RG, and in the specific compressed texture formats: GL_COMPRESSED_
RED_RGTC1, GL_COMPRESSED_SIGNED_RED_RGTC1, GL_
COMPRESSED_RG_RGTC2, and GL_COMPRESSED_SIGNED_RG_RGTC2,
and for sized depth and stencil formats, OpenGL version 3.0 added:
GL_DEPTH_COMPONENT16, GL_DEPTH_COMPONENT24, GL_DEPTH_
COMPONENT32F, and GL_DEPTH24_STENCIL8, and GL_DEPTH32F_
STENCIL8 for packed stencil-depth dual-channel texels.
OpenGL version 3.1 added support for signed normalized values (which
are mapped the range [-1,1]), and are specified for internalFormat with the
tokens: GL_R8_SNORM, GL_R16_SNORM, GL_RG8_SNORM, GL_RG16_
SNORM, GL_RGB8_SNORM, GL_RGB16_SNORM, GL_RGBA8_SNORM,
GL_RGBA16_SNORM.
The internalFormat may request a specific resolution of components. For
example, if internalFormat is GL_R3_G3_B2, you are asking that texels be 3
bits of red, 3 bits of green, and 2 bits of blue. By definition, GL_INTENSITY,
GL_LUMINANCE, GL_LUMINANCE_ALPHA, GL_DEPTH_COMPONENT,
GL_RGB, GL_RGBA, GL_SRGB, GL_SRGB_ALPHA, GL_SLUMINANCE,
GL_SLUMINANCE_ALPHA, and the compressed forms of the above
tokens are lenient, because they do not ask for a specific resolution. (For
compatibility with the OpenGL release 1.0, the numeric values 1, 2, 3, and 4
for internalFormat are equivalent to the symbolic constants GL_LUMINANCE,
GL_LUMINANCE_ALPHA, GL_RGB, and GL_RGBA, respectively.)
The width and height parameters give the dimensions of the texture image;
border indicates the width of the border, which is either 0 (no border)
or 1 (and must be 0 for version 3.1 implementations). For OpenGL
implementations that do not support version 2.0 or greater, both width
and height must have the form 2m+2b, where m is a non-negative integer
(which can have a different value for width than for height) and b is the
value of border. The maximum size of a texture map depends on the
implementation of OpenGL, but it must be at least 64 u64 (or 66 u66
with borders). For OpenGL implementations supporting version 2.0
and greater, textures may be of any size. The format and type parameters
describe the format and data type of the texture image data. They have the

Specifying the Texture 403
As you can see by the myriad of accepted values, the internal format of a tex-
ture image may affect the performance of texture operations. For example,
some implementations perform texturing faster with GL_RGBA than with
GL_RGB, because the color components align to processor memory better.
Since this varies, you should check specific information about your imple-
mentation of OpenGL.
The internal format of a texture image also may control how much
memory a texture image consumes. For example, a texture of internal
format GL_RGBA8 uses 32 bits per texel, while a texture of internal format
GL_R3_G3_B2 uses only 8 bits per texel. Of course, there is a corresponding
trade-off between memory consumption and color resolution.
A GL_DEPTH_COMPONENT texture stores depth values, as compared to
colors, and is most often used for rendering shadows (as described in
“Depth Textures” on page 483). Similarly a GL_DEPTH_STENCIL texture
stores depth and stencil values in the same texture.
Textures specified with an internal format of GL_SRGB, GL_SRGB8,
GL_SRGB_ALPHA, GL_SRGB8_ALPHA8, GL_SLUMINANCE_ALPHA,
same meaning as they do for glDrawPixels(). (See “Imaging Pipeline” in
Chapter 8.) In fact, texture data is in the same format as the data used by
glDrawPixels(), so the settings of glPixelStore*() and glPixelTransfer*()
are applied. (In Example 9-1, the call
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
is made because the data in the example isn’t padded at the end of each
texel row.) The format parameter can be GL_COLOR_INDEX, GL_DEPTH_
COMPONENT, GL_RGB, GL_RGBA, GL_RED, GL_GREEN, GL_BLUE,
GL_ALPHA, GL_LUMINANCE, or GL_LUMINANCE_ALPHA—that is,
the same formats available for glDrawPixels() with the exception of
GL_STENCIL_INDEX. OpenGL version 3.0 additionally permits the
following formats: GL_DEPTH_STENCIL, GL_RG, GL_RED_INTEGER,
GL_GREEN_INTEGER, GL_BLUE_INTEGER, GL_ALPHA_INTEGER,
GL_RG_INTEGER, GL_RGB_INTEGER, GL_RGBA_INTEGER, GL_BGR_
INTEGER, and GL_BGRA_INTEGER.
Similarly, the type parameter can be GL_BYTE, GL_UNSIGNED_BYTE,
GL_SHORT, GL_UNSIGNED_SHORT, GL_INT, GL_UNSIGNED_INT,
GL_FLOAT, GL_BITMAP, or one of the packed pixel data types.
Finally, texels contains the texture image data. This data describes the
texture image itself as well as its border.

404 Chapter 9: Texture Mapping
GL_SLUMINANCE8_ALPHA8, GL_SLUMINANCE, GL_SLUMINANCE8,
GL_COMPRESSED_SRGB, GL_COMPRESSED_SRGB_ALPHA,
GL_COMPRESSED_SLUMINANCE, or GL_COMPRESSED_SLUMINANCE_
ALPHA) are expected to have their red, green, and blue color components
specified in the sRGB color space (officially known as the International
Electrotechnical Commission IEC standard 61966-2-1). The sRGB color
space is approximately the same as the 2.2 gamma-corrected linear RGB
color space. For sRGB textures, the alpha values in the texture should not
be gamma corrected.
For internal formats with the suffixes of “F”, “I”, or “UI”, the format of a
texel is stored in a floating-point value, signed integer, or unsigned integer,
respectively, of the specified number of bits (e.g., GL_R16F would store a single
channel texture with each texel being a 16-bit floating-point value). All of these
formats were added in OpenGL Version 3.0. For these formats, the values are
not mapped into the range [0,1], but rather are allowed their full numeric
precision. One other special format that involves floating-point values is the
packed shared-exponent format, which specifies the red, green, and blue values
as floating-point values, all of which have the same exponent value. All of these
formats are described in the online appendix Appendix J, “Floating-Point
Formats for Textures, Framebuffers, and Renderbuffers.”1
Integer internal texture formats (those with an “I” or “UI” suffix) require
their input data to match the specified integer size.
Signed-normalized values specified with internal formats including
GL_*_SNORM are converted into the range [-1,1].
Although texture mapping results in color-index mode are undefined, you
can still specify a texture with a GL_COLOR_INDEX image. In that case,
pixel-transfer operations are applied to convert the indices to RGBA values
by table lookup before they’re used to form the texture image.
If your OpenGL implementation supports the Imaging Subset and any of its
features are enabled, the texture image will be affected by those features. For
example, if the two-dimensional convolution filter is enabled, then the
convolution will be performed on the texture image. (The convolution may
change the image’s width and/or height.)
For OpenGL versions prior to Version 2.0, the number of texels for both the
width and the height of a texture image, not including the optional border,
must be a power of 2. If your original image does not have dimensions that
fit that limitation, you can use the OpenGL Utility Library routine
gluScaleImage() to alter the sizes of your textures.
1This appendix is available online at http://www.opengl-redbook.com/appendices/.

Specifying the Texture 405
Note: In GLU 1.3, gluScaleImage() supports packed pixel formats (and
their related data types), but likely does not support those of OpenGL
Version 3.0 and later.
The framebuffer itself can also be used as a source for texture data.
glCopyTexImage2D() reads a rectangle of pixels from the framebuffer and
uses that rectangle as texels for a new texture.
int gluScaleImage(GLenum format, GLint widthin, GLint heightin,
GLenum typein, const void *datain, GLint widthout,
GLint heightout, GLenum typeout, void *dataout);
Scales an image using the appropriate pixel-storage modes to unpack the
data from datain. The format,typein, and typeout parameters can refer to
any of the formats or data types supported by glDrawPixels(). The image
is scaled using linear interpolation and box filtering (from the size
indicated by widthin and heightin to widthout and heightout), and the
resulting image is written to dataout, using the pixel GL_PACK* storage
modes. The caller of gluScaleImage() must allocate sufficient space for
the output buffer. A value of 0 is returned on success, and a GLU error
code is returned on failure.
void glCopyTexImage2D(GLenum target, GLint level,
GLint internalFormat, GLint x, GLint y,
GLsizei width, GLsizei height, GLint border);
Creates a two-dimensional texture, using framebuffer data to define the
texels. The pixels are read from the current GL_READ_BUFFER and are
processed exactly as if glCopyPixels() had been called, but instead of going
to the framebuffer, the pixels are placed into texture memory. The settings
of glPixelTransfer*() and other pixel-transfer operations are applied.
The target parameter must be one of the constants GL_TEXTURE_2D,
GL_TEXTURE_CUBE_MAP_POSITIVE_X, GL_TEXTURE_CUBE_MAP_
NEGATIVE_X, GL_TEXTURE_CUBE_MAP_POSITIVE_Y, GL_TEXTURE_
CUBE_MAP_NEGATIVE_Y, GL_TEXTURE_CUBE_MAP_POSITIVE_Z, or
GL_TEXTURE_CUBE_MAP_NEGATIVE_Z (see “Cube Map Textures” on
page 465 for information about use of the *CUBE_MAP* constants), or
GL_TEXTURE_1D_ARRAY (see “Texture Arrays” on page 419). The level,
internalFormat, and border parameters have the same effects that they have
for glTexImage2D(). The texture array is taken from a screen-aligned pixel

406 Chapter 9: Texture Mapping
If your OpenGL implementation is Version 3.0 or later, you can use
framebuffer objects to effectively perform the same operation as
glCopyPixels2D() by rendering directly into texture memory. This
process is described in detail in “Framebuffer Objects” in Chapter 10.
The next sections give more detail about texturing, including the use of
the target, border, and level parameters. The target parameter can be used
to query accurately the size of a texture (by creating a texture proxy with
glTexImage*D()) and whether a texture possibly can be used within the
texture resources of an OpenGL implementation. Redefining a portion of a
texture is described in “Replacing All or Part of a Texture Image” on page 408.
One- and three-dimensional textures are discussed in “Texture Rectangles” on
page 412 and “Three-Dimensional Textures” on page 414, respectively. The
texture border, which has its size controlled by the border parameter, is
detailed in “Compressed Texture Images” on page 420. The level parameter is
used to specify textures of different resolutions and is incorporated into the
special technique of mipmapping, which is explained in “Mipmaps: Multiple
Levels of Detail” on page 423. Mipmapping requires understanding how to
filter textures as they are applied; filtering is covered on page 434.
Texture Proxy
To an OpenGL programmer who uses textures, size is important. Texture
resources are typically limited, and texture format restrictions vary among
OpenGL implementations. There is a special texture proxy target to evalu-
ate whether your OpenGL implementation is capable of supporting a par-
ticular texture format at a particular texture size.
glGetIntegerv(GL_MAX_TEXTURE_SIZE,...) tells you a lower bound on the
largest width or height (without borders) of a texture image; typically, the
size of the largest square texture supported. For 3D textures, GL_MAX_3D_
TEXTURE_SIZE may be used to query the largest allowable dimension (width,
height, or depth, without borders) of a 3D texture image. For cube map
textures, GL_MAX_CUBE_MAP_TEXTURE_SIZE is similarly used.
rectangle with the lower left corner at coordinates specified by the (x,y)
parameters. The width and height parameters specify the size of this pixel
rectangle. For OpenGL implementations that do not support Version 2.0,
both width and height must have the form 2m+2b, where m is a non-
negative integer (which can have a different value for width than for height)
and b is the value of border. For implementations supporting OpenGL
Version 2.0 and greater, textures may be of any size.

Specifying the Texture 407
However, use of any of the GL_MAX*TEXTURE_SIZE queries does not
consider the effect of the internal format or other factors. A texture image
that stores texels using the GL_RGBA16 internal format may be using
64 bits per texel, so its image may have to be 16 times smaller than an image
with the GL_LUMINANCE4 internal format. Textures requiring borders or
mipmaps further reduce the amount of available memory.
A special placeholder, or proxy, for a texture image allows the program to
query more accurately whether OpenGL can accommodate a texture of a
desired internal format.
For instance, to find out whether there are enough resources available for
a standard 2D texture, call glTexImage2D() with a target parameter of
GL_PROXY_TEXTURE_2D and the given level, internalFormat, width, height,
border, format, and type. For a proxy, you should pass NULL as the pointer
for the texels array. (For a cube map, use glTexImage2D() with the target
GL_PROXY_TEXTURE_CUBE_MAP. For one- or three-dimensional textures,
texture rectangles, and texture arrays, use the corresponding routines and
symbolic constants.)
After the texture proxy has been created, query the texture state variables
with glGetTexLevelParameter*(). If there aren’t enough resources to
accommodate the texture proxy, the texture state variables for width,
height, border width, and component resolutions are set to 0.
void glGetTexLevelParameter{if}v(GLenum target, GLint level,
GLenum pname,TYPE *params);
Returns in params texture parameter values for a specific level of detail,
specified as level.target defines the target texture and is GL_TEXTURE_1D,
GL_TEXTURE_2D, GL_TEXTURE_3D, GL_TEXTURE_CUBE_MAP_
POSITIVE_X, GL_TEXTURE_CUBE_MAP_NEGATIVE_X, GL_TEXTURE_
CUBE_MAP_POSITIVE_Y, GL_TEXTURE_CUBE_MAP_NEGATIVE_Y,
GL_TEXTURE_CUBE_MAP_POSITIVE_Z, GL_TEXTURE_CUBE_MAP_
NEGATIVE_Z, GL_TEXTURE_1D_ARRAY, GL_TEXTURE_2D_ARRAY,
GL_TEXTURE_RECTANGLE, GL_PROXY_TEXTURE_1D, GL_PROXY_
TEXTURE_1D_ARRAY, GL_PROXY_TEXTURE_2D, GL_PROXY_TEXTURE_
2D_ARRAY, GL_PROXY_TEXTURE_3D, GL_PROXY_TEXTURE_CUBE_
MAP, or GL_PROXY_TEXTURE_RECTANGLE. (GL_TEXTURE_CUBE_MAP
is not valid, because it does not specify a particular face of a cube map.)
Accepted values for pname are GL_TEXTURE_WIDTH, GL_TEXTURE_
HEIGHT, GL_TEXTURE_DEPTH, GL_TEXTURE_BORDER, GL_TEXTURE_
INTERNAL_FORMAT, GL_TEXTURE_RED_SIZE, GL_TEXTURE_GREEN_
SIZE, GL_TEXTURE_BLUE_SIZE, GL_TEXTURE_ALPHA_SIZE, GL_
TEXTURE_LUMINANCE_SIZE, and GL_TEXTURE_INTENSITY_SIZE.

408 Chapter 9: Texture Mapping
Example 9-2 demonstrates how to use the texture proxy to find out if there
are enough resources to create a 64u64 texel texture with RGBA components
with 8 bits of resolution. If this succeeds, then glGetTexLevelParameteriv()
stores the internal format (in this case, GL_RGBA8) into the variable format.
Example 9-2 Querying Texture Resources with a Texture Proxy
GLint width;
glTexImage2D(GL_PROXY_TEXTURE_2D, 0, GL_RGBA8,
64, 64, 0, GL_RGBA, GL_UNSIGNED_BYTE, NULL);
glGetTexLevelParameteriv(GL_PROXY_TEXTURE_2D, 0,
GL_TEXTURE_WIDTH, &width);
Note: There is one major limitation with texture proxies: The texture proxy
answers the question of whether a texture is capable of being loaded
into texture memory. The texture proxy provides the same answer,
regardless of how texture resources are currently being used. If other
textures are using resources, then the texture proxy query may respond
affirmatively, but there may not be enough resources to make your
texture resident (that is, part of a possibly high-performance working
set of textures). The texture proxy does not answer the question of
whether there is sufficient capacity to handle the requested texture.
(See “Texture Objects” for more information about managing resident
textures.)
Replacing All or Part of a Texture Image
Creating a texture may be more computationally expensive than modify-
ing an existing one. Often it is better to replace all or part of a texture
image with new information, rather than create a new one. This can be
helpful for certain applications, such as using real-time, captured video
images as texture images. For that application, it makes sense to create a
single texture and use glTexSubImage2D() to replace repeatedly the tex-
ture data with new video images. Also, there are no size restrictions for
glTexSubImage2D() that force the height or width to be a power of 2.
(This is helpful for processing video images, which generally do not have
sizes that are powers of 2. However, you must load the video images into
an initial, larger image that must have 2n texels for each dimension, and
adjust texture coordinates for the subimages.)
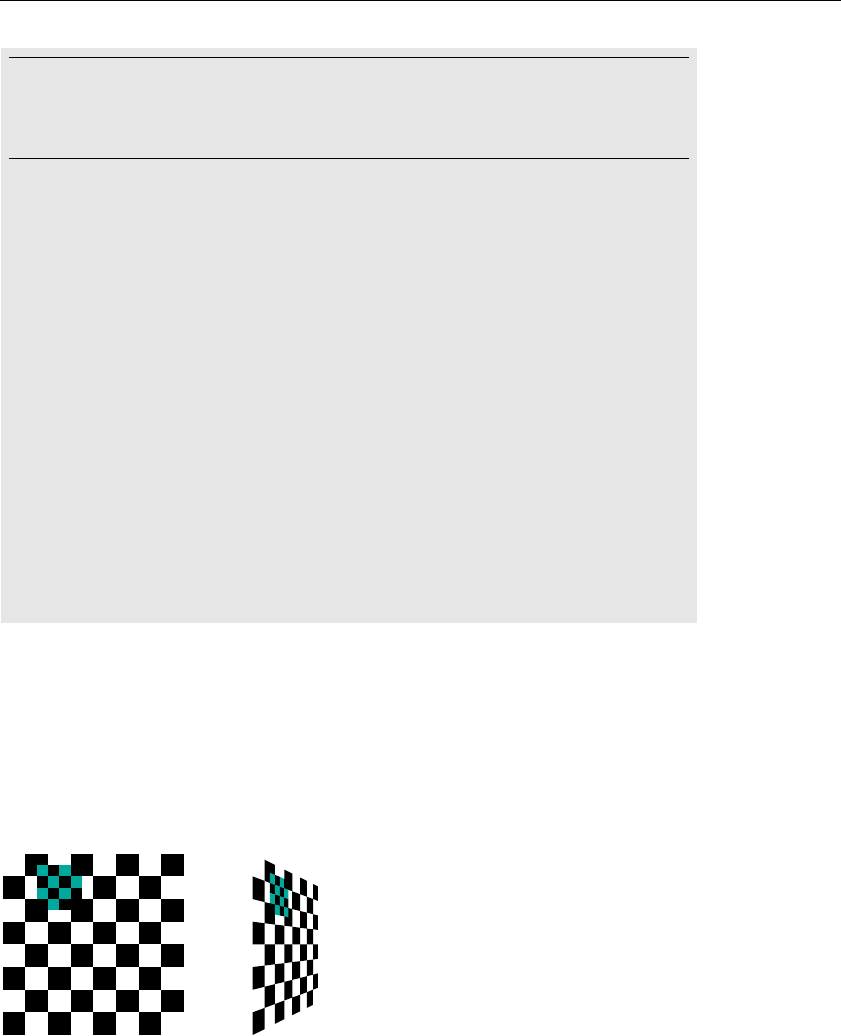
Specifying the Texture 409
In Example 9-3, some of the code from Example 9-1 has been modified
so that pressing the ‘s’ key drops a smaller checkered subimage into the
existing image. (The resulting texture is shown in Figure 9-3.) Pressing
the ‘r’ key restores the original image. Example 9-3 shows the two routines,
makeCheckImages() and keyboard(), that have been substantially changed.
(See “Texture Objects” for more information about glBindTexture().)
void glTexSubImage2D(GLenum target, GLint level, GLint xoffset,
GLint yoffset, GLsizei width, GLsizei height,
GLenum format, GLenum type,
const GLvoid *texels);
Defines a two-dimensional texture image that replaces all or part of
a contiguous subregion (in 2D, it’s simply a rectangle) of the current,
existing two-dimensional texture image. The target parameter must be set
to one of the same options that are available for glCopyTexImage2D.
The level,format, and type parameters are similar to the ones used for
glTexImage2D().level is the mipmap level-of-detail number. It is not
an error to specify a width or height of 0, but the subimage will have no
effect. format and type describe the format and data type of the texture
image data. The subimage is also affected by modes set by glPixelStore*()
and glPixelTransfer*() and other pixel-transfer operations.
texels contains the texture data for the subimage. width and height are the
dimensions of the subregion that is replacing all or part of the current
texture image. xoffset and yoffset specify the texel offset in the x- and
y-directions—with (0, 0) at the lower left corner of the texture—and
specify where in the existing texture array the subimage should be placed.
This region may not include any texels outside the range of the originally
defined texture array.
Figure 9-3 Texture with Subimage Added

410 Chapter 9: Texture Mapping
Example 9-3 Replacing a Texture Subimage: texsub.c
/* Create checkerboard textures */
#define checkImageWidth 64
#define checkImageHeight 64
#define subImageWidth 16
#define subImageHeight 16
static GLubyte checkImage[checkImageHeight][checkImageWidth][4];
static GLubyte subImage[subImageHeight][subImageWidth][4];
void makeCheckImages(void)
{
int i, j, c;
for (i = 0; i < checkImageHeight; i++) {
for (j = 0; j < checkImageWidth; j++) {
c = (((i&0x8)==0) ^ ((j&0x8)==0))*255;
checkImage[i][j][0] = (GLubyte) c;
checkImage[i][j][1] = (GLubyte) c;
checkImage[i][j][2] = (GLubyte) c;
checkImage[i][j][3] = (GLubyte) 255;
}
}
for (i = 0; i < subImageHeight; i++) {
for (j = 0; j < subImageWidth; j++) {
c = (((i&0x4)==0) ^ ((j&0x4)==0))*255;
subImage[i][j][0] = (GLubyte) c;
subImage[i][j][1] = (GLubyte) 0;
subImage[i][j][2] = (GLubyte) 0;
subImage[i][j][3] = (GLubyte) 255;
}
}
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘s’:
case ‘S’:
glBindTexture(GL_TEXTURE_2D, texName);
glTexSubImage2D(GL_TEXTURE_2D, 0, 12, 44,
subImageWidth, subImageHeight, GL_RGBA,
GL_UNSIGNED_BYTE, subImage);
glutPostRedisplay();
break;
case ‘r’:

Specifying the Texture 411
case ‘R’:
glBindTexture(GL_TEXTURE_2D, texName);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA,
checkImageWidth, checkImageHeight, 0,
GL_RGBA, GL_UNSIGNED_BYTE, checkImage);
glutPostRedisplay();
break;
case 27:
exit(0);
break;
default:
break;
}
}
Once again, the framebuffer itself can be used as a source for texture data—
this time, a texture subimage. glCopyTexSubImage2D() reads a rectangle
of pixels from the framebuffer and replaces a portion of an existing texture
array. (glCopyTexSubImage2D() is something of a cross between
glCopyTexImage2D() and glTexSubImage2D().)
void glCopyTexSubImage2D(GLenum target, GLint level, GLint xoffset,
GLint yoffset, GLint x, GLint y,
GLsizei width, GLsizei height);
Uses image data from the framebuffer to replace all or part of a contiguous
subregion of the current, existing two-dimensional texture image. The
pixels are read from the current GL_READ_BUFFER and are processed
exactly as if glCopyPixels() had been called, but instead of going to the
framebuffer, the pixels are placed into texture memory. The settings of
glPixelTransfer*() and other pixel-transfer operations are applied.
The target parameter must be set to one of the same options that are avail-
able for glCopyTexImage2D.level is the mipmap level-of-detail number.
xoffset and yoffset specify the texel offset in the x- and y-directions—with
(0, 0) at the lower left corner of the texture—and specify where in the
existing texture array the subimage should be placed. The subimage tex-
ture array is taken from a screen-aligned pixel rectangle with the lower left
corner at coordinates specified by the (x,y) parameters. The width and
height parameters specify the size of this subimage rectangle.
For OpenGL Version 3.1, a GL_INVALID_VALUE error is generated if target
is GL_TEXTURE_RECTANGLE, and level is not zero.

412 Chapter 9: Texture Mapping
Texture Rectangles
OpenGL Version 3.1 added textures that are addressed by their texel
locations, and not normalized texture coordinates. These textures, specified
by a target of GL_TEXTURE_RECTANGLE, are very useful when you want a
direct mapping of texels to pixels during rendering. A few restrictions apply
when using texture rectangles, as they are called: No mipmap-based filtering
is done (e.g,. texture rectangles may not have mipmaps), nor can they be
compressed.
One-Dimensional Textures
Sometimes a one-dimensional texture is sufficient—for example, if you’re
drawing textured bands where all the variation is in one direction. A one-
dimensional texture behaves as a two-dimensional one with height =1, and
without borders along the top and bottom. All the two-dimensional texture
and subtexture definition routines have corresponding one-dimensional
routines. To create a simple one-dimensional texture, use glTexImage1D().
For a sample program that uses a one-dimensional texture map, see
Example 9-8.
If your OpenGL implementation supports the Imaging Subset and if the one-
dimensional convolution filter is enabled (GL_CONVOLUTION_1D), then
the convolution is performed on the texture image. (The convolution may
change the width of the texture image.) Other pixel operations may also be
applied.
To replace all or some of the texels of a one-dimensional texture, use
glTexSubImage1D().
void glTexImage1D(GLenum target, GLint level, GLint internalFormat,
GLsizei width, GLint border, GLenum format,
GLenum type, const GLvoid *texels);
Defines a one-dimensional texture. All the parameters have the same meanings
as for glTexImage2D(), except that texels is now a one-dimensional array. As
before, for OpenGL implementations that do not support OpenGL Version 2.0
or greater, the value of width is 2m (or 2m+ 2, if there’s a border), where m is a
non-negative integer. You can supply mipmaps and proxies (set target to GL_
PROXY_TEXTURE_1D), and the same filtering options are available as well.

Specifying the Texture 413
To use the framebuffer as the source of a new one-dimensional texture
or a replacement for an old one-dimensional texture, use either
glCopyTexImage1D() or glCopyTexSubImage1D().
void glTexSubImage1D(GLenum target, GLint level, GLint xoffset,
GLsizei width, GLenum format,
GLenum type, const GLvoid *texels);
Defines a one-dimensional texture array that replaces all or part of
a contiguous subregion (in 1D, a row) of the current, existing one-
dimensional texture image. The target parameter must be set to
GL_TEXTURE_1D.
The level,format, and type parameters are similar to the ones used for
glTexImage1D().level is the mipmap level-of-detail number. format
and type describe the format and data type of the texture image data.
The subimage is also affected by modes set by glPixelStore*(),
glPixelTransfer*(), or other pixel-transfer operations.
texels contains the texture data for the subimage. width is the number of
texels that replace part or all of the current texture image. xoffset specifies
the texel offset in the existing texture array where the subimage should be
placed.
void glCopyTexImage1D(GLenum target, GLint level,
GLint internalFormat, GLivnt x, GLint y,
GLsizei width, GLint border);
Creates a one-dimensional texture using framebuffer data to define the
texels. The pixels are read from the current GL_READ_BUFFER and are
processed exactly as if glCopyPixels() had been called, but instead of
going to the framebuffer, the pixels are placed into texture memory.
The settings of glPixelStore*() and glPixelTransfer*() are applied.
The target parameter must be set to the constant GL_TEXTURE_1D. The
level, internalFormat, and border parameters have the same effects that they
have for glCopyTexImage2D(). The texture array is taken from a row of
pixels with the lower left corner at coordinates specified by the (x,y)
parameters. The width parameter specifies the number of pixels in this
row. For OpenGL implementations that do not support Version 2.0, the
value of width is 2m (or 2m+ 2 if there’s a border), where m is a non-
negative integer.

414 Chapter 9: Texture Mapping
Three-Dimensional Textures
Advanced
Three-dimensional textures are most often used for rendering in medical
and geoscience applications. In a medical application, a three-dimensional
texture may represent a series of layered computed tomography (CT) or
magnetic resonance imaging (MRI) images. To an oil and gas researcher,
a three-dimensional texture may model rock strata. (Three-dimensional
texturing is part of an overall category of applications, called volume
rendering. Some advanced volume rendering applications deal with voxels,
which represent data as volume-based entities.)
Due to their size, three-dimensional textures may consume a lot of texture
resources. Even a relatively coarse three-dimensional texture may use 16 or
32 times the amount of texture memory that a single two-dimensional tex-
ture uses. (Most of the two-dimensional texture and subtexture definition
routines have corresponding three-dimensional routines.)
A three-dimensional texture image can be thought of as layers of two-
dimensional subimage rectangles. In memory, the rectangles are arranged in a
sequence. To create a simple three-dimensional texture, use glTexImage3D().
Note: There are no three-dimensional convolutions in the Imaging Subset.
However, 2D convolution filters may be used to affect three-
dimensional texture images.
void glCopyTexSubImage1D(GLenum target, GLint level, GLint xoffset,
GLint x, GLint y, GLsizei width);
Uses image data from the framebuffer to replace all or part of a contiguous
subregion of the current, existing one-dimensional texture image. The
pixels are read from the current GL_READ_BUFFER and are processed
exactly as if glCopyPixels() had been called, but instead of going to the
framebuffer, the pixels are placed into texture memory. The settings of
glPixelTransfer*() and other pixel-transfer operations are applied.
The target parameter must be set to GL_TEXTURE_1D. level is the mipmap
level-of-detail number. xoffset specifies the texel offset and where to put
the subimage within the existing texture array. The subimage texture
array is taken from a row of pixels with the lower left corner at coordinates
specified by the (x,y) parameters. The width parameter specifies the
number of pixels in this row.
Advanced
Specifying the Texture 415
For a portion of a program that uses a three-dimensional texture map, see
Example 9-4.
Example 9-4 Three-Dimensional Texturing: texture3d.c
#define iWidth 16
#define iHeight 16
#define iDepth 16
static GLubyte image [iDepth][iHeight][iWidth][3];
static GLuint texName;
/* Create a 16x16x16x3 array with different color values in
* each array element [r, g, b]. Values range from 0 to 255.
*/
void makeImage(void)
{
int s, t, r;
for (s = 0 ; s < 16 ; s++)
for (t = 0 ; t < 16 ; t++)
for (r = 0 ; r < 16 ; r++) {
image[r][t][s][0] = s * 17;
image[r][t][s][1] = t * 17;
image[r][t][s][2] = r * 17;
}
}
void glTexImage3D(GLenum target, GLint level, GLint internalFormat,
GLsizei width, GLsizei height, GLsizei depth,
GLint border, GLenum format, GLenum type,
const GLvoid *texels);
Defines either a three-dimensional texture or an array of two-dimensional
textures. All the parameters have the same meanings as for glTexImage2D(),
except that texels is now a three-dimensional array, and the parameter depth
has been added for 3D textures. For GL_TEXTURE_2D_ARRAY, depth
represents the length of the texture array. If the OpenGL implementation does
not support Version 2.0, the value of depth is 2m (or 2m + 2, if there’s a border),
where m is a non-negative integer. For OpenGL 2.0 implementations, the
power-of-two dimension requirement has been eliminated. You can supply
mipmaps and proxies (set target to GL_PROXY_TEXTURE_3D), and the same
filtering options are available as well.

416 Chapter 9: Texture Mapping
/* Initialize state: the 3D texture object and its image
*/
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
glEnable(GL_DEPTH_TEST);
makeImage();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glGenTextures(1, &texName);
glBindTexture(GL_TEXTURE_3D, texName);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_WRAP_S, GL_CLAMP);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_WRAP_T, GL_CLAMP);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_WRAP_R, GL_CLAMP);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
glTexImage3D(GL_TEXTURE_3D, 0, GL_RGB, iWidth, iHeight,
iDepth, 0, GL_RGB, GL_UNSIGNED_BYTE, image);
}
To replace all or some of the texels of a three-dimensional texture, use
glTexSubImage3D().
texels contains the texture data for the subimage. width, height, and depth
specify the size of the subimage in texels. xoffset, yoffset, and zoffset specify
void glTexSubImage3D(GLenum target, GLint level, GLint xoffset,
GLint yoffset, GLint zoffset, GLsizei width,
GLsizei height, GLsizei depth, GLenum format,
GLenum type, const GLvoid *texels);
Defines a three-dimensional texture array that replaces all or part of a
contiguous subregion of the current, existing three-dimensional texture
image. The target parameter must be set to GL_TEXTURE_3D.
The level,format, and type parameters are similar to the ones used for
glTexImage3D().level is the mipmap level-of-detail number. format
and type describe the format and data type of the texture image
data. The subimage is also affected by modes set by glPixelStore*(),
glPixelTransfer*(), and other pixel-transfer operations.

Specifying the Texture 417
the texel offset indicating where to put the subimage within the existing
texture array.
To use the framebuffer as the source of replacement for a portion of an
existing three-dimensional texture, use glCopyTexSubImage3D().
Pixel-Storage Modes for Three-Dimensional Textures
Pixel-storage values control the row-to-row spacing of each layer (in other
words, of one 2D rectangle). glPixelStore*() sets pixel-storage modes, with
parameters such as *ROW_LENGTH, *ALIGNMENT, *SKIP_PIXELS, and
*SKIP_ROWS (where * is either GL_UNPACK_ or GL_PACK_), which control
referencing of a subrectangle of an entire rectangle of pixel or texel data.
(These modes were previously described in “Controlling Pixel-Storage
Modes” on page 347.)
The aforementioned pixel-storage modes remain useful for describing two
of the three dimensions, but additional pixel-storage modes are needed
to support referencing of subvolumes of three-dimensional texture image
data. New parameters, *IMAGE_HEIGHT and *SKIP_IMAGES, allow the
routines glTexImage3D(),glTexSubImage3D(), and glGetTexImage()
to delimit and access any desired subvolume.
void glCopyTexSubImage3D(GLenum target, GLint level, GLint xoffset,
GLint yoffset, GLint zoffset, GLint x,
GLint y, GLsizei width, GLsizei height);
Uses image data from the framebuffer to replace part of a contiguous
subregion of the current, existing three-dimensional texture image. The
pixels are read from the current GL_READ_BUFFER and are processed
exactly as if glCopyPixels() had been called, but instead of going to the
framebuffer, the pixels are placed into texture memory. The settings of
glPixelTransfer*() and other pixel-transfer operations are applied.
The target parameter must be set to GL_TEXTURE_3D. level is the mipmap
level-of-detail number. The subimage texture array is taken from a screen-
aligned pixel rectangle with the lower left corner at coordinates specified
by the (x,y) parameters. The width and height parameters specify the size
of this subimage rectangle. xoffset, yoffset, and zoffset specify the texel
offset indicating where to put the subimage within the existing texture
array. Since the subimage is a two-dimensional rectangle, only a single
slice of the three-dimensional texture (the slice at zoffset) is replaced.
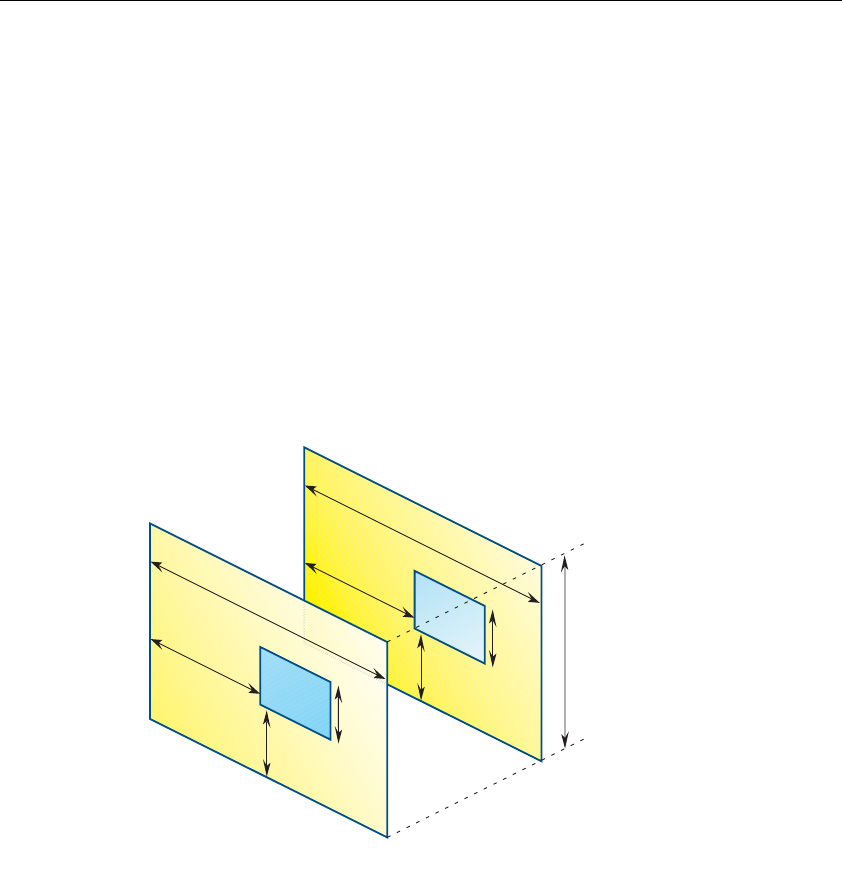
418 Chapter 9: Texture Mapping
If the three-dimensional texture in memory is larger than the subvolume
that is defined, you need to specify the height of a single subimage with the
*IMAGE_HEIGHT parameter. Also, if the subvolume does not start with
the very first layer, the *SKIP_IMAGES parameter needs to be set.
*IMAGE_HEIGHT is a pixel-storage parameter that defines the height (num-
ber of rows) of a single layer of a three-dimensional texture image. If the
*IMAGE_HEIGHT value is zero (a negative number is invalid), then the
number of rows in each two-dimensional rectangle is the value of height,
which is the parameter passed to glTexImage3D() or glTexSubImage3D().
(This is commonplace because *IMAGE_HEIGHT is zero, by default.) Other-
wise, the height of a single layer is the *IMAGE_HEIGHT value.
Figure 9-4 shows how *IMAGE_HEIGHT determines the height of an image
(when the parameter height determines only the height of the subimage.)
This figure shows a three-dimensional texture with only two layers.
*SKIP_IMAGES defines how many layers to bypass before accessing the first
data of the subvolume. If the *SKIP_IMAGES value is a positive integer (call
the value n), then the pointer in the texture image data is advanced that
many layers (n * the size of one layer of texels). The resulting subvolume starts
at layer n and is several layers deep—how many layers deep is determined by
the depth parameter passed to glTexImage3D() or glTexSubImage3D(). If the
Layer 1
Subimage
in Layer 1
*SKIP_PIXELS
*ROW_LENGTH
*SKIP_ROWS
Height
Layer 0
Subimage
in Layer 0
*SKIP_PIXELS
*ROW_LENGTH
*SKIP_ROWS
Height
*IMAGE_HEIGHT
Figure 9-4 *IMAGE_HEIGHT Pixel-Storage Mode
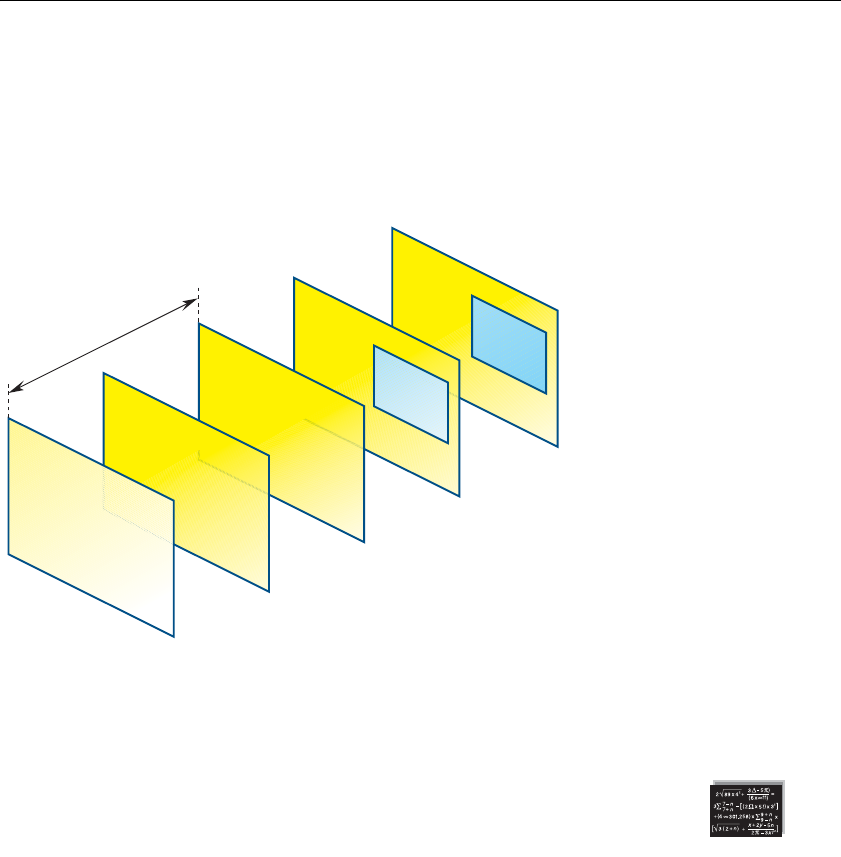
Specifying the Texture 419
*SKIP_IMAGES value is zero (the default), then accessing the texel data begins
with the very first layer described in the texel array.
Figure 9-5 shows how the *SKIP_IMAGES parameter can bypass several
layers to get to where the subvolume is actually located. In this example,
*SKIP_IMAGES == 3, and the subvolume begins at layer 3.
Texture Arrays
Advanced
For certain applications, you may have a number of one- or two-
dimensional textures that you might like to access simultaneously within
the confines of a draw call. For instance, suppose you’re authoring a game
that features multiple characters of basically the same geometry, but each of
which has its own costume. Without the OpenGL Version 3.0 feature of
texture arrays, you would probably use a set of calls similar to the technique
used in Example 9-5.
The call to glBindTexture() for each draw call could have performance
implications for the application if the texture objects needed to be updated
in the OpenGL server (due to perhaps a shortage of texture storage resources).
Layer 4
Subimage
in Layer 4
Layer 3
Layer 2
Layer 1
Layer 0
Subimage
in Layer 3
*SKIP_IMAGES
Figure 9-5 *SKIP_IMAGES Pixel-Storage Mode
Advanced

420 Chapter 9: Texture Mapping
Texture arrays allow you to combine a collection of one- or two-dimensional
textures, all of the same size, in a texture of the next higher dimension
(e.g., an array of two-dimensional textures becomes something of a three-
dimensional texture). If you were to try using a three-dimensional texture
to store a collection of two-dimensional textures, you would encounter a
few inconveniences: The indexing texture coordinate—r in this case—is
normalized to the range [0,1]. To access the third texture in a stack of seven,
you would need to pass .35714 (or thereabouts) to access what you would
probably like to access as “2” (textures are indexed from zero, just like “C”).
Texture arrays permit this type of texture selection.
Additionally, texture arrays allow suitable mipmap filtering within the
texture accessed by the index. In comparison, a three-dimensional texture
would filter between the texture “slices,” likely in a way that doesn’t return
the results you were hoping for.
Compressed Texture Images
Texture maps can be stored internally in a compressed format to possibly
reduce the amount of texture memory used. A texture image can either be
compressed as it is being loaded or loaded directly in its compressed form.
Compressing a Texture Image While Loading
To have OpenGL compress a texture image while it’s being downloaded,
specify one of the GL_COMPRESSED_* enumerants for the internalformat
parameter. The image will automatically be compressed after the texels have
been processed by any active pixel-store (See “Controlling Pixel-Storage
Modes”) or pixel-transfer modes (See “Pixel-Transfer Operations”).
Once the image has been loaded, you can determine if it was compressed,
and into which format, using the following:
GLboolean compressed;
GLenum textureFormat;
GLsizei imageSize;
glGetTexLevelParameteriv(GL_TEXTURE_2D, GL_TEXTURE_COMPRESSED,
&compressed);
if (compressed == GL_TRUE) {

Specifying the Texture 421
glGetTexLevelParameteriv(GL_TEXTURE_2D,
GL_TEXTURE_INTERNAL_FORMAT, &textureFormat);
glGetTexLevelParameteriv(GL_TEXTURE_2D,
GL_TEXTURE_COMPRESSED_IMAGE_SIZE, &imageSize);
}
Loading a Compressed Texture Images
OpenGL doesn’t specify the internal format that should be used for
compressed textures; each OpenGL implementation is allowed to specify a
set of OpenGL extensions that implement a particular texture compression
format. For compressed textures that are to be loaded directly, it’s important
to know their storage format and to verify that the texture’s format is
available in your OpenGL implementation.
To load a texture stored in a compressed format, use the
glCompressedTexImage*D() calls.
void glCompressedTexImage1D(GLenum target, GLint level,
GLenum internalformat, GLsizei width,
GLint border, GLsizei imageSize,
const GLvoid *texels);
void glCompressedTexImage2D(GLenum target, GLint level,
GLenum internalformat, GLsizei width,
GLsizei height, GLint border,
GLsizei imageSize, const GLvoid *texels);
void glCompressedTexImage3D(GLenum target, GLint level,
GLenum internalformat, GLsizei width,
GLsizei height, GLsizei depth,
GLint border, GLsizei imageSize,
const GLvoid *texels);
Defines a one-, two-, or three-dimensional texture from a previously
compressed texture image.
Use the level parameter if you’re supplying multiple resolutions of
the texture map; with only one resolution, level should be 0. (See
“Mipmaps: Multiple Levels of Detail” for more information about using
multiple resolutions.)
internalformat specifies the format of the compressed texture image. It
must be a supported compression format of the implementation loading
the texture, otherwise a GL_INVALID_ENUM error is specified. To deter-
mine supported compressed texture formats, see Appendix B for details.

422 Chapter 9: Texture Mapping
Additionally, compressed textures can be used, just like uncompressed
texture images, to replace all or part of an already loaded texture. Use the
glCompressedTexSubImage*D() calls.
width,height, and depth represent the dimensions of the texture image for
one-, two-, and three-dimensional texture images, respectively. As with
uncompressed textures, border indicates the width of the border, which is either
0 (no border) or 1. Each value must have the form 2m+ 2b, where m is a non-
negative integer and b is the value of border. For OpenGL 2.0 implementations,
the power-of-two dimension requirement has been eliminated.
For OpenGL Version 3.1, a GL_INVALID_ENUM error is generated if target
is GL_TEXTURE_RECTANGLE, or GL_PROXY_TEXTURE_RECTANGLE for
glCompressedTexImage2D().
void glCompressedTexSubImage1D(GLenum target, GLint level,
GLint xoffset, GLsizei width,
GLenum format, GLsizei imageSize,
const GLvoid *texels);
void glCompressedTexSubImage2D(GLenum target, GLint level,
GLint xoffset, GLint yoffet,
GLsizei width, GLsizei height,
GLsizei imageSize,
const GLvoid *texels);
void glCompressedTexSubImage3D(GLenum target, GLint level,
GLint xoffset GLint yoffset,
GLint zoffset, GLsizei width,
GLsizei height, GLsizei depth,
GLsizei imageSize,
const GLvoid *texels);
Defines a one-, two-, or three-dimensional texture from a previously
compressed texture image.
The xoffset,yoffset, and zoffset parameters specify the pixel offsets for
the respective texture dimension where to place the new image inside
of the texture array.
width,height, and depth specify the size of the one-, two-, or three-
dimensional texture image to be used to update the texture image.
imageSize specifies the number of bytes stored in the texels array.

Specifying the Texture 423
Using a Texture’s Borders
Advanced
If you need to apply a larger texture map than your implementation of
OpenGL allows, you can, with a little care, effectively make larger textures by
tiling with several different textures. For example, if you need a texture twice
as large as the maximum allowed size mapped to a square, draw the square as
four subsquares, and load a different texture before drawing each piece.
Since only a single texture map is available at one time, this approach might
lead to problems at the edges of the textures, especially if some form of linear
filtering is enabled. The texture value to be used for pixels at the edges must be
averaged with something beyond the edge, which, ideally, should come from
the adjacent texture map. If you define a border for each texture whose texel
values are equal to the values of the texels at the edge of the adjacent texture
map, then the correct behavior results when linear filtering takes place.
To do this correctly, notice that each map can have eight neighbors—one
adjacent to each edge and one touching each corner. The values of the
texels in the corner of the border need to correspond with the texels in the
texture maps that touch the corners. If your texture is an edge or corner of
the whole tiling, you need to decide what values would be reasonable to put
in the borders. The easiest reasonable thing to do is to copy the value of the
adjacent texel in the texture map with glTexSubImage2D().
A texture’s border color is also used if the texture is applied in such a way
that it only partially covers a primitive. (See “Repeating and Clamping
Textures” on page 452 for more information about this situation.)
Note: Texture borders are not supported in OpenGL Version 3.1 and later.
When specifying a texture in those implementations, the value of the
border must be 0.
Mipmaps: Multiple Levels of Detail
Advanced
Textured objects can be viewed, like any other objects in a scene, at different
distances from the viewpoint. In a dynamic scene, as a textured object
moves farther from the viewpoint, the texture map must decrease in size
along with the size of the projected image. To accomplish this, OpenGL
has to filter the texture map down to an appropriate size for mapping onto
the object, without introducing visually disturbing artifacts, such as
Advanced
Advanced

424 Chapter 9: Texture Mapping
shimmering, flashing, and scintillation. For example, to render a brick wall,
you may use a large texture image (say 128u128 texels) when the wall is
close to the viewer. But if the wall is moved farther away from the viewer
until it appears on the screen as a single pixel, then the filtered textures may
appear to change abruptly at certain transition points.
To avoid such artifacts, you can specify a series of prefiltered texture maps
of decreasing resolutions, called mipmaps, as shown in Figure 9-6. The term
mipmap was coined by Lance Williams, when he introduced the idea in his
paper “Pyramidal Parametrics” (SIGGRAPH 1983 Proceedings). Mip stands
for the Latin multum in parvo, meaning “many things in a small place.”
Mipmapping uses some clever methods to pack image data into memory.
Original texture
Prefiltered images
1/4
1/16 1/64
etc
1 pixel
Figure 9-6 Mi
p
ma
p
s

Specifying the Texture 425
Note: To acquire a full understanding of mipmaps, you need to understand
minification filters, which are described in “Filtering” on page 434.
When using mipmapping, OpenGL automatically determines which tex-
ture map to use based on the size (in pixels) of the object being mapped.
With this approach, the level of detail in the texture map is appropriate
for the image that’s drawn on the screen—as the image of the object gets
smaller, the size of the texture map decreases. Mipmapping requires some
extra computation and texture storage area; however, when it’s not used,
textures that are mapped onto smaller objects might shimmer and flash as
the objects move.
To use mipmapping, you must provide all sizes of your texture in powers of
2 between the largest size and a 1 u1 map. For example, if your highest-
resolution map is 64 u16, you must also provide maps of size 32 u8, 16 u4,
8u2, 4 u1, 2 u1, and 1 u1. The smaller maps are typically filtered and
averaged-down versions of the largest map in which each texel in a smaller
texture is an average of the corresponding 4 texels in the higher-resolution
texture. (Since OpenGL doesn’t require any particular method for calculat-
ing the lower-resolution maps, the differently sized textures could be totally
unrelated. In practice, unrelated textures would make the transitions
between mipmaps extremely noticeable, as in Plate 20.)
To specify these textures, call glTexImage2D() once for each resolution of
the texture map, with different values for the level,width,height, and image
parameters. Starting with zero, level identifies which texture in the series is
specified; with the previous example, the highest-resolution texture of size
64 u16 would be declared with level =0, the 32u8 texture with level =1,
and so on. In addition, for the mipmapped textures to take effect, you need
to choose the appropriate filtering method as described in “Filtering” on
page 434.
Note: This description of OpenGL mipmapping avoids detailed discussion
of the scale factor (known as O) between texel size and polygon size.
This description also assumes default values for parameters related to
mipmapping. To see an explanation of O and the effects of mipmap-
ping parameters, see “Calculating the Mipmap Level” on page 430
and “Mipmap Level of Detail Control” on page 431.
Example 9-5 illustrates the use of a series of six texture maps decreasing in
size from 32 u32 to 1 u1. This program draws a rectangle that extends from
the foreground far back in the distance, eventually disappearing at a point,
as shown in Plate 20. Note that the texture coordinates range from 0.0 to
8.0, so 64 copies of the texture map are required to tile the rectangle—eight
in each direction. To illustrate how one texture map succeeds another, each
map has a different color.

426 Chapter 9: Texture Mapping
Example 9-5 Mipmap Textures: mipmap.c
GLubyte mipmapImage32[32][32][4];
GLubyte mipmapImage16[16][16][4];
GLubyte mipmapImage8[8][8][4];
GLubyte mipmapImage4[4][4][4];
GLubyte mipmapImage2[2][2][4];
GLubyte mipmapImage1[1][1][4];
static GLuint texName;
void makeImages(void)
{
int i, j;
for (i = 0; i < 32; i++) {
for (j = 0; j < 32; j++) {
mipmapImage32[i][j][0] = 255;
mipmapImage32[i][j][1] = 255;
mipmapImage32[i][j][2] = 0;
mipmapImage32[i][j][3] = 255;
}
}
for (i = 0; i < 16; i++) {
for (j = 0; j < 16; j++) {
mipmapImage16[i][j][0] = 255;
mipmapImage16[i][j][1] = 0;
mipmapImage16[i][j][2] = 255;
mipmapImage16[i][j][3] = 255;
}
}
for (i = 0; i < 8; i++) {
for (j = 0; j < 8; j++) {
mipmapImage8[i][j][0] = 255;
mipmapImage8[i][j][1] = 0;
mipmapImage8[i][j][2] = 0;
mipmapImage8[i][j][3] = 255;
}
}
for (i = 0; i < 4; i++) {
for (j = 0; j < 4; j++) {
mipmapImage4[i][j][0] = 0;
mipmapImage4[i][j][1] = 255;
mipmapImage4[i][j][2] = 0;
mipmapImage4[i][j][3] = 255;
}
}
for (i = 0; i < 2; i++) {
for (j = 0; j < 2; j++) {

Specifying the Texture 427
mipmapImage2[i][j][0] = 0;
mipmapImage2[i][j][1] = 0;
mipmapImage2[i][j][2] = 255;
mipmapImage2[i][j][3] = 255;
}
}
mipmapImage1[0][0][0] = 255;
mipmapImage1[0][0][1] = 255;
mipmapImage1[0][0][2] = 255;
mipmapImage1[0][0][3] = 255;
}
void init(void)
{
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_FLAT);
glTranslatef(0.0, 0.0, -3.6);
makeImages();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glGenTextures(1, &texName);
glBindTexture(GL_TEXTURE_2D, texName);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST_MIPMAP_NEAREST);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, 32, 32, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage32);
glTexImage2D(GL_TEXTURE_2D, 1, GL_RGBA, 16, 16, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage16);
glTexImage2D(GL_TEXTURE_2D, 2, GL_RGBA, 8, 8, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage8);
glTexImage2D(GL_TEXTURE_2D, 3, GL_RGBA, 4, 4, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage4);
glTexImage2D(GL_TEXTURE_2D, 4, GL_RGBA, 2, 2, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage2);
glTexImage2D(GL_TEXTURE_2D, 5, GL_RGBA, 1, 1, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage1);
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);
glEnable(GL_TEXTURE_2D);
}
void display(void)
{

428 Chapter 9: Texture Mapping
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBindTexture(GL_TEXTURE_2D, texName);
glBegin(GL_QUADS);
glTexCoord2f(0.0, 0.0); glVertex3f(-2.0, -1.0, 0.0);
glTexCoord2f(0.0, 8.0); glVertex3f(-2.0, 1.0, 0.0);
glTexCoord2f(8.0, 8.0); glVertex3f(2000.0, 1.0, -6000.0);
glTexCoord2f(8.0, 0.0); glVertex3f(2000.0, -1.0, -6000.0);
glEnd();
glFlush();
}
Building Mipmaps in Real Applications
Example 9-5 illustrates mipmapping by making each mipmap a different
color so that it’s obvious when one map is replaced by another. In a real
situation, you define mipmaps such that the transition is as smooth as
possible. Thus, the maps of lower resolution are usually filtered versions
of an original, high-resolution texture map.
There are several ways to create mipmaps using OpenGL features. In the
most modern versions of OpenGL (i.e., Version 3.0 and later), you can use
glGenerateMipmap(), which will build the mipmap stack for the current
texture image (see “Texture Objects” and its discussion of glBindTexture())
bound to a specific texture target.
The use of glGenerateMipmap() makes explicit which mipmaps you would
like, and puts them under the control of the OpenGL implementation. If
you don’t have access to a Version 3.0 or later implementation, you can still
int glGenerateMipmap(GLenum target);
Generates a complete set of mipmaps for the texture image associated
with target, which must be one of: GL_TEXTURE_1D, GL_TEXTURE_2D,
GL_TEXTURE_3D, GL_TEXTURE_1D_ARRAY, GL_TEXTURE_2D_ARRAY,
or GL_TEXTURE_CUBE_MAP.
The mipmap levels constructed are controlled by the GL_TEXTURE_
BASE_LEVEL, and GL_TEXTURE_MAX_LEVEL (see “Mipmap Level of
Detail Control” on page 431 for details describing these values). If those
values are left to their defaults, an entire mipmap stack down to a single-
texel texture map is created. The filtering method used in creating each
successive level is implementation dependent.
A GL_INVALID_OPERATION error will be generated if target is GL_TEXTURE_
CUBE_MAP, and not all cube map faces are initialized and consistent.

Specifying the Texture 429
have OpenGL generate mipmaps for you. Use glTexParameter*() to set GL_
GENERATE_MIPMAP to GL_TRUE; then any change to the texels (interior
or border) of a BASE_LEVEL mipmap will automatically cause all textures at
all mipmap levels from BASE_LEVEL+1 to MAX_LEVEL to be recomputed
and replaced. Textures at all other mipmap levels, including at BASE_LEVEL,
remain unchanged.
Note: In OpenGL Version 3.1 and later, use of GL_GENERATE_MIPMAP has
been replaced with the more explicit glGenerateMipmap() routine.
Trying to set GL_GENERATE_MIPMAP on a texture object in Version
3.1 will generate a GL_INVALID_OPERATION error.
Finally, if you are using an older OpenGL implementation (any version
prior to 1.4), you would need to construct the mipmap stack manually,
without OpenGL’s aid. However, because mipmap construction is such an
important operation, the OpenGL Utility Library contains routines that can
help you manipulate of images to be used as mipmapped textures.
Assuming you have constructed the level 0, or highest-resolution,
map, the routines gluBuild1DMipmaps(),gluBuild2DMipmaps(), and
gluBuild3DMipmaps() construct and define the pyramid of mipmaps
down to a resolution of 1 u 1 (or 1, for one-dimensional, or 1 u 1 u 1, for
three-dimensional). If your original image has dimensions that are not
exact powers of 2, gluBuild*DMipmaps() helpfully scales the image to the
nearest power of 2. Also, if your texture is too large, gluBuild*DMipmaps()
reduces the size of the image until it fits (as measured by the GL_PROXY_
TEXTURE mechanism).
int gluBuild1DMipmaps(GLenum target, GLint internalFormat,
GLint width, GLenum format, GLenum type,
const void *texels);
int gluBuild2DMipmaps(GLenum target, GLint internalFormat,
GLint width, GLint height, GLenum format,
GLenum type, const void *texels);
int gluBuild3DMipmaps(GLenum target, GLint internalFormat,
GLint width, GLint height, GLint depth,
GLenum format, GLenum type, const void *texels);
Constructs a series of mipmaps and calls glTexImage*D() to load the images.
The parameters for target,internalFormat,width,height,depth,format,type, and
texels are exactly the same as those for glTexImage1D(),glTexImage2D(),
and glTexImage3D(). A value of 0 is returned if all the mipmaps are
constructed successfully; otherwise, a GLU error code is returned.

430 Chapter 9: Texture Mapping
With increased control over level of detail (using BASE_LEVEL, MAX_
LEVEL, MIN_LOD, and MAX_LOD), you may need to create only a subset
of the mipmaps defined by gluBuild*DMipmaps(). For example, you may
want to stop at a 4 u4 texel image, rather than go all the way to the smallest
1u1 texel image. To calculate and load a subset of mipmap levels, call
gluBuild*DMipmapLevels().
Calculating the Mipmap Level
Computing which level of mipmap to texture a particular polygon depends
on the scale factor between the texture image and the size of the polygon
to be textured (in pixels). Let’s call this scale factor U and also define a sec-
ond value, O, where O=log
2U + lodbias. (Since texture images can be multi-
dimensional, it is important to clarify that U is the maximum scale factor of
all dimensions.)
lodbias is the level-of-detail bias, a constant value set by glTexEnv*() to
adjust O. (For information about how to use glTexEnv*() to set level-of-
detail bias, see “Texture Functions” on page 444.) By default, lodbias = 0.0,
which has no effect. It’s best to start with this default value and adjust in
small amounts, if needed.
int gluBuild1DMipmapLevels(GLenum target, GLint internalFormat,
GLint width, GLenum format,
GLenum type, GLint level, GLint base,
GLint max, const void *texels);
int gluBuild2DMipmapLevels(GLenum target, GLint internalFormat,
GLint width, GLint height, GLenum format,
GLenum type, GLint level, GLint base,
GLint max, const void *texels);
int gluBuild3DMipmapLevels(GLenum target, GLint internalFormat,
GLint width, GLint height, GLint depth,
GLenum format, GLenum type,
GLint level, GLint base, GLint max,
const void *texels);
Constructs a series of mipmaps and calls glTexImage*D() to load the
images. level indicates the mipmap level of the texels image. base and max
determine which mipmap levels will be derived from texels. Otherwise,
the parameters for target,internalFormat,width,height,depth,format,type, and
texels are exactly the same as those for glTexImage1D(),glTexImage2D(),
and glTexImage3D(). A value of 0 is returned if all the mipmaps are
constructed successfully; otherwise, a GLU error code is returned.
Specifying the Texture 431
If Od0.0, then the texture is smaller than the polygon, so a magnification
filter is used. If O> 0.0, then a minification filter is used. If the
minification filter selected uses mipmapping, then O indicates the
mipmap level. (The minification-to-magnification switchover point is
usually at O= 0.0, but not always. The choice of mipmapping filter may
shift the switchover point.)
For example, if the texture image is 64 u64 texels and the polygon size is
32 u32 pixels, then U= 2.0 (not 4.0), and therefore O= 1.0. If the texture
image is 64 u32 texels and the polygon size is 8 u16 pixels, then U=8.0
(x scales by 8.0, y by 2.0; use the maximum value) and therefore O=3.0.
Mipmap Level of Detail Control
By default, you must provide a mipmap for every level of resolution, down
to 1 texel in every dimension. For some techniques, you want to avoid rep-
resenting your data with very small mipmaps. For instance, you might use
a technique called mosaicing, where several smaller images are combined on
a single texture. One example of mosaicing is shown in Figure 9-7, where
many characters are on a single texture, which may be more efficient than
creating a texture image for each character. To map only a single letter from
the texture, you make smart use of texture coordinates to isolate the letter
you want.
If you have to supply very small mipmaps, the lower-resolution mipmaps of
the mosaic crush together detail from many different letters. Therefore, you
may want to set restrictions on how low your resolution can go. Generally,
you want the capability to add or remove levels of mipmaps as needed.
Another visible mipmapping problem is popping—the sudden transition
from using one mipmap to using a radically higher- or lower-resolution
mipmap, as a mipmapped polygon becomes larger or smaller.
A B C D E F G H
I J K L M N O P
Q R S T U V W X
Y Z 1 2 3 4 5 6
7 8 9 0 ! @ # $
% ^ & * ( ) - +
[ ] { } | / \ ?
< > ; : . , ~ “
Texture
Polygon
T
Figure 9-7 Using a Mosaic Texture

432 Chapter 9: Texture Mapping
Note: Many mipmapping features were introduced in later versions of
OpenGL. Check the version of your implementation to see if a
particular feature is supported. In some versions, a particular feature
may be available as an extension.
To control mipmapping levels, the constants GL_TEXTURE_BASE_LEVEL,
GL_TEXTURE_MAX_LEVEL, GL_TEXTURE_MIN_LOD, and GL_TEXTURE_
MAX_LOD are passed to glTexParameter*(). The first two constants (for
brevity, shortened to BASE_LEVEL and MAX_LEVEL in the remainder of this
section) control which mipmap levels are used and therefore which levels
need to be specified. The other two constants (shortened to MIN_LOD and
MAX_LOD) control the active range of the aforementioned scale factor O
These texture parameters address several of the previously described prob-
lems. Effective use of BASE_LEVEL and MAX_LEVEL may reduce the num-
ber of mipmaps that need to be specified and thereby streamline texture
resource usage. Selective use of MAX_LOD may preserve the legibility of a
mosaic texture, and MIN_LOD may reduce the popping effect with higher-
resolution textures.
BASE_LEVEL and MAX_LEVEL are used to set the boundaries for which
mipmap levels are used. BASE_LEVEL is the level of the highest-resolution
(largest texture) mipmap level that is used. The default value for BASE_
LEVEL is 0. However, you may later change the value for BASE_LEVEL, so
that you add additional higher-resolution textures “on the fly.” Similarly,
MAX_LEVEL limits the lowest-resolution mipmap to be used. The default
value for MAX_LEVEL is 1000, which almost always means that the
smallest-resolution texture is 1 texel.
To set the base and maximum mipmap levels, use glTexParameter*()
with the first argument set to GL_TEXTURE_1D, GL_TEXTURE_2D, GL_
TEXTURE_3D, or GL_TEXTURE_CUBE_MAP, depending on your textures.
The second argument is one of the parameters described in Table 9-1. The
third argument denotes the value for the parameter.
Parameter Description Values
GL_TEXTURE_BASE_
LEVEL
level for highest-resolution texture
(lowest numbered mipmap level) in use
any non-
negative integer
GL_TEXTURE_MAX_
LEVEL
level for smallest-resolution texture
(highest numbered mipmap level) in use
any non-
negative integer
Table 9-1 Mipmapping Level Parameter Controls

Specifying the Texture 433
The code in Example 9-6 sets the base and maximum mipmap levels to 2 and
5, respectively. Since the image at the base level (level 2) has a 64 u32 texel
resolution, the mipmaps at levels 3, 4, and 5 must have the appropriate
lower resolution.
Example 9-6 Setting Base and Maximum Mipmap Levels
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_BASE_LEVEL, 2);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAX_LEVEL, 5);
glTexImage2D(GL_TEXTURE_2D, 2, GL_RGBA, 64, 32, 0, GL_RGBA,
GL_UNSIGNED_BYTE, image1);
glTexImage2D(GL_TEXTURE_2D, 3, GL_RGBA, 32, 16, 0, GL_RGBA,
GL_UNSIGNED_BYTE, image2);
glTexImage2D(GL_TEXTURE_2D, 4, GL_RGBA, 16, 8, 0, GL_RGBA,
GL_UNSIGNED_BYTE, image3);
glTexImage2D(GL_TEXTURE_2D, 5, GL_RGBA, 8, 4, 0, GL_RGBA,
GL_UNSIGNED_BYTE, image4);
Later on, you may decide to add additional higher-or lower-resolution
mipmaps. For example, you may add a 128 u64 texel texture to this set
of mipmaps at level 1, but you must remember to reset BASE_LEVEL.
Note: For mipmapping to work, all mipmaps between BASE_LEVEL and the
largest possible level, inclusive, must be loaded. The largest possible
level is the smaller of either the value for MAX_LEVEL or the level
at which the size of the mipmap is only 1 texel (either 1, 1 u1, or
1u1u1). If you fail to load a necessary mipmap level, then texturing
may be mysteriously disabled. If you are mipmapping and texturing
does not appear, ensure that each required mipmap level has been
loaded with a legal texture.
As with BASE_LEVEL and MAX_LEVEL, glTexParameter*() sets MIN_LOD
and MAX_LOD. Table 9-2 lists possible values.
Parameter Description Values
GL_TEXTURE_MIN_LOD minimum value for O(scale
factor of texture image versus
polygon size)
any value
GL_TEXTURE_MAX_LOD maximum value for Oany value
Table 9-2 Mipmapping Level-of-Detail Parameter Controls

434 Chapter 9: Texture Mapping
The following code is an example of using glTexParameter*() to specify the
level-of-detail parameters:
glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MIN_LOD, 2.5);
glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MAX_LOD, 4.5);
MIN_LOD and MAX_LOD provide minimum and maximum values for O
(the scale factor from texture image to polygon) for mipmapped minification,
which indirectly specifies which mipmap levels are used.
If you have a 64 u64 pixel polygon and MIN_LOD is the default value of
0.0, then a level 0 64 u64 texel texture map may be used for minification
(provided BASE_LEVEL = 0; as a rule, BASE_LEVEL dMIN_LOD). However,
if MIN_LOD is set to 2.0, then the largest texture map that may be used for
minification is 16 u16 texels, which corresponds to O= 2.0.
MAX_LOD has influence only if it is less than the maximum O (which is
either MAX_LEVEL or where the mipmap is reduced to 1 texel). In the case
of a 64 u64 texel texture map, O= 6.0 corresponds to a 1 u1 texel mipmap.
In the same case, if MAX_LOD is 4.0, then no mipmap smaller than 4 u4
texels will be used for minification.
You may find that a MIN_LOD that is fractionally greater than BASE_LEVEL
or a MAX_LOD that is fractionally less than MAX_LEVEL is best for reducing
visual effects (such as popping) related to transitions between mipmaps.
Filtering
Texture maps are square or rectangular, but after being mapped to a polygon
or surface and transformed into screen coordinates, the individual texels of
a texture rarely correspond to individual pixels of the final screen image.
Depending on the transformations used and the texture mapping applied,
a single pixel on the screen can correspond to anything from a tiny portion
of a texel (magnification) to a large collection of texels (minification), as
shown in Figure 9-8. In either case, it’s unclear exactly which texel values
should be used and how they should be averaged or interpolated. Conse-
quently, OpenGL allows you to specify any of several filtering options to
determine these calculations. The options provide different trade-offs
between speed and image quality. Also, you can specify independently
the filtering methods for magnification and minification.
In some cases, it isn’t obvious whether magnification or minification is
called for. If the texture map needs to be stretched (or shrunk) in both the
x- and y- directions, then magnification (or minification) is needed. If the
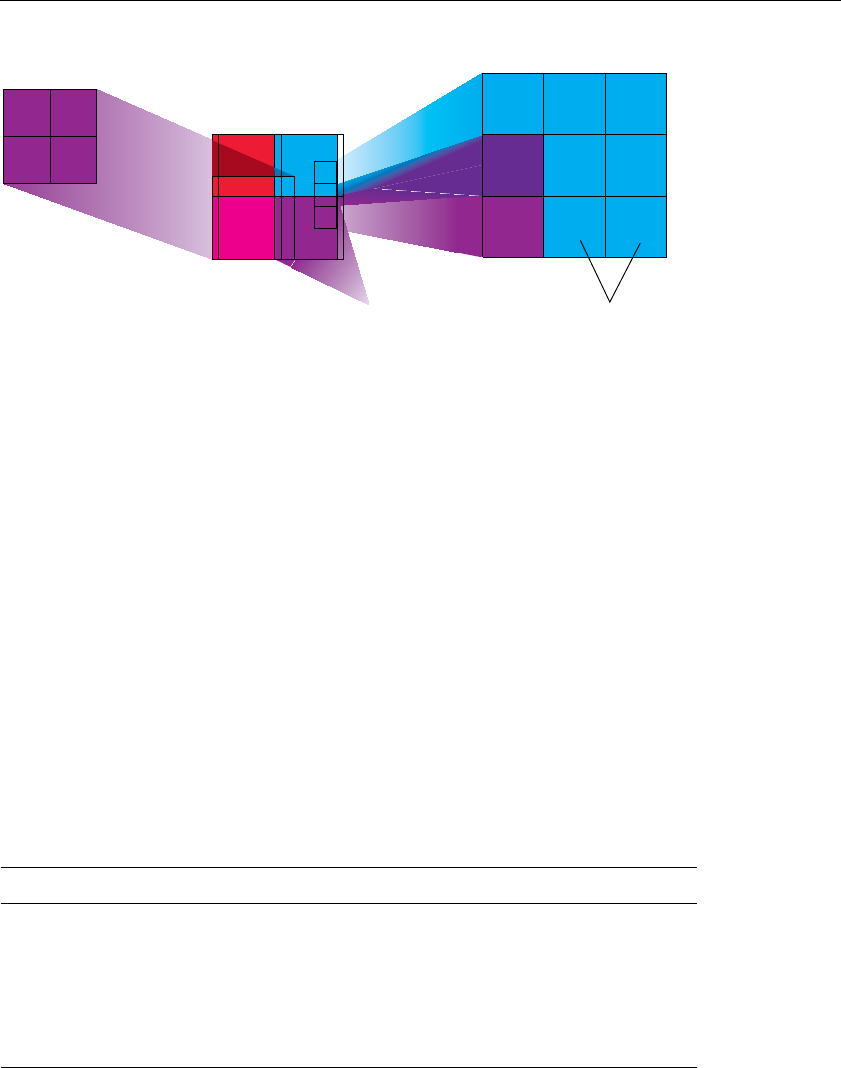
Filtering 435
texture map needs to be stretched in one direction and shrunk in the other,
OpenGL makes a choice between magnification and minification that in
most cases gives the best result possible. It’s best to try to avoid these situa-
tions by using texture coordinates that map without such distortion. (See
“Computing Appropriate Texture Coordinates” on page 450.)
The following lines are examples of how to use glTexParameter*() to
specify the magnification and minification filtering methods:
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
The first argument to glTexParameter*() is GL_TEXTURE_1D, GL_
TEXTURE_2D, GL_TEXTURE_3D, or GL_TEXTURE_CUBE_MAP, whichever
is appropriate. For the purposes of this discussion, the second argument is
either GL_TEXTURE_MAG_FILTER, or GL_TEXTURE_MIN_FILTER, to indi-
cate whether you’re specifying the filtering method for magnification or
minification. The third argument specifies the filtering method; Table 9-3
lists the possible values.
Parameter Values
GL_TEXTURE_MAG_FILTER GL_NEAREST or GL_LINEAR
GL_TEXTURE_MIN_FILTER GL_NEAREST, GL_LINEAR,
GL_NEAREST_MIPMAP_NEAREST,
GL_NEAREST_MIPMAP_LINEAR,
GL_LINEAR_MIPMAP_NEAREST, or
GL_LINEAR_MIPMAP_LINEAR
Table 9-3 Filtering Methods for Magnification and Minification
Magnification
Texture
Polygon
Polygon
Minification
Pixels
Texel
Figure 9-8 Texture Magnification and Minification

436 Chapter 9: Texture Mapping
If you choose GL_NEAREST, the texel with coordinates nearest the center of
the pixel is used for both magnification and minification. This can result in
aliasing artifacts (sometimes severe). If you choose GL_LINEAR, a weighted
linear average of the 2 u2 array of texels that lie nearest to the center of the
pixel is used, again for both magnification and minification. (For three-
dimensional textures, it’s a 2 u2u2 array; for one-dimensional, it’s an
average of 2 texels.) When the texture coordinates are near the edge of the
texture map, the nearest 2 u2 array of texels might include some that are
outside the texture map. In these cases, the texel values used depend on
which wrapping mode is in effect and whether you’ve assigned a border
for the texture. (See “Repeating and Clamping Textures” on page 452.)
GL_NEAREST requires less computation than GL_LINEAR and therefore
might execute more quickly, but GL_LINEAR provides smoother results.
With magnification, even if you’ve supplied mipmaps, only the base level
texture map is used. With minification, you can choose a filtering method
that uses the most appropriate one or two mipmaps, as described in the next
paragraph. (If GL_NEAREST or GL_LINEAR is specified with minification,
only the base level texture map is used.)
As shown in Table 9-3, four additional filtering options are available when
minifying with mipmaps. Within an individual mipmap, you can choose
the nearest texel value with GL_NEAREST_MIPMAP_NEAREST, or you can
interpolate linearly by specifying GL_LINEAR_MIPMAP_NEAREST. Using
the nearest texels is faster but yields less desirable results. The particular
mipmap chosen is a function of the amount of minification required, and
there’s a cutoff point from the use of one particular mipmap to the next.
To avoid a sudden transition, use GL_NEAREST_MIPMAP_LINEAR or
GL_LINEAR_MIPMAP_LINEAR for linear interpolation of texel values from
the two nearest best choices of mipmaps. GL_NEAREST_MIPMAP_LINEAR
selects the nearest texel in each of the two maps and then interpolates
linearly between these two values. GL_LINEAR_MIPMAP_LINEAR uses
linear interpolation to compute the value in each of two maps and then
interpolates linearly between these two values. As you might expect, GL_
LINEAR_MIPMAP_LINEAR generally produces the highest-quality results,
but it requires the most computation and therefore might be the slowest.
Caution: If you request a mipmapped texture filter, but you have not supplied
a full and consistent set of mipmaps (all correct-sized texture images
between GL_TEXTURE_BASE_LEVEL and GL_TEXTURE_MAX_
LEVEL), OpenGL will, without any error, implicitly disable
texturing. If you are trying to use mipmaps and no texturing
appears at all, check the texture images at all your mipmap levels.

Texture Objects 437
Some of these texture filters are known by more popular names. GL_NEAREST
is often called point sampling. GL_LINEAR is known as bilinear sampling,
because for two-dimensional textures, a 2 u2 array of texels is sampled.
GL_LINEAR_MIPMAP_LINEAR is sometimes known as trilinear sampling,
because it is a linear average between two bilinearly sampled mipmaps.
Note: The minification-to-magnification switchover point is usually at
O= 0.0, but is affected by the type of minification filter you choose.
If the current magnification filter is GL_LINEAR and the minification
filter is GL_NEAREST_MIPMAP_NEAREST or GL_NEAREST_MIPMAP_
LINEAR, then the switch between filters occurs at O= 0.5. This pre-
vents the minified texture from looking sharper than its magnified
counterpart.
Nate Robins’ Texture Tutorial
If you have downloaded Nate Robins’ suite of tutorial programs, now
run the texture tutorial. (For information on how and where to download
these programs, see “Errata” on page xlii.) With this tutorial, you can
experiment with the texture-mapping filtering method, switching between
GL_NEAREST and GL_LINEAR.
Texture Objects
A texture object stores texture data and makes it readily available. You may
control many textures and go back to textures that have been previously
loaded into your texture resources. Using texture objects is usually the
fastest way to apply textures, resulting in big performance gains, because it
is almost always much faster to bind (reuse) an existing texture object than
it is to reload a texture image using glTexImage*D().
Also, some implementations support a limited working set of high-
performance textures. You can use texture objects to load your most
often used textures into this limited area.
To use texture objects for your texture data, take these steps:
1. Generate texture names.
2. Initially bind (create) texture objects to texture data, including the
image arrays and texture properties.
3. If your implementation supports a working set of high-performance
textures, see if you have enough space for all your texture objects. If
there isn’t enough space, you may wish to establish priorities for each
texture object so that more often used textures stay in the working set.

438 Chapter 9: Texture Mapping
4. Bind and rebind texture objects, making their data currently available
for rendering textured models.
Naming a Texture Object
Any nonzero unsigned integer may be used as a texture name. To avoid
accidentally reusing names, consistently use glGenTextures() to provide
unused texture names.
glIsTexture() determines if a texture name is actually in use. If a texture
name was returned by glGenTextures() but has not yet been bound (calling
glBindTexture() with the name at least once), then glIsTexture() returns
GL_FALSE.
Creating and Using Texture Objects
The same routine, glBindTexture(), both creates and uses texture objects.
When a texture name is initially bound (used with glBindTexture()), a new
texture object is created with default values for the texture image and tex-
ture properties. Subsequent calls to glTexImage*(),glTexSubImage*(),
glCopyTexImage*(),glCopyTexSubImage*(),glTexParameter*(), and
void glGenTextures(GLsizei n, GLuint *textureNames);
Returns n currently unused names for texture objects in the array
textureNames. The names returned in textureNames do not have to be a
contiguous set of integers.
The names in textureNames are marked as used, but they acquire texture
state and dimensionality (1D, 2D, or 3D) only when they are first bound.
Zero is a reserved texture name and is never returned as a texture name by
glGenTextures().
GLboolean glIsTexture(GLuint textureName);
Returns GL_TRUE if textureName is the name of a texture that has been
bound and has not been subsequently deleted, and returns GL_FALSE if
textureName is zero or textureName is a nonzero value that is not the name
of an existing texture.

Texture Objects 439
glPrioritizeTextures() store data in the texture object. The texture object
may contain a texture image and associated mipmap images (if any),
including associated data such as width, height, border width, internal
format, resolution of components, and texture properties. Saved texture
properties include minification and magnification filters, wrapping modes,
border color, and texture priority.
When a texture object is subsequently bound once again, its data becomes
the current texture state. (The state of the previously bound texture is
replaced.)
In Example 9-7, two texture objects are created in init(). In display(), each
texture object is used to render a different four-sided polygon.
Example 9-7 Binding Texture Objects: texbind.c
#define checkImageWidth 64
#define checkImageHeight 64
static GLubyte checkImage[checkImageHeight][checkImageWidth][4];
static GLubyte otherImage[checkImageHeight][checkImageWidth][4];
static GLuint texName[2];
void makeCheckImages(void)
{
void glBindTexture(GLenum target, GLuint textureName);
glBindTexture() does three things. When using the textureName of an
unsigned integer other than zero for the first time, a new texture object is
created and assigned that name. When binding to a previously created
texture object, that texture object becomes active. When binding to a
textureName value of zero, OpenGL stops using texture objects and returns
to the unnamed default texture.
When a texture object is initially bound (that is, created), it assumes the
dimensionality of target, which is GL_TEXTURE_1D, GL_TEXTURE_2D,
GL_TEXTURE_3D, GL_TEXTURE_CUBE_MAP, GL_TEXTURE_1D_ARRAY,
GL_TEXTURE_2D_ARRAY, GL_TEXTURE_RECTANGLE, or GL_TEXTURE_
BUFFER. Immediately on its initial binding, the state of the texture object
is equivalent to the state of the default target dimensionality at the
initialization of OpenGL. In this initial state, texture properties such as
minification and magnification filters, wrapping modes, border color, and
texture priority are set to their default values.

440 Chapter 9: Texture Mapping
int i, j, c;
for (i = 0; i < checkImageHeight; i++) {
for (j = 0; j < checkImageWidth; j++) {
c = (((i&0x8)==0)^((j&0x8)==0))*255;
checkImage[i][j][0] = (GLubyte) c;
checkImage[i][j][1] = (GLubyte) c;
checkImage[i][j][2] = (GLubyte) c;
checkImage[i][j][3] = (GLubyte) 255;
c = (((i&0x10)==0)^((j&0x10)==0))*255;
otherImage[i][j][0] = (GLubyte) c;
otherImage[i][j][1] = (GLubyte) 0;
otherImage[i][j][2] = (GLubyte) 0;
otherImage[i][j][3] = (GLubyte) 255;
}
}
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
glEnable(GL_DEPTH_TEST);
makeCheckImages();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glGenTextures(2, texName);
glBindTexture(GL_TEXTURE_2D, texName[0]);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, checkImageWidth,
checkImageHeight, 0, GL_RGBA, GL_UNSIGNED_BYTE,
checkImage);
glBindTexture(GL_TEXTURE_2D, texName[1]);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);

Texture Objects 441
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, checkImageWidth,
checkImageHeight, 0, GL_RGBA, GL_UNSIGNED_BYTE,
otherImage);
glEnable(GL_TEXTURE_2D);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBindTexture(GL_TEXTURE_2D, texName[0]);
glBegin(GL_QUADS);
glTexCoord2f(0.0, 0.0); glVertex3f(-2.0, -1.0, 0.0);
glTexCoord2f(0.0, 1.0); glVertex3f(-2.0, 1.0, 0.0);
glTexCoord2f(1.0, 1.0); glVertex3f(0.0, 1.0, 0.0);
glTexCoord2f(1.0, 0.0); glVertex3f(0.0, -1.0, 0.0);
glEnd();
glBindTexture(GL_TEXTURE_2D, texName[1]);
glBegin(GL_QUADS);
glTexCoord2f(0.0, 0.0); glVertex3f(1.0, -1.0, 0.0);
glTexCoord2f(0.0, 1.0); glVertex3f(1.0, 1.0, 0.0);
glTexCoord2f(1.0, 1.0); glVertex3f(2.41421, 1.0, -1.41421);
glTexCoord2f(1.0, 0.0); glVertex3f(2.41421, -1.0, -1.41421);
glEnd();
glFlush();
}
Whenever a texture object is bound once again, you may edit the contents
of the bound texture object. Any commands you call that change the
texture image or other properties change the contents of the currently
bound texture object as well as the current texture state.
In Example 9-7, after completion of display(), you are still bound to the
texture named by the contents of texName[1]. Be careful that you don’t call
a spurious texture routine that changes the data in that texture object.
When mipmaps are used, all related mipmaps of a single texture image must
be put into a single texture object. In Example 9-5, levels 0–5 of a mip-
mapped texture image are put into a single texture object named texName.
Cleaning Up Texture Objects
As you bind and unbind texture objects, their data still sits around some-
where among your texture resources. If texture resources are limited, deleting
textures may be one way to free up resources.

442 Chapter 9: Texture Mapping
A Working Set of Resident Textures
Some OpenGL implementations support a working set of high-performance
textures, which are said to be resident. Typically, these implementations
have specialized hardware to perform texture operations and a limited
hardware cache to store texture images. In this case, using texture objects is
recommended, because you are able to load many textures into the working
set and then control them.
If all the textures required by the application exceed the size of the cache,
some textures cannot be resident. If you want to find out if a single texture
is currently resident, bind its object, and then call glGetTexParameter*v()
to determine the value associated with the GL_TEXTURE_RESIDENT state.
If you want to know about the texture residence status of many textures, use
glAreTexturesResident().
Note that glAreTexturesResident() returns the current residence status.
Texture resources are very dynamic, and texture residence status may change
void glDeleteTextures(GLsizei n, const GLuint *textureNames);
Deletes n texture objects, named by elements in the array textureNames.
The freed texture names may now be reused (for example, by
glGenTextures()).
If a texture that is currently bound is deleted, the binding reverts to the
default texture, as if glBindTexture() were called with zero for the value
of textureName. Attempts to delete nonexistent texture names or the
texture name of zero are ignored without generating an error.
GLboolean glAreTexturesResident(GLsizei n,
const GLuint *textureNames,
GLboolean *residences);
Queries the texture residence status of the n texture objects, named in
the array textureNames.residences is an array in which texture residence
status is returned for the corresponding texture objects in the array
textureNames. If all the named textures in textureNames are resident, the
glAreTexturesResident() function returns GL_TRUE, and the contents
of the array residences are undisturbed. If any texture in textureNames is
not resident, then glAreTexturesResident() returns GL_FALSE, and the
elements in residences, which correspond to nonresident texture objects
in textureNames, are also set to GL_FALSE.
Compatibility
Extension
glAreTextures
Resident

Texture Objects 443
at any time. Some implementations cache textures when they are first used.
It may be necessary to draw with the texture before checking residency.
If your OpenGL implementation does not establish a working set of high-
performance textures, then the texture objects are always considered
resident. In that case, glAreTexturesResident() always returns GL_TRUE
and basically provides no information.
Texture Residence Strategies
If you can create a working set of textures and want to get the best texture
performance possible, you really have to know the specifics of your imple-
mentation and application. For example, with a visual simulation or video
game, you have to maintain performance in all situations. In that case, you
should never access a nonresident texture. For these applications, you want
to load up all your textures on initialization and make them all resident. If
you don’t have enough texture memory available, you may need to reduce
the size, resolution, and levels of mipmaps for your texture images, or you
may use glTexSubImage*() to repeatedly reuse the same texture memory.
Note: If you have several short-lived textures of the same size, you can use
glTexSubImage*() to reload existing texture objects with different
images. This technique may be more efficient than deleting textures
and reestablishing new textures from scratch.
For applications that create textures “on the fly,” nonresident textures
may be unavoidable. If some textures are used more frequently than others,
you may assign a higher priority to those texture objects to increase their
likelihood of being resident. Deleting texture objects also frees up space.
Short of that, assigning a lower priority to a texture object may make it first
in line for being moved out of the working set, as resources dwindle.
glPrioritizeTextures() is used to assign priorities to texture objects.
void glPrioritizeTextures(GLsizei n, const GLuint *textureNames,
const GLclampf *priorities);
Assigns the n texture objects, named in the array textureNames, the texture
residence priorities in the corresponding elements of the array priorities.
The priority values in the array priorities are clamped to the range [0.0, 1.0]
before being assigned. Zero indicates the lowest priority (textures least
likely to be resident), and 1 indicates the highest priority.
glPrioritizeTextures() does not require that any of the textures in
textureNames be bound. However, the priority might not have any effect
on a texture object until it is initially bound.
Compatibility
Extension
glPrioritizeTextures

444 Chapter 9: Texture Mapping
glTexParameter*() also may be used to set a single texture’s priority, but
only if the texture is currently bound. In fact, use of glTexParameter*() is
the only way to set the priority of a default texture.
If texture objects have equal priority, typical implementations of OpenGL
apply a least recently used (LRU) strategy to decide which texture objects to
move out of the working set. If you know that your OpenGL implementa-
tion uses this algorithm, then having equal priorities for all texture objects
creates a reasonable LRU system for reallocating texture resources.
If your implementation of OpenGL doesn’t use an LRU strategy for texture
objects of equal priority (or if you don’t know how it decides), you can
implement your own LRU strategy by carefully maintaining the texture
object priorities. When a texture is used (bound), you can maximize its
priority, which reflects its recent use. Then, at regular (time) intervals, you
can degrade the priorities of all texture objects.
Note: Fragmentation of texture memory can be a problem, especially if
you’re deleting and creating numerous new textures. Although it
may be possible to load all the texture objects into a working set by
binding them in one sequence, binding them in a different sequence
may leave some textures nonresident.
Texture Functions
In each of the examples presented so far in this chapter, the values in the
texture map have been used directly as colors to be painted on the surface
being rendered. You can also use the values in the texture map to modulate
the color in which the surface would be rendered without texturing or to
combine the color in the texture map with the original color of the surface.
You choose texturing functions by supplying the appropriate arguments to
glTexEnv*().
void glTexEnv{if}(GLenum target, GLenum pname,TYPE param);
void glTexEnv{if}v(GLenum target, GLenum pname, const TYPE *param);
Sets the current texturing function. target must be either GL_TEXTURE_
FILTER_CONTROL or GL_TEXTURE_ENV.
If target is GL_TEXTURE_FILTER_CONTROL, then pname must be
GL_TEXTURE_LOD_BIAS, and param is a single, floating-point value used
to bias the mipmapping level-of-detail parameter.
Compatibility
Extension
glTexEnv and all
associated tokens

Texture Functions 445
Note: This is only a partial list of acceptable values for glTexEnv*(),
excluding texture combiner functions. For complete details about
GL_COMBINE and a complete list of options for pname and param
for glTexEnv*(), see “Texture Combiner Functions” on page 472 and
Table 9-8.
The combination of the texturing function and the base internal format
determines how the textures are applied for each component of the texture.
The texturing function operates on selected components of the texture
and the color values that would be used with no texturing. (Note that the
selection is performed after the pixel-transfer function has been applied.)
Recall that when you specify your texture map with glTexImage*D(), the
third argument is the internal format to be selected for each texel.
There are six base internal formats: GL_ALPHA, GL_LUMINANCE, GL_
LUMINANCE_ALPHA, GL_INTENSITY, GL_RGB, and GL_RGBA. Other
internal formats (such as GL_LUMINANCE6_ALPHA2 or GL_R3_G3_B2)
specify desired resolutions of the texture components and can be matched
to one of these six base internal formats.
Texturing calculations are ultimately in RGBA, but some internal formats
are not in RGB. Table 9-4 shows how the RGBA color values are derived
from different texture formats, including the less obvious derivations.
If target is GL_TEXTURE_ENV and if pname is GL_TEXTURE_ENV_MODE,
then param is one of GL_DECAL, GL_REPLACE, GL_MODULATE,
GL_BLEND, GL_ADD, or GL_COMBINE, which specifies how texture
values are combined with the color values of the fragment being processed.
If pname is GL_TEXTURE_ENV_COLOR, then param is an array of 4
floating-point numbers (R, G, B, A) which denotes a color to be used
for GL_BLEND operations.
If target is GL_POINT_SPRITE and if pname is GL_COORD_REPLACE, then
setting param to GL_TRUE will enable the iteration of texture coordinates
across a point sprite. Texture coordinates will remain constant across the
primitive if param is set to GL_FALSE.
Base Internal Format Derived Source Color (R, G, B, A)
GL_ALPHA (0, 0, 0, A)
GL_LUMINANCE (L, L, L, 1)
Table 9-4 Deriving Color Values from Different Texture Formats

446 Chapter 9: Texture Mapping
Table 9-5 and Table 9-6 show how a texturing function (except for GL_
COMBINE) and base internal format determine the texturing application
formula used for each component of the texture.
In Table 9-5 and Table 9-6, note the following use of subscripts:
•s indicates a texture source color, as determined in Table 9-4.
•f indicates an incoming fragment value.
•c indicates values assigned with GL_TEXTURE_ENV_COLOR.
• No subscript indicates a final, computed value.
In these tables, multiplication of a color triple by a scalar means multiplying
each of the R, G, and B components by the scalar; multiplying (or adding)
two color triples means multiplying (or adding) each component of the
second by (or to) the corresponding component of the first.
GL_LUMINANCE_ALPHA (L, L, L, A)
GL_INTENSITY (I, I, I, I)
GL_RGB (R, G, B, 1)
GL_RGBA (R, G, B, A)
Base Internal Format GL_REPLACE
Function
GL_MODULATE
Function
GL_DECAL
Function
GL_ALPHA C = Cf
A = As
C = Cf
A = AfAs
undefined
GL_LUMINANCE C = Cs
A = Af
C = CfCs
A = Af
undefined
GL_LUMINANCE_ALPHA C = Cs
A = As
C = CfCs
A = AfAs
undefined
GL_INTENSITY C = Cs
A = Cs
C = CfCs
A = AfCs
undefined
Table 9-5 Replace, Modulate, and Decal Texture Functions
Base Internal Format Derived Source Color (R, G, B, A)
Table 9-4 (continued) Deriving Color Values from Different Texture Formats
Texture Functions 447
The replacement texture function simply takes the color that would have
been painted in the absence of any texture mapping (the fragment’s color),
tosses it away, and replaces it with the texture color. You use the replace-
ment texture function in situations where you want to apply an opaque
texture to an object—such as, for example, if you were drawing a soup can
with an opaque label.
The decal texture function is similar to replacement, except that it works for
only the RGB and RGBA internal formats, and it processes alpha differently.
With the RGBA internal format, the fragment’s color is blended with the
texture color in a ratio determined by the texture alpha, and the fragment’s
alpha is unchanged. The decal texture function may be used to apply an
alpha blended texture, such as an insignia on an airplane wing.
GL_RGB C = Cs
A = Af
C = CfCs
A = Af
C = Cs
A = Af
GL_RGBA C = Cs
A = As
C = CfCs
A = AfAs
C = Cf(1 As) + CsAs
A = Af
Base Internal Format GL_BLEND Function GL_ADD Function
GL_ALPHA C = Cf
A = AfAs
C = Cf
A = AfAs
GL_LUMINANCE C = Cf(1 Cs) + CcCs
A = Af
C = Cf + Cs
A = Af
GL_LUMINANCE_ALPHA C = Cf(1 Cs) + CcCs
A = AfAs
C = Cf + Cs
A = AfAs
GL_INTENSITY C = Cf(1 Cs) + CcCs
A = Af(1 As) + AcAs
C = Cf + Cs
A = Af + As
GL_RGB C = Cf(1 Cs) + CcCs
A = Af
C = Cf + Cs
A = Af
GL_RGBA C = Cf(1 Cs) + CcCs
A = AfAs
C = Cf + Cs
A = AfAs
Table 9-6 Blend and Add Texture Functions
Base Internal Format GL_REPLACE
Function
GL_MODULATE
Function
GL_DECAL
Function
Table 9-5 (continued) Replace, Modulate, and Decal Texture Functions

448 Chapter 9: Texture Mapping
For modulation, the fragment’s color is modulated by the contents of
the texture map. If the base internal format is GL_LUMINANCE, GL_
LUMINANCE_ALPHA, or GL_INTENSITY, the color values are multiplied by
the same value, so the texture map modulates between the fragment’s color
(if the luminance or intensity is 1) to black (if it’s 0). For the GL_RGB and
GL_RGBA internal formats, each of the incoming color components is
multiplied by a corresponding (possibly different) value in the texture. If
there’s an alpha value, it’s multiplied by the fragment’s alpha. Modulation
is a good texture function for use with lighting, since the lit polygon color
can be used to attenuate the texture color. Most of the texture-mapping
examples in the color plates use modulation for this reason. White, specular
polygons are often used to render lit, textured objects, and the texture
image provides the diffuse color.
The additive texture function simply adds the texture color to the fragment
color. If there’s an alpha value, it’s multiplied by the fragment alpha, except
for the GL_INTENSITY format, where the texture’s intensity is added to
the fragment alpha. Unless the texture and fragment colors are carefully
chosen, the additive texture function easily results in oversaturated or
clamped colors.
The blending texture function is the only function that uses the color
specified by GL_TEXTURE_ENV_COLOR. The luminance, intensity, or color
value is used somewhat like an alpha value to blend the fragment’s color
with the GL_TEXTURE_ENV_COLOR. (See “Sample Uses of Blending” in
Chapter 6 for the billboarding example, which uses a blended texture.)
Nate Robins’ Texture Tutorial
If you have downloaded Nate Robins’ suite of tutorial programs, run the
texture tutorial. Change the texture-mapping environment attribute and
see the effects of several texture functions. If you use GL_MODULATE, note
the effect of the color specified by glColor4f(). If you choose GL_BLEND,
see what happens if you change the color specified by the env_color array.
Assigning Texture Coordinates
As you draw your texture-mapped scene, you must provide both object
coordinates and texture coordinates for each vertex. After transformation,
the object’s coordinates determine where on the screen that particular
vertex is rendered. The texture coordinates determine which texel in the

Assigning Texture Coordinates 449
texture map is assigned to that vertex. In exactly the same way that colors
are interpolated between two vertices of shaded polygons and lines, texture
coordinates are interpolated between vertices. (Remember that textures are
rectangular arrays of data.)
Texture coordinates can comprise one, two, three, or four coordinates.
They’re usually referred to as the s-, t-, r-, and q-coordinates to distinguish
them from object coordinates (x, y, z, and w) and from evaluator coordi-
nates (u and v; see Chapter 12). For one-dimensional textures, you use the
s-coordinate; for two-dimensional textures, you use s and t; and for three-
dimensional textures, you use s,t, and r. The q-coordinate, like w, is typically
given the value 1 and can be used to create homogeneous coordinates; it’s
described as an advanced feature in “The q-Coordinate.” The command
to specify texture coordinates, glTexCoord*(), is similar to glVertex*(),
glColor*(), and glNormal*()—it comes in similar variations and is used
the same way between glBegin() and glEnd() pairs. Usually, texture-
coordinate values range from 0 to 1; values can be assigned outside this
range, however, with the results described in “Repeating and Clamping
Textures.”
The next subsection discusses how to calculate appropriate texture coordi-
nates. Instead of explicitly assigning them yourself, you can choose to have
texture coordinates calculated automatically by OpenGL as a function of
void glTexCoord{1234}{sifd}(TYPE coords);
void glTexCoord{1234}{sifd}v(const TYPE *coords);
Sets the current texture coordinates (s, t, r, q). Subsequent calls to
glVertex*() result in those vertices being assigned the current texture
coordinates. With glTexCoord1*(), the s-coordinate is set to the specified
value, t and r are set to 0, and q is set to 1. Using glTexCoord2*() allows
you to specify s and t;r and q are set to 0 and 1, respectively. With
glTexCoord3*(),q is set to 1 and the other coordinates are set as specified.
You can specify all coordinates with glTexCoord4*(). Use the appropriate
suffix (s, i, f, or d) and the corresponding value for TYPE (GLshort, GLint,
GLfloat, or GLdouble) to specify the coordinates’ data type. You can
supply the coordinates individually, or you can use the vector version of
the command to supply them in a single array. Texture coordinates are
multiplied by the 4 u4 texture matrix before any texture mapping occurs.
(See “The Texture Matrix Stack” on page 481.) Note that integer texture
coordinates are interpreted directly, rather than being mapped to the
range [1, 1] as normal coordinates are.
Compatibility
Extension
glTexCoord

450 Chapter 9: Texture Mapping
the vertex coordinates. (See “Automatic Texture-Coordinate Generation”
on page 457.)
Nate Robins’ Texture Tutorial
If you have Nate Robins’ texture tutorial, run it, and experiment with the
parameters of glTexCoord2f() for the four different vertices. See how you
can map from a portion of the entire texture. (What happens if you make a
texture coordinate less than 0 or greater than 1?)
Computing Appropriate Texture Coordinates
Two-dimensional textures are square or rectangular images that are typically
mapped to the polygons that make up a polygonal model. In the simplest
case, you’re mapping a rectangular texture onto a model that’s also rectan-
gular—for example, your texture is a scanned image of a brick wall, and
your rectangle represents a brick wall of a building. Suppose the brick wall
is square and the texture is square, and you want to map the whole texture
to the whole wall. The texture coordinates of the texture square are (0, 0),
(1, 0), (1, 1), and (0, 1) in counterclockwise order. When you’re drawing the
wall, just give those four coordinate sets as the texture coordinates as you
specify the wall’s vertices in counterclockwise order.
Now suppose that the wall is two-thirds as high as it is wide, and that the
texture is again square. To avoid distorting the texture, you need to map the
wall to a portion of the texture map so that the aspect ratio of the texture
is preserved. Suppose that you decide to use the lower two-thirds of the
texture map to texture the wall. In this case, use texture coordinates of
(0, 0), (1, 0), (1, 2/3), and (0, 2/3) for the texture coordinates, as the wall
vertices are traversed in a counterclockwise order.
As a slightly more complicated example, suppose you’d like to display a tin
can with a label wrapped around it on the screen. To obtain the texture, you
purchase a can, remove the label, and scan it in. Suppose the label is 4 units
tall and 12 units around, which yields an aspect ratio of 3 to 1. Since tex-
tures must have aspect ratios of 2n to 1, you can either simply not use the
top third of the texture, or you can cut and paste the texture until it has the
necessary aspect ratio. Suppose you decide not to use the top third. Now
suppose the tin can is a cylinder approximated by 30 polygons of length
4 units (the height of the can) and width 12/30 (1/30 of the circumference
of the can). You can use the following texture coordinates for each of the
30 approximating rectangles:
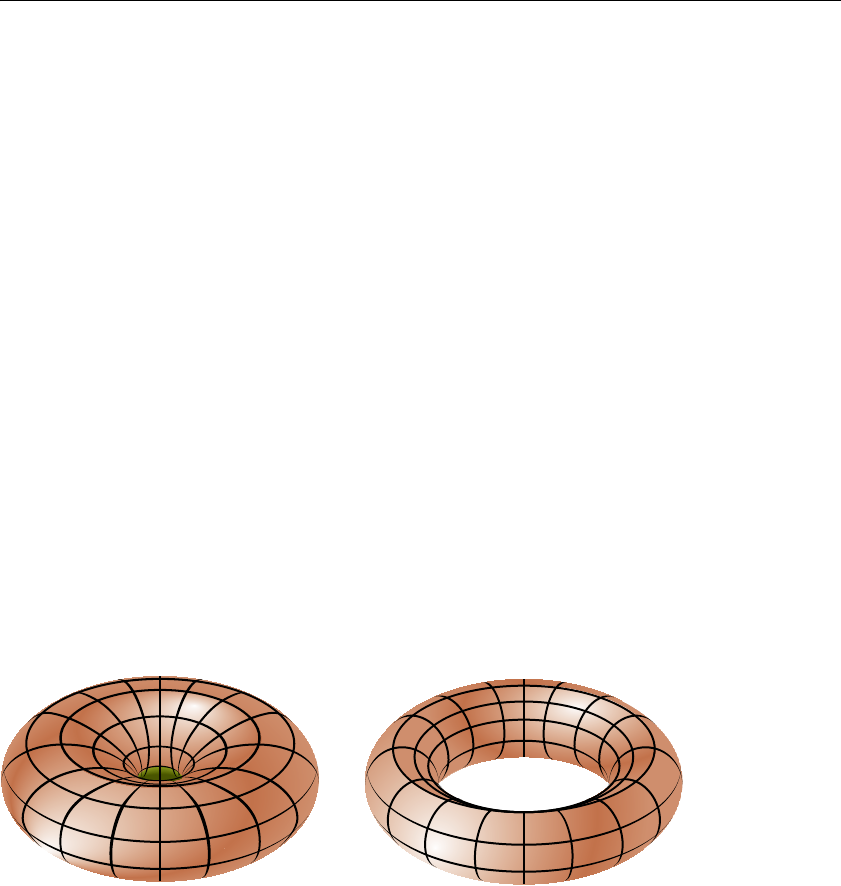
Assigning Texture Coordinates 451
1: (0, 0), (1/30, 0), (1/30, 2/3), (0, 2/3)
2: (1/30, 0), (2/30, 0), (2/30, 2/3), (1/30, 2/3)
3: (2/30, 0), (3/30, 0), (3/30, 2/3), (2/30, 2/3)
. . .
30: (29/30, 0), (1, 0), (1, 2/3), (29/30, 2/3)
Only a few curved surfaces such as cones and cylinders can be mapped to a
flat surface without geodesic distortion. Any other shape requires some
distortion. In general, the higher the curvature of the surface, the more
distortion of the texture is required.
If you don’t care about texture distortion, it’s often quite easy to find a rea-
sonable mapping. For example, consider a sphere whose surface coordinates
are given by (cos T cos I, cos Tsin I, sin T), where 0 dTd2S and 0 dIdS.
The T-I rectangle can be mapped directly to a rectangular texture map, but
the closer you get to the poles, the more distorted the texture is. The entire
top edge of the texture map is mapped to the north pole, and the entire
bottom edge to the south pole. For other surfaces, such as that of a torus
(doughnut) with a large hole, the natural surface coordinates map to the
texture coordinates in a way that produces only a little distortion, so it
might be suitable for many applications. Figure 9-9 shows two toruses, one
with a small hole (and therefore a lot of distortion near the center) and one
with a large hole (and only a little distortion).
If you’re texturing spline surfaces generated with evaluators (see Chapter 12),
the u and v parameters for the surface can sometimes be used as texture
coordinates. In general, however, there’s a large artistic component to
successful mapping of textures to polygonal approximations of curved
surfaces.
Figure 9-9 Texture-Map Distortion

452 Chapter 9: Texture Mapping
Repeating and Clamping Textures
You can assign texture coordinates outside the range [0, 1] and have them
either clamp or repeat in the texture map. With repeating textures, if you
have a large plane with texture coordinates running from 0.0 to 10.0 in
both directions, for example, you’ll get 100 copies of the texture tiled
together on the screen. During repeating, the integer parts of texture coor-
dinates are ignored, and copies of the texture map tile the surface. For most
applications in which the texture is to be repeated, the texels at the top of
the texture should match those at the bottom, and similarly for the left and
right edges.
A “mirrored” repeat is available, where the surface tiles “flip-flop.” For
instance, within texture coordinate range [0, 1], a texture may appear
oriented from left-to-right (or top-to-bottom or near-to-far), but the
“mirrored” repeat wrapping reorients the texture from right-to-left for
texture coordinate range [1, 2], then back again to left-to-right for coordi-
nates [2, 3], and so on.
Another possibility is to clamp the texture coordinates: Any values greater
than 1.0 are set to 1.0, and any values less than 0.0 are set to 0.0. Clamping
is useful for applications in which you want a single copy of the texture to
appear on a large surface. If the texture coordinates of the surface range
from 0.0 to 10.0 in both directions, one copy of the texture appears in the
lower left corner of the surface.
If you are using textures with borders or have specified a texture border
color, both the wrapping mode and the filtering method (see “Filtering” on
page 434) influence whether and how the border information is used.
If you’re using the filtering method GL_NEAREST, the closest texel in the
texture is used. For most wrapping modes, the border (or border color) is
ignored. However, if the texture coordinate is outside the range [0, 1] and
the wrapping mode is GL_CLAMP_TO_BORDER, then the nearest border
texel is chosen. (If no border is present, the constant border color is used.)
If you’ve chosen GL_LINEAR as the filtering method, a weighted combi-
nation in a 2 u2 array (for two-dimensional textures) of color data is used
for texture application. If there is a border or border color, the texture and
border colors are used together, as follows:
• For the wrapping mode GL_REPEAT, the border is always ignored. The
2u2 array of weighted texels wraps to the opposite edge of the texture.
Thus, texels at the right edge are averaged with those at the left edge,
and top and bottom texels are also averaged.

Assigning Texture Coordinates 453
• For the wrapping mode GL_CLAMP, the texel from the border (or
GL_TEXTURE_BORDER_COLOR) is used in the 2 u2 array of weighted
texels.
• For the wrapping mode GL_CLAMP_TO_EDGE, the border is always
ignored. Texels at or near the edge of the texture are used for texturing
calculations, but not the border.
• For the wrapping mode GL_CLAMP_TO_BORDER, if the texture coor-
dinate is outside the range [0, 1], then only border texels (or if no
border is present, the constant border color) are used for texture appli-
cation. Near the edge of texture coordinates, texels from both the bor-
der and the interior texture may be sampled in a 2 u2 array.
If you are using clamping, you can avoid having the rest of the surface
affected by the texture. To do this, use alpha values of 0 for the edges (or
borders, if they are specified) of the texture. The decal texture function
directly uses the texture’s alpha value in its calculations. If you are using one
of the other texture functions, you may also need to enable blending with
good source and destination factors. (See “Blending” in Chapter 6.)
To see the effects of wrapping, you must have texture coordinates that
venture beyond [0.0, 1.0]. Start with Example 9-1, and modify the texture
coordinates for the squares by mapping the texture coordinates from 0.0 to
4.0, as follows:
glBegin(GL_QUADS);
glTexCoord2f(0.0, 0.0); glVertex3f(-2.0, -1.0, 0.0);
glTexCoord2f(0.0, 4.0); glVertex3f(-2.0, 1.0, 0.0);
glTexCoord2f(4.0, 4.0); glVertex3f(0.0, 1.0, 0.0);
glTexCoord2f(4.0, 0.0); glVertex3f(0.0, -1.0, 0.0);
glTexCoord2f(0.0, 0.0); glVertex3f(1.0, -1.0, 0.0);
glTexCoord2f(0.0, 4.0); glVertex3f(1.0, 1.0, 0.0);
glTexCoord2f(4.0, 4.0); glVertex3f(2.41421, 1.0, -1.41421);
glTexCoord2f(4.0, 0.0); glVertex3f(2.41421, -1.0, -1.41421);
glEnd();
With GL_REPEAT wrapping, the result is as shown in Figure 9-10.
Figure 9-10 Repeating a Texture
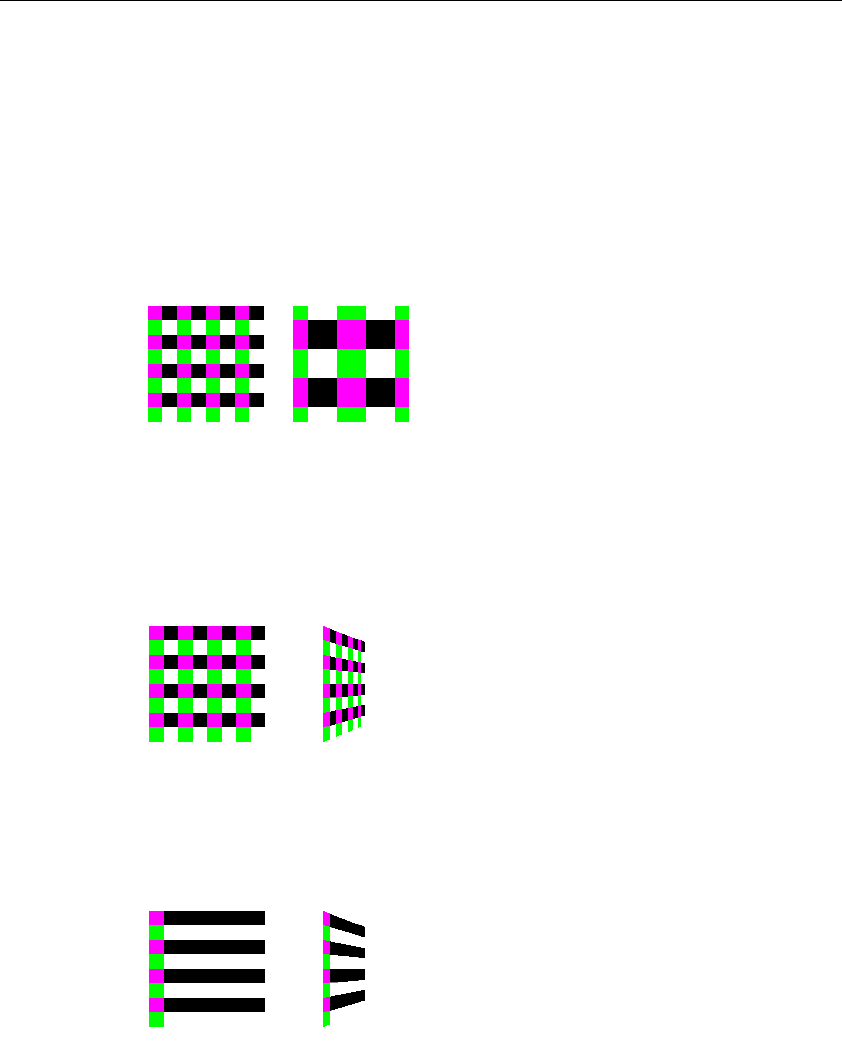
454 Chapter 9: Texture Mapping
In this case, the texture is repeated in both the s- and t- directions, since the
following calls are made to glTexParameter*():
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
Some OpenGL implementations support GL_MIRRORED_REPEAT wrapping,
which reverses orientation at every integer texture coordinate boundary.
Figure 9-11 shows the contrast between ordinary repeat wrapping (left) and
the mirrored repeat (right).
In Figure 9-12, GL_CLAMP is used for each direction. Where the texture
coordinate s or t is greater than one, the texel used is from where each
texture coordinate is exactly one.
Wrapping modes are independent for each direction. You can also clamp in
one direction and repeat in the other, as shown in Figure 9-13.
Figure 9-11 Comparing GL_REPEAT to GL_MIRRORED_REPEAT
Figure 9-12 Clamping a Texture
Figure 9-13 Repeating and Clamping a Texture
Assigning Texture Coordinates 455
You’ve now seen several arguments for glTexParameter*(), which are
summarized as follows.
void glTexParameter{if}(GLenum target, GLenum pname,TYPE param);
void glTexParameter{if}v(GLenum target, GLenum pname,
const TYPE *param);
void glTexParameterI{i ui}v(GLenum target, GLenum pname,
const TYPE *param);
Sets various parameters that control how a texture is treated as it’s applied
to a fragment or stored in a texture object. The target parameter is GL_
TEXTURE_1D, GL_TEXTURE_2D, GL_TEXTURE_3D, GL_TEXTURE_1D_
ARRAY, GL_TEXTURE_2D_ARRAY, GL_TEXTURE_CUBE_MAP, and GL_
TEXTURE_RECTANGLE to match the intended texture. The possible
values for pname and param are shown in Table 9-7. You can use the vector
version of the command to supply an array of values for GL_TEXTURE_
BORDER_COLOR, or you can supply individual values for other
parameters using the nonvector version. If values are supplied as integers
using glTexParameterf*(), they’re converted to floating-point numbers
according to Table 4-1; they’re also clamped to the range [0, 1]. Integer
values passed into glTexParameterI*() are not converted. Likewise, if
integer values are supplied using glTexParameterI*() to set floating-point
parameters, they are converted as described in Table 4-1.
Parameter Values
GL_TEXTURE_WRAP_S GL_CLAMP, GL_CLAMP_TO_EDGE,
GL_CLAMP_TO_BORDER, GL_REPEAT,
GL_MIRRORED_REPEAT
GL_TEXTURE_WRAP_T GL_CLAMP, GL_CLAMP_TO_EDGE,
GL_CLAMP_TO_BORDER, GL_REPEAT,
GL_MIRRORED_REPEAT
GL_TEXTURE_WRAP_R GL_CLAMP, GL_CLAMP_TO_EDGE,
GL_CLAMP_TO_BORDER, GL_REPEAT,
GL_MIRRORED_REPEAT
GL_TEXTURE_MAG_FILTER GL_NEAREST, GL_LINEAR
Table 9-7 glTexParameter*() Parameters
Compatibility
Extension
GL_CLAMP
GL_TEXTURE_
BORDER_COLOR
GL_GENERATE_
MIPMAP
GL_TEXTURE_
PRIORITY

456 Chapter 9: Texture Mapping
Try This
Figures 9-12 and 9-13 are drawn using GL_NEAREST for the minification
and magnification filters. What happens if you change the filter values to
GL_LINEAR? The resulting image should look more blurred.
Border information may be used while calculating texturing. For the
simplest demonstration of this, set GL_TEXTURE_BORDER_COLOR to
GL_TEXTURE_MIN_FILTER GL_NEAREST, GL_LINEAR,
GL_NEAREST_MIPMAP_NEAREST,
GL_NEAREST_MIPMAP_LINEAR,
GL_LINEAR_MIPMAP_NEAREST,
GL_LINEAR_MIPMAP_LINEAR
GL_TEXTURE_BORDER_COLOR any four values in [0.0, 1.0] (for non-integer
texture formats), or signed or unsigned integer
values (for integer texture formats)
GL_TEXTURE_PRIORITY [0.0, 1.0] for the current texture object
GL_TEXTURE_MIN_LOD any floating-point value
GL_TEXTURE_MAX_LOD any floating-point value
GL_TEXTURE_BASE_LEVEL any non-negative integer
GL_TEXTURE_MAX_LEVEL any non-negative integer
GL_TEXTURE_LOD_BIAS any floating-point value
GL_DEPTH_TEXTURE_MODE GL_RED, GL_LUMINANCE, GL_INTENSITY,
GL_ALPHA
GL_TEXTURE_COMPARE_MODE GL_NONE, GL_COMPARE_REF_TO_TEXTURE
(for Version 3.0 and later), or
GL_COMPARE_R_TO_TEXTURE (for versions
up to and including Version 2.1)
GL_TEXTURE_COMPARE_FUNC GL_LEQUAL, GL_GEQUAL, GL_LESS,
GL_GREATER, GL_EQUAL, GL_NOTEQUAL,
GL_ALWAYS, GL_NEVER
GL_GENERATE_MIPMAP GL_TRUE, GL_FALSE
Parameter Values
Table 9-7 (continued) glTexParameter*() Parameters
Try This
Automatic Texture-Coordinate Generation 457
a noticeable color. With the filters set to GL_NEAREST and the wrapping
mode set to GL_CLAMP_TO_BORDER, the border color affects the textured
object (for texture coordinates beyond the range [0, 1]). The border also
affects the texturing with the filters set to GL_LINEAR and the wrapping
mode set to GL_CLAMP.
What happens if you switch the wrapping mode to GL_CLAMP_TO_EDGE
or GL_REPEAT? In both cases, the border color is ignored.
Nate Robins’ Texture Tutorial
Run the Nate Robins’ texture tutorial and see the effects of the wrapping
parameters GL_REPEAT and GL_CLAMP. You will need to make the texture
coordinates at the vertices (parameters to glTexCoord2f()) less than 0
and/or greater than 1 to see any repeating or clamping effect.
Automatic Texture-Coordinate Generation
You can use texture mapping to make contours on your models or to simu-
late the reflections from an arbitrary environment on a shiny model. To
achieve these effects, let OpenGL automatically generate the texture coordi-
nates for you, rather than explicitly assign them with glTexCoord*(). To gen-
erate texture coordinates automatically, use the command glTexGen().
void glTexGen{ifd}(GLenum coord, GLenum pname,TYPE param);
void glTexGen{ifd}v(GLenum coord, GLenum pname, const TYPE *param);
Specifies the functions for automatically generating texture coordinates.
The first parameter, coord, must be GL_S, GL_T, GL_R, or GL_Q to indicate
whether texture coordinate s, t, r, or q is to be generated. The pname
parameter is GL_TEXTURE_GEN_MODE, GL_OBJECT_PLANE, or
GL_EYE_PLANE. If it’s GL_TEXTURE_GEN_MODE, param is an integer
(or, in the vector version of the command, points to an integer) that
is one of GL_OBJECT_LINEAR, GL_EYE_LINEAR, GL_SPHERE_MAP,
GL_REFLECTION_MAP, or GL_NORMAL_MAP. These symbolic constants
determine which function is used to generate the texture coordinate.
With either of the other possible values for pname,param is a pointer to
an array of values (for the vector version) specifying parameters for the
texture-generation function.
Compatibility
Extension
glTexGen and all
accpted tokens.

458 Chapter 9: Texture Mapping
The different methods of texture-coordinate generation have different uses.
Specifying the reference plane in object coordinates is best when a texture
image remains fixed to a moving object. Thus, GL_OBJECT_LINEAR would
be used for putting a wood grain on a tabletop. Specifying the reference
plane in eye coordinates (GL_EYE_LINEAR) is best for producing dynamic
contour lines on moving objects. GL_EYE_LINEAR may be used by special-
ists in the geosciences who are drilling for oil or gas. As the drill goes deeper
into the ground, the drill may be rendered with different colors to repre-
sent the layers of rock at increasing depths. GL_SPHERE_MAP and GL_
REFLECTION_MAP are used mainly for spherical environment mapping,
and GL_NORMAL_MAP is used for cube maps. (See “Sphere Map” on
page 463 and “Cube Map Textures” on page 465.)
Creating Contours
When GL_TEXTURE_GEN_MODE and GL_OBJECT_LINEAR are specified,
the generation function is a linear combination of the object coordinates of
the vertex (xo, yo, zo, wo):
generated coordinate = p1x0 + p2y0 + p3z0 + p4w0
The p1, ..., p4 values are supplied as the param argument to glTexGen*v(),
with pname set to GL_OBJECT_PLANE. With p1, ..., p4 correctly normalized,
this function gives the distance from the vertex to a plane. For example, if
p2 = p3 = p4 = 0 and p1 = 1, the function gives the distance between the ver-
tex and the plane x = 0. The distance is positive on one side of the plane,
negative on the other, and zero if the vertex lies on the plane.
Initially, in Example 9-8, equally spaced contour lines are drawn on a teapot;
the lines indicate the distance from the plane x = 0. The coefficients for the
plane x = 0 are in this array:
static GLfloat xequalzero[] = {1.0, 0.0, 0.0, 0.0};
Since only one property is being shown (the distance from the plane), a
one-dimensional texture map suffices. The texture map is a constant green
color, except that at equally spaced intervals it includes a red mark. Since
the teapot is sitting on the xy-plane, the contours are all perpendicular to its
base. Plate 18 shows the picture drawn by the program.
In the same example, pressing the ‘s’ key changes the parameters of the
reference plane to
static GLfloat slanted[] = {1.0, 1.0, 1.0, 0.0};

Automatic Texture-Coordinate Generation 459
The contour stripes are parallel to the plane x + y + z = 0, slicing across the
teapot at an angle, as shown in Plate 18. To restore the reference plane to its
initial value, x = 0, press the ‘x’ key.
Example 9-8 Automatic Texture-Coordinate Generation: texgen.c
#define stripeImageWidth 32
GLubyte stripeImage[4*stripeImageWidth];
static GLuint texName;
void makeStripeImage(void)
{
int j;
for (j = 0; j < stripeImageWidth; j++) {
stripeImage[4*j] = (GLubyte) ((j<=4) ? 255 : 0);
stripeImage[4*j+1] = (GLubyte) ((j>4) ? 255 : 0);
stripeImage[4*j+2] = (GLubyte) 0;
stripeImage[4*j+3] = (GLubyte) 255;
}
}
/* planes for texture-coordinate generation */
static GLfloat xequalzero[] = {1.0, 0.0, 0.0, 0.0};
static GLfloat slanted[] = {1.0, 1.0, 1.0, 0.0};
static GLfloat *currentCoeff;
static GLenum currentPlane;
static GLint currentGenMode;
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_SMOOTH);
makeStripeImage();
glPixelStorei(GL_UNPACK_ALIGNMENT, 1);
glGenTextures(1, &texName);
glBindTexture(GL_TEXTURE_1D, texName);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MAG_FILTER,
GL_LINEAR);
glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MIN_FILTER,
GL_LINEAR);

460 Chapter 9: Texture Mapping
glTexImage1D(GL_TEXTURE_1D, 0, GL_RGBA, stripeImageWidth, 0,
GL_RGBA, GL_UNSIGNED_BYTE, stripeImage);
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);
currentCoeff = xequalzero;
currentGenMode = GL_OBJECT_LINEAR;
currentPlane = GL_OBJECT_PLANE;
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, currentGenMode);
glTexGenfv(GL_S, currentPlane, currentCoeff);
glEnable(GL_TEXTURE_GEN_S);
glEnable(GL_TEXTURE_1D);
glEnable(GL_CULL_FACE);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_AUTO_NORMAL);
glEnable(GL_NORMALIZE);
glFrontFace(GL_CW);
glCullFace(GL_BACK);
glMaterialf(GL_FRONT, GL_SHININESS, 64.0);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glRotatef(45.0, 0.0, 0.0, 1.0);
glBindTexture(GL_TEXTURE_1D, texName);
glutSolidTeapot(2.0);
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-3.5, 3.5, -3.5*(GLfloat)h/(GLfloat)w,
3.5*(GLfloat)h/(GLfloat)w, -3.5, 3.5);
else
glOrtho(-3.5*(GLfloat)w/(GLfloat)h,
3.5*(GLfloat)w/(GLfloat)h, -3.5, 3.5, -3.5, 3.5);

Automatic Texture-Coordinate Generation 461
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘e’:
case ‘E’:
currentGenMode = GL_EYE_LINEAR;
currentPlane = GL_EYE_PLANE;
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, currentGenMode);
glTexGenfv(GL_S, currentPlane, currentCoeff);
glutPostRedisplay();
break;
case ‘o’:
case ‘O’:
currentGenMode = GL_OBJECT_LINEAR;
currentPlane = GL_OBJECT_PLANE;
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, currentGenMode);
glTexGenfv(GL_S, currentPlane, currentCoeff);
glutPostRedisplay();
break;
case ‘s’:
case ‘S’:
currentCoeff = slanted;
glTexGenfv(GL_S, currentPlane, currentCoeff);
glutPostRedisplay();
break;
case ‘x’:
case ‘X’:
currentCoeff = xequalzero;
glTexGenfv(GL_S, currentPlane, currentCoeff);
glutPostRedisplay();
break;
case 27:
exit(0);
break;
default:
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);

462 Chapter 9: Texture Mapping
glutInitWindowSize(256, 256);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutMainLoop();
return 0;
}
You enable texture-coordinate generation for the s-coordinate by passing
GL_TEXTURE_GEN_S to glEnable(). To generate other coordinates, enable
them with GL_TEXTURE_GEN_T, GL_TEXTURE_GEN_R, or GL_TEXTURE_
GEN_Q. Use glDisable() with the appropriate constant to disable coordi-
nate generation. Also note the use of GL_REPEAT to cause the contour lines
to be repeated across the teapot.
The GL_OBJECT_LINEAR function calculates the texture coordinates in
the model’s coordinate system. Initially, in Example 9-8, the GL_OBJECT_
LINEAR function is used, so the contour lines remain perpendicular to the
base of the teapot, no matter how the teapot is rotated or viewed. However,
if you press the ‘e’ key, the texture-generation mode is changed from
GL_OBJECT_LINEAR to GL_EYE_LINEAR, and the contour lines are calcu-
lated relative to the eye coordinate system. (Pressing the ‘o’ key restores
GL_OBJECT_LINEAR as the texture-generation mode.) If the reference plane
is x = 0, the result is a teapot with red stripes parallel to the yz-plane from
the eye’s point of view, as shown in Plate 18. Mathematically, you are mul-
tiplying the vector (p1p2p3p4) by the inverse of the modelview matrix to
obtain the values used to calculate the distance to the plane. The texture
coordinate is generated with the following function:
generated coordinate = p1’xe + p2’ye + p3’ze + p4’we
where (p1’p
2’p
3’p
4’) = (p1p2p3p4)M1
In this case, (xe, ye, ze, we) are the eye coordinates of the vertex, and p1, ...,
p4 are supplied as the param argument to glTexGen*(), with pname set to
GL_EYE_PLANE. The primed values are calculated only at the time they’re
specified, so this operation isn’t as computationally expensive as it looks.
In all these examples, a single texture coordinate is used to generate con-
tours. s,t, and (if needed) r texture coordinates can be generated indepen-
dently, however, to indicate the distances to two or three different planes.
With a properly constructed two- or three-dimensional texture map, the
resulting two or three sets of contours can be viewed simultaneously. For an

Automatic Texture-Coordinate Generation 463
added level of complexity, you can mix generation functions. For example,
you can calculate the s-coordinate using GL_OBJECT_LINEAR, and the
t-coordinate using GL_EYE_LINEAR.
Sphere Map
Advanced
The goal of environment mapping is to render an object as if it were
perfectly reflective, so that the colors on its surface are those reflected to
the eye from its surroundings. In other words, if you look at a perfectly
polished, perfectly reflective silver object in a room, you see the reflections
of the walls, floor, and other items in the room from the object. (A classic
example of using environment mapping is the evil, morphing cyborg in the
film Terminator 2.) The objects whose reflections you see depend on the
position of your eye and on the position and surface angles of the silver
object. To perform environment mapping, all you have to do is create an
appropriate texture map and then have OpenGL generate the texture
coordinates for you.
Environment mapping is an approximation based on the assumption that
the items in the environment are far away in comparison with the surfaces
of the shiny object—that is, it’s a small object in a large room. With this
assumption, to find the color of a point on the surface, take the ray from
the eye to the surface, and reflect the ray off the surface. The direction of
the reflected ray completely determines the color to be painted there.
Encoding a color for each direction on a flat texture map is equivalent to
putting a polished perfect sphere in the middle of the environment and
taking a picture of it with a camera that has a lens with a very long focal
length placed far away. Mathematically, the lens has an infinite focal length
and the camera is infinitely far away. The encoding therefore covers a
circular region of the texture map, tangent to the top, bottom, left, and
right edges of the map. The texture values outside the circle make no
difference, because they are never accessed in environment mapping.
To make a perfectly correct environment texture map, you need to obtain
a large silvered sphere, take a photograph of it in some environment with
a camera located an infinite distance away and with a lens that has an infinite
focal length, and scan in the photograph. To approximate this result, you can
use a scanned-in photograph of an environment taken with an extremely
wide-angle (or fish-eye) lens. Plate 21 shows a photograph taken with such a
lens and the results when that image is used as an environment map.
Advanced

464 Chapter 9: Texture Mapping
Once you’ve created a texture designed for environment mapping, you
need to invoke OpenGL’s environment-mapping algorithm. This algorithm
finds the point on the surface of the sphere with the same tangent surface
as that of the point on the object being rendered, and it paints the object’s
point with the color visible on the sphere at the corresponding point.
To generate automatically the texture coordinates to support environment
mapping, use this code in your program:
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
glTexGeni(GL_T, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
glEnable(GL_TEXTURE_GEN_S);
glEnable(GL_TEXTURE_GEN_T);
The GL_SPHERE_MAP constant creates the proper texture coordinates for
the environment mapping. As shown, you need to specify it for both the
s- and t-directions. However, you don’t have to specify any parameters for
the texture-coordinate generation function.
The GL_SPHERE_MAP texture function generates texture coordinates using
the following mathematical steps:
1. u is the unit vector pointing from the origin to the vertex (in eye
coordinates).
2. n’ is the current normal vector, after transformation to eye
coordinates.
3. r is the reflection vector, (rx ry rz)T, which is calculated by u – 2n’n’Tu.
4. An interim value, m, is calculated by
5. Finally, the s and t texture coordinates are calculated by
and
.
m = 2 r2 + r2+ (rz + 1)2
x y
s = r /m + 1
x2
t = r /m + 1
y2

Automatic Texture-Coordinate Generation 465
Cube Map Textures
Advanced
Cube map textures are a special technique that uses a set of six two-
dimensional texture images to form a texture cube centered at the origin.
For each fragment, the texture coordinates (s, t, r) are treated as a direction
vector, with each texel representing what on the texture cube is “seen” from
the origin. Cube maps are ideal for environment, reflection, and lighting
effects. Cube maps can also wrap a spherical object with textures,
distributing texels relatively evenly on all its sides.
The cube map textures are supplied by calling glTexImage2D() six times,
with the target argument indicating the face of the cube (+X, X, +Y, Y, +Z,
or Z). As the name implies, each cube map texture must have the same
dimensions so that a cube is formed with the same number of texels on each
side, as shown in this code, where imageSize has been set to a power of 2:
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X, 0, GL_RGBA,
imageSize, imageSize, 0, GL_RGBA, GL_UNSIGNED_BYTE, image1);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_X, 0, GL_RGBA,
imageSize, imageSize, 0, GL_RGBA, GL_UNSIGNED_BYTE, image4);
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_Y, 0, GL_RGBA,
imageSize, imageSize, 0, GL_RGBA, GL_UNSIGNED_BYTE, image2);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_Y, 0, GL_RGBA,
imageSize, imageSize, 0, GL_RGBA, GL_UNSIGNED_BYTE, image5);
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_Z, 0, GL_RGBA,
imageSize, imageSize, 0, GL_RGBA, GL_UNSIGNED_BYTE, image3);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_Z, 0, GL_RGBA,
imageSize, imageSize, 0, GL_RGBA, GL_UNSIGNED_BYTE, image6);
Useful cube map texture images may be generated by setting up a (real or
synthetic) camera at the origin of a scene and taking six “snapshots” with
90-degree field-of-view, oriented along the positive and negative axes. The
“snapshots” break up the entire 3D space into six frustums, which intersect
at the origin.
Cube map functionality is orthogonal to many other texturing operations,
so cube maps work with standard texturing features, such as texture
borders, mipmaps, copying images, subimages, and multitexturing. There is
a special proxy texture target for cube maps (GL_PROXY_TEXTURE_CUBE_
MAP) because a cube map generally uses six times as much memory as an
ordinary 2D texture. Texture parameters and texture objects should be
established for the entire cube map as a whole, not for the six individual
Advanced

466 Chapter 9: Texture Mapping
cube faces. The following code is an example of setting wrapping and
filtering methods with the target GL_TEXTURE_CUBE_MAP:
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S,
GL_REPEAT);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T,
GL_REPEAT);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R,
GL_REPEAT);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
To determine which texture (and texels) to use for a given fragment, the
current texture coordinates (s, t, r) first select one of the six textures, based
upon which of s, t, and rhas the largest absolute value (major axis) and
its sign (orientation). The remaining two coordinates are divided by the
coordinate with the largest value to determine a new (s’, t’), which is used to
look up the corresponding texel(s) in the selected texture of the cube map.
Although you can calculate and specify the texture coordinates explicitly,
this is generally laborious and unnecessary. Almost always, you’ll want to
use glTexGen*() to automatically generate cube map texture coordinates,
using one of the two special texture coordinate generation modes:
GL_REFLECTION_MAP or GL_NORMAL_MAP.
GL_REFLECTION_MAP uses the same calculations (until step 3 of the
sphere-mapping coordinate computation described in “Sphere Map”
on page 463) as the GL_SPHERE_MAP texture coordinate generation to
determine (rx ry rz) for use as (s, t, r). The reflection map mode is well-suited
for environment mapping as an alternative to sphere mapping.
GL_NORMAL_MAP is particularly useful for rendering scenes with infinite
(or distant local) light sources and diffuse reflection. GL_NORMAL_MAP
uses the model-view matrix to transform the vertex’s normal into eye
coordinates. The resulting (nx ny nz) becomes texture coordinates (s, t, r).
In Example 9-9, the normal map mode is used for texture generation and
cube map texturing is also enabled.
Example 9-9 Generating Cube Map Texture Coordinates: cubemap.c
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, GL_NORMAL_MAP);
glTexGeni(GL_T, GL_TEXTURE_GEN_MODE, GL_NORMAL_MAP);
glTexGeni(GL_R, GL_TEXTURE_GEN_MODE, GL_NORMAL_MAP);

Multitexturing 467
glEnable(GL_TEXTURE_GEN_S);
glEnable(GL_TEXTURE_GEN_T);
glEnable(GL_TEXTURE_GEN_R);
/* turn on cube map texturing */
glEnable(GL_TEXTURE_CUBE_MAP);
Multitexturing
During standard texturing, a single texture image is applied once to a poly-
gon. Multitexturing allows several textures to be applied, one by one in a
pipeline of texture operations, to the same polygon. There is a series of
texture units, where each texture unit performs a single texturing operation
and successively passes its result onto the next texture unit, until all defined
units are completed. Figure 9-14 shows how a fragment might undergo four
texturing operations—one for each of four texture units.
Multitexturing enables advanced rendering techniques, such as lighting
effects, decals, compositing, and detail textures.
Texture
unit 0
Texture
image 0
Texture
unit 1
Texture
image 1
Texture
unit 2
Texture
image 2
Texture
unit 3
Texture
image 3
Fragment
color input
to texturing
Fragment
color output
after texturing
Figure 9-14 Multitexture Processing Pipeline

468 Chapter 9: Texture Mapping
Steps in Multitexturing
To write code that uses multitexturing, perform the following steps:
Note: In feedback mode, multitexturing is undefined beyond the first
texture unit.
1. For each texturing unit, establish the texturing state, including texture
image, filter, environment, coordinate generation, and matrix. Use
glActiveTexture() to change the current texture unit. This is discussed
further in the next subsection, “Establishing Texture Units.” You may
also call glGetIntegerv(GL_MAX_TEXTURE_UNITS,...) to see how
many texturing units are available on your implementation. In a
worst-case scenario, there are at least two texture units.
2. During vertex specification, use glMultiTexCoord*() to specify more
than one texture coordinate per vertex. A different texture coordinate
may be used for each texturing unit. Each texture coordinate will be
used during a different texturing pass. Automatic texture-coordinate
generation and specification of texture coordinates in vertex arrays are
special cases of this situation. The special cases are described in “Other
Methods of Texture-Coordinate Specification” on page 471.
Establishing Texture Units
Multitexturing introduces multiple texture units, which are additional
texture application passes. Each texture unit has identical capabilities and
houses its own texturing state, including the following:
•Texture image
• Filtering parameters
• Environment application
• Texture matrix stack
• Automatic texture-coordinate generation
• Vertex-array specification (if needed)
Each texture unit combines the previous fragment color with its texture
image, according to its texture state. The resulting fragment color is passed
onto the next texture unit, if it is active.
To assign texture information to each texture unit, the routine
glActiveTexture() selects the current texture unit to be modified. After
that, calls to glTexImage*(),glTexParameter*(),glTexEnv*(),glTexGen*(),

Multitexturing 469
and glBindTexture() affect only the current texture unit. Queries of these
texture states also apply to the current texture unit, as well as queries of the
current texture coordinates and current raster texture coordinates.
If you use texture objects, you can bind a texture to the current texture unit.
The current texture unit has the values of the texture state contained within
the texture object (including the texture image).
The following code fragment, Example 9-10, has two distinct parts. In the
first part, two ordinary texture objects are created (assume the arrays texels0
and texels1 define texture images). In the second part, the two texture
objects are used to set up two texture units.
Example 9-10 Initializing Texture Units for Multitexturing: multitex.c
/* Two ordinary texture objects are created */
GLuint texNames[2];
glGenTextures(2, texNames);
glBindTexture(GL_TEXTURE_2D, texNames[0]);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, 32, 32, 0, GL_RGBA,
GL_UNSIGNED_BYTE, texels0);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
glBindTexture(GL_TEXTURE_2D, texNames[1]);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, 16, 16, 0, GL_RGBA,
GL_UNSIGNED_BYTE, texels1);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S,
GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T,
GL_CLAMP_TO_EDGE);
/* Use the two texture objects to define two texture units
* for use in multitexturing. */
glActiveTexture(GL_TEXTURE0);
glEnable(GL_TEXTURE_2D);
void glActiveTexture(GLenum texUnit);
Selects the texture unit that is currently modified by texturing routines.
texUnit is a symbolic constant of the form GL_TEXTUREi, where i is in the
range from 0 to k1, and k is the maximum number of texture units.

470 Chapter 9: Texture Mapping
glBindTexture(GL_TEXTURE_2D, texNames[0]);
glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);
glMatrixMode(GL_TEXTURE);
glLoadIdentity();
glTranslatef(0.5f, 0.5f, 0.0f);
glRotatef(45.0f, 0.0f, 0.0f, 1.0f);
glTranslatef(-0.5f, -0.5f, 0.0f);
glMatrixMode(GL_MODELVIEW);
glActiveTexture(GL_TEXTURE1);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, texNames[1]);
glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);
When a textured polygon is now rendered, it is rendered with two texturing
units. In the first unit, the texels0 texture image is applied with nearest texel
filtering, repeat wrapping, replacement texture environment, and a texture
matrix that rotates the texture image. After the first unit is completed, the
newly textured polygon is sent onto the second texture unit (GL_TEXTURE1),
where it is processed with the texels1 texture image with linear filtering,
edge clamping, modulation texture environment, and the default identity
texture matrix.
Note: Operations to a texture attribute group (using glPushAttrib(),
glPushClientAttrib(),glPopAttrib(), or glPopClientAttrib()) save
or restore the texture state of all texture units (except for the texture
matrix stack).
Specifying Vertices and Their Texture Coordinates
With multitexturing, it isn’t enough to have one set of texture coordinates
per vertex. You need to have one set for each texture unit for each vertex.
Instead of using glTexCoord*(), you must use glMultiTexCoord*(), which
specifies the texture unit, as well as the texture coordinates.
In Example 9-11, a triangle is given the two sets of texture coordinates
necessary for multitexturing with two active texture units.
void glMultiTexCoord{1234}{sifd}(GLenum texUnit,TYPE coords);
void glMultiTexCoord{1234}{sifd}v(GLenum texUnit, const TYPE *coords);
Sets the texture-coordinate data (s, t, r, q) in coords for use with the texture
unit texUnit. The enumerated values for texUnit are the same as for
glActiveTexture().
Compatibility
Extension
glMultiTexCoord

Multitexturing 471
Example 9-11 Specifying Vertices for Multitexturing
glBegin(GL_TRIANGLES);
glMultiTexCoord2f(GL_TEXTURE0, 0.0, 0.0);
glMultiTexCoord2f(GL_TEXTURE1, 1.0, 0.0);
glVertex2f(0.0, 0.0);
glMultiTexCoord2f(GL_TEXTURE0, 0.5, 1.0);
glMultiTexCoord2f(GL_TEXTURE1, 0.5, 0.0);
glVertex2f(50.0, 100.0);
glMultiTexCoord2f(GL_TEXTURE0, 1.0, 0.0);
glMultiTexCoord2f(GL_TEXTURE1, 1.0, 1.0);
glVertex2f(100.0, 0.0);
glEnd();
Note: If you are multitexturing and you use glTexCoord*(), you are setting
the texture coordinates for the first texture unit. In other words,
using glTexCoord*() is equivalent to using glMultiTexCoord*
(GL_TEXTURE0,...).
In the rare case that you are multitexturing a bitmap or image rectangle, you
need to associate several texture coordinates with each raster position.
Therefore, you must call glMultiTexCoord*() several times, once for each
active texture unit, for each glRasterPos*() or glWindowPos*() call. (Since
there is only one current raster position for the entire bitmap or image
rectangle, there is only one corresponding texture coordinate per unit, so
the aesthetic possibilities are extremely limited.)
Other Methods of Texture-Coordinate Specification
Explicitly calling glMultiTexCoord*() is only one of three ways to specify
texture coordinates when multitexturing. The other two ways are to use
automatic texture-coordinate generation (with glTexGen*()) or vertex
arrays (with glTexCoordPointer()).
If you are multitexturing and using automatic texture-coordinate genera-
tion, then glActiveTexture() directs which texture unit is affected by the
following automatic texture-coordinate generation routines:
• glTexGen*(...)
• glEnable(GL_TEXTURE_GEN_*)
• glDisable(GL_TEXTURE_GEN_*)
If you are multitexturing and specifying texture coordinates in vertex
arrays, then glClientActiveTexture() directs the texture unit for which
glTexCoordPointer() specifies its texture-coordinate data.

472 Chapter 9: Texture Mapping
Reverting to a Single Texture Unit
If you are using multitexturing and want to return to a single texture unit,
then you need to disable texturing for all units, except for texture unit 0,
with code as shown in Example 9-12.
Example 9-12 Reverting to Texture Unit 0
/* disable texturing for other texture units */
glActiveTexture (GL_TEXTURE1);
glDisable (GL_TEXTURE_2D);
glActiveTexture (GL_TEXTURE2);
glDisable (GL_TEXTURE_2D);
/* make texture unit 0 current */
glActiveTexture (GL_TEXTURE0);
Texture Combiner Functions
Advanced
OpenGL has evolved from its early focus on vertex processing (transforma-
tion, clipping) toward more concern with rasterization and fragment oper-
ations. Texturing functionality is increasingly exposed to the programmer
to improve fragment processing.
In addition to multipass texture techniques, flexible texture combiner func-
tions provide the programmer with finer control over mixing fragments
with texture or other color values. Texture combiner functions support
high-quality texture effects, such as bump mapping, more realistic specular
lighting, and texture fade effects (such as interpolating between two tex-
tures). A combiner function takes color and alpha data from up to three
sources and processes them, generating RGBA values as output for subse-
quent operations.
glTexEnv*() is used extensively to configure combiner functions. In
“Texture Functions,” you encountered an abbreviated description of
glTexEnv*(), and now here’s the complete description:
void glClientActiveTexture(GLenum texUnit);
Selects the current texture unit for specifying texture-coordinate data with
vertex arrays. texUnit is a symbolic constant of the form GL_TEXTUREi,
with the same values that are used for glActiveTexture().
Compatibility
Extension
glClientActive
Texture
Advanced

Texture Combiner Functions 473
void glTexEnv{if}(GLenum target, GLenum pname,TYPE param);
void glTexEnv{if}v(GLenum target, GLenum pname, const TYPE *param);
Sets the current texturing function. target must be either GL_TEXTURE_
FILTER_CONTROL or GL_TEXTURE_ENV.
If target is GL_TEXTURE_FILTER_CONTROL, then pname must be
GL_TEXTURE_LOD_BIAS, and param is a single, floating-point value
used to bias the mipmapping level-of-detail parameter.
If target is GL_TEXTURE_ENV, acceptable values for the second and
third arguments (pname and param) are listed in Table 9-8. If pname is
GL_TEXTURE_ENV_MODE, param specifies how texture values are com-
bined with the color values of the fragment being processed. Several envi-
ronment modes (GL_BLEND, GL_COMBINE, GL_COMBINE_RGB, and
GL_COMBINE_ALPHA) determine whether other environment modes are
useful.
If the texture environment mode is GL_BLEND, then the GL_TEXTURE_
ENV_COLOR setting is used.
If the texture environment mode is GL_COMBINE, then the GL_COMBINE_
RGB, GL_COMBINE_ALPHA, GL_RGB_SCALE, or GL_ALPHA_SCALE
parameters are also used. For the GL_COMBINE_RGB function, the
GL_SOURCEi_RGB and GL_OPERANDi_RGB parameters (where i is 0, 1,
or 2) also may be specified. Similarly for the GL_COMBINE_ALPHA
function, GL_SOURCEi_ALPHA and GL_OPERANDi_ALPHA may be
specified.
glTexEnv pname glTexEnv param
GL_TEXTURE_ENV_MODE GL_DECAL, GL_REPLACE, GL_MODULATE,
GL_BLEND, GL_ADD, or GL_COMBINE
GL_TEXTURE_ENV_COLOR array of 4 floating-point numbers: (R, G, B, A)
GL_COMBINE_RGB GL_REPLACE, GL_MODULATE, GL_ADD,
GL_ADD_SIGNED, GL_INTERPOLATE,
GL_SUBTRACT, GL_DOT3_RGB, or GL_DOT3_RGBA
GL_COMBINE_ALPHA GL_REPLACE, GL_MODULATE, GL_ADD,
GL_ADD_SIGNED, GL_INTERPOLATE, or
GL_SUBTRACT
Table 9-8 Texture Environment Parameters If target Is GL_TEXTURE_ENV
Compatibility
Extension
glTexEnv and all
accepted tokens

474 Chapter 9: Texture Mapping
Here are the steps for using combiner functions. If you are multitexturing,
you may use a different combiner function for every texture unit and thus
repeat these steps for each unit.
• To use any combiner function, you must call
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE);
• You should specify how you want RGB or alpha values to be combined
(see Table 9-9). For instance, Example 9-13 directs the current texture
unit to subtract RGB and alpha values of one source from another
source.
Example 9-13 Setting the Programmable Combiner Functions
glTexEnvf(GL_TEXTURE_ENV, GL_COMBINE_RGB, GL_SUBTRACT);
glTexEnvf(GL_TEXTURE_ENV, GL_COMBINE_ALPHA, GL_SUBTRACT);
GL_SRCi_RGB or
GL_SRCi_ALPHA
(where i is 0, 1, or 2)
GL_TEXTURE, GL_TEXTUREn (where n denotes
the nth texture unit and multitexturing is enabled),
GL_CONSTANT, GL_PRIMARY_COLOR, or
GL_PREVIOUS
GL_OPERANDi_RGB
(where i is 0, 1, or 2)
GL_SRC_COLOR, GL_ONE_MINUS_SRC_COLOR,
GL_SRC_ALPHA, or GL_ONE_MINUS_SRC_ALPHA
GL_OPERANDi_ALPHA
(where i is 0, 1, or 2)
GL_SRC_ALPHA, or GL_ONE_MINUS_SRC_ALPHA
GL_RGB_SCALE floating-point color scaling factor
GL_ALPHA_SCALE floating-point alpha scaling factor
glTexEnv param Combiner Function
GL_REPLACE Arg0
GL_MODULATE (default) Arg0 * Arg1
GL_ADD Arg0 + Arg1
GL_ADD_SIGNED Arg0 + Arg1 – 0.5
GL_INTERPOLATE Arg0 * Arg2 + Arg1 * (1 – Arg2)
Table 9-9 GL_COMBINE_RGB and GL_COMBINE_ALPHA Functions
glTexEnv pname glTexEnv param
Table 9-8 (continued) Texture Environment Parameters If target Is GL_TEXTURE_

Texture Combiner Functions 475
Note: GL_DOT3_RGB and GL_DOT3_RGBA are used only for
GL_COMBINE_RGB and not used for GL_COMBINE_ALPHA.
The GL_DOT3_RGB and GL_DOT3_RGBA modes differ subtly. With
GL_DOT3_RGB, the same dot product is placed into all three (R, G, B)
values. For GL_DOT3_RGBA, the result is placed into all four (R, G, B, A).
• Specify the source for the ith argument of the combiner function with
the constant GL_SOURCEi_RGB. The number of arguments (up to three)
depends upon the type of function chosen. As shown in Table 9-9,
GL_SUBTRACT requires two arguments, which may be set with the
following code:
Example 9-14 Setting the Combiner Function Sources
glTexEnvf(GL_TEXTURE_ENV, GL_SRC0_RGB, GL_TEXTURE);
glTexEnvf(GL_TEXTURE_ENV, GL_SRC1_RGB, GL_PREVIOUS);
When pname is GL_SOURCEi_RGB, these are your options for param along
with how the source is determined:
– GL_TEXTURE—the source for the ith argument is the texture of the
current texture unit
– GL_TEXTUREn—the texture associated with texture unit n. (If you
use this source, texture unit n must be enabled and valid, or the
result will be undefined.)
– GL_CONSTANT—the constant color set with GL_TEXTURE_
ENV_COLOR
– GL_PRIMARY_COLOR—the incoming fragment to texture unit 0,
which is the fragment color, prior to texturing
– GL_PREVIOUS—the incoming fragment from the previous texture
unit (for texture unit 0, this is the same as GL_PRIMARY_COLOR)
GL_SUBTRACT Arg0 – Arg1
GL_DOT3_RGB
GL_DOT3_RGBA
4 * ((Arg0r – 0.5) * (Arg1r – 0.5) +
(Arg0g – 0.5) * (Arg1g – 0.5) +
(Arg0b – 0.5) * (Arg1b – 0.5))
glTexEnv param Combiner Function
Table 9-9 (continued) GL_COMBINE_RGB and GL_COMBINE_ALPHA Functions

476 Chapter 9: Texture Mapping
If you suppose that the GL_SUBTRACT combiner code in Example 9-14 is
set for texture unit 2, then the output from texture unit 1 (GL_PREVIOUS,
Arg1) is subtracted from texture unit 2 (GL_TEXTURE, Arg0).
• Specify which values (RGB or alpha) of the sources are used and how
they are used:
– GL_OPERANDi_RGB matches the corresponding GL_SOURCEi_RGB
and determines the color values for the current GL_COMBINE_
RGB function. If GL_OPERANDi_RGB is pname, then param must
be one of GL_SRC_COLOR, GL_ONE_MINUS_SRC_COLOR,
GL_SRC_ALPHA, or GL_ONE_MINUS_SRC_ALPHA.
– Similarly, GL_OPERANDi_ALPHA matches the corresponding
GL_SOURCEi_ALPHA and determines the alpha values for the
current GL_COMBINE_ALPHA function. However, param is limited
to either GL_SRC_ALPHA or GL_ONE_MINUS_SRC_ALPHA.
When GL_SRC_ALPHA is used for the GL_COMBINE_RGB function, the
alpha values for the combiner source are interpreted as R, G, B values. In
Example 9-15, the three R, G, B components for Arg2 are (0.4, 0.4, 0.4).
Example 9-15 Using an Alpha Value for RGB Combiner Operations
static GLfloat constColor[4] = {0.1, 0.2, 0.3, 0.4};
glTexEnvfv(GL_TEXTURE_ENV, GL_TEXTURE_ENV_COLOR, constColor);
glTexEnvf(GL_TEXTURE_ENV, GL_SRC2_RGB, GL_CONSTANT);
glTexEnvf(GL_TEXTURE_ENV, GL_OPERAND2_RGB, GL_SRC_ALPHA);
In Example 9-15, if the operand had instead been GL_SRC_COLOR, the
RGB components would be (0.1, 0.2, 0.3). For GL_ONE_MINUS* modes,
a value’s complement (either 1–color or 1–alpha) is used for combiner
calculations. In Example 9-15, if the operand is GL_ONE_MINUS_SRC_
COLOR, the RGB components are (0.9, 0.8, 0.7). For GL_ONE_MINUS_
SRC_ALPHA, the result is (0.6, 0.6, 0.6).
• Optionally choose RGB or alpha scaling factors. The defaults are
glTexEnvf(GL_TEXTURE_ENV, GL_RGB_SCALE, 1.0);
glTexEnvf(GL_TEXTURE_ENV, GL_ALPHA_SCALE, 1.0);
• Finally draw the geometry, ensuring vertices have associated texture
coordinates.

Texture Combiner Functions 477
The Interpolation Combiner Function
The interpolation function helps illustrate texture combiners, because it
uses the maximum number of arguments and several source and operand
modes. Example 9-16 is a portion of the sample program combiner.c.
Example 9-16 Interpolation Combiner Function: combiner.c
/* for use as constant texture color */
static GLfloat constColor[4] = {0.0, 0.0, 0.0, 0.0};
constColor[3] = 0.2;
glTexEnvfv(GL_TEXTURE_ENV, GL_TEXTURE_ENV_COLOR, constColor);
glBindTexture(GL_TEXTURE_2D, texName[0]);
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE);
glTexEnvf(GL_TEXTURE_ENV, GL_COMBINE_RGB, GL_INTERPOLATE);
glTexEnvf(GL_TEXTURE_ENV, GL_SRC0_RGB, GL_TEXTURE);
glTexEnvf(GL_TEXTURE_ENV, GL_OPERAND0_RGB, GL_SRC_COLOR);
glTexEnvf(GL_TEXTURE_ENV, GL_SRC1_RGB, GL_PREVIOUS);
glTexEnvf(GL_TEXTURE_ENV, GL_OPERAND1_RGB, GL_SRC_COLOR);
glTexEnvf(GL_TEXTURE_ENV, GL_SRC2_RGB, GL_CONSTANT);
glTexEnvf(GL_TEXTURE_ENV, GL_OPERAND2_RGB, GL_SRC_ALPHA);
/* geometry is now rendered */
In Example 9-16, there is only one active texture unit. Since GL_
INTERPOLATE is the combiner function, there are three arguments, and
they are combined with the following formula: (Arg0 * Arg2) + (Arg1 *
(1 – Arg2)). The three arguments are as follows:
•Arg0, GL_TEXTURE, the texture image associated with the
currently bound texture object (texName[0])
•Arg1, GL_PREVIOUS, the result of the previous texture unit, but
since this is texture unit 0, GL_PREVIOUS is the fragment prior to
texturing
•Arg2, GL_CONSTANT, a constant color; currently (0.0, 0.0, 0.0, 0.2)
The interpolated result you get is a weighted blending of the texture image
and the untextured fragment. Because GL_SRC_ALPHA is specified for
GL_OPERAND2_RGB, the alpha value of the constant color (Arg2)serves
as the weighting.
If you run the sample program combiner.c, you’ll see 20 percent of the
texture blended with 80 percent of a smooth-shaded polygon. combiner.c
also varies the alpha value of the constant color, so you’ll see the results of
different weightings.
478 Chapter 9: Texture Mapping
Examining the interpolation function explains why several of the OpenGL
default values were chosen. The third argument for interpolation is
intended as weight for the two other sources. Since interpolation is the only
combiner function to use three arguments, it’s safe to make GL_CONSTANT
the default for Arg2. At first glance, it may seem odd that the default value
for GL_OPERAND2_RGB is GL_SRC_ALPHA. But the interpolation weight is
usually the same for all three color components, so using a single value
makes sense, and taking it from the alpha value of the constant is
convenient.
Applying Secondary Color after Texturing
While applying a texture to a typical fragment, only a primary color is
combined with the texel colors. The primary color may be the result of
lighting calculations or glColor*().
After texturing, but before fog calculations, sometimes a secondary color is
also applied to a fragment. Application of a secondary color may result in a
more realistic highlight on a textured object.
Secondary Color When Lighting Is Disabled
If lighting is not enabled and the color sum mode is enabled (by
glEnable(GL_COLOR_SUM)), then the current secondary color (set by
glSecondaryColor*()) is added to the post-texturing fragment color.
glTexEnv pname Initial Value for param
GL_SRC0_RGB GL_TEXTURE
GL_SRC1_RGB GL_PREVIOUS
GL_SRC2_RGB GL_CONSTANT
GL_OPERAND0_RGB GL_SRC_COLOR
GL_OPERAND1_RGB GL_SRC_COLOR
GL_OPERAND2_RGB GL_SRC_ALPHA
Table 9-10 Default Values for Some Texture Environment Modes
Point Sprites 479
glSecondaryColor*() accepts the same data types and interprets values the
same way that glColor*() does. (See Table 4-1 on page 198.) Secondary
colors may also be specified in vertex arrays.
Secondary Specular Color When Lighting Is Enabled
Texturing operations are applied after lighting, but blending specular
highlights with a texture’s colors usually lessens the effect of lighting. As
discussed earlier (in “Selecting a Lighting Model” on page 227), you can cal-
culate two colors per vertex: a primary color, which consists of all nonspec-
ular contributions, and a secondary color, which is a sum of all specular
contributions. If specular color is separated, the secondary (specular) color
is added to the fragment after the texturing calculation.
Note: If lighting is enabled, the secondary specular color is applied,
regardless of the GL_COLOR_SUM mode, and any secondary color
set by glSecondaryColor*() is ignored.
Point Sprites
While OpenGL supports antialiasing of points with a point size greater than
one (as set with glPointSize()), the visual results may not be precisely what
your application requires. Point sprites allow better control over the shading
of large points. By default, when point sprites are enabled, every fragment
in the sprite is assigned the same state as the vertex that initiated the point’s
rendering. Point sprites modify how fragment data is generated by iterating
texture coordinates across the fragments of the expanded point.
void glSecondaryColor3{b s i f d ub us ui}(TYPE r,TYPE g,TYPE b);
void glSecondaryColor3{b s i f d ub us ui}v(const TYPE *values);
Sets the red, green, and blue values for the current secondary color. The
first suffix indicates the data type for parameters: byte, short, integer,
float, double, unsigned byte, unsigned short, or unsigned integer. If there
is a second suffix, v, then values is a pointer to an array of values of the
given data type.
Compatibility
Extension
glSecondaryColor
GL_COLOR_SUM

480 Chapter 9: Texture Mapping
To enable point sprites, call glEnable() with a parameter of GL_POINT_
SPRITE. This will cause OpenGL to ignore the current settings for point
antialiasing. Each fragment in the point will be assigned the associated
vertex data, and those values will be used in shading.
Note: OpenGL Version 3.1 renders all points as if point sprites were enabled.
glTexEnv() and all of the parameters associated with point sprites
have been removed.
To enable the iteration of texture coordinates across the point sprite,
you need to call glTexEnv*(GL_POINT_SPRITE, GL_COORD_REPLACE,
GL_TRUE). This needs to be done for each texture unit with a texture map
that you want applied to the sprite. Figure 9-15 illustrates the differences
between antialiased points and texture-mapped point sprites. On the left
is an image of a 10-pixel antialiased point. The right image is a 10-pixel
texture-mapped point sprite.
Figure 9-15 Comparison of Antialiased Points and Textured Point Sprites
The texture coordinates for point sprites are automatically assigned by
OpenGL during rasterization. Figure 9-16 illustrates how texture coordinates
are assigned to the point sprite. The stexture coordinate increases from zero
to one from left to right across the fragments of the sprite. However, for t
texture coordinates, values are controlled by where the sprite’s texture-
coordinate origin is specified. Control of the origin is specified by calling
glPointParameter() with GL_POINT_SPRITE_COORD_ORIGIN and setting
the value to either GL_LOWER_LEFT or GL_UPPER_LEFT.
When the sprite origin is specified to be the GL_LOWER_LEFT, the
t-coordinate increases from zero to one going from bottom to top of the
sprite. Conversely, when the value is specified to be GL_UPPER_LEFT, the
t-coordinate increases from zero to one going from top to bottom.
Example 9-17 demonstrates a 10-pixel-wide point sprite with an applied
texture map.
The Texture Matrix Stack 481
Example 9-17 Configuring a Point Sprite for Texture Mapping: sprite.c
glPointSize(10.0);
glTexEnvi(GL_POINT_SPRITE, GL_COORD_REPLACE, GL_TRUE);
glPointParameteri(GL_POINT_SPRITE_COORD_ORIGIN, GL_LOWER_LEFT);
glEnable(GL_POINT_SPRITE);
The Texture Matrix Stack
Advanced
Just as your model coordinates are transformed by a matrix before being
rendered, texture coordinates are multiplied by a 4 u4 matrix before any
texture mapping occurs. By default, the texture matrix is the identity, so the
texture coordinates you explicitly assign or those that are automatically
generated remain unchanged. By modifying the texture matrix while
redrawing an object, however, you can make the texture slide over the
surface, rotate around it, stretch and shrink, or any combination of the
three. In fact, since the texture matrix is a completely general 4 u4 matrix,
effects such as perspective can be achieved.
The texture matrix is actually the top matrix on a stack, which must have a
stack depth of at least two matrices. All the standard matrix-manipulation
GL_LOWER_LEFT
(0,0)
(1,1)
GL_UPPER_LEFT
(0,0)
(1,1)
F
F
Figure 9-16 Assignment of Texture Coordinates Based on the Setting of
GL_POINT_SPRITE_COORD_ORIGIN
Advanced

482 Chapter 9: Texture Mapping
commands such as glPushMatrix(),glPopMatrix(),glMultMatrix(), and
glRotate*() can be applied to the texture matrix. To modify the current
texture matrix, you need to set the matrix mode to GL_TEXTURE, as
follows:
glMatrixMode(GL_TEXTURE); /* enter texture matrix mode */
glRotated(...);
/* ... other matrix manipulations ... */
glMatrixMode(GL_MODELVIEW); /* back to modelview mode */
The q-Coordinate
The mathematics of the fourth texture coordinate, q, are similar to the
w-coordinate of the (x, y, z, w) object coordinates. When the four texture
coordinates (s, t, r, q) are multiplied by the texture matrix, the resulting
vector (s’, t’, r’, q’) is interpreted as homogeneous texture coordinates. In
other words, the texture map is indexed by s’/q’,t’/q’, and r’/q’.
You can make use of q in cases where more than one projection or perspec-
tive transformation is needed. For example, suppose you want to model a
spotlight that has some nonuniform pattern—brighter in the center, per-
haps, or noncircular, because of flaps or lenses that modify the shape of the
beam. You can emulate shining such a light onto a flat surface by making a
texture map that corresponds to the shape and intensity of a light, and then
projecting it onto the surface in question using projection transformations.
Projecting the cone of light onto surfaces in the scene requires a perspective
transformation (qz 1), since the lights might shine on surfaces that aren’t
perpendicular to them. A second perspective transformation occurs because
the viewer sees the scene from a different (but perspective) point of view.
(See Plate 28 for an example; and see “Fast Shadows and Lighting Effects
Using Texture Mapping” by Mark Segal, Carl Korobkin, Rolf van Widenfelt,
Jim Foran, and Paul Haeberli, SIGGRAPH 1992 Proceedings [Computer
Graphics, 26:2, July 1992, pp. 249–252] for more details.)
Another example might arise if the texture map to be applied comes from a
photograph that itself was taken in perspective. As with spotlights, the final
view depends on the combination of two perspective transformations.
Nate Robins’ Texture Tutorial
In Nate Robins’ texture tutorial, you can use the popup menu to view the
4u4 texture matrix, make changes in matrix values, and then see their
effects.
Compatibility
Extension
GL_TEXTURE

Depth Textures 483
Depth Textures
Advanced
After lighting a surface (see Chapter 5), you’ll soon notice that OpenGL
light sources don’t cast shadows. The color at each vertex is calculated
without regard to any other objects in the scene. To have shadows, you need
to determine and record which surfaces (or portions of the surfaces) are
occluded from a direct path to a light source.
A multipass technique using depth textures provides a solution to render-
ing shadows. If you temporarily move the viewpoint to the light source
position, you notice that everything you see is lit—there are no shadows
from that perspective. A depth texture provides the mechanism to save the
depth values for all “unshadowed” fragments in a shadow map. As you ren-
der your scene, if you compare each incoming fragment to the correspond-
ing depth value in the shadow map, you can choose what to render,
depending upon whether it is or isn’t shadowed. The idea is similar to the
depth test, except that it’s done from the point of view of the light source.
The condensed description is as follows:
1. Render the scene from the point of view of the light source. It doesn’t
matter how the scene looks; you only want the depth values. Create a
shadow map by capturing the depth buffer values and storing them in
a texture map (shadow map).
2. Generate texture coordinates with (s,t) coordinates referencing loca-
tions within the shadow map, with the third texture coordinate (r), as
the distance from the light source. Then draw the scene a second time,
comparing the r value with the corresponding depth texture value to
determine whether the fragment is lit or in shadow.
The following sections provide a more detailed discussion, along with
sample code illustrating each of the steps.
Creating a Shadow Map
The first step is to create a texture map of depth values. You create this by
rendering the scene with the viewpoint positioned at the light source’s
position. Example 9-18 calls glGetLightfv() to obtain the current light
source position, calculates an up-vector, and then uses it as the viewing
transformation.
Advanced

484 Chapter 9: Texture Mapping
Example 9-18 begins by setting the viewport size to match that of the
texture map. It then sets up the appropriate projection and viewing
matrices. The objects for the scene are rendered, and the resulting depth
image is copied into texture memory for use as a shadow map. Finally, the
viewport is reset to it’s original size and position.
Note a few more points:
• The projection matrix controls the shape of the light’s “lampshade.”
The variables lightFovy and lightAspect in the gluPerspective() control
the size of the lampshade. A small lightFovy value will be more like a
spotlight, and a larger value will be more like a floodlight.
• The near and far clipping planes for the light (lightNearPlane and
lightFarPlane) are used to control the precision of the depth values.
Try to keep the separation between the near and far planes as small
as possible to maximize the precision of the values.
• After the depth values have been established in the depth buffer, you
want to capture them and put them into a GL_DEPTH_COMPONENT
format texture map. Example 9-18 uses glCopyTexImage2D() to make
a texture image from the depth buffer contents. As with any texture,
ensure that the image width and height are powers of two.
Example 9-18 Rendering Scene with Viewpoint at Light Source: shadowmap.c
GLint viewport[4];
GLfloat lightPos[4];
glGetLightfv(GL_LIGHT0, GL_POSITION, lightPos);
glGetIntegerv(GL_VIEWPORT, viewport);
glViewport(0, 0, SHADOW_MAP_WIDTH, SHADOW_MAP_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_PROJECTION);
glPushMatrix();
glLoadIdentity();
gluPerspective(lightFovy, lightAspect, lightNearPlane,
lightFarPlane);
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
glLoadIdentity();

Depth Textures 485
gluLookAt(lightPos[0], lightPos[1], lightPos[2],
lookat[0], lookat[1], lookat[2],
up[0], up[1], up[2]);
drawObjects();
glPopMatrix();
glMatrixMode(GL_PROJECTION);
glPopMatrix();
glMatrixMode(GL_MODELVIEW);
glCopyTexImage2D(GL_TEXTURE_2D, 0, GL_DEPTH_COMPONENT, 0, 0,
SHADOW_MAP_WIDTH, SHADOW_MAP_HEIGHT, 0);
glViewport(viewport[0], viewport[1],
viewport[2], viewport[3]);
Generating Texture Coordinates and Rendering
Now use glTexGen*() to automatically generate texture coordinates that
compute the eye-space distance from the light source position. The value of
the r coordinate should correspond to the distance from the primitives to
the light source. You can do this by using the same projection and viewing
transformations that you used to create the shadow map. Example 9-19 uses
the GL_MODELVIEW matrix stack to do all the matrix computations.
Note that the generated (s, t, r, q) texture coordinates and the depth values
in the shadow map are not similarly scaled. The texture coordinates are
generated in eye coordinates, so they fall in the range [1, 1]. The depth
values in the texels are within [0, 1]. Therefore, an initial translation and
scaling maps the texture coordinates into the same range of values as the
shadow map.
Example 9-19 Calculating Texture Coordinates: shadowmap.c
GLfloat tmpMatrix[16];
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
glLoadIdentity();
glTranslatef(0.5, 0.5, 0.0);
glScalef(0.5, 0.5, 1.0);
gluPerspective(lightFovy, lightAspect,
lightNearPlane, lightFarPlane);
gluLookAt(lightPos[0], lightPos[1], lightPos[2],
lookat[0], lookat[1], lookat[2],
up[0], up[1], up[2]);

486 Chapter 9: Texture Mapping
glGetFloatv(GL_MODELVIEW_MATRIX, tmpMatrix);
glPopMatrix();
transposeMatrix(tmpMatrix);
glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, GL_OBJECT_LINEAR);
glTexGeni(GL_T, GL_TEXTURE_GEN_MODE, GL_OBJECT_LINEAR);
glTexGeni(GL_R, GL_TEXTURE_GEN_MODE, GL_OBJECT_LINEAR);
glTexGeni(GL_Q, GL_TEXTURE_GEN_MODE, GL_OBJECT_LINEAR);
glTexGenfv(GL_S, GL_OBJECT_PLANE, &tmpMatrix[0]);
glTexGenfv(GL_T, GL_OBJECT_PLANE, &tmpMatrix[4]);
glTexGenfv(GL_R, GL_OBJECT_PLANE, &tmpMatrix[8]);
glTexGenfv(GL_Q, GL_OBJECT_PLANE, &tmpMatrix[12]);
glEnable(GL_TEXTURE_GEN_S);
glEnable(GL_TEXTURE_GEN_T);
glEnable(GL_TEXTURE_GEN_R);
glEnable(GL_TEXTURE_GEN_Q);
In Example 9-20, before the scene is rendered for the second and final time,
the texture comparison mode GL_COMPARE_R_TO_TEXTURE instructs
OpenGL to compare the fragment’s r-coordiate with the texel value. If the
rdistance is less than or equal to (the comparison function GL_LEQUAL)
the texel value, there is nothing between this fragment and the light source,
and it is effectively treated as having a luminance value of one. If the com-
parison fails, then there is another primitive between this fragment and the
light source, so this fragment is shadowed and has an effective luminance
of zero.
Example 9-20 Rendering Scene Comparing r Coordinate: shadowmap.c
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S,
GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T,
GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_COMPARE_FUNC,
GL_LEQUAL);
glTexParameteri(GL_TEXTURE_2D, GL_DEPTH_TEXTURE_MODE,
GL_LUMINANCE);
glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_COMPARE_MODE,
GL_COMPARE_R_TO_TEXTURE);
glEnable(GL_TEXTURE_2D);

Depth Textures 487
This technique can produce some unintended visual artifacts:
• Self-shadowing, whereby an object incorrectly casts a shadow upon
itself, is a common problem.
• Aliasing of the projected texture, particularly in the regions farthest
from the light sources, can occur. Using higher resolution shadow
maps can help reduce the aliasing.
• GL_MODULATE mode, when used with depth texturing, may cause
sharp transitions between shadowed and unshadowed regions.
Unfortunately, there are no steadfast rules for overcoming these issues.
Some experimentation may be required to produce the best-looking image.
This page intentionally left blank

489
Chapter 10
10.The Framebuffer
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Understand the buffers that make up the framebuffer and how
they’re used
• Clear selected buffers and enable them for writing
• Control the parameters of the scissor, alpha, stencil, and depth tests
that are applied to pixels
• Use occlusion queries to determine if objects will be visible
• Perform dithering and logical operations
• Use the accumulation buffer for such purposes as scene antialiasing
• Create and use framebuffer objects for advanced techniques, and to
minimizing copying of data between buffers
Note: In OpenGL Version 3.1, some of the techniques and functions
described in this chapter were removed through deprecation. The
concepts are still relevant, but are available using more modern
features.

490 Chapter 10: The Framebuffer
An important goal of almost every graphics program is to draw pictures on
the screen. The screen is composed of a rectangular array of pixels, each
capable of displaying a tiny square of color at that point in the image. After
the rasterization stage (including texturing and fog), the data is not yet
pixels—just fragments. Each fragment has coordinate data that corresponds
to a pixel, as well as color and depth values. Then each fragment undergoes
a series of tests and operations, some of which have been previously
described (see “Blending” in Chapter 6), and others that are discussed in
this chapter.
If the tests and operations are survived, the fragment values are ready to
become pixels. To draw these pixels, you need to know what color they are,
which is the information that’s stored in the color buffer. Whenever data is
stored uniformly for each pixel, such storage for all the pixels is called a
buffer. Different buffers might contain different amounts of data per pixel,
but within a given buffer, each pixel is assigned the same amount of data.
A buffer that stores a single bit of information about pixels is called a
bitplane, and the number of bitplanes in a buffer is usually called its “depth”
(not to be confused with a pixel’s depth value, which is used in depth-buffer
testing, as described in “Depth Test” later in this chapter).
As shown in Figure 10-1, the lower left pixel in an OpenGL window is pixel
(0, 0), corresponding to the window coordinates of the lower left corner of
the 1 u1 region occupied by this pixel. In general, pixel (x, y) fills the region
bounded by x on the left, x+ 1 on the right, y on the bottom, and y+ 1 on
the top.
3.0
2.0
1.0
0.0
0.0 1.0 2.0 3.0
Pixel
(2, 1)
Lower left corner
of the window
x window coordinate
y window
coordinate
Figure 10-1 Region Occupied by a Pixel

491
As an example of a buffer, let’s look more closely at the color buffer, which
holds the color information that’s to be displayed on the screen. Assume
that the screen is 1280 pixels wide and 1024 pixels high and that it’s a full
24-bit color screen—in other words, that there are 224 (or 16,777,216) dif-
ferent colors that can be displayed. Since 24 bits translates to 3 bytes (8 bits
per byte), the color buffer in this example has to store at least 3 bytes of data
for each of the 1,310,720 (1280*1024) pixels on the screen. A particular
hardware system might have more or fewer pixels on the physical screen as
well as more or less color data per pixel. Any particular color buffer, how-
ever, has the same amount of data saved for each pixel on the screen.
The color buffer is only one of several buffers that hold information about a
pixel. For example, in “A Hidden-Surface Removal Survival Kit” on page 205,
you learned that the depth buffer holds depth information for each pixel.
The color buffer itself can consist of several subbuffers. The framebuffer on
a system comprises all of these buffers. With the exception of the color
buffer(s), you don’t view these other buffers directly; instead, you use them
to perform such tasks as hidden-surface elimination, antialiasing of an
entire scene, stenciling, drawing smooth motion, and other operations.
This chapter describes all the buffers that can exist in an OpenGL imple-
mentation and explains how they’re used. It also discusses the series of tests
and pixel operations that are performed before any data is written to the
viewable color buffer. Finally, for completeness, the chapter concludes by
explaining how to use the accumulation buffer, which holds images that are
drawn into the color buffer. Originally, the accumulation buffer was mar-
ginally more capable of storing higher-precision color values. With OpenGL
Version 3.0, color buffers that support native floating-point values were
introduced, which effectively makes the accumulation buffer obsolete,
though not necessarily the techniques that were enabled by it. These can
easily be implemented on floating-point buffers.
This chapter has the following major sections.
• “Buffers and Their Uses” describes the possible buffers, what they’re
for, and how to clear them and enable them for writing.
• “Testing and Operating on Fragments” explains the scissor, alpha,
stencil, and depth tests that occur after a pixel’s position and color have
been calculated but before this information is drawn on the screen.
Several operations—blending, dithering, and logical operations—can
also be performed before a fragment updates the screen.
• “The Accumulation Buffer” describes how to perform several advanced
techniques using the accumulation buffer. These techniques include
antialiasing an entire scene, using motion blur, and simulating photo-
graphic depth of field.
Chapter 10: The Framebuffer

492 Chapter 10: The Framebuffer
• “Framebuffer Objects” discusses a new type of object in OpenGL
Version 3.0 that enables rendering to occur in buffers other than the
color buffer displayed on the screen. They enable off-screen rendering
and the ability to update texture maps using render-to-texture.
Version 1.4 of OpenGL added
• Stencil operations GL_INCR_WRAP and GL_DECR_WRAP.
Version 3.0 enhanced support by adding
• Framebuffer objects for off-screen and render-to-texture capabilities.
• sRGB-formatted framebuffers for rendering.
Version 3.1 modified the feature set by
• Removing support for the accumulation and auxiliary buffers.
Buffers and Their Uses
An OpenGL system can manipulate the following buffers:
• Color buffers: front-left, front-right, back-left, back-right, and any
number of auxiliary color buffers
• Depth buffer
•Stencil buffer
• Accumulation buffer
Your particular OpenGL implementation determines which buffers are
available and how many bits per pixel each buffer holds. Additionally, you
can have multiple visuals, or window types, that have different buffers
available. Table 10-1 lists the parameters to use with glGetIntegerv() to query
your OpenGL system about per-pixel buffer storage for a particular visual.
Note: If you’re using the X Window System, you’re guaranteed, at a mini-
mum, to have a visual with one color buffer for use in RGBA mode,
with associated stencil, depth, and accumulation buffers that have
color components of nonzero size. Also, if your X Window System
implementation supports a Pseudo-Color visual, you are also guaran-
teed to have one OpenGL visual that has a color buffer for use in

Buffers and Their Uses 493
color-index mode, with associated depth and stencil buffers. You’ll
probably want to use glXGetConfig() to query your visuals; see
Appendix C for more information about this routine.
Color Buffers
The color buffers are the ones to which you usually draw. They contain
either color-index or RGB color data and may also contain alpha values. An
OpenGL implementation that supports stereoscopic viewing has left and
right color buffers for the left and right stereo images. If stereo isn’t sup-
ported, only the left buffers are used. Similarly, double-buffered systems
have front and back buffers, and a single-buffered system has the front
buffers only. Every OpenGL implementation must provide a front-left
color buffer.
Optional, nondisplayable auxiliary color buffers may also be supported.
OpenGL doesn’t specify any particular uses for these buffers, so you can
define and use them however you please. For example, you might use them
for saving an image that you use repeatedly. Then, rather than redrawing
the image, you can just copy it from an auxiliary buffer into the usual color
buffers. (See the description of glCopyPixels() in “Reading, Writing, and
Copying Pixel Data” on page 333 for more information about how to
do this.)
Parameter Meaning
GL_RED_BITS, GL_GREEN_BITS,
GL_BLUE_BITS, GL_ALPHA_BITS
number of bits per R, G, B, or A component in
the color buffers
GL_INDEX_BITS number of bits per index in the color buffers
GL_DEPTH_BITS number of bits per pixel in the depth buffer
GL_STENCIL_BITS number of bits per pixel in the stencil buffer
GL_ACCUM_RED_BITS,
GL_ACCUM_GREEN_BITS,
GL_ACCUM_BLUE_BITS,
GL_ACCUM_ALPHA_BITS
number of bits per R, G, B, or A component in
the accumulation buffer
Table 10-1 Query Parameters for Per-Pixel Buffer Storage

494 Chapter 10: The Framebuffer
Note: In OpenGL Version 3.0, color-index mode rendering and auxiliary
buffers were deprecated; these features were entirely removed from
OpenGL in Version 3.1. They are available as part of the GL_ARB_
compatibility extension, if your OpenGL implementation supports
this extension.
You can use GL_STEREO or GL_DOUBLEBUFFER with glGetBooleanv()
to find out if your system supports stereo (that is, has left and right
buffers) or double-buffering (front and back buffers). To find out how
many, if any, auxiliary buffers are present, use glGetIntegerv() with
GL_AUX_BUFFERS.
Depth Buffer
The depth buffer stores a depth value for each pixel. As described in
“A Hidden-Surface Removal Survival Kit” on page 205, depth is usually
measured in terms of distance to the eye, so pixels with larger depth-buffer
values are overwritten by pixels with smaller values. This is just a useful
convention, however, and the depth buffer’s behavior can be modified as
described in “Depth Test” on page 510. The depth buffer is sometimes called
the z buffer (the z comes from the fact that x- and y-values measure horizon-
tal and vertical displacement on the screen, and the z-value measures dis-
tance perpendicular to the screen).
Stencil Buffer
One use for the stencil buffer is to restrict drawing to certain portions of the
screen, just as a cardboard stencil can be used with a can of spray paint to
make fairly precise painted images. For example, if you want to draw an
image as it would appear through an odd-shaped windshield, you can store
an image of the windshield’s shape in the stencil buffer, and then draw the
entire scene. The stencil buffer prevents anything that wouldn’t be visible
through the windshield from being drawn. Thus, if your application is a
driving simulation, you can draw all the instruments and other items inside
the automobile once, and as the car moves, only the outside scene need be
updated.
Accumulation Buffer
The accumulation buffer holds RGBA color data just as the color buffers do
in RGBA mode. (The results of using the accumulation buffer in color-index
mode are undefined.) It’s typically used for accumulating a series of images
into a final, composite image. With this method, you can perform
Buffers and Their Uses 495
operations such as scene antialiasing by supersampling an image and then
averaging the samples to produce the values that are finally painted into the
pixels of the color buffers. You don’t draw directly into the accumulation
buffer; accumulation operations are always performed in rectangular blocks,
which are usually transfers of data to or from a color buffer.
Clearing Buffers
In graphics programs, clearing the screen (or any of the buffers) is typically
one of the most expensive operations you can perform—on a 1280 u1024
monitor, it requires touching well over a million pixels. For simple graphics
applications, the clear operation can take more time than the rest of the
drawing. If you need to clear not only the color buffer but also the depth
and stencil buffers, the clear operation can be three times as expensive.
To address this problem, some machines have hardware that can clear more
than one buffer at once. The OpenGL clearing commands are structured
to take advantage of such architectures. First, you specify the values to be
written into each buffer to be cleared. Then you issue a single command to
perform the clear operation, passing in a list of all the buffers to be cleared.
If the hardware is capable of simultaneous clears, they all occur at once;
otherwise, the buffers are cleared sequentially.
The following commands set the clearing values for each buffer:
void glClearColor(GLclampf red, GLclampf green, GLclampf blue,
GLclampf alpha);
void glClearIndex(GLfloat index);
void glClearDepth(GLclampd depth);
void glClearStencil(GLint s);
void glClearAccum(GLfloat red, GLfloat green, GLfloat blue,
GLfloat alpha);
Specifies the current clearing values for the color buffer (in RGBA mode),
the color buffer (in color-index mode), the depth buffer, the stencil buffer,
and the accumulation buffer. The GLclampf and GLclampd types (clamped
GLfloat and clamped GLdouble) are clamped to be between 0.0 and 1.0.
The default depth-clearing value is 1.0; all the other default clearing
values are 0. The values set with the clear commands remain in effect until
they’re changed by another call to the same command.
Compatibility
Extension
glClearIndex
glClearAccum

496 Chapter 10: The Framebuffer
After you’ve selected your clearing values and you’re ready to clear the
buffers, use glClear();
Advanced
If you’re using multiple draw buffers—particularly those that have floating-
point or non-normalized integer pixel formats—you can clear each
individually bound buffer using glClearBuffer*() functions, which were
introduced in OpenGL Version 3.0. Unlike functions such as glClearColor()
and glClearDepth(), which set a clear value within OpenGL that’s used
when glClear() is called, glClearBuffer*() uses the values passed to it to
immediately clear the bound drawing buffers.
void glClear(GLbitfield mask);
Clears the specified buffers. The value of mask is the bitwise logical OR of
some combination of GL_COLOR_BUFFER_BIT, GL_DEPTH_BUFFER_BIT,
GL_STENCIL_BUFFER_BIT, and GL_ACCUM_BUFFER_BIT to identify
which buffers are to be cleared. GL_COLOR_BUFFER_BIT clears either the
RGBA color buffer or the color-index buffer, depending on the mode of
the system at the time. When you clear the color or color-index buffer, all
the color buffers that are enabled for writing (see the next section) are
cleared. The pixel ownership test, scissor test, and dithering, if enabled,
are applied to the clearing operation. Masking operations, such as
glColorMask() and glIndexMask(), are also effective. The alpha test,
stencil test, and depth test do not affect the operation of glClear().
void glClearBuffer{fi ui}v(GLenum buffer, GLint drawbuffer,
const TYPE *value);
Clears the buffer indexed by drawbuffer associated with buffer to value.
buffer must be one of GL_COLOR, GL_DEPTH, or GL_STENCIL.
If buffer is GL_COLOR, drawbuffer specifies an index to a particular draw
buffer, and value is a four-element array containing for clear color. If the
buffer indexed by drawbuffer has multiple draw buffers (as specified by a
call to glDrawBuffers()), all draw buffers are cleared to value.
If buffer is GL_DEPTH or GL_STENCIL, drawbuffer must be zero, and value
is a single-element array containing an appropriate clear value (subject to
clamping and type conversion for depth values, and masking and type
conversion for stencil values).
Compatibility
Extension
GL_ACCUM_
BUFFER_BIT
Advanced

Buffers and Their Uses 497
To reduce the number of functions calls associated with using multiple
draw buffers, you can call glClearBufferfi() to simultaneously clear the
depth and stencil buffers (which is effectively equivalent to calling
glClearBuffer*() twice—once for the depth buffer and once for the stencil
buffer):
Selecting Color Buffers for Writing and Reading
The results of a drawing or reading operation can go into or come from any
of the color buffers: front, back, front-left, back-left, front-right, back-right,
or any of the auxiliary buffers. You can choose an individual buffer to be the
drawing or reading target. For drawing, you can also set the target to draw
into more than one buffer at the same time. You use glDrawBuffer() to
select the buffers to be written and glReadBuffer() to select the buffer as
the source for glReadPixels(),glCopyPixels(),glCopyTexImage*(), and
glCopyTexSubImage*().
If you are using double-buffering, you usually want to draw only in the back
buffer (and swap the buffers when you’re finished drawing). In some situa-
tions, you might want to treat a double-buffered window as though it were
single-buffered by calling glDrawBuffer(GL_FRONT_AND_BACK) to
enable you to draw to both front and back buffers at the same time.
A GL_INVALID_ENUM is generated if buffer is not one of the accepted
values listed above. GL_INVALID_VALUE is generated if buffer is GL_
COLOR, and drawbuffer is less than zero, or greater than or equal to GL_
MAX_DRAW_BUFFERS; or if buffer is GL_DEPTH, or GL_STENCIL, and
drawbuffer is not zero. Finally, a GL_INVALID_OPERATION is set if buffer
is GL_COLOR, and applied to a color-index mode buffer.
void glClearBufferfi(GLenum buffer, GLint drawbuffer,
GLfloat depth, GLint stencil);
Clear both the depth and stencil buffers of the currently bound framebuffer
simultaneously (which may be faster on some implementations). buffer
must be GL_DEPTH_STENCIL, and drawbuffer must be zero. depth and
stencil will be used as the clear values for the respective buffers.
A GL_INVALID_ENUM is generated if buffer is not GL_DEPTH_STENCIL.
and a GL_INVALID_VALUE is generated if drawbuffer is not zero.

498 Chapter 10: The Framebuffer
glDrawBuffer() is also used to select buffers to render stereo images
(GL*LEFT and GL*RIGHT) and to render into auxiliary buffers (GL_AUXi).
Note: You can enable drawing to nonexistent buffers as long as you enable
drawing to at least one buffer that does exist. If none of the specified
buffers exists, an error results.
void glDrawBuffer(GLenum mode);
void glDrawBuffers(GLsizei n, const GLenum *buffers);
Selects the color buffers enabled for writing or clearing and disables
buffers enabled by previous calls to glDrawBuffer(). More than one buffer
may be enabled at one time. The value of mode can be one of the
following:
GL_FRONT GL_FRONT_LEFT GL_AUXi
GL_BACK GL_FRONT_RIGHT GL_FRONT_AND_BACK
GL_LEFT GL_BACK_LEFT GL_NONE
GL_RIGHT GL_BACK_RIGHT GL_COLOR_
ATTACHMENTi
Arguments that omit LEFT or RIGHT refer to both the left and right stereo
buffers; similarly, arguments that omit FRONT or BACK refer to both. The
i in GL_AUXi is a digit identifying a particular auxiliary buffer.
By default, mode is GL_FRONT for single-buffered contexts and GL_BACK
for double-buffered contexts.
OpenGL Version 2.0 added the glDrawBuffers() routine, which specifies
multiple color buffers capable of receiving color values. buffers is an
array of buffer enumerates. Only GL_NONE, GL_FRONT_LEFT,
GL_FRONT_RIGHT, GL_BACK_LEFT, GL_BACK_RIGHT, and GL_AUXi
are accepted.
With OpenGL Version 3.0’s addition of framebuffer objects, GL_COLOR_
ATTACHMENTi was added to specify which color renderbuffers are draw
targets when OpenGL is bound to a user-defined framebuffer object.
If the fixed-function OpenGL pipeline is used for generating fragment
colors, each of the specified buffers receives the same color value. If a
fragment shader is employed and specifies output to multiple buffers, then
each buffer will be written with the color specified in the shader’s output.
See “Rendering to Multiple Output Buffers” in Chapter 15 for details.
Compatibility
Extension
GL_AUXi
Buffers and Their Uses 499
Note: You must enable reading from a buffer that exists or an error results.
Masking Buffers
Before OpenGL writes data into the enabled color, depth, or stencil buffers,
a masking operation is applied to the data, as specified with one of the
following commands. A bitwise logical AND is performed with each mask
and the corresponding data to be written.
void glReadBuffer(GLenum mode);
Selects the color buffer enabled as the source for reading pixels for
subsequent calls to glReadPixels(),glCopyPixels(),glCopyTexImage*(),
glCopyTexSubImage*(), and glCopyConvolutionFilter*(), and disables
buffers enabled by previous calls to glReadBuffer(). The value of mode can
be one of the following:
GL_FRONT GL_FRONT_LEFT GL_AUXi
GL_BACK GL_FRONT_RIGHT GL_COLOR_ATTACHMENTi
GL_LEFT GL_BACK_LEFT
GL_RIGHT GL_BACK_RIGHT
The buffers for glReadBuffer() are the same as those described for
glDrawBuffer(). By default, mode is GL_FRONT for single-buffered
contexts and GL_BACK for double-buffered contexts.
Use GL_COLOR_ATTACHMENTi with OpenGL Versions 3.0 and later
when reading from a user-defined framebuffer object. The value of i must
be between 0 and GL_MAX_COLOR_ATTACHMENTS (as returned by
calling glGetIntegerv())
void glIndexMask(GLuint mask);
void glColorMask(GLboolean red, GLboolean green, GLboolean blue,
GLboolean alpha);
void glColorMaski(GLuint buf, GLboolean red, GLboolean green,
GLboolean blue, GLboolean alpha);
void glDepthMask(GLboolean flag);
void glStencilMask(GLuint mask);
void glStencilMaskSeparate(GLenum face, GLuint mask);
Sets the masks used to control writing into the indicated buffers. The mask
set by glIndexMask() applies only in color-index mode. If a 1 appears
Compatibility
Extension
GL_AUXi
Compatibility
Extension
glIndexMask

500 Chapter 10: The Framebuffer
You can do plenty of tricks with color masking in color-index mode. For
example, you can use each bit in the index as a different layer and set up
interactions between arbitrary layers with appropriate settings of the color
map. You can create overlays and underlays, and do so-called color-map
animations. (See Chapter 14 for examples of using color masking.) Masking
in RGBA mode is useful less often, but you can use it for loading separate
image files into the red, green, and blue bitplanes, for example.
You’ve seen one use for disabling the depth buffer in “Three-Dimensional
Blending with the Depth Buffer” on page 263. Disabling the depth buffer
for writing can also be useful if a common background is desired for a series
of frames, and you want to add some features that may be obscured by parts
of the background. For example, suppose your background is a forest, and
you would like to draw repeated frames with the same trees, but with
objects moving among them. After the trees are drawn and their depths
recorded in the depth buffer, the image of the trees is saved, and the new
items are drawn with the depth buffer disabled for writing. As long as the
new items don’t overlap each other, the picture is correct. To draw the next
frame, restore the image of the trees and continue. You don’t need to restore
the values in the depth buffer. This trick is most useful if the background is
extremely complex—so complex that it’s much faster just to recopy the
image into the color buffer than to recompute it from the geometry.
Masking the stencil buffer can allow you to use a multiple-bit stencil buffer
to hold multiple stencils (one per bit). You might use this technique to
in mask, the corresponding bit in the color-index buffer is written; if a 0
appears, the bit isn’t written. Similarly, glColorMask() affects drawing in
RGBA mode only. The red,green,blue, and alpha values control whether
the corresponding component is written. (GL_TRUE means it is written.
If flag is GL_TRUE for glDepthMask(), the depth buffer is enabled for writ-
ing; otherwise, it’s disabled. The mask for glStencilMask() is used for
stencil data in the same way as the mask is used for color-index data in
glIndexMask(). The default values of all the GLboolean masks are
GL_TRUE, and the default values for the two GLuint masks are all 1’s.
OpenGL Version 2.0 includes the glStencilMaskSeparate() function that
allows separate mask values for front- and back-facing polygons.
OpenGL Version 3.0 added the glColorMaski() function to allow setting
of the color mask for an individual buffer specified by buf when rendering
to multiple color buffers (see “Selecting Color Buffers for Writing and
Reading” on page 497 for more details on using multiple buffers).

Testing and Operating on Fragments 501
perform capping as explained in “Stencil Test” on page 504 or to implement
the Game of Life as described in “Life in the Stencil Buffer” on page 664.
Note: The mask specified by glStencilMask() controls which stencil bit-
planes are written. This mask isn’t related to the mask that’s specified
as the third parameter of glStencilFunc(), which specifies which bit-
planes are considered by the stencil function.
Testing and Operating on Fragments
When you draw geometry, text, or images on the screen, OpenGL per-
forms several calculations to rotate, translate, scale, determine the lighting,
project the object(s) into perspective, execute a vertex shader, figure out
which pixels in the window are affected, and determine the colors in which
those pixels should be drawn. Many of the earlier chapters in this book pro-
vide some information about how to control these operations. After
OpenGL determines that an individual fragment should be generated and
what its color should be, several processing stages remain that control how
and whether the fragment is drawn as a pixel into the framebuffer. For
example, if it’s outside a rectangular region or if it’s farther from the view-
point than the pixel that’s already in the framebuffer, it isn’t drawn. In
another stage, the fragment’s color is blended with the color of the pixel
already in the framebuffer.
This section describes both the complete set of tests that a fragment must
pass before it goes into the framebuffer and the possible final operations
that can be performed on the fragment as it’s written. The tests and opera-
tions occur in the following order; if a fragment is eliminated in an early
test, none of the later tests or operations takes place:
1. Scissor test
2. Alpha test
3. Stencil test
4. Depth test
5. Blending
6. Dithering
7. Logical operations
All of these tests and operations are described in detail in the following
subsections.

502 Chapter 10: The Framebuffer
Scissor Test
You can define a rectangular portion of your window and restrict drawing
to take place within it by using the glScissor() command. If a fragment lies
inside the rectangle, it passes the scissor test.
The scissor test is just a version of a stencil test using a rectangular region
of the screen. It’s fairly easy to create a blindingly fast hardware imple-
mentation of scissoring, while a given system might be much slower at
stenciling—perhaps because the stenciling is performed in software.
Advanced
An advanced use of scissoring is performing nonlinear projection. First
divide the window into a regular grid of subregions, specifying viewport
and scissor parameters that limit rendering to one region at a time. Then
project the entire scene to each region using a different projection matrix.
To determine whether scissoring is enabled and to obtain the values
that define the scissor rectangle, you can use GL_SCISSOR_TEST with
glIsEnabled() and GL_SCISSOR_BOX with glGetIntegerv().
Alpha Test
In RGBA mode, the alpha test allows you to accept or reject a fragment
based on its alpha value. The alpha test is enabled and disabled by passing
GL_ALPHA_TEST to glEnable() and glDisable(). To determine whether the
alpha test is enabled, use GL_ALPHA_TEST with glIsEnabled().
Note: The alpha fragment test was deprecated in OpenGL Version 3.0,
and replaced in OpenGL Version 3.1 by discarding fragments in a
fragment shader using the discard operation. See the description of
discard in “Flow Control Statements” on page 705.
void glScissor(GLint x, GLint y, GLsizei width, GLsizei height);
Sets the location and size of the scissor rectangle (also known as the scissor
box). The parameters define the lower left corner (x,y) and the width and
height of the rectangle. Pixels that lie inside the rectangle pass the scissor
test. Scissoring is enabled and disabled by passing GL_SCISSOR_TEST to
glEnable() and glDisable(). By default, the rectangle matches the size of
the window and scissoring is disabled.
Advanced
Compatibility
Extension
GL_ALPHA_TEST

Testing and Operating on Fragments 503
If enabled, the test compares the incoming alpha value with a reference
value. The fragment is accepted or rejected depending on the result of the
comparison. Both the reference value and the comparison function are set
with glAlphaFunc(). By default, the reference value is 0, the comparison
function is GL_ALWAYS, and the alpha test is disabled. To obtain the alpha
comparison function or reference value, use GL_ALPHA_TEST_FUNC or
GL_ALPHA_TEST_REF with glGetIntegerv().
One application for the alpha test is implementation of a transparency
algorithm. Render your entire scene twice, the first time accepting only
fragments with alpha values of 1, and the second time accepting fragments
with alpha values that aren’t equal to 1. Turn the depth buffer on during
both passes, but disable depth buffer writing during the second pass.
Another use might be to make decals with texture maps whereby you can
see through certain parts of the decals. Set the alphas in the decals to 0.0
void glAlphaFunc(GLenum func, GLclampf ref);
Sets the reference value and comparison function for the alpha test. The
reference value ref is clamped to be between 0 and 1. The possible values
for func and their meanings are listed in Table 10-2.
Parameter Meaning
GL_NEVER never accept the fragment
GL_ALWAYS always accept the fragment
GL_LESS accept fragment if fragment alpha < reference alpha
GL_LEQUAL accept fragment if fragment alpha d reference alpha
GL_EQUAL accept fragment if fragment alpha = reference alpha
GL_GEQUAL accept fragment if fragment alpha t reference alpha
GL_GREATER accept fragment if fragment alpha > reference alpha
GL_NOTEQUAL accept fragment if fragment alpha z reference alpha
Table 10-2 glAlphaFunc() Parameter Values
Compatibility
Extension
glAlphaFunc

504 Chapter 10: The Framebuffer
where you want to see through, set them to 1.0 otherwise, set the reference
value to 0.5 (or anything between 0.0 and 1.0), and set the comparison
function to GL_GREATER. The decal has see-through parts, and the values
in the depth buffer aren’t affected. This technique, called billboarding, is
described in “Sample Uses of Blending” on page 258.
Stencil Test
The stencil test takes place only if there is a stencil buffer. (If there is no
stencil buffer, the stencil test always passes.) Stenciling applies a test that
compares a reference value with the value stored at a pixel in the stencil
buffer. Depending on the result of the test, the value in the stencil buffer is
modified. You can choose the particular comparison function used, the
reference value, and the modification performed with the glStencilFunc()
and glStencilOp() commands.
void glStencilFunc(GLenum func, GLint ref, GLuint mask);
void glStencilFuncSeparate(GLenum face,
GLenum func, GLint ref, GLuint mask);
Sets the comparison function (func), the reference value (ref), and a mask
(mask) for use with the stencil test. The reference value is compared
with the value in the stencil buffer using the comparison function, but
the comparison applies only to those bits for which the corresponding
bits of the mask are 1. The function can be GL_NEVER, GL_ALWAYS,
GL_LESS, GL_LEQUAL, GL_EQUAL, GL_GEQUAL, GL_GREATER, or
GL_NOTEQUAL. If it’s GL_LESS, for example, then the fragment passes if
ref is less than the value in the stencil buffer. If the stencil buffer contains
s bitplanes, the low-order s bits of mask are bitwise ANDed with the value
in the stencil buffer and with the reference value before the comparison
is performed. The masked values are all interpreted as non-negative val-
ues. The stencil test is enabled and disabled by passing GL_STENCIL_TEST
to glEnable() and glDisable(). By default, func is GL_ALWAYS, ref is 0,
mask is all 1s, and stenciling is disabled.
OpenGL 2.0 includes the glStencilFuncSeparate() function that allows
separate stencil function parameters to be specified for front- and back-
facing polygons.

Testing and Operating on Fragments 505
“With saturation” means that the stencil value will clamp to extreme
values. If you try to decrement zero with saturation, the stencil value
remains zero. “Without saturation” means that going outside the
indicated range wraps around. If you try to decrement zero without
saturation, the stencil value becomes the maximum unsigned integer
value (quite large!).
Stencil Queries
You can obtain the values for all six stencil-related parameters by using the
query function glGetIntegerv() and one of the values shown in Table 10-3.
You can also determine whether the stencil test is enabled by passing
GL_STENCIL_TEST to glIsEnabled().
void glStencilOp(GLenum fail, GLenum zfail, GLenum zpass);
void glStencilOpSeparate(GLenum face, GLenum fail, GLenum zfail,
GLenum zpass);
Specifies how the data in the stencil buffer is modified when a fragment
passes or fails the stencil test. The three functions fail,zfail, and zpass
can be GL_KEEP, GL_ZERO, GL_REPLACE,GL_INCR, GL_INCR_WRAP,
GL_DECR, GL_DECR_WRAP, or GL_INVERT. They correspond to
keeping the current value, replacing it with zero, replacing it with the
reference value, incrementing it with saturation, incrementing it without
saturation, decrementing it with saturation, decrementing it without
saturation, and bitwise-inverting it. The result of the increment and
decrement functions is clamped to lie between zero and the maximum
unsigned integer value (2s 1 if the stencil buffer holds s bits).
The fail function is applied if the fragment fails the stencil test; if it passes,
then zfail is applied if the depth test fails and zpass is applied if the depth
test passes, or if no depth test is performed. (See “Depth Test” on
page 510.) By default, all three stencil operations are GL_KEEP.
OpenGL 2.0 includes the glStencilOpSeparate() function that allows
separate stencil tests to be specified for front- and back-facing polygons.

506 Chapter 10: The Framebuffer
Stencil Examples
Probably the most typical use of the stencil test is to mask out an irregularly
shaped region of the screen to prevent drawing from occurring within it (as
in the windshield example in “Buffers and Their Uses”). To do this, fill the
stencil mask with 0’s, and then draw the desired shape in the stencil buffer
with 1’s. You can’t draw geometry directly into the stencil buffer, but you
can achieve the same result by drawing into the color buffer and choosing
a suitable value for the zpass function (such as GL_REPLACE). (You can use
glDrawPixels() to draw pixel data directly into the stencil buffer.) When-
ever drawing occurs, a value is also written into the stencil buffer (in this
case, the reference value). To prevent the stencil-buffer drawing from affecting
the contents of the color buffer, set the color mask to zero (or GL_FALSE).
You might also want to disable writing into the depth buffer.
After you’ve defined the stencil area, set the reference value to 1, and set the
comparison function such that the fragment passes if the reference value is
equal to the stencil-plane value. During drawing, don’t modify the contents
of the stencil planes.
Example 10-1 demonstrates how to use the stencil test in this way. Two
toruses are drawn, with a diamond-shaped cutout in the center of the scene.
Within the diamond-shaped stencil mask, a sphere is drawn. In this example,
drawing into the stencil buffer takes place only when the window is re-
drawn, so the color buffer is cleared after the stencil mask has been created.
Query Value Meaning
GL_STENCIL_FUNC stencil function
GL_STENCIL_REF stencil reference value
GL_STENCIL_VALUE_MASK stencil mask
GL_STENCIL_FAIL stencil fail action
GL_STENCIL_PASS_DEPTH_FAIL stencil pass and depth buffer fail action
GL_STENCIL_PASS_DEPTH_PASS stencil pass and depth buffer pass action
Table 10-3 Query Values for the Stencil Test

Testing and Operating on Fragments 507
Example 10-1 Using the Stencil Test: stencil.c
#define YELLOWMAT 1
#define BLUEMAT 2
void init(void)
{
GLfloat yellow_diffuse[] = { 0.7, 0.7, 0.0, 1.0 };
GLfloat yellow_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat blue_diffuse[] = { 0.1, 0.1, 0.7, 1.0 };
GLfloat blue_specular[] = { 0.1, 1.0, 1.0, 1.0 };
GLfloat position_one[] = { 1.0, 1.0, 1.0, 0.0 };
glNewList(YELLOWMAT, GL_COMPILE);
glMaterialfv(GL_FRONT, GL_DIFFUSE, yellow_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, yellow_specular);
glMaterialf(GL_FRONT, GL_SHININESS, 64.0);
glEndList();
glNewList(BLUEMAT, GL_COMPILE);
glMaterialfv(GL_FRONT, GL_DIFFUSE, blue_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, blue_specular);
glMaterialf(GL_FRONT, GL_SHININESS, 45.0);
glEndList();
glLightfv(GL_LIGHT0, GL_POSITION, position_one);
glEnable(GL_LIGHT0);
glEnable(GL_LIGHTING);
glEnable(GL_DEPTH_TEST);
glClearStencil(0x0);
glEnable(GL_STENCIL_TEST);
}
/* Draw a sphere in a diamond-shaped section in the
* middle of a window with 2 tori.
*/
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
/* draw blue sphere where the stencil is 1 */
glStencilFunc(GL_EQUAL, 0x1, 0x1);
glStencilOp(GL_KEEP, GL_KEEP, GL_KEEP);
glCallList(BLUEMAT);
glutSolidSphere(0.5, 15, 15);

508 Chapter 10: The Framebuffer
/* draw the tori where the stencil is not 1 */
glStencilFunc(GL_NOTEQUAL, 0x1, 0x1);
glPushMatrix();
glRotatef(45.0, 0.0, 0.0, 1.0);
glRotatef(45.0, 0.0, 1.0, 0.0);
glCallList(YELLOWMAT);
glutSolidTorus(0.275, 0.85, 15, 15);
glPushMatrix();
glRotatef(90.0, 1.0, 0.0, 0.0);
glutSolidTorus(0.275, 0.85, 15, 15);
glPopMatrix();
glPopMatrix();
}
/* Whenever the window is reshaped, redefine the
* coordinate system and redraw the stencil area.
*/
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
/* create a diamond shaped stencil area */
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
gluOrtho2D(-3.0, 3.0, -3.0*(GLfloat)h/(GLfloat)w,
3.0*(GLfloat)h/(GLfloat)w);
else
gluOrtho2D(-3.0*(GLfloat)w/(GLfloat)h,
3.0*(GLfloat)w/(GLfloat)h, -3.0, 3.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glClear(GL_STENCIL_BUFFER_BIT);
glStencilFunc(GL_ALWAYS, 0x1, 0x1);
glStencilOp(GL_REPLACE, GL_REPLACE, GL_REPLACE);
glBegin(GL_QUADS);
glVertex2f(-1.0, 0.0);
glVertex2f(0.0, 1.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, -1.0);
glEnd();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0, (GLfloat) w/(GLfloat) h, 3.0, 7.0);

Testing and Operating on Fragments 509
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0, 0.0, -5.0);
}
/* Main Loop
* Be certain to request stencil bits.
*/
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB |
GLUT_DEPTH | GLUT_STENCIL);
glutInitWindowSize(400, 400);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
The following examples illustrate other uses of the stencil test. (See
Chapter 14 for additional ideas.)
• Capping—Suppose you’re drawing a closed convex object (or several of
them, as long as they don’t intersect or enclose each other) made up of
several polygons, and you have a clipping plane that may or may not
slice off a piece of it. Suppose that if the plane does intersect the object,
you want to cap the object with some constant-colored surface, rather
than see the inside of it. To do this, clear the stencil buffer to zeros, and
begin drawing with stenciling enabled and the stencil comparison
function set always to accept fragments. Invert the value in the stencil
planes each time a fragment is accepted. After all the objects are drawn,
regions of the screen where no capping is required have zeros in the
stencil planes, and regions requiring capping are nonzero. Reset the
stencil function so that it draws only where the stencil value is nonzero,
and draw a large polygon of the capping color across the entire screen.
• Overlapping translucent polygons—Suppose you have a translucent
surface that’s made up of polygons that overlap slightly. If you simply
use alpha blending, portions of the underlying objects are covered by
more than one transparent surface, which doesn’t look right. Use the
stencil planes to make sure that each fragment is covered by at most
one portion of the transparent surface. Do this by clearing the stencil

510 Chapter 10: The Framebuffer
planes to zeros, drawing only when the stencil plane is zero, and
incrementing the value in the stencil plane when you draw.
• Stippling—Suppose you want to draw an image with a stipple pattern.
(See “Displaying Points, Lines, and Polygons” on page 55 for more
information about stippling.) You can do this by writing the stipple
pattern into the stencil buffer and then drawing conditionally on
the contents of the stencil buffer. After the original stipple pattern is
drawn, the stencil buffer isn’t altered while drawing the image, so the
object is stippled by the pattern in the stencil planes.
Depth Test
For each pixel on the screen, the depth buffer keeps track of the distance
between the viewpoint and the object occupying that pixel. Then, if the
specified depth test passes, the incoming depth value replaces the value
already in the depth buffer.
The depth buffer is generally used for hidden-surface elimination. If a new
candidate color for that pixel appears, it’s drawn only if the corresponding
object is closer than the previous object. In this way, after the entire scene
has been rendered, only objects that aren’t obscured by other items remain.
Initially, the clearing value for the depth buffer is a value that’s as far from
the viewpoint as possible, so the depth of any object is nearer than that
value. If this is how you want to use the depth buffer, you simply have to
enable it by passing GL_DEPTH_TEST to glEnable() and remember to clear
the depth buffer before you redraw each frame. (See “Clearing Buffers” on
page 495.) You can also choose a different comparison function for the
depth test with glDepthFunc().
void glDepthFunc(GLenum func);
Sets the comparison function for the depth test. The value for func
must be GL_NEVER, GL_ALWAYS, GL_LESS, GL_LEQUAL, GL_EQUAL,
GL_GEQUAL, GL_GREATER, or GL_NOTEQUAL. An incoming fragment
passes the depth test if its z-value has the specified relation to the value
already stored in the depth buffer. The default is GL_LESS, which means
that an incoming fragment passes the test if its z-value is less than that
already stored in the depth buffer. In this case, the z-value represents the
distance from the object to the viewpoint, and smaller values mean that
the corresponding objects are closer to the viewpoint.

Testing and Operating on Fragments 511
Occlusion Query
Advanced
The depth buffer determines visibility on a per-pixel basis. For performance
reasons, it would be nice to be able to determine if a geometric object is
visible before sending all of its (perhaps complex) geometry for rendering.
Occlusion queries enable you to determine if a representative set of geometry
will be visible after depth testing.
This is particularly useful for complex geometric objects with many
polygons. Instead of rendering all of the geometry for a complex object, you
might render its bounding box or another simplified representation that
require less rendering resources. If OpenGL returns that no fragments or
samples would have been modified by rendering that piece of geometry,
you know that none of your complex object will be visible for that frame,
and you can skip rendering that object for the frame.
The following steps are required to utilize occlusion queries:
1. (Optional) Generate a query id for each occlusion query that you need.
2. Specify the start of an occlusion query by calling glBeginQuery().
3. Render the geometry for the occlusion test.
4. Specify that you’ve completed the occlusion query by calling
glEndQuery().
5. Retrieve the number of samples that passed the depth test.
In order to make the occlusion query process as efficient as possible, you’ll
want to disable all rendering modes that will increase the rendering time
but won’t change the visibility of a pixel.
Generating Query Objects
An occlusion query object identifier is just an unsigned integer. While not
strictly necessary, it’s a good practice to have OpenGL generate a set of ids
for your use. glGenQueries() will generate the requested number of unused
query ids for your subsequent use.
Advanced

512 Chapter 10: The Framebuffer
You can also determine if an identifier is currently being used as an
occlusion query by calling glIsQuery().
Initiating an Occlusion Query Test
To specify geometry that’s to be used in an occlusion query, merely bracket
the rendering operations between calls to glBeginQuery() and glEndQuery(),
as demonstrated in Example 10-2.
Example 10-2 Rendering Geometry with Occlusion Query: occquery.c
glBeginQuery(GL_SAMPLES_PASSED, Query);
glBegin(GL_TRIANGLES);
glVertex3f( 0.0, 0.0, 1.0);
glVertex3f(-1.0, 0.0, 0.0);
glVertex3f( 1.0, 0.0, 0.0);
glEnd();
glEndQuery(GL_SAMPLES_PASSED);
All OpenGL operations are available while an occlusion query is active, with
the exception of glGenQueries() and glDeleteQueries(), which will raise a
GL_INVALID_OPERATION error.
void glGenQueries(GLsizei n, GLuint *ids);
Returns n currently unused names for occlusion query objects in the array
ids The names returned in ids do not have to be a contiguous set of
integers.
The names returned are marked as used for the purposes of allocating
additional query objects, but only acquire valid state once they have been
specified in a call to glBeginQuery().
Zero is a reserved occlusion query object name and is never returned as a
valid value by glGenQueries().
GLboolean glIsQuery(GLuint id);
Returns GL_TRUE if id is the name of an occlusion query object. Returns
GL_FALSE if id is zero or if id is a nonzero value that is not the name of a
buffer object.

Testing and Operating on Fragments 513
Determining the Results of an Occlusion Query
Once you’ve completed rendering the geometry for the occlusion
query, you need to retrieve the results. This is done with a call to
glGetQueryObject[u]iv(), as shown in Example 10-3, which will return
the number of fragments, or samples, if you’re using multisampling (see
“Alpha and Multisampling Coverage” on page 279 for details).
Example 10-3 Retrieving the Results of an Occlusion Query: occquery.c
count = 1000; /* counter to avoid a possible infinite loop */
while (!queryReady && count--) {
glGetQueryObjectiv(Query, GL_QUERY_RESULT_AVAILABLE,
&queryReady);
}
void glBeginQuery(GLenum target, GLuint id);
Specifies the start of an occlusion query operation. target must be
GL_SAMPLES_PASSED. id is an unsigned integer identifier for this
occlusion query operation.
void glEndQuery(GLenum target);
Ends an occlusion query. target must be GL_SAMPLES_PASSED.
void glGetQueryObjectiv(GLenum id, GLenum pname,
GLint *params);
void glGetQueryObjectuiv(GLenum id, GLenum pname,
GLuint *params);
Queries the state of an occlusion query object. id is the name of a query
object. If pname is GL_QUERY_RESULT, then params will contain the
number of fragments or samples (if multisampling is enabled) that passed
the depth test, with a value of zero representing the object being entirely
occluded.
There may be a delay in completing the occlusion query operation. If
pname is GL_QUERY_RESULT_AVAILABLE, params will contain GL_TRUE
if the results for query id are available, or GL_FALSE otherwise.

514 Chapter 10: The Framebuffer
if (queryReady) {
glGetQueryObjectiv(Query, GL_QUERY_RESULT, &samples);
fprintf(stderr, " Samples rendered: %d\n", samples);
}
else {
fprintf(stderr, " Result not ready ... rendering
anyways\n");
samples = 1; /* make sure we render */
}
if (samples > 0)
glDrawArrays(GL_TRIANGLE_FAN, 0, NumVertices);
Cleaning Up Occlusion Query Objects
After you’ve completed your occlusion query tests, you can release the
resources related to those queries by calling glDeleteQueries().
Conditional Rendering
Advanced
One of the issues with occlusion queries is that they require OpenGL to
pause processing geometry and fragments, count the number of affected
samples in the depth buffer, and return the value to your application.
Stopping modern graphics hardware in this manner usually
catastrophically affects performance in performance-sensitive
applications. To eliminate the need to pause OpenGL’s operation,
conditional rendering allows the graphics server (hardware) to decide if
an occlusion query yielded any fragments, and to render the intervening
commands. Conditional rendering is enabled by surrounding the
rendering operations you would have conditionally executed using the
results of glGetQuery*().
void glDeleteQueries(GLsizei n, const GLuint *ids);
Deletes n occlusion query objects, named by elements in the array ids. The
freed query objects may now be reused (for example, by glGenQueries()).
Advanced
Testing and Operating on Fragments 515
The code shown in Example 10-4 completely replaces the sequence of code
in Example 10-3. Not only it the code more compact, it is far more efficient
as it completely removes the results query to the OpenGL server, which is a
major performance inhibitor.
Example 10-4 Rendering Using Conditional Rendering: condrender.c
glBeginConditionalRender(Query, GL_QUERY_WAIT);
glDrawArrays(GL_TRIANGLE_FAN, 0, NumVertices);
glEndConditionalRender();
Blending, Dithering, and Logical Operations
Once an incoming fragment has passed all the tests described in “Testing
and Operating on Fragments,” it can be combined with the current con-
tents of the color buffer in one of several ways. The simplest way, which is
also the default, is to overwrite the existing values. Alternatively, if you’re
using RGBA mode and you want the fragment to be translucent or anti-
aliased, you might average its value with the value already in the buffer
(blending). On systems with a small number of available colors, you might
want to dither color values to increase the number of colors available at the
cost of a loss in resolution. In the final stage, you can use arbitrary bitwise
logical operations to combine the incoming fragment and the pixel that’s
already written.
void glBeginConditionalRender(GLuint id, GLenum mode);
void glEndConditionalRender(void);
Delineates a sequence of OpenGL rendering commands that may be
discarded based on the results of the occlusion query object id.mode
specifies how the OpenGL implementation uses the results of the occlusion
query, and must be one of: GL_QUERY_WAIT, GL_QUERY_NO_WAIT,
GL_QUERY_BY_REGION_WAIT, or GL_QUERY_BY_REGION_NO_WAIT.
A GL_INVALID_VALUE is set if id is not an existing occlusion query. A
GL_INVALID_OPERATION is generated if glBeginConditionalRender()
is called while a conditional rendering sequence is in operation; if
glEndConditionalRender() is called when no conditional render is
underway; if id is the name of a occlusion query object with a target
different than GL_SAMPLES_PASSED; or if id is the name of an occlusion
query in progress.
516 Chapter 10: The Framebuffer
Blending
Blending combines the incoming fragment’s R, G, B, and alpha values with
those of the pixel already stored at the location. Different blending opera-
tions can be applied, and the blending that occurs depends on the values of
the incoming alpha value and the alpha value (if any) stored at the pixel.
(See “Blending” on page 251 for an extensive discussion of this topic.)
Control of blending is available on a per-buffer basis starting with OpenGL
Version 3.0, using the following commands:
To determine if blending is enabled for a particular buffer, use
glIsEnabledi().
Dithering
On systems with a small number of color bitplanes, you can improve the
color resolution at the expense of spatial resolution by dithering the color
in the image. Dithering is like halftoning in newspapers. Although The New
Yor k Tim es has only two colors—black and white—it can show photographs
by representing the shades of gray with combinations of black and white
dots. Comparing a newspaper image of a photo (having no shades of gray)
with the original photo (with grayscale) makes the loss of spatial resolution
obvious. Similarly, systems with a small number of color bitplanes may
dither values of red, green, and blue on neighboring pixels for the
appearance of a wider range of colors.
void glEnablei(GLenum target, GLuint index);
void glDisablei(GLenum target, GLuint index);
Enables or disables blending for buffer index.target must be GL_BLEND.
A GL_INVALID_VALUE is generated if index is greater than or equal to
GL_MAX_DRAW_BUFFERS.
GLboolean glIsEnabledi(GLenum target, GLuint index);
Specifies whether target is enabled for buffer index.
For OpenGL Version 3.0, target must be GL_BLEND, or a GL_INVALID_
ENUM is generated.
A GL_INVALID_VALUE is generated if index is outside of the range
supported for target.

Testing and Operating on Fragments 517
The dithering operation that takes place is hardware-dependent; all OpenGL
allows you to do is to turn it on and off. In fact, on some machines, enabling
dithering might do nothing at all, which makes sense if the machine already
has high color resolution. To enable and disable dithering, pass GL_DITHER
to glEnable() and glDisable(). Dithering is enabled by default.
Dithering applies in both RGBA and color-index mode. The colors or color
indices alternate in some hardware-dependent way between the two nearest
possibilities. For example, in color-index mode, if dithering is enabled and
the color index to be painted is 4.4, then 60 percent of the pixels may be
painted with index 4, and 40 percent of the pixels with index 5. (Many dith-
ering algorithms are possible, but a dithered value produced by any algo-
rithm must depend on only the incoming value and the fragment’s x- and
y-coordinates.) In RGBA mode, dithering is performed separately for each
component (including alpha). To use dithering in color-index mode, you
generally need to arrange the colors in the color map appropriately in ramps;
otherwise, bizarre images might result.
Logical Operations
The final operation on a fragment is the logical operation, such as an OR,
XOR, or INVERT, which is applied to the incoming fragment values (source)
and/or those currently in the color buffer (destination). Such fragment
operations are especially useful on bit-blt-type machines, on which the pri-
mary graphics operation is copying a rectangle of data from one place in the
window to another, from the window to processor memory, or from mem-
ory to the window. Typically, the copy doesn’t write the data directly into
memory but instead allows you to perform an arbitrary logical operation on
the incoming data and the data already present; then it replaces the existing
data with the results of the operation.
Since this process can be implemented fairly cheaply in hardware, many
such machines are available. As an example of using a logical operation,
XOR can be used to draw on an image in an undoable way; simply XOR the
same drawing again, and the original image is restored. As another example,
when using color-index mode, the color indices can be interpreted as bit
patterns. Then you can compose an image as combinations of drawings on
different layers, use writemasks to limit drawing to different sets of
bitplanes, and perform logical operations to modify different layers.
You enable and disable logical operations by passing GL_INDEX_LOGIC_
OP or GL_COLOR_LOGIC_OP to glEnable() and glDisable() for color-
index mode or RGBA mode, respectively. You also must choose among
the 16 logical operations with glLogicOp(), or you’ll just get the effect of
518 Chapter 10: The Framebuffer
the default value, GL_COPY. (For backward compatibility with OpenGL
Version 1.0, glEnable(GL_LOGIC_OP) also enables logical operation in
color-index mode.)
The Accumulation Buffer
Note: The accumulation buffer was removed through deprecation from
OpenGL Version 3.1. Some of the techniques described in this
chapter in prior editions—full-scene antialiasing, principally—have
been replaced by other techniques (see “Alpha and Multisampling
Coverage” on page 279). The remaining techniques are easy to
implement using floating-point pixel formats in the framebuffer—a
feature added in OpenGL Version 3.0. The concepts of these
techniques are similar to those mentioned here.
void glLogicOp(GLenum opcode);
Selects the logical operation to be performed, given an incoming (source)
fragment and the pixel currently stored in the color buffer (destination).
Table 10-4 shows the possible values for opcode and their meaning (s
represents source and d destination). The default value is GL_COPY.
Parameter Operation Parameter Operation
GL_CLEAR 0 GL_AND s d
GL_COPY sGL_OR s d
GL_NOOP dGL_NAND ¬(s d)
GL_SET 1 GL_NOR ¬(s d)
GL_COPY_INVERTED ¬sGL_XOR s XOR d
GL_INVERT ¬dGL_EQUIV ¬(s XOR d)
GL_AND_REVERSE s ¬d GL_AND_INVERTED ¬s d
GL_OR_REVERSE s ¬d GL_OR_INVERTED ¬s d
Table 10-4 Sixteen Logical Operations

The Accumulation Buffer 519
Advanced
The accumulation buffer can be used for such things as scene antialiasing,
motion blur, simulating photographic depth of field, and calculating the
soft shadows that result from multiple light sources. Other techniques are
possible, especially in combination with some of the other buffers. (See The
Accumulation Buffer: Hardware Support for High-Quality Rendering by Paul
Haeberli and Kurt Akeley [SIGGRAPH 1990 Proceedings, pp. 309–318] for
more information about uses for the accumulation buffer.)
OpenGL graphics operations don’t write directly into the accumulation
buffer. Typically, a series of images is generated in one of the standard color
buffers, and these images are accumulated, one at a time, into the accumu-
lation buffer. When the accumulation is finished, the result is copied back
into a color buffer for viewing. To reduce rounding errors, the accumulation
buffer may have higher precision (more bits per color) than the standard
color buffers. Rendering a scene several times obviously takes longer than
rendering it once, but the result is higher quality. You can decide what
trade-off between quality and rendering time is appropriate for your
application.
You can use the accumulation buffer the same way a photographer can use
film for multiple exposures. A photographer typically creates a multiple
exposure by taking several pictures of the same scene without advancing
the film. If anything in the scene moves, that object appears blurred. Not
surprisingly, a computer can do more with an image than a photographer
can do with a camera. For example, a computer has exquisite control over
the viewpoint, but a photographer can’t shake a camera a predictable and
controlled amount. (See “Clearing Buffers” on page 495 for information
about how to clear the accumulation buffer; use glAccum() to control it.)
void glAccum(GLenum op, GLfloat value);
Controls the accumulation buffer. The op parameter selects the operation,
and value is a number to be used in that operation. The possible operations
are GL_ACCUM, GL_LOAD, GL_RETURN, GL_ADD, and GL_MULT:
• GL_ACCUM reads each pixel from the buffer currently selected for
reading with glReadBuffer(), multiplies the R, G, B, and alpha
values by value, and adds the resulting values to the accumulation
buffer.
Advanced
Compatibility
Extension
glAccum and all
accepted tokens
• GL_LOAD is the same as GL_ACCUM, except that the values replace
those in the accumulation buffer, rather than being added to them.
• GL_RETURN takes values from the accumulation buffer, multiplies
them by value, and places the results in the color buffer(s) enabled
for writing.
• GL_ADD and GL_MULT simply add and multiply, respectively, the
value of each pixel in the accumulation buffer to or by value and then
return it to the accumulation buffer. For GL_MULT, value is clamped
to be in the range [1.0, 1.0]. For GL_ADD, no clamping occurs.
Motion Blur
Similar methods can be used to simulate motion blur, as shown in Plate 7
and Figure 10-2. Suppose your scene has some stationary and some moving
objects in it, and you want to make a motion-blurred image extending over
a small interval of time. Set up the accumulation buffer in the same way, but
instead of jittering the images spatially, jitter them temporally. The entire
scene can be made successively dimmer by calling
glAccum(GL_MULT, decayFactor);
as the scene is drawn into the accumulation buffer, where decayFactor is a
number from 0.0 to 1.0. Smaller numbers for decayFactor cause the object to
appear to be moving faster. You can transfer the completed scene, with the
object’s current position and a “vapor trail” of previous positions, from the
accumulation buffer to the standard color buffer with
glAccum(GL_RETURN, 1.0);
The image looks correct even if the items move at different speeds or if some
of them are accelerated. As before, the more jitter points (temporal, in this
case) you use, the better the final image, at least up to the point where you
begin to lose resolution because of the finite precision in the accumulation
buffer. You can combine motion blur with antialiasing by jittering in both
the spatial and temporal domains, but you pay for higher quality with
longer rendering times.
520 Chapter 10: The Framebuffer
Depth of Field
A photograph made with a camera is in perfect focus only for items lying in
a single plane a certain distance from the film. The farther an item is from

this plane, the more out of focus it is. The depth of field for a camera is a
region about the plane of perfect focus where items are out of focus by a
small enough amount.
Under normal conditions, everything you draw with OpenGL is in focus
(unless your monitor is bad; in which case, everything is out of focus). The
accumulation buffer can be used to approximate what you would see in a
photograph, where items are increasingly blurred as their distance from
the plane of perfect focus increases. It isn’t an exact simulation of the
effects produced in a camera, but the result looks similar to what a camera
would produce.
Figure 10-2 Motion-Blurred Object
The Accumulation Buffer 521
To achieve this result, draw the scene repeatedly using calls with different
argument values to glFrustum(). Choose the arguments so that the position
of the viewpoint varies slightly around its true position and so that each
frustum shares a common rectangle that lies in the plane of perfect focus,
as shown in Figure 10-3. The results of all the renderings should be averaged
in the usual way using the accumulation buffer.
Plate 10 shows an image of five teapots drawn using the depth-of-field
effect. The gold teapot (second from the left) is in focus, and the other
teapots get progressively blurrier, depending on their distance from the
focal plane (gold teapot). The code used to draw this image is shown in
Example 10-5 (which assumes that accPerspective() and accFrustum() are
defined as described in Example 10-5). The scene is drawn eight times, each
with a slightly jittered viewing volume, by calling accPerspective(). As
you recall, with scene antialiasing, the fifth and sixth parameters jitter the
viewing volumes in the x- and y-directions. For the depth-of-field effect,
however, you want to jitter the volume while holding it stationary at the
focal plane. The focal plane is the depth value defined by the ninth (last)
parameter to accPerspective(), which is z = 5.0 in this example. The amount
of blur is determined by multiplying the x and y jitter values (seventh and
eighth parameters of accPerspective()) by a constant. Determining the con-
stant is not a science; experiment with values until the depth of field is as

522 Chapter 10: The Framebuffer
pronounced as you want. (Note that in Example 10-5, the fifth and sixth
parameters to accPerspective() are set to 0.0, so scene antialiasing is
turned off.)
Example 10-5 Depth-of-Field Effect: dof.c
void init(void)
{
GLfloat ambient[] = { 0.0, 0.0, 0.0, 1.0 };
GLfloat diffuse[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat position[] = { 0.0, 3.0, 3.0, 0.0 };
A
BNormal (nonjittered) view
Plane in focus
A
BJittered at point A
A
BJittered at point B
Figure 10-3 Jittered Viewing Volume for Depth-of-Field Effects

The Accumulation Buffer 523
GLfloat lmodel_ambient[] = { 0.2, 0.2, 0.2, 1.0 };
GLfloat local_view[] = { 0.0 };
glLightfv(GL_LIGHT0, GL_AMBIENT, ambient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, diffuse);
glLightfv(GL_LIGHT0, GL_POSITION, position);
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, lmodel_ambient);
glLightModelfv(GL_LIGHT_MODEL_LOCAL_VIEWER, local_view);
glFrontFace(GL_CW);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_AUTO_NORMAL);
glEnable(GL_NORMALIZE);
glEnable(GL_DEPTH_TEST);
glClearColor(0.0, 0.0, 0.0, 0.0);
glClearAccum(0.0, 0.0, 0.0, 0.0);
/* make teapot display list */
teapotList = glGenLists(1);
glNewList(teapotList, GL_COMPILE);
glutSolidTeapot(0.5);
glEndList();
}
void renderTeapot(GLfloat x, GLfloat y, GLfloat z,
GLfloat ambr, GLfloat ambg, GLfloat ambb,
GLfloat difr, GLfloat difg, GLfloat difb,
GLfloat specr, GLfloat specg, GLfloat specb, GLfloat shine)
{
GLfloat mat[4];
glPushMatrix();
glTranslatef(x, y, z);
mat[0] = ambr; mat[1] = ambg; mat[2] = ambb; mat[3] = 1.0;
glMaterialfv(GL_FRONT, GL_AMBIENT, mat);
mat[0] = difr; mat[1] = difg; mat[2] = difb;
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat);
mat[0] = specr; mat[1] = specg; mat[2] = specb;
glMaterialfv(GL_FRONT, GL_SPECULAR, mat);
glMaterialf(GL_FRONT, GL_SHININESS, shine*128.0);
glCallList(teapotList);
glPopMatrix();
}

524 Chapter 10: The Framebuffer
void display(void)
{
int jitter;
GLint viewport[4];
glGetIntegerv(GL_VIEWPORT, viewport);
glClear(GL_ACCUM_BUFFER_BIT);
for (jitter = 0; jitter < 8; jitter++) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
accPerspective(45.0,
(GLdouble) viewport[2]/(GLdouble) viewport[3],
1.0, 15.0, 0.0, 0.0,
0.33*j8[jitter].x, 0.33*j8[jitter].y, 5.0);
/* ruby, gold, silver, emerald, and cyan teapots */
renderTeapot(-1.1, -0.5, -4.5, 0.1745, 0.01175,
0.01175, 0.61424, 0.04136, 0.04136,
0.727811, 0.626959, 0.626959, 0.6);
renderTeapot(-0.5, -0.5, -5.0, 0.24725, 0.1995,
0.0745, 0.75164, 0.60648, 0.22648,
0.628281, 0.555802, 0.366065, 0.4);
renderTeapot(0.2, -0.5, -5.5, 0.19225, 0.19225,
0.19225, 0.50754, 0.50754, 0.50754,
0.508273, 0.508273, 0.508273, 0.4);
renderTeapot(1.0, -0.5, -6.0, 0.0215, 0.1745, 0.0215,
0.07568, 0.61424, 0.07568, 0.633,
0.727811, 0.633, 0.6);
renderTeapot(1.8, -0.5, -6.5, 0.0, 0.1, 0.06, 0.0,
0.50980392, 0.50980392, 0.50196078,
0.50196078, 0.50196078, .25);
glAccum(GL_ACCUM, 0.125);
}
glAccum(GL_RETURN, 1.0);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
}
/* Main Loop
* Be certain you request an accumulation buffer.
*/
int main(int argc, char** argv)
{

The Accumulation Buffer 525
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB |
GLUT_ACCUM | GLUT_DEPTH);
glutInitWindowSize(400, 400);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Soft Shadows
To accumulate soft shadows resulting from multiple light sources, render
the shadows with one light turned on at a time, and accumulate them
together. This can be combined with spatial jittering to antialias the scene
at the same time. (See “Shadows” on page 658 for more information about
drawing shadows.)
Jittering
If you need to take 9 or 16 samples to antialias an image, you might think
that the best choice of points is an equally spaced grid across the pixel. Sur-
prisingly, this is not necessarily true. In fact, sometimes it’s a good idea to
take points that lie in adjacent pixels. You might want a uniform distribu-
tion or a normalized distribution, clustering toward the center of the pixel.
In addition, Table 10-5 shows a few sets of reasonable jittering values to be
used for some selected sample counts. Most of the examples in this table are
uniformly distributed in the pixel, and all lie within the pixel.
Count Values
2 {0.25, 0.75}, {0.75, 0.25}
3 {0.5033922635, 0.8317967229}, {0.7806016275, 0.2504380877},
{0.2261828938, 0.4131553612}
4 {0.375, 0.25}, {0.125, 0.75}, {0.875, 0.25}, {0.625, 0.75}
Table 10-5 Sample Jittering Values

526 Chapter 10: The Framebuffer
Framebuffer Objects
Advanced
Up to this point, all of our discussion regarding buffers has focused
on the buffers provided by the windowing system, as you requested
when you called glutCreateWindow() (and configured by your call to
glutInitDisplayMode()). Although you can quite successfully use any
technique with just those buffers, quite often various operations require
moving data between buffers superfluously. This is where framebuffer
5 {0.5, 0.5}, {0.3, 0.1}, {0.7, 0.9}, {0.9, 0.3}, {0.1, 0.7}
6 {0.4646464646, 0.4646464646}, {0.1313131313, 0.7979797979},
{0.5353535353, 0.8686868686}, {0.8686868686, 0.5353535353},
{0.7979797979, 0.1313131313}, {0.2020202020, 0.2020202020}
8 {0.5625, 0.4375}, {0.0625, 0.9375}, {0.3125, 0.6875}, {0.6875, 0.8125},
{0.8125, 0.1875}, {0.9375, 0.5625}, {0.4375, 0.0625}, {0.1875, 0.3125}
9 {0.5, 0.5}, {0.1666666666, 0.9444444444}, {0.5, 0.1666666666},
{0.5, 0.8333333333}, {0.1666666666, 0.2777777777},
{0.8333333333, 0.3888888888}, {0.1666666666, 0.6111111111},
{0.8333333333, 0.7222222222}, {0.8333333333, 0.0555555555}
12 {0.4166666666, 0.625}, {0.9166666666, 0.875}, {0.25, 0.375},
{0.4166666666, 0.125}, {0.75, 0.125}, {0.0833333333, 0.125}, {0.75, 0.625},
{0.25, 0.875}, {0.5833333333, 0.375}, {0.9166666666, 0.375},
{0.0833333333, 0.625}, {0.583333333, 0.875}
16 {0.375, 0.4375}, {0.625, 0.0625}, {0.875, 0.1875}, {0.125, 0.0625},
{0.375, 0.6875}, {0.875, 0.4375}, {0.625, 0.5625}, {0.375, 0.9375},
{0.625, 0.3125}, {0.125, 0.5625}, {0.125, 0.8125}, {0.375, 0.1875},
{0.875, 0.9375}, {0.875, 0.6875}, {0.125, 0.3125}, {0.625, 0.8125}
Count Values
Table 10-5 (continued) Sample Jittering Values
Advanced

Framebuffer Objects 527
objects enter the picture (as part of OpenGL Version 3.0). Using framebuffer
objects, you can create our own framebuffers and use their attached
renderbuffers to minimize data copies and optimize performance.
Framebuffer objects are quite useful for performing off-screen-rendering,
updating texture maps, and engaging in buffer ping-ponging (a data-transfer
techniques used in GPGPU).
The framebuffer that is provided by the windowing system is the only
framebuffer that is available to the display system of your graphics server—
that is, it is the only one you can see on your screen. It also places
restrictions on the use of the buffers that were created when your window
opened. By comparison, the framebuffers that your application creates
cannot be displayed on your monitor; they support only off-screen rendering.
Another difference between window-system-provided framebuffers and
framebuffers you create is that those managed by the window system
allocate their buffers—color, depth, stencil, and accumulation—when your
window is created. When you create an application-managed framebuffer
object, you need to create additional renderbuffers that you associate with
the framebuffer objects you created. The buffers with the window-system-
provided buffers can never be associated with an application-created
framebuffer object, and vice versa.
To allocate an application-generated framebuffer object name, you need to
call glGenFramebuffers() which will allocate an unused identifier for the
framebuffer object. As compared to some other objects within OpenGL
(e.g., texture objects and display lists), you always need to use an name
returned from glGenFramebuffers().
Allocating a framebuffer object name doesn’t actually create the
framebuffer object or allocate any storage for it. Those tasks are handled
through a call to glBindFramebuffer().glBindFramebuffer() operates in a
similar manner to many of the other glBind*() routines you’ve seen in
OpenGL. The first time it is called for a particular framebuffer, it causes
void glGenFramebuffers(GLsize n, GLuint *ids);
Allocate n unused framebuffer object names, and return those names in ids.

528 Chapter 10: The Framebuffer
storage for the object to be allocated and initialized. Any subsequent calls
will bind the provided framebuffer object name as the active one.
As with all of the other objects you have encountered in OpenGL,
you can release an application-allocated framebuffer by calling
glDeleteFramebuffers(). That function will mark the framebuffer object’s
name as unallocated and release any resources associated with the
framebuffer object.
For completeness, you can determine whether a particular unsigned integer
is an application-allocated framebuffer object by calling glIsFramebuffer():.
void glBindFramebuffer(GLenum target, GLuint framebuffer);
Specifies either a framebuffer for either reading or writing. When target
is GL_DRAW_FRAMEBUFFER, framebuffer specifies the destination
framebuffer for rendering. Similarly, when target is set to GL_READ_
FRAMEBUFFER, framebuffer specifies the source of read operations. Passing
GL_FRAMEBUFFER for target sets both the read and write framebuffer
bindings to framebuffer.
framebuffer must either be zero, which binds target to the default; a
window-system provided framebuffer; or a framebuffer object generated
by a call to glGenFramebuffers().
A GL_INVALID_OPERATION error is generated if framebuffer is neither
zero nor a valid framebuffer object previously generated by calling
glGenFramebuffers(), but not deleted by calling glDeleteFramebuffers().
void glDeleteFramebuffers(GLsize n, const GLuint *ids);
Deallocates the n framebuffer objects associated with the names provided
in ids. If a framebuffer object is currently bound (i.e., its name was passed
to the most recent call to glBindFramebuffer()), and is deleted, the
framebuffer target is immediately bound to id zero (the window-system
provided framebuffer), and the framebuffer object is released.
No errors are generated by glDeleteFramebuffers(). Unused names or
zero are simply ignored.
GLboolean glIsFramebuffer(GLuint framebuffer);

Framebuffer Objects 529
Once a framebuffer object is created, you still can’t do much with it. You
need to provide a place for drawing to go and reading to come from; those
places are called framebuffer attachments. We’ll discuss those in more detail
after we examine renderbuffers, which are one type of buffer you can attach
to a framebuffer object.
Renderbuffers
Renderbuffers are effectively memory managed by OpenGL that contains
formatted image data. The data that a renderbuffer holds takes meaning
once it is attached to a framebuffer object, assuming that the format of the
image buffer matches what OpenGL is expecting to render into (e.g., you
can’t render colors into the depth buffer).
As with many other buffers in OpenGL, the process of allocating and
deleting buffers is similar to what you’ve seen before. To create a new
renderbuffer, you would call glGenRenderbuffers().
Likewise, a call to glDeleteRenderbuffers() will release the storage
associated with a renderbuffer.
Returns GL_TRUE if framebuffer is the name of a framebuffer returned
from glGenFramebuffers(). Returns GL_FALSE if framebuffer is zero (the
window-system default framebuffer) or a value that’s either unallocated or
been deleted by a call to glDeleteFramebuffers().
void glGenRenderbuffers(GLsizei n, GLuint *ids);
Allocate n unused renderbuffer object names, and return those names in
ids. Names are unused until bound with a call to glBindRenderbuffer().
void glDeleteRenderbuffers(GLsizei n, const GLuint *ids);
Deallocates the n renderbuffer objects associated with the names provided
in ids. If one of the renderbuffers is currently bound and passed to
glDeleteRenderbuffers(), a binding of zero replaces the binding at the
current framebuffer attachment point, in addition to the renderbuffer
being released.
No errors are generated by glDeleteRenderbuffers(). Unused names or
zero are simply ignored.

530 Chapter 10: The Framebuffer
Likewise, you can determine whether a name represents a valid renderbuffer
by calling glIsRenderbuffer().
Similar to the process of binding a framebuffer object so that you can
modify its state, you call glBindRenderbuffer() to affect a renderbuffer’s
creation and to modify the state associated with it, which includes the
format of the image data that it contains.
Creating Renderbuffer Storage
When you first call glBindRenderbuffer() with an unused renderbuffer
name, the OpenGL server creates a renderbuffer with all its state
information set to the default values. In this configuration, no storage has
been allocated to store image data. Before you can attach a renderbuffer to
a framebuffer and render into it, you need to allocate storage and specify its
image format. This is done by calling either glRenderbufferStorage() or
glRenderbufferStorageMultisample().
void glIsRenderbuffer(GLuint renderbuffer);
Returns GL_TRUE if renderbuffer is the name of a renderbuffer returned
from glGenRenderbuffers(). Returns GL_FALSE if renderbuffer is zero (the
window-system default framebuffer) or a value that’s either unallocated or
been deleted by a call to glDeleteRenderbuffers().
void glBindRenderbuffer(GLenum target, GLuint renderbuffer);
Creates a renderbuffer and associates it with the name renderbuffer.target
must be GL_RENDERBUFFER. renderbuffer must either be zero, which
removes any renderbuffer binding, or a name that was generated by a call
to glGenRenderbuffers(); otherwise, a GL_INVALID_OPERATION error
will be generated.
void glRenderbufferStorage(GLenum target, GLenum internalformat,
GLsizei width, GLsizei height);
void glRenderbufferStorageMultisample(GLenum target,
GLsizei samples, GLenum internalformat, GLsizei width,
GLsizei height);

Framebuffer Objects 531
Allocates storage for image data for the bound renderbuffer. target must be
GL_RENDERBUFFER. For a color-renderable buffer, internalformat must be
one of: GL_RED, GL_R8, GL_R16, GL_RG, GL_RG8, GL_RG16, GL_RGB,
GL_R3_G3_B2, GL_RGB4, GL_RGB5, GL_RGB8, GL_RGB10, GL_RGB12,
GL_RGB16, GL_RGBA, GL_RGBA2, GL_RGBA4, GL_RGB5_A1, GL_RGBA8,
GL_RGB10_A2, GL_RGBA12, GL_RGBA16, GL_SRGB, GL_SRGB8,
GL_SRGB_ALPHA, GL_SRGB8_ALPHA8,GL_R16F, GL_R32F, GL_RG16F,
GL_RG32F, GL_RGB16F, GL_RGB32F, GL_RGBA16F, GL_RGBA32F,
GL_R11F_G11F_B10F, GL_RGB9_E5, GL_R8I, GL_R8UI, GL_R16I,
GL_R16UI, GL_R32I, GL_R32UI, GL_RG8I, GL_RG8UI, GL_RG16I,
GL_RG16UI, GL_RG32I, GL_RG32UI, GL_RGB8I, GL_RGB8UI,
GL_RGB16I, GL_RGB16UI, GL_RGB32I, GL_RGB32UI, GL_RGBA8I,
GL_RGBA8UI, GL_RGBA16I, GL_RGBA16UI, GL_RGBA32I. OpenGL
version 3.1 adds the additional following formats: GL_R8_SNORM,
GL_R16_SNORM, GL_RG8_SNORM, GL_RG16_SNORM, GL_RGB8_
SNORM, GL_RGB16_SNORM, GL_RGBA8_SNORM, GL_RGBA16_SNORM.
To use a renderbuffer as a depth buffer, it must be depth-renderable, which
is specified by setting internalformat to either GL_DEPTH_COMPONENT,
GL_DEPTH_COMPONENT16, GL_DEPTH_COMPONENT32, GL_DEPTH_
COMPONENT32, or GL_DEPTH_COMPONENT32F.
For use exclusively as a stencil buffer, internalformat should be specified
as either GL_STENCIL_INDEX, GL_STENCIL_INDEX1, GL_STENCIL_
INDEX4, GL_STENCIL_INDEX8, or GL_STENCIL_INDEX16.
For packed depth-stencil storage, internalformat must be GL_DEPTH_
STENCIL, which allows the renderbuffer to be attached as the depth
buffer, stencil buffer, or at the combined depth-stencil attachment point.
width and height specify the size of the renderbuffer in pixels, and samples
specifies the number of multisample samples per pixel. Setting samples to
zero in a call to glRenderbufferStorageMultisample() is identical to
calling glRenderbufferStorage().
A GL_INVALID_VALUE is generated if width or height is greater than the
value returned when querying GL_MAX_RENDERBUFFER_SIZE, or if
samples is greater than the value returned when querying GL_MAX_
SAMPLES. A GL_INVALID_OPERATION is generated if internalformat is a
signed- or unsigned-integer format (e.g., a format containing a “I”, or “UI”
in its token), and samples is not zero, and the implementation doesn’t
support multisampled integer buffers. Finally, if the renderbuffer size and
format combined exceed the available memory able to be allocated, then
a GL_OUT_OF_MEMORY error is generated.

532 Chapter 10: The Framebuffer
Example 10-6 Creating an RGBA Color Renderbuffer: fbo.c
glGenRenderbuffers( 1, &color );
glBindRenderbuffer( GL_RENDERBUFFER, color );
glRenderbufferStorage( GL_RENDERBUFFER, GL_RGBA, 256, 256 );
Once you have created storage for your renderbuffer, you need to attach it
to a framebuffer object before you can render into it.
Framebuffer Attachments
When you render, you can send the results of that rendering to a number
of places:
• The color buffer to create an image, or even multiple color buffers if
you’re using multiple render targets (see “Special Output Values” in
Chapter 15)
• The depth buffer to store occlusion information
• The stencil buffer for storing per-pixel masks to control rendering
Each of those buffers represents a framebuffer attachment, to which you
can attach suitable image buffers that you later render into, or read from.
The possible framebuffer attachment points are listed in Table 10-6.
Currently, there are two types of rendering surfaces you can associate with
one of those attachments: renderbuffers and a level of a texture image.
Attachment Name Description
GL_COLOR_ATTACHMENTiThe ith color buffer. i can range from
zero (the default color buffer) to
GL_MAX_COLOR_ATTACHMENTS–1
GL_DEPTH_ATTACHMENT The depth buffer
GL_STENCIL_ATTACHMENT The stencil buffer
GL_DEPTH_STENCIL_ATTACHMENT A special attachment for packed depth-
stencil buffers (which require the
renderbuffer to have been allocated as a
GL_DEPTH_STENCIL pixel format)
Table 10-6 Framebuffer Attachments

Framebuffer Objects 533
We’ll first discuss attaching a renderbuffer to a framebuffer object, which is
done by calling glFramebufferRenderbuffer().
In Example 10-7, we create and attach two renderbuffers: one for color, and
the other for depth. We then proceed to render, and finally copy the results
back to the window-system-provided framebuffer to display the results. You
might use this technique to generate frames for a movie rendering off-
screen, where you don’t have to worry about the visible framebuffer being
corrupted by overlapping windows or someone resizing the window and
interrupting rendering.
One important point to remember is that you might need to reset the
viewport for each framebuffer before rendering, particularly if the size of
your application-defined framebuffers differs from the window-system
provided framebuffer.
Example 10-7 Attaching a Renderbuffer for Rendering: fbo.c
enum { Color, Depth, NumRenderbuffers };
GLuint framebuffer, renderbuffer[NumRenderbuffers]
void
init()
{
glGenRenderbuffers( NumRenderbuffers, renderbuffer );
glBindRenderbuffer( GL_RENDERBUFFER, renderbuffer[Color] );
glRenderbufferStorage( GL_RENDERBUFFER, GL_RGBA, 256, 256 );
void glFramebufferRenderbuffer(GLenum target, GLenum attachment,
GLenum renderbuffertarget, GLuint renderbuffer);
Attaches renderbuffer to attachment of the currently bound framebuffer
object. target must either be GL_READ_FRAMEBUFFER, GL_DRAW_
FRAMEBUFFER, or GL_FRAMEBUFFER (which is equivalent to GL_DRAW_
FRAMEBUFFER).
attachment is one of GL_COLOR_ATTACHMENTi, GL_DEPTH_
ATTACHMENT, GL_STENCIL_ATTACHMENT, or GL_DEPTH_STENCIL_
ATTACHMENT.
renderbuffertarget must be GL_RENDERBUFFER, and renderbuffer must
either be zero, which removes any renderbuffer attachment at attachment,
or a renderbuffer name returned from glGenRenderbuffers(), or a GL_
INVALID_OPERATION error is generated.

534 Chapter 10: The Framebuffer
glBindRenderbuffer( GL_RENDERBUFFER, renderbuffer[Depth] );
glRenderbufferStorage( GL_RENDERBUFFER, GL_DEPTH_COMPONENT24,
256, 256 );
glGenFramebuffers( 1, &framebuffer );
glBindFramebuffer( GL_DRAW_FRAMEBUFFER, framebuffer );
glFramebufferRenderbuffer( GL_DRAW_FRAMEBUFFER,
GL_COLOR_ATTACHMENT0, GL_RENDERBUFFER,
renderbuffer[Color] );
glFramebufferRenderbuffer( GL_DRAW_FRAMEBUFFER,
GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER,
renderbuffer[Depth] );
glEnable( GL_DEPTH_TEST );
}
void
display()
{
/* Prepare to render into the renderbuffer */
glBindFramebuffer( GL_DRAW_FRAMEBUFFER, framebuffer );
glViewport( 0, 0, 256, 256 );
/* Render into renderbuffer */
glClearColor( 1.0, 0.0, 0.0, 1.0 );
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
/* Do other rendering */
/* Set up to read from the renderbuffer and draw to
** window-system framebuffer */
glBindFramebuffer( GL_READ_FRAMEBUFFER, framebuffer );
glBindFramebuffer( GL_DRAW_FRAMEBUFFER, 0 );
glViewport(0, 0, windowWidth, windowHeight);
glClearColor( 0.0, 0.0, 1.0, 1.0 );
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
/* Do the copy */
glBlitFramebuffer( 0, 0, 255, 255, 0, 0, 255, 255,
GL_COLOR_BUFFER_BIT, GL_NEAREST );
glutSwapBuffers();
}

Framebuffer Objects 535
Another very common use for framebuffer objects is to update textures
dynamically. You might do this to indicate changes in a surface’s
appearance (such as bullet holes in a wall in a game) or to update values in
a lookup table if you’re doing GPGPU-like computations. In these cases, you
bind a level of a texture map as the framebuffer attachment, as compared to
a renderbuffer. After rendering, the texture map can be detached from the
framebuffer so that it can be used in subsequent rendering.
Note: Nothing prevents you from reading from a texture that is
simultaneously bound as a framebuffer attachment for writing. In
this scenario, called a framebuffer rendering loop, the results are
undefined for both operations. That is, the values returned from
sampling the bound texture map, as well as the values written into
the texture level while bound, will likely be incorrect.
void glFramebufferTexture1D(GLenum target, GLenum attachment,
GLenum texturetarget, GLuint texture, GLint level);
void glFramebufferTexture2D(GLenum target, GLenum attachment,
GLenum texturetarget, GLuint texture, GLint level);
void glFramebufferTexture3D(GLenum target, GLenum attachment,
GLenum texturetarget, GLuint texture, GLint level,
GLint layer);
Attaches a level of a texture objects as a rendering attachment to a
framebuffer object. target must be either GL_READ_FRAMEBUFFER,
GL_DRAW_FRAMEBUFFER, or GL_FRAMEBUFFER (which is equivalent to
GL_DRAW_FRAMEBUFFER). attachment must be one of the framebuffer
attachment points: GL_COLOR_ATTACHMENTi, GL_DEPTH_
ATTACHMENT, GL_STENCIL_ATTACHMENT, or GL_DEPTH_STENCIL_
ATTACHMENT (in which case, the internal format of the texture must be
GL_DEPTH_STENCIL).
For glFramebufferTexture1D(),texturetarget must be GL_TEXTURE_1D,
if texture is not zero. For glFramebufferTexture2D(),texturetarget must
be GL_TEXTURE_2D, GL_TEXTURE_RECTANGLE, GL_TEXTURE_CUBE_
MAP_POSITIVE_X, GL_TEXTURE_CUBE_MAP_POSITIVE_Y, GL_
TEXTURE_CUBE_MAP_POSITIVE_Z, GL_TEXTURE_CUBE_MAP_
NEGATIVE_X, GL_TEXTURE_CUBE_MAP_NEGATIVE_Y, GL_TEXTURE_
CUBE_MAP_NEGATIVE_Z, and for glFramebufferTexture3D()
texturetarget must be GL_TEXTURE_3D.

536 Chapter 10: The Framebuffer
Similar to the previous example, Example 10-8 demonstrates the process
of dynamically updating a texture, using the texture after its update is
completed, and then rendering with it later.
Example 10-8 Attaching a Texture Level as a Framebuffer Attachment: fbotexture.c
GLuint framebuffer, texture;
void
init()
{
GLuint renderbuffer;
/* Create an empty texture */
glGenTextures( 1, &texture );
glBindTexture( GL_TEXTURE_2D, texture );
glTexImage2D( GL_TEXTURE_2D, 0, GL_RGBA8, TexWidth,
TexHeight, 0, GL_RGBA, GL_UNSIGNED_BYTE, NULL );
/* Create a depth buffer for our framebuffer */
glGenRenderbuffers( 1, &renderbuffer );
glBindRenderbuffer( GL_RENDERBUFFER, renderbuffer );
If texture is zero, indicating that any texture bound to attachment is
released, and no subsequent bind to attachment is made. In this case,
texturetarget,level, and layer are ignored.
If texture is not zero, it must be the name of an existing texture object
(created with glGenTextures()), with texturetarget matching the texture
type (e.g., GL_TEXTURE_1D, etc.) associated with the texture object, or if
texture is a cube map, then texturetarget must be one of the cube map face
targets: GL_TEXTURE_CUBE_MAP_POSITIVE_X, GL_TEXTURE_CUBE_
MAP_POSITIVE_Y, GL_TEXTURE_CUBE_MAP_POSITIVE_Z, GL_
TEXTURE_CUBE_MAP_NEGATIVE_X, GL_TEXTURE_CUBE_MAP_
NEGATIVE_Y, GL_TEXTURE_CUBE_MAP_NEGATIVE_Z, otherwise, a GL_
INVALID_OPERATION error is generated.
level represents the mipmap level of the associated texture image to be
attached as a render target, and for three-dimensional textures, layer
represents the layer of the texture to be used. If texturetarget is GL_
TEXTURE_RECTANGLE (from OpenGL version 3.1), then level must
be zero.

Framebuffer Objects 537
glRenderbufferStorage( GL_RENDERBUFFER, GL_DEPTH_COMPONENT24,
TexWidth, TexHeight );
/* Attach the texture and depth buffer to the framebuffer */
glGenFramebuffers( 1, &framebuffer );
glBindFramebuffer( GL_DRAW_FRAMEBUFFER, framebuffer );
glFramebufferTexture2D( GL_DRAW_FRAMEBUFFER,
GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, texture, 0 );
glFramebufferRenderbuffer( GL_DRAW_FRAMEBUFFER,
GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, renderbuffer );
glEnable( GL_DEPTH_TEST );
}
void
display()
{
/* Render into the renderbuffer */
glBindFramebuffer( GL_DRAW_FRAMEBUFFER, framebuffer );
glViewport( 0, 0, TexWidth, TexHeight );
glClearColor( 1.0, 0.0, 1.0, 1.0 );
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
/* Do other rendering */
/* Generate mipmaps of our texture */
glGenerateMipmap( GL_TEXTURE_2D );
/* Bind to the window-system framebuffer, unbinding from
** the texture, which we can use to texture other objects */
glBindFramebuffer( GL_FRAMEBUFFER, 0 );
glViewport( 0, 0, windowWidth, windowHeight );
glClearColor( 0.0, 0.0, 1.0, 1.0 );
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
/* Render using the texture */
glEnable( GL_TEXTURE_2D );
...
glutSwapBuffers();
}

538 Chapter 10: The Framebuffer
Framebuffer Completeness
Given the myriad of combinations between texture and buffer formats,
and between framebuffer attachments, various situations can arise that
prevent the completion of rendering when you are using application-
defined framebuffer objects. After modifying the attachments to a
framebuffer object, it’s best to check the framebuffer’s status by calling
glCheckFramebufferStatus().
The errors representing the various violations of framebuffer configurations
are listed in Table 10-7.
Of the listed errors, GL_FRAMEBUFFER_UNSUPPORTED is very
implementation dependent, and may be the most complicated to debug.
void glFramebufferTextureLayer(GLenum target, GLenum attachment,
GLuint texture, GLint level, GLint layer);
Attaches a layer of a three-dimensional texture, or a one- or two-
dimensional array texture as a framebuffer attachment, in a similar
manner to glFramebufferTexture3D().
target must be one of GL_READ_FRAMEBUFFER, GL_DRAW_
FRAMEBUFFER, or GL_FRAMEBUFFER (which is equivalent to GL_DRAW_
FRAMEBUFFER). attachment must be one of GL_COLOR_ATTACHMENTi,
GL_DEPTH_ATTACHMENT, GL_STENCIL_ATTACHMENT, or GL_DEPTH_
STENCIL_ATTACHMENT.
texture must be either zero, indicating that the current binding for the
attachment should be released, or a texture object name (as returned from
glGenTextures()). level indicates the mipmap level of the texture object,
and layer represents which layer of the texture (or array element) should
be bound as an attachment.
GLenum glCheckFramebufferStatus(GLenum target);
Returns one of the framebuffer completeness status enums listed in
Table 10-7. target must be one of GL_READ_FRAMEBUFFER, GL_DRAW_
FRAMEBUFFER, or GL_FRAMEBUFFER (which is equivalent to GL_DRAW_
FRAMEBUFFER).
If glCheckFramebufferStatus() generates an error, zero is returned.

Framebuffer Objects 539
Copying Pixel Rectangles
While glCopyPixels() has been the default routine for replicating blocks of
pixels since OpenGL Version 1.0, as OpenGL expanded its rendering facilities,
a more substantial pixel-copying routine was required. glBlitFramebuffer(),
described below, subsumes the operations of glCopyPixels() and
glPixelZoom() in a single, enhanced call. glBlitFramebuffer() allows greater
pixel filtering during the copy operation, much in the same manner as
texture mapping (in fact, the same filtering operations, GL_NEAREST and
GL_LINEAR are used during the copy). Additionally, this routine is aware of
multisampled buffers, and supports copying between different framebuffers
(as controlled by framebuffer objects).
Framebuffer Completeness
Status Enum Description
GL_FRAMEBUFFER_COMPLETE The framebuffer and its attachments match the
rendering or reading state required.
GL_FRAMEBUFFER_UNDEFINED The bound framebuffer is specified to be the
default framebuffer (i.e., glBindFramebuffer()
with zero specified as the framebuffer), and the
default framebuffer doesn’t exist.
GL_FRAMEBUFFER_
INCOMPLETE_ATTACHMENT
A necessary attachment to the bound
framebuffer is uninitialized
GL_FRAMEBUFFER_
INCOMPLETE_MISSING_
ATTACHMENT
There are no images (e.g., texture layers or
renderbuffers) attached to the framebuffer.
GL_FRAMEBUFFER_
INCOMPLETE_DRAW_BUFFER
Every drawing buffer (e.g., GL_DRAW_BUFFERi
as specified by glDrawBuffers()) has an
attachment.
GL_FRAMEBUFFER_
INCOMPLETE_READ_BUFFER
An attachment exists for the buffer specified
for the buffer specified by glReadBuffer().
GL_FRAMEBUFFER_
UNSUPPORTED
The combination of images attached to the
framebuffer object is incompatible with the
requirements of the OpenGL implementation.
GL_FRAMEBUFFER_
INCOMPLETE_MULTISAMPLE
The number of samples for all images across
the framebuffer’s attachments do not match.
Table 10-7 Errors returned by glCheckFramebufferStatus()

540 Chapter 10: The Framebuffer
void glBlitFramebuffer(GLint srcX0, GLint srcY0,
GLint srcX1, GLint srcY1, GLint dstX0, GLint dstY0,
GLint dstX1, GLint dstY1, GLbitfield buffers,
GLenum filter);
Copies a rectangle of pixel values from one region of the read framebuffer
to another region of the draw framebuffer, potentially resizing, reversing,
converting, and filtering the pixels in the process. srcX0,srcY0,srcX1,
srcY1 represent the source region where pixels are sourced from, and
written to the rectangular region specified by dstX0,dstY0,dstX1,dstY1.
buffers is the bitwise-or of GL_COLOR_BUFFER_BIT, GL_DEPTH_BUFFER_
BIT, and GL_STENCIL_BUFFER_BIT, which represent the buffers in which
the copy should occur. Finally, filter specifies the method of interpolation
done if the two rectangular regions are different sizes, and must be one of
GL_NEAREST or GL_LINEAR; no filtering is applied if the regions are the
same size.
If there are multiple color draw buffers (See “Rendering to Multiple Output
Buffers” on page 729), each buffer receives a copy of the source region.
If srcX1 < srcX0, or dstX1 < dstX0, the image is reversed in the horizontal
direction. Likewise, if srcY1 < srcY0 or dstY1 < dstY0, the image is reverse
in the vertical direction. However, If both the source and destination sizes
are negative in the same direction, no reversal is done.
If the source and destination buffers are of different formats, conversion of
the pixel values is done in most situations. However, if the read color buffer
is a floating-point format, and any of the write color buffers are not, or vice
verse; and if the read color buffer is a signed (unsigned) integer format and
not all of the draw buffers are signed (unsigned) integer values, the call will
generate a GL_INVALID_OPERATION, and no pixels will be copied.
Multisampled buffers also have an effect on the copying of pixels. If the
source buffer is multisampled, and the destination is not, the samples are
resolved to a single pixel value for the destination buffer. Conversely, if
the source buffer is not multisampled, and the destination is, the source
pixel’s data is replicated for each sample. Finally, if both buffers are
multisampled and the number of samples for each buffer is the same, the
samples are copied without modification. However, if the buffers have a
different number of samples, no pixels are copied, and a GL_INVALID_
OPERATION error is generated.
A GL_INVALID_VALUE error is generated if buffers has other bits set than
those permitted, or if filter is other than GL_LINEAR or GL_NEAREST.

541
Chapter 11
11.Tessellators and Quadrics
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Render concave filled polygons by first tessellating them into convex
polygons, which can be rendered using standard OpenGL routines
• Use the OpenGL Utility Library to create quadrics objects to render and
model the surfaces of spheres and cylinders, and to tessellate disks
(circles) and partial disks (arcs)
Note: In OpenGL Version 3.1, some of the techniques and functions
described in this chapter—particularly those relating to quadric
objects—were likely affected by deprecation. While many of these
features can be found in the GLU library, they rely on OpenGL
functions that were removed.

542 Chapter 11: Tessellators and Quadrics
The OpenGL Library (GL) is designed for low-level operations, both stream-
lined and accessible to hardware acceleration. The OpenGL Utility Library
(GLU) complements the OpenGL library, supporting higher-level operations.
Some of the GLU operations are covered in other chapters. Mipmapping
(gluBuild*DMipmaps()) and image scaling (gluScaleImage()) are discussed
along with other facets of texture mapping in Chapter 9. Several matrix trans-
formation GLU routines (gluOrtho2D(),gluPerspective(),gluLookAt(),
gluProject(),gluUnProject(), and gluUnProject4()) are described in
Chapter 3. The use of gluPickMatrix() is explained in Chapter 13. The
GLU NURBS facilities, which are built atop OpenGL evaluators, are covered
in Chapter 12. Only two GLU topics remain: polygon tessellators and quad-
ric surfaces; these topics are discussed in this chapter.
To optimize performance, the basic OpenGL renders only convex polygons,
but the GLU contains routines for tessellating concave polygons into con-
vex ones, which the basic OpenGL can handle. Where the basic OpenGL
operates on simple primitives, such as points, lines, and filled polygons, the
GLU can create higher-level objects, such as the surfaces of spheres, cylin-
ders, and cones.
This chapter has the following major sections.
• “Polygon Tessellation” explains how to tessellate concave polygons
into easier-to-render convex polygons.
• “Quadrics: Rendering Spheres, Cylinders, and Disks” describes how to
generate spheres, cylinders, circles and arcs, including data such as
surface normals and texture coordinates.
Polygon Tessellation
As discussed in “Describing Points, Lines, and Polygons” in Chapter 2,
OpenGL can directly display only simple convex polygons. A polygon is
simple if the edges intersect only at vertices, there are no duplicate vertices,
and exactly two edges meet at any vertex. If your application requires the
display of concave polygons, polygons containing holes, or polygons with
intersecting edges, these polygons must first be subdivided into simple
convex polygons before they can be displayed. Such subdivision is called
tessellation, and the GLU provides a collection of routines that perform
tessellation. These routines take as input arbitrary contours, which describe
hard-to-render polygons, and they return some combination of triangles,
triangle meshes, triangle fans, and lines.
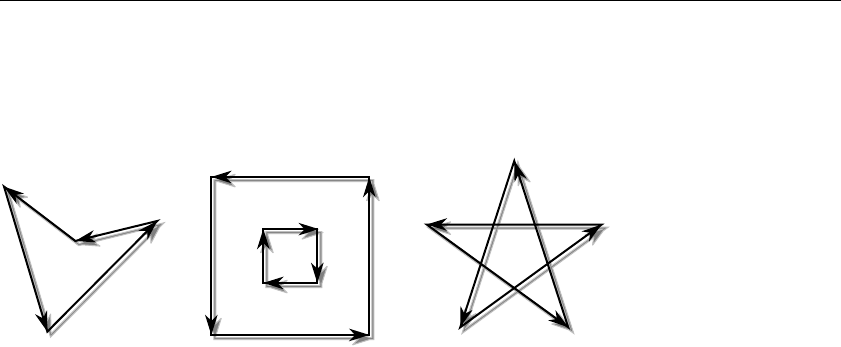
Polygon Tessellation 543
Figure 11-1 shows some contours of polygons that require tessellation:
from left to right, a concave polygon, a polygon with a hole, and a self-
intersecting polygon.
If you think a polygon may need tessellation, follow these typical steps:
1. Create a new tessellation object with gluNewTess().
2. Use gluTessCallback() several times to register callback functions
to perform operations during the tessellation. The trickiest case
for a callback function is when the tessellation algorithm detects an
intersection and must call the function registered for the GLU_TESS_
COMBINE callback.
3. Specify tessellation properties by calling gluTessProperty(). The most
important property is the winding rule, which determines the regions
that should be filled and those that should remain unshaded.
4. Create and render tessellated polygons by specifying the contours
of one or more closed polygons. If the data for the object is static,
encapsulate the tessellated polygons in a display list. (If you don’t have
to recalculate the tessellation repeatedly, using display lists is more
efficient.)
5. If you need to tessellate something else, you may reuse your
tessellation object. If you are forever finished with your tessellation
object, you may delete it with gluDeleteTess().
Note: The tessellator described here was introduced in Version 1.2 of the
GLU. If you are using an older version of the GLU, you must use
routines described in “Describing GLU Errors” on page 557. To query
which version of GLU you have, use gluGetString(GLU_VERSION),
Figure 11-1 Contours That Require Tessellation

544 Chapter 11: Tessellators and Quadrics
which returns a string with your GLU version number. If you don’t
seem to have gluGetString() in your GLU, then you have GLU 1.0,
which did not yet have the gluGetString() routine.
Creating a Tessellation Object
As a complex polygon is being described and tessellated, it has associated
data, such as the vertices, edges, and callback functions. All this data is tied
to a single tessellation object. To perform tessellation, your program first
has to create a tessellation object using the routine gluNewTess().
A single tessellation object can be reused for all your tessellations. This
object is required only because library routines might need to do their own
tessellations, and they should be able to do so without interfering with
any tessellation that your program is doing. It might also be useful to have
multiple tessellation objects if you want to use different sets of callbacks
for different tessellations. A typical program, however, allocates a single
tessellation object and uses it for all its tessellations. There’s no real need to
free it, because it uses a small amount of memory. On the other hand, it
never hurts to be tidy.
Tessellation Callback Routines
After you create a tessellation object, you must provide a series of callback
routines to be called at appropriate times during the tessellation. After
specifying the callbacks, you describe the contours of one or more polygons
using GLU routines. When the description of the contours is complete, the
tessellation facility invokes your callback routines as necessary.
Any functions that are omitted are simply not called during the tessellation,
and any information they might have returned to your program is lost. All
are specified by the single routine gluTessCallback().
GLUtesselator* gluNewTess(void);
Creates a new tessellation object and returns a pointer to it. A null pointer
is returned if the creation fails.

Polygon Tessellation 545
void gluTessCallback(GLUtesselator *tessobj, GLenum type, void (*fn)());
Associates the callback function fn with the tessellation object tessobj. The
type of the callback is determined by the parameter type, which can be
GLU_TESS_BEGIN, GLU_TESS_BEGIN_DATA, GLU_TESS_EDGE_FLAG,
GLU_TESS_EDGE_FLAG_DATA, GLU_TESS_VERTEX, GLU_TESS_VERTEX_
DATA, GLU_TESS_END, GLU_TESS_END_DATA, GLU_TESS_COMBINE,
GLU_TESS_COMBINE_DATA, GLU_TESS_ERROR, or GLU_TESS_ERROR_
DATA. The 12 possible callback functions have the following prototypes:
GLU_TESS_BEGIN void begin(GLenum type);
GLU_TESS_BEGIN_DATA void begin(GLenum type,
void *user_data);
GLU_TESS_EDGE_FLAG void edgeFlag(GLboolean flag);
GLU_TESS_EDGE_FLAG_DATA void edgeFlag(GLboolean flag,
void *user_data);
GLU_TESS_VERTEX void vertex(void *vertex_data);
GLU_TESS_VERTEX_DATA void vertex(void *vertex_data,
void *user_data);
GLU_TESS_END void end(void);
GLU_TESS_END_DATA void end(void *user_data);
GLU_TESS_COMBINE void combine(
GLdouble coords[3],
void *vertex_data[4],
GLfloat weight[4],
void **outData);
GLU_TESS_COMBINE_DATA void combine(
GLdouble coords[3],
void *vertex_data[4],
GLfloat weight[4],
void **outData,
void *user_data);
GLU_TESS_ERROR void error(GLenum errno);
GLU_TESS_ERROR_DATA void error(GLenum errno,
void *user_data);

546 Chapter 11: Tessellators and Quadrics
To change a callback routine, simply call gluTessCallback() with the new
routine. To eliminate a callback routine without replacing it with a new one,
pass gluTessCallback() a null pointer for the appropriate function.
As tessellation proceeds, the callback routines are called in a manner
similar to how you use the OpenGL commands glBegin(),glEdgeFlag*(),
glVertex*(), and glEnd(). (See “Marking Polygon Boundary Edges” in
Chapter 2 for more information about glEdgeFlag*().) The combine call-
back is used to create new vertices where edges intersect. The error callback
is invoked during the tessellation only if something goes wrong.
For every tessellator object created, a GLU_TESS_BEGIN callback is invoked
with one of four possible parameters: GL_TRIANGLE_FAN, GL_TRIANGLE_
STRIP, GL_TRIANGLES, or GL_LINE_LOOP. When the tessellator decom-
poses the polygons, the tessellation algorithm decides which type of trian-
gle primitive is most efficient to use. (If the GLU_TESS_BOUNDARY_ONLY
property is enabled, then GL_LINE_LOOP is used for rendering.)
Since edge flags make no sense in a triangle fan or triangle strip, if there is
a callback associated with GLU_TESS_EDGE_FLAG that enables edge flags,
the GLU_TESS_BEGIN callback is called only with GL_TRIANGLES. The
GLU_TESS_EDGE_FLAG callback works exactly analogously to the OpenGL
glEdgeFlag*() call.
After the GLU_TESS_BEGIN callback routine is called and before the call-
back associated with GLU_TESS_END is called, some combination of the
GLU_TESS_EDGE_FLAG and GLU_TESS_VERTEX callbacks is invoked (usually
by calls to gluTessVertex(), which is described on page 555). The associated
edge flags and vertices are interpreted exactly as they are in OpenGL
between glBegin() and the matching glEnd().
If something goes wrong, the error callback is passed a GLU error number.
A character string describing the error is obtained using the routine
gluErrorString(). (See “Describing GLU Errors” on page 557 for more
information about this routine.)
Example 11-1 shows a portion of tess.c, in which a tessellation object is
created and several callbacks are registered.
Example 11-1 Registering Tessellation Callbacks: tess.c
#ifndef CALLBACK
#define CALLBACK
#endif

Polygon Tessellation 547
/* a portion of init() */
tobj = gluNewTess();
gluTessCallback(tobj, GLU_TESS_VERTEX, glVertex3dv);
gluTessCallback(tobj, GLU_TESS_BEGIN, beginCallback);
gluTessCallback(tobj, GLU_TESS_END, endCallback);
gluTessCallback(tobj, GLU_TESS_ERROR, errorCallback);
/* the callback routines registered by gluTessCallback() */
void CALLBACK beginCallback(GLenum which)
{
glBegin(which);
}
void CALLBACK endCallback(void)
{
glEnd();
}
void CALLBACK errorCallback(GLenum errorCode)
{
const GLubyte *estring;
estring = gluErrorString(errorCode);
fprintf(stderr, "Tessellation Error: %s\n", estring);
exit(0);
}
Note: Type casting of callback functions is tricky, especially if you wish to
make code that runs equally well on Microsoft Windows and UNIX.
To run on Microsoft Windows, programs that declare callback func-
tions, such as tess.c, need the symbol CALLBACK in the declarations
of functions. The trick of using an empty definition for CALLBACK
(as demonstrated below) allows the code to run well on both
Microsoft Windows and UNIX:
#ifndef CALLBACK
#define CALLBACK
#endif
void CALLBACK callbackFunction(...) {
....
}
In Example 11-1, the registered GLU_TESS_VERTEX callback is simply
glVertex3dv(), and only the coordinates at each vertex are passed along.
However, if you want to specify more information at every vertex, such as

548 Chapter 11: Tessellators and Quadrics
a color value, a surface normal vector, or a texture coordinate, you’ll have
to make a more complex callback routine. Example 11-2 shows the start of
another tessellated object, further along in program tess.c. The registered
function vertexCallback() expects to receive a parameter that is a pointer
to six double-length floating-point values: the x-,y-, and z-coordinates and
the red, green, and blue color values for that vertex.
Example 11-2 Vertex and Combine Callbacks: tess.c
/* a different portion of init() */
gluTessCallback(tobj, GLU_TESS_VERTEX, vertexCallback);
gluTessCallback(tobj, GLU_TESS_BEGIN, beginCallback);
gluTessCallback(tobj, GLU_TESS_END, endCallback);
gluTessCallback(tobj, GLU_TESS_ERROR, errorCallback);
gluTessCallback(tobj, GLU_TESS_COMBINE, combineCallback);
/* new callback routines registered by these calls */
void CALLBACK vertexCallback(GLvoid *vertex)
{
const GLdouble *pointer;
pointer = (GLdouble *) vertex;
glColor3dv(pointer+3);
glVertex3dv(vertex);
}
void CALLBACK combineCallback(GLdouble coords[3],
GLdouble *vertex_data[4],
GLfloat weight[4], GLdouble **dataOut )
{
GLdouble *vertex;
int i;
vertex = (GLdouble *) malloc(6 * sizeof(GLdouble));
vertex[0] = coords[0];
vertex[1] = coords[1];
vertex[2] = coords[2];
for (i = 3; i < 6; i++)
vertex[i] = weight[0] * vertex_data[0][i]
+ weight[1] * vertex_data[1][i]
+ weight[2] * vertex_data[2][i]
+ weight[3] * vertex_data[3][i];
*dataOut = vertex;
}

Polygon Tessellation 549
Example 11-2 also shows the use of the GLU_TESS_COMBINE callback.
Whenever the tessellation algorithm examines the input contours, detects
an intersection, and decides it must create a new vertex, the GLU_TESS_
COMBINE callback is invoked. The callback is also called when the tessellator
decides to merge features of two vertices that are very close to one another.
The newly created vertex is a linear combination of up to four existing
vertices, referenced by vertex_data[0..3] in Example 11-2. The coefficients
of the linear combination are given by weight[0..3]; these weights sum to
1.0. coords gives the location of the new vertex.
The registered callback routine must allocate memory for another vertex, per-
form a weighted interpolation of data using vertex_data and weight, and return
the new vertex pointer as dataOut.combineCallback() in Example 11-2 inter-
polates the RGB color value. The function allocates a six-element array, puts
the x-,y-, and z-coordinates in the first three elements, and then puts the
weighted average of the RGB color values in the last three elements.
User-Specified Data
Six kinds of callbacks can be registered. Since there are two versions of each
kind of callback, there are 12 callbacks in all. For each kind of callback, there
is one with user-specified data and one without. The user-specified data is
given by the application to gluTessBeginPolygon() and is then passed,
unaltered, to each *DATA callback routine. With GLU_TESS_BEGIN_DATA,
the user-specified data may be used for “per-polygon” data. If you specify
both versions of a particular callback, the callback with user_data is used,
and the other is ignored. Therefore, although there are 12 callbacks, you can
have a maximum of six callback functions active at any one time.
For instance, Example 11-2 uses smooth shading, so vertexCallback()
specifies an RGB color for every vertex. If you want to do lighting and
smooth shading, the callback would specify a surface normal for every
vertex. However, if you want lighting and flat shading, you might specify
only one surface normal for every polygon, not for every vertex. In that
case, you might choose to use the GLU_TESS_BEGIN_DATA callback and
pass the vertex coordinates and surface normal in the user_data pointer.
Tessellation Properties
Prior to tessellation and rendering, you may use gluTessProperty() to set
several properties to affect the tessellation algorithm. The most important

550 Chapter 11: Tessellators and Quadrics
and complicated of these properties is the winding rule, which determines
what is considered “interior” and “exterior.”
Winding Numbers and Winding Rules
For a single contour, the winding number of a point is the signed number
of revolutions we make around that point while traveling once around the
contour (where a counterclockwise revolution is positive and a clockwise
revolution is negative). When there are several contours, the individual
winding numbers are summed. This procedure associates a signed integer
value with each point in the plane. Note that the winding number is the
same for all points in a single region.
void gluTessProperty(GLUtesselator *tessobj, GLenum property,
GLdouble value);
For the tessellation object tessobj, the current value of property is set to
value.property is GLU_TESS_BOUNDARY_ONLY, GLU_TESS_TOLERANCE,
or GLU_TESS_WINDING_RULE.
If property is GLU_TESS_BOUNDARY_ONLY, value is either GL_TRUE or
GL_FALSE. When it is set to GL_TRUE, polygons are no longer tessellated
into filled polygons; line loops are drawn to outline the contours that
separate the polygon interior and exterior. The default value is GL_FALSE.
(See gluTessNormal() to see how to control the winding direction of the
contours.)
If property is GLU_TESS_TOLERANCE, value is a distance used to calculate
whether two vertices are close enough together to be merged by the
GLU_TESS_COMBINE callback. The tolerance value is multiplied by
the largest coordinate magnitude of an input vertex to determine the
maximum distance any feature can move as a result of a single merge
operation. Feature merging may not be supported by your implementa-
tion, and the tolerance value is only a hint. The default tolerance value
is zero.
The GLU_TESS_WINDING_RULE property determines which parts of the
polygon are on the interior and which are on the exterior and should not
be filled. value can be GLU_TESS_WINDING_ODD (the default), GLU_
TESS_WINDING_NONZERO, GLU_TESS_WINDING_POSITIVE, GLU_
TESS_WINDING_NEGATIVE, or GLU_TESS_WINDING_ABS_GEQ_TWO.
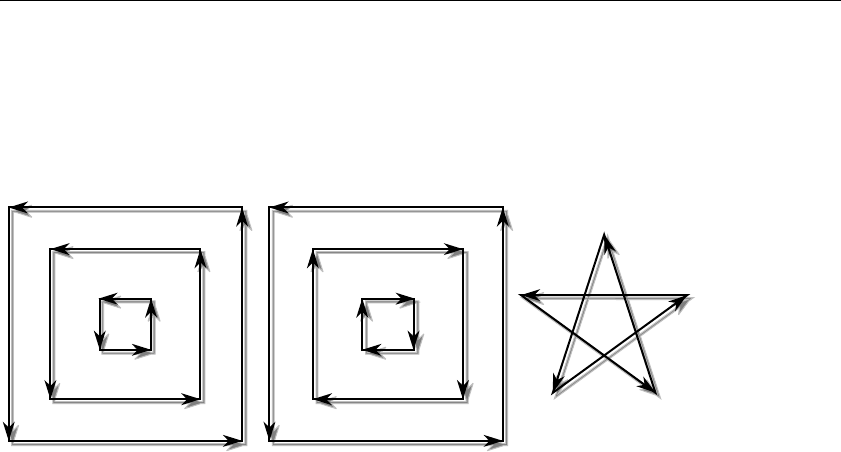
Polygon Tessellation 551
Figure 11-2 shows three sets of contours and winding numbers for points
inside those contours. In the set at the left, all three contours are counter-
clockwise, so each nested interior region adds 1 to the winding number. In
the middle set, the two interior contours are drawn clockwise, so the wind-
ing number decreases and actually becomes negative.
The winding rule classifies a region as inside if its winding number belongs
to the chosen category (odd, nonzero, positive, negative, or “absolute value
greater than or equal to 2”). The odd and nonzero rules are common ways
to define the interior. The positive, negative, and “absolute value t 2” wind-
ing rules have some limited use for polygon CSG (computational solid
geometry) operations.
The program tesswind.c demonstrates the effects of winding rules. The four
sets of contours shown in Figure 11-3 are rendered. The user can then cycle
through the different winding rule properties to see their effects. For each
winding rule, the dark areas represent interiors. Note the effects of clockwise
and counterclockwise winding.
CSG Uses for Winding Rules
GLU_TESS_WINDING_ODD and GLU_TESS_WINDING_NONZERO are the
most commonly used winding rules. They work for the most typical cases
of shading.
The winding rules are also designed for CSG operations, making it easy to
find the union, difference, or intersection (Boolean operations) of several
contours.
1
2
3
1
0
-1 11
1
11
2
Figure 11-2 Winding Numbers for Sample Contours
552 Chapter 11: Tessellators and Quadrics
First, assume that each contour is defined so that the winding number is 0
for each exterior region and 1 for each interior region. (Each contour must
not intersect itself.) Under this model, counterclockwise contours define
the outer boundary of the polygon, and clockwise contours define holes.
Contours may be nested, but a nested contour must be oriented oppositely
from the contour that contains it.
1
2
3
1
0
-1
1
2
321 4321
Contours and
Winding
Numbers
Winding Rules
Odd
Nonzero
Positive
Negative
ABS_GEQ_TWO
Unfilled
Unfilled
Unfilled Unfilled
Figure 11-3 How Winding Rules Define Interiors

Polygon Tessellation 553
If the original polygons do not satisfy this description, they can be con-
verted to this form by first running the tessellator with the GLU_TESS_
BOUNDARY_ONLY property turned on. This returns a list of contours satis-
fying the restriction just described. By creating two tessellator objects, the
callbacks from one tessellator can be fed directly as input to the other.
Given two or more polygons of the preceding form, CSG operations can be
implemented as follows:
• UNION—To calculate the union of several contours, draw all input
contours as a single polygon. The winding number of each resulting
region is the number of original polygons that cover it. The union
can be extracted by using the GLU_TESS_WINDING_NONZERO or
GLU_TESS_WINDING_POSITIVE winding rule. Note that with the
nonzero winding rule, we would get the same result if all contour
orientations were reversed.
• INTERSECTION—This works only for two contours at a time. Draw a
single polygon using two contours. Extract the result using GLU_TESS_
WINDING_ABS_GEQ_TWO.
• DIFFERENCE—Suppose you want to compute A diff (B union C union
D). Draw a single polygon consisting of the unmodified contours from
A, followed by the contours of B, C, and D, with their vertex order
reversed. To extract the result, use the GLU_TESS_WINDING_POSITIVE
winding rule. (If B, C, and D are the result of a GLU_TESS_BOUNDARY_
ONLY operation, an alternative to reversing the vertex order is to use
gluTessNormal() to reverse the sign of the supplied normal.)
Other Tessellation Property Routines
There are also complementary routines, which work alongside
gluTessProperty().gluGetTessProperty() retrieves the current values of
tessellator properties. If the tessellator is being used to generate wireframe
outlines instead of filled polygons, gluTessNormal() can be used to
determine the winding direction of the tessellated polygons.
void gluGetTessProperty(GLUtesselator *tessobj, GLenum property,
GLdouble *value);
For the tessellation object tessobj, the current value of property is returned to
value. Values for property and value are the same as for gluTessProperty().

554 Chapter 11: Tessellators and Quadrics
If you have some knowledge about the location and orientation of the input
data, then using gluTessNormal() can increase the speed of the tessellation.
For example, if you know that all polygons lie on the xy-plane, call
gluTessNormal(tessobj, 0, 0, 1).
As stated above, the default normal is (0, 0, 0), and its effect is not immedi-
ately obvious. In this case, it is expected that the input data lies approximately
in a plane, and a plane is fitted to the vertices, no matter how they are truly
connected. The sign of the normal is chosen so that the sum of the signed
areas of all input contours is non-negative (where a counterclockwise con-
tour has a positive area). Note that if the input data does not lie approxi-
mately in a plane, then projection perpendicular to the computed normal
may substantially change the geometry.
Polygon Definition
After all the tessellation properties have been set and the callback actions
have been registered, it is finally time to describe the vertices that comprise
input contours and tessellate the polygons.
Calls to gluTessBeginPolygon() and gluTessEndPolygon() surround the
definition of one or more contours. When gluTessEndPolygon() is called,
the tessellation algorithm is implemented, and the tessellated polygons are
void gluTessNormal(GLUtesselator *tessobj, GLdouble x, GLdouble y,
GLdouble z);
For the tessellation object tessobj,gluTessNormal() defines a normal vec-
tor, which controls the winding direction of generated polygons. Before
tessellation, all input data is projected into a plane perpendicular to the
normal. Then, all output triangles are oriented counterclockwise, with
respect to the normal. (Clockwise orientation can be obtained by revers-
ing the sign of the supplied normal.) The default normal is (0, 0, 0).
void gluTessBeginPolygon(GLUtesselator *tessobj, void *user_data);
void gluTessEndPolygon(GLUtesselator *tessobj);
Begins and ends the specification of a polygon to be tessellated and
associates a tessellation object, tessobj, with it. user_data points to a user-
defined data structure, which is passed along all the GLU_TESS_*_DATA
callback functions that have been bound.

Polygon Tessellation 555
generated and rendered. The callback functions and tessellation properties
that were bound and set to the tessellation object using gluTessCallback()
and gluTessProperty() are used.
In practice, a minimum of three vertices is needed for a meaningful contour.
In the program tess.c, a portion of which is shown in Example 11-3, two
polygons are defined. One polygon is a rectangular contour with a triangular
hole inside, and the other is a smooth-shaded, self-intersecting, five-pointed
star. For efficiency, both polygons are stored in display lists. The first poly-
gon consists of two contours; the outer one is wound counterclockwise,
and the “hole” is wound clockwise. For the second polygon, the star array
contains both the coordinate and color data, and its tessellation callback,
vertexCallback(), uses both.
It is important that each vertex is in a different memory location because
the vertex data is not copied by gluTessVertex(); only the pointer (vertex_
data) is saved. A program that reuses the same memory for several vertices
may not get the desired result.
Note: In gluTessVertex(), it may seem redundant to specify the vertex coor-
dinate data twice, for both the coords and vertex_data parameters;
however, both are necessary. coords refers only to the vertex coordi-
nates. vertex_data uses the coordinate data, but may also use other
information for each vertex.
void gluTessBeginContour(GLUtesselator *tessobj);
void gluTessEndContour(GLUtesselator *tessobj);
Begins and ends the specification of a closed contour, which is a portion of
a polygon. A closed contour consists of zero or more calls to gluTessVertex(),
which defines the vertices. The last vertex of each contour is
automatically linked to the first.
void gluTessVertex(GLUtesselator *tessobj, GLdouble coords[3],
void *vertex_data);
Specifies a vertex in the current contour for the tessellation object. coords
contains the three-dimensional vertex coordinates, and vertex_data is a
pointer that’s sent to the callback associated with GLU_TESS_VERTEX or
GLU_TESS_VERTEX_DATA. Typically, vertex_data contains vertex coordi-
nates, surface normals, texture coordinates, color information, or what-
ever else the application may find useful.

556 Chapter 11: Tessellators and Quadrics
Example 11-3 Polygon Definition: tess.c
GLdouble rect[4][3] = {50.0, 50.0, 0.0,
200.0, 50.0, 0.0,
200.0, 200.0, 0.0,
50.0, 200.0, 0.0};
GLdouble tri[3][3] = {75.0, 75.0, 0.0,
125.0, 175.0, 0.0,
175.0, 75.0, 0.0};
GLdouble star[5][6] = {250.0, 50.0, 0.0, 1.0, 0.0, 1.0,
325.0, 200.0, 0.0, 1.0, 1.0, 0.0,
400.0, 50.0, 0.0, 0.0, 1.0, 1.0,
250.0, 150.0, 0.0, 1.0, 0.0, 0.0,
400.0, 150.0, 0.0, 0.0, 1.0, 0.0};
startList = glGenLists(2);
tobj = gluNewTess();
gluTessCallback(tobj, GLU_TESS_VERTEX, glVertex3dv);
gluTessCallback(tobj, GLU_TESS_BEGIN, beginCallback);
gluTessCallback(tobj, GLU_TESS_END, endCallback);
gluTessCallback(tobj, GLU_TESS_ERROR, errorCallback);
glNewList(startList, GL_COMPILE);
glShadeModel(GL_FLAT);
gluTessBeginPolygon(tobj, NULL);
gluTessBeginContour(tobj);
gluTessVertex(tobj, rect[0], rect[0]);
gluTessVertex(tobj, rect[1], rect[1]);
gluTessVertex(tobj, rect[2], rect[2]);
gluTessVertex(tobj, rect[3], rect[3]);
gluTessEndContour(tobj);
gluTessBeginContour(tobj);
gluTessVertex(tobj, tri[0], tri[0]);
gluTessVertex(tobj, tri[1], tri[1]);
gluTessVertex(tobj, tri[2], tri[2]);
gluTessEndContour(tobj);
gluTessEndPolygon(tobj);
glEndList();
gluTessCallback(tobj, GLU_TESS_VERTEX, vertexCallback);
gluTessCallback(tobj, GLU_TESS_BEGIN, beginCallback);
gluTessCallback(tobj, GLU_TESS_END, endCallback);
gluTessCallback(tobj, GLU_TESS_ERROR, errorCallback);
gluTessCallback(tobj, GLU_TESS_COMBINE, combineCallback);
glNewList(startList + 1, GL_COMPILE);
glShadeModel(GL_SMOOTH);

Polygon Tessellation 557
gluTessProperty(tobj, GLU_TESS_WINDING_RULE,
GLU_TESS_WINDING_POSITIVE);
gluTessBeginPolygon(tobj, NULL);
gluTessBeginContour(tobj);
gluTessVertex(tobj, star[0], star[0]);
gluTessVertex(tobj, star[1], star[1]);
gluTessVertex(tobj, star[2], star[2]);
gluTessVertex(tobj, star[3], star[3]);
gluTessVertex(tobj, star[4], star[4]);
gluTessEndContour(tobj);
gluTessEndPolygon(tobj);
glEndList();
Deleting a Tessellation Object
If you no longer need a tessellation object, you can delete it and free all
associated memory with gluDeleteTess().
Tessellation Performance Tips
For best performance, remember these rules:
• Cache the output of the tessellator in a display list or other user
structure. To obtain the post-tessellation vertex coordinates, tessellate
the polygons while in feedback mode. (See “Feedback” in Chapter 13.)
•Use gluTessNormal() to supply the polygon normal.
• Use the same tessellator object to render many polygons, rather than
allocate a new tessellator for each one. (In a multithreaded, multi-
processor environment, you may get better performance using several
tessellators.)
Describing GLU Errors
The GLU provides a routine for obtaining a descriptive string for an error
code. This routine is not limited to tessellation but is also used for NURBS
and quadrics errors, as well as for errors in the base GL. (See “Error
void gluDeleteTess(GLUtesselator *tessobj);
Deletes the specified tessellation object, tessobj, and frees all associated
memory.
558 Chapter 11: Tessellators and Quadrics
Handling” in Chapter 14 for information about OpenGL’s error-handling
facility.)
Backward Compatibility
If you are using the 1.0 or 1.1 version of GLU, you have a much less power-
ful tessellator. The 1.0/1.1 tessellator handles only simple nonconvex poly-
gons or simple polygons containing holes. It does not properly tessellate
intersecting contours (no COMBINE callback) or process per-polygon data.
The 1.0/1.1 tessellator still works in either GLU 1.2 or 1.3, but its use is no
longer recommended.
The 1.0/1.1 tessellator has some similarities to the current tessellator.
gluNewTess() and gluDeleteTess() are used for both tessellators. The main
vertex specification routine remains gluTessVertex(). The callback mecha-
nism is controlled by gluTessCallback(), although only five callback func-
tions can be registered, a subset of the current 12.
Here are the prototypes for the 1.0/1.1 tessellator:
void gluBeginPolygon(GLUtriangulatorObj *tessobj);
void gluNextContour(GLUtriangulatorObj *tessobj, GLenum type);
void gluEndPolygon(GLUtriangulatorObj *tessobj);
The outermost contour must be specified first, and it does not require an
initial call to gluNextContour(). For polygons without holes, only one
contour is defined, and gluNextContour() is not used. If a polygon has
multiple contours (that is, holes or holes within holes), the contours
are specified one after the other, each preceded by gluNextContour().
gluTessVertex() is called for each vertex of a contour.
For gluNextContour(),type can be GLU_EXTERIOR, GLU_INTERIOR,
GLU_CCW, GLU_CW, or GLU_UNKNOWN. These serve only as hints to
the tessellation. If you get them right, the tessellation might go faster. If
you get them wrong, they’re ignored, and the tessellation still works. For
polygons with holes, one contour is the exterior contour and the other is
the interior. The first contour is assumed to be of type GLU_EXTERIOR.
Choosing clockwise or counterclockwise orientation is arbitrary in three
dimensions; however, there are two different orientations in any plane,
and the GLU_CCW and GLU_CW types should be used consistently. Use
GLU_UNKNOWN if you don’t have a clue.

Quadrics: Rendering Spheres, Cylinders, and Disks 559
It is highly recommended that you convert GLU 1.0/1.1 code to the new
tessellation interface for GLU 1.2 by following these steps:
1. Change references to the major data structure type from
GLUtriangulatorObj to GLUtesselator. In GLU 1.2, GLUtriangulatorObj
and GLUtesselator are defined to be the same type.
2. Convert gluBeginPolygon() to two commands: gluTessBeginPolygon()
and gluTessBeginContour(). All contours must be explicitly started,
including the first one.
3. Convert gluNextContour() to both gluTessEndContour() and
gluTessBeginContour(). You have to end the previous contour before
starting the next one.
4. Convert gluEndPolygon() to both gluTessEndContour() and
gluTessEndPolygon(). The final contour must be closed.
5. Change references to constants to gluTessCallback(). In GLU 1.2,
GLU_BEGIN, GLU_VERTEX, GLU_END, GLU_ERROR, and
GLU_EDGE_FLAG are defined as synonyms for GLU_TESS_BEGIN,
GLU_TESS_VERTEX, GLU_TESS_END, GLU_TESS_ERROR, and
GLU_TESS_EDGE_FLAG.
Quadrics: Rendering Spheres, Cylinders, and Disks
The base OpenGL Library provides support only for modeling and
rendering simple points, lines, and convex filled polygons. Neither 3D
objects nor commonly used 2D objects such as circles are directly available.
Throughout this book, you’ve been using GLUT to create some 3D objects.
The GLU also provides routines to model and render tessellated, polygonal
approximations for a variety of 2D and 3D shapes (spheres, cylinders, disks,
and parts of disks), which can be calculated with quadric equations. This
includes routines for drawing the quadric surfaces in a variety of styles and
orientations. Quadric surfaces are defined by the following general
quadratic equation:
a1x2 + a2y2 + a3z2 + a4xy + a5yz + a6xz + a7x + a8y + a9z + a10 = 0

560 Chapter 11: Tessellators and Quadrics
(See David Rogers’ Procedural Elements for Computer Graphics, New York, NY:
McGraw-Hill, 1985.) Creating and rendering a quadric surface is similar to
using the tessellator. To use a quadrics object, follow these steps:
1. To create a quadrics object, use gluNewQuadric().
2. Specify the rendering attributes for the quadrics object (unless you’re
satisfied with the default values).
a. Use gluQuadricOrientation() to control the winding direction
and differentiate the interior from the exterior.
b. Use gluQuadricDrawStyle() to choose between rendering the
object as points, lines, or filled polygons.
c. For lit quadrics objects, use gluQuadricNormals() to specify one
normal per vertex or one normal per face. The default specifies that
no normals are generated at all.
d. For textured quadrics objects, use gluQuadricTexture() if you want
to generate texture coordinates.
3. Prepare for problems by registering an error-handling routine with
gluQuadricCallback(). Then, if an error occurs during rendering, the
routine you’ve specified is invoked.
4. Now invoke the rendering routine for the desired type of quadrics
object: gluSphere(),gluCylinder(),gluDisk(), or gluPartialDisk(). For
best performance for static data, encapsulate the quadrics object in a
display list.
5. When you’re completely finished with it, destroy this object with
gluDeleteQuadric(). If you need to create another quadric, it’s best to
reuse your quadrics object.
Managing Quadrics Objects
A quadrics object consists of parameters, attributes, and callbacks that are
stored in a data structure of type GLUquadricObj. A quadrics object may
generate vertices, normals, texture coordinates, and other data, all of which
may be used immediately or stored in a display list for later use. The follow-
ing routines create, destroy, and report errors in a quadrics object.

Quadrics: Rendering Spheres, Cylinders, and Disks 561
For GLU_ERROR, fn is called with one parameter, which is the error code.
gluErrorString() can be used to convert the error code into an ASCII string.
Controlling Quadrics Attributes
The following routines affect the kinds of data generated by the quadrics
routines. Use these routines before you actually specify the primitives.
Example 11-4, quadric.c, on page 565, demonstrates changing the drawing
style and the kinds of normals generated as well as creation of quadrics
objects, error handling, and drawing the primitives.
GLU_POINT and GLU_LINE specify that primitives should be rendered as
a point at every vertex or a line between each pair of connected vertices.
GLUquadricObj* gluNewQuadric(void);
Creates a new quadrics object and returns a pointer to it. A null pointer is
returned if the routine fails.
void gluDeleteQuadric(GLUquadricObj *qobj);
Destroys the quadrics object qobj and frees up any memory used by it.
void gluQuadricCallback(GLUquadricObj *qobj, GLenum which,
void (*fn)());
Defines a function fn to be called in special circumstances. GLU_ERROR is
the only legal value for which, so fn is called when an error occurs. If fn is
NULL, any existing callback is erased.
void gluQuadricDrawStyle(GLUquadricObj *qobj, GLenum drawStyle);
For the quadrics object qobj,drawStyle controls the rendering style. Legal
values for drawStyle are GLU_POINT, GLU_LINE, GLU_SILHOUETTE, and
GLU_FILL.

562 Chapter 11: Tessellators and Quadrics
GLU_SILHOUETTE specifies that primitives are rendered as lines, except
that edges separating coplanar faces are not drawn. This is most often used
for gluDisk() and gluPartialDisk().
GLU_FILL specifies rendering by filled polygons, where the polygons are
drawn in a counterclockwise fashion with respect to their normals. This
may be affected by gluQuadricOrientation().
For gluSphere() and gluCylinder(), the definitions of outside and inside are
obvious. For gluDisk() and gluPartialDisk(), the positive z side of the disk
is considered to be outside.
gluQuadricNormals() is used to specify when to generate normal vectors.
GLU_NONE means that no normals are generated, and is intended for use
without lighting. GLU_FLAT generates one normal for each facet, which is
often best for lighting with flat shading. GLU_SMOOTH generates one
normal for every vertex of the quadric, which is usually best for lighting
with smooth shading.
void gluQuadricOrientation(GLUquadricObj *qobj, GLenum orientation);
For the quadrics object qobj,orientation is either GLU_OUTSIDE (the
default) or GLU_INSIDE, which controls the direction in which normals
are pointing.
void gluQuadricNormals(GLUquadricObj *qobj, GLenum normals);
For the quadrics object qobj,normals is GLU_NONE (the default),
GLU_FLAT, or GLU_SMOOTH.
void gluQuadricTexture(GLUquadricObj *qobj,
GLboolean textureCoords);
For the quadrics object qobj,textureCoords is either GL_FALSE (the default)
or GL_TRUE. If the value of textureCoords is GL_TRUE, then texture coor-
dinates are generated for the quadrics object. The manner in which the
texture coordinates are generated varies, depending on the type of quad-
rics object rendered.

Quadrics: Rendering Spheres, Cylinders, and Disks 563
Quadrics Primitives
The following routines actually generate the vertices and other data that
constitute a quadrics object. In each case, qobj refers to a quadrics object
created by gluNewQuadric().
Note: The cylinder is not closed at the top or bottom. The disks at the base
and at the top are not drawn.
void gluSphere(GLUquadricObj *qobj, GLdouble radius, GLint slices,
GLint stacks);
Draws a sphere of the given radius, centered around the origin, (0, 0, 0).
The sphere is subdivided around the z-axis into a number of slices (similar
to longitude) and along the z-axis into a number of stacks (latitude).
If texture coordinates are also generated by the quadrics facility, the
t-coordinate ranges from 0.0 at z = radius to 1.0 at z = radius, with t
increasing linearly along longitudinal lines. Meanwhile, s ranges from 0.0
at the +y axis, to 0.25 at the +x axis, to 0.5 at the y axis, to 0.75 at the
x axis, and back to 1.0 at the +y axis.
void gluCylinder(GLUquadricObj *qobj, GLdouble baseRadius,
GLdouble topRadius, GLdouble height,
GLint slices, GLint stacks);
Draws a cylinder oriented along the z-axis, with the base of the cylinder
at z = 0 and the top at z = height. Like a sphere, the cylinder is subdivided
around the z-axis into a number of slices and along the z-axis into a
number of stacks.baseRadius is the radius of the cylinder at z = 0. topRadius
is the radius of the cylinder at z = height. If topRadius is set to 0, then a
cone is generated.
If texture coordinates are generated by the quadrics facility, then the
t-coordinate ranges linearly from 0.0 at z = 0 to 1.0 at z = height. The s
texture coordinates are generated the same way as they are for a sphere.

564 Chapter 11: Tessellators and Quadrics
Note: For all quadrics objects, it’s better to use the *Radius,height, and
similar arguments to scale them, rather than the glScale*() com-
mand, so that the unit-length normals that are generated don’t have
to be renormalized. Set the rings and stacks arguments to values other
than 1 to force lighting calculations at a finer granularity, especially
if the material specularity is high.
Example 11-4 shows each of the quadrics primitives being drawn, as well as
the effects of different drawing styles.
void gluDisk(GLUquadricObj *qobj, GLdouble innerRadius,
GLdouble outerRadius, GLint slices, GLint rings);
Draws a disk on the z = 0 plane, with a radius of outerRadius and a concen-
tric circular hole with a radius of innerRadius. If innerRadius is 0, then no
hole is created. The disk is subdivided around the z-axis into a number of
slices (like slices of pizza) and also about the z-axis into a number of con-
centric rings.
With respect to orientation, the +z side of the disk is considered to be
“outside”; that is, any normals generated point along the +z axis. Other-
wise, the normals point along the z axis.
If texture coordinates are generated by the quadrics facility, then the
texture coordinates are generated linearly such that where R = outerRadius,
the values for s and t at (R, 0, 0) are (1, 0.5), at (0, R, 0) they are (0.5, 1), at
(R, 0, 0) they are (0, 0.5), and at (0, R, 0) they are (0.5, 0).
void gluPartialDisk(GLUquadricObj *qobj, GLdouble innerRadius,
GLdouble outerRadius, GLint slices, GLint rings,
GLdouble startAngle, GLdouble sweepAngle);
Draws a partial disk on the z = 0 plane. A partial disk is similar to a
complete disk, in terms of outerRadius,innerRadius,slices, and rings. The
difference is that only a portion of a partial disk is drawn, starting from
startAngle through startAngle +sweepAngle (where startAngle and sweepAngle
are measured in degrees, where 0 degrees is along the +y axis, 90 degrees
along the +x axis, 180 along the y axis, and 270 along the x axis).
A partial disk handles orientation and texture coordinates in the same way
as a complete disk.

Quadrics: Rendering Spheres, Cylinders, and Disks 565
Example 11-4 Quadrics Objects: quadric.c
#ifndef CALLBACK
#define CALLBACK
#endif
GLuint startList;
void CALLBACK errorCallback(GLenum errorCode)
{
const GLubyte *estring;
estring = gluErrorString(errorCode);
fprintf(stderr, “Quadric Error: %s\n”, estring);
exit(0);
}
void init(void)
{
GLUquadricObj *qobj;
GLfloat mat_ambient[] = { 0.5, 0.5, 0.5, 1.0 };
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat mat_shininess[] = { 50.0 };
GLfloat light_position[] = { 1.0, 1.0, 1.0, 0.0 };
GLfloat model_ambient[] = { 0.5, 0.5, 0.5, 1.0 };
glClearColor(0.0, 0.0, 0.0, 0.0);
glMaterialfv(GL_FRONT, GL_AMBIENT, mat_ambient);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, model_ambient);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_DEPTH_TEST);
/* Create 4 display lists, each with a different quadric object.
* Different drawing styles and surface normal specifications
* are demonstrated.
*/
startList = glGenLists(4);
qobj = gluNewQuadric();
gluQuadricCallback(qobj, GLU_ERROR, errorCallback);
gluQuadricDrawStyle(qobj, GLU_FILL); /* smooth shaded */

566 Chapter 11: Tessellators and Quadrics
gluQuadricNormals(qobj, GLU_SMOOTH);
glNewList(startList, GL_COMPILE);
gluSphere(qobj, 0.75, 15, 10);
glEndList();
gluQuadricDrawStyle(qobj, GLU_FILL); /* flat shaded */
gluQuadricNormals(qobj, GLU_FLAT);
glNewList(startList+1, GL_COMPILE);
gluCylinder(qobj, 0.5, 0.3, 1.0, 15, 5);
glEndList();
gluQuadricDrawStyle(qobj, GLU_LINE); /* wireframe */
gluQuadricNormals(qobj, GLU_NONE);
glNewList(startList+2, GL_COMPILE);
gluDisk(qobj, 0.25, 1.0, 20, 4);
glEndList();
gluQuadricDrawStyle(qobj, GLU_SILHOUETTE);
gluQuadricNormals(qobj, GLU_NONE);
glNewList(startList+3, GL_COMPILE);
gluPartialDisk(qobj, 0.0, 1.0, 20, 4, 0.0, 225.0);
glEndList();
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glEnable(GL_LIGHTING);
glShadeModel(GL_SMOOTH);
glTranslatef(-1.0, -1.0, 0.0);
glCallList(startList);
glShadeModel(GL_FLAT);
glTranslatef(0.0, 2.0, 0.0);
glPushMatrix();
glRotatef(300.0, 1.0, 0.0, 0.0);
glCallList(startList+1);
glPopMatrix();
glDisable(GL_LIGHTING);
glColor3f(0.0, 1.0, 1.0);
glTranslatef(2.0, -2.0, 0.0);
glCallList(startList+2);

Quadrics: Rendering Spheres, Cylinders, and Disks 567
glColor3f(1.0, 1.0, 0.0);
glTranslatef(0.0, 2.0, 0.0);
glCallList(startList+3);
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-2.5, 2.5, -2.5*(GLfloat)h/(GLfloat)w,
2.5*(GLfloat)h/(GLfloat)w, -10.0, 10.0);
else
glOrtho(-2.5*(GLfloat)w/(GLfloat)h,
2.5*(GLfloat)w/(GLfloat)h, -2.5, 2.5, -10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case 27:
exit(0);
break;
}
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutMainLoop();
return 0;
}
This page intentionally left blank

569
Chapter 12
12.Evaluators and NURBS
Chapter Objectives
Advanced
After reading this chapter, you’ll be able to do the following:
• Use OpenGL evaluator commands to draw basic curves and surfaces
• Use the GLU’s higher-level NURBS facility to draw more complex
curves and surfaces and to return data on the vertices of geometric
objects, which result from the tessellation of the curves and surfaces
Note that this chapter presumes a number of prerequisites; they’re listed in
“Prerequisites” on page 571.
Note: In OpenGL Version 3.1, all of the techniques and functions described
in this chapter were removed through deprecation. Even though
some of this functionality is part of the GLU library, it relies on
functionality that has been removed from the core OpenGL library.
Advanced

570 Chapter 12: Evaluators and NURBS
At the lowest level, graphics hardware draws points, line segments, and
polygons, which are usually triangles and quadrilaterals. Smooth curves
and surfaces are drawn by approximating them with large numbers of small
line segments or polygons. However, many useful curves and surfaces can
be described mathematically by a small number of parameters such as a few
control points. Saving the 16 control points for a surface requires much less
storage than saving 1000 triangles together with the normal vector infor-
mation at each vertex. In addition, the 1000 triangles only approximate the
true surface, but the control points accurately describe the real surface.
Evaluators provide a way to specify points on a curve or surface (or part
of one) using only the control points. The curve or surface can then be
rendered at any precision. In addition, normal vectors can be calculated for
surfaces automatically. You can use the points generated by an evaluator
in many ways—to draw dots where the surface would be; to draw a
wireframe version of the surface; or to draw a fully lighted, shaded, and
even textured version.
You can use evaluators to describe any polynomial or rational polynomial
splines or surfaces of any degree. These include almost all splines and spline
surfaces in use today, including B-splines, NURBS (Non-Uniform Rational
B-Spline) surfaces, Bézier curves and surfaces, and Hermite splines. Since
evaluators provide only a low-level description of the points on a curve or
surface, they’re typically used underneath utility libraries that provide a
higher-level interface to the programmer. The GLU’s NURBS facility is such
a higher-level interface—the NURBS routines encapsulate extensive compli-
cated code. Much of the final rendering is done with evaluators, but for
some conditions (trimming curves, for example) the NURBS routines use
planar polygons for rendering.
This chapter contains the following major sections:
• “Prerequisites” discusses what knowledge is assumed for this chapter. It
also gives several references where you can obtain this information.
• “Evaluators” explains how evaluators work and how to control them
using the appropriate OpenGL commands.
• “The GLU NURBS Interface” describes the GLU routines for creating,
rendering, and returning the tessellated vertices of NURBS curves and
surfaces.

Prerequisites 571
Prerequisites
Evaluators make splines and surfaces that are based on a Bézier (or Bernstein)
basis. The defining formulas for the functions in this basis are given in this
chapter, but the discussion doesn’t include derivations or even lists of all
their interesting mathematical properties. If you want to use evaluators to
draw curves and surfaces using other bases, you must know how to convert
your basis to a Bézier basis. In addition, when you render a Bézier surface or
part of it using evaluators, you need to determine the granularity of your
subdivision. Your decision needs to take into account the trade-off between
high-quality (highly subdivided) images and high speed. Determining an
appropriate subdivision strategy can be quite complicated—too complicated
to be discussed here.
Similarly, a complete discussion of NURBS is beyond the scope of this book.
The GLU NURBS interface is documented here, and programming examples
are provided for readers who already understand the subject. In what
follows, you already should know about NURBS control points, knot
sequences, and trimming curves.
If you lack some of these prerequisites, the following references will help:
• Farin, Gerald E., Curves and Surfaces for Computer-Aided Geometric
Design, Fourth Edition. San Diego, CA: Academic Press, 1996.
• Farin, Gerald E., NURB Curves and Surfaces: From Projective Geometry to
Practical Use. Wellesley, MA: A. K. Peters Ltd., 1995.
• Farin, Gerald E., editor, NURBS for Curve and Surface Design, Society for
Industrial and Applied Mathematics, Philadelphia, PA, 1991.
• Hoschek, Josef, and Dieter Lasser, Fundamentals of Computer Aided
Geometric Design. Wellesley, MA: A. K. Peters Ltd., 1993.
• Piegl, Les, and Wayne Tiller, The NURBS Book. New York, NY: Springer-
Verlag, 1995.
Note: Some terms used in this chapter might have slightly different
meanings in other books on spline curves and surfaces, since there
isn’t total agreement among the practitioners of this art. Generally,
the OpenGL meanings are a bit more restrictive. For example, OpenGL
evaluators always use Bézier bases; in other contexts, evaluators
might refer to the same concept, but with an arbitrary basis.

572 Chapter 12: Evaluators and NURBS
Evaluators
A Bézier curve is a vector-valued function of one variable
C(u) = [X(u)Y(u)Z(u)]
where u varies in some domain (say [0, 1]). A Bézier surface patch is a vector-
valued function of two variables
S(u,v) = [X(u,v)Y(u,v)Z(u,v)]
where u and v can both vary in some domain. The range isn’t necessarily
three-dimensional as shown here. You might want two-dimensional output
for curves on a plane or texture coordinates, or you might want four-
dimensional output to specify RGBA information. Even one-dimensional
output may make sense for gray levels.
For each u (or u and v, in the case of a surface), the formula for C() (or S())
calculates a point on the curve (or surface). To use an evaluator, first define
the function C() or S(), enable it, and then use the glEvalCoord1() or
glEvalCoord2() command instead of glVertex*(). This way, the curve or
surface vertices can be used just as any other vertices are used—to form
points or lines, for example. In addition, other commands automatically
generate a series of vertices that produce a regular mesh uniformly spaced
in u (or in u and v). One- and two-dimensional evaluators are similar, but
the description is somewhat simpler in one dimension, so that case is
discussed first.
One-Dimensional Evaluators
This subsection presents an example of using one-dimensional evaluators to
draw a curve. It then describes the commands and equations that control
evaluators.
One-Dimensional Example: A Simple Bézier Curve
The program shown in Example 12-1 draws a cubic Bézier curve using four
control points, as shown in Figure 12-1.

Evaluators 573
Example 12-1 Bézier Curve with Four Control Points: bezcurve.c
GLfloat ctrlpoints[4][3] = {
{ -4.0, -4.0, 0.0}, { -2.0, 4.0, 0.0},
{2.0, -4.0, 0.0}, {4.0, 4.0, 0.0}};
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glShadeModel(GL_FLAT);
glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
glEnable(GL_MAP1_VERTEX_3);
}
void display(void)
{
int i;
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINE_STRIP);
for (i = 0; i <= 30; i++)
glEvalCoord1f((GLfloat) i/30.0);
glEnd();
/* The following code displays the control points as dots. */
glPointSize(5.0);
glColor3f(1.0, 1.0, 0.0);
glBegin(GL_POINTS);
for (i = 0; i < 4; i++)
glVertex3fv(&ctrlpoints[i][0]);
glEnd();
glFlush();
}
Figure 12-1 Bézier Curve

574 Chapter 12: Evaluators and NURBS
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-5.0, 5.0, -5.0*(GLfloat)h/(GLfloat)w,
5.0*(GLfloat)h/(GLfloat)w, -5.0, 5.0);
else
glOrtho(-5.0*(GLfloat)w/(GLfloat)h,
5.0*(GLfloat)w/(GLfloat)h, -5.0, 5.0, -5.0, 5.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}
A cubic Bézier curve is described by four control points, which appear in this
example in the ctrlpoints[][] array. This array is one of the arguments for
glMap1f(). The other arguments for this command are:
GL_MAP1_VERTEX_3 Specifies that three-dimensional control points
are provided and that three-dimensional vertices
should be produced
0.0 Low value of parameter u
1.0 High value of parameter u
3 The number of floating-point values to advance in
the data between one control point and the next
4 The order of the spline, which is the degree plus 1: in
this case, the degree is 3 (since this is a cubic curve)
&ctrlpoints[0][0] Pointer to the first control point’s data

Evaluators 575
Note that the second and third arguments control the parameterization of
the curve—as the variable u ranges from 0.0 to 1.0, the curve goes from one
end to the other. The call to glEnable() enables the one-dimensional
evaluator for three-dimensional vertices.
The curve is drawn in the routine display() between the glBegin() and glEnd()
calls. Since the evaluator is enabled, giving the command glEvalCoord1f()
is just like issuing a glVertex() command with the coordinates of a vertex
on the curve corresponding to the input parameter u.
Defining and Evaluating a One-Dimensional Evaluator
The Bernstein polynomial of degree n (or order n+ 1) is given by
If Pi represents a set of control points (one-, two-, three-, or even four-
dimensional), then the equation
represents a Bézier curve as u varies from 0.0 to 1.0. To represent the same
curve but allowing u to vary between u1 and u2 instead of 0.0 and 1.0,
evaluate
The command glMap1() defines a one-dimensional evaluator that uses
these equations.
Bn(u) =
(
n
)
ui(1−u)n−i
ii
C(u) =B
n(u) P
i i
i = 0
n
C
(
u−u1
)
u2− u1

576 Chapter 12: Evaluators and NURBS
void glMap1{fd}(GLenum target,TYPE u1,TYPE u2, GLint stride,
GLint order, const TYPE *points);
Defines a one-dimensional evaluator. The target parameter specifies what
the control points represent, as shown in Table 12-1, and therefore how
many values need to be supplied in points. The points can represent
vertices, RGBA color data, normal vectors, or texture coordinates. For
example, with GL_MAP1_COLOR_4, the evaluator generates color data
along a curve in four-dimensional (RGBA) color space. You also use the
parameter values listed in Table 12-1 to enable each defined evaluator
before you invoke it. Pass the appropriate value to glEnable() or
glDisable() to enable or disable the evaluator.
The second two parameters for glMap1*(),u1 and u2, indicate the range
for the variable u. The variable stride is the number of single- or double-
precision values (as appropriate) in each block of storage. Thus, it’s an
offset value between the beginning of one control point and the
beginning of the next.
The order is the degree plus 1, and it should agree with the number of
control points. The points parameter points to the first coordinate of the
first control point. Using the example data structure for glMap1*(), use
the following for points:
(GLfloat *)(&ctlpoints[0].x)
Parameter Meaning
GL_MAP1_VERTEX_3 x, y, z vertex coordinates
GL_MAP1_VERTEX_4 x, y, z, w vertex coordinates
GL_MAP1_INDEX color index
GL_MAP1_COLOR_4 R, G, B, A
GL_MAP1_NORMAL normal coordinates
GL_MAP1_TEXTURE_COORD_1 s texture coordinates
GL_MAP1_TEXTURE_COORD_2 s, t texture coordinates
GL_MAP1_TEXTURE_COORD_3 s, t, r texture coordinates
GL_MAP1_TEXTURE_COORD_4 s, t, r, q texture coordinates
Table 12-1 Types of Control Points for glMap1*()
Compatibility
Extension
glMap1 and any
tokens accepted
by it

Evaluators 577
More than one evaluator can be evaluated at a time. If you have both a
GL_MAP1_VERTEX_3 and a GL_MAP1_COLOR_4 evaluator defined and
enabled, for example, then calls to glEvalCoord1() generate both a position
and a color. Only one of the vertex evaluators can be enabled at a time,
although you might have defined both of them. Similarly, only one of the
texture evaluators can be active. Otherwise, however, evaluators can be used
to generate any combination of vertex, normal, color, and texture-coordinate
data. If you define and enable more than one evaluator of the same type,
the one of highest dimension is used.
Use glEvalCoord1*() to evaluate a defined and enabled one-
dimensional map.
For evaluated vertices, generation of values for color, color index,
normal vectors, and texture coordinates is done by evaluation. Calls
to glEvalCoord*() do not use the current values for color, color index,
normal vectors, and texture coordinates. glEvalCoord*() also leaves those
values unchanged.
Defining Evenly Spaced Coordinate Values in One Dimension
You can use glEvalCoord1() with any values of u, but by far the most
common practice is to use evenly spaced values, as shown previously in
Example 12-1. To obtain evenly spaced values, define a one-dimensional
grid using glMapGrid1*() and then apply it using glEvalMesh1().
void glEvalCoord1{fd}(TYPE u);
void glEvalCoord1{fd}v(const TYPE *u);
Causes evaluation of the enabled one-dimensional maps. The argument u
is the value (or a pointer to the value, in the vector version of the
command) of the domain coordinate.
void glMapGrid1{fd}(GLint n,TYPE u1,TYPE u2);
Defines a grid that goes from u1 to u2 in n steps, which are evenly
spaced.
Compatibility
Extension
glEvalCoord1
Compatibility
Extension
glMapGrid1
578 Chapter 12: Evaluators and NURBS
Two-Dimensional Evaluators
In two dimensions, everything is similar to the one-dimensional case, except
that all the commands must take two parameters, u and v, into account.
Points, colors, normals, or texture coordinates must be supplied over a
surface instead of a curve. Mathematically, the definition of a Bézier surface
patch is given by
where the Pij values are a set of mn control points, and the Bi functions are
the same Bernstein polynomials for one dimension. As before, the Pij values
can represent vertices, normals, colors, or texture coordinates.
The procedure for using two-dimensional evaluators is similar to the
procedure for one dimension:
1. Define the evaluator(s) with glMap2*().
2. Enable them by passing the appropriate value to glEnable().
3. Invoke them either by calling glEvalCoord2() between a glBegin()
and glEnd() pair or by specifying and then applying a mesh with
glMapGrid2() and glEvalMesh2().
void glEvalMesh1(GLenum mode, GLint p1, GLint p2);
Applies the currently defined map grid to all enabled evaluators. The mode
can be either GL_POINT or GL_LINE, depending on whether you want to
draw points or a connected line along the curve. The call has exactly the
same effect as issuing a glEvalCoord1() for each of the steps from p1 to
p2, inclusive, where 0 dp1,p2 dn. Programmatically, it’s equivalent to
glBegin(GL_POINTS); /* OR glBegin(GL_LINE_STRIP); */
for (i = p1; i <= p2; i++)
glEvalCoord1(u1 + i*(u2-u1)/n);
glEnd();
except that if i = 0 or i = n, then glEvalCoord1() is called with exactly u1
or u2 as its parameter.
Compatibility
Extension
glEvalMesh1
S(u, v) = Bn(u) Bm(v) P
i j ij
n
i = 0
m
j = 0
Evaluators 579
Defining and Evaluating a Two-Dimensional Evaluator
Use glMap2*() and glEvalCoord2*() to define and then invoke a two-
dimensional evaluator.
void glMap2{fd}(GLenum target,TYPE u1,TYPE u2, GLint ustride,
GLint uorder, TYPE v1,TYPE v2, GLint vstride,
GLint vorder,TYPE points);
The target parameter can have any of the values in Table 12-1, except that
the string MAP1 is replaced with MAP2. As before, these values are also
used with glEnable() to enable the corresponding evaluator. Minimum
and maximum values for both uand v are provided as u1,u2,v1, and v2.
The parameters ustride and vstride indicate the numbers of single- and
double-precision values (as appropriate) between independent settings for
these values, allowing users to select a subrectangle of control points out
of a much larger array. For example, if the data appears in the form
GLfloat ctlpoints[100][100][3];
and you want to use the 4 u4 subset beginning at ctlpoints[20][30],
choose ustride to be 100*3 and vstride to be 3. The starting point, points,
should be set to &ctlpoints[20][30][0]. Finally, the order parameters, uorder
and vorder, can be different—allowing patches that are cubic in one
direction and quadratic in the other, for example.
void glEvalCoord2{fd}(TYPE u, TYPE v);
void glEvalCoord2{fd}v(const TYPE *values);
Causes evaluation of the enabled two-dimensional maps. The arguments
uand v are the values (or a pointer to the values u and v, in the vector
version of the command) for the domain coordinates. If either of the
vertex evaluators is enabled (GL_MAP2_VERTEX_3 or GL_MAP2_
VERTEX_4), then the normal to the surface is computed analytically.
This normal is associated with the generated vertex if automatic normal
generation has been enabled by passing GL_AUTO_NORMAL to
glEnable(). If it’s disabled, the corresponding enabled normal map is
used to produce a normal. If no such map exists, the current normal
is used.
Compatibility
Extension
glMap2 and any
tokens accepted
by it
Compatibility
Extension
glEvalCoord2
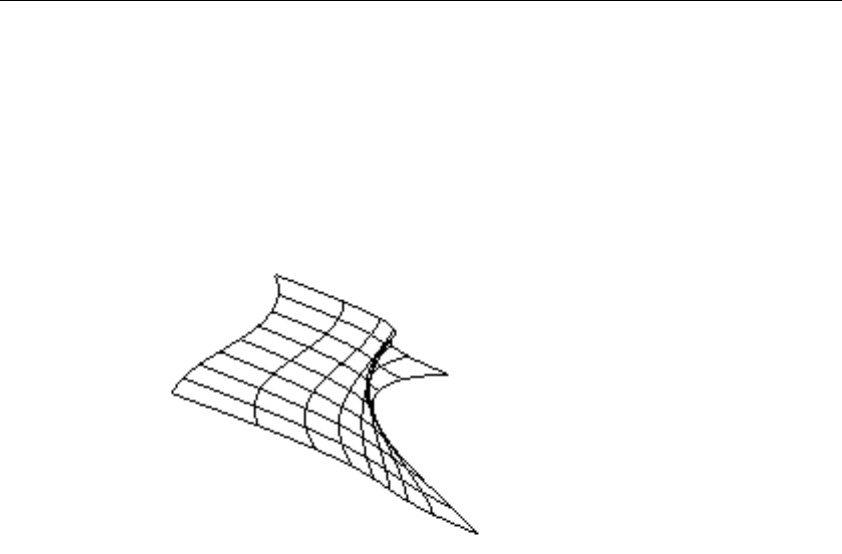
580 Chapter 12: Evaluators and NURBS
Two-Dimensional Example: A Bézier Surface
Example 12-2 draws a wireframe Bézier surface using evaluators, as shown
in Figure 12-2. In this example, the surface is drawn with nine curved lines
in each direction. Each curve is drawn as 30 segments. To get the whole
program, add the reshape() and main() routines from Example 12-1.
Example 12-2 Bézier Surface: bezsurf.c
GLfloat ctrlpoints[4][4][3] = {
{{-1.5, -1.5, 4.0}, {-0.5, -1.5, 2.0},
{0.5, -1.5, -1.0}, {1.5, -1.5, 2.0}},
{{-1.5, -0.5, 1.0}, {-0.5, -0.5, 3.0},
{0.5, -0.5, 0.0}, {1.5, -0.5, -1.0}},
{{-1.5, 0.5, 4.0}, {-0.5, 0.5, 0.0},
{0.5, 0.5, 3.0}, {1.5, 0.5, 4.0}},
{{-1.5, 1.5, -2.0}, {-0.5, 1.5, -2.0},
{0.5, 1.5, 0.0}, {1.5, 1.5, -1.0}}
};
void display(void)
{
int i, j;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glPushMatrix();
glRotatef(85.0, 1.0, 1.0, 1.0);
for (j = 0; j <= 8; j++) {
glBegin(GL_LINE_STRIP);
Figure 12-2 Bézier Surface
Evaluators 581
for (i = 0; i <= 30; i++)
glEvalCoord2f((GLfloat)i/30.0, (GLfloat)j/8.0);
glEnd();
glBegin(GL_LINE_STRIP);
for (i = 0; i <= 30; i++)
glEvalCoord2f((GLfloat)j/8.0, (GLfloat)i/30.0);
glEnd();
}
glPopMatrix();
glFlush();
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4,
0, 1, 12, 4, &ctrlpoints[0][0][0]);
glEnable(GL_MAP2_VERTEX_3);
glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_FLAT);
}
Defining Evenly Spaced Coordinate Values in Two Dimensions
In two dimensions, the glMapGrid2*() and glEvalMesh2() commands
are similar to the one-dimensional versions, except that both u and v
information must be included.
void glMapGrid2{fd}(GLint nu,TYPE u1,TYPE u2,
GLint nv,TYPE v1,TYPE v2);
void glEvalMesh2(GLenum mode, GLint i1,
GLint i2, GLint j1, GLint j2);
Defines a two-dimensional map grid that goes from u1 to u2 in nu evenly
spaced steps, goes from v1 to v2 in nv steps (glMapGrid2*()), and then
applies this grid to all enabled evaluators (glEvalMesh2()). The only sig-
nificant difference from the one-dimensional versions of these two com-
mands is that in glEvalMesh2(), the mode parameter can be GL_FILL as
well as GL_POINT or GL_LINE. GL_FILL generates filled polygons using
the quad-mesh primitive. Stated precisely, glEvalMesh2() is nearly equiv-
alent to one of the following three code fragments. (It’s nearly equivalent
because when i is equal to nu, or j to nv, the parameter is exactly equal to
u2 or v2, not to u1 + nu(u2 u1)/nu, which might be slightly different
due to round-off error.)
Compatibility
Extension
glMapGrid2
glEvalMesh2

582 Chapter 12: Evaluators and NURBS
glBegin(GL_POINTS); /* mode == GL_POINT */
for (i = nu1; i <= nu2; i++)
for (j = nv1; j <= nv2; j++)
glEvalCoord2(u1 + i*(u2-u1)/nu, v1+j*(v2-v1)/nv);
glEnd();
or
for (i = nu1; i <= nu2; i++) { /* mode == GL_LINE */
glBegin(GL_LINES);
for (j = nv1; j <= nv2; j++)
glEvalCoord2(u1 + i*(u2-u1)/nu, v1+j*(v2-v1)/nv);
glEnd();
}
for (j = nv1; j <= nv2; j++) {
glBegin(GL_LINES);
for (i = nu1; i <= nu2; i++)
glEvalCoord2(u1 + i*(u2-u1)/nu, v1+j*(v2-v1)/nv);
glEnd();
}
or
for (i = nu1; i < nu2; i++) { /* mode == GL_FILL */
glBegin(GL_QUAD_STRIP);
for (j = nv1; j <= nv2; j++) {
glEvalCoord2(u1 + i*(u2-u1)/nu, v1+j*(v2-v1)/nv);
glEvalCoord2(u1 + (i+1)*(u2-u1)/nu, v1+j*(v2-v1)/nv);
glEnd();
}
Example 12-3 shows the differences necessary to draw the same Bézier
surface as in Example 12-2, but using glMapGrid2() and glEvalMesh2() to
subdivide the square domain into a uniform 8 u8 grid. This program also
adds lighting and shading, as shown in Figure 12-3.
Example 12-3 Lit, Shaded Bézier Surface Using a Mesh: bezmesh.c
void initlights(void)
{
GLfloat ambient[] = {0.2, 0.2, 0.2, 1.0};
GLfloat position[] = {0.0, 0.0, 2.0, 1.0};
GLfloat mat_diffuse[] = {0.6, 0.6, 0.6, 1.0};
GLfloat mat_specular[] = {1.0, 1.0, 1.0, 1.0};
GLfloat mat_shininess[] = {50.0};
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);

Evaluators 583
glLightfv(GL_LIGHT0, GL_AMBIENT, ambient);
glLightfv(GL_LIGHT0, GL_POSITION, position);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glRotatef(85.0, 1.0, 1.0, 1.0);
glEvalMesh2(GL_FILL, 0, 20, 0, 20);
glPopMatrix();
glFlush();
}
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glEnable(GL_DEPTH_TEST);
glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4,
0, 1, 12, 4, &ctrlpoints[0][0][0]);
glEnable(GL_MAP2_VERTEX_3);
glEnable(GL_AUTO_NORMAL);
glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
initlights();
}
Figure 12-3 Lit, Shaded Bézier Surface Drawn with a Mesh

584 Chapter 12: Evaluators and NURBS
Using Evaluators for Textures
Example 12-4 enables two evaluators at the same time: The first generates
three-dimensional points on the same Bézier surface as in Example 12-3,
and the second generates texture coordinates. In this case, the texture
coordinates are the same as the u- and v-coordinates of the surface, but a
special flat Bézier patch must be created to do this.
The flat patch is defined over a square with corners at (0, 0), (0, 1), (1, 0),
and (1, 1); it generates (0, 0) at corner (0, 0), (0, 1) at corner (0, 1), and so
on. Since it’s of order 2 (linear degree plus 1), evaluating this texture at the
point (u, v) generates texture coordinates (s, t). It’s enabled at the same
time as the vertex evaluator, so both take effect when the surface is drawn
(see Plate 19). If you want the texture to repeat three times in each
direction, change every 1.0 in the array texpts[][][] to 3.0. Since the texture
wraps in this example, the surface is rendered with nine copies of the
texture map.
Example 12-4 Using Evaluators for Textures: texturesurf.c
GLfloat ctrlpoints[4][4][3] = {
{{ -1.5, -1.5, 4.0}, { -0.5, -1.5, 2.0},
{0.5, -1.5, -1.0}, {1.5, -1.5, 2.0}},
{{ -1.5, -0.5, 1.0}, { -0.5, -0.5, 3.0},
{0.5, -0.5, 0.0}, {1.5, -0.5, -1.0}},
{{ -1.5, 0.5, 4.0}, { -0.5, 0.5, 0.0},
{0.5, 0.5, 3.0}, {1.5, 0.5, 4.0}},
{{ -1.5, 1.5, -2.0}, { -0.5, 1.5, -2.0},
{0.5, 1.5, 0.0}, {1.5, 1.5, -1.0}}
};
GLfloat texpts[2][2][2] = {{{0.0, 0.0}, {0.0, 1.0}},
{{1.0, 0.0}, {1.0, 1.0}}};
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
glEvalMesh2(GL_FILL, 0, 20, 0, 20);
glFlush();
}
#define imageWidth 64
#define imageHeight 64
GLubyte image[3*imageWidth*imageHeight];

Evaluators 585
void makeImage(void)
{
int i, j;
float ti, tj;
for (i = 0; i < imageWidth; i++) {
ti = 2.0*3.14159265*i/imageWidth;
for (j = 0; j < imageHeight; j++) {
tj = 2.0*3.14159265*j/imageHeight;
image[3*(imageHeight*i+j)] =
(GLubyte) 127*(1.0+sin(ti));
image[3*(imageHeight*i+j)+1] =
(GLubyte) 127*(1.0+cos(2*tj));
image[3*(imageHeight*i+j)+2] =
(GLubyte) 127*(1.0+cos(ti+tj));
}
}
}
void init(void)
{
glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4,
0, 1, 12, 4, &ctrlpoints[0][0][0]);
glMap2f(GL_MAP2_TEXTURE_COORD_2, 0, 1, 2, 2,
0, 1, 4, 2, &texpts[0][0][0]);
glEnable(GL_MAP2_TEXTURE_COORD_2);
glEnable(GL_MAP2_VERTEX_3);
glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
makeImage();
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_DECAL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
glTexImage2D(GL_TEXTURE_2D, 0, 3, imageWidth, imageHeight, 0,
GL_RGB, GL_UNSIGNED_BYTE, image);
glEnable(GL_TEXTURE_2D);
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_FLAT);
}

586 Chapter 12: Evaluators and NURBS
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-4.0, 4.0, -4.0*(GLfloat)h/(GLfloat)w,
4.0*(GLfloat)h/(GLfloat)w, -4.0, 4.0);
else
glOrtho(-4.0*(GLfloat)w/(GLfloat)h,
4.0*(GLfloat)w/(GLfloat)h, -4.0, 4.0, -4.0, 4.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glRotatef(85.0, 1.0, 1.0, 1.0);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
return 0;
}
The GLU NURBS Interface
Although evaluators are the only OpenGL primitives available to draw
curves and surfaces directly, and even though they can be implemented
very efficiently in hardware, they’re often accessed by applications through
higher-level libraries. The GLU provides a NURBS interface built on top of
the OpenGL evaluator commands.

The GLU NURBS Interface 587
A Simple NURBS Example
If you understand NURBS, writing OpenGL code to manipulate NURBS
curves and surfaces is relatively easy, even with lighting and texture mapping.
Perform the following steps to draw NURBS curves or untrimmed NURBS
surfaces. (See “Trimming a NURBS Surface” on page 601 for information
about trimmed surfaces.)
1. If you intend to use lighting with a NURBS surface, call glEnable()
with GL_AUTO_NORMAL to generate surface normals automatically.
(Or you can calculate your own.)
2. Use gluNewNurbsRenderer() to create a pointer to a NURBS object,
which is referred to when creating your NURBS curve or surface.
3. If desired, call gluNurbsProperty() to choose rendering values, such as
the maximum size of lines or polygons that are used to render your
NURBS object. gluNurbsProperty() can also enable a mode, where
the tessellated geometric data can be retrieved through the callback
interface.
4. Call gluNurbsCallback() if you want to be notified when an error is
encountered. (Error checking may slightly degrade performance but is
still highly recommended.) gluNurbsCallback() may also be used to
register the functions to call to retrieve the tessellated geometric data.
5. Start your curve or surface by calling gluBeginCurve() or
gluBeginSurface().
6. Generate and render your curve or surface. Call gluNurbsCurve() or
gluNurbsSurface() at least once with the control points (rational or
nonrational), knot sequence, and order of the polynomial basis func-
tion for your NURBS object. You might call these functions additional
times to specify surface normals and/or texture coordinates.
7. Call gluEndCurve() or gluEndSurface() to complete the curve or
surface.
Example 12-5 renders a NURBS surface in the shape of a symmetrical hill,
with control points ranging from 3.0 to 3.0. The basis function is a cubic
B-spline, but the knot sequence is nonuniform, with a multiplicity of 4 at
each endpoint, causing the basis function to behave as a Bézier curve in
each direction. The surface is lighted, with a dark gray diffuse reflection
and white specular highlights. Figure 12-4 shows the surface as a lit
wireframe.
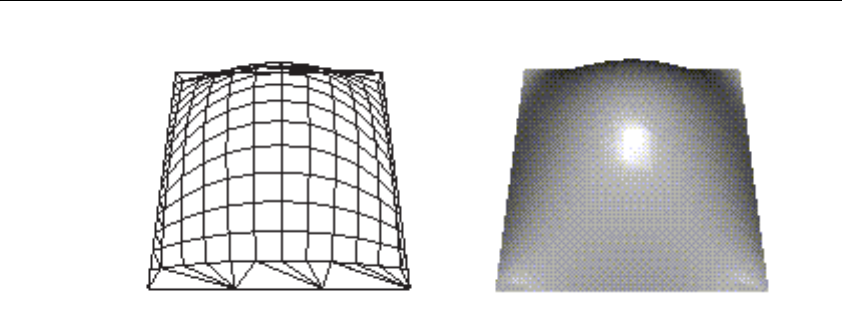
588 Chapter 12: Evaluators and NURBS
Example 12-5 NURBS Surface: surface.c
#ifndef CALLBACK
#define CALLBACK
#endif
GLfloat ctlpoints[4][4][3];
int showPoints = 0;
GLUnurbsObj *theNurb;
void init_surface(void)
{
int u, v;
for (u = 0; u < 4; u++) {
for (v = 0; v < 4; v++) {
ctlpoints[u][v][0] = 2.0*((GLfloat)u - 1.5);
ctlpoints[u][v][1] = 2.0*((GLfloat)v - 1.5);
if ( (u == 1 || u == 2) && (v == 1 || v == 2))
ctlpoints[u][v][2] = 3.0;
else
ctlpoints[u][v][2] = -3.0;
}
}
}
void CALLBACK nurbsError(GLenum errorCode)
{
const GLubyte *estring;
Figure 12-4 NURBS Surface

The GLU NURBS Interface 589
estring = gluErrorString(errorCode);
fprintf(stderr, “Nurbs Error: %s\n”, estring);
exit(0);
}
void init(void)
{
GLfloat mat_diffuse[] = { 0.7, 0.7, 0.7, 1.0 };
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat mat_shininess[] = { 100.0 };
glClearColor(0.0, 0.0, 0.0, 0.0);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_DEPTH_TEST);
glEnable(GL_AUTO_NORMAL);
glEnable(GL_NORMALIZE);
init_surface();
theNurb = gluNewNurbsRenderer();
gluNurbsProperty(theNurb, GLU_SAMPLING_TOLERANCE, 25.0);
gluNurbsProperty(theNurb, GLU_DISPLAY_MODE, GLU_FILL);
gluNurbsCallback(theNurb, GLU_ERROR, nurbsError);
}
void display(void)
{
GLfloat knots[8] = {0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0};
int i, j;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glRotatef(330.0, 1., 0., 0.);
glScalef(0.5, 0.5, 0.5);
gluBeginSurface(theNurb);
gluNurbsSurface(theNurb,
8, knots, 8, knots,
4 * 3, 3, &ctlpoints[0][0][0],
4, 4, GL_MAP2_VERTEX_3);

590 Chapter 12: Evaluators and NURBS
gluEndSurface(theNurb);
if (showPoints) {
glPointSize(5.0);
glDisable(GL_LIGHTING);
glColor3f(1.0, 1.0, 0.0);
glBegin(GL_POINTS);
for (i = 0; i < 4; i++) {
for (j = 0; j < 4; j++) {
glVertex3f(ctlpoints[i][j][0],
ctlpoints[i][j][1], ctlpoints[i][j][2]);
}
}
glEnd();
glEnable(GL_LIGHTING);
}
glPopMatrix();
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0, (GLdouble)w/(GLdouble)h, 3.0, 8.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0, 0.0, -5.0);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key) {
case ‘c’:
case ‘C’:
showPoints = !showPoints;
glutPostRedisplay();
break;
case 27:
exit(0);
break;
default:
break;
}
}

The GLU NURBS Interface 591
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutKeyboardFunc(keyboard);
glutMainLoop();
return 0;
}
Managing a NURBS Object
As shown in Example 12-5, gluNewNurbsRenderer() returns a new NURBS
object, whose type is a pointer to a GLUnurbsObj structure. You must make
this object before using any other NURBS routine. When you’re done with
a NURBS object, you may use gluDeleteNurbsRenderer() to free up the
memory that was used.
Controlling NURBS Rendering Properties
A set of properties associated with a NURBS object affects the way the object
is rendered. These properties include how the surface is rasterized (for
example, filled or wireframe), whether the tessellated vertices are displayed
or returned, and the precision of tessellation.
GLUnurbsObj* gluNewNurbsRenderer(void);
Creates a new NURBS object, nobj, and returns a pointer to the new object,
or zero, if OpenGL cannot allocate memory for a new NURBS object.
void gluDeleteNurbsRenderer(GLUnurbsObj *nobj);
Destroys the NURBS object nobj.

592 Chapter 12: Evaluators and NURBS
void gluNurbsProperty(GLUnurbsObj *nobj, GLenum property,
GLfloat value);
Controls attributes of a NURBS object, nobj. The property argument
specifies the property and can be GLU_DISPLAY_MODE, GLU_NURBS_
MODE, GLU_CULLING, GLU_SAMPLING_METHOD, GLU_SAMPLING_
TOLERANCE, GLU_PARAMETRIC_TOLERANCE, GLU_U_STEP, GLU_V_
STEP, or GLU_AUTO_LOAD_MATRIX. The value argument indicates what
the property should be.
For the property GLU_DISPLAY_MODE, the default value is GLU_FILL,
which causes the surface to be rendered as polygons. If GLU_OUTLINE_
POLYGON is used for the display-mode property, only the outlines of
polygons created by tessellation are rendered. GLU_OUTLINE_PATCH
renders the outlines of patches and trimming curves. (See “Creating a
NURBS Curve or Surface” on page 595.)
The property GLU_NURBS_MODE controls whether the tessellated vertices
are simply rendered (the default value, GLU_NURBS_RENDERER) or
whether the callback interface is activated to allow the tessellated data
to be returned (if value is GLU_NURBS_TESSELLATOR). For details, see
“Getting Primitives Back from the NURBS Tessellator” on page 597.
GLU_CULLING can speed up performance by not performing tessellation
if the NURBS object falls completely outside the viewing volume; set this
property to GL_TRUE to enable culling (the default is GL_FALSE).
Since a NURBS object is rendered as primitives, it’s sampled at different
values of its parameter(s) (u and v) and broken down into small line
segments or polygons for rendering. If property is GLU_SAMPLING_
METHOD, then value is set to GLU_PATH_LENGTH (which is the default),
GLU_PARAMETRIC_ERROR, GLU_DOMAIN_DISTANCE, GLU_OBJECT_
PATH_LENGTH, or GLU_OBJECT_PARAMETRIC_ERROR, which specifies
how a NURBS curve or surface should be tessellated. When value is set
to GLU_PATH_LENGTH, the surface is rendered so that the maximum
length, in pixels, of the edges of tessellated polygons is no greater than
that specified by GLU_SAMPLING_TOLERANCE. When value is set to
GLU_PARAMETRIC_ERROR, then the quantity specified by GLU_
PARAMETRIC_TOLERANCE is the maximum distance, in pixels, between
tessellated polygons and the surfaces they approximate.

The GLU NURBS Interface 593
Avalue of GLU_OBJECT_PATH_LENGTH is similar to GLU_PATH_LENGTH,
except that the maximum length (the value of GLU_SAMPLING_
TOLERANCE) of a tessellated primitive is measured in object space, not
pixels. Similarly, GLU_OBJECT_PARAMETRIC_ERROR is related to
GLU_PARAMETRIC_ERROR, except that GLU_PARAMETRIC_
TOLERANCE measures the maximum distance between tessellated
polygons and the surfaces they approximate, in object space, not in pixels.
When value is set to GLU_DOMAIN_DISTANCE, the application specifies,
in parametric coordinates, how many sample points per unit length are
taken in the u- and v-dimensions, using the values for GLU_U_STEP and
GLU_V_STEP.
If property is GLU_SAMPLING_TOLERANCE and the sampling method is
GLU_PATH_LENGTH or GLU_OBJECT_PATH_LENGTH, value controls the
maximum length, in pixels or object space units, respectively, that should
be used for tessellated polygons. For example, the default value of 50.0
makes the largest sampled line segment or polygon edge 50.0 pixels long
or 50.0 units long in object space. If property is GLU_PARAMETRIC_
TOLERANCE and the sampling method is GLU_PARAMETRIC_ERROR
or GLU_OBJECT_PARAMETRIC_ERROR, value controls the maximum
distance, in pixels or object space, respectively, between the tessellated
polygons and the surfaces they approximate. For either sampling method,
the default value for GLU_PARAMETRIC_TOLERANCE is 0.5. For
GLU_PARAMETRIC_ERROR, this value makes the tessellated polygons
within one-half pixel of the approximated surface. (For GLU_OBJECT_
PARAMETRIC_ERROR, the default value of 0.5 doesn’t have the same
obvious meaning.)
If the sampling method is GLU_DOMAIN_DISTANCE and property is
either GLU_U_STEP or GLU_V_STEP, then value is the number of sample
points per unit length taken along the u- or v-dimension, respectively, in
parametric coordinates. The default for both GLU_U_STEP and GLU_V_
STEP is 100.
The GLU_AUTO_LOAD_MATRIX property determines whether the pro-
jection matrix, modelview matrix, and viewport are downloaded from the
OpenGL server (GL_TRUE, the default), or whether the application must
supply these matrices with gluLoadSamplingMatrices() (GL_FALSE).

594 Chapter 12: Evaluators and NURBS
Note: Several of the NURBS properties (the GLU_NURBS_MODE and
its nondefault value GLU_NURBS_TESSELLATOR, and the object
space sampling methods GLU_OBJECT_PATH_LENGTH and GLU_
OBJECT_PARAMETRIC_ERROR) are introduced in GLU Version 1.3.
Prior to GLU 1.3, these NURBS properties existed as vendor-specific
extensions, if at all. Make sure you check the GLU version before you
attempt to use these properties.
If you need to query the current value of a NURBS property, you may use
gluGetNurbsProperty().
Handling NURBS Errors
Since there are 37 different errors specific to NURBS functions, it’s a good
idea to register an error callback to let you know if you’ve stumbled into one
of them. In Example 12-5, the callback function was registered with
gluNurbsCallback(theNurb, GLU_ERROR, (GLvoid (*)()) nurbsError);
void gluLoadSamplingMatrices(GLUnurbsObj *nobj,
const GLfloat modelMatrix[16],
const GLfloat projMatrix[16],
const GLint viewport[4]);
If the GLU_AUTO_LOAD_MATRIX is turned off, the modelview and projec-
tion matrices and the viewport specified in gluLoadSamplingMatrices()
are used to compute sampling and culling matrices for each NURBS curve
or surface.
void gluGetNurbsProperty(GLUnurbsObj *nobj, GLenum property,
GLfloat *value);
Given the property to be queried for the NURBS object nobj, returns its
current value.

The GLU NURBS Interface 595
In Example 12-5, the nurbsError() routine was registered as the error
callback function:
void CALLBACK nurbsError(GLenum errorCode)
{
const GLubyte *estring;
estring = gluErrorString(errorCode);
fprintf(stderr, “Nurbs Error: %s\n”, estring);
exit(0);
}
In GLU 1.3, additional NURBS callback functions have been added to return
post-tessellation values back to the program (instead of rendering them).
For more information on these new callbacks, see “Getting Primitives Back
from the NURBS Tessellator” on page 597.
Creating a NURBS Curve or Surface
To render a NURBS surface, gluNurbsSurface() is bracketed by
gluBeginSurface() and gluEndSurface(). The bracketing routines save and
restore the evaluator state.
void gluNurbsCallback(GLUnurbsObj *nobj, GLenum which,
void (*fn)(GLenum errorCode));
which is the type of callback; for error checking, it must be GLU_ERROR.
When a NURBS function detects an error condition, fn is invoked with the
error code as its only argument. errorCode is one of 37 error conditions,
named GLU_NURBS_ERROR1 through GLU_NURBS_ERROR37. Use
gluErrorString() to describe the meaning of these error codes.
void gluBeginSurface(GLUnurbsObj *nobj);
void gluEndSurface(GLUnurbsObj *nobj);
After gluBeginSurface(), one or more calls to gluNurbsSurface() defines
the attributes of the surface. Exactly one of these calls must have a surface
type of GL_MAP2_VERTEX_3 or GL_MAP2_VERTEX_4 to generate
vertices. Use gluEndSurface() to end the definition of a surface. Trimming
of NURBS surfaces is also supported between gluBeginSurface() and
gluEndSurface(). (See “Trimming a NURBS Surface” on page 601.)

596 Chapter 12: Evaluators and NURBS
void gluNurbsSurface(GLUnurbsObj *nobj, GLint uknot_count,
GLfloat *uknot, GLint vknot_count, GLfloat *vknot,
GLint u_stride, GLint v_stride, GLfloat *ctlarray,
GLint uorder, GLint vorder, GLenum type);
Describes the vertices (or surface normals or texture coordinates) of a
NURBS surface, nobj. Several of the values must be specified for both u
and v parametric directions, such as the knot sequences (uknot and
vknot), knot counts (uknot_count and vknot_count), and the order of
the polynomial (uorder and vorder) for the NURBS surface. Note that
the number of control points isn’t specified. Instead, it’s derived by
determining the number of control points along each parameter as
the number of knots minus the order. Then, the number of control
points for the surface is equal to the number of control points in each
parametric direction, multiplied by one another. The ctlarray argument
points to an array of control points.
The last parameter, type, is one of the two-dimensional evaluator types.
Commonly, you might use GL_MAP2_VERTEX_3 for nonrational or GL_
MAP2_VERTEX_4 for rational control points, respectively. You might also
use other types, such as GL_MAP2_TEXTURE_COORD_* or GL_MAP2_
NORMAL to calculate and assign texture coordinates or surface normals.
For example, to create a lighted (with surface normals) and textured
NURBS surface, you may need to call this sequence:
gluBeginSurface(nobj);
gluNurbsSurface(nobj, ..., GL_MAP2_TEXTURE_COORD_2);
gluNurbsSurface(nobj, ..., GL_MAP2_NORMAL);
gluNurbsSurface(nobj, ..., GL_MAP2_VERTEX_3);
gluEndSurface(nobj);
The u_stride and v_stride arguments represent the number of floating-
point values between control points in each parametric direction. The
evaluator type, as well as its order, affects the u_stride and v_stride values.
In Example 12-5, u_stride is 12 (4*3) because there are three coordinates
for each vertex (set by GL_MAP2_VERTEX_3) and four control points in
the parametric v-direction; v_stride is 3 because each vertex has three
coordinates, and the v control points are adjacent to one another in
memory.

The GLU NURBS Interface 597
Drawing a NURBS curve is similar to drawing a surface, except that all cal-
culations are done with one parameter, u, rather than two. Also, for curves,
gluBeginCurve() and gluEndCurve() are the bracketing routines.
Getting Primitives Back from the NURBS Tessellator
By default, the NURBS tessellator breaks down a NURBS object into geometric
lines and polygons, and then renders them. In GLU 1.3, additional callback
functions have been added, so instead of rendering the post-tessellation
values, they can be returned for use by the application.
To do this, call gluNurbsProperty() to set the GLU_NURBS_MODE property
to the value GLU_NURBS_TESSELLATOR. The other necessary step is to call
gluNurbsCallback() several times to register callback functions, which the
NURBS tessellator will now call.
void gluBeginCurve(GLUnurbsObj *nobj);
void gluEndCurve(GLUnurbsObj *nobj);
After gluBeginCurve(), one or more calls to gluNurbsCurve() define the
attributes of the surface. Exactly one of these calls must have a surface
type of GL_MAP1_VERTEX_3 or GL_MAP1_VERTEX_4 to generate
vertices. Use gluEndCurve() to end the definition of a surface.
void gluNurbsCurve(GLUnurbsObj *nobj, GLint uknot_count,
GLfloat *uknot, GLint u_stride, GLfloat *ctlarray,
GLint uorder, GLenum type);
Defines a NURBS curve for the object nobj. The arguments have the
same meaning as those for gluNurbsSurface(). Note that this routine
requires only one knot sequence and one declaration of the order of
the NURBS object. If this curve is defined within a gluBeginCurve()/
gluEndCurve() pair, then the type can be any of the valid one-
dimensional evaluator types (such as GL_MAP1_VERTEX_3 or
GL_MAP1_VERTEX_4).

598 Chapter 12: Evaluators and NURBS
To change a callback routine, call gluNurbsCallback() with the new routine.
To eliminate a callback routine without replacing it, pass gluNurbsCallback()
a null pointer for the appropriate function.
void gluNurbsCallback(GLUnurbsObj *nobj, GLenum which,
void (*fn)());
nobj is the NURBS object to be tessellated. which is the enumerant
identifying the callback function. If the property GLU_NURBS_MODE is set
to GLU_NURBS_TESSELLATOR, then 12 possible callback functions (in
addition to GLU_ERROR) are available. (If GLU_NURBS_MODE is set to
the default GLU_NURBS_RENDERER value, then only GLU_ERROR is
active.) The 12 callbacks have the following enumerants and prototypes:
GLU_NURBS_BEGIN void begin(GLenum type);
GLU_NURBS_BEGIN_DATA void begin(GLenum type,
void *userData);
GLU_NURBS_TEXTURE_COORD void texCoord(
GLfloat *tCrd);
GLU_NURBS_TEXTURE_COORD_DATA void texCoord(
GLfloat *tCrd,
void *userData);
GLU_NURBS_COLOR void color(GLfloat *color);
GLU_NURBS_COLOR_DATA void color(GLfloat *color,
void *userData);
GLU_NURBS_NORMAL void normal(GLfloat *nml);
GLU_NURBS_NORMAL_DATA void normal(GLfloat *nml,
void *userData);
GLU_NURBS_VERTEX void vertex(GLfloat *vertex);
GLU_NURBS_VERTEX_DATA void vertex(GLfloat *vertex,
void *userData);
GLU_NURBS_END void end(void);
GLU_NURBS_END_DATA void end(void *userData);

The GLU NURBS Interface 599
Six of the callback functions allow the user to pass some data to it. To specify
that user data, you must call gluNurbsCallbackData().
As tessellation proceeds, the callback routines are called in a manner similar
to that in which you use the OpenGL commands glBegin(),glTexCoord*(),
glColor*(),glNormal*(),glVertex*(), and glEnd(). During the GLU_NURBS_
TESSELLATOR mode, the curve or surface is not directly rendered, but you
can capture the vertex data passed as parameters to the callback functions.
To demonstrate these new callbacks, Example 12-6 and Example 12-7 show
portions of surfpoints.c, which is a modification of the earlier surface.c
program. Example 12-6 shows part of the init() subroutine, where the
NURBS object is created, GLU_NURBS_MODE is set to perform the
tessellation, and the callback functions are registered.
Example 12-6 Registering NURBS Tessellation Callbacks: surfpoints.c
void init(void)
{
/* only a portion of init() shown here--several lines deleted */
theNurb = gluNewNurbsRenderer();
gluNurbsProperty(theNurb, GLU_NURBS_MODE,
GLU_NURBS_TESSELLATOR);
gluNurbsProperty(theNurb, GLU_SAMPLING_TOLERANCE, 100.0);
gluNurbsProperty(theNurb, GLU_DISPLAY_MODE, GLU_FILL);
gluNurbsCallback(theNurb, GLU_ERROR, nurbsError);
gluNurbsCallback(theNurb, GLU_NURBS_BEGIN, beginCallback);
gluNurbsCallback(theNurb, GLU_NURBS_VERTEX, vertexCallback);
gluNurbsCallback(theNurb, GLU_NURBS_NORMAL, normalCallback);
gluNurbsCallback(theNurb, GLU_NURBS_END, endCallback);
}
Example 12-7 shows the callback functions of surfpoints.c. In these
callbacks, printf() statements act as diagnostics to show what rendering
directives and vertex data are returned from the tessellator. In addition,
the post-tessellation data is resubmitted to the pipeline for ordinary
rendering.
void gluNurbsCallbackData(GLUnurbsObj *nobj,
void *userData);
nobj is the NURBS object to be tessellated. userData is the data to be passed
to the callback functions.

600 Chapter 12: Evaluators and NURBS
Example 12-7 The NURBS Tessellation Callbacks: surfpoints.c
void CALLBACK beginCallback(GLenum whichType)
{
glBegin(whichType); /* resubmit rendering directive */
printf("glBegin(");
switch (whichType) { /* print diagnostic message */
case GL_LINES:
printf("GL_LINES)\n"); break;
case GL_LINE_LOOP:
printf("GL_LINE_LOOP)\n"); break;
case GL_LINE_STRIP:
printf("GL_LINE_STRIP)\n"); break;
case GL_TRIANGLES:
printf("GL_TRIANGLES)\n"); break;
case GL_TRIANGLE_STRIP:
printf("GL_TRIANGLE_STRIP)\n"); break;
case GL_TRIANGLE_FAN:
printf("GL_TRIANGLE_FAN)\n"); break;
case GL_QUADS:
printf("GL_QUADS)\n"); break;
case GL_QUAD_STRIP:
printf("GL_QUAD_STRIP)\n"); break;
case GL_POLYGON:
printf("GL_POLYGON)\n"); break;
default:
break;
}
}
void CALLBACK endCallback()
{
glEnd(); /* resubmit rendering directive */
printf("glEnd()\n");
}
void CALLBACK vertexCallback(GLfloat *vertex)
{
glVertex3fv(vertex); /* resubmit tessellated vertex */
printf("glVertex3f (%5.3f, %5.3f, %5.3f)\n",
vertex[0], vertex[1], vertex[2]);
}
void CALLBACK normalCallback(GLfloat *normal)
{
glNormal3fv(normal); /* resubmit tessellated normal */
printf("glNormal3f (%5.3f, %5.3f, %5.3f) ",
normal[0], normal[1], normal[2]);
}

The GLU NURBS Interface 601
Trimming a NURBS Surface
To create a trimmed NURBS surface with OpenGL, start as if you were
creating an untrimmed surface. After calling gluBeginSurface() and
gluNurbsSurface() but before calling gluEndSurface(), start a trim by
calling gluBeginTrim().
You can create two kinds of trimming curves: a piecewise linear curve with
gluPwlCurve() or a NURBS curve with gluNurbsCurve(). A piecewise linear
curve doesn’t look like what is conventionally called a curve, because it’s a
series of straight lines. A NURBS curve for trimming must lie within the unit
square of parametric (u, v) space. The type for a NURBS trimming curve is
usually GLU_MAP1_TRIM2. Less often, the type is GLU_MAP1_TRIM3,
where the curve is described in a two-dimensional homogeneous space
(u’, v’, w’) by (u, v) = (u’/w’, v’/w’).
You need to consider the orientation of trimming curves—that is, whether
they’re counterclockwise or clockwise—to make sure you include the desired
part of the surface. If you imagine walking along a curve, everything to the
left is included and everything to the right is trimmed away. For example,
if your trim consists of a single counterclockwise loop, everything inside the
loop is included. If the trim consists of two nonintersecting counterclock-
wise loops with nonintersecting interiors, everything inside either of them
void gluBeginTrim(GLUnurbsObj *nobj);
void gluEndTrim(GLUnurbsObj *nobj);
Marks the beginning and end of the definition of a trimming loop. A
trimming loop is a set of oriented, trimming curve segments (forming a
closed curve) that defines the boundaries of a NURBS surface.
void gluPwlCurve(GLUnurbsObj *nobj, GLint count, GLfloat *array,
GLint stride, GLenum type);
Describes a piecewise linear trimming curve for the NURBS object nobj.
There are count points on the curve, and they’re given by array. The type
can be either GLU_MAP1_TRIM_2 (the most common) or GLU_MAP1_
TRIM_3 ((u, v, w) homogeneous parameter space). The value of type
determines whether stride is 2 or 3. stride represents the number of
floating-point values to the next vertex in array.
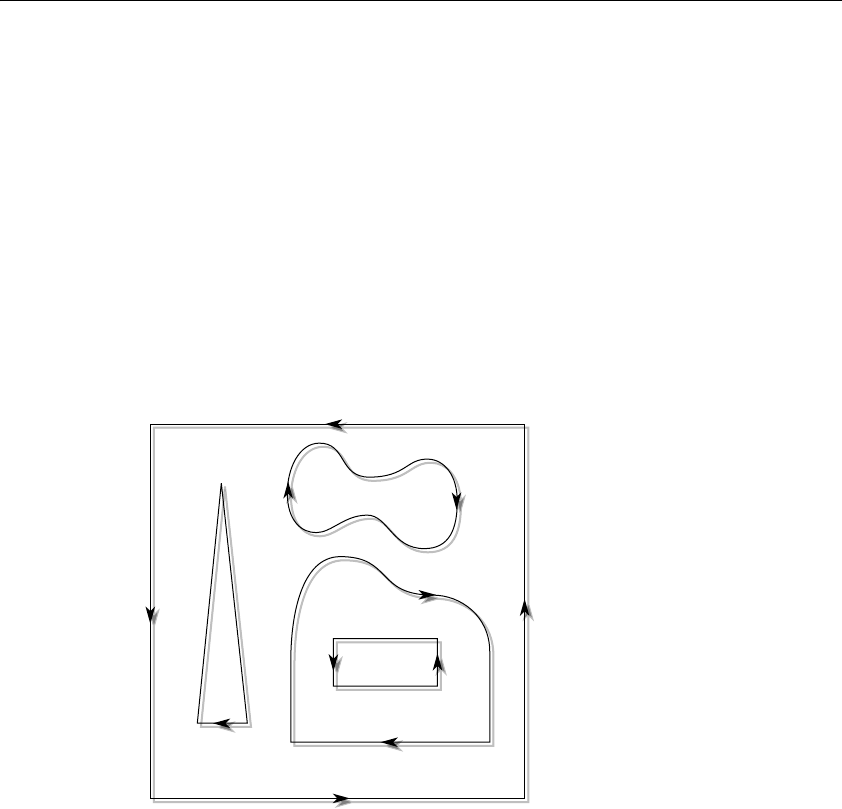
602 Chapter 12: Evaluators and NURBS
is included. If it consists of a counterclockwise loop with two clockwise
loops inside it, the trimming region has two holes in it. The outermost trim-
ming curve must be counterclockwise. Often, you run a trimming curve
around the entire unit square to include everything within it, which is what
you get by default by not specifying any trimming curves.
Trimming curves must be closed and nonintersecting. You can combine
trimming curves, as long as the endpoints of the trimming curves meet to
form a closed curve. You can nest curves, creating islands that float in space.
Be sure to get the curve orientations right. For example, an error results if
you specify a trimming region with two counterclockwise curves, one
enclosed within the other: the region between the curves is to the left of one
and to the right of the other, so it must be both included and excluded,
which is impossible. Figure 12-5 illustrates a few valid possibilities.
Figure 12-6 shows the same small hill shown in Figure 12-4, but with
a trimming curve that’s a combination of a piecewise linear curve and
a NURBS curve. The program that creates this figure is similar to the one
shown in Example 12-5; the differences are in the routines shown in
Example 12-8.
A
B
C
D
E
gluBeginSurface();
gluNurbsSurface(...);
gluBeginTrim();
gluPwlCurve(...); /* A */
gluEndTrim();
gluBeginTrim();
gluPwlCurve(...); /* B */
gluEndTrim();
gluBeginTrim();
gluNurbsCurve(...); */ C */
gluEndTrim();
gluBeginTrim();
gluNurbsCurve(...); */ D */
gluPwlCurve(...); /* D */
gluEndTrim();
gluBeginTrim();
gluPwlCurve(...); /* E */
gluEndTrim();
gluEndSurface();
Figure 12-5 Parametric Trimming Curves

The GLU NURBS Interface 603
Example 12-8 Trimming a NURBS Surface: trim.c
void display(void)
{
GLfloat knots[8] = {0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0};
GLfloat edgePt[5][2] = /* counter clockwise */
{{0.0, 0.0}, {1.0, 0.0}, {1.0, 1.0}, {0.0, 1.0},
{0.0, 0.0}};
GLfloat curvePt[4][2] = /* clockwise */
{{0.25, 0.5}, {0.25, 0.75}, {0.75, 0.75}, {0.75, 0.5}};
GLfloat curveKnots[8] =
{0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0};
GLfloat pwlPt[3][2] = /* clockwise */
{{0.75, 0.5}, {0.5, 0.25}, {0.25, 0.5}};
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
glRotatef(330.0, 1., 0., 0.);
glScalef(0.5, 0.5, 0.5);
gluBeginSurface(theNurb);
gluNurbsSurface(theNurb, 8, knots, 8, knots,
4 * 3, 3, &ctlpoints[0][0][0],
4, 4, GL_MAP2_VERTEX_3);
gluBeginTrim(theNurb);
gluPwlCurve(theNurb, 5, &edgePt[0][0], 2,
GLU_MAP1_TRIM_2);
gluEndTrim(theNurb);
gluBeginTrim(theNurb);
gluNurbsCurve(theNurb, 8, curveKnots, 2,
&curvePt[0][0], 4, GLU_MAP1_TRIM_2);
Figure 12-6 Trimmed NURBS Surface

604 Chapter 12: Evaluators and NURBS
gluPwlCurve(theNurb, 3, &pwlPt[0][0], 2,
GLU_MAP1_TRIM_2);
gluEndTrim(theNurb);
gluEndSurface(theNurb);
glPopMatrix();
glFlush();
}
In Example 12-8, gluBeginTrim() and gluEndTrim() bracket each trim-
ming curve. The first trim, with vertices defined by the array edgePt[][], goes
counterclockwise around the entire unit square of parametric space. This
ensures that everything is drawn, provided it isn’t removed by a clockwise
trimming curve inside of it. The second trim is a combination of a NURBS
trimming curve and a piecewise linear trimming curve. The NURBS curve
ends at the points (0.9, 0.5) and (0.1, 0.5), where it is met by the piecewise
linear curve, forming a closed clockwise curve.

605
Chapter 13
13.Selection and Feedback
Chapter Objectives
After reading this chapter, you’ll be able to do the following:
• Create applications that allow the user to select a region of the screen
or pick an object drawn on the screen
• Use the OpenGL feedback mode to obtain the results of rendering
calculations
Note: In OpenGL Version 3.1, all of the techniques and functions described
in this chapter were removed through deprecation. Even though
some of this functionality is part of the GLU library, it relies on
functionality that has been removed from the core OpenGL library

606 Chapter 13: Selection and Feedback
Some graphics applications simply draw static images of two- and three-
dimensional objects. Other applications allow the user to identify objects
on the screen and then to move, modify, delete, or otherwise manipulate
those objects. OpenGL is designed to support exactly such interactive appli-
cations. Since objects drawn on the screen typically undergo multiple rota-
tions, translations, and perspective transformations, it can be difficult for
you to determine which object a user is selecting in a three-dimensional
scene. To help you, OpenGL provides a selection mechanism that automat-
ically tells you which objects are drawn inside a specified region of the win-
dow. You can use this mechanism together with a special utility routine to
determine which object within the region the user is specifying, or picking,
with the cursor.
Selection is actually a mode of operation for OpenGL; feedback is another
such mode. In feedback mode, you use your graphics hardware and OpenGL
to perform the usual rendering calculations. Instead of using the calculated
results to draw an image on the screen, however, OpenGL returns (or feeds
back) the drawing information to you. For example, if you want to draw
three-dimensional objects on a plotter rather than the screen, you would
draw the items in feedback mode, collect the drawing instructions, and
then convert them to commands the plotter can understand.
In both selection and feedback modes, drawing information is returned to
the application rather than being sent to the framebuffer, as it is in render-
ing mode. Thus, the screen remains frozen—no drawing occurs—while
OpenGL is in selection or feedback mode. In these modes, the contents of
the color, depth, stencil, and accumulation buffers are not affected. This
chapter explains each of these modes in its own section:
• “Selection” discusses how to use selection mode and related routines to
allow a user of your application to pick an object drawn on the screen.
• “Feedback” describes how to obtain information about what would be
drawn on the screen and how that information is formatted.
Selection
Typically, when you’re planning to use OpenGL’s selection mechanism, you
first draw your scene into the framebuffer, and then you enter selection
mode and redraw the scene. However, once you’re in selection mode, the
contents of the framebuffer don’t change until you exit selection mode.
When you exit selection mode, OpenGL returns a list of the primitives that
intersect the viewing volume. (Remember that the viewing volume is

Selection 607
defined by the current modelview and projection matrices and any
additional clipping planes, as explained in Chapter 3.) Each primitive that
intersects the viewing volume causes a selection hit. The list of primitives is
actually returned as an array of integer-valued names and related data—the
hit records—that correspond to the current contents of the name stack. You
construct the name stack by loading names onto it as you issue primitive
drawing commands while in selection mode. Thus, when the list of names
is returned, you can use it to determine which primitives might have been
selected on the screen by the user.
In addition to this selection mechanism, OpenGL provides a utility routine
designed to simplify selection in some cases by restricting drawing to a
small region of the viewport. Typically, you use this routine to determine
which objects are drawn near the cursor, so that you can identify which
object the user is picking. (You can also delimit a selection region by
specifying additional clipping planes. Remember that these planes act in
world space, not in screen space.) Since picking is a special case of selection,
selection is described first in this chapter, and then picking.
The Basic Steps
To use the selection mechanism, you need to perform the following steps:
1. Specify the array to be used for the returned hit records with
glSelectBuffer().
2. Enter selection mode by specifying GL_SELECT with glRenderMode().
3. Initialize the name stack using glInitNames() and glPushName().
4. Define the viewing volume you want to use for selection. Usually this
is different from the viewing volume you originally used to draw the
scene, so you probably want to save and then restore the current
transformation state with glPushMatrix() and glPopMatrix().
5. Alternately issue primitive drawing commands and commands to
manipulate the name stack so that each primitive of interest is
assigned an appropriate name.
6. Exit selection mode and process the returned selection data (the hit
records).
The following two paragraphs describe glSelectBuffer() and glRenderMode().
In the next subsection, the commands for manipulating the name stack are
described.

608 Chapter 13: Selection and Feedback
Creating the Name Stack
As mentioned in the preceding subsection, the name stack forms the basis
for the selection information that’s returned to you. To create the name
stack, first initialize it with glInitNames(), which simply clears the stack,
and then add integer names to it while issuing corresponding drawing
commands. As you might expect, the commands to manipulate the stack
allow you to push a name onto it (glPushName()), pop a name off of it
(glPopName()), and replace the name at the top of the stack with a different
one (glLoadName()). Example 13-1 shows what your name-stack manipu-
lation code might look like with these commands.
void glSelectBuffer(GLsizei size, GLuint *buffer);
Specifies the array to be used for the returned selection data. The buffer
argument is a pointer to an array of unsigned integers into which the data
is put, and size indicates the maximum number of values that can be
stored in the array. You need to call glSelectBuffer() before entering
selection mode.
GLint glRenderMode(GLenum mode);
Controls whether the application is in rendering, selection, or feedback
mode. The mode argument can be GL_RENDER (the default), GL_
SELECT, or GL_FEEDBACK. The application remains in a given mode
until glRenderMode() is called again with a different argument. Before
selection mode is entered, glSelectBuffer() must be called to specify
the selection array. Similarly, before feedback mode is entered,
glFeedbackBuffer() must be called to specify the feedback array. The
return value for glRenderMode() has meaning if the current render
mode (that is, not the mode parameter) is either GL_SELECT or GL_
FEEDBACK. The return value is the number of selection hits or the
number of values placed in the feedback array when either mode is
exited; a negative value means that the selection or feedback array has
overflowed. You can use GL_RENDER_MODE with glGetIntegerv() to
obtain the current mode.
Compatibility
Extension
glSelectBuffer
glRenderMode
Selection 609
Example 13-1 Creating a Name Stack
glInitNames();
glPushName(0);
glPushMatrix(); /* save the current transformation state */
/* create your desired viewing volume here */
glLoadName(1);
drawSomeObject();
glLoadName(2);
drawAnotherObject();
glLoadName(3);
drawYetAnotherObject();
drawJustOneMoreObject();
glPopMatrix(); /* restore the previous transformation state*/
In this example, the first two objects to be drawn have their own names,
and the third and fourth objects share a single name. With this setup, if
either or both of the third and fourth objects cause a selection hit, only one
hit record is returned to you. You can have multiple objects share the same
name if you don’t need to differentiate between them when processing the
hit records.
void glInitNames(void);
Clears the name stack so that it’s empty.
void glPushName(GLuint name);
Pushes name onto the name stack. Pushing a name beyond the capacity
of the stack generates the error GL_STACK_OVERFLOW. The name
stack’s depth can vary among different OpenGL implementations, but
it must be able to contain at least 64 names. You can use the parameter
GL_NAME_STACK_DEPTH with glGetIntegerv() to obtain the depth of
the name stack.
void glPopName(void);
Pops one name off the top of the name stack. Popping an empty stack
generates the error GL_STACK_UNDERFLOW.
Compatibility
Extension
glInitNames
glPushName
glPopName
glLoadName
610 Chapter 13: Selection and Feedback
Calls to glPushName(),glPopName(), and glLoadName() are ignored if
you’re not in selection mode. You might find that it simplifies your code to
use these calls throughout your drawing code, and then use the same drawing
code for both selection and normal rendering modes.
The Hit Record
In selection mode, a primitive that intersects the viewing volume causes a
selection hit. Whenever a name-stack manipulation command is executed
or glRenderMode() is called, OpenGL writes a hit record into the selection
array if there’s been a hit since the last time the stack was manipulated or
glRenderMode() was called. With this process, objects that share the same
name—for example, an object composed of more than one primitive—
don’t generate multiple hit records. Also, hit records aren’t guaranteed to
be written into the array until glRenderMode() is called.
Note: In addition to geometric primitives, valid raster position coordinates
produced by glRasterPos() or glWindowPos() cause a selection hit.
Also, during selection mode, if culling is enabled and a polygon is
processed and culled, then no hit occurs.
Each hit record consists of the following four items, in the order shown:
• The number of names on the name stack when the hit occurred.
• Both the minimum and maximum window-coordinate z-values of all
vertices of the primitives that have intersected the viewing volume
since the last recorded hit. These two values, which lie in the range
[0, 1], are each multiplied by 232 1 and rounded to the nearest
unsigned integer.
• The contents of the name stack at the time of the hit, with the
bottommost element first.
void glLoadName(GLuint name);
Replaces the value at the top of the name stack with name. If the stack
is empty, which it is right after glInitNames() is called, glLoadName()
generates the error GL_INVALID_OPERATION. To avoid this, if the stack
is initially empty, call glPushName() at least once to put something on
the name stack before calling glLoadName().

Selection 611
When you enter selection mode, OpenGL initializes a pointer to the beginning
of the selection array. Each time a hit record is written into the array, the
pointer is updated accordingly. If writing a hit record would cause the
number of values in the array to exceed the size argument specified with
glSelectBuffer(), OpenGL writes as much of the record as will fit in the
array and sets an overflow flag. When you exit selection mode with
glRenderMode(), this command returns the number of hit records that
were written (including a partial record if there was one), clears the name
stack, resets the overflow flag, and resets the stack pointer. If the overflow
flag has been set, the return value is 1.
A Selection Example
In Example 13-2, four triangles (a green, a red, and two yellow triangles,
created by calling drawTriangle()) and a wireframe box representing the
viewing volume (drawViewVolume()) are drawn on the screen. Then
the triangles are rendered again (selectObjects()), but this time in selection
mode. The corresponding hit records are processed in processHits(), and
the selection array is printed out. The first triangle generates a hit, the
second one doesn’t, and the third and fourth ones together generate a
single hit.
Example 13-2 Selection Example: select.c
void drawTriangle(GLfloat x1, GLfloat y1, GLfloat x2,
GLfloat y2, GLfloat x3, GLfloat y3, GLfloat z)
{
glBegin(GL_TRIANGLES);
glVertex3f(x1, y1, z);
glVertex3f(x2, y2, z);
glVertex3f(x3, y3, z);
glEnd();
}
void drawViewVolume(GLfloat x1, GLfloat x2, GLfloat y1,
GLfloat y2, GLfloat z1, GLfloat z2)
{
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINE_LOOP);
glVertex3f(x1, y1, -z1);
glVertex3f(x2, y1, -z1);
glVertex3f(x2, y2, -z1);
glVertex3f(x1, y2, -z1);
glEnd();

612 Chapter 13: Selection and Feedback
glBegin(GL_LINE_LOOP);
glVertex3f(x1, y1, -z2);
glVertex3f(x2, y1, -z2);
glVertex3f(x2, y2, -z2);
glVertex3f(x1, y2, -z2);
glEnd();
glBegin(GL_LINES); /* 4 lines */
glVertex3f(x1, y1, -z1);
glVertex3f(x1, y1, -z2);
glVertex3f(x1, y2, -z1);
glVertex3f(x1, y2, -z2);
glVertex3f(x2, y1, -z1);
glVertex3f(x2, y1, -z2);
glVertex3f(x2, y2, -z1);
glVertex3f(x2, y2, -z2);
glEnd();
}
void drawScene(void)
{
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(40.0, 4.0/3.0, 1.0, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(7.5, 7.5, 12.5, 2.5, 2.5, -5.0, 0.0, 1.0, 0.0);
glColor3f(0.0, 1.0, 0.0); /* green triangle */
drawTriangle(2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -5.0);
glColor3f(1.0, 0.0, 0.0); /* red triangle */
drawTriangle(2.0, 7.0, 3.0, 7.0, 2.5, 8.0, -5.0);
glColor3f(1.0, 1.0, 0.0); /* yellow triangles */
drawTriangle(2.0, 2.0, 3.0, 2.0, 2.5, 3.0, 0.0);
drawTriangle(2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -10.0);
drawViewVolume(0.0, 5.0, 0.0, 5.0, 0.0, 10.0);
}
void processHits(GLint hits, GLuint buffer[])
{
unsigned int i, j;
GLuint names, *ptr;
printf(“hits = %d\n”, hits);
ptr = (GLuint *) buffer;

Selection 613
for (i = 0; i < hits; i++) { /* for each hit */
names = *ptr;
printf(“ number of names for hit = %d\n”, names); ptr++;
printf(“ z1 is %g;”, (float) *ptr/0x7fffffff); ptr++;
printf(“ z2 is %g\n”, (float) *ptr/0x7fffffff); ptr++;
printf(“ the name is “);
for (j = 0; j < names; j++) { /* for each name */
printf(“%d “, *ptr); ptr++;
}
printf(“\n”);
}
}
#define BUFSIZE 512
void selectObjects(void)
{
GLuint selectBuf[BUFSIZE];
GLint hits;
glSelectBuffer(BUFSIZE, selectBuf);
(void) glRenderMode(GL_SELECT);
glInitNames();
glPushName(0);
glPushMatrix();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0.0, 5.0, 0.0, 5.0, 0.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glLoadName(1);
drawTriangle(2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -5.0);
glLoadName(2);
drawTriangle(2.0, 7.0, 3.0, 7.0, 2.5, 8.0, -5.0);
glLoadName(3);
drawTriangle(2.0, 2.0, 3.0, 2.0, 2.5, 3.0, 0.0);
drawTriangle(2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -10.0);
glPopMatrix();
glFlush();
hits = glRenderMode(GL_RENDER);
processHits(hits, selectBuf);
}

614 Chapter 13: Selection and Feedback
void init(void)
{
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_FLAT);
}
void display(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
drawScene();
selectObjects();
glFlush();
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(200, 200);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Picking
As an extension of the process described in the preceding section, you can
use selection mode to determine if objects are picked. To do this, you use a
special picking matrix in conjunction with the projection matrix to restrict
drawing to a small region of the viewport, typically near the cursor. Then
you allow some form of input, such as clicking a mouse button, to initiate
selection mode. With selection mode established and with the special
picking matrix used, objects that are drawn near the cursor cause selection
hits. Thus, during picking, you’re typically determining which objects are
drawn near the cursor.

Selection 615
Picking is set up almost exactly the same as regular selection mode with the
following major differences:
• Picking is usually triggered by an input device. In the following code
examples, pressing the left mouse button invokes a function that
performs picking.
• You use the utility routine gluPickMatrix() to multiply the current
projection matrix by a special picking matrix. This routine should
be called prior to multiplying a standard projection matrix (such as
gluPerspective() or glOrtho()). You’ll probably want to save the
contents of the projection matrix first, so the sequence of operations
may look like this:
glMatrixMode(GL_PROJECTION);
glPushMatrix();
glLoadIdentity();
gluPickMatrix(...);
gluPerspective, glOrtho, gluOrtho2D, or glFrustum
/* ... draw scene for picking ; perform picking ... */
glPopMatrix();
Another completely different way to perform picking is described in
“Object Selection Using the Back Buffer” in Chapter 14. This technique uses
color values to identify different components of an object.
void gluPickMatrix(GLdouble x, GLdouble y, GLdouble width,
GLdouble height, GLint viewport[4]);
Creates a projection matrix that restricts drawing to a small region of
the viewport and multiplies that matrix onto the current matrix stack.
The center of the picking region is (x, y) in window coordinates, typically
the cursor location. width and height define the size of the picking region
in screen coordinates. (You can think of the width and height as the
sensitivity of the picking device.) viewport[] indicates the current viewport
boundaries, which can be obtained by calling
glGetIntegerv(GL_VIEWPORT, GLint *viewport);

616 Chapter 13: Selection and Feedback
Advanced
The net result of the matrix created by gluPickMatrix() transforms the
clipping region into the unit cube 1d (x,y,z)d 1 (or wd (wx,wy,wz)dw).
The picking matrix effectively performs an orthogonal transformation that
maps the clipping region to the unit cube. Since the transformation is
arbitrary, you can make picking work for different sorts of regions—for
example, for rotated rectangular portions of the window. In certain situations,
you might find it easier to specify additional clipping planes to define the
picking region.
Example 13-3 illustrates simple picking. It also demonstrates how to use
multiple names to identify different components of a primitive; in this case,
the row and column of a selected object. A 3 u3 grid of squares is drawn,
with each square a different color. The board[3][3] array maintains the
current amount of blue for each square. When the left mouse button is
pressed, the pickSquares() routine is called to identify which squares were
picked by the mouse. Two names identify each square in the grid—one
identifies the row, and the other the column. Also, when the left mouse
button is pressed, the colors of all squares under the cursor position change.
Example 13-3 Picking Example: picksquare.c
int board[3][3]; /* amount of color for each square */
/* Clear color value for every square on the board */
void init(void)
{
int i, j;
for (i = 0; i < 3; i++)
for (j = 0; j < 3; j ++)
board[i][j] = 0;
glClearColor(0.0, 0.0, 0.0, 0.0);
}
void drawSquares(GLenum mode)
{
GLuint i, j;
for (i = 0; i < 3; i++) {
if (mode == GL_SELECT)
glLoadName(i);
for (j = 0; j < 3; j ++) {
if (mode == GL_SELECT)
glPushName(j);
glColor3f((GLfloat) i/3.0, (GLfloat) j/3.0,
(GLfloat) board[i][j]/3.0);
Advanced

Selection 617
glRecti(i, j, i+1, j+1);
if (mode == GL_SELECT)
glPopName();
}
}
}
/* processHits prints out the contents of the
* selection array.
*/
void processHits(GLint hits, GLuint buffer[])
{
unsigned int i, j;
GLuint ii, jj, names, *ptr;
printf(“hits = %d\n”, hits);
ptr = (GLuint *) buffer;
for (i = 0; i < hits; i++) { /* for each hit */
names = *ptr;
printf(“ number of names for this hit = %d\n”, names);
ptr++;
printf(“ z1 is %g;”, (float) *ptr/0x7fffffff); ptr++;
printf(“ z2 is %g\n”, (float) *ptr/0x7fffffff); ptr++;
printf(“ names are “);
for (j = 0; j < names; j++) { /* for each name */
printf(“%d “, *ptr);
if (j == 0) /* set row and column */
ii = *ptr;
else if (j == 1)
jj = *ptr;
ptr++;
}
printf(“\n”);
board[ii][jj] = (board[ii][jj] + 1) % 3;
}
}
#define BUFSIZE 512
void pickSquares(int button, int state, int x, int y)
{
GLuint selectBuf[BUFSIZE];
GLint hits;
GLint viewport[4];

618 Chapter 13: Selection and Feedback
if (button != GLUT_LEFT_BUTTON || state != GLUT_DOWN)
return;
glGetIntegerv(GL_VIEWPORT, viewport);
glSelectBuffer(BUFSIZE, selectBuf);
(void) glRenderMode(GL_SELECT);
glInitNames();
glPushName(0);
glMatrixMode(GL_PROJECTION);
glPushMatrix();
glLoadIdentity();
/* create 5x5 pixel picking region near cursor location */
gluPickMatrix((GLdouble) x, (GLdouble) (viewport[3] - y),
5.0, 5.0, viewport);
gluOrtho2D(0.0, 3.0, 0.0, 3.0);
drawSquares(GL_SELECT);
glMatrixMode(GL_PROJECTION);
glPopMatrix();
glFlush();
hits = glRenderMode(GL_RENDER);
processHits(hits, selectBuf);
glutPostRedisplay();
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
drawSquares(GL_RENDER);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, 3.0, 0.0, 3.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
int main(int argc, char** argv)
{

Selection 619
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(100, 100);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutMouseFunc(pickSquares);
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Picking with Multiple Names and a Hierarchical Model
Multiple names can also be used to choose parts of a hierarchical object in
a scene. For example, if you were rendering an assembly line of automobiles,
you might want the user to move the mouse to pick the third bolt on the
left front wheel of the third car in line. A different name can be used to
identify each level of hierarchy: which car, which wheel, and finally which
bolt. As another example, one name can be used to describe a single molecule
among other molecules, and additional names can differentiate individual
atoms within that molecule.
Example 13-4 is a modification of Figure 3-4, which draws an automobile
with four identical wheels, each of which has five identical bolts. Code has
been added to manipulate the name stack with the object hierarchy.
Example 13-4 Creating Multiple Names
draw_wheel_and_bolts()
{
long i;
draw_wheel_body();
for (i = 0; i < 5; i++) {
glPushMatrix();
glRotate(72.0*i, 0.0, 0.0, 1.0);
glTranslatef(3.0, 0.0, 0.0);
glPushName(i);
draw_bolt_body();
glPopName();
glPopMatrix();
}
}

620 Chapter 13: Selection and Feedback
draw_body_and_wheel_and_bolts()
{
draw_car_body();
glPushMatrix();
glTranslate(40, 0, 20); /* first wheel position*/
glPushName(1); /* name of wheel number 1 */
draw_wheel_and_bolts();
glPopName();
glPopMatrix();
glPushMatrix();
glTranslate(40, 0, -20); /* second wheel position */
glPushName(2); /* name of wheel number 2 */
draw_wheel_and_bolts();
glPopName();
glPopMatrix();
/* draw last two wheels similarly */
}
Example 13-5 uses the routines in Example 13-4 to draw three different
cars, numbered 1, 2, and 3.
Example 13-5 Using Multiple Names
draw_three_cars()
{
glInitNames();
glPushMatrix();
translate_to_first_car_position();
glPushName(1);
draw_body_and_wheel_and_bolts();
glPopName();
glPopMatrix();
glPushMatrix();
translate_to_second_car_position();
glPushName(2);
draw_body_and_wheel_and_bolts();
glPopName();
glPopMatrix();
glPushMatrix();
translate_to_third_car_position();
glPushName(3);
draw_body_and_wheel_and_bolts();
glPopName();
glPopMatrix();
}

Selection 621
Assuming that picking is performed, the following are some possible name-
stack return values and their interpretations. In these examples, at most one
hit record is returned; also, d1 and d2 are depth values.
2d1 d2 2 1 Car 2, wheel 1
1d1 d2 3Car 3 body
3d1 d2 1 1 0 Bolt 0 on wheel 1 on car 1
empty The pick was outside all cars
The last interpretation assumes that the bolt and wheel don’t occupy the
same picking region. A user might well pick both the wheel and the bolt,
yielding two hits. If you receive multiple hits, you have to decide which hit
to process, perhaps by using the depth values to determine which picked
object is closest to the viewpoint. The use of depth values is explored further
in the next subsection.
Picking and Depth Values
Example 13-6 demonstrates how to use depth values when picking to
determine which object is picked. This program draws three overlapping
rectangles in normal rendering mode. When the left mouse button is
pressed, the pickRects() routine is called. This routine returns the cursor
position, enters selection mode, initializes the name stack, and multiplies
the picking matrix with the current orthographic projection matrix. A
selection hit occurs for each rectangle the cursor is over when the left mouse
button is clicked. Finally, the contents of the selection buffer are examined
to identify which named objects were within the picking region near the
cursor.
The rectangles in this program are drawn at different depth, or z-, values.
Since only one name is used to identify all three rectangles, only one hit can
be recorded. However, if more than one rectangle is picked, that single hit
has different minimum and maximum z-values.
Example 13-6 Picking with Depth Values: pickdepth.c
void init(void)
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_FLAT);
glDepthRange(0.0, 1.0); /* The default z mapping */
}

622 Chapter 13: Selection and Feedback
void drawRects(GLenum mode)
{
if (mode == GL_SELECT)
glLoadName(1);
glBegin(GL_QUADS);
glColor3f(1.0, 1.0, 0.0);
glVertex3i(2, 0, 0);
glVertex3i(2, 6, 0);
glVertex3i(6, 6, 0);
glVertex3i(6, 0, 0);
glEnd();
if (mode == GL_SELECT)
glLoadName(2);
glBegin(GL_QUADS);
glColor3f(0.0, 1.0, 1.0);
glVertex3i(3, 2, -1);
glVertex3i(3, 8, -1);
glVertex3i(8, 8, -1);
glVertex3i(8, 2, -1);
glEnd();
if (mode == GL_SELECT)
glLoadName(3);
glBegin(GL_QUADS);
glColor3f(1.0, 0.0, 1.0);
glVertex3i(0, 2, -2);
glVertex3i(0, 7, -2);
glVertex3i(5, 7, -2);
glVertex3i(5, 2, -2);
glEnd();
}
void processHits(GLint hits, GLuint buffer[])
{
unsigned int i, j;
GLuint names, *ptr;
printf(“hits = %d\n”, hits);
ptr = (GLuint *) buffer;
for (i = 0; i < hits; i++) { /* for each hit */
names = *ptr;
printf(“ number of names for hit = %d\n”, names); ptr++;
printf(“ z1 is %g;”, (float) *ptr/0x7fffffff); ptr++;

Selection 623
printf(“ z2 is %g\n”, (float) *ptr/0x7fffffff); ptr++;
printf(“ the name is “);
for (j = 0; j < names; j++) { /* for each name */
printf(“%d “, *ptr); ptr++;
}
printf(“\n”);
}
}
#define BUFSIZE 512
void pickRects(int button, int state, int x, int y)
{
GLuint selectBuf[BUFSIZE];
GLint hits;
GLint viewport[4];
if (button != GLUT_LEFT_BUTTON || state != GLUT_DOWN)
return;
glGetIntegerv(GL_VIEWPORT, viewport);
glSelectBuffer(BUFSIZE, selectBuf);
(void) glRenderMode(GL_SELECT);
glInitNames();
glPushName(0);
glMatrixMode(GL_PROJECTION);
glPushMatrix();
glLoadIdentity();
/* create 5x5 pixel picking region near cursor location */
gluPickMatrix((GLdouble) x, (GLdouble) (viewport[3] - y),
5.0, 5.0, viewport);
glOrtho(0.0, 8.0, 0.0, 8.0, -0.5, 2.5);
drawRects(GL_SELECT);
glPopMatrix();
glFlush();
hits = glRenderMode(GL_RENDER);
processHits(hits, selectBuf);
}
624 Chapter 13: Selection and Feedback
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
drawRects(GL_RENDER);
glFlush();
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei) w, (GLsizei) h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0.0, 8.0, 0.0, 8.0, -0.5, 2.5);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
int main(int argc, char **argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(200, 200);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutMouseFunc(pickRects);
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Try This
• Modify Example 13-6 to add additional calls to glPushName() so that
multiple names are on the stack when the selection hit occurs. What
will the contents of the selection buffer be?
•By default, glDepthRange() sets the mapping of the z-values to
[0.0, 1.0]. Try modifying the glDepthRange() values and see how these
modifications affect the z-values that are returned in the selection
array.
Try This

Selection 625
Hints for Writing a Program That Uses Selection
Most programs that allow a user to edit geometric objects interactively
provide a mechanism for the user to pick items or groups of items for
editing. For two-dimensional drawing programs (for example, text editors,
page-layout programs, and circuit-design programs), it might be easier to
do your own picking calculations instead of using the OpenGL picking
mechanism. Often, it’s easy to find bounding boxes for two-dimensional
objects and to organize them in some hierarchical data structure to speed
up searches. For example, picking that uses the OpenGL style in a VLSI
layout program containing millions of rectangles can be relatively slow.
However, using simple bounding-box information when rectangles are
typically aligned with the screen could make picking in such a program
extremely fast. The code is probably simpler to write, too.
As another example, since only geometric objects cause hits, you might
want to create your own method for picking text. Setting the current raster
position is a geometric operation, but it effectively creates only a single
pickable point at the current raster position, which is typically at the lower
left corner of the text. If your editor needs to manipulate individual
characters within a text string, some other picking mechanism must be
used. You could draw little rectangles around each character during picking
mode, but it’s almost certainly easier to handle text as a special case.
If you decide to use OpenGL picking, organize your program and its data
structures so that it’s easy to draw appropriate lists of objects in either selec-
tion or normal drawing mode. This way, when the user picks something,
you can use the same data structures for the pick operation that you use to
display the items on the screen. Also, consider whether you want to allow
the user to select multiple objects. One way to do this is to store a bit for
each item, indicating whether it’s selected (this method, however, requires
you to traverse your entire list of items to find the selected items). You
might find it useful to maintain a list of pointers to selected items to speed
up this search. It’s probably a good idea to keep the selection bit for each
item as well, because when you’re drawing the entire picture, you might
want to draw selected items differently (for example, in a different color or
within a selection box). Finally, consider the selection user interface. You
might want to allow the user to
• Select an item
• Sweep-select a group of items

626 Chapter 13: Selection and Feedback
• Add an item to the selection
• Add a sweep selection to the current selections
• Delete an item from a selection
• Choose a single item from a group of overlapping items
A typical solution for a two-dimensional drawing program might work as
follows:
1. All selection is done by pointing with the mouse cursor and using the
left mouse button. In the steps that follow, cursor means the cursor tied
to the mouse, and button means the left mouse button.
2. Clicking on an item selects it and deselects all other currently selected
items. If the cursor is on top of multiple items, the smallest is selected.
(In three dimensions, there are many other strategies for disambiguat-
ing a selection.)
3. Clicking down where there is no item, holding the button down while
dragging the cursor, and then releasing the button selects all the items
in a screen-aligned rectangle whose corners are determined by the cursor
positions when the button went down and where it came up. This is
called a sweep selection. All items not in the swept-out region are dese-
lected. (You must decide whether an item is selected only if it’s completely
within the sweep region, or if any part of it falls within the region. The
“completely within” strategy usually works best.)
4. If the Shift key is held down and the user clicks on an item that isn’t
currently selected, that item is added to the selected list. If the clicked-
on item is selected, it’s deleted from the selection list.
5. If a sweep selection is performed with the Shift key pressed, the items
swept out are added to the current selection.
6. In an extremely cluttered region, it’s often hard to do a sweep
selection. When the button goes down, the cursor might lie on top of
some item, and normally that item would be selected. You can make
any operation a sweep selection, but a typical user interface interprets a
button down on an item plus a mouse motion as a select-plus-drag
operation. To solve this problem, you can have an enforced sweep
selection by holding down, say, the Alt key. With this procedure, the
following set of operations constitutes a sweep selection: Alt button
down, sweep, button up. Items under the cursor when the button goes
down are ignored.

Feedback 627
7. If the Shift key is held during this sweep selection, the items enclosed
in the sweep region are added to the current selection.
8. Finally, if the user clicks on multiple items, select just one of them. If
the cursor isn’t moved (or maybe not moved more than a pixel), and
the user clicks again in the same place, deselect the item originally
selected, and select a different item under the cursor. Use repeated
clicks at the same point to cycle through all the possibilities.
Different rules can apply in particular situations. In a text editor, you
probably don’t have to worry about characters on top of each other, and
selections of multiple characters are always contiguous characters in the
document. Thus, you need to mark only the first and last selected characters
to identify the complete selection. With text, often the best way to handle
selection is to identify the positions between characters, rather than the
characters themselves. This allows you to have an empty selection when the
beginning and end of the selection are between the same pair of characters;
it also allows you to put the cursor before the first character in the
document or after the final one with no special-case code.
In a three-dimensional editor, you might provide ways to rotate and zoom
between selections, so sophisticated schemes for cycling through the
possible selections might be unnecessary. On the other hand, selection in
three dimensions is difficult because the cursor’s position on the screen
usually gives no indication of its depth.
Feedback
Feedback is similar to selection in that once you’re in either mode, no pixels
are produced and the screen is frozen. Drawing does not occur; instead,
information about primitives that would have been rendered is sent back to
the application. The key difference between selection and feedback modes
is the information that is sent back. In selection mode, assigned names are
returned to an array of integer values. In feedback mode, information about
transformed primitives is sent back to an array of floating-point values.
The values sent back to the feedback array consist of tokens that specify
what type of primitive (point, line, polygon, image, or bitmap) has been
processed and transformed, followed by vertex, color, or other data for
that primitive. The values returned are fully transformed by lighting and
viewing operations. Feedback mode is initiated by calling glRenderMode()
with GL_FEEDBACK as the argument.
628 Chapter 13: Selection and Feedback
Here’s how you enter and exit feedback mode:
1. Call glFeedbackBuffer() to specify the array to hold the feedback
information. The arguments for this command describe what type of
data and how much of it is written into the array.
2. Call glRenderMode() with GL_FEEDBACK as the argument to enter
feedback mode. (For this step, you can ignore the value returned by
glRenderMode().) After this point, primitives aren’t rasterized to
produce pixels until you exit feedback mode, and the contents of the
framebuffer don’t change.
3. Draw your primitives. While issuing drawing commands, you can
make several calls to glPassThrough() to insert markers into the
returned feedback data and thus facilitate parsing.
4. Exit feedback mode by calling glRenderMode() with GL_RENDER as
the argument if you want to return to normal drawing mode. The
integer value returned by glRenderMode() is the number of values
stored in the feedback array.
5. Parse the data in the feedback array.
void glFeedbackBuffer(GLsizei size, GLenum type, GLfloat *buffer);
Establishes a buffer for the feedback data: buffer is a pointer to an array
where the data is stored. The size argument indicates the maximum
number of values that can be stored in the array. The type argument
describes the information fed back for each vertex in the feedback
array; its possible values and their meanings are shown in Table 13-1.
glFeedbackBuffer() must be called before feedback mode is entered. In
the table, k is 1 in color-index mode and 4 in RGBA mode.
type Argument Coordinates Color Texture Total Values
GL_2D x,y-- 2
GL_3D x,y,z-- 3
GL_3D_COLOR x,y,zk-3 + k
GL_3D_COLOR_TEXTURE x,y,zk47 + k
GL_4D_COLOR_TEXTURE x,y,z,wk48 + k
Table 13-1 glFeedbackBuffer() type Values
Compatibility
Extension
glFeedbackBuffer
and all associated
tokens

Feedback 629
Note: When multitexturing is supported, feedback returns only the texture
coordinates of texture unit 0.
The Feedback Array
In feedback mode, each primitive that would be rasterized (or each call to
glBitmap(),glDrawPixels(), or glCopyPixels(), if the raster position is
valid) generates a block of values that’s copied into the feedback array. The
number of values is determined by the type argument of glFeedbackBuffer(),
as listed in Table 13-1. Use the appropriate value for the type of primitives
you’re drawing: GL_2D or GL_3D for unlit two- or three-dimensional prim-
itives; GL_3D_COLOR for lit, three-dimensional primitives; and GL_3D_
COLOR_TEXTURE or GL_4D_COLOR_TEXTURE for lit, textured, three- or
four-dimensional primitives.
Each block of feedback values begins with a code indicating the primitive
type, followed by values that describe the primitive’s vertices and associated
data. Entries are also written for pixel rectangles. In addition, pass-through
markers that you’ve explicitly created can be returned in the array; the next
subsection explains these markers in more detail. Table 13-2 shows the syntax
for the feedback array; remember that the data associated with each returned
vertex is as described in Table 13-1. Note that a polygon can have n vertices
returned. Also, the x-, y-, and z-coordinates returned by feedback are win-
dow coordinates; if w is returned, it’s in clip coordinates. For bitmaps and
pixel rectangles, the coordinates returned are those of the current raster
position. In Table 13-2, note that GL_LINE_RESET_TOKEN is returned only
when the line stipple is reset for that line segment.
Primitive Type Code Associated Data
Point GL_POINT_TOKEN vertex
Line GL_LINE_TOKEN or GL_LINE_
RESET_TOKEN
vertex vertex
Polygon GL_POLYGON_TOKEN n vertex vertex ... vertex
Bitmap GL_BITMAP_TOKEN vertex
Pixel Rectangle GL_DRAW_PIXEL_TOKEN or
GL_COPY_PIXEL_TOKEN
vertex
Pass-through GL_PASS_THROUGH_TOKEN a floating-point number
Table 13-2 Feedback Array Syntax

630 Chapter 13: Selection and Feedback
Using Markers in Feedback Mode
Feedback occurs after transformations, lighting, polygon culling, and
interpretation of polygons by glPolygonMode(). It might also occur after
polygons with more than three edges are broken up into triangles (if your
particular OpenGL implementation renders polygons by performing this
decomposition). Thus, it might be hard for you to recognize the primitives
you drew in the feedback data you receive. To help parse the feedback data,
call glPassThrough() as needed in your sequence of drawing commands to
insert a marker. You might use the markers to separate the feedback values
returned from different primitives, for example. This command causes
GL_PASS_THROUGH_TOKEN to be written into the feedback array,
followed by the floating-point value you pass in as an argument.
A Feedback Example
Example 13-7 demonstrates the use of feedback mode. This program draws
a lit, three-dimensional scene in normal rendering mode. Then, feedback
mode is entered, and the scene is redrawn. Since the program draws lit,
untextured, three-dimensional objects, the type of feedback data is GL_3D_
COLOR. Since RGBA mode is used, each unclipped vertex generates seven
values for the feedback buffer: x, y, z, r, g, b, and a.
In feedback mode, the program draws two lines as part of a line strip and
then inserts a pass-through marker. Next, a point is drawn at (100.0,
100.0, 100.0), which falls outside the orthographic viewing volume and
thus doesn’t put any values into the feedback array. Finally, another pass-
through marker is inserted, and another point is drawn.
void glPassThrough(GLfloat token);
Inserts a marker into the stream of values written into the feedback array,
if called in feedback mode. The marker consists of the code GL_PASS_
THROUGH_TOKEN followed by a single floating-point value, token. This
command has no effect when called outside of feedback mode. Calling
glPassThrough() between glBegin() and glEnd() generates a GL_
INVALID_OPERATION error.
Compatibility
Extension
glPassThrough

Feedback 631
Example 13-7 Feedback Mode: feedback.c
void init(void)
{
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
}
void drawGeometry(GLenum mode)
{
glBegin(GL_LINE_STRIP);
glNormal3f(0.0, 0.0, 1.0);
glVertex3f(30.0, 30.0, 0.0);
glVertex3f(50.0, 60.0, 0.0);
glVertex3f(70.0, 40.0, 0.0);
glEnd();
if (mode == GL_FEEDBACK)
glPassThrough(1.0);
glBegin(GL_POINTS);
glVertex3f(-100.0, -100.0, -100.0); /* will be clipped */
glEnd();
if (mode == GL_FEEDBACK)
glPassThrough(2.0);
glBegin(GL_POINTS);
glNormal3f(0.0, 0.0, 1.0);
glVertex3f(50.0, 50.0, 0.0);
glEnd();
glFlush();
}
void print3DcolorVertex(GLint size, GLint *count,
GLfloat *buffer)
{
int i;
printf(“ “);
for (i = 0; i < 7; i++) {
printf(“%4.2f “, buffer[size-(*count)]);
*count = *count - 1;
}
printf(“\n”);
}

632 Chapter 13: Selection and Feedback
void printBuffer(GLint size, GLfloat *buffer)
{
GLint count;
GLfloat token;
count = size;
while (count) {
token = buffer[size-count]; count--;
if (token == GL_PASS_THROUGH_TOKEN) {
printf(“GL_PASS_THROUGH_TOKEN\n”);
printf(“ %4.2f\n”, buffer[size-count]);
count--;
}
else if (token == GL_POINT_TOKEN) {
printf(“GL_POINT_TOKEN\n”);
print3DcolorVertex(size, &count, buffer);
}
else if (token == GL_LINE_TOKEN) {
printf(“GL_LINE_TOKEN\n”);
print3DcolorVertex(size, &count, buffer);
print3DcolorVertex(size, &count, buffer);
}
else if (token == GL_LINE_RESET_TOKEN) {
printf(“GL_LINE_RESET_TOKEN\n”);
print3DcolorVertex(size, &count, buffer);
print3DcolorVertex(size, &count, buffer);
}
}
}
void display(void)
{
GLfloat feedBuffer[1024];
GLint size;
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0.0, 100.0, 0.0, 100.0, 0.0, 1.0);
glClearColor(0.0, 0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
drawGeometry(GL_RENDER);
glFeedbackBuffer(1024, GL_3D_COLOR, feedBuffer);
(void) glRenderMode(GL_FEEDBACK);
drawGeometry(GL_FEEDBACK);

Feedback 633
size = glRenderMode(GL_RENDER);
printBuffer(size, feedBuffer);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(100, 100);
glutInitWindowPosition(100, 100);
glutCreateWindow(argv[0]);
init();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Running this program generates the following output:
GL_LINE_RESET_TOKEN
30.00 30.00 0.00 0.84 0.84 0.84 1.00
50.00 60.00 0.00 0.84 0.84 0.84 1.00
GL_LINE_TOKEN
50.00 60.00 0.00 0.84 0.84 0.84 1.00
70.00 40.00 0.00 0.84 0.84 0.84 1.00
GL_PASS_THROUGH_TOKEN
1.00
GL_PASS_THROUGH_TOKEN
2.00
GL_POINT_TOKEN
50.00 50.00 0.00 0.84 0.84 0.84 1.00
Thus, the line strip drawn with these commands results in two primitives:
glBegin(GL_LINE_STRIP);
glNormal3f(0.0, 0.0, 1.0);
glVertex3f(30.0, 30.0, 0.0);
glVertex3f(50.0, 60.0, 0.0);
glVertex3f(70.0, 40.0, 0.0);
glEnd();
The first primitive begins with GL_LINE_RESET_TOKEN, which indicates
that the primitive is a line segment and that the line stipple is reset. The
second primitive begins with GL_LINE_TOKEN, so it’s also a line segment,
but the line stipple isn’t reset and hence continues from where the previous
line segment left off. Each of the two vertices for these lines generates seven
values for the feedback array. Note that the RGBA values for all four vertices

634 Chapter 13: Selection and Feedback
in these two lines are (0.84, 0.84, 0.84, 1.0), which is a very light gray color
with the maximum alpha value. These color values are a result of the
interaction of the surface normal and lighting parameters.
Since no feedback data is generated between the first and second pass-
through markers, you can deduce that any primitives drawn between the
first two calls to glPassThrough() were clipped out of the viewing volume.
Finally, the point at (50.0, 50.0, 0.0) is drawn, and its associated data is
copied into the feedback array.
Note: In both feedback and selection modes, information about objects is
returned prior to any fragment tests. Thus, objects that would not be
drawn due to failure of the scissor, alpha, depth, or stencil test may
still have their data processed and returned in both feedback and
selection modes.
Try This
Make changes in Example 13-7 to see how they affect the feedback values
that are returned. For example, change the coordinate values of glOrtho().
Change the lighting variables, or eliminate lighting altogether and change
the feedback type to GL_3D. Or, add more primitives to see what other
geometric objects (such as filled polygons) contribute to the feedback array.
Try This

635
Chapter 14
14.Now That You Know
Chapter Objectives
This chapter doesn’t have objectives in the same way that previous chapters
do. It’s simply a collection of topics that describe ideas you might find
useful for your application. Some topics, such as error handling, don’t fit
into other categories, but are too short for an entire chapter.
OpenGL is a collection of low-level tools; now that you know about those
tools, you can use them to implement higher-level functions. This chapter
presents several examples of such higher-level capabilities.

636 Chapter 14: Now That You Know
This chapter discusses a variety of techniques based on OpenGL commands
that illustrate some of the not-so-obvious uses to which you can put these
commands. The examples presented are in no particular order and aren’t
related to each other. The idea is to read the section headings and skip to
the examples that you find interesting. For your convenience, the headings
are listed and explained briefly here.
Note: Most of the examples in the rest of this guide are complete and can
be compiled and run as is. In this chapter, however, there are no
complete programs, and you have to do a bit of work on your own to
make them run.
• “Error Handling” tells you how to check for OpenGL error conditions.
• “Which Version Am I Using?” describes how to find out details about
your implementation, including the version number. This can be
useful for writing applications that can run on earlier versions of
OpenGL.
• “Extensions to the Standard” presents techniques for identifying and
using extensions (which are either specific to a vendor or approved by
the Khronos OpenGL ARB Working Group) to the OpenGL standard.
• “Cheesy Translucency” explains how to use polygon stippling to
achieve translucency; this is particularly useful when no blending
hardware is available.
• “An Easy Fade Effect” shows how to use polygon stippling to create the
effect of a fade into the background.
• “Object Selection Using the Back Buffer” describes how to use the back
buffer in a double-buffered system to handle simple object picking.
• “Cheap Image Transformation” discusses how to draw a distorted
version of a bitmapped image by drawing each pixel as a quadrilateral.
• “Displaying Layers” explains how to display multiple layers of different
materials and indicate where the materials overlap.
• “Antialiased Characters” describes how to draw smoother fonts.
• “Drawing Round Points” describes how to draw near-round points.
• “Interpolating Images” shows how to blend smoothly from one image
to another.
• “Making Decals” explains how to draw two images, where one is a sort
of decal that should always appear on top of the other.

Error Handling 637
• “Drawing Filled, Concave Polygons Using the Stencil Buffer” tells you
how to draw concave polygons, nonsimple polygons, and polygons
with holes by using the stencil buffer.
• “Finding Interference Regions” describes how to determine where
three-dimensional pieces overlap.
• “Shadows” describes how to draw shadows of lit objects.
• “Hidden-Line Removal” discusses how to draw a wireframe object with
hidden lines removed by using the stencil buffer.
• “Texture Mapping Applications” describes several clever uses for tex-
ture mapping, such as rotating and warping images.
• “Drawing Depth-Buffered Images” tells you how to combine images in
a depth-buffered environment.
• “Dirichlet Domains” explains how to find the Dirichlet domain of a set
of points using the depth buffer.
• “Life in the Stencil Buffer” explains how to implement the Game of
Life using the stencil buffer.
• “Alternative Uses for glDrawPixels() and glCopyPixels()” describes how
to use these two commands for such effects as fake video, airbrushing,
and transposed images.
Error Handling
The truth is, your program will make mistakes. Use of error-handling
routines is essential during development and is highly recommended for
commercially released applications (unless you can give a 100 percent
guarantee your program will never generate an OpenGL error condition.
Get real!). OpenGL has simple error-handling routines for the base GL and
GLU libraries.
When OpenGL detects an error (in either the base GL or GLU), it records a
current error code. The command that caused the error is ignored, so it has
no effect on the OpenGL state or on the framebuffer contents. (If the error
recorded was GL_OUT_OF_MEMORY, however, the results of the command
are undefined.) Once recorded, the current error code isn’t cleared—that
is, additional errors aren’t recorded—until you call the query command
glGetError(), which returns the current error code. After you’ve queried
and cleared the current error code, or if there’s no error to begin with,
glGetError() returns GL_NO_ERROR.

638 Chapter 14: Now That You Know
It is strongly recommended that you call glGetError() at least once in each
display() routine. Table 14-1 lists the basic defined OpenGL error codes.
There are also 37 GLU NURBS errors (with nondescriptive constant names,
GLU_NURBS_ERROR1, GLU_NURBS_ERROR2, and so on); 14 tessellator
errors (GLU_TESS_MISSING_BEGIN_POLYGON, GLU_TESS_MISSING_
END_POLYGON, GLU_TESS_MISSING_BEGIN_CONTOUR, GLU_TESS_
MISSING_END_CONTOUR, GLU_TESS_COORD_TOO_LARGE, GLU_TESS_
NEED_COMBINE_CALLBACK, along with eight errors generically named
GLU_TESS_ERROR*); and GLU_INCOMPATIBLE_GL_VERSION. Also, the
GLU defines the error codes GLU_INVALID_ENUM, GLU_INVALID_VALUE,
and GLU_OUT_OF_MEMORY, which have the same meanings as the related
OpenGL codes.
GLenum glGetError(void);
Returns the value of the error flag. When an error occurs in either the GL
or the GLU, the error flag is set to the appropriate error code value. If
GL_NO_ERROR is returned, there has been no detectable error since the
last call to glGetError() or since the GL was initialized. No other errors are
recorded until glGetError() is called, the error code is returned, and the
flag is reset to GL_NO_ERROR.
Error Code Description
GL_INVALID_ENUM GLenum argument out of range
GL_INVALID_VALUE numeric argument out of range
GL_INVALID_OPERATION operation illegal in current state
GL_INVALID_FRAMEBUFFER_
OPERATION
framebuffer object is not complete
GL_STACK_OVERFLOW command would cause a stack overflow
GL_STACK_UNDERFLOW command would cause a stack underflow
GL_OUT_OF_MEMORY not enough memory left to execute command
GL_TABLE_TOO_LARGE specified table is too large
Table 14-1 OpenGL Error Codes

Which Version Am I Using? 639
To obtain a printable, descriptive string corresponding to either a GL or
GLU error code, use the GLU routine gluErrorString().
In Example 14-1, a simple error-handling routine is shown.
Example 14-1 Querying and Printing an Error
GLenum errCode;
const GLubyte *errString;
while ((errCode = glGetError()) != GL_NO_ERROR) {
errString = gluErrorString(errCode);
fprintf (stderr, “OpenGL Error: %s\n”, errString);
}
Note: The string returned by gluErrorString() must not be altered or freed
by the application.
Which Version Am I Using?
The portability of OpenGL applications is one of OpenGL’s attractive fea-
tures. However, new versions of OpenGL introduce new features, and if you
use new features, you may have problems running your code on older ver-
sions of OpenGL. In addition, you may want your application to perform
equally well on a variety of implementations. For example, you might make
texture mapping the default rendering mode on one machine, but have
only flat shading on another. You can use glGetString() to obtain release
information about your OpenGL implementation.
const GLubyte* gluErrorString(GLenum errorCode);
Returns a pointer to a descriptive string that corresponds to the OpenGL
or GLU error number passed in errorCode.
const GLubyte* glGetString(GLenum name);
Returns a pointer to a string that describes an aspect of the OpenGL
implementation. name can be one of the following: GL_VENDOR,
GL_RENDERER, GL_VERSION, GL_SHADING_LANGUAGE_VERSION,
or GL_EXTENSIONS.
Compatibility
Extension
GL_EXTENSIONS

640 Chapter 14: Now That You Know
GL_VENDOR returns the name of the company responsible for the OpenGL
implementation. GL_RENDERER returns an identifier of the renderer,
which is usually the hardware platform. For more about GL_EXTENSIONS,
see the section “Extensions to the Standard.”
GL_VERSION and GL_SHADING_LANGUAGE_VERSION return a string
that identifies the version number of your implementation of OpenGL. The
version string is laid out as follows:
<version number><space><vendor-specific information>
The version number is of the form
major_number.minor_number
or
major_number.minor_number.release_number
where the numbers all have one or more digits. The vendor-specific infor-
mation is optional. For example, if this OpenGL implementation is from
the fictitious XYZ Corporation, the string returned might be
1.2.4 XYZ-OS 3.2
which means that this implementation is XYZ’s fourth release of an OpenGL
library that conforms to the specification for OpenGL Version 1.2. It prob-
ably also means that this is release 3.2 of XYZ’s proprietary operating
system.
At runtime, another way to query the OpenGL version is to call
glGetIntegerv() with GL_MAJOR_VERSION and GL_MINOR_VERSION,
which will return the major and minor nubmer, respectively, as in would be
returned in string form from glGetString(). At compile time, you can use the
preprocessor statement #ifdef to look for the symbolic constants named
GL_VERSION_m_n, where m, and n corresponed to the major- and minor-
version numbers. For example, the preprocessor token GL_VERSION_3_0,
represent OpenGL version 3.0. If a particular token is present, that indicates
that all versions up to, and including that version are available—at least for
compilation. You should always check the version and extension strings at
runtime to make sure the functionality you need is present in the imple-
mentation that you’re using..
Note: If running from client to server, such as when performing indirect
rendering with the OpenGL extension to the X Window System, the
client and server may be different versions. If your client version is
ahead of your server, your client might request an operation that is
not supported on your server.

Extensions to the Standard 641
Utility Library Version
gluGetString() is a query function for the Utility Library (GLU) and is
similar to glGetString().
Note that gluGetString() was not available in GLU 1.0. Another way to
query the GLU version number is to look for the symbolic constant
GLU_VERSION_1_3. The absence of the constant GLU_VERSION_1_3
means that you have GLU 1.2 or an earlier version. The same principle is
true for constants GLU_VERSION_1_1 and GLU_VERSION_1_2.
Also note that GLU extensions are different from OpenGL extensions.
Window System Extension Versions
For window system extensions for OpenGL, such as GLX, WGL, PGL, and
AGL, there are similar routines (such as glXQueryExtensionString()) for
querying version information. See Appendix D for more information.
(The aforementioned glXQueryExtensionString() and related routines
were introduced with GLX 1.1 and are not supported with GLX 1.0.)
Extensions to the Standard
OpenGL has a formal written specification that describes the operations
that comprise the library. An individual vendor or a group of vendors may
decide to add additional functionality to their released implementation.
Function and symbolic constant names clearly indicate whether a feature is
part of the OpenGL standard, a vendor-specific extension, or an OpenGL
extension approved by the Khronos OpenGL ARB Working Group.
To make a vendor-specific name, the vendor appends a company identifier
(in uppercase) and, if needed, additional information, such as a machine
name. For example, if XYZ Corporation wants to add a new function and
symbolic constant, they might be of the form glCommandXYZ() and
GL_DEFINITION_XYZ. If XYZ Corporation wants to have an extension
const GLubyte* gluGetString(GLenum name);
Returns a pointer to a string that describes an aspect of the OpenGL
implementation. name can be GLU_VERSION or GLU_EXTENSIONS.

642 Chapter 14: Now That You Know
that is available only on its FooBar graphics board, the names might be
glCommandXYZfb() and GL_DEFINITION_XYZ_FB.
If two or more vendors agree to implement the same extension, then
the functions and constants are suffixed with the more generic EXT
(glCommandEXT() and GL_DEFINITION_EXT).
Similarly, if the OpenGL ARB approves an extension, the functions
and constants are suffixed with ARB (glCommandARB() and
GL_DEFINITION_ARB).
Determining Supported Extensions
There are a number of ways of determining which extensions are supported
on your OpenGL implementation:
• If your OpenGL version is less than 3.0, call glGetString(GL_
EXTENSIONS), which returns a space-separated list of every extension
supported by your implementation.
• To see whether a particular extension is supported, if you have GLU 1.3
or greater, you can call gluCheckExtension(), which returns a Boolean
value indicating support for that extension.
• If you are using OpenGL Version 3.0 or later, you can call
glGetStringi(), which returns a single string corresponding to the
extension string associated with the index provided.
GLboolean gluCheckExtension(char *extName,
const GLubyte *extString);
Returns GL_TRUE if extName is found in extString, or GL_FALSE if it isn’t.
const GLubyte *glGetStringi(GLenum target, GLuint index);
Returns the string associated with index for the indexed state target.
target must be GL_EXTENSIONS. index must be a value between zero and
GL_NUM_EXTENSIONS-1, as queried by glGetIntegerv().
There is no specified ordering of extension strings; the order may vary
across OpenGL implementations, or across different contexts within a
single implementation.
A GL_INVALID_VALUE error is generated if index is less than zero, or
greater than or equal to GL_NUM_EXTENSIONS.

Extensions to the Standard 643
Note: In OpenGL Version 3.1, glGetString() will no longer accept
GL_EXTENSIONS. You must use glGetStringi() to obtain the list
of extensions.
If you are using the GLEW library for managing extensions, it provides a
convenient mechanism for verifying extensions: It defines a Boolean
variable with a name identical to the extension string entry (e.g.,
“GL_ARB_multitexture”).
If you have GLU 1.3, you can use gluCheckExtension() to see whether a
specified extension is supported.
gluCheckExtension() can check OpenGL and GLX extension strings, as
well as GLU extension strings.
Prior to GLU 1.3, to find out if a specific extension is supported, use the
code in Example 14-2 to search through the list and match the extension
name. QueryExtension() returns GL_TRUE if the string is found, or
GL_FALSE if it isn’t.
Example 14-2 Determining if an Extension Is Supported (Prior to GLU 1.3)
static GLboolean QueryExtension(char *extName)
{
char *p = (char *) glGetString(GL_EXTENSIONS);
char *end;
if (p == NULL)
return GL_FALSE;
end = p + strlen(p);
while (p < end) {
int n = strcspn(p, “ “);
if ((strlen(extName)==n) && (strncmp(extName,p,n)==0)) {
return GL_TRUE;
}
p += (n + 1);
}
return GL_FALSE;
}
Extensions to the Standard for Microsoft Windows (WGL)
If you need access to an extension function on a Microsoft Windows
platform, you should
• Create conditional code based on the symbolic constant, which
identifies the extension.

644 Chapter 14: Now That You Know
• Query the previously discussed extension string at run-time.
•Use wglGetProcAddress() to locate the pointer to the extension
function.
Example 14-3 demonstrates how to find a fictitious extension named
glSpecialEXT(). Note that the conditional code (#ifdef) verifies the
definition of GL_EXT_special. If the extension is available, a data type (in
this case, PFNGLSPECIALEXTPROC) is specifically defined for the function
pointer. Finally, wglGetProcAddress() obtains the function pointer.
Example 14-3 Locating an OpenGL Extension with wglGetProcAddress()
#ifdef GL_EXT_special
PFNGLSPECIALEXTPROC glSpecialEXT;
#endif
/* somewhere later in the code */
#ifdef GL_EXT_special
glSpecialEXT = (PFNGLSPECIALEXTPROC)
wglGetProcAddress("glSpecialEXT");
assert(glSpecialEXT != NULL);
#endif
Cheesy Translucency
You can use polygon stippling to simulate a translucent material. This is
an especially good solution for systems that don’t have blending hard-
ware. Since polygon stipple patterns are 32 u32 bits, or 1024 bits, you can
go from opaque to transparent in 1023 steps. (In practice, that’s many
more steps than you need.) For example, if you want a surface that lets
through 29 percent of the light, simply make up a stipple pattern in which
29 percent (roughly 297) of the pixels in the mask are 0 and the rest are 1.
Even if your surfaces have the same translucency, don’t use the same stip-
ple pattern for each one, because they cover exactly the same bits on the
screen. Make up a different pattern for each surface by randomly selecting
the appropriate number of pixels to be 0. (See “Displaying Points, Lines,
and Polygons” in Chapter 2 for more information about polygon
stippling.)
If you don’t like the effect with random pixels turned on, you can use reg-
ular patterns, but they don’t work as well when transparent surfaces are

An Easy Fade Effect 645
stacked. This is often not a problem, because most scenes have relatively
few translucent regions that overlap. In a picture of an automobile with
translucent windows, your line of sight can go through at most two win-
dows, and usually it’s only one.
An Easy Fade Effect
Suppose you have an image that you want to fade gradually to some back-
ground color. Define a series of polygon stipple patterns, each of which has
more bits turned on so that they represent denser and denser patterns. Then
use these patterns repeatedly with a polygon large enough to cover the
region over which you want to fade. For example, suppose you want to fade
to black in 16 steps. First define 16 different pattern arrays:
GLubyte stips[16][4*32];
Then load them in such a way that each has one-sixteenth of the pixels in
a 32 u32 stipple pattern turned on and that the bitwise OR of all the stipple
patterns is all 1’s. After that, the following code does the trick:
draw_the_picture();
glColor3f(0.0, 0.0, 0.0); /* set color to black */
for (i = 0; i < 16; i++) {
glPolygonStipple(&stips[i][0]);
draw_a_polygon_large_enough_to_cover_the_whole_region();
}
In some OpenGL implementations, you might get better performance by
first compiling the stipple patterns into display lists. During your initializa-
tion, do something like this:
#define STIP_OFFSET 100
for (i = 0; i < 16; i++) {
glNewList(i+STIP_OFFSET, GL_COMPILE);
glPolygonStipple(&stips[i][0]);
glEndList();
}
Then, replace this line in the first code fragment
glPolygonStipple(&stips[i][0]);
with
glCallList(i);

646 Chapter 14: Now That You Know
By compiling the command to set the stipple into a display list, OpenGL
might be able to rearrange the data in the stips[ ][ ] array into the hardware-
specific form required for maximum stipple-setting speed.
Another application for this technique is if you’re drawing a changing
picture and want to leave some blur behind that gradually fades out to give
some indication of past motion. For example, suppose you’re simulating a
planetary system and you want to leave trails on the planets to show recent
portions of their paths. Again, assuming you want to fade in 16 steps, set up
the stipple patterns as before (using the display-list version, say), and have
the main simulation loop look something like this:
current_stipple = 0;
while (1) { /* loop forever */
draw_the_next_frame();
glCallList(current_stipple++);
if (current_stipple == 16) current_stipple = 0;
glColor3f(0.0, 0.0, 0.0); /* set color to black */
draw_a_polygon_large_enough_to_cover_the_whole_region();
}
Each time through the loop, you clear one-sixteenth of the pixels. Any pixel
that hasn’t had a planet on it for 16 frames is certain to be cleared to black.
Of course, if your system supports blending in hardware, it’s easier to blend
in a certain amount of background color with each frame. (See “Displaying
Points, Lines, and Polygons” in Chapter 2 for polygon stippling details,
Chapter 7 for more information about display lists, and “Blending” in
Chapter 6 for information about blending.)
Object Selection Using the Back Buffer
Although the OpenGL selection mechanism (see “Selection” in Chapter 13)
is powerful and flexible, it can be cumbersome to use. Often, the situation
is simple: Your application draws a scene composed of a substantial number
of objects; the user points to an object with the mouse, and the application
needs to find the item under the tip of the cursor.
One way to do this requires your application to be running in double-buffer
mode. When the user picks an object, the application redraws the entire
scene in the back buffer, but instead of using the normal colors for objects,
it encodes some kind of object identifier for each object’s color. The appli-
cation then simply reads the pixel under the cursor, and the value of that
pixel encodes the number of the picked object. If many picks are expected

Cheap Image Transformation 647
for a single, static picture, you can read the entire color buffer once and
look in your copy for each attempted pick, rather than read each pixel
individually.
Note that this scheme has an advantage over standard selection in that it
picks the object that’s in front if multiple objects appear at the same pixel,
one behind the other. Since the image with false colors is drawn in the
back buffer, the user never sees it; you can redraw the back buffer (or copy
it from the front buffer) before swapping the buffers. In color-index mode,
the encoding is simple: Send the object identifier as the index. In RGBA
mode, encode the bits of the identifier into the R, G, and B components.
Be aware that you can run out of identifiers if there are too many objects
in the scene. For example, suppose you’re running in color-index mode on
a system that has 4-bit buffers for color-index information (16 possible dif-
ferent indices) in each of the color buffers, but the scene has thousands of
pickable items. To address this issue, the picking can be done in a few
passes. To think about this in concrete terms, assume there are fewer than
4096 items, so all the object identifiers can be encoded in 12 bits. In the
first pass, draw the scene using indices composed of the 4 high-order bits,
and then use the second and third passes to draw the middle 4 bits and
the 4 low-order bits. After each pass, read the pixel under the cursor,
extract the bits, and pack them together at the end to get the object
identifier.
With this method, the picking takes three times as long, but that’s often
acceptable. Note that after you have the 4 high-order bits, you eliminate
15/16 of all objects, so you really need to draw only 1/16 of them for the
second pass. Similarly, after the second pass, 255 of the 256 possible items
have been eliminated. The first pass thus takes about as long as drawing a
single frame does, but the second and third passes can be up to 16 and
256 times as fast.
If you’re trying to write portable code that works on different systems,
break up your object identifiers into chunks that fit on the lowest
common denominator of those systems. Also, keep in mind that your
system might perform automatic dithering in RGB mode. If this is the
case, turn off dithering.
Cheap Image Transformation
If you want to draw a distorted version of a bitmapped image (perhaps
simply stretched or rotated, or perhaps drastically modified by some

648 Chapter 14: Now That You Know
mathematical function), there are many possibilities. You can use the image
as a texture map, which allows you to scale, rotate, or otherwise distort the
image. If you just want to scale the image, you can use glPixelZoom().
In many cases, you can achieve good results by drawing the image of each
pixel as a quadrilateral. Although this scheme doesn’t produce images as
nice as those you would get by applying a sophisticated filtering algorithm
(and it might not be sufficient for sophisticated users), it’s a lot quicker.
To make the problem more concrete, assume that the original image is m
pixels by n pixels, with coordinates chosen from [0, m 1] u [0, n 1]. Let
the distortion functions be x(m, n) and y(m, n). For example, if the distor-
tion is simply a zooming by a factor of 3.2, then x(m, n) =3.2m and
y(m, n) =3.2Þn. The following code draws the distorted image:
glShadeModel(GL_FLAT);
glScale(3.2, 3.2, 1.0);
for (j=0; j < n; j++) {
glBegin(GL_QUAD_STRIP);
for (i=0; i <= m; i++) {
glVertex2i(i,j);
glVertex2i(i, j+1);
set_color(i,j);
}
glEnd();
}
This code draws each transformed pixel in a solid color equal to that pixel’s
color and scales the image size by 3.2. The routine set_color() stands for
whatever the appropriate OpenGL command is to set the color of the image
pixel.
The following is a slightly more complex version that distorts the image
using the functions x(i, j) and y(i, j):
glShadeModel(GL_FLAT);
for (j=0; j < n; j++) {
glBegin(GL_QUAD_STRIP);
for (i=0; i <= m; i++) {
glVertex2i(x(i,j), y(i,j));
glVertex2i(x(i,j+1), y(i,j+1));
set_color(i,j);
}
glEnd();
}

Displaying Layers 649
An even better distorted image can be drawn with the following code:
glShadeModel(GL_SMOOTH);
for (j=0; j < (n-1); j++) {
glBegin(GL_QUAD_STRIP);
for (i=0; i < m; i++) {
set_color(i,j);
glVertex2i(x(i,j), y(i,j));
set_color(i,j+1);
glVertex2i(x(i,j+1), y(i,j+1));
}
glEnd();
}
This code smoothly interpolates color across each quadrilateral. Note that
this version produces one fewer quadrilateral in each dimension than do
the flat-shaded versions, because the color image is being used to specify
colors at the quadrilateral vertices. In addition, you can antialias the
polygons with the appropriate blending function (GL_SRC_ALPHA,
GL_ONE) to get an even nicer image.
Displaying Layers
In some applications, such as semiconductor layout programs, you want to
display multiple layers of different materials and indicate where the mate-
rials overlap each other.
As a simple example, suppose you have three different substances that can
be layered. At any point, eight possible combinations of layers can occur, as
shown in Table 14-2.
Layer 1 Layer 2 Layer 3 Color
0 absent absent absent black
1 present absent absent red
2 absent present absent green
3 present present absent blue
4 absent absent present pink
Table 14-2 Eight Combinations of Layers

650 Chapter 14: Now That You Know
You want your program to display eight different colors, depending on the
layers present. One arbitrary possibility is shown in the last column of the
table. To use this method, use color-index mode and load your color map
so that entry 0 is black, entry 1 is red, entry 2 is green, and so on. Note that
if the numbers from 0 through 7 are written in binary, the 4 bit is turned on
whenever layer 3 appears, the 2 bit whenever layer 2 appears, and the 1 bit
whenever layer 1 appears.
To clear the window, set the writemask to 7 (all three layers) and set the
clearing color to 0. To draw your image, set the color to 7, and when you
want to draw something in layer n, set the writemask to n. In other types of
applications, it might be necessary to erase selectively in a layer, in which
case you would use the writemasks just discussed, but set the color to 0
instead of 7. (See “Masking Buffers” in Chapter 10 for more information
about writemasks.)
Antialiased Characters
Using the standard technique for drawing characters with glBitmap(),
drawing each pixel of a character is an all-or-nothing affair—the pixel is
either turned on or not. If you’re drawing black characters on a white back-
ground, for example, the resulting pixels are either black or white, never
a shade of gray. Much smoother, higher-quality images can be achieved if
intermediate colors are used when rendering characters (grays, in this
example).
Assuming that you’re drawing black characters on a white background,
imagine a highly magnified picture of the pixels on the screen, with a high-
resolution character outline superimposed on it, as shown in the left-hand
diagram in Figure 14-1.
5 present absent present yellow
6 absent present present white
7 present present present gray
Layer 1 Layer 2 Layer 3 Color
Table 14-2 (continued) Eight Combinations of Layers

Antialiased Characters 651
Notice that some of the pixels are completely enclosed by the character’s
outline and should be painted black, some pixels are completely outside the
outline and should be painted white, but many pixels should ideally be
painted some shade of gray, where the darkness of the gray corresponds to
the amount of black in the pixel. If this technique is used, the resulting
image on the screen looks better.
If speed and memory usage are of no concern, each character can be drawn
as a small image instead of as a bitmap. If you’re using RGBA mode, how-
ever, this method might require up to 32 bits per pixel of the character to
be stored and drawn, instead of the 1 bit per pixel for a standard character.
Alternatively, you could use one 8-bit index per pixel and convert these
indices to RGBA by table lookup during transfer. In many cases, a compro-
mise is possible that allows you to draw the character with a few gray levels
between black and white (say, two or three), and the resulting font descrip-
tion requires only 2 or 3 bits per pixel of storage.
The numbers in the right-hand diagram in Figure 14-1 indicate the
approximate percentage coverage of each pixel: 0 means approximately
empty, 1 means approximately one-third coverage, 2 means two-thirds,
and 3 means completely covered. If pixels labeled 0 are painted white,
pixels labeled 3 are painted black, and pixels labeled 1 and 2 are painted
Figure 14-1 Antialiased Characters

652 Chapter 14: Now That You Know
one-third and two-thirds black, respectively, the resulting character
looks quite good. Only 2 bits are required to store the numbers 0, 1, 2,
and 3, so for 2 bits per pixel, four levels of gray can be saved.
There are basically two methods of implementing antialiased characters,
depending on whether you’re in RGBA mode or color-index mode.
In RGBA mode, define three different character bitmaps, corresponding to
where 1, 2, and 3 appear in Figure 14-1. Set the color to white, and clear for
the background. Set the color to one-third gray (RGB = (0.666, 0.666, 0.666)),
and draw all the pixels with a 1 in them. Then set RGB = (0.333, 0.333,
0.333), draw with the 2 bitmap, and use RGB = (0.0, 0.0, 0.0) for the 3
bitmap. What you’re doing is defining three different fonts and redrawing
the string three times, where each pass fills in the bits of the appropriate
color densities.
In color-index mode, you can do exactly the same thing, but if you’re will-
ing to set up the color map correctly and use writemasks, you can get away
with only two bitmaps per character and two passes per string. In the pre-
ceding example, set up one bitmap that has a 1 wherever 1 or 3 appears in
the character. Set up a second bitmap that has a 1 wherever 2 or 3 appears.
Load the color map so that 0 gives white, 1 gives light gray, 2 gives dark gray,
and 3 gives black. Set the color to 3 (11 in binary) and the writemask to 1,
and draw the first bitmap. Then change the writemask to 2, and draw the
second. Where 0 appears in Figure 14-1, nothing is drawn in the frame-
buffer. Where 1, 2, and 3 appear, 1, 2, and 3 appear in the framebuffer.
For this example with only four gray levels, the savings are small—two
passes instead of three. If eight gray levels were used instead of four, the
RGBA method would require seven passes, and the color-map masking
technique would require only three. With 16 gray levels, the comparison
is 15 passes to four passes. (See “Masking Buffers” in Chapter 10 for more
information about writemasks, and “Bitmaps and Fonts” in Chapter 8 for
more information about drawing bitmaps.)
Try This
• Can you imagine how to do RGBA rendering using no more images
than the optimized color-index case?
Hint: How are RGB fragments normally merged into the color buffer when
antialiasing is desired?
Try This

Making Decals 653
Drawing Round Points
Draw near-round, aliased points by enabling point antialiasing, turning
blending off, and using an alpha function that passes only fragments with
alpha greater than 0.5. (See “Antialiasing” and “Blending” in Chapter 6 for
more information about these topics.)
Interpolating Images
Suppose you have a pair of images (where image can mean a bitmap image
or a picture generated using geometry in the usual way), and you want to
blend smoothly from one to the other. This can be done easily using the
alpha component and appropriate blending operations. Let’s say you want
to accomplish the blending in 10 steps, where image A is shown in frame 0
and image B is shown in frame 9. The obvious approach is to draw image A
with an alpha of (9 i)/9 and image B with an alpha of i/9 in frame i.
The problem with this method is that both images must be drawn in each
frame. A faster approach is to draw image A in frame 0. To get frame 1, blend
in 1/9 of image B and 8/9 of what’s there. For frame 2, blend in 1/8 of image
B with 7/8 of what’s there. For frame 3, blend in 1/7 of image B with 6/7 of
what’s there, and so on. For the last step, you’re just drawing 1/1 of image
B blended with 0/1 of what’s left, yielding image B exactly.
To see that this works, if for frame i you have
and you blend in B/(9 i) with (8 i)/(9 i) of what’s there, you get
(See “Blending” in Chapter 6.)
Making Decals
Suppose you’re drawing a complex three-dimensional picture using depth-
buffering to eliminate the hidden surfaces. Suppose further that one part of
(9 − i)A+ iB
9 9
(9 − i)A+ iB
9 9 = 9 −(i+ 1) A +(i+ 1) B
9 9
B +8− i
9 −i 9 −i

654 Chapter 14: Now That You Know
your picture is composed of coplanar figures A and B, where figure B is a sort
of decal that should always appear on top of figure A.
Your first approach might be to draw figure B after you’ve drawn figure A,
setting the depth-buffering function to replace fragments when their depth
is greater than or equal to the value stored in the depth buffer (GL_GEQUAL).
Owing to the finite precision of the floating-point representations of the
vertices, however, round-off error can cause figure B to be sometimes a bit
in front of and sometimes a bit behind figure A. Here’s one solution to this
problem:
1. Disable the depth buffer for writing, and render A.
2. Enable the depth buffer for writing, and render B.
3. Disable the color buffer for writing, and render A again.
4. Enable the color buffer for writing.
Note that during the entire process, the depth-buffer test is enabled. In
Step 1, A is rendered wherever it should be, but none of the depth-buffer
values are changed; thus, in Step 2, wherever B appears over A, B is
guaranteed to be drawn. Step 3 simply makes sure that all of the depth
values under A are updated correctly, but since RGBA writes are disabled, the
color pixels are unaffected. Finally, Step 4 returns the system to the default
state (writing is enabled in both the depth buffer and the color buffer).
If a stencil buffer is available, the following, simpler technique can be used:
1. Configure the stencil buffer to write 1 if the depth test passes, and 0
otherwise. Render A.
2. Configure the stencil buffer to make no stencil value change, but to
render only where stencil values are 1. Disable the depth-buffer test
and its update. Render B.
With this method, it’s not necessary to initialize the contents of the stencil
buffer at any time, because the stencil values of all pixels of interest (that is,
those rendered by A) are set when A is rendered. Be sure to reenable the
depth test and disable the stencil test before additional polygons are drawn.
(See “Selecting Color Buffers for Writing and Reading,” “Depth Test,” and
“Stencil Test” in Chapter 10.)

Drawing Filled, Concave Polygons Using the Stencil Buffer 655
Drawing Filled, Concave Polygons Using the
Stencil Buffer
Consider the concave polygon 1234567 shown in Figure 14-2. Imagine that
it’s drawn as a series of triangles: 123, 134, 145, 156, and 167, all of which
are shown in the figure. The heavier line represents the original polygon
boundary. Drawing all these triangles divides the buffer into nine regions A,
B, C, ..., I, where region I is outside all the triangles.
In the text of the figure, each of the region names is followed by a list of the
triangles that cover it. Regions A, D, and F make up the original polygon;
note that these three regions are covered by an odd number of triangles.
Every other region is covered by an even number of triangles (possibly zero).
Thus, to render the inside of the concave polygon, you need to render only
regions that are enclosed by odd numbers of triangles. This can be done
using the stencil buffer, with a two-pass algorithm.
First, clear the stencil buffer and disable writing into the color buffer. Next,
draw each of the triangles in turn, using the GL_INVERT function in the
stencil buffer. (For best performance, use triangle fans.) This flips the value
1
2
3
4
6
5
7
A
B
D
C
E
GF
H
*A:
B:
C:
*D:
E:
*F:
G:
H:
I:
134
123 134
134 145
134 145 156
123 134 145 156
156
123 156
156 167
(none)
Figure 14-2 Concave Polygon

656 Chapter 14: Now That You Know
between zero and a nonzero value every time a triangle that covers a pixel
is drawn. After all the triangles are drawn, if a pixel is covered an even
number of times, the value in the stencil buffers is zero; otherwise, it’s
nonzero. Finally, draw a large polygon over the whole region (or redraw the
triangles), but allow drawing only where the stencil buffer is nonzero.
Note: There’s a slight generalization of the preceding technique, where you
don’t need to start with a polygon vertex. In the 1234567 example,
let P be any point on or off the polygon. Draw the triangles: P12, P23,
P34, P45, P56, P67, and P71. Regions covered by odd numbers of
triangles are inside; other regions are outside. This is a generalization
in that if P happens to be one of the polygon’s edges, one of the
triangles is empty.
This technique can be used to fill both nonsimple polygons (polygons
whose edges cross each other) and polygons with holes. The following
example illustrates how to handle a complicated polygon with two regions,
one four-sided and one five-sided. Assume further that there’s a triangular
hole and a four-sided hole (it doesn’t matter in which regions the holes lie).
Let the two regions be abcd and efghi, and let the holes be jkl and mnop.
Let z be any point in the plane. Draw the following triangles:
zab zbc zcd zda zef zfg zgh zhi zie zjk zkl zlj zmn zno zop zpm
Mark regions covered by odd numbers of triangles as in, and those covered
by even numbers as out. (See “Stencil Test” in Chapter 10 for more
information about the stencil buffer.)
Finding Interference Regions
If you’re designing a mechanical part made from smaller three-dimensional
pieces, you often want to display regions in which the pieces overlap. In
many cases, such regions indicate design errors where parts of a machine
interfere with each other. In the case of moving parts, this process can be
even more valuable, because a search for interfering regions can be done
through a complete mechanical cycle of the design. The method for doing
this is complicated, and the description here might be too brief. Complete
details can be found in the paper Interactive Inspection of Solids: Cross-sections
and Interferences, by Jarek Rossignac, Abe Megahed, and Bengt-Olaf
Schneider (SIGGRAPH 1992 Proceedings).
The method is related to the capping algorithm described in “Stencil Test”
in Chapter 10. The idea is to pass an arbitrary clipping plane through the

Finding Interference Regions 657
objects that you want to test for interference, and then determine when a
portion of the clipping plane is inside more than one object at a time. For a
static image, the clipping plane can be moved manually to highlight inter-
fering regions; for a dynamic image, it might be easier to use a grid of clip-
ping planes to search for all possible interferences.
Draw each of the objects you want to check and clip them against the clip-
ping plane. Note which pixels are inside the object at that clipping plane
using an odd-even count in the stencil buffer, as explained in “Drawing
Filled, Concave Polygons Using the Stencil Buffer.” (For properly formed
objects, a point is inside the object if a ray drawn from that point to the eye
intersects an odd number of surfaces of the object.) To find interferences,
you need to find pixels in the framebuffer where the clipping plane is in the
interiors of two or more regions at once; in other words, in the intersection
of the interiors of any pair of objects.
If multiple objects need to be tested for mutual intersection, store one bit
every time some intersection appears, and another bit wherever the clip-
ping buffer is inside any of the objects (the union of the objects’ interiors).
For each new object, determine its interior, find the intersection of that
interior with the union of the interiors of the objects so far tested, and keep
track of the intersection points. Then add the interior points of the new
object to the union of the other objects’ interiors.
You can perform the operations described in the preceding paragraph by
using different bits in the stencil buffer together with various masking
operations. Three bits of stencil buffer are required per pixel—one for the
toggling to determine the interior of each object, one for the union of all
interiors discovered so far, and one for the regions in which interference has
occurred so far. To make this discussion more concrete, assume that the
1 bit of the stencil buffer is for toggling between interior and exterior, the
2 bit is the running union, and the 4 bit is for interferences so far. For each
object that you’re going to render, clear the 1 bit (using a stencil mask of 1
and clearing to 0), then toggle the 1 bit by keeping the stencil mask as 1 and
using the GL_INVERT stencil operation.
You can find intersections and unions of the bits in the stencil buffers using
the stenciling operations. For example, to make bits in buffer 2 be the union
of the bits in buffers 1 and 2, mask the stencil to those 2 bits, and draw
something over the entire object with the stencil function set to pass if any-
thing nonzero occurs. This happens if the bits in buffer 1, in buffer 2, or in
both are turned on. If the comparison succeeds, write a 1 in buffer 2. Also,
make sure that drawing in the color buffer is disabled. An intersection

658 Chapter 14: Now That You Know
calculation is similar—set the function to pass only if the value in the two
buffers is equal to 3 (bits turned on in both buffers 1 and 2). Write the result
into the correct buffer. (See “Stencil Test” in Chapter 10.)
Shadows
Every possible projection of three-dimensional space to three-dimensional
space can be achieved with a suitable 4 u4 invertible matrix and homoge-
neous coordinates. If the matrix isn’t invertible but has rank 3, it projects
three-dimensional space onto a two-dimensional plane. Every such possible
projection can be achieved with a suitable rank-3 4 u4 matrix. To find the
shadow of an arbitrary object on an arbitrary plane from an arbitrary light
source (possibly at infinity), you need to find a matrix representing that
projection, multiply it on the matrix stack, and draw the object in the
shadow color. Keep in mind that you need to project onto each plane that
you’re calling the “ground.”
As a simple illustration, assume the light is at the origin, and the equation
of the ground plane is ax +by +cz +d= 0. Given a vertex S = (sx, sy, sz,1),
the line from the light through S includes all points DS, where D is an
arbitrary real number. The point where this line intersects the plane
occurs when
D(asx +bsy +csz)+d=0,
so
D = d/(asx +bsy +csz).
Plugging this back into the line, we get
d(sx, sy, sz)/(asx + bsy + csz)
for the point of intersection.
The matrix that maps S to this point for every S is
This matrix can be used if you first translate the world so that the light is at
the origin.
d–000
0d–00
00 d–0
abc
0

Hidden-Line Removal 659
If the light is from an infinite source, all you have is a point S and a direction
D = (dx, dy, dz). Points along the line are given by
S + DD
Proceeding as before, the intersection of this line with the plane is given by
a(sx + Ddx)+b(sy + Ddy)+c(sz+Ddz)+d=0
Solving for D, plugging that back into the equation for a line, and then
determining a projection matrix gives
This matrix works given the plane and an arbitrary direction vector. There’s
no need to translate anything first. (See Chapter 3 and Appendix C.)
Hidden-Line Removal
If you want to draw a wireframe object with hidden lines removed, one
approach is to draw the outlines using lines and then fill the interiors of the
polygons making up the surface with polygons having the background
color. With depth-buffering enabled, this interior fill covers any outlines
that would be obscured by faces closer to the eye. This method would work,
except that there’s no guarantee that the interior of the object falls entirely
inside the polygon’s outline; in fact, it might overlap it in various places.
There’s an easy, two-pass solution using either polygon offset or the stencil
buffer. Polygon offset is usually the preferred technique, since polygon
offset is almost always faster than stencil buffer. Both methods are described
here, so you can see how both approaches to the problem work.
Hidden-Line Removal with Polygon Offset
To use polygon offset to accomplish hidden-line removal, the object is
drawn twice. The highlighted edges are drawn in the foreground color,
using filled polygons but with the polygon mode GL_LINE, to rasterize the
polygons as wireframe edges. Then the filled polygons are drawn with the
bdyucdzu+b–dxuc–dxud–dxu
a–dyuadxucdzu+c–dyud–dyu
a–dzub–dzuadxubdyu+d–dzu
000adxub+dyucdzu+

660 Chapter 14: Now That You Know
default polygon mode, which fills the interior of the wireframe, and with
enough polygon offset to nudge the filled polygons a little farther from
the eye. With the polygon offset, the interior recedes just enough that the
highlighted edges are drawn without unpleasant visual artifacts.
glEnable(GL_DEPTH_TEST);
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
set_color(foreground);
draw_object_with_filled_polygons();
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
glEnable(GL_POLYGON_OFFSET_FILL);
glPolygonOffset(1.0, 1.0);
set_color(background);
draw_object_with_filled_polygons();
glDisable(GL_POLYGON_OFFSET_FILL);
You may have to adjust the amount of offset needed (for wider lines, for
example). (See “Polygon Offset” in Chapter 6 for more information.)
Hidden-Line Removal with the Stencil Buffer
Using the stencil buffer for hidden-line removal is a more complicated pro-
cedure. For each polygon, you’ll need to clear the stencil buffer and then
draw the outline in both the framebuffer and the stencil buffer. Then, when
you fill the interior, enable drawing only where the stencil buffer is still
clear. To avoid doing an entire stencil-buffer clear for each polygon, an easy
way to clear it is simply to draw 0’s into the buffer using the same polygon
outline. In this way, you need to clear the entire stencil buffer only once.
For example, the following code represents the inner loop you might use to
perform such hidden-line removal. Each polygon is outlined in the fore-
ground color, filled with the background color, and then outlined again in
the foreground color. The stencil buffer is used to keep the fill color of each
polygon from overwriting its outline. To optimize performance, the stencil
and color parameters are changed only twice per loop by using the same
values both times the polygon outline is drawn.
glEnable(GL_STENCIL_TEST);
glEnable(GL_DEPTH_TEST);
glClear(GL_STENCIL_BUFFER_BIT);
glStencilFunc(GL_ALWAYS, 0, 1);
glStencilOp(GL_INVERT, GL_INVERT, GL_INVERT);
set_color(foreground);
for (i=0; i < max; i++) {

Texture Mapping Applications 661
outline_polygon(i);
set_color(background);
glStencilFunc(GL_EQUAL, 0, 1);
glStencilOp(GL_KEEP, GL_KEEP, GL_KEEP);
fill_polygon(i);
set_color(foreground);
glStencilFunc(GL_ALWAYS, 0, 1);
glStencilOp(GL_INVERT, GL_INVERT, GL_INVERT);
outline_polygon(i);
}
(See “Stencil Test” in Chapter 10.)
Texture Mapping Applications
Texture mapping is quite powerful, and it can be used in some interesting
ways. Here are a few advanced applications of texture mapping:
• Antialiased text—Define a texture map for each character at a relatively
high resolution, and then map them onto smaller areas using the
filtering provided by texturing. This also makes text appear correctly
on surfaces that aren’t aligned with the screen, but are tilted and have
some perspective distortion.
• Antialiased lines—These can be done like antialiased text: make the
line in the texture several pixels wide, and use texture filtering to
antialias the lines.
• Image scaling and rotation—If you put an image into a texture map
and use that texture to map onto a polygon, rotating and scaling the
polygon effectively rotates and scales the image.
• Image warping—Store the image as a texture map, but map it to some
spline-defined surface (using evaluators). As you warp the surface, the
image follows the warping.
• Projecting images—Put the image in a texture map, and project it as a
spotlight, creating a slide projector effect. (See “The q-Coordinate” in
Chapter 9 for more information about how to model a spotlight using
textures.)
(See Chapter 3 for information about rotating and scaling, Chapter 9 for
more information about creating textures, and Chapter 12 for details on
evaluators.)

662 Chapter 14: Now That You Know
Drawing Depth-Buffered Images
For complex static backgrounds, the rendering time for the geometric
description of the background can be greater than the time it takes to draw
a pixel image of the rendered background. If there’s a fixed background
and a relatively simple changing foreground, you may want to draw the
background and its associated depth-buffered version as an image, rather
than render it geometrically. The foreground might also consist of items
that are time-consuming to render, but whose framebuffer images and
depth buffers are available. You can render these items into a depth-buffered
environment using a two-pass algorithm.
For example, if you’re drawing a model of a molecule made of spheres, you
might have an image of a beautifully rendered sphere and its associated
depth-buffer values that were calculated using Phong shading or ray-tracing
or some other scheme that isn’t directly available through OpenGL. To draw
a complex model, you might be required to draw hundreds of such spheres,
which should be depth-buffered together.
To add a depth-buffered image to the scene, first draw the image’s depth-
buffer values into the depth buffer using glDrawPixels(). Then enable
depth-buffering, set the writemask to 0 so that no drawing occurs, and
enable stenciling such that the stencil buffers are drawn whenever a write
to the depth buffer occurs.
Then draw the image into the color buffer, masked by the stencil buffer
you’ve just written so that writing occurs only when there’s a 1 in the stencil
buffer. During this write, set the stenciling function to zero out the stencil
buffer so that it’s automatically cleared when it’s time to add the next image
to the scene. If the objects are to be moved nearer to or farther from the
viewer, you need to use an orthographic projection; in such cases, you use
GL_DEPTH_BIAS with glPixelTransfer*() to move the depth image. (See
“Coordinate System Survival Kit” in Chapter 2, “Depth Test” and “Stencil
Test” in Chapter 10, and Chapter 8 for details on glDrawPixels() and
glPixelTransfer*().)
Dirichlet Domains
Given a set S of points in a plane, the Dirichlet domain or Voronoi polygon
of one of the points is the set of all points in the plane closer to that point
than to any other point in the set S. These points provide the solutions to
Dirichlet Domains 663
many problems in computational geometry. Figure 14-3 shows outlines of
the Dirichlet domains for a set of points.
If for each point in S, you draw a depth-buffered cone with its apex at the
point in a different color than each of the points in S, the Dirichlet domain
for each point is drawn in that color. The easiest way to do this is to precom-
pute a cone’s depth in an image and use the image as the depth-buffer val-
ues as described in the preceding section,“Drawing Depth-Buffered Images.”
You don’t need an image to draw into the framebuffer as in the case of
shaded spheres, however. While you’re drawing into the depth buffer, use
the stencil buffer to record the pixels where drawing should occur by first
clearing it and then writing nonzero values wherever the depth test suc-
ceeds. To draw the Dirichlet region, draw a polygon over the entire window,
but enable drawing only where the stencil buffers are nonzero.
You can do this perhaps more easily by rendering cones of uniform color
with a simple depth buffer, but a good cone might require thousands of
1
3
4
2
5
6
7
•
•
•
•
•
•
•
Figure 14-3 Dirichlet Domains
664 Chapter 14: Now That You Know
polygons. The technique described in this section can render higher-quality
cones much more quickly. (See “A Hidden-Surface Removal Survival Kit” in
Chapter 5 and “Depth Test” in Chapter 10.)
Life in the Stencil Buffer
The Game of Life, invented by John Conway, is played on a rectangular grid
in which each grid location is either “alive” or “dead.” To calculate the next
generation from the current one, count the number of live neighbors for
each grid location (the eight adjacent grid locations are neighbors). A grid
location is alive in generation n+ 1 if it was alive in generation n and has
exactly two or three live neighbors, or if it was dead in generation n and
has exactly three live neighbors. In all other cases, it is dead in generation
n+ 1. This game generates some incredibly interesting patterns given
different initial configurations. (See Martin Gardner, “Mathematical
Games,” Scientific American, vol. 223, no. 4, October 1970, pp. 120–123.)
Figure 14-4 shows six generations from a game.
Figure 14-4 Six Generations from the Game of Life

Alternative Uses for glDrawPixels() and glCopyPixels() 665
One way to create this game using OpenGL is to use a multipass algorithm.
Keep the data in the color buffer, one pixel for each grid point. Assume that
black (all zeros) is the background color, and that the color of a live pixel is
nonzero. Initialize by clearing the depth and stencil buffers to zero, set the
depth-buffer writemask to zero, and set the depth comparison function so
that it passes on not-equal. To iterate, read the image off the screen, enable
drawing into the depth buffer, and set the stencil function so that it
increments whenever a depth comparison succeeds but leaves the stencil
buffer unchanged otherwise. Disable drawing into the color buffer.
Next, draw the image eight times, and offset one pixel in each vertical,
horizontal, and diagonal direction. When you’re done, the stencil buffer
contains a count of the number of live neighbors for each pixel. Enable
drawing to the color buffer, set the color to the color for live cells, and set
the stencil function to draw only if the value in the stencil buffer is 3 (three
live neighbors). In addition, if this drawing occurs, decrement the value in
the stencil buffer. Then draw a rectangle covering the image; this paints
each cell that has exactly three live neighbors with the “alive” color.
At this point, the stencil buffers contain 0, 1, 2, 4, 5, 6, 7, and 8, and the
values under the 2’s are correct. The values under 0, 1, 4, 5, 6, 7, and 8 must
be cleared to the “dead” color. Set the stencil function to draw whenever the
value is not 2 and to zero the stencil values in all cases. Then draw a large
polygon of the “dead” color across the entire image. You’re done.
For a usable demonstration program, you might want to zoom the grid
up to a size larger than a single pixel; it’s hard to see detailed patterns with
a single pixel per grid point. (See “Coordinate System Survival Kit” in
Chapter 2, and “Depth Test” and “Stencil Test” in Chapter 10.)
Alternative Uses for glDrawPixels() and
glCopyPixels()
You might think of glDrawPixels() as a way to draw a rectangular region of
pixels to the screen. Although this is often what it’s used for, some other
interesting uses are outlined here:
• Video—Even if your machine doesn’t have special video hardware,
you can display short movie clips by repeatedly drawing frames with
glDrawPixels() in the same region of the back buffer and then swap-
ping the buffers. The size of the frames you can display with reasonable

666 Chapter 14: Now That You Know
performance using this method depends on your hardware’s drawing
speed, so you might be limited to 100 u100 pixel movies (or smaller) if
you want smooth fake video.
• Airbrush—In a paint program, your airbrush (or paintbrush) shape can
be simulated using alpha values. The color of the paint is represented
as the color values. To paint with a circular brush in blue, repeatedly
draw a blue square with glDrawPixels() where the alpha values are
largest in the center and taper to zero at the edges of a circle centered
in the square. Draw using a blending function that uses alpha of the
incoming color and (1 alpha) of the color already at the pixel. If the
alpha values in the brush are all much less than 1, you have to paint
over an area repeatedly to get a solid color. If the alpha values are near
1, each brush stroke pretty much obliterates the colors underneath.
• Filtered zooms—If you zoom a pixel image by a nonintegral amount,
OpenGL effectively uses a box filter, which can lead to rather severe
aliasing effects. To improve the filtering, jitter the resulting image by
amounts less than a pixel and redraw it multiple times, using alpha
blending to average the resulting pixels. The result is a filtered zoom.
• Transposing images—You can swap same-size images in place with
glCopyPixels() using the XOR operation. With this method, you can
avoid having to read the images back into processor memory. If A and
B represent the two images, the operation looks like this:
a. A = A XOR B
b. B = A XOR B
c. A = A XOR B

667
Chapter 15
15.The OpenGL Shading Language
Chapter Objectives
This chapter discusses the OpenGL Shading Language. GLSL, as the OpenGL
Shading Language is commonly called, is a programming language for
creating programmable shaders. Introduced as a part of OpenGL version 2.0,
the OpenGL Shading Language enables applications to explicitly specify the
operations used in processing vertices and fragments. Additionally, GLSL
helps unlock the computation power of modern hardware implementations
of OpenGL.
After reading this chapter, you’ll be able to do the following:
• Understand the structure and components of programmable shaders
written in the OpenGL Shading Language
• Integrate programmable shaders into OpenGL programs
• Use exclusively shader-based techniques, including transform
feedback, uniform blocks, and texture buffers

668 Chapter 15: The OpenGL Shading Language
This chapter includes discussions of features in versions 1.30 and 1.40 of the
OpenGL Shading Language, which are the versions associated with OpenGL
versions 3.0 and 3.1, respectively. Just as OpenGL Version 3.1 removed the
functionality deprecated in Version 3.0, so GLSL 1.40 removed features
from GLSL 1.30. Those features are available if your implementation
supports the GL_ARB_compatibility extension. This chapter discusses
shaders in the context of GLSL 1.30.
The OpenGL Graphics Pipeline and Programmable
Shading
You can think of the internal operation of OpenGL as two machines—one
for processing vertices, the other for fragments—with dials and switches
on the front of each machine. You control each machine’s operation by
flipping switches and twisting dials, but the internal operation of the
machines is “fixed”; that is, you can’t change the order of operations
inside of the machine, and you’re limited to the features that were built
into the machine. This mode of operation for OpenGL is commonly called
the fixed-function pipeline, and is described in detail in Appendix E, “Order
of Operations.”1 Figure 15-1 illustrates the basic architecture of the
OpenGL fixed-function pipeline.
Figure 15-1 Overview of the OpenGL Fixed-Function Pipeline
OpenGL 2.0 augmented the fixed-function pipeline approach by adding a
programmable shading pipeline, where you can control the processing of
vertices and fragments with small programs, called shaders, written in a
special language called The OpenGL Shading Language, or GLSL for short.
1This appendix is available online at http://www.opengl-redbook.com/appendices/.
Ver tex
Processing
Machine
Fragment
Processing
Machine
Framebuffer
Pixel
Data
Ver tex
Data

The OpenGL Graphics Pipeline and Programmable Shading 669
In an application, you can use both the fixed-function and programmable
pipelines for processing data, but not simultaneously. When you use a
shader for processing, the corresponding portion of the fixed-function
pipeline is disabled. In Version 3.1, the fixed-function pipeline was removed
through deprecation. If your implementation supports the GL_ARB_
compatibility extension its functionality is made available in that extension.
While programmable shaders are not new to computer graphics, accessibility
to them became available in interactive graphics libraries such as OpenGL
only a few years ago. Just like the field of computer graphics itself,
techniques for programmable shaders constitute a huge subject, and this
chapter does not attempt to teach the theory behind programmable shaders.
Rather, it covers the language available for authoring shaders available in
OpenGL and how to integrate those shaders into an OpenGL application.
For more information on programmable shading, you may want to broaden
your knowledge of the subject with these supplemental works:
•The RenderMan Companion: A Programmer’s Guide to Realistic Computer
Graphics by Steve Upstill (Addison-Wesley, 1990)—while this text
describes Pixar’s RenderMan shader language (which is one of the
predominant programmable shader languages used for computer-
generated images in the movie industry), it describes the basics of
programmable shading and presents much of the theory and practice
of using shaders to generate images.
•Real-Time Shading by John C. Hart, Wolfgang Heidrich, Michael
McCool, and Marc Olano (AK Peters, Ltd., 2002)—this modern text
describes the latest advancements in programmable shading on
graphics hardware and provides a survey of different techniques and
implementations of programmable shaders.
•The GPU Gems series (Addison-Wesley)—these books describe many
shader implementation tricks and techniques.
This section begins with a discussion of how shaders affect the processing
of vertices and fragments. We continue describing what’s required to
integrate shaders to your OpenGL program, and then introduce writing
shaders in GLSL. For all of the details on the OpenGL shading language,
please see:
•The OpenGL Shading Language Specification, versions 1.30 and 1.40 by
John Kessenich (available for download from http://www.opengl.org)
•The OpenGL Shading Language, 3rd editon, by Randi Rost and Bill
Licea-Kane, with contributions by Dan Ginsburg, John M. Kessenich,
Barthold Lichtenbelt, Hugh Malan, and Mike Weiblen (Addison-
Wesley, 2009)
670 Chapter 15: The OpenGL Shading Language
Vertex Processing
Figure 15-2 illustrates the processing of a vertex through the OpenGL
pipeline. The shaded area indicates the functions of the vertex processing
pipeline that are replaced by a vertex shader.
When the fixed-function pipeline processes a vertex, it’s responsible for
providing the following values that are used for rasterization:
•Eye-space coordinates
• Primary and secondary colors
• Texture coordinates
• Fog coordinates
•Point size
Depending upon which features you have enabled, the vertex pipeline may
not update all of those values. Those values are computed based on the
input of the application through calls like glVertex*() and the other vertex
data calls.
Clipping
Primitive
Setup
ModelView
Matrix
Projection
Matrix
Normal
Matrix
TexGen/Texture
Matrix
Normal
Vector
Color
Values
Texture
Coordinates
Fog
Coordinates
Ve r te x
Coordinates
Functional Stages
Subsumed by a
Vertex Shader
Figure 15-2 Vertex Processing Pipeline

The OpenGL Graphics Pipeline and Programmable Shading 671
Not all operations in the vertex pipeline are replaced when you use a shader.
After the execution of the shader, the following operations still occur, just
as if the vertex were processed by the fixed-function pipeline:
• Perspective division
• Viewport mapping
•Primitive assembly
• Frustum and user clipping
• Backface culling
• Two-sided lighting selection
• Polygon-mode processing
• Polygon offset
• Depth range clamping
Fragment Processing
Similarly, Figure 15-3 illustrates the pixel processing part of the OpenGL
pipeline. Once again, the shaded region indicates the functionality replaced
by a fragment shader.
Framebuffer
Primary and
Secondary Color
Summation
Per-Pixel Fog
Application
Fragment
Tests
Texture
Mapping
From Geometric
Primitive Setup
Bitmaps/Pixel
Rectangles
Figure 15-3 Fragment Processing Pipeline

672 Chapter 15: The OpenGL Shading Language
Similar to vertex shaders, fragment shaders take over the processing of
fragments. The operations subsumed in a fragment shader are:
• Texel retrieval for texture application
• Texture application
•Fogging
• Primary and secondary color summation
The operations that OpenGL does regardless of the application of a
fragment shader are:
• Flat or smooth shading (which controls how values are
interpolated across fragments)
• Pixel coverage computations
• Pixel ownership tests
• Scissor operations
• Stipple-pattern application (deprecated in OpenGL Version 3.0;
removed in Version 3.1)
• Alpha test (in OpenGL versions up to and including 3.0.
Version 3.1 removed this test, replacing it with functionality
available in a fragment shader)
• Depth test
•Stencil test
•Alpha blending
• Logical operations on pixels
• Dithering of color values
•Color masking
Using GLSL Shaders
A Sample Shader
Example 15-1 shows a simple vertex shader. It transforms a point’s position
by simulating acceleration due to gravity. While not every detail will make
sense at the moment, hopefully you’ll be able to understand the basic flow
of what’s going on.

Using GLSL Shaders 673
Example 15-1 A Sample GLSL (Version 1.30) Vertex Shader
#version 130
uniform float t; // Time (passed in from the application)
attribute vec4 vel; // Particle velocity
const vec4 g = vec4( 0.0, -9.80, 0.0 );
void main()
{
vec4 position = gl_Vertex;
position += t*vel + t*t*g;
gl_Position = gl_ModelViewProjectionMatrix * position;
}
The above preceeding is written using GLSL version 1.30 (you can tell by the
#version 130), which is compatible with OpenGL Version 3.0. Minor
changes are required to make it a version 1.40 shader, as demonstrated in
Example 15-2.
Example 15-2 The Same GLSL Vertex Shader (Version 1.40)
#version 140
uniform float t; // Time (passed in from the application)
uniform mat4 MVP; // Combined modelview and projection matrices
in vec4 pos; // Particle position (as a homogenous coordinate)
in vec4 vel; // Particle velocity
const vec4 g = vec4( 0.0, -9.80, 0.0 );
void main()
{
vec4 position = pos;
position += t*vel + t*t*g;
gl_Position = MVP * position;
}
OpenGL / GLSL Interface
Writing shaders for use with OpenGL programs is similar to using a
compiler-based language like “C.” You have a compiler analyze your
program, check it for errors, and then translate it into object code. Next,

674 Chapter 15: The OpenGL Shading Language
a collection of object files are combined together in a linking phase
generating an executable program. Using GLSL shaders in your program
is a similar process, except that the compiler and linker are part of the
OpenGL driver.
Figure 15-4 illustrates the steps required to create GLSL shader objects and
link them together to create an executable shader program.
When you want to use a vertex or fragment shader in your application,
you’ll need to do the following sequence of steps:
For each shader object:
1. Create a shader object.
2. Compile your shader source into the object.
3. Verify that your shader successfully compiled.
Executable
Shader
Program
Shader
Object Shader
Object
Shader
Program
Shader
Source
Character
Strings
glShader Source
glCompileShader
glCreateShader
glAttachShader
glCreateProgram
glLinkProgram
glUseProgram
•
•
•
Figure 15-4 Shader Creation Flowchart
Using GLSL Shaders 675
Then, to link multiple shader objects into a shader program, you’ll:
1. Create a shader program.
2. Attach the appropriate shader objects to the shader program.
3. Link the shader program.
4. Verify that the shader link phase completed successfully.
5. Use the shader for vertex or fragment processing.
Why create multiple shader objects? Just as you might reuse a function in
different programs, the same idea applies to GLSL programs. Common
routines that you create might be usable in multiple shaders. Instead of
having to compile several large shaders with lots of common code, you’ll
merely link the appropriate shader objects together into a shader program.
To create a shader object, call glCreateShader().
Once you have created a shader object, you need associate the source code
of the shader with that object created by glCreateShader(). This is done by
calling glShaderSource().
GLuint glCreateShader(GLenum type);
Allocates a shader object. type must be either GL_VERTEX_SHADER or
GL_FRAGMENT_SHADER. The return value is either a non-zero integer or
zero if an error occurred.
void glShaderSource(GLuint shader, GLsizei count,
const GLchar **string, const GLint *length);
Associates the source of a shader with a shader object shader.string is
an array of count GLchar strings that compose the shader’s source. The
character strings in string may be optionally null-terminated. length can be
one of three values. If length is NULL, then it’s assumed that each string
provided in string is null-terminated. Otherwise, length has count elements,
each of which specifies the length of the corresponding entry in string. If
the value of an element in the array length is a positive integer, the value
represents the number of characters in the corresponding string element.
If the value is negative for particular elements, then that entry in string is
assumed to be null-terminated.

676 Chapter 15: The OpenGL Shading Language
To compile a shader object’s source, use glCompileShader().
Similar to when you compile a “C” program, you need to determine if
the compilation finished successfully. A call to glGetShaderiv(), with an
argument of GL_COMPILE_STATUS, will return the status of the compilation
phase. If GL_TRUE is returned, the compilation succeeded, and the object can
be linked into a shader program. If the compilation failed, you can determine
what the error was by retrieving the compilation log. glGetShaderInfoLog()
will return an implementation-specific set of messages describing the
compilation errors. The current size of the error log can be queried by
calling glGetShaderiv() with an argument of GL_INFO_LOG_LENGTH.
Once you have created and compiled all of the necessary shader objects,
you will need to link them together to create an executable shader program.
This process is similar in nature to creating shader objects. First, you’ll need
to create a shader program to which you can attach the shader objects.
Using glCreateProgram(), a shader program will be returned for further
processing.
void glCompileShader(GLuint shader);
Compiles the source code for shader. The results of the compilation can be
queried by calling glGetShaderiv() with an argument of GL_COMPILE_
STATUS.
void glGetShaderInfoLog(GLuint shader, GLsizei bufSize,
GLsizei *length, char *infoLog);
Returns the log associated with the last compilation of a shader object.
shader specifies which shader object to query. The log is returned as a null-
terminated character string of length characters in the buffer infoLog. The
maximum return size of the log is specified in bufSize.
If length is NULL, infoLog’s length is not returned.
GLuint glCreateProgram();
Creates an empty shader program. The return value is either a non-zero
integer, or zero if an error occurred.

Using GLSL Shaders 677
Once you have your shader program, you’ll need to populate it with
the necessary shader objects to create the executable program. This is
accomplished by attaching a shader object to the program by calling
glAttachShader().
For parity, if you need to remove a shader object from a program to modify
the shader’s operation, detach the shader object by calling glDetachShader()
with the appropriate shader object identifier.
After all the necessary shader objects have been attached to the shader
program, you will need to link the objects for an executable program. This
is accomplished by calling glLinkProgram().
As with shader objects, there’s a chance that the linking phase may fail due
to errors in the attached shader objects. You can query the result of the link
operation’s success by calling glGetProgramiv() with an argument of
GL_LINK_STATUS. If GL_TRUE was returned, the link was successful, and
you’re able to specify the shader program for use in processing vertices or
fragments. If the link failed, represented by GL_FALSE being returned, then
void glAttachShader(GLuint program, GLuint shader);
Associates the shader object, shader, with the shader program, program. A
shader object can be attached to a shader program at any time, although
its functionality will only be available after a successful link of the shader
program. A shader object can be attached to multiple shader programs
simultaneously.
void glDetachShader(GLuint program, GLuint shader);
Removes the association of a shader object, shader, from the shader
program, program. If shader is detached from program and had been
previously marked for deletion (by calling glDeleteShader()), it is deleted
at that time.
void glLinkProgram(GLuint program);
Processes all shader objects attached to program to generate a completed
shader program. The result of the linking operation can be queried by
calling glGetProgramiv() with GL_LINK_STATUS. GL_TRUE is returned
for a successful link; GL_FALSE is returned otherwise.

678 Chapter 15: The OpenGL Shading Language
you can determine the cause of the failure by retrieving the program link
information log by calling glGetProgramLog().
After a successful program link, you can engage the vertex or fragment
program by calling glUseProgram() with the program’s object handle. To
revert back to using the fixed-function pipeline, pass zero as the program
object.
Example 15-3 illustrates creating and linking a vertex shader in GLSL. The
process is virtually identical for fragment shaders.
Example 15-3 Creating and Linking GLSL shaders
GLuint shader, program;
GLint compiled, linked;
void glGetProgramInfoLog(GLuint program, GLsizei bufSize,
GLsizei *length, char *infoLog);
Returns the log associated with the last compilation of a shader program.
program specifies which shader program to query. The log is returned as a
null-terminated character string of length characters in the buffer infoLog.
The maximum return size of the log is specified in bufSize.
If length is NULL, infoLog’s length is not returned.
void glUseProgram(GLuint program);
Uses program for either vertex or fragment processing, depending upon
the type of shader created with glCreateShader(). If program is zero, no
shader is used for processing, and OpenGL reverts to fixed-function
operation (in OpenGL Version 3.1, as there is no fixed-function pipeline,
the results are undefined, but no error is generated).
While a program is in use, it can have new shader objects attached,
compile attached shader objects, or detach previously attached objects.
It may also be relinked. If the link phase is successful, the newly linked
shader program replaces the previously active program. If the link fails,
the currently bound shader program remains active and is not replaced
until either a new program is specified with glUseProgram() or the
program is successfully relinked.

Using GLSL Shaders 679
const GLchar* shaderSrc[] = {
“void main()”
“{“
“ gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;”
“}”
};
shader = glCreateShader(GL_VERTEX_SHADER);
glShaderSource(shader, 1, shaderSrc, NULL);
glCompileShader(shader);
glGetShaderiv(shader, GL_COMPILE_STATUS, &compiled );
if (!compiled) {
GLint length;
GLchar* log;
glGetShaderiv(shader, GL_INFO_LOG_LENGTH,
&length );
log = (GLchar*) malloc(length);
glGetShaderInfoLog(shader, length, &length, log);
fprintf(stderr, “compile log = ‘%s’\n”, log);
free(log);
}
program = glCreateProgram();
glAttachShader(program, shader);
glLinkProgram(program);
glGetProgramiv(program, GL_LINK_STATUS, &linked );
if (linked) {
glUseProgram(program);
} else {
GLint length;
GLchar* log;
glGetProgramiv(progam, GL_INFO_LOG_LENGTH, &length );
log = (GLchar*) malloc(length);
glGetProgramInfoLog(program, length, &length, log);
fprintf(stderr, “link log = ‘%s’\n”, log);
free(log);
}

680 Chapter 15: The OpenGL Shading Language
To release the resources related to shader objects and programs, you can
delete those objects by calling the respective deletion function. If either the
shader program or object is currently active when it’s deleted, the object is
only marked for deletion. It is deleted when the program is no longer in use,
or the shader object is detached from all shader program objects.
To determine if an identifier is currently in use as either a shader program
or object, calling glIsProgram() or glIsShader() will return a boolean value
indicating if the identifier is in use.
To aid in shader development, the OpenGL call glValidateProgram() can
help verify that a shader will execute given the current OpenGL state.
Depending upon the underlying OpenGL implementation, program
validation may also return hints about performance characteristics or other
useful information specific to that shader’s execution for that OpenGL
implementation. You would validate a program in the same manner you
void glDeleteShader(GLuint shader);
Deletes shader. If shader is currently linked to one or more active shader
programs, the object is tagged for deletion and deleted once the shader
program is no longer being used by any shader program.
void glDeleteProgram(GLuint program);
Deletes program immediately if not currently in use in any context, or
tagged for deletion when the program is no longer in use by any contexts.
GLboolean glIsProgram(GLuint program);
Returns GL_TRUE if program is the name of a shader program. If program
is zero, or non-zero and not the name of a shader object, GL_FALSE is
returned.
GLboolean glIsShader(GLuint shader);
Returns GL_TRUE if shader is the name of a shader object. If shader is zero,
or non-zero and not the name of a shader object, GL_FALSE is returned.

Creating Shaders with GLSL 681
would compile it by merely calling glValidateProgram() once all of the
necessary shader objects were attached to the shader program. Similarly,
you can query the results of the validation step by calling glGetProgramiv()
with an argument of GL_VALIDATE_STATUS.
The OpenGL Shading Language
This section provides an overview of the shading language used within
OpenGL, commonly called GLSL. GLSL shares many traits with C++ and
Java, and is used for authoring both vertex and fragment shaders, although
certain features are only available for one type of shader. We will first
describe GLSL’s requirements, types, and other language constructs that are
shared between vertex and fragment shaders, and then discuss the features
unique to each type of shader.
Creating Shaders with GLSL
The Starting Point
A shader program, just like a “C” program, starts execution in main(). Every
GLSL shader program begins life as:
void
main()
{
// Your code goes here
}
The “//” construct is a comment and terminates at the end of the current
line. “C”-type, multi-line comments—the /* and */ type—are also supported.
void glValidateProgram(GLuint program);
Validates program against the current OpenGL state settings. After
validation, the value of GL_VALIDATE_STATUS will be set to either GL_
TRUE, indicating that the program will execute in the current OpenGL
environment, or GL_FALSE otherwise. The value of GL_VALIDATE_
STATUS status can be queried by calling glGetProgramiv().

682 Chapter 15: The OpenGL Shading Language
However, unlike ANSI “C,” main() does not return an integer value; it is
declared void.
While this is a perfectly legal GLSL vertex- or fragment-shader program that
compiles and even runs, its functionality leaves something to be desired.
We will continue by describing variables and their operation.
Also, as with C and its derivative languages, statements are terminated with
a semicolon.
Declaring Variables
GLSL is a strongly typed language; that is, every variable must be declared
and have an associated type. Variable names conform to the same rules as
those for C: You can use letters, numbers, and the underscore character
(_) to compose variable names. A digit cannot be the first character in a
variable name.
Table 15-1 shows the basic types available in GLSL.
An additional set of types is named samplers, which are used as opaque
handles for accessing texture maps. The various types of samplers and their
uses are discussed in “Accessing Texture Maps in Shaders” on page 707.
Note: An OpenGL implementation is not required to implement these
types as stringently as one might like. As long as their operation
is semantically and operationally correct, the underlying
implementation may vary. For example, integers may be stored in
floating-point registers. It is not a good idea to assume particular
numeric outcomes, such as the maximum-sized integer value
being 215, based upon these types.
Type Description
float IEEE-like floating-point value
int signed integer value
uint unsigned integer value
bool Boolean value
Table 15-1 Basic Data Types in GLSL

Creating Shaders with GLSL 683
Variable Scoping
While all variables must be declared, they may be declared any time before
their use (unlike “C,” where they must be the first statements in a block of
code). The scoping rules of GLSL closely parallel those of C++:
• Variables declared outside of any function definition have global scope
and are visible to all functions within the shader program.
• Variables declared within a set of curly braces (e.g., function definition,
block following a loop or “if” statement, and so on) exist within the
scope of those braces only.
• Loop iteration variables, such as i in the loop
for (int i = 0; i < 10; ++i) {
// loop body
}
are only scoped for the body of the loop.
Variable Initialization
Variables may also be initialized when declared. For example:
int i, numParticles = 1500;
float force, g = -9.8;
bool falling = true;
Integer constants may be expressed as octal, decimal, or hexadecimal
values. An optional minus sign before a numeric value negates the constant,
and a trailing ‘u’ or ‘U’ denotes an unsigned integer value.
Floating-point values must include a decimal point, unless described in
scientific format (e.g., 3E-7), and may optionally include an ‘f’ or ‘F’ suffix
as in “C.”
Boolean values are either true or false, and can be initialized to either of those
values or as the result of a operation that resolves to a boolean expression.
Constructors
As mentioned, GLSL is a strongly typed language, even more so than C++.
In general, there is no implicit conversion between values, except in a few
cases. For example,
int f = 10.0;
will result in a compilation error due to assigning a constant floating-point
value to an integer variable. Integer values and vectors will be implicitly

684 Chapter 15: The OpenGL Shading Language
converted into the equivalent floating-point value or vector. Any other
conversion of values requires using a conversion function (a C++-like
constructor). For example,
float f = 10.0;
int ten = int(f);
uses the int() function to do the conversion. Likewise, the other types
also have conversion functions: float(),uint(),bool(). These functions also
illustrate another feature of GLSL: operator overloading, whereby each
function takes various input types, but all use the same base function name.
We will discuss more on functions in a bit.
Aggregate Types
Three of GLSL’s primitive types can be combined to better match core
OpenGL’s data values and to ease computational operations.
First, GLSL supports vectors of two, three, or four dimensions for each of the
primitive types. Also, matrices of floats are available. Table 15-2 lists the
valid vector and matrix types.
Matrix types that list both dimensions, such as mat4x3, use the first value
to specify the number of columns, the second the number of rows.
Variables declared with these types can be initialized similar to their scalar
counterparts:
vec3 velocity = vec3(0.0, 2.0, 3.0);
Base Type 2-D vec 3-D vec 4-D vec Matrix Types
float vec2 vec3 vec4 mat2, mat3, mat4
mat2x2, mat2x3, mat2x4,
mat3x2, mat3x3, mat3x4
mat4x2, mat4x3, mat4x4
int ivec2 ivec3 ivec4 —
uint uvec2 uvec3 uvec4 —
bool bvec2 bvec3 bvec4 —
Table 15-2 GLSL Vector and Matrix Types

Creating Shaders with GLSL 685
and converting between types is equally accessible:
ivec3 steps = ivec3(velocity);
Vector constructors can also be used to truncate or lengthen a vector. If a
longer vector is passed into the constructor of a smaller vector, the vector is
truncated to the appropriate length.
vec4 color;
vec3 RGB = vec3(color); // now RGB only has three elements
Likewise, vectors are lengthened in somewhat the same manner. Scalar
values can be promoted to vectors, as in
vec3 white = vec3(1.0); // white = ( 1.0, 1.0, 1.0 )
vec4 translucent = vec4(white, 0.5);
Matrices are constructed in the same manner and can be initialized to either
a diagonal matrix or a fully populated matrix.
In the case of diagonal matrices, a single value is passed into the constructor,
and the diagonal elements of the matrix are set to that value, with all others
being set to zero, as in
Matrices can also be created by specifying the value of every element in the
matrix in the constructor. Values can be specified by combinations of scalars
and vectors, as long as enough values are provided, and each column is
specified in the same manner. Additionally, matrices are specified in
column-major order, meaning the values are used to populate columns
before rows (which is the opposite of how “C” initializes two-dimensional
arrays).
For example, we could initialize a 3 u3 matrix in any of the following ways:
mat3 M = mat3(1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0 );
vec3 column1 = vec3(1.0, 2.0, 3.0);
vec3 column2 = vec3(4.0, 5.0, 6.0);
vec3 column3 = vec3(7.0, 8.0, 9.0);
mat3 M = mat3(column1, column2, column3);
mmat34.0
4.0 0.0 0.0
0.0 4.0 0.0
0.0 0.0 4.0
==

686 Chapter 15: The OpenGL Shading Language
or even
vec2 column1 = vec2(1.0, 2.0);
vec2 column2 = vec2(4.0, 5.0);
vec2 column3 = vec2(7.0, 8.0);
mat3 M = mat3(column1, 3.0,
column2, 6.0,
column3, 9.0);
all yielding the same matrix
Accessing Elements in Vectors and Matrices
The individual elements of vectors and matrices can be accessed and
assigned. Vectors support two types of element access: a named-component
method and an array-like method. Matrices use a two-dimensional array-
like method.
Components of a vector can be accessed by name, as in
float red = color.r;
float v_y = velocity.y;
or using a zero-based index scheme. The following yield identical results to
the above:
float red = color[0];
float v_y = velocity[1];
In fact, as shown in Table 15-3, there are three sets of component names
available, all of which do the same thing. The multiple sets are useful for
clarifying the operations that you’re doing.
Component Accessors Description
(x, y, z, w) components associated with positions
(r, g, b, a) components associated with colors
(s, t, p, q) components associated with texture coordinates
Table 15-3 Vector Component Accessors
M
1.0 4.0 7.0
2.0 5.0 8.0
3.0 6.0 9.0
=

Creating Shaders with GLSL 687
A common use for component-wise access to vectors is for swizzling
components, as you might do with colors, perhaps for color space
conversion. For example, you could do the following to specify a luminance
value based on the red component of an input color:
vec3 luminance = color.rrr;
Likewise, if you needed to move components around in a vector, you
might do:
color = color.abgr; // reverse the components of a color
The only restriction is that only one set of components can be used with a
variable in one statement. That is, you can’t do:
vec4 color = otherColor.rgz;// Error: ‘z’ is from a
// different group
Also, a compile-time error will be raised if you attempt to access an element
that’s outside of what the type supports. For example,
vec2 pos;
float zPos = pos.z; // Error: no ‘z’ component in 2D vectors
Matrix elements can be accessed using the array notation. Either a single
scalar value or an array of elements can be accessed from a matrix:
mat4 m = mat4(2.0);
vec4 zVec = m[2];
float yScale = m[1][1]; // or m[1].y works as well
Structures
You can also logically group together collections of different types in a
structure. Structures are convenient for passing groups of associated data
into functions. When a structure is defined, it automatically creates a new
type, and implicitly defines a constructor function that takes the types of
the elements of the structure as parameters.
struct Particle {
float lifetime;
vec3 position;
vec3 velocity;
};
Particle p = Particle(10.0, pos, vel); // pos, vel are vec3’s
Likewise, to reference elements of a structure, use the familiar “dot”
notation as you would in “C.”

688 Chapter 15: The OpenGL Shading Language
Arrays
GLSL also supports one-dimensional arrays of any type, including
structures. As with “C,” arrays are indexed using brackets ([ ]). The range of
elements in an array of size n is 0 ... n1. Unlike “C,” however, negative
array indices are not permitted, nor are two-dimensional arrays.
Arrays can be declared sized or unsized. You might use an unsized array as
a forward declaration of an array variable and later redeclare it to the
appropriate size. Array declarations use the bracket notation, as in:
float coeff[3]; // an array of 3 floats
float[3] coeff; // same thing
int indices[]; // unsized. Redeclare later with a size
Arrays are first-class types in GLSL, meaning they have constructors and can
be used as function parameters and return types. To statically initialize an
array of values, you would use a constructor in the following manner:
float coeff[3] = float[3]( 2.38, 3.14, 42.0 );
The dimension value on the constructor is optional.
Additionally, similar to Java, GLSL arrays have an implicit method for
reporting their number of elements: the length() method. If you would like
to operate on all the values in an array, here is an example using the
length() method:
for ( int i = 0; i < coeff.length(); ++i ) {
coeff[i] *= 2.0;
}
Storage Qualifiers
Types can also have modifiers that affect their behavior. There are four
modifiers defined in GLSL, as shown in Table 15-4.
Type Modifier Description
const Labels a variable as a read-only, compile-time constant.
in Specifies that the variable is an input to the shader stage.
out Specifies that the variable is an output from a shader stage.
uniform Specifies that the value is passed to the shader from the
application and is constant across a given primitive.
Table 15-4 GLSL Type Modifiers

Creating Shaders with GLSL 689
Note: In GLSL versions prior to 1.30, vertex shader input variables were
qualified with the keyword “attribute.” Likewise, fragment shader
input variables (which correspond to vertex shader outputs) were
qualified with the “varying” keyword. In anticipation of potentially
adding more shading stages, both of those keywords were replaced by
the more generic “in” and “out” variations. In Version 1.40, both
“attribute” and “varying” were removed (though they remain
accessible using the GL_ARB_compatibility extension).
All storage qualifiers are valid for globally scoped variables. Additionally,
const is applicable to local variables and function parameters.
Const Storage Qualifier
Just as with “C,” the const type modifier indicates that the variable is read-
only. For example, the statement
const float Pi = 3.141529
sets the variable Pi to an approximation of S. With the addition of the const
modifier, it becomes an error to write to a variable after its declaration, so
they must be initialized when declared.
In Storage Qualifier
The in modifier is used to qualify inputs into a shader stage. Those inputs
may be vertex attributes (for vertex shaders) or interpolated variables (for
fragment shaders).
Fragment shaders can further qualify their input values using some
additional keywords that are valid only in combination with the in
keyword. Those keywords are described in Table 15-5.
in Keyword Qualifier Description
centroid Forces the sampling of a fragment input variable to be
within the area covered by the primitive for the pixel
when multisampling is enabled.
smooth Interpolates the fragment input variable in a
perspective-correct manner.
Table 15-5 Additional in Keyword Qualifiers (for Fragment Shader Inputs)

690 Chapter 15: The OpenGL Shading Language
For example, if you would like a flat-shaded, centroid-sampled fragment
input, you would specify
flat centroid in fragment;
in your fragment shader.
Out Storage Qualifier
The out modifier is used to qualify outputs from a shader stage—for
example, the transformed homogenous coordinates from a vertex shader, or
the final fragment color from a fragment shader.
Vertex shaders can further qualify their output values using the centroid
keyword, which has the same meaning here as for fragment inputs. In
addition, any vertex shader output qualified by centroid must have a
matching fragment shader input variable that is also centroid qualified (i.e.,
the fragment shader has to have a variable with the identical declaration as
in the vertex shader).
Uniform Storage Qualifier
The uniform modifier specifies that a variable’s value will be specified by the
application before the shader’s execution and does not change across the
primitive being processed. Uniform variables are shared between vertex and
fragment shaders and must be declared as global variables. Any type of
variable, including structures and arrays, can be specified as uniform.
Consider a shader that uses an additional color in shading a primitive. You
might declare a uniform variable to pass that information into your shaders.
In the shaders, you would make the declaration:
uniform vec4 BaseColor;
Within your shaders, you can reference BaseColor by name, but to set its
value in your application, you need to do a little extra work. The GLSL
flat Doesn’t interpolate the fragment input (i.e., the input
will be the same for all fragments, as in flat shading).
noperspective Linearly interpolates the fragment variable.
in Keyword Qualifier Description
Table 15-5 Additional in Keyword Qualifiers (for Fragment Shader Inputs)
Table 15.5 (continued) Additional in Keyword Qualifiers (for Fragment Shader Inputs)

Creating Shaders with GLSL 691
compiler creates a table of all uniform variables when it links your shader
program. To set BaseColor’s value from your application, you need to obtain
the index of BaseColor in the table, which is done using the
glGetUniformLocation() routine.
Once you have the associated index for the uniform variable, you can set the
value of the uniform variable using the glUniform*() or glUniformMatrix*()
routines.
GLint glGetUniformLocation(GLuint program, const char *name)
Returns the index of the uniform variable name associated with the shader
program.name is a null-terminated character string with no spaces. A value
of minus one (1) is returned if name does not correspond to a uniform
variable in the active shader program, or if a reserved shader variable name
(those starting with gl_ prefix) is specified.
name can be a single variable name, an element of an array (by including
the appropriate index in brackets with the name), or a field of a structure
(by specifying name, then “.” followed by the field name, as you would in
the shader program). For arrays of uniform variables, the index of the first
element of the array may be queried either by specifying only the array
name (for example, “arrayName”), or by specifying the index to the first
element of the array (as in “arrayName[0]”).
The returned value will not change unless the shader program is relinked
(see glLinkProgram()).
void glUniform{1234}{if ui}(GLint location,TYPE value);
void glUniform{1234}{if ui}v(GLint location, GLsizei count,
const TYPE *values);
void glUniformMatrix{234}fv(GLint location, GLsizei count,
GLboolean transpose, const GLfloat *values);
void glUniformMatrix{2x3,2x4,3x2,3x4,4x2,4x3}fv(GLint location,
GLsizei count, GLboolean transpose,
const GLfloat *values);
Sets the value for the uniform variable associated with the index location
The vector form loads count sets of values (from one to four values,
depending upon which glUniform*() call is used) into the uniform

692 Chapter 15: The OpenGL Shading Language
Example 15-4 demonstrates obtaining a uniform variable’s index and
assigning values.
Example 15-4 Obtaining a Uniform Variable’s Index and Assigning Values
GLint timeLoc; /* Uniform index for variable “time” in shader */
GLfloat timeValue; /* Application time */
timeLoc = glGetUniformLocation(program, “time”);
glUniform1f(timeLoc, timeValue);
Uniform variables can also be declared within named uniform blocks that
enable sharing and other features for shaders. Those uniform variables
aren’t accessible using the routines we just discussed, and they require usage
of other routines described in the next section.
Uniform Blocks
Advanced
As your shader programs become more complex, it’s likely that the number
of uniform variables they use will increase. Often the same uniform value is
variables starting location. If location is the start of an array, count
sequential elements of the array are loaded.
The floating-point forms can be used to load a single float, a floating-point
vector, an array of floats, or an array of vectors of floats.
The integer forms can be used to update a single integer, an integer vector,
an array of integers, or an array of integer vectors. Additionally, individual
and arrays of texture samplers can also be loaded.
For glUniformMatrix{234}fv(),count sets of 2 u2, 3 u3, or 4 u4 matrices
are loaded from values.
For glUniformMatrix{2x3,2x4,3x2,3x4,4x2,4x3}fv(),count sets of like-
dimensioned matrices are loaded from values. If transpose is GL_TRUE,
values are specified in row-major order (like arrays in “C”); or if GL_FALSE
is specified, values are taken to be in column-major order (ordered in the
same manner as glLoadMatrix()).
Advanced

Uniform Blocks 693
used within several shader programs. As uniform locations are generated
when a shader is linked (i.e., when glLinkProgram() is called), the indices
may change, even though (to you) the values of the uniform variables
are identical. Uniform buffer objects provide a method to optimize both
accessing uniform variables and enabling sharing of uniform values across
shader programs.
As you might imagine, that given uniform variables can exist both in your
application and in a shader, you’ll need to both modify your shaders and
use OpenGL routines to set up uniform buffer objects.
Note: Uniform blocks were added into OpenGL Version 3.1.
Specifying Uniform Variables Blocks in Shaders
To access a collection of uniform variables using routines such as
glMapBuffer() (see “Buffer Objects” in Chapter 2 for more details), you
need to slightly modify their declaration in your shader. Instead of
declaring each uniform variable individually, you group them, just as you
would do in a structure, in a uniform block. A uniform block is specified
using the uniform keyword. You then enclose all the variables you want in
that block within a pair of braces, as shown in Example 15-5.
Example 15-5 Declaring a Uniform Variable Block
uniform Matrices {
mat4 ModelView;
mat4 Projection;
mat4 Color;
};
All types, with the exception of samplers, are permitted to be within a
uniform block. Additionally, uniform blocks must be declared at global
scope.
Uniform Block Layout Control
A variety of qualifiers are available to specify how to lay out the variables
within a uniform block. These qualifiers can be used either for each
individual uniform block or to specify how all subsequent uniform blocks
are arranged (after specifying a layout declaration). The possible qualifiers
are detailed in Table 15-6.

694 Chapter 15: The OpenGL Shading Language
For example, to specify that a single uniform block is shared and has row-
major matrix storage, you would declare it in the following manner:
layout (shared, row_major) uniform { ... };
The multiple qualifying options must be separated by commas within the
parentheses. To affect the layout of all subsequent uniform blocks, use the
following construct:
layout (packed, column_major) uniform;
With this specification, all uniform blocks declared after that line will use
that layout until the global layout is changed, or unless they include a
layout override specific to their declaration.
Accessing Uniform Variables Declared in a Uniform Block
While uniform blocks are named, the uniform variables declared within
them are not qualified by that name. That is, a uniform block doesn’t
scope a uniform variable’s name, so declaring two variables of the same
name within two uniform blocks of different names will cause an error.
Using the block name is not necessary when accessing a uniform variable,
however.
Layout Qualifier Description
shared Specify that the uniform block is shared among
multiple programs. (This is the default sharing
setting).
packed Lay out the uniform block to minimize its
memory use; however, this generally disables
sharing across programs.
std140 Use the default layout as described in the
OpenGL specification for uniform blocks.
row_major Cause matrices in the uniform block to be stored
in a row-major element ordering.
column_major Specify matrices should be stored in a column-
major element ordering. (This is the default
ordering.)
Table 15-6 Layout Qualifiers for Uniform Blocks

Uniform Blocks 695
Accessing Uniform Blocks from Your Application
Because uniform variables form a bridge to share data between shaders
and your application, you need to find the offsets of the various uniform
variables inside the named uniform blocks in your shaders. Once you know
the location of those variables, you can initialize them with data, just as you
would any type of buffer object (using calls such as glBufferData(), for
example).
To start, let’s assume that you already know the names of the uniform blocks
used inside the shaders in your application. The first step in initializing
the uniform variables in your uniform block is to obtain the index of the
block for a given program. Calling glGetUniformBlockIndex() returns an
essential piece of information required to complete the mapping of uniform
variables into your application’s address space.
To initialize a buffer object to be associated with your uniform block, you’ll
need to bind a buffer object to a GL_UNIFORM_BUFFER target using the
glBindBuffer() routine (see “Creating Buffer Objects” in Chapter 2 for
details).
Once we have a buffer object initialized, we need to determine
how large to make it to accommodate the variables in the named
uniform block from our shader. To do so, we use the routine
glGetActiveUniformBlockiv(), requesting the GL_UNIFORM_BLOCK_
DATA_SIZE, which returns the size of the block as generated by the
compiler (the compiler may decide to eliminate uniform variables that
aren’t used in the shader, depending on which uniform block layout
you’ve selected). glGetActiveUniformBlockiv() can be used to obtain
other parameters associated with a named uniform block. See “The
Query Commands” in Appendix B for the complete list of options.
After obtaining the index of the uniform block, we need to associate a buffer
object with that block. The most common method for doing so is to call
GLuint glGetUniformBlockIndex(GLuint program,
const char *uniformBlockName)
Returns the index of the named uniform block specified by
uniformBlockName associated with program. If uniformBlockName is not
a valid uniform block of program, GL_INVALID_INDEX is returned.

696 Chapter 15: The OpenGL Shading Language
either glBindBufferRange() or, if all the buffer storage is used for the
uniform block, glBindBufferBase().
Once the association between a named uniform block and a buffer object is
made, you can initialize or change values in that block by using any of the
commands that affect a buffer’s values, as described in “Updating Data
Values in Buffer Objects” in Chapter 2.
You may also want to specify the binding for a particular named uniform
block to a buffer object, as compared to the process of allowing the linker
to assign a block binding and then querying the value of that assignment
after the fact. You might follow this approach if you have numerous shader
programs will share a uniform block. It avoids having the block be assigned
a different index for each program. To explicitly control a uniform block’s
binding, call glUniformBlockBinding() before calling glLinkProgram().
void glBindBufferRange(GLenum target, GLuint index, GLuint buffer,
GLintptr offset, GLsizeiptr size);
void glBindBufferBase(GLenum target, GLuint index, GLuint buffer);
Associates the buffer object buffer with the named uniform block
associated with index.target can either be GL_UNIFORM_BUFFER (for
uniform blocks) or GL_TRANSFORM_FEEDBACK_BUFFER (for use with
transform feedback; see “Transform Feedback” on page 722). index is the
index associated with a uniform block. offset and size specify the starting
index and range of the buffer that is to be mapped to the uniform buffer.
Calling glBindBufferBase() is identical to calling glBindBufferRange()
with offset equal to zero and size equal to the size of the buffer object.
These calls can generate various OpenGL errors: A GL_INVALID_VALUE is
generated if size is less than zero; if offset + size is greater than the size of
the buffer; if either offset or size is not a multiple of 4; or if index is less than
zero, or greater than or equal to the value returned when querying GL_
MAX_UNIFORM_BUFFER_BINDINGS.
GLint gUniformBlockBinding(GLuint program,
GLuint uniformBlockIndex,
GLuint uniformBlockBinding)
Explicitly assigns uniformBlockIndex to uniformBlockBinding for program.

Uniform Blocks 697
The layout of uniform variables in a named uniform block is controlled by
the layout qualifier specified when the block was compiled and linked. If
you used the default layout specification, you will need to determine the
offset and date-store size of each variable in the uniform block. To do so,
you will use the pair of calls: glGetUniformIndices(), to retrieve the index
of a particular named uniform variable, and glGetActiveUniformsiv(), to
get the offset and size for that particular index, as shown in Example 15-6.
Example 15-6 Initializing Uniform Variables in a Named Uniform Block: ubo.c
/* Vertex and fragment shaders that share a block of uniforms
** named “Uniforms” */
const char* vShader = {
“#version 140\n”
“uniform Uniforms {“
“ vec3 translation;”
“ float scale;”
“ vec4 rotation;”
“ bool enabled;”
“};”
“in vec2 vPos;”
“in vec3 vColor;”
“out vec4 fColor;”
“void main()”
“{“
“ vec3 pos = vec3( vPos, 0.0 );”
“ float angle = radians( rotation[0] );”
“ vec3 axis = normalize( rotation.yzw );”
“ mat3 I = mat3( 1.0 );”
“ mat3 S = mat3( 0, -axis.z, axis.y, “
void glGetUniformIndices(GLuint program, GLsizei uniformCount,
const char **uniformNames, GLuint *uniformIndices);
Returns the indices associated with the uniformCount uniform variables
specified by name in the array uniformNames in the array uniformIndices
for program. Each name in uniformNames is assumed to be NULL
terminated, and both uniformNames and uniformIndices have uniformCount
elements in each array.
If a name listed in uniformNames is not the name of an active uniform
variables, the value GL_INVALID_INDEX is returned in the corresponding
element in uniformIndices.

698 Chapter 15: The OpenGL Shading Language
“ axis.z, 0, -axis.x, “
“ -axis.y, axis.x, 0 );”
“ mat3 uuT = outerProduct( axis, axis );”
“ mat3 rot = uuT + cos(angle)*(I - uuT) + sin(angle)*S;”
“ pos *= scale;”
“ pos *= rot;”
“ pos += translation;”
“ fColor = vec4( scale, scale, scale, 1 );”
“ gl_Position = vec4( pos, 1 );”
“}”
};
const char* fShader = {
“#version 140\n”
“uniform Uniforms {“
“ vec3 translation;”
“ float scale;”
“ vec4 rotation;”
“ bool enabled;”
“};”
“in vec4 fColor;”
“out vec4 color;”
“void main()”
“{“
“ color = fColor;”
“}”
};
/* Helper function to convert GLSL types to storage sizes */
size_t
TypeSize( GLenum type )
{
size_t size;
#define CASE( Enum, Count, Type ) \
case Enum: size = Count * sizeof(Type); break
switch( type ) {
CASE( GL_FLOAT, 1, GLfloat );
CASE( GL_FLOAT_VEC2, 2, GLfloat );
CASE( GL_FLOAT_VEC3, 3, GLfloat );
CASE( GL_FLOAT_VEC4, 4, GLfloat );
CASE( GL_INT, 1, GLint );
CASE( GL_INT_VEC2, 2, GLint );
CASE( GL_INT_VEC3, 3, GLint );
CASE( GL_INT_VEC4, 4, GLint );
CASE( GL_UNSIGNED_INT, 1, GLuint );

Uniform Blocks 699
CASE( GL_UNSIGNED_INT_VEC2, 2, GLuint );
CASE( GL_UNSIGNED_INT_VEC3, 3, GLuint );
CASE( GL_UNSIGNED_INT_VEC4, 4, GLuint );
CASE( GL_BOOL, 1, GLboolean );
CASE( GL_BOOL_VEC2, 2, GLboolean );
CASE( GL_BOOL_VEC3, 3, GLboolean );
CASE( GL_BOOL_VEC4, 4, GLboolean );
CASE( GL_FLOAT_MAT2, 4, GLfloat );
CASE( GL_FLOAT_MAT2x3, 6, GLfloat );
CASE( GL_FLOAT_MAT2x4, 8, GLfloat );
CASE( GL_FLOAT_MAT3, 9, GLfloat );
CASE( GL_FLOAT_MAT3x2, 6, GLfloat );
CASE( GL_FLOAT_MAT3x4, 12, GLfloat );
CASE( GL_FLOAT_MAT4, 16, GLfloat );
CASE( GL_FLOAT_MAT4x2, 8, GLfloat );
CASE( GL_FLOAT_MAT4x3, 12, GLfloat );
default:
fprintf( stderr, “Unknown type: 0x%x\n”, type );
exit( EXIT_FAILURE );
break;
}
#undef CASE
return size;
}
void
init()
{
GLuint program;
glClearColor( 1, 0, 0, 1 );
/* Compile and load vertex and fragment shaders (see
** LoadProgram.c */
program = LoadProgram( vShader, fShader );
glUseProgram( program );
/* Initialize uniform values in uniform block “Uniforms” */
{
GLuint uboIndex;
GLint uboSize;
GLuint ubo;
GLvoid *buffer;
/* Find the uniform buffer index for “Uniforms”, and
** determine the block’s sizse*/

700 Chapter 15: The OpenGL Shading Language
uboIndex = glGetUniformBlockIndex( program, “Uniforms” );
glGetActiveUniformBlockiv( program, uboIndex,
GL_UNIFORM_BLOCK_DATA_SIZE, &uboSize );
buffer = malloc( uboSize );
if ( buffer == NULL ) {
fprintf( stderr, “Unable to allocate buffer\n” );
exit( EXIT_FAILURE );
}
else {
enum { Translation, Scale, Rotation,
Enabled, NumUniforms };
/* Values to be stored in the buffer object */
GLfloat scale = 0.5;
GLfloat translation[] = { 0.1, 0.1, 0.0 };
GLfloat rotation[] = { 90, 0.0, 0.0, 1.0 };
GLboolean enabled = GL_TRUE;
/* Since we know the names of the uniforms
** in our block, make an array of those values */
const char* names[NumUniforms] = {
“translation”,
“scale”,
“rotation”,
“enabled”
};
/* Query the necessary attributes to determine
** where in the buffer we should write
** the values */
GLuint indices[NumUniforms];
GLint size[NumUniforms];
GLint offset[NumUniforms];
GLint type[NumUniforms];
glGetUniformIndices( program, NumUniforms,
names, indices );
glGetActiveUniformsiv( program, NumUniforms, indices,
GL_UNIFORM_OFFSET, offset );
glGetActiveUniformsiv( program, NumUniforms, indices,
GL_UNIFORM_SIZE, size );
glGetActiveUniformsiv( program, NumUniforms, indices,
GL_UNIFORM_TYPE, type );

Uniform Blocks 701
/* Copy the uniform values into the buffer */
memcpy( buffer + offset[Scale], &scale,
size[Scale] * TypeSize(type[Scale]) );
memcpy( buffer + offset[Translation], &translation,
size[Translation] * TypeSize(type[Translation]) );
memcpy( buffer + offset[Rotation], &rotation,
size[Rotation] * TypeSize(type[Rotation]) );
memcpy( buffer + offset[Enabled], &enabled,
size[Enabled] * TypeSize(type[Enabled]) );
/* Create the uniform buffer object, initialize
** its storage, and associated it with the shader
** program */
glGenBuffers( 1, &ubo );
glBindBuffer( GL_UNIFORM_BUFFER, ubo );
glBufferData( GL_UNIFORM_BUFFER, uboSize,
buffer, GL_STATIC_RAW );
glBindBufferBase( GL_UNIFORM_BUFFER, uboIndex, ubo );
}
}
...
}
Computational Invariance
GLSL does not guarantee that two identical computations in different
shaders will result in exactly the same value. The situation is no different
than for computational applications executing on the CPU, where the
order of compiled instructions may result in tiny differences due to the
accumulation order of instructions. These tiny errors may be an issue for
multipass algorithms that expect positions to be computed exactly the
same for each shader pass. GLSL has a method of enforcing this type of
invariance between shaders by using the invariant keyword.
invariant Qualifier
The invariant qualifier may be applied to any output varying variables of a
vertex shader. The variable may be a built-in variable or a user-defined one.
For example:
invariant gl_Position;
invariant centroid varying vec3 Color;

702 Chapter 15: The OpenGL Shading Language
As you may recall, varying variables are used to pass data from a vertex
shader into a fragment shader. Invariant variables must be declared
invariant in both the vertex and fragment shader. The invariant keyword
may be applied at any time before use of the variable in the shader and may
be used to modify previously declared variables.
For debugging, it may be useful to impose invariance on all varying
variables in shader. This can be accomplished by using the vertex shader
preprocessor pragma
#pragma STDGL invariant(all)
Global invariance in this manner is useful for debugging; however, it may
likely have an impact on the shader’s performance. Guaranteeing invariance
usually disables optimizations that may have been performed by the GLSL
compiler.
Statements
The real work in a shader is done by computing values and making
decisions. In the same manner as C++, GLSL has a rich set of operators for
constructing arithmetic operations for computing values and a standard set
of logical constructs for controlling shader execution.
Arithmetic Operations
No text describing a language is complete without the mandatory table of
operator precedence (see Table 15-7). The operators are ordered in decreasing
precedence. In general, the types being operated on must be the same, and
for vector and matrices, the operands must be of the same dimension.
Precedence Operators Accepted Types Description
1 ( ) — Grouping of operations
2[]
f( )
. (period)
++ --
arrays
functions
structures
int, float, vec*, mat*
Array subscripting
Function calls and constructors
Structure field or method access
Post-increment and -decrement
3 ++ --
+ - !
int, float, vec*, mat*
int, float, vec*, mat*
Pre-increment and -decrement
Unary operations: explicit positive
or negative value, negation
Table 15-7 GLSL Operators and Their Precedence

Uniform Blocks 703
Note: This table lists all currently implemented operators of GLSL. Various
operations that exist in C++ (%, the modulus operator, for example)
are currently reserved but not implemented in GLSL.
Overload Operators
Most operators in GLSL are overloaded, meaning that they operate on a
varied set of types. Specifically, arithmetic operations (including pre- and
post-increment and -decrement) for vectors and matrices are well-defined
in GLSL. For example, to multiply a vector and a matrix (recalling that the
order of terms is important—matrix multiplication is non-commutative, for
all you math-heads), use the following operation:
vec3 v;
mat3 m;
vec3 result = v * m;
The normal restrictions apply, that the dimensionality of the matrix and
the vector must match. Additionally, scalar multiplication with a vector and
matrix will produce the expected result. One notable exception is that the
multiplication of two vectors will result in component-wise multiplication
4 * / int, float, vec*, mat* Multiplicative operations
5 + - int, float, vec*, mat* Additive operations
6 < > <= >= int, float, vec*, mat* Relational operations
7 == != int, float, vec*, mat* Equality operations
8 && bool Logical and operation
9 ^^ bool Logical exclusive-or operation
10 || bool Logical or operation
11 a ? b : c bool
int, float, vec*, mat*
Selection operation (inline “if”
operation; if (a) then (b) else (c))
12 =
+= -=
*= /=
int, float, vec*, mat* Assignment
Arithmetic assignment
13 , (comma) — Sequence of operations
Precedence Operators Accepted Types Description
Table 15-7 (continued) GLSL Operators and Their Precedence

704 Chapter 15: The OpenGL Shading Language
of components; however, multiplying two matrices will result in normal
matrix multiplication.
vec2 a, b, c;
mat2 m, u, v;
c = a * b; //c = ( a.x*b.x, a.y*b.y )
m = u * v; //m = (u00*v00+u01*v10u00*v01+u01*v11
u01*v00+u11*v10u10*v01+u11*v11 )
Additional common vector operations (e.g., dot and cross products) are sup-
ported by function calls, as well as various per-component operations on
vectors and matrices.
Logical Operations
GLSL’s logical control structures are the popular if-then-else and switch
statements. As with the “C” language the else clause is optional, and
multiple statements require a block.
if ( truth ) {
// true clause
} else {
// false clause
}
Similar to the situation in C, switch statements are available (starting with
GLSL 1.30) in their familiar form:
switch( int_value ) {
case n:
// statements
break;
case m:
// statements
break;
default:
// statements
break;
}
GLSL switch statements also support “fall-through” cases—a case statement
that does not end with a break statement. They do require a break for the
final case in the block (before the closing brace).

Uniform Blocks 705
Looping Constructs
GLSL supports the familiar “C” form of for,while, and do ... while loops.
The for loop permits the declaration of the loop iteration variable in the
initialization clause of the for loop. The scope of iteration variables declared
in this manner is only for the lifetime of the loop.
for (int i = 0; i < 10; ++i ) {
...
}
while (n < 10) {
...
}
do {
...
} while (n < 10);
Flow Control Statements
Additional control statements beyond conditionals and loops are available
in GLSL. Table 15-8 describes available flow-control statements.
Statement Description
break Terminates execution of the block of a loop, and
continues execution after the scope of that block.
continue Terminates the current iteration of the enclosing block
of a loop, resuming execution with the next iteration of
the loop.
return [result] Returns from the current subroutine, optionally
providing a value to be returned from the function
(assuming return value matches the return type of the
enclosing function).
discard Discards the current fragment and ceases shader
execution. Discard statements are only valid in fragment
shader programs.
Table 15-8 GLSL Flow-Control Statements

706 Chapter 15: The OpenGL Shading Language
The discard statement is available only in fragment programs. The
execution of the fragment shader may be terminated at the execution of the
discard statement, but this is implementation dependent.
Functions
Functions permit you to replace occurrences of common code with a
function call. This, of course, allows for smaller code, and less chances for
errors. GLSL defines a number of built-in functions, which are listed in
Appendix I, “Built-In OpenGL Shading Language Variables and Functions,”2
as well as support for user-defined functions. User-defined functions can be
defined in a single shader object, and reused in multiple shader programs.
Declarations
Function declaration syntax is very similar to “C,” with the exception of the
access modifiers on variables:
returnType functionName([accessModifier] type1 variable1,
[accessModifier] type2 varaible2,
... )
{
// function body
return returnValue; // unless returnType is void
}
Function names can be any combination of letters, numbers, and the
underscore character, with the exception that it can neither begin with a
digit nor with gl_.
Return types can be any built-in GLSL type and user-defined structure;
arrays are not available as return values. If a function doesn’t return a value,
its return type is void.
Parameters to functions can be of any type, including arrays (which must
specify their size).
Functions must be either declared, or prototyped, before their use. Just as in
C++, the compiler must have seen the function’s definition before its use or an
error will be raised. If a function is used in a shader object other than the one
where it’s defined, a prototype must be declared. A prototype is merely the
function’s signature without its accompanying body. Here’s a simple example:
float HornerEvalPolynomial(float coeff[10], float x);
2This appendix is available online at http://www.opengl-redbook.com/appendices/.

Accessing Texture Maps in Shaders 707
Parameters Access Modifiers
While functions in GLSL are able to modify and return values after their
execution, there’s no concept of a pointer or reference, as in “C” or C++.
Rather, parameters of functions have associated access modifiers indicating
if the value should be copied into, or out of, a function after execution.
Table 15-9 describes the available parameter access modifiers in GLSL.
The in keyword is optional. If a variable does not include an access
modifier, then an “in” modifier is implicitly added to the parameter’s
declaration. However, if the variable’s value needs to be copied out of a
function, it must either be tagged with an “out” (for write-only variables) or
an “inout” (for read-write variables). Writing to an variable not tagged with
one of these modifiers will generate a compile-time error.
Additionally, to verify at compile time that a function doesn’t modify an
input-only variable, adding a “const in” modifier will cause the compiler to
check that the variable is not written to in the function.
Using OpenGL State Values in GLSL Programs
Almost all values that you set in using the OpenGL API are accessible from
within vertex and fragment shader programs. A comprehensive list of GLSL
built-in variables is provided in Appendix I, “Built-In OpenGL Shading
Language Variables and Functions.”3
Accessing Texture Maps in Shaders
GLSL also supports accessing texture maps in both vertex and fragment
shaders. To access a texture map, GLSL makes an association between an
Access Modifier Description
in value copied into a function (default if not specified)
const in read-only value copied into a function
out value copied out of a function (undefined upon
entrance into the function)
inout value copied into and out of a function
Table 15-9 GLSL Function Parameter Access Modifiers
3This appendix is available online at http://www.opengl-redbook.com/appendices/.

708 Chapter 15: The OpenGL Shading Language
active texture unit (see “Steps in Multitexturing” in Chapter 9) configured
in the OpenGL application, and a variable declared in a shader. Such
variables use one of the sampler data types shown in Table 15-10 to allow
the shader program access to the texture map’s data. The dimensions of the
associated texture map must match the type of the sampler.
Sampler Name Description
sampler1D
isampler1D
usample1D
Accesses a 1D texture map
sampler2D
isampler2D
usampler2D
Accesses a 2D texture map
sampler3D
isampler3D
usampler3D
Accesses a 3D texture map
samplerCube
isamplerCube
usamplerCube
Accesses a cube map (for reflection mapping)
sampler1DArray
isampler1DArray
usampler1DArray
Accesses an array of 1D texture maps
sampler2DArray
isampler2DArray
usampler2DArray
Accesses an array of 2D texture maps
sampler2DRect
isampler2DRect
usampler2DRect
Accesses a 2D texture rectangle
sampler1DShadow Accesses a 1D shadow map
sampler2DShadow Accesses a 2D shadow map
samplerCubeShadow Accesses a cube map of shadowmaps
sampler1DArrayShadow Accesses an array of 1D shadow maps
sampler2DArrayShadow Accesses an array of 2D shadow maps
Table 15-10 Fragment Shader Texture Sampler Types

Accessing Texture Maps in Shaders 709
Samplers must be declared as uniform variables in the shader and must have
their value assigned from within the OpenGL application. Samplers may
also be used as parameters in functions, but must be used with samplers of
matching type.
Samplers must have a texture unit assigned to them before their use in a
shader, and can only be initialized by glUniform1i(), or glUniform1iv(), with
the index of the texture unit that the sampler should use (see Example 15-7).
Example 15-7 Associating Texture Units with Sampler Variables
GLint texSampler; /* sampler index for shader variable “tex” */
texSampler = glGetUniformLocation(program, “tex”);
glUniform1i(texSampler, 2); /* Set “tex” to use GL_TEXTURE2 */
Accessing Textures in GLSL
Sampling a texture map from within a GLSL shader uses the sampler
variable that you’ve declared and associated with a texture unit. There
are a number of texture access routines (described in “Texture Lookup
Functions” in Appendix I, “Built-in OpenGL Shading Language Variables
and Functions,”4) for accessing all OpenGL supported texture map types.
In Example 15-8, we sample the two-dimensional texture map associated
with the sampler2D variable tex, and combine the results with the fragment’s
color, providing the same results as using GL_MODULATE mode for the
texture environment mode.
Example 15-8 Sampling a Texture Within a GLSL Shader
uniform sampler2D tex;
void main()
{
gl_FragColor = gl_Color * texture2D(tex, gl_TexCoord[0].st);
}
sampler2DRectShadow Accesses a 2D shadow texture rectangle
samplerBuffer
isamplerBuffer
usamplerBuffer
Accesses a texture buffer
4This appendix is available online at http://www.opengl-redbook.com/appendices/.
Sampler Name Description
Table 15-10 (continued) Fragment Shader Texture Sampler Types

710 Chapter 15: The OpenGL Shading Language
Even though the example seems simple, that’s truly all there is to do. However,
much more interesting applications are enabled when the values in a texture
map do not necessarily represent colors, but other data used for subsequent
computation after retrieving the results from the texture map. Specifically, one
application is using the values in one texture map as indices into another,
described in “Dependent Texture Reads” below. The same results can be
accomplished using the combiner texture environment (see “Texture
Combiner Functions” in Chapter 9), but are much simpler to do using shaders.
The results you compute after sampling a texture are controlled by the code
you write in your shader, but how the texture map is sampled is still con-
trolled by the state settings in your application. For example, you control
whether a texture map contains mipmaps, and how those mipmaps are
sampled, as well as the filters used for resolving the returned texel values
(basically, the parameters you set with glTexParameter*()). From inside
the shader, you can control the biasing of mipmap selection, and using
projective-texture techniques (see Appendix I, “Built-In OpenGL Shading
Language Variables and Functions,”5 for details and suitable functions).
Dependent Texture Reads
During the execution of a shader that employs texture mapping, you’ll use
texture coordinates to specify locations in texture maps and retrieve the
resulting texel values. While texture coordinates are supplied for each active
texture unit, you can use any values you might like as texture coordinates
(assuming matching dimensionality) for use with a sampler, including
values you may have just sampled from another texture map. Passing the
results of one texture access as texture coordinates into another texture
access operation is generally termed a dependent texture read, indicating that
the results of the second operation are dependent on the first operation.
This is easy to implement in GLSL and is illustrated in Example 15-9.
Example 15-9 Dependent Texture Reads in GLSL
uniform sampler1D coords;
uniform sampler3D volume;
void main()
{
vec3 texCoords = texture1D(coords, gl_TexCoord[0].s);
vec3 volumeColor = texture3D(volume, texCoords);
...
}
5This appendix is available online at http://www.opengl-redbook.com/appendices/.

Shader Preprocessor 711
Texture Buffers
Advanced
While GLSL makes arrays available, both as statically initialized values
inside shaders, and as collections of values presented as an array in a
uniform variable, you might occasionally need an array that exceeds the
size limits available in those two options. Previous to OpenGL Version 3.1,
you would have likely stored such a table of values in a texture map, and
then manipulate the texture coordinates to obtain access to the values you
wanted in the texture, usually in a less than straightforward manner. A
more intuitive and direct solution to that data storage problem is the texture
buffer. A texture buffer is a special type of buffer object, similar to a one-
dimensional texture, that you can index using an integer value (like a
normal array index) in your shader, but that offers the more expansive
resources of texture memory, thereby allowing larger data sets.
You create a texture buffer just as you would any other buffer object. First
you call glBindBuffer() with a target of GL_TEXTURE_BUFFER to create the
object, and then you call glBufferData() (for example) to initialize its data.
To bind that buffer to a texture buffer, you call glTexBuffer().
Similar to other texture maps, you specify which texture unit to associate
the texture buffer with by calling glActiveTexture().
Shader Preprocessor
The first step in compilation of a GLSL shader is parsing by the preprocessor.
Similar to the “C” preprocessor, there are a number of directives for creating
conditional compilation blocks and defining values. However, unlike the
“C” preprocessor, there is no file inclusion (#include).
void glTexBuffer(GLenum target, GLenum internalFormat, GLuint buffer);
Associates the buffer object buffer with target, causing the format of the
data in buffer to be interpreted as having the format of internalFormat.
target must be GL_TEXTURE_BUFFER, and internalFormat may be any of
the sized texture formats: G, GL_R8, GL_R16, GL_R16F, GL_R32F, GL_R8I,
GL_R16I, GL_R32I, GL_R8UI, GL_R16UI, GL_R32UI, GL_RG8, GL_RG16,
GL_RG16F, GL_RG32F, GL_RG8I, GL_RG16I, GL_RG32I, GL_RG8UI,
GL_RG16UI, GL_RG32UI, GL_RGBA8, GL_RGBA16, GL_RGBA16F,
GL_RGBA32F, GL_RGBA8I, GL_RGBA16I, GL_RGBA32I, GL_RGBA8UI,
GL_RGBA16UI, GL_RGBA32UI.
Advanced

712 Chapter 15: The OpenGL Shading Language
Preprocessor Directives
Table 15-11 lists the preprocessor directives accepted by the GLSL
preprocessor and their functions.
Macro Definition
The GLSL preprocessor allows macro definition in much the same manner
as the “C” preprocessor, with the exception of the string substitution and
concatenation facilities. Macros might define a single value, as in
#define NUM_ELEMENTS 10
or with parameters like
#define LPos(n) gl_LightSource[(n)].position
Additionally, there are several predefined macros for aiding in diagnostic
messages (that you might issue with the #error directive, for example), as
shown in Table 15-12.
Preprocessor Directive Description
#define
#undef
Control the definition of constants and macros
similar to the C preprocessor
#if
#ifdef
#ifndef
#else
#elif
#endif
Conditional code management similar to the
C preprocessor, including the defined operator.
Conditional expressions evaluate integer
expressions and defined values (as specified by
#define) only.
#error text Cause the compiler to insert text (up to the first
newline character) into the shader information log
#pragma options Control compiler specific options
#extension options Specify compiler operation with respect to
specified GLSL extensions
#version number Mandate a specific version of GLSL version support
#line options Control diagnostic line numbering
Table 15-11 GLSL Preprocessor Directives

Shader Preprocessor 713
Likewise, macros (excluding those defined by GLSL) may be undefined by
using the #undef directive. For example
#undef LPos
Preprocessor Conditionals
Identical to the processing by the “C” preprocessor, the GLSL preprocessor
provides conditional code inclusion based on macro definition and integer
constant evaluation.
Macro definition may be determined in two ways: Either using the #ifdef
directive
#ifdef NUM_ELEMENTS
...
#endif
or using the defined operator with the #if or #elif directives
#if defined(NUM_ELEMENTS) && NUM_ELEMENTS > 3
...
#elif NUM_ELEMENTS < 7
...
#endif
Compiler Control
The #pragma directive provides the compiler additional information
regarding how you would like your shaders compiled.
Macro Definition
__LINE__ Line number defined by one more than the number of
newline characters processed and modified by the #line
directive
__FILE__ Source string number currently being processed
__VERSION__ Integer representation of the OpenGL Shading Language
version
Table 15-12 GLSL Preprocessor Predefined Macros

714 Chapter 15: The OpenGL Shading Language
Optimization Compiler Option
The optimize option instructs the compiler to enable or disable
optimization of the shader from the point where the directive resides
forward in the shader source. You can enable or disable optimization by
issuing either
#pragma optimize(on)
and
#pragma optimize(off)
respectively. These options may only be issued outside of a function
definition. By default, optimization is enabled for all shaders.
Debug Compiler Option
The debug option enables or disables additional diagnostic output of the
shader. You can enable or disable debugging by issuing either
#pragma debug(on)
and
#pragma debug(off)
respectively. Similar to the optimize option, these options may only be
issued outside of a function definition, and by default, debugging is
disabled for all shaders.
Global Shader Compilation Option
One final #pragma directive is available, STDGL. This option is currently used
to enable invariance in the output of varying values. See “invariant
Qualifier” on page 701 for details.
Extension Processing in Shaders
GLSL, like OpenGL itself, may be enhanced by extensions. As vendors may
include extensions specific to their OpenGL implementation, it’s useful to
have some control over shader compilation in light of possible extensions
that a shader may use.
The GLSL preprocessor uses the #extension directive to provide
instructions to the shader compiler regarding how extension availability

Vertex Shader Specifics 715
should be handled during compilation. For any, or all, extensions, you can
specify how you would like the compiler to proceed with compilation.
#extension extension_name : <directive>
where extensions_name uses the same extension name returned by calling
glGetString(GL_EXTENSIONS) or
#extension all : <directive>
to affect the behavior of all extensions.
The options available are shown in Table 15-13.
Vertex Shader Specifics
You can send data from your application into a vertex program using several
mechanisms:
• By using the standard OpenGL vertex data interface (those calls that
are legal between a glBegin() and a glEnd()), such as glVertex*(),
glNormal*(), and so on. These values can vary on a per-vertex basis
and are considered to be built-in attribute variables.
• By declaring uniform variables. These values remain constant across a
geometric primitive.
Directive Description
require Flag an error if the extension is not supported, or if the all
extension specification is used.
enable Give a warning if the particular extensions specified are not
supported, or flag an error if the all extension specification is
used.
warn Give a warning if the particular extensions specified are not
supported, or give a warning if any extension use is detected
during compilation.
disable Disable support for the particular extensions listed (that is, have
the compiler act as if the extension is not supported even if it
is) or all extensions if all is present, issuing warnings and
errors as if the extension were not present.
Table 15-13 GLSL Extension Directive Modifiers
716 Chapter 15: The OpenGL Shading Language
• By declaring attribute variables, which can be updated on a per-vertex
basis, in addition to the standard vertex state. (This is effectively the
only method for specifying vertex attributes in OpenGL Version 3.1,
unless the GL_ARB_compatibility extension is available to you.)
Likewise, a vertex program must output some data (and optionally update
other variables) for continued processing by the remaining vertex
processing by the OpenGL pipeline, and possibly an accompanying
fragment program.
The outputs that need to be written include:
•gl_Position, which must be updated by the vertex program and
contain the homogeneous coordinate of the vertex after modelview
and projection transformation.
• Various other built-in variables that are declared varying for passing
data into the fragment pipeline. These include colors, texture
coordinates, and other per-fragment data. They are described in
“Varying Output Variables” on page 721.
• User-defined varying variables.
Figure 15-5 illustrates the inputs and outputs of a vertex program.
gl_Position
gl_FrontColor
gl_BackColor
gl_FrontSecondaryColor
gl_BackSecondaryColor
gl_TexCoord[n]
gl_FogFragCoord
gl_PointSize
gl_ClipVertex
User-defined
varying
variables
gl_Vertex
gl_Normal
gl_Color
gl_SecondaryColor
gl_TexCoordn
gl_FogCoord
User-defined
uniform
variables
User-defined
vertex
attributes
Ver tex
Shader
Figure 15-5 GLSL Vertex Shader Input and Output Variables

Vertex Shader Specifics 717
Built-In Attribute Input Variables
Table 15-14 shows variables representing those that are globally available in
a vertex shader. The variables reflect the current OpenGL state, as set by the
corresponding routine.
User-Defined Attribute Variables
User-defined attribute variables are global variables that associate values
passed from the OpenGL application to a vertex shader executing within
the OpenGL implementation.
Attribute variables can be defined as float, floating-point vectors (vec*), or
matrices (mat*).
Hint: In general, attribute variables are implemented as vec4’s internal to
OpenGL. If you have a number of single floating-point variables that
you wish to use as vertex attributes, consider combining those values
into one or more vec* structures. While declaring a single float is
supported, it uses an entire vec4 to represent the single value.
Variable Type Specifying function Description
gl_Vertex vec4 glVertex Vertex’s world-space
coordinate
gl_Color vec4 glColor Primary color value
gl_SecondaryColor vec4 glSecondaryColor Secondary color value
gl_Normal vec4 glNormal Lighting normal
gl_MultiTexCoordnvec4 glMultiTexCoord( n, ... ); Texture unit n’s texture
coordinates, with n = 0
... 7.
gl_FogCoord float glFogCoord Fog coordinate
gl_VertexID int —Index of current vertex
since the start of the
last rendering call
gl_InstanceID int glDrawArraysInstanced
glDrawElementsInstanced
The instance ID for the
associated primitives
Table 15-14 Vertex Shader Attribute Global Variables

718 Chapter 15: The OpenGL Shading Language
To use user-defined attribute variables, OpenGL needs to know how to
match the name of the variable you specified in your shader program with
values that you pass into a shader. Similar to how OpenGL handles uniform
variables, when a shader program is linked, the linker generates a table of
variable names for attribute variables. To determine the maximum number
of user-defined vertex attributes, call glGetIntegerv() with a parameter of
GL_MAX_VERTEX_ATTRIBS.
To determine which index you need to update for the respective variable in
the vertex program, you’ll call glGetAttribLocation(), with the name of
your variable, and the index corresponding to that name will be returned.
For example, in a vertex shader, you might declare
varying vec3 displacement;
Assuming that the shader compiled and linked appropriately, you would
determine the index of “displacement” by calling:
int index = glGetAttribLocation(program, “displacement”);
You can also explicitly set the binding of an attribute variable to an index
using the glBindAttribLocation() call; however, this must be done before
the shader program is linked.
GLint glGetAttribLocation(GLuint program, const char *name);
Returns the index associated with name for the shader program.name must
be a null-terminated character string matching the declaration in program.
If name is not an active variable, or it’s the name of a built-in attribute
variable, or an error occurs, a value of 1 is returned.
void glBindAttribLocation(GLint program, GLuint index,
const char *name);
Explicitly specifies which index location name should be assigned the next
time program is linked. index must be an integer between zero and GL_
MAX_VERTEX_ATTRIBS 1, and name must be a null-terminated string.
Built-in attribute variables (those beginning with gl_) will generate a
GL_INVALID_OPERATION error.

Vertex Shader Specifics 719
To set the value associated with the returned index, you’ll use a version of
the glVertexAttrib*() function.
While attribute variables are floating point, there’s no restriction on the
type of input data used to initialize their values. Specifically, integer-type
input values can be normalized into the range of zero to one, using
glVertexAttrib4N*(), before being assigned into the attribute variable.
Scalar (single-value), vector, and matrix attribute values can be set using
glVertexAttrib*(). For the matrix case, multiple calls are required. In
particular, for a matrix of dimension n, you would call glVertexAttrib*(),
with indices: index, index+1, ..., index+n1.
Vertex shaders also augment the vertex array facility (see “Vertex Arrays”
on page 70). As with other types of vertex data, values for vertex attribute
variables can be stored in vertex arrays and updated by calling
glDrawArrays(),glArrayElement(), and so on. To specify the array to
be used to update a variable’s value, call glVertexAttribPointer().
void glVertexAttrib{1234}{sfd}(GLuint index,TYPE values);
void glVertexAttrib{123}{sfd}v(GLuint index, const TYPE *values);
void glVertexAttrib4{bsifd ub us ui}v(GLuint index,TYPE values);
void glVertexAttrib4Nub(GLuint index,TYPE values);
void glVertexAttrib4N{bsi ub us ui}v(GLuint index, const TYPE *values);
void glVertexAttribI{1234}{i ui}(GLuint index,TYPE values);
void glVertexAttribI4{bsi ub us ui}v(GLint index, const TYPE *values);
Specifies the values for vertex attribute variables associated with index to
values. For calls that do not explicitly set all four values, default values
of 0.0 (0 for signed- and unsigned-integer values) will be set for the y- and
z-coordinates, and 1.0 (1 for signed- and unsigned-integer values) for the
w-coordinate.
Specifying values for index zero is identical to calling glVertex*(), with the
same values.
The normalized version will convert integer input values into the range
zero to one, using the mappings specified in Table 4-1 on page 198.
Matrices are updated by specifying consecutive values for index.values
specified will be used to update the respective columns of the matrix.

720 Chapter 15: The OpenGL Shading Language
As with other types of vertex arrays, specifying the array is only one part of
the process. Each client-side vertex array needs to be enabled. Compared to
using glEnableClientState(), arrays of vertex attributes are enabled by
calling glEnableVertexAttribArray().
Special Output Variables
The values shown in Table 15-15 are available for writing (and reading after
being written) in a vertex shader. gl_Position specifies the vertex’s final
position upon exit of the vertex shader and is required to be written in the
shader.
void glVertexAttribPointer(GLuint index, GLint size, GLenum type,
GLboolean normalized, GLsizei stride,
const GLvoid* pointer);
Specifies where the data values for index can be accessed. pointer is the
memory address of the first set of values in the array. size represents the
number of components to be updated per vertex. type specifies the data
type (GL_SHORT, GL_INT, GL_FLOAT, or GL_DOUBLE) of each element in
the array. normalized indicates that the vertex data should be normalized
before being stored (in the same manner as glVertexAttrib4N*()). stride is
the byte offset between consecutive elements in the array. If stride is 0, the
data is assumed to be tightly packed.
void glEnableVertexAttribArray(GLuint index);
void glDisableVertexAttribArray(GLuint index);
Specifies that the vertex array associated with variable index be enabled
or disabled. index must be a value between 0 and GL_MAX_VERTEX_
ATTRIBS 1.
Variable Name Type Description
gl_Position vec4 Transformed vertex position (in eye coordinates).
gl_PointSize float Point size of vertex.
gl_ClipVertex vec4 Vertex position to be used with user-defined clipping
planes. This value must be in the same coordinate
system as the clipping planes: eye-coordinates or
object-coordinates.
Table 15-15 Vertex Shader Special Global Variables

Vertex Shader Specifics 721
While you’re able to set the output vertex position to any homogenous
coordinate you might like, the final value of gl_Position is usually
computed within a vertex program as:
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
Or, if you’re employing a multipass algorithm (one rendering multiple
images from the same geometry) that needs to have the results of the vertex
shader and fixed function pipeline be consistent, set gl_Position using the
following code:
gl_Position = ftransform();
gl_PointSize controls the output size of a point, similar to glPointSize(),
but on a per-vertex basis. To control the size of points from within vertex
programs, call glEnable() with a value of GL_VERTEX_PROGRAM_POINT_
SIZE, which overrides any current point size that may have been specified.
User-defined clipping planes, as specified by glClipPlane(), can be used by
writing a homogeneous coordinate into the gl_ClipVertex variable. For
clipping to proceed correctly, the clipping plane specified and the coordinate
written into gl_ClipVertex must be in the same coordinate space. The
common space for clipping is eye-coordinates. You can transform the
current vertex into eye-coordinates for clipping by executing:
gl_ClipVertex = gl_ModelViewMatrix * gl_Vertex;
Varying Output Variables
Table 15-16 represents those variables that can be written to in a vertex
shader and have their values readable in a fragment shader. The values
in the fragment shader are iterated across the fragments (or samples, if
multisampling) of the primitives.
Variable Name Type Description
gl_FrontColor vec4 Primary color to be used for front-facing
primitives
gl_BackColor vec4 Primary color to be used for back-facing
primitives
gl_FrontSecondaryColor vec4 Secondary color to be used for front-facing
primitives
Table 15-16 Vertex Shader Varying Global Variables

722 Chapter 15: The OpenGL Shading Language
A vertex shader has the capability of setting both the front- and back-face
color values for a vertex. Be default, regardless of the values set from within
a vertex shader, the front-facing color will be chosen. This behavior can be
modified by calling glEnable(), with a value of GL_VERTEX_PROGRAM_
TWO_SIDE, which causes OpenGL to select colors based on the orientation
of the underlying primitive.
Texture Mapping in Vertex Shaders
Texture mapping is available in vertex shaders. Using textures in vertex
shaders is identical to the process described in “Accessing Textures in GLSL”
on page 709, with one minor exception. Automatic mipmap selection is not
done in vertex shaders. However, you can manually select which mipmap
level using the texture*Lod routines in GLSL.
To determine if your implementation is capable of using textures in vertex
shaders, query GL_MAX_VERTEX_TEXTURE_IMAGE_UNITS using
glIntegerv(). If a nonzero value is returned, texturing is supported.
Transform Feedback
Advanced
Transform feedback allows an application to record the transformed
primitives generated by rendering (and before clipping) using a vertex
shader, into a buffer object, somewhat similar to the situation described
in “Feedback” in Chapter 13, but with more flexible control of the data
recorded.
gl_BackSecondaryColor vec4 Secondary color to be used for back-facing
primitives
gl_TexCoord[n]vec4nth Texture coordinate values
gl_FogFragCoord vec4 Fragment fog coordinate value
Variable Name Type Description
Table 15-16 (continued) Vertex Shader Varying Global Variables
Advanced

Transform Feedback 723
Using transform feedback is a two-step process:
1. Specifying the mapping of outputs of a vertex shader into one or more
buffer objects.
2. Rendering while in transform feedback mode.
To accomplish step 1, we’ll call glTransformFeedbackVaryings() before
linking our vertex shader. This function will set the output ordering of the
varyings that we want to capture and specify how the data will be written out.
Once the program has been successfully linked, and the ordering of
varyings set, we can attach buffer objects to receive the transformed
outputs. To bind a buffer, we use glBindBufferRange() (or
glBindBufferBase()), associating the appropriate number of buffers if the
bufferMode was set to GL_SEPARATE_ATTRIBS, or a single buffer if the
bufferMode was set to GL_INTERLEAVED_ATTRIBS. The size of the buffer (as
specified either by glBindBufferRange() or when the buffer was sized by
calling glBufferData(), for example) dictates the number of attribute values
recorded for the specified primitives. When the available buffer space is
exhausted, no more primitives will be recorded.
To capture the transformed output, you enter transform feedback mode by
calling glBeginTransformFeedback(), and specifying the type of primitives
you would like recorded, as described in Table 15-17. The complete set of
specified varyings is written for each vertex (up to space limitations in the
buffer).
void glTransformFeedbackVaryings(GLuint program, GLsizei count,
const char **varyings, GLenum bufferMode);
Assigns the ordering for count varying variables specified by (null-
terminated) names in the array varyings for program.bufferMode must be
either GL_SEPARATE_ATTRIBS, which specifies that the varyings should
be written to count separate buffer objects, or GL_INTERLEAVED_ATTRIBS,
which writes the count varying values contiguously into a single buffer
object.
A program may fail to link if count exceeds the number of available
varyings for output. A GL_INVALID_VALUE error will be generated if
program is not a valid program object, or if bufferMode is set to GL_
SEPARATE_ATTRIBS and count is greater than the value returned for a
query of GL_MAX_TRANSFORM_FEEDBACK_SEPARATE_ATTRIBS.

724 Chapter 15: The OpenGL Shading Language
You then issue rendering commands. Vertices are transformed by your
shader, and the varying variables you specified in step 1 are recorded.
Example 15-10 illustrates the process of capturing vertex values, surface
normals, and texture coordinates using transform feedback. Note that the
input consists of only the vertex positions; all of the other values are
generated by the vertex shader.
Example 15-10 Using Transform Feedback to Capture Geometric Primitives: xfb.c
GLuint
LoadTransformFeedbackShader(const char* vShader, GLsizei count,
const GLchar** varyings)
{
GLuint shader, program;
GLint completed;
Transform Feedback Primitive Type Permitted OpenGL Primitive Type
GL_POINTS GL_POINTS
GL_LINES GL_LINES
GL_LINE_LOOP
GL_LINE_STRIP
GL_TRIANGLES GL_TRIANGLES
GL_TRIANGLE_FAN
GL_TRAINGLE_STRIP
GL_QUADS
GL_QUAD_STRIP
GL_POLYGONS
Table 15-17 Transform Feedback Primitives and Their Permitted OpenGL
Rendering Types
void glBeginTransformFeedback(GLenum primitiveMode);
void glEndTransformFeedback(void);
Enters and exits transform feedback mode. primitiveMode must be one of
GL_POINTS, GL_LINES, or GL_TRIANGLES, which represents the type of
output written to the associated buffer objects.
A GL_INVALID_OPERATION error is generated if a command renders an
OpenGL primitive type that is incompatible with the current transform
feedback mode.

Transform Feedback 725
program = glCreateProgram();
/*
** --- Load and compile the vertex shader ---
*/
if (vShader != NULL) {
shader = glCreateShader(GL_VERTEX_SHADER);
glShaderSource(shader, 1, &vShader, NULL);
glCompileShader(shader);
glGetShaderiv(shader, GL_COMPILE_STATUS, &completed);
if (!completed) {
GLint len;
char* msg;
glGetShaderiv(shader, GL_INFO_LOG_LENGTH, &len);
msg = (char*) malloc(len);
glGetShaderInfoLog(shader, len, &len, msg);
fprintf(stderr, "Vertex shader compilation ”
“failure:\n%s\n", msg);
free(msg);
glDeleteProgram(program);
exit(EXIT_FAILURE);
}
glAttachShader(program, shader);
}
glTransformFeedbackVaryings(program, count, varyings,
GL_INTERLEAVED_ATTRIBS);
/*
** --- Link program ---
*/
glLinkProgram(program);
glGetProgramiv(program, GL_LINK_STATUS, &completed);
if (!completed) {
GLint len;
char* msg;
glGetProgramiv(program, GL_INFO_LOG_LENGTH, &len);
msg = (char*) malloc(len);
glGetProgramInfoLog(program, len, &len, msg);

726 Chapter 15: The OpenGL Shading Language
fprintf(stderr, "Program link failure:\n%s\n", msg);
free(msg);
glDeleteProgram(program);
exit(EXIT_FAILURE);
}
return program;
}
void
init()
{
/* Vertex shader generating our output values */
const char vShader[] = {
"#version 140\n" "in vec2 coords;"
"out vec2 texCoords;"
"out vec3 normal;"
"void main() {"
" float angle = radians(coords[0]);"
" normal = vec3(cos(angle), sin(angle), 0.0);"
" texCoords = normal.xy;"
" gl_Position = vec4(normal.xy, coords[1], 1.0);"
"}"
};
/* List (and ordering) of varying values written to the
** transform buffer */
const char *varyings[] = {
"texCoords",
"normal",
"gl_Position"
};
GLuint program;
GLuint query;
GLint count;
/* Load shader program and set up varyings */
program = LoadTransformFeedbackShader(vShader, 3,
varyings);
glUseProgram(program);
glGenQueries(1, &query);
/* Bind to transform-feedback buffer */

Fragment Shader Specifics 727
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 0, xfb);
glBeginQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN,
query);
glBeginTransformFeedback(GL_POINTS);
glDrawArrays(GL_POINTS, 0, 2*(NumSlices+1));
glEndTransformFeedback();
glEndQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN);
glGetQueryObjectiv(query, GL_QUERY_RESULT, &count);
fprintf(stderr, "%d primitives written\n", count);
...
}
Fragment Shader Specifics
Like vertex programs, your OpenGL application can send data directly to a
fragment program, as well as having OpenGL provide values for use in your
program. All of that data, along with the inputs into a fragment shader,
result in the final color and depth value of a fragment. After execution of a
fragment shader, the computed values continue through the OpenGL
fragment pipeline to the fragment test and blending stages.
Figure 15-6 describes the inputs and outputs of a fragment programs.
Figure 15-6 Fragment Shader Built-In Variables
gl_FragCoord
gl_Color
gl_SecondaryColor
gl_TexCoord[n]
gl_FogFragCoord
gl_FrontFacing
gl_FragColor
gl_FragDepth
gl_FragData[n]
discard
fragment
User-defined
uniform
variables
User-defined
vertex
attributes
Fragment
Shader

728 Chapter 15: The OpenGL Shading Language
Input Values
Fragment shaders receive the iterated values of the final vertex pipeline
outputs. These include the fragment’s position, resolved primary and
secondary colors, a set of texture coordinates, and a fog coordinate distance
for the fragment. All of these values are described in Table 15-18.
Special Output Values
Input values are combined in a fragment program to produce the final
values for fragment, as shown in Table 15-19.
Variable Type Description
gl_FragCoord vec4 (Read only) Position of the fragment, including
the z-component, which represents the fixed-
function computed depth value
gl_FrontFacing bool (Read only) Specifies if the fragment belongs to
a front-facing primitive
gl_Color vec4 Primary color of the fragment
gl_SecondayColor vec4 Secondary color of the fragment
gl_TexCoord[n]vec4 nth texture coordinates for the fragment
gl_FogFragCoord float Fragment’s fog coordinate, either specified as
the z-coordinate of the primitive in eye space or
the interpolated fog coordinate
gl_PointCoord vec2 Fragment’s location for a point sprite in the
range [0.0, 1.0]. The value is undefined if the
current primitive is not a point sprite or if point
sprites are disabled
Table 15-18 Fragment Shader Varying Global Variables
Variable Type Description
gl_FragColor vec4 Final color of the fragment
gl_FragDepth float Final depth of the fragment
gl_FragData[n] vec4 Data value written to the nth data buffer
Table 15-19 Fragment Shader Output Global Variables

Fragment Shader Specifics 729
gl_FragColor is the final color of the fragment. While writing to
gl_FragColor isn’t required output from a fragment program, the results of
the final fragment color for writing into the color buffer are undefined.
gl_FragDepth is the final depth of the fragment and is utilized in the depth
test. While you cannot modify the (x, y) coordinate of a fragment, the depth
value can be modified.
Finally, additional data may be written from a fragment program.
The gl_FragData array allows for the writing of various data into extra
buffers, as described below.
Rendering to Multiple Output Buffers
A fragment shader may output values to multiple buffers simultaneously
using the gl_FragData array. Writing a value into array element
gl_FragData[n] will cause the color to be written into the appropriate
fragment in the buffer in element n of the array passed to glDrawBuffers().
A fragment shader may write to either gl_FragColor or gl_FragData in a
shader, but not both.
User-Defined Fragment Shader Outputs
You might find that using relatively nondescript names such as
gl_FragColor is not suitable for specifying the output of your shader.
While GLSL doesn’t care, the next programmer to look at your code
(which you probably forgot to comment) might not immediately
understand that your shader does not output a color, but rather the
results of evaluating a Bessel function of the second kind (or some other
mathematical archana).
With GLSL version 1.30, you can give more suitable names to the outputs
from your fragment shaders, and you can control the mapping of those
outputs to the various bound drawing buffers. You can either specify the
mapping of fragment output name to a buffer before linking or query the
program after linking to determine the layout of variables.
To use the first approach, call glBindFragDataLocation() before calling
glLinkProgram().

730 Chapter 15: The OpenGL Shading Language
After linking, you can retrieve the mapping by calling
glGetFragDataLocation():
void glBindFragDataLocation(GLuint program, GLuint colorNumber,
const char *name);
Specifies the output of fragment variable name should be written to color
buffer colorNumber for GLSL program. This affects only programs that have
not yet been linked.
A GL_INVALID_VALUE error is generated if colorNumber is less than zero
or greater than the value returned when querying GL_MAX_DRAW_
BUFFERS. A GL_INVALID_OPERATION error is generated if name begins
with gl_.
GLint glGetFragDataLocation(GLuint program, const char *name);
Returns the color buffer index associated with the output of name from
GLSL program.
A GL_INVALID_OPERATION error is generated if program did not
successfully link, and glGetFragDataLocation() is called. A value of –1 is
returned if name is not a fragment program output associated with
program or if another error occurred.
731
Appendix A
A.
Basics of GLUT: The OpenGL Utility Toolkit
This appendix describes a subset of the OpenGL Utility Toolkit (GLUT)
originally developed by Mark Kilgard. We use an open-source version of
GLUT named freeglut (http://freeglut.sourceforge.net/) developed by
Pawel W. Olszta, with contributions from Andreas Umbach and Steve Baker.
GLUT has become a popular library for OpenGL programmers because it
standardizes and simplifies window and event management. GLUT has
been ported atop a variety of OpenGL implementations, including both the
X Window System and Microsoft Windows.
This appendix has the following major sections:
• “Initializing and Creating a Window”
• “Handling Window and Input Events”
• “Loading the Color Map”
• “Initializing and Drawing Three-Dimensional Objects”
• “Managing a Background Process”
• “Running the Program”
(See “How to Obtain the Sample Code” on page xli for information about
how to obtain the source code for GLUT.)

732 Appendix A: Basics of GLUT: The OpenGL Utility Toolkit
With GLUT, your application structures its event handling to use callback
functions. (This method is similar to using the Xt Toolkit, also known as the
X Intrinsics, with a widget set.) For example, first you open a window and
register callback routines for specific events. Then you create a main loop
without an exit. In that loop, if an event occurs, its registered callback func-
tions are executed. On completion of the callback functions, flow of control
is returned to the main loop.
Initializing and Creating a Window
Before you can open a window, you must specify its characteristics. Should
it be single-buffered or double-buffered? Should it store colors as RGBA val-
ues or as color indices? Where should it appear on your display? To specify
the answers to these questions, call glutInit(),glutInitDisplayMode(),
glutInitWindowSize(), and glutInitWindowPosition() before you call
glutCreateWindow() to open the window.
void glutInit(int argc, char **argv);
glutInit() should be called before any other GLUT routine, because it
initializes the GLUT library. glutInit() will also process command line
options, but the specific options are window system dependent. For the
X Window System, -iconic, -geometry, and -display are examples of com-
mand line options, processed by glutInit(). (The parameters to glutInit()
should be the same as those to main().)
void glutInitDisplayMode(unsigned int mode);
Specifies a display mode (such as RGBA or color-index, or single- or
double-buffered) for windows created when glutCreateWindow() is
called. You can also specify that the window have an associated depth,
stencil, and/or accumulation buffer. The mask argument is a bitwise ORed
combination of GLUT_RGBA or GLUT_INDEX, GLUT_SINGLE or GLUT_
DOUBLE, and any of the buffer-enabling flags: GLUT_DEPTH, GLUT_
STENCIL, or GLUT_ACCUM. For example, for a double-buffered, RGBA-
mode window with a depth and stencil buffer, use GLUT_DOUBLE |
GLUT_RGBA | GLUT_DEPTH | GLUT_STENCIL. The default value is
GLUT_RGBA | GLUT_SINGLE (an RGBA, single-buffered window).

Handling Window and Input Events 733
Handling Window and Input Events
After the window is created, but before you enter the main loop, you should
register callback functions using the following routines.
void glutInitContextVersion(int majorVersion, int minorVersion);
Specifies the major and minor versions of the OpenGL implementation
that you want a context created for. To use OpenGL Version 3.0 or greater,
you need to call this routine before calling glutCreateWindow(), due to the
different context creation semantics introduced by OpenGL Version 3.0.
void glutInitWindowSize(int width, int height);
void glutInitWindowPosition(int x, int y);
Requests windows created by glutCreateWindow() to have an initial size
and position. The arguments (x, y) indicate the location of a corner of the
window, relative to the entire display. width and height indicate the win-
dow’s size (in pixels). The initial window size and position are hints and
may be overridden by other requests.
int glutCreateWindow(char *name);
Opens a window with previously set characteristics (display mode, width,
height, and so on). The string name may appear in the title bar if your
window system does that sort of thing. The window is not initially dis-
played until glutMainLoop() is entered, so do not render into the win-
dow until then.
The value returned is a unique integer identifier for the window. This
identifier can be used for controlling and rendering to multiple windows
(each with an OpenGL rendering context) from the same application.
void glutDisplayFunc(void (*func)(void));
Specifies the function that’s called whenever the contents of the window need
to be redrawn. The contents of the window may need to be redrawn when the
window is initially opened, when the window is popped and window damage
is exposed, and when glutPostRedisplay() is explicitly called.

734 Appendix A: Basics of GLUT: The OpenGL Utility Toolkit
void glutReshapeFunc(void (*func)(int width, int height));
Specifies the function that’s called whenever the window is resized or
moved. The argument func is a pointer to a function that expects two
arguments, the new width and height of the window. Typically, func calls
glViewport(), so that the display is clipped to the new size, and it rede-
fines the projection matrix so that the aspect ratio of the projected image
matches the viewport, avoiding aspect ratio distortion. If glutReshape-
Func() isn’t called or is deregistered by passing NULL, a default reshape
function is called, which calls glViewport(0,0,width,height).
void glutKeyboardFunc(void (*func)(unsigned char key, int x, int y));
Specifies the function, func, that’s called when a key that generates an
ASCII character is pressed. The key callback parameter is the generated
ASCII value. The x and y callback parameters indicate the location of the
mouse (in window-relative coordinates) when the key was pressed.
void glutMouseFunc(void (*func)(int button, int state, int x, int y));
Specifies the function, func, that’s called when a mouse button is pressed
or released. The button callback parameter is GLUT_LEFT_BUTTON,
GLUT_MIDDLE_BUTTON, or GLUT_RIGHT_BUTTON. The state callback
parameter is either GLUT_UP or GLUT_DOWN, depending on whether
the mouse has been released or pressed. The x and y callback parameters
indicate the location (in window-relative coordinates) of the mouse when
the event occurred.
void glutMotionFunc(void (*func)(int x, int y));
Specifies the function, func, that’s called when the mouse pointer moves
within the window while one or more mouse buttons are pressed. The x
and y callback parameters indicate the location (in window-relative coor-
dinates) of the mouse when the event occurred.
void glutPostRedisplay(void);
Marks the current window as needing to be redrawn. At the next
opportunity, the callback function registered by glutDisplayFunc() will
be called.

Initializing and Drawing Three-Dimensional Objects 735
Loading the Color Map
If you’re using color-index mode, you might be surprised to discover there’s
no OpenGL routine to load a color into a color-lookup table. This is because
the process of loading a color map depends entirely on the window system.
GLUT provides a generalized routine to load a single color index with an
RGB value, glutSetColor().
Initializing and Drawing Three-Dimensional Objects
Many sample programs in this guide use three-dimensional models to
illustrate various rendering properties. The following drawing routines are
included in GLUT to avoid having to reproduce the code to draw these
models in each program. The routines render all their graphics in immedi-
ate mode. Each three-dimensional model comes in two flavors: wireframe
without surface normals, and solid with shading and surface normals. Use
the solid version when you’re applying lighting. Only the teapot generates
texture coordinates.
void glutSetColor(GLint index, GLfloat red, GLfloat green, GLfloat blue);
Loads the index in the color map, index, with the given red,green, and blue
values. These values are normalized to lie in the range [0.0, 1.0].
void glutWireSphere(GLdouble radius, GLint slices, GLint stacks);
void glutSolidSphere(GLdouble radius, GLint slices, GLint stacks);
void glutWireCube(GLdouble size);
void glutSolidCube(GLdouble size);
void glutWireTorus(GLdouble innerRadius, GLdouble outerRadius,
GLint nsides, GLint rings);
void glutSolidTorus(GLdouble innerRadius, GLdouble outerRadius,
GLint nsides, GLint rings);

736 Appendix A: Basics of GLUT: The OpenGL Utility Toolkit
Managing a Background Process
You can specify a function that’s to be executed if no other events are
pending—for example, when the event loop would otherwise be idle—with
glutIdleFunc(). This is particularly useful for continuous animation or
other background processing.
void glutWireIcosahedron(void);
void glutSolidIcosahedron(void);
void glutWireOctahedron(void);
void glutSolidOctahedron(void);
void glutWireTetrahedron(void);
void glutSolidTetrahedron(void);
void glutWireDodecahedron(GLdouble radius);
void glutSolidDodecahedron(GLdouble radius);
void glutWireCone(GLdouble radius, GLdouble height, GLint slices,
GLint stacks);
void glutSolidCone(GLdouble radius, GLdouble height, GLint slices,
GLint stacks);
void glutWireTeapot(GLdouble size);
void glutSolidTeapot(GLdouble size);
void glutIdleFunc(void (*func)(void));
Specifies the function, func, to be executed if no other events are pending.
If NULL (zero) is passed in, execution of func is disabled.

Running the Program 737
Running the Program
After all the setup is completed, GLUT programs enter an event processing
loop, glutMainLoop().
void glutMainLoop(void);
Enters the GLUT processing loop, never to return. Registered callback
functions will be called when the corresponding events instigate them.
This page intentionally left blank

740 Appendix B: State Variables
The Query Commands
In addition to the basic commands to obtain the values of simple state vari-
ables (commands such as glGetIntegerv() and glIsEnabled(), which are
described in “Basic State Management” in Chapter 2), there are other spe-
cialized commands to return more complex state variables. The prototypes
for these specialized commands are listed here. Some of these routines, such
as glGetError() and glGetString(), have been discussed in more detail else-
where in the book.
To find out when you need to use these commands and their corresponding
symbolic constants, use the tables in the next section, “OpenGL State
Variables.”
void glGetActiveAttrib(GLuint program, GLuint index, GLsizei bufSize,
GLsizei *length, GLint *size, GLenum *type,
char *name);
void glGetActiveUniformBlockiv(GLuint program,
GLuint uniformBlockIndex, GLenum pname,
GLint *params);
GLint glGetActiveUniformName(GLuint program,
GLuint uniformIndex, GLsizei bufSize,
GLsizei *length, char *uniformName)
void glGetActiveUniformsiv(GLuint program, GLsizei uniformCount,
const GLuint *uniformIndices, GLenum pname,
GLint *params)
void glGetAttachedShaders(GLuint program, GLsizei maxCount,
GLsizei *count, GLuint *shaders);
void glGetBufferSubData(GLenum target, GLintptr offset,
GLsizeiptr size, GLvoid* data);
void glGetBufferParameteriv(GLenum target, GLenum pname,
GLint *params);
void glGetBufferPointerv(GLenum target, GLenum pname,
GLvoid **pointer);
void glGetClipPlane(GLenum plane, GLdouble *equation);
void glGetColorTable(GLenum target, GLenum pname, GLenum type,
GLvoid *table);

The Query Commands 741
void glGetColorTableParameter{if}v(GLenum target, GLenum pname,
TYPE *params);
void glGetCompressedTexImage(GLenum target, GLint lod,
GLvoid *pixels);
void glGetConvolutionFilter(GLenum target, GLenum format,
GLenum type, GLvoid *image);
void glGetConvolutionParameter{if}v(GLenum target, GLenum pname,
TYPE *params);
GLenum glGetError(void);
void glGetHistogram(GLenum target, GLboolean reset, GLenum format,
GLenum type, GLvoid *values);
void glGetHistogramParameter{if}v(GLenum target, GLenum pname,
TYPE *params);
void glGetLight{if}v(GLenum light, GLenum pname,TYPE *params);
void glGetMap{ifd}v(GLenum target, GLenum query,TYPE *v);
void glGetMaterial{if}v(GLenum face, GLenum pname,TYPE *params);
void glGetMinmax(GLenum target, GLboolean reset, GLenum format,
GLenum type, GLvoid *values);
void glGetMinmaxParameter{if}v(GLenum target, GLenum pname,
TYPE *params);
void glGetPixelMap{f ui us}v(GLenum map,TYPE *values);
void glGetPolygonStipple(GLubyte *mask);
void glGetProgramInfoLog(GLuint program, GLsizei bufSize,
GLsizei *length, GLchar *infoLog);
void glGetProgramiv(GLuint program, GLenum pname, GLint *params);
void glGetQueryiv(GLenum target, GLenum pname, GLint *params);
void glGetQueryObjectiv(GLuint id, GLenum pname, GLint *params);
void glGetQueryObjectuiv(GLuint id, GLenum pname, GLuint *params);
void glGetSeparableFilter(GLenum target, GLenum format,
GLenum type, GLvoid *row, GLvoid *column,
GLvoid *span);

742 Appendix B: State Variables
void glGetShaderInfoLog(GLuint shader, GLsizei bufSize, GLsizei *length,
GLchar *infoLog);
void glGetShaderiv(GLuint shader, GLenum pname, GLint *params);
void glGetShaderSource(GLuint shader, GLsizei bufSize, GLsizei *length,
GLchar *source);
const GLubyte * glGetString(GLenum name);
const GLubyte * glGetStringi(GLenum name, GLuint index);
void glGetTexEnv{if}v(GLenum target, GLenum pname,TYPE *params);
void glGetTexGen{ifd}v(GLenum coord, GLenum pname,TYPE *params);
void glGetTexImage(GLenum target, GLint level, GLenum format,
GLenum type, GLvoid *pixels);
void glGetTexLevelParameter{if}v(GLenum target, GLint level,
GLenum pname,TYPE *params);
void glGetTexParameter{if}v(GLenum target, GLenum pname,
TYPE *params);
void glGetUniform{if}v(GLuint program, GLint location, TYPE *params);
void glGetVertexAttrib{ifd}v(GLuint index, GLenum pname,
TYPE *params);
void glGetVertexAttribPointerv(GLuint index, GLenum pname,
GLvoid **pointer);
GLboolean glIsBuffer(GLuint buffer);
GLboolean glIsList(GLuint list);
GLboolean glIsProgram(GLuint program);
GLboolean glIsQuery(GLuint id);
GLboolean glIsShader(GLuint shader);
GLboolean glIsTexture(GLuint texObject);
void gluGetNurbsProperty(GLUnurbsObj *nobj, GLenum property,
GLfloat *value);
const GLubyte * gluGetString(GLenum name);
void gluGetTessProperty(GLUtesselator *tess, GLenum which,
GLdouble *data);

OpenGL State Variables 743
OpenGL State Variables
The following pages contain tables that list the names of queryable state
variables. For each variable, the tables list a description of it, its attribute
group, its initial or minimum value, and the suggested glGet*() command
to use for obtaining it. State variables that can be obtained using
glGetBooleanv(),glGetIntegerv(),glGetFloatv(), or glGetDoublev() are
listed with just one of these commands—the one that’s most appropriate
given the type of data to be returned. (Some vertex-array variables can be
queried only with glGetPointerv().) These state variables can’t be obtained
using glIsEnabled(). However, state variables for which glIsEnabled() is
listed as the query command can also be obtained using glGetBooleanv(),
glGetIntegerv(),glGetFloatv(), and glGetDoublev(). State variables for
which any other command is listed as the query command can be obtained
only by using that command.
Note: When querying texture state, such as GL_TEXTURE_MATRIX, in
an implementation where the GL_ARB_multitexture extension is
defined, the values returned reference the currently active texture
unit only. See “Multitexturing” on page 467 for details.
If one or more attribute groups are listed, the state variable belongs to the
listed group or groups. If no attribute group is listed, the variable doesn’t
belong to any group. glPushAttrib(),glPushClientAttrib(),glPopAttrib(),
and glPopClientAttrib() may be used to save and restore all state values
that belong to an attribute group (see “Attribute Groups” in Chapter 2 for
more information).
All queryable state variables have initial values; however, those that are
implementation-dependent may not have an initial value listed. If no
initial value is listed, you need to consult the section where that variable is
discussed.
More detail on all of the query functions and values is available online at
http://www.opengl.org/sdk/docs/man.

744 Appendix B: State Variables
Current Values and Associated Data
State Variable Description Attribute
Group
Initial Value Get Command
GL_CURRENT_COLOR Current color current (1, 1, 1, 1) glGetIntegerv(),
glGetFloatv()
GL_CURRENT_SECONDARY_COLOR Current secondary color current (0, 0, 0, 1) glGetIntegerv(),
glGetFloatv()
GL_CURRENT_INDEX Current color index current 1 glGetIntegerv(),
glGetFloatv()
GL_CURRENT_TEXTURE_COORDS Current texture coordinates current (0, 0, 0, 1) glGetFloatv()
GL_CURRENT_NORMAL Current normal current (0, 0, 1) glGetFloatv()
GL_CURRENT_FOG_COORD Current fog coordinate current 0 glGetIntegerv(),
glGetFloatv()
GL_CURRENT_RASTER_POSITION Current raster position current (0, 0, 0, 1) glGetFloatv()
GL_CURRENT_RASTER_DISTANCE Current raster distance current 0 glGetFloatv()
GL_CURRENT_RASTER_COLOR Color associated with raster
position
current (1, 1, 1, 1) glGetIntegerv(),
glGetFloatv()
GL_CURRENT_RASTER_SECONDARY_
COLOR
Secondary color associated with
raster position
current (0, 0, 0, 1) glGetIntegerv(),
glGetFloatv()
Table B-1 State Variables for Current Values and Associated Data

OpenGL State Variables 745
GL_CURRENT_RASTER_INDEX Color index associated with
raster position
current 1 glGetIntegerv(),
glGetFloatv()
GL_CURRENT_RASTER_TEXTURE_COORDS Texture coordinates associated
with raster position
current (0, 0, 0, 1) glGetFloatv()
GL_CURRENT_RASTER_POSITION_VALID Raster position valid bit current GL_TRUE glGetBooleanv()
GL_EDGE_FLAG Edge flag current GL_TRUE glGetBooleanv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-1 (continued) State Variables for Current Values and Associated Data

746 Appendix B: State Variables
Vertex Array Data State (Not Included in Vertex Array Object State)
Vertex Array Object State
State Variable Description Attribute Group Initial Value Get Command
GL_CLIENT_ACTIVE_TEXTURE Active texture unit, for
texture-coordinate array
vertex-array GL_TEXTURE0 glGetIntegerv()
GL_ARRAY_BUFFER_BINDING Current buffer binding vertex-array 0 glGetIntegerv()
GL_PRIMITIVE_RESTART Primitive restart enable — GL_FALSE glIsEnabled()
GL_PRIMITIVE_RESTART_INDEX Primitive restart index
value
— 0 glGetIntegerv()
Table B-2 Vertex Array Data State Variables
State Variable Description Attribute
Group
Initial Value Get Command
GL_VERTEX_ARRAY Vertex array enable vertex-array GL_FALSE glIsEnabled()
GL_VERTEX_ARRAY_BINDING Vertex array object
binding
vertex-array 0 glGetIntegerv()
GL_VERTEX_ARRAY_SIZE Coordinates per vertex vertex-array 4 glGetIntegerv()
GL_VERTEX_ARRAY_TYPE Type of vertex coordinates vertex-array GL_FLOAT glGetIntegerv()
Table B-3 Vertex Array Object State Variables

OpenGL State Variables 747
GL_VERTEX_ARRAY_STRIDE Stride between vertices vertex-array 0 glGetIntegerv()
GL_VERTEX_ARRAY_POINTER Pointer to the vertex array vertex-array NULL glGetPointerv()
GL_NORMAL_ARRAY Normal array enable vertex-array GL_FALSE glIsEnabled()
GL_NORMAL_ARRAY_TYPE Type of normal
coordinates
vertex-array GL_FLOAT glGetIntegerv()
GL_NORMAL_ARRAY_STRIDE Stride between normals vertex-array 0 glGetIntegerv()
GL_NORMAL_ARRAY_POINTER Pointer to the normal
array
vertex-array NULL glGetPointerv()
GL_FOG_COORD_ARRAY Fog coordinate array
enable
vertex-array GL_FALSE glIsEnabled()
GL_FOG_COORD_ARRAY_TYPE Type of fog coordinate
components
vertex-array GL_FLOAT glGetIntegerv()
GL_FOG_COORD_ARRAY_STRIDE Stride between fog
coordinates
vertex-array 0 glGetIntegerv()
GL_FOG_COORD_ARRAY_POINTER Pointer to the fog
coordinate array
vertex-array NULL glGetPointerv()
GL_COLOR_ARRAY RGBA color array enable vertex-array GL_FALSE glIsEnabled()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-3 (continued) Vertex Array Object State Variables

748 Appendix B: State Variables
GL_COLOR_ARRAY_SIZE Color components per
vertex
vertex-array 4 glGetIntegerv()
GL_COLOR_ARRAY_TYPE Type of color components vertex-array GL_FLOAT glGetIntegerv()
GL_COLOR_ARRAY_STRIDE Stride between colors vertex-array 0 glGetIntegerv()
GL_COLOR_ARRAY_POINTER Pointer to the color array vertex-array NULL glGetPointerv()
GL_SECONDARY_COLOR_ARRAY Secondary color array
enable
vertex-array GL_FALSE glIsEnabled()
GL_SECONDARY_COLOR_ARRAY_SIZE Secondary color
components per vertex
vertex-array 3 glGetIntegerv()
GL_SECONDARY_COLOR_ARRAY_TYPE Type of secondary color
components
vertex-array GL_FLOAT glGetIntegerv()
GL_SECONDARY_COLOR_ARRAY_
STRIDE
Stride between secondary
colors
vertex-array 0 glGetIntegerv()
GL_SECONDARY_COLOR_ARRAY_
POINTER
Pointer to the secondary
color array
vertex-array NULL glGetPointerv()
GL_INDEX_ARRAY Color-index array enable vertex-array GL_FALSE glIsEnabled()
GL_INDEX_ARRAY_TYPE Type of color indices vertex-array GL_FLOAT glGetIntegerv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-3 (continued) Vertex Array Object State Variables

OpenGL State Variables 749
GL_INDEX_ARRAY_STRIDE Stride between color
indices
vertex-array 0 glGetIntegerv()
GL_INDEX_ARRAY_POINTER Pointer to the index array vertex-array NULL glGetPointerv()
GL_TEXTURE_COORD_ARRAY Texture-coordinate array
enable
vertex-array GL_FALSE glIsEnabled()
GL_TEXTURE_COORD_ARRAY_SIZE Texture coordinates per
element
vertex-array 4 glGetIntegerv()
GL_TEXTURE_COORD_ARRAY_TYPE Type of texture
coordinates
vertex-array GL_FLOAT glGetIntegerv()
GL_TEXTURE_COORD_ARRAY_STRIDE Stride between texture
coordinates
vertex-array 0 glGetIntegerv()
GL_TEXTURE_COORD_ARRAY_POINTER Pointer to the texture-
coordinate array
vertex-array NULL glGetPointerv()
GL_VERTEX_ATTRIB_ARRAY_ENABLED Vertex attrib array enable vertex-array GL_FALSE glGetVertexAttribiv()
GL_VERTEX_ATTRIB_ARRAY_SIZE Vertex attrib array size vertex-array 4 glGetVertexAttribiv()
GL_VERTEX_ATTRIB_ARRAY_STRIDE Vertex attrib array stride vertex-array 0 glGetVertexAttribiv()
GL_VERTEX_ATTRIB_ARRAY_TYPE Vertex attrib array type vertex-array GL_FLOAT glGetVertexAttribiv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-3 (continued) Vertex Array Object State Variables

750 Appendix B: State Variables
GL_VERTEX_ATTRIB_ARRAY_
NORMALIZED
Vertex attrib array
normalized
vertex-array GL_FALSE glGetVertexAttribiv()
GL_VERTEX_ATTRIB_ARRAY_INTEGER Vertex attrib array has
unconverted integer
values
vertex-array GL_FALSE glGetVertexAttribiv()
GL_VERTEX_ATTRIB_ARRAY_POINTER Vertex attrib array pointer vertex-array NULL glGetVertexAttrib
Pointer()
GL_EDGE_FLAG_ARRAY Edge flag array enable vertex-array GL_FALSE glIsEnabled()
GL_EDGE_FLAG_ARRAY_STRIDE Stride between edge flags vertex-array 0 glGetIntegerv()
GL_EDGE_FLAG_ARRAY_POINTER Pointer to the edge-flag
array
vertex-array NULL glGetPointerv()
GL_ARRAY_BUFFER_BINDING Current buffer binding vertex-array 0 glGetIntegerv()
GL_VERTEX_ARRAY_BUFFER_BINDING Vertex array buffer binding vertex-array 0 glGetIntegerv()
GL_NORMAL_ARRAY_BUFFER_BINDING Normal array buffer
binding
vertex-array 0 glGetIntegerv()
GL_COLOR_ARRAY_BUFFER_BINDING Color array buffer binding vertex-array 0 glGetIntegerv()
GL_INDEX_ARRAY_BUFFER_BINDING Index array buffer binding vertex-array 0 glGetIntegerv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-3 (continued) Vertex Array Object State Variables

OpenGL State Variables 751
GL_TEXTURE_COORD_ARRAY_BUFFER_
BINDING
Texture-coordinate array
buffer binding
vertex-array 0 glGetIntegerv()
GL_EDGE_FLAG_ARRAY_BUFFER_
BINDING
Edge flag array buffer
binding
vertex-array 0 glGetIntegerv()
GL_SECONDARY_COLOR_ARRAY_
BUFFER_BINDING
Secondary color array
buffer binding
vertex-array 0 glGetIntegerv()
GL_FOG_COORD_ARRAY_BUFFER_
BINDING
Fog-coordinate array
buffer binding
vertex-array 0 glGetIntegerv()
GL_ELEMENT_ARRAY_BUFFER_BINDING Element array buffer
binding
vertex-array 0 glGetIntegerv()
GL_VERTEX_ATTRIB_ARRAY_BUFFER_
BINDING
Vertex attribute array
buffer binding
vertex-array 0 glGetVertexAttribiv()
GL_VERTEX_ARRAY_BINDING Current vertex array object
binding
vertex-array 0 glGetIntegerv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-3 (continued) Vertex Array Object State Variables

752 Appendix B: State Variables
State Variable Description Attribute
Group
Initial Value Get Command
GL_BUFFER_SIZE Buffer data size — 0 glGetBufferParameteriv()
GL_BUFFER_USAGE Buffer usage pattern — GL_STATIC_DRAW glGetBufferParameteriv()
GL_BUFFER_ACCESS Buffer access flag — GL_READ_WRITE glGetBufferParameteriv()
GL_BUFFER_ACCESS_FLAGS Extended buffer access
flags
— 0 glGetBufferParameteriv()
GL_BUFFER_MAPPED Buffer map flag — GL_FALSE glGetBufferParameteriv()
GL_BUFFER_MAP_POINTER Mapped buffer pointer — NULL glGetBufferPointerv()
GL_BUFFER_MAP_OFFSET Start of mapped buffer
range
— 0 glGetBufferParameteriv()
GL_BUFFER_MAP_LENGTH Size of mapped buffer
range
— 0 glGetBufferParameteriv()
Table B-4 Vertex Buffer Object State Variables

OpenGL State Variables 753
Transformation
State Variable Description Attribute
Group
Initial Value Get Command
GL_COLOR_MATRIX Color matrix stack — Identity glGetFloatv()
GL_TRANSPOSE_COLOR_MATRIX Stack of transposed color
matrices
— Identity glGetFloatv()
GL_MODELVIEW_MATRIX Modelview matrix stack — Identity glGetFloatv()
GL_TRANSPOSE_MODELVIEW_MATRIX Stack of transposed
modelview matrices
— Identity glGetFloatv()
GL_PROJECTION_MATRIX Projection matrix stack — Identity glGetFloatv()
GL_TRANSPOSE_PROJECTION_MATRIX Stack of transposed
projection matrices
— Identity glGetFloatv()
GL_TEXTURE_MATRIX Texture matrix stack — Identity glGetFloatv()
GL_TRANSPOSE_TEXTURE_MATRIX Stack of transposed texture
matrices
— Identity glGetFloatv()
GL_VIEWPORT Viewport origin and extent viewport — glGetIntegerv()
GL_DEPTH_RANGE Depth range near and far viewport 0, 1 glGetFloatv()
GL_COLOR_MATRIX_STACK_DEPTH Color matrix stack pointer — 1 glGetIntegerv()
Table B-5 Transformation State Variables

754 Appendix B: State Variables
GL_MODELVIEW_STACK_DEPTH Modelview matrix stack
pointer
— 1 glGetIntegerv()
GL_PROJECTION_STACK_DEPTH Projection matrix stack
pointer
— 1 glGetIntegerv()
GL_TEXTURE_STACK_DEPTH Texture matrix stack pointer — 1 glGetIntegerv()
GL_MATRIX_MODE Current matrix mode transform GL_MODELVIEW glGetIntegerv()
GL_NORMALIZE Current normal
normalization on/off
transform/
enable
GL_FALSE glIsEnabled()
GL_RESCALE_NORMAL Current normal rescaling
on/off
transform/
enable
GL_FALSE glIsEnabled()
GL_CLIP_DISTANCEi (replacing GL_
CLIP_PLANEi in Version 3.0 and greater)
User clipping-plane
coefficients
transform (0, 0, 0, 0) glGetClipPlane()
GL_CLIP_DISTANCEi (replacing GL_
CLIP_PLANEi in Version 3.0 and greater)
ith user clipping plane
enabled
transform/
enable
GL_FALSE glIsEnabled()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-5 (continued) Transformation State Variables

OpenGL State Variables 755
Coloring
State Variable Description Attribute
Group
Initial Value Get Command
GL_FOG_COLOR Fog color fog (0, 0, 0, 0) glGetFloatv()
GL_FOG_INDEX Fog index fog 0 glGetFloatv()
GL_FOG_DENSITY Exponential fog density fog 1.0 glGetFloatv()
GL_FOG_START Linear fog start fog 0.0 glGetFloatv()
GL_FOG_END Linear fog end fog 1.0 glGetFloatv()
GL_FOG_MODE Fog mode fog GL_EXP glGetIntegerv()
GL_FOG True if fog enabled fog/enable GL_FALSE glIsEnabled()
GL_FOG_COORD_SRC Source of coordinates for
fog calculation
fog GL_FRAGMENT_
DEPTH
glGetIntegerv()
GL_COLOR_SUM True if color sum is enabled fog/enable GL_FALSE glIsEnabled()
GL_SHADE_MODEL glShadeModel() setting lighting GL_SMOOTH glGetIntegerv()
GL_CLAMP_VERTEX_
COLOR
Vertex clamping color lighting/
enable
GL_TRUE glGetIntegerv()
GL_CLAMP_FRAGMENT_
COLOR
Fragment clamping color color-buffer/
enable
GL_FIXED_ONLY glGetIntegerv()
GL_CLAMP_READ_COLOR Read color clamping color-buffer/
enable
GL_FIXED_ONLY glGetIntegerv()
Table B-6 Coloring State Variables

756 Appendix B: State Variables
Lighting
See also Tables 5-1 and 5-3 for initial values.
State Variable Description Attribute
Group
Initial Value Get Command
GL_LIGHTING True if lighting is enabled lighting
/enable
GL_FALSE glIsEnabled()
GL_COLOR_MATERIAL True if color tracking is enabled lighting GL_FALSE glIsEnabled()
GL_COLOR_MATERIAL_PARAMETER Material properties tracking
current color
lighting GL_AMBIENT_
AND_DIFFUSE
glGetIntegerv()
GL_COLOR_MATERIAL_FACE Face(s) affected by color
tracking
lighting GL_FRONT_
AND_BACK
glGetIntegerv()
GL_AMBIENT Ambient material color lighting (0.2, 0.2, 0.2, 1.0) glGetMaterialfv()
GL_DIFFUSE Diffuse material color lighting (0.8, 0.8, 0.8, 1.0) glGetMaterialfv()
GL_SPECULAR Specular material color lighting (0.0, 0.0, 0.0, 1.0) glGetMaterialfv()
GL_EMISSION Emissive material color lighting (0.0, 0.0, 0.0, 1.0) glGetMaterialfv()
GL_SHININESS Specular exponent of material lighting 0.0 glGetMaterialfv()
GL_LIGHT_MODEL_AMBIENT Ambient scene color lighting (0.2, 0.2, 0.2, 1.0) glGetFloatv()
GL_LIGHT_MODEL_LOCAL_VIEWER Viewer is local lighting GL_FALSE glGetBooleanv()
Table B-7 Lighting State Variables

OpenGL State Variables 757
GL_LIGHT_MODEL_TWO_SIDE Use two-sided lighting lighting GL_FALSE glGetBooleanv()
GL_LIGHT_MODEL_COLOR_
CONTROL
Color control lighting GL_SINGLE_
COLOR
glGetIntegerv()
GL_AMBIENT Ambient intensity of light ilighting (0.0, 0.0, 0.0, 1.0) glGetLightfv()
GL_DIFFUSE Diffuse intensity of light ilighting — glGetLightfv()
GL_SPECULAR Specular intensity of light ilighting — glGetLightfv()
GL_POSITION Position of light ilighting (0.0, 0.0, 1.0, 0.0) glGetLightfv()
GL_CONSTANT_ATTENUATION Constant attenuation factor lighting 1.0 glGetLightfv()
GL_LINEAR_ATTENUATION Linear attenuation factor lighting 0.0 glGetLightfv()
GL_QUADRATIC_ATTENUATION Quadratic attenuation factor lighting 0.0 glGetLightfv()
GL_SPOT_DIRECTION Spotlight direction of light ilighting (0.0, 0.0, 1.0) glGetLightfv()
GL_SPOT_EXPONENT Spotlight exponent of light ilighting 0.0 glGetLightfv()
GL_SPOT_CUTOFF Spotlight angle of light ilighting 180.0 glGetLightfv()
GL_LIGHTiTrue if light i enabled lighting
/enable
GL_FALSE glIsEnabled()
GL_COLOR_INDEXES ca,cd, and cs for color-index
lighting
lighting 0, 1, 1 glGetMaterialfv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-7 (continued) Lighting State Variables

758 Appendix B: State Variables
Rasterization
State Variable Description Attribute Group Initial Value Get Command
GL_POINT_SIZE Point size point 1.0 glGetFloatv()
GL_POINT_SMOOTH Point antialiasing on point/enable GL_FALSE glIsEnabled()
GL_POINT_SPRITE Point sprite enable point/enable GL_FALSE glIsEnabled()
GL_POINT_SIZE_MIN Attenuated minimum point
size
point 0.0 glGetFloatv()
GL_POINT_SIZE_MAX Attenuated maximum point
size
point See Note a at
end of table.
glGetFloatv()
GL_POINT_FADE_THRESHOLD_
SIZE
Threshold for alpha
attenuation
point 1.0 glGetFloatv()
GL_POINT_DISTANCE_
ATTENUATION
Attenuation coefficients point 1, 0, 0 glGetFloatv()
GL_POINT_SPRITE_COORD_
ORIGIN
Origin orientation for point
sprites
point GL_UPPER_LEFT glGetIntegerv()
GL_LINE_WIDTH Line width line 1.0 glGetFloatv()
GL_LINE_SMOOTH Line antialiasing on line/enable GL_FALSE glIsEnabled()
GL_LINE_STIPPLE_PATTERN Line stipple line 1’s glGetIntegerv()
GL_LINE_STIPPLE_REPEAT Line stipple repeat line 1 glGetIntegerv()
Table B-8 Rasterization State Variables

OpenGL State Variables 759
GL_LINE_STIPPLE Line stipple enable line/enable GL_FALSE glIsEnabled()
GL_CULL_FACE Polygon culling enabled polygon/enable GL_FALSE glIsEnabled()
GL_CULL_FACE_MODE Cull front-/back-facing
polygons
polygon GL_BACK glGetIntegerv()
GL_FRONT_FACE Polygon front-face CW/CCW
indicator
polygon GL_CCW glGetIntegerv()
GL_POLYGON_SMOOTH Polygon antialiasing on polygon/enable GL_FALSE glIsEnabled()
GL_POLYGON_MODE Polygon rasterization mode
(front and back)
polygon GL_FILL glGetIntegerv()
GL_POLYGON_OFFSET_FACTOR Polygon offset factor polygon 0 glGetFloatv()
GL_POLYGON_OFFSET_UNITS Polygon offset units polygon 0 glGetFloatv()
GL_POLYGON_OFFSET_POINT Polygon offset enable for GL_
POINT mode rasterization
polygon/enable GL_FALSE glIsEnabled()
GL_POLYGON_OFFSET_LINE Polygon offset enable for GL_
LINE mode rasterization
polygon/enable GL_FALSE glIsEnabled()
GL_POLYGON_OFFSET_FILL Polygon offset enable for GL_
FILL mode rasterization
polygon/enable GL_FALSE glIsEnabled()
GL_POLYGON_STIPPLE Polygon stipple enable polygon/enable GL_FALSE glIsEnabled()
— Polygon stipple pattern polygon-stipple 1’s glGetPolygon
Stipple()
a. The initial value of GL_POINT_SIZE_MAX is the maximum of GL_ALIASED_POINT_SIZE_RANGE and GL_SMOOTH_POINT_SIZE_RANGE.
State Variable Description Attribute Group Initial Value Get Command
Table B-8 (continued) Rasterization State Variables

760 Appendix B: State Variables
Multisampling
State Variable Description Attribute Group Initial Value Get Command
GL_MULTISAMPLE Multisample rasterization multisample/
enable
GL_TRUE glIsEnabled()
GL_SAMPLE_ALPHA_TO_COVERAGE Modify coverage from alpha multisample/
enable
GL_FALSE glIsEnabled()
GL_SAMPLE_ALPHA_TO_ONE Set alpha to maximum multisample/
enable
GL_FALSE glIsEnabled()
GL_SAMPLE_COVERAGE Mask to modify coverage multisample/
enable
GL_FALSE glIsEnabled()
GL_SAMPLE_COVERAGE_VALUE Coverage mask value multisample 1 glGetFloatv()
GL_SAMPLE_COVERAGE_INVERT Invert coverage mask value multisample GL_FALSE glGetBooleanv()
Table B-9 Multisampling

OpenGL State Variables 761
Texturing
State Variable Description Attribute
Group
Initial Value Get Command
GL_COMPRESSED_TEXTURE_
FORMATS
List of supported compressed
texture formats
— varies glGetIntegerv()
GL_TEXTURE_xTrue if x (dimensional) texturing is
enabled (x is 1D, 2D, or 3D)
texture/
enable
GL_FALSE glIsEnabled()
GL_TEXTURE_xx-D texture image at level of detail
i(x is 1D, 2D, or 3D)
— — glGetTexImage()
GL_TEXTURE_1D_ARRAY 1D texture array image at row i— — glGetTexImage()
GL_TEXTURE_2D_ARRAY 2D texture array image at slice i— — glGetTexImage()
GL_TEXTURE_RECTANGLE Rectangular texture image at LOD 0 — — glGetTexImage()
GL_TEXTURE_BINDING_xTexture object bound to GL_
TEXTURE_x (x is 1D, 2D, or 3D)
texture 0 glGetIntegerv()
GL_TEXTURE_BINDING_1D_
ARRAY
Texture object bound to GL_
TEXTURE_1D_ARRAY
texture 0 glGetIntegerv()
GL_TEXTURE_BINDING_2D_
ARRAY
Texture object bound to GL_
TEXTURE_2D_ARRAY
texture 0 glGetIntegerv()
GL_TEXTURE_BINDING_
RECTANGLE
Texture object bound to GL_
TEXTURE_RECTANGLE
— 0 glGetIntegerv()
Table B-10 Texturing State Variables

762 Appendix B: State Variables
GL_TEXTURE_BINDING_
CUBE_MAP
Texture object bound to GL_
TEXTURE_CUBE_MAP
texture 0 glGetIntegerv()
GL_TEXTURE_BUFFER_DATA_
STORE_BINDING
Buffer object bound as the data
store for the active image unit’s
buffer texture
— 0 glGetTexLevelParameter()
GL_TEXTURE_COMPRESSED True if texture map is stored
internally in a compressed format
— GL_FALSE glGetTexLevelParameter*()
GL_TEXTURE_COMPRESSED_
IMAGE_SIZE
Number of bytes in compressed
texture image array
— 0 glGetTexLevelParameter*()
GL_TEXTURE_CUBE_MAP True if cube map texturing is
enabled
texture/
enable
GL_FALSE glIsEnabled()
GL_TEXTURE_CUBE_MAP_
POSITIVE_X
+x face cube map texture image at
level of detail i
— — glGetTexImage()
GL_TEXTURE_CUBE_MAP_
NEGATIVE_X
-x face cube map texture image at
level of detail i
— — glGetTexImage()
GL_TEXTURE_CUBE_MAP_
POSITIVE_Y
+y face cube map texture image at
level of detail i
— — glGetTexImage()
GL_TEXTURE_CUBE_MAP_
NEGATIVE_Y
-y face cube map texture image at
level of detail i
— — glGetTexImage()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-10 (continued) Texturing State Variables

OpenGL State Variables 763
GL_TEXTURE_CUBE_MAP_
POSITIVE_Z
+z face cube map texture image at
level of detail i
— — glGetTexImage()
GL_TEXTURE_CUBE_MAP_
NEGATIVE_Z
-z face cube map texture image at
level of detail i
— — glGetTexImage()
GL_TEXTURE_BORDER_COLOR Texture border color texture (0, 0, 0, 0) glGetTexParameter*()
GL_TEXTURE_MIN_FILTER Texture minification function texture GL_NEAREST_
MIPMAP_
LINEAR
glGetTexParameter*()
GL_TEXTURE_MAG_FILTER Texture magnification function texture GL_LINEAR glGetTexParameter*()
GL_TEXTURE_WRAP_S Texture coord S wrap mode texture GL_REPEAT glGetTexParameter*()
GL_TEXTURE_WRAP_T Texture coord T wrap mode
(2D, 3D, cube map textures only)
texture GL_REPEAT glGetTexParameter*()
GL_TEXTURE_WRAP_R Texture coord R wrap mode
(3D textures only)
texture GL_REPEAT glGetTexParameter*()
GL_TEXTURE_PRIORITY Texture object priority texture 1 glGetTexParameter*()
GL_TEXTURE_RESIDENT Texture residency texture varies glGetTexParameteriv()
GL_TEXTURE_MIN_LOD Minimum level of detail texture 1000 glGetTexParameterfv()
GL_TEXTURE_MAX_LOD Maximum level of detail texture 1000 glGetTexParameterfv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-10 (continued) Texturing State Variables

764 Appendix B: State Variables
GL_TEXTURE_BASE_LEVEL Base texture array texture 0 glGetTexParameterfv()
GL_TEXTURE_MAX_LEVEL Maximum texture array level texture 1000 glGetTexParameterfv()
GL_TEXTURE_LOD_BIAS Texture level-of-detail bias texture 0.0 glGetTexParameterfv()
GL_DEPTH_TEXTURE_MODE Depth texture mode texture GL_
LUMINANCE
glGetTexParameteriv()
GL_TEXTURE_COMPARE_MODE Texture comparison mode texture GL_NONE glGetTexParameteriv()
GL_TEXTURE_COMPARE_FUNC Texture comparison function texture GL_LEQUAL glGetTexParameteriv()
GL_GENERATE_MIPMAP Automatic mipmap generation texture GL_FALSE glGetTexParameter*()
GL_TEXTURE_WIDTH Texture image i’s width — 0 glGetTexLevelParameter*()
GL_TEXTURE_HEIGHT 2D/3D texture image i’s height — 0 glGetTexLevelParameter*()
GL_TEXTURE_DEPTH 3D texture image i’s depth — 0 glGetTexLevelParameter*()
GL_TEXTURE_BORDER Texture image i’s border width — 0 glGetTexLevelParameter*()
GL_TEXTURE_INTERNAL_
FORMAT
Texture image i’s internal image
format
—GL_RGBA or
GL_R8
glGetTexLevelParameter*()
GL_TEXTURE_COMPONENTS Texture image i’s internal image
format
— 1 glGetTexLevelParameter*()
GL_TEXTURE_RED_SIZE Texture image i’s red resolution — 0 glGetTexLevelParameter*()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-10 (continued) Texturing State Variables

OpenGL State Variables 765
GL_TEXTURE_GREEN_SIZE Texture image i’s green resolution — 0 glGetTexLevelParameter*()
GL_TEXTURE_BLUE_SIZE Texture image i’s blue resolution — 0 glGetTexLevelParameter*()
GL_TEXTURE_ALPHA_SIZE Texture image i’s alpha resolution — 0 glGetTexLevelParameter*()
GL_TEXTURE_LUMINANCE_SIZE Texture image i’s luminance
resolution
— 0 glGetTexLevelParameter*()
GL_TEXTURE_INTENSITY_SIZE Texture image i’s intensity
resolution
— 0 glGetTexLevelParameter*()
GL_TEXTURE_DEPTH_SIZE Texture image i’s depth resolution — 0 glGetTexLevelParameter*()
GL_SHARED_SIZE Shared exponent field resolution — 0 glGetTexLevelParameter*()
GL_TEXTURE_RED_TYPE Texture image i’s red type — GL_NONE glGetTexLevelParameter*()
GL_TEXTURE_GREEN_TYPE Texture image i’s green type — GL_NONE glGetTexLevelParameter*()
GL_TEXTURE_BLUE_TYPE Texture image i’s blue type — GL_NONE glGetTexLevelParameter*()
GL_TEXTURE_ALPHA_TYPE Texture image i’s alpha type — GL_NONE glGetTexLevelParameter*()
GL_TEXTURE_LUMINANCE_
TYPE
Texture image i’s luminance type — GL_NONE glGetTexLevelParameter*()
GL_TEXTURE_INTENSITY_TYPE Texture image i’s intensity type — GL_NONE glGetTexLevelParameter*()
GL_TEXTURE_DEPTH_TYPE Texture image i’s depth type — GL_NONE glGetTexLevelParameter*()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-10 (continued) Texturing State Variables

766 Appendix B: State Variables
GL_TEXTURE_COMPRESSED True, if texture image has a
compressed internal format
— GL_FALSE glGetTexLevelParameter*()
GL_TEXTURE_COMPRESSED_
IMAGE_SIZE
Size (in GLubyte) of compressed
texture image
— 0 glGetTexLevelParameter*()
GL_COORD_REPLACE Coordinate replacement enable point GL_FALSE glTexEnviv()
GL_ACTIVE_TEXTURE Active texture unit texture GL_TEXTURE0 glGetIntegerv()
GL_TEXTURE_ENV_MODE Texture application function texture GL_MODULATE glGetTexEnviv()
GL_TEXTURE_ENV_COLOR Texture environment color texture (0, 0, 0, 0) glGetTexEnvfv()
GL_TEXTURE_LOD_BIAS Texture level of detail bias texture 0.0 glGetTexEnvfv()
GL_TEXTURE_GEN_xTexgen enabled (x is S, T, R,
or Q)
texture/
enable
GL_FALSE glIsEnabled()
GL_EYE_PLANE Texgen plane equation coefficients texture — glGetTexGenfv()
GL_OBJECT_PLANE Texgen object linear coefficients texture — glGetTexGenfv()
GL_TEXTURE_GEN_MODE Function used for texgen texture GL_EYE_
LINEAR
glGetTexGeniv()
GL_COMBINE_RGB RGB combiner function texture GL_MODULATE glGetTexEnviv()
GL_COMBINE_ALPHA Alpha combiner function texture GL_MODULATE glGetTexEnviv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-10 (continued) Texturing State Variables

OpenGL State Variables 767
GL_SRC0_RGB RGB source 0 texture GL_TEXTURE glGetTexEnviv()
GL_SRC1_RGB RGB source 1 texture GL_PREVIOUS glGetTexEnviv()
GL_SRC2_RGB RGB source 2 texture GL_CONSTANT glGetTexEnviv()
GL_SRC0_ALPHA Alpha source 0 texture GL_TEXTURE glGetTexEnviv()
GL_SRC1_ALPHA Alpha source 1 texture GL_PREVIOUS glGetTexEnviv()
GL_SRC2_ALPHA Alpha source 2 texture GL_CONSTANT glGetTexEnviv()
GL_OPERAND0_RGB RGB operand 0 texture GL_SRC_
COLOR
glGetTexEnviv()
GL_OPERAND1_RGB RGB operand 1 texture GL_SRC_
COLOR
glGetTexEnviv()
GL_OPERAND2_RGB RGB operand 2 texture GL_SRC_ALPHA glGetTexEnviv()
GL_OPERAND0_ALPHA Alpha operand 0 texture GL_SRC_ALPHA glGetTexEnviv()
GL_OPERAND1_ALPHA Alpha operand 1 texture GL_SRC_ALPHA glGetTexEnviv()
GL_OPERAND2_ALPHA Alpha operand 2 texture GL_SRC_ALPHA glGetTexEnviv()
GL_RGB_SCALE RGB post-combiner scaling texture 1.0 glGetTexEnviv()
GL_ALPHA_SCALE Alpha post-combiner scaling texture 1.0 glGetTexEnviv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-10 (continued) Texturing State Variables

768 Appendix B: State Variables
Pixel Operations
State Variable Description Attribute Group Initial Value Get Command
GL_SCISSOR_TEST Scissoring enabled scissor/enable GL_FALSE glIsEnabled()
GL_SCISSOR_BOX Scissor box scissor — glGetIntegerv()
GL_ALPHA_TEST Alpha test enabled color-buffer/
enable
GL_FALSE glIsEnabled()
GL_ALPHA_TEST_FUNC Alpha test function color-buffer GL_ALWAYS glGetIntegerv()
GL_ALPHA_TEST_REF Alpha test reference value color-buffer 0 glGetIntegerv()
GL_STENCIL_TEST Stenciling enabled stencil-
buffer/enable
GL_FALSE glIsEnabled()
GL_STENCIL_FUNC Stencil function stencil-buffer GL_ALWAYS glGetIntegerv()
GL_STENCIL_VALUE_MASK Stencil mask stencil-buffer 1’s glGetIntegerv()
GL_STENCIL_REF Stencil reference value stencil-buffer 0 glGetIntegerv()
GL_STENCIL_FAIL Stencil fail action stencil-buffer GL_KEEP glGetIntegerv()
GL_STENCIL_PASS_DEPTH_FAIL Stencil depth-buffer fail action stencil-buffer GL_KEEP glGetIntegerv()
GL_STENCIL_PASS_DEPTH_PASS Stencil depth-buffer pass action stencil-buffer GL_KEEP glGetIntegerv()
GL_STENCIL_BACK_FUNC Back stencil function stencil-buffer GL_ALWAYS glGetIntegerv()
Table B-11 Pixel Operations

OpenGL State Variables 769
GL_STENCIL_BACK_VALUE_
MASK
Back stencil mask stencil-buffer 1’s glGetIntegerv()
GL_STENCIL_BACK_REF Back stencil reference value stencil-buffer 0 glGetIntegerv()
GL_STENCIL_BACK_FAIL Back stencil fail action stencil-buffer GL_KEEP glGetIntegerv()
GL_STENCIL_BACK_PASS_
DEPTH_FAIL
Back stencil depth-buffer fail action stencil-buffer GL_KEEP glGetIntegerv()
GL_STENCIL_BACK_PASS_
DEPTH_PASS
Back stencil depth-buffer pass
action
stencil-buffer GL_KEEP glGetIntegerv()
GL_DEPTH_TEST Depth buffer enabled depth-buffer/
enable
GL_FALSE glIsEnabledi()
GL_DEPTH_FUNC Depth-buffer test function depth-buffer GL_LESS glGetIntegerv()
GL_BLEND Blending enabled for draw buffer icolor-buffer/
enable
GL_FALSE glIsEnabled()
GL_BLEND_SRC_RGB Blending source RGB function color-buffer GL_ONE glGetIntegerv()
GL_BLEND_SRC_ALPHA Blending source alpha function color-buffer GL_ONE glGetIntegerv()
GL_BLEND_DST_RGB Blending destination RGB function color-buffer GL_ZERO glGetIntegerv()
GL_BLEND_DST_ALPHA Blending destination alpha
function
color-buffer GL_ZERO glGetIntegerv()
State Variable Description Attribute Group Initial Value Get Command
Table B-11 (continued) Pixel Operations

770 Appendix B: State Variables
GL_BLEND_EQUATION_RGB RGB blending equation color-buffer GL_FUNC_ADD glGetIntegerv()
GL_BLEND_EQUATION_ALPHA Alpha blending equation color-buffer GL_FUNC_ADD glGetIntegerv()
GL_BLEND_COLOR Constant blend color color-buffer (0, 0, 0, 0) glGetFloatv()
GL_FRAMEBUFFER_SRGB sRGB update and blending enabled color-buffer/
enable
GL_FALSE glIsEnabled()
GL_DITHER Dithering enabled color-buffer/
enable
GL_TRUE glIsEnabled()
GL_INDEX_LOGIC_OP Color index logical operation
enabled
color-buffer/
enable
GL_FALSE glIsEnabled()
GL_COLOR_LOGIC_OP RGBA color logical operation
enabled
color-buffer/
enable
GL_FALSE glIsEnabled()
GL_LOGIC_OP_MODE Logical operation function color-buffer GL_COPY glGetIntegerv()
State Variable Description Attribute Group Initial Value Get Command
Table B-11 (continued) Pixel Operations

OpenGL State Variables 771
Framebuffer Control
State Variable Description Attribute Group Initial
Value
Get Command
GL_DRAW_BUFFERiBuffers selected for color icolor-buffer — glGetIntegerv()
GL_DRAW_BUFFER Buffers selected for color 0 color-buffer — glGetIntegerv()
GL_INDEX_WRITEMASK Color-index writemask color-buffer 1’s glGetIntegerv()
GL_COLOR_WRITEMASK Color write enabled; R, G, B, or A for
draw buffer i
color-buffer GL_TRUE glGet
Booleani_v()
GL_DEPTH_WRITEMASK Depth buffer enabled for writing depth-buffer GL_TRUE glGetBooleanv()
GL_STENCIL_WRITEMASK Front stencil buffer writemask stencil-buffer 1’s glGetIntegerv()
GL_STENCIL_BACK_
WRITEMASK
Back stencil buffer writemask stencil-buffer 1’s glGetIntegerv()
GL_COLOR_CLEAR_VALUE Color-buffer clear value (RGBA mode) color-buffer (0, 0, 0, 0) glGetFloatv()
GL_INDEX_CLEAR_VALUE Color-buffer clear value (color-index
mode)
color-buffer 0 glGetFloatv()
GL_DEPTH_CLEAR_VALUE Depth-buffer clear value depth-buffer 1 glGetIntegerv()
GL_STENCIL_CLEAR_VALUE Stencil-buffer clear value stencil-buffer 0 glGetIntegerv()
GL_ACCUM_CLEAR_VALUE Accumulation-buffer clear value accum-buffer 0 glGetFloatv()
Table B-12 Framebuffer Control State Variables

772 Appendix B: State Variables
Framebuffer Object State
State Variable Description Attribute
Group
Initial Value Get Command
GL_DRAW_FRAMEBUFFER_
BINDING
Framebuffer object bound to GL_DRAW_
FRAMEBUFFER
— 0 glGetIntegerv()
GL_READ_FRAMEBUFFER_
BINDING
Framebuffer object bound to GL_READ_
FRAMEBUFFER
— 0 glGetIntegerv()
GL_DRAW_BUFFERiDraw buffer selected for color output icolor-
buffer
—glGetIntegerv()
GL_READ_BUFFER Read source buffer pixel — glGetIntegerv()
GL_FRAMEBUFFER_
ATTACHMENT_OBJECT_TYPE
Type of image attached to framebuffer
attachment point
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_OBJECT_NAME
Name of object attached to framebuffer
attachment point
— 0 glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_TEXTURE_
LEVEL
Mipmap level of texture image attached, if
object attached is a texture
— 0 glGetFramebuffer
Attachment
Parameteriv()
Table B-13 Framebuffer Object State Variables

OpenGL State Variables 773
GL_FRAMEBUFFER_
ATTACHMENT_TEXTURE_
CUBE_MAP_FACE
Cubemap face of texture image attached, if
object attached is a cubemap texture
—GL_
TEXTURE_
CUBE_MAP_
POSITIVE_X
glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_TEXTURE_
LAYER
Layer of texture image attached, if
attached object is a 3D texture
— 0 glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_COLOR_
ENCODING
Encoding of components in the attached
image
— — glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_COMPONENT_
TYPE
Type of components in the attached image — — glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_RED_SIZE
Size in bits of attached image’s red
component
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_GREEN_SIZE
Size in bits of attached image’s green
component
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_BLUE_SIZE
Size in bits of attached image’s blue
component
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-13 (continued) Framebuffer Object State Variables

774 Appendix B: State Variables
GL_FRAMEBUFFER_
ATTACHMENT_ALPHA_SIZE
Size in bits of attached image’s alpha
component
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_DEPTH_SIZE
Size in bits of attached image’s depth
component
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
GL_FRAMEBUFFER_
ATTACHMENT_STENCIL_SIZE
Size in bits of attached image’s stencil
component
— GL_NONE glGetFramebuffer
Attachment
Parameteriv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-13 (continued) Framebuffer Object State Variables

OpenGL State Variables 775
Renderbuffer Object State
State Variable Description Attribute
Group
Initial Value Get Command
GL_RENDERBUFFER_BINDING Renderbuffer object bound to GL_
RENDERBUFFER
— 0 glGetIntegerv()
GL_RENDERBUFFER_WIDTH Width of renderbuffer — 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_HEIGHT Height of renderbuffer — 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_
INTERNAL_FORMAT
Internal format of renderbuffer — GL_RGBA glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_RED_SIZE Size in bits of renderbuffer image’s red
component
— 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_GREEN_
SIZE
Size in bits of renderbuffer image’s green
component
— 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_BLUE_
SIZE
Size in bits of renderbuffer image’s blue
component
— 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_ALPHA_
SIZE
Size in bits of renderbuffer image’s alpha
component
— 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_DEPTH_
SIZE
Size in bits of renderbuffer image’s depth
component
— 0 glGetRenderbuffer
Parameteriv()
Table B-14 Renderbuffer Object State Variables
776 Appendix B: State Variables
Pixels
GL_RENDERBUFFER_STENCIL_
SIZE
Size in bits of renderbuffer image’s stencil
component
— 0 glGetRenderbuffer
Parameteriv()
GL_RENDERBUFFER_SAMPLES Number of samples — 0 glGetRenderbuffer
Parameteriv()
State Variable Description Attribute
Group
Initial Value Get Command
GL_UNPACK_SWAP_BYTES Value of GL_UNPACK_SWAP_BYTES pixel-store GL_FALSE glGetBooleanv()
GL_UNPACK_LSB_FIRST Value of GL_UNPACK_LSB_FIRST pixel-store GL_FALSE glGetBooleanv()
GL_UNPACK_IMAGE_HEIGHT Value of GL_UNPACK_IMAGE_HEIGHT pixel-store 0 glGetIntegerv()
GL_UNPACK_SKIP_IMAGES Value of GL_UNPACK_SKIP_IMAGES pixel-store 0 glGetIntegerv()
GL_UNPACK_ROW_LENGTH Value of GL_UNPACK_ROW_LENGTH pixel-store 0 glGetIntegerv()
GL_UNPACK_SKIP_ROWS Value of GL_UNPACK_SKIP_ROWS pixel-store 0 glGetIntegerv()
GL_UNPACK_SKIP_PIXELS Value of GL_UNPACK_SKIP_PIXELS pixel-store 0 glGetIntegerv()
Table B-15 Pixel State Variables
State Variable Description Attribute
Group
Initial Value Get Command
Table B-14 (continued) Renderbuffer Object State Variables

OpenGL State Variables 777
GL_UNPACK_ALIGNMENT Value of GL_UNPACK_ALIGNMENT pixel-store 4 glGetIntegerv()
GL_PIXEL_PACK_BUFFER_
BINDING
Pixel pack buffer binding pixel-store 0 glGetIntegerv()
GL_PIXEL_UNPACK_BUFFER_
BINDING
Pixel unpack buffer binding pixel-store 0 glGetIntegerv()
GL_PACK_SWAP_BYTES Value of GL_PACK_SWAP_BYTES pixel-store GL_FALSE glGetBooleanv()
GL_PACK_LSB_FIRST Value of GL_PACK_LSB_FIRST pixel-store GL_FALSE glGetBooleanv()
GL_PACK_IMAGE_HEIGHT Value of GL_PACK_IMAGE_HEIGHT pixel-store 0 glGetIntegerv()
GL_PACK_SKIP_IMAGES Value of GL_PACK_SKIP_IMAGES pixel-store 0 glGetIntegerv()
GL_PACK_ROW_LENGTH Value of GL_PACK_ROW_LENGTH pixel-store 0 glGetIntegerv()
GL_PACK_SKIP_ROWS Value of GL_PACK_SKIP_ROWS pixel-store 0 glGetIntegerv()
GL_PACK_SKIP_PIXELS Value of GL_PACK_SKIP_PIXELS pixel-store 0 glGetIntegerv()
GL_PACK_ALIGNMENT Value of GL_PACK_ALIGNMENT pixel-store 4 glGetIntegerv()
GL_MAP_COLOR True if colors are mapped pixel GL_FALSE glGetBooleanv()
GL_MAP_STENCIL True if stencil values are mapped pixel GL_FALSE glGetBooleanv()
GL_INDEX_SHIFT Value of GL_INDEX_SHIFT pixel 0 glGetIntegerv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-15 (continued) Pixel State Variables

778 Appendix B: State Variables
GL_INDEX_OFFSET Value of GL_INDEX_OFFSET pixel 0 glGetIntegerv()
GL_x_SCALE Value of GL_x_SCALE; x is GL_RED,
GL_GREEN, GL_BLUE, GL_ALPHA, or
GL_DEPTH
pixel 1 glGetFloatv()
GL_x_BIAS Value of GL_x_BIAS; x is GL_RED,
GL_GREEN, GL_BLUE, GL_ALPHA, or
GL_DEPTH
pixel 0 glGetFloatv()
GL_COLOR_TABLE True if color table lookup is enabled pixel/
enable
GL_FALSE glIsEnabled()
GL_POST_CONVOLUTION_
COLOR_TABLE
True if post convolution color table lookup
is enabled
pixel/
enable
GL_FALSE glIsEnabled()
GL_POST_COLOR_MATRIX_
COLOR_TABLE
True if post color matrix color table lookup
is enabled
pixel/
enable
GL_FALSE glIsEnabled()
GL_COLOR_TABLE Color tables — empty glGetColorTable()
GL_COLOR_TABLE_FORMAT Color tables’ internal image format — GL_RGBA glGetColorTable
Parameteriv()
GL_COLOR_TABLE_WIDTH Color tables’ specified width — 0 glGetColorTable
Parameteriv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-15 (continued) Pixel State Variables

OpenGL State Variables 779
GL_COLOR_TABLE_x_SIZE Color table component resolution;
x is RED, GREEN, BLUE,
ALPHA, LUMINANCE, or
INTENSITY
— 0 glGetColorTable
Parameteriv()
GL_COLOR_TABLE_SCALE Scale factors applied to color table entries pixel (1, 1, 1, 1) glGetColorTable
Parameterfv()
GL_COLOR_TABLE_BIAS Bias values applied to color table entries pixel (0, 0, 0, 0) glGetColorTable
Parameterfv()
GL_CONVOLUTION_1D True if 1D convolution is enabled pixel/
enable
GL_FALSE glIsEnabled()
GL_CONVOLUTION_2D True if 2D convolution is enabled pixel/
enable
GL_FALSE glIsEnabled()
GL_SEPARABLE_2D True if separable 2D convolution is
enabled
pixel/
enable
GL_FALSE glIsEnabled()
GL_CONVOLUTION_1D 1D convolution filter — empty glGetConvolution
Filter()
GL_CONVOLUTION_2D 2D convolution filter — empty glGetConvolution
Filter()
GL_SEPARABLE_2D 2D separable convolution filter — empty glGetSeparable
Filter()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-15 (continued) Pixel State Variables

780 Appendix B: State Variables
GL_CONVOLUTION_
BORDER_COLOR
Convolution border color pixel (0, 0, 0, 0) glGetConvolution
Parameterfv()
GL_CONVOLUTION_
BORDER_MODE
Convolution border mode pixel GL_REDUCE glGetConvolution
Parameteriv()
GL_CONVOLUTION_
FILTER_SCALE
Scale factors applied to convolution filter
entries
pixel (1, 1, 1, 1) glGetConvolution
Parameterfv()
GL_CONVOLUTION_
FILTER_BIAS
Bias values applied to convolution filter
entries
pixel (0, 0, 0, 0) glGetConvolution
Parameterfv()
GL_CONVOLUTION_FORMAT Convolution filter internal format — GL_RGBA glGetConvolution
Parameteriv()
GL_CONVOLUTION_WIDTH Convolution filter width — 0 glGetConvolution
Parameteriv()
GL_CONVOLUTION_HEIGHT Convolution filter height — 0 glGetConvolution
Parameteriv()
GL_POST_CONVOLUTION_
x_SCALE
Component scale factors after
convolution; x is RED, GREEN, BLUE, or
ALPHA
pixel 1 glGetFloatv()
GL_POST_CONVOLUTION_
x_BIAS
Component bias values after convolution;
x is RED, GREEN, BLUE, or ALPHA
pixel 0 glGetFloatv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-15 (continued) Pixel State Variables

OpenGL State Variables 781
GL_POST_COLOR_MATRIX_
x_SCALE
Component scale factors after color
matrix; x is RED, GREEN, BLUE, or ALPHA
pixel 1 glGetFloatv()
GL_POST_COLOR_MATRIX_
x_BIAS
Component bias values after color matrix;
x is RED, GREEN, BLUE, or ALPHA
pixel 0 glGetFloatv()
GL_HISTOGRAM True if histogramming is enabled pixel/
enable
GL_FALSE glIsEnabled()
GL_HISTOGRAM Histogram table — empty glGetHistogram()
GL_HISTOGRAM_WIDTH Histogram table width — 0 glGetHistogram
Parameteriv()
GL_HISTOGRAM_FORMAT Histogram table internal format — GL_RGBA glGetHistogram
Parameteriv()
GL_HISTOGRAM_x_SIZE Histogram table component resolution;
x is RED, GREEN, BLUE, ALPHA, or
LUMINANCE
— 0 glGetHistogram
Parameteriv()
GL_HISTOGRAM_SINK True if histogramming consumes pixel
groups
— GL_FALSE glGetHistogram
Parameteriv()
GL_MINMAX True if minmax is enabled pixel/
enable
GL_FALSE glIsEnabled()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-15 (continued) Pixel State Variables

782 Appendix B: State Variables
GL_MINMAX Minmax table — See Note a
at the end
of table.
glGetMinmax()
GL_MINMAX_FORMAT Minmax table internal format — GL_RGBA glGetMinmax
Parameteriv()
GL_MINMAX_SINK True if minmax consumes pixel groups — GL_FALSE glGetMinmax
Parameteriv()
GL_ZOOM_X x zoom factor pixel 1.0 glGetFloatv()
GL_ZOOM_Y y zoom factor pixel 1.0 glGetFloatv()
GL_PIXEL_MAP_xglPixelMap() translation tables;
x is a map name from Table 8-1
—0’s glGetPixelMap*()
GL_PIXEL_MAP_x_SIZE Size of glPixelMap() translation table x— 1 glGetIntegerv()
GL_READ_BUFFER Read source buffer pixel — glGetIntegerv()
a. Min table initially set to maximum representable values. Max table set to minimum representable values.
State Variable Description Attribute
Group
Initial Value Get Command
Table B-15 (continued) Pixel State Variables

OpenGL State Variables 783
Evaluators
State Variable Description Attribute Group Initial Value Get Command
GL_ORDER 1D map order — 1 glGetMapiv()
GL_ORDER 2D map orders — 1, 1 glGetMapiv()
GL_COEFF 1D control points — — glGetMapfv()
GL_COEFF 2D control points — — glGetMapfv()
GL_DOMAIN 1D domain endpoints — — glGetMapfv()
GL_DOMAIN 2D domain endpoints — — glGetMapfv()
GL_MAP1_x1D map enables: x is map type eval/enable GL_FALSE glIsEnabled()
GL_MAP2_x2D map enables: x is map type eval/enable GL_FALSE glIsEnabled()
GL_MAP1_GRID_DOMAIN 1D grid endpoints eval 0, 1 glGetFloatv()
GL_MAP2_GRID_DOMAIN 2D grid endpoints eval 0, 1; 0, 1 glGetFloatv()
GL_MAP1_GRID_SEGMENTS 1D grid divisions eval 1 glGetFloatv()
GL_MAP2_GRID_SEGMENTS 2D grid divisions eval 1, 1 glGetFloatv()
GL_AUTO_NORMAL True if automatic normal
generation is enabled
eval/enable GL_FALSE glIsEnabled()
Table B-16 Evaluator State Variables

784 Appendix B: State Variables
Shader Object State
State Variable Description Attribute Group Initial Value Get Command
GL_SHADER_TYPE Type of shader (vertex or
fragment)
— — glGetShaderiv()
GL_DELETE_STATUS Shader flagged for deletion — GL_FALSE glGetShaderiv()
GL_COMPILE_STATUS Last compilation status — GL_FALSE glGetShaderiv()
— Information log for shader
objects
— empty string glGetShaderInfoLog()
GL_INFO_LOG_LENGTH String length of shader
information log
— 0 glGetShaderiv()
— Source code for a shader — empty string glGetShaderSource()
GL_SHADER_SOURCE_LENGTH String length of shader
source code
— 0 glGetShaderiv()
Table B-17 Shader Object State Variables

OpenGL State Variables 785
Program Object State
State Variable Description Attribute Group Initial Value Get Command
GL_CURRENT_PROGRAM Name of current program object — 0 glGetIntegerv()
GL_DELETE_STATUS Program object deleted — GL_FALSE glGetProgramiv()
GL_LINK_STATUS Last link attempt succeeded — GL_FALSE glGetProgramiv()
GL_VALIDATE_STATUS Last validate attempt succeeded — GL_FALSE glGetProgramiv()
GL_ATTACHED_SHADERS Number of attached shader
objects
— 0 glGetProgramiv()
— Shader objects attached — empty glGetAttachedShaders()
— Info log for program object — empty glGetProgramInfoLog()
GL_INFO_LOG_LENGTH Length of info log — 0 glGetProgramiv()
GL_ACTIVE_UNIFORMS Number of active uniforms — 0 glGetProgramiv()
— Location of active uniforms — — glGetUniformLocation()
— Size of active uniform — — glGetActiveUniform()
— Type of active uniform — — glGetActiveUniform()
— Name of active uniform — empty glGetActiveUniform()
GL_ACTIVE_UNIFORM_
MAX_LENGTH
Maximum active uniform name
length
— 0 glGetProgramiv()
Table B-18 Program Object State Variables

786 Appendix B: State Variables
— Uniform value — 0 glGetUniform()
GL_ACTIVE_ATTRIBUTES Number of active attributes — 0 glGetProgramiv()
— Location of active generic
attribute
— — glGetAttribLocation()
— Size of active attribute — — glGetActiveAttrib()
— Type of active attribute — — glGetActiveAttrib()
— Name of active attribute — empty glGetActiveAttrib()
GL_ACTIVE_ATTRIBUTE_
MAX_LENGTH
Maximum active attribute name
length
— 0 glGetProgramiv()
GL_TRANSFORM_
FEEDBACK_BUFFER_MODE
Transform feedback mode for the
program
—GL_
INTERLEAV
ED_ATTRIBS
glGetProgramiv()
GL_TRANSFORM_
FEEDBACK_VARYINGS
Number of varyings to stream to
buffer objects
— 0 glGetProgramiv()
GL_TRANSFORM_
FEEDBACK_VARYING_
MAX_LENGTH
Maximum transform feedback
varying name length
— 0 glGetProgramiv()
— Size of each transform feedback
varying variable
— — glGetTransformFeedback
Varying()
State Variable Description Attribute Group Initial Value Get Command
Table B-18 (continued) Program Object State Variables

OpenGL State Variables 787
— Type of each transform feedback
varying variable
— — glGetTransformFeedback
Varying()
— Name of each transform feedback
varying variable
— — glGetTransformFeedback
Varying()
GL_UNIFORM_BUFFER_
BINDING
Uniform buffer object bound to
to the context
— 0 glGetIntegerv()
GL_UNIFORM_BUFFER_
BINDING
Uniform buffer object bound to a
specific context binding point
— 0 glGetIntegeri_v()
GL_ACTIVE_UNIFORM_
BLOCKS
Number of active uniform blocks — 0 glGetProgramiv()
GL_ACTIVE_UNIFORM_
BLOCK_MAX_NAME_
LENGTH
Length of longest active uniform
block name
— 0 glGetProgramiv()
GL_UNIFORM_TYPE Type of active uniform — — glGetActiveUniformsiv()
GL_UNIFORM_SIZE Size of active uniform — — glGetActiveUniformsiv()
GL_UNIFORM_NAME_
LENGTH
Uniform name length — — glGetActiveUniformsiv()
GL_UNIFORM_BLOCK_
INDEX
Uniform block index — — glGetActiveUniformsiv()
GL_UNIFORM_OFFSET Uniform buffer offset — — glGetActiveUniformsiv()
State Variable Description Attribute Group Initial Value Get Command
Table B-18 (continued) Program Object State Variables

788 Appendix B: State Variables
GL_UNIFORM_ARRAY_
STRIDE
Uniform buffer array stride — — glGetActiveUniformsiv()
GL_UNIFORM_MATRIX_
STRIDE
Uniform buffer intra-matrix
stride
— — glGetActiveUniformsiv()
GL_UNIFORM_IS_ROW_
MAJOR
Is uniform a row-major matrix? — — glGetActiveUniformsiv()
GL_UNIFORM_BLOCK_
BINDING
Uniform buffer binding point
associated with the specified
uniform block
— 0 glGetActiveUniform
Blockiv()
GL_UNIFORM_BLOCK_
DATA_SIZE
Size of storage needed to hold
uniform block’s data
— — glGetActiveUniform
Blockiv()
GL_UNIFORM_BLOCK_
ACTIVE_UNIFORMS
Number of active uniforms in the
specified uniform block
— — glGetActiveUniform
Blockiv()
GL_UNIFORM_BLOCK_
ACTIVE_UNIFORMS_
INDICES
Array of active uniform indices of
the specified uniform block
— — glGetActiveUniform
Blockiv()
GL_UNIFORM_BLOCK_
REFERENCED_BY_VERTEX_
SHADER
True if uniform block is actively
referenced by the vertex stage
— 0 glGetActiveUniform
Blockiv()
GL_UNIFORM_BLOCK_
REFERENCED_BY_
FRAGMENT_SHADER
True if uniform block is actively
referenced by the fragment stage
— 0 glGetActiveUniform
Blockiv()
State Variable Description Attribute Group Initial Value Get Command
Table B-18 (continued) Program Object State Variables

OpenGL State Variables 789
Query Object State
Transform Feedback State
State Variable Description Attribute Group Initial Value Get Command
GL_QUERY_RESULT Query object result — 0 glGetQueryObject
uiv()
GL_QUERY_RESULT_AVAILABLE Is the query object’s
result available?
— GL_FALSE glGetQueryObject
uiv()
Table B-19 Query Object State Variables
State Variable Description Attribute Group Initial Value Get Command
GL_TRANSFORM_FEEDBACK_
BUFFER_BINDING
Buffer object bound to
generic bind point for
transform feedback
— 0 glGetIntegerv()
GL_TRANSFORM_FEEDBACK_
BUFFER_BINDING
Buffer object bound to
each transform feedback
attribute stream
— 0 glGetIntegeri_v()
GL_TRANSFORM_FEEDBACK_
BUFFER_START
Starting offset of range
bound for each
transform feedback
attribute stream
— 0 glGetIntegeri_v()
Table B-20 Transform Feedback State Variables

790 Appendix B: State Variables
GL_TRANSFORM_FEEDBACK_
BUFFER_SIZE
Size of range bound for
each transform feedback
attribute stream
— 0 glGetIntegeri_v()
GL_TRANSFORM_FEEDBACK_
INTERLEAVED_COMPONENTS
Maximum number of
components to write to a
single buffer in
interleaved mode
— 64 glGetIntegerv()
GL_TRANSFORM_FEEDBACK_
SEPARATE_ATTRIBS
Maximum number of
separate varying
attributes that can be
captured in transform
feedback
— 4 glGetIntegerv()
GL_TRANSFORM_FEEDBACK_
SEPARATE_COMPONENTS
Maximum number of
separate varying
components in separate
mode
— 4 glGetIntegerv()
State Variable Description Attribute Group Initial Value Get Command
Table B-20 (continued) Transform Feedback State Variables

OpenGL State Variables 791
Vertex Shader State
Hints
State Variable Description Attribute Group Initial Value Get Command
GL_VERTEX_PROGRAM_TWO_SIDE Two-sided color mode enable GL_FALSE glIsEnabled()
GL_CURRENT_VERTEX_ATTRIB Generic vertex attribute current (0, 0, 0, 1) glGetVertex
Attribfv()
GL_VERTEX_PROGRAM_POINT_SIZE Point size mode enable GL_FALSE glIsEnabled()
Table B-21 Vertex Shader State Variables
State Variable Description Attribute
Group
Initial Value Get Command
GL_PERSPECTIVE_CORRECTION_HINT Perspective correction hint hint GL_DONT_CARE glGetIntegerv()
GL_POINT_SMOOTH_HINT Point smooth hint hint GL_DONT_CARE glGetIntegerv()
GL_LINE_SMOOTH_HINT Line smooth hint hint GL_DONT_CARE glGetIntegerv()
GL_POLYGON_SMOOTH_HINT Polygon smooth hint hint GL_DONT_CARE glGetIntegerv()
GL_FOG_HINT Fog hint hint GL_DONT_CARE glGetIntegerv()
GL_GENERATE_MIPMAP_HINT Mipmap generation hint hint GL_DONT_CARE glGetIntegerv()
Table B-22 Hint State Variables

792 Appendix B: State Variables
Implementation-Dependent Values
GL_TEXTURE_COMPRESSION_HINT Texture compression hint hint GL_DONT_CARE glGetIntegerv()
GL_FRAGMENT_SHADER_DERIVATIVE_
HINT
Fragment shader derivative
accuracy hint
hint GL_DONT_CARE glGetIntegerv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
GL_MAX_LIGHTS Maximum number of lights — 8 glGetIntegerv()
GL_MAX_CLIP_DISTANCES (which
replaces GL_MAX_CLIP_PLANES in Version
3.0 and greater)
Maximum number of user clipping
planes
—6 glGetIntegerv()
GL_MAX_COLOR_MATRIX_STACK_DEPTH Maximum color matrix stack depth — 2 glGetIntegerv()
GL_MAX_MODELVIEW_STACK_DEPTH Maximum modelview-matrix stack
depth
— 32 glGetIntegerv()
GL_MAX_PROJECTION_STACK_DEPTH Maximum projection-matrix stack
depth
—2 glGetIntegerv()
Table B-23 Implementation-Dependent State Variables
State Variable Description Attribute
Group
Initial Value Get Command
Table B-22 (continued) Hint State Variables

OpenGL State Variables 793
GL_MAX_TEXTURE_STACK_DEPTH Maximum depth of texture matrix
stack
—2 glGetIntegerv()
GL_SUBPIXEL_BITS Number of bits of subpixel precision in
x and y
—4 glGetIntegerv()
GL_MAX_3D_TEXTURE_SIZE See discussion in “Texture Proxy” in
Chapter 9
— 16 glGetIntegerv()
GL_MAX_TEXTURE_SIZE See discussion in “Texture Proxy” in
Chapter 9
— 64 glGetIntegerv()
GL_MAX_ARRAY_TEXTURE_LAYERS Maximum number of layers for texture
arrays
— 256 glGetIntegerv()
GL_MAX_TEXTURE_LOD_BIAS Maximum absolute texture level of
detail bias
—2.0 glGetFloatv()
GL_MAX_CUBE_MAP_TEXTURE_SIZE Maximum cube map texture image
dimension
— 16 glGetIntegerv()
GL_MAX_RENDERBUFFER_SIZE Maximum width and height of
renderbuffers
— 1024 glGetIntegerv()
GL_MAX_PIXEL_MAP_TABLE Maximum size of a glPixelMap()
translation table
— 32 glGetIntegerv()
GL_MAX_NAME_STACK_DEPTH Maximum selection-name stack depth — 64 glGetIntegerv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

794 Appendix B: State Variables
GL_MAX_LIST_NESTING Maximum display-list call nesting — 64 glGetIntegerv()
GL_MAX_EVAL_ORDER Maximum evaluator polynomial order — 8 glGetIntegerv()
GL_MAX_VIEWPORT_DIMS Maximum viewport dimensions — — glGetIntegerv()
GL_MAX_ATTRIB_STACK_DEPTH Maximum depth of the attribute stack — 16 glGetIntegerv()
GL_MAX_CLIENT_ATTRIB_STACK_DEPTH Maximum depth of the client attribute
stack
— 16 glGetIntegerv()
GL_NUM_COMPRESSED_TEXTURE_
FORMATS
Number of supported texture
compression formats
—— glGetIntegerv()
GL_AUX_BUFFERS Number of auxiliary buffers — 0 glGetBooleanv()
GL_RGBA_MODE True if color buffers store RGBA — — glGetBooleanv()
GL_INDEX_MODE True if color buffers store indices — — glGetBooleanv()
GL_DOUBLEBUFFER True if front and back buffers exist — — glGetBooleanv()
GL_STEREO True if left and right buffers exist — — glGetBooleanv()
GL_ALIASED_POINT_SIZE_RANGE Range (low to high) of aliased point
sizes
—1, 1 glGetFloatv()
GL_SMOOTH_POINT_SIZE_RANGE Range (low to high) of antialiased
point sizes
—1, 1 glGetFloatv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

OpenGL State Variables 795
GL_SMOOTH_POINT_SIZE_GRANULARITY Antialiased point-size granularity — — glGetFloatv()
GL_ALIASED_LINE_WIDTH_RANGE Range (low to high) of aliased line
widths
—1, 1 glGetFloatv()
GL_SMOOTH_LINE_WIDTH_RANGE Range (low to high) of antialiased line
widths
—1, 1 glGetFloatv()
GL_SMOOTH_LINE_WIDTH_
GRANULARITY
Antialiased line-width granularity — — glGetFloatv()
GL_MAX_CONVOLUTION_WIDTH Maximum width of convolution filter — 3 glConvolution
Parameteriv()
GL_MAX_CONVOLUTION_HEIGHT Maximum height of convolution filter — 3 glConvolution
Parameteriv()
GL_MAX_ELEMENTS_INDICES Recommended maximum number of
glDrawRangeElements() indices
—— glGetIntegerv()
GL_MAX_ELEMENTS_VERTICES Recommended maximum number of
glDrawRangeElements() vertices
—— glGetIntegerv()
GL_MAX_TEXTURE_UNITS Maximum number of texture units
(not to exceed 32)
—2 glGetIntegerv()
GL_SAMPLE_BUFFERS Number of multisample buffers — 0 glGetIntegerv()
GL_SAMPLES Coverage mask size — 0 glGetIntegerv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

796 Appendix B: State Variables
GL_MAX_SAMPLES Maximum number of multisample
samples
—4
GL_MAX_COLOR_ATTACHMENTS Maximum number of framebuffer
object color attachment points
—8
GL_COMPRESSED_TEXTURE_FORMATS Enumerated compressed texture
formats
—— glGetIntegerv()
GL_NUM_COMPRESSED_TEXTURE_
FORMATS
Number of enumerated compressed
texture formats
—0 glGetIntegerv()
GL_QUERY_COUNTER_BITS Number of bits in the occlusion query
counter
— — glGetQueryiv()
GL_EXTENSIONS Supported extensions — — glGetStringi()
GL_NUM_EXTENSIONS Number of supported extensions — — glGetIntegerv()
GL_MAJOR_VERSION Major version number — — glGetIntegerv()
GL_MINOR_VERSION Minor version number — — glGetIntegerv()
GL_CONTEXT_FLAGS Value for full- or forward-compatible
context flag
—— glGetIntegerv()
GL_RENDERER Renderer string — — glGetString()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

OpenGL State Variables 797
GL_SHADING_LANGUAGE_VERSION OpenGL Shading Language (GLSL)
version
— — glGetString()
GL_VENDOR Vendor string — — glGetString()
GL_VERSION Version string — — glGetString()
GL_MAX_VERTEX_ATTRIBS Number of active vertex attributes — 16 glGetIntegerv()
GL_MAX_VERTEX_UNIFORM_
COMPONENTS
Number of words for vertex shader
uniform variables
— 512 glGetIntegerv()
GL_MAX_VARYING_COMPONENTS
(which replaces GL_MAX_VARYING_
FLOATS in Version 3.0 and greater)
Number of floats for varying variables — 32 glGetIntegerv()
GL_MAX_COMBINED_TEXTURE_IMAGE_
UNITS
Total number of texture units
accessible by OpenGL
—2 glGetIntegerv()
GL_MAX_VERTEX_TEXTURE_IMAGE_
UNITS
Number of texture image units
accessible by a vertex shader
—0 glGetIntegerv()
GL_MAX_TEXTURE_IMAGE_UNITS Number of texture image units
accessible by fragment processing
—2 glGetIntegerv()
GL_MAX_TEXTURE_COORDS Number of texture-coordinate sets — 2 glGetIntegerv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

798 Appendix B: State Variables
GL_MAX_TEXTURE_BUFFER_SIZE Number of addressable texels for buffer
textures
— 65536 glGetIntegerv()
GL_MAX_RECTANGLE_TEXTURE_SIZE Maximum width and height of
rectangular textures
— 1024 glGetIntegerv()
GL_MAX_FRAGMENT_UNIFORM_
COMPONENTS
Number of words for fragment shader
uniform variables
— 64 glGetIntegerv()
GL_MIN_PROGRAM_TEXEL_OFFSET Minimum texel offset allowed in texel
lookup
— –8 glGetIntegerv()
GL_MAX_PROGRAM_TEXEL_OFFSET Maximum texel offset allowed in texel
lookup
—7 glGetIntegerv()
GL_MAX_DRAW_BUFFERS Maximum number of active draw
buffers
— 1+ glGetIntegerv()
GL_MAX_VERTEX_UNIFORM_BLOCKS Maximum number of vertex uniform
buffers per program
— 12 glGetIntegerv()
GL_MAX_FRAGMENT_UNIFORM_BLOCKS Maximum number of fragment
uniform buffers per program
— 12 glGetIntegerv()
GL_MAX_COMBINED_UNIFORM_BLOCKS Maximum number of combined
uniform buffers per program
— 24 glGetIntegerv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

OpenGL State Variables 799
GL_MAX_UNIFORM_BUFFER_BINDINGS Maximum number of uniform buffer
binding points per context
— 24 glGetIntegerv()
GL_MAX_UNIFORM_BLOCK_SIZE Maximum size in machine units of a
uniform block
— 16384 glGetIntegerv()
GL_UNIFORM_BUFFER_OFFSET_
ALIGNMENT
Minimum required alignment for
uniform buffer sizes and offsets
—1 glGetIntegerv()
GL_MAX_VERTEX_UNIFORM_
COMPONENTS
Number of words for vertex shader
uniform variables in default uniform
block
—1 glGetIntegerv()
GL_MAX_FRAGMENT_UNIFORM_
COMPONENTS
Number of words for fragment shader
uniform variables in default uniform
block
—1 glGetIntegerv()
GL_MAX_COMBINED_VERTEX_
UNIFORM_COMPONENTS
Number of words for vertex shader
uniform variables in all uniform blocks
(including the default uniform block)
—1 glGetIntegerv()
GL_MAX_COMBINED_FRAGMENT_
UNIFORM_COMPONENTS
Number of words for fragment shader
uniform variables in all uniform blocks
(including the default uniform block)
—1 glGetIntegerv()
State Variable Description Attribute
Group
Minimum
Value
Get Command
Table B-23 (continued) Implementation-Dependent State Variables

800 Appendix B: State Variables
Implementation-Dependent Pixel Depths
Miscellaneous
State Variable Description Attribute
Group
Minimum
Value
Get Command
GL_x_BITS Number of bits in x color buffer component
(x is one of RED, GREEN, BLUE, ALPHA, or INDEX)
— — glGetIntegerv()
GL_DEPTH_BITS Number of depth-buffer bitplanes — — glGetIntegerv()
GL_STENCIL_BITS Number of stencil bitplanes — — glGetIntegerv()
GL_ACCUM_x_BITS Number of bits in x accumulation buffer component
(x is one of RED, GREEN, BLUE, or ALPHA)
— — glGetIntegerv()
Table B-24 Implementation-Dependent Pixel-Depth State Variables
State Variable Description Attribute
Group
Initial Value Get Command
GL_LIST_BASE Setting of glListBase() list 0 glGetIntegerv()
GL_LIST_INDEX Number of display list under
construction; 0 if none
— 0 glGetIntegerv()
GL_LIST_MODE Mode of display list under construction;
undefined if none
— 0 glGetIntegerv()
Table B-25 Miscellaneous State Variables

OpenGL State Variables 801
GL_ATTRIB_STACK_DEPTH Attribute stack pointer — 0 glGetIntegerv()
GL_CLIENT_ATTRIB_STACK_DEPTH Client attribute stack pointer — 0 glGetIntegerv()
GL_NAME_STACK_DEPTH Name stack depth — 0 glGetIntegerv()
GL_RENDER_MODE glRenderMode() setting — GL_RENDER glGetIntegerv()
GL_SELECTION_BUFFER_POINTER Pointer to selection buffer select 0 glGetPointerv()
GL_SELECTION_BUFFER_SIZE Size of selection buffer select 0 glGetIntegerv()
GL_FEEDBACK_BUFFER_POINTER Pointer to feedback buffer feedback 0 glGetPointerv()
GL_FEEDBACK_BUFFER_SIZE Size of feedback buffer feedback 0 glGetIntegerv()
GL_FEEDBACK_BUFFER_TYPE Type of feedback buffer feedback GL_2D glGetIntegerv()
— Current error code(s) — 0 glGetError()
GL_CURRENT_QUERY Active occlusion query ID — 0 glGetQueryiv()
GL_COPY_READ_BUFFER Buffer object bound to copy buffer
“read” bind point
— 0 glGetIntegerv()
GL_COPY_WRITE_BUFFER Buffer object bound to copy buffer
“write” bind point
— 0 glGetIntegerv()
GL_TEXTURE_BUFFER Buffer object bound to texture buffer
bind point
— 0 glGetIntegerv()
State Variable Description Attribute
Group
Initial Value Get Command
Table B-25 (continued) Miscellaneous State Variables
This page intentionally left blank
803
Appendix C
C.Homogeneous Coordinates and
Transformation Matrices
This appendix presents a brief discussion of homogeneous coordinates.
It also lists the forms of the transformation matrices used for rotation,
scaling, translation, perspective projection, and orthographic projection.
These topics are introduced and discussed in Chapter 3. For a more
detailed discussion of these subjects, see almost any book on three-
dimensional computer graphics—for example, Computer Graphics:
Principles and Practice, by Foley, van Dam, Feiner, and Hughes (Addison-
Wesley, 1990); or a text on projective geometry—for example, The Real
Projective Plane, by H. S. M. Coxeter, 2nd ed. (Cambridge University Press,
1961). In the discussion that follows, the term homogeneous coordinates
always means three-dimensional homogeneous coordinates, although
projective geometries exist for all dimensions.
This appendix has the following major sections:
• “Homogeneous Coordinates”
•“Transformation Matrices”

804 Appendix C: Homogeneous Coordinates and Transformation Matrices
Homogeneous Coordinates
OpenGL commands usually deal with two- and three-dimensional vertices,
but in fact all are treated internally as three-dimensional homogeneous ver-
tices comprising four coordinates. Every column vector (x, y, z, w)T repre-
sents a homogeneous vertex if at least one of its elements is nonzero. If the
real number a is nonzero, then (x, y, z, w)T and (ax, ay, az, aw)T represent
the same homogeneous vertex. (This is just like fractions: x/y = (ax)/(ay).) A
three-dimensional Euclidean space point (x, y, z)T becomes the homoge-
neous vertex with coordinates (x, y, z, 1.0)T, and the two-dimensional
Euclidean point (x, y)T becomes (x, y, 0.0, 1.0)T.
As long as w is nonzero, the homogeneous vertex (x, y, z, w)T corresponds
to the three-dimensional point (x/w, y/w, z/w)T. If w = 0.0, it corresponds to
no Euclidean point, but rather to some idealized “point at infinity.” To under-
stand this point at infinity, consider the point (1, 2, 0, 0), and note that the
sequence of points (1, 2, 0, 1), (1, 2, 0, 0.01), and (1, 2.0, 0.0, 0.0001) corre-
sponds to the Euclidean points (1, 2), (100, 200), and (10,000, 20,000). This
sequence represents points rapidly moving toward infinity along the line
2x=y. Thus, you can think of (1, 2, 0, 0) as the point at infinity in the direc-
tion of that line.
Note: OpenGL might not handle homogeneous clip coordinates with w < 0
correctly. To be sure that your code is portable to all OpenGL systems,
use only non-negative w-values.
Transforming Vertices
Vertex transformations (such as rotations, translations, scaling, and shear-
ing) and projections (such as perspective and orthographic) can all be
represented by applying an appropriate 4 u4 matrix to the coordinates rep-
resenting the vertex. If v represents a homogeneous vertex and M is a 4 u4
transformation matrix, then Mv is the image of v under the transformation
by M. (In computer-graphics applications, the transformations used are
usually nonsingular—in other words, the matrix M can be inverted. This
isn’t required, but some problems arise with singular matrices.)
After transformation, all transformed vertices are clipped so that x,y, and z
are in the range [w,w] (assuming w > 0). Note that this range corresponds
in Euclidean space to [1.0, 1.0].

Transformation Matrices 805
Transforming Normals
Normal vectors aren’t transformed in the same way as vertices or position
vectors are. Mathematically, it’s better to think of normal vectors not as vec-
tors, but as planes perpendicular to those vectors. Then, the transformation
rules for normal vectors are described by the transformation rules for per-
pendicular planes.
A homogeneous plane is denoted by the row vector (a, b, c, d), where at least
one of a, b, c, and d is nonzero. If q is a nonzero real number, then (a, b, c, d)
and (qa, qb, qc, qd) represent the same plane. A point (x, y, z, w)T is on the
plane (a, b, c, d) if ax +by +cz +dw =0. (If w = 1, this is the standard descrip-
tion of a Euclidean plane.) In order for (a, b, c, d) to represent a Euclidean
plane, at least one of a,b, or c must be nonzero. If they’re all zero, then (0,
0, 0, d) represents the “plane at infinity,” which contains all the “points at
infinity.”
If p is a homogeneous plane and v is a homogeneous vertex, then the
statement “v lies on plane p” is written mathematically as pv = 0, where pv
is normal matrix multiplication. If M is a nonsingular vertex transformation
(that is, a 4 u4 matrix that has an inverse M1), then pv = 0 is equivalent to
pM1Mv = 0, so Mv lies in the plane pM1. Thus, pM1 is the image of the
plane under the vertex transformation M.
If you like to think of normal vectors as vectors instead of as the planes
perpendicular to them, let v and n be vectors such that v is perpendicular
to n. Then, nTv = 0. Thus, for an arbitrary nonsingular transformation M,
nTM1Mv = 0, which means that nTM1 is the transpose of the transformed
normal vector. Thus, the transformed normal vector is (M1)Tn. In other
words, normal vectors are transformed by the inverse transpose of the
transformation that transforms points. Whew!
Transformation Matrices
Although any nonsingular matrix M represents a valid projective transfor-
mation, a few special matrices are particularly useful. These matrices are
listed in the following subsections.
806 Appendix C: Homogeneous Coordinates and Transformation Matrices
Translation
The call glTranslate*(x, y, z) generates T, where
Scaling
The call glScale*(x, y, z) generates S, where
Notice that S1 is defined only if x,y, and z are all nonzero.
Rotation
The call glRotate*(a, x, y, z) generates R as follows:
Let v = (x, y, z)T, and u = v/||v|| = (x’, y’, z’)T.
Also let
Then
T = and T−1 =
1 0 0 x
0 1 0 y
0 0 1 z
0 0 0 1
1 0 0 −x
0 1 0 −y
0 0 1 −z
0 0 0 1
S = and S−1 =
x 0 0 0
0y 0 0
0 0 z 0
0 0 0 1
1 0 0 0
x
01 0 0
y
0 0 1 0
z
0 0 0 1
S = and M = uuT + (cos a) (I−uuT) + (sin a)S
0 −z' y'
z' 0−x'
−y' x' 0
R =
m m m 0
m m m 0
m m m 0
0 0 0 1

Transformation Matrices 807
where m represent the elements from M, which is the 3 u3 matrix defined
on the preceding page. The R matrix is always defined. If x=y=z=0,
then R is the identity matrix. You can obtain the inverse of R,R1, by
substituting a for a, or by transposition.
The glRotate*() command generates a matrix for rotation about an
arbitrary axis. Often, you’re rotating about one of the coordinate axes; the
corresponding matrices are as follows:
As before, the inverses are obtained by transposition.
Perspective Projection
The call glFrustum(l, r, b, t, n, f ) generates R, where
R is defined as long as lzr,tzb, and nzf.
glRotate*(a, 1, 0, 0):
1 0 0 0
0 cos a−sin a 0
0 sin a cos a0
0 0 0 1
glRotate*(a, 0, 1, 0):
cos a 0 sin a 0
0 1 0 0
−sin a0 cos a0
0 0 0 1
glRotate*(a, 0, 0, 1):
cos a−sin a00
sin a cos a 0 0
0 0 1 0
0 0 0 1
R
2n
rl–
----------0rl+
rl–
----------0
02n
tb–
---------- tb+
tb–
-----------0
00 fn+–
fn–
------------------- 2fn–
fn–
-----------
00 1–0
and R1–
rl–
2n
----------00
rl+
2n
----------
0tb–
2n
---------- 0tb+
2n
-----------
00 0 1–
00 fn––
2fn
-------------------fn+
2fn
-----------
==
808 Appendix C: Homogeneous Coordinates and Transformation Matrices
Orthographic Projection
The call glOrtho(l, r, b, t, n, f ) generates R, where
R is defined as long as lzr,tzb, and nzf.
R
2
rl–
----------00rl+
rl–
----------–
02
tb–
---------- 0tb+
tb–
-----------–
00 2–
fn–
-----------fn+
fn–
-----------–
000 1
and R1–
rl–
2
----------00
rl+
2
----------
0tb–
2
---------- 0tb+
2
-----------
00
fn–
2–
-----------nf+
2
-----------
00 0 1
==
809
Appendix D
D.OpenGL and Window Systems
OpenGL is available on many different platforms and works with many
different window systems. It is designed to complement window systems,
not duplicate their functionality. Therefore, OpenGL performs geometric
and image rendering in two and three dimensions, but it does not manage
windows or handle input events.
However, the basic definitions of most window systems don’t support a
library as sophisticated as OpenGL, with its complex and diverse pixel
formats, including depth, stencil, and accumulation buffers, as well as
double-buffering. For most window systems, some routines are added to
extend the window system to support OpenGL.
This appendix introduces the extensions defined for several window and
operating systems: the X Window System, the Apple Mac OS, and Microsoft
Windows. You need to have some knowledge of the window systems to
fully understand this appendix.
This appendix has the following major sections:
• “Accessing New OpenGL Functions”
• “GLX: OpenGL Extension for the X Window System”
• “AGL: OpenGL Extensions for the Apple Macintosh”
• “WGL: OpenGL Extension for Microsoft
Windows 95/98/NT/ME/2000/XP”

810 Appendix D: OpenGL and Window Systems
Accessing New OpenGL Functions
OpenGL is changing all the time. The manufacturers of OpenGL graphics
hardware add new extensions and the Khronos OpenGL ARB Working Group
approve those extensions and merge them into the core of OpenGL. Since
each manufacturer needs to be able to update its version of OpenGL, the
header files (like gl.h), and the library you use to compile (like opengl32.lib,
on Microsoft Windows, for example) may be out of sync with the latest ver-
sion. This would likely cause errors when compiling (or more specifically,
linking) your application.
To help you work around this problem, a mechanism for accessing the new
functions was added to each of the window system libraries. This method
varies among the different window systems, but the idea is the same in all
cases. You will need to retrieve function pointers for the functions that you
want to use. You need to do this only if the function is not available
explicitly from your library (you’ll know when it isn’t; you’ll get a linker
error).
Each window system has its own function for getting an OpenGL function
pointer; check the respective section in this appendix for specifics.
Here is an example for Microsoft Windows:
#include <windows.h> /* for wglGetProcAddress() */
#include “glext.h”
PFNGLBINDPROGRAMARBPROC glBindProgramARB;
void
init(void)
{
glBindProgramARB = (PFNGLBINDPROGRAMARB)
wglGetProcAddress(“glBindProgramARB”);
...
}
The function pointer type—in this case, PFNGLBINDPROGRAMARBPROC—
is defined in glext.h, as are all of the enumerants that you pass into
OpenGL functions. If the returned value is zero (effectively a NULL
pointer), the function is not available in the OpenGL implementation
that your program is using.
GLUT includes a similar routine, glutGetProcAddress(), which simply
wraps the window-system dependent routine.

Accessing New OpenGL Functions 811
It’s not sufficient in all cases to merely retrieve a function pointer to
determine if functionality is present. To verify that the extension the
functionality is defined from is available, check the extension string (see
“The Query Commands” in Appendix B for details).
GLEW: The OpenGL Extension Wrangler
To simplify both verifying extension support and dealing with the
associated function pointers, we recommend using the open-source GLEW
library (http://glew.sourceforge.net/) developed by Milan Ikits and
Marcelo Magallon, which manages this process simply and elegantly.
To incorporate GLEW into your applications, follow these three simple
steps:
1. Replace the OpenGL and glext.h header files with those of GLEW:
glew.h
2. Initialize GLEW by calling glewInit() after you’ve created your
window (or more specifically, your OpenGL context). This causes
GLEW to query and retrieve all available function pointers from your
implementation as well as to provide a convenient set of variables for
determining whether a particular version or extension is supported.
3. Verify that the extension containing the functionality you want to use
is available. GLEW provides a set of Boolean variables named after the
extension (for example, GL_ARB_map_buffer_range is the variable
name for the OpenGL map buffer range extension). If the variable’s
value is true, you can use the extension’s functions.
Here’s a short example using our init() routine, which is executed after
calling glutCreateWindow():
#include <GLEW.h>
void
init()
{
GLuint vao;
glewInit(); // Initialize the GLEW library
if ( GLEW_VERSION_3_0 ) {
// We know that we’re using OpenGL Version 3.0, and
// that vertex array objects are supported

812 Appendix D: OpenGL and Window Systems
glGenVertexArrays( 1, &vao );
glBindVertexArray( vao );
}
// Initialize and bind all other vertex arrays
...
}
We can use one of GLEW’s variables, GLEW_VERSION_3_0, in this case to
determine our OpenGL version and make decisions about use of features.
GLX: OpenGL Extension for the X Window System
In the X Window System, OpenGL rendering is made available as an exten-
sion to X in the formal X sense. GLX is an extension to the X protocol (and
its associated API) for communicating OpenGL commands to an extended
X server. Connection and authentication are accomplished with the
normal X mechanisms.
As with other X extensions, there is a defined network protocol for OpenGL’s
rendering commands encapsulated within the X byte stream, so client-
server OpenGL rendering is supported. Since performance is critical in
three-dimensional rendering, the OpenGL extension to X allows OpenGL
to bypass the X server’s involvement in data encoding, copying, and inter-
pretation, and instead render directly to the graphics pipeline.
GLX Version 1.3 introduces several sweeping changes, starting with the new
GLXFBConfig data structure, which describes the GLX framebuffer config-
uration (including the depth of the color buffer components, and the types,
quantities, and sizes of the depth, stencil, accumulation, and auxiliary buff-
ers). The GLXFBConfig structure describes these framebuffer attributes for
a GLXDrawable rendering surface. (In X, a rendering surface is called a
Drawable.)
GLX 1.3 also provides for three types of GLXDrawable surfaces: GLXWindow,
GLXPixmap, and GLXPbuffer. A GLXWindow is on-screen; a GLXPixmap
or GLXPbuffer is off-screen. Because a GLXPixmap has an associated
X pixmap, both X and GLX may render into a GLXPixmap. GLX may be the
only way to render into a GLXPbuffer. The GLXPbuffer is intended to store
pixel data in nonvisible framebuffer memory. (Off-screen rendering isn’t
guaranteed to be supported for direct renderers.)

GLX: OpenGL Extension for the X Window System 813
GLX version 1.4 increased support for framebuffer configuration by adding
drawable configuration options for number of buffers and samples for
multisampled drawables.
The X Visual is an important data structure for maintaining pixel format
information about an OpenGL window. A variable of data type XVisualInfo
keeps track of pixel format information, including pixel type (RGBA or
color-index), single- or double-buffering, resolution of colors, and presence
of depth, stencil, and accumulation buffers. The standard X Visuals (for
example, PseudoColor, and TrueColor) do not describe the pixel format
details, so each implementation must extend the number of X Visuals
supported.
In GLX 1.3, a GLXWindow has an X Visual, associated with its GLXFBConfig.
For a GLXPixmap or a GLXPbuffer, there may or may not be a similar
associated X Visual. Prior to GLX 1.3, all surfaces (windows or pixmaps) were
associated with an X Visual. (Prior to 1.3, Pbuffers were not part of GLX.)
The GLX routines are discussed in more detail in the OpenGL Reference
Manual. Integrating OpenGL applications with the X Window System and
the Motif widget set is discussed in great detail in OpenGL Programming
for the X Window System by Mark Kilgard (Addison-Wesley, 1996), which
includes full source code examples. If you absolutely want to learn about
the internals of GLX, you may want to read the GLX specification, which
can be found at
http://www.opengl.org/developers/documentation/glx.html
Initialization
Use glXQueryExtension() and glXQueryVersion() to determine whether
the GLX extension is defined for an X server and, if so, which version is
present. glXQueryExtensionsString() returns extension information about
the client-server connection. glXGetClientString() returns information
about the client library, including extensions and version number.
glXQueryServerString() returns similar information about the server.
glXChooseFBConfig() returns a pointer to an array of GLXFBConfig
structures describing all GLX framebuffer configurations that meet the
client’s specified attributes. You may use glXGetFBConfigAttrib() to query
a framebuffer configuration about its support of a particular GLX attribute.
You may also call glXGetVisualFromFBConfig() to retrieve the X visual
associated with a GLXFBConfig.

814 Appendix D: OpenGL and Window Systems
Creation of rendering areas varies slightly, depending on the type of draw-
able. For a GLXWindow, first create an X Window with an X visual that
corresponds to the GLXFBConfig. Then use that X Window when calling
glXCreateWindow(), which returns a GLXWindow. Similarly for a
GLXPixmap, first create an X Pixmap with a pixel depth that matches the
GLXFBConfig. Then use that Pixmap when calling glXCreatePixmap() to
create a GLXPixmap. A GLXPbuffer does not require an X Window or an
X Pixmap; just call glXCreatePbuffer() with the appropriate GLXFBConfig.
Note: If you are using GLX 1.2 or earlier, you do not have a GLXFBConfig
structure. Instead, use glXChooseVisual(), which returns a pointer
to an XVisualInfo structure describing the X visual that meets the
client’s specified attributes. You can query a visual about its support
of a particular OpenGL attribute with glXGetConfig(). To render to
an off-screen pixmap, you must use the earlier
glXCreateGLXPixmap() routine.
Accessing OpenGL Functions
To access function pointers for extensions and new features in the
X Window System, use the glXGetProcAddress() function. This function
is defined in the glxext.h header file, which can be downloaded from the
OpenGL Web site.
Controlling Rendering
Several GLX routines are provided for creating and managing an OpenGL
rendering context. Routines are also provided for such tasks as handling
GLX events, synchronizing execution between the X and OpenGL streams,
swapping front and back buffers, and using an X font.
Managing an OpenGL Rendering Context
An OpenGL rendering context is created with either glXCreateNewContext()
or glXCreateContextAttribsARB(), whose use is required in OpenGL
Version 3.0 and greater. One of the arguments to these routines allows you
to request a direct rendering context that bypasses the X server as described
previously. (To perform direct rendering, the X server connection must be
local, and the OpenGL implementation needs to support direct rendering.)
Another argument also allows display-list and texture-object indices and
definitions to be shared by multiple rendering contexts. You can determine
whether a GLX context is direct with glXIsDirect().

GLX: OpenGL Extension for the X Window System 815
glXMakeContextCurrent() binds a rendering context to the current
rendering thread and also establishes two current drawable surfaces. You
can draw into one of the current drawable surfaces and read pixel data
from the other drawable. In many situations, the draw and read drawables
refer to the same GLXDrawable surface. glXGetCurrentContext() returns
the current context. You can also obtain the current draw drawable
with glXGetCurrentDrawable(), the current read drawable with
glXGetCurrentReadDrawable(), and the current X Display with
glXGetCurrentDisplay(). You can use glXQueryContext() to determine
the current values for context attributes.
Only one context can be current for any thread at any one time. If you have
multiple contexts, you can copy selected groups of OpenGL state variables
from one context to another with glXCopyContext(). When you’re
finished with a particular context, destroy it with glXDestroyContext().
Note: If you are using GLX 1.2 or earlier, use glXCreateContext() to create
a rendering context and glXMakeCurrent() to make it current. You
cannot declare a drawable as a separate read drawable, so you do not
have glXGetCurrentReadDrawable().
Handling GLX Events
GLX 1.3 introduces GLX events, which are returned in the event stream of
standard X11 events. GLX event handling has been added specifically to deal
with the uncertainty of the contents of a GLXPbuffer, which may be clob-
bered at any time. In GLX 1.3, you may use glXSelectEvent() to select only
one event with GLX_PBUFFER_CLOBBER_MASK. With standard X event
handling routines, you can now determine if a portion of a GLXPbuffer (or
GLXWindow) has been damaged and then take steps, if desired, to recover.
(Also, you can call glXGetSelectedEvent() to find out if you are already
monitoring this GLX event.)
Synchronizing Execution
To prevent X requests from executing until any outstanding OpenGL
rendering is completed, call glXWaitGL(). Then, any previously issued
OpenGL commands are guaranteed to be executed before any X rendering
calls made after glXWaitGL(). Although the same result can be achieved
with glFinish(),glXWaitGL() doesn’t require a round-trip to the server and
thus is more efficient in cases where the client and server are on separate
machines.

816 Appendix D: OpenGL and Window Systems
To prevent an OpenGL command sequence from executing until any out-
standing X requests are completed, use glXWaitX(). This routine guarantees
that previously issued X rendering calls are executed before any OpenGL
calls made after glXWaitX().
Swapping Buffers
For drawables that are double-buffered, the front and back buffers can be
exchanged by calling glXSwapBuffers(). An implicit glFlush() is done as
part of this routine.
Using an X Font
A shortcut for using X fonts in OpenGL is provided with the command
glXUseXFont(). This routine builds display lists, each of which calls
glBitmap() for each requested character from the specified font and font size.
Cleaning Up Drawables
Once rendering is completed, you can destroy the drawable surface with
the appropriate call to glXDestroyWindow(),glXDestroyPixmap(), or
glXDestroyPbuffer(). (These routines are not available prior to GLX 1.3,
although there is glXDestroyGLXPixmap(), which is similar to
glXDestroyPixmap().)
GLX Prototypes
Initialization
Determine whether the GLX extension is defined on the X server:
Bool glXQueryExtension( Display *dpy, int *errorBase,
int *eventBase );
Query version and extension information for client and server:
Bool glXQueryVersion( Display *dpy, int *major, int *minor );
const char* glXGetClientString( Display *dpy, int name );
const char* glXQueryServerString( Display *dpy, int screen,
int name );
const char* glXQueryExtensionsString( Display *dpy, int screen );

GLX: OpenGL Extension for the X Window System 817
Obtain available GLX framebuffer configurations:
GLXFBConfig * glXGetFBConfigs( Display *dpy, int screen,
int *nelements );
GLXFBConfig * glXChooseFBConfig( Display *dpy, int screen,
const int attribList, int *nelements );
Query a GLX framebuffer configuration for attribute or X Visual
information:
int glXGetFBConfigAttrib( Display *dpy, GLXFBConfig config,
int attribute, int *value );
XVisualInfo * glXGetVisualFromFBConfig( Display *dpy,
GLXFBConfig config );
Create surfaces that support rendering (both on-screen and off-screen):
GLXWindow glXCreateWindow( Display *dpy,
GLXFBConfig config, Window win, const int *attribList );
GLXPixmap glXCreatePixmap( Display *dpy, GLXFBConfig config,
Pixmap pixmap, const int *attribList );
GLXPbuffer glXCreatePbuffer( Display *dpy, GLXFBConfig config,
const int *attribList );
Obtain a pointer to an OpenGL function:
__GLXextFuncPtr glXGetProcAddress(const char* funcName);
Controlling Rendering
Manage and query an OpenGL rendering context:
GLXContext glXCreateNewContext( Display *dpy,
GLXFBConfig config, int renderType, GLXContext shareList,
Bool direct );
GLXContext glXCreateContextAttribsARB (Display *dpy,
GLXFBConfig config, GLXContext shareList, Bool direct,
const int *attribs);
Bool glXMakeContextCurrent( Display *dpy,
GLXDrawable drawable, GLXDrawable read, GLXContext context );
void glXCopyContext( Display *dpy, GLXContext source,
GLXContext dest, unsigned long mask );

818 Appendix D: OpenGL and Window Systems
Bool glXIsDirect( Display *dpy, GLXContext context );
GLXContext glXGetCurrentContext( void );
Display* glXGetCurrentDisplay( void );
GLXDrawable glXGetCurrentDrawable( void );
GLXDrawable glXGetCurrentReadDrawable( void );
int glXQueryContext( Display *dpy, GLXContext context,
int attribute, int *value );
void glXDestroyContext( Display *dpy, GLXContext context );
Ask to receive and query GLX events:
int glXSelectEvent( Display *dpy, GLXDrawable drawable,
unsigned long eventMask );
int glXGetSelectedEvent( Display *dpy, GLXDrawable drawable,
unsigned long *eventMask );
Synchronize execution:
void glXWaitGL( void );
void glXWaitX( void );
Exchange front and back buffers:
void glXSwapBuffers( Display *dpy, GLXDrawable drawable );
Use an X font:
void glXUseXFont( Font font, int first, int count, int listBase );
Clean up drawables:
void glXDestroyWindow( Display *dpy, GLXWindow win );
void glXDestroyPixmap( Display *dpy, GLXPixmap pixmap );
void glXDestroyPbuffer( Display *dpy, GLXPbuffer pbuffer );
Deprecated GLX Prototypes
The following routines have been deprecated in GLX 1.3. If you are using
GLX 1.2 or a predecessor, you may need to use several of these routines.

AGL: OpenGL Extensions for the Apple Macintosh 819
Obtain the desired visual:
XVisualInfo* glXChooseVisual( Display *dpy, int screen,
int *attribList );
int glXGetConfig( Display *dpy, XVisualInfo *visual, int attrib,
int *value );
Manage an OpenGL rendering context:
GLXContext glXCreateContext( Display *dpy, XVisualInfo *visual,
GLXContext shareList, Bool direct );
Bool glXMakeCurrent( Display *dpy, GLXDrawable drawable,
GLXContext context );
Perform off-screen rendering:
GLXPixmap glXCreateGLXPixmap( Display *dpy,
XVisualInfo *visual, Pixmap pixmap );
void glXDestroyGLXPixmap( Display *dpy, GLXPixmap pix );
AGL: OpenGL Extensions for the Apple Macintosh
This section covers the routines defined as the OpenGL extension to the
Apple Macintosh (AGL). An understanding of the way the Macintosh
handles graphics rendering is required. The OpenGL Programming Guide
for Mac OS X contains a complete reference for using OpenGL within
Apple’s Mac OS X operating system (accessible on the Internet at
http://developer.apple.com/DOCUMENTATION/GraphicsImaging/
Conceptual/OpenGL-MacProgGuide/opengl_intro/opengl_intro.html.)
In addition to AGL, Mac OS X supports other interfaces for OpenGL: CGL
(Core OpenGL API), which is a low-level interface to OpenGL contexts
(not recommended for novice users); and NSOpenGL* routines, which are
part of Cocoa, Apple’s set of media APIs. We only describe AGL in this
appendix, and refer the interested reader to Apple’s Developer Web site:
http://developer.apple.com/.
The data type AGLPixelFormat (the AGL equivalent to XVisualInfo)
maintains pixel information, including pixel type (RGBA or color index);
single- or double-buffering; resolution of colors; and presence of depth,
stencil, and accumulation buffers.

820 Appendix D: OpenGL and Window Systems
Initialization
Use aglGetVersion() to determine which version of AGL for the Macintosh
is available.
The capabilities of underlying graphics devices and your requirements for
rendering buffers are resolved using aglChoosePixelFormat(). It returns an
AGLPixelFormat structure or NULL, depending on whether or not your
requirements can be accommodated.
Rendering and Contexts
Several AGL routines are provided for creating and managing an OpenGL
rendering context. You can use such a context to render into either a win-
dow or an off-screen graphics world. Routines are also provided that allow
you to swap front and back rendering buffers; adjust buffers in response to
a move, resize, or graphics device change event; and use Macintosh fonts.
For software rendering (and, in some cases, hardware-accelerated render-
ing), the rendering buffers are created in the system memory space.
Managing an OpenGL Rendering Context
An OpenGL rendering context is created (at least one context per window
being rendered into) with aglCreateContext(). This takes the pixel format
you selected as a parameter and uses it to initialize the context.
Use aglSetDrawable() to attach the context to the drawable and then
aglSetCurrentContext() to make a rendering context current. Only one
context can be current for a thread of control at any time. This indicates
which drawable is to be rendered into and which context to use with it. It’s
possible for more than one context to be used (not simultaneously) with a
particular drawable. Two routines allow you to determine the current
rendering context and drawable being rendered into:
aglGetCurrentContext() and aglGetDrawable().
If you have multiple contexts, you can copy selected groups of OpenGL
state variables from one context to another with aglCopyContext(). When
a particular context is no longer needed, it should be destroyed by calling
aglDestroyContext().

AGL: OpenGL Extensions for the Apple Macintosh 821
On-Screen Rendering
To render on-screen, first create a pixel format. Create a context based
on this pixel format and attach the context to the window with
aglSetDrawable(). The buffer rectangle can be modified by calling
aglSetInteger(AGL_BUFFER_RECT, ...).
Off-Screen Rendering
To render off-screen, create a pixel format with the AGL_OFFSCREEN
attribute. Create a context based on this pixel format and attach the context
to the screen with aglSetOffScreen().
Full-Screen Rendering
To render full-screen, create a pixel format with the AGL_FULLSCREEN
attribute. Create a context based on this pixel format and attach the context
to the screen with aglSetFullScreen().
Swapping Buffers
For drawables that are double-buffered (as per the pixel format of the
current rendering context), call aglSwapBuffers() to exchange the
front and back buffers. The swap rectangle can be modified by calling
aglSetInteger(AGL_SWAP_RECT, ...). An implicit glFlush() is performed
as part of this routine.
Updating the Rendering Buffers
The Apple Macintosh toolbox requires you to perform your own event
handling and does not provide a way for libraries to hook into the event
stream automatically. So that the drawables maintained by OpenGL
can adjust to changes in drawable size, position, and pixel depth,
aglUpdateContext() is provided.

822 Appendix D: OpenGL and Window Systems
This routine must be called by your event processing code whenever one of
these events occurs in the current drawable. Ideally, the scene should be
re-rendered after an update call to take into account the changes made to
the rendering buffers.
Using an Apple Macintosh Font
A shortcut for using Macintosh fonts is provided with aglUseFont().
This routine builds display lists, each of which calls glBitmap() for each
requested character from the specified font and font size.
Error Handling
An error-handling mechanism is provided for the Apple Macintosh
OpenGL extension. When an error occurs, you can call aglGetError() to
get a more precise description of what caused the error.
AGL Prototypes
Initialization
Determine version information:
void aglGetVersion( GLint *major, GLint *minor );
Determine available pixel formats:
AGLPixelFormat aglCreatePixelFormat( const GLint *attribs );
AGLPixelFormat aglChoosePixelFormat( const AGLDevice *gdevs,
GLint ndev, const GLint *attribs );
GLboolean aglDescribePixelFormat( AGLPixelFormat pix,
GLint attrib, GLint *value );
void aglDestroyPixelFormat( AGLPixelFormat pix );
AGLPixelFormat aglNextPixelFormat( AGLPixelFormat pix );
AGLDevice *aglDevicesOfPixelFormat( AGLPixelFormat pix,
GLint *ndevs );

AGL: OpenGL Extensions for the Apple Macintosh 823
Renderer information functions:
AGLRendererInfo aglQueryRendererInfo( const AGLDevice *gdevs,
GLint ndev );
void aglDestroyRendererInfo( AGLRendererInfo rend );
AGLRendererInfo aglNextRendererInfo( AGLRendererInfo rend );
GLboolean aglDescribeRenderer( AGLRendererInfo rend,
GLint prop, GLint *value );
Controlling Rendering
Manage OpenGL rendering contexts:
AGLContext aglCreateContext( AGLPixelFormat pix,
AGLContext share );
GLboolean aglDestroyContext( AGLContext ctx );
GLboolean aglCopyContext( AGLContext src, AGLContext dst,
GLuint mask );
GLboolean aglUpdateContext( AGLContext ctx );
Current state functions:
GLboolean aglSetCurrentContext( AGLContext ctx );
AGLContext aglGetCurrentContext( void );
Drawable functions:
GLboolean aglSetDrawable( AGLContext ctx, AGLDrawable draw );
GLboolean aglSetOffScreen( AGLContext ctx, GLsizei width,
GLsizei height, GLsizei rowbytes, GLvoid *baseaddr );
GLboolean aglSetFullScreen( AGLContext ctx, GLsizei width,
GLsizei height, GLsizei freq, GLint device );
AGLDrawable aglGetDrawable( AGLContext ctx );
Virtual screen functions:
GLboolean aglSetVirtualScreen( AGLContext ctx, GLint screen );
GLint aglGetVirtualScreen( AGLContext ctx );

824 Appendix D: OpenGL and Window Systems
Configure global library option:
GLboolean aglConfigure( GLenum pname, GLuint param );
Swap function:
void aglSwapBuffers( AGLContext ctx );
Per context options:
GLboolean aglEnable( AGLContext ctx, GLenum pname );
GLboolean aglDisable( AGLContext ctx, GLenum pname );
GLboolean aglIsEnabled( AGLContext ctx, GLenum pname );
GLboolean aglSetInteger( AGLContext ctx, GLenum pname,
const GLint *params );
GLboolean aglGetInteger( AGLContext ctx, GLenum pname,
GLint *params );
Font function:
GLboolean aglUseFont( AGLContext ctx, GLint fontID, Style face,
GLint size, GLint first, GLint count, GLint base );
Error functions:
GLenum aglGetError( void );
const GLubyte *aglErrorString( GLenum code );
Soft reset function:
void aglResetLibrary( void );
WGL: OpenGL Extension for Microsoft
Windows 95/98/NT/ME/2000/XP
OpenGL rendering is supported on systems that run any modern version
of Microsoft Windows (from Windows 95 and later). The functions and
routines of the Win32 library are necessary to initialize the pixel format and
control rendering, and for access to extensions for OpenGL. Some routines,
which are prefixed by wgl, extend Win32 so that OpenGL can be fully
supported.

WGL: OpenGL Extension for Microsoft Windows 95/98/NT/ME/2000/XP 825
For Win32/WGL, the PIXELFORMATDESCRIPTOR is the key data structure
for maintaining pixel format information about the OpenGL window.
A variable of data type PIXELFORMATDESCRIPTOR keeps track of pixel
information, including pixel type (RGBA or color-index); single- or
double-buffering; resolution of colors; and presence of depth, stencil, and
accumulation buffers.
To get more information about WGL, you may want to start with technical
articles available through the Microsoft Developer Network Web site.
Initialization
Use GetVersion() or the newer GetVersionEx() to determine version
information. ChoosePixelFormat() tries to find a PIXELFORMAT
DESCRIPTOR with specified attributes. If a good match for the requested
pixel format is found, then SetPixelFormat() should be called for actual
use of the pixel format. You should select a pixel format in the device con-
text before creating a rendering context.
If you want to find out details about a given pixel format, use
DescribePixelFormat() or, for overlays or underlays,
wglDescribeLayerPlane().
Accessing OpenGL Functions
To access function pointers for extensions and new features in Microsoft
Windows, use the wglGetProcAddress() function. This function is defined
in the wingdi.h header file, which is automatically included when you
include windows.h in your application.
Controlling Rendering
Several WGL routines are provided for creating and managing an OpenGL
rendering context, rendering to a bitmap, swapping front and back buffers,
finding a color palette, and using either bitmap or outline fonts.
Managing an OpenGL Rendering Context
wglCreateContext() and wglCreateContextAttribsARB() (the latter for
use with OpenGL Version 3.0 and greater) create an OpenGL rendering
context for drawing on the device in the selected pixel format of the device

826 Appendix D: OpenGL and Window Systems
context. (To create an OpenGL rendering context for overlay or underlay
windows, use wglCreateLayerContext() instead.) To make a rendering
context current, use wglMakeCurrent();wglGetCurrentContext() returns
the current context. You can also obtain the current device context with
wglGetCurrentDC(). You can copy some OpenGL state variables from
one context to another with wglCopyContext() or make two contexts
share the same display lists and texture objects with wglShareLists().
When you’re finished with a particular context, destroy it with
wglDestroyContext().
Accessing OpenGL Extensions
Use wglGetProcAddress() to access implementation-specific OpenGL
extension procedure calls. To determine which extensions are supported
by your implementation, use glGetString(GL_EXTENSIONS).
wglGetProcAddress(), when passed the exact name of the extension
returned from glGetString(), returns a function pointer for the extension
procedure call, or returns NULL if the extension is not supported.
OpenGL Rendering to a Bitmap
Win32 has a few routines for allocating (and deallocating) bitmaps, to
which you can render OpenGL directly. CreateDIBitmap() creates a
device-dependent bitmap (DDB) from a device-independent bitmap (DIB).
CreateDIBSection() creates a device-independent bitmap (DIB) that appli-
cations can write to directly. When finished with your bitmap, you can use
DeleteObject() to free it up.
Synchronizing Execution
If you want to combine GDI and OpenGL rendering, be aware that there
are no equivalents to functions such as glXWaitGL(),glXWaitX(), and
pglWaitGL() in Win32. Although glXWaitGL() has no equivalent in Win32,
you can achieve the same effect by calling glFinish(), which waits until all
pending OpenGL commands are executed, or by calling GdiFlush(), which
waits until all GDI drawing has been completed.
Swapping Buffers
For windows that are double-buffered, the front and back buffers can be
exchanged by calling SwapBuffers() or wglSwapLayerBuffers(); the latter
is used for overlays and underlays.

WGL: OpenGL Extension for Microsoft Windows 95/98/NT/ME/2000/XP 827
Finding a Color Palette
To access the color palette for the standard (nonlayer) bitplanes, use the
standard GDI functions to set the palette entries. For overlay or underlay
layers, use wglRealizeLayerPalette(), which maps palette entries from
a given color-index layer plane into the physical palette or initializes
the palette of an RGBA layer plane. wglGetLayerPaletteEntries() and
wglSetLayerPaletteEntries() are used to query and set the entries in
palettes of layer planes.
Using a Bitmap or Outline Font
WGL has two routines, wglUseFontBitmaps() and wglUseFontOutlines(),
for converting system fonts for use with OpenGL. Both routines build a dis-
play list for each requested character from the specified font and font size.
WGL Prototypes
Initialization
Determine version information:
BOOL GetVersion( LPOSVERSIONINFO lpVersionInformation );
BOOL GetVersionEx( LPOSVERSIONINFO lpVersionInformation );
Pixel format availability, selection, and capability:
int ChoosePixelFormat( HDC hdc,
CONST PIXELFORMATDESCRIPTOR * ppfd );
BOOL SetPixelFormat( HDC hdc, int iPixelFormat,
CONST PIXELFORMATDESCRIPTOR * ppfd );
int DescribePixelFormat( HDC hdc, int iPixelFormat, UINT nBytes,
LPPIXELFORMATDESCRIPTOR ppfd );
BOOL wglDescribeLayerPlane( HDC hdc, int iPixelFormat,
int iLayerPlane, UINT nBytes, LPLAYERPLANEDESCRIPTOR plpd );
Obtain a pointer to an OpenGL function:
PROC wglGetProcAddress(LPCSTR funcName);

828 Appendix D: OpenGL and Window Systems
Controlling Rendering
Manage or query an OpenGL rendering context:
HGLRC wglCreateContext( HDC hdc );
HGLRC wglCreateContextAttribsARB( HDC hdc,
HGLRC hShareContext, const int *attribList )
HGLRC wglCreateLayerContext( HDC hdc, int iLayerPlane );
BOOL wglShareLists( HGLRC hglrc1, HGLRC hglrc2 );
BOOL wglDeleteContext( HGLRC hglrc );
BOOL wglCopyContext( HGLRC hglrcSource, HGLRC hlglrcDest,
UINT mask );
BOOL wglMakeCurrent( HDC hdc, HGLRC hglrc );
HGLRC wglGetCurrentContext( VOID );
HDC wglGetCurrentDC( VOID );
Access implementation-dependent extension procedure calls:
PROC wglGetProcAddress( LPCSTR lpszProc );
Access and release the bitmap of the front buffer:
HBITMAP CreateDIBitmap( HDC hdc,
CONST BITMAPINFOHEADER *lpbmih, DWORD fdwInit,
CONST VOID *lpbInit, CONST BITMAPINFO *lpbmi,
UINT fuUsage );
HBITMAP CreateDIBSection( HDC hdc, CONST BITMAPINFO *pbmi,
UINT iUsage, VOID *ppvBits, HANDLE hSection,
DWORD dwOffset );
BOOL DeleteObject( HGDIOBJ hObject );
Exchange front and back buffers:
BOOL SwapBuffers( HDC hdc );
BOOL wglSwapLayerBuffers( HDC hdc, UINT fuPlanes );

WGL: OpenGL Extension for Microsoft Windows 95/98/NT/ME/2000/XP 829
Find a color palette for overlay or underlay layers:
int wglGetLayerPaletteEntries( HDC hdc, int iLayerPlane,
int iStart, int cEntries, CONST COLORREF *pcr );
int wglSetLayerPaletteEntries( HDC hdc, int iLayerPlane, int iStart
int cEntries, CONST COLORREF *pcr );
BOOL wglRealizeLayerPalette( HDC hdc, int iLayerPlane,
BOOL bRealize );
Use a bitmap or an outline font:
BOOL wglUseFontBitmaps( HDC hdc, DWORD first, DWORD count,
DWORD listBase );
BOOL wglUseFontOutlines( HDC hdc, DWORD first, DWORD count,
DWORD listBase, FLOAT deviation, FLOAT extrusion, int format,
LPGLYPHMETRICSFLOAT lpgmf );
This page intentionally left blank
831
Glossary
API
An abbreviation of “application-programming interface.”
accumulation buffer
Memory (bitplanes) that is used to accumulate a series of images gener-
ated in the color buffer. Using the accumulation buffer may significantly
improve the quality of the image, but also take correspondingly longer
to render. The accumulation buffer is used for effects such as depth of field,
motion blur, and full-scene antialiasing.
aliasing
A rendering technique that assigns to pixels the color of the primitive being
rendered, regardless of whether that primitive covers all or only a portion
of the pixel’s area. This results in jagged edges, or jaggies.
alpha
A fourth color component. The alpha component is never displayed
directly and is typically used to control color blending. By convention,
OpenGL alpha corresponds to the notion of opacity, rather than transpar-
ency, meaning that an alpha value of 1.0 implies complete opacity, and an
alpha value of 0.0 complete transparency.
ambient
Ambient light is nondirectional and distributed uniformly throughout
space. Ambient light falling upon a surface approaches from all directions.
The light is reflected from the object independent of surface location and
orientation, with equal intensity in all directions.

832 Glossary
animation
Generating repeated renderings of a scene, with smoothly changing view-
point and/or object positions, quickly enough so that the illusion of motion
is achieved. OpenGL animation is almost always done using double-
buffering.
antialiasing
A rendering technique that assigns pixel colors based on the fraction of the
pixel’s area that’s covered by the primitive being rendered. Antialiased
rendering reduces or eliminates the jaggies that result from aliased
rendering.
application-specific clipping
Clipping of primitives against planes in eye coordinates; the planes are
specified by the application using glClipPlane().
ARB Imaging Subset
The collection of OpenGL extensions for processing pixel rectangles.
Imaging Subset operations include color table lookups, color matrix
transformations, image convolutions, and image statistics.
attenuation
The property of light that describes how a light’s intensity diminishes over
distance.
attribute group
A set of related state variables, which OpenGL can save or restore together
at one time.
back faces
See faces.
bit
Binary digit. A state variable having only two possible values: 0 or 1. Binary
numbers are constructions of one or more bits.
bitmap
A rectangular array of bits. Also, the primitive rendered by the glBitmap()
command, which uses its bitmap parameter as a mask.

Glossary 833
bitplane
A rectangular array of bits mapped one-to-one with pixels. The framebuffer
is a stack of bitplanes.
blending
Reduction of two color components to one component, usually as a linear
interpolation between the two components.
buffer
A group of bitplanes that store a single component (such as depth or green)
or a single index (such as the color index or the stencil index). Sometimes
the red, green, blue, and alpha buffers together are referred to as the color
buffer, rather than the color buffers.
buffer object
A vertex array located in the GL’s server memory, as opposed to the client
application’s memory. Vertex data and indices stored in buffer objects may
render considerably faster than the equivalent client-side versions.
byte swapping
The process of exchanging the ordering of bytes in a (usually integer)
variable type (i.e., int,short, etc.)
C
God’s programming language.
C++
The object-oriented programming language of a pagan deity.
client
The computer from which OpenGL commands are issued. The computer
that issues OpenGL commands can be connected via a network to a differ-
ent computer that executes the commands, or commands can be issued and
executed on the same computer. See also server.
client memory
The main memory (where program variables are stored) of the client
computer.

834 Glossary
clip coordinates
The coordinate system that follows transformation by the projection matrix
and precedes perspective division. View-volume clipping is done in clip
coordinates, but application-specific clipping is not.
clipping
Elimination of the portion of a geometric primitive that’s outside the half-
space defined by a clipping plane. Points are simply rejected if outside. The
portion of a line or polygon that’s outside the half-space is eliminated, and
additional vertices are generated as necessary to complete the primitive
within the clipping half-space. Geometric primitives and the current raster
position (when specified) are always clipped against the six half-spaces
defined by the left, right, bottom, top, near, and far planes of the view vol-
ume. Applications can specify optional application-specific clipping planes
to be applied in eye coordinates.
color index
A single value that represents a color by name, rather than by value. OpenGL
color indices are treated as continuous values (for example, floating-point
numbers), while operations such as interpolation and dithering are per-
formed on them. Color indices stored in the framebuffer are always integer
values, however. Floating-point indices are converted to integers by round-
ing to the nearest integer value.
color-index mode
An OpenGL context is in color-index mode if its color buffers store color
indices, rather than red, green, blue, and alpha color components.
color-lookup table
A one-dimensional image used to substitute RGBA color components in an
image pixel.
color map
A table of index-to-RGB mappings that’s accessed by the display hardware.
Each color index is read from the color buffer, converted to an RGB triple
by lookup in the color map, and sent to the monitor.
color matrix
The 4 u4 matrix used to transform RGBA pixel values when passed into
the Imaging Subset. Color matrices are particularly useful in color space
conversions.

Glossary 835
components
Single, continuous (for example, floating-point) values that represent
intensities or quantities. Usually, a component value of zero represents the
minimum value or intensity, and a component value of one represents the
maximum value or intensity, although other ranges are sometimes used.
Because component values are interpreted in a normalized range, they
are specified independent of actual resolution. For example, the RGB
triple (1, 1, 1) is white, regardless of whether the color buffers store 4, 8,
or 12 bits each.
Out-of-range components are typically clamped to the normalized range,
not truncated or otherwise interpreted. For example, the RGB triple
(1.4, 1.5, 0.9) is clamped to (1.0, 1.0, 0.9) before it’s used to update the color
buffer. Red, green, blue, alpha, and depth are always treated as components,
never as indices.
concave
A polygon that is not convex. See convex.
context
A complete set of OpenGL state variables. Note that framebuffer contents are
not part of OpenGL state, but that the configuration of the framebuffer (and
any associated renderbuffers) is.
convex
A polygon is convex if no straight line in the plane of the polygon intersects
the polygon more than twice.
convex hull
The smallest convex region enclosing a specified group of points. In two
dimensions, the convex hull is found conceptually by stretching a rubber
band around the points so that all of the points lie within the band.
convolution filter
One- or two-dimensional images that are used for computing the weighted
average of pixel images.
convolution kernel
See convolution filter.

836 Glossary
coordinate system
In n-dimensional space, a set of n linearly independent vectors anchored to
a point (called the origin). A group of coordinates specifies a point in space
(or a vector from the origin) by indicating how far to travel along each
vector to reach the point (or tip of the vector).
culling
The process of eliminating a front face or back face of a polygon so that it
isn’t drawn.
current matrix
A matrix that transforms coordinates in one coordinate system to coordi-
nates of another system. There are three current matrices in OpenGL: The
modelview matrix transforms object coordinates (coordinates specified by
the programmer) to eye coordinates; the perspective matrix transforms eye
coordinates to clip coordinates; the texture matrix transforms specified or
generated texture coordinates as described by the matrix. Each current
matrix is the top element on a stack of matrices. Each of the three stacks can
be manipulated with OpenGL matrix-manipulation commands.
current raster position
A window coordinate position that specifies the placement of an image
primitive when it’s rasterized. The current raster position and other current
raster parameters are updated when glRasterPos() is called.
decal
A method of calculating color values during texture application, where the
texture colors replace the fragment colors or, if alpha blending is enabled,
the texture colors are blended with the fragment colors, using only the
alpha value.
deprecated
The identification of a function entry point, or feature exposed as a token
passed into a function call, that is slated for potential removal in future
versions of the API.
depreciation model
The plan used for the identification and potential removal of features from
the OpenGL library. The depreciation model was introduced with OpenGL
Version 3.0, and the first features were removed from the API in Version 3.1.

Glossary 837
depth
Generally refers to the z window coordinate.
depth buffer
Memory that stores the depth value at every pixel. To perform hidden-
surface removal, the depth buffer records the depth value of the object that
lies closest to the observer at every pixel. The depth value of every new
fragment uses the recorded value for depth comparison and must pass the
comparison test before being rendered.
depth-cuing
A rendering technique that assigns color based on distance from the
viewpoint.
diffuse
Diffuse lighting and reflection accounts for the direction of a light source.
The intensity of light striking a surface varies with the angle between the
orientation of the object and the direction of the light source. A diffuse
material scatters that light evenly in all directions.
directional light source
See infinite light source.
display list
A named list of OpenGL commands. Display lists are always stored on the
server, so display lists can be used to reduce network traffic in client-server
environments. The contents of a display list may be preprocessed and might
therefore execute more efficiently than the same set of OpenGL commands
executed in immediate mode. Such preprocessing is especially important
for computing intensive commands such as NURBS or polygon tessellation.
dithering
A technique for increasing the perceived range of colors in an image at the
cost of spatial resolution. Adjacent pixels are assigned differing color values;
when viewed from a distance, these colors seem to blend into a single
intermediate color. The technique is similar to the halftoning used in black-
and-white publications to achieve shades of gray.

838 Glossary
double-buffering
OpenGL contexts with both front and back color buffers are double-
buffered. Smooth animation is accomplished by rendering into only the
back buffer (which isn’t displayed), and then causing the front and back
buffers to be swapped. See glutSwapBuffers() in “Motion = Redraw + Swap”
in Chapter 1Appendix A.
edge flag
A Boolean value at a vertex that marks whether that vertex precedes a
boundary edge. glEdgeFlag*() may be used to mark an edge as not on the
boundary. When a polygon is drawn in GL_LINE mode, only boundary
edges are drawn.
element
A single component or index.
emission
The color of an object that is self-illuminating or self-radiating. The
intensity of an emissive material is not attributed to any external light
source.
evaluated
The OpenGL process of generating object-coordinate vertices and
parameters from previously specified Bézier equations.
execute
An OpenGL command is executed when it’s called in immediate mode or
when the display list that it’s a part of is called.
extension
A new feature of OpenGL that hasn’t been added into the core of OpenGL.
An extension does not have to be supported by every OpenGL implemen-
tation, as compared to core OpenGL functions, which are supported for
every OpenGL implementation. There are different types of extensions,
based upon how broadly supported the functionality is. Generally, exten-
sions supported only by a single company’s OpenGL implementation will
have a name that includes an abbreviation of the company name. If more
companies adopt the extension, its name will change from the abbreviation

Glossary 839
to a string that includes the letters, EXT; for example, GL_EXT_polygon_
offset. If OpenGL’s governing body, the Khronos OpenGL ARB Working
Group (or ARB, for short) reviews and approves the extension, its name will
change once again. For example, a reviewed extension that was approved
by the ARB is GL_ARB_multitexture.
eye coordinates
The coordinate system that follows transformation by the modelview
matrix and precedes transformation by the projection matrix. Lighting and
application-specific clipping are done in eye coordinates.
faces
The sides of a polygon. Each polygon has two faces: a front face and a back
face. Only one face or the other is ever visible in the window. Whether the
back or front face is visible is effectively determined after the polygon is
projected onto the window. After this projection, if the polygon’s edges are
directed clockwise, one of the faces is visible; if directed counterclockwise,
the other face is visible. Whether clockwise corresponds to front or back
(and counterclockwise corresponds to back or front) is determined by the
OpenGL programmer.
feedback
OpenGL’s mechanism for allowing an application to retrieve information
about which geometric and imaging primitives that would have rasterized
to the window. No pixels are updated in feedback mode.
filtering
The process of combining pixels or texels to obtain a higher or lower
resolution version of an input image or texture.
fixed-function pipeline
The processing model where the order of operations that OpenGL uses on
vertices and fragments is fixed by the implementation. A programmer’s
control over its operation is limited by setting state values and enabling or
disabling operations. See programmable graphics pipeline.
flat shading
Refers to a primitive colored with a single, constant color across its extent,
rather than smoothly interpolated colors across the primitive. See Gouraud
shading.

840 Glossary
fog
A rendering technique that can be used to simulate atmospheric effects such
as haze, fog, and smog by fading object colors to a background color based
on distance from the viewer. Fog also aids in the perception of distance from
the viewer, giving a depth cue.
fonts
Groups of graphical character representations generally used to display
strings of text. The characters may be roman letters, mathematical symbols,
Asian ideograms, Egyptian hieroglyphics, and so on.
fragment
Fragments are generated by the rasterization of primitives. Each fragment
corresponds to a single pixel and includes color, depth, and sometimes
texture-coordinate values.
framebuffer
All the buffers of a given window or context. Sometimes includes all the
pixel memory of the graphics hardware accelerator.
framebuffer attachment
A connection point in a framebuffer object that makes an association
between allocated image storage (which might be a texture map level, a
renderbuffer, pixel buffer object, or any of the other types of object storage
in OpenGL), and a rendering target, such as a color buffer, the depth buffer,
or the stencil buffer.
front faces
See faces.
frustum
The view volume warped by perspective division.
gamma correction
A function applied to colors stored in the framebuffer to correct for the
nonlinear response of the eye (and sometimes of the monitor) to linear
changes in color-intensity values.

Glossary 841
geometric model
The object-coordinate vertices and parameters that describe an object. Note
that OpenGL doesn’t define a syntax for geometric models, but rather a
syntax and semantics for the rendering of geometric models.
geometric object
See geometric model.
geometric primitive
A point, a line, or a polygon.
GLSL
The short name for The OpenGL Shading Language.
GLX
The window system interface for OpenGL on the X Window System.
GPU
The abbreviation for Graphics Processing Unit.
GPGPU
The short name for General-Purpose computing on GPUs, which is the field
of techniques attempting to do general computation (algorithms that you
would normally execute on a CPU) on graphics processors.
Gouraud shading
Smooth interpolation of colors across a polygon or line segment. Colors are
assigned at vertices and linearly interpolated across the primitive to produce
a relatively smooth variation in color. Also called smooth shading.
group
Each pixel of an image in client memory is represented by a group of one,
two, three, or four elements. Thus, in the context of a client memory image,
a group and a pixel are the same thing.
half-spaces
A plane divides space into two half-spaces.

842 Glossary
hidden-line removal
A technique to determine which portions of a wireframe object should be
visible. The lines that comprise the wireframe are considered to be edges of
opaque surfaces, which may obscure other edges that are farther away from
the viewer.
hidden-surface removal
A technique to determine which portions of an opaque, shaded object
should be visible and which portions should be obscured. A test of the
depth coordinate, using the depth buffer for storage, is a common method
of hidden-surface removal.
histogram
A database of the distribution of pixel values in an image. The results of the
histogram process are counts of unique pixel values.
homogeneous coordinates
A set of n+1 coordinates used to represent points in n-dimensional
projective space. Points in projective space can be thought of as points in
Euclidean space together with some points at infinity. The coordinates are
homogeneous because a scaling of each of the coordinates by the same
nonzero constant doesn’t alter the point that the coordinates refer to.
Homogeneous coordinates are useful in the calculations of projective
geometry, and thus in computer graphics, where scenes must be projected
onto a window.
image
A rectangular array of pixels, either in client memory or in the framebuffer.
image primitive
A bitmap or an image.
immediate mode
Execution of OpenGL commands when they’re called, rather than from a
display list. No immediate-mode bit exists; the mode in immediate mode
refers to use of OpenGL, rather than to a specific bit of OpenGL state.

Glossary 843
index
A single value that’s interpreted as an absolute value rather than as a nor-
malized value in a specified range (as is a component). Color indices are the
names of colors, which are dereferenced by the display hardware using the
color map. Indices are typically masked, rather than clamped when out of
range. For example, the index 0xf7 is masked to 0x7 when written to a 4-bit
buffer (color or stencil). Color indices and stencil indices are always treated
as indices, never as components.
indices
Preferred plural of index. (The choice between the plural forms indices or
indexes—as well as matrices or matrixes and vertices or vertexes—has
engendered much debate between the authors and principal reviewers of
this guide. The authors’ compromise solution is to use the -ices form, but to
state clearly for the record that the use of indice [sic], matrice [sic], and
vertice [sic] for the singular forms is an abomination.)
infinite light source
A directional source of illumination. The radiating light from an infinite
light source strikes all objects as parallel rays.
instance id
A identifier available in vertex shaders for identifying a unique group of
primitives. In GLSL, the instance id is provided in the monotonically
increasing variable gl_InstanceID.
instanced rendering
Drawing multiple copies of the same set of geometry, varying a unique
identifier for each copy of the geometry. See instance id.
interleaved
A method of storing vertex arrays whereby heterogeneous types of data (i.e.,
vertex, normals, texture coordinates, etc.) are grouped together for faster
retrieval.
interpolation
Calculation of values (such as color or depth) for interior pixels, given the
values at the boundaries (such as at the vertices of a polygon or a line).

844 Glossary
IRIS GL
Silicon Graphics’ proprietary graphics library, developed from 1982
through 1992. OpenGL was designed with IRIS GL as a starting point.
jaggies
Artifacts of aliased rendering. The edges of primitives that are rendered with
aliasing are jagged, rather than smooth. A near-horizontal aliased line, for
example, is rendered as a set of horizontal lines on adjacent pixel rows,
rather than as a smooth, continuous line.
jittering
A pseudo-random displacement (shaking) of the objects in a scene, used in
conjunction with the accumulation buffer to achieve special effects.
kernel
See convolution kernel.
level of detail
The process of creating multiple copies of an object or image with different
levels of resolution. See also mipmap.
lighting
The process of computing the color of a vertex based on current lights,
material properties, and lighting-model modes.
line
A straight region of finite width between two vertices. (Unlike
mathematical lines, OpenGL lines have finite width and length.) Each
segment of a strip of lines is itself a line.
local light source
A source of illumination that has an exact position. The radiating light from
a local light source emanates from that position. Other names for a local
light source are point light source or positional light source. A spotlight is a
special kind of local light source.
local viewer mode
An OpenGL light model mode that accurately computes the vector from a
vertex to the eye. For performance reasons, local viewer mode is not enabled,
and an approximation to the real vector is used for lighting computations.

Glossary 845
logical operation
Boolean mathematical operations between the incoming fragment’s RGBA
color or color-index values and the RGBA color or color-index values
already stored at the corresponding location in the framebuffer. Examples
of logical operations include AND, OR, XOR, NAND, and INVERT.
luminance
The perceived brightness of a surface. Often refers to a weighted average of
red, green, and blue color values that indicates the perceived brightness of
the combination.
material
A surface property used in computing the illumination of a surface.
matrices
Preferred plural of matrix. See indices.
matrix
A two-dimensional array of values. OpenGL matrices are all 4 u4, though
when stored in client memory they’re treated as 1 u16 single-dimension
arrays.
minmax
The process of computing the minimum and maximum pixel values in an
image using the Imaging Subset.
mipmap
A reduced resolution version of a texture map, used to texture a geometric
primitive whose screen resolution differs from the resolution of the source
texture map.
modelview matrix
The 4 u4 matrix that transforms points, lines, polygons, and raster
positions from object coordinates to eye coordinates.
modulate
A method of calculating color values during texture application whereby
the texture and the fragment colors are combined.

846 Glossary
monitor
The device that displays the image in the framebuffer.
motion blurring
A technique that uses the accumulation buffer to simulate what appears on
film when you take a picture of a moving object or when you move the
camera while taking a picture of a stationary object. In animations without
motion blur, moving objects can appear jerky.
multitexturing
The process of applying several texture images to a single primitive. The
images are applied one after another, in a pipeline of texturing operations.
network
A connection between two or more computers that enables each to transfer
data to and from the others.
nonconvex
A polygon is nonconvex if a line exists in the plane of the polygon that
intersects the polygon more than twice.
normal
A three-component plane equation that defines the angular orientation,
but not position, of a plane or surface.
normal vectors
See normal.
normalized
To normalize a normal vector, divide each of the components by the square
root of the sum of their squares. Then, if the normal is thought of as a vector
from the origin to the point (nx’, ny’, nz’), this vector has unit length.
factor = sqrt(nx2 + ny2 + nz2)
nx’ = nx / factor
ny’ = ny / factor
nz’ = nz / factor

Glossary 847
NURBS
Non-Uniform Rational B-Spline. A common way to specify parametric
curves and surfaces. (See GLU NURBS routines in Chapter 12.)
object
An object-coordinate model that’s rendered as a collection of primitives.
object coordinates
Coordinate system prior to any OpenGL transformation.
off-screen rendering
The process of drawing into a framebuffer that is not directly displayed to
the visible screen.
The OpenGL Shading Language
The language used for authoring shader program. Also commonly known as
the GLSL.
orthographic
Nonperspective (or parallel) projection, as in some engineering drawings,
with no foreshortening.
outer product
A process that produces a matrix from two vectors. For the matrix A, which
is the outer product of the vectors u and v,Aij = uivj.
pack
The process of converting pixel colors from a buffer into the format
requested by the application.
parameters
Values passed as arguments to OpenGL commands. Sometimes parameters
are passed by reference to an OpenGL command.
perspective correction
An additional calculation for texture coordinates to fix texturing artifacts
for a textured geometric rendered in a perspective projection.
perspective division
The division of x,y, and z by w, carried out in clip coordinates.

848 Glossary
picking
A form of selection that uses a rectangular region (usually near the cursor
location) to determine which primitives to select.
ping-pong buffers
AGPGPU technique of writing values to a buffer (usually a texture map) that
is immediately rebound as a texture map to be read from to do a subsequent
computation. Effectively, you can consider the buffer written-to, and
subsequently read-from as being a collection of temporary values. Ping-
ponging buffers is usually done using framebuffer objects.
pixel
Picture element. The bits at location (x, y) of all the bitplanes in the frame-
buffer constitute the single pixel (x, y). In an image in client memory, a pixel
is one group of elements. In OpenGL window coordinates, each pixel cor-
responds to a 1.0 u1.0 screen area. The coordinates of the lower left corner
of the pixel are (x, y), and of the upper right corner are (x + 1, y+ 1).
point
An exact location in space, which is rendered as a finite-diameter dot.
point light source
See local light source.
polygon
A near-planar surface bounded by edges specified by vertices. Each triangle
of a triangle mesh is a polygon, as is each quadrilateral of a quadrilateral
mesh. The rectangle specified by glRect*() is also a polygon.
polygon offset
A technique to modify depth-buffer values of a polygon when additional
geometric primitives are drawn with identical geometric coordinates.
positional light source
See local light source.
primitive
A point, a line, a polygon, a bitmap, or an image. (Note: Not just a point, a
line, or a polygon!)

Glossary 849
projection matrix
The 4 u4 matrix that transforms points, lines, polygons, and raster
positions from eye coordinates to clip coordinates.
proxy texture
A placeholder for a texture image, which is used to determine if there are
enough resources to support a texture image of a given size and internal
format resolution.
programmable graphics pipeline
The mode of operation where the processing of vertices,fragments, and their
associated data (texture coordinates, for example) is under the control of
shader programs specified by the programmer.
quadrilateral
A polygon with four edges.
rasterization
Converts a projected point, line, or polygon, or the pixels of a bitmap or
image, to fragments, each corresponding to a pixel in the framebuffer. Note
that all primitives are rasterized, not just points, lines, and polygons.
rectangle
A quadrilateral whose alternate edges are parallel to each other in object
coordinates. Polygons specified with glRect*() are always rectangles; other
quadrilaterals might be rectangles.
rendering
Conversion of primitives specified in object coordinates to an image in the
framebuffer. Rendering is the primary operation of OpenGL—it’s what
OpenGL does.
render-to-texture
A technique where the storage for a texture map is used as a destination for
rendering (i.e., a renderbuffer). Render-to-texture enables a more efficient
method for updating texture maps than rendering into the color buffer, and
copy the results into texture memory, saving the copy operation.

850 Glossary
renderbuffer
An allocation of memory in the OpenGL server for the storage of pixel
values. Renderbuffers are used as a destination for rendering, as well as able
to be as texture maps without requiring a copy of the renderbuffer’s data.
resident texture
A texture image that is cached in special, high-performance texture mem-
ory. If an OpenGL implementation does not have special, high-performance
texture memory, then all texture images are deemed resident textures.
RGBA
Red, green, blue, alpha.
RGBA mode
An OpenGL context is in RGBA mode if its color buffers store red, green,
blue, and alpha color components, rather than color indices.
scissoring
A fragment clipping test. Fragments outside of a rectangular scissor region
are rejected.
selection
The process of determining which primitives intersect a 2D region or 3D
volume defined by matrix transformations.
separable filter
A form of 2D convolution filter that can be represented by two 1D vectors.
The 2D separable filter is determined by computing the outer product of the
two vectors.
server
The computer on which OpenGL commands are executed. This might differ
from the computer from which commands are issued. See client.
shader program
A set of instructions written in a graphics shading language (The OpenGL
Shading Language, also called GLSL) that control the processing of graphics
primitives.

Glossary 851
shading
The process of interpolating color within the interior of a polygon, or
between the vertices of a line, during rasterization.
shininess
The exponent associated with specular reflection and lighting. Shininess
controls the degree with which the specular highlight decays.
single-buffering
OpenGL contexts that don’t have back color buffers are single-buffered. You
can use these contexts for animation, but take care to avoid visually
disturbing flashes when rendering.
singular matrix
A matrix that has no inverse. Geometrically, such a matrix represents a
transformation that collapses points along at least one line to a single point.
smooth shading
See Gouraud shading.
specular
Specular lighting and reflection incorporates reflection off shiny objects
and the position of the viewer. Maximum specular reflectance occurs when
the angle between the viewer and the direction of the reflected light is zero.
A specular material scatters light with greatest intensity in the direction of
the reflection, and its brightness decays, based upon the exponential value
shininess.
spotlight
A special type of local light source that has a direction (where it points to)
as well as a position. A spotlight simulates a cone of light, which may have
a fall-off in intensity, based upon distance from the center of the cone.
sprite
A screen-aligned graphics primitive. Sprites are usually represented as
either a single vertex that is expanded to cover many pixels around the
transformed vertex, or as a quadrilateral its vertices specified so that it is
perpendicular to the viewing direction (or put another way, parallel to the
image plane).

852 Glossary
sRGB color space
An RGB color space standard specified by the International Electrotechnical
Commission (IEC) that matches the color intensity outputs of monitors
and printers better than a linear RGB space. The sRGB approximately
corresponds to gamma correcting RGB (but not alpha) values using a
gamma value of 2.2. See IEC standard 61966-2-1 for all of the gory details.
stencil buffer
Memory (bitplanes) that is used for additional per-fragment testing, along
with the depth buffer. The stencil test may be used for masking regions,
capping solid geometry, and overlapping translucent polygons.
stereo
Enhanced three-dimensional perception of a rendered image by computing
separate images for each eye. Stereo requires special hardware, such as two
synchronized monitors or special glasses, to alternate viewed frames for
each eye. Some implementations of OpenGL support stereo by including
both left and right buffers for color data.
stipple
A one- or two-dimensional binary pattern that defeats the generation of
fragments where its value is zero. Line stipples are one-dimensional and are
applied relative to the start of a line. Polygon stipples are two-dimensional
and are applied with a fixed orientation to the window.
tessellation
Reduction of a portion of an analytic surface to a mesh of polygons, or of a
portion of an analytic curve to a sequence of lines.
texel
A texture element. A texel is obtained from texture memory and represents
the color of the texture to be applied to a corresponding fragment.
texture mapping
The process of applying an image (the texture) to a primitive. Texture
mapping is often used to add realism to a scene. For example, you can apply
a picture of a building facade to a polygon representing a wall.
texture matrix
The 4 u4 matrix that transforms texture coordinates from the coordinates
in which they’re specified to the coordinates that are used for interpolation
and texture lookup.

Glossary 853
texture object
A named cache that stores texture data, such as the image array, associated
mipmaps, and associated texture parameter values: width, height, border
width, internal format, resolution of components, minification and
magnification filters, wrapping modes, border color, and texture priority.
textures
One- or two-dimensional images that are used to modify the color of
fragments produced by rasterization.
texture unit
When multitexturing, as part of an overall multiple pass application of tex-
ture images, a texture unit controls one processing step for a single texture
image. A texture unit maintains the texturing state for one texturing pass,
including the texture image, filter, environment, coordinate generation,
and matrix stack. Multitexturing consists of a chain of texture units.
transformations
The warping of spaces. In OpenGL, transformations are limited to projec-
tive transformations that include anything that can be represented by a
4u4 matrix. Such transformations include rotations, translations, (non-
uniform) scalings along the coordinate axes, perspective transformations,
and combinations of these.
triangle
A polygon with three edges. Triangles are always convex.
uniform variable
A type of variable used in vertex or fragment shaders that doesn’t change its
value across a set of primitives (either a single primitive, or the collection of
primitives specified by a single draw call).
uniform buffer object
A type of buffer object that encapsulates a set of uniform variables, making
access and update of that collection of uniform variables much faster with
less function call overhead.
unpack
The process of converting pixels supplied by an application to OpenGL’s
internal format.

854 Glossary
vertex
A point in three-dimensional space.
vertex array
A block of vertex data (vertex coordinates, texture coordinates, surface
normals, RGBA colors, color indices, and edge flags) may be stored in an
array and then used to specify multiple geometric primitives through the
execution of a single OpenGL command.
vertices
Preferred plural of vertex. See indices.
viewpoint
The origin of either the eye- or the clip-coordinate system, depending on
context. (For example, when discussing lighting, the viewpoint is the origin
of the eye-coordinate system. When discussing projection, the viewpoint is
the origin of the clip-coordinate system.) With a typical projection matrix,
the eye-coordinate and clip-coordinate origins are at the same location.
view volume
The volume in clip coordinates whose coordinates satisfy the following
three conditions:
wd x d w
wd y d w
wd z d w
Geometric primitives that extend outside this volume are clipped.
VRML
VRML stands for Virtual Reality Modeling Language, which is (according to
the VRML Mission Statement) “a universal description language for multi-
participant simulations.” VRML is specifically designed to allow people to
navigate through three-dimensional worlds that are placed on the World
Wide Web. The first versions of VRML are subsets of the Open Inventor
file format with additions to allow hyperlinking to the Web (to URLs—
Universal Resource Locators).
window
A subregion of the framebuffer, usually rectangular, whose pixels all have
the same buffer configuration. An OpenGL context renders to a single
window at a time.

Glossary 855
window-aligned
When referring to line segments or polygon edges, implies that these are
parallel to the window boundaries. (In OpenGL, the window is rectangular,
with horizontal and vertical edges.) When referring to a polygon pattern,
implies that the pattern is fixed relative to the window origin.
window coordinates
The coordinate system of a window. It’s important to distinguish between
the names of pixels, which are discrete, and the window-coordinate
system, which is continuous. For example, the pixel at the lower left corner
of a window is pixel (0, 0); the window coordinates of the center of this
pixel are (0.5, 0.5, z). Note that window coordinates include a depth, or z,
component, and that this component is continuous as well.
wireframe
A representation of an object that contains line segments only. Typically,
the line segments indicate polygon edges.
working set
On machines with special hardware that increases texture performance, this
is the group of texture objects that are currently resident. The performance
of textures within the working set outperforms the textures outside the
working set.
X Window System
A window system used by many of the machines on which OpenGL is
implemented. GLX is the name of the OpenGL extension to the X Window
System. (See Appendix D.)
This page intentionally left blank

857
Index
Numbers
3D Computer Graphics, 390
A
accumulation buffer, 492, 494, 519–525
clearing, 36, 495
depth-of-field effect, use for, 521–525
examples of use, 519
motion blur, use for, 520
sample program with depth-of-field effect,
522
AGL, 15
aglChoosePixelFormat(), 820, 822
aglConfigure(), 824
aglCopyContext(), 820, 823
aglCreateContext(), 820, 823
aglDescribePixelFormat(), 822
aglDescribeRenderer(), 823
aglDestroyContext(), 820, 823
aglDestroyPixelFormat(), 822
aglDestroyRendererInfo(), 823
aglDevicesOfPixelFormat(), 822
aglDisable(), 824
aglEnable(), 824
aglErrorString(), 824
aglGetCurrentContext(), 820, 823
aglGetDrawable(), 820, 823
aglGetError(), 824
aglGetInteger(), 824
aglGetVersion(), 820, 822
aglGetVirtualScreen(), 823
aglIsEnabled(), 824
aglNextPixelFormat(), 822
aglNextRendererInfo(), 823
aglQueryRendererInfo(), 823
aglResetLibrary(), 824
aglSetCurrentContext(), 820, 823
aglSetDrawable(), 820, 821, 823
aglSetFullScreen(), 821, 823
aglSetInteger(), 821, 824
aglSetOffScreen(), 821, 823
aglSetVirtualScreen(), 823
aglSwapBuffers(), 821, 824
aglUpdateContext(), 821, 823
aglUseFont(), 824
airbrushing, 666
Akeley, Kurt, 519
aliasing, see antialiasing
alpha, 251
destination alpha, 280
material properties, 233
multisampling coverage, 279
texture image data type, 445
alpha blending, see blending
alpha test, 503
querying current values, 503
rendering pipeline stage, 14
ambient
contribution to lighting equation, 243
global light, 228, 242
light, 207, 208, 216
material properties, 209, 233
animation, 22–25
antialiasing, 267–280
accumulation buffer used for, 520–??
characters (by masking), 650
characters (by texturing), 661
color-index mode, 272
coverage values, 267
enabling for points or lines, 269
enabling for polygons, 280
lines, 267, 269–275

858 Index
antialiasing, continued
lines (by texturing), 661
points, 269–275, 653
polygons, 280
RGBA mode, 270
sample program in color-index mode, 272
sample program in RGBA mode, 270
Apple Interface to OpenGL, see AGL
ARB imaging subset, 367–388
architectural applications
orthographic parallel projection, use of,
156
arcs, 559
array elements, see vertex arrays
aspect ratio
perspective projection, 155
viewport transformation, 159
atmospheric effects, see fog
attenuation of light, 217–218
attribute groups, 110–112
client, 110
list of, 743–800
multitexturing, with, 470
server, 110
stack depth, obtaining, 111
stacks, 110
auxiliary buffers, 493, 498
B
back-facing polygons, 61
culling, 62
material property, specifying, 232
two-sided lighting, 229
background, 34–37
color, 34
drawing a fixed, 500, 662
background processing, 736
backward compatibility
tessellation, 558
basis functions, 571, 572
Bernstein
basis, 571
polynomial, 575
Bézier
basis, 571, 572
curve, 575
sample program using mesh for surface,
582
sample program which draws curve, 573
sample program which draws surface, 580
BGR and BGRA pixel formats, 336
billboarding, 259, 504
bitmaps, 322–329
display lists cache bitmap data, 303
distorting, 648
drawing, 327
feedback mode, 629
fonts, used for, 324, 331
imaging pipeline operations, 344
ordering of data in, 325
origin of, 328
sample program, 324
sample program that creates a font, 331
size of, 325
bitplanes, 190, 490
displayable colors, number of, 192
blending, 251–264, 516
antialiasing polygons, 280
controlling blending on a per-buffer basis,
516
coverage calculations for antialiasing, 267
destination alpha, 280
differences among releases, 250
enabling, 255
enabling for antialiasing, 269
equation, 255
factors (source and destination), 252
images, 653
ordering polygons before drawing, 263

Index 859
rendering pipeline stage, 14
sample program for three-dimensional, 264
sample program with blended polygons,
261
texture function, 448
three dimensions, in, 263
uses of, 258
buffer object, 833
buffer objects
binding, 93
creating, 92
deleting, 102
flushing a mapped buffer range, 100
initializing with data, 94
mapping a buffer, 97, 98
partial copy, 101
replacing data, 96
unmapping a buffer, 97
buffer, see framebuffer
C
C programming language, 8
CAD/CAM, see computer-aided design
camera analogy, 126–127
environment mapping, 463
viewport transformations, 158
capping, see computational solid geometry
characters
antialiasing, 661
circles, 559
clearing buffers, 36
clearing the color buffer, 35
clearing the framebuffer, 34–37, 495–496
affected by scissoring, dithering, and
masking, 496
client-server, see networked operation
clip coordinates, 128, 170
feedback mode, 629
clip planes
user defined, 169
clipping, 158
interference regions found using clipping
planes, 657
overview, 125
primitives in rendering pipeline, 12
viewing volume, 153
clipping planes
additional clipping planes, 128, 168–172
far, 154–156, 162
near, 154–156, 162
querying number of additional, 170
sample program with additional clipping
planes, 170
color
alpha values, 251
background, 34
cube showing blended RGB values, 189
current raster color, 329
human perception, 187
RGBA values for, 38, 188
specifying, 37
specifying for tessellation, 548
specifying in color-index mode, 199
specifying in RGBA mode, 197
color buffer, 188, 190, 491, 492, 493
clearing, 36
masking, 499
color map, 188, 193
loading for antialiasing, 272
loading for smooth shading, 202
loading, using GLUT, 735
size of, 194
color matrix, 382–383
example, 382
post transform scale and bias, 383
sample program, 382
color sum mode, 478

860 Index
color tables, 369–371
proxies, 374
replacing part of, 373
sample program, 371
specifying, 369
color-index mode, 193–195
changing between RGBA mode
and, 196
choosing between RGBA mode and, 195
coverage calculations for
antialiasing, 267
dithering, 517
layering with writemasks, 500
lighting, 246–247
lighting calculations in, 247
texturing limitations, 396, 404
vertex arrays, specifying values with, 74
combiner functions, 472–478
command syntax, 7–9
compositing images, 259
compositing transformations, 172–179
computational solid geometry
capping, 509
difference of several contours, 553
interference regions, 656
intersection of two contours, 553
union of several contours, 553
Computer Graphics: Principles and Practice, xl,
187, 191, 803
computer-aided design
orthographic parallel projection, use of,
156
concave polygons
GLU tessellation, 542
stencil buffer, drawing with the, 655
cones, 559, 736
improving rendering of, 664
constant attenuation, 218
contours, 458
control points, 570, 574, 578, 587
convex polygons, 43
convolutions, 374–382
1d filters, 380
2d filters, 374
border modes, 381
post convolution scale and bias, 382
sample program, 376
separable filters, 378
Conway, John, 664
coordinate systems
grand, fixed, 139, 148, 172
local, 139, 148, 172, 176
simple 2D, 40–41
coordinates
see clip coordinates, depth coordinates, eye
coordinates, homogeneous
coordinates, normalized device
coordinates, object coordinates, q
texture coordinates, texture
coordinates, w coordinates, or window
coordinates
coverage, pixel, 267
Coxeter, H. S. M., 803
cross product, 151
CSG, see computational solid geometry
cube maps, 465
culling, 61–62
enabling, 62
rendering pipeline stage, 12
selection mode, 610
curves and curved surfaces, 45
also see evaluators or NURBS
Curves and Surfaces for Computer-Aided
Geometric Design, 571
cylinders, 559
D
data types
RGBA color conversion, 197
special OpenGL, 8
texture data, 403

Index 861
decals, 503, 654
polygon offset used for, 294
texture function, 447
deprecation mechanism, 27
depth buffer, 206, 492, 494
also see hidden-surface removal
background, using masking for a common,
500
blending, use for three-dimensional, 263
clearing, 36, 206, 495
decals, for, 654
Dirichlet domains, for, 663
drawing static backgrounds, 662
masking, 499
pixel data, 342, 353
depth coordinates, 129, 161
perspective division, 161
picking use, 621
polygon offset, 293–296
rendering pipeline stage for depth-range
operations, 12
sample program with picking, 621
selection hit records, 610
depth test, 510
also see depth buffer
rendering pipeline stage, 14
depth-cuing, see fog
depth-of-field effect, 521–525
sample program, 522
destination factor, see blending
determing object coordinates from window
coordinates, 180, 182
diffuse
contribution to lighting
equation, 243
light, 208, 216
material properties, 209, 233
directional light source, 217
Dirichlet domains, 663
disks, 559
display lists, 33, 299
changing mode settings, 319
compiling, 307
creating, 305
deleting, 311
disadvantages, 304, 310
error handling, 306
executing, 305, 310
executing multiple, 312
font creation, 313, 329
hierarchical, 310
immediate mode, mixing with, 310
indices for, obtaining, 306
naming, 306
nesting, 310
nesting limit, querying, 310
networked operation, 309
querying use of an index, 311
rendering pipeline stage, 11
sample program creating a font, 314
sample program for creating, 299, 305
sharing among rendering contexts, 814, 826
state variables saved and restored, 319
tessellation, use with, 557
uses for, 303, 319
vertex-array data, 309
what can be stored in, 308
distorted images, 647
texture images, 451
dithering, 192–193, 516
and clearing, 496
rendering pipeline stage, 14
dot product
lighting calculations, use in, 243
texture combiner function, 475
double-buffering, 23–25
automatic glFlush(), 39
changing between single-buffering and, 196
object selection using the back buffer, 646
querying its presence, 494

862 Index
drawing
clearing the window, 34
forcing completion of, 38
icosahedron, 115
points, 48
polygons, 48, 61
preparing for, 34
rectangles, 45
spheres, cylinders, and disks, 559–567
drawing pixel data, see pixel data
Duff, Tom, 259
E
edge flags, 67–68
tessellated polygons generate, 546
vertex arrays, specifying values with, 74
emission, 208, 234, 241
enabling
alpha test, 502
antialiasing of points or lines, 269
antialiasing polygons, 280
blending, 255
color material properties mode, 237
color sum mode, 478
culling, 62
depth test, 510
dithering, 193, 517
evaluators, 575, 579
fog, 281
lighting, 231
line stippling, 57
logical operations, 517
multisampling, 276
normal vectors for evaluated surfaces,
automatic generation of, 579, 587
polygon offset, 294
polygon stippling, 63
rescaling normals, 70, 212
stencil test, 504
texture coordinate generation, 462
texturing, 396, 399
unit length normal vectors ensured, 70,
212
endianness, 349
environment mapping, 463, 465
errata, xlii
error handling, 637–639
error string description, 639
evaluators, 572–586
basis functions, 571, 575
evenly spaced values, 577, 581
one-dimensional, 572
rendering pipeline stage, 11
sample program using mesh for 2D Bézier
surface, 582
sample program which draws 1D Bézier
curve, 573
sample program which draws 2D Bézier
surface, 580
sample program which generates texture
coordinates, 584
texture coordinates, generating, 584
two-dimensional, 580
event management, using GLUT, 21
extensions
Microsoft Windows and
wglGetProcAddress(), 643
vendor-specific, 641
eye coordinates, 128, 170
texture coordinate generation, 458, 462
F
fade effect, 645
Farin, Gerald E., 571
feedback, 627–634
array contents, 633
pass-through markers, 630
querying current rendering mode, 608
returned data, 629

Index 863
sample program, 631
steps to perform, 628
tessellation, obtaining vertex data after, 557
Feiner, Steven K., xl, 803
field of view, 132
calculate, using trigonometry to, 163
filtering, 434–436
mipmapped textures, 424–429, 436
texture border colors, 452
flat shading, 200
flight simulation
fog, use of, 281
flushing, 38
fog, 280–291
blending factors, 284
color-index mode, 285
density, 285
enabling, 281
equations, 284
fog coordinates, 288
hints, 281
RGBA mode, 285
sample program in color-index mode, 286
sample program in RGBA mode, 281
sample program with fog coordinates, 289
Foley, James D., xl, 187, 191, 803
fonts, 329–332
antialiased characters (by masking), 650
antialiased characters (by texturing), 661
bitmapped, 331
creating with display lists, 313
drawing, 328
drawing as bitmaps, 324
multi-byte, 330
same program, 331
sample program using multiple display
lists, 314
X fonts, using, 816
Foran, Jim, 482
foreshortening, perspective, 153
fragments, 14, 490
alpha test, 503
blending, 251
depth test, 510
rendering pipeline operations, 14
scissor test, 502
tests, 501–518
texture functions, 446
framebuffer, 190, 491
capacity per pixel, 492
clearing, 495–496
copying pixel data within, 333, 342, 344
enabling for reading, 497
enabling for writing, 497
minimum configuration with the X
Window System, 492
querying color resolution, 190
reading pixel data from, 333, 335
writing pixel data to, 333, 341
framebuffer objects, 13
freeglut, xli, 15
front-facing polygons, 61
specifying material property for, 232
two-sided lighting, 229
frustum, 153
ftp (file-transfer protocol) site
GLX specification, 813
Fundamentals of Computer Aided Geometric
Design, 571
G
Game of Life, 664
gamma correction, 191
Gardner, Martin, 664
geometric primitives, 42–53
rendering pipeline stage, 12
geosciences
use of texturing in applications, 458

864 Index
giraffe, 194
GL_VERTEX_PROGRAM_POINT_SIZE, 721
GL_VERTEX_PROGRAM_TWO_SIDE, 722
glAccum(), 519
glActiveTexture(), 469
glAlphaFunc(), 503
glAreTexturesResident(), 442
glArrayElement(), 77
legal between glBegin() and glEnd(), 52
Glassner, Andrew S., xl
glAttachShader(), 677
glBegin(), 47, 48, 546
restrictions, 51
glBeginConditionalRender(), 515
glBeginQuery(), 513
glBeginTransformFeedback(), 724
glBindAttribLocation(), 718
glBindBuffer(), 93
glBindBufferBase(), 696
glBindBufferRange(), 696
glBindFragDataLocation(), 730
glBindFramebuffer(), 528
glBindRenderbuffer(), 530
glBindTexture(), 399, 439
multitexturing, 469
glBindVertexArray()
vertex array objects, 105
glBitmap(), 324, 327, 816
feedback mode, 629
fonts, used for, 331
imaging pipeline operations, 344
pixel-storage modes effect, 347
glBlendColor*(), 254
glBlendEquation(), 255
glBlendEquationSeparate(), 255
glBlendFunc(), 253
glBlendFuncSeparate(), 253
glBlitFramebuffer(), 540
glBufferData(), 94
glBufferSubData(), 96
glCallList(), 302, 305, 310
legal between glBegin() and glEnd(), 52
glCallLists(), 312
fonts, use for, 329
legal between glBegin() and glEnd(), 52
sample program, 331
glCheckFramebufferStatus(), 538
glClampColor(), 198
glClear(), 35, 36, 496
depth buffer, clearing the, 206
glClearAccum(), 36, 495
glClearBuffer*(), 496
glClearBufferfi(), 497
glClearColor(), 35, 36, 495
glClearDepth(), 35, 495
glClearIndex(), 36, 199, 495
fog, use with, 286
glClearStencil(), 36, 495
glClientActiveTexture(), 472
glClipPlane(), 169
glColor*(), 38, 197
legal between glBegin() and glEnd(), 51
glColorMask(), 496, 499
glColorMaski(), 499
glColorMaterial(), 237
glColorPointer(), 74
glColorSubTable(), 373
glColorTable(), 369
glColorTableParameter(), 371
glCompileShader(), 676
glCompressedTexImage1D(), 421
glCompressedTexImage2D(), 421
glCompressedTexImage3D(), 421
glCompressedTexSubImage1D(), 422
glCompressedTexSubImage2D(), 422
glCompressedTexSubImage3D(), 422
glConvolutionFilter1D(), 380
glConvolutionFilter2D(), 375

Index 865
glConvolutionParameter*(), 381
glCopyBufferSubData(), 101
glCopyColorSubTable(), 373
glCopyColorTable(), 372
glCopyConvolutionFilter1D(), 380
glCopyConvolutionFilter2D(), 378
glCopyPixels(), 333, 342
alternative uses, 665
feedback mode, 629
glReadBuffer() effect, 499
imaging pipeline operations, 344
pixel-transfer modes effect, 352
glCopyTexImage1D(), 413
glReadBuffer() effect, 499
pixel-transfer modes effect, 352
glCopyTexImage2D(), 405
glReadBuffer() effect, 499
pixel-transfer modes effect, 352
glCopyTexSubImage1D(), 414
glReadBuffer() effect, 499
pixel-transfer modes effect, 352
glCopyTexSubImage2D(), 411
glReadBuffer() effect, 499
pixel-transfer modes effect, 352
glCopyTexSubImage3D(), 417
pixel-transfer modes effect, 352
glCreateProgram(), 676
glCreateShader(), 675
glCullFace(), 62
glDeleteBuffers(), 102
glDeleteFramebuffers(), 528
glDeleteLists(), 312, 330
glDeleteProgram(), 680
glDeleteQueries(), 514
glDeleteRenderbuffers(), 529
glDeleteShader(), 680
glDeleteTextures(), 442
glDeleteVertexArrays(), 109
glDepthFunc(), 510
glDepthMask(), 499
blending opaque and translucent objects,
264
glDepthRange(), 161
gluUnProject(), relationship to, 180
glWindowPos*() effect, 326
glDetachShader(), 677
glDisable(), 10, 54
glDisableClientState(), 73
glDisablei(), 516
glDisableVertexAttribArray(), 720
glDrawArrays(), 82
glDrawBuffer(), 341, 343, 498
glDrawBuffers(), 498
glDrawElements(), 78
glDrawPixels(), 333, 340, 506, 662
alternative uses, 665
feedback mode, 629
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glDrawRangeElements(), 81
version, 33
glEdgeFlag*(), 68
legal between glBegin() and glEnd(), 52
glEdgeFlagPointer(), 74
glEnable(), 10, 54, 213
also see enabling
glEnableClientState(), 52, 72
glEnablei(), 516
glEnableVertexAttribArray(), 720
glEnd(), 47, 48, 546
restrictions, 51
glEndConditionalRender(), 515
glEndList(), 301, 305, 307
glEndQuery(), 513
glEndTransformFeedback(), 724
glEvalCoord*(), 577
legal between glBegin() and glEnd(), 52
used instead of glVertex*(), 572, 575

866 Index
glEvalCoord2*(), 579
glEvalMesh1(), 578
glEvalMesh2(), 581
glEvalPoint*()
legal between glBegin() and glEnd(), 52
glext.h, 16
glFeedbackBuffer(), 628
glRenderMode(), use with, 608
glFinish(), 40
glFlush(), 39, 816
glFlushMappedBufferRange(), 100
glFog*(), 284
glFogCoord*(), 288
glFogCoordPointer(), 74
glFramebufferRenderbuffer(), 533
glFramebufferTexture1D(), 535
glFramebufferTexture2D(), 535
glFramebufferTexture3D(), 535
glFramebufferTextureLayer(), 538
glFrontFace(), 62
glFrustum(), 133, 153, 154
glGenBuffers(), 92
glGenerateMipmap(), 428
glGenFramebuffers(), 527
glGenLists(), 301, 306
fonts, use for, 330
glGenQueries(), 512
glGenRenderbuffers(), 529
glGenTextures(), 399, 438
glGenVertexArrays(), 105
glGetAttachedShaders(), 740
glGetAttribLocation(), 718
glGetBooleanv(), 10, 54, 743
double-buffering support, querying, 494
stereo support, querying, 494
glGetBufferParameteriv(), 740
glGetBufferPointerv(), 740
glGetBufferSubData(), 740
glGetClipPlane(), 740
glGetColorTable(), 740
pixel-storage modes effect, 347
glGetColorTableParameter*(), 741
glGetCompressedTexImage(), 741
glGetConvolutionFilter(), 741
pixel-storage modes effect, 347
glGetConvolutionParameter*(), 741
glGetDoublev(), 10, 54, 743
glGetError(), 10, 638, 741
glGetFloatv(), 10, 54, 743
line width attributes, obtaining, 57
glGetFragDataLocation(), 730
glGetHistogram(), 385, 741
pixel-storage modes effect, 347
glGetHistogramParameter*(), 741
glGetIntegerv(), 10, 54, 743
alpha test information, obtaining, 503
attribute stack depth, obtaining, 111
clipping planes, obtaining number of
additional, 170
color resolution, obtaining, 190
display list nesting limit, obtaining, 310
matrix stack depth, obtaining, 167
maximum texture size, obtaining, 406
name stack depth, obtaining, 609
pixel map information, obtaining, 355
rendering mode, obtaining current, 608
stencil-related values, obtaining, 505
vertex array range values, obtaining, 81
glGetLight*(), 10, 741
glGetMap*(), 741
glGetMaterial*(), 741
glGetMinmax(), 387, 741
pixel-storage modes effect, 347
glGetMinmaxParameter*(), 741
glGetPixelMap(), 741
glGetPointerv(), 10, 54, 743
glGetPolygonStipple(), 10, 741
glGetProgramInfoLog(), 678

Index 867
glGetProgramiv(), 741
glGetProgramLogInfo(), 741
glGetQueryiv(), 741
glGetQueryObject*(), 513
glGetQueryObjectiv(), 741
glGetQueryObjectuiv(), 741
glGetSeparableFilter(), 741
pixel-storage modes effect, 347
glGetShaderInfoLog(), 676, 742
glGetShaderiv(), 742
glGetShaderSource(), 742
glGetString(), 639, 742
glGetStringi(), 642
glGetTexEnv*(), 742
glGetTexGen*(), 742
glGetTexImage(), 742
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glGetTexLevelParameter*(), 407, 742
glGetTexParameter*(), 742
texture residency, obtaining, 442
glGetUniform*(), 742
glGetUniformBlockIndex(), 695
glGetUniformIndices(), 697
glGetUniformLocation(), 691
glGetVertexAttrib*(), 742
glGetVertexAttribPointerv(), 742
glHint()
fog use, 281
texture use, 400
glHistogram(), 384
glIndex(), 199
glIndex*()
fog, use with, 286
legal between glBegin() and glEnd(), 51
glIndexMask(), 496, 499
glIndexPointer(), 74
glInitNames(), 607, 608, 609
glInterleavedArrays(), 89
glIsBuffer(), 93, 742
glIsEnabled(), 10, 54, 743
glIsFramebuffer(), 528
glIsList(), 312, 742
glIsProgram(), 680, 742
glIsQuery(), 512, 742
glIsRenderbuffer(), 530
glIsShader(), 680, 742
glIsTexture(), 438, 742
glIsVertexArray(), 110
glLight*(), 213, 214, 215, 220
glLightModel*(), 228
glLineStipple(), 57
glLineWidth(), 56
glLinkProgram(), 677
glListBase(), 312
fonts, use for, 330
sample program, 331
glLoadIdentity(), 133, 135, 145
viewing transformations, use
before, 131
glLoadMatrix*(), 134, 135
glLoadName(), 608, 610
glLoadTransposeMatrix*(), 134, 136
glLogicOp(), 256, 518
glMap*(), 574
glMap1*(), 576
glMap2*(), 579
glMapBuffer(), 97
glMapBufferRange(), 98
glMapGrid1*(), 577
glMapGrid2*(), 581
glMaterial*(), 214, 232
legal between glBegin() and glEnd(), 51
glMatrixMode(), 133, 135
use with matrix stacks, 166
glMinmax(), 387
glMultiDrawArrays(), 83
version, 33

868 Index
glMultiDrawElements(), 80
version, 33
glMultiTexCoord*(), 470
glMultMatrix*(), 134, 135
glMultTransposeMatrix*(), 134, 136
glNewList(), 301, 305, 307
glNormal*()
legal between glBegin() and glEnd(), 51
glNormal3*(), 69
glNormalPointer(), 74
glOrtho(), 157
picking matrix use, 615
glPassThrough(), 628, 630
glPixelMap*(), 354
glPixelStore*(), 347, 417
cannot be stored in display lists, 309
polygon stippling, 63
texture image data, effect on, 403, 405,
409, 411, 413, 416, 421, 422
glPixelTransfer*(), 352, 662
texture image data, effect on, 403, 405,
409, 411, 413, 416, 421, 422
glPixelZoom(), 356, 648
glPointParameter*(), 292
glPointSize(), 55, 721
glPolygonMode(), 61
antialiasing, effect on, 280
polygon offset, use with, 294
glPolygonOffset(), 294
glPolygonStipple(), 63
pixel-storage modes effect, 347
glPopAttrib(), 10, 111, 318, 470, 743
glPopClientAttrib(), 10, 112, 470, 743
glPopMatrix(), 166, 176, 223, 318
restore orientation of coordinate systems,
179
selection, use with, 607
glPopName(), 608, 609
glPrimitiveRestartIndex(), 84
glPrioritizeTextures(), 443
glPushAttrib(), 10, 111, 318, 470, 743
glPushClientAttrib(), 10, 112, 470, 743
glPushMatrix(), 166, 176, 223, 318
save orientation of coordinate systems, 179
selection, use with, 607
glPushName(), 607, 608, 609
glRasterPos*(), 324, 325
images, for positioning, 333
multitexturing, with, 471
selection hit, 610
glReadBuffer(), 342, 499
glReadPixels(), 333, 335
glReadBuffer() effect, 499
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glRect*(), 45
glRenderbufferStorage(), 530
glRenderbufferStorageMultisample(), 530
glRenderMode(), 607, 608, 610, 628
glResetHistogram(), 386
glResetMinmax(), 388
glRotate*(), 142, 172, 175
glSampleCoverage(), 279
glScale*(), 131, 142, 175
glScissor(), 502
glSecondaryColor*(), 479
glSecondaryColorPointer(), 74
glSelectBuffer(), 607, 608
display lists, cannot be stored in, 309
glSeparableFilter2D(), 379
glShadeModel(), 200
glShaderSource(), 675
glStencilFunc(), 504
glStencilFuncSeparate(), 504
glStencilMask(), 499
glStencilMaskSeparate(), 499
glStencilOp(), 505
glStencilOpSeparate(), 505

Index 869
glTexBuffer(), 711
glTexCoord*(), 400, 449
legal between glBegin() and glEnd(), 52
texture unit 0, for, 471
glTexCoordPointer(), 74
glTexEnv*(), 399, 444, 473
level of detail bias, 430
multitexturing, 468
glTexGen*(), 457
cube maps, 466
environment mapping, 464
multitexturing, 468, 471
glTexImage1D(), 412
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glTexImage2D(), 399, 400
cube map textures, 465
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
specifying mipmaps, 425
glTexImage3D(), 415
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glTexParameter*(), 399, 455
automatic mipmap regeneration, 429
mipmap level of detail, controlling, 433
mipmap levels, controlling base and
maximum, 432
multitexturing, 468
specifying filtering methods, 435
glTexSubImage1D(), 413
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glTexSubImage2D(), 409
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glTexSubImage3D(), 416
pixel-storage modes effect, 347
pixel-transfer modes effect, 352
glTranslate*(), 141, 172, 175
GLU, 3, 15, 542
drawing spheres, cylinders, and disks,
559–567
error string description, 639
obsolete routines
gluBeginPolygon(), 558
gluEndPolygon(), 558
gluNextContour(), 558
quadrics, 559–567
tessellation, 44, 542–559
version numbers, obtaining, 641
gluBeginCurve(), 587, 597
gluBeginSurface(), 587, 595
gluBeginTrim(), 601
gluBuild1DMipmapLevels(), 430
gluBuild1DMipmaps(), 429
gluBuild2DMipmapLevels(), 430
gluBuild2DMipmaps(), 429
gluBuild3DMipmapLevels(), 430
gluBuild3DMipmaps(), 429
gluCheckExtension(), 642
gluCylinder(), 560, 563
gluDeleteNurbsRenderer(), 591
gluDeleteQuadric(), 560, 561
gluDeleteTess(), 557, 558
gluDisk(), 560, 564
gluEndCurve(), 587, 597
gluEndSurface(), 587, 595
gluEndTrim(), 601
gluErrorString(), 561, 595, 639
polygon tessellation, 546
gluGetNurbsProperty(), 594, 742
gluGetString(), 641, 742
gluGetTessProperty(), 553, 742
gluLoadSamplingMatrices(), 594
gluLookAt(), 129, 131, 149, 172
gluNewNurbsRenderer(), 587, 591
gluNewQuadric(), 560, 561
gluNewTess(), 544, 558
glUniform*(), 691

870 Index
glUniformBlockBinding(), 696
glUniformMatrix*(), 691
glUnmapBuffer(), 97
gluNurbsCallback(), 587, 595, 598
gluNurbsCallbackData(), 599
gluNurbsCurve(), 587, 597
gluNurbsProperty(), 587, 592
returning tessellated data, 597
gluNurbsSurface(), 587, 596
gluOrtho2D(), 158
resized windows, use with, 41
gluPartialDisk(), 560, 564
gluPerspective(), 133, 156, 172
picking matrix use, 615
gluPickMatrix(), 615
gluProject(), 183
gluPwlCurve(), 601
gluQuadricCallback(), 560, 561
gluQuadricDrawStyle(), 560, 561
gluQuadricNormals(), 560, 562
gluQuadricOrientation(), 560, 562
gluQuadricTexture(), 560, 562
gluScaleImage(), 405
glUseProgram(), 678
gluSphere(), 560, 563
GLUT, 15, 731–737
basic functions, 17–22
event management, 21
glutCreateWindow(), 19, 733
glutDisplayFunc(), 19, 733
glutIdleFunc(), 21, 736
glutInit(), 18, 732
glutInitContextFlags(), 19
glutInitContextVersion(), 18
glutInitDisplayMode(), 18, 732
glutInitWindowPosition(), 18, 733
glutInitWindowSize(), 18, 733
glutKeyboardFunc(), 21, 734
glutMainLoop(), 19, 737
glutMotionFunc(), 21, 734
glutMouseFunc(), 21, 734
glutPostRedisplay(), 19, 302, 734
glutReshapeFunc(), 21, 734
simple example, 40
glutSetColor(), 18, 199, 247, 735
smooth shading, use for, 202
glutSolidCone(), 736
glutSolidCube(), 21, 735
glutSolidDodecahedron(), 736
glutSolidIcosahedron(), 736
glutSolidOctahedron(), 736
glutSolidSphere(), 21, 735
glutSolidTeapot(), 736
glutSolidTetrahedron(), 736
glutSolidTorus(), 735
glutSwapBuffers(), 25
glutWireCone(), 736
glutWireCube(), 21, 735
glutWireDodecahedron(), 736
glutWireIcosahedron(), 736
glutWireOctahedron(), 736
glutWireSphere(), 21, 172, 735
glutWireTeapot(), 736
glutWireTetrahedron(), 736
glutWireTorus(), 735
multisampling, 276
window management, 40
gluTessBeginContour(), 555
gluTessBeginPolygon(), 554
gluTessCallback(), 545, 555, 558
gluTessEndContour(), 555
gluTessEndPolygon(), 554
gluTessNormal(), 553, 554, 557
gluTessProperty(), 550, 555
gluTessVertex(), 555, 558
gluUnProject(), 180, 183
gluUnProject4(), 182
glValidateProgram(), 681

Index 871
glVertex*(), 46
legal between glBegin() and glEnd(), 51
using glEvalCoord*() instead, 572
glVertexAttrib*(), 719
glVertexAttrib4N*(), 719
glVertexAttribI*(), 719
glVertexAttribPointer(), 720
glVertexPointer(), 52, 74
glViewport(), 134, 159
using with resized windows, 41
glWindowPos*(), 326
multitexturing, with, 471
selection hit, 610
GLX, 15, 813
ftp site for GLX specification, 813
glXChooseFBConfig(), 813, 817
glXChooseVisual(), 814, 819
glXCopyContext(), 815, 817
glXCreateContext(), 815, 819
glXCreateGLXPixmap(), 814, 819
glXCreateNewContext(), 814, 817
glXCreatePbuffer(), 814, 817
glXCreatePixmap(), 814, 817
glXCreateWindow(), 814, 817
glXDestroyContext(), 815, 818
glXDestroyGLXPixmap(), 816, 819
glXDestroyPbuffer(), 816, 818
glXDestroyPixmap(), 816, 818
glXDestroyWindow(), 816, 818
glXGetClientString(), 813, 816
glXGetConfig(), 493, 814, 819
glXGetCurrentContext(), 815, 818
glXGetCurrentDisplay(), 815, 818
glXGetCurrentDrawable(), 815, 818
glXGetCurrentReadDrawable(), 815, 818
glXGetFBConfigAttrib(), 813, 817
glXGetFBConfigs(), 817
glXGetProcAddress(), 814, 817
glXGetSelectedEvent(), 815, 818
glXGetVisualFromFBConfig(), 813, 817
glXIsDirect(), 814, 818
glXMakeContextCurrent(), 815, 817
glXMakeCurrent(), 815, 819
glXQueryContext(), 815, 818
glXQueryExtension(), 813, 816
glXQueryExtensionsString(), 813, 816
glXQueryServerString(), 813, 816
glXQueryVersion(), 813, 816
glXSelectEvent(), 815, 818
glXSwapBuffers(), 25, 816, 818
glXUseXFont(), 816, 818
glXWaitGL(), 815, 818
glXWaitX(), 816, 818
glXQueryExtensionString(), 641
Gouraud shading, see smooth shading
H
Haeberli, Paul, 482, 519
haze, see fog
header files, 15
Version 3.1, 17
hidden-line removal, 659
polygon offset used for, 294
hidden-surface removal, 205–207, 510
hierarchical models, 164, 310
picking, 619–621
highlights, see specular
hints, 268
fog, 281
perspective correction, 268, 400
histogram, 383–386
reseting, 384, 386
retrieving, 384
sample program, 385
hits (selection), see selection (hit records)
holes in polygons, 43, 656
homogeneous coordinates, 42, 804
Hoschek, Josef, 571
Hughes, John F., xl, 803

872 Index
I
icosahedron, drawing, 115
identity matrix, 131, 135, 145
illumination, see lighting
images, 322, 333–343
also see pixel data
blending, 653
compositing, 252
distorted, 647
imaging pipeline, 343–359
interpolating between, 653
magnifying or reducing, 356
nonrectangular, 259
projecting, 661
sample code which draws an image, 341
sample program which draws, copies, and
zooms an image, 357
scaling and rotating, 661
sources of, 333
superimposing, 654
transposing, 666
warping, 661
imaging pipeline, see images (imaging pipeline)
imaging subset, 367–388
texture images, effect on, 404, 412
immediate mode, 33, 298
display lists, mixing with, 310
infinite light source, 217
input events
handling, using GLUT, 21
intensity
texture image data type, 445
Interactive Inspection of Solids: Cross-sections
and Interferences, 656
interference regions, 656
interleaved arrays, 88
interpolating
color values and texture coordinates, 268,
449
texture combiner function, 477
J
jaggies, 267
jittering, 525
K
Kilgard, Mark, xli, 15, 731, 813
Korobkin, Carl, 482
L
Lasser, Dieter, 571
layers, drawing, 649
Life, Game of, 664
light sources, 214–227
ambient light, 208, 216
contribution to lighting equation, 242
diffuse light, 208, 216
directional, 217
display lists cache values, 303
infinite light source, 217
local light source, 217
maximum number of sources, 213
moving along with the viewpoint, 225
moving light sources, 221–226
multiple light sources, 220
performance tips, 213
positional, 217
rendering pipeline stage, 12
RGBA values, 209
sample program that moves the light
source, 224
specifying a light source, 213
specular light, 208
spotlights, 219–220
stationary, 222
lighting
also see light sources, material properties
ambient light, 207
approximation of the real world, 207
attenuation, 217–218

Index 873
calculations in color-index mode, 247
color-index mode, 246–247
default values, using, 214
display lists cache values, 303
enabling, 213, 214
enabling and disabling, 231
equation that calculates lighting, 241
global ambient light, 228, 242
lighting model, 227–230
lighting model, specifying a, 213
rendering pipeline stage, 12
sample program introducing lighting, 210
specular color separated, 230, 245, 479
steps to perform, 210
two-sided materials, 229
viewer, local or infinite, 229
line segment, 43
linear attenuation, 218
lines, 43
antialiasing, 269–275, 661
connected closed loop, specifying, 48, 50
connected strip, specifying, 48, 50
feedback mode, 629
querying line width, 57
sample program with wide, stippled lines,
59
specifying, 48, 50
stippling, 57
tessellated polygons decomposed
into, 546
width, 56
local light source, 217
logical operations
rendering pipeline stage, 14
transposing images, using for, 666
lookup table, see color map
luminance, 336, 362
pixel data formats for, 338, 346
texture image data type, 445
M
magnifying images, 356
masking, 499
antialiasing characters, 652
layers, drawing, 649
rendering pipeline stage, 14
material properties, 214, 231–240
ambient, 209, 233
changing a single parameter with
glColorMaterial(), 237
changing material properties, 235
diffuse, 209, 233
display lists cache values, 303
emission, 208, 234, 241
enabling color material properties mode,
237
rendering pipeline stage, 12
RGBA values, 210
sample program which changes material
properties, 235
sample program which uses
glColorMaterial(), 238
shininess, 234
specular, 209, 234
two-sided lighting, 229
matrix
choosing which matrix is current, 135
column-major ordering, 136
current, 131
display lists cache matrix operations, 303
identity, 131, 135, 145
loading, 135
loading transposed, 136
modelview, 128, 135
multiplying matrices, 135
multiplying transposed matrices, 136
NURBS, specifying for sampling, 593
orthographic parallel projection, 808
perspective projection, 807
projection, 133, 135

874 Index
matrix, continued
rotation, 806
row-major ordering, 136
scaling, 806
texture, 481
transformation pipeline, 126
transformations of homogeneous
coordinates, 804
translation, 806
matrix stack, 164–168
choosing which matrix stack is current,
166
modelview, 167
popping, 166
projection, 168
pushing, 166
querying stack depth, 167
texture, 481
Megahed, Abe, 656
Microsoft
callback functions on Windows, 547
Microsoft Win32, see Win32
Microsoft Windows 95/98/NT, 15, 824
Microsoft Windows to OpenGL interface,
see WGL
minmax, 387–388
reseting, 387, 388
retrieving results, 387
sample program, 388
mipmapping, 424–429
automated generation, 429
base and maximum levels, 432
level of detail control, 431
minification filters, 436
texture objects for mipmaps, 441
mirroring objects, see scaling
modeling transformations, 131, 137, 140–145
camera analogy, 126
connection to viewing transformations,
131
example, 143
rotation, 142
rotation matrix, 806
sample program, 145
scaling, 142
scaling matrix, 806
translation, 141
translation matrix, 806
models
rendering wireframe and solid, 21, 735
modelview matrix, 128, 135
arbitrary clipping planes, effect on, 169
stack, 167
mosaicing, 431
motion blur, 520
stippling, with, 646
motion, see animation
movie clips, 665
multiple layers
displaying with overlap, 649
multisampling, 275–279
fading point primitives, 292
sample program, 276
multitexturing, 467–472
N
name stack, 607–611
creating, 608
initializing, 608
loading, 608
multiple names, 619–621
popping, 608
pushing, 608
querying maximum depth, 609
networked operation, 39–40
attribute groups, saving and restoring, 110
display lists, 309
versions, 640

Index 875
Non-Uniform Rational B-Splines, see NURBS
nonplanar polygons, 44
normal vectors, 68–70, 212
calculating length, 70
cross product, calculating normalized, 117
enabling automatic unit length division,
70, 212
matrix transformations, 128
normalized, 70
NURBS, generating for, 596
quadrics, generated for, 562
rendering pipeline stage, 12
specifying, 69
tessellation, specifying for, 548
transformations, 805
uniform rescaling, 70
vertex arrays, specifying values with, 74
normal, see normal vectors
normalized device coordinates, 128
NURB Curves and Surfaces, 571
NURBS, 586–604
creating a NURBS curve or surface,
595–597
creating a NURBS object, 591
culling, 592
deleting a NURBS object, 591
display list use, 302
error handling, 594
method of display (lines or filled
polygons), 592
normal vectors, generating, 596
properties, controlling NURBS, 591
querying property value, 594
references, 571
sample program which draws a lit NURBS
surface, 588
sample program with a trimmed surface,
603
sampling precision, 592
source for matrices, 593
steps to use, 587
texture coordinate generation, 596
trimming, 601–604
NURBS Book, The, 571
NURBS for Curve and Surface Design, 571
NURBS tessellator
sample code, 599, 600
O
object coordinates, 128
texture coordinate generation, 458
objects, see models
occlusion queries
conditional rendering, 515
occlusion query, 511
opacity, 252
OpenGL contexts, 27
OpenGL Extension to the X Window System,
see GLX
OpenGL Programming for the X Window System,
xli, 813
OpenGL Reference Manual, xl, 813
OpenGL Utility Library, see GLU
OpenGL Utility Toolkit, see GLUT
orthographic parallel projection, 133,
156–157
matrix, 808
outer product, 378
outlined polygons, 61, 68
polygon offset solution, 293
overlapping objects, 656
P
packed pixel data, 338–339
painting, 252, 258, 666
partial disks, 559
pass-through markers, 630

876 Index
performance tips
clearing the window, 36
display lists, 302
flushing the pipeline, 38
fog, 281
hints, 268
light source attenuation, effect of, 218
light sources, effect of additional, 213
NURBS and display lists, 302
pixel data alignment, 350
pixel data, drawing, 366
polygon restrictions, 44
polygon subdivision, 114
removing hidden surfaces, 207
tessellation and display lists, 302
tessellation, use of, 557
texture images, internal format of, 403
texture objects, 437
two-sided lighting, 230
perspective projection, 153–156
correction hint, 268, 400
depth coordinates, effect on, 161
matrix, 807
perspective division, 128
picking, 614–624
back buffer for, using the, 646
depth coordinates, 621
hierarchical models, 619–621
projection matrix, special, 615
sample program, 616
sample program with depth coordinates,
621
strategies, 625
sweep selection, 626
Piegl, Les, 571
pipeline
imaging, 343–359
rendering, 10–14
vertex transformation, 126
pixel
coverage, 267
pixel data, 322, 333–343
also see images
BGR and BGRA formats, 336
byte alignment, 350
byte swapping, 348
copying within the framebuffer, 13, 333,
342, 344
depth buffer pixel data, 342, 353
drawing or reading a subrectangle of, 349
drawing process in detail, 359–361
endianness, 349
feedback mode, 629
formats for reading or drawing, 335
formats for storing in memory, 338, 346
mapping, 13, 354–355
packed, 338–339
packing into processor memory, 13,
346–348
performance tips, 366
pipeline operations, 13, 343–359
pixel zoom, 356
querying pixel mapping information, 355
reading from the framebuffer, 333, 335
reading process in detail, 361–362
sample code which draws an image, 341
sample program that uses a pixel buffer
object for storage, 364
sample program which draws, copies, and
zooms pixel data, 357
stencil buffer pixel data, 338, 354
storage modes, 347, 417–419
transfer modes, 13, 352, 445
unpacking from processor memory, 13,
346–348
writing to the framebuffer, 333, 341
point light source, see positional light source
point parameters, 291
sample program, 292

Index 877
points, 42
antialiasing, 269–275, 653
drawing, 48
feedback mode, 629
point parameters, 291
round, 269–275, 653
size, 55
specifying, 48, 50
polygon offset, 293–296
depth slope of a polygon, 295
enabling, 294
hidden-line removal, 659
sample program, 296
shadowing use, 484
polygonal approximations to surfaces, 113
polygons, 43
boundary edges, 67–68
concave, drawing filled, 542, 655
convex, 43
culling the faces, 61
drawing, 48
drawing as points, lines, or filled, 61
feedback mode, 629
front and back faces, 61
holes in, 43
non-convex, 44, 67
nonplanar, 44
polygon mode, 12, 61
reversing the faces, 61
self-intersecting, 549
simple, 43
specifying, 48, 51
stippling, 63
tessellation, specifying for, 554
Voronoi, 663
positional light source, 217
primitives
geometric, 42–53
raster, 322
priority of texture objects, 443
Procedural Elements for Computer Graphics, 560
programs
aaindex.c, 272
aargb.c, 270
alpha3D.c, 264
alpha.c, 261
bezcurve.c, 573
bezmesh.c, 582
bezsurf.c, 580
checker.c, 398
clip.c, 170
colormat.c, 238
colormatrix.c, 382
colortable.c, 371
combiner.c, 477
convolution.c, 376
cube.c, 130
cubemap.c, 466
dof.c, 522
drawf.c, 324
feedback.c, 631
fog.c, 281
fogcoord.c, 289
fogindex.c, 286
font.c, 331
histogram.c, 385
image.c, 357
light.c, 210
lines.c, 59
list.c, 305
material.c, 235
minmax.c, 388
mipmap.c, 426
model.c, 145
movelight.c, 224
multisamp.c, 276
multitex.c, 469
pboimage.c, 364

878 Index
programs, continued
pickdepth.c, 621
picksquare.c, 616
planet.c, 173
pointp.c, 292
polyoff.c, 296
quadric.c, 565
robot.c, 177
select.c, 611
shadowmap.c, 484–486
smooth.c, 200
sprite.c, 481
stencil.c, 507
stroke.c, 314
surface.c, 588
surfpoints.c, 599, 600
tess.c, 548, 556
texbind.c, 439
texgen.c, 459
texsub.c, 410
texture3d.c, 415
texturesurf.c, 584
torus.c, using a display list, 299
trim.c, 603
unproject.c, 180
projecting images, 661
projection matrix, 133, 135
matrix stack, 168
orthographic parallel projection matrix, 808
perspective projection matrix, 807
shadows created with, 658
projection transformation
centered along view vector, 156
off-axis perspective, 154
parallel projection, 157
perspective, 154, 156
three-dimensional orthographic, 157
projection transformations, 132, 152–158
camera lens analogy, 126
orthographic parallel, 133, 156–157
perspective, 153–156
picking, 615
texturing effects, 482
two-dimensional orthographic, 158
proxies
color table, see color table proxies, 374
proxy textures, 406
cube maps, 465
Q
q texture coordinates, 482
quadratic attenuation, 218
quadrics, 559–567
creating an object, 560
destroying an object, 560
drawing as points, lines, and filled
polygons, 561
error handling, 561
normal vectors, generating, 562
orientation, 562
quadratic equation, 559
sample program, 565
steps to use, 560
texture coordinates, generating, 562
quadrilateral
specifying, 48
strip, specifying, 48, 51
R
raster position, 325
after drawing a bitmap, 327
current, 325
current raster color, 329
current, obtaining the, 326
selection hit, 610
transformation of, 326
rasterization, 190, 490
rendering pipeline stage, 14

Index 879
readImage(), 372
reading pixel data, see pixel data
Real Projective Plane, The, 803
rectangles
specifying, 45
reducing images, 356
reflecting objects, see scaling
reflection, see material properties
reflective objects, see environment mapping
refresh, screen, 22
removing hidden surfaces, see hidden-surface
removal
rescaling normals, 70, 212
resident textures, 408, 442
management strategies, 443
querying residence status, 442
RGBA mode, 191
changing between color-index mode and,
196
choosing between color-index mode and,
195
coverage calculations for antialiasing, 267
data type conversion, 197
light source colors, 209
lighting calculations in, 241
material property values, 210
vertex arrays, specifying values with, 74
Robins, Nate, xlii, 145, 151, 158, 179, 227,
236, 437, 448, 450, 457, 482
robot arm example, 175–179
Rogers, David, 560
Rossignac, Jarek, 656
rotating images, 661
rotation, 142
matrix, 806
S
scaling, 142
matrix, 806
scaling images, 661
Schneider, Bengt-Olaf, 656
Scientific American, 664
scissor test, 502
and clearing, 496
rendering pipeline stage, 14
secondary color, 478–479
specular, 230, 245
Segal, Mark, 482
selection, 606–627
back buffer for, using the, 646
hit records, 610
programming tips, 625
querying current rendering mode, 608
sample program, 611
steps to perform, 607
sweep selection, 626
shading
flat, 200
sample program with smooth shading, 200
smooth, 200
specifying shading model, 200
shadows, 241, 525, 658
shininess, 234
also see environment mapping
silhouette edges, 114
smoke, see fog
smooth shading, 200
solar system example, 172–175
source factor, see blending
specifying the background color, 36
specifying the depth buffer clear value, 35
specular
contribution to lighting equation, 244
light, 208
material properties, 209, 234
secondary specular color, 230, 245, 479
sphere map, 463
spheres, 559, 735
split-screen
multiple viewports, 159

880 Index
spotlights, see light sources
state attributes
perserving, 111
preserving vertex arrays, 112
reverting, 111
reverting vertex arrays, 112
state machine, 9–10
state variables, 53
attribute groups, 110–112
display list execution, effect of, 318
enable and disable states, 54
list of, 743–800
querying, 54
stencil buffer, 492, 494
clearing, 36, 495
concave polygons, for drawing, 655
decals, for, 654
Dirichlet domains, for, 663
Game of Life, for the, 664
hidden-line removal, 660
masking, 499
pixel data, 338, 354
stencil test, 504–510
examples of using, 506
interference regions found using clipping
planes, 657
querying stencil parameters, 505
rendering pipeline stage, 14
sample program, 507
stereo, 494, 498
querying its presence, 494
stippling
display lists cache stipple patterns, 303
enabling line stippling, 57
enabling polygon stippling, 63
fade effect, use for, 645
line pattern reset, 58, 629, 633
lines, 57
polygons, 63
sample program with line stipple, 59
stencil test, use of, 510
translucency, use to simulate, 644
stitching, 294
stretching objects, see scaling
stride
vertex arrays, 76, 89
subdivision, 113–121
generalized, 120
icosahedron example, 118
recursive, 119
subimages, 408–411, 413, 416
superimposing images, 654
surface normals, see normal vectors
surfaces, see evaluators or NURBS
swapping buffers, see double-buffering
syntax, see command syntax
T
Terminator 2, 463
tessellation, 44, 542–559
backward compatibility with obsolete
routines, 558
begin and end callback routines, 546
callback routines, 544–549
combine callback routine, 546, 549
contours, specifying, 554
converting code to use the GLU 1.2
tessellator, 559
creating an object, 544
decomposition into geometric primitives,
546
deleting objects, 557
display list use, 302
edge flag generation, 546
error handling, 546
interior and exterior, determining,
550–553
intersecting contours combined, 546, 549

Index 881
performance tips, 557
polygons, specifying, 554
properties, 550–554
reuse of objects, 544, 557
reversing winding direction, 554
sample code, 548, 556
user-specified data, 549
vertices, specifying, 547, 555
winding rules, 550–553
texels, 14, 391
text, see characters
texture coordinates, 400, 448–464
assigning manually, 448
clamping, 452–455
computing manually, 450
cube maps, 466
enabling automatic generation of, 462
environment mapping, automatic
generation for, 464
evaluators, generated by, 584
generating automatically, 457–464
multitexturing, special situations with, 471
NURBS, generating for, 596
q coordinate, 482
quadrics, generated for, 562
reference planes, specifying, 458
rendering pipeline stage, 12
repeating, 452–455
sample program with texture coordinate
generation, 459
tessellation, specifying for, 548
vertex arrays, specifying values with, 74
wrapping modes, 452–455
texture functions, 444–448
add, 448
blend, 448
blending color, 448
decal, 399, 447
fragment operations, 446
level of detail bias, 444
modulate, 448
pixel-transfer modes effect, 445
replace, 447
texture internal format, interaction with,
446
texture images
alpha data, 445
borders, 423, 452
components, 401
data types, 403
distorting, 451
framebuffer as a source of, 405, 411, 413,
417
imaging pipeline operations, 345
intensity data, 445
internal format, 401
luminance data, 445
mipmaps, 424–429
multitexturing, 468
one-dimensional, 412–414
performance affected by internal format,
403
power of 2 size restriction, 404
proxy textures, 406
querying maximum size, 406
residence status, 442
resident textures, 408, 442
resident textures, management strategies
of, 443
sample program with mipmaps, 426
sample program with subimages, 410
specifying, 400–423
subimages, 408–411, 413, 416
three-dimensional, 414–419
working set of textures, 408, 437, 442
texture mapping
sample program using 3D textures, 415
texture mapping, see texturing
texture matrix, 481

882 Index
texture objects, 399, 437–442
binding, 438
creating, 438
data which can be stored in, 439
deleting, 441
fragmentation of texture memory, 444
least-recently used (LRU) strategy, 444
mipmaps, 441
naming, 438
performance tips, 437
priority, 443
rendering pipeline, 13
sample program, 398
sample program with multiple texture
objects, 439
sharing among rendering contexts, 814,
826
steps to perform, 437
using, 438
texturing
also see texture coordinates, texture
functions, texture images, texture
matrix, and texture objects
antialiasing characters, 661
antialiasing lines, 661
blending, 259
border colors, treatment of, 452
color-index mode limitations, 396, 404
combiner functions, 472–478
compressed textures, 420
creating contours, 458
cube maps, 465
decals with alpha testing, 503
differences among releases, 393
enabling, 396, 399
filtering, 434–436
image transformations, 661
mipmapping, 424–429, 436
mosaic texture, 431
multitexturing, 467–472
perspective correction hint, 400
popping visual artifact, 431
rendering pipeline stage, 13
sample code using point sprites, 481
sample code with a depth texture, 484–486
sample code with combiner functions, 477
sample code with multitexturing, 469
sample program, 398
sample program with cube maps, 466
sample program with evaluated, Bézier
surface, 584
sample program with mipmapping, 426
sample program with texture coordinate
generation, 459
sample uses for, 661
simulating shadows or spotlights, 482
specular color separated, 230, 245, 479
sphere map, 463
steps to perform, 396
3D Computer Graphics: A User’s Guide for
Artists and Designers, xl
3D models, rendering, 21, 735
Tiller, Wayne, 571
tips, programming
selection and picking, 625
transformations, 162
transformations
also see modeling transformations,
projection transformations, viewing
transformations, and viewport
transformations
combining multiple, 172–179
display lists cache transformations, 303
general-purpose commands, 134
matrices, 805–808
modeling, 137, 140–145
ordering correctly, 137–140
overview, 125
projection, 132, 152–158
reversing the geometric processing
pipeline, 180

Index 883
sample program, 130
sample program combining modeling
transformations, 173, 177
sample program for modeling
transformations, 145
sample program showing reversal of
transformation pipeline, 180
troubleshooting, 162–164
units, 156
viewing, 137, 146–151
viewport, 134, 158–160
translation, 141
matrix, 806
translucent objects, 252, 644
stencil test, creating with the, 510
transparent objects, 252
creating with the alpha test, 503
transposing images, 666
triangle
fan, specifying, 48
specifying, 48, 50
strip, specifying, 48, 50
tessellated polygons decomposed into, 546
trimming
curves and curved surfaces, 601–604
sample program, 603
tutorials
on-line, xlii
two-sided lighting, 229
U
up-vector, 131
Utility Library, OpenGL, see GLU
Utility Toolkit, OpenGL, see GLUT
V
van Dam, Andries, xl, 187, 191, 803
van Widenfelt, Rolf, 482
vendor-specific extensions, 641
versions, 639–641
GLU, 641
vertex, 42
also see vertex arrays
evaluators, generating with, 572
feedback mode, 629
per-vertex operations pipeline stage, 12
specifying, 46
tessellation, specifying for, 547, 555
transformation pipeline, 126
vertex arrays, 70–91
dereference a list of array elements, 78, 80,
81
dereference a sequence of array elements,
82, 83
dereference a single element, 77
differences among releases, 33
disabling, 73
display list use, 309
enabling, 72
interleaved arrays, 88
interleaved arrays, specifying, 89
multitexturing texture coordinates, 471
querying, 743
querying range values, 81
restarting primitives, 83–??, 84, ??–86
reuse of vertices, 79
specifying data, 73
steps to use, 71
stride between data, 76, 89
vertex-array objects, 104–??, 109, ??–110
vertex-arrays objects, 105
video
fake, 665
flipping an image with glPixelZoom(), 356
textured images, 408
viewing
camera analogy, 126–127

884 Index
viewing transformations, 130, 137, 146–151
connection to modeling transformations,
131
default position, 131
different methods, 151
pilot view, 152
polar view, 152
tripod analogy, 126
up-vector, 131
viewing volume, 153
clipping, 158, 168
viewpoint
lighting, for, 229
viewport transformations, 129, 134, 158–160
photograph analogy, 126
rendering pipeline stage, 12
visual simulation
fog, use of, 281
Voronoi polygons, 663
W
w coordinates, 42, 129, 134
lighting, use with, 217
perspective division, 161
warping images, 661
Watt, Alan, 390
web sites, xl
errata list, xlii
Microsoft Developer Network, 825
WGL, 15, 825
wglCopyContext(), 826, 828
wglCreateContext(), 825, 828
wglCreateLayerContext(), 826, 828
wglDeleteContext(), 828
wglDescribeLayerPlane(), 825, 827
wglDestroyContext(), 826
wglGetCurrentContext(), 826, 828
wglGetCurrentDC(), 826, 828
wglGetLayerPaletteEntries(), 827, 829
wglGetProcAddress(), 828
wglMakeCurrent(), 826, 828
wglRealizeLayerPalette(), 827, 829
wglSetLayerPaletteEntries(), 829
wglShareLists(), 826, 828
wglSwapLayerBuffers(), 826, 828
wglUseFontBitmaps(), 827, 829
wglUseFontOutlines(), 827, 829
wglGetProcAddress(), 644
Williams, Lance, 424
Win32
ChoosePixelFormat(), 825, 827
CreateDIBitmap(), 826, 828
CreateDIBSection(), 826, 828
DeleteObject(), 826, 828
DescribePixelFormat(), 825, 827
GetVersion(), 825, 827
GetVersionEx(), 825, 827
SetPixelFormat(), 825, 827
SwapBuffers(), 826, 828
winding, 62
winding rules, 550–553
computational solid geometry, used for,
551
reversing winding direction, 554
window coordinates, 129, 158
feedback mode, 629
polygon offset, 294
raster position, 326
window management
glViewport() called, when window resized,
159
using GLUT, 40
working set of textures, 408, 437, 442
fragmentation of texture memory, 444
writemask, see masking (buffers)
writing pixel data, see pixel data (drawing)
www.opengl.org, xl

Index 885
X
X Window System, 15, 813
client-server rendering, 5
minimum framebuffer configuration, 492
X Visual, 196, 813
Z
z buffer, see depth buffer
z coordinates, see depth coordinates
zooming images, 356
filtered, 666
This page intentionally left blank
1
Appendix E
E.Order of Operations
This book describes all the operations performed between initial specifica-
tion of vertices and final writing of fragments into the framebuffer. The
chapters of this book are arranged in an order that facilitates learning, rather
than in the exact order in which these operations are actually performed.
Sometimes the exact order of operations doesn’t matter—for example, sur-
faces can be converted to polygons and then transformed, or transformed
first and then converted to polygons, with identical results—and different
implementations of OpenGL might do things differently.
This appendix describes a possible order; any implementation is required to
yield equivalent results. If you want more details than are presented here,
see the OpenGL Specification at http://www.opengl.org/registry/.
This appendix has the following major sections:
• “Overview”
• “Geometric Operations”
• “Pixel Operations”
• “Fragment Operations”
• “Odds and Ends”
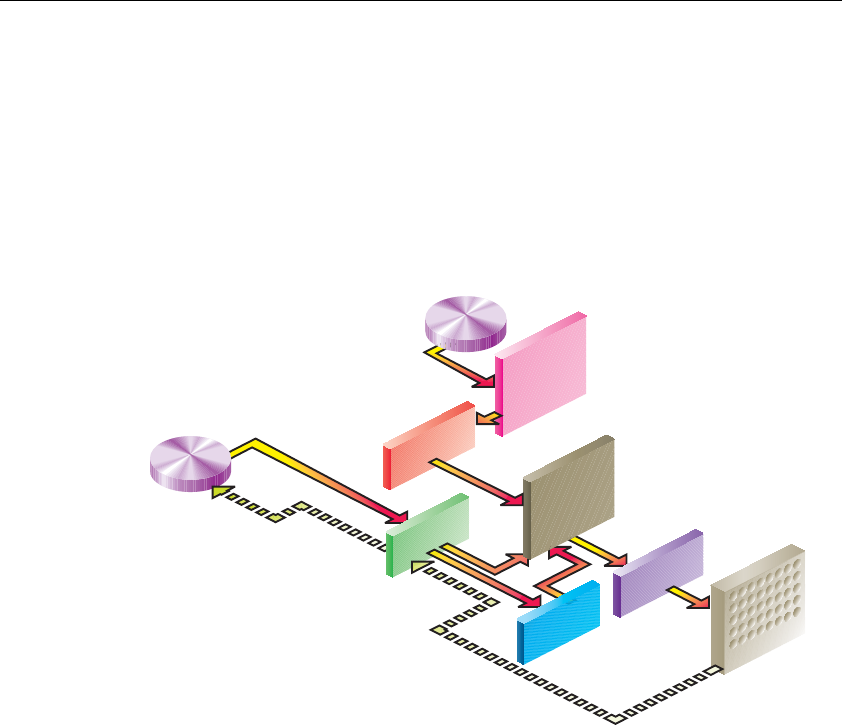
2Appendix E: Order of Operations
Overview
This section gives an overview of the order of operations. Shown in
Figure E-1 is a schematic representation of the fixed-function OpenGL
pipeline. Geometric data (vertices, lines, and polygons) follows the path
through the row of boxes that include evaluators and per-vertex operations,
while pixel data (pixels, images, and bitmaps) is treated differently for part
of the process. Both types of data undergo the rasterization and per-fragment
operations before the final pixel data is written into the framebuffer.
All data, whether it describes geometry or pixels, can be saved in a display
list or processed immediately. When a display list is executed, the data is
sent from the display list just as if it were sent by the application.
All geometric primitives are eventually described by vertices. If evaluators
are used, that data is converted to vertices and treated as vertices from then
on. Vertex data may also be stored in and used from specialized vertex
arrays. Per-vertex calculations are performed on each vertex, followed by
rasterization to fragments. For pixel data, pixel operations are performed,
and the results are stored in the texture memory, used for polygon stippling,
or rasterized to fragments.
Ver tex
shading
and primitive
assembly
Pixel
data
Ver tex
data
Pixel
operations
Rasterization
Per-fragment
operations
Framebuffer
Texture
assembly
Fragment
shading
Figure E-1 The Fixed-Function Pipeline’s Order of Operations
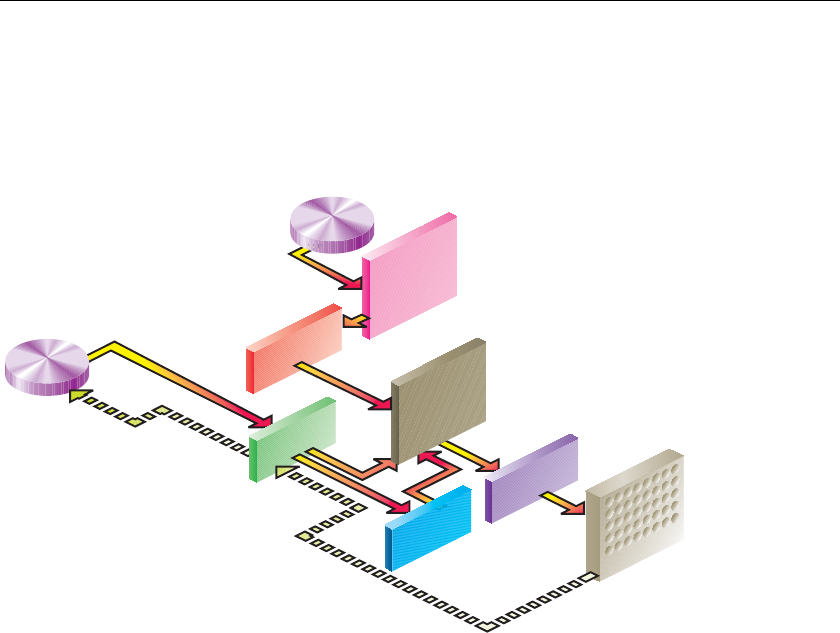
Geometric Operations 3
Finally, the fragments are subjected to a series of per-fragment operations,
after which the final pixel values are drawn into the framebuffer.
This model differs only slightly for the programmable pipeline available in
OpenGL Version 3.1 and greater, as illustrated in Figure E-2.
Figure E-2 The Programmable Pipeline’s Order of Operations
Geometric Operations
Geometric data, whether it comes from a display list, an evaluator, the ver-
tices of a rectangle, or is in the form of raw data, consists of a set of vertices
and the type of primitive it describes (a vertex, line, or polygon). Vertex
data includes not only the (x, y, z, w) coordinates, but also other vertex
attributes: a normal vector, texture coordinates, primary and secondary
RGBA colors, a color index, material properties, edge-flag data, or entirely
generic values assigned meaning in a programmable vertex shader. All of
these elements except the vertex’s coordinates can be specified in any
order, and default values exist as well. As soon as a vertex rendering com-
mand (e.g., glVertex*(), glDrawArrays(), glDrawElements()) is issued, the
components are padded, if necessary, to four dimensions (using z = 0 and
w = 1), and the current values of all the elements are associated with the
Ver tex
shading
and primitive
assembly
Pixel
data
Ver tex
data
Pixel
operations
Rasterization
Per-fragment
operations
Framebuffer
Texture
assembly
Fragment
shading

4Appendix E: Order of Operations
vertex. The complete set of vertex data is then processed. (If vertex arrays
are used, vertex data may be batch processed, and processed vertices may
be reused.)
Per-Vertex Operations
In the fixed-function pipeline mode, the per-vertex operations stage of pro-
cessing, each vertex’s spatial coordinates are transformed by the modelview
matrix, while the normal vector is transformed by that matrix’s inverse
transpose and renormalized if specified. If automatic texture generation is
enabled, new texture coordinates are generated from the transformed ver-
tex coordinates, and they replace the vertex’s old texture coordinates. The
texture coordinates are then transformed by the current texture matrix and
passed on to the primitive assembly step.
Meanwhile, the lighting calculations, if enabled, are performed using the
transformed vertex and normal vector coordinates and the current material,
lights, and lighting model. These calculations generate new colors or indi-
ces that are clamped or masked to the appropriate range and passed on to
the primitive assembly step.
For vertex shader programs, the above sequence of operations is replaced
by the execution of the user-defined shader, which must update the
vertex’s position, and may update the primary and secondary colors for the
primitives front- and back-facing colors, associated texture coordinates,
and fog coordinates. Additionally, the point size, and vertex position to be
used with user-defined clip planes may also be updated.
Primitive Assembly
Primitive assembly varies, depending on whether the primitive is a point, a
line, or a polygon. If flat shading is enabled, the colors or indices of all the
vertices in a line or polygon are set to the same value. If special clipping
planes are defined and enabled, they’re used to clip primitives of all three
types. (The clipping-plane equations are transformed by the inverse trans-
pose of the modelview matrix when they’re specified.) Point clipping sim-
ply passes or rejects vertices; line or polygon clipping can add additional
vertices, depending on how the line or polygon is clipped. After this clip-
ping, the spatial coordinates of each vertex are transformed by the projec-
tion matrix, and the results are clipped against the standard viewing planes
x = rw,y = rw, and z = rw.

Pixel Operations 5
If selection is enabled, any primitive not eliminated by clipping generates a
selection-hit report, and no further processing is performed. Without selec-
tion, perspective division by w occurs and the viewport and depth-range
operations are applied. Also, if the primitive is a polygon, it’s then subjected
to a culling test (if culling is enabled). A polygon might convert to vertices
or lines, depending on the polygon mode.
Finally, points, lines, and polygons are rasterized to fragments, taking into
account polygon or line stipples, line width, and point size. Rasterization
involves determining which squares of an integer grid in window coordi-
nates are occupied by the primitive. If antialiasing is enabled, coverage (the
portion of the square that is occupied by the primitive) is also computed.
Color and depth values are also assigned to each such square. If polygon off-
set is enabled, depth values are slightly modified by a calculated offset
value.
Pixel Operations
Pixels from host memory or pixel unpack buffers are first unpacked into the
proper number of components. The OpenGL unpacking facility handles a
number of different formats. Next, the data is scaled, biased, and processed
using a pixel map. The results are clamped to an appropriate range, depend-
ing on the data type, and then either written in the texture memory for use
in texture mapping or rasterized to fragments.
If pixel data is read from the framebuffer, pixel-transfer operations (scale,
bias, mapping, and clamping) are performed. The results are packed into an
appropriate format and then returned to processor memory.
The pixel-copy operation is similar to a combination of the unpacking and
transfer operations, except that packing and unpacking are unnecessary,
and only a single pass is made through the transfer operations before the
data is written back into the framebuffer.
Texture Memory
Texture images can be specified from framebuffer memory, as well as
processor memory. All or a portion of a texture image may be replaced.
Texture data may be stored in texture objects, which can be loaded into
texture memory. If there are too many texture objects to fit into texture

6Appendix E: Order of Operations
memory at the same time, the textures that have the highest priorities
remain in the texture memory.
Fragment Operations
In the fixed-function mode, if texturing is enabled, a texel is generated from
texture memory for each fragment from every enabled texture unit (by
means of glActiveTexture()) and is applied to the fragment. Then fog
calculations are performed, if they’re enabled, followed by the application
of coverage (antialiasing) values, if antialiasing is enabled.
If a fragment shader program is enabled, texture sampling and application,
per-pixel fog computations, and alpha-value assignment may be done in
the fragment shader. Assuming the fragment was not discarded by the
fragment shader, the fragment’s color will be updated with the color
assigned in the fragment shader, which may include the combination of
colors generated from the iterated primary and secondary colors, texture
application, fog computations, or other color values. The depth value for
the fragment may be also be updated and any associated fragment data may
also be updated.
Next comes scissoring, followed by the alpha test (in RGBA mode only, and
for OpenGL versions to Version 3.0), the stencil test, and the depth-buffer
test. If in RGBA mode, blending is performed. Blending is followed by dith-
ering and logical operation. All these operations may be disabled.
The fragment is then masked by a color mask or an index mask, depending
on the mode, and drawn into the appropriate buffer. If fragments are being
written into the stencil or depth buffer, masking occurs after the stencil and
depth tests, and the results are drawn into the framebuffer without perform-
ing the blending, dithering, or logical operation.
Odds and Ends
For the fixed-function pipeline, matrix operations deal with the current
matrix stack, which can be the modelview, the projection, or the texture
matrix stack. If the Imaging subset is included in the implementation, a
color matrix stack will also be present. The commands glMultMatrix*(),
glLoadMatrix*(), and glLoadIdentity() are applied to the top matrix on
the stack, while glTranslate*(),glRotate*(),glScale*(),glOrtho(), and
glFrustum() are used to create a matrix that’s multiplied by the top matrix.

Odds and Ends 7
When the modelview matrix is modified, its inverse transpose is also gener-
ated for normal vector transformation.
The commands that set the current raster position are treated exactly like a
vertex command up until the point when rasterization would occur. At this
point, the value is saved and used in the rasterization of pixel data.
The various glClear() commands bypass all operations except scissoring,
dithering, and writemasking.
This page intentionally left blank
1
Appendix F
F.Programming Tips
This appendix lists some tips and guidelines that you might find useful.
Keep in mind that these tips are based on the intentions of the designers of
OpenGL, not on any experience with actual applications and implementa-
tions. This appendix has the following major sections:
• “OpenGL Correctness Tips”
• “OpenGL Performance Tips”
• “GLX Tips”

2Appendix F: Programming Tips
OpenGL Correctness Tips
• Perform error checking often. Call glGetError() at least once each time
the scene is rendered to make certain error conditions are noticed
while you are developing your application. Once development is
completed, removing the error checking can help improve
performance.
• Do not count on the error behavior of an OpenGL implementation—it
might change in a future release of OpenGL. For example, OpenGL 1.1
ignores matrix operations invoked between glBegin() and glEnd()
commands, but a future version might not. Put another way, OpenGL
error semantics may change between upward-compatible revisions.
• Check the extension string to verify that any extensions you want to
use are supported. This is particularly relevant for routines that must be
accessed through a function pointer retrieved by functions such as
glXGetProcAddress() or wglGetProcAddress().
• If you need to collapse all geometry to a single plane, use the projec-
tion matrix. If the modelview matrix is used, OpenGL features that
operate in eye coordinates (such as lighting and application-defined
clipping planes) might fail.
• Do not make extensive changes to a single matrix. For example, do not
animate a rotation by continually calling glRotate*() with an incre-
mental angle. Rather, use glLoadIdentity() to initialize the given
matrix for each frame, and then call glRotate*() with the desired
complete angle for that frame.
• Count on multiple passes through a rendering database to generate the
same pixel fragments only if this behavior is guaranteed by the invari-
ance rules established for a compliant OpenGL implementation. (See
Appendix G for details on the invariance rules.) Otherwise, a different
set of fragments might be generated.
• Do not expect errors to be reported while a display list is being defined.
The commands within a display list generate errors only when the list
is executed.
• Place the frustum’s near plane as far from the viewpoint as possible to
optimize the operation of the depth buffer.
• Call glFlush() to force all previous OpenGL commands to be executed.
Do not count on glGet*() or glIs*() to flush the rendering stream.
Query commands flush as much of the stream as is required to return
valid data but don’t guarantee completion of all pending rendering
commands.

OpenGL Correctness Tips 3
• Turn dithering off when rendering predithered images (for example,
when glCopyPixels() is called).
• Make use of the full range of the accumulation buffer. For example,
if accumulating four images, scale each by one-quarter as it is
accumulated.
• If exact two-dimensional rasterization is desired, you must carefully
specify both the orthographic projection and the vertices of primitives
that are to be rasterized. The orthographic projection should be speci-
fied with integer coordinates, as shown in the following example:
gluOrtho2D(0, width, 0, height);
where width and height are the dimensions of the viewport. Given this
projection matrix, polygon vertices and pixel image positions should
be placed at integer coordinates to rasterize predictably. For example,
glRecti(0, 0, 1, 1) reliably fills the lower left pixel of the viewport, and
glRasterPos2i(0, 0) reliably positions an unzoomed image at the lower
left of the viewport. Point vertices, line vertices, and bitmap positions
should be placed at half-integer locations, however. For example, a line
drawn from (x1, 0.5) to (x2, 0.5) will be reliably rendered along the
bottom row of pixels into the viewport, and a point drawn at (0.5, 0.5)
will reliably fill the same pixel as glRecti(0, 0, 1, 1).
An optimum compromise that allows all primitives to be specified at
integer positions, while still ensuring predictable rasterization, is to
translate x and y by 0.375, as shown in the following code fragment.
Such a translation keeps polygon and pixel image edges safely away
from the centers of pixels, while moving line vertices close enough to
the pixel centers.
glViewport(0, 0, width, height);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0, width, 0, height);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.375, 0.375, 0.0);
/* render all primitives at integer positions */
• Avoid using negative w vertex coordinates and negative q texture
coordinates. OpenGL might not clip such coordinates correctly and
might make interpolation errors when shading primitives defined by
such coordinates.

4Appendix F: Programming Tips
• Do not assume the precision of operations based on the data types
of parameters to OpenGL commands. For example, if you are using
glRotated(), you should not assume that the geometric processing
pipeline maintains double-precision floating-point accuracy during its
operation. It is possible that the parameters to glRotated() are con-
verted to a different data type before processing.
OpenGL Performance Tips
Following are some performance tips for your consideration, regardless of
whether of which rendering pipeline (i.e., fixed-function or programmable)
you’re using. Generally speaking, these tips will help improve the
performance of any application:
• Try to minimize state changes during rendering by grouping primitives
of like OpenGL state. When you issue a draw call (e.g., glVertex(),
glDrawArrays()), OpenGL does an internal state validation check,
usually called validation. Validation can be an expensive operation in
terms of performance, so it benefits your application’s performance to
minimize validations.
• Use query functions when your application requires just a few state
values for its own computations. If your application requires several
state values from the same attribute group, use glPushAttrib() and
glPopAttrib() to save and restore them.
• Some OpenGL implementations benefit from storing vertex data in
vertex arrays. Use of vertex arrays reduces function call overhead. Some
implementations can improve performance by engaging in batch
processing or reusing processed vertices.
• Generate object names (e.g., by calling glGen*()), rather than
assigning names of your own choosing. This practice is required for
OpenGL Version 3.1 and greater, but in versions prior to OpenGL
Version 3.1, user-assigned object names require a lookup in internal
implementation-specific tables (and almost always on the host CPU,
as compared to the GPU). This lookup may add significant overhead
to binding objects if a large number of names are used, especially if
identical names are used for different types of objects (e.g., if a texture
object and a pixel-buffer object use the same unsigned-integer value).
• In many cases, using indexed vertex arrays rendered with
glDrawElements() may take advantage of hardware caching of
transformed vertices.

OpenGL Performance Tips 5
• If the situation allows it, use gl*TexSubImage() to replace all or part of
an existing texture image, rather than the more costly operations of
deleting and creating an entire new image.
• If your OpenGL implementation supports a high-performance working
set of resident textures, try to make all of your textures resident—that
is, make them fit into the high-performance texture memory. If neces-
sary, reduce the size or internal format resolution of your textures until
they all fit into memory. If such a reduction creates intolerably fuzzy
textured objects, you may give some textures lower priority, which
will, when push comes to shove, leave them out of the working set.
• If you need to render the same pixel rectangle multiple times, store
the image in a texture map and render it by using a screen-aligned
quadrilateral rather than by calling glDrawPixels().
•Use a single glClear() call per frame if possible. Do not use glClear() to
clear small subregions of the buffers; use this routine only for complete
or nearly complete clears.
•Call glFinish() only when you are measuring the execution time of
OpenGL rendering. Remove this function from your program once
you’re done making measurements.
• OpenGL commands are automatically flushed (as if you had called
glFlush()) when a double-buffered window is swapped.
When using the fixed-function pipeline, here are some performance
considerations to keep in mind:
•Use glColorMaterial() when only a single material property is being
varied rapidly (at each vertex, for example). Use glMaterial() for
infrequent changes or when more than a single material property is
being varied rapidly.
•Use glLoadIdentity() to initialize a matrix, rather than load your own
copy of the identity matrix.
• Use specific matrix calls such as glRotate*(),glTranslate*(), and
glScale*(), rather than compose your own rotation, translation, or
scale matrices and call glMultMatrix().
• Use texture objects to encapsulate texture data. Place all the
glTexImage*() calls (including mipmaps) required to completely
specify a texture and the associated glTexParameter*() calls (which set
texture properties) into a texture object. Bind this texture object to
select the texture.

6Appendix F: Programming Tips
• Use evaluators even for simple surface tessellations to minimize
network bandwidth in client–server environments.
• Provide unit-length normals if it’s possible to do so, and avoid the
overhead of GL_NORMALIZE. Avoid using glScale*() when doing
lighting because it almost always requires that GL_NORMALIZE be
enabled.
•Set glShadeModel() to GL_FLAT if smooth shading isn’t required.
• Use a single call to glBegin(GL_TRIANGLES) to draw multiple
independent triangles, rather than calling glBegin(GL_TRIANGLES)
multiple times or calling glBegin(GL_POLYGON). Even if only a single
triangle is to be drawn, use GL_TRIANGLES, rather than GL_POLYGON.
Use a single call to glBegin(GL_QUADS) in the same manner, rather
than calling glBegin(GL_POLYGON) repeatedly. Likewise, use a single
call to glBegin(GL_LINES) to draw multiple independent line segments,
rather than calling glBegin(GL_LINES) multiple times.
• Favor the use of vertex buffer objects over display lists.
• In general, use the vector forms of commands to pass precomputed
data, and use the scalar forms of commands to pass values that are
computed near call time.
• Be sure to disable expensive rasterization and per-fragment operations
when drawing or copying images. OpenGL will even apply textures to
pixel images if asked.
• Unless absolutely necessary, avoid having different front and back
polygon modes.
When you’re using vertex or fragment shaders in your applications, here are
some tips that may help improve the application’s performance:
• Pack individual scalar values (such as uniform variables or vertex
attributes) into vector data types. In the case of uniform variables,
when the GLSL linker resolves scalar values, they are assigned unique
uniform vector values, even if only a single component of the vector is
used. Helping the linker out by making that mapping explicit in your
shader may improve performance.
• Using uniform buffer objects (in particular, the shader variety) will
help significantly reduce the overhead of loading uniform variables
when changing between shaders.

GLX Tips 7
GLX Tips
•Use glXWaitGL(), rather than glFinish(), to force X rendering com-
mands to follow GL rendering commands.
• Likewise, use glXWaitX(), rather than XSync(), to force GL rendering
commands to follow X rendering commands.
• Be careful when using glXChooseVisual(), because Boolean selections
are matched exactly. Since some implementations won’t export visu-
als with all combinations of Boolean capabilities, you should call
glXChooseVisual() several times with different Boolean values before
you give up. For example, if no single-buffered visual with the required
characteristics is available, check for a double-buffered visual with the
same capabilities. It might be available, and it’s easy to use.
This page intentionally left blank
1
Appendix G
G.OpenGL Invariance
OpenGL is not a pixel-exact specification. It therefore doesn’t guarantee an
exact match between images produced by different OpenGL implementa-
tions. However, OpenGL does specify exact matches, in some cases, for
images produced by the same implementation. This appendix describes the
invariance rules that define these cases.

2Appendix G: OpenGL Invariance
The obvious and most fundamental case is repeatability. A conforming
OpenGL implementation generates the same results each time a specific
sequence of commands is issued from the same initial conditions. Although
such repeatability is useful for testing and verification, it’s often not useful
to application programmers, because it’s difficult to arrange for equivalent
initial conditions. For example, rendering a scene twice, the second time
after swapping the front and back buffers, doesn’t meet this requirement.
Therefore, repeatability can’t be used to guarantee a stable, double-buffered
image.
A simple and useful algorithm that counts on invariant execution is erasing
a line by redrawing it in the background color. This algorithm works only if
rasterizing the line results in the same fragment (x, y) pairs being generated
in both the foreground and background color cases. OpenGL requires that
the coordinates of the fragments generated by rasterization be invariant
with respect to framebuffer contents; which color buffers are enabled for
drawing; the values of matrices other than those on the tops of the matrix
stacks; the scissor parameters; all writemasks; all clear values; the current
color, index, normal, texture coordinates, and edge-flag values; the current
raster color, raster index, and raster texture coordinates; and the material
properties. It is further required that exactly the same fragments be gener-
ated, including the fragment color values, when framebuffer contents, color
buffer enables, matrices other than those on the tops of the matrix stacks,
the scissor parameters, writemasks, or clear values differ.
OpenGL further suggests, but doesn’t require, that fragment generation be
invariant with respect to the matrix mode, the depths of the matrix stacks,
the alpha test parameters (other than alpha test enable), the stencil param-
eters (other than stencil enable), the depth test parameters (other than
depth test enable), the blending parameters (other than enable), the logical
operation (but not logical operation enable), and the pixel-storage and
pixel-transfer parameters. Because invariance with respect to several enables
isn’t recommended, you should use other parameters to disable functions
when invariant rendering is required. For example, to render invariantly with
blending enabled and disabled, set the blending parameters to GL_ONE
and GL_ZERO to disable blending, rather than call glDisable(GL_BLEND).
Alpha testing, stencil testing, depth testing, and the logical operation all
can be disabled in this manner.
Finally, OpenGL requires that per-fragment arithmetic, such as blending
and the depth test, is invariant to all OpenGL states except the state that
directly defines it. For example, the only OpenGL parameters that affect
how the arithmetic of blending is performed are the source and destination
blend parameters and the blend enable parameter. Blending is invariant to

Appendix G: OpenGL Invariance 3
all other state changes. This invariance holds for the scissor test, the alpha
test, the stencil test, the depth test, blending, dithering, logical operations,
and buffer writemasking.
As a result of all these invariance requirements, OpenGL can guarantee that
images rendered into different color buffers, either simultaneously or
separately using the same command sequence, are pixel-identical. This
holds for all the color buffers in the framebuffer or all the color buffers in
an off-screen buffer, but it isn’t guaranteed between the framebuffer and off-
screen buffers.
This page intentionally left blank
Appendix H
H.Calculating Normal Vectors
This appendix describes how to calculate normal vectors for surfaces.
You need to define normals to use the OpenGL lighting facility, which
is described in Chapter 5. “Normal Vectors” in Chapter 2 introduces nor-
mals and the OpenGL command for specifying them. This appendix goes
through the details of calculating them. It has the following major sections:
• “Finding Normals for Analytic Surfaces”
• “Finding Normals from Polygonal Data”
1

Since normals are perpendicular to a surface, you can find the normal at a
particular point on a surface by first finding the flat plane that just touches
the surface at that point. The normal is the vector that’s perpendicular to
that plane. On a perfect sphere, for example, the normal at a point on the
surface is in the same direction as the vector from the center of the sphere
to that point. For other types of surfaces, there are other, better means of
determining the normals, depending on how the surface is specified.
Recall that smooth curved surfaces are approximated by large numbers of
small flat polygons. If the vectors perpendicular to these polygons are used
as the surface normals in such an approximation, the surface appears fac-
eted, since the normal direction is discontinuous across the polygonal
boundaries. In many cases, however, an exact mathematical description
exists for the surface, and true surface normals can be calculated at every
point. Using the true normals improves the rendering considerably, as
shown in Figure H-1. Even if you don’t have a mathematical description,
you can do better than the faceted look shown in the figure. The two major
sections in this appendix describe how to calculate normal vectors for these
two cases:
• “Finding Normals for Analytic Surfaces” explains what to do when you
have a mathematical description of a surface.
• “Finding Normals from Polygonal Data” covers the case in which you
have only the polygonal data to describe a surface.
2Appendix H: Calculating Normal Vectors
Figure H-1 Rendering with Polygonal Normals versus True Normals

Finding Normals for Analytic Surfaces 3
Finding Normals for Analytic Surfaces
An analytic surface is a smooth, differentiable surface that is described by
a mathematical equation (or set of equations). In many cases, the easiest
surfaces to find normals for are analytic surfaces for which you have an
explicit definition in the following form:
V(s, t) = [ X(s, t)Y(s, t)Z(s, t) ]
where s and t are constrained to be in some domain, and X,Y, and Z are
differentiable functions of two variables. To calculate the normal, find
which are vectors tangent to the surface in the s- and t-directions. The cross
product
is perpendicular to both and, hence, to the surface. The following shows
how to calculate the cross product of two vectors. (Watch out for the
degenerate cases where the cross product has zero length.)
You should probably normalize the resulting vector. To normalize a vector
[xyz], calculate its length
and divide each component of the vector by the length.
As an example of these calculations, consider the analytic surface
V(s, t) = [ s2t3 3st ]
From this we have
[vx vy vz]
x
[wx wy wz] = [(vy wz−wyvz) (wx vz−vxwz) (vx wy−wxvy)]
Length = x2 + y2 + z2

4Appendix H: Calculating Normal Vectors
For example, when s =1 and t = 2, the corresponding point on the surface
is (1, 8, 1), and the vector (24, 2, 24) is perpendicular to the surface at that
point. The length of this vector is 34, so the unit normal vector is (24/34,
2/34, 24/34) = (0.70588, 0.058823, 0.70588).
For analytic surfaces that are described implicitly, as F(x, y, z) = 0, the prob-
lem is harder. In some cases, you can solve for one of the variables, say
z=G(x, y), and put it in the explicit form given previously:
Then continue as described earlier.
If you can’t get the surface equation in an explicit form, you might be able
to make use of the fact that the normal vector is given by the gradient
evaluated at a particular point (x, y, z). Calculating the gradient might be
easy, but finding a point that lies on the surface can be difficult. As an
example of an implicitly defined analytic function, consider the equation
of a sphere of radius 1 centered at the origin:
x2 + y2 + z2 1 = 0
This means that
F(x,y,z) = x2 + y2 + z2 1
which can be solved for z to yield
Thus, normals can be calculated from the explicit form
as described previously.
V(s, t) = [ s t G(s, t) ]
z = +1− x2− y2
V(s, t)= [s t 1 − s2− t2]

Finding Normals from Polygonal Data 5
If you could not solve for z, you could have used the gradient
as long as you could find a point on the surface. In this case, it’s not so hard
to find a point—for example, (2/3, 1/3, 2/3) lies on the surface. Using the
gradient, the normal at this point is (4/3, 2/3, 4/3). The unit-length normal
is (2/3, 1/3, 2/3), which is the same as the point on the surface, as expected.
Finding Normals from Polygonal Data
As mentioned previously, you often want to find normals for surfaces that
are described with polygonal data such that the surfaces appear smooth
rather than faceted. In most cases, the easiest way to do this (although it
might not be the most efficient way) is to calculate the normal vectors for
each of the polygonal facets and then average the normals for neighboring
facets. Use the averaged normal for the vertex that the neighboring facets
have in common. Figure H-2 shows a surface and its polygonal approxima-
tion. (Of course, if the polygons represent the exact surface and aren’t
merely an approximation—if you’re drawing a cube or a cut diamond, for
example—don’t do the averaging. Calculate the normal for each facet as
described in the following paragraphs, and use that same normal for each
vertex of the facet.)
To find the normal for a flat polygon, take any three vertices v1,v2, and v3
of the polygon that do not lie in a straight line. The cross product
[v1v2]u [v2v3]
is perpendicular to the polygon. (Typically, you want to normalize the
resulting vector.) Then you need to average the normals for adjoining facets
to avoid giving too much weight to one of them. For instance, in the exam-
ple shown in Figure H-2, if n1,n2,n3, and n4 are the normals for the four
polygons meeting at point P, calculate n1+n2+n3+n4 and then normalize
it. (You can get a better average if you weight the normals by the size of the
angles at the shared intersection.) The resulting vector can be used as the
normal for point P.
F = 2x 2y 2z
∇
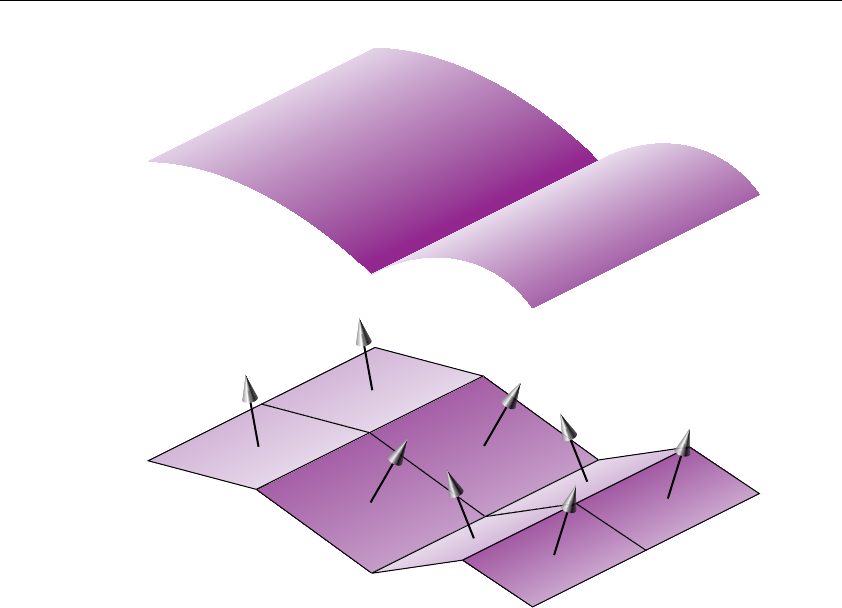
6Appendix H: Calculating Normal Vectors
Sometimes, you need to vary this method for particular situations. For
instance, at the boundary of a surface (such as point Q in Figure H-2), you
might be able to choose a better normal based on your knowledge of how
the surface should look. Sometimes the best you can do is average the
polygon normals on the boundary as well. Similarly, some models have
some smooth parts and some sharp corners (point R is on such an edge in
Figure H-2). In this case, the normals on either side of the crease shouldn’t
be averaged. Instead, polygons on one side of the crease should be drawn
with one normal, and polygons on the other side with another.
n1
n3n2
n4
Q
P
R
Figure H-2 Averaging Normal Vectors

1
Appendix I
I.Built-In OpenGL Shading Language
Variables and Functions
The OpenGL Shading Language, commonly called the “GLSL,” defines
a number of variables for matching OpenGL state and large set of
convenience functions. This appendix1 provides a complete list of GLSL
built-in variables and functions.
1This appendix is adapted from The OpenGLShading Language Specification (Versions 1.30 and
1.40) by John Kessenich.

2Appendix I: Built-In OpenGL Shading Language Variables and Functions
The OpenGL Shading Language has been updated including deprecating
and removing some features.
Version 1.30 of GLSL added numerous new functions and data types, while
maintaining complete backward compatibility with previous versions of
GLSL. No features were removed through deprecation, although various
variables and state were deprecated.
Version 1.40, while aligning with the removed features of OpenGL,
removed several features as well. Those removed features are made available
again if the GL_ARB_compatibility extension is available with your
implementation. Removed features (which are supported with the
compatibility extension) are listed in the margin.
Variables
For OpenGL versions up to and including 3.0, much of the OpenGL
state associated with the fixed-function pipeline that an application can
configure is also available as variables from within a GLSL shader. The next
sections describe all state variables available to shaders, and any restrictions
on their use.
Vertex Shader Input Attribute Variables
Table I-1 lists the set of global attribute values reflecting the per-vertex input
data that can be accessed exclusively from within a vertex shader. Almost
all of these values were deprecated in Version 1.30.
Variable Name Type Specifying Function Description
gl_Vertex vec4 glVertex Vertex’s world-space
coordinate
gl_Color vec4 glColor Primary color value
gl_SecondaryColor vec4 glSecondaryColor Secondary color value
gl_Normal vec3 glNormal Lighting normal
Table I-1 Global Vertex Shader Attribute Variables
Compatibility
Extension
gl_Vertex
gl_Color
gl_
SecondaryColor
gl_Normal
gl_
MultiTexCoordn

Variables 3
Vertex Shader Special Output Variables
The following variables are used in later stages of the vertex processing
pipeline, and are only available in vertex shaders.
In particular, the gl_Position variable is the only required output of vertex
shaders, and specifies the final, projected position of the input vertex.
Generally, this is accomplished by directly multiplying the input vertex by
the combined modelview and projection transformations, as in the
following example:
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
Table I-2 enumerates the special output variables of a vertex shader.
gl_MultiTexCoordnvec4 glMultiTexCoord( n, })Texture unit n’s texture
coordinates, with
n = 0 ... 7.
gl_FogCoord float glFogCoord Fog coordinate
gl_VertexID int —Index value of current
vertex
gl_InstanceID int —Instance index of
current rendering
primitive
Variable Name Type Description
gl_Position vec4 Transformed vertex position.
gl_PointSize float Point size (in pixels) of output vertex. This
value overrides the current OpenGL setting if
glEnable(GL_VERTEX_PROGRAM_POINT_SIZE);
has been called.
gl_ClipDistance[] float Distances from the vertex to each clipping plane.
(This variable replaces gl_ClipVertex from
GLSL 1.20.)
Table I-2 Special Vertex Shader Output Variables
Variable Name Type Specifying Function Description
Table I-1 (continued) Global Vertex Shader Attribute Variables
Compatibility
Extension
gl_ClipVertex
4Appendix I: Built-In OpenGL Shading Language Variables and Functions
Vertex Shader Output Varying Variables
While user-defined varying variables are shared between vertex and
fragment shaders, certain OpenGL-defined varying variables are accessible
only in vertex shader, with their values being assigned to a unique set of
(corresponding, but differently named) varying values that are available
only in fragment shaders.
Table I-3 lists the variables that are only available in vertex shaders.
Table I-4 lists the set of input varying variables available in fragment
shaders.
Variable Name Type Description
gl_FrontColor vec4 Primary color to be used for front-facing
primitives
gl_BackColor vec4 Primary color to be used for back-facing
primitives
gl_FrontSecondaryColor vec4 Secondary color to be used for front-facing
primitives
gl_BackSecondaryColor vec4 Secondary color to be used for back-facing
primitives
gl_TexCoord[n] vec4 nth Texture coordinates values
gl_FogFragCoord vec4 Fragment fog coordinate value
Table I-3 Varying Vertex Shader Output Variables
Variable Name Type Description
gl_Color vec4 Primary color of the fragment
gl_SecondaryColor bool Secondary color of the fragment
gl_TexCoord[n] vec4 nth Texture coordinates for the fragment
gl_FogFragCoord float Fragment’s fog coordinate
gl_PointCoord vec2 Fragment’s coordinates when point sprites are
enabled
Table I-4 Varying Fragment Shader Input Variables
Compatibility
Extension
gl_Front*Color
gl_Back*Color
gl_TexCoord
gl_FogFragCoord
Compatibility
Extension
gl_*Color
gl_TexCoord
gl_FogFragCoord

Variables 5
Built-In Implementation Constants
Most implementation-dependent maximum values are reflected as constant
integer variables accessible in both vertex and fragment shaders. The
variables listed in Table I-5 represent the minimum capabilities of an
OpenGL implementation, and all are represented as a single constant
integer expression.
Variable Name Default
Value
Description
gl_MaxLights 8 Number of lights
gl_MaxClipPlanes 6 Number of user-defined clipping
planes
gl_MaxTextureUnits 16 Number of texture units
gl_MaxTextureCoords 2 Number of texture-coordinates
supported.
gl_MaxVertexAttribs 16 Number of vec4 sets of vertex
attributes
gl_MaxVertexUniformComponents 1024 Number of vec4 uniform
variables available for a vertex
shader
gl_MaxVaryingFloats 64 Number of varying float variables
gl_MaxVertexTextureImageUnits 16 Number of texture units available
from within a vertex shader
gl_MaxCombinedTextureImageUnits 16 Total number of texture units
available for both vertex and
fragment shaders
gl_MaxTextureImageUnits 16 Number of texture units available
from within a fragment shader
gl_MaxFragmentUniformComponents 1024 Number of vec4 uniform
variables available from a
fragment shader
Table I-5 Implementation Maximum Value Variables
Compatibility
Extension
gl_MaxClipPlanes
gl_MaxVarying
Floats
6Appendix I: Built-In OpenGL Shading Language Variables and Functions
Built-In Uniform State Variables
The following sets of variables are available in both vertex and fragment
shaders, and reflect the OpenGL state settings specified by the application.
Note: All built-in uniform state, with the exception of gl_DepthRange,
was deprecated in GLSL 1.30, and effectively removed. All of the
functionality is available if your implementation includes the
GL_ARB_compatibility extension.
Transformation Matrix State
The following variables represent the matrix transformation states
of OpenGL. Various matrices are derived from the values set within an
OpenGL application. For example, lighting normals (see “Define Normal
Vectors for Each Vertex of Every Object” in Chapter 5) are transformed by
the inverse-transpose of the upper-left 3 u3 part of the modelview matrix,
which is automatically computed for you when changes are made to the
modelview matrix and presented using the gl_NormalMatrix variable.
Derived matrices (particularly those involving matrix inverses) may be
undefined if the source matrix is ill-conditioned or singular.
Table I-6 lists the available matrices in GLSL.
gl_MaxDrawBuffers 8 Number of buffers available
for simultaneous output from
within a fragment shader using
gl_FragData
gl_MaxClipDistances 8 Number of distances to user-
defined clipping planes
Variable Name Type Description
gl_ModelViewMatrix mat4 Current modelview matrix
gl_ProjectionMatrix mat4 Current projection matrix
Table I-6 Transformation Matrix Variables
Variable Name Default
Value
Description
Table I-5 (continued) Implementation Maximum Value Variables
Compatibility
Extension
All fixed-function
matrices

Variables 7
gl_ModelViewProjectionMatrix mat4 Product of the modelview and
projection matrices
gl_TextureMatrix[n] mat4 Texture matrix for texture
unit n. The maximum
dimension of the array is
gl_MaxTextureCoords.
gl_NormalMatrix mat3 Inverse-transpose of the upper
3u3 of the modelview matrix
gl_ModelViewMatrixInverse mat4 Inverse of the modelview
matrix
gl_ProjectionMatrixInverse mat4 Inverse of the projection
matrix
gl_ModelViewProjectionMatrixInverse mat4 Inverse of combined
modelview and projection
matrices
gl_TextureMatrixInverse[n] mat4 Inverse of texture matrix n
gl_ModelViewMatrixTranspose mat4 Transpose of the modelview
matrix
gl_ProjectionMatrixTranspose mat4 Transpose of the projection
matrix
gl_ModelViewProjectionMatrixTranspose mat4 Inverse of the combined
modelview and projection
matrix
gl_TextureMatrixTranspose[n] mat4 Transpose of texture
matrix n
gl_ModelViewMatrixInverseTranspose mat4 Inverse-transpose of the
modelview matrix
gl_ProjectionMatrixInverseTranspose mat4 Inverse-transpose of the
projection matrix
gl_ModelViewProjection
MatrixInverseTranspose
mat4 Inverse-transpose of the
combined modelview and
projection matrix
gl_TextureMatrixInverseTranspose[n] mat4 Inverse-transpose of texture
matrix n
Variable Name Type Description
Table I-6 (continued) Transformation Matrix Variables

8Appendix I: Built-In OpenGL Shading Language Variables and Functions
Lighting Normal Normalization State
Vertex normals can be normalized within a shader by using the normalize()
function. However, if normals were uniformly scaled (all calls to glScale()
had the same values for x,y, and z), they could be normalized by a simple
scaling operation (thus saving the potentially expensive square root
operation required by normalize()). The scaling factor is stored in:
uniform float gl_NormalScale;
and applied as
vec3 normal = gl_NormalScale * gl_Normal;
Depth Range State
Access to the depth range values (as set by glDepthRange()) can be accessed
using:
struct gl_DepthRangeParameters {
float near;
float far;
float diff;
};
uniform gl_DepthRangeParameters gl_DepthRange;
Table I-7 provides descriptions for each of the depth range variables.
User-Defined Clipping Planes
Access to the user-defined clipping planes (as specified by glClipPlane())
can be accessed in a shader through the array:
uniform vec4 gl_ClipPlane[gl_MaxClipPlanes];
Variable Name Type Description
gl_DepthRange.near float Depth value that vertices at the near
clipping plane are mapped to
gl_DepthRange.far float Depth value that vertices at the far clipping
plane are mapped to
gl_DepthRange.diff float Difference between the near and far depth
range values, computed as (far – near)
Table I-7 Depth Range Variables
Compatibility
Extension
gl_ClipPlanes

Variables 9
Point Parameter
Parameters controlling the size and shading of points are controlled by the
state set by calling glPointParameter(). The following structure allows
access to all point parameter settings:
struct gl_PointParameters {
float size;
float sizeMin;
float sizeMax;
float fadeThresholdSize;
float distanceConstantAttenuation;
float distanceLinearAttenuation;
float distanceQuadraticAttenuation;
};
uniform gl_PointParameters gl_Point;
The variables associated with point sizes and parameters are listed in
Table I-8.
Variable Name Type Description
gl_Point.size float Current point-size setting
gl_Point.sizeMin float Minimum value for derived
point sizes
gl_Point.sizeMax float Maximum value for derived
point sizes
gl_Point.fadeThresholdSize float Threshold value for selecting
whether to fade a point’s
alpha value
gl_Point.distanceConstantAttenuation float Constant coefficient for point
attenuation computations
gl_Point.distanceLinearAttenuation float Linear coefficient for point
attenuation computations
gl_Point.distanceQuadraticAttenuation float Quadratic coefficient for
point attenuation
computations
Table I-8 Point Size and Attenuation Variables
Compatibility
Extension
gl_Point

10 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Material State
Material state, as specified by calling glMaterial(), can be queried by
utilizing the values in the following structure, which stores material
properties for both the front- and back-material state:
struct gl_MaterialParameters {
vec4 emission;
vec4 ambient;
vec4 diffuse;
vec4 specular;
float shininess;
};
uniform gl_MaterialParameters gl_FrontMaterial;
uniform gl_MaterialParameters gl_BackMaterial;
Table I-9 lists the material variables and their descriptions.
Lighting State
The state associated with each light in OpenGL is stored in the following
structure. For this section, the notation described in “The Mathematics of
Lighting” on page 240 is used.
struct gl_LightSourceParameters {
vec4 ambient;
vec4 diffuse;
vec4 specular;
vec4 position;
Variable Name Type Description
gl_FrontMaterial.emission
gl_BackMaterial.emission
vec4 Emission color for material
gl_FrontMaterial.ambient
gl_BackMaterial.ambient
vec4 Ambient color for material
gl_FrontMaterial.diffuse
gl_BackMaterial.diffuse
vec4 Diffuse color for material
gl_FrontMaterial.specular
gl_BackMaterial.specular
vec4 Specular color for material
gl_FrontMaterial.shininess
gl_BackMaterial.shininess
float Shininess color for material
Table I-9 Lighting Material Variables
Compatibility
Extension
gl_FrontMaterial
gl_BackMaterial
Compatibility
Extension
gl_LightSource
gl_LightModel
gl_
FrontLightProduct
gl_
BackLightProduct

Variables 11
vec4 halfVector;
vec3 spotDirection;
float spotExponent;
float spotCutoff;
float spotCosCutoff;
float constantAttenuation;
float linearAttenuation;
float quadraticAttenuation;
};
uniform gl_LightSourceParameters gl_LightSource[gl_MaxLights];
Table I-10 provides a list of the parameters associated with each light source
available in a shader.
Variable Name Type Description
gl_LightSource[n].ambient vec4 Ambient color for light n
gl_LightSource[n].diffuse vec4 Diffuse color for light n
gl_LightSource[n].specular vec4 Specular color for light n
gl_LightSource[n].position vec4 World-coordinate position for
light n
gl_LightSource[n].halfVector vec4 Lighting half-vector for light n
gl_LightSource[n].spotDirection vec3 Spotlight direction for light n
gl_LightSource[n].spotExponent float Spotlight exponent for light n
gl_LightSource[n].spotCutoff float Spotlight cutoff angle for
light n
gl_LightSource[n].spotCosCutoff float Cosine of the spotlight cutoff
angle for light n
gl_LightSource[n].constantAttenuation float Constant coefficient for
attenuation computation for
light n
gl_LightSource[n].linearAttenuation float Linear coefficient for
attenuation computation for
light n
gl_LightSource[n].quadraticAttenuation float Quadratic coefficient for
attenuation computation for
light n
Table I-10 Light Source Variables

12 Appendix I: Built-In OpenGL Shading Language Variables and Functions
The following structure contains the values for the light-model parameters.
struct gl_LightModelParameters {
vec4 ambient;
};
uniform gl_LightModelParameters gl_LightModel;
The values associated with the light model are described in Table I-11.
To help reduce the computation required for computing the colors based on
OpenGL’s Phone lighting model, the non-light dependent terms of the
lighting equation (the emission and ambient material terms) combined
with the light model ambient value are cached in the following structure
and are described in Table I-12.
struct gl_LightModelProducts {
vec4 sceneColor;
};
uniform gl_LightModelProducts gl_FrontLightModelProduct;
uniform gl_LightModelProducts gl_BackLightModelProduct;
Similarly, various products of constant factors of the material and lights are
cached in the following structure and described in Table I-13.
struct gl_LightProducts
vec4 ambient;
vec4 diffuse;
vec4 specular;
};
Variable Name Type Description
gl_LightModel.ambient vec4 Light model’s ambient color
Table I-11 Light Model Variables
Variable Name Type Description
gl_FrontLightModelProduct.sceneColor
gl_BackLightModelProduct.sceneColor
vec4 emissionmaterial + ambientmaterial *
ambientlight model
Table I-12 Cached Light Model Value Variables

Variables 13
uniform gl_LightProducts gl_FrontLightProduct[gl_MaxLights];
uniform gl_LightProducts gl_BackLightProduct[gl_MaxLights];
Texture Environment State
The texture environment color (as specified by glTexEnv()) for each texture
unit is available by accessing:
uniform vec4 gl_TextureEnvColor[gl_MaxTextureImageUnits];
Texture Coordinate Generation State
The user-defined planes for texture coordinate generation are available
by accessing the following sets of values, one for each set of texture
coordinates:
uniform vec4 gl_EyePlaneS[gl_MaxTextureCoords];
uniform vec4 gl_EyePlaneT[gl_MaxTextureCoords];
uniform vec4 gl_EyePlaneR[gl_MaxTextureCoords];
uniform vec4 gl_EyePlaneQ[gl_MaxTextureCoords];
uniform vec4 gl_ObjectPlaneS[gl_MaxTextureCoords];
uniform vec4 gl_ObjectPlaneT[gl_MaxTextureCoords];
uniform vec4 gl_ObjectPlaneR[gl_MaxTextureCoords];
uniform vec4 gl_ObjectPlaneQ[gl_MaxTextureCoords];
Fog
The state associated with fog and atmospheric effects (see “Fog” in
Chapter 6) in OpenGL is stored in the following structure and described
in Table I-14.
Variable Name Type Description
gl_FrontLightProduct[n].ambient
gl_BackLightProduct[n].ambient
vec4 ambientmaterial ambientlight
gl_FrontLightProduct[n].diffuse
gl_BackLightProduct[n].diffuse
vec4 (max {L · n, 0}) diffuselight
diffusematerial
gl_FrontLightProduct[n].specular
gl_BackLightProduct[n].specular
vec4 (max {s·n, 0})shininess
specularlight specularmaterial
Table I-13 Cached Light Product Value Variables
Compatibility
Extension
gl_EyePlane*
gl_ObjectPlane*
Compatibility
Extension
gl_Fog
14 Appendix I: Built-In OpenGL Shading Language Variables and Functions
struct gl_FogParameters {
vec4 color;
float density;
float start;
float end;
float scale;
};
uniform gl_FogParameters gl_Fog;
Built-In Functions
Angle Conversion and Trigonometric Functions
Table I-15 describes the trigonometric functions available in GLSL shaders.
Angles are measured in radians, and the following commands operate on
each component separately. TYPE represents one of float, vec2, vec3, or vec4.
Variable Name Type Description
gl_Fog.color vec4 Fog color
gl_Fog.density float Fog density
gl_Fog.start float Starting distance for linear fog
gl_Fog.end float Ending distance for linear fog
gl_Fog.scale float Scaling factor for linear fog. This value is
computed as
Table I-14 Fog Variables and Cached Values
Function Syntax Description
TYPE radians(TYPE degrees)Returns
TYPE degrees(TYPE radians)Returns
Table I-15 Angle Conversion and Trigonometric Functions
scale 1
end start–
----------------------------=
S
180
---------
©¹
§·
degrees
180
S
---------
©¹
§·
radians

Built-In Functions 15
TYPE sin(TYPE angle) Returns the sine of angle
TYPE cos(TYPE angle) Returns the cosine of angle
TYPE tan(TYPE angle) Returns the tangent of angle
TYPE asin(TYPE x) Returns the arcsine (sin–1) of x. The range of
values returned by this function is [–S/2, S/2],
and the result is undefined if |x| > 1.
TYPE acos(TYPE x) Returns the arccosine (cos–1) of x. The range of
values returned by this function is [0, S], and
the result is undefined if |x| > 1.
TYPE atan(TYPE y,TYPE x) Returns the arctangent (tan–1) of y/x. The signs
of x and y are used to determine what
quadrant the angle is in. The range of values
returned by this function is [–S,S], and the
result is undefined if x and yare both 0.
TYPE atan(TYPE y_over_x) Returns the arctangent (tan–1) of y_over_x. The
range of values returned by this function is
[–S/2, S/2]
TYPE sinh(TYPE x) Returns the hyperbolic sine of x, which is
defined as
TYPE cosh(TYPE x) Returns the hyperbolic cosine of x, which is
defined as
TYPE tanh(TYPE x) Returns the hyperbolic tangent of x, which is
defined as
TYPE asinh(TYPE x) Returns the arc (inverse) hyperbolic sine of x.
TYPE acosh(TYPE x) Returns the arc (inverse) hyperbolic cosine
of x.
TYPE atanh(TYPE x) Returns the arc (inverse) hyperbolic tanget
of x.
Function Syntax Description
Table I-15 (continued) Angle Conversion and Trigonometric Functions
exex–
–
2
------------------
exex–
+
2
------------------
xsinh
xcosh
--------------------
16 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Transcendental Functions
Table I-16 lists the logarithmic and exponential functions available
in GLSL. The commands operate on each component separately. TYPE
represents one of float, vec2, vec3, or vec4.
Basic Numerical Functions
Table I-17 lists the basic numerical functions that GLSL supports. Each
command operates on each component separately. TYPE represents one of
float, vec2, vec3, or vec4. iTYPE represents one of int, ivec2, ivec3, or ivec4.
Similarly, uTYPE represents one of uint, uvec2, uvec3, or uvec4.
Function Syntax Description
TYPE pow(TYPE x,TYPE y) Returns xy. Results are undefined if x < 0, or if
x = 0 and yd0
TYPE exp(TYPE x) Returns ex.
TYPE log(TYPE x) Returns ln(x). Results are undefined if xd 0
TYPE exp2(TYPE x) Returns 2x.
TYPE log2(TYPE x) Returns log2(x). Results are undefined if xd 0.
TYPE sqrt(TYPE x) Returns . Results are undefined if x d0.
TYPE inversesqrt(TYPE x)Returns . Results are undefined if xd0.
Table I-16 Transcendental Functions
Function Syntax Description
TYPE abs(TYPE x)
iTYPE abs(iTYPE x
Returns
TYPE sign(TYPE x)
iTYPE sign(iTYPE x)Returns
Table I-17 Basic Numerical Functions
x
1
x
-------
x
1x0!
0x0=
1–x0
¯
°
®
°

Built-In Functions 17
TYPE floor(TYPE x) Returns a value equal to the nearest
integer that is less than or equal to x
TYPE ceil(TYPE x) Returns a value equal to the nearest
integer that is greater than or equal to x
TYPE fract(TYPE x) Returns x - floor(x)
TYPE trunc(TYPE x) Returns the nearest integer to x whose
absolute value is not greater than the
absolute value of x
TYPE round(TYPE x) Returns the nearest integer to x rounded
in an implementation-dependent
manner, presumably using the fastest
computational approach.
TYPE roundEven(TYPE x) Returns the nearest even integer to x by
adding 0.5. For example, 3.5 and 4.5,
would both round to 4.0.
TYPE mod(TYPE x, float y)
TYPE mod(TYPE x,TYPE y)
Returns the floating-point modulus:
x – y floor (x/y)
TYPE modf(TYPE x, out TYPE i) Returns the fractional part of x and sets
i to the integer part of x. Both the return
value and i will have the same sign as x.
TYPE min(TYPE x,TYPE y)
TYPE min(TYPE x, float y)
iTYPE min(iTYPE x, iTYPE y)
iTYPE min(iTYPE x, int y)
uTYPE min(uTYPE x,uTYPE y)
uTYPE min(uTYPE x, uint y)
Returns x < y ? x : y;
TYPE max(TYPE x,TYPE y)
TYPE max(TYPE x, float y)
iTYPE max(iTYPE x, iTYPE y)
iTYPE max(iTYPE x, int y)
uTYPE max(uTYPE x,uTYPE y)
uTYPE max(uTYPE x, uint y)
Returns x > y ? x : y;
Function Syntax Description
Table I-17 (continued) Basic Numerical Functions

18 Appendix I: Built-In OpenGL Shading Language Variables and Functions
TYPE clamp(TYPE x,TYPE minVal,
TYPE maxVal)
TYPE clamp(TYPE x, float minVal,
float maxVal)
iTYPE clamp(iTYPE x, iTYPE minVal,
iTYPE maxVal)
iTYPE clamp(iTYPE x, int minVal,
int maxVal)
uTYPE clamp(uTYPE x, uTYPE minVal,
uTYPE maxVal)
uTYPE clamp(uTYPE x, uint minVal,
uint maxVal)
Returns
min(max(x, minVal), maxVal)
TYPE mix(TYPE x,TYPE y,TYPE a)
TYPE mix(TYPE x,TYPE y, float a)
Returns x (1 – a) + y a
TYPE mix(TYPE x,TYPE y,bvec a) Returns ai ? xi : yi for each component
of a.
TYPE step(TYPE edge,TYPE x)
TYPE step(float edge,TYPE x)
Returns x < edge ? 0.0 : 1.0;
TYPE smoothstep(TYPE edge0,
TYPE edge1, TYPE x)
TYPE smoothstep(float edge0,
float edge1, TYPE x)
Returns
where
bvec isnan(TYPE x) Returns true if x is NaN (not a number),
false otherwise.
bvec isinf(TYPE x) Returns true if x is either positive or
negative infinity (based on the
underlying floating-point
representation), false otherwise.
Function Syntax Description
Table I-17 (continued) Basic Numerical Functions
0.0 xedge0d
t32t2
–edge0x edge1
1.0 xedge1t
¯
°
®
°
tx edge0–
edge1edge0–
------------------------------------=

Built-In Functions 19
Vector-Operation Functions
Table I-18 describes the vector operations in GLSL. The following
commands operate on their arguments as vectors. Where not explicitly
specified, TYPE represents one of: float, vec2, vec3, or vec4.
Function Syntax Description
float length(TYPE x) Returns the length of vector x:
sqrt (x[0] x[0] + x[1] x[1] + ...)
float distance(TYPE p0,TYPE p1) Returns the distance between p0 and p1:
length (p0 – p1)
float dot(TYPE x,TYPE y) Returns the dot product of xand y:
result = x[0] y[0] + x[1] y[1] + ...
vec3 cross(vec3 x, vec3 y) Returns the cross product of x and y, i.e.,
result.x = x[1] y[2] - y[1] x[2]
result.y = x[2] y[0] - y[2] x[0]
result.z = x[0] y[1] - y[0] x[1]
TYPE normalize(TYPE x) Returns a vector in the same direction as x
but with a length of 1.
vec4 ftransform() Returns the transformed input vertex such
that it matches the output of the fixed-
function vertex pipeline.
TYPE faceforward(TYPE N,
TYPE I,TYPE Nref)
Returns dot (Nref,I) < 0 ? N : –N
TYPE reflect(TYPE I,TYPE N) Returns the reflection direction for incident
vector I, given the normalized surface
orientation vector N:
result = I – 2 dot(N, I)N
TYPE refract(TYPE I,TYPE N,
float eta)
Returns the refracted vector R, given the
normalized incident vector I, normalized
surface normal N, and ratio of indices of
refraction eta. The refracted vector is
computed in the following manner:
Table I-18 Vector-Operation Functions
Compatibility
Extension
ftransform()
k1eta21N
ˆI
ˆ
x
2
––=
R0k0
eta I
ˆetaN
ˆI
ˆ
xk+N
ˆ
–k0!
¯
®
=

20 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Matrix Functions
As compared to standard matrix multiplication, which is defined using
the operator, the matrixCompMult() routine, described in Table I-19,
produces a component-wise multiplication of two equally dimensioned
matrices.
Function Syntax Description
mat matrixCompMult(mat x, mat y) Multiply matrix xby matrix y
component-wise, i.e., resultij is the
scalar product of xij and yij.
mat2 outerProduct(vec2 c, vec2 r)
mat3 outerProduct(vec3 c, vec3 r)
mat4 outerProduct(vec4 c, vec4 r)
mat2x3 outerProduct(vec3 c, vec2 r)
mat3x2 outerProduct(vec2 c, vec3 r)
mat2x4 outerProduct(vec4 c, vec2 r)
mat4x2 outerProduct(vec2 c, vec4 r)
mat3x4 outerProduct(vec4 c, vec3 r)
mat4x3 outerProduct(vec3 c, vec4 r)
Generates a cur matrix by computing
the outer matrix product (also called
the tensor product).
mat2 transpose(mat2 m)
mat3 transpose(mat3 m)
mat4 transpose(mat4 m)
mat2x3 transpose(mat3x2 m)
mat3x2 transpose(mat2x3 m)
mat2x4 transpose(mat4x2 m)
mat4x2 transpose(mat2x4 m)
mat3x4 transpose(mat4x3 m)
mat4x3 transpose(mat3x4 m)
Return the transpose of the matrix m.
The input matrix is not modified.
Table I-19 Matrix Functions

Built-In Functions 21
Vector-Component Relational Functions
The following functions produce a vector of Boolean values representing
the results of the specified operation conducted on each pair of components
from the input vectors. TYPE represents any of vec2, vec3, vec4, ivec2,
ivec3, ivec4, uvec2, uvec3, or uvec4 in the prototypes below, or a Boolean
vector when explicitly specified. The input vectors must be of the same
type, and the Boolean vector returned, represented by bvec below, will have
the same size at the input vectors.
Table I-20 describes the accepted vector functions.
Texture Lookup Functions
Texture lookup functions are available to both vertex and fragment shaders
if supported by the underlying OpenGL implementation. All of these
Function Syntax Description
bvec lessThan(TYPE x, TYPE y) Returns the component-wise
compare of x<y.
bvec lessThanEqual(TYPE x, TYPE y) Returns the component-wise
compare of xdy.
bvec greaterThan(TYPE x, TYPE y) Returns the component-wise
compare of x>y.
bvec greaterThanEqual(TYPE x, TYPE y) Returns the component-wise
compare of xty.
bvec equal(TYPE x, TYPE y)
bvec equal(bvec x, bvec y)
Returns the component-wise
compare of x== y.
bvec notEqual(TYPE x, TYPE y)
bvec notEqual(bvec x, bvec y)
Returns the component-wise
compare of x!= y.
bool any(bvec x) Returns true if any component of x
is true.
bool all(bvec x) Returns true only if all components
of xare true.
bvec not(bvec x) Returns the component-wise
logical complement of x.
Table I-20 Vector Component Operation Functions

22 Appendix I: Built-In OpenGL Shading Language Variables and Functions
functions rely on the use of samplers, which provide a handle for accessing
the texture map specified by the application using the OpenGL API. The
different types of samplers are detailed in “Accessing Texture Maps in
Shaders” in Chapter 15.
In the following tables, sampler types (e.g., floating point, signed, and
unsigned integer) are generically represented by “SAMPLER” with the
specific texture type appended (e.g., SAMPLER2DArray). Likewise, optional
parameters are denoted in square brackets ([...]).
The functions in Tables I-29 through I-32 provide access to textures through
samplers, as set up through the OpenGL API. Texture properties such as size,
pixel format, number of dimensions, filtering method, number of mip-map
levels, depth comparison, and so on are also defined by OpenGL API calls.
Such properties are taken into account as the texture is accessed via the
built-in functions defined below.
Texture Sizes Access Functions
The following routines will return the sizes (as a set of integers) for each
dimension of a texture level (lod):
Function Syntax Description
int textureSize(SAMPLER1D sampler, int lod)
ivec2 textureSize(SAMPLER2D sampler, int lod)
ivec3 textureSize(SAMPLER3D sampler, int lod)
ivec2 textureSize(SAMPLERCube sampler, int lod)
int textureSize(SAMPLER1DShadow sampler, int lod)
ivec2 textureSize(SAMPLER2DShadow sampler, int lod)
ivec2 textureSize(SAMPLERCubeShadow sampler, int lod)
ivec2 textureSize(SAMPLER1DArray sampler, int lod)
ivec3 textureSize(SAMPLER2DArray sampler, int lod)
ivec2 textureSize(SAMPLER1DArrayShadow sampler, int lod)
ivec3 textureSize(SAMPLER2DArrayShadow sampler, int lod)
Added in GLSL 1.40:
ivec2 textureSize(SAMPLER2DRect sampler, int lod)
ivec2 textureSize(SAMPLER2DRectShadow sampler, int lod)
int textureSize(SAMPLERBuffer sampler, int lod)
Returns the
dimensions of the
specified lod for the
texture addressed
by sampler. For
multi-dimensional
textures, the width,
height, and depth
of the texture (or
the number of
layers for array
textures) are
returned in that
order.
Table I-21 Texture Size Access Functions

Built-In Functions 23
Basic Texture Access Functions
The following functions use the provided texture coordinates to retrieve a
texel from the texture map associated with sampler.
All forms are accepted by fragment shaders. Functions with the bias
parameter are not accepted in vertex shaders.
The optional bias parameter is used to alter which mipmap is sampled (see
“Calculating the Mipmap Level” in Chapter 9). If a bias value is provided
while accessing a texture that does not contain mipmaps, the texture is
accessed directly, and the value is ignored. The bias forms of the texture
functions are available only in fragment shaders.
Function Syntax Description
gvec4 texture(SAMPLER1D sampler, float coord
[, float bias])
gvec4 texture(SAMPLER2D sampler, vec2 coord
[, float bias])
gvec4 texture(SAMPLER3D sampler, vec3 coord
[, float bias])
gvec4 texture(SAMPLERCube sampler, vec3 coord
[, float bias])
float texture(SAMPLER1DShadow sampler,
vec3 coord [, float bias])
float texture(SAMPLER2DShadow sampler,
vec3 coord [, float bias])
float texture(SAMPLERCubeShadow sampler,
vec4 coord [, float bias])
gvec4 texture(SAMPLER1DArray sampler,
vec2 coord [, float bias])
gvec4 texture(SAMPLER2DArray sampler,
vec3 coord [, float bias])
float texture(SAMPLER1DArrayShadow sampler,
vec3 coord [, float bias])
float texture(SAMPLER2DArrayShadow sampler,
vec4 coord
Added in GLSL 1.40:
gvec4 texture(SAMPLER2DRect sampler, vec2 coord)
float texture(SAMPLER2DRectShadow sampler,
vec3 coord)
Samples the texture
associated with sampler at
the coordinate coord, adding
bias to the computed
mipmap level-of-detail.
Table I-22 Basic Texture Access Functions

24 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Texture Lookup Functions Using a Constant Coordinate Offset
Sample a texture using a constant offset that is applied to the texture
coordinates provided. If a bias value is specified, it is added to the mipmap
lod parameter before sampling. The bias form is not valid in vertex shaders.
Function Syntax Description
gvec4 textureOffset(SAMPLER1D sampler,
float coord, int offset [, float bias])
gvec4 textureOffset(SAMPLER2D sampler,
vec2 coord, ivec2 offset [, float bias])
gvec4 textureOffset(SAMPLER3D sampler,
vec3 coord, ivec3 offset [, float bias])
float textureOffset(
SAMPLER1DShadow sampler,
vec3 coord, int offset,
[, float bias])
float textureOffset(
SAMPLER2DShadow sampler,
vec3 coord, ivec2 offset,
[, float bias])
gvec4 textureOffset(
SAMPLER1DArray sampler,
vec2 coord, int offset [, float bias])
gvec4 textureOffset(
SAMPLER2DArray sampler,
vec2 coord, ivec2 offset [, float bias])
gvec4 textureOffset(
SAMPLER1DArrayShadow sampler,
vec2 coord, int offset [, float bias])
Added in GLSL 1.40:
gvec4 textureOffset(SAMPLER2DRect sampler,
vec2 coord, ivec2 offset)
float textureOffset(
SAMPLER2DShadow sampler,
vec3 coord, ivec2 offset)
Sample a texture offsetting the
provided coordinates. The range of
offset values is implementation
dependent, and may be queried by
the application (not the shader,
however) by querying the values
GL_MIN_PROGRAM_TEXEL_
OFFSET, and GL_MAX_PROGRAM_
TEXEL_OFFSET.
The offset value is not applied to
the layer value for Array samplers.
Table I-23 Constant Texture-Coordinate Offset Texture Access Functions

Built-In Functions 25
Single Texel Fetch Functions
The following functions retrieve a single texel (without filtering) from a
texture. The *Offset forms offset the supplied texture coordinates by an
offset, similar to the textureOffset() functions.
Function Syntax Description
gvec4 texelFetch(SAMPLER1D sampler,
int coord, int lod)
gvec4 texelFetch(SAMPLER2D sampler,
ivec2 coord, int lod)
gvec4 texelFetch(SAMPLER3D sampler,
ivec3 coord, int lod)
gvec4 texelFetch(SAMPLER1DArray
sampler, ivec2 coord, int lod)
gvec4 texelFetch(SAMPLER2DArray
sampler, ivec3 coord, int lod)
Added in GLSL 1.40:
gvec4 texelFetch(SAMPLER2DRect
sampler, ivec2 coord)
gvec4 texelFetch(SAMPLERBuffer
sampler, int coord)
Retrieve a single unfiltered texel from a
texture map addressed by coord from the
level-of-detail lod.
gvec4 texelFetchOffset(SAMPLER1D
sampler, int coord, int lod, int
offset)
gvec4 texelFetchOffset(SAMPLER2D
sampler, ivec2 coord, int lod, int
offset)
gvec4 texelFetchOffset(SAMPLER3D
sampler, ivec3 coord, int lod, int
offset)
gvec4 texelFetchOffset(
SAMPLER1DArray sampler,
ivec2 coord, int lod, int offset)
gvec4 texelFetchOffset(
SAMPLER2DArray sampler,
ivec3 coord, int lod, int offset)
gvec4 texelFetchOffset(
SAMPLER2DRect sampler,
ivec2 coord, int offset)
Retrieve a single unfiltered texel from a
texture map addressed by coord from the
level-of-detail lod. Texture coordinates
are offset using the values specified in
offset.
Table I-24 Single Texel Texture Access Functions

26 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Projected Texture Access Functions
The following functions retrieve a texel from the texture map associated
with sampler. Before the texel is retrieved, all components of the input
texture coordinate, coord, are divided by the last coordinate.
All forms are accepted by fragment shaders. Functions with the bias
parameter are not accepted in vertex shaders.
Once again, the optional bias parameter is used to alter which mipmap is
sampled (see “Calculating the Mipmap Level” in Chapter 9). If a bias value
is provided while accessing a texture that does not contain mipmaps, the
texture is accessed directly and the value is ignored. The bias forms of the
texture functions are available only in fragment shaders.
The *Offset forms apply the specified offset, similar to the operation of the
texelOffset() routines, to the provided coordinates before the projective
divide and texture sampling.
Function Syntax Description
gvec4 textureProj(SAMPLER1D sampler,
vec2 coord [, float bias])
gvec4 textureProj(SAMPLER1D sampler,
vec4 coord [, float bias])
gvec4 textureProj(SAMPLER2D sampler,
vec3 coord [, float bias])
gvec4 textureProj(SAMPLER2D sampler,
vec4 coord [, float bias])
gvec4 textureProj(SAMPLER3D sampler,
vec4 coord [, float bias])
float textureProj(SAMPLER1DShadow
sampler, vec4 coord [, float bias])
gvec4 textureProj(SAMPLER2D sampler,
vec4 coord [, float bias])
Added in GLSL 1.40:
gvec4 textureProj(SAMPLER2DRect
sampler, vec3 coord)
gvec4 textureProj(SAMPLER2DRect
sampler, vec4 coord)
float textureProj(
SAMPLER2DRectShadow sampler,
vec4 coord)
Sample a texture with projection.
Texture coordinates are divided by
the last component of coord before
sampling. For shadow maps, the third
component of the divided coordinate
is used as the shadow map reference
value.
Table I-25 Projected Texture Access Functions

Built-In Functions 27
Explicit Texture LOD Access Functions
The following functions retrieve texels only from a single mipmap level
explicitly specified by the lod parameter.
The *Offset forms apply the specified offset, similar to the operation of the
texelOffset() routines, to the provided coordinates before texture sampling.
gvec4 textureProjOffset(SAMPLER1D
sampler, vec2 coord, int offset [,
float bias])
gvec4 textureProjOffset(SAMPLER1D
sampler, vec4 coord, int offset [,
float bias])
gvec4 textureProjOffset(SAMPLER2D
sampler, vec3 coord, ivec2 offset [,
float bias])
gvec4 textureProjOffset(SAMPLER2D
sampler, vec4 coord, ivec2 offset [,
float bias])
gvec4 textureProjOffset(SAMPLER3D
sampler, vec4 coord, ivec3 offset [,
float bias])
float textureProjOffset(
SAMPLER1DShadow sampler,
vec4 coord, int offset [, float bias])
gvec4 textureProjOffset(SAMPLER2D
sampler, vec4 coord, ivec2 offset [,
float bias])
Added in GLSL 1.40:
gvec4 textureProjOffset(
SAMPLER2DRect sampler, vec3
coord, ivec2 offset)
gvec4 textureProjOffset(
SAMPLER2DRect sampler, vec4
coord, ivec2 offset)
float textureProjOffset(
SAMPLERRectShadow sampler,
vec4 coord, ivec2 offset)
Sample a texture with projection.
Texture coordinates are divided by
the last component of coord before
sampling. For shadow maps, the third
component of the divided coordinate
is used as the shadow map reference
value.
Function Syntax Description
Table I-25 (continued) Projected Texture Access Functions

28 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Function Syntax Description
gvec4 textureLod(SAMPLER1D sampler, float
coord, float lod)
gvec4 textureLod(SAMPLER2D sampler, vec2
coord, float lod)
gvec4 textureLod(SAMPLER3D sampler, vec3
coord, float lod)
gvec4 textureLod(SAMPLERCube sampler, vec3
coord, float lod)
gvec4 textureLod(SAMPLER1DShadow sampler,
vec3 coord, float lod)
gvec4 textureLod(SAMPLER2DShadow sampler,
vec3 coord, float lod)
gvec4 textureLod(SAMPLER1DArray sampler, vec2
coord, float lod)
gvec4 textureLod(SAMPLER2DArray sampler, vec2
coord, float lod)
gvec4 textureLod(SAMPLER1DArrayShadow
sampler, vec2 coord, float lod)
Sample from the single
mipmap level specified by lod.
These calls also set all partial
derivatives associated with
mipmap-level interpolation
to zero.
gvec4 textureLodOffset(SAMPLER1D sampler,
float coord, float lod, int offset)
gvec4 textureLodOffset(SAMPLER2D sampler,
vec2 coord, float lod, ivec2 offset)
gvec4 textureLodOffset(SAMPLER3D sampler,
vec3 coord, float lod, ivec3 offset)
float textureLodOffset(
SAMPLER1DShadow sampler, vec3 coord,
float lod, ivec offset)
float textureLodOffset(
SAMPLER2DShadow sampler, vec3 coord,
float lod, ivec offset)
gvec4 textureLodOffset(
SAMPLER1DArray sampler, vec2 coord,
float lod, ivec offset)
gvec4 textureLodOffset(
SAMPLER2DArray sampler, vec2 coord,
float lod, ivec offset)
float textureLodOffset(
SAMPLER1DArrayShadow sampler, vec2
coord, float lod, ivec offset)
Sample from the single
mipmap level specified by lod,
using the coordinates supplied
in coord after being offset by the
values supplied in offset. These
calls also set all partial
derivatives associated with
mipmap-level interpolation
to zero.
Table I-26 Explicit Texture LOD Access Functions

Built-In Functions 29
Explicit Gradient Texture Access Functions
The following functions sample a texture using the user-supplied gradients
in the mipmap level determination. The *Offset forms apply the specified
offset, similar to the operation of the texelOffset() routines, to the provided
coordinates before texture sampling.
Function Syntax Description
gvec4 textureGrad(SAMPLER1D sampler,
float coord, float dPdx, float dPdy)
gvec4 textureGrad(SAMPLER2D sampler,
vec2 coord, vec2 dPdx, vec2 dPdy)
gvec4 textureGrad(SAMPLER3D sampler,
vec3 coord, vec3 dPdx, vec3 dPdy)
gvec4 textureGrad(SAMPLERCube sampler,
vec3 coord, vec3 dPdx, vec3 dPdy)
float textureGrad(SAMPLER1DShadow sampler,
vec3 coord, float dPdx, float dPdy)
float textureGrad(SAMPLER2DShadow sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
float textureGrad(SAMPLERCubeShadow sampler,
vec4 coord, vec3 dPdx, vec3 dPdy)
gvec4 textureGrad(SAMPLER1DArray sampler,
vec2 coord, float dPdx, float dPdy)
gvec4 textureGrad(SAMPLER2DArray sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
float textureGrad(SAMPLER1DArrayShadow sampler,
vec3 coord, float dPdx, float dPdy)
float textureGrad(SAMPLER2DShadow sampler,
vec4 coord, vec2 dPdx, vec2 dPdy)
Added in GLSL 1.40:
gvec4 textureGrad(SAMPLER2DRect sampler,
vec2 coord, vec2 dPdx, vec2 dPdy)
float textureGrad(SAMPLER2DRectShadow sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
Sample a texture using
the provided explicit
gradients. The partial
derivatives are with
respect to the window x
and y coordinates.
Table I-27 Explicit Gradient Texture Access Functions

30 Appendix I: Built-In OpenGL Shading Language Variables and Functions
gvec4 textureGradOffset(SAMPLER1D sampler,
float coord, float dPdx, float dPdy)
gvec4 textureGradOffset(SAMPLER2D sampler,
vec2 coord, vec2 dPdx, vec2 dPdy)
gvec4 textureGradOffset(SAMPLER3D sampler,
vec3 coord, vec3 dPdx, vec3 dPdy)
gvec4 textureGradOffset(SAMPLERCube sampler,
vec3 coord, vec3 dPdx, vec3 dPdy)
float textureGradOffset(SAMPLER1DShadow sampler,
vec3 coord, float dPdx, float dPdy)
float textureGradOffset(SAMPLER2DShadow sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
float textureGradOffset(SAMPLERCubeShadow
sampler, vec4 coord, vec3 dPdx, vec3 dPdy)
gvec4 textureGradOffset(SAMPLER1DArray sampler,
vec2 coord, float dPdx, float dPdy)
gvec4 textureGradOffset(SAMPLER2DArray sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
float textureGradOffset(SAMPLER1DArrayShadow
sampler, vec3 coord, float dPdx, float dPdy)
float textureGradOffset(SAMPLER2DShadow sampler,
vec4 coord, vec2 dPdx, vec2 dPdy)
Added in GLSL 1.40:
gvec4 textureGradOffset(SAMPLER2DRect sampler,
vec2 coord, vec2 dPdx, vec2 dPdy)
float textureGradOffset(SAMPLER2DShadow sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
Sample a texture using the
provided explicit gradient
values. The provided offset
is applied to the texture
coordinates before
sampling.
Function Syntax Description
Table I-27 (continued) Explicit Gradient Texture Access Functions

Built-In Functions 31
Combination Texture Access Functions
The following routines provide combinations of the other routines for
texture access. For example, the textureProjLod() function does a
projective texture sample on a single mipmap level. As always, the *Offset()
variants apply a coordinate offset before sampling the texture, similar to
textureOffset().
Function Syntax Description
gvec4 textureProjLod(SAMPLER1D sampler,
vec2 coord, float lod)
gvec4 textureProjLod(SAMPLER1D sampler,
vec4 coord, float lod)
gvec4 textureProjLod(SAMPLER2D sampler,
vec3 coord, float lod)
gvec4 textureProjLod(SAMPLER2D sampler,
vec4 coord, float lod)
gvec4 textureProjLod(SAMPLER3D sampler,
vec4 coord, float lod)
float textureProjLod(SAMPLER1DShadow sampler,
vec4 coord, float lod)
float textureProjLod(SAMPLER2DShadow sampler,
vec4 coord, float lod)
Sample a texture using a
projective lookup within
an explicit LOD.
gvec4 textureProjLodOffset(SAMPLER1D sampler, vec2
coord, float lod, int offset)
gvec4 textureProjLodOffset(SAMPLER1D sampler, vec4
coord, float lod, int offset)
gvec4 textureProjLodOffset(SAMPLER2D sampler, vec3
coord, float lod, ivec2 offset)
gvec4 textureProjLodOffset(SAMPLER2D sampler,
vec4 coord, float lod, ivec2 offset)
gvec4 textureProjLodOffset(SAMPLER3D sampler, vec4
coord, float lod, ivec3 offset)
float textureProjLodOffset(
SAMPLER1DShadow sampler, vec4 coord,
float lod, int offset)
float textureProjLodOffset(
SAMPLER2DShadow sampler, vec4 coord,
float lod, ivec2 offset)
Sample a texture using a
projective lookup within
an explicit LOD,
offsetting the supplied
coordinates.
Table I-28 Projected, LOD, and Gradient Combined Texture Access Functions

32 Appendix I: Built-In OpenGL Shading Language Variables and Functions
gvec4 textureProjGrad(SAMPLER1D sampler,
vec2 coord, float dPdx, float dPdy)
gvec4 textureProjGrad(SAMPLER1D sampler,
vec4 coord, float dPdx, float dPdy)
gvec4 textureProjGrad(SAMPLER2D sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
gvec4 textureProjGrad(SAMPLER2D sampler,
vec4 coord, vec2 dPdx, vec2 dPdy)
gvec4 textureProjGrad(SAMPLER3D sampler,
vec4 coord, vec3 dPdx, vec3 dPdy)
float textureProjGrad(SAMPLER1DShadow sampler,
vec4 coord, float dPdx, float dPdy)
float textureProjGrad(SAMPLER2DShadow sampler,
vec4 coord, float dPdx, float dPdy)
Added in GLSL 1.40:
gvec4 textureProjGrad(SAMPLER2DRect sampler,
vec3 coord, vec2 dPdx, vec2 dPdy)
gvec4 textureProjGrad(SAMPLER2DRect sampler,
vec4 coord, vec2 dPdx, vec2 dPdy)
float textureProjGrad(SAMPLER2DRectShadow sampler,
vec4 coord, float dPdx, float dPdy)
Sample a texture using a
projective lookup with an
explicit gradient.
Function Syntax Description
Table I-28 (continued) Projected, LOD, and Gradient Combined Texture
Table I-28 (continued) Projected, LOD, and Gradient Combined Texture Access
Functions

Built-In Functions 33
Deprecated Texture Access Functions
The following set of functions were deprecated in GLSL Version 1.30, but
had not been removed from the language as of the time of this book’s
publication.
Projective Texture Access Functions
The following functions retrieve a texel from the texture map associated
with sampler. Before the texel is retrieved, all components of the input
texture coordinate, coord, are divided by the last coordinate.
gvec4 textureProjGradOffset(SAMPLER1D sampler,
vec2 coord, float dPdx, float dPdy, int offset)
gvec4 textureProjGradOffset(SAMPLER1D sampler,
vec4 coord, float dPdx, float dPdy, int offset)
gvec4 textureProjGradOffset(SAMPLER2D sampler,
vec3 coord, vec2 dPdx, vec2 dPdy, ivec2 offset)
gvec4 textureProjGradOffset(SAMPLER2D sampler,
vec4 coord, vec2 dPdx, vec2 dPdy, ivec2 offset)
gvec4 textureProjGradOffset(SAMPLER3D sampler,
vec4 coord, vec3 dPdx, vec3 dPdy, ivec3 offset)
float textureProjGradOffset(
SAMPLER1DShadow sampler, vec4 coord,
float dPdx, float dPdy, int offset)
float textureProjGradOffset(
SAMPLER2DShadow sampler, vec4 coord,
vec2 dPdx, vec2 dPdy, ivec2 offset)
Added in GLSL 1.40:
gvec4 textureProjGradOffset(SAMPLER2DRect sampler,
vec3 coord, vec2 dPdx, vec2 dPdy,
ivec2 offset)
gvec4 textureProjGradOffset(SAMPLER2DRect
sampler, vec4 coord, vec2 dPdx, vec2 dPdy,
ivec2 offset)
float textureProjGradOffset(
SAMPLER2DRectShadow sampler,
vec4 coord, vec2 dPdx, vec2 dPdy, ivec2 offset)
Sample a texture using a
projective lookup with an
explicit gradient.,
offsetting the supplied
coordinates.
Function Syntax Description
Table I-28 (continued) Projected, LOD, and Gradient Combined Texture
Table I-28 (continued) Projected, LOD, and Gradient Combined Texture Access
Functions

34 Appendix I: Built-In OpenGL Shading Language Variables and Functions
All forms are accepted by fragment shaders. Functions with the bias
parameter are not accepted in vertex shaders.
Once again, The optional bias parameter is used to alter which mipmap is
sampled (see “Calculating the Mipmap Level” in Chapter 9). If a bias value
is provided while accessing a texture that does not contain mipmaps, the
texture is accessed directly and the value is ignored. The bias forms of the
texture functions are only available in fragment shaders.
Function Syntax Description
vec4 texture1D(sampler1D sampler,
float coord)
vec4 texture1D(sampler1D sampler,
float coord, float bias)
Samples a one-dimensional texture map,
with optional mipmap-level biasing
vec4 texture2D(sampler2D sampler,
vec2 coord)
vec4 texture2D(sampler2D sampler,
vec2 coord, float bias)
Samples a two-dimensional texture map,
with optional mipmap-level biasing
vec4 texture3D(sampler3D sampler,
vec3 coord)
vec4 texture3D(sampler3D sampler,
vec3 coord, float bias)
Samples a three-dimensional texture
map, with optional mipmap-level
biasing
Table I-29 Deprecated Basic Texture Access Functions
Function Syntax Description
vec4 texture1DProj(sampler1D sampler,
vec2 coord)
vec4 texture1DProj(sampler1D sampler,
vec4 coord)
vec4 texture1DProj(sampler1D sampler,
vec2 coord, float bias)
vec4 texture1DProj(sampler1D sampler,
vec4 coord, float bias)
Samples a one-dimensional texture
map, with optional mipmap-level
biasing. The input texture coordinate
is divided by the last texture
coordinates (coord.s for the vec2 call;
coord.q for the vec4 call).
Table I-30 Projective Texture Access Functions

Built-In Functions 35
Vertex Shader Texture Access Functions
Texel retrieval in vertex shaders does not include the automatic
computation of a mipmap level, as happens in a fragment shader. The
following functions allow for the sampling of mipmapped textures by
vertex shaders by providing an mipmap level-of-detail, or lod value (see
“Calculating the Mipmap Level” in Chapter 9 for how to compute the level-
of-detail value).
The vertex shader versions of the texture access functions are available in
non-projective and projective forms (those calls that include “Proj” in the
name. The input texture coordinates for the projective forms are processed
as described in “Projective Texture Access Functions” on page 33.
vec4 texture2DProj(sampler2D sampler,
vec3 coord)
vec4 texture2DProj(sampler2D sampler,
vec4 coord)
vec4 texture2DProj(sampler2D sampler,
vec3 coord, float bias)
vec4 texture2DProj(sampler2D sampler,
vec4 coord, float bias)
Samples a two-dimensional texture
map, with optional mipmap-level
biasing. The input texture coordinate
is divided by the last texture
coordinates (coord.t for the vec2 call;
coord.q for the vec4 call).
vec4 texture3DProj(sampler3D sampler,
vec4 coord)
vec4 texture3DProj(sampler3D sampler,
vec4 coord, float bias)
Samples a three-dimensional texture
map, with optional mipmap-level
biasing. The input texture coordinate
is divided by the last texture
coordinates (coord.p for the vec2 call;
coord.q for the vec4 call).
Function Syntax Description
vec4 texture1DLod(sampler1D sampler,
float coord, float lod)
vec4 texture1DProjLod(sampler1D sampler, vec2
coord, float lod)
vec4 texture1DProjLod(sampler1D sampler, vec4
coord, float lod)
Samples a one-dimensional
texture map by specifying the
mipmap level-of-detail.
Table I-31 Vertex Shader Texture Access Functions
Function Syntax Description
Table I-30 Projective Texture Access Functions

36 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Cube-Map Texture Access Functions
Retrieve the texel at input texture coordinate, coord, in the cube map texture
currently bound to sampler. The direction of coord is used to select which
face to do a two-dimensional texture lookup in.
Shadow-Map Texture Access Functions
If a non-shadow texture call is made to a sampler that represents a depth
texture with depth comparisons turned on, then results are undefined. If a
shadow texture call is made to a sampler that represents a depth texture
with depth comparisons turned off, then results are undefined. If a shadow
texture call is made to a sampler that does not represent a depth texture,
then results are undefined.
vec4 texture2DLod(sampler2D sampler,
vec2 coord, float lod)
vec4 texture2DProjLod(sampler2D sampler, vec3
coord, float lod)
vec4 texture2DProjLod(sampler2D sampler, vec4
coord, float lod)
Samples a two-dimensional
texture map by specifying the
mipmap level-of-detail.
vec4 texture3DLod(sampler3D sampler,
vec3 coord, float lod)
vec4 texture3DProjLod(sampler3D sampler, vec4
coord, float lod)
Samples a three-dimensional
texture map by specifying the
mipmap level-of-detail.
Function Syntax Description
vec4 textureCube(samplerCube sampler,
vec3 coord)
vec4 textureCube(samplerCube sampler,
vec3 coord, float bias)
vec4 textureCubeLod(samplerCube sampler,
vec3 coord, float lod)
Samples a cube-mapped texture,
with optional bias (fragment
shader only) or lod parameters.
Table I-32 Cube-Map Texture Access Functions
Function Syntax Description
Table I-31 (continued) Vertex Shader Texture Access Functions

Built-In Functions 37
Fragment Processing Functions
Table I-34 describes the functions for accessing a fragment’s derivative,
which are computed as the fragments of the underlying geometric primitive
are rasterized.
Function Syntax Description
vec4 shadow1D(sampler1DShadow sampler,
vec3 coord)
vec4 shadow2D(sampler2DShadow sampler,
vec3 coord)
vec4 shadow1D(sampler1DShadow sampler,
vec3 coord, float bias)
vec4 shadow2D(sampler2DShadow sampler,
vec3 coord, float bias)
vec4 shadow1DProj(sampler1DShadow sampler,
vec4 coord)
vec4 shadow2DProj(sampler2DShadow sampler,
vec4 coord)
vec4 shadow1DProj(sampler1DShadow sampler,
vec4 coord, float bias)
vec4 shadow2DProj(sampler2DShadow sampler,
vec4 coord, float bias)
vec4 shadow1DLod(sampler1DShadow sampler,
vec3 coord, float lod)
vec4 shadow2DLod(sampler2DShadow sampler,
vec3 coord, float lod)
vec4 shadow1DProjLod(sampler1DShadow sampler,
vec4 coord, float lod)
vec4 shadow2DProjLod(sampler2DShadow sampler,
vec4 coord, float lod)
Sample a shadow depth
map. The functions
utilizing the bias
parameter are only
available in fragment
shaders.
The LOD and projective
versions of the
functions process
texture coordinates
similarly to other LOD
and projective
functions, respectively.
Table I-33 Shadow-Map Texture Access Functions
Function Syntax Description
TYPE dFdx(TYPE p) Returns the derivative in the x-direction.
TYPE dFdy(TYPE p) Returns the derivative in the y-direction
TYPE fwidth(TYPE p)Returns
Table I-34 Fragment Derivative Functions
dFdx p dFdy p+

38 Appendix I: Built-In OpenGL Shading Language Variables and Functions
Noise Functions
The stochastic noise functions described in Table I-35 are available in both
vertex and fragment shaders. The computed noise values returned are
pseudo-random, but repeatable provided the same random number seed
is used.
Function Syntax Description
float noise1(TYPE x) Returns a 1D noise value based on the input value x.
vec2 noise2(TYPE x) Returns a 2D noise value based on the input value x.
vec3 noise3(TYPE x) Returns a 3D noise value based on the input value x.
vec4 noise4(TYPE x) Returns a 4D noise value based on the input value x.
Table I-35 Random-Noise Generation Functions
1
Appendix J
J.Floating-Point Formats for Textures,
Framebuffers, and Renderbuffers
This appendix will describe the floating-point formats used for pixel storage
in framebuffers and renderbuffers, and texel storage in textures. It has the
following major sections:
• “Floating-Point Formats Used in OpenGL”

2Appendix J: Floating-Point Formats for Textures, Framebuffers, and Renderbuffers
Floating-Point Formats Used in OpenGL
In addition to the normal 32-bit single-precision floating-point values you
are used to using when you declare a GLfloat in your application, OpenGL
supports reduced-precision floating-point representations for storing data
more compactly than its 32-bit representation. In many instances, your
floating-point data may not require the entire dynamic range of a 32-bit
float, and storing or processing data in a reduced-precision format may save
memory, and increase data transfer rates.
OpenGL supports three reduce-precision floating-point formats: 16-bit
(signed) floating-point values, and 10- and 11-bit unsigned floating-point
values. Table J-1 describes the bit-layout of each representation, and the
associated pixel formats
16-bit Floating-Point Values
For signed 16-bit floating-point values, the minimum and maximum values
that can be represented are (about) 6.103u10-5, and 65504.0, respectively.
The following routine, F32toF16(), will convert a single, full-precision
32-bit floating-point value to a 16-bit reduced-precision form (stored as an
unsigned-short integer)
#define F16_EXPONENT_BITS 0x1F
#define F16_EXPONENT_SHIFT 10
#define F16_EXPONENT_BIAS 15
#define F16_MANTISSA_BITS 0x3ff
#define F16_MANTISSA_SHIFT (23 - F16_EXPONENT_SHIFT)
#define F16_MAX_EXPONENT \
(F16_EXPONENT_BITS << F16_EXPONENT_SHIFT)
Floating-
point
Type
Associated Pixel Formats Sign bit Number of
Exponents
Bits
Number of
Mantissa Bits
16-bit GL_RGB16F,
GL_RGBA16F
15 10
11-bit GL_R11F_G11F_B10F
(red and green components)
05 6
10-bit GL_R11F_G11F_B10F
(blue component)
05 5
Table J-1 Reduced-Precision Floating-Point Formats

Floating-Point Formats Used in OpenGL 3
GLushort
F32toF16(GLfloat val)
{
GLuint f32 = (*(GLuint *) &val);
GLushort f16 = 0;
/* Decode IEEE 754 little-endian 32-bit floating-point value
*/
int sign = (f32 >> 16) & 0x8000;
/* Map exponent to the range [-127,128] */
int exponent = ((f32 >> 23) & 0xff) - 127;
int mantissa = f32 & 0x007fffff;
if (exponent == 128) { /* Infinity or NaN */
f16 = sign | F16_MAX_EXPONENT;
if (mantissa) f16 |= (mantissa & F16_MANTISSA_BITS);
}
else if (exponent > 15) { /* Overflow - flush to Infinity */
f16 = sign | F16_MAX_EXPONENT;
}
else if (exponent > -15) { /* Representable value */
exponent += F16_EXPONENT_BIAS;
mantissa >>= F16_MANTISSA_SHIFT;
f16 = sign | exponent << F16_EXPONENT_SHIFT | mantissa;
}
else {
f16 = sign;
}
return f16;
}
Likewise, F16toF32() converts from the reduced-precision floating-point
form into a normal 32-bit floating-point value.
#define F32_INFINITY 0x7f800000
GLfloat
F16toF32(GLushort val)
{
union {
GLfloat f;
GLuint ui;
} f32;
int sign = (val & 0x8000) << 15;
int exponent = (val & 0x7c00) >> 10;
int mantissa = (val & 0x03ff);

4Appendix J: Floating-Point Formats for Textures, Framebuffers, and Renderbuffers
f32.f = 0.0;
if (exponent == 0) {
if (mantissa != 0) {
const GLfloat scale = 1.0 / (1 << 24);
f32.f = scale * mantissa;
}
}
else if (exponent == 31) {
f32.ui = sign | F32_INFINITY | mantissa;
}
else {
GLfloat scale, decimal;
exponent -= 15;
if (exponent < 0) {
scale = 1.0 / (1 << -exponent);
}
else {
scale = 1 << exponent;
}
decimal = 1.0 + (float) mantissa / (1 << 10);
f32.f = scale * decimal;
}
if (sign) f32.f = -f32.f;
return f32.f;
}
10- and 11-bit Unsigned Floating-Point Values
For normalized color values in the range [0, 1], unsigned 10- and 11-bit
floating-point formats may provide a more compact format with better
dynamic range than either floating-point values, or OpenGL’s unsigned
integer pixel formats. The maximum representable values are 65204 and
64512, respectively.
Routines for converting floating-point values into 10-bit unsigned floating-
point values, and vice versa are shown below.
#define UF11_EXPONENT_BIAS 15
#define UF11_EXPONENT_BITS 0x1F
#define UF11_EXPONENT_SHIFT 6
#define UF11_MANTISSA_BITS 0x3F
#define UF11_MANTISSA_SHIFT (23 - UF11_EXPONENT_SHIFT)

Floating-Point Formats Used in OpenGL 5
#define UF11_MAX_EXPONENT \
(UF11_EXPONENT_BITS << UF11_EXPONENT_SHIFT)
GLushort
F32toUF11(GLfloat val)
{
GLuint f32 = (*(GLuint *) &val);
GLushort uf11 = 0;
/* Decode little-endian 32-bit floating-point value */
int sign = (f32 >> 16) & 0x8000;
/* Map exponent to the range [-127,128] */
int exponent = ((f32 >> 23) & 0xff) - 127;
int mantissa = f32 & 0x007fffff;
if (sign) return 0;
if (exponent == 128) { /* Infinity or NaN */
uf11 = UF11_MAX_EXPONENT;
if (mantissa) uf11 |= (mantissa & UF11_MANTISSA_BITS);
}
else if (exponent > 15) { /* Overflow - flush to Infinity */
uf11 = UF11_MAX_EXPONENT;
}
else if (exponent > -15) { /* Representable value */
exponent += UF11_EXPONENT_BIAS;
mantissa >>= UF11_MANTISSA_SHIFT;
uf11 = exponent << UF11_EXPONENT_SHIFT | mantissa;
}
return uf11;
}
#define F32_INFINITY 0x7f800000
GLfloat
UF11toF32(GLushort val)
{
union {
GLfloat f;
GLuint ui;
} f32;
int exponent = (val & 0x07c0) >> UF11_EXPONENT_SHIFT;
int mantissa = (val & 0x003f);

6Appendix J: Floating-Point Formats for Textures, Framebuffers, and Renderbuffers
f32.f = 0.0;
if (exponent == 0) {
if (mantissa != 0) {
const GLfloat scale = 1.0 / (1 << 20);
f32.f = scale * mantissa;
}
}
else if (exponent == 31) {
f32.ui = F32_INFINITY | mantissa;
}
else {
GLfloat scale, decimal;
exponent -= 15;
if (exponent < 0) {
scale = 1.0 / (1 << -exponent);
}
else {
scale = 1 << exponent;
}
decimal = 1.0 + (float) mantissa / 64;
f32.f = scale * decimal;
}
return f32.f;
}
For completeness, we present similar routines for converting 10-bit
unsigned floating-point values.
#define UF10_EXPONENT_BIAS 15
#define UF10_EXPONENT_BITS 0x1F
#define UF10_EXPONENT_SHIFT 5
#define UF10_MANTISSA_BITS 0x3F
#define UF10_MANTISSA_SHIFT (23 - UF10_EXPONENT_SHIFT)
#define UF10_MAX_EXPONENT \
(UF10_EXPONENT_BITS << UF10_EXPONENT_SHIFT)
GLushort
F32toUF10(GLfloat val)
{
GLuint f32 = (*(GLuint *) &val);
GLushort uf10 = 0;
/* Decode little-endian 32-bit floating-point value */
int sign = (f32 >> 16) & 0x8000;

Floating-Point Formats Used in OpenGL 7
/* Map exponent to the range [-127,128] */
int exponent = ((f32 >> 23) & 0xff) - 127;
int mantissa = f32 & 0x007fffff;
if (sign) return 0;
if (exponent == 128) { /* Infinity or NaN */
uf10 = UF10_MAX_EXPONENT;
if (mantissa) uf10 |= (mantissa & UF10_MANTISSA_BITS);
}
else if (exponent > 15) { /* Overflow - flush to Infinity */
uf10 = UF10_MAX_EXPONENT;
}
else if (exponent > -15) { /* Representable value */
exponent += UF10_EXPONENT_BIAS;
mantissa >>= UF10_MANTISSA_SHIFT;
uf10 = exponent << UF10_EXPONENT_SHIFT | mantissa;
}
return uf10;
}
#define F32_INFINITY 0x7f800000
GLfloat
UF10toF32(GLushort val)
{
union {
GLfloat f;
GLuint ui;
} f32;
int exponent = (val & 0x07c0) >> UF10_EXPONENT_SHIFT;
int mantissa = (val & 0x003f);
f32.f = 0.0;
if (exponent == 0) {
if (mantissa != 0) {
const GLfloat scale = 1.0 / (1 << 20);
f32.f = scale * mantissa;
}
}
else if (exponent == 31) {
f32.ui = F32_INFINITY | mantissa;
}

8Appendix J: Floating-Point Formats for Textures, Framebuffers, and Renderbuffers
else {
GLfloat scale, decimal;
exponent -= 15;
if (exponent < 0) {
scale = 1.0 / (1 << -exponent);
}
else {
scale = 1 << exponent;
}
decimal = 1.0 + (float) mantissa / 64;
f32.f = scale * decimal;
}
return f32.f;
}

2Appendix K: RGTC Compressed Texture Format
RGTC Overview
The RGTC compressed texture format is a standardized compression format
for one- and two-component textures. It is a block-based format where
collections of 4 u4 texel squares that are compressed into a 64-bit
encodings for each component. The first two bytes of an encoding for a
channel represent representative values, which may be linearly combined
to compute the color of any pixel in the 4 u4 block. The remaining 48-bits
represent 16 three-bit codes used to determine the appropriate linear
combination of the two representative values.
Textures compressed using the RGTC format must have a width and height
that are multiples of four pixels. Any pixels that fall outside of the multiple-
of-four width or height are ignored on decompression.
The RGTC format includes four encodings depending on the number of
components in the image, and the sign of the texel data, as shown in Table K-1.
Encoding RGTC Images
The following routine will encode a one-component 4 u4 block of
GLubyte pixels into an RGTC bit-field representing the compressed pixels,
as described in The OpenGL Graphics System: A Specification, Appendix D
(Version 3.1).
RGTC Format Description
GL_COMPRESSED_RED_RGTC1 Single-channel 8-bit unsigned
image data
GL_COMPRESSED_SIGNED_RED_RGTC1 Single-channel 8-bit signed image
data
GL_COMPRESSED_RG_RTGC2 Two-channel 8-bit per
component unsigned image data
GL_COMPRESSED_SIGNED_RG_RGTC2 Two-channel 8-bit per
component signed image data
Table K-1 The RTGC Compressed Image Formats

RGTC Overview 3
GLubyte*
RGTCEncode( const GLubyte pixels[4][4] )
{
int i, j, r, c, idx;
GLubyte min = 0xff, max = 0x00; /* range for current 4x4
block */
GLubyte codes[4][4];
GLbyte group = 0;
static GLubyte encoded[8];
unsigned long long *bits;
/* Note which group of codes were using
** in our encoding.
**
** Group[0] ==> red_0 > red_1
** Group[1] ==> red_0 <= red_1
*/
const GLubyte Group[2] = { 0x00, 0x80 };
const GLubyte Mask[2] = { 0x07, 0x38 };
const GLubyte Shift[2] = { 0, 3 };
/* compute min & max pixel values */
for ( i = 0; i < 4; ++i ) {
for ( j = 0; j < 4; ++j ) {
GLubyte val = pixels[i][j];
if ( min > val ) min = val;
if ( max < val ) max = val;
}
}
if ( min == max ) {
/* Constant color across the block - we'll use the
** first set of codes (red_0 > red_1), and set
** all bits to be code 0 */
encoded[0] = min;
encoded[1] = max;
encoded[2] = 0x00;
encoded[3] = 0x00;
encoded[4] = 0x00;
encoded[5] = 0x00;
encoded[6] = 0x00;
encoded[7] = 0x00;
}

4Appendix K: RGTC Compressed Texture Format
else {
GLfloat d1 = (max - min) / 7.0;
GLfloat d2 = (max - min) / 5.0;
GLubyte *pptr = (GLubyte*) pixels;
GLubyte *cptr = (GLubyte*) codes;
for ( i = 0; i < 16; ++i, ++pptr, ++cptr ) {
GLfloat v1 = (*pptr - min) / d1;
GLfloat v2 = (*pptr - min) / d2;
GLubyte ip1 = (GLubyte) v1;
GLubyte ip2 = (GLubyte) v2;
GLfloat fp1 = v1 - ip1;
GLfloat fp2 = v2 - ip2;
enum { MinCode = 0, MaxCode = 1 };
if ( fp1 > 0.5 ) {
fp1 -= 0.5;
ip1 += 1;
}
if ( fp2 > 0.5 ) {
fp2 -= 0.5;
ip1 += 1;
}
if ( ip1 == 0 ) {
*cptr = MinCode;
}
else if ( ip1 == 7 ) {
*cptr = MaxCode;
}
else {
*cptr = (ip2 << Shift[1]) | (ip1 << Shift[0]);
}
if ( fp1 < fp2 ) {
/* The current pixel's closer to one of the
** seventh range partitoning values */
*cptr |= Group[0];
++group;
}

RGTC Overview 5
else {
/* Here, the current pixel's closer to
** one of the fifth range partitonings
** values */
*cptr |= Group[1];
--group;
}
}
}
group = (group >= 0) ? 0 : 1;
bits = (unsigned long long*) encoded;
for ( i = 0; i < 4; ++i ) {
for ( j = 0; j < 4; ++j ) {
GLubyte shift = 3*(4*j+i);
GLubyte code;
unsigned long long mask;
code = codes[i][j] & Mask[group];
code >>= Shift[group];
mask = code << shift;
*bits |= mask;
}
}
if ( group == 0 ) {
encoded[0] = max;
encoded[1] = min;
}
else {
encoded[0] = min;
encoded[1] = max;
}
}
return encoded;
}
This page intentionally left blank

2Appendix L: std140 Uniform Buffer Layout
Using the std140 Layout Qualifier
Generally, when you group a number of uniform variables in a uniform
buffer object, you need to query the offset (and format and type, if you
don’t know those values from the shader source). For large collections of
uniforms, this process can result in needed to make many queries. The
std140 layout qualifier requests that the GLSL shader compiler organize the
variables in uniform block according to a set of rules, where you can
predictably compute the offset of any member in the block, knowing its
type and offset. This feature is only available with GLSL Version 1.40 at the
time of this writing (but will presumably be backward compatible with
future versions of GLSL).
In order to qualify a block to use the std140 layout, you need to add layout
directive to its declaration, as demonstrated below:
layout (std140) uniform UniformBlock {
// declared variables
};
std140 Layout Rules
The set of rules shown in Table L-1 are used by the GLSL compiler to layout
members in a std140-qualified uniform block. The offsets of members in
the block are accumulated based on the sizes of the previous members in the
block (those declared before the variable in question), and the starting
offset. The starting offset of the first member is always zero.
Variable Type Variable Size/Offset
Scalar variable type (bool, int, uint,
float)
Size of the scalar in basic machine types
(e.g., sizeof(GLfloat))
Two-element vector (bvec2, ivec2,
uvec2, vec2)
Twice the size of the underlying scalar
type
Three-element vector (bvec3, ivec3,
uvec3, vec3)
Four-element vector (bvec4, ivec4,
uvec4 vec2)
Four times the size of the underlying
scalar type
Table L-1 std140 Layout Rules

std140 Layout Rules 3
An array of scalars or vectors Each element in the array is the size of
the underlying type, and the offset of
any element is its index (using zero-
based indexing) times the elements size.
The entire array is padded to be a
multiple of the size of a vec4.
Single, or arrays of column-major
matrices of size C columns and R rows
Stored as an array of C vectors each with
R components, and potentially padded
like other arrays.
If the variable is an array of M column-
major matrices, it is stored as an array of
MuC vectors each with R components
(and potentially padded).
Single, or arrays of row-major matrices
with R rows and C columns
Stored as an array of R vectors each with
Ccomponents, and potentially padded
like other arrays.
If the variable is an array of M column-
major matrices, it is stored as an array of
MuR vectors each with Ccomponents
(and potentially padded).
A single structure definition, or an array
of structures
Offsets and sizes of the structure’s
members are computed using the
preceding rules. The structure’s size will
be padded out to a multiple of the size of
a vec4.
An array of structures’ offsets are
computed considering the alignment
and padding of the individual
structures, with structure member’s
offsets computed using the preceding
rules.
Variable Type Variable Size/Offset
Table L-1 (continued) std140 Layout Rules

Your purchase of
OpenGL® Programming Guide, Seventh Edition,
includes access to
a free online edition for 45 days through the Safari Books Online subscription service.
Nearly every Addison-Wesley Professional book is available online through Safari Books
Online, along with more than 5,000 other technical books and videos from publishers
such as Cisco Press, Exam Cram, IBM Press, O’Reilly, Prentice Hall, Que, and Sams.
SAFARI BOOKS ONLINE allows you to search for a specifi c answer, cut and paste
code, download chapters, and stay current with emerging technologies.
Activate your FREE Online Edition at
www.informit.com/safarifree
STEP 1: Enter the coupon code: CSMWAZG.
STEP 2: New Safari users, complete the brief registration form.
Safari subscribers, just log in.
If you have diffi culty registering on Safari or accessing the online edition,
please e-mail customer-service@safaribooksonline.com
FREE Online
Edition