Oscillator Design Guide For ST Microcontrollers Application
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 23
- 1 Quartz crystal properties and model
- 2 Oscillator theory
- 3 Pierce oscillator
- 4 Pierce oscillator design
- 5 Easy guideline for the selection of suitable crystal and external components
- 6 Some recommended crystals for STM32™ microcontrollers
- 7 Some recommended crystals for STM8A/S microcontrollers
- 8 Some PCB hints
- 9 Conclusion
- 10 Revision history

April 2010 Doc ID 15287 Rev 3 1/23
AN2867
Application note
Oscillator design guide
for ST microcontrollers
Introduction
Most designers are familiar with oscillators (Pierce-Gate topology), but few really
understand how they operate, let alone how to properly design an oscillator. In practice,
most designers do not even really pay attention to the oscillator design until they realize the
oscillator does not operate properly (usually when it is already being produced). This should
not happen. Many systems or projects are delayed in their deployment because of a crystal
not working as intended. The oscillator should receive its proper amount of attention during
the design phase, well before the manufacturing phase. The designer would then avoid the
nightmare scenario of products being returned.
This application note introduces the Pierce oscillator basics and provides some guidelines
for a good oscillator design. It also shows how to determine the different external
components and provides guidelines for a good PCB for the oscillator.
This document finally contains an easy guideline to select suitable crystals and external
components, and it lists some recommended crystals (HSE and LSE) for STM32™ and
STM8A/S microcontrollers in order to quick start development.
www.st.com

Contents AN2867
2/23 Doc ID 15287 Rev 3
Contents
1 Quartz crystal properties and model . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2 Oscillator theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3 Pierce oscillator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4 Pierce oscillator design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
4.1 Feedback resistor RF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
4.2 Load capacitor CL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.3 Gain margin of the oscillator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.4 Drive level DL and external resistor RExt calculation . . . . . . . . . . . . . . . . 12
4.4.1 Calculating drive level DL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.4.2 Another drive level measurement method . . . . . . . . . . . . . . . . . . . . . . . 13
4.4.3 Calculating external resistor RExt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
4.5 Startup time . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
4.6 Crystal pullability . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5 Easy guideline for the selection of suitable crystal
and external components . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
6 Some recommended crystals for STM32™ microcontrollers . . . . . . . 16
6.1 HSE part . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
6.1.1 Part numbers of recommended 8 MHz crystals . . . . . . . . . . . . . . . . . . . 16
6.1.2 Part numbers of recommended 8 MHz ceramic resonators . . . . . . . . . 16
6.1.3 Part numbers of recommended 25 MHz crystals
(Ethernet applications) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
6.1.4 Part numbers of recommended 14.7456 MHz crystals (audio
applications) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
6.2 LSE part . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
7 Some recommended crystals for STM8A/S microcontrollers . . . . . . . 19
7.1 Part numbers of recommended crystal oscillators . . . . . . . . . . . . . . . . . . 19
7.2 Part numbers of recommended ceramic resonators . . . . . . . . . . . . . . . . 19
8 Some PCB hints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

List of tables AN2867
4/23 Doc ID 15287 Rev 3
List of tables
Table 1. Example of equivalent circuit parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Table 2. Typical feedback resistor values for given frequencies . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Table 3. EPSON®. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Table 4. HOSONIC ELECTRONIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Table 5. CTS®. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Table 6. FOXElectronics®. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Table 7. Recommendable condition (for consumer). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Table 8. Recommendable condition (for CAN bus) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Table 9. HOSONIC ELECTRONIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Table 10. FOXElectronics®. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Table 11. CTS®. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Table 12. FOXElectronics®. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Table 13. ABRACON™ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Table 14. EPSON TOYOCOM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Table 15. JFVNY® . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Table 16. KDS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Table 17. KYOCERA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Table 18. Recommendable conditions (for consumer) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Table 19. Recommendable conditions (for CAN-BUS). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Table 20. Document revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

AN2867 List of figures
Doc ID 15287 Rev 3 5/23
List of figures
Figure 1. Quartz crystal model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Figure 2. Impedance representation in the frequency domain. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Figure 3. Oscillator principle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Figure 4. Pierce oscillator circuitry . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Figure 5. Inverter transfer function. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Figure 6. Current drive measurement with a current probe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Figure 7. Recommended layout for an oscillator circuit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

Quartz crystal properties and model AN2867
6/23 Doc ID 15287 Rev 3
1 Quartz crystal properties and model
A quartz crystal is a piezoelectric device transforming electric energy to mechanical energy
and vice versa. The transformation occurs at the resonant frequency. The quartz crystal can
be modeled as follows:
Figure 1. Quartz crystal model
C0: represents the shunt capacitance resulting from the capacitor formed by the electrodes
Lm: (motional inductance) represents the vibrating mass of the crystal
Cm: (motional capacitance) represents the elasticity of the crystal
Rm: (motional resistance) represents the circuit losses
The impedance of the crystal is given by the following equation (assuming that Rm is
negligible):
(1)
Figure 2 represents the impedance in the frequency domain.
Figure 2. Impedance representation in the frequency domain
Fs is the series resonant frequency when the impedance Z = 0. Its expression can be
deduced from equation (1) as follows:
(2)
Q
C0
RmCm
Lm
ai15833
Zj
w
----w2LmCm1–
C0Cm
+()w2LmCmC0
–
----------------------------------------------------------------
×=
FsFa
Impedance
Inductive behavior:
the quartz oscillates
Area of parallel
resonance: Fp
Capacitive behavior:
no oscillation
Phase (deg)
Frequency
Frequency
+90
–90
ai15834
Fs
1
2πLmCm
---------------------------=
AN2867 Quartz crystal properties and model
Doc ID 15287 Rev 3 7/23
Fa is the anti-resonant frequency when impedance Z tends to infinity. Using equation (1), it is
expressed as follows:
(3)
The region delimited by Fs and Fa is usually called the area of parallel resonance (shaded
area in Figure 2). In this region, the crystal operates in parallel resonance and behaves as
an inductance that adds an additional phase equal to 180 ° in the loop. Its frequency Fp (or
FL: load frequency) has the following expression:
(4)
From equation (4), it appears that the oscillation frequency of the crystal can be tuned by
varying the load capacitor CL. This is why in their datasheets, crystal manufacturers indicate
the exact CL required to make the crystal oscillate at the nominal frequency.
Ta bl e 1 gives an example of equivalent crystal circuit component values to have a nominal
frequency of 8 MHz.
Using equations (2), (3) and (4) we can determine Fs, Fa and Fp of this crystal:
and .
If the load capacitance CL at the crystal electrodes is equal to 10 pF, the crystal will oscillate
at the following frequency: .
To have an oscillation frequency of exactly 8 MHz, CL should be equal to 4.02 pF.
Table 1. Example of equivalent circuit parameters
Equivalent component Value
Rm8 Ω
Lm14.7 mH
Cm0.027 pF
C05.57 pF
FaFs1Cm
C0
--------+=
FpFs1Cm
2C
0CL
+()
-----------------------------+
⎝⎠
⎛⎞
=
Fs7988768 Hz=
Fa8008102 Hz=
Fp7995695 Hz=
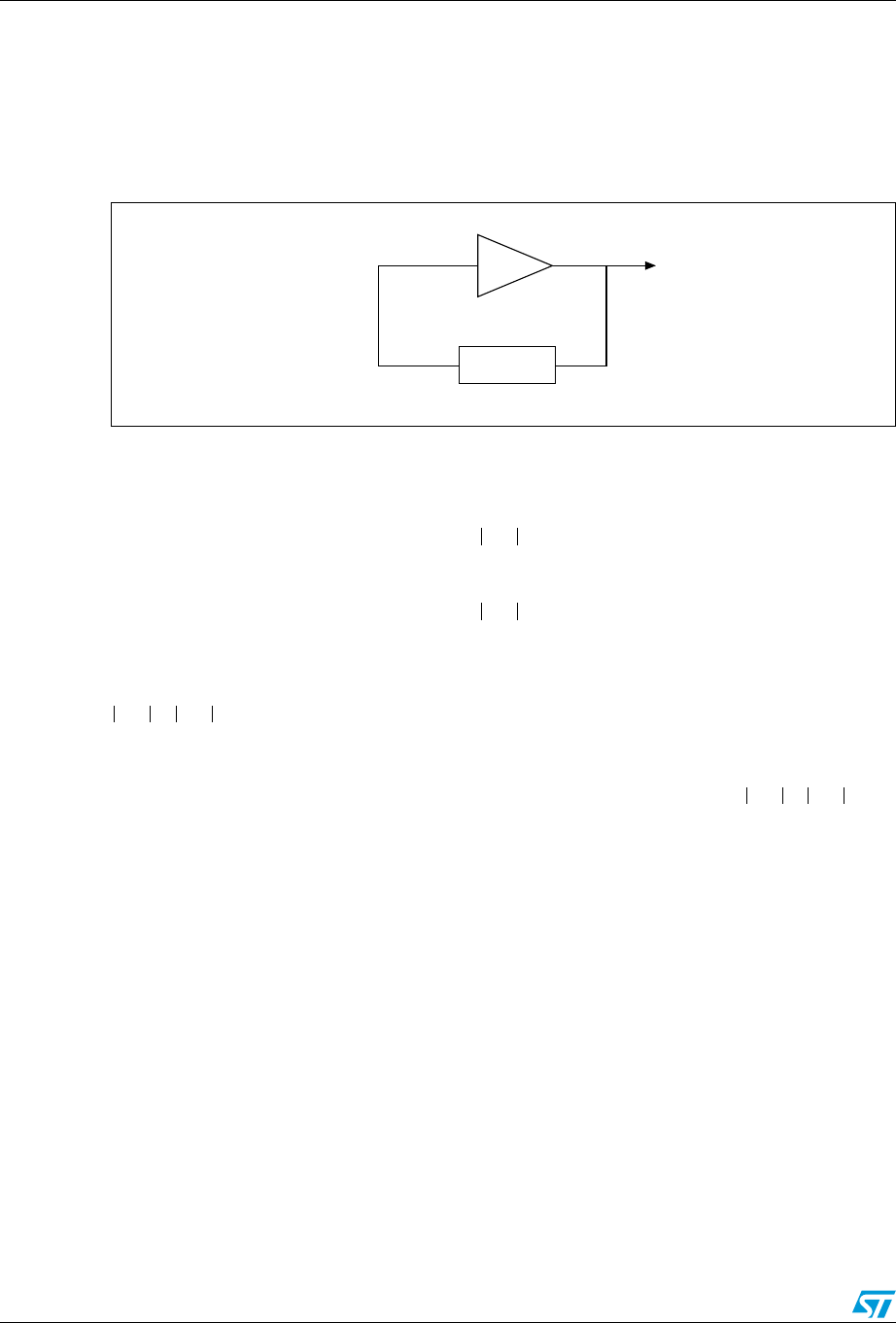
Oscillator theory AN2867
8/23 Doc ID 15287 Rev 3
2 Oscillator theory
An oscillator consists of an amplifier and a feedback network to provide frequency selection.
Figure 3 shows the block diagram of the basic principle.
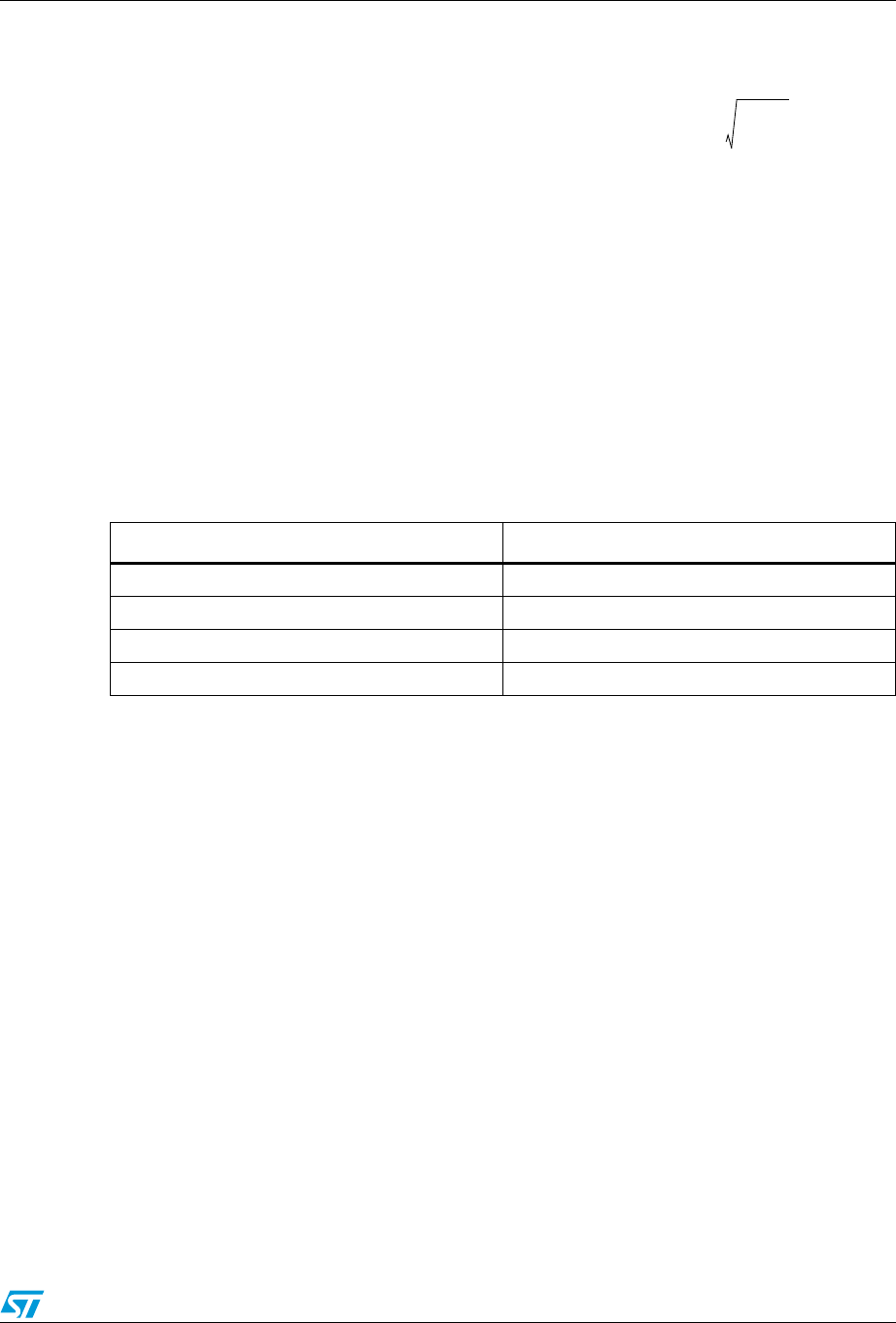
Figure 3. Oscillator principle
Where:
●A(f) is the complex transfer function of the amplifier that provides energy to keep the
oscillator oscillating.
●B(f) is the complex transfer function of the feedback that sets the oscillator frequency.
To oscillate, the following Barkhausen conditions must be fulfilled. The closed-loop gain
should be greater than 1 and the total phase shift of 360 ° is to be provided:
and
The oscillator needs initial electric energy to start up. Power-up transients and noise can
supply the needed energy. However, the energy level should be high enough to trigger
oscillation at the required frequency. Mathematically, this is represented by |,
which means that the open-loop gain should be much higher than 1. The time required for
the oscillations to become steady depends on the open-loop gain.
Meeting the oscillation conditions is not enough to explain why a crystal oscillator starts to
oscillate. Under these conditions, the amplifier is very unstable, any disturbance introduced
in this positive feedback loop system makes the amplifier unstable and causes oscillations
to start. This may be due to power-on, a disable-to enable sequence, the thermal noise of
the crystal, etc. It is also important to note that only noise within the range of serial-to
parallel frequency can be amplified. This represents but a little amount of energy, which is
why crystal oscillators are so long to start up.
Passive feedback element
A(f)
Active element
B(f)
ai15835
Af() Af() ejfαf()
⋅=
Bf() Bf() ejfβf()
⋅=
Af() Bf()⋅1≥
αf() βf()+2π=
Af() Bf()⋅1»
AN2867 Pierce oscillator
Doc ID 15287 Rev 3 9/23
3 Pierce oscillator
Pierce oscillators are commonly used in applications because of their low consumption, low
cost and stability.
Figure 4. Pierce oscillator circuitry
Inv: the internal inverter that works as an amplifier
Q: crystal quartz or a ceramic resonator
RF: internal feedback resistor
RExt: external resistor to limit the inverter output current
CL1 and CL2: are the two external load capacitors
Cs: stray capacitance is the addition of the MCU pin capacitance (OSC_IN and OSC_OUT)
and the PCB capacitance: it is a parasitical capacitance.
RExt
RF
Q
CL1 CL2
Microcontroller
Inv
Cs
ai15836
OSC_OUTOSC_IN
Pierce oscillator design AN2867
10/23 Doc ID 15287 Rev 3
4 Pierce oscillator design
This section describes the different parameters and how to determine their values in order
to be more conversant with the Pierce oscillator design.
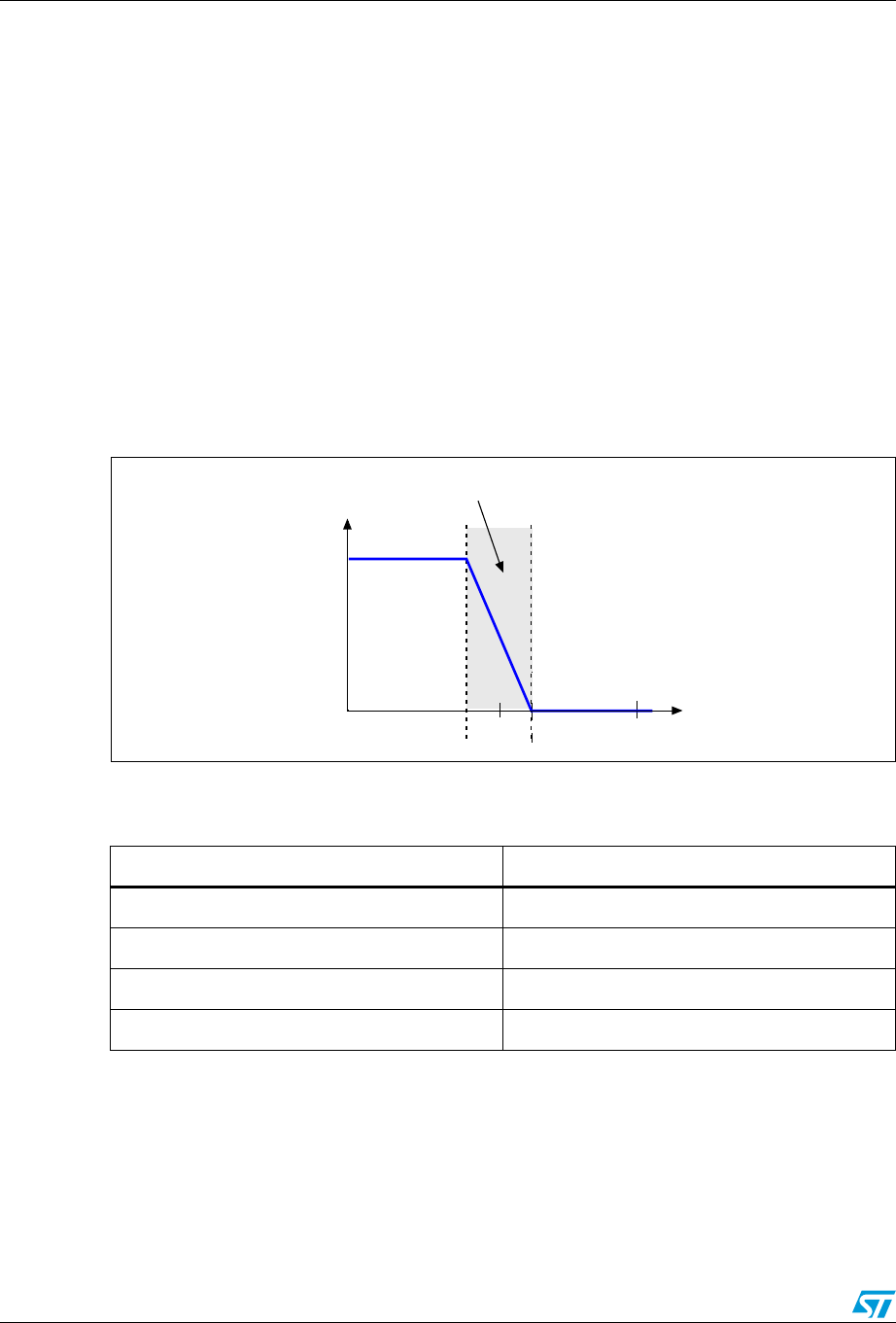
4.1 Feedback resistor RF
In most of the cases in ST microcontrollers, RF is embedded in the oscillator circuitry. Its role
is to make the inverter act as an amplifier. The feedback resistor is connected between Vin
and Vout so as to bias the amplifier at Vout = Vin and force it to operate in the linear region
(shaded area in Figure 5). The amplifier amplifies the noise (for example, the thermal noise
of the crystal) within the range of serial to parallel frequency (Fa, Fa). This noise causes the
oscillations to start up. In some cases, if RF is removed after the oscillations have stabilized,
the oscillator continues to operate normally.
Figure 5. Inverter transfer function
Ta bl e 2 provides typical values of RF
.
Table 2. Typical feedback resistor values for given frequencies
Frequency Feedback resistor range
32.768 kHz 10 to 25 MΩ
1 MHz 5 to 10 MΩ
10 MHz 1 to 5 MΩ
20 MHz 470 kΩ to 5 MΩ
~V
DD
/2 V
DD
V
DD
Linear area: the inverter acts as an amplifier
Saturation
region
Saturation
region
V
out
V
in
ai15837

AN2867 Pierce oscillator design
Doc ID 15287 Rev 3 11/23
4.2 Load capacitor CL
The load capacitance is the terminal capacitance of the circuit connected to the crystal
oscillator. This value is determined by the external capacitors CL1 and CL2 and the stray
capacitance of the printed circuit board and connections (Cs). The CL value is specified by
the crystal manufacturer. Mainly, for the frequency to be accurate, the oscillator circuit has to
show the same load capacitance to the crystal as the one the crystal was adjusted for.
Frequency stability mainly requires that the load capacitance be constant. The external
capacitors CL1 and CL2 are used to tune the desired value of CL to reach the value specified
by the crystal manufacturer.
The following equation gives the expression of CL:
Example of CL1 and CL2 calculation:
For example if the CL value of the crystal is equal to 15 pF and, assuming that Cs = 5 pF,
then:
. That is: .
4.3 Gain margin of the oscillator
The gain margin is the key parameter that determines whether the oscillator will start up or
not. It has the following expression:
, where:
●gm is the transconductance of the inverter (in mA/V for the high-frequency part or in
µA/V for the low-frequency part: 32 kHz).
●gmcrit (gm critical) depends on the crystal parameters.
Assuming that CL1 = CL2, and assuming that the crystal sees the same CL on its pads
as the value given by the crystal manufacturer, gmcrit is expressed as follows:
, where ESR = equivalent series resistor
According to the Eric Vittoz theory: the impedance of the motional RLC equivalent circuit of
a crystal is compensated by the impedance of the amplifier and the two external
capacitances.
To satisfy this theory, the inverter transconductance (gm) must have a value gm > gmcrit. In
this case, the oscillation condition is reached. A gain margin of 5 can be considered as a
minimum to ensure an efficient startup of oscillations.
For example, to design the oscillator part of a microcontroller that has a gm value equal to
25 mA/V, we choose a quartz crystal (from Fox) that has the following characteristics:
frequency = 8 MHz, C0 = 7 pF, CL = 10 pF, ESR = 80 Ω.. Will this crystal oscillate with this
microcontroller?
Let us calculate gmcrit:
CL
CL1 CL2
×
CL1 CL2
+
--------------------------- Cs
+=
CLCs
–CL1 CL2
×
CL1 CL2
+
--------------------------- 10 pF==
CL1 C
L2
=20 pF=
gainminarg
gm
gmcrit
---------------=
gmcrit 4ESR×2πF()
2
×C0CL
+()
2
×=
gmcrit 480 2π× 86
×10×()
2
×× 712–
×10 10 12–
×10+()
2
×0.23 mA V⁄==
Pierce oscillator design AN2867
12/23 Doc ID 15287 Rev 3
Calculating the gain margin gives:
The gain margin is very sufficient to start the oscillation and the “gain margin greater than 5”
condition is reached. The crystal will oscillate normally.
If an insufficient gain margin is found (gain margin < 5) the oscillation condition is not
reached and the crystal will not start up. You should then try to select a crystal with a lower
ESR or/and with a lower CL.
4.4 Drive level DL and external resistor RExt calculation
The drive level and external resistor value are closely related. They will therefore be
addressed in the same section.
4.4.1 Calculating drive level DL
The drive level is the power dissipated in the crystal. It has to be limited otherwise the quartz
crystal can fail due to excessive mechanical vibration. The maximum drive level is specified
by the crystal manufacturer, usually in mW. Exceeding this maximum value may lead to the
crystal being damaged.
The drive level is given by the following formula: , where:
●ESR is the equivalent series resistor (specified by the crystal manufacturer):
●IQ is the current flowing through the crystal in RMS. This current can be displayed on
an oscilloscope as a sine wave. The current value can be read as the peak-to-peak
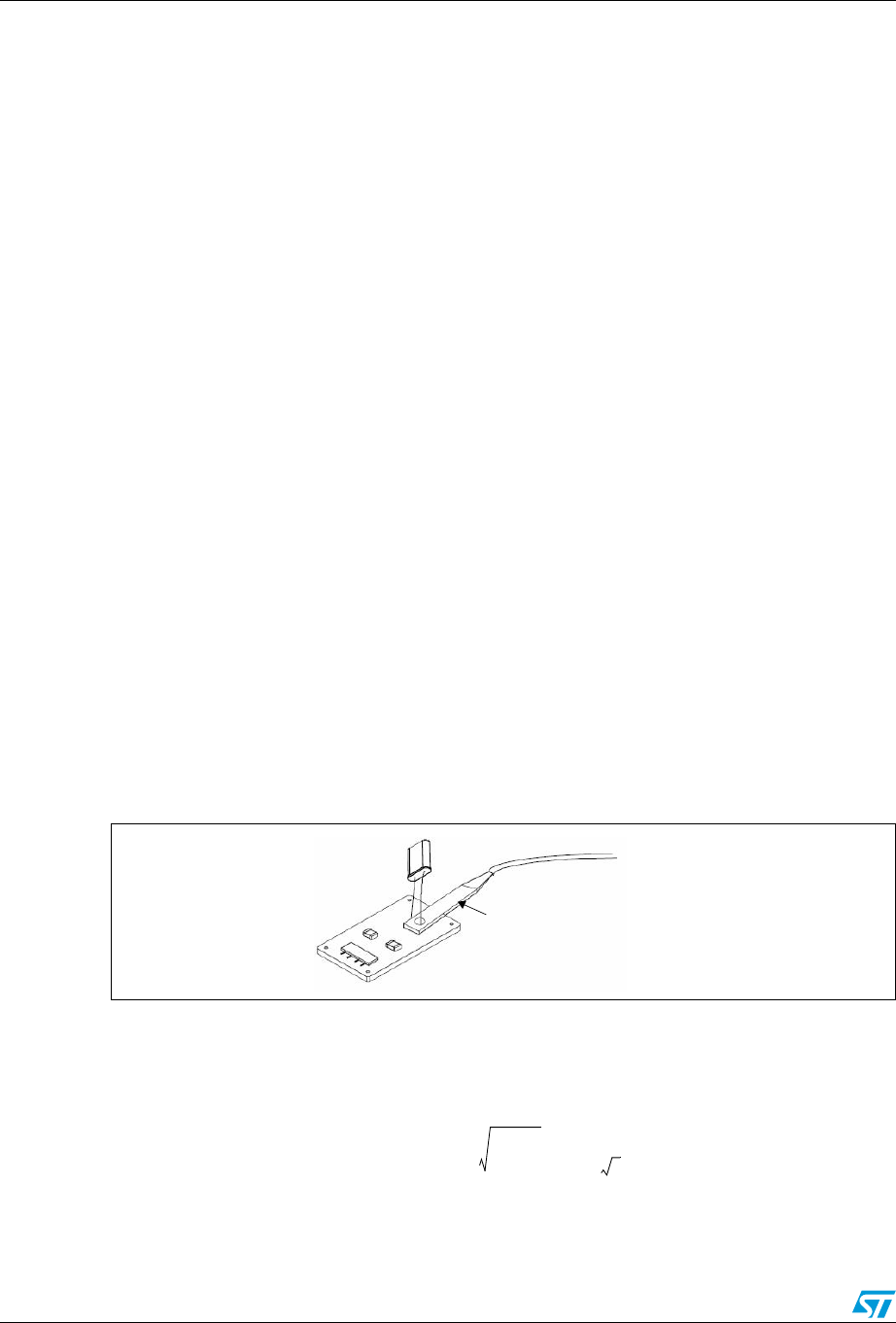
value (IPP). When using a current probe (as shown in Figure 6), the voltage scale of an
oscilloscope may be converted into 1mA/1mV.
Figure 6. Current drive measurement with a current probe
So as described previously, when tuning the current with the potentiometer, the current
through the crystal does not exceed IQmax RMS (assuming that the current through the
crystal is sinusoidal).
Thus IQmax RMS is given by:
gainminarg
gm
gmcrit
---------------25
0.23
----------- 107===
DL ESR IQ
2
×=
ESR Rm1C0
CL
-------+
⎝⎠
⎛⎞
2
×=
Crystal
ai15838
To oscilloscope
Current probe
IQmaxRMS DLmax
ESR
----------------- IQmaxPP
22
------------------------==

AN2867 Pierce oscillator design
Doc ID 15287 Rev 3 13/23
Therefore the current through the crystal (peak-to-peak value read on the oscilloscope)
should not exceed a maximum peak-to-peak current (IQmaxPP) equal to:
Hence the need for an external resistor (RExt) (refer to Section 4.4.3) when IQ exceeds
IQmaxPP. The addition of RExt then becomes mandatory and it is added to ESR in the
expression of IQmax.
4.4.2 Another drive level measurement method
The drive level can be computed as:
DL= I²QRMS × ESR, where IQRMS is the RMS AC current.
This current can be calculated by measuring the voltage swing at the amplifier input with a
low-capacitance oscilloscope probe (no more than 1 pF). The amplifier input current is
negligible with respect to the current through CL1, so we can assume that the current
through the crystal is equal to the current flowing through CL1. Therefore the RMS voltage at
this point is related to the RMS current by:
, with:
●F = crystal frequency
●, where: Vpp is the voltage peak-to-peak measured at CL1 level
●Ctot = CL1 + (Cs/2) + Cprobe where:
–C
L1 is the external load capacitor at the amplifier input
–C
s is the stray capacitance
–C
probe is the probe capacitance)
Therefore the drive level, DL, is given by: .
This DL value must not exceed the drive level specified by the crystal manufacturer.
4.4.3 Calculating external resistor RExt
The role of this resistor is to limit the drive level of the crystal. With CL2, it forms a low-pass
filter that forces the oscillator to start at the fundamental frequency and not at overtones
(prevents the oscillator from vibrating at 3, 5, 7 etc. times the fundamental frequency). If the
power dissipated in the crystal is higher than the value specified by the crystal manufacturer,
the external resistor RExt becomes mandatory to avoid overdriving the crystal. If the power
dissipated in the selected quartz is less than the drive level specified by the crystal
manufacturer, the insertion of RExt is not recommended and its value is then 0 Ω..
An initial estimation of RExt is obtained by considering the voltage divider formed by
RExt/CL2. Thus, the value of RExt is equal to the reactance of CL2.
Therefore: .
Let us put:
●oscillation frequency F = 8 MHz
●CL2 = 15 pF
Then:
IQmaxPP 2 2DL
max
×
ESR
----------------------------×=
IQRMS 2πFV
RMS
×Ctot
×=
VRMS
Vpp
22
-----------=
DL ESR πF×Ctot
×()
2
×Vpp
()
2
×
2
------------------------------------------------------------------------------------=
RExt
1
2πFC2
------------------=
RExt 1326 Ω=

Pierce oscillator design AN2867
14/23 Doc ID 15287 Rev 3
The recommended way of optimizing RExt is to first choose CL1 and CL2 as explained earlier
and to connect a potentiometer in the place of RExt. The potentiometer should be initially set
to be approximately equal to the capacitive reactance of CL2. It should then be adjusted as
required until an acceptable output and crystal drive level are obtained.
Caution: After calculating RExt it is recommended to recalculate the gain margin (refer to Section 4.3:
Gain margin of the oscillator) to make sure that the addition of RExt has no effect on the
oscillation condition. That is, the value of RExt has to be added to ESR in the expression of
gmcrit and gm >> gmcrit must also remain true:
gm >> gmcrit = 4 × (ESR + RExt) × (2 × PI × F)² × (C0 + CL)²
Note: If RExt is too low, there is no power dissipation in the crystal. If RExt is too high, there is no
oscillation: the oscillation condition is not reached.
4.5 Startup time
It is the time that take the oscillations to start and become stable. This time is longer for a
quartz than for a ceramic resonator. It depends on the external components: CL1 and CL2.
The startup time also depends on the crystal frequency and decreases as the frequency
rises. It also depends on the type of crystal used: quartz or ceramic resonator (the startup
time for a quartz is very long compared to that of a ceramic resonator). Startup problems are
usually due to the gain margin (as explained previously) linked to CL1 and CL2 being too
small or too large, or to ESR being too high.
The startup times of crystals for frequencies in the MHz range are within the ms range.
The startup time of a 32 kHz crystal is within the 1 s to 5 s range.
4.6 Crystal pullability
Pullability refers to the change in frequency of a crystal in the area of usual parallel
resonance. It is also a measure of its frequency change for a given change in load
capacitance. A decrease in load capacitance causes an increase in frequency. Conversely,
an increase in load capacitance causes a decrease in frequency. Pullability is given by the
following formula:
Pullability PPM pF⁄()
Cm
6
×10
2C
0CL
+()
2
×
---------------------------------------=

AN2867 Easy guideline for the selection of suitable crystal and external components
Doc ID 15287 Rev 3 15/23
5 Easy guideline for the selection of suitable crystal
and external components
This section gives a recommended procedure to select suitable crystal/external
components. The whole procedure is divided into three main steps:
Step1: Calculate the gain margin
(please refer to Section 4.3: Gain margin of the oscillator)
●Choose a crystal and go to the references (chosen crystal + microcontroller
datasheets)
●Calculate the oscillator gain margin and check if it greater than 5:
If Gain margin < 5, the crystal is not suitable, choose another with a lower ESR or/and
a lower CL. Redo step 1.
If Gain margin > 5, go to step 2.
Step2: Calculate the external load capacitors
(please refer to Section 4.2: Load capacitor CL)
Calculate CL1 and CL2 and check if they match the exact capacitor value on market or not:
●If you found the exact capacitor value then the oscillator will oscillate at the exact
expected frequency. You can proceed to step 3.
●If you did not find the exact value and:
– frequency accuracy is a key issue for you, you can use a variable capacitor to
obtain the exact value. Then you can proceed to step 3.
– frequency accuracy is not critical for you, choose the nearest value found on
market and go to step 3.
Step3: Calculate the drive level and external resistor
(please refer to Section 4.4: Drive level DL and external resistor RExt calculation)
●Compute DL and check if is greater or lower than DLcrystal:
–If DL < DL
crystal, no need for an external resistor. Congratulations you have found
a suitable crystal.
–If DL > DL
crystal, you should calculate RExt in order to have: DL < DLcrystal. You
should then recalculate the gain margin taking RExt into account.
If you find that gain margin > 5, congratulations, you have found a suitable crystal.
If not, then this crystal will not work and you have to choose another. Return to
step 1 to run the procedure for the new crystal.

Some recommended crystals for STM32™ microcontrollers AN2867
16/23 Doc ID 15287 Rev 3
6 Some recommended crystals for STM32™
microcontrollers
6.1 HSE part
6.1.1 Part numbers of recommended 8 MHz crystals
6.1.2 Part numbers of recommended 8 MHz ceramic resonators
Ta bl e 7 and Ta b le 8 give the references of recommended CERALOCK® ceramic resonator
for the STM32™ microcontrollers provided and certified by Murata.
Table 3. EPSON®
Part number ESR CLC0Gain margin Package
MA-406 or MA-505 or MA-506 (8 MHz) 80 Ω10 pF 5 pF 137.4 SMD
Table 4. HOSONIC ELECTRONIC
Part number ESR CLC0Gain margin Package
HC-49S-8 MHz 80 Ω10 pF 7 pF 107 Through-hole
Table 5. CTS®
Part number ESR CLC0Gain margin Package
ATS08 A 60 Ω20 pF 7 pF 56.9 Through-hole
ATS08ASM 60 Ω20 pF 7 pF 56.9 SMD
Table 6. FOXElectronics®
Part number ESR CLC0Gain margin Package
FOXSLF/080-20 80 Ω20 pF 7 pF 43.1 Through-hole
FOXSDLF/080-20 80 Ω20 pF 7 pF 43.1 SMD
PFXLF/080-20 80 Ω20 pF 7 pF 43.1 SMD
Table 7. Recommendable condition (for consumer)
Part number CLPackage
CSTCE8M00G55-R0 Embedded load capacitors CL1 = CL2 = 33 pF SMD
Table 8. Recommendable condition (for CAN bus)
Part number CLPackage
CSTCE8M00G15C**-R0(1)
1. Refer to the datasheet of the resonator for details on the two asterisks.
Embedded load capacitors CL1 = CL2 = 33 pF SMD
AN2867 Some recommended crystals for STM32™ microcontrollers
Doc ID 15287 Rev 3 17/23
For other Murata resonators recommended for STM32 microcontrollers, please refer to the
following link:
http://search.murata.co.jp/Ceramy/ICListAction.do?sKeyHin=STM32&sKeyMak=ST-
MICROELECTRONICS&sLang=en&sParam=STM32
6.1.3 Part numbers of recommended 25 MHz crystals
(Ethernet applications)
6.1.4 Part numbers of recommended 14.7456 MHz crystals (audio
applications)
Table 9. HOSONIC ELECTRONIC
Part number ESR CLC0Gain margin Package
6FA25000F10M11 40 Ω10pF 7pF 21.91 SMD
SA25000F10M11 40 Ω10pF 7pF 21.91 Through-hole
Table 10. FOXElectronics®
Part number ESR CLC0Gain margin Package
FOXSLF/250F-20 30 Ω20 pF 7 pF 11.58 Through-hole
FOXSDLF/250F-20 30 Ω20 pF 7 pF 11.58 SMD
PFXLF250F-20 30 Ω20 pF 7 pF 11.58 SMD
Table 11. CTS®
Part number ESR CLC0Gain margin Package
ATS25A 30 Ω20 pF 7 pF 11.58 Through-hole
ATS25ASM 30 Ω20 pF 7 pF 11.58 SMD
Table 12. FOXElectronics®
Part number ESR CLC0Gain margin Package
FOXSLF/147-20 40 Ω20 pF 7 pF 24.97 Through-hole
FOXSDLF/147-20 40 Ω20 pF 7 pF 24.97 SMD
Table 13. ABRACON™
Part number ESR CLC0Gain margin Package
ABMM2-14.7456 MHz 50 Ω18 pF 7 pF 29.3 SMD
Some recommended crystals for STM32™ microcontrollers AN2867
18/23 Doc ID 15287 Rev 3
6.2 LSE part
For the LSE part of STM32™ microcontrollers, it is recommended to use a crystal with
CL<7pF.
Table 14. EPSON TOYOCOM
Part number ESR CLC0Gain margin Package
C-2-Type 35 kΩ6 pF 2 pF 13.5 Through-hole
C-4-Type 55 kΩ6 pF 2 pF 8.5 Through-hole
Table 15. JFVNY®
Part number ESR CLC0Gain margin Package
DT-38G06 30 kΩ6 pF 1.3 pF 18.44 Through-hole
MC306G06 50 kΩ6 pF 2 pF 9.3 SMD
Table 16. KDS
Part number ESR CLC0Gain margin Package
SM-26F 80 kΩ6 pF 1.1 pF 7.3 Through-hole
AN2867 Some recommended crystals for STM8A/S microcontrollers
Doc ID 15287 Rev 3 19/23
7 Some recommended crystals for STM8A/S
microcontrollers
7.1 Part numbers of recommended crystal oscillators
7.2 Part numbers of recommended ceramic resonators
Ta bl e 1 8 and Ta b le 1 9 give the references of recommended CERALOCK® ceramic
resonators for the STM8A microcontrollers provided and certified by Murata.
Table 17. KYOCERA
Part number Freq. ESR CL Drive level (DL)
CX5032GA08000H0QSWZZ 8 MHz 300 Ω max 12 pF 500 µW max
CX5032GA16000H0QSWZZ 16 MHz 100 Ω max 12 pF 300 µW max
CX8045GA08000H0QSWZZ 8 MHz 200 Ω max 12 pF 500 µW max
CX8045GA16000H0QSWZZ 16 MHz 50 Ω max 12 pF 300 µW max
Table 18. Recommendable conditions (for consumer)
Part number Freq. CL
CSTCR4M00G55B-R0 4 MHz CL1 = CL2 = 39 pF
CSTCE8M00G55A-R0 8 MHz CL1 = CL2 = 33 pF
CSTCE16M0G55A-R0 16 MHz CL1 = CL2 = 15 pF
Table 19. Recommendable conditions (for CAN-BUS)
Part number Freq. CL
CSTCR4M00G15C**-R0 4 MHz CL1 = CL2 = 39 pF
CSTCR8M00G15C**-R0 8 MHz CL1 = CL2 = 33 pF
CSTCE16M0V13C**-R0 16 MHz CL1 = CL2 = 15 pF
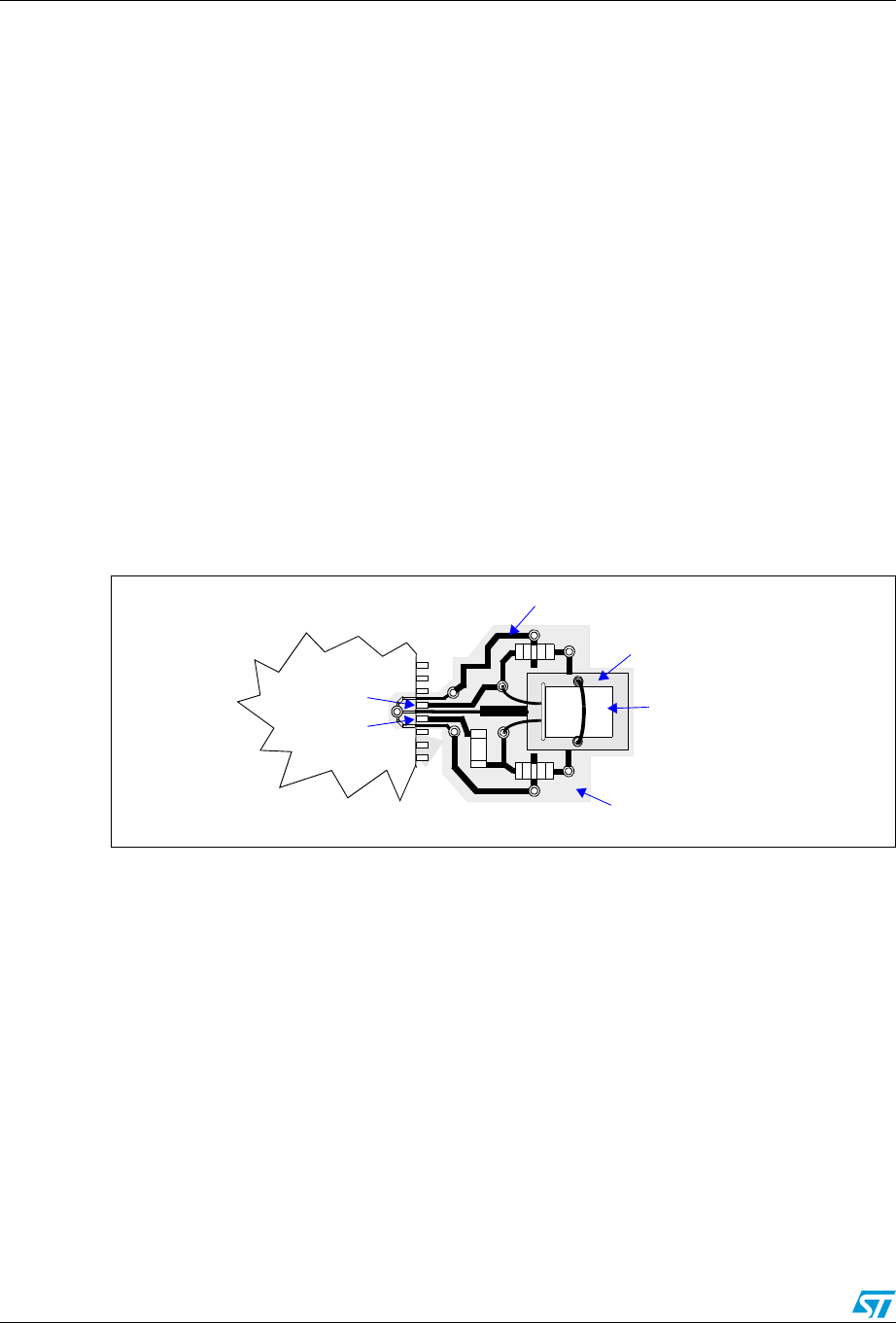
Some PCB hints AN2867
20/23 Doc ID 15287 Rev 3
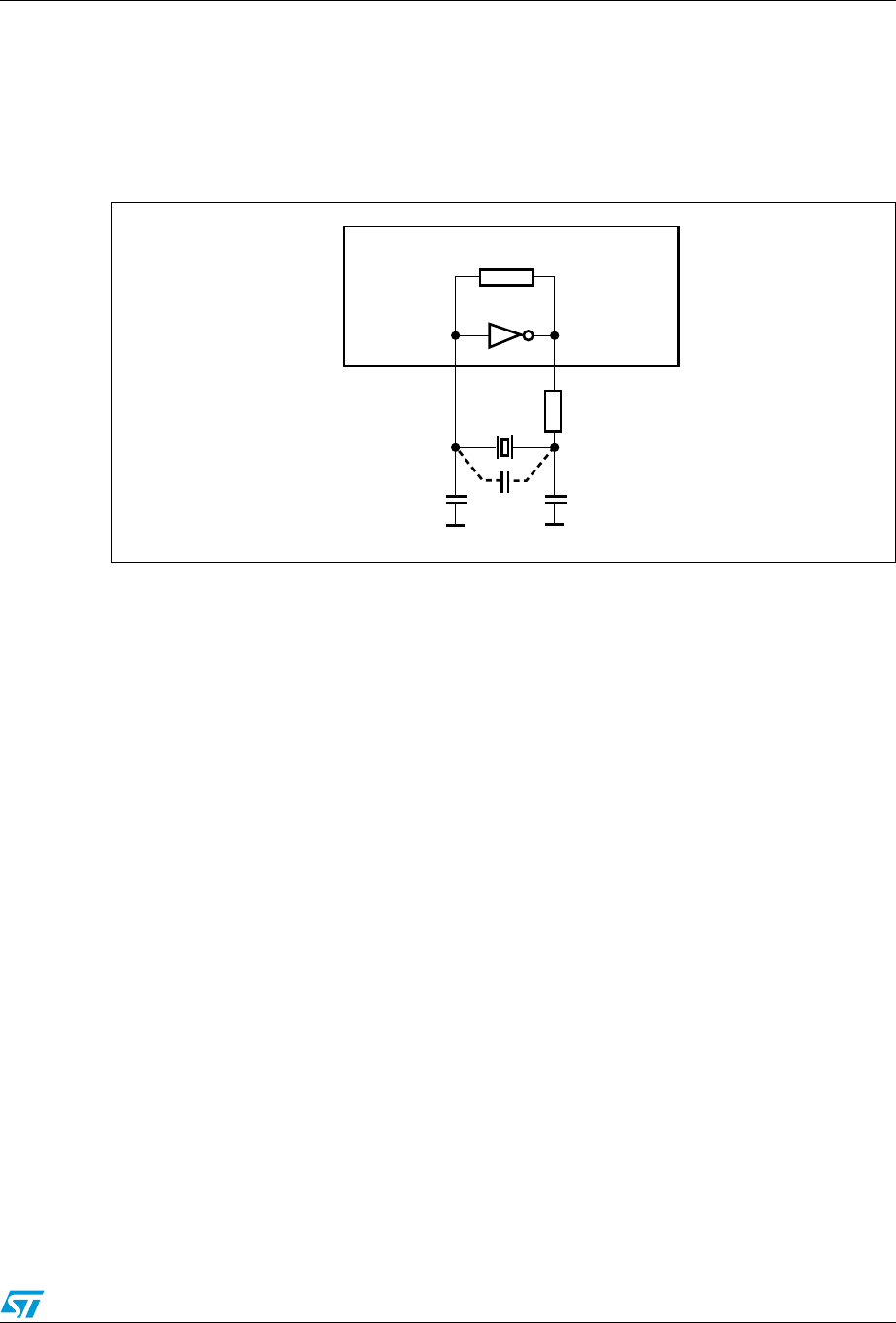
8 Some PCB hints
1. High values of stray capacitance and inductances must be avoided as much as
possible as they might give rise to an undesired mode of oscillation and lead to startup
problems.
In addition, high-frequency signals should be avoided near the oscillator circuitry.
2. Reduce trace lengths as much as possible.
3. Use ground planes to isolate signals and reduce noise. For instance, the use of a local
ground plane on the PCB layer immediately below the crystal guard ring is a good
solution to isolate the crystal from undesired coupling with signals on other PCB layers
(crosstalk). Note that the ground plane is needed in the vicinity of the crystal only and
not on the entire board (see Figure 7.).
4. The VSS paths can also be routed as shown in Figure 7. In this way, the VSS paths
isolate the oscillator input from the output and the oscillator from adjacent circuitry. The
unterminated VSS paths that end under CL1 and CL2 are not in contact with the ground
shield under the quartz. All VSS vias in Figure 7 are connected to the local ground
plane (except for the quartz pads).
5. Use decoupling capacitors between each VDD path and the closest VSS path to reduce
noise.
Figure 7. Recommended layout for an oscillator circuit
Note: RExt is mandatory only if the dissipated power in the crystal exceeds the drive level specified
by the crystal manufacturer. Otherwise, its value is 0
Ω
(refer to Section 4.4: Drive level DL
and external resistor RExt calculation for more details).
C
L2
R
Ext
(1)
OSC_OUT
OSC_IN
Microcontroller
C
L1 Ground shield
ai15839
V
SS
paths
Quartz
Local ground plane (other layer)

AN2867 Conclusion
Doc ID 15287 Rev 3 21/23
9 Conclusion
The most important parameter is the gain margin of the oscillator, which determines if the
oscillator will start up or not. This parameter has to be calculated at the beginning of the
design phase to choose the suitable crystal for the application. The second parameter is the
value of the external load capacitors that have to be selected in accordance with the CL
specification of the crystal (provided by the crystal manufacturer). This determines the
frequency accuracy of the crystal. The third parameter is the value of the external resistor
that is used to limit the drive level. In the 32 kHz oscillator part, however, it is not
recommended to use an external resistor.
Because of the number of variables involved, in the experimentation phase you should use
components that have exactly the same properties as those that will be used in production.
Likewise, you should work with the same oscillator layout and in the same environment to
avoid unexpected behavior and therefore save time.

Revision history AN2867
22/23 Doc ID 15287 Rev 3
10 Revision history
Table 20. Document revision history
Date Revision Changes
20-Jan-2009 1 Initial release.
10-Nov-2009 2
DL formula corrected in Section 4.4.2: Another drive level
measurement method.
Package column added to all tables in Section 6: Some
recommended crystals for STM32™ microcontrollers.
Recommended part numbers updated in Section 6.1: HSE part and
Section 6.2: LSE part.
Section 6.1.3: Part numbers of recommended 25 MHz crystals
(Ethernet applications) added.
Section 6.1.4: Part numbers of recommended 14.7456 MHz crystals
(audio applications) added.
27-Apr-2010 3 Added Section 7: Some recommended crystals for STM8A/S
microcontrollers.

AN2867
Doc ID 15287 Rev 3 23/23
Please Read Carefully:
Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the
right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any
time, without notice.
All ST products are sold pursuant to ST’s terms and conditions of sale.
Purchasers are solely responsible for the choice, selection and use of the ST products and services described herein, and ST assumes no
liability whatsoever relating to the choice, selection or use of the ST products and services described herein.
No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this
document refers to any third party products or services it shall not be deemed a license grant by ST for the use of such third party products
or services, or any intellectual property contained therein or considered as a warranty covering the use in any manner whatsoever of such
third party products or services or any intellectual property contained therein.
UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED
WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED
WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE (AND THEIR EQUIVALENTS UNDER THE LAWS
OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.
UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT
RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING
APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJURY,
DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE
GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.
Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void
any warranty granted by ST for the ST product or service described herein and shall not create or extend in any manner whatsoever, any
liability of ST.
ST and the ST logo are trademarks or registered trademarks of ST in various countries.
Information in this document supersedes and replaces all information previously supplied.
The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.
© 2010 STMicroelectronics - All rights reserved
STMicroelectronics group of companies
Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germany - Hong Kong - India - Israel - Italy - Japan -
Malaysia - Malta - Morocco - Philippines - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America
www.st.com
