M2 PS 32 Solutions
User Manual: M2
Open the PDF directly: View PDF ![]() .
.
Page Count: 3
NYS COMMON CORE MATHEMATICS CURRICULUM
M2
Lesson 32
GEOMETRY
Lesson 32: Using Trigonometry to Find Side Lengths of an Acute Triangle
Date: 10/28/14
482
© 2014 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
Exit Ticket Sample Solutions
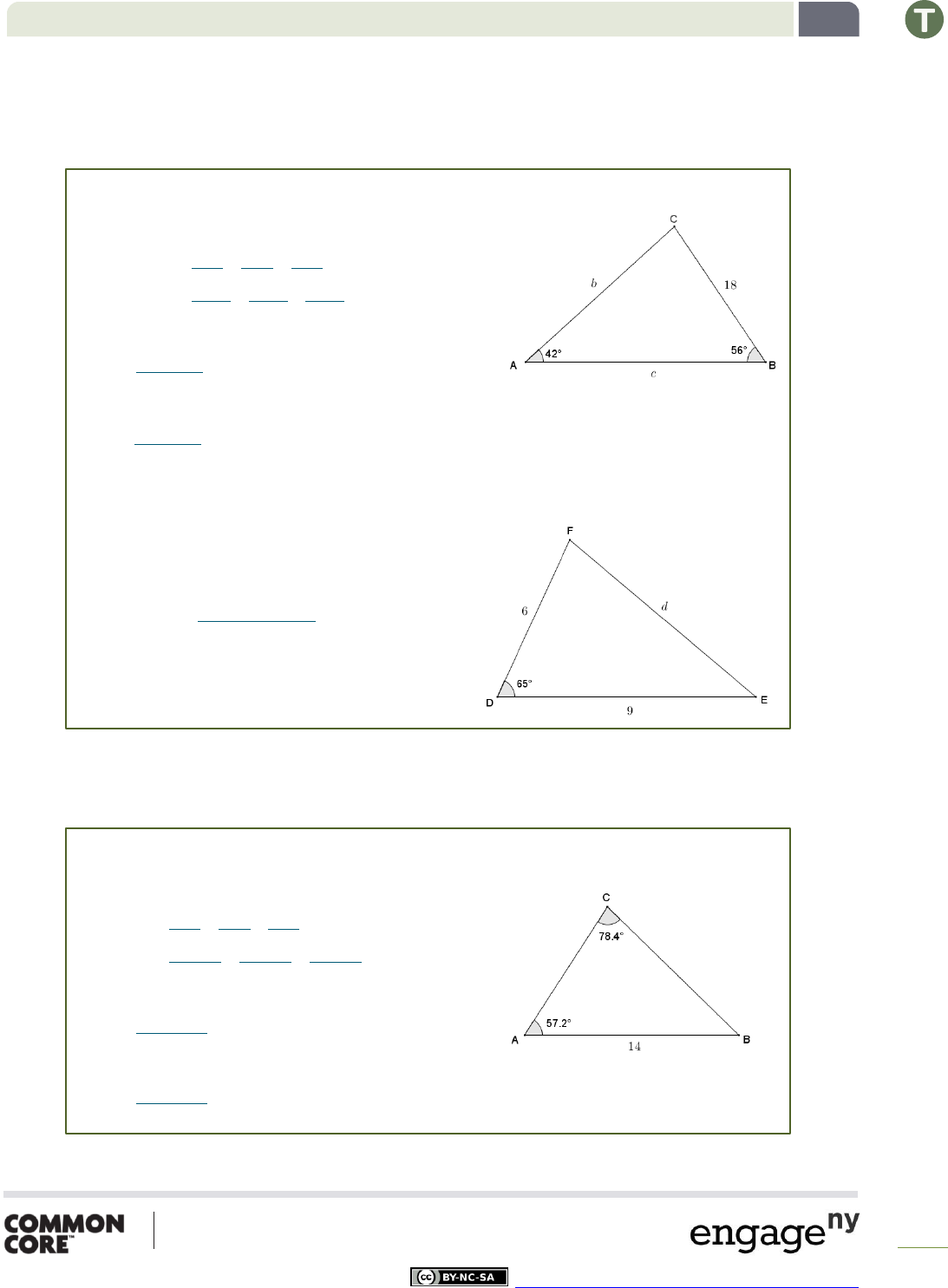
Use the law of sines to find lengths and in the triangle below. Round answers to the nearest tenth as necessary. 1.
Given , use the law of cosines to find the length of the side marked to the nearest tenth. 2.
Problem Set Sample Solutions
1. Given , , , and , calculate the measure of angle to the nearest tenth of a
degree, and use the law of sines to find the lengths of and to the nearest tenth.
By the angle sum of a triangle, .
NYS COMMON CORE MATHEMATICS CURRICULUM
M2
Lesson 32
GEOMETRY
Lesson 32: Using Trigonometry to Find Side Lengths of an Acute Triangle
Date: 10/28/14
483
© 2014 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
Calculate the area of to the nearest square unit.
2. Given , , and , calculate the measure of , and use the Law of Sines to find the lengths of
and
to the nearest hundredth.
By the angle sum of a triangle, .
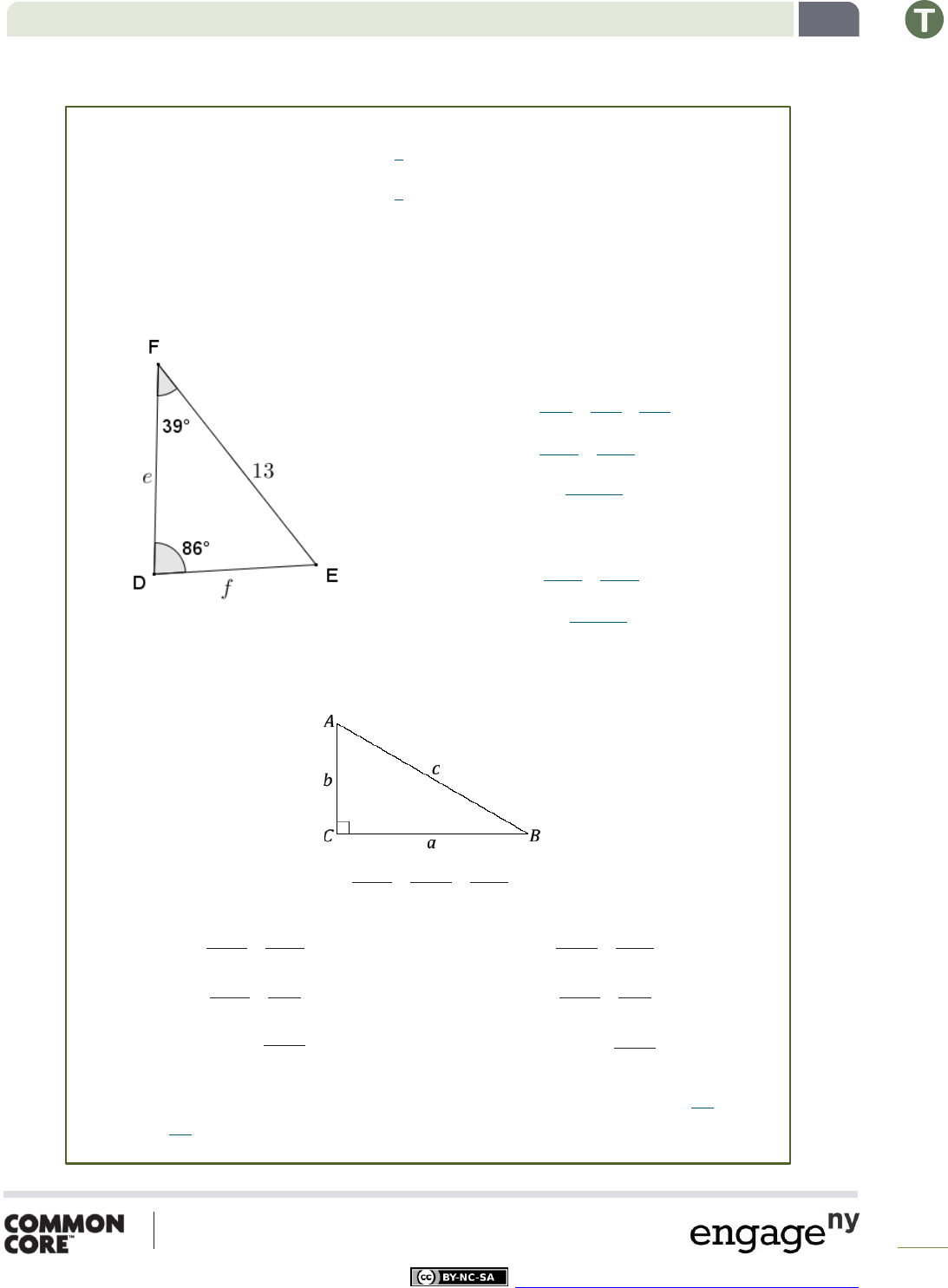
3. Does the law of sines apply to a right triangle? Based on , the following ratios were set up according to the
law of sines.
Fill in the partially completed work below:
What conclusions can we draw?
The law of sines does apply to a right triangle. We get the formulas that are equivalent to
and
, where and are the measures of the acute angles of the right triangle.
NYS COMMON CORE MATHEMATICS CURRICULUM
M2
Lesson 32
GEOMETRY
Lesson 32: Using Trigonometry to Find Side Lengths of an Acute Triangle
Date: 10/28/14
484
© 2014 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
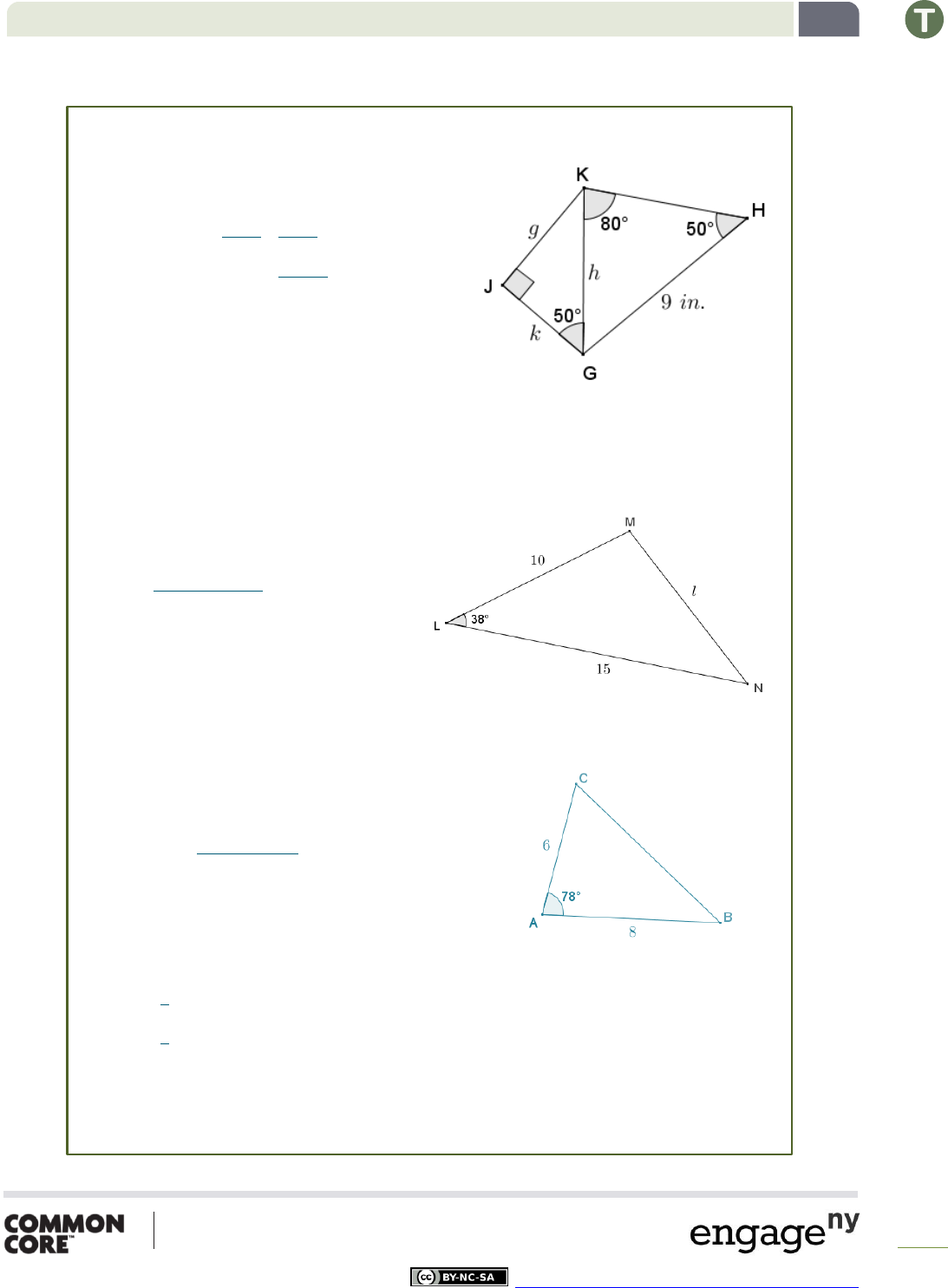
4. Given quadrilateral , , , , is a right angle and , use the Law
of Sines to find the length of , and then find the lengths of
and
to the nearest tenth of an inch.
By the angle sum of a triangle, ; therefore,
is an isosceles triangle since its base 's have equal
measure.
5. Given triangle , , , and , use the Law of Cosines to find the length of
to the
nearest tenth.
6. Given triangle , , , and . Draw a diagram of triangle , and use the law of cosines
to find the length of
.
The length of
is approximately .
Calculate the area of triangle .
The area of triangle is approximately square units.