Paradis Rdebuts_RO Rdebuts RO
User Manual: Paradis-rdebuts_RO
Open the PDF directly: View PDF ![]() .
.
Page Count: 79

R pentru incepatori
Emmanuel Paradis
Institututul de Stiinte ale Evolutiei
Universitatea din Montpellier II
F-34095 Montpellier c´edex 05
Franta
E-mail: paradis@isem.univ-montp2.fr
I thank Julien Claude, Christophe Declercq, ´
Elodie Gazave, Friedrich Leisch,
Louis Luangkesron, Fran¸cois Pinard, and Mathieu Ros for their comments and
suggestions on earlier versions of this document. I am also grateful to all the
members of the R Development Core Team for their considerable efforts in
developing R and animating the discussion list ‘rhelp’. Thanks also to the
R users whose questions or comments helped me to write “R for Beginners”.
Special thanks to Jorge Ahumada for the Spanish translation.
c
2002, 2005, Emmanuel Paradis (August 10, 2013)
Permission is granted to make and distribute copies, either in part or in
full and in any language, of this document on any support provided the above
copyright notice is included in all copies. Permission is granted to translate
this document, either in part or in full, in any language provided the above
copyright notice is included.
Traducerea si adaptarea textului in limba romana cu acordul autorului:
Ana Maria Dobre
Multumiri: Multumiri echipei R-omania, cea care se ocupa de sustinerea
R Project in Romania. Aceasta documentatie face parte din activitatile de
cercetare ale echipei R-omania Team: www.r-project.ro
Contents
1 Introducere 1
2 Cateva concepte de baza 3
2.1 Cum functioneaza R ........................ 3
2.2 Crearea, listarea si stergerea obiectelor din memorie ...... 5
2.3 Suportul online ........................... 7
3 Date in R 10
3.1 Obiecte ............................... 10
3.2 Citirea datelor dintr-un fisier ................... 12
3.3 Salvarea datelor ........................... 16
3.4 Generarea datelor .......................... 17
3.4.1 Secvente regulate ...................... 17
3.4.2 Secvente aleatoare ..................... 19
3.5 Manipularea obiectelor ....................... 20
3.5.1 Crearea obiectelor ..................... 20
3.5.2 Convertirea obiectelor ................... 25
3.5.3 Operatori .......................... 27
3.5.4 Accesarea valorilor unui obiect: sistemul de indexare . . 28
3.5.5 Accesarea valorilor unui obiect cu nume ......... 31
3.5.6 Editorul de date ...................... 32
3.5.7 Functii aritmetice simple ................. 33
3.5.8 Calcul matriceal ...................... 36
4 Grafice in R 38
4.1 Gestionarea graficelor ....................... 38
4.1.1 Deschiderea catorva instrumente grafice ......... 38
4.1.2 Impartirea unui grafic ................... 39
4.2 Functiile grafice ........................... 42
4.3 Comenzi de grafice de nivel scazut ................ 43
4.4 Parametri grafici .......................... 45
4.5 Un exemplu practic ......................... 46
4.6 Pachetele grid si lattice ....................... 50
5 Analiza statistica in R 58
5.1 Un exemplu simplu de analiza a variantei ............ 58
5.2 Formulele .............................. 59
5.3 Functii generice ........................... 61
5.4 Pachete ............................... 64

1 Introducere
Scopul prezentei documentatii este de a oferi un punct de plecare pentru cei
nou interesati de R. Am ales sa scot in evidenta in intelegerea modului in care
functioneaza R, cu intentia unui incepator, mai degraba decat a unui expert,
utilizarea acestuia. Avand in vedere ca posibilitatile acoperite de R sunt vaste,
este util unui incepator sa obtina notiuni si concepte de baza ˆın scopul de a
progresa cu usurinta. Am incercat sa simplific explicatiile cat de mult am
putut pentru a le face usor de inteles de catre toti cititorii, dand in acelasi
timp detalii utile, uneori exemplificate cu tabele.
R este un sistem pentru analize statistice si grafice creat de catre Ross Ihaka
si Robert Gentleman 1. R este in egala masura software si limbaj considerat
a fi un dialect al limbajului S creat de catre AT&T Bell Laboratories. S este
disponibil sub forma software-ului S-PLUS comercializat de catre Insightful2.
Exista diferente importante intre designul R-ului si al S-ului: cei care doresc
sa afle mai multe despre acest aspect pot citi articolul scris de catre Ihaka &
Gentleman (1996) sau R-FAQ3, o copie a acestuia fiind integrata in R.
R este distribuit in mod gratuit sub licenta GNU General Public Licence4;
dezvoltarea precum si distributialui sunt in grija catorva statisticieni cunoscuti
sub denumirea generica de R Development Core Team.
R este disponibil sub cateva forme: sursele (dezvoltate in special in C si
proceduri in Fortran), esentiale pentru Unix si Linux sau cateva fisiere binare
predefinite pentru Windows, Linux si Macintosh. Fisierele necesare pentru
instalarea R, fie din surse sau din fisiere binare predefinite sunt distribuite
pe site-ul Comprehensive R Archive Network (CRAN)5unde se gasesc si in-
structiunile pentru instalare. In ceea ce priveste variantele de Linux (Debian,
. . . ), fisierele binare sunt in general disponibile pentu majoritatea versiunilor;
cautati pe site-ul CRAN daca este necesar.
R are o multime de functii pentru analiza statistica si grafica; cele re-
cente au vizualizare instantanee in propria fereastra si pot fi salvate in diferite
formate (jpg, png, bmp, ps, pdf, emf, pictex, xfig; formatele disponibile pot
depinde de sistemul de operare). Rezultatele unei analize statistice sunt afisate
pe ecran, cateva rezultate intermediare (probabilitati, coeficienti de regresie,
valori reziduale, . . . ) pot fi salvate, scrise intr-un fisier, sau folosite in analize
ulterioare.
Limbajul R permite utilizatorului, spre exemplu, sa programeze grupurile
de instructiuni pentru analiza succesiva a seturilor de date. De asemenea este
1Ihaka R. & Gentleman R. 1996. R: a language for data analysis and graphics. Journal
of Computational and Graphical Statistics 5: 299–314.
2Vezi http://www.insightful.com/products/splus/default.asp pentru mai multe informatii
3http://cran.r-project.org/doc/FAQ/R-FAQ.html
4Pentru mai multe informatii: http://www.gnu.org/
5http://cran.r-project.org/
1

posibila combinarea intr-un singur program a mai multor functii statistice
pentru a efectua analize mai complexe. Utilizatorii R pot beneficia de o gama
larga de programe intocmite pentru S si care sunt disponibile pe Internet6,
majoritatea putand fi folosite direct in R.
La prima vedere, R poate parea prea complex pentru un non-specialist.
Lucrurile nu stau insa astfel. In realitate, o caracteristica de seama a lui
R este chiar flexibilitatea sa. In timp ce un software clasic afiseaza imediat
rezultatele unei analize, R memoreaza aceste rezultate intr-un ”obiect”, astfel
ca o analiza poate fi efectuata fara afisarea vreunui rezultat. Utilizatorul poate
ramane surprins din aceasta cauza, insa o asemenea particularitate este foarte
utila. Intr-adevar, utilizatorul poate extrage doar partea din rezultat de care
este interesat. Spre exemplu, daca cineva ruleaza o serie de 20 de regresii si
vrea sa compare diferiti coeficienti de regresie, R poate afisa numai coeficientii
estimati: astfel rezultatul poate avea o singura linie, in timp ce un software
clasic poate deschide 20 de ferestre cu rezultate. Vom vedea si alte exemple
ce ilustreaza flexibilitatea lui R in comparatie cu software-urile traditionale.
6Spre exemplu: http://stat.cmu.edu/S/
2
2 Cateva concepte de baza
Odata ce R a fost instalat pe computer, software-ul poate fi lansat prin fisierul
executabil corespunzator. Prompt-ul, implicit ‘>’, indica faptul ca R asteapta
comenzile operatorului. La utilizarea in Windows a programului Rgui.exe,
cateva comenzi (accesarea suportului online, deschiderea fisierelor,. . . ) pot
fi executate prin meniurile derulante. In aceasta etapa, un utilizator nou isi
poate pune intrebarea ≪Ce e de facut acum ? ≫. Este, intr-adevar, foarte
util sa cunoasteti cateva lucruri de baza atunci cand utilizati R pentru prima
data, iar acest fapt va fi demonstrat in cele ce urmeaza.
Vom vedea, pe scurt, cum functioneaza R. Apoi, vom descrie operatorul
“assign”, operator care permite crearea obiectelor, vom arata cum se orga-
nizeaza obiectele in memorie si cum se utilizeaza suportul online care este
foarte util atunci cand rulati R.
2.1 Cum functioneaza R
Faptul ca R este un limbaj ii poate face pe unii dintre utilizatori sa gandeasca
”Eu nu pot face programare”. Acest argument nu este solid din doua mo-
tive. In primul rand, R este un limbaj interpretat, nu unul compilat, ceea ce
presupune ca toate comenzile introduse prin tastatura sunt direct executate
fara sa fie necesara redactarea unui program complet asa cum se intampla in
majoritatea limbajelor de programare (C, Fortran, Pascal, . . . ).
In al doilea rand, sintaxa R este foarte simpla si intuitiva. Spre exemplu,
o regresie liniara poate fi efectuata cu ajutorul comenzii lm(y ~ x) care in-
seamna “adecvarea modelului liniar avand yca variabila de raspuns si xca
predictor”. In R, pentru a putea fi executata, o functie trebuie intotdeauna sa
fie scrisa cu paranteze, chiar daca nu este nimic scris intre acestea (de exemplu,
ls()). Daca se tasteaza numele unei functii fara sa fie urmat de paranteze, R
va afisa continutul functiei. In aceasta documentatie, numele functiilor sunt in
general scrise cu paranteze pentru a le distinge de alte obiecte, daca nu cumva
textul indica altfel.
Atunci cand R ruleaza, variabilele, datele, functiile, rezultatele, etc, sunt
retinute in memoria activa a computerului sub forma unor obiecte cu un anu-
mit nume. Utilizatorul poate actiona asupra acestor obiecte prin intermediul
operatorilor (aritmetici, logici, de comparatie, . . . ) si functiilor (chiar ele fiind
considerate obiecte). Utilizarea operatorilor este relativ intuitiva, mai tarziu
vom detalia acest aspect (p. 27). O functie R poate fi redata astfel:
3
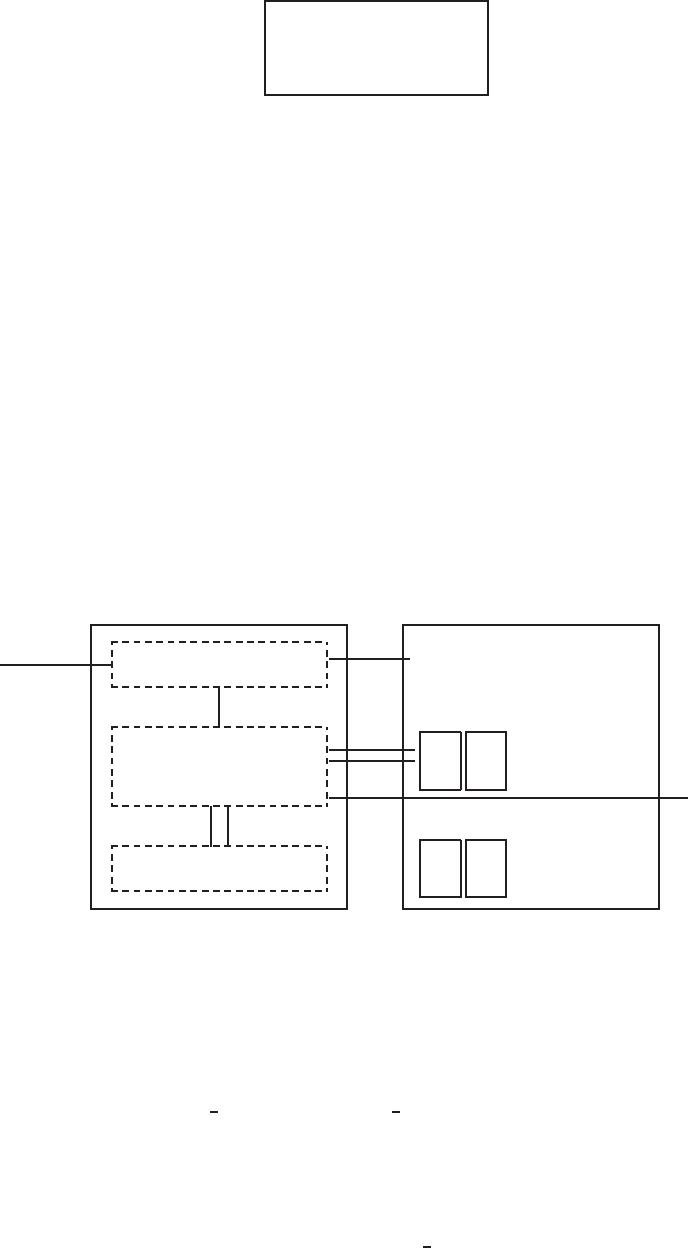
argumente −→
optiuni −→
functie
↑
argumente implicite
=⇒rezultat
Argumentele pot fi obiecte (“date”, formule, expresii, . . . ), cateva putand
fi definite implicit in cadrul functiei; aceste valori implicite pot fi modificate
de catre utilizator prin optiuni specifice. O functie R poate sa nu aiba nevoie
de argument: fie toate argumentele sunt definite implicit (iar valorile lor pot
fi modificate prin optiuni), fie nici un argument nu este definit in functie. Mai
tarziu vom vedea mai multe detalii despre utilizarea si construirea functiilor
(p. 70). Prezenta descriere este suficienta pentru moment ca sa intelegem cum
functioneaza R.
Toate actiunile din R sunt executate asupra obiectelor retinute in memoria
activa a computerului: nu sunt utilizate fisiere temporare (Fig. 1). Citirea si
scrierea fisierelor sunt utilizate pentru input-ul si output-ul datelor si rezul-
tatelor (grafice, . . . ). Utilizatorul executa functiile prin intermediul catorva
comenzi. Rezultatele sunt afisate direct pe ecran, memorate intr-un obiect,
sau scrise pe disc (in special pentru grafice). Din moment ce rezultatele sunt
obiecte, pot fi considerate ca date si analizate ca atare. Fisierele de date pot
fi citite de pe hard-disk-ul local sau de pe un server la distanta prin Internet.
functii si operatori
❄
obiecte de date
❄
✻
✏
✏
✏
✏✮ ❳❳❳❳❳❳
❳③
obiecte de rezultate
.../library/base/
/stast/
/graphics/
...
biblioteca de
functii
✛
fisiere
de date
✛✲
internet
✛
PS JPEG . . .
tastatura
mouse ✲
comenzi
ecran
Memoria activa Hard disk
Figure 1: O vedere schematica asupra modului in care functioneaza R
Functiile disponibile utilizatorului sunt stocate in biblioteca localizata pe
disc in folderul numit R HOME/library (R HOME este folderul unde este in-
stalat R). Acest folder contine pachete de functii, care sunt la randul lor struc-
turate in foldere. Pachetul numit base este, oarecum, baza R si contine functiile
de baza ale limbajului, in special pentru a citi si a manipula datele. Fiecare
pachet are un folder numit R cu un fisier cu denumirea pachetului (de exem-
plu, pentru pachetul base, acesta este fisierul R HOME/library/base/R/base).
4

Acest fisier contine toate functiile pachetului.
Una dintre cele mai simple comenzi este tastarea unui nume de obiect
pentru a afisa continutul sau. De exemplu, daca un obiect ncontine valoarea
10:
> n
[1] 10
Cifra 1 dintre paranteze indica faptul ca afisajul incepe cu primul element al
lui n. Aceasta comanda este o utilizare implicita a functiei print iar exemplul
de mai sus este similar cu print(n) (in unele situatii, functia print trebuie
sa fie utilizata explicit, cum ar fi in cadrul unei functii sau al unui ciclu).
Numele unui obiect poate incepe cu o litera (A–Z and a–z) si poate include
litere, cifre (0–9), puncte (.) si underline ( ). R face diferenta intre majuscule
si minuscule in numele obiectelor, astfel ca xsi Xpot fi doua nume de obiecte
distincte (chiar si in Windows).
2.2 Crearea, listarea si stergerea obiectelor din memorie
Un obiect poate fi creat prin operatorul ”assign” care este scris ca o sageata
cu un semn de minus si o paranteza; acest simbol poate fi orientat de la stanga
la dreapta sau invers:
> n <- 15
> n
[1] 15
> 5 -> n
> n
[1] 5
> x <- 1
> X <- 10
> x
[1] 1
> X
[1] 10
Daca obiectul exista deja, valoarea sa precedenta va fi stearsa (modificarea
are efect numai asupra obiectelor din memoria activa, nu si asupra datelor
de pe disc). Valoarea atribuita in acest mod poate fi rezultatul unei operatii
si/sau al unei functii:
> n <- 10 + 2
> n
[1] 12
> n <- 3 + rnorm(1)
> n
[1] 2.208807
5
Functia rnorm(1) genereaza o valoare aleatoare normala de medie zero si
varianta unitara (p. 19). De retinut ca puteti doar sa tastati o expresie fara
sa atribuiti valoarea sa unui obiect, rezultatul afisat astfel nefiind retinut in
memorie:
> (10 + 2) * 5
[1] 60
Atribuirea va fi omisa in exemple daca nu este necesara pentru intelegere.
Functia ls listeaza obiectele din memorie: doar numele obiectelor sunt
afisate.
> name <- "Carmen"; n1 <- 10; n2 <- 100; m <- 0.5
> ls()
[1] "m" "n1" "n2" "name"
De remarcat ca se pot utiliza semi-coloane pentru separarea comenzilor
distincte pe aceeasi linie. Daca dorim sa listam doar obiectele care contin un
anumit caracter in numele lor, poate fi utilizata optiunea pattern (care poate
fi prescurtata cu pat):
> ls(pat = "m")
[1] "m" "name"
Pentru a restrictiona listarea caracterelor ale caror nume incep cu un anumit
caracter:
> ls(pat = "^m")
[1] "m"
Functia ls.str afiseaza unele detalii despre obiectele din memorie:
> ls.str()
m : num 0.5
n1 : num 10
n2 : num 100
name : chr "Carmen"
Optiunea pattern poate fi utilizata in acelasi mod ca si ls. O alta optiune
utila a lui ls.str este max.level care specifica nivelul detalierii pentru afis-
area obiectelor compuse. In mod implicit, ls.str afiseaza detaliile obiectelor
din memorie, inclusiv coloane de secvente de date, matrici si liste, care pot
avea ca rezultat un afisaj lung. Putem evita afisarea tuturor acestor detalii
prin optiunea max.level = -1:
> M <- data.frame(n1, n2, m)
> ls.str(pat = "M")
M : ‘data.frame’: 1 obs. of 3 variables:
6
$ n1: num 10
$ n2: num 100
$ m : num 0.5
> ls.str(pat="M", max.level=-1)
M : ‘data.frame’: 1 obs. of 3 variables:
Pentru a sterge obiectele din memorie, folosim functia rm:rm(x) sterge
obiectul x,rm(x,y) sterge ambele obiecte xsi y,rm(list=ls()) sterge toate
obiectele din memorie; aceleasi optiuni mentionate pentru functia ls() pot fi
utilizate pentru a sterge in mod selectiv cateva obiecte: rm(list=ls(pat="^m")).
2.3 Suportul online
Suportul online al lui R ofera informatii foarte utile cu privire la modul in
care se utilizeaza functiile. Suportul este disponibil direct printr-o functie, ca
de exemplu:
> ?lm
va afisa, in cadrul R, pagina de asistenta pentru functia lm() (model liniar).
Comenzile help(lm) si help("lm") au acelasi efect. Cea din urma trebuie
utilizata pentru a accesa suportul cu caractere non-conventionale:
> ?*
Error: syntax error
> help("*")
Arithmetic package:base R Documentation
Arithmetic Operators
...
Prin apelarea suportului se deschide o pagina (aceasta depinde de sistemul
de operare) cu informatii generale pe primul rand cum ar fi numele pachetului
in cadrul caruia se afla functia sau operatorii respectivi. Apoi urmeaza un
titlu urmat de sectiuni care ofera informatii detaliate.
Descriere: o scurta descriere.
Utilizare: in cazul unei functii, precizeaza numele cu toate argumentele sale
si optiunile posibile (cu valorile corespunzatoare implicite); pentru un
operator precizeaza utilizarea specifica.
Argumente: in cazul unei functii, detaliaza fiecare argument al sau.
Detalii: descriere detaliata.
Valoare: daca este cazul, tipul obiectului returnat de functie sau operator.
Vezi si: alte pagini de suport apropiate sau similare cu cea actuala.
7
Exemple: cateva exemple care pot fi executate in general fara deschiderea
suportului cu functia example.
Pentru incepatori, este bine sa se consulte sectiunea Exemple. In general,
este util sa se citeasca cu atentie sectiunea Argumente. Pot fi intalnite si
alte sectiuni, cum ar fi Note,Referinte sau Autor(i).
In mod implicit, functia help cauta doar in pachetele care sunt incarcate
in memorie. Optiunea try.all.packages, care in mod implicit este FALSE,
permite cautarea in toate pachetele daca valoarea sa este TRUE:
> help("bs")
No documentation for ’bs’ in specified packages and libraries:
you could try ’help.search("bs")’
> help("bs", try.all.packages = TRUE)
Help for topic ’bs’ is not in any loaded package but
can be found in the following packages:
Package Library
splines /usr/lib/R/library
De retinut ca in acest caz pagina de suport a functiei bs nu este afisata.
Utilizatorul poate afisa paginile de suport pentru un pachet neincarcat in
memorie utilizand optiunea package:
> help("bs", package = "splines")
bs package:splines R Documentation
B-Spline Basis for Polynomial Splines
Description:
Generate the B-spline basis matrix for a polynomial spline.
...
Pagina de suport in format html (citita, de exemplu, cu Netscape) este
afisata prin:
> help.start()
O cautare prin cuvinte-cheie este posibila cu acest suport html. Sec-
tiunea Vezi si contine linkuri hypertext catre alte pagini suport pentru func-
tii. Cautarea prin cuvinte-cheie este de asemenea posibila in R prin func-
tia help.search. Cea din urma apare pentru un anumit topic, ca un sir
de caractere, in paginile de suport ale tuturor pachetelor instalate. De ex-
emplu, help.search("tree") va afisa o lista de functii pe care paginile de
suport le numesc “tree”. De retinut ca, in cazul in care cateva pachete au
fost recent instalate, poate fi utila reimprospatarea bazei de date utilizate
8
de help.search folosind optiunea rebuild (de ex., help.search("tree",
rebuild = TRUE)).
Functia apropos gaseste toate functiile ale caror nume contin sirul de car-
actere dat ca argument; se cauta doar in pachetele incarcate in memorie :
> apropos(help)
[1] "help" ".helpForCall" "help.search"
[4] "help.start"
9

3 Date in R
3.1 Obiecte
Am vazut ca R lucreaza cu obiecte care sunt, desigur, caracterizate de numele
lor si de continut, dar si de atribute care specifica tipul datelor reprezentate
in obiect. Pentru a intelege utilitatea acestor atribute, considerati o variabila
care poate lua valorile 1, 2, sau 3: o asemenea variabila poate fi de tip integer
(de exemplu, numarul oualelor dintr-un cuib) sau codificarea unei variabile
categoriale (de exemplu, sexul unor populatii de crustacei: masculin, feminin,
sau hermafrodit).
Este clar ca analiza statistica a acestei variabile nu va fi aceeasi in ambele
cazuri: in R, atributele unui obiect dau informatia necesara. In termeni mai
tehnici si mai generali, actiunea unei functii asupra unui obiect depinde de
atributele acestuia din urma.
Toate obiectele au doua atribute intrinseci:categoria si lungimea. Cate-
goria reprezinta tipul de baza al elementelor obiectului; exista patru categorii
principale: numeric, caracter, complex7, si logic (FALSE or TRUE). Exista si alte
categorii insa acestea nu reprezinta date, ca de exemplu functia sau expresia.
Lungimea este numarul de elemente ale obiectului. Pentru a afisa categoria si
lungimea unui obiect, se pot utiliza functiile mode si, respectiv, length:
> x <- 1
> mode(x)
[1] "numeric"
> length(x)
[1] 1
> A <- "Gomphotherium"; compar <- TRUE; z <- 1i
> mode(A); mode(compar); mode(z)
[1] "character"
[1] "logical"
[1] "complex"
Indiferent de categorie, datele lipsa sunt reprezentate de NA (not available).
O valoare numerica foarte mare poate fi specificata cu ajutorul unei notatii
exponentiale:
> N <- 2.1e23
> N
[1] 2.1e+23
R reprezinta in mod corect valori numerice infinite, cum ar fi ±∞ cu Inf
si -Inf, sau valori nenumerice cu NaN (not a number).
7Categoria complex nu va fi tratata in aceasta documentatie.
10

> x <- 5/0
> x
[1] Inf
> exp(x)
[1] Inf
> exp(-x)
[1] 0
> x - x
[1] NaN
O valoare a categoriei de tip caracter este introdusa cu ghilimele duble
". Este posibil sa includa ultimul caracter in valoare daca acesta urmeaza un
backslash \. Cele doua caractere \"vor fi tratate impreuna in mod specific
de cateva functii, cum ar fi cat pentru afisarea pe ecran, sau write.table
pentru scrierea pe hard-disk (p. 16, optiunea qmethod a acestei functii).
> x <- "Double quotes \" delimitate R’s strings."
> x
[1] "Double quotes \" delimitate R’s strings."
> cat(x)
Double quotes " delimitate R’s strings.
Ca o alternativa, variabilele de tip caracter pot fi delimitate cu ghilimele
simple (’); in acest caz nu este necesar sa inlocuim ghilimelele duble cu
backslash-uri (insa trebuie sa existe ghilimele simple!):
> x <- ’Double quotes " delimitate R\’s strings.’
> x
[1] "Double quotes \" delimitate R’s strings."
Tabelul urmator prezinta un rezumat al tipurilor de obiecte ce reprezinta
date.
obiect tipuri mai multe tipuri
posibile in
acelasi obiect
vector numeric, caracter, complex sau logic Nu
factor numeric sau caracter Nu
sir numeric, caracter, complex sau logic Nu
matrice numeric, caracter, complex sau logic Nu
secventa de date numeric, caracter, complex sau logic Da
ts numeric, caracter, complex sau logic Nu
lista numeric, caracter, complex, logic, Da
functie, expresie, . . .
11

Un vector este o variabila in sensul general valabil. Un factor este o vari-
abila categoriala. Un sir este un tabel cu kdimensiuni, o matrice fiind un
caz particular de sir cu k= 2. De retinut ca elementele unui sir sau ale unei
matrici sunt toate de acelasi tip. O secventa de date este un tabel compus din
unul sau cativa vectori si/sau factori de aceeasi lungime dar posibil de tipuri
diferite. Un ‘ts’ este un set de date de serii de timp ce contine atribute adi-
tionale cum ar fi frecventa si datele. Nu in ultimul rand, o lista poate contine
orice tip de obiect, inclusiv liste!
In cazul unui vector, tipul sau/si lungimea sunt suficiente pentru a descrie
datele. In cazul altor obiecte, sunt necesare alte informatii care sunt date
de atribute non-intrinseci. Dintre aceste atribute, putem mentiona dim, ce
corespunde dimensiunilor unui obiect. De exemplu, o matrice cu 2 linii si 2
coloane are pentru dim perechea de valori [2, 2], insa lungimea sa este 4.
3.2 Citirea datelor dintr-un fisier
Pentru scrierea si citirea in fisiere, R utilizeaza folderul de lucru. Pentru a gasi
acest folder, comanda getwd() (obtine folderul de lucru) poate fi utilizata, iar
folderul de lucru poate fi schimbat cu setwd("C:/data") sau setwd("/home/-
paradis/R"). Este necesar sa atribuim calea unui fisier daca acesta nu se afla
in folderul de lucru.8
R poate citi date stocate in fisiere text (ASCII) cu urmatoarele functii:
read.table (care are cateva variante, vezi mai jos), scan si read.fwf. R
poate de asemenea sa citeasca fisiere in alte formate (Excel, SAS, SPSS, . . . )
si sa acceseze baze de date de tip SQL, insa functiile necesare nu se afla in
pachetul base. Aceste functionalitati sunt foarte eficiente pentru o utilizare
mai avansata a R, insa ne vom opri aici la citirea fisierelor in format ASCII.
Functia read.table are ca efect crearea unei secvente de date, iar aceasta
este modalitatea principala de citire a datelor in forma tabelara. De exemplu,
pentru un fisier numit data.dat, comanda:
> mydata <- read.table("data.dat")
va crea o secventa de date numita mydata, iar fiecare variabila va fi numita,
implicit, V1,V2, . . . si poate fi accesata individual prin mydata$V1,mydata$V2,
. . . , sau prin mydata["V1"],mydata["V2"], . . . , sau, inca o alta varianta,
prin mydata[, 1],mydata[,2 ], . . . 9Exista cateva optiuni ale caror valori
implicite (de ex. cele utilizate de R daca sunt omise de utilizator) sunt detaliate
in tabelul urmator:
8In Windows, este utila crearea unui shortcut al Rgui.exe apoi editarea proprietatilor si
schimbarea folderului in campul “Start in:” sub tab-ul “Short-cut”: acest folder va deveni
folderul de lucru daca R este pornit din acest shortcut.
9Exista o diferenta: mydata$V1 si mydata[, 1] sunt vectori in timp ce mydata["V1"]
este o secventa de date. Vom vedea mai tarziu (p. 20) cateva detalii privind manipularea
obiectelor.
12
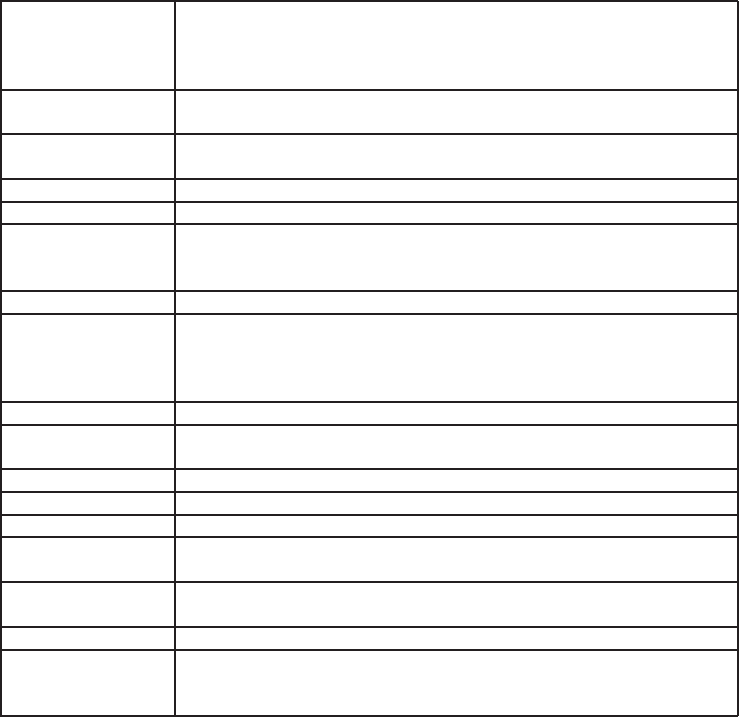
read.table(file, header = FALSE, sep = "", quote = "\"’", dec = ".",
row.names, col.names, as.is = FALSE, na.strings = "NA",
colClasses = NA, nrows = -1,
skip = 0, check.names = TRUE, fill = !blank.lines.skip,
strip.white = FALSE, blank.lines.skip = TRUE,
comment.char = "#")
fisier numele fisierului (intre "" sau o variabila de tip caracter), posibil
cu calea sa (simbolul \nu este permis si trebuie inlocuit cu /, chiar
si in Windows), sau acces la distanta catre un fisier de tip URL
(http://...)
header o variabila de tip logic (FALSE sau TRUE) ce indica daca fisierul con-
tine numele variabilelor pe prima linie
sep campul separator folosit in fisier, de exemplu sep="\t" daca este o
tabulare
quote caracterele folosite pentru a cita variabilele de tip caracter
dec caracterul utilizat pentru zecimale
row.names un vector cu numele liniilor care poate fi un vector de tip caracter,
sau numar ( sau nume) a unei variabile din fisier (implicit: 1,2,3,
...)
col.names un vector cu numele variabilelor (implicit: V1,V2,V3, ...)
as.is controleaza conversia variabilelor de tip caracter in factori (daca
este FALSE) le pastreaza caractere (TRUE); as.is poate fi vector de
tip logic, numeric sau caracter cu mentionarea variabilelor ce trebuie
pastrate ca si caractere
na.strings valoarea atribuita datelor lipsa (convertita in NA)
colClasses un vector de tip caracter ce returneaza clasele ce trebuie atribuite
coloanelor
nrows numarul maxim de linii de citit (valorile negative sunt ignorate)
skip numarul de linii de omis inainte de citirea datelor
check.names pentru TRUE, verifica daca numele variabilei este valid pentru R
fill daca TRUE si toate liniile nu au acelasi numar de variabile, sunt
adaugate “blank-uri”
strip.white (conditional to sep) pentru TRUE, sterge spatiile in plus dinaintea si
dupa variabilele de tip caracter
blank.lines.skip pentru TRUE, ignora liniile “blank”
comment.char caracter ce defineste comentariile din fisierul de date, restul liniei de
dupa acest caracter este ignorat (pentru a dezactiva acest argument,
utilizati comment.char = "")
Variantele read.table sunt eficiente din moment ce au diferite valori im-
plicite:
read.csv(file, header = TRUE, sep = ",", quote="\"", dec=".",
fill = TRUE, ...)
read.csv2(file, header = TRUE, sep = ";", quote="\"", dec=",",
fill = TRUE, ...)
read.delim(file, header = TRUE, sep = "\t", quote="\"", dec=".",
fill = TRUE, ...)
13
read.delim2(file, header = TRUE, sep = "\t", quote="\"", dec=",",
fill = TRUE, ...)
Functia scan este mai flexibila decat read.table. O diferenta consta in
posibilitatea specificarii tipului variabilelor, ca de exemplu:
> mydata <- scan("data.dat", what = list("", 0, 0))
citeste in fisierul data.dat trei variabile, prima este de tip caracter iar ur-
matoarele doua sunt de tip numeric. O alta diferenta importanta este aceea
ca scan() poate fi utilizat pentru crearea diferitelor obiecte, vectori, matrici,
secvente de date, liste, . . . In exemplul de mai sus, mydata este o lista de
trei vectori. In mod implicit, daca what este omis, scan() creaza un vector
numeric. Daca datele citite nu corespund tipului asteptat (nici cel implicit,
nici cel specificat de what), este afisat un mesaj de eroare. Optiunile sunt
urmatoarele:
scan(file = "", what = double(0), nmax = -1, n = -1, sep = "",
quote = if (sep=="\n") "" else "’\"", dec = ".",
skip = 0, nlines = 0, na.strings = "NA",
flush = FALSE, fill = FALSE, strip.white = FALSE, quiet = FALSE,
blank.lines.skip = TRUE, multi.line = TRUE, comment.char = "",
allowEscapes = TRUE)
14

file numele fisierului (intre ""), posibil si calea sa (the symbol \nu este
permis si trebuie sa fie inlocuit de /, chiar si in Windows), sau cu
acces la distanta la un fisier de tip URL (http://...); daca file="",
datele sunt introduse prin tastatura (accesul este incheiat de o linie
blank)
what specifica tipul datelor (implicit numeric)
nmax numarul datelor de citit, sau, daca what este de tip lista, numarul
liniilor de citit (implicit, scan citeste datele pana la sfarsitul fisieru-
lui)
nnumarul datelor de citit (implicit, fara limita)
sep campul separator utilizat in fisier
quote caracterele utilizate pentru citarea variabilelor de tip caracter
dec caracterul utilizat pentru zecimale
skip numarul de linii omise inainte de citirea datelor
nlines numarul de linii de citit
na.string valoarea atribuita datelor lipsa (convertita ca NA)
flush o valoare logica, pentru TRUE,scan sare la linia urmatoare odata ce
numarul de coloane a fost atins (permite utilizatorului sa adauge
comentarii in fisierul de date)
fill daca TRUE si toate liniile nu au acelasi numar de variabile, sunt
adaugate ”blank-uri”
strip.white (conditional to sep) pentru TRUE, sterge spaiile in plus dinainte si
dupa variabilele de tip caracter
quiet o valoare logica, pentru FALSE,scan afiseaza o linie ce arata cam-
purile care au fost citite
blank.lines.skip pentru TRUE, ignora liniile blank
multi.line daca what este de tip lista, specifica daca variabilele aceleiasi inreg-
istrari sunt afisate pe o singura linie in fisier (FALSE)
comment.char un caracter ce defineste comentariile in fisierul de date, restul liniei
ce urmeaza dupa acest caracter este ignorat (in mod implicit este
dezactivat)
allowEscapes precizeaza care dintre C-style nu este (e.g., ‘\t’) procesat (cel im-
plicit) sau citit ca si verbatim
Functia read.fwf poate fi utilizata pentru citirea unor date intr-un fisier
in format de dimensiune fixa:
read.fwf(file, widths, header = FALSE, sep = "\t",
as.is = FALSE, skip = 0, row.names, col.names,
n = -1, buffersize = 2000, ...)
Optiunile sunt aceleasi ca pentru read.table(), cu
exceptia widths care specifica dimensiunea campurilor
(buffersize este numarul maxim de linii citite simul-
tan). De exemplu, daca un fisier numit data.txt contine
datele indicate in partea dreapta, datele pot fi citite cu
urmatoarea comanda:
A1.501.2
A1.551.3
B1.601.4
B1.651.5
C1.701.6
C1.751.7
> mydata <- read.fwf("data.txt", widths=c(1, 4, 3))
> mydata
V1 V2 V3
1 A 1.50 1.2
15

2 A 1.55 1.3
3 B 1.60 1.4
4 B 1.65 1.5
5 C 1.70 1.6
6 C 1.75 1.7
3.3 Salvarea datelor
Functia write.table scrie intr-un fisier un obiect, in mod caracteristic o
secventa de date dar si alte tipuri de obiecte (vector, matrice, . . . ). Argu-
mentele si optiunile sunt urmatoarele:
write.table(x, file = "", append = FALSE, quote = TRUE, sep = " ",
eol = "\n", na = "NA", dec = ".", row.names = TRUE,
col.names = TRUE, qmethod = c("escape", "double"))
xnumele obiectului ce urmeaza a fi scris
file numele fisierului (in mod implicit obiectul este afisat pe ecran)
append pentru TRUE adauga datele fara sa le stearga pe acelea posibil existente in
fisier
quote un vector de tip numeric sau logic: pentru TRUE variabilele de tip caracter
si cele de tip factor sunt scrise intre "", altfel vectorul numeric indica
numarul de variabile de scris intre "" (in ambele cazuri numele variabilelor
sunt scrise intre "" dar nu si pentru quote = FALSE)
sep separatorul de campuri utilizat in fisier
eol caracterul utilizat la sfarsitul fiecarei linii ("\n")
na caracterul utilizat pentru date lipsa
dec caracterul utilizat pentru zecimale
row.names o valoare logica ce indica daca numele liniilor sunt scrise in fisier
col.names numele coloanelor
qmethod specifica, pentru quote=TRUE, modul in care ghilimelele "incluse in vari-
abilele de tip caracter sunt tratate: pentru "escape" (sau "e", implicit)
fiecare "este inlocuit de \", pentru "d" fiecare "este inlocuit de ""
Pentru a scrie mai simplu un obiect intr-un fisier, poate fi utilizata comanda
write(x, file="data.txt"), unde xeste numele obiectului (care poate fi
vector, matrice, sau un sir). Exista doua optiuni: nc (sau ncol) care defineste
numarul de coloane din fisier (in mod implicit nc=1 daca xeste de tip caracter,
nc=5 pentru alte tipuri) si append (de tip logic) pentru a adauga datele fara
stergerea celor posibil existente in fisier (TRUE) sau stergerea lor daca fisierul
exista deja (FALSE, in mod implicit).
Pentru a inregistra un grup de obiecte de orice tip, putem utiliza comanda
save(x, y, z, file= "xyz.RData"). Pentru a usura transferul de date din-
tre diferite aparate, poate fi utilizata optiunea ascii = TRUE. Datele (care
sunt numite in aceasta faza workspace in jargon R) pot fi incarcate mai tarziu
in memorie cu load("xyz.RData"). Functia save.image() este un shortcut
pentru save(list =ls(all=TRUE), file=".RData").
16
3.4 Generarea datelor
3.4.1 Secvente regulate
O secventa regulata de obiecte integer, de exemplu de la 1 la 30, poate fi
generata astfel:
> x <- 1:30
Vectorul rezultat xare 30 de elemente. Operatorul ‘:’ are prioritate printre
operatorii aritmetici in cadrul unei expresii:
> 1:10-1
[1] 0 1 2 3 4 5 6 7 8 9
> 1:(10-1)
[1] 1 2 3 4 5 6 7 8 9
Functia seq poate genera secvente de numere reale dupa cum urmeaza:
> seq(1, 5, 0.5)
[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
unde primul numar indica inceputul secventei, al doilea sfarsitul, iar al treilea
cresterea utilizata pentru generarea secventei. Se mai poate utiliza si:
> seq(length=9, from=1, to=5)
[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Se pot atribui direct valorile utilizand functia c:
> c(1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5)
[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
De asemenea este posibil, daca se doreste introducerea unor date prin
tastatura, sa se utilizeze functia scan cu optiunile implicite precum urmeaza:
> z <- scan()
1: 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
10:
Read 9 items
> z
[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Functia rep creaza un vector cu toate elementele identice:
> rep(1, 30)
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Functia sequence creaza o serie de secvente de obiecte integer terminata
fiecare cu numerele date ca argumente:
17
> sequence(4:5)
[1] 1 2 3 4 1 2 3 4 5
> sequence(c(10,5))
[1] 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5
Functia gl (eng. generates levels) este foarte folositoare intrucat genereaza
serii regulate de factori. Utilizarea acestei functii este redata gl(k, n), unde
keste numarul de niveluri (sau clase) si neste numarul de raspunsuri in fiecare
nivel. Pot fi utilizate doua optiuni: length pentru a specifica numarul de date
generate si labels pentru a specifica numele nivelurilor factorului. Exemple:
> gl(3, 5)
[1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
Levels: 1 2 3
> gl(3, 5, length=30)
[1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
Levels: 1 2 3
> gl(2, 6, label=c("Male", "Female"))
[1] Male Male Male Male Male Male
[7] Female Female Female Female Female Female
Levels: Male Female
> gl(2, 10)
[1] 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
Levels: 1 2
> gl(2, 1, length=20)
[1] 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2
Levels: 1 2
> gl(2, 2, length=20)
[1] 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2
Levels: 1 2
expand.grid() creaza o secventa de date cu toate combinatiile de vectori
sau factori dati ca argumente:
> expand.grid(h=c(60,80), w=c(100, 300), sex=c("Male", "Female"))
h w sex
1 60 100 Male
2 80 100 Male
3 60 300 Male
4 80 300 Male
5 60 100 Female
6 80 100 Female
7 60 300 Female
8 80 300 Female
18

3.4.2 Secvente aleatoare
teorema functia
Gaussian (normal) rnorm(n, mean=0, sd=1)
exponential rexp(n, rate=1)
gamma rgamma(n, shape, scale=1)
Poisson rpois(n, lambda)
Weibull rweibull(n, shape, scale=1)
Cauchy rcauchy(n, location=0, scale=1)
beta rbeta(n, shape1, shape2)
‘Student’ (t)rt(n, df)
Fisher–Snedecor (F)rf(n, df1, df2)
Pearson (χ2)rchisq(n, df)
binomial rbinom(n, size, prob)
multinomial rmultinom(n, size, prob)
geometric rgeom(n, prob)
hipergeometric rhyper(nn, m, n, k)
logistic rlogis(n, location=0, scale=1)
lognormal rlnorm(n, meanlog=0, sdlog=1)
negativ binomial rnbinom(n, size, prob)
uniform runif(n, min=0, max=1)
statistica Wilcoxon rwilcox(nn, m, n),rsignrank(nn, n)
In statistica este necesar sa se poata genera date aleatoare, iar R poate
face asta pentru o gama larga de functii de densitate de probabilitate. Aceste
functii sunt de forma rfunc (n, p1, p2, ...), unde func indica probabili-
tatea distributiei, nnumarul de date generate, iar p1,p2, . . . sunt valorile
parametrilor distributiei. Tabelul de mai sus ofera detalii pentru fiecare tip
de distributie si valorile posibile implicite (daca nicio valoare implicita nu este
indicata, inseamna ca parametrul trebuie precizat de catre utilizator).
Majoritatea acestor functii au echivalente obtinute prin inlocuirea literei r
cu d,psau qpentru a obtine, densitatea de probabilitate (dfunc (x, ...)),
distributia cumulativa de probabilitate (pfunc (x, ...)), respectiv valoarea
quantilei (qfunc (p, ...), cu 0 <p<1). Ultimele seturi de functii pot fi
utilizate pentru a gasi valorile critice sau P-values ale testelor statistice. Spre
exemplu, valorile critice pentru testul t bilateral urmand o distributie normala
de 5% au limitele:
> qnorm(0.025)
[1] -1.959964
> qnorm(0.975)
[1] 1.959964
Pentru testul t unilateral, qnorm(0.05) si 1 -
qnorm(0.95) vor fi utilizate in functie de forma ipotezei alternative.
Valoarea P-value a unui test, cu χ2= 3.84 si df = 1, este:
19
> 1 - pchisq(3.84, 1)
[1] 0.05004352
3.5 Manipularea obiectelor
3.5.1 Crearea obiectelor
Anterior am prezentat diferite metode de creare a obiectelor utilizand oper-
atorul de atribuire; tipul si categoria obiectelor create astfel sunt in general
implicit determinate. Este posibila crearea unui obiect si specificarea modului
sau, a lungimii, categoriei, etc. Aceasta maniera este interesanta din perspec-
tiva manipularii obiectelor. Este posibila, spre exemplu, crearea unui obiect
‘gol’ si modificarea elementelor sale in mod succesiv, ceea ce este mai eficient
decat combinarea elementelor sale cu c(). Sistemul de indexare poate fi folosit
aici, asa cum vom vedea mai tarziu (p. 28).
Poate fi de asemenea foarte convenabila crearea unor obiecte din altele
deja existente. De exemplu, daca se doreste adecvarea unei serii de modele,
se pune formula intr-o lista, iar apoi se extrag succesiv elementele pentru a le
insera in functia lm.
In aceasta etapa a studierii R-ului, interesul pentru invatarea urmatoarelor
functionalitati este atat practic cat si didactic. Constructia explicita a obiectelor
ofera o intelegere mai buna a structurii lor si ne permite sa avansam catre niste
notiuni anterior mentionate.
Vector. Functia vector, care are doua argumente mode si length, creaza un
vector ale carui elemente au o valoare dependenta de tipul specificat ca
argument: 0 pentru numeric, FALSE pentru logic, sau "" pentru carac-
ter. Functiile urmatoare au exact acelasi efect si au pentru un singur
argument lungimea vectorului: numeric(),logical(), si character().
Factor. Un factor include nu doar valorile corespunzatoare variabilei catego-
riale, ci si diferitele niveluri posibile ale acelei variabile (chiar daca nu
exista in date). Functia factor creaza un factor cu urmatoarele optiuni:
factor(x, levels = sort(unique(x), na.last = TRUE),
labels = levels, exclude = NA, ordered = is.ordered(x))
levels specifica posibilele niveluri ale factorului (in mod implicit valorile
unice ale vectorului x), labels defineste numele nivelurilor, exclude
valorile lui xpentru excluderea din niveluri si ordered este un argument
logic ce specifica daca nivelurile factorului sunt ordonate. Rechemarea
lui xeste de tip numeric sau caracter. Urmeaza cateva exemple.
> factor(1:3)
[1] 1 2 3
Levels: 1 2 3
20
> factor(1:3, levels=1:5)
[1] 1 2 3
Levels: 1 2 3 4 5
> factor(1:3, labels=c("A", "B", "C"))
[1] A B C
Levels: A B C
> factor(1:5, exclude=4)
[1] 1 2 3 NA 5
Levels: 1 2 3 5
Functia levels extrage posibilele niveluri ale unui factor:
> ff <- factor(c(2, 4), levels=2:5)
> ff
[1] 2 4
Levels: 2 3 4 5
> levels(ff)
[1] "2" "3" "4" "5"
Matrice. O matrice este de fapt un vector cu un atribut aditional (dim) care
la randul lui este un vector numeric de lungime 2 si defineste numarul de
linii si coloane ale matricii. O matrice poate fi creata cu functia matrix:
matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE,
dimnames = NULL)
Optiunea byrow indica daca valorile date de data trebuie sa completeze
succesiv coloanele (varianta implicita) sau liniile (pentru TRUE). Op-
tiunea dimnames permite atribuirea de nume liniilor si coloanelor.
> matrix(data=5, nr=2, nc=2)
[,1] [,2]
[1,] 5 5
[2,] 5 5
> matrix(1:6, 2, 3)
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
> matrix(1:6, 2, 3, byrow=TRUE)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
O alta modalitate de creare a unei matrici este atribuirea de valori core-
spunzatoare atributului dim (care este initial NULL):
21
> x <- 1:15
> x
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
> dim(x)
NULL
> dim(x) <- c(5, 3)
> x
[,1] [,2] [,3]
[1,] 1 6 11
[2,] 2 7 12
[3,] 3 8 13
[4,] 4 9 14
[5,] 5 10 15
Secventa de date. Am vazut pana acum ca o secventa de date este cre-
ata implicit de functia read.table; de asemenea este posibila crearea
unei secvente de date cu functia data.frame. Vectorii astfel inclusi in
secventa de date trebuie sa fie de aceeasi lungime, sau daca unul dintre
ei este mai scurt, este “reciclat” de un anumit numar de ori:
> x <- 1:4; n <- 10; M <- c(10, 35); y <- 2:4
> data.frame(x, n)
x n
1 1 10
2 2 10
3 3 10
4 4 10
> data.frame(x, M)
x M
1 1 10
2 2 35
3 3 10
4 4 35
> data.frame(x, y)
Error in data.frame(x, y) :
arguments imply differing number of rows: 4, 3
Daca un factor este inclus in secventa de date, trebuie sa fie de aceeasi
lungime cu vectorul(vectorii). Este posibila schimbarea numelor coloanelor
cu, spre exemplu, data.frame(A1=x, A2=n). De asemenea se pot atribui
nume liniilor cu optiunea row.names care trebuie sa fie, bineinteles, un
vector de tip caracter si cu lungimea egala cu numarul de linii ale secven-
tei de date. De retinut ca secventele de date au un atribut dim similar
cu matricile.
List. O lista este creata intr-un mod similar cu secventele de date prin functia
list. Nu exista nicio limitare asupra obiectelor care sa poata fi inclusa.
22
Spre deosebire de data.frame(), numele obiectelor nu sunt luate im-
plicit; atribuirea vectorilor xsi yse ilustreaza in exemplul urmator:
> L1 <- list(x, y); L2 <- list(A=x, B=y)
> L1
[[1]]
[1] 1 2 3 4
[[2]]
[1] 2 3 4
> L2
$A
[1] 1 2 3 4
$B
[1] 2 3 4
> names(L1)
NULL
> names(L2)
[1] "A" "B"
Serii de timp. Functia ts creaza un obiect de clasa "ts" dintr-un vector
(serii de timp singulare) sau dintr-o matrice (serii de timp multivariate) si
cateva optiuni care caracterizeaza seriile. Optiunile, cu valorile implicite,
sunt urmatoarele:
ts(data = NA, start = 1, end = numeric(0), frequency = 1,
deltat = 1, ts.eps = getOption("ts.eps"), class, names)
23
data un vector sau o matrice
start timpul primei observatii, fie ca este un numar sau un
vector de doua numere intregi (vezi exemplul de mai sus)
end timpul ultimei observatii specificat in acelasi mod ca si
start
frequency numarul de observatii pe unitate de timp
deltat fractiunea perioadei de esantionare dintre observatii suc-
cesive (ex. 1/12 pentru date lunare); doar o frequency
sau deltat trebuie atribuite
ts.eps toleranta pentru comparatia seriilor. Frecventele sunt
considerate egale daca diferentele lor sunt mai mici decat
ts.eps
class clasa atribuita obiectului; cea implicita este "ts" pentru
o serie singulara si c("mts", "ts") pentru serii multi-
variate
names un vector de tip caracter cu numele seriilor individuale
in cazul seriilor multivariate; in mod implicit numele
coloanelor data sau Series 1,Series 2, . . .
Cateva exemple de serii de timp create cu ts:
> ts(1:10, start = 1959)
Time Series:
Start = 1959
End = 1968
Frequency = 1
[1] 1 2 3 4 5 6 7 8 9 10
> ts(1:47, frequency = 12, start = c(1959, 2))
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1959 1 2 3 4 5 6 7 8 9 10 11
1960 12 13 14 15 16 17 18 19 20 21 22 23
1961 24 25 26 27 28 29 30 31 32 33 34 35
1962 36 37 38 39 40 41 42 43 44 45 46 47
> ts(1:10, frequency = 4, start = c(1959, 2))
Qtr1 Qtr2 Qtr3 Qtr4
1959 1 2 3
1960 4 5 6 7
1961 8 9 10
> ts(matrix(rpois(36, 5), 12, 3), start=c(1961, 1), frequency=12)
Series 1 Series 2 Series 3
Jan 1961 8 5 4
Feb 1961 6 6 9
Mar 1961 2 3 3
Apr 1961 8 5 4
May 1961 4 9 3
Jun 1961 4 6 13
24
Jul 1961 4 2 6
Aug 1961 11 6 4
Sep 1961 6 5 7
Oct 1961 6 5 7
Nov 1961 5 5 7
Dec 1961 8 5 2
Expresia. Obiectele de tip expresie au un rol fundamental in R. O expresie
este o serie de caractere care au sens pentru R. Toate comenzile valide
sunt expresii. Atunci cand o comanda este introdusa direct prin tas-
tatura, esteevaluata de catre R si executata daca este valida. In multe
cazuri, este necesara construirea unei expresii fara evaluarea ei: aceasta
este ceea ce executa functia expression. Este, de asemenea, posibila
evaluarea ulterioara a expresiei cu eval().
> x <- 3; y <- 2.5; z <- 1
> exp1 <- expression(x / (y + exp(z)))
> exp1
expression(x/(y + exp(z)))
> eval(exp1)
[1] 0.5749019
Expresiile pot fi utilizate, odata cu alte obiecte, la includerea ecuatiilor
in grafice (p. 44). O expresie poate fi creata dintr-o variabila de tip
caracter. Cateva functii recunosc expresiile ca argumente, de exemplu D
care returneaza derivate partiale:
> D(exp1, "x")
1/(y + exp(z))
> D(exp1, "y")
-x/(y + exp(z))^2
> D(exp1, "z")
-x * exp(z)/(y + exp(z))^2
3.5.2 Convertirea obiectelor
Cititorul a realizat cu siguranta ca diferentele dintre cateva tipuri de obiecte
sunt mici; prin urmare este logic ca este posibila convertirea unui obiect dintr-
un tip in altul prin schimbarea unor atribute ale sale. O asemenea conversie
va fi efectuata cu o functie de tipul as.something . R (versiunea 2.1.0) are, in
pachetele base si utils, 98 astfel de functii, astfel ca nu vom aprofunda aceste
detalii aici.
Rezultatul unei conversii depinde, evident, de atributele obiectului conver-
tit. In general, conversia urmeaza reguli intuitive. Pentru conversia tipurilor,
tabelul urmator ofera o privire de ansamblu.
25

Conversie in Functia Reguli
numeric as.numeric FALSE →0
TRUE →1
"1","2", . . . →1, 2, . . .
"A", . . . →NA
logic as.logical 0→FALSE
other numbers →TRUE
"FALSE","F" →FALSE
"TRUE","T" →TRUE
other characters →NA
caracter as.character 1, 2, . . . →"1","2", . . .
FALSE →"FALSE"
TRUE →"TRUE"
Exista functii speciale pentru convertirea tipurilor obiectelor (as.matrix,
as.ts,as.data.frame,as.expression, . . . ). Aceste functii vor modifica alte
atribute in afara de tip in timpul conversiei. Rezultatele sunt, din nou, intu-
itive in general. O situatie frecvent intalnita este conversia factorilor in valori
numerice. In acest caz, R face conversia cu o codare numerica a nivelurilor
factorului:
> fac <- factor(c(1, 10))
> fac
[1] 1 10
Levels: 1 10
> as.numeric(fac)
[1] 1 2
Aceasta are inteles atunci cand se considera un factor de tip caracter:
> fac2 <- factor(c("Male", "Female"))
> fac2
[1] Male Female
Levels: Female Male
> as.numeric(fac2)
[1] 2 1
De retinut ca rezultatul nu este NA, asa cum ar fi fost de asteptat conform
tabelului de mai sus.
Pentru a converti factorul de tip numeric intr-un vector numeric cu pas-
trarea nivelurilor asa cum erau specificate, trebuie convertit intai in caracter,
apoi in numeric.
> as.numeric(as.character(fac))
[1] 1 10
26

Aceasta procedura este foarte utila daca intr-un fisier o variabila numerica
are si valori nenumerice. Am vazut ca read.table() intr-o asemenea situatie
data, va citi, implicit, aceasta coloana ca si factor.
3.5.3 Operatori
Anterior am observat ca exista trei tipuri principale de operatori in R10
Operatori
Aritmetici De comparatie Logici
+adunare <mai mic ! x NU logic
-scadere >mai mare x & y SI logic
*inmultire <= mai mic sau egal x && y id.
/impartire >= mai mare sau egal x|ySAU logic
^ridicare la putere == egal x|| yid.
%% modul != diferit de xor(x, y) SAU exclusiv
%/% impartire cu rest
Operatorii aritmetici si de comparatie actioneaza asupra a doua elemente
(x + y,a < b). Operatorii aritmetici actioneaza nu doar asupra variabilelor
de tip numeric sau complex, dar si asupra variabilelor logice; in cazul din urma,
valorile logice sunt fortat transformate in numerice. Operatorii de comparatie
pot fi aplicati oricarui tip: ei returneaza una sau cateva valori logice.
Operatorii logici sunt aplicati unui (!) sau unor obiecte de tip logic si
returneaza una (sau mai multe) valori logice. Operatorii “SI” si “SAU” exista
sub doua forme: cel simplu actioneaza asupra fiecarui element din obiect si re-
turneaza tot atatea valori logice cate comparatii s-au facut; cel dublu opereaza
asupra primului element al obiectului.
Este necesara utilizarea operatorului “SI” pentru a specifica o inegalitate
de tipul 0 < x < 1 care va fi codata prin: 0 < x & x < 1. Expresia 0 < x <
1este valida, dar nu va returna rezultatul asteptat: din moment ce operatorii
sunt identici, vor fi executati succesiv de la stanga la dreapta. Comparatia 0
< x este executata prima si returneaza o valoare de tip logic care este apoi
comparata cu 1 (TRUE sau FALSE < 1): in aceasta situatie, valoarea logica este
implicit transformata in tip numeric (1sau 0 < 1).
> x <- 0.5
> 0 < x < 1
[1] FALSE
Operatorii de comparatie opereaza pe fiecare element al ambelor obiecte
de comparat (recicland valorile celei mai scurte daca este necesar) si astfel
returneaza un obiect de aceeasi lungime. Pentru a compara ‘in intregime’
doua obiecte, sunt disponibile doua functii: identical si all.equal.
10 Caracterele urmatoare sunt de asemenea operatori in R: $,@,[,[[,:,?,<-,<<-,=,::.
Un tabel de operatori ce descrie regulile cu precadere poate fi gasit cu ?Syntax.
27
> x <- 1:3; y <- 1:3
> x == y
[1] TRUE TRUE TRUE
> identical(x, y)
[1] TRUE
> all.equal(x, y)
[1] TRUE
Functia identical compara reprezentarea interna a datelor si returneaza
TRUE daca obiectele sunt identice si FALSE in caz contrar. Functia all.equal
compara “egalitatea apropiata” a doua obiecte si returneaza TRUE sau afiseaza
un sumar al diferentelor. Cea de-a doua functie ia in considerare aproximarea
calculului procesului atunci cand compara valori numerice. Compararea valo-
rilor numerice pe un computer este uneori plina de suprize!
> 0.9 == (1 - 0.1)
[1] TRUE
> identical(0.9, 1 - 0.1)
[1] TRUE
> all.equal(0.9, 1 - 0.1)
[1] TRUE
> 0.9 == (1.1 - 0.2)
[1] FALSE
> identical(0.9, 1.1 - 0.2)
[1] FALSE
> all.equal(0.9, 1.1 - 0.2)
[1] TRUE
> all.equal(0.9, 1.1 - 0.2, tolerance = 1e-16)
[1] "Mean relative difference: 1.233581e-16"
3.5.4 Accesarea valorilor unui obiect: sistemul de indexare
Sistemul de indexare este o cale eficienta si flexibila de a accesa in mod selectiv
elementele unui obiect; poate fi atat numeric cat si logic. Pentru a accesa, spre
exemplu, a treia valoare a unui vector x, introducem x[3] care poate fi folosit
atat pentru a extrage cat si pentru a schimba aceasta valoare:
> x <- 1:5
> x[3]
[1] 3
> x[3] <- 20
> x
[1] 1 2 20 4 5
Chiar indexul poate fi un vector de tip numeric:
> i <- c(1, 3)
28
> x[i]
[1] 1 20
Daca xeste o matrice sau o secventa de date, valoarea liniei isi a coloanei j
este accesata cu x[i, j]. Pentru a accesa toate valorile ale unei anumite linii
sau coloane, trebuie sa se omita indexul corespunzator (fara a uita virgula!):
> x <- matrix(1:6, 2, 3)
> x
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
> x[, 3] <- 21:22
> x
[,1] [,2] [,3]
[1,] 1 3 21
[2,] 2 4 22
> x[, 3]
[1] 21 22
Cu siguranta ati observat ca ultimul rezultat este un vector si nu o matrice.
R va returna implicit un obiect cu dimensiunea cea mai mica posibila. Acest
fapt se poate schimba cu optiunea drop a carei valoare implicita este TRUE:
> x[, 3, drop = FALSE]
[,1]
[1,] 21
[2,] 22
Acest sistem de indexare este schematizat in siruri, cu un numar de indici
egal cu numarul de dimensiuni ale sirului (de exemplu, un sir de dimensiune
3: x[i, j, k],x[, , 3],x[, , 3, drop = FALSE], si asa mai departe).
Poate fi util de retinut ca indexarea se face cu paranteze patrate, in timp ce
parantezele rotunde sunt utilizate pentru argumentele unei functii:
> x(1)
Error: couldn’t find function "x"
Indexarea poate fi utilizata de asemenea pentru a suprima unul sau mai
multe linii sau coloane utilizand valori negative. De exemplu, x[-1, ] va
suprima prima linie, in timp ce x[-c(1, 15), ] va face acelasi lucru pentru
linia 1 si linia 15. Utilizand matricea definita mai sus:
> x[, -1]
[,1] [,2]
[1,] 3 21
[2,] 4 22
29
> x[, -(1:2)]
[1] 21 22
> x[, -(1:2), drop = FALSE]
[,1]
[1,] 21
[2,] 22
Pentru vectori, matrici si siruri, este posibila accesarea valorilor unui ele-
ment cu o expresie de comparatie ca in indexul:
> x <- 1:10
> x[x >= 5] <- 20
> x
[1] 1 2 3 4 20 20 20 20 20 20
> x[x == 1] <- 25
> x
[1] 25 2 3 4 20 20 20 20 20 20
O utilizare practica a indexarii logice este, de exemplu, posibilitatea selec-
tarii elementelor cu sot ale unei variabile intregi:
> x <- rpois(40, lambda=5)
> x
[1]594776451135715392252
[21]46654534333773814214
> x[x %% 2 == 0]
[1] 4 6 4 2 2 2 4 6 6 4 4 8 4 2 4
Prin urmare, acest sistem de indexare utilizeaza valorile logice returnate,
in exemplele de mai sus, prin operatori de comparatie. Aceste valori logice
pot fi calculate in prealabil, urmand sa fie reciclate daca este necesar:
> x <- 1:40
> s <- c(FALSE, TRUE)
> x[s]
[1] 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
Indexarea logica poate fi utilizata si cu secvente de date, insa cu grija, din
moment ce coloane diferite din secventa de date pot avea tipuri diferite.
In cazul listelor, accesarea diferitelor elemente (care pot fi orice tip de
obiect) este efectuata fie cu paranteze patrate simple fie cu duble: diferenta
este ca prin parantezele simple se returneaza o lista, in timp ce parantezele
duble extrag obiectul dintr-o lista. Rezultatul poate fi indexat asa cum s-a
prezentat anterior pentru vectori, matrici, etc. Spre exemplu, daca al treilea
obiect al unei liste este vector, valoarea ia sa poate fi accesata utilizand
my.list[[3]][i], daca este un sir de dimensiune 3 utilizand my.list[[3]][i,
j, k] si asa mai departe. O alta diferenta este aceea ca my.list[1:2] va re-
turna o lista cu primele doua elemente din lista originala, desi my.list[[1:2]]
nu va da rezultatul asteptat.
30
3.5.5 Accesarea valorilor unui obiect cu nume
Numele sunt etichete ale elementelor unui obiect, prin urmare sunt de tip
caracter. Ele sunt in general atribute optionale. Exista cateva tipuri de nume
(names,colnames,rownames,dimnames).
Numele unui vector sunt memorate intr-un vector de aceeasi lungime cu
obiectul si pot fi accesate cu functia names.
> x <- 1:3
> names(x)
NULL
> names(x) <- c("a", "b", "c")
> x
a b c
1 2 3
> names(x)
[1] "a" "b" "c"
> names(x) <- NULL
> x
[1] 1 2 3
Pentru matrici si secvente de date, colnames si rownames sunt etichetele
pentru coloane si, respectiv linii. Acestea pot fi accesate atat cu functiile lor
corespunzatoare, cat si cu dimnames care returneaza o lista cu ambii vectori.
> X <- matrix(1:4, 2)
> rownames(X) <- c("a", "b")
> colnames(X) <- c("c", "d")
> X
c d
a 1 3
b 2 4
> dimnames(X)
[[1]]
[1] "a" "b"
[[2]]
[1] "c" "d"
Pentru siruri, numele dimensiunilor pot fi accesate cu dimnames:
> A <- array(1:8, dim = c(2, 2, 2))
> A
, , 1
[,1] [,2]
[1,] 1 3
31
[2,] 2 4
, , 2
[,1] [,2]
[1,] 5 7
[2,] 6 8
> dimnames(A) <- list(c("a", "b"), c("c", "d"), c("e", "f"))
> A
, , e
c d
a 1 3
b 2 4
, , f
c d
a 5 7
b 6 8
Daca elementele unui obiect au nume, acestea pot fi extrase utilizandu-
le sub forma de indici. De fapt, aceasta poarta numele de ‘subsetting’ mai
degraba decat ‘extraction’ din moment ce sunt pastrate atributele obiectului
original. De exemplu, daca o secventa de date DF contine variabilele x,ysi z,
comanda DF["x"] va returna o secventa de date doar cu x;DF[c("x", "y")]
va returna o secventa de date cu ambele variabile. Aceasta functioneaza si cu
liste daca elementele acesteia au nume.
Asa cum constata cititorul, indexul utilizat aici este un vector de tip car-
acter. Ca si vectorii numerici sau logici observati mai sus, acest vector poate
fi definit in prealabil si apoi utilizat pentru extragere. Pentru a extrage un
vector sau un factor dintr-o secventa de date, se poate utiliza operatorul $
(e.g., DF$x). Acesta functioneaza si in cazul listelor.
3.5.6 Editorul de date
Se poate utiliza o fila grafica pentru editarea unui obiect de “date”. De exem-
plu, daca Xeste o matrice, comanda data.entry(X) va lansa un editor grafic
si se vor putea modifica valori prin selectarea celulelor respective, or to addsau
se vor putea adauga coloane noi sau linii.
Functia data.entry modifica direct obiectul dat ca argument fara sa fie
nevoie sa i se atribuie rezultatul. Pe de alta parte, functia de returneaza o
lista cu obiectele date ca argumente si posibil modificate. Acest rezultat este
afisat pe ecran in mod implicit, insa, ca pentru majoritatea functiilor, poate
fi atribuit unui obiect.
Detaliile privind utilizarea editorului de date depind de sistemul de operare.
32
3.5.7 Functii aritmetice simple
Exista numeroase functii in R pentru a manipula datele. Deja am studiat-
o pe cea mai simpla, ccare concateneaza obiectele listate in paranteze. De
exemplu:
> c(1:5, seq(10, 11, 0.2))
[1] 1.0 2.0 3.0 4.0 5.0 10.0 10.2 10.4 10.6 10.8 11.0
Vectorii pot fi manipulati cu expresii aritmetice clasice:
> x <- 1:4
> y <- rep(1, 4)
> z <- x + y
> z
[1] 2 3 4 5
Pot fi adunati vectori de lungimi diferite; in acest caz, este reciclat cel mai
scurt vector. Exemple:
> x <- 1:4
> y <- 1:2
> z <- x + y
> z
[1] 2 4 4 6
> x <- 1:3
> y <- 1:2
> z <- x + y
Warning message:
longer object length
is not a multiple of shorter object length in: x + y
> z
[1] 2 4 4
De remercat ca R returneaza un mesaj de atentionare si nu un mesaj de
eroare, chiar daca operatia a fost efectuata. Daca vrem sa adunam (sau sa
inmultim) aceeasi valoare tuturor elementelor unui vector:
> x <- 1:4
> a <- 10
> z <- a * x
> z
[1] 10 20 30 40
Functiile disponibile in R pentru manipularea datelor sunt prea numeroase
pentru a fi enumerate aici. Se pot gasi toate functiile matematice de baza
(log,exp,log10,log2,sin,cos,tan,asin,acos,atan,abs,sqrt, . . . ),
functiile speciale (gamma,digamma,beta,besselI, . . . ), ca si alte diverse
33
functii utilizate in statistica. Cateva dintre aceste functii sunt prezentate in
tabelul urmator.
34

sum(x) suma elementelor lui x
prod(x) produsul elementelor lui x
max(x) maximul elementelor lui x
min(x) minimul elementelor lui x
which.max(x) returneaza indexul celui mai mare element al lui x
which.min(x) returneaza indexul celui mai mic element al lui x
range(x) id. than c(min(x), max(x))
length(x) numarul elementelor lui x
mean(x) media elementelor lui x
median(x) mediana elementelor lui x
var(x) sau cov(x) dispersia elementelor lui x(calculata cu n−1); daca xeste o
matrice sau o secventa de date, matricea varianta-covarianta
este calculata
cor(x) matricea corelatie a lui xdaca este o matrice sau o secventa de
date (1 daca xeste un vector)
var(x, y) sau cov(x, y) dispersia dintre xsi y, sau dintre coloanele lui xsi ale lui y
daca sunt matrici sau secvente de date
cor(x, y) corelatie liniara intre xsi y,sau matricea corelatiei daca sunt
matrici sau secvente de date
Aceste functii returneaza o singura valoare (deci un vector de lungime
unu), cu exceptia range care returneaza un vector de lungime doi, si var,cov,
si cor care pot returna o matrice. Functiile urmatoare returneaza rezultate
mai complexe.
round(x, n) rotunjeste elementele lui xcu nzecimale
rev(x) inverseaza elementele lui x
sort(x) sorteaza elementele lui xin ordine crescatoare; pentru sortare in ordine
descrescatoare: rev(sort(x))
rank(x) ordoneaza elementele lui x
log(x, base) calculeaza logaritmul lui xin baza base
scale(x) daca xeste o matrice, centreaza si reduce datele; doar pentru
centrare se foloseste optiunea center=FALSE, doar pentru reducere
scale=FALSE (in mod implicit center=TRUE, scale=TRUE)
pmin(x,y,...) un vector cu elementul ireprezentand minimul dintre x[i],y[i], . . .
pmax(x,y,...) id. pentru maxim
cumsum(x) un vector cu elementul ireprezentand suma de la x[1] la x[i]
cumprod(x) id. pentru produs
cummin(x) id. pentru minim
cummax(x) id. pentru maxim
match(x, y) returneaza un vector de aceeasi lungime cu xcu elementele lui xcare
se afla in y(NA altfel)
which(x == a) returneaza un vector cu indicii lui xoperatorul de comparatie este
adevarat (TRUE), in acest exemplu valorile lui ipentru care x[i] ==
a( argumentul acestei functii trebuie sa fie o variabila de tip logic)
choose(n, k) calculeaza combinari de kluate cate nrepetari = n!/[(n−k)!k!]
na.omit(x) suprima observatiile cu date lipsa (NA) (suprima linia corespunzatoare
daca xeste o matrice sau o secventa de date)
35

na.fail(x) returneaza un mesaj de eroare daca xcontine cel putin un NA
unique(x) daca xeste un vector sau o secventa de date, returneaza un obiect
similar insa u elementele duble suprimate
table(x) returneaza un tabel cu numerele diferitelor valori ale lui x(specific
pentru cele de tip integer sau factor)
table(x, y) tabel de contingenta al lui xsi y
subset(x, ...) returneaza o selectie a lui xprivitoare la criteriul (..., specifica com-
paratiilor : x$V1 < 10); daca xeste o secventa de date, optiunea
select permita ca variabilele sa fie pastrate (sau restranse folosind
un semn de minus)
sample(x, size) reesantioneaza aleatoriu si fara inlocuire size elemente din vectorul
x, optiunea replace = TRUE permite reesantionarea fara inlocuire
3.5.8 Calcul matriceal
R ofera facilitati pentru calcule si manipulari ale matricilor. Functiile rbind
si cbind imbina matrici tinand cont de linii sau coloane, respectiv:
> m1 <- matrix(1, nr = 2, nc = 2)
> m2 <- matrix(2, nr = 2, nc = 2)
> rbind(m1, m2)
[,1] [,2]
[1,] 1 1
[2,] 1 1
[3,] 2 2
[4,] 2 2
> cbind(m1, m2)
[,1] [,2] [,3] [,4]
[1,] 1 1 2 2
[2,] 1 1 2 2
Operatorul care realizeaza produsul a doua matrici este ‘%*%’. De exemplu,
considerand cele doua matrici m1 si m2 de mai sus:
> rbind(m1, m2) %*% cbind(m1, m2)
[,1] [,2] [,3] [,4]
[1,] 2 2 4 4
[2,] 2 2 4 4
[3,] 4 4 8 8
[4,] 4 4 8 8
> cbind(m1, m2) %*% rbind(m1, m2)
[,1] [,2]
[1,] 10 10
[2,] 10 10
36
Transpusa unei matrici este efectuata cu functia t; aceasta functie este
valabila si pentru secvente de date.
Functia diag poate fi utilizata pentru a extrage sau a modifica diagonala
unei matrici, sau pentru a construi diagonala unei matrici.
> diag(m1)
[1] 1 1
> diag(rbind(m1, m2) %*% cbind(m1, m2))
[1] 2 2 8 8
> diag(m1) <- 10
> m1
[,1] [,2]
[1,] 10 1
[2,] 1 10
> diag(3)
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
> v <- c(10, 20, 30)
> diag(v)
[,1] [,2] [,3]
[1,] 10 0 0
[2,] 0 20 0
[3,] 0 0 30
> diag(2.1, nr = 3, nc = 5)
[,1] [,2] [,3] [,4] [,5]
[1,] 2.1 0.0 0.0 0 0
[2,] 0.0 2.1 0.0 0 0
[3,] 0.0 0.0 2.1 0 0
R are si cateva functii speciale pentru calcule cu matrici. Putem men-
tiona solve pentru inversarea unei matrici, qr pentru descompunere, eigen
pentru calculul numarului caracteristic si vectorului propriu, si svd pentru
descompunerea valorilor singulare.
37

4 Grafice in R
R ofera o varietate remarcabila de grafice. Pentru a va face o idee, puteti
incerca demo(graphics) sau demo(persp). Nu putem detalia aici posibili-
tatile R-ului in materie de grafice, din moment ce fiecare functie grafica are
un numar mare de optiuni ce fac foarte flexibila producerea de grafice.
Modul in care functioneaza functiile grafice provine mai ales de la schema
prezentata la inceputul acestui document. Rezultatul unei functii grafice nu
poate fi atribuit unui obiect11 insa este trimis unui instrument grafic. Un
instrument grafic este o fereastra grafica sau un fisier.
Exista doua tipuri de functii grafice: functii de grafice prin puncte de nivel
ridicat care creaza un grafic nou, si functii de grafice prin puncte de nivel scazut
care adauga elemente unui grafic existent. Graficele sunt produse cu referire
la parametri grafici care sunt definiti in mod implicit si pot fi modificati cu
functia par.
Vom vedea in primul rand cum se gestioneaza graficele si instrumentele
grafice; apoi vom detalia oarecum functiile grafice si parametrii. Apoi vom
vedea un exemplu practic de utilizare a acestor functionalitati in producerea
graficelor. In incheiere, vom expune pachetele grid si lattice ale caror func-
tionare este diferita de cele mentionate anterior.
4.1 Gestionarea graficelor
4.1.1 Deschiderea catorva instrumente grafice
Atunci cand este executata o functie grafica, daca nu este deschis un instru-
ment grafic, R deschide o fereastra grafica in care afiseaza graficul. Un instru-
ment grafic poate fi deschis cu functia potrivita. Lista instrumentelor grafice
disponibile depinde de sistemul de operare. Ferestrele grafice sunt numite X11
in Unix/Linux si ferestre in Windows. In toate cazurile, se poate deschide
o fereastra grafica prin comanda x11() care functioneaza si in Windows din
cauza unui nume de imprumut referitor la comanda windows(). Un instru-
ment grafic care este un fisier va fi deschis cu o functie specifica formatului:
postscript(),pdf(),png(), . . . Lista cu instrumente grafice disponibile
poate fi afisata cu ?device.
Ultimul instrument deschis devine instrumentul grafic activ pe care toate
graficele ulterioare sunt afisate. Functia dev.list() afiseaza lista instru-
mentelor deschise:
> x11(); x11(); pdf()
11 Exista cateva exceptii: hist() si barplot() produce si rezultate numerice de tip lista
sau matrici.
38
> dev.list()
X11 X11 pdf
234
Cifrele afisate sunt numerele instrumentului care trebuie utilizat pentru a
schimba instrumentul activ. Pentru a afla instrumentul activ:
> dev.cur()
pdf
4
si pentru a schimba instrumentul activ:
> dev.set(3)
X11
3
Functia dev.off() inchide un instrument: in mod implicit este inchis
instrumentul activ, in caz contrar acesta este cel al carui numar este dat ca
argument al functiei. R afiseaza apoi numarul noului instrument activ:
> dev.off(2)
X11
3
> dev.off()
pdf
4
Doua caracteristici specifice versiunii de Windows a R-ului merita a fi
mentionate: un instrument Windows Metafile care poate si deschis cu functia
win.metafile, si un meniu “History” afisat atunci cand fereastra grafica este
selectata ce permite inregistrarea tuturor graficelor intocmite in timpul unei
sesiuni (in mod implicit, sistemul de inregistrare este oprit; utilizatorul il poate
porni facand click pe “Recording” in acest meniu).
4.1.2 Impartirea unui grafic
Functia split.screen imparte instrumentul graficului activ. De exemplu:
> split.screen(c(1, 2))
imparte instrumentul in doua parti care pot fi selectate cu screen(1) sau
screen(2);erase.screen() sterge ultimul grafic desenat. O parte din in-
strument poate fi impartita la randul ei cu split.screen() ducand la posi-
bilitatea de a face aranjamente mai complexe.
Aceste functii sunt incompatibile cu altele (sum ar fi layout sau coplot)
si nu trebuie utilizate in cadrul mai multe instrumente grafice. Utilizarea lor
trebuie sa se limiteze, spre exemplu, la explorarea grafica a datelor.
39

Functia layout imparte fereastra grafica activa in cateva parti in care
graficele vor fi afisate succesiv. Argumentul sau principal este o matrice cu
numere intregi ce indica numerele “sub-ferestrelor”. De exemplu, pentru a
imparti instrumentul in patru parti egale:
> layout(matrix(1:4, 2, 2))
De asemenea este posibila crearea acestei matrici inainte, permitand o
vizualizare mai buna a modului de impartire a instrumentului:
> mat <- matrix(1:4, 2, 2)
> mat
[,1] [,2]
[1,] 1 3
[2,] 2 4
> layout(mat)
Pentru a vizualiza impartirea creata, se poate utiliza functia layout.show
cu numarul de sub-ferestre ca argument (in acest caz 4). In acest exemplu,
vom avea:
> layout.show(4)
1
2
3
4
Exemplele urmatoare ilustreaza cateva dintre posibilitatile oferite de layout().
> layout(matrix(1:6, 3, 2))
> layout.show(6)
1
2
3
4
5
6
> layout(matrix(1:6, 2, 3))
> layout.show(6)
1
2
3
4
5
6
> m <- matrix(c(1:3, 3), 2, 2)
> layout(m)
> layout.show(3)
1
2
3
40
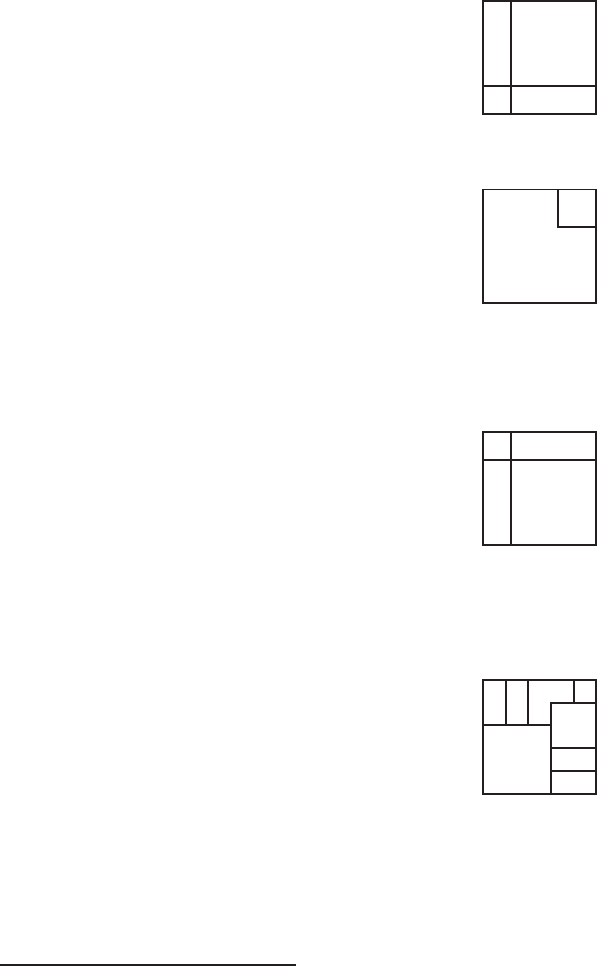
In toate aceste exemple, nu am utilizat optiunea byrow a functiei matrix(),
sub-ferestrele fiind asftel numerotate sub forma de coloane; se poate specifica
doar matrix(..., byrow=TRUE) astfel incat sub-ferestrele sa fie numerotate
sub forma de randuri. Numerele din matrice pot fi alocate in orice ordine, de
exemplu, matrix(c(2, 1, 4, 3), 2, 2).
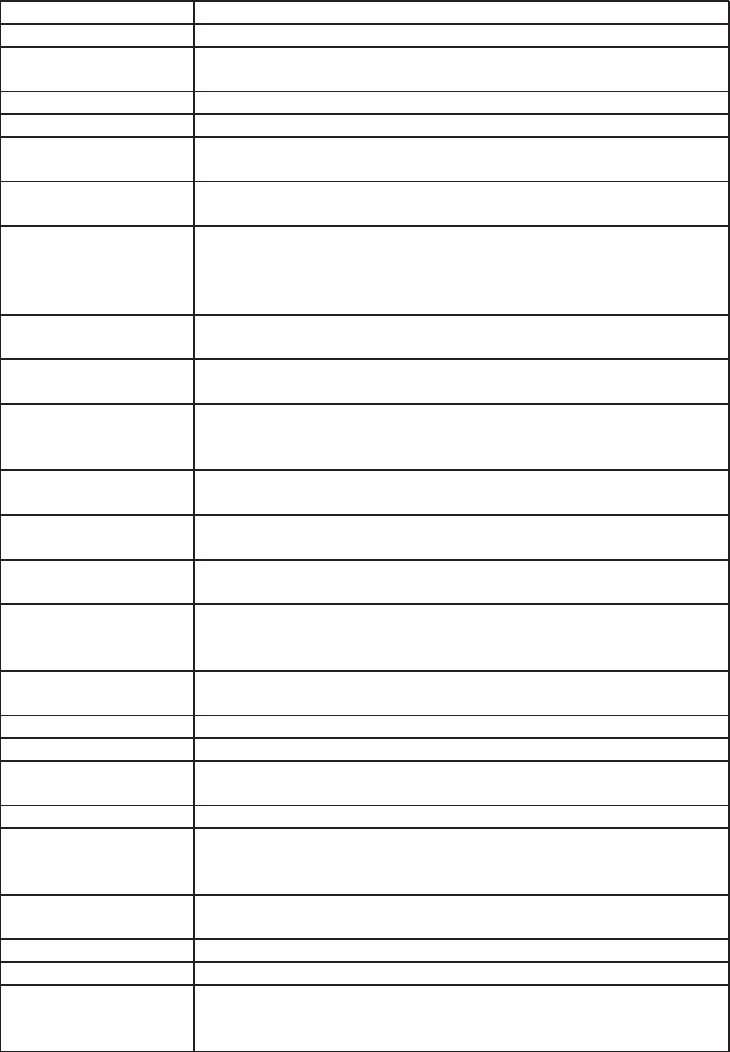
In mod implicit, layout() imparte instrumentul in inaltimi si latimi fixe:
aceasta se poate modifica prin optiunile widths si heights. Aceste dimensiuni
sunt date in mod relativ12. Exemple:
> m <- matrix(1:4, 2, 2)
> layout(m, widths=c(1, 3),
heights=c(3, 1))
> layout.show(4)
1
2
3
4
> m <- matrix(c(1,1,2,1),2,2)
> layout(m, widths=c(2, 1),
heights=c(1, 2))
> layout.show(2)
1
2
In cele din urma, numerele din matrice pot include zero-uri oferind posi-
bilitatea de a face impartiri complexe (sau chiar esoterice).
> m <- matrix(0:3, 2, 2)
> layout(m, c(1, 3), c(1, 3))
> layout.show(3) 1
2
3
> m <- matrix(scan(), 5, 5)
1: 0 0 3 3 3 1 1 3 3 3
11: 0 0 3 3 3 0 2 2 0 5
21: 4 2 2 0 5
26:
Read 25 items
> layout(m)
> layout.show(5)
1
2
3
4
5
12 Ele pot fi date in centimetri, vezi ?layout.
41
4.2 Functiile grafice
In cele ce urmeaza vom face o prezentare generala a functiilor grafice de nivel
ridicat din R.
plot(x) grafic al valorilor lui x(pe axa y) ordonate pe axa x
plot(x, y) grafic bidimensional al lui x(pe axa x) si y(pe axa y)
sunflowerplot(x,
y)
id. insa punctele de coordonate similare sunt desenate ca o floare
ce are numarul de petale egal cu numarul de puncte
pie(x) grafic circular
boxplot(x) boxplot
stripchart(x) grafic al valorilor lui xpe o linie (o alternativa la boxplot()
pentru esantioanele de dimensiuni mici)
coplot(x~y |z) grafic bidimensional al lui xsi ypentru valori individuale (sau
interval de valori) ale lui z
interaction.plot
(f1, f2, y)
pentru f1 si f2 factori, graficele mediilor lui y(pe axa y) rapor-
tate la valorile lui f1 (pe axa x) si ale lui f2 (curbe diferite);
optiunea fun permite alegerea unei sumarizari statistice a lui y
(in mod implicit fun=mean)
matplot(x,y) grafic bidimensional a primei coloane a lui xvs. a primei coloane
a lui y, a doua a lui xvs. a doua a lui y, etc.
dotchart(x) pentru xsecventa de date, face graficul de tip puncte (grafice
ingramadite linie de linie si coloana de coloana)
fourfoldplot(x) vizualizeaza, cu sferturi de cerc, relatia dintre doua variabile
dihotomice pentru populatii diferite (xtrebuie sa fie un sir cu
dim=c(2, 2, k), sau o matrice cu dim=c(2, 2) pentru k= 1)
assocplot(x) grafic Cohen–Friendly ce arata abaterile de la indenepdenta ran-
durilor si coloanelor intr-un tabel de contingenta bidimensional
mosaicplot(x) grafic ‘mozaic’ al valorilor reziduale ale unei regresii logaritmice
a unui tabel de contingenta
pairs(x) pentru xmatrice sau secventa de date, creaza toate graficele
bivariate posibile dintre coloanele lui x
plot.ts(x) pentru xobiect de clasa "ts", creaza graficul lui xraportate la
timp, xpoate fi multivariat insa seriile trebuie sa aiba aceleasi
frecvente si date
ts.plot(x) id. insa xeste multivariat iar seriile pot avea date diferite si
trebuie sa aiba aceeasi frecventa
hist(x) histograma frecventelor lui x
barplot(x) histograma valorilor lui x
qqnorm(x) cuantilele lui xraportate la valorile asteptate sub o regula nor-
mala
qqplot(x, y) cuantilele lui yraportate la cuantilele lui x
contour(x, y, z) grafic contur (datele sunt interpolate pentru a desena curbele),
xsi ytrebuie sa fie vectori si ztrebuie sa fie matrice astfel incat
dim(z)=c(length(x), length(y)) (xsi ypot fi omise)
filled.contour (x,
y, z)
id. insa zonele dintre contururi sunt colorate, existand si o leg-
enda a culorilor
image(x, y, z) id. insa zona curenta este reprezentata prin culori
persp(x, y, z) id. insa in perspectiva
stars(x) pentru xmatrice sau secventa de date, creaza un grafic cu seg-
mente sau o stea in care fiecare rand al lui xeste reprezentat de
o stea iar coloanele sunt lungimile segmentelor
42
symbols(x, y, ...) deseneaza, la coordonatele date de xsi y, simboluri (cercuri,
patrate, dreptunghiuri, stele, termometre sau “boxplot-uri”) ale
caror dimensiuni, culori, etc, sunt specificate de argumente su-
plimentare
termplot(mod.obj) graficul efectelor (partiale) ale unui model de regresie (mod.obj)
Pentru fiecare functie, optiunile pot fi gasite in suportul on-line din R.
cateva dintre aceste optiuni sunt identice pentru cateva functii grafice; mai jos
sunt prezentate cele principale (cu valorile posibile implicite):
add=FALSE if TRUE suprapune graficul peste cel anterior (daca acesta
exista)
axes=TRUE if FALSE nu deseneaza axele si caseta
type="p" specifica tipul graficului, "p": puncte, "l": linii, "b":
puncte unite prin linii, "o": id. insa liniile sunt peste
puncte, "h": linii verticale, "s": trepte, datele sunt
reprezentate prin varful liniilor verticale, "S": id. insa
datele sunt reprezentate prin baza liniilor verticale
xlim=, ylim= specifica limitele de jos si de sus a axelor, de exemplu cu
xlim=c(1, 10) sau xlim=range(x)
xlab=, ylab= denumeste axele; trebuie sa fie variabile de tip caracter
main= titlul principal; trebuie sa fie variabila de tip caracter
sub= subtitlu (scris cu un font mai mic)
4.3 Comenzi de grafice de nivel scazut
R are un set de functii grafice care afecteaza un grafic deja existent: ele sunt
numite comenzi de grafice de nivel scazut. Iata care sunt principalele:
points(x, y) adauga puncte (poate fi utilizata optiunea type=)
lines(x, y) id. insa adauga linii
text(x, y, labels,
...)
adauga text dat de labels la coordonatele (x,y); o varianta des
folosita este: plot(x, y, type="n"); text(x, y, names)
mtext(text,
side=3, line=0,
...)
adauga text dat de text la marginea specificata de side (vezi
axis() mai jos); line specifica linia din zona graficului
segments(x0, y0,
x1, y1)
deseneaza linii de la punctele (x0,y0) la punctele (x1,y1)
arrows(x0, y0,
x1, y1, angle= 30,
code=2)
id. cu sageti catre punctele (x0,y0) daca code=2, catre punctele
(x1,y1) daca code=1, sau ambele daca code=3;angle controleaza
unghiul dintre axa sagetii si limita capului sagetii
abline(a,b) deseneaza o linie de panta bsi segment a
abline(h=y) deseneaza o linie orizontala la ordonata y
abline(v=x) deseneaza o linie verticala la abcisa x
abline(lm.obj) deseneaza linia regresiei data de lm.obj (vezi sectiunea 5)
43

rect(x1, y1, x2,
y2)
deseneaza un dreptunghi ale carui limite din stanga, dreapta,
sus si jos sunt x1,x2,y1, si respectiv y2
polygon(x, y) deseneaza un poligon ce uneste punctele de coordonate date de
xsi y
legend(x, y,
legend)
adauga legenda la punctul (x,y) cu simbolurile date de legend
title() adauga un titlu si optional un subtitlu
axis(side, vect) adauga o axa la baza (side=1), in stanga (2), sus (3), sau in
dreapta (4); vect (optional) abcisa (sau ordonatele) unde sunt
desenate marcajele
box() adauga o caseta in jurul graficului curent
rug(x) deseneaza datele xpe axa xca linii verticale mici
locator(n,
type="n", ...)
returneaza coordonatele (x, y) pe care utilizatorul a facut click
cu mouse-ul de nori pe grafic; de asemenea deseneaza sim-
boluri (type="p") sau linii (type="l") referitoare la parametri
grafici optionali (...); in mod implicit nu este desenat nimic
(type="n")
De remercat posibilitatea de a adauga expresii matematice pe un grafic cu
text(x, y, expression(...)), acolo unde functia expression transforma
argumentele sale intr-o ecuatie matematica De exemplu,
> text(x, y, expression(p == over(1, 1+e^-(beta*x+alpha))))
va afisa, pe grafic, urmatoare ecuatie la punctul de coordonate (x, y):
p = 1
1 + e−(βx+α)
Pentru a include o variabila intr-o expresie putem utiliza functiile substitute
si as.expression; de exemplu pentru a include valoarea lui R2(calculata an-
terior si memorata intr-un obiect numit Rsquared):
> text(x, y, as.expression(substitute(R^2==r, list(r=Rsquared))))
va afisa pe grafic la punctul de coordonate (x, y):
R2= 0.9856298
Pentru a afisa doar trei zecimale, comanda se poate modifica dupa cum urmeaza:
> text(x, y, as.expression(substitute(R^2==r,
+ list(r=round(Rsquared, 3)))))
si va afisa:
R2= 0.986
In cele din urma, pentru a scrie R cu font italic:
> text(x, y, as.expression(substitute(italic(R)^2==r,
+ list(r=round(Rsquared, 3)))))
R2= 0.986
44
4.4 Parametri grafici
In plus fata de comenzile de grafice de nivel scazut, prezentarea graficelor poate
fi imbunatatita cu prezentarea parametrilor grafici. Acestia pot fi utilizati
fie ca optiuni ale functiilor grafice (insa nu functioneaza pentru toate), sau
impreuna cu functia par pentru a schimba permanent parametrii grafici, astfel
ca graficele consecutive vor fi desenate in raport cu parametrii specificati de
utilizator. Spre exemplu, comanda urmatoare:
> par(bg="yellow")
va avea ca rezultat desenarea graficelor consecutive cu un fundal galben. Ex-
ista 73 de parametri grafici, cativa dintre ei avand functii similare. Lista
completa a acestor parametri poate fi citita cu ?par; in urmatorul tabel sunt
prezentati cei mai uzuali.
adj controleaza alinierea textului fata de limita stanga a textului astfel incat 0este
aliniat stanga, 0.5 este centrat, 1este aliniat dreapta, valorile >1 muta textul
inspre stanga, iar valorile negative inspre dreapta; pentru doua valori date
(e.g., c(0, 0)) a doua controleaza alinierea verticala fata de nivelul textului
bg specifica culoarea fundalului (e.g., bg="red",bg="blue"; lista celor 657 de
culori disponibile este afisata cu colors())
bty controleaza tipul casetei desenate in jurul graficului, valorile permise fiind: "o",
"l","7","c","u" ou "]" (caseta arata conform caracterului corespunzator);
pentru bty="n" caseta nu este trasata
cex o valoarea ce controleaza dimensiunea textului si simbolurilor fata de cele
implicite; parametrii urmatori au acelasi control pentru numerele de pe axe,
cex.axis, etichetele axelor, cex.lab, titlu, cex.main, si subtitlu, cex.sub
col controleaza culoarea simbolurilor; ca si pentru cex exista: col.axis,col.lab,
col.main,col.sub
font o valoare integer care controleaza stilul textului (1: normal, 2: italic, 3: bold,
4: bold italic); ca si pentru cex exista: font.axis,font.lab,font.main,
font.sub
las o valoare integer care controleaza orientarea etichetelor axelor (0: paralel cu
axele, 1: orizontal, 2: perpendicular pe axe, 3: vertical)
lty controleaza tipul liniilor, poate fi de tip integer (1: neintrerupt, 2: striat (eng.
dashed), 3: punctat (eng. dotted), 4: striat si punctat (eng. dotdash), 5:
punctat lung (eng. longdash), 6: punctat de doua ori (eng. twodash)), sau
de tip sir de pana la 8 caractere (intre "0" si "9") care specifica alternativ
lungimea, in puncte sau pixeli, a elementelor desenate si ale spatiilor goale, de
exemplu lty="44" ca avea acelasi efect cu lty=2
lwd o valoare numerica ce controleaza lungimea liniilor
mar un vector de 4 valori numerice care controleaza spatiul dintre axe si limita grafi-
cului de forma c(bottom, left, top, right), valorile implicite sunt c(5.1,
4.1, 4.1, 2.1)
mfcol un vector de forma c(nr,nc) care imparte fereastra graficului intr-o matrice
cu nr linii si nc coloane, graficele fiind apoi desenate in coloane (vezi sectiunea
4.1.2)
mfrow id. insa graficele sunt apoi desenate in linie (vezi sectiunea 4.1.2)
pch controleaza tipul simbolului, fie ca este un integer intre 1 si 25, sau orice alt
caracter fara "" (Fig. 2)
45

*?Xa
1 2 345678 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 "*" "?" "." "X" "a"
Figure 2: Simbolurile de reprezentare grafica in R (pch=1:25). Culorile au fost
obtinute cu optiunile col="blue", bg="yellow", a doua optiune are efect
numai asupra simbolurilor 21–25. Poate fi utilizat orice caracter (pch="*",
"?",".", . . . ).
ps o valoarea de tip integer ce controleaza dimensiunea in puncte a textului si
simbolurilor
pty un caracter ce specifica tipul zonei reprezentate grafic, "s": patrat (eng.
square), "m": maximal
tck o valoare care specifica lungimea marcajelor de pe axe ca parte a celei mai
mici lungimi sau inaltimi a graficului; pentru tck=1 este desenata o grila
tcl id. insa ca parte a inaltimii unei linii de text (in mod implicit tcl=-0.5)
xaxt pentru xaxt="n" axa xeste setata insa nu desenata (util impreuna cu
axis(side=1, ...))
yaxt pentru yaxt="n" axa yeste setata insa nu desenata (util impreuna cu
axis(side=2, ...))
4.5 Un exemplu practic
Pentru a ilustra functionalitatile grafice ale lui R, vom considera un exemplu
simplu de grafic bidimensional de 10 perechi de variabile aleatoare. Aceste
valori au fost generate cu:
> x <- rnorm(10)
> y <- rnorm(10)
Graficul dorit va fi obtinut cu plot(); se va introduce comanda:
> plot(x, y)
46

−0.5 0.0 0.5 1.0
−1.0 −0.5 0.0 0.5
x
y
Figure 3: Functia plot utilizata fara optiuni.
iar graficul va fi reprezentat in instrumentul grafic activ. Rezultatul este aratat
in Fig. 3. In mod implicit, R creaza grafice intr-un mod “inteligent”: spatiile
dintre marcajele de pe axe, plasarea etichetelor, etc, sunt calculate astfel incat
graficul rezultat sa fie cat mai inteligibil posibil.
Cu toate acestea, utilizatorul poate schimba modul in care este prezentat
un grafic, de exemplu, pentru a il adapta la un sablon editorial, sau pentru a ii
oferi o amprenta personala pentru o discutie/prezentare. Cel mai simplu mod
de a schimba prezentarea unui grafic este de a adauga optiuni care sa modifice
argumentele implicite. In exemplul nostru, putem modifica semnificativ figura
dupa cum urmeaza:
plot(x, y, xlab="Ten random values", ylab="Ten other values",
xlim=c(-2, 2), ylim=c(-2, 2), pch=22, col="red",
bg="yellow", bty="l", tcl=0.4,
main="How to customize a plot with R", las=1, cex=1.5)
Rezultatul este in Fig. 4. Vom detalia fiecare optiune folosita. In primul
rand, xlab si ylab schimba etichetele axelor care, in mod implicit, au fost
numele variabilelor. Apoi, xlim si ylim ne permit sa definim limitele pe ambele
axe13. Parametrul grafic pch este utilizat aici ca o optiune: pch=22 specifica un
patrat cu fundal si contur ce pot fi diferite si care sunt date decol si respectiv
bg. Tabelul de parametri grafici prezinta intelesul modificarilor executate de
bty,tcl,las si cex. In cele din urma, un titlu poate fi adaugat cu optiunea
main.
13 In mod implicit, R adauga 4% pe fiecare parte a limitei axei. Acesta manifestare poate
fi alterata prin setarea parametrilor grafici xaxs="i" si yaxs="i" (pot fi trecuti ca optiuni
in plot()).
47
−2 −1 0 1 2
−2
−1
0
1
2
How to customize a plot with R
Ten random values
Ten other values
Figure 4: Functia plot utilizata cu optiunile.
Parametrii grafici si functiile de grafice de nivel scazut ne permit sa avansam
in prezentarea unui grafic. Asa acum am vazut anterior, cativa parametri
grafici nu pot fi trecuti ca argumente intr-o functie ca plot. Vom modifica
acum cativa dintre acesti parametri cu par(), asadar este necesara introduc-
erea catorva comenzi. Atunci cand parametri grafici sunt schimbati, este utila
salvarea valorilor initiale in prealabil pentru a le putea reda ulterior. Mai jos
sunt prezentate comenzile utilizate pentru a obtine Fig. 5.
opar <- par()
par(bg="lightyellow", col.axis="blue", mar=c(4, 4, 2.5, 0.25))
plot(x, y, xlab="Ten random values", ylab="Ten other values",
xlim=c(-2, 2), ylim=c(-2, 2), pch=22, col="red", bg="yellow",
bty="l", tcl=-.25, las=1, cex=1.5)
title("How to customize a plot with R (bis)", font.main=3, adj=1)
par(opar)
Vom detalia actiunile rezultate din aceste comenzi. In primul rand, parametrii
grafici impliciti sunt copiati intr-o lista numita aici opar. Vor fi modificati
apoi trei parametri: bg pentru culoarea fundalului, col.axis pentru culoarea
numerelor de pe axe si mar pentru dimensiunile marginilor din jurul zonei
graficului. Graficul este desenat intr-un mod asemanator Fig. 4. Modificarile
marginilor permit utilizarea spatiului din jurul zonei graficului. Titlul este
adaugat aici cu functia grafica de nivel scazut title care permite utilizarea
unor parametrii ca argumente fara a modifica restul graficului. In cele din
urma, parametrii grafici initiali sunt redati cu ultima comanda.
Acum, controlul este total! In Fig. 5, R inca determina cateva lucruri, cum
ar fi numarul de marcaje de pe axe, sau spatiul dintre titlu si zona graficului.
48
−2 −1 0 1 2
−2
−1
0
1
2
Ten random values
Ten other values
How to customize a plot with R (bis)
Figure 5: Functiile par,plot si title.
Vom vedea in cele ce urmeaza cum sa controlam total prezentarea graficului.
Modalitatea utilizata aici este de a reprezenta un grafic “gol”(eng. blank)
cu plot(..., type="n"), apoi de a adauga puncte, axe, etichete, etc, cu
functii grafice de nivel scazut. Vom considera cateva aranjamente cum ar fi
schimbarea culorii zonei graficului. Comenzile sunt prezentate mai jos, iar
graficul rezultat se afla in Fig. 6.
opar <- par()
par(bg="lightgray", mar=c(2.5, 1.5, 2.5, 0.25))
plot(x, y, type="n", xlab="", ylab="", xlim=c(-2, 2),
ylim=c(-2, 2), xaxt="n", yaxt="n")
rect(-3, -3, 3, 3, col="cornsilk")
points(x, y, pch=10, col="red", cex=2)
axis(side=1, c(-2, 0, 2), tcl=-0.2, labels=FALSE)
axis(side=2, -1:1, tcl=-0.2, labels=FALSE)
title("How to customize a plot with R (ter)",
font.main=4, adj=1, cex.main=1)
mtext("Ten random values", side=1, line=1, at=1, cex=0.9, font=3)
mtext("Ten other values", line=0.5, at=-1.8, cex=0.9, font=3)
mtext(c(-2, 0, 2), side=1, las=1, at=c(-2, 0, 2), line=0.3,
col="blue", cex=0.9)
mtext(-1:1, side=2, las=1, at=-1:1, line=0.2, col="blue", cex=0.9)
par(opar)
Ca si mai inainte, parametrii grafici impliciti sunt salvati, iar culoarea
fundalului si marginile sunt modificate. Graficul este apoi desenat cu type="n"
pentru a nu trasa puncetele, xlab="", ylab="" pentru a nu scrie etichetele
49
How to customize a plot with R (ter)
Ten random values
Ten other values
−2 0 2
−1
0
1
Figure 6: Un grafic “hand-made”.
axelor, iar xaxt="n", yaxt="n" pentru a nu desena axele. Va rezulta crearea
cadranului din jurul zonei graficului, si definirea axelor fata de xlim si ylim.
De remercat ca am fi putut utiliza optiunea axes=FALSE insa in acest caz nici
axele nici cadrulnu ar fi putut fi desenate.
Elementele sunt apoi adaugate in zona graficului definita cu cateva functii
grafice de nivel scazut. Inainte de a adauga punctele, culoarea din interiorul
zonei graficului este schimbata cu rect(): dimensiunile dreptunghiului sunt
selectate astfel incat sa fie considerabil mai mare decat zona graficului.
Punctele sunt reprezentate cu points(); a fost utilizat un nou simbol.
Axele sunt adaugate cu axis(): vectorul dat ca argument secund specifica
coordonatele marcajelor. Optiunea labels=FALSE specifica ca nu poate fi
scrisa nicio eticheta langa marcaje. Aceasta optiune accepta si un vector de
tip caracter, spre exemplu labels=c("A", "B", "C").
Titlul este adaugat cu title(), insa fontul este putin modificat. Notatiile
de pe axe sunt scrise cu mtext() (text marginal). Primul argument al acestei
functii este un vector de tip caracter ce urmeaza a fi scris. Optiunea line
indica distanta de la zona graficului (in mod implicit line=0)la coordonata.
A doua apelare a functiei mtext() utilizeaza valoarea implicita a lui side (3).
Celelalte doua apelari ale functiei mtext() trec ca prim argument un vector
numeric: acesta va fi convertit in caracter.
4.6 Pachetele grid si lattice
Pachetele grid si lattice implementeaza sistemele de tip grila si latice. Grila este
un nou mod grafic cu sistem propriu de parametri grafici care sunt distincti
fata de cei studiati anterior. Principalele doua diferente dintre grila si graficele
50

de baza sunt:
•un mod mai flexibil de a imparti instrumentele grafice utilizand viewports
care poate fi superior (obiectele grafice pot fi chiar impartite intre zone
distincte predefinite ale unui spatiu de afisare, de ex., sageti);
•obiectele grafice (grob) pot fi modificate sau sterse dintr-un grafic fara
a fi necesara re-desenarea intregului grafic (asa cum se cere in cazul
graficelor de baza).
Graficele de tip grila nu pot fi de obicei unite sau combinate cu graficele
de baza (Pachetul gridBase trebuie utilizat pentru aceasta). In orice caz, este
posibila utilizarea ambelor moduri grafice in aceeasi sesiune in cadrul aceluiasi
instrument grafic.
Latice este in fond implementarea in cadrul R a graficelor Trellis din S-
PLUS. Trellis este un mod de vizualizare a datelor multidimensionale in mod
special corespunzator explorarii relatiilor sau interactiunilor dintre variabile14.
Principala ideea din spatele latice (si al Trellis) este aceea a graficelor de condi-
tionari multiple: un grafic bidimensional va fi impartit in cateva grafice tinand
cont de valorile unei a treia variabile. Functia coplot utilizeaza o modalitate
similara, insa latice ofera functionalitati mai vaste. Latice utilizeaza modul
grafic de tip grila.
Cele mai multe functii din lattice considera o formula ca principalul lor
argument15, de exemplu y~x. Formula y ~ x | z presupune ca graficul lui
yraportat la xsa fie reprezentat in cateva grafice tinand cont de valorile lui
z.
Tabelul urmator prezinta principalele functii ale pachetului lattice. For-
mula data ca argument este formula tipic necesara, insa toate aceste functii
accepta o formula conditionala (y ~ x | z) ca argument principal; in ultimul
caz, un grafic multiplu, raportat la valorile lui z, este reprezentat asa cum se
va vedea in exemplele de mai jos.
14 http://cm.bell-labs.com/cm/ms/departments/sia/project/trellis/index.html
15 plot() accepta de asemenea o formula ca argument principal: pentru xsi ydoi vectori
de aceeasi lungime, plot(y ~ x) si plot(x, y) vor genera grafice identice.
51
barchart(y ~ x) histograma valorilor lui yin raport cu cele ale lui x
bwplot(y ~ x) grafic “box-and-whiskers”
densityplot(~ x) graficul functiilor de densitate
dotplot(y ~ x) grafic punctat Cleveland (grafice ingramadite linie de
linie si coloana de coloana)
histogram(~ x) histograma frecventelor lui x
qqmath(~ x) cuantilele lui xraportate la valorile asteptate sub o dis-
tributie teoretica
stripplot(y ~ x) grafic unidimensional, xtrebuie sa fie numeric, ypoate fi
un factor
qq(y ~ x) cuantile pentru compararea a doua distributii, xtrebuie
sa fie numeric, ytrebuie sa fie numeric, caracter sau fac-
tor insa trebuie sa aiba doua ‘niveluri’
xyplot(y ~ x) grafice bidimensionale (cu multe functionalitati)
levelplot(z ~ x*y)
contourplot(z ~ x*y)
grafic colorat al valorilor lui zla coordonatele date de x
si y(x,ysi zau toate aceeasi lungime)
cloud(z ~ x*y) grafic de perspectiva 3-D (puncte)
wireframe(z ~ x*y) id. (suprafata)
splom(~ x) matrice de grafice bidimensionale
parallel(~ x) grafic de coordonate paralele
In continuare vom vedea cateva exemple pentru a ilustra cateva aspecte ale
pachetului lattice. Pachetul se incarca in memorie prin comanda library(lattice)
astfel incat functiile sa poata fi accesate.
Vom incepe cu graficele functiilor de densitate. Asemenea grafice pot fi
create cu densityplot(~ x) care va reprezenta o curba a functiei de densi-
tate empirica cu punctele corespunzatoare observatiilor pe axa x(similar cu
rug()). Exemplul nostru va fi putin mai complicat pe fiecare grafic cu su-
perpozitia curbelor densitatii empirice si a celor prezise prin regula normala.
Este necesara folosirea argumentului panel care defineste ce e reprezentat pe
fiecare grafic. Comenzile sunt urmatoarele:
n <- seq(5, 45, 5)
x <- rnorm(sum(n))
y <- factor(rep(n, n), labels=paste("n =", n))
densityplot(~ x | y,
panel = function(x, ...) {
panel.densityplot(x, col="DarkOliveGreen", ...)
panel.mathdensity(dmath=dnorm,
args=list(mean=mean(x), sd=sd(x)),
col="darkblue")
})
Primele trei linii ale comenzii genereaza un esantion aleatoriu de variabile
normal independente care este impartit in sub-esantioane de marime egala cu
5, 10, 15, . . . , si 45. Apoi se apeleaza functia densityplot ce produce cate
un grafic pentru fiecare sub-esantion. panel ia ca argument o functie. In
exemplul nostru, am definit o functie care apeleaza doua functii pre-definite
in lattice:panel.densityplot pentru a desena functia de densitate empirica
si panel.mathdensity pentru a desena functia de densitate prezisa de regula
52

x
Density
0
0.1
0.2
0.3
0.4
0.5
0.6
−4 −2 0 2 4
n = 5
n = 10
−4 −2 0 2 4
n = 15
n = 20
n = 25
0
0.1
0.2
0.3
0.4
0.5
0.6
n = 30
0
0.1
0.2
0.3
0.4
0.5
0.6
n = 35
n = 40
−4 −2 0 2 4
n = 45
Figure 7: Functia densityplot.
normala. Functia panel.densityplot este chemata in mod implicit daca
nu este dat niciun argument in panel: comanda densityplot (~ x | y) ar
rezulta in acelasi grafic similar Fig. 7insa fara curbele albastre.
Exemplele urmatoare sunt preluate, mai mult sau mai putin modificate,
din suportul pachetului lattice si utilizeaza cateva seturi de date disponibile
in R: localizarile a 1000 de cutremure in apropierea insulelor Fiji si cateva
masuratori ale florilor facute pe trei specii de iris.
Fig. 8arata localizarea geografica a cutremurelor raportate la adancime.
Comenzile necesarepentru acest grafic sunt urmatoarele:
data(quakes)
mini <- min(quakes$depth)
maxi <- max(quakes$depth)
int <- ceiling((maxi - mini)/9)
inf <- seq(mini, maxi, int)
quakes$depth.cat <- factor(floor(((quakes$depth - mini) / int)),
labels=paste(inf, inf + int, sep="-"))
xyplot(lat ~ long | depth.cat, data = quakes)
Prima comanda incarca setul de date quakes in memorie. Urmatoarele
cinci comenzi creaza un factor prin impartirea adancimii (variabila depth) in
noua intervale egale: nivelurile acestui factor sunt etichetate cu cea mai mica
si cea mai mare limita a acestor intervale. Apoi se poate chema functia xyplot
cu formula corespunzatoare si argumentul data ce indica unde functia xyplot
trebuie sa caut variabilele16.
16 plot() nu poate lua ca argument data, locatia variabilelor trebuie mentionata explicit,
de exemplu plot(quakes$long ~ quakes$lat).
53
long
lat
−40
−35
−30
−25
−20
−15
−10
165 170 175 180 185
40−112
112−184
165 170 175 180 185
184−256
256−328
328−400
−40
−35
−30
−25
−20
−15
−10
400−472
−40
−35
−30
−25
−20
−15
−10
472−544
544−616
165 170 175 180 185
616−688
Figure 8: Functia xyplot cu setul de date“quakes”(cutremure).
In cazul setului de date iris, intrepatrunderea in cadrul diferitelor este
suficient de mica astfel incat pot fi reprezentate grafic ca in figura (Fig. 9).
Comenzile sunt urmatoarele:
data(iris)
xyplot(
Petal.Length ~ Petal.Width, data = iris, groups=Species,
panel = panel.superpose,
type = c("p", "smooth"), span=.75,
auto.key = list(x = 0.15, y = 0.85)
)
Apelarea functiei xyplot este un pic mai complexa in cazul de fata de-
cat in cel anterior si utilizeaza cateva optiuni detaliate in cele ce urmeaza.
Optiunea groups, asa cum ii sugereaza numele, defineste grupuri care vor fi
utilizate de alte optiuni. Am vazut deja optiunea panel care defineste modul
in care diferitele grupuri vor fi reprezentate pe grafic: am utilizat o functie
pre-definita panel.superpose pentru a suprapune grupurile pe acelasi grafic.
Nu este trecuta nicio optiune in panel.superpose, culorile implicite vor fi
utilizate pentru a distinge grupurile. Optiunea type, similar plot(), speci-
fica modul in care datele sunt reprezentate, insa aici putem da cateva argu-
mente ca vector: "p" pentru a desena punctele si "smooth" pentru a desena o
curba aplatizata al carei grad de aplatizare este specificat de span. Optiunea
auto.key adauga o legenda graficului: este necesara mentionarea, sub forma
de lista, a coordonatelor in care legenda va fi reprezentata. De remercat ca
aceste coordonate sunt legate de dimensiunea graficului (adica in [0, 1]).
Acum vom ilustra functia splom cu acelasi set de date iris. Urmatoarele
comenzi au fost utilizate pentru a crea Fig. 10:
54
Petal.Width
Petal.Length
oo
o
o
o
o
o
o
o
o o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o o
o
o
oo oo o
o
o
o
oo
o
ooo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
o
o o
o
o
o
o
o
o
o
o
oo o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
1
2
3
4
5
6
7
0 0.5 1 1.5 2 2.5
setosa
versicolor
virginica
Figure 9: Functia xyplot cu setul de date “iris”.
splom(
~iris[1:4], groups = Species, data = iris, xlab = "",
panel = panel.superpose,
auto.key = list(columns = 3)
)
Principalul argument este de data aceasta o matrice (primele patru coloane
ale setului iris). Rezultatul este setul de grafice bidimensionale posibile din-
tre coloanele matricii, ca in cazul functiei pairs. In mod implicit, splom
adauga textul “Scatter Plot Matrix” sub axa x: pentru a evita acest lucru, a
fost utilizata optiunea xlab="". Celelalte optiuni sunt similare cu exemplul
anterior, cu exceptia columns = 3 pentru auto.key care este specificata astfel
incat legenda sa fie afisata pe trei coloane.
Fig. 10 ar putea fi creata cu pairs(), insa ultima functie nu poate crea
grafice conditionale ca in Fig. 11. Codul utilizat este relativ simplu:
splom(~iris[1:3] | Species, data = iris, pscales = 0,
varnames = c("Sepal\nLength", "Sepal\nWidth", "Petal\nLength"))
Intrucat sub-graficele sunt relativ mici, am adaugat doua optiuni pentru
a imbunatati lizibilitatea figurii: pscales = 0 sterge marcajele de pe axe
(toate sub-graficele sunt desenate pe aceeasi scala), iar numele variabilelor au
fost redefinite pentru a le afisa pe doua linii ("\n" codul pentru o linie goala
intr-un sir de tip caracter).
Ultimul exemplu foloseste metoda coordonatelor paralele pentru analiza
exploratorie a datelor multidimensionale. Variabilele sunt aranjate pe o axa
(e.g., the y-axis), iar valorile observate sunt reprezentate pe cealalta axa (vari-
abilele sunt masurate similar, de ex., prin standardizarea lor). Valorile diferite
55

Sepal.Length
5
5
6
6
7
7
88
o
oo
ooo
o
o
o
o
o
oo
o
oo
o
o
o
o
oo
o
oo
o ooo
o
o
ooo
oo
o
o
o
oo
oo
oo
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
oo
o
oooo
oo
o
o
oo o
o
o
o
o
o
o
oo
o
o
o
ooo
o
o
o
o
o
o
oo
o
o
o
o
o
o
oo
oo
o
o
oo
o
o
o
o
oo
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
ooo
ooo
o
o
o
o
o
oo
o
o
o
o
o
oo
o
oo
o
o
o
o
o
o
o
o
o
oo
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
oo
oo
oo
o
o
oo
o
o
ooo
oo
o
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
oo
o
o
oo
oo
o
o
oo
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
oo
o
oo
o
o
o
o
oo
o
o
o
o o
oo
o
o
o
oo
o
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
oo
oo
oo
ooo
oo
o
ooo oo
o
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
o
o
oo
o
o
o
o
o
o
oo
oo
o
o
oo
o
o
o
o
oo
o
o
oo
oo
o
o
o
o
o
o
o
o
oo
o
o
ooo
ooo
o
o
o
o
o
o
o
o o
oo
o
o
oo
o
o
o
o
oo
o
o
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
ooo o
o
oo
o
o
o
o
o
o
o
oo o
o
o
o
o
o
o
o
oooo
o
o
o
oo
oo
o
o
o
o
o
o
o
o
o
o
o
o
o o
o
o
o
o
o
oo o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o o
o
oo
o
oooo
o
oo
o
o
o
o
oooo
o
o
o
o
o
o
o
o
Sepal.Width
2
2
2.5
2.5
3
3
3.5
3.5
4
4
4.5 4.5
o
o
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
ooo o
o
oo
o
o
o
o
o
o
o
oo o
o
o
o
o
o
o
o
o
o
oo
o
o
ooo
o o
o
o
o
o
o
oo
o
o
o
o
o
oo
o
o
o
o
o
o
o o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o o
o
oo
o
oo
oo
o
oo o
o
o
o
oooo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
oo
o
o
o
o
o
o
o
o
ooo
o
o
oo
o
o
oo
o
o
o
oooo
o
o
o
o
o
o
ooo
oo
o
ooo
o o
o
o
o
o
o
o
o
o
o
o
o
ooo
o
o
o
o
o
ooo
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
oo
oo
o
oo
o
o
o
o
oo oo
o
oo
o
o
o
o
o
oo
o
ooo
oo
oo o
o
o
oo
o
o
oo
oo
o
oo
oooo
o
oo oo o
o
oo
o
oo
ooo o
o
oo
oo
o
o
oo
oo
oo
o
o
o
oo
o
o
o
o
ooo
o
o
o
o
oooo
o
o
o
o
oo
o
o o o
o
o
o
oo
o
o
ooo o
o
o
o
o
o
oo
o
o
o
oo
o
oo
o
oo
o
o
o
oo
o
o
o
oo
o
ooooo
o
o
oo
o
o
oo
ooo
o
o
o
oo
o
o
oo o
ooo
o
o
oo o
o
o
ooo
o
oo
o
oo
o
oo
o oo
o
oo o oo
oooo
oooo o oo
oo
oo
o
o
o
o
oo
oo
o
o
o
oo
oo
o
o
o
o
oo
o
o
oooo
oo
o
o
o
oo
oo o
o
oo
ooo
o
o
o oo
o
o
o
o
o
o
oo
o
o
o
oo
o
oo
ooo
o
o
o
oo
o
o
o
o
o
oo
oo
oo
o
o
ooo
o
oo
o
oo
oo
o
ooo
o
Petal.Length
1
1
2
2
3
3
4
4
4
4
5
5
6
6
77
oo
o
o
oo
o
o
o
oo
o
o
ooo
o
o
o
o
oo
oo
o
o o
o
o
oo ooo
o
o
o
oo
oooo o
o
o
o
o
o
o
oo
o
oo
oo
o
oo
oo
oo
o
oo
oo
o
o
o
o
ooo
oo
o
oo
oo
o
oo
o
o
o
o
oo
o
o
ooo
o
o
o
o
o
o
oo
o
o
o
oo
o
oo
oo
o
o
oo
oo
o
o
o
o
o
o
oo
ooo
o
o
ooo
o
ooo
oo
oo
o
ooo
o
oooo o o
ooo ooo
oo o
oo
o oo o
o
o
o
oo
ooooo o
oooo o
o
o o
oo
o
o
o
ooo oo
o
o o
oo
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
oo
oooo
o
o
o
o
oo
o
ooo
ooo
oo
o
o
o
o
o o
oo
o
oo
o
oo
ooo
o
o
oo
o
oo
o
o
o
o
o
o o
o
o
ooo
o
o
oo
o
o
o
o
o
oo
o
oo
o
o
o
o
oo
o
o
oo oo o o
o
oo ooo
oo ooo
o oo
oo
o
o
oo ooooo o
oooo oo
o ooo o
oo
ooo oo
o
oo
oo
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
o
o
oooo
o
o
o
o
oo
ooo
o
o oooo
o
o
oo
oo
oo
o
oo
o
o
o
ooo
o
o
oo
o
oo
o
o
o
o
o
oo
o
o
oo o
o
o
oo
o
o
o
oo
oo
o
o
o
o
oo
o
oo
o
o
oooooo
o
oo
o
oo
oo
ooo
ooo
o
o
o
o
oo
o
oooo
o
o
oooo
o
oo
oo
o
oo
o
oooo
o
oo
oo
o
o
o
o
o
o
o
o
o
oo
o
o
o
o
o
oo
o
o
oo
o
o
oo
o
o
o
o
o
o
oooo
o
o
o
o
o
oo
oo
o
oo
o
oo
ooo
o
o
o
o
o
o
o
o
o
o
o
o
o o
o
o
ooo
o
o
oo
o
oo
o
o
oo
o
o
o
o
o
o
o
o
o
o
o
Petal.Width
0
0
0.5
0.5
1
1
1.5
1.5
2
2
2.5 2.5
Setosa Versicolor Virginica
Figure 10: Functia splom cu setul de date “iris” (1).
Scatter Plot Matrix
Sepal
Length
Sepal
Width
Petal
Length
setosa
Sepal
Length
Sepal
Width
Petal
Length
versicolor
Sepal
Length
Sepal
Width
Petal
Length
virginica
Figure 11: Functia splom cu setul de date “iris” (2).
56
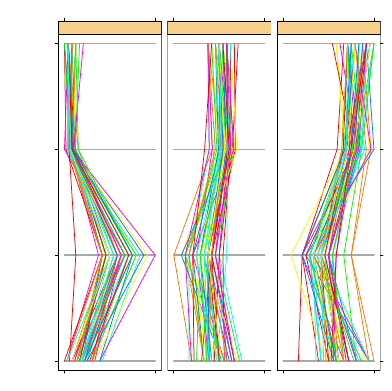
Sepal.Length
Sepal.Width
Petal.Length
Petal.Width
Min Max
setosa
versicolor
Min Max
Min Max
virginica
Figure 12: Functia parallel cu setul de date “iris”.
ale aceleiasi observatii sunt unite printr-o linie. Folosind setul de date iris,
Fig. 12 este obtinuta prin urmatorul cod:
parallel(~iris[, 1:4] | Species, data = iris, layout = c(3, 1))
57
5 Analiza statistica in R
Mai mult decat crearea de grafice, este imposibil sa avansam in detalierea
posibilitatilor oferite de R in privinta analizelor statistice. Scopul este de a
oferi cateva referinte pentru a contura o idee asupra particularitatilor R-ului
in a efectua analiza de date.
Pachetul stats contine functii pentru o gama larga de analize statistice
de baza: teste clasice, modele liniare (inclusiv regresii liniare, modele liniare
generalizate si analiza variantei), distributii, sumarizari statistice, clustere ier-
arhice, analiza seriilor de timp, metoda celor mai mici patrate si analiza statis-
tica multidimensionala. Alte metode statistice sunt disponibile in multe alte
pachete. Cateva dintre ele sunt distribuite odata cu instalarea de baza a R-
ului si sunt etichetate ca recommended, (recomandate) iar multe alte pachete
suntcontributed (contribuite) si trebuie instalate de catre utilizator.
Vom incepe cu un exemplu simplu care nu cere niciun alt pachet in afara
de stats pentru a introduce modalitatea generala de analiza de date in R. Apoi,
vom detalia cateva notiuni, formula (eng. formulae) si functii generale (eng.
generic functions), care sunt utile indiferent de tipul de analiza efectuata. Vom
incheia cu o prezentare generala a pachetelor.
5.1 Un exemplu simplu de analiza a variantei
Functia pentru analiza variantei in pachetul stats este aov. Pentru a o exem-
plifica, vom considera un set de date distribuite cu R: InsectSprays. Sase
insecticide au fost testate; variabila de raspuns a fost numarul de insecte.
Fiecare insecticid a fost testat de 12 ori, astfel au rezultat 72 de observatii.
Nu vom considera explorarea grafica a datelor, insa ne vom focusa pe o sim-
pla analiza a variantei variabilei de raspuns in raport cu insecticidul. Dupa
incarcarea datelor din memorie cu functia data, analiza este efectuata dupa o
extragere de radical a variabilei de raspuns:
> data(InsectSprays)
> aov.spray <- aov(sqrt(count) ~ spray, data = InsectSprays)
Principalul (si cel obligatoriu) argument al functiei aov este o formula care
specifica variabila de raspuns in partea stanga a simbolului tilde ~si vari-
abila independenta in partea dreapta. Optiunea data = InsectSprays speci-
fica faptul ca variabilele trebuie sa se afle in secventa de date InsectSprays.
Aceasta sintaxa este echivalenta cea de mai jos:
> aov.spray <- aov(sqrt(InsectSprays$count) ~ InsectSprays$spray)
sau cu (in cazul in care cunoastem numerele coloanelor variabilelor):
58
> aov.spray <- aov(sqrt(InsectSprays[, 1]) ~ InsectSprays[, 2])
Este de preferat sa utilizam prima sintaxa intrucat este mai clara.
Rezultatele nu sunt afisate din moment ce sunt atribuite obiectului numit
aov.spray. Apoi vom utiliza cateva functii pentru a extrage rezultatele, spre
exemplu print pentru a afisa un scurt sumar al analizei (in special parametri
estimati) si summary pentru a afisa mai multe detalii (inclusiv testele statis-
tice):
> aov.spray
Call:
aov(formula = sqrt(count) ~ spray, data = InsectSprays)
Terms:
spray Residuals
Sum of Squares 88.43787 26.05798
Deg. of Freedom 5 66
Residual standard error: 0.6283453
Estimated effects may be unbalanced
> summary(aov.spray)
Df Sum Sq Mean Sq F value Pr(>F)
spray 5 88.438 17.688 44.799 < 2.2e-16 ***
Residuals 66 26.058 0.395
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Trebuie amintit ca tastarea numelui unui obiect ca o comanda este similara
cu print(aov.spray). O reprezentare grafica a rezultatelor poate fi facuta
cu plot() sau termplot(). Inainte de a tasta plot(aov.spray) vom imparti
graficele in patru parti astfel incat cele patru grafice diagnostic sa fie create
pe acelasi grafic. Comenzile sunt urmatoarele:
> opar <- par()
> par(mfcol = c(2, 2))
> plot(aov.spray)
> par(opar)
> termplot(aov.spray, se=TRUE, partial.resid=TRUE, rug=TRUE)
iar graficele rezultate se afla in figurile 13 si 14.
5.2 Formulele
Formulele sunt elementul-cheie in analizele statistice in R: notatia utilizata este
aceeasi pentru (aproape) toate functiile. O formula este in mod caracteristic
de forma y ~ model unde yeste raspunsul analizat si model este un set de
59
1.5 2.5 3.5
−1.5 0.0 1.0
Fitted values
Residuals
Residuals vs Fitted
27 39
25
−2 −1 0 1 2
−2 0 1 2
Theoretical Quantiles
Standardized residuals
Normal Q−Q plot
27
39
25
1.5 2.5 3.5
0.0 0.5 1.0 1.5
Fitted values
Standardized residuals
Scale−Location plot
27 39
25
0 20 40 60
0.00 0.04 0.08
Obs. number
Cook’s distance
Cook’s distance plot
27
39
25
Figure 13: Reprezentarea grafica a rezultatelor functiei aov cu plot().
termeni pentru care cativa parametri urmeaza sa fie estimati. Acesti termeni
sunt separati cu simboluri aritmetice insa aici au un sens particular.
a+b efectul aditiv al lui asi b
Xdaca Xeste o matrice, aceasta specifica un efect aditiv al
fiecarei coloane, adica X[,1]+X[,2]+...+X[,ncol(X)];
cateva dintre coloane pot fi selectate cu indici numerici
(ex., X[,2:4])
a:b efectul de impartire dintre asi b
a*b efecte aditive si de impartire (identice cu a+b+a:b)
poly(a, n) polinomul ade gradul n
^n include toate impartirile pana la n, ex. (a+b+c)^2 este
identic cu a+b+c+a:b+a:c+b:c
b %in% a efectele lui bsunt incluse in a(identic cu a+a:b, sau a/b)
-b sterge efectul lui b, de exemplu: (a+b+c)^2-a:b este
identic cu a+b+c+a:c+b:c
-1 y~x-1 este o regresie prin origine (id. pentru y~x+0 sau
0+y~x)
1 y~1 adecveaza un model fara efecte (doar termenul liber
- eng. intercept)
offset(...) adauga un efect modelului fara a estima vreun parametru
(e.g., offset(3*x))
Observam ca operatorii aritmetici din R au sensuri diferite intr-o formula
fata de sensul pe care il au in expresii. De exemplu, formula y~x1+x2 defineste
modelul y=β1x1+β2x2+α, nu (daca operatorul +ar avea sensul obisnuit)
y=β(x1+x2)+α. Pentru a include operatiile aritmetice intr-o formula, putem
utiliza functia I: formula y~I(x1+x2) defineste modelul y=β(x1+x2)+α. In
60
0 1 2 3 4 5 6
−3 −2 −1 0 1 2
spray
Partial for spray
Figure 14: Reprezentarea grafica a rezultatelor functiei aov cu termplot().
mod similar, pentru a defini modelul y=β1x+β2x2+α, vom utiliza formula y
~ poly(x, 2) (nu y ~ x + x^2). In orice caz, este posibila includerea unei
functii intr-o formula pentru a transforma o variabila asa cum am vazut mai
sus in exemplul cu analiza variantei sprayurilor de insecte.
Pentru analize de variante, aov() accepta o sintaxa particulara pentru a
defini efectele aleatoare. De exemplu, y ~ a + Error(b) se refera la efectele
aditive ale termenului fix asi ale celui aleator b.
5.3 Functii generice
Ne amintim faptul ca functiile R actioneaza asupra atributelor obiectelor posi-
bil trecute ca si argumente. Clasa este un atribut care are nevoie de putina
atentie aici. Este un lucru obisnuit ca functiile statistice din R sa returneze
un obiect cu acelasi nume ca si clasa sa (de ex., aov returneaza un obiect
de clasa "aov",lm returneaza un obiect de clasa "lm"). Functiile pe care le
putem utiliza ulterior pentru a extrage rezultatele vor actiona asupra clasei
obiectului. Aceste functii sunt denumite functii generice.
De exemplu, functia utilizata cel mai frecvent pentru a extrage rezultatele
din analize este summary care afiseaza rezutatele detaliate. Indiferent daca
obiectul dat ca argument este de clasa "lm" (model liniar) sau "aov" (anal-
iza variantei), este evident ca informatia afisata nu va fi aceeasi. Avantajul
functiilor generice este ca sintaxa este aceeasi pentru toate clasele.
Un obiect ce contine rezultatele unei analize este in general o lista, iar
modul in care este afisat este determinat de clasa lui. Am studiat deja aceasta
notiune conform careia actiunea unei functii depinde de tipul de obiect dat
61
ca argument. Este o caracteristica specifica R17. Tabelul urmator prezinta
principalele functii generice ce pot fi utilizate pentru a extrage informatia din
obiectele rezultate dintr-o analiza. Varianta utilizata in mod obisnuit a acestor
functii este:
> mod <- lm(y ~ x)
> df.residual(mod)
[1] 8
print returneaza un sumar pe scurt
summary returneaza un sumar detaliat
df.residual returneaza numarul rezidual de grade de libertate
coef returneaza coeficientii estimati (uneori cu abaterile standard corespunza-
toare)
residuals returneaza reziduurile
deviance returneaza abaterea medie patratica de selectie
fitted returneaza valorile adecvate
logLik calculeaza logaritm din probabilitate si numarul parametrilor
AIC calculeaza criteriul Akaike sau AIC (depinde de logLik())
O functie precum aov sau lm returneaza o lista cu elemente diferite core-
spunzatoare rezultatelor analizei. Daca luam exemplul nostru de analiza a
variantei cu setul de date InsectSprays, putem vedea structura obiectului
returnat de aov:
> str(aov.spray, max.level = -1)
List of 13
- attr(*, "class")= chr [1:2] "aov" "lm"
O alta modalitate de a vizualiza aceasta structura este afisarea numelor
obiectului:
> names(aov.spray)
[1] "coefficients" "residuals" "effects"
[4] "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "contrasts"
[10] "xlevels" "call" "terms"
[13] "model"
Elementele pot fi apoi extrase asa cum am vazut deja:
> aov.spray$coefficients
(Intercept) sprayB sprayC sprayD
3.7606784 0.1159530 -2.5158217 -1.5963245
sprayE sprayF
-1.9512174 0.2579388
17 Exista peste 100 de functii generice in R.
62
summary() creaza de asemenea o lista care, in cazul aov(), este un tabel
de teste:
> str(summary(aov.spray))
List of 1
$ :Classes anova and ‘data.frame’: 2 obs. of 5 variables:
..$ Df : num [1:2] 5 66
..$ Sum Sq : num [1:2] 88.4 26.1
..$ Mean Sq: num [1:2] 17.688 0.395
..$ F value: num [1:2] 44.8 NA
..$ Pr(>F) : num [1:2] 0 NA
- attr(*, "class")= chr [1:2] "summary.aov" "listof"
> names(summary(aov.spray))
NULL
Functiile generice nu actioneaza in general asupra obiectelor: ele apeleaza
functia potrivita referitoare la clasa argumentului. O functie apelata de una
generica este o metoda in jargonul R. In mod schematic, o metoda este con-
struita ca generic.cls , unde cls este clasa obiectului. De exemplu, in cazul
summary, putem afisa metodele corespunzatoare:
> apropos("^summary")
[1] "summary" "summary.aov"
[3] "summary.aovlist" "summary.connection"
[5] "summary.data.frame" "summary.default"
[7] "summary.factor" "summary.glm"
[9] "summary.glm.null" "summary.infl"
[11] "summary.lm" "summary.lm.null"
[13] "summary.manova" "summary.matrix"
[15] "summary.mlm" "summary.packageStatus"
[17] "summary.POSIXct" "summary.POSIXlt"
[19] "summary.table"
Putem observa diferenta pentru aceasta functie generica in cazul unei re-
gresii liniare, comparativ cu analiza variantei, printr-un mic exemplu simulat:
> x <- y <- rnorm(5)
> lm.spray <- lm(y ~ x)
> names(lm.spray)
[1] "coefficients" "residuals" "effects"
[4] "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "xlevels"
[10] "call" "terms" "model"
> names(summary(lm.spray))
[1] "call" "terms" "residuals"
[4] "coefficients" "sigma" "df"
[7] "r.squared" "adj.r.squared" "fstatistic"
[10] "cov.unscaled"
63

Tabelul urmator arata cateva functii generice care executa analize supli-
mentare ale unui obiect rezultat dintr-o alta analiza, principalul argument
fiind obiectul din urma, insa in unele cazuri este necesar inca un argument,
spre exemplupredict sau update.
add1 testeaza in mod succesiv toti termenii care pot fi adaugati unui model
drop1 testeaza in mod succesiv toti termenii care pot fi eliminati dintr-un model
step selecteaza un model cu AIC (apeleaza add1 si drop1)
anova calculeaza tabelul analizei variantei sau abaterea media patratica pentru
unul sau mai multe modele
predict calculeaza valorile estimate pentru date noi intr-un model adecvat
update re-adecveaza un model cu o noua formula sau date noi
Exista si cateva functii-utilitate care extrag informatii dintr-un obiect sau
formula a unui model, cum ar fi alias care gaseste termenii dependenti liniar
intr-un model liniar specificat de o formula.
In final, exista bineinteles, functii grafice precum plot care afiseaza diverse
diagnostice, sau termplot (vezi exemplul de mai sus); desi aceasta din urma
nu este functie generica, apeleaza predict.
5.4 Pachete
Tabelul urmator prezinta pachetele standard care sunt distribuite cu instalarea
de baza a R. Cateva sunt incarcate in memorie atunci cand R este pornit;
aceasta lista se poate afisa cu functia search:
> search()
[1] ".GlobalEnv" "package:methods"
[3] "package:stats" "package:graphics"
[5] "package:grDevices" "package:utils"
[7] "package:datasets" "Autoloads"
[9] "package:base"
Celelalte pachete pot fi utilizate dupa ce sunt incarcate:
> library(grid)
Lista functiilor dintr-un pachet poate fi afisata cu:
> library(help = grid)
sau prin rasfoirea suportului in format html. Informatia referitoare la fiecare
functie poate fi accesata asa cum am prezentat anterior. (p. 7).
64

Package Description
base functii de baza R
datasets seturi de date de baza R
grDevices instrumente grafice pentru grafice de baza si grafice tip retea
graphics grafice de baza
grid grafice tip retea
methods definitia metodelor si claselor pentru obiecte R si instru-
mente de programare
splines functii si clase pentru regresia tip ”spline”
stats functii statistice
stats4 functii statistice ce utilizeaza clase S4
tcltk functii pentru interfata R cu elemente de interfata grafica
cu utilizatorul ale Tcl/Tk
tools instrumente pentru dezvoltarea si administrarea pachetelor
utils functii utilitare R
Multe pachete contribuite sunt adaugate listei de metode de analiza statis-
tica disponibile in R. Ele sunt distribuite separat si trebuie instalate si incar-
cate in R. Lista completa a pachetelor contribuite, cu descrierile corespunza-
toare, este disponibila pe site-ul CRAN 18. Cateva dintre aceste pachete sunt
recomandate intrucat acopera metodele statistice frecvent utilizate in analiza
de date. Pachetele recomandate sunt deseori distribuite cu instalarea de baza
a R. Ele sunt descrise pe scurt in tabelul urmator.
Pachet Descriere
boot metode de re-esantionare si bootstraping
class metode de clasificare
cluster metode de clustering
foreign functii pentru citirea datelor stocate in diferite formate (S3,
Stata, SAS, Minitab, SPSS, Epi Info)
KernSmooth metode pentru liniarizare kernel si estimarea densitatii (in-
clusiv kernel-uri bidimensionale)
lattice Grafice tip retea (Trellis)
MASS contine multe functii, instrumente si seturi de date din bib-
liotecile “Statistica moderna aplicata cu S” de Venables &
Ripley
mgcv modele aditive generalizate
nlme modele liniare si neliniare de efecte mixte
nnet retele neurale si modele logistice liniare multinomiale
rpart partitionare recursiva
spatial analize spatiale (“kriging”, covarianta spatiala, . . . )
survival analiza datelor de supravietuire
18 http://cran.r-project.org/src/contrib/PACKAGES.html
65

Exista alte doua colectii principale de pachete R: Omegahat Project for
Statistical Computing19 care se axeaza pe aplicatii web-based si interfete in-
tre software-uri si limbaje, si Bioconductor Project20 specializat in aplicatii
bioinformatice (in special pentru analiza micro-datelor).
Procedura de instalare a unui pachet depinde de sistemul de operare si de
tipul de instalare a R - din surse sau fisiere binare precompilate. In situatia
din urma, este recomandata utilizarea pachetelor pre-compilate disponibile pe
website-ul CRAN. In Windows, fisierul binar Rgui.exe are un meniu numit
“Packages” ce permite instalarea pachetelor prin internet de pe website-ul
CRAN, sau din fisiere tip arhiva de pe diskul local.
Daca R a fost compilat, un pachet poate fi instalat din sursa sa care este
distribuita ca un fisier cu extensia ‘.tar.gz’. Spre exemplu, daca dorim sa
instalam pachetul gee, vom descarca intai fisierul gee 4.13-6.tar.gz (numarul
4.13-6 indica versiunea pachetului; in general este disponibila pe CRAN o
singura versiune). Vom tasta apoi in sistem (nu in R) comanda:
R CMD INSTALL gee_4.13-6.tar.gz
Exista cateva functii generale utile pentru a gestiona pachetele, cum ar
fi: installed. packages,CRAN.packages, sau download.packages. De
asemnenea este util sa tastam frecvent comanda:
> update.packages()
care verifica versiunile pachetelor instalate cu cele disponibile pe CRAN (aceasta
comanda poate fi apelata din meniul “Packages” in Windows). Utilizatorul
poate apoi sa actualizeze pachetele cu versiuni mai recente decat cele instalate
pe computer.
19 http://www.omegahat.org/R/
20 http://www.bioconductor.org/
66
6 Programarea cu R in pratica
Acum, dupa ce am prezentat o vedere de ansamblu asupra functionalitatilor
R-ului, ne vom intoarce la limbaj si programare. Vom vedea cateva idei simple
care pot fi utilizate in practica.
6.1 Bucle si vectorizari
Un avantaj al lui R fata de alte software-uri cu meniuri pull-down menus este
posibilitatea programarii seriilor de analize simple care vor fi executate in mod
succesiv. Acest aspect este comun tuturor limbajelor de calculatoare, insa R
are cateva caracteristici particulare ce fac programarea mai usoara pentru
non-specialisti.
Ca si alte limbaje, R are cateva structuri de control care sunt diferite fata
de cele din limbajul C. Sa presupunem ca avem un vector x, si pentru fiecare
element al lui xcu valoarea b, dorim sa atribuim valoarea 0 unei alte variabile
y, altfel 1. Vom crea intai un vector yde aceeasi lungime cu x:
y <- numeric(length(x))
for (i in 1:length(x)) if (x[i] == b) y[i] <- 0 else y[i] <- 1
Cateva instructiuni pot fi executate daca sunt plasate in interiorul aco-
ladelor:
for (i in 1:length(x)) {
y[i] <- 0
...
}
if (x[i] == b) {
y[i] <- 0
...
}
O alta situatie posibila este executarea unei instructiuni cat timp o anumita
conditie este adevarata:
while (myfun > minimum) {
...
}
Cu toate acestea, buclele si structurile de control pot fi evitate in ma-
joritatea situatiilor datorita unei caracteristici a R-ului: vectorizarea. Vector-
izarea face ca buclele sa fie implicite in expresie, si exista multe cazuri pentru
a ilustra acest lucru. Vom considera adunarea a doi vectori:
67
> z <- x + y
Aceasta adunare poate fi scrisa cu o bucla, asa cum este posibil in majori-
tatea limbajelor:
> z <- numeric(length(x))
> for (i in 1:length(z)) z[i] <- x[i] + y[i]
In acest caz, este necesar sa cream in prealabil un vector zdatorita utilizarii
sistemului de indexare. Realizam ca aceasta bucla explicita va functiona doar
daca xsi yau aceeasi lungime: trebuie schimbat daca aceasta conditie nu este
indeplinita, cu toate ca prima expresie va functiona in toate situatiile.
Executiile conditionale (if ... else) pot fi evitate prin utilizarea in-
dexarii logice; ne vom intoarce la exemplul anterior:
> y[x == b] <- 0
> y[x != b] <- 1
In afara de faptul ca sunt mai simple, expresiile vectorizate sunt mai efi-
ciente din punct de vedere al computerizarii, in special pentru date de dimen-
siuni mari.
Exista si cateva functii de tipul ‘apply’ care evita scrierea buclelor. apply
actioneaza asupra randurilor si/sau coloanelor unei matrici, sintaxa sa fiind
apply(X, MARGIN, FUN, ...), unde Xeste o matrice, MARGIN arata daca
se considera randurile (1), coloanele (2), sau ambele (c(1, 2)), FUN este o
functie (sau un operator, insa in acest caz trebuie specificat in paranteze)
pentru aplicare, iar ... sunt alte argumente optionale pentru FUN. In cele ce
urmeaza prezentam un exemplu simplu.
> x <- rnorm(10, -5, 0.1)
> y <- rnorm(10, 5, 2)
> X <- cbind(x, y) # the columns of X keep the names "x" and "y"
> apply(X, 2, mean)
x y
-4.975132 4.932979
> apply(X, 2, sd)
x y
0.0755153 2.1388071
lapply() actioneaza asupra unei liste: sintaxa sa este similara cu cea a
functieiapply si returneaza o lista.
> forms <- list(y ~ x, y ~ poly(x, 2))
> lapply(forms, lm)
[[1]]
Call:
68
FUN(formula = X[[1]])
Coefficients:
(Intercept) x
31.683 5.377
[[2]]
Call:
FUN(formula = X[[2]])
Coefficients:
(Intercept) poly(x, 2)1 poly(x, 2)2
4.9330 1.2181 -0.6037
sapply() este o varianta flexibila a functiei lapply(), care poate avea ca
argument un vector sau o matrice, si returneaza rezultatul intr-o forma mai
prietenoasa pentru utilizator, in general un tabel.
6.2 Scrierea unui program in R
In mod caracteristic, un program R este scris intr-un fisier salvat in format
ASCII si denumit cu extensia ‘.R’. O situatie tipica in care un program este
necesar este atunci cand utilizatorul doreste sa execute aceleasi secvente de
instructiuni de cateva ori. In primul nostru exemplu, dorim sa cream ace-
lasi grafic pentru trei specii diferite de pasari, datele aflandu-se in trei fisiere
diferite. Vom proceda pas cu pas si vom vedea diferite moduri de a programa
aceasta problema simpla.
In primul rand, vom crea programul nostru in cel mai intuitiv mod prin
executarea in mod sucesiv a comenzilor necesare, avand grija sa impartim in
prealabil instrumentul grafic.
layout(matrix(1:3, 3, 1)) # partition the graphics
data <- read.table("Swal.dat") # read the data
plot(data$V1, data$V2, type="l")
title("swallow") # add a title
data <- read.table("Wren.dat")
plot(data$V1, data$V2, type="l")
title("wren")
data <- read.table("Dunn.dat")
plot(data$V1, data$V2, type="l")
title("dunnock")
Caracterul ‘#’ este utilizat pentru a adauga comentarii intr-un program:
R va trece apoi la linia urmatoare.
69
Problema acestui program este ca poate deveni destul de lung daca dorim
sa adaugam alte specii. Mai mult decat atat, cateva comenzi sunt executate
de cateva ori, astfel ca pot fi grupate impreuna si executate dupa schimbarea
catorva argumente. Strategia aplicata aici este atribuirea acestor argumente
unor vectori de tip caracter, si utilizarea indecsilor pentru accesarea acestor
valori diferite.
layout(matrix(1:3, 3, 1)) # partition the graphics
species <- c("swallow", "wren", "dunnock")
file <- c("Swal.dat" , "Wren.dat", "Dunn.dat")
for(i in 1:length(species)) {
data <- read.table(file[i]) # read the data
plot(data$V1, data$V2, type="l")
title(species[i]) # add a title
}
De remarcat ca aici nu exista ghilimele inainte si dupa file[i] in read.table()
din moment ce acest argument este de tip caracter.
Programul nostru este acum mai compact. Este mai simplu sa adaugam
alte specii din moment ce vectorii ce contin speciile si numele fisierelor se afla
la inceputul programului.
Programele de mai sus vor functiona corect daca fisierele de date ‘.dat’ sunt
localizate in folderul de lucru al R, altfel utilizatorul trebuie fie sa schimbe
folderul de lucru, fie sa specifice calea in program (spre exemplu: file <-
"/home/paradis/data/Swal.dat"). Daca programul este scris in fisierul My-
birds.R, va fi apelat prin tastarea urmatoarei comenzi:
> source("Mybirds.R")
Ca pentru orice date de intrare provenite dintr-un fisier, este necesar sa
specificam calea de acces daca fisierul nu se afla in folderul de lucru
6.3 Scrierea functiilor proprii
Am constatat deja ca majoritatea executiilor in R sunt facute prin functii ale
caror argumente sunt trecute intre paranteze. Utilizatorii pot scrie propriile
lor functii, iar acestea vor avea exact aceleasi proprietati ca celelalte functii
din R.
Scrierea propriilor functii permite o utilizare eficienta, flexibila si rationala
a R-ului. Ne vom intoarce la exemplul nostru de citire a catorva date urmate de
reprezentare grafica. daca dorim sa facem aceasta operatie in situatii diferite,
poate fi o idee buna sa scriem o functie:
myfun <- function(S, F)
{
data <- read.table(F)
70
plot(data$V1, data$V2, type="l")
title(S)
}
Pentru a fi executata, aceasta functie trebuie sa fie incarcata in memorie,
iar aceasta se poate realiza in cateva moduri. Liniile functiei pot fi introduse
direct din tastatura, ca orice alta comanda, sau copiate cu copy-paste dintr-
un editor. Daca functia a fost salvata intr-un fisier text, poate fi incarcata
cu source() ca orice alt program. Daca utilizatorul doreste sa incarce cateva
functii de fiecare data cand R este lansat, acestea pot fi salvate intr-un spatiu
de lucru .RData care va fi incarcat in memorie daca se afla in folderul de
lucru. O alta posibilitate este de a configura fisierul ‘.Rprofile’ sau ‘Rprofile’
(vezi ?Startup pentru detalii). In cele din urma, este posibila crearea unui
pachet, insa acest aspect nu va fi prezentat aici (vezi manualul “Writing R
Extensions”).
Odata ce functia este incarcata, vom putea sa citim datele si sa le reprezen-
tam grafic printr-o singura comanda, spre exemplu cu myfun("swallow",
"Swal.dat"). Astfel, avem acum o a treia versiune a programului nostru:
layout(matrix(1:3, 3, 1))
myfun("swallow", "Swal.dat")
myfun("wren", "Wrenn.dat")
myfun("dunnock", "Dunn.dat")
Putem utiliza de asemenea sapply(), ceea ce conduce la a patra versiune
a programului:
layout(matrix(1:3, 3, 1))
species <- c("swallow", "wren", "dunnock")
file <- c("Swal.dat" , "Wren.dat", "Dunn.dat")
sapply(species, myfun, file)
In R, nu este necesara declararea variabilelor utilizate in cadrul functiei.
Atunci cand o functie este executata, R utilizeaza o regula denumita domeniu
lexic - eng. lexical scoping pentru a decide daca un obiect este local functiei
sau global. Pentru a intelege acest mecanism, vom considera functia simpla
de mai jos:
> foo <- function() print(x)
> x <- 1
> foo()
[1] 1
Denumirea xnu este utilizata pentru a crea un obiect in cadrul foo(), asa
incat R va cauta in mediul propriu daca exista un obiect denumit x, si va afisa
valoarea sa (altfel, un mesaj de eroare este afisat, iar executia este intrerupta).
Daca xeste utilizat ca nume al unui obiect in cadrul unei functii, valoarea
lui xnu este utilizata in mediul global.
71

> x <- 1
> foo2 <- function() { x <- 2; print(x) }
> foo2()
[1] 2
> x
[1] 1
De aceasta data print() utilizeaza obiectul xcare este definit in cadrul
mediului sau, adica a mediului foo2.
Cuvantul “propriu” de mai sus este important. In cele doua functii date
ca exemplu, exista doua medii: cel global si cel al functiei foo sau foo2. Daca
sunt trei sau mai multe medii in serie, cautarea obiectelor este facuta progresiv
de la un anumit mediu la cel propriu, si asa mai departe, pana la cel global.
Sunt doua moduri de specificare a argumentelor unei functii: dupa pozitiile
lor sau dupa numele lor (numite si argumente caracterizate). De exemplu, vom
considera o functie cu trei argumente:
foo <- function(arg1, arg2, arg3) {...}
foo() poate fi executata fara a utiliza numele arg1, . . . , daca obiectele
corespunzatoare sunt plasate in pozitia corecta, de exemplu: foo(x, y, z).
In orice caz, pozitia nu are importanta daca numele argumentelor sunt uti-
lizate, de ex. foo(arg3 = z, arg2 = y, arg1 = x). O alta caractristica a
functiilor R-ului este posibilitatea utilizarii valorilor implicite in definitiile lor.
Spre exemplu:
foo <- function(arg1, arg2 = 5, arg3 = FALSE) {...}
Comenzile foo(x),foo(x, 5, FALSE), si foo(x, arg3 = FALSE) vor avea
exact acelasi rezultat. Utilizarea valorilor implicite in definitia unei functii
este folositoare, in special atunci cand se folosesc argumente caracterizate (de
ex. schimbarea unei singure valori implicite cum ar fi foo(x, arg3 = TRUE)).
Pentru a conclude aceasta sectiune, vom vedea un alt exemplu care nu
este pur statistic, insa ilustreaza flexibilitatea R-ului. Consideram ca dorim sa
studiem comportamentul unui model neliniar: modelul lui Ricker definit de:
Nt+1 =Ntexp r1−Nt
K
Acest model este larg utilizat in dinamica populatiei, in special in cea a
pestilor. Utilizand o functie, dorim sa simulam acest model cu privire la rata
cresterii rsi numarul initial al populatiei N0(capacitatea maxima Keste
adesea egala cu 1 iar aceasta valoare va fi luata ca implicita); rezultatele vor fi
afisate ca grafic de numere raportate la timp. Vom adauga o optiune pentru
a permite utilizatorului sa afiseze doar numerele in ultimii cativa pasi (in mod
implicit toate rezultatele vor fi reprezentate grafic). Functia de mai jos poate
executa aceasta analiza numerica a modelului Ricker.
72
ricker <- function(nzero, r, K=1, time=100, from=0, to=time)
{
N <- numeric(time+1)
N[1] <- nzero
for (i in 1:time) N[i+1] <- N[i]*exp(r*(1 - N[i]/K))
Time <- 0:time
plot(Time, N, type="l", xlim=c(from, to))
}
Incercati cu:
> layout(matrix(1:3, 3, 1))
> ricker(0.1, 1); title("r = 1")
> ricker(0.1, 2); title("r = 2")
> ricker(0.1, 3); title("r = 3")
73

7 Literatura de specialitate R
Manuale. Cateva manuale sunt integrate in R HOME/doc/manual/:
•An Introduction to R [R-intro.pdf],
•R Installation and Administration [R-admin.pdf],
•R Data Import/Export [R-data.pdf],
•Writing R Extensions [R-exts.pdf],
•R Language Definition [R-lang.pdf].
Fisierele pot fi in formate diferite (pdf, html, texi, . . . ) in functie de
tipul instalarii.
FAQ. R este distribuit si cu sectiunea FAQ (Frequently Asked Questions)
localizata in folderul R HOME/doc/html/. O versiune a R-FAQ este in
mod regulat actualizata pe site-ul CRAN:
http://cran.r-project.org/doc/FAQ/R-FAQ.html
Resurse on-line Site-ul CRAN Web gazduieste cateva documente, resurse
bibliografice si linkuri catre alte site-uri. Exista si o lista de publicatii
(carti si articole) despre R sau metode statistice21 si cateva documente
si tutoriale scrise de catre utilizatorii R 22.
Liste de adrese Exista patru liste de discutii despre R; pentru a va abona, a
trimite un mesaj, sau a citi arhivele accesati: http://www.R-project.org/mail.html.
Lista generala de discutii ‘r-help’ este o sursa interesanta de informatii
pentru utilizatorii R (celelalte trei liste sunt dedicate anuntarilor de noi
versiuni si sunt pentru dezvoltatori). Multi utilizatori au trimis catre ‘r-
help’ functii sau programe care pot fi gasite in arhive. Daca intampinati
o problema in R, este important sa parcurgeti urmatorii pasi inainte de
a trimite un mesaj catre ‘r-help’:
1. cititi cu atentie suportul on-line (utilizand motorul de cautare);
2. cititi R-FAQ;
3. cautati in arhivele ‘r-help’ la adresa mai sus mentionata, sau uti-
lizand unul dintre motoarele de cautare dezvoltate pe cateva site-
uri23;
4. cititi “ghidul de postare”24 inainte de a trimite o intrebare.
21 http://www.R-project.org/doc/bib/R-publications.html
22 http://cran.r-project.org/other-docs.html
23 Adresele acestor site-uri sunt enumerate la http://cran.r-project.org/search.html
24 http://www.r-project.org/posting-guide.html
74

R News. Jurnalul electronic R News isi propune sa fie o punte de legatura
intre listele de discutii electronice si publicatiile stiintifice traditionale.
Prima editie a fost publicata in ianuarie 200125.
Citarea R intr-o publicatie Daca doriti sa faceti referire catre R intr-o
publicatie, trebuie sa citati urmatoarea referinta:
R Development Core Team (2005). R: A language and envi-
ronment for statistical computing. R Foundation for Statisti-
cal Computing, Vienna, Austria. ISBN 3-900051-07-0, URL:
http://www.R-project.org.
25 http://cran.r-project.org/doc/Rnews/
75