Practical Guide To Quantitative Finance Interview
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 212 [warning: Documents this large are best viewed by clicking the View PDF Link!]



First Edition
Xinfeng Zhou
Edited by Brett Jiu


To
the memory
of
my
sister, Xinli Zhou
©Copyright 2008 by Xinfeng Zhou, http://www.quantfinanceinterviews.com
All right reserved.
No part
of
this book may be reproduced or transmitted in any form or
by
any means,
electronic or mechanical, including photocopying, recording or by any information
storage and retrieval system, without the written permission
of
the Publisher, except
where permitted by law.


Table
of
Contents
Chapter 1 General Principles ......................................................................................... 1
1.
Build a broad knowledge base .................................................
....
.................................................. 1
2.
Practice your interview skills .......................
..
.
..
........................
..
...................................
..
.............. 1
3. Listen carefully .................
..
.........................
..
................................................................
..
..
............ 2
4. Speak your mind .
....
...
..
...
..
.............................
..
.......
..
....
.........
..
................................
..
..................
..
2
5. Make reasonable assumptions ......................
..
................................................................................ 2
Chapter 2 Brain Teasers ................................................................................................. 3
2.1
Problem Simplification ......................................................... ................................... 3
Screwy pirates ...................
..
............................................................
..
..
..
............................................. 3
Tiger
and
sheep ....... ............................................
..
............................................................................. 4
2.2 Logic Reasoning ...................................................................................................... 5
River crossing .................................................................................
..
.
..
..........................
..
.
..
............... 5
Birthday problem .............................................
..
.
..
...........................
..
.
..
..............................
..
..
........... 5
Card
game
.........................................................................................
..
..
........................
..
................... 6
Burning ropes ..................................................
..
.
..
........................................................
..
....
................ 7
Defective ball ......
..
..
............
..
.....
..
.......................
..
.
..
...
..
............
..
..
..
.
..
....................
.. ..
...................
..
... 7
Trailing zeros ...................................................................................
...
............................................... 9
Horse race ...................................................................................................................
..
..
..
................. 9
Infinite sequence ...............................................
.. ..
...........................................................................
10
2.3 Thinking Out
of
the Box ....................................................
..
....................
..
.. ..
........
10
Box packing ....................................................................................
..
...
..
..........................................
10
Calendar cubes .
..
..............................................................................
...
..
.......................
..
..................
11
Door
to
offer ......................................................................................
..
..
........................
..
................
12
Message delivery ...............................................................................
..
..
.........................
..
...............
13
Last ball ...............................
..
..........................
.. ..
.................................................................. ..........
13
Light switches ...................................................
..
..
.............................
..
..
.........................
..
..
.............
14
Quant salary ....................................................................................
..
...
..
..........................................
15
2.4 Application
of
Symmetry ......................
..
.....................................................
..
.......
15
Coin piles .
..
.
..
..
.........................
...
....
..
...
..
.
..
........................................................
..
.......
..
.......
..
...........
15
Mislabeled bags ............................................................................................................................... 16
Wise men ...........................................................................................
..
.
..
......................
...
..
..............
17
2.5 Series Summation ..................................................................................................
17
Clock pieces .........................................................
..
.............................
.. ..
.........................................
18
Missing integers ................................................
..
.
..
.....................
..
...............................
..
..................
18
Counterfeit coins I ..............................
..
.........................................
..
..............................
..
................
19
2.6 The Pigeon Hole Principle .......................................................................
...
........... 20
Matching socks ................................................................................................................................
21
Handshakes ........................
....
..........................................................................................
..
..............
21
Have
we
met before? ...........................................................................
..
...............................
..
.........
21
Ants
on
a square ...........................
..
..
....................................................
..
.......................................... 22
Counterfeit coins II ..........................
..
.................
..
................................
..
.......................
..
................ 22

Contents
2.7 Modular Arithmetic .............................. .
..
...................................................
..
..
........ 23
Prisoner problem ................
..
............................................................
..
............................
..
................
24
Division
by
9 .................................................................................
..
................................................ 25
Chameleon colors ............................................................................
..
...............................
..
............. 26
2.8 Math Induction .....................................
..
................................................................ 27
Coin split problem ..........................................................................
..
............................................... 27
Chocolate
bar
problem ....................................................................................................
..
............... 28
Race track .............................................................................................................................
..
......... 29
2.9 Proof by Contradiction ........................
..
..
........................... ....................................
31
Irrational number
..
..............................................
..
.........................
..
.
..
................... ..
..
....
..
.. ..
............
31
Rainbow hats .....................................................................................................................
..
............
31
Chapter 3 Calculus and Linear Algebra ...................................................................... 33
3.1
Limits and Derivatives
..
......................
..
...
................................................
..
..
..
........ 33
Basics
of
derivatives ........................................................................
..
..............................................
33
Maximum and minimum .... ...............................................................
..
...........................
..
............... 34
L'Hospital's rule .................................................................................................................
..
........... 35
3.2 Integration ............................................
.. ..
......................
...
..........................
..
..
....... 36
Basics
of
integration ........................................................................................................
..
..............
36
Applications
of
integration .................................................................
..
............................
..
............. 38
Expected value using integration ......................................................
..
...............................
..
............
40
3.3 Partial Derivatives and Multiple Integrals ............................................................ .40
3.4 Important Calculus Methods ..................................................................
...
............ .41
Taylor's series ......................................................................................
..
..........................................
41
Newton's method .............................................................................
..
..............................................
44
Lagrange multipliers ........................................................................................................................ 45
3.5 Ordinary Differential Equations ....... ...
..
....
..
.......
..
..........
....
.......
..
.............
..
........... .46
Separable differential equations ..........................
..
...........................................................
..
.............. 4 7
First-order linear differential equations ..........................................................................
..
............... 4 7
Homogeneous linear equations .......................................................
..
............................................... 48
Nonhomogeneous linear equations ..................................................................................................
49
3.6 Linear Algebra ............
..
.......................
..
........................
..
.. ..
...................
..
............. 50
Vectors .................
..
...
.. ..
................................... ..........
..
.
..
...................
..
...............................
..
........... 50
QR
decomposition ......
..
..............................................
..
..... ...............
..
............................................. 52
Determinant, eigenvalue
and
eigenvector .........................................
..
................................
..
........... 53
Positive semidefinite/definite matrix .................................................
..
...............................
..
...........
56
LU decomposition and Cholesky decomposition ...........................................................
..
............... 57
Chapter 4 Probability Theory .......................................................................................
59
4.1
Basic Probability Definitions and Set Operations ..............
..
.......................
..
......... 59
Coin toss game .................................................................................................................................
61
Card game .........................................................
..
...........................................................
..
................
61
Drunk passenger ...............................................................................
..
.
..
.......................................... 62
ii

A Practical Guide
To
Quantitative Finance Interviews
N points on a circle ............
..
............................................................................................................ 63
4.2 Combinatorial Analysis .................................................
..
.........................
..
........... 64
Poker hands ........................
..
............................................................................................................ 65
Hopping rabbit .. .....
..
................ ...........
..
..............................
..
..............................
..
........................... 66
Screwy pirates 2 .............................................................................................................
..
................ 6 7
Chess tournament. ............................................
..
................................... ........................................... 68
Application letters ..............
..
......................................................................................... ................... 69
Birthday problem .............................................................................................................................
71
I
OOth
digit ...........................
..
........................................................................................ ...................
71
Cubic
of
integer ............................................................................................................................... 72
4.3 Conditional Probability and Bayes' formula .................
..
.......................
..
..
........... 72
Boys and girls ...................................................................................
..
............................................. 73
All-girl world? ................................................................................................................................. 74
Unfair coin .......................................................... ............................................................................. 74
Fair probability from an unfair coin ................................................................................................. 75
Dart game ......................................................................................................................................... 75
Birthday line ....................................................... .........................................................................
..
.. 76
Dice order ........................................................................................................................................ 78
Monty Hall problem ............................................. ............................. ............................................... 78
Amoeba population .............................................. ............................................................................ 79
Candies in a
jar
................................................................................................................................ 79
Coin toss game .................................................... .............................................................. ...............
80
Russian roulette series ......................................... .............................................................. ...............
81
Aces .................................................................... ............................................................................. 82
Gambler's ruin problem ....................................... ............................................................................
83
Basketball scores .............................................................................................................................. 84
Cars on road ....................................................................................................................... .............. 85
4.4 Discrete and Continuous Distributions .......................................................
..
......... 86
Meeting probability .......................................................................................................................... 88
Probability
of
triangle ................................
..
...... .................................................
..
........................... 89
Property
of
Poisson process
..
..............................................................................................
..
........... 90
Moments
of
normal distribution ........................................................ ................................. .............
91
4.5 Expected Value, Variance & Covariance ......................
..
...................................... 92
Connecting noodles .......................................................................................................................... 93
Optimal hedge ratio .............................................. ........................................................................... 94
Dice game ........................................................ .............................. .................................................. 94
Card game ........................................................... ...............
..
............................................................ 95
Sum
of
random variables
..
.................................... ............................
..
......................... .................... 95
Coupon collection .............................................................................. .......................... .................... 97
Joint default probability ....................................... ............................................................................ 98
4.6 Order Statistics ............................................................................................
..
........ 99
Expected value
of
max and min ............................................................................................ ........... 99
Correlation
of
max and min ........................
..
.............. ................................................................... 100
Random ants ...................................................... ............................................................................ l 02
Chapter 5 Stochastic Process and Stochastic Calculus ............................................ 105
iii

Contents
5
.1
Markov Chain ...........
..
..............................................................................
..
.........
105
Gambler's ruin problem ....
..
..........................................................................................
..
........ ....... 107
Dice question ....................
..
..........................................................................................
..
............... 108
Coin triplets ...................................................................................................................... .. ........... l 09
Color balls ........................................................
..
................................
..
..........................................
113
5.2 Martingale
and
Random walk .........................................
..
....................... ............
115
Drunk man ..................................................................................................................................... 116
Dice game ..........................
.. ..
...........................................................
..
............................... ..
..
........ 117
Ticket line .........................................................................................
..
........................................... 117
Coin sequence .........
..
.
..
.................................................................................................................. 119
5.3 Dynamic Programming ........................
..
.........................
..
..........
..
..........
..
..
..
.......
121
Dynamic programming (DP) algorithm ........................................... .................................... .......... 122
Dice game ........................................................................................... ................................ ........... 123
World series ........................................................................................... ........................................ 123
Dynamic dice
game
....................................................................................................................... 126
Dynamic card
game
....................................................................................................................... 127
5.4 Brownian Motion and Stochastic Calculus .........
..
...................................
..
.
..
....... 129
Brownian motion ...............................................................................
..
.......................................... 129
Stopping time/ first passage time .......................................................... .........................................
131
Ito's
lemrna ........................
..
.......................................................................................................... 135
Chapter 6 Finance ........................................................................................................ 137
6.1. Option Pricing .......................................
..
......................
..
.
..
.....................
..
..
..
...... 137
Price direction
of
options ............................................................................................................... 137
Put-call parity ...................
..
.............................
..
................................
..
..........................................
138
American v.s. European options ........................................................
..
.......................................... 139
Black-Scholes-Merton differential equation .......... ........................................................................ 142
Black-Scholes formula ...................................................................................................................
143
6.2. The Greeks ...........................................
..
........................
..
...........................
..
...... 149
Delta .................................................................................................
..
........................................... 149
Gamma ...............................................................
..
.......................................................................... 152
Theta ....
..
............................
..
............................................................................................. ............. 154
Vega ...... ............................................................................................
..
........................................... 156
6.3. Option Portfolios and Exotic Options ....
..
..
....................................
..
........
..
.........
158
Bull spread ..............................................
..
.
..
.....
..
..
..
..........................
..
........................................... 159
Straddle .......................................................................................................................................... 159
Binary options ................................................................................................................................ 160
Exchange options ...........................................................................................................................
161
6.4. Other Finance Questions .....................
..
.
..
......................... ..................................
163
Portfolio optimization .........
..
............ .
..
.......................... ..
.. ..
............................
..
.................... ........
163
Value
at
risk .. .........
..
.............
..
.............................................
..
............... .........................
..
.............. 164
Duration and convexity ..................................................................................................
..
..............
165
Forward and futures ....................................................................................................................... 167
Interest rate models ...........
..
.................................................................. ......................................... 168
IV

A Practical Guide
To
Quantitative Finance Interviews
Chapter 7 Algorithms and Numerical Methods ....................................................... 171
7.1. Algorithms ..................
..
.......................
..
.........................
..
..................................
171
Number swap ................................................................................................................................. 172
Unique elements .................... ............................................................
..
..........................................
173
Homer's algorithm ......................................................................................................................... 174
Moving average ...................................................
..
........................................................................ 174
Sorting algorithm ...............................................
..
.......................................................................... 174
Random permutation ..........................................
..
...............................
..
......................................... 176
Search algorithm ................................................
..
..........................
..
.............................................. 177
Fibonacci numbers ... .............................
..
....................................................................................... 179
Maximum contiguous subarray ..........................
....
.............................
..
......................................... 180
7 .2. The Power
of
Two ..........................................................
..
..................... ............. 182
Power
of
2? .................................................................................................................................... 182
Multiplication by 7 ...........................................
..
..............................................................
..
............ 182
Probability simulation ..........................................................................
..
......................
..
.
..
............. 182
Poisonous wine .............................................................................................................. ................ 183
7.3 Numerical Methods ........................................................
..
................................... 184
Monte Carlo simulation ...................................................................
..
...............................
..
........... 184
Finite difference method .....
..
...............................................................
..
.......................
..
............... 189
v


Preface
This book will prepare you for quantitative finance interviews
by
helping you zero in on
the key concepts that are frequently tested in such interviews. In this book we analyze
solutions to more than 200 real interview problems and provide valuable insights into
how to ace quantitative interviews. The book covers a variety
of
topics that you are
likely to encounter in quantitative interviews: brain teasers, calculus, linear algebra,
probability, stochastic processes and stochastic calculus, finance and programming.
Professionals and students seeking to pursue a career in quantitative finance or related
quantitative fields will benefit most from thoroughly reading this book. In recent years,
we have seen a dramatic surge
in
demand for talents with strong quantitative skills from
investment banks, investment management firms, hedge funds, financial software
vendors and financial consulting companies.
As
a result, quant, an umbrella description
that encompasses quantitative analysts, quantitative researchers, quantitative strategists,
quantitative traders, and quantitative developers, has become an attractive career choice.
Dozens
of
financial engineering or computational finance programs have been
established in the last few years to educate professionals for quantitative finance jobs.
Graduates with backgrounds
in
finance, mathematics, physics, computer sciences, and
various engineering majors are contending for quant jobs as well. Naturally, the
competition is fierce. To be a successful candidate, you have to distinguish yourself
from many other excellent applicants.
In general, a successful candidate for a quantitative finance position is expected to have
a strong mathematics background (in probability, statistics, stochastic calculus, etc.),
solid programming skills and basic to intermediate-level finance knowledge. Most
candidates find quantitative interviews, or at least some interview problems, challenging.
Quantitative interviews cover a broad range
of
mathematics, finance and programming
topics that the candidates may have never used
or
even encountered in their daily work
or study. Moreover, most interview problems require strong problem-solving skills,
beyond reciting formulas or doing simple calculations. A successful candidate needs a
combination
of
knowledge and problem-solving skills in order
to
excel in quantitative
interviews. This is precisely what this book provides!
This book addresses these aspects
by
reviewing the necessary finance and mathematical
concepts that serve as tools to structure and solve interview problems. Since it includes
most
of
the topics used
by
quantitative interviewers, it presupposes some basic
preparation in mathematics, statistics, finance, and programming.
I also strongly recommend that you try to solve each problem on your own first before
reading the answer. Working out solutions on your own will help you improve your
problem-solving skills and help you quickly identify common approaches to tackling
quantitative problems.

Needless to say, you are likely to encounter some problems in interviews that are similar
to or exactly the same as the problems in this book. After all, the book covers many
essential quantitative topics using real interview problems. However, the goal
of
the
book
is
not to teach you how to game the system by remembering the answers!
In
fact,
just memorizing answers may not help much in your interview process. Unless you truly
understand the underlying concepts and can analyze the problems yourself, you will fail
to elaborate on the solutions and will be ill-equipped to answer many other problems
that use similar concepts. (Besides, many experienced quantitative interviewers are good
at
catching those who have simply memorized "canned" answers.)
This
is
exactly the reason why I make significant effort to review essential concepts, to
present solution strategies, and to analyze the solutions in detail instead
of
simply
providing answers to problems. Furthermore, although the building blocks can be
learned, how one analyzes problems and implements these concepts usually makes a big
difference-and
these are the skills you can acquire through practice, practice and
practice.
I realize that there may be better methods to solve some
of
the problems presented in
this book.
It
is entirely possible that despite my best efforts some inadvertent errors may
have crept
in
. Please email me at xinfeng@quantfinanceinterviews.com
if
you have a
better approach to solving some
of
these problems or find errors. I will be grateful for
your feedback and will post corrections and your constructive feedback on the book's
companion website http://www.quantfinanceinterviews.
com
. The website is a joint
venture with my editor, Brett Jiu. You will also find some extra interview problems
with answers that we have gathered.
I sincerely hope that you enjoy solving these problems and are successful in your
interviews.
Xinfeng Zhou

Notations
v
3
s.t.
a
/\b
avb
n
for each/for every/for all
there exists
therefore
whenever A is true, B is also true
such that
the minimum
of
a and b
the maximum
of
a and b
TIX;
X1
XX
2
X··
·
XXn
i=I
n!
x%y
<1>
J
f(x)dx
r
f(x)dx
N(µ,
a2)
cdf
pd/
n
factorial
of
nonnegative integer n, n ! =
f1
i ( 0 ! =
I)
modulo operation
empty set
indefinite integral
of
f(x)
definite integral
of
f(x)
from a to b
max(x, 0)
i=I
normal distribution with mean µ and variance a2
cumulative density function
probability density function


Chapter 1 General Principles
Let us begin this book by exploring five general principles that will be extremely helpful
in
your interview process.
From
my experience on both sides
of
the interview table,
these general guidelines will better prepare you for job interviews and will likely make
you a successful candidate.
1.
Build a broad knowledge base
The length and the style
of
quant interviews differ from firm to firm. Landing a quant
job may mean enduring hours
of
bombardment with brain teaser, calculus, linear algebra,
probability theory, statistics, derivative pricing, or programming problems. To be a
successful candidate, you need to have broad knowledge in mathematics, finance and
programmmg.
Will all these topics be relevant for your future quant job? Probably not. Each specific
quant position often requires only limited knowledge in these domains. General problem
solving skills
may
make more difference than specific knowledge. Then why are
quantitative interviews so comprehensive? There are at least two reasons for this:
The first reason
is
that interviewers often have diverse backgrounds. Each interviewer
has his or her own favorite topics that are often related to his or her own educational
background or work experience. As a result, the topics you will be tested
on
are likely
to
be very broad. The second reason is more fundamental. Your problem solving
skills-a
crucial requirement for any quant
job-is
often positively correlated to the breadth
of
your knowledge. A basic understanding
of
a broad range
of
topics often helps you better
analyze problems, explore alternative approaches, and come
up
with efficient solutions.
Besides, your responsibility
may
not be restricted to your own projects. You will be
expected to contribute as a member
of
a bigger team. Having broad knowledge will help
you contribute to the team's success as well.
The key here
is
"basic understanding." Interviewers do not expect you to be an expert on
a specific
subject-unless
it happens to be your PhD thesis. The knowledge used
in
interviews, although broad, covers mainly essential concepts. This is exactly the reason
why most
of
the books I refer to in the following chapters have the word "introduction"
or "first" in the title.
If
I am allowed to give only one suggestion to a candidate, it will be
know
the
basics very well.
2.
Practice your interview skills
The interview process starts long before you step into an interview room.
In
a sense, the
success or failure
of
your interview is often determined before the first question is asked.
Your solutions to interview problems may fail to reflect your true intelligence and

General Principles
knowledge
if
you are unprepared. Although a complete review
of
quant interview
problems
is
impossible and unnecessary, practice does improve your interview skills.
Furthermore, many
of
the behavioral, technical and resume-related questions can be
anticipated. So prepare yourself for potential questions long before you enter an
interview room.
3. Listen carefully
You should be an active listener in interviews so that you understand the problems well
before you attempt to answer them.
If
any aspect
of
a problem is not clear to you,
politely ask for clarification.
If
the problem is more than a couple
of
sentences,
jot
down
the key words to help you remember all the information. For complex problems,
interviewers often give away some clues when they explain the problem. Even the
assumptions they give may include some information as to how to approach the problem.
So listen carefully and make sure you get the necessary information.
4. Speak your mind
When you analyze a problem and explore different ways to solve it, never do it silently.
Clearly demonstrate your analysis and write down the important steps involved
if
necessary. This conveys your intelligence to the interviewer and shows that you are
methodical and thorough. In case that you
go
astray, the interaction will also give your
interviewer the opportunity to correct the course and provide you with some hints.
Speaking your mind does not mean explaining every tiny detail.
If
some conclusions are
obvious to you, simply state the conclusion without the trivial details. More often than
not, the interviewer uses a problem to test a specific concept/approach. You should focus
on demonstrating your understanding
of
the key concept/approach instead
of
dwelling
on less relevant details.
5. Make reasonable assumptions
In real job settings, you are unlikely to have all the necessary information
or
data
you'd
prefer to have before you build a model and make a decision. In interviews,
interviewers may not give you all the necessary assumptions either. So it is up to you to
make reasonable assumptions. The keyword here is reasonable. Explain your
assumptions to the interviewer so that you will get immediate feedback. To solve
quantitative problems, it is crucial that you can quickly make reasonable assumptions
and design appropriate frameworks to solve problems based on the assumptions.
We are now ready to review basic concepts
in
quantitative finance subject areas and
have
fun
solving real-world interview problems!
2

Chapter 2 Brain Teasers
In
this chapter, we cover problems that only require common sense, logic, reasoning, and
basic-no
more than high school
level-math
knowledge to solve. In a sense, they are
real brain teasers
as
opposed to mathematical problems in disguise. Although these brain
teasers do not require specific math knowledge, they are
no
less difficult than other
quantitative interview problems. Some
of
these problems test your analytical and general
problem-solving skills; some require you to think out
of
the box; while others ask you to
solve the problems using fundamental math techniques in a creative way. In this chapter,
we review some interview problems to explain the general themes
of
brain teasers that
you are likely to encounter in quantitative interviews.
2.
1 Problem Simplification
If
the original problem is so complex that you cannot come up with an immediate
solution, try to identify a simplified version
of
the problem and start with it. Usually you
can start with the simplest sub-problem and gradually increase the complexity. You do
not need to have a defined plan
at
the beginning. Just try to solve the simplest cases and
analyze your reasoning. More often than not, you will find a pattern that will guide you
through the whole problem.
Screwy pirates
Five pirates looted a chest full
of
100 gold coins. Being a bunch
of
democratic pirates,
they agree on the following method to divide the loot:
The most senior pirate will propose a distribution
of
the coins. All pirates, including the
most senior pirate, will then vote.
If
at
least 50%
of
the pirates (3 pirates in this case)
accept the proposal, the gold
is
divided as proposed.
If
not, the most senior pirate will be
fed
to shark and the process starts over with the next most senior pirate
...
The process is
repeated until a plan is approved. You can assume that all pirates are perfectly rational:
they want to stay alive first and to get as much gold as possible second. Finally, being
blood-thirsty pirates, they want to have fewer pirates on the boat
if
given a choice
between otherwise equal outcomes.
How will the gold coins be divided in the end?
Solution:
If
you have not studied game theory or dynamic programming, this strategy
problem
may
appear to be daunting.
If
the problem with 5 pirates seems complex, we
can always start with a simplified version
of
the problem by reducing the number
of
pirates. Since the solution to I-pirate case
is
trivial, let's start with 2 pirates. The senior

Brain Teasers
pirate (labeled as 2) can claim all the gold since he will always get 50%
of
the votes
from himself and pirate 1
is
left with nothing.
Let's add a more senior pirate,
3.
He
knows that
if
his plan
is
voted down, pirate 1 will
get nothing. But
if
he offers private 1 nothing, pirate 1 will be happy to kill him.
So
pirate 3 will offer private 1 one coin and keep the remaining
99
coins, in which strategy
the plan will have 2 votes from pirate 1 and 3.
If
pirate 4 is added, he knows that
if
his plan is voted down, pirate 2 will get nothing. So
pirate 2 will settle for one coin
if
pirate 4 offers one. So pirate 4 should offer pirate 2
one
coin and keep the remaining 99 coins and his plan will be approved with 50%
of
the
votes from pirate 2 and 4.
Now we finally come to the 5-pirate case. He knows that
if
his plan is voted down, both
pirate 3 and pirate 1 will get nothing. So he only needs to offer pirate 1 and pirate 3 one
coin each to get their votes and keep the remaining 98 coins.
If
he divides the coins this
way, he will have three out
of
the five votes: from pirates 1 and 3
as
well as himself.
Once we start with a simplified version and add complexity to it, the answer becomes
obvious. Actually after the case n =
5,
a clear pattern has emerged and we do not need to
stop at 5 pirates. For any
2n
+ 1 pirate case (n should be less than 99 though), the most
senior pirate will offer pirates
1,
3,
· ·
·,
and 2n
-1
each one coin and keep the rest for
himself.
Tiger and sheep
One hundred tigers and one sheep are put on a magic island that only has grass. Tigers
can eat grass, but they would rather eat sheep. Assume: A. Each time only one tiger can
eat one sheep, and that tiger itself will become a sheep after it eats the sheep. B. All
tigers are smart and perfectly rational and they want to survive. So will the sheep
be
eaten?
Solution: 100
is
a large number, so again let's start with a simplified version
of
the
problem.
If
there
is
only 1 tiger ( n = 1 ), surely it will eat the sheep since it does not need
to worry about being eaten. How about 2 tigers? Since both tigers are perfectly rational,
either tiger probably would do some thinking
as
to what will happen
if
it eats the sheep.
Either tiger is probably thinking:
if
I eat the sheep, I will become a sheep; and then I will
be eaten by the other tiger. So to guarantee the highest likelihood
of
survival, neither
tiger will eat the sheep.
If
there are 3 tigers, the sheep will be eaten since each tiger will realize that once it
changes to a sheep, there will be 2 tigers left and it will not
be
eaten. So the first tiger
that thinks this through will eat the sheep.
If
there are 4 tigers, each tiger will understand
4

A Practical Guide
To
Quantitative Finance Interviews
that
if
it eats the sheep, it will tum to a sheep. Since there are 3 other tigers, it will be
eaten. So to guarantee the highest likelihood
of
survival, no tiger will eat the sheep.
Following the same logic,
we
can naturally show that
if
the number
of
tigers
is
even, the
sheep will not be eaten.
If
the number is odd, the sheep will be eaten. For the case
n = l 00, the sheep will not be eaten.
2.2 Logic Reasoning
River crossing
Four people,
A,
B, C and D need to get across a river. The only way to cross the river
is
by
an
old bridge, which holds at most 2 people at a time. Being dark, they can't cross the
bridge without a torch,
of
which they only have one. So each pair can only walk at the
speed
of
the slower person. They need to get all
of
them across to the other side as
quickly as possible. A is the slowest and takes
10
minutes to cross; B takes 5 minutes; C
takes 2 minutes; and D takes 1 minute.
What
is
the minimum time to get all
of
them across to the other side?1
Solution: The key point is to realize that the l 0-minute person should go with the 5-
minute person and this should not happen in the first crossing, otherwise one
of
them
have to go back.
So
C
and
D should go across first (2 min); then send D back (lmin); A
and B go across (
10
min); send C back (2min); C and D go across again (2 min).
It
takes
17
minutes
in
total. Alternatively, we can send C back first and then D back in
the second round, which takes
17
minutes as well.
Birthday problem
You and your colleagues know that your boss
A's
birthday
is
one
of
the following
10
dates:
Mar 4, Mar 5, Mar 8
Jun 4, Jun 7
Sep
1,
Sep 5
Dec
1,
Dec 2, Dec 8
A told you only the month
of
his birthday, and told your colleague
Conly
the day. After
that, you first said: "I
don't
know
A's
birthday; C
doesn't
know it either." After hearing
1 Hint: The key is to realize that A and B should get across the bridge together.
5

Brain Teasers
what you said, C replied: "I didn't know
A's
birthday, but now I know it." You smiled
and said: "Now I know it, too." After looking at the
10
dates and hearing your comments,
your administrative assistant wrote down
A's
birthday without asking any questions. So
what did the assistant write?
Solution: Don't let the "he said, she said" part confuses
you.
Just interpret the logic
behind each individual's comments and try your best to derive useful information from
these comments.
Let D be the day
of
the month
of
A's
birthday, we have
De{l,2,4,5,7,8}
.
If
the
birthday
is
on a unique day, C will know the
A's
birthday immediately. Among possible
Ds, 2 and 7 are unique days. Considering that you are sure that C does not know
A's
birthday, you must infer that the day the C was told
of
is not 2 or 7. Conclusion: the
month is not June or December.
(If
the month had been June, the day C was told
of
may
have been 2;
ifthe
month had been December, the day C was told
of
may have been 7.)
Now C knows that the month must be either March
or
September. He immediately
figures out
A's
birthday, which means the day must be unique in the March and
September list.
It
means
A's
birthday cannot be Mar 5, or Sep 5. Conclusion: the
birthday must be Mar 4, Mar 8 or Sep
1.
Among these three possibilities left, Mar 4 and Mar 8 have the same month. So
if
the
month you have is March, you still cannot figure out
A's
birthday. Since you can figure
out
A's
birthday,
A's
birthday must be Sep
1.
Hence, the assistant must have written Sep
1.
Card game
A casino offers a card game using a normal deck
of
52 cards. The rule is that you
tum
over two cards each time. For each pair,
if
both are black, they go to the dealer's pile;
if
both are red, they go to your pile;
if
one black and one red, they are discarded. The
process is repeated until you two go through all
52
cards.
If
you have more cards in your
pile, you win $100; otherwise (including ties) you get nothing. The casino allows you to
negotiate the price you want to pay for the game. How much would you be willing to
pay to play this game?2
Solution: This surely
is
an insidious casino. No matter how the cards are arranged, you
and the dealer will always have the same number
of
cards in your piles. Why? Because
each pair
of
discarded cards have one black card and one red card, so equal number
of
2 Hint: Try to approach the problem using symmetry. Each discarded pair has one black and one red card.
What does that tell you as to the number
of
black and red cards in the rest two piles?
6

A Practical Guide To Quantitative Finance Interviews
red and black cards are discarded. As a result, the number
of
red cards left for you and
the number
of
black cards left for the dealer are always the same. The dealer always
wins! So we should not pay anything to play the game.
Burning ropes
You have two ropes, each
of
which takes I hour to bum. But either rope has different
densities at different points, so there's no guarantee
of
consistency in the time it takes
different sections within the rope to
bum
. How do you use these two ropes to measure
45
minutes?
Solution: This
is
a classic brain teaser question. For a rope that takes x minutes to bum,
if
you light both ends
of
the rope simultaneously, it takes x I 2 minutes
to
bum. So we
should light both ends
of
the first rope and light one end
of
the second rope. 30 minutes
later, the first rope will get completely burned, while that second rope now becomes a
30-min rope. At that moment,
we
can light the second rope at the other end (with the
first end still burning), and when it is burned out, the total time is exactly
45
minutes.
Defective ball
You have
12
identical balls. One
of
the balls is heavier OR lighter than the rest (you
don't know which). Using just a balance that can only show you which side
of
the tray
is
heavier, how can you determine which ball is the defective one with 3 measurements?3
Solution: This weighing problem is another classic brain teaser and is still being asked
by many interviewers. The total number
of
balls often ranges from 8
to
more than
100.
Here we use n =
12
to show the fundamental approach. The key is to separate the
original group (as well as any intermediate subgroups) into three sets instead
of
two. The
reason is that the comparison
of
the first two groups always gives information about the
third group.
Considering that the solution is wordy to explain, I draw a tree diagram in Figure
2.1
to
show the approach in detail. Label the balls 1 through
12
and separate them to three
groups with 4 balls each. Weigh balls
1,
2, 3, 4 against balls 5, 6, 7,
8.
Then we go on to
explore two possible scenarios: two groups balance, as expressed using an
"="
sign, or
1,
3 Hint: First do it for 9 identical balls and use only 2 measurements, knowing that one is heavier than the
rest.
7

Brain Teasers
2,
3,
4 are lighter than 5, 6, 7,
8,
as expressed using an
"<"
sign. There is no need to
explain the scenario that
1,
2, 3, 4 are heavier than 5, 6, 7,
8.
(Why?4)
If
the two groups balance, this immediately tells us that the defective ball is in
9,
10,
11
and 12, and it is either lighter
(l)
or heavier (H) than other balls. Then we take 9,
10
and
11
from
group 3 and compare balls
9,
10
with 8,
11.
Here we have already figured out
that 8 is a normal ball.
If
9,
IO
are lighter, it must mean either 9 or
10
isl
or
11
is
H.
In
which case, we just compare 9 with
10.
If
9 is lighter, 9 is the defective one and it is
L;
if
9 and
10
balance, then
11
must
be
defective and H;
If
9 is heavier,
10
is the defective
one and it is L.
lf9,
IO
and 8,
11
balance,
12
is the defective one.
lf9
,
10
is heavier, than
either 9 or
10
is
H,
or
11
is
L.
You can easily follow the tree in Figure 2.1 for further analysis and it is clear from the
tree that all possible scenarios can be resolved in 3 measurements.
I /2/3/4 L
or
5/617/8 H 9/ I0/11/
12
Lor
H
l/2L
or
6H
4L
or
7/8H 5H
or
3L
9/IOLor
l
IH
12Lorl211
9/IOfl
or
11
L
IL
6H
2L
8H
4L
7H
3L
5H
9L
l
IH
IOL
12H 12L IOH I
IL
9H
Figure
2.1
Tree diagram to identify the defective ball in 12 balls
In
general
if
you have the information as to whether the defective ball is heavier or
4 Here is where the symmetry idea comes
in.
Nothing makes the I, 2, 3, 4 or 5, 6, 7, 8 labels special.
If
I, 2,
3, 4 are heavier than 5, 6, 7, 8, let's just exchange the labels
of
these two groups. Again
we
have the case
of
I, 2, 3, 4 being lighter than 5, 6, 7,
8.
8

A Practical Guide
To
Quantitative Finance Interviews
lighter, you can identify the defective ball among up to
3n
balls using no more than n
measurements since each weighing reduces the problem size by 2/3.
If
you have no
information as to whether the defective ball is heavier or lighter, you can identify the
defective ball among up
to
(3n
-
3)
I 2 balls using no more than n measurements.
Trailing zeros
How many trailing zeros are there in
100!
(factorial
of
100)?
Solution: This is an easy problem. We know that each pair
of
2 and 5 will give a trailing
zero.
If
we perform prime number decomposition on all the numbers in 100!, it is
obvious that the frequency
of
2 will far outnumber
of
the frequency
of
5.
So
the
frequency
of
5 determines the number
of
trailing zeros. Among numbers
1,
2, · · ·, 99, and
100, 20 numbers are divisible by 5 (
5,
10, · · ·, 100
).
Among these 20 numbers, 4 are
divisible by 52 ( 25, 50,
75,
100
).
So
the total frequency
of
5
is
24 and there are 24
trailing zeros.
Horse race
There are
25
horses, each
of
which runs at a constant speed that
is
different from the
other horses'. Since the track only has 5 lanes, each race can have at most 5 horses.
If
you need to find the 3 fastest horses, what is the minimum number
of
races needed to
identify them?
Solution: This problem tests your basic analytical skills.
To
find the 3 fastest horses,
surely all horses need to be tested. So a natural first step is to divide the horses to 5
groups (with horses 1-5, 6-10, 11-15, 16-20, 21-25
in
each group). After 5 races, we will
have the order within each group, let's assume the order follows the order
of
numbers
(e.g., 6 is the fastest and
IO
is
the slowest
in
the 6-10 group)5. That means 1, 6,
11,
16
and
21
are the fastest within each group.
Surely the last two horses within each group are eliminated. What else can we infer? We
know that within each group,
if
the fastest horse ranks 5th
or
4th among 25 horses, then
all horses in that group cannot be in top 3;
if
it ranks the 3rd, no other horse in that group
can be in the top 3;
if
it ranks the 2nd, then
one
other horse in that group
may
be in top 3;
if
it ranks the first, then two other horses in that group may be in top
3.
5 Such an assumption does not affect the generality
of
the solution.
If
the order is not
as
described,
just
change the labels
of
the horses.
9

Brain Teasers
So
let's
race horses 1, 6,
11,
16
and
21. Again
with
out loss
of
generality,
let's
assume
the order is
1,
6, 11, 16 and 21.
Then
we immediately know that horses 4-5, 8-10, 12-15,
16-20 and 21-25 are eliminated. Since 1
is
fastest among all the horses, 1 is in. We need
to determine which two among horses 2, 3, 6, 7
and
11
are in top 3, which only takes one
extra race.
So all together we
need
7 races (in 3 rounds) to identify the 3 fastest horses.
Infinite sequence
If
x /\ x
/\
x
/\
x
/\
x · · · = 2 , where x /\ y =
xY,
what is x ?
Solution: This
problem
appears to
be
difficult,
but
a simple analysis will give
an
elegant
solution. What do
we
have from the original equation?
limx/\x/\x/\x/\x···=2<=>limx/\x/\x/\x/\x···=2.
In
other words, as
n
terms
n-1
terms
adding
or
minus one x
/\
should
yield
the same result.
so x
/\
x
/\
x
/\
x
/\
x · · · = x
/\
(x
/\
x
/\
x /\ x · · ·) = x
/\
2 = 2 x =
J2.
2.3 Thinking Out
of
the Box
Box packing
Can you pack
53
bricks
of
dimensions
1x1x4
into a 6 x 6 x 6 box?
Solution: This
is
a nice problem extended from a popular chess board problem. In that
problem, you have a 8 x 8 chess
board
with two small squares at the opposite diagonal
comers removed.
You
have many bricks with dimension 1 x
2.
Can
you pack
31
bricks
into the remaining
62
squares?
(An
alternative question is whether you can
cover
all
62
squares using bricks without any bricks overlapping with each other or sticking out
of
the board, which requires a similar analysis.)
A real chess board figure surely helps the visualization. As shown in Figure 2.2, when a
chess board
is
filled with alternative black
and
white squares, both squares at the
opposite diagonal
comers
have the same color.
If
you put a 1 x 2 brick on the board, it
will always cover
one
black square and one white square.
Let's
say it's the
two
black
comer
squares were removed, then the rest
of
the board can fit at most 30 bricks since
we only have 30
black
squares left (and each brick requires one black square). So to
pack
31
bricks is
out
of
the question. To cover all 62 squares without overlapping or
overreaching, we
must
have exactly 3 I bricks. Yet
we
have proved that
31
bricks cannot
10

A Practical Guide
To
Quantitative Finance Interviews
fit in the 62 squares left, so you cannot find a way to fill in all 62 squares without
overlapping or overreaching.
Removed
Removed
+-
Figure 2.2 Chess board with alternative black and white squares
Just as any good trading strategy,
if
more and more people
get
to know it and replicate it,
the effectiveness
of
such a strategy will disappear.
As
the chess board problem becomes
popular, many interviewees simply commit it to memory (after all, it's easy to remember
the answer). So some ingenious interviewer came
up
with the newer version to test your
thinking process, or at least your ability
to
extend your knowledge to new problems.
lfwe
look at the total volume in this
30
problem,
53
bricks have a volume
of
212, which
is
smaller then the box's volume 216. Yet
we
can show it is impossible to pack all the
bricks into the box using a similar approach as the chess board problem. Let's imagine
that the 6 x 6 x 6 box is actually comprised
of
small 2 x 2 x 2 cubes. There should be 27
small cubes. Similar to the chess board (but in
30),
imagine that
we
have black cubes
and white cubes
alternates-it
does take a little
30
visualization.
So
we have either 14
black cubes &
13
white cubes
or
13
black cubes &
14
white cubes. For any
1x1x4
brick
that we pack into the box, half (
1x1x2)
of
it must
be
in a black 2 x 2 x 2 cube and the
other half must be in a white 2 x 2 x 2 cube. The problem is that each 2 x 2 x 2 cube can
only be used
by
4
of
the
1x1
x 4 bricks. So for the color with
13
cubes, be it black
or
white, we can only use them for 52
1x1x4
tubes. There is no way to place the 53th
brick. So we cannot pack
53
bricks
of
dimensions 1x1x4 into a 6 x 6 x 6 box.
Calendar cubes
You just had two dice custom-made. Instead
of
numbers 1 - 6, you place single-digit
numbers on the faces
of
each dice so that every morning
you
can arrange the dice in a
way as to make the two front faces show the current day
of
the month. You must use
both dice (in other words, days 1 - 9 must
be
shown as
01
-09), but you can switch the
11

Brain Teasers
order
of
the dice
if
you
want. What numbers do
you
have to put on the six faces
of
each
of
the two dice to achieve that?
Solution: The days
of
a month include
11
and 22, so both dice must have 1 and
2.
To
express single-digit days,
we
need
to
have at least a 0
in
one dice. Let's put a 0 in dice
one first. Considering that we need to express all single digit days and dice two cannot
have all the digits from 1 - 9, it's necessary to have a 0
in
dice two as well in order to
express all single-digit days.
So far we have assigned the following numbers:
! Dice one
Dice two I : I
If
we can assign all the rest
of
digits 3,
4,
5,
6,
7, 8, and 9 to the rest
of
the faces, the
problem is solved.
But
there are 7 digits left. What can we do?
Here's
where you need to
think out
of
the box.
We
can use a 6 as a 9 since they will never be needed at the same
time! So, simply
put
3, 4, and 5
on
one dice and 6,
7,
and 8
on
the other dice, and the
final numbers on the two dice are:
Dice one 1 2 0 3 4 5
Dice two 1 2 0 6 7 8
Door
to offer
You are facing two doors. One leads to your job offer and the other leads to exit. In front
of
either door
is
a guard. One guard always tells lies and the other always tells the truth.
You can only ask one guard one yes/no question. Assuming you do want to get the job
offer, what question will you ask?
Solution: This is another classic brain teaser (maybe a little out-of-date
in
my opinion).
One popular answer is to ask one gua
rd
: "Would the other guard say that you are
guarding the door to the offer?"
If
he
answers yes, choose the other
door;
if
he answers
no, choose
the
door this guard is standing
in
front of.
There are two possible scenarios:
I . Truth teller guards the door to offer; Liar guards the door to exit.
2. Truth teller guards the door
to
exit; Liar guards the door to offer.
If
we ask a guard a direct question such as "Are you guarding the door to the offer?" For
scenario I, both guards will answer yes; for scenario 2, both guards will answer no. So a
12

A Practical Guide
To
Quantitative Finance Interviews
direct question does not help us solve the problem. The
key
is to involve both guards in
the questions as the popular answer does. For scenario
1,
if
we happen to choose the
truth teller, he will answer no since the liar will say no;
if
we happen to choose the liar
guard,
he
will answer yes since the truth teller will say no. For scenario 2,
if
we happen
to choose the truth teller, he will answer yes since the liar will say yes;
if
we happen to
choose the liar guard,
he
will answer no since the truth teller with say yes. So for both
scenarios,
if
the answer
is
no, we choose that door;
if
the answer
is
yes, we choose the
other door.
Message delivery
You need to communicate with your colleague
in
Greenwich via a messenger service.
Your documents are sent
in
a padlock box. Unfortunately the messenger service
is
not
secure, so anything inside an unlocked box will be lost (including any locks you place
inside the box) during the delivery. The high-security padlocks you and your colleague
each use have only one
key
which the person placing the lock owns. How can you
securely send a document to your colleague?6
Solution:
If
you
have a document to deliver, clearly you cannot deliver it in an unlocked
box. So the first step
is
to deliver it to Greenwich in a locked box. Since you are the
person who has the key to that lock, your colleague cannot open the box to get the
document. Somehow you need to remove the lock before he can get the document,
which means the box should be sent back to you before your colleague can get the
document.
So what can he do before he sends back the box?
He
can place a second lock on the box,
which
he
has the key
to!
Once
the box
is
back to you,
you
remove your own lock and
send the box back to your colleague. He opens his own lock and gets the document.
Last ball
A bag has
20
blue balls and 14 red balls. Each time
you
randomly take two balls out.
(Assume each ball in the bag has equal probability
of
being taken). You do not put these
two balls back. Instead,
if
both balls have the same color, you add a blue ball to the bag;
if
they have different colors, you add a red ball to the bag. Assume that you have an
unlimited supply
of
blue and red balls,
if
you keep on repeating this process, what will
be the color
of
the last ball left in the bag?
7 What
if
the
bag
has 20 blue balls and l 3 red
balls instead?
6 Hint: You
can
have more than
one
lock on the box.
7 Hint: Consider the changes in the number
ofred
and blue balls after each step.
13

Brain Teasers
Solution: Once you understand the hint, this problem should be an easy one. Let (B, R)
represent the number
of
blue balls and red balls in the bag.
We
can take a look what will
happen after two balls are taken out.
Both balls are blue: (B, R)
(B-1,
R)
Both balls are red: (B, R)
(B
+
1,
R-2)
One red and one blue: (B, R)
(B
-1,
R)
Notice that R either stays the same
or
decreases by 2, so the number
of
red balls will
never become odd
if
we begin with
14
red balls. We also know that the total number
of
balls decreases by one each time until only one ball is left. Combining the information
we have, the last ball must be a blue one. Similarly, when we start with odd number
of
red balls, the final ball must be a red one.
Light switches
There is a light bulb inside a room and four switches outside. All switches are currently
at
off
state and only one switch controls the light bulb. You may tum any number
of
switches on
or
off
any number
of
times you want. How many times do you need to go
into the room to figure out which switch controls the light bulb?
Solution: You may have seen the classical version
of
this problem with 3 light bulbs
inside the room and 3 switches outside. Although this problem is slightly modified, the
approach
is
exact the same. Whether the light
is
on and
off
is binary, which only allows
us
to
distinguish two switches.
If
we have another binary factor, there are 2 x 2 = 4
possible combinations
of
scenarios, so we can distinguish 4 switches. Besides light, a
light bulb also emits heat and becomes hot after the bulb has been lit for some time. So
we can use the on/off and cold/hot combination to decide which one
of
the four switches
controls the light.
Tum on switches 1 and
2;
move on to solve some other puzzles
or
do whatever you like
for a while; tum
off
switch 2 and turn on switch 3; get into the room quickly, touch the
bulb and observe whether the light is on
or
off.
The light bulb is on and hot -switch 1 controls the light;
The light bulb is
off
and hot -switch 2 controls the light;
The light bulb is on and cold -switch 3 controls the light;
The light bulb is
off
and cold -switch 4 controls the light.
14

A Practical Guide
To
Quantitative Finance Interviews
Quant salary
Eight quants from different banks are getting together for drinks. They are all interested
in knowing the average salary
of
the group. Nevertheless, being cautious and humble
individuals, everyone prefers not
to
disclose his or her
own
salary to the group. Can you
come
up
with a strategy for the quants to calculate the average salary without knowing
other people's salaries?
Solution: This is a light-hearted problem and has more than one answer. One approach is
for the first quant
to
choose a random number, adds it
to
his/her salary and gives it to the
second quant. The second quant will add his/her own salary
to
the result and give it to
the third quant; ... ; the eighth quant will add his/her
own
salary to the result and give it
back
to
the first quant. Then the first quant will deduct the "random" number from the
total and divide the "real" total by 8 to yield the average salary.
You may be wondering whether this strategy has any use except being a good brain
teaser to test interviewees.
It
does have applications in practice. For example, a third
party data provider collect fund holding position data (securities owned by a fund and
the number
of
shares) from all participating firms and then distribute the information
back to participants. Surely most participants
do
not want others to figure out what they
are holding.
If
each position in the fund has the same fund ID every day, it's easy to
reverse-engineer the fund from the holdings and to replicate the strategy. So different
random numbers (or more exactly pseudo-random numbers since the provider knows
what number is added to the fund ID
of
each position and complicated algorithm
is
involved to make the mapping one to one) are added to the fund ID
of
each position in
the funds before distribution. As a result, the positions in the same fund appear to have
different fund IDs. That prevents participants from re-constructing other funds. Using
this approach, the participants can share market information and remain anonymous at
the same time.
2.4 Application
of
Symmetry
Coin piles
Suppose that you are blind-folded in a room and are told that there are 1000 coins on the
floor. 980
of
the coins have tails up and the other 20 coins have heads
up.
Can you
separate the coins into two piles so to guarantee both piles have equal number
of
heads?
Assume that you cannot tell a coin's side
by
touching it, but you are allowed
to
tum over
any number
of
coins.
Solution:
Let's
say that we separate the 1000 coins into two piles with n coins in one pile
and 1000 -n coins in the other.
If
there are m coins in the first pile with heads up, there
15

Brain Teasers
must be 20 -m coins in the second pile with heads up. We also know that there are
n -m coins in the first pile with tails up. We clearly cannot guarantee that m = 10 by
simply adjusting
n.
What other options do we have? We can
tum
over coins
if
we want to. Since we have no
way
of
knowing what a coin's side is, it
won't
guarantee anything
if
we selectively flip
coins. However,
if
we flip all the coins in the first pile, all heads become tails and all
tails become heads. As a result, it will have
n-m
heads and m tails (symmetry). So, to
start, we need to make the number
of
tails in the original first pile equal to the number
of
heads in the second pile; in other words, to make n -m =
20-
m.
n = 20 makes the
equation hold.
If
we take 20 coins at random and tum them all over, the number
of
heads
among these turned-over 20 coins should be the same as the number
of
heads among the
other 980 coins.
Mislabeled bags
You are given three bags
of
fruits. One has apples in it; one has oranges in it; and one
has a mix
of
apples and oranges in it. Each bag has a label on it (apple, orange or mix).
Unfortunately, your manager tells you that ALL bags are mislabeled. Develop a strategy
to identify the bags by taking out minimum number
of
fruits? You can take any number
of
fruits from any bags.8
Solution: The key here is to use the fact that ALL bags are mislabeled. For example, a
bag labeled with apple must contain either oranges only or a mix
of
oranges and apples.
Let's look at the labels: orange, apple, mix (orange+ apple). Have you realized that the
orange label and the apple label are symmetric?
If
not, let me explain it in detail:
If
you
pick a fruit from the bag with the orange label and it's an apple (orange apple), then
the bag is either all apples or a mix.
If
you pick a fruit from the bag with the apple label
and
it's
an orange (apple orange), then the bag is either an orange bag or a mix.
Symmetric labels are not exciting and are unlikely to be the correct approach. So let's try
the bag with the mix label and get one fruit from
it.
If
the fruit we get is an orange, then
we know that bag is actually orange
(It
cannot be a mix
of
oranges and apples since we
know the bag's label is wrong). Since the bag with the apple label cannot be apple only,
it must be the mix bag. And the bag with the orange label must be the apple bag.
Similarly, for the case that apples are in the bag with the mix label, we can figure out all
the bags using one single pick.
8 The problem struck me as a word game when I first saw
it.
But it does test a candidate's attention to
details besides his or her logic reasoning skills.
16

A Practical Guide
To
Quantitative Finance Interviews
Wise men
A sultan has captured 50 wise men. He has a glass currently standing bottom down.
Every minute he calls one
of
the wise men who can choose either to
tum
it over (set it
upside down
or
bottom down) or to do nothing. The wise men will be called randomly,
possibly for
an
infinite number
of
times. When someone called to the sultan correctly
states that all wise men have already been called to the sultan at least once, everyone
goes free. But
if
his statement is wrong, the sultan puts everyone to death. The wise men
are allowed to communicate only once before they get imprisoned into separate rooms
(one per room). Design a strategy that lets the wise men go free.
Solution: For the strategy to work, one wise man, let's call him the spokesman, will state
that every one has been called. What does that tell us?
1.
All the other 49 wise men are
equivalent (symmetric). 2. The spokesman is different from the other 49 men. So
naturally those 49 equivalent wise men should act in the same way and the spokesman
should act differently.
Here is one
of
such strategies: Every one
of
the 49 (equivalent) wise men should flip the
glass upside down the first time that he sees the glass bottom down. He does nothing
if
the glass is already upside down
or
he has flipped the glass once. The spokesman should
flip the glass bottom down each time he sees the glass upside down and he should do
nothing
if
the glass is already bottom down. After he does the 49th flip, which means all
the other 49 wise men have been called, he can declare that all the wise
men
have been
called.
2.5 Series Summation
Here is a famous story about the legendary mathematician/physicist Gauss: When he
was a child, his teacher gave the children a boring assignment to add the numbers from 1
to 100. To the amazement
of
the teacher, Gauss turned in his answer in less than a
minute. Here is his approach:
100
:Ln=
1 +
2+
·
··
+
99+
100
n=I + + + +
100
:Ln
=
100+
99+···+
2 + 1
! ! ! !
100
100xl01
2Ln
=
101+101+···+101+101=
101x100
:Ln
=---
2
n=I n =I
17

Brain Teasers
This approach can
be
generalized to any integer N: f n = N ( N + 1
)
n=I
2
The summation formula for consecutive squares may not be as intuitive:
f n2 =
N(N
+1)(2N
+1) = N3 + N2 +
N.
n=I
6 3 2 6
N
But
if
we correctly guess that L n2 =
aN
3 +
bN
2 +
cN
+ d and apply the initial
conditions
N=l
l=a+b+c+d
N = 2 5 =
8a
+
4b
+ 2c + d
n=I
we will have the solution that
a=
1/3, b =
112
, c =
116,
d = 0. We can then easily show
that the same equation applies to all N by induction.
Clock pieces
A clock (numbered 1 -
12
clockwise) fell
off
the wall and broke into three pieces. You
find that the sums
of
the numbers
on
each piece are equal. What are the numbers on each
piece? (No strange-shaped piece is allowed.)
12
12x13
Solution: Using the summation equation, L n = 78. So the numbers on each
n=I
2
piece must sum up to 26. Some interviewees mistakenly assume that the numbers on
each piece have to
be
continuous because no strange-shaped piece is allowed. It' s easy to
see that 5,
6,
7 and 8 add up to 26. Then the interviewees' thinking gets stuck because
they cannot find more consecutive numbers that add up
to
26.
Such an assumption is not correct since
12
and 1 are continuous on a clock. Once that
wrong assumption is removed, it becomes clear that
12+1=13
and
11+2=13.
So the
second piece is 11, 12, 1 and 2; the third piece is 3, 4, 9 and
10
.
Missing integers
Suppose we have 98 distinct integers from I to I 00. What is a good way to find out the
two missing integers (within [
l,
100])?
18

A Practical Guide To Quantitative Finance Interviews
Solution: Denote the missing integers as x and
y,
and the existing ones are z1, • •
·,
z
98
•
Applying the summation equations, we have
100
98
100x101
98
L n = x + y + L
z;
=>
x + y = -
L,
z;
n=I
i=I 2
i=I
Using these two equations, we can easily solve x and y.
If
you
implement this strategy
using a computer program, it is apparent that the algorithm has a complexity
of
O(n) for
two missing integers in 1 to
n.
Counterfeit coins I
There are
10
bags with 100 identical coins in each bag. In all bags but one, each coin
weighs
10
grams. However, all the coins
in
the counterfeit bag weigh either 9 or
11
grams. Can you find the counterfeit bag
in
only
one
weighing, using a digital scale that
tells the exact weight? 9
Solution: Yes, we
can
identify the counterfeit
bag
using one measurement.
Take
1 coin
out
of
the first bag, 2 out
of
the second bag, 3 out the third bag, · ·
·,
and
10
coins out
of
10
the tenth bag. All together, there are
Ln
=
55
coins.
If
there were no counterfeit coins,
i=I
they should weigh
550
grams.
Let's
assume the i-th bag is the counterfeit bag, there will
be i counterfeit coins, so the final weight will
be
550 ± i. Since i is distinct for each bag,
we can identify the counterfeit coin bag as well as whether the counterfeit coins are
lighter
or
heavier than the real coins using 550 ±
i.
This is not the only answer: we can choose other numbers
of
coins from each
bag
as long
as they are all different numbers.
Glass balls
You are holding two glass balls in a 100-story building.
If
a ball is thrown out
of
the
window, it will not break
if
the floor number is less than X,
and
it will always break
if
9 Hint: In order to find the counterfeit coin bag in one weighing,
the
number
of
coins from
each
bag must
be different.
If
we
use the same number
of
coins from two bags, symmetry will prevent you from
distinguish these two bags
if
one is the counterfeit coin bag.
19

Brain Teasers
the floor number is equal to or greater than X. You would like to determine X. What is
the strategy that will minimize the number
of
drops for the worst case scenario?
10
Solution: Suppose that
we
have a strategy with a maximum
of
N throws. For the first
throw
of
ball one, we can
try
the N-th floor.
If
the ball breaks, we can start to try the
second ball from the first floor and increase the floor number by one until the second
ball breaks. At most, there are N
-1
floors to test. So a maximum
of
N throws are
enough to cover all possibilities.
If
the first ball thrown out
of
N-th floor does not break,
we have N
-1
throws left. This time we can only increase the floor number
by
N
-1
for
the first ball since the second ball can only cover N -2 floors
if
the first ball breaks.
If
the first ball thrown out
of
(2N-1 )th floor does not break, we have N -2 throws left. So
we can only increase the floor number by N -2 for the first ball since the second ball
can only cover N -3 floors
if
the first ball breaks ...
Using such logic, we can see that the number
of
floors that these two balls can cover
with a maximum
of
N throws is N + ( N
-1)
+ .. · + 1 = N ( N +
1)
I 2 . In order to cover 100
stories, we need to have
N(N
+ 1)/
2:?:
100.
Taking the smallest integer, we have N = 14.
Basically, we start the first ball on the 14th floor,
if
the ball breaks,
we
can use the
second ball to try floors l,
2,
· · ·,
13
with a maximum throws
of
14
(when the 13th or the
14th floor is X).
If
the first ball does not break,
we
will try the first ball on the
14+(14-1)=27th
floor.
If
it breaks, we can use the second ball to cover floors
15,
16,
.. ·, 26 with a total maximum throws
of
14
as well...
2.6 The Pigeon Hole Principle
Here
is
the basic version
of
the Pigeon Hole Principle:
if
you have fewer pigeon holes
than pigeons and you put every pigeon in a pigeon hole, then at least one pigeon hole has
more than one pigeon. Basically it says that
if
you have n holes and more than n+ 1
pigeons, at least 2 pigeons have to share one
of
the holes. The generalized version
is
that
if
you have n holes and at least
mn
+ 1 pigeons,
at
least m
+I
pigeons have to share one
of
the holes. These simple and intuitive ideas are surprisingly useful in many problems.
Here we will use some examples to show their applications.
10
Hint: Assume we design a strategy with N maximum throws. If the first ball is thrown once, the second
ball can cover N -I floors;
if
the first ball is thrown twice, the second ball can cover N -2 floors ...
20

A Practical Guide To Quantitative Finance Interviews
Matching socks
Your drawer contains 2 red socks, 20 yellow socks
and
31
blue socks. Being a busy and
absent-minded MIT student, you just randomly grab a number
of
socks out
of
the draw
and
try
to find a matching pair. Assume each sock has equal probability
of
being
selected, what is the minimum number
of
socks you need to grab in order to guarantee a
pair
of
socks
of
the same color?
Solution: This question is
just
a variation
of
the even simpler version
of
two-color-socks
problem, in which case you only need 3. When you have 3 colors
(3
pigeon holes), by
the Pigeon Hole Principle, you will need to have 3
+ 1 = 4 socks ( 4 pigeons) to guarantee
that at least two socks have the same color (2 pigeons share a hole).
Handshakes
You are invited
to
a welcome party with 25 fellow team members. Each
of
the fellow
members shakes hands with you to welcome
you.
Since a number
of
people
in
the room
haven't met each other, there's a lot
of
random handshaking among others as well.
If
you
don't know the total number
of
handshakes, can
you
say with certainty that there are at
least two people present who shook hands with exactly the same number
of
people?
Solution: There are 26 people
at
the party and each shakes hands with from
I-since
everyone shakes hands with
you-to
25 people. In other words, there are 26 pigeons and
25 holes. As a result,
at
least two people must have shaken hands with exactly the same
number
of
people.
Have we met before?
Show me that, ifthere are 6 people at a party, then either at least 3 people met each other
before the party, or at least 3 people were strangers before the party.
Solution: This question appears
to
be a complex one and interviewees often get puzzled
by what the interviewer exactly wants. But once
you
start
to
analyze possible scenarios,
the answer becomes obvious.
Let's say that you are the 6th person at the party. Then by generalized Pigeon Hole
Principle (Do we even need that for such an intuitive conclusion?), among the remaining
5 people, we conclude that either at least 3 people
met
you or at least 3 people did not
meet you. Now let's explore these two mutually exclusive and collectively exhaustive
scenarios:
Case
1:
Suppose that at least 3 people have met you before.
21

Brain Teasers
If
two people in this group met each other,
you
and the pair
(3
people)
met
each other.
If
no pair among these people met each other, then these people ( 2 3 people) did not meet
each other. In either sub-case, the conclusion holds.
Case
2:
Suppose at least 3 people have not
met
you before.
If
two people in this group did not meet each other, you and the pair (3 people) did not
meet each other.
If
all pairs among these people knew each other, then these people ( 2 3
people) met each other. Again, in either sub-case, the conclusion holds.
Ants on a square
There are
51
ants on a square with side length
of
1.
If
you have a glass with a radius
of
1/7, can you put your glass at a position on the square to guarantee that the glass
encompasses at least 3 ants?
11
Solution: To guarantee that the glass encompasses at least 3 ants, we can separate the
square into 25 smaller areas. Applying the generalized Pigeon Hole Principle, we can
show that at least one
of
the areas must have at least 3 ants. So we only need to make
sure that the glass is large enough to cover
any
of
the 25 smaller areas. Simply separate
the area into 5 x 5 smaller squares with side length
of
115
each will do since a circle with
radius
of
117
can cover a square
12
with side length
1/5.
Counterfeit coins
II
There are 5 bags with l 00 coins
in
each bag. A coin can weigh 9 grams, l 0 grams
or
11
grams. Each bag contains coins
of
equal weight, but we do not know what type
of
coins
a bag contains. You have a digital scale (the kind that tells the exact weight). How many
times do you need to use the scale to determine which type
of
coin each bag contains?
13
Solution:
If
the answer for 5 bags
is
not obvious, let's start with the simplest version
of
the
problem-I
bag.
We
only need to take one coin to weigh
it.
Now we
can
move on to
2 bags. How many coins do we need to take from bag 2 in order to determine the coin
types
of
bag l and bag 2? Considering that there are three possible types for bag
1,
we
will need three coins from bag
2;
two coins won't do. For notation simplicity,
let's
change the number/weight for three types to -I, 0 and l (by removing the mean 10).
If
11
Hint: Separate the square into 25 smaller areas; then at least one area has 3 ants in it.
12 A circle with radius r can cover a square with side length
up
to
,/2
rand
,/2
;:::
1.414.
13
Hint: Start with a simpler problem. What
if
you
have
two bags
of
coins instead
of
5,
how
many coins do
you need from each bag to find the type
of
coins in either bag? What is the minimum difference in coin
numbers? Then how about three bags?
22

A Practical
Guide
To
Quantitative Finance Interviews
we only use 2 coins from bag
2,
the final sum for 1 coin from bag 1 and 2 coins from
bag 2 ranges from
-3
to 3 (7 pigeon holes). At the same time
we
have 9 ( 3 x
3)
possible
combinations for the weights
of
coins in bag I and bag 2 (9 pigeons). So at least two
combinations will yield the same final sum (9>7, so at least two pigeons need to share
one hole), and we can not distinguish them.
If
we use 3 coins from bag 2, then the sum
ranges from -4 to 4, which is possible to cover all 9 combinations. The following table
exactly shows that all possible combinations yield different sums:
Sum
1 coin, bag 1
N
-I
0 I
0.0
=
-I
-4 -3 -2
.,;
c
·c;
0
-I
0 I
u
t")
I 2 3 4
Cl
and C2 represent the weights
of
coins from bag 1
and
2 respectively.
Then how about 3 bags? We are going to have 33 = 27 possible combinations. Surely an
indicator ranging from
-13
to
13
will cover it and we will need 9 coins from bag 3. The
possible combinations are shown in the following table:
Sum
C2
=-1
C2=0
C2=1
t")
-I
0 I
-I
0 I
-I
0 I
0.0
=
.;;
-I
-13 -12
-II
-IO
-9 -8 -7 -6
-5
c
·c;
0 -4 -3 -2
-I
0 I 2 3 4
u
O'I
I 5 6 7 8 9 10
11
12
13
CJ,
C2,
and
CJ
represent the weights
of
coins from bag
1,
2,
and
3 respectively.
Following this logic, it is easy to see that we will need 27 coins from bag 4 and
81
coins
from bag
5.
So the answer is to take 1, 3, 9, 27 and
81
coins from bags I, 2, 3, 4, and 5,
respectively, to determine which type
of
coins each bag contains using a single weighing.
2. 7 Modular Arithmetic
The modulo operation---denoted
as
x%y
or x mod
y-finds
the remainder
of
division
of
number x
by
another number y. For simpicility, we only consider the case where y is a
positive integer. For example,
5%3
= 2. An intuitive property
of
modulo operation is
23

Brain Teasers
that
if
x1
%y
= x2
%y,
then (
x,
-x
2
)%y
= 0. From this property
we
can also show that
x%y,
(x+I)%y,
···,
and
(x+
y-1)%y
are all different numbers.
Prisoner problem
One hundred prisoners are given the chance to be set free tomorrow. They are all told
that each will be given a red or blue hat to wear. Each prisoner can see everyone else's
hat but not his own. The hat colors are assigned randomly and once the hats are placed
on top
of
each prisoner's head they cannot communicate with one another in any form, or
else they are immediately executed. The prisoners will be called out in random order and
the prisoner called out will guess the color
of
his hat. Each prisoner declares the color
of
his hat so that everyone else can hear it.
If
a prisoner guesses correctly the color
of
his
hat, he is set free immediately; otherwise he is executed.
They are given the night to come
up
with a strategy among themselves to save as many
prisoners as possible. What is the best strategy they can adopt and how many prisoners
can they guarantee to save?
14
Solution: At least 99 prisoners can be saved.
The key lies in the first prisoner who can see everyone else's
hat.
He declares his hat to
be red
if
the number
of
red hats he sees is odd. Otherwise he declares his hat to be blue.
He will have a
1/2
chance
of
having guessed correctly. Everyone else is able to deduce
his own hat color combining the knowledge whether the number
of
red hats
is
odd
among 99 prisoners (excluding the first) and the color
of
the other 98 prisoners
(excluding the first and himself). For example,
if
the number
of
red hats is odd among
the other 99 prisoners. A prisoner wearing a red hat will see even number
of
red hats in
the other
98
prisoners (excluding the first and himself) and deduce that he
is
wearing a
red hat.
The two-color case is easy, isn't it? What
if
there are 3 possible hat colors: red, blue, and
white? What is the best strategy they can adopt and how many prisoners can they
guarantee to save?
15
Solution: The answer is still that at least 99 prisoners will be saved. The difference is
that the first prisoner now only has
1/3
chance
of
survival. Let's use the following
scoring system:
red=O,
green= I, and blue=2. The first prisoner counts the total score for
14
Hint: The first prisoner can see the number
of
red and blue hats
of
all other 99 prisoners. One color has
odd number
of
counts and the other has even number
of
counts.
15
Hint: That a number is odd simply means x%2 = 1 . Here we have 3 colors, so you may want to consider
x%3 instead.
24

A Practical Guide
To
Quantitative Finance Interviews
the rest
of
99 prisoners and calculates s%3.
If
the remainder is 0, he announces red;
if
the remainder is
1,
green; 2, blue. He has 1/3 chance
of
living, but all
the
rest
of
the
prisoners can determine his own score (color) from the remainder.
Let's
consider a
prisoner i among 99 prisoners (excluding the first prisoner). He can calculate the total
score (x)
of
all other 98 prisoners. Since
(x
+ 0)%3, ( x +
1)
%3, and ( x +
2)
%3 are all
different, so from the remainder that the first prisoner gives (for the
99
prisoners
including i), he can determine his own score (color). For example,
if
prisoner i sees that
there are 32 red, 29 green and
37
blue in those 98 prisoners (excluding the first and
himself). The total score
of
those 98 prisoners is 103.
If
the first prisoner announces that
the remainder is 2 (green), then prisoner i knows his
own
color
is
green
(1) since
only
104%3 = 2 among 103, 104 and
105.
Theoretically, a similar strategy
can
be extended to any
number
of
colors. Surely that
requires all prisoners to have exceptional memory and calculation capability.
Division by 9
Given an arbitrary integer, come
up
with a rule
to
decide whether it is divisible by 9 and
prove it.
Solution: Hopefully
you
still remember the rules from your high school
math
class. Add
up all the digits
of
the integer.
If
the sum is divisible by 9,
then
the integer is divisible
by
9; otherwise the integer is not divisible by
9.
But
how do we prove it?
Let's
express the original integer as a
=a)
on
+
an_,
10n-I
+ .
..
+a,
10
1
+Go.
Basically we
State that
if
an+
an-I
+ · · · + a1 + a0 =
9x
( X is a integer), then the a is divisible by 9 as
well. The
proof
is straightforward:
For any
a=a)On+an_,10n-i+···+a,IO'+a
0, let
b=a-(an+an_,+···+a,+a
0
).
We
have b=an(lOn
-l)+an_,(lon-i
-l)+···+a,(10
1
-l)=a-9x,
which is divisible by 9
since all
(1
Ok
-1),
k =
1,-
·
·,n
are divisible by 9. Because both
band
9x are divisible by 9,
a=
b +
9x
must be divisible by 9 as well.
(Similarly you can also show that
a=
(-lY
an
+
(-lf-
1
an-i
+ · · · +
(-1)
1
a,+
a0 = 1
lx
is the
necessary and sufficient condition for a to be divisible by 11.)
25

Brain Teasers
Chameleon colors
A remote island has three types
of
chameleons with the following population:
13
red
chameleons,
15
green chameleons and
17
blue chameleons. Each time two chameleons
with different colors meet, they would change their color to the third color.
For
example,
if
a green chameleon meets a red chameleon, they both change their color to blue.
Is
it
ever possible for all chameleons to become the same color? Why
or
why not?
16
Solution:
It
is not possible for all chameleons to become the same color. There are
several approaches to proving this conclusion. Here we discuss two
of
them.
Approach
1.
Since the numbers 13,
15
and
17
are "large" numbers, we can simplify the
problem
to
0, 2
and
4 for three colors. (To see this, you need to realize that
if
combination
(m
+
1,
n +
1,
p +
1)
can be converted
to
the same color, combination
(m,n,p)
can be converted
to
the same color as well.) Can a combination (0,2,4) be
converted
to
a combination
(0,0,6)?
The answer is NO,
as
shown in Figure 2.3:
(0,
2,
4)
(I,
2,
30
Figure 2.3 chameleon color combination transitions from (0, 2,
4)
Actually combination
(1,
2,
3)
is equivalent to combination (0,
1,
2), which can only be
converted to another (0,1,2) but will never reach (0,0,3).
Approach
2.
A different, and more fundamental approach, is to realize that in order for
all the chameleons to become the same color, at certain intermediate stage, two colors
must have the same number. To see this, just imagine
the
stage before a final stage.
It
must has the combination (1,1,x).
For
chameleons
of
two different colors to have the
same number, their module
of
3 must be the same
as
well. We start with
15
= 3x,
13
= 3 y +
l,
and
17
=
3z
+ 2 chameleon, when two chameleons
of
different colors meet,
we will have three possible scenarios:
16 Hint: consider the numbers
in
module
of
3.
26

A Practical Guide To Quantitative Finance Interviews
{
(3x +
2,3y,3z
+
1)
= (3x',3y'+ 1,3z'+ 2), one
ymeetsonez
(3x,3y+
l,3z
+ 2)
=>
(3(x-1)
+
2,3(y
+ 1),3z +
1)
=
(3x',3y'+
1,3z'+
2),
onexmeetsonez
(3(x-1)
+2,3y,3(z
+
1)
+
1)
=
(3x',3y'+
1,3z'+ 2), onexmeetsone y
So the pattern is preserved and
we
will never get two colors to have the same module
of
3.
In
other words, we cannot make two colors have the same number. As a result, the
chameleons cannot become the same color. Essentially, the relative change
of
any pair
of
colors after two chameleons meet is either 0 or
3.
In order for all the chameleons to
become one color, at least one pair's difference must be a multiple
of
3.
2.8 Math Induction
Induction is one
of
the most powerful and commonly-used
proof
techniques in
mathematics, especially discrete mathematics. Many problems that involve integers can
be solved using induction. The general steps for proof
by
induction are the following:
• State that the proof uses induction and define an appropriate predicate P(n).
• Prove the base case
P(l),
or any other smallest number n for the predicate to be true.
• Prove that P(n) implies P(n +
1)
for every integer
n.
Alternatively, in a strong
induction argument, you prove that P(l), P(2),
···,
and
P(n)
together imply
P(n+
1).
In most cases, the real difficulty lies not in the induction step, but to formulate the
problem
as
an induction problem and come up with the appropriate predicateP(n). The
simplified version
of
the problem can often help you identify P(n).
Coin split problem
You split 1000 coins into two piles and count the number
of
coins in each pile.
If
there
are x coins in pile one and y coins in pile two, you multiple x by y to get xy. Then you
split both piles further, repeat the same counting and multiplication process, and add the
new multiplication results to the original. For example, you split x to
x,
andx2, y to y,
andy
2, then the sum is
xy+x,x
2 + y1y2• The same process
is
repeated until you only
have piles
of
1 stone each. What is the final sum? (The final 1
's
are not included in the
sum.) Prove that you always get the same answer no matter how the piles are divided.
27

Brain Teasers
Solution: Let n be the number
of
the coins and
f(n)
be the final sum.
It
is unlikely that
a solution will jump to our mind since the number n = 1000
is
a large number.
If
you
aren't sure how to approach the problem, it never hurts to begin with the simplest cases
and try to find a pattern. For this problem, the base case has n = 2. Clearly the only split
is 1 + 1 and the final sum is I. When n =
3,
the first split is 2 + 1 and we have
xy
= 2 and
the 2-coin pile will further give an extra multiplication result
1,
so the final sum is 3.
This analysis also gives the hint that when n coins are split into x and n -x coins, the
total sum will be
f(n)=x(n-x)+f(x)+f(n-x).
4 coins can be split into
2+2
or
3+1. For either case we can apply
x(n-x)+
f(x)+
f(n-x)
and yields the same final
sum6.
Claim: For n coins, independent
of
intermediate splits, the final sum is n( n -
I)
. 17
2
So how do
we
prove it? The answer should
be
clear to you: by strong induction.
We
have proved the claim for the base cases n =
2,
3,
4. Assume the claim is true for
n =
2,
· · ·, N -I coins, we need to prove that it holds for n = N coins as well. Again we
apply the equation
f(n)
=
x(n-x)+
f(x)+
f(n-x).
If
N coins are split
intox
coins and
N -x coins, we have
f (
N)
=
x(
N -
x)
+ f (
x)
+ f ( N -
x)
N(N-1)
(N
-x)(N-x-1)
N(N-1)
=x(N-x)+
+
=---
2 2 2
So indeed it holds for n = N as well and
f(n)
=
n(n-l)
is true for any n
2.
Applying
2
the conclusion to n=lOOO, we have
/(n)=1000x999/2.
Chocolate bar problem
A chocolate bar has 6 rows and 8 columns (
48
small 1x1 squares). You break it into
individual squares by making a number
of
breaks. Each time, break one rectangle into
two smaller rectangles. For example, in the first step you can break the
6x8
chocolate
bar into a 6 x 3 one and a 6 x 5 one. What is the total number
of
breaks needed in order
to break the chocolate bar into 48 small squares?
17
.f(2)
=
l,
.f(3)-
/(2)
= 2 and
/(4)-/(3)
= 3 should give you enough hint to realize the pattern is
n(n
-1)
.f(n)=l+2+···+(n-l)=
.
2
28

A Practical Guide
To
Quantitative Finance Interviews
Solution: Let m be the number
of
the rows
of
the chocolate bar and n be the number
of
columns. Since there
is
nothing special for the case m = 6 and n =
8,
we should find a
general solution for all m and
n.
Let's begin with the base case where m = 1 and n =
1.
The number
of
breaks needed is clearly
0.
For
m > 1 and n =
1,
the number
of
breaks is
m
-1;
similarly for m = 1 and n >
1,
the number
of
breaks is n
-1.
So
for any m and n,
if
we break the chocolate into m rows first, which takes m
-1
breaks, and then break
each row into n small pieces, which takes
m(
n -l) breaks, the total number
of
breaks is
( m
-1)
+ m( n
-1)
= mn -
I.
If
we breaks it into n columns first and then break each
column into m small pieces, the total number
of
breaks is also mn
-1.
But
is
the total
number
of
breaks always
mn
-l for other sequences
of
breaks?
Of
course it
is.
We
can
prove it using strong induction.
We have shown the number
of
breaks is mn
-1
for base cases m
1,
n = 1 and
m =
1,
n;;:::
1.
To prove it for a general m x n case, Jet's assume the statement is true for
cases where rows < m, columns n and rows
m,
columns <
n.
If
the first break is
along a row and
it
is broken into two smaller pieces m x n1 and m x
(n
-n1
),
then the
total number
of
breaks is
l+(mxn
1
-l)+(mx(n-n,)-l)=mn-1.
Here
we
use the
results for m, columns <
n.
Similarly,
if
it is broken into two pieces m1 x n and
( m -m1) x n, the total number
of
breaks is 1 + (
m,
x n
-1)
+ ( ( m -m1) x n
-1)
= mn
-1.
So
the total number
of
breaks is always mn
-1
in
order to break the chocolate bar into
mx
n small pieces. For the case m = 6 and n =
8,
the number
of
breaks is 47.
Although induction
is
the standard approach used to solve this problem, there is actually
a simpler solution
if
you've noticed
an
important fact: the number
of
pieces always
increases
by
1 with each break since it always breaks one piece into
two.
In the
beginning, we have a single piece. In the end, we will have mn pieces. So the number
of
breaks must be mn
-1.
Race track
Suppose that you are on a one-way circular race track. There are N gas cans randomly
placed
on
different locations
of
the track and the total sum
of
the gas in these cans is
enough for your car to run exactly one circle. Assume that your car has no gas in the gas
tank initially, but you can put your car at any location on the track and you can pick up
the gas cans along the way to fill
in
your gas tank. Can you choose a starting
position on the track so that your car can complete the entire circle?1
18
Hint: Start with N =
l,
2 and solve the problem using induction.
29

Brain Teasers
Solution:
If
you get stuck as to how to solve the problem, again start with the simplest
cases
(N
=
1,
2) and consider using an induction approach. Without loss
of
generality,
let's assume that the circle has circumference
of
1.
For
N =
1,
the problem is trivial. Just
start at where the gas can is. For N = 2, The problem is still simple.
Let's
use a figure to
visualize the approach. As shown
in
Figure 2.4A, the amount
of
gas
in can 1
and
can 2,
expressed as the distance the car can travel, are x, and x2 respectively, so x, + x2 =
1.
The corresponding segments are y, and y2, so y, + y2 =
1.
Since
x,
+ x2 = 1 and
y, + y2 =
1,
we must have x, y,
or
x2 y2 (
x,
< y, and x2 <
Yi
cannot both
be
true).
If
x,
y, , we can start at gas can
1,
which has enough gas to reach
gas
can 2, and get more
gas from gas can 2 to finish the whole circle. Otherwise, we will
just
start at gas can 2
and pick up gas can 1 along the way to finish the whole circle.
Yt
A
Figure 2.4 Gas can locations on the cycle and segments between gas cans
The argument for N = 2 also gives
us
the hint for the induction step. Now we want to
show that
if
the statement holds for N = n, then the same statement also holds for
N = n +
1.
As shown m Figure
2.48,
we have x1 + x2 + · · · +
xn+i
= 1 and
y, + y2 + · · · +
Yn+t
= 1 for N = n +
1.
So there must exist at least
one
i, that
has
X;
Y;·
That means whenever the car reaches
X;,
it can reach
x;+i
with more gas
(For i = n +
1,
it goes to i
=I
instead). In other words, we can actually "combine"
x;
and
x;+i
to one gas can at the position
of
x;
with an amount
of
gas
X;
+
X;+i
(and eliminate
the gas can i
+I
).
But
such combination reduces the N = n
+I
problem to N = n, for
30

A Practical
Guide
To
Quantitative Finance Interviews
which the statement holds. So the statement also holds for N = n +
1.
Hence we can
always choose a starting position on the track
to
complete the entire circle for any
N.
There
is
also an alternative approach to this problem that provides a solution to the
starting point. Let's imagine that you have another car with enough gas
to
finish the
circle. You put that car at the position
of
a randomly chosen gas can and drive the car for
a full circle. Whenever you reach a gas can (including at the initial position), you
measure the amount
of
gas in your gas tank before you add the gas from the can to your
gas tank. After you finish the circle, read through your measurement records and find the
lowest measurement. The gas can position corresponding
to
the lowest measurement
should be your starting position
if
the car has
no
gas initially.
(It
may take some thinking
to fully understand this argument.
I'd
recommend that you again draw a figure and give
this argument some careful thoughts
if
you don't find the reasoning obvious.)
2.9 Proof
by
Contradiction
In a proof by contradiction or indirect proof, you show that
if
a proposition were false,
then some logical contradiction or absurdity would follow. Thus, the proposition must be
true.
Irrational number
Can you prove that
J2
is an irrational number? A rational number is a number that can
be expressed as a ratio
of
two integers; otherwise it is irrational.
Solution: This is a classical example
of
proof
by
contradiction.
If
.J2
is not an irrational
number, it can be expressed as a ratio
of
two integers m and
n.
If
m and n have any
common factor,
we
can remove it by dividing both m and n by the common factor. So in
the end, we will have a pair
of
m and n that have no common factors.
(It
is called
irreducible fraction.) Since m
In
=
.J2,
we have m2 = 2n2• So m2 must
be
an even
number and m must be an even number as well. Let's express m as 2x, where
xis
an
integer, since m
is
even. Then m2 =
4x
2 and
we
also have n2 = 2x2, which means n
must be even as well. But that both m and n are even contradicts the earlier statement
that m and n have
no
common factors. So
.J2
must be an irrational number.
Rainbow hats
Seven prisoners are given the chance to be set free tomorrow. An executioner will put a
hat on each prisoner's head. Each hat can be one
of
the seven colors
of
the rainbow and
the hat colors are assigned completely at the executioner's discretion. Every prisoner can
31

Brain Teasers
see the hat colors
of
the other six prisoners, but not his own. They cannot communicate
with others
in
any form, or else they are immediately executed. Then each prisoner
writes down his guess
of
his own hat color.
If
at least one prisoner correctly guesses the
color
of
his hat, they all will be set free immediately; otherwise they will be executed.
They are given the night to come up with a strategy. Is there a strategy that they can
guarantee that they will be set free?
19
Solution: This problem is often perceived to be more difficult than the prisoner problem
in the modular arithmetic section. In the previous prisoner problem, the prisoners can
hear others' guesses. So one prisoner's declaration gives all the necessary information
other prisoners need. In this problem, prisoners
won't
know what others' guesses are. To
solve the problem, it does require an aha moment. The key
to
the aha moment is given
by
the hint. Once you realize that
if
we code the colors to 0-6, (
tx,
J%7
must
be
among 0,
1,
2, 3, 4, 5 or 6 as well. Then each prisoner
i-let's
label them as 0-6 as
well-should
give a guess
g;
so that the sum
of
g;
and the rest
of
6 prisoners' hat color
codes will give a remainder
of
i when divided by 7, where
g;
is a unique number
between 0 and
6.
For
example, prisoner O's guess should make
(g
0 +
IxkJ%7
= 0.
k;tO
This way, we can guarantee at least one
of
g;
=
X;
for i = 0, I,
2,
3,
4,
5,
6.
We
can
easily prove this cone I us ion
by
contradiction.
If
g, *
x,,
then ( t
x,
J % 7 * i
(since
(g;
+ L
xk
J % 7 * i and
g;
and
X;
are both between 0 and 6). But
if
K * X; for all
kot1
i 0, l,2,3,4,5, and 6, then (
t,x,
J%7*0,1
,
2,3,4,5,6,
which is clearly impossible. So
at least one
of
g;
must equal to x; . As a result, using this strategy, they are guaranteed
to be set free.
19
Hint: Let's assign the 7 colors
of
rainbow with code 0-6 and
X;
be the color code
of
prisoner
i.
Then
(
t,x,
)%7
must be 0,
1,
2, 3, 4, 5
or
6.
How many guesses can 7 prisoners make?
32

Chapter
3
Calculus
and
Linear
Algebra
Calculus and linear algebra lay the foundation for many advanced math topics used in
quantitative finance. So be prepared to answer some calculus or linear algebra
problems-many
of
them may be incorporated into more complex
problems-in
quantitative interviews. Since most
of
the tested calculus and linear algebra knowledge
is easy to grasp, the marginal benefit far outweighs the time you spend brushing up your
knowledge on
key
subjects.
If
your memory
of
calculus or linear algebra is a little rusty,
spend some time reviewing your college textbooks!
Needless to say, it
is
extremely difficult to condense any calculus/linear algebra books
into one chapter. Neither is it
my
intention to
do
so. This chapter focuses only on some
of
the core concepts
of
calculus/linear algebra that are frequently occurring
in
quantitative interviews. And unless necessary, it does so without covering the proof,
details
or
even caveats
of
these concepts.
If
you are not familiar with any
of
the concepts,
please refer to your favorite calculus/linear algebra books for details.
3.
1
Limits
and
Derivatives
Basics
of
derivatives
Let's begin with some basic definitions and equations used in limits and derivatives.
Although the notations may be different, you can find these materials in any calculus
textbook.
Derivative: Let y =
f(x),
then f '(x) = dy = lim
L\y
= lim
f(x
+
f(x)
dJC
d.1---tO
d.1---tO
The
product
rule:
If
u = u(x) and v = v(x) and their respective derivatives exist,
d(uv)
dv
du
---;;;-
= u
dx
+ v dx,
(uv)'
=
u'v+
uv'
. d
(u)
( du
dv)f
2
The
quotient
rule:
dx
= v
dx
-u dx v , (
U)
1 = U
1
V -
UV
1
v v2
.
ey
The
cham
rule:
If
y =
f(u(x))
and u =
u(x),
then -=
--
dx du
dx
The generalized
power
rule
:
dyn
= nyn-t
dy
for "if n O
dx
dx
Some useful equations:

Calculus and Linear Algebra
ln( ab) =
ln
a + ln b
ex
= lim(l +
n->oo
lim sinx = l
x lim(l + xl = l + kx for any k
lim(ln x
Ix')
= 0 for any r > 0 lim
x'
e-x = 0 for any r
x
)00
!!_e" =
e"
du da"
=(a"
lna)
du
dx dx
dx
dx
d l du
u'
-lnu=--=-
dx u
dx
u
d . d . d 2
-sm
x = cos
x,
-cos
x = - sm
x,
-tan
x = sec x
dx
dx
dx
What
is
the derivative
of
y = ln
x'"x
?1
Solution: This is a good problem to test your knowledge
of
basic derivative
formulas-
specifically, the chain rule and the product rule.
Let
u=lny=ln(lnx
1
"x)=lnxxln(lnx).
Applying the chain rule and the product rule,
we have
du=
d(ln
y)
=
_!_
dy = d(ln
x)
x ln(lnx) +
ln
xx
d(ln(lnx))
= ln(lnx) +
dx
dx
y
dx
dx
dx x x ln x
. d(ln(ln
x))
. . .
To denve , we agam use the cham rule by settmg v =
ln
x:
dx
d(ln(ln
x))
d(ln v) dv l I I
----''-------'- = = - x - =
--
dx
dv
dx
v x x ln x ·
:.
_!_dy
dy
=y(ln(lnx)+l)=lnx'"x
(ln(lnx)+l).
y dx x
xlnx
dx
x x
Maximum and minimum
Derivative f
'(x)
is
essentially the slope
of
the tangent line to the curve y =
f(x)
and
the instantaneous rate
of
change (velocity)
of
y with respect to x. At point x = c,
if
1 Hint: To calculate the derivative
of
functions with the format y = f
(x)',
it is common to take natural
logs on both sides and then take the derivative, since
d(ln
y)
I dx
=I
I y x dy I
dx.
34

A Practical Guide
To
Quantitative Finance Interviews
f
'(
c) > 0, f (
x)
is an increasing function at
c;
if
f '(
c)
< 0, f (
x)
is a decreasing
function at c.
Local maximum or minimum: suppose
that
f(x)
is differentiable at c and is defined
on
an open interval containing
c.
If
/(c)
is either a local maximum value
or
a local
minimum value
of
f(x),
then J '(c) =
0.
Second Derivative test: Suppose the secondary derivative
of
f(x),
f "(x), is
continuous near c.
If
f '(c) = 0 and
f"(c)
> 0, then
f(x)
has a local minimum at c;
if
f '(c) = 0
and
/"(c)
<
0,
then.
f(x)
has a local maximum
at
c.
Without calculating the numerical results,
can
you tell
me
which number is larger,
eli
or
::re
?2
Solution:
Let's
take natural logs
of
eli
and
::r
e.
On
the left side we have
::r
In
e,
on the
right side
we
have e ln
::r.
If
eli
>::re,
eli
>
::re
<=>
::r
x
In
e >
ex
In
::r
<=>
ln
e >
In
::r.
e
::r
Is it true?
That
depends on whether
f(x)
=
lnx
is an increasing
or
decreasing function
x
ti T k. h d . . f
/(
) h J
'(
) 1/ x x x -
In
x
1-
ln x
rom e to
::r.
a mg t e envattve o x , we ave x = 2 = 2 ,
x x
which is less than 0 when x > e
(lnx
> 1 ). In fact,
f(x)
has global maximum when
In
e ln
::r
x = e for all x >
0.
So ->
--
and
eli
>
::re
.
e
::r
Alternative approach:
If
you are familiar
with
the Taylor's series, which
we
will discuss
ao
1 x x 2 x3
in Section 3 .4, you can apply Taylor's series to
ex
: ex = L -= 1
+-+-
+-+
· · · So
n=O
n ! 1 ! 2 ! 3 !
ex>
1 + x,
Vx
>
0.
Let x =
::r
I
e-1,
then eJr!e I e >
::r
I e
<=>
eJr
!e >
::r
<=>
eli
>::r
e.
L'Hospital's rule
Suppose that functions
f(x)
and
g(x)
are differentiable at x and that limg'(a)-:;:. 0.
x-->a
Further suppose that
lim/(a)
= 0
and
limg(a)
= 0
or
that
limf(a)
±oo
and
x-+a
x-7-a x
-+
a
2 Hint: Again consider taking natural logs
on
both sides;
In
a >
In
b a > b since
In
x is a
monotonously increasing function.
35

Calculus and Linear Algebra
limg(a)
±oo,
then lim
f(x)
= lim f '(x). L'Hospital's rule converts the limit from
x-+a
x-+a
g(x)
x-+a
g '(x)
an indeterminate form to a determinate form.
What is the limit
of
ex I x2 as x
oo,
and what is the limit
of
x2
In
x as x o+?
x
Solution:
lim;
is a typical example
of
L'Hospital's rule since lim
ex
=
oo
and
X-><0
X
X-+«>
limx
2 =
oo.
Applying L'Hospital's rule, we have
x-+oo
lim f
(x)
= lim
ex
= lim f
'(x)
= lim
!t.__.
x-+a
g(x)
x-+oo
x2
X-+00
g '(x)
X-+OO
2x
The result still has the property that lim f (x) = lim
ex
=
oo
and lim
g(x)
= lim
2x
=
oo,
so
x-+OO
X---?00
x-+oo
X-+OO
we can apply the
L'
Hospital's rule again:
lim
f(x)
=lime:
= lim f '(x) =
lim!t.__
= lim
d(ex)/
dx = =
oo.
x-+oog(x)
x...+oox
x-+oog'(x)
x-+oo2x
x-+ood(2x)/dx
x-+«>
2
At first look, L 'Hospital's rule does not appear to be applicable to lim x2
In
x since
it's
x-+0+
not in the format
of
lim f
(x).
However, we can rewrite the original limit
as
lim
x-+a
g(x)
x-+0+
x-
and it becomes obvious that lim
x-
2 =
oo
and lim ln x = -oo. So we can now apply
X-+0+
L'Hospital's rule:
l.
21
1
.
lnx
1
.
d(lnx)/
dx 1
.
l/
x 1
. x2 0
1mx
nx=
1m-=
1m
=
1m
=
1m-=
x
x-+o+
x-
2
x-+o·
d ( x -2) I dx
x-+o+
-2
I x3
x-+o+
-2
3.
2 Integration
Basics
of
integration
Again, let's begin with some basic definitions and equations used in integration.
If
we can find a function
F(x)
with derivative
f(x),
then we call
F(x)
an
antiderivative
of
f (
x)
.
If
f(x)=F'(x),
[f(x)=
[F'(x)dx=[F(x)t=F(b)-F(a)
36

A Practical Guide
To
Quantitative Finance Interviews
dFdx(x)
--
f(x),
F(
)
F(
) r
/(
)d
a =y"=> x
=ya+
t t
Uk+I
The generalized power rule in reverse:
Ju*
du=
--
+ c (k
'*
1),
where c
is
any
k+l
constant.
Integration by substitution:
J
/(g(x))
· g
'(x)dx
= J
f(u)du
with u =
g(x),
du=
g
'(x)dx
Substitution in definite integrals:
r6
/(g(x))
· g '(x)dx =
r<b>
f(u)du
l,
Jg(u)
Integration by parts: fudv =
uv-
J vdu
A.
What is the integral ofln(x)?
Solution: This is an example
of
integration by parts. Let u =
ln
x and v =
x,
we
have
d ( uv) = vdu +
udv
=
(xx
1
Ix
)dx +
ln
xdx
,
:.
flnxdx
=
xlnx-
fdx
=
xlnx-x+c,
where c is any constant.
B.
What
is
the integral
of
sec(x) from x = 0 to x =
Jr
I
6?
Solution: Clearly this problem is directly related
to
differentiation/integration
of
trigonometric functions. Although there are derivative functions for all basic
trigonometric functions, we only need to remember two
of
them: x =cos
x,
dx
=-sin
x. The rest can be derived using the product rule or the quotient rule. For
dx
example,
dsecx
d(l/
cosx)
sinx
---=
=--=secxtanx
dx
dx
cos2 x '
dtanx
d(sinx/cosx)
cos2
x+sin
2 x 2
dx =
dx
= cos2 x
=sec
x.
d(secx+
tanx)
------=sec
x(sec x
+tan
x).
dx
37

Calculus and Linear Algebra
Since the (sec x + tan
x)
term occurs in the derivative, we also have
din
I
secx+tanx
I
secx(secx+
tanx)
-------=
=secx
dx
(secx+
tanx)
=>
J sec x
=In
I sec x + tan x I +c
and
r'
6
secx
=
ln(sec(JZ"
I 6) +
tan(JZ"
I 6))-ln(sec(O) + tan(O))
=In(
J3)
Applications
of
integration
A. Suppose that two cylinders each with radius 1 intersect at right angles and their
centers also intersect. What is the volume
of
the intersection?
Solution: This problem is an application
of
integration to volume calculation.
For
these
applied problems, the most difficult part is to correctly formulate the integration. The
general integration function to calculate 3D volume is V = r
A(z)dz
where
A(z)
is the
I
cross-sectional area
of
the solid cut
by
a plane perpendicular to the z-axis at coordinate
z.
The
key
here is to find the right expression for cross-sectional area A as a function
of
z.
Figure 3.1 gives us a clue.
If
you cut the intersection
by
a horizontal plane, the cut will
be a square with side-length
-(2z}2.
Taking advantage
of
symmetry, we can
calculate the total volume as
An alternative approach requires even better 3D imagination.
Let's
imagine a sphere that
is inscribed inside
both
cylinders, so it is inscribed inside the intersection as well. The
sphere should have a radius
of
r I 2.
At
each cut perpendicular to the z-axis, the circle
from the sphere is inscribed
in
the square from the intersection as well. So
Acircte = A.,quure· Since
it's
true for all z values, we have
V,phere =
-j-
JZ"(
5"
)3 = V;ntersection
=>
V;ntersection = 16 / 3r3 = 16 / 3 ·
38

A Practical Guide
To
Quantitative Finance Interviews
Figure
3.1
Interaction
of
two cylinders
B. The snow began to fall some time before noon at a constant rate. The city
of
Cambridge sent out a snow plow at noon
to
clear Massachusetts A venue from MIT to
Harvard. The plow removed snow at a constant volume per minute.
At
1 pm, it had
moved 2 miles and at 2 pm, 3 miles. When did the snow begin to fall?
Solution: Let's denote noon as time 0 and assume snow began to fall T hours before
noon. The speed at which the plow moves is inversely related to the vertical cross-
sectional area
of
the snow: v = c1 I A(t), where
vis
the speed
of
the plow,
c,
is a constant
representing the volume
of
snow that the plow can remove every hour
and
A(t)
is the
cross-sectional area
of
the snow.
If
t
is
defined as the time after noon, we also have
A(t)
= c2 (t +
T),
where c2 is the rate
of
cross-sectional area increase per hour (since the
snow falls at a constant rate). So v =
c,
=
c2
(t+T)
t+T
c
integration, we have
1
c
(l+T)
--dt=cln(l+T)-clnT
=cln
--
= 2,
T+t
T
1
i2
c
(2+T)
--dt=cln(2+T)-clnT=cln
--
=3
T+t
T
From these two equations, we get
c
where
c=-'
Cz
Taking the
39

Calculus and Linear Algebra
Overall, this question, although fairly straightforward, tests analytical skills, integration
knowledge and algebra knowledge.
Expected value using integration
Integration
is
used extensively to calculate the unconditional
or
conditional expected
value
of
continuous random variables. In Chapter 4, we will demonstrate its value in
probability and statistics. Here we
just
use one example
to
show its application:
If
Xis
a standard normal random variable, X -N(O,
1),
what
is
E[X
IX>
O]?
Solution: SinceX -N(O,
1),
the probability density function
of
x is
f(x)
=
Jk
e-
112
x2
and we have
E[X
Ix>
O]
= r
xf(x)dx
= r x b
e-
112
x2
dx.
Because
d(-112x
2
)=-x
and where c is an arbitrary constant, it is
obvious that we can use integration by substitution by letting u =
-1I2x
2• Replace
e-
112
x2 with
eu
and
xdx
with
-du,
we have
r I
-1
1
2x
2dx _ r I ud _ 1 [ u
]--<X)
_ I
(0
1)
_ I h [ u
]--<X)
x
J2ii
e --.ffii e u --& e 0 --
J2ii
--J2ii , w ere e 0
ts
determined
by
x = 0=> u = 0 and x =
oo
=>
u =
-oo.
:.
E[XIX>0]=1/J2;
3.3 Partial Derivatives
and
Multiple Integrals
Partial derivative:
w=f(x
,y)=> 8
8
if
(x
0
,y
0
)=
lim
=ix
x
&->0
. • . a2 f a
af
02
J a
af
a
Bf
Second order partial derivatives: -=
-(-),
--
=
-(-)
=
-(-)
8x
2
ax
ax
axay ax
By
By
ax
The general chain rule: Suppose that
w=
f(xl'x
2
,-··,x",)
and that each
of
variables
xi'
x2, • •
·,
x"'
is a function
of
the variables ti' t2, • •
·,
tn.
If
all these functions have
· fi d · I d . . h
aw aw
Bx
1
aw
ax
2
aw
ax
contmuous 1rst-or
er
part1a envatives, t en -
=--+--+···+--"'
ior
Bt;
ax,
Bt;
Bx
2
Bt;
Bx"'
at;
each i, I
-5::
i
-5::
n.
40

A Practical Guide To Quantitative Finance Interviews
Changing Cartesian integrals into polar integrals: The variables in two-dimension
plane can be mapped into polar coordinates: x = r cos
B,
y = r sin
B.
Tthe integration in a
continuous polar region R is converted to
JfJ(x,y)dxdy
=
Jf
J(rcosB,rsinB)rdrdB.
R R
Calculate r e-x
212
dx.
Solution: Hopefully you happen to remember that the probability density function (pdf)
of
the standard normal distribution is
f(x)
= e-x
212
. By definition, we have
v2Jr
If
you've forgotten the
pdf
of
the standard normal distribution or
if
you are specifically
asked to prove ( e-x
21
2
dx
=I,
you will need to use polar integrals
to
solve the
v2tr
problem:
(
e-x212dx
(
e-y212dy
= ( (
e-(x2+/i12dxdy
= r
1"
e-<r2cos2B
+r2
sin2e)12rdrd(}
= r
1"
e-r212rdrdB= -r e-r212d(-r
2/
2)1"
dB
=
-[
e-r212
I [ = 2Jr
3.4 Important Calculus Methods
Taylor's series
One-dimensional Taylor's series expands function
f(x)
as the sum
of
a series using the
derivatives
at
a point x = x0 :
41

Calculus and Linear Algebra
f
"(O)
J<n>(O)
If
X0 =
0,
f(x)
=
f(O)+
+···+
n!
xn
+···
Taylor's series are often used to represent functions in power series terms. For example,
Taylor's series for three common transcendental functions,
ex,
sin x and cos x , at
x0 = 0 are
x
"'
1 x
x2
x3
e
=L-=1+-+-+-+···
n=O
n !
1!
2 ! 3 ! '
•
oo
(-IYx2n+1
x3
xs
x1
smx=
L
=x--+---+···
n=O
(2n+l)!
3!
5!
7!
'
oo
(-If
x2n
x2 x4 x6
COSX=
L
=1--+---+···
n=O
(2n)!
2!
4!
6!
The Taylor's series can also be expressed as the sum
of
the nth-degree Taylor
f
"(x)
fn>(x)
polynomial T,,(x) =
f(x
0)+
J'(x
0
)(x-x
0)+ 0
(x-x
0)2
+·
·· + 0
(x-x
0f and
2!
n!
a remainder Rn(x):
f(x)
= Tn(x) + Rn(x).
fn+'>C)
For some i between
Xo
and x, Rn(x) = x I
X-Xo
r+I.
Let
Mbe
the maximum
of
(n+l)!
Mx
I
X-X
ln+I
IJ<n+I)
(x)I
for all i between x0 and x, we get constraint
!Rn
(x)I:::;;
0
(n
+ l)!
A. What is i;?
Solution: The solution to this problem uses Euler's formula,
e;o
=cos
e + i
sine,
which
can be proven using Taylor's series. Let's look at the proof. Applying Taylor's series to
e;e, cos e and
sine,
we have
iB
ie
(ie)2 (ie)3 (ie)4 . e e 2 . e3 e4 . es
e
=1+-+--+--+--+···=1+1----1-+-+1-+···
I!
2!
3!
4!
I!
2!
3!
4!
5!
e2 e4 e6
cos e =
1-
-+-
- - + · · ·
2!
4!
6!
. e3 es e1 . . . e . e 3 • es . e1
sm e =
e-
-+-
- - + · · · l sm e =
l-
-1-+
l-
-1-
+ · · ·
3!
5!
7!
I!
3!
5!
7!
42

A Practical Guide
To
Quantitative Finance Interviews
Combining these three series, it is apparent that
eiB
=cos
e + i
sine.
When 8 = :1r, the equation becomes
eiJC
= cos
:1r
+ i sin
:1r
=
-1.
When 8 =
:1r
I
2,
the
equation becomes
eiJC
12
=cos(
Jr
I
2)
+ i sin (Jr I
2)
=
i.
3 So In i =
In
(
eiJCl
2) =
i:1r
I 2.
Hence,
tn(i)
= i ln i =
i(i:1r
I 2)
=-Jr
I 2 i; = e-JC
12
•
B. Prove (l +
xf
1 +
nx
for all x >
-1
and for all integers n
2.
Solution: Let f
(x)
= (l +
xf.
It is clear that 1 +
nx
is the first two terms in the Taylor's
series
of
f(x)
with x0 =
0.
So
we
can consider solving this problem using Taylor's
sen
es.
For
Xo
= 0 we have (l +
xr
= 1 for
'ef
n
2.
The first and secondary derivatives
off
(x)
are f '(x) = n(l +
xf-'
and f "(x) =
n(n-1)(1
+
xy-
2• Applying Taylor's series, we have
f(x)
=
f(x
0
)+
f'(x
0
)(x-x
0
)+
/"Ci)
(x-x
0
)2
=
f(O)+
f'(O)x+
f"(i)
x2
2!
2!
'
= 1 +
nx+
n(n-1)(1
+xr-
2 x2
where x
:::;;
i
:::;;
0
if
x < 0 and x i 0
if
x > 0 .
Since x
>-1
andn
2, we have n > 0,
(n-1)
> 0,
(l+iy-
2 > 0, x2
0.
Hence,
n(n-l)(l+xr-
2x2 and
f(x)=(l+xY
>l+nx.
If
Taylor's series does not jump to your mind, the condition that n is an integer may give
you the hint that
you
can try the induction method. We can rephrase the problem as: for
every integer n
2,
prove
(1
+
xY
:2::
1 + nx for x >
-1
.
The base case: show (l + x y 1 +
nx,
V x >
-1
when n = 2, which can be easily proven
since
(I
2x,
Vx
>-1.
The induction step: show that
if
(1
+
xY
:2::
1 + nx,
'efx
>
-1
when n = k, the same
statement holds for n = k + 1:
(1
+
x)k+i
:2::
1 + (k + l)x,
Vx
>
-1.
This step is
straightforward as well.
3 Clearly they satisfy equation (
e'"'
)'
=
i'
=
e"
=
-1.
43

Calculus and Linear Algebra
(1
+
x)k+i
=(I+
x)k
(1
+ x)
(1
+loc)(l + x) = 1
+(k
+ l)x+loc2,
'fifx
>
-1
So the statement holds for all integers n 2 when x >
-1.
Newton's method
Newton's method, also known as the Newton-Raphson method or the Newton-Fourier
method, is an iterative process for solving the equation
f(x)
= 0.
It
begins with an initial
value x0 and applies the iterative step
xn+i
=
xn
-
f(xn)
to solve
f(x)
= 0
if
Xpx2
,.
..
f'(xJ
converge.4
Convergence
of
Newton's method is not guaranteed, especially when the starting point
is far away from the correct solution. For Newton's method to converge, it is often
necessary that the initial point is sufficiently close to the root;
f(x)
must be
differentiable around the root. When it does converge, the convergence rate is quadratic,
which means
lxn+i
-x
11
::;;
c5<1, where x1 is the solution to
f(x)
=
0.
(xn
-xi)
A. Solve x2 = 37 to the third digit.
Solution: Let
f(x)
= x2
-37,
the original problem
is
equivalent to solving
f(x)
=
0.
x0 = 6 is a natural initial guess. Applying Newton's method, we have
= _
f(x
0) = _
-37
= 6_
36-37
= 6 083
x1 x0 x0 • •
f'(x
0) 2x0 2 x 6
( 6.0832 = 37.00289, which is very close
to
37.)
If
you do not remember Newton's method, you can directly apply Taylor's series for
function
f(x)
=
J-;
with
f'(x)
=
+x-
112
:
/(37)
/(36)+
f '(36)(37-36) =
6+
I
112
= 6.083.
4 The iteration equation comes from the first-order Taylor's series:
((
)
!(
) f
'(
)(
) 0 f
(x
. )
x z x +
xx
-x
=
=:>x
=x---
•
1111
II
•
II
n•l
H
11•1
n
f'(x)
44

A Practical Guide
To
Quantitative Finance Interviews
Alternatively, we can use algebra since it is obvious that the solution should be slightly
higher than
6.
We have (6 +
y)
2 =
If
we ignore the y2 term,
which is small, then y = 0.083 and x = 6 + y = 6.083.
B. Could you explain some root-finding algorithms to solve
f(x)
=
0?
Assume
f(x)
is
a differentiable function.
Solution: Besides Newton's method, the bisection method and the secant method are two
alternative methods for root-finding. 5
Bisection method is an intuitive root-finding algorithm. It starts with two initial values
a0and b0 such that
f(a
0) < 0 and
f(b
0) >
0.
Since
f(x)
is differentiable, there must be
an x between a0 and b0 that makes
f(x)
=
0.
At each step, we check the sign
of
f((an+bn)/2).
If
f((an+bn)/2)<0,
we set
bn+I
=bn
and
an+I
=(an+bn)/2;
If
f((an+bJ!2)>0,
we set
an+I
=an and
bn+I
=(an+bJ/2;
If
J((an+bJ!2)=0,
or its
absolute value is within allowable error, the iteration stops and x =
(an
+
bn)
I
2.
The
x
-x
bisection method converges linearly,
n+i
f
<5<1,
which means it is slower than
xn-xf
Newton's method. But once you find an a0/ b0 pair, convergence is guaranteed.
Secant method starts with two initial values x0, x1 and applies the iterative step
xn+I
=
xn
-
xn
-xn-I
f(xJ.
It replaces the f
'(xJ
in Newton's method with a
f(xJ-
f(xn-1)
linear approximation f (
xn)
-f ( xn-i) . Compared with Newton's method, it does not
xn
-xn-1
require the calculation
of
derivative
f'(xJ,
which makes it valuable
if
f '(x) is difficult
to calculate. Its convergence rate is (
1+JS)I2,
which makes it faster than the bisection
method but slower than Newton's method. Similar to Newton's method, convergence
is
not guaranteed
if
initial values are not close to the root.
Lagrange multipliers
The method
of
Lagrange multipliers is a common technique used to find local
maximums/minimums
of
a multivariate function with one
or
more constraints.
6
5 Newton's method is also used in optimization-including multi-dimensional optimization
problems-to
find local minimums
or
maximums.
45

Calculus and Linear Algebra
Let
f(x,,
x2,
···,
xJ
be a function
of
n variables
x=(x"
x2,
···,
xJ
with gradient
vector
Vf(x)
= ( , , · ·
·,
!.
) . The necessary condition for maximizing or
minimizing
f(x)
subject
to
a set
of
k constraints
is
that'\lf(x)+A,Vg,(x)+A..iVg
2(x)+···+A.k'\lgk(x)=O, where A,,···,A.k are called the
Lagrange multipliers.
What is the distance from the origin to the plane
2x
+ 3 y +
4z
=
12
?
Solution: The distance (D) from the origin to a plane is the minimum distance between
the origin and points on the plane. Mathematically, the problem can be expressed as
min D2
=J(x,y,z)=x
2
+y2+z
2
s.t.
g(x,y,z)=2x+3y+4z-12=0
Applying the Lagrange multipliers, we have
qf
+A.
OJ
=
2x+
2A.
= 0
ax ax
.IL=-24/29
ar
+.IL
ar
=
2y+
3.IL
= 0
ay ay
ar
+.IL
OJ
=
2x
+
4.IL
= 0
az
az
x = 24 I 29
__..._
D =
(1i)2
(.J£)2
(
48
)2
=
___,,
29
+
29
+
29
y =
36129
v29
2x+3y+4z-12
= 0 z =
48/29
In general, for a plane with equation
ax+
by+
cz
=
d,
the distance to the origin
is
D=
ldl
.Ja2
+b2 +c2
3.
5 Ordinary Differential Equations
In
this section, we cover four typical differential equation patterns that are commonly
seen in interviews.
6 The method
of
Lagrange multipliers is a special case
of
Karush-Kuhn-Tucker (KKT) conditions, which
reveals the necessary conditions for the solutions to constrained nonlinear optimization problems.
46

A Practical Guide
To
Quantitative Finance Interviews
Separable differential equations
A separable differential equation has the form
dy
=
g(x)h(y)
. Since it is separable, we
dx
can express the original equation as dy =
g(x)dx.
Integrating both sides, we have the
h(y)
solution f
dy
= f
g(x)dx.
h(y)
A.
Solve ordinary differential equation y
'+
6xy
=
0,
y(O) = l
Solution: Let
g(x)
=
-6x
and
h(y)
=
y,
we have dy =
-6xdx
. Integrate both sides
of
y
the equation:
fdy
=
f-6xdx
lny=-3x
2
+c
y=e-
3x2
+",
where c is a constant.
y
Plugging in the initial condition y(O) =
1,
we have c = O and y = e-3x2•
B. Solve ordinary differential equation
y'
= x -Y .
7
x+y
Solution: Unlike the last example, this equation is not separable in its current form. But
we can use a change
of
variable to tum it into a separable differential equation. Let
z = x +
y,
then the original differential equation is converted to
d ( z -x) = x - ( z -
x)
dz -l = 2x -l
zdz
=
2xdx
fzdz
=
f2xdx
+ c
dx z dx z
(x+
y)
2 = z2 = 2x2
+c
y2 +
2xy-x
2 = c
First-order linear differential equations
A first-order differential linear equation has the form
dy
+
P(x)y
= Q(x). The standard
dx
approach to solving a first-order differential equation
is
to identify a suitable function
l(x)
, called an integrating factor, such that
l(x)(y'+
P(x)y)
=
l(x)y'+
l(x)P(x)y
7 Hint: Introduce variable z = x +
y.
47

Calculus and Linear Algebra
=(I(x)y)';
Then
we
have
(I(x)y)'
=
l(x)Q(x)
and
we can integrate both sides to solve
J
l(x)Q(x)dx
for
y:
I(x)y
= J
I(x)Q(x)dx
=>
y = .
I(x)
The integrating factor,
l(x),
must satisfy
dl(x)
=
I(x)P(x),
which means
l(x)
is
a
dx
separable differential equation with general solution
J(x)
=
ef
P<xldx. 8
Solve ordinary different equation
y'+
y
y(l)
=I,
where x > 0.
x x
Solution: This
is
a typical example
of
first-order linear equations with
P(x)
=
_!_
and
x
I JP(x)dx
Jo
/ x)dx 1 1
Q(x)
= - 2•
So
l(x)
= e = e =
e"x
= x and we have
l(x)Q(x)
=-.
x x
:.
l(x)(y'+
P(x)y)
= (
xy
)'
=
I(x)Q(x)
=I
Ix
Taking integration
on
both sides,
xy
= J
(l/
x)dx
=
lnx+c
=>
y =
lnx+c.
x
Plugging in y(l)
=I,
we
get c
=I
and
y = ln x +
1.
x
Homogeneous linear equations
A homogenous linear equation is a second-order differential equation with the form
d2 d
c(x)y
=
0.
dx
dx
It
is easy
to
show that,
if
y, and y2 are linearly independent solutions to the
homogeneous linear equation, then any
y(x)=c,y,(x)+c
2y2
(x),
where c1 and c2 are
arbitrary constants, is a solution to the homogeneous linear equation as well.
When a, b and c
(a
-:t:.
0 ) are constants instead
of
functions
of
x, the homogenous
linear equation has closed form solutions:
Let 'i and r2 be the roots
of
the characteristic equation ar2 +
br
+ c = O ,9
8 The constant c
is
not needed
in
this case since
it
just scales both sides
of
the equation
by
a factor.
48

A Practical Guide
To
Quantitative Finance Interviews
2.
If
1j
and r2 are real and
1j
= r2 = r, then the general solution
is
y = c1
erx
+ c2xerx;
3.
If
1j
and r2 are complex numbers
a±
ip,
then the general solution is
y = eax (c1 COS fJx + C2 sin
fJx).
It
is
easy to verify that the general solutions indeed satisfy the homogeneous linear
solutions by taking the first and secondary derivatives
of
the general solutions.
What is the solution
of
ordinary differential equation y
"+
y '+ y =
0?
Solution:
In
this specific case, we have
a=
b = c = 1 and b2
-4ac
=
-3
< 0 , so we have
complex roots r =
-1I2
± f3 I
2i
(a
=
-1I2,
f3
= f3 I 2
),
and
the general solution
to
the
differential equation is therefore
y =
eax(c
1
cospx+c
2
sinpx)
=
e-
112
x { c1
cos(.J3I2x)+c
2 sin(.J3 /
2x)
).
Nonhomogeneous linear equations
Unlike a homogenous linear equation a d2
-;'
+ b
dy
+ cy = 0, a nonhomogeneous linear
dx dx
equation a d2
3:
+ b
dy
+
cy
=
d(x)
has
no
closed-form solution. But
if
we
can find a
dx
dx
d2
dy
particular solution
yP(x)
for
a;,
+b
dx
+cy=d(x),
then
y=yP(x)+
y/x),
where
Yi:(x) is the general solution
of
the homogeneous equation a d2
3:
+b
dy
+cy
=0,
dx dx IS a
general solution
of
the nonhomogeneous equation a d2
3:
+ b
dy
+ cy =
d(x).
dx dx
9 A d . . ' b 0 h . b d . c I
-b
+
.J
b'
-4ac
qua
rat1c
equation
ar
+ r + c = as roots given y qua
rat1c
a r = - . You
2a
should either commit the formula to memory or
be
able to derive it using
(r
+ b I 2a)' =
(b'
-
4ac)
I
4a'.
49

Calculus and Linear Algebra
Although it may
be
difficult to identify a particular solution y P (
x)
in
general, in the
special case when
d(x)
is a simple polynomial, the particular solution is often a
polynomial
of
the same degree.
What is the solution
of
ODEs y
"+
y
'+
y = l and y
"+
y
'+
y =
x?
Solution:
In
these ODEs, we again have
a=
b = c = 1 and b2
-4ac
=
-3
< 0,
so
we have
complex solutions r =
-1I2
±
..f3
I
2i
(a
=
-1
I2, p =
..f3
I
2)
and the general solution is
y = e-
112
x { c1
cos(
.J3
I
2x)
+c
2 sin(
.J3
I
2x)
).
What is a particular solution for y
"+
y
'+
y = 1? Clearly y = l is.
So
the solution
to
y"+
y'+
y=1
is
To find a particular solution for y
"+
y
'+
y =
x,
Let
y P
(x)
= mx +
n,
then we have
So
the particular solution is
x-1
and
the solution
to
y
"+
y
'+
y = x is
y = y P(x) +
yg(x)
=
e-
112
x {
c,
cos(
.J3
I
2x)
+ c2 sin(
.J3
I
2x))
+(x-1).
3.
6 Linear Algebra
Linear algebra is extensively used in applied quantitative finance because
of
its role in
statistics, optimization, Monte Carlo simulation, signal processing, etc. Not surprisingly,
it is also a comprehensive mathematical field that covers many topics.
In
this section, we
discuss several topics that have significant applications in statistics and numerical
methods.
Vectors
An n x l (column) vector
is
a one-dimensional array.
It
can represent the coordinates
of
a point in the
Rn
(n-dimensional) Euclidean space.
50

A Practical Guide
To
Quantitative Finance Interviews
Inner product/dot product: the inner product (or dot product)
of
two
Rn
vectors x and
n
y is defined as L
X;Y;
=
xr
y
i=I
Euclidean
norm:
llxll
=ffx;
llx-yll
XTy
Then angle B between
Rn
vectors x and y has the property that cos B =
llxll
llYll
. x and Y
are orthogonal
if
xr
y =
0.
The correlation coefficient
of
two random variables can be
viewed as the cosine
of
the angle between them in Euclidean space ( p =cos(}).
There are 3 random variables
x,
y and z. The correlation between x and y is 0.8 and the
correlation between x and z is 0.8. What is the maximum and minimum correlation
between
y and z?
Solution: We can consider random variables
x,
y and z as vectors. Let B be the angle
between x and
y,
then we have cos B =
Px,
y = 0.8. Similarly the angle between x and z is
B as well. For y and z to have the maximum correlation, the angle between them needs
to be the smallest. In this case, the minimum angle is 0 (when vector y and z are
in
the
same direction) and the correlation
is
1.
For
the minimum correlation, we want the
maximum angle between
y and z, which is the case shown in Figure 3.2.
'
If
you
still
remember
some
trigonometry,
all
you
need
is that
cos(2B) = (cos8)2
-(sin
8)
2
= 0.82
-0.6
2 = 0.28
0.8
Otherwise,
you can
solve
the
problem
using
Pythagoras's
Theorem:
0.8x1.2 =
y z cos2B=
.J1
2
-0.96
2 = 0.28
0.6 0.6
Figure 3.2 Minimum correlation and maximum angle between vectors y and z
51

Calculus and Linear
Algebra
QR decomposition
QR decomposition: For each non-singular n x n matrix A, there
is
a unique pair
of
orthogonal matrix Q and upper-triangular matrix R with positive diagonal elements such
that A
=QR.
io
QR decomposition is often used to solve linear systems
Ax=
b when A is a non-singular
matrix. Since Q is an orthogonal matrix, Q-' =
QT
and QRx = b
Rx=
QT
b. Because R
is an upper-triangular matrix,
we
can begin with
xn
(the equation is simply
Rn,nxn
=(QT b
)n
),
and recursively calculate all
X;,
'Iii=
n,
n
-1,
···,I.
If
the programming language you are using does not have a function for the linear least
squares regression, how would you design an algorithm
to
do so?
Solution: The linear least squares regression is probably the most widely used statistical
analysis method.
Let's
go
over a standard approach to solving linear least squares
regressions using matrices. A simple linear regression with n observations can be
expressed as
Y;
=
/3
0
x;,o
+
/3
1
x;,
1 + ·
··
+
/3P_
1
x;,p-I +
si'
'Iii=
1,···,n,
where
X;o
=
1,
'Iii,
1s
the intercept
term and
x;,t
• • •
·,
xi,p- I are p
-1
exogenous regressors.
The goal
of
the linear least squares regression is to find a set
of
f3
=
[/3
0,
/3"
···,Pp-if
n
that makes the smallest.
Let's
express the linear regression in matrix format:
i=I
Y=X/3+&, where Y=[Yi,Yz,-··,f;,f and &=[s"&2,-··,&nf are both
nxl
column
vectors; X
is
a n x p matrix with each column representing a regressor (including the
intercept)
and
each row representing an observation. Then the problem becomes
n
min f
(/3)
=min L s;2 =
min(Y
-X
/3)r (Y -X
/3)
/)
/)
i=l
/)
10
A nonsingular matrix Q is called an orthogonal matrix
if
Q ' =
Q'.
Q is orthogonal
if
and only
if
the
columns (and rows)
of
Q form
an
orthonormal
set
of
vectors in R". The Gram-Schmidt
orthonormalization process (often
improved
to increase numerical stability) is often used for QR
decomposition. Please
refer
to a linear
algebra
textbook
if
you
are interested in the Gram-Schmidt process.
52

A Practical Guide To Quantitative Finance Interviews
To minimize the function
/(/3),
taking the first derivative' 1
of
f(/3)
with respect to
/3,
we have
/'(/3)
=
2Xr
(Y
-X
fl)=
0
(Xr
X)/J
=
xrY,
where
(Xr
X)
is a p x p
symmetric matrix and
xry
is a p x I column vector.
Let A =
(Xr
X)
and b =
xrY,
then the problem becomes
Afl
= b, which can
be
solved
using
QR
decomposition as we described.
Alternatively,
if
the programming language has a function for matrix inverse, we can
directly calculate
fl
as
fl=
(XT
xr'
XTY.
12
Since we are discussing linear regressions,
it's
worthwhile to point out the assumptions
behind the linear least squares regression (a common statistics question at interviews):
1.
The relationship between Y and
Xis
linear: Y = X
f3
+
&.
2.
E[&;]=O,
Vi=l,-··,n.
3. var(&;)=a2,
i=l,-··,n
(constant variance), andE[&;&J]=O,i;tj (uncorrelated
errors).
4.
No
perfect multicollinearity:
p(x;,x)
;t
±1,
i ;t j where
p(xi'x
1) is the
correlation
of
regressors
X;
and
xr
5.
& and
X;
are independent.
Surely in practice, some
of
these assumptions are violated and the simple linear least
squares regression is no longer the best linear unbiased estimator (BLUE). Many
econometrics books dedicate significant chapters to addressing the effects
of
assumption
violations and corresponding remedies.
Determinant, eigenvalue and eigenvector
Determinant: Let A be an n x n matrix with elements
{A;),
where i, j =
1,
· ·
·,
n.
The
determinant
of
A is defined as a scalar: det(A) =
Lfll(p)a
1
.p
1a2
.p
2 ···an.p., where
p
p
=(pl'
p2, •
··,
Pn) is any permutation
of
(I, 2, · ·
·,
n); the sum is taken
over
all
n!
possible permutations; and
11
To do that, you do need a little knowledge about matrix derivatives. Some
of
the important derivative
equations for vectors/matrices are
oa'
x = ox' a
=a,
ox
ox
o(Ax +
b)'
C(Dx
+e)
=A'
C(Dx
+e)
+
D'
C'
(Ax+
b),
ax
oAx
ox'
Ax
T 02
x'
Ax
a;=
A,
----;--- =
(A
+ A)x,
axax'
= 2A,
12
The matrix inverse introduces large numerical error
if
the matrix is close to singular or badly scaled.
53

Calculus and Linear Algebra
{I,
if
p can be coverted to natural order by even number
of
exchanges
lf/(p)=
. .
-1, 1f p can be coverted to natural order by odd number
of
exchanges
For example, determinants
of
2 x 2 and 3 x 3 matrices can
be
calculated as
de{[:
!
])
=ad
-be,
de{[:
:
rn
=
aei
+ bfg + cdh
-ceg-
ajh-
bdi.
13
I
Determinant properties: det(Ar) = det(A), det(AB) = det(A)det(B), det(A-1) =
--
det(A)
Eigenvalue: Let A be
an
n x n matrix. A real number
A.
is called
an
eigenvalue
of
A
if
there exists a nonzero vector x in
Rn
such that
Ax
= Ax. Every nonzero vector x
satisfying this equation
is
called an eigenvector
of
A associated with the eigenvalue
A.
.
Eigenvalues and eigenvectors are crucial concepts
in
a variety
of
subjects such as
ordinary differential equations, Markov chains, principal component analysis (PCA), etc.
The importance
of
determinant lies in its relationship to eigenvalues/eigenvectors.
14
The determinant
of
matrix A -
Al,
where I is an n x n identity matrix with ones on the
main diagonal and zeros elsewhere,
is
called the characteristic polynomial
of
A. The
equation det(A -
Al)=
0
is
called the characteristic equation
of
A. The eigenvalues
of
A are the real roots
of
the characteristic equation
of
A. Using the characteristic equation,
n n
we can also show that
A,A.i
···An = det(A) and
LA;=
trace(
A)=
IA;,;·
A
is
diagonalizable
if
and only
if
it has linearly independent eigenvectors.
15
Let
A,,
Ai,
· ·
·,
An
be the eigenvalues
of
A, x1, x2, • •
·,
xn
be the corresponding eigenvectors.
and X = [ x1 I x2 I··· I xn], then
X-
1
AX=
13
In
practice, determinant
is
usually not solved by the sum
of
all permutations because it is
computationally inefficient.
LU
decomposition and cofactors are often used to calculate determinants
instead.
14
Determinant can also be applied to matrix inverse
and
linear equations as well.
15
If
all n eigenvalues are real and distinct, then the eigenvectors are independent and A is diagonalizable.
54

A Practical Guide
To
Quantitative Finance Interviews
If
matrix A = [ what are the eigenvalues and eigenvectors
of
A?
Solution: This is a simple example
of
eigenvalues and eigenvectors.
It
can be solved
using three related approaches:
Approach
A:
Apply the definition
of
eigenvalues and eigenvectors directly.
Let.!
be an eigenvalue and x = [
::]
be its corresponding eigenvector.
By
definition, we
have
So either
A.
=
3,
in which case x1 = x2 (plug
A.
= 3 into equation 2x1 + x2 =
A.x
1
) and the
d.
l.
d . .
[I/
.Ji]
0 . h. h h
correspon
mg
norma
1ze
eigenvector
1s
I /
.J2
,
or
x1 + x2 = , m w
1c
case t e
normalized eigenvector is [
11
and
A.=
1 (plug x2 =
-x
1 into equation
-1/v2
2x1
+x
2 =
A.x
1
).
Approach
B:
Use equationdet(A-A./) =
0.
det( A -
A.I)
= 0
:::::::>
(2 -
A.
)(2 -
A.)
-1
=
0.
Solving the equation, we have
A,
= 1 and
Ai
= 3. Applying the eigenvalues to
Ax=
A.x,
we
can
get the corresponding
eigenvectors.
n n
Approach C: Use equations
A,
·Ai···
An
= det(A) and
LA;
=trace(
A)=
LA;,;·
i=I
det(A) =
2x
2-1x1=3
and trace(A) =
2x2
= 4.
A,xAi=3}
{A,=l
So we have
:::::::>
• Again apply the eigenvalues to Ax =
A.x,
and we
A,+Ai=4 Ai=3
can get the corresponding eigenvectors.
55

Calculus and Linear Algebra
Positive semidefinite/definite matrix
When A is a symmetric n x n matrix, as in the cases
of
covariance and correlation
matrices, all the eigenvalues
of
A are real numbers. Furthermore, all eigenvectors that
belong to distinct eigenvalues
of
A are orthogonal.
Each
of
the following conditions is a necessary and sufficient condition to make a
symmetric matrix A positive semidefinite:
1.
xr
Ax
0 for any n x 1 vector x .
2. All eigenvalues
of
A are nonnegative.
3. All the upper left (or lower right) submatrices
AK,
K =
1,
· ·
·,
n have nonnegative
determinants.
16
Covariance/correlation matrices
must
also be positive semidefinite.
If
there is
no
perfect
linear dependence among random variables, the covariance/correlation matrix must also
be positive definite. Each
of
the following conditions is a necessary and sufficient
condition to make a symmetric matrix A positive definite:
1.
xr
Ax
> 0 for any nonzero n x 1 vector x .
2. All eigenvalues
of
A are positive.
3. All the
upper
left (or lower right) submatrices
AK,
K =
1,
·
·.,
n have positive
determinants.
There are 3 random variables x, y
and
z. The correlation between x and y is 0.8 and the
correlation between x and z is 0.8. What is the maximum and minimum correlation
between
y and z?
Solution: The problem can be solved using the positive semidefiniteness property
of
the
correlation matrix.
Let the correlation between
y and z
be
p , then the correlation matrix for
x,
y and z is
p
0.8
0.8
0.81
p .
1
p
16
A necessary, but not sufficient, condition for matrix A to be positive semidifinite
is
that A has no
negative diagonal elements.
56

A Practical Guide
To
Quantitative Finance Interviews
det(P)
0
;
8
J)+o.8xdei([
0
;
8
=
(1-
p2
)-0.8
x
(0.8-0.8p)
+ 0.8x
(0.8p-0.8)
=
-0.28
+ l
.28p-
p2
;;:::
0
So the maximum correlation between y and z is
1,
the minimum is 0.28.
LU decomposition and Cholesky decomposition
Let A be a nonsingular n x n matrix. LU decomposition expresses A as the product
of
a
lower and upper triangular matrix:
A=
LU.
17
LU
decomposition can be use to solve
Ax=
b and calculate the determinant
of
A:
n n
LUx = b
Ux
=
y,
Ly=
b;
det(A) = det(L)det(U)
=II
L;,;f]
uj,j"
i=I
j=I
When A is a symmetric positive definite matrix, Cholesky decomposition expresses A
as A =
RT
R, where R is a unique upper-triangular matrix with positive diagonal entries.
Essentially, it is a
LU
decomposition with the property L =UT.
Cholesky decomposition is useful in Monte Carlo simulation to generate correlated
random variables as shown in the following problem:
How do you generate two N(O,l) (standard normal distribution) random variables with
correlation p
if
you have a random number generator for standard normal distribution?
Solution: Two _N(O,l) random variables
xP
x2
with a correlation p can
be
generated
from independent N(O,
1)
random variables z1, z2 using the following equations:
X1
=Z1
X2
=
PZ1
+ p2
Z2
It
is easy to confirm that var( x1
) = var( z1
) =
1,
var( x2) = p2
var( z1
) +
(1-
p2) var( z2) =
1,
and cov(xpx2) = cov(z1
,pz
1
+ p2
z2) = cov(z1
,pz
1
) =
p.
This approach is a basic example using Cholesky decomposition to generate correlated
random numbers. To generate correlated random variables that follow an-dimensional
17
LU decomposition occurs naturally in Gaussian elimination.
57

Calculus and Linear Algebra
multivariate normal distribution X =
[X"
X2
,-··,XJT
N(µ,
I)
with mean
µ = [µ,, µ2, • •
·,
µn
f and covariance matrix I (a n x n positive definite matrix)
18
, we can
decompose the covariance matrix I into
RT
R and generate n independent
N(O,
1)
random variables
z"
z2,
···,
zn.
Let vector Z = [z,, z2
,-··,znf,
then X can be generated
asX=µ+RTZ.
19
Alternatively, X can also be generated using another important matrix decomposition
called singular value decomposition (SVD):
For
any n x p matrix X, there exists a
factorization
of
the form X =
UD
VT,
where U and V are n x p and p x p orthogonal
matrices, with columns
of
U spanning the column space
of
X, and the columns
of
V
spanning the row space; D is a p x p diagonal matrix called the singular values
of
X.
For a positive definite covariance matrix, we have V = U and L =
UDUT.
Furthermore,
D is the diagonal matrix
of
eigenvalues
A,,
Ai,
· ·
·,
A,n
and U
is
the matrix
of
n
corresponding eigenvectors. Let D
112
be a diagonal matrix with diagonal elements
Ji;,
JI;.,
···,
Ji:,
then it
1s
clear that D =
(D
112 )2 = (D
112
)(D
112 f and
I=
UD
112
(UD
112
)T.
Again,
if
we generate a vector
of
n independent N(O,
1)
random
variables Z =
[z"
z2
,.
• •
,zJ
7
',
X can be generated as X = µ + (UD
112
)Z.
18
Th
bb"l"
d · f 1· ·
Id"
"b
· ·
cxp(-'.<x-µ)'I'(x-µ))
e pro a 1 tty enstty o mu ttvanate
nonna
1stn utton ts
f(x)
=
. ( 21i
19
In general,
if
y
=AX+
h, where A and
bare
constant, then the covariance matriceI:,.,. =
Ar
......
A'
.
58

Chapter 4 Probability Theory
Chances are that
you
will
face
at least a couple
of
probability problems in most
quantitative interviews. Probability theory
is
the foundation
of
every aspect
of
quantitative finance.
As
a result, it has become a popular topic in quantitative interviews.
Although good intuition and logic can help you solve many
of
the probability problems,
having a thorough understanding
of
basic probability theory will provide you with clear
and concise solutions to most
of
the problems you are likely
to
encounter. Furthermore,
probability theory is extremely valuable
in
explaining some
of
the seemingly-
counterintuitive results. Armed with a little knowledge, you will find that many
of
the
interview problems are no more than disguised textbook problems.
So we dedicate this chapter to reviewing basic probability theory that is not only broadly
tested in interviews
but
also likely to be helpful for your future career. 1 The knowledge
is applied to real interview problems to demonstrate the power
of
probability theory.
Nevertheless, the necessity
of
knowledge in
no
way
downplays the role
of
intuition and
logic. Quite the contrary, common sense and sound judgment are always crucial for
analyzing and solving either interview or real-life problems. As you will see in the
following sections, all the techniques we discussed in Chapter 2 still play a vital role in
solving many
of
the probability problems.
Let's have some
fun
playing the odds.
4. 1 Basic Probability Definitions
and
Set
Operations
First
let's
begin with some basic definitions and notations used in probability. These
definitions and notations may seem dry without
examples-which
we
will present
momentarily-yet
they are crucial to our understanding
of
probability theory. In
addition, it will lay a solid ground for us to systematically approach probability
problems.
Outcome
(w): the outcome
of
an experiment or trial.
Sample space/Probability space
(0):
the set
of
all possible outcomes
of
an experiment.
1 As I have emphasized in Chapter 3, this book does not teach probability or any other math topics due to
the space
limit-it
is
not
my
goal to
do
so, either. The
book
gives a summary
of
the frequently-tested
knowledge and shows
how
it can
be
applied to a wide range
of
real interview problems. The knowledge
used in this chapter
is
covered by most introductory probability books. It
is
always helpful to pick up one
or two classic probability books
in
case you want to refresh your memory
on
some
of
the topics. My
personal favorites are First Course in Probability by Sheldon Ross and Introduction
to
Probability by
Dimitri P. Bertsekas and John
N.
Tsitsiklis.

Probability Theory
P(w):
Probability
of
an outcome ( P(w) 0, V
men,
L P(m) = 1
).
(OE!l
Event: A set
of
outcomes and a subset
of
the sample space.
P(A):
Probability
of
an event A, P(A) = L P(m).
roEA
Au
B:
Union
Au
B is the set
of
outcomes in event A
or
in event B (or both).
An
B
or
AB : Intersection A n B (or AB )
is
the set
of
outcomes
in
both A and
B.
Ac:
The complement
of
A, which is the event "not A".
Mutually
Exclusive:
An
B =
ct>
where
ct>
is an empty set.
Forany
mutually exclusive events E,, £2
,.
• •
E"
,
P(
Q
E;)
= t P(E;).
Random
variable:
A function that maps
each
outcome
(ro)
in the sample space (Q) into
the set
of
real numbers.
Let's use the rolling
of
a six-sided dice to explain these definitions and notations. A roll
of
a dice has 6 possible outcomes (mapped
to
a random variable):
1,
2, 3,
4,
5, or
6.
So
the sample space Q is {1,2,3,4,5,6} and the probability
of
each outcome is
116
(assuming a fair dice). We can define an event A representing the event that the outcome
is an odd number A =
{1,
3, 5}, then the complement
of
A is
Ac
=
{2,
4,
6}
. Clearly
P(
A) =
P(l)
+ P(3) +
P(
5) = 1I2. Let B be the event that
the
outcome is larger than
3:
B =
{4,
5,
6}.
Then the union is
Au
B =
{1,
3,
4,
5,
6}
and the intersection is
An
B =
{5}.
One popular random variable called indicator variable (a binary dummy
variable) for event A is defined as the following:
{
1,
if
X E
{1,
3,
5}
I A = . Basically I A = 1
when
A occurs and I A = 0
if
A'.
occurs. The
0,
if
{1,
3,
5}
expected value
of
I A is
£[I
A]=
P(A).
Now, time for some examples.
60

A Practical Guide
To
Quantitative Finance Interviews
Coin toss game
Two gamblers are playing a coin toss game. Gambler A has
(n
+
1)
fair coins; B has n
fair coins. What is the probability that A will have more heads than B
if
both flip all their
coins?2
Solution: We have yet to cover all the powerful tools probability theory offers. What do
we have now? Outcomes, events, event probabilities, and surely our reasoning
capabilities! The one extra coin makes A different from B.
If
we remove a coin from
A,
A and B will become symmetric. Not surprisingly, the symmetry will give us a lot
of
nice properties.
So
let's
remove the last coin
of
A and compare the number
of
heads
in
A's
first n coins with
B's
n coins. There are three possible outcomes:
£1:
A's
n coins have more heads than
B's
n coins;
£2:
A's
n coins have equal number
of
heads as
B's
n coins;
£3:
A's
n coins have fewer heads than
B's
n coins.
By symmetry, the probability that A has more heads is equal
to
the probability that B has
more heads.
So
we
have
P(E
1) =
P(E
3
).
Let's
denoteP(E
1) =
P(E
3) = xand
P(E
2) = y.
Since L
P(
m) =
1,
we have
2x
+ y =
1.
For event £1, A will always have more heads
men
than B no matter what
A's
(n+l)th
coin's side is; for event £3, A will have no more
heads than B
no
matter what
A's
(n+l)th
coin's side
is.
For event £2,
A's
(n+l)th
coin does make a difference.
If
it's
a head, which happens with probability 0.5, it will
make A have more heads than
B.
So the
(n
+ l)th coin increases the probability that A
has more heads than B by 0.5 y and the total probability that A has more heads
is
x+0.5y=x+0.5(1-2x)=0.5
when A has
(n+l)
coins.
Card game
A casino offers a simple card game. There are 52 cards
in
a deck with 4 cards for each
jack queen king ace
value 2,
3,
4,
5,
6,
7, 8, 9,
10,
J,
Q,
K,
A.
Each time the cards are thoroughly shuffled
(so each card has equal probability
of
being selected). You pick up a card from the deck
and the dealer picks another one without replacement.
If
you have a larger number, you
win;
if
the numbers are equal or yours is smaller, the house
wins-as
in
all other casinos,
the house always has better odds
of
winning. What is your probability
of
winning?
2 Hint: What are the possible results (events)
if
we compare the number
of
heads in
A's
first n coins with
B's
n coins? By making
the
number
of
coins equal, we can take advantage
of
symmetry. For each event,
what will happen
if
A's
last coin is a head?
Or
a tail?
61

Probability Theory
Solution: One answer to this problem
is
to consider all
13
different outcomes
of
your
card. The card can have a value 2,
3,
···,A
and each has 1/13
of
probability. With a
value
of
2, the probability
of
winning is 0/51; with a value
of
3, the probability
of
winning is 4/51 (when
the
dealer picks a 2);
...
; with a value
of
A, the probability
of
winning is 48/51 (when the dealer picks a 2, 3, · · ·, or K).
So
your probability
of
. . .
wmnmg
ts
1 ( 0 4
48)
4 4 12x13 8
iix
51+51+···+51
=
13x51x(O+l+···+l
2
)=13x51
x 2
=17·
Although this is a straightforward solution and it elegantly uses the sum
of
an integer
sequence, it is not the most efficient way to solve the problem.
If
you have got
the
core
spirits
of
the coin tossing problem, you may approach the problem by considering three
different outcomes:
E,
: Your card has a number larger than the dealer's;
£2 : Your card has a number equal to the dealer's;
£3: Your card has a number lower than the dealer's.
Again by symmetry, P(E,) =
P(E
3
).
So
we only need to figure out
P(E
2
),
the
probability that two cards have equal value.
Let's
say you have randomly selected a card.
Among the remaining
51
cards, only 3 cards will have the same value as your card. So
the probability that the
two
cards have equal value
is
3/51. As a result, the probability
that you win is
P(
E,)
= (
1-
P(
E2
))
I 2 =
(1-
3 I 51) I 2 = 8I17.
Drunk passenger
A line
of
100
airline passengers are waiting to board a plane. They each hold a ticket to
one
of
the 100 seats on that flight. For convenience, let's say that the n-th passenger in
line has a ticket for the seat number
n.
Being drunk, the first person in line picks a
random seat (equally likely for each seat). All
of
the other passengers are sober, and will
go
to
their proper seats unless it is already occupied;
In
that case, they will randomly
choose a free seat. You're person number 100. What
is
the probability that you end up
in your seat (i.e., seat #100) ?3
Solution: Let's consider seats
#1
and #100. There are
two
possible outcomes:
3 Hint:
If
you are trying to
use
complicated conditional probability to solve the problem,
go
back and think
again.
If
you decide to start with a simpler version
of
the problem, starting with two passengers and
increasing the number
of
passengers to show a pattern by induction, you can solve the problem more
efficiently. But the problem
is
much simpler than that. Focus on events and symmetry
and
you will have
an intuitive answer.
62

£1 : Seat # 1 is taken before # 100;
£2 : Seat # 100 is taken before #
1.
A Practical Guide To Quantitative Finance Interviews
If
any
passenger
takes seat # 100 before # 1 is taken, surely you will not
end
up
in you
own seat.
But
if
any passenger takes # 1 before #
100
is taken,
you
will definitely
end
up
in you
own
seat.
By
symmetry,
either
outcome has a probability
of
0.5. So the
probability that you
end
up
in your
seat
is 50%.
In case
this
over-simplified version
of
reasoning is not clear
to
you, consider the
following detailed explanation:
If
the
drunk
passenger takes
#1
by
chance, then
it's
clear
all the
rest
of
the passengers will
have
the correct seats.
If
he takes # 100, then you will
not get
your
seat. The probabilities
that
he takes #1
or
#100 are equal. Otherwise assume
that he
takes
the n-th seat, where n is a number
between
2 and 99. Everyone between 2
and
(n-1)
will get his
own
seat.
That
means the
n-th
passenger essentially becomes the
new
"drunk"
guy with designated
seat
#1.
If
he chooses #1, all the rest
of
the passengers
will have the correct seats.
If
he
takes
# 100,
then
you
will
not
get your seat. (The
probabilities that he takes # 1 or #
100
are again equal.) Otherwise he will
just
make
another passenger
down
the line the
new
"drunk"
guy
with designated seat # 1
and
each
new
"drunk"
guy has equal probability
of
taking #1
or
#100. Since
at
all
jump
points
there's
an
equal probability for the
"drunk"
guy
to
choose seat #1
or
100,
by
symmetry,
the probability that you, as the
lOOth
passenger,
will
seat in #100 is 0.5.
N points on a circle
Given N points drawn randomly on
the
circumference
of
a circle,
what
is the probability
that they
are
all within a semicircle?4
Solution:
Let's
start
at
one
point
and
clockwise label the points as
1,
2, · ·
·,
N . The
probability that all the remaining N
-1
points
from
2 to N are in the clockwise
semicircle starting at
point
1 (That is,
if
point 1 is
at
12:00, points 2 to N are all
between 12:00 and 6:00) is 1I2N-i. Similarly the probability that a clockwise semicircle
starting
at
any
point
i,
where i e {2, · ·
·,
N} contains all the other N
-1
points is also
1/
2N-I.
Claim: the events that all the other N
-1
points
are
in the clockwise semicircle starting
at
point i, i =
1,
2, · ·
·,
N are mutually exclusive.
In
other
words,
if
we,
starting
at
point i
and proceeding clockwise along the circle, sequentially encounters points i +
1,
i + 2, · · ·,
N,
1,
· ·
·,
i
-1
in
half
a circle, then starting
at
any
other
point
j,
we
cannot encounter all
4 Hint: Consider the events that starting from a point n, you
can
reach all the rest
of
the points on the circle
clockwise, n E
{I,
...
,
N}
in a semicircle. Are these events mutually exclusive?
63

Probability Theory
other points within a clockwise semicircle. Figure 4.1 clearly demonstrates this
conclusion.
If
starting at point i and proceeding clockwise along the circle,
we
sequentially encounter points i +
1,
i + 2, ·
·.,
N,
1,
·
·.,
i
-1
within
half
a circle, the
clockwise arc between i
-1
and i must be no less than
half
a circle.
If
we
start at any
other point, in order to reach all other points clockwise, the clockwise arc between i
-1
and i are always included. So we cannot reach all points within a clockwise semicircle
starting from any other points. Hence, all these events are mutually exclusive and
we
have
P(QE}
t.P(E;)=>P(QE}
Nxl/2"-'
N
12"-'
The same argument can be extended to any arcs that have a length less than half a circle.
If
the ratio
of
the arc length to the circumference
of
the circle is x ( x
1I2
), then the
probability
of
all N points fitting into the arc is N x
xN-i.
,
<x
' ' ' ' ' ' ' ' ' ' ' ' ' ' '
i-1
Figure 4.1 N points fall in a clockwise semicircle starting from i
4.2 Combinatorial Analysis
Many problems in probability theory can be solved by simply counting the number
of
different ways that a certain event can occur. The mathematic theory
of
counting is
often referred to as combinatorial analysis (or combinatorics).
In
this section,
we
will
cover the basics
of
combinatorial analysis.
Basic principle
of
counting: Let S be a set
of
length-k sequences.
If
there are
64

A Practical Guide
To
Quantitative Finance Interviews
• n1 possible first entries,
• n2 possible second entries for each first entry,
• n3 possible third entries for each combination
of
first and second entries, etc.
Then there are a total
of
n1 • n2
· · ·
nk
possible outcomes.
Permutation: A rearrangement
of
objects into distinct sequence (i.e., order matters).
Property: There are n ! different permutations
of
n objects,
of
which n1 are
n1
!n2
!.
..
nr
!
alike, n2 are alike, · ·
·,
nr
are alike.
Combination: An unordered collection
of
objects (i.e., order doesn't matter).
Property: There are
(nJ
= n ! different combinations
of
n distinct objects taken
r
(n-r)!r!
r at a time.
Binomial theorem:
(x+
yy
=
:t(nJxk
yn-k
k;O
k
Inclusion-Exclusion Principle:
P(E
1 u £2) =
P(E
1) +
P(E
2
)-
P(E
1
Ei)
P(E
1 u £2 u £3) =
P(E
1) +
P(E
2) +
P(E
3
)-P(E
1
E2
)-P(E
1
E3
)-P(E
2E3) +
P(E
1
E2E3)
and more generally,
N
P(E
1
u£
2 u
...
uEN)
=
_LP(E;)-
I P(E;1
E;
2
)+···+(-1y+
1 I P(E;1
E;
2 • • •
E;,)+···
i=I i1
<i2 i1
<i2 < ... i,
+
(-1t+I
P(E1E2
...
EN)
where
""'"'
P(E;
E;
···E;)
has
(NJ
terms.
£..J
1 2 , r
i1
<i
1<
..
.ir
Poker hands
Poker is a card game in which each player gets a hand
of
5 cards. There are 52 cards in a
deck. Each card has a value and belongs
to
a suit. There are
13
values,
jack queen king ace spade club
hean
diamond
2,
3,
4,
5,
6, 7,
8,
9, 10,
J,
Q,
K,
A,
and four suits, • ,
"',
• , • .
65

Probability Theory
What are the probabilities
of
getting hands with four-of-a-kind
(four
of
the five cards
with the same value)? Hands with a full house (three cards
of
one value and two cards
of
another value)? Hands with two pairs?
Solution: The number
of
different
hands
of
a five-card draw is the number
of
5-element
subsets
of
a 52-element so total
number
of
hands ( 5
5
2) 2, 598, 960.
Hands with a four-of-a-kind: First
we
can choose the value
of
the
four cards with the
same value, there are
13
choices.
The
5th card
can
be any
of
the rest 48 cards (12
choices for values
and
4 choices for suits). So the
number
of
hands with four-of-a kind is
13x48
=
624.
Hands with a Full House: In sequence we need
to
choose the value
of
the triple,
13
choices; the suits
of
the
triple,
(;)
choices; the value
of
the pair, 12 choices;
and
the
suits
of
the pair, ( choices.
So
the number
of
hands
with
full house
is
13x(;)xl2xG)
13x4x
12x6
3,
744.
Hands with Two Pairs: In sequence
we
need to choose the
values
of
the two pairs,
choices; the suits
of
the first pair, ( choices; the suits
of
the
second pair, (
choices; and the remaining card,
44
(
52-4
x 2, since the last cards can not have the
same value as either pair) choices.
So
the number
of
hands with
two
pairs is
78x6x6x
To calculate the probability
of
each,
we
only need
to
divide the
number
of
hands
of
each
kind
by
the total possible number
of
hands.
Hopping rabbit
A rabbit sits at the
bottom
of
a staircase with n stairs. The rabbit
can
hop up only one
or
two stairs at a time.
How
many different ways are there for the rabbit to ascend to the
top
of
the stairs?5
5 Hint: Consider an induction approach. Before the final hop to reach
then-th
stair, the rabbit can be at
either the (n-1 )th stair
or
the (n-2)th stair assuming n > 2.
66

A Practical Guide
To
Quantitative Finance Interviews
Solution: Let's begin with the simplest cases
and
consider solving the problem for any
number
of
stairs using induction. For n
=I
, there
is
only one way and f
(1)
=I.
For
n = 2, we can have one 2-stair hop or two I-stair hops. So f (2) =
2.
For any n >
2,
there are always two possibilities for the last hop, either it's a I-stair
hop
or a 2-stair
hop.
In
the former case, the rabbit
is
at
(n-1)
before reaching n, and it
has
f(n
-1)
ways to
reach (n
-1).
In
the latter case, the rabbit is at
(n-2)
before reaching n, and it has
f(n-2)
ways to reach
(n-2).
So
we
have
f(n)=f(n-2)+/(n-l).
Using this
function we can calculate
f(n)
for n =
3,
4,
· · ·
6
Screwy pirates 2
Having peacefully divided the loot (in chapter 2), the pirate team goes
on
for more
looting and expands the group to
11
pirates.
To
protect their hard-won treasure, they
gather together to
put
all the loot in a safe. Still being a democratic bunch, they decide
that only a majority -any majority -
of
them together can open the safe.
So
they
ask a locksmith to put a certain number
of
locks
on
the safe. To access the treasure,
every lock needs to be opened. Each lock can have multiple keys; but each key only
opens one lock. The locksmith can give more than one key to each pirate.
What is the smallest number
of
locks needed? And
how
many keys must each pirate
carry?7
Solution: This problem
is
a good example
of
the application
of
combinatorial analysis
in
information sharing and cryptography. A general version
of
the problem was explained
in
a 1979 paper
"How
to Share a Secret"
by
Adi Shamir. Let's randomly select 5 pirates
from the I I-member group; there must be a lock that none
of
them has the key
to.
Yet
any
of
the other 6 pirates must have the key to this lock since any 6 pirates can open all
locks. In other words,
we
must have a "special" lock
to
which none
of
the 5 selected
pirates has a key and the other 6 pirates all have keys. Such 5-pirate groups are randomly
selected. So for each combination
of
5 pirates, there must be such a "special" lock. The
minimum number
of
locks needed is
(I
I)
=
__!__!_!_
= 462 locks. Each lock has 6 keys,
5 5!6!
which are given to a unique 6-member subgroup. So each pirate must have
462x6
---
= 252 keys. That's surely a lot
of
locks to put
on
a safe
and
a lot
of
keys for
11
each pirate to carry.
6 You may have recognized that the sequence is a sequence
of
Fibonacci numbers.
7 Hint: every subgroup
of
6 pirates should have the same key to a unique lock that the other 5 pirates do
not have.
67

Probability Theory
Chess tournament
A chess tournament has
2n
players with skills 1 > 2 > · · · >2".
It
is
organized
as
a
knockout tournament, so that after each round only the winner proceeds to the next
round. Except for the final, opponents in each round are drawn at random. Let's also
assume that when two players meet in a game, the player with better skills always wins.
What's the probability that players 1 and 2 will meet
in
the final?8
Solution: There are at least two approaches to solve the problem. The standard approach
applies multiplication rule based on conditional probability, while a counting approach
is far more efficient. (We will cover conditional probability in detail
in
the
next
section.)
Let's begin with the conditional probability approach, which is easier to grasp. Since
there are
2n
players, the tournament will have n rounds (including the final). For round
1,
players 2,3,-··,2n each have 2n1
_ 1 probability to be 1
's
rival, so the probability that
1 d 2 d . d 1 .
2n
-2
2x(2n-l
-1)
C
d"
. h 1 d 2 d
an o not meet m roun is
--
= . on ition on t at
an
o not
2n
-1
2n
-1
meet in round
1,
2n-i
players proceed to the
2nd
round and the conditional probability
2n-l
- 2 2 X
(2n-
2
-1)
that 1 and 2 will
not
meet in round 2
is
1 = 1 • We can repeat the same
2n-
-1
2n-
-1
process until the
(n
-l)th round, in which there are 22 (=
2n
I
2n-
2) players left and the
conditional probability that 1 and 2 will not meet in round ( n
-1)
is
22
-2
2x(2
2-1
-l)
=----
22-1
22
-1
Let E1 be the event that 1 and 2 do not meet in round
1;
E2 be the event that 1 and 2 do not meet in rounds
1and2;
En-i
be the event that 1 and 2 do not meet in round
1,
2,
· · ·, n
-1.
Apply the multiplication rule, we have
P(l
and 2 meet in the nth
game)=
P(E
1) x
P(E
2 I E1) x · · · x P(En-i I E1E2 • • •
En_
2)
2 X
(2n-l
-
J)
2 X (2n-2
-J)
2 X (22
-l
-1)
2n-I
= X
X···X
=--
2n
-l
2n-I
- l 22 - )
2n
-1
8 Hint: Consider separating the players to two 2•-' subgroups. What will happen
if
player 1 and 2 in the
same group?
Or
not in the same group?
68

A Practical Guide
To
Quantitative Finance Interviews
Now let's
move
on to the counting approach. Figure
4.2A
is the general case
of
what
happens in the final. Player 1 always wins,
so
he will
be
in the final. From the figure, it
is obvious that
2n
players are separated to two
2n-i
-player subgroups and each group
will have one player reaching the final. As shown in Figure
4.28,
for player 2 to reach
the final, he/she must
be
in a different subgroup from
1.
Since
any
of
the remaining
players in 2,
3,
· ·
·,
2n
are likely to be
one
of
the
(2n-i
-
1)
players in the same subgroup
as player 1
or
one
of
the
2n-i
players in the subgroup different from player 1, the
probability that 2
is
in a different subgroup from 1
and
that I and 2
will
meet in the final
is simply Clearly,
the
counting approach provides not only a simpler solution
but
2n
-1
also more insight to the problem.
General Case
nth
round I
/\
(n-l)th
round 1 +
?
I
t
+
?
/\
? +
?
2n-I
players
2n-I
players
A
1 & 2 in the Final
1
nth round I
/\
(n-l)thround
1 +
?
t
+
2
/\
2 +
?
2n-I
players
2n-I
players
B
Figure 4.2A The general case of separating
2"
players into
2"-
1-player subgroups;
4.28
The special case with players 1 and 2 in different groups
Application letters
You're sending
job
applications to 5 firms: Morgan Stanley, Lehman Brothers, UBS,
Goldman Sachs, and Merrill Lynch.
You
have 5 envelopes
on
the table neatly typed with
names
and
addresses
of
people at these 5 firms.
You
even
have
5 cover letters
personalized to each
of
these
firms.
Your
3-year-old
tried
to be helpful and stuffed
each
cover letter into each
of
the
envelopes for you. Unfortunately she randomly put letters
69

Probability Theory
into envelopes without realizing that the letters are personalized. What is the probability
that all 5 cover letters are mailed to the wrong firms?9
Solution: This problem is a classic example for the Inclusion-Exclusion Principle. In fact,
a more general case is an example
in
Ross' textbook
First
Course in Probability.
Let's denote by E;, i = l,··
·,5
the event that the i-th letter has
the
correct envelope. Then
P ( is the probability that at least one letter has
the
correct envelope and
1-P(
is the probability that all letters have the wrong envelopes.
P(
can
be calculated using the Inclusion-Exclusion Principle:
t.P(E,)-
P(E1E2
···E,)
It's obvious thatP(E;)
=_!_
,
Vi=
1,-··,5. So
i:P(E;)
= 1.
5 i=I
P(E;,E;) is the event that both letter
i,
and letter i2 have
the
correct envelope. The
probability that i1 has the correct envelope is 1I5; Conditioned on that i1 has the correct
envelope, the probability that i2 has the correct envelope
is
1I4
(there are only 4
envelopes left).
So
P(E,.E;
)=_!_x-
1
-=
(5-2
)!.
I 2 5
5-1
5!
There are (5J = 5! members
of
P(E;,E;)
in
LP(E;,E;),
so we have
2
2!(5-2)!
i1<i2
"f\'p(£
.£ .
)=(5-2)!x
5!
=J__
t:
11
12
5!
2!(5-2)!
2!
Similarly we have
"f\'
P(E;
E;
E;)
=
_!__,
.
L...i.
I 2 ) 3 I
I
P(E
E
···E
)=-
' 2 5
5!
I1<I2<l.1
•
1
"f\'
P(E.
E.
E..
E)
=-,
and
L...i
,,
'2
,,
'•
4 I
i1<i:!
<iJ<
i4
•
9 Hint: The complement is that at least one letter is mailed to the correct
firm
.
70

A Practical Guide
To
Quantitative Finance Interviews
:.
__
I
+_!_=!2_
i=I 1
2!
3!
4!
5!
30
So the probability that all 5 letters are mailed to the wrong firms is
1-
P
(.:_p;)
=
!.!_.
i=I 30
Birthday problem
How many people do we need in a class to make the probability that two people have the
same birthday more than 1/2? (For simplicity, assume 365 days a year.)
Solution: The number is surprisingly small: 23. Let's say
we
have n people in the class.
Without any restrictions, we have 365 possibilities for each individual's birthday. The
basic principle
of
counting tells us that there are
365n
possible sequences.
We want to find the number
of
those sequences that have no duplication
of
birthdays.
For the first individual, we can choose any
of
the 365 days; but for the second, only 364
remaining choices left, ... , for the rth individual, there are 365 -r
+I
choices. So for n
people there are 365 x 364 x · · · x
(365-
n +
1)
possible sequences where no two
individuals have the same birthday.
We
need to have 365 x 364 x · · · x (365 -n
+I)
< 1/ 2
365n
for the odds to be in our favor. The smallest such n is 23.
100th digit
What
is
the 1
OOth
digit to the right
of
the decimal point in the decimal representation
of
(1
+
.fi.)3000
?10
Solution:
If
you still have not figure out the solution from the hint, here is one more hint:
(1
+
J2
r +
(1-
.Ji.
r is an integer when n = 3000.
Applying the binomial theorem for ( x +
yr
, we have
n
(nJ
k n
(nJ
k n
(nJ
k
k
in-kJ2
= L k
in-k.fi_
+ L k
in-kJ2
k-0
k=2j.OSJS!!_ k=2J+l,OSJ<!!_
2 2
10
Hint:
(1
+
.J2
)2 +
(1-
.J2
)2 = 6 . What will happen to
(1-
.J2
)2n as n becomes large?
71

Probability Theory
n
(nJ
k
So
(1
+
J2
r +
(1
-
J2.
y = 2 L k 1
n-k
J2.
' which
is
always an integer.
It
is easy to
2
see that
0<(1-J2.)
3000 <<10-100• So the
100thdigitof(l+J2r
mustbe9.
Cubic of integer
Let x be
an
integer between 1 and
10
12
, what
is
the probability that the cubic
of
x ends
with 11?
11
Solution:
All
integers can be expressed as x =
a+
1
Ob,
where a is the last digit
of
x.
Applying the binomial theorem, we have x3 = (a + 1
Ob
)3 = a3 +
30a
2
b + 300ab2 + 1000b3•
The unit digit
of
x3 only depends on a3• So a3 has a unit digit
of
1.
Only a = 1 satisfies
this requirement and a3 =
1.
Since a3 =
1,
the tenth digit only depends on
30a
2
b = 30b.
So we must have that 3b ends in
1,
which requires the last digit
of
b to be
7.
Consequently, the last two digits
of
x should be 71, which has a probability
of
1 % for
integers between I and
10
12
•
4.3 Conditional Probability
and
Bayes' formula
Many financial transactions are responses to probability adjustments based on
new-and
most likely incomplete-information. Conditional probability surely is one
of
the most
popular test subjects in quantitative interviews. So in this section, we focus on basic
conditional probability definitions and theorems.
Conditional probability
P(A
I
B):
If
P(B)
>
0,
then
P(A
I
B)
=
P(AB)
is
the fraction
P(B)
of
B outcomes that are also A outcomes.
11
Hint: The last two digits
of
x3 only depend on the last two digits
of
x.
72

A Practical Guide To Quantitative Finance Interviews
Law
of
total orobabilitv: for any mutually exclusive events {
F;}
, i =
1,
2, · · ·,
n,
whose
n
union is the entire sample space (
F;
n F1
=<I>,
Vi
-:1;
j;
LJ
F;
= n
),
we
have
i =I
n
P(E)
=
P(EF;)+P(EF
2) + ·
··
+P(EFn)
=LP(£
I
F;)P(F;)
i=I
=
P(E
I
F;)P(F;)
+
P(E
I F;_)P(F
2) + ·
··
+
P(E
I Fn)P(F,,)
Independent events:
P(EF)
=
P(E)P(F)
=>
P(EFc)
=
P(E)P(Fc).
Independence is a symmetric relation: X is independent
of
Y
<=>
Y is independent
of
X.
P(E
I
F.
)P(F.)
8 ' F I
P(F.
I
£)
--
J J
ayes
ormu
a:
J n
if
F;, i =
1,
·
·.,
n, are mutually
L
P(E
IF;
)P(F;)
i=l
exclusive events whose union is the entire sample space.
As the following examples will demonstrate, not all conditional probability problems
have intuitive solutions. Many demand logical analysis instead.
Boys and girls
Part A. A company is holding a dinner for working mothers with at least one son. Ms.
Jackson, a mother with two children, is invited. What is the probability that both
children are boys?
Solution: The sample space
of
two children
is
given by
0=
{(b,b),(b,g),(g,b),(g,g)}
(e.g.,
(g,
b) means the older child is a girl and the younger child a boy), and each
outcome has the same probability. Since Ms. Jackson is invited, she has at least one son.
Let B be the event that at least one
of
the children is a boy and A be the event that both
children are boys, we have
P(A
I B) =
P(A
nB)
=
P(
{(b,b)}) =
_11_4
=
_!_
P(B)
P(
{(b,b),(b,g),(g,b)}) 3 I 4 3
Part
B.
Your new colleague,
Ms.
Parker is known to have two children.
If
you see her
walking with one
of
her children and that child
is
a boy, what
is
the probability that both
children are boys?
73

Probability Theory
Solution: the other child
is
equally likely to be a boy
or
a girl (independent
of
the
boy
you've seen), so the probability that both children are boys is 1/2.
Notice the subtle difference between part A and part
B.
In part A, the problem essentially
asks given there is at least one boy in two children, what is the conditional probability
that both children are boys. Part B asks that given
one
child is a boy, what
is
the
conditional probability that the other child is also a boy. For both parts, we need to
assume that each child is equal likely to be a boy or a girl.
All-girl world?
In a primitive society, every couple prefers to have a
baby
girl. There is a 50% chance
that each child they have is a girl, and the genders
of
their children are mutually
independent.
If
each couple insists on having more children until they get a girl and once
they have a girl they will stop having more children, what will eventually happen to the
fraction
of
girls in this society?
Solution:
It
was surprising that many
interviewees-include
many who studied
probability-have
the misconception that there will be more girls. Do not let the
word
"prefer" and a wrong intuition misguide you. The fraction
of
baby girls are driven
by
nature, or at least the X and Y chromosomes, not by the couples' preference. You only
need to look at the key information: 50% and independence. Every new-born child has
equal probability
of
being a boy or a girl regardless
of
the gender
of
any other children.
So the fraction
of
girls born is always 50% and the fractions
of
girls in the society will
stay stable at 50%.
Unfair coin
You are given 1000 coins. Among them, 1 coin has heads on both sides. The other 999
coins are fair coins. You randomly choose a coin and toss it
10
times. Each time, the
coin turns up heads. What is the probability that the coin you choose is the unfair one?
Solution: This is a classic conditional probability question that uses
Bayes'
theorem.
Let
A be the event that the chosen coin
is
the unfair one, then
A"
is
the event that the chosen
coin is a fair one. Let B be the event that all ten tosses
tum
up heads. Apply
Bayes'
theorem we have P( A I
B)
=
P(
B I
A)P(
A)
=
P(
B I
A)P(
A)
P(B)
P(B
I
A)P(A)
+
P(B
I
A")P(A")
The priors are
P(
A)
= 1/1000 and
P(
A")
= 99911000.
If
the coin is unfair,
it
always
turns up heads, so
P(B
I
A)=
1.
If
the coin is fair, each time it has
1/2
probability turning
74

A Practical Guide
To
Quantitative Finance interviews
up heads. So
P(B
I
A")=
(1I2)
10
= 111024. Plug in all the available information and we
have the answer:
P(AIB)-
P(BIA)P(A)
= 1/lOOOxl
P(B
I A)P(A) +
P(B
I A'
)P(A')
1/1000x1+999/1000x1I1024
Fair probability from an unfair coin
If
you have an unfair coin, which may bias toward either heads or tails at an unknown
probability, can you generate even odds using this coin?
Solution: Unlike fair coins, we clearly can not generate even odds with one toss using an
unfair coin.
How
about using 2 tosses? Let
PH
be the probability the coin will yield
head, and
Pr
be the probability the coin will yield tails (
pH
+ Pr = 1
).
Consider two
independent tosses. We have four possible outcomes HH,
HT,
TH
and TT with
probabilities
P(HH)
=
PHPH,
P(HT)
=
PHPr>
P(TH)
=Pr
PH' and
P(TT)
=Pr
Pr.
So we have
P(HT)
=P(TH)
. By assigning
HT
to winning and
TH
to losing, we can
generate even odds.
12
Dart game
Jason throws two darts at a dartboard, aiming for the center. The second dart lands
farther from the center than the first.
If
Jason throws a third dart aiming for the center,
what is the probability that the third throw
is
farther from the center than the first?
Assume Jason's skillfulness is constant.
Solution: A standard answer directly applies the conditional probability by enumerating
all possible outcomes.
If
we
rank the three darts' results from the best (A) to the worst
(C), there are 6 possible outcomes with equal probability:
12
I should point out that this simple approach is not the most efficient approach since I am disregarding
the cases HH and TT. When the coin has high bias (one side is far more likely than the other side to occur),
the method may take many runs to generate one useful result. For more complex algorithm that increasing
efficiency, please refer to Tree Algorithms
for
Unbiased Coin Tossing with a Biased Coin by Quentin
F.
Stout and Bette L. Warren, Annals
of
Probability 12 ( 1984), pp. 212-222.
75

Probability Theory
Outcome 1 2 3 4 5 6
1st throw A B A c B c
2nd throw B A c A c B
3rd throw c c B B A A
The information from the first two throws eliminates outcomes 2, 4 and
6.
Conditioned
on outcomes
1,
3, and 5, the outcomes that the 3rd throw is worse than the 1st throw are
outcomes 1 and
3.
So there is 2/3 probability that the third throw is farther from the
center than the first.
This approach surely is reasonable. Nevertheless, it is not an efficient approach. When
the number
of
darts is small, we can easily enumerate all outcomes. What
if
it is a more
complex version
of
the original problem:
Jason throws n ( n 2
5)
darts at a dartboard, aiming for the center. Each subsequent dart
is farther from the center than the first dart.
If
Jason throws the
(n
+ l)th dart, what is the
probability that it
is
also farther from the center than his first?
This question is equivalent to a simple question: what is the probability that the
(n
+ 1)th
throw is not the best among all
(n
+
1)
throws? Since the 1st throw is the best among the
first n throws, essentially I
am
saying the event that the
(n
+ l)th throw is the best
of
all
( n +
1)
throws (let's call it
An+i
) is independent
of
the event that the 1st throw is the best
of
the first n throws (let's call it A1
).
In fact,
An+i
is independent
of
the order
of
the first
n throws. Are these two events really independent? The answer is a resounding yes.
If
it
is not obvious to you that
An+i
is independent
of
the order
of
the first n throws, let's look
at it another way: the order
of
the first n throws is independent
of
An
+i • Surely this claim
is conspicuous. But independence is symmetric! Since the probability
of
An+i
is
1/(n+1),
the probability that
(n
+
l)th
throw is not the best
is
n /
(n
+
1)
.
13
For the original version, three darts are thrown independently, they each have a
1/3
chance
of
being the best throw. As long as the third dart is not the best throw, it will be
worse than the first dart. Therefore the answer
is
2/3.
Birthday line
At a movie theater, a whimsical manager announces that she will give a free ticket to the
first person
in
line whose birthday is the same as someone who has already bought a
ticket. You are given the opportunity to choose any position
in
line. Assuming that you
13
Here you can again use symmetry argument: each throw is equally likely to
be
the best.
76

A Practical Guide
To
Quantitative Finance Interviews
don't know anyone else's birthday and all birthdays are distributed randomly throughout
the year (assuming 365
dals
in a year), what position in line gives you the largest chance
of
getting the free ticket?
1
Solution:
If
you have solved the problem that no two people have the same birthday in
an n-people group, this new problem is just a small extension. Assume that you choose
to be the n-th person in line. In order for you to get the free ticket, all
of
the first n
-1
individuals in line must have different birthdays and your birthday needs to be the same
as one
of
those n
-1
individuals.
p(n)
=
p(first
n-1
peoplehavenosamebirthday) x
p(yours
among those n
-1
birthdays)
365
x 364 x · · · (365 -n + 2) n
-1
365n-i
365
It
is intuitive to argue that when n is small, increasing n will increase your chance
of
getting the free ticket since the increase
of
p (yours
among
those n
-1
birthdays) is
more significant than the decrease in
p(first
n-1
peoplehavenosamebirthday).
So
when n is small, we have
P(n)
>
P(n-1).
As n increases, gradually the negative impact
of
p
(first
n
-1
people
have
no
same
birthday) will catch
up
and at a certain point we
will have
P(n+l)<P(n).
So we need to find such
an
n that satisfies
P(n)>P(n-1)
and
P(n)
>
P(n
+ 1).
P(n
-
l)
= 365 x 364 x ... x
365-(n
-3)
x n -2
365 365 365 365
P(n)=
365 x 364
X···x
365-(n-2)
x
n-1
365 365 365
365
P(n+l)=
365 x 364 X···X
365-(n-2)
x
365-(n-1)
x_!!_
365 365 365 365 365
P(n)>P(n-1)=>
x-->--
2
365 365 365 n -3n -
363
< 0
365-(n-2)
n-1
n-21
Hence,
=>
=>
n = 20
P(n) > P(n +
1)
n-1
>
365-(n-l)
x--"-
n'
-n-365
> 0 }
365
365
365
You should be the 20th person in line.
14
Hint:
If
you are the n-th person in line, to get the free ticket, the first
(n-I)
people in line must not have
the same birthday and you must have the same birthday as one
of
them.
77

Probability Theory
Dice order
We throw 3 dice one by one. What is the probability that we obtain 3 points in strictly
increasing order?
15
Solution: To have 3 points
in
strictly increasing order, first all three points must be
different numbers. Conditioned
on
three different numbers, the probability
of
strictly
increasing order is simply l I 3 ! = l I 6 (one specific sequence out
of
all possible
permutations). So
we
have
P = P(different numbers
in
all three throws) x P(increasing orderl3 different numbers)
=
(Ix2-x-i)x_J__
= 5 I 54
6 6 6
Monty Hall problem
Monty Hall problem is a probability puzzle based
on
an old American show Let's Make
a Deal. The problem is named after the show's host. Suppose you're on the show now,
and you're given the choice
of
3 doors. Behind one door
is
a car; behind the other two,
goats. You don't
know
ahead
of
time what
is
behind each
of
the doors.
You pick one
of
the doors and announce
it.
As soon as you pick the door, Monty opens
one
of
the other two doors that he knows has a goat behind it. Then
he
gives you the
option to either keep your original choice or switch to the third door. Should you switch?
What is the probability
of
winning a car
if
you switch?
Solution:
If
you
don't
switch, whether you win
or
not is independent
of
Monty's action
of
showing you a goat, so your probability
of
winning
is
1/3
. What
if
you switch? Many
would argue that since there are only two doors left after Monty shows a door with goat,
the probability
of
winning
is
1/2.
But
is this argument correct?
If
you look at the problem from a different perspective, the answer becomes clear. Using
a switching strategy, you
win
the
car
if
and only
if
you originally pick a door with a goat,
which has a probability
of
2/3 (You pick a door with a goat, Monty shows a door with
another goat, so the one you switch
to
must have a car behind it).
If
you originally
picked the door with the car, which has a probability
of
113,
you
will lose by switching.
So your probability
of
winning by switching
is
actually 2/3.
15
Hint:
To
obtain 3 points in strictly increasing order, the 3 points must be different. For 3 different points
in a sequence, strictly increasing order is
one
of
the possible permutations.
78

A Practical Guide To Quantitative Finance Interviews
Amoeba population
There is a one amoeba in a pond. After every minute the amoeba may die, stay the same,
split into two or split into three with equal probability. All its offspring,
if
it has any, will
behave the same (and independent
of
other amoebas). What is the probability the
amoeba population will die out?
Solution: This is just another standard conditional probability problem once you realize
we need to derive the probability conditioned on what happens to the amoeba one
minute later. Let
P(E)
be the probability that the amoeba population will die
out
and
apply the law
of
total probability conditioned on what happens to the amoeba one
minute later:
For the original amoeba, as stated
in
the question, there are four possible mutually
exclusive events each with probability 1/4. Let's denote
F;
as the event the amoeba dies;
F2
as
the event that it stays the same;
F;
as the event that it splits into two; F4 as the
event that it splits into three. For event
F;,
P(
E I F;) = I since no amoeba is left.
P(E
I F2) =
P(E)
since the state
is
the same as the beginning. For
F;,
there are two
amoebas; either behaves the same as the original one. The total amoeba population will
die only
if
both amoebas die out. Since they are independent, the probability that they
both will die out
is
P(E)
2• Similarly we have
P(F
4) = P(E)3. Plug in all the numbers,
the equation becomes
P(E)=
1/4xl+I/4
x
P(E)+1/4xP(E)
2
+1/4xP(E)
3• Solve
this equation with the restriction 0 <
P(E)
<I,
and
we
will get
P(E)
=
J2-I
0.414
(The other two roots
of
the equation are I and
-J2
-1 ).
Candies in a jar
You are taking out candies one by one from a
jar
that has I 0 red candies, 20 blue candies,
and 30 green candies in it. What
is
the probability that there are at least 1 blue candy and
1 green candy left in the
jar
when you have taken out all the red candies?
16
Solution:
At
first look, this problem appears
to
be
a combinatorial one. However, a
conditional probability approach gives a much more intuitive answer. Let
T,,
and
16
Hint:
If
there are at least I blue candy and 1 green candy left, the last red candy must have been
removed before the last blue candy and the last green candy in the sequence
of
60 candies. What is the
probability that the blue candy is the last one in the 60-candy sequence? Conditioned on that, what is the
probability that the last green candy
is
the last one in
the
30-candy sequence (10 red, 20 green)? What
if
the green candy is the last one in the 60-candy sequence?
79

Probability Theory
be the number that the last red, blue, and green candies are taken out respectively.
To
have at least 1 blue candy and 1 green candy left when all the red candies are taken out,
we need to have
T,.
<
T,,
and
T,.
<
Tg.
In
other words, we want to derive
P(T,.
<
T,,
n
Tr
<
Tg)
. There are two mutually exclusive events that satisfy
T,.
<
T,,
and
T,.
<
Tg
:
T,.
<
T,,
<
Tg
and
T,.
<
Tg
<
T,,
.
:.
P(T,.
<T,,nT,. <Tg)=P(T,.
<T,,
<Tg
<T,,)
T,.
<
T,,
<
Tg
means that the last candy
is
green (
Tg
= 60
).
Since each
of
the 60 candies
are equally likely to be the last candy and among them
30
are green ones, we have
P(Tg
= 60) = 30 . Conditioned on
Tg
= 60,
we
need
P(Tr
<
T,,
I
Tg
= 60). Among the
30
60
red and blue candies, each candy
is
again equally likely to be the last candy and there are
20 blue candies, so
P(T,.
<
T,,
I
Tg
= 60) =
20
and
P(Tr
<
T,,
<
Tg)
=
30
x
20
. Similarly,
30
60
30
20
30
we have
P(T
<Tg
<T,,)=-x-.
r 60 40
Hence,
30
20
20
30
7
P(T <
T,,
n T <
Tg)
=
P(T,.
<
7;,
<
Tg)
+
P(T,.
<
Tg
<
7;,)
= - x - + - x - = - .
r r 60
30
60
40
12
Coin toss game
Two players, A and B, alternatively toss a fair coin
(A
tosses the coin first, then B tosses
the coin, then
A,
then B .. . ). The sequence
of
heads and tails
is
recorded.
If
there is a
head followed by a tail (HT subsequence), the game ends and the person who tosses the
tail wins. What is the probability that A wins the game?
17
Solution: Let
P(A)
be the probability that A wins; then the probability that B wins is
P(
B) =
1-
P(
A).
Let's condition P( A) on
A's
first toss, which has
1I2
probability
of
H
(heads) and 1/ 2 probability
of
T (tails).
P(A) =
1/2P(A
I
H)
+
l/2P(A
IT)
If
A's
first toss is
T,
then B essentially becomes the first to toss (An
His
required for the
HT subsequence). So we have
P(
A
IT)
=
P(
B)
=
1-
P(
A).
If
A's
first toss ends in H, let's further condition on B's first toss. B has 1/2 probability
of
getting
T,
in that case A loses. For the I I 2 probability that B gets
H,
B essentially
17
Hint: condition
on
the result
of
A's
first toss and use symmetry.
80

A Practical Guide To Quantitative Finance Interviews
becomes the first one to toss
an
H.
In that case, A has (
1-
P(
A I
H))
probability
of
winning. So
P(
A I
H)
=
1I2
x 0 + l I 2 ( 1 -
P(
A I
H))
P(
A I
H)
=
1I3
Combining all the available information, we have
P(A)
=
1/
2x
113+ 1/
2(1-P(A))
P(A)
= 419.
Sanity check: we can see that
P(A)
<
1I2,
which is reasonable since A cannot
win
in his
first toss, yet B has 1/4 probability to win in her first toss.
Russian roulette series
Let's play a traditional version
of
Russian roulette. A single bullet is put into a 6-
chamber revolver. The barrel is randomly spun so that each chamber is equally likely to
be under the hammer. Two players take turns to pull the
trigger-with
the gun
unfortunately pointing
at
one's own
head-without
further spinning until the gun goes
off
and the person who gets killed loses.
If
you, one
of
the players, can choose to
go
first
or second, how will
you
choose? And what is your probability
of
loss?
Solution: Many people have the wrong impression that the first person has higher
probability ofloss. After all, the first player has a
116
chance
of
getting killed in the first
round before the second player starts. Unfortunately, this is one
of
the few times that
intuition is wrong. Once the barrel is spun, the position
of
the bullet is fixed.
If
you go
first, you lose
if
and
only
if
the bullet is in chamber
1,
3 and
5.
So the probability that
you lose is the same as the second player, 1/2.
In
that sense, whether to go first
or
second
does not matter.
Now,
let's
change the rule slightly.
We
will spin the barrel again after every trigger pull.
Will you choose to
be
the first or the second player? And what is your probability
of
loss?
Solution: The difference is that each run now becomes independent. Assume that the
first player's probability
of
losing is
p,
then the second player's probability
of
losing is
1-
p.
Let's
condition the probability
on
the first person's first trigger pull. He has 1/6
probability
of
losing in this run. Otherwise, he essentially becomes the second player in
the game with new (conditional) probability
of
losing
1-
p. That happens with
probability 5/6. That gives us p =
1xI/6
+(I
-
p)
x 5 I 6
=>
p = 6111.
So
you should
choose to be the second player and have 5I11 probability
of
losing.
If
instead
of
one bullet, two bullets are randomly
put
in the chamber. Your opponent
played the first and he was alive after the first trigger pull. You are given the option
whether to spin the barrel. Should
you
spin the barrel?
81

Probability Theory
Solution:
if
you spin the barrel, the probability that you will lose in this round
is
2/6.
If
you don't spin the barrel, there are only 5 chambers left and your probability oflosing in
this round (conditioned on that your opponent survived) is 2/5.
So
you should spin the
barrel.
What
if
the two bullets are randomly put in two consecutive positions?
If
your opponent
survived his first round, should you spin the barrel?
Solution: Now we have to condition our probability on the fact that the positions
of
the
two bullets are consecutive. As shown in Figure 4.3, let's label the empty chambers as
1,
2, 3 and 4; label the ones with bullets 5
and
6.
Since your opponent survived the first
round, the possible position he encountered is
1,
2,
3
or
4 with equal probability. With
1/4 chance, the next one
is
a bullet (the position was 4). So
if
you don't spin, the chance
of
survival is 3/4.
If
you spin the barrel, each position has equal probability
of
being
chosen, and your chance
of
survival
is
only 2/3. So you should not spin the barrel.
0)
Figure 4.3 Russian roulette with two consecutive bullets.
Aces
Fifty-two cards are randomly distributed to 4 players with each player getting
13
cards.
What
is
the probability that each
of
them will have
an
ace?
Solution: The problem can be answered using standard counting methods. To distribute
52 cards to 4 players with 13 cards each has 52 ! permutations.
If
each player
13!13!13!13!
82

A Practical Guide
To
Quantitative Finance Interviews
needs to have one ace,
we
can distribute the aces first, which has 4 ! ways. Then we
48!
distribute the rest 48 cards to 4 players with
12
cards each, which has
-----
12!l2!l2!l2
!
permutations. So the probability that each
of
them will have an Ace is
4
!x
48! 7 52!
=52x39x26xQ,
12!12!12!12! 13!13!13!13! 52
51
50 49
The logic becomes clearer
if
we use a conditional probability approach. Let's begin with
any one
of
the four aces; it has probability 52 I
52
=I
of
belonging to a pile. The second
ace can be any
of
the remaining
51
cards, among which 39 belong to a pile different
from the first ace.
So
the probability that the second ace is not in the pile
of
the first ace
is 39 I
51
.
Now
there are 50 cards left, among which 26 belong to the other two piles. So
the conditional probability that the third ace
is
in one
of
the other 2 piles given the first
two aces are already in different piles is
26
I
50.
Similarly, the conditional probability
that the fourth ace
is
in the pile different from the first three aces given that the first
three aces are in different piles
is
13
I 49 .
So
the probability that each pile has an ace
is
Ix
39 x 26
51
50
49
Gambler's ruin problem
A gambler starts with an initial fortune
of
i dollars. On each successive game, the
gambler wins
$1
with probability
p,
0 < p <
I,
or loses
$1
with probability q =
1-
p . He
will stop
if
he either accumulates N dollars or loses all his money. What is the
probability that he will end
up
with N dollars?
Solution: This is a classic textbook probability problem called the Gambler's Ruin
Problem. Interestingly, it is still widely used in quantitative interviews.
From any initial state i (the dollars the gambler has),
0:::;;
i:::;;
N,
let
P;
be
the probability
that the gambler's fortune will reach N instead
of
0. The next state is either i
+I
with
probability p
or
i
-1
with probability q.
So
we have
P,
=
pP,.,
+qP,_,
=>
P,.,
-P,
=;
(P,-P,_,
) = (; J
(P,_,
-P,_, ) =
...
= (;
)'
(J:-P,
)
We also have the boundary probabilities
Po
= 0 and
PN
= I .
So starting from
Pi,
we can successively evaluate as an expression
of
Pi
:
83

Probability Theory
Extending this expression to
PN,
we have
[ q
(qJN-1]
{1-(q/p)N
Pi,ifq/p*l
PN
= 1 = 1 + - + ... + -
Pi
=
1-
q
Ip
P P
NI>i,
if
q
Ip
= 1
=>Pi=
1-(q/p)N'
q p =>P;=
1-(q/p)N
1'
p
{
l-q/p
zif
I
*1
{l-(qlpYp
zif
*112
l!N,
ifqlp=l
i/N,
if
p=l/2
Basketball scores
A basketball player is taking 100 free throws. She scores one point
if
the ball passes
through the hoop and zero point
if
she misses. She has scored on
her
first throw
and
missed on her second. For each
of
the following throw the probability
of
her scoring is
the fraction
of
throws she has made so far. For example,
if
she has scored 23 points after
the 40th throw, the probability that she will score in the
41
th throw is 23/40. After 100
throws (including the first and the second), what is the probability that she scores exactly
50 baskets?
18
Solution: Let
(n,k),
1 k n, be the event that the player scores k baskets after n
throws and
P,,,k
=
P(
(n,k)
) . The solution is surprisingly simple
if
we use an induction
approach starting with n = 3. The third throw has 1/2 probability
of
scoring.
So
we have
= 1I2 and = 1I2.
For
the case when n = 4, let's apply the law
of
total
probability
18
Hint: Again, do not let the number 100 scares you. Start with smallest n, solve the problem; try to find a
pattern by increasing n; and prove the pattern using induction.
84

A Practical Guide To Quantitative Finance Interviews
2 1 1 1
P((4,l)
I (3,1)) x +
P((4,l)
I (3,2)) =
3x2+
Ox
2 = 3
1 1 1 1 1
=
P((4,2)
I (3,1)) x
P..
31 +
P((4,2)
I (3,2)) x =
-x-+-x-
= -
' .
'3232
3
1 2 1 1
=
P((4,3)
I (3,1)) 1 +
P((4,3)
I (3,2)) x = 0
x-+-x-
= -
. . ' 2 3 2 3
The results indicate that P k = - 1
-,
V k =
1,
2, · · ·, n -1 , and give the hint that the law
of
n,
n-1
total probability can be used
in
the induction step.
Induction step: given that
Pk=
-1
-,
Vk
=
1,
2,···,
n-1,
n,
n-1
we need to prove
p = 1 = 1 V k =
1,
2,
.. ·, n. To show it, simply apply the law
of
total
n+l.k
(n+l)-1
n
probability:
P,,+i,k =
P(
miss I (n, k)) P,,,k +
P(
score I (n,
k-1))
P,,,k-I
=(l-:)
+
=;
The equation
is
also applicable
to
the
P,,+
1,1 and
P,,+i,n•
although in these cases k -I = 0
n
and
(1-kn)=o,
respectively.
So
we have
P*=-
1
-,
Vk=l,2,
..
.,n-land
Vn"?.2.
n ,
n-I
Hence,
Pioo
50 =
1199
.
Cars on road
If
the probability
of
observing at least one car on a highway during any 20-minute time
interval is 609/625, then what
is
the probability
of
observing at least one car during any
5-minute time interval? Assume that the probability
of
seeing a car at any moment is
uniform (constant) for the entire 20 minutes.
Solution: We can break down the 20-minute interval into a sequence
of
4 non-
overlapping 5-minute intervals. Because
of
constant default probability
(of
observing a
car), the probability
of
observing a car in any 5-minute interval is constant. Let's denote
the probability to be
p,
then the probability that in any 5-minute interval we do not
observe a car is I - p .
85

Probability Theory
The
probability that
we
do
not
observe
any
car
in all four
of
such independent 5-minute
intervals is
(1-
p )4 =
1-609
I 625 = 16 I 625, which gives p = 3 I
5.
4.4 Discrete and Continuous Distributions
In
this section, we review a variety
of
distribution functions for random variables
that
are widely used in quantitative modeling. Although it
may
not
be necessary to memorize
the properties
of
these distributions, having
an
intuitive understanding
of
the
distributions
and
having the ability to quickly derive important properties are valuable
skills in practice.
As
usual,
let's
begin
with
the
theories:
Common function
of
random
variables
Table 4.1 summarizes
how
the basic properties
of
discrete and continuous
random
variables are defined
or
calculated. These
are
the basics
you
should
commit
to
memory
.
Random variable
ill
Discrete Continuous
19
Cumulative distribution function/cdf
F(a)
=
P{X
F(a)
=
[f(x)dx
Probability mass function
/pmf
pmf: d
p(x)
=
P{X
=
x}
pdf:
f(x)
=-F(x)
Probabil!!Y_
dens!!Y_
function dx
Expected value/ E[
X]
L
xp(x)
(xf(x)dx
x:p(x)>O
Expected value
of
g(X)/
E[g(X)]
L
g(x)p(x)
(g(x)f(x)dx
x:p(x)>O
Variance
of
XI var(
X)
E[(X
-E[X])
2] =
E[X
2
]-(E[X])
2
Standard deviation
of
XI
std(X)
.Jvar(X)
Table 4.1 Basic properties
of
discrete and continuous random variables
Discrete
random
variables
Table 4.2 includes some
of
the most widely-used discrete distributions. Discrete uniform
random variable represents
the
occurrence
of
a value
between
number a and b
when
all
values in the set {a,
a+l,-
· ·,
b}
have equal probability. Binomial random variable
represents the
number
of
successes in a sequence
of
n experiments
when
each trial is
19
For continuous random variables,
P(X
=
x)
= 0,
\Ix
E
(-00,00),
so
P{X
x} =
P{X
<
x}.
86
A Practical Guide To Quantitative Finance Interviews
independently a success with probability p . Poisson random variable represents the
number
of
events occurring in a fixed period
of
time with the expected number
of
occurrences At when events occur with a
known
average rate A and are independent
of
the time since the last event. Geometric random variable represents the trial number (n)
to get the first success
when
each trial is independently a success with probability
p.
Negative Binomial random variable represents the trial number to get to the r-th success
when each trial is independently a success
with
probability p .
Name Probability mass function (pmf)
E[X]
var(X)
1 x =
a,a+
1,.··,b
b+a
(b-a+l)
2
-1
Uniform P(x) = ,
--
b-a+l
2
12
Binomial P(x)
=(:
)p'(I-
Pr-',
x = 0,1,. ·
.,n
np
np(l-
p)
Poisson
P(x)=
e_,i,
(A.t}"
x = 0,
1,
.. .
20
A.t
At
x!
,
P(x)
=
(1-
py-'
p,
x = 1,2,
...
1
1-
p
Geometric -
p
p2
Negative (
x-1)
r
r(l-
p)
P(x)=
pr(l-py-r,
x=r,r+l,-··
-
Binomial
r-1
p
p2
Table 4.2 Probability mass function, expected value and variance of discrete random
variables
Continuous random variables
Table 4.3 includes some
of
the
commonly
encountered continuous distributions.
Uniform distribution describes a random variable uniformly distributed
over
the interval
[a,
b].
Because
of
the central limit theorem, normal distribution/Gaussian distribution is
by
far the
most
popular continuous distribution. Exponential distribution models the
arrival time
of
an event
if
it has a
constant
arrival rate
A.
. Gamma distribution with
parameters (a,
A.)
often arises, in practice,
as
the distribution
of
the amount
of
time one
has to wait until a total
of
n events occur. Beta distributions are used to model events
20 Here we use the product
of
arrival rate
A.
and time t to define the parameter (expected value) since it is
the definition used in many Poisson process studies.
87

Probability Theory
that are constrained within a defined interval. By adjusting the shape parameters a and
p,
it can model different shapes
of
probability density functions.21
Name Probability density function (pdf)
E[X]
var(X)
Uniform 1
aS.xS.b
b+a
(b-a)
2
--
'
--
b-a
2
12
1
-(x-µ)2
Normal
ez;r-
x E (-oo,
oo)
µ
a2
.[i;a
'
Exponential A
-AX
e '
I/
A.
1/ A,2
Gamma
A.e-A.x (A-xt-1
r(a)
,
r(a)=
r
e-yya-i
a/A,
al
A-
2
r(a
+ fi)
xa-1
(1-
x)p-1
O<x<l
a
ap
Beta
--
r(a)r(p)
'
a+p
(a+
p +
l)(a
+
/J)
2
Table 4.3 Probability density function, expected value and variance
of
continuous
random variables
Meeting probability
Two bankers each arrive at the station at some random time between 5:00 am and 6:00
am (arrival time for either banker is uniformly distributed). They stay exactly five
minutes and then leave. What is the probability they will meet on a given day?
Solution: Assume banker A arrives X minutes after 5:00 am and B arrives Y minutes after
5:00 am. X and Y are independent uniform distribution between 0 and 60. Since both
only stay exactly five minutes, as shown in Figure 4.4, A and B meet
if
and only
if
1x-r1::::;5.
So the probability that A and B will meet is simply the area
of
the shadowed region
divided by the area
of
the square (the rest
of
the region can be combined
to
a square with
size len
th
55
):
60x60-2x(l/2x55x55)
=
(60+55)x(60-55)
= 23 .
g
@x@
@x@
IM
21
For example, beta distribution is widely used
in
modeling loss given default in risk management.
lfyou
are familiar with Bayesian statistics, you will also recognize it as a popular conjugate prior function.
88
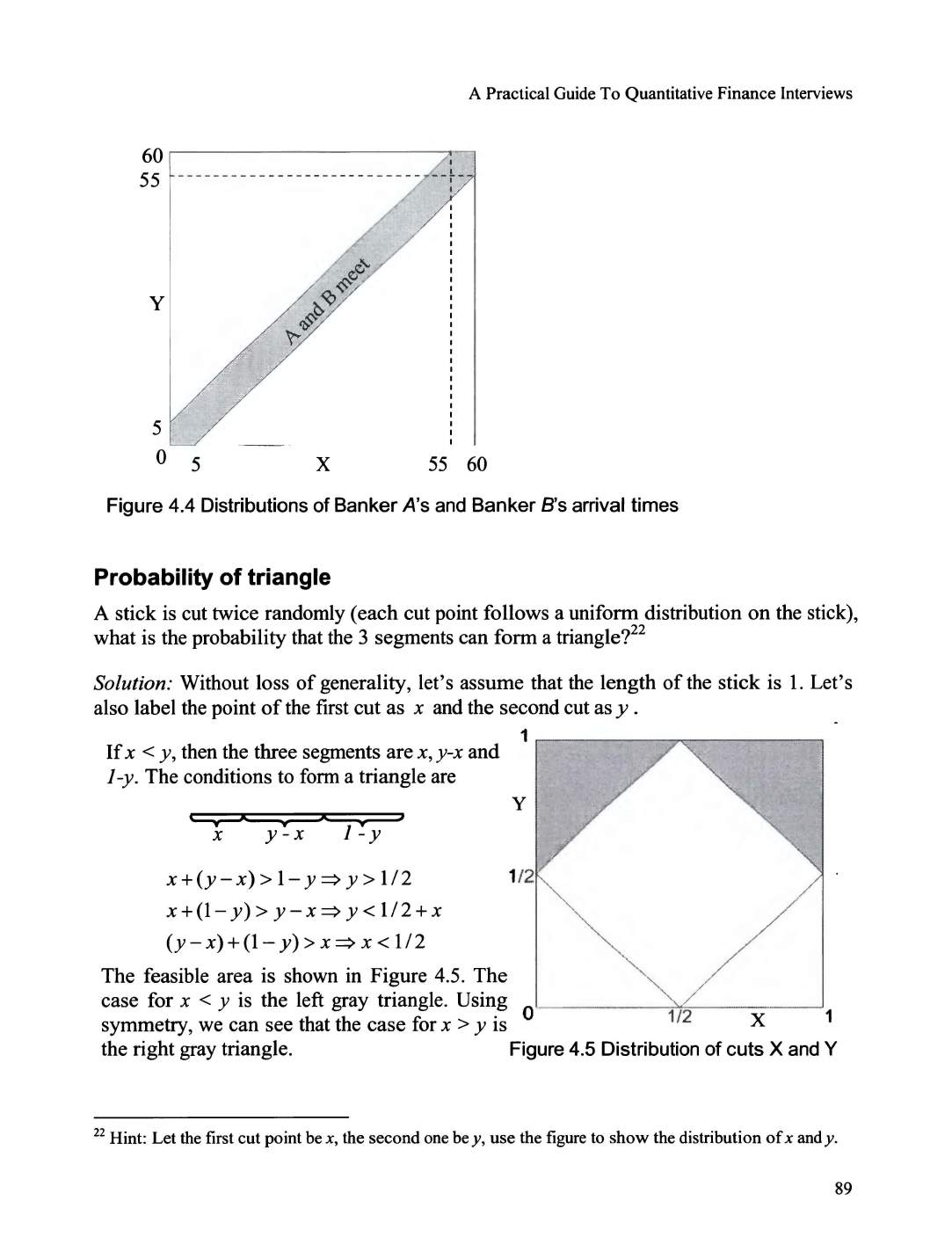
A Practical Guide
To
Quantitative Finance Interviews
60
55
y
5 x
55
60
Figure 4.4 Distributions
of
Banker
A's
and Banker B's arrival times
Probability
of
triangle
A stick is cut twice randomly (each cut point follows a uniform distribution
on
the stick),
what is the probability that the 3 segments can form a triangle?22
Solution: Without loss
of
generality, let's assume that the length
of
the stick is
1.
Let's
also label the point
of
the first cut
as
x and the second cut as y .
If
x <
y,
then the three segments are
x,y-x
and
1-y. The conditions to form a triangle are
A
¥
x
y-x
x+(y-x)
>
1-
y
=>
y > 112
x +
(1-
y)
> y -x
=>
y <
1I2
+ x
(y-
x)
+
(1-
y)
> x
=>
x < 112
The feasible area is shown in Figure 4.5. The
1
.--------.,,...------..,,...,,....
y
case for x < y is the left gray triangle. Using
symmetry, we can see that the case for x > y is 1
12
X 1
the right gray triangle. Figure 4.5 Distribution
of
cuts
X and Y
22 Hint: Let the first cut point be x, the second one
bey,
use the figure to
show
the distribution
of
x and y.
89

Probability Theory
The total shadowed area represents the region where 3 segments can form a triangle,
which is 1/4
of
the square. So the probability is
114.
Property
of
Poisson process
You
are waiting for a bus at a bus station. The buses arrive at the station according to a
Poisson process
with
an average arrival time
of
10 minutes
(.A
= 0.1 I min).
If
the buses
have been running for a long time and you arrive at the bus station at a random time,
what is your expected waiting time? On average,
how
many minutes ago did the last bus
leave?
Solution: Considering the importance
of
jump-diffusion processes in derivative pricing
and the role
of
Poisson processes in studying
jump
processes,
let's
elaborate more on
exponential random variables and the Poison process. Exponential distribution is widely
used to model the time interval between independent events
that
happen at a constant
( . 1 ) 1
/()
{Ae-"'
(t
0)
Th d . 1 . .
1/
1
average rate arr1va rate
11.:
t = . e expecte
amva
time is
/L
0
(t
< 0)
and the variance is 1IA2• Using integration, we
can
calculate the
cdf
of
an exponential
distribution to be
F(t)
=
P(r
s;
t)
=
l-e-'
1 and
P(r
>
t)
= e_,,, where r is
the
random
variable for arrival time. One unique property
of
exponential distribution is
memorylessness: P { r > s + t I r > s} =
P(
r > t}.
23
That means
if
we have waited for s
time units, the extra waiting time
has
the same distribution
as
the
waiting time when we
start
at
time
0.
When the arrivals
of
a series
of
events each independently follow an exponential
distribution with arrival rate
A.,
the
number
of
arrivals between time 0 and t can be
-A.I
At'
modeled as a Poisson process
P(N(t)
=
x)
= e , x = 0,
1,
· · ·
24
The expected
x!
number
of
arrivals is At and the variance is also At. Because
of
the memoryless nature
of
exponential distribution, the number
of
arrivals between time s and t is also a Poisson
e-.l(t-s)
(
A(t-S)
r
process x!
Taking advantage
of
the memoryless property
of
exponential distribution, we know that
the expected waiting time is 1 I A = 10 min.
If
you
look back in time, the memoryless
property stills applies. So on average, the last bus arrived
10
minutes ago as well.
23
P{r
>
s+t
Ir>
s}
=
e-.<(s+i>
I
e--<.•
=
e_,.,
= P(x >
t}
24
More rigorously,
N(t)
is defined as a right-continuous function.
90

A Practical Guide
To
Quantitative Finance Interviews
This is another example that your intuition may misguide you. You may be wondering
that
if
the last bus on average arrived 10 minutes ago and the next bus on average will
arrive
10
minutes later, shouldn't the average arrival time be 20 minutes instead
of
10?
The explanation to the apparent discrepancy is that when you arrive at a random time,
you are more likely
to
arrive in a long time interval between two bus arrivals than in a
short one. For example,
if
one interval between two bus arrivals is 30 minutes and
another is 5 minutes, you are more likely to arrive at a time during that 30-minute
interval rather than 5-minute interval. In fact,
if
you arrive at a random time, the
E[X
2]
expected residual life (the time for the next bus to arrive) is for a general
2E[X]
distribution.
25
Moments
of
normal distribution
If
X follows standard normal distribution ( X -N (0,
1)
), what is
£[
xn]
for n =
1,
2, 3
and4?
Solution: The first to fourth moments
of
the standard normal distribution are essentially
the mean, the variance, the skewness and the kurtosis. So you probably have
remembered that the answers are 0,
1,
0 (no skewness), and 3, respectively.
Standard normal distribution has
pdf
f(x)
= e-x
212
• Using simple symmetry we
'\/27r
have E[xn] = (
xn
e-x
212
dx = 0 when n is odd. For n =
2,
integration by parts are
'\/27r
often used.
To
solve
E[Xn]
for any integer
n,
an approach using moment generating
functions may be a better choice. Moment generating functions are defined as
{
Le'
..
p(x),
M(t)
= E[e1
x]
= x
(
e'x
f(x)dx,
if
x
is
discrete
if
x
is
continuous
Sequentially taking derivative
of
M(t),
we get one frequently-used property
of
M(t):
M'(t)
= !
E[e
1
x]
=
E[Xe
1
x]
=>
M'(O) =
E[X],
M"(t)
= !
E[Xe'x]
=
E[X
2e1
x]=>M"(O)
=
E[X
2
],
25 The residual life is explained in Chapter 3 of"Discrete Stochastic Process" by Robert G. Gallager.
91

Probability Theory
and Mn(O) = E[Xn],
Vn
l in general.
We can use this property to solve E[Xn] for X -
N(O,
1)
. For standard normal
distribution
M(t)=E[e
1
x]=
(e
1
x
v2ff
v2ff
(
.}z;
e-<x-1)
212 is the
pdf
of
normal distribution X -
N(t,
1), so (
f(x)dx
= 1 ).
Taking derivatives, we have
M'(t)
= te12
12
= 0, M"(t) = e
1212
+ t2e1
212
M"(O) = e0=1,
4.5 Expected Value, Variance & Covariance
Expected value, variance and covariance are indispensable in estimating returns and
risks
of
any investments. Naturally, they are a popular test subject in interviews as well.
The basic knowledge includes the following:
If
E[x;] is finite for all
i=l,
..
.,
n, then
E[X
1 + ..
·+X
n
]=E[X
1
]+
..
·+E[XJ.
The
relationship holds whether the
x;
's
are independent
of
each other
or
not.
If
X and Yare independent, then
E[g(X)h(Y)]
= E[g(x)]E[h(Y)].
Covariance:
Cov(X,Y)
=
E[(X
-E[X])(Y-E[Y])]
=
E[XY]-E[X]E[Y].
.
Cov(X
Y)
Correlation:
p(X,Y)
= '
Var(X) Var(Y)
If
X and Y are independent,
Cov(X,
Y)
= 0 and
p(X
,
Y)
= 0.
26
General rules
of
variance and covariance:
n m n m
=
Yi)
i=I
j=I
i=I
j=I
n n
Var(LX;)=
L:var(
X
;)+2LL
Cov(X;,X
; )
i<j
26 The reverse
is
not true.
p(
X,
Y)
= 0 only means X and Y are uncorrelated; they may well
be
dependent.
92

A Practical Guide
To
Quantitative Finance Interviews
Conditional expectation and variance
For discrete distribution:
E[g(X)
I Y =
y]
=
Lg(x)Pxir(x
I
y)
=
Lg(x)p(X
= x I Y =
y)
x x
For continuous distribution:
E[g(X)
I Y =
y]
=
[,g(x)fx
1
r(x
I y)dx
Law
of
total expectation:
{
IE[X
I Y =
y]p(Y
=
y),
for discrete Y
E[X]
=
E[E[X
I
Y]]
= y
(
£[
X I Y = y ]fr
(y
)dy, for continuous Y
Connecting noodles
You have I 00 noodles in your soup bowl. Being blindfolded, you are told to take two
ends
of
some noodles (each
end
on any noodle has the same probability
of
being chosen)
in your bowl and connect them. You continue until there are no free ends. The number
of
loops formed
by
the noodles this way is stochastic. Calculate the expected number
of
circles.
Solution: Again do not be frightened by the large number 100.
If
you have no clue how
to start, let's begin with the simplest case where n
=I.
Surely you have only one choice
(to connect both ends
of
the noodle), so
E[/(l)]
=I.
How about 2 noodles? Now you
(
4)
4 x 3
have 4 ends ( 2 x
2)
and you can connect any two
of
them. There are 2 = - 2
-= 6
combinations. Among them, 2 combinations will connect both ends
of
the same noodle
together and yield I circle and I noodle. The other 4 choices will yield a single noodle.
So the expected number
of
circles is
£[/(2)]
=
2/
6 x
(1+£[/(I)])+416
x
E[/(l)]
=I
I 3
+£[/(I)]=
I I
3+
1.
We now move
on
to 3 noodles with ( = 6 ; 5 = I 5 choices. Among them, 3 choices
will yield 1 circle and 2 noodles; the other 12 choices will yield 2 noodles only, so
E[/(3)]
=
3/15
x
(I+
£[/(2)])
+
12/15x
E[/(2)]
= 115+
E[/(2)]
=
115+1/3+1.
See the pattern? For any n noodles, we will have
£[/
(n)] =
1+1I3+1I5
+···+I
/(2n
-1),
which can be easily proved by induction. Plug I 00 in, we will have the answer.
93

Probability Theory
Actually after the 2-noodle case, you probably have found the key to this question.
If
you start with n noodles, among ( 2
2
n)
= n ( 2 n -
1)
possible combinations, we have
n = - 1
-probability to yield 1 circle and n - I noodles and 2n -2 probability
n(2n-I)
2n-l
2n-l
to yield
n-1
noodles only, so
E[f(n)]
=
E[/(n-1)]+-
1- . Working backward, you
2n-1
can get the final solution as well.
Optimal hedge ratio
You just bought one share
of
stock A and want to hedge it by shorting stock B. How
many shares
of
B should you short to minimize the variance
of
the hedged position?
Assume that the variance
of
stock
A's
return is
o-3;
the variance
of
B's return is a;;
their correlation coefficient is p.
Solution: Suppose that we short h shares
of
B,
the variance
of
the portfolio return is
var(rA
-hrs)=
o-3
-2phaAas
+ h2
a;
The best hedge ratio should minimize
var(rA
-hrs)·
Take the first order partial
derivative with respect to
hand
set it to zero:
ovar
=
-2pa
A
as
+2ha;
=0
h = p
aA
.
Oh
O"s
To confirm it's the minimum, we can also check the second-order partial derivative:
82
var -
2o-
2 > O So Indeed when h
=pa
A, the hedge portfolio has the minimum
Oh
2 -S • O"s
variance.
Dice game
Suppose that you roll a dice. For each roll, you are paid the face value.
If
a roll gives 4, 5
or
6, you can roll the dice again. Once you get I, 2 or 3, the game stops. What
is
the
expected payoff
of
this game?
Solution: This is an example
of
the law
of
total expectation. Clearly your payoff will
be
different depending on the outcome
of
first roll. Let
E[X]
be your expected payoff and
Y be the outcome
of
your first throw. You have 1/2 chance to get YE
{I,
2,
3},
in which
case the expected value
is
the expected face value 2, so
E[X
I YE
{I,
2,3}] =
2;
you have
94

A Practical Guide To Quantitative Finance Interviews
112
chance to get YE {4,5,
6},
in which case you get expected face value 5 and extra
throw(s). The extra throw(s) essentially means
you
start the game again and have
an
extra expected value
E[
X]
. So we have E[ X I Y E ( 4,
5,
6)] = 5 +
E[
X].
Apply the law
of
total expectation, we have
E[X]
=
E[E[X
I Y]] =
+x
2
+tx(5+
E[X])
=>
E[X]
= 7 .
27
Card game
What is the expected number
of
cards that need to be turned
over
in a regular 52-card
deck in order to see the first ace?
Solution: There are 4 aces and 48 other cards. Let's label them as card l,
2,
· · ·, 48. Let
{
1,
if
card i is turned over before 4 aces
x-
i -0, otherwise
The total number
of
cards that need to be turned over in order to see the first ace
is
a a
x = 1 + L
xi'
so we have
E[
X]
= 1 +
LE[
XJ
As
shown in the following sequence,
i=I
i=l
each card i is equally likely to be in one
of
the five regions separated by 4 aces:
1A2A3A4A5
So the probability that card i appears before all 4 aces
is
115,
and
we
have
E[
Xi]
= 1I5.
48
Therefore,
E[X]
= 1
+LE[
Xi]=
1+48/
5 =
10
.
6.
i=I
This is just a special case for random ordering
of
m ordinary cards and n special cards.
The expected position
of
the first special card is 1 + f E[
Xi]
= 1 +
__!!!__
.
i=l
n + 1
Sum
of
random variables
Assume that
XI,
X2, .. ·, and
xn
are independent and identically-distributed (IID)
random variables with uniform distribution between 0 and
1.
What
is
the probability
that S = X + X + · · · + X < 1 ?28
n I 2 n - •
27 You will also see that the problem can be solved using
Wald's
equality in Chapter
5.
28 Hint: start with the simplest case where n
=l,
2, and 3.
Try
to find a general formula and prove it using
induction.
95
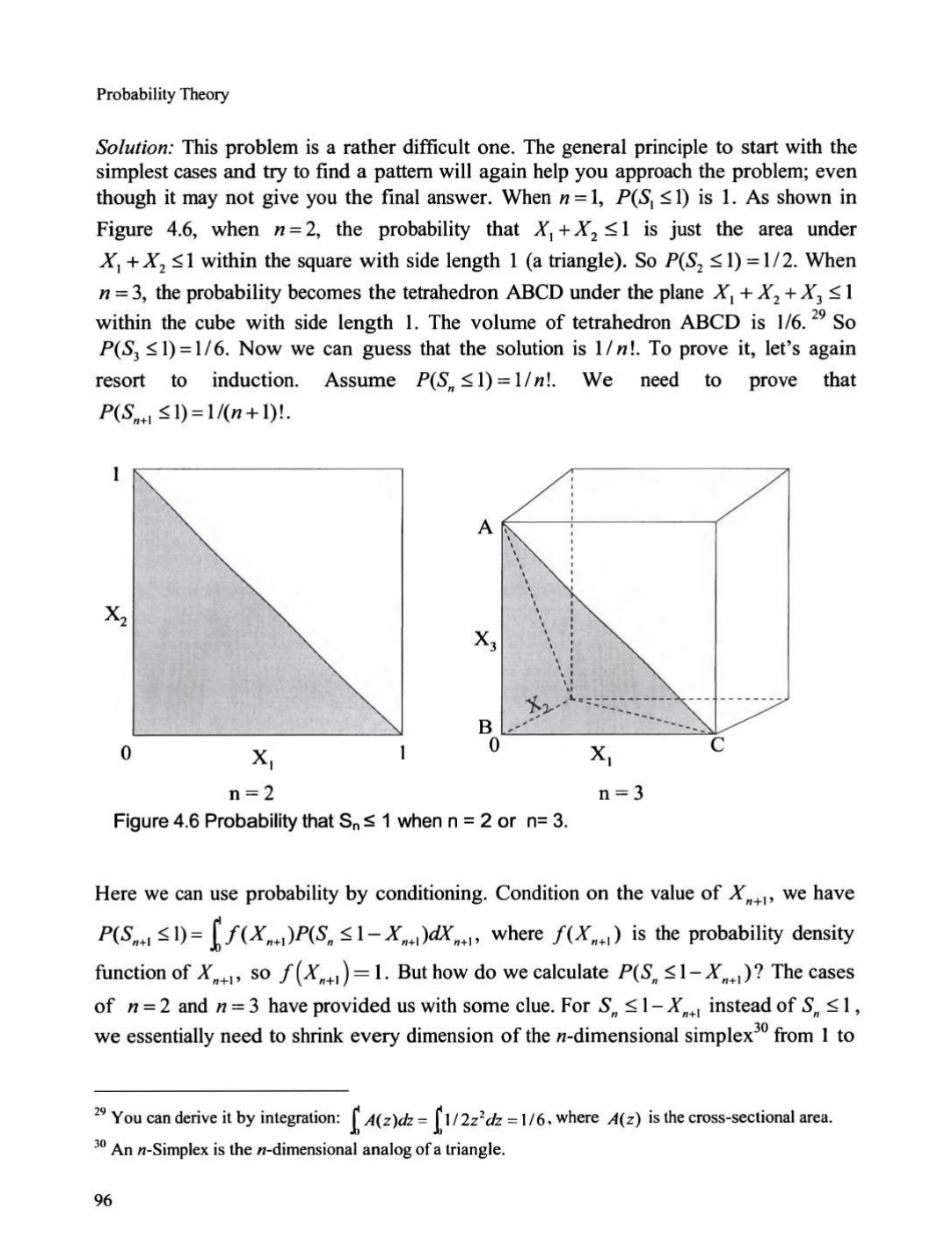
Probability Theory
Solution: This problem
is
a rather difficult one. The general principle to start with the
simplest cases and
try
to
find a pattern will again help you approach the problem; even
though it may
not
give you the final answer. When n =
1,
P(S
1 ::; l) is
1.
As shown in
Figure 4.6,
when
n =
2,
the probability that
X,
+ X2
::;
1 is just the area under
X1
+X
2
::;1
within the square with side length 1 (a triangle).
So
P(S
2
::;
1)
= 1/2. When
n =
3,
the probability becomes the tetrahedron ABCD under the plane X1 + X2 + X3 ::; 1
within the cube with side length
1.
The volume
of
tetrahedron ABCD is
1/6.
29 So
P(S
3 ::;
1)
=I
I
6.
Now
we
can guess that the solution is 1
In!.
To
prove it, let's again
resort
to
induction. Assume P(Sn::;
1)
=
11
n!.
We
need to prove that
P(Sn+i
:s;l)=l/(n+l)!.
A ,
\
\
\
\
\
\
\
\
\
\
\
.
\
\
" .
I '
' .
\ I
I I
,.
"
Jv·'-<
=:::
:::::::_-_-
__
B
0 x,
n=3
Figure 4.6 Probability that
Sn
s:
1 when n = 2
or
n=
3.
Here we
can
use probability
by
conditioning. Condition on the value
of
X
n+i,
we
have
P(Sn+i
::;])=
lf(Xn+i)P(Sn
::;I-Xn+JdXn+P where
f(Xn+i)
is the probability density
function
of
xn+I' so f ( xn+I) =
1.
But how do we calculate
P(Sn
::;
1-
xn+I)? The cases
of
n = 2 and n = 3 have provided
us
with some clue. For
Sn
::;
1-Xn+i instead
of
Sn
::;
1,
we
essentially need
to
shrink every dimension
of
the n-dimensional simplex30 from 1 to
29 You can derive it
by
integration:
f.
A(z)dz
=
f.1
/2z
2dz
=I
/6,
where A(z)
is
the cross-sectional area.
30 An n-Simplex
is
the n-dimensional analog
of
a triangle.
96

A Practical Guide To Quantitative Finance Interviews
1-
x
n+i
· So its volume should be
(1-
x
n+I
r instead
of
_!_.
Plugging in these results,
n! n!
h
P(s
<l)=
rO-Xn+itdX
=_!_[
(l-Xn+1f+
1
]1
=_!_x_l_=
1
We
ave
n+I
-
.b
n+I
n! n!
n+l
0 n!
n+l
(n+l)!
So the general result is true for n + 1 as well and we have
P(Sn
::;
1)
= 1
In!.
Coupon collection
There are N distinct types
of
coupons in cereal boxes and each type, independent
of
prior
selections, is equally likely to be in a box.
A.
If
a child wants to collect a complete set
of
coupons with at least one
of
each type,
how many coupons (boxes) on average are needed to make such a complete set?
B.
If
the child has collected n coupons, what is the expected number
of
distinct coupon
types?31
Solution: For part
A,
let
X;,
i =
1,
2,
· ·
·,
N , be the number
of
additional coupons needed
to obtain the i-th type after
(i-1)
distinct types have been collected. So the total number
N
of
coupons needed is X = X1 + X2 + · · · + X N = L Xi .
i=I
For any
i,
i-1
distinct types
of
coupons have already been collected.
It
follows that a
new coupon will be
of
a different type with probability
1-
(i
-1)
IN=
(N
-i +
1)
IN.
Essentially to obtain the i-th distinct type, the random variable X; follows a geometric
distribution with p =
(N
-i
+ 1)/ N and E[X;] = N
/(N
-i
+
1)
. For example,
if
i = 1, we
simply have
Xi
=
E[
Xi] = 1 .
N N N ( 1 1
1)
:. E[X]=
LE[Xi]=
L .
=N
-+-+···+-.
i=I
i=I N
-1
+ 1 N N
-1
1
31
Hint: For part A, let
X;
be the number
of
extra coupons collected to get the i-th distinct coupon after
i-1
types
of
distinct coupons have been collected. Then the total expected number
of
coupons to collect
N
all distinct types is
E[X]
= L
E[X;].
For part B, which is the expected probability (P) that the i-th
i=1
coupon type is not in the n coupons?
97

Probability Theory
For part B, let Y be the number
of
distinct types
of
coupons in the set
of
n coupons. We
introduce indicator random variables I;, i =
1,
2,
· · ·,
N,
where
{
I;
=
1,
if
at least one coupon
of
the i-th type
is
in the set
of
n coupons
I;
= 0, otherwise
N
So
we
have Y
=I,+
/2
+···+IN
=_LI;
i=l
For each collected coupon, the probability that it
is
not the i-th coupon type is N -
l.
N
Since all n coupons are independent, the probability that none
of
the n coupons is the i-th
( N -1
)n
( N
-1
)n
coupon type is P(I; = 0) = N and we have
£[/;]
=
P(l,
=
1)
=
1-
N
:. E[Y]=
:tE[/;]=N-N(N-l)n.32
i=I N
Joint default probability
If
there
is
a 50% probability that bond A will default next year and a 30% probability
that bond B will default. What is the range
of
probability that at least one bond defaults
and what
is
the range
of
their correlation?
Solution: The range
of
probability that at least one bond defaults
is
easy to find. To have
the largest probability, we can assume whenever A defaults, B does not default;
whenever B defaults, A does not default.
So
the maximum probability that at least one
bond defaults
is
50% + 30% =
80%.
(The result only applies
if
P(A)
+
P(B)
'.5:
1
).
For
the minimum, we can assume whenever A defaults, B also defaults. So the minimum
probability that at least one bond defaults is 50%.
To calculate the corresponding correlation, let I A and I 8 be the indicator for the event
that bond A/B defaults next year and p
AB
be their correlation. Then we have
E[I
A]=
0.5,
E[I
8] = 0.3,
var(JJ
=PA
x
(1-
p
A)=
0.25, var(/
8) = 0.21.
32 A similar question:
if
you randomly put
18
balls into I 0 boxes, what is the expected number
of
empty
boxes?
98

A Practical Guide To Quantitative Finance Interviews
P(A
or
B defaults)= E[JA]+E[/8
]-E[JA/
8]
= E[J A ] + E[J
8 ] - (
E[
I A
]E[J
8] -
cov(/
A
,I
8
))
= 0.5
+0.3-(0.5
x
0.3-
PAB(jA(jB)
=
0.65-.J0.21/
2pAB
For the maximum probability, we
have
0.65-.J0.21I2pA
8 = 0.8
=>
PAn
= -J3i7.
For the minimum probability, we have
0.65-.J0.21I2pA
8 =
0.5
=>
PAn
=
.J3i7.
In this problem, do
not
start with
P(A
or
B defaults)=0.65-.J0.2112pA8 and
try
to set
p A8 = ± 1 to calculate the maximum and minimum probability since the correlation
cannot
be
±I.
The range
of
correlation is restricted
to
[
-.J3i7,
..J377]
.
4.
6
Order
Statistics
LetXbe
a random variable with cumulative distribution function Fx(x). We
can
derive
the distribution function for the minimum
I:,
= min(
xi'
x
2'
...
' x
n)
and for the maximum
Zn=
max(XpX
2
,-··,Xn)
of
n IID random variables with
cdf
Fx(x)as
P(I:,
x)
=
(P(X
x)Y
=>I-Fr
(x) =
(1-Fx(x)Y
=>fr
(x) =
efx
(x)(I-Fx(x)y-i
n n
P(Zn
x)
=
(P(X
x)Y
=>
Fz"
(x) =
(Fx(x)Y
=>
fz" (x) = nfx(x)(Fx (x)y-i
Expected value
of
max and min
Let
XPX
2
,-··,Xn
be 110 random variables with uniform distribution between 0 and
1.
What are the cumulative distribution function, the probability density function and
expected value
of
Zn=
max(XpX
2
,-··,Xn)?
What
are the cumulative distribution
function, the probability density function and expected value
of
Yn
= min(X1
,X
2, • •
·,
Xn)?
Solution: This is a direct test
of
textbook knowledge. For uniform distribution
on
[O,
1],
Fx(x) = x and
fx(x)
=
1.
Applying
Fx(x)
and
fx(x)
to Zn=
max(X
1
,X
2,
..
·,Xn)
we
have
P(Zn
x)
=
(P(X
x)Y
=>
F2" (x) =
(Fx(x)f
=
Xn
=>
fz"
(x) = nfx(x)(Fx(x)y-1 =
nxn-1
99

Probability Theory
1 1 n [
n+I
]'
n
and E[Zn]=
xfz
(x)dx=
nxndx=-
x
=-.
n
n+l
0
n+l
P(Y,,
;?:
x) = (P(X;?:
x)Y
=>Fr
" (x) =
1-(1-
Fx
(x)f
=
1-(1-
xY
=>fr"
(x)
= nfx
(x)(l-Fx
(x)f-
1 =
n(l-xy-'
and
E[Y,,]=
rnx(l-xf-'dx=
rn(l-y)yn-ldx=[yn]I
__
n_[Yn+i]'
=-1-
.
.b .b
0
n+l
0
n+l
Correlation
of
max and min
Let
X1 and X2
be
IID random variables
with
uniform distribution
between
0 and 1,
Y =
min(XpX
2)
and
Z =
max(X"X
2
).
What
is the probability
of
Y;:::
y given that
Z $ z for any
y,
z E
[O,
l]?
What
is the correlation
of
Y
and
Z?
Solution: This problem
is
another demonstration that a figure is worth a thousand words.
As
shown in Figure 4.7, the probability that Z z is simply the square
with
side length
z. So Since
Z=max(X
1
,X
2) and
Y=min(X
1
,X
2
),
we
must have
Y $ Z for any
pair
of
X,
and
X2• So
if
y >
z,
P(Y y I Z z) = 0.
For
y z, that X,
and X2 satisfies
Y;:::y
and
Z$z
is the
square
with vertices
(y,y),(z,y),(z
,z),
and
(y,z),
which
has
an
area
(z-
y)
2• So
P(Y;:::
y n Z $ z) =
(z
-y)2• Hence
{ (z -
y)
2 I z2,
if
0 $ z $ 1
and
0 $ y $ z
P(Y;:::
y I Z $
z)
= 0, otherwise
Now let's move
on
to calculate the correlation
of
Y and
Z.
corr(Y,Z) = cov(Y,Z) =
E[fZ]-
E[Y]E[Z]
std(Y) xstd(Z) J E[Y2]-E[Y]2 x
100
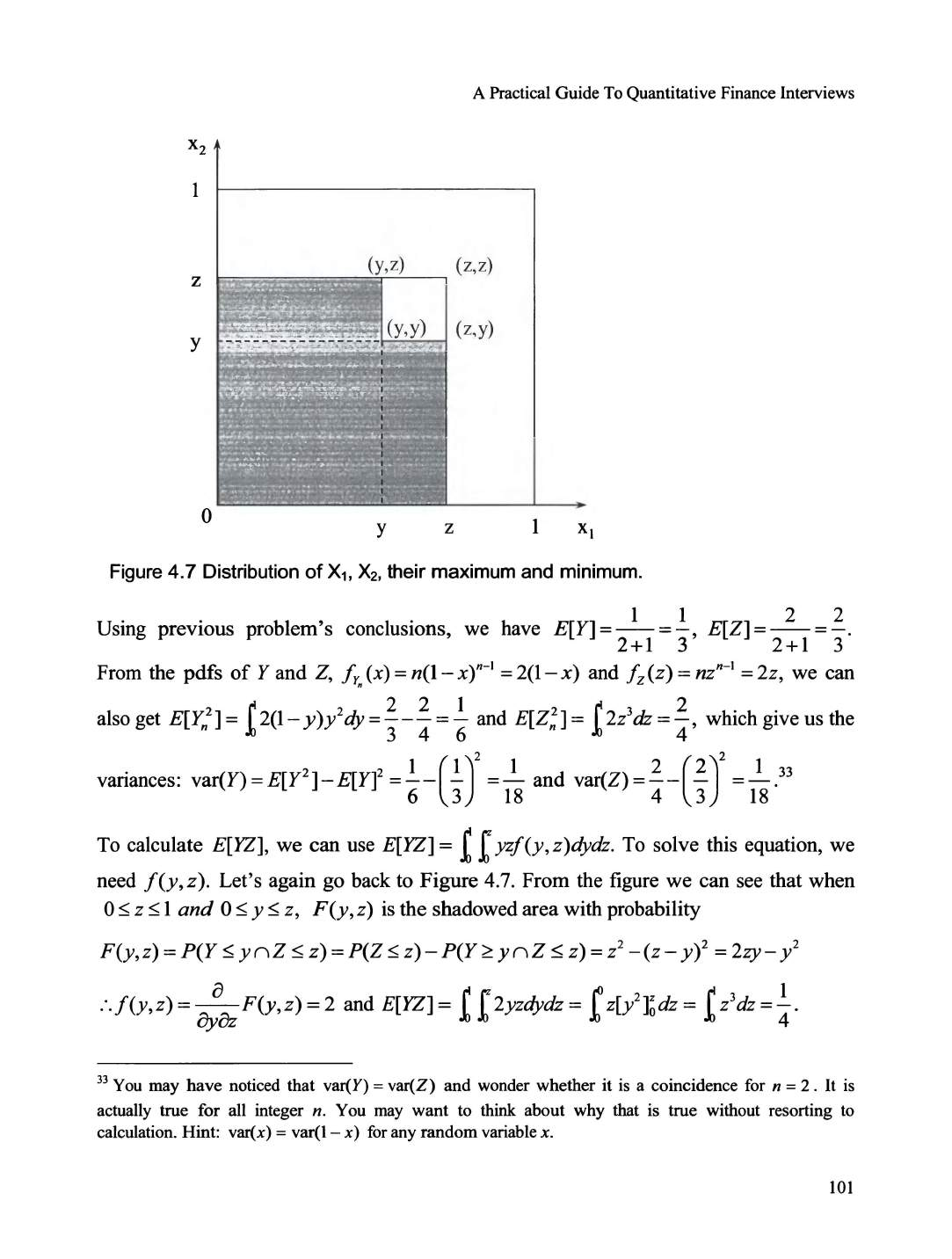
A Practical Guide To Quantitative Finance Interviews
I
z
y
0 y z I
Figure
4.7
Distribution
of
X1,
X2,
their maximum and minimum.
Using previous problem's conclusions, we have
E[Y]=-
1
-=.!.,
E[Z]=-
2
-=3..
2+1 3
2+1
3
From the pdfs
of
Y and Z, fr. (x) =
n(l-
xt-
1 =
2(1-x)
and /2(z) = nzn-i = 2z, we can
also get E[Yn2] =
r'
2(1-
y)y
2dy =
3__3_
=
_.!._
and
E[Z;]
=
r'
2z3dz =
3..,
which give us the
1 3 4 6 1 4
variances: var(Y)=E[Y2
]-E[Y]
2
=--
-
=-and
var(Z)=--
- =
1 ( 1 ) 2 1 2 ( 2 ) 2 1
33
6 3
18
4 3
18
To
calculate E[fZ], we can use E[.YZ] = ! r
To
solve this equation, we
need
f(y,z).
Let's again go back to Figure 4.7. From the figure we can see that when
0:::;
z:::;
1
and
0:::;
y:::;
z,
F(y,z)
is the shadowed area with probability
F(y,z)
= P(Y:::;
ynZ:::;
z)
= P(Z:::;
z)-P(Y
ynZ:::;
z) = z2
-(z-
y)
2 =
2zy-
y2
:.f(y,z)
=
;az
F(y,z)
= 2 and E[.YZ] = ! r = r = ! z3
dz
=
33
You
may
have
noticed that var(Y) = var(Z) and wonder whether it
is
a coincidence for n =
2.
It
is
actually true for all integer n. You
may
want to think about why that is true without resorting to
calculation. Hint: var(x) = var(l -x)
for
any random variable x.
101

Probability Theory
An alternative and simpler approach to calculate
E[fZ]
is again to take advantage
of
symmetry. Notice that no matter x1
:::::
x2 or x1 > x2, we always have
yz
= x1x2
( z = max(x1
,x
2) and y = min(xpx2)
).
11
1 1 1
:.E[fZ]=
X1X2dx1dx2
=E[X1]E[X2]=-X-=-.
2 2 4
1 cov(Y
Z)
1
Hence cov(Y,
Z)
=
E[rz]-
E[Y]E[Z]
= - and corr(Y,
Z)
=
'.J
=
36 var(Y) x var(Z) 2
Sanity check: That Y and Z have positive autocorrelation make sense since when Y
becomes large, Z tends to become large as well ( Z Y ).
Random ants
500 ants are randomly put
on
a 1-foot string (independent uniform distribution for
each
ant between 0 and 1
).
Each ant randomly moves toward one end
of
the string (equal
probability to the left or right) at constant speed
of
1 foot/minute until it falls
off
at one
end
of
the string. Also assume that the size
of
the ant is infinitely small. When two ants
collide head-on, they both immediately change directions and keep
on
moving
at
I
foot/min. What is the expected time for all ants to fall
off
the string?34
Solution: This problem is often perceived to be a difficult one. The following
components contribute to the complexity
of
the problem: The ants are randomly located;
each ant can go either direction; an ant needs to change direction when it meets another
ant. To solve the problem, let's tackle these components.
When two ants collide head-on, both immediately change directions. What does it mean?
The following diagram illustrates the key point:
Before collision: After switch
When an ant A collides with another ant B, both switch direction. But
if
we exchange the
ants' labels, it's like that the collision never happens. A continues to move
to
the right
and B moves to the left. Since the labels are randomly assigned anyway, collisions
make
no difference to the result. So we can assume that when two ants meet, each just keeps
on going
in
its original direction. What about the random direction that each ant chooses?
Once the collision is removed, we can use symmetry to argue that it makes no difference
which direction that an ant goes either. That means
if
an
ant
is
put at the x-th foot, the
34
Hint:
If
we switch the label
of
two ants that collide with each other, it's like that the collision
never
happened.
102

A Practical Guide To Quantitative Finance Interviews
expected value for it to fall
off
is
just
x min.
If
it goes in the other direction, simply set x
to
1-
x. So the original problem
is
equivalent
to
the following:
What is the expected value
of
the maximum
of
500 IID random variables with uniform
distribution between 0 and
1?
Clearly the answer is 499 min, which
is
the expected time for all ants to fall
off
the
500
string.
103


Chapter 5 Stochastic Process and Stochastic Calculus
In this chapter, we cover a few
topics-Markov
chain, random walk and martingale,
dynamic programming-that are often not included
in
introductory probability courses.
Unlike basic probability theory, these tools may not be considered to be standard
requirements for quantitative researchers/analysts. But a good understanding
of
these
topics can simplify your answers to many interview problems and give you an edge in
the interview process. Besides, once you learn the basics, you'll find many interview
problems turning into fun-to-solve math puzzles.
5.
1 Markov Chain
A Markov chain is a sequence
of
random variables X0
,X
1
,.
•
.,xn,
...
with the Markov
property that given the present state, the future states and the past states are independent:
P{Xn+i=jlXn=i,Xn_
1
=in_
1
,···,X
0
=i
0
}=pij=P{Xn+i=JIXn=i}
for all n, i0,
···,
in-1'
i, and
j,
where i, j E
{l,
2, .. .,
M}
represent the state space S = {s" s2,
..
.,
sM}
of
x.
In other words, once the current state
is
known, past history has no bearing
on
the future.
For a homogenous Markov chain, the transition probability from state i to state j does
not depend on n.
1 A Markov chain with M states can be completely described by
an
M x M transition matrix P and the initial probabilities
P(X
0) •
P11
P1
2
P1M
Transition matrix:
P={Pu}=
P 21
P22
P2M where the transition
'
pij
IS
PM1
PM
2
PMM
probability from state i to state
j.
M
Initialprobabilities:
P(X
0
)=(P(X
0
=l)
,
P(X
0
=2),
.. .,
P(X
0
=M)),
LP(X
0
=i)=l.
i:I
The
probability
of
a path:
P(X,
= i,'
X2
= i2
...
'
xn
=in
I
Xo
=
io)
=
pioi1
pi1i2
.. . P
;n
_l
in
Transition graph: A transition graph is often used to express the transition matrix
graphically. The transition graph is more intuitive than the matrix, and it emphasizes
1
In
this chapter, we only consider finite-state homogenous Markov chains (i.e., transition probabilities do
not change over time).

Stochastic Process and Stochastic Calculus
possible and impossible transitions. Figure
5.1
shows the transition graph and the
transition matrix
of
a Markov chain with four states:
1 0.5 ; 2 3 4
'-·
o.s
[f
os
II
0 0.5 0 0.5 l
< > 0.5 0 0.25 0.25 2
P=
0 0.4 0.4 0.2 3
0.25 0.4 0 0 0 1 4
0.4
Figure
5.1
Transition graph and transition matrix
of
the Play
Classification
of
states
State j
is
accessible from state i
if
there
is
a directed path in the transition graph from i to
j
(::In
such that
Pt>>
0). Let
TiJ
= min(n :Xn = j I X0 = i), then
P(TiJ
<
oo)
>
0)
if
and
only
if
state j is accessible from state
i.
States i and j
communicate
if
i is accessible
from}
and} is accessible from
i.
In Figure 5.1, state 3 and 1 communicate. State 4 is
accessible form state
l,
but they do not communicate since state 1
is
not accessible from
state 4.
We say that state i is
recurrent
if
for every state j that is accessible from i, i
is
also
accessible from j (VJ,
P(TiJ
<
oo)
> 0
=>
P(TiJ
<
oo)
= 1
).
A state is called
transient
if
it is
not recurrent (
::3},
P(TiJ
<
oo)
> 0 and P(I';j <
oo)
< 1
).
In Figure 5.1, only state 4 is
recurrent. States
1,
2 and 3 are all transient since 4 is accessible from 1/2/3, but 1/2/3 are
not accessible from 4.
Absorbing
Markov
chains: A state i is called absorbing
if
it is impossible to leave this
state (
P;;
=
l,
piJ
= 0,
VJ
* i
).
A Markov chain
is
absorbing
if
it has at least one absorbing
state and
if
from every state it is possible to go to an absorbing state. In Figure 5. I, state
4 is an absorbing state. The corresponding Markov chain is an absorbing Markov chain.
Equations for
absorption
probability: The probability to reach a specific absorbing
state s, a1
,.
•
·,
aM,
are unique solutions to equations
a_,
=I,
a;
= 0 for all absorbing
M
state(s) i * s, and
a;=
Iajpii
for all transient states
i.
These equations can be easily
106

A Practical Guide To Quantitative Finance Interviews
derived using the law
of
total probability
by
conditioning
the
absorption probabilities
on
the next state.
Equations
for the expected time
to
absorption: The expected times
to
absorption,
µ1
,.
•
·,
µ
M,
are unique solutions to the equations
µ;
= 0
for
all absorbing state( s) i and
m
µ; = 1
+I,
pijµj
for
all transient states
i.
These equations can be easily derived using
the
j=l
law
of
total expectation by conditioning
the
expected times to absorption on the next
state. The number 1 is added since it takes
one
step to reach the next state.
Gambler's
ruin
problem
Player M has
$1
and player N has $2. Each game gives the winner
$1
from
the other.
As
a better player, M wins 2/3
of
the games. They play until
one
of
them
is
bankrupt. What
is
the probability that M wins?
Solution: The most difficult part
of
Markov chain problems often lies
in
how to choose
the right state space
and
define the transition probabilities
Py
's,
Vi,
j.
This problem has
fairly straightforward states. You can define the state space as the combination
of
the
money that player M
has
($m) and the money that player N has ($n):
{(m,n)} = {(3,0),(2,1),(1,2),(0,3)}. (Neither m nor n can
be
negative since the whole
game stops when one
of
them goes bankrupt.) Since
the
sum
of
the dollars
of
both
players is always $3,
we
can actually simplify the state space using only
m:
{m}
= {0,1,2,3}.
The transition graph
and
the corresponding transition matrix are shown
in
Figure 5.2.
[
Po.o
Po.1
Po.2
Po,31
I l 0
I
1/3
2/3 l I 0
r£J
P={Jt}=
P1.o
P1.1
P1.2
P1,J
= K 1
l 2 3
P2.o
P2.1
P2.2
P2.J
0 K
l/3
2/3
P2.o
P2.1
P2.2
P2.J
0 0
0 x
0 l
Figure 5.2 Transition matrix and transition graph
for
Gambler's ruin problem
The initial state
is
X0 = 1
(M
has
$1
at the beginning). At state
1,
the next state is 0
(M
loses a game) with probability
1/3
and 2
(M
wins a game) with probability 2/3.
So
Pi.o
=113 and p1
,2
=213.
Similarly we can get p2,1 =113 and p2,3 =213. Both state 3
(Mwins the whole game) and state 0 (Mloses the whole game) are absorbing states.
To calculate the probability that M reaches absorbing state 3,
we
can apply absorption
probability equations:
107

Stochastic Process and Stochastic Calculus
3 3
a3 =
1,
a0 = 0 , and a1 =
"""'
p,
1
.a1
.,
a2 =
"""'
p2 .a .
£..J
'
£..J
,.f .I
j=O j=O
Plugging
in
the transition probabilities using either the transition graph
or
transition
matnx,
we
have
. a1 = 1/ 3 x 0 + 2 I 3 x a2} { a1 = 417
a2 = 1/ 3 x a1 + 2 I 3 x 1 a2 = 617
So, starting from $1, player M has 417 probability
of
winning.
Dice question
Two players bet on roll(s)
of
the total
of
two standard six-face dice. Player A bets that a
sum
of
12
will occur first. Player B bets that two consecutive
7s
will occur first. The
players keep rolling the dice and record the sums until one player wins. What is the
probability that A will win?
Solution: Many
of
the simple Markov chain problems can
be
solved using pure
conditional probability argument.
It
is
not surprising considering that Markov chain is
defined as conditional probability:
P{X
1 =
1·
1 X = i X 1 = i 1 • • • X0 = i0} = p
..
=
P{X
1 =
1·
1 X =
i}
n+
n '
n-
n-
' ' y n+ n ·
So let's first solve the problem using conditional probability arguments. Let
P(A)
be
the
probability that A wins. Conditioning
P(A)
on
the first throw's sum
F,
which
has
three
possible outcomes F =
12,
F = 7 and F
{7,
12},
we
have
P(A)
=
P(A
IF=
12)P(F
=
12)
+
P(A
IF=
7)P(F
=
7)+
P(A
{7,12})P(F
{7,
12})
Then we tackle each component on the right hand side. Using simple permutation, we
can easily see that
P(F=12)=1136,
P(F=7)=6136,
Also it
is obvious that
P(AIF=12)=1
and (The
game
essentially
starts over again.) To calculate
P(A
IF=
7), we need to further condition on the second
throw's total, which again has three possible outcomes: E = 12, E =
7,
and E {7,12}.
P(A
IF=
7) =
P(A
IF=
7,E
= 12)P(E =
12
IF=
7)+P(A
IF=
7,E
=
7)P(E
=
71F=7)
+
P(A
IF=
7, E
{7,12}
)P(E
{7,
12}
IF=
7)
=
P(A
IF=
7,E
=
12)x1/36+
P(A
IF
=7,E
=
7)x6/36
=
1x1I36+0x
6136
+
P(A)x
29 I 36 = l
/36+
29 I
36P(A)
Here the second equation relies on the independence between the second and the first
rolls.
If
F = 7 and E =
12,
A wins;
if
F = 7 and E = 7, A loses;
if
F = 7 and
108

A Practical Guide
To
Quantitative Finance Interviews
E
!l
{7,12}, the game essentially starts
over
again. Now we have all the necessarily
information for
P(
A)
. Plugging it into the original equation, we have
P(A)
=
P(A
IF=
I
2)P(F
= 12) +
P(A
IF=
7)P(F
= 7) +
P(A
IF
!l
{7,
12}
)P(F
!l
{7,
12})
=Ix
1/36
+
6136x
(1/36 + 29
/36P(A))
+ 29
/36P(A)
Solving the equation, we get
P(
A)
=
7I13
.
This approach, although logically solid, is not intuitively appealing.
Now
let's
try a
Markov chain approach. Again the key part is to choose the right state space
and
define
the transition probabilities.
It
is apparent that
we
have two absorbing states, 12 (A wins)
and
7-7 (B wins), at least two transient states, S (starting state) and 7 (one 7 occurs, yet
no
12
or
7-7 occurred).
Do
we
need any other states? Theoretically, you can have other
states. In fact,
you
can
use
all combination
of
the outcomes
of
one roll
and
two
consecutive rolls as states to construct a transition matrix and you will get the same final
result. Nevertheless, we want to consolidate as many equivalent states as possible. As
we
just
discussed
in
the conditional probability approach,
if
no 12 has occurred and the
most recent roll did not yield 7, we essentially go back to the initial starting state S. So
all
we
need are states S, 7,
7-
7 and 12. The transition graph and probability to reach state
12 are shown
in
Figure 5.3.
6/36
cfil)1
7
Probability to absorption state
12
a12
=I,
a1-1
= 0 }
as=
l/36
x I
+6/36
x a7 +
29/36x
as 7 /13
a7
=l
/
36xl+6/36x0+29/36xas
Figure 5.3 Transition graph and probability to absorption
for
dice rolls
Here the transition probability is again derived from conditional probability arguments.
Yet the transition graph makes the process crystal clear.
Coin triplets
Part
A.
If
you keep
on
tossing a fair coin,
what
is the expected number
of
tosses such
that you can have
HHH
(heads heads heads) in a row?
What
is the expected number
of
tosses to have
THH
(tails heads heads) in a row?
Solution: The most difficult part
of
Markov chain is, again, to choose the right state
space. For the
HHH
sequence, the state space is straightforward. We only need four
states: S (for the starting state when no coin is tossed
or
whenever a T turns
up
before
HHH),
H,
HH,
and
HHH.
The transition
graph
is
109

Stochastic Process and Stochastic Calculus
At
state
S,
after a coin toss, the state will stay at S when the toss gives a
T.
If
the toss
gives an
H,
the state becomes
H.
At state
H,
it has 1/2 probability goes back to state S
if
the next toss is
T;
otherwise, it goes to state
HH.
At state HH, it also has
112
probability
goes back
to
state S
if
the next toss is
T;
otherwise, it reaches the absorbing state
HHH.
So we have the following transition probabilities:
Ps.s
=
t,
Ps.H
=
t,
PH
.s
=
t,
PH.HH
=
+,
PHH,s
=
+,
PHH,HHH
=
+,
and
PHHH
,
HHH
=
1.
We are interested in the expected number
of
tosses to get
HHH,
which is the expected
time to absorption starting from state
S.
Applying the standard equations for the
expected time to absorption, we have
µs=l+±µs+tµ11
µH
=I
+!µs
+t
µHH
µHH
=
l+tµs
+t
µHHll
µHHH
=0
So from the starting state, the expected number
of
tosses to get HHH is
14.
Similarly for expected time to reach
THH,
we can construct the following transition
graph and estimate the corresponding expected time to absorption:
112
An
1/2
1/21\)
\__W
µs = 1 +I µs +I
µr
µr
= 1
+fµr
+f
µrH
µ711
= 1 + I
µT
+ I
µTHI/
µTHH
= 0
So from the starting state
S,
the expected number
of
tosses to get
THH
is
8.
µs
=8
µT
=4
µTH
= 2
µ71111 = 0
Part B. Keep flipping a fair coin until either HHH or
THH
occurs in the sequence. What
is the probability that you get an HHH subsequence before
THH?
2
2 Hint: This problem does not require the drawing
of
a Markov chain. Just think about the relationship
between
an
HHH
pattern and a
THH
pattern. How can we get an
HHH
sequence before a
THH
sequence?
110

A Practical Guide To Quantitative Finance Interviews
Solution:
Let's
try a standard Markov chain approach. Again the focus is on choosing
the right state space.
In
this case,
we
begin with starting state
S.
We only need ordered
subsequences
of
either
HHH
or THH. After one coin is flipped,
we
have either state
Tor
H. After two flips, we have states
TH
and HH. We
do
not need
TT
(which is equivalent
to T for this problem)
or
HT
(which is also equivalent to T as well). For three coin
sequences, we only
need
THH and
HHH
states,
which
are both absorbing states. Using
these states, we can build the following transition graph:
1/2
in
112
A(\•
Cf)
({)
®
@J
112
Figure 5.4 Transition graph
of
coin tosses to reach
HHH
or
THH
We want to get the probability
to
reach absorbing state
HHH
from the starting state
S.
Applying the equations for absorption probability,
we
have
aHHH
=
1,
arHH
= 0
as
=tar
+taH
ar
=tar
+taTH,
aH
=tar
+faHH
aTH
=tar
+taTHH•aHH
=tar
+taHHH
ar
=0,aTH
=0
a -I
s-8
a =
.l
H 4
a -I
HH
-2
So
the probability that we end up with the
HHH
pattern is
1/8.
This problem actually has a special feature that renders the calculation unnecessary. You
may have noticed that
ar
= 0. Once a tail occurs,
we
will always
get
THH
before HHH.
The reason is that the last two coins in THH is
HH,
which is the first two coins in
sequence HHH. In fact, the only way that the sequence reaches state
HHH
before
THH
is that we get three consecutive
Hs
in the beginning. Otherwise, we always have a T
before the first
HH
sequence and always end
in
THH
first. So
if
we don't start the coin
flipping sequence with
HHH,
which has a probability
of
118,
we will always have
THH
beforeHHH.
Part C. (Difficult)
Let's
add more fun to the triplet game. Instead
of
fixed triplets for the
two players, the new game allows both to choose their own triplets. Player 1 chooses a
triplet first and announces it; then player 2 chooses a different triplet. The players again
toss the coins until one
of
the two triplet sequences appears. The player whose chosen
triplet appears first wins the game.
111
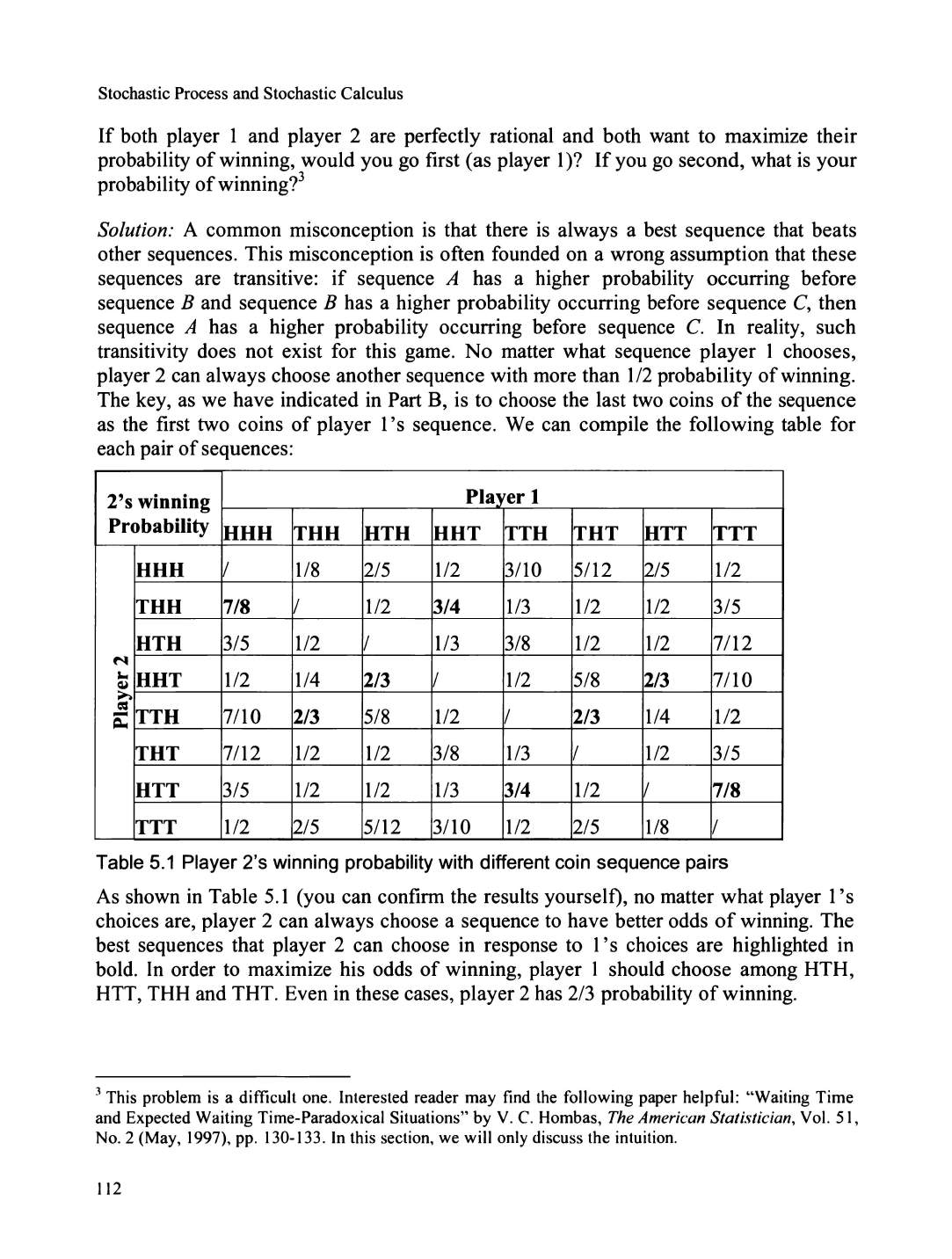
Stochastic Process
and
Stochastic Calculus
If
both player 1 and player 2 are perfectly rational and both want to maximize their
probability
of
winning, would you go first
(as
player 1 )?
If
you go second, what is your
probability
of
winning?3
Solution: A common misconception is that there is always a best sequence that beats
other sequences. This misconception is often founded on a wrong assumption that these
sequences are transitive:
if
sequence A has a higher probability occurring before
sequence B and sequence B has a higher probability occurring before sequence
C,
then
sequence A has a higher probability occurring before sequence
C.
In
reality, such
transitivity does not exist for this game.
No
matter what sequence
player
1 chooses,
player 2 can always choose another sequence with more than l/2 probability
of
winning.
The key, as we have indicated in Part B, is to choose the last two coins
of
the sequence
as the first two coins
of
player
l's
sequence. We can compile the following table for
each pair
of
sequences:
2's winning Plaver 1
Probability
HHH
THH
HTH
HHT
TTH
THT
HTT
TTT
HHH
I l/8
215
l/2
3/10 5/12
215
112
THH
7/8 v 1/2 3/4 l/3 1/2 l/2
315
HTH
315
l/2
11
l/3 3/8
l/2
l/2 7/12
M
""
HHT
1/2 1/4
2/3
11
1/2 5/8
2/3
7110
;;...
=
TTH
7/10
2/3
5/8
l/2
v 2/3
l/4
112
=::
TUT
7/12
112
1/2 3/8
1/3
I l/2
315
HTT
315
l/2
1/2 l/3 3/4 1/2
11
7/8
TTT
1/2
215
5112
3/10
l/2
215
1/8
I
Table
5.1
Player 2's winning probability with different coin sequence pairs
As shown
in
Table
5.1
(you can confirm the results yourself), no matter what player
l's
choices are, player 2 can always choose a sequence to have better odds
of
winning. The
best sequences that player 2 can choose in response to 1
's
choices are highlighted in
bold.
In
order to maximize his odds
of
winning, player I should choose among HTH,
HTT, THH and THT. Even in these cases, player 2 has 2/3 probability
of
winning.
3 This problem is a difficult one. Interested reader
ma
y find the following paper helpful: "Waiting
Time
and
Expected Wailing Time-Paradoxical Situations"
by
V.
C. Hombas, The American Statistician, Vol.
51,
No. 2 (May, 1997). pp. 130-133. In this section,
we
will only discuss the intuition.
112

A Practical Guide
To
Quantitative Finance Interviews
Color balls
A box contains n balls
of
n different colors. Each time, you randomly select a pair
of
balls, repaint the first to match the second, and put the pair back into the box. What
is
the expected number
of
steps until all balls
in
the box are
of
the same color? (Very
difficult)
Solution: Let
Nn
be the number
of
steps needed to make all balls the same color, and let
F;,
i =
1,
2, · ·
·,
n, be the event that all balls have color i in the end. Applying the law
of
total expectation,
we
have
Since all the colors are symmetric (i.e., they should have equivalent properties), we have
P[F;]
=
PIF2J
= ... =
P[Fn]
= l
In
and E[Nn] =
E[Nn
IF;]=
E[Nn
I
F2]
= E[Nn I
Fn].
That
means we can assume that all the balls have color l in the end and use
E[Nn
IF;] to
represent E[Nn].
So how do we calculate E[Nn
IF;]?
Not
surprisingly, use a Markov chain. Since we
only consider event
F;,
color l is different from other colors and colors
2,
· · ·, n
become equivalent. In other words, any pairs
of
balls that have no color l ball involved
are equivalent and any pairs with a color l ball and a ball
of
another color are equivalent
if
the order is the same as well.
So
we only need to use the number
of
balls that have
color l as the states. Figure 5.5 shows the transition graph.
Figure 5.5 Transition graph
for
all n balls
to
become color 1
Staten
is
the only absorbing state. Notice that there is
no
state
0,
otherwise it will never
reach
F;
. In fact, all the transition probability
is
conditioned on
F;
as well, which makes
the transition probability
P;,;+i
I
F;
higher than the unconditional probability
P;,;+i
and
P;,;-i
IF;
lower than
P;,;-i
· For example,
Pi,o
IF;
= 0 and
Pi,o
=
1/
n.
(Without
conditioning, each ball is likely
to
be the second ball, so color l has l
In
probability
of
being the second ball.) Using the conditional transition probability, the problem
essentially becomes expected time to absorption with system equations:
E[N; IF;]= l +
E[N;-1
IF;] x I';,;-1
IF;
+E[N; I F;]x
P;,;
IF;+
E[N;+1
I F;]x I';,;+1 IF;·
113

Stochastic Process and Stochastic Calculus
To calculate
P;,;-i
IF;, let's rewrite the probability as P(xk+i = i
-11
xk
=
i,
F; ),
V k = 0,
1,
..
,,
to make the derivation step clearer:
P(
. II
'F)
P(xk=i,xk+
1
=i-1,F;)
x
=1-
x
=l
k+1
k ' i P(xk =
i,F;)
P(F;
lxk+I
=i-1,xk
=i)xP(xk+I
=i-llxk
=i)xP(xk
=i)
P(F; I
xk
=
i)
x P(xk =
i)
_ P(F;
lxk+I
=i-l)xP(xk+I
=i-llxk
=i)
P(F; I
xk
=
i)
i-1
i(n-i)
-
x----
= n
n(n-l)_(n-i)x(i-1)
i/n
n(n-1)
The first equation
is
simply the definition
of
conditional probability; the second equation
is the application
of
Bayes' theorem; the third equation applies the Markov property. To
derive P(F; I
xk
=
i)
= i
In,
we again need to use symmetry.
We
have shown that
if
all
the balls have different colors, then we have P[
F;]
=
P[
F2] =
..
· = P[ Fn] =
I/
n.
What is
the probability
of
ending in a given color, labeled as c,
if
i
of
the balls are
of
color
c?
It
is simply i
In
. To see that, we can label the color
of
each
of
the i balls
of
color c as
cJ, j =
1,
..
·,i
(even though they are in fact the same color). Now
it's
obvious that all
balls will end with color
cJ
with probability 1
In.
The probability for c is the sum
of
probabilities
of
c/s,
which gives the result i
In.
Similarly we have P(F; I
xk+I
=
i-1)
=
(i-1)/
n.
For
P(xk+I
=
i-1
I
xk
=
i),
we use a
basic counting method. There are
n(n
-1)
possible permutations to choose 2 balls out
of
n balls. In order for one color 1 ball to change color, the second ball must be color
1,
which has i choices; the first ball needs to be another color, which has
(n-i)
choices.
S
P(
. l I
.)
i(n
-i)
o
xk+I
= z -
xk
= z = .
n(n
-1)
Applying the same principles, we can get
. .
(n-i)x2i
. .
(n-i)x(i+l)
P(xk+i
=1lxk
=1,F;)=
, P(xk+i
=1+llxk
=1,F;)=
.
n(n-1)
n(n-1)
Plugging into
E[
N;
I
F;]
and simplifying
E[
N;
I F;] as Z;, we have
(n-i)
x
2ix
Z; =
n(n-1)
+
(n-i)(i
+ l)Z;+i +
(n-i)(i-
l)Z;_1•
114

A Practical Guide To Quantitative Finance Interviews
Using these recursive system equations and the boundary condition Zn= 0, we can get
Z1=(n-l)2.4
5.2
Martingale
and
Random walk
Random walk: The process
{Sn;
n
1}
is called a random walk
if
{X;;i
1}
are IID
(identical and independently distributed) random variables and
Sn=
X,
+···Xn,
where
n =
1,
2, · · · The term comes from the fact that
we
can think
of
Sn
as the position
at
time
n for a walker who makes successive random steps
X,,
X2, • • •
If
X;
takes values 1 and
-1
with probabilities p and 1 - p respectively,
Sn
is called a
simple
random
walk with parameter
p.
Furthermore,
if
p = f, the process
Sn
ts
a
symmetric random walk. For symmetric random walk,
it's
easy to show that
E[Sn] = 0 and var(Sn) =
E[S;]-E[Sn]
2 = E[S;] = n .5
Symmetric random walk is the process that is most often tested
in
quantitative
interviews. The interview questions on random walk often revolve around finding the
first n for which
Sn
reaches a defined threshold
a,
or the probability that
Sn
reaches
a for any given value
of
n .
Martingale: a martingale {
Zn;n
1}
is a stochastic process with the properties that
E[I
Zn
I]<
oo
for all n and
E[Zn+I
I
Zn=
zn,Zn-t =
zn_
1
,-··,Z
1 = z1] =
zn.
The property
of
a
martingale can be extended to E[
Zm;
m > n I Zn= zn,Zn-I =
zn-P
· ·
·,Z,
= z1] =
zn,
which
means the conditional expected value
of
future
Zm
is the current value
Zn.
6
A symmetric random walk is a martingale. From the definition
of
the symmetric random
{
Sn
+ 1 with probability
112
walk we have
Sn+i
= . . . , so E[Sn+i
ISn
=sn,···,S
1
=s
1
]=sn.
s n
-1
wt
th probab1hty 1/2
Since
E[S:+i
-(n
+
1)]
= t[(Sn +
1)
2 +(Sn
-1)2]-(n
+
1)
=
s;-n,
s;
-n is a martingale
as
well.
4 Even this step is not straightforward. You need to plug in the
ts
and try a few cases starting with
i = n -
I.
The
pattern will emerge and you can see that all the terms containing
z._,,
z._,.
··
·,
Z2 cancel out.
5 Induction again can be used for its proof. Var(S,) = Var(Z,)
=I.
Induction step:
If
Var(S.) = n, then
we
have Var(S.,,) = Var(S. +
x.,,)
= Var(S.) + Var(x.,,) = n
+I
since x
••
, is independent
of
Sn.
6 Do not confuse a martingale process with a Markov process. A martingale does
not
need to be a Markov
process; a Markov process does not need to
be
a martingale process, either.
115

Stochastic Process and Stochastic Calculus
Stopping rule: For an experiment with a set
of
IID random variables X1
,X
2
,-··,
a
stopping rule for {X;;i
1}
is a positive integer-value random variable N (stopping time)
such that for each n >
l,
the event {N
:5:
n}
is independent
of
Xn+i•Xn+
2
,···
. Basically it
says that whether to stop at n depends only
on
X1
,X
2
,··
·,Xn
(i.e., no look ahead).
Wald's Equality: Let N be a stopping rule for IID random variables
XPX
2
,-··
and let
SN
= X, + X2 + · · · + X N , then E[
SN]
= E[ X]E[
N].
Since it is an
important-yet
relatively little
known-theorem,
let's briefly review its
proof. Let
In
be the indicator function
of
the event {N n}. So
SN
can
be
written as
SN=
LX)n,
where
In
=1
if
and
In
=0
if
N:5:n-1.
n=I
From the definition
of
stopping rules, we know that
In
is independent
of
Xn,
Xn+i
• · · ·
(it only depends on XI' X2,
···,
Xn_
1
).
So
E[X)n]=E[Xn]E[In]=E[X]E[In]
and
E[SN
l = E[t,x.1"] =
t.E[
X/"]
=
t.E[
X]E[I.] =
E[
xJt,E[
/"] =
E[X]E[N]
.7
A martingale stopped at a stopping time is a martingale.
Drunk man
A drunk man is at the 17th meter
of
a 100-meter-long bridge. He has a
50%
probability
of
staggering forward or backward one meter each step. What is the probability that he
will make it to the end
of
the bridge (the
lOOth
meter) before the beginning (the
0th
meter)? What is the expected number
of
steps he takes
to
reach either the beginning
or
the end
of
the bridge?
Solution: The probability part
of
the
problem-often
appearing in different
disguises-is
among the most popular martingale problems asked
by
quantitative interviewers.
Interestingly, few people use a clear-cut martingale argument. Most candidates either
use Markov chain with two absorbing states or treat it as a special version
of
the
gambler's ruin problem with p = 1I2. These approaches yield the correct results
in
the
end, yet a martingale argument is not only simpler but also illustrates the insight behind
the problem.
7 For detailed proof and applications
of
Wald's Equality, please refer to the book Disc:rete Stochastic
Processes by Robert
G.
Gallager.
116

A Practical Guide
To
Quantitative Finance Interviews
Let's set the current
pos1t10n
(the 17th meter) to
O;
then the problem becomes a
symmetric random walk that stops at either
83
or -17.
We
also know that both
Sn
and
-n are martingales. Since a martingale stopped at a stopping time
is
a martingale,
s N and -N (where s N =
xi
+ x 2 + ... + x N with N being the stopping time) are
martingales
as
well. Let
pa
be the probability that it stops at a =
83,
p
/3
be
the
probability it stops at
-/3
=
-17
( p
/3
=
1-
pa), and N
be
the stopping time. Then
we
have
E[
SN]
=
pa
X
83-
(1-
pa) X
17
= S0 = 0 } { p = 0.17
-N]
= E[pa x
83
2
+(1-
Pa) x
17
2
]-E[N]
=
sg
-0
= 0
=>
=
1441
Hence, the probability that
he
will make it to the end
of
the bridge (the 1
OOth
meter)
before reaching the beginning is 0.17, and the expected number
of
steps he takes to
reach either the beginning or the end
of
the bridge is
1441.
We
can easily extend the solution to a general case: a symmetric random walk starting
from 0 that stops at either a
(a
>
0)
or
-/3
( p > 0
).
The probability that it stops at a
instead
of
-/3
is
Pa
=
f3
/(a+
jJ). The expected stopping time to reach either a or
-/3
is
E[
N]
= ajJ.
Dice game
Suppose that you roll a dice. For each roll, you are paid the face value.
If
a roll gives
4,
5
or 6, you can roll the dice again.
If
you get
1,
2 or
3,
the game stops. What
is
the
expected payoff
of
this game?
Solution: In Chapter 4,
we
used the law
of
total expectation to solve the problem. A
simpler approach-requiring more
knowledge-is
to apply Wald's Equality since
the
problem has clear stopping rules. For each roll, the process has
1/2
probability
of
stopping. So the stopping time N follows a geometric distribution with p =
1I2
and
we
have
E[N]
=II
p =
2.
For each roll, the expected face value is
E[X]
= 7 I
2.
The total
expected payoff
is
E[SN] =
E[X]E[N]
= 7
/2x
2 =
7.
Ticket line
At a theater ticket office, 2n people are waiting to buy tickets. n
of
them have only
$5
bills and the other n people have only
$10
bills. The ticket seller has
no
change
to
start
117

Stochastic Process and Stochastic Calculus
with.
If
each person buys one $5 ticket, what is the probability that all people will be
able to buy their tickets without having
to
change positions?
Solution: This problem is often considered to be a difficult one. Although many can
correctly formulate the problem, few can solve the problem using the reflection
principle.8 This problem is one
of
the many cases where a broad knowledge makes a
difference.
Assign + 1 to the n people with $5 bills and
-1
to the n people with $10 bills. Consider
the process as a walk. Let (a,b) represent that after a steps, the walk ends at
b.
So we
start at (0,0) and reaches (2n,O)after
2n
steps. For these 2n steps, we need to choose n
steps as
+l,
so there are (2
nJ
= 2n! possible paths.
We
are interested in the paths that
n n!n!
have the property b
0,
VO<
a<
2n steps.
It's
easier to calculate the number
of
complement paths that reach b =
-1,
30
<a<
2n. As shown in Figure 5.6,
if
we reflect
the path across the line y =
-1
after a path first reaches -1, for every path that reaches
(2n, 0) at step 2n, we have one corresponding reflected path that reaches (2n, -2) at
step 2n. For a path to reach
(2n,-
2),
there are (n
-1)
steps
of+
1 and
(n
+
1)
steps
of
-1.
So there are ( 2n J = 2n ! such paths. The number
of
paths that have the
n-1
(n-l)!(n+l)!
property b =
-1,
30
<
a<
2n, given that the path reaches (2n, 0) is also ( 2n J and the
n-1
number
of
paths that have the property b 0, VO<
a<
2n is
(
2nJ
( 2n J
(2nJ
n
(2nJ
1
(2nJ
n -
n-l
= n -
n+l
n =
n+l
n ·
Hence, the probability that all people will be able to buy their tickets without having to
change positions is 1/(n+1).
8 Consider a random walk starting at
a,
S
=a,
and reaching h
inn
steps: S =
h.
Denote N
(a,b)
as
the
0
II
n
number
of
possible paths from
(0,a)
to
(n,h)
and as the number possible paths from (0,a) to
(n,h)
that at some step k ( k >
O,
), S, =
O;
in other words,
N:'(a,b)
are the paths that contain
(
k,
0),
:30
< k < n.
The
reflection
principle
says that
if
a,
h >
0,
then
(a,
h) =
N,,
(-a,
h
).
The proof
is
intuitive: for each path (0,
a)
to (k,
0),
there
is
a one-to-one corresponding path from (0,
-a)
to (k,
0).
118
A Practical Guide To Quantitative Finance Interviews
b
-1
------------------
-2
Figure 5.6 Reflected paths: the dashed line is the reflection
of
the solid line
after it reaches
-1
Coin sequence
Assume that you have a fair coin. What is the expected number
of
coin tosses to get n
heads in a row?
Solution: Let
E[f(n)]
be the expected number
of
coin tosses to get n heads in a row.
In
the Markov chain section, we discussed the case where n = 3 (to get the pattern HHH).
For any integer
n,
we
can consider an induction approach. Using the Markov chain
approach, we can
easy
get that
E[/(l)]
=
2,
E[/(2)]
= 6 and
E[/(3)]
=
14.
A natural
guess for the general formula
is
that
£[/(n)]
=
2n+I
-2.
As always, let's prove the
formula using induction. We have shown the formula is true for n = 1,2,3. So we only
need to prove that
if
E[f(n)]
=
2n+I
-2,
E[f(n
+
1)]
=
2n+
2
-2.
The following diagram
shows how to prove that the equation holds for
E[f(n
+
1)]:
__
_.
P=l/2
P=l/2
The state before (n +
1)
heads in a
row
(denoted as (n +
l)H)
must be n heads in a row
(denoted as nH
).
It takes an expected
E[f
( n)] =
2n+I
- 2 tosses to reach nH.
Conditioned on state
nH,
there is a 1/2 probability it will go to
(n+l)H
(the new toss
yields
H)
and the process stops. There is also a 1/2 probability that it will
go
to the
119

Stochastic Process
and
Stochastic Calculus
starting state 0 (the new toss yields 1) and we need another expected
E[f
(n
+
1)]
tosses
to reach (n+
l)H.
So we have
E[f(n
+
1)]
= E[F(n)]
+txl
+
+x
E[f(n+
1)]
E[/(n+l)]
=
2x
E[F(n)]+ 2 = r+2
-2
General Martingale approach:
Let's
use
HH
· · ·
Hn
to explain a general approach for the
expected time to get any coin sequence by exploring the stopping times
of
martingales.9
Imagine a gambler has
$1
to bet on a sequence
of
n heads (
HH
· · ·
Hn
) in a fair game
with the following rule: Bets are placed on
up
to n consecutive games (tosses) and each
time the gambler bets all his money (unless he goes bankrupt). For example,
if
H
appears at the first game, he will have
$2
and he will put all $2 into the second game. He
stops playing either when he loses a game
or
when
he
wins n games in a roll, in which
case he collects
$2n
(with probability I I
2n
). Now let's imagine, instead
of
one gambler,
before each toss a new gambler joins the game and bets on the same sequence
of
n heads
with a bankroll
of
$1
as well. After the i-th game, i gamblers have participated in the
game and the total amount
of
money they have put in the game should be $i. Since each
game is fair, the expected value
of
their total bankroll is $i as well. In other words,
if
we
denote
x;
as the amount
of
money all the participating gamblers have after the i-th game,
then
(x;
-i)
is a martingale.
Now, let's add a stopping rule: the whole game will stop
if
one
of
the gamblers becomes
the first to get n heads in a roll. A martingale stopped at a stopping time is a martingale.
So we still have E[(x;
-i)]
= 0.
If
the sequence stops after the i-th toss ( i n ), the
(i-
n + 1)-th player is the (first) player who gets n heads in a roll with
payoff
2n.
So all
the
(i
-
n)
players before him went bankrupt; the
{i-
n + 2) -th player gets ( n
-1)
heads
in a roll with
payoff
2n-J ;
...
; the i-th player gets one head with payoff 2. So the total
payoff
is
fixed and
X;
=
2n
+
2n-I
+ · · · + i =
r+I
-2 .
Hence, E[(x; -i)] = 2n+I -
2-
E[i]
= 0
E[i]
= 2n+I
-2.
This approach can be applied to any coin
sequences-as
well as dice sequences or any
sequences with arbitrary number
of
elements. For example, let's consider the sequence
HHTTHH. We can again use a stopped martingale process for sequence
HHTTHH.
The
gamblers join the game one by one before each toss to bet on the same sequence
HHTTHH
until one gambler becomes the first to get the sequence
HHITHH.
If
the
sequence stops after the i-th toss, the
{i-
5)th
gambler gets the
HHTTHH
with payoff
9
If
you prefer more details about the approach, please refer to "A Martingale Approach
to
the Study
of
Occurrence
of
Sequence Patterns in Repeated Experiments" by Shuo-Yen Robert Li, The Annals
of
Probability, Vol. 8, No. 6 (Dec., 1980), pp. 1171-1176.
120

A Practical Guide To Quantitative Finance Interviews
26. All the
(i
-6) players before him went bankrupt; the
(i
-4)th
player loses in the
second toss (HT); the
(i-3)th
player and the
(i
-2)th player lose in the first toss
(D;
the
(i
-l)th player gets sequence
HH
with payoff 22 and the i-th player gets H with
payoff
2.
Hence, E[(x;
-i)]
= 26 + 22 + 21 -
E[i]
= 0
E[i]
= 70.
5.3 Dynamic Programming
Dynamic Programming refers to a collection
of
general methods developed to solve
sequential, or multi-stage, decision problems.
10
It is an extremely versatile tool with
applications in fields such as finance, supply chain management and airline scheduling.
Although theoretically simple, mastering dynamic programming algorithms requires
extensive mathematical prerequisites and rigorous logic. As a result, it is often perceived
to be one
of
the most difficult graduate level courses.
Fortunately, the dynamic programming problems you are likely to encounter in
interviews-although
you often may not recognize them as
such-are
rudimentary
problems. So in this section we will focus on the basic logic used in dynamic
programming and apply it to several interview problems. Hopefully the solutions to
these examples will convey the gist and the power
of
dynamic programming.
A discrete-time dynamic programming model includes two inherent components:
1.
The
underlying discrete-time dynamic
system
A dynamic programming problem can always be divided into stages with a decision
required at each stage. Each stage has a number
of
states associated with it. The decision
at one stage transforms the current state into a state in the next stage (at some stages and
states, the decision may be trivial
if
there is only one choice).
Assume that the problem has N + 1 stages (time periods). Following the convention, we
label these stages as
0,
1,
· · ·, N
-1,
N.
At any stage k, 0 k N
-1,
the state transition
can
be
expressed as
xk+i
= f (xk, uk, wk), where
xk
is the state
of
system at stage
k;
11
uk
is the decision selected at stage
k;
w*
is a random parameter (also called disturbance).
'0 This section barely scratches the surface
of
dynamic programming. For up-to-date dynamic
programming topics,
I'd
recommend the book Dynamic Programming
and
Optimal Control
by
Professor
Dimitri
P.
Bertsekas.
11
In general,
xk
can
incorporate all past relevant information. In our discussion, we only consider the
present information
by
assuming Markov property.
121

Stochastic Process and Stochastic Calculus
Basically the state
of
next stage
xk+i
is determined as a function
of
the current state
xk,
current decision
uk
(the choice we make at stage k from the available options) and the
random variable
wk
(the probability distribution
of
wk
often depends on
xk
and
uk
).
2. A cost
(or
profit)
function
that
is additive
over
time.
Except for the last stage (N), which has a cost/profit g N ( x
N)
depending only
on
x
N,
the
costs at all other stages gk(xk,uk,
wk)
can depend on
xk,
uk, and
wk.
So
the total
N-1
cost/profit is
gN(xN)+
Lgk(xk,uk,wk)}.
The goal
of
optimization is to select strategies/policies for the decision sequences
tr*=
{u
0 *,-··,uN-i
*}
that minimize expected cost (or maximize expected profit):
N-1
J,...(x0
)=minE{gN(xN)+
Lgk(xk'uk'wk)}.
,..
k=O
Dynamic programming (DP) algorithm
The dynamic programming algorithm relies
on
an idea called the
Principle
of
Optimality:
If
tr*=
{u
0
*,-··,uN _
1
*}
is the optimal policy for the original dynamic
programming problem, then the tail policy
tr;*=
{u;
*,-· ·,uN-i
*}
must be optimal for the
NI
tail subproblem E {g N (xN) + L
gk
(xk,
uk,
wk)} .
k-i
NI
DP
algorithm:
To
solve the basic problem J,...(x0
)=minE{g
N
(xN)+
Lgk(xk,uk,wk)},
,..
k-0
start with J N(xN) = gN(xN), and go backwards minimizing cost-to-go function Jk(xk):
Jk(xk)=
min E{gk(xk,uk ,
wk)+Jk+i(f(xk'uk,wk))},k=O,-··,N-1.
Then the J0(x0)
11,cU,(.r,)
..-,
generated from this algorithm is the expected optimal cost.
Although the algorithm looks complicated, the intuition is straightforward.
For
dynamic
programming problems, we should start with optimal policy for every possible state
of
the final stage (which has the highest amount
of
information and least amount
of
uncertainty) first and then work backward towards earlier stages by applying the tail
policies and cost-to-go functions until you reach the initial stage.
Now let's use several examples to show how the DP algorithm is applied.
122

A Practical Guide To Quantitative Finance Interviews
Dice game
You can roll a 6-side dice up to 3 times. After
the
first or the second roll,
if
you
get a
number
x,
you can decide either to get x dollars
or
to choose to continue rolling. But
once you decide
to
continue, you forgo the number you just rolled.
If
you get to the third
roll,
you'll
just get x dollars
if
the third number is x and the game stops.
What
is the
game worth and what is your strategy?
Solution: This
is
a simple dynamic programming strategy game.
As
all dynamic
programming questions, the key is to start with the final stage and work backwards. For
this question, it is the stage where you have forgone the first two rolls.
It
becomes a
simple dice game
with
one roll. Face values 1, 2, 3, 4, 5, and 6 each have a
1/6
probability and your expected payoff is $3.5.
Now let's go back one step. Imagine that you are at the point after the second roll, for
which you can choose either
to
have a third roll
with
an expected payoff
of
$3.5
or
keep
the current face value. Surely you will keep the face value
if
it is larger than 3. 5; in other
words, when you get
4,
5 or 6, you stop rolling.
When
you get
1,
2 or 3, you keep rolling.
So your expected
payoff
before the second roll
is
3I6x3.5+1I6
x ( 4 + 5 + 6) = $4.25.
Now let's go back one step further. Imagine that
you
are at the point after the first roll,
for which you can choose either to have a second roll with expected payoff $4.25 (when
face value is
1,
2,
3
or
4) or keep the current face value. Surely you will keep the face
value
if
it is larger than 4.25; In other words, when you get 5
or
6, you stop rolling.
So
your expected payoff before the first roll is 4 I 6 x 4.25 + 1I6 x ( 5 + 6) = $14 I 3 .
This backward approach----called tail policy in dynamic
programming-gives
us the
strategy and also the expected value
of
the game
at
the initial stage, $14/3.
World series
The Boston Red Sox
and
the Colorado Rockies are playing in the World Series finals.
In
case you are not familiar with the World Series, there are a maximum
of
7 games and
the first team that wins 4 games claims the championship. You have $100 dollars to
place a double-or-nothing bet on the Red Sox.
Unfortunately, you can only bet on each individual game, not the series as a whole. How
much should you bet
on
each game
so
that
if
the
Red
Sox wins the whole series, you win
exactly $100, and
if
Red
Sox loses,
you
lose exactly $100?
Solution: Let
(i,j)
represents the state that the
Red
Sox has won i games and the
Rockies has
wonj
games, and let f (i,
j)
be our
net
payoff, which can be negative when
we lose money, at state
(i,j)
. From the rules
of
the game, we know that there may be
between 4 and 7 games in total. We need to decide on a strategy so that whenever the
123

Stochastic Process and Stochastic Calculus
series
is
over, our final net payoff is either + 100---when Red Sox wins the
championship--or
-100-when
Red Sox loses.
In
other words, the state space
of
the
final stage includes {(4,0), (4,1), (4,2), (4,3)} with payoff
f(i,})=100
and
{(0,4), (1,4), (2,4), (3,4)} with payoff
f(i,j)
= -100. As all dynamic programming
questions, the key is to start with the final stage and work
backwards-even
though in
this case the number
of
stages is not fixed.
For
each state
(i,
j),
if
we
bet $y on the Red
Sox for the next game, we will have
(f(i,
j)
+
y)
ifthe
Red Sox wins and the state goes
to (i +
1,
}),
or
(f
(i,
})-
y)
if
the Red Sox loses and the state goes to
(i,
j +I). So
clearly we have
f(i
+
1,
J)
= f (i,
J)
+
y}
{f
(i,
J)
=(JU+
1,
J)
+
f(i,
J +
1))
I
2.
f(i,
j+l)=f(i,
j)-y
y=(f(i+l,
j)-f(i,
}+1))12
For example, we have
/(3,
3) =
/(
4, 3
)+
/(
3, 4) = lOO-IOO
=0.
Let's
set
up a table
2 2
with the columns representing i and the rows representing
j.
Now we have all the
information to fill in
/(4,
0),
/(4,
I),
/(4,
3),
/(4,
2), f(O, 4), f
(1,
4),
/(2,
4),
/(3,
4), as well as
/(3,3).
Similarly we can also fill in all
f(i,j)
for the states where
i = 3 or j = 3 as shown in Figure 5.7. Going further backward,
we
can fill
in
the net
payoffs at every possible state. Using equation
y=(f(i+l,
j)-f(i,
}+1))12,
we
can
also calculate the bet we need to place at each state, which is essentially
our
strategy.
If
you are not accustomed to the table format, Figure 5.8 redraws it as a binomial tree, a
format you should be familiar with.
If
you consider that the boundary conditions are
/(4,
0),
/(4,
I),
/(4,
3),
/(4,
2), f(O, 4),
/(1,
4),
/(2,
4), and
/(3,
4), the
underlying asset either increases by 1 or decrease by I after each step,
and
there
is
no
interest, then the problem becomes a simple binomial tree problem and the bet
we
place
each time
is
the delta
in
dynamic hedging. In fact, both European options
and
American
options can be solved numerically using dynamic programming approaches.
124
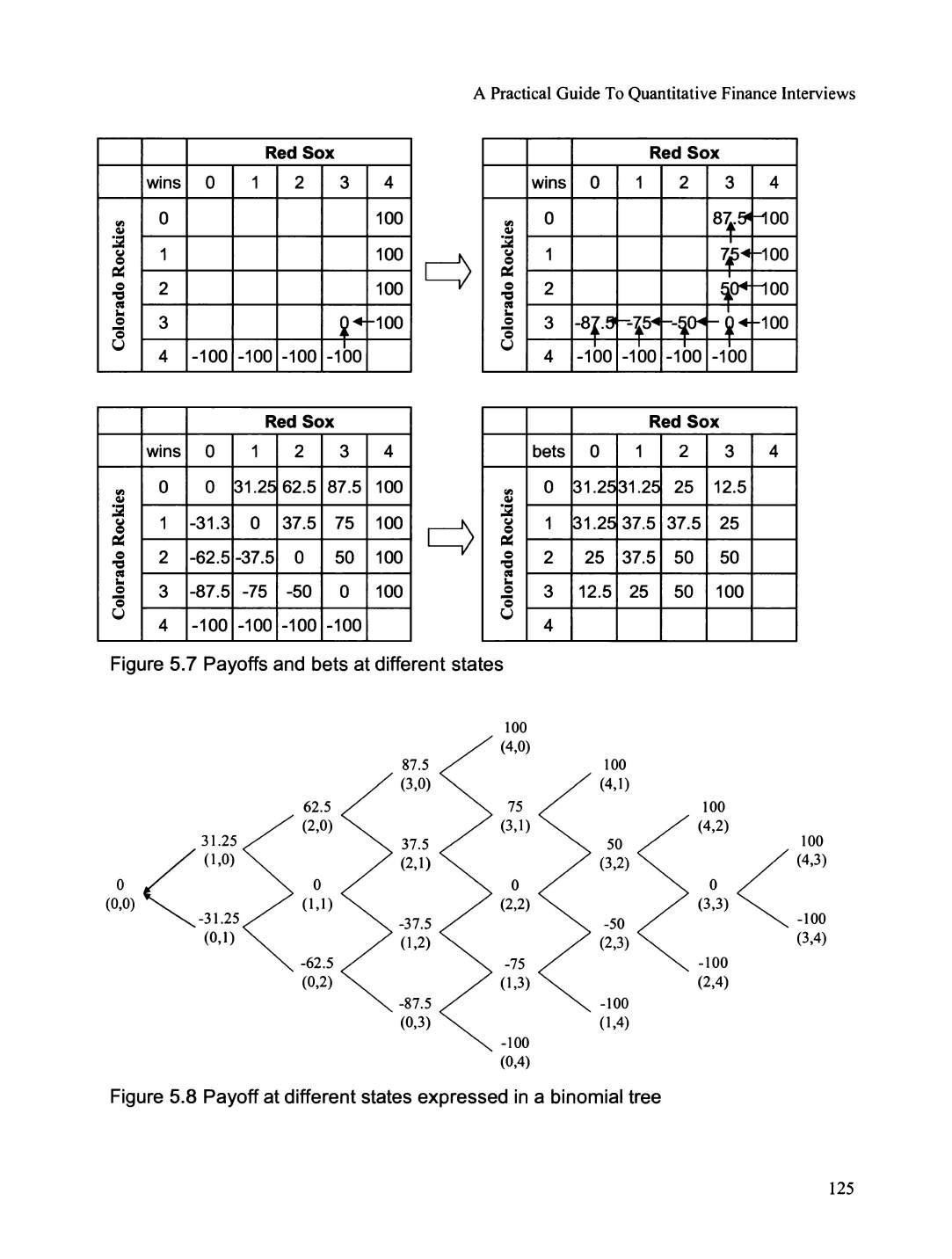
A Practical Guide To Quantitative Finance Interviews
Red Sox Red
Sox
wins 0 1 2 3 4 wins 0 1 2 3 4
"'
0 100
"'
0 00
:.:2
1 100
CJ
=
= 2 100
'Cl
:.:2
1
Q
CJ
=
= 2 00
'Cl
= =
"'
3
1·
t-100
=
cs
u 4 -100 -100 -100 -100
"'
= 3
cs
u 4 -100 -100 -100 -100
Red Sox Red
Sox
wins 0 1 2 3 4 bets 0 1 2 3 4
"'
0 0 62.5 87.5 100
"'
0 25 12.5
:.:2
1 -31.3 0 37.5 75 100
:.:2
37.5 37.5 25
CJ
1
=
= 2 -62.5 -37.5 0 50 100
'Cl = 2 25 37.5 50 50
'Cl
=
"'
3 -87.5 -50 100
= -75 0
cs
=
"'
= 3 12.5 25 50 100
cs
u 4 -100 -100 -100 -100 u 4
Figure
5.
7 Payoffs and bets
at
different states
100
(4,0)
87.5 100
(3
,0) (4,
1)
62.5
75
100
(2,0) (3, I) (4,2)
31.25 37.5 50 100
0 < (1,0) (2,1) (3,2) 0 < (4,3)
0 0
(0,0)
(I,
I)
(2,2) (3,3)
-31.25 -37.5 -50 -100
(0,1) (1,2) (2,3) (3,4)
-62.5 -75 -100
(0,2) (1,3) (2,4)
-87.5 -100
(0,3) (1,4)
-100
(0,4)
Figure 5.8 Payoff
at
different states expressed
in
a binomial tree
125

Stochastic Process and Stochastic Calculus
Dynamic dice game
A casino comes up with a fancy dice game.
It
allows
you
to roll a dice as many times as
you want unless a 6 appears. After each roll,
if
1 appears, you will win $1;
if
2 appears,
you will
win
$2;
...
;
if
5 appears, you win $5; but
if
6 appears all the moneys you have
won in the game
is
lost and the game stops. After each roll,
if
the dice number is 1-5,
you can decide whether to keep the money or keep
on
rolling.
How
much are you
willing to pay to play the game
(if
you are risk neutral)?12
Solution: Assuming that we have accumulated n dollars, the decision to have another
roll
or
not depends on the expected profit versus expected loss.
If
we decide to have an
extra roll, our expected
payoff
will become
1 l 1 1 1 1 5
-(n+
1)+-(n+2)+-(n
+3)+-(n+
4)+-(n+5)+-x
0 =
-n+
2.5.
6 6 6 6 6 6 6
We have another roll
if
the expected
payoff
n + 2.5 >
n,
which means that we should
6
keep rolling
if
the money is no more than $14. Considering that we will stop rolling
when n
15,
the maximum
payoff
of
the game is $19 (the dice rolls a 5 after reaching
the state
n=l4
). We then have the following:
/(19)=19,
/(18)=18,
/(17)=17,
/(16)
=
16,
and
/(15)
=
15.
When
n:::;;
14,
we will keep on rolling, so
E[f(n)
In:::;;
14]
=
_!..
t
E[f(n
+ i)]. Using this equation, we can calculate the value for
6
i;I
E[f(n)]
recursively for all n =
14,
13,
···,
0. The results are summarized
in
Table 5.2.
Since
E[/(O)]
= 6.15, we are willing to
pay
at
most $6.15 for the game.
n
19
18
17
16 15 14
13 12
I I 10
Elf0ll
19.00 18.00 17.00 16.00 15.00 14.17 13.36 12.59 11.85 11.16
n 9 8 7 6 5 4 3 2 I 0
Elt02J.
10.52 9.91 9.34 8.80 8.29 7.81 7.36 6.93 6.53 6.15
Table 5.2 Expected payoff
of
the game when the player has accumulated n dollars
12
Hint:
If
you decide to have another roll, the expected amount you have after the roll should be higher
than the amount before the roll. As the number
of
dollars increases, you risk losing more money
if
a 6
appears. So when the amount
of
dollar reaches a certain number, you should stop rolling.
126

A Practical Guide To Quantitative Finance Interviews
Dynamic card game
A casino offers yet another card game with the standard
52
cards (26 red, 26 black). The
cards are thoroughly shuffled and the dealer draws cards one
by
one. (Drawn cards are
not returned to the deck.) You can ask the dealer to stop at any time you like. For each
red card drawn, you win $1; for each black card drawn, you lose $1. What is the optimal
stopping rule in terms
of
maximizing expected
payoff
and how much are you willing
to
pay for this game?
Solution:
It
is another problem perceived
to
be difficult by many interviewees. Yet it is a
simple dynamic programming problem. Let (b,
r)
represent the number
of
black and red
cards left in the deck, respectively.
By
symmetry, we have
red cards drawn -black cards drawn = black cards left -red cards left = b -r
At each (b,
r),
we face the decision whether to stop or keep on playing.
If
we
ask the
dealer to stop at (b, r), the
payoff
is
b-r
.
If
we keep
on
going, there is
_b_
b+r
probability that the next card will be
black-in
which case the state changes to
(b-1,
r)-and
_r_
probability that the next card will be
red-in
which case the state
b+r
changes to (b,
r-1).
We will stop
if
and only
if
the expected payoff
of
drawing more
cards is less than b -r. That also gives
us
the system equation:
E[f(b,r)]
=
max(b-r,
_b_E[f(b-l,r)]+-r-[f(b,r-1)]).
13
b+r
b+r
As shown in Figure 5.9 (next page), using the boundary conditions
/(0,
r)
=
0,
f(b,
O)=b,
'Vb,
r=O,
1,
···,
26,
and
the system equation for
E[f(b,
r)],
we can
recursively calculate
E[f(b,
r)] for all pairs
of
band
r.
The expected payoff at the beginning
of
the game is E
[!
(26, 26)] = $2.62.
13
You probably have recognized this system equation as the one
for
American options. Essentially you
decide whether you want to exercise the option at state (b,
r).
127

Stochastic Process and Stochastic Calculus
f(b,r) Number
of
Black
Cards
Left
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17 18
19
20
21
22
23
24 25
26
0 1 2 3 4 5 6 7 8 9
10
11
12 13 14 15 16
17
18 19
20
21
22
23 24 25 26
1 0 0.50 1 2 3 4 5 6 7 8 9 10
11
12
13
14
15 16
17 18 19
20
21
22 23 24 25
2 0 0.33
0.67
1.20 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17 18 19
20
21
22 23
24
3 0 0.25 0.50 0.85 1.34 2 3 4 5 6 7 8 9 10
11
12
13
14 15 16
17
18 19
20
21
22
23
14
0 0.20 0 .
40
0.66 1.00 1.44 2.07 3 4 5 6 7 8 9
10
11
12 13 14 15 16 17
18
19 20
21
22
5 0 0.17 0.33 0.54 0.79 1.12 1.
55
2.15 3 4 5 6 7 8 9 10
11
12 13
14
15
16 17
18
19
20
21
I&
0 0.14
0.29
0.45 0.66 0.91 1.23 1.66 2.23 3 4 5 6 7 8 9
10
11 12 13 14 15
16
17 18 19 20
17
0 0.13 0.25 0.39 0.56 0.76 1.01 1.
34
1.75 2.30 3 4 5 6 7 8 9 10 11 12 13 14
15
16 17 18 19
8 0 0.11 0.22 0.35 0.49 0.66 0.86 1.11 1.43 1.84 2.36 3.05 4 5 6 7 8 9 10 11 12 13 14
15
16
17
18
=
19
0 0.10 0 .
20
0.31 0.43 0.58 0.75 0.
95
1.21 1.52 1.92 2.43 3.10 4 5 6 7 8 9 10
11
12
13
14 15 16 17
CD
_,
10
0 0.09 0 .
18
0.28 0.39 0.52 0.66 0.
83
1.04 1.30 1.61 2.
00
2.50 3.15 4 5 6 7 8 9 10
11
12 13
14
15
16
Ill
'E
11 0 0.
08
0.17 0.26 0.35 0.46 0.
59
0.74 0.
91
1.12 1.38 1.69 2.08 2.57 3.20 4 5 6 7 8 9 10
11
12 13 14 15
"
(.)
12 0 0.
08
0.15 0.24 0.32 0.
42
0.54 0.
66
0.81 0.99 1.20 1.46 1.77 2.15 2.
63
3.24 4 5 6 7 8 9
10
11
12 13 14
"O
GI
a::
13 0 0.07 0.14 0.22 0.30 0.39 0.49 0.
60
0.73 0.89 1.06 1.28 1.53 1.84 2.22 2.70 3.28 4.03 5 6 7 8 9 10
11
12 13
....
0
14
0 0.07 0.13 0.
20
0.28 0.36 0.
45
0.
55
0.67 0.80 0.
95
1.13 1.35 1.60 1.91 2.
29
2.75 3.33 4.
06
5 6 7 8 9
10
11
12
...
CD
15
0 0.06 0.13 0.19 0.26 0.33 0.42 0.51 0.61 0.73 0.
86
1.02 1.20 1.42 1.
67
1.98 2.36 2.81 3.
38
4.09 5 6 7 8 9
10
11
..a
E 0.24 0.31 0 .
39
0.47 0.57 0.67 0.
79
0.93 1.08 1.27 1.
48
1.74 2.05 2.42 2.
87
3.43 4.13
:I
16
0 0.06
0.12
0.18 5 6 7 8 9 10
z 17 0
006
0.
11
0.17 0.
23
029
0.36 0.44 0.53 0.62 0.73 0.
85
0.99 1.15 1.
33
1.55 1.81 2.11 2.
48
2.
93
3.48 4.16 5 6 7 8 9
18 0 0.
05
0.11 0 .16 0.22 0.
28
0.34 0.41 0.49 0.58 0.
67
0.78 0.90 1.
04
1.
21
1.39 1.61 1.87 2.
17
2.
54
2.
99
3.53 4.19 5 6 7 8
19
0 0.05 0.10 0.15 0.
20
0.26 0.32 0.39 0.46 0.54 0.63 0.73 0.84 0.96 1.10 1.26 1.45 1.67 1.93 2.24 2.60 3.04 3.57 4.
22
5.
01
6 7
120
0 0.05
0.10
0.14 0.19 0.25 0.31 0.37 0.43 0.51 0.59 0.68 0.78 0.89 1.01 1.16 1.
32
1.51 1.
73
1.99 2.30 2.66 3 .
09
3.
62
4.
25
5.03 6
121
0 0.05 0 .
09
0.14 0.19 0.24 0.
29
0.
35
0.41 0.48 0.
55
0.63 0.72 0.83 0.
94
1.07 1.21 1.38 1.57 1.79 2.05 2.
35
2.
72
3
.1
5 3.
66
4.28 5.
05
22
0 0.04 0.09 0.13 0.18 0.23 0.28 0.
33
0.39 0.
45
0.52 0.60 0.68 0.77 0 .
87
0.99 1.12 1.26 1.43 1.62 1.85 2.
11
2.
41
2.
77
3.20 3.
71
4.32
23 0 0.04 0.
08
0.13 0.17 0.22 0.26 0.
32
0.
37
0.43 0.49 0.56 0 .
64
0.72 0 .82 0.92 1.
04
1.17 1.32 1.48 1.68 1.90 2.16 2.47 2.82 3.25 3.75
24 0 0.04 0.08 0.12 0.16 0.
21
0.25 0.30 0.35 0.
41
0.47 0.53 0.
60
0.68 0.77 0.86 0.97 1.
08
1.
22
1.
37
1.54 1.73 1.
96
2.22 2.52 2.
88
3.30
j25 0 0.04 0.08 0.12 0.16 0.20 0.24 0.
29
0.34 0.39 0.45 0.
51
0.57 0.64 0.72 0.
81
0 .
90
1.01 1.13 1.
26
1.
42
1.59 1.
78
2.01 2.
27
2.57 2.93
0 0.04 0.07 0.
11
0.15 0.19 0 .
23
0.
28
0.32 0.37 0.
43
0.48 0.54 0.61 0.
68
0.76 0.85 0.95 1.
06
1.18 1.
31
1.46 1.64 1.83 2.
06
2.
32
2.
62
Figure
5.9
Expected
payoffs
at different
states
(b,
r)
128

A Practical Guide To Quantitative Finance Interviews
5.4 Brownian Motion
and
Stochastic Calculus
In this section, we briefly go over some problems for stochastic calculus, the counterpart
of
stochastic processes in continuous space. Since the basic definitions and theorems
of
Brownian motion and stochastic calculus are directly used as interview problems, we'll
simply integrate them into the problems instead
of
starting with an overview
of
definitions and theorems.
Brownian motion
A. Define and enumerate some properties
of
a Brownian motion?1
Solution: This is the most basic Brownian motion question. Interestingly,
part
of
the
definition, such
as
W(O) =
0,
and some properties are
so
obvious that we often fail to
recite all the details.
A continuous stochastic process
W(t),
t
0,
is a Brownian motion
if
• W(O)=O;
• The increments
of
the process
W(t,)-W(O),
W(t2
)-W(t
1
),
···,
W(tJ-W(tn_
1
),
t,
t2
::;;
• • •
tn
are independent;
• Each
of
these increments
is
normally distributed with distribution
W(t;+
1
)-W(t;)
-N(O,
f;+i
-t;).
Some
of
the important properties
of
Brownian motion are the following: continuous (no
jumps);
E[W(t)]
=
O;
E[W(t)
2] = t;
W(t)-
N(O,t); martingale property
E[W(t+s)IW(t)]=W(t);
cov(W(s),W(t))=s,
'v'O<s<t;
and Markov property (in
continuous space).
There are two other important martingales related to Brownian motion that are valuable
tools in many applications.
•
Y(t)
= W(t)2
-t
is a martingale.
•
Z(t)
= exp{...1.W(t)-tA.2
1},
where
A.
is
any
constant
and
W(t)
1s
a Brownian
motion, is a martingale. (Exponential martingale).
1 A Brownian motion is often denoted as B,. Alternatively it is denoted as
W(t)
since it is a Wiener
process. In this section,
we
use both notations interchangeably so that you get familiar with both.
129

Stochastic Process
and
Stochastic Calculus
We'll
show a
proof
of
the first martingale using Ito's lemma in the
next
section. A
sketch for the exponential martingale is the following:2
E[
Z(t
+s)]
=
E[
exp {
2(W(t)
+ W(s)
)-tA-
2
(t
+ s)}]
=exp{
exp{-!-1
2s}
E[
exp{2W(s)} J
=
Z,
exp{-tA-
2
s}exp{t-1
2
s}
=
z,
B. What is the correlation
of
a Brownian motion and its square?
Solution: The solution to this problem is surprisingly simple.
At
time
t,
B,
N(O,t),
by
symmetry,
E[B,]
= 0 and
E[B:]
=
0.
Applying the equation for covanance
Cov(X,Y)
=
E[XY]-E[X]E[Y],
we have
Cov(B
1,B,2) =
E[B,3]-E[B,]E[B/]
=
0-0
= 0.
So the correlation
of
a Brownian motion and its square is 0, too.
C. Let
B,
be a Brownian motion. What is the probability that
B,
> 0 and B2 <
0?
Solution: A standard solution takes advantage
of
the fact that
B,
-N(O, I), and B2 -
B,
is independent
of
B"
which is again a normal distribution: B2 -
B,
N(O,
1).
If
B,
= x > 0 , then for B2 <
0,
we must have B2 -
B,
<
-x.
P(B,
>0,B
2
<O)=P(B,
>0,B
2
-B,
<-B,)
= r
Ji;
e-x212dx
(Ji;
e-y212dy
= r [
e-(x'+/)12dxdy
= r
r7/4Jr
7
!4tr-3!2tr[-e-r2
1
2]00
=_!_
.l.i12,,
2tr
2tr
0 8
But do we really need the integration step?
If
we
fully take advantage
of
the
facts that
B,
and B2
-B,
are two 110 N(O, I), the answer is no. Using conditional probability and
independence,
we
can reformulate the equation as
P(B, >
O,B
2 <
0)
= P(B, > O)P(B2
-B,
< O)P(I B2
-B,
l>I
B,
I)
=l/2xl/2xl/2=118
2
W(s)-N(O,s).
So
E[exp{'1.W(s)}] is the
moment
generating function
of
normal random variable
N(O,s).
130
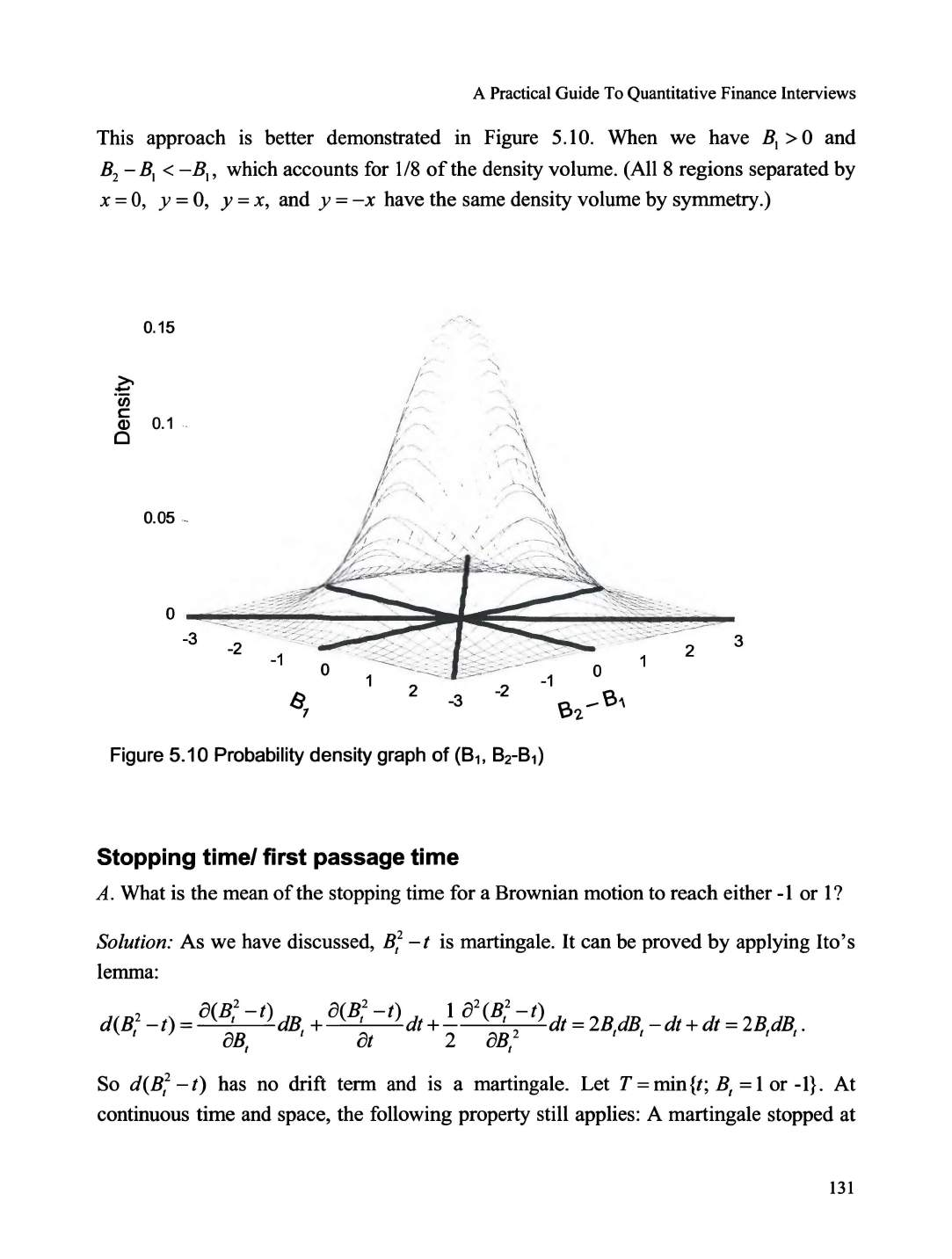
A Practical Guide To Quantitative Finance Interviews
This approach is better demonstrated in Figure 5.10. When
we
have B1 > 0 and
B2
-B
1 <
-B,,
which accounts for 1/8
of
the density volume. (All 8 regions separated by
x = 0, y = 0, y = x, and y
=-x
have
the
same density volume
by
symmetry.)
0.15
,_
' '-.
l
·u;
I
c /
'"
Q) 0.1
-,
0 f
I "
0.05 -
Figure 5.10 Probability density graph
of
(81'
8r81)
Stopping time/ first passage time
A. What is the mean
of
the
stopping time for a Brownian motion to reach either
-1
or
1?
Solution:
As
we have discussed,
B}
-t
is martingale.
It
can be proved
by
applying
Ito's
lemma:
d(Bl2
-t)
= B(B
12
-t)
dBi+ o(B,2
-t)
dt+!
82
(B
12
2-t)
dt
=
2BldBI
-dt+
dt
= 2B,dB,.
at
2
So
d(B
1
2
-t)
has no drift term and is a martingale.
Let
T=min{t;
B1
=1
or
-1}.
At
continuous time and space, the following property still applies: A martingale stopped
at
131

Stochastic Process and Stochastic Calculus
a stopping time is a martingale! So
Bi
-T is a martingale and E
[Bi
-T J =
Bg
-0 = 0.
The probability that
B,
hits 1 or
-1
is
1,
so
Bi=
1
=>
E[T]
=
E[
Bi]=
I.
B. Let W (t) be a standard Wiener process and
rx
( x >
0)
be the first passage time to
level x (
rx
= min{t;
W(t)
=
x}
). What is the probability density function
of
rx
and the
expected value
of
rx
?
Solution: This is a textbook problem that
is
elegantly solved using the reflection
principle, so we will simply summarize the explanation. For any Wiener process paths
that reach x before t (
rx
t ), they have equal probability ending above x or below x at
time t, The explanation lies in the reflection
principle.
As
shown in Figure 5.11, for each path that reaches x before t and is at a level
y above x at time
t,
we can switch the sign
of
any move starting from
rx
and the
reflected path will end at
2x-
y that is below x at time
t.
For a standard Wiener process
(Brownian motion), both paths have equal probability.
P(rx
t)
= P(rx t, W(t):?.
x)
+ P(rx
t,
W(t)
x) =
2P(rx
t, W(t):?.
x)
= 2P(W(t):?.
x)
= 2 r
e-w2
121
dw
,.
...;2;rt
:.
r:
m
"2m
Jx1v1
"2;r
Take the derivative with respect
to
t, we have
r ( ) dP{rx
t}
dP{rx
t}
d(x
I
Ji)
2N
'(
I r.) x _
3
12
xe-x
2121
\.I
O
Jr
t = = = X
vt
X-f
::::>
,
vX
> .
'
dt
d(x/
Ji)
dt
2
t.&i
From part
A,
it's easy to show that the expected stopping time
to
reach either a
(a>
0)
or
-/3
(
f3
>
0)
is
again
E[
N]
=
af3.
The expected first passage time to level x is
3
lf
we define
M(I)
=max
W(s),
then
P(r
:s;
t)
if
and only
if
M(t)?.
x. Taking the derivative
of
P(r,
:s;
t)
with respect to x, we can derive the probability density function
of
M(t)
.
132
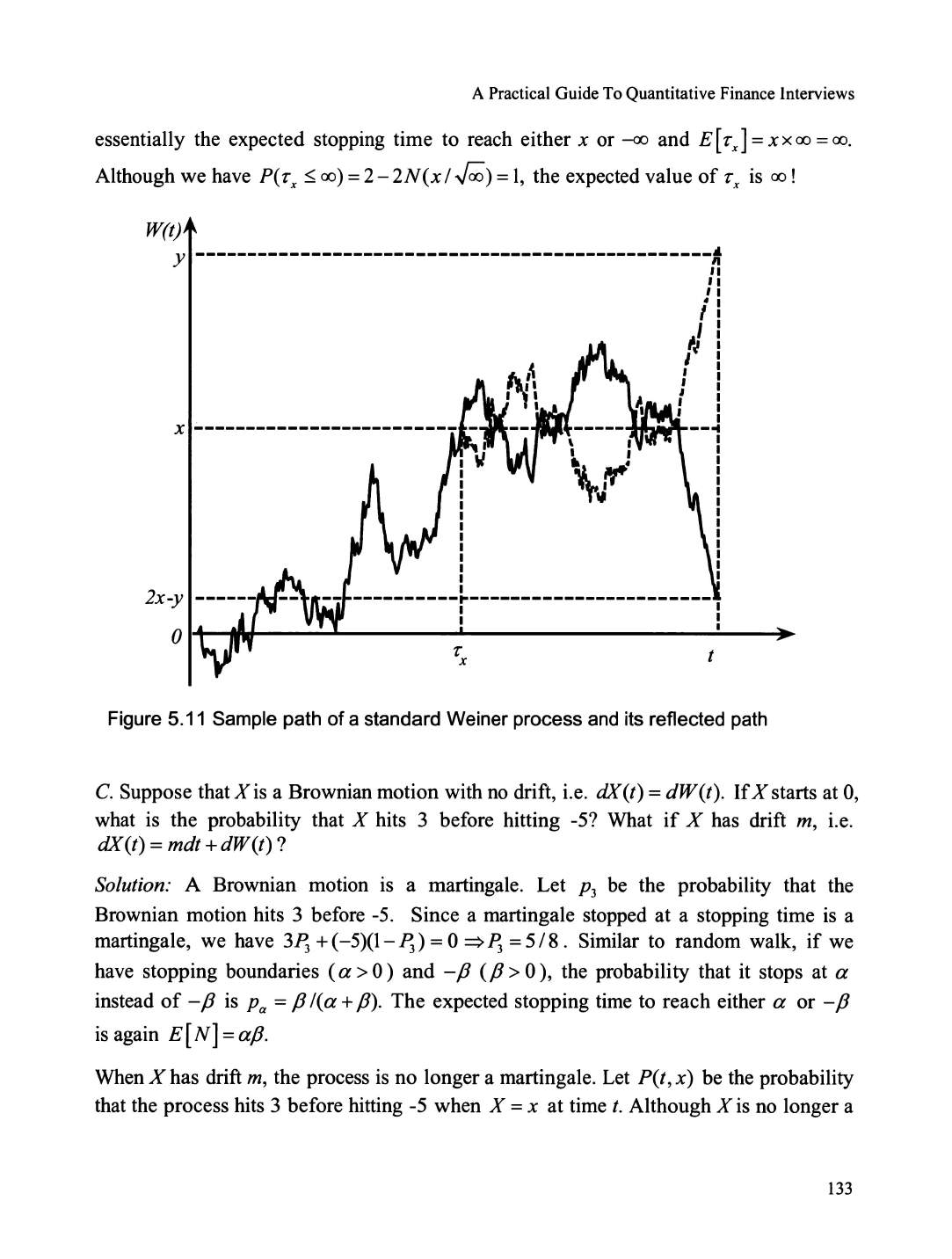
A Practical Guide To Quantitative Finance Interviews
essentially the expected stopping time to reach either x
or
-oo
and E [
rx]
=xx
oo
=
oo.
Although
we
have P(
rx
oo)
=
2-
2N(x
1,
the expected value
of
rx
is
oo
!
W(t)
y _________________________________________________ ,
I
I
I
•
2x-y
I
i
/
I
I
I
I
I
----------r-----------------------.
I I
.......
r
x t
Figure 5.11 Sample path
of
a standard Weiner process and its reflected path
C.
Suppose that
Xis
a Brownian motion with
no
drift, i.e.
dX(t)
=
dW(t).
If
X starts at 0,
what is the probability that X hits 3 before hitting -5? What
if
X has drift m, i.e.
dX(t)
=
mdt
+
dW(t)?
Solution: A Brownian motion is a martingale. Let p3 be the probability that the
Brownian motion hits 3 before -5. Since a martingale stopped at a stopping time is a
martingale, we have +
(-5)(1-
= 0 = 5 I 8 . Similar to random walk,
if
we
have stopping boundaries
(a>
0)
and
-P
(p > 0 ), the probability that it stops at a
instead
of
-P is
Pa
= P
/(a+
p).
The
expected stopping time to reach either a
or
-P
is again
E[
N]
=
ap.
When X has drift m, the process is
no
longer a martingale. Let
P(t,
x)
be the probability
that the process hits 3 before hitting -5 when X = x
at
time
t.
Although
Xis
no longer a
133

Stochastic Process and Stochastic Calculus
martingale process, it is still a Markov process. So
P(t,x)
=
P(x)
is actually independent
oft.
Applying the Feynman-Kac equation4,
we
have
mP,.(x)+l/2Pxx(x)=O
for
-5<x<3.
We also have boundary conditions that
P(3)
= I and
P(-5)
=
0.
mP,.(x)
+II
2Pxx(x) = 0 is a homogeneous linear differential equation with two real roots:
1j
= 0 and r2 =
-2m.
So the general solution is
P(
x)
= c1
e0x + c2
e-
2
mx
= c1 + c2
e-
2
mx
•
Applying the boundary conditions, we have
' 2
=>
1
=>
P(O)=c
+c
=----
{C
+C
e-6m
= 1
{C
=
-elOm
/(e-6m
-elOm)
elOm
-1
c,
+c2e10m
=O
C2=ll(e-6m_elOm) I 2 e'°m-e-6m
A different and simpler approach takes advantage
of
the exponential martingale:
Z(t)=exp{A.W(t)-tA.
2
1}.
Since
W(t)=X(t)-mt,
X(t)-mt
is a Brownian motion as
well. Applying the exponential martingale, we have E
[exp
(
A.(X
-
mt)-t
A.
2
t)
J
=I
for
any constant
.A..
To remove the terms including time t,
we
can set
A.=
-2m
and the
equation becomes
E[
exp(-2mX)]
=I.
Since a martingale stopped at a stopping time is
elOm
-1
a martingale, we have
exp(-2mx3)+
(1-
= 1
=>
iom
-6m.
e
-e
D. Suppose that
Xis
a generalized Weiner process
dX
= dt + dW(t), where W(t) is a
Brownian motion. What is the probability that
Xever
reaches -1?
Solution: To solve this problem, we again can use the equation
E[
exp(-2mX)J
= 1
from the previous problem with m =
l.
It
may not be obvious since
we
only have
one
apparent boundary,
-1.
To
apply the stopping time,
we
also need a corresponding
positive boundary. To address this problem, we can simply use
+oo
as the positive
boundary and the equation becomes
4 Let X
be
an Ito process given by equation
dX
(I)
= /J(t,
X)dt
+
y(
t,
X
)dW
and f
(x)
be
a function
of
X.
Define function V
(I.
x)
=
E[f
( X,. ) I
X,
=
x].
then V
(I.
x)
is a martingale process that satisfies the partial
av
av
1 , a1v
differential equation
-+
/J(t,x)-+-y
·
(1,x)-
= 0 and terminal condition
V(T,
x)
=
f(x)
for all
a1
as
2
as'
x.
134

A Practical Guide
To
Quantitative Finance Interviews
Ito's lemma
Ito's lemma is the stochastic counterpart
of
the chain rule in ordinary calculus. Let
X(t)
be an Ito process satisfying
dX(t)=fi(t,X)dt+y(t,X)dW(t),
and
f(X(t),t)
be a
twice-differentiable function
of
X(t)
and
t.
Then
f(X(t),t)
is an Ito process satisfying
.
of
of
1 02f
Dnft
rate=-+
fi(t,X)-+-y
2
(t,X)-
2
ot
ox 2 ox
A.
Let
B,
be a Brownian motion and
z,
=
.JiB,.
What is the mean and variance
of
Z,?
Is
z,
a martingale process?
Solution: As a Brownian motion,
B,
N(O,
t),
which is symmetric about 0. Since
Ji
is
a constant
at
t,
Z,
=.Ji
B,
is symmetric about 0 and has mean 0 and variance
t x var(B,) = t2• More exactly, Z, N(O, t2) .
Although Z, has unconditional expected value 0, it is not a martingale. Applying Ito's
r:
az az
02
z _
r:
lemma to
Z,
=
viB,,
we have dZ,
=-
1
dB,
+-
1
dt+tx--;
dt
=tt
1
12
B1
dt+vtdB
1•
aB,
at
oB,
For all the cases that
B,
:;e
0,
which has probability
1,
the drift term
tr
112
B,dt is not
zero.5 Hence, the process
Z,
=
.JiB,
is not a martingale process.
B. Let W(t) be a Brownian motion. Is W(t)3 a martingale process?
5 A generalized Wiener process
dx
=
a(x,
t)dt
+
b(x,
t)dW(t)
is
a martingale process
if
and only
if
the
drift term has coefficient
a(x,t)
= 0.
135

Stochastic Process
and
Stochastic Calculus
Solution: Applying Ito's lemma to
f(W(t),
t)=W(t)
3, we have 8
1 =3W(t)2
8W(t)
'
8/ 82/
ar=O,
8W(t)2
=6W(t),
and
df(W(t),
t)=3W(t)dt+3W(t)
2
dW(t).
So again for the
cases
W(t)
:;t
0,
which has probability
1,
the drift term is not zero. Hence,
W(t)
3 is not a
martingale process.
136

Chapter 6 Finance
It
used
to
be common for candidates with no finance knowledge to get hired into
quantitative finance positions. Although this still happens for candidates with specialized
knowledge that is in high demand, it's more likely that you are required, or at least
expected, to have a basic grasp
of
topics in finance. So you should expect
to
answer
some finance questions and be judged on
your
answers.
Besides classic textbooks,' there are a few interview books
in
the market
to
help you
prepare for finance interviews.2
If
you want to get prepared for general finance problems,
you may want to read a finance interview book
to
get a feel for what types
of
questions
are asked. The focus
of
this chapter is more on the intuitions and mathematics behind
derivative pricing instead
of
basic finance knowledge. Derivative problems are popular
choices in quantitative
interviews-even
for divisions that are not directly related to
derivative
markets-because
these problems are complex enough to test your
understanding
of
quantitative finance.
6.
1.
Option Pricing
Let's begin with some notations that we will use in the following sections.
T:
maturity date;
t:
the current time; r = T -t : time to maturity; S : stock price at time
t;
r: continuous risk-free interest rate;
y:
continuous dividend yield; a: annualized asset
volatility; c: price
of
a European call;
p:
price
of
a European put;
C:
price
of
an
American call;
P:
price
of
an American put; D: present value, at
t,
of
future dividends;
K:
strike price; PV: present value at
t.
Price direction of options
How do vanilla European/ American option prices change when
S,
K, r ,
a,
r,
or D
changes?
Solution: The payoff
of
a call is max(S -
K,
0) and the payoff
of
a put is max(K -S,
0).
A European option can only be exercised at the expiration time, while an American
option can
be
exercised at any time before maturity. Intuitively we can figure out that
the price
of
a European/ American call should decrease when the strike price increases
1 For basic finance theory and financial market knowledge, I recommend Investments
by
Zvi Bodie, Alex
Kane and Alan J. Marcus. For derivatives, Options, Futures and Other Derivatives
by
John C. Hull is a
classic.
If
you
want
to gain a deeper understanding
of
stochastic calculus and derivative pricing,
I'd
recommend Stochastic Calculus
for
Finance (Volumes I and II)
by
Steven
E.
Shreve.
2 For example, Vault Guide to Finance Interviews and Vault Guide
to
Advanced
and
Quantitative
Finance Interviews.

Finance
since a call with a higher strike has no
higher-and
sometimes
lower-payoff
than a call
with a lower strike. Using similar analyses, we summarize the effect
of
changing market
conditions on an option's value in Table 6.1.
The impact
of
time to maturity on the price
of
a European call/put is uncertain.
If
there is
a large dividend payoff between two different maturity dates, a European call with
shorter maturity that expires before the ex-dividend date may be worth more than a call
with longer maturity. For deep in-the-money European puts, the one with shorter
maturity
is
worth more since it can be exercised earlier (time value
of
the money).
Variable Euro ean call American call American Put
Stock nee
Strike
nee
Time to maturi
Volatilit
Risk-free rate
Dividends
Table
6.1
Impact
of
S,
K,
r ,
a,
r,
and
Don
option prices
r:
increase; t : decrease;?: increase
or
decrease
It
is
also worth noting that Table
6.1
assumes that only one factor changes value while
all others stay the same, which in practice may not
be
realistic since some
of
the factors
are related. For example, a large decrease in interest rate often triggers a stock market
rally and increases the stock price, which has an opposite effect on option value.
Put-call parity
Put-call parity: c + K-rr = p + S -
D,
where the European call option and the European
put option have the same underlying security, the same maturity T and the same strike
price K. Since p
2::
0, we can also derive boundaries for
c,
S -D -Ke-rr c
S,
from
the put-call parity.
For American options, the equality no longer holds and it becomes two inequalities:
S-D-K:::;
S-K-rr.
Can you write down the put-call parity for European options on non-dividend paying
stocks and prove it?
138

A Practical Guide
To
Quantitative Finance Interviews
Solution: The put-call parity for European options
on
non-dividend paying stocks is
c + K-rr = p + S. We can treat the left side
of
the equation as portfolio
A-a
call and a
zero-coupon bond with face value
K-and
the right side as portfolio
B-a
put and the
underlying stock, which is a protective put. Portfolio A has payoff
max(ST-K,O)+K=max(SroK)
at maturity
T;
portfolio B has payoff
max(K-SroO)+ST
=max(SroK) at
T.
Since both portfolios have the same payoff at T
and no payoff between t and
T,
the no-arbitrage argument3 dictates that they must have
the same value at
t.
Hence,
c+
K-r• = p +
S.
If
we rearrange the put-call parity equation into c -p =
S-K-r',
it will give us different
insight. The portfolio on the left side
of
the
equation-long
a call and short a
put-has
the payoff max(
ST
-
K,
0)-
max( K -
Sro
0) =
ST
-
K,
which
is
the payoff
of
a forward
with delivery price K. A forward with delivery price K has present value S -K-rr.
So
we
again have the put-call parity c -p = S -K-r•. This expression shows that when the
strike price K =
sr•
(forward price), a call has the same value as put; when K <
srr,
a
call has higher value; and when K >
sr•,
a put has higher value.
American v.s. European options
A. Since American options can be exercised at any time before maturity, they are often
more valuable than European options with the same characteristics. But when the stock
pays no dividend, the theoretical price for an American call and European call should be
the same since it is never optimal to exercise the American call. Why should you never
exercise an American call on a non-dividend paying stock before maturity?
Solution: There are a number
of
solutions to this popular problem.
We
present three
arguments for the conclusion.
Argument I.
If
you exercises the call option, you will only get the intrinsic value
of
the
call S
-K.
The price
of
the American/European call also includes time value, which
is
positive for a call on a non-dividend paying stock. So the investor is better
off
selling the
option than exercising it before maturity.
In fact,
if
we
rearrange the put-call parity for European options, we have
c =
S-K-r'
+ p =
(S-K)+(K-K-r')+
p. The value
of
a European call on a non-
dividend paying stock includes three components: the first component is the intrinsic
value
S-K;
the second component is the time value
of
the strike
(if
you exercise now,
3 A set
of
transactions is an arbitrage opportunity
if
the initial investment
'.S
O;
payoff
2':
O;
and
at
least one
of
the inequalities is strict.
139

Finance
you pay K now instead
of
K at the maturity date, which is lower in present value); and
the third component is the value
of
the put, which is often considered
to
be
a protection
against falling stock price. Clearly the second and the third components are both positive.
So the European call should be worth more than its intrinsic value. Considering that the
corresponding American call is worth at least as much as the European call, it is worth
more than its intrinsic value as well. As a result, it is not optimal to exercise the
American call before maturity.
Argument
2.
Let's compare two different strategies.
In
strategy
1,
we exercise the call
option4 at time t
(t
< n and receive cash S
-K.
Alternatively, we can keep the call,
short the underlying stock and lend K dollars with interest rate r (the cash proceedings
from the short sale,
S,
is larger than K). At the maturity date
T,
we exercise the call
if
it's
in the money, close the short position and close the lending. Table 6.2 shows the cash
flow
of
such a strategy:
It
clearly shows that at time t, we have the same cash flow as exercising the call,
S-K.
But at time
T,
we always have positive cash flow as well. So this strategy is clearly
better than exercising the call at time
t.
By
keeping the call alive, the extra benefit can be
realized at maturity.
T
Cash flow t ST
SK
Sr>K
Call 0 0
Sr-K
Short Stock s
-Sr
-Sr
Lend
Katt
-K
Kerr Kerr
Total
S-K
Ke
rr
-ST>
0 Kerr
-K
> 0
Table 6.2 Payoff
of
an
alternative strategy without exercising the call
Argument
3.
Let's
use a mathematical argument relying
on
risk-neutral pricing and
Jensen's
inequality-if/(X)
is a convex function, 5 then From
Figure 6.
1,
it's
obvious that the payoff
(if
exercised when S > K )
of
a call option
C(S)
= (S -
Kf
is a convex function
of
stock price with property
4 We assume S > K in our discussion. Otherwise, the call surely should not be exercised.
5 A function
/(X)
is
convex
if
and only
O<A.<I.
If
f "(x) >
0,
Vx, then
/(X)
is
convex.
140
A Practical Guide
To
Quantitative Finance Interviews
Let S1 = S and S2 =
0,
then C(A.S)::;
A.C(S)
+ (1-A. )C(O) =
A.C(S)
since
C(O)
=
0.
c
AC(S1)+(
l-A)C(S2)
C(AS1+{l-A)S2)
0
Figure
6.1
Payoff
of
a European call option
s
If
the option is exercised at time t, the payoff at t is C(S, -
K).
If
it is not exercised until
maturity, the discounted expected payoff (to t) is .E[e-r'C(ST)] under risk-neutral
measure. Under risk-neutral probabilities,
we
also have
E[
ST]
= S,er•.
where the inequality is from Jensen's inequality.
Let s =errs, and
A=
e-rr,
we
have
C(A.S)
= C(S,)
::;e-r•
c(
er•
s,)::;
e-rr
E[
C(ST)] .
Since the discounted payoff e-rr
E[
C(ST)] is no less than
C(S,)
for any t::; T under the
risk neutral measure, it is never optimal to exercise the option before expiration.
I should point out that the
payoff
of
a put is also a convex function
of
the stock price.
But it is often optimal to exercise an American put on a non-dividend paying stock. The
difference is thatP(O) =
K,
so it does not have the property that
P(A.S)::;
A.P(S).
In fact,
P(A.S)
A.P(S). So the argument for American calls does not apply to American puts.
Similar analysis can also show that early exercise
of
an American call option for
dividend-paying stocks
is
never optimal except possibly for the time right before an ex-
dividend date.
B.
A European put option
on
a non-dividend paying stock with strike price $80 is
currently priced at $8 and a put option on the same stock with strike price $90 is priced
at $9. Is there an arbitrage opportunity existing in these two options?
141

Finance
Solution:
In
the last problem, we mentioned that the payoff
of
a put is a convex function
in stock price. The price
of
a put option as a function
of
the strike price is a convex
function
as
well. Since a put option with strike 0 is worthless,
we
always have
P(O)
+
1P(K)
=
1P(K)
>
P(1K).
For this specific problem, we should have 8/
9xP(90)=8/9x9=8>P(80)
. Since the
put option with strike price $80 is currently price at 8, it is overpriced and we should
short it.
The
overall arbitrage portfolio is to short 9 units
of
put with K = $80 and long 8
units
of
put with K = 90. At time 0, the initial cash flow is 0. At the maturity date, we
have three possible scenarios:
90, payoff= 0 (No put is exercised.)
90 >
ST
80,
payoff=
8 x
(90-
ST) > 0 (Puts with K =
90
are exercised.)
ST
< 80, payoff= 8 x (90-ST
)-9
x
(80-
ST)=
ST
> 0 (All puts are exercised.)
The final payoff 0 with positive probability that payoff >
0.
So
it is clearly
an
arbitrage opportunity.
Black-Scholes-Merton differential equation
Can you write down the Black-Scholes-Merton differential equation and briefly explain
how to derive it?
Solution:
If
the evolution
of
the stock price is a geometric Brownian motion,
dS
= µSdt+(J"SdW(t), and the derivative V = V(S,t) is a function
of
Sand
t,
then
applying Ito's lemma yields:
dV=(av
+µSav
dW(t), where W(t)isaBrownianmotion.
at
as
2
as
as
The Black-Scholes-Merton differential equation is a partial differential equation that
.
av
av
1 a1v
should be satisfied by
V:
-+rS-+-(J"
2S2
--
2
=rV.
at
as
2
as
To derive the Black-Scholes-Merton differential equation, we build a portfolio with two
components: long one unit
of
the derivative and short
av
unit
of
the underlying stock.
as
Then the portfolio has value n = V -
av
S and the change
of
n follows equation
as
142

A Practical Guide
To
Quantitative Finance Interviews
dTI
=
dV
-
av
dS
as
av
av
1 a2v
av
av
=
(-+
µS-+-a
2
S2-2
)dt
+aS-dW(t)--(µSdt
+ aSdW(t))
at
as
2 as as as
=(av
+_!_a2
s2
a2V )dt
at 2
as
2
It is apparent that this portfolio is risk-free since it has no diffusion term. It should have
risk-free rate
of
return as well: dTI =
r(V
-
av
S)dt. Combining these results
we
have
as
av
1 2 2 a2v
av av
av
1 2 2 a1v
(at
+2a S as2 )dt =
r(V
-as S)dt
=>
at + rS
as
+2a S
as
2 = rV,
which is the Black-Scholes-Merton differential equation.
The Black-Scholes-Merton differential equation is a special case
of
the discounted
Feynman-Kac theorem. The discounted Feynman-Kac theorem builds
the
bridge
between stochastic differential equations and partial differential equations
and
applies to
all Ito processes in general:
Let X be an Ito process given
by
equation
dX(t)
=
fl(t,X)dt
+
y(t,X)dW(t)
and
/(x)
be a function
of
X.
Define function V(t,x) = E[e-r(T-t>f(Xr) I X1 = x], then
V(t,x)
is a
martingale process that satisfies the partial differential equation
av
av
1 a1v
-+
f3(t,x)-+-y
2
(t,x)-
2 =
rV(t,x)
at
ax
2
ax
and boundary condition
V(T,x)
=
f(x)
for all x.
Under risk-neutral measure,
dS=rSdt+aSdW(t).
Let
S=X,
f3(t,X)=rS
and
y(t,
X)
= aS, then the discounted Feynman-Kac equation becomes the Black-Scholes-
M . 1 .
av
s
av
1 2s2 a1v
erton 11erentia equation
-+r
-+-a
-=rV.
at as 2
as
2
Black-Scholes formula
The Black-Scholes formula for European calls
and
puts with continuous dividend yield y
1s:
143

Finance
d = ln(Se-Y' I
K)+(r+
a2 I
2)r
= ln(S I
K)+(r-y+a
2 I
2)r
h 1
a../r
a../r
w ere
d
_ln(SIK)+(r-y-a
2
12)r
-d-
r
2-
r - ,
avr
avr
N(x)
is
the
cdf
of
the standard normal distribution and N
'(x)
is the
pdf
of
the standard
normal distribution:
N(x)
= (
tb-
e-y2
12
dy
and
N'(x) =
tb-
e-x
212
•
v2ff
v2K
If
the underlying asset
is
a futures contract, then yield y =
r.
If
the underlying asset
is
a
foreign currency, then yield y =
rl,
where r1 is the foreign risk-free interest rate.
A. What are the assumptions behind the Black-Scholes formula?
Solution: The original Black-Scholes formula for European calls and puts consists
of
the
equations c =
SN
(
d,)
-Ke-rr N ( d
2) and p =
Ke-rr
N
(-d
2) -
SN
(
-d,
), which require the
following assumptions:
1.
The stock pays no dividends.
2. The risk-free interest rate is constant and known.
3.
The stock price follows a geometric Brownian motion with constant
driftµ
and
volatility a: dS =
µSdt+aSdW(t).
4. There are no transaction costs or taxes; the proceeds
of
short selling can be fully
invested.
5. All securities are perfectly divisible.
6. There are no risk-free arbitrage opportunities.
B.
How
can
you derive the Black-Scholes formula for a European call on a non-dividend
paying stock using risk-neutral probability measure?
Solution: The Black-Scholes formula for a European call on a non-dividend paying
stock is
c = SN(d,
)-Ke-r•
N(d
2
),
where
d,
= ln(S /
K)
+
CT
2
12
)r
and d2 =
d,
-
a../r.
a r
144

A Practical Guide To Quantitative Finance Interviews
Under the risk-neutral probability measure, the drift
of
stock price becomes the risk-free
interest rate
r(t):
dS =
r(t)Sdt
+
aSdW(t).
Risk-neutral measure allows the option to be
priced as the discounted value
of
its expected
payoff
with the risk-free interest rate:
[
-(
r(u)du
]
V(t) = E e V(T)
S(t)
,
0::;
t
T,
where
V(T)
is the payoff at maturity
T.
When r is constant, the formula can
be
further simplified as
V(t)=e-rrE[V(T)IS(t)].
Under risk-neutral probabilities,
dS
= rSdt + CYSdW(t). Applying
Ito's
lemma, we get
d(ln(S))
=
(r-CY
2
/2)dt
+
adW(t)
=>
ln
ST
-
N(lnS
+
(r-CY
2 I
2)r,
a2
r).
So ST=
se<r-cril
2
)r+cr.fi&'
where c -N(O,
1).
For a European option, we have
V (T) = {
se<r-cri
t2)r+cr.fic
-
K'
if
se<r-ui
t2)r+cr.fil·
> K
0, otherwise
S
(r-cri
12)r+cr.fic
K ln(K
IS)-
(r-
a2 I
2)r
_ d d
e >
=>c>
1
--
2an
avr
E[V(T)
Is]=
E[
max(
ST
-K,O)
Is]=
.c
(se<r-cri
12
>r+crJT&
-K)-
1
-e-&i
12
dc
di
Jf;
-S
rr
[ 1
+·-.ficr)i
12d
K [ 1 -ci/2d
-e
--e
c -
--e
c
di
J2;
di
J2;
Let & =
c-a.J;,
then
de
=di,
c =
-d
2
=>
&
=-d
2
-a.J;
=-d,
and we have
S
rr
[ 1
-(c-Jrcr)i
12d
-S
rr
[ 1 -&i/2d- S
rr
(d
)
e r;:;-e c -e r;:;-e c = e N 1 ,
di
"27!
d1
"27l
Ki
ld2
v2Jr
:. E[V(T)] =Serr
N(
d1
)-KN(d
2) and V(t) =
e-rr
E[V(T)]
=SN
( d,
)-Ke-rr
N(d
2)
From the derivation process, it is also obvious that
1-N(-d
2) =
N(d
2)
is
the risk-
neutral probability that the call option finishes in the money.
C. How do you derive the Black-Scholes formula for a European call option
on
a non-
dividend paying stock
by
solving the Black-Scholes-Merton differential equation?
145

Finance
Solution:
You can skip this problem
if
you
don't
have background in partial differential
equations (PDE). One approach to solving the problem is
to
convert the Black-Scholes-
Merton differential equation to a heat equation and then apply the boundary conditions
to the heat equation to derive the Black-Scholes formula.
Let
y=lnS
(S=eY)and
f=T-t then
av
=-av
av
=av
dy
=_!_aV
and
'
at
af
'
as
ay
ds
s
ay
a
2
v = av(av)=
av(_!_
avJ=.=!.
av+_!_
av(avJ=.=!.
av
+-1
a
2
v .6
as
2
as
as
as
s
ay
s2
ay
s
as
ay
s2
ay
s2
ay
2
av
av
1 2 2 a
2
v
The Black-Scholes-Merton differential equation
-+
rS-+-CT
S
---rV
= 0
at
as
2
as
2
can be converted to -
-+
r--CT
-+-CT
---rV
=
0.
av
( 1
2)av
1
2a
2
v
af
2
ay
2
ay
2
Let
u=er•v,
the equation
becomes--+
r--CT
2
-+-CT
2-2
=0.
- .
au
( 1 )
au
I a
1
u
af
2
ay
2
ay
Finally, let x=y+(r- and
au
au
r=f,
then
-=-
and
ay
ax
au
au
( I 2)
au
h. h
ti
h .
-=-+
r--CT
-,
w
1c
trans orms t e equation to
af
ar
2
ax
S h . . I . b h t/d"ffu . .
au
I 2
a1u
F h
o t e ongma equation ecomes a ea 1
s1on
equation - = -
CT
-2 . or eat
ar
2
ax
.
au
I 2
a1u
h ( ) .
ti
. f . d . bl
equation - = -
CT
-2 , w ere u = u x, r
1s
a unction o time r an space vana
ex,
ar
2
ax
with boundary condition
u(x,0)
= u0(x), the solution is
I i ( (x-1/1)2} 7
u(x,
r)
=
,-;;---
!-o
u
0
(1/f
)exp
-2 l/f.
v2JrrCT
00
2CT
r
6 The
Jog
is taken to convert the geometric Brownian motion to an arithmetic Brownian motion; r = T -t
is used to convert the equation from a backward equation to a forward equation with initial condition at
r = 0 (the boundary condition at t = T r = 0
).
146

A Practical Guide
To
Quantitative Finance Interviews
For European calls, the boundary condition is u0 (ST)= max
(ST
-
K,
0 ).
S=exp(x-(r-0.5o-
2
)x-).
When
X=lfl
and
r=O,
ST
=e'll.
u(S,r)=u(x
,
r)=
(max(ell'-K,O)exp(
27rTO"
2o-
T r
= I
(ell'
jdV'
27rTO"
!nK
2o-
T r
Vf-X
Let c =
o-Ji,
dVf
then
de=
,--
,
Cf.YT
exp[-(x-V1)
2
J=e-c
212 and when
2o-
2r
-l
K
_1n(KIS)-(r-o-
2
/2)r
_ d
Vt-
n '
&-
r
--
2
o-vr
Now, it's clear that the equation for u(S,
r)
is exactly the same
as
the equation for
E[V(T)IS]
in question
B.
Hence, we have
V(S,t)=e-r'u(S,r)=SN(d
1
)-Ke-r'N(d
2)
as
well.
D. Assume zero interest rate and a stock with current price at
$1
that pays no dividend.
When the price hits level
$H
( H > 1)
for
the first time you can exercise the option and
receive
$1.
What is this option worth
to
you today?
Solution: First let's use a brute-force approach to solve the problem by assuming that
the stock price follows a geometric Brownian motion under risk-neutral measure:
dS
= rSdt + o-SdW(t). Since r =
0,
dS
=
aSdW(t)
=>
d(ln S) =
-to-
2
dt
+ o-dW(t).
When t =
0,
we
have S0=1=>ln(S0
)=0.
Ou
1 a
1u
7 The
fundamental
solution to heat equation -=
--
with initial condition u0(1/')
=/(If/)
is
OT
2
ax
2
u(x,t)=
[__..,p(x,
=lfl)f(lf/)dl/',
where
p(x
,
=x/x
0
=If/)=
&exp{-(x-11')2
/2t}.
For detailed discussion about heat equation, please refer to The Mathematics
of
Financial Derivatives by
Paul Wilmott, Sam Howison, and
Jeff
Dewynne.
147

Finance
Hence,
ln
S =
-to-
21 + o-W(t)
=>
ln S +
to-
2t =
W(t)
is a Brownian motion.
O'"
Whenever S reaches $H, the payoff is
$1.
Because the interest rate
is
0,
the discounted
payoff
is
also
$1
under risk-neutral measure. So the value
of
the option
is
the probability
that S ever reaches $H, which is equivalent to the probability that
In
S ever reaches
lnH.
Again we can apply the exponential martingale
Z(t)
= exp{A.W(t)-tA.2
1}
as
we
[ { 1nS+1-o-2t
}]
didinChapter5:
E[Z(t)]=E
exp
A.
o-
2
-fA.
2t
=l.
To remove the terms including time t,
we
can set
A.=
a and the equation becomes
E[
exp(lnS)]
=I.
The Let P be the probability that
lnS
ever reaches
lnH
(using
-oo
as the negative boundary for stopping time), we have
Pexp(lnH)+(l-P)exp(-oo)
=
Px
H =
1=>P=1/
H.
So the probability that
Sever
reaches
$His
l/H
and the price
of
the option should be
$1/H. Notice that S is a martingale under the risk-neutral measure; 8 but
In
S has a
negative drift. The reason
is
that
In
S follows a (symmetrical) normal distribution, but S
itself follows a lognormal distribution, which is positively skewed. As T oo, although
the expected value
of
Sr is I, the probability that Sr 1 actually approaches 0.
It
is simpler to use a no-arbitrage argument to derive the price. In order to pay
$1
when
the stock price hits $H,
we
need to buy 1 I H shares
of
the stock (at
$1
I H). So the option
should be worth
no
more than
$1
I H. Yet
if
the option price C
is
less than $1/ H
( C < 1 I H
=>
CH
< 1 ),
we
can buy an option by borrowing C shares
of
the stock. The
initial investment is 0. Once the stock price hits $H,
we
will excise the option and return
the stock by buying C shares at price $H, which gives payoff I -
CH
>
0.
That means
we
have no initial investment, yet we have possible positive future payoff, which
is
contradictory to the no arbitrage argument. So the price cannot be less than
$1
I H. Hence,
the price
is
exactly $1/H.
E. Assume a non-dividend paying stock follows a geometric Brownian motion. What is
the value
of
a contract that at maturity T pays the inverse
of
the stock price observed at
the maturity?
8 Once we recognize that S
is
a martingale under the risk neutral measure, we do not need
the
assumption
that S follows a geometric Brownian motion. S has two boundaries for stopping: 0 and H.
The
boundary
conditions are
/(0)
= o and
/(//)
=
1.
Using the martingale, the probability that
it
will
ever
reaches
His
P x II +
(I
-
P)
x 0 =
S,,
= I
=>
P = I I H .
148

A Practical Guide To Quantitative Finance Interviews
Solution: Under risk-neutral measure
dS
= rSdt + aSdW(t). Apply Ito's lemma to
(
av
av
1 a2
v J
av
dV
=
-rS
+-+--
2 a2S2
dt+-aSdW(t)
1
as
a1
2
as
as
V=-:
S
(I
12
) I
=
--
2
rS+0+--
3 a2S2
dt--
2
aSdW(t)=(-r+a
2
)Vdt-aVdW(t)
S
2S
S
So V follows a geometric Brownian motion as well and we
can
apply Ito's lemma to
lnV:
d(ln
V)
=
-(-r+
a2) +
0---
2 a2 dt
+-adW(t)=
-r+-a
2
dt-adW(t).
(
v 1 v2 J v ( 1 )
v 2 v v 2
Discounting the
payoff
by
e-rr,
we
have V = e-rr E
[VT]
=
i,
e-
2
rr
+ a 2
r.
6.
2.
The
Greeks
All Greeks are first-order
or
second-order partial derivatives
of
the option price with
respect to different underlying factors, which are used to measure the
risks-as
well as
potential
returns-of
the
financial derivative. The following Greeks for a derivative
fare
routinely used by financial institutions:
Bf
82
f
Bf Bf
Bf
Gamma:
r=-·
Theta:
0=-·
Vega:
v=-·
Rho:
p=-
as
' 8S2 '
Bt
'
Ba
'
Br
Delta
For a European call
with
dividend
yieldy:
d = e-yr
N(d
1)
For a European put
with
dividend
yieldy:
d
=-e-yr[l-N(d
1
)]
A. What is the delta
of
a European call option on a non-dividend paying stock? How do
you derive the delta?
Solution: The delta
of
a European call on a non-dividend paying stock has a clean
expression: d =
N(d
1
).
For the derivation, though, many make
the
mistake
by
treating
149

Finance
N(d
1)and
N(d
2) as constants in the call pricing formula
c=SN(d
1
)-Ke-r'N(d
2
)and
simply taking the partial derivative on S to yield
N(d
1
).
The
derivation step
is
actually
more complex than that since both
N(d
1) and
N(d
2) are functions
of
S through d1 and
d2• Sothecorrectpartialderivativeis
ac
=N(d
1
)+Sxj_N(d
1
)-Ke-r•
j_N(d
2
).
as
as
as
Take the partial derivative with respect
to
S for N ( d1) and N ( d2) 9:
j_N(d)=N'(d)j_d
=-l-e-d
?
12x
I = I e-d,
21
2
as
I I
as
I .J2; Sa.f;
Sa.J27ri
j_N(d
)=N'(d
)j_d
=-l-e-d?t2x
I = I
e-
(
d1-u..fT)212
as
2 2
as
2 .J2; sa.J;
sa.J2;rr
1
-d
1
2 / 2
u./Td
1
-u
2
r/
2 1
-d
1
2 / 2 S
rr
= e e e = e
x-e
Sa.J2;; K
a s a _ a
So we have r'
-N(d
2
)=0.
Hence, the
as
K
as
as
ac
ac
last two components
of-
cancel out and -=
N(d
1
).
as
as
B. What
is
your estimate
of
the delta
of
an at-the-money call on a stock without dividend?
What will happen
to
delta as the at-the-money option approaches maturity date?
Solution: For an at-the-money European call, the stock price equals the strike price.
(r
+ a2 I
2)r
r a r · ·
= c
=(-+-)vr
>0
and
8.=N(d
1
)>0.5.
As
shown m Figure
avr
a 2
6.2, all at-the-money call options indeed have
!-:..
> 0.5 and the longer the maturity, the
higher
the!-:...
As
T-t-;O,
which is also
a 2
shown
in
Figure 6.2 ( T = I 0 days). The same argument is true for calls
on
stock with
continuous dividend rate y
if
r > y .
Figure 6.2 also shows that when
Sis
large
(S
>>
K
),
!-:..
approaches
I.
Furthermore, the
shorter the maturity, the faster the delta approaches
1.
On the other hand,
if
Sis
small
( S
<<
K ),
!-:..
approaches 0 and the shorter the maturity, the faster the delta approaches 0.
9 d = d
-a/;=>
N '(d ) =
§_e<r-
y
>r
N
'(d)
Bd2
=ad,
2 1 2 K 1 •
as
as
150
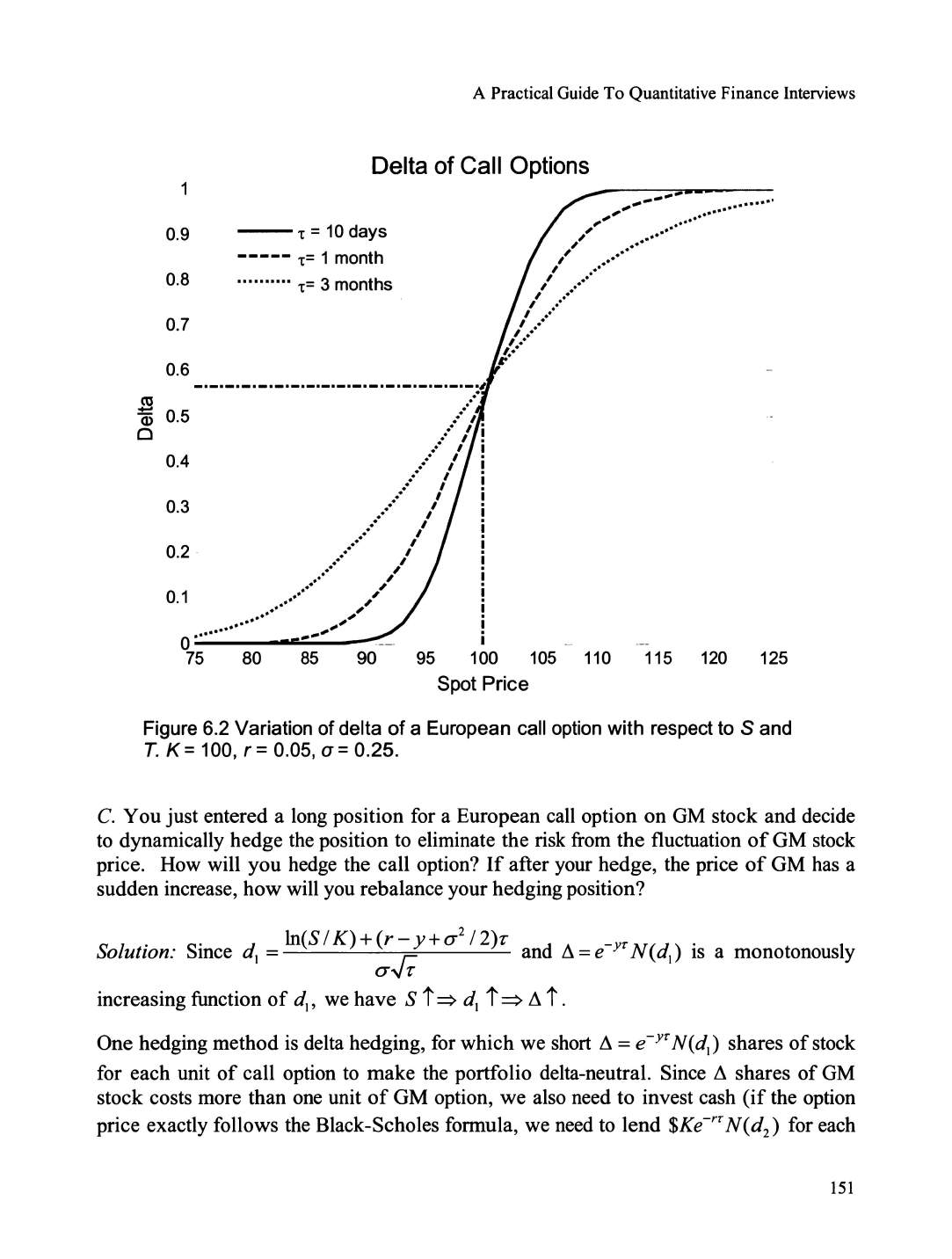
A Practical Guide
To
Quantitative Finance Interviews
1
0.9
0.8
0.7
0.6
Delta
of
Call Options
--.=
10days
-----
t=
1 month
••••••••••
t=
3 months
-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·-·"
.·•
----
..
,......
.
..
················
,
..
,
....
'
,'
..
··
..
..
/
...
··
I
.•
,
.·•
I •• •
I
.•
I
.•
I •• •
I•"
,
..
·
s
Q)
0.5
..
···I
•" I
.•
I
0
0.4
0.3
0.2
0.1
•• • I
•" I
.•
I
••• I
•• I
•• I
•• • I
•"
I
.•
I
...
··
,'
•"
I
..
· ,
...
··
,'
..
,
..
· ,
...
···
·····
;"'
o····"···
__
,,
75 80 85
90
95
100
Spot Price
105
110 115
120
125
Figure 6.2 Variation of delta
of
a European call option with respect to S and
T.
K = 100, r = 0.05,
a=
0.25.
C.
You just entered a long position for a European call option
on
GM
stock and decide
to dynamically hedge the position to eliminate the risk from the fluctuation
of
GM stock
price. How will you hedge the call option?
If
after your hedge, the price
of
GM has a
sudden increase,
how
will you rebalance your hedging position?
Solution: Since d1 = ln(S /
K)
+
(r
Jf + a2 12
)'
and
/).
= e-yr
N(d
1) is a monotonously
a r
increasing function
of
d1, we have S t d1 t
=>
/).
t .
One hedging method is delta hedging, for which we
e-yr
N(d
1) shares
of
stock
for each unit
of
call option to make the portfolio delta-neutral. Since
/).
shares
of
GM
stock costs more than one unit
of
GM option,
we
also need to invest cash
(if
the option
price exactly follows the Black-Scholes formula, we need to lend $Ke-rr
N(d
2) for each
151

Finance
unit
of
option) in the money market.
If
there is a sudden increase in
S,
d1 increases and
increases as well. That means
we
need to short more
stock
and lend
more
cash
(Ke-rr
N(d
2) also increases).
The delta hedge
only
replicates
the
value and
the
slope
of
the
option.
To
hedge the
curvature
of
the option, we will
need
to hedge
gamma
as well.
D.
Can
you estimate the value
of
an
at-the-money call on a non-dividend
paying
stock?
Assume the interest rate is low
and
the call has
short
maturity.
Solution: When
S=K,
we
have
c=S(N(d
1
)-e-rrN(d
2
)).
In a low-interest
environment, r 0
and
e-rr
1,
so
c
S(N(d,)-N(d
2
)).
We
also have
N(d,
)-N(d
2) =
f"i
e-
112
x2
dx,
12
v27r
r
a,-
r
ar
where d2
=(a
-2
)vr
and d1
=(a
+2)vr
.
For
a small r, a typical a for
stocks(<
40%
per
year) and a
short
maturity(< 3 months),
both d2 and d1 are close
to
0.
For
example,
if
r = 0.03,
a=
0.3, and T
=I
I 6 year, then
d -0 02 d
-I/id?
-0 98
2 -- • an e - . .
In practice, this approximation is
used
by some volatility traders to estimate the implied
volatility
of
an at-the-money option.
(The approximation
e-
112
x2 1
causes
a small overestimation since
e-
112
x2 <
1;
but the
approximation
-e-rr
K
-K
causes
a small underestimation.
To
some extent, the two
opposite effects cancel out and the overall approximation is fairly accurate.)
Gamma
For
a European call/put with dividend yield
y:
r = N
'(
d,
S0a T
152

A Practical Guide
To
Quantitative Finance Interviews
What happens to the gamma
of
an
at-the-money European option when it approaches its
maturity?
Solution: From the put-call parity, it is obvious that a call and a put with identical
characteristics have the same gamma (since r = 0 for both the cash position and the
underlying stock). Taking the partial derivative
of
the
/1
of
a call option with respect to
N'(d
)e-y•
S
We
haver=
I
'
Sa/;
'
So for plain vanilla call and put options, gamma is always positive.
Figure
6.3
shows that gamma is high when options are at the money, which
is
the stock
price region that
/1
changes rapidly with
S.
If
S
<<
K
or
S
>>
K (deep in the money or
out
of
the money), gamma approaches 0 since
/1
stays constant at I or 0.
The gamma
of
options with shorter maturities approaches 0 much faster than options
with longer maturities
as
S moves away from K.
So
for deep in-the-money or deep out-
of-the-money options, longer maturity means higher gamma. In contrast,
if
the stock
prices are close to the strike price (at the money)
as
the maturity nears, the slope
of
delta
for an at-the-money call becomes steeper and steeper. So for options close
to
the strike
price, shorter-term options have higher gammas.
As r
0,
an at-the-money call/put has r
--+
oo
(
/1
becomes a step function). This can
be shown from the formula
of
gamma for a European call/put with no dividend,
r = N'(d1).
Sa/;.
When S =
K,
d1 = lim(
!.._
+
a)/;
0 lim N
'(
d1) • The numerator is I I
.J2;;
T-40
a 2
T-40
V 2Jr
yet the denominator has a limit
limSa/;--+
0, so r
oo.
In other words, When t =
T,
T--+0
delta becomes a step function. This phenomenon makes hedging at-the-money options
difficult when t T since delta is extremely sensitive to changes in
S.
153
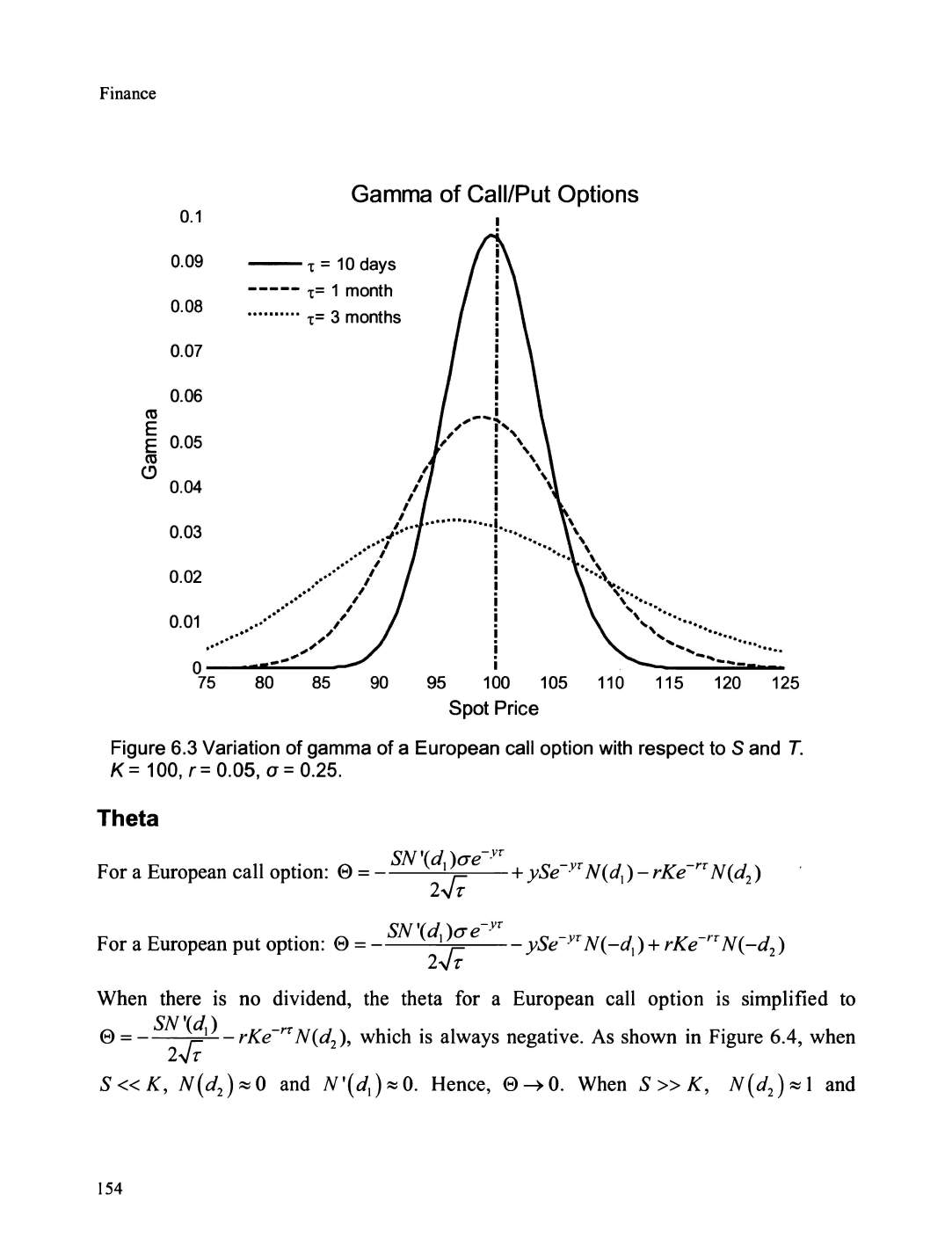
Finance
ro
E
E
ro
C)
Gamma
of
Call/Put Options
0.1
0.09
0.08
0.07
0.06
0.05
0.
04
0.03
0.02
0.01
-.=
10days
-----
t=
1 month
..........
t=
3 months
I
I
I
I
I
I
..
,
..
···I
..
·
··
,
....
/
,.•
I
••
• I
,o'
I
.··
,
...
,
..
··
,
··
···
,,
......
o--..a.:;;-;,...
___
75
80 85
90
95
100
105 110 115 120 125
Spot Price
Figure 6.3 Variation
of
gamma
of
a European call option with respect to
Sand
T.
K = 100,
r=
0.05,
a=
0.25.
Theta
SN'(d
)ae-
yr
For a European call option: 0 = -
J;
+ ySe-yr N ( d1) - rKe-rr N ( d2)
2 r
SN'(d
)ae-
yr
For a European put option: 0 =
J";
ySe-yr
N(-di)
+
rKe-r
r
N(-d
2)
2 r
When there is no dividend, the theta for a European call option is simplified to
0 = - rKe-rr
N(d
2
),
which is always negative. As shown in Figure 6.4, when
S<<K,
and Hence, When
S>>K,
and
154
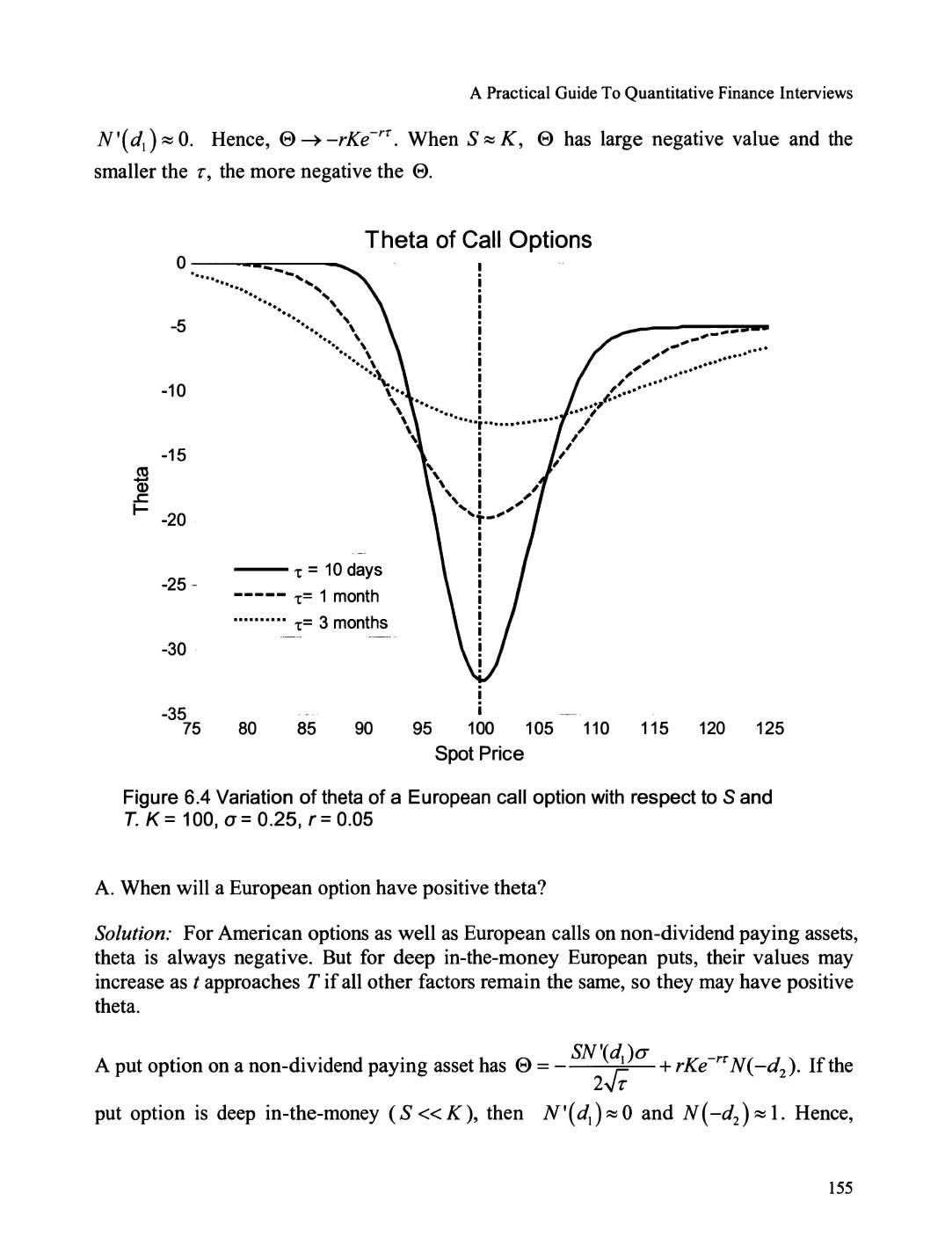
A Practical Guide To Quantitative Finance Interviews
Hence, When 0 has large negative value and the
smaller the r, the more negative the
0.
.I:.
-5
-10
-15
·····
...
I-
-20
-25 -
-30
-35
75
Theta
of
Call Options
...
..
..
..
..
..
..
..
..
--
't
= 10 days
-----
't=
1 month
.........
•
't=
3 months
80
85
90
_.,---
_.,,,,
....
,,,,
·····
,
,,
·········
...
...
•-;'
///
95
100 105
110
115
120
125
Spot Price
Figure 6.4 Variation
of
theta
of
a European call option with respect to
Sand
T.
K = 100,
a=
0.25,
r=
0.05
A.
When will a European option have positive theta?
Solution: For American options as well as European calls on non-dividend paying assets,
theta
is
always negative. But for deep in-the-money European puts, their values may
increase as t approaches T
if
all other factors remain the same, so they may have positive
theta.
A put option on a non-dividend paying asset has 0 = -
SN'<j!cr
+ rKe-rr
N(-d
2
).
If
the
2 r
put option is deep in-the-money
(S<<K),
then and Hence,
155

Finance
0 rKe-r• > 0.
That's
also the reason why it can be optimal to exercise a deep in-the-
money American put before maturity.
For
deep in-the-money European call options with high dividend yield,
the
theta can
be
positive as well.
If
a call option with high dividend yield is deep in-the-money ( S
>>
K ),
so the component
ySe-Y'N(d
1) can
make
0 positive.
B. You just entered a long position for a call option on
GM
and hedged
the
position
by
shorting GM shares to make the portfolio
delta
neutral.
If
there is an immediate increase
or
decrease
in
GM's
stock price, what will happen to the value
of
your portfolio? Is it an
arbitrage opportunity? Assume that GM does not pay dividends.
Solution: A position in the underlying asset has zero gamma. So the portfolio is delta-
neutral and long gamma. Therefore, either
an
immediate increase
or
decrease in the
GM
stock price will increase the portfolio value. The convexity (positive gamma) enhances
returns when there is a large move in the stock price in either direction.
Nevertheless, it is not an arbitrage opportunity.
It
is a trade-off between gamma and
theta instead.
From
the Black-Scholes-Merton differential equation, the portfolio V
. .
av
av
l a2v 1
satisfies the equation
-+rS-+-o-
2S2
--
2 =
+-o-
2S2r =
rV.
For a delta-
at
as
2
as
2
neutral portfolio,
we
have
E>
+
_!_
a2
s2r = r
V.
This indicates that gamma
and
theta often
2
have opposite signs. For example, when
an
at-the-money call approaches maturity,
gamma
is
large and positive, so theta is large and negative. Our delta neutral portfolio
has positive
gamma
and negative theta.
That
means
if
the price does
not
move, the
passage
of
time will result in a lower portfolio value unless we rebalance. So the
portfolio does not provide an arbitrage opportunity.
Vega
For European options: v =
ac
=
ap
= Se-Y'
./;
N
'(
d1)
aa
aa
At-the-money options are most sensitive to volatility change, so they have higher vegas
than either in-the-money or out-of-the-money options. The vegas
of
all options decrease
as time
to
expiration becomes shorter (
J-:;
0 ) since a long-term option
is
more
sensitive to change in volatility.
A. Explain implied volatility and volatility smile. What is the implication
of
volatility
156

A Practical
Guide
To
Quantitative Finance Interviews
smile for the Black-Scholes pricing model?
Solution: Implied volatility is the volatility that makes the model option price equal to
the market option price. Volatility smile describes the relationship between the implied
volatility
of
the options and the strike prices for a given asset. For currency options,
implied volatilities tend to be higher for in-the-money and out-of-the-money options
than for at-the-money options. For equity, volatility often decreases as the strike price
increases (also called volatility skew). The Black-Scholes model assumes that the asset
price follows a lognormal distribution with constant volatility. In reality, volatilities are
neither constant nor deterministic. In fact, the volatility is a stochastic process itself.
Furthermore, there may be jumps
in
asset prices.
B.
You have to price a European call option either with a constant volatility 30% or by
drawing volatility from a random distribution with a mean
of
30%.
Which option would
be more expensive?
Solution: Many would simply argue that stochastic volatility makes the stock price
more volatile, so the call price
is
more valuable when the volatility is drawn from a
random distribution. Mathematically, the underlying argument
is
that the price
of
a
European call option
is
a convex function
of
volatility and
as
a result
e (
E[
al)
::;;
E [ e( a)], where a
is
the random variable representing volatility and e is the
call option price. Is the underlying argument correct?
It's
correct in most, but not all,
cases.
If
the call price e is always a convex function
of
a,
then 0.
Be
is the
Ba
Ba
Vega
of
the option. For a European call option,
Be
,-
, ( 2 )
v = - = S v
TN
( d1) = exp
-d
1 I 2 .
Ba
'\/2tr
The secondary partial derivative is called Volga. For a European call option,
Ba
B2e
= exp(-d12 I
2)
d1d2
= v
d1d2.
Ba
2
.&
a a
v
is
always positive. For most out-of-the-money call options, both d1 and d2 are
negative; for most in-the-money call options, both d1 and d2 are positive.
So
d1
d2
> 0
in most cases and e
is
a convex function
of
a when d1
d2 > 0. But theoretically, we can
have conditions that d1 > 0 and d2 < 0 and < 0 when the option is close to being
Ba
157

Finance
at-the-money. So the function
is
not always convex. In those cases, the option with
constant volatility may have a higher value.
C.
The Black-Scholes formula for non-dividend paying stocks assumes that the stock
follows a geometric Brownian motion. Now assume that you don't know the stochastic
process followed by the stock price, but you have the European call prices for all
(continuous) strike prices K. Can you determine the risk-neutral probability density
function
of
the stock price at time
T?
Solution: The payoff a European call at its maturity date is Max(
ST
-
K,
0).
Therefore
under risk-neutral measure, we have c = e-rr i (s
-K)fs
(s)ds, where
fs
(s) is the
JK
r r
probability density function
of
ST
under the risk-neutral probability measure. Taking the
first and second derivatives
of
c with respect to K,
10
we have
ac
= e-rr F
(s-K)fs
(s)ds
aK
aKk
r
=e-rr
f'a(s-K)
f.
(s)ds-e-rr(K-K)xl
JK
aK
Sr
= e-rr
J;
-fsr
(s)ds
and
82
c = =
e-rT
F
-f.
(s)ds
=
e-rT
f.
(K).
aK
2
aK aK
aK
JK
Sr
Sr
Hence the risk-neutral probability density function is
f.s
(K)
=err
82
c
2.
r
aK
6.3. Option Portfolios and Exotic Options
In addition to the pricing and properties
of
vanilla European
and
American options, you
may be expected to be familiar with the construction and payoff
of
basic option-based
trading strategies---covered call, protective put, bull/bear spread, butterfly spread,
straddle, etc. Furthermore,
if
you are applying for a derivatives-related position, you
JO
To calculate the derivatives requires the Leibniz integral rule, a fonnula for differentiating a definite
integral whose limits are functions
of
the differential variable:
a
r(z)
!(z)
af(x,
z)
ab aa
-
f(x,z)dx
= ·
dx+
f(b(z),z)--f(a(z),z)-
az
•(zl
(z)
az
az
az
158

A Practical Guide To Quantitative Finance Interviews
should also have a good understanding
of
pricing and hedging
of
some
of
the common
exotic
derivatives-binary
option, barrier option, Asian option, chooser option, etc.
Bull spread
What are the price boundaries for a bull call spread?
Solution: A bull call spread is a portfolio with two options: long a call c1 with strike K1
and short a call c2 with strike K2
(K
1 < K2
).
The cash flow
of
a bull spread is
summarized in table 6.3.
Cash flow Time 0
Matur!!Y_T
ST::;
Kl
Kl<
ST
<K2
ST
Long c1
-c1
0
ST-Kl
ST-Kl
Short c2
C2
0 0
-(ST
-K
2)
Total C2
-c
1
<0
0
ST-Kl
K2-KI
Table 6.3 Cash flows
of
a bull call spread.
Since K1 < K2, the initial cash flow is negative. Considering that the final payoff
is
bounded by K2
-KP
the price
of
the spread, c1
-c
2, is bounded by e-rT(K2
-K
1
).
Besides, the payoff is also bounded
by
K2
; K1 ST' so the price is also bounded by
2
Straddle
Explain what a straddle is and when
you
want
to
purchase a straddle.
Solution: A straddle includes long positions in both a call option
and
a put option with
the same strike price K and maturity date T on the same stock.
The
payoff
of
a long
straddle is I
ST
-K I · So a straddle may be used to
bet
on large stock price moves. In
practice, a straddle
is
also used
as
a trading strategy for making bets on volatility.
If
an
investor believes that the realized (future) volatility should be much higher than the
implied volatility
of
call and put options, he
or
she will purchase a straddle. For example,
159

Finance
the value
of
an at-the-money call or put is almost a linear function
of
volatility.
If
the
investor purchases an at-the-money straddle, both the call and the put options have the
price c p where
O';
is the implied volatility.
If
the realized volatility
O'r
>
O';,
both options are undervalued. When the market prices converge
to
the prices
with the realized volatility, both the call and the put will become more valuable.
Although initially a straddle with an at-the-money call and an at-the-money put (
K = S )
has a delta close to 0, as the stock price moves away from the strike price, the delta is no
longer close to 0 and the investor is exposed
to
stock price movements. So a straddle is
not a pure bet on stock volatility. For a pure bet on volatility,
it
is
better to use volatility
swaps or variance swaps.
11
For example, a variance swap pays Nx(O'; -Kvar), where N
is the notional value,
O';
is the realized variance and
Kvar
is the strike for the variance.
Binary options
What is the price
of
a binary (cash-or-nothing digital) European call option on a non-
dividend paying stock
if
the stock price follows a geometric Brownian motion?
How
would you hedge a cash-or-nothing call option and what's the limitation
of
your hedging
strategy?
Solution: A cash-or-nothing call option with strike price K pays
$1
if
the asset price is
above the strike price at the maturity date, otherwise it pays nothing. The price
of
the
option is c8 = e
r•
N(d
2)
if
the underlying asset is a non-dividend paying stock. As we
have discussed
in
the derivation
of
the Black-Scholes formula,
N(d
2) is the probability
that a vanilla call option finishes in the money under the risk-neutral measure. So its
discounted value is
e-r•
N(d
2
).
Theoretically, a cash-or-nothing call option can be hedged using the standard delta
hedging strategy. Since =
ac
8 =
e-r•
N '( d2) 1 , a long position
in
a cash-or-
as
nothing call option can be hedged by shorting
e-r•
N '( d2) shares (and a risk-free
SO'
r
money market position). Such a hedge works well when the difference between S and K
is large and r is not close to 0. But when the option is approaching maturity T ( r
0)
11
For detailed discussion about volatility swaps, please refer to the paper "More Than You Ever Wanted
to Know about Volatility Swaps" by Kresimir Demeterfi, et al. The paper shows that a variance swap can
be approximated by a portfolio
of
straddles with proper weights inversely proportional to
Ilk.
160

A Practical Guide
To
Quantitative Finance Interviews
and the stock price
Sis
close to K,
"'1.
is extremely volatile
12
and small changes in the
stock price cause very large changes in
"'1..
In
these cases, it
is
practically impossible to
hedge a cash-or-nothing call option by delta hedging.
We can also approximate a digital option using a bull spread with two calls.
If
call
options are available for all strike prices and there are no transaction costs, we can long
I I
2&
call options with strike price K -& and short I I
2c
call options with strike price
K +
&.
The payoff
of
the bull spread
is
the same
as
the digital call option
if
ST
K -&
(both have payoff 0) or
ST
K + & (both have payoff
$1
).
When K -& <
ST
< K + & ,
their payoffs are different. Nevertheless,
if
we
set & 0, such a strategy will exactly
replicate the digital call. So it provides another way
of
hedging a digital call option. This
hedging strategy suffers its own drawback. In practice, not all strike prices are traded in
the market. Even
if
all strike prices were traded in the market, the number
of
options
needed for hedging, I
I
2&,
will be large in order to keep c small.
Exchange options
How would you price an exchange call option that pays max (
ST,i
-
ST,
2,
0)
at maturity.
Assume that S1 and S2 are non-dividend paying stocks and both follow geometric
Brownian motions with correlation p.
Solution: The solution to this problem uses change
of
numeraire. Numeraire means a
unit
of
measurement. When we express the price
of
an asset, we usually use the local
currency as the numeraire. But for modeling purposes, it is often easier to use a different
asset as the numeraire. The only requirement for a numeraire is that it must always be
positive.
The payoff
of
the exchange option depends on both
ST
I (price
of
SI
at maturity date n
and
sT,2
(price
of
s2
at
n,
so it appears that we need two geometric Brownian motions:
dS
1 = µ1S1dt +
o-
1S1
dW,,
1
dS
2 = µ1S2dt +
o-
2S2
dW,,
2
Yet
if
we use S1
as
the numeraire,
we
can convert the problem to just one geometric
Brownian motion. The final payoff is max (
sT,2
-
sT,I
• 0) =
sT,I
max (
-1,
oJ.
When
T ,I
1
-n
12 S K and r 0
=>
ln(S I
K)
0
=>
d1
(r
I
a+
0.5a)J";
0
=>
!!..
e I
oo.
v2tr
Savr
161

Finance
SI
and s2 are geometrical Browian motions, f = s2 is a geometric Brownian motion as
SI
well. One intuitive explanation
is
that both
In
S1 and ln S2 follow normal distributions,
so
ln
f = ln S2 -ln S1 follows a normal distribution as well and f follows a lognormal
distribution. More rigorously, we can apply the Ito's lemma to f = S2 :
SI
dif=
af
dS +
af
dS
+1._82f(dS)2+1._a21(dS
)2+
a2f
dSdS
as
1
as
2 2
as
2 1 2
as
2 2
as
as
1 2
I 2 I 2 I 2
s2 s2 s2 d s2 d 2 s 2 d s 2 d
=-µI
-dt-
0"1
-dW,.I
+
µ2
-t +
0'2
-
W,.2
+
0'1
-
t-
P0"10'2
-t
SI
SI
SI
SI
SI SI
= (
µ2
-
µ1
+
0"1
2
-
P0"10"2)
fdt
-aJdW,,1 +
D"
2
fdW,,2
= (µ2 -
µ1+0-1
2
-
P0"10"2
)fdt
+ -2pa10"2
+a;
x
fdW,,3
To make f = - 2 a martmgale, set µ2 -µ1
+ a1 -
pa
1
a2
= 0 and we have E
-·-
= - 2 ,
S . 2
-[ST2
l S
SI
ST
.I
SI
s
and
___!2:_
is
a martingale under the new measure. The value
of
the exchange option using
S11
S,
as the numeraire is
C,
(
;,::
-1,
0 J J which is just the value
ofa
call option
with underlying asset price S = S2 , strike price K =
1,
interest rate r = 0, and volatility
SI
So its value IS where
I
_
In
( S2 I S1) + d _ d _ r h
d1 -
.Jr
and 2 -1
av
r. T e payoff
of
the exchange option
O'
s r
expressed in local currency is S1
Cs
= S2
N(d
1
)-S
1
N(d
2
).
162

A Practical Guide To Quantitative Finance Interviews
6.4. Other Finance Questions
Besides option pricing problems, a variety
of
other quantitative finance problems are
tested in quantitative interviews as well. Many
of
these problems tend
to
be position-
specific. For example,
if
you are applying for a risk management job, prepare to answer
questions about VaR; for fixed-income jobs, get ready
to
answer questions about interest
rate models.
As
I explained in Chapter
1,
it always helps
if
you grasp the basic
knowledge before the interview. In this section,
we
use several examples to show some
typical interview problems.
Portfolio optimization
You
are constructing a simple portfolio using two stocks A and
B.
Both have the same
expected return
of
12%. The standard deviation
of
A's
return is 20% and the standard
deviation
of
B's
return is 30%; the correlation
of
their returns is
50%.
How will you
allocate your investment between these
two
stocks to minimize the risk
of
your portfolio?
Solution: Portfolio optimization has always been a crucial topic for investment
management
firms.
Harry Markowitz's mean-variance portfolio theory
is
by far the most
well-known and well-studied portfolio optimization model. The essence
of
the mean-
variance portfolio theory assumes that investors prefer (I) higher expected returns for a
given level
of
standard deviation/variance and (2) lower standard deviations/variances
for a given level
of
expected return. Portfolios that provide the minimum standard
deviation for a given expected return are termed efficient portfolios. The expected return
and the variance
of
a portfolio with N assets can
be
expressed as
T
µP
=w1µ1
+w2µ2
+
··
·+wNµN
=w
µ
N
var(rP) =
La}w;
2 +
Z:aifwiwJ
=
wr
L:
w
i=l
i*}
where
wi'
Vi=
1,-
· ·, N , is the weight
of
the i-th asset in the portfolio;
µ;,Vi
=
I,···,
N,
is
the expected return
of
the i-th asset;
0"
;2 is the variance
of
i-th asset's return;
aif =
pifa;a
1
is
the covariance
of
the returns
of
the i-th and
thej-th
assets and
pif
is their
correlation; w is an N x I column vector
of
w;
's; µ is an N x 1 column vector
ofµ;
's;
L
is
the covariance matrix
of
the returns
of
N assets, an N x N matrix.
Since the optimal portfolio minimizes the variance
of
the return for a given level
of
expected return, the efficient portfolio can be formulated as the following optimization
problem:
163

Finance
min wTLw
w , where e is an N x 1 vector with all elements equal
to
1.
13
S
.(.
WTµ
= µ
P,
WT
e = 1
For this specific problem, the expected returns are 12% for both stocks.
So
µP
is always
12% no matter
what
wA
and w8 (
wA
+ w8 = 1) are. The variance
of
the portfolio is
()
22
222
var
rP
=o-AwA
+a
8w8 +
PA
.BaAa8
wAw
8
+a;(l-wA)2
+2pA,BO"AO"BWA(l-wA)
Taking the derivative
of
var(rP) with respect to
wA
and setting it to zero,
we
have
avar(rp) 2 2
---=
2aAwA
-20-8(1-wA)
+2pA BO"AaB(l-wA)-2pA
BO"AO"BWA
= 0
aw
. .
A
So we should invest
617
of
the money
in
stock A and 1/7 in stock
B.
Value at risk
Briefly explain
what
VaR is. What is the potential drawback
of
using
VaR
to measure
the risk
of
derivatives?
Solution: Value at Risk (VaR) and stress test---or more general scenario
analysis-are
two important aspects
of
risk management. In the Financial
Risk
Manager Handbook,
14
VaR is defined as the following: VAR is the maximum loss over a target horizon such
that there is a low, pre-specified probability that the actual loss will be larger.
Given a confidence level a E (0,
1),
the VaR can be implicitly defined as
a=
[
xf(x)dx,
where x is the dollar profit (loss) and f
(x)
is its probability density
VaR
function.
In
practice, a is often set to 95%
or
99%. VaR is
an
extremely popular choice
in financial risk management since it summarizes the risk to a single dollar number.
C-µ
B
13
The optimal weights have closed form solution
w*
=AL
1e +
y:L
-1
µ,
where
A.=
P
D
µA-8
I I I 2
r =
I'
' A = e
IL
-e > 0, B = e
IL
µ'
c = µ
'L
µ > 0, D =
Ac
-B .
D
14
Financial
Ri.'>k
Manager Handbook by Phillippe Jorion
is
a comprehensive book covering different
aspects
of
risk management. A classic book for VaR is Value at Risk, also by Philippe Jori on.
164

A Practical Guide To Quantitative Finance Interviews
Mathematically, it is simply the (negative) first or fifth percentile
of
the profit
distribution.
As a percentile-based measure on the profit distribution, VaR does not depend on the
shape
of
the tails before (and after) probability
1-
a,
so it does
not
describe the loss on
the left tail. When the profit/loss distribution is far from a normal distribution, as in the
cases
of
many derivatives, the tail portion has a large impact
on
the risk, and
VaR
often
does not reflect the real risk.
15
For example, let's consider a short position
in
a credit
default swap. The underlying asset is bond A with a
$1
M notional value. Further assume
that A has a 3% default probability and the loss given default is 100% (no recovery).
Clearly
we
are facing the credit risk
of
bond A. Yet
if
we
use 95% confidence level,
VaR(A) = 0 since the probability
of
default
is
less than 5%.
Furthermore, VaR is not sub-additive and
is
not a coherent measure
of
risk, which
means that when we combine two positions A and B to form a portfolio
C,
we
do not
always have VaR(C) VaR(A)+ VaR(B). For example,
if
we
add
a short position in a
credit default swap
on
bond B with a
$IM
notional value. B also has a
3%
default
probability independent
of
A and the loss given default is 100%. Again we have
VaR(B) = 0. When A and B form a portfolio
C,
the probability that at least one bond will
default becomes So
VaR(C)=$1M>VaR(A)+VaR(B).
Lack
of
sub-additivity directly contradicts the intuitive idea that diversification reduces
risk. So it is a theoretical drawback
of
VaR.
(Sub-additivity
is
one property
of
a coherent risk measure. A risk measure
p(X)
is
considered coherent
if
the following conditions holds:
p(X
+ Y)
p(X)
+
p(Y);
p(aX)=ap(X),
Va>O;
if
and
p(X+k)=p(X)-k
for any
constant k.
It
is defined
in
Coherent Measure
of
Risk
by Artzner, P., et al., Mathematical
Finance, 9 (3):203-228. Conditional
VaR
is
a coherent risk measure.)
Duration and convexity
The duration
of
a bond is defined as D = _
_!_
dP,
where P is the price
of
the bond and y
p dy
is yield to maturity. The convexity
of
a bond is defined as C =
_!_
d2 Applying
p dy
Taylor's expansion, M when is small, M
p 2 p
For a fixed-rate bond with coupon rate c and time-to-maturity
T:
15
Stress test is often used as a complement
to
VaR
by
estimating the tail risk.
165

Finance
Another important concept is dollar duration:
$D
= -
dP
= P x D. Many market
dy
participants use a concept called
DVO
1:
D
VO
1 = -
dP
, which measures
the
10,000x
cry
price change
when
the yield changes by
one
basis point.
For
some
bond
derivatives,
such as swaps, dollar duration is especially important. A
swap
may have value P = 0,
in
which case dollar duration is more meaningful than duration.
When n bonds with values
P;,
i =
1,
···,
n,
and
Durations
Di
(convexities Ci) form a
portfolio, the duration
of
the portfolio is the value-weighted average
of
the
durations
of
n p n p n
the components: D = L
_!_Di
( C = L _!_Ci), where P =LP;· The dollar duration
of
i=I
p
i=I
p
i=I
n
the portfolio is simply the sum
of
the dollar durations
of
the
components:
$D
=
L$Di.
i=I
What are the price and duration
of
an inverse floater with face value $100 and annual
coupon rate
30%
-3r
that matures in 5 years? Assume that the coupons are paid
semiannually and the current yield curve is flat at 7 .5%.
Solution: The
key
to solving basic fixed-income problems is cash flow replication.
To
price a fixed-income security
with
exotic structures,
if
we
can replicate its cash flow
using a portfolio
of
fundamental bond types such as fixed-rate coupon bonds (including
zero-coupon bonds) and floating-rate bonds, no-arbitrage arguments give
us
the
following conclusions:
Price
of
the exotic security= Price
of
the replicating portfolio
Dollar duration
of
the exotic security = Dollar duration
of
the
replicating portfolio
To replicate the described inverse floater,
we
can use a portfolio constructed by shorting
3 floating rate bonds, which is worth $100 each, and longing 4 fixed-rate bonds with a
7.
5% annual coupon rate,
which
is worth $100 each as well. The coupon rate
of
a
floating-rate bond is adjusted every 0.5 years payable in arrear: the coupon rate paid
at
t + 0.5 y is determined at
t.
The
cash flows
of
both positions and the whole portfolio are
summarized in
the
following table.
It
is
apparent that the total cash flows
of
the portfolio
are the same as the described inverse floater. So the price
of
the inverse float is the price
of
the replicating portfolio: P;nverse = $100.
166

A Practical Guide
To
Quantitative Finance Interviews
Cash flow YearO Year 0.5 ...
Year4.5
Year
5
Short 3 floating- 300
-150r
0
-300-150r
rate
bonds
...
4.S
Long 4 bonds
with
-400
15
15
400+15
7.5%
COU_QOn
rate ...
Total -100
15-150r
0 ... 30-300r.i
The dollar duration
of
the inverse floater is
the
same as
the
dollar duration
of
the
portfolio as well: $Dinverse = 4 x
$D
fu:ed
-3 x
$D
floating. Since
the
yield
curve
is flat,
r0 =
7.5%
and the floating-rate
bond
is always worth $103.75 (after the payment
of
$3.75,
the
price
of
the
floating-rate bond
is
$100)
at
year 0.5,
and
the dollar duration
16
is
$ -
d(103.75/(l+y
/2)) _ 103.75 - 0.5 -
Djloating
--
-0.5x
2
-lOOx
-48.19.
dy
(1+
y/2)
l+
y/2
Th
· f
fi
d bo d · P
c/
2
lOO
h · h ·
e
pnce
o a
1xe
-rate n is = + z
r,
w ere
Tis
t e matunty
l=I
(1+y
I
2)'
(1+yI2)
of
the
bond
. So the dollar duration
of
the fixed-rate bond is
$D
= _
dP
= 1
('I.!._
c I 2 + lOOT J =
410
.
64
.
fixed
dy
1+y/2
l=I 2
(1+y/2)'
(1+Y/2)
2T
So
$Dinverse
= 4 x
$D
fu:ed -3 x
$D
floating = 1498 and
the
duration
of
the inverse floater is
Dinverse = $Dinverse / P;nverse = 14.98.
Forward and futures
What's
the
difference between futures and forwards?
If
the
price
of
the underlying asset
is strongly positively correlated
with
interest rates, and the interest rates are stochastic,
which
one
has higher price: futures
or
forwards?
Why?
Solution: Futures contracts are exchange-traded standardized contracts; forward
contracts are over-the-counter agreements so
they
are more flexible. Futures contracts
are marked-to-market daily; forwards contacts
are
settled at
the
end
of
the contract term.
16
The initial duration
of
a floating rate bond is the same as the duration
of
a six-month zero coupon bond.
167

Finance
If
the interest rate is deterministic, futures and forwards have the same theoretical price:
F =
se<r+u-y)r,
where u represents all the storage costs and y represents dividend yield
for investment assets, convenience yield for commodities and foreign risk-free interest
rate for foreign currencies.
The mark-to-market property
of
futures makes their values differ from forwards when
interest rates vary unpredictably (as they do in the real world). As the life
of
a futures
contract increases, the differences between forward and futures contracts may become
significant.
If
the futures price is positively correlated with the interest rate, the
increases
of
the futures price tend to occur the same time when interest rate
is
high.
Because
of
the mark-to-market feature, the investor who longs the futures has an
immediate profit that can be reinvested at a higher rate. The loss tends to
occur
when the
interest rate
is
low so that it can be financed at a low rate.
So
a futures contract
is
more
valuable than the forward when its value is positively correlated with interest rates and
the futures price should
be
higher.
Interest rate models
Explain some
of
the basic interest rate models and their differences.
Solution:
In
general, interest rate models can be separated into two categories: short-rate
models and forward-rate models. The short-rate models describe the evolution
of
the
instantaneous interest rate
R(t)
as stochastic processes, and the forward rate models
(e.g., the one-
or
two-factor Heath-Jarrow-Morton model) capture the dynamics
of
the
whole forward rate curve. A different classification separates interest rate models into
arbitrage-free models and equilibrium models. Arbitrage-free models take the current
term structure--constructed from most liquid
bonds-and
are arbitrage-free with respect
to the current market prices
of
bonds. Equilibrium models, on the other hand,
do
not
necessarily match the current term structure.
Some
of
the simplest short-rate models are the Vasicek model, the Cox-Ingersoll-Ross
model,
the
Ho-Lee model, and the Hull-White model.
Equilibrium short-rate models
Vasicek model:
dR(t)
=
a(b-R(t)
)dt
+
adW(t)
When R(t) > b, the drift rate is negative; when
R(t)
<
b,
the drift rate
is
positive. So the
Vasicek model has the desirable property
of
mean-reverting towards long-term average
b. But with constant volatility, the interest rate has positive probability
of
being negative,
which
is
undesirable.
Cox-Ingersoll-Ross model:
dR(t)
=a(
b-R(t))
dt
R(u)
dW(t)
168

A Practical Guide
To
Quantitative Finance Interviews
The Cox-Ingersoll-Ross model keeps the mean-reversion property
of
the Vasicek model.
But the diffusion rate
a)R(u)
addresses the drawback
of
Vasicek model by
guaranteeing that the short rate is positive.
No-arbitrage short-rate models
Ho-Lee model:
dr
=
B(t)dt+adz
The Ho-Lee model is the simplest no-arbitrage short-rate model where B(t) is a time-
dependent drift. B(t) is adjusted to make the model match the current rate curve.
Hull-White model: dR(t)
=a(
b(t)-R(t)
)dt
+
adW(t)
The Hull-White model has a structure similar to the Vasicek model. The difference is
that
b(t)
is
a time-dependent variable in the Hull-White model to make it fit the current
term structure.
169


Chapter 7 Algorithms and Numerical Methods
Although the percentage
of
time that a quant spends on programming varies with the job
function (e.g., quant analyst/researcher versus quant developer) and firm culture, a
typical quant generally devotes part
of
his
or
her time to implementing models through
programming. Therefore, programming skill test is often
an
inherent part
of
the
quantitative interview.
To a great extent, the programming problems asked in quantitative interviews are similar
to those asked in technology interviews. Not surprisingly, many
of
these problems are
platform-
or
language-specific. Although C++ and Java still dominate the market, we've
seen a growing diversification to other programming languages such as Matlab, SAS,
S-
Plus, and
R.
Since there are many existing books and websites dedicated to technology
interviews, this chapter will not give a comprehensive review
of
programming problems.
Instead, it discusses some algorithm problems and numerical methods that are favorite
topics
of
quantitative interviews.
7.
1.
Algorithms
In programming, the analysis
of
algorithm complexity often uses asymptotic analysis
that ignores machine-dependent constants and studies the running time T(n)
-the
number
of
primitive operations such as addition, multiplication, and
comparison-as
the
number
of
inputs n -
oo.
1
Three
of
the most important notations in algorithm complexity are big- 0 notation, Q
notation and 0 notation:
O(g(n))
= {
/(n):
there exist positive constants c and n0 such that 0
5:
f(n)
5:
cg(n)
for
all n n0 } •
It
is
the asymptotic upper bound
of
f ( n
).
n(g(n)) = {
f(n):
there exist positive constants c and n0 such that 0
5:
cg(n)
5:
f(n)
for
all n n0 } •
It
is
the asymptotic lower bound
of
f ( n
).
E>(g(n)) = {
/(n):
there exist positive constants c1, c2, and n0 such that
c1
g(n)
5:
f(n)
5:
c2
g(n)
for all n n0
}.
It is the asymptotic tight bound
of
f(n).
Besides notations, it is also important to explain two concepts in algorithm complexity:
1
If
you want to review basic algorithms, I highly recommend "Introduction to Algorithm" by Thomas
H.
Cormen, Charles
E.
Leiserson, Ronald
L.
Rivest and Clifford Stein.
It
covers all the theories discussed in
this section and includes many algorithms frequently appearing in interviews.

Algorithms and Numerical Methods
Worst-case
running
time
W(n):
an upper bound on the running time for any n inputs.
Average-case
running
time
A(n):
the expected running time
if
the n inputs are
randomly selected.
For many algorithms,
W(n)
and
A(n)
have the same
O(g(n)).
But as
we
will discuss
in some problems, they may well be different and their relative importance often
depends on the specific problem at hand.
A problem with n inputs can often be split into a subproblems with n I b inputs
in
each
subproblem. This paradigm is commonly called divide-and-conquer.
If
it takes
f(n)
primitive operations
to
divide the problem into subproblems and
to
merge the solutions
of
the subproblems, the running time can be expressed as a recurrence equation
T(n)
=
aT(n
I b) +
f(n),
where a
2::
1,
b >
1,
and
f(n)
0.
The
master
theorem
is a valuable tool in finding the tight bound for recurrence
equation
T(n)=aT(nlb)+f(n):
If
f(n)=O(n
10
gba-c)
for some constant e>O,
T(n)
=
e(
n
10
gba),
since
f(n)
grows slower than n
10
gba.
If
f(n)
=
e(
n10g6a
logk
n)
for
some k 0,
T(n)
=
e(
n
10
gha
logk+I
n),
since
/(n)
and n10g6a grow at similar rates.
If
f(n)
=
n(
n
10
gha+c)
for some constant e > 0, and
af
(n
I
b)
cf(n)
for some constant
c
<I,
T(n) =
0(/(n)),
since
f(n)
grows faster than n
10
gha.
Let's use binary search
to
show the application
of
the master theorem. To find an
element
in
an array,
if
the numbers in the array are sorted
(a,
a2 $ · · · an), we can use
binary search: The algorithm starts with
al
ntl
J'
If
al
nt
2
J = x, the search stops.
If
alnt
2J > x, we only need
to
search
a"·
.. ,aln12_1
J.
If
alnt
2J < x, we only need
to
search
alntl+IJ,.
.. ,an. Each time we can reduce the number
of
elements
to
search by half after
making one comparison. So we have a = I, b =
2,
and f ( n) = I. Hence,
f(n)
=
e(
n
10
g
21
log0
n)
and the binary search has complexity 0(1ogn).
Number swap
How
do
you swap two integers, i and
j,
without using additional storage space?
Solution: Comparison and swap are the basic operations for many algorithms. The most
common technique for swap uses a temporary variable, which unfortunately
is
forbidden
in this problem since the temporary variable requires additional storage space. A simple
172

A Practical Guide To Quantitative Finance Interviews
mathematic approach is to store the sum
of
i and} first, then extract i's value and assign
it
to
j and finally assign
j's
value to
i.
The implementation
is
shown in the following
code:2
void
swap(int
&i I
int
&j) {
i i + j ;
//st
o
re
the
sum
o f i
and
j
j i -j ;
//chan
ge j
to
i's
va
lue
i i -j ; / /
change
i
to
j's
va
lue
An alternative solution uses bitwise XOR (") function by taking advantage
of
the fact
that x " x = 0 and 0 " x =
x:
void
swap(int
&i
I
int
&j) {
i i j ;
j j
i;
//
j i "
(j
"
i)
i
i i j ;
Iii
(i
"
j)
A i j
Unique elements
If
you are given a sorted array, can you write some code to extract the unique elements
from the array? For example,
if
the array
is
[1,
1,
3, 3,
3,
5,
5,
5, 9, 9,
9,
9], the unique
elements should be [1, 3, 5, 9].
Solution: Let a be an n-element sorted array with elements a0 a1 · · · an-I. Whenever
we
encounter a new element
a;
in
the sorted array, its value is different from its
previous element
(a;
*
aH
). Using this property we can easily extract the unique
elements. One implementation in C++ is shown as the following function:3
template
<class
T>
vector<T>
unique(T
a[],
int
n)
{
vector<T>
vec;
/ / v
ector
used
to
avoid
resi
z i n g
problem
vec.reserve(n);
//r
e s
er
ver
to
a
vo
id
r
ea
ll
o
ca
tio
n
vec
.
push_back(a[O]);
for(int
i=l;
i<n;
++i)
2 This chapter uses C++ to demonstrate some implementations. For other problems, the algorithms are
described using pseudo codes.
The following is a one-line equivalent function for swapping two integers.
It
is not recommend, though, as
it lacks clarity .
void
swap(int
&i,
int
&j) {
i-=j=(i+=j)-j;
);
3 I should point out that
C++
STL has general algorithms for this basic operation: unique and unique_copy.
173

Algorithms and Numerical Methods
if(a[i]
!=
a[i-1])
vec.push_back(a[i]);
return
vec;
Horner's algorithm
Write an algorithm to compute y =
Ao
+ A,x + + A
3x3 + · · · +
Anxn.
Solution: A
nai"ve
approach calculates each component
of
the
polynomial
and
adds them
up, which takes
O(n
2) number
of
multiplications. We
can
use
Homer's
algorithm to
reduce the number
of
multiplications to O(n). The algorithm expresses the original
polynomial as y = ( ( ( (Anx +
An-i
)x +
An_
2) x +
···
+Ai)
x
+A,)
x
+Ao
and sequentially
calculate
Bn
=An,
Bn-I
=
Bnx
+An_,, · · ·, B0 = B,x
+Ao·
We have y = B0
with
at most n
multiplications.
Moving average
Given a large array A
of
length m, can
you
develop
an
efficient algorithm to build
another array containing the n-element moving average
of
the original array
(B,,···,Bn-i
=NA,
B;
=(Ai-n+i
+Ai-n+
2
+···+A;)
ln, '\li=n,
···
, m)?
Solution: When we calculate the moving average
of
the next n consecutive numbers,
we
can
reuse the previously computed moving average. Just multiply that average by n,
subtract the first number
in
that moving average and then
add
the new number, and you
have the new sum. Dividing
the
new sum
by
n yields the
new
moving average. Here is
the pseudo-code for calculating the moving average:
S=
A[l]
+ · ·· + A[n]; B[n] = S/n;
for (i=n+ I
tom)
{ S =
S-
A[i-n] + A[i]; B[i] = S/n; }
Sorting algorithm
Could you explain three sorting algorithms to sort n distinct values
A,,···,
An
and
analyze the complexity
of
each algorithm?
Solution: Sorting is a fundamental process that is directly
or
indirectly implemented in
many programs. So a variety
of
sorting algorithms have been developed for different
174

A Practical Guide
To
Quantitative Finance Interviews
purposes. Here
let's
discuss three such algorithms: insertion sort, merge sort and quick
sort.
Insertion
sort: Insertion sort uses an incremental approach. Assume that we have sorted
subarray
A[l,
...
, i-1].
We
insert element
A;
into the appropriate place in
A[l,
...
, i-1],
which yields sorted subarray
A[l,
...
, i]. Starting with i = 1 and increases i step by step
to n,
we
will have a fully sorted array. For each step, the expected number
of
comparisons
is
i I 2 and the worst-case number
of
comparisons
is
i.
So
we
have
A(n)
=
e(t,u
2)
=
0(n
2)
and
W(n)
=
e(t.;)
=
0(n
2).
Merge
sort: Merge sort uses the divide-and-conquer paradigm.
It
divides the array into
two subarrays each with n
I 2 items and sorts each subarray. Unless the subarray is small
enough (with no more than a few elements), the subarray is again divided for sorting.
Finally, the sorted subarrays are merged
to
form a single sorted array.
The algorithm can be expressed as the following pseudocode:
mergesort(A, beginindex, endindex)
if
begin index < endindex
then centerindex (beginindex + endindex )/2
mergel <- mergesort(A, beginindex, centerindex)
merge2 <- mergesort(A, centerindex + 1, endindex)
merge( merge
1,
merge2)
The merge
of
two sorted arrays with n/2 elements each into one array takes
E>(n)
primitive operations. The running time T(n) follows the following recursive function:
T(n) =
{2T(n/
2) +
E>(n),
if
n > 1
1,
if
n = 1 ·
Applying the master theorem to T(n) with
a=
2,
b =
2,
and
f(n)
=
E>(n),
we have
f(n)
=
e(
n
10
gba
log0 n ).
So
T(n) =
E>(n
logn).
For
merge sort, A(n) and
W(n)
are the
same as T(n).
Quicksort: Quicksort is another recursive sorting method.
It
chooses one
of
the
elements, A;, from the sequence and compares all other values with it. Those elements
smaller than
A;
are put in a subarray to the left
of
A;;
those elements larger than
A;
are
put in a subarray to the right
of
A;. The algorithm is then repeated on both subarrays
(and any subarrays from them) until all values are sorted.
175

Algorithms and Numerical Methods
In the worst case, quicksort requires the same number
of
comparisons as the insertion
sort. For example,
if
we always choose the first element in the array (subarray) and
compare all other elements with it, the worst case happens
when
A1,
···,An
are already
sorted. In such cases, one
of
the subarray is empty and the
other
has n -1 element. Each
step only reduces the subarray size by one. Hence, W (
n) =
El
(
t,
i)
=
0(
n2
).
To
estimate the average-case running time, let's assume that the initial ordering is
random so that each comparison is likely to be any pair
of
elements chosen from
A1,
···,An.
If
we suspect that the original sequence
of
elements has a certain pattern, we
can always randomly permute the sequence first with complexity
0(n)
as explained in
--
the next problem. Let
AP
and
Aq
be
the
pth
and qth element ( 1
:::;
p < q
n)
in the final
---
sorted array. There are q -p + 1 numbers between
AP
and Aq. The probability that
AP
--
.......
-
and
Aq
is compared is the probability that
Aq
is compared with
AP
before
Ap
+i • ·
·,
or
Aq-i
is compared with either
AP
or
Aq
(otherwise,
AP
and
Aq
are separated into
different subarrays and will not be compared), which happens with probability
P(p,q)
= 2 (you can again use the symmetry argument to derive this probablity).
q-
p
+I
n
q-1
n
q-1
( 2 )
The total expected number
of
comparison is A(n) = =
q-
p+
1
=
8(nlgn).
Although theoretically quicksort can be slower than merge sort in the worst cases, it is
often as fast as,
if
not faster than, merge sort.
Random permutation
A.
If
you have a random number generator that can generate random numbers from
either discrete
or
continuous uniform distributions, how
do
you shuffle a deck
of
52
cards so that every permutation is equally likely?
Solution: A simple algorithm to permute n elements is random permutation
by
sorting.
It
assigns a random number to each card and then sorts the cards in order
of
their assigned
random numbers. 4 By symmetry, every possible order (out
of
n!
possible ordered
sequences) is equally likely. The complexity is determined
by
the sorting step, so the
4
If
we use the continuous uniform distribution, theoretically any two random numbers have zero
probability
of
being equal.
176

A Practical Guide To Quantitative Finance Interviews
running time
is
E>(n
log n). For a small n, such as n =
52
in a deck
of
cards, the
complexity E>(nlogn) is acceptable. For large
n,
we
may want to use a faster algorithm
known as the Knuth shuffle. For n elements A[l], · ·
·,
A[n], the Knuth shuffle uses the
following loop
to
generate a random permutation:
for
(i=l
ton)
swap(A[i], A[Random(i, n)]),
where Random(i,
n)
is a random number from the discrete uniform distribution between
i and
n.
The Knuth shuffle has a complexity
of
E>(n)
and
an
intuitive interpretation. In the first
step, each
of
the n cards has equal probability
of
being chosen as the first card since the
card number is chosen from the discrete uniform distribution between 1 and n; in the
second step, each
of
the remaining n -1 cards elements has equal probability
of
being
chosen as the second card; and so on. So naturally each ordered sequence has 1
In!
probability.
B. You have a file consisting
of
characters. The characters in the file can be read
sequentially, but the length
of
the file is unknown. How do you pick a character so that
every character in the file has equal probability
of
being chosen?
Solution:
Let's
start with picking the first character.
If
there is a second character, we
keep the first character with probability 1/2 and replace the pick with the second
character with probability
112
.
If
there is a third character, we keep the pick (from the
first two characters) with probability 2/3 and replace the pick with the third character
with probability 1/3. The same process is continued until the final character. In other
words, let
Cn
be the character that
we
pick after we have scanned n characters and the
(n + l)th character exists, the probability
of
keeping the pick
is
_n_
and the probability
n+l
of
switching to the (n + l)th character is -1
-.
Using simple induction, we can easily
n+l
prove that each character has 1/ m probability
of
being chosen
if
there are m characters.
Search algorithm
A. Develop an algorithm to
find
both the minimum and the maximum
of
n numbers
using no more than 3n/2 comparisons.
Solution:
For
an unsorted array
of
n numbers, it takes
n-1
comparisons to identify
either the minimum
or
the maximum
of
the array. However, it takes at most 3n/2
comparisons to identify both the minimum and the maximum.
If
we separate the
elements to n/2 pairs, compare the elements in each pair and put the smaller one in group
177

Algorithms and Numerical Methods
A and the larger one in group B. This step takes n I 2 comparisons. Since the minimum
of
the whole array must be in group A and the maximum must be in
group
B, we only
need to find the minimum in A and the maximum in B, either
of
which takes n I 2 - 1
comparisons. So the total number
of
comparisons is at most 3n/2.5
B.
You are given an array
of
numbers. From the beginning
of
the array to some position,
all elements are zero; after that position, all elements are nonzero.
If
you
don't know the
size
of
the array, how do you find the position
of
the first nonzero element?
Solution: We can start with the 1st element;
if
it is zero, we check the
2nd
element;
if
the
2nd element is zero, we check the 4th element. .. The process is repeated until the ith
. 2; +
2i-l
step when the
2'
th element is nonzero.
Then
we check the th element.
If
it is
2
2; +
2i-l
zero, the search range is limited to the elements between the th element
and
2
the 2; th element; otherwise the search range is limited to the elements between the
. 2; +
2i-l
2'-1
th element and the th element.
..
Each time,
we
cut the range by half. This
2
method is basically a binary search.
If
the first nonzero element is
at
position
n,
the
algorithm complexity is
E>(log
n
).
C.
You have a square grid
of
numbers. The numbers in each row increase from left
to
right. The numbers in each column increase from top to bottom. Design
an
algorithm to
find a given number from the grid. What is the complexity
of
your algorithm?
Solution: Let A
be
an n x n matrix representing the grid
of
numbers and x
be
the number
we want to find in the grid. Begin the search with the last column from top to bottom:
A1
.n,
· ·
·,
An.n·
If
the number is found, then stop the search.
If
An.n < x, x is not in the
grid
and the search stops as well.
If
A;,n < x <
A;+
i.n• then we know that all the numbers in
rows l, · · ·, i are less than x and are eliminated as well.6
Then
we search
the
(i
+ l)th
row
from right to left.
If
the number is found in the
(i
+ l)th row, the search stops.
If
A1
,;+i > x, x is not
in
the grid since all the number in rows i + l and above are larger than
x.
If
A;+i.J+I > x >
Ai+l.J'
we eliminate all the numbers in columns j +
1,-
· -,n. Then
we
can search along column from A;+i.J towards An.J until
we
find x (or x does not exist in
5 Slight adjustment needs to be made
if
n is odd,
but
the upper bound 3n/2 still applies.
" i can be 0, which means x <
A1..,
in
which case
we
can
search the first row from right to left.
178

A Practical Guide
To
Quantitative Finance Interviews
the grid)
or
a k that makes Ak.J < x <
Ak+l,J
and then
we
search left along the row k + 1
from
Ak+
1 . towards
Ak+i
i
...
Using this algorithm, the search takes at most 2n steps. So
,}
'
its complexity is O(n).
Fibonacci numbers
Consider the following
C++
program for producing Fibonacci numbers:
int
Fibonacci(int
n)
if
(n
<=
0)
return
O;
else
if
(n==l)
return
l;
else
return
Fibonacci(n-l)+Fibonacci(n-2);
If
for some large
n,
it takes 100 seconds to compute Fibonacci(n), how long will it take
to compute Fibonacci(n+ 1 ), to the nearest second? Is this algorithm efficient? How
would you calculate Fibonacci numbers?
Solution: This C++ function uses a rather inefficient recursive method
to
calculate
Fibonacci numbers. Fibonacci numbers are defined as the following recurrence:
Po
= 0,
F;
=I,
F,.
=
Fn-1
+
Fn-
2' Vn
'C::.
2
(1+v'5f-(1-J5f
F has closed-formed solution
Fn
=
r;
, which can be easily proven
n
2nv5
using induction. From the function, it is clear that
T(O)
=I,
T(l)
=
1,
T(n) =
T(n-1)
+
T(n-2)
+I.
So the running time is a proportional to a sequence
of
Fibonacci numbers as well. For a
r;
T(n+l)
J5
+I
.
large n,
(1-
v :J y
0,
so .
If
it takes I 00 seconds to compute
T(n) 2
v'5+1
Fibonacci(n), the time to compute Fibonacci(n+l) is 2
seconds.7
7
</J
=
J5
+
1
is
called the golden ratio.
2
179

Algorithms and Numerical Methods
The recursive algorithm has exponential complexity 0 ( (
,/5
2
+
1
J}
which is surely
inefficient. The reason is that it fails to effectively use the information from Fibonacci
numbers with smaller n in the Fibonacci number sequence.
If
we compute F0,
F;,
· · ·,
Fn
in sequence using the definition, the running time has complexity
0(n).
An algorithm called recursive squaring can further reduce the complexity to
0(log
n).
Since = x and = ,
we
can show that
[
Fn+I
Fn
]
[l
l]
[
F,,
Fn-1
]
[F2
F;
]
[l
1]
Fn
Fn-1
I 0
Fn-1
Fn-2
F;
Fo
I 0
[
F,,+,
Fn
] = [ 1 1
Jn
using induction. Let A = [ 1 1
],
we can again apply the divide-
F,,
Fn-i
I 0 I 0
{
An
12
x
An
12
if
n is even
and-conquer paradigm to calculate
An
:
An
= _
1>
12
'<
_,
12
. . . The
A(n
x A n ) x A
if
n IS odd
'
multiplication
of
two
2x2
matrices has complexity 0(1). So
T(n)=T(n/2)+0(1).
Applying the master theorem, we have
T(n)
=
0(logn).
Maximum contiguous subarray
Suppose you have a one-dimensional array A with length n that contains both positive
and negative numbers. Design an algorithm to find the maximum sum
of
any contiguous
j
subarray A[i,j]
of
A:
V(i,j)
=
LA[x],
l-5:
i
5:
j
n.
x
=-
i
Solution: Almost all trading systems need such an algorithm to calculate maximum run-
up or maximum drawdown
of
either real trading books
or
simulated strategies. Therefore
this is a favorite algorithm question
of
interviewers, especially interviewers at hedge
funds and trading desks.
The most apparent algorithm
is
an
O(n
2) algorithm that sequentially calculates the
V(i,j)
's
from scratch using the following equations:
j
V(i,i) =
A[i]
when j = i and
V(i,j)
=
LA[x]
=
V(i,j-1)
+ A[j] when j > i .
x-i
As the
V(i,j)
's
are calculated, we also keep track
of
the maximum
of
V(i,j)
as well as
the corresponding subarray indices i
andj.
180

A Practical Guide
To
Quantitative Finance Interviews
A more efficient approach uses the divide-and-conquer paradigm. Let' s define
i
T(i)
=
LA[x]
and T(O) = 0,
then
V(i,j)
=
T(j)-T(i-1),
Vl
-5,
i
-5,
j
-5,
n . Clearly for
x=I
any fixed
j,
when
T(i-1)
is minimized,
V(i,j)
is maximized. So the maximum
subarray ending
at}
is
Vmax
=T(J)-Tmin
where
Tmin
=min(T(l)
,-
·-,T(j-1))
.
lfwe
keep
track
of
and update
Vmax
and
Tmin
as j increases, we can develop the following O(n)
algorithm:
T = A[l];
Vmax
= A[l];
Tmin
=min(O,T)
For
j = 2
ton
{ T = T + A[j];
If
T <
Tmin
, then
Tmin
= T;
}
Return
Vmax;
The following is a corresponding
C++
function that returns V
max
and indices i and j
given
an
array and its length:
double
maxSubarray(double
A[],
int
len,
int
&i,
int
&j)
double
T=A[O],
Vmax=A[O];
d o
ubl
e
Tmin
=
min(O.O,
T);
for(int
k=l;
k<len
;
++k)
T+=A[k];
if
(T-Tmin
> Vmax)
{Vmax=T-Tmin;
j=k
; }
if
(T<Tmin)
{Tmin=T;
i=
(k+l
<
j)?
(k
+
l):j;}
return
Vmax;
Applying it to the following array
A,
double
A[]={l.0,2.0,-5
.
0,4.0,-3.0,
2 .
0,
6.0,
-5.0,
-1.0};
int
i =
0,
j
=0;
181

Algorithms and Numerical Methods
double
Vmax =
maxSubarray(A,
sizeof(a)/sizeof(A[l]),
i,
j);
will give V
max
=
9,
i = 3 and j =
6.
So the subarray
is
[ 4.0, -3.0, 2.0, 6.0].
7.
2.
The Power
of
Two
There are only 10 kinds
of
people in the
world-those
who know binary, and those who
don't.
If
you happen to get this joke, you probably know that computers operate using
the binary (base-2) number system. Instead
of
decimal digits 0-9, each bit (binary digit)
has only two possible values: 0 and I. Binary representation
of
numbers gives some
interesting properties that are widely explored in practice
and
makes it an interesting
topic to test
in
interviews.
Powerof2
How do you determine whether
an
integer is a power
of2?
Solution: Any integer x =
2n
( n
0)
has a single bit (the (n + l)th bit from the right) set
to I. For example, 8 ( = 23) is expressed as 0 · · · 0 l 000. It is also easy to see that
2n
-1
has all the n bits from the right set to
l.
For example, 7 is expressed as 0···00111 . So
2n
and
2n
-I
do not share any common bits. As a result, x &
(x-1)
=
0,
where & is a
bitwise AND operator,
is
a simple way to identify whether the integer x
is
a power
of
2.
Multiplication by 7
Give a fast way to multiply an integer by 7 without using the multiplication (*) operator?
Solution:
(x
<< 3) -x, where
<<
is the bit-shift left operator. x
<<
3
is
equivalent to x*8.
Hence (x <<
3)-
xis
x*7.8
Probability simulation
You are given a fair coin. Can you design a simple game using the fair coin so that your
probability
of
winning
is
p, 0 < p <
I?
9
x The result could be wrong
if<<
causes an overflow.
9 Hint: Computer stores binary numbers instead
of
decimal ones; each digit
in
a binary number can be
simulated using a fair coin.
182

A Practical Guide
To
Quantitative Finance Interviews
Solution: The key to this problem is to realize that p E (0,
1)
can also be expressed as a
binary number and each digit
of
the binary number can be simulated using a fair coin.
First, we can express the probability p as binary number:
P = O.p1p2 • • •
Pn
=Pi
2-
1 + p2r2 + · · · +
Pnr",
P;
E
{0,1},
'\Ji=
1,
2,
···,
n.
Then, we can start tossing the fair coin, and count heads as 1 and tails as 0. Let
s;
E
{0,1}
be the result
of
the i-th toss starting from i =
1.
After each toss, we compare
P;
with
s;
.
If
s;
< P;, we win and the coin tossing stops.
If
s;
>
P;
,
we
lose and the coin tossing
stops.
If
s;
=
P;
, we continue to toss more coins. Some p values (e.g., I /3) are infinite
series when expressed as a binary number ( n
oo
).
In
these cases, the probability to
reach
s;
-:t:-
P;
is 1 as i increases.
If
the sequence is finite, (e.g.,
114=0.0
I)
and
we reach
the final stage with
s"
=
Pn
, we lose (e.g., for
114,
only the sequence
00
will be
classified as a win; all other three sequences 01, 10 and
11
are classified as a loss). Such
a simulation will give us probability p
of
winning.
Poisonous wine
You've got 1000 bottles
of
wines for a birthday party. Twenty hours before the party,
the winery sent you an urgent message that one bottle
of
wine was poisoned. You
happen to have
IO
lab mice that can be used to test whether a bottle
of
wine is poisonous.
The poison
is
so strong that any amount will kill a mouse in exactly
18
hours. But before
the death on the 18th hour, there are no other symptoms.
Is
there a sure way that you can
find the poisoned bottle using the 10 mice before the party?
Solution:
If
the mice can be tested sequentially to eliminate
half
of
the bottles each time,
the problem becomes a simple binary search problem. Ten mice can identify the
poisonous bottle in up to
1024
bottles
of
wines. Unfortunately, since the symptom won't
show up until
18
hours later and we only have
20
hours, we cannot sequentially test the
mice. Nevertheless, the binary search idea still applies. All integers between 1 and 1000
can be expressed in 10-bit binary format. For example, bottle 1000 can
be
labeled as
1111101000 since 1000 = 2
9 + 2
8 + 2
7 + 2
6 + 2
5 + 2
3 .
Now let mouse I take a sip from every bottle that has a I in the first bit (the lowest bit
on the right); let mouse 2 take a sip from every bottle with a 1 in the second bit; ... ;and,
finally, let mouse
10
take a sip from every bottle with a 1 in the 10th bit (the highest bit).
Eighteen hours later,
if
we line up the mice from the highest to the lowest bit and treat a
live mouse as 0 and a dead mouse as I,
we
can easily back track the label
of
the
poisonous bottle.
For
example,
if
the 6th, 7th, and 9th mice are dead and all others are
alive, the line-up gives the sequence 0I01100000 and the label for the poisonous bottle
is 28 + 26 + 25
=352.
183

Algorithms and Numerical Methods
7.3 Numerical Methods
The prices
of
many financial instruments do not have closed-form analytical solutions.
The valuation
of
these financial instruments relies on a variety
of
numerical methods. In
this section, we discuss the application
of
Monte Carlo simulation and finite difference
methods.
Monte Carlo simulation
Monte Carlo simulation
is
a method for iteratively evaluating a deterministic model
using random numbers with appropriate probabilities
as
inputs.
For
derivative pricing, it
simulates a large number
of
price paths
of
the underlying assets with probability
corresponding to the underlying stochastic process (usually under risk-neutral measure),
calculates the discounted payoff
of
the derivative for each path, and averages the
discounted payoffs to yield the derivative price. The validity
of
Monte Carlo simulation
relies on the law
of
large numbers.
Monte-Carlo simulation can be used
to
estimate derivative prices
if
the payoffs only
depend on the final values
of
the underlying assets, and it can be adapted to estimate
prices
if
the payoffs are path-dependent as well. Nevertheless, it cannot
be
directly
applied to American options
or
any other derivatives with early exercise options.
A. Explain how you can use Monte Carlo simulation to price a European call option?
Solution:
If
we assume that stock price follows a geometric Brownian motion,
we
can
simulate possible stock price paths. We can split the time between t
and
T into N
equally-spaced time steps. 10 So
D..t
=
T-t
and
t;
=t+/)..txi, for
i=0,1,2,···,N.
We
N
then simulate the stock price paths under risk-neutral probability using equation
s. = s.
e(r-u
212
)<M>+uJ6ic;
where c.
's
are IID random variables from standard normal
I t-1 ' I
distribution. Let's say that we simulate M paths and each one yields a stock price Sr.k'
where k =
I,
2, · ·
·,
M,
at maturity date
T.
'°
For European options, we can simply set
N=l.
But
for
more general options, especially the path-
dependent ones, we want to have small time steps and therefore N should be large.
184

A Practical Guide To Quantitative Finance Interviews
The estimated price
of
the European call is the present value
of
the expected payoff,
M
:Lmax(Sr,k
-K,0)
which
can
be
calculated as C =
e-r<T-i>
"""k_.=
1
------
M
B.
How
do
you generate random variables that follow
N(µ,a
2) (normal distribution
with
mean
µ and variance a2)
if
your
computer can only generate random variables
that follow continuous unifonn distribution between 0 and 1?
Solution: This is a great question to test the basic knowledge
of
random number
generation, the foundation
of
Monte Carlo simulation. The solution to this question can
be dissected to two steps:
1.
Generate random variable
of
x N(O,l)
from
uniform
random
number generator
using
inverse transform method and rejection method.
2.
Scale x to µ +
ax
to generate the final random variables
that
follow N
(µ,
a2) •
The
second
step
is
straightforward;
the
first step deserves some explanations. A popular
approach to generating random variables is the inverse transform method:
For
any
continuous random variable X with cumulative density function F ( U =
F(X)
), the
random variable X
can
be
defined as the inverse function
of
U: X =
F-
1
(U),
0,:::;;
U
,:::;;
1.
It
is
obvious that X =
F-
1(U) is a one-to-one function
with
0,:::;;
U,:::;;
1.
So any
continuous random variable can be generated using the following process:
• Generate a
random
number u from the standard uniform distribution.
• Compute the value x such that u =
F(x)
as the
random
number from the
distribution described by
F.
For this model to work,
F-
1
(U)
must
be
computable. For standard normal distribution,
( l
-x
212
dx
h · fu . h l . 1 l .
U =
F(X)
=
r::;-
e . T e mverse
nchon
as
no
ana yhca so
ut10n.
v2tr
Theoretically, we
can
come up with the one-to-one mapping
of
X to U as the numeric
solution
of
ordinary differential equation
F'(x)
=
f(x)
=
tb-
e-x
212 using numerical
v2tr
integration method
such
as the Euler method.
11
Yet
this approach is less efficient than
the rejection method:
11
To integrate y =
F(x)
with first derivative
y'
= f (x)
and
a known initial value y0 =
F(x
0 ) , the Euler
method chooses a small step size h ( h
can
be
positive
or
negative) to sequentially approximate y values:
185

Algorithms and Numerical Methods
Some random variables have
pdf
f(x),
but no analytical solution for
F-
1
(U).
In these
cases, we can use a random variable with
pdf
g(y)
and Y =
c-'(U)
to help generate
random variables with
pdf
/(x).
Assume that
Mis
a constant such that f
(y)
M,
'Vy.
g(y)
We can implement the following acceptance-rejection method:
• Sampling step: Generate random variable y from
g(y)
and a random variable v
from standard uniform distribution
[O,
1]
.
• Acceptance/rejection step:
If
v
f(y)
, accept x =
y;
otherwise, repeat the
Mg(y)
sampling step.
12
An exponential random variable (g(x)=A-e--<..-) with A-=l has
cdfu=G(x)=l-e-x.
So the inverse function has analytical solution x = - log(l -
u)
and a random variable
with exponential distribution can be conveniently simulated. For standard normal
distribution,
f(x)
= e-··212 ,
...;2;r
f(x)
=
/2ex-x212
<
/2e-(x-1)2
1
2+112
/2e1
1
2::::::::
1.32,
'VO<
X <
00
g(x)
·{;'
v;
v;
So we can choose M = 1.32 and
use
the acceptance-rejection method to generate
x -N(O,
1)
random variables and scale them to
N(µ,a
2) random variables.
C.
Can you explain a
few
variance reduction techniques to improve the efficiency
of
Monte Carlo simulation?
Solution: Monte Carlo simulation, in its basic form,
is
the mean
of
IID random variables
- l M
t;,.Y;,-··,YM:
Y Since the expected value
of
each
Y;
is unbiased, the
M i =I
estimator f is unbiased
as
well.
If
Var(Y)
=a
and we generate IID f;, then
Var(Y)
=a
I
JM,
where
Mis
the number
of
simulations.
Not
surprisingly, Monte Carlo
F(x
0 + h) =
F(x
0) +
f(x
0) x h,
F(x
0 + 2h) =
F(x
0 +
h)
+
f(x
0 + h) x
h,
· ·
·.
The initial value
of
the
cdfof
a standard normal can be F(O) = 0.5.
Ix
f(y)
I'
P(X
x)
I'
12
P(X
x)
ex:
g(y)-·--dy
= M
f(y)dy
=>
F(x)
= =
f(y)dy
' Mg(y) '
P(X
< oo) '
186

A Practical Guide
To
Quantitative Finance Interviews
simulation is computationally intensive
if
a
is
large. Thousands or even millions
of
simulations are often required to get the desired accuracy. Depending on the specific
problems, a variety
of
methods have been applied
to
reduce variance.
Antithetic variable: For each series
of
e;
's, calculate its corresponding payoff
Y(
e,, · · ·, e
N)
. Then reverse the sign
of
all
e;
's and calculate the corresponding payoff
Y(-e,,-··,-eN).
When
Y(e,,···,eN)
and
Y(-e"
..
·,-eN)
are negatively correlated, the
variance
is
reduced.
Moment matching: Specific samples
of
the random variable may not match the
population distribution well. We can draw a large set
of
samples first and then rescale
the samples to make the samples' moments (mean and variance are the most commonly
used) match the desired population moments.
Control variate:
If
we want to price a derivative X and there is a closely related
derivative Y that has an analytical solution, we can generate a series
of
random numbers
and use the same random sequences to price both X and Y to yield X and
Y.
Then X can
be estimated as X + (Y -i). Essentially
we
use (Y -
f)
to correct the estimation error
of
A
x.
Importance sampling: To estimate the expected value
of
h(x)
from
distribution/(x),
instead
of
drawing x from
distribution/(x),
we can draw x from distribution g(x) and
use Monte Carlo simulation to estimate expected value
of
h(x)f(x):
g(x)
E x [h(x)] =
Jh(x)f(x)dx
=
Jh(x)f(x)
g(x)dx
= E x [
h(x)f
(x)]·
13
f<
> g(x)
g<
>
g(x)
If
h(x)f(x)
has a smaller variance than
h(x),
then importance sampling can result in a
g(x)
more efficient estimator. This method is better explained using a deep out-of-the-money
option as an example.
If
we directly use risk-neutral f (ST) as the distribution, most
of
the simulated paths will yield
h(ST)
= 0 and as a result the estimation variance will be
large.
If
we introduce a distribution g(ST) that has much wider span (fatter tail for ST),
more simulated paths will have positive h(ST). The scaling factor
f(x)
will keep the
g(x)
estimator unbiased, but the approach will have lower variance.
13 Importance sampling is essentially a variance reduction method
using
a change
of
measure.
187

Algorithms and Numerical Methods
Low-discrepancy sequence: Instead
of
using random samples, we can generate a
deterministic sequence
of
"random variable" that represents the distribution. Such low-
discrepancy sequences may make the convergence rate 1
IM
.
D.
If
there is no closed-form pricing formula for an option, how would you estimate its
delta and gamma?
Solution: As we have discussed in problem A, the prices
of
options with or without
closed-form pricing formulas can be derived using Monte Carlo simulation. The same
methods can also be used to estimate delta and gamma by slightly changing the current
underlying price from S to S
±JS,
where
JS
is a small positive value. Run Monte
Carlo simulation for all three starting prices S -
JS,
S and S +
JS,
we will get their
corresponding option prices
/(S-JS),
/(S)
and
/(S
+JS).
.
Jf
/(S+JS)-/(S-JS)
Estimated delta:
!:!,.
= - =
--------
JS
2JS
. d
(/(S
+JS)-
f(S)
)-(/(S)-
/(S
-JS))
Estimate gamma:
f'
= 2
JS
To reduce variance, it's often better to use the same random number sequences to
estimate
/(S-JS),
/(S)
and
f(S
+JS).
14
E.
How do you use Monte Carlo simulation to estimate
;r?
Solution: Estimation
of
;r is a classic example
of
Monte Carlo simulation. One standard
method to estimate ;r is to randomly select points in the unit square (x and y are
independent uniform random variables between 0 and
1)
and determine the ratio
of
points that are within the circle x2 + y2 s
1.
For simplicity, we focus on the first quadrant.
As shown in Figure 7 .1, any points within the circle satisfy the equation
x;
2 + l s 1 . The
percentage
of
the points within the circle is proportional
to
its area:
p = Number
of
(
X;,
y;)
within
X;
2 +
y}
s 1 =
I/
4
;r
= =
4
p .
Number
of
(xpy;)
within the square
1x1
4
So we generate a large number
of
independent (x,
y)
points, estimate the ratio
of
the
points within the circle
to
the points in the square, and multiply the ratio by 4 to yield an
estimation
of
Jr.
Figure
7.1
uses only 1000 points for illustration. With today's
14
The method may not work well
if
the
payoff
function
is
not continuous.
188
A Practical Guide
To
Quantitative Finance Interviews
computing power, we can easily generate millions
of
(x,
y)
pairs to estimate
ff
with
good precision. 1,000 simulations with 1,000,000 (x,
y)
points each using Matlab took
less than 1 minute on a laptop and gave an average estimation
of
ff
as 3.1416 with
standard deviation 0.0015.
0.9
0.8
0.7
0.6
>-
0.5
0.4
0.3
0.2
0.1 .
0
0 0.2
.
.,
-
.......
. .
..
,,,.
.
..
;•
• •
&.'
•
.,
,
.....
'
..
,..
..
..
0.4
x
••I
!t.
• • I
• fL_t.
0.6
. ,
.....
_
......
-.
.,
.
...
. .
••••••
•
••
·<-.
0.8
••
:f:·
•
•
Figure 7
.1
A Monte Carlo simulation method
to
estimate
rr
Finite difference method
The finite difference method is another popular numerical technique for derivative
pricing.
It
numerically solves a differential equation to estimate the price
of
a derivative
by discretizing the time and the price
of
the underlying security. We can convert the
Black-Scholes-Merton equation, a second order nonlinear partial differential equation, to
a heat diffusion equation (as we did in Chapter
6).
This new equation, expressed as a
function
of
r (time to maturity)
andx
(a function
of
the price
of
the underlying security),
is a general differential equation for derivatives. The difference between various
derivatives lies in the boundary conditions.
By
building a grid
of
x and r and using the
boundary conditions,
we
can recursively calculate u at every x and r using finite
difference methods.
A. Can you briefly explain finite difference methods?
Solution: There are several version
of
finite difference methods used in practice. Let's
briefly go over the explicit difference method, the implicit difference method and the
189
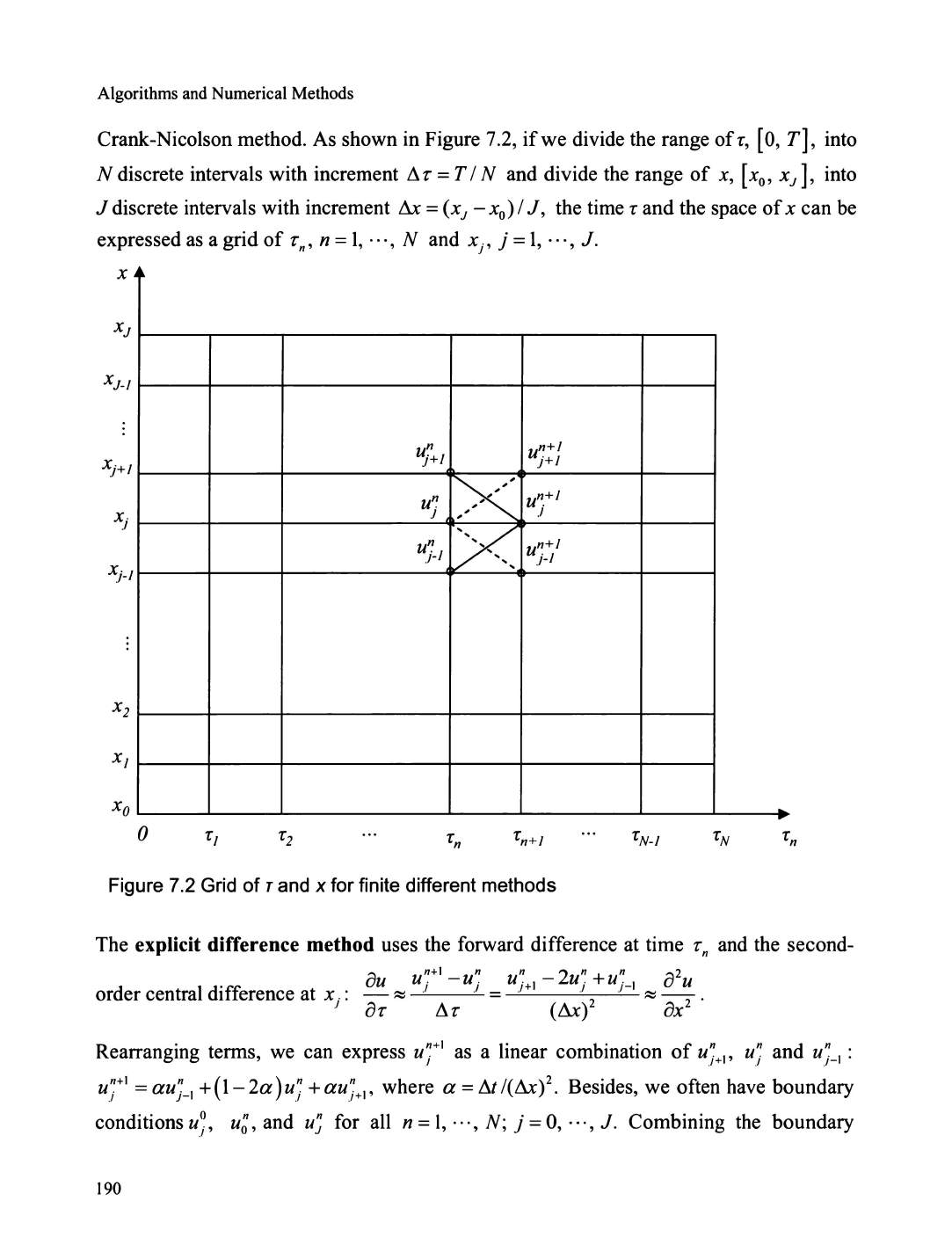
Algorithms and Numerical Methods
Crank-Nicolson method. As shown in Figure 7.2,
if
we
divide the range
of
r,
[O,
T],
into
N discrete intervals with increment
/1
r =
TI
N and divide the range
of
x, [ x0, x J ] , into
J discrete intervals with increment
l1x
= (xJ
-x
0) I
J,
the
timer
and the space
of
x can be
expressed as a grid
of
rn,
n = l,
···,
N and x1, j
=I,··.,
J .
x
x .
.I
X;-I
Xo
•
0
n
un
.I
u'! I
.1-
un+/
j+/
Un.+/
.I
un+I
j-1
Figure 7.2 Grid of
rand
x for finite different methods
...
The explicit difference method uses the forward difference at time
rn
and the second-
8u
Un+I
-Un
Un+I
-2Un
+Un_I
82U
order central difference at x .: - 1 1 -1 1 1 -
1
Br
11r -
(11x)
2 -
8x
2 •
Rearranging terms, we can express
un+i
as a linear combination
of
un+"
un
and
un_
1 :
J J J J
un+I
=
+(1-2a)un
+
aun
+
I'
where
a=
11t
/(11x)
2• Besides, we often have boundary
J J J .I
conditions
u;,
and for all n
=I,
·
·.,
N;
j = 0, ·
·.,
J . Combining the boundary
190

A Practical Guide
To
Quantitative Finance Interviews
conditions and equation u;+'
=au;_,
+(1-2a)u;
+au;+,,
we can estimate all
u;'s
on
the grid.
The implicit difference method uses the backward difference at time
tn+i
and the
a n+I n
u u .
-u.
second-order central difference at
x.
: -
:::::
1 1
J
ar
!l.r
The Crank-Nicolson method uses the central difference at time (t" +tn+1) 12 and the
second-order central difference at x1:
a
Un+I
-U"
} (
u"
-2u"
+Un
Un+I
-2Un+I +
Un+I
J
a2
U ; ;
;+I
;
;-I
;+I
;
;-1
U
-::::::
=-
+
:::::::--
a,
!l.r 2 (/l.x)2 (/l.x)2 8x2 •
B.
If
you are solving a parabolic partial differential equation using the explicit finite
difference method, is it worse to have too many steps in the time dimension or too many
steps in the space dimension?
Solution: The equation for the explicit finite difference method is
u;+'
=au;_,+(1-2a)u;+au;
+" where
a=l1t/(/l.x)
2• For the explicit finite difference
method to be stable, we need to have
1-
2a
> 0 l1t
/(!l.x)
2 < 1I2.
So
a small l1t (i.e.,
many time steps) is desirable, but a small !l.x (too many space steps) may make
l1t /(/l.x)2 > 1I2 and the results unstable.
In
that sense, it
is
worse to have too many steps
in the space dimension.
In
contrast, the implicit difference method is always stable and
convergent.
191


Index
absorbing Markov chain, 106
absorbing state,
113
absorption probability, 107
algorithm complexity, 171
analytical skills, 9
antithetic variable, 187
average-case running time,
172
Bayes' Formula,
73
binary option,
160
binomial theorem, 65,
71
bisection method,
45
bitwise XOR,
173
Black-Scholes formula, 143
Black-Scholes-Merton differential
equation, 142
boundary condition, 115
Brownian motion, 129
bull spread, 159
Cartesian integral,
41
chain rule, 33, 34
characteristic equation,
54
Cholesky decomposition, 57
coherent risk measure, 165
combination,
65
conditional probability, 68, 72, 75, 83
continuous distribution, 87
control variate,
187
convex function,
140
convexity, 165
correlation, 92
covariance,92
Cox-Ingersoll-Ross model,
168
Crank-Nicolson method,
191
cross-sectional area, 3 8
delta, 149
derivative, 33,
35
determinant, 5 3
diagonalizable,
54
discounted Feynman-Kac equation, 143
discrete distribution, 86
divide-and-conquer, 180
dollar duration, 166
duration,
165
dynamic programming,
121
dynamic programming algorithm, 122
eigenvalue, 54
eigenvector, 54
European put,
13
7
event, 60,
63
exchange option,
161
expected time to absorption, 110
expected times to absorption, 107
expected value, 86
explicit difference method, 190
exponential martingale, 129
Feynman-Kac equation,
134
Fibonacci numbers, 179
finite difference method, 189
first passage time,
131
first-order differential linear equation,
47
fixed-rate coupon bond, 166
floating-rate bond, 166
forwards,
167
futures,
167
Gamma, 149
general chain rule, 40
generalized power rule,
33
heat equation, 146
Ho-Lee model, 168
homogenous linear equation,
48
Homer's
algorithm, 174
Hull-White model, 168
implicit difference method,
191
importance sampling, 187
Inclusion-Exclusion Principle, 65
independence, 73
induction, 27, 29
insertion sort, 175
integration, 36
193

integration by parts, 37
integration by substitution, 37, 40
interest rate model, 168
intersection, 60
inverse floater, 166
Ito's lemma,
13
5
Jensen's inequality, 140
jump-diffusion process, 90
L'Hospital's rule, 36
Lagrange multipliers, 45
law
of
total expectation, 93, 113
Law
of
total probability,
73
linear least squares, 52
linear regression, 53
logic, 6
low-discrepancy sequence, 188
LU
decomposition, 57
Markov chain, 105
Markov property, 105, 114
mark-to-market, 168
martingale,
115
master theorem, 1 72
maximum, 35
maximum drawdown, 180
merge sort, 175
minimum, 35
module, 26
modulo operation, 23
moment generating function,
91
moment matching, 187
Monte Carlo simulation, 184
moving average, 174
multiplication rule:, 72
mutually exclusive, 60, 63
Newton's method, 44
Newton-Raphson method, 44
nonhomogeneous linear equation, 49
normal distribution,
91
numerical method, 184
order statistics,
99
orting algorithm, 174
out
of
the box, 3,
12
194
outcome, 59
partial derivative, 40
partial differential equations, 146
permutation, 65
Pigeon Hole Principle, 20,
21
Poison process, 90
Poisson process, 90
polar integral,
41
portfolio optimization, 163
positive definite, 56
positive semidefinite, 56
principle
of
counting,
64
Principle
of
Optimality, 122
probability density function, 41,
86
probability mass function, 86
probability space, 59
product rule, 34, 37
product rule:, 33
proof by contradiction, 31
put-call parity,
138
QR decomposition, 52
quicksort, 175
quotient rule, 33, 37
random permutation, 176
random variable, 60
random walk,
115
reflection principle, 118, 132
replicating portfolio, 166
Rho,
149
running time,
171
sample space, 59
secant method, 45
separable differential equation, 47
simplified version, 3, 4
singular value decomposition, 58
state space, 107
stopping rule, 116
straddle, 159
sub-additivity,
165
summation equation,
18
symmetric random walk, I
15
symmetry, 16

system equation, 127
Taylor's series, 42, 43
Theta, 149
transition graph, I
05, I 09,
111
transition matrix, 105
union,
60
uropean call,
137
Value at Risk,
164
A Practical Guide
To
Quantitative Finance Interviews
variance reduction, 186
Vasicek model, 168
vector,
51
Vega,
149
Volga,
157
Wald's
Equality, 116
worst-case running time,
172
195

II
I I I
Ill
llll
1111111111111111111111111111111
18555154R00119
Made
in
the
USA
San Hernardino.
C'
A
19
January
2015