Robotics Toolbox 10.3 User Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 437 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Preface
- Functions by category
- Introduction
- Functions and classes
- about
- angdiff
- angvec2r
- angvec2tr
- Arbotix
- Bicycle
- bresenham
- Bug2
- chi2inv_rtb
- circle
- colnorm
- ctraj
- delta2tr
- DHFactor
- diff2
- distancexform
- Dstar
- DXform
- e2h
- edgelist
- EKF
- ETS2
- ETS3
- eul2jac
- eul2r
- eul2tr
- gauss2d
- h2e
- homline
- homtrans
- ishomog
- ishomog2
- isrot
- isrot2
- isunit
- isvec
- jsingu
- jtraj
- LandmarkMap
- Lattice
- Link
- lspb
- mdl_ball
- mdl_baxter
- mdl_cobra600
- mdl_coil
- mdl_fanuc10L
- mdl_hyper2d
- mdl_hyper3d
- mdl_irb140
- mdl_irb140_mdh
- mdl_jaco
- mdl_KR5
- mdl_LWR
- mdl_M16
- mdl_mico
- mdl_motomanHP6
- mdl_nao
- mdl_offset6
- mdl_onelink
- mdl_p8
- mdl_phantomx
- mdl_planar1
- mdl_planar2
- mdl_planar2_sym
- mdl_planar3
- mdl_puma560
- mdl_puma560akb
- mdl_quadrotor
- mdl_S4ABB2p8
- mdl_simple6
- mdl_stanford
- mdl_stanford_mdh
- mdl_twolink
- mdl_twolink_mdh
- mdl_twolink_sym
- mdl_ur10
- mdl_ur3
- mdl_ur5
- models
- mplot
- mstraj
- mtraj
- Navigation
- numcols
- numrows
- oa2r
- oa2tr
- ParticleFilter
- peak
- peak2
- PGraph
- pickregion
- plot2
- plot_arrow
- plot_box
- plot_circle
- plot_ellipse
- plot_homline
- plot_point
- plot_poly
- plot_sphere
- plot_vehicle
- plotbotopt
- plotp
- plotvol
- Plucker
- polydiff
- Polygon
- PoseGraph
- Prismatic
- PrismaticMDH
- PRM
- qplot
- Quaternion
- r2t
- randinit
- RandomPath
- RangeBearingSensor
- Revolute
- RevoluteMDH
- rot2
- rotx
- roty
- rotz
- rpy2jac
- rpy2r
- rpy2tr
- RRT
- rt2tr
- rtbdemo
- RTBPlot
- RTBPose
- runscript
- SE2
- SE3
- Sensor
- SerialLink
- skew
- skewa
- SO2
- SO3
- startup_rtb
- stlRead
- t2r
- tb_optparse
- tpoly
- tr2angvec
- tr2delta
- tr2eul
- tr2jac
- tr2rpy
- tr2rt
- tranimate
- tranimate2
- transl
- transl2
- trchain
- trchain2
- trexp
- trexp2
- trinterp
- trinterp2
- tripleangle
- trlog
- trnorm
- trot2
- trotx
- troty
- trotz
- trplot
- trplot2
- trprint
- trprint2
- trscale
- Twist
- Unicycle
- unit
- UnitQuaternion
- Vehicle
- vex
- vexa
- VREP
- VREP_arm
- VREP_camera
- VREP_mirror
- VREP_obj
- wtrans
- xaxis
- xyzlabel
- yaxis
Robotics Toolbox
for MATLAB
Release 10
Peter Corke

Preface
This, the tenth major release of the Toolbox, represent-
ing over twenty five years of continuous development
and a substantial level of maturity. This version corre-
sponds to the second edition of the book “Robotics, Vi-
sion & Control, second edition” published in June 2017
– RVC2.
This MATLAB R
Toolbox has a rich collection of func-
tions that are useful for the study and simulation of
robots: arm-type robot manipulators and mobile robots.
For robot manipulators, functions include kinematics,
trajectory generation, dynamics and control. For mobile
robots, functions include path planning, kinodynamic
planning, localization, map building and simultaneous
localization and mapping (SLAM).
The Toolbox makes strong use of classes to represent robots and such things as sen-
sors and maps. It includes Simulink R
models to describe the evolution of arm or
mobile robot state over time for a number of classical control strategies. The Tool-
box also provides functions for manipulating and converting between datatypes such
as vectors, rotation matrices, unit-quaternions, quaternions, homogeneous transforma-
tions and twists which are necessary to represent position and orientation in 2- and
3-dimensions.
The code is written in a straightforward manner which allows for easy understanding,
perhaps at the expense of computational efficiency. If you feel strongly about computa-
tional efficiency then you can always rewrite the function to be more efficient, compile
the M-file using the MATLAB compiler, or create a MEX version.
The bulk of this manual is auto-generated from the comments in the MATLAB code
itself. For elaboration on the underlying principles, extensive illustrations and worked
examples please consult “Robotics, Vision & Control, second edition” which provides
a detailed discussion (720 pages, nearly 500 figures and over 1000 code examples) of
how to use the Toolbox functions to solve many types of problems in robotics.
Robotics Toolbox for MATLAB 3 Copyright c
Peter Corke 2017

Robotics Toolbox for MATLAB 4 Copyright c
Peter Corke 2017
Functions by category
Homogeneous transforma-
tions 3D
angvec2r...........................18
angvec2tr..........................19
eul2r...............................75
eul2tr..............................76
ishomog ........................... 78
isrot...............................79
isunit..............................80
oa2r..............................140
oa2tr ............................. 141
rotx .............................. 223
roty .............................. 224
rotz...............................224
rpy2r.............................225
rpy2tr.............................226
tr2angvec.........................340
tr2eul.............................342
tr2rpy.............................343
transl.............................346
trchain............................348
trexp..............................349
trinterp ........................... 351
tripleangle........................352
trlog..............................353
trnorm............................354
trotx..............................355
troty..............................355
trotz..............................356
trprint ............................ 359
trscale............................361
Homogeneous transforma-
tions 2D
ishomog2..........................79
isrot2..............................80
rot2 .............................. 223
transl2............................347
trchain2...........................348
trexp2............................350
trinterp2..........................352
trot2..............................354
trprint2...........................360
Homogeneous transforma-
tion utilities
r2t................................209
rt2tr..............................230
t2r................................337
tr2rt..............................344
Homogeneous points and
lines
e2h................................48
h2e................................77
homline............................77
homtrans...........................78
Differential motion
delta2tr............................37
eul2jac.............................75
rpy2jac...........................225
skewa.............................313
skew..............................313
tr2delta...........................341
tr2jac.............................342
vexa..............................397
Robotics Toolbox for MATLAB 5 Copyright c
Peter Corke 2017

vex...............................397
wtrans............................430
Trajectory generation
ctraj...............................37
jtraj................................81
lspb................................99
mstraj ............................ 129
mtraj.............................130
tpoly ............................. 339
trinterp2..........................352
trinterp ........................... 351
Pose representation classes
Quaternion........................199
RTBPose..........................233
SE2..............................243
SE3..............................251
SO2..............................314
SO3..............................321
Twist.............................361
UnitQuaternion....................371
Serial-link manipulator
DHFactor..........................38
Link...............................88
PrismaticMDH....................192
Prismatic..........................189
RevoluteMDH.....................220
Revolute..........................218
SerialLink.friction . . . . . . . . . . . . . . . . . 280
SerialLink.nofriction . . . . . . . . . . . . . . . 300
SerialLink.perturb . . . . . . . . . . . . . . . . . 302
SerialLink.plot . . . . . . . . . . . . . . . . . . . . 303
SerialLink.teach . . . . . . . . . . . . . . . . . . . 310
SerialLink.........................270
Models
mdl_KR5.........................107
mdl_LWR.........................108
mdl_S4ABB2p8...................119
mdl_ball..........................100
mdl_baxter........................100
mdl_cobra600.....................101
mdl_coil..........................102
mdl_hyper2d......................103
mdl_hyper3d......................104
mdl_irb140_mdh . . . . . . . . . . . . . . . . . . 105
mdl_irb140........................105
mdl_jaco..........................106
mdl_mico.........................109
mdl_nao..........................110
mdl_p8...........................113
mdl_phantomx.................... 113
mdl_planar1.......................114
mdl_planar2.......................115
mdl_planar3.......................116
mdl_puma560akb . . . . . . . . . . . . . . . . . . 117
mdl_puma560.....................116
mdl_quadrotor.....................118
mdl_stanford_mdh . . . . . . . . . . . . . . . . . 121
mdl_stanford......................120
mdl_twolink_mdh . . . . . . . . . . . . . . . . . 122
mdl_twolink_sym . . . . . . . . . . . . . . . . . . 124
mdl_twolink.......................122
mdl_ur10.........................125
mdl_ur3 .......................... 126
mdl_ur5 .......................... 127
models............................127
Kinematics
DHFactor..........................38
ETS2..............................58
ETS3..............................66
SerialLink.fkine . . . . . . . . . . . . . . . . . . . 280
SerialLink.ikine6s . . . . . . . . . . . . . . . . . 287
SerialLink.ikine . . . . . . . . . . . . . . . . . . . 284
SerialLink.jacob0 . . . . . . . . . . . . . . . . . . 295
SerialLink.jacobe . . . . . . . . . . . . . . . . . . 296
SerialLink.maniplty . . . . . . . . . . . . . . . . 298
jsingu..............................81
trchain2...........................348
trchain............................348
Dynamics
SerialLink.accel . . . . . . . . . . . . . . . . . . . 273
SerialLink.cinertia . . . . . . . . . . . . . . . . . 275
SerialLink.coriolis . . . . . . . . . . . . . . . . . 276
SerialLink.fdyn . . . . . . . . . . . . . . . . . . . . 278
SerialLink.gravload . . . . . . . . . . . . . . . . 283
SerialLink.inertia . . . . . . . . . . . . . . . . . . 292
Robotics Toolbox for MATLAB 6 Copyright c
Peter Corke 2017

SerialLink.itorque. . . . . . . . . . . . . . . . . .294
SerialLink.rne.....................309
wtrans............................430
Mobile robot
Bicycle ............................28
LandmarkMap......................82
Navigation........................131
RandomPath ...................... 210
RangeBearingSensor . . . . . . . . . . . . . . . 213
Sensor............................268
Unicycle..........................367
Vehicle...........................389
plot_vehicle.......................174
Localization
EKF...............................49
ParticleFilter......................141
PoseGraph........................188
Path planning
Bug2..............................33
DXform............................45
Dstar..............................41
Lattice.............................85
PRM.............................195
RRT..............................227
Graphics
circle..............................36
mplot.............................128
plot2 ............................. 166
plot_arrow........................166
plot_box..........................167
plot_circle........................168
plot_ellipse........................169
plot_homline......................170
plot_point.........................171
plot_poly......................... 172
plot_sphere........................173
plotp ............................. 175
plotvol............................176
qplot ............................. 198
tranimate2........................345
tranimate..........................344
trplot2............................358
trplot.............................356
xaxis.............................430
xyzlabel .......................... 431
yaxis.............................431
Utility
PGraph...........................148
Plucker...........................176
Polygon...........................183
RTBPlot..........................232
about..............................17
angdiff.............................17
bresenham ......................... 33
chi2inv_rtb.........................35
colnorm............................36
diff2...............................39
distancexform......................40
edgelist............................48
gauss2d............................77
isunit..............................80
isvec...............................81
numcols .......................... 139
numrows..........................140
peak2.............................148
peak..............................147
pickregion ........................ 165
polydiff...........................183
randinit...........................209
runscript..........................242
stlRead...........................337
tb_optparse........................338
unit...............................371
Demonstrations
rtbdemo...........................231
Examples
plotbotopt.........................175
Robotics Toolbox for MATLAB 7 Copyright c
Peter Corke 2017

Robotics Toolbox for MATLAB 8 Copyright c
Peter Corke 2017
Contents
Preface..................................... 2
Functionsbycategory............................. 5
1 Introduction 8
1.1 ChangesinRTB10........................... 8
1.1.1 Incompatible changes . . . . . . . . . . . . . . . . . . . . . . 8
1.1.2 Newfeatures .......................... 9
1.1.3 Enhancements ......................... 10
1.2 How to obtain the Toolbox . . . . . . . . . . . . . . . . . . . . . . . 12
1.2.1 From.mltbxfile ........................ 12
1.2.2 From.zipfile.......................... 12
1.2.3 MATLAB OnlineTM ...................... 13
1.2.4 Simulink R
........................... 13
1.2.5 Documentation......................... 14
1.3 Compatible MATLAB versions . . . . . . . . . . . . . . . . . . . . . 14
1.4 Useinteaching ............................. 14
1.5 Useinresearch ............................. 14
1.6 Support ................................. 15
1.7 Relatedsoftware ............................ 15
1.7.1 Robotics System ToolboxTM .................. 15
1.7.2 Octave ............................. 15
1.7.3 Machine Vision toolbox . . . . . . . . . . . . . . . . . . . . 16
1.8 Contributing to the Toolboxes . . . . . . . . . . . . . . . . . . . . . 16
1.9 Acknowledgements........................... 16
2 Functions and classes 17
about...................................... 17
angdiff..................................... 17
angvec2r.................................... 18
angvec2tr ................................... 19
Arbotix .................................... 19
Bicycle .................................... 28
bresenham................................... 33
Bug2...................................... 33
chi2inv_rtb .................................. 35
circle...................................... 36
colnorm .................................... 36
ctraj ...................................... 37
Robotics Toolbox for MATLAB 9 Copyright c
Peter Corke 2017

CONTENTS CONTENTS
delta2tr .................................... 37
DHFactor ................................... 38
diff2...................................... 39
distancexform................................. 40
Dstar...................................... 41
DXform.................................... 45
e2h....................................... 48
edgelist .................................... 48
EKF...................................... 49
ETS2 ..................................... 58
ETS3 ..................................... 66
eul2jac..................................... 75
eul2r...................................... 75
eul2tr ..................................... 76
gauss2d .................................... 77
h2e....................................... 77
homline .................................... 77
homtrans.................................... 78
ishomog.................................... 78
ishomog2 ................................... 79
isrot ...................................... 79
isrot2 ..................................... 80
isunit...................................... 80
isvec...................................... 81
jsingu ..................................... 81
jtraj ...................................... 81
LandmarkMap................................. 82
Lattice..................................... 85
Link...................................... 88
lspb ...................................... 99
mdl_ball.................................... 100
mdl_baxter .................................. 100
mdl_cobra600................................. 101
mdl_coil.................................... 102
mdl_fanuc10L................................. 102
mdl_hyper2d ................................. 103
mdl_hyper3d ................................. 104
mdl_irb140 .................................. 105
mdl_irb140_mdh ............................... 105
mdl_jaco.................................... 106
mdl_KR5 ................................... 107
mdl_LWR................................... 108
mdl_M16 ................................... 108
mdl_mico ................................... 109
mdl_motomanHP6 .............................. 110
mdl_nao.................................... 110
mdl_offset6 .................................. 111
mdl_onelink.................................. 112
mdl_p8 .................................... 113
mdl_phantomx ................................ 113
Robotics Toolbox for MATLAB 10 Copyright c
Peter Corke 2017

CONTENTS CONTENTS
mdl_planar1.................................. 114
mdl_planar2.................................. 115
mdl_planar2_sym............................... 115
mdl_planar3.................................. 116
mdl_puma560................................. 116
mdl_puma560akb............................... 117
mdl_quadrotor................................. 118
mdl_S4ABB2p8................................ 119
mdl_simple6.................................. 120
mdl_stanford ................................. 120
mdl_stanford_mdh .............................. 121
mdl_twolink.................................. 122
mdl_twolink_mdh............................... 122
mdl_twolink_sym............................... 124
mdl_ur10 ................................... 125
mdl_ur3.................................... 126
mdl_ur5.................................... 127
models..................................... 127
mplot ..................................... 128
mstraj ..................................... 129
mtraj...................................... 130
Navigation................................... 131
numcols.................................... 139
numrows.................................... 140
oa2r ...................................... 140
oa2tr...................................... 141
ParticleFilter.................................. 141
peak...................................... 147
peak2 ..................................... 148
PGraph .................................... 148
pickregion................................... 165
plot2...................................... 166
plot_arrow................................... 166
plot_box.................................... 167
plot_circle................................... 168
plot_ellipse .................................. 169
plot_homline ................................. 170
plot_point ................................... 171
plot_poly ................................... 172
plot_sphere .................................. 173
plot_vehicle.................................. 174
plotbotopt ................................... 175
plotp...................................... 175
plotvol..................................... 176
Plucker .................................... 176
polydiff .................................... 183
Polygon .................................... 183
PoseGraph................................... 188
Prismatic ................................... 189
PrismaticMDH ................................ 192
Robotics Toolbox for MATLAB 11 Copyright c
Peter Corke 2017

CONTENTS CONTENTS
PRM...................................... 195
qplot...................................... 198
Quaternion................................... 199
r2t ....................................... 209
randinit .................................... 209
RandomPath.................................. 210
RangeBearingSensor ............................. 213
Revolute.................................... 218
RevoluteMDH................................. 220
rot2 ...................................... 223
rotx ...................................... 223
roty ...................................... 224
rotz ...................................... 224
rpy2jac..................................... 225
rpy2r...................................... 225
rpy2tr ..................................... 226
RRT ...................................... 227
rt2tr ...................................... 230
rtbdemo .................................... 231
RTBPlot.................................... 232
RTBPose ................................... 233
runscript.................................... 242
SE2 ...................................... 243
SE3 ...................................... 251
Sensor..................................... 268
SerialLink................................... 270
skew...................................... 313
skewa ..................................... 313
SO2 ...................................... 314
SO3 ...................................... 321
startup_rtb................................... 336
stlRead .................................... 337
t2r ....................................... 337
tb_optparse .................................. 338
tpoly...................................... 339
tr2angvec ................................... 340
tr2delta .................................... 341
tr2eul ..................................... 342
tr2jac ..................................... 342
tr2rpy ..................................... 343
tr2rt ...................................... 344
tranimate ................................... 344
tranimate2................................... 345
transl...................................... 346
transl2..................................... 347
trchain..................................... 348
trchain2 .................................... 348
trexp...................................... 349
trexp2 ..................................... 350
trinterp..................................... 351
Robotics Toolbox for MATLAB 12 Copyright c
Peter Corke 2017

CONTENTS CONTENTS
trinterp2.................................... 352
tripleangle................................... 352
trlog...................................... 353
trnorm..................................... 354
trot2...................................... 354
trotx...................................... 355
troty...................................... 355
trotz ...................................... 356
trplot...................................... 356
trplot2..................................... 358
trprint ..................................... 359
trprint2 .................................... 360
trscale ..................................... 361
Twist...................................... 361
Unicycle.................................... 367
unit ...................................... 371
UnitQuaternion ................................ 371
Vehicle..................................... 389
vex....................................... 397
vexa ...................................... 397
VREP ..................................... 398
VREP_arm .................................. 414
VREP_camera................................. 418
VREP_mirror ................................. 423
VREP_obj................................... 426
wtrans..................................... 430
xaxis...................................... 430
xyzlabel.................................... 431
yaxis...................................... 431
Robotics Toolbox for MATLAB 13 Copyright c
Peter Corke 2017
Chapter 1
Introduction
1.1 Changes in RTB 10
RTB 10 is largely backward compatible with RTB 9.
1.1.1 Incompatible changes
•The class Vehicle no longer represents an Ackerman/bicycle vehicle model.
Vehicle is now an abstract superclass of Bicycle and Unicycle which
represent car-like and differentially-steered vehicles respectively.
•The class LandmarkMap replaces PointMap.
•Robot-arm forward kinematics now returns an SE3 object rather than a 4 ×4
matrix.
•The Quaternion class used to represent both unit and non-unit quaternions
which was untidy and confusing. They are now represented by two classes
UnitQuaternion and Quaternion.
•The method to compute the arm-robot Jacobian in the end-effector frame has
been renamed from jacobn to jacobe.
•The path planners, subclasses of Navigation, the method to find a path has
been renamed from path to query.
•The Jacobian methods for the RangeBearingSensor class have been re-
named to Hx,Hp,Hw,Gx,Gz.
•The function se2 has been replaced with the class SE2. On some platforms
(Mac) this is the same file. Broadly similar in function, the former returns a
3×3 matrix, the latter returns an object.
•The function se3 has been replaced with the class SE3. On some platforms
(Mac) this is the same file. Broadly similar in function, the former returns a
4×4 matrix, the latter returns an object.
Robotics Toolbox for MATLAB 14 Copyright c
Peter Corke 2017

CHAPTER 1. INTRODUCTION 1.1. CHANGES IN RTB 10
RTB 9 RTB 10
Vehicle Bicycle
Map LandmarkMap
jacobn jacobe
path query
H_x Hx
H_xf Hp
H_w Hw
G_x Gx
G_z Gz
Table 1.1: Function and method name changes
These changes are summarized in Table 1.1.
1.1.2 New features
•SerialLinkplot3d() renders realistic looking 3D models of robots. STL
models from the package ARTE by Arturo Gil (https://arvc.umh.es/
arte) are now included with RTB, by kind permission.
•ETS2 and ETS3 packages provide a gentle (non Denavit-Hartenberg) introduc-
tion to robot arm kinematics, see Chapter 7 for details.
•Distribution as an .mltbx format file.
•A comprehensive set of functions to handle rotations and transformations in 2D,
these functions end with the suffix 2, eg. transl2,rot2,trot2 etc.
•Matrix exponentials are handled by trexp,trlog,trexp2 and trlog2.
•The class Twist represents a twist in 3D or 2D. Respectively, it is a 6-vector
representation of the Lie algebra se(3), or a 3-vector representation of se(2).
•The method SerialLink.jointdynamics returns a vector of tf objects
representing the dynamics of the joint actuators.
•The class Lattice is a kino-dynamic lattice path planner.
•The class PoseGraph solves graph relaxation problems and can be used for
bundle adjustment and pose graph SLAM.
•The class Plucker represents a line using Plücker coordinates.
•The folder RST contains Live Scripts that demonstrate some capabilities of the
MATLAB Robotics System ToolboxTM.
•The folder symbolic contains Live Scripts that demonstrate use of the MAT-
LAB Symbolic Math ToolboxTM for deriving Jacobians used in EKF SLAM
(vehicle and sensor), inverse kinematics for a 2-joint planar arm and solving for
roll-pitch-yaw angles given a rotation matrix.
•All the robot models, prefixed by mdl_, now reside in the folder models.
Robotics Toolbox for MATLAB 15 Copyright c
Peter Corke 2017

1.1. CHANGES IN RTB 10 CHAPTER 1. INTRODUCTION
•New robot models include Universal Robotics UR3, UR5 and UR10; and Kuka
light weight robot arm.
•A new folder data now holds various data files as used by examples in RVC2:
STL models, occupancy grids, Hershey font, Toro and G2O data files.
Since its inception RTB has used matrices1to represent rotations and transformations
in 2D and 3D. A trajectory, or sequence, was represented by a 3-dimensional matrix,
eg. 4 ×4×N. In RTB10 a set of classes have been introduced to represent orientation
and pose in 2D and 3D: SO2,SE2,SO3,SE3 and UnitQuaternion. These classes
are fairly polymorphic, that is, they share many methods and operators2. All have a
number of static methods that serve as constructors from particular representations. A
trajectory is represented by a vector of these objects which makes code easier to read
and understand. Overloaded operators are used so the classes behave in a similar way
to native matrices3. The relationship between the classical Toolbox functions and the
new classes are shown in Fig 1.1.
You can continue to use the classical functions. The new classes have methods with
the names of classical functions to provide similar functionality. For instance
>> T = transl(1,2,3); % create a 4x4 matrix
>> trprint(T) % invoke the function trprint
>> T = SE3(1,2,3); % create an SE3 object
>> trprint(T) % invoke the method trprint
>> T.T % the equivalent 4x4 matrix
>> double(T) % the equivalent 4x4 matrix
>> T = SE3(1,2,3); % create a pure translation SE3 object
>> T2 = T*T; % the result is an SE3 object
>> T3 = trinterp(T, 5); % create a vector of five SE3 objects
>> T3(1) % the first element of the vector
>> T3*T % each element of T3 multiplies T, giving a vector of five SE3 objects
1.1.3 Enhancements
•Dependencies on the Machine Vision Toolbox for MATLAB (MVTB) have been
removed. The fast dilation function used for path planning is now searched for
in MVTB and the MATLAB Image Processing Toolbox (IPT) and defaults to a
provided M-function.
•A major pass over all code and method/function/class documentation.
•Reworking and refactoring all the manipulator graphics, work in progress.
•An “app" is included: tripleangle which allows graphical experimentation
with Euler and roll-pitch-yaw angles.
•A tidyup of all Simulink models. Red blocks now represent user settable param-
eters, and shaded boxes are used to group parts of the models.
1Early versions of RTB, before 1999, used vectors to represent quaternions but that changed to an object
once objects were added to the language.
2For example, you could substitute objects of class SO3 and UnitQuaternion with minimal code
change.
3The capability is extended so that we can element-wise multiple two vectors of transforms, multiply one
transform over a vector of transforms or a set of points.
Robotics Toolbox for MATLAB 16 Copyright c
Peter Corke 2017
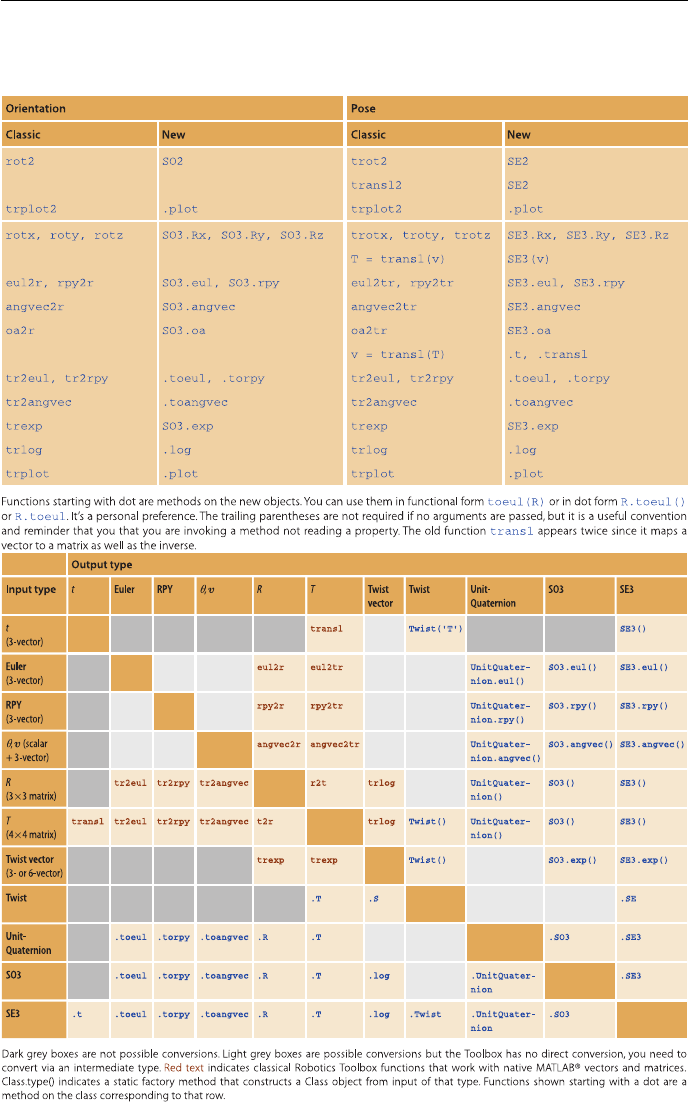
CHAPTER 1. INTRODUCTION 1.1. CHANGES IN RTB 10
Figure 1.1: (top) new and classic methods for representing orientation and pose, (bot-
tom) functions and methods to convert between representations. Reproduced from
“Robotics, Vision & Control, second edition, 2017”
Robotics Toolbox for MATLAB 17 Copyright c
Peter Corke 2017

1.2. HOW TO OBTAIN THE TOOLBOX CHAPTER 1. INTRODUCTION
•RangeBearingSensor animation
•All the java code that supports the DHFactor functionality now lives in the
folder java. The Makefile in there can be used to recompile the code. There
are java version issues and the shipped class files are built to java 1.7 which
allows operation
1.2 How to obtain the Toolbox
The Robotics Toolbox is freely available from the Toolbox home page at
http://www.petercorke.com
The file is available in MATLABtoolbox format (.mltbx) or zip format (.zip).
1.2.1 From .mltbx file
Since MATLAB R2014b toolboxes can be packaged as, and installed from, files with
the extension .mltbx. Download the most recent version of robot.mltbx or
vision.mltbx to your computer. Using MATLAB navigate to the folder where
you downloaded the file and double-click it (or right-click then select Install). The
Toolbox will be installed within the local MATLAB file structure, and the paths will be
appropriately configured for this, and future MATLAB sessions.
1.2.2 From .zip file
Download the most recent version of robot.zip or vision.zip to your computer. Use
your favourite unarchiving tool to unzip the files that you downloaded. To add the
Toolboxes to your MATLAB path execute the command
>> addpath RVCDIR ;
>> startup_rvc
where RVCDIR is the full pathname of the folder where the folder rvctools was
created when you unzipped the Toolbox files. The script startup_rvc adds various
subfolders to your path and displays the version of the Toolboxes. After installation
the files for both Toolboxes reside in a top-level folder called rvctools and beneath
this are a number of folders:
robot The Robotics Toolbox
vision The Machine Vision Toolbox
common Utility functions common to the Robotics and Machine Vision Toolboxes
simulink Simulink blocks for robotics and vision, as well as examples
contrib Code written by third-parties
If you already have the Machine Vision Toolbox installed then download the zip file to
the folder above the existing rvctools directory, and then unzip it. The files from
this zip archive will properly interleave with the Machine Vision Toolbox files.
Robotics Toolbox for MATLAB 18 Copyright c
Peter Corke 2017
CHAPTER 1. INTRODUCTION 1.2. HOW TO OBTAIN THE TOOLBOX
You need to setup the path every time you start MATLAB but you can automate this by
setting up environment variables, editing your startup.m script, using pathtool
and saving the path, or by pressing the “Update Toolbox Path Cache" button under
MATLAB General preferences. You can check the path using the command path or
pathtool.
A menu-driven demonstration can be invoked by
>> rtbdemo
1.2.3 MATLAB OnlineTM
The Toolbox works well with MATLAB OnlineTM which lets you access a MATLAB
session from a web browser, tablet or even a phone. The key is to get the RTB files
into the filesystem associated with your Online account. The easiest way to do this is
to install MATLAB DriveTM from MATLAB File Exchange or using the Get Add-Ons
option from the MATLAB GUI. This functions just like Google Drive or Dropbox,
a local filesystem on your computer is synchronized with your MATLAB Online ac-
count. Copy the RTB files into the local MATLAB Drive cache and they will soon be
synchronized, invoke startup_rvc to setup the paths and you are ready to simulate
robots on your mobile device or in a web browser.
1.2.4 Simulink R
Simulink R
is the block diagram simulation environment for MATLAB.
Common blocks
roblocks Block palette
Robot manipulator arms
sl_rrmc Resolved-rate motion control
sl_rrmc2 Resolved-rate motion control (relative)
sl_ztorque Robot collapsing under gravity
sl_jspace Joint space control
sl_ctorque Computed torque control
sl_fforward Torque feedforward control
sl_opspace Operational space control
sl_sea Series-elastic actuator
vloop_test Puma 560 velocity loop
ploop_test Puma 560 position loop
Mobile ground robot
sl_braitenberg Braitenberg vehicle moving to a source
sl_lanechange Lane changing control
sl_drivepoint Drive to a point
sl_driveline Drive to a line
sl_drivepose Drive to a pose
sl_pursuit Drive along a path
Flying robot
sl_quadrotor Quadrotor control
sl_quadrotor_vs Control visual servoing to a target
Robotics Toolbox for MATLAB 19 Copyright c
Peter Corke 2017

1.3. COMPATIBLE MATLAB VERSIONS CHAPTER 1. INTRODUCTION
1.2.5 Documentation
This document robot.pdf is a comprehensive manual that describes all functions in
the Toolbox. It is auto-generated from the comments in the MATLAB code and is fully
hyperlinked: to external web sites, the table of content to functions, and the “See also”
functions to each other.
The same documentation is available online in alphabetical order at http://www.
petercorke.com/RTB/r10/html/index_alpha.html or by category at http:
//www.petercorke.com/RTB/r10/html/index.html. Documentation is
also available via the MATLAB help browser, under supplemental software, as “Robotics
Toolbox".
1.3 Compatible MATLAB versions
The Toolbox has been tested under R2016b and R2017aPRE. Compatibility problems
are increasingly likely the older your version of MATLAB is.
1.4 Use in teaching
This is definitely encouraged! You are free to put the PDF manual (robot.pdf or
the web-based documentation html/*.html on a server for class use. If you plan to
distribute paper copies of the PDF manual then every copy must include the first two
pages (cover and licence).
Link to other resources such as MOOCs or the Robot Academy can be found at www.
petercorke.com/moocs.
1.5 Use in research
If the Toolbox helps you in your endeavours then I’d appreciate you citing the Toolbox
when you publish. The details are:
@book{Corke17a,
Author = {Peter I. Corke},
Note = {ISBN 978-3-319-54413-7},
Edition = {Second},
Publisher = {Springer},
Title = {Robotics, Vision \& Control: Fundamental Algorithms in {MATLAB}},
Year = {2017}}
or
P.I. Corke, Robotics, Vision & Control: Fundamental Algorithms in MAT-
LAB. Second edition. Springer, 2017. ISBN 978-3-319-54413-7.
which is also given in electronic form in the CITATION file.
Robotics Toolbox for MATLAB 20 Copyright c
Peter Corke 2017

CHAPTER 1. INTRODUCTION 1.6. SUPPORT
1.6 Support
There is no support! This software is made freely available in the hope that you find it
useful in solving whatever problems you have to hand. I am happy to correspond with
people who have found genuine bugs or deficiencies but my response time can be long
and I can’t guarantee that I respond to your email.
I can guarantee that I will not respond to any requests for help with assignments
or homework, no matter how urgent or important they might be to you. That’s
what your teachers, tutors, lecturers and professors are paid to do.
You might instead like to communicate with other users via the Google Group called
“Robotics and Machine Vision Toolbox”
http://tiny.cc/rvcforum
which is a forum for discussion. You need to signup in order to post, and the signup
process is moderated by me so allow a few days for this to happen. I need you to write a
few words about why you want to join the list so I can distinguish you from a spammer
or a web-bot.
1.7 Related software
1.7.1 Robotics System ToolboxTM
The Robotics System ToolboxTM (RST) from MathWorks is an official and supported
product. System toolboxes (see also the Computer Vision System Toolbox) are aimed
at developers of systems. RST has a growing set of functions for mobile robots, arm
robots, ROS integration and pose representations but its design (classes and functions)
and syntax is quite different to RTB. A number of examples illustrating the use of RST
are given in the folder RST as Live Scripts (extension .mlx), but you need to have the
Robotics System ToolboxTM installed in order to use it.
1.7.2 Octave
GNU Octave (www.octave.org) is an impressive piece of free software that implements
a language that is close to, but not the same as, MATLAB. The Toolboxes will not work
well with Octave, though with Octave 4 the incompatibilities are greatly reduced. An
old version of the arm-robot functions described in Chap. 7–9 have been ported to
Octave and this code is distributed in RVCDIR/robot/octave.
Many Toolbox functions work just fine under Octave. Three important classes (Quater-
nion, Link and SerialLink) will not work so modified versions of these classes is pro-
vided in the subdirectory called Octave. Copy all the directories from Octave to the
main Robotics Toolbox directory. The Octave port is now quite dated and not recently
tested – it is offered in the hope that you might find it useful.
Robotics Toolbox for MATLAB 21 Copyright c
Peter Corke 2017

1.8. CONTRIBUTING TO THE TOOLBOXES CHAPTER 1. INTRODUCTION
1.7.3 Machine Vision toolbox
Machine Vision toolbox (MVTB) for MATLAB. This was described in an article
@article{Corke05d,
Author = {P.I. Corke},
Journal = {IEEE Robotics and Automation Magazine},
Month = nov,
Number = {4},
Pages = {16-25},
Title = {Machine Vision Toolbox},
Volume = {12},
Year = {2005}}
and provides a very wide range of useful computer vision functions and is used to il-
lustrate principals in the Robotics, Vision & Control book. You can obtain this from
http://www.petercorke.com/vision. More recent products such as MAT-
LABImage Processing Toolbox and MATLABComputer Vision System Toolbox pro-
vide functionality that overlaps with MVTB.
1.8 Contributing to the Toolboxes
I am very happy to accept contributions for inclusion in future versions of the toolbox.
You will, of course, be suitably acknowledged (see below).
1.9 Acknowledgements
I have corresponded with a great many people via email since the first release of this
Toolbox. Some have identified bugs and shortcomings in the documentation, and even
better, some have provided bug fixes and even new modules, thankyou. See the file
CONTRIB for details.
Giorgio Grisetti and Gian Diego Tipaldi for the core of the pose graph solver. Ar-
turo Gil for allowing me to ship the STL robot models from ARTE. Jörn Malzahn has
donated a considerable amount of code, his Robot Symbolic Toolbox for MATLAB.
Bryan Moutrie has contributed parts of his open-source package phiWARE to RTB,
the remainder of that package can be found online. Other mentions to Gautam Sinha,
Wynand Smart for models of industrial robot arm, Paul Pounds for the quadrotor and
related models, Paul Newman for inspiring the mobile robot code, and Giorgio Grissetti
for inspiring the pose graph code.
Robotics Toolbox for MATLAB 22 Copyright c
Peter Corke 2017

Chapter 2
Functions and classes
about
Compact display of variable type
about(x) displays a compact line that describes the class and dimensions of x.
about xas above but this is the command rather than functional form
Examples
>> a=1;
>> about a
a [double] : 1x1 (8 bytes)
>> a = rand(5,7);
>> about a
a [double] : 5x7 (280 bytes)
See also
whos
angdiff
Difference of two angles
angdiff(th1,th2) is the difference between angles th1 and th2 on the circle. The result
is in the interval [-pi pi). Either or both arguments can be a vector:
Robotics Toolbox for MATLAB 23 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•If th1 is a vector, and th2 a scalar then return a vector where th2 is modulo
subtracted from the corresponding elements of th1.
•If th1 is a scalar, and th2 a vector then return a vector where the corresponding
elements of th2 are modulo subtracted from th1.
•If th1 and th2 are vectors then return a vector whose elements are the modulo
difference of the corresponding elements of th1 and th2.
angdiff(th) as above but th=[th1 th2].
angdiff(th) is the equivalent angle to th in the interval [-pi pi).
Notes
•If th1 and th2 are both vectors they should have the same orientation, which the
output will assume.
angvec2r
Convert angle and vector orientation to a rotation matrix
R=angvec2r(theta,v) is an orthonormal rotation matrix (3 ×3) equivalent to a rota-
tion of theta about the vector v.
Notes
•If theta == 0 then return identity matrix.
•If theta 6=0 then vmust have a finite length.
See also
angvec2tr,eul2r,rpy2r,tr2angvec,trexp,SO3.angvec
Robotics Toolbox for MATLAB 24 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
angvec2tr
Convert angle and vector orientation to a homogeneous trans-
form
T=angvec2tr(theta,v) is a homogeneous transform matrix (4 ×4) equivalent to a
rotation of theta about the vector v.
Note
•The translational part is zero.
•If theta == 0 then return identity matrix.
•If theta 6=0 then vmust have a finite length.
See also
angvec2r,eul2tr,rpy2tr,angvec2r,tr2angvec,trexp,SO3.angvec
Arbotix
Interface to Arbotix robot-arm controller
A concrete subclass of the abstract Machine class that implements a connection over a
serial port to an Arbotix robot-arm controller.
Methods
Arbotix Constructor, establishes serial communications
delete Destructor, closes serial connection
getpos Get joint angles
setpos Set joint angles and optionally speed
setpath Load a trajectory into Arbotix RAM
relax Control relax (zero torque) state
setled Control LEDs on servos
gettemp Temperature of motors
writedata1 Write byte data to servo control table
writedata2 Write word data to servo control table
readdata Read servo control table
Robotics Toolbox for MATLAB 25 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
command Execute command on servo
flush Flushes serial data buffer
receive Receive data
Example
arb=Arbotix(’port’, ’/dev/tty.usbserial-A800JDPN’, ’nservos’, 5);
q = arb.getpos();
arb.setpos(q + 0.1);
Notes
•This is experimental code.
•Considers the robot as a string of motors, and the last joint is assumed to be the
gripper. This should be abstracted, at the moment this is done in RobotArm.
•Connects via serial port to an Arbotix controller running the pypose sketch.
See also
Machine,RobotArm
Arbotix.Arbotix
Create Arbotix interface object
arb =Arbotix(options) is an object that represents a connection to a chain of Arbotix
servos connected via an Arbotix controller and serial link to the host computer.
Options
‘port’, P Name of the serial port device, eg. /dev/tty.USB0
‘baud’, B Set baud rate (default 38400)
‘debug’, D Debug level, show communications packets (default 0)
‘nservos’, N Number of servos in the chain
Robotics Toolbox for MATLAB 26 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.a2e
Convert angle to encoder
E= ARB.A2E(a) is a vector of encoder values Ecorresponding to the vector of joint
angles a. TODO:
•Scale factor is constant, should be a parameter to constructor.
Arbotix.char
Convert Arbotix status to string
C= ARB.char() is a string that succinctly describes the status of the Arbotix controller
link.
Arbotix.command
Execute command on servo
R= ARB.COMMAND(id,instruc) executes the instruction instruc on servo id.
R= ARB.COMMAND(id,instruc,data) as above but the vector data forms the
payload of the command message, and all numeric values in data must be in the range
0 to 255.
The optional output argument Ris a structure holding the return status.
Notes
•id is in the range 0 to N-1, where N is the number of servos in the system.
•Values for instruc are defined as class properties INS_*.
•If ‘debug’ was enabled in the constructor then the hex values are echoed to the
screen as well as being sent to the Arbotix.
•If an output argument is requested the serial channel is flushed first.
See also
Arbotix.receive,Arbotix.flush
Robotics Toolbox for MATLAB 27 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.connect
Connect to the physical robot controller
ARB.connect() establish a serial connection to the physical robot controller.
See also
Arbotix.disconnect
Arbotix.disconnect
Disconnect from the physical robot controller
ARB.disconnect() closes the serial connection.
See also
Arbotix.connect
Arbotix.display
Display parameters
ARB.display() displays the servo parameters in compact single line format.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Arbotix object and the command has no trailing semicolon.
See also
Arbotix.char
Robotics Toolbox for MATLAB 28 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.e2a
Convert encoder to angle
a= ARB.E2A(E) is a vector of joint angles acorresponding to the vector of encoder
values E.
TODO:
•Scale factor is constant, should be a parameter to constructor.
Arbotix.flush
Flush the receive buffer
ARB.FLUSH() flushes the serial input buffer, data is discarded.
s= ARB.FLUSH() as above but returns a vector of all bytes flushed from the channel.
Notes
•Every command sent to the Arbotix elicits a reply.
•The method receive() should be called after every command.
•Some Arbotix commands also return diagnostic text information.
See also
Arbotix.receive,Arbotix.parse
Arbotix.getpos
Get position
p= ARB.GETPOS(id) is the position (0-1023) of servo id.
p= ARB.GETPOS([]) is a vector (1 ×N) of positions of servos 1 to N.
Notes
•N is defined at construction time by the ‘nservos’ option.
Robotics Toolbox for MATLAB 29 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Arbotix.e2a
Arbotix.gettemp
Get temperature
T= ARB.GETTEMP(id) is the tempeature (deg C) of servo id.
T= ARB.GETTEMP() is a vector (1 ×N) of the temperature of servos 1 to N.
Notes
•N is defined at construction time by the ‘nservos’ option.
Arbotix.parse
Parse Arbotix return strings
ARB.PARSE(s) parses the string returned from the Arbotix controller and prints di-
agnostic text. The string scontains a mixture of Dynamixel style return packets and
diagnostic text.
Notes
•Every command sent to the Arbotix elicits a reply.
•The method receive() should be called after every command.
•Some Arbotix commands also return diagnostic text information.
See also
Arbotix.flush,Arbotix.command
Robotics Toolbox for MATLAB 30 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.readdata
Read byte data from servo control table
R= ARB.READDATA(id,addr) reads the successive elements of the servo control
table for servo id, starting at address addr. The complete return status in the structure
R, and the byte data is a vector in the field ‘params’.
Notes
•id is in the range 0 to N-1, where N is the number of servos in the system.
•If ‘debug’ was enabled in the constructor then the hex values are echoed to the
screen as well as being sent to the Arbotix.
See also
Arbotix.receive,Arbotix.command
Arbotix.receive
Decode Arbotix return packet
R= ARB.RECEIVE() reads and parses the return packet from the Arbotix and returns
a structure with the following fields:
id The id of the servo that sent the message
error Error code, 0 means OK
params The returned parameters, can be a vector of byte values
Notes
•Every command sent to the Arbotix elicits a reply.
•The method receive() should be called after every command.
•Some Arbotix commands also return diagnostic text information.
•If ‘debug’ was enabled in the constructor then the hex values are echoed
Robotics Toolbox for MATLAB 31 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.relax
Control relax state
ARB.RELAX(id) causes the servo id to enter zero-torque (relax state) ARB.RELAX(id,
FALSE) causes the servo id to enter position-control mode ARB.RELAX([]) causes
servos 1 to N to relax ARB.RELAX() as above ARB.RELAX([], FALSE) causes ser-
vos 1 to N to enter position-control mode.
Notes
•N is defined at construction time by the ‘nservos’ option.
Arbotix.setled
Set LEDs on servos
ARB.led(id,status) sets the LED on servo id to on or off according to the status
(logical).
ARB.led([], status) as above but the LEDs on servos 1 to N are set.
Notes
•N is defined at construction time by the ‘nservos’ option.
Arbotix.setpath
Load a path into Arbotix controller
ARB.setpath(jt) stores the path jt (P×N) in the Arbotix controller where P is the
number of points on the path and N is the number of robot joints. Allows for smooth
multi-axis motion.
See also
Arbotix.a2e
Robotics Toolbox for MATLAB 32 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.setpos
Set position
ARB.SETPOS(id,pos) sets the position (0-1023) of servo id. ARB.SETPOS(id,pos,
SPEED) as above but also sets the speed.
ARB.SETPOS(pos) sets the position of servos 1-N to corresponding elements of the
vector pos (1 ×N). ARB.SETPOS(pos, SPEED) as above but also sets the velocity
SPEED (1 ×N).
Notes
•id is in the range 1 to N
•N is defined at construction time by the ‘nservos’ option.
•SPEED varies from 0 to 1023, 0 means largest possible speed.
See also
Arbotix.a2e
Arbotix.writedata1
Write byte data to servo control table
ARB.WRITEDATA1(id,addr,data) writes the successive elements of data to the
servo control table for servo id, starting at address addr. The values of data must be
in the range 0 to 255.
Notes
•id is in the range 0 to N-1, where N is the number of servos in the system.
•If ‘debug’ was enabled in the constructor then the hex values are echoed to the
screen as well as being sent to the Arbotix.
See also
Arbotix.writedata2,Arbotix.command
Robotics Toolbox for MATLAB 33 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Arbotix.writedata2
Write word data to servo control table
ARB.WRITEDATA2(id,addr,data) writes the successive elements of data to the
servo control table for servo id, starting at address addr. The values of data must be
in the range 0 to 65535.
Notes
•id is in the range 0 to N-1, where N is the number of servos in the system.
•If ‘debug’ was enabled in the constructor then the hex values are echoed to the
screen as well as being sent to the Arbotix.
See also
Arbotix.writedata1,Arbotix.command
Bicycle
Car-like vehicle class
This concrete class models the kinematics of a car-like vehicle (bicycle or Ackerman
model) on a plane. For given steering and velocity inputs it updates the true vehicle
state and returns noise-corrupted odometry readings.
Methods
Bicycle constructor
add_driver attach a driver object to this vehicle
control generate the control inputs for the vehicle
deriv derivative of state given inputs
init initialize vehicle state
f predict next state based on odometry
Fx Jacobian of f wrt x
Fv Jacobian of f wrt odometry noise
update update the vehicle state
run run for multiple time steps
step move one time step and return noisy odometry
Robotics Toolbox for MATLAB 34 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Plotting/display methods
char convert to string
display display state/parameters in human readable form
plot plot/animate vehicle on current figure
plot_xy plot the true path of the vehicle
Vehicle.plotv plot/animate a pose on current figure
Properties (read/write)
x true vehicle state: x, y, theta (3 ×1)
V odometry covariance (2 ×2)
odometry distance moved in the last interval (2 ×1)
rdim dimension of the robot (for drawing)
L length of the vehicle (wheelbase)
alphalim steering wheel limit
maxspeed maximum vehicle speed
T sample interval
verbose verbosity
x_hist history of true vehicle state (N×3)
driver reference to the driver object
x0 initial state, restored on init()
Examples
Odometry covariance (per timstep) is
V = diag([0.02, 0.5*pi/180].^2);
Create a vehicle with this noisy odometry
v = Bicycle( ’covar’, diag([0.1 0.01].^2 );
and display its initial state
v
now apply a speed (0.2m/s) and steer angle (0.1rad) for 1 time step
odo = v.step(0.2, 0.1)
where odo is the noisy odometry estimate, and the new true vehicle state
v
We can add a driver object
v.add_driver( RandomPath(10) )
which will move the vehicle within the region -10<x<10, -10<y<10 which we can
see by
v.run(1000)
Robotics Toolbox for MATLAB 35 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
which shows an animation of the vehicle moving for 1000 time steps between randomly
selected wayoints.
Notes
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
Reference
Robotics, Vision & Control, Chap 6 Peter Corke, Springer 2011
See also
RandomPath,EKF
Bicycle.Bicycle
Vehicle object constructor
v=Bicycle(options) creates a Bicycle object with the kinematics of a bicycle (or Ack-
erman) vehicle.
Options
‘steermax’, M Maximu steer angle [rad] (default 0.5)
‘accelmax’, M Maximum acceleration [m/s2] (default Inf)
‘covar’, C specify odometry covariance (2 ×2) (default 0)
‘speedmax’, S Maximum speed (default 1m/s)
‘L’, L Wheel base (default 1m)
‘x0’, x0 Initial state (default (0,0,0) )
‘dt’, T Time interval (default 0.1)
‘rdim’, R Robot size as fraction of plot window (default 0.2)
‘verbose’ Be verbose
Notes
•The covariance is used by a “hidden” random number generator within the class.
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
Robotics Toolbox for MATLAB 36 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
Bicycle.char
Convert to a string
s= V.char() is a string showing vehicle parameters and state in a compact human
readable format.
See also
Bicycle.display
Bicycle.deriv
Time derivative of state
dx = V.deriv(T,x,u) is the time derivative of state (3 ×1) at the state x(3 ×1) with
input u(2 ×1).
Notes
•The parameter Tis ignored but called from a continuous time integrator such as
ode45 or Simulink.
Bicycle.f
Predict next state based on odometry
xn = V.f(x,odo) is the predicted next state xn (1 ×3) based on current state x(1 ×3)
and odometry odo (1 ×2) = [distance, heading_change].
xn = V.f(x,odo,w) as above but with odometry noise w.
Notes
•Supports vectorized operation where xand xn (N×3).
Robotics Toolbox for MATLAB 37 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Bicycle.Fv
Jacobian df/dv
J= V.Fv(x,odo) is the Jacobian df/dv (3 ×2) at the state x, for odometry input odo
(1 ×2) = [distance, heading_change].
See also
Bicycle.F,Vehicle.Fx
Bicycle.Fx
Jacobian df/dx
J= V.Fx(x,odo) is the Jacobian df/dx (3 ×3) at the state x, for odometry input odo
(1 ×2) = [distance, heading_change].
See also
Bicycle.f,Vehicle.Fv
Bicycle.update
Update the vehicle state
odo = V.update(u) is the true odometry value for motion with u=[speed,steer].
Notes
•Appends new state to state history property x_hist.
•Odometry is also saved as property odometry.
Robotics Toolbox for MATLAB 38 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
bresenham
Generate a line
p=bresenham(x1,y1,x2,y2) is a list of integer coordinates (2 ×N) for points lying
on the line segment joining the integer coordinates (x1,y1) and (x2,y2).
p=bresenham(p1,p2) as above but p1=[x1;y1] and p2=[x2;y2].
Notes
•Endpoint coordinates must be integer values.
Author
•Based on code by Aaron Wetzler
See also
icanvas
Bug2
Bug navigation class
A concrete subclass of the abstract Navigation class that implements the bug2 naviga-
tion algorithm. This is a simple automaton that performs local planning, that is, it can
only sense the immediate presence of an obstacle.
Methods
Bug2 Constructor
query Find a path from start to goal
plot Display the obstacle map
display Display state/parameters in human readable form
char Convert to string
Example
Robotics Toolbox for MATLAB 39 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
load map1 % load the map
bug = Bug2(map); % create navigation object
start = [20,10];
goal = [50,35];
bug.query(start, goal); % animate path
Reference
•Dynamic path planning for a mobile automaton with limited information on the
environment„ V. Lumelsky and A. Stepanov, IEEE Transactions on Automatic
Control, vol. 31, pp. 1058-1063, Nov. 1986.
•Robotics, Vision & Control, Sec 5.1.2, Peter Corke, Springer, 2011.
See also
Navigation,DXform,Dstar,PRM
Bug2.Bug2
Construct a Bug2 navigation object
b=Bug2(map,options) is a bug2 navigation object, and map is an occupancy grid,
a representation of a planar world as a matrix whose elements are 0 (free space) or 1
(occupied).
Options
‘goal’, G Specify the goal point (1 ×2)
‘inflate’, K Inflate all obstacles by K cells.
See also
Navigation.Navigation
Bug2.query
Find a path
B.query(start,goal,options) is the path (N×2) from start (1 ×2) to goal (1 ×2).
Row are the coordinates of successive points along the path. If either start or goal is []
Robotics Toolbox for MATLAB 40 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
the grid map is displayed and the user is prompted to select a point by clicking on the
plot.
Options
‘animate’ show a simulation of the robot moving along the path
‘movie’, M create a movie
‘current’ show the current position position as a black circle
Notes
•start and goal are given as X,Y coordinates in the grid map, not as MATLAB
row and column coordinates.
•start and goal are tested to ensure they lie in free space.
•The Bug2 algorithm is completely reactive so there is no planning method.
•If the bug does a lot of back tracking it’s hard to see the current position, use the
‘current’ option.
•For the movie option if M contains an extension a movie file with that extension
is created. Otherwise a folder will be created containing individual frames.
See also
animate
chi2inv_rtb
Inverse chi-squared function
x=chi2inv_rtb(p,n) is the inverse chi-squared cdf function of n-degrees of freedom.
Notes
•only works for n=2
•uses a table lookup with around 6 figure accuracy
•an approximation to chi2inv() from the Statistics & Machine Learning Toolbox
Robotics Toolbox for MATLAB 41 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
chi2inv
circle
Compute points on a circle
circle(C,R,options) plots a circle centred at C(1 ×2) with radius Ron the current
axes.
x=circle(C,R,options) is a matrix (2 ×N) whose columns define the coordinates
[x,y] of points around the circumferance of a circle centred at C(1 ×2) and of radius
R.
Cis normally 2 ×1 but if 3 ×1 then the circle is embedded in 3D, and xis N×3, but
the circle is always in the xy-plane with a z-coordinate of C(3).
Options
‘n’, N Specify the number of points (default 50)
colnorm
Column-wise norm of a matrix
cn =colnorm(a) is a vector (1×M) comprising the Euclidean norm of each column of
the matrix a(N×M).
See also
norm
Robotics Toolbox for MATLAB 42 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ctraj
Cartesian trajectory between two poses
tc =ctraj(T0,T1,n) is a Cartesian trajectory (4 ×4×n) from pose T0 to T1 with n
points that follow a trapezoidal velocity profile along the path. The Cartesian trajectory
is a homogeneous transform sequence and the last subscript being the point index, that
is, T(:,:,i) is the ith point along the path.
tc =ctraj(T0,T1,s) as above but the elements of s(n×1) specify the fractional dis-
tance along the path, and these values are in the range [0 1]. The ith point corresponds
to a distance s(i) along the path.
Notes
•If T0 or T1 is equal to [] it is taken to be the identity matrix.
•In the second case scould be generated by a scalar trajectory generator such as
TPOLY or LSPB (default).
•Orientation interpolation is performed using quaternion interpolation.
Reference
Robotics, Vision & Control, Sec 3.1.5, Peter Corke, Springer 2011
See also
lspb,mstraj,trinterp,UnitQuaternion.interp,SE3.ctraj
delta2tr
Convert differential motion to a homogeneous transform
T=delta2tr(d) is a homogeneous transform (4×4) representing differential translation
and rotation. The vector d=(dx, dy, dz, dRx, dRy, dRz) represents an infinitessimal
motion, and is an approximation to the spatial velocity multiplied by time.
Robotics Toolbox for MATLAB 43 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
tr2delta,SE3.delta
DHFactor
Simplify symbolic link transform expressions
f=dhfactor(s) is an object that encodes the kinematic model of a robot provided by
a string sthat represents a chain of elementary transforms from the robot’s base to its
tool tip. The chain of elementary rotations and translations is symbolically factored
into a sequence of link transforms described by DH parameters.
For example:
s = ’Rz(q1).Rx(q2).Ty(L1).Rx(q3).Tz(L2)’;
indicates a rotation of q1 about the z-axis, then rotation of q2 about the x-axis, transla-
tion of L1 about the y-axis, rotation of q3 about the x-axis and translation of L2 along
the z-axis.
Methods
base the base transform as a Java string
tool the tool transform as a Java string
command a command string that will create a SerialLink() object representing the specified kine-
matics
char convert to string representation
display display in human readable form
Example
>> s = ’Rz(q1).Rx(q2).Ty(L1).Rx(q3).Tz(L2)’;
>> dh = DHFactor(s);
>> dh
DH(q1+90, 0, 0, +90).DH(q2, L1, 0, 0).DH(q3-90, L2, 0, 0).Rz(+90).Rx(-90).Rz(-90)
>> r = eval( dh.command(’myrobot’) );
Notes
•Variables starting with q are assumed to be joint coordinates.
•Variables starting with L are length constants.
•Length constants must be defined in the workspace before executing the last line
above.
Robotics Toolbox for MATLAB 44 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•Implemented in Java.
•Not all sequences can be converted to DH format, if conversion cannot be achieved
an error is reported.
Reference
•A simple and systematic approach to assigning Denavit-Hartenberg parameters,
P.Corke, IEEE Transaction on Robotics, vol. 23, pp. 590-594, June 2007.
•Robotics, Vision & Control, Sec 7.5.2, 7.7.1, Peter Corke, Springer 2011.
See also
SerialLink
diff2
First-order difference
d=diff2(v) is the first-order difference (1 ×N) of the series data in vector v(1 ×N)
and the first element is zero.
d=diff2(a) is the first-order difference (M×N) of the series data in each row of the
matrix a(M×N) and the first element in each row is zero.
Notes
•Unlike the builtin function DIFF, the result of diff2 has the same number of
columns as the input.
See also
diff
Robotics Toolbox for MATLAB 45 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
distancexform
Distance transform
d=distancexform(im,options) is the distance transform of the binary image im. The
elements of dhave a value equal to the shortest distance from that element to a non-zero
pixel in the input image im.
d=distancexform(occgrid,goal,options) is the distance transform of the occupancy
grid occgrid with respect to the specified goal point goal = [X,Y]. The cells of the
grid have values of 0 for free space and 1 for obstacle. The resulting matrix dhas
cells whose value is the shortest distance to the goal from that cell, or NaN if the cell
corresponds to an obstacle (set to 1 in occgrid).
Options:
‘euclidean’ Use Euclidean (L2) distance metric (default)
‘cityblock’ Use cityblock or Manhattan (L1) distance metric
‘show’, dShow the iterations of the computation, with a delay of dseconds between frames.
‘noipt’ Don’t use Image Processing Toolbox, even if available
‘novlfeat’ Don’t use VLFeat, even if available
‘nofast’ Don’t use IPT, VLFeat or imorph, even if available.
Notes
•For the first case Image Processing Toolbox (IPT) or VLFeat will be used if avail-
able, searched for in that order. They use a 2-pass rather than iterative algorithm
and are much faster.
•Options can be used to disable use of IPT or VLFeat.
•If IPT or VLFeat are not available, or disabled, then imorph is used.
•If IPT, VLFeat or imorph are not available a slower M-function is used.
•If the ‘show’ option is given then imorph is used.
–Using imorph requires iteration and is slow.
–For the second case the Machine Vision Toolbox function imorph is re-
quired.
–imorph is a mex file and must be compiled.
•The goal is given as [X,Y] not MATLAB [row,col] format.
See also
imorph,DXform
Robotics Toolbox for MATLAB 46 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Dstar
D* navigation class
A concrete subclass of the abstract Navigation class that implements the D* navigation
algorithm. This provides minimum distance paths and facilitates incremental replan-
ning.
Methods
Dstar Constructor
plan Compute the cost map given a goal and map
query Find a path
plot Display the obstacle map
display Print the parameters in human readable form
char Convert to string% costmap_modify Modify the costmap
modify_cost Modify the costmap
Properties (read only)
distancemap Distance from each point to the goal.
costmap Cost of traversing cell (in any direction).
niter Number of iterations.
Example
load map1 % load map
goal = [50,30];
start=[20,10];
ds = Dstar(map); % create navigation object
ds.plan(goal) % create plan for specified goal
ds.query(start) % animate path from this start location
Notes
•Obstacles are represented by Inf in the costmap.
•The value of each element in the costmap is the shortest distance from the corre-
sponding point in the map to the current goal.
References
•The D* algorithm for real-time planning of optimal traverses, A. Stentz, Tech.
Rep. CMU-RI-TR-94-37, The Robotics Institute, Carnegie-Mellon University,
1994. https://www.ri.cmu.edu/pub_files/pub3/stentz_anthony__tony__1994_2/stentz_anthony__tony__1994_2.pdf
Robotics Toolbox for MATLAB 47 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•Robotics, Vision & Control, Sec 5.2.2, Peter Corke, Springer, 2011.
See also
Navigation,DXform,PRM
Dstar.Dstar
D* constructor
ds =Dstar(map,options) is a D* navigation object, and map is an occupancy grid,
a representation of a planar world as a matrix whose elements are 0 (free space) or 1
(occupied). The occupancy grid is coverted to a costmap with a unit cost for traversing
a cell.
Options
‘goal’, G Specify the goal point (2 ×1)
‘metric’, M Specify the distance metric as ‘euclidean’ (default) or ‘cityblock’.
‘inflate’, K Inflate all obstacles by K cells.
‘progress’ Don’t display the progress spinner
Other options are supported by the Navigation superclass.
See also
Navigation.Navigation
Dstar.char
Convert navigation object to string
DS.char() is a string representing the state of the Dstar object in human-readable form.
See also
Dstar.display,Navigation.char
Robotics Toolbox for MATLAB 48 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Dstar.modify_cost
Modify cost map
DS.modify_cost(p,C) modifies the cost map for the points described by the columns
of p(2×N) and sets them to the corresponding elements of C(1×N). For the particular
case where p(2×2) the first and last columns define the corners of a rectangular region
which is set to C(1 ×1).
Notes
•After one or more point costs have been updated the path should be replanned
by calling DS.plan().
See also
Dstar.set_cost
Dstar.plan
Plan path to goal
DS.plan(options) create a D* plan to reach the goal from all free cells in the map. Also
updates a D* plan after changes to the costmap. The goal is as previously specified.
DS.plan(goal,options) as above but goal given explicitly.
Options
‘animate’ Plot the distance transform as it evolves
‘progress’ Display a progress bar
Note
•If a path has already been planned, but the costmap was modified, then reinvok-
ing this method will replan, incrementally updating the plan at lower cost than a
full replan.
•The reset method causes a fresh plan, rather than replan.
Robotics Toolbox for MATLAB 49 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Dstar.reset
Dstar.plot
Visualize navigation environment
DS.plot() displays the occupancy grid and the goal distance in a new figure. The goal
distance is shown by intensity which increases with distance from the goal. Obstacles
are overlaid and shown in red.
DS.plot(p) as above but also overlays a path given by the set of points p(M×2).
See also
Navigation.plot
Dstar.reset
Reset the planner
DS.reset() resets the D* planner. The next instantiation of DS.plan() will perform a
global replan.
Dstar.set_cost
Set the current costmap
DS.set_cost(C) sets the current costmap. The cost map is the same size as the occu-
pancy grid and the value of each element represents the cost of traversing the cell. A
high value indicates that the cell is more costly (difficult) to traverese. A value of Inf
indicates an obstacle.
Notes
•After the cost map is changed the path should be replanned by calling DS.plan().
Robotics Toolbox for MATLAB 50 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Dstar.modify_cost
DXform
Distance transform navigation class
A concrete subclass of the abstract Navigation class that implements the distance trans-
form navigation algorithm which computes minimum distance paths.
Methods
DXform Constructor
plan Compute the cost map given a goal and map
query Find a path
plot Display the distance function and obstacle map
plot3d Display the distance function as a surface
display Print the parameters in human readable form
char Convert to string
Properties (read only)
distancemap Distance from each point to the goal.
metric The distance metric, can be ‘euclidean’ (default) or ‘cityblock’
Example
load map1 % load map
goal = [50,30]; % goal point
start = [20, 10]; % start point
dx = DXform(map); % create navigation object
dx.plan(goal) % create plan for specified goal
dx.query(start) % animate path from this start location
Notes
•Obstacles are represented by NaN in the distancemap.
•The value of each element in the distancemap is the shortest distance from the
corresponding point in the map to the current goal.
Robotics Toolbox for MATLAB 51 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•Robotics, Vision & Control, Sec 5.2.1, Peter Corke, Springer, 2011.
See also
Navigation,Dstar,PRM,distancexform
DXform.DXform
Distance transform constructor
dx =DXform(map,options) is a distance transform navigation object, and map is an
occupancy grid, a representation of a planar world as a matrix whose elements are 0
(free space) or 1 (occupied).
Options
‘goal’, G Specify the goal point (2 ×1)
‘metric’, M Specify the distance metric as ‘euclidean’ (default) or ‘cityblock’.
‘inflate’, K Inflate all obstacles by K cells.
Other options are supported by the Navigation superclass.
See also
Navigation.Navigation
DXform.char
Convert to string
DX.char() is a string representing the state of the object in human-readable form.
See also DXform.display, Navigation.char
Robotics Toolbox for MATLAB 52 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
DXform.plan
Plan path to goal
DX.plan(goal,options) plans a path to the goal given to the constructor, updates the
internal distancemap where the value of each element is the minimum distance from
the corresponding point to the goal.
DX.plan(goal,options) as above but goal is specified explicitly
Options
‘animate’ Plot the distance transform as it evolves
Notes
•This may take many seconds.
See also
Navigation.path
DXform.plot
Visualize navigation environment
DX.plot(options) displays the occupancy grid and the goal distance in a new figure.
The goal distance is shown by intensity which increases with distance from the goal.
Obstacles are overlaid and shown in red.
DX.plot(p,options) as above but also overlays a path given by the set of points p
(M×2).
Notes
•See Navigation.plot for options.
See also
Navigation.plot
Robotics Toolbox for MATLAB 53 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
DXform.plot3d
3D costmap view
DX.plot3d() displays the distance function as a 3D surface with distance from goal as
the vertical axis. Obstacles are “cut out” from the surface.
DX.plot3d(p) as above but also overlays a path given by the set of points p(M×2).
DX.plot3d(p,ls) as above but plot the line with the MATLAB linestyle ls.
See also
Navigation.plot
e2h
Euclidean to homogeneous
H=e2h(E) is the homogeneous version (K+1 ×N) of the Euclidean points E(K×N)
where each column represents one point in RK.
See also
h2e
edgelist
Return list of edge pixels for region
eg =edgelist(im,seed) is a list of edge pixels (2 ×N) of a region in the image im
starting at edge coordinate seed=[X,Y]. The edgelist has one column per edge point
coordinate (x,y).
eg =edgelist(im,seed,direction) as above, but the direction of edge following is
specified. direction == 0 (default) means clockwise, non zero is counter-clockwise.
Note that direction is with respect to y-axis upward, in matrix coordinate frame, not
image frame.
Robotics Toolbox for MATLAB 54 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
[eg,d] = edgelist(im,seed,direction) as above but also returns a vector of edge seg-
ment directions which have values 1 to 8 representing W SW S SE E NW N NW
respectively.
Notes
•Coordinates are given assuming the matrix is an image, so the indices are always
in the form (x,y) or (column,row).
•im is a binary image where 0 is assumed to be background, non-zero is an object.
•seed must be a point on the edge of the region.
•The seed point is always the first element of the returned edgelist.
•8-direction chain coding can give incorrect results when used with blobs founds
using 4-way connectivty.
Reference
•METHODS TO ESTIMATE AREAS AND PERIMETERS OF BLOB-LIKE
OBJECTS: A COMPARISON Luren Yang, Fritz Albregtsen, Tor Lgnnestad and
Per Grgttum IAPR Workshop on Machine Vision Applications Dec. 13-15, 1994,
Kawasaki
See also
ilabel
EKF
Extended Kalman Filter for navigation
Extended Kalman filter for optimal estimation of state from noisy measurments given
a non-linear dynamic model. This class is specific to the problem of state estimation
for a vehicle moving in SE(2).
This class can be used for:
•dead reckoning localization
•map-based localization
•map making
•simultaneous localization and mapping (SLAM)
Robotics Toolbox for MATLAB 55 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
It is used in conjunction with:
•a kinematic vehicle model that provides odometry output, represented by a Ve-
hicle sbuclass object.
•The vehicle must be driven within the area of the map and this is achieved by
connecting the Vehicle subclass object to a Driver object.
•a map containing the position of a number of landmark points and is represented
by a LandmarkMap object.
•a sensor that returns measurements about landmarks relative to the vehicle’s pose
and is represented by a Sensor object subclass.
The EKF object updates its state at each time step, and invokes the state update methods
of the vehicle object. The complete history of estimated state and covariance is stored
within the EKF object.
Methods
run run the filter
plot_xy plot the actual path of the vehicle
plot_P plot the estimated covariance norm along the path
plot_map plot estimated landmark points and confidence limits
plot_vehicle plot estimated vehicle covariance ellipses
plot_error plot estimation error with standard deviation bounds
display print the filter state in human readable form
char convert the filter state to human readable string
Properties
x_est estimated state
P estimated covariance
V_est estimated odometry covariance
W_est estimated sensor covariance
landmarks maps sensor landmark id to filter state element
robot reference to the Vehicle object
sensor reference to the Sensor subclass object
history vector of structs that hold the detailed filter state from each time step
verbose show lots of detail (default false)
joseph use Joseph form to represent covariance (default true)
Vehicle position estimation (localization)
Create a vehicle with odometry covariance V, add a driver to it, create a Kalman filter
with estimated covariance V_est and initial state covariance P0
veh = Vehicle(V);
veh.add_driver( RandomPath(20, 2) );
Robotics Toolbox for MATLAB 56 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ekf = EKF(veh, V_est, P0);
We run the simulation for 1000 time steps
ekf.run(1000);
then plot true vehicle path
veh.plot_xy(’b’);
and overlay the estimated path
ekf.plot_xy(’r’);
and overlay uncertainty ellipses
ekf.plot_ellipse(’g’);
We can plot the covariance against time as
clf
ekf.plot_P();
Map-based vehicle localization
Create a vehicle with odometry covariance V, add a driver to it, create a map with
20 point landmarks, create a sensor that uses the map and vehicle state to estimate
landmark range and bearing with covariance W, the Kalman filter with estimated co-
variances V_est and W_est and initial vehicle state covariance P0
veh = Bicycle(V);
veh.add_driver( RandomPath(20, 2) );
map = LandmarkMap(20);
sensor = RangeBearingSensor(veh, map, W);
ekf = EKF(veh, V_est, P0, sensor, W_est, map);
We run the simulation for 1000 time steps
ekf.run(1000);
then plot the map and the true vehicle path
map.plot();
veh.plot_xy(’b’);
and overlay the estimatd path
ekf.plot_xy(’r’);
and overlay uncertainty ellipses
ekf.plot_ellipse(’g’);
We can plot the covariance against time as
clf
ekf.plot_P();
Vehicle-based map making
Create a vehicle with odometry covariance V, add a driver to it, create a sensor that
uses the map and vehicle state to estimate landmark range and bearing with covariance
Robotics Toolbox for MATLAB 57 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
W, the Kalman filter with estimated sensor covariance W_est and a “perfect” vehicle
(no covariance), then run the filter for N time steps.
veh = Vehicle(V);
veh.add_driver( RandomPath(20, 2) );
map = LandmarkMap(20);
sensor = RangeBearingSensor(veh, map, W);
ekf = EKF(veh, [], [], sensor, W_est, []);
We run the simulation for 1000 time steps
ekf.run(1000);
Then plot the true map
map.plot();
and overlay the estimated map with 97% confidence ellipses
ekf.plot_map(’g’, ’confidence’, 0.97);
Simultaneous localization and mapping (SLAM)
Create a vehicle with odometry covariance V, add a driver to it, create a map with
20 point landmarks, create a sensor that uses the map and vehicle state to estimate
landmark range and bearing with covariance W, the Kalman filter with estimated co-
variances V_est and W_est and initial state covariance P0, then run the filter to estimate
the vehicle state at each time step and the map.
veh = Vehicle(V);
veh.add_driver( RandomPath(20, 2) );
map = PointMap(20);
sensor = RangeBearingSensor(veh, map, W);
ekf = EKF(veh, V_est, P0, sensor, W, []);
We run the simulation for 1000 time steps
ekf.run(1000);
then plot the map and the true vehicle path
map.plot();
veh.plot_xy(’b’);
and overlay the estimated path
ekf.plot_xy(’r’);
and overlay uncertainty ellipses
ekf.plot_ellipse(’g’);
We can plot the covariance against time as
clf
ekf.plot_P();
Then plot the true map
map.plot();
and overlay the estimated map with 3 sigma ellipses
ekf.plot_map(3, ’g’);
Robotics Toolbox for MATLAB 58 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
References
Robotics, Vision & Control, Chap 6, Peter Corke, Springer 2011
Stochastic processes and filtering theory, AH Jazwinski Academic Press 1970
Acknowledgement
Inspired by code of Paul Newman, Oxford University, http://www.robots.ox.ac.uk/ pnew-
man
See also
Vehicle,RandomPath,RangeBearingSensor,PointMap,ParticleFilter
EKF.EKF
EKF object constructor
E=EKF(vehicle,v_est,p0,options) is an EKF that estimates the state of the vehi-
cle (subclass of Vehicle) with estimated odometry covariance v_est (2 ×2) and initial
covariance (3 ×3).
E=EKF(vehicle,v_est,p0,sensor,w_est,map,options) as above but uses infor-
mation from a vehicle mounted sensor, estimated sensor covariance w_est and a map
(LandmarkMap class).
Options
‘verbose’ Be verbose.
‘nohistory’ Don’t keep history.
‘joseph’ Use Joseph form for covariance
‘dim’, D Dimension of the robot’s workspace.
•D scalar; X: -D to +D, Y: -D to +D
•D (1 ×2); X: -D(1) to +D(1), Y: -D(2) to +D(2)
•D (1 ×4); X: D(1) to D(2), Y: D(3) to D(4)
Notes
•If map is [] then it will be estimated.
Robotics Toolbox for MATLAB 59 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•If v_est and p0 are [] the vehicle is assumed error free and the filter will only
estimate the landmark positions (map).
•If v_est and p0 are finite the filter will estimate the vehicle pose and the landmark
positions (map).
•EKF subclasses Handle, so it is a reference object.
•Dimensions of workspace are normally taken from the map if given.
See also
Vehicle,Bicycle,Unicycle,Sensor,RangeBearingSensor,LandmarkMap
EKF.char
Convert to string
E.char() is a string representing the state of the EKF object in human-readable form.
See also
EKF.display
EKF.display
Display status of EKF object
E.display() displays the state of the EKF object in human-readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a EKF object and the command has no trailing semicolon.
See also
EKF.char
Robotics Toolbox for MATLAB 60 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
EKF.get_map
Get landmarks
p= E.get_map() is the estimated landmark coordinates (2 ×N) one per column. If the
landmark was not estimated the corresponding column contains NaNs.
See also
EKF.plot_map,EKF.plot_ellipse
EKF.get_P
Get covariance magnitude
E.get_P() is a vector of estimated covariance magnitude at each time step.
EKF.get_xy
Get vehicle position
p= E.get_xy() is the estimated vehicle pose trajectory as a matrix (N×3) where each
row is x, y, theta.
See also
EKF.plot_xy,EKF.plot_error,EKF.plot_ellipse,EKF.plot_P
EKF.init
Reset the filter
E.init() resets the filter state and clears landmarks and history.
Robotics Toolbox for MATLAB 61 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
EKF.plot_ellipse
Plot vehicle covariance as an ellipse
E.plot_ellipse() overlay the current plot with the estimated vehicle position covariance
ellipses for 20 points along the path.
E.plot_ellipse(ls) as above but pass line style arguments ls to plot_ellipse.
Options
‘interval’, I Plot an ellipse every I steps (default 20)
‘confidence’, C Confidence interval (default 0.95)
See also
plot_ellipse
EKF.plot_error
Plot vehicle position
E.plot_error(options) plot the error between actual and estimated vehicle path (x, y,
theta) versus time. Heading error is wrapped into the range [-pi,pi)
Options
‘bound’, S Display the confidence bounds (default 0.95).
‘color’, C Display the bounds using color C
LS Use MATLAB linestyle LS for the plots
Notes
•The bounds show the instantaneous standard deviation associated with the state.
Observations tend to decrease the uncertainty while periods of dead-reckoning
increase it.
•Set bound to zero to not draw confidence bounds.
•Ideally the error should lie “mostly” within the +/-3sigma bounds.
Robotics Toolbox for MATLAB 62 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
EKF.plot_xy,EKF.plot_ellipse,EKF.plot_P
EKF.plot_map
Plot landmarks
E.plot_map(options) overlay the current plot with the estimated landmark position (a
+-marker) and a covariance ellipses.
E.plot_map(ls,options) as above but pass line style arguments ls to plot_ellipse.
Options
‘confidence’, C Draw ellipse for confidence value C (default 0.95)
See also
EKF.get_map,EKF.plot_ellipse
EKF.plot_P
Plot covariance magnitude
E.plot_P() plots the estimated covariance magnitude against time step.
E.plot_P(ls) as above but the optional line style arguments ls are passed to plot.
EKF.plot_xy
Plot vehicle position
E.plot_xy() overlay the current plot with the estimated vehicle path in the xy-plane.
E.plot_xy(ls) as above but the optional line style arguments ls are passed to plot.
See also
EKF.get_xy,EKF.plot_error,EKF.plot_ellipse,EKF.plot_P
Robotics Toolbox for MATLAB 63 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
EKF.run
Run the filter
E.run(n,options) runs the filter for ntime steps and shows an animation of the vehicle
moving.
Options
‘plot’ Plot an animation of the vehicle moving
Notes
•All previously estimated states and estimation history are initially cleared.
ETS2
Elementary transform sequence in 2D
This class and package allows experimentation with sequences of spatial transforma-
tions in 2D.
import ETS2.*
a1 = 1; a2 = 1;
E = Rz(’q1’) *Tx(a1) *Rz(’q2’) *Tx(a2)
Operation methods
fkine forward kinematics
Information methods
isjoint test if transform is a joint
njoints the number of joint variables
structure a string listing the joint types
Robotics Toolbox for MATLAB 64 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Display methods
display display value as a string
plot graphically display the sequence as a robot
teach graphically display as robot and allow user control
Conversion methods
char convert to string
string convert to string with symbolic variables
Operators
* compound two elementary transforms
+ compound two elementary transforms
Notes
•The sequence is an array of objects of superclass ETS2, but with distinct sub-
classes: Rz, Tx, Ty.
•Use the command ‘clear imports’ after using ETS3.
See also
ETS3
ETS2.ETS2
Create an ETS2 object
E=ETS2(w,v) is a new ETS2 object that defines an elementary transform where w
is ‘Rz’, ‘Tx’ or ‘Ty’ and vis the paramter for the transform. If vis a string of the form
‘qN’ where N is an integer then the transform is considered to be a joint. Otherwise
the transform is a constant.
E=ETS2(e1) is a new ETS2 object that is a clone of the ETS2 object e1.
See also
ETS2.Rz,ETS2.Tx,ETS2.Ty
Robotics Toolbox for MATLAB 65 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ETS2.char
Convert to string
E.char() is a string showing transform parameters in a compact format. If E is a trans-
form sequence (1 ×N) then the string describes each element in sequence in a single
line format.
See also
ETS2.display
ETS2.display
Display parameters
E.display() displays the transform or transform sequence parameters in compact single
line format.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is an ETS2 object and the command has no trailing semicolon.
See also
ETS2.char
ETS2.find
Find joints in transform sequence
E.find(J) is the index in the transform sequence ETS (1 ×N) corresponding to the Jth
joint.
Robotics Toolbox for MATLAB 66 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ETS2.fkine
Forward kinematics
ETS.fkine(q,options) is the forward kinematics, the pose of the end of the sequence
as an SE2 object. q(1 ×N) is a vector of joint variables.
ETS.fkine(q,n,options) as above but process only the first nelements of the transform
sequence.
Options
‘deg’ Angles are given in degrees.
ETS2.isjoint
Test if transform is a joint
E.isjoint is true if the transform element is a joint, that is, its parameter is of the form
‘qN’.
ETS2.isprismatic
Test if transform is prismatic joint
E.isprismatic is true if the transform element is a joint, that is, its parameter is of the
form ‘qN’ and it controls a translation.
ETS2.mtimes
Compound transforms
E1 * E2 is a sequence of two elementary transform.
See also
ETS2.plus
Robotics Toolbox for MATLAB 67 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ETS2.n
Number of joints in transform sequence
E.njoints is the number of joints in the transform sequence.
Notes
•Is a wrapper on njoints, for compatibility with SerialLink object.
See also
ETS2.n
ETS2.njoints
Number of joints in transform sequence
E.njoints is the number of joints in the transform sequence.
See also
ETS2.n
ETS2.plot
Graphical display and animation
ETS.plot(q,options) displays a graphical animation of a robot based on the transform
sequence. Constant translations are represented as pipe segments, rotational joints as
cylinder, and prismatic joints as boxes. The robot is displayed at the joint angle q
(1 ×N), or if a matrix (M×N) it is animated as the robot moves along the M-point
trajectory.
Options
‘workspace’, W Size of robot 3D workspace, W = [xmn, xmx ymn ymx zmn zmx]
‘floorlevel’, L Z-coordinate of floor (default -1)
Robotics Toolbox for MATLAB 68 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘delay’, D Delay betwen frames for animation (s)
‘fps’, fps Number of frames per second for display, inverse of ‘delay’ option
‘[no]loop’ Loop over the trajectory forever
‘[no]raise’ Autoraise the figure
‘movie’, M Save an animation to the movie M
‘trail’, L Draw a line recording the tip path, with line style L
‘scale’, S Annotation scale factor
‘zoom’, Z Reduce size of auto-computed workspace by Z, makes robot look bigger
‘ortho’ Orthographic view
‘perspective’ Perspective view (default)
‘view’, V Specify view V=’x’, ‘y’, ‘top’ or [az el] for side elevations, plan view, or general view
by azimuth and elevation angle.
‘top’ View from the top.
‘[no]shading’ Enable Gouraud shading (default true)
‘lightpos’, L Position of the light source (default [0 0 20])
‘[no]name’ Display the robot’s name
‘[no]wrist’ Enable display of wrist coordinate frame
‘xyz’ Wrist axis label is XYZ
‘noa’ Wrist axis label is NOA
‘[no]arrow’ Display wrist frame with 3D arrows
‘[no]tiles’ Enable tiled floor (default true)
‘tilesize’, S Side length of square tiles on the floor (default 0.2)
‘tile1color’, C Color of even tiles [r g b] (default [0.5 1 0.5] light green)
‘tile2color’, C Color of odd tiles [r g b] (default [1 1 1] white)
‘[no]shadow’ Enable display of shadow (default true)
‘shadowcolor’, C Colorspec of shadow, [r g b]
‘shadowwidth’, W Width of shadow line (default 6)
‘[no]jaxes’ Enable display of joint axes (default false)
‘[no]jvec’ Enable display of joint axis vectors (default false)
‘[no]joints’ Enable display of joints
‘jointcolor’, C Colorspec for joint cylinders (default [0.7 0 0])
‘jointcolor’, C Colorspec for joint cylinders (default [0.7 0 0])
‘jointdiam’, D Diameter of joint cylinder in scale units (default 5)
‘linkcolor’, C Colorspec of links (default ‘b’)
‘[no]base’ Enable display of base ‘pedestal’
‘basecolor’, C Color of base (default ‘k’)
‘basewidth’, W Width of base (default 3)
The options come from 3 sources and are processed in order:
•Cell array of options returned by the function PLOTBOTOPT (if it exists)
•Cell array of options given by the ‘plotopt’ option when creating the SerialLink
object.
•List of arguments in the command line.
Many boolean options can be enabled or disabled with the ‘no’ prefix. The various
option sources can toggle an option, the last value encountered is used.
Robotics Toolbox for MATLAB 69 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Graphical annotations and options
The robot is displayed as a basic stick figure robot with annotations such as:
•shadow on the floor
•XYZ wrist axes and labels
•joint cylinders and axes
which are controlled by options.
The size of the annotations is determined using a simple heuristic from the workspace
dimensions. This dimension can be changed by setting the multiplicative scale factor
using the ‘mag’ option.
Figure behaviour
•If no figure exists one will be created and the robot drawn in it.
•If no robot of this name is currently displayed then a robot will be drawn in the
current figure. If hold is enabled (hold on) then the robot will be added to the
current figure.
•If the robot already exists then that graphical model will be found and moved.
Notes
•The options are processed when the figure is first drawn, to make different op-
tions come into effect it is neccessary to clear the figure.
•Delay betwen frames can be eliminated by setting option ‘delay’, 0 or ‘fps’, Inf.
•The size of the plot volume is determined by a heuristic for an all-revolute robot.
If a prismatic joint is present the ‘workspace’ option is required. The ‘zoom’
option can reduce the size of this workspace.
See also
ETS2.teach,SerialLink.plot3d
ETS2.plus
Compound transforms
E1 + E2 is a sequence of two elementary transform.
Robotics Toolbox for MATLAB 70 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
ETS2.mtimes
ETS2.string
Convert to string with symbolic variables
E.string is a string representation of the transform sequence where non-joint parameters
have symbolic names L1, L2, L3 etc.
See also
trchain
ETS2.structure
Show joint type structure
E.structure is a character array comprising the letters ‘R’ or ‘P’ that indicates the types
of joints in the elementary transform sequence E.
Notes
•The string will be E.njoints long.
See also
SerialLink.config
ETS2.teach
Graphical teach pendant
Allow the user to “drive” a graphical robot using a graphical slider panel.
ETS.teach(options) adds a slider panel to a current ETS plot. If no graphical robot
exists one is created in a new window.
ETS.teach(q,options) as above but the robot joint angles are set to q(1 ×N).
Robotics Toolbox for MATLAB 71 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘eul’ Display tool orientation in Euler angles (default)
‘rpy’ Display tool orientation in roll/pitch/yaw angles
‘approach’ Display tool orientation as approach vector (z-axis)
‘[no]deg’ Display angles in degrees (default true)
GUI
•The Quit (red X) button removes the teach panel from the robot plot.
Notes
•The currently displayed robots move as the sliders are adjusted.
•The slider limits are derived from the joint limit properties. If not set then for
–a revolute joint they are assumed to be [-pi, +pi]
–a prismatic joint they are assumed unknown and an error occurs.
See also
ETS2.plot
ETS3
Elementary transform sequence in 3D
This class and package allows experimentation with sequences of spatial transforma-
tions in 3D.
import +ETS3.*
L1 = 0; L2 = -0.2337; L3 = 0.4318; L4 = 0.0203; L5 = 0.0837; L6 = 0.4318;
E3 = Tz(L1) *Rz(’q1’) *Ry(’q2’) *Ty(L2) *Tz(L3) *Ry(’q3’) *Tx(L4) *Ty(L5) *Tz(L6)
Operation methods
fkine
Robotics Toolbox for MATLAB 72 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Information methods
isjoint test if transform is a joint
njoints the number of joint variables
structure a string listing the joint types
Display methods
display display value as a string
plot graphically display the sequence as a robot
teach graphically display as robot and allow user control
Conversion methods
char convert to string
string convert to string with symbolic variables
Operators
* compound two elementary transforms
+ compound two elementary transforms
Notes
•The sequence is an array of objects of superclass ETS3, but with distinct sub-
classes: Rx, Ry, Rz, Tx, Ty, Tz.
•Use the command ‘clear imports’ after using ETS2.
See also
ETS2
ETS3.ETS3
Create an ETS3 object
E=ETS3(w,v) is a new ETS3 object that defines an elementary transform where w
is ‘Rx’, ‘Ry’, ‘Rz’, ‘Tx’, ‘Ty’ or ‘Tz’ and vis the paramter for the transform. If vis a
Robotics Toolbox for MATLAB 73 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
string of the form ‘qN’ where N is an integer then the transform is considered to be a
joint and the parameter is ignored. Otherwise the transform is a constant.
E=ETS3(e1) is a new ETS3 object that is a clone of the ETS3 object e1.
See also
ETS2.Rz,ETS2.Tx,ETS2.Ty
ETS3.char
Convert to string
E.char() is a string showing transform parameters in a compact format. If E is a trans-
form sequence (1 ×N) then the string describes each element in sequence in a single
line format.
See also
ETS3.display
ETS3.display
Display parameters
E.display() displays the transform or transform sequence parameters in compact single
line format.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is an ETS3 object and the command has no trailing semicolon.
See also
ETS3.char
Robotics Toolbox for MATLAB 74 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ETS3.find
Find joints in transform sequence
E.find(J) is the index in the transform sequence ETS(1 ×N) corresponding to the Jth
joint.
ETS3.fkine
Forward kinematics
ETS.fkine(q,options) is the forward kinematics, the pose of the end of the sequence
as an SE3 object. q(1 ×N) is a vector of joint variables.
ETS.fkine(q,n,options) as above but process only the first nelements of the transform
sequence.
Options
‘deg’ Angles are given in degrees.
ETS3.isjoint
Test if transform is a joint
E.isjoint is true if the transform element is a joint, that is, its parameter is of the form
‘qN’.
ETS3.isprismatic
Test if transform is prismatic joint
E.isprismatic is true if the transform element is a joint, that is, its parameter is of the
form ‘qN’ and it controls a translation.
Robotics Toolbox for MATLAB 75 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ETS3.mtimes
Compound transforms
E1 * E2 is a sequence of two elementary transform.
See also
ETS3.plus
ETS3.n
Number of joints in transform sequence
E.njoints is the number of joints in the transform sequence.
Notes
•Is a wrapper on njoints, for compatibility with SerialLink object.
See also
ETS3.n
ETS3.njoints
Number of joints in transform sequence
E.njoints is the number of joints in the transform sequence.
See also
ETS2.n
Robotics Toolbox for MATLAB 76 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ETS3.plot
Graphical display and animation
ETS.plot(q,options) displays a graphical animation of a robot based on the transform
sequence. Constant translations are represented as pipe segments, rotational joints as
cylinder, and prismatic joints as boxes. The robot is displayed at the joint angle q
(1 ×N), or if a matrix (M×N) it is animated as the robot moves along the M-point
trajectory.
Options
‘workspace’, W Size of robot 3D workspace, W = [xmn, xmx ymn ymx zmn zmx]
‘floorlevel’, L Z-coordinate of floor (default -1)
‘delay’, D Delay betwen frames for animation (s)
‘fps’, fps Number of frames per second for display, inverse of ‘delay’ option
‘[no]loop’ Loop over the trajectory forever
‘[no]raise’ Autoraise the figure
‘movie’, M Save an animation to the movie M
‘trail’, L Draw a line recording the tip path, with line style L
‘scale’, S Annotation scale factor
‘zoom’, Z Reduce size of auto-computed workspace by Z, makes robot look bigger
‘ortho’ Orthographic view
‘perspective’ Perspective view (default)
‘view’, V Specify view V=’x’, ‘y’, ‘top’ or [az el] for side elevations, plan view, or general view
by azimuth and elevation angle.
‘top’ View from the top.
‘[no]shading’ Enable Gouraud shading (default true)
‘lightpos’, L Position of the light source (default [0 0 20])
‘[no]name’ Display the robot’s name
‘[no]wrist’ Enable display of wrist coordinate frame
‘xyz’ Wrist axis label is XYZ
‘noa’ Wrist axis label is NOA
‘[no]arrow’ Display wrist frame with 3D arrows
‘[no]tiles’ Enable tiled floor (default true)
‘tilesize’, S Side length of square tiles on the floor (default 0.2)
‘tile1color’, C Color of even tiles [r g b] (default [0.5 1 0.5] light green)
‘tile2color’, C Color of odd tiles [r g b] (default [1 1 1] white)
‘[no]shadow’ Enable display of shadow (default true)
‘shadowcolor’, C Colorspec of shadow, [r g b]
‘shadowwidth’, W Width of shadow line (default 6)
‘[no]jaxes’ Enable display of joint axes (default false)
‘[no]jvec’ Enable display of joint axis vectors (default false)
‘[no]joints’ Enable display of joints
‘jointcolor’, C Colorspec for joint cylinders (default [0.7 0 0])
‘jointcolor’, C Colorspec for joint cylinders (default [0.7 0 0])
‘jointdiam’, D Diameter of joint cylinder in scale units (default 5)
Robotics Toolbox for MATLAB 77 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘linkcolor’, C Colorspec of links (default ‘b’)
‘[no]base’ Enable display of base ‘pedestal’
‘basecolor’, C Color of base (default ‘k’)
‘basewidth’, W Width of base (default 3)
The options come from 3 sources and are processed in order:
•Cell array of options returned by the function PLOTBOTOPT (if it exists)
•Cell array of options given by the ‘plotopt’ option when creating the SerialLink
object.
•List of arguments in the command line.
Many boolean options can be enabled or disabled with the ‘no’ prefix. The various
option sources can toggle an option, the last value encountered is used.
Graphical annotations and options
The robot is displayed as a basic stick figure robot with annotations such as:
•shadow on the floor
•XYZ wrist axes and labels
•joint cylinders and axes
which are controlled by options.
The size of the annotations is determined using a simple heuristic from the workspace
dimensions. This dimension can be changed by setting the multiplicative scale factor
using the ‘mag’ option.
Figure behaviour
•If no figure exists one will be created and the robot drawn in it.
•If no robot of this name is currently displayed then a robot will be drawn in the
current figure. If hold is enabled (hold on) then the robot will be added to the
current figure.
•If the robot already exists then that graphical model will be found and moved.
Notes
•The options are processed when the figure is first drawn, to make different op-
tions come into effect it is neccessary to clear the figure.
•Delay betwen frames can be eliminated by setting option ‘delay’, 0 or ‘fps’, Inf.
Robotics Toolbox for MATLAB 78 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•The size of the plot volume is determined by a heuristic for an all-revolute robot.
If a prismatic joint is present the ‘workspace’ option is required. The ‘zoom’
option can reduce the size of this workspace.
See also
ETS3.teach,SerialLink.plot3d
ETS3.plus
Compound transforms
E1 + E2 is a sequence of two elementary transform.
See also
ETS3.mtimes
ETS3.string
Convert to string with symbolic variables
E.string is a string representation of the transform sequence where non-joint parameters
have symbolic names L1, L2, L3 etc.
See also
trchain
ETS3.structure
Show joint type structure
E.structure is a character array comprising the letters ‘R’ or ‘P’ that indicates the types
of joints in the elementary transform sequence E.
Notes
•The string will be E.njoints long.
Robotics Toolbox for MATLAB 79 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SerialLink.config
ETS3.teach
Graphical teach pendant
Allow the user to “drive” a graphical robot using a graphical slider panel.
ETS.teach(options) adds a slider panel to a current ETS plot. If no graphical robot
exists one is created in a new window.
ETS.teach(q,options) as above but the robot joint angles are set to q(1 ×N).
Options
‘eul’ Display tool orientation in Euler angles (default)
‘rpy’ Display tool orientation in roll/pitch/yaw angles
‘approach’ Display tool orientation as approach vector (z-axis)
‘[no]deg’ Display angles in degrees (default true)
GUI
•The Quit (red X) button removes the teach panel from the robot plot.
Notes
•The currently displayed robots move as the sliders are adjusted.
•The slider limits are derived from the joint limit properties. If not set then for
–a revolute joint they are assumed to be [-pi, +pi]
–a prismatic joint they are assumed unknown and an error occurs.
See also
ETS3.plot
Robotics Toolbox for MATLAB 80 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
eul2jac
Euler angle rate Jacobian
J=eul2jac(phi,theta,psi) is a Jacobian matrix (3 ×3) that maps Euler angle rates to
angular velocity at the operating point specified by the Euler angles phi,theta,psi.
J=eul2jac(eul) as above but the Euler angles are passed as a vector eul=[phi,theta,
psi].
Notes
•Used in the creation of an analytical Jacobian.
See also
rpy2jac,SerialLink.jacobe
eul2r
Convert Euler angles to rotation matrix
R=eul2r(phi,theta,psi,options) is an SO(3) orthonornal rotation matrix (3 ×3)
equivalent to the specified Euler angles. These correspond to rotations about the Z, Y,
Z axes respectively. If phi,theta,psi are column vectors (N×1) then they are assumed
to represent a trajectory and Ris a three-dimensional matrix (3 ×3×N), where the last
index corresponds to rows of phi,theta,psi.
R=eul2r(eul,options) as above but the Euler angles are taken from the vector (1 ×3)
eul = [phi theta psi]. If eul is a matrix (N×3) then Ris a three-dimensional matrix
(3 ×3×N), where the last index corresponds to rows of RPY which are assumed to be
[phi,theta,psi].
Options
‘deg’ Angles given in degrees (radians default)
Note
•The vectors phi,theta,psi must be of the same length.
Robotics Toolbox for MATLAB 81 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
eul2tr,rpy2tr,tr2eul,SO3.eul
eul2tr
Convert Euler angles to homogeneous transform
T=eul2tr(phi,theta,psi,options) is an SE(3) homogeneous transformation ma-
trix (4 ×4) with zero translation and rotation equivalent to the specified Euler angles.
These correspond to rotations about the Z, Y, Z axes respectively. If phi,theta,psi
are column vectors (N×1) then they are assumed to represent a trajectory and R is a
three-dimensional matrix (4 ×4×N), where the last index corresponds to rows of phi,
theta,psi.
R=eul2r(eul,options) as above but the Euler angles are taken from the vector (1 ×3)
eul = [phi theta psi]. If eul is a matrix (N×3) then Ris a three-dimensional matrix
(4 ×4×N), where the last index corresponds to rows of RPY which are assumed to be
[phi,theta,psi].
Options
‘deg’ Angles given in degrees (radians default)
Note
•The vectors phi,theta,psi must be of the same length.
•The translational part is zero.
See also
eul2r,rpy2tr,tr2eul,SE3.eul
Robotics Toolbox for MATLAB 82 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
gauss2d
Gaussian kernel
out =gauss2d(im,sigma,C) is a unit volume Gaussian kernel rendered into matrix
out (W×H) the same size as im (W×H). The Gaussian has a standard deviation of
sigma. The Gaussian is centered at C=[U,V].
h2e
Homogeneous to Euclidean
E=h2e(H) is the Euclidean version (K-1 ×N) of the homogeneous points H(K×N)
where each column represents one point in PK.
See also
e2h
homline
Homogeneous line from two points
L=homline(x1,y1,x2,y2) is a vector (3 ×1) which describes a line in homogeneous
form that contains the two Euclidean points (x1,y1) and (x2,y2).
Homogeneous points X (3 ×1) on the line must satisfy L’*X = 0.
See also
plot_homline
Robotics Toolbox for MATLAB 83 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
homtrans
Apply a homogeneous transformation
p2 =homtrans(T,p) applies the homogeneous transformation Tto the points stored
columnwise in p.
•If Tis in SE(2) (3 ×3) and
– p is 2 ×N(2D points) they are considered Euclidean (R2)
– p is 3 ×N(2D points) they are considered projective (p2)
•If Tis in SE(3) (4 ×4) and
– p is 3 ×N(3D points) they are considered Euclidean (R3)
– p is 4 ×N(3D points) they are considered projective (p3)
tp =homtrans(T,T1) applies homogeneous transformation Tto the homogeneous
transformation T1, that is tp=T*T1. If T1 is a 3-dimensional transformation then T
is applied to each plane as defined by the first two dimensions, ie. if T=N×Nand
T1=N×N×Mthen the result is N×N×M.
Notes
•Tis a homogeneous transformation defining the pose of {B}with respect to {A}.
•The points are defined with respect to frame {B}and are transformed to be with
respect to frame {A}.
See also
e2h,h2e,RTBPose.mtimes
ishomog
Test if SE(3) homogeneous transformation matrix
ishomog(T) is true (1) if the argument Tis of dimension 4 ×4 or 4 ×4×N, else false
(0).
ishomog(T, ‘valid’) as above, but also checks the validity of the rotation sub-matrix.
Robotics Toolbox for MATLAB 84 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The first form is a fast, but incomplete, test for a transform is SE(3).
See also
isrot,ishomog2,isvec
ishomog2
Test if SE(2) homogeneous transformation matrix
ishomog2(T) is true (1) if the argument Tis of dimension 3×3 or 3 ×3×N, else false
(0).
ishomog2(T, ‘valid’) as above, but also checks the validity of the rotation sub-matrix.
Notes
•The first form is a fast, but incomplete, test for a transform in SE(3).
See also
ishomog,isrot2,isvec
isrot
Test if SO(3) rotation matrix
isrot(R) is true (1) if the argument is of dimension 3 ×3 or 3 ×3×N, else false (0).
isrot(R, ‘valid’) as above, but also checks the validity of the rotation matrix.
Notes
•A valid rotation matrix has determinant of 1.
Robotics Toolbox for MATLAB 85 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
ishomog,isrot2,isvec
isrot2
Test if SO(2) rotation matrix
isrot2(R) is true (1) if the argument is of dimension 2 ×2 or 2 ×2×N, else false (0).
isrot2(R, ‘valid’) as above, but also checks the validity of the rotation matrix.
Notes
•A valid rotation matrix has determinant of 1.
See also
isrot,ishomog2,isvec
isunit
Test if vector has unit length
isunit(v) is true if the vector has unit length.
Notes
•A tolerance of 100eps is used.
Robotics Toolbox for MATLAB 86 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
isvec
Test if vector
isvec(v) is true (1) if the argument vis a 3-vector, else false (0).
isvec(v,L) is true (1) if the argument vis a vector of length L, either a row- or column-
vector. Otherwise false (0).
Notes
•Differs from MATLAB builtin function ISVECTOR, the latter returns true for
the case of a scalar, isvec does not.
•Gives same result for row- or column-vector, ie. 3 ×1 or 1 ×3 gives true.
See also
ishomog,isrot
jsingu
Show the linearly dependent joints in a Jacobian matrix
jsingu(J) displays the linear dependency of joints in a Jacobian matrix. This depen-
dency indicates joint axes that are aligned and causes singularity.
See also
SerialLink.jacobn
jtraj
Compute a joint space trajectory
[q,qd,qdd] = jtraj(q0,qf,m) is a joint space trajectory q(m×N) where the joint
coordinates vary from q0 (1×N) to qf (1×N). A quintic (5th order) polynomial is used
with default zero boundary conditions for velocity and acceleration. Time is assumed
Robotics Toolbox for MATLAB 87 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
to vary from 0 to 1 in msteps. Joint velocity and acceleration can be optionally returned
as qd (m×N) and qdd (m×N) respectively. The trajectory q,qd and qdd are m×N
matrices, with one row per time step, and one column per joint.
[q,qd,qdd] = jtraj(q0,qf,m,qd0,qdf) as above but also specifies initial qd0 (1 ×N)
and final qdf (1 ×N) joint velocity for the trajectory.
[q,qd,qdd] = jtraj(q0,qf,T) as above but the number of steps in the trajectory is
defined by the length of the time vector T(m×1).
[q,qd,qdd] = jtraj(q0,qf,T,qd0,qdf) as above but specifies initial and final joint
velocity for the trajectory and a time vector.
Notes
•When a time vector is provided the velocity and acceleration outputs are scaled
assumign that the time vector starts at zero and increases linearly.
See also
qplot,ctraj,SerialLink.jtraj
LandmarkMap
Map of planar point landmarks
A LandmarkMap object represents a square 2D environment with a number of land-
mark landmark points.
Methods
plot Plot the landmark map
landmark Return a specified map landmark
display Display map parameters in human readable form
char Convert map parameters to human readable string
Properties
map Matrix of map landmark coordinates 2 ×N
dim The dimensions of the map region x,y in [-dim,dim]
nlandmarks The number of map landmarks N
Robotics Toolbox for MATLAB 88 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Examples
To create a map for an area where X and Y are in the range -10 to +10 metres and with
50 random landmark points
map = LandmarkMap(50, 10);
which can be displayed by
map.plot();
Reference
Robotics, Vision & Control, Chap 6, Peter Corke, Springer 2011
See also
RangeBearingSensor,EKF
LandmarkMap.LandmarkMap
Create a map of point landmark landmarks
m=LandmarkMap(n,dim,options) is a LandmarkMap object that represents
nrandom point landmarks in a planar region bounded by +/-dim in the x- and y-
directions.
Options
‘verbose’ Be verbose
LandmarkMap.char
Convert map parameters to a string
s= M.char() is a string showing map parameters in a compact human readable format.
Robotics Toolbox for MATLAB 89 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
LandmarkMap.display
Display map parameters
M.display() displays map parameters in a compact human readable form.
Notes
•This method is invoked implicitly at the command line when the result of an ex-
pression is a LandmarkMap object and the command has no trailing semicolon.
See also
map.char
LandmarkMap.landmark
Get landmarks from map
f= M.landmark(k) is the coordinate (2 ×1) of the kth landmark (landmark).
LandmarkMap.plot
Plot the map
M.plot() plots the landmark map in the current figure, as a square region with dimen-
sions given by the M.dim property. Each landmark is marked by a black diamond.
M.plot(ls) as above, but the arguments ls are passed to plot and override the default
marker style.
Notes
•The plot is left with HOLD ON.
Robotics Toolbox for MATLAB 90 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
LandmarkMap.show
Show the landmark map
Notes
•Deprecated, use plot method.
LandmarkMap.verbosity
Set verbosity
M.verbosity(v) set verbosity to v, where 0 is silent and greater values display more
information.
Lattice
Lattice planner navigation class
A concrete subclass of the abstract Navigation class that implements the lattice planner
navigation algorithm over an occupancy grid. This performs goal independent planning
of kinematically feasible paths.
Methods
Lattice Constructor
plan Compute the roadmap
query Find a path
plot Display the obstacle map
display Display the parameters in human readable form
char Convert to string
Properties (read only)
graph A PGraph object describign the tree
Robotics Toolbox for MATLAB 91 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Example
lp = Lattice(); % create navigation object
lp.plan(’iterations’, 8) % create roadmaps
lp.query( [1 2 pi/2], [2 -2 0] ) % find path
lp.plot(); % plot the path
References
•Robotics, Vision & Control, Section 5.2.4, P. Corke, Springer 2016.
See also
Navigation,DXform,Dstar,PGraph
Lattice.Lattice
Create a Lattice navigation object
p=Lattice(map,options) is a probabilistic roadmap navigation object, and map is an
occupancy grid, a representation of a planar world as a matrix whose elements are 0
(free space) or 1 (occupied).
Options
‘grid’, G Grid spacing in X and Y (default 1)
‘root’, R Root coordinate of the lattice (2 ×1) (default [0,0])
‘iterations’, N Number of sample points (default Inf)
‘cost’, C Cost for straight, left, right (default [1,1,1])
‘inflate’, K Inflate all obstacles by K cells.
Other options are supported by the Navigation superclass.
Notes
•Iterates until the area defined by the map is covered.
See also
Navigation.Navigation
Robotics Toolbox for MATLAB 92 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Lattice.char
Convert to string
P.char() is a string representing the state of the Lattice object in human-readable form.
See also
Lattice.display
Lattice.plan
Create a lattice plan
P.plan(options) creates the lattice by iteratively building a tree of possible paths. The
resulting graph is kept within the object.
Options
‘iterations’, N Number of sample points (default Inf)
‘cost’, C Cost for straight, left, right (default [1,1,1])
Default parameter values come from the constructor
Lattice.plot
Visualize navigation environment
P.plot() displays the occupancy grid with an optional distance field.
Options
‘goal’ Superimpose the goal position if set
‘nooverlay’ Don’t overlay the Lattice graph
Robotics Toolbox for MATLAB 93 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Lattice.query
Find a path between two poses
P.query(start,goal) finds a path (N×3) from pose start (1 ×3) to pose goal (1 ×3).
The pose is expressed as [X,Y,THETA].
Link
manipulator Link class
A Link object holds all information related to a robot joint and link such as kinematics
parameters, rigid-body inertial parameters, motor and transmission parameters.
Constructors
Link general constructor
Prismatic construct a prismatic joint+link using standard DH
PrismaticMDH construct a prismatic joint+link using modified DH
Revolute construct a revolute joint+link using standard DH
RevoluteMDH construct a revolute joint+link using modified DH
Information/display methods
display print the link parameters in human readable form
dyn display link dynamic parameters
type joint type: ‘R’ or ‘P’
Conversion methods
char convert to string
Operation methods
A link transform matrix
friction friction force
nofriction Link object with friction parameters set to zero%
Robotics Toolbox for MATLAB 94 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Testing methods
islimit test if joint exceeds soft limit
isrevolute test if joint is revolute
isprismatic test if joint is prismatic
issym test if joint+link has symbolic parameters
Overloaded operators
+ concatenate links, result is a SerialLink object
Properties (read/write)
theta kinematic: joint angle
d kinematic: link offset
a kinematic: link length
alpha kinematic: link twist
jointtype kinematic: ‘R’ if revolute, ‘P’ if prismatic
mdh kinematic: 0 if standard D&H, else 1
offset kinematic: joint variable offset
qlim kinematic: joint variable limits [min max]
m dynamic: link mass
r dynamic: link COG wrt link coordinate frame 3 ×1
I dynamic: link inertia matrix, symmetric 3 ×3, about link COG.
B dynamic: link viscous friction (motor referred)
Tc dynamic: link Coulomb friction
G actuator: gear ratio
Jm actuator: motor inertia (motor referred)
Examples
L = Link([0 1.2 0.3 pi/2]);
L = Link(’revolute’, ’d’, 1.2, ’a’, 0.3, ’alpha’, pi/2);
L = Revolute(’d’, 1.2, ’a’, 0.3, ’alpha’, pi/2);
Notes
•This is a reference class object.
•Link objects can be used in vectors and arrays.
•Convenience subclasses are Revolute, Prismatic, RevoluteMDH and Prismat-
icMDH.
Robotics Toolbox for MATLAB 95 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
References
•Robotics, Vision & Control, P. Corke, Springer 2011, Chap 7.
See also
Link,Revolute,Prismatic,SerialLink,RevoluteMDH,PrismaticMDH
Link.Link
Create robot link object
This the class constructor which has several call signatures.
L=Link() is a Link object with default parameters.
L=Link(lnk) is a Link object that is a deep copy of the link object lnk and has type
Link, even if lnk is a subclass.
L=Link(options) is a link object with the kinematic and dynamic parameters specified
by the key/value pairs.
Options
‘theta’, TH joint angle, if not specified joint is revolute
‘d’, D joint extension, if not specified joint is prismatic
‘a’, A joint offset (default 0)
‘alpha’, A joint twist (default 0)
‘standard’ defined using standard D&H parameters (default).
‘modified’ defined using modified D&H parameters.
‘offset’, O joint variable offset (default 0)
‘qlim’, Ljoint limit (default [])
‘I’, I link inertia matrix (3 ×1, 6 ×1 or 3 ×3)
‘r’, R link centre of gravity (3 ×1)
‘m’, M link mass (1 ×1)
‘G’, G motor gear ratio (default 1)
‘B’, B joint friction, motor referenced (default 0)
‘Jm’, J motor inertia, motor referenced (default 0)
‘Tc’, T Coulomb friction, motor referenced (1 ×1 or 2 ×1), (default [0 0])
‘revolute’ for a revolute joint (default)
‘prismatic’ for a prismatic joint ‘p’
‘standard’ for standard D&H parameters (default).
‘modified’ for modified D&H parameters.
‘sym’ consider all parameter values as symbolic not numeric
Robotics Toolbox for MATLAB 96 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•It is an error to specify both ‘theta’ and ‘d’
•The joint variable, either theta or d, is provided as an argument to the A() method.
•The link inertia matrix (3 ×3) is symmetric and can be specified by giving a
3×3 matrix, the diagonal elements [Ixx Iyy Izz], or the moments and products
of inertia [Ixx Iyy Izz Ixy Iyz Ixz].
•All friction quantities are referenced to the motor not the load.
•Gear ratio is used only to convert motor referenced quantities such as friction
and interia to the link frame.
Old syntax
L=Link(dh,options) is a link object using the specified kinematic convention and
with parameters:
•dh = [THETA D A ALPHA SIGMA OFFSET] where SIGMA=0 for a revolute
and 1 for a prismatic joint; and OFFSET is a constant displacement between the
user joint variable and the value used by the kinematic model.
•dh = [THETA D A ALPHA SIGMA] where OFFSET is zero.
•dh = [THETA D A ALPHA], joint is assumed revolute and OFFSET is zero.
Options
‘standard’ for standard D&H parameters (default).
‘modified’ for modified D&H parameters.
‘revolute’ for a revolute joint, can be abbreviated to ‘r’ (default)
‘prismatic’ for a prismatic joint, can be abbreviated to ‘p’
Notes
•The parameter D is unused in a revolute joint, it is simply a placeholder in the
vector and the value given is ignored.
•The parameter THETA is unused in a prismatic joint, it is simply a placeholder
in the vector and the value given is ignored.
Examples
A standard Denavit-Hartenberg link
L3 = Link(’d’, 0.15005, ’a’, 0.0203, ’alpha’, -pi/2);
since ‘theta’ is not specified the joint is assumed to be revolute, and since the kinematic
convention is not specified it is assumed ‘standard’.
Robotics Toolbox for MATLAB 97 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Using the old syntax
L3 = Link([ 0, 0.15005, 0.0203, -pi/2], ’standard’);
the flag ‘standard’ is not strictly necessary but adds clarity. Only 4 parameters are
specified so sigma is assumed to be zero, ie. the joint is revolute.
L3 = Link([ 0, 0.15005, 0.0203, -pi/2, 0], ’standard’);
the flag ‘standard’ is not strictly necessary but adds clarity. 5 parameters are specified
and sigma is set to zero, ie. the joint is revolute.
L3 = Link([ 0, 0.15005, 0.0203, -pi/2, 1], ’standard’);
the flag ‘standard’ is not strictly necessary but adds clarity. 5 parameters are specified
and sigma is set to one, ie. the joint is prismatic.
For a modified Denavit-Hartenberg revolute joint
L3 = Link([ 0, 0.15005, 0.0203, -pi/2, 0], ’modified’);
Notes
•Link object is a reference object, a subclass of Handle object.
•Link objects can be used in vectors and arrays.
•The joint offset is a constant added to the joint angle variable before forward
kinematics and subtracted after inverse kinematics. It is useful if you want the
robot to adopt a ‘sensible’ pose for zero joint angle configuration.
•The link dynamic (inertial and motor) parameters are all set to zero. These must
be set by explicitly assigning the object properties: m, r, I, Jm, B, Tc.
•The gear ratio is set to 1 by default, meaning that motor friction and inertia will
be considered if they are non-zero.
See also
Revolute,Prismatic,RevoluteMDH,PrismaticMDH
Link.A
Link transform matrix
T= L.A(q) is an SE3 object representing the transformation between link frames when
the link variable qwhich is either the Denavit-Hartenberg parameter THETA (revolute)
or D (prismatic). For:
•standard DH parameters, this is from the previous frame to the current.
•modified DH parameters, this is from the current frame to the next.
Robotics Toolbox for MATLAB 98 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•For a revolute joint the THETA parameter of the link is ignored, and qused
instead.
•For a prismatic joint the D parameter of the link is ignored, and qused instead.
•The link offset parameter is added to qbefore computation of the transformation
matrix.
See also
SerialLink.fkine
Link.char
Convert to string
s= L.char() is a string showing link parameters in a compact single line format. If L
is a vector of Link objects return a string with one line per Link.
See also
Link.display
Link.display
Display parameters
L.display() displays the link parameters in compact single line format. If L is a vector
of Link objects displays one line per element.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Link object and the command has no trailing semicolon.
See also
Link.char,Link.dyn,SerialLink.showlink
Robotics Toolbox for MATLAB 99 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Link.dyn
Show inertial properties of link
L.dyn() displays the inertial properties of the link object in a multi-line format. The
properties shown are mass, centre of mass, inertia, friction, gear ratio and motor prop-
erties.
If L is a vector of Link objects show properties for each link.
See also
SerialLink.dyn
Link.friction
Joint friction force
f= L.friction(qd) is the joint friction force/torque (1×N) for joint velocity qd (1×N).
The friction model includes:
•Viscous friction which is a linear function of velocity.
•Coulomb friction which is proportional to sign(qd).
Notes
•The friction value should be added to the motor output torque, it has a negative
value when qd>0.
•The returned friction value is referred to the output of the gearbox.
•The friction parameters in the Link object are referred to the motor.
•Motor viscous friction is scaled up by G2.
•Motor Coulomb friction is scaled up by G.
•The appropriate Coulomb friction value to use in the non-symmetric case de-
pends on the sign of the joint velocity, not the motor velocity.
•The absolute value of the gear ratio is used. Negative gear ratios are tricky: the
Puma560 has negative gear ratio for joints 1 and 3.
See also
Link.nofriction
Robotics Toolbox for MATLAB 100 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Link.horzcat
Concatenate link objects
[L1 L2] is a vector that contains deep copies of the Link class objects L1 and L2.
Notes
•The elements of the vector are all of type Link.
•If the elements were of a subclass type they are convered to type Link.
•Extends to arbitrary number of objects in list.
See also
Link.plus
Link.islimit
Test joint limits
L.islimit(q) is true (1) if qis outside the soft limits set for this joint.
Note
•The limits are not currently used by any Toolbox functions.
Link.isprismatic
Test if joint is prismatic
L.isprismatic() is true (1) if joint is prismatic.
See also
Link.isrevolute
Robotics Toolbox for MATLAB 101 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Link.isrevolute
Test if joint is revolute
L.isrevolute() is true (1) if joint is revolute.
See also
Link.isprismatic
Link.issym
Check if link is a symbolic model
res = L.issym() is true if the Link L has any symbolic parameters.
See also
Link.sym
Link.nofriction
Remove friction
ln = L.nofriction() is a link object with the same parameters as L except nonlinear
(Coulomb) friction parameter is zero.
ln = L.nofriction(’all’) as above except that viscous and Coulomb friction are set to
zero.
ln = L.nofriction(’coulomb’) as above except that Coulomb friction is set to zero.
ln = L.nofriction(’viscous’) as above except that viscous friction is set to zero.
Notes
•Forward dynamic simulation can be very slow with finite Coulomb friction.
See also
Link.friction,SerialLink.nofriction,SerialLink.fdyn
Robotics Toolbox for MATLAB 102 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Link.plus
Concatenate link objects into a robot
L1+L2 is a SerialLink object formed from deep copies of the Link class objects L1
and L2.
Notes
•The elements can belong to any of the Link subclasses.
•Extends to arbitrary number of objects, eg. L1+L2+L3+L4.
See also
SerialLink,SerialLink.plus,Link.horzcat
Link.set.I
Set link inertia
L.I = [Ixx Iyy Izz] sets link inertia to a diagonal matrix.
L.I = [Ixx Iyy Izz Ixy Iyz Ixz] sets link inertia to a symmetric matrix with specified
inertia and product of intertia elements.
L.I = M set Link inertia matrix to M (3 ×3) which must be symmetric.
Link.set.r
Set centre of gravity
L.r = R sets the link centre of gravity (COG) to R (3-vector).
Link.set.Tc
Set Coulomb friction
L.Tc = F sets Coulomb friction parameters to [F -F], for a symmetric Coulomb friction
model.
Robotics Toolbox for MATLAB 103 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
L.Tc = [FP FM] sets Coulomb friction to [FP FM], for an asymmetric Coulomb friction
model. FP>0 and FM<0. FP is applied for a positive joint velocity and FM for a
negative joint velocity.
Notes
•The friction parameters are defined as being positive for a positive joint veloc-
ity, the friction force computed by Link.friction uses the negative of the friction
parameter, that is, the force opposing motion of the joint.
See also
Link.friction
Link.sym
Convert link parameters to symbolic type
LS = L.sym is a Link object in which all the parameters are symbolic (’sym’) type.
See also
Link.issym
Link.type
Joint type
c= L.type() is a character ‘R’ or ‘P’ depending on whether joint is revolute or prismatic
respectively. If L is a vector of Link objects return an array of characters in joint order.
See also
SerialLink.config
Robotics Toolbox for MATLAB 104 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
lspb
Linear segment with parabolic blend
[s,sd,sdd] = lspb(s0,sf,m) is a scalar trajectory (m×1) that varies smoothly from s0
to sf in msteps using a constant velocity segment and parabolic blends (a trapezoidal
velocity profile). Velocity and acceleration can be optionally returned as sd (m×1)
and sdd (m×1) respectively.
[s,sd,sdd] = lspb(s0,sf,m,v) as above but specifies the velocity of the linear segment
which is normally computed automatically.
[s,sd,sdd] = lspb(s0,sf,T) as above but specifies the trajectory in terms of the length
of the time vector T(m×1).
[s,sd,sdd] = lspb(s0,sf,T,v) as above but specifies the velocity of the linear segment
which is normally computed automatically and a time vector.
lspb(s0,sf,m,v) as above but plots s,sd and sdd versus time in a single figure.
Notes
•If mis given
–Velocity is in units of distance per trajectory step, not per second.
–Acceleration is in units of distance per trajectory step squared, not per sec-
ond squared.
•If Tis given then results are scaled to units of time.
•The time vector Tis assumed to be monotonically increasing, and time scaling
is based on the first and last element.
•For some values of vno solution is possible and an error is flagged.
References
•Robotics, Vision & Control, Chap 3, P. Corke, Springer 2011.
See also
tpoly,jtraj
Robotics Toolbox for MATLAB 105 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_ball
Create model of a ball manipulator
MDL_BALL creates the workspace variable ball which describes the kinematic char-
acteristics of a serial link manipulator with 50 joints that folds into a ball shape.
mdl_ball(n) as above but creates a manipulator with njoints.
Also define the workspace vectors:
q joint angle vector for default ball configuration
Reference
•"A divide and conquer articulated-body algorithm for parallel O(log(n)) calcu-
lation of rigid body dynamics, Part 2", Int. J. Robotics Research, 18(9), pp
876-892.
Notes
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_coil,SerialLink
mdl_baxter
Kinematic model of Baxter dual-arm robot
MDL_BAXTER is a script that creates the workspace variables left and right which
describes the kinematic characteristics of the two 7-joint arms of a Rethink Robotics
Baxter robot using standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
qd lower arm horizontal as per data sheet
Robotics Toolbox for MATLAB 106 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•SI units of metres are used.
References
“Kinematics Modeling and Experimental Verification of Baxter Robot” Z. Ju, C. Yang,
H. Ma, Chinese Control Conf, 2015.
See also
mdl_nao,SerialLink
mdl_cobra600
Create model of Puma 560 manipulator
MDL_PUMA560 is a script that creates the workspace variable p560 which describes
the kinematic and dynamic characteristics of a Unimation Puma 560 manipulator using
standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
qstretch arm is stretched out in the X direction
qn arm is at a nominal non-singular configuration
Notes
•SI units are used.
•The model includes armature inertia and gear ratios.
Reference
•“A search for consensus among model parameters reported for the PUMA 560
robot”, P. Corke and B. Armstrong-Helouvry, Proc. IEEE Int. Conf. Robotics
and Automation, (San Diego), pp. 1608-1613, May 1994.
Robotics Toolbox for MATLAB 107 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SerialRevolute,mdl_puma560akb,mdl_stanford
mdl_coil
Create model of a coil manipulator
MDL_COIL creates the workspace variable coil which describes the kinematic char-
acteristics of a serial link manipulator with 50 joints that folds into a helix shape.
mdl_ball(n) as above but creates a manipulator with njoints.
Also defines the workspace vectors:
q joint angle vector for default helical configuration
Reference
•"A divide and conquer articulated-body algorithm for parallel O(log(n)) calcu-
lation of rigid body dynamics, Part 2", Int. J. Robotics Research, 18(9), pp
876-892.
Notes
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_ball,SerialLink
mdl_fanuc10L
Create kinematic model of Fanuc AM120iB/10L robot
MDL_FANUC10L is a script that creates the workspace variable R which describes
the kinematic characteristics of a Fanuc AM120iB/10L robot using standard DH con-
ventions.
Robotics Toolbox for MATLAB 108 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Also defines the workspace vector:
q0 mastering position.
Notes
•SI units of metres are used.
Author
Wynand Swart, Mega Robots CC, P/O Box 8412, Pretoria, 0001, South Africa, wynand.swart@gmail.com
See also
mdl_irb140,mdl_m16,mdl_motomanHP6,mdl_puma560,SerialLink
mdl_hyper2d
Create model of a hyper redundant planar manipulator
MDL_HYPER2D creates the workspace variable h2d which describes the kinematic
characteristics of a serial link manipulator with 10 joints which at zero angles is a
straight line in the XY plane.
mdl_hyper2d(n) as above but creates a manipulator with njoints.
Also define the workspace vectors:
qz joint angle vector for zero angle configuration
R=mdl_hyper2d(n) functional form of the above, returns the SerialLink object.
[R,qz] = mdl_hyper2d(n) as above but also returns a vector of zero joint angles.
Notes
•All joint axes are parallel to z-axis.
•The manipulator in default pose is a straight line 1m long.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
Robotics Toolbox for MATLAB 109 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
mdl_hyper3d,mdl_coil,mdl_ball,mdl_twolink,SerialLink
mdl_hyper3d
Create model of a hyper redundant 3D manipulator
MDL_HYPER3D is a script that creates the workspace variable h3d which describes
the kinematic characteristics of a serial link manipulator with 10 joints which at zero
angles is a straight line in the XY plane.
mdl_hyper3d(n) as above but creates a manipulator with njoints.
Also define the workspace vectors:
qz joint angle vector for zero angle configuration
R=mdl_hyper3d(n) functional form of the above, returns the SerialLink object.
[R,qz] = mdl_hyper3d(n) as above but also returns a vector of zero joint angles.
Notes
•In the zero configuration joint axes alternate between being parallel to the z- and
y-axes.
•A crude snake or elephant trunk robot.
•The manipulator in default pose is a straight line 1m long.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_hyper2d,mdl_ball,mdl_coil,SerialLink
Robotics Toolbox for MATLAB 110 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_irb140
Create model of ABB IRB 140 manipulator
MDL_IRB140 is a script that creates the workspace variable irb140 which describes
the kinematic characteristics of an ABB IRB 140 manipulator using standard DH con-
ventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
qd lower arm horizontal as per data sheet
Reference
•“IRB 140 data sheet”, ABB Robotics.
•"Utilizing the Functional Work Space Evaluation Tool for Assessing a System
Design and Reconfiguration Alternatives" A. Djuric and R. J. Urbanic
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_fanuc10l,mdl_m16,mdl_motormanHP6,mdl_S4ABB2p8,mdl_puma560,Seri-
alLink
mdl_irb140_mdh
Create model of the ABB IRB 140 manipulator
MDL_IRB140_MOD is a script that creates the workspace variable irb140 which de-
scribes the kinematic characteristics of an ABB IRB 140 manipulator using modified
DH conventions.
Also define the workspace vectors:
Robotics Toolbox for MATLAB 111 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
qz zero joint angle configuration
Reference
•ABB IRB 140 data sheet
•"The modeling of a six degree-of-freedom industrial robot for the purpose of
efficient path planning", Master of Science Thesis, Penn State U, May 2009,
Tyler Carter
See also
mdl_irb140,mdl_puma560,mdl_stanford,mdl_twolink,SerialLink
Notes
•SI units of metres are used.
•The tool frame is in the centre of the tool flange.
•Zero angle configuration has the upper arm vertical and lower arm horizontal.
mdl_jaco
Create model of Kinova Jaco manipulator
MDL_JACO is a script that creates the workspace variable jaco which describes the
kinematic characteristics of a Kinova Jaco manipulator using standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
Reference
•“DH Parameters of Jaco” Version 1.0.8, July 25, 2013.
Robotics Toolbox for MATLAB 112 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_mico,mdl_puma560,SerialLink
mdl_KR5
Create model of Kuka KR5 manipulator
MDL_KR5 is a script that creates the workspace variable KR5 which describes the
kinematic characteristics of a Kuka KR5 manipulator using standard DH conventions.
Also define the workspace vectors:
qk1 nominal working position 1
qk2 nominal working position 2
qk3 nominal working position 3
Notes
•SI units of metres are used.
•Includes an 11.5cm tool in the z-direction
Author
•Gautam Sinha, Indian Institute of Technology, Kanpur.
See also
mdl_irb140,mdl_fanuc10l,mdl_motomanHP6,mdl_S4ABB2p8,mdl_puma560,Se-
rialLink
Robotics Toolbox for MATLAB 113 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_LWR
Create model of Kuka LWR manipulator
MDL_LWR is a script that creates the workspace variable KR5 which describes the
kinematic characteristics of a Kuka KR5 manipulator using standard DH conventions.
Also define the workspace vectors:
qz all zero angles
Notes
•SI units of metres are used.
Reference
•Identifying the Dynamic Model Used by the KUKA LWR: A Reverse Engineer-
ing Approach Claudio Gaz Fabrizio Flacco Alessandro De Luca ICRA 2014
See also
mdl_kr5,mdl_irb140,mdl_puma560,SerialLink
mdl_M16
Create model of Fanuc M16 manipulator
MDL_M16 is a script that creates the workspace variable m16 which describes the
kinematic characteristics of a Fanuc M16 manipulator using standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
qd lower arm horizontal as per data sheet
Robotics Toolbox for MATLAB 114 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•“Fanuc M-16iB data sheet”, http://www.robots.com/fanuc/m-16ib.
•"Utilizing the Functional Work Space Evaluation Tool for Assessing a System
Design and Reconfiguration Alternatives", A. Djuric and R. J. Urbanic
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_irb140,mdl_fanuc10l,mdl_motomanHP6,mdl_S4ABB2p8,mdl_puma560,Se-
rialLink
mdl_mico
Create model of Kinova Mico manipulator
MDL_MICO is a script that creates the workspace variable mico which describes the
kinematic characteristics of a Kinova Mico manipulator using standard DH conven-
tions.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
Reference
•“DH Parameters of Mico” Version 1.0.1, August 05, 2013. Kinova
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
Robotics Toolbox for MATLAB 115 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Revolute,mdl_jaco,mdl_puma560,mdl_twolink,SerialLink
mdl_motomanHP6
Create kinematic data of a Motoman HP6 manipulator
MDL_MotomanHP6 is a script that creates the workspace variable hp6 which describes
the kinematic characteristics of a Motoman HP6 manipulator using standard DH con-
ventions.
Also defines the workspace vector:
q0 mastering position.
Author
Wynand Swart, Mega Robots CC, P/O Box 8412, Pretoria, 0001, South Africa, wynand.swart@gmail.com
Notes
•SI units of metres are used.
See also
mdl_irb140,mdl_m16,mdl_fanuc10l,mdl_S4ABB2p8,mdl_puma560,SerialLink
mdl_nao
Create model of Aldebaran NAO humanoid robot
MDL_NAO is a script that creates several workspace variables
leftarm left-arm kinematics (4DOF)
rightarm right-arm kinematics (4DOF)
leftleg left-leg kinematics (6DOF)
rightleg right-leg kinematics (6DOF)
Robotics Toolbox for MATLAB 116 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
which are each SerialLink objects that describe the kinematic characteristics of the
arms and legs of the NAO humanoid.
Reference
•“Forward and Inverse Kinematics for the NAO Humanoid Robot”, Nikolaos Ko-
finas, Thesis, Technical University of Crete July 2012.
•“Mechatronic design of NAO humanoid” David Gouaillier etal. IROS 2009, pp.
769-774.
Notes
•SI units of metres are used.
•The base transform of arms and legs are constant with respect to the torso frame,
which is assumed to be the constant value when the robot is upright. Clearly if
the robot is walking these base transforms will be dynamic.
•The first reference uses Modified DH notation, but doesn’t explicitly mention
this, and the parameter tables have the wrong column headings for Modified DH
parameters.
•TODO; add joint limits
•TODO; add dynamic parameters
See also
mdl_baxter,SerialLink
mdl_offset6
A minimalistic 6DOF robot arm with shoulder offset
MDL_OFFSET6 is a script that creates the workspace variable off6 which describes
the kinematic characteristics of a simple arm manipulator with a spherical wrist and a
shoulder offset, using standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
Robotics Toolbox for MATLAB 117 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_simple6,mdl_puma560,mdl_twolink,SerialLink
mdl_onelink
Create model of a simple 1-link mechanism
MDL_ONELINK is a script that creates the workspace variable tl which describes the
kinematic and dynamic characteristics of a simple planar 1-link mechanism.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Notes
•SI units are used.
•It is a planar mechanism operating in the XY (horizontal) plane and is therefore
not affected by gravity.
•Assume unit length links with all mass (unity) concentrated at the joints.
References
•Based on Fig 3-6 (p73) of Spong and Vidyasagar (1st edition).
See also
mdl_twolink,mdl_planar1,SerialLink
Robotics Toolbox for MATLAB 118 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_p8
Create model of Puma robot on an XY base
MDL_P8 is a script that creates the workspace variable p8 which is an 8-axis robot
comprising a Puma 560 robot on an XY base. Joints 1 and 2 are the base, joints 3-8 are
the robot arm.
Also define the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
qstretch arm is stretched out in the X direction
qn arm is at a nominal non-singular configuration
Notes
•SI units of metres are used.
References
•Robotics, Vision & Control, 1st edn, P. Corke, Springer 2011. Sec 7.3.4.
See also
mdl_puma560,SerialLink
mdl_phantomx
Create model of PhantomX pincher manipulator
MDL_PHANTOMX is a script that creates the workspace variable px which describes
the kinematic characteristics of a PhantomX Pincher Robot, a 4 joint hobby class ma-
nipulator by Trossen Robotics.
Also define the workspace vectors:
qz zero joint angle configuration
Robotics Toolbox for MATLAB 119 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Uses standard DH conventions.
•Tool centrepoint is middle of the fingertips.
•All translational units in mm.
Reference
•http://www.trossenrobotics.com/productdocs/assemblyguides/phantomx-basic-robot-
arm.html
mdl_planar1
Create model of a simple planar 1-link mechanism
MDL_PLANAR1 is a script that creates the workspace variable p1 which describes the
kinematic characteristics of a simple planar 1-link mechanism.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Notes
•Moves in the XY plane.
•No dynamics in this model.
See also
mdl_planar2,mdl_planar3,SerialLink
Robotics Toolbox for MATLAB 120 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_planar2
Create model of a simple planar 2-link mechanism
MDL_PLANAR2 is a script that creates the workspace variable p2 which describes the
kinematic characteristics of a simple planar 2-link mechanism.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Notes
•Moves in the XY plane.
•No dynamics in this model.
See also
mdl_twolink,mdl_planar1,mdl_planar3,SerialLink
mdl_planar2_sym
Create model of a simple planar 2-link mechanism
MDL_PLANAR2 is a script that creates the workspace variable p2 which describes the
kinematic characteristics of a simple planar 2-link mechanism.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Notes
•Moves in the XY plane.
Robotics Toolbox for MATLAB 121 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•No dynamics in this model.
See also
mdl_twolink,mdl_planar1,mdl_planar3,SerialLink
mdl_planar3
Create model of a simple planar 3-link mechanism
MDL_PLANAR2 is a script that creates the workspace variable p3 which describes the
kinematic characteristics of a simple redundant planar 3-link mechanism.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Notes
•Moves in the XY plane.
•No dynamics in this model.
See also
mdl_twolink,mdl_planar1,mdl_planar2,SerialLink
mdl_puma560
Create model of Puma 560 manipulator
MDL_PUMA560 is a script that creates the workspace variable p560 which describes
the kinematic and dynamic characteristics of a Unimation Puma 560 manipulator using
standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
Robotics Toolbox for MATLAB 122 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
qr vertical ‘READY’ configuration
qstretch arm is stretched out in the X direction
qn arm is at a nominal non-singular configuration
Notes
•SI units are used.
•The model includes armature inertia and gear ratios.
Reference
•“A search for consensus among model parameters reported for the PUMA 560
robot”, P. Corke and B. Armstrong-Helouvry, Proc. IEEE Int. Conf. Robotics
and Automation, (San Diego), pp. 1608-1613, May 1994.
See also
SerialRevolute,mdl_puma560akb,mdl_stanford
mdl_puma560akb
Create model of Puma 560 manipulator
MDL_PUMA560AKB is a script that creates the workspace variable p560m which
describes the kinematic and dynamic characterstics of a Unimation Puma 560 manipu-
lator modified DH conventions.
Also defines the workspace vectors:
qz zero joint angle configuration
qr vertical ‘READY’ configuration
qstretch arm is stretched out in the X direction
Notes
•SI units are used.
Robotics Toolbox for MATLAB 123 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•“The Explicit Dynamic Model and Inertial Parameters of the Puma 560 Arm”
Armstrong, Khatib and Burdick 1986
See also
mdl_puma560,mdl_stanford_mdh,SerialLink
mdl_quadrotor
Dynamic parameters for a quadrotor.
MDL_QUADCOPTER is a script creates the workspace variable quad which describes
the dynamic characterstics of a quadrotor flying robot.
Properties
This is a structure with the following elements:
nrotors Number of rotors (1 ×1)
J Flyer rotational inertia matrix (3 ×3)
h Height of rotors above CoG (1 ×1)
d Length of flyer arms (1 ×1)
nb Number of blades per rotor (1 ×1)
r Rotor radius (1 ×1)
c Blade chord (1 ×1)
e Flapping hinge offset (1 ×1)
Mb Rotor blade mass (1 ×1)
Mc Estimated hub clamp mass (1 ×1)
ec Blade root clamp displacement (1 ×1)
Ib Rotor blade rotational inertia (1 ×1)
Ic Estimated root clamp inertia (1 ×1)
mb Static blade moment (1 ×1)
Ir Total rotor inertia (1 ×1)
Ct Non-dim. thrust coefficient (1 ×1)
Cq Non-dim. torque coefficient (1 ×1)
sigma Rotor solidity ratio (1 ×1)
thetat Blade tip angle (1 ×1)
theta0 Blade root angle (1 ×1)
theta1 Blade twist angle (1 ×1)
theta75 3/4 blade angle (1 ×1)
thetai Blade ideal root approximation (1 ×1)
Robotics Toolbox for MATLAB 124 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
a Lift slope gradient (1 ×1)
A Rotor disc area (1 ×1)
gamma Lock number (1 ×1)
Notes
•SI units are used.
References
•Design, Construction and Control of a Large Quadrotor micro air vehicle. P.Pounds,
PhD thesis, Australian National University, 2007. http://www.eng.yale.edu/pep5/P_Pounds_Thesis_2008.pdf
•This is a heavy lift quadrotor
See also
sl_quadrotor
mdl_S4ABB2p8
Create kinematic model of ABB S4 2.8robot
MDL_S4ABB2p8 is a script that creates the workspace variable s4 which describes the
kinematic characteristics of an ABB S4 2.8 robot using standard DH conventions.
Also defines the workspace vector:
q0 mastering position.
Author
Wynand Swart, Mega Robots CC, P/O Box 8412, Pretoria, 0001, South Africa, wynand.swart@gmail.com
See also
mdl_fanuc10l,mdl_m16,mdl_motormanHP6,mdl_irb140,mdl_puma560,SerialLink
Robotics Toolbox for MATLAB 125 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_simple6
A minimalistic 6DOF robot arm
MDL_SIMPLE6 is a script creates the workspace variable s6 which describes the kine-
matic characteristics of a simple arm manipulator with a spherical wrist and no shoulder
offset, using standard DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
Notes
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_offset6,mdl_puma560,SerialLink
mdl_stanford
Create model of Stanford arm
MDL_STANFORD is a script that creates the workspace variable stanf which describes
the kinematic and dynamic characteristics of the Stanford (Scheinman) arm.
Also defines the vectors:
qz zero joint angle configuration.
Note
•SI units are used.
•Gear ratios not currently known, though reflected armature inertia is known, so
gear ratios are set to 1.
Robotics Toolbox for MATLAB 126 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•Kinematic data from "Modelling, Trajectory calculation and Servoing of a com-
puter controlled arm". Stanford AIM-177. Figure 2.3
•Dynamic data from “Robot manipulators: mathematics, programming and con-
trol” Paul 1981, Tables 6.5, 6.6
•Dobrotin & Scheinman, "Design of a computer controlled manipulator for robot
research", IJCAI, 1973.
See also
mdl_puma560,mdl_puma560akb,SerialLink
mdl_stanford_mdh
Create model of Stanford arm using MDH conventions
MDL_STANFORD is a script that creates the workspace variable stanf which describes
the kinematic and dynamic characteristics of the Stanford (Scheinman) arm using mod-
ified Denavit-Hartenberg parameters.
Also defines the vectors:
qz zero joint angle configuration.
Notes
•SI units are used.
References
•Kinematic data from "Modelling, Trajectory calculation and Servoing of a com-
puter controlled arm". Stanford AIM-177. Figure 2.3
•Dynamic data from “Robot manipulators: mathematics, programming and con-
trol” Paul 1981, Tables 6.5, 6.6
See also
mdl_puma560,mdl_puma560akb,SerialLink
Robotics Toolbox for MATLAB 127 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_twolink
Create model of a 2-link mechanism
MDL_TWOLINK is a script that creates the workspace variable twolink which de-
scribes the kinematic and dynamic characteristics of a simple planar 2-link mechanism
moving in the xz-plane, it experiences gravity loading.
Also defines the vector:
qz corresponds to the zero joint angle configuration.
Notes
•SI units are used.
•It is a planar mechanism operating in the vertical plane and is therefore affected
by gravity (unlike mdl_planar2 in the horizontal plane).
•Assume unit length links with all mass (unity) concentrated at the joints.
References
•Based on Fig 3-6 (p73) of Spong and Vidyasagar (1st edition).
See also
mdl_twolink_sym,mdl_planar2,SerialLink
mdl_twolink_mdh
Create model of a 2-link mechanism using modified DH con-
vention
MDL_TWOLINK_MDH is a script that the workspace variable twolink which de-
scribes the kinematic and dynamic characteristics of a simple planar 2-link mechanism
using modified Denavit-Hartenberg conventions.
Robotics Toolbox for MATLAB 128 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Also defines the vector:
Robotics Toolbox for MATLAB 129 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
qz corresponds to the zero joint angle configuration.
Notes
•SI units of metres are used.
•It is a planar mechanism operating in the xz-plane (vertical) and is therefore not
affected by gravity.
References
•Based on Fig 3.8 (p71) of Craig (3rd edition).
See also
mdl_twolink,mdl_onelink,mdl_planar2,SerialLink
mdl_twolink_sym
Create symbolic model of a simple 2-link mechanism
MDL_TWOLINK_SYM is a script that creates the workspace variable twolink which
describes in symbolic form the kinematic and dynamic characteristics of a simple pla-
nar 2-link mechanism moving in the xz-plane, it experiences gravity loading. The
symbolic parameters are:
•link lengths: a1, a2
•link masses: m1, m2
•link CoMs in the link frame x-direction: c1, c2
•gravitational acceleration: g
•joint angles: q1, q2
•joint angle velocities: qd1, qd2
•joint angle accelerations: qdd1, qdd2
Robotics Toolbox for MATLAB 130 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•It is a planar mechanism operating in the vertical plane and is therefore affected
by gravity (unlike mdl_planar2 in the horizontal plane).
•Gear ratio is 1 and motor inertia is 0.
•Link inertias Iyy1, Iyy2 are 0.
•Viscous and Coulomb friction is 0.
References
•Based on Fig 3-6 (p73) of Spong and Vidyasagar (1st edition).
See also
mdl_puma560,mdl_stanford,SerialLink
mdl_ur10
Create model of Universal Robotics UR10 manipulator
MDL_UR5 is a script that creates the workspace variable ur10 which describes the
kinematic characteristics of a Universal Robotics UR10 manipulator using standard
DH conventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr arm along +ve x-axis configuration
Reference
•https://www.universal-robots.com/how-tos-and-faqs/faq/ur-faq/actual-center-of-mass-
for-robot-17264/
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
Robotics Toolbox for MATLAB 131 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
mdl_ur3,mdl_ur5,mdl_puma560,SerialLink
mdl_ur3
Create model of Universal Robotics UR3 manipulator
MDL_UR5 is a script that creates the workspace variable ur3 which describes the kine-
matic characteristics of a Universal Robotics UR3 manipulator using standard DH con-
ventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr arm along +ve x-axis configuration
Reference
•https://www.universal-robots.com/how-tos-and-faqs/faq/ur-faq/actual-center-of-mass-
for-robot-17264/
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_ur5,mdl_ur10,mdl_puma560,SerialLink
Robotics Toolbox for MATLAB 132 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
mdl_ur5
Create model of Universal Robotics UR5 manipulator
MDL_UR5 is a script that creates the workspace variable ur5 which describes the kine-
matic characteristics of a Universal Robotics UR5 manipulator using standard DH con-
ventions.
Also define the workspace vectors:
qz zero joint angle configuration
qr arm along +ve x-axis configuration
Reference
•https://www.universal-robots.com/how-tos-and-faqs/faq/ur-faq/actual-center-of-mass-
for-robot-17264/
Notes
•SI units of metres are used.
•Unlike most other mdl_xxx scripts this one is actually a function that behaves
like a script and writes to the global workspace.
See also
mdl_ur3,mdl_ur10,mdl_puma560,SerialLink
models
Summarise and search available robot models
models() lists keywords associated with each of the models in Robotics Toolbox.
models(query) lists those models that match the keyword query. Case is ignored in
the comparison.
m=models(query) as above but returns a cell array (N×1) of the names of the m-files
that define the models.
Robotics Toolbox for MATLAB 133 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Examples
models
models(’modified_DH’) % all models using modified DH notation
models(’kinova’) % all Kinova robot models
models(’6dof’) % all 6dof robot models
models(’redundant’) % all redundant robot models, >6 DOF
models(’prismatic’) % all robots with a prismatic joint
Notes
•A model is a file mdl_*.m in the models folder of the RTB directory.
•The keywords are indicated by a line ‘% MODEL: ’ after the main comment
block.
mplot
Plot time-series data
A convenience function for plotting time-series data held in a matrix. Each row is a
timestep and the first column is time.
mplot(y,options) plots the time series data y(N×M) in multiple subplots. The first
column is assumed to be time, so M-1 plots are produced.
mplot(T,y,options) plots the time series data y(N×M) in multiple subplots. Time is
provided explicitly as the first argument so M plots are produced.
mplot(s,options) as above but sis a structure. Each field is assumed to be a time series
which is plotted. Time is taken from the field called ‘t’. Plots are labelled according to
the name of the corresponding field.
mplot(w,options) as above but wis a structure created by the Simulink write to
workspace block where the save format is set to "Structure with time". Each field
in the signals substructure is plotted.
mplot(R,options) as above but Ris a Simulink.SimulationOutput object returned by
the Simulink sim() function.
Options
‘col’, C Select columns to plot, a boolean of length M-1 or a list of column indices in the range
1 to M-1
‘label’, L Label the axes according to the cell array of strings L
‘date’ Add a datestamp in the top right corner
Robotics Toolbox for MATLAB 134 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•In all cases a simple GUI is created which is invoked by a right clicking on one
of the plotted lines. The supported options are:
–zoom in the x-direction
–shift view to the left or right
–unzoom
–show data points
See also
plot2,plotp
mstraj
Multi-segment multi-axis trajectory
traj =mstraj(p,qdmax,tseg,q0,dt,tacc,options) is a trajectory (K×N) for N
axes moving simultaneously through M segment. Each segment is linear motion and
polynomial blends connect the segments. The axes start at q0 (1 ×N) and pass through
M-1 via points defined by the rows of the matrix p(M×N), and finish at the point
defined by the last row of p. The trajectory matrix has one row per time step, and one
column per axis. The number of steps in the trajectory K is a function of the number
of via points and the time or velocity limits that apply.
•p(M×N) is a matrix of via points, 1 row per via point, one column per axis.
The last via point is the destination.
•qdmax (1 ×N) are axis speed limits which cannot be exceeded,
•tseg (1 ×M) are the durations for each of the K segments
•q0 (1 ×N) are the initial axis coordinates
•dt is the time step
•tacc (1 ×1) is the acceleration time used for all segment transitions
•tacc (1 ×M) is the acceleration time per segment, tacc(i) is the acceleration time
for the transition from segment i to segment i+1. tacc(1) is also the acceleration
time at the start of segment 1.
traj =mstraj(segments,qdmax,q0,dt,tacc,qd0,qdf,options) as above but addi-
tionally specifies the initial and final axis velocities (1 ×N).
Robotics Toolbox for MATLAB 135 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘verbose’ Show details.
Notes
•Only one of qdmax or tseg can be specified, the other is set to [].
•If no output arguments are specified the trajectory is plotted.
•The path length K is a function of the number of via points, q0,dt and tacc.
•The final via point p(end,:) is the destination.
•The motion has M segments from q0 to p(1,:) to p(2,:) ... to p(end,:).
•All axes reach their via points at the same time.
•Can be used to create joint space trajectories where each axis is a joint coordi-
nate.
•Can be used to create Cartesian trajectories where the “axes” correspond to trans-
lation and orientation in RPY or Euler angle form.
See also
mtraj,lspb,ctraj
mtraj
Multi-axis trajectory between two points
[q,qd,qdd] = mtraj(tfunc,q0,qf,m) is a multi-axis trajectory (m×N) varying from
configuration q0 (1 ×N) to qf (1 ×N) according to the scalar trajectory function tfunc
in msteps. Joint velocity and acceleration can be optionally returned as qd (m×N)
and qdd (m×N) respectively. The trajectory outputs have one row per time step, and
one column per axis.
The shape of the trajectory is given by the scalar trajectory function tfunc which is
applied to each axis:
[S,SD,SDD] = TFUNC(S0, SF, M);
and possible values of tfunc include @lspb for a trapezoidal trajectory, or @tpoly for
a polynomial trajectory.
[q,qd,qdd] = mtraj(tfunc,q0,qf,T) as above but T(m×1) is a time vector which
dictates the number of points on the trajectory.
Robotics Toolbox for MATLAB 136 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•If no output arguments are specified q,qd, and qdd are plotted.
•When tfunc is @tpoly the result is functionally equivalent to JTRAJ except that
no initial velocities can be specified. JTRAJ is computationally a little more
efficient.
See also
jtraj,mstraj,lspb,tpoly
Navigation
Navigation superclass
An abstract superclass for implementing planar grid-based navigation classes.
Methods
Navigation Superclass constructor
plan Find a path to goal
query Return/animate a path from start to goal
plot Display the occupancy grid
display Display the parameters in human readable form
char Convert to string
isoccupied Test if cell is occupied
rand Uniformly distributed random number
randn Normally distributed random number
randi Uniformly distributed random integer
progress_init Create a progress bar
progress Update progress bar
progress_delete Remove progress bar
Properties (read only)
occgrid Occupancy grid representing the navigation environment
goal Goal coordinate
start Start coordinate
seed0 Random number state
Robotics Toolbox for MATLAB 137 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Methods that must be provided in subclass
plan Generate a plan for motion to goal
next Returns coordinate of next point along path
Methods that may be overriden in a subclass
goal_set The goal has been changed by nav.goal = (a,b)
navigate_init Start of path planning.
Notes
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
•A grid world is assumed and vehicle position is quantized to grid cells.
•Vehicle orientation is not considered.
•The initial random number state is captured as seed0 to allow rerunning an ex-
periment with an interesting outcome.
See also
Bug2,Dstar,Dxform,PRM,Lattice,RRT
Navigation.Navigation
Create a Navigation object
n=Navigation(occgrid,options) is a Navigation object that holds an occupancy grid
occgrid. A number of options can be be passed.
Options
‘goal’, G Specify the goal point (2 ×1)
‘inflate’, K Inflate all obstacles by K cells.
‘private’ Use private random number stream.
‘reset’ Reset random number stream.
‘verbose’ Display debugging information
‘seed’, S Set the initial state of the random number stream. S must be a proper random number
generator state such as saved in the seed0 property of an earlier run.
Robotics Toolbox for MATLAB 138 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•In the occupancy grid a value of zero means free space and non-zero means
occupied (not driveable).
•Obstacle inflation is performed with a round structuring element (kcircle) with
radius given by the ‘inflate’ option.
•Inflation requires either MVTB or IPT installed.
•The ‘private’ option creates a private random number stream for the methods
rand, randn and randi. If not given the global stream is used.
See also
randstream
Navigation.char
Convert to string
N.char() is a string representing the state of the navigation object in human-readable
form.
Navigation.display
Display status of navigation object
N.display() displays the state of the navigation object in human-readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Navigation object and the command has no trailing semicolon.
See also
Navigation.char
Robotics Toolbox for MATLAB 139 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Navigation.goal_change
Notify change of goal
Invoked when the goal property of the object is changed. Typically this is overriden in
a subclass to take particular action such as invalidating a costmap.
Navigation.isoccupied
Test if grid cell is occupied
N.isoccupied(pos) is true if there is a valid grid map and the coordinate pos (1 ×2) is
occupied. P=[X,Y] rather than MATLAB row-column coordinates.
N.isoccupied(x,y) as above but the coordinates given separately.
Navigation.message
Print debug message
N.message(s) displays the string sif the verbose property is true.
N.message(fmt,args) as above but accepts printf() like semantics.
Navigation.navigate_init
Notify start of path
N.navigate_init(start) is called when the query() method is invoked. Typically over-
riden in a subclass to take particular action such as computing some path parameters.
start (2×1) is the initial position for this path, and nav.goal (2×1) is the final position.
See also
Navigate.query
Robotics Toolbox for MATLAB 140 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Navigation.plot
Visualize navigation environment
N.plot(options) displays the occupancy grid in a new figure.
N.plot(p,options) as above but overlays the points along the path (2 ×M) matrix.
Options
‘distance’, D Display a distance field D behind the obstacle map. D is a matrix of the same size as
the occupancy grid.
‘colormap’, @f Specify a colormap for the distance field as a function handle, eg. @hsv
‘beta’, B Brighten the distance field by factor B.
‘inflated’ Show the inflated occupancy grid rather than original
Notes
•The distance field at a point encodes its distance from the goal, small distance is
dark, a large distance is bright. Obstacles are encoded as red.
•Beta value -1<B<0 to darken, 0<B<+1 to lighten.
See also
Navigation.plot_fg,Navigation.plot_bg
Navigation.plot_bg
Visualization background
N.plot_bg(options) displays the occupancy grid with occupied cells shown as red and
an optional distance field.
N.plot_bg(p,options) as above but overlays the points along the path (2 ×M) matrix.
Options
‘distance’, D Display a distance field D behind the obstacle map. D is a matrix of the same size as
the occupancy grid.
‘colormap’, @f Specify a colormap for the distance field as a function handle, eg. @hsv
‘beta’, B Brighten the distance field by factor B.
‘inflated’ Show the inflated occupancy grid rather than original
Robotics Toolbox for MATLAB 141 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘pathmarker’, M Options to draw a path point
‘startmarker’, M Options to draw the start marker
‘goalmarker’, M Options to draw the goal marker
Notes
•The distance field at a point encodes its distance from the goal, small distance is
dark, a large distance is bright. Obstacles are encoded as red.
•Beta value -1<B<0 to darken, 0<B<+1 to lighten.
See also
Navigation.plot,Navigation.plot_fg,brighten
Navigation.plot_fg
Visualization foreground
N.plot_fg(options) displays the start and goal locations if specified. By default the
goal is a pentagram and start is a circle.
N.plot_fg(p,options) as above but overlays the points along the path (2 ×M) matrix.
Options
‘pathmarker’, M Options to draw a path point
‘startmarker’, M Options to draw the start marker
‘goalmarker’, M Options to draw the goal marker
Notes
•In all cases M is a single string eg. ‘r*’ or a cell array of MATLAB LineSpec
options.
•Typically used after a call to plot_bg().
See also
Navigation.plot_bg
Robotics Toolbox for MATLAB 142 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Navigation.query
Find a path from start to goal using plan
N.query(start,options) animates the robot moving from start (2 ×1) to the goal
(which is a property of the object) using a previously computed plan.
x= N.query(start,options) returns the path (M×2) from start to the goal (which is a
property of the object).
The method performs the following steps:
•Initialize navigation, invoke method N.navigate_init()
•Visualize the environment, invoke method N.plot()
•Iterate on the next() method of the subclass until the goal is achieved.
Options
‘animate’ Show the computed path as a series of green dots.
Notes
•If start given as [] then the user is prompted to click a point on the map.
See also
Navigation.navigate_init,Navigation.plot,Navigation.goal
Navigation.rand
Uniformly distributed random number
R= N.rand() return a uniformly distributed random number from a private random
number stream.
R= N.rand(m) as above but return a matrix (m×m) of random numbers.
R= N.rand(L,m) as above but return a matrix (L×m) of random numbers.
Notes
•Accepts the same arguments as rand().
•Seed is provided to Navigation constructor.
Robotics Toolbox for MATLAB 143 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•Provides an independent sequence of random numbers that does not interfere
with any other randomised algorithms that might be used.
See also
Navigation.randi,Navigation.randn,rand,RandStream
Navigation.randi
Integer random number
i= N.randi(rm) returns a uniformly distributed random integer in the range 1 to rm
from a private random number stream.
i= N.randi(rm,m) as above but returns a matrix (m×m) of random integers.
i= N.randn(rm,L,m) as above but returns a matrix (L×m) of random integers.
Notes
•Accepts the same arguments as randi().
•Seed is provided to Navigation constructor.
•Provides an independent sequence of random numbers that does not interfere
with any other randomised algorithms that might be used.
See also
Navigation.rand,Navigation.randn,randi,RandStream
Navigation.randn
Normally distributed random number
R= N.randn() returns a normally distributed random number from a private random
number stream.
R= N.randn(m) as above but returns a matrix (m×m) of random numbers.
R= N.randn(L,m) as above but returns a matrix (L×m) of random numbers.
Robotics Toolbox for MATLAB 144 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Accepts the same arguments as randn().
•Seed is provided to Navigation constructor.
•Provides an independent sequence of random numbers that does not interfere
with any other randomised algorithms that might be used.
See also
Navigation.rand,Navigation.randi,randn,RandStream
Navigation.spinner
Update progress spinner
N.spinner() displays a simple ASCII progress spinner, a rotating bar.
Navigation.verbosity
Set verbosity
N.verbosity(v) set verbosity to v, where 0 is silent and greater values display more
information.
numcols
Number of columns in matrix
nc =numcols(m) is the number of columns in the matrix m.
Notes
•Readable shorthand for SIZE(m,2);
Robotics Toolbox for MATLAB 145 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
numrows,size
numrows
Number of rows in matrix
nr =numrows(m) is the number of rows in the matrix m.
Notes
•Readable shorthand for SIZE(m,1);
See also
numcols,size
oa2r
Convert orientation and approach vectors to rotation matrix
R=oa2r(o,a) is an SO(3) rotation matrix (3 ×3) for the specified orientation and
approach vectors (3 ×1) formed from 3 vectors such that R= [N o a] and N = oxa.
Notes
•The matrix is guaranteed to be orthonormal so long as oand aare not parallel.
•The vectors oand aare parallel to the Y- and Z-axes of the coordinate frame.
References
•Robot manipulators: mathematics, programming and control Richard Paul, MIT
Press, 1981.
Robotics Toolbox for MATLAB 146 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
rpy2r,eul2r,oa2tr,SO3.oa
oa2tr
Convert orientation and approach vectors to homogeneous
transformation
T=oa2tr(o,a) is an SE(3) homogeneous tranformation (4 ×4) for the specified orien-
tation and approach vectors (3 ×1) formed from 3 vectors such that R = [N o a] and N
=oxa.
Notes
•The rotation submatrix is guaranteed to be orthonormal so long as oand aare
not parallel.
•The translational part is zero.
•The vectors oand aare parallel to the Y- and Z-axes of the coordinate frame.
References
•Robot manipulators: mathematics, programming and control Richard Paul, MIT
Press, 1981.
See also
rpy2tr,eul2tr,oa2r,SE3.oa
ParticleFilter
Particle filter class
Monte-carlo based localisation for estimating vehicle pose based on odometry and ob-
servations of known landmarks.
Robotics Toolbox for MATLAB 147 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Methods
run run the particle filter
plot_xy display estimated vehicle path
plot_pdf display particle distribution
Properties
robot reference to the robot object
sensor reference to the sensor object
history vector of structs that hold the detailed information from each time step
nparticles number of particles used
x particle states; nparticles x 3
weight particle weights; nparticles x 1
x_est mean of the particle population
std standard deviation of the particle population
Q covariance of noise added to state at each step
L covariance of likelihood model
w0 offset in likelihood model
dim maximum xy dimension
Example
Create a landmark map
map = PointMap(20);
and a vehicle with odometry covariance and a driver
W = diag([0.1, 1*pi/180].^2);
veh = Vehicle(W);
veh.add_driver( RandomPath(10) );
and create a range bearing sensor
R = diag([0.005, 0.5*pi/180].^2);
sensor = RangeBearingSensor(veh, map, R);
For the particle filter we need to define two covariance matrices. The first is is the
covariance of the random noise added to the particle states at each iteration to represent
uncertainty in configuration.
Q = diag([0.1, 0.1, 1*pi/180]).^2;
and the covariance of the likelihood function applied to innovation
L = diag([0.1 0.1]);
Now construct the particle filter
pf = ParticleFilter(veh, sensor, Q, L, 1000);
which is configured with 1000 particles. The particles are initially uniformly dis-
tributed over the 3-dimensional configuration space.
Robotics Toolbox for MATLAB 148 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
We run the simulation for 1000 time steps
pf.run(1000);
then plot the map and the true vehicle path
map.plot();
veh.plot_xy(’b’);
and overlay the mean of the particle cloud
pf.plot_xy(’r’);
We can plot the standard deviation against time
plot(pf.std(1:100,:))
The particles are a sampled approximation to the PDF and we can display this as
pf.plot_pdf()
Acknowledgement
Based on code by Paul Newman, Oxford University, http://www.robots.ox.ac.uk/ pnew-
man
Reference
Robotics, Vision & Control, Peter Corke, Springer 2011
See also
Vehicle,RandomPath,RangeBearingSensor,PointMap,EKF
ParticleFilter.ParticleFilter
Particle filter constructor
pf =ParticleFilter(vehicle,sensor,q,L,np,options) is a particle filter that estimates
the state of the vehicle with a landmark sensor sensor.qis the covariance of the noise
added to the particles at each step (diffusion), Lis the covariance used in the sensor
likelihood model, and np is the number of particles.
Options
‘verbose’ Be verbose.
‘private’ Use private random number stream.
‘reset’ Reset random number stream.
Robotics Toolbox for MATLAB 149 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘seed’, S Set the initial state of the random number stream. S must be a proper random number
generator state such as saved in the seed0 property of an earlier run.
‘nohistory’ Don’t save history.
‘x0’ Initial particle states (N×3)
Notes
•ParticleFilter subclasses Handle, so it is a reference object.
•If initial particle states not given they are set to a uniform distribution over the
map, essentially the kidnapped robot problem which is quite unrealistic.
•Initial particle weights are always set to unity.
•The ‘private’ option creates a private random number stream for the methods
rand, randn and randi. If not given the global stream is used.
See also
Vehicle,Sensor,RangeBearingSensor,PointMap
ParticleFilter.char
Convert to string
PF.char() is a string representing the state of the ParticleFilter object in human-
readable form.
See also
ParticleFilter.display
ParticleFilter.display
Display status of particle filter object
PF.display() displays the state of the ParticleFilter object in human-readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a ParticleFilter object and the command has no trailing semicolon.
Robotics Toolbox for MATLAB 150 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
ParticleFilter.char
ParticleFilter.init
Initialize the particle filter
PF.init() initializes the particle distribution and clears the history.
Notes
•If initial particle states were given to the constructor the states are set to this
value, else a random distribution over the map is used.
•Invoked by the run() method.
ParticleFilter.plot_pdf
Plot particles as a PDF
PF.plot_pdf() plots a sparse PDF as a series of vertical line segments of height equal
to particle weight.
ParticleFilter.plot_xy
Plot vehicle position
PF.plot_xy() plots the estimated vehicle path in the xy-plane.
PF.plot_xy(ls) as above but the optional line style arguments ls are passed to plot.
ParticleFilter.run
Run the particle filter
PF.run(n,options) runs the filter for ntime steps.
Robotics Toolbox for MATLAB 151 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
Robotics Toolbox for MATLAB 152 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘noplot’ Do not show animation.
Notes
•All previously estimated states and estimation history is cleared.
peak
Find peaks in vector
yp =peak(y,options) are the values of the maxima in the vector y.
[yp,i] = peak(y,options) as above but also returns the indices of the maxima in the
vector y.
[yp,xp] = peak(y,x,options) as above but also returns the corresponding x-coordinates
of the maxima in the vector y.xis the same length as yand contains the corresponding
x-coordinates.
Options
‘npeaks’, N Number of peaks to return (default all)
‘scale’, S Only consider as peaks the largest value in the horizontal range +/- S points.
‘interp’, M Order of interpolation polynomial (default no interpolation)
‘plot’ Display the interpolation polynomial overlaid on the point data
Notes
•A maxima is defined as an element that larger than its two neighbours. The first
and last element will never be returned as maxima.
•To find minima, use peak(-V).
•The interp options fits points in the neighbourhood about the peak with an Mth
order polynomial and its peak position is returned. Typically choose M to be
even. In this case xp will be non-integer.
See also
peak2
Robotics Toolbox for MATLAB 153 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
peak2
Find peaks in a matrix
zp =peak2(z,options) are the peak values in the 2-dimensional signal z.
[zp,ij] = peak2(z,options) as above but also returns the indices of the maxima in the
matrix z. Use SUB2IND to convert these to row and column coordinates
Options
‘npeaks’, N Number of peaks to return (default all)
‘scale’, S Only consider as peaks the largest value in the horizontal and vertical range +/- S
points.
‘interp’ Interpolate peak (default no interpolation)
‘plot’ Display the interpolation polynomial overlaid on the point data
Notes
•A maxima is defined as an element that larger than its eight neighbours. Edges
elements will never be returned as maxima.
•To find minima, use peak2(-V).
•The interp options fits points in the neighbourhood about the peak with a paraboloid
and its peak position is returned. In this case ij will be non-integer.
See also
peak,sub2ind
PGraph
Graph class
g = PGraph() create a 2D, planar embedded, directed graph
g = PGraph(n) create an n-d, embedded, directed graph
Provides support for graphs that:
•are directed
Robotics Toolbox for MATLAB 154 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•are embedded in a coordinate system
•have symmetric cost edges (A to B is same cost as B to A)
•have no loops (edges from A to A)
•have vertices that are represented by integers VID
•have edges that are represented by integers EID
Methods
Constructing the graph
g.add_node(coord) add vertex, return vid
g.add_edge(v1, v2) add edge from v1 to v2, return eid
g.setcost(e, c) set cost for edge e
g.setdata(v, u) set user data for vertex v
g.data(v) get user data for vertex v
g.clear() remove all vertices and edges from the graph
Information from graph
g.edges(v) list of edges for vertex v
g.cost(e) cost of edge e
g.neighbours(v) neighbours of vertex v
g.component(v) component id for vertex v
g.connectivity() number of edges for all vertices
Display
g.plot() set goal vertex for path planning
g.highlight_node(v) highlight vertex v
g.highlight_edge(e) highlight edge e
g.highlight_component(c) highlight all nodes in component c
g.highlight_path(p) highlight nodes and edge along path p
g.pick(coord) vertex closest to coord
g.char() convert graph to string
g.display() display summary of graph
Robotics Toolbox for MATLAB 155 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Matrix representations
g.adjacency() adjacency matrix
g.incidence() incidence matrix
g.degree() degree matrix
g.laplacian() Laplacian matrix
Planning paths through the graph
g.Astar(s, g) shortest path from s to g
g.goal(v) set goal vertex, and plan paths
g.path(v) list of vertices from v to goal
Graph and world points
g.coord(v) coordinate of vertex v
g.distance(v1, v2) distance between v1 and v2
g.distances(coord) return sorted distances from coord to all vertices
g.closest(coord) vertex closest to coord
Object properties (read only)
g.n number of vertices
g.ne number of edges
g.nc number of components
Examples
g = PGraph();
g.add_node([1 2]’); % add node 1
g.add_node([3 4]’); % add node 1
g.add_node([1 3]’); % add node 1
g.add_edge(1, 2); % add edge 1-2
g.add_edge(2, 3); % add edge 2-3
g.add_edge(1, 3); % add edge 1-3
g.plot()
Notes
•Support for edge direction is rudimentary.
Robotics Toolbox for MATLAB 156 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.PGraph
Graph class constructor
g=PGraph(d,options) is a graph object embedded in ddimensions.
Options
‘distance’, M Use the distance metric M for path planning which is either ‘Euclidean’ (default) or
‘SE2’.
‘verbose’ Specify verbose operation
Notes
•Number of dimensions is not limited to 2 or 3.
•The distance metric ‘SE2’ is the sum of the squares of the difference in position
and angle modulo 2pi.
•To use a different distance metric create a subclass of PGraph and override the
method distance_metric().
PGraph.add_edge
Add an edge
E= G.add_edge(v1,v2) adds a directed edge from vertex id v1 to vertex id v2, and
returns the edge id E. The edge cost is the distance between the vertices.
E= G.add_edge(v1,v2,C) as above but the edge cost is C.
Notes
•If v2 is a vector add edges from v1 to all elements of v2
•Distance is computed according to the metric specified in the constructor.
See also
PGraph.add_node,PGraph.edgedir
Robotics Toolbox for MATLAB 157 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.add_node
Add a node
v= G.add_node(x) adds a node/vertex with coordinate x(D×1) and returns the integer
node id v.
v= G.add_node(x,vfrom) as above but connected by a directed edge from vertex
vfrom with cost equal to the distance between the vertices.
v= G.add_node(x,v2,C) as above but the added edge has cost C.
Notes
•Distance is computed according to the metric specified in the constructor.
See also
PGraph.add_edge,PGraph.data,PGraph.getdata
PGraph.adjacency
Adjacency matrix of graph
a= G.adjacency() is a matrix (N×N) where element a(i,j) is the cost of moving from
vertex i to vertex j.
Notes
•Matrix is symmetric.
•Eigenvalues of aare real and are known as the spectrum of the graph.
•The element a(I,J) can be considered the number of walks of one edge from
vertex I to vertex J (either zero or one). The element (I,J) of aNare the number
of walks of length N from vertex I to vertex J.
See also
PGraph.degree,PGraph.incidence,PGraph.laplacian
Robotics Toolbox for MATLAB 158 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.Astar
path finding
path = G.Astar(v1,v2) is the lowest cost path from vertex v1 to vertex v2.path is a
list of vertices starting with v1 and ending v2.
[path,C] = G.Astar(v1,v2) as above but also returns the total cost of traversing path.
Notes
•Uses the efficient A* search algorithm.
•The heuristic is the distance function selected in the constructor, it must be ad-
missible, meaning that it never overestimates the actual cost to get to the nearest
goal node.
References
•Correction to “A Formal Basis for the Heuristic Determination of Minimum Cost
Paths”. Hart, P. E.; Nilsson, N. J.; Raphael, B. SIGART Newsletter 37: 28-29,
1972.
See also
PGraph.goal,PGraph.path
PGraph.char
Convert graph to string
s= G.char() is a compact human readable representation of the state of the graph
including the number of vertices, edges and components.
PGraph.clear
Clear the graph
G.clear() removes all vertices, edges and components.
Robotics Toolbox for MATLAB 159 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.closest
Find closest vertex
v= G.closest(x) is the vertex geometrically closest to coordinate x.
[v,d] = G.closest(x) as above but also returns the distance d.
See also
PGraph.distances
PGraph.component
Graph component
C= G.component(v) is the id of the graph component that contains vertex v.
PGraph.componentnodes
Graph component
C= G.component(v) is the id of the graph component that contains vertex v.
PGraph.connectivity
Node connectivity
C= G.connectivity() is a vector (N×1) with the number of edges per vertex.
The average vertex connectivity is
mean(g.connectivity())
and the minimum vertex connectivity is
min(g.connectivity())
Robotics Toolbox for MATLAB 160 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.connectivity_in
Graph connectivity
C= G.connectivity() is a vector (N×1) with the number of edges per vertex.
The average vertex connectivity is
mean(g.connectivity())
and the minimum vertex connectivity is
min(g.connectivity())
PGraph.connectivity_out
Graph connectivity
C= G.connectivity() is a vector (N×1) with the number of edges per vertex.
The average vertex connectivity is
mean(g.connectivity())
and the minimum vertex connectivity is
min(g.connectivity())
PGraph.coord
Coordinate of node
x= G.coord(v) is the coordinate vector (D×1) of vertex id v.
PGraph.cost
Cost of edge
C= G.cost(E) is the cost of edge id E.
Robotics Toolbox for MATLAB 161 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.degree
Degree matrix of graph
d= G.degree() is a diagonal matrix (N×N) where element d(i,i) is the number of
edges connected to vertex id i.
See also
PGraph.adjacency,PGraph.incidence,PGraph.laplacian
PGraph.display
Display graph
G.display() displays a compact human readable representation of the state of the graph
including the number of vertices, edges and components.
See also
PGraph.char
PGraph.distance
Distance between vertices
d= G.distance(v1,v2) is the geometric distance between the vertices v1 and v2.
See also
PGraph.distances
PGraph.distances
Distances from point to vertices
d= G.distances(x) is a vector (1×N) of geometric distance from the point x(d×1) to
every other vertex sorted into increasing order.
Robotics Toolbox for MATLAB 162 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
[d,w] = G.distances(p) as above but also returns w(1 ×N) with the corresponding
vertex id.
Notes
•Distance is computed according to the metric specified in the constructor.
See also
PGraph.closest
PGraph.edata
Get user data for node
u= G.data(v) gets the user data of vertex vwhich can be of any type such as a number,
struct, object or cell array.
See also
PGraph.setdata
PGraph.edgedir
Find edge direction
d= G.edgedir(v1,v2) is the direction of the edge from vertex id v1 to vertex id v2.
If we add an edge from vertex 3 to vertex 4
g.add_edge(3, 4)
then
g.edgedir(3, 4)
is positive, and
g.edgedir(4, 3)
is negative.
See also
PGraph.add_node,PGraph.add_edge
Robotics Toolbox for MATLAB 163 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.edges
Find edges given vertex
E= G.edges(v) is a vector containing the id of all edges connected to vertex id v.
See also
PGraph.edgedir
PGraph.edges_in
Find edges given vertex
E= G.edges(v) is a vector containing the id of all edges connected to vertex id v.
See also
PGraph.edgedir
PGraph.edges_out
Find edges given vertex
E= G.edges(v) is a vector containing the id of all edges connected to vertex id v.
See also
PGraph.edgedir
PGraph.get.n
Number of vertices
G.n is the number of vertices in the graph.
Robotics Toolbox for MATLAB 164 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
PGraph.ne
PGraph.get.nc
Number of components
G.nc is the number of components in the graph.
See also
PGraph.component
PGraph.get.ne
Number of edges
G.ne is the number of edges in the graph.
See also
PGraph.n
PGraph.graphcolor
the graph
PGraph.highlight_component
Highlight a graph component
G.highlight_component(C,options) highlights the vertices that belong to graph com-
ponent C.
Robotics Toolbox for MATLAB 165 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘NodeSize’, S Size of vertex circle (default 12)
‘NodeFaceColor’, CNode circle color (default yellow)
‘NodeEdgeColor’, CNode circle edge color (default blue)
See also
PGraph.highlight_node,PGraph.highlight_edge,PGraph.highlight_component
PGraph.highlight_edge
Highlight a node
G.highlight_edge(v1,v2) highlights the edge between vertices v1 and v2.
G.highlight_edge(E) highlights the edge with id E.
Options
‘EdgeColor’, C Edge edge color (default black)
‘EdgeThickness’, T Edge thickness (default 1.5)
See also
PGraph.highlight_node,PGraph.highlight_path,PGraph.highlight_component
PGraph.highlight_node
Highlight a node
G.highlight_node(v,options) highlights the vertex vwith a yellow marker. If vis a
list of vertices then all are highlighted.
Options
‘NodeSize’, S Size of vertex circle (default 12)
‘NodeFaceColor’, C Node circle color (default yellow)
‘NodeEdgeColor’, C Node circle edge color (default blue)
Robotics Toolbox for MATLAB 166 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
PGraph.highlight_edge,PGraph.highlight_path,PGraph.highlight_component
PGraph.highlight_path
Highlight path
G.highlight_path(p,options) highlights the path defined by vector pwhich is a list of
vertex ids comprising the path.
Options
‘NodeSize’, S Size of vertex circle (default 12)
‘NodeFaceColor’, C Node circle color (default yellow)
‘NodeEdgeColor’, C Node circle edge color (default blue)
‘EdgeColor’, C Node circle edge color (default black)
‘EdgeThickness’, T Edge thickness (default 1.5)
See also
PGraph.highlight_node,PGraph.highlight_edge,PGraph.highlight_component
PGraph.incidence
Incidence matrix of graph
in = G.incidence() is a matrix (N×NE) where element in(i,j) is non-zero if vertex id i
is connected to edge id j.
See also
PGraph.adjacency,PGraph.degree,PGraph.laplacian
PGraph.laplacian
Laplacian matrix of graph
L= G.laplacian() is the Laplacian matrix (N×N) of the graph.
Robotics Toolbox for MATLAB 167 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Lis always positive-semidefinite.
•Lhas at least one zero eigenvalue.
•The number of zero eigenvalues is the number of connected components in the
graph.
See also
PGraph.adjacency,PGraph.incidence,PGraph.degree
PGraph.neighbours
Neighbours of a vertex
n= G.neighbours(v) is a vector of ids for all vertices which are directly connected
neighbours of vertex v.
[n,C] = G.neighbours(v) as above but also returns a vector Cwhose elements are the
edge costs of the paths corresponding to the vertex ids in n.
PGraph.neighbours_d
Directed neighbours of a vertex
n= G.neighbours_d(v) is a vector of ids for all vertices which are directly connected
neighbours of vertex v. Elements are positive if there is a link from vto the node
(outgoing), and negative if the link is from the node to v(incoming).
[n,C] = G.neighbours_d(v) as above but also returns a vector Cwhose elements are
the edge costs of the paths corresponding to the vertex ids in n.
PGraph.neighbours_in
Incoming neighbours of a vertex
n= G.neighbours(v) is a vector of ids for all vertices which are directly connected
neighbours of vertex v.
[n,C] = G.neighbours(v) as above but also returns a vector Cwhose elements are the
edge costs of the paths corresponding to the vertex ids in n.
Robotics Toolbox for MATLAB 168 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.neighbours_out
Outgoing neighbours of a vertex
n= G.neighbours(v) is a vector of ids for all vertices which are directly connected
neighbours of vertex v.
[n,C] = G.neighbours(v) as above but also returns a vector Cwhose elements are the
edge costs of the paths corresponding to the vertex ids in n.
PGraph.pick
Graphically select a vertex
v= G.pick() is the id of the vertex closest to the point clicked by the user on a plot of
the graph.
See also
PGraph.plot
PGraph.plot
Plot the graph
G.plot(opt) plots the graph in the current figure. Nodes are shown as colored circles.
Options
‘labels’ Display vertex id (default false)
‘edges’ Display edges (default true)
‘edgelabels’ Display edge id (default false)
‘NodeSize’, S Size of vertex circle (default 8)
‘NodeFaceColor’, C Node circle color (default blue)
‘NodeEdgeColor’, C Node circle edge color (default blue)
‘NodeLabelSize’, S Node label text sizer (default 16)
‘NodeLabelColor’, C Node label text color (default blue)
‘EdgeColor’, C Edge color (default black)
‘EdgeLabelSize’, S Edge label text size (default black)
‘EdgeLabelColor’, C Edge label text color (default black)
‘componentcolor’ Node color is a function of graph component
‘only’, N Only show these nodes
Robotics Toolbox for MATLAB 169 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PGraph.samecomponent
Graph component
C= G.component(v) is the id of the graph component that contains vertex v.
PGraph.setcoord
Coordinate of node
x= G.coord(v) is the coordinate vector (D×1) of vertex id v.
PGraph.setcost
Set cost of edge
G.setcost(E,C) set cost of edge id Eto C.
PGraph.setedata
Set user data for node
G.setdata(v,u) sets the user data of vertex vto uwhich can be of any type such as a
number, struct, object or cell array.
See also
PGraph.data
PGraph.setvdata
Set user data for node
G.setdata(v,u) sets the user data of vertex vto uwhich can be of any type such as a
number, struct, object or cell array.
Robotics Toolbox for MATLAB 170 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
PGraph.data
PGraph.vdata
Get user data for node
u= G.data(v) gets the user data of vertex vwhich can be of any type such as a number,
struct, object or cell array.
See also
PGraph.setdata
PGraph.vertices
Find vertices given edge
v= G.vertices(E) return the id of the vertices that define edge E.
pickregion
Pick a rectangular region of a figure using mouse
[p1,p2] = pickregion() initiates a rubberband box at the current click point and ani-
mates it so long as the mouse button remains down. Returns the first and last coordi-
nates in axis units.
Options
‘axis’, A The axis to select from (default current axis)
‘ls’, LS Line style for foreground line (default ‘:y’);
’bg’LS, Line style for background line (default ‘-k’);
‘width’, W Line width (default 2)
‘pressed’ Don’t wait for first button press, use current position
Robotics Toolbox for MATLAB 171 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Effectively a replacement for the builtin rbbox function which draws the box in
the wrong location on my Mac’s external monitor.
Author
Based on rubberband box from MATLAB Central written/Edited by Bob Hamans
(B.C.Hamans@student.tue.nl) 02-04-2003, in turn based on an idea of Sandra Mar-
tinka’s Rubberline.
plot2
Plot trajectories
Convenience function for plotting 2D or 3D trajectory data stored in a matrix with one
row per time step.
plot2(p) plots a line with coordinates taken from successive rows of p.pcan be N×2
or N×3.
If phas three dimensions, ie. N×2×Mor N×3×Mthen the M trajectories are
overlaid in the one plot.
plot2(p,ls) as above but the line style arguments ls are passed to plot.
See also
mplot,plot
plot_arrow
Draw an arrow in 2D or 3D
plot_arrow(p1,p2,options) draws an arrow from p1 to p2 (2 ×1 or 3 ×1).
plot_arrow(p,options) as above where the columns of p(2 ×2 or 3×2) define where
p=[p1 p2].
Robotics Toolbox for MATLAB 172 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
•All options are passed through to arrow3.
•MATLAB colorspec such as ‘r’ or ‘b–’
See also
arrow3
plot_box
Draw a box
plot_box(b,options) draws a box defined by b=[XL XR; YL YR] on the current plot
with optional MATLAB linestyle options LS.
plot_box(x1,y1,x2,y2,options) draws a box with corners at (x1,y1) and (x2,y2), and
optional MATLAB linestyle options LS.
plot_box(’centre’, P, ‘size’, W, options) draws a box with center at P=[X,Y] and with
dimensions W=[WIDTH HEIGHT].
plot_box(’topleft’, P, ‘size’, W, options) draws a box with top-left at P=[X,Y] and with
dimensions W=[WIDTH HEIGHT].
plot_box(’matlab’, BOX, LS) draws box(es) as defined using the MATLAB convention
of specifying a region in terms of top-left coordinate, width and height. One box is
drawn for each row of BOX which is [xleft ytop width height].
Options
‘edgecolor’ the color of the circle’s edge, Matlab color spec
‘fillcolor’ the color of the circle’s interior, Matlab color spec
‘alpha’ transparency of the filled circle: 0=transparent, 1=solid
•For an unfilled box any standard MATLAB LineStyle such as ‘r’ or ‘b—’.
•For an unfilled box any MATLAB LineProperty options can be given such as
‘LineWidth’, 2.
•For a filled box any MATLAB PatchProperty options can be given.
Robotics Toolbox for MATLAB 173 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The box is added to the current plot irrespective of hold status.
•Additional options LS are MATLAB LineSpec options and are passed to PLOT.
See also
plot_poly,plot_circle,plot_ellipse
plot_circle
Draw a circle
plot_circle(C,R,options) draws a circle on the current plot with centre C=[X,Y] and
radius R. If C=[X,Y,Z] the circle is drawn in the XY-plane at height Z.
If C(2 ×N) then N circles are drawn and H is N×1. If R(1 ×1) then all circles have
the same radius or else R(1 ×N) to specify the radius of each circle.
H=plot_circle(C,R,options) as above but return handles. For multiple circles His a
vector of handles, one per circle.
Animation
First draw the circle and keep its graphic handle, then alter it, eg.
H = PLOT_CIRCLE(C, R)
PLOT_ELLIPSE(C, R, ’alter’, H);
Options
‘edgecolor’ the color of the circle’s edge, Matlab color spec
‘fillcolor’ the color of the circle’s interior, Matlab color spec
‘alpha’ transparency of the filled circle: 0=transparent, 1=solid
‘alter’, Halter existing circles with handle H
•For an unfilled circle any standard MATLAB LineStyle such as ‘r’ or ‘b—’.
•For an unfilled circle any MATLAB LineProperty options can be given such as
‘LineWidth’, 2.
•For a filled circle any MATLAB PatchProperty options can be given.
Robotics Toolbox for MATLAB 174 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The circle(s) is added to the current plot irrespective of hold status.
See also
plot_ellipse,plot_box,plot_poly
plot_ellipse
Draw an ellipse or ellipsoid
plot_ellipse(E,options) draws an ellipse or ellipsoid defined by X’EX = 0 on the
current plot, centred at the origin. E(2 ×2) for an ellipse and E(2 ×3) for an ellipsoid.
plot_ellipse(E,C,options) as above but centred at C=[X,Y]. If C=[X,Y,Z] the ellipse
is parallel to the XY plane but at height Z.
H=plot_ellipse(E,C,options) as above but return graphic handle.
Animation
First draw the ellipse and keep its graphic handle, then alter it, eg.
H = PLOT_ELLIPSE(E, C, ’r’)
PLOT_ELLIPSE(C, R, ’alter’, H);
Options
‘confidence’, Cconfidence interval, range 0 to 1
‘alter’, Halter existing ellipses with handle H
‘npoints’, N use N points to define the ellipse (default 40)
‘edgecolor’ color of the ellipse boundary edge, MATLAB color spec
‘fillcolor’ the color of the circle’s interior, MATLAB color spec
‘alpha’ transparency of the fillcolored circle: 0=transparent, 1=solid
‘shadow’ show shadows on the 3 walls of the plot box
•For an unfilled ellipse any standard MATLAB LineStyle such as ‘r’ or ‘b—’.
•For an unfilled ellipse any MATLAB LineProperty options can be given such as
‘LineWidth’, 2.
•For a filled ellipse any MATLAB PatchProperty options can be given.
Robotics Toolbox for MATLAB 175 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•If A (2 ×2) draw an ellipse, else if A(3 ×3) draw an ellipsoid.
•The ellipse is added to the current plot irrespective of hold status.
•Shadow option only valid for ellipsoids.
•If a confidence interval is given the scaling factor is com;uted using an approxi-
mate inverse chi-squared function.
See also
plot_ellipse_inv,plot_circle,plot_box,plot_poly
plot_homline
Draw a line in homogeneous form
plot_homline(L,ls) draws a line in the current plot defined by L.X = 0 where L(3×1).
The current axis limits are used to determine the endpoints of the line. MATLAB line
specification ls can be set. If L(3 ×N) then N lines are drawn, one per column.
H=plot_homline(L,ls) as above but returns a vector of graphics handles for the lines.
Notes
•The line(s) is added to the current plot.
•The line(s) can be drawn in 3D axes but will always lie in the xy-plane.
See also
plot_box,plot_poly,homline
Robotics Toolbox for MATLAB 176 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
plot_point
Draw a point
plot_point(p,options) adds point markers to the current plot, where p(2 ×N) and
each column is the point coordinate.
Options
‘textcolor’, colspec Specify color of text
‘textsize’, size Specify size of text
‘bold’ Text in bold font.
‘printf’, {fmt, data}Label points according to printf format string and corresponding element of data
‘sequence’ Label points sequentially
‘label’, L Label for point
Additional options to PLOT can be used:
•standard MATLAB LineStyle such as ‘r’ or ‘b—’
•any MATLAB LineProperty options can be given such as ‘LineWidth’, 2.
Examples
Simple point plot
P = rand(2,4);
plot_point(P);
Plot points with markers
plot_point(P, ’*’);
Plot points with markers
plot_point(P, ’o’, ’MarkerFaceColor’, ’b’);
Plot points with square markers and labels 1 to 4
plot_point(P, ’sequence’, ’s’);
Plot points with circles and annotations P1 to P4
data = [1 2 4 8];
plot_point(P, ’printf’, {’ P%d’, data}, ’o’);
Notes
•The point(s) and annotations are added to the current plot.
•Points can be drawn in 3D axes but will always lie in the xy-plane.
Robotics Toolbox for MATLAB 177 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
plot,text
plot_poly
Draw a polygon
plot_poly(p,options) adds a polygon defined by columns of p(2 ×N), in the current
plot with default line style.
H=plot_poly(p,options) as above but processes additional options and returns a
graphics handle.
Animation
plot_poly(H,T) sets the pose of the polygon with handle Hto the pose given by T
(3 ×3 or 4 ×4).
Create a polygon that can be animated, then alter it, eg.
H = PLOT_POLY(P, ’animate’, ’r’)
PLOT_POLY(H, transl(2,1,0) );
options
‘fillcolor’,F the color of the circle’s interior, MATLAB color spec
‘alpha’, A transparency of the filled circle: 0=transparent, 1=solid.
‘edgecolor’,E edge color
‘animate’ the polygon can be animated
‘tag’, Tthe polygon is created with a handle graphics tag
•For an unfilled polygon any standard MATLAB LineStyle such as ‘r’ or ‘b—’.
•For an unfilled polygon any MATLAB LineProperty options can be given such
as ‘LineWidth’, 2.
•For a filled polygon any MATLAB PatchProperty options can be given.
Robotics Toolbox for MATLAB 178 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•If p(3 ×N) the polygon is drawn in 3D
•If not filled the polygon is a line segment, otherwise it is a patch object.
•The ‘animate’ option creates an hgtransform object as a parent of the polygon,
which can be animated by the last call signature above.
•The graphics are added to the current plot.
See also
plot_box,plot_circle,patch,Polygon
plot_sphere
Draw sphere
plot_sphere(C,R,ls) draws spheres in the current plot. Cis the centre of the sphere
(3 ×1), Ris the radius and ls is an optional MATLAB ColorSpec, either a letter or a
3-vector.
H=plot_sphere(C,R,color) as above but returns the handle(s) for the spheres.
H=plot_sphere(C,R,color,alpha) as above but alpha specifies the opacity of the
sphere where 0 is transparant and 1 is opaque. The default is 1.
If C(3 ×N) then N sphhere are drawn and His N×1. If R(1 ×1) then all spheres
have the same radius or else R(1 ×N) to specify the radius of each sphere.
Example
Create four spheres
plot_sphere( mkgrid(2, 1), .2, ’b’)
and now turn on a full lighting model
lighting gouraud
light
NOTES
•The sphere is always added, irrespective of figure hold state.
•The number of vertices to draw the sphere is hardwired.
Robotics Toolbox for MATLAB 179 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
plot_vehicle
Draw mobile robot pose
plot_vehicle(x,options) draws an oriented triangle to represent the pose of a mobile
robot moving in a planar world. The pose x(1 ×3) = [x,y,theta]. If xis a matrix
(N×3) then an animation of the robot motion is shown and animated at the specified
frame rate.
Animation mode
H=plot_vehicle(x,options) as above draws the robot and returns a handle.
plot_vehicle(x, ‘handle’, H) updates the pose x(1 ×3) of the previously drawn robot.
Image mode
plot_vehicle(x, ‘image’, IMG) where IMG is an RGB image that is scaled and centered
on the robot’s position. The vertical axis of the image becomes the x-axi in the plot, ie.
it is rotated. If you wish to specify the rotation then use
plot_vehicle(x, ‘image’, {IMG,R}) where R is the counterclockwise rotation angle in
degrees.
Options
‘scale’, S draw vehicle with length S x maximum axis dimension (default 1/60)
‘size’, S draw vehicle with length S
‘fillcolor’, F the color of the circle’s interior, MATLAB color spec
‘alpha’, A transparency of the filled circle: 0=transparent, 1=solid
‘box’ draw a box shape (default is triangle)
‘fps’, F animate at F frames per second (default 10)
‘image’, I use an image to represent the robot pose
‘retain’ when x(N×3) then retain the robots, leaving a trail
Notes
•The vehicle is drawn relative to the size of the axes, so set them first using axis().
•For backward compatibility, ‘fill’, is a synonym for ‘fillcolor’
Robotics Toolbox for MATLAB 180 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
See also
Vehicle.plot,plot_poly
plotbotopt
Define default options for robot plotting
A user provided function that returns a cell array of default plot options for the Seri-
alLink.plot method.
See also
SerialLink.plot
plotp
Plot trajectory
Convenience function to plot points stored columnwise.
plotp(p) plots a set of points p, which by Toolbox convention are stored one per col-
umn. pcan be 2 ×Nor 3 ×N. By default a linestyle of ‘bx’ is used.
plotp(p,ls) as above but the line style arguments ls are passed to plot.
See also
plot,plot2
Robotics Toolbox for MATLAB 181 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
plotvol
Set the bounds for a 2D or 3D plot
plotvol(w) creates a new axis, and sets the bounds for a 2D plot with X and Y spanning
the interval -wto w. The axes are labelled, grid is enabled, aspect ratio set to 1:1, and
hold is enabled for subsequent plots.
plotvol([XMIN XMAX YMIN YMAX]) as above but the X and Y axis limits are
explicitly provided.
plotvol([XMIN XMAX YMIN YMAX ZMIN ZMAX]) as above but the X, Y and Z
axis limits are explicitly provided.
See also
axis,xaxis,yaxis
Plucker
Plucker coordinate class
Concrete class to represent a line in Plucker coordinates.
Methods
line Return Plucker line coordinates (1 ×6)
side Side operator
origin_closest origin_distance distance mindist point pp L intersect
Operators
* Multiply Plucker matrix by a general matrix
| Side operator
Notes
•This is reference class object
Robotics Toolbox for MATLAB 182 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•Link objects can be used in vectors and arrays
References
•Ken Shoemake, “Ray Tracing News”, Volume 11, Number 1 http://www.realtimerendering.com/resources/RTNews/html/rtnv11n1.html#art3
Plucker.Plucker
Create Plucker object
p=Plucker(p1,p2) create a Plucker object that represents the line joining the 3D
points p1 (3 ×1) and p2 (3 ×1).
p=Plucker(’points’, p1,p2) as above.
p=Plucker(’planes’, PL1, PL2) create a Plucker object that represents the line formed
by the intersection of two planes PL1, PL2 (4 ×1).
p=Plucker(’wv’, W, V) create a Plucker object from its direction W (3 ×1) and
moment vectors V (3 ×1).
p=Plucker(’Pw’, p, W) create a Plucker object from a point p(3 ×1) and direction
vector W (3 ×1).
Plucker.char
Convert to string
s= P.char() is a string showing Plucker parameters in a compact single line format.
See also
Plucker.display
Plucker.closest
Point on line closest to given point
p= PL.closest(x) is the coordinate of a point on the line that is closest to the point x
(3 ×1).
[p,d] = PL.closest(x) as above but also returns the closest distance.
Robotics Toolbox for MATLAB 183 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Plucker.origin_closest
Plucker.display
Display parameters
P.display() displays the Plucker parameters in compact single line format.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Plucker object and the command has no trailing semicolon.
See also
Plucker.char
Plucker.double
Convert Plucker coordinates to real vector
PL.double() is a 6 ×1 vector comprising the moment and direction vectors.
Plucker.intersect
Line intersection
PL1.intersect(pl2) is zero if the lines intersect. It is positive if pl2 passes counter-
clockwise and negative if pl2 passes clockwise. Defined as looking in direction of
PL1
•———>
o o
•———>
counterclockwise clockwise
Robotics Toolbox for MATLAB 184 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Plucker.intersect_plane
Line intersection with plane
x= PL.intersect_plane(p) is the point where the line intersects the plane p. Planes are
structures with a normal p.n (3 ×1) and an offset p.p (1 ×1) such that p.n x+p.p = 0.
x=[] if no intersection.
[x,T] = PL.intersect_plane(p) as above but also returns the line parameters (1 ×N) at
the intersection points.
See also
Plucker.point
Plucker.intersect_volume
Line intersects plot volume
p= PL.intersect_volume(bounds,line) returns a matrix (3 ×N) with columns that
indicate where the line intersects the faces of the plot volume specified in terms of
[xmin xmax ymin ymax zmin zmax]. The number of columns N is either 0 (the line is
outside the plot volume) or 2. LINE is a structure with elements .p (3 ×1) a point on
the line and .v a vector parallel to the line.
[p,T] = PL.intersect_volume(bounds,line) as above but also returns the line parame-
ters (1 ×N) at the intersection points.
See also
Plucker.point
Plucker.L
Skew matrix form of the line
L= PL.L() is the Plucker matrix, a 4 ×4 skew-symmetric matrix representation of the
line.
Robotics Toolbox for MATLAB 185 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•For two homogeneous points P and Q on the line, PQ’-QP’ is also skew symmet-
ric.
Plucker.line
Plucker line coordinates
P.line() is a 6-vector representation of the Plucker coordinates of the line.
See also
Plucker.v,Plucker.w
Plucker.mindist
Minimum distance between two lines
d= PL1.mindist(pl2) is the minimum distance between two Plucker lines PL1 and
pl2.
Plucker.mtimes
Plucker composition
PL * M is the product of the Plucker matrix and M (4 ×N).
M * PL is the product of M (N×4) and the Plucker matrix.
Plucker.or
Operator form of side operator
P1 | P2 is the side operator which is zero whenever the lines P1 and P2 intersect or are
parallel.
Robotics Toolbox for MATLAB 186 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Plucker.side
Plucker.origin_closest
Point on line closest to the origin
p= PL.origin_closest() is the coordinate of a point on the line that is closest to the
origin.
See also
Plucker.origin_distance
Plucker.origin_distance
Smallest distance from line to the origin
p= PL.origin_distance() is the smallest distance of a point on the line to the origin.
See also
Plucker.origin_closest
Plucker.plot
Plot a line
PL.plot(options) plots the Plucker line within the current plot volume.
PL.plot(b,options) as above but plots within the plot bounds b= [XMIN XMAX
YMIN YMAX ZMIN ZMAX].
Options
•are passed to plot3.
Robotics Toolbox for MATLAB 187 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
plot3
Plucker.point
Point on line
p= PL.point(L) is a point on the line, where Lis the parametric distance along the
line from the principal point of the line.
See also
Plucker.pp
Plucker.pp
Principal point of the line
p= PL.pp() is a point on the line.
Notes
•Same as Plucker.point(0)
See also
Plucker.point
Plucker.side
Plucker side operator
x=SIDE(p1,p2) is the side operator which is zero whenever the lines p1 and p2
intersect or are parallel.
Robotics Toolbox for MATLAB 188 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Plucker.or
polydiff
Differentiate a polynomial
pd =polydiff(p) is a vector of coefficients of a polynomial (1 ×N-1) which is the
derivative of the polynomial p(1 ×N).
p = [3 2 -1];
polydiff(p)
ans =
6 2
See also
polyval
Polygon
Polygon class
A general class for manipulating polygons and vectors of polygons.
Methods
plot Plot polygon
area Area of polygon
moments Moments of polygon
centroid Centroid of polygon
perimeter Perimter of polygon
transform Transform polygon
inside Test if points are inside polygon
intersection Intersection of two polygons
difference Difference of two polygons
union Union of two polygons
xor Exclusive or of two polygons
Robotics Toolbox for MATLAB 189 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
display print the polygon in human readable form
char convert the polgyon to human readable string
Properties
vertices List of polygon vertices, one per column
extent Bounding box [minx maxx; miny maxy]
n Number of vertices
Notes
•This is reference class object
•Polygon objects can be used in vectors and arrays
Acknowledgement
The methods: inside, intersection, difference, union, and xor are based on code written
by:
Kirill K. Pankratov, kirill@plume.mit.edu, http://puddle.mit.edu/ glenn/kirill/saga.html
and require a licence. However the author does not respond to email regarding the
licence, so use with care, and modify with acknowledgement.
Polygon.Polygon
Polygon class constructor
p=Polygon(v) is a polygon with vertices given by v, one column per vertex.
p=Polygon(C,wh) is a rectangle centred at Cwith dimensions wh=[WIDTH, HEIGHT].
Polygon.area
Area of polygon
a= P.area() is the area of the polygon.
See also
Polygon.moments
Robotics Toolbox for MATLAB 190 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Polygon.centroid
Centroid of polygon
x= P.centroid() is the centroid of the polygon.
See also
Polygon.moments
Polygon.char
String representation
s= P.char() is a compact representation of the polgyon in human readable form.
Polygon.difference
Difference of polygons
d= P.difference(q) is polygon P minus polygon q.
Notes
•If polygons P and qare not intersecting, returns coordinates of P.
•If the result dis not simply connected or consists of several polygons, resulting
vertex list will contain NaNs.
Polygon.display
Display polygon
P.display() displays the polygon in a compact human readable form.
See also
Polygon.char
Robotics Toolbox for MATLAB 191 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Polygon.inside
Test if points are inside polygon
in =p.inside(p) tests if points given by columns of p(2 ×N) are inside the polygon.
The corresponding elements of in (1 ×N) are either true or false.
Polygon.intersect
Intersection of polygon with list of polygons
i= P.intersect(plist) indicates whether or not the Polygon P intersects with
i(j) = 1 if p intersects polylist(j), else 0.
Polygon.intersect_line
Intersection of polygon and line segment
i= P.intersect_line(L) is the intersection points of a polygon P with the line segment
L=[x1 x2; y1 y2]. i(2 ×N) has one column per intersection, each column is [x y]’.
Polygon.intersection
Intersection of polygons
i= P.intersection(q) is a Polygon representing the intersection of polygons P and q.
Notes
•If these polygons are not intersecting, returns empty polygon.
•If intersection consist of several disjoint polygons (for non-convex P or q) then
vertices of iis the concatenation of the vertices of these polygons.
Robotics Toolbox for MATLAB 192 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Polygon.moments
Moments of polygon
a= P.moments(p,q) is the pqth moment of the polygon.
See also
Polygon.area,Polygon.centroid,mpq_poly
Polygon.perimeter
Perimeter of polygon
L= P.perimeter() is the perimeter of the polygon.
Polygon.plot
Draw polygon
P.plot() draws the polygon P in the current plot.
P.plot(ls) as above but pass the arguments ls to plot.
Notes
•The polygon is added to the current plot.
Polygon.transform
Transform polygon vertices
p2 = P.transform(T) is a new Polygon object whose vertices have been transformed
by the SE(2) homgoeneous transformation T(3 ×3).
Robotics Toolbox for MATLAB 193 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Polygon.union
Union of polygons
i= P.union(q) is a polygon representing the union of polygons P and q.
Notes
•If these polygons are not intersecting, returns a polygon with vertices of both
polygons separated by NaNs.
•If the result P is not simply connected (such as a polygon with a “hole”) the re-
sulting contour consist of counter- clockwise “outer boundary” and one or more
clock-wise “inner boundaries” around “holes”.
Polygon.xor
Exclusive or of polygons
i= P.union(q) is a polygon representing the exclusive-or of polygons P and q.
Notes
•If these polygons are not intersecting, returns a polygon with vertices of both
polygons separated by NaNs.
•If the result P is not simply connected (such as a polygon with a “hole”) the re-
sulting contour consist of counter- clockwise “outer boundary” and one or more
clock-wise “inner boundaries” around “holes”.
PoseGraph
Pose graph
PoseGraph.PoseGraph
the file data
we assume g2o format
Robotics Toolbox for MATLAB 194 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VERTEX*vertex_id X Y THETA
EDGE*startvertex_id endvertex_id X Y THETA IXX IXY IYY IXT IYT ITT
vertex numbers start at 0
PoseGraph.linear_factors
the ids of the vertices connected by the kth edge
id_i=eids(1,k); id_j=eids(2,k);
extract the poses of the vertices and the mean of the edge
v_i=vmeans(:,id_i);
v_j=vmeans(:,id_j);
z_ij=emeans(:,k);
Prismatic
Robot manipulator prismatic link class
A subclass of the Link class for a prismatic joint defined using standard Denavit-
Hartenberg parameters: holds all information related to a robot link such as kinematics
parameters, rigid-body inertial parameters, motor and transmission parameters.
Constructors
Prismatic construct a prismatic joint+link using standard DH
Information/display methods
display print the link parameters in human readable form
dyn display link dynamic parameters
type joint type: ‘R’ or ‘P’
Conversion methods
char convert to string
Robotics Toolbox for MATLAB 195 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Operation methods
A link transform matrix
friction friction force
nofriction Link object with friction parameters set to zero%
Testing methods
islimit test if joint exceeds soft limit
isrevolute test if joint is revolute
isprismatic test if joint is prismatic
issym test if joint+link has symbolic parameters
Overloaded operators
+ concatenate links, result is a SerialLink object
Properties (read/write)
theta kinematic: joint angle
d kinematic: link offset
a kinematic: link length
alpha kinematic: link twist
jointtype kinematic: ‘R’ if revolute, ‘P’ if prismatic
mdh kinematic: 0 if standard D&H, else 1
offset kinematic: joint variable offset
qlim kinematic: joint variable limits [min max]
m dynamic: link mass
r dynamic: link COG wrt link coordinate frame 3 ×1
I dynamic: link inertia matrix, symmetric 3 ×3, about link COG.
B dynamic: link viscous friction (motor referred)
Tc dynamic: link Coulomb friction
G actuator: gear ratio
Jm actuator: motor inertia (motor referred)
Notes
•Methods inherited from the Link superclass.
•This is reference class object
•Link class objects can be used in vectors and arrays
Robotics Toolbox for MATLAB 196 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
References
•Robotics, Vision & Control, P. Corke, Springer 2011, Chap 7.
See also
Link,Revolute,SerialLink
Prismatic.Prismatic
Create prismatic robot link object
L=Prismatic(options) is a prismatic link object with the kinematic and dynamic pa-
rameters specified by the key/value pairs using the standard Denavit-Hartenberg con-
ventions.
Options
‘theta’, TH joint angle
‘a’, A joint offset (default 0)
‘alpha’, A joint twist (default 0)
‘standard’ defined using standard D&H parameters (default).
‘modified’ defined using modified D&H parameters.
‘offset’, O joint variable offset (default 0)
‘qlim’, Ljoint limit (default [])
‘I’, I link inertia matrix (3 ×1, 6 ×1 or 3 ×3)
‘r’, R link centre of gravity (3 ×1)
‘m’, M link mass (1 ×1)
‘G’, G motor gear ratio (default 1)
‘B’, B joint friction, motor referenced (default 0)
‘Jm’, J motor inertia, motor referenced (default 0)
‘Tc’, T Coulomb friction, motor referenced (1 ×1 or 2 ×1), (default [0 0])
‘sym’ consider all parameter values as symbolic not numeric
Notes
•The joint extension, d, is provided as an argument to the A() method.
•The link inertia matrix (3 ×3) is symmetric and can be specified by giving a
3×3 matrix, the diagonal elements [Ixx Iyy Izz], or the moments and products
of inertia [Ixx Iyy Izz Ixy Iyz Ixz].
•All friction quantities are referenced to the motor not the load.
•Gear ratio is used only to convert motor referenced quantities such as friction
Robotics Toolbox for MATLAB 197 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
and interia to the link frame.
See also
Link,Prismatic,RevoluteMDH
PrismaticMDH
Robot manipulator prismatic link class for MDH convention
A subclass of the Link class for a prismatic joint defined using modified Denavit-
Hartenberg parameters: holds all information related to a robot link such as kinematics
parameters, rigid-body inertial parameters, motor and transmission parameters.
Constructors
PrismaticMDH construct a prismatic joint+link using modified DH
Information/display methods
display print the link parameters in human readable form
dyn display link dynamic parameters
type joint type: ‘R’ or ‘P’
Conversion methods
char convert to string
Operation methods
A link transform matrix
friction friction force
nofriction Link object with friction parameters set to zero%
Testing methods
islimit test if joint exceeds soft limit
Robotics Toolbox for MATLAB 198 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
isrevolute test if joint is revolute
isprismatic test if joint is prismatic
issym test if joint+link has symbolic parameters
Overloaded operators
+ concatenate links, result is a SerialLink object
Properties (read/write)
theta kinematic: joint angle
d kinematic: link offset
a kinematic: link length
alpha kinematic: link twist
jointtype kinematic: ‘R’ if revolute, ‘P’ if prismatic
mdh kinematic: 0 if standard D&H, else 1
offset kinematic: joint variable offset
qlim kinematic: joint variable limits [min max]
m dynamic: link mass
r dynamic: link COG wrt link coordinate frame 3 ×1
I dynamic: link inertia matrix, symmetric 3 ×3, about link COG.
B dynamic: link viscous friction (motor referred)
Tc dynamic: link Coulomb friction
G actuator: gear ratio
Jm actuator: motor inertia (motor referred)
Notes
•Methods inherited from the Link superclass.
•This is reference class object
•Link class objects can be used in vectors and arrays
•Modified Denavit-Hartenberg parameters are used
References
•Robotics, Vision & Control, P. Corke, Springer 2011, Chap 7.
See also
Link,Prismatic,RevoluteMDH,SerialLink
Robotics Toolbox for MATLAB 199 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PrismaticMDH.PrismaticMDH
Create prismatic robot link object using MDH notaton
L=PrismaticMDH(options) is a prismatic link object with the kinematic and dy-
namic parameters specified by the key/value pairs using the modified Denavit-Hartenberg
conventions.
Options
‘theta’, TH joint angle
‘a’, A joint offset (default 0)
‘alpha’, A joint twist (default 0)
‘standard’ defined using standard D&H parameters (default).
‘modified’ defined using modified D&H parameters.
‘offset’, O joint variable offset (default 0)
‘qlim’, Ljoint limit (default [])
‘I’, I link inertia matrix (3 ×1, 6 ×1 or 3 ×3)
‘r’, R link centre of gravity (3 ×1)
‘m’, M link mass (1 ×1)
‘G’, G motor gear ratio (default 1)
‘B’, B joint friction, motor referenced (default 0)
‘Jm’, J motor inertia, motor referenced (default 0)
‘Tc’, T Coulomb friction, motor referenced (1 ×1 or 2 ×1), (default [0 0])
‘sym’ consider all parameter values as symbolic not numeric
Notes
•The joint extension, d, is provided as an argument to the A() method.
•The link inertia matrix (3 ×3) is symmetric and can be specified by giving a
3×3 matrix, the diagonal elements [Ixx Iyy Izz], or the moments and products
of inertia [Ixx Iyy Izz Ixy Iyz Ixz].
•All friction quantities are referenced to the motor not the load.
•Gear ratio is used only to convert motor referenced quantities such as friction
and interia to the link frame.
See also
Link,Prismatic,RevoluteMDH
Robotics Toolbox for MATLAB 200 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PRM
Probabilistic RoadMap navigation class
A concrete subclass of the abstract Navigation class that implements the probabilistic
roadmap navigation algorithm over an occupancy grid. This performs goal independent
planning of roadmaps, and at the query stage finds paths between specific start and goal
points.
Methods
PRM Constructor
plan Compute the roadmap
query Find a path
plot Display the obstacle map
display Display the parameters in human readable form
char Convert to string
Example
load map1 % load map
goal = [50,30]; % goal point
start = [20, 10]; % start point
prm = PRM(map); % create navigation object
prm.plan() % create roadmaps
prm.query(start, goal) % animate path from this start location
References
•Probabilistic roadmaps for path planning in high dimensional configuration spaces,
L. Kavraki, P. Svestka, J. Latombe, and M. Overmars, IEEE Transactions on
Robotics and Automation, vol. 12, pp. 566-580, Aug 1996.
•Robotics, Vision & Control, Section 5.2.4, P. Corke, Springer 2011.
See also
Navigation,DXform,Dstar,PGraph
Robotics Toolbox for MATLAB 201 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
PRM.PRM
Create a PRM navigation object
p=PRM(map,options) is a probabilistic roadmap navigation object, and map is an
occupancy grid, a representation of a planar world as a matrix whose elements are 0
(free space) or 1 (occupied).
Options
‘npoints’, N Number of sample points (default 100)
‘distthresh’, D Distance threshold, edges only connect vertices closer than D (default 0.3
max(size(occgrid)))
Other options are supported by the Navigation superclass.
See also
Navigation.Navigation
PRM.char
Convert to string
P.char() is a string representing the state of the PRM object in human-readable form.
See also
PRM.display
PRM.plan
Create a probabilistic roadmap
P.plan(options) creates the probabilistic roadmap by randomly sampling the free space
in the map and building a graph with edges connecting close points. The resulting graph
is kept within the object.
Robotics Toolbox for MATLAB 202 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
Robotics Toolbox for MATLAB 203 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘npoints’, N Number of sample points (default is set by constructor)
‘distthresh’, D Distance threshold, edges only connect vertices closer than D (default set by construc-
tor)
PRM.plot
Visualize navigation environment
P.plot() displays the roadmap and the occupancy grid.
Options
‘goal’ Superimpose the goal position if set
‘nooverlay’ Don’t overlay the PRM graph
Notes
•If a query has been made then the path will be shown.
•Goal and start locations are kept within the object.
PRM.query
Find a path between two points
P.query(start,goal) finds a path (M×2) from start to goal.
qplot
Plot robot joint angles
qplot(q) is a convenience function to plot joint angle trajectories (M×6) for a 6-axis
robot, where each row represents one time step.
The first three joints are shown as solid lines, the last three joints (wrist) are shown as
dashed lines. A legend is also displayed.
qplot(T,q) as above but displays the joint angle trajectory versus time given the time
vector T(M×1).
Robotics Toolbox for MATLAB 204 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
jtraj,plotp,plot
Quaternion
Quaternion class
A quaternion is 4-element mathematical object comprising a scalar s, and a vector v
and is typically written: q = s <<vx, vy, vz>>.
A quaternion of unit length can be used to represent 3D orientation and is implemented
by the subclass UnitQuaternion.
Constructors
Quaternion general constructor
Quaternion.pure pure quaternion
Display methods
display print in human readable form
Operation methods
inv inverse
conj conjugate
norm norm, or length
unit unitized quaternion
inner inner product
Conversion methods
char convert to string
double quaternion elements as 4-vector
matrix quaternion as a 4 ×4 matrix
Overloaded operators
Robotics Toolbox for MATLAB 205 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
q*q2 quaternion (Hamilton) product
s*q elementwise multiplication of quaternion by scalar
q/q2 q*q2.inv
qnq to power n (integer only)
q+q2 elementwise sum of quaternion elements
q-q2 elementwise difference of quaternion elements
q1==q2 test for quaternion equality
q16=q2 test for quaternion inequalityq = rx*ry*rz;
Properties (read only)
s real part
v vector part
Notes
•Quaternion objects can be used in vectors and arrays.
References
•Animating rotation with quaternion curves, K. Shoemake, in Proceedings of
ACM SIGGRAPH, (San Fran cisco), pp. 245-254, 1985.
•On homogeneous transforms, quaternions, and computational efficiency, J. Funda,
R. Taylor, and R. Paul, IEEE Transactions on Robotics and Automation, vol. 6,
pp. 382-388, June 1990.
•Robotics, Vision & Control, P. Corke, Springer 2011.
See also
UnitQuaternion
Quaternion.Quaternion
Construct a quaternion object
Q = Quaternion is a zero quaternion
Q = Quaternion([S V1 V2 V3]) is a quaternion formed by specifying directly its 4
elements
q=Quaternion(s,v) is a quaternion formed from the scalar sand vector part v(1 ×3)
Robotics Toolbox for MATLAB 206 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The constructor is not vectorized, it cannot create a vector of Quaternions.
Quaternion.char
Convert to string
s= Q.char() is a compact string representation of the quaternion’s value as a 4-tuple.
If Q is a vector then shas one line per element.
Quaternion.conj
Conjugate of a quaternion
qi = Q.conj() is a quaternion object representing the conjugate of Q.
Notes
•Conjugatation changes the sign of the vector component.
See also
Quaternion.inv
Quaternion.display
Display quaternion
Q.display() displays a compact string representation of the quaternion’s value as a 4-
tuple. If Q is a vector then S has one line per element.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Quaternion object and the command has no trailing semicolon.
•The vector part is displayed with double brackets << 1, 0, 0 >> to distinguish
it from a UnitQuaternion which displays as <1, 0, 0 >
Robotics Toolbox for MATLAB 207 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•If Q is a vector of Quaternion objects the elements are displayed on consecutive
lines.
See also
Quaternion.char
Quaternion.double
Convert a quaternion to a 4-element vector
v= Q.double() is a row vector (1 ×4) comprising the quaternion elements, scalar then
vector. If Q is a vector (1 ×N) of Quaternion objects then vis a matrix (N×4) with
rows corresponding to the Quaternion elements.
elements [s vx vy vz].
Quaternion.eq
Test quaternion equality
Q1==Q2 is true if the quaternions Q1 and Q2 are equal.
Notes
•Overloaded operator ‘==’.
•This method is invoked for unit Quaternions where Q and -Q represent the equiv-
alent rotation, so non-equality does not mean rotations are not equivalent.
•If Q1 is a vector of quaternions, each element is compared to Q2 and the result
is a logical array of the same length as Q1.
•If Q2 is a vector of quaternions, each element is compared to Q1 and the result
is a logical array of the same length as Q2.
•If Q1 and Q2 are vectors of the same length, then the result is a logical array of
the same length.
See also
Quaternion.ne
Robotics Toolbox for MATLAB 208 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Quaternion.inner
Quaternion inner product
v= Q1.inner(q2) is the inner (dot) product of two vectors (1 ×4), comprising the
elements of Q1 and q2 respectively.
Notes
•Q1.inner(Q1) is the same as Q1.norm().
See also
Quaternion.norm
Quaternion.inv
Invert a quaternion
qi = Q.inv() is a quaternion object representing the inverse of Q.
Notes
•Is vectorized.
See also
Quaternion.conj
Quaternion.isequal
Test quaternion element equality
ISEQUAL(q1,q2) is true if the quaternions q1 and q2 are equal.
Notes
•Used by test suite verifyEqual in addition to eq().
•Invokes eq().
Robotics Toolbox for MATLAB 209 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Quaternion.eq
Quaternion.matrix
Matrix representation of Quaternion
m= Q.matrix() is a matrix (4 ×4) representation of the Quaternion Q.
Quaternion, or Hamilton, multiplication can be implemented as a matrix-vector prod-
uct, where the column-vector is the elements of a second quaternion:
matrix(Q1) *double(Q2)’
Notes
•This matrix is not unique, other matrices will serve the purpose for multiplica-
tion, see https://en.wikipedia.org/wiki/Quaternion#Matrix_representations
•The determinant of the matrix is the norm of the quaternion to the fourth power.
See also
Quaternion.double,Quaternion.mtimes
Quaternion.minus
Subtract quaternions
Q1-Q2 is a Quaternion formed from the element-wise difference of quaternion ele-
ments.
Q1-V is a Quaternion formed from the element-wise difference of Q1 and the vector
V (1 ×4).
Notes
•Overloaded operator ‘-’
•This is not a group operator, but it is useful to have the result as a quaternion.
Robotics Toolbox for MATLAB 210 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Quaternion.plus
Quaternion.mpower
Raise quaternion to integer power
QNis the Quaternion Q raised to the integer power N.
Notes
•Overloaded operator extasciicircum
•Computed by repeated multiplication.
•If the argument is a unit-quaternion, the result will be a unit quaternion.
See also
Quaternion.mtimes
Quaternion.mrdivide
Quaternion quotient.
Q1/Q2 is a quaternion formed by Hamilton product of Q1 and inv(Q2).
Q/S is the element-wise division of quaternion elements by the scalar S.
Notes
•Overloaded operator ‘/’
•For case Q1/Q2 both can be an N-vector, result is elementwise division.
•For case Q1/Q2 if Q1 scalar and Q2 a vector, scalar is divided by each element.
•For case Q1/Q2 if Q2 scalar and Q1 a vector, each element divided by scalar.
See also
Quaternion.mtimes,Quaternion.mpower,Quaternion.plus,Quaternion.minus
Robotics Toolbox for MATLAB 211 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Quaternion.mtimes
Multiply a quaternion object
Q1*Q2 is a quaternion formed by the Hamilton product of two quaternions.
Q*S is the element-wise multiplication of quaternion elements by the scalar S.
S*Q is the element-wise multiplication of quaternion elements by the scalar S.
Notes
•Overloaded operator ‘*’
•For case Q1*Q2 both can be an N-vector, result is elementwise multiplication.
•For case Q1*Q2 if Q1 scalar and Q2 a vector, scalar multiplies each element.
•For case Q1*Q2 if Q2 scalar and Q1 a vector, each element multiplies scalar.
See also
Quaternion.mrdivide,Quaternion.mpower
Quaternion.ne
Test quaternion inequality
Q1 6=Q2 is true if the quaternions Q1 and Q2 are not equal.
Notes
•Overloaded operator ‘6=’
•Note that for unit Quaternions Q and -Q are the equivalent rotation, so non-
equality does not mean rotations are not equivalent.
•If Q1 is a vector of quaternions, each element is compared to Q2 and the result
is a logical array of the same length as Q1.
•If Q2 is a vector of quaternions, each element is compared to Q1 and the result
is a logical array of the same length as Q2.
•If Q1 and Q2 are vectors of the same length, then the result is a logical array of
the same length.
Robotics Toolbox for MATLAB 212 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Quaternion.eq
Quaternion.new
Construct a new quaternion
qn = Q.new() constructs a new Quaternion object of the same type as Q.
qn = Q.new([S V1 V2 V3]) as above but specified directly by its 4 elements.
qn = Q.new(s,v) as above but specified directly by the scalar sand vector part v(1×3)
Notes
•Polymorphic with UnitQuaternion and RTBPose derived classes.
Quaternion.norm
Quaternion magnitude
qn =q.norm(q) is the scalar norm or magnitude of the quaternion q.
Notes
•This is the Euclidean norm of the quaternion written as a 4-vector.
•A unit-quaternion has a norm of one.
See also
Quaternion.inner,Quaternion.unit
Quaternion.plus
Add quaternions
Q1+Q2 is a Quaternion formed from the element-wise sum of quaternion elements.
Q1+V is a Quaternion formed from the element-wise sum of Q1 and the vector V
(1 ×4).
Robotics Toolbox for MATLAB 213 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Overloaded operator ‘+’
•This is not a group operator, but it is useful to have the result as a quaternion.
See also
Quaternion.minus
Quaternion.pure
Construct a pure quaternion
q=Quaternion.pure(v) is a pure quaternion formed from the vector v(1 ×3) and has
a zero scalar part.
Quaternion.set.s
Set scalar component
Q.s = S sets the scalar part of the Quaternion object to S.
Quaternion.set.v
Set vector component
Q.v = V sets the vector part of the Quaternion object to V (1 ×3).
Quaternion.unit
Unitize a quaternion
qu = Q.unit() is a UnitQuaternion object representing the same orientation as Q.
Notes
•Is vectorized.
Robotics Toolbox for MATLAB 214 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Quaternion.norm,UnitQuaternion
r2t
Convert rotation matrix to a homogeneous transform
T=r2t(R) is an SE(2) or SE(3) homogeneous transform equivalent to an SO(2) or
SO(3) orthonormal rotation matrix Rwith a zero translational component. Works for
Tin either SE(2) or SE(3):
•if Ris 2 ×2 then Tis 3 ×3, or
•if Ris 3 ×3 then Tis 4 ×4.
Notes
•Translational component is zero.
•For a rotation matrix sequence (K×K×N) returns a homogeneous transform
sequence (K+1 ×K+1 ×N).
See also
t2r
randinit
Reset random number generator
RANDINIT resets the defaul random number stream.
See also
RandStream
Robotics Toolbox for MATLAB 215 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RandomPath
Vehicle driver class
Create a “driver” object capable of steering a Vehicle subclass object through random
waypoints within a rectangular region and at constant speed.
The driver object is connected to a Vehicle object by the latter’s add_driver() method.
The driver’s demand() method is invoked on every call to the Vehicle’s step() method.
Methods
init reset the random number generator
demand speed and steer angle to next waypoint
display display the state and parameters in human readable form
char convert to string
plot
Properties
goal current goal/waypoint coordinate
veh the Vehicle object being controlled
dim dimensions of the work space (2 ×1) [m]
speed speed of travel [m/s]
dthresh proximity to waypoint at which next is chosen [m]
Example
veh = Bicycle(V);
veh.add_driver( RandomPath(20, 2) );
Notes
•It is possible in some cases for the vehicle to move outside the desired region, for
instance if moving to a waypoint near the edge, the limited turning circle may
cause the vehicle to temporarily move outside.
•The vehicle chooses a new waypoint when it is closer than property closeenough
to the current waypoint.
•Uses its own random number stream so as to not influence the performance of
other randomized algorithms such as path planning.
Robotics Toolbox for MATLAB 216 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Reference
Robotics, Vision & Control, Chap 6, Peter Corke, Springer 2011
See also
Vehicle,Bicycle,Unicycle
RandomPath.RandomPath
Create a driver object
d=RandomPath(d,options) returns a “driver” object capable of driving a Vehicle
subclass object through random waypoints. The waypoints are positioned inside a
rectangular region of dimension dinterpreted as:
•dscalar; X: -dto +d, Y: -dto +d
•d(1 ×2); X: -d(1) to +d(1), Y: -d(2) to +d(2)
•d(1 ×4); X: d(1) to d(2), Y: d(3) to d(4)
Options
‘speed’, S Speed along path (default 1m/s).
‘dthresh’, dDistance from goal at which next goal is chosen.
See also
Vehicle
RandomPath.char
Convert to string
s= R.char() is a string showing driver parameters and state in in a compact human
readable format.
Robotics Toolbox for MATLAB 217 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RandomPath.demand
Compute speed and heading to waypoint
[speed,steer] = R.demand() is the speed and steer angle to drive the vehicle toward
the next waypoint. When the vehicle is within R.dtresh a new waypoint is chosen.
See also
Vehicle
RandomPath.display
Display driver parameters and state
R.display() displays driver parameters and state in compact human readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a RandomPath object and the command has no trailing semicolon.
See also
RandomPath.char
RandomPath.init
Reset random number generator
R.init() resets the random number generator used to create the waypoints. This enables
the sequence of random waypoints to be repeated.
Notes
•Called by Vehicle.run.
Robotics Toolbox for MATLAB 218 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
randstream
RangeBearingSensor
Range and bearing sensor class
A concrete subclass of the Sensor class that implements a range and bearing angle
sensor that provides robot-centric measurements of landmark points in the world. To
enable this it holds a references to a map of the world (LandmarkMap object) and a
robot (Vehicle subclass object) that moves in SE(2).
The sensor observes landmarks within its angular field of view between the minimum
and maximum range.
Methods
reading range/bearing observation of random landmark
h range/bearing observation of specific landmark
Hx Jacobian matrix with respect to vehicle pose dh/dx
Hp Jacobian matrix with respect to landmark position dh/dp
Hw Jacobian matrix with respect to noise dh/dw
g feature position given vehicle pose and observation
Gx Jacobian matrix with respect to vehicle pose dg/dx
Gz Jacobian matrix with respect to observation dg/dz
Properties (read/write)
W measurement covariance matrix (2 ×2)
interval valid measurements returned every intervalth call to reading()
landmarklog time history of observed landmarks
Reference
Robotics, Vision & Control, Chap 6, Peter Corke, Springer 2011
Robotics Toolbox for MATLAB 219 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Sensor,Vehicle,LandmarkMap,EKF
RangeBearingSensor.RangeBearingSensor
Range and bearing sensor constructor
s=RangeBearingSensor(vehicle,map,options) is an object representing a range and
bearing angle sensor mounted on the Vehicle subclass object vehicle and observing an
environment of known landmarks represented by the LandmarkMap object map. The
sensor covariance is W (2 ×2) representing range and bearing covariance.
The sensor has specified angular field of view and minimum and maximum range.
Options
‘covar’, W covariance matrix (2 ×2)
‘range’, xmax maximum range of sensor
‘range’, [xmin xmax] minimum and maximum range of sensor
‘angle’, TH angular field of view, from -TH to +TH
‘angle’, [THMIN THMAX] detection for angles betwen THMIN and THMAX
‘skip’, K return a valid reading on every Kth call
‘fail’, [TMIN TMAX] sensor simulates failure between timesteps TMIN and TMAX
‘animate’ animate sensor readings
See also
options for Sensor constructor
See also
RangeBearingSensor.reading,Sensor.Sensor,Vehicle,LandmarkMap,EKF
RangeBearingSensor.g
Compute landmark location
p= S.g(x,z) is the world coordinate (2 ×1) of a feature given the observation z(1 ×2)
from a vehicle state with x(3 ×1).
Robotics Toolbox for MATLAB 220 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
RangeBearingSensor.Gx,RangeBearingSensor.Gz
RangeBearingSensor.Gx
Jacobian dg/dx
J= S.Gx(x,z) is the Jacobian dg/dx (2 ×3) at the vehicle state x(3 ×1) for sensor
observation z(2 ×1).
See also
RangeBearingSensor.g
RangeBearingSensor.Gz
Jacobian dg/dz
J= S.Gz(x,z) is the Jacobian dg/dz (2 ×2) at the vehicle state x(3 ×1) for sensor
observation z(2 ×1).
See also
RangeBearingSensor.g
RangeBearingSensor.h
Landmark range and bearing
z= S.h(x,k) is a sensor observation (1 ×2), range and bearing, from vehicle at pose x
(1 ×3) to the kth landmark.
z= S.h(x,p) as above but compute range and bearing to a landmark at coordinate p.
z= s.h(x) as above but computes range and bearing to all map features. zhas one row
per landmark.
Robotics Toolbox for MATLAB 221 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Noise with covariance W (propertyW) is added to each row of z.
•Supports vectorized operation where XV (N×3) and z(N×2).
•The landmark is assumed visible, field of view and range liits are not applied.
See also
RangeBearingSensor.reading,RangeBearingSensor.Hx,RangeBearingSensor.Hw,Range-
BearingSensor.Hp
RangeBearingSensor.Hp
Jacobian dh/dp
J= S.Hp(x,k) is the Jacobian dh/dp (2 ×2) at the vehicle state x(3 ×1) for map
landmark k.
J= S.Hp(x,p) as above but for a landmark at coordinate p(1 ×2).
See also
RangeBearingSensor.h
RangeBearingSensor.Hw
Jacobian dh/dw
J= S.Hw(x,k) is the Jacobian dh/dw (2 ×2) at the vehicle state x(3 ×1) for map
landmark k.
See also
RangeBearingSensor.h
Robotics Toolbox for MATLAB 222 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RangeBearingSensor.Hx
Jacobian dh/dx
J= S.Hx(x,k) returns the Jacobian dh/dx (2 ×3) at the vehicle state x(3 ×1) for map
landmark k.
J= S.Hx(x,p) as above but for a landmark at coordinate p.
See also
RangeBearingSensor.h
RangeBearingSensor.reading
Choose landmark and return observation
[z,k] = S.reading() is an observation of a random visible landmark where z=[R,THETA]
is the range and bearing with additive Gaussian noise of covariance W (property W). k
is the index of the map feature that was observed.
The landmark is chosen randomly from the set of all visible landmarks, those within
the angular field of view and range limits. If no valid measurement, ie. no features
within range, interval subsampling enabled or simulated failure the return is z=[] and
k=0.
Notes
•Noise with covariance W (property W) is added to each row of z.
•If ‘animate’ option set then show a line from the vehicle to the landmark
•If ‘animate’ option set and the angular and distance limits are set then display
that region as a shaded polygon.
•Implements sensor failure and subsampling if specified to constructor.
See also
RangeBearingSensor.h
Robotics Toolbox for MATLAB 223 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Revolute
Robot manipulator Revolute link class
A subclass of the Link class for a revolute joint defined using standard Denavit-Hartenberg
parameters: holds all information related to a revolute robot link such as kinematics pa-
rameters, rigid-body inertial parameters, motor and transmission parameters.
Constructors
Revolute construct a revolute joint+link using standard DH
Information/display methods
display print the link parameters in human readable form
dyn display link dynamic parameters
type joint type: ‘R’ or ‘P’
Conversion methods
char convert to string
Operation methods
A link transform matrix
friction friction force
nofriction Link object with friction parameters set to zero%
Testing methods
islimit test if joint exceeds soft limit
isrevolute test if joint is revolute
isprismatic test if joint is prismatic
issym test if joint+link has symbolic parameters
Overloaded operators
+ concatenate links, result is a SerialLink object
Robotics Toolbox for MATLAB 224 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Properties (read/write)
theta kinematic: joint angle
d kinematic: link offset
a kinematic: link length
alpha kinematic: link twist
jointtype kinematic: ‘R’ if revolute, ‘P’ if prismatic
mdh kinematic: 0 if standard D&H, else 1
offset kinematic: joint variable offset
qlim kinematic: joint variable limits [min max]
m dynamic: link mass
r dynamic: link COG wrt link coordinate frame 3 ×1
I dynamic: link inertia matrix, symmetric 3 ×3, about link COG.
B dynamic: link viscous friction (motor referred)
Tc dynamic: link Coulomb friction
G actuator: gear ratio
Jm actuator: motor inertia (motor referred)
Notes
•Methods inherited from the Link superclass.
•This is reference class object
•Link class objects can be used in vectors and arrays
References
•Robotics, Vision & Control, P. Corke, Springer 2011, Chap 7.
See also
Link,Prismatic,RevoluteMDH,SerialLink
Revolute.Revolute
Create revolute robot link object
L=Revolute(options) is a revolute link object with the kinematic and dynamic pa-
rameters specified by the key/value pairs using the standard Denavit-Hartenberg con-
ventions.
Options
Robotics Toolbox for MATLAB 225 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘d’, D joint extension
‘a’, A joint offset (default 0)
‘alpha’, A joint twist (default 0)
‘standard’ defined using standard D&H parameters (default).
‘modified’ defined using modified D&H parameters.
‘offset’, O joint variable offset (default 0)
‘qlim’, Ljoint limit (default [])
‘I’, I link inertia matrix (3 ×1, 6 ×1 or 3 ×3)
‘r’, R link centre of gravity (3 ×1)
‘m’, M link mass (1 ×1)
‘G’, G motor gear ratio (default 1)
‘B’, B joint friction, motor referenced (default 0)
‘Jm’, J motor inertia, motor referenced (default 0)
‘Tc’, T Coulomb friction, motor referenced (1 ×1 or 2 ×1), (default [0 0])
‘sym’ consider all parameter values as symbolic not numeric
Notes
•The joint angle, theta, is provided as an argument to the A() method.
•The link inertia matrix (3 ×3) is symmetric and can be specified by giving a
3×3 matrix, the diagonal elements [Ixx Iyy Izz], or the moments and products
of inertia [Ixx Iyy Izz Ixy Iyz Ixz].
•All friction quantities are referenced to the motor not the load.
•Gear ratio is used only to convert motor referenced quantities such as friction
and interia to the link frame.
See also
Link,Prismatic,RevoluteMDH
RevoluteMDH
Robot manipulator Revolute link class for MDH convention
A subclass of the Link class for a revolute joint defined using modified Denavit-Hartenberg
parameters: holds all information related to a revolute robot link such as kinematics pa-
rameters, rigid-body inertial parameters, motor and transmission parameters.
Constructors
RevoluteMDH construct a revolute joint+link using modified DH
Robotics Toolbox for MATLAB 226 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Information/display methods
display print the link parameters in human readable form
dyn display link dynamic parameters
type joint type: ‘R’ or ‘P’
Conversion methods
char convert to string
Operation methods
A link transform matrix
friction friction force
nofriction Link object with friction parameters set to zero%
Testing methods
islimit test if joint exceeds soft limit
isrevolute test if joint is revolute
isprismatic test if joint is prismatic
issym test if joint+link has symbolic parameters
Overloaded operators
+ concatenate links, result is a SerialLink object
Properties (read/write)
theta kinematic: joint angle
d kinematic: link offset
a kinematic: link length
alpha kinematic: link twist
jointtype kinematic: ‘R’ if revolute, ‘P’ if prismatic
mdh kinematic: 0 if standard D&H, else 1
offset kinematic: joint variable offset
qlim kinematic: joint variable limits [min max]
m dynamic: link mass
r dynamic: link COG wrt link coordinate frame 3 ×1
I dynamic: link inertia matrix, symmetric 3 ×3, about link COG.
B dynamic: link viscous friction (motor referred)
Robotics Toolbox for MATLAB 227 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Tc dynamic: link Coulomb friction
G actuator: gear ratio
Jm actuator: motor inertia (motor referred)
Notes
•Methods inherited from the Link superclass.
•This is reference class object
•Link class objects can be used in vectors and arrays
•Modified Denavit-Hartenberg parameters are used
References
•Robotics, Vision & Control, P. Corke, Springer 2011, Chap 7.
See also
Link,PrismaticMDH,Revolute,SerialLink
RevoluteMDH.RevoluteMDH
Create revolute robot link object using MDH notation
L=RevoluteMDH(options) is a revolute link object with the kinematic and dynamic
parameters specified by the key/value pairs using the modified Denavit-Hartenberg
conventions.
Options
‘d’, D joint extension
‘a’, A joint offset (default 0)
‘alpha’, A joint twist (default 0)
‘standard’ defined using standard D&H parameters (default).
‘modified’ defined using modified D&H parameters.
‘offset’, O joint variable offset (default 0)
‘qlim’, Ljoint limit (default [])
‘I’, I link inertia matrix (3 ×1, 6 ×1 or 3 ×3)
‘r’, R link centre of gravity (3 ×1)
‘m’, M link mass (1 ×1)
‘G’, G motor gear ratio (default 1)
‘B’, B joint friction, motor referenced (default 0)
Robotics Toolbox for MATLAB 228 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘Jm’, J motor inertia, motor referenced (default 0)
‘Tc’, T Coulomb friction, motor referenced (1 ×1 or 2 ×1), (default [0 0])
‘sym’ consider all parameter values as symbolic not numeric
Notes
•The joint angle, theta, is provided as an argument to the A() method.
•The link inertia matrix (3 ×3) is symmetric and can be specified by giving a
3×3 matrix, the diagonal elements [Ixx Iyy Izz], or the moments and products
of inertia [Ixx Iyy Izz Ixy Iyz Ixz].
•All friction quantities are referenced to the motor not the load.
•Gear ratio is used only to convert motor referenced quantities such as friction
and interia to the link frame.
See also
Link,Prismatic,RevoluteMDH
rot2
SO(2) Rotation matrix
R=rot2(theta) is an SO(2) rotation matrix (2 ×2) representing a rotation of theta
radians.
R=rot2(theta, ‘deg’) as above but theta is in degrees.
See also
SE2,trot2,isrot2,trplot2,rotx,roty,rotz,SO2
rotx
Rotation about X axis
R=rotx(theta) is an SO(3) rotation matrix (3 ×3) representing a rotation of theta
radians about the x-axis.
Robotics Toolbox for MATLAB 229 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
R=rotx(theta, ‘deg’) as above but theta is in degrees.
See also
roty,rotz,angvec2r,rot2,SO3.Rx
roty
Rotation about Y axis
R=roty(theta) is an SO(3) rotation matrix (3 ×3) representing a rotation of theta
radians about the y-axis.
R=roty(theta, ‘deg’) as above but theta is in degrees.
See also
rotx,rotz,angvec2r,rot2,SO3.Ry
rotz
Rotation about Z axis
R=rotz(theta) is an SO(3) rotation matrix (3 ×3) representing a rotation of theta
radians about the z-axis.
R=rotz(theta, ‘deg’) as above but theta is in degrees.
See also
rotx,roty,angvec2r,rot2,SO3.Rx
Robotics Toolbox for MATLAB 230 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
rpy2jac
Jacobian from RPY angle rates to angular velocity
J=rpy2jac(rpy,options) is a Jacobian matrix (3 ×3) that maps ZYX roll-pitch-yaw
angle rates to angular velocity at the operating point rpy=[R,P,Y].
J=rpy2jac(R,p,y,options) as above but the roll-pitch-yaw angles are passed as
separate arguments.
Options
‘xyz’ Use XYZ roll-pitch-yaw angles
‘yxz’ Use YXZ roll-pitch-yaw angles
Notes
•Used in the creation of an analytical Jacobian.
See also
eul2jac,SerialLink.JACOBE
rpy2r
Roll-pitch-yaw angles to rotation matrix
R=rpy2r(roll,pitch,yaw,options) is an SO(3) orthonornal rotation matrix (3 ×3)
equivalent to the specified roll, pitch, yaw angles angles. These correspond to rotations
about the Z, Y, X axes respectively. If roll,pitch,yaw are column vectors (N×1)
then they are assumed to represent a trajectory and Ris a three-dimensional matrix
(3 ×3×N), where the last index corresponds to rows of roll,pitch,yaw.
R=rpy2r(rpy,options) as above but the roll, pitch, yaw angles are taken from the
vector (1 ×3) rpy=[roll,pitch,yaw]. If rpy is a matrix (N×3) then Ris a three-
dimensional matrix (3 ×3×N), where the last index corresponds to rows of rpy which
are assumed to be [roll,pitch,yaw].
Options
Robotics Toolbox for MATLAB 231 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Rotations about X, Y, Z axes (for a robot gripper)
‘yxz’ Rotations about Y, X, Z axes (for a camera)
Note
•Toolbox rel 8-9 has the reverse angle sequence as default.
•ZYX order is appropriate for vehicles with direction of travel in the X direction.
XYZ order is appropriate if direction of travel is in the Z direction.
See also
tr2rpy,eul2tr
rpy2tr
Roll-pitch-yaw angles to homogeneous transform
T=rpy2tr(roll,pitch,yaw,options) is an SE(3) homogeneous transformation matrix
(4 ×4) with zero translation and rotation equivalent to the specified roll, pitch, yaw
angles angles. These correspond to rotations about the Z, Y, X axes respectively. If roll,
pitch,yaw are column vectors (N×1) then they are assumed to represent a trajectory
and R is a three-dimensional matrix (4 ×4×N), where the last index corresponds to
rows of roll,pitch,yaw.
T=rpy2tr(rpy,options) as above but the roll, pitch, yaw angles are taken from the
vector (1 ×3) rpy=[roll,pitch,yaw]. If rpy is a matrix (N×3) then R is a three-
dimensional matrix (4 ×4×N), where the last index corresponds to rows of rpy which
are assumed to be roll,pitch,yaw].
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Rotations about X, Y, Z axes (for a robot gripper)
‘yxz’ Rotations about Y, X, Z axes (for a camera)
Note
•Toolbox rel 8-9 has the reverse angle sequence as default.
•ZYX order is appropriate for vehicles with direction of travel in the X direction.
Robotics Toolbox for MATLAB 232 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
XYZ order is appropriate if direction of travel is in the Z direction.
See also
tr2rpy,rpy2r,eul2tr
RRT
Class for rapidly-exploring random tree navigation
A concrete subclass of the abstract Navigation class that implements the rapidly ex-
ploring random tree (RRT) algorithm. This is a kinodynamic planner that takes into
account the motion constraints of the vehicle.
Methods
RRT Constructor
plan Compute the tree
query Compute a path
plot Display the tree
display Display the parameters in human readable form
char Convert to string
Properties (read only)
graph A PGraph object describign the tree
Example
goal = [0,0,0];
start = [0,2,0];
veh = Bicycle(’steermax’, 1.2);
rrt = RRT(veh, ’goal’, goal, ’range’, 5);
rrt.plan() % create navigation tree
rrt.query(start, goal) % animate path from this start location
References
•Randomized kinodynamic planning, S. LaValle and J. Kuffner, International
Journal of Robotics Research vol. 20, pp. 378-400, May 2001.
Robotics Toolbox for MATLAB 233 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
•Probabilistic roadmaps for path planning in high dimensional configuration spaces,
L. Kavraki, P. Svestka, J. Latombe, and M. Overmars, IEEE Transactions on
Robotics and Automation, vol. 12, pp. 566-580, Aug 1996.
•Robotics, Vision & Control, Section 5.2.5, P. Corke, Springer 2011.
See also
Navigation,PRM,DXform,Dstar,PGraph
RRT.RRT
Create an RRT navigation object
R=RRT.RRT(veh,options) is a rapidly exploring tree navigation object for a vehicle
kinematic model given by a Vehicle subclass object veh.
R=RRT.RRT(veh,map,options) as above but for a region with obstacles defined by
the occupancy grid map.
Options
‘npoints’, N Number of nodes in the tree (default 500)
‘simtime’, T Interval over which to simulate kinematic model toward random point (default 0.5s)
‘goal’, P Goal position (1 ×2) or pose (1 ×3) in workspace
‘speed’, S Speed of vehicle [m/s] (default 1)
‘root’, RConfiguration of tree root (3 ×1) (default [0,0,0])
‘revcost’, C Cost penalty for going backwards (default 1)
‘range’, RSpecify rectangular bounds of robot’s workspace:
•Rscalar; X: -Rto +R, Y: -Rto +R
•R(1 ×2); X: -R(1) to +R(1), Y: -R(2) to +R(2)
•R(1 ×4); X: R(1) to R(2), Y: R(3) to R(4)
Other options are provided by the Navigation superclass.
Notes
•‘range’ option is ignored if an occupacy grid is provided.
Reference
•Robotics, Vision & Control Peter Corke, Springer 2011. p102.
Robotics Toolbox for MATLAB 234 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Vehicle,Bicycle,Unicycle
RRT.char
Convert to string
R.char() is a string representing the state of the RRT object in human-readable form.
RRT.plan
Create a rapidly exploring tree
R.plan(options) creates the tree roadmap by driving the vehicle model toward random
goal points. The resulting graph is kept within the object.
Options
‘goal’, P Goal pose (1 ×3)
‘ntrials’, N Number of path trials (default 50)
‘noprogress’ Don’t show the progress bar
‘samples’ Show progress in a plot of the workspace
•‘.’ for each random point x_rand
•‘o’ for the nearest point which is added to the tree
•red line for the best path
Notes
•At each iteration we need to find a vehicle path/control that moves it from a
random point towards a point on the graph. We sample ntrials of random steer
angles and velocities and choose the one that gets us closest (computationally
slow, since each path has to be integrated over time).
Robotics Toolbox for MATLAB 235 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RRT.plot
Visualize navigation environment
R.plot() displays the navigation tree in 3D, where the vertical axis is vehicle heading
angle. If an occupancy grid was provided this is also displayed.
RRT.query
Find a path between two points
x= R.path(start,goal) finds a path (N×3) from pose start (1×3) to pose goal (1×3).
The pose is expressed as [x,Y,THETA].
R.path(start,goal) as above but plots the path in 3D, where the vertical axis is vehicle
heading angle. The nodes are shown as circles and the line segments are blue for
forward motion and red for backward motion.
Notes
•The path starts at the vertex closest to the start state, and ends at the vertex
closest to the goal state. If the tree is sparse this might be a poor approximation
to the desired start and end.
See also
RRT.plot
rt2tr
Convert rotation and translation to homogeneous transform
TR =rt2tr(R,t) is a homogeneous transformation matrix (N+1 ×N+1) formed from
an orthonormal rotation matrix R(N×N) and a translation vector t(N×1). Works for
Rin SO(2) or SO(3):
•If Ris 2 ×2 and tis 2 ×1, then TR is 3 ×3
•If Ris 3 ×3 and tis 3 ×1, then TR is 4 ×4
For a sequence R(N×N×K) and t(N×K) results in a transform sequence (N+1 ×
N+1 ×K).
Robotics Toolbox for MATLAB 236 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The validity of Ris not checked
See also
t2r,r2t,tr2rt
rtbdemo
Robot toolbox demonstrations
rtbdemo displays a menu of toolbox demonstration scripts that illustrate:
•fundamental datatypes
–rotation and homogeneous transformation matrices
–quaternions
–trajectories
•serial link manipulator arms
–forward and inverse kinematics
–robot animation
–forward and inverse dynamics
•mobile robots
–kinematic models and control
–path planning (D*, PRM, Lattice, RRT)
–localization (EKF, particle filter)
–SLAM (EKF, pose graph)
–quadrotor control
rtbdemo(T) as above but waits for Tseconds after every statement, no need to push
the enter key periodically.
Notes
•By default the scripts require the user to periodically hit <Enter>in order to
move through the explanation.
•Some demos require Simulink
Robotics Toolbox for MATLAB 237 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RTBPlot
Plot utilities for Robotics Toolbox
RTBPlot.box
Draw a box
BPX(ax,R,extent,color,offset,options) draws a cylinder parallel to axis ax (’x’, ‘y’
or ‘z’) of side length Rbetween extent(1) and extent(2).
RTBPlot.cyl
Draw a cylinder
CYL(ax,R,extent,color,offset,options) draws a cylinder parallel to axis ax (’x’, ‘y’
or ‘z’) of radius Rbetween extent(1) and extent(2).
options are passed through to surf.
See also
surf,RTBPlot.box
RTBPlot.install_teach_panel
robot like object, has n fkine animate methods
Robotics Toolbox for MATLAB 238 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RTBPose
Superclass for SO2, SO3, SE2, SE3
This abstract class provides common methods for the 2D and 3D orientation and pose
classes: SO2, SE2, SO3 and SE3.
Methods
dim dimension of the underlying matrix
isSE true for SE2 and SE3
issym true if value is symbolic
plot graphically display coordinate frame for pose
animate graphically display coordinate frame for pose
print print the pose in single line format
display print the pose in human readable matrix form
char convert to human readable matrix as a string
double convert to real rotation or homogeneous transformation matrix
simplify apply symbolic simplification to all elements
Operators
+ elementwise addition, result is a matrix
- elementwise subtraction, result is a matrix
multiplication within group, also SO3 x vector
/ multiplication within group by inverse
== test equality
6=test inequality
A number of compatibility methods give the same behaviour as the classic RTB func-
tions:
tr2rt convert to rotation matrix and translation vector
t2r convert to rotation matrix
trprint print single line representation
trprint2 print single line representation
trplot plot coordinate frame
trplot2 plot coordinate frame
tranimate aimate coordinate frame
Robotics Toolbox for MATLAB 239 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Multiplication and division with normalization operations are performed in the
subclasses.
•SO3 is polymorphic with UnitQuaternion making it easy to change rotational
representations.
•If the File Exchange function cprintf is available it is used to print the matrix in
color: red for rotation and blue for translation.
See also
SO2,SO3,SE2,SE3
RTBPose.animate
Animate a coordinate frame
RTBPose.animate(p1,p2,options) animates a 3D coordinate frame moving from
pose p1 to pose p2, which can be SO3 or SE3.
RTBPose.animate(p,options) animates a coordinate frame moving from the identity
pose to the pose prepresented by any of the types listed above.
RTBPose.animate(pv,options) animates a trajectory, where pv is a vector of SO2,
SO3, SE2, SE3 objects.
Compatible with matrix function tranimate(T), tranimate(T1, T2).
Options (inherited from tranimate)
‘fps’, fps Number of frames per second to display (default 10)
‘nsteps’, n The number of steps along the path (default 50)
‘axis’, A Axis bounds [xmin, xmax, ymin, ymax, zmin, zmax]
‘movie’, M Save frames as files in the folder M
‘cleanup’ Remove the frame at end of animation
‘noxyz’ Don’t label the axes
‘rgb’ Color the axes in the order x=red, y=green, z=blue
‘retain’ Retain frames, don’t animate
Additional options are passed through to TRPLOT.
See also
tranimate
Robotics Toolbox for MATLAB 240 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RTBPose.char
Convert to string
s= P.char() is a string showing homogeneous transformation elements as a matrix.
See also
RTBPose.display
RTBPose.dim
Dimension
n= P.dim() is the dimension of the group object, 2 for SO2, 3 for SE2 and SO3, and 4
for SE3.
RTBPose.display
Display a pose
P.display() displays the pose.
Notes
•This method is invoked implicitly at the command line when the result of an ex-
pression is an RTBPose subclass object and the command has no trailing semi-
colon.
•If the function cprintf is found is used to colorise the matrix, rotational elements
in red, translational in blue.
See also
SO2,SO3,SE2,SE3
Robotics Toolbox for MATLAB 241 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RTBPose.double
Convert to matrix
T= P.double() is a matrix representation of the pose P, either a rotation matrix or a
homogeneous transformation matrix.
If P is a vector (1 ×N) then Twill be a 3-dimensional array (M×M×N).
Notes
•If the pose is symbolic the result will be a symbolic matrix.
RTBPose.isSE
Test if pose
P.isSE() is true if the object is of type SE2 or SE3.
RTBPose.issym
Test if pose is symbolic
P.issym() is true if the pose has symbolic rather than real values.
RTBPose.minus
Subtract poses
P1-P2 is the elementwise difference of the matrix elements of the two poses. The result
is a matrix not the input class type since the result of subtraction is not in the group.
RTBPose.mrdivide
Compound SO2 object with inverse
R = P/Q is a pose object representing the composition of the pose object P by the
inverse of the pose object Q, which is matrix multiplication of their equivalent matrices
with the second one inverted.
Robotics Toolbox for MATLAB 242 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
If either, or both, of P or Q are vectors, then the result is a vector.
If P is a vector (1 ×N) then R is a vector (1 ×N) such that R(i) = P(i)/Q.
If Q is a vector (1 ×N) then R is a vector (1 ×N) such thatR(i) = P/Q(i).
If both P and Q are vectors (1×N) then R is a vector (1×N) such that R(i) = P(i)/R(i).
See also
RTBPose.mtimes
RTBPose.mtimes
Compound pose objects
R = P*Q is a pose object representing the composition of the two poses described by
the objects P and Q, which is multiplication of their equivalent matrices.
If either, or both, of P or Q are vectors, then the result is a vector.
If P is a vector (1 ×N) then R is a vector (1 ×N) such that R(i) = P(i)*Q.
If Q is a vector (1 ×N) then R is a vector (1 ×N) such thatR(i) = P*Q(i).
If both P and Q are vectors (1×N) then R is a vector (1 ×N) such that R(i) = P(i)*R(i).
W = P*V is a column vector (2 ×1) which is the transformation of the column vector
V (2 ×1) by the rotation described by the SO2 object P. P can be a vector and/or V can
be a matrix, a columnwise set of vectors.
If P is a vector (1 ×N) then W is a matrix (2 ×N) such that W(:,i) = P(i)*V.
If V is a matrix (2×N) V is a matrix (2×N) then W is a matrix (2×N) such that W(:,i)
= P*V(:,i).
If P is a vector (1 ×N) and V is a matrix (2 ×N) then W is a matrix (2 ×N) such that
W(:,i) = P(i)*V(:,i).
See also
RTBPose.mrdivide
RTBPose.plot
Draw a coordinate frame (compatibility)
trplot(p,options) draws a 3D coordinate frame represented by pwhich is SO2, SO3,
SE2 or SE3.
Robotics Toolbox for MATLAB 243 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Compatible with matrix function trplot(T).
Options are passed through to trplot or trplot2 depending on the object type.
See also
trplot,trplot2
RTBPose.plus
Add poses
P1+P2 is the elementwise summation of the matrix elements of the two poses. The
result is a matrix not the input class type since the result of addition is not in the group.
RTBPose.print
Compact display of pose
P.print(options) displays the homogoneous transform in a compact single-line format.
If P is a vector then each element is printed on a separate line.
Options are passed through to trprint or trprint2 depending on the object type.
See also
trprint,trprint2
RTBPose.simplify
Symbolic simplification
p2 = P.simplify() applies symbolic simplification to each element of internal matrix
representation of the pose.
See also
simplify
Robotics Toolbox for MATLAB 244 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RTBPose.t2r
Get rotation matrix (compatibility)
R=t2r(p) returns the rotation matrix corresponding to the pose pwhich is either SE2
or SE3.
Compatible with matrix function R=t2r(T)
RTBPose.tr2rt
Split rotational and translational components (compatibility)
[R,t] = tr2rt(p) returns the rotation matrix and translation vector corresponding to the
pose pwhich is either SE2 or SE3.
Compatible with matrix function [R,t] = tr2rt(T)
RTBPose.tranimate
Animate a coordinate frame (compatibility)
TRANIMATE(p1,p2,options) animates a 3D coordinate frame moving from pose
p1 to pose p2, which can be SO2, SO3, SE2 or SE3.
TRANIMATE(p,options) animates a coordinate frame moving from the identity pose
to the pose prepresented by any of the types listed above.
TRANIMATE(pv,options) animates a trajectory, where pv is a vector of SO2, SO3,
SE2, SE3 objects.
Compatible with matrix function tranimate(T), tranimate(T1, T2).
Options (inherited from tranimate)
‘fps’, fps Number of frames per second to display (default 10)
‘nsteps’, n The number of steps along the path (default 50)
‘axis’, A Axis bounds [xmin, xmax, ymin, ymax, zmin, zmax]
‘movie’, M Save frames as files in the folder M
‘cleanup’ Remove the frame at end of animation
‘noxyz’ Don’t label the axes
‘rgb’ Color the axes in the order x=red, y=green, z=blue
‘retain’ Retain frames, don’t animate
Robotics Toolbox for MATLAB 245 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Additional options are passed through to TRPLOT.
See also
RTBPose.animate,tranimate
RTBPose.trplot
Draw a coordinate frame (compatibility)
trplot(p,options) draws a 3D coordinate frame represented by pwhich is SO2, SO3,
SE2, SE3.
Compatible with matrix function trplot(T).
Options (inherited from trplot)
‘handle’, h Update the specified handle
‘color’, C The color to draw the axes, MATLAB colorspec C
‘noaxes’ Don’t display axes on the plot
‘axis’, A Set dimensions of the MATLAB axes to A=[xmin xmax ymin ymax zmin zmax]
‘frame’, F The coordinate frame is named {F}and the subscript on the axis labels is F.
‘framelabel’, F The coordinate frame is named {F}, axes have no subscripts.
‘text_opts’, opt A cell array of MATLAB text properties
‘axhandle’, A Draw in the MATLAB axes specified by the axis handle A
‘view’, V Set plot view parameters V=[az el] angles, or ‘auto’ for view toward origin of coordi-
nate frame
‘length’, s Length of the coordinate frame arms (default 1)
‘arrow’ Use arrows rather than line segments for the axes
‘width’, w Width of arrow tips (default 1)
‘thick’, t Thickness of lines (default 0.5)
‘perspective’ Display the axes with perspective projection
‘3d’ Plot in 3D using anaglyph graphics
‘anaglyph’, A Specify anaglyph colors for ‘3d’ as 2 characters for left and right (default colors ‘rc’):
chosen from r)ed, g)reen, b)lue, c)yan, m)agenta.
‘dispar’, D Disparity for 3d display (default 0.1)
‘text’ Enable display of X,Y,Z labels on the frame
‘labels’, L Label the X,Y,Z axes with the 1st, 2nd, 3rd character of the string L
‘rgb’ Display X,Y,Z axes in colors red, green, blue respectively
‘rviz’ Display chunky rviz style axes
See also
RTBPose.plot,trplot
Robotics Toolbox for MATLAB 246 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
RTBPose.trplot2
Draw a coordinate frame (compatibility)
trplot2(p,options) draws a 2D coordinate frame represented by p
Compatible with matrix function trplot2(T).
Options (inherited from trplot)
‘handle’, h Update the specified handle
‘axis’, A Set dimensions of the MATLAB axes to A=[xmin xmax ymin ymax]
‘color’, c The color to draw the axes, MATLAB colorspec
‘noaxes’ Don’t display axes on the plot
‘frame’, F The frame is named {F}and the subscript on the axis labels is F.
‘framelabel’, F The coordinate frame is named {F}, axes have no subscripts.
‘text_opts’, opt A cell array of Matlab text properties
‘axhandle’, A Draw in the MATLAB axes specified by A
‘view’, V Set plot view parameters V=[az el] angles, or ‘auto’ for view toward origin of coordi-
nate frame
‘length’, s Length of the coordinate frame arms (default 1)
‘arrow’ Use arrows rather than line segments for the axes
‘width’, w Width of arrow tips
See also
RTBPose.plot,trplot2
RTBPose.trprint
Compact display of homogeneous transformation (compati-
bility)
trprint(p,options) displays the homogoneous transform in a compact single-line for-
mat. If pis a vector then each element is printed on a separate line.
Compatible with matrix function trprint(T).
Options (inherited from trprint)
‘rpy’ display with rotation in roll/pitch/yaw angles (default)
‘euler’ display with rotation in ZYX Euler angles
‘angvec’ display with rotation in angle/vector format
Robotics Toolbox for MATLAB 247 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘radian’ display angle in radians (default is degrees)
‘fmt’, f use format string f for all numbers, (default %g)
‘label’, l display the text before the transform
See also
RTBPose.print,trprint
RTBPose.trprint2
Compact display of homogeneous transformation (compati-
bility)
trprint2(p,options) displays the homogoneous transform in a compact single-line for-
mat. If pis a vector then each element is printed on a separate line.
Compatible with matrix function trprint2(T).
Options (inherited from trprint2)
‘radian’ display angle in radians (default is degrees)
‘fmt’, f use format string f for all numbers, (default %g)
‘label’, l display the text before the transform
See also
RTBPose.print,trprint2
runscript
Run an M-file in interactive fashion
runscript(script,options) runs the M-file script and pauses after every executable line
in the file until a key is pressed. Comment lines are shown without any delay between
lines.
Options
Robotics Toolbox for MATLAB 248 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘delay’, D Don’t wait for keypress, just delay of D seconds (default 0)
‘cdelay’, D Pause of D seconds after each comment line (default 0)
‘begin’ Start executing the file after the comment line %%begin (default false)
‘dock’ Cause the figures to be docked when created
‘path’, P Look for the file script in the folder P (default .)
‘dock’ Dock figures within GUI
‘nocolor’ Don’t use cprintf to print lines in color (comments black, code blue)
Notes
•If no file extension is given in script, .m is assumed.
•A copyright text block will be skipped and not displayed.
•If cprintf exists and ‘nocolor’ is not given then lines are displayed in color.
•Leading comment characters are not displayed.
•If the executable statement has comments immediately afterward (no blank lines)
then the pause occurs after those comments are displayed.
•A simple ‘-’ prompt indicates when the script is paused, hit enter.
•If the function cprintf() is in your path, the display is more colorful. You can get
this file from MATLAB File Exchange.
•If the file has a lot of boilerplate, you can skip over and not display it by giving
the ‘begin’ option which searchers for the first line starting with %%begin and
commences execution at the line after that.
See also
eval
SE2
Representation of 2D rigid-body motion
This subclasss of SO2 <RTBPose is an object that represents an SE(2) rigid-body
motion.
Constructor methods
SE2 general constructor
SE2.exp exponentiate an se(2) matrix
Robotics Toolbox for MATLAB 249 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE2.rand random transformation
new new SE2 object
Information and test methods
dim* returns 2
isSE* returns true
issym* true if rotation matrix has symbolic elements
isa check if matrix is SE2
Display and print methods
plot* graphically display coordinate frame for pose
animate* graphically animate coordinate frame for pose
print* print the pose in single line format
display* print the pose in human readable matrix form
char* convert to human readable matrix as a string
Operation methods
det determinant of matrix component
eig eigenvalues of matrix component
log logarithm of rotation matrix
inv inverse
simplify* apply symbolic simplication to all elements
interp interpolate between poses
Conversion methods
check convert object or matrix to SE2 object
theta return rotation angle
double convert to rotation matrix
R convert to rotation matrix
SE2 convert to SE2 object with zero translation
T convert to homogeneous transformation matrix
t translation column vector
Compatibility methods
isrot2* returns false
ishomog2* returns true
tr2rt* convert to rotation matrix and translation vector
Robotics Toolbox for MATLAB 250 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
t2r* convert to rotation matrix
trprint2* print single line representation
trplot2* plot coordinate frame
tranimate2* animate coordinate frame
transl2 return translation as a row vector
Static methods
check convert object or matrix to SO2 object
SE2.SE2
Construct an SE(2) object
Constructs an SE(2) pose object that contains a 3 ×3 homogeneous transformation
matrix.
T=SE2() is a null relative motion
T=SE2(x,y) is an object representing pure translation defined by xand y
T=SE2(xy) is an object representing pure translation defined by xy (2 ×1). If xy
(N×2) returns an array of SE2 objects, corresponding to the rows of xy.
T=SE2(x,y,theta) is an object representing translation, xand y, and rotation, angle
theta.
T=SE2(xy,theta) is an object representing translation, xy (2 ×1), and rotation, angle
theta
T=SE2(xyt) is an object representing translation, xyt(1) and xyt(2), and rotation,
angle xyt(3). If xyt (N×3) returns an array of SE2 objects, corresponding to the rows
of xyt.
T=SE2(R) is an object representing pure rotation defined by the orthonormal rotation
matrix R(2 ×2)
T=SE2(R,xy) is an object representing rotation defined by the orthonormal rotation
matrix R(2 ×2) and position given by xy (2 ×1)
T=SE2(T) is an object representing translation and rotation defined by the homoge-
neous transformation matrix T(3×3). If T(3 ×3×N) returns an array of SE2 objects,
corresponding to the third index of T
T=SE2(T) is an object representing translation and rotation defined by the SE2 ob-
ject T, effectively cloning the object. If T(N×1) returns an array of SE2 objects,
corresponding to the index of T
Robotics Toolbox for MATLAB 251 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘deg’ Angle is specified in degrees
Notes
•Arguments can be symbolic
•The form SE2(xy) is ambiguous with SE2(R) if xy has 2 rows, the second form
is assumed.
•The form SE2(xyt) is ambiguous with SE2(T) if xyt has 3 rows, the second form
is assumed.
SE2.check
Convert to SE2
q=SE2.check(x) is an SE2 object where xis SE2 or 3 ×3 homogeneous transforma-
tion matrix.
SE2.exp
Construct SE2 object from Lie algebra
p=SE2.exp(se2) creates an SE2 object by exponentiating the se(2) argument (3 ×3).
SE2.get.t
Get translational component
P.t is a column vector (2×1) representing the translational component of the rigid-body
motion described by the SE2 object P.
Notes
•If P is a vector the result is a MATLAB comma separated list, in this
case use P.transl().
Robotics Toolbox for MATLAB 252 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SE2.transl
SE2.interp
Interpolate between SO2 objects
P1.interp(p2,s) is an SE2 object representing interpolation between rotations repre-
sented by SE3 objects P1 and p2.svaries from 0 (P1) to 1 (p2). If sis a vector (1 ×N)
then the result will be a vector of SE2 objects.
Notes
•It is an error if S is outside the interval 0 to 1.
See also
SO2.angle
SE2.inv
Inverse of SE2 object
q=inv(p) is the inverse of the SE2 object p.p*qwill be the identity matrix.
Notes
•This is formed explicitly, no matrix inverse required.
SE2.isa
Test if matrix is SE(2)
SE2.ISA(T) is true (1) if the argument Tis of dimension 3 ×3 or 3 ×3×N, else false
(0).
SE2.ISA(T, true’) as above, but also checks the validity of the rotation sub-matrix.
Robotics Toolbox for MATLAB 253 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The first form is a fast, but incomplete, test for a transform in SE(3).
•There is ambiguity in the dimensions of SE2 and SO3 in matrix form.
See also
SO3.ISA,SE2.ISA,SO2.ISA,ishomog2
SE2.log
Lie algebra
se2 = P.log() is the Lie algebra augmented skew-symmetric matrix (3 ×3) correspond-
ing to the SE2 object P.
See also
SE2.Twist,logm
SE2.new
Construct a new object of the same type
p2 = P.new(x) creates a new object of the same type as P, by invoking the SE2 con-
structor on the matrix x(3 ×3).
p2 = P.new() as above but defines a null motion.
Notes
•Serves as a dynamic constructor.
•This method is polymorphic across all RTBPose derived classes, and allows easy
creation of a new object of the same class as an existing one.
See also
SE3.new,SO3.new,SO2.new
Robotics Toolbox for MATLAB 254 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE2.rand
Construct a random SE(2) object
SE2.rand() is an SE2 object with a uniform random translation and a uniform random
orientation. Random numbers are in the interval 0 to 1.
See also
rand
SE2.SE3
Lift to 3D
q= P.SE3() is an SE3 object formed by lifting the rigid-body motion described by the
SE2 object P from 2D to 3D. The rotation is about the z-axis, and the translational is
within the xy-plane.
See also
SE3
SE2.set.t
Set translational component
P.t = TV sets the translational component of the rigid-body motion described by the
SE2 object P to TV (2 ×1).
Notes
•TV can be a row or column vector.
•If TV contains a symbolic value then the entire matrix is converted to symbolic.
Robotics Toolbox for MATLAB 255 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE2.SO2
Extract SO(2) rotation
q=SO2(p) is an SO2 object that represents the rotational component of the SE2 rigid-
body motion.
See also
SE2.R
SE2.T
Get homogeneous transformation matrix
T= P.T() is the homogeneous transformation matrix (3 ×3) associated with the SE2
object P, and has zero translational component. If P is a vector (1 ×N) then T(3 ×3×
N) is a stack of rotation matrices, with the third dimension corresponding to the index
of P.
See also
SO2.T
SE2.transl
Get translational component
tv = P.transl() is a row vector (1 ×2) representing the translational component of the
rigid-body motion described by the SE2 object P. If P is a vector of objects (1 ×N)
then tv (N×2) will have one row per object element.
SE2.Twist
Convert to Twist object
tw = P.Twist() is the equivalent Twist object. The elements of the twist are the unique
elements of the Lie algebra of the SE2 object P.
Robotics Toolbox for MATLAB 256 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SE2.log,Twist
SE2.xyt
Construct SE2 object from Lie algebra
xyt = P.xyt() is a column vector (3 ×1) comprising the minimum three parameters of
this rigid-body motion [x; y; theta] with translation (x,y) and rotation theta.
SE3
SE(3) homogeneous transformation class
This subclasss of SE3 <SO3 <RTBPose is an object that represents an SE(3) rigid-
body motion
T=se3() is an SE(3) homogeneous transformation (4×4) representing zero translation
and rotation.
T=se3(x,y,z) as above represents a pure translation.
T= SE3.rx(theta) as above represents a pure rotation about the x-axis.
Constructor methods
SE3 general constructor
SE3.exp exponentiate an se(3) matrix
SE3.angvec rotation about vector
SE3.eul rotation defined by Euler angles
SE3.oa rotation defined by o- and a-vectors
SE3.rpy rotation defined by roll-pitch-yaw angles
SE3.rx rotation about x-axis
SE3.Ry rotation about y-axis
SE3.Rz rotation about z-axis
SE3.rand random transformation
new new SE3 object
Information and test methods
dim* returns 4
Robotics Toolbox for MATLAB 257 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
isSE* returns true
issym* true if rotation matrix has symbolic elements
isidentity true for null motion
SE3.isa check if matrix is SO2
Display and print methods
plot* graphically display coordinate frame for pose
animate* graphically animate coordinate frame for pose
print* print the pose in single line format
display* print the pose in human readable matrix form
char* convert to human readable matrix as a string
Operation methods
det determinant of matrix component
eig eigenvalues of matrix component
log logarithm of rotation matrixr>=0 && r<=1ub
inv inverse
simplify* apply symbolic simplication to all elements
Ad adjoint matrix (6 ×6)
increment update pose based on incremental motion
interp interpolate poses
velxform compute velocity transformation
interp interpolate between poses
ctraj Cartesian motion
Conversion methods
SE3.check convert object or matrix to SE3 object
double convert to rotation matrix
R return rotation matrix
SO3 return rotation part as an SO3 object
Tconvert to homogeneous transformation matrix
UnitQuaternion convert to UnitQuaternion object
toangvec convert to rotation about vector form
toeul convert to Euler angles
torpy convert to roll-pitch-yaw angles
t translation column vector
tv translation column vector for vector of SE3
Compatibility methods
homtrans apply to vector
Robotics Toolbox for MATLAB 258 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
isrot* returns false
ishomog* returns true
tr2rt* convert to rotation matrix and translation vector
t2r* convert to rotation matrix
trprint* print single line representation
trplot* plot coordinate frame
tranimate* animate coordinate frame
tr2eul convert to Euler angles
tr2rpy convert to roll-pitch-yaw angles
trnorm normalize the rotation matrix
transl return translation as a row vector
* means inherited from RTBPose
Operators
+ elementwise addition, result is a matrix
- elementwise subtraction, result is a matrix
multiplication within group, also group x vector
.* multiplication within group followed by normalization
/ multiply by inverse
./ multiply by inverse followed by normalization
== test equality
6=test inequality
Properties
n normal (x) vector
o orientation (y) vector
a approach (z) vector
t translation vector
For single SE3 objects only, for a vector of SE3 objects use the equivalent methods
t translation as a 3 ×1 vector (read/write)
R rotation as a 3 ×3 matrix (read/write)
Methods
tv return translations as a 3 ×Nvector
Robotics Toolbox for MATLAB 259 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The properies R, t are implemented as MATLAB dependent properties. When
applied to a vector of SE3 object the result is a comma-separated list which can
be converted to a matrix by enclosing it in square brackets, eg [T.t] or more
conveniently using the method T.transl
See also
SO3,SE2,RTBPose
SE3.SE3
Create an SE(3) object
Constructs an SE(3) pose object that contains a 4 ×4 homogeneous transformation
matrix.
T=SE3() is a null relative motion
T=SE3(x,y,z) is an object representing pure translation defined by x,yand z.
T=SE3(xyz) is an object representing pure translation defined by xyz (3 ×1). If xyz
(N×3) returns an array of SE3 objects, corresponding to the rows of xyz
T=SE3(R,xyz) is an object representing rotation defined by the orthonormal rotation
matrix R(3 ×3) and position given by xyz (3 ×1)
T=SE3(T) is an object representing translation and rotation defined by the homoge-
neous transformation matrix T(3×3). If T(3 ×3×N) returns an array of SE3 objects,
corresponding to the third index of T
T=SE3(T) is an object representing translation and rotation defined by the SE3 ob-
ject T, effectively cloning the object. If T(N×1) returns an array of SE3 objects,
corresponding to the index of T
Options
‘deg’ Angle is specified in degrees
Notes
•Arguments can be symbolic
Robotics Toolbox for MATLAB 260 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.Ad
Adjoint matrix
a= S.Ad() is the adjoint matrix (6 ×6) corresponding to the SE(3) value S.
See also
Twist.ad
SE3.angvec
Construct an SE(3) object from angle and axis vector
R=SE3.angvec(theta,v) is an orthonormal rotation matrix (3 ×3) equivalent to a
rotation of theta about the vector v.
Notes
•If theta == 0 then return identity matrix.
•If theta 6=0 then vmust have a finite length.
See also
SO3.angvec,eul2r,rpy2r,tr2angvec
SE3.check
Convert to SE3
q=SE3.check(x) is an SE3 object where xis SE3 object or 4 ×4 homogeneous trans-
formation matrix.
Robotics Toolbox for MATLAB 261 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.ctraj
Cartesian trajectory between two poses
tc = T0.ctraj(T1,n) is a Cartesian trajectory defined by a vector of SE3 objects (1 ×n)
from pose T0 to T1, both described by SE3 objects. There are npoints on the trajectory
that follow a trapezoidal velocity profile along the trajectory.
tc =CTRAJ(T0,T1,s) as above but the elements of s(n×1) specify the fractional dis-
tance along the path, and these values are in the range [0 1]. The ith point corresponds
to a distance s(i) along the path.
Notes
•In the second case scould be generated by a scalar trajectory generator such as
TPOLY or LSPB (default).
•Orientation interpolation is performed using quaternion interpolation.
Reference
Robotics, Vision & Control, Sec 3.1.5, Peter Corke, Springer 2011
See also
lspb,mstraj,trinterp,ctraj,UnitQuaternion.interp
SE3.delta
SE3 object from differential motion vector
T=SE3.delta(d) is an SE3 pose object representing differential translation and rota-
tion. The vector d=(dx, dy, dz, dRx, dRy, dRz) represents an infinitessimal motion, and
is an approximation to the spatial velocity multiplied by time.
See also
SE3.todelta,SE3.increment,tr2delta
Robotics Toolbox for MATLAB 262 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.eul
Construct an SE(3) object from Euler angles
p=SE3.eul(phi,theta,psi,options) is an SE3 object equivalent to the specified Euler
angles with zero translation. These correspond to rotations about the Z, Y, Z axes
respectively. If phi,theta,psi are column vectors (N×1) then they are assumed to
represent a trajectory then pis a vector (1 ×N) of SE3 objects.
p=SE3.eul2R(eul,options) as above but the Euler angles are taken from consecutive
columns of the passed matrix eul = [phi theta psi]. If eul is a matrix (N×3) then they
are assumed to represent a trajectory then pis a vector (1 ×N) of SE3 objects.
Options
‘deg’ Compute angles in degrees (radians default)
Note
•The vectors phi,theta,psi must be of the same length.
See also
SO3.eul,SE3.rpy,eul2tr,rpy2tr,tr2eul
SE3.exp
SE3 object from se(3)
SE3.exp(sigma) is the SE3 rigid-body motion given by the se(3) element sigma (4 ×
4).
SE3.exp(exp(S) as above, but the se(3) value is expressed as a twist vector (6 ×1).
SE3.exp(sigma,theta) as above, but the motion is given by sigma*theta where sigma
is an se(3) element (4 ×4) whose rotation part has a unit norm.
Notes
•wraps trexp.
Robotics Toolbox for MATLAB 263 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
trexp
SE3.homtrans
Apply transformation to points
P.homtrans(v) applies SE3 pose object P to the points stored columnwise in v(3 ×N)
and returns transformed points (3 ×N).
Notes
•P is an SE3 object defining the pose of {A}with respect to {B}.
•The points are defined with respect to frame {A}and are transformed to be with
respect to frame {B}.
•Equivalent to P*vusing overloaded SE3 operators.
See also
RTBPose.mtimes,homtrans
SE3.increment
Apply incremental motion to an SE3 pose
p1 = P.increment(d) is an SE3 pose object formed by applying the incremental motion
vector d(1 ×6) in the frame associated with SE3 pose P.
See also
SE3.todelta,delta2tr,tr2delta
SE3.interp
Interpolate SE3 poses
P1.interp(p2,s) is an SE3 object representing an interpolation between poses repre-
sented by SE3 objects P1 and p2.svaries from 0 (P1) to 1 (p2). If sis a vector (1 ×N)
Robotics Toolbox for MATLAB 264 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
then the result will be a vector of SO3 objects.
P1.interp(p2,n) as above but returns a vector (1 ×n) of SE3 objects interpolated be-
tween P1 and p2 in nsteps.
Notes
•The rotational interpolation (slerp) can be interpretted as interpolation along a
great circle arc on a sphere.
•It is an error if S is outside the interval 0 to 1.
See also
trinterp,UnitQuaternion
SE3.inv
Inverse of SE3 object
q=inv(p) is the inverse of the SE3 object p.p*qwill be the identity matrix.
Notes
•This is formed explicitly, no matrix inverse required.
SE3.isa
Test if a homogeneous transformation
SE3.ISA(T) is true (1) if the argument Tis of dimension 4 ×4 or 4 ×4×N, else false
(0).
SE3.ISA(T, ‘valid’) as above, but also checks the validity of the rotation sub-matrix.
Notes
•The first form is a fast, but incomplete, test for a transform in SE(3).
Robotics Toolbox for MATLAB 265 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SO3.ISA,SE2.ISA,SO2.ISA
SE3.isidentity
Apply incremental motion to an SE(3) pose
P.isidentity() is true of the SE3 object P corresponds to null motion, that is, its homo-
geneous transformation matrix is identity.
SE3.log
Lie algebra
se3 = P.log() is the Lie algebra expressed as an augmented skew-symmetric matrix
(4 ×4) corresponding to the SE3 object P.
See also
SE3.logs,SE3.Twist,trlog,logm
SE3.logs
Lie algebra
se3 = P.log() is the Lie algebra expressed as vector (1 ×6) corresponding to the SE2 ob-
ject P. The vector comprises the translational elements followed by the unique elements
of the skew-symmetric rotation submatrix.
See also
SE3.log,SE3.Twist,trlog,logm
Robotics Toolbox for MATLAB 266 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.new
Construct a new object of the same type
p2 = P.new(x) creates a new object of the same type as P, by invoking the SE3 con-
structor on the matrix x(4 ×4).
p2 = P.new() as above but defines a null motion.
Notes
•Serves as a dynamic constructor.
•This method is polymorphic across all RTBPose derived classes, and allows easy
creation of a new object of the same class as an existing one.
See also
SO3.new,SO2.new,SE2.new
SE3.oa
Construct an SE(3) object from orientation and approach vec-
tors
p=SE3.oa(o,a) is an SE3 object for the specified orientation and approach vectors
(3×1) formed from 3 vectors such that R = [N o a] and N = oxa, with zero translation.
Notes
•The rotation submatrix is guaranteed to be orthonormal so long as oand aare
not parallel.
•The vectors oand aare parallel to the Y- and Z-axes of the coordinate frame.
References
•Robot manipulators: mathematis, programming and control Richard Paul, MIT
Press, 1981.
Robotics Toolbox for MATLAB 267 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
rpy2r,eul2r,oa2tr,SO3.oa
SE3.rand
Construct a random SE(3) object
SE3.rand() is an SE3 object with a uniform random translation and a uniform random
RPY/ZYX orientation. Random numbers are in the interval 0 to 1.
See also
rand
SE3.rpy
Construct an SE(3) object from roll-pitch-yaw angles
p=SE3.rpy(roll,pitch,yaw,options) is an SE3 object equivalent to the specified roll,
pitch, yaw angles angles with zero translation. These correspond to rotations about the
Z, Y, X axes respectively. If roll,pitch,yaw are column vectors (N×1) then they are
assumed to represent a trajectory then pis a vector (1 ×N) of SE3 objects.
p=SE3.rpy(rpy,options) as above but the roll, pitch, yaw angles angles angles are
taken from consecutive columns of the passed matrix rpy = [roll,pitch,yaw]. If rpy
is a matrix (N×3) then they are assumed to represent a trajectory and pis a vector
(1 ×N) of SE3 objects.
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Rotations about X, Y, Z axes (for a robot gripper)
‘yxz’ Rotations about Y, X, Z axes (for a camera)
See also
SO3.rpy,SE3.eul,tr2rpy,eul2tr
Robotics Toolbox for MATLAB 268 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.Rx
Rotation about X axis
p=SE3.Rx(theta) is an SE3 object representing a rotation of theta radians about the
x-axis.
p=SE3.Rx(theta, ‘deg’) as above but theta is in degrees.
See also
SE3.Ry,SE3.Rz,rotx
SE3.Ry
Rotation about Y axis
p=SE3.Ry(theta) is an SE3 object representing a rotation of theta radians about the
y-axis.
p=SE3.Ry(theta, ‘deg’) as above but theta is in degrees.
See also
SE3.Ry,SE3.Rz,rotx
SE3.Rz
Rotation about Z axis
p=SE3.Rz(theta) is an SE3 object representing a rotation of theta radians about the
z-axis.
p=SE3.Rz(theta, ‘deg’) as above but theta is in degrees.
See also
SE3.Ry,SE3.Rz,rotx
Robotics Toolbox for MATLAB 269 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.set.t
Get translation vector
T = P.t is the translational part of SE3 object as a 3-element column vector.
Notes
•If applied to a vector will return a comma-separated list, use .transl() instead.
See also
SE3.transl,transl
SE3.SO3
Convert rotational component to SO3 object
P.SO3 is an SO3 object representing the rotational component of the SE3 pose P. If P
is a vector (N×1) then the result is a vector (N×1).
SE3.T
Get homogeneous transformation matrix
T= P.T() is the homogeneous transformation matrix (3 ×3) associated with the SO2
object P, and has zero translational component. If P is a vector (1 ×N) then T(3 ×3×
N) is a stack of rotation matrices, with the third dimension corresponding to the index
of P.
See also
SO2.T
Robotics Toolbox for MATLAB 270 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.toangvec
Convert to angle-vector form
[theta,v] = P.toangvec(options) is rotation expressed in terms of an angle theta (1 ×1)
about the axis v(1 ×3) equivalent to the rotational part of the SE3 object P.
If P is a vector (1 ×N) then theta (K×1) is a vector of angles for corresponding
elements of the vector and v(K×3) are the corresponding axes, one per row.
Options
‘deg’ Return angle in degrees
Notes
•If no output arguments are specified the result is displayed.
See also
angvec2r,angvec2tr,trlog
SE3.todelta
Convert SE(3) object to differential motion vector
d=SE3.todelta(p0,p1) is the (6 ×1) differential motion vector (dx, dy, dz, dRx, dRy,
dRz) corresponding to infinitessimal motion (in the p0 frame) from SE(3) pose p0 to
p1. .
d=SE3.todelta(p) as above but the motion is with respect to the world frame.
Notes
•dis only an approximation to the motion, and assumes that p0≈p1 or p≈eye(4,4).
•can be considered as an approximation to the effect of spatial velocity over a a
time interval, average spatial velocity multiplied by time.
See also
SE3.increment,tr2delta,delta2tr
Robotics Toolbox for MATLAB 271 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SE3.toeul
Convert to Euler angles
eul = P.toeul(options) are the ZYZ Euler angles (1 ×3) corresponding to the rotational
part of the SE3 object P. The 3 angles eul=[PHI,THETA,PSI] correspond to sequential
rotations about the Z, Y and Z axes respectively.
If P is a vector (1 ×N) then each row of eul corresponds to an element of the vector.
Options
‘deg’ Compute angles in degrees (radians default)
‘flip’ Choose first Euler angle to be in quadrant 2 or 3.
Notes
•There is a singularity for the case where THETA=0 in which case PHI is arbi-
trarily set to zero and PSI is the sum (PHI+PSI).
See also
SO3.toeul,SE3.torpy,eul2tr,tr2rpy
SE3.torpy
Convert to roll-pitch-yaw angles
rpy = P.torpy(options) are the roll-pitch-yaw angles (1 ×3) corresponding to the ro-
tational part of the SE3 object P. The 3 angles rpy=[R,P,Y] correspond to sequential
rotations about the Z, Y and X axes respectively.
If P is a vector (1 ×N) then each row of rpy corresponds to an element of the vector.
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Return solution for sequential rotations about X, Y, Z axes
‘yxz’ Return solution for sequential rotations about Y, X, Z axes
Robotics Toolbox for MATLAB 272 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•There is a singularity for the case where P=pi/2 in which case R is arbitrarily set
to zero and Y is the sum (R+Y).
See also
SE3.torpy,SE3.toeul,rpy2tr,tr2eul
SE3.transl
Get translation vector
T= P.transl() is the translational part of SE3 object as a 3-element row vector. If P is
a vector (1 ×N) then
the rows of T(M×3) are the translational component of the
corresponding pose in the sequence.
[x,y,z] = P.transl() as above but the translational part is returned as three components.
If P is a vector (1 ×N) then x,y,z(1 ×N) are the translational components of the cor-
responding pose in the sequence.
Notes
•The .t method only works for a single pose object, on a vector it returns a comma-
separated list.
See also
SE3.t,transl
SE3.tv
Return translation for a vector of SE3 objects
P.tv is a column vector (3×1) representing the translational part of the SE3 pose object
P. If P is a vector of SE3 objects (N×1) then the result is a matrix (3×N) with columns
corresponding to the elements of P.
Robotics Toolbox for MATLAB 273 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SE3.t
SE3.Twist
Convert to Twist object
tw = P.Twist() is the equivalent Twist object. The elements of the twist are the unique
elements of the Lie algebra of the SE3 object P.
See also
SE3.logs,Twist
SE3.velxform
Velocity transformation
Transform velocity between frames. A is the world frame, B is the body frame and C
is another frame attached to the body. PAB is the pose of the body frame with respect
to the world frame, PCB is the pose of the body frame with respect to frame C.
J= PAB.velxform() is a 6 ×6 Jacobian matrix that maps velocity from frame B to
frame A.
J= PCB.velxform(’samebody’) is a 6 ×6 Jacobian matrix that maps velocity from
frame C to frame B. This is also the adjoint of PCB.
Sensor
Sensor superclass
An abstract superclass to represent robot navigation sensors.
Methods
plot plot a line from robot to map feature
display print the parameters in human readable form
char convert to string
Robotics Toolbox for MATLAB 274 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Properties
robot The Vehicle object on which the sensor is mounted
map The PointMap object representing the landmarks around the robot
Reference
Robotics, Vision & Control, Peter Corke, Springer 2011
See also
RangeBearingSensor,EKF,Vehicle,LandmarkMap
Sensor.Sensor
Sensor object constructor
s=Sensor(vehicle,map,options) is a sensor mounted on a vehicle described by the
Vehicle subclass object vehicle and observing landmarks in a map described by the
LandmarkMap class object map.
Options
‘animate’ animate the action of the laser scanner
‘ls’, LS laser scan lines drawn with style ls (default ‘r-’)
‘skip’, I return a valid reading on every Ith call
‘fail’, T sensor simulates failure between timesteps T=[TMIN,TMAX]
Notes
•Animation shows a ray from the vehicle position to the selected landmark.
Sensor.char
Convert sensor parameters to a string
s= S.char() is a string showing sensor parameters in a compact human readable format.
Robotics Toolbox for MATLAB 275 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Sensor.display
Display status of sensor object
S.display() displays the state of the sensor object in human-readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Sensor object and the command has no trailing semicolon.
See also
Sensor.char
Sensor.plot
Plot sensor reading
S.plot(J) draws a line from the robot to the Jth map feature.
Notes
•The line is drawn using the linestyle given by the property ls
•There is a delay given by the property delay
SerialLink
Serial-link robot class
A concrete class that represents a serial-link arm-type robot. Each link and joint in the
chain is described by a Link-class object using Denavit-Hartenberg parameters (stan-
dard or modified).
Constructor methods
SerialLink general constructor
L1+L2 construct from Link objects
Robotics Toolbox for MATLAB 276 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Display/plot methods
animate animate robot model
display print the link parameters in human readable form
dyn display link dynamic parameters
edit display and edit kinematic and dynamic parameters
getpos get position of graphical robot
plot display graphical representation of robot
plot3d display 3D graphical model of robot
teach drive the graphical robot
Testing methods
islimit test if robot at joint limit
isconfig test robot joint configuration
issym test if robot has symbolic parameters
isprismatic index of prismatic joints
isrevolute index of revolute joints
isspherical test if robot has spherical wrist
Conversion methods
char convert to string
sym convert to symbolic parameters
todegrees convert joint angles to degrees
toradians convert joint angles to radians
SerialLink.SerialLink
Create a SerialLink robot object
R=SerialLink(links,options) is a robot object defined by a vector of Link class
objects which includes the subclasses Revolute, Prismatic, RevoluteMDH or Prismat-
icMDH.
R=SerialLink(options) is a null robot object with no links.
R=SerialLink([R1 R2 ...], options) concatenate robots, the base of R2 is attached to
the tip of R1. Can also be written as R1*R2 etc.
R=SerialLink(R1,options) is a deep copy of the robot object R1, with all the same
properties.
R=SerialLink(dh,options) is a robot object with kinematics defined by the ma-
trix dh which has one row per joint and each row is [theta d a alpha] and joints are
Robotics Toolbox for MATLAB 277 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
assumed revolute. An optional fifth column sigma indicate revolute (sigma=0) or pris-
matic (sigma=1). An optional sixth column is the joint offset.
Options
‘name’, NAME set robot name property to NAME
‘comment’, COMMENT set robot comment property to COMMENT
‘manufacturer’, MANUF set robot manufacturer property to MANUF
‘base’, T set base transformation matrix property to T
‘tool’, T set tool transformation matrix property to T
‘gravity’, G set gravity vector property to G
‘plotopt’, P set default options for .plot() to P
‘plotopt3d’, P set default options for .plot3d() to P
‘nofast’ don’t use RNE MEX file
Examples
Create a 2-link robot
L(1) = Link([ 0 0 a1 pi/2], ’standard’);
L(2) = Link([ 0 0 a2 0], ’standard’);
twolink = SerialLink(L, ’name’, ’two link’);
Create a 2-link robot (most descriptive)
L(1) = Revolute(’d’, 0, ’a’, a1, ’alpha’, pi/2);
L(2) = Revolute(’d’, 0, ’a’, a2, ’alpha’, 0);
twolink = SerialLink(L, ’name’, ’two link’);
Create a 2-link robot (least descriptive)
twolink = SerialLink([0 0 a1 0; 0 0 a2 0], ’name’, ’two link’);
Robot objects can be concatenated in two ways
R = R1 *R2;
R = SerialLink([R1 R2]);
Note
•SerialLink is a reference object, a subclass of Handle object.
•SerialLink objects can be used in vectors and arrays
•Link subclass elements passed in must be all standard, or all modified, dh pa-
rameters.
•When robots are concatenated (either syntax) the intermediate base and tool
transforms are removed since general constant transforms cannot be represented
in Denavit-Hartenberg notation.
Robotics Toolbox for MATLAB 278 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Link,Revolute,Prismatic,RevoluteMDH,PrismaticMDH,SerialLink.plot
SerialLink.A
Link transformation matrices
s= R.A(J,q) is an SE3 object (4 ×4) that transforms between link frames for the Jth
joint. qis a vector (1 ×N) of joint variables. For:
•standard DH parameters, this is from frame {J-1}to frame {J}.
•modified DH parameters, this is from frame {J}to frame {J+1}.
s= R.A(jlist,q) as above but is a composition of link transform matrices given in the
list jlist, and the joint variables are taken from the corresponding elements of q.
Exmaples
For example, the link transform for joint 4 is
robot.A(4, q4)
The link transform for joints 3 through 6 is
robot.A(3:6, q)
where q is 1 ×6 and the elements q(3) .. q(6) are used.
Notes
•Base and tool transforms are not applied.
See also
Link.A
SerialLink.accel
Manipulator forward dynamics
qdd = R.accel(q,qd,torque) is a vector (N×1) of joint accelerations that result from
applying the actuator force/torque (1 ×N) to the manipulator robot R in state q(1 ×N)
and qd (1 ×N), and N is the number of robot joints.
Robotics Toolbox for MATLAB 279 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
If q,qd,torque are matrices (K×N) then qdd is a matrix (K×N) where each row is
the acceleration corresponding to the equivalent rows of q,qd,torque.
qdd = R.accel(x) as above but x=[q,qd,torque] (1 ×3N).
Note
•Useful for simulation of manipulator dynamics, in conjunction with a numerical
integration function.
•Uses the method 1 of Walker and Orin to compute the forward dynamics.
•Featherstone’s method is more efficient for robots with large numbers of joints.
•Joint friction is considered.
References
•Efficient dynamic computer simulation of robotic mechanisms, M. W. Walker
and D. E. Orin, ASME Journa of Dynamic Systems, Measurement and Control,
vol. 104, no. 3, pp. 205-211, 1982.
See also
SerialLink.fdyn,SerialLink.rne,SerialLink,ode45
SerialLink.animate
Update a robot animation
R.animate(q) updates an existing animation for the robot R. This will have been cre-
ated using R.plot(). Updates graphical instances of this robot in all figures.
Notes
•Called by plot() and plot3d() to actually move the arm models.
•Used for Simulink robot animation.
See also
SerialLink.plot
Robotics Toolbox for MATLAB 280 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SerialLink.char
Convert to string
s= R.char() is a string representation of the robot’s kinematic parameters, showing
DH parameters, joint structure, comments, gravity vector, base and tool transform.
SerialLink.cinertia
Cartesian inertia matrix
m= R.cinertia(q) is the N×NCartesian (operational space) inertia matrix which
relates Cartesian force/torque to Cartesian acceleration at the joint configuration q,
and N is the number of robot joints.
See also
SerialLink.inertia,SerialLink.rne
SerialLink.collisions
Perform collision checking
C= R.collisions(q,model) is true if the SerialLink object R at pose q(1 ×N) inter-
sects the solid model model which belongs to the class CollisionModel. The model
comprises a number of geometric primitives with an associated pose.
C= R.collisions(q,model,dynmodel,tdyn) as above but also checks dynamic colli-
sion model dynmodel whose elements are at pose tdyn.tdyn is an array of transfor-
mation matrices (4 ×4×P), where P = length(dynmodel.primitives). The Pth plane of
tdyn premultiplies the pose of the Pth primitive of dynmodel.
C= R.collisions(q,model,dynmodel) as above but assumes tdyn is the robot’s tool
frame.
Trajectory operation
If qis M×Nit is taken as a pose sequence and Cis M×1 and the collision value
applies to the pose of the corresponding row of q.tdyn is 4x4xMxP.
Robotics Toolbox for MATLAB 281 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Requires the pHRIWARE package which defines CollisionModel class. Avail-
able from: https://github.com/bryan91/pHRIWARE .
•The robot is defined by a point cloud, given by its points property.
•The function does not currently check the base of the SerialLink object.
•If model is [] then no static objects are assumed.
Author
Bryan Moutrie
See also
CollisionModel,SerialLink
SerialLink.coriolis
Coriolis matrix
C= R.coriolis(q,qd) is the Coriolis/centripetal matrix (N×N) for the robot in config-
uration qand velocity qd, where N is the number of joints. The product C*qd is the
vector of joint force/torque due to velocity coupling. The diagonal elements are due
to centripetal effects and the off-diagonal elements are due to Coriolis effects. This
matrix is also known as the velocity coupling matrix, since it describes the disturbance
forces on any joint due to velocity of all other joints.
If qand qd are matrices (K×N), each row is interpretted as a joint state vector, and
the result (N×N×K) is a 3d-matrix where each plane corresponds to a row of qand
qd.
C= R.coriolis(qqd) as above but the matrix qqd (1 ×2N) is [q qd].
Notes
•Joint viscous friction is also a joint force proportional to velocity but it is elimi-
nated in the computation of this value.
•Computationally slow, involves N2/2 invocations of RNE.
See also
SerialLink.rne
Robotics Toolbox for MATLAB 282 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SerialLink.display
Display parameters
R.display() displays the robot parameters in human-readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a SerialLink object and the command has no trailing semicolon.
See also
SerialLink.char,SerialLink.dyn
SerialLink.dyn
Print inertial properties
R.dyn() displays the inertial properties of the SerialLink object in a multi-line format.
The properties shown are mass, centre of mass, inertia, gear ratio, motor inertia and
motor friction.
R.dyn(J) as above but display parameters for joint Jonly.
See also
Link.dyn
SerialLink.edit
Edit kinematic and dynamic parameters
R.edit displays the kinematic parameters of the robot as an editable table in a new
figure.
R.edit(’dyn’) as above but also includes the dynamic parameters in the table.
Robotics Toolbox for MATLAB 283 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The ‘Save’ button copies the values from the table to the SerialLink manipulator
object.
•To exit the editor without updating the object just kill the figure window.
SerialLink.fdyn
Integrate forward dynamics
[T,q,qd] = R.fdyn(tmax,ftfun) integrates the dynamics of the robot over the time
interval 0 to tmax and returns vectors of time T(K×1), joint position q(K×N) and
joint velocity qd (K×N). The initial joint position and velocity are zero. The torque
applied to the joints is computed by the user-supplied control function ftfun:
TAU = FTFUN(T, Q, QD)
where q(1 ×N) and qd (1 ×N) are the manipulator joint coordinate and velocity state
respectively, and Tis the current time.
[ti,q,qd] = R.fdyn(T,ftfun,q0,qd0) as above but allows the initial joint position q0
(1 ×N) and velocity qd0 (1x) to be specified.
[T,q,qd] = R.fdyn(T1, ftfun,q0,qd0, ARG1, ARG2, ...) allows optional arguments
to be passed through to the user-supplied control function:
TAU = FTFUN(T, Q, QD, ARG1, ARG2, ...)
For example, if the robot was controlled by a PD controller we can define a function to
compute the control
function tau = myftfun(t, q, qd, qstar, P, D)
tau = P*(qstar-q) + D*qd;
and then integrate the robot dynamics with the control
[t,q] = robot.fdyn(10, @myftfun, qstar, P, D);
Note
•This function performs poorly with non-linear joint friction, such as Coulomb
friction. The R.nofriction() method can be used to set this friction to zero.
•If ftfun is not specified, or is given as 0 or [], then zero torque is applied to the
manipulator joints.
•The MATLAB builtin integration function ode45() is used.
Robotics Toolbox for MATLAB 284 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SerialLink.accel,SerialLink.nofriction,SerialLink.rne,ode45
SerialLink.fellipse
Force ellipsoid for seriallink manipulator
R.fellipse(q,options) displays the force ellipsoid for the robot R at pose q. The ellip-
soid is centered at the tool tip position.
Options
‘2d’ Ellipse for translational xy motion, for planar manipulator
‘trans’ Ellipsoid for translational motion (default)
‘rot’ Ellipsoid for rotational motion
Display options as per plot_ellipse to control ellipsoid face and edge
color and transparency.
Example
To interactively update the force ellipsoid while using sliders to change the robot’s
pose:
robot.teach(’callback’, @(r,q) r.fellipse(q))
Notes
•The ellipsoid is tagged with the name of the robot prepended to “.fellipse”.
•Calling the function with a different pose will update the ellipsoid.
See also
SerialLink.jacob0,SerialLink.vellipse,plot_ellipse
Robotics Toolbox for MATLAB 285 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SerialLink.fkine
Forward kinematics
T= R.fkine(q,options) is the pose of the robot end-effector as an SE3 object for the
joint configuration q(1 ×N).
If qis a matrix (K×N) the rows are interpreted as the generalized joint coordinates
for a sequence of points along a trajectory. q(i,j) is the jth joint parameter for the ith
trajectory point. In this case Tis a an array of SE3 objects (K) where the subscript is
the index along the path.
[T,all] = R.fkine(q) as above but all (N) is a vector of SE3 objects describing the pose
of the link frames 1 to N.
Options
‘deg’ Assume that revolute joint coordinates are in degrees not radians
Note
•The robot’s base or tool transform, if present, are incorporated into the result.
•Joint offsets, if defined, are added to qbefore the forward kinematics are com-
puted.
•If the result is symbolic then each element is simplified.
See also
SerialLink.ikine,SerialLink.ikine6s
SerialLink.friction
Friction force
tau = R.friction(qd) is the vector of joint friction forces/torques for the robot moving
with joint velocities qd.
The friction model includes:
•Viscous friction which is a linear function of velocity.
•Coulomb friction which is proportional to sign(qd).
Robotics Toolbox for MATLAB 286 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The friction value should be added to the motor output torque, it has a negative
value when qd>0.
•The returned friction value is referred to the output of the gearbox.
•The friction parameters in the Link object are referred to the motor.
•Motor viscous friction is scaled up by G2.
•Motor Coulomb friction is scaled up by G.
•The appropriate Coulomb friction value to use in the non-symmetric case de-
pends on the sign of the joint velocity, not the motor velocity.
•The absolute value of the gear ratio is used. Negative gear ratios are tricky: the
Puma560 has negative gear ratio for joints 1 and 3.
See also
Link.friction
SerialLink.gencoords
Vector of symbolic generalized coordinates
q= R.gencoords() is a vector (1 ×N) of symbols [q1 q2 ... qN].
[q,qd] = R.gencoords() as above but qd is a vector (1 ×N) of symbols [qd1 qd2 ...
qdN].
[q,qd,qdd] = R.gencoords() as above but qdd is a vector (1 ×N) of symbols [qdd1
qdd2 ... qddN].
See also
SerialLink.genforces
SerialLink.genforces
Vector of symbolic generalized forces
q= R.genforces() is a vector (1 ×N) of symbols [Q1 Q2 ... QN].
Robotics Toolbox for MATLAB 287 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SerialLink.gencoords
SerialLink.getpos
Get joint coordinates from graphical display
q= R.getpos() returns the joint coordinates set by the last plot or teach operation on
the graphical robot.
See also
SerialLink.plot,SerialLink.teach
SerialLink.gravjac
Fast gravity load and Jacobian
[tau,jac0] = R.gravjac(q) is the generalised joint force/torques due to gravity tau (1 ×
N) and the manipulator Jacobian in the base frame jac0 (6×N) for robot pose q(1×N),
where N is the number of robot joints.
[tau,jac0] = R.gravjac(q,grav) as above but gravitational acceleration is given explic-
itly by grav (3 ×1).
Trajectory operation
If qis M×Nwhere N is the number of robot joints then a trajectory is assumed where
each row of qcorresponds to a robot configuration. tau (M×N) is the generalised
joint torque, each row corresponding to an input pose, and jac0 (6 ×N×M) where
each plane is a Jacobian corresponding to an input pose.
Notes
•The gravity vector is defined by the SerialLink property if not explicitly given.
•Does not use inverse dynamics function RNE.
•Faster than computing gravity and Jacobian separately.
Robotics Toolbox for MATLAB 288 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Author
Bryan Moutrie
See also
SerialLink.pay,SerialLink,SerialLink.gravload,SerialLink.jacob0
SerialLink.gravload
Gravity load on joints
taug = R.gravload(q) is the joint gravity loading (1 ×N) for the robot R in the joint
configuration q(1 ×N), where N is the number of robot joints. Gravitational accelera-
tion is a property of the robot object.
If qis a matrix (M×N) each row is interpreted as a joint configuration vector, and the
result is a matrix (M×N) each row being the corresponding joint torques.
taug = R.gravload(q,grav) as above but the gravitational acceleration vector grav is
given explicitly.
See also
SerialLink.gravjac,SerialLink.rne,SerialLink.itorque,SerialLink.coriolis
SerialLink.ikcon
Inverse kinematics by optimization with joint limits
q= R.ikcon(T) are the joint coordinates (1×N) corresponding to the robot end-effector
pose Twhich is an SE3 object or homogenenous transform matrix (4 ×4), and N is the
number of robot joints.
[q,err] = robot.ikcon(T) as above but also returns err which is the scalar final value of
the objective function.
[q,err,exitflag] = robot.ikcon(T) as above but also returns the status exitflag from
fmincon.
[q,err,exitflag] = robot.ikcon(T,q0) as above but specify the initial joint coordinates
q0 used for the minimisation.
[q,err,exitflag] = robot.ikcon(T,q0,options) as above but specify the options for
fmincon to use.
Robotics Toolbox for MATLAB 289 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Trajectory operation
In all cases if Tis a vector of SE3 objects (1 ×M) or a homogeneous transform se-
quence (4 ×4×M) then returns the joint coordinates corresponding to each of the
transforms in the sequence. qis M×Nwhere N is the number of robot joints. The
initial estimate of qfor each time step is taken as the solution from the previous time
step.
err and exitflag are also M×1 and indicate the results of optimisation for the corre-
sponding trajectory step.
Notes
•Requires fmincon from the MATLAB Optimization Toolbox.
•Joint limits are considered in this solution.
•Can be used for robots with arbitrary degrees of freedom.
•In the case of multiple feasible solutions, the solution returned depends on the
initial choice of q0.
•Works by minimizing the error between the forward kinematics of the joint angle
solution and the end-effector frame as an optimisation. The objective function
(error) is described as:
sumsqr( (inv(T)*robot.fkine(q) - eye(4)) *omega )
Where omega is some gain matrix, currently not modifiable.
Author
Bryan Moutrie
See also
SerialLink.ikunc,fmincon,SerialLink.ikine,SerialLink.fkine
SerialLink.ikine
Inverse kinematics by optimization without joint limits
q= R.ikine(T) are the joint coordinates (1×N) corresponding to the robot end-effector
pose Twhich is an SE3 object or homogenenous transform matrix (4 ×4), and N is the
number of robot joints.
This method can be used for robots with any number of degrees of freedom.
Robotics Toolbox for MATLAB 290 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘ilimit’, L maximum number of iterations (default 500)
‘rlimit’, L maximum number of consecutive step rejections (default 100)
‘tol’, Tfinal error tolerance (default 1e-10)
‘lambda’, L initial value of lambda (default 0.1)
‘lambdamin’, M minimum allowable value of lambda (default 0)
‘quiet’ be quiet
‘verbose’ be verbose
‘mask’, M mask vector (6 ×1) that correspond to translation in X, Y and Z, and rotation about
X, Y and Z respectively.
‘q0’, qinitial joint configuration (default all zeros)
‘search’ search over all configurations
‘slimit’, L maximum number of search attempts (default 100)
‘transpose’, A use Jacobian transpose with step size A, rather than Levenberg-Marquadt
Trajectory operation
In all cases if Tis a vector of SE3 objects (1 ×M) or a homogeneous transform se-
quence (4 ×4×M) then returns the joint coordinates corresponding to each of the
transforms in the sequence. qis M×Nwhere N is the number of robot joints. The
initial estimate of qfor each time step is taken as the solution from the previous time
step.
Underactuated robots
For the case where the manipulator has fewer than 6 DOF the solution space has more
dimensions than can be spanned by the manipulator joint coordinates.
In this case we specify the ‘mask’ option where the mask vector (1 ×6) specifies the
Cartesian DOF (in the wrist coordinate frame) that will be ignored in reaching a solu-
tion. The mask vector has six elements that correspond to translation in X, Y and Z,
and rotation about X, Y and Z respectively. The value should be 0 (for ignore) or 1.
The number of non-zero elements should equal the number of manipulator DOF.
For example when using a 3 DOF manipulator rotation orientation might be unimpor-
tant in which case use the option: ‘mask’, [1 1 1 0 0 0].
For robots with 4 or 5 DOF this method is very difficult to use since orientation is
specified by Tin world coordinates and the achievable orientations are a function of
the tool position.
References
•Robotics, Vision & Control, P. Corke, Springer 2011, Section 8.4.
Robotics Toolbox for MATLAB 291 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•This has been completely reimplemented in RTB 9.11
•Does NOT require MATLAB Optimization Toolbox.
•Solution is computed iteratively.
•Implements a Levenberg-Marquadt variable step size solver.
•The tolerance is computed on the norm of the error between current and desired
tool pose. This norm is computed from distances and angles without any kind of
weighting.
•The inverse kinematic solution is generally not unique, and depends on the initial
guess Q0 (defaults to 0).
•The default value of Q0 is zero which is a poor choice for most manipulators (eg.
puma560, twolink) since it corresponds to a kinematic singularity.
•Such a solution is completely general, though much less efficient than specific
inverse kinematic solutions derived symbolically, like ikine6s or ikine3.
•This approach allows a solution to be obtained at a singularity, but the joint
angles within the null space are arbitrarily assigned.
•Joint offsets, if defined, are added to the inverse kinematics to generate q.
•Joint limits are not considered in this solution.
•The ‘search’ option peforms a brute-force search with initial conditions chosen
from the entire configuration space.
•If the ‘search’ option is used any prismatic joint must have joint limits defined.
See also
SerialLink.ikcon,SerialLink.ikunc,SerialLink.fkine,SerialLink.ikine6s
SerialLink.ikine3
Inverse kinematics for 3-axis robot with no wrist
q= R.ikine3(T) is the joint coordinates (1 ×3) corresponding to the robot end-effector
pose Trepresented by the homogenenous transform. This is a analytic solution for a
3-axis robot (such as the first three joints of a robot like the Puma 560).
q= R.ikine3(T,config) as above but specifies the configuration of the arm in the form
of a string containing one or more of the configuration codes:
‘l’ arm to the left (default)
‘r’ arm to the right
‘u’ elbow up (default)
Robotics Toolbox for MATLAB 292 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘d’ elbow down
Notes
•The same as IKINE6S without the wrist.
•The inverse kinematic solution is generally not unique, and depends on the con-
figuration string.
•Joint offsets, if defined, are added to the inverse kinematics to generate q.
Trajectory operation
In all cases if Tis a vector of SE3 objects (1 ×M) or a homogeneous transform se-
quence (4 ×4×M) then returns the joint coordinates corresponding to each of the
transforms in the sequence. qis M×3.
Reference
Inverse kinematics for a PUMA 560 based on the equations by Paul and Zhang From
The International Journal of Robotics Research Vol. 5, No. 2, Summer 1986, p. 32-44
Author
Robert Biro with Gary Von McMurray, GTRI/ATRP/IIMB, Georgia Institute of Tech-
nology 2/13/95
See also
SerialLink.FKINE,SerialLink.IKINE
SerialLink.ikine6s
Analytical inverse kinematics
q= R.ikine(T) are the joint coordinates (1×N) corresponding to the robot end-effector
pose Twhich is an SE3 object or homogenenous transform matrix (4 ×4), and N is the
number of robot joints. This is a analytic solution for a 6-axis robot with a spherical
wrist (the most common form for industrial robot arms).
If Trepresents a trajectory (4 ×4×M) then the inverse kinematics is computed for
all M poses resulting in q(M×N) with each row representing the joint angles at the
corresponding pose.
Robotics Toolbox for MATLAB 293 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
q= R.IKINE6S(T,config) as above but specifies the configuration of the arm in the
form of a string containing one or more of the configuration codes:
‘l’ arm to the left (default)
‘r’ arm to the right
‘u’ elbow up (default)
‘d’ elbow down
‘n’ wrist not flipped (default)
‘f’ wrist flipped (rotated by 180 deg)
Trajectory operation
In all cases if Tis a vector of SE3 objects (1 ×M) or a homogeneous transform se-
quence (4 ×4×M) then R.ikcon() returns the joint coordinates corresponding to each
of the transforms in the sequence.
Notes
•Treats a number of specific cases:
–Robot with no shoulder offset
–Robot with a shoulder offset (has lefty/righty configuration)
–Robot with a shoulder offset and a prismatic third joint (like Stanford arm)
–The Puma 560 arms with shoulder and elbow offsets (4 lengths parameters)
–The Kuka KR5 with many offsets (7 length parameters)
•The inverse kinematics for the various cases determined using ikine_sym.
•The inverse kinematic solution is generally not unique, and depends on the con-
figuration string.
•Joint offsets, if defined, are added to the inverse kinematics to generate q.
•Only applicable for standard Denavit-Hartenberg parameters
Reference
•Inverse kinematics for a PUMA 560, Paul and Zhang, The International Journal
of Robotics Research, Vol. 5, No. 2, Summer 1986, p. 32-44
Author
•The Puma560 case: Robert Biro with Gary Von McMurray, GTRI/ATRP/IIMB,
Georgia Institute of Technology, 2/13/95
Robotics Toolbox for MATLAB 294 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•Kuka KR5 case: Gautam Sinha, Autobirdz Systems Pvt. Ltd., SIDBI Office,
Indian Institute of Technology Kanpur, Kanpur, Uttar Pradesh.
See also
SerialLink.fkine,SerialLink.ikine,SerialLink.ikine_sym
SerialLink.ikine_sym
Symbolic inverse kinematics
q= R.IKINE_SYM(k,options) is a cell array (C×1) of inverse kinematic solutions
of the SerialLink object ROBOT. The cells of qrepresent the different possible con-
figurations. Each cell of qis a vector (N×1), and the Jth element is the symbolic
expression for the Jth joint angle. The solution is in terms of the desired end-point
pose of the robot which is represented by the symbolic matrix (3 ×4) with elements
nx ox ax tx
ny oy ay ty
nz oz az tz
where the first three columns specify orientation and the last column specifies transla-
tion.
k<= N can have only specific values:
•2 solve for translation tx and ty
•3 solve for translation tx, ty and tz
•6 solve for translation and orientation
Options
‘file’, F Write the solution to an m-file named F
Example
mdl_planar2
sol = p2.ikine_sym(2);
length(sol)
ans =
2 % there are 2 solutions
s1 = sol{1} % is one solution
q1 = s1(1); % the expression for q1
q2 = s1(2); % the expression for q2
Robotics Toolbox for MATLAB 295 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•Robot manipulators: mathematics, programming and control Richard Paul, MIT
Press, 1981.
•The kinematics of manipulators under computer control, D.L. Pieper, Stanford
report AI 72, October 1968.
Notes
•Requires the MATLAB Symbolic Math Toolbox.
•This code is experimental and has a lot of diagnostic prints.
•Based on the classical approach using Pieper’s method.
SerialLink.ikinem
Numerical inverse kinematics by minimization
q= R.ikinem(T) is the joint coordinates corresponding to the robot end-effector pose
Twhich is a homogenenous transform.
q= R.ikinem(T,q0,options) specifies the initial estimate of the joint coordinates.
In all cases if Tis 4 ×4×Mit is taken as a homogeneous transform sequence and
R.ikinem() returns the joint coordinates corresponding to each of the transforms in the
sequence. qis M×Nwhere N is the number of robot joints. The initial estimate of q
for each time step is taken as the solution from the previous time step.
Options
‘pweight’, P weighting on position error norm compared to rotation error (default 1)
‘stiffness’, S Stiffness used to impose a smoothness contraint on joint angles, useful when N is large
(default 0)
‘qlimits’ Enforce joint limits
‘ilimit’, L Iteration limit (default 1000)
‘nolm’ Disable Levenberg-Marquadt
Notes
•PROTOTYPE CODE UNDER DEVELOPMENT, intended to do numerical in-
verse kinematics with joint limits
•The inverse kinematic solution is generally not unique, and depends on the initial
guess q0 (defaults to 0).
Robotics Toolbox for MATLAB 296 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•The function to be minimized is highly nonlinear and the solution is often trapped
in a local minimum, adjust q0 if this happens.
•The default value of q0 is zero which is a poor choice for most manipulators (eg.
puma560, twolink) since it corresponds to a kinematic singularity.
•Such a solution is completely general, though much less efficient than specific
inverse kinematic solutions derived symbolically, like ikine6s or ikine3.% - Uses
Levenberg-Marquadt minimizer LMFsolve if it can be found, if ‘nolm’ is not
given, and ‘qlimits’ false
•The error function to be minimized is computed on the norm of the error between
current and desired tool pose. This norm is computed from distances and angles
and ‘pweight’ can be used to scale the position error norm to be congruent with
rotation error norm.
•This approach allows a solution to obtained at a singularity, but the joint angles
within the null space are arbitrarily assigned.
•Joint offsets, if defined, are added to the inverse kinematics to generate q.
•Joint limits become explicit contraints if ‘qlimits’ is set.
See also
fminsearch,fmincon,SerialLink.fkine,SerialLink.ikine,tr2angvec
SerialLink.ikunc
Inverse manipulator by optimization without joint limits
q= R.ikunc(T) are the joint coordinates (1×N) corresponding to the robot end-effector
pose Twhich is an SE3 object or homogenenous transform matrix (4 ×4), and N is the
number of robot joints.
[q,err] = robot.ikunc(T) as above but also returns err which is the scalar final value of
the objective function.
[q,err,exitflag] = robot.ikunc(T) as above but also returns the status exitflag from
fminunc.
[q,err,exitflag] = robot.ikunc(T,q0) as above but specify the initial joint coordinates
q0 used for the minimisation.
[q,err,exitflag] = robot.ikunc(T,q0,options) as above but specify the options for
fminunc to use.
Robotics Toolbox for MATLAB 297 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Trajectory operation
In all cases if Tis a vector of SE3 objects (1 ×M) or a homogeneous transform se-
quence (4 ×4×M) then returns the joint coordinates corresponding to each of the
transforms in the sequence. qis M×Nwhere N is the number of robot joints. The
initial estimate of qfor each time step is taken as the solution from the previous time
step.
err and exitflag are also M×1 and indicate the results of optimisation for the corre-
sponding trajectory step.
Notes
•Requires fminunc from the MATLAB Optimization Toolbox.
•Joint limits are not considered in this solution.
•Can be used for robots with arbitrary degrees of freedom.
•In the case of multiple feasible solutions, the solution returned depends on the
initial choice of q0
•Works by minimizing the error between the forward kinematics of the joint angle
solution and the end-effector frame as an optimisation. The objective function
(error) is described as:
sumsqr( (inv(T)*robot.fkine(q) - eye(4)) *omega )
Where omega is some gain matrix, currently not modifiable.
Author
Bryan Moutrie
See also
SerialLink.ikcon,fmincon,SerialLink.ikine,SerialLink.fkine
SerialLink.inertia
Manipulator inertia matrix
i= R.inertia(q) is the symmetric joint inertia matrix (N×N) which relates joint torque
to joint acceleration for the robot at joint configuration q.
If qis a matrix (K×N), each row is interpretted as a joint state vector, and the re-
sult is a 3d-matrix (N×N×K) where each plane corresponds to the inertia for the
corresponding row of q.
Robotics Toolbox for MATLAB 298 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•The diagonal elements i(J,J) are the inertia seen by joint actuator J.
•The off-diagonal elements i(J,K) are coupling inertias that relate acceleration on
joint J to force/torque on joint K.
•The diagonal terms include the motor inertia reflected through the gear ratio.
See also
SerialLink.RNE,SerialLink.CINERTIA,SerialLink.ITORQUE
SerialLink.isconfig
Test for particular joint configuration
R.isconfig(s) is true if the robot has the joint configuration string given by the string s.
Example:
robot.isconfig(’RRRRRR’);
See also
SerialLink.config
SerialLink.islimit
Joint limit test
v= R.islimit(q) is a vector of boolean values, one per joint, false (0) if q(i) is within
the joint limits, else true (1).
Notes
•Joint limits are not used by many methods, exceptions being:
–ikcon() to specify joint constraints for inverse kinematics.
–by plot() for prismatic joints to help infer the size of the workspace
Robotics Toolbox for MATLAB 299 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Link.islimit
SerialLink.isspherical
Test for spherical wrist
R.isspherical() is true if the robot has a spherical wrist, that is, the last 3 axes are
revolute and their axes intersect at a point.
See also
SerialLink.ikine6s
SerialLink.issym
Test if SerialLink object is a symbolic model
res = R.issym() is true if the SerialLink manipulator R has symbolic parameters
Authors
Joern Malzahn, (joern.malzahn@tu-dortmund.de)
SerialLink.itorque
Inertia torque
taui = R.itorque(q,qdd) is the inertia force/torque vector (1 ×N) at the specified joint
configuration q(1 ×N) and acceleration qdd (1 ×N), and N is the number of robot
joints. taui = INERTIA(q)*qdd.
If qand qdd are matrices (K×N), each row is interpretted as a joint state vector, and
the result is a matrix (K×N) where each row is the corresponding joint torques.
Note
•If the robot model contains non-zero motor inertia then this will included in the
result.
Robotics Toolbox for MATLAB 300 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SerialLink.inertia,SerialLink.rne
SerialLink.jacob0
Jacobian in world coordinates
j0 = R.jacob0(q,options) is the Jacobian matrix (6×N) for the robot in pose q(1 ×N),
and N is the number of robot joints. The manipulator Jacobian matrix maps joint
velocity to end-effector spatial velocity V = j0*QD expressed in the world-coordinate
frame.
Options
‘rpy’ Compute analytical Jacobian with rotation rate in terms of XYZ roll-pitch-yaw angles
‘eul’ Compute analytical Jacobian with rotation rates in terms of Euler angles
‘exp’ Compute analytical Jacobian with rotation rates in terms of exponential coordinates
‘trans’ Return translational submatrix of Jacobian
‘rot’ Return rotational submatrix of Jacobian
Note
•End-effector spatial velocity is a vector (6 ×1): the first 3 elements are trans-
lational velocity, the last 3 elements are rotational velocity as angular velocity
(default), RPY angle rate or Euler angle rate.
•This Jacobian accounts for a base and/or tool transform if set.
•The Jacobian is computed in the end-effector frame and transformed to the world
frame.
•The default Jacobian returned is often referred to as the geometric Jacobian.
See also
SerialLink.jacobe,jsingu,deltatr,tr2delta,jsingu
Robotics Toolbox for MATLAB 301 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SerialLink.jacob_dot
Derivative of Jacobian
jdq = R.jacob_dot(q,qd) is the product (6 ×1) of the derivative of the Jacobian (in
the world frame) and the joint rates.
Notes
•This term appears in the formulation for operational space control XDD = J(q)QDD
+ JDOT(q)qd
•Written as per the reference and not very efficient.
References
•Fundamentals of Robotics Mechanical Systems (2nd ed) J. Angleles, Springer
2003.
•A unified approach for motion and force control of robot manipulators: The
operational space formulation
O Khatib, IEEE Journal on Robotics and Automation, 1987.
See also
SerialLink.jacob0,diff2tr,tr2diff
SerialLink.jacobe
Jacobian in end-effector frame
je = R.jacobe(q,options) is the Jacobian matrix (6 ×N) for the robot in pose q, and N
is the number of robot joints. The manipulator Jacobian matrix maps joint velocity to
end-effector spatial velocity V = je*QD in the end-effector frame.
Options
‘trans’ Return translational submatrix of Jacobian
‘rot’ Return rotational submatrix of Jacobian
Robotics Toolbox for MATLAB 302 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Was joacobn() is earlier version of the Toolbox.
•This Jacobian accounts for a tool transform if one is set.
•This Jacobian is often referred to as the geometric Jacobian.
•Prior to release 10 this function was named jacobn.
References
•Differential Kinematic Control Equations for Simple Manipulators, Paul, Shi-
mano, Mayer, IEEE SMC 11(6) 1981, pp. 456-460
See also
SerialLink.jacob0,jsingu,delta2tr,tr2delta
SerialLink.jointdynamics
Transfer function of joint actuator
tf = R.jointdynamic(q) is a vector of N continuous-time transfer function objects that
represent the transfer function 1/(Js+B) for each joint based on the dynamic parameters
of the robot and the configuration q(1 ×N). N is the number of robot joints.
%tf = R.jointdynamic(q, QD) as above but include the linearized effects of Coulomb
friction when operating at joint velocity QD (1 ×N).
Notes
•Coulomb friction is ignoredf.
See also
tf,SerialLink.rne
Robotics Toolbox for MATLAB 303 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SerialLink.jtraj
Joint space trajectory
q= R.jtraj(T1,t2,k,options) is a joint space trajectory (k×N) where the joint coordi-
nates reflect motion from end-effector pose T1 to t2 in ksteps, where N is the number
of robot joints. T1 and t2 are SE3 objects or homogeneous transformation matrices
(4 ×4). The trajectory qhas one row per time step, and one column per joint.
Options
‘ikine’, F A handle to an inverse kinematic method, for example F = @p560.ikunc. Default is
ikine6s() for a 6-axis spherical wrist, else ikine().
Notes
•Zero boundary conditions for velocity and acceleration are assumed.
•Additional options are passed as trailing arguments to the inverse kinematic func-
tion, eg. configuration options like ‘ru’.
See also
jtraj,SerialLink.ikine,SerialLink.ikine6s
SerialLink.maniplty
Manipulability measure
m= R.maniplty(q,options) is the manipulability index (scalar) for the robot at the
joint configuration q(1 ×N) where N is the number of robot joints. It indicates dexter-
ity, that is, how isotropic the robot’s motion is with respect to the 6 degrees of Cartesian
motion. The measure is high when the manipulator is capable of equal motion in all
directions and low when the manipulator is close to a singularity.
If qis a matrix (m×N) then m(m×1) is a vector of manipulability indices for each
joint configuration specified by a row of q.
[m,ci] = R.maniplty(q,options) as above, but for the case of the Asada measure re-
turns the Cartesian inertia matrix ci.
R.maniplty(q) displays the translational and rotational manipulability.
Two measures can be computed:
Robotics Toolbox for MATLAB 304 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•Yoshikawa’s manipulability measure is based on the shape of the velocity ellip-
soid and depends only on kinematic parameters (default).
•Asada’s manipulability measure is based on the shape of the acceleration ellip-
soid which in turn is a function of the Cartesian inertia matrix and the dynamic
parameters. The scalar measure computed here is the ratio of the smallest/largest
ellipsoid axis. Ideally the ellipsoid would be spherical, giving a ratio of 1, but in
practice will be less than 1.
Options
‘trans’ manipulability for transational motion only (default)
‘rot’ manipulability for rotational motion only
‘all’ manipulability for all motions
‘dof’, D D is a vector (1×6) with non-zero elements if the corresponding DOF is to be included
for manipulability
‘yoshikawa’ use Yoshikawa algorithm (default)
‘asada’ use Asada algorithm
Notes
•The ‘all’ option includes rotational and translational dexterity, but this involves
adding different units. It can be more useful to look at the translational and
rotational manipulability separately.
•Examples in the RVC book (1st edition) can be replicated by using the ‘all’
option
References
•Analysis and control of robot manipulators with redundancy, T. Yoshikawa, Robotics
Research: The First International Symposium (m. Brady and R. Paul, eds.), pp.
735-747, The MIT press, 1984.
•A geometrical representation of manipulator dynamics and its application to arm
design, H. Asada, Journal of Dynamic Systems, Measurement, and Control, vol.
105, p. 131, 1983.
•Robotics, Vision & Control, P. Corke, Springer 2011.
See also
SerialLink.inertia,SerialLink.jacob0
Robotics Toolbox for MATLAB 305 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SerialLink.mtimes
Concatenate robots
R = R1 * R2 is a robot object that is equivalent to mechanically attaching robot R2 to
the end of robot R1.
Notes
•If R1 has a tool transform or R2 has a base transform these are discarded since
DH convention does not allow for general intermediate transformations.
SerialLink.nofriction
Remove friction
rnf = R.nofriction() is a robot object with the same parameters as R but with non-linear
(Coulomb) friction coefficients set to zero.
rnf = R.nofriction(’all’) as above but viscous and Coulomb friction coefficients set to
zero.
rnf = R.nofriction(’viscous’) as above but viscous friction coefficients are set to zero.
Notes
•Non-linear (Coulomb) friction can cause numerical problems when integrating
the equations of motion (R.fdyn).
•The resulting robot object has its name string prefixed with ‘NF/’.
See also
SerialLink.fdyn,Link.nofriction
SerialLink.pay
Joint forces due to payload
tau = R.PAY(w,J) returns the generalised joint force/torques due to a payload wrench
w(1 ×6) and where the manipulator Jacobian is J(6 ×N), and N is the number of
robot joints.
Robotics Toolbox for MATLAB 306 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
tau = R.PAY(q,w,f) as above but the Jacobian is calculated at pose q(1 ×N) in the
frame given by fwhich is ‘0’ for world frame, ‘e’ for end-effector frame.
Uses the formula tau =J’w, where wis a wrench vector applied at the end effector, w
= [Fx Fy Fz Mx My Mz]’.
Trajectory operation
In the case qis M×Nor Jis 6 ×N×Mthen tau is M×Nwhere each row is the
generalised force/torque at the pose given by corresponding row of q.
Notes
•Wrench vector and Jacobian must be from the same reference frame.
•Tool transforms are taken into consideration when f= ‘e’.
•Must have a constant wrench - no trajectory support for this yet.
Author
Bryan Moutrie
See also
SerialLink.paycap,SerialLink.jacob0,SerialLink.jacobe
SerialLink.paycap
Static payload capacity of a robot
[wmax,J] = R.paycap(q,w,f,tlim) returns the maximum permissible payload wrench
wmax (1 ×6) applied at the end-effector, and the index of the joint Jwhich hits its
force/torque limit at that wrench. q(1 ×N) is the manipulator pose, wthe payload
wrench (1 ×6), fthe wrench reference frame (either ‘0’ or ‘e’) and tlim (2 ×N) is a
matrix of joint forces/torques (first row is maximum, second row minimum).
Trajectory operation
In the case qis M×Nthen wmax is M×6 and Jis M×1 where the rows are the
results at the pose given by corresponding row of q.
Robotics Toolbox for MATLAB 307 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Wrench vector and Jacobian must be from the same reference frame
•Tool transforms are taken into consideration for f= ‘e’.
Author
Bryan Moutrie
See also
SerialLink.pay,SerialLink.gravjac,SerialLink.gravload
SerialLink.payload
Add payload mass
R.payload(m,p) adds a payload with point mass mat position pin the end-effector
coordinate frame.
R.payload(0) removes added payload
Notes
•An added payload will affect the inertia, Coriolis and gravity terms.
•Sets, rather than adds, the payload. Mass and CoM of the last link is overwritten.
See also
SerialLink.rne,SerialLink.gravload
SerialLink.perturb
Perturb robot parameters
rp = R.perturb(p) is a new robot object in which the dynamic parameters (link mass
and inertia) have been perturbed. The perturbation is multiplicative so that values are
multiplied by random numbers in the interval (1-p) to (1+p). The name string of the
perturbed robot is prefixed by ‘p/’.
Robotics Toolbox for MATLAB 308 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Useful for investigating the robustness of various model-based control schemes. For
example to vary parameters in the range +/- 10 percent is:
r2 = p560.perturb(0.1);
See also
SerialLink.rne
SerialLink.plot
Graphical display and animation
R.plot(q,options) displays a graphical animation of a robot based on the kinematic
model. A stick figure polyline joins the origins of the link coordinate frames. The
robot is displayed at the joint angle q(1 ×N), or if a matrix (M×N) it is animated as
the robot moves along the M-point trajectory.
Options
‘workspace’, W Size of robot 3D workspace, W = [xmn, xmx ymn ymx zmn zmx]
‘floorlevel’, L Z-coordinate of floor (default -1)
‘delay’, D Delay betwen frames for animation (s)
‘fps’, fps Number of frames per second for display, inverse of ‘delay’ option
‘[no]loop’ Loop over the trajectory forever
‘[no]raise’ Autoraise the figure
‘movie’, M Save an animation to the movie M
‘trail’, L Draw a line recording the tip path, with line style L
‘scale’, S Annotation scale factor
‘zoom’, Z Reduce size of auto-computed workspace by Z, makes robot look bigger
‘ortho’ Orthographic view
‘perspective’ Perspective view (default)
‘view’, V Specify view V=’x’, ‘y’, ‘top’ or [az el] for side elevations, plan view, or general view
by azimuth and elevation angle.
‘top’ View from the top.
‘[no]shading’ Enable Gouraud shading (default true)
‘lightpos’, L Position of the light source (default [0 0 20])
‘[no]name’ Display the robot’s name
‘[no]wrist’ Enable display of wrist coordinate frame
‘xyz’ Wrist axis label is XYZ
‘noa’ Wrist axis label is NOA
‘[no]arrow’ Display wrist frame with 3D arrows
‘[no]tiles’ Enable tiled floor (default true)
‘tilesize’, S Side length of square tiles on the floor (default 0.2)
‘tile1color’, C Color of even tiles [r g b] (default [0.5 1 0.5] light green)
‘tile2color’, C Color of odd tiles [r g b] (default [1 1 1] white)
Robotics Toolbox for MATLAB 309 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘[no]shadow’ Enable display of shadow (default true)
‘shadowcolor’, C Colorspec of shadow, [r g b]
‘shadowwidth’, W Width of shadow line (default 6)
‘[no]jaxes’ Enable display of joint axes (default false)
‘[no]jvec’ Enable display of joint axis vectors (default false)
‘[no]joints’ Enable display of joints
‘jointcolor’, C Colorspec for joint cylinders (default [0.7 0 0])
‘pjointcolor’, C Colorspec for prismatic joint boxes (default [0.4 1 .03])
‘jointdiam’, D Diameter of joint cylinder in scale units (default 5)
‘linkcolor’, C Colorspec of links (default ‘b’)
‘[no]base’ Enable display of base ‘pedestal’
‘basecolor’, C Color of base (default ‘k’)
‘basewidth’, W Width of base (default 3)
The options come from 3 sources and are processed in order:
•Cell array of options returned by the function PLOTBOTOPT (if it exists)
•Cell array of options given by the ‘plotopt’ option when creating the SerialLink
object.
•List of arguments in the command line.
Many boolean options can be enabled or disabled with the ‘no’ prefix. The various
option sources can toggle an option, the last value encountered is used.
Graphical annotations and options
The robot is displayed as a basic stick figure robot with annotations such as:
•shadow on the floor
•XYZ wrist axes and labels
•joint cylinders and axes
which are controlled by options.
The size of the annotations is determined using a simple heuristic from the workspace
dimensions. This dimension can be changed by setting the multiplicative scale factor
using the ‘mag’ option.
Figure behaviour
•If no figure exists one will be created and the robot drawn in it.
•If no robot of this name is currently displayed then a robot will be drawn in the
current figure. If hold is enabled (hold on) then the robot will be added to the
current figure.
•If the robot already exists then that graphical model will be found and moved.
Robotics Toolbox for MATLAB 310 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Multiple views of the same robot
If one or more plots of this robot already exist then these will all be moved according
to the argument q. All robots in all windows with the same name will be moved.
Create a robot in figure 1
figure(1)
p560.plot(qz);
Create a robot in figure 2
figure(2)
p560.plot(qz);
Now move both robots
p560.plot(qn)
Multiple robots in the same figure
Multiple robots can be displayed in the same plot, by using “hold on” before calls to
robot.plot().
Create a robot in figure 1
figure(1)
p560.plot(qz);
Make a clone of the robot named bob
bob = SerialLink(p560, ’name’, ’bob’);
Draw bob in this figure
hold on
bob.plot(qn)
To animate both robots so they move together:
qtg = jtraj(qr, qz, 100);
for q=qtg’
p560.plot(q’);
bob.plot(q’);
end
Making an animation
The ‘movie’ options saves the animation as a movie file or separate frames in a folder
•‘movie’,’file.mp4’ saves as an MP4 movie called file.mp4
•‘movie’,’folder’ saves as files NNNN.png into the specified folder
–The specified folder will be created
–NNNN are consecutive numbers: 0000, 0001, 0002 etc.
–To convert frames to a movie use a command like:
Robotics Toolbox for MATLAB 311 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
ffmpeg -r 10 -i %04d.png out.avi
Notes
•The options are processed when the figure is first drawn, to make different op-
tions come into effect it is neccessary to clear the figure.
•The link segments do not neccessarily represent the links of the robot, they are a
pipe network that joins the origins of successive link coordinate frames.
•Delay betwen frames can be eliminated by setting option ‘delay’, 0 or ‘fps’, Inf.
•By default a quite detailed plot is generated, but turning off labels, axes, shadows
etc. will speed things up.
•Each graphical robot object is tagged by the robot’s name and has UserData that
holds graphical handles and the handle of the robot object.
•The graphical state holds the last joint configuration
•The size of the plot volume is determined by a heuristic for an all-revolute robot.
If a prismatic joint is present the ‘workspace’ option is required. The ‘zoom’
option can reduce the size of this workspace.
See also
SerialLink.plot3d,plotbotopt,SerialLink.animate,SerialLink.teach
SerialLink.plot3d
Graphical display and animation of solid model robot
R.plot3d(q,options) displays and animates a solid model of the robot. The robot is
displayed at the joint angle q(1 ×N), or if a matrix (M×N) it is animated as the robot
moves along the M-point trajectory.
Options
‘color’, C A cell array of color names, one per link. These are mapped to RGB using color-
name(). If not given, colors come from the axis ColorOrder property.
‘alpha’, A Set alpha for all links, 0 is transparant, 1 is opaque (default 1)
‘path’, P Overide path to folder containing STL model files
‘workspace’, W Size of robot 3D workspace, W = [xmn, xmx ymn ymx zmn zmx]
‘floorlevel’, L Z-coordinate of floor (default -1)
Robotics Toolbox for MATLAB 312 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘delay’, D Delay betwen frames for animation (s)
‘fps’, fps Number of frames per second for display, inverse of ‘delay’ option
‘[no]loop’ Loop over the trajectory forever
‘[no]raise’ Autoraise the figure
‘movie’, M Save frames as files in the folder M
‘scale’, S Annotation scale factor
‘ortho’ Orthographic view (default)
‘perspective’ Perspective view
‘view’, V Specify view V=’x’, ‘y’, ‘top’ or [az el] for side elevations, plan view, or general view
by azimuth and elevation angle.
‘[no]wrist’ Enable display of wrist coordinate frame
‘xyz’ Wrist axis label is XYZ
‘noa’ Wrist axis label is NOA
‘[no]arrow’ Display wrist frame with 3D arrows
‘[no]tiles’ Enable tiled floor (default true)
‘tilesize’, S Side length of square tiles on the floor (default 0.2)
‘tile1color’, C Color of even tiles [r g b] (default [0.5 1 0.5] light green)
‘tile2color’, C Color of odd tiles [r g b] (default [1 1 1] white)
‘[no]jaxes’ Enable display of joint axes (default true)
‘[no]joints’ Enable display of joints
‘[no]base’ Enable display of base shape
Notes
•Solid models of the robot links are required as STL files (ascii or binary) with
extension .stl.
•The solid models live in RVCTOOLS/robot/data/ARTE.
•Each STL model is called ‘linkN’.stl where N is the link number 0 to N
•The specific folder to use comes from the SerialLink.model3d property
•The path of the folder containing the STL files can be overridden using the ‘path’
option
•The height of the floor is set in decreasing priority order by:
–‘workspace’ option, the fifth element of the passed vector
–‘floorlevel’ option
–the lowest z-coordinate in the link1.stl object
Authors
•Peter Corke, based on existing code for plot().
•Bryan Moutrie, demo code on the Google Group for connecting ARTE and RTB.
Robotics Toolbox for MATLAB 313 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Acknowledgments
•STL files are from ARTE: A ROBOTICS TOOLBOX FOR EDUCATION by
Arturo Gil (https://arvc.umh.es/arte) are included, with permission.
•The various authors of STL reading code on file exchange, see stlRead.m
See also
SerialLink.plot,plotbotopt3d,SerialLink.animate,SerialLink.teach,stlRead
SerialLink.plus
Append a link objects to a robot
R+L is a SerialLink object formed appending a deep copy of the Link L to the Seri-
alLink robot R.
Notes
•The link L can belong to any of the Link subclasses.
•Extends to arbitrary number of objects, eg. R+L1+L2+L3+L4.
See also
Link.plus
SerialLink.qmincon
Use redundancy to avoid joint limits
qs = R.qmincon(q) exploits null space motion and returns a set of joint angles qs
(1 ×N) that result in the same end-effector pose but are away from the joint coordinate
limits. N is the number of robot joints.
[q,err] = R.qmincon(q) as above but also returns err which is the scalar final value of
the objective function.
[q,err,exitflag] = R.qmincon(q) as above but also returns the status exitflag from fmin-
con.
Robotics Toolbox for MATLAB 314 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Trajectory operation
In all cases if qis M×Nit is taken as a pose sequence and R.qmincon() returns the
adjusted joint coordinates (M×N) corresponding to each of the poses in the sequence.
err and exitflag are also M×1 and indicate the results of optimisation for the corre-
sponding trajectory step.
Notes
•Requires fmincon from the MATLAB Optimization Toolbox.
•Robot must be redundant.
Author
Bryan Moutrie
See also
SerialLink.ikcon,SerialLink.ikunc,SerialLink.jacob0
SerialLink.rne
Inverse dynamics
tau = R.rne(q,qd,qdd,options) is the joint torque required for the robot R to achieve
the specified joint position q(1×N), velocity qd (1×N) and acceleration qdd (1 ×N),
where N is the number of robot joints.
tau = R.rne(x,options) as above where x=[q,qd,qdd] (1 ×3N).
[tau,wbase] = R.rne(x,grav,fext) as above but the extra output is the wrench on the
base.
Options
‘gravity’, G specify gravity acceleration (default [0,0,9.81])
‘fext’, W specify wrench acting on the end-effector W=[Fx Fy Fz Mx My Mz]
‘slow’ do not use MEX file
Robotics Toolbox for MATLAB 315 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Trajectory operation
If q,qd and qdd (M×N), or x(M×3N) are matrices with M rows representing a
trajectory then tau (M×N) is a matrix with rows corresponding to each trajectory
step.
MEX file operation
This algorithm is relatively slow, and a MEX file can provide better performance. The
MEX file is executed if:
•the ‘slow’ option is not given, and
•the robot is not symbolic, and
•the SerialLink property fast is true, and
•the MEX file frne.mexXXX exists in the subfolder rvctools/robot/mex.
Notes
•The torque computed contains a contribution due to armature inertia and joint
friction.
•See the README file in the mex folder for details on how to configure MEX-file
operation.
•The M-file is a wrapper which calls either RNE_DH or RNE_MDH depending
on the kinematic conventions used by the robot object, or the MEX file.
•If a model has no dynamic parameters set the result is zero.
See also
SerialLink.accel,SerialLink.gravload,SerialLink.inertia
SerialLink.teach
Graphical teach pendant
Allow the user to “drive” a graphical robot using a graphical slider panel.
R.teach(options) adds a slider panel to a current robot plot. If no graphical robot exists
one is created in a new window.
R.teach(q,options) as above but the robot joint angles are set to q(1 ×N).
Robotics Toolbox for MATLAB 316 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘eul’ Display tool orientation in Euler angles (default)
‘rpy’ Display tool orientation in roll/pitch/yaw angles
‘approach’ Display tool orientation as approach vector (z-axis)
‘[no]deg’ Display angles in degrees (default true)
‘callback’, CB Set a callback function, called with robot object and joint angle vector: CB(R, q)
Example
To display the velocity ellipsoid for a Puma 560
p560.teach(’callback’, @(r,q) r.vellipse(q));
GUI
•The specified callback function is invoked every time the joint configuration
changes. the joint coordinate vector.
•The Quit (red X) button removes the teach panel from the robot plot.
Notes
•If the robot is displayed in several windows, only one has the teach panel added.
•All currently displayed robots move as the sliders are adjusted.
•The slider limits are derived from the joint limit properties. If not set then for
–a revolute joint they are assumed to be [-pi, +pi]
–a prismatic joint they are assumed unknown and an error occurs.
See also
SerialLink.plot,SerialLink.getpos
SerialLink.trchain
Convert to elementary transform sequence
s= R.TRCHAIN(options) is a sequence of elementary transforms that describe the
kinematics of the serial link robot arm. The string scomprises a number of tokens of
the form X(ARG) where X is one of Tx, Ty, Tz, Rx, Ry, or Rz. ARG is a joint variable,
or a constant angle or length dimension.
For example:
Robotics Toolbox for MATLAB 317 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
>> mdl_puma560
>> p560.trchain
ans =
Rz(q1)Rx(90)Rz(q2)Tx(0.431800)Rz(q3)Tz(0.150050)Tx(0.020300)Rx(-90)
Rz(q4)Tz(0.431800)Rx(90)Rz(q5)Rx(-90)Rz(q6)
Options
‘[no]deg’ Express angles in degrees rather than radians (default deg)
‘sym’ Replace length parameters by symbolic values L1, L2 etc.
See also
trchain,trotx,troty,trotz,transl,DHFactor
SerialLink.vellipse
Velocity ellipsoid for seriallink manipulator
R.vellipse(q,options) displays the velocity ellipsoid for the robot R at pose q. The
ellipsoid is centered at the tool tip position.
Options
‘2d’ Ellipse for translational xy motion, for planar manipulator
‘trans’ Ellipsoid for translational motion (default)
‘rot’ Ellipsoid for rotational motion
Display options as per plot_ellipse to control ellipsoid face and edge color and trans-
parency.
Example
To interactively update the velocity ellipsoid while using sliders to change the robot’s
pose:
robot.teach(’callback’, @(r,q) r.vellipse(q))
Notes
•The ellipsoid is tagged with the name of the robot prepended to “.vellipse”.
•Calling the function with a different pose will update the ellipsoid.
Robotics Toolbox for MATLAB 318 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SerialLink.jacob0,SerialLink.fellipse,plot_ellipse
skew
Create skew-symmetric matrix
s=skew(v) is a skew-symmetric matrix formed from v.
If v(1 ×1) then s=
| 0 -v |
| v 0 |
and if v(1 ×3) then s=
| 0 -vz vy |
| vz 0 -vx |
|-vy vx 0 |
Notes
•This is the inverse of the function VEX().
•These are the generator matrices for the Lie algebras so(2) and so(3).
References
•Robotics, Vision & Control: Second Edition, Chap 2, P. Corke, Springer 2016.
See also
skewa,vex
skewa
Create augmented skew-symmetric matrix
s=skewa(v) is an augmented skew-symmetric matrix formed from v.
If v(1 ×3) then s=
Robotics Toolbox for MATLAB 319 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
| 0 -v3 v1 |
| v3 0 v2 |
| 0 0 0 |
and if v(1 ×6) then s=
| 0 -v6 v5 v1 |
| v6 0 -v4 v2 |
|-v5 v4 0 v3 |
| 0 0 0 0 |
Notes
•This is the inverse of the function VEXA().
•These are the generator matrices for the Lie algebras se(2) and se(3).
•Map twist vectors in 2D and 3D space to se(2) and se(3).
References
•Robotics, Vision & Control: Second Edition, Chap 2, P. Corke, Springer 2016.
See also
skew,vex,Twist
SO2
Representation of 2D rotation
This subclasss of RTBPose is an object that represents an SO(2) rotation
Constructor methods
SO2 general constructor
SO2.exp exponentiate an so(2) matrix
SO2.rand random orientation
new new SO2 object
Information and test methods
dim* returns 2
Robotics Toolbox for MATLAB 320 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
isSE* returns false
issym* true if rotation matrix has symbolic elements
isa check if matrix is SO2
Display and print methods
plot* graphically display coordinate frame for pose
animate* graphically animate coordinate frame for pose
print* print the pose in single line format
display* print the pose in human readable matrix form
char* convert to human readable matrix as a string
Operation methods
det determinant of matrix component
eig eigenvalues of matrix component
log logarithm of rotation matrix
inv inverse
simplify* apply symbolic simplication to all elements
interp interpolate between rotations
Conversion methods
check convert object or matrix to SO2 object
theta return rotation angle
double convert to rotation matrix
R convert to rotation matrix
SE2 convert to SE2 object with zero translation
T convert to homogeneous transformation matrix with zero translation
Compatibility methods
isrot2* returns true
ishomog2* returns false
trprint2* print single line representation
trplot2* plot coordinate frame
tranimate2* animate coordinate frame
* means inherited from RTBPose
Robotics Toolbox for MATLAB 321 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Operators
+ elementwise addition, result is a matrix
- elementwise subtraction, result is a matrix
multiplication within group, also group x vector
/ multiply by inverse
== test equality
6=test inequality
See also
SE2,SO3,SE3,RTBPose
SO2.SO2
Construct an SO(2) object
p=SO2() is an SO2 object representing null rotation.
p=SO2(theta) is an SO2 object representing rotation of theta radians. If theta is a
vector (N) then pis a vector of objects, corresponding to the elements of theta.
p=SO2(theta, ‘deg’) as above but with theta degrees.
p=SO2(R) is an SO2 object formed from the rotation matrix R(2 ×2)
p=SO2(T) is an SO2 object formed from the rotational part of the homogeneous
transformation matrix T(3 ×3)
p= SO2(Q) is an SO2 object that is a copy of the SO2 object Q. %
See also
rot2,SE2,SO3
SO2.angle
Rotation angle
theta = P.angle() is the rotation angle, in radians, associated with the SO2 object P.
Robotics Toolbox for MATLAB 322 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO2.char
Convert to string
s= P.char() is a string containing rotation matrix elements.
See also
RTB.display
SO2.check
Convert to SO2
q=SO2.check(x) is an SO2 object where xis SO2, 2 ×2, SE2 or 3 ×3 homogeneous
transformation matrix.
SO2.det
Determinant of SO2 object
det(p) is the determinant of the SO2 object pand should always be +1.
SO2.eig
Eigenvalues and eigenvectors
E=eig(p) is a column vector containing the eigenvalues of the the rotation matrix of
the SO2 object p.
[v,d] = eig(p) produces a diagonal matrix dof eigenvalues and a full matrix vwhose
columns are the corresponding eigenvectors so that A*v=v*d.
See also
eig
Robotics Toolbox for MATLAB 323 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO2.exp
Construct SO2 object from Lie algebra
p=SO2.exp(so2) creates an SO2 object by exponentiating the se(2) argument (2 ×2).
SO2.interp
Interpolate between SO2 objects
P1.interp(p2,s) is an SO2 object representing interpolation between rotations repre-
sented by SO2 objects P1 and p2.svaries from 0 (P1) to 1 (p2). If sis a vector (1 ×N)
then the result will be a vector of SO2 objects.
Notes
•It is an error if S is outside the interval 0 to 1.
See also
SO2.angle
SO2.inv
Inverse of SO2 object
q=inv(p) is the inverse of the SO2 object p.p*qwill be the identity matrix.
Notes
•This is simply the transpose of the matrix.
SO2.isa
Test if matrix is SO(2)
SO2.ISA(T) is true (1) if the argument Tis of dimension 2 ×2 or 2 ×2×N, else false
(0).
Robotics Toolbox for MATLAB 324 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO2.ISA(T,true) as above, but also checks the validity of the rotation matrix, ie. its
determinant is +1.
Notes
•The first form is a fast, but incomplete, test for a transform in SE(3).
See also
SO3.ISA,SE2.ISA,SE2.ISA,ishomog2
SO2.log
Lie algebra
so2 = P.log() is the Lie algebra skew-symmetric matrix (2 ×2) corresponding to the
SO2 object P.
SO2.new
Construct a new object of the same type
p2 = P.new(x) creates a new object of the same type as P, by invoking the SO2 con-
structor on the matrix x(2 ×2).
p2 = P.new() as above but defines a null motion.
Notes
•Serves as a dynamic constructor.
•This method is polymorphic across all RTBPose derived classes, and allows easy
creation of a new object of the same class as an existing one.
See also
SE3.new,SO3.new,SE2.new
Robotics Toolbox for MATLAB 325 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO2.R
Get rotation matrix
R= P.R() is the rotation matrix (2×2) associated with the SO2 object P. If P is a vector
(1 ×N) then R(2 ×2×N) is a stack of rotation matrices, with the third dimension
corresponding to the index of P.
See also
SO2.T
SO2.rand
Construct a random SO(2) object
SO2.rand() is an SO2 object with a uniform random orientation. Random numbers
are in the interval 0 to 1.
See also
rand
SO2.SE2
Convert to SE2 object
q= P.SE2() is an SE2 object formed from the rotational component of the SO2 object
P and with a zero translational component.
See also
SE2
Robotics Toolbox for MATLAB 326 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO2.T
Get homogeneous transformation matrix
T= P.T() is the homogeneous transformation matrix (3 ×3) associated with the SO2
object P, and has zero translational component. If P is a vector (1 ×N) then T(3 ×3×
N) is a stack of rotation matrices, with the third dimension corresponding to the index
of P.
See also
SO2.T
SO2.theta
Rotation angle
theta = P.theta() is the rotation angle, in radians, associated with the SO2 object P.
Notes
•Deprecated, use angle() instead.
SO3
Representation of 3D rotation
This subclasss of RTBPose is an object that represents an SO(3) rotation
Constructor methods
SO3 general constructor
SO3.exp exponentiate an so(3) matrix
SO3.angvec rotation about vector
SO3.eul rotation defined by Euler angles
SO3.oa rotation defined by o- and a-vectors
SO3.rpy rotation defined by roll-pitch-yaw angles
SO3.Rx rotation about x-axis
SO3.Ry rotation about y-axis
Robotics Toolbox for MATLAB 327 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO3.Rz rotation about z-axis
SO3.rand random orientation
new new SO3 object
Information and test methods
dim* returns 3
isSE* returns false
issym* true if rotation matrix has symbolic elements
Display and print methods
plot* graphically display coordinate frame for pose
animate* graphically animate coordinate frame for pose
print* print the pose in single line format
display* print the pose in human readable matrix form
char* convert to human readable matrix as a string
Operation methods
det determinant of matrix component
eig eigenvalues of matrix component
log logarithm of rotation matrix
inv inverse
simplify* apply symbolic simplication to all elements
interp interpolate between rotations
Conversion methods
SO3.check convert object or matrix to SO3 object
theta return rotation angle
double convert to rotation matrix
R convert to rotation matrix
SE3 convert to SE3 object with zero translation
T convert to homogeneous transformation matrix with zero translation
UnitQuaternion convert to UnitQuaternion object
toangvec convert to rotation about vector form
toeul convert to Euler angles
torpy convert to roll-pitch-yaw angles
Compatibility methods
Robotics Toolbox for MATLAB 328 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
isrot* returns true
ishomog* returns false
trprint* print single line representation
trplot* plot coordinate frame
tranimate* animate coordinate frame
tr2eul convert to Euler angles
tr2rpy convert to roll-pitch-yaw angles
trnorm normalize the rotation matrix
Static methods
check convert object or matrix to SO2 object
exp exponentiate an so(3) matrix
isa check if matrix is 3 ×3
angvec rotation about vector
eul rotation defined by Euler angles
oa rotation defined by o- and a-vectors
rpy rotation defined by roll-pitch-yaw angles
Rx rotation about x-axis
Ry rotation about y-axis
Rz rotation about z-axis
* means inherited from RTBPose
Operators
+ elementwise addition, result is a matrix
- elementwise subtraction, result is a matrix
multiplication within group, also group x vector
.* multiplication within group followed by normalization
/ multiply by inverse
./ multiply by inverse followed by normalization
== test equality
6=test inequality
Properties
n normal (x) vector
o orientation (y) vector
a approach (z) vector
Robotics Toolbox for MATLAB 329 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SE2,SO2,SE3,RTBPose
SO3.SO3
Construct an SO(2) object
p=SO3() is an SO3 object representing null rotation.
p=SO3(R) is an SO3 object formed from the rotation matrix R(3 ×3)
p=SO3(T) is an SO3 object formed from the rotational part of the homogeneous
transformation matrix T(4 ×4)
p= SO3(Q) is an SO3 object that is a copy of the SO3 object Q. %
See also
SE3,SO2
SO3.angvec
Construct an SO(3) object from angle and axis vector
R=SO3.angvec(theta,v) is an orthonormal rotation matrix (3 ×3) equivalent to a
rotation of theta about the vector v.
Notes
•If theta == 0 then return identity matrix.
•If theta 6=0 then vmust have a finite length.
See also
SE3.angvec,eul2r,rpy2r,tr2angvec
Robotics Toolbox for MATLAB 330 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO3.check
Convert to SO3
q=SO3.check(x) is an SO3 object where xis SO3 object or 3×3 orthonormal rotation
matrix.
SO3.det
Determinant of SO3 object
det(p) is the determinant of the SO3 object pand should always be +1.
SO3.eig
Eigenvalues and eigenvectors
E=eig(p) is a column vector containing the eigenvalues of the the rotation matrix of
the SO3 object p.
[v,d] = eig(p) produces a diagonal matrix dof eigenvalues and a full matrix vwhose
columns are the corresponding eigenvectors so that A*v=v*d.
See also
eig
SO3.eul
Construct an SO(3) object from Euler angles
p=SO3.eul(phi,theta,psi,options) is an SO3 object equivalent to the specified Euler
angles. These correspond to rotations about the Z, Y, Z axes respectively. If phi,theta,
psi are column vectors (N×1) then they are assumed to represent a trajectory then pis
a vector (1 ×N) of SO3 objects.
R=SO3.eul(eul,options) as above but the Euler angles are taken from consecutive
columns of the passed matrix eul = [phi theta psi]. If eul is a matrix (N×3) then they
are assumed to represent a trajectory then pis a vector (1 ×N) of SO3 objects.
Robotics Toolbox for MATLAB 331 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Options
‘deg’ Compute angles in degrees (radians default)
Note
•The vectors phi,theta,psi must be of the same length.
See also
SO3.rpy,SE3.eul,eul2tr,rpy2tr,tr2eul
SO3.exp
Construct SO3 object from Lie algebra
p=SO3.exp(so2) creates an SO3 object by exponentiating the se(2) argument (2 ×2).
SO3.get.a
Get approach vector
P.a is the approach vector (3 ×1), the third column of the rotation matrix, which is the
z-axis unit vector.
See also
SO3.n,SO3.o
SO3.get.n
Get normal vector
P.n is the normal vector (3 ×1), the first column of the rotation matrix, which is the
x-axis unit vector.
Robotics Toolbox for MATLAB 332 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SO3.o,SO3.a
SO3.get.o
Get orientation vector
P.o is the orientation vector (3 ×1), the second column of the rotation matrix, which is
the y-axis unit vector..
See also
SO3.n,SO3.a
SO3.interp
Interpolate between SO3 objects
P1.interp(p2,s) is an SO3 object representing a slerp interpolation between rotations
represented by SO3 objects P1 and p2.svaries from 0 (P1) to 1 (p2). If sis a vector
(1 ×N) then the result will be a vector of SO3 objects.
P1.interp(p2,n) as above but returns a vector (1 ×n) of SO3 objects interpolated be-
tween P1 and p2 in nsteps.
Notes
•It is an error if S is outside the interval 0 to 1.
See also
UnitQuaternion
SO3.inv
Inverse of SO3 object
q=inv(p) is the inverse of the SO3 object p.p*qwill be the identity matrix.
Robotics Toolbox for MATLAB 333 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•This is simply the transpose of the matrix.
SO3.isa
Test if a rotation matrix
SO3.ISA(R) is true (1) if the argument is of dimension 3 ×3 or 3 ×3×N, else false
(0).
SO3.ISA(R, ‘valid’) as above, but also checks the validity of the rotation matrix.
Notes
•The first form is a fast, but incomplete, test for a rotation in SO(3).
See also
SE3.ISA,SE2.ISA,SO2.ISA
SO3.log
Lie algebra
se2 = P.log() is the Lie algebra augmented skew-symmetric matrix (3 ×3) correspond-
ing to the SE2 object P.
See also
SE2.Twist,trlog
SO3.new
Construct a new object of the same type
p2 = P.new(x) creates a new object of the same type as P, by invoking the SO3 con-
structor on the matrix x(3 ×3).
p2 = P.new() as above but defines a null rotation.
Robotics Toolbox for MATLAB 334 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Serves as a dynamic constructor.
•This method is polymorphic across all RTBPose derived classes, and allows easy
creation of a new object of the same class as an existing one.
See also
SE3.new,SO2.new,SE2.new
SO3.oa
Construct an SO(3) object from orientation and approach vec-
tors
p=SO3.oa(o,a) is an SO3 object for the specified orientation and approach vectors
(3 ×1) formed from 3 vectors such that R = [N o a] and N = oxa.
Notes
•The rotation matrix is guaranteed to be orthonormal so long as oand aare not
parallel.
•The vectors oand aare parallel to the Y- and Z-axes of the coordinate frame.
References
•Robot manipulators: mathematis, programming and control Richard Paul, MIT
Press, 1981.
See also
rpy2r,eul2r,oa2tr,SE3.oa
SO3.R
Get rotation matrix
R= P.R() is the rotation matrix (3×3) associated with the SO3 object P. If P is a vector
(1 ×N) then R(3 ×3×N) is a stack of rotation matrices, with the third dimension
corresponding to the index of P.
Robotics Toolbox for MATLAB 335 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
SO3.T
SO3.rand
Construct a random SO(3) object
SO3.rand() is an SO3 object with a uniform random RPY/ZYX orientation. Random
numbers are in the interval 0 to 1.
See also
rand
SO3.rdivide
Compound SO3 object with inverse and normalize
P./Q is the composition, or matrix multiplication of SO3 object P by the inverse of
SO3 object Q. If either of P or Q are vectors, then the result is a vector where each
element is the product of the object scalar and the corresponding element in the object
vector. If both P and Q are vectors they must be of the same length, and the result is
the elementwise product of the two vectors.
See also
SO3.mrdivide,SO3.times,trnorm
SO3.rpy
Construct an SO(3) object from roll-pitch-yaw angles
p=SO3.rpy(roll,pitch,yaw,options) is an SO3 object equivalent to the specified
roll, pitch, yaw angles angles. These correspond to rotations about the Z, Y, X axes
respectively. If roll,pitch,yaw are column vectors (N×1) then they are assumed to
represent a trajectory then pis a vector (1 ×N) of SO3 objects.
p=SO3.rpy(rpy,options) as above but the roll, pitch, yaw angles angles angles are
taken from consecutive columns of the passed matrix rpy = [roll,pitch,yaw]. If rpy
Robotics Toolbox for MATLAB 336 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
is a matrix (N×3) then they are assumed to represent a trajectory and pis a vector
(1 ×N) of SO3 objects.
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Rotations about X, Y, Z axes (for a robot gripper)
‘yxz’ Rotations about Y, X, Z axes (for a camera)
See also
SO3.eul,SE3.rpy,tr2rpy,eul2tr
SO3.Rx
Rotation about X axis
p=SO3.Rx(theta) is an SO3 object representing a rotation of theta radians about the
x-axis.
p=SO3.Rx(theta, ‘deg’) as above but theta is in degrees.
See also
SO3.Ry,SO3.Rz,rotx
SO3.Ry
Rotation about Y axis
p=SO3.Ry(theta) is an SO3 object representing a rotation of theta radians about the
y-axis.
p=SO3.Ry(theta, ‘deg’) as above but theta is in degrees.
See also
SO3.Rx,SO3.Rz,roty
Robotics Toolbox for MATLAB 337 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO3.Rz
Rotation about Z axis
p=SO3.Rz(theta) is an SO3 object representing a rotation of theta radians about the
z-axis.
p=SO3.Rz(theta, ‘deg’) as above but theta is in degrees.
See also
SO3.Rx,SO3.Ry,rotz
SO3.SE3
Convert to SEe object
q= P.SE3() is an SE3 object with a rotational component given by the SO3 object P,
and with a zero translational component.
See also
SE3
SO3.T
Get homogeneous transformation matrix
T= P.T() is the homogeneous transformation matrix (4 ×4) associated with the SO3
object P, and has zero translational component. If P is a vector (1 ×N) then T(4 ×4×
N) is a stack of rotation matrices, with the third dimension corresponding to the index
of P.
See also
SO3.T
Robotics Toolbox for MATLAB 338 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO3.times
Compound SO3 objects and normalize
R = P.*Q is an SO3 object representing the composition of the two rotations described
by the SO3 objects P and Q, which is matrix multiplication of their orthonormal rota-
tion matrices followed by normalization.
If either, or both, of P or Q are vectors, then the result is a vector.
If P is a vector (1 ×N) then R is a vector (1 ×N) such that R(i) = P(i).*Q.
If Q is a vector (1 ×N) then R is a vector (1 ×N) such thatR(i) = P.*Q(i).
If both P and Q are vectors (1×N) then R is a vector (1×N) such that R(i) = P(i).*R(i).
See also
RTBPose.mtimes,SO3.divide,trnorm
SO3.toangvec
Convert to angle-vector form
[theta,v] = P.toangvec(options) is rotation expressed in terms of an angle theta (1 ×1)
about the axis v(1 ×3) equivalent to the rotational part of the SO3 object P.
If P is a vector (1 ×N) then theta (K×1) is a vector of angles for corresponding
elements of the vector and v(K×3) are the corresponding axes, one per row.
Options
‘deg’ Return angle in degrees
Notes
•If no output arguments are specified the result is displayed.
See also
angvec2r,angvec2tr,trlog
Robotics Toolbox for MATLAB 339 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
SO3.toeul
Convert to Euler angles
eul = P.toeul(options) are the ZYZ Euler angles (1 ×3) corresponding to the rotational
part of the SO3 object P. The 3 angles eul=[PHI,THETA,PSI] correspond to sequential
rotations about the Z, Y and Z axes respectively.
If P is a vector (1 ×N) then each row of eul corresponds to an element of the vector.
Options
‘deg’ Compute angles in degrees (radians default)
‘flip’ Choose first Euler angle to be in quadrant 2 or 3.
Notes
•There is a singularity for the case where THETA=0 in which case PHI is arbi-
trarily set to zero and PSI is the sum (PHI+PSI).
See also
SO3.torpy,eul2tr,tr2rpy
SO3.torpy
Convert to roll-pitch-yaw angles
rpy = P.torpy(options) are the roll-pitch-yaw angles (1 ×3) corresponding to the ro-
tational part of the SO3 object P. The 3 angles rpy=[R,P,Y] correspond to sequential
rotations about the Z, Y and X axes respectively.
If P is a vector (1 ×N) then each row of rpy corresponds to an element of the vector.
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Return solution for sequential rotations about X, Y, Z axes
‘yxz’ Return solution for sequential rotations about Y, X, Z axes
Robotics Toolbox for MATLAB 340 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•There is a singularity for the case where P=pi/2 in which case R is arbitrarily set
to zero and Y is the sum (R+Y).
See also
SO3.toeul,rpy2tr,tr2eul
SO3.tr2eul
Convert to Euler angles (compatibility)
rpy = P.tr2eul(options) is a vector (1 ×3) of ZYZ Euler angles equivalent to the rota-
tion P (SO3 object).
Notes
•Overrides the classic RTB function tr2eul for an SO3 object.
•All the options of tr2eul apply.
See also
tr2eul
SO3.tr2rpy
Convert to RPY angles (compatibility)
rpy = P.tr2rpy(options) is a vector (1 ×3) of roll-pitch-yaw angles equivalent to the
rotation P (SO3 object).
Notes
•Overrides the classic RTB function tr2rpy for an SO3 object.
•All the options of tr2rpy apply.
•Defaults to ZYX order.
Robotics Toolbox for MATLAB 341 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
tr2rpy
SO3.trnorm
Normalize rotation (compatibility)
R= P.trnorm() is an SO3 object equivalent to P but normalized (guaranteed to be
orthogonal).
Notes
•Overrides the classic RTB function trnorm for an SO3 object.
See also
trnorm
SO3.UnitQuaternion
Convert to UnitQuaternion object
q= P.UnitQuaternion() is a UnitQuaternion object equivalent to the rotation de-
scribed by the SO3 object P.
See also
UnitQuaternion
startup_rtb
Initialize MATLAB paths for Robotics Toolbox
Adds demos, data, and examples to the MATLAB path, and adds also to Java class
path.
Robotics Toolbox for MATLAB 342 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•This sets the paths for the current session only.
•To make the settings persistent across sessions you can:
–Add this script to your MATLAB startup.m script.
–After running this script run PATHTOOL and save the path.
See also
path,addpath,pathtool,javaaddpath
stlRead
reads any STL file not depending on its format
[v,f,n,name] = stlread(fileName) reads the STL format file (ASCII or binary) and
returns vertices V, faces F, normals N and NAME is the name of the STL object (NOT
the name of the STL file).
Authors
•from MATLAB File Exchange by Pau Micó, https://au.mathworks.com/matlabcentral/fileexchange/51200-
stltools
•Copyright (c) 2015, Pau Micó
•Copyright (c) 2013, Adam H. Aitkenhead
•Copyright (c) 2011, Francis Esmonde-White
t2r
Rotational submatrix
R=t2r(T) is the orthonormal rotation matrix component of homogeneous transforma-
tion matrix T. Works for Tin SE(2) or SE(3)
•If Tis 4 ×4, then Ris 3 ×3.
•If Tis 3 ×3, then Ris 2 ×2.
Robotics Toolbox for MATLAB 343 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•For a homogeneous transform sequence (K×K×N) returns a rotation matrix
sequence (K-1 ×K-1 ×N).
•The validity of rotational part is not checked
See also
r2t,tr2rt,rt2tr
tb_optparse
Standard option parser for Toolbox functions
optout =tb_optparse(opt,arglist) is a generalized option parser for Toolbox func-
tions. opt is a structure that contains the names and default values for the options, and
arglist is a cell array containing option parameters, typically it comes from VARAR-
GIN. It supports options that have an assigned value, boolean or enumeration types
(string or int).
The software pattern is:
function(a, b, c, varargin)
opt.foo = false;
opt.bar = true;
opt.blah = [];
opt.stuff = {};
opt.choose = {’this’, ’that’, ’other’};
opt.select = {’#no’, ’#yes’};
opt = tb_optparse(opt, varargin);
Optional arguments to the function behave as follows:
‘foo’ sets opt.foo := true
‘nobar’ sets opt.foo := false
‘blah’, 3 sets opt.blah := 3
‘blah’, {x,y}sets opt.blah := {x,y}
‘that’ sets opt.choose := ‘that’
‘yes’ sets opt.select := (the second element)
‘stuff’, 5 sets opt.stuff to {5}
‘stuff’, {’k’,3}sets opt.stuff to {’k’,3}
and can be given in any combination.
If neither of ‘this’, ‘that’ or ‘other’ are specified then opt.choose := ‘this’. Alternatively
if:
Robotics Toolbox for MATLAB 344 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
opt.choose = {[], ’this’, ’that’, ’other’};
then if neither of ‘this’, ‘that’ or ‘other’ are specified then opt.choose := []
If neither of ‘no’ or ‘yes’ are specified then opt.select := 1.
Note:
•That the enumerator names must be distinct from the field names.
•That only one value can be assigned to a field, if multiple values are required
they must placed in a cell array.
•To match an option that starts with a digit, prefix it with ‘d_’, so the field ‘d_3d’
matches the option ‘3d’.
•opt can be an object, rather than a structure, in which case the passed options are
assigned to properties.
The return structure is automatically populated with fields: verbose and debug. The
following options are automatically parsed:
‘verbose’ sets opt.verbose := true
‘verbose=2’ sets opt.verbose := 2 (very verbose)
‘verbose=3’ sets opt.verbose := 3 (extremeley verbose)
‘verbose=4’ sets opt.verbose := 4 (ridiculously verbose)
‘debug’, N sets opt.debug := N
‘showopt’ displays opt and arglist
‘setopt’, S sets opt := S, if S.foo=4, and opt.foo is present, then opt.foo is set to 4.
The allowable options are specified by the names of the fields in the structure opt. By
default if an option is given that is not a field of opt an error is declared.
[optout,args] = tb_optparse(opt,arglist) as above but returns all the unassigned op-
tions, those that don’t match anything in opt, as a cell array of all unassigned arguments
in the order given in arglist.
[optout,args,ls] = tb_optparse(opt,arglist) as above but if any unmatched option
looks like a MATLAB LineSpec (eg. ‘r:’) it is placed in ls rather than in args.
[objout,args,ls] = tb_optparse(opt,arglist,obj) as above but properties of obj with
matching names in opt are set.
tpoly
Generate scalar polynomial trajectory
[s,sd,sdd] = tpoly(s0,sf,m) is a scalar trajectory (m×1) that varies smoothly from s0
to sf in msteps using a quintic (5th order) polynomial. Velocity and acceleration can
be optionally returned as sd (m×1) and sdd (m×1) respectively.
Robotics Toolbox for MATLAB 345 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
tpoly(s0,sf,m) as above but plots s,sd and sdd versus time in a single figure.
[s,sd,sdd] = tpoly(s0,sf,T) as above but the trajectory is computed at each point in the
time vector T(m×1).
[s,sd,sdd] = tpoly(s0,sf,T,qd0,qd1) as above but also specifies the initial and final
velocity of the trajectory.
Notes
•If mis given
–Velocity is in units of distance per trajectory step, not per second.
–Acceleration is in units of distance per trajectory step squared, not per sec-
ond squared.
•If Tis given then results are scaled to units of time.
•The time vector Tis assumed to be monotonically increasing, and time scaling
is based on the first and last element.
Reference:
Robotics, Vision & Control Chap 3 Springer 2011
See also
lspb,jtraj
tr2angvec
Convert rotation matrix to angle-vector form
[theta,v] = tr2angvec(R,options) is rotation expressed in terms of an angle theta
(1 ×1) about the axis v(1 ×3) equivalent to the orthonormal rotation matrix R(3 ×3).
[theta,v] = tr2angvec(T,options) as above but uses the rotational part of the homoge-
neous transform T(4 ×4).
If R(3 ×3×K) or T(4 ×4×K) represent a sequence then theta (K×1)is a vector of
angles for corresponding elements of the sequence and v(K×3) are the corresponding
axes, one per row.
Options
‘deg’ Return angle in degrees
Robotics Toolbox for MATLAB 346 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•For an identity rotation matrix both theta and vare set to zero.
•The rotation angle is always in the interval [0 pi], negative rotation is handled by
inverting the direction of the rotation axis.
•If no output arguments are specified the result is displayed.
See also
angvec2r,angvec2tr,trlog
tr2delta
Convert homogeneous transform to differential motion
d=tr2delta(T0,T1) is the differential motion (6 ×1) corresponding to infinitessimal
motion (in the T0 frame) from pose T0 to T1 which are homogeneous transformations
(4 ×4) or SE3 objects. d=(dx, dy, dz, dRx, dRy, dRz).
d=tr2delta(T) as above but the motion is with respect to the world frame.
Notes
•dis only an approximation to the motion T, and assumes that T0≈T1 or T≈eye(4,4).
•can be considered as an approximation to the effect of spatial velocity over a a
time interval, average spatial velocity multiplied by time.
Reference
•Robotics, Vision & Control 2nd Edition, p67
See also
delta2tr,skew
Robotics Toolbox for MATLAB 347 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
tr2eul
Convert homogeneous transform to Euler angles
eul =tr2eul(T,options) are the ZYZ Euler angles (1 ×3) corresponding to the rota-
tional part of a homogeneous transform T(4×4). The 3 angles eul=[PHI,THETA,PSI]
correspond to sequential rotations about the Z, Y and Z axes respectively.
eul =tr2eul(R,options) as above but the input is an orthonormal rotation matrix R
(3 ×3).
If R(3×3×K) or T(4×4×K) represent a sequence then each row of eul corresponds
to a step of the sequence.
Options
‘deg’ Compute angles in degrees (radians default)
‘flip’ Choose first Euler angle to be in quadrant 2 or 3.
Notes
•There is a singularity for the case where THETA=0 in which case PHI is arbi-
trarily set to zero and PSI is the sum (PHI+PSI).
•Translation component is ignored.
See also
eul2tr,tr2rpy
tr2jac
Jacobian for differential motion
J=tr2jac(tab) is a Jacobian matrix (6 ×6) that maps spatial velocity or differential
motion from frame {A}to frame {B}where the pose of {B}relative to {A}is repre-
sented by the homogeneous transform tab (4 ×4).
J=tr2jac(tab, ‘samebody’) is a Jacobian matrix (6 ×6) that maps spatial velocity or
differential motion from frame {A}to frame {B}where both are attached to the same
moving body. The pose of {B}relative to {A}is represented by the homogeneous
transform tab (4 ×4).
Robotics Toolbox for MATLAB 348 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
wtrans,tr2delta,delta2tr,SE3.velxform
tr2rpy
Convert a homogeneous transform to roll-pitch-yaw angles
rpy =tr2rpy(T,options) are the roll-pitch-yaw angles (1 ×3) corresponding to the
rotation part of a homogeneous transform T. The 3 angles rpy=[R,P,Y] correspond to
sequential rotations about the Z, Y and X axes respectively.
rpy =tr2rpy(R,options) as above but the input is an orthonormal rotation matrix R
(3 ×3).
If R(3×3×K) or T(4 ×4×K) represent a sequence then each row of rpy corresponds
to a step of the sequence.
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Return solution for sequential rotations about X, Y, Z axes
‘yxz’ Return solution for sequential rotations about Y, X, Z axes
Notes
•There is a singularity for the case where P=pi/2 in which case Ris arbitrarily set
to zero and Y is the sum (R+Y).
•Translation component is ignored.
•Toolbox rel 8-9 has the reverse default angle sequence as default
See also
rpy2tr,tr2eul
Robotics Toolbox for MATLAB 349 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
tr2rt
Convert homogeneous transform to rotation and translation
[R,t] = tr2rt(TR) splits a homogeneous transformation matrix (N×N) into an or-
thonormal rotation matrix R(M×M) and a translation vector t(M×1), where N=M+1.
Works for TR in SE(2) or SE(3)
•If TR is 4 ×4, then Ris 3 ×3 and T is 3 ×1.
•If TR is 3 ×3, then Ris 2 ×2 and T is 2 ×1.
A homogeneous transform sequence TR (N×N×K) is split into rotation matrix se-
quence R(M×M×K) and a translation sequence t(K×M).
Notes
•The validity of Ris not checked.
See also
rt2tr,r2t,t2r
tranimate
Animate a coordinate frame
tranimate(p1,p2,options) animates a 3D coordinate frame moving from pose X1 to
pose X2. Poses X1 and X2 can be represented by:
•homogeneous transformation matrices (4 ×4)
•orthonormal rotation matrices (3 ×3)
tranimate(x,options) animates a coordinate frame moving from the identity pose to
the pose xrepresented by any of the types listed above.
tranimate(xseq,options) animates a trajectory, where xseq is any of
•homogeneous transformation matrix sequence (4 ×4×N)
•orthonormal rotation matrix sequence (3 ×3×N)
Options
Robotics Toolbox for MATLAB 350 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘fps’, fps Number of frames per second to display (default 10)
‘nsteps’, n The number of steps along the path (default 50)
‘axis’, A Axis bounds [xmin, xmax, ymin, ymax, zmin, zmax]
‘movie’, M Save frames as a movie or sequence of frames
‘cleanup’ Remove the frame at end of animation
‘noxyz’ Don’t label the axes
‘rgb’ Color the axes in the order x=red, y=green, z=blue
‘retain’ Retain frames, don’t animate
Additional options are passed through to TRPLOT.
Notes
•Uses the Animate helper class to record the frames.
See also
trplot,animate,SE3.animate
tranimate2
Animate a coordinate frame
tranimate2(p1,p2,options) animates a 3D coordinate frame moving from pose X1 to
pose X2. Poses X1 and X2 can be represented by:
•homogeneous transformation matrices (4 ×4)
•orthonormal rotation matrices (3 ×3)
tranimate2(x,options) animates a coordinate frame moving from the identity pose to
the pose xrepresented by any of the types listed above.
tranimate2(xseq,options) animates a trajectory, where xseq is any of
•homogeneous transformation matrix sequence (4 ×4×N)
•orthonormal rotation matrix sequence (3 ×3×N)
Options
‘fps’, fps Number of frames per second to display (default 10)
‘nsteps’, n The number of steps along the path (default 50)
‘axis’, A Axis bounds [xmin, xmax, ymin, ymax, zmin, zmax]
Robotics Toolbox for MATLAB 351 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘movie’, M Save frames as a movie or sequence of frames
‘cleanup’ Remove the frame at end of animation
‘noxyz’ Don’t label the axes
‘rgb’ Color the axes in the order x=red, y=green, z=blue
‘retain’ Retain frames, don’t animate
Additional options are passed through to TRPLOT.
Notes
•Uses the Animate helper class to record the frames.
See also
trplot,animate,SE3.animate
transl
Create or unpack an SE(3) translational homogeneous trans-
form
Create a translational SE(3) matrix
T=transl(x,y,z) is an SE(3) homogeneous transform (4 ×4) representing a pure
translation of x,yand z.
T=transl(p) is an SE(3) homogeneous transform (4 ×4) representing a translation of
p=[x,y,z]. If p(M×3) it represents a sequence and T(4 ×4×M) is a sequence of
homogeneous transforms such that T(:,:,i) corresponds to the ith row of p.
Extract the translational part of an SE(3) matrix
p=transl(T) is the translational part of a homogeneous transform Tas a 3-element
column vector. If T(4 ×4×M) is a homogeneous transform sequence the rows of p
(M×3) are the translational component of the corresponding transform in the sequence.
[x,y,z] = transl(T) is the translational part of a homogeneous transform Tas three
components. If T(4 ×4×M) is a homogeneous transform sequence then x,y,z(1 ×M)
are the translational components of the corresponding transform in the sequence.
Robotics Toolbox for MATLAB 352 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Somewhat unusually this function performs a function and its inverse. An his-
torical anomaly.
See also
SE3.t,SE3.transl
transl2
Create or unpack an SE(2) translational homogeneous trans-
form
Create a translational SE(2) matrix
T=transl2(x,y) is an SE(2) homogeneous transform (3×3) representing a pure trans-
lation.
T=transl2(p) is a homogeneous transform representing a translation or point p=[x,y].
If p(M×2) it represents a sequence and T(3 ×3×M) is a sequence of homogenous
transforms such that T(:,:,i) corresponds to the ith row of p.
Extract the translational part of an SE(2) matrix
p=transl2(T) is the translational part of a homogeneous transform as a 2-element
column vector. If T(3 ×3×M) is a homogeneous transform sequence the rows of p
(M×2) are the translational component of the corresponding transform in the sequence.
Notes
•Somewhat unusually this function performs a function and its inverse. An his-
torical anomaly.
See also
SE2.t,rot2,ishomog2,trplot2,transl
Robotics Toolbox for MATLAB 353 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
trchain
Chain 3D transforms from string
T=trchain(s,q) is a homogeneous transform (4×4) that results from compounding a
number of elementary transformations defined by the string s. The string scomprises
a number of tokens of the form X(ARG) where X is one of Tx, Ty, Tz, Rx, Ry, or Rz.
ARG is the name of a variable in MATLAB workspace or qJ where J is an integer in
the range 1 to N that selects the variable from the Jth column of the vector q(1 ×N).
For example:
trchain(’Rx(q1)Tx(a1)Ry(q2)Ty(a3)Rz(q3)’, [1 2 3])
is equivalent to computing:
trotx(1) *transl(a1,0,0) *troty(2) *transl(0,a3,0) *trotz(3)
Notes
•Variables list in the string must exist in the caller workspace.
•The string can contain spaces between elements, or on either side of ARG.
•Works for symbolic variables in the workspace and/or passed in via the vector q.
•For symbolic operations that involve use of the value pi, make sure you define it
first in the workspace: pi = sym(’pi’);
See also
trchain2,trotx,troty,trotz,transl,SerialLink.trchain,ets
trchain2
Chain 2D transforms from string
T=trchain2(s,q) is a homogeneous transform (3 ×3) that results from compounding
a number of elementary transformations defined by the string s. The string scomprises
a number of tokens of the form X(ARG) where X is one of Tx, Ty or R. ARG is the
name of a variable in MATLAB workspace or qJ where J is an integer in the range 1 to
N that selects the variable from the Jth column of the vector q(1 ×N).
For example:
trchain(’R(q1)Tx(a1)R(q2)Ty(a3)R(q3)’, [1 2 3])
is equivalent to computing:
Robotics Toolbox for MATLAB 354 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
trot2(1) *transl2(a1,0) *trot2(2) *transl2(0,a3) *trot2(3)
Notes
•The string can contain spaces between elements or on either side of ARG.
•Works for symbolic variables in the workspace and/or passed in via the vector q.
•For symbolic operations that involve use of the value pi, make sure you define it
first in the workspace: pi = sym(’pi’);
See also
trchain,trot2,transl2
trexp
matrix exponential for so(3) and se(3)
For so(3)
R=trexp(omega) is the matrix exponential (3 ×3) of the so(3) element omega that
yields a rotation matrix (3 ×3).
R=trexp(omega,theta) as above, but so(3) motion of theta*omega.
R=trexp(s,theta) as above, but rotation of theta about the unit vector s.
R=trexp(w) as above, but the so(3) value is expressed as a vector w(1 ×3) where w
=s*theta. Rotation by ||w|| about the vector w.
For se(3)
T=trexp(sigma) is the matrix exponential (4 ×4) of the se(3) element sigma that
yields a homogeneous transformation matrix (4 ×4).
T=trexp(tw) as above, but the se(3) value is expressed as a twist vector tw (1 ×6).
T=trexp(sigma,theta) as above, but se(3) motion of sigma*theta, the rotation part
of sigma (4 ×4) must be unit norm.
T=trexp(tw,theta) as above, but se(3) motion of tw*theta, the rotation part of tw
(1 ×6) must be unit norm.
Robotics Toolbox for MATLAB 355 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Efficient closed-form solution of the matrix exponential for arguments that are
so(3) or se(3).
•If theta is given then the first argument must be a unit vector or a skew-symmetric
matrix from a unit vector.
•Angle vector argument order is different to ANGVEC2R.
References
•Robotics, Vision & Control: Second Edition, Chap 2, P. Corke, Springer 2016.
•“Mechanics, planning and control” Park & Lynch, Cambridge, 2017.
See also
angvec2r,trlog,trexp2,skew,skewa,Twist
trexp2
matrix exponential for so(2) and se(2)
SO(2)
R=trexp2(omega) is the matrix exponential (2 ×2) of the so(2) element omega that
yields a rotation matrix (2 ×2).
R=trexp2(theta) as above, but rotation by theta (1 ×1).
SE(2)
T=trexp2(sigma) is the matrix exponential (3 ×3) of the se(2) element sigma that
yields a homogeneous transformation matrix (3 ×3).
T=trexp2(tw) as above, but the se(2) value is expressed as a vector tw (1 ×3).
T=trexp2(sigma,theta) as above, but se(2) rotation of sigma*theta, the rotation part
of sigma (3 ×3) must be unit norm.
T=trexp(tw,theta) as above, but se(2) rotation of tw*theta, the rotation part of tw
must be unit norm.
Robotics Toolbox for MATLAB 356 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Efficient closed-form solution of the matrix exponential for arguments that are
so(2) or se(2).
•If theta is given then the first argument must be a unit vector or a skew-symmetric
matrix from a unit vector.
References
•Robotics, Vision & Control: Second Edition, Chap 2, P. Corke, Springer 2016.
•“Mechanics, planning and control” Park & Lynch, Cambridge, 2017.
See also
trexp,skew,skewa,Twist
trinterp
Interpolate SE(3) homogeneous transformations
T=trinterp(T0,T1,s) is a homogeneous transform (4 ×4) interpolated between T0
when s=0 and T1 when s=1. T0 and T1 are both homogeneous transforms (4 ×4).
Rotation is interpolated using quaternion spherical linear interpolation (slerp). If s
(N×1) then T(4 ×4×N) is a sequence of homogeneous transforms corresponding to
the interpolation values in s.
T=trinterp(T1,s) as above but interpolated between the identity matrix when s=0 to
T1 when s=1.
See also
ctraj,SE3.interp,UnitQuaternion,trinterp2
Robotics Toolbox for MATLAB 357 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
trinterp2
Interpolate SE(2) homogeneous transformations
T=trinterp2(T0,T1,s) is a homogeneous transform (3 ×3) interpolated between T0
when s=0 and T1 when s=1. T0 and T1 are both homogeneous transforms (3 ×3). If s
(N×1) then T(3 ×3×N) is a sequence of homogeneous transforms corresponding to
the interpolation values in s.
T=trinterp2(T1,s) as above but interpolated between the identity matrix when s=0
to T1 when s=1.
See also
trinterp,SE3.interp,UnitQuaternion
tripleangle
Visualize triple angle rotations
TRIPLEANGLE, by itself, displays a simple GUI with three angle sliders and a set of
axes showing three coordinate frames. The frames correspond to rotation after the first
angle (red), the first and second angles (green) and all three angles (blue).
tripleangle(options) as above but with options to select the rotation axes.
Options
‘rpy’ Rotation about axes x, y, z (default)
‘euler’ Rotation about axes z, y, z
‘ABC’ Rotation about axes A, B, C where A,B,C are each one of x,y or z.
Other options relevant to TRPLOT can be appended.
Notes
•All angles are displayed in units of degrees.
•Requires a number of .stl files in the examples folder.
•Buttons select particular view points.
•Checkbutton enables display of the gimbals (on by default)
Robotics Toolbox for MATLAB 358 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•This file originally generated by GUIDE.
See also
rpy2r,eul2r,trplot
trlog
logarithm of SO(3) or SE(3) matrix
s=trlog(R) is the matrix logarithm (3 ×3) of R(3 ×3) which is a skew symmetric
matrix corresponding to the vector theta*w where theta is the rotation angle and w
(3 ×1) is a unit-vector indicating the rotation axis.
[theta,w] = trlog(R) as above but returns directly theta the rotation angle and w(3×1)
the unit-vector indicating the rotation axis.
s=trlog(T) is the matrix logarithm (4 ×4) of T(4 ×4) which has a (3 ×3) skew sym-
metric matrix upper left submatrix corresponding to the vector theta*wwhere theta
is the rotation angle and w(3 ×1) is a unit-vector indicating the rotation axis, and a
translation component.
[theta,twist] = trlog(T) as above but returns directly theta the rotation angle and a
twist vector (6 ×1) comprising [v w].
Notes
•Efficient closed-form solution of the matrix logarithm for arguments that are
SO(3) or SE(3).
•Special cases of rotation by odd multiples of pi are handled.
•Angle is always in the interval [0,pi].
References
•“Mechanics, planning and control” Park & Lynch, Cambridge, 2016.
See also
trexp,trexp2,Twist
Robotics Toolbox for MATLAB 359 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
trnorm
Normalize a rotation matrix
rn =trnorm(R) is guaranteed to be a proper orthogonal matrix rotation matrix (3 ×3)
which is “close” to the non-orthogonal matrix R(3 ×3). If R= [N,O,A] the O and A
vectors are made unit length and the normal vector is formed from N = O x A, and then
we ensure that O and A are orthogonal by O = A x N.
tn =trnorm(T) as above but the rotational submatrix of the homogeneous transforma-
tion T(4 ×4) is normalised while the translational part is passed unchanged.
If R(3 ×3×K) or T(4 ×4×K) represent a sequence then rn and tn have the same
dimension and normalisation is performed on each plane.
Notes
•Only the direction of A (the z-axis) is unchanged.
•Used to prevent finite word length arithmetic causing transforms to become ‘un-
normalized’.
See also
oa2tr,SO3.trnorm,SE3.trnorm
trot2
SE2 rotation matrix
T=trot2(theta) is a homogeneous transformation (3 ×3) representing a rotation of
theta radians.
T=trot2(theta, ‘deg’) as above but theta is in degrees.
Notes
•Translational component is zero.
Robotics Toolbox for MATLAB 360 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
rot2,transl2,ishomog2,trplot2,trotx,troty,trotz,SE2
trotx
Rotation about X axis
T=trotx(theta) is a homogeneous transformation (4 ×4) representing a rotation of
theta radians about the x-axis.
T=trotx(theta, ‘deg’) as above but theta is in degrees.
Notes
•Translational component is zero.
See also
rotx,troty,trotz,trot2,SE3.Rx
troty
Rotation about Y axis
T=troty(theta) is a homogeneous transformation (4 ×4) representing a rotation of
theta radians about the y-axis.
T=troty(theta, ‘deg’) as above but theta is in degrees.
Notes
•Translational component is zero.
Robotics Toolbox for MATLAB 361 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
roty,trotx,trotz,trot2,SE3.Ry
trotz
Rotation about Z axis
T=trotz(theta) is a homogeneous transformation (4 ×4) representing a rotation of
theta radians about the z-axis.
T=trotz(theta, ‘deg’) as above but theta is in degrees.
Notes
•Translational component is zero.
See also
rotz,trotx,troty,trot2,SE3.Rz
trplot
Draw a coordinate frame
trplot(T,options) draws a 3D coordinate frame represented by the homogeneous trans-
form T(4 ×4).
H=trplot(T,options) as above but returns a handle.
trplot(R,options) as above but the coordinate frame is rotated about the origin accord-
ing to the orthonormal rotation matrix R(3 ×3).
H=trplot(R,options) as above but returns a handle.
H=trplot() creates a default frame EYE(3,3) at the origin and returns a handle.
Robotics Toolbox for MATLAB 362 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Animation
Firstly, create a plot and keep the the handle as per above.
trplot(H,T) moves the coordinate frame described by the handle Hto the pose T
(4 ×4).
Options
‘handle’, h Update the specified handle
‘color’, C The color to draw the axes, MATLAB colorspec C
‘noaxes’ Don’t display axes on the plot
‘axis’, A Set dimensions of the MATLAB axes to A=[xmin xmax ymin ymax zmin zmax]
‘frame’, F The coordinate frame is named {F}and the subscript on the axis labels is F.
‘framelabel’, F The coordinate frame is named {F}, axes have no subscripts.
‘text_opts’, opt A cell array of MATLAB text properties
‘axhandle’, A Draw in the MATLAB axes specified by the axis handle A
‘view’, V Set plot view parameters V=[az el] angles, or ‘auto’ for view toward origin of coordi-
nate frame
‘length’, s Length of the coordinate frame arms (default 1)
‘arrow’ Use arrows rather than line segments for the axes
‘width’, w Width of arrow tips (default 1)
‘thick’, t Thickness of lines (default 0.5)
‘perspective’ Display the axes with perspective projection
‘3d’ Plot in 3D using anaglyph graphics
‘anaglyph’, A Specify anaglyph colors for ‘3d’ as 2 characters for left and right (default colors ‘rc’):
chosen from r)ed, g)reen, b)lue, c)yan, m)agenta.
‘dispar’, D Disparity for 3d display (default 0.1)
‘text’ Enable display of X,Y,Z labels on the frame
‘labels’, L Label the X,Y,Z axes with the 1st, 2nd, 3rd character of the string L
‘rgb’ Display X,Y,Z axes in colors red, green, blue respectively
‘rviz’ Display chunky rviz style axes
Examples
trplot(T, ’frame’, ’A’)
trplot(T, ’frame’, ’A’, ’color’, ’b’)
trplot(T1, ’frame’, ’A’, ’text_opts’, {’FontSize’, 10, ’FontWeight’, ’bold’})
trplot(T1, ’labels’, ’NOA’);
h = trplot(T, ’frame’, ’A’, ’color’, ’b’);
trplot(h, T2);
3D anaglyph plot
trplot(T, ’3d’);
Notes
•Multiple frames can be added using the HOLD command
Robotics Toolbox for MATLAB 363 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
•The ‘rviz’ option is equivalent to ‘rgb’, ‘notext’, ‘noarrow’, ‘thick’, 5.
•The ‘arrow’ option requires arrow3 from FileExchange.
trplot2
Plot a planar transformation
trplot2(T,options) draws a 2D coordinate frame represented by the SE(2) homoge-
neous transform T(3 ×3).
H=trplot2(T,options) as above but returns a handle.
H=trplot2() creates a default frame EYE(2,2) at the origin and returns a handle.
Animation
Firstly, create a plot and keep the the handle as per above.
trplot2(H,T) moves the coordinate frame described by the handle Hto the SE(2) pose
T(3 ×3).
Options
‘handle’, h Update the specified handle
‘axis’, A Set dimensions of the MATLAB axes to A=[xmin xmax ymin ymax]
‘color’, c The color to draw the axes, MATLAB colorspec
‘noaxes’ Don’t display axes on the plot
‘frame’, F The frame is named {F}and the subscript on the axis labels is F.
‘framelabel’, F The coordinate frame is named {F}, axes have no subscripts.
‘text_opts’, opt A cell array of Matlab text properties
‘axhandle’, A Draw in the MATLAB axes specified by A
‘view’, V Set plot view parameters V=[az el] angles, or ‘auto’ for view toward origin of coordi-
nate frame
‘length’, s Length of the coordinate frame arms (default 1)
‘arrow’ Use arrows rather than line segments for the axes
‘width’, w Width of arrow tips
Examples
trplot2(T, ’frame’, ’A’)
trplot2(T, ’frame’, ’A’, ’color’, ’b’)
trplot2(T1, ’frame’, ’A’, ’text_opts’, {’FontSize’, 10, ’FontWeight’, ’bold’})
Robotics Toolbox for MATLAB 364 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Multiple frames can be added using the HOLD command
•The arrow option requires the third party package arrow3 from File Exchange.
•When using the form TRPLOT(H, ...) to animate a frame it is best to set the axis
bounds.
•The ‘arrow’ option requires arrow3 from FileExchange.
See also
trplot
trprint
Compact display of homogeneous transformation
trprint(T,options) displays the homogoneous transform in a compact single-line for-
mat. If Tis a homogeneous transform sequence then each element is printed on a
separate line.
s=trprint(T,options) as above but returns the string.
trprint Tis the command line form of above, and displays in RPY format.
Options
‘rpy’ display with rotation in ZYX roll/pitch/yaw angles (default)
‘xyz’ change RPY angle sequence to XYZ
‘yxz’ change RPY angle sequence to YXZ
‘euler’ display with rotation in ZYZ Euler angles
‘angvec’ display with rotation in angle/vector format
‘radian’ display angle in radians (default is degrees)
‘fmt’, f use format string f for all numbers, (default %g)
‘label’, l display the text before the transform
Examples
>> trprint(T2)
t = (0,0,0), RPY/zyx = (-122.704,65.4084,-8.11266) deg
>> trprint(T1, ’label’, ’A’)
A:t = (0,0,0), RPY/zyx = (-0,0,-0) deg
Robotics Toolbox for MATLAB 365 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•If the ‘rpy’ option is selected, then the particular angle sequence can be specified
with the options ‘xyz’ or ‘yxz’. ‘zyx’ is the default.
See also
tr2eul,tr2rpy,tr2angvec
trprint2
Compact display of SE2 homogeneous transformation
trprint2(T,options) displays the homogoneous transform in a compact single-line
format. If Tis a homogeneous transform sequence then each element is printed on a
separate line.
s=trprint2(T,options) as above but returns the string.
TRPRINT Tis the command line form of above, and displays in RPY format.
Options
‘radian’ display angle in radians (default is degrees)
‘fmt’, f use format string f for all numbers, (default %g)
‘label’, l display the text before the transform
Examples
>> trprint2(T2)
t = (0,0), theta = -122.704 deg
See also
trprint
Robotics Toolbox for MATLAB 366 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
trscale
Homogeneous transformation for pure scale
T=trscale(s) is a homogeneous transform (4 ×4) corresponding to a pure scale
change. If sis a scalar the same scale factor is used for x,y,z, else it can be a 3-vector
specifying scale in the x-, y- and z-directions.
Twist
SE(2) and SE(3) Twist class
A Twist class holds the parameters of a twist, a representation of a rigid body displace-
ment in SE(2) or SE(3).
Methods
S twist vector (1 ×3 or 1 ×6)
se twist as (augmented) skew-symmetric matrix (3 ×3 or 4 ×4)
T convert to homogeneous transformation (3 ×3 or 4 ×4)
R convert rotational part to matrix (2 ×2 or 3 ×3)
exp synonym for T
ad logarithm of adjoint
pitch pitch of the screw, SE(3) only
pole a point on the line of the screw
theta rotation about the screw
line Plucker line object representing line of the screw
display print the Twist parameters in human readable form
char convert to string
Conversion methods
SE convert to SE2 or SE3 object
double convert to real vector
Overloaded operators
* compose two Twists
multiply Twist by a scalar
Robotics Toolbox for MATLAB 367 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Properties (read only)
v moment part of twist (2 ×1 or 3 ×1)
w direction part of twist (1 ×1 or 3 ×1)
References
•“Mechanics, planning and control” Park & Lynch, Cambridge, 2016.
See also
trexp,trexp2,trlog
Twist.Twist
Create Twist object
tw =Twist(T) is a Twist object representing the SE(2) or SE(3) homogeneous trans-
formation matrix T(3 ×3 or 4 ×4).
tw =Twist(v) is a twist object where the vector is specified directly.
3D CASE::
tw =Twist(’R’, A, Q) is a Twist object representing rotation about the axis of direction
A (3 ×1) and passing through the point Q (3 ×1).
tw =Twist(’R’, A, Q, P) as above but with a pitch of P (distance/angle).
tw =Twist(’T’, A) is a Twist object representing translation in the direction of A
(3 ×1).
2D CASE::
tw =Twist(’R’, Q) is a Twist object representing rotation about the point Q (2 ×1).
tw =Twist(’T’, A) is a Twist object representing translation in the direction of A
(2 ×1).
Notes
The argument ‘P’ for prismatic is synonymous with ‘T’.
Robotics Toolbox for MATLAB 368 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Twist.ad
Logarithm of adjoint
TW.ad is the logarithm of the adjoint matrix of the corresponding homogeneous trans-
formation.
See also
SE3.Ad
Twist.char
Convert to string
s= TW.char() is a string showing Twist parameters in a compact single line format. If
TW is a vector of Twist objects return a string with one line per Twist.
See also
Twist.display
Twist.display
Display parameters
L.display() displays the twist parameters in compact single line format. If L is a vector
of Twist objects displays one line per element.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Twist object and the command has no trailing semicolon.
See also
Twist.char
Robotics Toolbox for MATLAB 369 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Twist.double
Return the twist vector
double(tw) is the twist vector in se(2) or se(3) as a vector (1 ×3 or 1 ×6).
Notes
•Sometimes referred to as the twist coordinate vector.
Twist.exp
Convert twist to homogeneous transformation
TW.exp is the homogeneous transformation equivalent to the twist (3 ×3 or 4 ×4).
TW.exp(theta) as above but with a rotation of theta about the twist.
Notes
•For the second form the twist must, if rotational, have a unit rotational compo-
nent.
See also
Twist.T,trexp,trexp2
Twist.line
Line of twist axis in Plucker form
TW.line is a Plucker object representing the line of the twist axis.
Notes
•For 3D case only.
Robotics Toolbox for MATLAB 370 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Plucker
Twist.mtimes
Multiply twist by twist or scalar
TW1 * TW2 is a new Twist representing the composition of twists TW1 and TW2.
TW * S with its twist coordinates scaled by scalar S.
Twist.pitch
Pitch of the twist
TW.pitch is the pitch of the Twist as a scalar in units of distance per radian.
Notes
•For 3D case only.
Twist.pole
Point on the twist axis
TW.pole is a point on the twist axis (2 ×1 or 3 ×1).
Notes
•For pure translation this point is at infinity.
Twist.S
Return the twist vector
TW.S is the twist vector in se(2) or se(3) as a vector (3 ×1 or 6 ×1).
Robotics Toolbox for MATLAB 371 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Sometimes referred to as the twist coordinate vector.
Twist.SE
Convert twist to SE2 or SE3 object
TW.SE is an SE2 or SE3 object representing the homogeneous transformation equiva-
lent to the twist.
See also
Twist.T,SE2,SE3
Twist.se
Return the twist matrix
TW.se is the twist matrix in se(2) or se(3) which is an augmented skew-symmetric
matrix (3 ×3 or 4 ×4).
Twist.T
Convert twist to homogeneous transformation
TW.T is the homogeneous transformation equivalent to the twist (3 ×3 or 4 ×4).
TW.T(theta) as above but with a rotation of theta about the twist.
Notes
•For the second form the twist must, if rotational, have a unit rotational compo-
nent.
See also
Twist.exp,trexp,trexp2
Robotics Toolbox for MATLAB 372 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Twist.theta
Twist rotation
TW.theta is the rotation (1 ×1) about the twist axis in radians.
Unicycle
vehicle class
This concrete class models the kinematics of a differential steer vehicle (unicycle
model) on a plane. For given steering and velocity inputs it updates the true vehicle
state and returns noise-corrupted odometry readings.
Methods
init initialize vehicle state
f predict next state based on odometry
step move one time step and return noisy odometry
control generate the control inputs for the vehicle
update update the vehicle state
run run for multiple time steps
Fx Jacobian of f wrt x
Fv Jacobian of f wrt odometry noise
gstep like step() but displays vehicle
plot plot/animate vehicle on current figure
plot_xy plot the true path of the vehicle
add_driver attach a driver object to this vehicle
display display state/parameters in human readable form
char convert to string
Class methods
plotv plot/animate a pose on current figure
Properties (read/write)
x true vehicle state: x, y, theta (3 ×1)
V odometry covariance (2 ×2)
odometry distance moved in the last interval (2 ×1)
Robotics Toolbox for MATLAB 373 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
rdim dimension of the robot (for drawing)
L length of the vehicle (wheelbase)
alphalim steering wheel limit
maxspeed maximum vehicle speed
T sample interval
verbose verbosity
x_hist history of true vehicle state (N×3)
driver reference to the driver object
x0 initial state, restored on init()
Examples
Odometry covariance (per timstep) is
V = diag([0.02, 0.5*pi/180].^2);
Create a vehicle with this noisy odometry
v = Bicycle( ’covar’, diag([0.1 0.01].^2 );
and display its initial state
v
now apply a speed (0.2m/s) and steer angle (0.1rad) for 1 time step
odo = v.step(0.2, 0.1)
where odo is the noisy odometry estimate, and the new true vehicle state
v
We can add a driver object
v.add_driver( RandomPath(10) )
which will move the vehicle within the region -10<x<10, -10<y<10 which we can
see by
v.run(1000)
which shows an animation of the vehicle moving for 1000 time steps between randomly
selected wayoints.
Notes
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
Reference
Robotics, Vision & Control, Chap 6 Peter Corke, Springer 2011
Robotics Toolbox for MATLAB 374 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
RandomPath,EKF
Unicycle.Unicycle
Unicycle object constructor
v=Unicycle(va,options) creates a Unicycle object with actual odometry covariance
va (2 ×2) matrix corresponding to the odometry vector [dx dtheta].
Options
‘W’, W Wheel separation [m] (default 1)
‘vmax’, S Maximum speed (default 5m/s)
‘x0’, x0 Initial state (default (0,0,0) )
‘dt’, T Time interval
‘rdim’, R Robot size as fraction of plot window (default 0.2)
‘verbose’ Be verbose
Notes
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
Unicycle.char
Convert to a string
s= V.char() is a string showing vehicle parameters and state in a compact human
readable format.
See also
Unicycle.display
Robotics Toolbox for MATLAB 375 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Unicycle.deriv
be called from a continuous time integrator such as ode45 or
Simulink
Unicycle.f
Predict next state based on odometry
xn = V.f(x,odo) is the predicted next state xn (1 ×3) based on current state x(1 ×3)
and odometry odo (1 ×2) = [distance, heading_change].
xn = V.f(x,odo,w) as above but with odometry noise w.
Notes
•Supports vectorized operation where xand xn (N×3).
Unicycle.Fv
Jacobian df/dv
J= V.Fv(x,odo) is the Jacobian df/dv (3 ×2) at the state x, for odometry input odo
(1 ×2) = [distance, heading_change].
See also
Unicycle.F,Vehicle.Fx
Unicycle.Fx
Jacobian df/dx
J= V.Fx(x,odo) is the Jacobian df/dx (3 ×3) at the state x, for odometry input odo
(1 ×2) = [distance, heading_change].
See also
Unicycle.f,Vehicle.Fv
Robotics Toolbox for MATLAB 376 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Unicycle.update
Update the vehicle state
odo = V.update(u) is the true odometry value for motion with u=[speed,steer].
Notes
•Appends new state to state history property x_hist.
•Odometry is also saved as property odometry.
unit
Unitize a vector
vn =unit(v) is a unit-vector parallel to v.
Note
•Reports error for the case where vis non-symbolic and norm(v) is zero
UnitQuaternion
unit quaternion class
A UnitQuaternion is a compact method of representing a 3D rotation that has computa-
tional advantages including speed and numerical robustness. A quaternion has 2 parts,
a scalar s, and a vector v and is typically written: q = s <vx, vy, vz>.
A UnitQuaternion is one for which s2+vx2+vy2+vz2= 1. It can be considered as a
rotation by an angle theta about a unit-vector V in space where
q = cos (theta/2) < v sin(theta/2)>
Robotics Toolbox for MATLAB 377 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Constructors
UnitQuaternion general constructor
UnitQuaternion.eul constructor, from Euler angles
UnitQuaternion.rpy constructor, from roll-pitch-yaw angles
UnitQuaternion.angvec constructor, from (angle and vector)
UnitQuaternion.omega constructor for angle*vector
UnitQuaternion.Rx constructor, from x-axis rotation
UnitQuaternion.Ry constructor, from y-axis rotation
UnitQuaternion.Rz constructor, from z-axis rotation
UnitQuaternion.vec constructor, from 3-vector
Display methods
display print in human readable form
plot plot a coordinate frame representing orientation of quaternion
animate animates a coordinate frame representing changing orientation of quaternion sequence
Operation methods
inv inverse
conj conjugate
unit unitized quaternion
dot derivative of quaternion with angular velocity
norm norm, or length
inner inner product
angle angle between two quaternions
interp interpolation (slerp) between two quaternions
UnitQuaternion.qvmul multiply unit-quaternions in 3-vector form
Conversion methods
char convert to string
double convert to 4-vector
matrix convert to 4 ×4 matrix
tovec convert to 3-vector
R convert to 3 ×3 rotation matrix
T convert to 4 ×4 homogeneous transform matrix
toeul convert to Euler angles
torpy convert to roll-pitch-yaw angles
toangvec convert to angle vector form
SO3 convert to SO3 class
SE3 convert to SE3 class
Robotics Toolbox for MATLAB 378 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Overloaded operators
q*q2 quaternion (Hamilton) product
q.*q2 quaternion (Hamilton) product followed by unitization
q*s quaternion times scalar
q/q2 q*q2.inv
q./q2 q*q2.inv followed by unitization
q/s quaternion divided by scalar
qnq to power n (integer only)
q+q2 elementwise sum of quaternion elements (result is a Quaternion)
q-q2 elementwise difference of quaternion elements (result is a Quaternion)
q1==q2 test for quaternion equality
q16=q2 test for quaternion inequality
Properties (read only)
s real part
v vector part
Notes
•Many methods and operators are inherited from the Quaternion superclass.
•UnitQuaternion objects can be used in vectors and arrays.
•A subclass of Quaternion
•The + and - operators return a Quaternion object not a UnitQuaternion
since the result is not, in general, a valid UnitQuaternion.
•For display purposes a Quaternion differs from a UnitQuaternion by using <<
>> notation rather than < >.
•To a large extent polymorphic with the SO3 class.
References
•Animating rotation with quaternion curves, K. Shoemake, in Proceedings of
ACM SIGGRAPH, (San Fran cisco), pp. 245-254, 1985.
•On homogeneous transforms, quaternions, and computational efficiency, J. Funda,
R. Taylor, and R. Paul, IEEE Transactions on Robotics and Automation, vol. 6,
pp. 382-388, June 1990.
•Robotics, Vision & Control, P. Corke, Springer 2011.
Robotics Toolbox for MATLAB 379 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Quaternion,SO3
UnitQuaternion.UnitQuaternion
Create a unit quaternion object
Construct a UnitQuaternion from various other orientation representations.
q=UnitQuaternion() is the identitity UnitQuaternion 1<0,0,0>representing a null
rotation.
q=UnitQuaternion(q1) is a copy of the UnitQuaternion q1, if q1 is a Quaternion it
is normalised.
q=UnitQuaternion(s,v) is a unit quaternion formed by specifying directly its scalar
and vector parts which are normalised.
q=UnitQuaternion([sV1 V2 V3]) is a quaternion formed by specifying directly its
4 elements which are normalised.
q=Quaternion(R) is a UnitQuaternion corresponding to the SO(3) orthonormal ro-
tation matrix R(3 ×3). If R(3 ×3×N) is a sequence then q(N×1) is a vector of
Quaternions corresponding to the elements of R.
q=Quaternion(T) is a UnitQuaternion equivalent to the rotational part of the SE(3)
homogeneous transform T(4 ×4). If T(4 ×4×N) is a sequence then q(N×1) is a
vector of Quaternions corresponding to the elements of T.
Notes
•Only the Rand Tforms are vectorised.
See also UnitQuaternion.eul, UnitQuaternion.rpy, UnitQuaternion.angvec, UnitQuater-
nion.omega, UnitQuaternion.Rx, UnitQuaternion.Ry, UnitQuaternion.Rz.
UnitQuaternion.angle
Angle between two UnitQuaternions
Q1.theta(q2) is the angle (in radians) between two UnitQuaternions Q1 and q2.
Notes
•Either or both Q1 and q2 can be a vector.
Robotics Toolbox for MATLAB 380 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•Metrics for 3D rotations: comparison and analysis Du Q. Huynh J.Math Imaging
Vis. DOFI 10.1007/s10851-009-0161-2
See also
Quaternion.angvec
UnitQuaternion.angvec
Construct from angle and rotation vector
q=UnitQuaternion.angvec(th,v) is a UnitQuaternion representing rotation of th
about the vector v(3 ×1).
See also
UnitQuaternion.omega
UnitQuaternion.animate
Animate a quaternion object
Q.animate(options) animates a quaternion array Q as a 3D coordinate frame.
Q.animate(qf,options) animates a 3D coordinate frame moving from orientation Q to
orientation qf.
Options
Options are passed to tranimate and include:
‘fps’, fps Number of frames per second to display (default 10)
‘nsteps’, n The number of steps along the path (default 50)
‘axis’, A Axis bounds [xmin, xmax, ymin, ymax, zmin, zmax]
‘movie’, M Save frames as files in the folder M
‘cleanup’ Remove the frame at end of animation
‘noxyz’ Don’t label the axes
‘rgb’ Color the axes in the order x=red, y=green, z=blue
‘retain’ Retain frames, don’t animate
Robotics Toolbox for MATLAB 381 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Additional options are passed through to TRPLOT.
See also
tranimate,trplot
UnitQuaternion.char
Convert to string
s= Q.char() is a compact string representation of the quaternion’s value as a 4-tuple.
If Q is a vector then shas one line per element.
See also
Quaternion.char
UnitQuaternion.dot
Quaternion derivative
qd = Q.dot(omega) is the rate of change in the world frame of a body frame with
attitude Q and angular velocity OMEGA (1 ×3) expressed as a quaternion.
Notes
•This is not a group operator, but it is useful to have the result as a quaternion.
Reference
•Robotics, Vision & Control, 2nd edition, Peter Corke, Chap 3.
See also
UnitQuaternion.dotb
Robotics Toolbox for MATLAB 382 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
UnitQuaternion.dotb
Quaternion derivative
qd = Q.dot(omega) is the rate of change in the body frame of a body frame with
attitude Q and angular velocity OMEGA (1 ×3) expressed as a quaternion.
Notes
•This is not a group operator, but it is useful to have the result as a quaternion.
Reference
•Robotics, Vision & Control, 2nd edition, Peter Corke, Chap 3.
See also
UnitQuaternion.dot
UnitQuaternion.eul
Construct from Euler angles
q=UnitQuaternion.eul(phi,theta,psi,options) is a UnitQuaternion representing
rotation equivalent to the specified Euler angles angles. These correspond to rotations
about the Z, Y, Z axes respectively.
q=UnitQuaternion.eul(eul,options) as above but the Euler angles are taken from
the vector (1 ×3) eul = [phi theta psi]. If eul is a matrix (N×3) then qis a vector
(1 ×N) of UnitQuaternion objects where the index corresponds to rows of eul which
are assumed to be [phi,theta,psi].
Options
‘deg’ Compute angles in degrees (radians default)
Notes
•Is vectorised, see eul2r for details.
Robotics Toolbox for MATLAB 383 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
UnitQuaternion.rpy,eul2r
UnitQuaternion.increment
Update quaternion by angular displacement
qu = Q.increment(omega) updates Q by a rotation which is given as a spatial displace-
ment omega (3 ×1) whose direction is the rotation axis and magnitude is the amount
of rotation.
See also
tr2delta
UnitQuaternion.interp
Interpolate UnitQuaternions
qi = Q.scale(s,options) is a UnitQuaternion that interpolates between a null rotation
(identity quaternion) for s=0 to Q for s=1.
qi = Q.interp(q2,s,options) as above but interpolates a rotation between Q for s=0
and q2 for s=1.
If sis a vector qi is a vector of UnitQuaternions, each element corresponding to se-
quential elements of s.
Options
‘shortest’ Take the shortest path along the great circle
Notes
•This is a spherical linear interpolation (slerp) that can be interpretted as interpo-
lation along a great circle arc on a sphere.
•It is an error if sis outside the interval 0 to 1.
Robotics Toolbox for MATLAB 384 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
References
•Animating rotation with quaternion curves, K. Shoemake, in Proceedings of
ACM SIGGRAPH, (San Fran cisco), pp. 245-254, 1985.
See also
ctraj
UnitQuaternion.inv
Invert a UnitQuaternion
qi = Q.inv() is a UnitQuaternion object representing the inverse of Q.
Notes
•Is vectorized, can operate on a vector of UnitQuaternion objects.
UnitQuaternion.mrdivide
Divide unit quaternions
Q1/Q2 is a UnitQuaternion object formed by Hamilton product of Q1 and
inv(q2) where Q1 and q2 are both UnitQuaternion objects.
Notes
•Overloaded operator ‘/’
•For case Q1/q2 both can be an N-vector, result is elementwise division.
•For case Q1/q2 if Q1 scalar and q2 a vector, scalar is divided by each element.
•For case Q1/q2 if q2 scalar and Q1 a vector, each element divided by scalar.
•If the dividend and divisor are UnitQuaternions, the quotient will be a unit quater-
nion.
Robotics Toolbox for MATLAB 385 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
Quaternion.mtimes,Quaternion.mpower,Quaternion.plus,Quaternion.minus
UnitQuaternion.mtimes
Multiply unit quaternions
Q1*Q2 is a UnitQuaternion object formed by Hamilton product
of Q1 and Q2 where Q1 and Q2 are both UnitQuaternion objects.
Q*V is a vector (3 ×1) formed by rotating the vector V (3 ×1)by the UnitQuaternion Q.
Notes
•Overloaded operator ‘*’
•For case Q1*Q2 both can be an N-vector, result is elementwise multiplication.
•For case Q1*Q2 if Q1 scalar and Q2 a vector, scalar multiplies each element.
•For case Q1*Q2 if Q2 scalar and Q1 a vector, each element multiplies scalar.
•For case Q*V where Q (1 ×N) and V (3 ×N), result (3 ×N) is elementwise
product of UnitQuaternion and columns of V.
•For case Q*V where Q (1 ×1) and V (3 ×N), result (3 ×N) is the product of the
UnitQuaternion by each column of V.
•For case Q*V where Q (1 ×N) and V (3 ×1), result (3 ×N) is the product of
each element of Q by the vector V.
See also
Quaternion.mrdivide,Quaternion.mpower,Quaternion.plus,Quaternion.minus
UnitQuaternion.new
Construct a new unit quaternion
qn = Q.new() constructs a new UnitQuaternion object of the same type as Q.
qn = Q.new([S V1 V2 V3]) as above but specified directly by its 4 elements.
Robotics Toolbox for MATLAB 386 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
qn = Q.new(s,v) as above but specified directly by the scalar sand vector part v(1×3)
Notes
•Polymorphic with Quaternion and RTBPose derived classes.
UnitQuaternion.omega
Construct from angle times rotation vector
q=UnitQuaternion.omega(w) is a UnitQuaternion representing rotation of |w| about
the vector w(3 ×1).
See also
UnitQuaternion.angvec
UnitQuaternion.plot
Plot a quaternion object
Q.plot(options) plots the quaternion as an oriented coordinate frame.
H= Q.plot(options) as above but returns a handle which can be used for animation.
Animation
Firstly, create a plot and keep the the handle as per above.
Q.plot(’handle’, H) updates the coordinate frame described by the handle Hto the
orientation of Q.
Options
Options are passed to trplot and include:
‘color’, C The color to draw the axes, MATLAB colorspec C
‘frame’, F The frame is named {F}and the subscript on the axis labels is F.
‘view’, V Set plot view parameters V=[az el] angles, or ‘auto’ for view toward origin of coordi-
nate frame
‘handle’, h Update the specified handle
Robotics Toolbox for MATLAB 387 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
See also
trplot
UnitQuaternion.q2r
Convert UnitQuaternion to homogeneous transform
T=q2tr(q)
Return the rotational homogeneous transform corresponding to the unit quaternion q.
See also: TR2Q
UnitQuaternion.qvmul
Multiply unit quaternions defined by vector part
qv =UnitQuaternion.QVMUL(qv1,qv2) multiplies two unit-quaternions defined
only by their vector components qv1 and qv2 (3 ×1). The result is similarly the vector
component of the product (3 ×1).
See also
UnitQuaternion.tovec,UnitQuaternion.vec
UnitQuaternion.R
Convert to orthonormal rotation matrix
R= Q.R() is the equivalent SO(3) orthonormal rotation matrix (3 ×3). If Q represents
a sequence (N×1) then Ris 3 ×3×N.
See also
UnitQuaternion.T,UnitQuaternion.SO3
Robotics Toolbox for MATLAB 388 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
UnitQuaternion.rdivide
Divide unit quaternions and unitize
Q1./Q2 is a UnitQuaternion object formed by Hamilton product of Q1 and
inv(q2) where Q1 and q2 are both UnitQuaternion objects. The result is explicitly
unitized.
Notes
•Overloaded operator ‘.*’
•For case Q1./q2 both can be an N-vector, result is elementwise division.
•For case Q1./q2 if Q1 scalar and q2 a vector, scalar is divided by each element.
•For case Q1./q2 if q2 scalar and Q1 a vector, each element divided by scalar.
See also
Quaternion.mtimes
UnitQuaternion.rpy
Construct from roll-pitch-yaw angles
q=UnitQuaternion.rpy(roll,pitch,yaw,options) is a UnitQuaternion representing
rotation equivalent to the specified roll, pitch, yaw angles angles. These correspond to
rotations about the Z, Y, X axes respectively.
q=UnitQuaternion.rpy(rpy,options) as above but the angles are given by the passed
vector rpy = [roll,pitch,yaw]. If rpy is a matrix (N×3) then qis a vector (1 ×N)
of UnitQuaternion objects where the index corresponds to rows of rpy which are
assumed to be [roll,pitch,yaw].
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Return solution for sequential rotations about X, Y, Z axes.
‘yxz’ Return solution for sequential rotations about Y, X, Z axes.
Robotics Toolbox for MATLAB 389 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
UnitQuaternion.Rx
Construct from rotation about x-axis
q=UnitQuaternion.Rx(angle) is a UnitQuaternion representing rotation of angle
about the x-axis.
q=UnitQuaternion.Rx(angle, ‘deg’) as above but THETA is in degrees.
See also
UnitQuaternion.Ry,UnitQuaternion.Rz
UnitQuaternion.Ry
Construct from rotation about y-axis
q=UnitQuaternion.Ry(angle) is a UnitQuaternion representing rotation of angle
about the y-axis.
q=UnitQuaternion.Ry(angle, ‘deg’) as above but THETA is in degrees.
See also
UnitQuaternion.Rx,UnitQuaternion.Rz
UnitQuaternion.Rz
Construct from rotation about z-axis
q=UnitQuaternion.Rz(angle) is a UnitQuaternion representing rotation of angle
about the z-axis.
q=UnitQuaternion.Rz(angle, ‘deg’) as above but THETA is in degrees.
See also
UnitQuaternion.Rx,UnitQuaternion.Ry
Robotics Toolbox for MATLAB 390 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
UnitQuaternion.SE3
Convert to SE3 object
x= Q.SE3() is an SE3 object with equivalent rotation and zero translation.
Notes
•The translational part of the SE3 object is zero
•If Q is a vector then an equivalent vector of SE3 objects is created.
See also
UnitQuaternion.SE3,SE3
UnitQuaternion.SO3
Convert to SO3 object
x= Q.SO3() is an SO3 object with equivalent rotation.
Notes
•If Q is a vector then an equivalent vector of SO3 objects is created.
See also
UnitQuaternion.SE3,SO3
UnitQuaternion.T
Convert to homogeneous transformation matrix
T= Q.T() is the equivalent SE(3) homogeneous transformation matrix (4 ×4). If Q is
a sequence (N×1) then Tis 4 ×4×N.
Notes:
•Has a zero translational component.
Robotics Toolbox for MATLAB 391 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
UnitQuaternion.R,UnitQuaternion.SE3
UnitQuaternion.times
Multiply a quaternion object and unitize
Q1.*Q2 is a UnitQuaternion object formed by Hamilton product of Q1 and
Q2. The result is explicitly unitized.
Notes
•Overloaded operator ‘.*’
•For case Q1.*Q2 both can be an N-vector, result is elementwise multiplication.
•For case Q1.*Q2 if Q1 scalar and Q2 a vector, scalar multiplies each element.
•For case Q1.*Q2 if Q2 scalar and Q1 a vector, each element multiplies scalar.
See also
Quaternion.mtimes
UnitQuaternion.toangvec
Convert to angle-vector form
th = Q.angvec(options) is the rotational angle, about some vector, corresponding to
this quaternion.
[th,v] = Q.angvec(options) as above but also returns a unit vector parallel to the rota-
tion axis.
Q.angvec(options) prints a compact single line representation of the rotational angle
and rotation vector corresponding to this quaternion.
Options
‘deg’ Display/return angle in degrees rather than radians
Robotics Toolbox for MATLAB 392 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•Due to the double cover of the quaternion, the returned rotation angles will be in
the interval [-2pi, 2pi).
•If Q is a UnitQuaternion vector then print one line per element.
•If Q is a UnitQuaternion vector (1 ×N) then th (1 ×N) and v(N×3).
UnitQuaternion.toeul
Convert to roll-pitch-yaw angle form.
eul = Q.toeul(options) are the Euler angles (1 ×3) corresponding to the UnitQuater-
nion. These correspond to rotations about the Z, Y, Z axes respectively. eul = [PHI,THETA,PSI].
Options
‘deg’ Compute angles in degrees (radians default)
Notes
•There is a singularity for the case where THETA=0 in which case PHI is arbi-
trarily set to zero and PSI is the sum (PHI+PSI).
See also
UnitQuaternion.toeul,tr2rpy
UnitQuaternion.torpy
Convert to roll-pitch-yaw angle form.
rpy = Q.torpy(options) are the roll-pitch-yaw angles (1 ×3) corresponding to the
UnitQuaternion. These correspond to rotations about the Z, Y, X axes respectively.
rpy = [ROLL, PITCH, YAW].
Options
‘deg’ Compute angles in degrees (radians default)
‘xyz’ Return solution for sequential rotations about X, Y, Z axes
‘yxz’ Return solution for sequential rotations about Y, X, Z axes
Robotics Toolbox for MATLAB 393 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•There is a singularity for the case where P=pi/2 in which case R is arbitrarily set
to zero and Y is the sum (R+Y).
See also
UnitQuaternion.toeul,tr2rpy
UnitQuaternion.tovec
Convert to unique 3-vector
v= Q.tovec() is a vector (1 ×3) that uniquely represents the UnitQuaternion. The
scalar component can be recovered by 1 - norm(v) and will always be positive.
Notes
•UnitQuaternions have double cover of SO(3) so the vector is derived from the
quaternion with positive scalar component.
•This vector representation of a UnitQuaternion is used for bundle adjustment.
See also
UnitQuaternion.vec,UnitQuaternion.qvmul
UnitQuaternion.tr2q
Convert homogeneous transform to a UnitQuaternion
q=tr2q(T)
Return a UnitQuaternion corresponding to the rotational part of the homogeneous
transform T.
Robotics Toolbox for MATLAB 394 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
UnitQuaternion.vec
Construct from 3-vector
q=UnitQuaternion.vec(v) is a UnitQuaternion constructed from just its vector com-
ponent (1 ×3) and the scalar part is 1 - norm(v) and will always be positive.
Notes
•This unique and concise vector representation of a UnitQuaternion is used for
bundle adjustment.
See also
UnitQuaternion.tovec,UnitVector.qvmul
Vehicle
Abstract vehicle class
This abstract class models the kinematics of a mobile robot moving on a plane and with
a pose in SE(2). For given steering and velocity inputs it updates the true vehicle state
and returns noise-corrupted odometry readings.
Methods
Vehicle constructor
add_driver attach a driver object to this vehicle
control generate the control inputs for the vehicle
f predict next state based on odometry
init initialize vehicle state
run run for multiple time steps
run2 run with control inputs
step move one time step and return noisy odometry
update update the vehicle state
Plotting/display methods
char convert to string
Robotics Toolbox for MATLAB 395 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
display display state/parameters in human readable form
plot plot/animate vehicle on current figure
plot_xy plot the true path of the vehicle
Vehicle.plotv plot/animate a pose on current figure
Properties (read/write)
x true vehicle state: x, y, theta (3 ×1)
V odometry covariance (2 ×2)
odometry distance moved in the last interval (2 ×1)
rdim dimension of the robot (for drawing)
L length of the vehicle (wheelbase)
alphalim steering wheel limit
speedmax maximum vehicle speed
T sample interval
verbose verbosity
x_hist history of true vehicle state (N×3)
driver reference to the driver object
x0 initial state, restored on init()
Examples
If veh is an instance of a Vehicle class then we can add a driver object
veh.add_driver( RandomPath(10) )
which will move the vehicle within the region -10<x<10, -10<y<10 which we can
see by
veh.run(1000)
which shows an animation of the vehicle moving for 1000 time steps between randomly
selected wayoints.
Notes
•Subclass of the MATLAB handle class which means that pass by reference se-
mantics apply.
Reference
Robotics, Vision & Control, Chap 6 Peter Corke, Springer 2011
See also
Bicycle,Unicycle,RandomPath,EKF
Robotics Toolbox for MATLAB 396 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Vehicle.Vehicle
Vehicle object constructor
v=Vehicle(options) creates a Vehicle object that implements the kinematic model of
a wheeled vehicle.
Options
‘covar’, C specify odometry covariance (2 ×2) (default 0)
‘speedmax’, S Maximum speed (default 1m/s)
‘L’, L Wheel base (default 1m)
‘x0’, x0 Initial state (default (0,0,0) )
‘dt’, T Time interval (default 0.1)
‘rdim’, R Robot size as fraction of plot window (default 0.2)
‘verbose’ Be verbose
Notes
•The covariance is used by a “hidden” random number generator within the class.
•Subclasses the MATLAB handle class which means that pass by reference se-
mantics apply.
Vehicle.add_driver
Add a driver for the vehicle
V.add_driver(d) connects a driver object dto the vehicle. The driver object has one
public method:
[speed, steer] = D.demand();
that returns a speed and steer angle.
Notes
•The Vehicle.step() method invokes the driver if one is attached.
See also
Vehicle.step,RandomPath
Robotics Toolbox for MATLAB 397 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Vehicle.char
Convert to string
s= V.char() is a string showing vehicle parameters and state in a compact human
readable format.
See also
Vehicle.display
Vehicle.control
Compute the control input to vehicle
u= V.control(speed,steer) is a control input (1×2) = [speed,steer] based on provided
controls speed,steer to which speed and steering angle limits have been applied.
u= V.control() as above but demand originates with a “driver” object if one is attached,
the driver’s DEMAND() method is invoked. If no driver is attached then speed and steer
angle are assumed to be zero.
See also
Vehicle.step,RandomPath
Vehicle.display
Display vehicle parameters and state
V.display() displays vehicle parameters and state in compact human readable form.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a Vehicle object and the command has no trailing semicolon.
See also
Vehicle.char
Robotics Toolbox for MATLAB 398 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Vehicle.init
Reset state
V.init() sets the state V.x := V.x0, initializes the driver object (if attached) and clears
the history.
V.init(x0) as above but the state is initialized to x0.
Vehicle.plot
Plot vehicle
The vehicle is depicted graphically as a narrow triangle that travels “point first” and
has a length V.rdim.
V.plot(options) plots the vehicle on the current axes at a pose given by the current
robot state. If the vehicle has been previously plotted its pose is updated.
V.plot(x,options) as above but the robot pose is given by x(1 ×3).
H= V.plotv(x,options) draws a representation of a ground robot as an oriented triangle
with pose x(1 ×3) [x,y,theta]. His a graphics handle.
V.plotv(H,x) as above but updates the pose of the graphic represented by the handle
Hto pose x.
Options
‘scale’, S Draw vehicle with length S x maximum axis dimension
‘size’, S Draw vehicle with length S
‘color’, C Color of vehicle.
‘fill’ Filled
Notes
•The last two calls are useful if animating multiple robots in the same figure.
See also
Vehicle.plotv,plot_vehicle
Robotics Toolbox for MATLAB 399 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Vehicle.plot_xy
Plots true path followed by vehicle
V.plot_xy() plots the true xy-plane path followed by the vehicle.
V.plot_xy(ls) as above but the line style arguments ls are passed to plot.
Notes
•The path is extracted from the x_hist property.
Vehicle.plotv
Plot ground vehicle pose
H=Vehicle.plotv(x,options) draws a representation of a ground robot as an oriented
triangle with pose x(1 ×3) [x,y,theta]. His a graphics handle. If x(N×3) is a matrix
it is considered to represent a trajectory in which case the vehicle graphic is animated.
Vehicle.plotv(H,x) as above but updates the pose of the graphic represented by the
handle Hto pose x.
Options
‘scale’, S Draw vehicle with length S x maximum axis dimension
‘size’, S Draw vehicle with length S
‘fillcolor’, C Color of vehicle.
‘fps’, F Frames per second in animation mode (default 10)
Example
Generate some path 3 ×N
p = PRM.plan(start, goal);
Set the axis dimensions to stop them rescaling for every point on the path
axis([-5 5 -5 5]);
Now invoke the static method
Vehicle.plotv(p);
Robotics Toolbox for MATLAB 400 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•This is a class method.
See also
Vehicle.plot
Vehicle.run
Run the vehicle simulation
V.run(n) runs the vehicle model for ntimesteps and plots the vehicle pose at each step.
p= V.run(n) runs the vehicle simulation for ntimesteps and return the state history
(n×3) without plotting. Each row is (x,y,theta).
See also
Vehicle.step,Vehicle.run2
Vehicle.run2
run the vehicle simulation with control inputs
p= V.run2(T,x0,speed,steer) runs the vehicle model for a time Twith speed speed
and steering angle steer.p(N×3) is the path followed and each row is (x,y,theta).
Notes
•Faster and more specific version of run() method.
•Used by the RRT planner.
See also
Vehicle.run,Vehicle.step,RRT
Robotics Toolbox for MATLAB 401 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Vehicle.step
Advance one timestep
odo = V.step(speed,steer) updates the vehicle state for one timestep of motion at
specified speed and steer angle, and returns noisy odometry.
odo = V.step() updates the vehicle state for one timestep of motion and returns noisy
odometry. If a “driver” is attached then its DEMAND() method is invoked to compute
speed and steer angle. If no driver is attached then speed and steer angle are assumed
to be zero.
Notes
•Noise covariance is the property V.
See also
Vehicle.control,Vehicle.update,Vehicle.add_driver
Vehicle.update
Update the vehicle state
odo = V.update(u) is the true odometry value for motion with u=[speed,steer].
Notes
•Appends new state to state history property x_hist.
•Odometry is also saved as property odometry.
Vehicle.verbosity
Set verbosity
V.verbosity(a) set verbosity to a.a=0 means silent.
Robotics Toolbox for MATLAB 402 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
vex
Convert skew-symmetric matrix to vector
v=vex(s) is the vector which has the corresponding skew-symmetric matrix s.
In the case that s(2 ×2) then vis 1 ×1
S=|0 -v|
| v 0 |
In the case that s(3 ×3) then vis 3 ×1.
| 0 -vz vy |
S = | vz 0 -vx |
|-vy vx 0 |
Notes
•This is the inverse of the function SKEW().
•Only rudimentary checking (zero diagonal) is done to ensure that the matrix is
actually skew-symmetric.
•The function takes the mean of the two elements that correspond to each unique
element of the matrix.
References
•Robotics, Vision & Control: Second Edition, Chap 2, P. Corke, Springer 2016.
See also
skew,vexa
vexa
Convert augmented skew-symmetric matrix to vector
v=vexa(s) is the vector which has the corresponding augmented skew-symmetric
matrix s.
vis 1 ×3 in the case that s(3 ×3) =
Robotics Toolbox for MATLAB 403 Copyright c
Peter Corke 2017
CHAPTER 2. FUNCTIONS AND CLASSES
| 0 -v3 v1 |
| v3 0 v2 |
| 0 0 0 |
vis 1 ×6 in the case that s(6 ×6) =
| 0 -v6 v5 v1 |
| v6 0 -v4 v2 |
|-v5 v4 0 v3 |
| 0 0 0 0 |
Notes
•This is the inverse of the function SKEWA().
•The matrices are the generator matrices for se(2) and se(3).
•This function maps se(2) and se(3) to twist vectors.
References
•Robotics, Vision & Control: Second Edition, Chap 2, P. Corke, Springer 2016.
See also
skewa,vex,Twist
VREP
V-REP simulator communications object
A VREP object holds all information related to the state of a connection to an instance
of the V-REP simulator running on this or a networked computer. Allows the creation
of references to other objects/models in V-REP which can be manipulated in MATLAB.
This class handles the interface to the simulator and low-level object handle operations.
Methods throw exception if an error occurs.
Methods
gethandle get handle to named object
getchildren get children belonging to handle
getobjname get names of objects
Robotics Toolbox for MATLAB 404 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
object return a VREP_obj object for named object
arm return a VREP_arm object for named robot
camera return a VREP_camera object for named vosion sensor
hokuyo return a VREP_hokuyo object for named Hokuyo scanner
getpos return position of object given handle
setpos set position of object given handle
getorient return orientation of object given handle
setorient set orientation of object given handle
getpose return pose of object given handle
setpose set pose of object given handle
setobjparam_bool set object boolean parameter
setobjparam_int set object integer parameter
setobjparam_float set object float parameter
getobjparam_bool get object boolean parameter
getobjparam_int get object integer parameter
getobjparam_float get object float parameter
signal_int send named integer signal
signal_float send named float signal
signal_str send named string signal
setparam_bool set simulator boolean parameter
setparam_int set simulator integer parameter
setparam_str set simulator string parameter
setparam_float set simulator float parameter
getparam_bool get simulator boolean parameter
getparam_int get simulator integer parameter
getparam_str get simulator string parameter
getparam_float get simulator float parameter
delete shutdown the connection and cleanup
simstart start the simulator running
simstop stop the simulator running
simpause pause the simulator
getversion get V-REP version number
checkcomms return status of connection
pausecomms pause the comms
loadscene load a scene file
clearscene clear the current scene
loadmodel load a model into current scene
display print the link parameters in human readable form
char convert to string
See also
VREP_obj,VREP_arm,VREP_camera,VREP_hokuyo
Robotics Toolbox for MATLAB 405 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.VREP
VREP object constructor
v=VREP(options) create a connection to an instance of the V-REP simulator.
Options
‘timeout’, T Timeout T in ms (default 2000)
‘cycle’, C Cycle time C in ms (default 5)
‘port’, P Override communications port
‘reconnect’ Reconnect on error (default noreconnect)
‘path’, P The path to VREP install directory
Notes
•The default path is taken from the environment variable VREP
VREP.arm
Return VREP_arm object
V.arm(name) is a factory method that returns a VREP_arm object for the V-REP robot
object named NAME.
Example
vrep.arm(’IRB 140’);
See also
VREP_arm
VREP.camera
Return VREP_camera object
V.camera(name) is a factory method that returns a VREP_camera object for the V-
REP vision sensor object named NAME.
Robotics Toolbox for MATLAB 406 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP_camera
VREP.char
Convert to string
V.char() is a string representation the VREP parameters in human readable foramt.
See also
VREP.display
VREP.checkcomms
Check communications to V-REP simulator
V.checkcomms() is true if a valid connection to the V-REP simulator exists.
VREP.clearscene
Clear current scene in the V-REP simulator
V.clearscene() clears the current scene and switches to another open scene, if none, a
new (default) scene is created.
See also
VREP.loadscene
VREP.delete
VREP object destructor
delete(v) closes the connection to the V-REP simulator
Robotics Toolbox for MATLAB 407 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.display
Display parameters
V.display() displays the VREP parameters in compact format.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a VREP object and the command has no trailing semicolon.
See also
VREP.char
VREP.getchildren
Find children of object
C= V.getchildren(H) is a vector of integer handles for the children of the V-REP
object denoted by the integer handle H.
VREP.gethandle
Return handle to VREP object
H= V.gethandle(name) is an integer handle for named V-REP object.
H= V.gethandle(fmt,arglist) as above but the name is formed from sprintf(fmt,ar-
glist).
See also
sprintf
Robotics Toolbox for MATLAB 408 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.getjoint
Get value of V-REP joint object
V.getjoint(H,q) is the position of joint object with integer handle H.
VREP.getobjname
Find names of objects
V.getobjname() will display the names and object handle (integers) for all objects in
the current scene.
name = V.getobjname(H) will return the name of the object with handle H.
VREP.getobjparam_bool
Get boolean parameter of a V-REP object
V.getobjparam_bool(H,param) gets the boolean parameter with identifier param of
object with integer handle H.
VREP.getobjparam_float
Get float parameter of a V-REP object
V.getobjparam_float(H,param) gets the float parameter with identifier param of
object with integer handle H.
VREP.getobjparam_int
Get integer parameter of a V-REP object
V.getobjparam_int(H,param) gets the integer parameter with identifier param of
object with integer handle H.
Robotics Toolbox for MATLAB 409 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.getorient
Get orientation of V-REP object
R= V.getorient(H) is the orientation of the V-REP object with integer handle Has a
rotation matrix (3 ×3).
EUL = V.getorient(H, ‘euler’, OPTIONS) as above but returns ZYZ Euler angles.
V.getorient(H,hrr) as above but orientation is relative to the position of object with
integer handle HR.
V.getorient(H,hrr, ‘euler’, OPTIONS) as above but returns ZYZ Euler angles.
Options
See tr2eul.
See also
VREP.setorient,VREP.getpos,VREP.getpose
VREP.getparam_bool
Get boolean parameter of the V-REP simulator
V.getparam_bool(name) is the boolean parameter with name name from the V-REP
simulation engine.
Example
v = VREP();
v.getparam_bool(’sim_boolparam_mirrors_enabled’)
See also
VREP.setparam_bool
Robotics Toolbox for MATLAB 410 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.getparam_float
Get float parameter of the V-REP simulator
V.getparam_float(name) gets the float parameter with name name from the V-REP
simulation engine.
Example
v = VREP();
v.getparam_float(’sim_floatparam_simulation_time_step’)
See also
VREP.setparam_float
VREP.getparam_int
Get integer parameter of the V-REP simulator
V.getparam_int(name) is the integer parameter with name name from the V-REP
simulation engine.
Example
v = VREP();
v.getparam_int(’sim_intparam_settings’)
See also
VREP.setparam_int
VREP.getparam_str
Get string parameter of the V-REP simulator
V.getparam_str(name) is the string parameter with name name from the V-REP sim-
ulation engine.
Robotics Toolbox for MATLAB 411 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Example
v = VREP();
v.getparam_str(’sim_stringparam_application_path’)
See also
VREP.setparam_str
VREP.getpos
Get position of V-REP object
V.getpos(H) is the position (1 ×3) of the V-REP object with integer handle H.
V.getpos(H,hr) as above but position is relative to the position of object with integer
handle hr.
See also
VREP.setpose,VREP.getpose,VREP.getorient
VREP.getpose
Get pose of V-REP object
T= V.getpose(H) is the pose of the V-REP object with integer handle Has a homoge-
neous transformation matrix (4 ×4).
T= V.getpose(H,hr) as above but pose is relative to the pose of object with integer
handle R.
See also
VREP.setpose,VREP.getpos,VREP.getorient
Robotics Toolbox for MATLAB 412 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.getversion
Get version of the V-REP simulator
V.getversion() is the version of the V-REP simulator server as an integer MNNNN
where M is the major version number and NNNN is the minor version number.
VREP.hokuyo
Return VREP_hokuyo object
V.hokuyo(name) is a factory method that returns a VREP_hokuyo object for the V-
REP Hokuyo laser scanner object named NAME.
See also
VREP_hokuyo
VREP.loadmodel
Load a model into the V-REP simulator
m= V.loadmodel(file,options) loads the model file file with extension .ttm into the
simulator and returns a VREP_obj object that mirrors it in MATLAB.
Options
‘local’ The file is loaded relative to the MATLAB client’s current folder, otherwise from the
V-REP root folder.
Example
vrep.loadmodel(’people/Walking Bill’);
Notes
•If a relative filename is given in non-local (server) mode it is relative to the V-
REP models folder.
Robotics Toolbox for MATLAB 413 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP.arm,VREP.camera,VREP.object
VREP.loadscene
Load a scene into the V-REP simulator
V.loadscene(file,options) loads the scene file file with extension .ttt into the simulator.
Options
‘local’ The file is loaded relative to the MATLAB client’s current folder, otherwise from the
V-REP root folder.
Example
vrep.loadscene(’2IndustrialRobots’);
Notes
•If a relative filename is given in non-local (server) mode it is relative to the V-
REP scenes folder.
See also
VREP.clearscene
VREP.mobile
Return VREP_mobile object
V.mobile(name) is a factory method that returns a VREP_mobile object for the V-REP
mobile base object named NAME.
See also
VREP_mobile
Robotics Toolbox for MATLAB 414 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.object
Return VREP_obj object
V.objet(name) is a factory method that returns a VREP_obj object for the V-REP ob-
ject or model named NAME.
Example
vrep.obj(’Walking Bill’);
See also
VREP_obj
VREP.pausecomms
Pause communcations to the V-REP simulator
V.pausecomms(p) pauses communications to the V-REP simulation engine if pis true
else resumes it. Useful to ensure an atomic update of simulator state.
VREP.setjoint
Set value of V-REP joint object
V.setjoint(H,q) sets the position of joint object with integer handle Hto the value q.
VREP.setjointtarget
Set target value of V-REP joint object
V.setjointtarget(H,q) sets the target position of joint object with integer handle Hto
the value q.
Robotics Toolbox for MATLAB 415 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.setjointvel
Set velocity of V-REP joint object
V.setjointvel(H,qd) sets the target velocity of joint object with integer handle Hto the
value qd.
VREP.setobjparam_bool
Set boolean parameter of a V-REP object
V.setobjparam_bool(H,param,val) sets the boolean parameter with identifier param
of object Hto value val.
VREP.setobjparam_float
Set float parameter of a V-REP object
V.setobjparam_float(H,param,val) sets the float parameter with identifier param of
object Hto value val.
VREP.setobjparam_int
Set Integer parameter of a V-REP object
V.setobjparam_int(H,param,val) sets the integer parameter with identifier param
of object Hto value val.
VREP.setorient
Set orientation of V-REP object
V.setorient(H,R) sets the orientation of V-REP object with integer handle Hto that
given by rotation matrix R(3 ×3).
V.setorient(H,T) sets the orientation of V-REP object with integer handle Hto rota-
tional component of homogeneous transformation matrix T(4 ×4).
V.setorient(H,E) sets the orientation of V-REP object with integer handle Hto ZYZ
Euler angles (1 ×3).
Robotics Toolbox for MATLAB 416 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
V.setorient(H,x,hr) as above but orientation is set relative to the orientation of object
with integer handle hr.
See also
VREP.getorient,VREP.setpos,VREP.setpose
VREP.setparam_bool
Set boolean parameter of the V-REP simulator
V.setparam_bool(name,val) sets the boolean parameter with name name to value val
within the V-REP simulation engine.
See also
VREP.getparam_bool
VREP.setparam_float
Set float parameter of the V-REP simulator
V.setparam_float(name,val) sets the float parameter with name name to value val
within the V-REP simulation engine.
See also
VREP.getparam_float
VREP.setparam_int
Set integer parameter of the V-REP simulator
V.setparam_int(name,val) sets the integer parameter with name name to value val
within the V-REP simulation engine.
Robotics Toolbox for MATLAB 417 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP.getparam_int
VREP.setparam_str
Set string parameter of the V-REP simulator
V.setparam_str(name,val) sets the integer parameter with name name to value val
within the V-REP simulation engine.
See also
VREP.getparam_str
VREP.setpos
Set position of V-REP object
V.setpos(H,T) sets the position of V-REP object with integer handle Hto T(1 ×3).
V.setpos(H,T,hr) as above but position is set relative to the position of object with
integer handle hr.
See also
VREP.getpos,VREP.setpose,VREP.setorient
VREP.setpose
Set pose of V-REP object
V.setpos(H,T) sets the pose of V-REP object with integer handle Haccording to ho-
mogeneous transform T(4 ×4).
V.setpos(H,T,hr) as above but pose is set relative to the pose of object with integer
handle hr.
Robotics Toolbox for MATLAB 418 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP.getpose,VREP.setpos,VREP.setorient
VREP.signal_float
Send a float signal to the V-REP simulator
V.signal_float(name,val) send a float signal with name name and value val to the
V-REP simulation engine.
VREP.signal_int
Send an integer signal to the V-REP simulator
V.signal_int(name,val) send an integer signal with name name and value val to the
V-REP simulation engine.
VREP.signal_str
Send a string signal to the V-REP simulator
V.signal_str(name,val) send a string signal with name name and value val to the
V-REP simulation engine.
VREP.simpause
Pause V-REP simulation
V.simpause() pauses the V-REP simulation engine. Use V.simstart() to resume the
simulation.
See also
VREP.simstart
Robotics Toolbox for MATLAB 419 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP.simstart
Start V-REP simulation
V.simstart() starts the V-REP simulation engine.
See also
VREP.simstop,VREP.simpause
VREP.simstop
Stop V-REP simulation
V.simstop() stops the V-REP simulation engine.
See also
VREP.simstart
VREP.youbot
Return VREP_youbot object
V.youbot(name) is a factory method that returns a VREP_youbot object for the V-REP
YouBot object named NAME.
See also
VREP_youbot
VREP_arm
Mirror of V-REP robot arm object
Mirror objects are MATLAB objects that reflect the state of objects in the V-REP envi-
ronment. Methods allow the V-REP state to be examined or changed.
Robotics Toolbox for MATLAB 420 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
This is a concrete class, derived from VREP_mirror, for all V-REP robot arm objects
and allows access to joint variables.
Methods throw exception if an error occurs.
Example
vrep = VREP();
arm = vrep.arm(’IRB140’);
q = arm.getq();
arm.setq(zeros(1,6));
arm.setpose(T); % set pose of base
Methods
getq get joint coordinates
setq set joint coordinates
setjointmode set joint control parameters
animate animate a joint coordinate trajectory
teach graphical teach pendant
Superclass methods (VREP_obj)
getpos get position of object
setpos set position of object
getorient get orientation of object
setorient set orientation of object
getpose get pose of object given
setpose set pose of object
can be used to set/get the pose of the robot base.
Superclass methods (VREP_mirror)
getname get object name
setparam_bool set object boolean parameter
setparam_int set object integer parameter
setparam_float set object float parameter
getparam_bool get object boolean parameter
getparam_int get object integer parameter
getparam_float get object float parameter
Robotics Toolbox for MATLAB 421 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Properties
n Number of joints
See also
VREP_mirror,VREP_obj,VREP_arm,VREP_camera,VREP_hokuyo
VREP_arm.VREP_arm
Create a robot arm mirror object
arm =VREP_arm(name,options) is a mirror object that corresponds to the robot
arm named name in the V-REP environment.
Options
‘fmt’, F Specify format for joint object names (default ‘%s_joint%d’)
Notes
•The number of joints is found by searching for objects with names systematically
derived from the root object name, by default named NAME_N where N is the
joint number starting at 0.
See also
VREP.arm
VREP_arm.animate
Animate V-REP robot
R.animate(qt,options) animates the corresponding V-REP robot with configurations
taken from consecutive rows of qt (M×N) which represents an M-point trajectory and
N is the number of robot joints.
Options
Robotics Toolbox for MATLAB 422 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
‘delay’, D Delay (s) betwen frames for animation (default 0.1)
‘fps’, fps Number of frames per second for display, inverse of ‘delay’ option
‘[no]loop’ Loop over the trajectory forever
See also
SerialLink.plot
VREP_arm.getq
Get joint angles of V-REP robot
ARM.getq() is the vector of joint angles (1 ×N) from the corresponding robot arm in
the V-REP simulation.
See also
VREP_arm.setq
VREP_arm.setjointmode
Set joint mode
ARM.setjointmode(m,C) sets the motor enable m(0 or 1) and motor control C(0 or
1) parameters for all joints of this robot arm.
VREP_arm.setq
Set joint angles of V-REP robot
ARM.setq(q) sets the joint angles of the corresponding robot arm in the V-REP simu-
lation to q(1 ×N).
See also
VREP_arm.getq
Robotics Toolbox for MATLAB 423 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP_arm.setqt
Set joint angles of V-REP robot
ARM.setq(q) sets the joint angles of the corresponding robot arm in the V-REP simu-
lation to q(1 ×N).
VREP_arm.teach
Graphical teach pendant
R.teach(options) drive a V-REP robot by means of a graphical slider panel.
Options
‘degrees’ Display angles in degrees (default radians)
‘q0’, q Set initial joint coordinates
Notes
•The slider limits are all assumed to be [-pi, +pi]
See also
SerialLink.plot
VREP_camera
Mirror of V-REP vision sensor object
Mirror objects are MATLAB objects that reflect the state of objects in the V-REP envi-
ronment. Methods allow the V-REP state to be examined or changed.
This is a concrete class, derived from VREP_mirror, for all V-REP vision sensor objects
and allows access to images and image parameters.
Methods throw exception if an error occurs.
Robotics Toolbox for MATLAB 424 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Example
vrep = VREP();
camera = vrep.camera(’Vision_sensor’);
im = camera.grab();
camera.setpose(T);
R = camera.getorient();
Methods
grab return an image from simulated camera
setangle set field of view
setresolution set image resolution
setclipping set clipping boundaries
Superclass methods (VREP_obj)
getpos get position of object
setpos set position of object
getorient get orientation of object
setorient set orientation of object
getpose get pose of object
setpose set pose of object
can be used to set/get the pose of the robot base.
Superclass methods (VREP_mirror)
getname get object name
setparam_bool set object boolean parameter
setparam_int set object integer parameter
setparam_float set object float parameter
getparam_bool get object boolean parameter
getparam_int get object integer parameter
getparam_float get object float parameter
See also
VREP_mirror,VREP_obj,VREP_arm,VREP_camera,VREP_hokuyo
Robotics Toolbox for MATLAB 425 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP_camera.VREP_camera
Create a camera mirror object
C=VREP_camera(name,options) is a mirror object that corresponds to the vision
senor named name in the V-REP environment.
Options
‘fov’, A Specify field of view in degreees (default 60)
‘resolution’, N Specify resolution. If scalar N×Nelse N(1)xN(2)
‘clipping’, Z Specify near Z(1) and far Z(2) clipping boundaries
Notes
•Default parameters are set in the V-REP environmen
•Can be applied to “DefaultCamera” which controls the view in the simulator
GUI.
See also
VREP_obj
VREP_camera.char
Convert to string
V.char() is a string representation the VREP parameters in human readable foramt.
See also
VREP.display
VREP_camera.getangle
Fet field of view for V-REP vision sensor
fov = C.getangle(fov) is the field-of-view angle to fov in radians.
Robotics Toolbox for MATLAB 426 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP_camera.setangle
VREP_camera.getclipping
Get clipping boundaries for V-REP vision sensor
C.getclipping() is the near and far clipping boundaries (1 ×2) in the Z-direction as a
2-vector [NEAR,FAR].
See also
VREP_camera.setclipping
VREP_camera.getresolution
Get resolution for V-REP vision sensor
R= C.getresolution() is the image resolution (1 ×2) of the vision sensor R(1)xR(2).
See also
VREP_camera.setresolution
VREP_camera.grab
Get image from V-REP vision sensor
im = C.grab(options) is an image (W×H) returned from the V-REP vision sensor.
C.grab(options) as above but the image is displayed using idisp.
Options
‘grey’ Return a greyscale image (default color).
Robotics Toolbox for MATLAB 427 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•V-REP simulator must be running.
•Color images can be quite dark, ensure good light sources.
•Uses the signal ‘handle_rgb_sensor’ to trigger a single image generation.
See also
idisp,VREP.simstart
VREP_camera.setangle
Set field of view for V-REP vision sensor
C.setangle(fov) set the field-of-view angle to fov in radians.
See also
VREP_camera.getangle
VREP_camera.setclipping
Set clipping boundaries for V-REP vision sensor
C.setclipping(near,far) set clipping boundaries to the range of Z from near to far.
Objects outside this range will not be rendered.
See also
VREP_camera.getclipping
VREP_camera.setresolution
Set resolution for V-REP vision sensor
C.setresolution(R) set image resolution to R×Rif Ris a scalar or R(1)xR(2) if it is a
2-vector.
Robotics Toolbox for MATLAB 428 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•By default V-REP cameras seem to have very low (32 ×32) resolution.
•Frame rate will decrease as frame size increases.
See also
VREP_camera.getresolution
VREP_mirror
V-REP mirror object class
Mirror objects are MATLAB objects that reflect the state of objects in the V-REP envi-
ronment. Methods allow the V-REP state to be examined or changed.
This abstract class is the root class for all V-REP mirror objects.
Methods throw exception if an error occurs.
Methods
getname get object name
setparam_bool set object boolean parameter
setparam_int set object integer parameter
setparam_float set object float parameter
getparam_bool get object boolean parameter
getparam_int get object integer parameter
getparam_float get object float parameter
remove remove object from scene
display display object info
char convert to string
Properties (read only)
h V-REP integer handle for the object
name Name of the object in V-REP
vrep Reference to the V-REP connection object
Robotics Toolbox for MATLAB 429 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Notes
•This has nothing to do with mirror objects in V-REP itself which are shiny re-
flective surfaces.
See also
VREP_obj,VREP_arm,VREP_camera,VREP_hokuyo
VREP_mirror.VREP_mirror
Construct VREP_mirror object
obj =VREP_mirror(name) is a V-REP mirror object that represents the object named
name in the V-REP simulator.
VREP_mirror.char
Convert to string
OBJ.char() is a string representation the VREP parameters in human readable foramt.
See also
VREP.display
VREP_mirror.display
Display parameters
OBJ.display() displays the VREP parameters in compact format.
Notes
•This method is invoked implicitly at the command line when the result of an
expression is a VREP object and the command has no trailing semicolon.
Robotics Toolbox for MATLAB 430 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP.char
VREP_mirror.getname
Get object name
OBJ.getname() is the name of the object in the VREP simulator.
VREP_mirror.getparam_bool
Get boolean parameter of V-REP object
OBJ.getparam_bool(id) is the boolean parameter with id of the corresponding V-REP
object.
See also VREP_mirror.setparam_bool, VREP_mirror.getparam_int, VREP_mirror.getparam_float.
VREP_mirror.getparam_float
Get float parameter of V-REP object
OBJ.getparam_float(id) is the float parameter with id of the corresponding V-REP
object.
See also VREP_mirror.setparam_bool, VREP_mirror.getparam_bool, VREP_mirror.getparam_int.
VREP_mirror.getparam_int
Get integer parameter of V-REP object
OBJ.getparam_int(id) is the integer parameter with id of the corresponding V-REP
object.
See also VREP_mirror.setparam_int, VREP_mirror.getparam_bool, VREP_mirror.getparam_float.
Robotics Toolbox for MATLAB 431 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP_mirror.setparam_bool
Set boolean parameter of V-REP object
OBJ.setparam_bool(id,val) sets the boolean parameter with id to value val within the
V-REP simulation engine.
See also VREP_mirror.getparam_bool, VREP_mirror.setparam_int, VREP_mirror.setparam_float.
VREP_mirror.setparam_float
Set float parameter of V-REP object
OBJ.setparam_float(id,val) sets the float parameter with id to value val within the
V-REP simulation engine.
See also VREP_mirror.getparam_float, VREP_mirror.setparam_bool, VREP_mirror.setparam_int.
VREP_mirror.setparam_int
Set integer parameter of V-REP object
OBJ.setparam_int(id,val) sets the integer parameter with id to value val within the
V-REP simulation engine.
See also VREP_mirror.getparam_int, VREP_mirror.setparam_bool, VREP_mirror.setparam_float.
VREP_obj
V-REP mirror of simple object
Mirror objects are MATLAB objects that reflect objects in the V-REP environment.
Methods allow the V-REP state to be examined or changed.
This is a concrete class, derived from VREP_mirror, for all V-REP objects and allows
access to pose and object parameters.
Robotics Toolbox for MATLAB 432 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
Example
vrep = VREP();
bill = vrep.object(’Bill’); % get the human figure Bill
bill.setpos([1,2,0]);
bill.setorient([0 pi/2 0]);
Methods throw exception if an error occurs.
Methods
getpos get position of object
setpos set position of object
getorient get orientation of object
setorient set orientation of object
getpose get pose of object
setpose set pose of object
Superclass methods (VREP_mirror)
getname get object name
setparam_bool set object boolean parameter
setparam_int set object integer parameter
setparam_float set object float parameter
getparam_bool get object boolean parameter
getparam_int get object integer parameter
getparam_float get object float parameter
display print the link parameters in human readable form
char convert to string
See also
VREP_mirror,VREP_obj,VREP_arm,VREP_camera,VREP_hokuyo
VREP_obj.VREP_obj
VREP_obj mirror object constructor
v=VREP_base(name) creates a V-REP mirror object for a simple V-REP object type.
Robotics Toolbox for MATLAB 433 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
VREP_obj.getorient
Get orientation of V-REP object
V.getorient() is the orientation of the corresponding V-REP object as a rotation matrix
(3 ×3).
V.getorient(’euler’, OPTIONS) as above but returns ZYZ Euler angles.
V.getorient(base) is the orientation of the corresponding V-REP object relative to the
VREP_obj object base.
V.getorient(base, ‘euler’, OPTIONS) as above but returns ZYZ Euler angles.
Options
See tr2eul.
See also
VREP_obj.setorient,VREP_obj.getopos,VREP_obj.getpose
VREP_obj.getpos
Get position of V-REP object
V.getpos() is the position (1 ×3) of the corresponding V-REP object.
V.getpos(base) as above but position is relative to the VREP_obj object base.
See also
VREP_obj.setpos,VREP_obj.getorient,VREP_obj.getpose
VREP_obj.getpose
Get pose of V-REP object
V.getpose() is the pose (4 ×4) of the the corresponding V-REP object.
V.getpose(base) as above but pose is relative to the pose the VREP_obj object base.
Robotics Toolbox for MATLAB 434 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
See also
VREP_obj.setpose,VREP_obj.getorient,VREP_obj.getpos
VREP_obj.setorient
Set orientation of V-REP object
V.setorient(R) sets the orientation of the corresponding V-REP to rotation matrix R
(3 ×3).
V.setorient(T) sets the orientation of the corresponding V-REP object to rotational
component of homogeneous transformation matrix T(4 ×4).
V.setorient(E) sets the orientation of the corresponding V-REP object to ZYZ Euler
angles (1 ×3).
V.setorient(x,base) as above but orientation is set relative to the orientation of VREP_obj
object base.
See also
VREP_obj.getorient,VREP_obj.setpos,VREP_obj.setpose
VREP_obj.setpos
Set position of V-REP object
V.setpos(T) sets the position of the corresponding V-REP object to T(1 ×3).
V.setpos(T,base) as above but position is set relative to the position of the VREP_obj
object base.
See also
VREP_obj.getpos,VREP_obj.setorient,VREP_obj.setpose
VREP_obj.setpose
Set pose of V-REP object
V.setpose(T) sets the pose of the corresponding V-REP object to T(4 ×4).
Robotics Toolbox for MATLAB 435 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
V.setpose(T,base) as above but pose is set relative to the pose of the VREP_obj object
base.
See also
VREP_obj.getpose,VREP_obj.setorient,VREP_obj.setpos
wtrans
Transform a wrench between coordinate frames
wt =wtrans(T,w) is a wrench (6 ×1) in the frame represented by the homogeneous
transform T(4 ×4) corresponding to the world frame wrench w(6 ×1).
The wrenches wand wt are 6-vectors of the form [Fx Fy Fz Mx My Mz]’.
See also
tr2delta,tr2jac
xaxis
Set X-axis scaling
xaxis(max) set x-axis scaling from 0 to max.
xaxis(min,max) set x-axis scaling from min to max.
xaxis([min max]) as above.
xaxis restore automatic scaling for x-axis.
See also
yaxis
Robotics Toolbox for MATLAB 436 Copyright c
Peter Corke 2017

CHAPTER 2. FUNCTIONS AND CLASSES
xyzlabel
Label X, Y and Z axes
XYZLABEL label the x-, y- and z-axes with ‘X’, ‘Y’, and ‘Z’ respectiveley
yaxis
Y-axis scaling
yaxis(max) set y-axis scaling from 0 to max.
yaxis(min,max) set y-axis scaling from min to max.
yaxis([min max]) as above.
yaxis restore automatic scaling for y-axis.
See also
yaxis
Robotics Toolbox for MATLAB 437 Copyright c
Peter Corke 2017
