SMI Tech Guide 2015

User Manual:

Open the PDF directly: View PDF .
Page Count: 180 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Technical Guide

An Assessment of College and Career Math

Readiness Across Grades K–Algebra ll

Technical Guide

Excepting those parts intended for classroom use, no part of this publication may be reproduced in whole or in part, or stored in a retrieval system, or transmitted

in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without written permission of the publisher. For information regarding

permission, write to Scholastic Inc., 557 Broadway, New York, NY 10012. Scholastic Inc. grants teachers who have purchased SMI College & Career permission to

reproduce from this book those pages intended for use in their classrooms. Notice of copyright must appear on all copies of copyrighted materials.

ISBN-13: 978-0-545-79640-8

ISBN-10: 0-545-79640-7

SCHOLASTIC, SCHOLASTIC ACHIEVEMENT MANAGER, and associated logos are trademarks and/or registered trademarks of Scholastic Inc.

QUANTILE, QUANTILE FRAMEWORK, LEXILE, and LEXILE FRAMEWORK are registered trademarks of MetaMetrics, Inc.

Other company names, brand names, and product names are the property and/or trademarks of their respective owners.

2 SMI College & Career

Table of Contents

Introduction ...................................................................................7

Features of Scholastic Math Inventory College & Career ........................................9

Rationale for and Uses of Scholastic Math Inventory College & Career ..........................10

Limitations of Scholastic Math Inventory College & Career .....................................13

Theoretical Foundations and Validity of the Quantile Framework for Mathematics .............15

The Quantile Framework for Mathematics Taxonomy ..........................................17

The Quantile Framework Field Study .........................................................22

The Quantile Scale .........................................................................31

Validity of the Quantile Framework for Mathematics ...........................................36

Relationship of Quantile Framework to Other Measures of Mathematics Understanding...........37

Using SMI College & Career...................................................................43

Administering the Test ......................................................................45

Interpreting Scholastic Math Inventory College & Career Scores ................................52

Using SMI College & Career Results..........................................................61

SMI College & Career Reports to Support Instruction ..........................................62

Development of SMI College & Career.........................................................65

Specifications of the SMI College & Career Item Bank .........................................66

SMI College & Career Item Development .....................................................69

SMI College & Career Computer-Adaptive Algorithm ...........................................74

Reliability ....................................................................................81

QSC Quantile Measure—Measurement Error .................................................82

SMI College & Career Standard Error of Measurement .........................................83

Validity.......................................................................................87

Content Validity ............................................................................89

Construct-Identification Validity..............................................................90

Conclusion.................................................................................91

References ...................................................................................93

Appendices ..................................................................................99

Appendix 1: QSC Descriptions and Standards Alignment ..................................... 100

Appendix 2: Norm Reference Table (spring percentiles) ...................................... 131

Appendix 3: Reliability Studies............................................................. 132

Appendix 4: Validity Studies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136

Table of Contents

Table of Contents 3

Figures

FIGURE 1 ........................................11

Growth Report.

FIGURE 2 ........................................28

Rasch achievement estimates of N = 9,656 students with

complete data.

FIGURE 3 ........................................29

Box and whisker plot of the Rasch ability estimates (using

the Quantile scale) for the final sample of students with

outfit statistics less than 1.8 (N = 9,176).

FIGURE 4 ........................................30

Box and whisker plot of the Rasch ability estimates (using

the Quantile scale) of the 685 Quantile Framework items for

the final sample of students (N = 9,176).

FIGURE 5 ........................................32

Relationship between reading and mathematics scale scores

on a norm-referenced assessment linked to the Lexile scale

in reading.

FIGURE 6 ........................................33

Relationship between grade level and mathematics

performance on the Quantile Framework field study and

other mathematics assessments.

FIGURE 7 ........................................41

A continuum of mathematical demand for Kindergarten

through precalculus textbooks (box plot percentiles: 5th,

25th, 50th, 75th, and 95th).

FIGURE 8 ........................................46

SMI College & Career’s four-function calculator and scientific

calculator.

FIGURE 9 ........................................47

SMI College & Career Grades 3–5 Formula Sheet.

FIGURE 10.......................................47

SMI College & Career Grades 6–8 Formula Sheet.

FIGURE 11.......................................48

SMI College & Career Grades 9–11 Formula Sheets.

FIGURE 12.......................................51

Sample administration of SMI College & Career for a fourth-

grade student.

FIGURE 13.......................................53

Normal distribution of scores described in percentiles,

stanines, and NCEs.

FIGURE 14.......................................57

Student-mathematical demand discrepancy and predicted

success rate.

FIGURE 15.......................................63

Instructional Planning Report.

FIGURE 16.......................................76

The Start phase of the SMI College & Career computer-

adaptive algorithm.

FIGURE 17.......................................78

The Step phase of the SMI College & Career computer-

adaptive algorithm.

FIGURE 18.......................................79

The Stop phase of the SMI College & Career computer-

adaptive algorithm.

FIGURE 19.......................................85

Distribution of SEMs from simulations of student

SMI College & Career scores, Grade 5.

FIGURE 20......................................156

SMI Validation Study, Phase I: SMI Quantile measures

displayed by location and grade.

FIGURE 21......................................157

SMI Validation Study, Phase II: SMI Quantile measures

displayed by location and grade.

FIGURE 22......................................157

SMI Validation Study, Phase II: SMI Quantile measures

displayed by grade.

FIGURE 23......................................158

SMI Validation Study, Phase III: SMI Quantile measures

displayed by location and grade.

FIGURE 24......................................158

SMI Validation Study, Phase III: SMI Quantile measures

displayed by grade.

Tables

TABLE 1.........................................23

Field study participation by grade and gender.

TABLE 2.........................................23

Test form administration by level.

TABLE 3.........................................24

Summary item statistics from the Quantile Framework

field study.

TABLE 4.........................................27

Mean and median Quantile measure for N 5 9,656

students with complete data.

TABLE 5.........................................29

Mean and median Quantile measure for the final set of

N 5 9,176 students.

TABLE 6.........................................37

Results from field studies conducted with the Quantile

Framework.

TABLE 7.........................................38

Results from linking studies conducted with the Quantile

Framework.

TABLE 8.........................................58

Success rates for a student with a Quantile measure of 750Q

and skills of varying difficulty (demand).

List of Figures and Tables

4 SMI College & Career

Table of Contents

TABLE 9.........................................58

Success rates for students with different Quantile measures

of achievement for a task with a Quantile measure of 850Q.

TABLE 10........................................60

SMI College & Career performance level ranges by grade.

TABLE 11........................................67

Designed strand profile for SMI: Kindergarten through

Grade 11 (Algebra II).

TABLE 12........................................73

Actual strand profile for SMI after item writing and review.

TABLE 13.......................................134

SMI Marginal reliability estimates, by district and overall.

TABLE 14.......................................135

SMI test-retest reliability estimates over a one-week period,

by grade.

TABLE 15.......................................139

SMI Validation Study—Phase I: Descriptive statistics for

the SMI Quantile measures.

TABLE 16.......................................140

SMI Validation Study—Phase I: Means and standard

deviations for the SMI Quantile measures, by gender.

TABLE 17.......................................140

SMI Validation Study—Phase I: Means and standard

deviations for the SMI Quantile measures, by race/ethnicity.

TABLE 18.......................................143

SMI Validation Study—Phase II: Descriptive statistics for the

SMI Quantile measures (spring administration).

TABLE 19.......................................144

SMI Validation Study—Phase II: Means and standard

deviations for the SMI Quantile measures, by gender

(spring administration).

TABLE 20.......................................145

SMI Validation Study—Phase II: Means and standard

deviations for the SMI Quantile measures, by race/ethnicity

(spring administration).

TABLE 21.......................................147

SMI Validation Study—Phase III: Descriptive statistics for

the SMI Quantile measures (spring administration).

TABLE 22.......................................149

SMI Validation Study—Phase III: Means and standard

deviations for the SMI Quantile measures, by gender

(spring administration).

TABLE 23.......................................150

SMI Validation Study—Phase III: Means and standard

deviations for the SMI Quantile measures, by race/ethnicity

(spring administration).

TABLE 24.......................................152

Harford County Public Schools—Intervention study means

and standard deviation for the SMI Quantile measures.

TABLE 25.......................................152

Raytown Consolidated School District No. 2—FASTT Math

intervention program participation means and standard

deviations for the SMI Quantile measures.

TABLE 26.......................................153

Inclusion in math intervention program means and

standard deviations for the SMI Quantile measures.

TABLE 27.......................................153

Gifted and Talented status means and standard deviations

for the SMI Quantile measures.

TABLE 28.......................................154

Gifted and Talented status means and standard deviations

for the SMI Quantile measures.

TABLE 29.......................................155

Special Education status means and standard deviations

for the SMI Quantile measures.

TABLE 30.......................................155

Special Education status means and standard deviations

for the SMI Quantile measures.

TABLE 31.......................................159

Correlations among the Decatur School District test scores.

TABLE 32.......................................159

Correlations between SMI Quantile measures and Harford

County Public Schools test scores.

TABLE 33.......................................160

Alief Independent School District—descriptive statistics for

SMI Quantile measures and 2010 TAKS mathematics scores,

by grade.

TABLE 34.......................................161

Alief Independent School District—descriptive statistics for

SMI Quantile measures and 2011 TAKS mathematics scores,

by grade.

TABLE 35.......................................162

Brevard Public Schools—descriptive statistics for SMI Quantile

measures and 2010 FCAT mathematics scores, by grade.

TABLE 36.......................................162

Brevard Public Schools—descriptive statistics for SMI Quantile

measures and 2011 FCAT mathematics scores, by grade.

TABLE 37.......................................163

Cabarrus County Schools—descriptive statistics for SMI

Quantile measures and 2010 NCEOG mathematics scores, by

grade.

TABLE 38.......................................163

Cabarrus County Schools—descriptive statistics for SMI

Quantile measures and 2011 NCEOG mathematics scores, by

grade.

TABLE 39.......................................164

Clark County School District—descriptive statistics for SMI

Quantile measures and 2010 CRT mathematics scores, by

grade.

List of Figures and Tables (continued)

Table of Contents 5

Table of Contents

TABLE 40.......................................164

Clark County School District—descriptive statistics for SMI

Quantile measures and 2011 CRT mathematics scores, by grade.

TABLE 41.......................................165

Harford County Public Schools—descriptive statistics for SMI

Quantile measures and 2010 MSA mathematics scores, by

grade.

TABLE 42.......................................165

Harford County Public Schools—descriptive statistics for SMI

Quantile measures and 2011 MSA mathematics scores, by

grade.

TABLE 43.......................................166

Kannapolis City Schools—descriptive statistics for SMI

Quantile measures and 2010 NCEOG mathematics scores, by

grade.

TABLE 44.......................................166

Kannapolis City Schools—descriptive statistics for SMI

Quantile measures and 2011 NCEOG mathematics scores, by

grade.

TABLE 45.......................................167

Killeen Independent School District—descriptive statistics for

SMI Quantile measures and 2011 TAKS mathematics scores,

by grade.

TABLE 46.......................................168

Description of longitudinal panel across districts, by grade.

TABLE 47.......................................168

Description of longitudinal panel across districts, by grade

for students with at least three Quantile measures.

TABLE 48.......................................169

Results of regression analyses for longitudinal panel,

across grades.

TABLE 49.......................................172

Alief Independent School District—bilingual means and

standard deviations for the SMI Quantile measures.

TABLE 50.......................................172

Cabarrus County Schools—English language learners (ELL)

means and standard deviations for the SMI Quantile

measures.

TABLE 51.......................................173

Alief ISD—English as a second language (ESL) means and

standard deviations for the SMI Quantile measures.

TABLE 52.......................................173

Alief ISD—limited English proficiency (LEP) status means

and standard deviations for the SMI Quantile measures.

TABLE 53.......................................173

Clark County School District—limited English proficiency

(LEP) status means and standard deviations for the SMI

Quantile measures.

TABLE 54.......................................173

Kannapolis City Schools—limited English proficiency (LEP)

status means and standard deviations for the SMI Quantile

measures.

TABLE 55.......................................174

Harford County Public Schools—English language learners

(ELL) means and standard deviations for the SMI Quantile

measures.

TABLE 56.......................................174

Kannapolis City Schools—limited English proficiency (LEP)

means and standard deviations for the SMI Quantile

measures.

TABLE 57.......................................174

Killeen ISD—limited English proficiency (LEP) means and

standard deviations for the SMI Quantile measures.

TABLE 58.......................................175

Alief ISD—Economically disadvantaged means and standard

deviations for the SMI Quantile measures.

TABLE 59.......................................175

Harford County Public Schools—Economically disadvantaged

means and standard deviations for the SMI Quantile

measures.

TABLE 60.......................................176

Killeen Independent School District—Economically

disadvantaged means and standard deviations for the SMI

Quantile measures.

TABLE 61.......................................177

Alief Independent School District—descriptive statistics for

SMI Quantile measures and 2010 TAKS reading scores, by

grade.

TABLE 62.......................................177

Brevard Public Schools—descriptive statistics for SMI

Quantile measures and 2010 FCAT reading scores, by grade.

TABLE 63.......................................178

Cabarrus County Schools—descriptive statistics for SMI

Quantile measures and 2010 NCEOG reading scores, by

grade.

TABLE 64.......................................178

Kannapolis City Schools—descriptive statistics for SMI

Quantile measures and 2010 NCEOG reading scores,

by grade.

TABLE 65.......................................179

Clark County School District—descriptive statistics for SMI

Quantile measures and 2010 CRT reading scores, by grade.

TABLE 66.......................................179

Alief Independent School District—descriptive statistics for

SMI Quantile measures and 2011 TAKS reading scores, by

grade.

Features of Scholastic Math Inventory College & Career............................9

Rationale for and Uses of Scholastic Math Inventory College & Career ......... 10

Limitations of Scholastic Math Inventory College & Career....................... 13

Introduction

8 SMI College & Career

Introduction

Scholastic Math InventoryTM College & Career, developed by Scholastic Inc., is an objective assessment of a

student’s readiness for mathematics instruction from Kindergarten through Algebra II (or High School Integrated

Math III), which is commonly considered an indicator of college and career readiness. SMI College & Career

quantifies a student’s path to and through high school mathematics and can be administered to students in Grades

K–12. A computer-adaptive test, SMI College & Career delivers test items targeted to students’ ability level. The

measurement system for SMI College & Career is the Quantile® Framework for Mathematics and, while SMI College

& Career can be used for several instructional purposes, a completed SMI College & Career administration yields a

Quantile® measure for each student. Teachers and administrators can use the students’ Quantile measures to:

• Conduct universal screening: identify the degree to which students are ready for instruction on certain

mathematical concepts and skills

• Differentiate instruction: provide targeted support for students at their readiness level

• Monitor growth: gauge students’ developing understandings of mathematics in relation to the objective

measure of algebra readiness and Algebra II completion and to being on track for college and career at the

completion of high school

The Quantile Framework for Mathematics, developed by MetaMetrics, Inc., is a scientifically based scale of

mathematics skills and concepts. The Quantile Framework helps educators measure student progress as well as

forecast student development by providing a common metric for mathematics concepts and skills and for students’

abilities. A Quantile measure refers to both the level of difficulty of the mathematical skills and concepts and a

student’s readiness for instruction.

SMI was developed during 2008–2010 and launched in Summer 2010. Additional items were added in 2011 and

again in 2013. Studies of SMI validity began in 2009. For a more robust validity analysis, Phase II of the SMI

validation study was conducted during the 2009–2010 school year. Phase III of the validity study was completed in

2012 with data collected from the 2010–2011 school year.

This technical guide is intended to provide users with the broad research foundation essential for deciding how SMI

College & Career should be administered and what kinds of inferences can be drawn from the results pertaining

to students’ mathematical achievement. In addition, this guide describes the development and psychometric

characteristics of this assessment and the Quantile Framework.

Introduction 9

Introduction

Features of Scholastic Math Inventory College & Career

SMI College & Career is a research-based universal screener and growth monitor designed to measure students’

readiness for instruction. The assessment is computer-based and features two components:

• The actual student test, which is computer adaptive, with more than 5,000 items

• The management system, Scholastic Achievement Manager, where enrollments are managed and

customized features and data reports can be accessed

SMI College & Career Test

When students are assessed with SMI College & Career, they receive a single measure—a Quantile measure—that

indicates their instructional readiness for calibrated content to and through Algebra II/High School Integrated Math

III. As a computer-adaptive test, SMI College & Career provides items based on students’ previous responses. This

format allows students to be tested on a large range of skills and concepts in a shorter amount of time and yields a

highly accurate score.

SMI College & Career can be completed in 20–40 minutes and is presented in three parts: Math Fact Screener (for

Kindergarten and Grade 1 an Early Numeracy Screener, which tests students on counting and quantity comparison,

is used), Practice Test, and Scored Test.

The Math Fact Screener is a simple and fast test focused on basic addition and multiplication skills. Once students

demonstrate relative mastery of math facts, they will not experience this part of the assessment again.

The Practice Test is a three- to five-question test calibrated far below the students’ current grade level. The purpose

of this part is to ensure students can interact with a computer test successfully and to provide them an opportunity

to practice with the tools provided in the assessment. Teachers can allow students to skip this part of the test after

its first administration.

The Scored Test part of the assessment produces Quantile measures for the students. In this part, students engage

with at least 25 and as many as 45 test items that follow a consistent four-option, multiple-choice format. Items are

presented in a simple, straightforward format with clear unambiguous language. Because of the depth of the item

bank, students do not see the same item twice in the same administration or in the next two administrations. Items

at the lowest level are sampled from Kindergarten and Grade 1 mathematical skills and topics; items at the highest

level are sampled from Algebra II/High School Integrated Math III topics. Some items may include mathematical

representations such as diagrams, graphs, tables, and charts. Optional calculators and formula sheets are included

in the program. Calculators will not be visible for problems whose purpose is computational proficiency. Providing

students with paper and pencil during their assessment is recommended. All assessments can be saved and

accessed at another time for completion. This feature is important for students with extended time accommodations.

10 SMI College & Career

Introduction

Scholastic Achievement Manager

Scholastic Achievement Manager (SAM) is the data backbone for all Scholastic technology programs, including SMI

College & Career. In SAM, educators can manage enrollment, create classes, and assign usernames and passwords.

SAM also provides teachers and administrators with nine template reports that support this formative assessment

with actionable data for teachers, students, parents, and administrators. These reports feature a growth report that

provides a quantifiable trajectory to and through Algebra II/High School Integrated Math III—a course cited as the

gatekeeper to college and career readiness—and provide a tool to differentiate math instruction by linking Quantile

measures to classroom resources and basal math textbooks.

There are over 5,000 test items that were rigorously developed to connect to a Quantile measure. When students are

tested with SMI College & Career, they are tested on items that represent five content strands (Number & Operations;

Algebraic Thinking, Patterns, and Proportional Reasoning; Geometry, Measurement, and Data; Statistics & Probability

[Grades 6–11 only]; and Expressions & Equations, Algebra, and Functions [Grades 6–11 only]) and receive a single

measure—a Quantile measure—that indicates their instructional readiness for calibrated content.

Scholastic Central

Scholastic Central puts your assessment calendar, data snapshots and news regarding student performance and

usage, instructional recommendations, and professional learning resources all in one centralized location to make it

easy to assess and plan instruction.

Leadership Dashboard

Administrators access the Leadership Dashboard on Scholastic Central to view high-level data snapshots and data

analytics for the schools using SMI College & Career. Follow up with individual schools for appropriate intervention to

increase student performance to proficiency.

You can use the Leadership Dashboard to:

• View Performance Level and Growth data snapshots, with pop-up information and a table of detailed data

by school

• Filter school- and district-level data by demographics

• View resources for Implementation Success Factors

• Schedule and view reports

Rationale for and Uses of Scholastic Math Inventory College & Career

A comprehensive program of mathematics education includes curriculum, assessment, and instruction.

• Curriculum is the planned set of standards and materials that are intended for implementation during the

academic year.

• Instruction is the enacting of curriculum; it is when students build new concepts and skills.

• Assessment should inform instruction by describing skills and concepts students are ready to learn.

The challenge for educators is meeting the demand of curriculum in a classroom of diverse learners. This challenge

is met when the curriculum unfolds in a way that all students make progress. Typically, the best starting point for

instruction is to identify the skills and concepts that each student is ready to learn.

SMI College & Career provides educators with information related to the difficulty of skills and concepts, as well as

the increasing difficulty of content progressions. This information is found in the SMI skills and concepts database at

www.scholastic.com/SMI.

Introduction 11

Introduction

An SMI College & Career test reports students’ Quantile measures. In the SMI College & Career reports, student test

results are aligned with specific skills and concepts that are appropriate for instruction. For example, Figure 1 depicts

a report that specifies growth in the skills and concepts that a student is ready to learn and links those concepts to the

Common Core State Standards identification number and other Quantile-based instructional information.

FIGURE 1. Growth Report.

Printed by: Teacher

GROWTH

Page 1 of 1

Printed on: 2/22/2015

CLASS: 3rd Period

School: Lincoln Middle School

Teacher: Sarah Foster

Grade: 5

Time Period: 12/13/14–02/22/15

Growth Report

FIRST TEST LAST TEST

STUDENT GRADE DATE

QuAnTilE®

MEAsurE/

PErforMAncE

lEvEl

DATE

QuAnTilE®

MEAsurE/

PErforMAncE

lEvEl

GROWTH IN QUANTILE® MEASURE

Gainer, Jacquelyn 5 12/13/14 925Q P02/22/15 1100Q A 175Q

Hartsock, Shalanda 5 12/13/14 595Q B02/22/15 750Q B 155Q

Cho, Henry 5 12/13/14 955Q P02/22/15 1100Q A 155Q

Cooper, Maya 5 12/13/14 700Q B02/22/15 820Q P 120Q

Robinson, Tiffany 5 12/13/14 390Q BB u 02/22/15 485Q BB 95Q

Cocanower, Jaime 5 12/13/14 640Q B02/22/15 710Q B 70Q

Garcia, Matt 5 12/13/14 615Q B02/22/15 680Q B 65Q

Terrell, Walt 5 12/13/14 670Q B02/22/15 720Q B 50Q

Enoki, Jeanette 5u 12/13/14 750Q P02/22/15 800Q B 50Q

Collins, Chris 5u 12/13/14 855Q Pu 02/22/15 890Q P 35Q

Morris, Timothy 5 12/13/14 620Q B02/22/15 650Q B 30Q

Ramirez, Jeremy 5u 12/13/14 580Q B 02/22/15 600Q B 20Q

KEY

USING THE DATA

Purpose:

This report shows changes in student

performance and growth on SMI over time.

Follow-Up:

Provide opportunities to challenge students who show

signicant growth. Provide targeted intervention and support

to students who show little growth.

YEAR-END PROFICIENCY RANGES

GRADE K 10Q–175Q GRADE 5 820Q–1020Q GRADE 9 1140Q–1325Q

GRADE 1 260Q–450Q GRADE 6 870Q–1125Q GRADE 10 1220Q–1375Q

GRADE 2 405Q–600Q GRADE 7 950Q–1175Q GRADE 11 1350Q–1425Q

GRADE 3 625Q–850Q GRADE 8 1030Q–1255Q GRADE 12 1390Q–1505Q

GRADE 4 715Q–950Q

EM Emerging Mathematician

ADVANCED

PROFICIENT

BASIC

BELOW BASIC

u Test taken in less than 15 minutes

12 SMI College & Career

Introduction

After an initial assessment with SMI College & Career, it is possible to monitor progress, predict the student’s

likelihood of success when instructed on mathematical skills and concepts, and report on actual student growth

toward the objective of algebra completion and, by extension, college and career readiness.

Students’ Quantile measures indicate their readiness for instruction on skills and concepts within a range of 50Q

above and below their Quantile measure. Students should be successful at independent practice with skills and

concepts that are about 150Q to 250Q below their Quantile measure. With SMI College & Career test results,

educators can choose materials and resources for targeted instruction and practice.

On a school-wide or instructional level, SMI College & Career results can be used to screen for intervention and

acceleration, measure progress at benchmarking intervals, group students for differentiated instruction, provide an

indication of outcomes on summative assessments, provide an independent measure of programmatic success, and

inform district decision making.

SMI supports school districts’ efforts to accelerate the learning path of struggling students. State educational

agencies (SEAs), local educational agencies (LEAs), and schools can use Title 1, Part A funds associated with

the American Recovery and Reinvestment Act of 2009 (ARRA) to identify, create, and structure opportunities and

strategies to strengthen education, drive school reform, and improve the academic achievement of at-risk students

using funds under Title I, Part A of the Elementary and Secondary Education Act of 1965 (ESEA) (US Department of

Education, 2009). Tiered intervention strategies can be used to provide support for students who are “at risk” of not

meeting state performance levels that define “proficient” achievement.

One such tiered approach is Response to Intervention (RTI), which involves providing the most appropriate

instruction, services, and scientifically based interventions to struggling students—with increasing intensity at each

tier of instruction (Cortiella, 2005).

As an academic assessment that can be used as a universal screener of all students, SMI College & Career can

also be used to identify those students who are “at risk” and provide student grouping recommendations for

appropriate instruction. SMI College & Career can be administered three to five times per year to monitor students’

growth. Regular monitoring of students’ progress is critical in determining if a student should move from one tier of

intervention to another and to determine the effectiveness of the intervention.

Introduction 13

Introduction

Another instructional approach supported by SMI College & Career is differentiated instruction in the Tier I classroom

(Tomlinson, 2001). By providing direct instructional recommendations for each student or each group of students and

linking those recommendations to the skills and concepts of the Quantile Framework, SMI College & Career provides

data to target and pace instruction.

Limitations of Scholastic Math Inventory College & Career

SMI College & Career utilizes an algorithm to ensure that each assessment is targeted to measure the readiness for

instruction of each student. Teachers and administrators can use the results to identify the mathematic skills and

concepts that are most appropriate for their students.

However, as with any assessment, SMI College & Career is one source of evidence about a student’s mathematical

understandings. Obviously, impactful decisions are best made when using multiple sources of evidence. Other

sources include student work such as homework and unit test results, state test data, adherence to mathematics

curriculum and pacing guides, student motivation, and teacher judgment.

One measure of student performance, taken on one day, is never sufficient to make high-stakes, student-

specific decisions such as summer school placement or retention.

The Quantile Framework for Mathematics Taxonomy ............................. 17

The Quantile Framework Field Study................................................. 22

The Quantile Scale...................................................................... 31

Validity of the Quantile Framework for Mathematics .............................. 36

Relationship of Quantile Framework to Other Measures of Mathematics

Understanding........................................................................... 37

Theoretical Foundation

and Validity of the Quantile

Framework for Mathematics

16 SMI College & Career

Theoretical Foundation

Theoretical Foundation and Validity of the Quantile

Framework for Mathematics

The Quantile Framework is the backbone on which the mathematical skills and concepts assessed in SMI College

& Career are mapped. The Quantile Framework is a scale that describes a student’s mathematical achievement.

Similar to how degrees on a thermometer measure temperature, the Quantile Framework uses a common metric—

the Quantile—to scientifically measure a student’s ability to reason mathematically, monitor a student’s readiness

for mathematics instruction, and locate a student on its taxonomy of mathematical skills, concepts, and applications.

The Quantile Framework uses this common metric to measure many different aspects of education in mathematics.

The same metric can be applied to measure the materials used in instruction, to calibrate the assessments used to

monitor instruction, and to interpret the results that are derived from the assessments. The result is an anchor to

which resources, concepts, skills, and assessments can be connected.

There are dozens of mathematics tests that measure a common construct and report results in proprietary, non-

exchangeable metrics. Not only are all of the tests using different units of measurement, but all use different scales

on which to make measurements. Consequently, it is difficult to connect the test results with materials used in the

classroom. The alignment of materials and linking of assessments with the Quantile Framework enables educators,

parents, and students to communicate and improve mathematics learning. The benefits of having a common metric

include being able to:

• Develop individual multiyear growth trajectories that denote a developmental continuum from the early

elementary level to Algebra II and Precalculus. The Quantile scale is vertically constructed, so the meaning

of a Quantile measure is the same regardless of grade level.

• Monitor and report student growth that meets the needs of state-initiated accountability systems

• Help classroom teachers make day-to-day instructional decisions that foster acceleration and growth

toward algebra readiness and through the next several years of secondary mathematics

To develop the Quantile Framework, the following preliminary tasks were undertaken:

• Building a structure of mathematical performance that spans the developmental continuum from

Kindergarten content through Geometry, Algebra II, and Precalculus content

• Developing a bank of items that had been field tested

• Developing the Quantile scale (multiplier and anchor point) based on the calibrations of the field-test

items

• Validating the measurement of mathematics achievement as defined by the Quantile Framework

Each of these tasks is described in the sections that follow. The implementation of the Quantile Framework in the

development of SMI College & Career, as well as the use of SMI College & Career and the interpretation of results, is

described in later sections of this guide.

Theoretical Foundation 17

Theoretical Foundation

The Quantile Framework for Mathematics Taxonomy

To develop a framework of mathematical performance, an initial structure needs to be established. The structure of

the Quantile Framework is organized around two guiding principles—(1) mathematics is a content area, and

(2) learning mathematics is developmental in nature.

The National Mathematics Advisory Panel report (2008, p. xix) recommended the following:

To prepare students for Algebra, the curriculum must simultaneously develop conceptual understanding,

computational fluency, and problem-solving skills . . . [t]hese capabilities are mutually supportive, each

facilitating learning of the others. Teachers should emphasize these interrelations; taken together, conceptual

understanding of mathematical operations, fluent execution of procedures, and fast access to number

combinations jointly support effective and efficient problem solving.

When developing the Quantile Framework, MetaMetrics recognized that in order to adequately address the

scope and complexity of mathematics, multiple proficiencies and competencies must be assessed. The Quantile

Framework is an effort to recognize and define a developmental context of mathematics instruction. This notion is

consistent with the National Council of Teachers of Mathematics’ (NCTM) conclusions about the importance of school

mathematics for college and career readiness presented in Administrator's Guide: Interpreting the Common Core

State Standards to Improve Mathematics Education, published in 2011.

Strands as Sub-domains of Mathematical Content

A strand is a major subdivision of mathematical content. The strands describe what students should know and be

able to do. The National Council of Teachers of Mathematics (NCTM) publication Principles and Standards for School

Mathematics (2000, hereafter NCTM Standards) outlined ten standards—five content standards and five process

standards. These content standards are Number and Operations, Algebra, Geometry, Measurement, and Data

Analysis and Probability. The process standards are Communications, Connections, Problem Solving, Reasoning, and

Representation.

As of March 2014, the Common Core State Standards for Mathematics (CCSS) have been adopted in 44 states,

the Department of Defense Education Activity, Washington DC, Guam, the Northern Mariana Islands, and the US

Virgin Islands. The CCSS identify critical areas of mathematics that students are expected to learn each year from

Kindergarten through Grade 8. The critical areas are divided into domains that differ at each grade level and include

Counting and Cardinality, Operations and Algebraic Thinking, Number and Operations in Base Ten, Number and

Operations—Fractions, Ratios and Proportional Relationships, the Number System, Expressions and Equations,

Functions, Measurement and Data, Statistics and Probability, and Geometry. The CCSS for Grades 9–12 are

organized by six conceptual categories: Number and Quantity, Algebra, Functions, Modeling, Geometry, and Statistics

and Probability (NGA Center & CCSSO, 2010a).

The six strands of the Quantile Framework bridge the Content Standards of the NCTM Standards and the domains

specified in the CCSS.

1. Number Sense. Students with number sense are able to understand a number as a specific amount,

a product of factors, and the sum of place values in expanded form. These students have an in-depth

understanding of the base-ten system and understand the different representations of numbers.

2. Numerical Operations. Students perform operations using strategies and standard algorithms on different

types of numbers but also use estimation to simplify computation and to determine how reasonable their

results are. This strand also encompasses computational fluency.

18 SMI College & Career

Theoretical Foundation

3. Geometry. The characteristics, properties, and comparison of shapes and structures are covered by

geometry, including the composition and decomposition of shapes. Not only does geometry cover abstract

shapes and concepts, but it provides a structure that can be used to observe the world.

4. Algebra and Algebraic Thinking. The use of symbols and variables to describe the relationships between

different quantities is covered by algebra. By representing unknowns and understanding the meaning

of equality, students develop the ability to use algebraic thinking to make generalizations. Algebraic

representations can also allow the modeling of an evolving relationship between two or more variables.

5. Data Analysis and Probability. The gathering of data and interpretation of data are included in data

analysis, probability, and statistics. The ability to apply knowledge gathered using mathematical methods to

draw logical conclusions is an essential skill addressed in this strand.

6. Measurement. The description of the characteristics of an object using numerical attributes is covered by

measurement. The strand includes using the concept of a unit to determine length, area, and volume in the

various systems of measurement, and the relationship between units of measurement within and between

these systems.

The Quantile Skill and Concept

Within the Quantile Framework, a Quantile Skill and Concept, or QSC, describes a specific mathematical skill or

concept a student can acquire. These QSCs are arranged in an orderly progression to create a taxonomy called the

Quantile scale. Examples of QSCs include:

1. Know and use addition and subtraction facts to 10 and understand the meaning of equality

2. Use addition and subtraction to find unknown measures of nonoverlapping angles

3. Determine the effects of changes in slope and/or intercepts on graphs and equations of lines

The QSCs used within the Quantile Framework were developed during Spring 2003, for Grades 1–8, Grade 9

(Algebra I), and Grade 10 (Geometry). The framework was extended to Algebra II and revised during Summer and Fall

2003. The content was finally extended to include material typically taught in Kindergarten and Grade 12

(Precalculus) during the Summer and Fall 2007.

The first step in developing a content taxonomy was to review the curricular frameworks from the following sources:

• NCTM Principles and Standards for School Mathematics (National Council of Teachers of Mathematics,

2000)

• Mathematics Framework for the 2005 National Assessment of Educational Progress: Prepublication Edition

(NAGB, 2005)

• North Carolina Standard Course of Study (Revised in 2003 for Kindergarten through Grade 12) (NCDPI, 1996)

Theoretical Foundation 19

Theoretical Foundation

• California Mathematics Framework and state assessment blueprints: Mathematics Framework for California

Public Schools: Kindergarten Through Grade Twelve (2000 Revised Edition), Mathematics Content Standards

for California Public Schools: Kindergarten Through Grade Twelve (December 1997), blueprints document

for the Star Program California Standards Tests: Mathematics (California Department of Education, adopted

by SBE October 9, 2002), and sample items for the California Mathematics Standards Tests (California

Department of Education, January 2002).

• Florida Sunshine State Standards: Sunshine State Standards Grade Level Expectations for Mathematics,

Grade 2 through Grade 10. The Sunshine State Standards “are the centerpiece of a reform effort in Florida

to align curriculum, instruction, and assessment” (Florida Department of Education, 2007, p. 1).

• Illinois: The Illinois Learning Standards for Mathematics. Goals 6 through 10 emphasize the following:

Number and Operations, Measurement, Algebra, Geometry, and Data Analysis and Statistics—Mathematics

Performance Descriptors, Grades 1–5 and Grades 6–12 (2002).

• Texas Essential Knowledge and Skills: Texas Essential Knowledge and Skills for Mathematics (TEKS)

was adopted by the Texas State Board of Education and became effective on September 1, 1998. The

TEKS, a state-mandated curriculum, was “specifically designed to help students to make progress . . . by

emphasizing the knowledge and skills most critical for student learning” (TEA, 2002, p. 4).

The review of the content frameworks resulted in the development of a list of QSCs spanning mathematical

knowledge from Kindergarten through Grade 12 (college and career readiness or precalculus). Each QSC is aligned

with one of the six content strands. Currently, there are approximately 549 QSCs, which can be viewed and searched

at www.scholastic.com/SMI or www.Quantiles.com.

Each QSC consists of a description of the content, a unique identification number, the grade at which it typically first

appears, and the strand with which it is associated.

20 SMI College & Career

Theoretical Foundation

Quantile Item Bank

The second task in the development of the Quantile Framework for Mathematics was to develop and field-test a

bank of items that could be used in future linking studies and calibration and development projects. Item bank

development for the Quantile Framework went through several stages—content specification, item writing and

review, field-testing and analyses, and final evaluation.

Content Specification

Each QSC developed during the design of the Quantile Framework was paired with a particular strand and identified

as typically being taught at a particular grade level. The curricular frameworks from Florida, North Carolina, Texas,

and California were synthesized to identify the appropriate grade level for each QSC. If a QSC was included in any of

these state frameworks, it was then added to the list of QSCs for the item bank utilized in the Quantile Framework

field study.

During Summer and Fall 2003, more than 1,400 items were developed to assess the QSCs associated with content

extending from first grade through Algebra II. The items were written and reviewed by mathematics educators

trained to develop multiple-choice items (Haladyna, 1994). Each item was associated with a strand and a QSC. In the

development of the Quantile Framework item bank, the reading demand of the items was kept as low as possible to

ensure that the items were testing mathematics achievement and not reading.

Item Writing and Review

Item writers were teachers of, and item-development specialists who had experience with, mathematics education

at various levels. Employing individuals with a range of experiences helped to ensure that the items were valid

measures. Item writers were provided with training materials concerning the development of multiple-choice

items and the Quantile Framework. Included in the item-writing materials were incorrect and ineffective items that

illustrated the criteria used to evaluate items, along with corrections based on those criteria. The final phase of item-

writer training was a short practice session with three items.

Item writers were given additional training related to sensitivity issues. Some item-writing materials address these

issues and identify areas to avoid when selecting passages and developing items. These materials were developed

based on work published concerning universal design and fair access, including the issues of equal treatment of the

sexes, fair representation of minority groups, and fair representation of disabled individuals.

Theoretical Foundation 21

Theoretical Foundation

A group of specialists representing various perspectives—test developers, editors, curriculum specialists, and

mathematics specialists—reviewed and edited the items. These individuals examined each item for sensitivity

issues and for the quality of the response options. During the second stage of the item review process, items were

approved, approved with edits, or deleted.

Field Testing and Analyses

The next stage in the development of the Quantile item bank was the field-testing of all of the items. First, individual

test items were compiled into leveled assessments distributed to groups of students. The data gathered from these

assessments were then analyzed using a variety of statistical methods. The final result was a bank of test items

appropriately placed within the Quantile scale, suitable for determining the mathematical achievement of students

on this scale.

Assessments for Field Testing

Assessment forms were developed for 10 levels for the purposes of field-testing. Levels 2 though 8 were aligned

with the typical content taught in Grades 2–8. Level 9 was aligned with the typical content taught in Algebra I. Level

10 was aligned with the typical content taught in Geometry. Finally, Level 11 was aligned with the typical content

taught in Algebra II. A total of 30 test forms were developed (three per assessment level), and each test form was

composed of 30 items.

Creating the taxonomy of QSCs across all grade levels involved linking the field test forms such that the concepts

and difficulty levels between tests overlapped. This was achieved by designating a linking set of items for each

grade level. These items were administered to the originally intended grade and were also placed on off-grade forms

(above or below one grade).

With the structure of the test forms established, the forms needed to be populated with the appropriate items. First,

a pool of items was formed from the items developed during the item-writing phase. The repository consisted of

66 items for each grade level, from Grade 2 to Algebra II (10 levels total). Of these, 54 items were designated on-

grade-level items and would only appear on test forms for that particular grade level. The remaining 12 items were

designated linking items and could appear on test forms one grade level above or below the level of the item.

The final field tests were composed of 686 unique items. Besides the 660 items mentioned above, two sets of 12

linking items were developed to serve as below-level items for Grade 2 and above-level items for Algebra II. Two

additional Algebra II items were developed to ensure coverage of all the QSCs at that level.

22 SMI College & Career

Theoretical Foundation

The three test forms for each grade level were developed using a domain-sampling model in which items were

randomly assigned within the QSC to a test form. To achieve the goal of linking the test forms within a grade level,

as well as across grade levels, the linking items were utilized as follows: Each test form contained six items from the

linking set at the same grade level as the test form. For across-grade linking, four items were added to each field-

test form from the below-grade linking set, and two items were added to each field-test form from the above-grade

linking set. In conclusion, the linking items were used such that test items overlapped on two forms within the same

grade level and on two or more forms from different grade levels.

Linking the test levels vertically (across grades) employed a common-item test design (design in which items are

used on multiple forms). In this design, multiple tests are given to nonrandom groups, and a set of common items

is included in the test administration to allow some statistical adjustments for possible sample-selection bias. This

design is most advantageous where the number of items to be tested (treatments) is large and the consideration of

cost (in terms of time) forces the experiment to be smaller than is desired (Cochran & Cox, 1957).

The Quantile Framework Field Study

The Quantile Framework field study was conducted in February 2004. Thirty-seven schools from 14 districts across

six states (California, Indiana, Massachusetts, North Carolina, Utah, and Wisconsin) agreed to participate in the study.

Data were received from 34 of the schools (two elementary schools and one middle school did not return data). A

total of 9,847 students in Grades 2 through 12 were tested. The number of students tested per school ranged from

74 to 920. The schools were diverse in terms of geographic location, size, and type of community (e.g., suburban;

small town, small city, or rural communities; and urban). See Table 1 for information about the sample at each grade

level and the total sample. See Table 2 for test administration forms by level.

Rulers were provided to students; protractors were provided to students administered test levels 3–11. Formula

sheets were provided on the back of the test booklet for students administered levels 5–8, 10, and 11. The use of

calculators was permitted on the second part of each test. Students administered level 5 and below could use a

four-function calculator, and students administered level 6 and above could use a scientific calculator. Administration

time was about 45 minutes at each grade level. Students administered the level 2 test could have the test read

aloud, and mark in the test booklet, if that was the typical form of assessment in the classroom.

Theoretical Foundation 23

Theoretical Foundation

TABLE 1. Field study participation by grade and gender.

Grade Sample Size (N) Percent Female (N) Percent Male (N)

2 1,283 48.1 (562) 51.9 (606)

3 1,354 51.9 (667) 48.1 (617)

4 1,454 47.7 (622) 52.3 (705)

5 1,344 48.9 (622) 51.1 (650)

6 976 47.7 (423) 52.3 (463)

7 1,250 49.8 (618) 50.2 (622)

8 1,015 51.9 (518) 48.1 (481)

9 489 52.0 (252) 48.0 (233)

10 259 48.6 (125) 51.4 (132)

11 206 49.3 (101) 50.7 (104)

12 143 51.7 (74) 48.3 (69)

Missing 74 39.1 (9) 60.9 (14)

Total 9,847 49.6 (4,615) 50.4 (4,696)

TABLE 2. Test form administration by level.

Test Level NMissing Form A Form B Form C

2 1,283 4 453 430 397

3 1,354 7 561 387 399

4 1,454 17 616 419 402

5 1,344 3 470 448 423

6 917 13 322 293 289

7 1,309 6 462 429 411

8 1,181 16 387 391 387

9 415 4 141 136 134

10 226 5 73 77 71

11 313 10 102 101 100

Missing 51 31 9 8 3

Total 9,847 116 3,596 3,119 3,016

24 SMI College & Career

Theoretical Foundation

At the conclusion of the field test, complete data was available from 9,678 students. Data were deleted if the test

level or the test form was not indicated on the answer sheet, or if the answer sheet was blank. These field-test data

were analyzed using both the classical measurement model and the Rasch (one-parameter logistic item response

theory) model. Item statistics and descriptive information (item number, field-test form and item number, QSC, and

answer key) were printed for each item and attached to the item record. The item record contained the statistical,

descriptive, and historical information for an item, a copy of the item as it appeared on the test forms, any comments

by reviewers, and the psychometric notations. Each item had a separate item record.

Field-Test Analyses—Classical Measurement

For each item, the p-value (percent correct) and the point-biserial correlation between the item score (correct

response) and the total test score were computed. Point-biserial correlations were also computed between each of

the incorrect responses and the total score. In addition, frequency distributions of the response choices (including

omits) were tabulated (both actual counts and percents).

Point-biserial correlations provide an estimate of the relationship of ability as measured by a specific item and ability

as measured by the overall test. All items were retained for further analyses during the development of the Quantile

scale using the Rasch item response theory model. Items with point-biserial correlations less than 0.10 were

removed from the item bank for future linking studies. Table 3 displays the summary items statistics.

TABLE 3. Summary item statistics from the Quantile Framework field study.

Level Number of

Items Tested

Mean p-value

(Range)

Mean Correct Response

Point-Biserial Correlation

(Range)

Mean Incorrect Responses

Point-Biserial Correlation

(Range)

2 90 0.583 (0.12–0.95) 0.322 (–0.15–0.56) –0.209 (–0.43–0.12)

3 90 0.532 (0.11–0.93) 0.256 (–0.08–0.52) –0.221 (–0.54–0.02)

4 90 0.552 (0.12–0.92) 0.242 (–0.21–0.50) –0.222 (–0.48–0.12)

5 90 0.535 (0.12–0.95) 0.279 (–0.05–0.50) –0.225 (–0.45–0.05)

6 90 0.515 (0.04–0.86) 0.244 (–0.08–0.45) –0.218 (–0.46–0.09)

7 90 0.438 (0.10–0.77) 0.294 (–0.12–0.56) –0.207 (–0.46–0.25)

8 90 0.433 (0.10–0.81) 0.257 (–0.15–0.50) –0.201 (–0.45–0.13)

9 90 0.396 (0.10–0.79) 0.208 (–0.19–0.52) –0.193 (–0.53–0.22)

10 90 0.511 (0.01–0.97) 0.193 (–0.26–0.53) –0.205 (–0.55–0.18)

11 90 0.527 (0.09–0.98) 0.255 (–0.09–0.51) –0.223 (–0.52–0.07)

Theoretical Foundation 25

Theoretical Foundation

Field-Test Analyses—Bias

Differential item functioning (DIF) examines the relationship between the score on an item and group membership,

while controlling for achievement. The Mantel-Haenszel procedure is a widely used methodology to examine

differential item functioning. (Roussos, Schnipke, & Pashley, 1999, p. 293). The Mantel-Haenszel procedure examines

DIF by examining j 2 3 2 contingency tables, where j is the number of different levels of achievement actually

accomplished by the examinees (actual total scores received on the test). The focal group is the group of interest

and the reference group serves as a basis for comparison for the focal group (Camilli & Shepard, 1994; Dorans &

Holland, 1993).

The Mantel-Haenszel chi-square statistic tests the alternative hypothesis that there is a linear association between

the row variable (score on the item) and the column variable (group membership). The Mantel-Haenszel x2

distribution has one degree of freedom and is determined as:

QMH 5 (n 2 1)r

2 (Equation 1)

where r

2 is the Pearson correlation between the row variable and the column variable (SAS Institute Inc., 1985).

The Mantel-Haenszel Log Odds Ratio statistic is used to determine the direction of DIF and can be calculated

using SAS. This measure is obtained by combining the odds ratios,

, across levels with the formula for weighted

averages (Camilli & Shepard, 1994).

For the gender analyses, males (approximately 50.4% of the population) were defined as the reference group and

females (approximately 49.6% of the population) were defined as the focal group.

The results from the Quantile Framework field study were reviewed for inclusion on future linking studies. The

following statistics were reviewed for each item: p-value, point-biserial correlation, and DIF estimates. Items that

exhibited extreme statistics were considered biased and removed from the item bank (47 out of 685).

From the studies conducted with the Quantile Framework item bank (Palm Beach County [FL] linking study,

Mississippi linking study, Department of Defense/TerraNova linking study, and Wyoming linking study), approximately

6.9% of the items in any one study were flagged as exhibiting DIF using the Mantel-Haenszel statistic and the

t-statistic from Winsteps. For each linking study the following steps were used to review the items: (1) flag the items

exhibiting DIF, (2) review the flagged items to determine if the content of the item is something that all students are

expected to know, and (3) make a decision to retain or delete the item.

26 SMI College & Career

Theoretical Foundation

Field-Test Analyses—Rasch Item Response Theory

Classical test theory has two basic shortcomings: (1) the use of item indices whose values depend on the particular

group of examinees from which they were obtained, and (2) the use of examinee achievement estimates that depend

on the particular choice of items selected for a test. The basic premises of item response theory (IRT) overcome

these shortcomings by predicting the performance of an examinee on a test item based on a set of underlying

abilities (Hambleton & Swaminathan, 1985). The relationship between an examinee’s item performance and the

set of traits underlying item performance can be described by a monotonically increasing function called an item

characteristic curve (ICC). This function specifies that as the level of the trait increases, the probability of a correct

response to an item increases.

The conversion of observations into measures can be accomplished using the Rasch (1980) model, which states

a requirement for the way item difficulties (calibrations) and observations (count of correct items) interact in a

probability model to produce measures. The Rasch item response theory model expresses the probability that a

person (n ) answers a certain item (i ) correctly by the following relationship (Hambleton & Swaminathan, 1985;

Wright & Linacre, 1994):

Pni 5 e

2 di

1 1 e

2 di

(Equation 2)

where di is the difficulty of item i (i 5 1, 2, . . ., number of items),

bn is the achievement of person n (n 5 1, 2, . . ., number of persons),

bn 2 di is the difference between the achievement of person n and the difficulty of item i, and

Pni is the probability that examinee n responds correctly to item i.

The Rasch measurement model assumes that item difficulty is the only item characteristic that influences the

examinee’s performance. In other words, all items are equally discriminating in their ability to identify low-achieving

persons and high achieving persons (Bond & Fox, 2001; Hambleton, Swaminathan, & Rogers, 1991). In addition, the

lower asymptote is zero, which specifies that examinees of very low achievement have zero probability of correctly

answering the item. The Rasch model has the following assumptions:

(1) unidimensionality —only one construct is assessed by the set of items

(2) local independence —when abilities influencing test performance are held constant, an examinee’s

responses to any pair of items are statistically independent (conditional independence, i.e., the only

reason an examinee scores similarly on several items is because of his or her achievement, not because

the items are correlated)

Theoretical Foundation 27

Theoretical Foundation

The Rasch model is based on fairly restrictive assumptions, but it is appropriate for criterion-referenced

assessments.

For the Quantile Framework field study, all students and items were submitted to a Winsteps analysis using a logit

convergence criterion of 0.0001 and a residual convergence criterion of 0.001. Items that a student skipped were

treated as missing, rather than being treated as incorrect. Only students who responded to at least 20 items were

included in the analyses (22 students were omitted, 0.22%).

The Quantile measure comes from multiplying the logit value by 180 and is anchored at 656Q. The multiplier and

the anchor point will be discussed in a later section. Table 4 shows the mean and median Quantile measures for all

students with complete data at each grade level. While there is not a monotonically increasing trend in the mean and

median Quantile measures (note that the measure for Grade 6 is higher than the measure for Grade 7), the measures

are not significantly different. Results from other studies (e.g., PASeries Math) did exhibit a monotonically increasing

function.

TABLE 4. Mean and median Quantile measure for N 5 9,656 students with complete data.

Grade Level NMean Quantile Measure

(Standard Deviation)

Median Quantile

Measure

2 1,275 320.68 (189.11) 323

3 1,339 511.41 (157.69) 516

4 1,427 655.45 (157.50) 667

5 1,337 790.06 (167.71) 771

6 959 871.82 (153.02) 865

7 1,244 860.52 (174.16) 841

8 1,004 929.01 (157.63) 910

9 482 958.69 (152.81) 953

10 251 1019.97 (162.87) 1005

11 200 1127.34 (178.57) 1131

12 138 1185.90 (189.19) 1164

28 SMI College & Career

Theoretical Foundation

Figure 2 shows the relationship between grade level and Quantile measure. The box and whisker plot shows the

score progression from grade to grade (the x axis). Across all 9,656 students, the correlation between grade and

Quantile measure was 0.76 in this initial filed study.

FIGURE 2. Rasch achievement estimates of N 5 9,656 students with complete data.

Quantile Measure

2500

2400

2300

2200

2100

100

200

300

400

500

600

700

800

900

1000

1100

1200

1300

1400

1500

1600

1700

1800

1900

2000

Grade Distribution

2 3 4 5 6 7 8 9 10 11 12

SMI_TG_028

All students with outfit mean square statistics greater than or equal to 1.8 were removed from further analyses. A

total of 480 students (4.97%) were removed from further analyses. The number of students removed ranged from

8.47% (108) in Grade 2 to 2.29% (22) in Grade 6 with a mean percent decrease of 4.45% per grade.

All remaining students (9,176) and all items were analyzed with Winsteps using a logit convergence criterion of

0.0001 and a residual convergence criterion of 0.001. Items that a student skipped were treated as missing, rather

than being treated as incorrect. Only students who responded to at least 20 items were included in the analyses.

Table 5 shows the mean and median Quantile measures for the final set of students at each grade level. Figure 3

shows the results from the final set of students. The correlation between grade and Quantile measure is 0.78 for this

interim field study.

Theoretical Foundation 29

Theoretical Foundation

TABLE 5. Mean and median Quantile measure for the final set of N 5 9,176 students.

Grade Level NMedian Logit Value Mean (Median)

Quantile Measure

2 1,167 –2.800 289.03 (292)

3 1,260 –1.650 502.18 (499)

4 1,352 –0.780 652.60 (656)

5 1,289 0.000 795.25 (796)

6 937 0.430 880.77 (874)

7 1,181 0.370 877.75 (863)

8 955 0.810 951.41 (942)

9 466 1.020 982.62 (980)

10 244 1.400 1044.08 (1048)

11 191 2.070 1160.49 (1169)

12 134 2.295 1219.87 (1210)

FIGURE 3. Box and whisker plot of the Rasch ability estimates (using the Quantile scale) for

the final sample of students with outfit statistics less than 1.8 (N 5 9,176).

SMI_TG_029

Grade Distribution

2 3 4 5 6 7 8 9 10 11 12

Quantile Measure

2500

2400

2300

2200

2100

100

200

300

400

500

600

700

800

900

1000

1100

1200

1300

1400

1500

1600

1700

1800

1900

2000

30 SMI College & Career

Theoretical Foundation

Figure 4 shows the distribution of item difficulties based on the final sample of students. For this analysis, missing

data were treated as skipped items and not counted as wrong. There is a gradual increase in difficulty when items

are sorted by the test level for which they were written. This distribution appears to be nonlinear, which is consistent

with other studies. The correlation between grade level for which the item was written and the Quantile measure of

the item was 0.80.

FIGURE 4. Box and whisker plot of the Rasch ability estimates (using the Quantile scale) of

the 685 Quantile Framework items for the final sample of students (N 5 9,176).

SMI_TG_030

Quantile Measure

2500

2400

2300

2200

2100

100

200

300

400

500

600

700

800

900

1000

1100

1200

1300

1400

1500

1600

1700

1800

1900

2000

Grade Level of Item (from item number)

1234567891011

The field testing of the items written for the Quantile Framework indicates a strong correlation between the grade

level of the item and the item difficulty.

Theoretical Foundation 31

Theoretical Foundation

The Quantile Scale

For development of the Quantile scale, two features needed to be defined:

(1) the scale multiplier (conversion factor from the Rasch model)

(2) the anchor point

Once the scale is defined, it can be used to assign Quantile measures to individual Quantile Skills and Concepts, or

QSCs, as well as clusters of QSCs.

Generating the Quantile Scale

As described in the previous section, the Rasch item response theory model (Wright & Stone, 1979) was used to

estimate the difficulties of items and the abilities of persons on the logit scale. The calibrations of the items from the

Rasch model are objective in the sense that the relative difficulties of the items remain the same across different

samples (specific objectivity). When two items are administered to the same individual, it can be determined which

item is harder and which one is easier. This ordering should hold when the same two items are administered to a

second person.

The problem is that the location of the scale is not known. General objectivity requires that scores obtained from

different test administrations be tied to a common zero; absolute location must be sample independent (Stenner,

1990). To achieve general objectivity instead of simply specific objectivity, the theoretical logit difficulties must be

transformed to a scale where the ambiguity regarding the location of zero is resolved.

The first step in developing the Quantile scale was to determine the conversion factor needed to transform logits

from the Rasch model into Quantile scale units. A vast amount of research has already been conducted on the

relationship between a student’s achievement in reading and the Lexile® scale. Therefore, the decision was made to

examine the relationship between reading and mathematics scales used with other assessments.

The median scale score for each grade level on a norm-referenced assessment linked with the Lexile scale is

plotted in Figure 5 using the same conversion equation for both reading and mathematics. Based on Figure 5, it was

concluded that the same conversion factor used with the Lexile scale could be used with the Quantile scale.

32 SMI College & Career

Theoretical Foundation

FIGURE 5. Relationship between reading and mathematics scale scores on a norm-

referenced assessment linked to the Lexile scale in reading.

SMI_TG_032

2400

2200

200

400

600

800

1000

1200

10 2 3 4 5 6 7 8 9 10 11 12 13

Grade Level

Lexile Scale Calibration

Reading Math

The second step in developing a Quantile scale with a fixed zero was to identify an anchor point for the scale. Given

the number of students at each grade level in the field study, and the fact that state assessment programs typically

test students in Grades 4 or 5, it was concluded that the scale should be anchored between Grades 4 and 5.

Median performance at the end of Grade 3 on the Lexile scale is 590L. Median performance at the end of Grade 4

on the Lexile scale is 700L. The Quantile Framework field study was conducted in February, and this point would

correspond to six months (0.6 years) into the school year. To determine the location of the scale, a value of 66

Quantile scale units was added to the median performance at the end of Grade 3 to reflect the growth of students in

Grade 4 prior to the field study (700 2 590 5 110; 110 3 0.6 5 66).

Therefore, the value of 656Q was used for the location of Grade 4 median performance. The anchor point was

validated with other assessment data and collateral data from the Quantile Framework field study (see Figure 6).

Theoretical Foundation 33

Theoretical Foundation

FIGURE 6. Relationship between grade level and mathematics performance on the Quantile

Framework field study and other mathematics assessments.

SMI_TG_033

2400

2200

200

400

600

800

1000

1200

1400

10 2 3 4 5 6 7 8 9 10 11 12

Grade Level

Quantile Measure

SAT-10 Math QF Median TN Math (S) TN Math (W)

As a result of the above analyses, a linear equation of the form

[(Logit 2 Anchor Logit) 3 180] 1 656 5 Quantile measure (Equation 3)

was used to convert logit difficulties to Quantile measures where the anchor logit is the median for Grade 4 in the

Quantile Framework field study.

34 SMI College & Career

Theoretical Foundation

Knowledge Clusters

The next step was to use the Quantile Framework to estimate the Quantile measure of each QSC. Having a measure

for each QSC on the Quantile scale will then allow the difficulty of skills and concepts and the complexity of other

resources to be evaluated. The Quantile measure of a QSC estimates the solvability, or a prediction of how difficult

the skill or concept will be for a learner.

The QSCs also fall into Knowledge Clusters along a content continuum. Recall that the Quantile Framework is a

content taxonomy of mathematical skills and concepts. Knowledge Clusters are a family of skills, like building

blocks, that depend one upon the other to connect and demonstrate how understanding of a mathematical topic

is founded, supported, and extended along the continuum. The Knowledge Clusters illustrate the interconnectivity

of the Quantile Framework and the natural progression of mathematical skills (content trajectory) needed to solve

increasingly complex problems.

The Quantile measures and Knowledge Clusters for QSCs were determined by a group of three to five subject-matter

experts (SMEs). Each SME has had classroom experience at multiple developmental levels, has completed graduate-

level courses in mathematics education, and understands basic psychometric concepts and assessment issues.

For the development of Knowledge Clusters, certain terminology was developed to describe relationships between

the QSCs.

• A target QSC is the skill or concept that is the focus of instruction.

• A prerequisite QSC is a QSC that describes a skill or concept that provides a building block necessary for

another QSC. For example, adding single-digit numbers is a prerequisite for adding two-digit numbers.

• A supplemental QSC is a QSC that describes associated skills or knowledge that assists and enriches

the understanding of another QSC. For example, two supplemental QSCs are: multiplying two fractions and

determining the probability of compound events.

• An impending QSC describes a skill or concept that will further augment understanding, building on

another QSC. An impending QSC for using division facts is simplifying equivalent fractions.

Each target QSC was classified with prerequisite QSCs and supplemental QSCs or was identified as a foundational

QSC. As a part of a taxonomy, QSCs are either a single link in a chain of skills that lead to the understanding of

larger mathematical concepts, or they are the first step toward such an understanding. A QSC that is classified as

foundational requires only general readiness to learn.

The SMEs examined each QSC to determine where the specific QSC comes in the content continuum based on

their classroom experience, instructional resources (e.g., textbooks), and other curricular frameworks (e.g., NCTM

Standards). The process called for each SME to independently review the QSC and develop a draft Knowledge

Cluster. The second step consisted of the three to five SMEs meeting and reviewing the draft clusters. Through

discussion and consensus, the SMEs developed the final Knowledge Cluster.

Once the Knowledge Cluster for a QSC was established, the information was used when determining the Quantile

measure of a QSC, as described below. If necessary, Knowledge Clusters are reviewed and refined if the Quantile

measures of the QSCs in the cluster are not monotonically increasing (steadily increasing) or there is not an

instructional explanation for the pattern.

Theoretical Foundation 35

Theoretical Foundation

Quantile Measures of Quantile Skills and Concepts

The Quantile Framework is a theory-referenced measurement system of mathematical understanding. As such,

a QSC Quantile measure represents the “typical” difficulty of all items that could be written to represent the QSC

and the collection of items can be thought of as an ensemble of the all of the items that could be developed for a

specific skill or concept. During 2002, Stenner, Burdick, Sanford, and Burdick (2006) conducted a study to explore

the “ensemble” concept to explain differences across reading items with the Lexile Framework® for Reading. The

theoretical Lexile measure of a piece of text is the mean theoretical difficulty of all items associated with the text.

Stenner and his colleagues state that the “Lexile Theory replaces statements about individual items with statements

about ensembles. The ensemble interpretation enables the elimination of irrelevant details. The extra-theoretical

details are taken into account jointly, not individually, and, via averaging, are removed from the data text explained

by the theory” (p. 314). The result is that when making text-dependent generalizations, text readability can be

measured with high accuracy and the uncertainty in expected comprehension is largely due to the unreliability in

reader measures.

While expert judgment alone could be used to scale the QSCs, empirical scaling is more replicable. Actual

performance by students on an assessment was used to determine the Quantile measure of a QSC empirically. The

process employed items and data from two national field studies:

• Quantile Framework field study (686 items, N 5 9,647, Grades 2 through Algebra II) as described earlier in

this guide

• PASeries Mathematics field study (7,080 items, N 5 27,329, Grades 2 through 9/Algebra I), which is

described in the PASeries Mathematics Technical Manual (MetaMetrics, 2005)

The items initially associated with each QSC were reviewed by SMEs and accepted for inclusion in the set of items,

moved to another QSC, or not included in the set. The following criteria were used:

• Items must be responded to by at least 50 examinees, administered at the target grade level, and have a

point-biserial correlation greater than or equal to 0.16.

• Grade levels for items must match the grade level of the introduction of the skill or concept as derived from

the national review of curricular frameworks (described on pages 9 and 10 of this document).

• Items must cover only appropriate introductory material for instruction of concept (e.g., the first night’s

homework after introducing the topic, or the A and B level exercises in a textbook) based on consensus of

the SMEs.

Once the set of items meeting the inclusion criteria was identified, the set of items was reviewed to ensure that the

curricular breadth of the QSC was covered. If the group of SMEs considered the set of items to be acceptable, then

the Quantile measure of the QSC was calculated empirically. The Quantile measure of a QSC is defined as the mean

Quantile measure of items that met the criteria.

The final step in the process was to review the Quantile measure of the QSC in relationship to the Quantile measures

of the QSCs identified as prerequisite and supplemental to the QSC. If the group of SMEs did not consider the set

of items to be acceptable, then the Quantile measure of the QSC was estimated and assigned a Quantile zone.

By assigning a Quantile zone instead of a Quantile measure to these QSCs, the SMEs were able to provide a valid

estimate of the skill or concept’s difficulty.

36 SMI College & Career

Theoretical Foundation

In 2007, with the extension of the Quantile Framework to include Kindergarten and Precalculus, the Quantile

measures of the QSCs were reviewed. Where additional items had been tested and the data was available, estimated

QSC Quantile measures were calculated. In 2014, a large data set from the administration of SMI was analyzed to

examine the relationship between the original QSC Quantile measures and empirical QSC means from the items

administered. The overall correlation between QSC Quantile measures and empirically estimated Quantile measures

was 0.98 (N 5 7,993 students). Based on the analyses, 12 QSCs were identified with larger-than-expected

deviations given the “ensemble” interpretation of a QSC Quantile measure. Each QSC was reviewed in terms of the

SMI items that generated the data, linking studies where the QSC was employed, and data from other assessments

developed employing the Quantile Framework. Of the 12 QSCs identified, it was concluded that the Quantile

measure of nine of the QSCs should be recalculated. Five of the QSCs are targeted for Kindergarten and Grade 1

and the current data set provided data to calculate a Quantile measure (the Quantile measure for the QSC had been

previously estimated). The other four QSC Quantile measures were revised because the type of “typical” item and

the technology used to assess the skill or concept had shifted from the time that the QSC Quantile measure was

established in 2004 (QSCs: 79, 654, 180, and 217). Three of the QSC Quantile measures were not changed (QSC:

134, 604, 408) because (1) some of the SMI items did not reflect the intent of the QSC, or (2) not enough items were

tested to indicate that the Quantile measure should be recalculated.

Validity of the Quantile Framework for Mathematics

Validity is the extent to which a test measures what its authors or users claim it measures. Specifically, test validity

concerns the appropriateness of inferences “that can be made on the basis of observations or test results” (Salvia

& Ysseldyke, 1998, p. 166). The 1999 Standards for Educational and Psychological Testing (American Educational

Research Association, American Psychological Association, & National Council on Measurement in Education, 1999)

state that “validity refers to the degree to which evidence and theory support the interpretations of test scores

entailed in the uses of tests” (p. 9). In other words, a valid test measures what it is supposed to measure.

Stenner, Smith, and Burdick state that “[t]he process of ascribing meaning to scores produced by a measurement

procedure is generally recognized as the most important task in developing an educational or psychological

measure, be it an achievement test, interest inventory, or personality scale” (1983). For the Quantile Framework,

which measures student understanding of mathematical skills and concepts, the most important aspect of validity

that should be examined is construct-identification validity. This global form of validity encompassing content-

description and criterion-prediction validity may be evaluated for the Quantile Framework for Mathematics by

examining how well Quantile measures relate to other measures of mathematical achievement.

Relationship of Quantile Measures to Other Measures of Mathematical Understandings

Scores from tests purporting to measure the same construct, for example “mathematical achievement,” should be

moderately correlated (Anastasi, 1982). Table 6 presents the results from field studies conducted with the Quantile

Framework while the Quantile scale was being developed. For each of the tests listed, student mathematics scores

were strongly correlated, with correlation coefficients around 0.70, with Quantile measures from the Quantile

Framework field study. This suggests that measures derived from the Quantile Framework meet the moderate-

correlation requirement described by Anastasi (1982).

Theoretical Foundation 37

Theoretical Foundation

TABLE 6. Results from field studies conducted with the Quantile Framework.

Standardized Test Grades in Study NCorrelation between Test

Score and Quantile Measure

RIT and Measures of Academic Progress

(MAP by NWEA) 4 & 5 94 0.69

North Carolina End-of-Grade Tests

(Mathematics) 4 & 5 341 0.73

Relationship of Quantile Framework to Other Measures of

Mathematics Understanding

The Quantile Framework for Mathematics has been linked with several standardized tests of mathematics

achievement. When assessment scales are linked, a common frame of reference can be used to interpret the test

results. This frame of reference can be “used to convey additional normative information, test-content information,

and information that is jointly normative and content-based. For many test uses . . . [this frame of reference] conveys

information that is more crucial than the information conveyed by the primary score scale” (Petersen, Kolen, &

Hoover, 1993, p. 222).

When two score scales are linked, the linking function can be used to provide a context for understanding the results

of the assessments. It is often difficult to explain what mathematical skills a student actually understands based on

the results of a mathematics test. Typical questions regarding assessment measures are:

• “If a student scores 1200 on the mathematics assessment, what does this mean?”

• “Based on my students’ test results, what math concepts can they understand and do?”

Once a linkage is established with an assessment that covers specific concepts and skills, then the results of the

assessment can be explained and interpreted in the context of the specific concepts a student can understand and

skills the student has mastered.

Table 7 presents the results from linking studies conducted with the Quantile Framework. For each of the tests

listed, student mathematics scores were reported using the test’s scale, as well as by Quantile measures. This dual

reporting provides a rich, criterion-related frame of reference for interpreting the standardized test scores. Each

student who takes one of the standardized tests can receive, in addition to norm- or criterion-referenced test results,

information related to the specific QTaxons on which he or she is ready to be instructed.

Table 7 also shows that measures derived from the Quantile Framework are more than moderately correlated to

other measures of mathematical understanding. The correlation coefficients were around 0.90 for all but one of the

tests studied.

38 SMI College & Career

Theoretical Foundation

TABLE 7. Results from linking studies conducted with the Quantile Framework.

Standardized Test Grades in Study NCorrelation Between Test

Score and Quantile Measure

Mississippi Curriculum Test,

Mathematics (MCT) 2–8 7,039 0.89

TerraNova (CTB/McGraw-Hill) 3, 5, 7, 9 6,356 0.92

Texas Assessment of Knowledge

and Skills (TAKS) 3–11 14,286 0.69–0.78*

Proficiency Assessments for

Wyoming Students (PAWS) 3, 5, 8, and 11 3,923 0.87

Progress in Math (PiM) 1–8 4,692 0.92

Progress Toward Standards (PTS3) 3–8 and 10 8,544 0.86–0.90*

Comprehensive Testing Program (CTP4) 3, 5, and 7 802 0.90

North Carolina End-of-Grade and North

Carolina End-of-Course (NCEOG/NCEOC) 3, 5, and 7; A1, G, A2 5,069 0.88–0.90*

Comprehensive Testing Progressing

(CTP4—ERB) 3, 5, and 7 953 0.87 to 0.90

Kentucky Core Content Tests (KCCT) 3–8 and 11 12,660 0.80 to 0.83*

Oklahoma Core Competency Tests (OCCT) 3–8 5,649 0.81 to 0.85*

Iowa Assessments 2, 4, 6, 8, and 10 7,365 0.92

Virginia Standards of Learning (SOL) 3–8, A1, G, and A2 12,470 0.86 to 0.89*

Kentucky Performance Rating for

Educational Progress (K-PREP) 3–8 6,859 0.81 to 0.85*

North Carolina ACT 11 3,320 0.90

North Carolina READY End-of-Grade/

End-of-Course Tests (NC EOG/NC EOC) 3, 4, 6, 8, and A1/I1 10,903 0.87 to 0.90*

* Separate conversion equations were derived for each grade/course.

Theoretical Foundation 39

Theoretical Foundation

Multidimensionality of Quantile Framework Items

Test dimensionality is defined as the minimum number of abilities or constructs measured by a set of test items.

A construct is a theoretical representation of an underlying trait, concept, attribute, process, and/or structure that

a test purports to measure (Messick, 1993). A test can be considered to measure one latent trait, construct, or

ability (in which case it is called unidimensional); or a combination of abilities (in which case it is referred to as

multidimensional). The dimensional structure of a test is intricately tied to the purpose and definition of the construct

to be measured. It is also an important factor in many of the models used in data analyses. Though many of the

models assume unidimensionality, this assumption cannot be strictly met because there are always other cognitive,

personality, and test-taking factors that have some level of impact on test performance (Hambleton & Swaminathan,

1985).

The complex nature of mathematics and the curriculum standards most states have adopted also contribute

to unintended dimensionality. Application and process skills, the reading demand of items, and the use of

calculators could possibly add features to an assessment beyond what the developers intended. In addition, the

NCTM Standards, upon which many states have based curricula, describe the growth of students’ mathematical

development across five content standards: Number and Operations, Algebra, Geometry, Measurement, and Data

Analysis and Probability. These standards, or sub-domains of mathematics, are useful in organizing mathematics

instruction in the classroom. These standards could represent different constructs and thereby introduce more

sources of dimensionality to tests designed to assess these standards.

Investigation of Dimensionality of Mathematics Assessments

A recent study conducted by Burg (2007) analyzed the dimensional structure of mathematical achievement tests

aligned to the NCTM content standards. Since there is not a consensus within the measurement community on a

single method to determine dimensionality, Burg employed four different methods for assessing dimensionality:

(1) exploring the conditional covariances (DETECT)

(2) assessment of essential unidimensionality (DIMTEST)

(3) item factor analysis (NOHARM)

(4) principal component analysis (WINSTEPS)

40 SMI College & Career

Theoretical Foundation

All four approaches have been shown to be effective indices of dimensional structure. Burg analyzed Grades 3–8

data from the Quantile Framework field study previously described.

Each set of on-grade items for a test form from Grades 3–8 were analyzed for possible sources of dimensionality

related to the five mathematical content strands. The analyses were also used to compare test structures across

grades. The results indicated that although mathematical achievement tests for Grades 3–8 are complex and exhibit

some multidimensionality, the sources of dimensionality are not related to the content strands. The complexity of the

data structure, along with the known overlap of mathematical skills, suggests that mathematical achievement tests

could represent a fundamentally unidimensional construct. While these sub-domains of mathematics are useful for

organizing instruction, developing curricular materials such as textbooks, and describing the organization of items on

assessments, they do not describe a significant psychometric property of the test or impact the interpretation of the

test results. Mathematics, as measured by the SMI, can be described as one construct with various sub-domains.

These findings support the NCTM Connections Standard, which states that all students (prekindergarten through

Grade 12) should be able to make and use connections among mathematical ideas and see how the mathematical

ideas interconnect. Mathematics can be best described as an interconnection of overlapping skills with a high

degree of correlation across the mathematical topics, skills, and strands.

Furthermore, these findings support the goals of the Common Core State Standards (CCSS) for Mathematics by

providing the foundations of a growth model by which a single measure can inform progress toward college and

career readiness.

College and Career Preparedness in Mathematics

There is increasing recognition of the importance of bridging the gap that exists between K–12 and higher education

and other postsecondary endeavors. Many state and policy leaders have formed task forces and policy committees

such as P-20 councils.

The Common Core State Standards for Mathematics were designed to enable all students to become college and

career ready by the end of high school while acknowledging that students are on many different pathways to this

goal: “One of the hallmarks of the Common Core State Standards for Mathematics is the specification of content that

all students must study in order to be college and career ready. This ‘college and career ready line’ is a minimum

for all students” (NGA Center & CCSSO, 2010b, p. 4). The CCSS for Mathematics suggest that “college and career

ready” means completing a sequence that covers Algebra I, Geometry, and Algebra II (or equivalently, Integrated

Mathematics 1, 2, and 3) during the middle school and high school years; and, leads to a student’s promotion

into more advanced mathematics by their senior year. This has led some policy makers to generally equate the

successful completion of Algebra II as a working definition of college and career ready. Exactly how and when this

content must be covered is left to the states to designate in their implementations of the CCSS for Mathematics

throughout K–12.

Theoretical Foundation 41

Theoretical Foundation

The mathematical demand of a mathematical textbook (in Quantile measures) quantitatively defines the level of

mathematical achievement that a student needs in order to be ready for instruction on the mathematical content

of the textbook. Assigning QSCs and Quantile measures to a textbook is done through a calibration process.

Textbooks were analyzed at the lesson level and the calibrations were completed by subject matter experts (SMEs)

experienced with the Quantile Framework and with the mathematics taught in mathematics classrooms. The intent

of the calibration process is to determine the mathematical demand presented in the materials. Textbooks contain a

variety of activities and lessons. In addition, some textbook lessons may include a variety of skills. Only one Quantile

measure is calculated per lesson and is obtained through analyzing the Quantile measures of the QSCs that have

been mapped to the lesson. This Quantile measure represents the composite task demand of the lesson.

MetaMetrics has calibrated more than 41,000 instructional materials (e.g., textbook lessons, instructional resources)

across the K–12 mathematics curriculum. Figure 7 shows the continuum of calibrated textbook lessons from

Kindergarten through precalculus where the median of the distribution for precalculus is 1350Q. The range between

the first quartile and the median of the first three chapters of precalculus textbooks is from 1200Q to 1350Q. This

range describes an initial estimate of the mathematical achievement level needed to be ready for mathematical

instruction corresponding to the “college and career readiness” standard in the Common Core State Standards for

Mathematics.

FIGURE 7. A continuum of mathematical demand for Kindergarten through precalculus

textbooks (box plot percentiles: 5th, 25th, 50th, 75th, and 95th).

SMI_TG_041

Quantile Measure

Mathematics Continuum 2010

1600

1400

1200

1000

800

600

400

200

2200

2400

Kindergarten

Grade 1

Grade 2

Grade 3

Grade 4

Grade 5

Grade 6

Grade 7

Grade 8

Algebra 1

Geometry

Algebra 2

PreCalculus

Administering the Test ................................................................. 45

Interpreting Scholastic Math Inventory College & Career Scores ................ 52

Using SMI College & Career Results.................................................. 61

SMI College & Career Reports to Support Instruction ............................. 62

Using SMI College & Career

44 SMI College & Career

Using SMI College & Career

The Scholastic Math Inventory College & Career (SMI College & Career) is a computer-adaptive mathematics test

that provides a measure of students’ readiness for mathematics instruction in the form a Quantile measure. The

results of the test can be used to measure how well students understand, and are likely to be successful with

various grade-appropriate mathematical skills and topics. SMI College & Career is designed to be administered three

to five times during a school year.

SMI College & Career consists of a bank of more than 5,000 four-option, multiple-choice items that represent

different mathematics concepts and topics. While the items span the five content standards, more than 75% of

the items for Kindergarten through Grade 8 are associated with Number & Operations (K–8); Algebraic Thinking,

Patterns, and Proportional Reasoning (K–8); and Expressions & Equations, Algebra, and Functions (6–8). In Grades 9

through 11 the focus shifts so that approximately 60% of the items in the Grade 9 and 11 item banks are associated

with Expressions & Equations, Algebra, and Functions, and approximately 60% of the items in the Grade 10 item

bank are associated with Geometry, Measurement, and Data. The weighting of content by grade was designed to

reflect the priorities expressed in the CCSSM and latest state mathematics standards. The items cover a wide range

of presentations, such as computational items, word problems and story problems, graphs, tables, figures, and other

representations.

The SMI Professional Learning Guide provides suggestions for test administration and an overview of Scholastic

Achievement Manager (SAM) features. It also includes information on how SMI College & Career can be implemented

in a variety of instructional environments including in Response to Intervention implementations. The guide provides

a detailed explanation of each SMI College & Career report and how SMI College & Career data can be used to

differentiate instruction in the core curriculum classroom.

All the documentation, installation guides, technical manuals, software manuals, and all technical updates provided

in the program are available for download on the Scholastic Product Support site. The address to that site is:

http://edproductsupport.scholastic.com/ts/product/smi/.

After installation, the first step in using SMI College & Career is the Scholastic Achievement Manager, or SAM—the

learning management system for all Scholastic technology programs. Educators use SAM to collect and organize

student-produced data. SAM helps educators understand and implement data-driven instruction by:

• Managing student rosters

• Generating reports that capture student performance at various levels of aggregation (student, classroom,

group, grade, school, and district)

• Locating helpful resources for classroom instruction and aligning the instruction to standards

• Communicating student progress to parents, teachers, and administrators

The SMI Professional Learning Guide also provides teachers with information on how to use the results from SMI

College & Career in the classroom. Teachers can use the reported Quantile measures to determine appropriate

instructional support materials for their students. Information related to best practices for test administration,

interpreting reports, and using Quantile measures in the classroom is also provided.

Using SMI College & Career 45

Using SMI College & Career

Administering the Test

SMI College & Career can be administered multiple times during the school year. Typically, SMI College & Career

should be administered three times during the school year—at the beginning, the middle, and the end—to monitor

students’ progress in developing mathematical understandings. Within an intervention program, SMI College &

Career can be administered every eight weeks. SMI College & Career should be administered no more than three

to five times per year in order to allow sufficient growth in between testing sessions. The tests are intended to be

untimed, and typically students take 20 to 40 minutes to complete the test.

SMI College & Career can be administered in a group setting or individually—wherever computers are available. The

test can also be administered on mobile devices. The setting should be quiet and free from distractions. Teachers

should make sure that students have the computer skills needed to complete the test and have scratch paper and

pencils.

Students log on to the program with usernames and passwords. The practice items in the assessment are provided

to ensure that students understand the directions, know how to use the computer to take the test, and are not

encountering server connectivity issues. In this section, students are introduced to the calculators and formula

sheets that are available for certain items within SMI College & Career. Calculators and specific formula sheets are

available based on the grade level of the item.

SMI College & Career includes two types of on-screen calculators depicted in Figure 8. Items written for Grade 5 and

lower are supported by a four-function calculator. Items written for Grade 6 and higher are supported by a scientific

calculator. Students in Grades 8 and above may use graphing calculators, which are not provided by the program.

These students should be provided access to their own graphing calculators with functionality similar to that of

a TI-84. When the purpose of the item is computational, SMI College & Career disables the use of the calculator

automatically. The student should become familiar with the calculator while completing the Practice Test items.

Administrators can turn off the calculator globally for the assessment. This option is often selected in states where

calculators are not permitted on high stakes exams. However, turning the calculator off may extend the time

students take on the assessment and may impact results. For the most comparable results, it is suggested that a

policy decision is made at the district level concerning calculator access in SMI College & Career.

46 SMI College & Career

Using SMI College & Career

FIGURE 8. SMI College & Career’s four-function calculator (left) and scientific calculator (right).

SMI_TG_046

5 64

Clear

5 64

Clear

)

(

x^y

!§

SMI College & Career also includes three on-screen Formula Sheets that include useful equations. There is a Formula

Sheet available for items written for Grades 3–5 (see Figure 9), Grades 6–8 (see Figure 10), and Grades 9–11 (see

Figure 11). Items written for Grade 2 and lower do not need a Formula Sheet. The student can review the Formula

Sheet before taking the Practice Test items. SAM allows an administrator to turn off the Formula Sheet. However,

turning the Formula Sheet off increases the demand on the student to solve the problems, and the decision to

provide access to the Formula Sheet should be determined globally at the district level.

Using SMI College & Career 47

Using SMI College & Career

FIGURE 9. SMI College & Career Grades 3–5 Formula Sheet.

SMI_TG_046-A

Perimeter

Square: P 5 4 3 s

Rectangle: P 5 (2 3 l ) 1 (2 3 w )

Area

Square: A 5 s 3 s

Rectangle: A 5 l 3 w

Volume

Cube: V 5 s 3 s 3 s

Rectangle prism: V 5 B 3 h or V 5 l 3 w 3 h

FIGURE 10. SMI College & Career Grades 6–8 Formula Sheet.

SMI_TG_047

Area

Triangle: A 5 bh

Parallelogram: A 5 bh

Trapezoid: A 5 (b1 1 b2 )h

Circle: A 5 r2

Circumference of a circle

C 5 2 r or C 5 d

Surface Area

Prism: SA 5 sum of the areas of all faces

Pyramid: SA 5 sum of the areas of all faces

Cylinder: SA 5 2 r2 1 2 r h

Volume

Cube: V 5 s3

Prism: V 5 Bh

Cylinder: V 5 r2h

Cone: V 5 r2h

Sphere: V 5 r3

–

ø 3.14 or ø

Simple Interest

I 5 Prt

Pythagorean Theorem

c2 5 a2 1 b2

–

p p

48 SMI College & Career

Using SMI College & Career

FIGURE 11. SMI College & Career Grades 9–11 Formula Sheets.

SMI_TG_048

Area

Triangle: A 5 bh

Parallelogram: A 5 bh

Trapezoid: A 5 (b1 1 b2 )h

Circle: A 5 r2

Circumference of a circle

C 5 2 r or C 5 d

Volume

Prism: V 5 Bh

Cylinder: V 5 r2h

Cone: V 5 r2h

Sphere: V 5 r3

Pythagorean Theorem

c2 5 a2 1 b2

–

Sum of the interior angles

of a polygon with n sides

S 5 (n 2 2)(180°)

Measure of an exterior angle

of a regular polygon with n sides

m/ 5

Compound Interest

A 5 P(1 1 )nt

Exponential Growth/Decay

A 5 A0ek(t 2 t0) 1 B0

Expected value

V 5 p1x1 1 p2x2 1 … 1 pnxn

Quadratic Formula

Solution of ax2 1 bx 1 c 5 0 is

360˚

–

x 52a

!§§§

2b 6b2 2 4ac

SMI_TG_048-A

Distance Formula

d 5

Arithmetic Sequence

an 5 a1 1 (n 2 1)d

Geometric Sequence

an 5 a1rn 2 1

Combinations of n Objects

Taken r at a Time

nCr 5

Permutations of n Objects

Taken r at a Time

nPr 5

Binomial Theorem

(a 1 b)n 5 nC0anb0 1 nC1a(n 2 1)b1 1

n C2a(n 2 2)b2 1 … 1 nCna0bn

Pythagorean Identity

sin2 1 cos2 5 1

Law of Sines

Law of Cosines

a2 5 b2 1 c2 2 2bccos A

b2 5 a2 1 c2 2 2accos B

c2 5 a2 1 b2 2 2abcos C

Heron’s Formula

A 5 where

s 5 (a 1b 1c)

sin A

–

AB c

!§§§§§§§§

s(s 2a)(s 2b)(s 2c)

u u

5sin B

–

b5sin C

–

!§§§§§

(x22x1)2 1 (y22y1)2

n !

r!(n 2 r)!

n !

(n 2 r)!

Using SMI College & Career 49

Using SMI College & Career

Targeting

Prior to testing, it is strongly suggested that the teacher or administrator inputs information into the SAM on the

known ability of students. The categories are:

• Undetermined

• Far below level

• Below level

• On level

• Above level

• Far above level

If the student’s ability is unknown, then the teacher or administrators should select undetermined. The default setting

for this feature is on grade level.

This targeting information is used by the SMI College & Career algorithm to determine the starting point for the

student. The value of this setting is to ensure that struggling students receive a question at a lower proficiency level.

For example the following levels will provide grade-level questions that are associated with the indicated percentile:

• Undetermined—50th%

• Far below level—5th%

• Below level—25th%

• On level—50th%

• Above level—75th%

• Far above level—90th%

Targeting applies only to the first administration of SMI College & Career. The second administration of the test will

start with a question at the Quantile measure received from the previous test administration.

Student Interaction With SMI College & Career

The student experience with SMI College & Career consists of three parts:

• Math Fact Screener

• Practice Test

• Scored Test

Math Fact Screener

The first part of SMI College & Career is the Math Fact Screener and is used at all grade levels. The Math Fact

Screener consists of an Early Numeracy Screener for counting and quantity comparison for students in Kindergarten

and Grade 1, items related to addition facts for Grades 2 and 3, and both addition and multiplication facts for Grades

4 and above. The facts presented do not change from grade to grade. The results of the Math Fact Screener are

not used in either the SMI College & Career algorithm or in determining a student’s SMI College & Career Quantile

measure. The screener performs a separate assessment of a student’s potential math fact knowledge and facility.

The Math Fact Screener consists of three parts (does not apply to the Early Numeracy Screener): the typing warm-

up, addition facts, and multiplication facts. During the typing warm-up, students practice typing in four different

values to ensure that they understand the interface used during the Math Fact Screener. Students then give the sums

for 10 addition facts; and, for students in Grades 4 and above, the product for a sampling of 10 multiplication facts.

50 SMI College & Career

Using SMI College & Career

An item is visible on the screen for up to 10 seconds. If the item is not answered in 10 seconds, it is counted as

incorrect and a new item is displayed. Although the item is visible for 10 seconds, students have only five seconds

to correctly respond to each item in the Math Fact Screener. If an answer is correct, but is not entered within five

seconds, then the question is counted as incorrect. Students do not see a time on the computer screen. There is no

time limit for counting an answer correct for the Early Numeracy Screener. The program records the student answer

and the time it took to respond to the fact. Students must answer 80% (eight out of 10) of the items correctly to pass

the Math Fact Screener. Students in Grade 3 and below must respond correctly to 80% of the addition items to pass

the Math Fact Screener. Students in Grade 4 and above must respond correctly to 80% of the addition items and

80% of the multiplication items.

The addition and multiplication sections are considered separately. A student who passes one section of the Math

Fact Screener will not be administered that section again.

SAM reports the Math Fact Screener results to the administrator at both the student and group levels. These reports

indicate that the student may need work on basic math facts.

Practice Test

The SMI College & Career Practice Test consists of three to five items that are significantly below the student’s

mathematical performance level (approximately 10th percentile for nominal grade level). The practice items are

administered during the student’s first experience with SMI College & Career at the beginning of each school year, unless

the teacher or administrator has configured their program settings in SAM such that the practice test is a part of every test.

Practice items are designed to ensure that the student understands the directions and knows how to use the

computer to take the test. It also introduces the use of the calculators and the Formula Sheets embedded within

SMI College & Career. Typically, students will see three items. The program will extend the student experience to

five items, however, if the student incorrectly responds to two or more of the initial three items. The student may be

asked to contact his teacher to ensure that he understands how to engage with the program.

Scored SMI College & Career Test

The final part of the students’ interaction is the SMI College & Career test administration. The initial test item is

selected for the student based on his or her grade level and the teacher’s estimate of his or her mathematical ability.

The first item of the first administration is one grade level below the student grade. The estimated math ability can

be set only for the first administration. During the test, the SMI College & Career algorithm is designed to adapt the

selection of test items according to the student’s responses. After the student responds to the first question, the test

then steps up or down according to the student’s performance. When the test has enough information to adequately

estimate the student’s readiness for mathematics instruction, the test stops and the student’s Quantile measure is

reported.

The process described above is detailed into three phases called Start, Step, and Stop. In the Start phase, the SMI

College & Career algorithm determines the best point on the Quantile scale to begin testing the student. The more

information SMI College & Career has about the student, the more accurate the results. For more accurate results

from the first administration, the practice of “targeting the student” is suggested. Initially, a student can be targeted

using: (1) the student’s grade level, and (2) the teacher’s estimate of the student’s ability in mathematics. For

successive administrations of SMI College & Career, the student’s prior Quantile measure plus an estimated amount

of assumed growth based on the time in between administrations is used for targeting. While it is not necessary

for a teacher to assign an estimated achievement level, assigning one will produce more accurate results; the

SAM default setting is “undetermined.” The teacher cannot set the math ability after the first test. For the student

whose test administration is illustrated in Figure 12, the teacher entered the student’s grade and an estimate of the

student’s mathematics achievement.

Using SMI College & Career 51

Using SMI College & Career

The second phase, Step, controls the selection of items presented to the student. If the only targeting information

entered was the student’s grade level, then the student is presented with an item that has a Quantile measure at

the 100Q below the 50th percentile for his or her grade. If more information about the student’s mathematical ability

was entered, then the student is presented with an item more closely aligned to the student’s “true” ability. If the

student answers the item correctly, then the student is presented with an item that is more difficult. If the student

answers the item incorrectly, then an item that is easier is presented. An SMI College & Career score (Quantile

measure) for the student is updated after the student responds to each item. The SMI College & Career algorithm will

always maintain a progression of items across the content strands.

Figure 12 shows how SMI College & Career may present items during a typical administration. The first item

presented to a student had a Quantile measure of 610, or measured 610Q. Because the item was answered

correctly, the next item was more difficult (740Q). Because this item was answered incorrectly, the third item

measured 630Q. Because this item was answered correctly, the next item was harder (710Q). Note as the number

of items administered increases, the differences between the Quantile measures of subsequent items decreases in

order to more accurately place a student on the Quantile Framework.

FIGURE 12. Sample administration of SMI College & Career for a fourth-grade student.

Quantile Measure

Item Number

SMI_TG_051

750

730

710

690

670

650

630

610

0 5 10 15 20 25 30

The final phase, Stop, controls the termination of the test. In SMI College & Career, students will be presented with

25 to 45 items. The exact number of items a student receives depends on how accurately the student responds to

the items presented. In addition, the number of items presented to the student is affected by how well the test was

targeted in the beginning. Well-targeted tests begin with less measurement error, and therefore need to present the

student with fewer items. In Figure 12, the student was well targeted and performed with reasonable consistency,

so only 25 items were administered. It can be inferred that the experience of taking a targeted test is optimal for

the students in terms of both proper challenging and maintaining motivation. A well-targeted test brings out the best

in students.

52 SMI College & Career

Using SMI College & Career

Interpreting Scholastic Math Inventory College & Career Scores

Results from SMI College & Career are reported as scale scores (Quantile measures). This scale extends from

Emerging Mathematician (below 0Q) to above 1600Q. The score is determined by the difficulty of the items a student

answered both correctly and incorrectly. Scale scores can be used to report the results of both criterion-referenced

tests and norm-referenced tests.

There are many reasons to use scale scores rather than raw scores to report test results. Scale scores overcome

the disadvantage of many other types of scores (e.g., percentiles and raw scores) in that equal differences

between scale score points represent equal differences in achievement. Each question on a test has a unique

level of difficulty. Therefore, answering 23 items correctly on one form of a test requires a slightly different level

of achievement than answering 23 items correctly on another form of the test. But receiving a scale score (in this

case, a Quantile measure) of 675Q on one form of a test represents the same level of mathematics understanding as

receiving a scale score of 675Q on another form of the test.

SMI College & Career provides both criterion-referenced and norm-referenced interpretations of the Quantile

measure. Norm-referenced interpretations of test results, often required for accountability purposes, indicate how

well the student’s performance on the assessment compares to other, similar students’ results. Criterion-referenced

interpretations of test results provide a rich frame of reference that can be used to guide instruction and skills

acquisition for optimal student mathematical development.

Norm-Referenced Interpretations

A norm-referenced interpretation of a test score expresses how a student performed on the test compared to other

students of the same age or grade. Norm-referenced interpretations of mathematics achievement test results,

however, do not provide any information about mathematical skills or topics a student has or has not mastered. For

accountability purposes, percentiles, stanines, and normal curve equivalents (NCEs) are used to report test results

when making comparisons (norm-referenced interpretations). For a comparison of these measures, refer to

Figure 13.

Using SMI College & Career 53

Using SMI College & Career

FIGURE 13. Normal distribution of scores described in percentiles, stanines, and NCEs.

SMI_TG_053

Percent of area

under the normal curve

Normal curve equivalent scores (NCEs)

Percentiles

Stanines

1 2 95 15 18 18 15 2 159

1 10 20 30 40 50 60 9580 9070

1 2 3 4 5 6 8 97

1 10 20 30 40 50 60 9980 9070

The percentile rank of a score indicates the percentage of scores lower than or equal to that score. Percentile ranks

range from 1 to 99. For example, if a student scores at the 65th percentile, it means that she performed as well as or

better than 65% of the norm group. Real differences in performance are greater at the ends of the percentile range

than in the middle. Percentile ranks of scores can be compared across two or more distributions. Percentile ranks,

however, cannot be used to determine differences in relative rank because the intervals between adjacent percentile

ranks do not necessarily represent equal raw score intervals. Note that the percentile rank does not refer to the

percentage of items answered correctly.

A normal curve equivalent (NCE) is a normalized student score with a mean of 50 and a standard deviation of 21.06.

NCEs range from 1 to 99. NCEs allow comparisons between different tests for the same student or group of students

and between different students on the same test. NCEs have many of the same characteristics as percentile

ranks, but have the additional advantage of being based on an interval scale. That is, the difference between two

consecutive scores on the scale has the same meaning throughout the scale. NCEs are required by many categorical

funding agencies (for example, Title I).

54 SMI College & Career

Using SMI College & Career

A stanine is a standardized student score with a mean of 5 and a standard deviation of 2. Stanines range from 1 to 9.

In general, stanines of 1 to 3 are considered below average, stanines of 4 to 6 are considered average, and stanines of

7 to 9 are considered above average. A difference of 2 between the stanines for two measures indicates that the two

measures are significantly different. Stanines, like percentiles, indicate a student’s relative standing in a norm group.

Normative information can be useful and is often required at the aggregate levels for program evaluation. Appendix 2

contains normative data (spring percentiles) for students in Grades K–12 at selected levels of performance.

To develop normative data, the results from a linking study with the Quantile Framework on a sample of more than

250,000 students from across the country were examined. Approximately 80% of the students attended public

school, and approximately 20% attended private or parochial schools. The students in the normative population

consisted of 19.8% African American, 2.7% Asian, 9.2% Hispanic, and 68.3% Other (includes White, Native

American, Other, and Multiracial). Approximately 6% of the students were eligible for the free or reduced-price lunch

program. Approximately half of the students attended public schools where more than half of the students were

eligible for Title I funding (either school-wide or targeted assistance).

Using SMI College & Career 55

Using SMI College & Career

Criterion-Referenced Interpretations

An important feature of the Quantile Framework is that it also provides criterion-referenced interpretations of every

measure. A criterion-referenced interpretation of a test score compares the specific knowledge and skills measured

by the test to the student’s proficiency with the same knowledge and skills. Criterion-referenced scores have

meaning in terms of what the student knows and can do, rather than in relation to the performance of a peer group.

The power of SMI College & Career as a criterion-reference test is amplified by the design and meaning of the

Quantile Framework. When the student’s mathematics ability is equal to the mathematical demand of the task,

the Quantile Theory forecasts that the student will demonstrate a 50% success rate on that task and is ready for

instruction related to that skill or concept. When 20 such tasks are given to this student, one expects one-half of

the responses to be correct. If the task is too difficult for the student, then the probability is less than 50% that the

response to the task will be correct. These tasks are skills and concepts for which the student likely does not have

the background knowledge required. Similarly, when the difficulty level of the task is less than a student’s measure,

then the probability is greater than 50% that the response will be correct. These tasks are skills and concepts are

ones that the student is likely to have already mastered.

Because the Quantile Theory provides complementary procedures for measuring achievement and mathematical

skills, the scale can be used to match a student’s level of understanding with other mathematical skills and concepts

with which the student is forecast to have a high understanding rate. Identifying skills that students are ready to

learn is critical not only to developing overall mathematics learning, but also to creating a positive mathematical

experience that can motivate and change attitudes about mathematics in general.

Assessment of mathematics learning is a key component in the classroom. This assessment takes on many different

models and styles depending on the purpose of the assessment. It can range from asking key questions during class

time, to probing critical thinking and reasoning of students’ answers, to asking students to record their mathematical

learning, to developing well-designed multiple-choice formats. As a progress monitoring tool, SMI College & Career

provides feedback to teachers throughout the school year that can be connected with typical end-of-the-year

proficiency ranges since multiple assessments are connected to the same reporting scale.

56 SMI College & Career

Using SMI College & Career

Forecasting Student Understanding and Success Rates

A student with a Quantile measure of 600Q who is to be instructed on mathematical tasks calibrated at 600Q is

expected to have a 50% success rate on the tasks and a 50% understanding rate of the skills and concepts. This

50% rate is the basis for selecting tasks employing skills and concepts for instruction targeted to the student’s

mathematical achievement. If the mathematical demand of a task is less than the student measure, the success rate

will exceed 50%. If the mathematical demand is much less, the success rate will be much greater. The difference in

Quantile scale units between student achievement and mathematical demand governs understanding and success.

This section gives more explicit information on predicting success rates.

If all of the tasks associated with a 400Q Quantile Skill and Concept had the same difficulty, the understanding

rate resulting from the 200Q difference between the 600Q student and the 400Q mathematical demand could

be determined using the Rasch model equation (see Equation 2, p. 26). This equation describes the relationship

between the measure of a student’s level of mathematical understanding and the difficulty of the skills and concepts.

Unfortunately, understanding rates calculated using only this procedure would be biased because the difficulties of

the tasks associated with a skill or concept are not all the same. The average difficulty level of the tasks and their

variability both affect the success rate.

Figure 14 shows the general relationship between student-task discrepancy and predicted success rate. When

the Student Measure and the task mathematical demand are the same, then the predicted success rate is 50%

and the student is ready for instruction on the skill or concept. If a student has a measure of 600Q and the task’s

mathematical demand is 400Q, the difference is 200Q. According to Figure 14, a difference of +200Q (Student

Measure minus task difficulty) indicates a predicted success rate of approximately 75%. Also note that a difference

of –200Q indicates a predicted success rate of about 25%.

Using SMI College & Career 57

Using SMI College & Career

The subjective experience between 25%, 50%, and 75% understanding or success varies greatly. A student with

a Quantile measure of 1000Q being instructed on QSCs with measures of 1000Q will likely have a successful

instructional experience—he or she has about a 50% rate of understanding with the background knowledge needed

to learn and apply the new information. Teachers working with such a student report that the student can engage

with the skills and concepts that are the focus of the instruction and, as a result of the instruction, are able to solve

problems utilizing those skills. In short, such students appear to understand what they are learning. A student

with a measure of 1000Q being instructed on QSCs with measures of 1200Q has about a 25% understanding

rate and encounters so many unfamiliar skills and difficult concepts so that the learning is frequently lost. Such

students report frustration and seldom engage in instruction at this level of understanding. Finally, a student with

a Quantile measure of 1000Q being instructed on QSCs with measures of 800Q has about a 75% understanding

rate and reports being able to engage with the skills and concepts with minimal instruction. He or she is able to

solve complex problems related to the skills and concepts, is able to connect the skills and concepts with skills and

concepts from other strands, and experiences automaticity of skills.

FIGURE 14. Student-mathematical demand discrepancy and predicted success rate.

SMI_TG_057

Predicted Success Rate

Student achievement—Task difﬁculty (in Quantiles)

21000

100%

90%

80%

70%

60%

50%

40%

30%

20%

10%

2750 2500 2250 0 250 500 750 1000

58 SMI College & Career

Using SMI College & Career

Table 8 gives an example of the predicted understanding or success rates for specific skills for a specific student.

Table 9 shows success rates for one specific skill calculated for different student achievement measures.

TABLE 8. Success rates for a student with a Quantile measure of 750Q and skills of varying

difficulty (demand).

Student

Mathematics

Achievement

Skill

Demand

Skill Description Predicted

Understanding

750Q 250Q Locate points on a number line. 90%

750Q 500Q Use order of operations, including parentheses, to

simplify numerical expressions. 75%

750Q 750Q Translate between models or verbal phrases and

algebraic expressions. 50%

750Q 1000Q Estimate and calculate areas with scale drawings

and maps. 25%

750Q 1250Q

Recognize and apply definitions and theorems

of angles formed when a transversal intersects

parallel lines.

10%

TABLE 9. Success rates for students with different Quantile measures of achievement for a

task with a Quantile measure of 850Q.

Student Mathematics

Achievement

Problems Related to “Locate points in all quadrants

of the coordinate plane using ordered pairs.”

Predicted

Understanding

350Q 850Q 10%

600Q 850Q 25%

850Q 850Q 50%

1100Q 850Q 75%

1350Q 850Q 90%

The primary utility of the Quantile Framework is its ability to forecast what happens when students engage in

mathematical tasks. The Quantile Framework makes a pointed success prediction every time a skill is chosen for a

student. There is error in skill measures, student measures, and their difference modeled as predicted success rates.

However, the error is sufficiently small that the judgments about the students, task demand, and success rates

are useful.

Using SMI College & Career 59

Using SMI College & Career

Performance Levels

The SMI performance levels were originally developed in 2009 using an iterative process. Each phase of the

development built upon previous discussions as well as incorporated new information as the process continued.

Performance levels were set for Grades 2–9. In 2013, Scholastic began the redevelopment of SMI College & Career to

align with the Common Core State Standards in Mathematics (NGA Center and CCSSO, 2010a) and expand the range of

use from Grade 2 through Algebra I to Kindergarten through Algebra II/High School Integrated Math 3. One aspect of this

redevelopment was to add performance standards for Kindergarten, Grade 1, Geometry/Math 2 (generally Grade 10),

and Algebra II/Math 3 (generally Grade 11). In order to add these additional grades based on the CCSSM demands and

to be consistent across all grade levels, the Grade 2–Algebra I standards were also modified.

The following sources of data were examined to develop the SRI College & Career performance standards:

• Student-based standards: North Carolina End-of-Grade and End-of-Course Math Assessments (North

Carolina Department of Public Instruction 2013 Quantile linking study, Grades 3–8 and Algebra I/Integrated 1,

MetaMetrics, Inc., 2013); Virginia Mathematics Standards of Learning Tests (Virginia Department of Education

2012 Quantile Linking Study, Grades 3–8, Algebra I and II, and Geometry, MetaMetrics, Inc., 2012c); Kentucky

Performance Rating for Educational Progress Math Test (Kentucky Department of Education 2012 Quantile

Linking Study, Grades 3–8, MetaMetrics, Inc., 2012b); National Assessment of Educational Progress—Math

(National Center for Educational Statistics “Lexile/Quantile Feasibility Study,” May 2011, Grades 4, 8, and 12,

MetaMetrics, Inc., 2011); and ACT Mathematics Tests administered in North Carolina (NCDPI and ACT 2012

Quantile linking study, Grade 11, MetaMetrics, Inc., 2012a)

• Resource-based standards: “2010 Math Text Continuum,” MetaMetrics, Inc., 2011, in “QF & CCR-2011.pdf”

The bottom of the “proficient” range for each grade level associated with the three states was examined and a

regression line was developed to smooth the data. The resulting function was similar to the top of the text continuum

range across the grade levels (75th percentile of lessons associated with the grade/course). This indicates that

students at this level should be ready for instruction on the more mathematically demanding topics at the end of the

school year, which is consistent with expectation. The top of the “proficient” range for each grade level associated

with the three states was examined and a regression line was developed to smooth the data. The proposed SMI

College & Career proficient range for each grade level was examined and compared with the Spring Quantile

percentile tables. This information was used to extrapolate to Kindergarten and Grades 1 and 2. These results are

consistent with the ranges associated with NAEP and ACT to define “college readiness.”

These proficient levels were used as starting points to define the ranges associated with the remaining three

performance levels for each grade level. Setting of these performance levels combined information about the QSC/

skill and concept difficulty as well as information related to the performance levels observed from previous Quantile

Framework linking studies. These levels were refined further based on discussion by educational and assessment

specialists. The policy descriptions for each of the performance levels used at each grade level are as follows:

60 SMI College & Career

Using SMI College & Career

• Advanced: Students scoring in this range exhibit superior performance on grade-level-appropriate skills

and concepts and, in terms of their mathematics development, may be considered on track for college

and career.

• Proficient: Students scoring in this range exhibit competent performance on grade-level-appropriate skills

and concepts and, in terms of their mathematics development, may be considered on track for college

and career.

• Basic: Students scoring in this range exhibit minimally competent performance on grade-level-appropriate

skills and concepts and, in terms of their mathematics development, may be considered marginally on track

for college and career.

• Below Basic: Students scoring in this range do not exhibit minimally competent performance on grade-

level-appropriate skills and concepts and, in terms of their mathematics development, are not considered

on track for college and career.

The final scores for each grade level and performance level used with SMI are presented in Table 10.

TABLE 10. SMI College & Career performance level ranges by grade (Spring Norms).

Grade Below Basic Basic Proficient Advanced

K EM*400–EM185 EM190–5 10–175 180 and Above

1 EM400–60 65–255 260–450 455 and Above

2 EM400–205 210–400 405–600 605 and Above

3 EM400–425 430–620 625–850 855 and Above

4 EM400–540 545–710 715–950 955 and Above

5 EM400–640 645–815 820–1020 1025 and Above

6 EM400–700 705–865 870–1125 1130 and Above

7 EM400–770 775–945 950–1175 1180 and Above

8 EM400–850 855–1025 1030–1255 1260 and Above

9 EM400–940 945–1135 1140–1325 1330 and Above

10 EM400–1020 1025–1215 1220–1375 1380 and Above

11 EM400–1150 1155–1345 1350–1425 1430 and Above

12 EM400–1190 1195–1385 1390–1505 1510 and Above

*Emerging Mathematician

Using SMI College & Career 61

Using SMI College & Career

Algebra Readiness and College and Career Readiness

In addition to describe performance in relation to describing general mathematical achievement, SMI College &

Career provides a Quantile measure that represents a student who is deemed ready for Algebra I. To determine this

value, the following information sources were examined: state standards for Grade 8 (before Algebra I) proficiency

(895Q to 1080Q), the SMI College & Career Grade 8 proficiency cutoff (1030Q), and the QSCs associated with the

algebra strand in Grades 8 and 9 (Grade 8: 700Q to 1190Q, Mean = 972.5Q; Grade 9: 700Q to 1350Q, Mean =

1082.0Q). It was concluded that a Quantile measure of 1030Q could be used to describe “readiness for Algebra I.”

The CCSS state that “[t]he high school portion of the Standards for Mathematical Content specifies the mathematics

all students should study for college and career readiness. These standards do not mandate the sequence of high

school courses. However, the organization of high school courses is a critical component to implementation of the

standards.

• a traditional course sequence (Algebra I, Geometry, and Algebra II)

• an integrated course sequence (Mathematics 1, Mathematics 2, Mathematics 3) . . .”

(NGA and CCSSO, 2010a, p. 84). To provide a Quantile measure that represents a student who is deemed ready

for the mathematics demands of college and career, the “Mathematics Continuum” presented in Figure 7 was

examined. The interquartile range for Algebra II is from 1200Q to 1350Q. It was concluded that a Quantile measure of

1350Q could be used to describe “readiness for college and career.”

Using SMI College & Career Results

SMI College & Career begins with the concept of targeted-level testing and makes a direct link with those measures

to instruction. With the Quantile Framework for Mathematics as the yardstick of skill difficulty, SMI College &

Career produces a measure that places skills, concepts, and students on the same scale. The Quantile measure

connects each student to mathematical resources—Knowledge Clusters, specific state standards, and the Common

Core State Standards for Mathematics, widely adopted basal textbooks, supplemental math materials, and math

intervention programs. Because SMI College & Career provides an accurate measure of where each student is in

his or her mathematical development, the instructional implications and skill success rate for optimal growth are

explicit. SMI College & Career targeted testing identifies for the student the mathematical skills and topics that are

appropriately challenging to him or her.

SMI College & Career provides a database that directly links Quantile measures and QSCs to all state standards

including the Common Core State Standards and hundreds of widely adopted textbooks and curricular resources.

This database also allows educators to target mathematical skills and concepts and unpack the Knowledge Cluster

associated with each Quantile Skill and Concept. The searchable database is found on www.Scholastic.com/SMI and

is one of the many of the supporting tools available at www.Quantiles.com.

62 SMI College & Career

Using SMI College & Career

SMI College & Career Reports to Support Instruction

The key benefit of SMI College & Career is its ability to generate immediate actionable data that can be used in the

classroom to monitor and interpret student progress. The Scholastic Achievement Manager (SAM) organizes and

analyzes the results gathered from student tests and presents this information in a series of clear, understandable,

actionable reports that can help educators track growth in mathematics achievement over time, evaluate progress

toward proficiency goals, and accomplish administrative tasks. SMI College & Career reports help educators

effectively assess where students are now and where they need to go. The SMI Professional Learning Guide

provides detailed descriptions of each of the SMI College & Career reports, which are designed to support four broad

functions: (1) progress monitoring, (2) instructional planning, (3) school-to-home communication, and (4) growth.

One key SMI College & Career report is the Instructional Planning Report (see Figure 15), which orders students by

percentile rank and places them into Performance Levels. In addition to identifying students in need of review and

fluency building in basic math facts, the report also provides instructional recommendation for students in the lower

Performance Levels. The instructional recommendations focus on Critical Foundations—those skills and concepts

that are most essential to accelerate students to grade-level proficiencies and college and career readiness. The

Critical Foundations are identified descriptively, by QSC number and description as well as the Common Core State

Standard identification number. Teachers can use this information to access Knowledge Clusters and textbook

alignments for intervention and differentiation purposes in the SMI Skills Database at www.scholastic.com/SMI.

Using SMI College & Career 63

Using SMI College & Career

FIGURE 15. Instructional Planning Report.

Printed by: Teacher

Page 1 of 5 Printed on: 2/22/2015

School: Williams Middle School

Teacher: Sarah Greene

Grade: 5

Time Period: 12/13/14–02/22/15

Instructional Planning Report

Class: 3rd Period

INSTRUCTIONAL

PLANNING

GROWTH

TRAJECTORY

INSTRUCTIONAL

PLANNING

ALERT

SCREENER NORMATIVE DATA

PERFORMANCE

LEVEL

STUDENTS GRADE ADDITION

MULTI

QUANTILE®

MEASURE DATE TEST TIME

(MIN)

PERCENTILE

RANK NCE STANINE

A Gainer, Jacquelyn 51100Q 02/22/15 35 95 77 7

A Cho, Henry 51100Q 02/22/15 25 95 77 7

P u Collins, Chris 5890Q 02/22/15 12 76 66 7

PKohlmeier, Ryan 5820Q 02/22/15 40 73 65 6

PCooper, Maya 5820Q 02/22/15 37 73 64 6

B Enoki, Jeanette 5800Q 02/22/15 39 71 63 6

B Hartsock, Shalanda 5750Q 02/22/15 33 70 59 4

B Terrell, Walt 5720Q 02/22/15 26 45 56 5

B Cocanower, Jaime 5710Q 02/22/15 38 45 53 5

B Garcia, Matt 5680Q 02/22/15 15 44 52 5

B Dixon, Ken 5660Q 02/22/15 35 41 47 5

B Morris, Timothy 5650Q 02/22/15 30 43 48 5

B u Blume, Joy 5640Q 02/22/15 9 39 45 5

B Ramirez, Jeremy 5600Q 02/22/15 37 37 45 4

BB u Robinson, Tiffany 5485Q 02/22/15 9 20 40 1

BB Williams, Anthony 5EM 02/22/15 35 10 26 1

USING THE DATA

Purpose:

This report provides instructional

recommendations for students at each

SMI performance level.

Follow-Up:

Use instructional recommendations to plan appropriate

support for students at each level.

KEY

EM Emerging Mathematician

A ADVANCED

P PROFICIENT

B BASIC

BB BELOW BASIC

Student may need to develop this skill

Student has acquired this skill

u Test taken in less than 15 minutes

YEAR-END PROFICIENCY RANGES

GRADE K 10Q–175Q GRADE 5 820Q–1020Q GRADE 9 1140Q–1325Q

GRADE 1 260Q–450Q GRADE 6 870Q–1125Q GRADE 10 1220Q–1375Q

GRADE 2 405Q–600Q GRADE 7 950Q–1175Q GRADE 11 1350Q–1425Q

GRADE 3 625Q–850Q GRADE 8 1030Q–1255Q GRADE 12 139Q–1505Q

GRADE 4 715Q–950Q

Aligning SMI College & Career Results With Classroom Instruction

To support teachers in the classroom in connecting the SMI College & Career results with classroom instructional

practices, the QSCs associated with each of the 12 SMI College & Career content grade levels are presented in

Appendix 1. (This Appendix is also available online at www.scholastic.com/SMI.) This information can be used to

match instruction with student Quantile measures to provide focused intervention to support whole-class instruction.

Educators can consult the Performance Level Growth Report or the Student Progress Report and identify the Quantile

measure of the Quantile Skill and Concept (QSC) to be taught to determine the likelihood that all students in the class

will have the prerequisite skills necessary for instruction on the topic. This information can be used to determine

how much scaffolding and support each student will need.

Development of SMI College & Career

Specifications of the SMI College & Career Item Bank ............................ 66

SMI College & Career Item Development ............................................ 69

SMI College & Career Computer-Adaptive Algorithm .............................. 74

66 SMI College & Career

Development of SMI College & Career

Scholastic Math Inventory College & Career was developed to assess a student’s readiness for mathematics

instruction and is based on the Quantile Framework for Mathematics. It is a computer-adaptive assessment and

individualizes for each student. SMI College & Career is designed for students from Kindergarten through Algebra II

(or High School Integrated Math III), which is commonly considered an indicator of college and career readiness. The

content covered ranges from skills typically taught in Kindergarten through content introduced in high school.

Specifications of the SMI College & Career Item Bank

The specifications for the SMI College & Career item bank were defined through an iterative process of developing

specifications, reviewing the specifications in relation to national curricular frameworks, and then revising the

specifications to better reflect the design principles of SMI College & Career. The specifications were developed by

curricular, instructional, and assessment specialists of Scholastic and MetaMetrics.

The SMI College & Career item specifications defined the items to be developed in terms of the strand covered, the

QSC assessed, and the targeted grade level. In addition, several other characteristics of the items, such as context,

reading demand, ethnicity, and gender were also considered to create a diverse item bank.

The SMI College & Career item bank specifications adhered to a strand variation that changed for different grade

level bands. Following the philosophy of the Common Core State Standards (CCSS) for Mathematics, the greatest

percentages of items in Kindergarten through Grade 5 assess topics in the Number & Operations strand. At Grade 6,

the emphasis shifts to the Algebraic Thinking, Patterns, and Proportional Reasoning strand and the Expressions &

Equations, Algebra, and Functions strand. Table 11 presents the design specifications for the SMI College & Career

item bank.

Development of SMI College & Career 67

Development of SMI College & Career

TABLE 11. Designed strand profile for SMI: Kindergarten through Grade 11 (Algebra II).

Number &

Operations

Algebraic

Thinking,

Patterns, and

Proportional

Reasoning

Geometry,

Measurement,

and Data

Statistics &

Probability

Expressions &

Equations, Algebra,

and Functions

Kindergarten 55% 25% 20% – –

Grade 1 50% 30% 20% – –

Grade 2 45% 30% 25% – –

Grade 3 40% 35% 25% – –

Grade 4 45% 35% 20% – –

Grade 5 65% 15% 20% – –

Grade 6 15% 35% 10% 10% 30%

Grade 7 15% 30% 10% 10% 35%

Grade 8 10% 5% 13% 7% 65%

Grade 9 5% 5% 10% 15% 65%

Grade 10 5% 5% 40% 10% 40%

Grade 11 5% 5% 20% 10% 60%

The QSCs previously listed for an SMI College & Career content grade level were compared with the Common Core

State Standards, which have been aligned with the Quantile Framework (alignment available at www.Quantiles.com).

Each standard was aligned with the appropriate QSC(s). There were several QSCs that spanned more than one grade

level of the CCSS. This resulted in additions and deletions to the list of QSCs associated with each SMI College &

Career content grade level.

Finally, the QSCs associated with each of the SMI College & Career grade level item banks were reviewed by SRI

International for alignment with the CCSS for Mathematics. Where necessary, QSCs were reviewed and added

or deleted. The QSCs associated with each of the 12 SMI College & Career content grade levels are presented in

Appendix 1.

68 SMI College & Career

Development of SMI College & Career

Within a content grade level of the SMI College & Career item bank, QSCs were weighted according to the amount

of classroom time or importance that a particular topic or skill is typically given in that grade based on the alignment

with the CCSS. A weight of 1 (small amount of time/minor topic), 2 (moderate amount of time/important topic), or 3

(large amount of time/critical topic) was assigned to each QSC within a grade by a subject matter expert (SME) and

reviewed by another SME. Within a grade, QSCs with a weight of 1 included fewer items than QSCs designated with

a weight of 3.

In addition to the mathematical content of the QSC, other features were considered in the SMI College & Career

item bank specifications as well. The item bank was designed so a range of items within a single QSC and grade

would be administered. Specifically this required the use of both computational problems as well as context/applied/

word/story problems. An emphasis was placed on having more computational items in comparison to the number of

context/applied/word problems. This emphasis was designed to minimize the importance of reading level and other

factors that might influence performance on the assessment, so that only mathematical achievement is measured.

Calculator availability was also determined by QSC. Some QSCs allow students the use of an online or personal

calculator, while for other QSCs the online calculator is not available or should not be used.

Development of SMI College & Career 69

Development of SMI College & Career

SMI College & Career Item Development

The SMI College & Career item bank is comprised of four-option, multiple-choice items. It is a familiar item type,

versatile and efficient in testing all levels of achievement, and most useful in computer-based testing (Downing,

2006). When properly written, this item type directly assesses specific student understandings for a particular

objective. That is, every item was written to assess one QSC and one standard only.

The item consists of a question (stem) and four options (responses). All the information required to answer a

question is contained in the stem and any associated graphic(s). Most stems are phrased “positively,” but a few

items use a “negative” (e.g., the use of the word not ) format. The number of negative items is minimal particularly in

the lower grades. When used, the word not is placed in bold/italics to emphasize its presence to the student. Stems

also incorporate several other formats, such as word problems; incomplete number sentences; solving equations;

and reading or interpreting figures, graphs, charts, and tables. Word problems require a student to read a short

context before answering a question. The reading demand is intentionally kept lower than the grade of the item to

assess the mathematical knowledge of the student and not his or her reading skills. All figures, graphs, charts, and

tables include titles and other descriptive information as appropriate.

Each item contains four responses (A, B, C, or D). Three of the responses are considered foils or distractors, and one,

and only one, response is the correct or best answer. Items were written so that the foils represented typical errors,

misconceptions, or miscalculations. Item writers were encouraged to write foils based on their own classroom

experiences and/or common error patterns documented in texts such as R.B. Ashlock’s book Error Patterns in

Computation (2010). Item writers were required to write rationales for each distractor.

In keeping with the findings and recommendation of the National Mathematics Advisory Panel, items were developed

with minimal “nonmathematical sources of influence on student performance” (2008, p. xxv). Unnecessary context

was avoided where possible and anything that could be considered culturally or economically biased was removed.

70 SMI College & Career

Development of SMI College & Career

Item writers for SMI College & Career were classroom teachers and other educators who had experience with the

everyday mathematics achievement of students at various levels and national mathematics curricular standards.

Using individuals with classroom teaching experience helped to ensure that the items were valid measures of

mathematics achievement. This ensured that items included not only the appropriate content but also considered the

appropriate grade level and typical errors used to develop plausible distractors.

The development of the SMI item bank consisted of four phases. Phase 1 occurred in Fall and Winter 2008, Phase 2

occurred in Fall 2011, Phase 3 occurred in Fall and Winter 2013, and Phase 4 occurred in the Summer of 2015.

Phase 1: Twenty-six individuals from nine different states developed items for Phase 1 of the SMI College & Career

item bank. The mean number of years of teaching experience for the item writers was 15.3 years. Over 60% of

the writers had a master’s degree, and all but one was currently certified in teaching. Approximately 70% of the

writers listed their current job title as “teacher,” and the other item writers were either curriculum specialists,

administrators, or retired. One writer was a professional item writer. The majority of the item writers were Caucasian

females, but 25% of the writers were male and 14% of the item writers described themselves as African American,

Asian, or Hispanic.

Phase 2: Four individuals developed items for Phase 2 of the SMI College & Career item bank. These individuals

were curriculum specialists at MetaMetrics with expertise in elementary school (1), middle school (2), and high

school (1). The number of years of classroom experience ranged from 2 to 30 years, and the number of years as

a MetaMetrics’ curriculum specialist ranged from 1 to 8 years. The four individuals had experience in developing

multiple mathematics assessments.

Phase 3: Eleven individuals developed items for Phase 3 of the SMI College & Career item bank. The mean number

of years of teaching experience for the item writers was 15.9 years. Over 45% of the writers had a master’s degree,

and all but one was currently certified in teaching. Approximately 37% of the writers listed their current job title as

“teacher,” and the other item writers were either curriculum specialists, administrators, or retired. One writer was a

professional item writer. The majority of the item writers were Caucasian females, but 27% of the writers were male.

Phase 4: All items that were added to SMI passed through several editorial rounds of review that were conducted by

an internal team of content experts. After being reviewed and edited in-house, the items were assigned QSCs and

Quantile measures by MetaMetrics Inc. in order to align to the Quantile Framework. All items were then reviewed by

an external team of teachers and content experts, who evaluated whether the content of the items and the language

used were appropriate for the targeted grade levels.

In addition, most new items being introduced into SMI have been field tested with small samples of SMI students.

This item pilot helped identify items that were more or less difficult than anticipated, with those items identified

either being removed or modified depending upon the results. All new items were also reviewed by teams of

teachers who evaluated whether the content of the items and the language used were appropriate for the targeted

grade level.

Development of SMI College & Career 71

Development of SMI College & Career

In all phases of item development, item writers were required to participate in a training that focused on guidelines

for writing SMI College & Career multiple-choice items and an introduction to the Quantile Framework. In addition,

each item writer was provided copies of the following:

• Webinar presentation (i.e., guidelines for item development)

• Mathematical Framework (NAEP, 2007)

• Calculator literacy information

• Standards for Evaluating Instructional Materials for Social Content (California Department of Education,

2000)

• Universal Design Checklist (Pearson Educational Measurement)

• List of names by gender and ethnicity identities as developed by Scholastic Inc.

Scholastic specified that item context represent a diverse population of students. In particular, if an item used a

student name, then there should be equal representation of males and females. Scholastic also provided guidelines

and specific names such that the names used in items would reflect ethnic and cultural diversity. The list of names

provided represented approximately 30% African American names, 30% Hispanic names, 25% European (not

Hispanic) names, 5% Asian names, and 10% Native American or other names.

Item writers were also given extensive training related to sensitivity issues. Part of the item writing materials

addressed these issues and identified areas to avoid when writing items. The following areas were covered:

violence and crime, depressing situations/death, offensive language, drugs/alcohol/tobacco, sex/attraction, race/

ethnicity, class, gender, religion, supernatural/magic, parent/family, politics, topics that are location specific, and

brand names or junk food. These materials were developed based on standards published by CTB/McGraw-Hill for

universal design and fair access—equal treatment of the sexes, fair representation of minority groups, and the fair

representation of disabled individuals (CTB/McGraw Hill, 1983).

72 SMI College & Career

Development of SMI College & Career

Item writers were initially asked to develop and submit 10 items. The items were then reviewed for content

alignment to the SMI College & Career curricular framework (QSC and, in the case of Phase 3 and 4 item

development, the CCSS), item format, grammar, and sensitivity. Based on this review, item writers received feedback.

Most item writers were then able to start writing assignments, but a few were required to submit additional items for

acceptance before an assignment was made.

All items were subjected to a multistep review process. First, items were reviewed by curriculum experts and edited

according to the item writing guidelines, QSC content, grade appropriateness, and sensitivity guidelines. The content

expert reviews also added detailed art specifications. Some items were determined to be incompatible with the QSC

and, during Phase 3 item development, the Common Core State Standards. These items were deemed unsuitable

and therefore rewritten. Whenever possible, items were edited and maintained in the item bank.

The next several steps in the item review process included a review of the items by a group of specialists

representing various perspectives. Test developers and editors examined each item for sensitivity issues, CCSS

alignment, QSC alignment, and grade match, as well as the quality of the response options. Upon the updating of all

edits and art specifications, items were presented to other reviewers to “cold solve.” That is, individuals who had

not participated in the review process thus far read and answered each item. Their answers were checked with

the correct answer denoted with the item. Any inconsistencies or suggested edits were reviewed and made when

appropriate.

At this point in the process, items were then submitted to Scholastic for review. Scholastic then sent the items for

external review to ensure that the item aligned with the QSC and also with the CCSS. Items were either “approved”

or “returned” with comments and suggestions for strengthening the item. Returned items were edited, reviewed

again, and then resubmitted unless the changes were extensive. Items with extensive changes were deleted and

another item was submitted.

Development of SMI College & Career 73

Development of SMI College & Career

SMI College & Career Review of Existing Item Bank

As part of the item development process for SMI College & Career, all previously developed SMI items were

reviewed. Each item was examined for its alignment with the QSC, alignment with the CCSS, grade appropriateness,

mathematical terminology, and language. All items that were added to SMI passed through several editorial rounds

of review that were conducted by an internal team of content experts. After being reviewed and edited in-house,

the items were assigned QSCs and Quantile measures in order to align to the Quantile Framework. All items were

subsequently reviewed by an external team of teachers and cognitive experts, who evaluated whether the content of

the items and the language used were appropriate for the targeted grade levels.

In addition, most new items being introduced into SMI have been field tested with small samples of SMI students

matched by grade level. This item field study helped identify items that were more or less difficult than anticipated,

with those items identified either being removed or modified depending upon the results. All new items were

also reviewed by teams of teachers who evaluated whether the content of the items and the language used were

appropriate for the targeted grade level.

SMI College & Career Final Item Bank Specifications

The final SMI College & Career item bank has a total of over 5,000 items. Following this extensive review process of

new and existing items, the item bank resulted in the final strand profiles shown in Table 12.

TABLE 12. Actual strand profile for SMI after item writing and review.

Number &

Operations

Algebraic

Thinking,

Patterns, and

Proportional

Reasoning

Geometry,

Measurement,

& Data

Statistics &

Probability

Expressions &

Equations, Algebra,

and Functions

Kindergarten 55% 15% 30% – –

Grade 1 40% 40% 20% – –

Grade 2 31% 28% 41% – –

Grade 3 37% 33% 30% – –

Grade 4 49% 21% 30% – –

Grade 5 70% 12% 18% – –

Grade 6 20% 25% 8% 13% 34%

Grade 7 22% 24% 21% 19% 14%

Grade 8 5% 3% 41% 12% 39%

Grade 9 4% 10% 14% 11% 61%

Grade 10 5% 2% 57% 6% 30%

Grade 11 2% 13% 15% 8% 62%

74 SMI College & Career

Development of SMI College & Career

SMI College & Career Computer-Adaptive Algorithm

School-wide tests are often administered at grade level to large groups of students in order to make decisions about

students and schools. Consequently, since all students in a grade are administered the same test, each test must

include a wide range of items to cover the needs of both low-achieving and high-achieving students. These wide-

range tests are often unable to measure some students as precisely as a more focused assessment could.

To provide the most accurate measure of a student’s mathematics developmental level, it is important to assess the

student’s current mathematical achievement. One method is to use as much background information as possible to

target a specific test level for each student. This information can consist of the student’s grade level and a teacher’s

judgment concerning the mathematical achievement of the student. This method requires the test administrator to

administer multiple test forms during one test session, which can be cumbersome and may introduce test security

problems.

With the widespread availability of computers in classrooms and schools, another, more efficient method is to

administer a test tailored to each student—computer-adaptive testing (CAT). Computer-adaptive testing is conducted

individually with the aid of a computer algorithm to select each item so that the greatest amount of information

about the student’s achievement is obtained before the next item is selected. SMI College & Career employs such a

methodology for testing online.

Many benefits of computer-adaptive testing have been described in educational literature (Stone & Lunz, 1994;

Wainer et al., 1990; Wang & Vispoel, 1998). Each test is tailored to the individual student and item selection is based

on the student’s achievement and responses to each question. The benefits also include the following:

• Increased efficiency—through reduced testing time and targeted testing

• Immediate scoring—a score can be reported as soon as the student finishes the test

• Control over item bank—because the test forms do not have to be physically developed, printed, shipped,

administered, or scored, a broader range of forms can be used

In addition, studies conducted by Hardwicke and Yoes (1984) and Schinoff and Steed (1988) provide evidence that

below-level students tend to prefer computer-adaptive tests because they do not discourage students by presenting

a large number of items that are too hard for them (cited in Wainer, 1993).

Development of SMI College & Career 75

Development of SMI College & Career

The computer-adaptive algorithm used with SMI College & Career is also based on the Rasch (one-parameter) item

response theory (IRT) model. An extensive discussion of this model was provided earlier in this guide, in connection

with the field test analyses used to develop the Quantile Framework itself. The same procedure used to determine

the Quantile measure of the students in the field study is used to determine the Quantile measure of a student

taking the SMI College & Career test. In short, the Rasch model uses an iterative procedure to calculate a student’s

score based on the differences between the desired score and the difficulty level of the items on the test and the

performance of the student on each item. The Quantile measure, based on this convergence within the Rasch model,

is recomputed with the addition of each new data point.

As described earlier, SMI College & Career uses a three-phase approach to assess a student’s level of mathematical

understanding—Start, Step, Stop. During test administration, the computer adapts the test continually according

to the student’s responses to the questions. The student starts the test; the test steps up or down according to

the student’s performance; and, when the computer has enough information about the student’s mathematical

achievement, the test stops.

The first phase, Start, determines the best point on the Quantile scale to begin testing the student. Figure 16

presents a flow chart of the Start phase of SMI College & Career. The algorithm requires several parameters before

it can begin selecting items. One requirement is a Student Measure, an initial value for a student’s understandings,

which is used as a starting point. For a student who is taking SMI College & Career for the first time, the student’s

initial Quantile measure will be based on either the teacher’s estimate of the student’s understanding or the default

value (the proficient level for the student’s grade). If a student has previously taken SMI College & Career, the

algorithm will use the Quantile measure from the last SMI administration.

Another required parameter is the effective grade level for each student. The effective grade level is typically the

grade level entered into the SAM system. However, if a student is at either the extreme high or low end of the

performance level, the algorithm will adjust the strand profile and the items to create an assessment that is better

targeted to the student, at one grade level above or below.

76 SMI College & Career

Development of SMI College & Career

FIGURE 16. The Start phase of the SMI College & Career computer-adaptive algorithm.

SMI_TG_076

Input student data

Grade level

Teacher judgment

Select item based on:

Strand

Grade level

QSC

Fact Fluency Screener

Practice Test items

Pass Practice Test?

Yes

Additional practice

test items

Initialize algorithm:

Strand proﬁle based on effective

grade level

Get interface help

from teacher

Development of SMI College & Career 77

Development of SMI College & Career

The second phase, Step, identifies which item a student will see. As shown in Figure 17, an item is selected according

to specific criteria and administered to a student. A Student Measure, or estimate of student understanding, is then

recalculated based on the student’s response. The algorithm selects another item based on the student’s performance

on the previous item, as well as other criteria meant to ensure coverage across content strands.

Items are selected using several criteria: strand, grade level, QSC, and difficulty. The effective grade level (typically

the actual grade level of the student) determines which strand profile and order is used throughout the test

administration. Once a strand is determined, the algorithm will select an appropriate QSC within that strand based

on a comparison of the Student Measure and the Skill Measure of the QSC. In other words, the algorithm searches to

find an item that matches both the strand designation and the performance level of the student. The number of times

a QSC is shown on a test is limited. In addition, the algorithm will screen items to prevent a student from seeing the

same item during consecutive test administrations.

The strand profile, which ensures that students respond to items from each of the five content strands, varies slightly

across grades. Using the SMI College & Career strand distribution described in Table 12, the first 13–14 items cover

all strands proportionally and then the process is repeated. For example, in Grade 3, students are administered

five items from the Number & Operations strand; five items from the Algebraic Thinking, Patterns & Proportional

Reasoning strand; and three items from the Geometry, Measurement, and Data strand. In Grade 9, students are

administered one item from each of the following strands: Numbers & Operations; Algebraic Thinking, Patterns &

Proportional Reasoning; and Geometry, Measurement, and Data. Then, students are administered two items from the

Statistics & Probability strand and nine items from the Expressions & Equations, Algebra, and Functions strand.

It is difficult to ascertain the ideal starting point for a student’s subsequent testing experience. The final score from

the previous administration provides a good initial reference point. However, it is also important that a student gain

some measure of early success during any test administration—that is one of the reasons why many fixed form

tests begin with relatively easier items. Scholastic has analyzed score decline data that indicated that students with

higher starting Student Scores (Quantile measure) tend to underperform on the early items in the test. This pattern

places greater stress on the algorithm’s ability to converge on a student’s “true” ability estimate. In addition, a lack

of success at the beginning of the assessment can also lead to motivational issues in some students. A series of

simulation studies conducted by Scholastic have shown that student score declines can be reduced significantly by

adjusting the starting item Quantile measure. At the beginning of any SMI College & Career administration, the first

item is presented at approximately 100Q below the student’s last estimated achievement level. It is believed this

early success will also set a positive tone for the remainder of the student’s testing session.

78 SMI College & Career

Development of SMI College & Career

FIGURE 17. The Step phase of the SMI College & Career computer-adaptive algorithm.

SMI_TG_078

Select item based on:

Strand

Grade level

QSC

Difﬁculty

Administer Item to Student

Find new ability estimate (b)

Adjust uncertainty (σ)

Has exit criteria been reached?

Begin Stop procedures

Yes

During the last phase, Stop, the SMI College & Career algorithm evaluates the exit criteria to determine if the

algorithm should end and the results should be reported. Figure 18 presents a flow chart of the Stop phase of

SMI College & Career. The program requires that students answer a minimum of 25 items, with 45 items being

administered on the initial administration of SMI College & Career. On successive administrations of SMI College

& Career, if the algorithm has enough information with 25 items to report a Student Measure with a small amount

of uncertainty, then the program ends. If more information is needed to minimize the measurement error, then up

to 20 more items are administered. Test reliability is influenced by many factors including the quality of the items,

testing conditions, and the student taking the test. In addition, after controlling for these factors reliability can also

be positively impacted by increasing the number of items on the test (Anastasi & Urbina, 1997). Scholastic has

conducted a series of simulation studies varying test length and found that increasing the test length significantly

decreases SEM. For most students the algorithm requires significantly less than 45 items to obtain an accurate

estimate of a student’s math achievement. However, for some students additional items may be needed in order to

obtain a stable and accurate estimate of their achievement. Extending the potential number of items that a student

might receive to 45 allows the algorithm a greater level of flexibility and improved accuracy for this group

of students.

Development of SMI College & Career 79

Development of SMI College & Career

FIGURE 18. The Stop phase of the SMI College & Career computer-adaptive algorithm.

SMI_TG_079

Select item based on:

Strand

Grade Level

QSC

Difﬁculty

Administer item to student

Find new ability estimate (b)

and adjust uncertainty (s)

Are stop conditions satisﬁed?

Number of items answered

Uncertainty is below speciﬁed level

Convert Student Measure

to Quantiles

Stop

Yes

QSC Quantile Measure—Measurement Error ....................................... 82

SMI College & Career Standard Error of Measurement ............................ 83

Reliability

82 SMI College & Career

Reliability

Reliability can be defined as “the degree to which test scores for a group of test takers are consistent over repeated

applications of a measurement procedure and hence are inferred to be dependable and repeatable for an individual

test taker” (Berkowitz, Wolkowitz, Fitch, & Kopriva, 2000). In reality, all test scores include some measure of error

(or level of uncertainty). This measurement error is related to many factors, such as the statistical model used to

compute the score, the items used to determine the score and the condition of the test taker when the test was

administered.

Reliability is a major consideration in evaluating any assessment procedure. Four sources of measurement error

should be examined for SMI College & Career:

(1) The proportion of test performance that is not due to error (marginal reliability)

(2) The consistency of test scores over time (alternate form/test-retest reliability)

(3) The error associated with a QSC Quantile measure, and

(4) The error associated with a student (standard error of measurement)

The first two sources of measurement error are typically used at the district level to describe the consistency

and comparability of scores. These studies will be conducted during the 2014–2015 school year. The last two

sources of measurement error are more associated with the interpretation and use of individual student results.

By quantifying the measurement error associated with these sources, the reliability of the test results can also

be quantified.

QSC Quantile Measure—Measurement Error

In a study of reading items, Stenner, Burdick, Sanford, and Burdick (2006) defined an ensemble to consist of all

of the items that could be developed from a selected piece of text. This hierarchical theory (items and their use

nested within the passage) is based on the notion of an ensemble as described by Einstein (1902) and Gibbs (1902).

Stenner and his colleagues investigated the ensemble differences across items, and it was determined that the

Lexile measure of a piece of text is equivalent to the mean difficulty of the items associated with the passage.

The Quantile Framework is an extension of this ensemble theory and defines the ensemble to consist of all of the

items that could be developed from a selected QSC at an introductory level. Each item that could be developed for

a QSC will have a slightly different level of difficulty from other items developed for the same QSC when tested with

students. These differences in difficulty can be due to such things as the wording in the stem, the level of the foils,

how diagnostic the foils are, the extent of graphics utilized in the item, etc. The Quantile measure of an item within

SMI College & Career is the mean difficulty level of the QSC ensemble.

Error may also be introduced when a QSC included at a certain grade level is not covered, or not covered at the

same grade level, in a particular state curriculum. Although the grade level objectives and expectations are very

similar across state curriculums, there are a handful of discrepancies that result in the same QSC being introduced

at different grade levels. For example, basic division facts are introduced in Grade 3 in some states while other state

curriculums consider it a Grade 4 topic.

Reliability 83

Reliability

SMI College & Career Standard Error of Measurement

One source of uncertainty in SMI College & Career scores is related to the individual student. Replication theory

describes the impact of retesting student performance using a different set of items (method) on a different

occasion (moment). Method and moment are random facets and are expected to vary with each replication of the

measurement process. Any calibrated set of items given on a particular day is considered interchangeable with any

other set of items given on another day within a two-week period.

The interchangeability of the item sets suggest there is no a priori basis for believing that one particular method-

moment combination will yield a higher or lower measure than any other. That is not to say that the resulting

measures are expected to be the same. On the contrary, they are expected to be different. It is unknown which

method-moment combination will in practice result in a more difficult testing situation. The anticipated variance

among replications due to method-moment combinations and their interactions is one source of measurement error.

A better understanding of how error due to replication comes about can be gained by describing some of the behavior

factors that may vary from administration to administration. Characteristics of the moment and context of measurement

can contribute to variation in replicate measures. Suppose, unknown to the test developer, scores increase with each

replication due to the student’s familiarity with the items and the format of the test, and therefore the results may not be

truly indicative of the student’s progress. This “occasion main effect” would be treated as error.

The mental state of the student at the time the test is administered can also be a source of error. Suppose Jessica

eats breakfast and rides the bus on Tuesdays and Thursdays, but on other days Jessica gets no breakfast and must

walk one mile to school. Some of the test administrations occur on what Jessica calls her “good days” and some

occur on her “bad days.” Variation in her mathematics performance due to these context factors contributes to error.

(For more information related to why scores change, see the paper entitled “Why Do Scores Change?” by Gary L.

Williamson (2004), available at www.Lexile.com.)

84 SMI College & Career

Reliability

The best approach to attaching uncertainty to a student’s measure is to replicate the item response record (i.e., simulate what would

happen if the reader were actually assessed again). Suppose eight-year-old José takes two 30-item SMI College & Career tests one

week apart. The occasions (the two different days) and the 30 items nested within each occasion can be independently replicated

(two-stage replication), and the resulting two measures averaged for each replicate. One thousand replications would result in a

distribution of replicate measures. The standard deviation of this distribution is the replicated standard error measurement, and

it describes uncertainty in measurement of José’s mathematics understandings by treating methods (items), moment (occasion

and context), and their interactions as error. Furthermore, in computing José’s mathematics measure and the uncertainty in that

measure, he is treated as an individual without reference to the performance of other students. This replication procedure allows

psychometricians to estimate an individual’s measurement error.

There is always some uncertainty associated with a student’s score because of the measurement error associated with test

unreliability. This uncertainty is known as the standard error of measurement (SEM). The magnitude of the SEM of an individual

student’s score depends on the following characteristics of the test (Hambleton et al., 1991):

• The number of test items—smaller standard errors are associated with longer tests

• The quality of the test items—in general, smaller standard errors are associated with highly discriminating items for which

correct answers cannot be obtained by guessing

• The match between item difficulty and student achievement—smaller standard errors are associated with tests composed

of items with difficulties approximately equal to the achievement of the student (targeted tests)

SMI College & Career was developed using the Rasch one-parameter item response theory model to relate a student’s ability to the

difficulty of the items. There is a certain amount of measurement error due to model misspecification (violation of model assumptions)

associated with each score on SMI College & Career. The computer algorithm that controls the administration of the assessment uses

a Bayesian procedure to estimate each student’s mathematical ability. This procedure uses prior information about students to control

the selection of items and the recalculation of each student’s understanding after responding to an item.

Compared to a fixed-form test where all students answer the same questions, a computer-adaptive test produces a different test for

every student. When students take a computer-adaptive test, they all receive approximately the same raw score or number of items

correct. This occurs because all students are answering questions that are targeted for their unique ability level—the questions are

neither too easy nor too hard. Because each student takes a unique test, the error associated with any one score or student is also

unique.

Reliability 85

Reliability

To examine the standard measurement error of SMI College & Career, a sample of four thousand Grade 5 students

was simulated. Every student had the same true ability of 700Q, and each student’s start ability was set in the range

of 550Q to 850Q. The test length was set uniformly to 30 items, and no tests were allowed to end sooner.

FIGURE 19. Distribution of SEMs from simulations of student SMI College & Career scores,

Grade 5.

SMI_TG_089

150

100

200

250

2300 2200 2100 0 100 200 300

Deviation from True Ability (Quantiles)

From the simulated test results in Figure 19, it can be seen that most of the score errors were small. Using the

results of the simulation, the initial standard error for an SMI College & Career score is estimated to be approximately

70Q. This means that on average, if a student takes the SMI College & Career three times, two out of three of the

student’s scores will be within 70 points of the student’s true readiness for mathematics instruction.

Content Validity .........................................................................89

Construct-Identification Validity...................................................... 90

Conclusion ............................................................................... 91

Validity

88 SMI College & Career

Validity

The validity of a test is the degree to which the test actually measures what it purports to measure. Validity provides

a direct check on how well the test fulfills its purpose. “The process of ascribing meaning to scores produced by

a measurement procedure is generally recognized as the most important task in developing an educational or

psychological measure, be it an achievement test, interest inventory, or personality scale” (Stenner, Smith, & Burdick,

1983). The appropriateness of any conclusion drawn from the results of a test is a function of the test’s validity.

According to Kane (2006), “to validate a proposed interpretation or use of test scores is to evaluate the rationale for

this interpretation or use” (p. 23).

Historically, validity has been categorized in three areas: content-description validity, criterion-prediction validity,

and construct-identification validity. Although the current argument-based approach to validity (Kane, 2006) reflects

principles inherent in all these areas, it is often convenient to organize discussions around the three areas separately.

Initially, the primary source of validity evidence for SMI College & Career comes from the examination of the content

and the degree to which the assessment could be said to measure mathematical understandings (construct-

identification validity evidence). As more data are collected and more studies are completed, additional validity

evidence can be described.

Validity 89

Validity

Content Validity

The content validity of a test refers to the adequacy with which relevant content has been sampled and represented

in the test. The content validity of SMI College & Career is based on the alignment between the content of the items

and the curricular framework used to develop SMI College & Career. Within SMI College & Career, each item was

aligned with a specific QSC in the Quantile Framework and with a specific standard in the Common Core State

Standards (CCSS) for Mathematics. The development of the Common Core State Standards Initiative (CCSSI) has

established a clear set of K–12 standards that will enable all students to become increasingly more proficient in

understanding and utilizing mathematics—with steady advancement to college and career readiness by high

school graduation.

The mathematics standards stress both procedural skill and conceptual understanding to prepare students for the

challenges of their postsecondary pursuits, not just to pass a test. They lay the groundwork for K–5 students to

learn about whole numbers, operations, fractions, and decimals, all of which are required to learn more challenging

concepts and procedures. The middle school standards build on the concepts and skills learned previously to provide

logical preparation for high school mathematics. The high school standards then assemble the skills taught in the

earlier grades challenging students to continue along productive learning progressions in order to develop more

sophisticated mathematical thinking and innovative problem-solving methods. Students who master the prescribed

mathematical skills and concepts through Grade 7 will be well prepared for algebra in Grade 8.

The mathematics standards outline eight practices that each student should develop in the early grades and then

master as they progress through middle and high school:

1. Make sense of problems and persevere in solving.

2. Reason abstractly and quantitatively.

3. Construct viable arguments and critique the reasoning of others.

4. Model with mathematics.

5. Use appropriate tools strategically.

6. Attend to precision.

7. Look for and make use of structure.

8. Look for and express regularity in repeated reasoning.

The Quantile Framework places the mathematics curriculum, teaching materials, and students on a common,

developmental scale, enabling educators to match students with instructional materials by readiness level,

forecast their understanding, and monitor their progress. To see the alignment, visit www.scholastic.com/SMI or

www.Quantiles.com.

Content validity was also built into SMI during its development. SMI was designed to measure readiness for

mathematical instruction. To this end, the tests were constructed with content skills in mind. All items were written

and reviewed by experienced classroom teachers to ensure that the content of the items was developmentally

appropriate and representative of classroom experiences.

For more information on the content validity of SMI and the Quantile Framework, please refer to the other

sections of this guide (section entitled “QSC Descriptions and Standards Alignment” in Appendix 1). SMI and the

Quantile Framework are the result of rigorous research and development by a large team of educational experts,

mathematicians, and assessment specialists.

90 SMI College & Career

Validity

Construct-Identification Validity

The construct-identification validity of a test is the extent to which the test may be said to measure a theoretical

construct or trait, such as readiness for mathematics instruction. It is expected that scores from a valid test of

mathematics skills should show expected:

1. Differences by age and/or grade

2. Differences among groups of students that traditionally show different or similar patterns of development in

mathematics (e.g., differences in socioeconomic levels, gender, ethnicity, etc.)

3. Relationships with other measures of mathematical understanding

Construct-identification validity is the most important aspect of validity related to SMI College & Career. SMI College

& Career is designed to measure the development of mathematical abilities; therefore, how well it measures

mathematical understanding and how well it measures the development of these mathematical understandings

must be examined.

Construct Validity From SMI Enterprise Edition

Evidence for the construct validity of SMI College & Career is provided by the body of research supporting SMI

Enterprise Edition collected between 2009 and 2011. SMI College & Career employs many of the items developed for

SMI and utilizes the same computer-adaptive testing algorithm and scoring and reporting protocols as were initially

developed for SMI.

Information and results of the validity studies conducted in three phases can be found in Appendix 4. The following

results were observed:

• Students classified as needing math intervention services scored significantly lower than students not

classified as needing math intervention services.

• Students classified as Gifted and Talented scored significantly higher than students not classified as Gifted

and Talented.

• Students classified as requiring Special Education services scored significantly lower than students not

requiring Special Education services.

• Student scores on SMI rose rapidly in elementary grades and leveled off in middle school depending on the

program being implemented (e.g., whole-class instruction versus remediation program). The developmental

nature of mathematics was demonstrated in these results.

• Student scores on SMI exhibited moderate correlations with state assessments of mathematics. The

within-grade correlations and the overall across-grades correlation (where appropriate) were moderate

as expected given the different mode of administration between the two tests (fixed, constant form for all

students within a grade on the state assessments, as compared to the SMI, which is a computer-adaptive

assessment that is tailored to each student’s level of achievement).

• Growth across a school year was constant across Grades 2–6 (approximately 0.6Q per day or approximately

108Q per year). With a small sample of students where data was collected over two years, a negative

correlation was observed between the student’s initial SMI Quantile measure and the amount grown over

the two school years. This negative correlation is consistent with the interpretation that lower-performing

students typically grow more than higher-performing students.

• For gender, there was no clear pattern in the differences in performance of males and females.

Validity 91

Validity

• For Race/Ethnicity, a significant difference was observed for most of the sites with the differences between

the mean differences as expected.

• For bilingual status, while a significant difference was observed for one site, the level of significance was

not strong and the differences were as expected with students not classified as bilingual scoring higher. For

ELL, ESL, and LEP status, a significant difference due to language proficiency classification was observed

for three of the sites, and the differences between the mean differences were as expected, with students

classified as needing EL services scoring lower.

• For economically disadvantaged classification, a significant difference due to FRPL status was observed for

one of the sites. The differences between the mean SMI Quantile measures were as expected with the “No”

classification scoring higher.

Construct Validity From the Quantile Framework

Evidence for the construct validity of SMI College & Career is provided by the body of research supporting the

Quantile Framework for Mathematics. The development of SMI College & Career utilized the Quantile Framework and

the calibration of items specified to previously field-tested and analyzed items. Item writers for SMI College & Career

were provided training on item development that matched the training used during the development of the Quantile

item bank, and item reviewers had access to all items from the Quantile item bank. These items had been previously

calibrated to the Quantile scale to ensure that items developed for SMI were theoretically consistent with other items

calibrated to the Quantile scale, and that they maintained their individual item calibrations.

Prior research has shown that test scores derived from items calibrated from the Quantile field study are highly

correlated with other assessments of mathematics achievement. The section in this technical report entitled “The

Theoretical Framework of Mathematics Achievement and the Quantile Framework for Mathematics” provides a

detailed description of the framework and the construct validity of the framework. The section also includes evidence

to support the fact that tests based upon the framework can accurately measure mathematics achievement.

Conclusion

The Scholastic Math Inventory and its reports of students’ readiness for mathematics instruction can be a powerful

tool for educators. However, it is imperative to remain cognizant of the fact that no one test should be the sole

determinant when making high-stakes decisions about students (e.g., summer school placement or retention). The

student’s background experiences, the curriculum in the prior grade or course, the textbook used, as well as direct

observation of each student’s mathematical achievement are all factors to take into consideration when making

these kinds of decisions.

References............................................................................... 94

References

94 SMI College & Career

References

American Educational Research Association, American Psychological Association, & National Council on

Measurement in Education (1999). Standards for educational and psychological testing. Washington, DC: American

Psychological Association.

Anastasi, A. (1982). Psychological testing (fifth edition). New York, NY: Macmillan Publishing Company, Inc.

Anastasi, A., & Urbina, S. (1997). Psychological testing (seventh edition), Upper Saddle River, NJ: Prentice Hall.

Ashlock, R.B. (2010). Error patterns in computation: Using error patterns to help each student learn (tenth edition).

Boston, MA: Allyn & Bacon.

Berkowitz, D., Wolkowitz, B., Fitch, R., & Kopriva, R. (2000). The use of tests as part of high-stakes decision-making

for students: A resources guide for educators and policy-makers. Washington, DC: US Department of Education.

[Available online: http://www.ed.gov/offices/OCR/testing/]

Bond, T.G., & Fox, C.M. (2001). Applying the Rasch model: Fundamental measurement in the human sciences.

Mahwah, NJ: Lawrence Erlbaum Associates.

Burg, S.S. (2007). An investigation of dimensionality across grade levels and effects on vertical linking for elementary

grade mathematics achievement tests. University of North Carolina, Chapel Hill.

California Department of Education (CDE). (1997, December). Mathematics content standards for California public

schools: Kindergarten through grade twelve. Sacramento, CA: Author.

California Department of Education (CDE). (2000). Mathematics framework for California public schools: Kindergarten

through grade twelve (Revised Edition). Sacramento, CA: Author.

California Department of Education (CDE). (2000). Standards for evaluating instructional materials for social content.

Sacramento, CA: Author.

California Department of Education (CDE). (2002, January). Sample items for the California Mathematics Standards

Tests. Sacramento, CA: Author.

California Department of Education (CDE). (2002, October). Blueprints document for the Star Program California

Standards Tests: Mathematics. Sacramento, CA: Author.

Camilli, G., & Shepard, L.A. (1994). Methods for identifying biased test items. Thousand Oaks, CA: Sage Publications, Inc.

Cochran, W., & Cox, G. (1957). Experimental designs (second edition). New York, NY: John Wiley & Sons, Inc.

Cortiella, C. (2005). A parent’s guide to response-to-intervention [Parent Advocacy Brief]. Retrieved April 22, 2009,

from http://www.ncld.org/images/stories/downloads/parent_center/rti_final.pdf

CTB/McGraw-Hill. (1983). Guidelines for bias-free publishing. Monterey, CA: Author.

Dorans, N.J., & Holland, P.W. (1993). DIF detection and description: Mantel-Haenszel and standardization. In P.W.

Holland and H. Wainer (Eds.), Differential item functioning (pp. 35–66). Hillsdale, NJ: Lawrence Erlbaum.

Downing, S.M. (2006). Selected-response item formats in test development. In S.M. Downing & T.M. Haladyna (Eds.),

Handbook of test development. Mahwah, NJ: Lawrence Erlbaum Associates.

Einstein, A. (1902). Ann. d. Phys., IV. Folge, 9, 417.

Florida Department of Education (FL DOE). (2007). Sunshine State Standards: Mathematics. Tallahassee, FL: Author.

Gibbs, J.W. (1902). Elementary principles in statistical mechanics. New Haven, CT: Yale University Press.

References 95

References

Green, B.F., Bock, R.D., Humphreys, L.G., Linn, R.L., & Reckase, M.D. (1984). Technical guidelines for assessing

computer adaptive tests. Journal of Educational Measurement, 21(4), 347–360.

Haladyna, T.M. (1994). Developing and validating multiple-choice test items. Hillsdale, NJ: Lawrence Erlbaum

Associates.

Hambleton, R.K., & Swaminathan, H. (1985). Item response theory: Principles and applications. Boston, MA: Kluwer-

Nijhoff.

Hambleton, R.K., Swaminathan, H., & Rogers, H.J. (1991). Fundamentals of item response theory. Newbury Park, CA:

Sage Publications, Inc.

Hardwicke, S.B., & Yoes, M.E. (1984). Attitudes and performance on computerized adaptive testing. San Diego, CA:

Rehab Group.

Illinois State Board of Education (ISBE). (2002). Mathematics performance descriptors, grades 1-5 and grades 6-12.

Springfield, IL: Author.

Kane, M.T. (2006). Validation. In R.L. Brennan (Ed.), Educational measurement (fourth edition, pp. 17–64). Westport,

CT: Praeger.

Linacre, J.M. (2010). A user’s guide to Winsteps ministep Rasch-model computer programs [Computer software and

manual]. Chicago: Winsteps.

Messick, S. (1993). Validity. In R.L. Linn (Ed.), Educational measurement (third edition, pp. 13–104). Washington, DC:

American Council on Education.

MetaMetrics, Inc. (2005). PASeries Mathematics technical manual. Iowa City, IA: Pearson Educational Measurement.

MetaMetrics, Inc. (2011). Lexile/Quantile Feasibility Study: A study to link NAEP Reading with The Lexile® Framework

for Reading and NAEP Mathematics with The Quantile® Framework for Mathematics. Durham, NC: Author.

MetaMetrics, Inc. (2012a). Linking the ACT® Mathematics with the Quantile® Framework: A study to link the ACT®

Mathematics Test administered in North Carolina with The Quantile® Framework for Mathematics. Durham, NC: Author.

MetaMetrics, Inc. (2012b). Linking the K-PREP Math Tests with the Quantile® Framework: A study to link the

Kentucky Performance Rating for Educational Progress Math Test with The Quantile® Framework for Mathematics.

Durham, NC: Author.

MetaMetrics, Inc. (2012c). Linking the Mathematics SOL Tests with the Quantile® Framework: A study to link the Virginia

Mathematics Standards of Learning Tests with The Quantile® Framework for Mathematics. Durham, NC: Author.

MetaMetrics, Inc. (2013). Linking the NC READY EOG Math/EOC Algebra I/Integrated I with the Quantile® Framework:

A study to link the North Carolina READY EOG Math/EOC Algebra I/Integrated I with The Quantile® Framework for

Mathematics. Durham, NC: Author.

National Assessment Governing Board (2005). Mathematics framework for the 2005 National Assessment of

Educational Progress (prepublication edition). Washington, DC: Author.

National Assessment Governing Board (NAGB). (2007, May). National Assessment of Educational Progress:

Mathematics framework for 2009 (Pre-publication Edition). Washington, DC: National Assessment Governing Board

and U.S. Department of Education.

National Council of Teachers of Mathematics (2000). Principles and standards for school mathematics. Reston, VA:

Author.

96 SMI College & Career

References

National Council of Teachers of Mathematics (2011). Administrator’s guide: Interpreting the Common Core State

Standards to improve mathematics education. Reston, VA: Author.

National Governors Association (NGA) and Council of Chief State School Officers (CCSSO). (2010a, June). Common

Core State Standards Initiative. Retrieved from http://www.corestandards.org/the-standards/

National Governors Association Center for Best Practices (NGA Center) & the Council of Chief State School

Officers (CCSSO). (2010b). Common Core State Standards for mathematics: Appendix A. Retrieved from

http://www.corestandards.org/assets/CCSSI_Mathematics_Appendix_A.pdf

National Mathematics Advisory Panel (2008). The final report of the National Mathematics Advisory Panel:

US Department of Education.

North Carolina Department of Public Instruction (NCDPI). (1996). North Carolina Standard Course of Study --

Mathematics. Raleigh, NC: Author.

Pearson Educational Measurement. (2003). Universal design checklist.

Petersen, N.S., Kolen, M.J., & Hoover, H.D. (1993). Scaling, norming, and equating. In R.L. Linn (Ed.), Educational

measurement (third edition). Phoenix, AZ: Oryx Press.

Rasch, G. (1980). Probabilistic models for some intelligence and attachment tests. Chicago, IL: The University of

Chicago Press.

Roussos, L., Schnipke, D., & Pashley, P. (1999). A generalized formula for the Mantel-Haenszel differential item

functioning parameter. Journal of Behavioral and Educational Statistics, 24, 293–322.

Salvia, J., & Ysseldyke, J.E. (1998). Assessment (seventh edition). Boston, MA: Houghton Mifflin Company.

SAS Institute, Inc. (1985). The FREQ procedure. In SAS users guide: Statistics, version 5 edition. Cary, NC: Author.

Schinoff, R.B., & Steed, L. (1988). The CAT program at Miami-Dade Community College. In D. Doucette (Ed.),

Computerized adaptive testing: The state of the art in assessment at three community colleges (pp. 25–36). Laguna

Hills, CA: League for Innovation in the Community College.

Stenner, A.J. (1990). Objectivity: Specific and general. Rasch Measurement Transactions, 4(111).

Stenner, A.J., Burdick, H., Sanford, E.E., & Burdick, D.S. (2006). How accurate are Lexile text measures? Journal of

Applied Measurement, 7 (3), 307–322.

Stenner, A.J., Smith, M.C., & Burdick, D.S. (1983). Toward a theory of construct definition. Journal of Educational

Measurement, 20 (4), 305–315.

Stone, G.E., & Lunz, M.E. (1994). The effect of review on the psychometric characteristics of computerized adaptive

tests. Applied Measurement in Education, 7, 211–222.

Texas Education Agency (TEA). (2002). Texas Essential Knowledge and Skills for mathematics. Austin, TX: Author.

Tomlinson, C.A., (2001). How to differentiate instruction in mixed-ability classrooms, second edition, Association for

Supervision and Curriculum Development.

US Department of Education, Office of Elementary and Secondary Education. (2009). GUIDANCE The American

Recovery and Reinvestment Act of 2009 (ARRA): Using Title I, Part A ARRA funds for grants to local educational

agencies to strengthen education, drive reform, and improve results for students. Retrieved May 14, 2014, from

http://www2.ed.gov/policy/gen/leg/recovery/guidance/titlei-reform.pdf

Wainer, H. (1993). Some practical considerations when converting a linearly administered test to an adaptive format.

Educational Researchers, 12 (1), 15–20.

References 97

References

Wainer, H., Dorans, N.J., Flaugher, R., Green, B.F., Mislevy, R.J., Steinburg, L., & Thissen, D. (1990). Computerized

adaptive testing: A primer. Hillsdale, NJ: Lawrence Erlbaum Associates.

Wang, T., & Vispoel, W.P. (1998). Properties of ability estimation methods in computerized adaptive testing. Journal of

Educational Measurement, 35, 109–135.

Williamson, G.L. (2004). Why do scores change? Durham, NC: MetaMetrics, Inc.

Williamson, G.L. (2006). What is expected growth? Durham, NC: MetaMetrics, Inc.

Wright, B.D., & Linacre, J.M. (1994). The Rasch model as a foundation for the Lexile Framework. Durham, NC:

MetaMetrics, Inc.

Wright, B.D., & Stone, M.H. (1979). Best Test Design. Chicago: MESA Press.

Appendix 1: QSC Descriptions and Standards Alignment ........................100

Appendix 2: Norm Reference Table (spring percentiles) .........................131

Appendix 3: Reliability Studies.......................................................132

Appendix 4: Validity Studies..........................................................136

Appendices

100 SMI College & Career

Appendices

Appendix 1: QSC Descriptions and Standards Alignment

Quantile

Measure QSC Description Strand CCSS ID QSC ID

EM260 Model the concept of addition for sums to 10. Number & Operations

K.OA.1,

K.OA.2,

K.OA.4

EM210 Read and write numerals using one-to-one

correspondence to match sets of 0 to 10. Number & Operations

K.CC.3,

K.CC.4.a,

K.CC.4.b,

K.CC.5

EM200 Use directional and positional words. Geometry, Measurement

& Data K.G.1 15

EM180 Describe likenesses and differences between and

among objects.

Geometry, Measurement

& Data K.G.4 16

EM150 Create and identify sets with greater than, less than, or

equal number of members by matching. Number & Operations K.CC.6 7

EM150 Describe, compare, and order objects using

mathematical vocabulary.

Geometry, Measurement

& Data

K.G.3,

K.MD.1,

K.MD.2,

1.MD.1,

1.MD.2

EM150 Know and use addition and subtraction facts to 10 and

understand the meaning of equality.

Algebraic Thinking,

Patterns & Proportional

Reasoning

K.OA.3,

K.OA.4,

K.OA.5,

1.OA.7

EM150 Measure length using nonstandard units. Geometry, Measurement

& Data

K.MD.1,

1.MD.1,

1.MD.2

581

EM130

Recognize the context in which addition or subtraction

is appropriate, and write number sentences to solve

number or word problems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

K.OA.1,

K.OA.2,

1.OA.1

EM110 Organize, display, and interpret information in concrete

or picture graphs.

Geometry, Measurement

& Data K.MD.3 20

EM110 Identify missing addends for addition facts.

Algebraic Thinking,

Patterns & Proportional

Reasoning

K.OA.4,

1.OA.1 75

EM100 Read and write numerals using one-to-one

correspondence to match sets of 11 to 100. Number & Operations

K.CC.3,

K.CC.4.a,

K.CC.4.b,

K.CC.5,

1.NBT.1

EM100 Identify, draw, and name basic shapes such as

triangles, squares, rectangles, hexagons, and circles.

Geometry, Measurement

& Data

K.G.1, K.G.2,

K.G.3, K.G.5,

2.G.1

536

Appendices 101

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

EM100 Tell time to the nearest hour and half-hour using digital

and analog clocks.

Geometry, Measurement

& Data 1.MD.3 1005

EM90 Group objects by 2s, 5s, and 10s in order to count. Number & Operations 1.OA.5 30

EM80

Rote count beginning at 1 or at another number by 1s,

and rote count by 2s, 5s, and 10s to 100 beginning at

2, 5, or 10.

Number & Operations

K.CC.1,

K.CC.2,

1.NBT.1

EM80 Add 3 single-digit numbers in number and word

problems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

1.OA.2 76

EM80 Identify and name spheres and cubes. Geometry, Measurement

& Data

K.G.1, K.G.2,

K.G.3 537

EM80 Know and use related addition and subtraction facts.

Algebraic Thinking,

Patterns & Proportional

Reasoning

1.OA.4 1003

EM60 Rote count 101 to 1,000. Number & Operations 1.NBT.1 65

EM60 Use models to determine properties of basic solid

figures (slide, stack, and roll).

Geometry, Measurement

& Data K.G.4 627

EM50 Sort a set of objects in one or more ways; explain. Geometry, Measurement

& Data K.MD.3 54

EM50 Read and write word names for whole numbers from

101 to 999. Number & Operations 2.NBT.3 68

EM40 Use addition and subtraction facts to 20. Number & Operations

1.OA.1,

1.OA.6,

2.OA.2

EM40

Use counting strategies to add and subtract within

100 that include counting forward, counting backward,

grouping, ten frames, and hundred charts.

Algebraic Thinking,

Patterns & Proportional

Reasoning

1.NBT.4,

1.NBT.6,

1.OA.2,

1.OA.5,

2.OA.1

617

EM20 Model the concept of subtraction using numbers less

than or equal to 10. Number & Operations K.OA.1,

K.OA.2 37

EM20 Identify and make figures with line symmetry. Geometry, Measurement

& Data 4.G.3 85

EM10 Represent numbers up to 100 in a variety of ways such

as tallies, ten frames, and other models. Number & Operations

K.CC.5,

K.NBT.1,

1.NBT.2.a,

1.NBT.2.b

EM10 Organize, display, and interpret information in picture

graphs and bar graphs using grids.

Geometry, Measurement

& Data

1.MD.4,

2.MD.10 61

102 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

EM10

Add 2- and 3-digit numbers with and without models

for number and word problems that do not require

regrouping.

Number & Operations

1.NBT.4,

1.NBT.5,

2.MD.5,

2.MD.6,

2.NBT.5,

2.NBT.6,

2.NBT.7,

2.NBT.8,

3.NBT.2,

3.MD.1,

3.MD.2

10 Use place value with ones and tens. Number & Operations

K.NBT.1,

1.NBT.2.a,

1.NBT.2.b,

1.NBT.2.c,

1.NBT.3,

1.NBT.4,

1.NBT.6

Use relationships between minutes, hours, days, weeks,

months, and years to describe time. Recognize the

meaning of a.m. and p.m. for the time of day.

Geometry, Measurement

& Data

2.MD.7,

3.MD.1 618

10 Compare and order sets and numerals up to 20,

including using symbol notation (>, <, =). Number & Operations

K.CC.4.c,

K.CC.7,

K.MD.3

1001

20 Measure weight using nonstandard units. Geometry, Measurement

& Data K.MD.1 582

20 Measure capacity using nonstandard units. Geometry, Measurement

& Data K.MD.1 583

20 Find the unknown in an addition or subtraction number

sentence.

Algebraic Thinking,

Patterns & Proportional

Reasoning

1.OA.8 1004

30 Use place value with hundreds. Number & Operations

2.NBT.1.a,

2.NBT.1.b,

2.NBT.3,

2.NBT.4,

2.NBT.5,

2.NBT.6,

2.NBT.7,

3.NBT.1,

3.NBT.2

40 Combine two- and three- dimensional simple figures to

create a composite figure.

Geometry, Measurement

& Data K.G.6, 1.G.2 542

50 Compare and order sets and numerals from 21 to 100,

including using symbol notation (>, <, =). Number & Operations 1.NBT.3 26

Appendices 103

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

Use models and appropriate vocabulary to determine

properties of basic plane figures (open or closed,

number of sides and vertices or corners).

Geometry, Measurement

& Data K.G.4, 1.G.1 1002

60 Identify odd and even numbers using objects.

Algebraic Thinking,

Patterns & Proportional

Reasoning

2.OA.3 70

70 Answer comparative and quantitative questions about

charts and graphs.

Geometry, Measurement

& Data

1.MD.4,

2.MD.10 59

70 Determine the value of sets of coins. Geometry, Measurement

& Data 2.MD.8 105

Subtract 2- and 3-digit numbers with and without

models for number and word problems that do not

require regrouping.

Number & Operations

1.NBT.5,

1.NBT.6,

2.MD.4,

2.MD.5,

2.MD.6,

2.NBT.5,

2.NBT.7,

2.NBT.8,

3.NBT.2,

3.MD.1,

3.MD.2

599

80 Represent a number in a variety of numerical ways.

Algebraic Thinking,

Patterns & Proportional

Reasoning

K.NBT.1,

K.OA.3,

K.OA.4,

K.CC.3,

1.OA.2,

1.OA.6,

2.OA.1

663

90 Add 2- and 3-digit numbers with and without models

for number and word problems that require regrouping. Number & Operations

1.NBT.4,

2.MD.5,

2.MD.6,

2.NBT.5,

2.NBT.6,

2.NBT.7,

3.NBT.2,

3.MD.1,

3.MD.2

598

100 Model the division of sets or the partition of figures into

two, three, or four equal parts (fair shares). Number & Operations 1.G.3, 2.G.3 38

100 Measure lengths in inches/centimeters using

appropriate tools and units.

Geometry, Measurement

& Data 3.MD.4 99

110 Identify odd and even numbers.

Algebraic Thinking,

Patterns & Proportional

Reasoning

2.OA.3 113

110 Skip count by 2s, 5s, and 10s beginning at any number. Number & Operations 2.NBT.2 1007

104 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

120 Indicate the value of each digit in any 2- or 3-digit

number. Number & Operations 2.NBT.1.b,

2.NBT.3 73

140 Relate standard and expanded notation to 3- and

4-digit numbers. Number & Operations 2.NBT.3,

2.NBT.4 110

150 Find the value of an unknown in a number sentence.

Algebraic Thinking,

Patterns & Proportional

Reasoning

2.MD.5,

2.OA.1,

3.OA.3,

3.OA.4,

3.OA.6,

4.OA.2,

4.OA.3

549

160 Identify and name basic solid figures: rectangular prism,

cylinder, pyramid, and cone; identify in the environment.

Geometry, Measurement

& Data K.G.1, K.G.2 46

160 Identify or generate numerical and geometric patterns;

correct errors in patterns or interpret pattern features.

Algebraic Thinking,

Patterns & Proportional

Reasoning

4.OA.5 91

160 Read and write word names for numbers from 1,000 to

9,999. Number & Operations 4.NBT.2 109

180 Use multiplication facts through 144.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.3,

3.OA.4,

3.OA.7

121

190 Represent fractions concretely and symbolically,

including representing whole numbers as fractions. Number & Operations

3.NF.1,

3.NF.2.a,

3.NF.2.b,

3.NF.3.c,

3.G.2

114

200 Organize, display, and interpret information in line plots

and tally charts.

Geometry, Measurement

& Data

1.MD.4,

2.MD.9 60

210 Compare and order numbers less than 10,000. Number & Operations 2.NBT.4 111

210 Tell time at the five-minute intervals. Geometry, Measurement

& Data 2.MD.7 541

210

Estimate, measure, and compare capacity using

appropriate tools and units in number and word

problems.

Geometry, Measurement

& Data

3.MD.2,

4.MD.2 650

Appendices 105

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

220 Use the commutative and associative properties to add

or multiply numerical expressions.

Algebraic Thinking,

Patterns & Proportional

Reasoning

1.NBT.4,

1.NBT.6,

1.OA.3,

2.NBT.5,

2.NBT.6,

2.NBT.7,

3.OA.5,

3.OA.9,

3.NBT.2,

3.NBT.3,

4.NBT.5,

4.NF.3.c,

5.MD.5.a,

5.NBT.7

161

240

Model multiplication in a variety of ways including

grouping objects, repeated addition, rectangular arrays,

skip counting, and area models.

Algebraic Thinking,

Patterns & Proportional

Reasoning

2.G.2, 2.OA.4,

3.OA.1,

3.OA.3,

4.NBT.5

118

240

Estimate, measure, and compare length using

appropriate tools and units in number and word

problems.

Geometry, Measurement

& Data

2.MD.1,

2.MD.2,

2.MD.3,

2.MD.4,

2.MD.5,

2.MD.9,

4.MD.2

649

250 Recognize the 2-dimensional elements of

3-dimensional figures.

Geometry, Measurement

& Data K.G.3 52

250 Identify, draw, and name shapes such as quadrilaterals,

trapezoids, parallelograms, rhombi, and pentagons.

Geometry, Measurement

& Data 2.G.1 83

250 Locate points on a number line. Number & Operations

2.MD.6,

3.NF.2a,

3.NF.2.b,

3.NF.3a,

3.MD.1

250

Subtract 2- and 3-digit numbers with and without

models for number and word problems that require

regrouping.

Number & Operations

2.MD.4,

2.MD.5,

2.MD.6,

2.NBT.5,

2.NBT.7,

3.NBT.2,

3.MD.1,

3.MD.2

117

270 Tell time to the nearest minute using digital and analog

clocks.

Geometry, Measurement

& Data 3.MD.1 1011

106 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

280 Use the identity properties for addition and

multiplication and the zero property for multiplication.

Algebraic Thinking,

Patterns & Proportional

Reasoning

1.NBT.4,

1.NBT.6,

2.NBT.5,

2.NBT.6,

2.NBT.7,

3.NBT.2,

3.NBT.3,

3.OA.5,

3.OA.9

119

300 Make different sets of coins with equivalent values. Geometry, Measurement

& Data 2.MD.8 106

300 Compare fractions with the same numerator or

denominator concretely and symbolically. Number & Operations 3.NF.3.d 538

300 Write an addition or a subtraction sentence that

represents a number or word problem; solve.

Algebraic Thinking,

Patterns & Proportional

Reasoning

2.MD.5,

2.OA.1 544

300 Multiply a 1-digit number by a 2-digit multiple of 10. Number & Operations 3.NBT.3 1010

310 Understand that many whole numbers factor in different

ways.

Algebraic Thinking,

Patterns & Proportional

Reasoning

4.OA.4 163

320

Model division in a variety of ways including sharing

equally, repeated subtraction, rectangular arrays, and

the relationship with multiplication.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.2,

3.OA.3,

3.OA.7,

4.NBT.6,

5.NBT.6,

5.NBT.7,

5.NF.3

120

320 Identify combinations of fractions that make one whole. Number & Operations 2.G.3, 3.G.2,

4.NF.3.a 540

330 Compare decimals (tenths and hundredths) with and

without models. Number & Operations 4.NF.7 156

330 Multiply a multidigit whole number by a 1-digit whole

number or a 2-digit multiple of 10. Number & Operations 4.NBT.5 165

350 Know and use division facts related to multiplication

facts through 144.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA3,

3.OA.4,

3.OA.6,

3.OA.7

162

360

Describe and demonstrate patterns in skip counting and

multiplication; continue sequences beyond memorized

or modeled numbers.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.9 129

360

Estimate, measure, and compare weight using

appropriate tools and units in number and word

problems.

Geometry, Measurement

& Data

3.MD.2,

4.MD.2 651

Appendices 107

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

360 Write an addition and subtraction sentence that

represents a two-step word problem; solve.

Algebraic Thinking,

Patterns & Proportional

Reasoning

2.OA.1 1006

370

Locate a point in Quadrant I of a coordinate grid given

an ordered pair; name the ordered pair for a point in

Quadrant I of a coordinate grid.

Geometry, Measurement

& Data

5.G.1, 5.G.2,

5.OA.3,

6.RP.3.a

138

390

Organize, display, and interpret information in tables

and graphs (frequency tables, pictographs, and line

plots).

Geometry, Measurement

& Data 3.MD.3 137

390 Write a multiplication or a division sentence that

represents a number or word problem; solve.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.3,

4.OA.1,

4.OA.2

607

390 Write a ratio or rate to compare two quantities.

Algebraic Thinking,

Patterns & Proportional

Reasoning

6.RP.1, 6.RP.2 654

400

Determine perimeter using concrete models,

nonstandard units, and standard units in number and

word problems.

Geometry, Measurement

& Data 3.MD.8 146

400

Identify and draw intersecting, parallel, skew, and

perpendicular lines and line segments. Identify

midpoints of line segments.

Geometry, Measurement

& Data 4.G.1 176

400 Model the concept of percent and relate to the value in

decimal or fractional form.

Algebraic Thinking,

Patterns & Proportional

Reasoning

6.RP.3.c 626

400

Write number sentences using any combination of

the four operations that represent a two-step word

problem; solve.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.8,

3.MD.3,

3.MD.8

1008

400

Use models to represent a fraction as a product of a

whole number and a unit fraction in number and word

problems.

Number & Operations

4.NF.4.a,

4.NF.4.b,

4.NF.4.c

1017

410 Round whole numbers to a given place value. Number & Operations 3.NBT.1,

4.NBT.3 660

420 Apply appropriate type of estimation for sums and

differences. Number & Operations 3.OA.8,

4.OA.3 153

440 Describe the probability of an chance event using a

fraction or ratio. Statistics & Probability 7.SP.5,

7.SP.8.a 185

450 Use benchmark numbers (zero, one-half, one) and

models to compare and order fractions. Number & Operations 3.NF.3.d,

4.NF.2 115

450 Divide using single-digit divisors with and without

remainders. Number & Operations 4.NBT.6 166

108 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

450

Use manipulatives, pictorial representations, and

appropriate vocabulary (e.g., polygon, side, angle,

vertex, diameter) to identify and compare properties of

plane figures.

Geometry, Measurement

& Data 2.G.1, 3.G.1 174

450

Determine the area of rectangles, squares, and

composite figures using nonstandard units, grids, and

standard units in number and word problems.

Geometry, Measurement

& Data

3.MD.5.a,

3.MD.5.b,

3.MD.6,

3.MD.7.b,

3.MD.7.d,

3.MD.8, 3.G.2,

4.MD.3

192

450

Use models to develop the relationship between the

total distance around a figure and the formula for

perimeter; find perimeter using the formula in number

and word problems.

Geometry, Measurement

& Data 4.MD.3 1018

460

Determine the value of sets of coins and bills using cent

sign and dollar sign appropriately. Create equivalent

amounts with different coins and bills.

Geometry, Measurement

& Data

2.MD.8,

4.MD.2 147

460

Read, write, and compare whole numbers from 10,000

to less than one million using standard and expanded

notation.

Number & Operations 4.NBT.2 152

470 Describe data using the mode. Statistics & Probability 6.SP.2 135

470 Estimate and compute the cost of items greater than

$1.00; make change.

Geometry, Measurement

& Data 2.MD.8 148

470 Rewrite and compare decimals to fractions (tenths and

hundredths) with and without models and pictures. Number & Operations 4.NF.6 157

470

Use concepts of positive numbers, negative numbers,

and zero (e.g., on a number line, in counting, in

temperature, in “owing”) to describe quantities in

number and word problems.

Number & Operations 6.NS.5,

6.NS.6.a 169

470

Read and write word names for rational numbers

in decimal form to the hundredths place or the

thousandths place.

Number & Operations 5.NBT.3.a 648

470

Apply appropriate types of estimation for number and

word problems that include estimating products and

quotients.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.8,

4.OA.3 1009

470 Indicate and compare the place value of each digit in a

multidigit whole number or decimal. Number & Operations 4.NBT.1,

5.NBT.1 1014

470 Add multidigit numbers with regrouping in number and

word problems. Number & Operations 4.NBT.4 1015

480 Organize, display, and interpret information in bar

graphs.

Geometry, Measurement

& Data 3.MD.3 134

Appendices 109

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

480 Organize, display, and interpret information in graphs

containing scales that represent multiple units.

Geometry, Measurement

& Data 3.MD.3 136

480

Use a coordinate grid to solve number and word

problems. Describe the path between given points on

the plane.

Geometry, Measurement

& Data 5.G.2 547

480 Model the concept of the volume of a solid figure using

cubic units.

Geometry, Measurement

& Data

5.MD.3.a,

5.MD.3.b,

5.MD.4,

5.MD.5.a,

6.G.2

630

480 Use addition and subtraction to find unknown measures

of nonoverlapping angles.

Geometry, Measurement

& Data 4.MD.7, 7.G.5 1019

490 Subtract multidigit numbers with regrouping in number

and word problems. Number & Operations 4.NBT.4 1016

500 Use order of operations including parentheses and other

grouping symbols to simplify numerical expressions.

Algebraic Thinking,

Patterns & Proportional

Reasoning

5.OA.1 167

520 Organize, display, and interpret information in line plots

with a horizontal scale in fractional units.

Geometry, Measurement

& Data

3.MD.4,

4.MD.4,

5.MD.2,

S.ID.1

1012

530 Estimate and compute products of whole numbers with

multidigit factors. Number & Operations 4.NBT.5,

5.NBT.5 170

530

Use manipulatives, pictorial representations, and

appropriate vocabulary (e.g., face, edge, vertex, and

base) to identify and compare properties of solid

figures.

Geometry, Measurement

& Data 2.G.1 175

530 Identify and draw angles (acute, right, obtuse, and

straight).

Geometry, Measurement

& Data 4.G.1 202

530 Use reasoning with equivalent ratios to solve number

and word problems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

6.RP.3.d 551

550

Graph or identify simple inequalities using symbol

notation ., ,, ø, ù, and Þ in number and word

problems.

Expressions & Equations,

Algebra, Functions 6.EE.8 604

560

Use grids to develop the relationship between the total

numbers of square units in a rectangle and the length

and width of the rectangle (l x w); find area using the

formula in number and word problems.

Geometry, Measurement

& Data

3.MD.7.a,

3.MD.7.c,

3.OA.5,

5.NF.4.b

191

110 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

560 Use the distributive property to represent and simplify

numerical expressions.

Algebraic Thinking,

Patterns & Proportional

Reasoning

3.OA.5,

3.MD.7.c,

4.NBT.5,

4.NBT.6,

5.NBT.6,

5.NBT.7,

6.NS.4

578

560 Identify the nets for prisms, pyramids, cylinders, and

cones in geometric and applied problems.

Geometry, Measurement

& Data 6.G.4 645

580 Estimate and compute sums and differences with

decimals. Number & Operations 5.NBT.7,

6.NS.3, 7.EE.3 201

580 Identify the number of lines of symmetry in a figure and

draw lines of symmetry.

Geometry, Measurement

& Data 4.G.3 615

580 Solve multistep number and word problems using the

four operations. Number & Operations 4.OA.3 1013

590 Add and subtract decimals using models and pictures

to explain the process and record the results. Number & Operations 5.NBT.7 158

590 Construct or complete a table of values to solve

problems associated with a given relationship.

Algebraic Thinking,

Patterns & Proportional

Reasoning

4.MD.1,

4.OA.5 180

590 Write equivalent fractions with smaller or larger

denominators. Number & Operations 4.NF.5,

5.NF.5.b 668

600 Find the fractional part of a whole number or fraction

with and without models and pictures. Number & Operations

5.NF.4.a,

5.NF.4.b,

5.NF.6.

160

600

Round decimals to a given place value; round fractions

and mixed numbers to a whole number or a given

fractional place value.

Number & Operations 5.NBT.4 164

600

Read, write, and compare numbers with decimal place

values to the thousandths place or numbers greater

than one million.

Number & Operations 5.NBT.3.a,

5.NBT.3.b 195

600 Use exponential notation and repeated multiplication to

describe and simplify exponential expressions.

Expressions & Equations,

Algebra, Functions 6.EE.1 220

600 Estimate products and quotients of decimals or of

mixed numbers.

Expressions & Equations,

Algebra, Functions 7.EE.3 669

610 Find multiples, common multiplies, and the least

common multiple of numbers; explain.

Algebraic Thinking,

Patterns & Proportional

Reasoning

4.OA.4,

6.NS.4 221

610 Distinguish between a population and a sample and

draw conclusions about the sample (random or biased). Statistics & Probability 7.SP.1, S.IC.1,

S.IC.3 314

Appendices 111

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

610 Model and identify mixed numbers and their equivalent

fractions. Number & Operations

4.NF.3.b,

4.NF.3.c,

5.NF.3

546

610

Identify and classify triangles according to the

measures of the interior angles and the lengths of the

sides; relate triangles based upon their hierarchical

attributes.

Geometry, Measurement

& Data

4.G.2, 5.G.3,

5.G.4 624

610 Estimate sums and differences with fractions and

mixed numbers. Number & Operations 5.NF.2, 7.EE.3 675

610 Recognize that a statistical question is one that will

require gathering data that has variability. Statistics & Probability 6.SP.1 1033

620 Identify the place value of each digit in a multidigit

numeral to the thousandths place. Number & Operations 5.NBT.1,

5.NBT.3a 154

620 Translate between models or verbal phrases and

numerical expressions.

Algebraic Thinking,

Patterns & Proportional

Reasoning

5.OA.2 1020

620

Add and subtract fractions and mixed numbers using

models and pictures to explain the process and record

the results in number and word problems.

Number & Operations 4.NF.3.d,

4.NF.5, 5.NF.2 1023

630

Use models to write equivalent fractions, including

using composition or decomposition or showing

relationships among halves, fourths, and eighths, and

thirds and sixths.

Number & Operations

3.NF.3.a,

3.NF.3.b,

4.NF.1

116

640 Calculate distances from scale drawings and maps.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.G.1 317

650

Solve one-step linear equations and inequalities and

graph solutions of the inequalities on a number line in

number and word problems.

Expressions & Equations,

Algebra, Functions 6.EE.7 208

650

Recognize and use patterns in powers of ten (with

or without exponents) to multiply and divide whole

numbers and decimals.

Number & Operations 5.NBT.2 633

670

Add and subtract fractions and mixed numbers with like

denominators (without regrouping) in number and word

problems.

Number & Operations

4.MD.4,

4.NF.3.a,

4.NF.3.b,

4.NF.3.c,

4.NF.3.d

199

680 Identify, draw, and name: points, rays, line segments,

lines, and planes.

Geometry, Measurement

& Data

4.G.1,

4.MD.5.a,

G.CO.1

173

680

Use models or points in the coordinate plane to

illustrate, recognize, or describe rigid transformations

(translations, reflections, and rotations) of plane figures.

Geometry, Measurement

& Data

G.CO.2,

G.CO.3 178

112 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

680

Name polygons by the number of sides. Distinguish

quadrilaterals based on properties of their sides

or angles; relate quadrilaterals based upon their

hierarchical attributes.

Geometry, Measurement

& Data

3.G.1, 4.G.2,

5.G.3, 5.G.4 620

690 Estimate and solve division problems with multidigit

divisors; explain solution. Number & Operations 5.NBT.6,

6.NS.2 171

690 Find factors, common factors, and the greatest common

factor of numbers; explain.

Algebraic Thinking,

Patterns & Proportional

Reasoning

4.OA.4,

6.NS.4 222

690 Solve two-step linear equations and inequalities and

graph solutions of the inequalities on a number line.

Expressions & Equations,

Algebra, Functions

7.EE.4.a,

7.EE.4.b,

7.G.5

275

700

Use geometric models and equations to investigate the

meaning of the square of a number and the relationship

to its positive square root. Know perfect squares to 625.

Algebraic Thinking,

Patterns & Proportional

Reasoning

8.EE.2,

N.RN.1 265

700 Multiply or divide two decimals or a decimal and a

whole number in number and word problems. Number & Operations 5.NBT.7,

6.NS.3 608

700 Determine the complement of an event. Statistics & Probability S.CP.1 646

710 Compare and order fractions using common numerators

or denominators. Number & Operations 4.NF.2 155

710

Convert fractions and terminating decimals to the

thousandths place to equivalent forms without models;

explain the equivalence.

Number & Operations 7.NS.2.d,

8.NS.1 196

710

Use remainders in problem-solving situations and

interpret the remainder with respect to the original

problem.

Number & Operations 4.OA.3 266

710

Represent division of a unit fraction by a whole number

or a whole number by a unit fraction using models to

explain the process in number and word problems.

Number & Operations

5.NF.7.a,

5.NF.7.b,

5.NF.5.c

1026

720 Read, write, or model numbers in expanded form using

decimal fractions or exponents. Number & Operations 5.NBT.3.a 226

720 Write a proportion to model a word problem; solve

proportions.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.RP.3 263

720

Estimate the square root of a number between two

consecutive integers with and without models. Use a

calculator to estimate the square root of a number.

Number & Operations 8.NS.2 297

720 Describe a data set by its number of observations, what

is being measured, and the units of measurement. Statistics & Probability 6.SP.5.a,

6.SP.5.b 1035

Appendices 113

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

720

Indicate the probability of a chance event with or

without models as certain, impossible, more likely, less

likely, or neither likely nor unlikely using benchmark

probabilities of 0, 1/2, and 1.

Statistics & Probability 7.SP.5,

7.SP.7.b 1045

740 Identify prime and composite numbers less than 100.

Algebraic Thinking,

Patterns & Proportional

Reasoning

4.OA.4 223

750 Describe the effect of operations on size and order of

numbers.

Algebraic Thinking,

Patterns & Proportional

Reasoning

5.OA.2,

5.NF.5.a,

5.NF.5.b

168

750

Identify and label the vertex, rays, and interior

and exterior of an angle. Use appropriate naming

conventions to identify angles.

Geometry, Measurement

& Data G.CO.1 203

750 Translate between models or verbal phrases and

algebraic expressions.

Expressions & Equations,

Algebra, Functions

6.EE.2.a,

N.Q.2,

A.SSE.1.a,

A.SSE.1.b

218

750

Determine the sample space for an event using

counting strategies (include tree diagrams,

permutations, combinations, and the Fundamental

Counting Principle).

Statistics & Probability 7.SP.8.a,

7.SP.8.b 251

750

Describe or compare the relationship between

corresponding terms in two or more numerical patterns

or tables of ratios.

Algebraic Thinking,

Patterns & Proportional

Reasoning

5.OA.3,

6.RP.3.a 1021

750 Multiply and divide decimals using models and pictures

to explain the process and record the results. Number & Operations 5.NBT.7 1022

770 Simplify numerical expressions that may contain

exponents.

Expressions & Equations,

Algebra, Functions 6.EE.2.c 236

770 Identify corresponding parts of similar and congruent

figures.

Geometry, Measurement

& Data

8.G.2, 8.G.4,

8.G.5 241

780 Analyze graphs, identify situations, or solve problems

with varying rates of change.

Expressions & Equations,

Algebra, Functions 8.F.5 209

780

Identify additive inverses (opposites) and multiplicative

inverses (reciprocals, including zero) and use them to

solve number and word problems.

Number & Operations

6.NS.6.a,

7.NS.1.a,

7.NS.1.b

623

780

Use geometric models and equations to investigate the

meaning of the cube of a number and the relationship

to its cube root.

Algebraic Thinking,

Patterns & Proportional

Reasoning

8.EE.2,

N.RN.1 1048

790 Add and subtract fractions and mixed numbers with

unlike denominators in number and word problems. Number & Operations

4.NF.5,

5.MD.2,

5.NF.1, 5.NF.2

231

790 Compare and order integers with and without models. Number & Operations 6.NS.7.b 235

114 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

790 Organize, display, and interpret information in

histograms. Statistics & Probability 6.SP.4,

S.ID.1 278

800 Describe data using the median. Geometry, Measurement

& Data

6.SP.2,

6.SP.5.c 183

800

Given a list of ordered pairs in a table or graph, identify

either verbally or algebraically the rule used to generate

and record the results.

Expressions & Equations,

Algebra, Functions 6.EE.9 244

800 Model or compute with integers using addition or

subtraction in number and word problems. Number & Operations 7.NS.1.b,

7.NS.1.c 261

800 Write a linear equation or inequality to represent a

given number or word problem; solve.

Expressions & Equations,

Algebra, Functions

6.EE.7,

7.EE.4.a,

7.EE.4.b,

A.CED.1,

A.CED.3

276

800

Organize, display, and interpret information in scatter

plots. Approximate a trend line and identify the

relationship as positive, negative, or no correlation.

Statistics & Probability 8.SP.1 311

800 Represent division of whole numbers as a fraction in

number and word problems. Number & Operations 5.NF.3 1024

800

Represent division of fractions and mixed numbers with

and without models and pictures in number and word

problems; describe the inverse relationship between

multiplication and division.

Number & Operations 6.NS.1 1028

800 Identify parts of a numerical or algebraic expression. Expressions & Equations,

Algebra, Functions 6.EE.2.b 1031

800

Interpret probability models for data from simulations

or for experimental data presented in tables and graphs

(frequency tables, line plots, bar graphs).

Statistics & Probability 7. SP.7.a,

7.SP.7.b 1046

800 Identify and use appropriate scales and intervals in

graphs and data displays.

Geometry, Measurement

& Data N.Q.1 1057

810

Write an equation to describe the algebraic relationship

between two defined variables in number and word

problems, including recognizing which variable is

dependent.

Expressions & Equations,

Algebra, Functions

6.EE.9,

F.BF.1.a 210

810

Draw circles; identify and determine the relationships

between the radius, diameter, chord, center, and

circumference.

Geometry, Measurement

& Data G.CO.1 237

810 Model or compute with integers using multiplication or

division in number and word problems. Number & Operations 7.NS.2.a,

7.NS.2.b 262

810 Identify linear and nonlinear relationships in data sets. Statistics & Probability 8.SP.1 572

Appendices 115

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

810

Determine and interpret the components of algebraic

expressions including terms, factors, variables,

coefficients, constants, and parts of powers in number

and word problems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

A.SSE.1.a,

A.SSE.1.b 1055

820 Multiply two fractions or a fraction and a whole number

in number and word problems. Number & Operations 5.NF.6,

5.MD.2 224

820

Convert measures of length, area, capacity, weight,

and time expressed in a given unit to other units in

the same measurement system in number and word

problems.

Geometry, Measurement

& Data

4.MD.1,

4.MD.2,

5.MD.1,

6.RP.3.d

258

820

Rewrite or simplify algebraic expressions including the

use of the commutative, associative, and distributive

properties, and inverses and identities in number and

word problems.

Expressions & Equations,

Algebra, Functions

6.EE.3,

6.EE.4,

7.EE.1, 7.EE.2

300

820

Locate, given the coordinates of, and graph points

which are the results of rigid transformations in all

quadrants of the coordinate plane; describe the path

of the motion using geometric models or appropriate

terms.

Geometry, Measurement

& Data

6.NS.6.b,

G.CO.2,

G.CO.4

616

820 Solve number and word problems using percent

proportion, percent equation, or ratios.

Algebraic Thinking,

Patterns & Proportional

Reasoning

6.RP.3.c,

7.RP.3 622

820

Determine the degree of a polynomial and indicate the

coefficients, constants, and number of terms in the

polynomial.

Expressions & Equations,

Algebra, Functions A.SSE.1.a 639

820

Use the commutative, associative, and distributive

properties, and inverses and identities to solve number

and word problems with rational numbers.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.NS.1.d,

7.NS.2.a,

7.NS.2.b,

7.NS.2.c

1039

830 Calculate unit rates in number and word problems,

including comparison of units rates.

Algebraic Thinking,

Patterns & Proportional

Reasoning

6.RP.2,

6.RP.3.b 233

830

Determine the probability from experimental results

or compare theoretical probabilities and experimental

results.

Statistics & Probability 7.SP.6 249

830 Use the definition of rational numbers to convert

decimals and fractions to equivalent forms. Number & Operations 7.NS.2.d,

8.NS.1 1040

840 Compare and order rational numbers with and without

models. Number & Operations 6.NS.7.a,

6.NS.7.b 260

840 Evaluate algebraic expressions in number and word

problems.

Expressions & Equations,

Algebra, Functions 6.EE.2.c 274

116 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

840

Use models to find volume for prisms and cylinders as

the product of the area of the base (B) and the height.

Calculate the volume of prisms in number and word

problems.

Geometry, Measurement

& Data

5.MD.5.a,

5.MD.5.b,

6.G.2, 7.G.6,

G.GMD.1

289

850 Describe data using the mean. Statistics & Probability 6.SP.2,

6.SP.5.c 214

850 Draw and measure angles using a protractor.

Understand that a circle measures 360 degrees.

Geometry, Measurement

& Data

4.MD.5.a,

4.MD.5.b,

4.MD.6

217

850 Locate points in all quadrants of the coordinate plane

using ordered pairs in number and word problems. Statistics & Probability

6.NS.6.b,

6.NS.6.c,

6.NS.8, 6.G.3

247

850

Describe, use, and compare real numbers. Use the

definition of rational numbers to derive and distinguish

irrational numbers.

Number & Operations 8.NS.1,

8.NS.2 564

850 Identify relations as directly proportional, linear, or

nonlinear using rules, tables, and graphs.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.RP.2.a,

8.F.3, 8.F.5 567

850 Use the discriminant to determine the number and

nature of the roots of a quadratic equation.

Expressions & Equations,

Algebra, Functions A.REI.4.b 591

860 Make predictions based on theoretical probabilities or

experimental results. Statistics & Probability 7.SP.6 316

860 Identify from a set of numbers which values satisfy a

given equation or inequality.

Expressions & Equations,

Algebra, Functions

6.EE.5,

6.EE.6, 6.EE.8 1032

870 Divide two fractions or a fraction and a whole number

in number or word problems. Number & Operations 5.MD.2,

6.NS.1 230

870 Calculate or estimate the percent of a number including

discounts, taxes, commissions, and simple interest.

Algebraic Thinking,

Patterns & Proportional

Reasoning

6.RP.3.c,

7.RP.3 264

870 Represent multiplication or division of mixed numbers

with and without models and pictures. Number & Operations 5.NF.6 1025

880 Describe cross-sectional views of three-dimensional

figures.

Geometry, Measurement

& Data

7.G.3,

G.GMD.4 556

880 Calculate unit rates of ratios that include fractions to

make comparisons in number and word problems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.RP.1 1037

880 Construct and interpret a two-way table to display two

categories of data from the same source. Statistics & Probability 8.SP.4 1054

880

Use set notation to describe domains, ranges, and

the intersection and union of sets. Identify cardinality

of sets, equivalent sets, disjoint sets, complement, or

subsets.

Expressions & Equations,

Algebra, Functions S.CP.1 1072

Appendices 117

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

890 Write equations to represent direct variation and use

direct variation to solve number and word problems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.RP.2.c,

A.CED.2 362

890 Perform multistep operations with rational numbers

(positive and negative) in number and word problems. Number & Operations

7.EE.3,

7.NS.1.b,

7.NS.1.c,

7.NS.1.d,

7.NS.2.a,

7.NS.3

642

890 Make predictions based on results from surveys and

samples. Statistics & Probability 7.SP.2 1043

900 Solve number and word problems involving percent

increase and percent decrease.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.RP.3 295

900 Graphically solve systems of linear equations. Expressions & Equations,

Algebra, Functions

8.EE.8.a,

8.EE.8.b,

8.EE.8.c,

A.REI.6

309

900

Use the distance formula to find the distance between

two points. Use the midpoint formula to find the

coordinates of the midpoint of a segment.

Geometry, Measurement

& Data

G.CO.11,

G.SRT.1.b,

G.GPE.4,

G.GPE.7

483

900

Use pictorial representations and appropriate

vocabulary to identify relationships with circles

(e.g., tangent, secant, concentric circles, inscribe,

circumscribe, semicircles, and minor and major arcs) in

number and word problems.

Geometry, Measurement

& Data

G.C.2, G.C.3,

G.MG.1 519

900 Determine the absolute value of a number with and

without models in number and word problems. Number & Operations 6.NS.7.c 636

900

Given a proportional relationship represented by tables,

graphs, models, or algebraic or verbal descriptions,

identify the unit rate (constant of proportionality).

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.RP.2.b,

7.RP.2.d 1038

910

Write whole numbers in scientific notation; convert

scientific notation to standard form; investigate the

uses of scientific notation.

Expressions & Equations,

Algebra, Functions 8.EE.3, 8.EE.4 259

910 Write a problem given a simple linear equation or

inequality.

Expressions & Equations,

Algebra, Functions

7.EE.4.a,

7.EE.4.b 277

910

Describe, extend, and analyze a wide variety of

geometric and numerical patterns, such as Pascal’s

triangle or the Fibonacci sequence.

Algebraic Thinking,

Patterns & Proportional

Reasoning

A.APR.5 308

920 Determine the probability of compound events (with and

without replacement). Statistics & Probability 7.SP.8.a,

7.SP.8.c 285

118 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

920 Use proportions to express relationships between

corresponding parts of similar figures.

Expressions & Equations,

Algebra, Functions 8.EE.6 292

920 Determine the quartiles or interquartile range for a set

of data. Statistics & Probability

6.SP.3,

6.SP.5.c,

S.ID.2

559

920 Multiply or divide with mixed numbers in number and

word problems. Number & Operations 5.NF.6 609

920

Determine the mean absolute deviation (MAD) for one

or more sets of data. Describe the meaning of MAD for

given data sets.

Statistics & Probability 6.SP.3,

6.SP.5.c 1000

920 Determine the volume of composite figures in number

and word problems.

Geometry, Measurement

& Data 5.MD.5.c 1027

920 Contrast statements about absolute values of integers

with statements about integer order. Number & Operations 6.NS.7.d 1030

920

Use frequency tables, dot plots, and other graphs to

determine the shape, center, and spread of a data

distribution.

Statistics & Probability

6.SP.2, 6.SP.3,

6.SP.4,

6.SP.5.a,

6.SP.5.b

1034

930

Generate a set of ordered pairs using a rule which is

stated in verbal, algebraic, or table form; generate a

sequence given a rule in verbal or algebraic form.

Algebraic Thinking,

Patterns & Proportional

Reasoning

5.OA.3,

6.RP.3.a 243

930

Investigate and determine the relationship between

the diameter and the circumference of a circle and the

value of pi; calculate the circumference of a circle.

Geometry, Measurement

& Data 7.G.4 254

930 Use ordered pairs derived from tables, algebraic rules,

or verbal descriptions to graph linear functions.

Expressions & Equations,

Algebra, Functions

7.RP.2.a,

8.EE.5,

8.F.3, 8.F.4,

A.REI.10,

F.IF.7.a

562

940

Recognize and extend arithmetic sequences and

geometric sequences. Identify the common difference

or common ratio.

Algebraic Thinking,

Patterns & Proportional

Reasoning

F.BF.2,

F.LE.1.a,

F.LE.2

656

940

Determine a simulation, such as random numbers,

spinners, and coin tosses, to model frequencies for

compound events.

Statistics & Probability

7.SP.8.c,

S.IC.2,

S.MD.6

1047

950

Describe data using or selecting the appropriate

measure of central tendency; choose a measure of

central tendency based on the shape of the data

distribution.

Statistics & Probability 6.SP.3,

6.SP.5.d 281

Appendices 119

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

950

Solve linear equations using the associative,

commutative, distributive, and equality properties and

justify the steps used.

Expressions & Equations,

Algebra, Functions

7.EE.4.a,

8.EE.7.a,

8.EE.7.b,

A.CED.1,

A.REI.1,

A.REI.3

332

950 Use dimensional analysis to rename quantities or rates. Geometry, Measurement

& Data

N.Q.1, N.Q.2,

G.MG.2 671

960 Organize, display, and interpret information in box-and-

whisker plots. Statistics & Probability 6.SP.4, S.ID.1 310

970 Approximate a linear model that best fits a set of data;

use the linear model to make predictions. Statistics & Probability

8.SP.2, 8.SP.3,

S.ID.6.a,

S.ID.6.c

565

970 Determine whether a linear equation has one solution,

infinitely many solutions, or no solution.

Expressions & Equations,

Algebra, Functions 8.EE.7.a 1049

970 Use appropriate units to model, solve, and estimate

multistep word problems.

Geometry, Measurement

& Data N.Q.1, N.Q.2 1056

980 Model and solve linear inequalities using the properties

of inequality in number and word problems.

Expressions & Equations,

Algebra, Functions

7.EE.4.b,

A.CED.1,

A.REI.3

644

990 Determine and use scale factors to reduce and enlarge

drawings on grids to produce dilations.

Geometry, Measurement

& Data

7.G.1, 8.G.3,

G.SRT.1.b 287

990

Determine precision unit, accuracy, and greatest

possible error of a measuring tool. Apply significant

digits in meaningful contexts.

Geometry, Measurement

& Data N.Q.3 322

990 Evaluate absolute value expressions. Numbers & Operations 6.NS.8,

7.NS.1.c 323

990

Write and solve systems of linear equations in two

or more variables algebraically in number and word

problems.

Expressions & Equations,

Algebra, Functions

8.EE.8.b,

8.EE.8.c,

A.REI.6,

A.CED.3

333

1000 Use rules of exponents to simplify numeric and

algebraic expressions.

Expressions & Equations,

Algebra, Functions

8.EE.1,

A.SSE.1.b,

A.SSE.2,

A.SSE.3.c

296

1000 Estimate and calculate using numbers expressed in

scientific notation.

Expressions & Equations,

Algebra, Functions 8.EE.3, 8.EE.4 298

1000 Identify and interpret the intercepts of a linear relation

in number and word problems.

Expressions & Equations,

Algebra, Functions

8.F.4, 8.SP.3,

F.IF.4, F.IF.7.a,

S.ID.7

307

1000

Recognize and apply algebra techniques to solve rate

problems including distance, work, density, and mixture

problems.

Expressions & Equations,

Algebra, Functions

F.LE.1.b,

A.REI.3,

G.MG.2

574

120 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1000 Estimate and calculate areas with scale drawings and

maps.

Algebraic Thinking,

Patterns & Proportional

Reasoning

7.G.1 585

1000 Solve a literal equation for an indicated variable. Expressions & Equations,

Algebra, Functions

A.CED.4,

A.REI.3 659

1000 Recognize conditions of side lengths that determine a

unique triangle, more than one triangle, or no triangle.

Geometry, Measurement

& Data 7.G.2 1041

1000

Recognize closure of number systems under a

collection of operations and their properties with and

without models; extend closure to analogous algebraic

systems.

Algebraic Thinking,

Patterns & Proportional

Reasoning

A.APR.1,

N.RN.3,

A.APR.7

1062

1010 Define and identify alternate interior, alternate exterior,

corresponding, adjacent and vertical angles.

Geometry, Measurement

& Data 7.G.5 240

1010

Use models to develop formulas for finding areas of

triangles, parallelograms, trapezoids, and circles in

number and word problems.

Geometry, Measurement

& Data 6.G.1 256

1010 Use models to investigate the concept of the

Pythagorean Theorem.

Geometry, Measurement

& Data 8.G.6 271

1020 Define and identify complementary and supplementary

angles.

Geometry, Measurement

& Data 7.G.5 239

1020

Graph quadratic functions. Identify and interpret

the intercepts, maximum, minimum, and the axis of

symmetry.

Expressions & Equations,

Algebra, Functions

F.IF.4, F.IF.7.a,

A.CED.2 335

1020 Solve quadratic equations using properties of equality. Expressions & Equations,

Algebra, Functions

A.CED.1,

A.REI.4.b,

N.CN.7

374

1030

Locate, given the coordinates of, and graph plane

figures which are the results of translations or

reflections in all quadrants of the coordinate plane.

Geometry, Measurement

& Data

8.G.1.a,

8.G.1.b,

8.G.1.c,

8.G.3, G.CO.4,

G.CO.5

270

1040

Calculate the areas of triangles, parallelograms,

trapezoids, circles, and composite figures in number

and word problems.

Geometry, Measurement

& Data

6.G.1, 7.G.4,

7.G.6 257

1040 Use nets or formulas to find the surface area of prisms,

pyramids, and cylinders in number and word problems.

Geometry, Measurement

& Data 6.G.4, 7.G.6 318

1040

Convert between different representations of relations

and functions using tables, the coordinate plane, and

algebraic or verbal statements.

Expressions & Equations,

Algebra, Functions

A.REI.10,

F.IF.4, F.LE.2,

A.CED.2

366

1040

Use properties, definitions, and theorems of angles

and lines to solve problems related to angle bisectors,

segment bisectors, and perpendicular bisectors.

Geometry, Measurement

& Data G.CO.9 491

Appendices 121

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1040

Use properties, definitions, and theorems to determine

the congruency or similarity of polygons in order to

solve problems.

Geometry, Measurement

& Data

G.CO.6,

G.SRT.2 497

1040 Use inverse, combined, and joint variation to solve

problems.

Expressions & Equations,

Algebra, Functions

A.CED.2,

A.CED.3 571

1040

Use the definition of a logarithm to convert between

logarithmic and exponential forms; evaluate logarithmic

expressions.

Expressions & Equations,

Algebra, Functions F.LE.4 1068

1050

Use the Pythagorean Theorem and its converse to

solve number and word problems, including finding the

distance between two points.

Geometry, Measurement

& Data

8.G.7, 8.G.8,

G.SRT.4,

G.SRT.8,

G.GPE.1,

G.GPE.7

302

1050 Determine algebraically or graphically the solutions of a

linear inequality in two variables.

Expressions & Equations,

Algebra, Functions

A.REI.3,

A.REI.12 306

1050 Add, subtract, and multiply polynomials.

Algebraic Thinking,

Patterns & Proportional

Reasoning

A.APR.1 325

1050

Evaluate expressions and use formulas to solve number

and word problems involving exponential functions;

classify exponential functions as exponential growth or

decay.

Expressions & Equations,

Algebra, Functions

A.SSE.3.c,

A.CED.1,

F.IF.8.b,

F.LE.1.c

339

1050 Determine the effects of changes in slope and/or

intercepts on graphs and equations of lines.

Expressions & Equations,

Algebra, Functions

F.BF.1.b,

F.BF.3 350

1050 Identify outliers and determine their effect on the mean,

median, and range of a set of data. Statistics & Probability

6.SP.3,

6.SP.5.c,

6.SP.5.d,

S.ID.3

561

1050

Select the appropriate measure of variability; choose a

measure of variability based on the presence of outliers,

clusters, and the shape of the data distribution.

Statistics & Probability 6.SP.5.d 1036

1060

Use models to investigate the relationship of the volume

of a cone to a cylinder and a pyramid to a prism with

the same base and height.

Geometry, Measurement

& Data

G.GMD.1,

G.GMD.3 319

1070

Use a variety of triangles, quadrilaterals, and other

polygons to draw conclusions about the sum of the

measures of the interior angles.

Geometry, Measurement

& Data

7.G.2, 8.G.5,

G.CO.10 204

1070

Locate, given the coordinates of, and graph plane

figures which are the results of rotations (multiples of

90 degrees) with respect to a given point.

Geometry, Measurement

& Data

8.G.1.a,

8.G.1.b,

8.G.1.c,

8.G.3, G.CO.4,

G.CO.5

303

122 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1070 Calculate the volume of cylinders, pyramids, and cones

in number and word problems.

Geometry, Measurement

& Data

7.G.6, 8.G.9,

G.GMD.3 320

1070

Use properties of triangles to solve problems related to

altitudes, perpendicular bisectors, angle bisectors, and

medians.

Geometry, Measurement

& Data G.CO.10 506

1070 Solve equations involving powers and roots by using

inverse relationships.

Expressions & Equations,

Algebra, Functions A.REI.4.b 569

1070 Use combinations and permutations to determine the

sample space of compound events. Statistics & Probability S.CP.9 588

1070 Make inferences about a population based on a sample

and compare variation in multiple samples. Statistics & Probability 7.SP.2 1042

1070

Verify how properties and relationships of geometric

figures are maintained or how they change through

transformations.

Geometry, Measurement

& Data

8.G.1.a,

8.G.1.b,

8.G.1.c, 8.G.2,

8.G.3, G.CO.4,

G.CO.6

1050

1070 Identify outliers and clusters in bivariate data in tables

and scatter plots. Statistics & Probability 8.SP.1 1053

1080 Write the equation of and graph linear relationships

given the slope and y-intercept.

Expressions & Equations,

Algebra, Functions 8.F.4, A.CED.2 345

1090 Find and interpret the maximum, the minimum, and the

intercepts of a quadratic function.

Expressions & Equations,

Algebra, Functions

F.IF.8.a,

A.SSE.3.b,

F.IF.4

375

1090

Find indicated terms, the common ratio, or the common

difference using recursive sequence formulas; write

recursive sequence formulas.

Expressions & Equations,

Algebra, Functions

F.IF.3, F.BF.1.a,

F.BF.2 464

1090 Describe or graph plane figures which are the results of

a sequence of transformations.

Geometry, Measurement

& Data

8.G.2, 8.G.4,

G.CO.3,

G.CO.5,

G.CO.7,

G.SRT.2, G.C.1

1051

1100

Derive a linear equation that models a set of data (line

of best fit) using calculators. Use the model to make

predictions.

Statistics & Probability S.ID.6.a,

S.ID.6.b 342

1100 Determine the measure of an angle in degree mode or

in radian mode.

Geometry, Measurement

& Data

G.C.5, F.TF.1,

F.TF.2 424

1100

Compare data and distributions of data, numerical

and contextual, to draw conclusions, considering the

measures of center and measures of variability.

Statistics & Probability 7.SP.3, 7.SP.4,

S.ID.2, S.ID.3 1044

Appendices 123

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1100 Calculate the surface area and volume of a sphere in

number and word problems.

Geometry, Measurement

& Data

8.G.9,

G.GMD.3 1052

1100 Describe three-dimensional figures generated by

rotations of plane figures in space.

Geometry, Measurement

& Data G.GMD.4 1064

1100

Express data in a two-way table. Calculate the marginal

distribution, marginal and conditional probabilities, or

basic probabilities.

Statistics & Probability S.ID.5, S.CP.4,

S.MD.7 1069

1110 Write the equation of and graph linear relationships

given two points on the line.

Expressions & Equations,

Algebra, Functions

F.LE.2,

A.CED.2 347

1110 Use slopes to determine if two lines are parallel or

perpendicular.

Geometry, Measurement

& Data

G.GPE.4,

G.GPE.5,

G.CO.11,

G.SRT.1.a

532

1120 Divide polynomials by monomial divisors. Expressions & Equations,

Algebra, Functions A.APR.6 326

1120 Graph absolute value functions and their corresponding

inequalities.

Expressions & Equations,

Algebra, Functions F.IF.4, F.IF.7.b 398

1120

Use properties, definitions, and theorems of

quadrilaterals (parallelograms, rectangles, rhombi,

squares, trapezoids, kites) to solve problems.

Geometry, Measurement

& Data G.CO.11 500

1120

Transform (translate, reflect, rotate, dilate) polygons in

the coordinate plane; describe the transformation in

simple algebraic terms.

Geometry, Measurement

& Data

8.G.3,

G.SRT.1.a,

G.SRT.1.b,

G.SRT.2

534

1120

Use properties, definitions, and theorems to solve

problems about rigid transformations and dilations of

plane figures.

Geometry, Measurement

& Data

G.SRT.1.a,

G.SRT.1.b,

G.SRT.2,

G.SRT.3

1063

1120

Find the coordinates of a point on a segment between

given endpoints that partitions the segment by a given

ratio.

Geometry, Measurement

& Data G.GPE.6 1065

1130 Factor quadratic polynomials, including special

products.

Expressions & Equations,

Algebra, Functions A.SSE.2 327

1130 Write the equation of and graph linear relationships

given the slope and one point on the line.

Expressions & Equations,

Algebra, Functions A.CED.2 346

1140

Find the slope of a line given two points on a line, a

table of values, the graph of the line, or an equation of

the line in number and word problems.

Expressions & Equations,

Algebra, Functions

8.EE.6, 8.F.4,

F.IF.6 343

1140

Describe the slope of a line given in the context of a

problem situation; compare rates of change in linear

relationships represented in different ways.

Expressions & Equations,

Algebra, Functions

8.EE.5, 8.F.2,

8.F.4, 8.F.5,

8.SP.3, F.IF.4,

F.LE.1.b,

S.ID.7

344

124 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1140 Solve quadratic equations by graphing. Expressions & Equations,

Algebra, Functions

A.CED.1,

A.REI.11 370

1140

Use properties of circles to solve number and word

problems involving arcs formed by central angles or

inscribed angles.

Geometry, Measurement

& Data G.C.5, G.MG.1 523

1150 Use properties of right triangles to solve problems using

the relationships in special right triangles.

Geometry, Measurement

& Data G.SRT.4 514

1150 Use measures of arcs or central angles to find arc

length or sector area of a circle.

Geometry, Measurement

& Data G.C.5, F.TF.1 529

1150 Interpret and compare properties of linear functions,

graphs, and equations.

Expressions & Equations,

Algebra, Functions

8.F.2, 8.F.5,

F.IF.4, F.IF.7.a 568

1150 Solve systems of linear inequalities. Expressions & Equations,

Algebra, Functions A.REI.12 674

1160

Use properties, definitions, and theorems of angles and

lines to solve problems related to adjacent, vertical,

complementary, supplementary, and linear pairs of

angles.

Geometry, Measurement

& Data G.CO.9 489

1160

Determine whether a system of equations has one

solution, multiple solutions, infinitely many solutions,

or no solution using graphs, tables, and algebraic

methods; compare solutions of systems of equations.

Expressions & Equations,

Algebra, Functions

A.REI.5,

A.REI.6,

G.GPE.5

1058

1170

Use properties of triangles to solve problems related

to similar triangles and the relationships of their

corresponding parts.

Geometry, Measurement

& Data

G.CO.10,

G.SRT.2,

G.SRT.3,

G.SRT.4,

G.SRT.5,

G.SRT.6

503

1170 Use properties of triangles to solve problems related to

isosceles and equilateral triangles.

Geometry, Measurement

& Data

G.CO.10,

G.SRT.4 505

1170 Describe and simplify imaginary and complex numbers. Number & Operations N.CN.1,

A.REI.4.b 595

1180 Divide one polynomial by another of a lower degree

using either synthetic division or the division algorithm.

Expressions & Equations,

Algebra, Functions A.APR.6 358

1180

Use and interpret function notation in number and word

problems; determine a value of the function given an

element of the domain.

Expressions & Equations,

Algebra, Functions

F.IF.1, F.IF.2,

F.IF.5 593

1180 Add, subtract, multiply, and divide functions. Expressions & Equations,

Algebra, Functions F.BF.1.b 594

1190

Define and distinguish between relations and functions,

dependent and independent variables, and domain

and range; identify whether relations are functions

numerically and graphically.

Expressions & Equations,

Algebra, Functions 8.F.1, F.IF.1 330

Appendices 125

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1190 Use properties of triangles to solve problems related to

congruent triangles and their corresponding parts.

Geometry, Measurement

& Data

G.CO.8,

G.CO.10,

G.SRT.5

504

1190

Given a specific interval, find the average rate of

change of a function using a table, graph, or algebraic

description.

Expressions & Equations,

Algebra, Functions F.IF.6 1060

1200 Identify and interpret zeros of a quadratic function using

factoring in algebraic and word problems.

Expressions & Equations,

Algebra, Functions

F.IF.8.a,

A.SSE.3.a,

A.REI.4.b

336

1200 Solve exponential equations by rewriting expressions

with like bases.

Expressions & Equations,

Algebra, Functions A.REI.3 354

1200 Solve quadratic equations using the quadratic formula. Expressions & Equations,

Algebra, Functions

A.REI.4.a,

A.REI.4.b,

N.CN.7,

A.CED.1

373

1200

Write the equation of and graph exponential equations

or functions, including f (x ) 5 abx and f (x ) 5 a (1 1 r )x,

in number and word problems; identify and interpret

critical values.

Expressions & Equations,

Algebra, Functions

A.CED.2,

F.IF.4, F.IF.7.e,

F.LE.2,

A.CED.1

400

1200

Use properties, definitions, and theorems of angles and

lines to solve problems related to the segment addition

postulate and the angle addition postulate.

Geometry, Measurement

& Data

G.CO.1,

G.CO.9,

G.GPE.6

490

1200 Use properties of circles to solve problems related to

the equation of a circle, its center, and radius length.

Geometry, Measurement

& Data

G.GPE.1,

G.GPE.4 518

1200 Write the equation of a line parallel or perpendicular to

a given line through a given point.

Expressions & Equations,

Algebra, Functions

G.GPE.5,

A.CED.2 533

1200 Describe the intervals for which a function is increasing

or decreasing.

Expressions & Equations,

Algebra, Functions F.IF.4 1059

1210 Perform basic operations with complex numbers and

graph complex numbers. Number & Operations N.CN.2 355

1210 Find the sum of a finite series and of an infinite

geometric series in number and word problems.

Expressions & Equations,

Algebra, Functions A.SSE.4 466

1210 Use properties of right triangles to solve problems using

the geometric mean.

Geometry, Measurement

& Data G.SRT.4 512

1210

Use rules of exponents to rewrite or simplify

expressions with rational exponents or radicals and

interpret their meaning.

Number & Operations

A.SSE.3.c,

N.RN.1,

N.RN.2,

F.IF.8.b.,

A.SSE.1.b

631

1210

Use theorems about congruent chords and arcs and the

relationships of a radius of a circle to a tangent to solve

problems.

Geometry, Measurement

& Data G.C.2 653

126 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1210 Complete the square to identify characteristics of

relations or functions and verify graphically.

Expressions & Equations,

Algebra, Functions

A.REI.4.a,

A.SSE.3.b,

G.GPE.1

658

1210

Distinguish between types of events (conditional,

mutually exclusive, independent, dependent, etc.).

Use the appropriate formula to determine probabilities

of random phenomena using the addition rule,

multiplication rule, or Venn diagrams.

Statistics & Probability

S.CP.2, S.CP.3,

S.CP.4, S.CP.5,

S.CP.6, S.CP.7,

S.CP.8, S.CP.9

1073

1220 Solve systems of equations or inequalities algebraically

and graphically that include nonlinear relationships.

Expressions & Equations,

Algebra, Functions

A.REI.7,

A.REI.11,

A.CED.2

441

1220

Use properties, definitions, and theorems of polygons

to solve problems related to the interior and exterior

angles of a convex polygon.

Geometry, Measurement

& Data

G.CO.11,

G.C.3 496

1220 Use trigonometric ratios to represent relationships in

right triangles to solve number and word problems.

Geometry, Measurement

& Data

G.SRT.6,

G.SRT.7,

G.SRT.8,

G.MG.1,

G.MG.2,

G.MG.3,

G.SRT.10,

F.TF.8

515

1220 Identify transformations on nonlinear parent functions

using function notation, algebraic equations, or graphs.

Expressions & Equations,

Algebra, Functions

F.BF.1.b,

F.BF.3 637

1230

Recognize the effect of scale factors or ratios on areas

and volumes of similar geometric figures; use formulas

to solve number and word problems.

Geometry, Measurement

& Data

G.MG.3,

G.GMD.1 530

1230

Classify functions as linear, quadratic, rational, etc.,

based on their tabular, graphical, verbal, or algebraic

description; compare properties of two or more

functions represented in different ways.

Expressions & Equations,

Algebra, Functions

F.IF.9, F.BF.2,

F.LE.1.a,

F.LE.1.b,

F.LE.1.c,

F.LE.3, F.IF.4

1061

1230

Compare theoretical probabilities to results fromany

simulations or experiments (may also include Law of

Large Numbers).

Statistics & Probability

S.IC.2,

S.MD.6,

S.MD.7

1074

1240

Examine the graph of a polynomial function to identify

properties including end behavior, real and non-real

zeros, odd and even degree, and relative maxima or

minima. Use the zeros and other properties to graph the

polynomial function.

Expressions & Equations,

Algebra, Functions

A.APR.3,

F.IF.4, F.IF.7.c 377

1240

Derive a quadratic or exponential function that models

a set of data (curve of best fit) using calculators. Use

the model to make predictions.

Statistics & Probability S.ID.6.a,

S.ID.6.b 408

Appendices 127

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1240 Describe and use the symmetry of a graph and

determine whether a function is even, odd, or neither.

Expressions & Equations,

Algebra, Functions F.BF.3, F.IF.4 432

1240 Define and use the normal distribution curve to model a

set of data; estimate the area under the curve. Statistics & Probability S.ID.4 479

1240 Use coordinate geometry to confirm properties of plane

figures.

Geometry, Measurement

& Data

G.GPE.4,

G.GPE.7 499

1240

Use various methods, including trigonometric

relationships or Heron’s Formula, to find the area of a

triangle in number and word problems.

Geometry, Measurement

& Data

G.SRT.8,

G.SRT.9 1071

1250

Describe graphically, algebraically, and verbally real-

world phenomena as functions; identify the independent

and dependent variables and any constraints of the

domain or range.

Expressions & Equations,

Algebra, Functions

F.IF.5, F.BF.1.a,

F.LE.5 365

1250 Graph a radical relation, function, or inequality. State

the domain and range.

Expressions & Equations,

Algebra, Functions

F.IF.7.b,

A.CED.2, F.IF.4 388

1250 Use summation notation to describe the sums in a

series to solve number and word problems.

Expressions & Equations,

Algebra, Functions A.SSE.4 465

1250 Use definitions and theorems of angles formed when a

transversal intersects parallel lines.

Geometry, Measurement

& Data 8.G.5, G.CO.9 492

1250

Use theorems related to the segments formed by

chords, secants, and tangents to solve number and

word problems.

Geometry, Measurement

& Data G.C.2, G.MG.1 524

1250 Write and solve quadratic inequalities graphically or

algebraically.

Expressions & Equations,

Algebra, Functions A.CED.1 589

1250 Identify the undefined values of rational algebraic

expressions.

Expressions & Equations,

Algebra, Functions

A.APR.7,

A.REI.2 638

1250 Determine or calculate residuals of a distribution. Statistics & Probability S.ID.6.b 1070

1250

Examine, interpret, or apply probability or game theory

strategies to determine the fairness of outcomes of

various situations, including games, economics, political

science, computer science, biology, etc.

Statistics & Probability S.MD.7 1075

1270 Solve quadratic equations by completing the square. Expressions & Equations,

Algebra, Functions

A.REI.4.a,

A.REI.4.b,

F.IF.8.a,

N.CN.7,

A.CED.1

372

1280

Use properties of triangles to solve problems related to

the segments parallel to one side of a triangle, including

segments joining the midpoints of two sides of a

triangle (midsegments).

Geometry, Measurement

& Data

G.CO.10,

G.SRT.4 509

1280 Use properties of parallel lines to solve problems

related to segments divided proportionally.

Geometry, Measurement

& Data G.CO.9 510

128 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1280 Write a quadratic equation or quadratic function given

its zeros.

Expressions & Equations,

Algebra, Functions

A.CED.1,

A.CED.2 662

1280

Describe the nature of the zeros of polynomial functions

using Descartes’s rule of signs, multiplicity, and the

Fundamental Theorem of Algebra using graphic and

algebraic methods.

Expressions & Equations,

Algebra, Functions N.CN.9 1076

1290 Determine measures of spread (standard deviation). Statistics & Probability S.ID.2, S.ID.4 477

1290 Expand binomial expressions that are raised to positive

integer powers using the binomial theorem.

Algebraic Thinking,

Patterns & Proportional

Reasoning

A.APR.5 586

1300 Analyze a function by decomposing it into simpler

functions.

Expressions & Equations,

Algebra, Functions F.IF.8.a 439

1300 Use the Law of Sines and Law of Cosines to solve

number and word problems involving triangles.

Geometry, Measurement

& Data

G.SRT.10,

G.SRT.11 664

1300

Factor a polynomial using grouping techniques by

recognizing quadratic form and forms of special

products, including factors with complex numbers.

Expressions & Equations,

Algebra, Functions

N.CN.8,

A.SSE.2,

A.APR.4,

F.IF.8.a

1066

1300 Calculate the reference angle from an angle in standard

position. Determine coterminal angles.

Geometry, Measurement

& Data F.TF.1, F.TF.2 1078

1310 Find sums, differences, products, and quotients of

rational algebraic expressions.

Algebraic Thinking,

Patterns & Proportional

Reasoning

A.APR.7 360

1320

Use graphs or compositions to establish the inverse

relationship between exponential and logarithmic

functions.

Expressions & Equations,

Algebra, Functions F.IF.7.e 401

1320

Find the inverse of a function or relation. Verify that

two functions are inverses using their graphs or

composition of functions.

Expressions & Equations,

Algebra, Functions F.BF.4.a 440

1320

Estimate or calculate the margin of error; determine the

size of the sample necessary for a desired margin of

error.

Statistics & Probability S.IC.4 1080

1330

Write and solve rational equations; identify extraneous

solutions, including checking the solution in the original

equation.

Expressions & Equations,

Algebra, Functions

A.REI.2,

A.CED.1 384

1340

Use the Rational Zero Theorem and the Remainder

Theorem to determine the rational solutions and factors

of a polynomial function.

Expressions & Equations,

Algebra, Functions

A.APR.2,

A.APR.3 378

1340

Compare distributions of univariate data or bivariate

data to draw conclusions; evaluate statements based

on data.

Statistics & Probability S.IC.5, S.IC.6 1081

Appendices 129

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1350 Write a polynomial equation given its solutions. Expressions & Equations,

Algebra, Functions

A.CED.1,

A.CED.2 381

1350

Write and solve radical equations and inequalities;

identify extraneous solutions, including checking the

solution in the original equation.

Expressions & Equations,

Algebra, Functions

A.REI.2,

A.CED.1 389

1350 Write and graph special functions (step, constant, and

piecewise) and identify the domain and range.

Expressions & Equations,

Algebra, Functions

F.IF.4, F.IF.5,

F.IF.7.b 670

1350

Use the definition of a parabola to identify

characteristics, write an equation, and graph the

relation.

Geometry, Measurement

& Data G.GPE.2 673

1350

Use rules for the mean and rules for the standard

deviation of random variables in order to determine the

effect linear operations have on the shape, center, and

spread of a data set.

Statistics & Probability S.IC.5 1079

1360

Determine the area and volume of figures using

right triangle relationships, including trigonometric

relationships in number and word problems.

Geometry, Measurement

& Data

G.MG.1,

G.MG.2,

G.MG.3

672

1380 Identify asymptotes, intercepts, holes, domain, and

range of a rational function and sketch the graph.

Expressions & Equations,

Algebra, Functions F.IF.4 383

1380

Write and solve rational inequalities; identify extraneous

solutions, including checking the solution in the original

equation.

Expressions & Equations,

Algebra, Functions A.CED.1 386

1380 Use a unit circle to define trigonometric functions and

evaluate trigonometric functions for a given angle.

Geometry, Measurement

& Data F.TF.2 420

1390

Find algebraically or approximate graphically or

numerically solutions of equations of the form f (x ) 5

g (x ) where f (x ) and g (x ) are linear, polynomial, rational,

radical, absolute value, exponential, logarithmic, or

trigonometric functions.

Expressions & Equations,

Algebra, Functions A.REI.11 1067

1400

Use models to make predictions and interpret the

correlation coefficient of the model; distinguish between

correlation and causation.

Statistics & Probability S.ID.8, S.ID.9 341

1410 Decompose rational expressions or rational functions,

including writing as partial fractions.

Expressions & Equations,

Algebra, Functions

A.SSE.2,

A.APR.6 1077

1420

Graph sine and cosine functions and identify the

domain, range, period, amplitude, midline, and phase

shift of the function.

Expressions & Equations,

Algebra, Functions

F.IF.4, F.IF.7.e,

F.TF.5 451

1460 Model periodic phenomena using trigonometric

functions.

Expressions & Equations,

Algebra, Functions F.TF.5 472

1480 Use trigonometric identities to verify relationships. Expressions & Equations,

Algebra, Functions F.TF.8 419

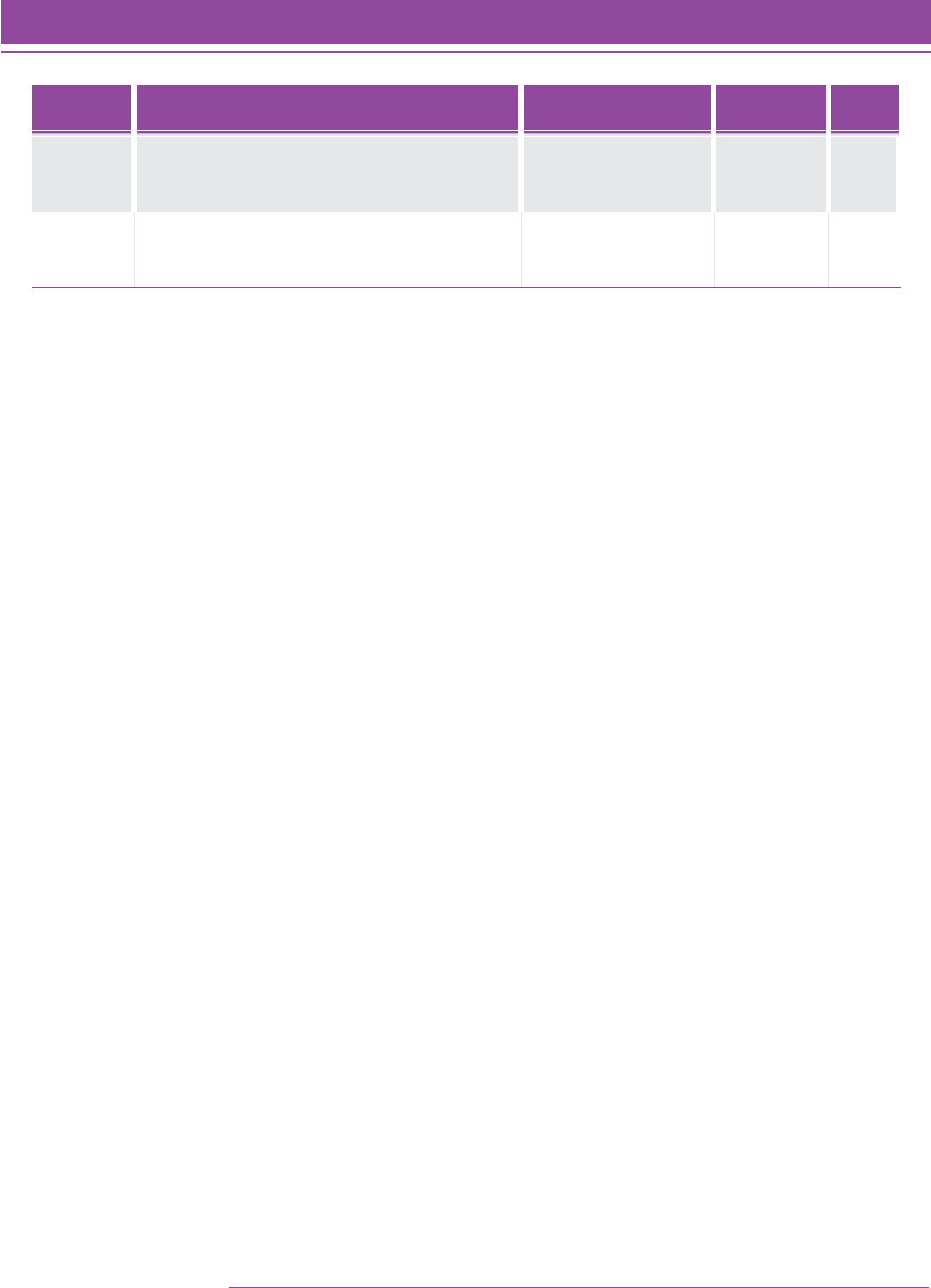
130 SMI College & Career

Appendices

Quantile

Measure QSC Description Strand CCSS ID QSC ID

1510

Graph tangent, cotangent, secant, and cosecant

functions and identify the domain, range, period, and

asymptotes of the function.

Expressions & Equations,

Algebra, Functions F.IF.4, F.IF.7.e 453

1540

Identify maximum and minimum points in terms of local

and global behavior; identify end behavior and other

critical values in functions and their graphs.

Expressions & Equations,

Algebra, Functions F.IF.4, F.IF.7.e 431

Appendices 131

Appendices

Appendix 2: Norm Reference Table (spring percentiles)

K12345678910 11 12

1 EM400Q EM310Q EM140Q 30Q 70Q 135Q 240Q 280Q 300Q 350Q 365Q 520Q 565Q

5 EM400Q EM195Q EM10Q 175Q 260Q 325Q 415Q 440Q 490Q 515Q 540Q 630Q 670Q

10 EM400Q EM115Q 65Q 250Q 350Q 415Q 505Q 525Q 590Q 610Q 655Q 730Q 760Q

25 EM270Q 15Q 175Q 375Q 480Q 550Q 645Q 665Q 730Q 760Q 810Q 890Q 910Q

35 EM210Q 75Q 230Q 430Q 535Q 610Q 700Q 730Q 795Q 830Q 880Q 960Q 980Q

50 EM125Q 140Q 290Q 495Q 605Q 690Q 775Q 815Q 880Q 915Q 970Q 1055Q 1075Q

65 EM45Q 210Q 360Q 560Q 670Q 760Q 845Q 885Q 965Q 1000Q 1055Q 1145Q 1165Q

75 10Q 260Q 405Q 605Q 720Q 815Q 895Q 945Q 1020Q 1065Q 1115Q 1205Q 1235Q

90 125Q 375Q 515Q 715Q 820Q 915Q 1000Q 1055Q 1140Q 1190Q 1240Q 1330Q 1370Q

95 180Q 455Q 585Q 790Q 885Q 980Q 1070Q 1115Q 1210Q 1270Q 1310Q 1400Q 1435Q

132 SMI College & Career

Appendices

Appendix 3: Reliability Studies

To be useful, a piece of information should be reliable—stable, consistent, and dependable. Reliability can be

defined as “the degree to which test scores for a group of test takers are consistent over repeated applications of

a measurement procedure and hence are inferred to be dependable and repeatable for an individual test taker”

(Berkowitz, Wolkowitz, Fitch, & Kopriva, 2000). In reality, all test scores include some measure of error (or level of

uncertainty).

Reliability is a major consideration in evaluating any assessment procedure. Two studies have been conducted with

an earlier version of SMI that, while not directly applicable to SMI College & Career, may be indicative of the level of

reliability that can be expected.

Appendices 133

Appendices

SMI Marginal Reliability

For a computer-adaptive test where there are no “fixed forms” (established test forms) and the items and tests

are calibrated using item response theory, the traditional measures of reliability are not appropriate (Green, Bock,

Humphreys, Linn, & Reckase, 1984). Fortunately, item response theory provides an index of reliability for an entire

test that does not require all children to be administered the same exact items. The marginal reliability is computed

by determining the proportion of test performance that is not due to error (i.e., the true score). Technically, the

marginal reliability is computed by subtracting the total variability in estimated ability by an error term, and dividing

this difference by the total estimated ability. As with traditional reliability (e.g., Cronbach alpha), the marginal

reliability is a coefficient between 0 and 1 that measures the proportion of the instrument score that is attributed to

the actual ability levels of the participants rather than aberrant “noise.” Thus, a marginal reliability that exceeds 0.80

provides evidence that the scores on a math test accurately separate or discriminate among test taker’s math ability.

Within Winsteps item analysis program (Linacre, 2010), the marginal reliability is calculated as the model reliability.

The model reliability estimate describes the upper bound of the “true” reliability of person ordering and is dependent

on sample ability variance, length of the test, number of categories per item, and sample-item targeting.

134 SMI College & Career

Appendices

A study was conducted to examine the marginal reliability of SMI test results. SMI was administered to 6,384

students across 13,630 administrations of the SMI in Grades 2–8 in six school districts across the nation. The data

was analyzed using Winsteps and the marginal (model) reliabilities are reported in Table 13. (For more information on

the sample, see the descriptions of the districts in Appendix 4, Phase II).

TABLE 13. SMI Marginal reliability estimates, by district and overall.

Grades Number of

Students (N)

Number of SMI

Administrations (N)

Number of SMI

Items Tested (N)

Marginal

Reliability

Alief (TX) 2–8 3,576 5,747 4,638 0.97

Brevard (FL) 2–6 381 1,591 3,297 0.98

Cabarrus (NC) 2–5 993 4,027 2,999 0.97

Clark (NV) 2–5 428 1,188 2,789 0.97

Harford (MD) 2–5 256 1,077 2,849 0.97

Kannapolis (NC) 5–6 750 1,751 3,087 0.96

All Students 2–8 6,384 13,630 4,721 0.97

Based upon these marginal reliability estimates, SMI is able to consistently order students and these estimates

provide an upper bound for all other estimates of the reliability of the SMI. The marginal reliability estimate does not

include “variability due to short-run random variation of the trait being measured or situational variance in the testing

conditions” (Green, Bock, Humphreys, Linn, & Reckase, 1984, p. 353). In order to examine variation in test scores

due to these sources of error, empirical studies need to be conducted. The next section describes a study designed

to examine the consistency of scores by re-administering the SMI on successive days with the criteria that items

presented to students are sampled without replacement.

Appendices 135

Appendices

SMI Test-Score Consistency

Test-retest reliability examines the extent to which two administrations of the same test yield similar results. The

closer the results, the greater the test-retest reliability of the assessment. A shortcoming of test-retest reliability

studies is the “practice effect” where respondents “learn” to answer the same questions in the first test and this

affects their responses in the next test. Alternate-form reliability examines the extent to which two equivalent forms

of an assessment yield the same results (i.e., students’ scores have the same rank order on both tests). In this

case, comparable (just not the same) items are administered at a common time. When taken together, alternate-

form reliability and test-retest reliability are estimates of test score consistency. Generally, correlation coefficients

estimating the reliability of an assessment ranging from 0.70 to 0.80 are considered as satisfactory or good.

A study was conducted to examine the stability and consistency of SMI test results. In the context of data collected

with a computer-adaptive assessment over a relatively short time period, correlations between test scores are

reflective of the test-retest reliability of alternate forms. SMI was administered twice to 223 students in Grades

4, 6, and 8 over a one-week period (April 29–30, 2010, and May 6, 2010) with 197 students completing both

administrations. Prior information used within the SMI scoring algorithm was reset after the first administration of

SMI. Of the matched sample, 54% were female (N 5 106), 21% were classified as black (N 5 41), 10% as Hispanic

(N 5 20), 7% as multiracial (N 5 13), and 62% as white (N 5 123).

Table 14 shows the test-retest reliability estimates for each grade level and across all grades over a one-week

period. The overall correlation between the two SMI Quantile measures was 0.78. Test-retest reliability coefficients

ranging from 0.70 to 0.80 are considered satisfactory.

TABLE 14. SMI test-retest reliability estimates over a one-week period, by grade.

Grade NSMI Test 1

Mean (SD)

SMI Test 2

Mean (SD)

Test-Retest

Correlation

4 77 695.32 (154.63) 681.95 (189.07) 0.79

6 66 801.52 (183.82) 812.20 (210.21) 0.70

8 54 887.78 (219.75) 920.74 (239.31) 0.73

Total 197 783.65 (199.23) 791.04 (231.22) 0.78

136 SMI College & Career

Appendices

Appendix 4: Validity Studies

The validity of a test is the degree to which the test actually measures what it purports to measure. Validity provides

a direct check on how well the test fulfills its purpose. The appropriateness of any conclusion drawn from the results

of a test is a function of the test’s validity. According to Kane (2006), “to validate a proposed interpretation or use of

test scores is to evaluate the rationale for this interpretation or use” (p. 23).

Initially, the primary source of validity evidence came from the examination of the content of SMI and the degree

to which the assessment could be said to measure mathematical understandings (construct-identification validity

evidence). Currently, data has been collected to further describe the validity (criterion-prediction and construct-

identification) of SMI. While not directly applicable to SMI College & Career, these studies may be indicative of the

level of reliability that can be expected.

Appendices 137

Appendices

SMI Validation Study—Phase I

Phase I of the SMI validation field study was conducted by Scholastic during summer and fall 2009, and data were

collected from four school districts across the United States. The validation study was designed to provide criterion

and construct validity for the SMI as a measure of a student’s mathematical understanding and provide answers to

the research questions. Next, the districts and their participation in the study are described.

Decatur Public School District 61 (Illinois)

Students attending a summer school program in 2009 from two middle schools in Decatur, Illinois, participated in a

study where the SMI was administered twice, approximately three weeks apart. This district also submitted scores

from its Statewide Assessment program, known as the Illinois Standards Achievement Test (ISAT), from 2008 and

2009 (administered in March).

Students in Grades 7 and 8 were placed in summer school if they had not met or exceeded ISAT scores from the

previous year in reading and/or math or if they failed one or more subjects in school. The district’s demographics

include: 65% economically disadvantaged; 45% white, 45% black, 2% Hispanic, 1% Asian, 8% multiracial.

In graphing the SMI Quantile 1 and Quantile 2 student data, several outliers were observed. Outliers were determined

by looking at the absolute rank difference between the SMI Quantile 1 and Quantile 2 measures. Those students with

difference scores of fewer than 40 points remained in the study.

Harford County Public Schools (Maryland)

Students from one elementary school in Harford County Public Schools, Maryland, were enrolled in an extended-

day intervention program. All but one student were assessed with the SMI in November 2009. The criteria used to

determine participation in the extended-day intervention included, but was not limited to, the SMI Quantile measure.

Student demographics in the district include 40% free or reduced-price lunch, but this varies by school due to

district SES diversity. There is a high military population, which affected the free or reduced-price lunch percentage,

as more students are eligible for free or reduced-price lunch since their families are not penalized for free housing.

The district ethnicity distribution is as follows: 40% African American, 40% Caucasian, 15% Latino, and 5% other

(including mixed ethnicities).

138 SMI College & Career

Appendices

Raytown Consolidated School District No. 2 (Missouri)

Students in three middle schools in Raytown School District, Missouri, participated in a summer school program in

2009. Because there were so few students in Grades 1–6 and Grade 8, only Grade 7 remained in the analysis.

The district chose to use SMI with two different groups of students. The first group consisted of students who used

the Math in Context program, the district’s standard summer school math program. In addition, seventh graders

in this cohort used FASTT Math every day for 10 minutes. The second group consisted of at-risk summer school

students who were simultaneously enrolled in the Math Academy, Math in Context, and FASTT Math. These students

were placed in Math Academy based on their grades, teacher recommendation, and STAR assessment.

Lexington Public Schools (Massachusetts)

One elementary and one middle school participated in this special study in the Lexington School District,

Massachusetts. The only variables available for this school district were the SMI scores and the state test from 2008

and 2009. The SMI was administered in October 2009, and the state tests were administered in March of each year.

The students participated in Everyday Math K–5 (Core) and in an intervention strategies program for Grades 6–8.

The following table summarizes all the locations with the number of students tested and the mean and standard

deviation on the SMI. A dash (-) indicates that data are not available. There were three weeks between the data

collected in the Decatur, Illinois, school district for the Quantile 1 and 2 measures.

Appendices 139

Appendices

TABLE 15. SMI Validation Study—Phase I: Descriptive statistics for the SMI Quantile

measures.

Grade 2 3 4 5

NMean (SD) NMean (SD) NMean (SD) NMean (SD)

Decatur, IL, SMI Q1 --------

Decatur, IL, SMI Q2 --------

Harford, MD 65 234.00

(151.94) 68 414.12

(155.08) 76 576.97

(152.23) 69 654.78

(178.22)

Raytown, MO --------

Lexington, MA - - - - 17 578.82

(182.96) - -

Grade 6 7 8

NMean (SD) NMean (SD) NMean (SD)

Decatur, IL, SMI Q1 - - 56 527.70

(217.26) 39 583.59

(255.31)

Decatur, IL, SMI Q2 - - 46 600.98

(181.42) 37 633.11

(215.99)

Harford, MD -- ---

Raytown, MO - - 268 658.60

(186.69) - -

Lexington, MA 21 865.00

(201.41) - - 16 1119.06

(87.54)

Note: Values based on five or fewer students have been excluded.

In each location, the following data were requested for each student:

1. SMI Quantile measure from Summer to November 2009 administration

2. State test scale scores and performance levels from Spring 2008 and Spring 2009

3. Student demographics (e.g., gender, grade, race/ethnicity, ELL status, free or reduced-price lunch status,

and math intervention status and program)

The following tables provide a demographic summary and the associated means and standard deviations of Quantile

measures for the associated students at the schools where data is available. Lexington School District did not

provide any demographic information.

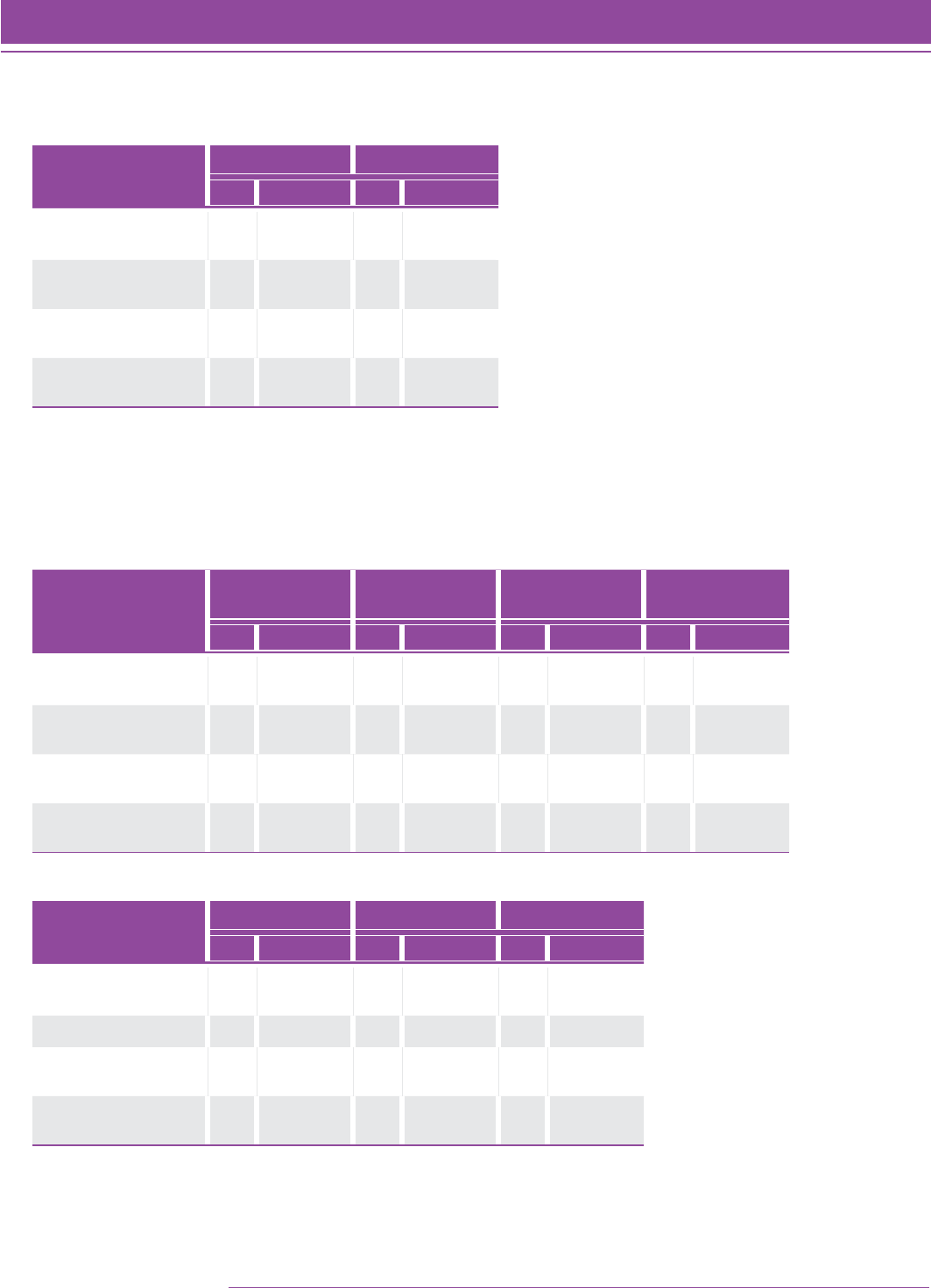
140 SMI College & Career

Appendices

TABLE 16. SMI Validation Study—Phase I: Means and standard deviations for the SMI

Quantile measures, by gender.

Gender Female Male

NMean (SD) NMean (SD)

Decatur, IL, SMI Q1 42 562.38

(231.93) 53 541.34

(237.34)

Decatur, IL, SMI Q2 38 591.71

(171.52) 45 635.22

(216.06)

Harford, MD 117 479.96

(217.00) 160 471.72

(230.95)

Raytown, MO 122 670.08

(181.12) 144 649.69

(192.55)

TABLE 17. SMI Validation Study—Phase I: Means and standard deviations for the SMI

Quantile measures, by race/ethnicity.

Race/Ethnicity African American American Indian/

Native American Asian Caucasian

NMean (SD) NMean (SD) NMean (SD) NMean (SD)

Decatur, IL, SMI Q1 58 561.66

(239.68) - - - - 30 553.50

(231.77)

Decatur, IL, SMI Q2 53 624.43

(179.18) - - - - 26 607.88

(240.62)

Harford, MD 95 481.05

(232.76) - - - - 139 480.54

(218.13)

Raytown, MO 139 633.31

(189.53) - - - - 109 680.69

(186.64)

Race/Ethnicity Pacific Islander Hispanic Multiracial

NMean (SD) NMean (SD) NMean (SD)

Decatur, IL, SMI Q1 - - - - 7 447.14

(196.04)

Decatur, IL, SMI Q2 - - - ---

Harford, MD - - 38 437.50

(237.58) - -

Raytown, MO - - 15 712.67

(126.53) - -

Note: Values based on five or fewer students have been excluded.

Appendices 141

Appendices

SMI Validation Study—Phase II

Phase II of the SMI validation field study was conducted by Scholastic during the 2009–2010 school year, and data

were collected from six school districts across the United States. The validation study was designed to provide

criterion-prediction and construct-identification validity for the SMI as a measure of a student’s readiness for

mathematics instruction and provide answers to the research questions. Next, the districts and their participation

is described.

Alief Independent School District (Texas)

Students in Grades 2–6 from four schools (Grades 2–4, three schools; Grades 5–6, one school) were administered

the SMI in December, February, and May of the 2009–2010 school year. In addition, students in Grades 3–6 were

administered the mathematics subtest of the Texas Assessment of Knowledge and Skills (TAKS) on April 26, 2010.

For Grades 2–4, bilingual students in one school were omitted from testing. For Grades 5–6, bilingual classrooms

were omitted from testing, and classes with lower-performing students and/or students classified as Special

Education were targeted for SMI testing.

Brevard Public Schools (Florida)

All students in Grades 2–6 from one school were administered the SMI in January, March, and May 2010. In addition,

students in Grades 3–6 were administered the mathematics subtest of the Florida Comprehensive Assessment Test

(FCAT) between March 9 and March 19, 2010. The mathematics instructional program consisted of FASTT Math

(used school-wide) and the Macmillan basal mathematics program, SuccessMaker® Math (used with students who

need additional support). Students were targeted for SuccessMaker Math instruction based upon their Quantile

measures and FCAT scores (lowest 25%). In addition, formative assessment was used in the classrooms with FASTT

Math software fluency data and CORE Math curriculum-based measures.

Cabarrus County Schools (North Carolina)

All students in Grades 2–5 from two schools were administered the SMI in February and April or May 2010. In

addition, students in Grades 3–5 were administered the mathematics subtest of the North Carolina End-of-Grade

Test (NCEOG) during the last three weeks of the school year (typically in May). The mathematics instructional

program consisted of Number Worlds, Everyday Math, First in Math, and Real Math (45-minute blocks per day). In

addition, formative assessment was used in the classrooms with AIMSWeb® M-CBM (Mathematics Curriculum-

Based Measurement). Students who were identified through the quarterly benchmarking assessment received

support from Title 1 staff. There was also a district-wide initiative for exploring Professional Learning Communities

(PLCs). In their PLCs, staff reviewed the quarterly assessments, identified students’ problem areas, and remediated

at the classroom level according to the common, formative assessment standards, and then intervened at the

student level accordingly.

142 SMI College & Career

Appendices

Clark County School District (Nevada)

All students in Grades 2–5 from one school were administered the SMI in November, January, February, and May of

the 2009–2010 school year, and scores were used to build an intervention program. In addition, students in Grades 3–5

were administered the mathematics subtest of the criterion-referenced tests (CRT) between February 16 and March

16. The mathematics intervention program consisted of FASTT Math and Do the Math. The school also uses interim

assessments that align with district benchmarks.

Harford County Public Schools (Maryland)

Students in Grades 2–5 from one school were administered the SMI in November, February, and May of the

2009–2010 school year. In addition, students in Grades 3–5 were administered the mathematics subtest of the

Maryland School Assessment (MSA) between March 8 and March 23, 2010. The mathematics instructional program

consisted of Dreambox, with Do the Math beginning in January 2010. All students used First in Math (mainly outside

the school day), and students participated in an extended-day program three times per week for a 45-minute

mathematics block. Students were able to do First in Math for an additional 15 minutes when class schedules

permitted. Intervention programs were designated as supplemental, but each classroom teacher completed targeted

instruction once per week as part of the Everyday Math program. In addition, formative assessment was used in the

classrooms with a modified version of the Unit Assessments in Everyday Math.

Kannapolis City Schools (North Carolina)

All students in Grades 5 and 6 from one school were administered the SMI in January, in March, and then for a third

time in Spring 2010. In addition, students were administered the mathematics subtest of the North Carolina End-of-

Grade Test (NCEOG) during the last three weeks of the school year (typically in May). The mathematics instructional

program was the standard curriculum, with SMI administered for assessment purposes only. Teacher teams created

a common assessment that could be used for formative assessment every four weeks. SMI Quantile measures

(along with NCEOG scores) were used to help teachers differentiate instruction, inform students’ Personal Education

Plans, and identify students in need of remediation. Student interventions included after-school tutoring programs

and teacher-developed interventions.

The following table summarizes all the locations, with the number of students tested and the mean and standard

deviation on the SMI. A dash (-) indicates that the data are not available.

Appendices 143

Appendices

TABLE 18. SMI Validation Study—Phase II: Descriptive statistics for the SMI

Quantile measures (spring administration).

Grade 2 3 4

NMean (SD) NMean (SD) NMean (SD)

Alief, TX 315 269.68

(149.72) 400 467.91

(159.78) 547 602.73

(158.14)

Brevard, FL 5320.00

(136.70) 101 371.53

(129.59) 94 583.67

(155.26)

Cabarrus, NC 154 287.18

(143.42) 283 481.96

(172.24) 279 604.43

(176.90)

Clark, NV 105 361.62

(139.76) 99 508.94

(197.22) 107 637.38

(147.00)

Harford, MD 64 360.31

(139.76) 59 555.93

(188.74) 67 698.81

(146.10)

Kannapolis, NC ------

Grade 5 6

NMean (SD) NMean (SD)

Alief, TX 282 646.35

(160.14) 283 744.58

(201.49)

Brevard, FL 90 679.56

(145.82) 91 787.09

(166.94)

Cabarrus, NC 277 711.70

(182.40) - -

Clark, NV 117 704.87

(180.96) - -

Harford, MD 66 761.59

(197.26) - -

Kannapolis, NC 368 678.29

(181.50) 382 803.17

(207.94)

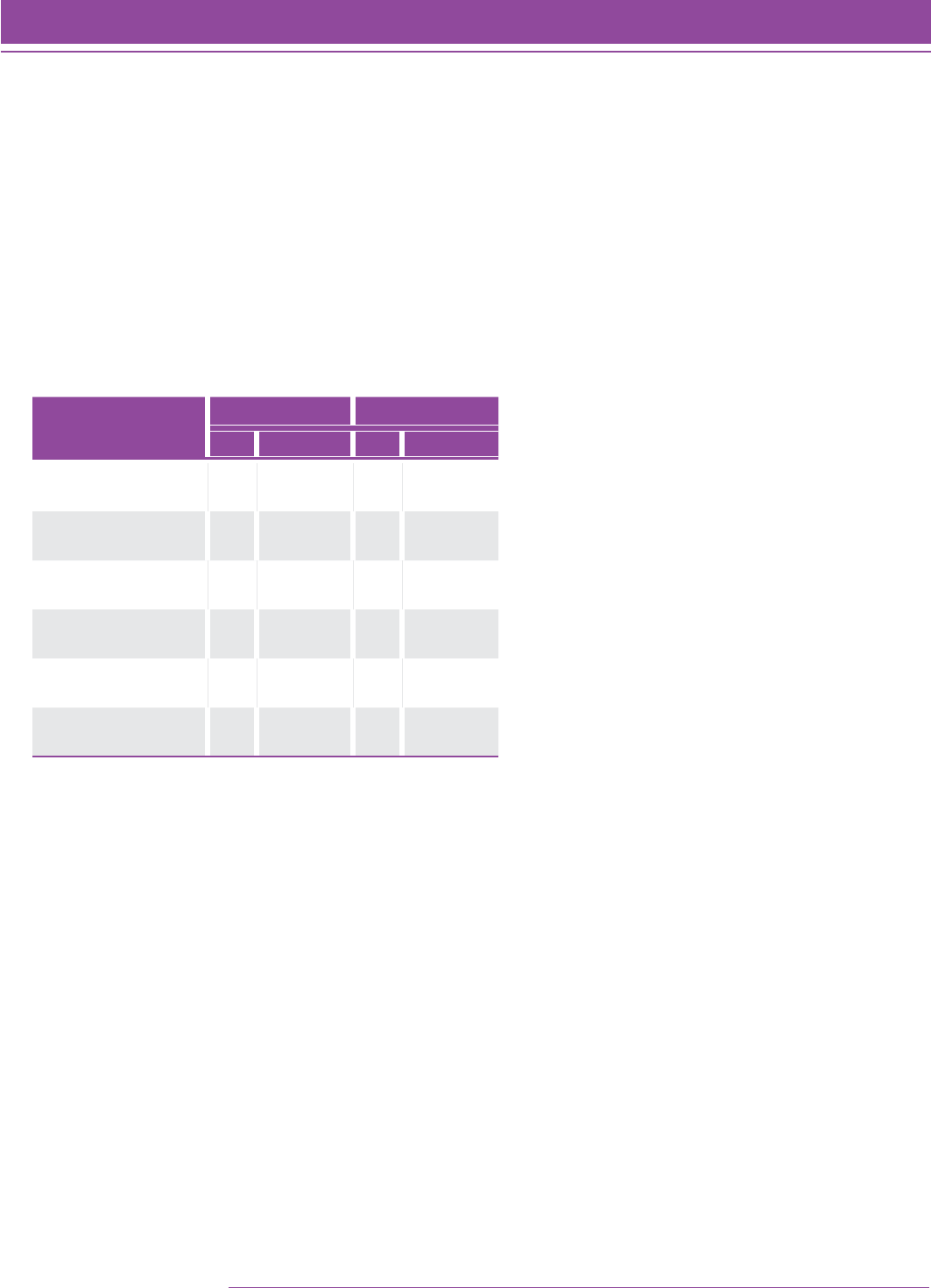
144 SMI College & Career

Appendices

In each location, data were requested for each student:

1. SMI Quantile measure from the 2009–2010 school year (fall, winter, and spring) administration

2. State test scale scores and performance levels from Spring 2008, Spring 2009, and Spring 2010

3. Student demographics (e.g., gender, grade, race/ethnicity, ELL status, free or reduced-price lunch status,

math intervention status and program)

The following tables provide a demographic summary and the associated means and standard deviations of Quantile

measures for the associated students at the schools where data is available. A dash (-) indicates that the data are

not available.

TABLE 19. SMI Validation Study—Phase II: Means and standard deviations for the SMI

Quantile measures, by gender (spring administration).

Gender Female Male

NMean (SD) NMean (SD)

Alief, TX 799 545.71

(229.09) 827 538.95

(221.40)

Brevard, FL 183 604.59

(218.72) 186 594,73

(215.42)

Cabarrus, NC 491 537.01

(218.23) 502 563.20

(227.40)

Clark, NV 139 614.28

(197.27) 173 633.50

(191.98)

Harford, MD 110 608.64

(215.14) 146 589.01

(239.72)

Kannapolis, NC 317 763.52

(179.75) 312 763.40

(195.98)

Appendices 145

Appendices

TABLE 20. SMI Validation Study—Phase II: Means and standard deviations for the SMI

Quantile measures, by race/ethnicity (spring administration).

Race/Ethnicity African American American Indian/

Native American Asian Caucasian

NMean (SD) NMean (SD) NMean (SD) NMean (SD)

Alief, TX ---- - ---

Brevard, FL 12 535.42

(252.12) - - 9 602.78

(207.49) 317 599.31

(214.83)

Cabarrus, NC 204 504.41

(213.74) - - 34 684.41

(227/80) 621 581.13

(216.27)

Clark, NV 15 496.67

(132.55) - - 5 704.00

(87.06) 154 695.94

(164.36)

Harford, MD 90 594.17

(232.32) - - 4 596.25

(211.83) 130 610.31

(224.42)

Kannapolis, NC 182 732.25

(184.69) - - - - 304 800.26

(182.90)

Race/Ethnicity Pacific Islander Hispanic Multiracial

NMean (SD) NMean (SD) NMean (SD)

Alief, TX ------

Brevard, FL - - 18 587.78

(257.34) 8713.13

(161.80)

Cabarrus, NC - - 92 421.96

(225.61) 38 484.34

(196.03)

Clark, NV - - 16 656.88

(169.01) - -

Harford, MD - - 30 542.33

(240.38) - -

Kannapolis, NC - - 143 724.93

(188.46) - -

146 SMI College & Career

Appendices

SMI Validation Study—Phase III

Phase III of the SMI validation field study was conducted by Scholastic during the 2010–2011 school year. Data

were collected from seven school districts across the United States. The validation study was designed to provide

criterion-prediction and construct-identification validity for the SMI as a measure of a student’s readiness for

mathematics instruction and provide answers to the research questions. Next, the districts and their participation

are described.

Alief Independent School District (Texas)

A sample of 5,073 students in Grades 2–8 from six schools (Grades 3–5, four schools; Grades 5–7, one school; and

Grades 7–8, one school) were administered the SMI in October, February, and May of the 2010–2011 school year. In

addition, students in Grades 3–8 were administered the mathematics subtest of the Texas Assessment of Knowledge

and Skills (TAKS) on April 1, 2011.

Brevard Public Schools (Florida)

A sample of 671 students in Grades 2–6 from one elementary school were administered the SMI in September,

January, and May of the 2010–2011 school year. In addition, students in Grades 3–6 were administered the

mathematics subtest of the Florida Comprehensive Assessment Test (FCAT) on April 13, 2011.

Cabarrus County Schools (North Carolina)

A sample of 1,148 students in Grades 2–5 from one elementary school were administered the SMI in late

September/early October, January, and late April/early May of the 2010–2011 school year. In addition, students

in Grades 3–5 were administered the mathematics subtest of the North Carolina End-of-Grade Test (NCEOG) on

May 11, 2011.

Clark County School District (Nevada)

A sample of 419 students in Grades 2–5 from one elementary school were administered the SMI in October, late

January/early February, and May of the 2010–2011 school year, and scores were used to build an intervention

program. In addition, students in Grades 3–5 were administered the mathematics subtest of the criterion-referenced

tests (CRT) on March 7, 2011.

Harford County Public Schools (Maryland)

A sample of 20,195 students in Grades 2–8 from 42 schools (33 elementary schools and 9 middle schools) were

administered the SMI in October/early November, January/February, and/or May/June of the 2010–2011 school year.

In addition, students in Grades 3–8 were administered the mathematics subtest of the Maryland School Assessment

(MSA) on March 15, 2011. Students in one elementary school (Grades 2–5) had data only for SMI and are, therefore,

not included in analyses for the complete sample for Harford County Public Schools.

Appendices 147

Appendices

Kannapolis City Schools (North Carolina)

A sample of 776 students in Grades 5 and 6 from one school were administered the SMI in February and May of the

2010–2011 school year. In addition, students were administered the mathematics subtest of the North Carolina End-

of-Grade Test (NCEOG) on May 1, 2011.

Killeen Independent School District (Texas)

A sample of 12,475 students in Grades 2–5 from 32 elementary schools were administered the SMI in late

September/early October, January/early February, and May of the 2010–2011 school year. In addition, students in

Grades 3–6 were administered the mathematics subtest of the Texas Assessment of Knowledge and Skills (TAKS)

on April 1 or May 1, 2011.

The following table summarizes all the locations, with the number of students tested and the mean and standard

deviation on the SMI. A dash (-) indicates that the data are not available.

TABLE 21. SMI Validation Study—Phase III: Descriptive statistics for the SMI

Quantile measures (spring administration).

Grade 2 3 4

NMean (SD) NMean (SD) NMean (SD)

Alief, TX 143 333.11

(130.73) 228 490.99

(170.78) 293 621.45

(142.38)

Brevard, FL 93 362.26

(113.57) 101 568.66

(167.03) 98 665.61

(149.81)

Cabarrus, NC 476 375.80

(148.21) 408 568.60

(203.25) 474 693.19

(193.52)

Clark, NV 75 340.40

(102.15) 101 544.80

(151.32) 103 644.27

(171.71)

Harford, MD 2,586 408.75

(166.18) 2,789 603.46

(201.76) 2,600 694.96

(166.61)

Kannapolis, NC ------

Killeen, TX 64 334.45

(147.92) 3,002 531.44

(147.61) 2,977 654.73

(135.79)

148 SMI College & Career

Appendices

TABLE 21. SMI Validation Study—Phase III: Descriptive statistics for the SMI

Quantile measures (spring administration). (continued)

Grade 5 6 7 8

NMean (SD) NMean (SD) NMean (SD) NMean (SD)

Alief, TX 89 678.09

(135.17) 94 758.14

(182.21) 286 773.02

(172.33) 152 762.11

(226.12)

Brevard, FL 88 802.44

(151.12) 92 863.32

(194.38) ----

Cabarrus, NC 506 802.59

(225.53) ------

Clark, NV 61 730.41

(144.83) ------

Harford, MD 2,784 799.88

(182.29) 2,182 850.01

(203.07) 2,161 877.64

(220.03) 2,219 939.06

(230.49)

Kannapolis, NC 321 712.49

(216.68) 301 815.93

(196.17) ----

Killeen, TX 2,786 740.24

(138.02) ------

In each location, data were requested for each student:

1. SMI Quantile measure from the 2009–2010 school year (fall, winter, and spring) administration

2. State test scale scores and performance levels from Spring 2008, Spring 2009, Spring 2010, and

Spring 2011

3. Student demographics (e.g., gender, grade, race/ethnicity, ELL status, free or reduced-price lunch status,

math intervention status and program)

The following tables provide a demographic summary and the associated means and standard deviations of Quantile

measures for the associated students at the schools where data is available. A dash (-) indicates that the data are

not available.

Appendices 149

Appendices

TABLE 22. SMI Validation Study—Phase III: Means and standard deviations for the SMI

Quantile measures, by gender (spring administration).

Gender Female Male

NMean (SD) NMean (SD)

Alief, TX 542 654.66

(181.30) 525 631.69

(197.24)

Brevard, FL 173 727.31

(195.74) 183 725.82

(202.48)

Cabarrus, NC* 289 679.36

(247.15) 306 656.91

(261.15)

Clark, NV 138 608.91

(180.53) 122 643.20

(163.07)

Harford, MD 8,280 717.69

(257.34) 8,868 730.23

(261.03)

Kannapolis, NC 331 773.47

(200.88) 346 750.06

(224.54)

Killeen, TX 4,350 636.57

(163.33) 4,479 638.35

(169.47)

* Minimum of five students per group to be reported

150 SMI College & Career

Appendices

TABLE 23. SMI Validation Study—Phase III: Means and standard deviations for the SMI

Quantile measures, by race/ethnicity (spring administration).*

Race/Ethnicity African American American Indian/

Native American Asian Caucasian

NMean (SD) NMean (SD) NMean (SD) NMean (SD)

Alief, TX 492 598.53

(203.86) - - 89 758.43

(185.19) 33 640.61

(200.94)

Brevard, FL 12 690.83

(251.14) - - - - 306 723.14

(200.60)

Cabarrus, NC** 114 606.01

(245.59) - - - - 422 670.98

(247.11)

Clark, NV 12 571.25

(191.41) - - 6 680.83

(146.27) 185 646.11

(165.01)

Harford, MD 3,084 647.60

(250.16) 54 714.26

(266.82) 549 797.20

(272.23) 11,669 746.84

(255.79)

Kannapolis, NC 188 716.06

(208.09) - - 8 848.13

(274.07) 296 798.26

(217.41)

Killeen, TX 3,180 616.98

(166.69) 114 651.14

(179.44) 347 690.78

(168.00) 2,762 659.11

(162.59)

Race/Ethnicity Pacific Islander Hispanic Multiracial

NMean (SD) NMean (SD) NMean (SD)

Alief, TX 11 570.45

(163.09) 738 677.99

(184.95) - -

Brevard, FL 9802. 22

(184.56) 17 750.00

(172.39) 11 774.55

(146.57)

Cabarrus, NC ------

Clark, NV 5652.00

(222.78) 34 508.38

(184.47) 15 663.33

(124.77)

Harford, MD 34 702.79

(242.99) 54 714.26

(266.82) 1,734 686.99

(262.83)

Kannapolis, NC - - 145 751.93

(199.35) 39 717.69

(203.42)

Killeen, TX 123 647.44

(147.66) 2,303 630.57

(166.07) - -

*Minimum of five students per group to be reported

**Omitted students classified as “3,” “4,” and “5” (N 5 59)

Appendices 151

Appendices

Construct-Identification Validity

The construct-identification validity of a test is the extent to which the test may be said to measure a theoretical

construct or trait, such as readiness for mathematics instruction. It is anticipated that scores from a valid test of

mathematics skills should show expected:

1. Differences by age and/or grade

2. Differences among groups of students that traditionally show different or similar patterns of development in

mathematics (e.g., differences in socioeconomic levels, gender, ethnicity, etc.)

3. Relationships with other measures of mathematical understanding

Construct-identification validity is the most important aspect of validity related to SMI. SMI is designed to measure

the development of mathematical abilities; therefore, how well it measures mathematical understanding and how

well it measures the development of these mathematical understandings must be examined.

Further Construct-Identification Validity

Convergent validity looks at the relationships between test scores and other criterion variables that the scores should

be related to (e.g., student characteristics, mathematical achievement grade equivalent, and remediation programs).

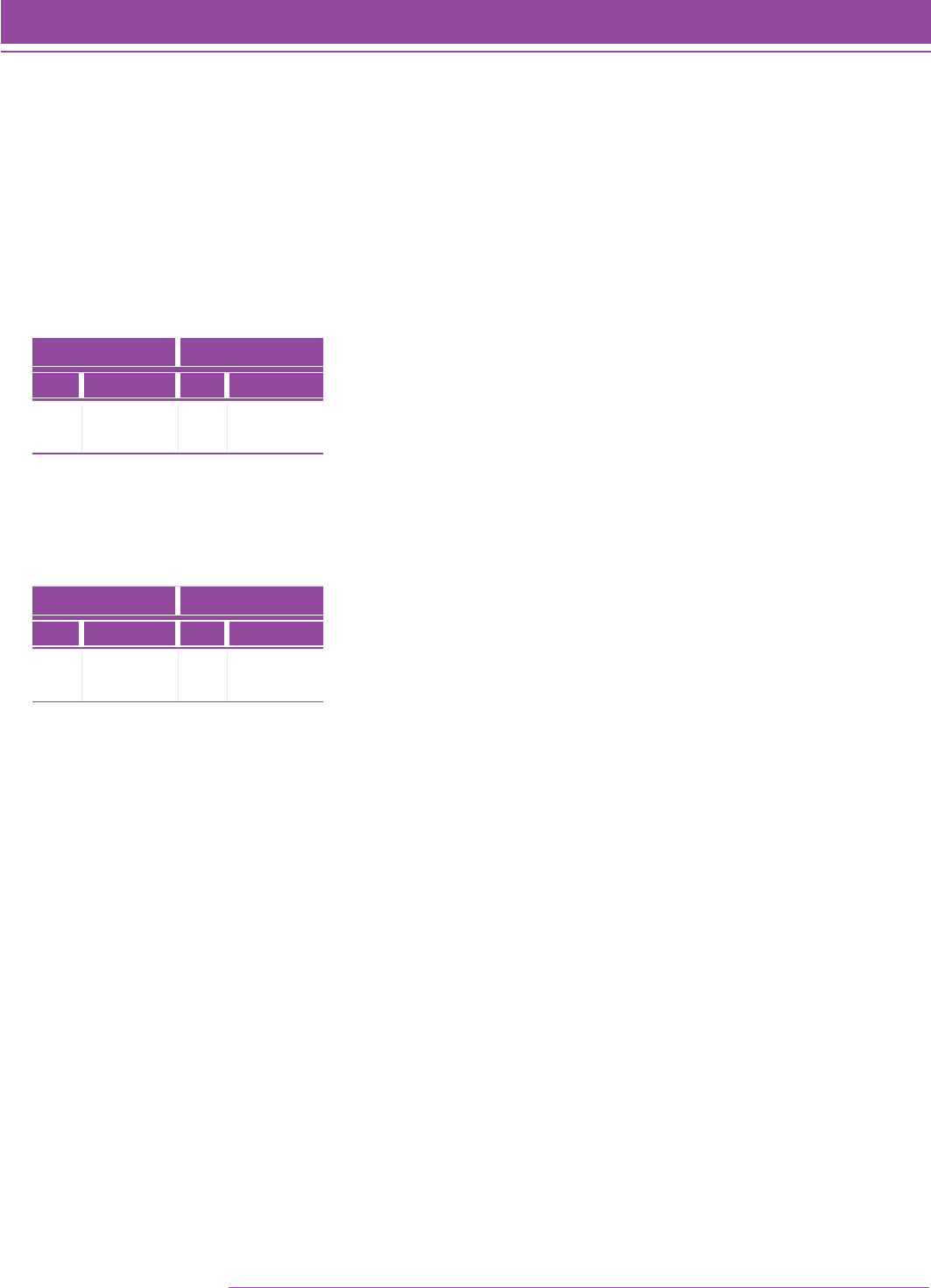
152 SMI College & Career

Appendices

Intervention Program

Because targeted mathematics intervention programs are specifically designed to improve students’ mathematical

achievement, an effective intervention would be expected to improve students’ mathematics test scores.

Participation in a math intervention program was collected from two of the Phase I sites (Decatur and Raytown). An

ANOVA was conducted for the data from each site, and a significant difference due to math intervention program

was observed for both of the sites (Harford, p < .05; Raytown, p < .0001). The differences between the mean SMI

Quantile measures are as expected.

TABLE 24. Harford County Public Schools—Intervention study means and standard

deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

26 561.92

(127.15) 252 467.42

(231.22)

p < 0.5

TABLE 25. Raytown Consolidated School District No. 2—FASTT Math intervention program

participation means and standard deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

60 564.50

(211.09) 206 686.58

(170.76)

p < .0001

During Phase III, information related to inclusion in a math intervention program was collected from four of the seven

sites (Alief, Brevard, Cabarrus, and Killeen) for students in Grades 2–6. As expected, students classified as needing

math intervention services scored significantly lower than students not classified as needing math intervention

services.

Appendices 153

Appendices

TABLE 26. Inclusion In math intervention program means and standard deviations for the

SMI Quantile measures.

School District

Number of Students

Classified as Needing

Math Intervention

Mean (SD) of

Math Intervention

Students

Number of Students

Not Classified as

Needing Math

Intervention

Mean (SD)

of Regular

Education

Students

Alief ISD 49 462.04 (140.60) 887 604.66 (173.45)

Brevard 70 578.93 (149.21) 199 716.23 (172.97)

Cabarrus County 67 524.93 (186.56) 528 685.95 (256.34)

Killeen ISD 2,737 569.67 (165.52) 6,092 667.93 (157.68)

p < .0001

Gifted and Talented Classification

Gifted and Talented (GT) classification information was collected in one of the Phase I sites (Harford) and three of the

Phase II sites (Alief, Harford, and Kannapolis). An ANOVA was conducted for the data from each site, and a significant

difference due to GT classification was observed for all of the sites (p < .0001). The differences between the mean

SMI Quantile measures are as expected.

TABLE 27. Gifted and Talented status means and standard deviations for the SMI Quantile

measures.

School District

Number of Students

Classified as Gifted

and Talented

Mean (SD) of

Gifted and

Talented Students

Number of Students

Not Classified as

Gifted and Talented

Mean (SD)

of Regular

Education

Students

Alief ISD 125 665.20 (186.95) 1500 531.98 (225.17)

Harford Co. (Phase I) 21 746.19 (160.55) 257 454.20 (215.27)

Harford Co. (Phase II) 18 854.72 (100.64) 238 577.98 (224.53)

Kannapolis City 57 977.54 (122.64) 572 742.12 (179.71)

p < .0001

154 SMI College & Career

Appendices

During Phase III, Gifted and Talented classification information was collected from four of the seven sites (Alief,

Brevard, Clark, and Killeen) for students in Grades 2–6. As expected, students classified as Gifted and Talented

scored significantly higher than students not classified as Gifted and Talented.

TABLE 28. Gifted and Talented status means and standard deviations for the SMI Quantile

measures.

School District

Number of Students

Classified as Gifted

and Talented

Mean (SD) of

Gifted and

Talented Students

Number of Students

Not Classified as

Gifted and Talented

Mean (SD)

of Regular

Education

Students

Alief ISD 103 720.19 (79.73) 833 581.99 (177.28)

Brevard 8 814.38 (45.63) 261 676.40 (178.39)

Clark County 22 768.41 (128.02) 243 613.31 (171.18)

Killeen ISD 425 784.38 (134.03) 8,404 630.04 (164.50)

p < .0300

Special Education Classification

Special Education status was collected in two of the Phase I sites (Decatur and Harford) and five of the Phase II

sites (Alief, Brevard, Cabarrus, Clark, and Kannapolis). An ANOVA was conducted for the data from each site, and a

significant difference due to Special Education status was observed for four of the sites (Alief, Cabarrus, Clark, and

Kannapolis; p < .0001). The differences between the mean SMI Quantile measures are as expected.

Appendices 155

Appendices

TABLE 29. Special Education status means and standard deviations for the SMI Quantile

measures.

School District

Number of Students

Classified as Special

Education

Mean (SD) of

Special Education

Students

Number of Students

Not Classified as

Special Education

Mean (SD)

of Non-Special

Education

Students

Alief ISD 89 452.64 (224.86) 1,364 575.74 (218.44)

Cabarrus County 94 423.03 (210.47) 899 563.55 (220.38)

Clark County 31 491.45 (227.79) 281 639.66 (184.85)

Kannapolis City 44 660.00 (204.64) 558 774.76 (183.40)

p < .0001

During Phase III, Special Education status information was collected from three of the seven sites (Alief, Brevard, and

Killeen) for students in Grades 2–6. As expected, students classified as requiring Special Education services scored

significantly lower than students not requiring Special Education services.

TABLE 30. Special Education status means and standard deviations for the SMI Quantile

measures.

School District

Number of Students

Classified as Special

Education

Mean (SD) of

Special Education

Students

Number of Students

Not Classified as

Special Education

Mean (SD)

of Non-Special

Education

Students

Alief ISD 44 411.93 (218.19) 892 606.33 (167.23)

Brevard 48 596.15 (215.03) 221 698.82 (163.02)

Killeen ISD 954 522.77 (189.50) 7,875 651.37 (157.91)

p < .0002

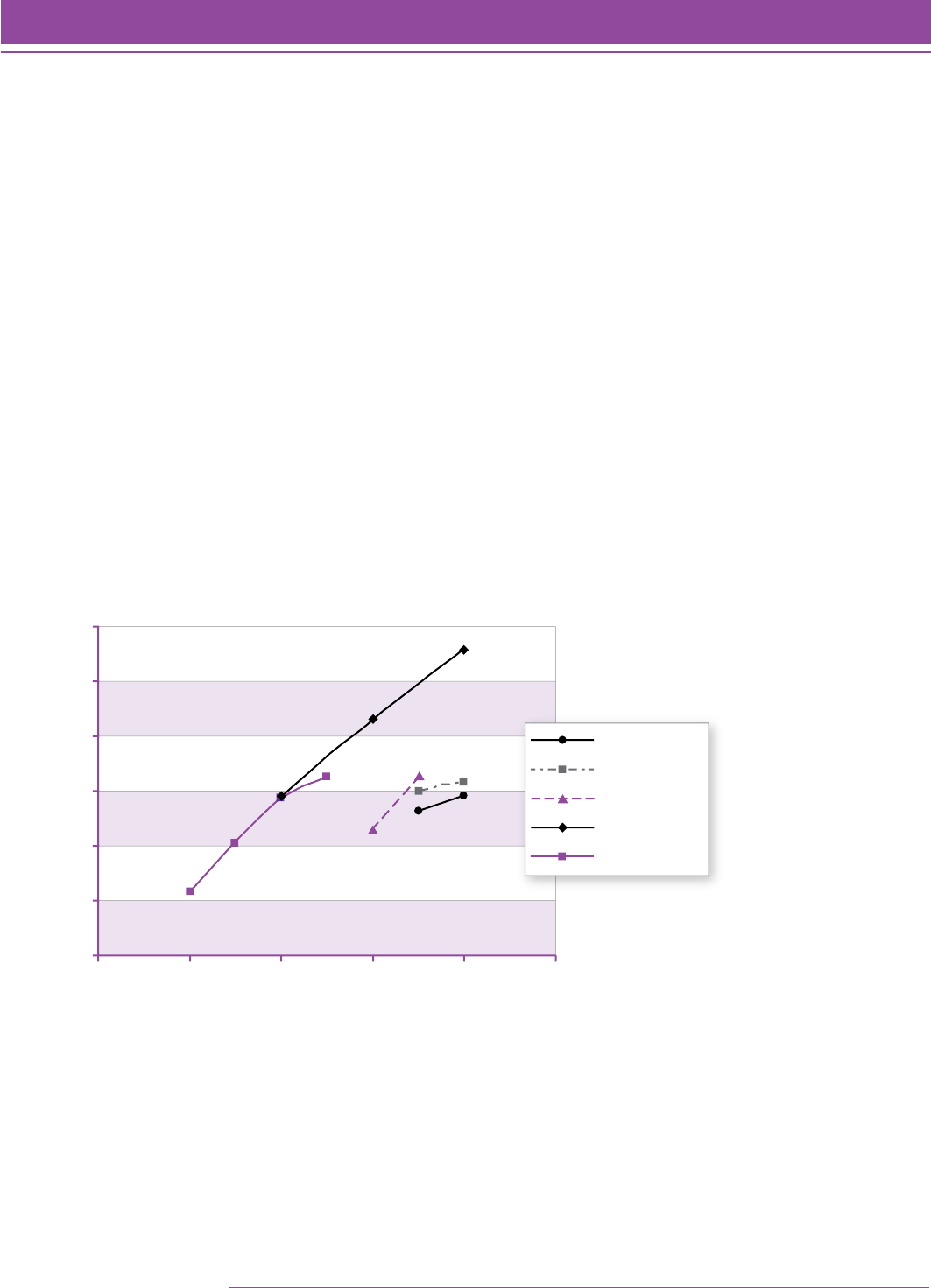
156 SMI College & Career

Appendices

Development of Mathematics Understandings

Mathematical understandings generally increase as a student progresses through school. They increase rapidly

during elementary school because students are specifically instructed in mathematics. In middle school,

mathematical achievement tends to grow at a slower rate because students begin to develop at various levels. SMI

was designed to assess the developmental nature of mathematical understandings.

Figure 20 shows the median performance on SMI for students at each location and grade level from the SMI

Validation Study—Phase I conducted during the 2008–2009 school year.

Figures 21 and 22 show the mean performance on SMI for students at each location and grade level from the SMI

Validation Study—Phase II conducted during the 2009–2010 school year.

Figures 23 and 24 show the mean performance on SMI for students at each location and grade level from the SMI

Validation Study—Phase III conducted during the 2010–2011 school year.

As predicted, student scores on SMI climb rapidly in elementary grades and level off in middle school depending

on the program being implemented (e.g., whole-class instruction versus remediation program). The developmental

nature of mathematics is demonstrated in these results. Graphing the multiple sets of results in each chart displays

that, in every study, the SMI scores are monotonically increasing as students move from grade to grade. This

important characteristic supports the property of how the SMI Quantile scale was created as well as the progressive

nature of mathematics.

FIGURE 20. SMI Validation Study, Phase I: SMI Quantile measures displayed by location

and grade.

SMI_TG_112

200

400

600

800

1000

1200

0246810

Grade

SMI Quantile measure

Illinois SMI1

Illinois SMI2

Raytown SMI

Massachusetts SMI

Maryland SMI

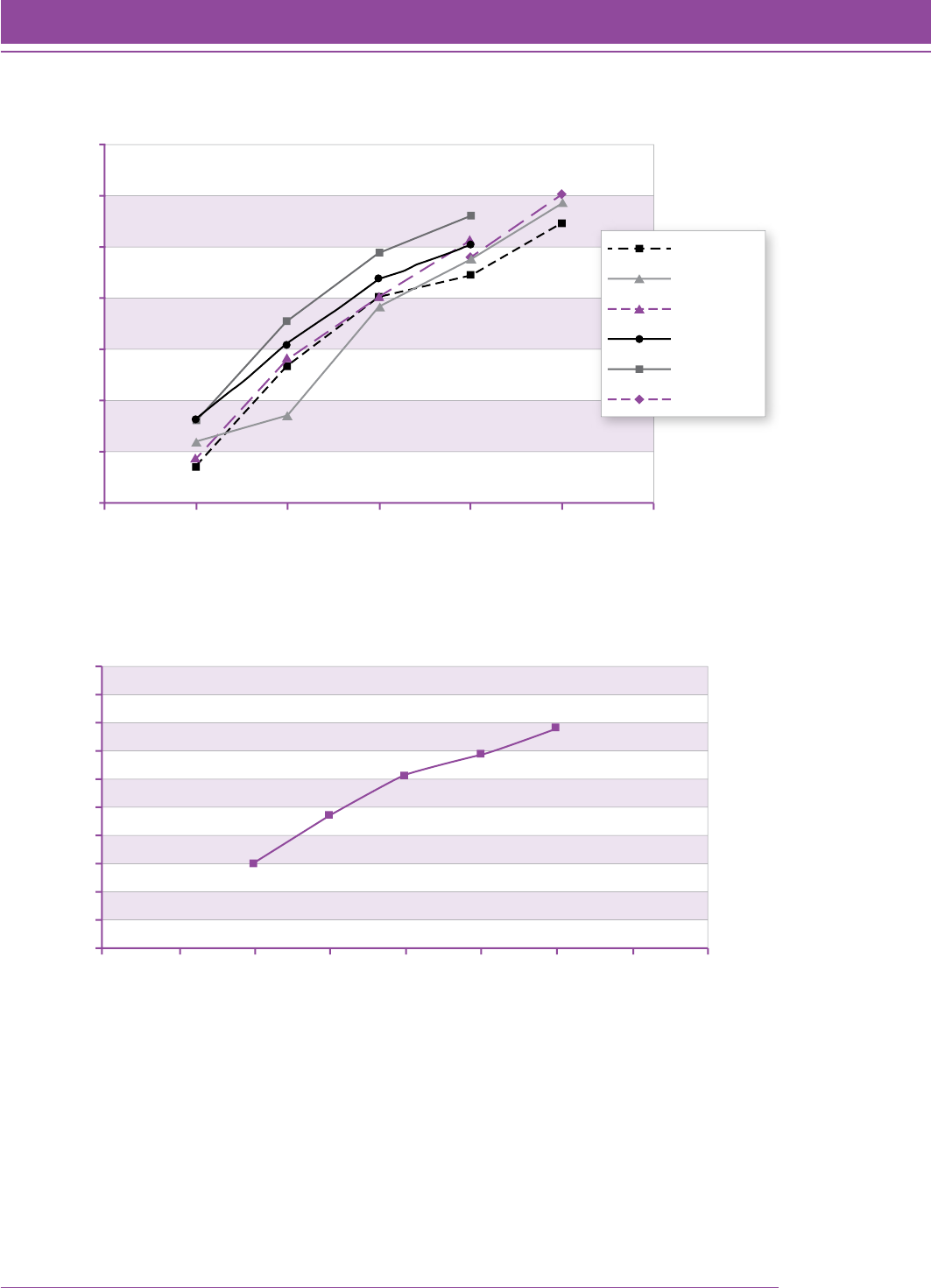
Appendices 157

Appendices

FIGURE 21. SMI Validation Study, Phase II: SMI Quantile measures displayed by location and

grade.

SMI_TG_113

300

200

400

500

600

700

800

900

1234567

Grade

SMI Quantile measure

Alief (TX)

Brevard (FL)

Cabarrus (NC)

Clark (NV)

Harford (MD)

Kannapolis (NC)

FIGURE 22. SMI Validation Study, Phase II: SMI Quantile measures displayed by grade.

SMI_TG_113-A

300

200

100

400

500

600

700

800

900

1000

012345678

Grade

SMI Quantile measure

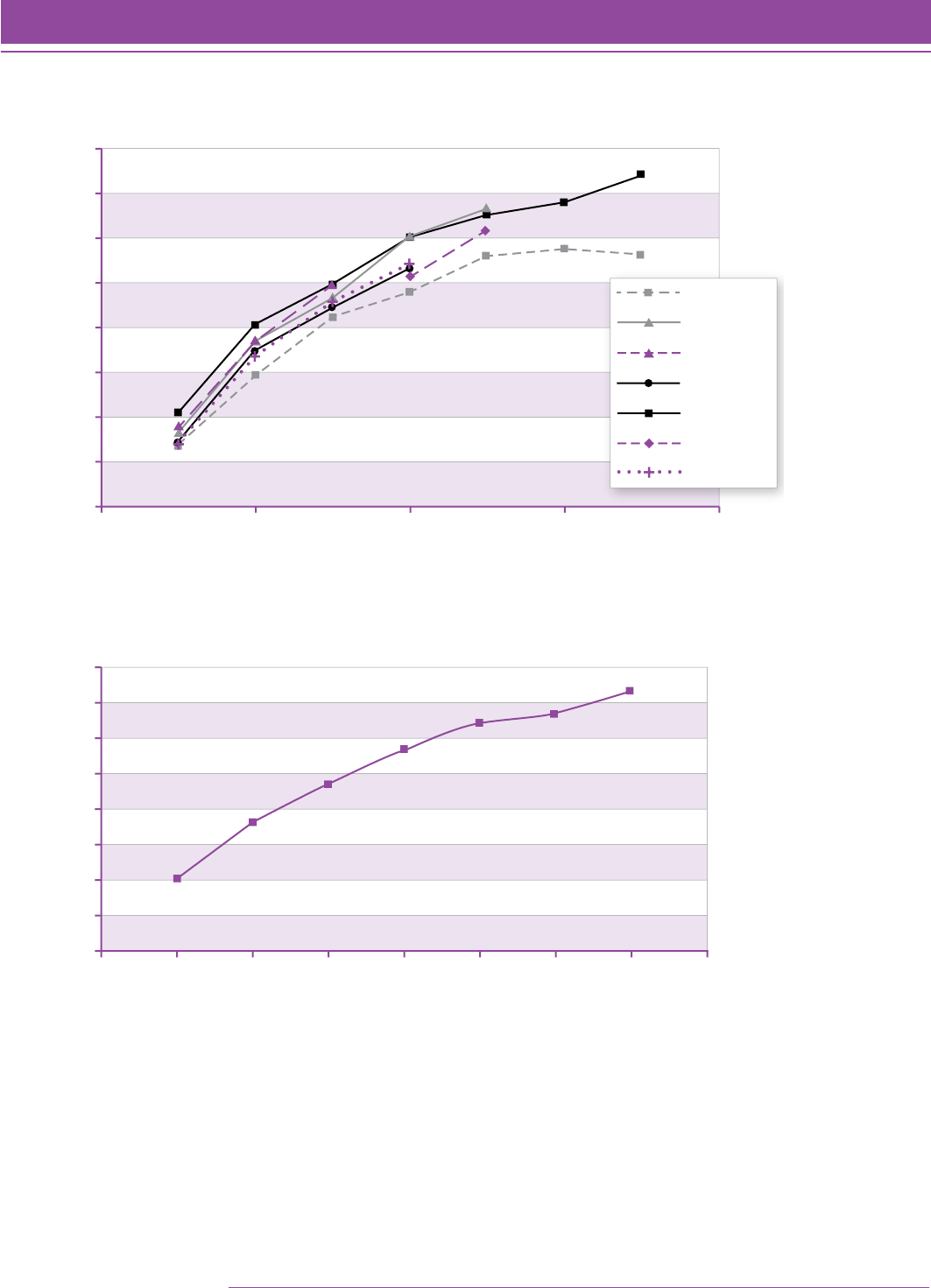
158 SMI College & Career

Appendices

FIGURE 23. SMI Validation Study, Phase III: SMI Quantile measures displayed by location and

grade.

SMI_TG_114

300

200

400

500

600

700

800

900

1000

135 9

Grade

SMI Quantile measure

Alief (TX)

Killeen (TX)

Brevard (FL)

Cabarrus (NC)

Clark (NV)

Harford (MD)

Kannapolis (NC)

FIGURE 24. SMI Validation Study, Phase III: SMI Quantile measures displayed by grade.

SMI_TG_114-A

300

200

400

500

600

700

800

900

1000

123456789

Grade

SMI Quantile measure

Appendices 159

Appendices

The Relationship Between SMI Scores and State Math Assessment Scores

State mathematics assessment data was collected in two of the Phase I sites (Decatur and Harford) and all six

of the Phase II sites (Alief, Brevard, Cabarrus, Clark, Harford, and Kannapolis). In general, SMI exhibited moderate

correlations (r 5 0.60 to 0.70) with state assessments of mathematics. The within-grade correlations and the overall

across-grades correlation (where appropriate) are moderate, as expected, given the different mode of administration

between the two tests (fixed, constant form for all students within a grade on the state assessments, as compared to

the SMI, which is a computer-adaptive assessment that is tailored to each student’s level of achievement).

Based on the data from Decatur (IL) Public School District described previously, the concurrent validity of SMI was

examined. Because ISAT is on a vertical scale, the data were collapsed across grades for analysis. The following

correlations indicate a strong relationship with the two administrations of the SMI Quantile measures. The ISAT 2008

and 2009 showed a moderate relationship with the SMI Quantile measures.

TABLE 31. Correlations among the Decatur Public School District test scores.

SMI Quantile 1 SMI Quantile 2

SMI Quantile 1 - -

SMI Quantile 2 0.81 -

ISAT 2008 0.60 0.61

ISAT 2009 0.60 0.62

During Phase I of the SMI Validation Study, in the Harford County Public Schools, the Maryland School Assessment

(MSA) is administered to all students in Grades 3–8 in March. It is not on a vertical scale, so the data for the state

test results could not be combined across grades. Both the mathematics and reading scores from the state test

were available. For the state tests, Grades 2–3 did not have scores. Grade 4 had state scores for 2009, and Grade 5

had scores for both 2008 and 2009. The correlation between the SMI Quantile measures and the MSA mathematics

scores are presented in Table 32.

TABLE 32. Correlations between SMI Quantile measures and Harford County

Public Schools test scores.

Grade 4 Grade 5

MSA 2008 - 0.67

MSA 2009 0.67 0.73

160 SMI College & Career

Appendices

In the Alief Independent School District (Texas), students in Grades 3–6 were administered the Texas Assessment of

Knowledge and Skills (TAKS) mathematics test on April 26, 2010, and students in Grades 3–6 also completed the

SMI within six weeks (89.1% of students).

TABLE 33. Alief Independent School District—descriptive statistics for SMI Quantile

measures and 2010 TAKS mathematics scores, by grade.

Grade N2010 TAKS Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 281 541.97 (72.29) 455.98 (143.77) 0.61

4 383 608.84 (72.52) 573.50 (137.76) 0.53

5 204 646.81 (75.70) 641.96 (148.29) 0.52

6 224 687.73 (70.04) 723.19 (187.44) 0.63

All 1,092 614.91 (88.96) 586.75 (179.11) 0.70

Again during the spring of the 2010–2011 school year, students in Grades 3–8 in the Alief ISD were administered the

Texas Assessment of Knowledge and Skills (TAKS) mathematics test, on April 4, 2011 (Grades 5 and 8), and April 26,

2011 (Grades 3, 4, 6, and 7), and students in Grades 3–8 also completed the SMI.

Appendices 161

Appendices

TABLE 34. Alief Independent School District—descriptive statistics for SMI Quantile

measures and 2011 TAKS mathematics scores, by grade.

Grade N2011 TAKS Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 348 576.10 (96.41) 493.54 (160.53) 0.69

4 401 648.60 (96.88) 629.98 (138.37) 0.63

5 85 658.64 (115.33) 683.74 (129.93) 0.37

6 90 717.41 (104.94) 761.96 (182.25) 0.70

7 283 698.04 (85.81) 774.31 (172.32) 0.58

8 134 709.91 (127.98) 766.24 (224.79) 0.38

All 1,341 664.50 (115.69) 652.25 (197.63) 0.68

In the Brevard Public Schools (Florida), students in Grades 3–6 were administered the mathematics part of the

Florida Comprehensive Assessment Test (FCAT) between March 9 and 19, 2010, and students also completed the

SMI within six weeks (97.0% of students).

162 SMI College & Career

Appendices

TABLE 35. Brevard Public Schools—descriptive statistics for SMI Quantile measures and

2010 FCAT mathematics scores, by grade.

Grade N2010 FCAT Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 5 1159.00 (270.07) 413.00 (101.71) 0.70

4 88 1550.00 (226.44) 522.44 (152.64) 0.63

5 87 1626.00 (187.80) 652.01 (129.03) 0.57

6 87 1738.00 (225.00) 782.01 (160.61) 0.69

All 267 1629.00 (235.97) 647.19 (183.39) 0.69

Again during the 2010–2011 school year, students in the Brevard Public Schools (Florida) in Grades 3–6 were

administered the mathematics part of the Florida Comprehensive Assessment Test (FCAT) between April 11 and 20,

2011, and students also completed the SMI.

TABLE 36. Brevard Public Schools—descriptive statistics for SMI Quantile measures and

2011 FCAT mathematics scores, by grade.

Grade N2011 FCAT Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

4 93 1543.00 (289.38) 579.41 (165.76) 0.80

5 93 1582.00 (237.55) 665.54 (151.65) 0.68

6 83 1759.00 (213.74) 810.54 (131.48) 0.79

7 88 1810.00 (247.78) 867.22 (194.91) 0.75

All 357 1669.00 (273.13) 726.53 (198.68) 0.80

In the Cabarrus County Schools (North Carolina), students in Grades 3–5 were administered the mathematics part

of the North Carolina End-of-Grade Tests (NCEOG) during the last three weeks of the school year, and students also

completed the SMI within six weeks (99.9% of students). The within-grade correlation for Grade 4 was lower

than expected.

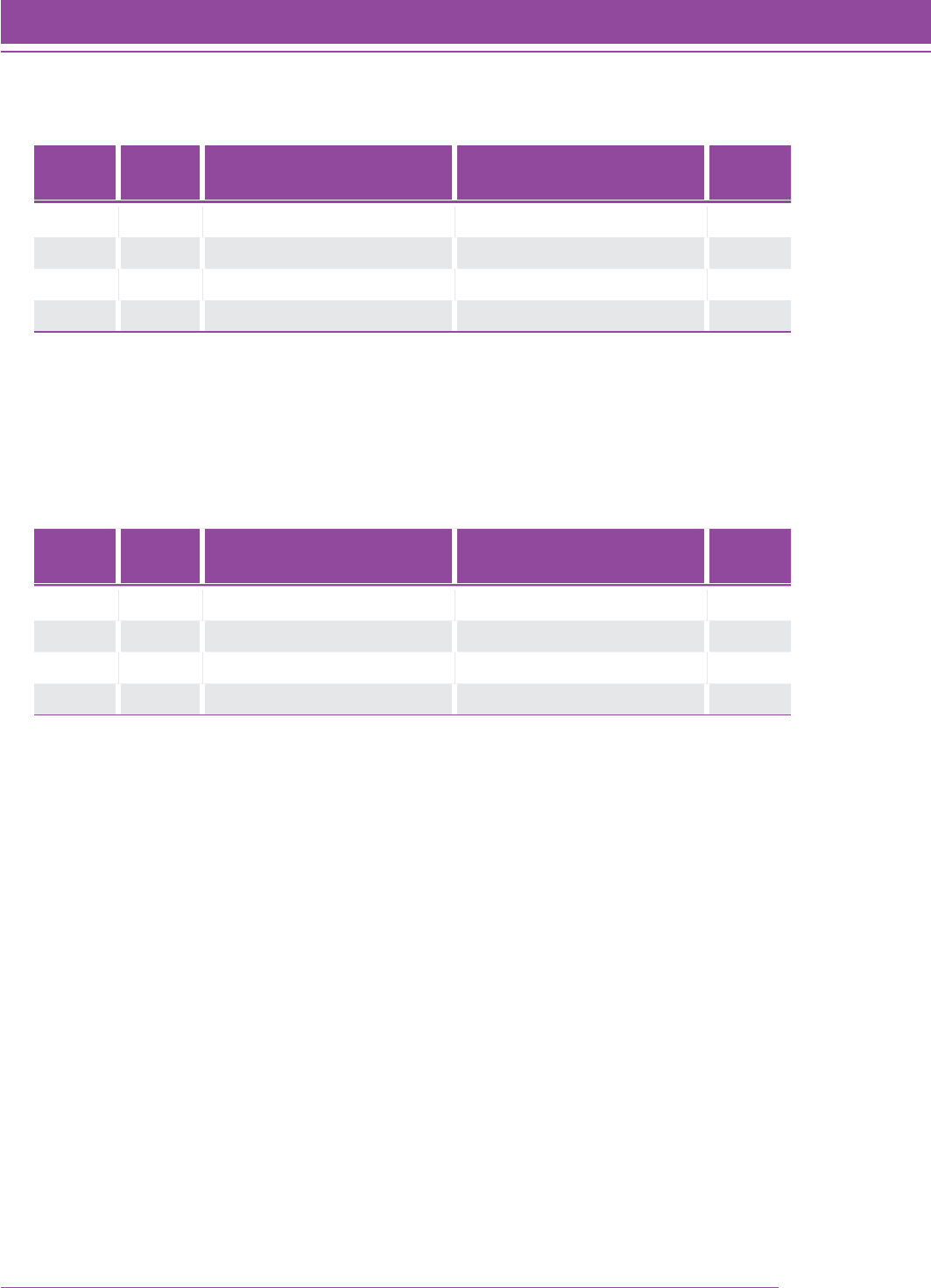
Appendices 163

Appendices

TABLE 37. Cabarrus County Schools—descriptive statistics for SMI Quantile measures and

2010 NCEOG mathematics scores, by grade.

Grade N2010 NCEOG Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 283 347.20 (10.98) 583.83 (201.38) 0.56

4 279 351.54 (10.25) 655.34 (184.50) 0.38

5 276 358.19 (9.30) 793.12 (196.33) 0.74

All 838 352.24 (11.16) 676.57 (212.53) 0.63

Again during the 2010–2011 school year, students in the Cabarrus County Schools in Grades 3–5 were administered

the mathematics part of the North Carolina End-of-Grade Tests (NCEOG) during the last three weeks of the school

year, and students also completed the SMI.

TABLE 38. Cabarrus County Schools—descriptive statistics for SMI Quantile measures and

2011 NCEOG mathematics scores, by grade.

Grade N2011 NCEOG Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 125 349.18 (10.29) 621.72 (193.29) 0.75

4 159 355.44 (9.75) 741.35 (180.15) 0.78

5 154 361.40 (8.56) 885.03 (202.70) 0.70

All 438 355.81 (10.67) 667.82 (254.48) 0.80

In the Clark County School District (Nevada), students in Grades 3–5 were administered the mathematics part of the

criterion-referenced tests (CRT) between February 16 and March 16, 2010, and students also completed the SMI

within seven to nine weeks (97.8% of students). The CRT is not reported on a vertical scale, so scores from Grades

3–5 cannot be combined for an overall correlation between CRT scale scores and SMI Quantile measures.

164 SMI College & Career

Appendices

TABLE 39. Clark County School District—descriptive statistics for SMI Quantile measures

and 2010 CRT mathematics scores, by grade.

Grade N2010 CRT Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 95 323.76 (64.36) 445.58 (173.49) 0.60

4 102 331.30 (46.03) 608.04 (146.37) 0.66

5 115 351.96 (84.52) 698.00 (173.57) 0.74

During Phase II, in the Harford County Public Schools (Maryland), students in Grades 3–5 were administered the

mathematics part of the Maryland School Assessment (MSA) between March 8 and 23, 2010, and students also

completed the SMI within six weeks (100.0% of students). The MSA is not reported on a vertical scale, so scores

from Grades 3–5 cannot be combined for an overall correlation between MSA scale scores and SMI Quantile

measures.

Again during the 2010–2011 school year, students in the Clark County School District in Grades 3–5 were

administered the mathematics part of the criterion-referenced tests (CRT) on March 7, 2011, and students also

completed the SMI.

TABLE 40. Clark County School District—descriptive statistics for SMI Quantile measures

and 2011 CRT mathematics scores, by grade.

Grade N2011 CRT Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 101 346.27 (64.33) 544.80 (151.32) 0.66

4 103 328.45 (50.68) 644.27 (171.71) 0.73

5 61 345.43 (84.95) 730.41 (144.83) 0.46

Appendices 165

Appendices

TABLE 41. Harford County Public Schools—descriptive statistics for SMI Quantile measures

and 2010 MSA mathematics scores, by grade.

Grade N2010 MSA Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 58 416.45 (34.15) 515.52 (167.28) 0.63

4 64 435.83 (33.40) 656.56 (140.56) 0.56

5 65 435.65 (37.57) 705.00 (178.80) 0.80

During Phase III (2010–2011 school year) in the Harford County Public Schools, students in Grades 3–5 were

administered the mathematics part of the Maryland School Assessment (MSA) between March 8 and 16, 2011, and

students also completed the SMI.

TABLE 42. Harford County Public Schools—descriptive statistics for SMI Quantile measures

and 2011 MSA mathematics scores, by grade.

Grade N2011 MSA Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 2,768 424.04 (37.07) 603.43 (201.73) 0.75

4 2,531 435.04 (37.87) 694.20 (165.71) 0.72

5 2,711 427.67 (31.84) 799.74 (182.14) 0.73

6 2,024 436.07 (37.24) 849.04 (203.77) 0.75

7 2,086 427.48 (34.89) 877.80 (219.64) 0.79

8 1,965 432.71 (35.56) 944.60 (230.80) 0.80

As in Cabarrus County Schools, students in Grades 5–6 in Kannapolis City Schools (North Carolina) were

administered the mathematics part of the North Carolina End-of-Grade Tests (NCEOG) during the last three weeks of

the school year, and students also completed the SMI within six weeks (93.0% of students).

166 SMI College & Career

Appendices

TABLE 43. Kannapolis City Schools—descriptive statistics for SMI Quantile measures and

2010 NCEOG mathematics scores, by grade.

Grade N2010 NCEOG Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

5 309 352.86 (8.51) 693.01 (172.44) 0.64

6 320 358.06 (8.32) 814.16 (174.10) 0.69

All 629 355.51 (8.80) 754.64 (183.45) 0.70

During Phase III of the SMI Validation Study (2010–2011 school year), students in Grades 5–6 in Kannapolis City

Schools were administered the mathematics part of the North Carolina End-of-Grade Tests (NCEOG) during the last

three weeks of the school year, and students also completed the SMI.

TABLE 44. Kannapolis City Schools—descriptive statistics for SMI Quantile measures and

2011 NCEOG mathematics scores, by grade.

Grade N2011 NCEOG Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

5 331 353.15 (8.76) 711.01 (214.20) 0.75

6 321 357.44 (8.28) 813.37 (200.14) 0.75

All 652 355.25 (8.79) 761.51 (213.46) 0.77

Appendices 167

Appendices

During the spring of the 2010–2011 school year, students in Grades 3–8 in Killeen ISD (Texas) were administered the

Texas Assessment of Knowledge and Skills (TAKS) mathematics test on April 4, 2011 (Grades 5 and 8), and April 26,

2011 (Grades 3, 4, 6, and 7), and students also completed the SMI.

TABLE 45. Killeen Independent School District—descriptive statistics for SMI Quantile

measures and 2011 TAKS mathematics scores, by grade.

Grade N2011 TAKS Math Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 2,801 581.88 (88.86) 531.44 (147.61) 0.65

4 2,713 649.67 (89.31) 654.73 (135.79) 0.61

5 2,483 708.15 (83.89) 740.24 (138.02) 0.53

All 7,997 644.54 (101.56) 637.47 (166.46) 0.71

Growth in Mathematical Understanding

“In the simplest terms, growth is change over time. To study growth, we measure a thing repeatedly on successive

occasions and draw conclusions about how it has changed” (Williamson, 2006). Growth in mathematical

understanding can be determined by examining the changes in SMI Quantile measures (an equal-interval scale).

Using the data collected during the SMI Validation Study—Phase II from six school districts, a data panel was

created consisting of students with two or more SMI Quantile measures. A total of 4,116 students were included in

the dataset. Table 46 describes the composition of the whole sample and Table 47 describes the composition of the

sample with three or more SMI Quantile measures.

168 SMI College & Career

Appendices

TABLE 46. Description of longitudinal panel across districts, by grade.

Grade NMean Number of

SMI Administrations

Mean Number of Days Between

SMI Administrations

2 533 2.6 85.3

3 843 2.6 80.6

4 1,001 2.6 82.6

5 1,062 2.4 91.4

6 677 2.7 80.0

All 4,116 2.6 84.2

TABLE 47. Description of longitudinal panel across districts, by grade for students with at

least three Quantile measures.

Grade NMean Number of

SMI Administrations

Mean Number of Days Between

SMI Administrations

2 293 3.0 84.3

3 462 3.0 78.0

4 594 3.0 79.7

5 431 3.1 76.4

6 471 3.0 70.4

All 2,251 3.0 77.4

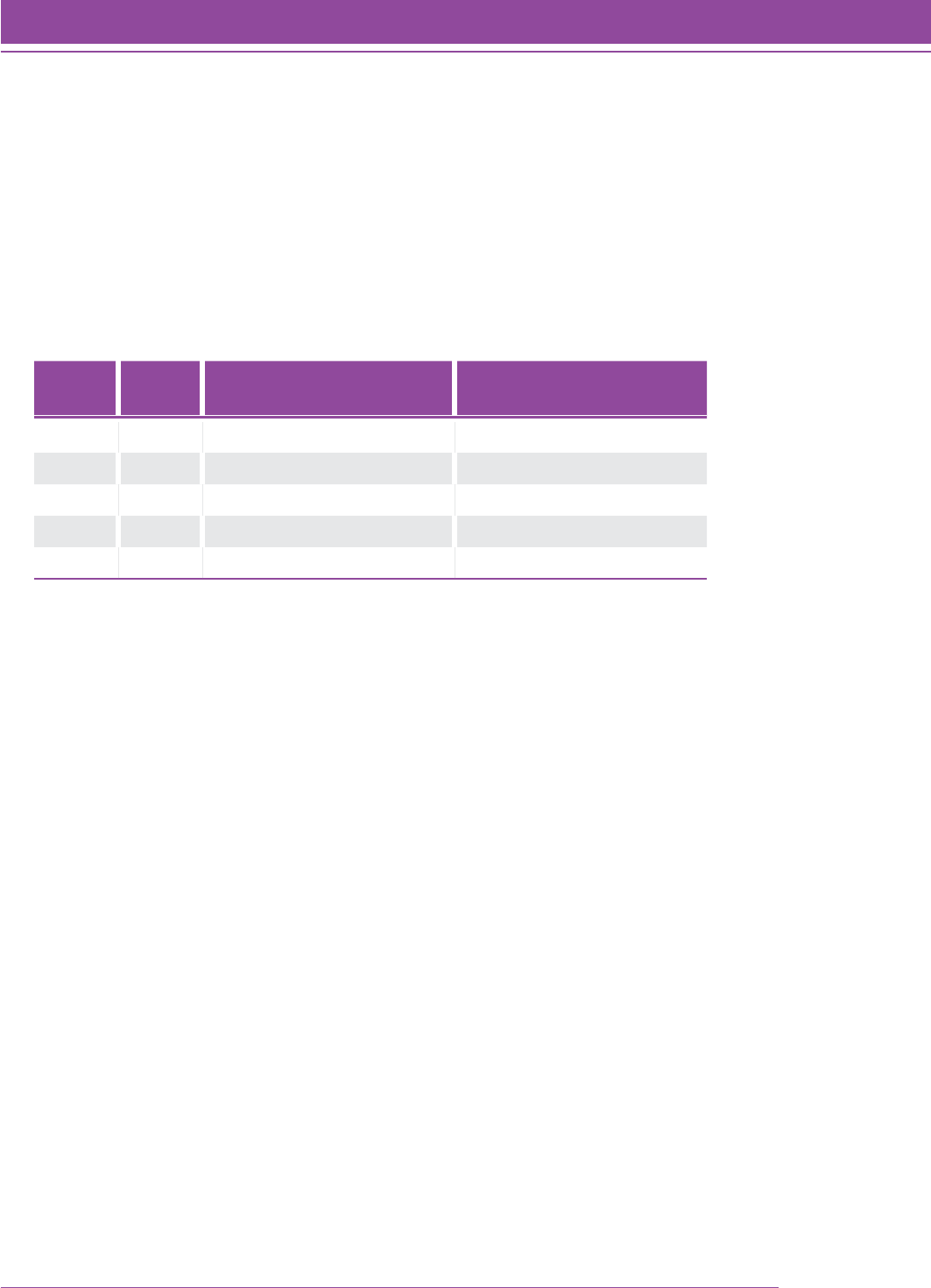
Appendices 169

Appendices

Given the short time span between initial and final assessments, a linear regression model was employed to

examine growth in mathematical understanding from the SMI Quantile measures. Of the panel, students with three

or more SMI Quantile measures (N 5 2,251, 51.4%) were used in the regression analyses. The slope of the linear

regression for each student describes the amount of growth in mathematical understanding per day. The growth

estimated from the SMI Quantile measures ranges from 0.5529 to 0.6790, with a mean (weighted) of 0.6138; or,

the expected growth in mathematical understanding, as measured by the SMI, is about 0.6Q per day (see Table 48).

Across grade levels, the R

2 statistics describing the percent of variance in SMI Quantile measures accounted for by

the linear model ranged from 52.3% in Grade 5 to 62.9% in Grade 2. Across Grades 2–6, the mean slope estimate is

significantly different from zero (p < 0.0001).

TABLE 48. Results of regression analyses for longitudinal panel, across grades.

Grade NSlope of Linear Regression

Mean (SD) R 2

2 293 0.6227 (0.7929) 0.6288

3 465 0.5853 (0.8690) 0.5603

4 594 0.6241 (0.8018) 0.5564

5 431 0.5529 (0.9106) 0.5231

6 471 0.6790 (1.0994) 0.5531

170 SMI College & Career

Appendices

The results in Table 48 describe the amount of growth that can be expected across a school year, which is consistent

across Grades 2–6 (approximately 0.6Q per day or approximately 108Q per year). These results are consistent with

other research conducted by MetaMetrics, with the Quantile Framework showing a near-linear trend between grade

level and mathematics achievement as measured on the Quantile scale.

During Phase III of the SMI Validation Study, growth was examined during the 2010–2011 school year. Data collected

during the fall administration of SMI was matched with data collected during the spring administration for a sample

of 10,178 students in Grades 2–6 from the seven sites. The average growth per day was estimated as 0.67Q (or

120.6Q per year) and ranged from 0.44Q per day in Grade 5 to 0.90Q per day in Grade 3 (the average growth during

the school year was 155.998Q and ranged from 101Q to 208Q).

A subsample of 752 students in Grades 2–6 from four sites (Alief, Brevard, Clark, and Harford) had data from both

the 2009–2010 school year and the 2010–2011 school year. This group of students grew, on average, 242Q over the

two school years (102Q in Year 1 and 153Q in Year 2). As expected, a negative correlation was observed between the

students’ initial status (SMI Quantile measure in Winter 2009) and the amount grown over the two school years

(r 5 2.486, p < .0001). This negative correlation is consistent with the interpretation that lower-performing

students typically grow more than higher-performing students.

Appendices 171

Appendices

Additional Aspects of Construct-Identification Validity

Discriminate validity looks at the relationships between test scores and other criterion variables that the scores

should not be related to (e.g., gender, race/ethnicity). Scores on assessments of mathematics ability are expected to

fluctuate according to some demographic characteristics of the students taking the test.

Gender

Gender information was collected in three of the Phase I sites (Decatur, Harford, and Raytown) and six of the

Phase II sites (Alief, Brevard, Cabarrus, Clark, Harford, and Kannapolis). An ANOVA was conducted for the data from

each site and a significant difference due to gender was not observed for any of the sites.

During Phase III of the SMI Validation Study, gender data were collected in the seven sites. An ANOVA was conducted

for the data from each site (results are presented in Table 22) and a significant difference due to gender was

observed in two of the seven sites (Alief, p < .0478; and Harford, p < .0015). The differences between the means

ranged from +22.97 (females performing higher than males) to 212.54 (males performing higher than females). As

expected, there is no clear pattern in the differences in performance of males and females on SMI.

Race/Ethnicity

Race/Ethnicity information was collected in three of the Phase I sites (Decatur, Harford, and Raytown) and five of the

Phase II sites (Brevard, Cabarrus, Clark, Harford, and Kannapolis). An ANOVA was conducted for the data from each

site (results are presented in Table 20) and a significant difference due to race/ethnicity was observed for three of

the sites (Cabarrus, p < .0001; Clark, p < .0001; and Kannapolis, p < .0001). The differences between the mean SMI

Quantile measures are as expected.

During Phase III of the SMI Validation Study, race/ethnicity information was collected in all seven of the sites. An

ANOVA was conducted for the data from each site (results are presented in Table 23) and a significant difference

due to race/ethnicity was observed for six of the seven sites (Alief, R

2 5 0.058, p < .0001; Cabarrus, R

2 5 0.057,

p < .0001; Clark, R

2 5 0.085, p < .0009; Harford, R

2 5 0.026, p < .0001; Kannapolis, R

25 0.031, p < .0009; and

Killeen, R

2 5 0.015, p < .0001). The differences between the mean SMI Quantile measures are as expected.

172 SMI College & Career

Appendices

Language Proficiency

Language proficiency is defined by participation in a bilingual instruction program or classification as English

language learner (ELL), English as a second language (ESL), or limited English proficiency (LEP). Data was collected

in one of the Phase I sites (Harford) and four of the Phase II sites (Alief, Cabarrus, Clark, and Kannapolis). For bilingual

status, an ANOVA was conducted for the data from Alief and a significant difference was not observed.

For bilingual status, an ANOVA was conducted for the Phase II data from Alief and a significant difference was

not observed. During Phase III, bilingual status was collected from two sites (Alief and Brevard) for students in

Grades 2–6. While a significant difference was observed for Alief, the level of significance is not strong and the

differences between the mean SMI Quantile measures are as expected.

TABLE 49. Alief Independent School District—bilingual means and standard deviations for

the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

249 577.83

(155.12) 687 604.21

(180.92)

p < .0412

For ELL, ESL, and LEP status, an ANOVA was conducted for the data from each site and a significant difference

due to language proficiency classification was observed for four of the sites (ELL: Cabarrus, p < .0001; ESL: Alief,

p < .01; LEP: Alief, Kannapolis, p < .0001; Clark, p < .01). The differences between the mean SMI Quantile measures

are as expected.

TABLE 50. Cabarrus County Schools—English language learners (ELL) means and standard

deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

75 393.67

(205.27) 918 563.04

(219.81)

p < .0001

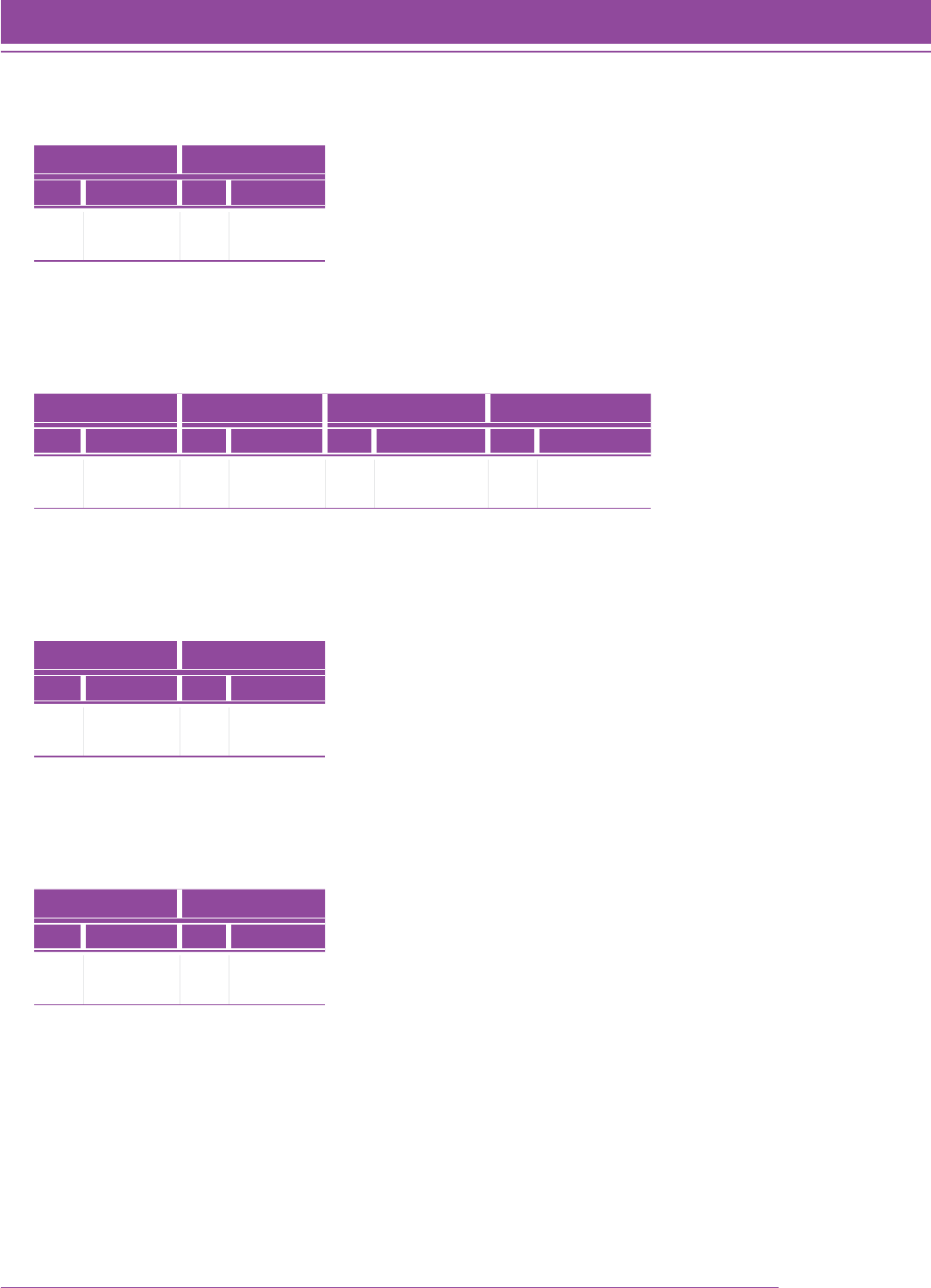
Appendices 173

Appendices

TABLE 51. Alief ISD—English as a second language (ESL) means and standard deviations for

the SMI Quantile measures.

0 1

NMean (SD) NMean (SD)

1,260 570.48

(220.42) 375 529.67

(212.43)

p < .01

TABLE 52. Alief ISD—limited English proficiency (LEP) status means and standard deviations

for the SMI Quantile measures.

Not-LEP LEP Exited LEP—Year 1 Exited LEP—Year 2

NMean (SD) NMean (SD) NMean (SD) NMean (SD)

120 748.12

(168.07) 414 501.87

(186.68) 130 632.19

(158.50) 105 755.05

(134.55)

p < .0001

TABLE 53. Clark County School District—limited English proficiency (LEP) status means and

standard deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

5398.00

(307.73) 307 628.63

(190.44)

p < .01

TABLE 54. Kannapolis City Schools—limited English proficiency (LEP) status means and

standard deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

66 660.45

(194.23) 544 776.16

(184.62)

p < .0001

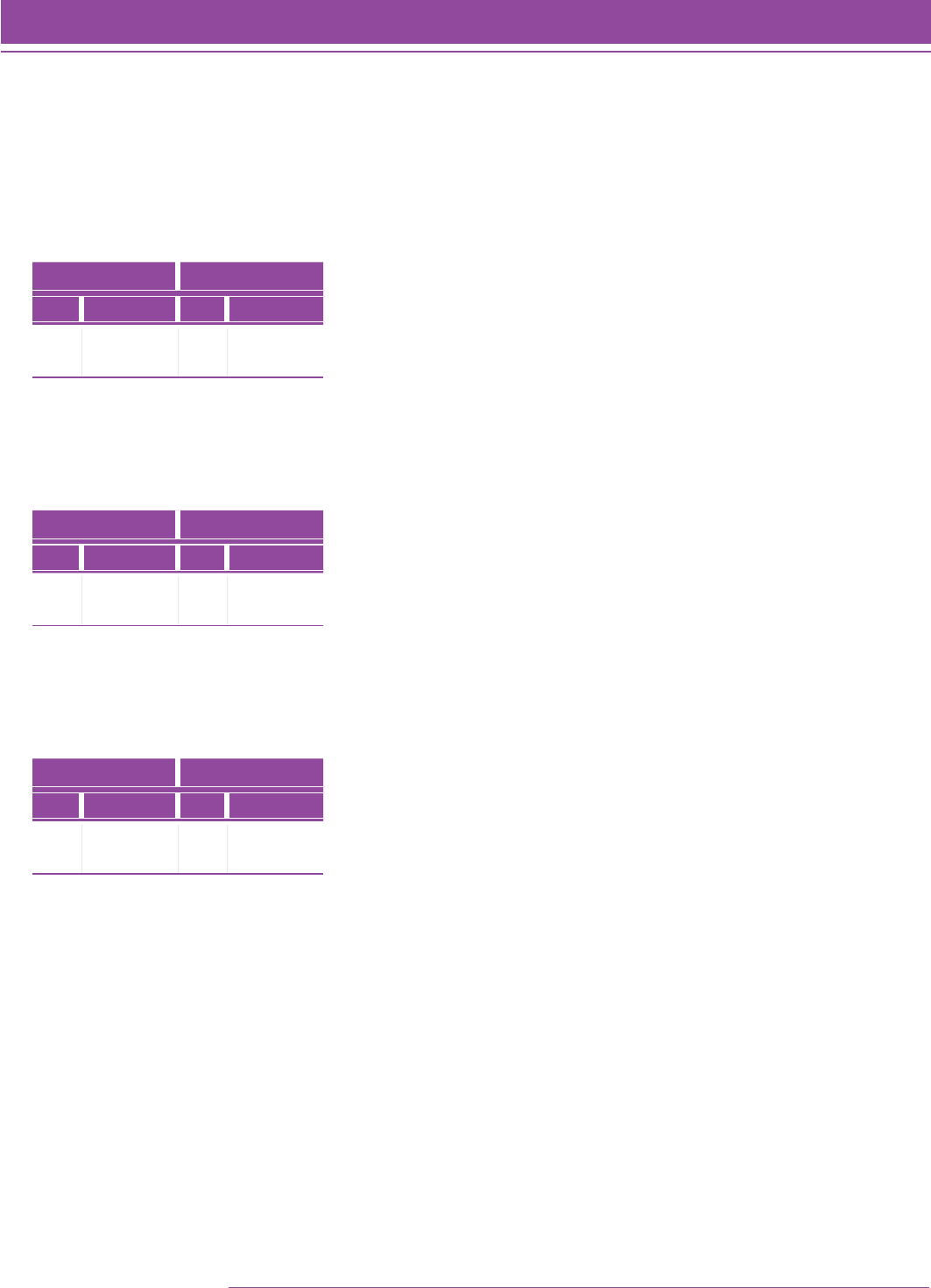
174 SMI College & Career

Appendices

For ELL, ESL, and LEP status during Phase III, an ANOVA was conducted for the Grades 2–6 data from

each site, and a significant difference due to language proficiency classification was observed for three of the sites

(ELL: Harford, p < .0001; LEP: Kannapolis, p < .0152; Killeen, p < .0001). The differences between the mean SMI

Quantile measures are as expected.

TABLE 55. Harford County Public Schools—English language learners (ELL) means

and standard deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

287 586.24

(239.28) 12,446 666.93

(239.62)

p < .0001

TABLE 56. Kannapolis City Schools—limited English proficiency (LEP) means and standard

deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

109 716.10

(206.92) 568 770.22

(213.77)

p < .0152

TABLE 57. Killeen ISD—limited English proficiency (LEP) means and standard deviations for

the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

794 587.69

(168.30) 8,035 642.39

(165.48)

p < .0001

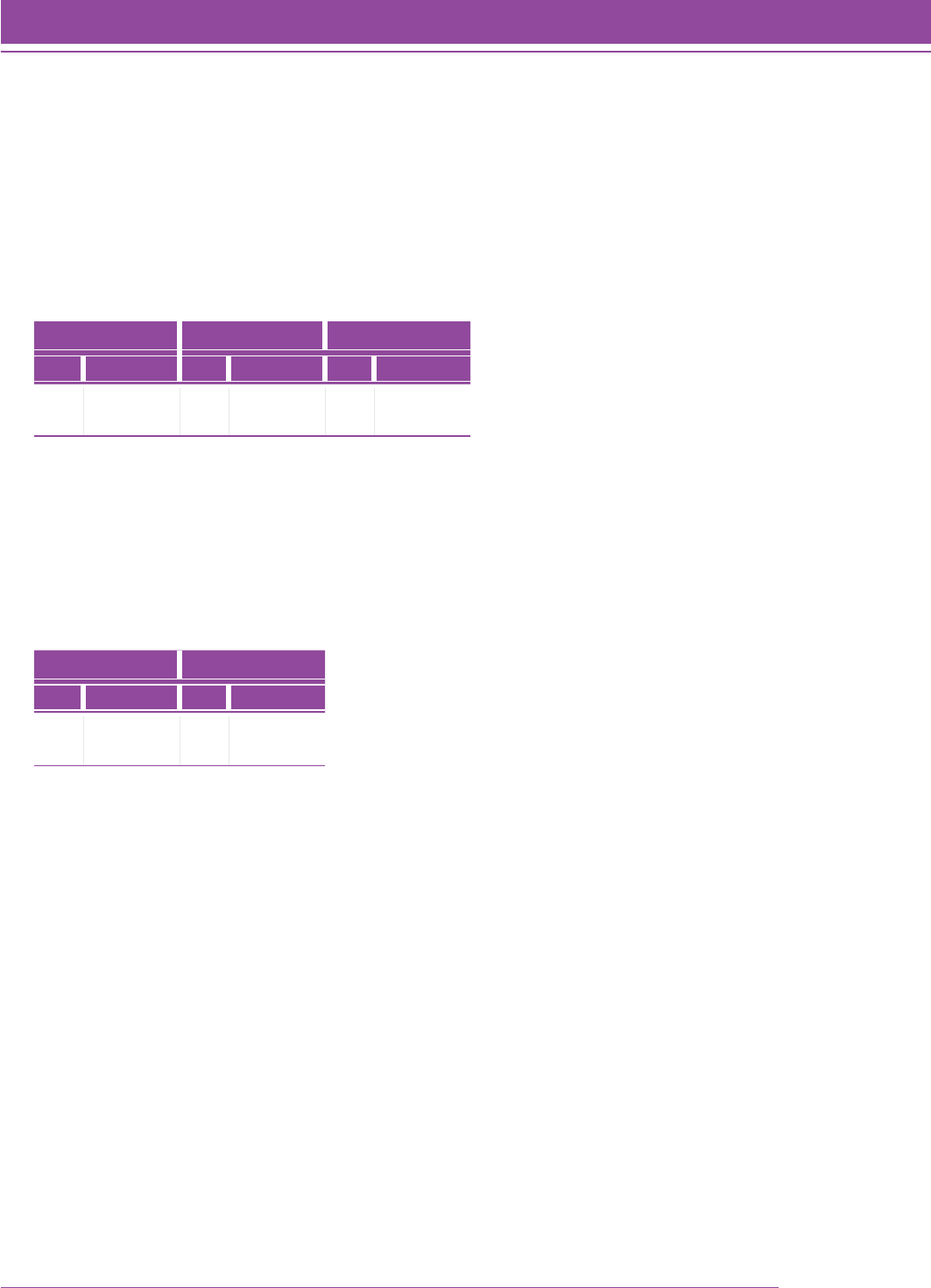
Appendices 175

Appendices

Economic Status

Economic status of students was defined by being classified as economically disadvantaged in the free or reduced-

price lunch (FRPL) program.

FRPL status was collected in one of the Phase I sites (Decatur) and two of the Phase II sites (Alief and Clark). An

ANOVA was conducted for the data from each site, and a significant difference due to FRPL status was observed for

one of the sites (Alief, p < .01). The differences between the mean SMI Quantile measures are as expected.

TABLE 58. Alief ISD—Economically disadvantaged means and standard deviations for the

SMI Quantile measures.

Free Reduced No

NMean (SD) NMean (SD) NMean (SD)

1,299 551.55

(218.30) 127 617.64

(200.96) 209 586.24

(229.15)

p < .01

Economically disadvantaged classification information was collected from two Phase II sites (Brevard and Harford).

An ANOVA was conducted for the data from each site and a significant difference due to FRPL status was observed

for one of the sites (Harford, p < .01). The differences between the mean SMI Quantile measures are as expected.

TABLE 59. Harford County Public Schools—Economically disadvantaged means and standard

deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

105 564.29

(225.34) 151 620.50

(229.86)

p < .01

During Phase III of the SMI Validation Study, economically disadvantaged classification information was collected

from three of the seven sites (Brevard, Harford, and Killeen). An ANOVA was conducted for the data from each site,

and a significant difference due to FRPL status was observed for one of the sites (Killeen, p < .01). The differences

between the mean SMI Quantile measures are as expected.

176 SMI College & Career

Appendices

TABLE 60. Killeen Independent School District—Economically disadvantaged means and

standard deviations for the SMI Quantile measures.

Yes No

NMean (SD) NMean (SD)

4,431 620.68

(165.35) 4,398 654.39

(165.89)

p < .01

Relationship Between SMI Quantile Measures and Assessments of Reading Comprehension

State mathematics assessment data was collected in two of the Phase I sites (Decatur and Harford) and all six of the

Phase II sites (Alief, Brevard, Cabarrus, Clark, Harford, and Kannapolis).

Interim reading assessment information was collected in one site during Phase I of the validation study. The

Maryland School Assessment (MSA) is administered to all students in Grades 3–8 in March. Additionally, Harford

County Public Schools had the Scholastic Reading Inventory (SRI) test scores available for this study. The reporting

score for the SRI is the Lexile measure. This score is on a vertical scale so these analyses were computed across

grades. The correlations among the SMI Quantile measures and SRI Lexile measures from 2009 ranged from 0.42 to

0.62 (Grade 2, r 5 0.62; Grade 3, r 5 0.42; Grade 4, r 5 0.47; and Grade 5, r 5 0.47), respectively, indicating that

the scores are minimally correlated.

State reading assessment results were collected from five of the six sites during Phase II of the validation study.

Table 61 presents the correlations between TAKS reading scale scores and SMI Quantile measures in Alief

Independent School District. Table 62 presents the correlations between FCAT reading scale scores and SMI Quantile

measures in Brevard Public Schools. Tables 63 and 64 present the correlations between NCEOG reading scale scores

and the SMI Quantile measures. As expected, all of the correlations are low and are lower than the correlations

between state math assessments results and SMI Quantile measures.

The one exception to this trend is the result for Clark County School District. Table 65 presents the correlations

between CRT reading scale scores and SMI Quantile measures for Clark County School District. The CRT is not

reported on a vertical scale, so scores from Grades 3 through 5 cannot be combined for an overall correlation

between CRT scale scores and SMI Quantile measures. The correlations between the CRT reading scale scores and

the SMI Quantile measures are higher than expected and closely approximate the correlations between the CRT

math scale scores and the SMI Quantile measures.

Appendices 177

Appendices

TABLE 61. Alief Independent School District—descriptive statistics for SMI Quantile

measures and 2010 TAKS reading scores, by grade.

Grade N2010 TAKS Reading Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 309 600.28 (84.34) 485.32 (145.67) 0.53

4 448 626.45 (77.64) 607.96 (142.87) 0.43

5 222 683.59 (61.94) 677.73 (142.89) 0.39

6 236 716.76 (80.93) 750.83 (186.38) 0.45

All 1,215 647.78 (88.83) 617.26 (178.72) 0.58

TABLE 62. Brevard Public Schools—descriptive statistics for SMI Quantile measures and

2010 FCAT reading scores, by grade.

Grade N2010 FCAT Reading Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 5 917.60 (282.50) 413.00 (101.71) 0.50

4 88 1466.00 (240.14) 522.44 (152.64) 0.50

5 87 1656.00 (240.76) 652.01 (129.03) 0.31

6 87 1720.00 (277.79) 782.01 (160.61) 0.56

All 267 1600.00 (290.21) 647.19 (183.39) 0.59

178 SMI College & Career

Appendices

TABLE 63. Cabarrus County Schools—descriptive statistics for SMI Quantile measures and

2010 NCEOG reading scores, by grade.

Grade N2010 NCEOG Reading Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 282 344.47 (11.08) 583.37 (201.59) 0.32

4 279 347.84 (9.09) 655.34 (184.50) 0.20

5 276 352.19 (9.34) 793.12 (196.33) 0.63

All 837 348.12 (10.37) 676.52 (212.66) 0.45

TABLE 64. Kannapolis City Schools—descriptive statistics for SMI Quantile measures and

2010 NCEOG reading scores, by grade.

Grade N2010 NCEOG Reading Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

5 309 348.28 (8.51) 693.01 (172.44) 0.53

6 320 354.09 (7.80) 814.16 (174.10) 0.56

All 629 351.24 (8.65) 754.64 (183.45) 0.59

Appendices 179

Appendices

TABLE 65. Clark County School District—descriptive statistics for SMI Quantile measures

and 2010 CRT reading scores, by grade.

Grade N2010 CRT Reading Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 95 330.32 (60.23) 445.58 (173.49) 0.61

4 102 348.19 (76.64) 608.04 (146.37) 0.60

5 115 324.32 (60.19) 698.00 (173.57) 0.59

State reading assessment results were collected from one of the seven sites during Phase III of the validation study

(Alief). Table 66 presents the correlations between TAKS reading scale scores and SMI Quantile measures in Alief

Independent School District for a sample of Grades 3 and 4 students. As expected, the correlations are low and are

lower than the correlations between state math assessments results and SMI Quantile measures.

TABLE 66. Alief Independent School District—descriptive statistics for SMI

Quantile measures and 2011 TAKS reading scores, by grade.

Grade N2011 TAKS Reading Scale Scores

Mean (SD)

SMI Quantile Measures

Mean (SD) r

3 110 593.83 (98.92) 493.87 (160.53) 0.57

4 115 646.32 (103.96) 629.98 (138.37) 0.40

All 225 620.00 (104.67) 652.25 (197.63) 0.54

SMI Tech Guide 2015

Navigation menu

Versions of this User Manual:

Views

Navigation