SS CP 65 1999 PT SL Example 001
User Manual: SS CP 65-1999 PT-SL Example 001
Open the PDF directly: View PDF ![]() .
.
Page Count: 6
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
SS CP 65-99 PT-SL EXAMPLE 001 - 1
SS CP 65-99 PT-SL EXAMPLE 001
Post-Tensioned Slab Design
PROBLEM DESCRIPTION
The purpose of this example is to verify the slab stresses and the required area of
mild steel strength reinforcing for a post-tensioned slab.
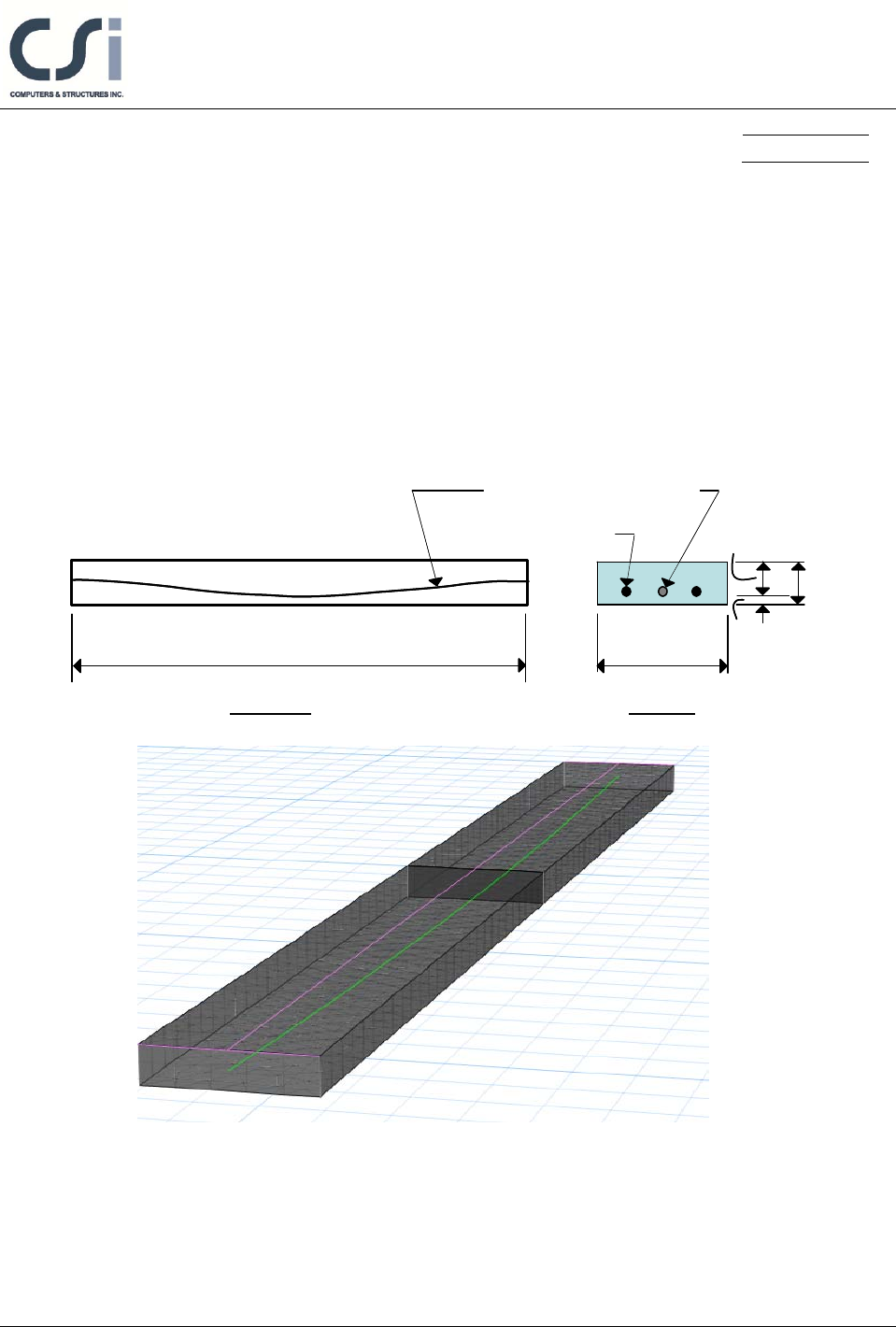
A one-way, simply supported slab is modeled in ETABS. The modeled slab is 254
mm thick by 914 mm wide and spans 9754 mm, as shown in shown in Figure 1.
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Figure 1 One-Way Slab

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
SS CP 65-99 PT-SL EXAMPLE 001 - 2
A 254-mm-wide design strip is centered along the length of the slab and has been
defined as an A-Strip. B-strips have been placed at each end of the span,
perpendicular to Strip-A (the B-Strips are necessary to define the tendon profile).
A tendon with two strands, each having an area of 99 mm2, has been added to the
A-Strip. The self weight and live loads have been added to the slab. The loads and
post-tensioning forces are as follows.
Loads: Dead = self weight, Live = 4.788 kN/m2
The total factored strip moments, required area of mild steel reinforcement, and
slab stresses are reported at the mid-span of the slab. Independent hand
calculations are compared with the ETABS results and summarized for verification
and validation of the ETABS results.
GEOMETRY, PROPERTIES AND LOADING
Thickness T, h = 254 mm
Effective depth d = 229 mm
Clear span L = 9754 mm
Concrete strength f 'c = 30 MPa
Yield strength of steel fy = 400 MPa
Prestressing, ultimate fpu = 1862 MPa
Prestressing, effective fe = 1210 MPa
Area of Prestress (single strand) Ap = 198 mm2
Concrete unit weight wc = 23.56 kN/m3
Modulus of elasticity Ec = 25000 N/mm3
Modulus of elasticity Es = 200,000 N/mm3
Poisson’s ratio = 0
Dead load wd = self kN/m2
Live load wl = 4.788 kN/m2
TECHNICAL FEATURES OF ETABS TESTED
Calculation of the required flexural reinforcement
Check of slab stresses due to the application of dead, live, and post-tensioning
loads
RESULTS COMPARISON
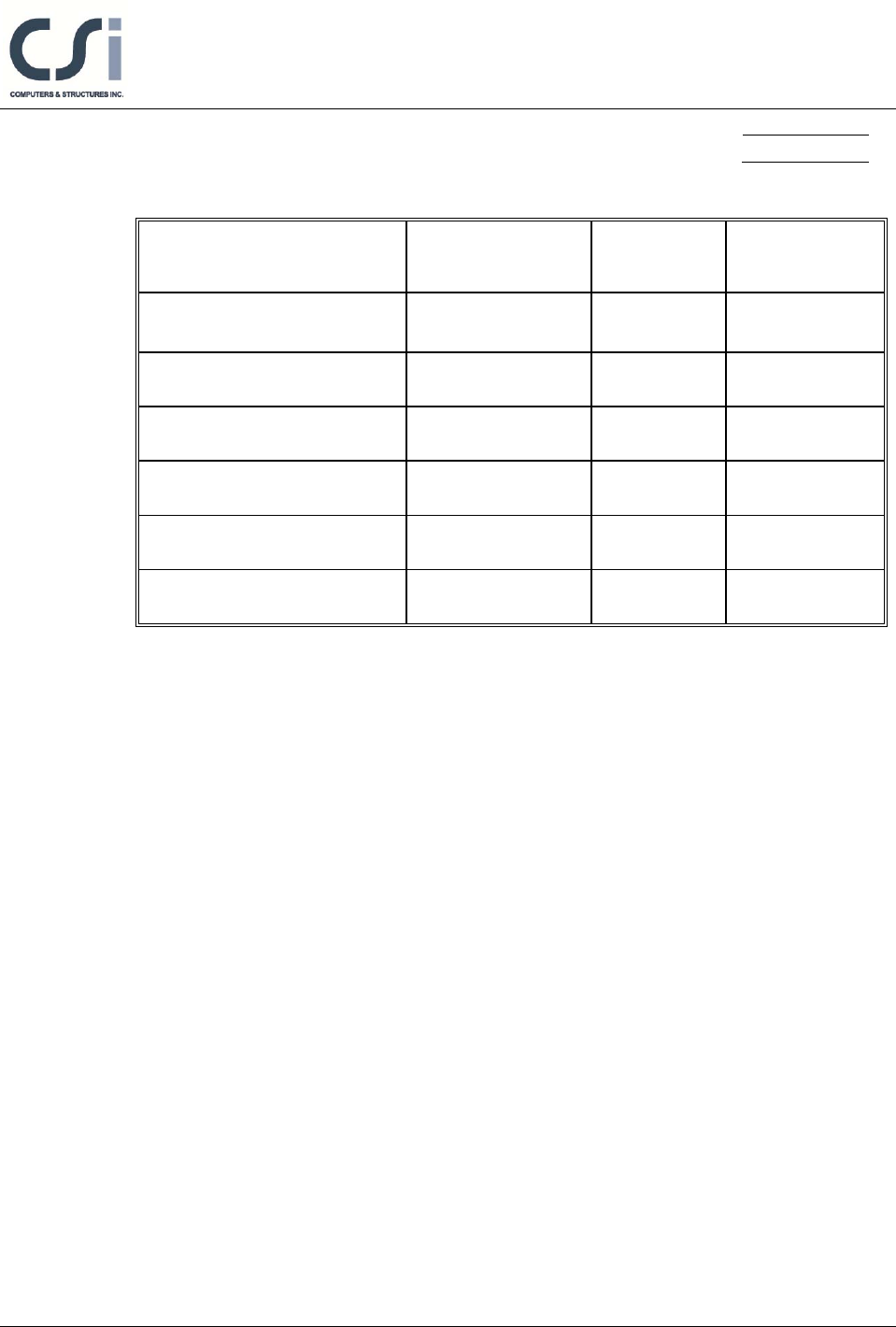
Table 1 shows the comparison of the ETABS total factored moments, required
mild steel reinforcing, and slab stresses with the independent hand calculations.
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
SS CP 65-99 PT-SL EXAMPLE 001 - 3
Table 1 Comparison of Results
FEATURE TESTED INDEPENDENT
RESULTS ETABS
RESULTS DIFFERENCE
Factored moment,
Mu (Ultimate) (kN-m) 174.4 174.4 0.00%
Area of Mild Steel req’d,
As (sq-cm) 19.65 19.80 0.76%
Transfer Conc. Stress, top
(D+PTI), MPa 5.058 5.057 -0.02%
Transfer Conc. Stress, bot
(D+PTI), MPa 2.839 2.839 0.00%
Normal Conc. Stress, top
(D+L+PTF), MPa 10.460 10.467 0.07%
Normal Conc. Stress, bot
(D+L+PTF), MPa 8.402 8.409 0.08%
COMPUTER FILE: SS CP 65-1999 PT-SL EX001.EDB
CONCLUSION
The ETABS results show an acceptable comparison with the independent results.
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
SS CP 65-99 PT-SL EXAMPLE 001 - 4
HAND CALCULATIONS:
Design Parameters:
Mild Steel Reinforcing Post-Tensioning
f’c = 30MPa fpu = 1862 MPa
fy = 400MPa fpy = 1675 MPa
Stressing Loss = 186 MPa
Long-Term Loss = 94 MPa
fi = 1490 MPa
fe = 1210 MPa
m, steel = 1.15
m, concrete = 1.50
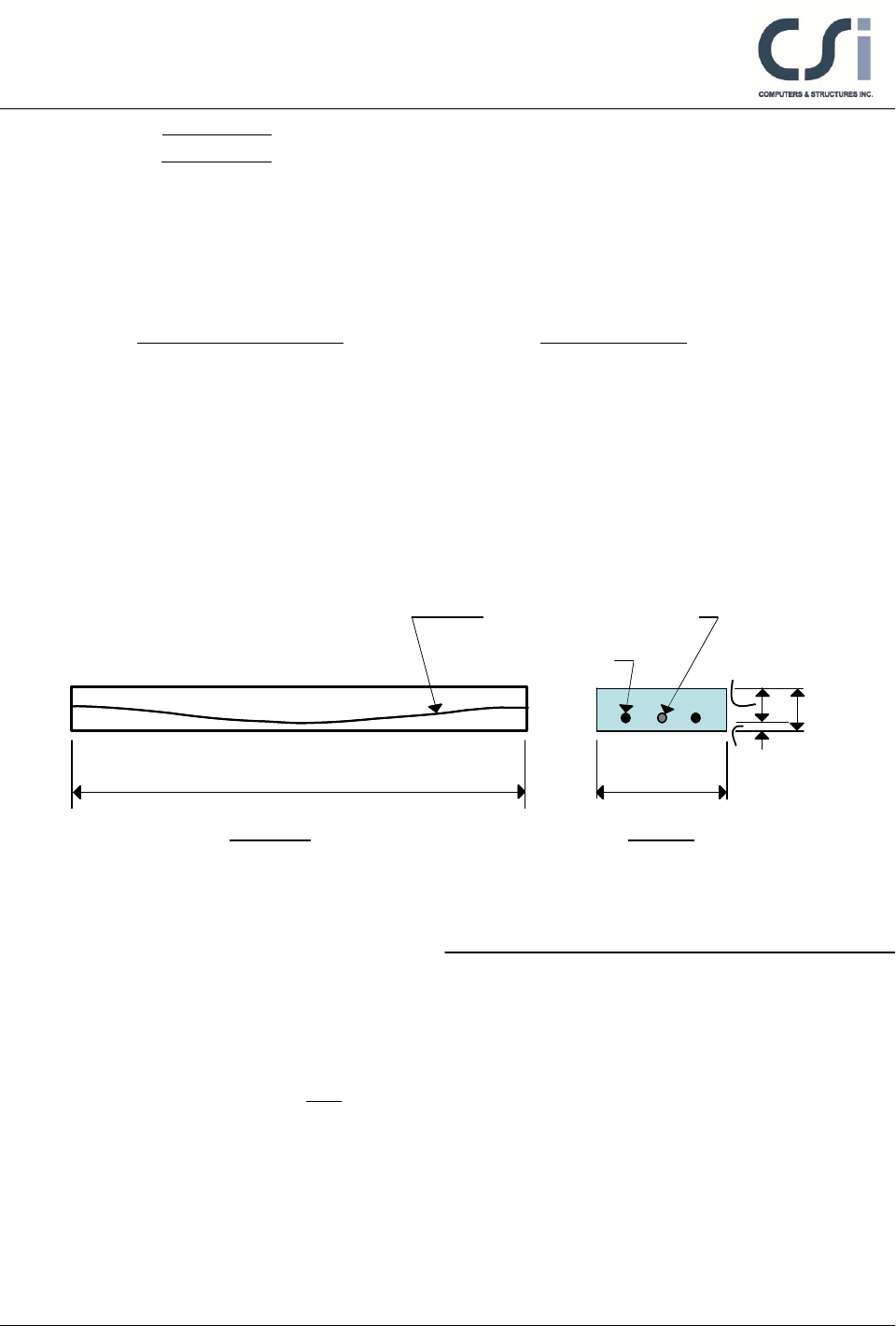
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Loads:
Dead, self-wt = 0.254 m 23.56 kN/m3 = 5.984 kN/m2 (D) 1.4 = 8.378 kN/m2 (Du)
Live, = 4.788 kN/m2 (L) 1.6 = 7.661 kN/m2 (Lu)
Total = 10.772 kN/m2 (D+L) = 16.039 kN/m2 (D+L)ult
=10.772 kN/m2 0.914 m = 9.846 kN/m,
u= 16.039 kN/m2 0.914 m = 14.659 kN/m
Ultimate Moment, 2
1
8
U
wl
M= 14.659 (9.754)2/8 = 174.4 kN-m

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
SS CP 65-99 PT-SL EXAMPLE 001 - 5
Ultimate Stress in strand, 7000 11.7
/
pu p
pb pe
cu
f
A
ffld fbd
7000 1862(198)
1210 1 1.7
9754/ 229 30(914)(229)
1358 MPa 0.7 1303 MPa
pu
f
K factor used to determine the effective depth is given as:
2
bdf
M
K
cu
= 2
174.4 0.1213
30000(0.914)(0.229) < 0.156
d
K
dz 95.0
9.0
25.05.0
= 192.2 mm
Ultimate force in PT,
,( ) 2 99 1303 1000 258.0 kN
ult PT P PS
FAf
Ultimate moment due to PT,
,,
( ) / 258.0 0.192 1.15 43.12 kN-m
ult PT ult PT
MFz
Net Moment to be resisted by As,
NET U PT
M
MM
174.4 43.12 131.28 kN-m
The area of tensile steel reinforcement is then given by:
0.87
NET
s
yX
M
A
f
z =
2
131.28 1 6 1965 mm
0.87 400 192 e
Check of Concrete Stresses at Midspan:
Initial Condition (Transfer), load combination (D+PTi) = 1.0D+0.0L+1.0PTI
Tendon stress at transfer = jacking stress stressing losses = 1490 186 = 1304 MPa
The force in the tendon at transfer, =
1304 197.4 1000 257.4 kN
Moment due to dead load,
2
5.984 0.914 9.754 8 65.04 kN-m
D
M
Moment due to PT,
(sag) 257.4 102 mm 1000 26.25 kN-m
PT PTI
MF
Stress in concrete,
257.4 65.04 26.23
0.254 0.914 0.00983
PTI D PT
FMM
fAS
where S = 0.00983m3
1.109 3.948 MPaf
5.058(Comp)max, 2.839(Tension)max
f

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
SS CP 65-99 PT-SL EXAMPLE 001 - 6
Normal Condition, load combinations: (D+L+PTF) = 1.0D+1.0L+1.0PTF
Tendon stress at normal = jacking stressing long-term = 1490 186 94 = 1210 MPa
The force in tendon at normal, =
1210 197.4 1000 238.9 kN
Moment due to dead load,
2
5.984 0.914 9.754 8 65.04 kN-m
D
M
Moment due to live load,
2
4.788 0.914 9.754 8 52.04 kN-m
L
M
Moment due to PT,
(sag) 238.9 102 mm 1000 24.37 kN-m
PT PTI
MF
Stress in concrete for (D+L+PTF),
238.8 117.08 24.37
0.254 0.914 0.00983
PTI D L PT
FM M
fAS
1 029 9 431
f
..
10.460(Comp)max, 8.402(Tension)maxf