P S312 2 Agouridas Solar Support Structure Analysis
User Manual: Solar Power Products
Open the PDF directly: View PDF ![]() .
.
Page Count: 11

3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
ANALYSIS OF SOLAR PANEL SUPPORT STRUCTURES
1A. Mihailidis, 1K. Panagiotidis, 1K. Agouridas*
1Lab. of Machine Elements & Machine Design, Dep. of Mechanical engineering, Aristotle
University of Thessaloniki, Greece
KEYWORDS
Solar array, frame structures
ABSTRACT
The use of renewable energy resources is increasing rapidly. Following this trend, the
implementation of large area solar arrays is considered to be a necessity. Several design
approaches of the supporting structures have been presented in order to achieve the
maximum overall efficiency. They are loaded mainly by aerodynamic forces. International
regulations as well as the competition between industries define that they must withstand the
enormous loads that result from air velocities over 120 km/h. Furthermore, they must have a
life expectancy of more than 20 years. In this paper, the analysis of two different design
approaches of solar panel support structures is presented. The analysis can be split in the
following steps.
1. Load calculation, which includes the creation of a simple CFD model using ANSA as pre-
processor and ANSYS-CFX as solver to determine the pressure distribution on the solar
panel area and the application of EUROCODE 1 to determine the resultant magnitude of
the forces acting on the surface of the solar panels.
2. Analysis of the structure, which includes the creation of a FE model using ANSA as pre-
processor. Loads calculated in the first step are applied to the model. As solver MSC
Nastran is used.
3. Identification of the structure critical points. According to the results weak points are
redesigned in order to increase the endurance.
1. INTRODUCTION, SUPPORT STRUCTURE DESIGNS
Nowadays the demand for clean, renewable energy sources is increasing. In order to collect
solar power effectively, it is necessary to use large areas of solar panels properly aligned to
the sun. A wide variety of design solutions is suggested so as to achieve maximum
efficiency. In this paper the analysis of two different design approaches are presented:
1. A fixed system that is mounted to a certain position as shown in Figure 1. The orientation
of the solar panel array is adapted to the installation site so that the efficiency of the
system is optimized.
2. An adjustable system that features mechanisms to enable it to be automatically rotated
around 2 axes as shown in Figure 2. This system has the advantage that light beams are
all day long normal to the surface of the panels.
The fact that these structures have to support a large area of solar panels (in both structures
the area is about 50m2), makes them vulnerable to wind action. Laws and regulations
prescribe that such structures must withstand air velocities over 120 km/h. Competition
among industries raises this limit to 140 km/h.
2. LOADS – BOUNDARY CONDITIONS
The main load of the support structures is caused by the wind action. Wind load has to be
calculated according to EUROCODE 1 (1). According to this regulation only the total wind
force is determined, and therefore it cannot be applied to a FE model directly. It has to be
distributed to node loads. On the other side, a CFD model results in the pressure distribution
that enables one to determine easily the required node loads. However, the total
aerodynamic force is different from that obtained by EUROCODE. The reason for this
deviation is that EUROCODE considers several effects such as season of the year,
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
installation site, required service life, and so on, whereas most CFD models do not.
Consequently both EUROCODE and CFD model must be used.
Figure 1 – Design A: Fixed support structure design (EXEL MAKMETAL)
Figure 2 – Design B: Adjustable support structure design (IRIS - PTOLEMEO)
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Load calculation
Wind direction is stochastic and therefore it is necessary to compute the pressure distribution
for a variety of wind directions, because it is usually very difficult to estimate which one is the
most critical. In the current analysis the following wind directions are considered 0, 15, 165
and 180 degrees. Figure 3 shows the CFD model and the boundary conditions for wind
direction angle 0 degrees.
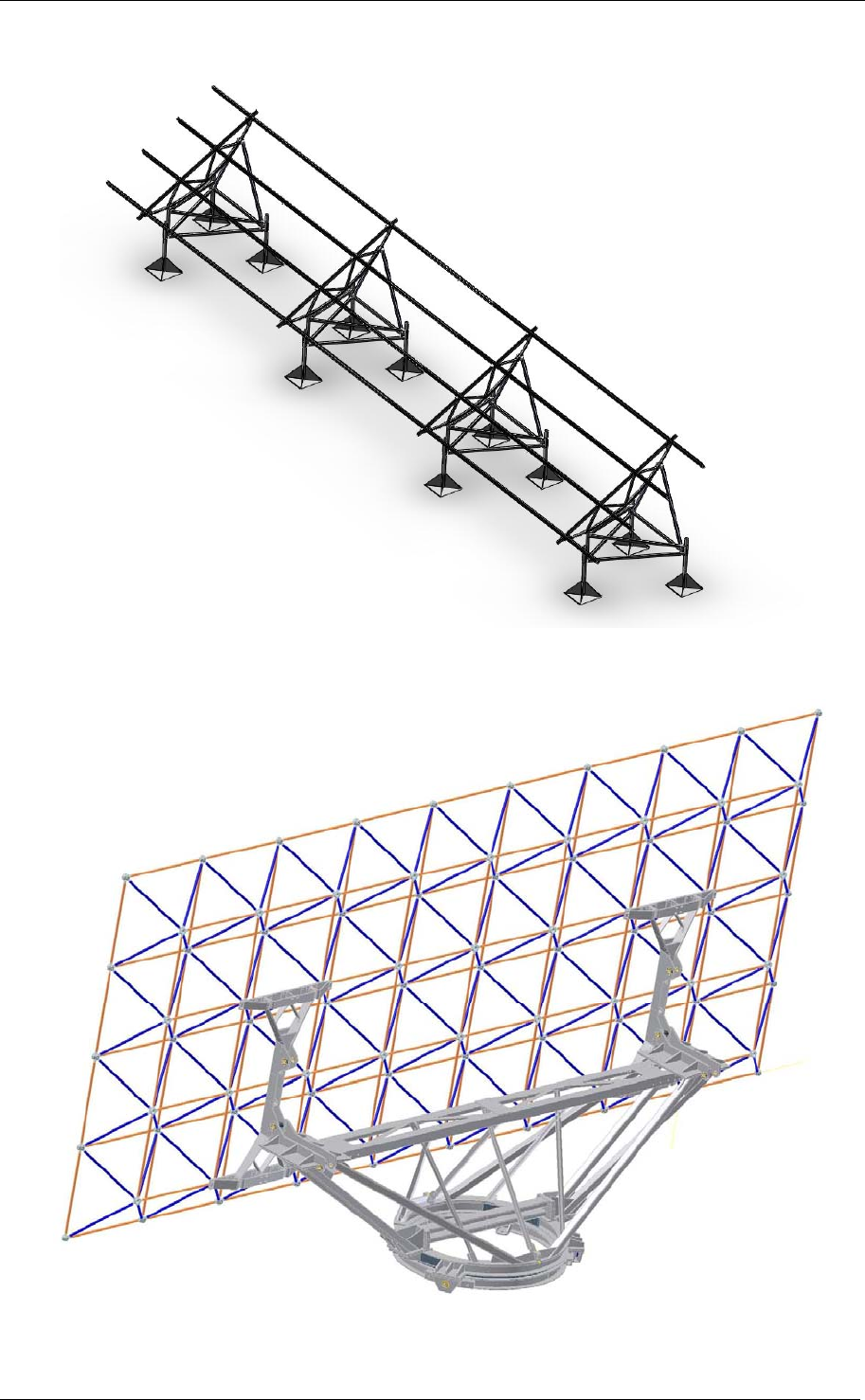
Figure 3 – Fluid model, boundary conditions:
1 Purple: Ground and plate
2 Green: Opening where the relative pressure is 0
3 Blue: Given velocity with vector normal to the control volume surface
The aerodynamic loads are caused mainly by the solar panel array whose thickness is very
small regarding its other dimensions. Therefore, it can be modelled as a thin plate consisting
of shell elements in a control volume. The dimensions of the control volume are chosen large
compared to the dimensions of the plate. The model was solved using the ANSYS-CFX.
Typical results are shown in Figures 4 and 5.
Figure 4 – CFX Results: Air Streamlines

3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Figure 5 – CFX Results: Pressure distribution on the front and the back of the plate
From these results the pressure distribution is obtained. Following, the resultant force and
the node loads can be determined.
The resultant force results from the summation of the loads acting on each node.
()
∑
=
+=
n
iCFXfiCFXbiCFX FFF
1
where:
CFX
F Resultant force obtained from CFD model
CFXbi
F Force on node i of the back side of the plate
CFXfi
F Force on node i of the front side of the plate
n Number of nodes
As mentioned earlier the total force according to EUROCODE Eu
F differs from that obtained
by the CFD model. A scaling factor C can then be calculated.
CFX
Eu
F
F
C=
The actually applied forces on the nodes are:
(
)
CFXfiCFXbinode FFCF
+
=
The procedure to import forces to the static model is the following:
1. Export forces from ANSYS-CFX
2. Export the geometry of the plate including the mesh from ANSA (2). The mesh must be
retained so that the position and the number of the nodes remain the same
3. Process of the forces by adding the force at the back and at the front node of the plate
scaled as mentioned above.
4. Compose the NASTRAN load file
5. Import the NASTRAN load file into the static FE model.
3. STRUCTURE MODELLING
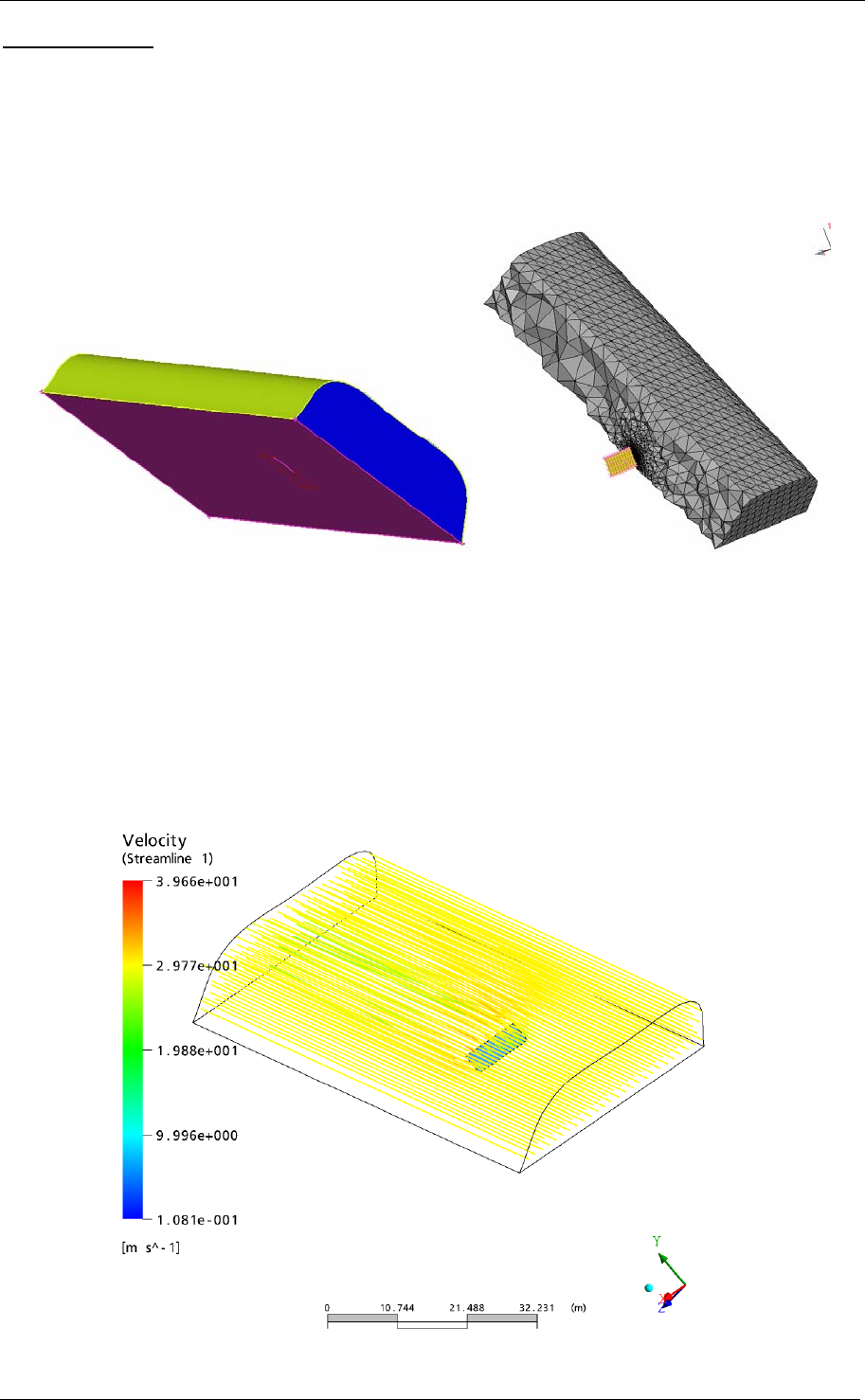
Since both structures designs consist only of thin-walled parts the 3-d solid parts imported
from the CAD file must be first translated to surfaces as shown in Figure 6.
Triangular and rectangular shell elements (CTRIAS and CTETRAS) (3) are used to model
the resulting surface.
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Figure 6 –Solid parts translated to surfaces
Figure 7 – Shell mesh
Figure 8 shows the modelling bolted connections. RB2 elements are used to constrain the
holes with the centre node and a CBAR element to model the body of the bolt. Since bolted
connections cannot support rotational loads, the torsional moment of inertia of the CBAR is
set to zero.
Figure 8 – Typical bolted connection
The space frame of Design B consists of nodes and tubes. The nodes are modeled as shell
elements and tubes as CBAR elements shown in Figure 9.
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Figure 9 – Space frame
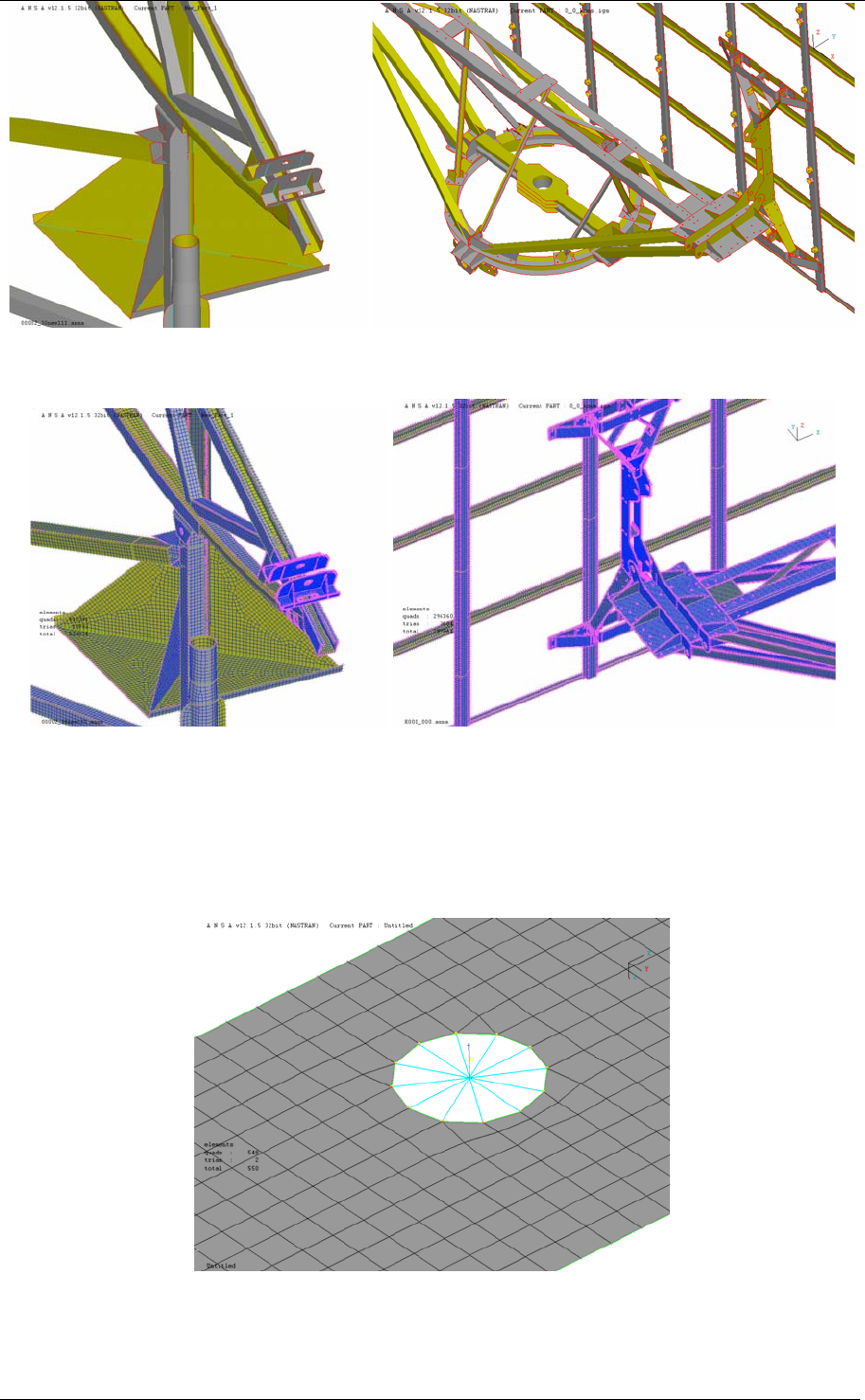
Critical welds are modeled according to the Hot Spot Stress analysis (4) as shown in Figure
10. This analysis requires that the stresses at certain positions are known, in order to
extrapolate the results and obtain the Hot Spot stress at the welding.
Figure 10 – Mesh used for Hot Spot Stress analysis
In modelling design A self-weight can be neglected, since it is supported by many rods
inserted in the ground. However the elastic properties of the ground have to be taken into
account. Depending on the installation site they must be determined by geotechnical
analysis.
Typical elastic properties are given in Figure 11.
Vertical stiffness 7000 kN/m
Horizontal stiffness 875 kN/m
Torsional stiffness 120 kNm/rad
Figure 11 - Constrains of the base of design A
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
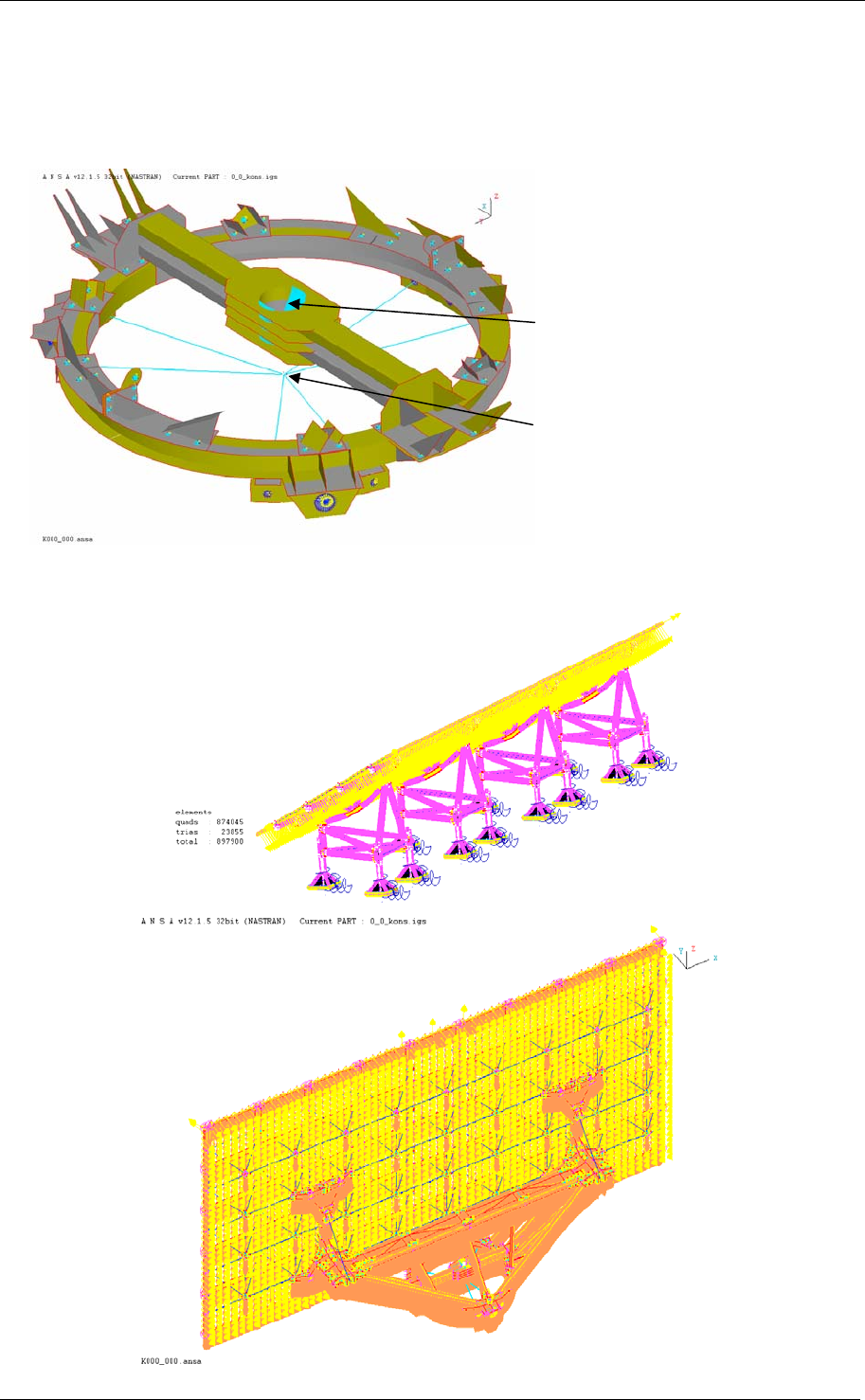
In design B the solar panels are attached to a space frame. It is connected by two hinges to
an auxiliary frame. In this way it can be rotated around the horizontal axis. The complete
support structure rest on three rollers in a circular guide. In this way it can be rotated around
the vertical axis. Calculations were carried out for several angles for both horizontal and
vertical axes. Moreover, the weight cannot be neglected in this design.
Figure 12 – Constrains design B
Constrained transnational de-
grees of freedom
Constrained rotational degree of
freedom (Driving motor is attached
here)
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Figure 13 – Final models ready to be solved
4. RESULTS
Both models were solved using MSC Nastran. The solution types chosen initially were 101 –
Linear Static and 106 – Non Linear Static taking into account large deformations and
assuming linear elastic material behaviour. The comparison showed that the non-Linear
solution resulted in only insignificantly better accuracy but required considerably more
computing time. Therefore, the Linear Static solution was chosen.
The assumption of a linear elastic material behaviour is justified by the fact that the allowable
maximum Von-Mises stress is set far below the yield stress, because the structure must
withstand the highly dynamic loads that actually occur.
The following Figures 14 – 18 show some problems of the initial designs and how they were
resolved.
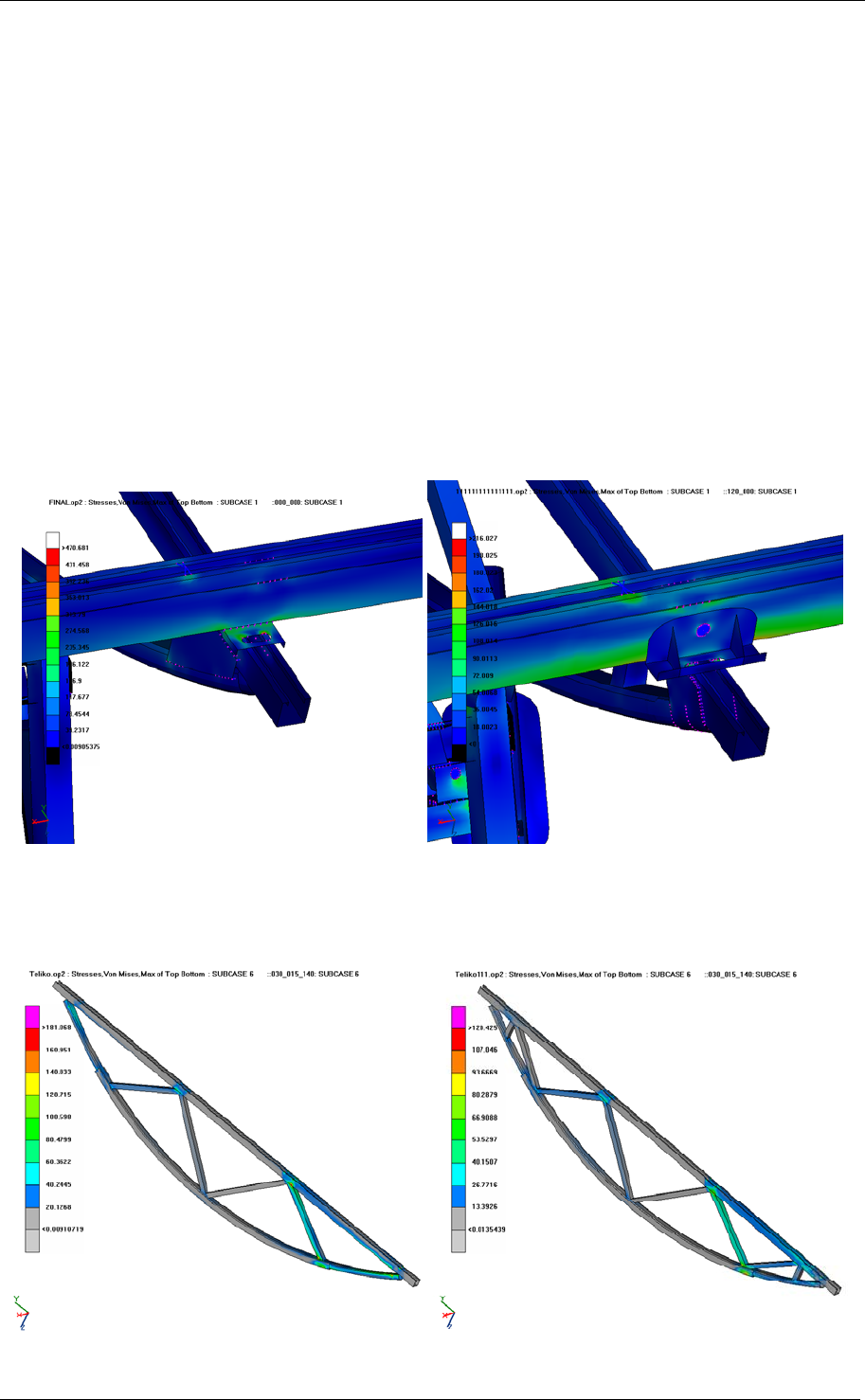
Figure 14 shows the initial design of the support of a longitudinal frame member. Since it is
fixed, the resulting stress field includes impermissible high values. In the improved design
shown on the right of the Figure 14, the maximum stress is significantly reduced, by fixing the
longitudinal member to a U – formed attachment by a single pin.
Figure 14 – Frame member support
The maximum stress in the transverse frame member was significantly reduced by a finer
triangulation near the end points as shown in Figure 15.
Figure 15 – Triangulation of the transverse frame member
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
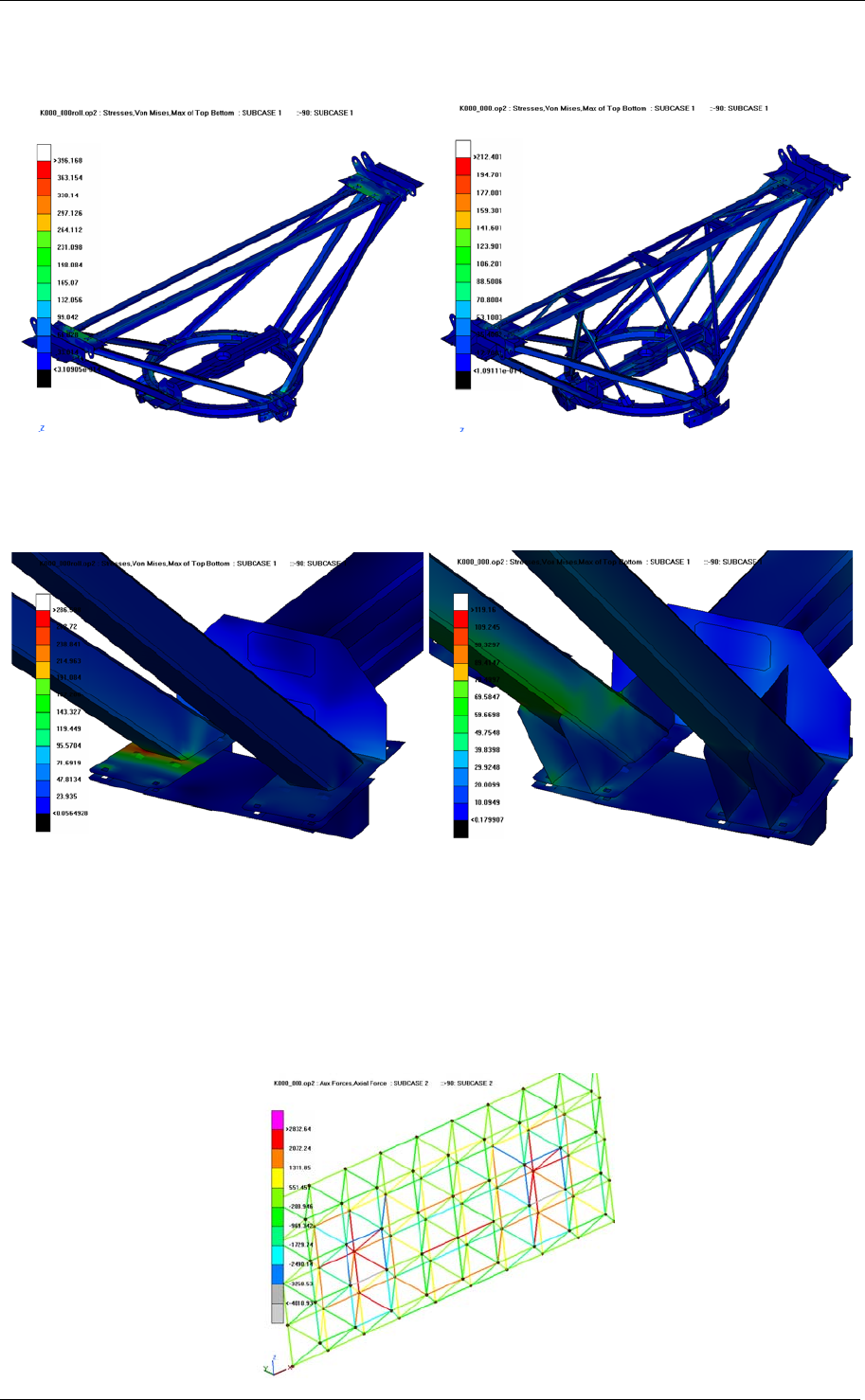
Figure 16 shows the reinforcements that were necessary to increase the load caring capacity
of the auxiliary frame design.
Figure 16 – Reinforcements of the auxiliary frame
Figure 17 shows that the maximum stress be could significantly reduced by adding properly
designed reinforcements.
Figure 17 – Reinforcements of weldings
The space frame of the design B consists, as mentioned above, from nodes and tubes.
Tubes can only be loaded by tensile or compressive forces. In the later case Von-Mises
stress as yield criterion is not enough for this part of the structure and buckling calculation is
also necessary.
Figure 18 shows the forces used for buckling calculation of the tubes.
3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Figure 18 – 1d Element forces used for buckling calculation
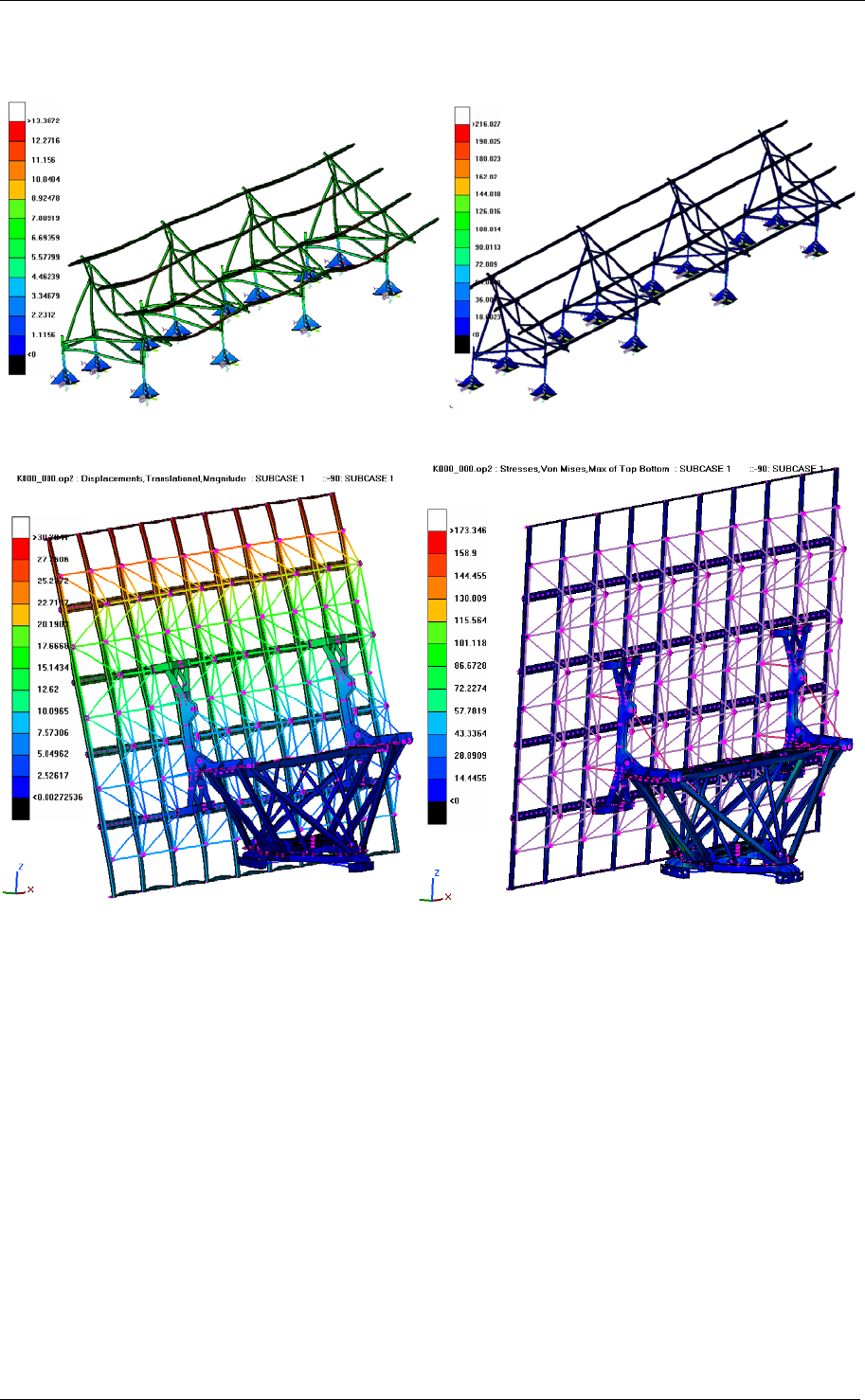
The following figures 19 and 20 show the deformation and the stress field of the final designs
of both structures.
Figure 19 – Deformation and stress field of design A
Figure 20 – Deformation and stress field of design B
5. CONCLUSIONS
Even fixed solar array support structures have sofisticated design, that needs to be analyzed
and often improved in order to withstand the wind load. The same applies of course to
adjustable designs to an even greater extend. The analysis has to be carried out for many
wind directions. Therefore, it is very important to employ productive software tools. The
designs presented in this paper were analyzed using ANSYS – CFX, ANSA, MSC NASTRAN
and META (5) in a very efficient way. Further, it was possible to omit the time-consuming
non-linear solutions, because comparative calculations showed that the accurancy gain
obtained by them is insignificand.
Figures 21 and 22 show the installed solar arrays.

3rd ANSA & μETA International Conference
September 9-11, 2009 Olympic Convention Centre, Porto Carras Grand Resort Hotel, Halkidiki Greece
Figure 21 – Design A
Figure 22 – Design B
REFERENCES
(1) Eurocode 1: Actions on structures - General actions - Part 1-4:Wind actions
(2) ANSA version 12.1.5 User’s Guide, BETA CAE Systems S.A., July 2008
(3) MSC.Nastran 2005 r3,Quick Reference Guide
(4) International Institute of Welding, Recommendations for fatigue design of welded
joints and components, June 2005
(5) μETA Postprocessor, version 6.2.0. User’s Guide, BETA CAE Systems S.A., June
2008