A Practical Guide To Designing Phase II Trials In Oncology (Statistics Practice) Sarah R. Brown, Walter M. Gregory, Christopher J. Twelves, Julia B
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 258 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- A Practical Guide to Designing Phase II Trials in Oncology
- 1 Introduction
- 2 Key points for consideration
- 3 Designs for single experimental therapies with a single arm
- 4 Designs for single experimental therapies including randomisation
- 5 Treatment selection designs
- 5.1 Including a control arm
- 5.1.1 One-stage designs
- 5.1.2 Two-stage designs
- 5.1.3 Multi-stage designs
- 5.1.4 Continuous monitoring designs
- 5.1.5 Decision-theoretic designs
- 5.1.6 Three-outcome designs
- 5.1.7 Phase II/III designs – same primary outcome measure at phase II and phase III
- 5.1.8 Phase II/III designs – different primary outcome measures at phase II and phase III
- 5.1.9 Randomised discontinuation designs
- 5.2 Not including a control arm
- 5.1 Including a control arm
- 6 Designs incorporating toxicity as a primary outcome
- 7 Designs evaluating targeted subgroups
- 8 ‘Chemo-radio-sensitisation’ in head and neck cancer
- 9 Combination chemotherapy in second-line treatment of non-small cell lung cancer
- 10 Selection by biomarker in prostate cancer
- 11 Dose selection in advanced multiple myeloma
- 12 Targeted therapy for advanced colorectal cancer
- 13 Phase II oncology trials: Perspective from industry
- References
- Index
- Statistics in Practice

StatiSticS in Practice
Sarah r. Brown
walter M. GreGory
chriS twelveS
Julia Brown
A Practical Guide
to Designing Phase II
Trials in Oncology
A Practical Guide to Designing
Phase II Trials in Oncology

STATISTICS IN PRACTICE
Series Advisors
Human and Biological Sciences
Stephen Senn
CRP-Sant´
e, Luxembourg
Earth and Environmental Sciences
Marian Scott
University of Glasgow, UK
Industry, Commerce and Finance
Wolfgang Jank
University of Maryland, USA
Founding Editor
Vic Barnett
Nottingham Trent University, UK
Statistics in Practice is an important international series of texts which provide
detailed coverage of statistical concepts, methods and worked case studies in specic
elds of investigation and study.
With sound motivation and many worked practical examples, the books show
in down-to-earth terms how to select and use an appropriate range of statistical
techniques in a particular practical eld within each title’s special topic area.
The books provide statistical support for professionals and research workers
across a range of employment elds and research environments. Subject areas cov-
ered include medicine and pharmaceutics; industry, nance and commerce; public
services; the earth and environmental sciences; and so on.
The books also provide support to students studying statistical courses applied to
the above areas. The demand for graduates to be equipped for the work environment
has led to such courses becoming increasingly prevalent at universities and colleges.
It is our aim to present judiciously chosen and well-written workbooks to meet
everyday practical needs. Feedback of views from readers will be most valuable to
monitor the success of this aim.
A complete list of titles in this series appears at the end of the volume.

A Practical Guide to Designing
Phase II Trials in Oncology
Sarah R. Brown
University of Leeds, UK
Walter M. Gregory
University of Leeds, UK
Chris Twelves
St James’s University Hospital, Leeds, UK
Julia Brown
University of Leeds, UK
This edition rst published 2014
© 2014 John Wiley & Sons, Ltd
Registered ofce
John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ,
United Kingdom
For details of our global editorial ofces, for customer services and for information about how to apply
for permission to reuse the copyright material in this book please see our website at www.wiley.com.
The right of the author to be identied as the author of this work has been asserted in accordance with the
Copyright, Designs and Patents Act 1988.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or
transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise,
except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of
the publisher.
Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may
not be available in electronic books.
Designations used by companies to distinguish their products are often claimed as trademarks. All brand
names and product names used in this book are trade names, service marks, trademarks or registered
trademarks of their respective owners. The publisher is not associated with any product or vendor
mentioned in this book.
Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in
preparing this book, they make no representations or warranties with respect to the accuracy or
completeness of the contents of this book and specically disclaim any implied warranties of
merchantability or tness for a particular purpose. It is sold on the understanding that the publisher is not
engaged in rendering professional services and neither the publisher nor the author shall be liable for
damages arising herefrom. If professional advice or other expert assistance is required, the services of a
competent professional should be sought.
Library of Congress Cataloging-in-Publication Data
A practical guide to designing phase II trials in oncology / [edited by] Sarah R. Brown,
Walter M. Gregory, Christopher Twelves, Julia Brown.
p. ; cm.
Includes bibliographical references and index.
ISBN 978-1-118-57090-6 (hardback)
I. Brown, Sarah R., editor of compilation. II. Gregory, Walter M., editor of compilation.
III. Twelves, Chris, editor of compilation. IV. Brown, Julia (Julia M.), editor of compilation.
[DNLM: 1. Clinical Trials, Phase II as Topic. 2. Antineoplastic Agents–therapeutic use.
3. Drug Evaluation–methods. 4. Neoplasms–drug therapy. QV 771.4]
RC271.C5
616.99′4061–dc23
2013041156
A catalogue record for this book is available from the British Library.
ISBN: 978-1-118-57090-6
Set in 10/12pt Times by Aptara Inc., New Delhi, India
1 2014
To Austin, from Sarah, for your continued support and
encouragement.
And to the many patients and their carers who take
part in clinical trials, often at the most difcult of
times, helping in the development of new and better
treatments for people with cancer now and
in the future.
Contents
Contributors xv
Foreword I xvii
Elizabeth A. Eisenhauer
Foreword II xix
Roger A’Hern
Preface xxi
1 Introduction 1
Sarah Brown, Julia Brown, Walter Gregory and Chris Twelves
1.1 The role of phase II trials in cancer 3
1.2 The importance of appropriate phase II trial design 5
1.3 Current use of phase II designs 6
1.4 Identifying appropriate phase II trial designs 7
1.5 Potential trial designs 9
1.6 Using the guidance to design your trial 10
2 Key points for consideration 12
Sarah Brown, Julia Brown, Marc Buyse, Walter Gregory, Mahesh Parmar and
Chris Twelves
2.1 Stage 1 – Trial questions 14
2.1.1 Therapeutic considerations 14
2.1.2 Primary intention of trial 16
2.1.3 Number of experimental treatment arms 17
2.1.4 Primary outcome of interest 18
2.2 Stage 2 – Design components 18
2.2.1 Outcome measure and distribution 18
2.2.2 Randomisation 21
2.2.3 Design category 26
2.3 Stage 3 – Practicalities 33
2.3.1 Practical considerations 33
2.4 Summary 35
viii CONTENTS
3 Designs for single experimental therapies with a single arm 36
Sarah Brown
3.1 One-stage designs 36
3.1.1 Binary outcome measure 36
3.1.2 Continuous outcome measure 38
3.1.3 Multinomial outcome measure 39
3.1.4 Time-to-event outcome measure 40
3.1.5 Ratio of times to progression 40
3.2 Two-stage designs 41
3.2.1 Binary outcome measure 41
3.2.2 Continuous outcome measure 50
3.2.3 Multinomial outcome measure 50
3.2.4 Time-to-event outcome measure 53
3.2.5 Ratio of times to progression 54
3.3 Multi-stage designs 55
3.3.1 Binary outcome measure 55
3.3.2 Continuous outcome measure 59
3.3.3 Multinomial outcome measure 59
3.3.4 Time-to-event outcome measure 60
3.3.5 Ratio of times to progression 60
3.4 Continuous monitoring designs 60
3.4.1 Binary outcome measure 60
3.4.2 Continuous outcome measure 63
3.4.3 Multinomial outcome measure 63
3.4.4 Time-to-event outcome measure 63
3.4.5 Ratio of times to progression 64
3.5 Decision-theoretic designs 64
3.5.1 Binary outcome measure 64
3.5.2 Continuous outcome measure 65
3.5.3 Multinomial outcome measure 65
3.5.4 Time-to-event outcome measure 65
3.5.5 Ratio of times to progression 65
3.6 Three-outcome designs 65
3.6.1 Binary outcome measure 65
3.6.2 Continuous outcome measure 66
3.6.3 Multinomial outcome measure 66
3.6.4 Time-to-event outcome measure 66
3.6.5 Ratio of times to progression 67
3.7 Phase II/III designs 67
4 Designs for single experimental therapies including randomisation 68
Sarah Brown
4.1 One-stage designs 68
4.1.1 Binary outcome measure 68
4.1.2 Continuous outcome measure 70
CONTENTS ix
4.1.3 Multinomial outcome measure 70
4.1.4 Time-to-event outcome measure 70
4.1.5 Ratio of times to progression 72
4.2 Two-stage designs 72
4.2.1 Binary outcome measure 72
4.2.2 Continuous outcome measure 73
4.2.3 Multinomial outcome measure 74
4.2.4 Time-to-event outcome measure 75
4.2.5 Ratio of times to progression 75
4.3 Multi-stage designs 75
4.3.1 Binary outcome measure 75
4.3.2 Continuous outcome measure 75
4.3.3 Multinomial outcome measure 75
4.3.4 Time-to-event outcome measure 76
4.3.5 Ratio of times to progression 76
4.4 Continuous monitoring designs 76
4.4.1 Binary outcome measure 76
4.4.2 Continuous outcome measure 76
4.4.3 Multinomial outcome measure 76
4.4.4 Time-to-event outcome measure 76
4.4.5 Ratio of times to progression 76
4.5 Three-outcome designs 77
4.5.1 Binary outcome measure 77
4.5.2 Continuous outcome measure 77
4.5.3 Multinomial outcome measure 77
4.5.4 Time-to-event outcome measure 77
4.5.5 Ratio of times to progression 77
4.6 Phase II/III designs 77
4.6.1 Binary outcome measure 77
4.6.2 Continuous outcome measure 79
4.6.3 Multinomial outcome measure 80
4.6.4 Time-to-event outcome measure 81
4.6.5 Ratio of times to progression 81
4.7 Randomised discontinuation designs 82
4.7.1 Binary outcome measure 82
4.7.2 Continuous outcome measure 82
4.7.3 Multinomial outcome measure 82
4.7.4 Time-to-event outcome measure 82
4.7.5 Ratio of times to progression 82
5 Treatment selection designs 83
Sarah Brown
5.1 Including a control arm 84
5.1.1 One-stage designs 84
5.1.2 Two-stage designs 84
x CONTENTS
5.1.3 Multi-stage designs 88
5.1.4 Continuous monitoring designs 89
5.1.5 Decision-theoretic designs 89
5.1.6 Three-outcome designs 89
5.1.7 Phase II/III designs – same primary outcome measure at
phase II and phase III 89
5.1.8 Phase II/III designs – different primary outcome measures
at phase II and phase III 99
5.1.9 Randomised discontinuation designs 102
5.2 Not including a control arm 103
5.2.1 One-stage designs 103
5.2.2 Two-stage designs 106
5.2.3 Multi-stage designs 108
5.2.4 Continuous monitoring designs 109
5.2.5 Decision-theoretic designs 110
5.2.6 Three-outcome designs 110
5.2.7 Phase II/III designs – same primary outcome measure at
phase II and phase III 110
5.2.8 Randomised discontinuation designs 111
6 Designs incorporating toxicity as a primary outcome 112
Sarah Brown
6.1 Including a control arm 112
6.1.1 One-stage designs 112
6.1.2 Two-stage designs 114
6.1.3 Multi-stage designs 115
6.2 Not including a control arm 117
6.2.1 One-stage designs 117
6.2.2 Two-stage designs 118
6.2.3 Multi-stage designs 122
6.2.4 Continuous monitoring designs 125
6.3 Toxicity alone 126
6.3.1 One stage 126
6.3.2 Continuous monitoring 127
6.4 Treatment selection based on activity and toxicity 128
6.4.1 Two-stage designs 128
6.4.2 Multi-stage designs 129
6.4.3 Continuous monitoring designs 129
7 Designs evaluating targeted subgroups 131
Sarah Brown
7.1 One-stage designs 131
7.1.1 Binary outcome measure 131
CONTENTS xi
7.2 Two-stage designs 132
7.2.1 Binary outcome measure 132
7.3 Multi-stage designs 135
7.3.1 Binary outcome measure 135
7.3.2 Time-to-event outcome measure 137
7.4 Continuous monitoring designs 138
7.4.1 Binary outcome measure 138
7.4.2 Time-to-event outcome measure 139
8 ‘Chemo-radio-sensitisation’ in head and neck cancer 141
John Chester and Sarah Brown
Stage 1 – Trial questions 141
Therapeutic considerations 141
Primary intention of trial 142
Number of experimental treatment arms 142
Primary outcome of interest 142
Stage 2 – Design components 142
Outcome measure and distribution 142
Randomisation 143
Design category 143
Possible designs 144
Stage 3 – Practicalities 146
Practical considerations for selecting between designs 146
Proposed trial design 148
Summary 150
9 Combination chemotherapy in second-line treatment of non-small
cell lung cancer 151
Ornella Belvedere and Sarah Brown
Stage 1 – Trial questions 152
Therapeutic considerations 152
Primary intention of trial 152
Number of experimental treatment arms 152
Primary outcome of interest 152
Stage 2 – Design components 153
Outcome measure and distribution 153
Randomisation 153
Design category 153
Possible designs 154
Stage 3 – Practicalities 155
Practical considerations for selecting between designs 155
Proposed trial design 158
Summary 162
xii CONTENTS
10 Selection by biomarker in prostate cancer 163
Rick Kaplan and Sarah Brown
Stage 1 – Trial questions 164
Therapeutic considerations 164
Primary intention of trial 164
Number of experimental treatment arms 164
Primary outcome of interest 164
Stage 2 – Design components 165
Outcome measure and distribution 165
Randomisation 165
Design category 166
Possible designs 167
Stage 3 – Practicalities 168
Practical considerations for selecting between designs 168
Proposed trial design 170
Summary 171
11 Dose selection in advanced multiple myeloma 174
Sarah Brown and Steve Schey
Stage 1 – Trial questions 174
Therapeutic considerations 174
Primary intention of trial 175
Number of experimental arms 175
Primary outcome of interest 175
Stage 2 – Design components 176
Outcome measure and distribution 176
Randomisation 176
Design category 177
Possible designs 177
Stage 3 – Practicalities 178
Practical considerations for selecting between designs 178
Proposed trial design 181
Summary 182
12 Targeted therapy for advanced colorectal cancer 185
Matthew Seymour and Sarah Brown
Stage 1 – Trial questions 185
Therapeutic considerations 185
Primary intention of trial 186
Number of experimental treatment arms 186
Primary outcome of interest 186
Stage 2 – Design components 187
Outcome measure and distribution 187
Randomisation 187
CONTENTS xiii
Design category 188
Possible designs 189
Stage 3 – Practicalities 190
Practical considerations for selecting between designs 190
Proposed trial design 191
Summary 194
13 Phase II oncology trials: Perspective from industry 195
Anthony Rossini, Steven Green and William Mietlowski
13.1 Introduction 195
13.2 Commercial challenges, drivers and considerations 196
13.3 Selecting designs by strategy 197
13.3.1 Basic strategies addressed by phase II studies 198
13.3.2 Potential registration 198
13.3.3 Exploratory activity 203
13.3.4 Regimen selection 204
13.3.5 Phase II to support predicting success in phase III 206
13.3.6 Phase II safety trials 208
13.3.7 Prospective identication of target populations 209
13.4 Discussion 210
References 213
Index 227

Contributors
Sarah Brown Clinical Trials Research Unit, Leeds Institute of Clinical Trials
Research, University of Leeds, UK.
This book was collectively written by Sarah Brown with contributions from:
Ornella Belvedere Department of Oncology, York Hospital, York, UK.
Julia Brown Clinical Trials Research Unit, Leeds Institute of Clinical Trials
Research, University of Leeds, UK.
Marc Buyse International Drug Development Institute, Louvain-la-Neuve, Belgium.
John Chester Institute of Cancer and Genetics, School of Medicine, Cardiff Univer-
sity, and Honorary Consultant, Velindre Cancer Centre, Cardiff, UK.
Steven Green Novartis Pharma AG, Basel, Switzerland.
Walter Gregory Clinical Trials Research Unit, Leeds Institute of Clinical Trials
Research, University of Leeds, UK.
Rick Kaplan Medical Research Council Clinical Trials Unit at University College
London, University College London Hospital, and NIHR Cancer Research Network
Coordinating Centre, UK.
William Mietlowski Novartis Pharma AG, Basel, Switzerland.
Mahesh Parmar Medical Research Council Clinical Trials Unit at University
College London, and NIHR Cancer Research Network Coordinating Centre, UK.
Anthony Rossini Novartis Pharma AG, Basel, Switzerland.
Steve Schey Kings College, London, and Lead Myeloma Clinician, Kings College
Hospital, London, UK.
Matthew Seymour Leeds Institute of Cancer and Pathology, University of Leeds,
and NIHR Cancer Research Network, Leeds and National Cancer Research Institute,
London, UK.
Chris Twelves Leeds Institute of Cancer and Pathology, University of Leeds, and St
James’s University Hospital, Leeds, UK.
Foreword I
The past two decades have seen an unprecedented expansion in the knowledge about
the biological, immunological and molecular phenomena that drive malignancy. This
knowledge has subsequently been translated into a large number of potential anti-
cancer therapeutics and potential predictive or prognostic molecular markers that are
under evaluation in clinical trials.
A key component of the oncology clinical trials development process is the
bridge that must be crossed between the end of phase I evaluation of a drug, at
which time information on its recommended dose, schedule, pharmacokinetic and
pharmacodynamics effects in a small group of individuals is available, and the deni-
tive randomised efcacy trial of that drug in the appropriately dened population of
cancer patients.
This ‘bridge’ is provided by the phase II trial. Historically, phase II oncology stud-
ies sought evidence of sufcient drug efcacy (based on objective tumour response
in a specic cancer type) that large conrmatory phase III trials would be justied.
Those not meeting the efcacy bar would not be pursued in further studies in that
tumour type. In today’s highly competitive environment, the phase II study has come
under scrutiny – some have expressed the concern that too many ‘promising’ drugs
emerging from phase II studies yield negative phase III results, that clinical trial end-
points traditionally deployed in phase II may not be specic or sensitive enough for
today’s molecular-based agents to appropriately direct subsequent drug development
decisions, that efciency is lost if discrete phase II and phase III trials are designed
and that much more should be learned about predictive or selection biomarkers before
and during phase II to optimally guide phase III design.
Numerous papers and opinion pieces on these and other phase II–related topics
have been published in the past decade. Thus this new book by Brown and colleagues:
A Practical Guide to Designing Phase II Trials in Oncology is a welcome addition
to the literature. This comprehensive and well-written guide takes a logical and step-
by-step approach by reviewing and making recommendations on the key variables
that must be considered in phase II oncology trials. Some of these include tailoring
design components to the specic trial question, the approach to studies of single-
and combination-agent trials, when and how randomised and adaptive designs might
be deployed, patient selection and phase II trial endpoints. In addition, the book drills
into issues that may be unique to designs in several specic malignancies such as
xviii FOREWORD I
non-small cell lung cancer, prostate cancer and myeloma. Throughout, examples are
utilised as a means of providing context and guiding the reader.
What is clear is that the phase II oncology trial is not a singular or simple
construct. There is no formula for its design that meets all potential needs. These
trials the ‘shape-shifters’ of the cancer trial spectrum – how they are designed, the
endpoints that are utilised, and the population enrolled depends on the agent and its
associated biology, the type of cancer, the question the trial is intended to address
and how those results are intended to guide future decisions. This comprehensive text
provides much-needed practical information in this important area of clinical cancer
research.
Elizabeth A. Eisenhauer, MD, FRCPC
Head, Department of Oncology
Queen’s University
Kingston, ON, Canada
Foreword II
Twenty years ago, in the early 1990s, the term ‘phase II trial design’ was practically
synonymous with the Simon optimal and MINIMAX two-stage trials (1989) – designs
which have stood the test of time with their pragmatic trade-off between the need to
stop a trial early for inefcacy if response rates were low and the likely overshoot of
interim analysis points in small trials. The Gehan design was also widely used but
many statisticians were wary of designs which focussed on estimation but did not
have distinct success/failure rules which allowed error rates to be tightly specied.
The eld of phase II trial design has expanded rapidly since these early days,
particularly in oncology. Phase I trial design has also been extended over the years to
go beyond mere dose nding and frequently includes an expansion phase at the chosen
dose level which provides initial information on efcacy and pharmacodynamic
predictors of response. Ideally this should enhance the relevance of the subsequent
phase II trials.
This book presents a much-needed guide to contemporary phase II clinical trial
design. Over the years trial endpoints have diversied to include the greater use
of endpoints such as progression free survival that cater for treatments that may
not cause tumour shrinkage and are thought to act by halting cancer cell growth
rather than killing the cell (cytostatic rather than cytotoxic). Recognition of the
inaccuracies inherent in designing trials on the basis of the expected response gleaned
from historical data has also seen more focus on the use of randomisation and the
incorporation of a control group. The increasing emphasis on stratied medicine,
recognising the need to tailor treatments more closely to the biological characteristics
of the individual patient’s disease, has also led to phase II trials designed to address
this need.
The recognition of the division between phase IIa trials designed to investigate
efcacy and phase IIb trials, which focus on determining whether a phase III trial
is worth undertaking, has also been welcome. The latter have increased in size and
complexity in an effort to forestall the possibility of a negative phase III trial. It
has been suggested that as many as two out of every three phase III oncology trials
are negative – a situation which is of real concern, given that drug development is
increasing in expense and comparatively few gain regulatory approval. It is reassuring
to note the number of phase II/III designs that have been developed to closely link
the development of phase II and phase III, but in some situations this is not possible.
xx FOREWORD II
The Simon Optimal Design (Simon 1989) is perhaps the seminal phase II single
arm design, and it is salutary to see how frequently this design is used and has acted
as a springboard for the development of other designs. It is frequently possible to add
judiciously placed interim analyses to trials without increasing the number of patients
or having an adverse effect on the error rates – a manoeuvre which is worth bearing
in mind. For example, the two-stage Simon MINIMAX design, which minimises
the number of patients needed to assess a binary endpoint, is frequently the same
size as the one-stage exact design – on occasion, the MINIMAX design is even
marginally smaller than the single-stage design! The MINIMAX design illustrates
the point that an optional futility interim analysis can be built into a planned one-
stage trial of a binary endpoint without increasing the number of patients or adversely
affecting the error rates. Alternatively, note that a one-stage design can frequently
be converted into a two-stage design by including a futility interim analysis at N/2
(here Nis the xed sample single-stage trial size or could be the number of events
for a time-to-event endpoint). The trial would be stopped on the grounds of futility if
the primary endpoint parameter did not exceed the value under the null hypothesis.
This approach is seen in the design mentioned by Whitehead (2009, Section 4.2.1).
A general boundary rule that I have also used is the p≤0.001 rule (Peto–Haybittle)
and related to this are common-sense considerations that should not be overlooked.
For example, if ve or more responses in a 41-patient trial are needed to demonstrate
efcacy, as soon as ve responses have been observed the efcacy threshold for the
trial has been passed, and it is clear a phase III trial will be recommended. If the
toxicity prole is acceptable, the fact the efcacy criteria has been met should be
disseminated so that planning for the follow-on phase III trial can commence.
This book will act as a valuable reference source in addition to giving sound
practical guidance. The authors identify a number of areas that have not been explored;
for example, no references were identied for randomised trials with a multinomial
outcome measure (Section 4.1.3). Statisticians who read this book could perhaps ask
themselves which neglected areas they think deserve the highest priority. As regards
phase IIb designs, I would like to see a three-outcome version of the randomised
Simon (2001) design (Section 4.1.4) based on progression-free survival.
Roger A’Hern
Senior Statistician
Clinical Trials and Statistics Unit
Institute of Cancer Research
Sutton, United Kingdom
Preface
Phase II trials are a key element of the drug development process in cancer, rep-
resenting a transition from initial evaluation in relatively small phase I studies, not
only focused on safety but also increasingly incorporating translational studies, to
denitive assessment of efcacy often in large randomised phase III trials. Efcient
design of these early phase trials is crucial to informed decision-making regarding
the future of a drug’s development. There are a number of textbooks available that
discuss statistical issues in early phase clinical trials. These cover pharmacokinetics
and pharmacodynamics studies, through to late phase II trials, and discuss issues
around sample size calculation and methods of analysis. There are few, however,
which focus specically on phase II trials in cancer, and the many elements involved
in their design. Given the large number and variety of phase II trial designs, often
conceptually innovative, and involving multiple components, the purpose of this book
is to provide practical guidance to researchers on appropriate phase II trial design in
cancer.
This book provides an overview to clinical trial researchers of the steps involved
in designing a phase II trial, from the initial discussions regarding the trial idea itself,
through to identication of an appropriate phase II design. It is written as an aid
to facilitate ongoing interaction between clinicians and statisticians throughout the
design process, enabling informed decision-making and providing insight as to how
information provided by clinicians feeds into the statistical design of a trial. The book
acts both as a comprehensive summary resource of traditional and novel phase II trial
designs and as a step-by-step approach to identifying suitable designs.
We wanted to provide a practical and structured approach to identifying appro-
priate statistical designs for trial-specic design criteria, considering both academic
and industry perspectives. A comprehensive library of available phase II trial designs
is included, and practical examples of how to use the book as a resource to design
phase II trials in cancer are given. We have purposely omitted methodological detail
associated with statistical designs for phase II trials, as well as discussion of analysis,
that can be found elsewhere, including in the references for each of the designs listed
in the library of designs.
The book begins with an introduction to phase II trials in cancer and their role
within the drug development process. A structured thought process addressing the
key elements associated with identifying appropriate phase II trial designs is intro-
duced in Chapter 2, including therapeutic considerations, outcome measures and
xxii PREFACE
randomisation. Each of these elements is discussed in detail, describing the different
stages of the thought process around which the guidance is centred. The purpose of
this detailed information is to allow readers to narrow down the number of designs that
are relevant to their trial-specic design criteria. A comprehensive library of phase II
designs is presented in Chapters 3–7, categorised according to design criteria, and a
brief summary of each trial design available is included.
Chapters 8–12 outline a series of practical examples of designing phase II trials in
cancer, providing practical illustration from trial concept to using the library to select
an appropriate trial design. The examples give a avour of how one might apply the
process described within the book, highlighting that there is no ‘one size ts all’
approach to trial design and that there are often many design solutions available to
any one scenario. We hope the book will help researchers to shortlist their options
in order to select an appropriate design to their specic setting, acknowledging other
options that may be considered.
This book has been written predominantly by academic clinical trialists, involving
both clinicians and statisticians. Many of the issues and considerations described
from an academic point of view are, however, also relevant to trials sponsored by
the pharmaceutical industry. The nal chapter of this book describes the design of
phase II trials in cancer from the industry perspective. The commercial perspective
is described in detail, outlining the design processes for phase II trials according to
specic strategic goals. This highlights both the similarities and differences in the
approach to phase II trial design between academia and industry. In the academic
setting there may be more focus on the phase II trial itself and less on the overall
development programme of the drug, compared to industry where the trial is designed
as part of a programme-oriented clinical development plan.
The book is written for both clinicians and statisticians involved in the design
of phase II trials in cancer. Although some elements are written primarily with
statisticians in mind, the discussion around key concepts of phase II trial design,
as well as the practical examples, is accessible to scientists and clinicians involved
in clinical trial design. For those new to early phase trial design, the book provides
an introduction to the concepts behind informed decision-making in phase II trials,
offering a unique and practical learning tool. For those familiar with phase II trial
design, we hope the reader will benet from exposure to new, less familiar trial
designs, providing alternative options to those which they may have previously used.
The book may also be used by postgraduate students enrolled on statistics courses
including a clinical trial or medical module, providing a useful learning tool with
core information on phase II trial design.
We hope that readers will benet from the step-by-step approach described, as
well as from the library of designs presented, enabling informed decision-making
throughout the design process and focused guidance on designs that t researchers’
pre-specied criteria.
Finally, we would like to thank all our colleagues who have contributed to this
book, for their advice and support.

1
Introduction
Sarah Brown, Julia Brown, Walter Gregory
and Chris Twelves
Traditionally, cancer drug development can be dened by four clinical testing phases
(Figure 1.1):
∙Phase I is the rst clinical test of a new drug after pre-clinical laboratory
studies and is designed to assess the safety, toxicity and pharmacology of
differing doses of a new drug. Typically such studies involve a limited number
of patients and ask the question ‘Is this drug safe?’
∙Phase II studies are designed to answer the question ‘Is this drug active, and is
it worthy of further large-scale study?’ They predominantly address the short-
term activity of a new drug, as well as assessing further safety and toxicity.
Typically sample sizes for phase II studies range from tens to low hundreds of
patients.
∙Phase III trials are often large-scale trials of hundreds, even thousands, of
patients and are usually designed to formally evaluate whether a new drug is
more effective in terms of efcacy or toxicity than current treatments. Here the
focus generally is on long-term efcacy, with the aim of identifying practice-
changing new drugs.
∙Finally, phase IV studies are carried out once a drug is licensed or approved
for a specic indication. Within the pharmaceutical industry setting, phase
IV studies may be designed to collect long-term safety information; in the
academic setting, phase IV trials may investigate the efcacy of a drug outside
of its licensed indication.
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.

2 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
• Determine dose and
preliminary toxicity
• Sample size–low tens
Phase I
• Establish intermediate
activity
• Gain further toxicity
information
• Sample size–high
tens to hundreds
Phase II
• Validate efficacy and
obtain further
toxicity information
• Sample size–
hundreds to
thousands
Phase III
• Post-marketing
surveillance
Phase IV
Figure 1.1 Four clinical phases of drug development.
Presented in this way drug development may appear to be a straight line pathway, but
this is often not the case in practice, with much more time and money invested in large
phase III trials than in other stages of development. Likewise, the boundaries between
the different stages of drug development are increasingly blurred. For example, many
phase I trials treat an expanded cohort of patients at the recommended phase II dose
often at least in part to demonstrate proof of principle or seek evidence of activity.
In recent years a wide range of new ‘targeted’ cancer therapies have emerged with
well-dened mechanisms of action directed at specic molecular pathways relevant
to tumour growth and often anticipated to be used in combination with other standard
treatments. This contrasts with cytotoxic chemotherapy from which the traditional
four phases of cancer drug development emerged. Nevertheless, phase II cancer trials
retain their pivotal position between initial clinical testing and costly, time-consuming
denitive efcacy studies.
The process from pre-clinical development to new drug approval typically takes
up to 10 years and is estimated to cost hundreds of millions of dollars, although
there is some uncertainty over the true costs (Collier 2009). Cytotoxic therapies,
which lack a specic target and mechanism of action, often have a low therapeutic
index, and historically have high rates of failure during drug development due to
lack of efcacy and/or toxicity (Walker and Newell 2009). Although attrition rates
for targeted cancer therapies appear lower than those of cytotoxic drugs, more drugs
progress to expensive late stages of development before being abandoned in cancer
than other therapeutic areas (DiMasi and Grabowski 2007). These worrying statistics
have led to increased attention on clinical trial design, aiming to reduce the attrition
rate and improve the efciency of cancer drug development.
This book focuses on the high-risk transition between phase II and III clinical
trials and provides a practical guide for researchers designing phase II clinical trials
in cancer. There is a clear need for phase II trials that more accurately identify
potentially effective therapies that should move rapidly to phase III trials; perhaps
even more pressing is the need for earlier rejection of ineffective therapies before they
enter phase III testing. On this basis we aim to provide researchers with a detailed
background of the key elements associated with designing phase II trials in patients
with cancer, a thought process for identifying appropriate statistical designs and a
library of available phase II trial designs. The book is not intended to be proscriptive
or didactic, but instead aims to facilitate and encourage an interactive approach by
INTRODUCTION 3
the clinical researcher and the statistician, leading to a more informed approach to
designing phase II oncology trials.
1.1 The role of phase II trials in cancer
Phase II trials in cancer are primarily designed to assess the short-term activity of
new treatments and the potential to move these treatments forward for evaluation of
longer-term efcacy in large phase III studies. In this respect, the term ‘activity’ is
used to describe the ability of an investigational treatment to produce an impact on
a short-term or intermediate clinical outcome measure. We distinguish this from the
term ‘efcacy’ which we use to describe the ability of an investigational treatment
to produce a signicant impact on a longer-term clinical outcome measure such as
overall survival in a denitive phase III trial. Cancer phase II trials are therefore
invariably conducted in the metastatic or neo-adjuvant settings, where measurable
short-term assessments of activity are more easily obtained than in the adjuvant
setting. We focus on phase II trials in cancer, where assessments of ‘activity’ are
usually not immediate and cure not achievable. Nevertheless, many of the statistical
designs available for phase II cancer trials, and concepts discussed, may be applied
to other disease areas.
Phase II trials act as a screening tool to assess the potential efcacy of a new
treatment. That broad description incorporates many different types of phase II trials
including assessing not only traditional evidence of tumour response but also proof
of concept of biological activity, selection between potential doses for further devel-
opment, choosing between potential treatments for subsequent phase III testing and
demonstration that the addition of a new agent to an established treatment appears to
increase the activity of that treatment.
In 1982 Fleming stated that ‘Commonly the central objective of phase II clinical
trials is the assessment of the antitumor “therapeutic efcacy” of a specic treatment
regimen’ (Fleming 1982). More recently the objective of a phase II trial in an idealised
pathway has been described to ‘establish clinical activity and to roughly estimate
clinical response rate in patients’ (Machin and Campbell 2005). Others have taken
this a step further to claim ‘The objective of a phase II trial should not just be to
demonstrate that a new therapy is active, but that it is sufciently active to believe that
it is likely to be successful in pivotal trials’ (Stone et al. 2007a). A common feature
of phase II trials is that their aim is not primarily to provide denitive evidence of
treatment efcacy, as in a phase III study; rather, phase II trials aim to show that a
treatment has sufcient activity to warrant further investigation.
The International Conference on Harmonisation (ICH) Guideline E8: General
Considerations for Clinical Trials prefers to consider classication of study objec-
tives rather than specic trial phases, since multiple phases of trials may incorporate
similar objectives (ICH Expert Working Group 1997). The objectives associated with
phase II trials in the ICH guidance are predominantly to explore the use of the treat-
ment for its targeted indication; estimate or conrm dosage for subsequent studies;
and provide a basis for conrmatory study design, endpoints and methodologies.
4 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Additionally, however, ICH notes that phase II studies, on some occasions, may
incorporate human pharmacology (assessing tolerance; dening or describing
pharmacokinetics/pharmacodynamics; exploring drug metabolism and interactions;
assessing activity) or therapeutic conrmation (demonstrating/conrming efcacy;
establishing a safety prole; providing an adequate basis for assessing benet/risk
relationship for licensing; establishing a dose/response relationship).
These denitions have in common that oncology phase II trials act as an inter-
mediate step between phase I testing on a limited number of patients to establish the
safety of a new treatment and denitive phase III trials aiming to conrm the efcacy
of a new treatment in a large number of patients. The specic aims of a phase II trial
may, however, differ depending on the mechanism of action of the drug in question,
the amount of information currently available on the drug and the setting in which it
is being investigated (e.g. pharmaceutical industry vs. academia). Phase II trials can
be broadly grouped into phase IIa and phase IIb trials. A phase IIa trial may be seen
as seeking proof of concept in the sense of assessing activity of an investigational
drug that has completed phase I development or may investigate multiple doses of a
drug to determine the dose–response relationship. Phase IIa trials may be considered
learning trials and be followed by a decision-making ‘go/no-go’ phase IIb trial to
determine whether or not to proceed to phase III; phase IIb trials may include selec-
tion of a single treatment or dose from many and may include randomisation to a
control arm.
Dose–response can be evaluated throughout the early stages of drug development,
including phase II, but this book does not specically address studies where this is
the primary aim. Many designs are available to assess the dose–response relationship,
perhaps the simplest and most common being the randomised parallel dose–response
design incorporating a control arm and at least two differing dose levels. Cytotoxics
are usually given at the highest feasible dose, but investigating dose–response rela-
tionships may be important with targeted agents that are not necessarily best given
at the maximum possible dose. Such trials serve a number of objectives including
the conrmation of efcacy; the estimation of an appropriate dose; the identication
of optimal strategies for individual dose adjustments; the investigation of the shape
and location of the dose–response curve; and the determination of a maximal dose
beyond which additional benet would be unlikely to occur.
Considerations around choice of starting dose, study design and regulatory issues
in obtaining dose–response information are provided in the ICH Guideline E4: Dose
Response Information to Support Drug Registration (ICH Expert Working Group
1994). Such considerations are, however, outwith the remit of this book, which
focuses on phase II trials designed to assess activity of single-agent or combination
therapies or those designed to select the most active of multiple therapies. We do,
however, discuss phase II selection designs to identify the most active dose from a
number of pre-specied doses rather than specic issues around evaluating dose–
response relationships.
There are often signicant differences between trials conducted within the phar-
maceutical industry and those conducted within academia. Such differences are
predominantly associated with the approach to designing phase II trials, within
INTRODUCTION 5
a portfolio of research, and decision-making around the future development of a
compound or drug. Consequently, the way in which clinical trials are designed,
particularly in the early phase setting, will likely differ between the two environ-
ments. For example, in the academic setting, regardless of the specic aim of the
phase II trial (e.g. proof of concept, go/no-go), decision criteria are pre-specied
to correspond with the primary aim of the trial and form the criteria on which
decision-making and conclusions of the trial are based. Within the pharmaceutical
industry the same pre-dened study aims and objectives apply; however, decision-
making may be complicated by additional factors external to the phase II trial itself,
such as the presence of competitor compounds, patent life or company strategy.
There is inherent pressure within the pharmaceutical industry to achieve timely
regulatory approval and a license indication for a new drug. This does not apply
in the same way within the academic setting where, by the time a drug reaches
phase II testing, it may have been through considerable testing within the phar-
maceutical setting and perhaps be already licensed in alternative disease areas or
in differing combinations or schedules. There are, however, initiatives to facilitate
increased academic/pharmaceutical collaboration in the early stages of drug devel-
opment. Thus, more academic phase II trials may be conducted using novel agents
with only limited clinical data available, so thorough discussion of the aims and
design of these trials becomes even more pertinent. A detailed insight into the indus-
try approach to the design of phase II trials within a developing drug portfolio is
provided in Chapter 13. By contrast, the remainder of this book, including termi-
nology and practical examples of designing phase II trials, draws its focus from the
academic setting.
1.2 The importance of appropriate phase II
trial design
Design of phase II trials is a key aspect of the drug development process. Poor
design may lead to increased probabilities of a false-positive phase II trial resulting
in unnecessary investment in an unsuccessful phase III trial; or a false-negative phase
II resulting in the rejection of a potentially effective treatment. There is a pressing
need for phase II trials to more accurately identify those cancer therapies that will
ultimately be successful in phase III studies and to allow earlier rejection of ineffective
therapies before undertaking costly and time-consuming phase III trials.
As the development of new cancer drugs moves further away from conventional
cytotoxics and more into targeted therapies, the challenges and opportunities in
phase II trial design are ever greater. The choice of phase II design includes not only
statistical considerations, but also decisions regarding the aims of the trial, whether
or not to include randomisation, the choice of endpoints and the size of treatment
effects to be targeted. Each of these elements is critical to ensure the phase II trial
is designed and conducted efciently and that the results of the trial may be used to
make robust, informed decisions regarding future research.
6 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Some researchers have suggested moving directly from phase I to phase III in the
drug development process, on the basis that survival benet in phase III trials may
be observed in the absence of improved response rates therefore rendering phase II
irrelevant (Booth et al. 2008). The potential perils of this approach are demonstrated
by the INTACT1 and INTACT2 trials of getinib in chemotherapy-na¨
ıve advanced
non-small cell lung cancer (NSCLC) patients (Giaccone et al. 2004; Herbst et al.
2004). Phase I trials of getinib in combination with chemotherapy had shown
acceptable tolerability and getinib as monotherapy was active in phase II NSCLC
trials; however, phase II trials of getinib in combination with chemotherapy were
not performed. Subsequently, these two phase III NSCLC trials in over 2000 patients
failed to show improved efcacy with the addition of getinib to cisplatin-based
chemotherapy (Giaccone et al. 2004; Herbst et al. 2004). A conventional, single-arm
NSCLC trial of getinib in combination with chemotherapy may have avoided the
subsequent negative phase III trials. This experience highlights the importance of
designing and conducting appropriately designed and potentially novel phase II trials
prior to embarking on large-scale phase III trials.
1.3 Current use of phase II designs
Several systematic reviews have considered current use of designs in published phase
II trials in cancer (Lee and Feng 2005; Mariani and Marubini 2000; Perrone et al.
2003). Common approaches to trial design included single-arm studies with objective
response as the primary efcacy endpoint, utilising Simon’s two-staged hypothesis
testing methods (Simon 1989), and randomised trials based on single-arm designs
embedded in a randomised setting (Lee and Feng 2005). All highlighted a distinct
lack of detail regarding an identiable statistical design, and design characteristics,
as a marked weakness of many published phase II studies, raising the possibility
that low quality may bias study ndings. Also striking is the consistent use of a
limited number of the same phase II study designs, emphasising the need for better
understanding of alternative statistical designs. A key recommendation from these
reviews is better communication between statisticians and clinical trialists to increase
the use of newer statistical designs. Likewise, the need for ‘the development of
practical designs with good statistical properties and easily accessible computing
tools with friendly user interface’ (Lee and Feng 2005) is recognised as essential so
statisticians can implement these new designs.
In 2009 the Journal of Clinical Oncology (JCO) published an editorial making
recommendations for the types of phase II trials that they would consider for publi-
cation (Cannistra 2009). The differing aims of phase II trials according to the nature
of the treatment under investigation were identied, with discussion as to the likely
priority given to each trial design. The specic categories and outcomes of phase II
trials were
∙single-arm phase II studies that represent the rst evidence of activity of a new
drug class;
INTRODUCTION 7
∙phase II studies of novel agents that not only conrm a class effect, but also
provide evidence of extraordinary and unanticipated activity compared to prior
agents in the same class;
∙phase II studies of an agent or regimen with prior promise (based on previous
reports of clinical activity), but that are convincingly negative when studied
more rigorously;
∙phase II studies of a single-agent or combination that convincingly demonstrate
a new, serious and unanticipated toxicity signal, despite being a rational and
potentially active regimen;
∙phase II studies with biomarker correlates that validate mechanism of action,
provide convincing insight into novel predictive markers or permit enrichment
of patients most likely to benet from a novel agent;
∙randomised phase II studies such as randomised selection, randomised com-
parison and randomised discontinuation designs.
The consistent use of single-arm, two-stage, response-driven designs as depicted
in the systematic reviews described previously would not optimally cover the majority
of these trial scenarios. The categories listed above were intended to provide authors
with guidance as to the types of phase II trials most relevant to informing the design of
subsequent phase III trials. Such recommendations highlight the need for awareness of
the many components contributing to the design of phase II trials and the importance
of making informed decisions to achieve the objectives of a trial and ensure the results
are robust and interpretable.
1.4 Identifying appropriate phase II trial designs
This book aims to provide guidance to both the clinical researcher and statistician
on each of the key elements of phase II trial design, enabling an understanding of
how they inform the overall design process. Recommendations published by the
Clinical Trial Design Task Force of the National Cancer Institute Investigational
Drug Steering Committee (Seymour et al. 2010) and by the Methodology for the
Development of Innovative Cancer Therapies (MDICT) Task Force (Booth et al.
2008) provide guidance on current best practice for individual aspects of early clinical
trial design. General discussion of choice of endpoints and use of randomisation
is given for the differing settings of monotherapy and combination therapy trials
(Seymour et al. 2010), as well as in the specic context of targeted therapies (Booth
et al. 2008), and discussion on reporting of phase II trials is also provided. Neither set
of recommendations, however, provides detailed guidance on the statistical design
categories available for phase II trials. Here we aim to guide researchers in a step-
by-step manner through the thought process associated with each element of phase
II design, from initial trial concept to the identication of an appropriate statistical
design. With detailed discussion on each of the elements we aim to provide researchers
8 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
with a thorough understanding of the overall process and each of the stages involved,
therefore providing a more informed approach.
Central to this approach is an overall thought process, presented in detail in Chap-
ter 2 and outlined briey below. The approach consists of three stages, highlighting
eight key elements associated with identifying an appropriate phase II trial design:
∙Stage 1 – Trial questions:
◦Therapeutic considerations
◦Primary intention of trial
◦Number of experimental treatment arms
◦Primary outcome of interest
∙Stage 2 – Design components:
◦Outcome measure and distribution
◦Randomisation
◦Design category
∙Stage 3 – Practicalities:
◦Practical considerations
Each of these elements is discussed in detail in Chapter 2, and practical examples
of using this approach to design phase II cancer trials are provided in Chapters 8–12.
These elements were identied as being essential to the design of phase II trials in
cancer through a comprehensive literature review of available statistical methodology
for phase II trials (Brown et al. 2011). The thought process itself is iterative, such that
information obtained during discussion of each element may feed into and inform
later elements of the design. The starting point of any trial design should, however, be a
discussion between the clinical researcher and the statistician that primarily concerns
clinical factors relating to the specic treatment(s) under investigation (Stage 1).
Continued interaction between the clinician and the statistician is essential throughout
the design process.
Using the detail provided in Chapter 2, each of the elements is addressed in
turn and iteratively. Decisions made throughout the process enable the statistician to
narrow down the specic statistical designs appropriate to the pre-specied criteria.
These statistical designs are provided in Chapters 3–7, a library resource of statistical
designs, as introduced here. Each design is categorised to enable efcient navigation
and identication of appropriate designs. Designs are laid out taking into account
∙The use of randomisation including
◦Single-arm designs, arranged by design category and outcome measure –
Chapter 3
INTRODUCTION 9
◦Randomised designs, arranged by design category and outcome measure –
Chapter 4
◦Treatment selection designs, arranged by inclusion of a control arm, design
category and outcome measure – Chapter 5
∙The focus on both activity and toxicity, or toxicity alone, as the primary outcome
of interest – Chapter 6
∙The evaluation of treatment activity in targeted subgroups – Chapter 7
Within each of Chapters 3–5, where there is no identied literature for spe-
cic design category and outcome measure combinations, this is highlighted within
the relevant subsection. For example, there were no references identied discussing
single-arm trial designs specically focused on continuous outcome measures, there-
fore this subsection is included to highlight this to the reader. For Chapters 6 and 7,
only those specic design category and outcome measure combinations for which
references have been identied are listed, since generally there are fewer designs
focused on activity and toxicity and targeted subgroups.
In the majority of cases there will be more than one statistical design that suits the
pre-specied trial parameters determined via the thought process. In such cases, the
nal stage in the thought process, that of practical considerations, may allow a choice
to be made between the alternatives. On the other hand, that choice may be based
on previous experience or assessment of various trial scenarios by mathematical
modelling or simulation. Further detail on choosing between multiple designs is
provided in Chapter 2.
1.5 Potential trial designs
The statistical designs summarised in Chapters 3–7 were identied from a compre-
hensive literature review of phase II statistical design methodology conducted in
January 2008 and updated in January 2010 (Brown et al. 2011). Individual designs
were specically assessed to determine their ease of implementation. Designs were
dened as not easy to implement if
∙the data required to enable implementation were not likely to be available;
∙there was no sample size justication rendering the design difcult or impos-
sible to interpret;
∙criteria were not specied for the study being positive or negative as this makes
the trial of little if any use in taking a new treatment forward;
∙each patient needed to be assessed prior to the next patient being recruited, as
this will usually be prohibitively restrictive in a phase II cancer trial; and
∙the necessary statistical softwares were not detailed as being available and/or
insufcient detail was provided to enable implementation.
10 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
While this assessment of ease of implementation is inherently subjective, these
criteria reect the practicalities of design implementation.
Applying the above criteria, those designs classed as being easy to implement
are included in Chapters 3–7. This amounts to over 100 statistical designs, ranging
from Gehan’s original two-stage design published in 1961 (Gehan 1961) to com-
plex multi-arm, multi-stage designs of more recent years. Mariani and Marubini
highlighted researchers’ preferences for single-arm, two-stage designs (Mariani and
Marubini 2000); there are, however, a wealth of alternative designs available, ranging
from adaptations of Simon’s original two-stage design to incorporate adjustments for
over-/under-recruitment, to randomised trials with formal hypothesis testing between
experimental and control arms. The intention of this book is to present researchers
with the designs available to them for their specic trial, rather than to recommend
one design over another. In doing so we incorporate the well-established designs of
Gehan (1961), Fleming (1982) and Simon (1989), as well as bringing lesser known
designs to the attention of researchers, allowing the user to make informed choices
regarding trial design. A brief overview of each design identied is presented; how-
ever, the technical detail of each design is omitted and may be further evaluated by
considering the complete references, as appropriate.
With the continued development of targeted therapies in cancer, and a drive
towards personalised medicine, the role of biomarkers within phase II trials is an
important area for discussion. Where known biomarkers are available to identify
selected patient populations most likely to benet from an intervention, phase II trials
may be designed as enrichment trials, whereby only biomarker-positive patients are
included. In these cases, any of the statistical designs listed within Chapters 3–6
may be appropriate, focusing solely on the target population. Alternatively, when
selected populations are perhaps less well validated, biomarker-stratied designs
may be considered. Here both biomarker-positive and biomarker-negative subgroups
are explored within a trial, ensuring adequate numbers of patients within each cohort
to potentially detect differing treatment effect sizes. Such designs are listed within
Chapter 7. A more detailed discussion of the incorporation of biomarkers within phase
II trials in cancer is provided in Chapter 2. There have, however, been a number of
recently published articles in this area that may not be included in the library of
available statistical designs since they post-date the updated systematic review on
which the library is based. Where the incorporation of biomarkers is of particular
relevance to a trial design, the researcher may use the thought process described
within this book and should consider not only any appropriate designs identied in
Chapters 3–7, but also additional, more recent, designs specically intended for trials
incorporating biomarkers.
1.6 Using the guidance to design your trial
We present a thought process for the design of phase II trials in cancer, introduced
briey in Section 1.4, addressing the key elements associated with identifying an
appropriate trial design; each of these elements is discussed in detail in Chapter 2.
INTRODUCTION 11
The information in Chapter 2 will allow researchers to narrow down the number of
appropriate designs for their trial and then navigate to the relevant designs in Chapters
3–7, where a brief summary of each trial design is provided. The statistical theory
underpinning the designs detailed is published elsewhere (Mariani and Marubini
1996; Machin et al. 2008; Machin and Campbell 2005), as well as in the individual
papers referenced.
This process is illustrated in Chapters 8–12 by a series of practical, real-life exam-
ples of designing phase II trials in cancer following the thought process and library
of statistical designs. The examples are intended merely as pragmatic illustrations of
how one might apply the process described within the book; they should not be taken
as sole solutions to trial design under the particular settings presented. It is acknowl-
edged that there may be a number of appropriate designs available, and exploration
of various possibilities is encouraged. Examples are presented in the setting of head
and neck cancer, lung cancer, prostate cancer, myeloma and colorectal cancer. Each
example gives differing trial design scenarios highlighting various common issues
encountered when designing phase II trials in cancer. These examples demonstrate
the types of discussions expected between statisticians and clinicians in order to
extract the necessary information to design a phase II trial. They also provide practi-
cal advice regarding how choice of design may be made when several designs t the
trial-specic requirements.

2
Key points for consideration
Sarah Brown, Julia Brown, Marc Buyse, Walter
Gregory, Mahesh Parmar and Chris Twelves
Designing a phase II trial requires ongoing discussion between the clinician, statis-
tician and other members of the trial team, so the design can evolve on the basis of
information specic to each trial. Central to the approach of identifying an optimal
phase II trial design is the thought process introduced in Chapter 1, and presented
diagrammatically in Figure 2.1. The process provides an overview of the key stages
and elements for consideration during the phase II trial design process. Each of these
elements should be worked through in turn in an iterative manner as information
derived at earlier stages feeds in to design choices and decisions in the latter stages
and consideration of alternative designs.
The thought process is made up of three stages:
∙Stage 1 – Trial questions. This stage elicits information predominantly relating
to the trial itself in relation to the treatment under investigation, the primary
intention of the trial, number of arms and primary outcome of interest.
∙Stage 2 – Design components. The information from the rst stage feeds
into the discussions relating to design components considering the outcome
measure, randomisation (or not) and category of design, enabling attention to
be focused on the specic statistical designs relevant to the trial.
∙Stage 3 – Practicalities. Finally, practical considerations may inform which,
from a number of candidate trial designs, is the one best suited to a particular
situation.
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.

Targeted
subgroups
Stage1 – trial
questions
One-stage
Two-stage
Multi-stage
Continuous
monitoring
Decision-theoretic
Three-outcome
PhaseII/III
Randomised
discontinuation
Designcategory
Outcomemeasure
anddistribution
Binary(e.g.
response/no
response)
Multinomial
(e.g.CRvs.
PRvs.
SD/PD)
Continuous
(e.g.
biomarker)
Time-to-
event
Ratioof
timesto
progression
Primary
outcomeof
interest
Activity
Activityand
toxicityor
Toxicity
Primary
intentionof
trial
Proofof
concept
Go/no-go
decisionfor
phaseIII
Randomisation
Single arm(no
randomisation)
Randomisation
toexperimental
arms(selection)
Randomisation
incl.control,
withnoformal
comparison
(referencearm
only)
Randomisation
incl.control,
withformal
comparison
Practical
considerations
Availability/
robustnessof
priordata
Early
termination
forlackof
activity
Programming
requirements
Early
termination
forevidence
ofactivity
Numberof
experimental
treatmentarms
One
Morethan
one
Therapeutic
considerations
Mechanism
ofaction
Singleor
combination
therapy
Biomarker
dependent
(enrichment
orendpoint)
Aimof
treatment
Stage2 – design
components
Stage3 –
practicalities
Operating
characteristics
Figure 2.1 Thought process for identifying phase II trial designs.
14 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
This chapter works through each of the stages and components of Figure 2.1.
2.1 Stage 1 – Trial questions
2.1.1 Therapeutic considerations
The choice of trial design depends not only on statistical considerations, but more
importantly on the clinical factors relating to the treatment(s) and/or disease under
investigation. Discussion of these therapeutic considerations is essential to inform
decisions to be made later in the thought process. At the rst meeting between the
clinician and statistician, discussion of the following points will provide an overview
of the setting of the trial and the specic therapeutic issues to be incorporated into
the trial design.
2.1.1.1 Mechanism of action
An important question to ask when beginning the trial design process is ‘how does
this treatment work?’ The term ‘cytotoxic’ may be used to describe chemothera-
peutic agents, where tumour shrinkage or response is widely accepted as reecting
anti-cancer activity. Many new cancer therapies are, however, targeted at specic
molecular pathways relevant to tumour growth, apoptosis (programmed cell death)
or angiogenesis (new blood vessel formation). Such ‘targeted therapies’, including
tyrosine kinase inhibitors, monoclonal antibody therapies and immunotherapeutic
agents, may be ‘cytostatic’. Here, a change in tumour volume may not be the expected
outcome: in such cases, tumour stabilisation or delay in tumour progression may be
a more anticipated outcome.
The mechanism of action of the agent under investigation will inform many
subsequent decisions, including the choice of outcome measure and whether or not
the trial should be randomised.
2.1.1.2 Aim of treatment
The aim of the treatment under investigation should be considered both in the context
of its mechanism of action and the specic population of patients in which the
treatment is being considered.
It is important to consider the ultimate aim of treatment, which would inform the
outcome measures in future phase III studies, and how this relates to shorter term
aims that can be incorporated into phase II trials. For example, in a population of
patients with a relatively long median progression-free survival (PFS) and overall
survival (OS), the aim of a phase III trial may be to prolong further PFS and/or
OS. These would, however, be unrealistic short-term outcomes for a phase II trial;
tumour response, which may reect PFS or OS, can be an appropriate shrinkage aim
in a phase II trial. By contrast, where the prognosis is less good PFS may provide a
realistic short-term outcome in phase II.
KEY POINTS FOR CONSIDERATION 15
It is essential to consider how the longer term and shorter term aims of treatment
are related, to ensure an appropriate intermediate outcome measure is chosen in phase
II that provides a robust assessment of potential efcacy in subsequent phase III trials.
2.1.1.3 Single or combination therapy
It is important to ascertain whether the treatment under investigation will be given
as a single agent or in combination with another novel or established intervention.
This distinction can inform the decision as to whether or not randomisation should
be incorporated. Where an investigational agent, be it a conventional cytotoxic or a
targeted agent, is used in combination with another active treatment it can be very
difcult to distinguish the effect of the investigational agent from that of the standard
partner therapy; this distinction can be made easier by incorporating randomisation
(see Section 2.2.2 for further discussion).
Similarly, the assessment of toxicity for combination treatments should also be
addressed. Where the addition of an investigational therapy is expected to increase
both activity and toxicity to a potentially signicant degree, dual primary endpoints
may be considered to assess the ‘trade-off’ between greater activity and increased
toxicity (see Section 2.1.4 for further discussion).
2.1.1.4 Biomarker dependent
Biomarkers are an increasingly important part of clinical trials. They can be dened
as ‘a characteristic that is objectively measured and evaluated as an indicator of
normal biological processes, pathogenic processes, or pharmacologic responses to a
therapeutic intervention’ (Atkinson et al. 2001).
Biomarkers may be considered in the design of phase II trials in two ways.
First, a biomarker may serve as an outcome measure. The biomarker may be an
intermediate (primary) endpoint in a phase II trial provided it reects the activity of a
treatment and is associated with efcacy; this may form the basis for a stop/go decision
regarding a subsequent phase III trial. Decisions regarding the use of biomarkers as
primary outcome measures will feed into the decision regarding use of randomisation,
considering whether any historical data exist for the biomarker with the standard
treatment and the reliability of such data. Where a change in a biomarker reects
the biological activity of an agent, but is not predictive of the natural history of the
disease, this alone may be an appropriate endpoint for a proof of concept phase II trial;
in such cases a second, go/no-go phase IIb trial may be required to assess the impact
of the treatment on the cancer prior to a decision on proceeding to a phase III trial.
The use of biomarkers as outcome measures is discussed further in Section 2.2.1.
Second, in the era of targeted therapies a molecular characteristic of the tumour
that is relevant to the mechanism of action of the treatment under investigation may
serve as a biomarker to dene a specic subgroup of patients in whom an intervention
is anticipated to be effective. This has been done especially successfully in studies
of small molecules and monoclonal antibodies targeting HER-2 and related cell
surface receptors (Piccart-Gebhart et al. 2005; Slamon et al. 2001). The potential
16 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
for a biomarker to identify a subpopulation of patients may, however, only become
apparent after phase III investigation, as in the case of the monoclonal antibody
cetuximab in colon cancer where efcacy is limited to patients with no mutation in
the KRAS oncogene (Bokemeyer et al. 2009; Tol et al. 2009; Van Cutsem et al. 2009).
Where available, using a biomarker to enrich the population in a phase II trial in
this way can increase the likelihood of anti-tumour activity being identied, and thus
speed up drug development. By denition, when using a biomarker for population
enrichment, the resulting phase II population is not representative of the general
population. Interpreting outcomes in the enriched population may, therefore, be more
challenging as historical control data may be unreliable; randomisation incorporating
a control arm should be considered in such situations.
There are, however, potential risks with an over-reliance on biomarkers in phase
II trials. If the mode of action of a novel therapy has been incorrectly characterised,
the biomarker chosen for enrichment may be inappropriate and could lead to a
false-negative phase II trial because the wrong patient population has been treated.
Likewise, if a biomarker used to demonstrate proof of principle of biological activity
does not accurately reect the clinically relevant mode of action, the outcome of a
phase II trial may be misleading. When a biomarker is the primary endpoint for a trial
or used to enrich the patient population of patients it is vital that the biomarker be
adequately validated. Where there is insufcient evidence that a biomarker reliably
reects biological activity or identies an optimal patient group, measurement of
the biomarker in an unselected phase II trial population may be appropriate as a
hypothesis-generating exercise for future studies.
Approaches to trial design that incorporates biomarker stratication are discussed
further in Section 2.2.3.
2.1.2 Primary intention of trial
In this context, we dene the ‘intention’ of a trial not as the specic research question
but in the wider sense of classifying trials into two categories:
∙proof of concept, be that biological or therapeutic, or phase IIa;
∙go/no-go decision for further evaluation in a phase III trial, or phase IIb.
A proof of concept, or phase IIa, trial may be undertaken after completing a phase
I trial to screen the investigational treatment for initial evidence of activity. This may
then be followed by a go/no-go phase IIb trial to determine whether a phase III trial
is justied. Running two sequential phase II trials may, in some cases, be inefcient.
The Clinical Trial Design Task Force of the National Cancer Institute Investigational
Drug Steering Committee proposed that, where appropriate, proof of concept may be
embedded in a single go/no-go trial (Seymour et al. 2010).
A model that is increasingly relevant to the development of targeted anti-
cancer agents is to incorporate proof of concept translational imaging and/or
molecular/biomarker studies within the expanded cohort of patients treated at the
recommended phase II dose in a phase I trial. Where clear proof of concept can
KEY POINTS FOR CONSIDERATION 17
be demonstrated in this way, there is a blurring of the conventional divide between
phase I and IIa studies but the need remains for a subsequent phase IIb trial with the
intention of making a formal decision regarding further evaluation in a phase III trial.
While this specic point for consideration is not used to group the trial designs
given in Chapters 3–7, it is important in considering issues such as primary outcome
measures and the use of randomisation. Where a trial is designed as a proof of
concept study alone, it may be appropriate to conduct a single-arm trial to obtain
an estimate of the potential activity of a treatment to within an acceptable degree
of accuracy. Short-term clinical or biomarker outcomes may be appropriate to give
a preliminary assessment of activity prior to embarking on a larger scale phase IIb
study. Where the aim of the phase II trial is to determine whether or not to continue
evaluation of a treatment within a large-scale phase III trial, the ability to make formal
comparisons between experimental and standard treatments may be more appropriate,
to be more condent of that decision to proceed or not. Similarly, in phase IIb
trials outcome measures known to be strongly associated with the primary phase III
outcome measure are desirable for robust decision-making. Further discussion on the
choice of outcome measures and the use of randomisation is given in Sections 2.2.1
and 2.2.2, respectively.
2.1.3 Number of experimental treatment arms
Whereas historically phase II cancer trials invariably had a single-arm, an increasing
number now comprise multiple arms, one of which is often a ‘control’ standard
treatment arm. The most common randomised phase II cancer trial designs have a
single experimental arm with a control arm so the activity seen in the experimental
arm can be compared formally or informally with that seen in the control arm.
Randomisation may be appropriate where historical data on the outcome measure are
unreliable or when a novel agent is being added to an effective standard therapy (see
Section 2.2.2 for discussion).
Where multiple experimental treatments are available, or a single treatment that
may be effective using different doses or schedules, a phase II trial may be designed to
select which, if any, of these options should be taken forward for phase III evaluation.
Randomisation can also be used to evaluate multiple treatment strategies such as
the sequence of rst- and second-line treatments. In these settings assessment of
activity of each individual novel treatment, based on pre-specied minimal levels of
activity, can be assessed using treatment selection designs which are described in
Chapter 5.
Where multiple treatments are being investigated in a single phase II trial,
with each single treatment in a different subgroup of patients (e.g. treatment A
in biomarker-X-positive patients, and treatment B in biomarker-X-negative patients),
this should not be considered as a treatment selection trial since only one experi-
mental treatment is being investigated within each subgroup. For the purposes of
trial design, such trials fall under the ‘single experimental arm’ category. Further
discussion regarding trials of subgroups of patients is provided in Section 2.2.3.
18 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
2.1.4 Primary outcome of interest
The primary outcome of interest will depend on the existing evidence base and/or
stage of development of the treatment under investigation, its mechanism of action
and potential toxicity. Thus, information obtained from discussion of the therapeutic
considerations of the treatment is important in deciding the primary focus of the trial,
as well as incorporating data from previous studies of the same, or similar, treatments.
At this stage, for the purpose of categorising trial designs, the primary outcome of
interest is categorised as being either activity alone, or both activity and toxicity.
Designs are also available that address a third option, of considering toxicity alone as
the primary outcome measure in a phase II trial. These designs are incorporated with
those assessing both activity and toxicity and are described in Chapter 6. Discussion
regarding the specic primary clinical outcome measure is given in Section 2.2.1.
2.1.4.1 Activity
Where the toxicity of the investigational treatment is believed to be modest in the
context of phase II decision-making or the toxicity of agents in the same class is
well known, the primary phase II trial outcome measure will usually be anti-tumour
activity, with toxicity included amongst the secondary outcome measures.
2.1.4.2 Activity and toxicity (or toxicity alone)
If the toxicity prole of the investigational treatment, be it a single-agent or com-
bination therapy, is of particular concern, the activity and toxicity of the treatment
may be considered as joint primary outcome measures, such that the investigational
treatment must show both promising activity and an acceptable level of toxicity to
warrant further evaluation. Such designs allow incorporation of trade-offs between
pre-specied levels of increased activity and increased toxicity, to determine the
acceptability of a new treatment with respect to further evaluation in a phase III trial.
2.2 Stage 2 – Design components
2.2.1 Outcome measure and distribution
Emerging cancer treatments have many differing modes of action, which should be
reected in the choice of outcome measures used to assess their activity. While tumour
response according to Response Evaluation Criteria in Solid Tumours (RECIST)
(Eisenhauer et al. 2009) has historically been the most widely used primary outcome
measure, non-binary denitions or volumetric measures of response, measures of time
to an event such as disease progression or continuous markers such as biomarkers
may be more relevant when evaluating the activity of targeted or cytostatic agents
(Adjei et al. 2009; Booth et al. 2008; Dhani et al. 2009; Karrison et al. 2007; McShane
et al. 2009).
When choosing between the many possible primary outcome measures for a
phase II trial the key points to consider include the expected mechanism of action of
KEY POINTS FOR CONSIDERATION 19
the intervention under evaluation, the aim of treatment in the current population of
patients, whether there are any biomarker outcome measures available, the stage of
assessment in the drug development pathway (i.e. phase IIa or IIb) and the strength
of the association between the proposed phase II outcome measure and the primary
outcome measure that would be used in future phase III trials. The chosen outcome
measure should also be robust with respect to external factors such as investigator
bias and patient and/or data availability.
The primary outcome measure of a phase II trial should be chosen on the basis
that if a treatment effect is observed, this provides sufcient evidence that a treatment
effect on the phase III primary outcome is likely to be seen. The use of surro-
gate endpoints has been investigated in a number of disease areas, including breast
(Burzykowski et al. 2008), colorectal (Piedbois and Buyse 2008) and head and neck
cancer (Michiels et al. 2009). While the outcome measures used in phase II trials do
not need to full formal surrogacy criteria (Buyse et al. 2000) evidence of correlation
between the phase II and III outcome measures is important to ensure reliability in
decision-making at the end of a phase II trial.
The choice of primary outcome measures for a phase II trial reects the outcome
distribution. This section outlines the various options used to categorise phase II trial
designs within Chapters 3–7, according to the distribution of the chosen primary
outcome measure (as described in Chapter 1).
2.2.1.1 Binary
Response is usually evaluated via a continuous outcome measure, that is, the percent-
age change in tumour size. This is, however, typically dichotomised as ‘response’
versus ‘no response’ following RECIST criteria (Eisenhauer et al. 2009). Such binary
outcomes, categorised as ‘yes’ or ‘no’, may be used for any measure that can be
reduced to a dichotomous outcome including toxicity or change in a biomarker. Other
outcome measures that may be expressed as continuous, such as time to disease pro-
gression, are frequently dichotomised to reect an event rate, such as progression at
a xed time point.
In phase II studies of cytotoxic chemotherapy the biological rationale for response
as an indicator of anti-cancer activity is based in part on the natural history of
untreated cancers which grow, spread and ultimately cause death. Administration
of each cycle or dose of treatment kills a substantial proportion of tumour cells
(Norton and Simon 1977) and as such is linked to delaying death (Norton 2001).
These principles may be applicable to chemotherapeutic agents which target tumour
cell kill, and therefore the endpoint of response may be a relevant indicator of anti-
tumour activity.
There are inherent issues in the assessment of tumour response, associated with
investigator bias, inter-observer reliability and variation in observed response rates
over multiple trials (Therasse 2002). These may, to some degree, be alleviated by the
incorporation of independent central review of response assessments or the incor-
poration of a randomised control arm when historical response data are unreliable.
The use of classical response criteria for trials of drugs that may not cause tumour
20 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
shrinkage is likely to be inappropriate and raises questions over the design of phase
II trials and the endpoints being used (Twombly 2006). Measures of time to an event
such as disease progression or novel endpoints such as biomarkers may be more rel-
evant when evaluating the activity of newer targeted therapies. Nevertheless, because
most targeted or biological therapies are selected for clinical development on the
basis of pre-clinical data demonstrating at least some degree of tumour regression,
tumour response may remain an appropriate outcome measure for novel agents, as
acknowledged by two Task Force publications (Booth et al. 2008; Seymour et al.
2010).
2.2.1.2 Continuous
Continuous outcome measures such as tumour volume or biomarker response may
be appropriate and relevant outcome measures for consideration in studies of novel
agents (Adjei et al. 2009; Karrison et al. 2007; McShane et al. 2009). The use of
biomarkers in clinical trials is becoming increasingly common in the development
of targeted treatments with novel mechanisms of action. Only when a biomarker has
been validated as an outcome measure of activity, that is, when a clear relationship
has been established with a more conventional clinically relevant outcome measure,
should a biomarker be used as the primary outcome measure of a phase II trial.
The difculties in identifying validated biomarkers have been highlighted (McShane
et al. 2009), in addition to the need for technical validation and quality assurance
of the relevant assays. As discussed above, biomarkers may be dichotomised to
produce a binary outcome; statistical designs can, however, incorporate biomarkers
as a continuous outcome, which may often lead to more efcient trial design.
2.2.1.3 Multinomial
Multinomial outcome measures may offer an alternative to binary outcomes when
multiple levels of a clinical outcome may be of importance. For targeted or cytostatic
therapies, an alternative to binary tumour response (i.e. response vs. no response) that
remains objective may be the ordered categories of tumour response such as complete
response plus partial response versus stable disease versus progressive disease (Booth
et al. 2008; Dhani et al. 2009). Alternatively activity of an experimental therapy may
be evidenced by either a sufciently high response rate or a sufciently low early
progressive disease rate (Sun et al. 2009).
2.2.1.4 Time to event
Time to progression (TTP), time-to-treatment failure (TTF) or PFS may be considered
as appropriate outcome measures to assess the activity of treatments in phase II clinical
trials (Pazdur 2008).
∙TTP may be dened as the time from registration or randomisation into a
clinical trial to time of progressive disease;
KEY POINTS FOR CONSIDERATION 21
∙TTF may be dened as time from registration/randomisation to treatment dis-
continuation for any reason, including disease progression, treatment toxicity,
patient preference or death;
∙PFS may be dened as time from registration/randomisation to objective
tumour progression or death.
The use of these endpoints has increased in recent years as a means of assessing
the activity of targeted or cytostatic treatments, including cancer vaccines. While
TTP and PFS may better capture the activity of such agents, they do present their
own challenges. Trials incorporating TTP or PFS as the primary outcome measure
may be constrained by a lack of accurate historical time-to-event population data
with which to make comparisons. This limitation may be overcome by randomised,
comparative designs, but they inherently require larger sample sizes. TTP or PFS may
be inuenced by assessment bias in terms of frequency of assessment irrespective of
randomisation, highlighting the need to carefully consider the schedule of follow-up
assessments; increasingly, assessments are recommended at xed time points rather
than in relation to the number of cycles of treatment received to avoid such biases.
Additional time-to-event outcome measures may also be considered including, for
example, time to developing an SAE in trials primarily concerned with safety assess-
ment or time to a clinical event such as bone fracture in trials of drugs specically
acting against bone metastases.
2.2.1.5 Ratio of times to progression
One way to overcome the limitations of TTP and PFS as outcome measures with
regard to the challenges of unreliable historical data, and to avoid the need for
additional patient numbers in a randomised study, may be to use each patient as their
own control. The ratio of times to progression or ‘growth modulation index’ has been
proposed for trials in patients who have had at least one previous line of treatment
(Mick et al. 2000; Von Hoff 1998).
The growth modulation index (GMI) represents the ratio of the TTP on the current
investigational treatment relative to that on the previous line of ‘standard’ treatment,
that is, sequentially measured paired failure times for each patient. Although origi-
nally proposed in the 1990s, this outcome measure may be considered exploratory, as
it has not been widely used in phase II trials to date and relies on TTP data from the
previous line of treatment, the accuracy of which may be uncertain as it will usually
have been administered outside a clinical trial when assessments are less structured.
A GMI of 1.33 has been proposed as clinically relevant, but this threshold has not
been validated (Von Hoff 1998). Time-to-event ratios may, however, be worthy of
consideration as a phase II outcome measure where randomisation is not appropriate.
2.2.2 Randomisation
The use of randomisation in phase II trials is widely debated (Buyse 2000; Redman
and Crowley 2007; Yothers et al. 2006). Randomisation protects against selection bias,
22 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
balances treatment groups for prognostic factors and contributes towards ensuring a
valid comparison of the treatments under investigation, such that any treatment effect
observed can reasonably be attributed to the treatment under investigation and not
external confounding factors.
Although randomised phase III clinical trials provide the mainstay of evidence-
based clinical research, the use of randomisation within phase II is not so straight-
forward. Those opposed to randomisation in phase II trials argue that it can be
unacceptably restrictive from a resource perspective, as it inevitably requires at least
twice the number of patients (assuming 1:1 randomisation), increasing both the cost
and duration of the trial (Yothers et al. 2006). A further criticism is that where the
main purpose of randomisation is to balance for potential prognostic factors (of
which there may be many), this is unlikely to be achieved in randomised phase II
trials that are generally only modest in size (Redman and Crowley 2007). On the
other hand, those making the case for randomised phase II trials stress the inherent
problems of selection bias in uncontrolled trials (Buyse 2000). Therapeutic benets
are generally smaller than potential differences in outcome due to baseline patient
and disease characteristics; patient selection bias can, therefore, seriously confound
the interpretation of non-randomised phase II trials, and thus the decision to take a
treatment forward to phase III. This may not be a problem in a phase IIa trial of a
new cytotoxic that is simply screening to establish whether it has a pre-specied, and
often low, level of activity; bias is more of a challenge in a phase IIb trial where the
key question is whether a new treatment has a sufciently high level of activity to
warrant a large phase III trial.
For an increasing number of phase II studies, especially those of cytostatic or
targeted agents, where ‘traditional’ endpoints such as response rate are not likely
to be the most appropriate outcome measures, historical controls are problematic as
data for alternative endpoints such as PFS may not be available. Where such data do
exist, the population of patients on which the data are available must be considered
since patients entering phase II clinical trials will not be representative of the broader
patient population treated in routine practice from which historical outcome data
may be derived. It is, therefore, important that the patients from whom the historical
outcome data are derived are matched as closely as possible to the phase II population
in terms of baseline characteristics and disease biomarkers if used for enrichment.
If this is not possible, there is a strong argument to include randomisation against a
control arm within the phase II trial.
In the context of randomisation, another important point is whether the experimen-
tal therapy under investigation is to be delivered as a single agent or in combination.
Where an experimental therapy is given in combination with the current standard
treatment, it is very difcult to identify any additional activity of the experimen-
tal agent over and above that of the standard partner therapy unless a comparative
control arm is incorporated into the trial. Even if historical activity data do exist
for the standard therapy, patient selection and evolving patterns of patient care may
often render the interpretation of such data difcult. This should be considered in
detail when making the decision as to whether or not to incorporate a randomised
control arm.
KEY POINTS FOR CONSIDERATION 23
Although randomisation is increasingly being incorporated into phase II trial
design, it can take various forms. Simply because randomisation between experimen-
tal and control treatments is incorporated into a phase II trial does not automatically
imply that the two arms are formally statistically compared with sufcient power; the
reasons for randomisation should, therefore, be critically evaluated.
The statistical implications of conducting a single-arm or a randomised phase II
study have been evaluated in simulation studies. One study compared the results of
multi-centre single-arm and randomised phase II trials of the same sample size, where
the decision as to whether or not the experimental treatment was deemed successful
was based solely on it showing a higher response rate than in the historical control
population, or randomised control population, that is, no formally powered statistical
comparison was employed (Taylor et al. 2006). Where there was expected to be little
variability in response rates between centres, and both the variability and uncertainty
in the response rate for the control population were small, single-arm studies were
found to be adequate in terms of correct decision-making. However, with increased
variability and uncertainty in response rates for either the experimental or control
population, randomised studies were more likely to make the correct recommen-
dation regarding proceeding to phase III, and should be considered as a possible
option. A further study compared error rates between single-arm and randomised
comparative phase II trials, which reected more realistically the characteristics of
a phase II trial (Tang et al. 2010). Although sample sizes for the randomised tri-
als were at least double those of the single-arm trials, the false-positive error rates
(type I error) in single-arm trials were two to four times those projected when the
characteristics of the study patients differed from those of the historical controls;
by contrast, randomised trials remained close to the planned type I error. Statistical
power (type II error) remained stable for both designs despite differences in the patient
populations.
The impact of misspecication of the control data for either approach should be
considered in detail, for example, the impact of specifying a control response rate of,
say, 60% when in fact it may be as low as, say, 50%, or as high as 70%. In the single-
arm setting, the impact of such misspecication, potentially leading to increased
false-negative or false-positive results, is much higher than in the randomised setting
since there is no concurrent control arm against which to verify the initial control
assumptions made. Thus where there is uncertainty in the control data, the inclusion
of a control arm may be considered appropriate.
There is no one-size-ts-all approach to phase II trial design, and the theoretical
and practical implications of randomisation must be considered on a trial-by-trial
basis. Below we discuss the various randomisation options for phase II trial design
and provide examples of when each setting may be appropriate. Randomisation is
categorised within the thought process as
i. no randomisation (single-arm phase II trial);
ii. randomisation incorporating a control arm, no formally powered statistical
comparison intended;
24 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
iii. randomisation incorporating a control arm, formal comparison intended; and
iv. randomisation to multiple experimental treatments.
The use of randomised discontinuation designs is addressed separately in Section
2.2.3.
2.2.2.1 No randomisation
Chapter 3 outlines those designs that incorporate only a single experimental arm. The
results of most single-arm phase II trials are interpreted in the context of historical
control data. The reliability, or otherwise, of these historical data is one of the main
issues driving discussion about randomisation in phase II studies (Rubinstein et al.
2009; Vickers et al. 2007). Single-arm phase II designs have been reported that utilise
historical data but incorporate an estimate of potential variability arising from the
number of patients or trials from which those historical data have been derived, and
are presented in Chapter 3.
A single-arm study may be considered appropriate where
∙comparison with a control group is not relevant. For example, a phase IIa trial
designed to show proof of concept, where the intention is to obtain an initial
estimate of treatment activity to inform the design of a randomised phase IIb
trial;
∙the historical data are sufciently robust for the primary outcome measure as
to allow a reliable comparison, for example, a study of a single-agent cytotoxic
treatment with response rate as the primary outcome measure, conducted in
a broad population of patients with a common cancer refractory to standard
therapy.
2.2.2.2 Randomisation including a control arm
Randomisation including a control arm can be considered in two ways: randomisation
with no formal comparison between experimental and control arms and randomisation
with a formal comparison between experimental and control arms. Further discussion
of each of these is given below. Phase II trial designs incorporating randomisa-
tion between a single experimental therapy (or combination therapy) and a control
arm are presented in Chapter 4.
With no formal comparison
Those designs that incorporate a control arm with no formal comparison intended
as the primary decision-making assessment are highlighted in Chapter 4, as the
study is not designed to have sufcient power to detect statistically signicant dif-
ferences between treatment arms. This does not infer that a comparison may not be
made of outcomes between the arms; rather, that these comparisons be made with
the acknowledgement of reduced statistical power therefore providing additional
exploratory comparisons only. This approach may be appropriate if it is sufcient to
KEY POINTS FOR CONSIDERATION 25
simply show that the experimental treatment has activity within a certain range. Ran-
domisation provides a level of reassurance that the study population is representative
and guards against patient selection bias; this approach is more acceptable when at
least some historical data exist to further aid interpretation of the activity of the investi-
gational agent.
In the absence of formal comparison between treatment arms, the sample size may
simply be doubled compared to a single-arm study and decision-making at the end of
the trial based primarily on the results of the experimental arm, albeit in the context
of outcomes in the control arm. Data from the patients randomised to the control
arm can be more formally incorporated. For example, response rates in the control
arm may be compared to the historical control rates to determine whether they are
reective of the assumptions made when designing the trial (Buyse 2000; Herson and
Carter 1986).
It has been suggested that the use of a control arm as a reference arm only
should be avoided, particularly in trials of targeted or cytostatic agents, since it may
be difcult to interpret the results when unexpected outcomes are observed in the
control arm and when the sample size is not sufcient enough to permit direct formally
powered comparisons (Rubinstein et al. 2009). For example, if positive results were
observed in the experimental arm on the basis of pre-dened criteria, but higher than
expected activity was also observed in the control arm, does this call into question
the positive trial outcome? On the other hand, if the outcome of the experimental
arm is negative and the control arm also has a lower level of activity than expected,
should the apparent low activity of the experimental treatment be questioned? These
uncertainties may be mitigated by looking at both study arms in relation to appropriate
historical data, where available.
With formal comparison
When a phase II trial aims to determine more than whether the investigational agent
has activity within a broad range, or there are serious doubts about the accuracy
of historical control data, formal comparison between the control and experimental
treatment arms is preferred. The trade-off for increased reliability is inevitably a
larger sample size.
The level of statistical signicance within a comparative, randomised phase II
trial should be considered carefully as this will further impact on sample size. It is
acceptable to increase the type I error in a phase II trial compared to the typical 5%
level used within phase III trials, and error rates of up to 20% have been used. This
may enable more realistic sample sizes, and the error associated with incorrectly
declaring a non-active treatment worthy of further investigation in phase III (i.e. the
type I error) may be deemed more acceptable than that of incorrectly rejecting a
treatment that is active. It is, therefore, important to maintain the power associated
with the design of the trial.
Another consideration in the use of formally comparative phase II designs is
the feasibility of achieving the treatment difference that is being specied. While it
may be appropriate to target large treatment effects in some circumstances, this may
26 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
not be the case in others. The size of the clinically relevant treatment effect should,
therefore, be considered carefully to ensure the outcome assumptions are realistic
and not simply used as a method of reducing sample size.
It must also be stressed that with the use of formally comparative phase II designs,
a statistically signicant result at phase II would not usually obviate the need for a
subsequent phase III trial. In contrast to the short-term endpoints usually selected
in phase II trials, longer term endpoints such as PFS and OS are typically selected
in large-scale phase III trials. Additionally, in a relatively small randomised phase
II study only a limited number of patients will have received study drug so not all
clinically relevant toxicities may be identied and should therefore be studied further.
Information gained from the phase II trial may also inuence patient selection for
the denitive phase III study. Subsequent conrmatory phase III trials are, therefore,
usually required even after a statistically positive randomised phase II trial.
2.2.2.3 Randomisation to experimental arms (selection)
Where the aim of a phase II trial is to select which of several candidate investigational
treatments to take forward for further evaluation, randomisation may be incorporated
to randomise patients between several experimental treatments. Where historical
control data are either available or not relevant as discussed above, this will inuence
the decision as to whether or not a control arm is also incorporated, also as discussed
above.
2.2.3 Design category
Phase II statistical designs can be broadly separated into nine statistical design cate-
gories:
∙one-stage;
∙two-stage;
∙multi-stage (or group sequential);
∙continuous monitoring;
∙decision-theoretic;
∙three-outcome;
∙phase II/III;
∙randomised discontinuation; and
∙targeted subgroups.
These categories are not mutually exclusive. For example, a one-stage trial
may incorporate a three-outcome design, or analysis based on a decision-theoretic
approach. Where this is the case, designs have been listed according to their primary
design categorisation.
KEY POINTS FOR CONSIDERATION 27
A brief description of these nine categories is provided below, focusing on the
practical implementation of each design. Previous reviews have used alternative cat-
egories for phase II designs, focusing either on single-arm versus randomised studies
(Seymour et al. 2010) or specic designs such as randomised designs, enrichment
designs and adaptive Bayesian designs for trials of molecularly targeted agents only
(Booth et al. 2008). Mariani and Marubini also previously conducted a review of
the statistical methods available for phase II trials, categorising designs according to
one sample versus controlled, as well as according to the number of stages of assess-
ments, and focusing on a framework for trial analysis, that is, frequentist, Bayesian or
decision theoretic (Mariani and Marubini 1996). The grouping of trial designs within
this book adopts a similar design categorisation to Mariani and Marubini (Mariani
and Marubini 1996), but the thought process incorporates points for discussion prior
to making the specic design decision. Additional categories of design that Mariani
and Marubini (Mariani and Marubini 1996) did not consider are also included.
2.2.3.1 One-stage
A one-stage design utilises a xed sample of patients, recruited until the required
sample size is obtained. After the necessary follow-up of patients, analysis and
decision-making regarding proof of concept, whether to move to phase III or not, or
which treatment(s) to select to take forward to phase III, is made. One-stage designs
are relatively straightforward, avoiding complexities relating to recruitment strategies
if interim analyses are undertaken. They do not, however, allow for adaptations
such as early trial termination due to low levels of activity. Where the safety of a
treatment is well known, and data are already available to suggest activity, either for
a similar treatment or for the same treatment in an alternative population of patients,
a single-stage design may be appropriate since an interim ‘check’ may be deemed
unnecessary.
Where the experimental therapy is highly active, over and above the current
standard therapy, fewer patients may be required under a one-stage design than
other two- or multi-stage designs that incorporate early termination for lack of
activity only.
2.2.3.2 Two-stage
Under a two-stage design patients are recruited to the trial in two stages such that at
the end of the rst stage an interim analysis is performed and the trial may be stopped
for a number of reasons, including lack of activity, early evidence of activity or
unacceptable toxicity; otherwise, the trial continues to a second stage. Alternatively,
the interim analysis may be used to select which of several experimental treatments
to take forward to the second stage. Additional adaptations may be incorporated at
the end of the rst stage according to the specic trial design, for example, sample
size re-estimation.
Stopping rules are developed for each stage of the study to determine whether
to stop or continue, based on pre-specied operating characteristics relevant to the
28 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
specic trial and design. At the end of the study, data from both stages are typically
used in deciding how to proceed.
Two-stage designs are benecial in that the analysis at the end of the rst stage
may act as a ‘check’ on the treatment(s) under investigation, potentially exposing
fewer patients to an inactive treatment than would be exposed using a one-stage
design (i.e. under the null hypothesis of no treatment activity, two-stage designs may
be more efcient). There are, however, issues around patient recruitment while data
from the rst stage of the trial are being analysed. This is a particular issue if the
outcome of interest requires a substantial period of follow-up or observation, for
example, PFS requiring a specic number of events to be observed. During this time,
patients either continue to be recruited, therefore contributing to the second-stage
sample size, without the results of the rst stage being known, or recruitment is
suspended. Continuing recruitment avoids the trial losing momentum and may be
acceptable where recruitment is slow. If a trial is recruiting rapidly, however, the total
required number of patients may be entered to the second stage of the trial before the
rst-stage analysis is complete, rendering the two-stage design futile.
Careful thought must be given to these points when a two-stage design is being
considered. A compromise may be considered, which does not require a break in
recruitment but takes into account data from patients recruited during the follow-up
and analysis period of the rst-stage patients if required (Herndon 1998). If the rst-
stage analysis suggests stopping due to lack of activity, recruitment may be suspended
at this stage and an additional assessment performed incorporating data on all patients
recruited during the follow-up and analysis period to determine whether to stop the
trial permanently or to resume recruitment (see Chapter 3). Additionally, other two-
stage designs can be adapted when the attained sample size is different to the planned
sample size, especially if this results in over-recruitment, where the decision-making
criteria may be updated in line with the actual number of patients recruited (Chen
and Ng 1998; Green and Dahlberg 1992).
Due to the nature of two-stage designs, the total sample size requirement is not
xed, so a maximum sample size and an average sample number (ASN) are generally
specied, to account for possible early termination of the trial.
2.2.3.3 Multi-stage
Multi-stage designs, also known as group-sequential designs, are similar to the two-
stage designs described above, but with additional analyses throughout the course of
the trial. This allows more opportunities to terminate the trial, exposing fewer patients
to inactive and/or toxic treatments, or to accelerate the start of the phase III trial
through early termination of the phase II trial if sufcient evidence of activity is seen.
Additional adaptations may be incorporated at each stage, and again stopping rules are
developed for each stage of the study based on pre-specied operating characteristics
relevant to the specic trial. As with two-stage designs, multi-stage designs require
consideration of whether to continue recruitment whilst interim assessments are
underway. Again, due to the nature of multi-stage designs, a maximum sample size
and an ASN are generally specied.
KEY POINTS FOR CONSIDERATION 29
Two-stage or multi-stage designs are generally chosen because of their ability
to terminate a trial earlier than a xed sample one-stage design and may be seen to
allow a more cautious approach. This is useful when the activity of a treatment is
not known and/or toxicity is likely to be considerable. In this case a two-stage or
multi-stage design may be appropriate irrespective of the implications of continuing
or suspending recruitment. Where such caution is not necessary, a two-stage or multi-
stage design may not be appropriate, especially when either suspending or continuing
recruitment is problematic; in these cases, a one-stage design may be an alternative.
2.2.3.4 Continuous monitoring
With continuous monitoring designs the outcome of interest is assessed after each
individual patient’s primary outcome has been observed. The rationale behind this
design is generally to allow early termination of the trial in case of lack of activity. This
provides, therefore, a more cautious approach to trial design, allowing termination
as soon as possible rather than waiting for a pre-dened number of patients to
be recruited. Again, pre-dened stopping rules are required and determined via
the specic design operating characteristics. Recruitment may continue while the
outcomes are observed, but real-time reporting of outcomes is fundamental to this
design. This is not possible if the primary outcome requires a prolonged period of
observation as with PFS or even best response, both of which may not be available
for some months following the start of treatment. In such cases there is little to be
gained from continuous monitoring over a multi-stage design, since many additional
patients may be recruited before data from the ‘last’ patient can be analysed. This may
be less problematic where, for example, acute treatment toxicity is the key outcome
measure, as this can generally be assessed more quickly than activity.
2.2.3.5 Decision-theoretic
Decision-theoretic designs consider costs and gains associated with making incorrect
decisions at the end of the phase II trial and incorporate utility functions associated
with these costs and gains. Variables such as the total patient ‘horizon’, that is,
the likely number of patients who would be treated with an effective new drug as
standard therapy after completion of a successful phase III trial, before the next new,
more effective drug becomes available, are required (Sylvester 1988). If that patient
population is small, and especially if the likely cost of the new treatment high, there
may be a nancial imperative that the magnitude of the treatment effect sought in
the phase II study be large. Decisions are generally made at the end of the trial after
a xed number of patients have been recruited, as in a one-stage design, although
multi-stage designs may also be used. These designs allow decisions to be made based
on an all-round assessment of gain, as opposed to concentrating solely on clinical
activity (Sylvester and Staquet 1980).
Although the ability to incorporate information regarding costs and gains
associated with decisions made throughout a trial is clearly potentially useful,
decision-theoretic designs are rarely used in phase II oncology trials. This may reect

30 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
the difculty of identifying accurately the cost and patient horizon information that is
often required for their design and difculty in formulating realistic and interpretable
models.
2.2.3.6 Three-outcome
The three-outcome design may be seen as a sub-design of the one-, two- or multi-stage
designs (Storer 1992). The main characteristic of this design is that instead of there
being two possible outcomes at the end of the phase II trial, that is, reject the null
hypothesis or reject the alternative hypothesis, a third outcome is incorporated where
the trial is inconclusive on the basis of primary endpoint data. This approach may
be used when there is a region of uncertainty between, for example, a response rate
above which further investigation in phase III is warranted and a response rate below
which it is not. If the primary outcome measure data of such a trial are inconclusive,
the decision to move to phase III or not may be based on alternative outcome measures
such as safety or cost.
Three-outcome designs may be single arm or randomised. Upper and lower
stopping boundaries are developed for each stage of the study to determine whether
to stop, continue or declare the trial inconclusive. To calculate these boundaries,
in addition to the conventional type I and type II errors (𝛼and 𝛽, respectively),
two further errors must also be considered. The probability of correctly making
the decision to reject the null hypothesis when the alternative is true (𝜋) and the
probability of correctly making the decision to reject the alternative hypothesis when
the null is true (𝜂), are required. With these four errors specied one can then
determine the probability of incorrectly declaring an inconclusive result when in fact
the alternative hypothesis is true (𝛿) and the probability of incorrectly declaring an
inconclusive result when in fact the null hypothesis is true (𝜆). These differing error
rates are shown graphically in Figure 2.2, assuming a binary outcome measure of
success or failure. Here, nLand nUrepresent the lower and upper stopping boundaries,
respectively, for the number of successes observed; Nis the sample size; and p0and
p1represent the success rates associated with the null and alternative hypotheses,
respectively. Alternatively, the probabilities of concluding in favour of either the null
or alternative hypotheses when in fact the true response rate lies within the region of
uncertainty may be specied (Storer 1992).
Three-outcome designs generally require fewer patients than a typical two-
outcome design using the same design criteria. They may also be seen as better
reecting clinical reality than the typical two-outcome design where the decision
λ
ηπ
nL
α
β
δ
Np1
Np0nU
Figure 2.2 Probabilities associated with the three-outcome design.
KEY POINTS FOR CONSIDERATION 31
between accepting and rejecting the null hypothesis may be determined by a single
success or failure (i.e. a single stopping boundary).
2.2.3.7 Phase II/III
Phase II/III designs are used when the transition from phase II to III is required to be
seamless. Such designs typically allow data generated from the phase II component of
the trial to be incorporated in the nal phase III analysis. These trials are, therefore,
usually randomised, incorporating a control arm. Randomisation may be used to
select the ‘best’ of several treatments in the phase II component to be carried forward
into phase III or to decide whether or not to continue an individual experimental
treatment (single-agent or combination therapy) into the phase III component.
One of the main benets of these designs is that they reduce the total time required
for the study to progress through phases II and III compared to running separate trials.
Since data from the phase II component may also be incorporated in the phase III
analysis, patient resources are also reduced; this is a major benet in rarer cancers
or disease sub-types where the patient population is small. Where a limited number
of patients are available for trial recruitment, the optimal use of patient data is even
more crucial than usual.
Alternatively, where separate phase II and phase III trials are to be carried out, a
phase II trial allowing early termination for evidence of activity may be considered
appropriate, bringing forward the phase III trial and saving patient resource. Where
patient numbers are limited, various trial design scenarios should be investigated
to identify the design which is most efcient in terms of patient numbers whilst
providing sufciently robust results.
As with multi-stage designs, the issue of whether to continue or suspend recruit-
ment during the analysis of the phase II component arises. The trial risks losing
momentum if recruitment is suspended, but rapid recruitment during this period may
result in a substantial number of patients being entered into the phase III element,
rendering the phase II/III design futile in its attempts to reduce the number of patients
exposed prior to embarking on phase III. For these trials to be carried out successfully,
the funding body, be it academic or industry, must commit to the full phase II/III
package in the knowledge that the trial may terminate after the phase II component.
Often many more centres will participate in the phase III component than in the phase
II. Since the trial may terminate for lack of activity after the phase II component, the
early preparation of centre set-up to enable a smooth transition to phase III must be
weighed against this possibility of early termination.
Specic phase II/III designs are outlined in Chapters 3–7. An alternative approach
to designing a phase II/III trial is to use conventional stand-alone phase II designs to
make decisions as to whether to continue to phase III or not and incorporate these
into phase III seamlessly (Storer 1990). Typically in this case, the primary outcome
measure under investigation during phase II is different to the primary outcome
measure under investigation during the phase III component, to avoid the need to
adjust the type I error rate in the phase III component. Otherwise, when the same
outcome measure is used in both phases II and III, with a formal comparison between
control and experimental treatments at the end of phase II, this essentially becomes
32 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
a phase III trial with at least one interim analysis. This approach, using the same
endpoints, is not generally recommended since the phase III endpoint will usually
be a long-term outcome such as OS. A long follow-up period would, therefore, be
required for that endpoint to be assessed in the interim/phase II analysis. Multi-stage
approaches may, however, be based on the phase II outcome measure with subsequent
interim analyses within the phase III component based on the phase III endpoints.
Phase II/III designs are inevitably associated with patient and resource efcien-
cies, accelerating the transition between the two trial phases, and usually allowing
patients recruited to phase II to be incorporated in the phase III analysis. However, by
performing separate phase II and phase III trials the results of the phase II trial, and
lessons learned during its set-up and conduct, may be incorporated into the design of
the phase III trial. Changes to eligibility criteria or follow-up schedules, for example,
may be required for the phase III trial. Here separate phase II and III trials enable
these alterations to be made. Such an approach to the planning of current and future
trials may be benecial where experience with an experimental treatment is minimal,
or data for the control population of the disease area in question are minimal, enabling
additional learning between stages of the development pathway.
2.2.3.8 Randomised discontinuation
Randomised discontinuation, or enrichment, trial designs (Kopec et al. 1993; Rosner
et al. 2002; Stadler 2007) involve all study patients initially being treated with the
experimental treatment for a pre-dened period of time, and then assessed for response
to treatment. Typically, those with progressive disease come off study whilst patients
who are responding continue to receive the experimental agent; those with stable
disease are randomised to either continue the experimental treatment or discontinue
it and either remain off treatment or receive standard treatment depending on the
question being asked in the trial.
Such an approach may be appropriate when the specic population of patients
in which the experimental treatment is expected to be effective is unknown. For
example, when evaluating a targeted agent where the level of expression of the relevant
target required for potential activity is not known, a randomised discontinuation
design may allow de facto enrichment of the patient population. Against this, only a
limited proportion of the population recruited to the trial actually contributes to the
randomised part of the study. An overview of the randomised discontinuation design
is presented by Stadler, providing an example of where the design has been used
successfully, as well as providing a summary of the advantages and disadvantages of
the design (Stadler 2007).
The role of the randomised discontinuation design has been reviewed in detail
(Booth et al. 2008; Capra 2004; Freidlin and Simon 2005; Kopec et al. 1993; Rosner et
al. 2002; Rubinstein et al. 2009). The Methodology for the Development of Innovative
Cancer Therapies (MDICT) Task Force (Booth et al. 2008) considered the design as
being exploratory in nature due to lack of clarity on its role in oncology. One study
comparing the randomised discontinuation design with a comparative randomised
design showed that the randomised discontinuation design may be underpowered
in comparison to the traditional design due to the number of patients who start the
KEY POINTS FOR CONSIDERATION 33
investigational treatment who are not then randomised (Capra 2004). An accurate
estimate of the proportion of patients likely to enter randomisation is, therefore,
essential in planning the study sample size. By contrast, a second study concluded
that, although the randomised discontinuation design may be less efcient than the
classical randomised design in many settings, it can be useful in the early development
of targeted agents where a reliable assay to select patients expressing the target is not
available (Freidlin and Simon 2005). The randomised discontinuation design may
be especially appropriate when treatment benet is restricted to a select group of
patients who are not identiable at the start of the trial.
2.2.3.9 Targeted subgroups
In the era of targeted therapies it may be appropriate to investigate the activity of a
treatment in a specic subgroup of patients in whom the intervention is anticipated to
be effective. Alternatively, where the specic subgroup of patients is not determined,
or there is uncertainty about whether a biomarker accurately identies a ‘sensitive’
patient population, it may be appropriate to assess activity simultaneously in several
subgroups of patients according to biomarker characterisation. Population enrichment
for a specic biomarker in phase II trials was discussed in Section 2.1.1.4, highlighting
the risks associated with incorrect characterisation and the possibilities of false-
negative results, as well as issues surrounding the use of historical data.
Designs that incorporate subgroup stratication may be used to enable the
inclusion of separate cohorts of patients dened by the biomarker in question, or
populations dened by other disease sub-types or patient characteristics, ensuring that
adequate numbers are recruited into each cohort. Approaches incorporating stratica-
tion range from separate phase II trials within each stratication level, to hierarchical
Bayesian designs (Thall et al. 2003) and tandem two-stage methods where the exper-
imental treatment is rst tested in an unselected patient population, and if there is
insufcient activity in this overall group, the trial continues in a select population
(e.g. marker-positive patients) only (Pusztai et al. 2007). Trials may also be partially
enriched to include a larger proportion of, for example, biomarker-positive patients,
providing additional power to detect treatment effects in this targeted subgroup of
patients.
These designs are discussed in Chapter 7; however, as noted in Chapter 1, a
number of recent papers have been published on biomarker stratication (An et al.
2012; Buyse et al. 2011; Freidlin et al. 2012; Freidlin and Korn 2013; Jenkins et al.
2011; Lai et al. 2012; Mandrekar et al. 2013; Roberts and Ramakrishnan 2011;
Tournoux-Facon et al. 2011), therefore we encourage consideration of additional
literature outlining alternative designs available.
2.3 Stage 3 – Practicalities
2.3.1 Practical considerations
At this stage of the design process, when faced with a number of statistical designs
from which to choose, deciding which particular design is most appropriate to your
34 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
particular setting can be difcult. Although all the designs considered are deemed
easy to implement, this section focuses on key practical aspects.
2.3.1.1 Programming requirements
For each statistical design described in Chapters 3–7, the programming require-
ments have been considered. It is important that the statistical methodology can be
implemented easily and efciently, allowing the statistician to consider various trial
scenarios during the design process. Only those designs that detail availability of
programs, or for which sufcient information is provided to allow the design to be
implemented, have been incorporated in this book. Nevertheless, some designs may
still be easier to implement than others depending on the resources available.
2.3.1.2 Availability/robustness of prior data
It is essential to consider the design parameters that must be dened in order to
implement each design and the variability associated with each of these parameters.
There may be, for example, a paucity of data on the primary outcome measure for
patients receiving the current standard treatment in the particular trial setting, so what
is the impact of those historical data being unreliable? For example, if the response
rate with standard therapy is estimated to be 20%, a phase II study may aim for a
response rate of 30% with the experimental arm. If a randomised phase II trial is
powered on such a basis but the patients in the control arm have better outcomes than
expected, the study may be underpowered. On the other hand, if a single-arm study is
undertaken and the historical response rate is overestimated an active treatment may
be inappropriately discarded. The implication of misspecication of study parameters
may be investigated by simulation or may already be addressed within the specic
design publication. If a trial design is not robust with regard to misspecication, it
may be more appropriate to consider a design that allows either an estimate of the
variance of the parameter to be incorporated into the design or to select a different
outcome measure that is robust in the face of misspecication. Additionally there may
be a specic design parameter for which no reliable data are available, for example, an
estimate of the correlation between a change in a biomarker and a clinically relevant
outcome measure. Here it may be possible either to consider a design that does not
require the parameter in question or to simulate the performance of the design under
differing parameter assumptions.
2.3.1.3 Early termination
Typically in phase II trials, early termination of a trial is incorporated to ensure
the safety and appropriate treatment of patients, usually in the context of lack of
activity or unacceptable toxicity. Early termination when evidence of activity has
been demonstrated may not be deemed necessary given the desire to obtain as much
information on the treatment as possible to provide a more robust estimate of the
treatment’s activity to inform the design of subsequent trials. On the other hand,
KEY POINTS FOR CONSIDERATION 35
this may delay opening of subsequent phase III trials and there are designs that do
incorporate early termination for activity.
2.3.1.4 Operating characteristics
In phase II trials, a larger type I error than typically used in phase III trials (e.g. 5%
two sided) is generally accepted due to the nature of phase II trials. Type I errors
of up to 20% have been used where the consequences of incorrectly rejecting an
active treatment are deemed less acceptable than those of inappropriately continuing
to develop a treatment that will ultimately not be active. In such circumstances,
subsequent larger phase III studies would be expected to identify the treatment as
inactive, whereas if a treatment is rejected the situation may well not be remedied as a
phase III trial is unlikely. The selection of an appropriate type I error rate is, therefore,
crucial to the reliability of the trial results and the efcient development of new
treatments. While larger type I error rates allow smaller sample sizes, investigators
need to consider carefully whether it is appropriate to conduct a small phase II study
with a high risk of a false-positive result, and ‘negative’ subsequent phase III trial;
the alternative is a larger phase II study with a lesser chance of development of an
ultimately ‘negative’ phase III trial.
Since the primary aim of many phase II trials is to determine whether a treatment
has a pre-specied level of activity, the power of phase II studies should generally
remain high; in practice, this means a power of at least 80%.
2.4 Summary
This chapter provides guidance on decision-making when identifying a trial design
for a phase II trial (Figure 2.1). Clinical researchers and statisticians should consider
carefully each of the three stages of the thought process; additional resources should
be consulted where necessary, and discussion maintained between the clinician and
statistician. The guidance we offer is not intended to be exhaustive or proscriptive.
Further reading and discussion around specic areas relevant to each specic phase
II design element should always be encouraged.
Examples of using the thought process in practice are presented in Chapters 8–12
for various trial design scenarios. These are intended as practical examples of how
the thought process may be implemented.

3
Designs for single experimental
therapies with a single arm
Sarah Brown
3.1 One-stage designs
3.1.1 Binary outcome measure
Fleming (1982)
∙One-stage, binary outcome
∙Standard software available
Fleming proposes a one-stage, two-stage and multi-stage design requiring spec-
ication of response rates under the null and alternative hypotheses and type I and
II error rates. Decision criteria are based around rejecting the null hypothesis that
the response rate of the experimental treatment is not less than some pre-specied
response rate, typically dened as the expected response rate of the current historical
control treatment. Sample size is based on normal approximation to the binomial
distribution. This is a widely used design and programs are readily available (e.g.
Machin et al. 2008).
Fazzari et al. (2000)
∙One-stage, binary outcome
∙Requires programming
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
DESIGNS WITH A SINGLE ARM 37
Fazzari and colleagues propose modications to previously published phase II
designs. The modications include: incorporating a patient population that is more
representative of the intended phase III trial population, by reducing the eligibility
restrictions and increasing the number of centres; increasing the sample size to
allow more accurate estimates of the treatment activity; using an outcome measure
that is more representative of that to be used in phase III, recommending a k-year
progression-free survival (PFS) or overall survival (binary) outcome measure for
advanced-stage disease populations; taking the upper limit of the 75% condence
interval of the activity of previous treatments as the minimum activity required to be
observed to warrant moving to phase III. The methodology for the design of the study
is based on rejecting the minimum activity required from an x% condence interval
around the estimate of treatment activity with, say, 80% probability. Sample size is
generated using Monte Carlo simulation which will require programming.
A’Hern (2001)
∙One-stage, binary outcome
∙Standard software available
A’Hern presents an adaptation of Fleming’s design (Fleming 1982). Calculation
of sample sizes and cut-offs is based on exact binomial distributions as opposed to
normal approximation. Trials based on exact distributions are typically larger than
those using the normal approximation; however, they avoid the possibility that con-
dence intervals around the estimate of activity at the end of the trial will incorrectly
contain the lower rejection proportion due to approximation to the normal distribu-
tion. As for Fleming, this design is widely used and programs are readily available
for its implementation. The choice between Fleming and A’Hern should be based on
the sample sizes and the requirement for exact testing.
Chang et al. (2004)
∙One-stage, binary outcome
∙Pascal programs noted as being available from authors
Chang and colleagues propose a design whereby the sample size, and thus the
test statistic, is calculated using exact unconditional methods. This design may be
used when the historical control data are based on only a few patients (say up to
120). The number of patients on which the historical data are based is required to be
known as analyses take into account the pooled variance of the historical control and
experimental data. Tables and software are available to calculate sample sizes.
Mayo and Gajewski (2004)
∙One-stage, binary outcome
∙Requires programming
38 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Mayo and Gajewski propose sample size calculations for a single-arm single-stage
trial with binary outcome, using Bayesian informative priors (pessimistic/optimistic).
This is an extension of the two-stage designs proposed by Tan and Machin (2002).
Prior information regarding expected response rate and level of uncertainty in this
value is required to determine sample sizes using either the mode, median or mean
approach. Programming is required for the median and mean approaches, possible in
Matlab. Sample sizes will vary depending on the approach used.
Gajewski and Mayo (2006)
∙One-stage, binary outcome
∙Requires programming
Gajewski and Mayo describe Bayesian sample size calculations where conicting
opinions on prior information can be incorporated. Information required to design
the trial includes prior distributions, cut-off for the posterior probability that the true
response rate is greater than some pre-specied value and an error term relating to a
small increase in the target response rate. Sample size calculation is iterative; therefore
some computation is required to identify the design characteristics, for which no
software is detailed but for which formulae are given to enable implementation.
This design differs from the earlier design proposed by Mayo and Gajewski (2004)
as it allows incorporation of pessimistic and optimistic priors, as opposed to one
informative prior.
Vickers (2009)
∙One-stage, binary outcome
∙Stata programs given in appendix to manuscript
Vickers proposes a design using historical control data to generate a statistical
prediction model for phase II trial. The observed trial data for the experimental
arm are then compared to the predicted results to give an indication of whether
patients treated with the experimental agents are doing better than expected, based
on the prediction model. The authors note that the methodology hinges on quality
historical control data relevant to the patient population under study. Step-by-step
methodology is presented which incorporates bootstrapping on both the historical
data set and the observed data set and a comparison of the predicted and actual
outcomes. Example Stata code is given in the appendix to the manuscript to allow
implementation of the statistical analysis, as well as assessment of power.
3.1.2 Continuous outcome measure
No references identied.
DESIGNS WITH A SINGLE ARM 39
3.1.3 Multinomial outcome measure
Zee et al. (1999)
∙One-stage, multinomial outcome
∙Requires programming
Zee and colleagues propose single-stage and multi-stage single-arm designs con-
sidering a multinomial outcome, in the context of incorporating progressive disease
as well as response into the primary outcome measure. Analysis is based on the num-
ber of responses and progressions observed, compared with predetermined stopping
criteria. A computer program written in SAS identies the operating characteristics
of the designs. This is not noted as being available in the paper; however, detail is
given to allow implementation.
Lu et al. (2005)
∙One-stage, multinomial outcome
∙Programs may be available from authors
Lu and colleagues propose a design (one-stage or two-stage) to look at both
complete response (CR) and total response (or other such outcome measures whereby
observing one outcome implies the other outcome is also observed). The design
recommends a treatment for further investigation if either of the alternative hypotheses
is met (i.e. for CR or for total response) and rejects the treatment if neither is met.
The designs follow the general approach of Fleming’s single-stage (Fleming 1982)
or Simon’s two-stage (Simon 1989) approach whereby the number of CRs and total
responses are compared to identied stopping boundaries. Tables are provided for
some combinations of null and alternative hypotheses; however, formulae are given
and at the time of manuscript publication programs were in development. The design
differs from others in this section in that one outcome measure is a sub-outcome
measure of the other, whereas other designs consider discrete outcome measures
such as partial response (PR) versus CR.
Chang et al. (2007)
∙One-stage, multinomial outcome
∙Programs noted as being available from authors
Chang and colleagues propose a single-stage and a two-stage design for window
studies which aim to assess the potential activity of a new treatment in newly diag-
nosed patients. Treatment is given to patients for a short period of time before
standard chemotherapy, and each patient is assessed for response or early pro-
gression (both binary outcome measures). The alternative hypothesis is based on
40 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
both the response rate being above a pre-specied rate and the early progressive
disease rate being below a pre-specied rate. The outcomes follow a multino-
mial distribution. A SAS program is noted as being available from the authors to
identify designs.
Stallard and Cockey (2008)
∙One-stage, multinomial outcome
∙Programs noted as being available from author
Stallard and Cockey propose single-arm, one- and two-stage designs for ordered
categorical data, where the rejection region for the null hypothesis is dened based
on the likelihood ratio test. The null region over which the type I error is controlled
considers a weighting of the proportion of patients in each response category, in a
similar manner to that of Lin and Chen (2000). The focus of the paper is on response
with three levels; however, the design may be extended to more than three levels.
Programs are noted as being available from the rst author to allow identication of
designs.
3.1.4 Time-to-event outcome measure
No references identied.
3.1.5 Ratio of times to progression
Mick et al. (2000)
∙One-stage, ratio of times to progression
∙Requires programming
Mick and colleagues propose a design based on the growth modulation index
(ratio of time to progression of experimental treatment relative to that on the patients’
previous course of anti-cancer treatment). The outcome measure is novel and the
authors justify its use for trials of cytostatic treatments where outcome measures such
as tumour response may not be appropriate. Various values of the growth modulation
index for null and alternative hypotheses should be considered to explore design
parameters, as appropriate for the setting of the study. Each patient acts as their
own control. Information is required for each patient on their time to progression on
previous treatment, and an estimate of the correlation between the two times is needed.
The design is identied via simulation, which allows investigation of the effect of the
correlation estimate on the overall design. Although software is not detailed as being
available, this has been implemented in Splus, and detail is provided to allow design
implementation.
DESIGNS WITH A SINGLE ARM 41
3.2 Two-stage designs
3.2.1 Binary outcome measure
Gehan (1961)
∙Two-stage, binary outcome
∙Standard software available
∙Early termination for lack of activity
Gehan proposes one of the earliest designs to assess experimental treatments
in phase II trials. The methodology is based on the double sampling method and
considers a phase II trial composed of a ‘preliminary’ stage and a ‘follow-up’
stage. The preliminary stage assesses whether the treatment under investigation is
likely to be worth further investigation, using a condence interval approach to
exclude treatments with response rates below those of interest from further investi-
gation. The follow-up stage assesses the activity of the treatment with pre-specied
precision. The number of patients to be included in the follow-up stage is deter-
mined according to the number of responses observed during the rst stage. The
proposed design is intended to completely reject inactive treatments quickly, such
that if the response rate of interest is excluded from the condence interval at the
end of the rst stage, the trial is terminated early. Otherwise the trial continues.
In the second stage the activity of the treatment is estimated with given preci-
sion, rather than providing decision criteria for continuing to a further trial. On
this basis, this design may be seen as an estimation procedure for initial proof
of concept trials rather than trials to determine whether or not to proceed to
phase III.
Fleming (1982)
∙Two-stage, binary outcome
∙Standard software available for overall sample size
∙Early termination for activity or lack of activity
Fleming proposes a one-stage, two-stage and multi-stage design. The multi-stage
design addresses multiple testing considerations to allow early termination in case
of extreme results, employing the standard single-stage test procedure at the last
test. Tables are presented for specic design scenarios using the exact underlying
binomial probabilities rather than the normal approximation to these probabilities.
Programs are readily available to calculate the overall sample size for a one-stage
design (e.g. Machin et al. 2008), with sample sizes at each stage chosen to be approx-
imately equal. Termination at the end of each stage is permitted for activity or lack
of activity.
42 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Simon (1987)
∙Two-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
Simon introduces a two-stage design that is single arm with a binary outcome
whereby the sample size is minimised under a pre-specied expected response rate,
not necessarily the null or alternative response rate. Where this expected response rate
corresponds with the null hypothesis response rate, this design is equivalent to the
optimal design proposed in the subsequent paper summarised below (Simon 1989).
The current design is optimised by keeping the size of the rst stage small, making
the probability of rejecting an inactive drug high, and not allowing too high a sample
size in the second stage. Early termination is permitted at the end of stage 1 only
for lack of activity. A table is provided with limited design scenarios; however, the
designs detailed below (Simon’s optimal and minimax) are more widely used and
may be considered ahead of this earlier design.
Simon (1989)
∙Two-stage, binary outcome
∙Standard software available
∙Early termination for lack of activity
Simon proposes a single-arm two-stage design based on minimising the expected
number of patients under the null hypothesis (optimal), as well as an additional
design that minimises the maximum sample size (minimax). This is a well-known
and widely used two-stage design, based on null and alternative response rates, power
and signicance level, and the observed number of responses at the end of each stage
is used to assess stopping rules. The outcome of interest is binary and the trial may
only be terminated at the end of the rst stage for lack of activity. Extensive tables are
provided for different design scenarios and software is readily available (e.g. Machin
et al. 2008).
Green and Dahlberg (1992)
∙Two-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
The design described by Green and Dahlberg permits early termination for lack
of activity at the end of stage 1 when the alternative hypothesis is rejected at the 0.02
signicance level. At the end of the second stage a signicance level of 0.055 is used to
reject the null hypothesis and declare sufcient activity for further investigation. Some
DESIGNS WITH A SINGLE ARM 43
detail is given regarding stopping boundary and sample size calculation, although this
would need to be programmed and solved iteratively to nd the most suitable design.
This paper also discusses adaptations to the designs of Gehan (1961), Fleming (1982),
and Simon (1989), in the cases where the nal attained trial sample size differs from
the original planned design.
Heitjan (1997)
∙Two-stage, binary outcome
∙Programs noted as being available from the author
∙Early termination for activity or lack of activity
Heitjan proposes a design whereby decision-making is based on the ability to
persuade someone with extreme prior beliefs that the treatment under investigation
is either active or not. This requires specication of extreme priors. For a sceptic,
the probability that the experimental treatment is better than the standard treatment
must be at least some pre-specied value (e.g. 70%) for the treatment to be declared
active (known as the ‘persuade the pessimist probability’ PPP), and for an enthusiast,
the probability that the experimental treatment is worse than the standard treatment
must be at least some pre-specied value (e.g. 70%) for the treatment to be declared
inactive (known as the ‘persuade the optimist probability’ POP). Timing of interim
analyses can either be based on numbers of patients or time during the trial. Sample
size is justied by assessing the operating characteristics and calculating PPPs and
POPs of the design under various scenarios. Programs are noted as being available
upon request from the author. Early termination is permitted for activity or lack of
activity.
Herndon (1998)
∙Two-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
Herndon proposes a hybrid two-stage design that allows continuation of recruit-
ment while the results of the rst stage are being analysed. If the results of the rst
stage indicate the treatment is inactive, accrual is suspended and data are re-analysed
including data from all patients recruited to that time point. Otherwise, the design
continues to target recruitment for the second stage. The sample sizes for the rst
and second stages are chosen for practicality rather than via Simon’s optimal method,
with overall sample size calculated to maintain pre-specied type I and II errors for
study-specic null and alternative hypotheses. Critical values for suspending recruit-
ment, reinitiating or terminating recruitment and for declaring the treatment worthy
of further investigation at the end of stage 2 are calculated. To identify the critical
values a numerical search is required, for which formulae are provided. If the stage
44 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
I results indicate re-analysis using all patients to that time point, analysis follows
similar methodology to that proposed by Green and Dahlberg (1992), detailed above,
as does the analysis of stage II.
Chen and Ng (1998)
∙Two-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Chen and Ng propose a exible design that operates in the same manner as
Simon’s two-stage design (Simon 1989), but here the number of patients at the rst
and second stages can vary by up to eight patients to allow a period of grace in
halting recruitment (in a similar manner to that described by Green and Dahlberg
1992, detailed above). A FORTRAN program is noted as being available from the
authors to enable implementation, and tables are given for some scenarios.
Chang et al. (1999)
∙Two-stage, binary outcome
∙Requires programming
∙Early termination for activity or lack of activity
Chang and colleagues outline a design for continuous or binary outcomes that
takes into account the number of patients on whom historical control data are based.
This reects the fact that the variances of the historical control data and the experi-
mental data will differ. The trial may be terminated at the end of the rst stage for
either activity or lack of activity. Algorithms are used to determine critical values for
stopping, and sample size is calculated by multiplying the single-stage sample size
(formulae provided) by between 1.02 and 1.05.
Hanfelt et al. (1999)
∙Two-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Hanfelt and colleagues propose a modication to Simon’s two-stage design
(Simon 1989) that minimises the median number of patients required under the
null hypothesis, as opposed to the expected number of patients. A program is noted
as being available from the authors that performs the design search. The design differs
very little to that of Simon, other than when the response rate of the treatment is much
less than the null hypothesis rate. Termination at the end of the rst stage is for lack
of activity only.
DESIGNS WITH A SINGLE ARM 45
Shuster (2002)
∙Two-stage, binary outcome
∙Requires programming
∙Early termination for activity or lack of activity
The minimax design proposed by Shuster follows the same format as, for example,
Simon’s design (Simon 1989), although it allows early termination for activity at the
end of the rst stage, as well as for lack of activity. Sample sizes and cut-offs are
calculated based on exact type I and II errors, and the smallest expected maximum
sample size is calculated. The author shows that the proposed design generates the
smallest sample sizes under the null, alternative and maximum scenarios, compared
to Chang et al. (1987) and Fleming (1982). The author advises use of the proposed
minimax design when early termination for activity is benecial (giving as an example
the setting of paediatric cancer). A table of specic design scenarios is presented;
otherwise the design will require programming.
Tan and Machin (2002)
∙Two-stage, binary outcome
∙Standard software available
∙Early termination for lack of activity
Tan and Machin propose two Bayesian designs: the single threshold design (STD)
and the dual threshold design (DTD). The designs are intended to be user-friendly and
easily interpreted by those familiar with frequentist phase II designs. They provide
an alternative approach to the design, analysis and interpretation of phase II trial
data, allowing incorporation of relevant prior information and summarising results in
terms of the probability that a response proportion falls within a pre-specied region
of interest. The following design parameters are required: target response rate for
a new treatment; prior distribution for the experimental treatment being tested; the
minimum probability of the true response rate being at least the target response rate
at the end of stage 1 (for the STD, 𝜆1) and at the end of the study (𝜆2). For the DTD,
the lower response rate of no further interest is also required, and here 𝜆1 represents
the probability that the true response rate is lower than the rate of no further interest
at the end of stage 1.
The STD focuses on ensuring, at the end of the rst stage, that the nal response
rate of the drug has a reasonable probability of passing the target response rate at the
end of the trial. The DTD, however, focuses on ensuring, at the end of the rst stage,
that the nal response rate at the end of the trial is not below the response rate of no
further interest. Tables are given for a number of design scenarios and the designs
are compared with the frequentist approach of Simon (1989). Programs have been
developed and are available in Machin et al. (2008).
46 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Case and Morgan (2003)
∙Two-stage, binary outcome
∙Standard software available and programs noted as being available from authors
∙Early termination for lack of activity
Case and Morgan outline a design with survival outcomes which are dichotomised
to give survival probabilities at pre-specied time points of interest, incorporating all
available information. The design is aimed to avoid the drawbacks of extended follow-
up periods and breaks in recruitment during follow-up between stages. The design
does not require a halt in recruitment between stages as Nelson–Aalen estimates
of survival are used to incorporate all survival information up to the time point of
interest, at the time of interim analysis. Early termination is permitted only for lack
of activity. FORTRAN programs are noted as being available upon request from the
authors, to identify the optimal design, and the proposed design is also available in
Machin et al. (2008).
Jung et al. (2004)
∙Two-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Jung and colleagues propose a searching algorithm to identify admissible two-
stage designs based on Bayesian decision theory, incorporating a loss function which
is a weighted function of the expected number of patients and the maximum number
of patients required. A computer program, developed in Java and noted as being
available upon request from the authors, searches admissible designs (comparing the
expected loss to the Bayes risk) using information provided on the response rates
under null and alternative hypotheses, type I and II errors and maximum number
of patients available. Stopping rules are generated based on a minimum number of
responses required to be observed.
Lin and Shih (2004)
∙Two-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Lin and Shih propose an adaptive design which allows sample size to be adjusted
at the end of the rst stage, to account for uncertainty in the response rate under the
alternative hypothesis. Two potential response rates are pre-specied at the design
stage, and the adjustment made based on these. Tables are provided and software is
DESIGNS WITH A SINGLE ARM 47
noted as being available from the authors to compute sample size and cut-offs that
are not displayed.
Wang et al. (2005)
∙Two-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
Wang and colleagues propose a Bayesian version of Simon’s two-stage design
(Simon 1989), controlling frequentist type I and II error rates, as well as Bayesian
error rates measured using posterior distributions. The design therefore allows incor-
poration of commonly controlled error rates familiar with frequentists, as well as
enabling calculation of posterior probabilities regarding treatment activity. Stopping
at the end of stage I is permitted for lack of activity only. Sample sizes and stopping
boundaries for each stage are provided in tables for specic design scenarios, and the
design is compared with that of Simon (1989) and the STD and DTDs of Tan and
Machin (2002). The design requires programming to enable implementation.
Banerjee and Tsiatis (2006)
∙Two-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Banerjee and Tsiatis propose an adaptive design that is similar to Simon’s optimal
design (Simon 1989); however, the sample size and decision criteria of the second
stage depend on the outcome of the rst stage, and the trial may terminate at the
end of the rst stage for either activity or lack of activity. The sample size and
decision criteria of the second stage are computed using Bayesian decision theory,
minimising the average sample size under the null hypothesis. The design offers
a small sample size reduction over Simon’s optimal design (3–5%); however, the
authors note potential difculties in planning a trial where the total sample size is
unknown at the outset. Tables are given for various design scenarios, and software is
noted as being available on request.
Ye and Shyr (2007)
∙Two-stage, binary outcome
∙Programs available on website
∙Early termination for lack of activity
The design proposed by Ye and Shyr follows that of Simon (1989) but is designed
to balance the number of patients investigated in each of the stages. Attention is
48 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
focused on a binary response outcome measure although the design may be extended
to multiple correlated outcome measures (where more than one outcome can occur
for one patient). Tables are provided with various design scenarios and software is
available at www.vicc.org/biostatistics/ts/freqapp.php (last accessed August 2013).
The authors note that when there are few patients available, Simon’s minimax
design would be preferable. If the optimal and minimax designs have dramatically
imbalanced sample sizes between the two stages then the proposed design may be
preferable; otherwise Simon’s optimal design can be used as this minimises the sam-
ple size under the null hypothesis. Termination at the end of the rst stage is for lack
of activity only.
Litwin et al. (2007)
∙Two-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Litwin and colleagues describe a design based on the outcome measure of PFS
at two set time points. In the second stage of the design the success rate of a binary
outcome measure at a set time point t2 is considered, which is dependent upon the
success rate of a, possibly different, binary outcome measure at an earlier set time
point t1 (assessed at the end of stage 1), for example, the progression-free rate at
time t2, dependent upon the progression-free rate at time t1. The design incorporates
the possibility of stopping for either activity or lack of activity at the end of the rst
stage and proceeds as follows:
1. n1 patients are recruited to the study and followed to time t1 for PFS.
2. If there are too few patients who are progression-free at time t1 then the trial
is stopped early for lack of activity.
3. If there are sufcient patients who are progression-free at time t1 then accrual
continues to the second stage until a total of n2 patients are recruited. Patients
in the initial cohort who are progression-free at t1 continue on in the study.
4. At the end of the second stage (t2) all n2–n1 patients from the second stage
and all those patients progression-free at t1 are evaluated at time t2.
Programs are noted as being available upon request from the authors.
Wu and Shih (2008)
∙Two-stage, binary outcome
∙Requires programming for adaptations
∙Early termination for lack of activity
DESIGNS WITH A SINGLE ARM 49
Wu and Shih propose approaches to handling data that deviate from the pre-
specied Simon’s two-stage design (Simon 1989). The following scenarios are
considered:
∙Simon’s design ‘interrupted’, such that there is additional evaluation at the
following times:
a. before completion of the rst stage;
b. after the rst stage but before completion of the second stage;
c. before completion of the rst stage and again before completion of the
second stage.
∙Simon’s design ‘abandoned’, that is, the rst unscheduled assessment leads to
abandoning the original design and an adapted assessment schedule is devel-
oped.
Adaptations to stopping rules are presented as well as detail regarding adjusting
the p-value associated with decision-making under the deviated scenario. Adaptations
are based on the conditional probability of passing the rst stage and the conditional
power of rejecting the null hypothesis assuming the study continues to its nal stage.
No software is detailed; however, sufcient detail is given to allow the design to be
programmed for implementation.
Koyama and Chen (2008)
∙Two-stage, binary outcome
∙Programs available on website
∙Early termination for lack of activity
Koyama and Chen detail an adaptation to Simon’s two-stage design (Simon
1989) to allow proper inference when the actual sample size at stage 2 deviates
from the planned sample size. The methodology allows computation of updated
critical values for the second stage, based on the number of responses observed
in the rst stage, and adapted p-values, point estimates and condence intervals,
incorporating conditional power. Software is available at http://biostat.mc.vanderbilt.
edu/wiki/Main/TwoStageInference (last accessed August 2013).
Chi and Chen (2008)
∙Two-stage, binary outcome
∙Standard programs available as per Simon’s two-stage design (Simon 1989)
∙Early termination for activity or lack of activity
Chi and Chen propose a curtailed sampling adaptation to Simon’s two-stage
design (Simon 1989). The design allows earlier termination of the trial in the event that
50 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
the treatment is either very active or very inactive. Detail of the proposed adaptations
is presented and is easily implemented, using standard software to identify a design
via Simon’s methodology (Simon 1989). The design can offer substantial savings in
sample sizes when compared to continuing recruitment to the predetermined number
of patients under Simon’s design.
Sambucini (2008)
∙Two-stage, binary outcome
∙Programs noted as being available
∙Early termination for lack of activity
Sambucini proposes a Bayesian design which represents a predictive version of
the STD proposed by Tan and Machin (2002), taking into account the uncertainty
about the data that have not yet been observed, to identify optimal two-stage sample
sizes and cut-off values. A ‘design’ prior and an ‘analysis’ prior are required to
be specied to compute prior predictive distributions and posterior probabilities of
treatment activity, respectively. A program written in R is available to determine
optimal two-stage designs.
3.2.2 Continuous outcome measure
Chang et al. (1999)
∙Two-stage, continuous outcome
∙Requires programming
∙Early termination for activity or lack of activity
Chang and colleagues outline a design for continuous or binary outcomes that
takes into account the number of patients on whom historical control data are based.
This reects the fact that the variances of the historical control data and the experi-
mental data will differ. The trial may be terminated at the end of the rst stage for
either activity or lack of activity. Algorithms are used to determine critical values for
stopping, and sample size is calculated by multiplying the single-stage sample size
(formulae provided) by between 1.02 and 1.05.
3.2.3 Multinomial outcome measure
Zee et al. (1999)
∙Two-stage, multinomial outcome
∙Requires programming
∙Early termination for activity or lack of activity
DESIGNS WITH A SINGLE ARM 51
Zee and colleagues propose single-stage and multi-stage single-arm designs con-
sidering a multinomial outcome, in the context of incorporating progressive disease
as well as response into the primary outcome measure. Analysis is based on the num-
ber of responses and progressions observed, compared with predetermined stopping
criteria. A computer program written in SAS identies the operating characteristics
of the designs. This is not noted as being available in the paper; however, detail is
given to allow implementation.
Lin and Chen (2000)
∙Two-stage, multinomial outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Lin and Chen detail a design that considers both CRs and PRs in a trinomial
outcome, weighting CR as the more desirable outcome. Investigators must specify
overall response rates under the null and alternative hypotheses, and the proportion
that is attributable to CR. A weighted score is calculated at the end of each stage
and this is compared with predetermined cut-off boundaries as in Simon’s optimal
and minimax designs (to which this paper may be viewed as an extension) (Simon
1989). Tables are given for specic scenarios; however, programs are noted as being
available upon request from the authors.
Panageas et al. (2002)
∙Two-stage, multinomial outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Panageas and colleagues propose a single-arm two-stage design based on Simon’s
optimal design (Simon 1989), but with a trinomial outcome (e.g. CR vs. PR vs. non-
response). The design requires null and alternative response rates to be specied for
both CR and PR, that is, improvements in both categories are required. The optimal
design is identied iteratively, to minimise the expected sample size and to satisfy
the type I and II error rates. A computer program is noted as being available from
the authors, with specic design scenarios presented in tables. There is a marginal
saving on sample size over Simon’s design (Simon 1989). The design differs from
that of Zee et al. (1999), detailed above, since early termination is permitted for lack
of activity only and does not incorporate weighting of the different outcomes.
Lu et al. (2005)
∙Two-stage, multinomial outcome
∙Programs may be available from authors
∙Early termination for lack of activity
52 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Lu and colleagues propose a design (one-stage or two-stage) to look at both CR
and total response (or other such outcome measures whereby observing one outcome
implies the other outcome is also observed). The design recommends a treatment
for further investigation if either of the alternative hypotheses is met (i.e. for CR
or for total response) and rejects the treatment if neither is met. The designs follow
the general approach of Fleming’s single-stage (1982) or Simon’s two-stage (Simon
1989) approach whereby the number of CRs and total responses are compared to
identied stopping boundaries. Tables are provided for some combinations of null
and alternative hypotheses; however, formulae are given and at the time of manuscript
publication programs were in development. The design differs from others in this
section in that one outcome measure is a sub-outcome measure of the other, whereas
other designs consider discrete outcome measures such as PR versus CR.
Chang et al. (2007)
∙Two-stage, multinomial outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Chang and colleagues propose a single-stage and a two-stage design for win-
dow studies which aim to assess the potential activity of a new treatment in newly
diagnosed patients. Treatment is given to patients for a short period of time before
standard chemotherapy, and each patient is assessed for response or early progres-
sion (both binary outcome measures). The alternative hypothesis is based on both the
response rate being above a pre-specied rate and the early progressive disease rate
being below a pre-specied rate. The outcomes follow a multinomial distribution. A
SAS program is noted as being available from the authors to identify designs.
Gofn and Tu (2008)
∙Two-stage, multinomial outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Gofn and Tu outline an adaptation to the design proposed by Zee et al. (1999),
based on a simulation approach to determine design. The authors note that the previous
design of Zee was found to have lower power than intended (Freidlin et al. 2002;
Zee et al. 1999). In the proposed two-stage design decision criteria are based on
the proportion of patients with response and the proportion of patients with early
progressive disease, in an advanced disease setting. The alternative hypothesis is that
the response rate is sufciently high or the early progressive disease rate is sufciently
low. Simulation is used to determine the required stopping boundaries to satisfy pre-
specied design criteria. Programs are noted as being available upon request from
the authors. Early termination is permitted for lack of activity only.
DESIGNS WITH A SINGLE ARM 53
Kocherginsky et al. (2009)
∙Two-stage, multinomial outcome
∙Programs available from website
∙Early termination for lack of activity
Kocherginsky and colleagues outline a design to consider the proportion of
patients achieving response and the proportion of patients not progressing early.
The alternative hypothesis being tested is that the response rate is sufciently high or
the non-progression rate is sufciently high. Sample size is calculated via numerical
searching, with the initial sample size estimate calculated following Simon’s two-
stage design (Simon 1989) based on the response rate limits. A numerical search is
then performed over all combinations of design parameters to determine stopping
rules, evaluated by assessing the probability of early termination and the probability
of rejecting the null hypothesis. The design incorporates a thorough assessment of
the operating characteristics over a range of response and progression rates, to guard
against unexpectedly high false-positive rates under certain parameters. Programs
written in R to implement the numerical search are noted as being available from
http://health.bsd.uchicago.edu/lestore/biostatlab/ (last accessed July 2013). Early
termination is permitted for lack of activity only.
Stallard and Cockey (2008)
∙Two-stage, multinomial outcome
∙Programs noted as being available from author
∙Early termination for lack of activity
Stallard and Cockey propose single-arm, one- and two-stage designs for ordered
categorical data, where the rejection region for the null hypothesis is dened based
on the likelihood ratio test. The null region over which the type I error is controlled
considers a weighting of the proportion of patients in each response category, in a
similar manner to that of Lin and Chen (2000). The focus of the paper is on response
with three levels; however, the design may be extended to more than three levels.
Programs are noted as being available from the rst author to allow identication of
designs.
3.2.4 Time-to-event outcome measure
Case and Morgan (2003)
∙Two-stage, time-to-event outcome
∙Standard software available and programs noted as being available from authors
∙Early termination for lack of activity
54 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Case and Morgan outline a design with survival outcomes which are dichotomised
to give survival probabilities at pre-specied time points of interest, incorporating all
available information. The design is aimed to avoid the drawbacks of extended follow-
up periods and breaks in recruitment during follow-up between stages. The design
does not require a halt in recruitment between stages as Nelson–Aalen estimates
of survival are used to incorporate all survival information up to the time point of
interest, at the time of interim analysis. Early termination is permitted only for lack
of activity. FORTRAN programs are noted as being available upon request from the
authors, to identify the optimal design, and the proposed design is also available in
Machin et al. (2008).
Litwin et al. (2007)
∙Two-stage, time-to-event outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Litwin and colleagues describe a design based on the outcome measure of
progression-free survival at two set time points, that is, a binary outcome. In the
second stage of the design the success rate of a binary outcome measure at a set
time point t2 is considered, which is dependent upon the success rate of a, possibly
different, binary outcome measure at an earlier set time point t1 (assessed at the end
of stage 1), for example, the progression-free rate at time t2, dependent upon the
progression-free rate at time t1. The design incorporates the possibility of stopping
for either activity or lack of activity at the end of the rst stage and proceeds as
follows:
1. n1 patients are recruited to the study and followed to time t1 for PFS.
2. If there are too few patients who are progression-free at time t1 then the trial
is stopped early for lack of activity.
3. If there are sufcient patients who are progression-free at time t1 then accrual
continues to the second stage until a total of n2 patients are recruited. Patients
in the initial cohort who are progression-free at t1 continue on the study.
4. At the end of the second stage (t2) all n2–n1 patients from the second stage
and all those patients progression-free at t1 are evaluated at time t2.
Programs are noted as being available upon request from the authors.
3.2.5 Ratio of times to progression
No references identied.
DESIGNS WITH A SINGLE ARM 55
3.3 Multi-stage designs
3.3.1 Binary outcome measure
Herson (1979)
∙Multi-stage, binary outcome
∙Programs noted as being available from author
∙Early termination for lack of activity
Herson describes a Bayesian multi-stage design that considers early stopping
rules based on the predictive probability that a treatment will not be successful at
the end of the phase II trial. Early termination is therefore only permitted for lack
of activity. The design incorporates investigators’ prior information on the response
rate of the experimental treatment and condence in this prior information (via a
coefcient of variation). Early termination boundaries are calculated based on pre-
specied sample sizes ranging from 20 to 30 patients, and consideration is also given
to the expected sample size of a subsequent phase III trial. Programs are noted as
being available from the author.
Fleming (1982)
∙Multi-stage, binary outcome
∙Standard software available for overall sample size
∙Early termination for activity or lack of activity
Fleming proposes a one-stage, two-stage and multi-stage design. The multi-stage
design addresses multiple testing considerations to allow early termination in the case
of extreme results, employing the standard single-stage test procedure at the last test.
Tables are presented for specic design scenarios using the exact underlying binomial
probabilities rather than the normal approximation to these probabilities. Programs
are readily available to calculate the overall sample size for a one-stage design (e.g.
Machin et al. 2008), with sample sizes at each stage chosen to be approximately
equal. Termination at the end of each stage is permitted for activity or lack of activity.
Bellissant et al. (1990)
∙Multi-stage, binary outcome
∙Requires programming
∙Early termination for activity or lack of activity
Bellissant and colleagues apply the triangular test (TT) and sequential probability
ratio test (SPRT), previously used in phase III trials, to single-arm group-sequential
56 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
phase II trials with a binary outcome. An efcient score, Z, and Fisher’s information,
V, are calculated derived from the likelihood function. The log odds ratio statis-
tic is used as the measure of the difference between the actual success rate and
the null hypothesis rate. Formulae are given for the calculation of Zand Vas well
as for calculation of the stopping boundaries, whereby Zis seen as the difference
between observed and expected number of responses under the null hypothesis and
Vas the variance of Zunder the null hypothesis. Early termination is permitted for
either activity or lack of activity. Sample size is justied via the operating charac-
teristics of the TT and SPRT, and group sizes and number of stages are arbitrary,
ranging from 5 to 15 in the examples. The design requires programming to enable
implementation.
Chen et al. (1994)
∙Multi-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
Chen and colleagues propose a multi-stage design that is an extension of Gehan’s
two-stage design (Gehan 1961), where the chance of stopping early is increased if
the observed response rate is smaller than that of interest. It is noted that this design
is suitable for phase II trials that have high expected response rates, in contrast to
the design of Gehan where the chance of stopping a trial early is low if the response
rate of interest is above 0.3. Limited tables of designs are presented, therefore addi-
tional designs will require programming. Early termination is permitted for lack of
activity only.
Ensign et al. (1994)
∙Multi-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
Ensign and colleagues propose a single-arm three-stage design that is an extension
to the two-stage design of Simon (1989). At the end of the rst stage, the trial is
terminated if no responses are observed (i.e. for lack of activity). If at least one
response is observed, stages 2 and 3 are carried out as per Simon’s stages 1 and 2.
The sample sizes and cut-offs for stages 2 and 3 are determined to minimise the
expected sample size under the null hypothesis. A restriction is made that the rst
stage must include at least ve patients. Extensive tables are provided for designs
under differing scenarios; however, the design will need programming to enable
implementation outwith those provided.
DESIGNS WITH A SINGLE ARM 57
Thall and Simon (1994a)
∙Multi-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Thall and Simon present sample size calculations for their original Bayesian
continuous monitoring design (Thall and Simon 1994b). Adaptations to this design are
also provided. The impact of group-sequential monitoring, as opposed to continuous
monitoring, is assessed and it is found that assessment after every two, three or four
patients has little impact on results; however, reducing assessments much further can
increase the likelihood of inconclusive results. The rst adaptation considers early
stopping boundaries for inconclusive results. The second adaptation considers early
termination for lack of activity, which considers only lower stopping boundaries.
Software is noted as being available upon request to compute and implement each
of these designs, including the original continuous monitoring design (Thall and
Simon 1994b).
Tan and Xiong (1996)
∙Multi-stage, binary outcome
∙Programs available on website
∙Early termination for activity or lack of activity
Tan and Xiong propose a group-sequential (or continuous monitoring) design for
the assessment of a binary outcome in a single-arm trial, based on the sequential
conditional probability ratio test (SCPRT). The design is based around comparison to
a reference xed sample size test (RFSST) such as that proposed by Fleming (1982),
and the results that this would achieve, since it is desirable to preserve the power of
this test while incorporating additional opportunities to terminate the trial early. The
proposed design provides similar power to the xed sample size test, but allows more
opportunity to terminate the trial early (for activity or lack of activity). A FORTRAN
program is available via the website (http://lib.stat.cmu.edu/designs/scprtbin (last
accessed July 2013)) to compute the design characteristics.
Chen (1997)
∙Multi-stage, binary outcome
∙Program noted as being available from author
∙Early termination for lack of activity
Chen proposes an extension to Simon’s minimax and optimal two-stage designs
(Simon 1989), simply incorporating an additional stage. Tables are provided with
designs under various scenarios, and a FORTRAN program is noted as being available
58 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
from the author for other scenarios. When compared to Simon’s design, the three-stage
design sometimes has smaller expected sample size; however, this is not consistent.
Compared to Ensign’s three-stage design (Ensign et al. 1994), the proposed design
does not make restrictions on the size and cut-off for the rst stage.
Murray et al. (2004)
∙Multi-stage, binary outcome
∙Requires programming
∙Early termination for activity or lack of activity
Murray and colleagues detail calculation of stopping rules based on condence
interval estimation of the response rate at each stage. A table of specic design
scenarios is presented; however, the design requires programming to identify optimal
decision criteria for scenarios outwith the tables. The design is based on a pre-
specied xed sample size (i.e. no sample size calculation is performed) and a xed
number of stages (with xed sample size at each stage), with type I and II errors
evaluated for the resulting design. Early termination is permitted for either activity
or lack of activity. The design may be used when only a small number of patients
are available for study (30 patients considered in the motivating example) and exact
binomial calculations are employed.
Ayanlowo and Redden (2007)
∙Multi-stage, binary outcome
∙Requires programming
∙Early termination for lack of activity
Ayanlowo and Redden propose a stochastic curtailment design which is based
on the simple binomial test and considers the conditional probability of declaring a
treatment active at the end of the trial, conditional upon the responses observed to
date and the assumption that the alternative hypothesis is true. The design requires
programming to identify the points at which to conduct interim assessments. Sample
size determination is based on a binomial test. Stochastic curtailment adaptations to
Simon’s minimax and optimal design are also proposed (Simon 1989). While the
proposed designs provide more opportunity to stop a trial early due to an inactive
treatment, the authors suggest its use only when Simon’s minimax design is already
being considered, and when the trial is expected to recruit slowly and the outcome
may be observed relatively quickly.
Chen and Shan (2008)
∙Multi-stage, binary outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
DESIGNS WITH A SINGLE ARM 59
Chen and Shan outline a three-stage design, extending previous designs to allow
early termination for either activity or lack of activity (Chen 1997; Ensign et al.
1994; Simon 1989). Tables are given for optimal and minimax designs where the
difference in null and alternative hypothesis rates is 0.20 or 0.15, for a number of
scenarios. A C program is noted as being available from the authors to search for
designs under alternative scenarios. Comparing the proposed optimal and minimax
designs with those of Chen (1997), the designs presented in the current paper require
larger maximal sample size under the optimal design and similar maximal sample
size under the minimax design, but have a smaller average sample number in most
cases. Due to the ability to terminate early for either activity or lack of activity, the
probability of early termination at the rst stage and overall is higher for the current
designs compared to those of Chen (1997).
Lee and Liu (2008)
∙Multi-stage, binary outcome
∙Programs available from website
∙Early termination for lack of activity or activity
Lee and Liu outline a Bayesian group-sequential/continuous monitoring design
based on a binary outcome and the use of predictive probabilities (probability of a
positive result should the trial run to conclusion, given the interim data observed).
The design incorporates early termination for lack of activity, as well as activ-
ity. The continuous monitoring design is compared to Simon’s two-stage design
(Simon 1989). Under the proposed approach the probability of stopping the trial
early is higher, and in general, the expected sample size under the null hypothesis
is smaller. When assessing the design for robustness to deviation from continu-
ous monitoring, although the type I error rate is inated (usually less than 10%)
the design generally remains robust. The authors provide further considerations of
robustness to early termination, estimation bias and comparison to posterior probabil-
ity designs. Software is available from https://biostatistics.mdanderson.org/Software
Download/SingleSoftware.aspx?Software_Id=84 (last accessed July 2013) to allow
implementation.
3.3.2 Continuous outcome measure
No references identied.
3.3.3 Multinomial outcome measure
Zee et al. (1999)
∙Multi-stage, multinomial outcome
∙Requires programming
∙Early termination for activity or lack of activity
60 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Zee and colleagues propose single-stage and multi-stage single-arm designs con-
sidering a multinomial outcome, in the context of incorporating progressive disease
as well as response into the primary outcome measure. Analysis is based on the num-
ber of responses and progressions observed, compared with predetermined stopping
criteria. A computer program written in SAS identies the operating characteristics
of the designs. This is not noted as being available in the paper; however, detail is
given to allow implementation.
3.3.4 Time-to-event outcome measure
Cheung and Thall (2002)
∙Multi-stage, time-to-event outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Cheung and Thall propose a Bayesian sequential-adaptive procedure for contin-
uous monitoring, which may be extended to assessment after cohorts of more than
one patient, that is, multi-stage. The outcome measure of interest is a binary indica-
tor of a composite time-to-event outcome, utilising all the censored and uncensored
observations at each interim assessment. Continuous monitoring based on the approx-
imate posterior (CMAP) is used following Thall and Simon (1994b). The design can
incorporate multiple competing and non-competing outcomes. Early termination is
permitted for activity or lack of activity. R programs are noted as being available
from the authors to allow implementation of the design. This design enables data to
be incorporated on all patients at each interim assessment without all follow-up data
being obtained and may therefore be used when follow-up of each patient is for a
non-trivial period of time.
3.3.5 Ratio of times to progression
No references identied.
3.4 Continuous monitoring designs
3.4.1 Binary outcome measure
Thall and Simon (1994b)
∙Continuous monitoring, binary outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Thall and Simon propose a Bayesian continuous monitoring design to assess the
binary outcome of response in a single-arm trial. Information required includes prior
DESIGNS WITH A SINGLE ARM 61
information on the standard treatment, required improvement due to the experimental
treatment and minimum and maximum boundaries on sample size. A at prior is
assumed for the experimental treatment. Also required is a concentration parameter
for the experimental treatment, representing the amount of dispersion about the
mean of the experimental treatment. After the response outcome is observed on each
patient, the trial may be terminated for lack of activity, terminated for activity or
continued to the next patient (although this assessment is not required before the next
patient can be recruited). If the maximum sample size is obtained and neither of the
stopping boundaries for activity or lack of activity is crossed, the trial is declared
inconclusive. Stopping boundaries are calculated in terms of upper and lower posterior
probability limits, calculated by numerical integration. Designs should be assessed
by simulation to investigate the operating characteristics. Detail regarding software
and implementation is presented elsewhere (Thall and Simon 1994a).
Thall and Simon (1994a)
∙Continuous monitoring, binary outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Thall and Simon present sample size calculations for their original Bayesian con-
tinuous monitoring design (Thall and Simon 1994b) outlined above. Adaptations to
this design are also provided. The rst adaptation considers early stopping boundaries
for inconclusive results. The second adaptation considers early termination for lack
of activity, which considers only lower stopping boundaries. Software is noted as
being available upon request to compute and implement the designs, including the
original continuous monitoring design (Thall and Simon 1994b).
Tan and Xiong (1996)
∙Continuous monitoring, binary outcome
∙Programs available on website
∙Early termination for activity or lack of activity
Tan and Xiong propose a group-sequential (or continuous monitoring) design for
the assessment of a binary outcome in a single-arm trial, based on the SCPRT.
The design is based around comparison to a RFSST such as that proposed by
Fleming (1982), and the results that this would achieve, since it is desirable to
preserve the power of this test while incorporating additional opportunities to ter-
minate the trial early. The proposed design provides similar power to the xed
sample size test, but allows more opportunity to terminate the trial early (for
activity or lack of activity). A FORTRAN program is available via the website
(http://lib.stat.cmu.edu/designs/scprtbin (last accessed July 2013)) to compute the
design characteristics.
62 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Chen and Chaloner (2006)
∙Continuous monitoring, binary outcome
∙Programs noted as being available from authors
∙Early termination for lack of activity
Chen and Chaloner propose a stopping rule for a Bayesian continuous monitoring
design. Stopping rules are based on both the posterior probability that the failure rate
is unacceptably high and the posterior probability that the failure rate is acceptably
low, where these high and low values are derived from historical data. Patients are
recruited until either the stopping rules are met or a maximum sample size has been
recruited. Programs are noted as being available in R (via contacting the authors) to
enable computation of the stopping boundaries and operating characteristics based
on maximum sample size available, prior information on the experimental treatment,
null and alternative hypothesis rates and the upper and lower posterior probability
bounds. Early termination is permitted only for lack of activity.
Lee and Liu (2008)
∙Continuous monitoring, binary outcome
∙Programs available from website
∙Early termination for lack of activity or activity
Lee and Liu outline a Bayesian group-sequential/continuous monitoring design
based on a binary outcome and the use of predictive probabilities (probability of a
positive result should the trial run to conclusion, given the interim data observed).
The design incorporates early termination for lack of activity, as well as activ-
ity. The continuous monitoring design is compared to Simon’s two-stage design
(Simon 1989). Under the proposed approach the probability of stopping the trial
early is higher, and in general, the expected sample size under the null hypothesis
is smaller. When assessing the design for robustness to deviation from continu-
ous monitoring, although the type I error rate is inated (usually less than 10%)
the design generally remains robust. The authors provide further considerations of
robustness to early termination, estimation bias and comparison to posterior probabil-
ity designs. Software is available from https://biostatistics.mdanderson.org/Software
Download/SingleSoftware.aspx?Software_Id=84 (last accessed July 2013) to allow
implementation.
Johnson and Cook (2009)
∙Continuous monitoring, binary outcome
∙Programs available on website
∙Early termination for lack of activity or activity
DESIGNS WITH A SINGLE ARM 63
Johnson and Cook propose a Bayesian continuous monitoring design based
on formal hypothesis tests. They argue that, in contrast to Bayesian designs based
on posterior credible intervals, any misspecication of prior densities associated
with the alternative hypothesis cannot bias the trial results in favour of the null
hypothesis when the proposed formal hypothesis test approach is used. Analysis
is performed after data are available for each patient, and the trial may be termi-
nated early for activity or lack of activity. Software is available from https://bio
statistics.mdanderson.org/SoftwareDownload/SingleSoftware.aspx?Software_Id=94
(last accessed July 2013) which allows the trial to be designed according to user-
specied priors.
3.4.2 Continuous outcome measure
No references identied.
3.4.3 Multinomial outcome measure
No references identied.
3.4.4 Time-to-event outcome measure
Cheung and Thall (2002)
∙Continuous monitoring, time-to-event outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Cheung and Thall propose a Bayesian sequential-adaptive procedure for continu-
ous monitoring. The outcome measure of interest is a binary indicator of a composite
time-to-event outcome, utilising all the censored and uncensored observations at
each interim assessment. Continuous monitoring based on the approximate posterior
(CMAP) is used following Thall and Simon (1994b). The design can incorporate
multiple competing and non-competing outcomes. Early termination is permitted for
activity or lack of activity. R programs are noted as being available from the author
to allow implementation of the design. This design enables data to be incorporated
on all patients at each assessment without all follow-up data being obtained and may
therefore be used when follow-up of each patient is for a non-trivial period of time.
Thall et al. (2005)
∙Continuous monitoring, time-to-event outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
64 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Thall and colleagues propose Bayesian continuous monitoring designs that incor-
porate three time-to-event outcomes (death, disease progression and SAE). Various
amendments to the design are proposed, including randomisation, frequent interval
monitoring, alternative distribution assumptions and incorporation of interval cen-
soring for disease progression. The trial may be stopped early for lack of activity or
for activity. Simulations are performed to establish operating characteristics of the
designs. Programs are noted as being available from the authors upon request.
Johnson and Cook (2009)
∙Continuous monitoring, time-to-event outcome
∙Programs available on website
∙Early termination for lack of activity or activity
Johnson and Cook propose a Bayesian continuous monitoring design based
on formal hypothesis tests. They argue that, in contrast to Bayesian designs based
on posterior credible intervals, any misspecication of prior densities associated
with the alternative hypothesis cannot bias the trial results in favour of the null
hypothesis when the proposed formal hypothesis test approach is used. Analysis
is performed after data are available for each patient, and the trial may be termi-
nated early for activity or lack of activity. Software is available from https://bio
statistics.mdanderson.org/SoftwareDownload/SingleSoftware.aspx?Software_Id=94
(last accessed July 2013) which allows the trial to be designed according to user-
specied priors.
3.4.5 Ratio of times to progression
No references identied.
3.5 Decision-theoretic designs
3.5.1 Binary outcome measure
Sylvester and Staquet (1980)
∙Decision-theoretic, binary outcome
∙Requires programming
∙Early termination for activity or lack of activity
Sylvester and Staquet outline a decision-theoretic design whereby the sample
size and cut-off boundaries for decision-making in the phase II trial are calculated
based on the number of patients who would be expected to receive the experimental
treatment in a subsequent phase III trial, as well as prior probabilities of the response
proportions of the experimental treatment in the phase II trial. There are examples
DESIGNS WITH A SINGLE ARM 65
of specic design scenarios; however, the design would require programming to
enable implementation. Decision criteria are based on observing a given number of
responses. The design allows incorporation of interim assessments, at which the trial
may be terminated early for either activity or lack of activity.
3.5.2 Continuous outcome measure
No references identied.
3.5.3 Multinomial outcome measure
No references identied.
3.5.4 Time-to-event outcome measure
No references identied.
3.5.5 Ratio of times to progression
No references identied.
3.6 Three-outcome designs
3.6.1 Binary outcome measure
Lee et al. (1979)
∙Three-outcome design, binary outcome
∙Requires programming
∙Early termination for activity or lack of activity
Lee and colleagues present a two-stage, three-outcome design whereby the avail-
able sample size is pre-specied based on non-statistical considerations such as
patient availability, and the optimal design is identied based on given constraints.
The design is based on determining whether the true response rate is above or below
a single pre-specied response rate, incorporating the possibility to declare an incon-
clusive result. Tables are presented for a target 20% response rate only, with upper
and lower limits of 30% and 10%, respectively, for determining activity, lack of
activity or an inconclusive result. The paper is therefore somewhat impractical for
designs beyond this specic setting, without further work to implement for other
scenarios. The design may be seen to complement the condence interval approach
to estimating a response rate with given precision.
66 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Storer (1992)
∙Three-outcome design, binary outcome
∙Programs noted as being available from author
∙Early termination for activity or lack of activity
Storer proposes a three-outcome design that is an adaptation to single-, two- and
multi-stage designs such as those described by Fleming (1982). The event rate of
uncertainty is taken to be around the midpoint between the event rate of no interest
and the event rate of interest. As described in Chapter 2, various error rates are
required to be specied. Here the probabilities of concluding in favour of either the
null or alternative hypothesis when in fact the true response rate lies within the region
of uncertainty are required to be specied. These error rates are set to be equal under
this design. Programs are noted as being available to identify the design, upon request
from the author. Early termination is permitted for activity or lack of activity in the
two- and multi-stage designs.
Sargent et al. (2001)
∙Three-outcome design, binary outcome
∙Requires programming; programs may be available upon request
∙Early termination for lack of activity
Sargent and colleagues propose a single-stage (and two-stage) design with three
possible outcomes. As described in Chapter 2, various error rates are required to be
specied, corresponding to differing regions of the distribution curves presented in
Figure 2.2. Here specic probabilities for concluding uncertainty are specied under
both the null and alternative hypotheses (𝜆and 𝛿, respectively, in Figure 2.2), and
these may differ. Tables and formulae are provided for sample size and stopping rule
calculation. The design requires programming; however, programs may be available
upon request from the authors. Under the two-stage design, early termination is for
lack of activity only.
3.6.2 Continuous outcome measure
No references identied.
3.6.3 Multinomial outcome measure
No references identied.
3.6.4 Time-to-event outcome measure
No references identied.
DESIGNS WITH A SINGLE ARM 67
3.6.5 Ratio of times to progression
No references identied.
3.7 Phase II/III designs
There are no phase II/III designs listed in this chapter since these designs require a
control arm to be incorporated in the phase II trial, to enable a seamless transition to
phase III.

4
Designs for single experimental
therapies including
randomisation
Sarah Brown
The designs included in this chapter incorporate randomisation to a control arm with
the intention of a formally powered statistical comparison between the experimental
and control arms, as well as designs where incorporation of randomisation is primarily
to provide a calibration arm, with no statistical comparison formally powered. The
distinction between these approaches is presented for each design listed.
4.1 One-stage designs
4.1.1 Binary outcome measure
Herson and Carter (1986)
∙One-stage, binary outcome
∙No formally powered statistical comparison between arms
∙Requires programming
Herson and Carter consider the inclusion of a randomised calibration group
in single-stage phase II trials of a binary endpoint, in order to reduce the risk of
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 69
false-negative decision-making. Patients are randomised between current standard
treatment (calibration group) and the treatment under investigation. Results of the
calibration group are intended largely to assess the credibility of the outcome in the
experimental arm, that is, not for formal comparative purposes. Decision criteria are
based primarily on the experimental arm results; however, outcomes in the calibration
arm are also considered to address the initial assumptions made regarding the current
standard treatment. Thus the trial essentially constitutes two separate designs, one for
the experimental arm and one for the calibration arm. Due to the assessment of the
control arm results, the overall sample size of the trial may be between three and ve
times that of a non-calibrated design. An example is provided; however, the design
will require programming.
Thall and Simon (1990)
∙One-stage, binary outcome
∙No formally powered statistical comparison between arms
∙Requires programming
Thall and Simon outline a design that incorporates historical data, including
variability, into the design of the trial. A specic proportion of patients are randomised
to a control arm dependent upon the amount of historical control data available, the
degree of both inter-study and intra-study variability and the overall sample size of
the phase II study being planned (following formulae provided). The inclusion of a
sample of patients randomised to a control arm allows the precision of the response
rate in the experimental arm at the end of the trial to be maximised, relative to
the control. Sample size is determined iteratively and the design would need to be
programmed to allow implementation.
Stone et al. (2007b)
∙One-stage, binary outcome
∙Formally powered statistical comparison between arms
∙Standard software available
Stone et al. discuss the use of progressive disease rate at a given time point (as
well as overall progression-free survival) as an outcome measure in randomised phase
II trials of cytostatic agents. Formal comparison between the experimental treatment
and the control treatment is performed for superiority; however, larger type I error
rates than would be used in phase III are incorporated, and large treatment effects
are targeted. The use of relaxed type I errors and large targeted treatment effects
contribute to reduced sample sizes compared to phase III trials, and may therefore be
deemed more realistic for phase II trials.
70 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
4.1.2 Continuous outcome measure
Thall and Simon (1990)
∙One-stage, continuous outcome
∙No formally powered statistical comparison between arms
∙Requires programming
Thall and Simon outline a design that incorporates historical data, including
variability, into the design of the trial. A specic proportion of patients are randomised
to a control arm dependent upon the amount of historical control data available, the
degree of both inter-study and intra-study variability and the overall sample size of
the phase II study being planned (following formulae provided). The inclusion of a
sample of patients randomised to a control arm allows the precision of the outcome
estimate in the experimental arm at the end of the trial to be maximised, relative to
the control. Sample size is determined iteratively and the design would need to be
programmed to allow implementation.
Chen and Beckman (2009)
∙One-stage, continuous outcome
∙Formally powered statistical comparison between arms
∙Programming code provided
Chen and Beckman describe an approach to a randomised phase II trial design
that incorporates optimal error rates. Optimal type I and II errors for the design are
identied by means of an efciency score function which is based on initial proposed
error rates and the ratio of sample sizes between phases II and III. Sample size
calculation is performed using standard phase III-type approaches using the optimal
identied type I and II errors. Formal comparison with the control arm is incorporated.
The design considers cost efciency of the phase II and III trials, on the basis of the
ratio of sample sizes between phases II and III and the aprioriprobability of success
of the investigational treatment. An R program is provided in the appendix of the
manuscript to identify optimal designs.
4.1.3 Multinomial outcome measure
No references identied.
4.1.4 Time-to-event outcome measure
Simon et al. (2001)
∙One-stage, time-to-event outcome
∙Formally powered statistical comparison between arms
∙Standard software available
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 71
Simon and colleagues propose what is termed a randomised ‘phase 2.5’ trial
design, incorporating intermediate outcome measures such as progression-free sur-
vival. The design takes the approach of a phase III trial design, with a formally
powered statistical comparison with the control arm for superiority. It incorporates
a relaxed signicance level, large targeted treatment effects and intermediate out-
come measures, resulting in more pragmatic and feasible sample sizes than would be
required in a phase III trial. The design is straightforward, following the methodology
of phase III trials; however, it is important to note that this should only be used where
large treatment differences are realistic and should not be seen as a way to eliminate
phase III testing.
Stone et al. (2007b)
∙One-stage, time-to-event outcome
∙Formally powered statistical comparison between arms
∙Standard software available
Stone et al. discuss the use of progressive disease rate at a given time point, as
well as overall progression-free survival, as an outcome measure in randomised phase
II trials of cytostatic agents. Formal comparison between the experimental treatment
and the control treatment is performed for superiority; however, larger type I error
rates than would be used in phase III are incorporated, and large treatment effects
are targeted. The use of relaxed type I errors and large targeted treatment effects
contribute to reduced sample sizes compared to phase III trials, and may therefore be
deemed more realistic for phase II trials. This reects the designs described above
by Simon et al. in the setting of time-to-event outcomes, which are described by the
authors as ‘phase 2.5’ designs (Simon et al. 2001).
Chen and Beckman (2009)
∙One-stage, time-to-event outcome
∙Formally powered statistical comparison between arms
∙Programming code provided
Chen and Beckman describe an approach to a randomised phase II trial design
that incorporates optimal error rates. Optimal type I and II errors for the design are
identied by means of an efciency score function which is based on initial proposed
error rates and the ratio of sample sizes between phases II and III. Sample size
calculation is performed using standard phase III-type approaches using the optimal
identied type I and II errors. Formal comparison with the control arm is incorporated.
The design considers cost efciency of the phase II and III trials, on the basis of the
ratio of sample sizes between phases II and III and the aprioriprobability of success
of the investigational treatment. An R program is provided in the appendix of the
manuscript to identify optimal designs.
72 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
4.1.5 Ratio of times to progression
No references identied.
4.2 Two-stage designs
4.2.1 Binary outcome measure
Whitehead et al. (2009)
∙Two-stage, binary outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙Early termination for activity or lack of activity
Whitehead and colleagues outline a randomised controlled two-stage design with
normally distributed outcome measures that may be extended to the setting of binary
and ordinal outcomes. The design allows early termination for activity, or lack of
activity, and incorporates formal comparison between experimental and control arms.
At the interim assessment, which takes place after approximately half the total number
of patients have been recruited, sample size re-estimation may be incorporated if
necessary. The methodology employs approximations to the normal distribution since
sample sizes are generally large enough. No software is detailed as being available
to identify designs; however, programming is noted as being possible in SAS, and
detail is provided to allow its implementation. Simulation is also required to evaluate
potential designs.
Jung (2008)
∙Two-stage, binary outcome
∙Formally powered statistical comparison between arms
∙Programs noted as being available from author
∙Early termination for lack of activity
Jung proposes a randomised controlled extension to Simon’s optimal and minimax
designs (Simon 1989) in the context of a binary outcome measure (e.g. response). The
experimental arm is formally compared with the control arm and declared worthy of
further investigation only if there are sufciently more responders in the experimental
arm. Extensive tables are provided, and programs to identify designs not included in
tables are noted as being available upon request from the author. Extensions to the
design include unequal allocation, strict type I and II error control and randomisation
to more than one experimental arm.
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 73
Jung and George (2009)
∙Two-stage, binary outcome
∙Formally powered statistical comparison between arms
∙Requires minimal programming
∙Early termination for lack of efcacy
Jung and George propose methods of comparing treatment arms in a randomised
phase II trial, where the intention is either to determine whether a single treatment
is worthy of evaluation compared to a control or to select one treatment from many
for further evaluation. The phase II design for a single experimental treatment ver-
sus control is initially based on the evaluation of the control and experimental arms
independently following Simon’s two-stage design (Simon 1989), or similar. The
experimental treatment must rst be accepted via this evaluation, that is, compared
to historical control rates, and is then formally compared with the concurrent con-
trol arm. The experimental treatment is deemed worthy of further evaluation if the
treatment difference between the two arms is above some pre-dened value. No soft-
ware is detailed; however, detail is given which should allow implementation, and
sufcient examples are also provided. The initial two-stage design can be calculated
using standard software available for Simon’s two-stage design.
4.2.2 Continuous outcome measure
Whitehead et al. (2009)
∙Two-stage, continuous outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙Early termination for activity or lack of activity
Whitehead and colleagues outline a randomised controlled two-stage design with
normally distributed outcome measures. The design allows early termination for
activity, or lack of activity, and incorporates formal comparison between experimental
and control arms. At the interim assessment, which takes place after approximately
half the total number of patients have been recruited, sample size re-estimation may be
incorporated if necessary. The methodology employs approximations to the normal
distribution since sample sizes are generally large enough. No software is detailed as
being available to identify designs; however, programming is noted as being possible
in SAS, and detail is provided to allow its implementation. Simulation is also required
to evaluate potential designs. The authors note that the design may be extended to
binary and ordinal outcome measures.
74 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
4.2.3 Multinomial outcome measure
Whitehead et al. (2009)
∙Two-stage, multinomial outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙Early termination for activity or lack of activity
Whitehead and colleagues outline a randomised controlled two-stage design with
normally distributed outcome measures, which may be extended to binary and ordinal
outcome measures. The design allows early termination for activity, and lack of
activity, and incorporates formal comparison between experimental and control arms.
At the interim assessment, which takes place after approximately half the total number
of patients have been recruited, sample size re-estimation may be incorporated if
necessary. The methodology employs approximations to the normal distribution since
sample sizes are generally large enough. No software is detailed as being available
to identify designs; however, programming is noted as being possible in SAS, and
detail is provided to allow its implementation. Simulation is also required to evaluate
potential designs.
Sun et al. (2009)
∙Two-stage, multinomial outcome
∙Formally powered statistical comparison between arms
∙Software noted as being available from author
∙Early termination for lack of activity
Sun and colleagues propose a randomised two-stage design based on Zee’s single-
arm multi-stage design with multinomial outcome measure (Zee et al. 1999), adjusting
the rules such that a sufciently high response rate or a sufciently low early pro-
gressive disease rate should warrant further investigation of the treatment. Optimal
and minimax designs are proposed following the methodology of Simon (1989).
Differences in response and progressive disease rates between control and exper-
imental arms are compared, and the authors note that the intention of the phase
II trial is to screen for potential efcacy as opposed to identifying statistically
signicant differences. An extension is also proposed to the multi-arm selection
setting. Detail is given regarding how to implement the designs in practice, and
software is noted as being available by contacting the rst author to allow iden-
tication of designs. The design recommends a treatment for further investigation
when the response rate is sufciently high, or the early progressive disease rate is
sufciently low. Early termination is permitted for lack of activity only. The authors
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 75
also note that the design may be extended to studies monitoring safety and efcacy
simultaneously.
4.2.4 Time-to-event outcome measure
No references identied.
4.2.5 Ratio of times to progression
No references identied.
4.3 Multi-stage designs
4.3.1 Binary outcome measure
No references identied.
4.3.2 Continuous outcome measure
Cronin et al. (1999)
∙Multi-stage, continuous outcome
∙Formally powered statistical comparison between arms
∙Standard software available for sample size
∙Early termination for activity or lack of activity
Cronin and colleagues propose a Bayesian design for monitoring of phase II trials.
The design incorporates both sceptical and indifferent priors at each of the interim
analyses, according to the hypothesis being tested. Early termination is permitted for
activity or lack of activity, and as such, priors differ at interim and nal analysis.
Posterior distributions are updated at each analysis. When compared with frequentist
group-sequential methods, the proposed Bayesian methods performed at least as well
for the main purpose of detecting ineffective treatments early. The Bayesian method
was slowest to stop when the treatment had clear biological activity. The authors
note that the Bayesian method provides exibility to make changes to outcome
measures, analyses and original trial plans at interim analyses without introducing
theoretical statistical complications. Standard software is available for sample size
calculation.
4.3.3 Multinomial outcome measure
No references identied.
76 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
4.3.4 Time-to-event outcome measure
No references identied.
4.3.5 Ratio of times to progression
No references identied.
4.4 Continuous monitoring designs
4.4.1 Binary outcome measure
No references identied.
4.4.2 Continuous outcome measure
No references identied.
4.4.3 Multinomial outcome measure
No references identied.
4.4.4 Time-to-event outcome measure
Thall et al. (2005)
∙Continuous monitoring, time-to-event outcome
∙Formally powered statistical comparison between arms
∙Programs available from authors
∙Early termination for activity or lack of activity
Thall and colleagues propose Bayesian continuous monitoring designs that incor-
porate three time-to-event outcomes (death, disease progression and serious adverse
event). Various amendments to the initial proposed single-arm continuous moni-
toring design assuming exponential distribution are proposed (Cheung and Thall
2002), including randomisation, frequent interval monitoring, alternative distribution
assumptions and incorporation of interval censoring for disease progression. The trial
may be stopped early for lack of activity or for activity. Simulations are performed
to assess the performance of the design. Programs are noted as being available from
the authors upon request.
4.4.5 Ratio of times to progression
No references identied.
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 77
4.5 Three-outcome designs
4.5.1 Binary outcome measure
Hong and Wang (2007)
∙Three-outcome design, binary outcome measure
∙Formally powered statistical comparison between arms
∙Programs noted as being available from authors
∙Early termination for lack of activity
Hong and Wang detail both a single-stage and a two-stage three-outcome design
which extend that of Sargent et al. (2001) (Chapter 3) to a randomised comparative
design. The region of uncertainty falls around the middle region between the null
hypothesis that the difference in response rates between the arms is zero and the
alternative hypothesis that the difference is delta. In the two-stage design the trial
may only be terminated at the end of the rst stage for lack of activity. A SAS program
to identify the design is noted as being available on request from the authors.
4.5.2 Continuous outcome measure
No references identied.
4.5.3 Multinomial outcome measure
No references identied.
4.5.4 Time-to-event outcome measure
No references identied.
4.5.5 Ratio of times to progression
No references identied.
4.6 Phase II/III designs
4.6.1 Binary outcome measure
Storer (1990)
∙Phase II/III, binary outcome
∙No formal comparison with control in phase II
∙Standard software available for phase II, phase III requires programming
∙No early termination during phase II
78 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Storer proposes a phase II/III design with the same binary outcome at both stages.
This corresponds to a single-arm phase II design (e.g. A’Hern 2001) embedded in a
randomised phase III trial (i.e. randomisation takes place in phase II but the design
and primary decision-making are based on a single-arm design). The phase II decision
criteria are based on the results of the experimental arm only, as opposed to comparing
activity between the experimental and control arms. Sample size calculations for the
phase II aspect may be performed using standard available software for one-stage
designs, based on numerical searching to satisfy given type I and II errors and null
and alternative hypothesis response rates. Standard approaches to phase III sample
size calculation are used, with formulae provided to incorporate an adjustment for
the phase II/III design. This design may be used as a basis for phase II/III designs
whereby any single-arm phase II design is embedded in a phase III trial, including
where the outcome measure at phase III differs to that at phase II.
The design described above uses the same outcome measure at phase II as it does
at phase III. Although this may be seen as seamless phase II/III approach, in effect
it reects a phase III trial with an early interim analysis on the primary outcome
measure (albeit based on a single-arm design). In this setting, consideration should
be given to the most appropriate outcome measure to use for both the phase II and
phase III primary outcome. It is rare that efcacy in the phase III setting could be
claimed on the basis of a binary outcome; rather, a time-to-event outcome is usually
required in phase III trials.
Lachin and Younes (2007)
∙Phase II/III, binary outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙No early termination during phase II
Lachin and Younes outline a phase II/III design that incorporates different out-
come measures at phases II and III (with phase II being a shorter term outcome
measure). Joint distributions for the phase II and III outcomes are calculated, and
the design operating characteristics and sample sizes are calculated via iteration and
numerical integration. An estimate of the correlation between the two outcome mea-
sures is required. The design preserves the type I and II error rates, and patients
randomised during phase II are included in the phase III analysis. Analysis of the
phase II outcome measure considers a formal comparison for lack of activity only (or
excessive toxicity). Software is not detailed as being available; therefore, this design
would require programming to allow implementation.
Chow and Tu (2008)
∙Phase II/III, binary outcome
∙Formally powered statistical comparison between arms
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 79
∙Requires programming
∙No early termination during phase II
Chow and Tu present sample size formulae for seamless adaptive phase II/III
designs where the outcome measures at each phase differ, but the outcome measure
distributions remain the same (e.g. binary outcome in phase II, binary outcome in
phase III). This design is based on two separate studies, with differing endpoints and
durations, which are then combined. Data from patients in the phase II trial are used
to predict the phase III endpoint, for those patients, rather than continuing to follow
patients to observe the phase III endpoint. These data are then combined with the
data from the phase III trial. The relationship between the outcome measures at each
phase is required to be known and well established. This is an essential component
due to the predictive nature of the design. The design will require programming to
enable implementation.
4.6.2 Continuous outcome measure
Liu and Pledger (2005)
∙Phase II/III, continuous outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙No early termination during phase II
Liu and Pledger detail a phase II/III design for a single experimental treat-
ment compared to a control, as well as outlining a design in the dose-nding
context. In the single experimental treatment setting, the experimental treatment
is compared with the control treatment at the end of the phase II trial, based on
the short-term continuous outcome measure associated with the phase II trial. At
this stage, there is no break in recruitment during the analysis, and the sample
size for the phase III trial may be modied to allow estimation of the standard
deviation of the phase III outcome measure. Different phase II and III outcome
measures are used. At the end of the trial, the test statistics from the rst and sec-
ond stages (i.e. phases II and III) are combined. The treatment effect required to be
observed is the same for both short- and long-term outcome measures and needs to
be pre-specied, along with prior information on probability of success and stan-
dard deviation for each outcome measure. This information is used to generate the
operating characteristics of the design. Formulae are given which would need to
be implemented in order to identify the design. The design offers exibility in that
the second-stage (phase III) sample size may be calculated based on updated data
from the rst stage (phase II), and adaptation rules do not need to be specied
in advance.
80 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Lachin and Younes (2007)
∙Phase II/III, continuous outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙No early termination during phase II
Lachin and Younes outline a phase II/III design that incorporates different out-
come measures at phases II and III (with phase II being a shorter term outcome
measure). Joint distributions for the phase II and III outcomes are calculated, and
the design operating characteristics and sample sizes are calculated via iteration and
numerical integration. An estimate of the correlation between the two outcome mea-
sures is required. The design preserves the type I and II error rates, and patients
randomised during phase II are included in the phase III analysis. Analysis of the
phase II outcome measure considers a formal comparison for lack of activity only (or
excessive toxicity). Software is not detailed as being available; therefore, this design
would require programming to allow implementation. Detail is provided for binary
and continuous phase II outcome measures; however, extensions to time-to-event
outcomes are discussed.
Chow and Tu (2008)
∙Phase II/III, continuous outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙No early termination in phase II
Chow and Tu present sample size formulae for seamless adaptive phase II/III
designs where the outcome measures at each phase differ, but the outcome measure
distributions remain the same (e.g. binary outcome in phase II, binary outcome in
phase III). This design is based on two separate studies, with differing endpoints and
durations, which are then combined. Data from patients in the phase II trial are used
to predict the phase III endpoint, for those patients, rather than continuing to follow
patients to observe the phase III endpoint. These data are then combined with the
data from the phase III trial. The relationship between the outcome measures at each
phase is required to be known and well established. This is an essential component
due to the predictive nature of the design. The design will require programming to
enable implementation.
4.6.3 Multinomial outcome measure
No references identied.
RANDOMISED DESIGNS FOR SINGLE EXPERIMENTAL THERAPIES 81
4.6.4 Time-to-event outcome measure
Lachin and Younes (2007)
∙Phase II/III, time-to-event outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙No early termination during phase II
Lachin and Younes outline a phase II/III design that incorporates different out-
come measures at phases II and III (with phase II being a shorter term outcome
measure). Joint distributions for the phase II and III outcomes are calculated, and
the design operating characteristics and sample sizes are calculated via iteration and
numerical integration. An estimate of the correlation between the two outcome mea-
sures is required. The design preserves the type I and II error rates, and patients
randomised during phase II are included in the phase III analysis. Analysis of the
phase II outcome measure considers a formal comparison for lack of activity only (or
excessive toxicity). Software is not detailed as being available; therefore, this design
would require programming to allow implementation.
Chow and Tu (2008)
∙Phase II/III, time-to-event outcome
∙Formally powered statistical comparison between arms
∙Requires programming
∙No early termination in phase II
Chow and Tu present sample size formulae for seamless adaptive phase II/III
designs where the outcome measures at each phase differ, but the outcome measure
distributions remain the same (e.g. binary outcome in phase II, binary outcome in
phase III). This design is based on two separate studies, with differing endpoints and
durations, which are then combined. Data from patients in the phase II trial are used
to predict the phase III endpoint, for those patients, rather than continuing to follow
patients to observe the phase III endpoint. These data are then combined with the
data from the phase III trial. The relationship between the outcome measures at each
phase is required to be known and well established. This is an essential component
due to the predictive nature of the design. The design will require programming to
enable implementation.
4.6.5 Ratio of times to progression
No references identied.
82 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
4.7 Randomised discontinuation designs
4.7.1 Binary outcome measure
Kopec et al. (1993)
∙Randomised discontinuation, binary outcome
∙Formally powered statistical comparison between arms
∙Requires programming (can incorporate standard software)
∙No early termination
Kopec et al. introduce the randomised discontinuation design. All eligible patients
are initially treated with the investigational treatment for a pre-dened period of
time. At this time, all patients are assessed for response to treatment. Treatment
‘responders’ are randomised to either continue with the investigational treatment or
to discontinue the investigational treatment (and instead receive a placebo or current
standard treatment). A formal comparison is made between the experimental and
control arms at the end of the second stage (i.e. after randomisation). Formulae for
the calculation of response proportions are provided and are based on the sample
size needed for the randomised phase to assess relative activity. The design would
therefore need programming. Analysis may also be adapted to incorporate data from
patients in the rst stage, to adapt the response requirements for randomisation, for
example, to incorporate patients with stable disease or greater, as detailed by Rosner
et al. (2002). Alternatively, patients achieving response may continue with treatment,
those with progressive disease discontinue treatment and those with stable disease
are randomised (Stadler 2007). The current design, incorporating randomisation of
patients who are responding to treatment, may be more applicable to other disease
areas where life-threatening consequences of discontinuing treatment may be less
immediate, and there are fewer potential ethical implications associated with this.
4.7.2 Continuous outcome measure
No references identied.
4.7.3 Multinomial outcome measure
No references identied.
4.7.4 Time-to-event outcome measure
No references identied.
4.7.5 Ratio of times to progression
No references identied.

5
Treatment selection designs
Sarah Brown
The designs described within this chapter specically address the question of treat-
ment selection, that is, randomisation to multiple experimental treatment arms is
incorporated. It is, however, also possible to consider treatment selection using single-
arm or randomised phase II designs described in Chapters 3 and 4. In this respect the
aim is to show that each experimental treatment has sufcient activity (and tolerabil-
ity, if appropriate) before performing treatment selection. Treatment selection from
those experimental arms found to be sufciently active (and tolerable if appropriate)
may then take place, for example, using selection designs such as those described
by Sargent and Goldberg (2001) or Simon et al. (1985) (see Section 5.2.1 for further
details). These designs select the most active treatment with a pre-specied probabil-
ity of correct selection, according to the difference in activity observed between the
experimental arms. Such an approach, combining these selection designs with other
phase II designs, ensures that the treatments considered for selection have already
passed pre-specied minimum activity criteria (and possibly tolerability criteria),
prior to selection. Steinberg and Venzon provide an example of such an approach,
as described in Section 5.2.2 (Steinberg and Venzon 2002). The efciency of such
an approach, as compared with the alternative treatment selection designs described
within this chapter, should be considered in further detail on a trial-specic basis.
The designs within this chapter are organised as follows. First, designs including
a control arm are described in Section 5.1, organised by design category and by
outcome measure distribution. Second, in Section 5.2, designs that do not include
a control arm are presented, again by design category and by outcome measure.
Treatment selection designs that incorporate both activity and toxicity are presented
separately in Section 6.4.
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
84 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
5.1 Including a control arm
5.1.1 One-stage designs
5.1.1.1 Binary outcome measure
No references identied.
5.1.1.2 Continuous outcome measure
No references identied.
5.1.1.3 Multinomial outcome measure
Whitehead and Jaki (2009)
∙One-stage, multinomial outcome, control arm
∙Formal comparison with control for selection
∙Programs noted as being available from authors
∙No early termination
Whitehead and Jaki propose one- and two-stage designs for phase II trials based
on ordered category outcomes, when the aim of the trial is to select a single treatment
to take forward to phase III evaluation. The design is randomised to incorporate a
formal comparison with a control arm, and hypothesis testing is based on the Mann–
Whitney statistic. The treatment identied with the smallest p-value indicating a
treatment effect is selected as the treatment to take forward for further investigation.
Details of sample size and critical value calculation are provided, and R code is noted
as being available from the authors to allow implementation. Specication of the
worthwhile treatment effect and the small positive treatment effect that is not worth
further investigation are required to be specied.
5.1.1.4 Time-to-event outcome measure
No references identied.
5.1.1.5 Ratio of times to progression
No references identied.
5.1.2 Two-stage designs
5.1.2.1 Binary outcome measure
Jung (2008)
∙Two-stage, binary outcome, control arm
∙Formal comparison with control for selection
TREATMENT SELECTION DESIGNS 85
∙Programs noted as being available from author
∙Early termination for lack of activity
Jung proposes a randomised controlled extension to Simon’s optimal and mini-
max designs (Simon 1989), considering a binary outcome measure and incorporating
early termination for lack of activity. The experimental arms are compared with
the control arm at the end of stage 1 and treatments may be dropped for lack of
activity. More than one experimental arm may therefore be taken forward to stage
2. If no treatments show improved activity over the control arm at the end of stage
1 the trial may be terminated for lack of activity. At the end of stage 2, all arms
that pass the stage 2 cut-off boundaries compared to control are deemed worthy of
further investigation. The selection design is an extension to the design described
comparing a single experimental arm with a control. In the selection design the
family-wise error rate, the probability of erroneously accepting an inactive treat-
ment, is controlled. Programs to identify designs are available upon request from
the author.
Jung and George (2009)
∙Two-stage, binary outcome, control arm
∙Formal comparison with control for selection
∙Requires minimal programming
∙Early termination for lack of activity
Jung and George propose methods of comparing treatment arms in a randomised
phase II trial, where the intention is either to select one treatment from many for
further evaluation or to determine whether a single treatment is worthy of evaluation
compared to a control. The phase II design is based on a k-armed trial (with or with-
out a control arm for selection) with each arm designed for independent evaluation
following Simon’s two-stage design (Simon 1989), or similar, based on historical con-
trol data, that is, no comparison is made with the control arm at this stage. Different
designs (i.e. the same two-stage design but with different operating characteristics)
may be used for different arms in the independent evaluation if deemed necessary.
A treatment must be accepted via the independent evaluation before it can be con-
sidered for selection, at which point comparisons may be made with the control
arm. p-Values are calculated to represent the probability that the difference between
the arms being compared is at least some pre-dened minimal accepted difference,
given the actual difference observed. The outcome measure used to select the better
treatment is the same outcome measure used for evaluation of each arm indepen-
dently, for example, tumour response. No software is detailed; however, detail is
given which should allow implementation, and sufcient examples are also provided.
The initial two-stage design can be calculated using software available for Simon’s
two-stage design.
86 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
5.1.2.2 Continuous outcome measure
Levy et al. (2006)
∙Two-stage, continuous outcome, control arm
∙No formal comparison with control for selection
∙Requires programming
∙No early termination; treatment selection at the end of stage 1
Levy et al. propose a randomised two-stage futility design incorporating treatment
selection at the end of the rst stage. At the end of the rst stage the ‘best’ treatment is
selected based on the treatment with the highest/lowest (‘best’) mean outcome, that is,
no comparison with control is made here. Sample size for the rst stage is calculated
to give at least 80% probability of correct selection. Patients then continue to be
randomised between control and the selected treatment, and data from the rst stage
is incorporated into the second-stage futility analysis, incorporating a bias correction.
The null hypothesis is that the selected treatment reduces the mean response by at
least x% compared to control; the alternative hypothesis is that the selected treatment
reduces the mean response by less than x% compared to control (reecting a futility
design). Sample size and power calculation details are provided in appendices.
Shun et al. (2008)
∙Two-stage, continuous outcome, control arm
∙No formal comparison with control for treatment selection
∙Requires programming
∙No early termination at the end of stage 1
Shun et al. propose a phase II/III or two-stage treatment selection design where
a single treatment is selected from two at the end of the rst stage. Randomisation
incorporates a control arm, with the intention of formal comparison at the end of the
second stage only, that is, no formal comparison for treatment selection. Treatment
selection is based on the experimental treatment with the highest/lowest (‘best’)
mean outcome. A normal approximation approach is proposed to avoid complex
numerical integration requirements. The design assumes that the treatment effects
of the experimental treatments are not the same. The practical approach to timing
of interim analysis addresses the need to perform this early in order to avoid type
I error ination and the need to perform this late enough such that there is a high
probability of correctly selecting the better treatment. No software is noted as being
available; however, detail is provided to allow implementation and a detailed example
is given. The authors note that this design can be extended to binary and time-to-
event outcome measures if the correlation between the nal and interim test statistics
is known.
TREATMENT SELECTION DESIGNS 87
5.1.2.3 Multinomial outcome measure
Sun et al. (2009)
∙Two-stage, multinomial outcome, control arm
∙Formal comparison with control
∙Software noted as being available from author
∙Early termination for lack of activity; early treatment selection
Sun and colleagues propose a randomised two-stage design based on Zee’s single-
arm multi-stage design with multinomial outcome measure (Zee et al. 1999), adjusting
the rules such that a sufciently high response rate or a sufciently low early pro-
gressive disease rate should warrant further investigation of a treatment. Optimal and
minimax designs are proposed following the methodology of Simon (1989), incor-
porating comparison with a control arm. Differences in response and progressive
disease rates between control and experimental arms are compared. The authors note
that the intention of the phase II trial is to screen for potential efcacy as opposed
to identifying statistically signicant differences compared with control. Patients are
randomised between multiple experimental treatments and a control arm. At the end
of the rst stage only those treatments that pass the stopping boundaries for both
response and progressive disease are continued to the second stage. If there is clear
evidence that one treatment is better than the other, selection may take place at the
end of the rst stage. If, at the end of the second stage, there is no clear evidence
that one experimental treatment is better than the other both arms may be considered
for further evaluation. Detail is given regarding how to implement the designs in
practice, and software is noted as being available by contacting the rst author to
allow identication of designs. The authors also note that the design may be extended
to studies monitoring safety and efcacy simultaneously.
Whitehead and Jaki (2009)
∙Two-stage, multinomial outcome, control arm
∙Formal comparison with control for selection
∙Programs noted as being available from authors
∙No early termination
Whitehead and Jaki propose one- and two-stage designs for phase II trials based
on ordered category outcomes, when the aim of the trial is to select a single treatment
to take forward to phase III evaluation. The design is randomised to incorporate a
formal comparison with a control arm, and hypothesis testing is based on the Mann–
Whitney statistic. In the two-stage design, treatment selection takes place at the end of
stage 1 whereby the treatment with the smallest p-value indicating a treatment effect is
selected as the treatment to take forward to stage 2. In stage 2, patients are randomised
between the selected treatment and control only. The nal analysis at the end of stage
88 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
2 is based on all data available on patients in the control arm and the selected treatment
arm. Details of sample size and critical value calculation are provided, and R code
is noted as being available from the authors to allow implementation. Specication
of the worthwhile treatment effect and the small positive treatment effect that is not
worth further investigation are required to be specied.
5.1.2.4 Time-to-event outcome measure
No references identied.
5.1.2.5 Ratio of times to progression
No references identied.
5.1.3 Multi-stage designs
5.1.3.1 Binary outcome measure
No references identied.
5.1.3.2 Continuous outcome measure
Cheung (2009)
∙Multi-stage, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Requires programming
∙Early treatment selection and early termination for lack of activity
Cheung describes an adaptive multi-arm, multi-stage selection design incorpo-
rating a control arm and considering a normally distributed outcome measure. Two
multi-stage procedures are proposed: an extension of the sequential probability ratio
test (SPRT) with a maximum sample size and a truncated sequential elimination
procedure (ELIM). The SPRT method allows early selection of a treatment when
there is evidence of increased activity compared to control, whereas the ELIM pro-
cedure also allows early termination of arms for lack of activity. The proposed
procedures are compared with single-arm trials and the ELIM procedure is rec-
ommended over these, incorporating sample size reassessment at interim analyses.
Cohort sizes between interim assessments may range from 1 to 10 with little impact
on the design’s operating characteristics. Sample size formulae are provided which
will require implementing in order to identify the trial design.
5.1.3.3 Multinomial outcome measure
No references identied.
TREATMENT SELECTION DESIGNS 89
5.1.3.4 Time-to-event outcome measure
No references identied.
5.1.3.5 Ratio of times to progression
No references identied.
5.1.4 Continuous monitoring designs
No references identied.
5.1.5 Decision-theoretic designs
No references identied.
5.1.6 Three-outcome designs
No references identied.
5.1.7 Phase II/III designs – same primary outcome measure at
phase II and phase III
The designs outlined within this section incorporate the same primary outcome
measure for phase II assessment as that used for phase III. Although this may be
seen as a seamless phase II/III approach, in effect it reects a phase III trial with an
early interim analysis on the primary outcome measure. In this setting, consideration
should be given to the most appropriate outcome measure to use for both the phase II
and phase III primary outcome. It is rare that efcacy in the phase III setting could
be claimed on the basis of, for example, a binary outcome; rather, a time-to-event
outcome is usually required in phase III trials.
5.1.7.1 Binary outcome measure
Bauer et al. (1998)
∙Phase II/III, binary outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from authors
∙Early termination for efcacy at the end of phase II
Bauer and colleagues outline a simulation program for an adaptive two-stage
design with application to phase II/III and dose nding. Two outcomes may be con-
sidered, with one primary variable on which formal hypothesis testing is performed
and the other for which adaptations at the end of the rst stage may be based on.
The outcomes may be binary or continuous, or a combination. The same primary
outcome measure is used at each analysis. Simulation is required to identify the best
90 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
design according to various operating characteristics and the performance of different
designs. A program is detailed (the focus of the manuscript) to allow implementation,
which is noted as being available on request from the authors. At the end of the rst
stage the stage 1 hypothesis is tested, generating a p-value p1. At the end of the second
stage the stage 2 hypothesis is tested using only data obtained from patients in stage
2, generating a p-value p2. The overall hypothesis is then tested combining p1 and
p2 using Fisher’s combination test (Fisher 1932). Application is given to phase II/
III, with treatment selection at the end of stage 1: if the p-value is signicant that at
least one of the treatments is superior then the treatment with the ‘best’ outcome is
considered in phase III. The trial may also terminate early for efcacy at the end of
stage 1 if the p-value is signicant at the stage 2 signicance level.
Bauer and Kieser (1999)
∙Phase II/III, binary outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from author
∙Early termination for efcacy at the end of phase II
Bauer and Kieser detail a design that incorporates formal comparison of each of
the experimental arms with the control at the end of phase II (as well as testing whether
any of the treatments are superior to control). The same primary outcome measure is
used in both phases II and III. A xed sample size is used for phase II, however the
phase III sample size can be updated adaptively at the end of phase II. Stopping at the
end of phase II is permissible for either lack of efcacy or early evidence of efcacy.
The design also allows more than one treatment to be taken forward to phase III. At
the end of phase II the sample size may be re-estimated and the test statistics to use
at phase III are determined, according to the number of treatments taken forward and
the hypotheses to be tested. The decision criterion at the end of phase III is based on
Fisher’s combination test (Fisher 1932) whereby the p-values from both phases are
combined (as opposed to combining data from all patients). Simulation is required
as detailed in Bauer et al. (1998), as above. Examples are given in the dose-nding
setting and the authors note that the main advantage of this design is its exibility and
its control of the family-wise error rate. The design is similar to that detailed above
(Bauer et al. 1998) with the exception that the current paper gives more detail relating
to multiple comparisons between experimental treatments and control arm. When
considering either of these two designs, it is advised that both papers be considered
together since the software detailed in Bauer et al., above, is required to identify the
design proposed here.
Stallard and Todd (2003)
∙Phase II/III, binary outcome, control arm
∙Formal comparison with control for treatment selection
TREATMENT SELECTION DESIGNS 91
∙Programs noted as being available from authors
∙Early termination for efcacy at the end of phase II
Stallard and Todd propose a design whereby patients from phase II are incorpo-
rated in the phase III analysis, and treatment selection at the end of phase II is based
on the treatment with the largest test statistic using efcient scores and Fisher’s infor-
mation. A formal comparison is made between the selected treatment and control,
and the trial may be terminated early for lack of efcacy or superiority at this stage.
The type I error in the nal phase III analysis is adjusted for the treatment selection
in phase II. Overall sample size and phase II sample size are computed according to
group-sequential phase III designs such as those described by Whitehead (1997). A
computer program is noted as being available from the authors to calculate power for
stopping boundaries, according to pre-specied group sizes. The authors note that
the design is useful when one treatment is likely to be much better than the others at
phase II, as opposed to taking multiple treatments to phase III. Consideration should
also be given to the timing of the rst interim analysis (i.e. phase II assessment).
Too early and there is too little information, too late and there are too many patients
enrolled and thus potentially wasted resources.
Kelly et al. (2005)
∙Phase II/III, binary outcome, control arm
∙Formal comparison with control for treatment selection
∙Requires programming
∙Early termination for efcacy and lack of efcacy during phase II
Kelly and colleagues propose an adaptation to the design proposed by Stallard and
Todd (detailed above), such that more than one treatment may be selected at multiple
stages within the phase II part of the trial. Treatments are evaluated for selection
using Fisher’s information and an efcient score statistic which may be applied to
continuous, binary and failure time data. p-Values are calculated at each stage for
comparison of the best treatment with control. Only treatments within a pre-specied
margin of the efcient score statistic of the best treatment are continued to the next
stage, and all other treatments are dropped. Patients are randomised between control
and each of the treatments under investigation at each stage. The trial may stop for
efcacy or lack of efcacy at each stage. The example given is based on the use
of the triangular test described by Whitehead (1997), which uses expected Fisher’s
information to calculate operating characteristics.
Wang and Cui (2007)
∙Phase II/III, binary outcome, control arm
∙No formal comparison with control in phase II
92 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
∙Requires programming
∙No early termination during phase II
Wang and Cui outline a design whereby patients are randomised to each of
the experimental treatments under investigation and a control arm, using response-
adaptive randomisation (the paper is written in the context of dose selection but
could be applied to treatment selection). The allocation ratios are calculated based on
distance conditional powers (i.e. the probability that the event rate for the treatment
under investigation is larger than some pre-specied xed rate, based on the observed
data and the fact that some patients will not yet have had their outcome observed).
The treatment to which most patients have been randomised is deemed the most
efcacious at the end of the recruitment period. This selected treatment is then
formally compared with the control treatment, forming the phase III comparison.
This design uses binary outcome measures such as treatment response, for both the
phase II treatment selection and the phase III formal comparison; although it is noted
that continuous outcomes may be used. Simulation is required to investigate the
design parameters, with sample size calculated based on the phase III comparison.
The design may be implemented with the development of programs based on formulae
provided.
5.1.7.2 Continuous outcome measure
Bretz et al. (2006)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Minimal programming required
∙Early termination for efcacy or lack of efcacy at the end of phase II
Bretz and colleagues outline a phase II/III design which allows treatment selection
at the interim assessment (i.e. at the end of phase II). The design allows data from
the rst stage to be incorporated into the nal analysis. Formal comparisons between
control and experimental treatments are performed at the end of each stage. Early
termination is permitted at the end of the rst stage (i.e. at the end of phase II) for
lack of efcacy or for early evidence of efcacy. Also at this time, if the study is to
be continued to phase III, adaptations to the design of the trial may be made such as
sample size reassessment based on the data observed to date. Final analysis includes
data from both stages, with decision criteria based on a combination of test results
(i.e. using methods such as Fisher’s product test of the conditional error function).
The closure principle is incorporated, such that a hypothesis is only rejected if it
and all associated intersection hypotheses are also rejected. Sample size formulae are
given to allow calculation. The design may be extended to multiple stages, in which
case early termination during the phase II aspect may be incorporated.
TREATMENT SELECTION DESIGNS 93
Bauer et al. (1998)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from authors
∙Early termination for efcacy at the end of phase II
Bauer and colleagues outline a simulation program for an adaptive two-stage
design with application to phase II/III and dose nding. Two outcomes may be con-
sidered, with one primary variable on which formal hypothesis testing is performed
and the other for which adaptations at the end of the rst stage may be based on.
The outcomes may be binary or continuous, or a combination. The same primary
outcome measure is used at each analysis. Simulation is required to identify the best
design according to various operating characteristics and the performance of different
designs. A program is detailed (the focus of the manuscript) to allow implementation,
which is noted as being available on request from the authors. At the end of the rst
stage the stage 1 hypothesis is tested, generating a p-value p1. At the end of the
second stage the stage 2 hypothesis is tested using only data obtained from patients in
stage 2, generating a p-value p2. The overall hypothesis is then tested combining p1
and p2 using Fisher’s combination test (Fisher 1932). Application is given to phase
II/III, with treatment selection at the end of stage 1: if the p-value is signicant that
at least one of the treatments is superior then the treatment with the ‘best’ outcome
is considered in phase III. The trial may also terminate early for efcacy at the end
of stage 1 if the p-value is signicant at the stage 2 signicance level.
Bauer and Kieser (1999)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from author
∙Early termination for efcacy at the end of phase II
Bauer and Kieser detail a design that incorporates formal comparison of each
of the experimental arms with the control at the end of phase II (as well as testing
whether any of the treatments are superior to control). The same primary outcome
measure is used in both phases II and III. A xed sample size is used for phase II,
however the phase III sample size can be updated adaptively at the end of phase
II. Stopping at the end of phase II is permissible for either lack of efcacy or early
evidence of efcacy and is based on p-value calculation. The design also allows more
than one treatment to be taken forward to phase III. At the end of phase II the sample
size may be re-estimated and the test statistics to use at phase III are determined,
according to the number of treatments taken forward and the hypotheses to be tested.
The decision criterion at the end of phase III is based on Fisher’s combination test
94 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
(Fisher 1932) whereby the p-values from both phases are combined (as opposed to
combining data from all patients). Simulation is required as detailed in Bauer et al.
(1998), as above. Examples are given in the dose-nding setting and the authors
note that the main advantage of this design is its exibility and its control of the
family-wise error rate. The design is similar to that detailed above (Bauer et al. 1998)
with the exception that the current paper gives more detail relating to the multiple
comparisons between experimental treatments and control arm. When considering
either of these two designs, it is advised that both papers be considered together since
the software detailed in Bauer et al., above, is required to identify the design proposed
here.
Stallard and Todd (2003)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from authors
∙Early termination for efcacy at the end of phase II
Stallard and Todd propose a design whereby patients from phase II are incorpo-
rated in the phase III analysis, and treatment selection at the end of phase II is based
on the treatment with the largest test statistic using efcient scores and Fisher’s infor-
mation. A formal comparison is made between the selected treatment and control,
and the trial may be terminated early for lack of efcacy or superiority at this stage.
The type I error in the nal phase III analysis is adjusted for the treatment selection
in phase II. Overall sample size and phase II sample size are computed according to
group-sequential phase III designs such as those described by Whitehead (1997). A
computer program is noted as being available from the authors to calculate power for
stopping boundaries, according to pre-specied group sizes. The authors note that
the design is useful when one treatment is likely to be much better than the others at
phase II, as opposed to taking multiple treatments to phase III. Consideration should
also be given to the timing of the rst interim analysis (i.e. phase II assessment).
Too early and there is too little information, too late and there are too many patients
enrolled and thus potentially wasted resources.
Kelly et al. (2005)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Requires programming
∙Early termination for efcacy and lack of efcacy during phase II
Kelly and colleagues propose an adaptation to the design proposed by Stallard and
Todd (detailed above), such that more than one treatment may be selected at multiple
stages within the phase II part of the trial. Treatments are evaluated for selection
TREATMENT SELECTION DESIGNS 95
using Fisher’s information and an efcient score statistic which may be applied to
continuous, binary and failure time data. p-Values are calculated at each stage for
comparison of the best treatment with control. Only treatments within a pre-specied
margin of the efcient score statistic of the best treatment are continued to the next
stage, and all other treatments are dropped. Patients are randomised between control
and each of the treatments under investigation at each stage. The trial may stop for
efcacy or lack of efcacy at each stage. The example given is based on the use
of the triangular test described by Whitehead (1997), which uses expected Fisher’s
information to calculate operating characteristics.
Wang (2006)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Requires programming
∙Early termination for efcacy at the end of phase II
Wang proposes an adaptive design with treatment selection at the end of phase
II. Patients are randomised between control and each of the experimental treatments
under investigation in phase II. The design controls the overall type I error and allows
the conditional error function of the phase III trial to depend on the data observed
during phase II. Maximum sample sizes are required to be specied and simulations
performed to evaluate expected sample size. The identication of the optimal design
requires detailed numerical integration. At the end of the rst stage the treatment with
the largest test statistic is selected to take forward to phase III; however, the trial could
also be stopped at this point (i.e. at the end of phase II) for efcacy or lack of efcacy.
There is formal comparison between each of the experimental arms and the control
arm at the end of phase II, and as long as at least one experimental treatment has
sufcient activity, a treatment is selected for further testing in phase III (or selected
as being superior if signicant enough). The design has been implemented in R and
formulae are given to allow this to be implemented in other software, therefore the
design would need programming.
Wang and Cui (2007)
∙Phase II/III, continuous outcome, control arm
∙No formal comparison with control in phase II
∙Requires programming
∙No early termination during phase II
Wang and Cui outline a design whereby patients are randomised to each of
the experimental treatments under investigation and a control arm, using response-
adaptive randomisation (the paper is written in the context of dose selection but
could be applied to treatment selection). The allocation ratios are calculated based
96 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
on distance conditional powers (i.e. the probability that the treatment effect for the
treatment under investigation is larger than some pre-specied xed value, based on
the observed data and the fact that some patients will not yet have had their outcome
observed). The treatment to which most patients have been randomised is deemed the
most efcacious at the end of the recruitment period. This selected treatment is then
formally compared with the control treatment, forming the phase III comparison.
This design as detailed uses binary outcome measures such as treatment response, for
both the phase II treatment selection and the phase III formal comparison, although it
is noted that continuous outcomes may be used. Simulation is required to investigate
the design parameters, with sample size calculated based on the phase III comparison.
The design may be implemented with the development of programs based on formulae
provided.
Shun et al. (2008)
∙Phase II/III, continuous outcome, control arm
∙No formal comparison with control for treatment selection
∙Requires programming
∙No early termination at the end of phase II
Shun et al. propose a phase II/III or two-stage treatment selection design where
a single treatment is selected from two at the end of the rst stage. Randomisation
incorporates a control arm, with the intention of formal comparison at the end of the
second stage only, that is, no formal comparison for treatment selection. Treatment
selection is based on the experimental treatment with the highest/lowest (‘best’)
mean outcome. A normal approximation approach is proposed to avoid complex
numerical integration requirements. The design assumes that the treatment effects of
the experimental treatments are not the same. The practical approach to timing of
interim analysis addresses the need to perform this early in order to avoid type I error
ination, and the need to perform this late enough such that there is a high probability
of correctly selecting the better treatment. No software is noted as being available;
however, detail is provided to allow implementation and a detailed example is given.
The authors note that this design can be extended to binary and time-to-event outcome
measures if the correlation between the nal and interim test statistics is known.
5.1.7.3 Multinomial outcome measure
Whitehead and Jaki (2009)
∙Phase II/III, multinomial outcome, control arm
∙Formal comparison with control for selection
∙Programs noted as being available from authors
∙No early termination during phase II
TREATMENT SELECTION DESIGNS 97
Whitehead and Jaki propose one- and two-stage designs for phase II trials based
on ordered category outcomes, when the aim of the trial is to select a single treatment
to take forward to phase III evaluation. The authors note that the two-stage design
detailed may be applied to the phase II/III setting, although renements to the design
may be required including the use of different outcome measures for treatment selec-
tion and nal analysis. The design is randomised to incorporate a formal comparison
with a control arm, and hypothesis testing is based on the Mann–Whitney statistic.
In the phase II/III setting, treatment selection takes place at the end of stage 1, that
is, phase II, whereby the treatment with the smallest p-value indicating a treatment
effect is selected as the treatment to take forward to stage 2, that is, phase III. Early
termination for lack of activity is permitted at the end of phase II. During phase III,
patients are randomised between the selected treatment and control only. The nal
analysis at the end of phase III is based on all data available on patients in the con-
trol arm and the selected treatment arm. Details of sample size and critical value
calculation are provided, and R code is noted as being available from the authors
to allow implementation. Specication of the worthwhile treatment effect and the
small positive treatment effect that is not worth further investigation are required to
be specied.
5.1.7.4 Time-to-event outcome measure
Bauer and Kieser (1999)
∙Phase II/III, time-to-event outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from author
∙Early termination for efcacy at the end of phase II
Bauer and Kieser detail a design that incorporates formal comparison of each
of the experimental arms with the control at the end of phase II (as well as testing
whether any of the treatments are superior to control). The same primary outcome
measure is used in both phases II and III. A xed sample size is used for phase II,
however the phase III sample size can be updated adaptively at the end of phase
II. Stopping at the end of phase II is permissible for either lack of efcacy or early
evidence of efcacy and is based on p-value calculation. The design also allows more
than one treatment to be taken forward to phase III. At the end of phase II the sample
size may be re-estimated and the test statistics to use at phase III are determined,
according to the number of treatments taken forward and the hypotheses to be tested.
The decision criterion at the end of phase III is based on Fisher’s combination test
(Fisher 1932) whereby the p-values from both phases are combined (as opposed to
combining data from all patients). Simulation is required as detailed in Bauer et al.
(1998). Examples are given in the dose-nding setting and the authors note that the
main advantage of this design is its exibility and its control of the family-wise error
rate. When considering this design, it is advised that the detail provided by Bauer et al.
98 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
(1998) also be reviewed since this paper outlines the software required to identify the
design proposed here.
Stallard and Todd (2003)
∙Phase II/III, time-to-event outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from authors
∙Early termination for efcacy at the end of phase II
Stallard and Todd propose a design whereby patients from phase II are incorpo-
rated in the phase III analysis, and treatment selection at the end of phase II is based
on the treatment with the largest test statistic using efcient scores and Fisher’s infor-
mation. A formal comparison is made between the selected treatment and control,
and the trial may be terminated early for lack of efcacy or superiority at this stage.
The type I error in the nal phase III analysis is adjusted for the treatment selection
in phase II. Overall sample size and phase II sample size are computed according to
group-sequential phase III designs such as those described by Whitehead (1997). A
computer program is noted as being available from the authors to calculate power for
stopping boundaries, according to pre-specied group sizes. The authors note that
the design is useful when one treatment is likely to be much better than the others at
phase II, as opposed to taking multiple treatments to phase III. Consideration should
also be given to the timing of the rst interim analysis (i.e. phase II assessment).
Too early and there is too little information, too late and there are too many patients
enrolled and thus potentially wasted resources.
Kelly et al. (2005)
∙Phase II/III, time-to-event outcome, control arm
∙Formal comparison with control for treatment selection
∙Requires programming
∙Early termination for efcacy and lack of efcacy during phase II
Kelly and colleagues propose an adaptation to the design proposed by Stallard and
Todd (detailed above), such that more than one treatment may be selected at multiple
stages within the phase II part of the trial. Treatments are evaluated for selection
using Fisher’s information and an efcient score statistic which may be applied to
continuous, binary and failure time data. p-Values are calculated at each stage for
comparison of the best treatment with control. Only treatments within a pre-specied
margin of the efcient score statistic of the best treatment are continued to the next
stage, and all other treatments are dropped. Patients are randomised between control
and each of the treatments under investigation at each stage. The trial may stop for
efcacy or lack of efcacy at each stage. The example given is based on the use
TREATMENT SELECTION DESIGNS 99
of the triangular test described by Whitehead (1997), which uses expected Fisher’s
information to calculate operating characteristics.
5.1.7.5 Ratio of times to progression
No references identied.
5.1.8 Phase II/III designs – different primary outcome
measures at phase II and phase III
The literature described within this section considers designs whereby different pri-
mary outcome measures are used for phase II and for phase III. Here the phase II
primary outcome measure should be selected based on the discussions provided in
Chapter 2, as this is not intended to be used for phase III decision-making.
5.1.8.1 Binary outcome measure
Todd and Stallard (2005)
∙Phase II/III, binary outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from the authors
∙No early termination during phase II
Todd and Stallard describe a design where treatment selection occurs at the
rst interim assessment (phase II) based on comparison of a short-term outcome
measure for each of the treatments versus control. Patients are randomised to
each of the experimental treatments and control during phase II, and then to the
selected treatment and the control during phase III. Phase III is carried out in a
group-sequential manner, with the experimental treatment compared to control in
terms of a longer term outcome measure. Selection at phase II is based on the
treatment with the largest test statistic, that is, there is formal comparison with
control but the study may only be terminated for lack of activity at this stage. The
trial protocol remains the same throughout the study; therefore, patients in phase II
can be incorporated in phase III. Required treatment effects (clinically signicant),
treatment effects that are still desirable but not clinically signicant and expected
correlation between phase II and III outcome measures are all required to identify
the complete phase II/III design. Formulae are given and programs are noted as
being available from the authors to calculate stopping boundaries.
5.1.8.2 Continuous outcome measure
Todd and Stallard (2005)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
100 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
∙Programs noted as being available from authors
∙No early termination during phase II
Todd and Stallard describe a design where treatment selection occurs at the
rst interim assessment (phase II) based on comparison of a short-term outcome
measure for each of the treatments versus control. Patients are randomised to each
of the experimental treatments and control during phase II, and then to the selected
treatment and the control during phase III. Phase III is carried out in a group-
sequential manner, with the experimental treatment compared to control in terms of
a longer term outcome measure. Selection at phase II is based on the treatment with
the largest test statistic, that is, there is formal comparison with control but the study
may only be terminated for lack of activity at this stage. The trial protocol remains
the same throughout the study; therefore, patients in phase II can be incorporated in
phase III. Required treatment effects (clinically signicant), treatment effects that are
still desirable but not clinically signicant and expected correlation between phase II
and III outcome measures are all required to identify the complete phase II/III design.
Formulae are given and programs are noted as being available from the authors to
calculate stopping boundaries.
Liu and Pledger (2005)
∙Phase II/III, continuous outcome, control arm
∙Formal comparison with control for treatment selection
∙Requires programming
∙No early termination during phase II
Liu and Pledger detail a phase II/III design in the dose-nding context where
patients are randomised to different doses and a placebo–control with the intention
of dose selection, as well as an adaptive two-stage phase II/III design where the
intention of phase II is to determine whether or not to continue to phase III, for a
single experimental treatment. Short-term continuous outcome measures are used at
the end of phase II to ‘prune’ the doses and to perform sample size adjustment for
the second stage (phase III), and long-term continuous outcome measures are used to
estimate the dose–response curve to calculate trend statistics for the analysis of the
phase III (and also at the end of phase II). Patients continue to be randomised to all
doses for a short period of phase III during the rst analysis for dose selection at the
end of phase II (i.e. there is no break in recruitment for phase II analysis), at which
point more than one dose may be carried forward. The treatment effect required to be
observed is the same for both short- and long-term outcome measures and needs to be
pre-specied, along with prior information on probability of success for each dose,
standard deviation for each outcome measure, the time period between enrolment of
the rst patient and the rst analysis and the likely recruitment in this period. This
information is used to generate the operating characteristics of the design. Formulae
are given which would need to be implemented in order to identify the design. The
TREATMENT SELECTION DESIGNS 101
design offers exibility in that the second stage (phase III) sample size may be
calculated based on updated data from the rst stage (phase II), and adaptation rules
do not need to be specied in advance.
Shun et al. (2008)
∙Phase II/III, continuous outcome, control arm
∙No formal comparison with control for treatment selection
∙Requires programming
∙No early termination at the end of phase II
Shun et al. propose a phase II/III or two-stage treatment selection design where
a single treatment is selected from two at the end of the rst stage (i.e. phase II).
Randomisation incorporates a control arm, with the intention of formal comparison at
the end of the second stage only, that is, no formal comparison for treatment selection.
Treatment selection is based on the experimental treatment with the highest/lowest
(‘best’) mean outcome. A normal approximation approach is proposed to avoid
complex numerical integration requirements. Where a different outcome measure is
used during phase II for treatment selection, the correlation between the phase II
and III outcome measures must be specied. The design assumes that the treatment
effects of the experimental treatments are not the same. The practical approach to
timing of interim analysis addresses the need to perform this early in order to avoid
type I error ination, and the need to perform this late enough such that there is a
high probability of correctly selecting the better treatment. No software is noted as
being available; however, detail is provided to allow implementation and a detailed
example is given. The authors note that this design can be extended to binary and
time-to-event outcome measures if the correlation between the nal and interim test
statistics is known.
5.1.8.3 Multinomial outcome measure
No references identied.
5.1.8.4 Time-to-event outcome measure
Royston et al. (2003)
∙Phase II/III, time-to-event outcome, control arm
∙Formal comparison with control for treatment selection
∙Some programming required before using standard software
∙No early termination during phase II
Royston and colleagues outline a multi-arm, two-stage design aimed at iden-
tifying treatments worthy of further consideration at the end of the rst stage by
102 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
comparing each treatment with a control arm using an intermediate outcome measure
of treatment activity. Only those treatments showing sufcient improvement in activ-
ity over control are continued to the second stage, at the end of which the treatments
are each compared with control using an outcome measure of primary interest (i.e.
different to that used at the end of the rst stage). Data from both stages of the trial
are incorporated in the nal analysis at the end of stage 2. The design may be seen
to reect a seamless phase II/III design with treatment selection at the end of phase
II, allowing more than one treatment to be continued into phase III. In evaluating
the operating characteristics of the design, an estimate of the correlation between the
treatment effects on the intermediate and nal outcome measures is required. The
authors propose an empirical approach to identifying this correlation using bootstrap
resampling of previous data sets, thus the design requires data of this type to be
available in order to allow implementation.
Todd and Stallard (2005)
∙Phase II/III, time-to-event outcome, control arm
∙Formal comparison with control for treatment selection
∙Programs noted as being available from authors
∙No early termination during phase II
Todd and Stallard describe a design where treatment selection occurs at the
rst interim assessment (phase II) based on comparison of a short-term outcome
measure for each of the treatments versus control. Patients are randomised to
each of the experimental treatments and control during phase II, and then to the
selected treatment and the control during phase III. Phase III is carried out in a
group-sequential manner, with the experimental treatment compared to control in
terms of a longer term outcome measure. Selection at phase II is based on the
treatment with the largest test statistic, that is, there is formal comparison with
control but the study may only be terminated for lack of activity at this stage. The
trial protocol remains the same throughout the study therefore patients in phase II
can be incorporated in phase III. Required treatment effects (clinically signicant),
treatment effects that are still desirable but not clinically signicant and expected
correlation between phase II and III outcome measures are all required to identify
the complete phase II/III design. Formulae are given and programs are noted as
being available from the authors to calculate stopping boundaries.
5.1.8.5 Ratio of times to progression
No references identied.
5.1.9 Randomised discontinuation designs
No references identied.
TREATMENT SELECTION DESIGNS 103
5.2 Not including a control arm
5.2.1 One-stage designs
5.2.1.1 Binary outcome measure
Whitehead (1985)
∙One-stage, binary outcome, no control arm
∙Requires programming
∙No early termination
Whitehead discusses a phase II selection design when there are a number of
treatments available for study, currently and expected in the near future, and a xed
number of patients available over a period of time. Patients are randomised to the
treatments currently available and new treatments may be entered as they become
available. A given number of patients are recruited to each treatment and analysis takes
place when all treatments have been considered. The design, for which no software
is detailed but for which formulae are given to allow implementation, identies the
optimal number of treatments (t) and patients per treatment (n) such that nt =total
number of patients available. The examples given consider trials including around
10 treatments, 6 patients per treatment, that is, 60 patients in total. Analysis takes
the form of an appropriate statistical model, tting treatment as a covariate and
incorporating other prognostic variables as necessary. The treatment with the largest
estimated benecial effect is then selected for further investigation in phase III. The
design allows modication such that more than one treatment may be taken forward
and such that cut-off boundaries may be incorporated to ensure a pre-specied level
of success. Any outcome measure distribution may be considered. No control patients
are incorporated and no assessment of risk of a false-negative result is considered.
It is noted that when only a few treatments are to be tested and when the number of
patients available is plentiful, this design may be less appropriate.
Simon et al. (1985)
∙One-stage, binary outcome, no control arm
∙Software available
∙No early termination
Simon et al. detail a selection procedure based on correctly selecting the treatment
with the higher event rate when the difference in event rates is at least d,somepre-
specied amount. The design proposed will always select a treatment, even if the
differences are <d, but will do so with less assurance that the correct treatment is
being selected. The design does not include a pre-specied minimum level of activity;
however, it may be applied as an addition to another trial design establishing minimum
levels of activity prior to treatment selection (as described in the introduction to this
104 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
chapter). The design is easily implemented in statistical programming software such
as SAS and is available in Machin et al (2008).
Sargent and Goldberg (2001)
∙One-stage, binary outcome, no control arm
∙Requires programming
∙No early termination
Sargent and Goldberg propose a similar treatment selection design to Simon
et al., described above. The treatment with the higher event rate is selected when
the difference between treatments in the event rate is at least d(required to be pre-
specied). If the difference is less than d, other criteria for selection can be used.
Sample size is selected by considering the probability that the better treatment is
correctly selected. Treatments do not have to pass given boundaries for minimum
activity, it is simply necessary for one treatment to be better than the other by at
least d. Sample size can be reduced by incorporating allowance to correctly pick the
better treatment when the result is ambiguous, that is, when the difference between
treatments is less than d, assume that, for example, 50% of the time the better
treatment would correctly be chosen based on other criteria. As described for the
design proposed by Simon et al., this design does not need to operate alone and
can be used in conjunction with other trial designs to ensure minimum levels of
activity and to generate sample size. The design is easily implemented in statistical
programming software such as SAS.
5.2.1.2 Continuous outcome measure
Whitehead (1985)
∙One-stage, continuous outcome, no control arm
∙Requires programming
∙No early termination
Whitehead discusses a phase II selection design when there are a number of
treatments available for study, currently and expected in the near future, and a xed
number of patients available over a period of time. Patients are randomised to the
treatments currently available and new treatments may be entered as they become
available. A given number of patients are recruited to each treatment and analysis takes
place when all treatments have been considered. The design, for which no software
is detailed but for which formulae are given to allow implementation, identies the
optimal number of treatments (t) and patients per treatment (n) such that nt =total
number of patients available. The examples given consider trials including around
10 treatments, 6 patients per treatment, that is, 60 patients in total. Analysis takes
the form of an appropriate statistical model, tting treatment as a covariate and
TREATMENT SELECTION DESIGNS 105
incorporating other prognostic variables as necessary. The treatment with the largest
estimated benecial effect is then selected for further investigation in phase III. The
design allows modication such that more than one treatment may be taken forward
and such that cut-off boundaries may be incorporated to ensure a pre-specied level
of success. Any outcome measure distribution may be considered. No control patients
are incorporated and no assessment of risk of a false-negative result is considered.
It is noted that when only a few treatments are to be tested and when the number of
patients available is plentiful, this design may be less appropriate.
5.2.1.3 Multinomial outcome measure
No references identied.
5.2.1.4 Time-to-event outcome measure
Whitehead (1985)
∙One-stage, time-to-event outcome, no control arm
∙Requires programming
∙No early termination
Whitehead discusses a phase II selection design when there are a number of
treatments available for study, currently and expected in the near future, and a xed
number of patients available over a period of time. Patients are randomised to the
treatments currently available and new treatments may be entered as they become
available. A given number of patients are recruited to each treatment and analysis takes
place when all treatments have been considered. The design, for which no software
is detailed but for which formulae are given to allow implementation, identies the
optimal number of treatments (t) and patients per treatment (n) such that nt =total
number of patients available. The examples given consider trials including around
10 treatments, 6 patients per treatment, that is, 60 patients in total. Analysis takes
the form of an appropriate statistical model, tting treatment as a covariate and
incorporating other prognostic variables as necessary. The treatment with the largest
estimated benecial effect is then selected for further investigation in phase III. The
design allows modication such that more than one treatment may be taken forward
and such that cut-off boundaries may be incorporated to ensure a pre-specied level
of success. Any outcome measure distribution may be considered. No control patients
are incorporated and no assessment of risk of a false-negative result is considered.
It is noted that when only a few treatments are to be tested and when the number of
patients available is plentiful, this design may be less appropriate.
5.2.1.5 Ratio of times to progression
No references identied.
106 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
5.2.2 Two-stage designs
5.2.2.1 Binary outcome measure
Weiss and Hokanson (1984)
∙Two-stage, binary outcome, no control arm
∙Standard software available
∙Early termination for lack of activity
Weiss and Hokanson discuss the concept of integrated phase II trials to minimise
the enrolment of an excessive number of patients into trials of potentially ineffective
drugs. It is assumed that a number of treatments are available for investigation at the
same time, which are ranked to determine which treatment should be assessed rst in a
sequence of integrated trials. The rst cohort of n1patients are recruited to treatment 1
and followed up for response, during which the next cohort of n1patients are recruited
to treatment 2, and so on. If a pre-specied number of responses are observed in any
of the treatment arms from the rst n1patients in that cohort, recruitment to further
treatment arms is halted and a further n2patients are recruited to the treatment on
which the responses were observed, essentially following an integrated scheme of
multiple trials based on Gehan’s design (Gehan 1961). The aim of the process is to
assess each treatment individually for its inclusion in a phase III trial, as opposed
to selecting one of the treatments alone to investigate further. As such, at the end
of the integrated process, a number of treatments may be deemed worthy of further
investigation.
Steinberg and Venzon (2002)
∙Two-stage, binary outcome, no control arm
∙Requires programming if design not in tables
∙Early treatment selection permitted
Steinberg and Venzon propose an early selection design which may be used in
conjunction with a single-arm phase II trial design (to generate sample size; the
authors use Simon’s two-stage design as an example). The proposed design incorpo-
rates assessment of two experimental treatments at the end of stage 1, selecting
the superior treatment as the treatment with an event rate at least x% higher
than the other treatment, with probability of correct selection z(xand zrequire
pre-specifying). Tables are given to identify the required difference in number of
events observed between the two arms to select the superior treatment early. If
no treatment is selected at the end of stage 1, the trial continues to randomise
between the two treatments with selection at the end, otherwise if a treatment is
selected, the trial continues recruiting patients to that arm to the desired number of
patients under the underlying design. When used in combination with, for example,
TREATMENT SELECTION DESIGNS 107
Simon’s two-stage design, each treatment arm must independently pass the stop-
ping boundaries at each stage to be evaluable for selection. This design may be
considered over single-stage selection designs to enable treatment selection as early
as possible.
Logan (2005)
∙Two-stage, binary outcome, no control arm
∙Requires programming if design not in tables
∙Early termination for lack of activity
Logan proposes a two-stage selection design based on an adaptation of Simon’s
two-stage design (Simon 1989), as applied to a randomised selection trial. Treatments
that do not pass the stopping criteria at the end of the rst stage are dropped, and
the sample size for the second stage is adapted based on the number of treatments
remaining for stage 2, up to a maximum sample size. Since the second-stage sample
size is adaptive, the cut-off boundaries for the second stage are also dependent on the
number of treatments continuing. The intention is that at the end of the second stage,
additional selection criteria may be applied to those treatments successfully passing
the nal stopping criteria, in the case of more than one treatment. The proposed design
offers a saving in the total number of patients as compared to Simon’s designs, when
it is anticipated that not all treatments will be highly active. Tables of sample sizes and
stopping boundaries are presented for various scenarios; however, additional designs
require computing.
Jung and George (2009)
∙Two-stage, binary outcome, no control arm
∙Requires minimal programming
∙Early termination for lack of activity
Jung and George propose methods of comparing treatment arms in a randomised
phase II trial, where the intention is either to select one treatment from many for
further evaluation or to determine whether a single treatment is worthy of evaluation
compared to a control. The phase II design is based on a k-armed trial (with
or without a control arm for selection) with each arm designed for independent
evaluation following Simon’s two-stage design (Simon 1989), or similar, based on
historical control data. Different designs (i.e. the same two-stage design but with
different operating characteristics) may be used for different arms in the independent
evaluation if deemed necessary. A treatment must be accepted via the independent
evaluation before it can be considered for selection, at which point between-arm
comparisons are made. p-Values are calculated to represent the probability that the
difference between the arms being compared is at least some pre-dened minimal
accepted difference, given the actual difference observed. The outcome measure
108 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
used to select the better treatment is the same outcome measure used for evaluation
of each arm independently, for example, tumour response. No software is detailed;
however, detail is given which should allow implementation, and sufcient examples
are also provided. The initial two-stage design can be calculated using software
available for Simon’s two-stage design.
5.2.2.2 Continuous outcome measure
No references identied.
5.2.2.3 Multinomial outcome measure
No references identied.
5.2.2.4 Time-to-event outcome measure
No references identied.
5.2.2.5 Ratio of times to progression
No references identied.
5.2.3 Multi-stage designs
5.2.3.1 Binary outcome measure
Thall et al. (2000)
∙Multi-stage, binary outcome, no control arm
∙Requires programming (simulation programs noted as being available from
author)
∙No early termination (multi-stage randomisation)
Thall et al. outline a design for treatment strategy selection that incorporates
response-adaptive randomisation within each patient, that is, future treatment strate-
gies for each patient depend on the treatments they have already received, and their
responses. This design is multi-stage in nature since patients are randomised at vari-
ous stages throughout their treatment schedule. Sample size requires investigation via
simulation, and the authors note that sample size should be determined empirically
rather than using simpler methods. Response is categorised as success or failure,
the criteria for which can be different for different stages of treatment. The ‘best’
treatment strategy is selected as that with the largest estimated success probability,
which can be assessed by considering responses to multiple treatment strategies for
each patient.
TREATMENT SELECTION DESIGNS 109
5.2.3.2 Continuous outcome measure
No references identied.
5.2.3.3 Multinomial outcome measure
No references identied.
5.2.3.4 Time-to-event outcome measure
Cheung and Thall (2002)
∙Multi-stage, time-to-event outcome, no control arm
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Cheung and Thall propose a Bayesian sequential-adaptive procedure for contin-
uous monitoring, which may be extended to assessment after cohorts of more than
1 patient, that is, multi-stage. The outcome measure of interest is a binary indicator of
a composite time-to-event outcome, utilising all the censored and uncensored obser-
vations at each interim assessment. Continuous monitoring based on the approximate
posterior (CMAP) is used following Thall and Simon (1994b). The design can incor-
porate multiple competing and non-competing outcomes. Early termination of each
treatment is permitted for activity or lack of activity; however, a treatment may also
be dropped if it is inferior to the other treatments. Selection is based on the treatment
with the largest success probability. R programs are noted as being available from
the authors to allow implementation of the design. This design enables data to be
incorporated on all patients at each interim assessment without all follow-up data
being obtained and may therefore be used when follow-up of each patient is for a
non-trivial period of time.
5.2.3.5 Ratio of times to progression
No references identied.
5.2.4 Continuous monitoring designs
5.2.4.1 Binary outcome measure
No references identied.
5.2.4.2 Continuous outcome measure
No references identied.
5.2.4.3 Multinomial outcome measure
No references identied.
110 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
5.2.4.4 Time-to-event outcome measure
Cheung and Thall (2002)
∙Continuous monitoring, time-to-event outcome
∙Programs noted as being available from authors
∙Early termination for activity or lack of activity
Cheung and Thall propose a Bayesian sequential-adaptive procedure for contin-
uous monitoring, which may be extended to assessment after cohorts of more than
1 patient, that is, multi-stage. The outcome measure of interest is a binary indicator of
a composite time-to-event outcome, utilising all the censored and uncensored obser-
vations at each interim assessment. Continuous monitoring based on the approximate
posterior (CMAP) is used following Thall and Simon (1994b). The design can incor-
porate multiple competing and non-competing outcomes. Early termination of each
treatment is permitted for activity or lack of activity; however, a treatment may also
be dropped if it is inferior to the other treatments. Selection is based on the treatment
with the largest success probability. R programs are noted as being available from
the authors to allow implementation of the design. This design enables data to be
incorporated on all patients at each interim assessment without all follow-up data
being obtained, and may therefore be used when follow-up of each patient is for a
non-trivial period of time.
5.2.4.5 Ratio of times to progression
No references identied.
5.2.5 Decision-theoretic designs
No references identied.
5.2.6 Three-outcome designs
No references identied.
5.2.7 Phase II/III designs – same primary outcome measure at
phase II and phase III
As described in Section 5.1.7, the designs outlined within this section incorporate the
same primary outcome measure for phase II assessment as that used for phase III.
Although this may be seen as seamless phase II/III approach, in effect it reects a
phase III trial with an early interim analysis on the primary outcome measure. In this
setting, consideration should be given to the most appropriate outcome measure to
use for both the phase II and phase III primary outcomes. It is rare that efcacy in
the phase III setting could be claimed on the basis of, for example, a binary outcome;
rather, a time-to-event outcome is usually required in phase III trials.
TREATMENT SELECTION DESIGNS 111
5.2.7.1 Binary outcome measure
Whitehead (1986)
∙Phase II/III, binary outcome, no control arm in phase II
∙Program available
∙No early termination during phase II
Whitehead proposes a phase II/III selection design with a binary outcome at both
phases. Randomisation in phase II is between experimental treatments only, and the
treatment with the largest event rate is selected as the treatment to be taken forward
to phase III, where randomisation then occurs between the selected treatment and
a control. The selection of a treatment for phase III does not incorporate stopping
boundaries for minimum levels of activity. Sample size is based on maximum avail-
able and is justied in terms of the probability of observing a signicant result at
phase III. A FORTRAN program is written to determine the optimal split of patients
between phases II and III, and formulae are also provided in the appendices of the
manuscript to detail this.
5.2.7.2 Continuous outcome measure
No references identied.
5.2.7.3 Multinomial outcome measure
No references identied.
5.2.7.4 Time-to-event outcome measure
No references identied.
5.2.7.5 Ratio of times to progression
No references identied.
5.2.8 Randomised discontinuation designs
No references identied.

6
Designs incorporating toxicity
as a primary outcome
Sarah Brown
This chapter outlines the phase II designs available for trials where the primary
outcome of interest is a joint outcome of both activity and toxicity or where toxicity
is assessed alone. Section 6.1 outlines designs that incorporate a control arm, and
Section 6.2 outlines those designs with no control arm, both organised by design
category and by outcome measure distribution for the activity endpoint. Also, as
discussed in Chapter 2, designs are available that address the option of using toxicity
alone as the primary outcome measure in a phase II trial. These designs are described
in Section 6.3 and may be considered as an add-on to a trial designed to assess
activity. Finally, designs that incorporate both activity and toxicity for the purpose
of treatment selection, that is, where there are multiple experimental treatments, are
presented in Section 6.4.
6.1 Including a control arm
6.1.1 One-stage designs
6.1.1.1 Binary outcome measure
Thall and Cheng (1999)
∙One-stage, binary activity outcome, control arm
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 113
∙Formal comparison with control
∙Requires programming
Thall and Cheng outline a randomised controlled design to assess safety and
activity as a bivariate variable, quantifying treatment effect as a corresponding two-
dimensional parameter. The design considers the acceptable trade-off in toxicity for
increases in activity, that is, the acceptable increase in toxicity for a specic increase
in activity, and vice versa, and provides a formal comparison of the experimental
treatment with control. It is necessary to specify the control activity and toxicity
estimates and trade-offs that would be acceptable to warrant the experimental treat-
ment worthy of further investigation; more than one trade-off can be specied. The
association between toxicity and activity should also be specied in terms of an odds
ratio (OR) between the probability of toxicity when, for example, response occurs,
relative to no response, where an OR of 1 implies independence between toxicity
and response. The design presented is a one-stage design and is extended to multiple
stages in a subsequent paper (Thall and Cheng 2001). Programs are not detailed as
being available; however, detail is given to allow implementation, and programs may
be available by contacting the authors.
6.1.1.2 Time-to-event outcome measure
Thall and Cheng (1999)
∙One-stage, time-to-event activity outcome, control arm
∙Formal comparison with control
∙Requires programming
∙No early termination
Thall and Cheng outline a randomised controlled design to assess safety and
activity as a bivariate variable, quantifying treatment effect as a corresponding two-
dimensional parameter. The design considers the acceptable trade-off in toxicity for
increases in activity, that is, the acceptable increase in toxicity for a specic increase
in activity, and vice versa, and provides a formal comparison of the experimental
treatment with control. It is necessary to specify the control activity and toxicity
estimates and trade-offs that would be acceptable to warrant the experimental treat-
ment worthy of further investigation; more than one trade-off can be specied. The
association between toxicity and activity should also be specied. The main body of
the paper outlines the design in the context of a binary outcome for activity; however,
distribution theory for application with a time-to-event outcome is provided in the
appendix to the paper. The design presented is a one-stage design and is extended
to multiple stages in a subsequent paper (Thall and Cheng 2001). Programs are not
detailed as being available; however, detail is given to allow implementation, and
programs may be available by contacting the authors.
114 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
6.1.2 Two-stage designs
6.1.2.1 Binary outcome measure
Thall and Cheng (2001)
∙Two-stage, binary activity outcome, control arm
∙Formal comparison with control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Cheng extend the one-stage design outlined in Section 6.1.1 to the
two-stage and multi-stage settings (Thall and Cheng 1999). The design considers
the acceptable trade-offs in toxicity for increases in activity, that is, the acceptable
increase in toxicity for a specic increase in activity, and vice versa, and provides
a formal comparison of the experimental treatment with control. It is necessary
to specify the control activity and toxicity estimates and trade-offs that would be
acceptable to warrant the experimental treatment worthy of further investigation;
more than one trade-off can be specied. The association between toxicity and
activity should also be specied in terms of an OR between the probability of toxicity
when, for example, response occurs, relative to no response, where an OR of 1
implies independence between toxicity and response. Sample size is either minimised
under the null hypothesis of no treatment difference in activity and toxicity or the
maximum sample size is minimised if the trial continues to a second stage. In the
two-stage setting, termination at the end of stage 1 is permitted only for lack of
activity or unacceptably high toxicity. The authors also discuss application to the
single-arm phase II setting. No software is noted; however, detail is given to allow
implementation.
Sun et al. (2009)
∙Two-stage, binary activity outcome, control arm
∙Formal comparison with control
∙Software noted as being available from author
∙Early termination for lack of activity or unacceptably high toxicity
Sun and colleagues propose a randomised two-stage design for activity as the
primary outcome of a phase II trial, whereby a sufciently high response rate or a
sufciently low early progressive disease rate should warrant further investigation
of the treatment. This is assessed as a multinomial outcome. As such, the authors
note that the design may be extended to studies monitoring safety and efcacy
simultaneously. In this setting, the activity outcome may be considered as a binary
outcome measure. Optimal and minimax designs are proposed following the method-
ology of Simon (1989). Differences in response and toxicity rates between control
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 115
and experimental arms are compared, highlighting that the intention of the phase II
trial is to screen for potential efcacy as opposed to identifying statistically signi-
cant differences. Decision rules are based on observing a sufciently high response
rate or a sufciently low toxicity rate. An extension is also proposed to the multi-
arm selection setting. Detail is given regarding how to implement the designs in
practice, and software is noted as being available by contacting the rst author
to allow identication of designs. The design recommends a treatment for further
investigation when the response rate is sufciently high or the toxicity rate is suf-
ciently low. Early termination is permitted for lack of activity or unacceptably high
toxicity only.
6.1.2.2 Time-to-event outcome measure
Thall and Cheng (2001)
∙Two-stage, time-to-event activity outcome, control arm
∙Formal comparison with control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Cheng extend the one-stage design outlined in Section 6.1.1 to the
two-stage and multi-stage setting (Thall and Cheng 1999). The design considers
the acceptable trade-offs in toxicity for increases in activity, that is, the acceptable
increase in toxicity for a specic increase in activity, and vice versa, and provides
a formal comparison of the experimental treatment with control. It is necessary
to specify the control activity and toxicity estimates and trade-offs that would be
acceptable to warrant the experimental treatment worthy of further investigation;
more than one trade-off can be specied. The association between toxicity and
activity should also be specied. The example provided by the authors outlines the
design in the context of a binary outcome for activity; however, distribution theory
provided for the one-stage design may be applied for application in the setting of a
time-to-event outcome for activity (Thall and Cheng 1999). In the two-stage setting,
termination at the end of stage 1 is permitted only for lack of activity or unacceptably
high toxicity. The authors also discuss application to the single-arm phase II setting.
No software is noted; however, detail is given to allow implementation.
6.1.3 Multi-stage designs
6.1.3.1 Binary outcome measure
Thall and Cheng (2001)
∙Multi-stage, binary activity outcome, control arm
∙Formal comparison with control
116 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
∙Requires programming
∙Early termination for lack of activity or unacceptable toxicity, or early termi-
nation for activity and acceptable toxicity
Thall and Cheng extend the one-stage design outlined in Section 6.1.1 to the
two-stage and multi-stage setting (Thall and Cheng 1999). The design considers
the acceptable trade-offs in toxicity for increases in activity, that is, the acceptable
increase in toxicity for a specic increase in activity, and vice versa, and provides
a formal comparison of the experimental treatment with control. It is necessary
to specify the control activity and toxicity estimates and trade-offs that would be
acceptable to warrant the experimental treatment worthy of further investigation;
more than one trade-off can be specied. The association between toxicity and
activity should also be specied in terms of an OR between the probability of toxicity
when, for example, response occurs, relative to no response, where an OR of 1 implies
independence between toxicity and response. In the multi-stage setting, termination at
each interim assessment is permitted either for rejection of the alternative hypothesis
(i.e. unacceptable toxicity or lack of activity) or for rejection of the null hypothesis
(i.e. acceptable toxicity and activity). The authors also discuss application to the
single-arm phase II setting. No software is noted; however, detail is given to allow
implementation.
6.1.3.2 Time-to-event outcome measure
Thall and Cheng (2001)
∙Multi-stage, time-to-event activity outcome, control arm
∙Formal comparison with control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity or early
termination for activity and acceptable toxicity
Thall and Cheng extend the one-stage design outlined in Section 6.1.1 to the
two-stage and multi-stage setting (Thall and Cheng 1999). The design considers
the acceptable trade-offs in toxicity for increases in activity, that is, the acceptable
increase in toxicity for a specic increase in activity, and vice versa, and provides
a formal comparison of the experimental treatment with control. It is necessary
to specify the control activity and toxicity estimates and trade-offs that would be
acceptable to warrant the experimental treatment worthy of further investigation;
more than one trade-off can be specied. The association between toxicity and
activity should also be specied. The example provided by the authors outlines the
design in the context of a binary outcome for activity; however, distribution theory
provided for the one-stage design may be applied for application in the setting of
a time-to-event outcome for activity (Thall and Cheng 1999). In the multi-stage
setting, termination at each interim assessment is permitted either for rejection of the
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 117
alternative hypothesis (i.e. unacceptable toxicity or lack of activity) or for rejection
of the null hypothesis (i.e. acceptable toxicity and activity). The authors also discuss
application to the single-arm phase II setting. No software is noted; however, detail
is given to allow implementation.
6.2 Not including a control arm
6.2.1 One-stage designs
6.2.1.1 Binary outcome measure
Conaway and Petroni (1995)
∙One-stage, binary activity outcome, no control
∙Programs noted as being available from authors
Conaway and Petroni propose a single-arm, bivariate outcome design for use
when the sample size is limited to a small number of patients. The design considers
both response and toxicity (both binary variables) and may be one-stage, two-stage
or multi-stage. Estimation of the association between the activity and toxicity out-
comes is required, for example, in the form of the correlation or an OR between the
probability of toxicity when, for example, response occurs, relative to no response,
where an OR of 1 implies independence between toxicity and response. The authors
note that the design, with respect to power, is robust against misspecication of this
association parameter. Sample sizes and cut-off points are calculated via iteration to
satisfy the error criteria, and generally group sizes of fewer than 10 are not considered.
Programs to enable implementation are noted as being available from the authors.
Conaway and Petroni (1996)
∙One-stage, binary activity outcome, no control
∙Requires programming
Conaway and Petroni propose a single-stage (and a two-stage) design for a single-
arm trial in which both toxicity and activity (with reference to a response outcome) are
incorporated. A trade-off between the two outcomes, that is, the acceptable increase in
toxicity for a specic increase in activity, and vice versa, is incorporated based on the
I-divergence test statistic. Four outcomes are assumed (active/not toxic; active/toxic;
not active/toxic; not active/not toxic). The minimum response rate acceptable if there
were no toxicities and the maximum toxicity rate acceptable if there was 100%
response are required to be specied, as well as the OR for the dependence between
the two outcomes, that is, the probability of toxicity when response occurs, relative to
no response, where an OR of 1 implies independence between toxicity and response.
To determine the total sample sizes and the cut-off boundaries iteration is required,
where the cut-offs are based on the I-divergence test statistic. The authors recommend
that, in practice, several values of the OR be investigated to assess the sensitivity of
118 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
the design to misspecication in each setting. The authors note that the properties
of the design are generally unaffected by misspecication. This design differs from
their previous design (Conaway and Petroni 1995) which bases results on the overall
activity and toxicity rates, as opposed to considering the four outcomes described
above. Programs are not noted as being available from the authors; therefore, the
design may need programming for implementation.
Jin (2007)
∙One-stage, binary activity outcome, no control
∙Requires programming
Jin considers a single-stage design incorporating both activity and toxicity as
binary outcome measures, with extension to the two-stage setting. The design
allows a trade-off between toxicity and activity by controlling the marginal type
I errors for these two outcomes separately. Incorporating this additional control
inevitably increases sample size. There are four potential outcomes: active/not toxic;
active/toxic; not active/toxic; not active/not toxic which are summarised by means of
specication of the overall response rate and overall toxicity rate, as well as the OR
representing the association between the two, that is, the probability of toxicity when
response occurs, relative to no response, where an OR of 1 implies independence
between toxicity and response. The design is noted to be robust against misspeci-
cation of this OR. This design would need programming to enable implementation.
6.2.2 Two-stage designs
6.2.2.1 Binary outcome measure
Bryant and Day (1995)
∙Two-stage, binary activity outcome, no control
∙Standard software available
∙Early termination for lack of activity or unacceptably high toxicity
Bryant and Day propose a two-stage, single-arm design that incorporates both
toxicity and activity as binary outcome variables, in a design that reects that of
Simon’s two-stage design for a single outcome (Simon 1989). Tables are presented
for specic design scenarios, with further designs accessible via available software
(Machin et al. 2008). Early termination is permitted for unacceptably low activity
or unacceptably high toxicity only. The design assumes toxicity and activity are
independent; this is arguably unlikely to be the case for most trials; however, the
impact of incorrectly assuming independence was assessed and the design found to
be reasonably insensitive to this. Additionally Tournoux et al. (2007) note that this
design is more robust to misspecication of the relationship between toxicity and
activity than that proposed by Conaway and Petroni (1995).
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 119
Conaway and Petroni (1995)
∙Two-stage, binary activity outcome, no control
∙Programs noted as being available from authors
∙Early termination for lack of activity or unacceptably high toxicity
Conaway and Petroni propose a single-arm, bivariate outcome design for use
when the sample size is limited to a small number of patients. The design considers
both response and toxicity (both binary variables) and may be one-stage, two-stage
or multi-stage. Estimation of the association between the activity and toxicity out-
comes is required, for example, in the form of the correlation or an OR between the
probability of toxicity when, for example, response occurs, relative to no response,
where an OR of 1 implies independence between toxicity and response. The authors
note that the design, with respect to power, is robust against misspecication of this
association parameter. Sample sizes and cut-off points are calculated via iteration to
satisfy the error criteria, and generally group sizes of fewer than 10 are not considered.
Programs to enable implementation are noted as being available from the authors.
In the two-stage design, the trial may terminate for lack of activity or unacceptable
toxicity only, at the end of the rst stage.
Conaway and Petroni (1996)
∙Two-stage, binary activity outcome, no control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity
Conaway and Petroni propose a two-stage (and one-stage) design for a single-arm
trial in which both toxicity and activity (with reference to a response outcome) are
incorporated. A trade-off between the two outcomes, that is, the acceptable increase in
toxicity for a specic increase in activity, and vice versa, is incorporated based on the
I-divergence test statistic. Four outcomes are assumed (active/not toxic; active/toxic;
not active/toxic; not active/not toxic). The minimum response rate acceptable if there
were no toxicities and the maximum toxicity rate acceptable if there was 100%
response are required to be specied, as well as the OR for the dependence between
the two outcomes, that is, the probability of toxicity when response occurs, relative to
no response, where an OR of 1 implies independence between toxicity and response.
To determine the total sample sizes and the cut-off boundaries iteration is required,
where the cut-offs are based on the I-divergence test statistic. The authors recommend
that, in practice, several values of the OR be investigated to assess the sensitivity of
the design to misspecication in each setting. The authors note that the properties
of the design are generally unaffected by misspecication. This design differs from
their previous design (Conaway and Petroni 1995) which bases results on the overall
activity and toxicity rates, as opposed to considering the four outcomes described
120 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
above. Programs are not noted as being available from the authors; therefore, the
design may need programming for implementation.
Thall and Cheng (2001)
∙Two-stage, binary activity outcome, no control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Cheng propose a two-stage design incorporating a control arm, which
may be extended to the setting of a single-arm phase II trial incorporating both activity
and toxicity. The design considers the acceptable trade-offs in toxicity for increases
in activity, that is, the acceptable increase in toxicity for a specic increase in activity,
and vice versa. It is necessary to specify the historical control activity and toxicity
estimates and trade-offs that would be acceptable to warrant the experimental treat-
ment worthy of further investigation. The association between toxicity and activity
should also be specied. Termination at the end of the rst stage is for lack of activity
or unacceptable toxicity only. The procedure is generalised such that the hypothesis
that the experimental treatment provides an improvement in activity and no increase
in the toxicity rate may be considered; this differs form other designs that assume an
improvement in both outcomes. No software is detailed; therefore, this design would
need to be programmed to enable implementation.
Jin (2007)
∙Two-stage, binary activity outcome, no control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity
Jin describes a one-stage design incorporating both activity and toxicity as binary
outcome measures, with extension to the two-stage setting. The design allows a trade-
off between toxicity and activity by controlling the marginal type I errors for these
two outcomes separately. Incorporating this additional control inevitably increases
sample size. There are four potential outcomes: active/not toxic; active/toxic; not
active/toxic; not active/not toxic which are summarised by means of specication
of the overall response rate and overall toxicity rate, as well as the OR representing
the association between the two, that is, the probability of toxicity when response
occurs, relative to no response, where an OR of 1 implies independence between
toxicity and response. The design is noted to be robust against misspecication
of this OR. This design would need programming to enable implementation. In the
two-stage design, early termination is permitted for lack of activity or unacceptable
toxicity.
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 121
Wu and Liu (2007)
∙Two-stage, binary activity outcome, no control
∙Sample size calculation as per other designs
∙Early termination based on sample size re-estimation
Wu and Liu describe an adaptation to traditional designs incorporating both
toxicity and activity as binary outcome measures (e.g. Conaway and Petroni 1995).
The adaptation takes into account the possibility of misspecication of the OR for
the probability of toxicity when response occurs, relative to no response. The overall
sample size is calculated based on this OR, following the methods of previous designs
such as Conaway and Petroni (1995), using an initial estimate of the OR. An interim
assessment is performed after n1patients, chosen arbitrarily, at which point a sample
size re-estimation is performed based on the observed OR for these patients. In
this design, the purpose of the interim assessment is for sample size re-estimation
only, and the design does not incorporate early termination for lack of activity or
unacceptable toxicity at this stage. Type I and II errors are controlled and the trial
may be terminated at the end of the rst stage if the re-estimated sample size (nnew)is
less than that of the initial stage (i.e. nnew ≤n1). Programming requirements follow
the methods used to determine initial sample size with calculation of the OR at the
end of the rst stage to re-estimate sample size.
6.2.2.2 Time-to-event outcome measure
Thall and Cheng (2001)
∙Two-stage, time-to-event activity outcome, no control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Cheng propose a two-stage design incorporating a control arm, which
may be extended to the setting of a single-arm phase II trial incorporating both activity
and toxicity. The design considers the acceptable trade-offs in toxicity for increases
in activity, that is, the acceptable increase in toxicity for a specic increase in activity,
and vice versa. It is necessary to specify the historical control activity and toxicity
estimates and trade-offs that would be acceptable to warrant the experimental treat-
ment worthy of further investigation. The association between toxicity and activity
should also be specied. The procedure is generalised such that the hypothesis that
the experimental treatment provides an improvement in activity and no increase in
the toxicity rate may be considered; this differs from other designs that assume an
improvement in both outcomes. The example provided by the authors outlines the
design in the context of a binary outcome for activity; however, distribution theory
provided for the one-stage design may be applied for application in the setting of a
time-to-event outcome for activity (Thall and Cheng 1999). No software is detailed;
122 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
therefore, this design would need to be programmed to enable implementation. In the
two-stage design early termination at the end of stage 1 is permitted only for lack of
activity or unacceptably high toxicity.
6.2.3 Multi-stage designs
6.2.3.1 Binary outcome measure
Conaway and Petroni (1995)
∙Multi-stage, binary activity outcome, no control
∙Programs noted as being available from authors
∙Early termination for lack of activity or unacceptably high toxicity
Conaway and Petroni propose a single-arm, bivariate outcome design for use
when the sample size is limited to a small number of patients. The design considers
both response and toxicity (both binary variables) and may be one-stage, two-stage
or multi-stage. Estimation of the association between the activity and toxicity out-
comes is required, for example, in the form of the correlation or an OR between the
probability of toxicity when, for example, response occurs, relative to no response,
where an OR of 1 implies independence between toxicity and response. The authors
note that the design, with respect to power, is robust against misspecication of this
association parameter. Sample sizes and cut-off points are calculated via iteration to
satisfy the error criteria, and generally group sizes of fewer than 10 are not considered.
Programs to enable implementation are noted as being available from the authors. In
the multi-stage design, the trial may terminate for lack of activity or unacceptable
toxicity only, at the end of each stage.
Thall et al. (1996)
∙Multi-stage, binary activity outcome, no control
∙Programs noted as being available from author
∙Early termination for lack of activity or unacceptably high toxicity
Thall and colleagues outline a Bayesian multi-stage (or continuous monitor-
ing) design that considers both toxicity and activity in a single-arm trial, based on
trade-offs in toxicity for increased activity. Patients are considered to have one of
four possible outcomes (activity/no toxicity; activity/toxicity; no activity/no toxic-
ity; no activity/toxicity). The posterior distribution for the experimental treatment
is updated after every stage, and the trial may be terminated early for lack of
activity or unacceptable toxicity. Stopping rules are presented graphically for the
example presented within the paper. Simulation is used to determine the operating
characteristics of the design, including the probability of early termination and the
sample size distribution. Although the design requires group-sequential monitor-
ing (or continuous monitoring), software is noted as being available upon request
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 123
from the rst author, which provides all the information to design and implement
the trial.
Thall and Sung (1998)
∙Multi-stage, binary activity outcome, no control
∙Programs available on web
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Sung propose a Bayesian design that allows incorporation of multiple
outcomes, specically toxicity and activity, which is an extension of the design pro-
posed by Thall et al. (1995). Extensions include the design of a phase II equivalence
trial, whereby the phase II trial only requires to show that the experimental treatment
is no worse than the historical control data and that there is at least some possibility
of subsequently establishing conrmatory equivalence, or superiority, in a phase
III trial. Outcomes are categorised into klevels (e.g. toxicity, response; toxicity, no
response; no toxicity, response; no toxicity, no response). Dirichlet prior information
for each of the klevels is used to design the trial, and software is available at http://bio
statistics.mdanderson.org/SoftwareDownload/SingleSoftware.aspx?Software_Id=3
(last accessed June 2013).
Thall and Cheng (2001)
∙Multi-stage, binary activity outcome, no control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity or early
termination for activity and acceptable toxicity
Thall and Cheng propose a multi-stage design incorporating a control arm, which
may be extended to the setting of a single-arm phase II trial incorporating both activity
and toxicity. The design considers the acceptable trade-offs in toxicity for increases
in activity, that is, the acceptable increase in toxicity for a specic increase in activity,
and vice versa. It is necessary to specify the historical control activity and toxicity
estimates and trade-offs that would be acceptable to warrant the experimental treat-
ment worthy of further investigation. The association between toxicity and activity
should also be specied. In the multi-stage setting, termination at each interim assess-
ment is permitted either for rejection of the alternative hypothesis (i.e. unacceptable
toxicity or lack of activity) or for rejection of the null hypothesis (i.e. acceptable
toxicity and activity). The procedure is generalised such that the hypothesis that
the experimental treatment provides an improvement in activity and no increase in
the toxicity rate may be considered; this differs from other designs that assume an
improvement in both outcomes. No software is detailed; therefore, this design would
need to be programmed to enable implementation.
124 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Thall et al. (2003)
∙Multi-stage, binary activity outcome, no control
∙Programs noted as being available from authors
∙Early termination for lack of activity or unacceptably high toxicity
Thall and colleagues propose a hierarchical Bayesian design to investigate mul-
tiple disease sub-types in a single-arm trial (described in Chapter 7), for which detail
is given to extend this to incorporate both toxicity and activity outcome measures.
The design incorporates the probabilities of four possible outcomes: activity/no toxi-
city; activity/toxicity; no activity/no toxicity; no activity/toxicity. Differing treatment
effects may be targeted within differing disease sub-types. Data observed in each sub-
group of patients are used to provide information across all subgroups, thus ‘sharing’
data to update the posterior distributions across multiple disease sub-types. The trial
may be terminated early for lack of activity or unacceptable toxicity. Simulation is
required to update the posterior distribution after every group of patients; therefore,
the design is computationally intensive. Programs are noted as being available upon
request from the authors to allow simulation, and programs for computing stopping
boundaries are provided in the appendix to the manuscript.
6.2.3.2 Time-to-event outcome measure
Thall and Cheng (2001)
∙Multi-stage, time-to-event activity outcome, no control
∙Requires programming
∙Early termination for lack of activity or unacceptably high toxicity or early
termination for activity and acceptable toxicity
Thall and Cheng propose a multi-stage design incorporating a control arm, which
may be extended to the setting of a single-arm phase II trial incorporating both
activity and toxicity. The design considers the acceptable trade-offs in toxicity for
increases in activity, that is, the acceptable increase in toxicity for a specic increase
in activity, and vice versa. It is necessary to specify the historical control activity
and toxicity estimates and trade-offs that would be acceptable to warrant the exper-
imental treatment worthy of further investigation. The association between toxicity
and activity should also be specied. The procedure is generalised such that the
hypothesis that the experimental treatment provides an improvement in activity and
no increase in the toxicity rate may be considered; this differs from other designs
that assume an improvement in both outcomes. The example provided by the authors
outlines the design in the context of a binary outcome for activity; however, dis-
tribution theory provided for the one-stage design may be applied for application
in the setting of a time-to-event outcome for activity (Thall and Cheng 1999). No
software is detailed; therefore, this design would need to be programmed to enable
implementation. In the multi-stage setting, termination at each interim assessment is
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 125
permitted either for rejection of the alternative hypothesis (i.e. unacceptable toxicity
or lack of activity) or for rejection of the null hypothesis (i.e. acceptable toxicity
and activity).
6.2.4 Continuous monitoring designs
6.2.4.1 Binary outcome measure
Thall et al. (1996)
∙Continuous monitoring, binary activity outcome, no control
∙Programs noted as being available from author
∙Early termination for lack of activity or unacceptably high toxicity
Thall and colleagues outline a Bayesian continuous monitoring (or multi-stage)
design that considers both toxicity and activity in a single-arm trial, based on trade-
offs in toxicity for increased activity. Patients are considered to have one of four
possible outcomes (activity/no toxicity; activity/toxicity; no activity/no toxicity; no
activity/toxicity). The posterior distribution for the experimental treatment is updated
continuously after every stage, and the trial may be terminated early for lack of
activity or unacceptable toxicity. Stopping rules are presented graphically for the
example presented within the paper. Simulation is used to determine the operating
characteristics of the design, including the probability of early termination and the
sample size distribution. Although the design requires continuous monitoring (or
group-sequential monitoring), software is noted as being available upon request from
the rst author, which provides all the information to design and implement the trial.
Thall and Sung (1998)
∙Continuous monitoring, binary activity outcome, no control
∙Programs available on web
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Sung propose a Bayesian design that allows incorporation of multiple
outcomes, specically toxicity and activity, which is an extension of the design pro-
posed by Thall et al. (1995). Extensions include the design of a phase II equivalence
trial, whereby the phase II trial only requires to show that the experimental treatment
is no worse than the historical control data and that there is at least some possibility
of subsequently establishing conrmatory equivalence, or superiority, in a phase
III trial. Outcomes are categorised into klevels (e.g. toxicity, response; toxicity, no
response; no toxicity, response; no toxicity, no response). Dirichlet prior information
for each of the klevels is used to design the trial, and software is available at http://bio
statistics.mdanderson.org/SoftwareDownload/SingleSoftware.aspx?Software_Id=3
(last accessed June 2013).
126 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Thall et al. (2003)
∙Continuous monitoring, binary activity outcome, no control
∙Programs noted as being available from authors
∙Early termination for lack of activity or unacceptably high toxicity
Thall and colleagues propose a hierarchical Bayesian design to investigate mul-
tiple disease sub-types in a single-arm trial (described in Chapter 7), for which
detail is given to extend this to incorporate both toxicity and activity outcome mea-
sures. The design incorporates the probabilities of four possible outcomes: activity/
no toxicity; activity/toxicity; no activity/no toxicity; no activity/toxicity. Differing
treatment effects may be targeted within differing disease sub-types. Data observed
in each subgroup of patients are used to provide information across all subgroups, thus
‘sharing’ data to update the posterior distributions across multiple disease sub-types.
The trial may be terminated early for lack of activity or unacceptable toxicity. Sim-
ulation is required to update the posterior distribution after every group of patients;
therefore, the design is computationally intensive. Programs are noted as being avail-
able upon request from the authors to allow simulation, and programs for computing
stopping boundaries are provided in the appendix to the manuscript.
6.3 Toxicity alone
6.3.1 One stage
de Boo and Zielhuis (2004)
∙One-stage, binary toxicity outcome, control arm
∙Formal comparison with control
∙Programs noted as being available from authors
∙No early termination
de Boo and Zielhuis propose sample size calculations for single-stage, non-
inferiority trials of safety where toxicity probabilities are small. This design considers
toxicity alone and may be incorporated as an add-on to a trial designed to assess
activity, with toxicity assessed at the end of the trial. Details of computation are given
in the appendix of the manuscript, and a SAS program is noted as being available upon
request from the authors. Formal comparison between the experimental and control
arms is incorporated. Due to small toxicity probabilities and formal comparison,
the design can require large numbers of patients. Operating characteristics may be
investigated to assess design performance when incorporated as an add-on to an
activity trial (i.e. where sample size is determined according to the design of the
activity trial).
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 127
6.3.2 Continuous monitoring
Goldman (1987)
∙Continuous monitoring, binary toxicity outcome, no control
∙Requires programming
∙Early termination for unacceptably high toxicity
Goldman proposes stopping rules when monitoring toxicities (as a binary out-
come) in a single-arm, small study. The sequential probability ratio test (SPRT) is
used to calculate stopping rules as a function of the number of patients and events
(toxicities), to give a design of the form (–,a,b,c,... h) which is interpreted as fol-
lows: the trial should not stop after just one toxicity, but would stop if two toxicities
were observed in apatients, three in bpatients, . . . up to nine toxicities in hnumber
of patients. The design considers stopping boundaries of toxicity only and should
be adapted to ensure that the operating characteristics of the design are as close
to the required values as possible. Programming is therefore required to implement
this; however, it is noted that a program has been written, therefore this may be
available upon request. The author notes that this design is only relevant for small,
single-sample studies when early termination is for an excess of toxicities only. For
studies with large xed sample sizes, or multiple outcome testing, probabilities of
early termination may be better calculated using Monte Carlo simulation.
Goldman and Hannan (2001)
∙Continuous monitoring, binary toxicity outcome, no control
∙Programs noted as being available from authors and on web
∙Early termination for unacceptably high toxicity
Goldman and Hannan propose a continuous monitoring design that considers the
toxicity of a treatment and runs alongside a single-arm design for activity (i.e. this
is an add-on), as an adaptation to the earlier design of Goldman, described above
(Goldman 1987). It assumes activity is not continuously monitored. Sample size is
determined as per the primary activity design, and stopping rules for toxicity are
generated based on sample size, null and alternative toxicity rates and type I error.
A FORTRAN program is noted as being available from the authors to identify the
design. The design is of the form (–,a,b,c,... ,h) which is interpreted as follows:
the trial should not stop after just one toxicity, but would stop if two toxicities were
observed in apatients, three in bpatients, . . . up to nine toxicities in hnumber of
patients (as in the design described above). This design uses the original 1987 paper
and incorporates the algorithm into a larger FORTRAN program which also outputs
the average sample number (accounting for the possibility of early termination).
This is available at http://www.biostat.umn.edu/Projects/bounds/ (last accessed July
2013). Evaluation takes place whenever toxicity occurs, and the authors note that the
design performs well in up to 20–30 patients. This approach does not consider the
128 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
effect on the activity assumptions due to the additional toxicity monitoring, unlike
the design proposed by Ivanova et al. (2005; described below).
Ivanova et al. (2005)
∙Continuous monitoring, binary toxicity outcome, no control
∙Programs available on web
∙Early termination for unacceptably high toxicity
Ivanova and colleagues propose a continuous monitoring design for toxicity that
can be added on to a single-stage design for activity. Stopping boundaries are created
to assess toxicity after every patient and stop the trial early in the case of extreme toxic-
ity. Although the toxicity outcome does not need to be observed before the next patient
can be recruited, it does need to be monitored in real time as analysis is performed
after every patient. A xed sample size calculated as per the primary activity design is
required to calculate the stopping boundaries for toxicity. If the trial does not stop early
for toxicity then the decision criteria for phase III are based on the activity outcome at
the end of the trial. Outcomes of toxicity and response are binary, and details of esti-
mation of toxicity and response rates are given, for which the correlation between the
two outcome measures is required. These need to be considered at the design stage as
the evaluation of toxicity may result in bias of the estimate of response. It is noted that
unless toxicity and activity are highly correlated, there is little effect on the estimate
of response obtained by incorporating an additional toxicity assessment. This design
differs from that described by Goldman (1987) in that it uses O’Brien and Fleming or
Pocock stopping boundaries (O’Brien and Fleming 1979; Pocock 1977) instead of the
SPRT (which assumes open-ended samples) and considers calculation of unbiased
estimates of toxicity and response. Software to identify the design is available from
http://www.bios.unc.edu/distrib/gee/crossing/cp3/ (last accessed July 2013).
6.4 Treatment selection based on activity and toxicity
6.4.1 Two-stage designs
Sun et al. (2009)
∙Two-stage, activity and toxicity, control arm
∙Formally powered statistical comparison between arms
∙Software noted as being available from author
∙Early termination for lack of activity or unacceptably high toxicity
Sun and colleagues propose a randomised two-stage design based on Zee’s single-
arm multi-stage design with multinomial outcome measure (Zee et al. 1999). It is
noted that the design may be extended to studies monitoring safety and efcacy
simultaneously. Decision rules are based on observing a sufciently high response
DESIGNS INCORPORATING TOXICITY AS A PRIMARY OUTCOME 129
rate or a sufciently low toxicity rate. Optimal and minimax designs are proposed
following the methodology of Simon (1989). Differences in response and toxicity
between control and experimental arms are compared, with the intention of screening
for potential efcacy as opposed to identifying statistically signicant differences.
Patients are randomised between multiple experimental treatments and a control arm.
At the end of the rst stage only those treatments that pass the stopping boundaries
for both response and toxicity are continued to the second stage. If there is clear
evidence that one treatment is better than the other, selection may take place at the
end of the rst stage. If, at the end of the second stage, there is no clear evidence
that one experimental treatment is better than the other, both arms may be considered
for further evaluation. Detail is given regarding how to implement the designs in
practice, and software is noted as being available by contacting the rst author to
allow identication of designs.
6.4.2 Multi-stage designs
Thall and Sung (1998)
∙Multi-stage, activity and toxicity, no control arm
∙No formal comparison between arms
∙Programs available on web
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Sung propose a Bayesian design that allows incorporation of multiple
outcomes, specically toxicity and activity, which is noted to be an extension of Thall
et al. (1995). Designs can be single arm or multi-arm for treatment selection. The
outcomes are categorised into klevels (e.g. toxicity, response; toxicity, no response;
no toxicity, response; no toxicity, no response). Dirichlet prior information for each
of the klevels is used to design the trial, and software is available at http://bio
statistics.mdanderson.org/SoftwareDownload/SingleSoftware.aspx?Software_Id=3
(last accessed June 2013). Treatment selection is based on the approaches of
Simon et al. (1985) and Thall and Estey (1993), such that the treatment with,
for example, the highest response rate is correctly selected with a pre-specied
minimum probability. It is noted that it does take considerably more time to elicit
the required information for this design from clinicians than more standard designs;
however, once this has been established, the design reects a realistic representation
of scientic and clinical requirements.
6.4.3 Continuous monitoring designs
Thall and Sung (1998)
∙Continuous monitoring, activity and toxicity, no control arm
∙No formal comparison between arms
130 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
∙Programs available on web
∙Early termination for lack of activity or unacceptably high toxicity
Thall and Sung propose a Bayesian design that allows incorporation of multiple
outcomes, specically toxicity and activity, which is noted to be an extension of
Thall et al. (1995). Designs can be single arm or multi-arm for treatment selection.
An adaptation to the multi-stage design can be made to allow continuous monitoring.
The outcomes are categorised into klevels (e.g. toxicity, response; toxicity, no
response; no toxicity, response; no toxicity, no response). Dirichlet prior information
for each of the klevels is used to design the trial, and software is available at http://bio
statistics.mdanderson.org/SoftwareDownload/SingleSoftware.aspx?Software_Id=3
(last accessed June 2013). Treatment selection is based on the approaches of
Simon et al. (1985) and Thall and Estey (1993), such that the treatment with,
for example, the highest response rate is correctly selected with a pre-specied
minimum probability. It is noted that it does take considerably more time to elicit
the required information for this design from clinicians than more standard designs;
however, once this has been established, the design reects a realistic representation
of scientic and clinical requirements.

7
Designs evaluating targeted
subgroups
Sarah Brown
This chapter summarises those designs identied via the literature review that may
be used for the purpose of evaluating targeted subgroups of patients. As discussed
previously, there have been a number of recently published articles in this area that
have not been evaluated for inclusion here since they post-date the updated systematic
review on which the library is based. Where the incorporation of biomarkers are
of particular relevance to a trial design, the designs described within this chapter
should be considered; however, we encourage further review of more recent designs
specically intended for trials incorporating biomarkers.
7.1 One-stage designs
7.1.1 Binary outcome measure
A’Hern (2004)
∙One-stage, binary outcome
∙No control arm incorporated
∙Programs noted as being available from author
A’Hern outlines a single-arm, one-stage (and two-stage) design that takes into
account differing response likelihoods for different subgroups of patients, based on
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
132 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
the constant arcsine difference (CAD) between upper and lower response limits,
which has a constant variance. Null and alternative outcomes are specied for each
group and the CAD calculated and assumed constant across each group. In practice,
one species the null and alternative hypothesis values for a known prognostic group,
calculates the corresponding CAD and then calculates equivalent differences for other
prognostic groups, considering whether or not these differences would be clinically
realistic in other groups. Cut-off values for the distribution of CAD are calculated
during the trial, requiring an algorithm to be updated after each patient (towards the
end of recruitment), and therefore continuous monitoring is required. Programs are
noted as being available from the author to run this in excel.
London and Chang (2005)
∙One-stage, binary outcome
∙No control arm incorporated
∙Requires programming
London and Chang incorporate assessment of response rate within strata in their
proposed design. Two approaches are proposed: one for which the true proportion of
patients in each strata is assumed known (the unconditional approach) and one for
which this is assumed unknown (the conditional approach). A simulation algorithm
is provided to identify sample size and stopping rules for the unconditional approach,
and exact computation is used for the conditional approach. Details are provided
in the manuscript; however, both of the approaches will require programming. An
estimate of the accrual rate to each stratum is required initially to determine sample
size. If, during the course of the trial, the actual stratum proportions are very different
to the estimates used, a sample size adjustment may be required during the trial. In
general, the conditional approach is recommended, as an accurate estimate of the
proportion of patients in each stratum is not required and it is noted to be robust to
changes in the proportion of patients within each stratum if the observed proportions
are not too far away from the expected proportions. If researchers are very unsure of
the likely proportions, a number of differing proportions should be considered and
the most conservative sample size taken.
7.2 Two-stage designs
7.2.1 Binary outcome measure
A’Hern (2004)
∙Two-stage, binary outcome
∙No control arm incorporated
∙Programs noted as being available from author
∙Early termination for lack of activity
DESIGNS EVALUATING TARGETED SUBGROUPS 133
A’Hern outlines a single-arm, two-stage (and one-stage) design that takes into
account differing response likelihoods for different subgroups of patients, based on
the CAD between upper and lower response limits, which has a constant variance.
At the end of the rst stage the trial may terminate early for lack of activity. Null
and alternative outcomes are specied for each group and the CAD calculated and
assumed constant across each group. In practice, one species the null and alternative
hypothesis values for a known prognostic group, calculates the corresponding CAD
and then calculates equivalent differences for other prognostic groups, considering
whether or not these differences would be clinically realistic in other groups. Cut-
off values for the distribution of CAD are calculated during the trial, requiring an
algorithm to be updated after each patient (towards the end of recruitment), and
therefore continuous monitoring is required. Programs are noted as being available
from the author to run this in excel.
London and Chang (2005)
∙Two-stage, binary outcome
∙No control arm incorporated
∙Requires programming
∙Early termination for lack of activity
London and Chang incorporate assessment of response rate within strata in their
proposed design. Two approaches are proposed: one for which the true proportion of
patients in each strata is assumed known (the unconditional approach) and one for
which this is assumed unknown (the conditional approach). A simulation algorithm
is provided to identify sample size and stopping rules for the unconditional approach,
and exact computation is used for the conditional approach. Details are provided in
the manuscript; however, both of the approaches will require programming. An esti-
mate of the accrual rate to each stratum is required initially to determine sample size.
If, during the course of the trial, the actual stratum proportions are very different to the
estimates used, a sample size adjustment may be required during the trial. In general,
the conditional approach is recommended, as an accurate estimate of the proportion
of patients in each stratum is not required and it is noted to be robust to changes in
the proportion of patients within each stratum if the observed proportions are not too
far away from the expected proportions. If researchers are very unsure of the likely
proportions, a number of differing proportions should be considered and the most con-
servative sample size taken. For the two-stage unconditional approach the researcher
is required to specify the proportion of the overall type I and type II error rates to be
spent in the rst stage. Additionally, early termination for lack of activity is permitted.
Pusztai et al. (2007)
∙Two-stage, binary outcome
∙No control arm incorporated
134 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
∙Standard software available as per other designs
∙Early termination for lack of activity
Pustzai and colleagues detail a single-arm two-stage design that considers the
response to a single experimental treatment according to biomarker positivity. The
goal is to determine whether the drug is likely to have a certain level of activity in
unselected patients, and if it is below the level of interest at the end of the rst stage,
whether a particular patient selection method can enrich the responding population
to meet the targeted level of activity in a molecularly selected group. The marker
of interest needs to be specied before the trial begins, and more than one marker
may be considered (and analyses conducted separately). Sample size and stopping
boundaries are calculated as per other two-stage designs (e.g. Simon 1989). The trial
is implemented as follows:
1. Recruit as normal to a traditional two-stage design, regardless of marker eval-
uation.
2. If at the end of stage 1 there are sufcient number of responses to continue
to the next stage, continue as per traditional two-stage design, regardless of
marker evaluation.
3. If at the end of stage 1 there are too few responses, continue the study in
marker-positive patients only (there may be more than one marker under
investigation), with an additional intermediate stage.
4. Assuming (3), if at the end of the next stage there are still too few responses,
reject the drug for lack of activity, the marker has failed.
5. Assuming (3), if at the end of the next stage there are sufcient responses to
justify continuation, continue to next stage in this group of patients.
6. Assuming (5), complete nal stage of study to determine the activity of the
drug in this subset of patients.
Jones and Holmgren (2007)
∙Two-stage, binary outcome
∙No control arm incorporated
∙Standard software available
∙Early termination for lack of activity
Jones and Holmgren outline a two-stage design, assuming a biomarker of inter-
est is available at the start of the study and its prevalence is well established. It
incorporates marker positivity/negativity in an adaptive Simon’s two-stage design
(Simon 1989). The authors initially describe a basic approach to assessing treatment
DESIGNS EVALUATING TARGETED SUBGROUPS 135
activity in specic subgroups via two parallel two-stage designs. The adaptive parallel
two-stage design proceeds as follows:
1. Begin with two parallel two-stage designs.
2. If, at the end of stage 1, the experimental treatment is deemed sufciently active
in both marker-positive and marker-negative subgroups, the trial continues on
to the second stage in an unselected population.
3. If, at the end of stage 1, activity of the experimental treatment is restricted to
only the marker-positive subgroup, the trial continues on to the second stage
in marker-positive patients only.
As this design is an adapted Simon’s two-stage design, software is available to
calculate sample size and stopping boundaries, and early termination is permitted
for lack of activity only. The design differs from that proposed by Pusztai et al.
(2007) in that the biomarker and its prevalence are well established at the start of
the trial, and the investigation is of one biomarker only, not many. Additionally the
design considers marker-positive and marker-negative patients separately to begin
with, whereas the design proposed by Pustzai et al. considers all patients initially,
with grouping by marker positivity only if required.
7.3 Multi-stage designs
7.3.1 Binary outcome measure
Thall et al. (2003)
∙Multi-stage, binary outcome
∙No control arm incorporated
∙Programs provided in appendix to manuscript, and further simulation programs
noted as being available from authors
∙Early termination for lack of activity
Thall and colleagues propose a hierarchical Bayesian design to investigate mul-
tiple disease sub-types in a single-arm trial. The design incorporates either a binary
response outcome or a time-to-event outcome and may be conducted as either a
multi-stage or continuous monitoring design, whereby stopping rules are applied at
each assessment. Differing treatment effects may be targeted within differing disease
sub-types. Data observed in each subgroup of patients are used to provide information
across all subgroups, thus ‘sharing’ data to update the posterior distributions across
multiple disease sub-types. The trial may be terminated early for lack of activity,
and toxicity outcome measures may also be incorporated. Simulation is required to
update the posterior distribution after every group of patients; therefore, the design is
computationally intensive. Programs are noted as being available upon request from
136 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
the authors to allow simulation, and programs for computing stopping boundaries are
provided in the appendix to the manuscript.
Wathen et al. (2008)
∙Multi-stage, binary outcome
∙No control arm incorporated
∙Programs may be available from authors
∙Early termination for lack of activity
Wathen et al. outline a Bayesian design for single-arm multi-stage or continuous
monitoring trials incorporating either a binary or time-to-event outcome and account-
ing for patient heterogeneity. The proposed design generalises the approaches of Thall
et al. (2005) and Thall and Simon (1994b) using linear regression to incorporate a
treatment–subgroup interaction. Treatment effects to be detected may differ between
subgroups. Early termination for lack of activity is incorporated. The authors note
that in the case where a treatment–subgroup interaction is unlikely to occur, simpler
models may be sufcient and avoid the complexity of the proposed methodology.
Simulations are required to validate the design with regard to the false-negative error
rates and false-positive rates. The authors aim to provide free software for imple-
menting the proposed method, which is assumed to be available from the authors.
Le Blanc et al. (2009)
∙Multi-stage, binary outcome
∙No control arm incorporated
∙Standard software available
∙Early termination for lack of activity
Le Blanc et al. outline a group-sequential design that allows incorporation of
a wide population of patients when the specic target of a new drug is uncertain,
such that hypothesis testing and analyses consider multiple subgroups of patients.
Outcomes may be binary or the methodology adapted to time-to-event outcomes.
Testing for lack of activity occurs within each stratum, or across all strata, when
a pre-specied minimum number of patients have been accrued. Accrual may be
terminated for lack of activity within a stratum or the whole trial may be terminated if
the overall test for lack of activity is signicant. This may also be adapted in the case
where a specic subgroup is targeted as likely being the most active group, such that
demonstrating lack of activity in this subgroup indicates terminating the study overall.
Sample size calculations follow the two-stage design methodologies of Simon (1989),
Korn et al. (2008) (to incorporate weighting) or Thall et al. (2003), to determine
sample sizes within each stratum (total number of patients and minimum number of
patients before testing for lack of activity should begin) and overall. Additionally, for
DESIGNS EVALUATING TARGETED SUBGROUPS 137
time-to-event outcomes, large sample trials may follow the methodology of Lin et al.
(1996) or evaluate small sample sizes via simulation.
7.3.2 Time-to-event outcome measure
Thall et al. (2003)
∙Multi-stage, time-to-event outcome
∙No control arm incorporated
∙Programs provided in appendix to manuscript, and further simulation programs
noted as being available from authors
∙Early termination for lack of activity
Thall and colleagues propose a hierarchical Bayesian design to investigate mul-
tiple disease sub-types in a single-arm trial. The design incorporates either a binary
response outcome or time-to-event outcome and may be conducted as either a multi-
stage or continuous monitoring design, whereby stopping rules are applied at each
assessment. Differing treatment effects may be targeted within differing disease sub-
types. Data observed in each subgroup of patients are used to provide information
across all subgroups, thus ‘sharing’ data to update the posterior distributions across
multiple disease sub-types. The trial may be terminated early for lack of activity,
and toxicity outcome measures may also be incorporated. Simulation is required to
update the posterior distribution after every group of patients; therefore, the design is
computationally intensive. Programs are noted as being available upon request from
the authors to allow simulation, and programs for computing stopping boundaries are
provided in the appendix to the manuscript.
Wathen et al. (2008)
∙Multi-stage, time-to-event outcome
∙No control arm incorporated
∙Programs may be available from authors
∙Early termination for lack of activity
Wathen et al. outline a Bayesian design for single-arm multi-stage or continuous
monitoring trials incorporating either a binary or time-to-event outcome and account-
ing for patient heterogeneity. The proposed design generalises the approaches of Thall
and Simon (1994b) and Thall et al. (2005), using linear regression to incorporate a
treatment–subgroup interaction. Treatment effects to be detected may differ between
subgroups. Early termination for lack of activity is incorporated. The authors note
that in the case where a treatment–subgroup interaction is unlikely to occur, simpler
models may be sufcient and avoid the complexity of the proposed methodology.
Simulations are required to validate the design with regard to the false-negative error
138 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
rates and false-positive rates. The authors aim to provide free software for imple-
menting the proposed method, which is assumed to be available from the authors.
Le Blanc et al. (2009)
∙Multi-stage, time-to-event outcome
∙No control arm incorporated
∙Standard software available
∙Early termination for lack of activity
Le Blanc et al. outline a group-sequential design that allows incorporation of
a wide population of patients when the specic target of a new drug is uncertain,
such that hypothesis testing and analyses consider multiple subgroups of patients.
Outcomes may be binary or the methodology adapted to time-to-event outcomes.
Testing for lack of activity occurs within each stratum, or across all strata, when
a pre-specied minimum number of patients have been accrued. Accrual may be
terminated for lack of activity within a stratum or the whole trial may be terminated if
the overall test for lack of activity is signicant. This may also be adapted in the case
where a specic subgroup is targeted as likely being the most active group, such that
demonstrating lack of activity in this subgroup indicates terminating the study overall.
Sample size calculations follow the two-stage design methodologies of Simon (1989),
Korn et al. (2008) (to incorporate weighting) or Thall et al. (2003), to determine
sample sizes within each stratum (total number of patients and minimum number of
patients before testing for lack of activity should begin) and overall. Additionally, for
time-to-event outcomes, large sample trials may follow the methodology of Lin et al.
(1996) or evaluate small sample sizes via simulation.
7.4 Continuous monitoring designs
7.4.1 Binary outcome measure
Thall et al. (2003)
∙Continuous monitoring, binary outcome
∙No control arm incorporated
∙Programs provided in appendix to manuscript, and further simulation programs
noted as being available from authors
∙Early termination for lack of activity
Thall and colleagues propose a hierarchical Bayesian design to investigate mul-
tiple disease sub-types in a single-arm trial. The design incorporates either a binary
response outcome or time-to-event outcome and may be conducted as either a multi-
stage or continuous monitoring design, whereby stopping rules are applied at each
DESIGNS EVALUATING TARGETED SUBGROUPS 139
assessment. Differing treatment effects may be targeted within differing disease sub-
types. Data observed in each subgroup of patients are used to provide information
across all subgroups, thus ‘sharing’ data to update the posterior distributions across
multiple disease sub-types. The trial may be terminated early for lack of activity and
toxicity outcome measures may also be incorporated. Simulation is required to update
the posterior distribution after every patient; therefore, the design is computationally
intensive. Programs are noted as being available upon request from the authors to
allow simulation, and programs for computing stopping boundaries are provided in
the appendix to the manuscript.
Wathen et al. (2008)
∙Continuous monitoring, binary outcome
∙No control arm incorporated
∙Programs may be available from authors
∙Early termination for lack of activity
Wathen et al. outline a Bayesian design for single-arm multi-stage or continuous
monitoring trials incorporating either a binary or time-to-event outcome and account-
ing for patient heterogeneity. The proposed design generalises the approaches of Thall
and Simon (1994b) and Thall et al. (2005), using linear regression to incorporate a
treatment–subgroup interaction. Treatment effects to be detected may differ between
subgroups. Early termination for lack of activity is incorporated. The authors note
that in the case where a treatment–subgroup interaction is unlikely to occur, simpler
models may be sufcient and avoid the complexity of the proposed methodology.
Simulations are required to validate the design with regard to the false-negative error
rates and false-positive rates. The authors aim to provide free software for imple-
menting the proposed method, which is assumed to be available from the authors.
7.4.2 Time-to-event outcome measure
Thall et al. (2003)
∙Continuous monitoring, time-to-event outcome
∙No control arm incorporated
∙Programs provided in appendix to manuscript, and further simulation programs
noted as being available from authors
∙Early termination for lack of activity
Thall and colleagues propose a hierarchical Bayesian design to investigate mul-
tiple disease sub-types in a single-arm trial. The design incorporates either a binary
response outcome or time-to-event outcome and may be conducted as either a multi-
stage or continuous monitoring design, whereby stopping rules are applied at each
140 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
assessment. Differing treatment effects may be targeted within differing disease sub-
types. Data observed in each subgroup of patients are used to provide information
across all subgroups, thus ‘sharing’ data to update the posterior distributions across
multiple disease sub-types. The trial may be terminated early for lack of activity and
toxicity outcome measures may also be incorporated. Simulation is required to update
the posterior distribution after every patient; therefore, the design is computationally
intensive. Programs are noted as being available upon request from the authors to
allow simulation, and programs for computing stopping boundaries are provided in
the appendix to the manuscript.
Wathen et al. (2008)
∙Continuous monitoring, time-to-event outcome
∙No control arm incorporated
∙Programs may be available from authors
∙Early termination for lack of activity
Wathen et al. outline a Bayesian design for single-arm multi-stage or continuous
monitoring trials incorporating either a binary or time-to-event outcome and account-
ing for patient heterogeneity. The proposed design generalises the approaches of Thall
and Simon (1994b) and Thall et al. (2005), using linear regression to incorporate a
treatment–subgroup interaction. Treatment effects to be detected may differ between
subgroups. Early termination for lack of activity is incorporated. The authors note
that in the case where a treatment–subgroup interaction is unlikely to occur, simpler
models may be sufcient and avoid the complexity of the proposed methodology.
Simulations are required to validate the design with regard to the false-negative error
rates and false-positive rates. The authors aim to provide free software for imple-
menting the proposed method, which is assumed to be available from the authors.

8
‘Chemo-radio-sensitisation’
in head and neck cancer
John Chester and Sarah Brown
Drug A is a molecularly-targeted cytostatic agent directed against Epidermal Growth
Factor Receptor (EGFR), that was well tolerated as a single agent in phase I trials.
It is hypothesised to enhance the efcacy of radiotherapy for patients presenting
with locally-advanced head and neck squamous cell carcinoma (HNSCC), for whom
current standard treatment is radiotherapy alone. The patient population size is rel-
atively modest, but there are some historical data for treatment with radiotherapy
alone, in this population. Data are also available from a patient population with more
advanced disease in whom a previous phase III study with a similar molecularly-
targeted agent demonstrated efcacy and an acceptable toxicity prole, when used
in combination with radiotherapy. A phase II trial of drug A, in combination with
radiotherapy as primary treatment, is proposed to be run as an academic study within
a large collaborative group.
Stage 1 – Trial questions
Therapeutic considerations
Mechanism of action: Drug A is a molecularly-targeted cytostatic agent directed
against EGFR. It is believed to be primarily cytostatic as a single agent, but to act
synergistically with radiotherapy. It may therefore have both local radio-sensitising
and systemic anti-tumour effects.
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
142 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Aim of treatment: The ultimate aim of primary treatment for patients with locally-
advanced disease is cure. Since the combination of drug A with radiotherapy may
have both local and systemic anti-tumour effects, achieving radiological complete
remission and remaining both locally and systemically disease-free are appropriate
indicators of treatment activity.
Single or combination therapy: Drug A is given in combination with radiotherapy;
therefore, any activity of the combination therapy would need to be greater than that
of radiotherapy alone, the current standard treatment.
Biomarkers: There are no validated biomarkers associated with drug A or with
HNSCC, to allow patient enrichment or surrogate assessment of therapeutic activity.
Primary intention of trial
Proof of concept data are available from an earlier phase III study of a similar agent
in combination with radiotherapy, in the same tumour type, but in more advanced
disease. Combination therapy was shown to be tolerable and achieved improved
overall survival (OS) compared to radiotherapy alone in that setting. A proof of
concept study for drug A in combination with radiotherapy is therefore not deemed
necessary. Rather, the aim of the current trial is to make a go/no-go decision as to
whether or not to proceed to a phase III trial of the combination in patients with
locally-advanced HNSCC.
Number of experimental treatment arms
There is only one experimental treatment under investigation, so a treatment selection
trial is not required.
Primary outcome of interest
Drug A has an acceptable toxicity prole in single-agent studies. Similar agents have
been combined safely with radiotherapy in patients with more advanced disease,
and therefore the current combination is expected to have only minimal additional
toxicity or functional decit. While toxicity will form a secondary endpoint of the
phase II trial, the primary outcome of interest is activity.
Stage 2 – Design components
Outcome measure and distribution
Since drug A is a putative radio-sensitiser, the primary aim of combination with
radiotherapy is to eliminate local disease and minimise disease recurrence. Event-
free survival (EFS) is dened as the time from trial registration to rst event (i.e. local
or distant recurrence or death from any cause) and has been shown to be strongly
correlated with OS in patients with locally-advanced HNSCC (Michiels et al. 2009).
Patients who do not achieve complete remission are classed as having an event at time
‘CHEMO-RADIO-SENSITISATION’ IN HEAD AND NECK CANCER 143
zero. A binary outcome measure of being event-free at 8 months post-registration may
be assessed to reect treatment activity on both local and distant disease. This time
point corresponds with approximately 3 months after completion of radiotherapy
and provides a robust time point at which to assess disease status in the absence
of initial post-treatment radiological artefacts. Patients continue to be radiologically
assessed every 3 months for the rst year after completion of radiotherapy. Therefore
this specic time point of interest forms part of the measurement of the overall EFS
outcome. These outcome measures, both at 8 months and over the year following
completion of radiotherapy, reect relatively short-term assessments of treatment
activity, whereas the primary endpoint of a phase III trial would usually be the longer-
term endpoint of OS. Both the binary and overall time-to-event outcome measures
are therefore considered as possible primary outcome measures for the phase II trial.
The use of a time-to-event endpoint has the potential advantage of providing more
information about the pattern of disease recurrence, than simply dichotomising the
information at a single time point. However, there are a number of factors contributing
to the decision as to which outcome measure to choose as the primary assessment,
including available statistical designs, acceptable lengths of follow-up (i.e. follow-
up to 8 months only or continued follow-up until event occurrence), randomisation,
sample size and design operating characteristic requirements (i.e. type I and II errors).
Randomisation
Drug A is to be given in combination with radiotherapy, that is, another effective
treatment modality. It is important that any activity observed with the combination
may be attributed to the addition of drug A. Randomisation may, therefore, be incor-
porated to provide a more robust and reliable assessment of the additional benet
derived from the addition of drug A in this particular setting. Incorporating a formal
comparison between the arms will ensure decision-making at the end of phase II is
more statistically robust. This is particularly relevant here, since the primary aim of
the phase II trial is to make a go/no-go decision regarding proceeding to phase III.
While this approach may be more appropriate, at this stage we also consider designs
that incorporate randomisation without formally powered statistical comparison to
address all possibilities in this setting and allow further discussion with the clinicians.
Design category
It is important that multiple scenarios are considered when choosing the statistical
design, to assess how robust each of them is if outcomes in either the experimental or
control arm are not as expected. For example, if activity in the control arm is uncertain,
how well do the different trial designs cope with an under- or over-estimation of this
activity?
Rejected designs:
i. On the basis that proof of concept data for a similar molecularly-targeted
agent in combination with radiotherapy already exist, a two-stage or
144 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
multi-stage approach allowing for early termination for lack of activity was, in
this example, deemed unnecessary.
ii. Decision-theoretic approaches to trial design incorporate information on num-
ber of patients to be treated in future phase III trials, total number of patients
who may benet from the treatment in the future and costs of treatment.
Due to difculties in reliably determining such information in this situation, a
decision-theoretic approach was deemed inappropriate.
iii. Activity with radiotherapy alone is expected to be relatively high in this setting.
It is deemed appropriate to only proceed to a phase III trial with drug A if a
signicant, clinically-relevant improvement in activity is observed, over and
above that achieved with radiotherapy alone. A three-outcome design, which
allows an ‘inconclusive’ result to be identied for the primary endpoint, and
additional, secondary endpoints to be considered for the purpose of decision-
making, was therefore deemed inappropriate for this setting.
iv. Finally, randomised discontinuation designs were also rejected, on the basis
that the initial assessment of treatment activity is carried out on completion
of treatment. Randomised discontinuation designs are appropriate when it is
possible to randomise those patients who are, for example, responding to treat-
ment at a pre-specied, early assessment point, to either continue or discontinue
therapy, thus obtaining a randomised comparison of treatment versus no treat-
ment in responders. In this particular trial setting, this opportunity does not
arise as patients have only a single block of treatment, so this design is not
applicable. It may have been possible to randomise patients who responded to
initial radiotherapy to receive or not receive drug A; however, this would not
have addressed the central question of whether drug A enhances the activity of
radiotherapy.
Candidate designs: One-stage and phase II/III designs were considered as poten-
tial designs for the trial.
Possible designs
Thus far, we have determined that the phase II trial will be a randomised study,
addressing the go/no-go decision to proceed to a phase III trial, primarily on the basis
of activity. This will be assessed on the basis of either a binary outcome measure or
a time-to-event outcome measure. Having rejected other potential designs, as in the
previous section, the trial will have either a conventional one-stage phase II or phase
II/III statistical design. Phase II/III designs allow a relatively seamless transition
from phase II to III. They can be more efcient with regard to time, cost and patients,
than designing and running separate phase II and III trials. They are also particularly
valuable where patient numbers are limited, since it is possible to incorporate data
from patients recruited during phase II in the analysis of the phase III trial. However,
a potential limitation is that this design precludes incorporating lessons learnt in the
phase II trial when designing the subsequent phase III trial.
‘CHEMO-RADIO-SENSITISATION’ IN HEAD AND NECK CANCER 145
At this stage, two practical issues are particularly relevant. First, the investigators
wish to move rapidly to the phase III trial if there is sufcient evidence of activity.
Second, the eligible patient population is very precisely dened, so the available
patient population for trial recruitment will be limited. The rst point may clearly
be a wish of many investigators, but in this particular scenario moving rapidly to
phase III may be justied. Previous evidence already exists for the tolerability and
efcacy of a similar treatment, albeit in a more advanced disease setting. Therefore,
issues surrounding treatment acceptability in the current setting are not expected.
Similarly, on the basis of previous evidence in the more advanced setting, there is
a high expectation that treatment activity will be observed. In addition, the patient
population is well dened and a clear outline of the potential phase III trial protocol
is already in place.
The requirement to learn more about the treatment under investigation and the
specic target phase III population in order to determine or modify the design of
a subsequent phase III trial is therefore minimal. In this respect, it may be deemed
feasible to adopt a phase II/III trial design.
Having discussed these considerations in detail, it was ultimately decided that a
phase II/III design was most appropriate for the trial in question, with the phase II
element designed to have only a single stage.
Phase II/III trials can be designed by incorporating stand-alone phase II designs
into a phase III trial, as is the concept described by Storer (1990), and may incorporate
different primary outcome measures in each phase. In this respect, stand-alone, one-
stage phase II designs may be considered.
Reviewing the one-stage and phase II/III designs in Chapter 4 which t to a greater
or lesser extent the design requirements described above, the following designs may
be considered for this trial.
One-stage phase II designs to incorporate into phase II/III:
i. Herson and Carter (1986) – binary outcome, randomisation with no formal
comparison between treatment arms
ii. Thall and Simon (1990) – binary outcome, randomisation with no formal
comparison between treatment arms
iii. Stone et al. (2007b) and Simon et al. (2001) – time-to-event outcome, randomi-
sation with formal comparison between treatment arms
iv. Chen and Beckman (2009) – time-to-event outcome, randomisation with formal
comparison between treatment arms
Phase II/III:
v. Storer (1990) – binary outcome, randomisation with no formal comparison
between treatment arms in phase II
vi. Lachin and Younes (2007) – binary or time-to-event outcome, randomisation
with formal comparison between treatment arms for lack of activity
146 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
vii. Chow and Tu (2008) – binary or time-to-event outcome, randomisation with
formal comparison between treatment arms
Stage 3 – Practicalities
Practical considerations for selecting between designs
We now consider each of the above designs in turn.
i and ii. The designs of Herson and Carter and Thall and Simon each incorporate
a randomised control arm without the primary intention of formal comparison
of this group with the experimental arm. The purpose here is to provide an
assessment of the reliability of the results observed in the experimental arm,
reducing the inuence of bias from factors such as patient selection by having
a parallel control arm that puts the experimental arm results into context. With
these designs, the decision to proceed to phase III or not is, in theory, based
primarily on the results observed in the experimental arm of the trial. The
reliability of such a decision, to either claim or refute sufcient activity of the
experimental therapy with no formal comparison with the control arm at this
stage, may be questioned, especially given the requirement to move seamlessly
to phase III on the basis of these results. Additionally, in the design described by
Thall and Simon only a proportion of patients are randomised to the control arm,
determined to maximise the precision of the estimated experimental treatment
effect. In order to incorporate this design into a phase II/III trial, enabling
patients recruited during phase II to be incorporated in the phase III analysis,
an equal number of patients would be required in each of the control and
experimental arms, assuming randomisation on a 1:1 basis in phase III.
iii. Stone and colleagues describe a phase II design which is formally powered to
compare the treatment arm with the control arm, using relaxed type I errors and
potentially targeting large treatment effects. This reects the designs described
by Simon et al. in the setting of time-to-event outcomes, which are described
by the authors as ‘phase 2.5 screening’ designs, due to the use of phase III-type
designs but with type I error rates typically associated with phase II (Simon et al.
2001). By incorporating formal comparison with the control arm, the sample
size of the trial will inevitably increase. This should, however, be weighed
against the reliability of the decision-making criteria and compared with that
for the non-comparative phase II designs described in i and ii above.
iv. Chen and Beckman describe an approach to a randomised phase II trial design
that incorporates the ratio of sample sizes between phases II and III. Optimal
type I and II errors for the design are identied by means of an efciency
score function. Formal comparison with the control arm is incorporated. The
design considers cost efciency of the phase II and III trials, on the basis of
the ratio of sample sizes between phases II and III and the aprioriprobability
of success of the investigational treatment. Sufcient detail is provided within

‘CHEMO-RADIO-SENSITISATION’ IN HEAD AND NECK CANCER 147
the paper to allow implementation and an R program is provided to identify
optimal designs.
v. Storer describes the design of a phase II/III trial which corresponds to a single-
arm phase II trial design embedded in a randomised phase III trial, such that
patients are randomised between control and experimental arms during phase II.
However, decision-making is based primarily on the results of the experimental
arm. In this respect, the design is similar to those described for i and ii and
therefore the same considerations apply here.
vi. The randomised phase II/III design described by Lachin and Younes bases
the decision to progress to phase III on an assessment of futility at the end of
phase II. Incorporating the expected correlation between the phase II and III
outcomes, this design preserves the type I and II errors and enables patients
recruited during phase II to be included in the phase III analysis. From a
practical viewpoint, this design requires programming to determine sample
size and other operating characteristics.
vii. Chow and Tu propose a seamless phase II/III design for scenarios where there
is a well-established relationship between the phase II and III endpoints, that
is, the phase II endpoint is predictive of the phase III endpoint. This design is
based on two separate studies, with differing endpoints and durations, being
combined to derive the same objective. As such, data from the phase II trial are
used to predict the phase III endpoint, rather than continuing to follow patients,
to observe the endpoint. Moreover, in the current trial, we would want to obtain
data on both the phase II and phase III primary endpoints in both phases of the
trial, requiring longer follow-up of the patients recruited in phase II. For this
reason, the design of Chow and Tu is not appropriate for this trial.
Table 8.1 summarises the specic design requirements for the study, as well as
the desirable practical elements associated with design selection (relating to software
availability in this setting). After further discussion with the clinical team it is agreed
that incorporation of a formally powered statistical comparison between the treatment
arms is most appropriate in this setting. Bearing this in mind, the two designs that
t the specic study requirements and also have software available to allow easier
implementation are (iii) Stone et al. (2007b)/Simon et al. (2001) and (iv) Chen and
Beckman (2009). Due to lack of familiarity with the design described by Chen and
Table 8.1 Summary of practical considerations for each design.
Consideration i ii iii iv v vi vii
Required
1:1 randomisation Y N Y Y Y Y Y
Formal comparison with control N N Y Y N Y Y
Desirable
Statistical software/programs available N N Y Y Y N N
148 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Beckman, it was decided that further simulation work to explore this design in more
detail would be benecial. In this particular scenario we may choose the approach
described by Stone et al./Simon et al. since this may be immediately implemented.
Taking a pragmatic approach to designing this trial, the nal proposed statistical
design is a randomised phase II design following Stone et al. (2007b), embedded in
a phase III trial.
Proposed trial design
Giving further consideration to the primary endpoint of the phase II trial, it is important
to highlight that the intention of this study is ultimately to run seamlessly into a phase
III trial. Any patients entered into the phase II trial would, therefore, have exactly the
same eligibility criteria and be followed up in exactly the same manner as patients
entered in the phase III element, that is, patient follow-up within the trial would not
cease once the initial 8-month endpoint, described earlier, had been observed. In this
sense, the phase II trial accrues further data on overall EFS beyond the 8-month time
point. Since this overall time-to-event endpoint has been shown to be correlated with
OS in locally-advanced HNSCC, it seems prudent to incorporate as much information
on this endpoint as possible in phase II, rather than dichotomising the information at
a single time point and consequently ignoring data beyond this. We therefore chose
to use time-to-event EFS as the primary endpoint for the phase II trial, with a specic
evaluation of 8-month EFS as a secondary endpoint.
On the basis of previously published EFS data in a similar patient population,
the expected median EFS with radiotherapy alone is 1 year (Tobias et al. 2010).
In the more advanced setting, a reduction in hazard rate for EFS of 30% (95% CI
0.54–0.90) was observed with the addition of a similar molecularly-targeted agent to
radiotherapy alone, corresponding to a 27% reduction in hazard rate for OS. In order
to observe a slightly larger treatment effect in the current population, a reduction in
hazard rate for EFS of approximately 35% with the addition of drug A to radiotherapy
is targeted, corresponding to an improved median EFS of 6.5 months (from 12 to
18.5 months). Assuming patients are recruited over a 2-year period, with all patients
being followed up for a minimum of 8 months, our chosen design would require 84
patients per arm (with 96 events overall) to detect a hazard ratio of 0.65 with 80%
power and a one-sided 10% signicance level (i.e. there is a 10% chance that we
would declare the addition of drug A to radiotherapy superior to radiotherapy alone
on the basis of EFS, and thus continue into the phase III trial, when in fact there is
no difference).
The corresponding phase III component of the trial is designed to detect an
improvement in hazard rate for OS of 25%, that is, HR 0.75. Although there is
correlation between the phase II and III primary outcome measures, the correlation
between the treatment effects observed in each phase is not expected to be perfect.
Thus we would expect a smaller treatment effect on OS than on EFS. Median OS with
radiotherapy alone is expected to be approximately 2.6 years on the basis of previously
published data in a similar patient population (Tobias et al. 2010). With 80% power
Point of
consideration
Selection from
flow diagram
Rationale
behind
selection
Randomisation Design category Practical
considerations
Randomisation to
a control arm with
a formal
comparison
Drug A is given in
combination with
radiotherapy, the
current standard
of care. Need to
ensure improved
activity due to
addition or drug
A
Aim to make go/
no-go decision for
phase III
PhaseII/III: one-
stage phase II
design embedded
in a phase III trial
Small population
of patients, may
be difficult to
recruit
Phase III data
from similar agent
provide proof of
concept of
combination with
respect to activity
and toxicity:
multi-stage
approach may not
be necessary
Data obtained in
phase II to be
used in phase III
Randomised
phase II,
embedded in a
phase III trial
1:1 randomisation
Formal
comparison with
control
Software
available
to implement
Primary aim of
trial
Number of
experimental
treatment arms
Primary outcome
of interest
Outcome
measure and
distribution
Go/no‐go decision
for phase III
Proof of concept
data from studies
with a similar
agent in the same
tumour type, but
more advanced
disease setting
One experimental
arm
Only one
experimental
treatment for
consideration
Activity
Drug A has an
acceptable
toxicity profile in
single–agent
studies
Similar agents
have been
combined safely
with RT in more
advanced disease
Expected to have
minimal toxicity/
functional deficit
Binary – 8-month
event-free
proportion OR
Time-to-event –
event-free survival
Drug A acts as a
radio-sensitiser
and treatment
aims to eliminate
disease and
minimise
recurrence
Event-free
survival strongly
correlated with
overall survival
Binary outcome
requires shorter
follow-up; time-
to-event outcome
provides more
information
Therapeutic
considerations
No selection,
therapeutic
considerations
below
Patients with
locally-advanced
stage head and
neck cancer
Drug A is a
molecularly-
targeted agent
directed against
EGFR
Given with RT
may have both
local and systemic
anti-tumour
effects
No validated
biomarkers
associated with
drug A or disease
Figure 8.1 Summary of decision process in designing phase II trial of drug A in head and neck cancer.
150 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
and a 5% two-sided signicance level, 283 patients per arm are required (with
382 deaths overall), assuming 5-year follow-up. The phase II component therefore
comprises approximately 30% of the total sample size required for the whole phase
II/III trial.
Summary
This trial has been designed to assess the activity of the addition of a molecularly-
targeted cytostatic agent, drug A, to radiotherapy in locally-advanced HNSCC
patients. By taking into account therapeutic considerations associated with the
drug, the patient population, information regarding appropriate outcome measures
in HNSCC and the design of the subsequent phase III trial, we addressed the trial-
specic design requirements through each of the three stages featured in Figure 2.1
and described in Chapter 2. A summary of each of the elements addressed is pre-
sented in Figure 8.1. Working through the thought processes and taking an iterative
approach to the design of the trial, with ongoing discussion between the clinician and
statistician, we have designed a randomised, controlled, seamless phase II/III trial
which incorporates formal comparison between radiotherapy plus drug A and radio-
therapy alone, for the assessment of EFS as the primary phase II outcome measure,
in locally-advanced HNSCC patients.
We thank Dr Mehmet Senn for discussions around trial design.

9
Combination chemotherapy in
second-line treatment of
non-small cell lung cancer
Ornella Belvedere and Sarah Brown
Established treatment options for patients with advanced-stage non-small cell
lung cancer (NSCLC) previously treated with chemotherapy include single-agent
chemotherapy (i.e. docetaxel in unselected patients or pemetrexed in patients with
nonsquamous histology) and oral tyrosine kinase inhibitors (i.e. erlotinib or ge-
tinib) (Azzoli et al. 2009). The use of doublet chemotherapy is currently being
investigated using various chemotherapy combinations. Drug B is a cytotoxic with a
favourable toxicity prole and evidence of activity in combination with docetaxel in
the rst-line setting for NSCLC patients. To date, drug B has not been investigated
in second-line combination therapy. It is hypothesised that drug B, in combina-
tion with docetaxel, will improve the efcacy of docetaxel alone for patients with
advanced-stage NSCLC. The trial is proposed to run as an academic study in a
small number of centres with limited funding and relatively few patients; histori-
cal control data in this population are, however, available. A phase II trial of drug
B in combination with docetaxel is proposed to determine whether a larger phase
III trial should be planned and considered for funding by a much larger collabora-
tive group.
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
152 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Stage 1 – Trial questions
Therapeutic considerations
Mechanism of action: Drug B is a platinum-based cytotoxic agent expected to induce
tumour response. It has a lack of cross-resistance with other platinum-based agents
used in rst-line NSCLC, based on pre-clinical data. Its favourable toxicity prole,
along with evidence of activity in NSCLC in both pre-clinical and clinical studies
(Monnet et al. 1998), makes drug B a good candidate to combine with docetaxel
in NSCLC.
Aim of treatment: The ultimate goal of second-line therapy for NSCLC is to
prolong patients’ survival. Additionally, controlling disease-related symptoms and
improving quality of life are important in this setting. An appropriate early indicator
of treatment activity for combination chemotherapy which is expected to induce cell
kill is achieving radiological tumour response.
Single or combination therapy: Drug B is to be given in combination with doc-
etaxel, an active drug, therefore any activity of the combination therapy would need
to be shown as over and above that of docetaxel alone.
Biomarkers: There are no validated biomarkers associated with drug B or
with NSCLC, to allow patient enrichment or alternative assessment of therapeutic
activity.
Primary intention of trial
Proof of concept data are available for this combination as rst-line treatment for
NSCLC. A proof of concept study for drug B in combination with docetaxel is,
therefore, not deemed necessary. The aim of the current trial is to determine the
activity of drug B in combination with docetaxel in patients with NSCLC previously
treated with chemotherapy, to make a go/no-go decision as to whether or not to
proceed to a phase III trial.
Number of experimental treatment arms
There is only one experimental treatment under investigation therefore a selection
trial is not required.
Primary outcome of interest
Drug B has an acceptable toxicity prole in single-agent studies and has a mild
toxicity prole in combination with docetaxel when assessed in chemo-na¨
ıve patients.
Therefore, while toxicity will form a secondary endpoint of the phase II trial, the
primary outcome of interest is activity alone.
COMBINATION CHEMOTHERAPY IN NON-SMALL CELL LUNG CANCER 153
Stage 2 – Design components
Outcome measure and distribution
The primary aim of treatment in patients with advanced NSCLC previously treated
with chemotherapy is ultimately to prolong overall survival. Early indicators of
treatment activity are radiological tumour response, since the cytotoxic combination
treatment under investigation is expected to induce tumour cell kill, and progression-
free survival (PFS). The strength of the relationship between response rate, PFS and
overall survival in NSCLC has been investigated in patients with advanced NSCLC
(Mandrekar et al. 2010). PFS was shown to be more strongly correlated with overall
survival than response; however, the analysis is based on a limited number of trials,
some of which incorporate targeted therapies that may be expected to induce tumour
stabilisation rather than response. Since the focus of the current study is on cytotoxic
treatment, it was deemed appropriate to assess response rate as the primary outcome
measure. Thus, a binary outcome measure of the proportion of patients achieving at
least a conrmed partial response will be used.
Randomisation
Drug B is to be given in combination with docetaxel. It is important to be condent
that any apparent extra activity with the combination can reasonably be attributed to
the addition of drug B. Randomisation should, therefore, be incorporated to provide
robust and reliable results in this particular setting. Incorporating formal statisti-
cal comparison between the arms provides the most robust approach; however, as
acknowledged in Chapter 2, this requires a major increase in sample size compared
to single-arm phase II trials, unless a large treatment effect is targeted. Here, with the
trial proposed to run in a small number of centres and with relatively few patients,
formally powered comparison with single agent docetaxel may be prohibitive in
terms of sample size. There is a substantial body of historical data available on the
activity of docetaxel alone in second-line NSCLC, which can reliably inform the
expected response rate (Fossella et al. 2000; Hanna et al. 2004; Shepherd et al. 2000).
It may, however, be plausible to incorporate randomisation but with no formally pow-
ered comparison in this trial. As discussed in Chapter 2, without formal comparison
between the control and experimental arm, the sample size increase is more modest
than when a formal comparison is intended. In its simplest form, the sample size
may just be doubled, to allocate patients in a 1:1 ratio to control and experimen-
tal treatments. Here the control arm acts as a calibration group, and the inclusion
of randomisation reduces patient selection bias, thus providing greater condence
interpreting results of the experimental therapy.
Design category
It is important that multiple scenarios be considered when choosing the statistical
design, to assess how robust each of them is, if outcomes in either the experimental or
154 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
control arm are not as expected. For example, if activity in the control arm is uncertain,
how well do the different trial designs cope with an under- or over-estimation of this
activity?
Rejected designs:
i. Proof of concept data for the combination of drug B with docetaxel are avail-
able in the rst-line NSCLC setting. There is no reason to expect that the
combination will be less active than docetaxel alone; the safety prole of the
combination is known and will be monitored throughout the trial. On this
basis, two-stage, multi-stage and continuous monitoring approaches allowing
for early termination for lack of activity are not necessary.
ii. Decision-theoretic approaches to trial design incorporate information on num-
ber of patients to be treated in future phase III trials, total number of patients
who may benet from the treatment in the future and costs of treatment. Due
to difculties in reliably determining such data in this particular setting, a
decision-theoretic approach was deemed inappropriate.
iii. Randomised discontinuation designs were also rejected. In the context of com-
bination chemotherapy for NSCLC a randomised discontinuation design might
mean all patients initially receiving drug B and docetaxel, and those who
respond then being randomised to continue or stop drug B. Such a design
would not, however, truly evaluate the combination versus single-agent ques-
tion, as all participants would have received drug B and docetaxel.
iv. Finally, since the resources to run a phase III trial are not available and would
be contingent on the results of this study, the trial is intended as a stand-alone
phase II trial. Phase II/III designs may therefore also be discarded.
Candidate designs: One-stage and three-outcome designs were considered as
potential designs for the trial.
Possible designs
We have determined that the phase II trial will be a randomised trial, addressing the
go/no-go decision to proceed to a phase III trial, principally on the basis of activity.
This will be assessed using a binary outcome measure via either a one-stage or three-
outcome statistical design. It is expected that formal comparison between docetaxel
and docetaxel +drug B would result in a prohibitive sample size; nevertheless, these
designs are considered in order to explore the possibility of incorporating this. In order
to also consider randomisation with no formal comparison, that is, where the control
arm acts as calibration, single-arm trial designs are included with decision-making
criteria based primarily on the results of the experimental arm alone. Reviewing the
available designs in Chapters 3 and 4 which t these design parameters, the following
designs may to a greater or lesser extent be appropriate. Discussion as to selecting
between these specic designs is given in the next section.
COMBINATION CHEMOTHERAPY IN NON-SMALL CELL LUNG CANCER 155
One-stage:
From Chapter 3:
i. Fleming (1982) – single-arm design
ii. Fazzari et al. (2000) – single-arm design
iii. A’Hern (2001) – single-arm design
iv. Chang et al. (2004) – single-arm design
v. Mayo and Gajewski (2004) – single-arm design
vi. Gajewski and Mayo (2006) – single-arm design
vii. Vickers (2009) – single-arm design
From Chapter 4:
viii. Herson and Carter (1986) – randomisation with no formal comparison between
treatment arms
ix. Thall and Simon (1990) – randomisation with no formal comparison between
treatment arms
x. Stone et al. (2007b) – randomisation with formal comparison between treatment
arms
Three outcomes:
From Chapter 3:
xi. Storer (1992) – single-arm design
xii. Sargent et al. (2001) – single-arm design
From Chapter 4:
xiii. Hong and Wang (2007) – randomisation with formal comparison between
treatment arms
Stage 3 – Practicalities
Practical considerations for selecting between designs
The three-outcome designs listed above may be seen as sub-designs of a one-stage
design and may be used when there is a region of uncertainty between, for example,
the response rate that clearly warrants further investigation in phase III and one that
denitely does not. If the primary outcome measure of a three-outcome design trial is
inconclusive, the decision to move to phase III or not may be based on other factors,
such as safety or cost. Three-outcome designs may also require fewer patients than
some two-outcome designs using the same design criteria. In order to assess potential
savings in patient numbers and the impact on operating characteristics associated with
156 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
this, we consider below each of the one-stage and three-outcome designs relevant to
the proposed trial.
i. Fleming outlines a single-stage design based on rejecting the null hypothesis
that the response rate is less than or equal to a pre-specied value, typically that
associated with the current control arm. Sample size calculation assumes the
normal approximation to the binomial distribution; therefore, where small sam-
ple sizes are identied the robustness of this assumption may be questionable.
Software is readily available to implement this design.
ii. Fazzari et al. describe the design of a phase II trial based on estimating the phase
III outcome measure parameter and corresponding x% condence interval, with
decision criteria based around the upper bound of the condence interval. The
authors describe the design as an ‘intermediate trial between a screening phase
II manuscript and the phase III randomised comparative survival manuscript’
(Fazzari et al. 2000). This design is not appropriate to the current setting
since the ability to reliably predict the phase III endpoint of overall survival
based on response is questionable. The design requires programming to allow
implementation.
iii. The design of A’Hern is an adaptation of the Fleming design described above.
Here the sample size and decision criteria are based on the exact binomial
distribution and may therefore be more appropriate for small sample sizes.
Software is readily available to implement this design.
iv. Chang et al. propose a single-arm design that incorporates the number of
patients on which the historical control data are based. The design focuses
on performing an exact unconditional test comparing the observed historical
control event rate with the expected event rate in the experimental arm. The
authors note that in many cases the sample sizes determined were similar to
those derived under alternative single-arm non-comparative designs. Programs
are noted as being available from the authors.
v. Mayo and Gajewski propose a Bayesian single-arm design based on the use
of informative priors, either pessimistic or optimistic. Various approaches to
sample size calculation are detailed based on the mean, median or mode prior. It
is noted that these different approaches can result in very different trial designs,
which is largely due to the method of eliciting the prior information and its
interpretation. In the current setting where there are reliable historical control
data on single-agent docetaxel, and results using the combination, albeit in a
different clinical setting, this design may not be necessary or appropriate. The
design requires programming to allow implementation.
vi. The second design of Gajewski and Mayo is based on the use of conict-
ing prior information, whereby both pessimistic and optimistic assumptions
are incorporated. Sample size is determined via an iterative approach and
therefore requires some programming. As with the previous design, given the
available data in the current setting, the decision was taken to consider more
COMBINATION CHEMOTHERAPY IN NON-SMALL CELL LUNG CANCER 157
appropriate alternative designs. The design requires programming to allow
implementation.
vii. The design of Vickers uses historical control data to generate a statistical
prediction model to predict the results of the experimental arm in the current
trial. The observed results at the end of the trial are then compared with this
prediction. Where the historical control cohort is of a sufciently large size, the
resulting trial design using this methodology will require a similar number of
patients to a single-arm trial designed on the basis of comparison of proportions.
Given the historical control data available in the current setting are sufciently
large, and the additional complexities associated with building a prediction
model for the proposed design, a practical decision was made not to consider
this design. Stata programs are provided in the appendix to the manuscript.
viii. Herson and Carter incorporate a randomised control arm without formal com-
parison of this group with the experimental arm. The purpose here is to provide
an assessment of the reliability of the results observed in the experimental arm
and also to assess in detail the activity of the control arm. This allows evalu-
ation of the assumptions made in designing the trial and provides additional
information particularly in the event of rejecting the alternative hypothesis of
increased activity in the control arm. The overall design is a combination of
individual designs for each of the control and experimental arms and may result
in overall sample sizes of between three and ve times that of a non-calibrated
design. This relatively large increase in sample size is inefcient in the current
setting where there is a body of historical control data available. From a practi-
cal viewpoint, this design may also require programming to determine sample
size if operating characteristics do not equal those provided in the manuscript.
ix. In the design of Thall and Simon fewer patients are randomised to the control
arm than to the experimental arm to maximise the precision of the response
rate in the experimental arm relative to the control. The proportion randomised
to the control arm is dependent upon the amount of historical control data, the
degree of variability and the overall sample size of the phase II study being
planned (calculated using formulae provided). From a practical viewpoint, this
design requires programming to determine sample size and other operating
characteristics iteratively.
x. Stone and colleagues describe a phase II design which is formally powered
to compare the experimental arm with the control arm, using relaxed type I
errors and targeting large treatment effects, using typical designs considered
for phase III. This design will, therefore, result in larger sample sizes than
others. Software is readily available to implement this design.
Three outcomes:
xi. Storer proposes a three-outcome design adapted from a typical single-stage
design. Here, if the observed event rate is between that specied under the null
hypothesis (p1) and that specied under the alternative (p2), it is possible to
158 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
consider additional information before deciding either in favour of or against
the experimental arm. The event rate of uncertainty is taken to be around (p1+
p2)∕2. The error associated with incorrectly concluding in favour of either the
null or alternative hypotheses is specied under this event rate. Software is not
available for this method and would therefore require programming; a table of
various design scenarios is, however, given.
xii. Sargent et al. describe a three-outcome design similar to that described by
Storer. Here the errors associated with incorrectly declaring an inconclusive
result under the null and under the alternative hypotheses are specied and are
allowed to differ. This allows more exibility in the design of the trial. With the
addition of a region of uncertainty, sample sizes are typically less than those
derived under a two-outcome design with the same operating characteristics.
A table of various design scenarios is given; programs may be available from
the authors upon request.
xiii. Hong and Wang describe a randomised three-outcome design whereby
decision-making is based on the difference in the number of events observed
between the arms, with the null hypothesis that there is no difference. The
design incorporates formal comparison with the control arm. The region
of uncertainty for this three-outcome design falls around the middle region
between the null and alternative hypothesis (that the difference is at least Δ).
Software is noted as being available upon request from the authors to enable
the operating characteristics to be identied; we were, however, unable to
obtain this.
The key practical consideration in deciding between the designs described above
is the ability to implement the methodology to enable a comparison of sample sizes
and operating characteristics between the designs. Table 9.1 summarises the desirable
practical elements associated with design selection (relating to software availability in
this setting) and the additional considerations made in each of the summaries above.
The six designs that were therefore considered, that is, those with no additional
methodological complexities for this scenario and where software is available, are
(i) Fleming, (iii) A’Hern, (iv) Chang et al., (x) Stone et al. and (xii) Sargent et al.
Proposed trial design
The expected response rate with docetaxel alone in this setting is 7–10% (Fossella
et al. 2000; Hanna et al. 2004; Shepherd et al. 2000). To decide whether or not to
further investigate the activity of docetaxel +drug B in the phase III setting, a response
rate below which further investigation would not be warranted was set at 10%. The
targeted response rate of docetaxel +drug B was set at 30%, chosen as being the
minimal clinically-relevant response rate that would warrant further investigation of
this combination therapy, that is, a 20% absolute increase in response rate.
To consider each of the possible designs, the following operating characteristics
were dened. For the one-stage two-outcome designs, a one-sided type I error rate of

Table 9.1 Summary of practical considerations for each design.
Design
Consideration i ii iii iv v vi vii
Additional complexities
in methodological
approach?
NYNNYYY
Statistical software/
programs available
YNYYNNY
Other information – Based on phase
III primary
outcome
–Formal
comparison
with historical
control data
–––
Design
Consideration viii ix x xi xii xiii
Additional complexities
in methodological
approach?
NNNNNN
Statistical software/
programs available
NNYNYN
a
Other information Imbalanced
randomisation in
favour of control
– Incorporates
formal
comparison
– – Incorporates
formal
comparison
aNoted as being available upon request; however, we were unable to obtain.
160 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
5% and 80% power are used. For the three-outcome design, a one-sided type I error
rate, 𝛼, of 5% and 80% power (i.e. the probability of rejecting the null hypothesis when
the alternative is true) are again used; however, additional error rates of incorrectly
declaring an inconclusive result also require specifying (see Section 2.2.3.6 for full
details). The probability of incorrectly declaring an inconclusive result when in fact
the alternative hypothesis is true, 𝛿(i.e. response rate ≥30%), and the probability of
incorrectly declaring an inconclusive result when in fact the null hypothesis is true,
𝜆(i.e. response rate ≤10%), may be specied separately. In the current example we
take 𝛿=10% and 𝜆=15%. To maintain 80% power under the three-outcome design,
the probability of incorrectly rejecting the alternative hypothesis when in fact it is
true, 𝛽, is set to 10%.
Table 9.2 summarises the required sample sizes and associated stopping criteria
for the operating characteristics described earlier. The design based on Chang et al. is
taken from the published sample size tables, assuming historical control data available
for a minimum of 120 patients; it is acknowledged that there is in fact a much larger
body of data available for this population.
Considering each of the designs, that of Sargent et al. was chosen, including
randomisation to a control arm to guard against selection bias and provide a calibration
arm. The randomised design incorporating formal comparison (Stone et al. 2007b)
requires approximately twice the number of patients per arm compared to those
where no formal comparison is intended. Due to the prohibitive sample size of this
design for few study centres, this was not used. The sample sizes for the one-stage
designs of Fleming and A’Hern are comparable to that of the three-outcome design.
Although the design of Fleming requires one less patient per arm, the inclusion of the
Table 9.2 Summary of sample sizes and stopping rules under each design.
Design N(per arm) Stopping criteria
Stone et al. 49 Formal comparison; based on one-sided p-value <5%
Fleming 20 If at least 5/20 responses observed, further
investigation warranted
A’Hern 25 If at least 6/25 responses observed, further
investigation warranted
Chang et al. 29 Exact unconditional test of observed response rate
compared to historical control data
Sargent et al. 21 If number of responses observed in experimental arm
(r)is
∙≤3 – no further investigation warranted
∙≥5 – further investigation warranted
∙3<r<5 – inconclusive – consider alternative
outcomes
Point of
consideration
Selection
from flow
diagram
Rationale
behind
selection
Randomisation Design category Practical
considerations
Randomisation
to a control arm
with no formal
comparison
Drug B is given
in combination
with docetaxel,
the current
standard of care.
Need to ensure
improved
activity due to
addition of drug
B
Aim to make go/
no-go decision
for phase III
Small number of
patients
available
One-stage or
three-outcome
No interim
assessments of
activity required
Consider
incorporating
additional
outcome
measures in
decision-making
if appropriate
Three-outcome
Software
available to
implement
Provides degree
of flexibility in
decision-making
criteria
Primary aim of
trial
Number of
experimental
treatment arms
Primary
outcome of
interest
Outcome
measure and
distribution
Go/no-go
decision for
phase III
Proof of concept
data from
studies of
chemo-naïve
NSCLC patients
One
experimental
arm
Only one
experimental
treatment for
consideration
Activity
Drug B has an
acceptable
toxicity profile in
single-agent
studies
Mild toxicity
profile in
combination
with docetaxel
when assessed
in chemo-naïve
patients
Binary –
proportion
achieving
confirmed partial
response
Partial response
acts as early
indicator of
treatment
activity
Treatment given
for up to 18
weeks
Progression-free
survival
correlated with
overall survival
in study of small
number of trials
only, including
targeted agents
Therapeutic
considerations
No selection,
therapeutic
considerations
below
Patients with
advanced-stage
non-small cell
lung cancer
(NSCLC)
Drug B is a
platinum-based
cytotoxic agent
Response
provides short-
term indicator of
activity
No validated
biomarkers
associated with
drug B or disease
Figure 9.1 Summary of decision process in designing phase II trial of drug B in advanced NSCLC.
162 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
inconclusive region with just one additional patient per arm provides extra exibility
in this situation.
Summary
This trial has been designed to assess the activity of the addition of a platinum-
based cytotoxic agent, drug B, to docetaxel as second-line treatment for patients
with advanced NSCLC. By taking into account the therapeutic considerations asso-
ciated with the drug, the patient population, literature regarding appropriate outcome
measures in NSCLC and methodological issues associated with relevant statistical
designs, we addressed the trial-specic design requirements and practical consid-
erations listed in each of the three stages featured in Figure 2.1 and described in
Chapter 2. A summary of the discussions associated with each of the eight elements
is presented in Figure 9.1. Working through the thought process and taking an itera-
tive approach to the design of the trial, with ongoing discussion between the clinician
and statistician, a randomised, controlled, one-stage, three-outcome trial of docetaxel
plus drug B for second-line treatment of advanced NSCLC patients was chosen, with
response rate as the phase II primary outcome measure, incorporating randomisation
to a control arm of single-agent docetaxel for calibration only.
This trial was in fact designed, conducted, analysed and reported by the Alpe-
Adria Thoracic Oncology Multidisciplinary (ATOM) group (ATOM019) (Belvedere
et al. 2011).

10
Selection by biomarker in
prostate cancer
Rick Kaplan and Sarah Brown
There is currently no standard treatment for patients with biochemical-failure-only
prostate cancer following curative intent local therapy, the standard of care being
watchful waiting. Clinicians are, however, increasingly treating such patients with
androgen-deprivation therapies. These have an associated toxicity prole, and there
is no conclusive prospective evidence of clinical benet in this setting. There is,
therefore, a need to investigate novel strategies in these patients; immune-modulator
strategies may offer an alternative and less-toxic approach for patients with low
tumour burden. Vaccine C is a targeted active immunotherapy, hypothesised to control
tumour growth (indirectly reected by prostate specic antigen (PSA) levels) thus
potentially prolonging disease-free survival or, at a minimum, postponing exposure to
long-term androgen deprivation. The development pathway of treatments in prostate
cancer is important to consider in the design of clinical trials. In the setting of
biochemical-failure-only prostate cancer, the time from entering clinical development
to registration of successful treatments can be particularly long. Phase III trials in
this setting may use endpoints such as time to failure of hormone therapy, or time
to development of metastatic disease, as surrogates for overall survival. Even so,
such events may be uncommon and are delayed often by many years; Pound et al.
found that in some settings the median time to development of metastatic disease in
untreated men with rising PSA was 8 years (Pound et al. 1999). Thus, consideration
of the whole development pathway from phase I to registration is critical to ensure the
design of the most efcient clinical trials. In this setting, and example, consideration
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
164 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
is given to expanding the phase II trial immediately to phase III, should the vaccine
be shown to be associated with an encouraging level of activity.
Stage 1 – Trial questions
Therapeutic considerations
Mechanism of action: Vaccine C is a targeted active immunotherapy. It induces MUC1
antigen expression to induce both innate and adaptive immunity. The vaccine is likely
to be of interest for patients with low-volume tumours or patients with biochemical
failure only, since although these patients have other treatment options available
to them, they do not necessarily need them at this time. In addition, vaccines are
generally expected to be more effective when tumour volume is minimal.
Aim of treatment: The ultimate aim of treatment of patients with biochemical-
failure-only disease is reversal of rising levels of PSAs, so as to delay onset of disease,
delay of complications and improvement in metastatic disease-free survival.
Single or combination therapy: Vaccine C is given as a single agent.
Biomarkers: In this population of patients, the biomarker PSA is an appropriate
intermediate outcome measure of disease activity (see Section 10.2.1 for further dis-
cussion). There are no biomarkers associated with potential for benet from vaccine
C for the purpose of population enrichment.
Primary intention of trial
The overall aims of the trial are to rst identify an encouraging signal with vaccine
C to warrant further study and then to select a single dosing schedule to investigate
further in a randomised phase III trial. Proof of concept data are available for this
vaccine in non-small cell lung cancer, but not in prostate cancer, although studies of
similar agents have been performed. The trial aims to provide proof of concept data
in this setting as well as sufcient evidence of activity to make a go/no-go decision
as to whether or not to proceed to a phase III trial and to select the most active dose
of vaccine C to compare against watchful waiting in the phase III trial.
Number of experimental treatment arms
Two dosing schedules are to be considered: (1) weekly to week 7 then every 3 weeks
to week 36 or progressive disease (PD); (2) every 3 weeks to week 36 or PD. The
intention is not to show that one schedule is superior to the other, but to guide
selection so that the selected schedule is sufciently active to warrant investigation
in a randomised controlled phase III trial.
Primary outcome of interest
Safety and tolerability of the vaccine have been established in phase I trials, and
there have been previous phase II studies of the vaccine in non-small cell lung
cancer. Toxicity assessment is not thought appropriate as a primary outcome measure,
SELECTION BY BIOMARKER IN PROSTATE CANCER 165
since previous studies suggest this vaccine is less toxic than alternatives such as
androgen-deprivation therapy; toxicity will therefore form a secondary endpoint,
with the primary endpoint activity alone. Since the current standard of treatment for
these patients is watchful waiting, and these patients are asymptomatic, a substantial
improvement in activity is needed to warrant further investigation in a phase III trial.
The primary outcome of interest is therefore activity alone.
Stage 2 – Design components
Outcome measure and distribution
There are several outcome measures in trials of targeted therapies in prostate can-
cer (Stadler 2002). In this group of patients tumour burden is low and patients are
asymptomatic. These patients have biochemical-failure-only disease that often pre-
dates clinical progression by a considerable time; therefore, endpoints such as time
to development of metastatic disease are impractical due to the long follow-up times
required. PSA is a commonly used short-term biomarker of outcome in prostate can-
cer and may be an appropriate primary outcome in this setting. Although PSA has
not been shown to be a true surrogate for overall survival in the context of predicting
treatment effects, a strong correlation between PSA and overall survival has been
shown for the individual patient (Collette et al. 2005). A correlation was, however,
also shown for PSA response. PSA response has previously been used in phase II
trials, as an endpoint to determine when not to take a treatment forward for further
investigation, since if a patient does not achieve a PSA response, he is unlikely to
gain any further clinical benet from treatment. Using PSA response as a robust out-
come to reliably suggest further evaluation in phase III is warranted may, however,
be questioned. The use of PSA response relies on pre-dened denitions which may
not reect the longitudinal trajectory of PSA levels over time. By assessing PSA as
a continuous variable, and comparing changes over time, we may obtain more infor-
mation on the effect of treatment than we would by using a simple binary outcome
of PSA response. The use of PSA doubling time (PSA DT), derived from changes
in PSA over time, is a commonly referenced outcome measure that is signicantly
associated with risk of prostate cancer-specic mortality (Freedland et al. 2005). PSA
DT is dened as the natural log of 2 (0.693) divided by the estimate of the slope of the
regression line of log(PSA) over time. PSA DT data are more widely published than
change in PSA levels at a specic time point and provide an appropriate short-term
measure of the activity of the vaccine that does not rely on pre-dened response de-
nitions. We assess the pattern of change in PSA levels over time, with the expectation
that the use of vaccine C will increase the doubling time. Thus the outcome under
consideration is a continuous measure.
Randomisation
Vaccine C is given as a single agent. The current standard of care in this setting is
watchful waiting. With the additional complexities associated with giving patients a
166 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
treatment, such as possible side effects, additional hospital attendances, additional
clinical tests and so on, it is important that any treatment effect observed is substantial,
to justify the associated ‘medicalisation’. The primary outcome measure is PSA DT.
PSA levels are expected to rise in patients undergoing watchful waiting, and with the
use of vaccine C the rate of rise in PSA is expected to be reduced or even reversed,
and therefore PSA DT extended. Inclusion of a control arm is therefore essential to
allow comparable data regarding the trajectory of PSA levels over time, which may
be dependent upon baseline PSA levels and/or the variable natural history of prostate
cancers. It is, however, unlikely that a treatment would be taken forward to phase III if
it did not induce initial reductions in PSA levels; therefore, this may also be required
by the study sponsor.
There is a wide clinical range of behaviours for biochemical tumours, even more
so in prostate cancer than in other cancers. It is important to minimise the chance
of random selection of a cohort of patients with a particularly indolent biochemical
tumour which may not be applicable to the general disease population. The inclusion
of randomisation to a control arm of watchful waiting helps guard against this bias.
As previously highlighted, consideration is given to a phase II/III design to speed up
the drug development pathway in a setting where clinical events are delayed. In order
for such a design to be possible, whereby patients recruited to the phase II element are
also then included in the phase III component, it is essential that the control arm of the
phase III trial be incorporated from the beginning of the trial, that is, it is an essential
design criteria that randomisation is included in the phase II trial. Inclusion of a
control arm also allows direct comparison with each of the dosing schedules during
the phase II element thus providing a robust assessment of the decision as to whether
or not to proceed to phase III. This also follows the discussion of Stadler regarding
phase II trial design for trials of cytostatic treatments in prostate cancer (Stadler
2002). Randomisation with formal comparison will, therefore, be incorporated.
Design category
Rejected designs:
i. Currently there are only phase I data with this vaccine in this setting, although
phase II studies in non-small cell lung cancer have demonstrated its activity.
A two-stage, or multi-stage, design incorporates interim assessments of the
activity of the vaccine and can allow early termination for lack of activity,
or early selection of a dosing schedule, as well as assessment of safety and
tolerability. These designs may, therefore, be deemed appropriate due to the
limited experience with this vaccine to date and may allow early dose selection.
However, due to inherent logistical problems with multi-stage designs, espe-
cially the long follow-up period required before the primary outcome measure
is observed (relative to patient recruitment), designs with more than two stages
are not considered for this trial.
ii. Likewise, continuous monitoring designs are also not considered.
SELECTION BY BIOMARKER IN PROSTATE CANCER 167
iii. Since an interim assessment of activity is deemed useful in this setting, the use
of one-stage designs was also rejected.
iv. Decision-theoretic approaches to trial design incorporate information on num-
ber of patients to be treated in future phase III trials, total patient horizon and
costs of treatment. Due to difculties in reliably determining such information,
especially where the underlying disease has a relatively long natural history, a
decision-theoretic approach was not considered.
v. The overall aims of the trial are to rst identify an encouraging signal with
vaccine C to warrant further study and then to select a single dosing schedule
to investigate further in a randomised phase III trial. As previously discussed,
a substantial treatment effect must be observed compared to watchful waiting
alone, to warrant further study. On this basis, the three-outcome design may
not be suitable given this incorporates the possibility of an inconclusive result.
vi. Finally, randomised discontinuation designs were also rejected. They do not
lend themselves to dose selection studies, and given the consideration for the
trial to be expanded into a phase III trial, the use of a concurrent observation
control arm is necessary. This design was therefore not considered on this basis.
Candidate designs: Two-stage and phase II/III designs were considered as poten-
tial designs for the trial.
Possible designs
Thus far, we have determined that the phase II trial will be a randomised dose selection
study, addressing the go/no-go decision to proceed to a phase III trial with a selected
schedule of vaccine C, on the basis of activity. This will be assessed using the tumour
marker PSA as a continuous outcome measure to derive PSA DT, with the aim of
taking forward a single dose to phase III. The use of a phase II/III trial design is
of particular interest in this setting due to their associated efciencies. Phase II/III
designs allow a relatively seamless transition from phase II to phase III. They can
be more efcient with regard to time, cost and patients, than designing and running
separate phase II and III trials. They are particularly efcient where patient numbers
are limited or where the time taken to observe phase III events is particularly long,
since it is possible to incorporate data from patients recruited during phase II in the
analysis of the phase III trial. These considerations are relevant for the current study.
A relevant issue when considering the use of a phase II/III design is that this
may preclude the opportunity to learn between trial phases. The chance to reect
on the design of the phase II trial, for example, assessing the impact of issues such
as eligibility criteria, can be important when there may be uncertainties around
the design of the subsequent phase III trial. In this particular setting, the practical
issues associated with moving to phase III as quickly and efciently as possible, and
the ability to include phase II patients with long follow-up times in the phase III
component, outweigh the potential benets of pausing between phases. At the end
of the phase II component, recruitment may continue until the phase II analysis is
168 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
complete. At this time, should the decision to continue into phase III be conrmed,
a full review of the phase II component may be conducted to allow any necessary
amendments to the trial protocol.
As previously discussed, the use of a two-stage design allows an interim assess-
ment of activity, enabling the possibility to terminate the trial early for either activity
or lack of activity or enabling early dose selection. Early termination on the basis
that vaccine C is active is not appropriate as the aim is to choose between two poten-
tially active schedules. Early dose selection or termination for lack of activity may,
however, be useful.
Phase II/III trials can be designed by incorporating stand-alone phase II designs
into a phase III trial, described by Storer (1990), and may incorporate different
primary outcome measures in each phase. Stand-alone two-stage phase II selection
designs may therefore be included when considering phase II/III trials.
It is possible to conduct selection trials that are designed with go/no-go decision
criteria applied to each individual arm separately, after which only those arms deemed
sufciently active (i.e. passing the ‘go’ criteria) are compared for selection. Such an
approach is described by Simon et al. (1985) in the context of binary outcomes.
However, in order to minimise the number of designs to be considered and discussed
in this specic example, this approach will not be considered here. In practice, such
designs may be investigated further.
Reviewing the available two-stage and phase II/III treatment selection designs
in Chapter 5 which t the design parameters described above, the following designs
may be considered for this trial.
Two-stage phase II designs to incorporate into phase II/III:
i. Levy et al. (2006) – continuous outcome, randomisation with formal compari-
son with control
ii. Shun et al. (2008) – continuous outcome, randomisation with formal compar-
ison with control
Phase II/III (different primary outcome measures at phase II and phase III):
iii. Todd and Stallard (2005) – continuous outcome, randomisation with formal
comparison with control
iv. Liu and Pledger (2005) – continuous outcome, randomisation with formal
comparison with control
v. Shun et al. (2008) – continuous outcome, randomisation with formal compar-
ison with control
Stage 3 – Practicalities
Practical considerations for selecting between designs
We now consider each of the above designs in turn.
SELECTION BY BIOMARKER IN PROSTATE CANCER 169
i. The design of Levy et al. incorporates the ability to select a dosing regimen at
the end of the rst stage of the trial. Treatment selection is based on informal
comparison of the two dosing regimens, with no comparison to the control
for treatment selection. The treatment with the ‘best’ outcome (e.g. longest
mean PSA DT) is selected as the one to be taken forward for further study.
The sample size for the trial is calculated to ensure that the probability that the
better treatment is selected is at least 80%, when the true difference between
the treatments is a least 𝛿, a pre-specied minimal change. A futility analysis
is incorporated to compare the selected treatment with control. The design
requires programming as standard programs are not noted as being available.
ii. The design described by Shun et al. incorporates treatment selection at the end
of the rst stage, where the treatment with the ‘better’ outcome is selected, and
formal superiority comparison with the control at the end of the second stage,
conditional on the interim selection. No early termination for lack of activity
is proposed at the end of the rst stage. The probability of correctly selecting
the treatment with the most activity can be pre-specied in the design, as can
the timing of the rst-stage analysis. The design requires programming.
iii. Todd and Stallard describe a phase II/III design incorporating schedule selec-
tion at the end of phase II, which is conducted as a one-stage design. At the
end of phase II formal comparisons are made with the control arm and the
most superior schedule is selected; termination of the trial at this stage is
permitted only for lack of activity. Phase III is then conducted in a group-
sequential approach. Programs to calculate stopping boundaries are noted as
being available from the authors.
iv. Liu and Pledger propose a phase II/III design which assumes both the phase II
and III outcomes are continuous. Treatment selection occurs at the end of phase
II, which is conducted in a single stage. At this point, more than one treatment
can be selected, and adjustment of the phase III sample size is possible. The
design is described in the context of dose selection, whereby at the end of
phase II doses with unacceptable toxicity or low activity are dropped. The
design requires programming.
v. The design described by Shun et al. in the context of the phase II/III setting is
the same as that described above in the two-stage setting; however, treatment
selection is made at the end of the phase II component.
Table 10.1 summarises various requirements for the design of the trial, as well as
the desirable practical elements associated with design selection (relating to software
availability and early termination during phase II). Although none of the designs
incorporate early termination for lack of activity during the phase II element, the
design of Shun et al. does incorporate formal comparison with the control arm at
the end of phase II, with a superiority comparison, as does the design of Todd and
Stallard. Although the design of Todd and Stallard does not incorporate early schedule
selection during phase II, the formal comparison between the control arm and each of

170 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Table 10.1 Summary of practical considerations for each design.
Consideration i ii iii iv v
Required
Formal comparison with control YaYYYY
Two-stage phase II Y Y N N N
Desirable
Statistical software/programs available N N Y N N
Early termination for lack of activity
(during phase II)
NNNNN
aNon-superiority comparison.
the schedules to perform selection inherently makes the selection robust. Additionally,
the design of Todd and Stallard clearly outlines the approach to the group-sequential
phase III trial, incorporating multiple assessments of efcacy throughout the duration
of the trial, and has software available. Due to the additional detail provided with this
design and software availability, it was deemed appropriate to adopt the design of
Todd and Stallard, building an additional interim assessment of safety and tolerability
into the phase II element.
Proposed trial design
It is difcult to determine reliable estimates of PSA DT specically for the cohort of
men who, with their clinicians, would participate in a controlled trial of new treatment
versus no immediate intervention (i.e. watchful waiting), since such a cohort is likely a
very selected population of patients. On the assumption that men with doubling times
of <8 months (or their clinicians) may be most likely to opt for treatment intervention
and those with slow doubling times in excess of 12 months may decide they do not
want any treatment at this stage, we estimate mean PSA DT with watchful waiting in
the current trial to be approximately 8 months, with an associated standard deviation of
4 months. An increase in PSA DT of at least 4 months (50% increase), that is, average
doubling time with vaccine C 12 months, is deemed worthy of further consideration in
phase III. Under the design of Todd and Stallard, the standardised PSA DT difference
between each schedule and the control arm will be used as the measure of treatment
effect and corresponds to a target value of 1.0 (Todd and Stallard 2005). Using a 5%
one-sided signicance level and with 90% power, a total of 18 patients per arm are
required in the phase II trial. Accounting for a 20% dropout rate, a total of 66 patients
will be recruited (22 per arm) to the phase II component. Since the estimate of mean
doubling time in the control arm is somewhat unreliable, an interim assessment during
phase II will be conducted to evaluate whether an increase in sample size is required.
This will be performed by an independent data monitoring committee. Additionally,
ongoing assessments of safety and tolerability will be performed throughout the trial,
with no formal stopping rules applied to these endpoints.
SELECTION BY BIOMARKER IN PROSTATE CANCER 171
The trial is designed as a phase II/III trial using the group-sequential design of
Todd and Stallard (2005). At the end of the phase II component, when patients have
been followed up for at least 12 months to observe changes in PSA levels over time, a
formal comparison between the two dosing schedules of vaccine C and the control arm
of watchful waiting will be performed. A dosing schedule will be selected for further
evaluation in the phase III component if there is a statistically signicant increase in
PSA DT of at least 50%. If neither of the dosing schedules pass this boundary, the
trial may be terminated for lack of activity. Should both dosing schedules be found to
signicantly improve PSA DT, the schedule with the largest treatment effect estimate
may be selected, and patients will continue to be randomised between the selected
schedule and watchful waiting under the phase III component.
In this population of patients, median time to development of metastases is
approximately 8 years (Pound et al. 1999). In the current trial, upon further biochem-
ical progression after vaccine C or watchful waiting, patients may receive further
treatment to include androgen-deprivation therapy. Due to the long follow-up times
required to observe development of metastases, the phase III component is designed
to detect a clinically relevant improvement in time from randomisation to androgen
independence (TAI) with the use of the selected schedule of vaccine C, as the primary
outcome measure. Time to development of metastases (TDM) will be incorporated
as a long-term secondary endpoint. There is a paucity of data in this specic set-
ting from which to determine TAI; however, it is anticipated that in this population
of patients, the median time from androgen independence to distant metastases is
approximately 30 months (Smith et al. 2005). A median time from randomisation
to androgen independence for patients initially randomised to watchful waiting is
therefore assumed to be approximately 66 months (5 1
∕
5years). An improvement in
median TAI of 1.4 years with vaccine C is deemed clinically relevant, correspond-
ing to a hazard ratio of 0.8. A maximum of 1400 patients will be randomised to
receive either watchful waiting or the selected schedule of vaccine C, with a single
interim assessment for futility as described in detail by Todd and Stallard (2005),
and accounting for dropout. This design also provides sufcient power to detect an
improvement in median TDM from 8 to 10 years with vaccine C.
Summary
This trial has been designed to select an active dosing schedule of vaccine C to
take forward into phase III evaluation, for patients with biochemical-failure-only
prostate cancer. This phase II/III trial has been designed to reect the practical issues
associated with drug development in disease areas where long-term follow-up of
patients is required to observe sufcient data for phase III registration studies. A
statistically efcient phase II design has been identied to select the more active of
two dosing regimens of vaccine C to take forward in to the phase III component.
Taking into account therapeutic considerations associated with the vaccine, the
patient population, external literature regarding appropriate outcome measures in
prostate cancer, available outcome measure data and the development pathway of
Point of
consideration
Selection from
flow diagram
Rationale
behind
selection
Randomisation Design category Practical
considerations
Randomisation to
a control arm with
a formal
comparison
Current standard
of care watchful
waiting – need to
ensure
improvements in
PSA attributed to
vaccine C and not
confounding
factors such as
selection bias,
particularly as
change related to
baseline PSA
Aim to make go/
no-go decision for
phase III
May continue
directly to phase
III
Phase II/III: two-
stage phase II
design embedded
in a phase III trial
Two-stage
approach to allow
schedule selection
and interim
monitoring
Data obtained in
phase II to be
used in phase III
Randomised
phase II/III trial
Formal
comparison with
control for
schedule selection
(more robust to
misspecification)
Include interim
phase II safety
and tolerability
assessment, as
well as sample
size re-
assessment
Group-sequential
phase III
Primary aim of
trial
Number of
experimental
treatment arms
Primary outcome
of interest
Outcome
measure and
distribution
Proof of concept
and go/no-go
including schedule
selection
Two schedules for
consideration
Proof of concept
data available in
NSCLC only
Aim to provide
sufficiently robust
evidence to make
go/no-go decision
for phase III
Consideration to
expand
immediately into
phase III
Two
Two dosing
schedules for
consideration
Activity
Vaccine C has an
acceptable
toxicity profile in
phase I studies
Current standard
of care is watchful
waiting, therefore
need substantial
improvement in
activity
Continuous–PSA
doubling time
derived from
change in PSA over
time
Biochemical-
failure-only;
therefore long
follow-up times
required for, for
example, time to
metastases
PSA commonly
used short-term
biomarker
outcome
PSA strongly
correlated with
overall survival
Doubling time
data more widely
available
Therapeutic
considerations
No selection,
therapeutic
considerations
below
Patients with
biochemical-
failure-only
prostate cancer
Vaccine C is a
targeted active
immunotherapy,
given as single
agent
Aim to control
rising levels of
PSA and improve
metastatic
disease-free
survival
Biomarker PSA to
assess disease
outcome
Figure 10.1 Summary of decision process in designing phase II trial of vaccine C in prostate cancer.
SELECTION BY BIOMARKER IN PROSTATE CANCER 173
the vaccine, we addressed the trial-specic design requirements for each of the eight
points featured in Figure 2.1 and described in Chapter 2, as summarised in Figure 10.1.
Working through the thought process and taking an iterative approach to the design
of the trial, with ongoing discussion between the clinician and statistician, we have
designed a randomised, controlled, seamless phase II/III selection trial. Although
the design does not meet the exact initial specications (i.e. two-stage phase II),
the iterative process and review of available designs further informed the decision
process, resulting in an appropriate design, as determined by the trial team. This
highlights the benets of considering all available options and taking a practical
approach to trial design. The design incorporates dose schedule selection via formal
comparison with the current standard of care, watchful waiting, for the assessment
of PSA DT, derived from changes in PSA levels over time, as the primary phase II
outcome measure in biochemical-failure-only prostate cancer patients. Additionally,
the phase III component incorporates group-sequential assessment of the phase III
primary endpoint of time to androgen independence.

11
Dose selection in advanced
multiple myeloma
Sarah Brown and Steve Schey
The outlook for patients with multiple myeloma relapsing after optimal therapy with
thalidomide, lenalidomide and bortezomib is poor, and patients with disease refrac-
tory to initial treatments have an especially poor prognosis. There is no consensus
on the optimal therapy for these patients. Drug D is a uniquely structured alkylating
anti-tumour agent that lacks cross-resistance with other alkylating agents. There is
very good evidence to show that combinations of an alkylator, thalidomide and corti-
costeroid are effective in treating patients with relapsed/refractory multiple myeloma
(Facon et al. 2007; Palumbo et al. 2006, 2008). Drug D in combination with thalido-
mide and dexamethasone is therefore proposed as a combination therapy for phase II
investigation in this population of patients. Data are available suggesting that drug D
adds to the activity of other combination therapies; the optimal dose of drug D as com-
bination therapy is not, however, known. A dose selection study is proposed to con-
sider the optimal dose of drug D in combination with thalidomide and dexamethasone
(DTD). A phase II selection study of DTD (dose 1) versus DTD (dose 2) is proposed.
Stage 1 – Trial questions
Therapeutic considerations
Mechanism of action: Drug D is an alkylating agent which, when given in combination
with thalidomide and dexamethasone, is expected to induce disease response.
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
DOSE SELECTION IN ADVANCED MULTIPLE MYELOMA 175
Aim of treatment: The ultimate aim of treatment in this population of patients
is to improve overall survival. Whilst it may be demonstrated that a drug may be
active ex vivo, this is not of value unless it is at doses that can be achieved in vivo.
Progression-free and event-free survival may also be desirable endpoints. Whilst
activity can often be demonstrated ex vivo, for a drug to be effective as a treatment,
it needs to be shown that the drug can be delivered in patients at the dose required
without unacceptable toxicity. It is known from previous studies of similar treatments
that patients may have difculty receiving a full course of treatment due to cumulative
haematological toxicities. Such cumulative toxicity, emerging in later cycles, may not
be identied in phase I studies where the tolerability usually focuses on cycle 1. It is,
therefore, important to demonstrate not only anti-tumour activity, indicating potential
to improve overall survival, but also acceptable tolerability and the ability to deliver
the treatment, when recommending an optimal dose.
Single or combination therapy: Drug D is to be given in combination with thalido-
mide and dexamethasone.
Biomarkers: Although aberrant expression of phenotypic, cytogenetic or molec-
ular markers can be used to dene poor prognosis disease, there are no agreed
biomarkers consistently demonstrated to be associated with response or prognosis
for drug D, or with regard to outcome measures of disease activity in this setting,
to enable patient enrichment or alternative assessment of therapeutic activity. Para-
protein is used as a surrogate marker of tumour bulk in secretory myeloma whilst
the serum-free light chains can be utilised in the less common light-chain myeloma
or non-secretory disease. They are monitored serially during treatment to assess the
response to treatment but are less sensitive than immunophenotyping in identifying
minimal residual disease. Currently, there is a lack of robust, prospective data for the
use of alternative biomarkers but validation studies are ongoing.
Primary intention of trial
The primary objective of the study is to identify a dose of drug D given in combi-
nation with dexamethasone and thalidomide that is active and tolerable and can be
consistently delivered to patients with relapsed/refractory multiple myeloma, with
the intention of taking that combination forward into studies in newly diagnosed
patients. A randomised phase II selection trial incorporating proof of concept for the
de novo study is therefore proposed.
Number of experimental arms
Although there is only one experimental drug under investigation, there are two doses
of drug D being considered. There are, therefore, two experimental arms.
Primary outcome of interest
Drug D, and other similar drugs used to treat myeloma, may be associated with
cumulative toxicity. It is important to demonstrate that drug D in combination with
176 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
thalidomide and dexamethasone is both sufciently active and tolerable, in terms of
being deliverable; therefore, an assessment of tolerability is incorporated as a primary
outcome measure in this trial. This is seen as being equally as important as demon-
strating activity, therefore joint primary outcome measures of toxicity/tolerability and
activity will be used.
Stage 2 – Design components
Outcome measure and distribution
The tolerability of DTD may be measured by the ability to deliver drug D in full dose
and on time for at least two cycles, that is, a binary outcome measure. If a patient
is unable to receive the rst two cycles of treatment without any haematological
toxicities requiring dose delay or reduction, this is an indication that there are likely
to be future tolerability issues with the combination, requiring dose reductions or
delays.
Drug D is a cytotoxic agent expected to induce disease response. There are, unfor-
tunately, limited data regarding the use of surrogate endpoints associated with overall
survival in relapsed refractory multiple myeloma patients. However, overall response
rate, in combination with substantial response duration, has been recommended as
an appropriate endpoint for accelerated approval of new myeloma agents by the US
Food and Drug Administration (Anderson et al. 2005), and response rates (complete
response plus partial response) have been recommended as benchmark outcomes in
trials in the relapsed and refractory setting (Anderson et al. 2007). It was therefore
deemed appropriate to base the assessment of activity on the outcome measure of
partial response or, better, a binary outcome measure assessed over up to six cycles
of treatment with DTD.
Dual primary outcome measures of activity and tolerability will be assessed using
the endpoints of partial response or better and ability to tolerate at least two cycles
of treatment, respectively.
Randomisation
Randomisation will be performed between DTD (dose 1) and DTD (dose 2), for
the purpose of dose selection. Although drug D is to be given in combination with
both thalidomide and dexamethasone, there is no standard therapy available for this
population of patients.
As previously highlighted, the aim of the current trial is to identify a dose of drug
D in combination with thalidomide and dexamethasone that is sufciently active
and tolerable to warrant investigation in the de novo setting. It is expected that
the subsequent study in the de novo setting would be a further randomised trial,
with a conventional control arm to establish the benet, or otherwise, from drug D
administered at an optimal dose in combination with thalidomide and dexamethasone
compared to ‘standard therapy’. As such, no conventional ‘control’ arm is incorpo-
rated in the current trial, since the aim of the study is not to quantify the benet, or
DOSE SELECTION IN ADVANCED MULTIPLE MYELOMA 177
otherwise, of drug D in combination with thalidomide and dexamethasone, over and
above a current standard therapy, but to provide proof of concept data.
Historical control data are available from two large randomised phase III stud-
ies in a similar population of patients, providing initial data on which to base the
assumptions made within the current trial.
Design category
Rejected designs:
i. Upon discussion with the clinical investigators, it was decided that assessing
the data early in the trial was important to ensure the tolerability of the treatment
is not too low and that the activity is sufciently high. A one-stage design was
therefore rejected.
ii. Due to the nature of the primary activity outcome measure assessed over up
to six cycles of treatment, nal response results will not be available until
6 months after randomisation. For logistical reasons a multi-stage or contin-
uous monitoring design was deemed inappropriate, as they require data to be
available in a ‘real-time’ manner.
iii. As already noted, the follow-on study is expected to be in a different setting
to the current study, that is, de novo versus heavily pre-treated; therefore a
seamless phase II/III study would not be possible.
iv. Decision-theoretic approaches to trial design require information on number
of patients to be treated in future phase III trials, total patient horizon (number
of patients in the population who may potentially be treated with the new drug
were it approved) and costs of treatment. Since the subsequent study is expected
to be in a different setting, with different decision-theoretic parameters, such
an approach is again not appropriate.
v. A three-outcome design, which allows an ‘inconclusive’ result to be identied
for the primary endpoint, and additional, secondary, endpoints to be taken
into account, was also deemed inappropriate since a dual primary endpoint is
already being considered.
vi. Finally, randomised discontinuation designs were also considered but rejected
since the study does not aim to determine the additional benet of drug D over
thalidomide and dexamethasone. Moreover, a discontinuation design does not
suit a study aimed at evaluating different doses of a study drug.
Candidate designs: Two-stage designs were considered as potential designs for
the trial.
Possible designs
On the basis of the above exclusions and the requirement to assess tolerability and
activity at an interim time point, a two-stage trial design was chosen, incorporating
178 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
dose selection between DTD (dose 1) and DTD (dose 2), to select an optimal dose of
drug D in a subsequent study of DTD in the de novo setting. The trial will incorporate
joint primary outcome measures of toxicity/tolerability and activity.
It is possible to conduct selection trials designed with go/no-go decision criteria
that are applied to each individual arm, to ensure that only those arms sufciently
active (and tolerable), that is, passing the ‘go’ criteria, are compared for selection, as
opposed to simply selecting the dose with the better activity and tolerability. Such an
approach is described by Simon et al. (1985) and Sargent and Goldberg (2001), in
the context of binary outcomes, and will be considered here.
There are no two-stage designs for dual-endpoint selection trials described in
Section 6.4, which t the design parameters described above; however, the following
multi-stage design may be considered:
i. Thall and Sung (1998) – multi-stage design which may be adapted to incorpo-
rate just two stages
Additionally, applying the concept of Simon et al. (1985) or Sargent and Goldberg
(2001), the following two-stage designs for dual-endpoint single-arm trials may also
be considered (Section 6.2):
ii. Bryant and Day (1995)
iii. Conaway and Petroni (1995)
iv. Conaway and Petroni (1996)
v. Thall and Cheng (2001)
vi. Jin (2007)
vii. Wu and Liu (2007)
Stage 3 – Practicalities
Practical considerations for selecting between designs
We now consider each of the above designs in turn.
Dual-endpoint selection designs
i. Thall and Sung propose a Bayesian multi-stage design, which may be reduced
to incorporate just two stages, to assess multiple outcomes, for example, toxicity
and activity. They specically outline application of this design to randomised
phase II selection trials. Outcomes are categorised into klevels (e.g. active/not
toxic; active/toxic; not active/toxic; not active/not toxic) and priors based on
historical data. Clinicians need to provide information on the trade-off between
activity and toxicity, that is, the acceptable increase in toxicity for a specic
increase in activity. The joint probability of both a response and toxicity,
often specied in terms of a conditional probability or an odds ratio, should
be accounted for when assessing the operating characteristics of the design.
DOSE SELECTION IN ADVANCED MULTIPLE MYELOMA 179
The impact of this relationship between activity and toxicity was investigated
via example, varying the odds ratio between the probability of toxicity when
response occurs, relative to no response. The operating characteristics were
not sensitive to the relationship specied. Selection may be based on any
appropriate criterion applied at the end of the trial to those treatments not
terminated early due to unacceptably high toxicity or unacceptably low activity
(in the case where there is more than one treatment passing the rst stage). As
an example, selection may be based on the treatment with the highest response
rate and toxicity below a specic level, from those treatments not terminated
early. Software is available to allow implementation of the design.
Dual-endpoint single-arm designs (i.e. incorporating selection after assessment
of each individual arm)
ii. Bryant and Day propose a design that reects that of Simon’s two-stage design
for a single outcome measure (Simon 1989). Early termination for unacceptably
low activity or unacceptably high toxicity is incorporated at the end of the
rst stage. The design assumes toxicity and activity are independent. This
is arguably unlikely to be the case for most trials; however, the impact of
incorrectly assuming independence was assessed and the design found to be
reasonably insensitive to this. Software is available to enable implementation.
iii. Conaway and Petroni (1995) propose a design based on enumerating the exact
distribution for two binary endpoints. Estimation of the association between
the activity and toxicity outcomes is required, for example, in the form of the
correlation or an odds ratio. Early termination for unacceptably low activity
or unacceptably high toxicity is incorporated at the end of the rst stage. The
authors note that the design, with respect to power, is robust against misspec-
ication of the association parameter. Programs to enable implementation are
noted as being available from the author.
iv. The design proposed by Conaway and Petroni in 1996 incorporates assessment
of toxicity and activity based on the I-divergence test statistic incorporating
all four combinations of toxicity and activity described previously, allowing a
trade-off between activity and toxicity. This differs from their previous design
(Conaway and Petroni 1995) and the Bryant and Day design, which base results
on the overall activity and toxicity rates. An estimate of the association between
activity and toxicity is required; however, the authors note that the properties
of the test are reasonably unaffected by misspecication. Early termination
for unacceptably low activity or unacceptably high toxicity is incorporated at
the end of the rst stage. Programs are not noted as being available from the
authors; therefore, the design may need programming for implementation.
v. The design proposed by Thall and Cheng, in the setting with no control arm,
allows for assessment of improvement in activity with the experimental treat-
ment whilst not increasing toxicity, compared to historical control data. No
discussion is provided regarding the correlation between the endpoints and

180 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
robustness to misspecication of this relationship. The design would require
programming to enable implementation.
vi. Jin proposed an alternative test to that of Conaway and Petroni (1996), designed
to deal with trade-off between toxicity and activity by controlling the marginal
type I errors for these two outcomes separately. Incorporating this additional
control inevitably increases sample size. As for other designs, an estimate of
the association between the two outcome measures is required, and the design
is robust to misspecication with regard to statistical power. Early termination
for unacceptably low activity or unacceptably high toxicity is incorporated
at the end of the rst stage. This design would need programming to enable
implementation.
vii. Wu and Liu propose an adaptation to the designs proposed by, for example,
Conaway and Petroni (1995). The adaptation incorporates a sample size read-
justment at the end of the rst stage to allow for inaccuracy in the initial
specication of the association between activity and toxicity. In this respect,
the interim assessment focuses on sample size re-estimation rather than early
termination for lack of activity or unacceptable toxicity. Programming require-
ments are as for the original designs.
In the case of designs (ii)–(vii), the focus is to determine activity and tolerability
of each of the experimental regimens individually. In the case where both regimens
are found to be sufciently tolerable and active, additional secondary selection criteria
should be employed.
Table 11.1 provides a summary of the practical considerations for each design.
There are a number of designs in this example that are appropriate to the specic
requirements of the trial. Taking a practical approach for the purpose of this example,
we consider only those which are deemed robust to misspecication of the relationship
between the endpoints and for which software is available. This includes the following
designs: (i) Thall and Sung, (ii) Bryant and Day and (iii) Conaway and Petroni. In
reality, further exploration of the designs for which no software is available is also
recommended.
Table 11.1 Summary of practical considerations for each design.
Consideration i ii iii iv v vi vii
Required
Robust to misspecication
of relationship between
endpoints
Y Y Y Y Not discussed Y Y
Desirable
Statistical software/
programs available
YYYN N NN/A
a
aAvailability according to the original methods from which the sample size is adopted.
DOSE SELECTION IN ADVANCED MULTIPLE MYELOMA 181
Tournoux et al. (2007) compared the designs of Bryant and Day (1995) and
Conaway and Petroni (1995). The Bryant and Day design was more robust to mis-
specication of the relationship between activity and toxicity. We may therefore
choose between the Bayesian design of Thall and Sung which incorporates treatment
selection and the frequentist design of Bryant and Day which requires the use of
additional, secondary, selection procedures. Again taking a practical approach for
the purpose of this example, we present here the proposed trial design based on the
design described by Bryant and Day; however, the design presented by Thall and
Sung may equally be considered.
Using the Bryant and Day design requires the inclusion of an additional, sec-
ondary, selection approach should both dosing schedules be found to be sufciently
active and tolerable. Such designs are described by Simon et al. (1985) and Sargent
and Goldberg (2001) and are discussed in Chapter 5. In the current setting we propose
to perform selection on the basis of PFS, using the design of Sargent and Goldberg.
This design selects the dosing schedule with the higher PFS rate with a derived proba-
bility of correct selection only when the difference in PFS between the two schedules
is larger than a pre-specied value. In the case where the difference is less than this,
selection may be based on alternative criteria. This differs to the design described by
Simon et al. which will always select a schedule with higher PFS, regardless of the
magnitude of difference between the two arms, thus potentially leading to increased
probability of incorrect selection.
Proposed trial design
We rst consider the design for each dosing schedule individually, before moving to
regimen selection. Previously published data in a slightly less pre-treated population
of patients are available to provide estimates of historical control data (van de Donk
et al. 2011). Overall response rates were 60%. Since the population of patients
in the current trial is expected to be more heavily pre-treated than those in the
previous studies, a response rate of at least 50% with drug D in combination with
TD is targeted. A response rate of 20% is taken as the response rate below which
a dosing combination would be rejected. Considering tolerability rates, previous
data identied 20% of patients unable to tolerate treatment. For the purpose of the
current trial, a tolerability rate of 75% or less, that is, >25% intolerable, is taken
to be unacceptable and would lead to a recommendation of rejecting the dosing
combination. A tolerability rate of 90% is targeted with this regimen, that is, 10%
intolerability, a relative reduction of 50% compared to historical control data, deemed
clinically relevant.
After discussion with the clinicians it was agreed that the trial should be designed
with 90% power and 10% type I error rates for both activity and tolerability (i.e. 10%
chance that a dosing schedule is deemed active when in fact the response rate is <20%
and 10% chance a dosing schedule is deemed tolerable when in fact tolerability is
<75%). Implementing this design using software provided by Machin et al. (2008),
the corresponding design is as follows, for each arm separately.
182 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
∙Stage 1: Recruit 20 patients and follow up to observe response and tolerability.
If at least 4/20 patients achieve a response and at least 15/20 patients are able
to tolerate treatment, continue to stage 2. If there are three or fewer patients
who do not achieve a response, the dosing schedule is terminated early for lack
of activity; if there are 14 or fewer patients who are able to tolerate treatment,
the dosing schedule is terminated early for non-tolerability.
∙Stage 2: Recruit a further 24 patients to a total of 44 in each arm. Follow up to
observe response and tolerability. If at least 13/44 patients achieve a response
and at least 36/44 patients are able to tolerate treatment, the dosing schedule is
deemed sufciently active and tolerable. If there are 12 or fewer patients who
do not achieve a response, the dosing schedule is rejected for lack of activity;
if there are 35 or fewer patients who are able to tolerate treatment, the dosing
schedule is rejected for non-tolerability.
If only one of the dosing schedules successfully passes stage 2, this dosing
schedule will be selected for further investigation. In the case where both dosing
schedules successfully pass stage 2 and are deemed sufciently active and tolera-
ble to warrant further investigation, the selection criteria of Sargent and Goldberg
are applied, as previously described. It was agreed that the dosing schedule with
the higher PFS rate at 12 months should be selected only when the difference in
12-month PFS rates between the two arms is greater than 5%. A 25% PFS rate at
12 months with dose 1 and a 35% PFS rate with dose 2 were hypothesised based
on previously published data for drug D. With 44 patients per arm and observed
PFS rates of 25% and 35% in the dose 1 and 2 arms, respectively, the study would
correctly select the dose schedule with higher PFS rate with 81% probability (assum-
ing that in 50% of ambiguous cases the correct treatment would be selected), based
on PFS alone. If the difference is less than 5%, alternative selection criteria may
be considered.
Patients will be randomised on a 1:1 basis to receive either DTD (dose 1) or DTD
(dose 2), with a maximum of 88 patients randomised (44 per arm).
Summary
This trial has been designed to select the best dosing schedule of a cytotoxic agent,
drug D, when given in combination with thalidomide and dexamethasone in patients
with relapsed refractory multiple myeloma. Sufcient activity and tolerability of
dose 1 and dose 2 are initially incorporated to select between the two doses, with
additional, secondary, selection only in the case where both dosing schedules are
found sufciently active and tolerable. Schedule selection is then determined on the
basis of progression-free survival.
By taking into account therapeutic considerations associated with the drug,
the patient population and available historical control data and taking pragmatic
approaches to trial design, the specic design criteria associated with each of the
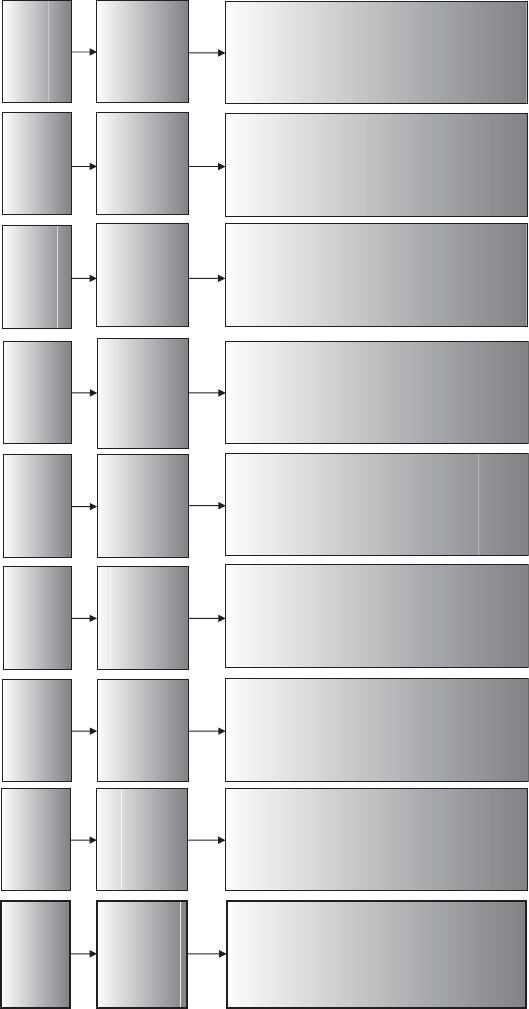
Pointof
consideration
Selectionfrom
flowdiagram
Rationale
behind
selection
Randomisation Designcategory Practical
considerations
Randomisationto
experimental
armsonly
Primaryaimto
selectmostactive
andtolerable
dose
Historicalcontrol
dataonless
heavily pretreated
patients
Subsequentphase
IItrialindenovo
settingtoinclude
randomisationto
control
Two stage
Necessaryto
includeearly
evaluationof
activityand
tolerability
Oneinterim
assessment
deemedsufficient
Two‐stage
activityand
tolerabilitywith
secondary
schedule
selection
Robustto
misspecification
ofrelationship
betweenactivity
andtolerability
Availablesoftware
Pragmatic
decisionfor
purposeof
example
Primaryaimof
trial
Numberof
experimental
treatmentarms
Primaryoutcome
ofinterest
Outcome
measureand
distribution
Proofofconcept
Primaryaimdose
selection
Intentiontotake
thecombination
forwardintostudy
ofnewly
diagnosed
patients
Twoexperimental
arms
Twodosing
schedulesfor
consideration
Activityand
toxicity
DrugDis
expectedtohave
associated
cumulative
toxicities
Needtoshow
bothsufficiently
activeand
tolerable
Dualbinary–
responseand
tolerabilityofat
leasttwocycles
DrugDexpected
toinduce
responsein
combinationwith
thalidomideand
dexamethasone
Response
recommendedas
benchmark
outcomein this
setting
Non‐tolerabilityof
firsttwocyclesis
anearlyindication
offuture
tolerabilityissues
Therapeutic
considerations
Noselection,
therapeutic
considerations
below
Patientswith
relapsed/
refractory
multiplemyeloma
DrugDisa
cytotoxicagent,
expectedto
induceresponse
Optimaldose
unclear
Associated
cumulative
toxicities
Novalidated
biomarkers
associatedwith
drugDordisease
Figure 11.1 Summary of decision process in designing phase II trial of drug D in multiple myeloma.
184 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
eight elements featured in Figure 2.1 and described in Chapter 2 are summarised in
Figure 11.1. Working through the thought process and taking an iterative approach
to the design of the trial, with ongoing discussion between the clinician and statisti-
cian, we have designed a randomised, phase II selection trial, for the selection of the
optimal dose of drug D in combination with thalidomide and dexamethasone (DTD)
in patients with relapsed refractory multiple myeloma.

12
Targeted therapy for advanced
colorectal cancer
Matthew Seymour and Sarah Brown
Drug E is a monoclonal antibody therapy targeting a cell surface receptor, ‘Receptor
X’, that is known to be involved in cell growth from some cancers. Retrospective
studies have shown that Receptor X is strongly expressed in around 5% of colorectal
cancers, and it is now hypothesised that drug E, given in combination with current
standard chemotherapy, will improve efcacy for patients with X-positive advanced
colorectal cancer (aCRC) after failure of rst-line chemotherapy. Receptor X is not
routinely measured in aCRC, so there are only limited historical data from previous
trials on which to base the expected control outcomes in this specic group. Phase
III clinical data are available for the efcacy of drug E in other solid tumours where
Receptor X is more commonly expressed, and it is hoped that a similar treatment
effect will occur in X-positive aCRC. Drug E has demonstrated an acceptable toxicity
prole in studies in other disease areas. A phase II trial of drug E in combination
with standard second-line chemotherapy, for Receptor-X-positive aCRC patients, is
proposed to determine whether to proceed to a larger phase III trial.
Stage 1 – Trial questions
Therapeutic considerations
Mechanism of action: Drug E is a monoclonal antibody directed against Receptor X.
It is believed to be primarily cytostatic as a single agent, but to act synergistically
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
186 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
with standard cytotoxic chemotherapy. In the setting of second-line treatment for
aCRC, classical cytotoxic chemotherapies are associated with low response rates due
to high levels of tumour resistance. It is, therefore, unrealistic to expect the addition
of drug E to chemotherapy to induce a high response rate. An assessment of disease
control, that is, progression-free survival (PFS), offers a more realistic measure of
the efcacy of this combination in this setting.
Aim of treatment: The ultimate aim of second-line treatment of patients with
advanced disease is to prolong overall survival. An early indicator of treatment
activity is the ability to prolong PFS, as discussed above.
Single or combination therapy: Drug E is given in combination with standard
second-line chemotherapy; to be relevant, therefore, the activity of the combination
therapy would need to be greater than that of chemotherapy alone.
Biomarkers: Drug E targets the specic cell surface receptor, Receptor X, so the
trial will be focused specically on patients with X-positive tumours. On the basis of
evidence in other disease areas, the drug is not expected to improve clinical outcomes
in patients with X-negative tumours; these patients will, therefore, be excluded. There
are no validated biomarkers associated with aCRC which may provide an alternative
assessment of therapeutic activity.
Primary intention of trial
There is conrmed clinical evidence of efcacy of drug E in other solid tumours
(breast and gastrointestinal cancer). Owing to the small population of patients avail-
able, the current phase II trial is designed to deliver proof of concept in this targeted
population of patients and a go/no-go decision for a subsequent phase III trial. It is
important to consider the most efcient trial designs due to the rarity of the target
population, as well as the length of time required for a drug to move from phase II
to phase III then into routine clinical practice. A pragmatic approach to designing
trials in these settings is essential, to ensure reliable and robust trial design, whilst
maintaining an efcient and achievable drug development pathway.
Number of experimental treatment arms
There is only one experimental treatment under investigation, so a selection trial is
not required.
Primary outcome of interest
Drug E has shown an acceptable toxicity prole in multiple studies in other solid
tumours. The current combination in aCRC is expected to have only minimal addi-
tional toxicity or functional decit. While toxicity will form a secondary endpoint of
the phase II trial, the primary outcome of interest is activity.
TARGETED THERAPY FOR ADVANCED COLORECTAL CANCER 187
Stage 2 – Design components
Outcome measure and distribution
In this heavily pre-treated population of patients, response rates to chemotherapy
are historically low and the addition of drug E is not expected to induce a high
response rate. The use of PFS as an indicator of activity may, therefore, be more
appropriate and clinically relevant. PFS is strongly correlated with overall survival in
patients with aCRC (Buyse et al. 2007), albeit predominantly in the setting of trials
of chemotherapeutic agents.
Chemotherapy plus drug E will be given for an initial period of 12 weeks, reect-
ing the initial treatment period of standard chemotherapy. After this point, patients
who have not progressed will continue to receive drug E until progression. Assess-
ments of disease status via CT scan will be carried out approximately 12-weekly
until disease progression. Median PFS with standard chemotherapy is approximately
4.8 months in patients with advanced colorectal cancer following rst-line therapy,
but data specically for patients with X-positive colorectal cancer are limited (see
Section 12.4 for further details). This population of patients represents a rare sub-
group of aCRC patients, so recruitment to the study will likely be slow. A binary
outcome dichotomising PFS at a single time point (i.e. the proportion of patients free
of disease progression at a specic time point) is worthy of consideration due to the
long period of recruitment and the requirement otherwise for all patients to be fol-
lowed up to disease progression. If inclusion of interim assessments during the trial
is being considered, however, the requirement to wait for all patients to be followed
up to the specic time point of interest before this can take place may be impractical.
The use of all time-to-event data up to and including the specic time point may be
considered a possibility in this setting. Conversely, PFS will be limited and the use
of a time-to-event outcome (i.e. overall PFS) may be preferable since this incorpo-
rates all available information from the trial and will further facilitate design of the
potential phase III trial that would have a time-to-event primary outcome measure.
Randomisation
Drug E is to be given in combination with standard chemotherapy. It is important
that any possible additional activity observed with the combination can reasonably
be attributed to the addition of drug E. In the absence of reliable historical control
data for this population of patients with X-positive aCRC, randomisation should be
incorporated to provide robust and reliable results. Randomisation will increase the
number of patients required with what is a rare sub-type of a more common cancer, so
it is also important to minimise the sample size in other ways. Since the trial is being
designed to provide sufcient data to determine whether to progress to a phase III trial,
randomisation is essential despite its impact on patient numbers. A key consideration
is the incorporation, or otherwise, of formal statistical comparison with control. While
this is preferable for the purpose of making a stop/go decision, to sufciently power
such a comparison with an acceptable type I error rate may be prohibitive within
188 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
such a rare population. On the other hand, an additional consideration is the targeted
treatment effect with the experimental treatment. In studies adding drug E to standard
chemotherapy in other disease areas, hazard ratios of between 0.5 and 0.7 have been
observed. When such large treatment effects are realistic, it may be feasible to perform
formal statistical comparisons between experimental and control arms, with limited
sample sizes.
Randomisation will, therefore, be incorporated, and the feasibility of including
a formally powered comparison with a control will be considered, with regard to
impact on sample size. Should drug E show a sufcient level of activity, a subsequent
randomised phase III trial with multiple interim assessments for lack of efcacy is
envisaged.
Design category
Especially where historical data may be unreliable it is important to consider multiple
scenarios when choosing the statistical design, to assess how robust each design is if
outcomes in either treatment arm are not as expected. For example, if activity in the
control arm is uncertain, how well do the different trial designs cope with an under-
or over-estimation of this activity?
Rejected designs:
i. Decision-theoretic approaches to trial design incorporate information on num-
ber of patients to be treated in future phase III trials, number of patients
potentially benetting from future treatment and costs of treatment. In this
particular setting, the costs associated with the current treatment are expected
to change in the near future due to patent expiry. The data are, therefore, not
reliable for the purpose of a decision-theoretic design and this design was
deemed inappropriate.
ii. Randomised discontinuation designs were also rejected, on the basis that the
initial assessment of treatment activity is carried out on completion of the rst
block of combination treatment, after which treatment is with single agent drug
E only. Although it may be possible for all patients to receive initial treatment
with drug E plus chemotherapy, to randomise patients free of progression
at 12 weeks to drug E versus no treatment is not the central question here.
Rather, the trial is designed to address the treatment schedule as a whole, that
is, initial combination therapy followed by single-agent maintenance therapy,
compared with chemotherapy alone, so a randomisation discontinuation design
was rejected.
iii. Due to the rarity of the subgroup of patients considered in this trial, and the
potential subsequent phase III trial, seamless phase II/III designs were deemed
inappropriate given the uncertainty regarding feasibility of recruiting large
numbers of patients.
iv. Studies in other solid tumours have shown large treatment effects, with haz-
ard ratios in the region of 0.5–0.7 with the addition of drug E to standard
TARGETED THERAPY FOR ADVANCED COLORECTAL CANCER 189
chemotherapy. With the addition of this monoclonal antibody to current
standard chemotherapy, there is no reason to expect that toxicity will be
reduced (although neither is it expected that signicant additional toxicities
will emerge), and the combination therapy will ultimately be more costly than
standard chemotherapy alone. A three-outcome design which enables alterna-
tive outcome measures such as toxicity and cost to be considered in the event
that the treatment effect is inconclusive (i.e. it lies within a ‘grey area’ between
declaring the treatment worthy of further investigation and not worthy of fur-
ther investigation) is not appropriate here since we do not expect either of these
measures to be reduced with the use of drug E.
v. As previously noted, the proportion of aCRC patients with X-positive disease
is low; therefore, recruitment is expected to be relatively slow. The ability
to build in early stopping boundaries for lack of activity is benecial in this
setting due to the potentially prolonged period of recruitment. On this basis
two-stage designs were felt preferable to one-stage designs that do not incor-
porate formal interim assessment and the opportunity for early cessation. The
use of a multi-stage design, or a continuous monitoring design, was con-
sidered but a single interim assessment was considered sufcient provided
recruitment could continue during the stage 1 analysis as the eligible patient
population is small and it is important not to ‘lose’ potential patients due to a halt
in recruitment.
Candidate designs: Two-stage designs were considered as potential designs for
the trial.
Possible designs
We have determined that the phase II trial will be a randomised trial, addressing both
the proof of concept of drug E in combination with standard chemotherapy and the
decision to proceed or not to phase III, on the basis of activity alone. This will be
assessed using the time-to-event outcome measure of PFS, either incorporating all
available data on PFS or enabling all available data up to and including a specic
time point to be incorporated. Thus we consider designs listed under time-to-event
outcome measures only. A two-stage statistical design will be used. Inclusion of
randomisation for the purpose of formally powered statistical comparison will be
addressed by taking a pragmatic approach to the necessary sample size in the context
of the target population being small but the potential treatment effect large. Single-
arm designs which enable randomisation for the purpose of calibration only, as well
as randomised designs incorporating formally powered comparison, are therefore
considered. Designs are identied from Chapter 3, single-arm trial designs that are
adapted to include a randomised reference arm, or from Chapter 4.
Reviewing the available designs in Chapters 3 and 4 which t these design
parameters, the following designs may be considered for this trial. Discussion as to
selecting between these specic designs is given in the next section.
190 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
From Chapter 3
i. Case and Morgan (2003)
ii. Litwin et al. (2007)
Although there are no two-stage designs listed in Chapter 4 with time-to-event end-
points, the principles of, for example, Herson and Carter (1986) or Buyse (2000) may
be incorporated into the designs listed above, to assess the credibility of the outcome
in the experimental arm. Alternatively, the one-stage designs from Chapter 4 noted
below may be considered, with an adaptation to incorporate an interim assessment
for lack of activity:
iii. Stone et al. (2007b) and Simon et al. (2001)
iv. Chen and Beckman (2009)
Stage 3 – Practicalities
Practical considerations for selecting between designs
We now consider each of the above designs in turn.
i. The design proposed by Case and Morgan incorporates a time-to-event out-
come measure whereby all information available at the time of the interim
analysis is included. This is achieved by identifying a specic time point of
interest at which the probability of PFS is assessed, in other words, a binary
outcome derived from the time-to-event outcome incorporating all available
data, including those patients with follow-up to less than the time point of
interest. This design does not require a halt to recruitment. Standard programs
are available for this design. Although a control arm may be included for the
purpose of calibration, this does not power the study for formal comparison of
the arms.
ii. The design of Litwin et al. is based on a time-to-event outcome measure at two
specic time points, that is, a binary outcome. This design does not incorporate
data for patients who have not yet been followed up to the specic time point
of interest at the interim assessment, and is therefore not considered further.
iii. Stone and colleagues describe a phase II design which is formally powered
to compare the experimental arm with the control arm, using relaxed type
I errors and potentially targeting large treatment effects. This reects the
designs described by Simon in the setting of time-to-event outcomes, which
are described by the authors as ‘phase 2.5 screening’ designs, due to the
use of phase III-type designs but with type I error rates typically associated
with phase II trials (Simon et al. 2001). By incorporating a formally powered
statistical comparison with the control arm, the sample size of the trial will
inevitably increase. This should, however, be weighed against the reliability of
TARGETED THERAPY FOR ADVANCED COLORECTAL CANCER 191
the decision-making criteria and compared with that for the non-comparative
phase II design described in (i) above. Standard software is available for this
design.
iv. Chen and Beckman describe an approach to a randomised phase II trial design
that incorporates the ratio of sample sizes between phases II and III. Optimal
type I and II errors for the design are identied by means of an efciency
score function. Formal comparison with the control arm is incorporated. The
design considers cost efciency of the phase II and III trials based on the
ratio of sample sizes between phases II and III and the aprioriprobability of
success of the investigational treatment, to determine the sample size for phase
II. Sufcient detail is provided within the paper to allow implementation and
an R program is provided to identify optimal designs. At this stage, however,
the design of the potential phase III trial is unclear, since the phase II study
is designed in part to provide data on feasibility of recruitment with such a
rare subgroup of patients. The design of Chen and Beckman is, therefore, not
considered further.
To distinguish between the designs incorporating no formal comparison (Case
and Morgan 2003) versus formal comparison (Stone et al. 2007b), we consider below
the required sample sizes, bearing in mind the need to include an interim assessment
for lack of activity using the design of Stone et al.
Proposed trial design
The primary assessment of activity is based on PFS. The trial is designed for
patients with X-positive aCRC after failure of rst-line chemotherapy. It is antic-
ipated that approximately 30% of patients will have progressed on rst-line therapy;
for these patients the estimated median PFS with standard second-line chemother-
apy is 2.6 months (Sobrero et al. 2008). The remaining 70% of patients are
expected to have progressed during a treatment break, or on intermittent therapy,
with rst-line chemotherapy; the estimated median PFS for these patients treated
with standard ‘re-challenge’ chemotherapy is 5.7 months (Adams et al. 2011). It is
acknowledged that the standard chemotherapy may, therefore, differ between these
two groups of patients. The expected median PFS of patients after rst-line ther-
apy in the current trial is approximately 4.8 months since we have no evidence
that Receptor X status is prognostic of outcome. In other disease areas, a reduc-
tion in hazard rate for PFS of 30–50% has been observed with the addition of
drug E to chemotherapy. In the current setting, a hazard ratio of 0.6 is targeted
(i.e. a reduction in hazard rate of 40%) with the addition of drug E to standard
chemotherapy. This corresponds to a targeted median PFS of 8 months in the experi-
mental arm.
The design of Case and Morgan requires a specic time point at which to assess
the progression-free probability; we select the 24-week time point. Corresponding
192 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
expected PFS probabilities at 24 weeks (5.5 months) post-randomisation are 45.2% in
the control arm (i.e. a probability of progression that would not be of further interest)
and 62.1% in the experimental arm (i.e. a probability of progression worthy of further
investigation).
We assume that patients are to be recruited over no more than a 3-year period
as more protracted recruitment risks loss of engagement from investigators and the
potential that the clinical question behind the trial will have changed if other new
treatments have become available. Power of 80% is selected to detect the targeted
treatment effect, with a 10% one-sided type I error for incorrectly declaring the
addition of drug E to standard chemotherapy worthy of further investigation.
Under the design of Case and Morgan we would require 51 patients in the exper-
imental arm, with an interim analysis taking place after 23 patients are recruited,
not accounting for dropout. This is based on minimising the expected duration of
accrual under the null hypothesis (Case and Morgan 2003). In order to incorporate
randomisation to a reference arm a 1:1 randomisation would simply double the sam-
ple size. Alternatively, an imbalanced randomisation such as 2:1 in favour of the
experimental arm may be favoured in this setting where the specic population of
patients is rare. This will provide sufcient data in the experimental arm whilst also
guarding against selection bias. It retains a reference arm against which the control
arm assumptions may be informally compared, but the design is not powered for
formal statistical comparison between the arms. In this particular example, includ-
ing a 2:1 randomisation between standard chemotherapy plus drug E and standard
chemotherapy alone without formal statistical comparison, a total of up to 77 patients
will be recruited (assuming successfully passing stage 1; chemotherapy plus drug E
n=51, chemotherapy alone n=26).
Under the design of Stone et al., we would require 40 patients per arm, that is, a
total of 80 patients, assuming all patients are followed up until disease progression
and for a minimum of 6 months. An interim assessment for lack of activity, based
on the design of Gehan (1961), would be incorporated to enable early termination of
the trial in the event that the PFS probability at 24 weeks post-randomisation is not
sufciently large enough in the experimental arm, to warrant continuation.
Comparing the two designs, we can see that the inclusion of formal comparison
between the arms increases the required sample size only marginally in this set-
ting. This is because the design of Stone et al. considers all the time-to-event data
through the 3 years of recruitment and additional follow-up, whereas the design of
Case and Morgan, although taking into account the time-to-event data prior to the
24-week time point, focuses on the survival probabilities at 24 weeks. The inclu-
sion of the additional data under the design of Stone et al. makes this a feasible
approach in this particular setting with a long recruitment period and a large tar-
geted treatment effect. Additionally, the inclusion of a formally powered statistical
comparison between treatment arms is more robust to uncertainty in the estimation
of activity of the control arm, at the design stage. This trial would therefore require
approximately 1600 patients to be screened over 3 years to identify 80 patients with
X-positive aCRC.
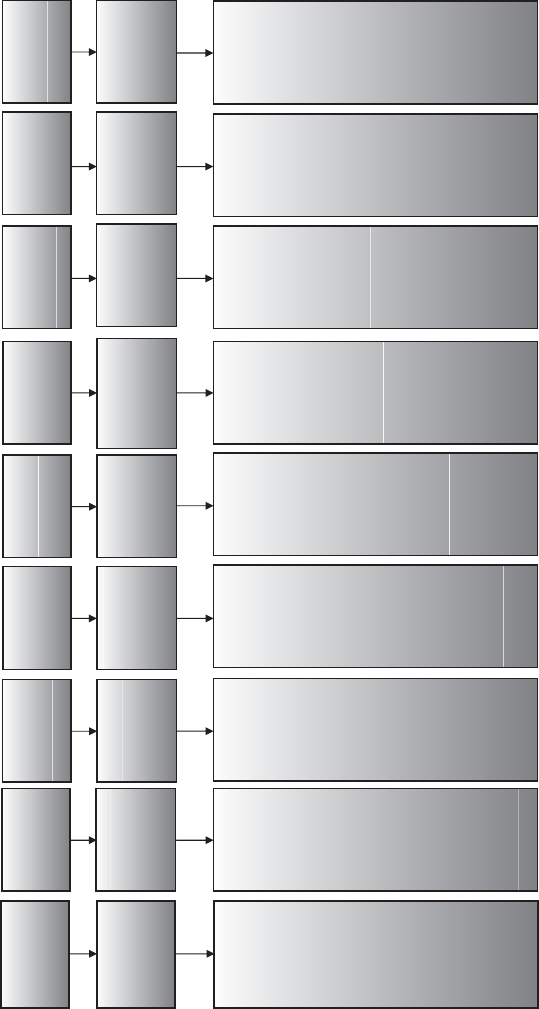
Pointof
consideration
Selection
fromflow
diagram
Rationale
behind
selection
Randomisation Designcategory Practical
considerations
Randomisation
toacontrolarm
withORwithout
formal
comparison
DrugEgivenin
combination
withstandard
chemotherapy
Raredisease
subgroup;
pragmatic
approachtotrial
designneeded
Largetreatment
effecttargeted,
thereforeformal
comparisonmay
notbe
prohibitive
Two-stage
Smallpopulation
ofpatients,may
bedifficultto
recruit
Requireinterim
assessmentfor
lackofactivity
Formal
comparisonwith
control,with
interim
assessment
Software
availableto
implement
Allows
incorporationof
allprogression
-freesurvival
data
Enableformal
comparison–
morerobust
Primaryaimof
trial
Numberof
experimental
treatmentarms
Primary
outcomeof
interest
Outcome
measureand
distribution
Proofofconcept
andgo/no-go
decisionfor
phaseIII
Targeted,rare
population
Proofofconcept
dataavailablein
othersolid
tumoursonly
Subsequent
studywould
formally
comparewith
standard
chemotherapy
One
experimental
arm
Onlyone
experimental
treatmentfor
consideration
Activity
DrugEhasan
acceptable
toxicityprofilein
otherdisease
areas
Expectedtohave
minimaltoxicity
/functional
deficit
Time-to-event–
progression-free
survival
Theadditionof
drugEto
standard
chemotherapy
aimstodelay
disease
progression
Heavilypre-
treated
population,
thereforehigh
responserates
unrealistic
Patientsreceive
experimental
treatment until
disease
progression
thereforewould
be followedup
Therapeutic
considerations
Noselection,
therapeutic
considerations
below
Patientswith
Receptor-X-
positive
advanced
colorectalcancer
requiring
second-line
chemotherapy
DrugEisa
monoclonal
antibody
directedagainst
Receptor-X
Givenwith
standard
chemotherapy
maydelay
disease
progression
Figure 12.1 Summary of decision process in designing phase II trial of drug E in Receptor-X-positive advanced colorectal cancer.
194 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
Summary
This trial has been designed to assess the activity of the addition of a monoclonal
antibody, drug E, to standard chemotherapy in patients with Receptor-X-positive
aCRC. By taking into account therapeutic considerations associated with the drug, the
rare patient population and mechanistic considerations associated with appropriate
outcome measures in aCRC, we addressed the trial-specic design requirements
through each of the three stages featured in Figure 2.1 and described in Chapter 2,
as summarised in Figure 12.1. Working through the thought process with ongoing
discussion between the clinician and statistician, we have designed a randomised,
controlled, two-stage trial, with PFS as the primary phase II outcome measure for
the assessment of chemotherapy plus drug E in Receptor-X-positive aCRC patients.
The trial is designed to provide both proof of concept data and a go/no-go decision
regarding whether or not to proceed to a larger randomised phase III trial.

13
Phase II oncology trials:
Perspective from industry
Anthony Rossini, Steven Green and William Mietlowski
13.1 Introduction
In oncology clinical development, phase II has the widest range of possible goals
which can be addressed at this stage. In contrast, there is general agreement for what
is to be done at phase I and phase III. Phase I generates the initial data used to select
a dose which can be used relatively safely in a larger population. Likewise, phase
III studies aim to establish evidence justifying efcacy and safety enabling health
authority approval. Generally, these designs focus on clinically relevant survival and
event-time endpoints. Phase II trials, on the other hand, have the simple but ill-dened
mission of providing evidence for one or more of the many possible strategic paths
between these two phases. Specically, the phase II programme must bridge between
the current knowledge about the initially established dosing regimen and the phase III
design to support registration. There are many possible paths, representing the many
approaches to learning about how to use a compound to treat cancer. The diversity
of clinical development paths can also be deduced from the range of clinical trial
designs described in this book. This chapter will focus on selecting phase II designs
originating in response to strategies embodied in a commercially oriented clinical
development plan (CDP).
Commercially sponsored trials are a component of a pre-specied, evolving,
comprehensive CDP. A CDP can be formally thought of as a document which frames
the development of a compound in terms of medical indications, staging of activities
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
196 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
and collection of data for justifying registration across possible indications. This
contains justication for components which the development team considers essential
to develop the compound. The choice of trial designs should address the CDP’s
objectives, conditional on previous results. The goal of the CDP is to provide a
roadmap of activities to efciently either deliver a commercially viable product or
terminate development early for futility and/or safety issues. A commercially viable
product requires both regulatory approval and agreement by payers to reimburse.
The selection process described in this chapter takes into account pharmaceutical
drug development challenges and drivers. These frame the constraints and require-
ments which inform the selection of the phase II design(s). The source for these
challenges arise both internally and externally and relate to both scientic and oper-
ational considerations. Internal clinical development decisions which impact phase
II include timing and prioritisation of the compound in relation to other compounds
in the portfolio. External clinical constraints and drivers include current medical
practice, payer approaches and competition from external compounds. Constraints
include both nancial resources and shared internal specialised employee skills which
are in limited supply and required for more sophisticated designs. Some parts of this
chapter are forward looking and represent practices which are not yet incorporated.
Other parts are retrospective and may be suboptimal or obsolete due to recent statis-
tical, clinical or regulatory landscape changes. This chapter just reects a snapshot
in time of current thinking.
Multiple options often exist for clinical development strategies at the planning
stage for the phase II programme, with acceleration and hesitation pressure coming
from both the development team and the external environment. The selection of one
or more strategies in the face of uncertainty informs the choice of phase II design(s)
to be implemented. The range of strategic goals that are addressed in this chapter
consists of those for potential registration, establishing exploratory activity, regimen
selection, prediction of phase III success, safety trials and prospective identication
of targeted populations. We next describe some of the commercial challenges and
drivers before discussing strategic considerations and how they can inform study
design selection.
13.2 Commercial challenges, drivers
and considerations
The environment for commercial clinical drug development can change frequently,
making xed as well as long-term planning difcult. New information arises regard-
ing science, competitors, regulators and payer organisation; payer organisation can
cause an extreme change in plans, from rapid acceleration to a complete halt of the
programme. In addition, corporate philosophy and goals, as well as organisational
structure, can also impact a development programme’s strategy.
Competition, both internal and external, is a difcult factor to manage. Competi-
tion can take the form of internal competition between indications for a compound’s
PERSPECTIVE FROM INDUSTRY 197
resources, as well as between compounds which address the same family of indica-
tions. The CDP should outline how to address this.
The approach in this chapter naturally emphasises strategic goals based on com-
mercial experience. These strategic goals reect both common, clinical and scientic
goals and relevant corporate nancial opportunities and challenges, since maintaining
positive cash ow, and the extent of that income source, will dictate potential oppor-
tunities and risks. For any publicly traded company, the value of the investigational
portfolio is intrinsically incorporated into the value of the stock price. A failed phase
III trial can strongly inuence the stock price of a company if this compound reects
a sizable portion of the stock price as well as an erosion of condence in the company
to register drugs. Decisions which benet the company are at the level of the clinical
trial, such as minimising patients who are exposed to toxic drugs via careful sample
size determination and interim analyses. Other decisions at the strategic level, includ-
ing selection of drugs with most appropriate benet/risk balance, and the efcient
development of viable therapies also benet both patients and society as a whole.
While this could be done formally using a decision-theoretic framework, it is often
informally managed.
13.3 Selecting designs by strategy
The CDP provides guidance in terms of overall goals and approaches for clinical
development. Since it has a strategic focus for approaching clinical development,
a selection of trial designs based on strategic deliverables is simpler for teams to
use. We rst give some examples of overall programme-level strategies that could
be under consideration, before moving forward with how a few common phase II
strategies are addressed.
Overall programme strategies are described differently from, and yet contain,
the phase II strategies which are being considered. For example, one increas-
ingly popular development strategy is to target a rare but well-characterised
oncological indication, register the compound for treatment in that setting and then
construct a series of interrelated development programmes to expand into different
indications. These expanded indications are selected by considering the targets which
represent a component of the tumour, unlike the original indication where the tar-
get is found more homogenously across the whole tumour. Another strategy is to
leverage chemical synergies and initially target a medium-sized indication based on
initial pre-clinical and phase I results, combined with how they may relate to existing
medical practice and needs. Other common strategies include pairing new treatments
with existing ones for combination therapies, as well as including in the initial plans
a focus on setting up a possible diagnostic/compound combination.
Phase II studies address the middle stage of these strategies. For each example
given above, multiple questions could be addressed depending on the specic tactical
implementation of the global CDP strategy. The rest of this section focuses on the
phase II-specic strategic aspects.
198 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
13.3.1 Basic strategies addressed by phase II studies
The summary within Table 13.1 illustrates some examples of matching trial design
options to development strategies. For each strategy, multiple phase II designs are
observed to have been employed, and some of these designs can be seen to have
addressed multiple strategic objectives. This table is just a historical view; proper
due diligence requires searching the literature for improvements and newer designs
which may include any of those listed within Chapters 3–7, understanding available
data in the specic setting and the current state of regulatory requirements and payer
opinions. Based on an internal review of phase II experiences, we have identied six
strategic goals that have occurred with high frequency, specically:
1. Determination of activity for registration
2. Determine exploratory activity
3. Selection of regimen (single and combination agents)
4. Prediction of phase III success
5. Safety characterisation
6. Prospective identication of target populations
A clinical development programme can have multiple phase II trials, sometimes
answering the same strategic question on a different topic (different safety foci,
different subgroups to characterise). Alternatively, a single phase II trial can address
multiple goals. We now cover each strategy and describe considerations as well as
some of the trial design features which are of increasing importance for each particular
strategy.
13.3.2 Potential registration
The rst strategic goal discussed is the accommodation of possible registration based
on strong positive early results. This could be considered a feasible strategic goal
based on pre-clinical data, phase I study results and the overall scientic and medical
rationale for development. The considerations in this section are primarily applicable
to situations when conditional or accelerated approval is based solely on phase
II or earlier trial data. Although this section primarily relates to trials designed for
registration, it also applies to registration from trials in which overwhelming evidence
of efcacy was observed although not planned for registration. Registration trials
designed to meet the usual requirement of ‘an adequate and well-controlled study’
are out of scope for this section; for example, we do not cover intended phase III
trials powered to detect clinically meaningful differences at the one-sided 2.5% level
of signicance.
13.3.2.1 Regulatory considerations
This strategic goal intersects regulatory and statistical considerations. It is critical
to remember that the regulatory environment is constantly changing and requires

Table 13.1 Roadmap for phase II: strategic situations.
Known at phase II planning Main goal of phase II study Major designs Major endpoints (most common)
Regimen likely to be active in
an unmet medical need
without approved or
available therapy, no major
safety issues
Determine potential for phase
II-based registration
(endpoint to confer clinical
benet)
Single-stage and two-stage
single-arm design
Randomised phase II
Overall tumour response rate
(e.g. durable CR)
PFS, OS (overwhelming
evidence of efcacy)
Phase I data available, dose
known but activity in
indication to be shown, not
suitable for phase II
registration, no major
safety issues
Determine biological activity
using a quick, intermediate
endpoint
Two-stage design, single arm
(Simon and Bayesian based)
Randomised phase II
Single-arm multinomial
Randomised two-stage multinomial
Randomised discontinuation
Growth modulation index (GMI)
(intra-patient PFS)
Overall tumour response rate
(CR/PR)
PFS, tumour markers, imaging
‘wet’ biomarker
Multinomial (CR/PR, SD, early
PD)
Duration of SD
GMI response rate (GMI ≥1.33)
Several potential regimens
(doses, schedules,
formulations, etc.) for
possible combination
development
Determine best regimen
(possibly a combination)
for subsequent randomised
controlled trial
Randomised Simon two stage
Randomised selection (Bayesian
and frequentist) with and without
control group
Randomised (combination add-on
vs. SOC)
Randomised modied factorial (no
control group)
Randomised factorial (add-on with
SOC)
Overall tumour response rate
PFS
Possibly pharmacodynamics
(continued)

Table 13.1 (Continued)
Known at phase II planning Main goal of phase II study Major designs Major endpoints (most common)
Regimen, indication known,
important to reduce risk in
phase III; not suitable for
phase II registration, no
major safety issues
Determine likelihood of
success in phase III using
suitable endpoint and
patient population in phase
II study
Randomised phase II
(Bayesian-based predictive
probability of success)
Phase III endpoints PFS, OS,
response rates
(haematological
malignancies)
Potential major safety
issue(s) representing
possible ‘no/go’
Better characterise safety
prole, especially major
safety issue(s), include
safety as co-primary
endpoint
Extension of two-stage designs
where safety and efcacy are
co-primary endpoints
Seamless phase I/II
Randomised phase II
Safety and efcacy (usually
overall tumour response rate)
Regimen, indication known
but not suitable for phase II
registration, no major
safety issues,
heterogeneous populations
dened by molecular
markers, histology, prior
treatment paradigms
Determine appropriate patient
subpopulation for phase III
trial
Adaptive targeted two-stage
design
‘Basket of indication’ design
Stratication and enrichment
designs
Overall tumour response rate
PFS
Pharmacodynamics
Entries given in Bold, used in Novartis trials, italics, used in other pharma, bold italics, academic trials or literature.
PERSPECTIVE FROM INDUSTRY 201
regular review during the overall clinical development process. For phase II trials
designed for registration, it is even more critical to review the most current regulatory
guidance and recent relevant regulatory events, and regulatory affairs specialists need
to be involved in design discussions.
Although regulatory approval based solely on phase II data still remains possible
in both the United States and European Union (EU), its applicability may now be
conned to indications for which there is no approved or available therapy and will
likely require demonstration of clear clinical benet and efcacy. One necessary but
not sufcient programme-related requirement is that the accelerated approval (phase
II) trial must be part of a well-conceived and comprehensive CDP. This CDP should
include at least two randomised phase III trials for the registered indication which
are planned as part of a post-marketing approval requirement. These phase III trials
should be enrolling patients at the time of accelerated approval. The conditional mar-
keting authorisation approval process in the EU is analogous to accelerated approval
in the United States. However, it must be renewed on an annual basis. This renewal
requires timely completion of studies demonstrating clinical benet. Health authority
meetings should be planned to conrm the adequacy of the registration plan including
post-marketing approval commitments. For example, registration using single-arm
trials based on objective tumour response rate may require evidence of strong pos-
itive benet/risk, require documentation of unmet medical need or represent a rare
indication.
If the planned phase II study for monotherapy or combination studies is intended
for potential registration, this should be conrmed with the health authorities prior
to the start of the study, for example, at the end of a phase I meeting. The brieng
documents should also contain a detailed description of the planned phase II trial
(detailed protocol synopsis), an overall CDP which includes concrete and viable
plans for post-approval conrmatory trial(s) and a discussion about the total number
of patients in the proposed submission to monitor safety (i.e. the size of the safety
database). At the present time, the protocol would need to be submitted for an FDA
Special Protocol Assessment (SPA), with content of the brieng documents similar
to those prepared to discuss phase II-based registration with the Committee for
Medicinal Products for Human Use (CHMP). They should provide evidence that the
planned development would meet the requisite statutory requirements for conditional
approval or approval under exceptional circumstances. For a single-arm trial, the
absolute minimum evidence could be, for example, clear documentation that the
investigated indication represents an unmet medical need (e.g. documentation that
patients had progressive disease under standard of care) or represents a rare indication
for which a randomised controlled trial is not feasible. Clearly, more evidence will
be warranted if there are questions from regulators or others who are weighing the
quality of the evidence.
While it is possible for a randomised controlled phase II trial to demonstrate
overwhelming evidence of efcacy, the standards are rather stringent (see Section
13.3.2.2). The screening randomised phase II trial should incorporate the same degree
of rigour as the planned phase III trials. Ideally, it should use the same endpoint and
patient population as the planned phase III trials.
202 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
13.3.2.2 Statistical considerations
The statistical considerations can be discussed in relation to the planned role of phase
II in the development strategy, that is, whether the phase II trials are specically
targeted for accelerated approval and/or conditional registration.
Trials planned for registration (accelerated approval and/or conditional regis-
tration) Regulatory and medical considerations generally drive the potential for
accelerated registration. The study designs commonly considered arise from the
unmet medical need/rare indication setting and include single-arm designs based on
objective tumour response, randomised uncontrolled phase II trials (e.g. two different
doses) and randomised controlled studies for rare diseases (if feasible). The single-
arm design may have one stage (if early termination for lack of efcacy is not a
concern because of phase I activity) or two stages (if early termination for futility is
a requirement).
Although statistical methodology is used to design the pivotal phase II study, drive
sample size considerations and provide operating characteristics, successful statistical
results may only be necessary and not sufcient for health authority approval. In the
uncontrolled setting, clinical considerations for the overall benet/risk are critical
considerations.
As the CHMP guidance (EMEA/357981/2005) stipulates, statistical support is
required to provide justication for ‘approval based on exceptional circumstances’.
Some of this is used to characterise the context of the design and indication; for
example, the sponsor’s inability to provide comprehensive efcacy and safety infor-
mation because the rarity of the indication must be established. Evaluation of sample
size requirements under various statistical scenarios may prove necessary to support
an exceptional circumstances claim. Relevant EMA guidance such as the CHMP
guidance on small populations, and the EMA workshop on methodological aspects
of clinical trials for efcacy evaluations in small populations, should be referenced
for possible alternative designs.
Trials not planned for registration but overwhelming evidence of efcacy
observed In addition to phase II trials planned for registration, it may be pos-
sible for a randomised controlled phase II trial designed for screening agents for
subsequent phase III studies to provide overwhelming evidence of efcacy that might
lead to registration. For example, if the primary efcacy endpoint and patient popu-
lation match what is planned for phase III, a strong positive outcome may render a
subsequent randomised controlled trial difcult to recruit and potentially unethical.
With respect to design characteristics, it has been suggested that the boundaries used
for interim monitoring of a randomised phase III trial be employed to determine
overwhelming evidence of efcacy from a randomised phase II trial. For example,
if there are one-quarter the number of events in the randomised phase II trial as
compared to a randomised phase III trial, then a one-sided p-value <0.00003 would
be required to claim efcacy, assuming O’Brien–Fleming boundaries are used for
interim monitoring at 25% of the information.
PERSPECTIVE FROM INDUSTRY 203
Implementation and design should address the exceptional circumstances upon
which the argument for registration is based. The impact on trial operations based
on different outcomes must be contemplated. The regulatory acceptance of a claim
based on a randomised controlled phase II trial not primarily or originally intended
for submission but in which overwhelming evidence of efcacy was observed might
be enhanced by pre-specifying this in the protocol. In this situation, consider provid-
ing a potential strategy for conrming an effect and for generating adequate safety
information.
13.3.3 Exploratory activity
The goal of exploratory activity trials (phase IIa) is to collect efcacy data to use in
planning for (or against) future randomised controlled trials. The phase IIa criteria
should be explicitly dened and reect the competitive environment and the appro-
priate level of evidence to decide on the merits of a subsequent larger randomised
controlled trial at a particular level of risk.
Risk calculations must, at least implicitly, incorporate expected returns. From a
pharmaceutical company perspective, the cost of not continuing development of a
‘good’ drug, in terms of expected future sales, might be much greater than continuing
with a bad drug. On one side, continuing development of a ‘bad’ drug results in
losses from the failed phase III trial as well as the lost opportunity of reallocating
resources for better drugs. On the other, potential prot from a new successful drug
could outweigh the potential losses from continuing with a useless or harmful drug;
this can encourage continuing development in the case of uncertainty.
If they exist, short-term endpoints which are well correlated with the primary
endpoint for registration should be considered as discussed in Chapter 2. This is still
true even if they are not causally related to the registration endpoint. This data can
help support a no-go decision (termination of development for the specic indication).
In addition, a successful phase IIa trial may use the results from these endpoints to
reassess the proposed future trial designs within the CDP.
Both single-arm and randomised trial designs (especially for combination agents)
may be used for phase IIa trials.
Bayesian and frequentist methods have been proposed for phase IIa trials. For
frequentist designs, the power of the pre-specied success criteria is key, since a
negative trial for the phase IIa endpoint may terminate an indication’s development.
As discussed above, the risks involved in termination of a development programme
require careful consideration. A greater type I error rate, increasing the tolerance for
allowing a poor development programme to continue, may be tolerated in this phase
IIa setting. For example, one-sided type I error rates as high as 20% have been used
for randomised phase IIa trials and one-sided type I error rates as high as 10% have
been used for internal single-arm phase IIa trials.
Bayesian methods can incorporate relevant historical information in a straight-
forward manner if it exists (Neuenschwander et al. 2010). Attention and preparation
should be given to prepare for concerns regarding the selection of historical data (prior
sensitivity) and operating characteristics under different scenarios, as previously
204 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
discussed in Chapter 2. However, reliable historical data for the phase IIa study might
not be available. If the trial relies on a functional imaging or molecular biomarker
or is limited to a targeted subpopulation, this information may not be available for
the standard of care. In other settings where historical information for the phase IIa
endpoint may be available, there may be concerns about inter-trial variability that
would indicate the need for a randomised phase IIa trial. Historical information is not
necessarily usable on a one-to-one substitution basis as a replacement for including
a control (active or placebo) arm in the study. In particular, a phase IIa trial for
a combination of a new drug added to a standard of care should be a randomised
comparison with the standard of care alone. One advantage to the Bayesian analysis
approach is that it can also provide estimates of the predictive probability of success
(PoS) in later trials. For further discussion of PoS refer to section 13.3.5.
Finally, we reiterate that data on potential phase III endpoints to support future
trial planning and programme-level decision-making should be collected even though
a short-term endpoint was chosen to design the phase IIa trial.
13.3.4 Regimen selection
Selection of a regimen for single-agent therapies tends to follow two strategies.
If there is sufcient evidence of activity in all proposed experimental regimens, a
randomised selection design without a control group may be used. Selection designs
try to determine the best regimen when several competing regimens are candidates for
a subsequent randomised controlled trial to study only the best regimen. For example,
there may be questions about the most appropriate dose, schedule, sequence and/or
formulation to compare with the standard of care. This aims to have a high chance
of selecting the best regimen (if it exists) for a subsequent randomised controlled
trial without requiring additional subjects in a placebo arm for comparison. The
other common design strategy is to incorporate historical or concurrent controls
in a traditional comparison design, potentially with the facility to drop ineffective
regimens early. Historical controls should be carefully considered for relevance, as
temporal changes in standard of care could increase bias, variance or both. Concurrent
controls may be required due to insufcient information on activity. Chapter 5 in this
book summarises additional design possibilities.
If there is a marked difference in response based on dose or regimen, selection
designs are straightforward for comparing regimes of a single compound. However,
it can be a valuable tool to select across compounds at the same stage of development.
In this instance, there are many challenges to implementing the rst strategy within
a company. In many pharmaceutical companies, project teams are usually set up to
develop individual drugs or drugs from the same family. Successful implementation
for cross-compound selection would require either close collaboration across teams
or an integrated indication team approach to development. This also applies to the
selection stage in the development of combination therapies
13.3.4.1 Adaptive designs and selection
Regimen selection during the phase II part of an adaptive phase II/III design is
one of the common adaptations cited by the proponents of the design. There are
PERSPECTIVE FROM INDUSTRY 205
many positive aspects for these designs which are found in the literature. To balance
out that view, we point out that the greatest obstacles to implementation of such
an adaptive phase II/III design are primarily logistic. For example, there must be
adequate rewalls in place to keep the project team blinded to the phase II results,
detailed pre-specied decision rules for selecting the best regimen to be chosen by
an independent group, usually a data monitoring committee (DMC), and one or more
meetings with the health authorities. The potential advantages from using an adaptive
phase II/III design with regimen selection during the phase II part should be weighed
against the intensive and time-consuming study start-up activities. There may also be
increased monitoring, more complex randomisation and potential issues concerning
operational bias. In addition, from a corporate perspective, the main decision-making
is allocated to an external DMC which reduces the exibility, in case of surprising
internal or external results which result in requiring major trial changes. As a result
phase II/III trials can have drawbacks when there is not so much existing knowledge
about the drug, target population and indication.
13.3.4.2 Dose selection for combination therapies
Combination therapies require additional critical consideration. Different agents are
often at different stages of development. Seldom do the agents have equal amounts
of prior information from internal clinical studies.
The intentional drug–drug interaction leads to considering a few subsequent
points. With respect to safety there may be a synergistic effect of the combination of
drugs leading to a higher incidence of severe acute and delayed toxicity relative to the
single-agent therapies, even if full doses were tolerable according to the individual
phase I studies. In addition, identifying predictive biomarkers for patient stratication
may be more challenging in the combination setting. For combinations where one or
more agent has been approved, the selection of the approved agent as a component
of the treatment should take into account the relative frequency of usage of this
agent globally as well as the pre-clinical and phase I evidence supporting the usage
of the combination with the investigational agent. For registration of a combination
therapy of two or more investigational agents the contribution to efcacy of each
component generally needs to be quantied to show evidence that any observed
clinical benet is not entirely attributable to only one of the two single agents.
Contributions of the components might be demonstrated in phase II based on a
surrogate or pharmacodynamic marker using a factorial design (U.S. Department of
Health and Human Services 2013).
Regimen selection in the setting of combination therapies with two or more
experiment compounds increases complexity. Three possible settings are (i) com-
bination of an investigational agent(s) with a standard of care; (ii) combination of
two (or more) investigational agents in an indication without a standard of care; and
(iii) combination of two (or more) investigational agents compared to a standard of
care. In all three settings we currently consider only randomised trial designs. Van
Glabbeke et al. (2002) claimed that ‘non-randomised Phase II studies of drug com-
binations are often meaningless, sometimes misleading’. They gave two examples
206 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
where use of non-randomised phase II combination studies may have led to mislead-
ing development. The rst was a study on dose-intensive chemotherapeutic regimens
for intermediate- and/or high-grade non-Hodgkin’s lymphoma. Here, ve subsequent
randomised trials versus a CHOP (or CHOP-like control) all showed no objective
benet but greater toxicity and toxic death rates relative to the standard arm. The
second was an autologous bone marrow transplantation (BMT) for breast cancer. In
this case, a denitive randomised phase III trial had accrual problems because of the
reports of uncontrolled phase II trials.
13.3.5 Phase II to support predicting success in phase III
Predicting success in phase III is an important strategic consideration for the drug
industry. In general, despite all of the introduced improvements in clinical develop-
ment, the rate of phase III failures is still high, and it is common for management to
be continually surprised by this. One of the reasons for this strategic goal is to manage
expectations on what will be obtained from phase III trials, and therefore using pre-
vious data to predict the likelihood of ‘success’ is very appealing. If there is still a lot
of uncertainty following phase II, then management must be aware of this so they can
make appropriate planning decisions. At the end of the day companies can live with
risk of ‘failure’ if it is well managed and spread appropriately across the portfolio.
Prospective thinking about the future success of a trial is an important part
of good decision-making. Considerations of probability of success (PoS) comprise
qualitative as well as quantitative aspects. There are various important qualitative
considerations, such as the choice of endpoint, patient population, disease setting
and dosing schedule. In order to be reasonably well calibrated, calculations of the
PoS should include all relevant sources of uncertainty. These comprise uncertainties
regarding the future data, the true underlying parameter of interest (e.g. a progression-
free survival (PFS) hazard ratio), between-trial heterogeneity and the relationship
between different endpoints in phases II and III.
From a predictive point of view, the most informative phase II design is a ran-
domised design with the same endpoint (PFS or overall survival (OS)) as in phase III.
For such a design, and a reasonably promising effect estimate in phase II (e.g. HR of
0.7 to 0.75), the PoS in phase III is approximately 60–70%. If a different endpoint is
considered for phase II, collecting information on the phase III endpoint, if feasible,
will be important. In summary,
∙not acknowledging relevant uncertainties leads to an overly optimistic estimate
for the PoS in phase III;
∙the largest uncertainties should be accounted for since they have the largest
impact;
∙a good outcome in phase II does not necessarily lead to higher probabilities of
success, in particular if between-trial heterogeneity is large.
A good quantitative estimate for the PoS is an important input for decision-
making. For example, in a multi-stage trial this probability may inform decisions at
PERSPECTIVE FROM INDUSTRY 207
interim to stop the trial early. Or, at the end of a phase II trial, the decision to go to
phase III may be easier if the chance to be successful is reasonably high. However,
formal quantications of the PoS have not been used systematically in the past, for
various reasons:
1. An assessment of the PoS in a future trial requires an understanding of future
data, that is, a prediction for the data in the upcoming trial.
2. The inherent difculty to make predictions. This is due to the fact that extrap-
olations are required from current data to future data, which are based on
assumptions that are essentially unveriable at the time when the prediction is
made. The standard assumption is that the future will be identical to the past.
To relax this fairly strong assumption means to introduce other assumptions
that may be equally difcult to justify.
3. The need to think (before starting phase II) about the design of the phase III
trial.
4. Technical difculties that are of a purely statistical or computational nature.
Points 1 and 2 above are scientically challenging. Predictions are one variant of
the problem of induction (Hacking 2001), one of the most difcult problems in the
empirical sciences. Predictions are inductive in the sense that there is no logical (or
deductive) way that allows to reliably extrapolate (1) from partial to full information
or (2) from the past to the future. The statistical/probabilistic approach to induction
provides a quantitative framework that combines mathematical rigour with good
judgement, the latter depending on the given context. To prospectively think about
upcoming phase III trials, point 3, can be quite a challenge too, as it requires teams to
think beyond phase II and may imply the involvement of health authorities at a fairly
early stage.
Predictive problems in clinical trials arise in different ways:
1. The least controversial prediction problem is within-trial prediction for the
same endpoint. This type of prediction may be of relevance at an interim stage
of a phase IIa study. For example, in a multi-stage single-arm phase II trial,
a prediction from the data on objective response rate (ORR) available at the
rst stage can be used to calculate the predictive distribution for the remaining
data, from which the PoS for phase II can be obtained. This probability can
be used to stop the trial, for futility and/or early success. Note that within-trial
prediction is relatively straightforward only under the assumption that there
is homogeneity over the different stages of the trial with regard to all relevant
factors that may inuence the outcome of the trial.
2. Between-trial prediction for the same endpoint is more difcult, because
(in its simplest form) it critically depends on the assumption that all relevant
factors that may inuence the outcome are equal (or at least sufciently similar)
for both trials. For example, in a randomised phase II trial using a time-to-event
208 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
endpoint (e.g. a PFS hazard ratio), the data at the end of the trial can be used
to predict data for an upcoming phase III trial of given design.
3. The quality of between-endpoint prediction depends on how predictive one
endpoint is for the other. For example, PFS data may be collected in a ran-
domised phase II trial, but OS will be used in phase III. Clearly, a proper
prediction for PoS in phase III depends on a good understanding of the degree
of correlation between PFS and OS. Therefore lack of knowledge between
the endpoints adds to the uncertainty about the prediction and increases the
challenges of planning across the portfolio, since risks of phase III failure are
less known.
The different types of extrapolations may arise in combination. For example, in a
phase II study with PFS as the primary endpoint, some limited information about OS
may be available. For this situation, between-trial (for PFS) and between-trial as well
as between-endpoint considerations (for OS) will inuence the PoS in phase III. The
level of uncertainty due to different endpoints depends also on the disease setting.
Prediction of future results in the context of clinical trials is an important use of
early phase data and, as noted in this section, requires some attention to detail.
13.3.6 Phase II safety trials
Historically, within the drug industry, trials set up to specically look at some aspect
of safety have been relatively uncommon and have often been motivated as a result
of health authority concerns. The evolving regulatory and reimbursement landscape
has changed the playing eld, and this drives development towards a situation where
safety and specic risks are assessed in a proactive ongoing basis. It is assumed that
the frequency of such studies will likely increase.
Although safety information is constantly monitored in all trials, sample size
determination is usually based upon efcacy, and formal early stopping rules related
to safety issues usually are not always clearly specied in phase II. Safety should be
investigated as a co-primary endpoint when the study drug shows some preliminary
efcacy but major safety concerns in the early stage of the development, or if the
experimental treatment has similar efcacy as the standard but may have a substantial
improvement of safety.
There are many advantages of collecting and studying safety data in phase II trials.
For example, the safety data from phase II trials are collected in a more specic and
controlled setting. Safety proles in the targeted population(s) can provide further
insight into the safety and efcacy relationship of the studied drug. Another example
is that long-term toxicities or safety trends can be collected and studied. Phase I
oncology trials usually have short duration and focus on the toxicities occurred in
the rst cycle in order to determine the maximum tolerated dose (MTD), and further
recommended phase II dose. Finally, a control arm can be included to compare the
safety prole of an investigational drug with the control of interest. Most of the
time, the control could be a standard of care that is available to the general patient
population.
PERSPECTIVE FROM INDUSTRY 209
The designs with both safety and efcacy as co-primary endpoints include, but
are not limited to, Bryant and Day (1995), Conaway and Petroni (1995) and Thall and
Cheng (2001) are discussed in more detail in Chapter 6. Additionally Hoering et al.
(2011) consider this in the phase I/II setting. One practical problem with many of
these designs is that dening toxicity as a binary variable can be clinically challenging
when several toxicities of various grades are of interest.
13.3.7 Prospective identication of target populations
The increasing awareness that cancers are actually very heterogeneous has driven the
development of targeted therapies which are effective in clearly dened and diag-
nosed populations. Although the number of potential patients may be reduced, this
possible income loss can be balanced out by both a more powerful and stronger
treatment effect (smaller and faster trials) and the likelihood of possible earlier
approval where the additional time on the market can lead to increased income.
A related challenge for pharmaceutical companies is that in many countries reim-
bursement must be justied, in that the payers require evidence for the population
which will benet most. Therefore, from a drug company point of view there is a
nancial imperative to ensure that the right set of patients are treated and that an
appropriate level of evidence of efcacy is provided to the health authorities in this
population.
Heterogeneity in treatment outcome is a common phenomenon in phase II clinical
trials, perhaps more so than in phase III. Sources of heterogeneity of clinical outcome
in response to an experimental treatment in phase II experiments can often be antic-
ipated. The use of biomarkers can be one attempt to prospectively account for and
control the variation. Without successful accommodation, the impact of unaccounted
heterogeneity can lead to biased inferences. This can result in the early rejection of
effective therapeutics or improper planning and failure in phase III experiments.
Two main design strategies, stratication and enrichment, are used (sometimes
together) to prospectively account for such heterogeneity, as has previously been
introduced in Chapter 2. First, enrichment strategies limit trial enrolment to patients
with specic marker proles. These should be used carefully and only in the presence
of substantial contextual evidence that the study drug will be ineffective in the
excluded patient subgroups. Second, stratication strategies enrol all comers but
assess treatment effects separately in mutually exclusive subgroups. Such studies
should be sized adequately to provide valid inferences about the effect (often benet–
risk) within each subgroup. For both of these approaches, adaptive and Bayesian
variations of these strategies may be more informative and allow greater exibility,
although requiring considerable upfront investment for planning and implementation.
The choice of a phase II design depends on the nature of the marker(s) likely
to affect treatment outcome in any given setting. Markers (single traits or signatures
of traits) that are informative for clinical outcome can be broadly categorised as
predictive, which are those that separate different populations in terms of the clinical
outcome of interest in response to a particular treatment; or prognostic, those that
separate different populations in terms of the clinical outcome of interest irrespective
210 A PRACTICAL GUIDE TO DESIGNING PHASE II TRIALS IN ONCOLOGY
of the treatment; or predictive–prognostic, when both predictive and prognostic effects
are observed.
Traditional approaches may be inadequate for a number of reasons. The main
issue with traditional ‘all-comers’ designs is that they exercise no control on the
subgroup composition of the set of patients studied. When the studied treatment is
effective only in selected subgroups, the measured treatment effect is diluted and can
lead to misleading conclusions and costly errors in development. This is particularly
true for targeted agents.
For multiple reasons it is often not possible to retrospectively calculate accurate
estimates of treatment effects within subgroups of interest (e.g. patients with a certain
biomarker-positive status). Sample sizes of phase II cancer trials are often fairly small,
so that there may be too few patients in a given subgroup (e.g. rare mutations) to draw
reliable inference. Furthermore, without prospective planning important predictive
traits may be confounded with other predictive/prognostic traits.
In comparative assessment of treatment benet, randomisation can be used to
achieve balance between treatment arms. However, in the case of predictive mark-
ers, without appropriate stratication there may still be important imbalances and
confounding of effects due to small sample sizes, and the trial may therefore yield
insufcient information to identify important subgroups.
For genetic and molecular markers, it is assumed that assays are available and have
reasonable turnaround time to allow each patient’s marker status to be established
upfront (i.e. before enrolment or start of treatment). Denition of indications and
hence designs for identifying indications are based on classication of biomarker
status into a few discrete categories (typically a dichotomy). Thus, while biomarker
status may be continuous, in most cases appropriate thresholds for classication need
to be established prior to implementing the proposed strategies.
The relative merits of the proposed strategies need to be assessed at the outset and
can be measured in terms of numbers of patients, time to completion of the trial or the
cost of the trial. These merits are impacted by factors including the relative treatment
effect in the biomarker-dened subgroups, the prevalence of these subgroups and the
accuracy and cost of the diagnostic and treatment. Phase II designs which may be
appropriate in the context of targeted subgroups are outlined in Chapter 7.
As a nal note, when indications are based on levels of predictive biomarkers,
co-development of reliable diagnostics for patient selection should start early. Failure
to start early enough will increase risk due to the need to bridge between a clinical
trial assay and a clinically and analytically validated diagnostic system.
13.4 Discussion
This chapter is intended to provide a strategic overview of programme-level decision-
making and the need to tailor phase II designs according to the CDP. It is also intended
to complement the other chapters in this book. By rening the strategic boundaries of
what the trial should support, and then working to select the best of the implementable
designs, this will result in more efcient trials which have a better chance to provide
PERSPECTIVE FROM INDUSTRY 211
answers. Sometimes these trials will be shorter or smaller, but hopefully they will
always be more decisive trials.
Phase II clinical trials play a critical role in understanding better how the com-
pound can be used to maintain or improve the health of a patient. During times of
rapid discovery of possible therapies, phase II trials can sometimes be viewed neg-
atively, as an attempt to correct early mistaken decisions about the indicated use of
the compound. During times when few compounds are being discovered, they can be
seen as an opportunity and means to patiently increase the probability of nding a
commercially viable and protable niche for the compound. The challenge in under-
standing the huge diversity of designs, along with the ever-evolving commercial and
medical landscape, makes the approach for proper selection interesting and difcult.
Disclaimer: The opinions expressed in this chapter are solely those of the authors
and not necessarily those of Novartis. Novartis does not guarantee the accuracy or
reliability of the information provided herein.

References
Adams, R.A., Meade, A.M., Seymour, M.T., Wilson, R.H., Madi, A., Fisher, D., Kenny,
S.L., Kay, E., Hodgkinson, E., Pope, M., Rogers, P., Wasan, H., Falk, S., Gollins,
S., Hickish, T., Bessell, E.M., Propper, D., Kennedy, M.J., Kaplan, R., Maughan, T.S.
and MRC COIN Trial Investigators 2011. Intermittent versus continuous oxaliplatin and
uoropyrimidine combination chemotherapy for rst-line treatment of advanced colorectal
cancer: results of the randomised phase 3 MRC COIN Trial. Lancet Oncology, 12(7),
642–653.
Adjei, A.A., Christian, M. and Ivy, P. 2009. Novel designs and end points for phase II clinical
trials. Clinical Cancer Research, 15(6), 1866–1872.
A’Hern, R.P. 2001. Sample size tables for exact single-stage phase II designs. Statistics in
Medicine, 20(6), 859–866.
A’Hern, R.P. 2004. Widening eligibility to phase II trials: constant arcsine difference phase II
trials. Controlled Clinical Trials, 25(3), 251–264.
An, M.W., Mandrekar, S.J. and Sargent, D.J. 2012. A 2-stage phase II design with direct
assignment option in stage II for initial marker validation. Clinical Cancer Research, 18(16),
4225–4233.
Anderson, K.C., Kyle, R.A., Rajkumar, S.V., Stewart, A.K., Weber, D. and Richardson, P.
2007. Clinically relevant end points and new drug approvals for myeloma. Leukemia, 22(2),
231–239.
Anderson, K.C., Pazdur, R. and Farrell, A.T. 2005. Development of effective new treatments
for multiple myeloma. Journal of Clinical Oncology, 23(28), 7207–7211.
Atkinson, A.J., Colburn, W.A., DeGruttola, V.G., DeMets, D.L., Downing, G.J., Hoth, D.F.,
Oates, J.A., Peck, C.C., Schooley, R.T., Spilker, B.A., Woodcock, J. and Zeger, S.L.
2001. Biomarkers and surrogate endpoints: preferred denitions and conceptual framework.
Clinincal Pharmacology and Therapeutics, 69(3), 89–95.
Ayanlowo, A.O. and Redden, D.T. 2007. Stochastically curtailed phase II clinical trials.
Statistics in Medicine, 26(7), 1462–1472.
Azzoli, C.G., Baker, S. Jr, Temin, S., Pao, W., Aliff, T., Brahmer, J., Johnson, D.H.,
Laskin, J.L., Masters, G., Milton, D., Nordquist, L., Pster, D.G., Piantadosi, S.,
Schiller, J.H., Smith, R., Smith, T.J., Strawn, J.R., Trent, D., Giaccone, G. and American
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
214 REFERENCES
Society of Clinical Oncology 2009. American Society of Clinical Oncology Clinical Practice
Guideline update on chemotherapy for stage IV non-small-cell lung cancer. Journal of
Clinical Oncology, 27(36), 6251–6266.
Banerjee, A. and Tsiatis, A.A. 2006. Adaptive two-stage designs in phase II clinical trials.
Statistics in Medicine, 25(19), 3382–3395.
Bauer, M., Bauer, P. and Budde, M. 1998. A simulation program for adaptive two stage
designs. Computational Statistics & Data Analysis, 26, 351–371.
Bauer, P. and Kieser, M. 1999. Combining different phases in the development of medical
treatments within a single trial. Statistics in Medicine, 18(14), 1833–1848.
Bellissant, E., Benichou, J. and Chastang, C. 1990. Application of the triangular test to phase
II cancer clinical trials. Statistics in Medicine, 9(8), 907–917.
Belvedere, O., Follador, A., Rossetto, C., Merlo, V., Defferrari, C., Sibau, A.M., Aita, M.,
Dal Bello, M.G., Meduri, S., Gaiardo, M., Fasola, G. and Grossi, F. 2011. A randomised
phase II study of docetaxel/oxaliplatin and docetaxel in patients with previously treated
non-small cell lung cancer: an Alpe-Adria Thoracic Oncology Multidisciplinary group trial
(ATOM 019). European Journal of Cancer, 47(11), 1653–1659.
Bokemeyer, C., Bondarenko, I., Makhson, A., Hartmann, J.T., Aparicio, J., de Braud, F.,
Donea, S., Ludwig, H., Schuch, G., Stroh, C., Loos, A.H., Zubel, A. and Koralewski, P.
2009. Fluorouracil, leucovorin, and oxaliplatin with and without cetuximab in the rst-line
treatment of metastatic colorectal cancer. Journal of Clinical Oncology, 27(5), 663–671.
Booth, C.M., Calvert, A.H., Giaccone, G., Lobbezoo, M.W., Eisenhauer, E.A. and Seymour,
L.K. 2008. Design and conduct of phase II studies of targeted anticancer therapy: recom-
mendations from the task force on methodology for the development of innovative cancer
therapies (MDICT). European Journal of Cancer, 44(1), 25–29.
Bretz, F., Schmidli, H., Konig, F., Racine, A. and Maurer, W. 2006. Conrmatory seamless
phase II/III clinical trials with hypotheses selection at interim: general concepts. Biometrical
Journal, 48(4), 623–634.
Brown, S.R., Gregory, W.M., Twelves, C.J., Buyse, M., Collinson, F., Parmar, M., Seymour,
M.T. and Brown, J.M. 2011. Designing phase II trials in cancer: a systematic review and
guidance. British Journal of Cancer, 105(2), 194–199.
Bryant, J. and Day, R. 1995. Incorporating toxicity considerations into the design of two-stage
phase II clinical trials. Biometrics, 51(4), 1372–1383.
Burzykowski, T., Buyse, M., Piccart-Gebhart, M.J., Sledge, G., Carmichael, J., Luck,
H.J., Mackey, J.R., Nabholtz, J.M., Paridaens, R., Biganzoli, L., Jassem, J., Bontenbal,
M., Bonneterre, J., Chan, S., Basaran, G.A. and Therasse, P. 2008. Evaluation of tumor
response, disease control, progression-free survival, and time to progression as potential
surrogate end points in metastatic breast cancer. Journal of Clinical Oncology, 26(12),
1987–1992.
Buyse, M. 2000. Randomized designs for early trials of new cancer treatments – an overview.
Drug Information Journal, 34(2) 387–396.
Buyse, M., Burzykowski, T., Carroll, K., Michiels, S., Sargent, D.J., Miller, L.L., Elfring,
G.L., Pignon, J.P. and Piedbois, P. 2007. Progression-free survival is a surrogate for survival
in advanced colorectal cancer. Journal of Clinical Oncology, 25(33), 5218–5224.
Buyse, M., Michiels, S., Sargent, D.J., Grothey, A., Matheson, A. and de Gramont, A. 2011.
Integrating biomarkers in clinical trials. Expert Review of Molecular Diagnostics, 11(2),
171–182.
REFERENCES 215
Buyse, M., Molenberghs, G., Burzykowski, T., Renard, D. and Geys, H. 2000. The validation
of surrogate endpoints in meta-analyses of randomized experiments. Biostatistics, 1(1), 49–
67.
Cannistra, S.A. 2009. Phase II trials in Journal of Clinical Oncology. Journal of Clinical
Oncology, 27(19), 3073–3076.
Capra, W.B. 2004. Comparing the power of the discontinuation design to that of the classic
randomized design on time-to-event endpoints. Controlled Clinical Trials, 25(2), 168–177.
Case, L.D. and Morgan, T.M. 2003. Design of phase II cancer trials evaluating survival
probabilities. BMC Medical Research Methodology, 3, 1–12.
Chang, M.N., Devidas, M. and Anderson, J. 2007. One- and two-stage designs for phase II
window studies. Statistics in Medicine, 26(13), 2604–2614.
Chang, M.N., Shuster, J.J. and Kepner, J.L. 1999. Group sequential designs for phase II trials
with historical controls. Controlled Clinical Trials, 20(4), 353–364.
Chang, M.N., Shuster, J.J. and Kepner, J.L. 2004. Sample sizes based on exact unconditional
tests for phase II clinical trials with historical controls. Journal of Biopharmaceutical
Statistics, 14(1), 189–200.
Chang, M.N., Therneau, T.M., Wieand, H.S. and Cha, S.S. 1987. Designs for group sequential
phase II clinical trials. Biometrics, 43(4), 865–874.
Chen, C. and Beckman, R.A. 2009. Optimal cost-effective designs of phase II proof of
concept trials and associated go-no go decisions. Journal of Biopharmaceutical Statistics,
19(3), 424–436.
Chen, C. and Chaloner, K. 2006. A Bayesian stopping rule for a single arm study: with a case
study of stem cell transplantation. Statistics in Medicine, 25(17), 2956–2966.
Chen, K. and Shan, M. 2008. Optimal and minimax three-stage designs for phase II oncology
clinical trials. Contemporary Clinical Trials, 29(1), 32–41.
Chen, S., Soong, S.J. and Wheeler, R.H. 1994. An efcient multiple-stage procedure for
phase II clinical trials that have high response rate objectives. Controlled Clinical Trials,
15(4), 277–283.
Chen, T.T. 1997. Optimal three-stage designs for phase II cancer clinical trials. Statistics in
Medicine, 16(23), 2701–2711.
Chen, T.T. and Ng, T.H. 1998. Optimal exible designs in phase II clinical trials. Statistics in
Medicine, 17(20), 2301–2312.
Cheung, Y.K. 2009. Selecting promising treatments in randomized phase II cancer trials with
an active control. Journal of Biopharmaceutical Statistics, 19(3), 494–508.
Cheung, Y.K. and Thall, P.F. 2002. Monitoring the rates of composite events with censored
data in phase II clinical trials. Biometrics, 58(1), 89–97.
Chi, Y. and Chen, C.M. 2008. Curtailed two-stage designs in phase II clinical trials. Statistics
in Medicine, 27(29), 6175–6189.
Chow, S.C. and Tu, Y.H. 2008. On two-stage seamless adaptive design in clinical trials.
Journal of the Formosan Medical Association, 107(Suppl 12), 52–60.
Collette, L., Burzykowski, T., Carroll, K.J., Newling, D., Morris, T. and Schroder, F.H. 2005.
Is prostate-specic antigen a valid surrogate end point for survival in hormonally treated
patients with metastatic prostate cancer? Joint Research of the European Organisation for
Research and Treatment of Cancer, the Limburgs Universitair Centrum, and AstraZeneca
Pharmaceuticals. Journal of Clinical Oncology, 23(25), 6139–6148.
216 REFERENCES
Collier, R. 2009. Drug development cost estimates hard to swallow. Canadian Medical Asso-
ciation Journal, 180(3), 279–280.
Committee for Medicinal Products for Human Use (CHMP) 2005. Guideline on Procedures
for the Granting of a Marketing Authorisation Under Exceptional Circumstances, pursuant
to Article 14 (8) of Regulation (EC) NO 726/2004 (EMEA/357981/2005).
Conaway, M.R. and Petroni, G.R. 1995. Bivariate sequential designs for phase II trials.
Biometrics, 51(2), 656–664.
Conaway, M.R. and Petroni, G.R. 1996. Designs for phase II trials allowing for a trade-off
between response and toxicity. Biometrics, 52(4), 1375–1386.
Cronin, K.A., Freedman, L.S., Lieberman, R., Weiss, H.L., Beenken, S.W. and Kelloff, G.J.
1999. Bayesian monitoring of phase II trials in cancer chemoprevention. Journal of Clinical
Epidemiology, 52(8), 705–711.
de Boo, T.M. and Zielhuis, G.A. 2004. Minimization of sample size when comparing two
small probabilities in a non-inferiority safety trial. Statistics in Medicine, 23(11), 1683–
1699.
Dhani, N., Tu, D., Sargent, D.J., Seymour, L. and Moore, M.J. 2009. Alternate endpoints
for screening phase II studies. Clinical Cancer Research, 15(6), 1873–1882.
DiMasi, J.A. and Grabowski, H.G. 2007. Economics of new oncology drug development.
Journal of Clinical Oncology, 25(2), 209–216.
Eisenhauer, E.A., Therasse, P., Bogaerts, J., Schwartz, L.H., Sargent, D., Ford, R., Dancey,
J., Arbuck, S., Gwyther, S., Mooney, M., Rubinstein, L., Shankar, L., Dodd, L., Kaplan,
R., Lacombe, D. and Verweij, J. 2009. New response evaluation criteria in solid tumours:
revised RECIST guideline (version 1.1). European Journal of Cancer, 45(2), 228–247.
Ensign, L.G., Gehan, E.A., Kamen, D.S. and Thall, P.F. 1994. An optimal three-stage design
for phase II clinical trials. Statistics in Medicine, 13(17), 1727–1736.
Facon, T., Mary, J.Y., Hulin, C., Benboubker, L., Attal, M., Pegourie, B., Renaud,
M., Harousseau, J.L., Guillerm, G., Chaleteix, C., Dib, M., Voillat, L., Maisonneuve,
H., Troncy, J., Dorvaux, V., Monconduit, M., Martin, C., Casassus, P., Jaubert, J.,
Jardel, H., Doyen, C., Kolb, B., Anglaret, B., Grosbois, B., Yakoub-Agha, I., Mathiot,
C., Avet-Loiseau, H. and Intergroupe Francophone du My´
elome 2007. Melphalan and
prednisone plus thalidomide versus melphalan and prednisone alone or reduced-intensity
autologous stem cell transplantation in elderly patients with multiple myeloma (IFM 99-06):
a randomised trial. Lancet, 370(9594), 1209–1218.
Fazzari, M., Heller, G. and Scher, H.I. 2000. The phase II/III transition. Toward the proof of
efcacy in cancer clinical trials. Controlled Clinical Trials, 21(4), 360–368.
Fisher, R.A. 1932. Statistical Methods for Research Workers, 4th edn. Oliver and Boyd,
Edinburgh.
Fleming, T.R. 1982. One-sample multiple testing procedure for phase II clinical trials. Bio-
metrics, 38, 143–151.
Fossella, F.V., DeVore, R., Kerr, R.N., Crawford, J., Natale, R.R., Dunphy, F., Kalman, L.,
Miller, V., Lee, J.S., Moore, M., Gandara, D., Karp, D., Vokes, E., Kris, M., Kim, Y.,
Gamza, F. and Hammershaimb, L. 2000. Randomized phase III trial of docetaxel versus
vinorelbine or ifosfamide in patients with advanced non-small-cell lung cancer previously
treated with platinum-containing chemotherapy regimens. The TAX 320 Non-Small Cell
Lung Cancer Study Group. [Erratum appears in Journal of Clinical Oncology 2004;22(1),
209]. Journal of Clinical Oncology, 18(12), 2354–2362.
REFERENCES 217
Freedland, S.J., Humphreys, E.B. and Mangold, L.A. 2005. Risk of prostate cancer-specic
mortality following biochemical recurrence after radical prostatectomy. Journal of American
Medical Association, 294(4), 433–439.
Freidlin, B., Dancey, J., Korn, E.L., Zee, B. and Eisenhauer, E. 2002. Multinomial phase II
trial designs. Journal of Clinical Oncology, 20(2), 599.
Freidlin, B. and Korn, E.L. 2013. Borrowing information across subgroups in phase II trials:
is it useful? Clinical Cancer Research, 19(6), 1326–1334.
Freidlin, B., McShane, L.M., Polley, M.Y. and Korn, E.L. 2012. Randomized phase II trial
designs with biomarkers. Journal of Clinical Oncology, 30(26), 3304–3309.
Freidlin, B. and Simon, R. 2005. Evaluation of randomized discontinuation design. Journal
of Clinical Oncology, 23(22), 5094–5098.
Gajewski, B.J. and Mayo, M.S. 2006. Bayesian sample size calculations in phase II clinical
trials using a mixture of informative priors. Statistics in Medicine, 25(15), 2554–2566.
Gehan, E.A. 1961. The determination of the number of patients required in a preliminary and
a follow-up trial of a new chemotherapeutic agent. Journal of Chronic Diseases, 13(4),
346–353.
Giaccone, G., Herbst, R.S., Manegold, C., Scagliotti, G., Rosell, R., Miller, V., Natale,
R.B., Schiller, J.H., von Pawel, J., Pluzanska, A., Gatzemeier, U., Grous, J., Ochs, J.S.,
Averbuch, S.D., Wolf, M.K., Rennie, P., Fandi, A. and Johnson, D.H. 2004. Getinib
in combination with gemcitabine and cisplatin in advanced non-small-cell lung cancer: a
phase III trial – INTACT 1. Journal of Clinical Oncology, 22(5), 777–784.
Gofn, J.R. and Tu, D. 2008. Phase II stopping rules that employ response rates and early
progression. Journal of Clinical Oncology, 26(22), 3715–3720.
Goldman, A.I. 1987. Issues in designing sequential stopping rules for monitoring side effects
in clinical trials. Controlled Clinical Trials, 8, 327–337.
Goldman, A.I. and Hannan, P.J. 2001. Optimal continuous sequential boundaries for monitor-
ing toxicity in clinical trials: a restricted search algorithm. Statistics in Medicine, 20(11),
1575–1589.
Green, S.J. and Dahlberg, S. 1992. Planned versus attained design in phase II clinical trials.
Statistics in Medicine, 11(7), 853–862.
Hacking, I. 2001. An Introduction to Probability and Inductive Logic. Cambridge University
Press.
Hanfelt, J.J., Slack, R.S. and Gehan, E.A. 1999. A modication of Simon’s optimal design for
phase II trials when the criterion is median sample size. Controlled Clinical Trials, 20(6),
555–566.
Hanna, N., Shepherd, F.A., Fossella, F.V., Pereira, J.R., De Marinis, F., von Pawel, J.,
Gatzemeier, U., Tsao, T.C., Pless, M., Muller, T., Lim, H.L., Desch, C., Szondy, K.,
Gervais, R., Shaharyar, Manegold, C., Paul, S., Paoletti, P., Einhorn, L. and Bunn, P.A.,
Jr 2004. Randomized phase III trial of pemetrexed versus docetaxel in patients with non-
small-cell lung cancer previously treated with chemotherapy. Journal of Clinical Oncology,
22(9), 1589–1597.
Heitjan, D.F. 1997. Bayesian interim analysis of phase II cancer clinical trials. Statistics in
Medicine, 16(16), 1791–1802.
Herbst, R.S., Giaccone, G., Schiller, J.H., Natale, R.B., Miller, V., Manegold, C., Scagliotti,
G., Rosell, R., Oliff, I., Reeves, J.A., Wolf, M.K., Krebs, A.D., Averbuch, S.D., Ochs,
J.S., Grous, J., Fandi, A. and Johnson, D.H. 2004. Getinib in combination with paclitaxel
218 REFERENCES
and carboplatin in advanced non-small-cell lung cancer: a phase III trial – INTACT 2.
Journal of Clinical Oncology, 22(5), 785–794.
Herndon, J.E. 1998. A design alternative for two-stage, phase II, multicenter cancer clinical
trials. Controlled Clinical Trials, 19(5), 440–450.
Herson, J. 1979. Predictive probability early termination plans for phase II clinical trials.
Biometrics, 35(4), 775–783.
Herson, J. and Carter, S.K. 1986. Calibrated phase II clinical trials in oncology. Statistics in
Medicine, 5(5), 441–447.
Hoering, A., Leblanc, M. and Crowley, J. 2011. Seamless phase I–II trial design for assessing
toxicity and efcacy for targeted agents. Clinical Cancer Research, 17(4), 640–646.
Hong, S. and Wang, Y. 2007. A three-outcome design for randomized comparative phase II
clinical trials. Statistics in Medicine, 26(19), 3525–3534.
ICH Expert Working Group 1994. International Conference on Harmonisation, Guideline on
Dose-Response Information to Support Drug Registration E4.
ICH Expert Working Group 1997. International Conference on Harmonisation, Guideline on
General Considerations for Clinical Trials E8.
Ivanova, A., Qaqish, B.F. and Schell, M.J. 2005. Continuous toxicity monitoring in phase II
trials in oncology. Biometrics, 61(2), 540–545.
Jenkins, M., Stone, A. and Jennison, C. 2011. An adaptive seamless phase II/III design for
oncology trials with subpopulation selection using correlated survival endpoints. Pharma-
ceutical Statistics, 10(4), 347–356.
Jin, H. 2007. Alternative designs of phase II trials considering response and toxicity. Contem-
porary Clinical Trials, 28(4), 525–531.
Johnson, V.E. and Cook, J.D. 2009. Bayesian design of single-arm phase II clinical trials with
continuous monitoring. Clinical Trials, 6(3), 217–226.
Jones, C.L. and Holmgren, E. 2007. An adaptive Simon two-stage design for phase 2 studies
of targeted therapies. Contemporary Clinical Trials, 28(5), 654–661.
Jung, S.H. 2008. Randomized phase II trials with a prospective control. Statistics in Medicine,
27(4), 568–583.
Jung, S.H. and George, S.L. 2009. Between-arm comparisons in randomized phase II trials.
Journal of Biopharmaceutical Statistics, 19(3), 456–468.
Jung, S.H., Lee, T., Kim, K. and George, S.L. 2004. Admissible two-stage designs for phase
II cancer clinical trials. Statistics in Medicine, 23(4), 561–569.
Karrison, T.G., Maitland, M.L., Stadler, W.M. and Ratain, M.J. 2007. Design of phase II
cancer trials using a continuous endpoint of change in tumor size: application to a study
of sorafenib and erlotinib in non small-cell lung cancer. Journal of the National Cancer
Institute, 99(19), 1455–1461.
Kelly, P.J., Stallard, N. and Todd, S. 2005. An adaptive group sequential design for phase
II/III clinical trials that select a single treatment from several. Journal of Biopharmaceutical
Statistics, 15(4), 641–658.
Kocherginsky, M., Cohen, E.E. and Karrison, T. 2009. Design of phase II cancer trials for
evaluation of cytostatic/cytotoxic agents. Journal of Biopharmaceutical Statistics, 19(3),
524–529.
Kopec, J.A., Abrahamowicz, M. and Esdaile, J.M. 1993. Randomized discontinuation trials:
utility and efciency. Journal of Clinical Epidemiology, 46(9), 959–971.
REFERENCES 219
Korn, E.L., Liu, P.Y., Lee, S.J., Chapman, J.A., Niedzwiecki, D., Suman, V.J., Moon, J.,
Sondak, V.K., Atkins, M.B., Eisenhauer, E.A., Parulekar, W., Markovic, S.N., Saxman, S.
and Kirkwood, J.M. 2008. Meta-analysis of phase II cooperative group trials in metastatic
stage IV melanoma to determine progression-free and overall survival benchmarks for future
phase II trials. Journal of Clinical Oncology, 26(4), 527–534.
Koyama, T. and Chen, H. 2008. Proper inference from Simon’s two-stage designs. Statistics
in Medicine, 27(16), 3145–3154.
Lachin, J.M. and Younes, N. 2007. A composite design for transition from a preliminary to a
full-scale study. Statistics in Medicine, 26(27), 5014–5032.
Lai, T.L., Lavori, P.W., Shih, M.C. and Sikic, B.I. 2012. Clinical trial designs for testing
biomarker-based personalized therapies. Clinical Trials, 9(2), 141–154.
Le Blanc, M., Rankin, C. and Crowley, J. 2009. Multiple histology phase II trials. Clinical
Cancer Research, 15(13), 4256–4262.
Lee, J.J. and Feng, L. 2005. Randomized phase II designs in cancer clinical trials: current
status and future directions. Journal of Clinical Oncology, 23(19), 4450–4457.
Lee, J.J. and Liu, D.D. 2008. A predictive probability design for phase II cancer clinical trials.
Clinical Trials, 5(2), 93–106.
Lee, Y.J., Staquet, M., Simon, R., Catane, R. and Muggia, F. 1979. Two-stage plans for
patient accrual in phase II cancer clinical trials. Cancer Treatment Reports, 63(11–12),
1721–1726.
Levy, G., Kaufmann, P., Buchsbaum, R., Montes, J., Barsdorf, A., Arbing, R., Battista, V.,
Zhou, X., Mitsumoto, H., Levin, B. and Thompson, J.L. 2006. A two-stage design for a
phase II clinical trial of coenzyme Q10 in ALS. Neurology, 66(5), 660–663.
Lin, D.Y., Shen, L., Ying, Z. and Breslow, N.E. 1996. Group sequential designs for monitoring
survival probabilities. Biometrics, 52(3), 1033–1041.
Lin, S.P. and Chen, T.T. 2000. Optimal two-stage designs for phase II clinical trials with
differentiation of complete and partial responses. Communications in Statistics-Theory and
Methods, 29(5–6), 923–940.
Lin, Y. and Shih, W.J. 2004. Adaptive two-stage designs for single-arm phase IIA cancer
clinical trials. Biometrics, 60(2), 482–490.
Litwin, S., Wong, Y.N. and Hudes, G. 2007. Early stopping designs based on progression-free
survival at an early time point in the initial cohort. Statistics in Medicine, 26(24), 4400–
4415.
Liu, Q. and Pledger, G.W. 2005. Phase 2 and 3 combination designs to accelerate drug
development. Journal of the American Statistical Association, 100(470), 493–502.
Logan, B.R. 2005. Optimal two-stage randomized phase II clinical trials. Clinical Trials, 2(1),
5–12.
London, W.B. and Chang, M.N. 2005. One- and two-stage designs for stratied phase II
clinical trials. Statistics in Medicine, 24(17), 2597–2611.
Lu, Y., Jin, H. and Lamborn, K.R. 2005. A design of phase II cancer trials using total and
complete response endpoints. Statistics in Medicine, 24(20), 3155–3170.
Machin, D. and Campbell, M.J. 2005. Design of Studies for Medical Research.JohnWiley&
Sons, Ltd, Chichester.
Machin, D., Campbell, M.J., Tan, S.-B. and Tan, S.-H. 2008. Sample Size Tables for Clinical
Studies, 3rd edn. Wiley-Blackwell.
220 REFERENCES
Mandrekar, S.J., An, M.W. and Sargent, D.J. 2013. A review of phase II trial designs for
initial marker validation. Contemporary Clinical Trials, Epub ahead of print.
Mandrekar, S.J., Qi, Y., Hillman, S.L., Allen Ziegler, K.L., Reuter, N.F., Rowland, K.M.,
Jr, Kuross, S.A., Marks, R.S., Schild, S.E. and Adjei, A.A. 2010. Endpoints in phase II
trials for advanced non-small cell lung cancer. Journal of Thoracic Oncology, 5(1), 3–9.
Mariani, L. and Marubini, E. 1996. Design and analysis of phase II cancer trials: a review of
statistical methods and guidelines for medical researchers. International Statistical Review,
64(1), 61–88.
Mariani, L. and Marubini, E. 2000. Content and quality of currently published phase II cancer
trials. Journal of Clinical Oncology, 18(2), 429–436.
Mayo, M.S. and Gajewski, B.J. 2004. Bayesian sample size calculations in phase II clinical
trials using informative conjugate priors. Controlled Clinical Trials, 25(2), 157–167.
McShane, L.M., Hunsberger, S. and Adjei, A.A. 2009. Effective incorporation of biomarkers
into phase II trials. Clinical Cancer Research, 15(6), 1898–1905.
Michiels, S., Le Maitre, A., Buyse, M., Burzykowski, T., Maillard, E., Bogaerts, J.,
Vermorken, J.B., Budach, W., Pajak, T.F., Ang, K.K., Bourhis, J. and Pignon, J.P.
2009. Surrogate endpoints for overall survival in locally advanced head and neck cancer:
meta-analyses of individual patient data. The Lancet Oncology, 10(4), 341–350.
Mick, R., Crowley, J.J. and Carroll, R.J. 2000. Phase II clinical trial design for noncytotoxic
anticancer agents for which time to disease progression is the primary endpoint. Controlled
Clinical Trials, 21(4), 343–359.
Monnet, I., Brienza, S., Hugret, F., Voisin, S., Gastiaburu, J., Saltiel, J.C., Soulie, P., Armand,
J.P., Cvitkovic, E. and de Cremoux, H. 1998. Phase II study of oxaliplatin in poor-prognosis
non-small cell lung cancer (NSCLC). ATTIT. Association pour le Traitement des Tumeurs
Intra Thoraciques. European Journal of Cancer, 34(7), 1124–1127.
Murray, S.C., Otterness, M.F., Forster, J.K., Catellier, D.J. and Koch, G.G. 2004. An
application of a multi-stage strategy involving condence intervals to evaluate whether a
response rate is favourable or not. Pharmaceutical Statistics, 3(1), 25–37.
Neuenschwander, B., Capkun-Niggli, G., Branson, M. and Spiegelhalter, D.J. 2010. Sum-
marizing historical information on controls in clinical trials. Clinical Trials, 7(1), 5–18.
Norton, L. 2001. Theoretical concepts and the emerging role of taxanes in adjuvant therapy.
The Oncologist, 6(Suppl 3), 30–35.
Norton, L. and Simon, R. 1977. Tumor size, sensitivity to therapy, and design of treatment
schedules. Cancer Treatment Reports, 61(7), 1307–1317.
O’Brien, P.C. and Fleming, T.R. 1979. A multiple testing procedure for clinical trials. Bio-
metrics, 35(3), 549–556.
Palumbo, A., Bringhen, S., Caravita, T., Merla, E., Capparella, V., Callea, V., Cangialosi, C.,
Grasso, M., Rossini, F., Galli, M., Catalano, L., Zamagni, E., Petrucci, M.T., De Stefano,
V., Ceccarelli, M., Ambrosini, M.T., Avonto, I., Falco, P., Ciccone, G., Liberati, A.M.,
Musto, P., Boccadoro, M. and Italian Multiple Myeloma Network, GIMEMA. 2006. Oral
melphalan and prednisone chemotherapy plus thalidomide compared with melphalan and
prednisone alone in elderly patients with multiple myeloma: randomised controlled trial.
Lancet, 367(9513), 825–831.
Palumbo, A., Bringhen, S., Liberati, A.M., Caravita, T., Falcone, A., Callea, V., Montanaro,
M., Ria, R., Capaldi, A., Zambello, R., Benevolo, G., Derudas, D., Dore, F., Cavallo,
F., Gay, F., Falco, P., Ciccone, G., Musto, P., Cavo, M. and Boccadoro, M. 2008. Oral
REFERENCES 221
melphalan, prednisone, and thalidomide in elderly patients with multiple myeloma: updated
results of a randomized controlled trial. Blood, 112(8), 3107–3114.
Panageas, K.S., Smith, A., Gonen, M. and Chapman, P.B. 2002. An optimal two-stage phase
II design utilizing complete and partial response information separately. Controlled Clinical
Trials, 23(4), 367–379.
Pazdur, R. 2008. Endpoints for assessing drug activity in clinical trials. The Oncologist,
13(Suppl 2), 19–21.
Perrone, F., Di Maio, M., De Maio, E., Maione, P., Ottaiano, A., Pensabene, M., Di
Lorenzo, G., Lombardi, A.V., Signoriello, G. and Gallo, C. 2003. Statistical design in
phase II clinical trials and its application in breast cancer. The Lancet Oncology, 4(5),
305–311.
Piccart-Gebhart, M.J., Procter, M., Leyland-Jones, B., Goldhirsch, A., Untch, M., Smith,
I., Gianni, L., Baselga, J., Bell, R., Jackisch, C., Cameron, D., Dowsett, M., Barrios,
C.H., Steger, G., Huang, C.S., Andersson, M., Inbar, M., Lichinitser, M., Lang, I.,
Nitz, U., Iwata, H., Thomssen, C., Lohrisch, C., Suter, T.M., Ruschoff, J., Suto, T.,
Greatorex, V., Ward, C., Straehle, C., McFadden, E., Dolci, M.S. and Gelber, R.D. 2005.
Trastuzumab after adjuvant chemotherapy in HER2-positive breast cancer. New England
Journal of Medicine, 353(16), 1659–1672.
Piedbois, P. and Buyse, M. 2008. Endpoints and surrogate endpoints in colorectal cancer: a
review of recent developments. Current Opinion in Oncology, 20(4), 466–471.
Pocock, S.J. 1977. Group sequential methods in the design and analysis of clinical trials.
Biometrika, 64(2), 191–199.
Pound, C.R., Partin, A.W., Eisenberger, M.A., Chan, D.W., Pearson, J.D. and Walsh, P.C.
1999. Natural history of progression after PSA elevation following radical prostatectomy.
Journal of American Medical Association, 281(17), 1591–1597.
Pusztai, L., Anderson, K. and Hess, K.R. 2007. Pharmacogenomic predictor discovery
in phase II clinical trials for breast cancer. Clinical Cancer Research, 13(20), 6080–
6086.
Redman, M. and Crowley, J. 2007. Small randomized trials. Journal of Thoracic Oncology,
2(1), 1–2.
Roberts, J.D. and Ramakrishnan, V. 2011. Phase II trials powered to detect tumor subtypes.
Clinical Cancer Research, 17(17), 5538–5545.
Rosner, G.L., Stadler, W. and Ratain, M.J. 2002. Randomized discontinuation design:
application to cytostatic antineoplastic agents. Journal of Clinical Oncology, 20(22),
4478–4484.
Royston, P., Parmar, M.K. and Qian, W. 2003. Novel designs for multi-arm clinical trials
with survival outcomes with an application in ovarian cancer. Statistics in Medicine, 22(14),
2239–2256.
Rubinstein, L., Crowley, J., Ivy, P., Leblanc, M. and Sargent, D. 2009. Randomized phase
II designs. Clinical Cancer Research, 15(6), 1883–1890.
Sambucini, V. 2008. A Bayesian predictive two-stage design for phase II clinical trials. Statistics
in Medicine, 27(8), 1199–1224.
Sargent, D.J., Chan, V. and Goldberg, R.M. 2001. A three-outcome design for phase II clinical
trials. Controlled Clinical Trials, 22(2), 117–125.
Sargent, D.J. and Goldberg, R.M. 2001. A exible design for multiple armed screening trials.
Statistics in Medicine, 20(7), 1051–1060.
222 REFERENCES
Seymour, L., Ivy, S.P., Sargent, D., Spriggs, D., Baker, L., Rubinstein, L., Ratain, M.J.,
Le Blanc, M., Stewart, D., Crowley, J., Groshen, S., Humphrey, J.S., West, P. and
Berry, D. 2010. The design of phase II clinical trials testing cancer therapeutics: consensus
recommendations from the Clinical Trial Design Task Force of the National Cancer Institute
Investigational Drug Steering Committee. Clinical Cancer Research, 16(6), 1764–1769.
Shepherd, F.A., Dancey, J., Ramlau, R., Mattson, K., Gralla, R., O’Rourke, M., Levitan,
N., Gressot, L., Vincent, M., Burkes, R., Coughlin, S., Kim, Y. and Berille, J. 2000.
Prospective randomized trial of docetaxel versus best supportive care in patients with non-
small-cell lung cancer previously treated with platinum-based chemotherapy. Journal of
Clinical Oncology, 18(10), 2095–2103.
Shun, Z., Lan, K.K. and Soo, Y. 2008. Interim treatment selection using the normal approxi-
mation approach in clinical trials. Statistics in Medicine, 27(4), 597–618.
Shuster, J. 2002. Optimal two-stage designs for single arm phase II cancer trials. Journal of
Biopharmaceutical Statistics, 12(1), 39–51.
Simon, R. 1987. How large should a phase II trial of a new drug be? Cancer Treatment Reports,
71(11), 1079–1085.
Simon, R. 1989. Optimal two-stage designs for phase II clinical trials. Controlled Clinical
Trials, 10(1), 1–10.
Simon, R., Wittes, R.E. and Ellenberg, S.S. 1985. Randomized phase II clinical trials. Cancer
Treatment Reports, 69(12), 1375–1381.
Simon, R.M., Steinberg, S.M., Hamilton, M., Hildesheim, A., Khleif, S., Kwak, L.W.,
Mackall, C.L., Schlom, J., Topalian, S.L. and Berzofsky, J.A. 2001. Clinical trial designs for
the early clinical development of therapeutic cancer vaccines. Journal of Clinical Oncology,
19(6), 1848–1854.
Slamon, D.J., Leyland-Jones, B., Shak, S., Fuchs, H., Paton, V., Bajamonde, A., Fleming,
T., Eiermann, W., Wolter, J., Pegram, M., Baselga, J. and Norton, L. 2001. Use of
chemotherapy plus a monoclonal antibody against HER2 for metastatic breast cancer that
overexpresses HER2. New England Journal of Medicine, 344(11), 783–792.
Smith, M.R., Kabbinavar, F., Saad, F., Hussain, A., Gittelman, M.C., Bilhartz, D.L.,
Wynne, C., Murray, R., Zinner, N.R., Schulman, C., Linnartz, R., Zheng, M., Goessl,
C., Hei, Y.J., Small, E.J., Cook, R. and Higano, C.S. 2005. Natural history of rising
serum prostate-specic antigen in men with castrate nonmetastatic prostate cancer. Journal
of Clinical Oncology, 23(13), 2918–2925.
Sobrero, A.F., Maurel, J., Fehrenbacher, L., Scheithauer, W., Abubakr, Y.A., Lutz, M.P.,
Vega-Villegas, M.E., Eng, C., Steinhauer, E.U., Prausova, J., Lenz, H.J., Borg, C.,
Middleton, G., Kr¨
oning, H., Luppi, G., Kisker, O., Zubel, A., Langer, C., Kopit, J. and
Burris, H.A. 2008. EPIC: phase III trial of cetuximab plus irinotecan after uoropyrimidine
and oxaliplatin failure in patients with metastatic colorectal cancer. Journal of Clinical
Oncology, 26(14), 2311–2319.
Stadler, W. 2002. New trial designs to assess antitumor and antiproliferative agents in prostate
cancer. Investigational New Drugs, 20(2), 201–208.
Stadler, W.M. 2007. The randomized discontinuation trial: a phase II design to assess growth-
inhibitory agents. Molecular Cancer Therapeutics, 6(4), 1180–1185.
Stallard, N. and Cockey, L. 2008. Two-stage designs for phase II cancer trials with ordinal
responses. Contemporary Clinical Trials, 29(6), 896–904.
Stallard, N. and Todd, S. 2003. Sequential designs for phase III clinical trials incorporating
treatment selection. Statistics in Medicine, 22(5), 689–703.
REFERENCES 223
Steinberg, S.M. and Venzon, D.J. 2002. Early selection in a randomized phase II clinical trial.
Statistics in Medicine, 21(12), 1711–1726.
Stone, A., Wheeler, C. and Barge, A. 2007a. Improving the design of phase II trials of
cytostatic anticancer agents. Contemporary Clinical Trials, 28(2), 138–145.
Stone, A., Wheeler, C., Carroll, K. and Barge, A. 2007b. Optimizing randomized phase II
trials assessing tumor progression. Contemporary Clinical Trials, 28(2), 146–152.
Storer, B.E. 1990. A sequential phase II/III trial for binary outcomes. Statistics in Medicine,
9(3), 229–235.
Storer, B.E. 1992. A class of phase II designs with three possible outcomes. Biometrics, 48(1),
55–60.
Sun, L.Z., Chen, C. and Patel, K. 2009. Optimal two-stage randomized multinomial designs
for phase II oncology trials. Journal of Biopharmaceutical Statistics, 19(3), 485–493.
Sylvester, R.J. 1988. A Bayesian approach to the design of phase II clinical trials. Biometrics,
44(3), 823–836.
Sylvester, R.J. and Staquet, M.J. 1980. Design of phase II clinical trials in cancer using
decision theory. Cancer Treatment Reports, 64(2–3), 519–524.
Tan, M. and Xiong, X. 1996. Continuous and group sequential conditional probability ratio
tests for phase II clinical trials. Statistics in Medicine, 15(19), 2037–2051.
Tan, S.B. and Machin, D. 2002. Bayesian two-stage designs for phase II clinical trials. Statistics
in Medicine, 21(14), 1991–2012.
Tang, H., Foster, N.R., Grothey, A., Ansell, S.M., Goldberg, R.M. and Sargent, D.J. 2010.
Comparison of error rates in single-arm versus randomized phase II cancer clinical trials.
Journal of Clinical Oncology, 28(11), 1936–1941.
Taylor, J.M., Braun, T.M. and Li, Z. 2006. Comparing an experimental agent to a standard
agent: relative merits of a one-arm or randomized two-arm phase II design. Clinical Trials,
3(4), 335–348.
Thall, P.F. and Cheng, S.C. 1999. Treatment comparisons based on two-dimensional safety
and efcacy alternatives in oncology trials. Biometrics, 55(3), 746–753.
Thall, P.F. and Cheng, S.C. 2001. Optimal two-stage designs for clinical trials based on safety
and efcacy. Statistics in Medicine, 20(7), 1023–1032.
Thall, P.F. and Estey, E.H. 1993. A Bayesian strategy for screening cancer treatments prior to
phase II clinical evaluation. Statistics in Medicine, 12(13), 1197–1211.
Thall, P.F., Millikan, R.E. and Sung, H.G. 2000. Evaluating multiple treatment courses in
clinical trials. Statistics in Medicine, 19(8), 1011–1028.
Thall, P.F. and Simon, R. 1990. Incorporating historical control data in planning phase II
clinical trials. Statistics in Medicine, 9(3), 215–228.
Thall, P.F. and Simon, R. 1994a. A Bayesian approach to establishing sample size and
monitoring criteria for phase II clinical trials. Controlled Clinical Trials, 15(6), 463–481.
Thall, P.F. and Simon, R. 1994b. Practical Bayesian guidelines for phase IIB clinical trials.
Biometrics, 50(2), 337–349.
Thall, P.F., Simon, R. and Estey, E.H. 1995. Bayesian sequential monitoring designs for
single-arm clinical trials with multiple outcomes. Statistics in Medicine, 14, 357–379.
Thall, P.F., Simon, R.M. and Estey, E.H. 1996. New statistical strategy for monitoring safety
and efcacy in single-arm clinical trials. Journal of Clinical Oncology, 14(1), 296–303.
Thall, P.F. and Sung, H.G. 1998. Some extensions and applications of a Bayesian strategy for
monitoring multiple outcomes in clinical trials. Statistics in Medicine, 17(14), 1563–1580.
224 REFERENCES
Thall, P.F., Wathen, J.K., Bekele, B.N., Champlin, R.E., Baker, L.H. and Benjamin, R.S.
2003. Hierarchical Bayesian approaches to phase II trials in diseases with multiple subtypes.
Statistics in Medicine, 22(5), 763–780.
Thall, P.F., Wooten, L.H. and Tannir, N.M. 2005. Monitoring event times in early phase
clinical trials: some practical issues. Clinical Trials, 2(6), 467–478.
Therasse, P. 2002. Measuring the clinical response. What does it mean? European Journal of
Cancer 38(14), 1817–1823.
Tobias, J.S., Monson, K., Gupta, N., MacDougall, H., Glaholm, J., Hutchison, I., Kadalayil,
L. and Hackshaw, A. 2010. Chemoradiotherapy for locally advanced head and neck cancer:
10-year follow-up of the UK Head and Neck (UKHAN1) trial. The Lancet Oncology, 11(1),
66–74.
Todd, S. and Stallard, N. 2005. A new clinical trial design combining phases 2 and 3: sequential
designs with treatment selection and a change of endpoint. Drug Information Journal, 39(2),
109–118.
Tol, J., Koopman, M., Cats, A., Rodenburg, C.J., Creemers, G.J., Schrama, J.G., Erdkamp,
F.L., Vos, A.H., van Groeningen, C.J., Sinnige, H.A., Richel, D.J., Voest, E.E., Dijkstra,
J.R., Vink-B¨
orger, M.E., Antonini, N.F., Mol, L., van Krieken, J.H., Dalesio, O. and Punt,
C.J. 2009. Chemotherapy, bevacizumab, and cetuximab in metastatic colorectal cancer. New
England Journal of Medicine, 360(6), 563–572.
Tournoux, C., De Rycke, Y., Medioni, J. and Asselain, B. 2007. Methods of joint evaluation
of efcacy and toxicity in phase II clinical trials. Contemporary Clinical Trials, 28(4),
514–524.
Tournoux-Facon, C., De Rycke, Y. and Tubert-Bitter, P. 2011. Targeting population entering
phase III trials: a new stratied adaptive phase II design. Statistics in Medicine, 30(8),
801–811.
Twombly, R. 2006. Criticism of tumor response criteria raises trial design questions. Journal
of the National Cancer Institute, 98(4), 232–234.
U.S. Department of Health and Human Services, Food and Drug Administration, Center for
Drug Evaluation and Research (CDER) 2013. Guidance for Industry: Codevelopment of
Two or More New Investigational Drugs for Use in Combination. Final Draft June 2013.
Available online at: http://www.fda.gov/Drugs/Guidance ComplianceRegulatoryInforma-
tion/Guidances/default.htm (accessed on 1 November 2013).
Van Cutsem, E., Kohne, C.H., Hitre, E., Zaluski, J., Chang Chien, C.R., Makhson, A.,
D’Haens, G., Pinter, T., Lim, R., Bodoky, G., Roh, J.K., Folprecht, G., Ruff, P.,
Stroh, C., Tejpar, S., Schlichting, M., Nippgen, J. and Rougier, P. 2009. Cetuximab and
chemotherapy as initial treatment for metastatic colorectal cancer. New England Journal of
Medicine, 360(14), 1408–1417.
van de Donk, N.W.C.J., Lokhorst, H.M., Dimopoulos, M., Cavo, M., Morgan, G., Einsele,
H., Kropff, M., Schey, S., Avet-Loiseau, H., Ludwig, H., Goldschmidt, H., Sonneveld, P.,
Johnsen, H.E., Blade, J., San-Miguel, J.F. and Palumbo, A. 2011. Treatment of relapsed
and refractory multiple myeloma in the era of novel agents. Cancer Treatment Reviews,
37(4), 266–283.
Van Glabbeke, M., Steward, W. and Armand, J.P. 2002. Non-randomised phase II trials of drug
combinations: often meaningless, sometimes misleading. Are there alternative strategies?
European Journal of Cancer, 38(5), 635–638.
Vickers, A.J. 2009. Phase II designs for anticancer botanicals and supplements. Journal of the
Society for Integrative Oncology, 7(1), 35–40.
REFERENCES 225
Vickers, A.J., Ballen, V. and Scher, H.I. 2007. Setting the bar in phase II trials: the use of
historical data for determining ‘go/no go’ decision for denitive phase III testing. Clinical
Cancer Research, 13(3), 972–976.
Von Hoff, D.D. 1998. There are no bad anticancer agents, only bad clinical trial designs –
Twenty-First Richard and Hinda Rosenthal Foundation Award Lecture. Clinical Cancer
Research, 4(5), 1079–1086.
Walker, I. and Newell, H. 2009. Do molecularly targeted agents in oncology have reduced
attrition rates? Nature Reviews Drug Discovery, 8(1), 15–16.
Wang, J. 2006. An adaptive two-stage design with treatment selection using the conditional
error function approach. Biometrical Journal, 48(4), 679–689.
Wang, L. and Cui, L. 2007. Seamless phase II/III combination study through response adaptive
randomization. Journal of Biopharmaceutical Statistics, 17(6), 1177–1187.
Wang, Y.G., Leung, D.H., Li, M. and Tan, S.B. 2005. Bayesian designs with frequentist
and Bayesian error rate considerations. Statistical Methods in Medical Research, 14(5),
445–456.
Wathen, J.K., Thall, P.F., Cook, J.D. and Estey, E.H. 2008. Accounting for patient hetero-
geneity in phase II clinical trials. Statistics in Medicine, 27(15), 2802–2815.
Weiss, G.B. and Hokanson, J.A. 1984. Advantages of integrated trials for performing multiple
phase II studies. Investigational New Drugs, 2(4), 409–414.
Whitehead, J. 1985. Designing phase II studies in the context of a programme of clinical
research. Biometrics, 41(2), 373–383.
Whitehead, J. 1986. Sample sizes for phase II and phase III clinical trials: an integrated
approach. Statistics in Medicine, 5(5), 459–464.
Whitehead, J. 1997. The Design and Analysis of Sequential Clinical Trials, 2nd edn. John
Wiley & Sons, Ltd, Chichester.
Whitehead, J. and Jaki, T. 2009. One- and two-stage design proposals for a phase II trial com-
paring three active treatments with control using an ordered categorical endpoint. Statistics
in Medicine, 28(5), 828–847.
Whitehead, J., Valdes-Marquez, E. and Lissmats, A. 2009. A simple two-stage design for
quantitative responses with application to a study in diabetic neuropathic pain. Pharmaceu-
tical Statistics, 8(2), 125–135.
Wu, C. and Liu, A. 2007. An adaptive approach for bivariate phase II clinical trial designs.
Contemporary Clinical Trials, 28(4), 482–486.
Wu, Y. and Shih, W.J. 2008. Approaches to handling data when a phase II trial deviates from
the pre-specied Simon’s two-stage design. Statistics in Medicine, 27(29), 6190–6208.
Ye, F. and Shyr, Y. 2007. Balanced two-stage designs for phase II clinical trials. Clinical
Trials, 4(5), 514–524.
Yothers, G., Wieand, H.S. and Freireich, E.J. 2006. Pro/Con: randomization in phase II
clinical trials. Clinical Advances in Hematology and Oncology, 4(10), 776–778.
Zee, B., Melnychuk, D., Dancey, J. and Eisenhauer, E. 1999. Multinomial phase II cancer
trials incorporating response and early progression. Journal of Biopharmaceutical Statistics,
9(2), 351–363.

Index
Academia, 4–5
Accelerated approval, 176, 198, 201,
202
Activity, exploratory, 196, 198,
203–204
A’Hern
(2001), 37, 155–160
(2004), 131–132
Alpe-Adria Thoracic Oncology
Multidisciplinary (ATOM) group,
162
Alternative hypothesis, 30, 157, 158,
160
Androgen deprivation, 163, 165,
171
Average sample number (ASN), 28, 59,
127
Ayanlowo and Redden (2007), 58
Banerjee and Tsiatis (2006), 47
Bauer et al. (1998), 89, 93
Bauer and Kieser (1999), 90, 93, 97
Bayesian, 27, 33, 38, 45–47, 50, 55, 57,
59–64, 75, 76, 109, 110, 122,
123–126, 129, 130, 135–140, 156,
178, 181, 203, 204, 209
Bellissant et al. (1990), 55
Binary outcome, 19–20, 36–50, 54–66,
68–69, 72–73, 77–79, 82, 84–85,
89–92, 99, 103–104, 106–108,
111, 112–121, 122–124, 125–128,
131–136, 138–139, 143–145, 148,
153–154, 165, 176, 181
Biomarker, 7, 10, 15–16, 17, 20, 33, 34,
133–135, 163–173, 203, 205,
209–210
Bretz et al. (2006), 92
Bryant and Day (1995), 118, 178–181
Case and Morgan (2003), 46, 53,
190–192
Categorical data, see Multinomial
outcome
Chang et al.
(1999), 44, 50
(2004), 37, 155–160
(2007), 39, 52
Chen (1997), 57
Chen and Beckman (2009), 70–71,
145–147, 190–192
Chen and Chaloner (2006), 62
Chen et al. (1994), 56
Chen and Ng (1998), 44
Chen and Shan (2008), 58
Cheung (2009), 88
Cheung and Thall
(2002), 60, 63, 109–110
Chi and Chen (2008), 49
Chow and Tu (2008), 78, 80–81,
145–147
Clinical development plan (CDP),
195–197, 201, 203, 210
A Practical Guide to Designing Phase II Trials in Oncology, First Edition.
Sarah R. Brown, Walter M. Gregory, Chris Twelves and Julia Brown.
© 2014 John Wiley & Sons, Ltd. Published 2014 by John Wiley & Sons, Ltd.
228 INDEX
Colorectal cancer, 11, 185–194
Combination therapy, 7, 15, 22, 24, 31,
142–150, 151–162, 174–184,
185–194, 197, 198, 203–205
Committee for Medicinal Products for
Human Use (CHMP), 201, 202
Conaway and Petroni
(1995), 117, 119, 122, 178–181
(1996), 117, 119, 178–181
Condence intervals, 37, 41, 49, 58, 65,
156
Continuous monitoring, 26, 29, 60–64,
76, 89, 109–110, 125–130, 132,
133, 138–140, 154, 166, 177, 189
Continuous outcome, 18–20, 38, 50,
59, 63, 65, 66, 70, 73, 75, 76, 77,
79–80, 82, 84, 86, 88, 92–96,
99–101, 104, 108, 109, 111, 165,
167, 168
Control arm, 16, 17, 22, 23, 24–26, 31,
34, 68–82, 83–102, 112–116, 126,
128–129, 146–147, 153–154,
157–160, 166–173, 176, 187, 190,
194, 201, 202, 204, 208
Correlation, 19, 34, 40, 78, 80, 81, 86,
96, 99, 100, 101, 102, 117, 119,
122, 128, 147, 148, 165, 179, 208
Costs of treatment, 29, 144, 154, 167,
177, 188
Critical values, 43, 44, 49, 50, 84, 88,
97. See also Stopping boundaries
Cronin et al. (1999), 75
Cytostatic therapies, 14, 18, 20, 21, 22,
25, 40, 69, 71, 141, 185. See also
Targeted therapies
Cytotoxic therapies, 2, 4, 5, 14, 15, 19,
22, 24, 151–153, 176, 186
de Boo and Zielhuis (2004), 126
Decision making, 4, 5, 15, 16–17, 18,
19, 22–25, 27, 28, 29, 30, 35,
143–147, 152–158, 164, 166, 167,
168, 178, 186, 187, 189, 191,
196–197, 203, 204, 205, 206
Decision-theoretic, 26, 29–30, 64, 89,
110, 144, 154, 167, 177, 188, 197
Dexamethasone, 174–184
Docetaxel, 151–162
Dose nding, 4, 79, 89, 90, 93, 94, 97,
100
Dose response, 4, 100
Drug development, 1–6, 16, 19, 166,
171, 186, 196
Dual threshold design, 45
Early termination, 27–29, 31, 34–35,
144, 154, 166–168, 169, 170,
179–180, 192, 202
Effect size, 10
Efcacy, 1–4, 15, 78, 87, 89, 90–95, 97,
98, 110, 115, 129, 145, 170, 185,
186, 188, 198, 201–203, 205, 208,
209
Eligibility criteria, 32, 37 148, 167
Enrichment, 7, 10, 16, 22, 27, 32, 33,
142, 152, 164, 175, 209
Ensign et al. (1994), 56
European Medicines Agency (EMEA),
202
Event-free survival, 142–143, 148, 175
False negative result, 5, 6, 16, 23
False positive result, 5, 23, 35
Fazzari et al. (2000), 36, 155–160
Fixed sample, 27, 29, 57, 58, 61, 90,
93, 97, 127, 128
Fleming (1982), 36, 41, 55, 155–160
Follow-up, 21, 28, 32, 41, 46, 54, 60,
63, 109, 110, 143, 147, 148,
165–167, 171, 190, 192
Food and Drug Administration (FDA),
176, 201
Frequentist, 45, 47, 75, 181, 203
Funding, 31
Futility, 86, 147, 169, 171, 196, 202,
207
Gajewski and Mayo (2006), 38,
155–160
Getinib, 6, 151
Gehan (1961), 41
Gofn and Tu (2008), 52
INDEX 229
Goldman (1987), 127
Goldman and Hannan (2001), 127
Go/no-go, 4, 5, 15, 16, 142–144, 152,
154, 164, 167, 168, 178, 186
Green and Dahlberg (1992), 42
Group sequential, 26, 28, 55, 57, 59,
61, 62, 75, 91, 94, 98, 99, 102,
122, 125, 136, 138, 170, 171.
See also Multi-stage
Growth modulation index, 21, 40,
199
Hanfelt et al. (1999), 44
Head and neck cancer/head and neck
squamous cell carcinoma
(HNSCC), 11, 19, 141–150
Heitjan (1997), 43
Herndon (1998), 43
Herson (1979), 55
Herson and Carter (1986), 68,
145–147, 155–160
Historical control data, 15, 16, 17, 19,
21, 22, 23, 24, 25, 26, 33, 34, 37,
38, 44, 50, 62, 69, 70, 73, 85, 107,
123, 125, 141, 151, 153, 156, 157,
160, 177, 178, 179, 181, 185, 187,
188, 203, 204
Hong and Wang (2007), 77, 155–160
Implementation, 9, 10, 27, 147, 156,
191, 197, 203–205, 209
Independent data monitoring
committee, 170, 205
Independent review, 19
INTACT1, 6
INTACT2, 6
Interactions, 136, 137, 139, 140, 205
Interim analysis, 27, 28, 31, 32, 54, 78,
86, 89, 91, 94, 96, 98, 101, 110,
170, 171, 177–180, 187–192, 197,
202, 207
International Conference on
Harmonization (ICH), 3, 4
Interpreting trial results, 7, 16, 22, 24,
25, 45, 153
Ivanova et al. (2005), 128
Jin (2007), 118, 120, 178–181
Johnson and Cook (2009), 62, 64
Jones and Holmgren (2007), 134
Jung (2008), 72, 84
Jung et al. (2004), 46
Jung and George (2009), 73, 85, 107
Kelly et al. (2005), 91, 94, 98
Kocherginsky et al. (2009), 53
Kopec et al. (1993), 82
Koyama and Chen (2008), 49
Lachin and Younes (2007), 78, 80–81,
145–147
Le Blanc et al. (2009), 136, 138
Lee et al. (1979), 65
Lee and Liu (2008), 59, 62
Levy et al. (2006), 86, 168–170
Lin and Chen (2000), 51
Lin and Shih (2004), 46
Litwin et al. (2007), 48, 54, 190–192
Liu and Pledger (2005), 79, 100,
168–170
Logan (2005), 107
London and Chang (2005), 132–133
Lu et al. (2005), 39, 51
Mayo and Gajewski (2004), 37,
155–160
Mechanism of action, 2, 4, 7, 14, 15,
18, 20, 141, 152, 164, 174, 185
Methodology for the Development of
Innovative Cancer Therapies
(MDICT) Task Force, 7, 32
Mick et al. (2000), 40
Minimax design, 42, 45, 48, 51, 57, 58,
59, 72, 74, 85, 87, 114, 129
Misspecication, 23, 34, 117–122,
179–181
Molecular targeted agents, 27, 141,
148. See also Targeted therapies
Monoclonal antibody therapy, 14, 15,
16, 185–194
Multi arm, 17, 26, 83, 163–173,
174–184, 204–205. See also
Treatment selection
230 INDEX
Multinomial outcome, 20, 39–40,
50–53, 59–60, 63, 65, 66, 70,
74–76, 77, 80, 82, 84, 87, 88,
96–97, 101, 105, 108, 109, 111,
114, 128
Multiple myeloma, 11, 174–184
Multi-stage, 26–29, 55–60, 66, 75, 88,
91, 92, 94, 98, 108–109, 115–117,
122–125, 129, 135–138, 144, 154,
166, 177, 178, 189, 206, 207
Murray et al. (2004), 58
National Cancer Institute, 7, 16
Non-small cell lung cancer (NSCLC),
6, 11, 151–162, 164, 166
Null hypothesis, 28, 30–31, 156–158,
160, 192
Objective response, 6, 207
Objectives, 3–5, 7, 196, 198
One-sided test, 148, 158, 160, 170, 192,
198, 202, 203
One-stage, 26–29, 36–40, 68–71, 78,
84, 103–105, 112–113, 117–118,
126, 131–132, 144, 145, 154–158,
160, 167, 169, 177, 189, 190, 202
Operating characteristics, 27–29, 35,
158–160
Optimal design, 42, 47, 48, 51, 52, 57,
58, 59, 72, 74, 85, 87, 114, 129
Ordered categorical outcome, see
Multinomial outcome
Overall survival, 3, 14, 142, 153, 156,
163, 165, 175, 176, 186, 187,
206
Panageas et al. (2002), 51
Patient population, 10, 14, 16, 19, 22,
23, 24, 25, 29, 31–33, 131–140,
141, 145, 148, 151, 160, 164, 166,
170, 171, 176–177, 181, 182, 186,
187–189, 192, 201, 202, 203, 205,
206, 208, 209–210
Pharmaceutical industry, 1, 4, 5,
195–211
Phase 2, 5, 71, 146, 190
phase I, 1, 2, 4, 6, 16, 17, 163, 175,
195, 197, 198, 200–202, 205, 208
Phase II/III, 26, 31, 32, 67, 77–88,
89–102, 110, 111, 144–150, 154,
166, 167–173, 177, 188, 204, 205
phase IIa, 4, 16, 19, 22, 24, 203, 204,
207
phase IIb, 4, 15–17, 19, 22, 24
phase III, 1–7, 14–19, 22, 23, 25–32,
35, 141–150, 163–173, 185–191,
195–198, 201–204, 206–209
phase IV, 1
Phases of drug development
Power, 23–25, 33, 35, 148, 160, 170,
187, 190, 192, 203
Practicalities, 8, 10, 12, 33–35,
146–148, 155–158, 168–170,
178–181, 190–191
Prediction (of outcomes), 38, 79, 80,
81, 147, 156–157, 196, 206–208,
209
Primary aim, 5, 16, 18, 24, 35,
142–143, 152, 164, 175, 186
Primary endpoint, 15–16, 17, 18–21,
24, 29, 30, 31, 34, 142–143, 145,
148, 152–153, 164–166, 175–178,
186–187, 203, 208
Probability of success (PoS), 200, 204,
206
Programming, 34, 147, 156–158, 169,
170, 179–180
Progression-free survival, 14, 20–22,
26, 29, 37, 48, 54, 69, 71, 153,
175, 181, 182, 186, 187, 189–192,
199, 200, 206, 208
Proof of concept, 3–5, 15–17, 24, 27,
41, 142, 143, 152, 154, 164, 175,
177, 186, 189, 194
Prostate cancer, 11, 163–173
Prostate Specic Antigen (PSA),
163–167, 169–173
Protocol, 145, 168, 201, 203
Publication guidance, 6–7
Pusztai et al. (2007), 133
INDEX 231
Radiotherapy, 141–150
Randomisation, 7, 8, 12, 15–17, 21–26,
31, 32–33, 68–82, 83, 86, 92, 95,
108, 111, 143, 145, 146, 147,
153–155, 159, 160, 165–166, 168,
171, 176–177, 187–189, 192, 205,
210
Randomised discontinuation, 7, 24, 26,
32–33, 82, 102, 111, 144, 154,
167, 177, 188, 199
rare, 187–191
Ratio of times to progression, 21, 40,
54, 60, 64, 65, 67, 72, 75–77, 81,
82, 84, 88, 89, 99, 102, 105, 108,
109, 110, 111
RECIST criteria, 18, 19
Recommended phase II dose, 2, 16,
208
Recruitment, 28, 29, 31, 32, 145–148,
166–167, 187–192
Reference arm, 25, 189, 192
Region of uncertainty, 30, 66, 77, 155,
158
Registration trials, 163, 195, 196,
198–203
Regulatory considerations/
requirements, 4, 196, 198, 201,
202
Response, 3, 6, 19, 20, 22, 23, 24, 25,
29, 30, 34, 152, 153, 155,
157–162, 176–182, 186, 187, 199,
200, 201, 202, 204, 207
Royston et al. (2003), 101
Safety, 21, 27, 30, 34, 154, 155, 164,
166, 170, 195, 196, 201, 203, 205,
208
Sambucini (2008), 50
Sample size, 1, 9, 23, 25–28, 30, 33,
35, 153, 154, 156, 157, 158, 160,
169, 170, 180, 187–192, 197, 202,
208, 210
Sargent et al. (2001), 66, 155–160
Sargent and Goldberg (2001), 104,
178–182
Screening, 3, 22, 146, 156, 190, 201,
202
Selection bias, 21, 22, 25, 153, 160,
192
Sequential probability ratio test
(SPRT)/Sequential conditional
probability ratio test (SCPRT),
55–57, 61, 88, 127–128
Shun et al. (2008), 86, 96, 101,
168–170
Shuster (2002), 45
Signicance level, 25, 148, 150, 170,
198. See also Type I error
Simon
(1987), 42
(1989), 42
Simon et al.
(1985), 103
(2001), 70, 145–147, 190–192
Simulation, 9, 23, 34, 148
Single arm, 6–10, 17, 23–25, 27, 30, 34,
36–67, 78, 83, 117–140, 153–157,
178, 179, 189, 199, 201–203, 207
Single threshold design, 45, 50
Software, 9, 34, 147, 156–158, 169,
170, 179, 180, 181
Stallard and Cockey (2008), 40, 53
Stallard and Todd (2003), 90, 94, 98
Statistical analysis, 27, 28, 31,
146–147, 167, 169, 204
Steinberg and Venzon (2002), 106
Stochastic curtailment, 58
Stone et al. (2007b), 69, 71, 145–147,
155–160, 190–192
Stopping rules/boundary, 27, 28, 29,
30, 31, 160, 171, 189, 208
Storer (1990), 66, 77, 145–147,
155–160
Stratied designs, 10, 33, 131–140,
200, 205, 209
Subgroups, 9, 10, 15, 17, 33, 131–140,
209, 210
Sun et al. (2009), 74, 87, 114, 128
Surrogate endpoints, 19, 163, 165, 175,
176, 205
232 INDEX
Sylvester and Staquet (1980), 64
Systematic review, 6–7, 10
Tan and Machin (2002), 45
Tan and Xiong (1996), 57, 61
Targeted subgroups, 9, 15, 26, 32, 33,
131–140, 185–192, 196, 203, 208,
210
Targeted therapies, 2, 3, 4, 5, 7, 10, 14,
15, 16, 18, 20, 21, 22, 25, 32, 33,
141–150, 163–173, 185–192,
209–210
Thalidomide, 174–184
Thall and Cheng
(1999), 112–113
(2001), 114–116, 120–121, 123–124,
178–181
Thalletal.
(1996), 122, 125
(2000), 108
(2003), 124, 126, 135, 137–139
(2005), 63, 76
Thall and Simon
(1990), 69–70, 145–147, 155–160
(1994a), 57, 61
(1994b), 60
Thall and Sung
(1998), 123, 125, 129–130, 178–181
Thought process, 7–14, 35, 150, 162,
173, 184, 194
Three-outcome, 26, 30, 65–66, 77, 89,
110, 144, 154–162, 167, 177, 189
Time to event outcome, 20, 21, 40,
53–54, 60, 63–64, 65, 66 70–71,
75–78, 81, 82, 84, 88, 89, 97–99,
101–102, 105, 108–111, 113, 115,
116, 121, 124, 137–140, 143–146,
148 187, 189, 190, 192
Time to progression, 20, 40
Time to treatment failure, 20
Todd and Stallard
(2005), 102, 99, 168–170
Toxicity, 1, 2, 7, 9, 15, 18, 19, 21, 27,
29, 34, 112–130, 135, 137, 139,
140, 142, 151, 152, 163–165,
175–184, 185–186, 189, 205, 206,
209
Trade-off, 15, 18, 25, 113–124,
178–180
Treatment selection, 4, 7, 9, 17, 26,
83–111, 128–130, 163–173,
174–184, 197, 198, 204–205
Triangular test, 55, 91, 95, 99
Tumour response, 3, 14, 18, 19, 20, 40,
152, 153, 199, 200, 201, 202.
See also Response
Tumour size/volume, 14, 19, 20
Two-sided test, 35, 150
Two-stage, 7, 10, 27–29, 33, 41–54,
72–74, 77, 84–87, 106–108,
114–115, 118–122, 128, 132–135,
138, 143, 154, 166–173, 177–184,
189–194, 199, 200, 202
Type I error, 23, 25, 30, 31, 35,
146–147, 157–158, 160, 180–181,
187, 190–192, 203
Type II error, 23, 30, 133. See also
Power
Vickers (2009), 38, 155–160
Wang (2006), 95
Wang and Cui (2007), 91, 95
Wang et al. (2005), 47
Wathen et al. (2008), 136–137,
139–140
Weiss and Hokanson (1984), 106
Whitehead (1985), 103–105
Whitehead (1986), 111
Whitehead and Jaki (2009), 84, 87,
96
Whitehead et al. (2009), 72–74
Wu and Liu (2007), 121, 178–181
Wu and Shih (2008), 48
Ye and Shyr (2007), 47
Zee et al. (1999), 39, 50, 59
Statistics in Practice
Human and Biological Sciences
Berger – Selection Bias and Covariate Imbalances in Randomized Clinical Trials
Berger and Wong – An Introduction to Optimal Designs for Social and Biomedical Research
Brown, Gregory, Twelves and Brown – A Practical Guide to Designing Phase II Trials in
Oncology
Brown and Prescott – Applied Mixed Models in Medicine, Second Edition
Carpenter and Kenward – Multiple Imputation and its Application
Carstensen – Comparing Clinical Measurement Methods
Chevret (Ed.) – Statistical Methods for Dose-Finding Experiments
Ellenberg, Fleming and DeMets – Data Monitoring Committees in Clinical Trials: A Practical
Perspective
Hauschke, Steinijans and Pigeot – Bioequivalence Studies in Drug Development: Methods
and Applications
K¨
all´
en – Understanding Biostatistics
Lawson, Browne and Vidal Rodeiro – Disease Mapping with Win-BUGS and MLwiN
Lesaffre, Feine, Leroux and Declerck – Statistical and Methodological Aspects of Oral Health
Research
Lui – Statistical Estimation of Epidemiological Risk
Marubini and Valsecchi – Analysing Survival Data from Clinical Trials and Observation
Studies
Millar – Maximum Likelihood Estimation and Inference: With Examples in R, SAS and
ADMB
Molenberghs and Kenward – Missing Data in Clinical Studies
Morton, Mengersen, Playford and Whitby – Statistical Methods for Hospital Monitoring
with R
O’Hagan, Buck, Daneshkhah, Eiser, Garthwaite, Jenkinson, Oakley and Rakow – Uncertain
Judgements: Eliciting Expert’s Probabilities
O’Kelly and Ratitch – Clinical Trials with Missing Data: A Guide for Practitioners
Parmigiani – Modeling in Medical Decision Making: A Bayesian Approach
Pintilie – Competing Risks: A Practical Perspective
Senn – Cross-over Trials in Clinical Research, Second Edition
Senn – Statistical Issues in Drug Development, Second Edition
Spiegelhalter, Abrams and Myles – Bayesian Approaches to Clinical Trials and Health-Care
Evaluation
Walters – Quality of Life Outcomes in Clinical Trials and Health-Care Evaluation
Welton, Sutton, Cooper and Ades – Evidence Synthesis for Decision Making in Healthcare
Whitehead – Design and Analysis of Sequential Clinical Trials, Revised Second Edition
Whitehead – Meta-Analysis of Controlled Clinical Trials
Willan and Briggs – Statistical Analysis of Cost Effectiveness Data
Winkel and Zhang – Statistical Development of Quality in Medicine
Earth and Environmental Sciences
Buck, Cavanagh and Litton – Bayesian Approach to Interpreting Archaeological Data
Chandler and Scott – Statistical Methods for Trend Detection and Analysis in the
Environmental Statistics
Glasbey and Horgan – Image Analysis in the Biological Sciences
Haas – Improving Natural Resource Management: Ecological and Political Models
Haas – Introduction to Probability and Statistics for Ecosystem Managers
Helsel – Nondetects and Data Analysis: Statistics for Censored Environmental Data
Illian, Penttinen, Stoyan and Stoyan – Statistical Analysis and Modelling of Spatial Point
Patterns
Mateu and Muller (Eds) – Spatio-Temporal Design: Advances in Efcient Data Acquisition
McBride – Using Statistical Methods for Water Quality Management
Webster and Oliver – Geostatistics for Environmental Scientists, Second Edition
Wymer (Ed.) – Statistical Framework for Recreational Water Quality Criteria and Monitoring
Industry, Commerce and Finance
Aitken – Statistics and the Evaluation of Evidence for Forensic Scientists, Second Edition
Balding – Weight-of-evidence for Forensic DNA Proles
Brandimarte – Numerical Methods in Finance and Economics: A MATLAB-Based
Introduction, Second Edition
Brandimarte and Zotteri – Introduction to Distribution Logistics
Chan – Simulation Techniques in Financial Risk Management
Coleman, Greeneld, Stewardson and Montgomery (Eds) – Statistical Practice in Business
and Industry
Frisen (Ed.) – Financial Surveillance
Fung and Hu – Statistical DNA Forensics
Gusti Ngurah Agung – Time Series Data Analysis Using EViews
Jank and Shmueli (Ed.) – Statistical Methods in e-Commerce Research
Kenett (Ed.) – Operational Risk Management: A Practical Approach to Intelligent Data
Analysis
Kenett (Ed.) – Modern Analysis of Customer Surveys: With Applications using R
Kenett and Zacks – Modern Industrial Statistics: With Applications in R, MINITAB and JMP,
Second Edition
Kruger and Xie – Statistical Monitoring of Complex Multivariate Processes: With
Applications in Industrial Process Control
Lehtonen and Pahkinen – Practical Methods for Design and Analysis of Complex Surveys,
Second Edition
Ohser and M¨
ucklich – Statistical Analysis of Microstructures in Materials Science
Pasiouras (Ed.) – Efciency and Productivity Growth: Modelling in the Financial Services
Industry
Pourret, Naim and Marcot (Eds) – Bayesian Networks: A Practical Guide to Applications
Ruggeri, Kenett and Faltin – Encyclopedia of Statistics and Reliability
Taroni, Aitken, Garbolino and Biedermann – Bayesian Networks and Probabilistic Inference
in Forensic Science
Taroni, Bozza, Biedermann, Garbolino and Aitken – Data Analysis in Forensic Science